Euler’s partition function
![]() $p(n)$
is the number of partitions of a nonnegative integer n and its generating function is given by
$p(n)$
is the number of partitions of a nonnegative integer n and its generating function is given by
 $$ \begin{align*} \sum_{n=0}^\infty p(n)q^n = \prod_{k=1}^\infty \frac{1}{1-q^k}, \quad |q| < 1. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty p(n)q^n = \prod_{k=1}^\infty \frac{1}{1-q^k}, \quad |q| < 1. \end{align*} $$
The properties of the function
![]() $p(n)$
, such as its asymptotic behaviour and its parity, have been an object of study for a long time. For instance, Ballantine and Merca [Reference Ballantine and Merca1] recently made a conjecture on when
$p(n)$
, such as its asymptotic behaviour and its parity, have been an object of study for a long time. For instance, Ballantine and Merca [Reference Ballantine and Merca1] recently made a conjecture on when
 $$ \begin{align*}\sum_{ak+1 \text{ is a square}}p(n-k)\end{align*} $$
$$ \begin{align*}\sum_{ak+1 \text{ is a square}}p(n-k)\end{align*} $$
is odd, which was proved by Hong and Zhang [Reference Hong and Zhang2].
The function
![]() $p(n)$
is linked to the divisor function
$p(n)$
is linked to the divisor function
 $$ \begin{align*}\sigma(n) := \sum_{d \mid n}d,\end{align*} $$
$$ \begin{align*}\sigma(n) := \sum_{d \mid n}d,\end{align*} $$
whose generating function is given by
 $$ \begin{align*} \sum_{n=1}^\infty \sigma(n)q^n = \sum_{n=1}^\infty \frac{nq^n}{1-q^n}. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty \sigma(n)q^n = \sum_{n=1}^\infty \frac{nq^n}{1-q^n}. \end{align*} $$
In particular,
![]() $p(n)$
and
$p(n)$
and
![]() $\sigma (n)$
satisfy the following convolution identities, which differ only in the values of
$\sigma (n)$
satisfy the following convolution identities, which differ only in the values of
![]() $p(0)$
and
$p(0)$
and
![]() $\sigma (0)$
:
$\sigma (0)$
:
 $$ \begin{align*} \sum_{k=-\infty}^\infty (-1)^kp(n-P_5(k)) &= \delta_{0,n}, \quad\text{with } p(0) = 1, \\ \sum_{k=-\infty}^\infty (-1)^k\sigma(n-P_5(k)) &= 0, \quad\text{with } \sigma(0) \text{ replaced by } n, \end{align*} $$
$$ \begin{align*} \sum_{k=-\infty}^\infty (-1)^kp(n-P_5(k)) &= \delta_{0,n}, \quad\text{with } p(0) = 1, \\ \sum_{k=-\infty}^\infty (-1)^k\sigma(n-P_5(k)) &= 0, \quad\text{with } \sigma(0) \text{ replaced by } n, \end{align*} $$
where
![]() $\delta _{ij}$
is the Kronecker delta and
$\delta _{ij}$
is the Kronecker delta and
![]() $P_m(k)$
is the kth generalised m-gonal number
$P_m(k)$
is the kth generalised m-gonal number
 $$ \begin{align} P_m(k) := \bigg(\frac m2 - 1\bigg)k^2 - \bigg(\frac m2 - 2 \bigg) k. \end{align} $$
$$ \begin{align} P_m(k) := \bigg(\frac m2 - 1\bigg)k^2 - \bigg(\frac m2 - 2 \bigg) k. \end{align} $$
Motivated by these identities as well as the fact that the divisor functions
![]() $\sigma (n)$
and
$\sigma (n)$
and
 $$ \begin{align*} \sigma_{\mathrm{odd}}(n) := \sum_{\substack{d \mid n \\ d \text{ odd}}} d, \end{align*} $$
$$ \begin{align*} \sigma_{\mathrm{odd}}(n) := \sum_{\substack{d \mid n \\ d \text{ odd}}} d, \end{align*} $$
where
![]() $\sigma _{\mathrm {odd}}(n) :=0$
for
$\sigma _{\mathrm {odd}}(n) :=0$
for
![]() $n \le 0$
, have the same parity, Merca [Reference Merca3] recently studied the relationship between
$n \le 0$
, have the same parity, Merca [Reference Merca3] recently studied the relationship between
![]() $\sigma _{\mathrm {odd}}(n)$
and the generalised m-gonal numbers. More specifically, he investigated for which positive integers m the following congruences hold for all
$\sigma _{\mathrm {odd}}(n)$
and the generalised m-gonal numbers. More specifically, he investigated for which positive integers m the following congruences hold for all
![]() $n \in \mathbb {Z}^+$
:
$n \in \mathbb {Z}^+$
:
 $$ \begin{align} \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_m(k)) &\equiv \begin{cases} n \pmod 2 & \text{if } n= P_m({\kern2pt}j), \, j \in \mathbb{Z}, \\ 0 \pmod 2 & \text{otherwise}, \\ \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_m(k)) &\equiv \begin{cases} n \pmod 2 & \text{if } n= P_m({\kern2pt}j), \, j \in \mathbb{Z}, \\ 0 \pmod 2 & \text{otherwise}, \\ \end{cases} \end{align} $$
 $$ \begin{align} \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_5(k)) &\equiv \begin{cases} n \pmod m & \text{if } n= P_5({\kern2pt}j), \, j \in \mathbb{Z}, \\ 0 \pmod m & \text{otherwise}, \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_5(k)) &\equiv \begin{cases} n \pmod m & \text{if } n= P_5({\kern2pt}j), \, j \in \mathbb{Z}, \\ 0 \pmod m & \text{otherwise}, \end{cases} \end{align} $$
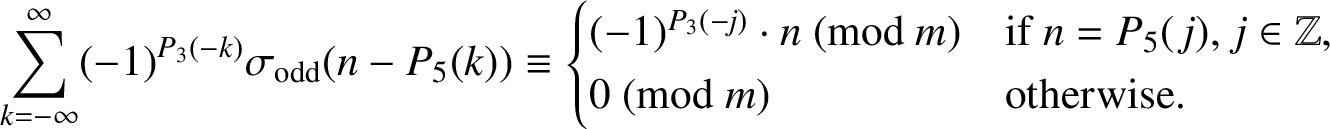 $$ \begin{align} \sum_{k=-\infty}^\infty (-1)^{P_3(-k)}\sigma_{\mathrm{odd}}(n-P_5(k)) &\equiv \begin{cases} (-1)^{P_3(-j)}\cdot n \pmod m & \text{if } n= P_5({\kern2pt}j), \, j \in \mathbb{Z}, \\ 0 \pmod m & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{k=-\infty}^\infty (-1)^{P_3(-k)}\sigma_{\mathrm{odd}}(n-P_5(k)) &\equiv \begin{cases} (-1)^{P_3(-j)}\cdot n \pmod m & \text{if } n= P_5({\kern2pt}j), \, j \in \mathbb{Z}, \\ 0 \pmod m & \text{otherwise}. \end{cases} \end{align} $$
In particular, Merca posed the following conjectures in [Reference Merca3].
Conjecture 1. The following are true.
Merca showed the ‘if’ condition for each of these conjectures. Using his work, we obtain the following theorem.
Theorem 2. Merca’s conjectures are true.
Proof. We begin by proving (ii). Merca showed that (3) holds if
![]() $m \in \{2,3,6\}$
[Reference Merca3, Theorem 3]. Hence, it suffices to show that if
$m \in \{2,3,6\}$
[Reference Merca3, Theorem 3]. Hence, it suffices to show that if
![]() $m \notin \{2,3,6\}$
, then there exists some
$m \notin \{2,3,6\}$
, then there exists some
![]() $n \in \mathbb {Z}^+$
such that
$n \in \mathbb {Z}^+$
such that
![]() $n \neq P_5({\kern2pt}j)$
for all
$n \neq P_5({\kern2pt}j)$
for all
![]() $j \in \mathbb {Z}$
and
$j \in \mathbb {Z}$
and
 $$ \begin{align} \sum_{k = -\infty}^\infty \sigma_{\mathrm{odd}}(n-P_5(k)) \not\equiv 0 \pmod m. \end{align} $$
$$ \begin{align} \sum_{k = -\infty}^\infty \sigma_{\mathrm{odd}}(n-P_5(k)) \not\equiv 0 \pmod m. \end{align} $$
Since
![]() $\sigma _{\mathrm {odd}}(n-P_5(k)) = 0$
whenever
$\sigma _{\mathrm {odd}}(n-P_5(k)) = 0$
whenever
![]() $n-P_5(k) \le 0$
, the sum in (5) is in fact finite and we easily compute
$n-P_5(k) \le 0$
, the sum in (5) is in fact finite and we easily compute
![]() $\sum _k \sigma _{\mathrm {odd}}(3-P_5(k)) = 6$
, where
$\sum _k \sigma _{\mathrm {odd}}(3-P_5(k)) = 6$
, where
![]() $3 \ne P_5({\kern2pt}j)$
for
$3 \ne P_5({\kern2pt}j)$
for
![]() $j \in \mathbb {Z}$
. Thus, (5) holds unless
$j \in \mathbb {Z}$
. Thus, (5) holds unless
![]() $6 \equiv 0 \pmod m$
. But this is the case only if
$6 \equiv 0 \pmod m$
. But this is the case only if
![]() $m \in \{2,3,6\}$
.
$m \in \{2,3,6\}$
.
Next, we prove (iii). Again, Merca proved that (4) holds if
![]() $m \in \{2,4\}$
[Reference Merca3, Theorem 4]. Hence, it suffices to show that if
$m \in \{2,4\}$
[Reference Merca3, Theorem 4]. Hence, it suffices to show that if
![]() $m \notin \{2,4\}$
, then there exists some
$m \notin \{2,4\}$
, then there exists some
![]() $n \in \mathbb {Z}^+$
such that
$n \in \mathbb {Z}^+$
such that
![]() $n\neq P_5({\kern2pt}j)$
for all
$n\neq P_5({\kern2pt}j)$
for all
![]() $j \in \mathbb {Z}$
and
$j \in \mathbb {Z}$
and
 $$ \begin{align} \sum_{k = -\infty}^\infty (-1)^{P_3(-k)} \sigma_{\mathrm{odd}}(n-P_5(k)) \not\equiv 0 \pmod m. \end{align} $$
$$ \begin{align} \sum_{k = -\infty}^\infty (-1)^{P_3(-k)} \sigma_{\mathrm{odd}}(n-P_5(k)) \not\equiv 0 \pmod m. \end{align} $$
We compute
![]() $\sum _k (-1)^{P_3(-k)} \sigma _{\mathrm {odd}}(3-P_5(k)) = 4$
, where
$\sum _k (-1)^{P_3(-k)} \sigma _{\mathrm {odd}}(3-P_5(k)) = 4$
, where
![]() $3 \ne P_5({\kern2pt}j)$
for
$3 \ne P_5({\kern2pt}j)$
for
![]() $j \in \mathbb {Z}$
, and so (6) holds unless
$j \in \mathbb {Z}$
, and so (6) holds unless
![]() $4 \equiv 0 \pmod {m}$
. But this is the case only if
$4 \equiv 0 \pmod {m}$
. But this is the case only if
![]() $m \in \{2,4\}$
.
$m \in \{2,4\}$
.
Finally, we prove (i). Since
![]() $\sigma _{\mathrm {odd}}(n)$
is odd if and only if n is a square or twice a square (see [Reference Merca3, page 3]),
$\sigma _{\mathrm {odd}}(n)$
is odd if and only if n is a square or twice a square (see [Reference Merca3, page 3]),
 $$ \begin{align} \sum_{n=1}^\infty \sigma_{\mathrm{odd}}(n)q^n \equiv \sum_{n=1}^\infty q^{n^2}+\sum_{n=1}^\infty q^{2n^2} \pmod 2. \end{align} $$
$$ \begin{align} \sum_{n=1}^\infty \sigma_{\mathrm{odd}}(n)q^n \equiv \sum_{n=1}^\infty q^{n^2}+\sum_{n=1}^\infty q^{2n^2} \pmod 2. \end{align} $$
The nth coefficient of
 $$ \begin{align*} \bigg(\sum_{\ell=1}^\infty \sigma_{\mathrm{odd}}(\ell)q^\ell\bigg)\bigg(\sum_{k=-\infty}^\infty q^{P_m(k)}\bigg) = \sum_{\ell=1}^\infty \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(\ell)q^{\ell+P_m(k)} {=} \sum_{n = 1}^\infty \bigg(\sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_m(k))\bigg)q^n \end{align*} $$
$$ \begin{align*} \bigg(\sum_{\ell=1}^\infty \sigma_{\mathrm{odd}}(\ell)q^\ell\bigg)\bigg(\sum_{k=-\infty}^\infty q^{P_m(k)}\bigg) = \sum_{\ell=1}^\infty \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(\ell)q^{\ell+P_m(k)} {=} \sum_{n = 1}^\infty \bigg(\sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_m(k))\bigg)q^n \end{align*} $$
is given by
![]() $\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(n-P_m(k))$
. On the other hand, the nth coefficient of
$\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(n-P_m(k))$
. On the other hand, the nth coefficient of
 $$ \begin{align*} \bigg(\sum_{\ell=1}^\infty q^{\ell^2}+\sum_{\ell=1}^\infty q^{2\ell^2}\bigg)\bigg(\sum_{k=-\infty}^\infty q^{P_m(k)}\bigg) = \sum_{\substack{\ell \ge 1 \\ k \in \mathbb{Z}}} (q^{\ell^2+P_m(k)}+q^{2\ell^2+P_m(k)}) \end{align*} $$
$$ \begin{align*} \bigg(\sum_{\ell=1}^\infty q^{\ell^2}+\sum_{\ell=1}^\infty q^{2\ell^2}\bigg)\bigg(\sum_{k=-\infty}^\infty q^{P_m(k)}\bigg) = \sum_{\substack{\ell \ge 1 \\ k \in \mathbb{Z}}} (q^{\ell^2+P_m(k)}+q^{2\ell^2+P_m(k)}) \end{align*} $$
is given by
![]() $a_m(n)+b_m(n)$
, where
$a_m(n)+b_m(n)$
, where
 $$ \begin{align*} a_m(n) = |A_m(n)| &:= \#\{(\ell,k) \in \mathbb{Z}^+\times \mathbb{Z}:\, \ell^2+P_m(k) = n\}, \\ b_m(n) = |B_m(n)| &:= \#\{(\ell,k) \in \mathbb{Z}^+\times \mathbb{Z}:\, 2\ell^2+P_m(k) = n\}. \end{align*} $$
$$ \begin{align*} a_m(n) = |A_m(n)| &:= \#\{(\ell,k) \in \mathbb{Z}^+\times \mathbb{Z}:\, \ell^2+P_m(k) = n\}, \\ b_m(n) = |B_m(n)| &:= \#\{(\ell,k) \in \mathbb{Z}^+\times \mathbb{Z}:\, 2\ell^2+P_m(k) = n\}. \end{align*} $$
Thus, due to (7),
 $$ \begin{align*} \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_m(k)) \equiv a_m(n)+b_m(n) \pmod 2. \end{align*} $$
$$ \begin{align*} \sum_{k=-\infty}^\infty \sigma_{\mathrm{odd}}(n-P_m(k)) \equiv a_m(n)+b_m(n) \pmod 2. \end{align*} $$
Suppose first that
![]() $m \ge 7$
. Then we claim that
$m \ge 7$
. Then we claim that
![]() $P_m(0) = 0, P_m(1) = 1$
and
$P_m(0) = 0, P_m(1) = 1$
and
![]() $P_m(k)> 3$
for all
$P_m(k)> 3$
for all
![]() $k \notin \{0,1\}$
. From (1), it is clear that
$k \notin \{0,1\}$
. From (1), it is clear that
![]() $P_m(0) = 0$
and
$P_m(0) = 0$
and
![]() $P_m(1) = 1$
. To see that
$P_m(1) = 1$
. To see that
![]() $P_m(k)> 3$
for all
$P_m(k)> 3$
for all
![]() $k \notin \{0,1\}$
, note that since the leading term of
$k \notin \{0,1\}$
, note that since the leading term of
![]() $P_m(x)$
is positive and its minimum is at
$P_m(x)$
is positive and its minimum is at
![]() $(m-4)/(2m-4)$
, where
$(m-4)/(2m-4)$
, where
![]() $0 < {(m-4)}/{(2m-4)} < 1$
, we have
$0 < {(m-4)}/{(2m-4)} < 1$
, we have
![]() $P_m(k) \ge P_m(2) = m \ge 7$
for
$P_m(k) \ge P_m(2) = m \ge 7$
for
![]() $k \ge 2$
and
$k \ge 2$
and
![]() $P_m(k) \ge P_m(-1) = m-3 \ge 4$
for
$P_m(k) \ge P_m(-1) = m-3 \ge 4$
for
![]() $k \le -1$
.
$k \le -1$
.
Now, let
![]() $n=3$
. Then the above shows that n is not a generalised m-gonal number for
$n=3$
. Then the above shows that n is not a generalised m-gonal number for
![]() $m \ge 7$
, and so for (2) to hold, we must have
$m \ge 7$
, and so for (2) to hold, we must have
![]() $\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_m(k)) \equiv 0 \pmod 2$
. If
$\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_m(k)) \equiv 0 \pmod 2$
. If
![]() $(\ell ,k) \in A_m(3)$
, then
$(\ell ,k) \in A_m(3)$
, then
![]() $\ell ^2 = 3-P_m(k)$
, so that in particular
$\ell ^2 = 3-P_m(k)$
, so that in particular
![]() $\ell ^2 \le 3$
, which forces
$\ell ^2 \le 3$
, which forces
![]() $\ell = 1$
. But then we must have
$\ell = 1$
. But then we must have
![]() $P_m(k) = 2$
, which we have seen to be impossible. Hence,
$P_m(k) = 2$
, which we have seen to be impossible. Hence,
![]() $A_m(3)$
is empty and
$A_m(3)$
is empty and
![]() $a_m(3) \equiv 0 \pmod 2$
. On the other hand, if
$a_m(3) \equiv 0 \pmod 2$
. On the other hand, if
![]() $(\ell ,k) \in B_m(3)$
, we must again have
$(\ell ,k) \in B_m(3)$
, we must again have
![]() $\ell = 1$
. It follows that
$\ell = 1$
. It follows that
![]() $P_m(k) = 1$
, which is the case if and only if
$P_m(k) = 1$
, which is the case if and only if
![]() $k = 1$
. Hence,
$k = 1$
. Hence,
![]() $B_m(3) = \{(1,1)\}$
and
$B_m(3) = \{(1,1)\}$
and
![]() $b_m(3) \equiv 1\pmod 2$
. We conclude that
$b_m(3) \equiv 1\pmod 2$
. We conclude that
![]() $\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_m(k)) \equiv a_m(3)+b_m(3)\equiv 1 \not \equiv 0 \pmod 2$
.
$\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_m(k)) \equiv a_m(3)+b_m(3)\equiv 1 \not \equiv 0 \pmod 2$
.
Merca showed that (2) holds for
![]() $m \in \{5,6\}$
and, for
$m \in \{5,6\}$
and, for
![]() $m \in \{1,2\}$
, the sum in (2) diverges; hence, it remains to consider
$m \in \{1,2\}$
, the sum in (2) diverges; hence, it remains to consider
![]() $m \in \{3,4\}$
. Suppose first that
$m \in \{3,4\}$
. Suppose first that
![]() $m = 3$
and note that
$m = 3$
and note that
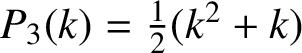 $P_3(k) = \tfrac 12(k^2+k)$
. We have
$P_3(k) = \tfrac 12(k^2+k)$
. We have
![]() $3 = P_3(-3) = P_3(2)$
, so for (2) to hold, we must have
$3 = P_3(-3) = P_3(2)$
, so for (2) to hold, we must have
![]() $\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_3(k)) \equiv 3 \equiv 1 \pmod 2$
. If
$\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_3(k)) \equiv 3 \equiv 1 \pmod 2$
. If
![]() $(\ell ,k) \in A_3(3)$
, then
$(\ell ,k) \in A_3(3)$
, then
![]() $\ell = 1$
and
$\ell = 1$
and
![]() $P_3(k) = 2$
, which is impossible. Hence,
$P_3(k) = 2$
, which is impossible. Hence,
![]() $A_3(3)$
is empty. If
$A_3(3)$
is empty. If
![]() $(\ell ,k) \in B_3(3)$
, then
$(\ell ,k) \in B_3(3)$
, then
![]() $\ell =1$
and
$\ell =1$
and
![]() $P_3(k) = 1$
, which is the case if and only if
$P_3(k) = 1$
, which is the case if and only if
![]() $k \in \{-2,1\}$
. It follows that
$k \in \{-2,1\}$
. It follows that
![]() $B_3(3) = \{(1,-2),(1,1)\}$
and
$B_3(3) = \{(1,-2),(1,1)\}$
and
![]() $\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_3(k)) \equiv a_3(3)+b_3(3) \equiv 0 \not \equiv 1 \pmod 2$
.
$\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(3-P_3(k)) \equiv a_3(3)+b_3(3) \equiv 0 \not \equiv 1 \pmod 2$
.
Finally, suppose that
![]() $m = 4$
and note that
$m = 4$
and note that
![]() $P_4(k) = k^2$
. Since
$P_4(k) = k^2$
. Since
![]() $4 = P_4(2)$
, for (2) to hold we must have
$4 = P_4(2)$
, for (2) to hold we must have
![]() $\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(4-P_4(k)) \equiv 4 \equiv 0 \pmod 2$
. If
$\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(4-P_4(k)) \equiv 4 \equiv 0 \pmod 2$
. If
![]() $(\ell ,k) \in A_4(4)$
, then either
$(\ell ,k) \in A_4(4)$
, then either
![]() $\ell = 1$
and
$\ell = 1$
and
![]() $P_4(k) = 3$
, which is impossible, or
$P_4(k) = 3$
, which is impossible, or
![]() $\ell = 2$
and
$\ell = 2$
and
![]() $P_4(k) = 0$
, which is the case if and only if
$P_4(k) = 0$
, which is the case if and only if
![]() $k = 0$
. Thus,
$k = 0$
. Thus,
![]() $A_4(4) = \{(2,0)\}$
. On the other hand, if
$A_4(4) = \{(2,0)\}$
. On the other hand, if
![]() $(\ell ,k) \in B_4(4)$
, then
$(\ell ,k) \in B_4(4)$
, then
![]() $\ell =1$
and
$\ell =1$
and
![]() $P_3(k) = 2$
, which is impossible. It follows that
$P_3(k) = 2$
, which is impossible. It follows that
![]() $B_4(4)$
is empty and
$B_4(4)$
is empty and
![]() $\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(4-P_4(k)) \equiv a_4(4)+b_4(4) \equiv 1 \not \equiv 0 \pmod 2$
.
$\sum _{k=-\infty }^\infty \sigma _{\mathrm {odd}}(4-P_4(k)) \equiv a_4(4)+b_4(4) \equiv 1 \not \equiv 0 \pmod 2$
.
Acknowledgements
We would like to thank Ken Ono for suggesting this project and for several helpful conversations. We thank William Craig and Badri Pandey, as well as the referee, for their comments on the exposition in this note.



