In time-to-event analyses, a competing-risks setting occurs when 1 or several events preclude the observation of an event of interest.Reference Wolkewitz, Cooper, Bonten, Barnett and Schumacher 1 , Reference Andersen, Geskus, de Witte and Putter 2 Recent studies have shown that this setting is of special importance when analyzing risk factors for nosocomial infections (NIs).Reference Wolkewitz 3 , Reference Weber, Cube, von, Sommer and Wolkewitz 4 For instance, a cohort study of hospitalized children in Kenya reported no association between burns and nosocomial bacteremia.Reference Aiken, Mturi and Njuguna 5 However, a complete competing-risks analysis would have detected an effect on length of stay, which would have yielded a cumulative risk 3 times higher for children with burns.Reference Wolkewitz, Cooper, Bonten, Barnett and Schumacher 1 , Reference Schumacher, Allignol, Beyersmann, Binder and Wolkewitz 6 This analysis is achieved by determining the influence of a risk factor on each separate competing event.Reference Wolkewitz, von Cube and Schumacher 7 The decreasing effect of a risk factor (eg, burns) on the rate of 1 event (eg, discharge from hospital) can have an increasing effect on the risk of experiencing a competing event (eg, nosocomial bacteremia). Therefore, ignoring competing risks when analyzing hospital-acquired infections can lead to biased results and incomplete conclusions.
When the covariate information is expensive or difficult to acquire, separate nested case-control (NCC) study designs can be used to ascertain the influence of risk factors on NIReference Obadia, Opatowski and Temime 8 , Reference O’Fallon, Kandell, Schreiber and D’Agata 9 and its competing events. An NCC requires the collection of covariate information for cases and time-matched controls that are a subset of the total available controls in the full cohort, thus achieving a reduction in time and resources. In traditional practice, controls would be sampled for each competing event and would only be included in the analysis of the competing event for which they were selected. However, SamuelsenReference Samuelsen 10 proposed pooling these controls together and employing a weighted Cox model so that all selected controls are used in the analysis of each competing event. This method led to improvements in precision over keeping the controls separated.
In this study, we adapted the methodology of Samuelsen and applied it to a common setting in hospital epidemiology. Our goal was to estimate the influence of potential risk factors on acquiring an NI and on the competing event of dying or being discharged without infection in 2 Spanish intensive care units (ICUs). By reusing controls from 1 initial sampling, we avoided the added effort of sampling with respect to every competing event (ie, “sample for one, analyze for all”). Furthermore, our extension requires additional data that are routinely collected (and not any additional covariate data), thus enabling a competing-risks reanalysis of previously conducted NCC studies. These improvements can be achieved with little cost to the researcher.
Methods
Data were collected from 6,563 admissions in 2 Spanish ICUs within the ENVIN-HELICS network. We removed 5 individuals from the original cohort due to missing values. Among the 6,563 patients admitted, 432 (6.58%) acquired an NI (ie, bloodstream infection, urinary tract infection, or pneumonia) and 762 (11.6%) died without acquiring an infection. However, 5,359 of 6,563 patients (81.6%) were discharged alive without acquiring an infection, and 10 (0.15%) were administratively censored. (Hereafter, we omit the “without acquiring an infection” description for death or discharge.) The 2 competing events we examined were the risk of acquiring an infection (defined as after 24 hours in the ICU) and the composite event of dying or being discharged. The influence of the Acute Physiology and Chronic Health Evaluation (APACHE) score on these competing events was of interest. For ease of analysis, the APACHE score was categorized into quartiles. Additionally, a dichotomous covariate for treatment with antibiotics within 48 hours of admission (ATB48H) was also analyzed. Entry and event or censoring times were needed for the entire cohort to perform a traditional NCC study. This ‘skeleton’ of information was required to select controls at the time of the event as well as to calculate inclusion probabilities.
Time-dynamic sampling
Incidence density sampling was employed to select a reduced sample (ie, subcohort) of the full cohort for statistical analysis. Figure 1 provides a visual representation of the sampling design. We randomly selected 1 control from the risk set each time a subject was observed to acquire an infection (ie, each time the vertical black lines cross the potential controls at each infection time). For example, patient 29 acquired an infection on day 5 and patients 30–50 were potential controls. Whether a subject is selected as a control had no bearing on their potential to be sampled again in the future; individuals may be controls at several infection times. Furthermore, a subject selected as a control may acquire an infection at a later follow-up time. For example, patient 49 was a potential control for both infection case 29 and 45 and later (on approximately day 14) acquired an infection.
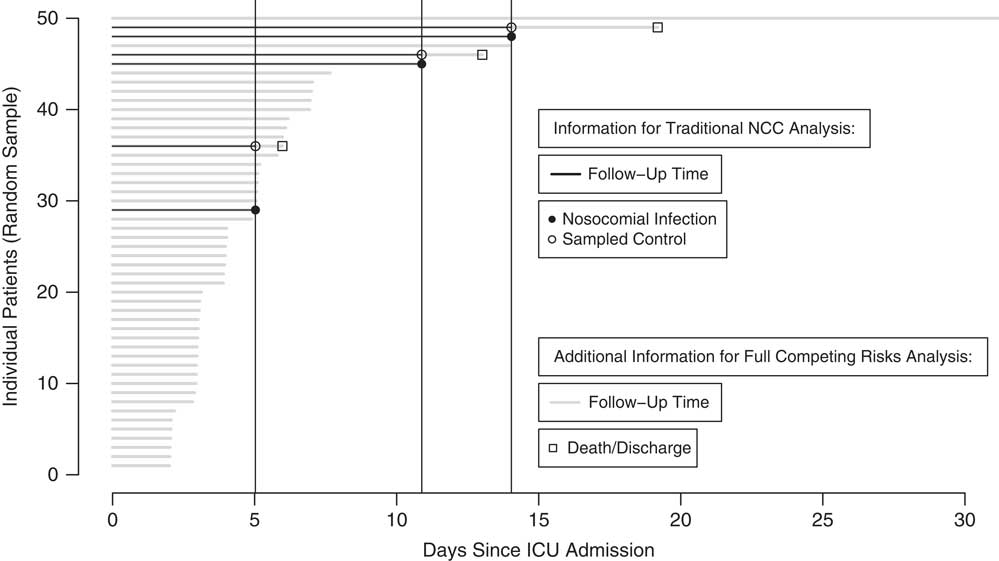
Fig. 1 Nested case-control (NCC) design using incidence density sampling for random sampling of 50 patients from Spanish ICU data. Comparison of information required for established NCC method and extended method. Covariate information collected for nosocomial infection cases and sampled controls.
Traditional analysis: NCC Design
Nosocomial infection cause-specific hazard ratio estimation. The normal practice for an NCC design is to employ a conditional logistic regression model using the time-matched case-control data. The required cases, controls, and follow-up time (black horizontal lines) information for the traditional analysis is shown in Fig. 1.
Inverse probability weighting (IPW) analysis: case-cohort design
Nosocomial infection, death or discharge cause-specific hazard ratio estimation, nosocomial infection risk ratio estimation
In step 1, “inverse probability weighting” calls for noncases in the sampled subcohort to be weighted with the inverse of their inclusion probabilities. This weighting compensates for controls not selected to the subcohort and thus attempts to reconstruct the original full cohort. Cases are weighted with 1. These weights are fixed for the entirety of the patient’s follow-up time. The time-matching can now be broken and the controls are reused at event times when they are at risk (akin to a case-cohort design).
SamuelsenReference Samuelsen 10 reviews 2 inclusion probability estimators. The first is a nonparametric Kaplan-Meier (KM) type estimator. The second is a standard logistic regression model-type weighting (generalized linear model, GLMReference Saarela, Kulathinal, Arjas and Läärä 11 ). The first step is to calculate these inclusion probabilities with the ‘skeleton’ from the underlying data.
In step 2, the inclusion probabilities from step 1 are subsequently used in a weighted Cox partial likelihood to estimate the cause-specific hazard ratio of interest (infection and death or discharge). The remaining competing event (death or discharge, or infection, respectively) is censored. APACHE score quartiles and a variable for antibiotic treatment within 48 hours (ATB48H) are included in the regression. Variance estimation is more complicated due to dependent factors in the weighted likelihood. For this reason, we used robust variances in our analyses.
For the NI risk estimates, the weights from step 1 were included in a log-binomial model. General estimating equations were used for variance estimation.
Results
Time-dynamic sampling
As a result of incidence density sampling, a subcohort of 864 individuals was selected for the traditional analysis. Several controls were sampled multiple times resulting in a subcohort of 760 distinct individuals for the weighted analysis. Among 760 infection cases, 432 (56.8%) were automatically included. Of all 760 cases, 2 cases (0.3%) were censored and 326 death or discharge cases (42.9%) were sampled with respect to infection. From the subcohort, 137 cases (18.0%) were in the first APACHE quartile, 189 (24.9%) were in the second, 184 (24.2%) were in the third, and 250 (32.9%) were in the fourth. Furthermore, 209 (27.5%) were treated with an antibiotic within 48 hours of admission, while 551 (72.5%) were not.
Figure 2 shows the weights assigned to the selected controls. Patients with longer stays in the ICU have a higher chance of being selected as a control (and consequently lower inverse probability weights) than patients with shorter stays. Thus, the weights are higher for sampling times early after admission and lower for later sampling times (when only patients with longer stays can be selected).
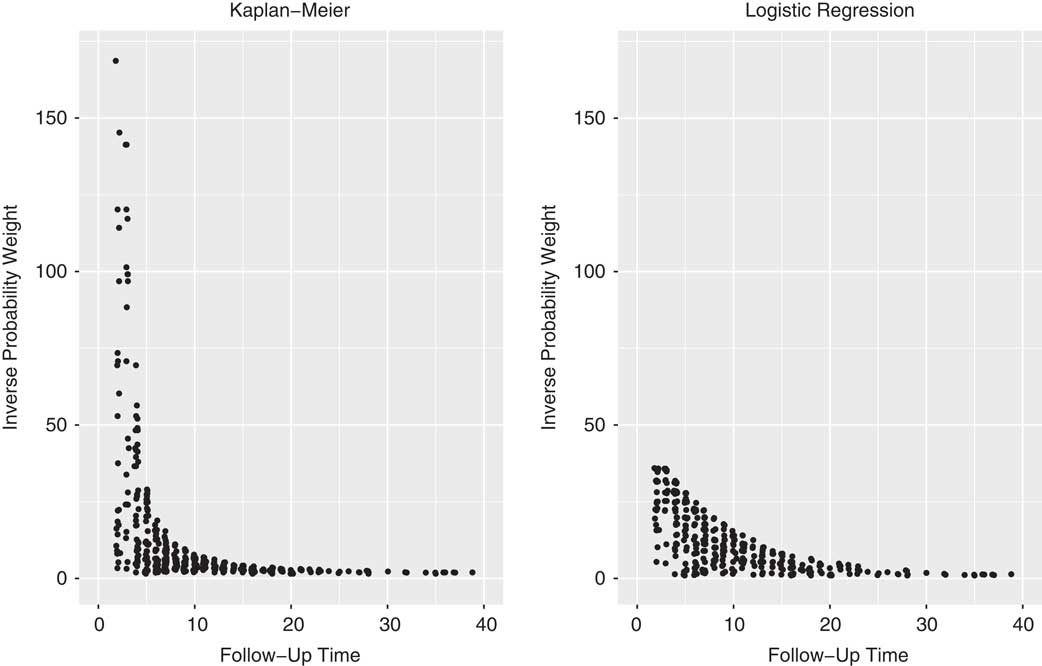
Fig. 2 Dots represent the weights of individual controls at the time they were sampled. For example, a patient with weight 10 represents 10 patients in the analysis. The aim of this weighting is to reconstruct the full cohort from the selected subcohort.
Infection cause-specific hazard analysis
Table 1 shows the results from the full cohort estimation (the “gold standard”) as well as the IPW and traditional estimation from a reduced cohort for the infection endpoint. From the full cohort, we can conclude that an increasing APACHE score is associated with an increasing hazard for acquire an infection. The same interpretation would result from the IPW and traditional methods, even though the reduced cohort estimates did not reach statistical significance (P <.05) for the second APACHE quartile. All 4 estimates indicate that antibiotic treatment within 48 hours is associated with a lower infection hazard. We observed little difference in accuracy and precision among the traditional, KM, and GLM estimates.
Table 1 Results from Analysis of Spanish ICU Data

Note. NI, nosocomial infection; HR, hazard ratio; CI, confidence interval; SE, standard error; RR, risk ratio; IPW, Cox partial likelihood with inverse probability weighting; KM, Kaplan Meier weights; GLM, logistic regression weights.
a Cause-specific hazard ratio for exposure
b Calculated with estimated standard errors for Cox regression and conditional logistic regression, calculated with robust standard errors for inverse probability weighting and log binomial model.
c Using log binomial model.
d Distinct patients.
e First APACHE quartile reference for second, third, and fourth APACHE quartiles.
f Cox regression.
g Conditional logistic regression.
h Antibiotic treatment within 48 hours of admission.
Death or discharge cause-specific hazard analysis
Table 1 shows the results for the full cohort and IPW estimation with reused controls for the combined death-or-discharge endpoint. Importantly, traditional estimation (conditional logistic regression) is not possible for this competing event with the given data. Here, IPW methods conform to the full cohort interpretation that higher APACHE scores have a statistically significant decreasing effect on death or discharge. The estimates for antibiotic treatment within 48 hours are also in agreement: full, 0.64 (95% CI, 0.60–0.69); KM, 0.64 (95% CI, 0.44–0.95); and GLM, 0.65 (95% CI, 0.53–0.81). The logistic regression weights have a slight advantage over the KM weights in precision.
Infection risk analysis
Using a log binomial model to predict risk, the IPW estimates are in good agreement with the full cohort estimates. Once again, traditional estimation is not possible for this analysis with the given data. Interestingly, we observed a far more pronounced influence of the fourth-quartile APACHE score on the risk ratio (6.92, full cohort) for acquiring a NI than on the corresponding hazard ratio (2.14, full cohort). This finding is explained by the strong decreasing effect a high APACHE score has on the death-or-discharge hazard; these patients stay longer in the ICU and thus have a higher risk of acquiring an NI. This phenomenon also explains the seemingly paradoxical result that ATB48H has a statistically significant decreasing influence on the NI hazard ratio (0.75) but no influence on the NI risk ratio. Again, ATB4H is associated with an increased length of stay in the ICU (decreased death-or-discharge hazard) and thus a greater risk of acquiring an infection.
Simulated data
In addition to the successful implementation of the methodology with prospectively collected real data from 2 Spanish ICUs, the methodology was also applied to simulated competing risks data with similarly impressive results (see Table 2). Both IPW methods match the accuracy and precision of the traditional method for the first simulated event while displaying good agreement with the full simulated cohort estimates for the second event and risk analysis. Software code in R for the real and simulated data analysis is provided in the supplemental material section.
Table 2 Results from Analysis of Simulated Data

Note. HR, hazard ratio; CI, confidence interval; SE, standard error; RR, risk ratio; IPW, Cox partial likelihood with inverse probability weighting; KM, Kaplan Meier weights; GLM, logistic regression weights.
a True event 1 HR, 2.00.
b True event 2 HR, 0.50.
c Cause-specific hazard ratio for exposure.
d Calculated with estimated standard errors for Cox regression and conditional logistic regression, calculated with robust standard errors for IPW and log binomial model.
e Using log binomial model.
f Distinct individuals.
g Cox regression.
h Conditional logistic regression.
Discussion
In this study, we adapted existing methods to perform a complete competing risks analysis on the occurrence of hospital acquired infections. This adapted method of reusing controls not only matched the accuracy and precision of traditional cause specific analyses for an event of interest but also extended it to provide competing event etiological and event-of-interest prediction analysis, which are 2 substantial improvements. Although the KM and GLM weights produced similar results, Fig. 2 illustrates that the nonparametric KM weights are more prone to extreme values, whereas the GLM weights have a smoothing effect on the weight distribution. We therefore recommend plotting and studying the weights of different approaches; extreme weights impact the robustness of the model. The only additional information required for this extension analysis was follow-up and event-type data that are routinely recorded for hospital patients. Considering that this information was likely recorded for previously conducted NCC studies, one could easily revisit these studies and enhance their results.
The method of reusing controls can be extended in several ways. Matching controls to cases on additional variables can both adjust for confounding and improve efficiency. For example, we could have matched controls in our Spanish ICU cohort by sex or age at admission. In reviewing the role of matching in case-control studies of antimicrobial resistance, Cerceo et alReference Cerceo, Lautenbach, Linkin, Bilker and Lee 12 emphasize the importance of accounting for study design matching in the analysis. The matching can be resolved in the inclusion probabilities and/or the regression analysis. Stoer and SamulesenReference Støer and Samuelsen 13 addressed this question by introducing strong correlations between matching variables and exposure–outcome in simulated data for a subsequent event setting. They found that adjusting for matching in the weight estimation had little influence on the estimates, whereas adjusting in the Cox regression was essential. Thus, we recommend including possible confounding variables in the weighted Cox model.
A further extension proposed by Wolkewitz et alReference Wolkewitz, Cooper, Palomar-Martinez, Olaechea-Astigarraga, Alvarez-Lerma and Schumacher 14 is conducting subdistribution incidence density sampling and estimating the cumulative incidence function by assuming a Fine and Gray model. In this variation, the patients are available for selection until their (potential) censoring time and the inclusion probability weights are subsequently adjusted. Simulation studies and application to the Spanish ICU data showed IPW estimation to be in good agreement with the full cohort (data not shown). The method could also be extended to a “subsequent event” setting where a second event is a subset of a first event. For example, the controls sampled with respect to acquiring infection (first event) could be reused to analyze death from hospital infection (second event).
Our study has some limitations. In some situations, breaking the time-matched risk sets is not recommended. BorganReference Borgan and Keogh 15 found that reusing controls when close matching is required (eg, in the presence of batch effects for biological samples) can lead to bias in simulation studies. Salim et alReference Salim, Yang and Reilly 16 found that in situations with little overlap in the distributions of the matching variables for 2 separate outcomes, reusing controls was less efficient than simply sampling new time-matched controls.
Ohneberg et alReference Ohneberg, Wolkewitz and Beyersmann 17 applied NCC and case-cohort designs to the same Spanish ICU data set and found that the NCC design had slight advantages in power and precision in assessing the effect of a dichotomous APACHE score on acquiring infection. A further comparison of a case-cohort design and an NCC design reusing controls in a setting with multiple outcomes is of certain interest. Our results indicate that an NCC design does not have the purported disadvantage in such a setting and that a full competing-risks analysis can be performed without collecting new data. This methodology provides a clear improvement over established NCC methods.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/ice.2018.186
Acknowledgments
We would like to thank the Spanish ICUs for their invaluable contribution to collecting the data.
Financial support
D.H. has received support from the Innovative Medicines Initiative Joint Undertaking (grant no. 115737-2, Combatting Bacterial Resistance in Europe—Molecules Against Gram-Negative Infections [COMBACTE-MAGNET]). This work was supported by the German Research Foundation (grant no. WO 1746/1-2 to M.W.). The funders had no role in data collection and analysis, decision to publish, or preparation of the manuscript.
Conflicts of interest
All authors report no conflicts of interest relevant to this article.






