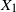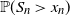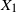1. Introduction
Moderateand large deviations of the sum of independent and identically distributed (i.i.d.) real-valued random variables have been investigated since the beginning of the 20th century. Kinchin [Reference Kinchin13] in 1929 was the first to give a result on large deviations of the sum of i.i.d. Bernoulli-distributed random variables. In 1933 Smirnov [Reference Smirnov23] improved this result, and in 1938 Cramér [Reference Cramér5] gave a generalization to sums of i.i.d. random variables satisfying the eponymous Cramér condition which requires the Laplace transform of the common distribution of the random variables to be finite in a neighborhood of zero. Cramér’s result was extended by Feller [Reference Feller8] to sequences of not necessarily identically distributed random variables under restrictive conditions (Feller considered only random variables taking values in bounded intervals), thus Cramér’s result does not follow from Feller’s result. A strengthening of Cramér’s theorem was given by Petrov [Reference Petrov20] together with a generalization to the case of non-identically distributed random variables. Improvements of Petrov’s result can be found in [Reference Petrov and Robinson21]. Deviations for sums of heavy-tailed i.i.d. random variables were studied by several authors: an early result appears in [Reference Linnik15], and more recent references are [Reference Borovkov2, Reference Borovkov and Borovkov3, Reference Denisov, Dieker and Shneer7, Reference Mikosch and Nagaev16].
In [Reference Nagaev17, Reference Nagaev18], A. V. Nagaev studied the case where the commom distribution of the i.i.d. random variables is absolutely continuous with respect to the Lebesgue measure with density
$p(t)\sim \exp\big\{{-}\left\lvert {t} \right\rvert^{1-\varepsilon}\big\}$
as
$\left\lvert {t} \right\rvert\to \infty$
, with
$\varepsilon \in (0,1)$
. He distinguished five exact-asymptotics results corresponding to five types of deviation speeds. These results were generalized in [Reference Nagaev19] to the case where the tail writes as
$\exp\big\{{-}t^{1-\varepsilon}L(t)\big\}$
, where
$\varepsilon \in (0,1)$
and L is a suitably slowly varying function at infinity. Such results can also be found in [Reference Borovkov2, Reference Borovkov and Borovkov3]. In [Reference Brosset, Klein, Lagnoux and Petit4], the authors considered the following setting. Let
$\varepsilon \in (0,1)$
and let X be a Weibull-like (or semiexponential, or stretched exponential) random variable, i.e. there exists
$q > 0$
such that
$\log \mathbb{P}(X \,\geqslant\, x) \sim -qx^{1-\varepsilon}$
as
$x\to \infty$
. Assume also that there exists
$\gamma > 0$
such that
$\mathbb{E}[|X|^{2+\gamma}] < \infty$
. For all
$n \in \mathbb{N}^*$
, let
$X_1$
,
$X_2$
, …,
$X_n$
be i.i.d. copies of X and set
$S_n=X_1+\dots+X_n$
. The asymptotic behavior of the large-deviation probability
$\mathbb{P}(S_n \,\geqslant\, x_n)$
is given for any positive sequence
$x_n \gg n^{1/2}$
. According to the asymptotics of
$x_n$
, three types of behavior emerge for
$\log \mathbb{P}(S_n \,\geqslant\, x_n)$
:
-
Maximal jump range [Reference Brosset, Klein, Lagnoux and Petit4, Theorem 1]: When
$x_n \gg n^{1/(1+\varepsilon)}$
,
$\log \mathbb{P}(S_n \,\geqslant\, x_n) \sim \log\mathbb{P}(\max(X_1,\ldots,X_n)\,\geqslant\, x_n).$
-
Gaussian range: [Reference Brosset, Klein, Lagnoux and Petit4, Theorem 2]: When
$n^{1/2}\ll x_n \ll n^{1/(1+\varepsilon)}$
,
$\log \mathbb{P}(S_n \,\geqslant\, x_n) \sim \log(1-\phi(n^{-1/2} x_n)),$
$\phi$
being the cumulative distribution function of the standard Gaussian law. -
Transition: [Reference Brosset, Klein, Lagnoux and Petit4, Theorem 3]: The case
$x_n = \Theta\big(n^{1/(1+\varepsilon)}\big)$
appears to be an interpolation between the Gaussian range and the maximal jump range.
The main contribution of the present paper is a generalization to triangular arrays of the results in [Reference Brosset, Klein, Lagnoux and Petit4, Reference Nagaev17, Reference Nagaev18]. Such a setting appears naturally in some combinatorial problems, such as those presented in [Reference Janson12], including hashing with linear probing. Since the 1980s, laws of large numbers have been established for triangular arrays [Reference Gut9–Reference Hu, Moricz and Taylor11]. Lindeberg’s condition is standard for the central limit theorem to hold for triangular arrays [Reference Billingsley1, Theorem 27.2]. Dealing with triangular arrays of light-tailed random variables, the Gärtner–Ellis theorem provides moderate- and large-deviation results. Deviations for sums of heavy-tailed i.i.d. random variables have been studied by several authors [Reference Borovkov2–Reference Brosset, Klein, Lagnoux and Petit4, Reference Linnik15, Reference Nagaev17–Reference Nagaev19], and a good survey can be found in [Reference Mikosch and Nagaev16]. Here, we focus on the particular case of semiexponential tails (treated in [Reference Borovkov2–Reference Brosset, Klein, Lagnoux and Petit4, Reference Nagaev17, Reference Nagaev18] for sums of i.i.d. random variables), generalizing the results to triangular arrays. See [Reference Klein, Lagnoux and Petit14] for an application to hashing with linear probing.
The paper is organized as follows. In Section 2 we state the main results, the proofs of which can be found in Section 3. The assumptions are discussed in Section 4. Section 5 is devoted to the study of the model of a truncated random variable which is a natural model of a triangular array. This kind of model appears in many proofs of large deviations. Indeed, when dealing with a random variable, the Laplace transform of which is not finite, a classical approach consists in truncating the random variable and letting the truncation go to infinity. In this model we exhibit various rate functions, especially non-convex ones.
2. Main results
In the following, for any sequences
$(x_n)_{n\,\geqslant\,1}$
and
$(y_n)_{n\,\geqslant\, 1}$
, it will be more convenient to write
$x_n \preccurlyeq y_n$
for
$x_n = O(y_n)$
as
$n \to \infty$
. For all
$n \,\geqslant\, 1$
, let
$Y_n$
be a centered real-valued random variable, and let
$N_n$
be a natural number. We assume that
$N_n \to \infty$
as
$n \to \infty$
. For all
$n \,\geqslant\, 1$
, let
$\left(Y_{n,i}\right)_{1 \,\leqslant\, i \,\leqslant\, N_n}$
be a family of i.i.d. random variables distributed as
$Y_n$
. Define, for all
$k \in [\![{1},{N_n}]\!]$
,
$T_{n,k}\mathrel{\mathop:}=\sum_{i=1}^{k} Y_{n,i}.$
To lighten the notation, let
$T_{n} \mathrel{\mathop:}= T_{n,N_{n}}$
.
Theorem 2.1. (Maximal jump range.) Let
$\varepsilon \in {\left({0},{1}\right)}$
,
$q > 0$
, and
$\alpha >1/(1+\varepsilon)$
. Assume that:
-
(H1) For all sequences
$(y_n)_{n\,\geqslant\, 1}$
such that
$N_n^{\alpha \varepsilon} \preccurlyeq y_n \preccurlyeq N_n^\alpha$
,
$\log \mathbb{P}(Y_n \,\geqslant\, y_n) \underset{n\to \infty}{\sim} -q y_n^{1-\varepsilon}$
. -
(H2)
$\mathbb{E}\big[Y_n^2\big] = o\Big(N_n^{\alpha(1+\varepsilon)-1}\Big)$
as
$n\to \infty$
.
Then, for all
$y \,\geqslant\, 0$
,
\begin{align*} \lim_{n \to \infty} \frac{1}{N_n^{\alpha(1-\varepsilon)}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q y^{1-\varepsilon} .\end{align*}
In this paper we have chosen to make explicit the deviations in terms of powers of
$N_n$
, as is now standard in large-deviation theory. Nevertheless, as in [Reference Brosset, Klein, Lagnoux and Petit4, Reference Nagaev17, Reference Nagaev18], the proof ofTheorem 2.1 immediately adapts to show that
$\log \mathbb{P}( T_{n} \,\geqslant\, x_n ) \underset{n\to \infty}{\sim} - q x_n^{1-\varepsilon}$
as soon as
$x_n \gg N_n^{1/(1+\varepsilon)}$
, assuming that
$\mathbb{E}\big[Y_n^2\big] = o\big(x_n^{1+\varepsilon}/N_n\big)$
as
$n\to \infty$
and that there exists
$\delta > 0$
such that, for all sequences
$(y_n)_{n\,\geqslant\, 1}$
such that
$x_n^{\varepsilon} \,\leqslant\, y_n \,\leqslant\, x_n(1+\delta)$
,
$\log\mathbb{P}(Y_n \,\geqslant\, y_n)\underset{n\to \infty}{\sim} -q y_n^{1-\varepsilon}$
. Theorems 2.2 and 2.3 adapt analogously.
Theorem 2.2. (Gaussian range.) Let
$\varepsilon \in {\left({0},{1}\right)}$
,
$q > 0$
,
$\sigma > 0$
, and
$\frac{1}{2} < \alpha < 1/(1+\varepsilon)$
. Suppose that (H1) holds together with:
-
(H2′)
$\mathbb{E}\big[Y_n^2\big]\underset{n\to \infty}{\longrightarrow} \sigma^2 .$
-
(H2+) There exists
$\gamma \in {\left({0},{1}\right]}$
such that
$\mathbb{E}\big[\left\lvert {Y_n} \right\rvert^{2+\gamma}\big]=o\Big(N_n^{\gamma(1-\alpha)}\Big)$
as
$n\to \infty$
.
Then, for all
$y \,\geqslant\, 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1} }\log \mathbb{P}( T_{n} \,\geqslant\, N_n^{\alpha} y ) = - \frac{y^2}{2\sigma^2}.\end{equation*}
Theorem 2.3. (Transition.) Let
$\varepsilon \in {\left({0},{1}\right)}$
,
$q > 0$
,
$\sigma > 0$
, and
$\alpha = 1/(1+\varepsilon)$
. Suppose that (H1), (H2′), and (H2
$^+$
) hold. Then, for all
$y \,\geqslant\, 0$
,
\begin{equation*} \lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1} }\log \mathbb{P}( T_{n} \,\geqslant\, N_n^\alpha y ) = - \inf_{0\,\leqslant\, t \,\leqslant\, 1} \biggl\{ q(1-t)^{1-\varepsilon} y^{1-\varepsilon}+\frac{t^2y^2}{2\sigma^2} \biggr\} \;=\!:\; - I(y) .\end{equation*}
Noticethat the speed of deviation is continuous in
$\alpha$
since, at the transition (
$\alpha = 1/(1+\varepsilon)$
),
$2\alpha-1=\alpha(1-\varepsilon)$
. Moreover, let us make explicit the rate function I. Let
$f(t)\mathrel{\mathop:}= q(1-t)^{1-\varepsilon} y^{1-\varepsilon}+{t^2y^2/}{(2\sigma^2)}$
. An easy computation shows that, if
$y \,\leqslant\, y_0\mathrel{\mathop:}= ((1-\varepsilon^2)(1+1/\varepsilon)^\varepsilon q\sigma^2)^{1/(1+\varepsilon)}$
, f is increasing and its minimum
$y^2/(2\sigma^2)$
is attained at
$t=1$
. If
$y>y_0$
, f has two local minima, at t(y) and at 1; the former corresponds to the smaller of the two roots in
${\left[{0},{1}\right]}$
of the equation
$f'(t) = 0$
, which is equivalent to
\begin{align*} t(1-t)^{\varepsilon}=\frac{(1-\varepsilon)q\sigma^2}{y^{1+\varepsilon}}. \end{align*}
If
$y_0< y\,\leqslant\, y_1\mathrel{\mathop:}= (1+\varepsilon)\left({q\sigma^2}/{(2\varepsilon)^{\varepsilon}}\right)^{1/(1+\varepsilon)}$
, then
$f(t(y))\,\geqslant\, f(1)$
; if
$y>y_1$
,
$f(t(y))< f(1)$
. As a consequence, for all
$y\,\geqslant\, 0$
,
\begin{align*}I(y) = \Bigg\{ \begin{array}{ll} \frac{y^2}{2\sigma^2} & \;\;\;\;\;\text{if}\; y\,\leqslant\, y_1 , \\[4pt] q(1-t(y))^{1-\varepsilon} y^{1-\varepsilon}+\frac{t(y)^2y^2}{2\sigma^2} & \;\;\;\;\;\text{if}\; y> y_1. \end{array} \end{align*}
Remark 2.1. Consider the following generalization of (H1). Let L be a slowly varying function and assume that:
-
(H1′) For all sequences
$(y_n)_{n\,\geqslant\, 1}$
such that
$N_n^{\alpha \varepsilon}/L(N_n^\alpha) \preccurlyeq y_n \preccurlyeq N_n^\alpha$
,
$\log \mathbb{P}(Y_n \,\geqslant\, y_n) \sim -L(y_n) y_n^{1-\varepsilon}$
.
Then, the proof of Theorem 2.1 (resp. Theorem 2.2) immediately adapts to show that if Assumptions (H1′) and (H2) (resp. (H1′), (H2′), and (H2
$^+$
)) hold, then, for all
$y \,\geqslant\, 0$
,
\begin{align*}\lim_{n \to \infty} \frac{1}{L(N_n^\alpha) N_n^{\alpha(1-\varepsilon)}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - y^{1-\varepsilon} .\end{align*}
(resp. the conclusion of Theorem 2.2 holds). However, Theorem 2.3 requires additional assumptions on L to handle such a generalization of (H1).
3. Proofs
3.1. Preliminary known results
First, we present a classical result, known as the principle of the largest term. The proof is standard (see, e.g., [Reference Dembo and Zeitouni6, Lemma 1.2.15]).
Lemma 3.1. (Principle of the largest term) Let
$(v_n)_{n\,\geqslant\, 1}$
be a positive sequence diverging to
$\infty$
, let r be a positive integer, and, for
$i \in [\![{1},{r}]\!]$
, let
$(a_{n,i})_{n\,\geqslant\, 1}$
be a sequence of non-negative numbers. Then,
\begin{equation*}\limsup_{n \to \infty} \frac{1}{v_n} \log \left(\sum_{i=1}^r a_{n,i}\right)=\max_{i=1,\dots,r}\left( \limsup_{n \to \infty} \frac{1}{v_n} \log a_{n,i}\right) .\end{equation*}
The next theorem is a unilateral version of the Gärtner–Ellis theorem, which was provedin [Reference Plachky and Steinebach22].
Theorem 3.1. (Unilateral Gärtner–Ellis theorem) Let
$(Z_n)_{n\,\geqslant\, 1}$
be a sequence of real-valued random variables, and let
$(v_n)_{n\,\geqslant\, 1}$
be a positive sequence diverging to
$\infty$
. Suppose that there exists a differentiable function
$\Lambda$
defined on
$\mathbb{R}_+$
such that
$\Lambda'$
is a (increasing) bijective function from
$\mathbb{R}_+$
to
$\mathbb{R}_+$
and, for all
$\lambda\,\geqslant\, 0$
,
\begin{equation*}\frac{1}{v_n} \log\mathbb{E}\bigl[ \textrm{e}^{v_n\lambda Z_n} \bigr] \underset{n\to\infty}{\longrightarrow} \Lambda(\lambda) .\end{equation*}
Then, for all
$z\,\geqslant\, 0$
,
\begin{equation*}-\inf_{t>z} \Lambda^*(t) \,\leqslant\, \liminf_{n\to\infty} \frac{1}{v_n}\log \mathbb{P}(Z_n>z) \,\leqslant\, \limsup_{n\to\infty} \frac{1}{v_n}\log \mathbb{P}(Z_n\,\geqslant\, z) \,\leqslant\, -\inf_{t\,\geqslant\, z} \Lambda^*(t) ,\end{equation*}
where, for all
$t\,\geqslant\, 0$
,
$\Lambda^*(t)\mathrel{\mathop:}= \sup \{ \lambda t -\Lambda(\lambda) ;\, \lambda \,\geqslant\, 0\}$
.
The proofs of Theorems 2.1, 2.2, and 2.3 are adaptations of those in [Reference Brosset, Klein, Lagnoux and Petit4] to the case of triangular arrays. We decided to detail these proofs here to introduce Sections 4 and 5, where the proofs are mainly sketched.
3.2. Proof of Theorem 2 (Maximal jump range)
Assume that Theorem 2.1 has been proved for
$y > 0$
. Then, the case
$y = 0$
follows by monotony. Indeed, for all
$y > 0$
,
\begin{align*}0 \,\geqslant\, \liminf_{n \to \infty} \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \mathbb{P}(T_{n} \,\geqslant\, 0) & \,\geqslant\, \lim_{n \to \infty} \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q y^{1-\varepsilon} \underset{y \to 0}{\longrightarrow} 0 .\end{align*}
From now on, we assume that
$y > 0$
. First, we define
\begin{align*} \mathbb{P}( T_{n} \,\geqslant\, N_n^{\alpha} y ) & = \mathbb{P}( T_{n} \,\geqslant\, N_n^{\alpha} y;\ \text{for all}\ i \in [\![{1},{N_n}]\!], \ Y_{n,i} < N_n^{\alpha} y) \nonumber \\ & \quad + \mathbb{P}( T_{n} \,\geqslant\, N_n^{\alpha} y;\ \text{there exists}\ i \in [\![{1},{N_n}]\!]\ \text{such that}\ Y_{n,i} \,\geqslant\, N_n^{\alpha} y) \nonumber \\ & \;=\!:\; P_n + R_n. .\end{align*}
Theorem 2.1 is a direct consequence of Lemmas 3.1, 3.2, and 3.3.
Lemma 3.2. Under (H1) and (H2), for
$\alpha > \frac{1}{2}$
and
$y > 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{ N_n^{\alpha(1-\varepsilon)} } \log R_n = -q y^{1-\varepsilon} .\end{equation*}
Proof of Lemma 3.2. Using (H1),
\begin{align*}\limsup_{n \to \infty} \frac{1}{ N_n^{\alpha(1-\varepsilon)} } \log R_n & \,\leqslant\, \lim_{n \to \infty} \frac{1}{ N_n^{\alpha(1-\varepsilon)} } \log (N_n \mathbb{P}(Y_n \,\geqslant\, N_n^{\alpha} y)) = - qy^{1-\varepsilon}. \end{align*}
Let us prove the converse inequality. Let
$\delta > 0$
. We have
$R_n \,\geqslant\, \mathbb{P}\left( T_{n} \,\geqslant\, N_n^{\alpha} y, Y_{n,1} \,\geqslant\, N_n^{\alpha} y\right)$
$ \,\geqslant\, \mathbb{P}\left( T_{n,N_{n-1}} \,\geqslant\, -N_n^\alpha\delta\right) \mathbb{P}(Y_n \,\geqslant\, N_n^{\alpha} (y +\delta))$
. By Chebyshev’s inequality, observe that
\begin{align*}\mathbb{P}( T_{n,N_{n-1}} \,\geqslant\, -{N_n}^{\alpha}\delta ) & \,\geqslant\, 1-\frac{\textrm{Var}(Y_n)}{N_n^{2\alpha-1}\delta^2} \to 1 ,\end{align*}
using (H2). Finally, by (H1), we get
\begin{align*}\liminf_{n \to \infty} \frac{1}{N_n^{\alpha(1-\varepsilon)}} \log R_n & \,\geqslant\, \lim_{n \to \infty} \frac{1}{N_n^{\alpha(1-\varepsilon)}} \log \mathbb{P}(Y_n \,\geqslant\, N_n^{\alpha}(y + \delta)) = - q (y + \delta)^{1-\varepsilon} .\end{align*}
We conclude by letting
$\delta \to 0$
.
Lemma 3.3. Under (H1) and (H2), for
$\alpha > 1/(1+\varepsilon)$
and
$y > 0$
,
\begin{equation*} \limsup_{n \to \infty} \frac{1}{ N_n^{\alpha(1-\varepsilon)} }\log P_n \,\leqslant\, -q y^{1-\varepsilon} .\end{equation*}
Proof of Lemma 3.3. For all
$q' \in {\left({0},{q}\right)}$
, we have
\begin{align*}P_n & = \mathbb{E}\left[ \textbf{1}_{T_{n} \,\geqslant\, N_n^\alpha y} \textbf{1}_{\forall i \in [\![{1},{N_n}]\!], Y_{n,i} < N_n^{\alpha} y} \right] \\ & \qquad\qquad\qquad\qquad\qquad\quad\leqslant\, \exp\left\{-q' (N_n^{\alpha} y)^{1-\varepsilon}\right\} \mathbb{E}\left[ \exp\left\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} Y_n\right\} \textbf{1}_{Y_n < N_n^{\alpha} y} \right]^{N_n} ,\end{align*}
using the inequality
$\textbf{1}_{x \,\geqslant\, 0} \,\leqslant\, \textrm{e}^x$
for the first indicator function above. If we prove that
$\mathbb{E}\left[ \exp\Big\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} Y_n\Big\} \textbf{1}_{Y_n < N_n^{\alpha} y} \right] \,\leqslant\, 1 + o \Big( N_n^{\alpha(1-\varepsilon)-1} \Big),$
then
$\log P_n \,\leqslant\, -q' (N_n^{\alpha} y)^{1-\varepsilon} + o\Big(N_n^{\alpha(1-\varepsilon)}\Big)$
and the conclusion follows by letting
$q' \to q$
. Write
\begin{align*}\mathbb{E} \left[ \exp\left\{\frac{q'}{(N_n^{\alpha} y)^{\varepsilon}} Y_n\right\} \textbf{1}_{Y_n < N_n^{\alpha} y} \right]& = \mathbb{E} \left[ \exp\left\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} Y_n\right\} \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}} \right] \\ & \quad + \mathbb{E} \left[ \exp\left\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} Y_n\right\} \textbf{1}_{N_n^{\alpha \varepsilon} \,\leqslant\, Y_n < N_n^{\alpha} y} \right].\end{align*}
First, using the fact that, for all
$x < q' y^{-\varepsilon}$
,
$\textrm{e}^x \,\leqslant\, 1 + x + \frac{1}{2}\textrm{e}^{q' y^{-\varepsilon}} x^2$
, and (H2), we get
\begin{align*}\mathbb{E} \left[ \exp\left\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} Y_n\right\} \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}} \right] & \,\leqslant\, \mathbb{E} \left[ \left(1 + \frac{q'}{(N_n^{\alpha} y)^{\varepsilon}}Y_n + \frac{(q')^2 \textrm{e}^{q' y^{-\varepsilon}}}{2 (N_n^{\alpha} y)^{2\varepsilon}}Y_n^2\right) \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}} \right]\\ & \,\leqslant\, 1 + \frac{(q')^2 \textrm{e}^{q' y^{-\varepsilon}}}{2}\cdot \frac{\mathbb{E}\big[Y_n^2\big]}{(N_n^{\alpha} y)^{2\varepsilon}} \nonumber \\ & = 1 + o (N_n^{\alpha(1-\varepsilon)-1}), \nonumber\end{align*}
the second inequality stemming from the following lemma.
Lemma 3.4. Under (H1), for all
$y > 0$
, for all
$q' < q$
there exists
$n_0(q') \,\geqslant\, 1$
such that, for all
$n \,\geqslant\, n_0(q')$
and for all
$u \in {\left[{N_n^{\alpha \varepsilon}},{N_n^\alpha y}\right]}$
,
$\log\mathbb{P}(Y_n\,\geqslant\, u)\,\leqslant\, -q' u^{1-\varepsilon}$
.
Proof of Lemma 3.4. By contraposition, if the conclusion of the lemma is false, we can construct a sequence
$(u_n)_{n \,\geqslant\, 1}$
such that, for all
$n \,\geqslant\, 1$
,
$u_n \in {\left[{N_n^{\alpha \varepsilon}},{N_n^\alpha y}\right]}$
and
$\log \mathbb{P}(Y_n\,\geqslant\, u_n) > -q' u_n^{1-\varepsilon}$
, whence (H1) is not satisfied.
Secondly, integrating by parts (Lebesgue–Stieljes version), we get
\begin{align*}\mathbb{E} &\left[ \exp\left\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} Y_n\right\} \textbf{1}_{N_n^{\alpha \varepsilon} \,\leqslant\, Y_n < N_n^{\alpha} y} \right] = \int_{N_n^{\alpha \varepsilon}}^{N_n^{\alpha} y} \exp\left\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} u\right\} \mathbb{P}(Y_n \in \textrm{d} u)\\ & = - \bigg[ \exp\bigg\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} u\bigg\} \mathbb{P}(Y_n \,\geqslant\, u) \bigg]_{N_n^{\alpha \varepsilon}}^{ N_n^{\alpha} y} + \frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}} \int_{N_n^{\alpha \varepsilon}}^{N_n^{\alpha} y} \exp\bigg\{\frac{q'}{ (N_n^{\alpha} y)^{\varepsilon}}u\bigg\} \mathbb{P}(Y_n \,\geqslant\, u) \, \textrm{d} u \\ & \,\leqslant\, \textrm{e}^{q' y^{-\varepsilon}} \mathbb{P}(Y_n \,\geqslant\, N_n^{\alpha \varepsilon}) + \frac{q'}{(N_n^{\alpha} y)^{\varepsilon}} \int_{N_n^{\alpha \varepsilon}}^{ N_n^{\alpha} y} \exp\bigg\{\frac{q'}{(N_n^{\alpha} y)^{\varepsilon}} u-q''u^{1-\varepsilon}\bigg\} \, \textrm{d} u \\ & \,\leqslant\, (1 + q'(N_n^{\alpha} y)^{1-\varepsilon}) \textrm{e}^{q' y^{-\varepsilon} - q''N_n^{\alpha \varepsilon (1-\varepsilon)}} \\ & = o\big(N_n^{\alpha(1-\varepsilon)-1}\big)\end{align*}
for n large enough, using (H1) and Lemma 3.4 with
$q''\in {\left({q'},{q}\right)}$
, and taking the supremum of
$u \mapsto q'(N_n^{\alpha} y)^{-\varepsilon} u-q''u^{1-\varepsilon}$
over
${\left[{N_n^{\alpha \varepsilon}},{N_n^{\alpha} y} \right]}$
. The proof of Lemma 3.3 is now complete.
3.3. Proof of Theorems 2.2 (Gaussian range) and 2.3 (Transition)
Theconclusions of Theorems 2.2 and 2.3 follow from Lemmas 3.5, 3.6, and 3.9 below, and the principle of the largest term (Lemma 3.1): Lemma 3.5 (resp. Lemma 3.6) provides the leading term in Theorem 2.2 (resp. in Theorem 2.3), and Lemma 3.9 bounds the remaining terms. The structure of the proof follows [Reference Brosset, Klein, Lagnoux and Petit4].
Let us fix
$y > 0$
. The result for
$y = 0$
follows by monotony (see the beginning of the proof of Theorem 2.1).
3.3.1 Principal estimates
For all
$m \in [\![{0},{N_n}]\!]$
, we define
\begin{align} \Pi_{n, m} & = \mathbb{P}\bigl( T_{n} \,\geqslant\, N_n^\alpha y;\\ & \qquad \qquad \qquad \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon};\; \text{for all}\ i \in [\![{m+1},{N_n}]\!], Y_{n,i} < N_n^{\alpha \varepsilon} \bigr) , \nonumber\end{align}
so that
\begin{align} \mathbb{P}( T_{n} \,\geqslant\, N_n^{\alpha} y ) & = \sum_{m=0}^{N_n} \binom{N_n}{m} \Pi_{n,m} .\end{align}
Lemma 3.5. Under (H1), (H2′), and (H2
$^+$
), for
$\frac{1}{2} < \alpha \,\leqslant\, 1/(1+\varepsilon)$
and
$y > 0$
,
\begin{align*} \lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \Pi_{n,0} = - \frac{y^2}{2\sigma^2} .\end{align*}
Proof of Lemma 3.5. For all
$n\,\geqslant\, 1$
, we introduce the variable
$Y^<_n$
distributed as
$\mathcal{L}(Y_n \mid Y_n < N_n^{\alpha \varepsilon})$
. Let
$T^<_n=\sum_{i=1}^{N_n} Y^{<}_{n,i}$
, where the
$Y^{<}_{n,i}$
are independent random variables distributed as
$Y^<_n$
. Then
$\Pi_{n,0}=\mathbb{P}(T^<_n \,\geqslant\, N_n^\alpha y) \mathbb{P}(Y_n < N_n^{\alpha \varepsilon})^{N_n}$
. On the one hand,
$\mathbb{P}(Y_n < N_n^{\alpha \varepsilon})^{N_n} \to 1$
by (H1). On the other hand, in order to apply the unilateral version of the Gärtner–Ellis theorem (Theorem 3.1), we compute, for
$u\,\geqslant\, 0$
,
\begin{align}\Lambda_n(u) & = \frac{1}{N_n^{2\alpha - 1}} \log \mathbb{E} \left[\exp\left\{\frac{u}{N_n^\alpha}T^<_n\right\}\right] \nonumber \\ & = N_n^{2(1-\alpha)} \log \mathbb{E} \left[\exp\left\{\frac{u}{N_n^{1-\alpha}}Y_n\right\} \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}}\right] - N_n^{2(1-\alpha)} \log \mathbb{P}(Y_n < N_n^{\alpha \varepsilon}) .\end{align}
By (H1), the second term above goes to 0. As for the first term, for
$\gamma \in {\left({0},{1}\right)}$
given by (H2
$^+$
), there exists a constant
$c>0$
such that, for all
$t \,\leqslant\, u$
,
$\left\lvert {\textrm{e}^t-1-t-t^2/2} \right\rvert\,\leqslant\, c\left\lvert {t} \right\rvert^{2+\gamma}$
, whence
\begin{align} \left\lvert {\left( \exp\left\{\frac{u}{N_n^{1-\alpha}}Y_n\right\} - 1 - \frac{u}{N_n^{1-\alpha}}Y_n - \frac{u^2}{2N_n^{2(1-\alpha)}}Y_n^2 \right) \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}}} \right\rvert & \\ &\!\!\!\!\!\! \,\leqslant\, \frac{c u^{2+\gamma}}{N_n^{(2+\gamma)(1-\alpha)}}\left\lvert {Y_n} \right\rvert^{2+\gamma}, \nonumber \end{align}
since
$\alpha(1+\varepsilon)\,\leqslant\, 1$
. Now,
\begin{align}\biggl| \mathbb{E} & \left[\exp\left\{\frac{u}{N_n^{1-\alpha}}Y_n\right\} \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}} \right] - \exp\left\{\frac{u^2 \sigma^2}{2 N_n^{2(1-\alpha)}}\right\} \biggr| \nonumber \\ & \,\leqslant\, \left| \mathbb{E}\left[ \left( \exp\left\{\frac{u}{N_n^{1-\alpha}}Y_n\right\} - 1 - \frac{u}{N_n^{1-\alpha}}Y_n - \frac{u^2}{2N_n^{2(1-\alpha)}} Y_n^2 \right) \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}} \right] \right| \nonumber \\ & \quad + \left| \mathbb{E} \left[ \left( 1 + \frac{u}{N_n^{1-\alpha}}Y_n + \frac{u^2}{2N_n^{2(1-\alpha)}}Y_n^2 \right) \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}} \right] - \left( 1 + \frac{u^2 \mathbb{E}\big[Y_n^2\big]}{2 N_n^{2(1-\alpha)}} \right) \right| \nonumber \\ & \quad + \left| \left( 1 + \frac{u^2 \mathbb{E}[Y_n^2]}{2 N_n^{2(1-\alpha)}} \right) - \exp\left\{\frac{u^2 \sigma^2}{2 N_n^{2(1-\alpha)}}\right\} \right| \nonumber \\ & = \left| \mathbb{E} \left[ \left( 1 + \frac{u}{N_n^{1-\alpha}}Y_n + \frac{u^2}{2N_n^{2(1-\alpha)}}Y_n^2 \right) \textbf{1}_{Y_n \,\geqslant\, N_n^{\alpha \varepsilon}} \right] \right| + o(N_n^{-2(1-\alpha)}) , \end{align}
using (3.4), (H2
$^+$
), the fact that
$\mathbb{E}[Y_n] = 0$
, a Taylor expansion of order 2 of the exponential function, and (H2′). Finally, for n large enough, applying Hölder’s inequality,
\begin{align}\left| \mathbb{E} \left[ \left( 1 + \frac{u}{N_n^{1-\alpha}}Y_n + \frac{u^2}{2N_n^{2(1-\alpha)}}Y_n^2 \right) \textbf{1}_{Y_n \,\geqslant\, N_n^{\alpha \varepsilon}} \right] \right| & \,\leqslant\, \mathbb{E}\big[Y_n^2 \textbf{1}_{Y_n \,\geqslant\, N_n^{\alpha \varepsilon}}\big] \nonumber \\ & \,\leqslant\, \mathbb{E}\big[\left\lvert {Y_n} \right\rvert^{2+\gamma}\big]^{2/(2+\gamma)} \mathbb{P}\big(Y_n \,\geqslant\, N_n^{\alpha \varepsilon}\big)^{\gamma/(2+\gamma)} \nonumber \\ & = o\big(N_n^{-2(1-\alpha)}\big) \end{align}
as a consequence of (H1) and (H2
$^+$
). Combining (3.3), (3.5), and (3.6), we get
\begin{align*}\Lambda_n(u) \underset{n \to \infty}{\longrightarrow} \frac{u^2\sigma^2}{2} \;=\!:\; \Lambda(u) ,\end{align*}
and the proof of Lemma 3.5 follows from the fact that
$\Lambda^*(y) = y^2 / (2 \sigma^2)$
.
Lemma 3.6. Under (H1), (H2′), and (H2
$^+$
), for
$\alpha = 1/(1+\varepsilon)$
and
$y > 0$
,
\begin{align*}\liminf_{n\to\infty} \frac{1}{N_n^{2 \alpha - 1}} \log \Pi_{n,1} \,\geqslant\, -I(y). \end{align*}
Proof of Lemma 3.6. Remember that for
$\alpha = 1/(1+\varepsilon)$
we have
$2 \alpha - 1 = \alpha(1 - \varepsilon)$
. So, for all
$t \in {\left({0},{1}\right)}$
,
\begin{align*}\frac{1}{N_n^{2 \alpha - 1}} \log \Pi_{n,1} & \,\geqslant\, \frac{1}{N_n^{2 \alpha - 1}} \log \mathbb{P}\bigl( T_{n,N_{n-1}} \,\geqslant\, N_n^\alpha ty;\ \text{for all}\ i \in [\![{1},{N_n-1}]\!], Y_{n,i} < N_n^{\alpha \varepsilon} \bigr) \\ & \quad + \frac{1}{N_n^{2 \alpha - 1}} \log \mathbb{P}\bigl(N_n^\alpha (1-t)y \,\leqslant\, Y^<_{n},N_{n} < N_n^\alpha y \bigr) \\ & \underset{n \to \infty}{\longrightarrow} - \frac{t^2y^2}{2\sigma^2} - q(1-t)^{1-\varepsilon} y^{1-\varepsilon} ,\end{align*}
by Lemma 3.5 (applied to the array
$(Y_{n,i})_{1\,\leqslant\, i \,\leqslant\, N_n-1}$
) and by (H1). Optimizing in
$t \in {\left({0},{1}\right)}$
provides the conclusion.
3.3.2 Two uniform bounds
Lemma 3.7. Under (H2′) and (H2
$^+$
), for all
$\delta \in {\left({0},{1}\right)}$
and
$y > 0$
, there exists
$n(\delta, y) \,\geqslant\, 1$
such that, for all
$n \,\geqslant\, n(\delta, y)$
, for all
$m \in [\![{0},{N_n}]\!]$
, for all
$u \in {\left[{0},{N_n^\alpha y}\right]}$
,
\begin{equation*}\log \mathbb{P}(T_{n,m} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} < N_n^{\alpha \varepsilon}) \,\leqslant\, - \frac{(1-\delta) u^2}{2 N_n \sigma^2} .\end{equation*}
Proof of Lemma 3.7. Using the fact that
$\textbf{1}_{t \,\geqslant\, 0} \,\leqslant\, \textrm{e}^t$
, for all
$\lambda > 0$
,
\begin{align*}\mathbb{P}\big(T_{n,m} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], \quad Y_{n,i} < N_n^{\alpha \varepsilon}\big) & \,\leqslant\, \textrm{e}^{-\lambda u} \mathbb{E}\big[\textrm{e}^{\lambda Y_n} \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}}\big]^m .\end{align*}
For
$\gamma \in {\left({0},{1}\right)}$
given by (H2
$^+$
), there exists
$c(y) > 0$
such that, for all
$s \,\leqslant\, y \sigma^{-2}$
, we have
$\textrm{e}^s \,\leqslant\, 1 + s + \frac{1}{2}s^2+c(y)|s|^{2+\gamma}$
. Hence, for
$\lambda \mathrel{\mathop:}= u (N_n\sigma^2)^{-1} \,\leqslant\, N_n^{-\alpha \varepsilon} y \sigma^{-2} $
,
\begin{align*}\mathbb{E}\big[\textrm{e}^{\lambda Y_n} \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}}\big] & \,\leqslant\, 1 + \frac{\lambda^2}{2} \mathbb{E}\big[Y_n^2\big] + c(y) \lambda^{2+\gamma} \mathbb{E}\big[\left\lvert {Y_n} \right\rvert^{2+\gamma}\big] = 1 + \frac{\lambda^2\sigma^2}{2}(1+\delta_n) ,\end{align*}
where
\begin{equation*}\delta_n \mathrel{\mathop:}= \biggl( \frac{\mathbb{E}\big[Y_n^2\big]}{\sigma^2} - 1 \biggr) + \frac{2 c(y) \lambda^\gamma}{\sigma^2} \mathbb{E}\big[\left\lvert {Y_n} \right\rvert^{2+\gamma}\big] .\end{equation*}
By (H2′), the first term in
$\delta_n$
goes to 0 as
$n \to \infty$
. Moreover,
$\lambda \,\leqslant\, N_n^{\alpha - 1} y \sigma^{-2}$
so, using (H2
$^+$
), we obtain that, for
$n \,\geqslant\, n(\delta, y)$
large enough,
$\left\lvert {\delta_n} \right\rvert \,\leqslant\, \delta$
. Finally, since
$m \,\leqslant\, N_n$
, we have, for
$n \,\geqslant\, n(\delta, y)$
,
\begin{align*} & \qquad\qquad\qquad\log \mathbb{P}(T_{n,m} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} < N_n^{\alpha \varepsilon}) \\ & \qquad\qquad\qquad\qquad\qquad\,\leqslant\, - \lambda u + \frac{N_n \lambda^2 \sigma^2}{2} (1+\delta) = - \frac{(1-\delta) u^2}{2 N_n \sigma^2}.\end{align*}
Lemma 3.8. Under (H1), for all
$\delta \in {\left({0},{1}\right)}$
and
$y>0$
, there exists
$n(\delta,y) \,\geqslant\, 1$
such that, for all
$n \,\geqslant\, n(\delta,y)$
, for all
$m \in [\![{1},{N_n}]\!]$
, for all
$u \in {\left[{0},{N_n^\alpha y}\right]}$
,
$\log \mathbb{P}(T_{n,m} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon}) \,\leqslant\, - (1 - \delta) q \bigl( u^{1-\varepsilon} + (m-1) (1-2^{-\varepsilon}) N_n^{\alpha \varepsilon (1-\varepsilon)} \bigr) .$
Proof of Lemma 3.8. Let q
′ be such that
$(1 - \delta) q < q' < q$
. First, we establish that there exists
$n_0(\delta)$
such that, for all
$n\,\geqslant\, n_0(\delta)$
,
\begin{align}& \mathbb{P}\big(T_{n,m} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon}\big)\\ & \!\!\,\leqslant\, \!\!\begin{cases}\exp\Big[ -q' m N_n^{\alpha \varepsilon(1 - \varepsilon)} \Big] & \text{if $u < m N_n^{\alpha \varepsilon}$} , \\[6pt](u^m + m) \exp\Big[ -q' \Big( \big(u-(m-1)N_n^{\alpha \varepsilon}\big)^{1-\varepsilon} + (m-1) N_n^{\alpha \varepsilon (1-\varepsilon)} \Big) \Big] \!\!\!\! & \text{if $m N_n^{\alpha \varepsilon} \,\leqslant\, u \,\leqslant\, N_n^\alpha y$.} \nonumber\end{cases} \end{align}
The result is trivial for
$u < m N_n^{\alpha \varepsilon}$
or
$m = 1$
, using Lemma 3.4. Now, we suppose
$u \,\geqslant\, m N_n^{\alpha \varepsilon}$
and
$m \,\geqslant\, 2$
. We have
\begin{align*}\mathbb{P}(T_{n,m} \,\geqslant\, u; &\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon}) \\ & \,\leqslant\, \mathbb{P}(T_{n,m} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], N_n^{\alpha \varepsilon} \,\leqslant\, Y_{n,i} < u) \\ & \quad + \mathbb{P}(\text{there exists}\ i_0 \in [\![{1},{m}]\!]\ \text{such that}\ Y_{n,i_{0}} \,\geqslant\, u - (m - 1) N_n^{\alpha \varepsilon}; \\ & \qquad \quad \ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon}) .\end{align*}
First,
\begin{align} \mathbb{P}(\text{there exists}\ i_0 \in & [\![{1},{m}]\!] \ \text{such that}\ Y_{n,i_{0}} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon}) \nonumber \\ & \,\leqslant\, m \mathbb{P}(Y_n \,\geqslant\, u - (m - 1) N_n^{\alpha \varepsilon}) \mathbb{P}(Y_n \,\geqslant\, N_n^{\alpha \varepsilon})^{m-1} \nonumber \\ & \,\leqslant\, m \exp \bigl[ -q' \bigl( (u - (m - 1) N_n^{\alpha \varepsilon})^{1-\varepsilon} + (m-1) N_n^{\alpha \varepsilon(1-\varepsilon)} \bigr) \bigr]\end{align}
as soon as
$n \,\geqslant\, n_1(\delta) \,\geqslant\, n_0(\delta)$
, where
$n_1(\delta)$
is the integer
$n_0(q')$
given by Lemma 3.4 (remember that
$N_n^{\alpha \varepsilon} \,\leqslant\, m N_n^{\alpha \varepsilon} \,\leqslant\, u \,\leqslant\, N_n^\alpha y$
). Secondly, denoting by
$a_i$
integers and q” a number such that
$q' < q'' < q$
,
\begin{align*}\mathbb{P}(T_{n,m} \,\geqslant\, u; \ \text{for all} &\ i \in [\![{1},{m}]\!], N_n^{\alpha \varepsilon} \,\leqslant\, Y_{n,i} < u - (m - 1) N_n^{\alpha \varepsilon}) \\[4pt] & = \int_{\forall i, N_n^{\alpha \varepsilon} \,\leqslant\, u_i < u} \textbf{1}_{u_1 + \dots + u_m \,\geqslant\, u} \prod_{i=1}^m \mathbb{P}(Y_n \in \textrm{d} u_i) \\[4pt] & \,\leqslant\, \sum_{\forall i, \left\lceil {N_n^{\alpha \varepsilon}} \right\rceil \,\leqslant\, a_i \,\leqslant\, \left\lceil {u} \right\rceil} \textbf{1}_{a_1 + \dots + a_m \,\geqslant\, u} \prod_{i=1}^m \mathbb{P}(a_i-1 < Y_n \,\leqslant\, a_i) \\[4pt] & \,\leqslant\, \sum_{\forall i, \left\lceil {N_n^{\alpha \varepsilon}} \right\rceil \,\leqslant\, a_i \,\leqslant\, \left\lceil {u} \right\rceil} \textbf{1}_{a_1 + \dots + a_m \,\geqslant\, u} \prod_{i=1}^m \textrm{e}^{-q''(a_i-1)^{1-\varepsilon}} \\[4pt] & \,\leqslant\, \int_{\forall i, N_n^{\alpha \varepsilon} \,\leqslant\, u_i < u+2} \textbf{1}_{u_1 + \dots + u_m \,\geqslant\, u} \prod_{i=1}^m \textrm{e}^{-q''(u_i-2)^{1-\varepsilon}} \, \textrm{d} u_i \\[4pt] & \,\leqslant\, \int_{\substack{\forall i, N_n^{\alpha \varepsilon} \,\leqslant\, u_i < u+2 \\ u_1 + \dots + u_m \,\geqslant\, u}} \textrm{e}^{-q'\Big(u_1^{1-\varepsilon} + \dots + u_m^{1-\varepsilon}\Big)} \, \textrm{d} u_1 \cdots \textrm{d} u_m ,\end{align*}
as soon as n is large enough (
$n \,\geqslant\, n_2(\delta) \,\geqslant\, n_1(\delta)$
) so that, for all
$v \,\geqslant\, N_n^{\alpha \varepsilon}$
,
$q''(v-2)^{1-\varepsilon} \,\geqslant\, q'v^{1-\varepsilon}$
. Now, the function
$s_m \colon (u_1, \dots, u_m) \mapsto u_1^{1-\varepsilon} + \dots + u_m^{1-\varepsilon}$
is concave, so
$s_m$
reaches its minimum on the domain of integration at the points where all the
$u_i$
equal
$N_n^{\alpha \varepsilon}$
, except one equal to
$u-(m-1)N_n^{\alpha \varepsilon}$
. Therefore,
\begin{align}& \mathbb{P}(T_{n,m} \,\geqslant\, u, \ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon})\\ & \qquad \qquad \qquad \qquad \qquad \quad \,\leqslant\, u^m \exp\bigl[ -q' \bigl( (u-(m-1)N_n^{\alpha \varepsilon})^{1-\varepsilon} + (m-1) N_n^{\alpha \varepsilon (1-\varepsilon)} \bigr) \bigr]. \nonumber\end{align}
Equations (3.8) and (3.9) yield (3.7).
The conclusion of Lemma 3.8 for
$u < m N_n^{\alpha \varepsilon}$
stems from (3.7) and the following easy inequality: for all
$m \,\geqslant\, 1$
,
$m^{1 - \varepsilon} + (m - 1)(1 - 2^{-\varepsilon}) \,\leqslant\, m$
. As for
$u \,\geqslant\, m N_n^{\alpha \varepsilon}$
, we notice that the function
$g(u) \mathrel{\mathop:}= - u^{1-\varepsilon} + (u-(m-1)N_n^{\alpha \varepsilon})^{1-\varepsilon} + (m-1) N_n^{\alpha \varepsilon (1-\varepsilon)}$
is increasing on
${\left[{m N_n^{\alpha \varepsilon}},{\infty}\right)}$
and
$g(m N_n^{\alpha \varepsilon}) = N_n^{\alpha \varepsilon (1-\varepsilon)} m(1-m^{-\varepsilon}) \,\geqslant\, N_n^{\alpha \varepsilon (1-\varepsilon)} (m-1) (1-2^{-\varepsilon}) ,$
so, using (3.7) and the fact that, for
$m \,\geqslant\, 1$
,
$u^m+m \,\leqslant\, (u+1)^m$
,
\begin{align*}\mathbb{P}(T_{n,m} \,\geqslant\, u, &\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon}) \\[4pt] & \,\leqslant\, (u+1)^m \exp\bigl[ -q'\bigl( u^{1-\varepsilon} + (m-1)(1-2^{-\varepsilon}) N_n^{\alpha \varepsilon (1-\varepsilon)} \bigr) \bigr] \\[4pt] & \,\leqslant\, \exp\bigl[ -(1 - \delta) q \bigl( u^{1-\varepsilon} + (m-1)(1-2^{-\varepsilon}) N_n^{\alpha \varepsilon (1-\varepsilon)} \bigr) \bigr]\end{align*}
as soon as
\begin{align*} \log(u+1) & \,\leqslant\, \log(N_n^\alpha y + 1) \\ & \,\leqslant\, \frac{1}{2} (q' - (1 - \delta)q) (1 - 2^{-\varepsilon}) N_n^{\alpha \varepsilon (1-\varepsilon)} \\ & \,\leqslant\, \frac{m-1}{m} (q' - (1 - \delta)q) (1-2^{-\varepsilon}) N_n^{\alpha \varepsilon (1-\varepsilon)} ,\end{align*}
i.e. for
$n \,\geqslant\, n(\delta,y) \,\geqslant\, n_2(\delta)$
.
3.3.3 Upper bound for the sum of the
$\Pi_{n, m}$
Using the uniform bounds of Lemmas 3.7 and 3.8, we are able to bound above the remaining term
$\sum_{m=1}^n \binom{n}{m} \Pi_{n,m}$
.
Lemma 3.9. Assume (H1), (H2′), and (H2
$^+$
). If
$\frac{1}{2} < \alpha < 1/(1+\varepsilon)$
, then, for all
$y > 0$
,
\begin{align*}\limsup_{n \to \infty} \frac{1}{N_n^{2\alpha - 1}} \log \sum_{m=1}^n \binom{n}{m} \Pi_{n,m} \,\leqslant\, - \frac{y}{2 \sigma^2} .\end{align*}
If
$\alpha = 1/(1+\varepsilon)$
, then, for all
$y > 0$
,
\begin{align*}\limsup_{n \to \infty} \frac{1}{N_n^{2\alpha - 1}} \log \sum_{m=1}^n \binom{n}{m} \Pi_{n,m} \,\leqslant\, - I(y) .\end{align*}
Proof of Lemma 3.9. Fix some integer
$r \,\geqslant\, 1$
. Noticing that
\begin{equation*}\left\{ {(a, b) \in (\mathbb{R}_+)^2} \mathrel{}\middle|\mathrel{} {a + b \,\geqslant\, 1} \right\} \subset \bigcup_{k=1}^r \bigg\{(a, b) \in (\mathbb{R}_+)^2 \, \Big\vert \, a \,\geqslant\, \frac{k-1}{r},\ b \,\geqslant\, 1-\frac{k}{r}\bigg\} ,\end{equation*}
we have, for all
$m \in [\![{1},{N_n}]\!]$
,
\begin{align*}\Pi_{n,m} & = \mathbb{P}\bigl( T_{n} \,\geqslant\, N_n^\alpha y;\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon} ; \\ & \qquad \ \text{for all}\ i \in [\![{m+1},{N_n}]\!], Y_{n,i} < N_n^{\alpha \varepsilon} \bigr) \\ & \,\leqslant\, \sum_{k=1}^r \mathbb{P}\biggl( T_{n,N_{n-m}} \,\geqslant\, \frac{k-1}{r} N_n^\alpha y ; \ \text{for all}\ i \in [\![{1},{n-m}]\!], Y_{n,i} < N_n^{\alpha \varepsilon} \biggr) \\ & \qquad \quad \times \mathbb{P}\biggl( T_{n,m} \,\geqslant\, \biggl( 1-\frac{k}{r} \biggr) N_n^\alpha y ; \ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon} \biggr) \\ & \,\leqslant\, \sum_{k=1}^r \exp\biggl[ -(1-\delta)\biggl( \frac{(k-1)^2 (N_n^\alpha y)^2}{2 N_n \sigma^2 r^2} \\ & \qquad \qquad \qquad \qquad \qquad + q \Bigl( \Bigl( 1 - \frac{k}{r} \Bigr) N_n^\alpha y \Bigr)^{1-\varepsilon} + q (m - 1)(1-2^{-\varepsilon}) N_n^{\alpha \varepsilon (1-\varepsilon)} \biggr) \biggr] ,\end{align*}
for n large enough, applying Lemmas 3.7 and 3.8. Hence,
\begin{align*}\log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} & \,\leqslant\, \log \sum_{k=1}^r \exp\biggl[ -(1-\delta)\biggl( N_n^{2 \alpha - 1}\frac{((k-1)/r)^2 y^2}{2 \sigma^2} \\ & \qquad \qquad \qquad \quad + q N_n^{\alpha(1 - \varepsilon)} \Bigl( \Bigl( 1 - \frac{k}{r} \Bigr) y \Bigr)^{1-\varepsilon} \biggr) \biggr] \\ & \quad + \log \sum_{m=1}^{N_n} \binom{N_n}{m} \textrm{e}^{-(1 - \delta) q (m - 1)(1-2^{-\varepsilon}) N_n^{\alpha \varepsilon (1-\varepsilon)}} ,\end{align*}
where the latter sum is bounded.
For
$\alpha \in {\big(\frac{1}{2},1/(1 + \varepsilon)\big)}$
, we have
$2 \alpha - 1 < \alpha(1 - \varepsilon)$
. Therefore, applying the principle of the largest term (Lemma 3.1), we get
\begin{equation*}\limsup_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \,\leqslant\, - (1-\delta) \Bigl( \frac{r-1}{r} \Bigr)^2 \frac{1}{2 \sigma^2} ,\end{equation*}
so, letting
$r \to \infty$
and
$\delta \to 0$
,
\begin{equation*}\limsup_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \,\leqslant\, - \frac{1}{2 \sigma^2} .\end{equation*}
For
$\alpha = 1/(1 + \varepsilon)$
, remember that
$2 \alpha - 1 = \alpha(1 - \varepsilon)$
. Therefore, applying the principle of the largest term (Lemma 3.1), we get
\begin{equation*}\limsup_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \,\leqslant\, - (1-\delta) \min_{k=1}^r \biggl( \biggl(\frac{k-1}{r}\biggr)^2\frac{y^2}{2 \sigma^2} + q \biggl( 1-\frac{k}{r} \biggr)^{1-\varepsilon} y^{1-\varepsilon} \biggr) ,\end{equation*}
so, letting
$r \to \infty$
and
$\delta \to 0$
,
\begin{equation*}\;\qquad \limsup_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \,\leqslant\, - \min_{t \in {\left[{0},{1}\right]}} \biggl( \frac{t^2 y^2}{2 \sigma^2} + q (1-t)^{1-\varepsilon} y^{1-\varepsilon} \biggr) = - I(y).\end{equation*}
Remark 3.1. Notice that, using the contraction principle, we can show that, for all fixed m, if
$\alpha \in {\big(\frac{1}{2},1/(1+\varepsilon)\big)}$
, then
\begin{align*}\lim_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}}\log \Pi_{n,m} = - \frac{y^2}{2 \sigma^2} , ;\end{align*}
and if
$\alpha = 1/(1+\varepsilon)$
, then
\begin{align*}\lim_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}}\log \Pi_{n,m} = - I(y) .\end{align*}
4. About the assumptions
Looking into the proof of Theorem 2.1, one can see that Assumption (H1) can be weakened and we may only assume the two conditions that follow.
Theorem 4.1. The conclusion of Theorem 2.1 holds under (H2) and:
-
(H1a) For all
$y_n = \Theta(N_n^\alpha)$
,
$\log \mathbb{P}(Y_n \,\geqslant\, y_n) \underset{n\to \infty}{\sim} -q y_n^{1-\varepsilon}$
. -
(H1b) For all
$N_n^{\alpha \varepsilon} \preccurlyeq y_n \preccurlyeq N_n^\alpha$
,
$\limsup\limits_{n\to \infty} y_n^{-(1-\varepsilon)} \log \mathbb{P}(Y_n \,\geqslant\, y_n) \,\leqslant\, -q$
.
Lemma 4.1. (H1a) is equivalent to:
-
(H1a′) For all
$y > 0$
,
$\log \mathbb{P}(Y_n \,\geqslant\, N_n^\alpha y) \underset{n\to \infty}{\sim} - q (N_n^\alpha y)^{1-\varepsilon}$
.
Proof of Lemma 4.1. If
$ N_n^\alpha c_1\,\leqslant\, y_n \,\leqslant\, N_n^\alpha c_2$
, then
$-qc_2 \,\leqslant\, N_n^{-\alpha(1-\varepsilon)} \log \mathbb{P}(Y_n \,\geqslant\, y_n) \,\leqslant\, -q c_1 .$
First, extract a convergent subsequence; then, again extract a subsequence such that
$N_n^{-\alpha} y_n$
is convergent and use (H1a) to show that
$N_n^{-\alpha(1-\varepsilon)} \log \mathbb{P}(Y_n \,\geqslant\, y_n)$
is convergent.
The following lemma is straightforward.
Lemma 4.2. (H1b) is equivalent to the conclusion of Lemma 3.4:
-
(H1b′) For all
$y > 0$
, for all
$q' < q$
, there exists
$n_0$
such that for all
$n \,\geqslant\, n_0$
and for all
$u \in {\left[{N_n^{\alpha \varepsilon}},{N_n^\alpha y}\right]}$
,
$\log\mathbb{P}(Y_n\,\geqslant\, u)\,\leqslant\, -q' u^{1-\varepsilon}$
.
Theorem 4.2. The conclusion of Theorem 2.1 holds under (H1a), (H1b), and
\begin{equation*}\mathbb{E}\big[\left\lvert {Y_n} \right\rvert^{2+\gamma}\big]/\mathbb{E}\big[\left\lvert {Y_n} \right\rvert^{2}\big]^{1+\gamma/2}=o\big(N_n^{\gamma/2}\big)\end{equation*}
as
$n\to \infty$
.
Proof of Theorem 4.2. The only modification in the proof is the minoration of
$R_n$
:
$R_n \,\geqslant\, \mathbb{P}\big(T_{n,N_{n-1}} \,\geqslant\, 0\big) \mathbb{P}(Y_n \,\geqslant\, N_n^{\alpha} y)$
. Now Lyapunov’s theorem [Reference Billingsley1, Theorem 27.3] applies, so
$\mathbb{P}\big(T_{n,N_{n-1}} \,\geqslant\, 0\big) \to \frac{1}{2}$
as
$n\to \infty$
.
As for Theorem 2.2, Assumption (H1) can be weakened and we may only assume (H1b), or even the following weaker assumption.
Theorem 4.3. The conclusion of Theorem 2.2 holds under (H2′), (H2
$^+$
), and:
-
(H1c) For all
$y > 0$
there exists
$q > 0$
and
$n_0$
such that, for all
$n \,\geqslant\, n_0$
and for all
$u \in {\left[{N_n^{\alpha \varepsilon}},{N_n^\alpha y}\right]}$
,
$\log \mathbb{P}(Y_n \,\geqslant\, u) \,\leqslant\, - q u^{1-\varepsilon}$
.
Finally, in Theorem 2.3, Assumption (H1) can be weakened and we may only assume (H1a) and (H1b).
5. Application: Truncated random variable
Let us consider a centered real-valued random variable Y, admitting a finite moment of order
$2+\gamma$
for some
$\gamma>0$
. Set
$\sigma^2 \mathrel{\mathop:}= \mathbb{E}\big[Y^2\big]$
. Now, let
$\beta > 0$
and
$c > 0$
. For all
$n \,\geqslant\, 1$
, let us introduce the truncated random variable
$Y_n$
defined by
$\mathcal{L}(Y_n) = \mathcal{L}\Big(Y \mid Y < N_n^\beta c\Big)$
. Such truncated random variables naturally appear in proofs of large-deviation results. For all
$n \,\geqslant\, 1$
, let
$N_n$
be a natural number. We assume that
$N_n \to \infty$
as
$n \to \infty$
. For all
$n \,\geqslant\, 1$
, let
$\left(Y_{n,i}\right)_{1 \,\leqslant\, i \,\leqslant\, N_n}$
be a family of i.i.d. random variables distributed as
$Y_n$
. Define, for all
$k \in [\![{1},{N_n}]\!]$
,
$T_{n,k}\mathrel{\mathop:}=\sum_{i=1}^{k} Y_{n,i} ,$
and let
$T_{n} \mathrel{\mathop:}= T_{n,N_{n}}$
.
If Y has a light-tailed distribution, i.e.
$\Lambda_Y(\lambda)\mathrel{\mathop:}= \log \mathbb{E}\big[\textrm{e}^{\lambda Y}\big]<\infty$
for some
$\lambda>0$
, then (the unilateral version of) the Gärtner–Ellis theorem (Theorem 3.1) applies: if
$\alpha\in {\left({1/2},{1}\right)}$
, then
\begin{equation*}\lim_{n\to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^\alpha y) = -\frac{y^2}{2\sigma^2} , \end{equation*}
and if
$\alpha=1$
, then
\begin{equation*}\lim_{n\to \infty} \frac{1}{N_n} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^\alpha y) = -\Lambda_Y^*(y)= -\sup_{\lambda\,\geqslant\, 0}\{\lambda y-\Lambda_Y(\lambda)\}.\end{equation*}
Note that we recover the same asymptotics as for the non-truncated random variable Y. In other words, the truncation does not affect the deviation behavior.
Now we consider the case where
$\log \mathbb{P}(Y \,\geqslant\, y) \sim -q y^{1-\varepsilon}$
for some
$q>0$
and
$\varepsilon \in {\left({0},{1}\right)}$
. In this case, the Gärtner–Ellis theorem does not apply directly; indeed, the Gärtner–Ellis theorem always provides a convex rate function (
$\Lambda^*$
in Theorem 3.1) but, as can be seen in Figures 1 to 3, some of the rate functions obtained are not convex. Observe that, as soon as
$y_n \to \infty$
,
\begin{align*}\limsup_{n \to \infty} \frac{1}{y_n^{1-\varepsilon}} \log \mathbb{P}(Y_n \,\geqslant\, y_n) & = \limsup_{n\to \infty} \frac{1}{y_n^{1-\varepsilon}} \left(\log \mathbb{P} \left(y_n \,\leqslant\, Y < N_n^\beta c\right)-\log \mathbb{P} \left(Y < N_n^\beta c\right)\right) \\ & \,\leqslant\, -q ,\end{align*}
so (H1b) is satisfied. If, moreover,
$y_n \,\leqslant\, N_n^\beta c'$
with
$c' < c$
, then
$\log \mathbb{P}(Y_n \,\geqslant\, y_n) \sim -q y_n^{1-\varepsilon}$
, so (H1) is satisfied for
$\alpha < \beta$
. In addition,
$\mathbb{E}[Y_n]$
,
$\mathbb{E}\big[(Y_n - \mathbb{E}[Y_n])^2\big]-\mathbb{E}\big[Y^2\big]$
, and
$\mathbb{E}\big[\left\lvert {Y_n - \mathbb{E}[Y_n]} \right\rvert^{2+\gamma}\big]-\mathbb{E}\big[Y^{2+\gamma}\big]$
are exponentially decreasing to zero. Therefore, (H2′) and (H2
$^+$
) are satisfied, and our Theorems 2.1, 2.2, 2.3, and 4.3 directly apply (to
$Y_n - \mathbb{E}[Y_n]$
) for
$\alpha < \max(\beta, 1/(1+\varepsilon))$
.
Figure 1. Representation of the rate functions. Here,
$q=1$
,
$\sigma^2=2$
,
$\varepsilon =1/2$
, and
$c=1$
. Left: Gaussian range. The typical event corresponds to the case where all the random variables are small but their sum has a Gaussian contribution. Center: Maximal jump range. The typical event corresponds to the case where one random variable contributes to the total sum (
$N_n^\alpha y$
), regardless of the others. We recover the random variable tail. Right: Truncated maximal jump range. The typical event corresponds to the case where
$N_n^{\alpha-\beta}y/c$
variables take the saturation value
$N_n^\beta c$
, regardless of the others.
Figure 2. Representation of the rate functions. Here,
$q=1$
,
$\sigma^2=1$
,
$\varepsilon =1/2$
, and
$c=1$
. Left: Transition 1. The typical event corresponds to the case where one random variable is large (
$N_n^\alpha (1-t(y)) y$
) and the sum of the others has a Gaussian contribution (two competing terms). Center: Transition 2. The typical event corresponds to the case where
$\left\lfloor {y/c} \right\rfloor$
random variables take the saturation value
$N_n^\beta c$
and one completes to get the total sum. Right: Transition 3. The typical event corresponds to the case where some random variables (a number of order
$N_n^{1-\beta(1+\varepsilon)}$
) take the saturation value
$N_n^\beta c$
, and the sum of the others has a Gaussian contribution (two competing terms).
For
$\alpha \,\geqslant\, \max(\beta, 1/(1+\varepsilon))$
, the proofs easily adapt to cover all cases. To expose the results, we separate the three cases
$\beta > 1/(1+\varepsilon)$
,
$\beta < 1/(1+\varepsilon)$
, and
$\beta = 1/(1+\varepsilon)$
. We provide the graphs of the exhibited rate functions (Figures 1 and 3) and a synthetic diagram (Figure 4).
Figure 3. Representation of the rate functions. Here,
$q=1$
,
$\sigma^2=1$
, and
$\varepsilon =1/2$
(so
$c_0=1$
). Left: Transition 1, for
$c \,\leqslant\, c_0$
(here,
$c=0.7$
). The typical event corresponds to the case where
$k_3(c, y)$
variables take the saturation value
$N^\beta c$
, and the sum of the others has a Gaussian contribution. Right: Transition 1, for
$c > c_0$
(here,
$c=2$
). The typical event corresponds to the case where
$k_2(c, y)$
variables take the saturation value
$N^\beta c$
, one is also large
$\big(N_n^\beta (1-t(y-k_2(c, y)c) )(y-k_2(c, y)c)\big)$
, and the sum of the others has a Gaussian contribution.
Figure 4. Speed and rate function diagram.
5.1. Case
$\beta {>} 1/(1+\varepsilon)$
5.1.1 Gaussian range
When
$\alpha < 1/(1+\varepsilon)$
Theorem 2.2 applies and, for all
$y \,\geqslant\, 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - \frac{y^2}{2\sigma^2} .\end{equation*}
5.1.2 Transition 1
When
$\alpha = 1/(1+\varepsilon)$
Theorem 2.3 applies and, for all
$y \,\geqslant\, 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - I_1(y) \mathrel{\mathop:}= - I(y)= - \inf_{0\,\leqslant\, t \,\leqslant\, 1} \biggl\{ q(1-t)^{1-\varepsilon} y^{1-\varepsilon}+\frac{t^2y^2}{2\sigma^2} \biggr\} .\end{equation*}
5.1.3 Maximal jump range
When
$1/(1+\varepsilon) < \alpha < \beta$
Theorem 2.1 applies and, for all
$y \,\geqslant\, 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{\alpha(1-\varepsilon)}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q y^{1-\varepsilon} .\end{equation*}
5.1.4 Transition 2
When
$\alpha = \beta$
, for all
$y \,\geqslant\, 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{\alpha(1-\varepsilon)}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y)= - I_2(c, y) \mathrel{\mathop:}= - q\left(\left\lfloor {y/c} \right\rfloor c^{1-\varepsilon} + (y - \left\lfloor {y/c} \right\rfloor c)^{1-\varepsilon} \right).\end{equation*}
Observe that
$I_2$
is continuous on
${\left({0},{\infty}\right)} \times {\left[{0},{\infty}\right)}$
. For all
$t > 0$
,
\begin{align*}\Pi_{n,0}&= \mathbb{P}\bigl(T_{n} \,\geqslant\, N_n^\alpha y;\ \text{for all}\ i \in [\![{1},{N_n}]\!], Y_{n,i} < N_n^{\alpha \varepsilon}\bigr) \\ & \,\leqslant\, \textrm{e}^{-ty N_n^{\alpha(1-\varepsilon)}} \mathbb{E}\bigl[ \textrm{e}^{t N_n^{-\alpha\varepsilon} Y_n} \textbf{1}_{Y_n < N_n^{\alpha \varepsilon}} \bigr]^{N_n} \\ & = \textrm{e}^{-tyN_n^{\alpha(1-\varepsilon)}(1+o(1))} ,\end{align*}
(see the proof of Theorem 2.1). Therefore, letting
$t \to \infty$
, Lemma 3.5 updates into
\begin{equation*}\frac{1}{N_n^{\alpha(1-\varepsilon)}} \log \Pi_{n,0} \underset{n \to \infty}{\longrightarrow} -\infty .\end{equation*}
For all fixed
$m \,\geqslant\, \left\lfloor {y/c} \right\rfloor + 1$
, let
$c' < c$
be such that
$\left\lfloor {y / c'} \right\rfloor + 1 \,\leqslant\, m$
. Then,
$\Pi_{n,m} \,\geqslant\, \mathbb{P}\bigl(\text{for all}\ i \in [\![{1},{\left\lfloor {y / c'}\right\rfloor}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha} c';\ \left[ Y_{n,\lfloor {y / c'} \rfloor} + 1\right] \,\geqslant\, N_n^\alpha(y - \left\lfloor {y / c'} \right\rfloor c') \bigr) ,$
so
\begin{equation*}\liminf_{n \to \infty} \frac{1}{N_n^{\alpha(1-\varepsilon)}} \log \Pi_{n,m} \,\geqslant\, -I_2(c', y) .\end{equation*}
Letting
$c' \to c$
, Lemma 3.6 updates into: for all
$m \,\geqslant\, \left\lfloor {y/c} \right\rfloor + 1$
,
\begin{equation*} \liminf_{n \to \infty} \frac{1}{N_n^{\alpha(1-\varepsilon)}} \log \Pi_{n,m} \,\geqslant\, -I_2(c, y) ,\end{equation*}
which provides a lower bound for the sum of the
$\Pi_{n, m}$
. To upper bound the sum of the
$\Pi_{n, m}$
, Lemma 3.7 still applies. Lemma 3.8 (more precisely (3.7)) adapts as follows: for all
$\delta \in {\left({0},{1}\right)}$
, there exists
$n(\delta) \,\geqslant\, 1$
such that, for all
$n \,\geqslant\, n(\delta)$
, for all
$m \,\geqslant\, 1$
, for all
$u \in {\left[{0},{N_n^\alpha y}\right]}$
,
\begin{align*}\log &\, \mathbb{P}(T_{n,m} \,\geqslant\, u;\ \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\alpha \varepsilon}) \\ & \,\leqslant\,\begin{cases}-q' m N_n^{\alpha \varepsilon(1 - \varepsilon)} & \text{if $u < m N_n^{\alpha \varepsilon}$} , \\-q' \bigl( l(N_n^\alpha c + 2)^{1 - \varepsilon} + (u - l(N_n^\alpha c + 2))^{1 - \varepsilon} \\ \qquad + (m - l - (m - l)^{1 - \varepsilon}) N_n^{\alpha \varepsilon(1 - \varepsilon)} \bigr) & \text{if $m N_n^{\alpha \varepsilon} \,\leqslant\, u < m N_n^\alpha c$} , \\-\infty & \text{if $m N_n^\alpha c \,\leqslant\, u$}\end{cases} \\ & \;=\!:\; - M(n, m, u) ,\end{align*}
with
\begin{equation*}l = \left\lfloor {\frac{u - m N_n^{\alpha \varepsilon}}{N_n^\alpha c + 2 - N_n^{\alpha \varepsilon}}} \right\rfloor .\end{equation*}
Here, following the proof of Lemma 3.8, the concave function
$s_m \colon (u_1, \dots, u_m) \mapsto u_1^{1-\varepsilon} + \dots + u_m^{1-\varepsilon}$
attains its minimum on the domain of integration at the points with all coordinates equal to
$N_n^{\alpha \varepsilon}$
, except for l coordinates equal to
$N_n^\alpha c + 2$
and one coordinate equal to
$u - l (N_n^\alpha c + 2) - (m - l - 1) N_n^{\alpha \varepsilon}$
. Finally, Lemma 3.9 adapts as follows: for
$\alpha(1 - \varepsilon)^2 < \gamma < \alpha(1 - \varepsilon)$
,
\begin{align*} & \limsup_{n \to \infty} \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \\ & \,\leqslant\, \limsup_{n \to \infty} \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \sum_{k=1}^r \sum_{m = 1}^{N_n} \exp\biggl[ -(1-\delta) N_n^{2 \alpha - 1}\frac{(k-1)^2 y^2}{2 \sigma^2 r^2} - M(n, m, (1 - k / r) N_n^\alpha y) \biggr] \\ & = \limsup_{n \to \infty} \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \sum_{m=1}^{N_n} \exp\biggl[- M(n, m, (1 - 1 / r) N_n^\alpha y) \biggr] ,\end{align*}
since
$2 \alpha - 1 > \alpha (1 - \varepsilon)$
and, for n large enough,
\begin{align*}\frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log & \sum_{m > N_n^\gamma} \exp\bigl[- M(n, m, (1 - 1 / r) N_n^\alpha y) \bigr] \\ & \,\leqslant\, \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \sum_{m > N_n^\gamma} \exp\bigl[- q' (m - l - (m - l)^{1 - \varepsilon}) N_n^{\alpha \varepsilon(1 - \varepsilon)} \bigr] \\ & \,\leqslant\, \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \sum_{m > N_n^\gamma} \exp\Bigl[- \frac{q}{2} m N_n^{\alpha \varepsilon(1 - \varepsilon)} \Bigr] \\ & \,\leqslant\, - \frac{q}{4} N_n^{\gamma - \alpha (1 - \varepsilon)^2} \\ & \underset{n \to \infty}{\longrightarrow} -\infty .\end{align*}
Now, for
$m \,\leqslant\, N_n^\gamma$
,
\begin{align*}M(n, m, & (1 - 1 / r) N_n^\alpha y) \\ & \,\geqslant\, N_n^{\alpha(1 - \varepsilon)} (1 - \delta) q \left(\left\lfloor {(1 - 1 / r)y/c} \right\rfloor c^{1-\varepsilon} + ((1 - 1 / r)y - \left\lfloor {(1 - 1 / r)y/c} \right\rfloor c)^{1-\varepsilon} \right) \\ & \quad + N_n^{\alpha \varepsilon(1 - \varepsilon)} (1 - \delta) q (m - \left\lfloor {y/c} \right\rfloor - m^{1 - \varepsilon}) \\ & \,\geqslant\, N_n^{\alpha(1 - \varepsilon)} (1 - \delta) I_2(c, (1 - 1 / r)y) + N_n^{\alpha \varepsilon(1 - \varepsilon)} (1 - \delta) q (m - \left\lfloor {y/c} \right\rfloor - m^{1 - \varepsilon}) .\end{align*}
Eventually,
\begin{align*}\limsup_{n \to \infty} &\ \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \\ & \,\leqslant\, - (1 - \delta) I_2(c, (1 - 1 / r)y) \\ & \quad + \limsup_{n \to \infty} \frac{1}{N_n^{\alpha(1 - \varepsilon)}} \log \sum_{m \,\leqslant\, N_n^\gamma} \exp\biggl[- (1 - \delta) q (m - \left\lfloor {y/c} \right\rfloor - m^{1 - \varepsilon}) N_n^{\alpha \varepsilon(1 - \varepsilon)} \biggr] \\ & = - (1 - \delta) I_2(c, (1 - 1 / r)y) ,\end{align*}
since the latter series is convergent. The result follows letting
$r \to \infty$
and
$\delta \to 0$
.
5.1.5 Truncated maximal jump range
When
$\beta < \alpha < \beta + 1$
and
$y \,\geqslant\, 0$
, or
$\alpha = \beta+1$
and
$y < c$
, the proof of Theorem 2.1 adapts and provides
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{\alpha-\beta\varepsilon}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q y c^{-\varepsilon} .\end{equation*}
The upper bound stems from
\begin{equation*}\mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) \,\leqslant\, \textrm{e}^{- qy c^{-\varepsilon} N_n^{\alpha-\beta\varepsilon}} \mathbb{E}\left[ \textrm{e}^{y c^{-\varepsilon} N_n^{-\beta\varepsilon} Y_n} \bigl(\textbf{1}_{Y_n < N_n^{\beta \varepsilon}} + \textbf{1}_{N_n^{\beta \varepsilon} \,\leqslant\, Y_n < N_n^\beta c}\bigr) \right]^{N_n}\end{equation*}
and the same lines as in the proof of Theorem 2.1. As for the lower bound, we write, for
$c' < c$
,
\begin{align*}\log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) & \,\geqslant\, \log \mathbb{P}(\text{for all}\ i \in [\![ 1, \lceil N_n^{\alpha-\beta} y/c' \rceil ]\!], Y_{n,i} \,\geqslant\, N_n^\beta c') \\ & \sim - N_n^{\alpha-\beta} y (c')^{-1} q (N_n^\beta c' )^{1-\varepsilon} \\ & = - N_n^{\alpha-\beta\varepsilon} q y (c')^{-\varepsilon} ,\end{align*}
and we recover the upper bound when
$c' \to c$
.
5.1.6 Trivial case
When
$\alpha=\beta+1$
and
$y \,\geqslant\, c$
, or
$\alpha > \beta+1$
, we obviously have
$\mathbb{P}(T_{n} \,\geqslant\, N_n^\alpha y) = 0$
.
5.2. Case
$\beta = 1/(1+\varepsilon)$
Here, Theorem 2.2 applies for
$\alpha < 1/(1+\varepsilon)$
. The notable fact is that the Gaussian range is extended: it spreads up to
$\alpha < 1-\beta\varepsilon$
.
5.2.1 Gaussian range
When
$\alpha < 1-\beta\varepsilon$
the proof of Theorem 2.2 adapts and, for all
$y \,\geqslant\, 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - \frac{y^2}{2\sigma^2} .\end{equation*}
As we said, the result for
$\alpha < 1/(1+\varepsilon)$
is a consequence of Theorem 2.2. Now, suppose
$\beta < 1/(1+\varepsilon) \,\leqslant\, \alpha <1-\beta\varepsilon$
. Here, we adapt the decomposition (3.1) and (3.2) as
\begin{equation*} \mathbb{P}( T_{n} \,\geqslant\, N_n^{\alpha} y ) = \sum_{m=0}^{N_n} \binom{N_n}{m} \Pi_{n,m} ,\end{equation*}
where, for all
$m \in [\![{0},{N_n}]\!]$
,
\begin{align*}\Pi_{n, m} & = \mathbb{P}\bigl( T_{n} \,\geqslant\, N_n^{\alpha} y;\; \text{for all}\ i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\beta \varepsilon};\; \text{for all}\ i \in [\![{m+1},{N_n}]\!], Y_{n,i} < N_n^{\beta \varepsilon} \bigr). \end{align*}
Lemma 3.5 works for
$\alpha < 1-\beta\varepsilon$
, adapting the proof with
$\mathcal{L}(Y^<_n) = \mathcal{L}\big(Y_n\ \big|\ Y_n < N_n^{\beta \varepsilon}\big)$
. To upper bound the sum of the
$\Pi_{n, m}$
, Lemma 3.7 still applies. Lemma 3.8 (more precisely (3.7)) adapts as follows: for all
$\delta \in {\left({0},{1}\right)}$
, there exists
$n(\delta) \,\geqslant\, 1$
such that, for all
$n \,\geqslant\, n(\delta)$
, for all
$m \,\geqslant\, 1$
, for all
$u \in {\left[{0},{N_n^\alpha y}\right]}$
,
\begin{align*}\log &\, \mathbb{P}(T_{n,m} \,\geqslant\, u;\ \text{for all} i \in [\![{1},{m}]\!], Y_{n,i} \,\geqslant\, N_n^{\beta \varepsilon}) \\ & \,\leqslant\,\begin{cases}-q' m N_n^{\beta \varepsilon(1 - \varepsilon)} & \text{if $u < m N_n^{\beta \varepsilon}$} , \\-q' \bigl( l\big(N_n^\beta c + 2\big)^{1 - \varepsilon} + \big(u - l\big(N_n^\beta c + 2\big)\big)^{1 - \varepsilon} \\ \qquad + (m - l - (m - l)^{1 - \varepsilon}) N_n^{\beta \varepsilon(1 - \varepsilon)} \big) & \text{if $m N_n^{\beta \varepsilon} \,\leqslant\, u < m N_n^\beta c$} , \\-\infty & \text{if $m N_n^\beta c \,\leqslant\, u$}\end{cases} \\ & \;=\!:\; - M(n, m, u) ,\end{align*}
with
\begin{equation*}l = \left\lfloor {\frac{u - m N_n^{\beta \varepsilon}}{N_n^\beta c + 2 - N_n^{\beta \varepsilon}}} \right\rfloor .\end{equation*}
Here, following the proof of Lemma 3.8, the concave function
$s_m \colon (u_1, \dots, u_m) \mapsto u_1^{1-\varepsilon} + \dots + u_m^{1-\varepsilon}$
reaches its minimum on the domain of integration at the points with all coordinates equal to
$N_n^{\beta \varepsilon}$
, except for l coordinates equal to
$N_n^\beta c + 2$
and one coordinate equal to
$u - l \big(N_n^\beta c + 2\big) - (m - l - 1) N_n^{\beta \varepsilon}$
. Finally, Lemma 3.9 adapts as follows: for
$2 \alpha - 1 - \beta \varepsilon(1 - \varepsilon) < \gamma < \alpha - \beta \varepsilon$
(note that
$2 \alpha - 1 < \alpha - \beta \varepsilon$
),
\begin{align*} & \limsup_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \\ & \,\leqslant\, \limsup_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{k=1}^r \exp\biggl[ -(1-\delta)\biggl( N_n^{2 \alpha - 1}\frac{((k-1)/r)^2 y^2}{2 \sigma^2} \biggr) \biggr] \\ & \qquad \qquad \qquad \qquad \qquad \times \sum_{m = 1}^{N_n} \textrm{e}^{- M(n, m, (1 - k / r) N_n^\alpha y)} .\end{align*}
For
$k \,\leqslant\, r - 1$
and n large enough,
\begin{align*}\frac{1}{N_n^{2 \alpha - 1}} &\log \sum_{m > N_n^\gamma} \textrm{e}^{- M(n, m, (1 - k / r) N_n^\alpha y)} \\ & \,\leqslant\, \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m > N_n^\gamma} \exp\bigl[- q' (m - l - (m - l)^{1 - \varepsilon}) N_n^{\beta \varepsilon(1 - \varepsilon)} \bigr] \\ & \,\leqslant\, \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m > N_n^\gamma} \exp\Bigl[- \frac{q}{2} m N_n^{\beta \varepsilon(1 - \varepsilon)} \Bigr] \\ & \,\leqslant\, - \frac{q}{4} N_n^{\gamma - (2 \alpha - 1 - \beta \varepsilon(1 - \varepsilon))} \\ & \underset{n \to \infty}{\longrightarrow} -\infty\end{align*}
and
\begin{align*}\frac{1}{N_n^{2 \alpha - 1}} & \log \sum_{m \,\leqslant\, N_n^\gamma} \textrm{e}^{- M(n, m, (1 - k / r) N_n^\alpha y)} \\ & \,\leqslant\, - (1 - \delta) q N_n^{\alpha - \beta \varepsilon - (2 \alpha - 1)} \left\lfloor {y / (rc)} \right\rfloor c^{1-\varepsilon} \\ & \quad + \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m \,\leqslant\, N_n^\gamma} \exp\bigl[ - (1 - \delta) q (m - l - (m - l)^{1 - \varepsilon}) N_n^{\beta \varepsilon(1 - \varepsilon)} \bigr] \\ & \underset{n \to \infty}{\longrightarrow} -\infty ,\end{align*}
since the latter series is convergent. Eventually,
\begin{align*}\limsup_{n \to \infty}& \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m=1}^{N_n} \binom{N_n}{m} \Pi_{n,m} \\ & \,\leqslant\, -(1-\delta) \frac{(1-1/r)^2 y^2}{2 \sigma^2} + \limsup_{n \to \infty} \frac{1}{N_n^{2 \alpha - 1}} \log \sum_{m=1}^{N_n} \textrm{e}^{- q' m N_n^{\beta \varepsilon (1 - \varepsilon)}} \\ & = -(1-\delta) \frac{(1-1/r)^2 y^2}{2 \sigma^2} ,\end{align*}
since the latter series is convergent. The result follows letting
$r \to \infty$
and
$\delta \to 0$
.
5.2.2 Transition 3
When
$\alpha = 1-\beta\varepsilon$
the proof of Theorem 2.3 adapts and, for all
$y \,\geqslant\, 0$
,
\begin{align*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = -I_3(c, y) &\mathrel{\mathop:}= - \inf_{0 \,\leqslant\, t \,\leqslant\, 1} \biggl\{ q(1-t) y c^{-\varepsilon} + \frac{t^2 y^2}{2\sigma^2} \biggr\} \\ & = - \begin{cases}\frac{y^2}{2\sigma^2} & \text{if $y \,\leqslant\, y_3(c)$} , \\\frac{qy}{c^\varepsilon} - \frac{q^2\sigma^2}{2c^{2\varepsilon}} & \text{if $y > y_3(c)$} ,\end{cases}\end{align*}
with
$y_3(c) \mathrel{\mathop:}= q\sigma^2 c^{-\varepsilon}$
.
5.2.3 Truncated maximal jump range
When
$1-\beta\varepsilon < \alpha < 1+\beta$
and
$y \,\geqslant\, 0$
, or
$\alpha = 1+\beta$
and
$y < c$
, as before, the proof of Theorem 2.1 adapts and
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{\alpha-\beta\varepsilon}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q y c^{-\varepsilon} .\end{equation*}
5.2.4 Trivial case
When
$\alpha=\beta+1$
and
$y \,\geqslant\, c$
, or
$\alpha > \beta+1$
, we obviously have
$\mathbb{P}(T_{n} \,\geqslant\, N_n^\alpha y) = 0$
.
5.3 Case
$\beta = 1/(1+\varepsilon)$
5.3.1 Gaussian range
When
$\alpha < 1/(1+\varepsilon) = \beta$
Theorem 2.2 applies and, for all
$y \,\geqslant\, 0$
,
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - \frac{y^2}{2\sigma^2} .\end{equation*}
5.3.2 Transition
${T_0}$
As in Section 2 after the statement of Theorem 2.3, we define t(y) and
$y_1$
for the function
$f(t)=q(1-t)^{1-\varepsilon} y^{1-\varepsilon}+{t^2y^2/}{(2\sigma^2)}$
. Define
$\tilde{t}(y) \mathrel{\mathop:}= 1$
for
$y< y_1$
and
$\tilde{t}(y)\mathrel{\mathop:}= t(y)$
for
$y \,\geqslant\, y_1$
, and notice that
$\tilde{t}$
is decreasing on
${\left[{y_1},{\infty}\right)}$
(and
$\tilde{t}(y) \to 0$
as
$y \to \infty$
). Set
$c_0 \mathrel{\mathop:}= (1-\tilde{t}(y_1))y_1 = (2\varepsilon q \sigma^2)^{1/(1+\varepsilon)}$
.
When
$\alpha = 1/(1+\varepsilon) = \beta$
and
$c \,\leqslant\, c_0$
, then
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q k_{0,1}(c, y) c^{1-\varepsilon} + \frac{(y - k_{0,1}(c, y)c)^2}{2 \sigma^2} \;=\!:\; -I_{0,1}(c, y) ,\end{equation*}
where
\begin{equation*}k_{0,1}(c, y) \mathrel{\mathop:}= \max\left( \left\lfloor {\frac{y-y_{0,1}(c)}{c}} \right\rfloor + 1, 0 \right) ,\qquad \text{and} \quad y_{0,1}(c) \mathrel{\mathop:}= \frac{c}{2} + q \sigma^2 c^{-\varepsilon}\end{equation*}
(
$y_{0,1}(c)$
is the unique solution in y of
$y^2 - (y - c)^2 = 2\sigma^2qc^{1-\varepsilon}$
).
When
$\alpha = 1/(1+\varepsilon) = \beta$
and
$c \,\geqslant\, c_0$
, then
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{2\alpha-1}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q k_{0,2}(c, y) c^{1-\varepsilon} + I(y - k_{0,2}(c, y)c) \;=\!:\; -I_{0,2}(c, y) ,\end{equation*}
where
\begin{equation*}k_{0,2}(c, y) \mathrel{\mathop:}= \max\left( \left\lfloor {\frac{y-y_{0,2}(c)}{c}} \right\rfloor + 1, 0 \right) ,\qquad \text{and} \quad y_{0,2}(c) \mathrel{\mathop:}= c + (1-\varepsilon)q\sigma^2c^{-\varepsilon}\end{equation*}
(
$y_{0,2}(c)$
is the unique solution in y of
$(1-\tilde{t}(y))y = c$
).
We remark that, for all
$c < c_0$
,
$y_{0,1}(c) > y_1$
, so the Gaussian range in the truncated case is extended compared with the range in the non-truncated case (where it stops at
$y_1$
). Moreover,
$y_{0,1}(c_0) = y_1 = y_{0,2}(c_0)$
and
$I_{0,1}(c_0, \cdot) = I_{0,2}(c_0, \cdot)$
(since
$I_1(y) = y^2/(2\sigma^2)$
for
$y \,\leqslant\, y_1$
).
5.3.3 Truncated maximal jump range
When
$1/(1+\varepsilon) = \beta < \alpha < \beta+1$
and
$y \,\geqslant\, 0$
, or
$\alpha = 1+\beta$
and
$y < c$
, as before, the proof of Theorem 2.1 adapts and
\begin{equation*}\lim_{n \to \infty} \frac{1}{N_n^{\alpha-\beta\varepsilon}} \log \mathbb{P}(T_{n} \,\geqslant\, N_n^{\alpha} y) = - q y c^{-\varepsilon} .\end{equation*}
5.3.4 Trivial case
When
$\alpha=\beta+1$
and
$y \,\geqslant\, c$
, or
$\alpha > \beta+1$
, we obviously have
$\mathbb{P}(T_{n} \,\geqslant\, N_n^\alpha y) = 0$
.
Acknowledgements
We gratefully thank the reviewers and the editor for their comments, criticisms, and advice, which greatly helped us to improve the manuscript and to make it more readable.
Funding Information
There are no funding bodies to thank relating to the creation of this article.
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
