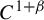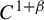1 Introduction
In this paper we establish that ‘fake’ stable holonomies inside ‘fake’ center-stable manifolds for sufficiently bunched
![]() $C^{1+\beta }$
diffeomorphisms are uniformly bi-Lipschitz and, in fact,
$C^{1+\beta }$
diffeomorphisms are uniformly bi-Lipschitz and, in fact,
![]() $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
. This establishes two folklore results in smooth ergodic theory, the primary motivation for this paper. We explain these two folklore results in the remainder of this introduction in order to motivate our main technical result.
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
. This establishes two folklore results in smooth ergodic theory, the primary motivation for this paper. We explain these two folklore results in the remainder of this introduction in order to motivate our main technical result.
1.1 Ergodicity of partially hyperbolic diffeomorphisms
In [Reference Burns and WilkinsonBW1], Burns and Wilkinson established the ergodicity (and K-property) of partially hyperbolic, center-bunched, essentially accessible,
![]() $C^2$
volume-preserving diffeomorphisms. This extends a number of earlier results, including [Reference Grayson, Pugh and ShubGPS, Reference Pugh and ShubPS2]. A similar result (with stronger center-bunching conditions) was announced for
$C^2$
volume-preserving diffeomorphisms. This extends a number of earlier results, including [Reference Grayson, Pugh and ShubGPS, Reference Pugh and ShubPS2]. A similar result (with stronger center-bunching conditions) was announced for
![]() $C^{1+\delta }$
-diffeomorphisms. However, it seems that the bunching condition given in [Reference Burns and WilkinsonBW1, Theorem 0.3] is possibly too weak for the method of proof. A proof of the technical result needed to establish [Reference Burns and WilkinsonBW1, Theorem 0.3] was circulated as an unpublished note in [Reference Burns and WilkinsonBW2]. It seems some of the details of the proof in [Reference Burns and WilkinsonBW2] are incorrect, specifically [Reference Burns and WilkinsonBW2, Lemma 1.1]. We replace this lemma with Lemma 3.1 below; however, we note that our Lemma 3.1 requires a stronger bunching condition imposed by condition (6) below. The results of this note replace the main result in [Reference Burns and WilkinsonBW2] and we obtain a proof of [Reference Burns and WilkinsonBW1, Theorem 0.3] (under a stronger bunching hypothesis).
$C^{1+\delta }$
-diffeomorphisms. However, it seems that the bunching condition given in [Reference Burns and WilkinsonBW1, Theorem 0.3] is possibly too weak for the method of proof. A proof of the technical result needed to establish [Reference Burns and WilkinsonBW1, Theorem 0.3] was circulated as an unpublished note in [Reference Burns and WilkinsonBW2]. It seems some of the details of the proof in [Reference Burns and WilkinsonBW2] are incorrect, specifically [Reference Burns and WilkinsonBW2, Lemma 1.1]. We replace this lemma with Lemma 3.1 below; however, we note that our Lemma 3.1 requires a stronger bunching condition imposed by condition (6) below. The results of this note replace the main result in [Reference Burns and WilkinsonBW2] and we obtain a proof of [Reference Burns and WilkinsonBW1, Theorem 0.3] (under a stronger bunching hypothesis).
We refer the reader to [Reference Burns and WilkinsonBW1] for definitions and complete arguments. Let M be a compact manifold and, for
![]() $\beta>0$
, let
$\beta>0$
, let
![]() $f\colon M\to M$
be a
$f\colon M\to M$
be a
![]() $C^{1+\beta }$
diffeomorphism. We assume f admits a continuous,
$C^{1+\beta }$
diffeomorphism. We assume f admits a continuous,
![]() $(Df)$
-equivariant partially hyperbolic splitting
$(Df)$
-equivariant partially hyperbolic splitting
in particular, there are continuous functions
with
![]() $\hat \nu (x), \nu (x) <1$
such that:
$\hat \nu (x), \nu (x) <1$
such that:
-
•
 $\mu (x) \|v\| < \|D_x f v\| < \nu (x) \|v\|$
, for all
$\mu (x) \|v\| < \|D_x f v\| < \nu (x) \|v\|$
, for all
 $v\in E^s(x)$
;
$v\in E^s(x)$
; -
•
 $\gamma (x) \|v\| < \|D_x f v\| < \hat \gamma (x ){}^{-1} \|v\| $
, for all
$\gamma (x) \|v\| < \|D_x f v\| < \hat \gamma (x ){}^{-1} \|v\| $
, for all
 $v\in E^c(x)$
;
$v\in E^c(x)$
; -
•
 $\hat \nu (x){}^{-1} \|v\| < \|D_x f v\| < \hat \mu (x){}^{-1} \|v\|$
, for all
$\hat \nu (x){}^{-1} \|v\| < \|D_x f v\| < \hat \mu (x){}^{-1} \|v\|$
, for all
 $v\in E^u(x)$
.
$v\in E^u(x)$
.
Theorem 1.1. Let
![]() $f\colon M\to M$
be a volume-preserving, essentially accessible, partially hyperbolic
$f\colon M\to M$
be a volume-preserving, essentially accessible, partially hyperbolic
![]() $C^{1+\beta } $
diffeomorphism. Let
$C^{1+\beta } $
diffeomorphism. Let
![]() $\bar \theta <\beta $
be such that
$\bar \theta <\beta $
be such that
Assume f satisfies the strong center-bunching hypothesis: there exists
![]() $0<\theta <\bar \theta $
such that for all
$0<\theta <\bar \theta $
such that for all
![]() $x\in M$
,
$x\in M$
,
and
Then f is ergodic and has the K-property.
In [Reference Burns and WilkinsonBW1, Theorem 0.3], the conclusion of Theorem 1.1 is asserted to hold under the bunching condition
where
![]() $\bar \theta $
satisfies (1). Since
$\bar \theta $
satisfies (1). Since
![]() $0<\max \{\nu (x), \hat \nu (x)\} <1$
, if
$0<\max \{\nu (x), \hat \nu (x)\} <1$
, if
![]() $\theta <\bar \theta $
we have
$\theta <\bar \theta $
we have
and (3) implies (4). In many applications one expects
![]() $\gamma (x)<1$
, whence
$\gamma (x)<1$
, whence
In particular, condition (2) is non-trivial even when (1) holds and the bunching condition (3) is strictly stronger than (4). Our proof seems to require a stronger bunching condition in (3) implied by the additional estimate (2).
For justification of Theorem 1.1, we refer the reader to the paragraph preceding [Reference Burns and WilkinsonBW1, Theorem 0.3]. See also the discussion in the paragraph preceding ‘Step 2’ on page 467 of [Reference Burns and WilkinsonBW1] where Theorem 2.4 below replaces [Reference Burns and WilkinsonBW1, Proposition 3.1(vii)].
We note that if
![]() $\bar \theta $
satisfies (1) then
$\bar \theta $
satisfies (1) then
![]() $\theta = \bar \theta \beta $
satisfies (2) and we have the following corollary.
$\theta = \bar \theta \beta $
satisfies (2) and we have the following corollary.
Corollary 1.2. If, in Theorem 1.1, we have
then f is ergodic and has the K-property.
Remark 1.3. Theorem 2.4 below establishes the smoothness of stable holonomies inside center-stable manifolds for a choice of ‘globalized’ dynamics. In the language of [Reference Burns and WilkinsonBW1], this establishes the smoothness of holonomy maps by fake stable manifolds inside fake center-stable manifolds. See the discussion in [Reference Burns and WilkinsonBW1, Proposition 3.1(vii)]. We note that dynamical coherence and the existence of ‘genuine’ center manifolds is neither assumed nor required in the proof of [Reference Burns and WilkinsonBW1].
In the case where the partially hyperbolic diffeomorphism
![]() $f\colon M\to M$
is dynamically coherent, one could likely adapt the proof of Theorem 2.4 to show that the holonomy maps by ‘genuine’ stable manifolds inside ‘genuine’ center-stable manifolds are
$f\colon M\to M$
is dynamically coherent, one could likely adapt the proof of Theorem 2.4 to show that the holonomy maps by ‘genuine’ stable manifolds inside ‘genuine’ center-stable manifolds are
![]() $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
.
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
.
We emphasize that in the case where
![]() $f\colon M\to M$
is dynamically coherent, the center-stable and center manifolds discussed in what follows are not the center-stable and center manifolds for the dynamics of f. In particular, while f might admit compact center manifolds, the ‘fake’ center manifolds we consider will never be compact.
$f\colon M\to M$
is dynamically coherent, the center-stable and center manifolds discussed in what follows are not the center-stable and center manifolds for the dynamics of f. In particular, while f might admit compact center manifolds, the ‘fake’ center manifolds we consider will never be compact.
1.2 Ledrappier–Young entropy formula
In two seminal papers [Reference Ledrappier and YoungLY1, Reference Ledrappier and YoungLY2], Ledrappier and Young established remarkable results relating the metric entropy of a
![]() $C^2$
diffeomorphism
$C^2$
diffeomorphism
![]() $f\colon M\to M$
of a compact manifold
$f\colon M\to M$
of a compact manifold
![]() $M,$
its Lyapunov exponents, and the geometry of conditional measures along unstable manifolds. In [Reference Ledrappier and YoungLY1], the Sinai–Ruelle–Bowen (SRB) property of measures satisfying the Pesin entropy formula is established for
$M,$
its Lyapunov exponents, and the geometry of conditional measures along unstable manifolds. In [Reference Ledrappier and YoungLY1], the Sinai–Ruelle–Bowen (SRB) property of measures satisfying the Pesin entropy formula is established for
![]() $C^2$
diffeomorphisms and measures with zero Lyapunov exponents. This extends Ledrappier’s result from [Reference LedrappierLed] which established the SRB property for hyperbolic measures invariant under
$C^2$
diffeomorphisms and measures with zero Lyapunov exponents. This extends Ledrappier’s result from [Reference LedrappierLed] which established the SRB property for hyperbolic measures invariant under
![]() $C^{1+\beta }$
diffeomorphisms satisfying the Pesin entropy formula. In [Reference Ledrappier and YoungLY2], a more general formula (in terms of Lyapunov exponents and transverse conditional dimensions) for the entropy
$C^{1+\beta }$
diffeomorphisms satisfying the Pesin entropy formula. In [Reference Ledrappier and YoungLY2], a more general formula (in terms of Lyapunov exponents and transverse conditional dimensions) for the entropy
![]() $h_{\mu }(f)$
of f with respect to a general ergodic f-invariant probability measure
$h_{\mu }(f)$
of f with respect to a general ergodic f-invariant probability measure
![]() $\mu $
is derived.
$\mu $
is derived.
As remarked in [Reference Ledrappier and YoungLY1, pp. 526], there is one crucial step in which the
![]() $C^2$
hypothesis rather than the
$C^2$
hypothesis rather than the
![]() $C^{1+\beta }$
hypothesis on the dynamics is used: establishing the Lipschitzness of unstable holonomies inside center-unstable sets. In [Reference Ledrappier and YoungLY2], the corresponding estimate is the Lipschitzness of the holonomies along intermediate unstable foliations inside the total unstable manifolds. In the case of hyperbolic measures, the entropy formula from [Reference Ledrappier and YoungLY2] is known to hold for
$C^{1+\beta }$
hypothesis on the dynamics is used: establishing the Lipschitzness of unstable holonomies inside center-unstable sets. In [Reference Ledrappier and YoungLY2], the corresponding estimate is the Lipschitzness of the holonomies along intermediate unstable foliations inside the total unstable manifolds. In the case of hyperbolic measures, the entropy formula from [Reference Ledrappier and YoungLY2] is known to hold for
![]() $C^{1+\beta }$
diffeomorphisms as it is sufficient to establish the Lipschitzness of
$C^{1+\beta }$
diffeomorphisms as it is sufficient to establish the Lipschitzness of
![]() $W^i$
holonomies inside the
$W^i$
holonomies inside the
![]() $W^{i+1}$
manifolds (corresponding to Lyapunov exponents
$W^{i+1}$
manifolds (corresponding to Lyapunov exponents
![]() $\lambda _i>\lambda _{i+1} >0$
) on Pesin sets; this Lipschitzness of holonomies along intermediate unstable manifolds was established in [Reference Barreira, Pesin and SchmelingBPS, Appendix]. However, the proof in [Reference Barreira, Pesin and SchmelingBPS, Appendix] does not imply Lipschitzness of unstable holonomies inside center-unstable sets which is essential in the proof of the main technical result of [Reference Ledrappier and YoungLY1]: that the entropy of f is ‘carried entirely by the unstable manifolds’; see [Reference Ledrappier and YoungLY1, Corollary 5.2]. The results of this note establish the Lipschitzness of unstable holonomies inside center-unstable sets which confirms that the results of [Reference Ledrappier and YoungLY1, Reference Ledrappier and YoungLY2] hold for
$\lambda _i>\lambda _{i+1} >0$
) on Pesin sets; this Lipschitzness of holonomies along intermediate unstable manifolds was established in [Reference Barreira, Pesin and SchmelingBPS, Appendix]. However, the proof in [Reference Barreira, Pesin and SchmelingBPS, Appendix] does not imply Lipschitzness of unstable holonomies inside center-unstable sets which is essential in the proof of the main technical result of [Reference Ledrappier and YoungLY1]: that the entropy of f is ‘carried entirely by the unstable manifolds’; see [Reference Ledrappier and YoungLY1, Corollary 5.2]. The results of this note establish the Lipschitzness of unstable holonomies inside center-unstable sets which confirms that the results of [Reference Ledrappier and YoungLY1, Reference Ledrappier and YoungLY2] hold for
![]() $C^{1+\beta }$
diffeomorphisms and invariant measures with zero Lyapunov exponents. See §4 for a brief formulation and justification of the Lipschitzness of unstable holonomies inside center-unstable sets.
$C^{1+\beta }$
diffeomorphisms and invariant measures with zero Lyapunov exponents. See §4 for a brief formulation and justification of the Lipschitzness of unstable holonomies inside center-unstable sets.
To formulate results, fix
![]() $\beta>0$
and let
$\beta>0$
and let
![]() $f\colon M\to M$
be a
$f\colon M\to M$
be a
![]() $C^{1+\beta }$
diffeomorphism of a compact k-dimensional manifold M. Let
$C^{1+\beta }$
diffeomorphism of a compact k-dimensional manifold M. Let
![]() $\mu $
be an ergodic, f-invariant Borel probability measure. We have the following generalizations of the main results of [Reference Ledrappier and YoungLY1, Reference Ledrappier and YoungLY2].
$\mu $
be an ergodic, f-invariant Borel probability measure. We have the following generalizations of the main results of [Reference Ledrappier and YoungLY1, Reference Ledrappier and YoungLY2].
Theorem 1.4. [Reference Ledrappier and YoungLY2, Theorem A]
![]() $h_{\mu }(f)$
satisfies the Pesin entropy formula if and only if
$h_{\mu }(f)$
satisfies the Pesin entropy formula if and only if
![]() $\mu $
has the SRB property.
$\mu $
has the SRB property.
Theorem 1.5. [Reference Ledrappier and YoungLY2, Theorem C
 ${\hspace{-0.2pt}}^\prime$
]
${\hspace{-0.2pt}}^\prime$
]
For a general ergodic, f-invariant probability measure
![]() $\mu $
, the entropy formula of [Reference Ledrappier and YoungLY2, Theorem C
$\mu $
, the entropy formula of [Reference Ledrappier and YoungLY2, Theorem C
![]() ${}^\prime$
] remains valid.
${}^\prime$
] remains valid.
1.3 Outline
In §2 we present an abstract setup in which the dynamics is assumed to be a perturbation of linear dynamics. Our main result, Theorem 2.2, establishes that stable holonomies are uniformly Lipschitz and, in fact,
![]() $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
under certain bunching conditions. We formulate our main result, Theorem 2.2, in a sufficiently abstract setting so that it may be applied to a number of settings. We reduce the proof of Theorem 2.2 to the special case of Theorem 2.4. Section 3 is then devoted to the proof of Theorem 2.4. In §4 we briefly formulate and justify the main technical fact needed to establish Theorems 1.4 and 1.5.
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
under certain bunching conditions. We formulate our main result, Theorem 2.2, in a sufficiently abstract setting so that it may be applied to a number of settings. We reduce the proof of Theorem 2.2 to the special case of Theorem 2.4. Section 3 is then devoted to the proof of Theorem 2.4. In §4 we briefly formulate and justify the main technical fact needed to establish Theorems 1.4 and 1.5.
2 Statement of main theorem
Our main result, Theorem 2.2 below, concerns the smoothness of stable holonomies inside center-stable manifolds for sequences of
![]() $C^{1+\beta }$
diffeomorphisms that are assumed to be perturbations of linear maps
$C^{1+\beta }$
diffeomorphisms that are assumed to be perturbations of linear maps
![]() $L_n\colon \mathbb {R}^k\to \mathbb {R}^k$
with prescribed hyperbolicity properties. We briefly explain the relationship between this setup and the results outlined above.
$L_n\colon \mathbb {R}^k\to \mathbb {R}^k$
with prescribed hyperbolicity properties. We briefly explain the relationship between this setup and the results outlined above.
Consider a
![]() $C^{1+\beta }$
diffeomorphism
$C^{1+\beta }$
diffeomorphism
![]() $f\colon M\to M$
of a compact manifold and
$f\colon M\to M$
of a compact manifold and
![]() $x\in M$
. Using exponential charts
$x\in M$
. Using exponential charts
![]() $\exp _x\colon T_xM\to M$
we identify the local dynamics of f near x with a
$\exp _x\colon T_xM\to M$
we identify the local dynamics of f near x with a
![]() $C^{1+\beta }$
diffeomorphism
$C^{1+\beta }$
diffeomorphism
![]() $f_x$
from a neighborhood of
$f_x$
from a neighborhood of
![]() $0$
in
$0$
in
![]() $T_xM $
to a neighborhood of
$T_xM $
to a neighborhood of
![]() $0$
in
$0$
in
![]() $T_{f(x)}M$
. Interpolating between
$T_{f(x)}M$
. Interpolating between
![]() $f_x$
and
$f_x$
and
![]() $D_xf$
via a bump function, we extend
$D_xf$
via a bump function, we extend
![]() $f_x$
to a
$f_x$
to a
![]() $C^{1+\beta }$
diffeomorphism
$C^{1+\beta }$
diffeomorphism
which coincides with
![]() $D_xf$
outside a neighborhood of the origin. Taking the domain of the bump function sufficiently small, we may further assume
$D_xf$
outside a neighborhood of the origin. Taking the domain of the bump function sufficiently small, we may further assume
![]() $\|F_x - D_xf\|_{C^1}$
and
$\|F_x - D_xf\|_{C^1}$
and
![]() $\|F_x{}^{-1} - (D_xf){}^{-1}\|_{C^1}$
are sufficiently small. If
$\|F_x{}^{-1} - (D_xf){}^{-1}\|_{C^1}$
are sufficiently small. If
![]() $\|F_x - D_xf\|_{C^1}$
and
$\|F_x - D_xf\|_{C^1}$
and
![]() $\|F_x{}^{-1} - (D_xf){}^{-1}\|_{C^1}$
are sufficiently small, hyperbolicity properties of
$\|F_x{}^{-1} - (D_xf){}^{-1}\|_{C^1}$
are sufficiently small, hyperbolicity properties of
![]() $Df$
along the orbit
$Df$
along the orbit
![]() $\{f^n(x): n\in \mathbb {Z}\}$
induce analogous hyperbolicity properties for the sequence of diffeomorphisms
$\{f^n(x): n\in \mathbb {Z}\}$
induce analogous hyperbolicity properties for the sequence of diffeomorphisms
![]() $\{F_{f^n(x)}:n\in \mathbb {Z}\}$
. In particular, if f admits a partially hyperbolic splitting then the sequence of maps
$\{F_{f^n(x)}:n\in \mathbb {Z}\}$
. In particular, if f admits a partially hyperbolic splitting then the sequence of maps
![]() $\{F_{f^n(x)}:n\in \mathbb {Z}\}$
admits a partially hyperbolic splitting. Moreover, if f satisfies bunching conditions as in (1), (2), and (3) then the sequence of maps
$\{F_{f^n(x)}:n\in \mathbb {Z}\}$
admits a partially hyperbolic splitting. Moreover, if f satisfies bunching conditions as in (1), (2), and (3) then the sequence of maps
![]() $\{F_{f^n(x)}:n\in \mathbb {Z}\}$
satisfy analogous bunching conditions.
$\{F_{f^n(x)}:n\in \mathbb {Z}\}$
satisfy analogous bunching conditions.
In the setting of non-uniformly hyperbolic dynamics, given a bi-regular point x for the derivative cocycle, one may perform a further sequence of coordinate changes on each
![]() $T_{f^n(x)}M$
; these are the so-called Lyapunov charts discussed in §4. Relative to these new coordinates one may assume the globalized dynamics
$T_{f^n(x)}M$
; these are the so-called Lyapunov charts discussed in §4. Relative to these new coordinates one may assume the globalized dynamics
![]() $\{F_{f^n(x)}: n\in \mathbb {Z}\}$
is uniformly partially hyperbolic and the hyperbolicity estimates are related to the Lyapunov exponents of the sequence of linear maps
$\{F_{f^n(x)}: n\in \mathbb {Z}\}$
is uniformly partially hyperbolic and the hyperbolicity estimates are related to the Lyapunov exponents of the sequence of linear maps
![]() $\{D_{f^n(x)} f: n\in \mathbb {Z}\}$
.
$\{D_{f^n(x)} f: n\in \mathbb {Z}\}$
.
We formulate our main theorem for dynamics
![]() $\{F_{f^n(x)}:n\in \mathbb {Z}\}$
that are perturbations of linear maps, usually thinking of them as globalizations of local dynamics in local coordinates. We establish smoothness of stable holonomies inside center-stable manifolds for these globalized dynamics. If f is a partially hyperbolic diffeomorphism satisfying sufficient bunching conditions then, in the language of [Reference Burns and WilkinsonBW1, Proposition 3.1], this establishes smoothness of ‘fake’ stable holonomies inside ‘fake’ center-stable manifolds associated to an orbit
$\{F_{f^n(x)}:n\in \mathbb {Z}\}$
that are perturbations of linear maps, usually thinking of them as globalizations of local dynamics in local coordinates. We establish smoothness of stable holonomies inside center-stable manifolds for these globalized dynamics. If f is a partially hyperbolic diffeomorphism satisfying sufficient bunching conditions then, in the language of [Reference Burns and WilkinsonBW1, Proposition 3.1], this establishes smoothness of ‘fake’ stable holonomies inside ‘fake’ center-stable manifolds associated to an orbit
![]() $\{f^n(x): n\in \mathbb {Z}\}$
.
$\{f^n(x): n\in \mathbb {Z}\}$
.
2.1 Setup
Fix
![]() $k\in \mathbb {N}$
and let
$k\in \mathbb {N}$
and let
![]() $\mathbb {R}^k$
be decomposed into subvector spaces
$\mathbb {R}^k$
be decomposed into subvector spaces
For each
![]() $n\in \mathbb {Z}$
, let
$n\in \mathbb {Z}$
, let
![]() $A_n\colon \mathbb {R}^s\to \mathbb {R}^s$
,
$A_n\colon \mathbb {R}^s\to \mathbb {R}^s$
,
![]() $B_n\colon \mathbb {R}^c\to \mathbb {R}^c$
, and
$B_n\colon \mathbb {R}^c\to \mathbb {R}^c$
, and
![]() $C_n\colon \mathbb {R}^u\to \mathbb {R}^u$
be invertible linear maps and let
$C_n\colon \mathbb {R}^u\to \mathbb {R}^u$
be invertible linear maps and let
 $$ \begin{align*} L_n = \left(\begin{array}{ccc}A_n & 0 & 0 \\0 & B_n & 0 \\0 & 0 & C_n\end{array}\right) \end{align*} $$
$$ \begin{align*} L_n = \left(\begin{array}{ccc}A_n & 0 & 0 \\0 & B_n & 0 \\0 & 0 & C_n\end{array}\right) \end{align*} $$
be the associated invertible linear map preserving the decomposition
![]() $\mathbb {R}^k= \mathbb {R}^s\oplus \mathbb {R}^c\oplus \mathbb {R}^u$
. We assume each component of the decomposition
$\mathbb {R}^k= \mathbb {R}^s\oplus \mathbb {R}^c\oplus \mathbb {R}^u$
. We assume each component of the decomposition
![]() $\mathbb {R}^k= \mathbb {R}^s\oplus \mathbb {R}^c\oplus \mathbb {R}^u$
is non-trivial, though the results can be formulated (with fewer conditions) in the case where
$\mathbb {R}^k= \mathbb {R}^s\oplus \mathbb {R}^c\oplus \mathbb {R}^u$
is non-trivial, though the results can be formulated (with fewer conditions) in the case where
![]() $\mathbb {R}^u$
is degenerate.
$\mathbb {R}^u$
is degenerate.
We assume there are constants
such that for every
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
-
(1)
 $e^{\eta ^{\prime }_n}\le m(A_n) \le \|A_n\| \le e^{\kappa ^{\prime }_n}$
,
$e^{\eta ^{\prime }_n}\le m(A_n) \le \|A_n\| \le e^{\kappa ^{\prime }_n}$
, -
(2)
 $e^{ \gamma ^{\prime }_n}\le m(B_n) \le \|B_n\| \le e^{ \hat \gamma ^{\prime }_n}$
,
$e^{ \gamma ^{\prime }_n}\le m(B_n) \le \|B_n\| \le e^{ \hat \gamma ^{\prime }_n}$
, -
(3)
 $e^{\hat \kappa ^{\prime }_n}\le m(C_n) \le \|C_n\| \le e^{ \hat \eta ^{\prime }_n}.$
$e^{\hat \kappa ^{\prime }_n}\le m(C_n) \le \|C_n\| \le e^{ \hat \eta ^{\prime }_n}.$
Here
![]() $\|\cdot \|$
is the operator norm induced by the standard norm on the corresponding Euclidean spaces and
$\|\cdot \|$
is the operator norm induced by the standard norm on the corresponding Euclidean spaces and
![]() $m(A) := \|A{}^{-1}\|^{-1}$
denotes the associated conorm of A. Throughout, we will further assume that
$m(A) := \|A{}^{-1}\|^{-1}$
denotes the associated conorm of A. Throughout, we will further assume that
![]() $\sup \{ \kappa ^{\prime }_n\}<0$
. We do not impose any assumptions on the signsFootnote
1
of
$\sup \{ \kappa ^{\prime }_n\}<0$
. We do not impose any assumptions on the signsFootnote
1
of
![]() $\gamma ^{\prime }_n$
,
$\gamma ^{\prime }_n$
,
![]() $\hat \gamma ^{\prime }_n, \hat \kappa ^{\prime }_n$
and
$\hat \gamma ^{\prime }_n, \hat \kappa ^{\prime }_n$
and
![]() $\hat \eta ^{\prime }_n$
.
$\hat \eta ^{\prime }_n$
.
We assume, moreover, that
Fix some
Anticipating perturbing the linear maps
![]() $L_n$
below, we set
$L_n$
below, we set
2.2 Bunching criteria
Fix
![]() $0<\beta <1$
, which will be the Hölder regularity of the derivatives of perturbations of
$0<\beta <1$
, which will be the Hölder regularity of the derivatives of perturbations of
![]() $L_n$
below. We assume that
$L_n$
below. We assume that
![]() $ \hat \gamma ' _n-\gamma ^{\prime }_n$
and
$ \hat \gamma ' _n-\gamma ^{\prime }_n$
and
![]() $\epsilon _0$
are sufficiently small so that there exists
$\epsilon _0$
are sufficiently small so that there exists
![]() $0<\bar \theta <\beta $
satisfying
$0<\bar \theta <\beta $
satisfying
and
![]() $\theta < \bar \theta $
with
$\theta < \bar \theta $
with
and
These are the analogues of (1), (2), and (3) above.
Condition (5) ensures that certain invariant distributions defined below are uniformly
![]() $\bar \theta $
-Hölder. Condition (7) is a standard bunching condition. Note that with
$\bar \theta $
-Hölder. Condition (7) is a standard bunching condition. Note that with
![]() $\theta =\bar \theta $
, (7) is the bunching condition stated in [Reference Burns and WilkinsonBW1, Theorem 0.3]. Our proof, however, requires a stronger bunching criteria imposed by (6). In particular, we use heavily (6) in our proof of Lemma 3.1 below. Note from (5) that
$\theta =\bar \theta $
, (7) is the bunching condition stated in [Reference Burns and WilkinsonBW1, Theorem 0.3]. Our proof, however, requires a stronger bunching criteria imposed by (6). In particular, we use heavily (6) in our proof of Lemma 3.1 below. Note from (5) that
![]() $\theta = \beta \bar \theta $
satisfies (6).
$\theta = \beta \bar \theta $
satisfies (6).
2.3 Family of perturbations
We introduce the dynamics
![]() $f_n$
we study for the remainder as
$f_n$
we study for the remainder as
![]() $C^1$
small perturbations of the linear maps
$C^1$
small perturbations of the linear maps
![]() $L_n$
. We begin with some notational conventions used throughout the paper.
$L_n$
. We begin with some notational conventions used throughout the paper.
2.3.1 Notational conventions
We let
![]() $\|\cdot \|$
denote the standard Euclidean norm on
$\|\cdot \|$
denote the standard Euclidean norm on
![]() $\mathbb {R}^k$
and write d for the induced distance. Given a subspace
$\mathbb {R}^k$
and write d for the induced distance. Given a subspace
![]() $U\subset \mathbb {R}^k$
, we write
$U\subset \mathbb {R}^k$
, we write
![]() $S U$
for the unit sphere in U relative to the Euclidean norm
$S U$
for the unit sphere in U relative to the Euclidean norm
![]() $\|\cdot \|$
. If
$\|\cdot \|$
. If
![]() $T\colon U\to V$
is linear we write
$T\colon U\to V$
is linear we write
![]() $ T_*\colon S U\to S V$
for the induced map. We recall that if
$ T_*\colon S U\to S V$
for the induced map. We recall that if
![]() $T\colon U\to V$
is a linear isomorphism with
$T\colon U\to V$
is a linear isomorphism with
![]() $a\le m(T)\le \|T\|\le b$
then
$a\le m(T)\le \|T\|\le b$
then
![]() $ T_* $
is bi-Lipschitz with constants
$ T_* $
is bi-Lipschitz with constants
![]() $b{}^{-1} a$
and
$b{}^{-1} a$
and
![]() $ba{}^{-1}$
. Finally, if
$ba{}^{-1}$
. Finally, if
![]() $N\subset \mathbb {R}^k$
is an embedded submanifold we write
$N\subset \mathbb {R}^k$
is an embedded submanifold we write
![]() $SN:= STN$
for the unit sphere bundle over N. Given a diffeomorphism
$SN:= STN$
for the unit sphere bundle over N. Given a diffeomorphism
![]() $g\colon N_1\to N_2$
, we write
$g\colon N_1\to N_2$
, we write
![]() $g_*\colon SN_1 \to S N_2$
for the renormalized derivative map
$g_*\colon SN_1 \to S N_2$
for the renormalized derivative map
 $$ \begin{align*} g_*(x,v) = \bigg(g(x), \frac{1}{ \|D_xg (v)\| }D_xg(v)\bigg). \end{align*} $$
$$ \begin{align*} g_*(x,v) = \bigg(g(x), \frac{1}{ \|D_xg (v)\| }D_xg(v)\bigg). \end{align*} $$
In what follows, we consider
![]() $C^{1+\beta }$
diffeomorphisms
$C^{1+\beta }$
diffeomorphisms
![]() $f\colon \mathbb {R}^k\to \mathbb {R}^k$
with uniform estimates on the
$f\colon \mathbb {R}^k\to \mathbb {R}^k$
with uniform estimates on the
![]() $(1+\beta )$
-norms: namely, viewing
$(1+\beta )$
-norms: namely, viewing
![]() $x\mapsto D_xf$
as a map from
$x\mapsto D_xf$
as a map from
![]() $\mathbb {R}^k$
to the space of linear maps, we assume that
$\mathbb {R}^k$
to the space of linear maps, we assume that
![]() $ \sup _{x\in \mathbb {R}^k } \|D_x f\|<\infty $
and that
$ \sup _{x\in \mathbb {R}^k } \|D_x f\|<\infty $
and that
![]() $Df$
is
$Df$
is
![]() $\beta $
-Hölder continuous with
$\beta $
-Hölder continuous with
 $$ \begin{align*} \mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}}(Df) := \sup_{x \neq y } \bigg\{\dfrac{ \| D_xf- D_y f \|} {d(x,y) ^{\beta}}\bigg\} <\infty. \end{align*} $$
$$ \begin{align*} \mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}}(Df) := \sup_{x \neq y } \bigg\{\dfrac{ \| D_xf- D_y f \|} {d(x,y) ^{\beta}}\bigg\} <\infty. \end{align*} $$
Given submanifolds
![]() $N_1$
and
$N_1$
and
![]() $N_2$
and a diffeomorphism
$N_2$
and a diffeomorphism
![]() $h\colon N_1\to N_2$
then, as the linear maps
$h\colon N_1\to N_2$
then, as the linear maps
![]() $D_{x} h$
and
$D_{x} h$
and
![]() $D_y h$
have different domains for
$D_y h$
have different domains for
![]() $x\neq y\in N_1$
, we define the Hölder variation of
$x\neq y\in N_1$
, we define the Hölder variation of
![]() $Dh$
and
$Dh$
and
![]() $h_*$
as functions between metric spaces: Assuming
$h_*$
as functions between metric spaces: Assuming
![]() $N_1$
has bounded diameter, define the
$N_1$
has bounded diameter, define the
![]() $\beta $
-Hölder variation of
$\beta $
-Hölder variation of
![]() $Dh \colon TN_1\to TN_2$
to be
$Dh \colon TN_1\to TN_2$
to be
 $$ \begin{align*}\mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}} (Dh) := \sup_{\substack{(x,v)\neq (y,u) \in SN_1 } }\bigg\{ \dfrac{ d(Dh(x,v),Dh (y,u)) }{d((x,v), (y,u)) ^{\beta}}\bigg\}\end{align*} $$
$$ \begin{align*}\mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}} (Dh) := \sup_{\substack{(x,v)\neq (y,u) \in SN_1 } }\bigg\{ \dfrac{ d(Dh(x,v),Dh (y,u)) }{d((x,v), (y,u)) ^{\beta}}\bigg\}\end{align*} $$
where, given
![]() $(x,v)$
and
$(x,v)$
and
![]() $(y,u)$
in
$(y,u)$
in
![]() $T\mathbb {R}^k$
, we write
$T\mathbb {R}^k$
, we write
Similarly define
![]() ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} ( h_*)$
. The
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} ( h_*)$
. The
![]() $C^{1+\beta }$
-norm of h is
$C^{1+\beta }$
-norm of h is
![]() $\max \{ \|h\|_{C^1}, {\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} ( Dh ) \}$
.
$\max \{ \|h\|_{C^1}, {\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} ( Dh ) \}$
.
2.3.2 Families of perturbations
For the remainder of §2 and throughout §3, we fix
![]() $f_n\colon \mathbb {R}^k\to \mathbb {R}^k$
to be a sequence of
$f_n\colon \mathbb {R}^k\to \mathbb {R}^k$
to be a sequence of
![]() $C^{1+\beta }$
diffeomorphisms with
$C^{1+\beta }$
diffeomorphisms with
![]() $f_n(0) = 0$
for each n. Fix
$f_n(0) = 0$
for each n. Fix
![]() $\epsilon '>0$
sufficiently small satisfying Proposition 2.1 below. We assume there is a
$\epsilon '>0$
sufficiently small satisfying Proposition 2.1 below. We assume there is a
![]() $C_0>1$
such that for each
$C_0>1$
such that for each
![]() $n\in \mathbb {Z}$
:
$n\in \mathbb {Z}$
:
-
(1)
 $\|f_n-L_n\|_{{C^1}}\le \epsilon '$
, and
$\|f_n-L_n\|_{{C^1}}\le \epsilon '$
, and
 $\|f_n{}^{-1} -L_n{}^{-1} \|_{{C^1}}\le \epsilon '$
;
$\|f_n{}^{-1} -L_n{}^{-1} \|_{{C^1}}\le \epsilon '$
; -
(2)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (Df_n)<C_0$
, and
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (Df_n)<C_0$
, and
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (Df_n{}^{-1})<C_0$
.
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (Df_n{}^{-1})<C_0$
.
Note then that for some
![]() $C_1\ge C_0>1$
we have:
$C_1\ge C_0>1$
we have:
-
(3)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}_{\mathrm {loc}} ( ( f_n)_*)\le C_1 $
, and
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}_{\mathrm {loc}} ( ( f_n)_*)\le C_1 $
, and
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}_{\mathrm {loc}} (( f_n{}^{-1})_* )\le C_1 $
;
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}_{\mathrm {loc}} (( f_n{}^{-1})_* )\le C_1 $
; -
(4)
 $\| (D_x f_n^{\pm 1})_*\|_{C^1}\le C_1$
and
$\| (D_x f_n^{\pm 1})_*\|_{C^1}\le C_1$
and
 $\|D_x f_n ^{\pm 1 } \| \le C_1$
for every x.
$\|D_x f_n ^{\pm 1 } \| \le C_1$
for every x.
Here,
![]() ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}_{\mathrm {loc}} ( f_*) $
is the local Hölder variation of
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}_{\mathrm {loc}} ( f_*) $
is the local Hölder variation of
![]() $f_*\colon S\mathbb {R}^k\to S\mathbb {R}^k$
defined as
$f_*\colon S\mathbb {R}^k\to S\mathbb {R}^k$
defined as
 $$ \begin{align*} \mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}}_{\mathrm{loc}} ( f_*) := \sup_{ 0<d((x,v), (y,u)) \le 1 }\bigg\{ \dfrac{ d(f_*(x,v),f_* (y,u)) }{d((x,v), (y,u)) ^{\beta}}\bigg\}. \end{align*} $$
$$ \begin{align*} \mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}}_{\mathrm{loc}} ( f_*) := \sup_{ 0<d((x,v), (y,u)) \le 1 }\bigg\{ \dfrac{ d(f_*(x,v),f_* (y,u)) }{d((x,v), (y,u)) ^{\beta}}\bigg\}. \end{align*} $$
Moreover, as it holds in all applications we have in mind, one may assume that
![]() $f_n(y) = L_n(y)$
for all y with
$f_n(y) = L_n(y)$
for all y with
![]() $\|y\|\ge 1$
.
$\|y\|\ge 1$
.
From the graph transform method, given
![]() $\epsilon '>0$
sufficiently small and a sequence
$\epsilon '>0$
sufficiently small and a sequence
![]() $f_n$
of diffeomorphisms as above, we may construct foliations of
$f_n$
of diffeomorphisms as above, we may construct foliations of
![]() $\mathbb {R}^k$
by pseudo-stable and pseudo-unstable manifolds. (See [Reference Hirsch, Pugh and ShubHPS, Theorem 5.1], [Reference Burns and WilkinsonBW1, Proposition 3.1], or [Reference Pugh and ShubPS1, Theorem 3.16] for more details.) To summarize, we have the following proposition.
$\mathbb {R}^k$
by pseudo-stable and pseudo-unstable manifolds. (See [Reference Hirsch, Pugh and ShubHPS, Theorem 5.1], [Reference Burns and WilkinsonBW1, Proposition 3.1], or [Reference Pugh and ShubPS1, Theorem 3.16] for more details.) To summarize, we have the following proposition.
Proposition 2.1. There exist
![]() $\beta '>\bar \theta $
and
$\beta '>\bar \theta $
and
![]() $\beta ">0$
so that for every sufficiently small
$\beta ">0$
so that for every sufficiently small
![]() $\epsilon '>0$
and every
$\epsilon '>0$
and every
![]() $C_0>1$
as above there is a
$C_0>1$
as above there is a
![]() $\hat C>0$
such that for every
$\hat C>0$
such that for every
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
![]() $\star = \{u,c,s,cu,cs\}$
, and
$\star = \{u,c,s,cu,cs\}$
, and
![]() $x\in \mathbb {R}^k$
there are manifolds
$x\in \mathbb {R}^k$
there are manifolds
![]() $W^{\star }_n(x)$
containing x with:
$W^{\star }_n(x)$
containing x with:
-
(1)
 $e^{\hat \kappa _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \eta _n} d(x,y) $
for
$e^{\hat \kappa _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \eta _n} d(x,y) $
for
 $y\in W^u_n(x)$
;
$y\in W^u_n(x)$
; -
(2)
 $e^{ \gamma _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \eta _n} d(x,y) $
for
$e^{ \gamma _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \eta _n} d(x,y) $
for
 $y\in W^{cu}_n(x)$
;
$y\in W^{cu}_n(x)$
; -
(3)
 $e^{ \gamma _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \gamma _n} d(x,y)$
for
$e^{ \gamma _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \gamma _n} d(x,y)$
for
 $y\in W^c_n(x)$
;
$y\in W^c_n(x)$
; -
(4)
 $e^{ \eta _n } d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \gamma _n } d(x,y)$
for
$e^{ \eta _n } d(x,y) \le d(f_n(x), f_n(y)) \le e^{\hat \gamma _n } d(x,y)$
for
 $y\in W^{cs}_n(x)$
;
$y\in W^{cs}_n(x)$
; -
(5)
 $e^{ \eta _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{ \kappa _n} d(x,y)$
for
$e^{ \eta _n} d(x,y) \le d(f_n(x), f_n(y)) \le e^{ \kappa _n} d(x,y)$
for
 $y\in W^s_n(x)$
;
$y\in W^s_n(x)$
; -
(6)
 $f_n (W^{\star }_n(x)) = W^{\star }_{n+1} (f_n(x))$
for every
$f_n (W^{\star }_n(x)) = W^{\star }_{n+1} (f_n(x))$
for every
 $x\in \mathbb {R}^k$
and
$x\in \mathbb {R}^k$
and
 $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
. -
(7) If
 $y\in W^{\star }_n(x)$
then
$y\in W^{\star }_n(x)$
then
 $W^{\star }_n(x) = W^{\star }_n(y)$
. In particular, the partition into
$W^{\star }_n(x) = W^{\star }_n(y)$
. In particular, the partition into
 $W^{\star }_n$
-manifolds foliates
$W^{\star }_n$
-manifolds foliates
 $\mathbb {R}^k$
; moreover, the partition into
$\mathbb {R}^k$
; moreover, the partition into
 $W^s_n$
-manifolds subfoliates each
$W^s_n$
-manifolds subfoliates each
 $W^{cs}_n(x)$
.
$W^{cs}_n(x)$
. -
(8) Each
 $W^{\star }_n(x)$
is the graph of a
$W^{\star }_n(x)$
is the graph of a
 $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
function
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
function
 $G^{\star } _n(x)\colon \mathbb {R}^{\star }\to (\mathbb {R}^{\star })^{\perp }$
with
$G^{\star } _n(x)\colon \mathbb {R}^{\star }\to (\mathbb {R}^{\star })^{\perp }$
with
 $\| D_uG^{\star } _n(x)\|\le \tfrac 1 3$
for all
$\| D_uG^{\star } _n(x)\|\le \tfrac 1 3$
for all
 $u\in \mathbb {R}^{\star }$
and
$u\in \mathbb {R}^{\star }$
and-
(a)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}( D G^{\star } _n(x)) \le \hat C$
for
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }}( D G^{\star } _n(x)) \le \hat C$
for
 $\star = s$
;
$\star = s$
; -
(b)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta '}}( D G^{\star } _n(x)) \le \hat C$
for
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta '}}( D G^{\star } _n(x)) \le \hat C$
for
 $\star = cs, c, cu$
;
$\star = cs, c, cu$
; -
(c)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta "}}( D G^{\star } _n(x)) \le \hat C$
for
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta "}}( D G^{\star } _n(x)) \le \hat C$
for
 $\star = u$
.
$\star = u$
.
Moreover, the functions
 $G_n^{\star } (x)$
depend continuously (in the
$G_n^{\star } (x)$
depend continuously (in the
 $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
topology) on x.
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
topology) on x. -
For a discussion of the
![]() $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
-regularity of individual leaves in property (8) (of Proposition 2.1), see for instance [Reference Pugh and ShubPS1, §6]. Note, in particular, that while the foliation of
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
-regularity of individual leaves in property (8) (of Proposition 2.1), see for instance [Reference Pugh and ShubPS1, §6]. Note, in particular, that while the foliation of
![]() $\mathbb {R}^k$
into
$\mathbb {R}^k$
into
![]() $W^{\star }_n$
-leaves is only continuous, each leaf
$W^{\star }_n$
-leaves is only continuous, each leaf
![]() $W^{\star }_n(x)$
is a uniformly
$W^{\star }_n(x)$
is a uniformly
![]() $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
-embedded submanifold.
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
-embedded submanifold.
Write
![]() $E^{\star }_n(x):= T_xW^{\star }_n(x)$
. From our choice of
$E^{\star }_n(x):= T_xW^{\star }_n(x)$
. From our choice of
![]() $\bar \theta>0$
satisfying (5), it follows (for example, from the
$\bar \theta>0$
satisfying (5), it follows (for example, from the
![]() $C^r$
-section theorem [Reference Hirsch, Pugh and ShubHPS, p. 30]; see also discussion following [Reference Burns and WilkinsonBW1]) that the tangent spaces
$C^r$
-section theorem [Reference Hirsch, Pugh and ShubHPS, p. 30]; see also discussion following [Reference Burns and WilkinsonBW1]) that the tangent spaces
![]() $E^{\star }_n(x)$
are Hölder continuous with exponent
$E^{\star }_n(x)$
are Hölder continuous with exponent
![]() $\bar \theta $
and constant uniform in
$\bar \theta $
and constant uniform in
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $n\in \mathbb {Z}$
for
$n\in \mathbb {Z}$
for
![]() $\star = cu, cs$
, and hence for
$\star = cu, cs$
, and hence for
![]() $\star = c$
. For
$\star = c$
. For
![]() $\star = s,u$
, the distributions
$\star = s,u$
, the distributions
![]() $E^{\star }_n(x)$
are Hölder continuous with exponent satisfying analogues of (5). As discussed in [Reference Pugh and ShubPS1, Theorem 6.6], each
$E^{\star }_n(x)$
are Hölder continuous with exponent satisfying analogues of (5). As discussed in [Reference Pugh and ShubPS1, Theorem 6.6], each
![]() $W^{cu}_n(x)$
is
$W^{cu}_n(x)$
is
![]() $C^{1+\beta '}$
whenever
$C^{1+\beta '}$
whenever
![]() $0<\beta '\le \beta $
satisfies
$0<\beta '\le \beta $
satisfies
Since
![]() $\eta _n<\gamma _n$
, we have
$\eta _n<\gamma _n$
, we have
and equation (5) implies each
![]() $W^{cu}_n(x)$
is
$W^{cu}_n(x)$
is
![]() $C^{1+\beta '}$
for some
$C^{1+\beta '}$
for some
![]() $\beta '>\bar \theta $
. Similarly, equation (5) implies each
$\beta '>\bar \theta $
. Similarly, equation (5) implies each
![]() $W^{cs}_n(x)$
is
$W^{cs}_n(x)$
is
![]() $C^{1+\beta '}$
for some
$C^{1+\beta '}$
for some
![]() $\beta '>\bar \theta $
; thus each
$\beta '>\bar \theta $
; thus each
![]() $W^{c}_n(x)$
is
$W^{c}_n(x)$
is
![]() $C^{1+\beta '}$
. We also note in the case where
$C^{1+\beta '}$
. We also note in the case where
![]() $\inf \{\hat \kappa _n\}>0$
, we may take
$\inf \{\hat \kappa _n\}>0$
, we may take
![]() $\beta "=\beta $
.
$\beta "=\beta $
.
We write
2.4
 $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
holonomies inside center-stable manifolds
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
holonomies inside center-stable manifolds
Fix
![]() $R>0$
. Fix
$R>0$
. Fix
![]() $p\in \mathbb {R}^k$
,
$p\in \mathbb {R}^k$
,
![]() $n\in \mathbb {Z}$
, and
$n\in \mathbb {Z}$
, and
![]() $q\in W^s_n(p,R)$
. Let
$q\in W^s_n(p,R)$
. Let
![]() $\hat D_1 $
and
$\hat D_1 $
and
![]() $\hat D_2$
be two uniformly
$\hat D_2$
be two uniformly
![]() $C^{1+\beta '}$
embedded,
$C^{1+\beta '}$
embedded,
![]() $\dim (\mathbb {R}^{cu})$
-dimensional manifolds without boundary and with
$\dim (\mathbb {R}^{cu})$
-dimensional manifolds without boundary and with
![]() $p\in \hat D_1$
and
$p\in \hat D_1$
and
![]() $q\in \hat D_2$
. We assume the diameter of each
$q\in \hat D_2$
. We assume the diameter of each
![]() $D_i$
is less than
$D_i$
is less than
![]() $1$
and that each subspace
$1$
and that each subspace
![]() $T_x\hat D_i$
is sufficiently transverse to
$T_x\hat D_i$
is sufficiently transverse to
![]() $\mathbb {R}^s$
: Given
$\mathbb {R}^s$
: Given
![]() $v\in T_x \hat D_i$
, write
$v\in T_x \hat D_i$
, write
![]() $v= v^s + v^{cu}$
where
$v= v^s + v^{cu}$
where
![]() $v^s\in \mathbb {R}^s$
and
$v^s\in \mathbb {R}^s$
and
![]() $v^{cu}\in \mathbb {R}^{cu}$
; we then assume
$v^{cu}\in \mathbb {R}^{cu}$
; we then assume
![]() $\|v^{cu}\|\ge 3 \|v^s\|$
. Let
$\|v^{cu}\|\ge 3 \|v^s\|$
. Let
![]() $D_1= W^{cs}_n(p)\cap \hat D_1$
and
$D_1= W^{cs}_n(p)\cap \hat D_1$
and
![]() $D_2= W^{cs}_n(q)\cap \hat D_2$
. Given
$D_2= W^{cs}_n(q)\cap \hat D_2$
. Given
![]() $x\in D_1$
, let
$x\in D_1$
, let
![]() $h_{D_1, D_2}(x)$
denote the unique point y in
$h_{D_1, D_2}(x)$
denote the unique point y in
![]() $D_2$
with
$D_2$
with
![]() $y\in W^s_n(x)$
if such a point exists. Note that the domain and codomain of
$y\in W^s_n(x)$
if such a point exists. Note that the domain and codomain of
![]() $h_{D_1, D_2}$
are open subsets of
$h_{D_1, D_2}$
are open subsets of
![]() $D_1$
and
$D_1$
and
![]() $D_2$
. By restriction of domain and codomain we may assume
$D_2$
. By restriction of domain and codomain we may assume
![]() $h_{D_1, D_2}\colon D_1 \to D_2$
is a homeomorphism.
$h_{D_1, D_2}\colon D_1 \to D_2$
is a homeomorphism.
Our main result is the following theorem.
Theorem 2.2. The map
![]() $h_{D_1, D_2}$
is a
$h_{D_1, D_2}$
is a
![]() $C^{1+\hat \alpha }$
diffeomorphism for some
$C^{1+\hat \alpha }$
diffeomorphism for some
![]() $\hat \alpha>0$
. Moreover, the
$\hat \alpha>0$
. Moreover, the
![]() $C^{1+\hat \alpha }$
-norm of
$C^{1+\hat \alpha }$
-norm of
![]() $ h_{D_1, D_2}$
is uniform across all choices of
$ h_{D_1, D_2}$
is uniform across all choices of
![]() $n,p,q,D_1$
, and
$n,p,q,D_1$
, and
![]() $D_2$
as above.
$D_2$
as above.
In particular, we have the following corollary.
Corollary 2.3. The map
![]() $h_{D_1, D_2}$
is bi-Lipschitz with Lipschitz constants uniform in all choices of
$h_{D_1, D_2}$
is bi-Lipschitz with Lipschitz constants uniform in all choices of
![]() $n,p,q,D_1$
, and
$n,p,q,D_1$
, and
![]() $D_2$
as above.
$D_2$
as above.
2.5 Main theorem
As discussed below, it is sufficient to prove a special case of Theorem 2.2.
Recall that each
![]() $W^c_n(x)$
is a uniformly
$W^c_n(x)$
is a uniformly
![]() $C^{1+\beta '}$
-embedded manifold and intersects
$C^{1+\beta '}$
-embedded manifold and intersects
![]() $W^s_n(y)$
for every
$W^s_n(y)$
for every
![]() $y\in W^{cs}_n(x)$
. Moreover, each
$y\in W^{cs}_n(x)$
. Moreover, each
![]() $E^{cu}_n(y)$
is uniformly transverse to both
$E^{cu}_n(y)$
is uniformly transverse to both
![]() $\mathbb {R}^s$
and
$\mathbb {R}^s$
and
![]() $E^s_n(y)$
. It suffices to prove Theorem 2.2 for the distinguished family of transversals to
$E^s_n(y)$
. It suffices to prove Theorem 2.2 for the distinguished family of transversals to
![]() $W^s_n$
given by the family of center manifolds. Given
$W^s_n$
given by the family of center manifolds. Given
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
![]() $p\in \mathbb {R}^k$
, and
$p\in \mathbb {R}^k$
, and
![]() $q\in W^s_n(p)$
, we write
$q\in W^s_n(p)$
, we write
![]() $h^s_{p,q,n}\colon W^c_n(p)\to W^c_n(q)$
for the stable holonomy map between center manifolds. More precisely, given
$h^s_{p,q,n}\colon W^c_n(p)\to W^c_n(q)$
for the stable holonomy map between center manifolds. More precisely, given
![]() $z\in W^c_n(p)$
, let
$z\in W^c_n(p)$
, let
As both
![]() $\{W _n^{s}(x): x\in W^{cs}_n(p)\}$
and
$\{W _n^{s}(x): x\in W^{cs}_n(p)\}$
and
![]() $\{W _n^{c}(x): x\in W^{cs}_n(p)\}$
subfoliate
$\{W _n^{c}(x): x\in W^{cs}_n(p)\}$
subfoliate
![]() $ W^{cs}_n(p)$
, it follows that
$ W^{cs}_n(p)$
, it follows that
![]() $h^s_{p,q,n}(z) \in W^{c}_n(q).$
Moreover, by the global transverseness of the manifolds, the maps
$h^s_{p,q,n}(z) \in W^{c}_n(q).$
Moreover, by the global transverseness of the manifolds, the maps
![]() $h^s_{p,q,n}$
have domain all of
$h^s_{p,q,n}$
have domain all of
![]() $W^c_n(p)$
and map onto
$W^c_n(p)$
and map onto
![]() $W^c_n(q).$
$W^c_n(q).$
The main result of this paper is the following theorem.
Theorem 2.4. There exist
![]() $0<R_0<1$
and
$0<R_0<1$
and
![]() $\hat \alpha>0$
with the following property. Let
$\hat \alpha>0$
with the following property. Let
![]() $p\in \mathbb {R}^k$
and
$p\in \mathbb {R}^k$
and
![]() $q\in W^s_n(p, R_0)$
. Then the holonomy map
$q\in W^s_n(p, R_0)$
. Then the holonomy map
is a
![]() $C^{1+ \hat \alpha }$
-diffeomorphism onto its image. Moreover, the
$C^{1+ \hat \alpha }$
-diffeomorphism onto its image. Moreover, the
![]() $C^{1+\hat \alpha }$
-norm of
$C^{1+\hat \alpha }$
-norm of
![]() $h^s_{p,q,n}$
is uniform across the choice of p, q and n.
$h^s_{p,q,n}$
is uniform across the choice of p, q and n.
The
![]() $R_0>0$
for which the theorem holds is given by criteria in §3.1.2 below.
$R_0>0$
for which the theorem holds is given by criteria in §3.1.2 below.
We recall that the composition of finitely many
![]() $C^{1+ \hat \alpha }$
diffeomorphisms is again a
$C^{1+ \hat \alpha }$
diffeomorphisms is again a
![]() $C^{1+ \hat \alpha }$
diffeomorphism. Since
$C^{1+ \hat \alpha }$
diffeomorphism. Since
![]() $R_0>0$
, for any fixed
$R_0>0$
, for any fixed
![]() $R>0$
and any
$R>0$
and any
![]() $q\in W^s_n(p, R)$
, the holonomy map
$q\in W^s_n(p, R)$
, the holonomy map
is the composition of finitely many
![]() $C^{1+ \hat \alpha }$
-diffeomorphisms and the
$C^{1+ \hat \alpha }$
-diffeomorphisms and the
![]() $C^{1+\hat \alpha }$
-norm of
$C^{1+\hat \alpha }$
-norm of
![]() $h^s_{p,q,n}$
is uniform across the choice of p, q and n.
$h^s_{p,q,n}$
is uniform across the choice of p, q and n.
Taking
![]() $\hat \alpha <\beta '$
and using that holonomies are uniformly
$\hat \alpha <\beta '$
and using that holonomies are uniformly
![]() $C^{1+\hat \alpha }$
, we use Journé’s theorem [Reference JournéJou] or related discussions in [Reference Pugh, Shub and WilkinsonPSW, §6] to conclude that leaves of the partition
$C^{1+\hat \alpha }$
, we use Journé’s theorem [Reference JournéJou] or related discussions in [Reference Pugh, Shub and WilkinsonPSW, §6] to conclude that leaves of the partition
![]() $\{W^s_n(x), x\in \mathbb {R}^k\}$
restrict to a
$\{W^s_n(x), x\in \mathbb {R}^k\}$
restrict to a
![]() $C^{1+\hat \alpha }$
-foliation inside each
$C^{1+\hat \alpha }$
-foliation inside each
![]() $W^{cs}_n(p)$
. The smoothness of holonomies for arbitrary transversals in Theorem 2.2 then follows by considering foliation charts. In particular, given arbitrary transversals
$W^{cs}_n(p)$
. The smoothness of holonomies for arbitrary transversals in Theorem 2.2 then follows by considering foliation charts. In particular, given arbitrary transversals
![]() $D_1 $
and
$D_1 $
and
![]() $D_2$
to
$D_2$
to
![]() $\{W^s_n(x), x\in W^{cs}_n(p) \}$
inside
$\{W^s_n(x), x\in W^{cs}_n(p) \}$
inside
![]() $W^{cs}_n(p)$
as above, it follows that the holonomy map
$W^{cs}_n(p)$
as above, it follows that the holonomy map
![]() $h^s_{D_1, D_2}$
is uniformly
$h^s_{D_1, D_2}$
is uniformly
![]() $C^{1+\hat \alpha }$
on its domain.
$C^{1+\hat \alpha }$
on its domain.
3 Proof of Theorem 2.4
We retain all notation from the previous section. In particular, fix
![]() $0<\theta < \bar \theta <\beta $
satisfying (5), (6), and (7).
$0<\theta < \bar \theta <\beta $
satisfying (5), (6), and (7).
3.1 Initial approximations, additional notation, and sequence of approximate holonomies
3.1.1 Initial approximations
Given
![]() $n\in \mathbb {Z}$
and arbitrary
$n\in \mathbb {Z}$
and arbitrary
![]() $p,q\in \mathbb {R}^k$
with
$p,q\in \mathbb {R}^k$
with
![]() $q\in W^s_n(p, 1)$
, we assume there exists a uniformly
$q\in W^s_n(p, 1)$
, we assume there exists a uniformly
![]() $C^{1+\beta '} $
initial approximation
$C^{1+\beta '} $
initial approximation
to the stable holonomy map
![]() $h_{p,q,n}^s$
with the following properties. There is a constant
$h_{p,q,n}^s$
with the following properties. There is a constant
![]() $C_2>1$
such that for every
$C_2>1$
such that for every
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
![]() $ p\in \mathbb {R}^k$
, and
$ p\in \mathbb {R}^k$
, and
![]() $q\in W^s(p,1)$
we have:
$q\in W^s(p,1)$
we have:
-
(1)
 $d(\pi _{p,q,n} (p), q)\le C_2 d(p,q)$
and
$d(\pi _{p,q,n} (p), q)\le C_2 d(p,q)$
and
 $d(p, \pi _{p,q,n} (p))\le C_2d(p,q)$
;
$d(p, \pi _{p,q,n} (p))\le C_2d(p,q)$
; -
(2)
 $d ((\pi _{p,q,n} )_*(v), v)\le C_2d(p,q)^{\bar \theta }$
for all
$d ((\pi _{p,q,n} )_*(v), v)\le C_2d(p,q)^{\bar \theta }$
for all
 $v\in SW^c_n(p)$
;
$v\in SW^c_n(p)$
; -
(3)
 $|\| D\pi _{p,q,n} \| - 1|\le C_2d(p,q)^{\bar \theta }$
;
$|\| D\pi _{p,q,n} \| - 1|\le C_2d(p,q)^{\bar \theta }$
; -
(4) if
 $p'\in W^c_n(p)$
and
$p'\in W^c_n(p)$
and
 $q'\in W^s_n(p', 1)\cap W^c_n(q)$
then
$q'\in W^s_n(p', 1)\cap W^c_n(q)$
then
 $\pi _{p,q,n} $
and
$\pi _{p,q,n} $
and
 $\pi _{p',q',n} $
coincide on
$\pi _{p',q',n} $
coincide on
 $W^c_n(p,1)\cap W^c_n(p',1)$
.
$W^c_n(p,1)\cap W^c_n(p',1)$
.
For instance, we may define such a system of approximating maps
![]() $\{\pi _{p,q,n}\}$
by linear projection: for
$\{\pi _{p,q,n}\}$
by linear projection: for
![]() $z\in W^c_n(p, 1)$
, define
$z\in W^c_n(p, 1)$
, define
![]() $\pi _{p,q,n} ( z)$
to be the unique point of intersection of
$\pi _{p,q,n} ( z)$
to be the unique point of intersection of
![]() $W^c_n(q)$
and
$W^c_n(q)$
and
![]() $ z + \mathbb {R}^u \oplus \mathbb {R}^s$
. One may verify that the above properties hold for this choice of
$ z + \mathbb {R}^u \oplus \mathbb {R}^s$
. One may verify that the above properties hold for this choice of
![]() $\pi _{p,q,n}$
.
$\pi _{p,q,n}$
.
3.1.2 Additional constants
Fix
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $0<\hat \theta < \theta < \bar \theta < \hat \beta <\beta $
for the remainder with
$0<\hat \theta < \theta < \bar \theta < \hat \beta <\beta $
for the remainder with
 $$ \begin{align} \sup \bigg\{ \frac{ (1+\alpha)(\hat\gamma _n- \gamma_n)}{-\kappa_n }\bigg\}<\hat \theta \end{align} $$
$$ \begin{align} \sup \bigg\{ \frac{ (1+\alpha)(\hat\gamma _n- \gamma_n)}{-\kappa_n }\bigg\}<\hat \theta \end{align} $$
and
 $$ \begin{align} \sup\bigg\{\dfrac{ \kappa_n}{\kappa_n- \gamma_n}\theta\bigg\} <\hat \beta. \end{align} $$
$$ \begin{align} \sup\bigg\{\dfrac{ \kappa_n}{\kappa_n- \gamma_n}\theta\bigg\} <\hat \beta. \end{align} $$
The existence of such
![]() $\alpha $
and
$\alpha $
and
![]() $\hat \theta $
follow from (7); the existence of such a
$\hat \theta $
follow from (7); the existence of such a
![]() $\hat \beta $
follows from (6). Set
$\hat \beta $
follows from (6). Set
![]() $\bar \kappa = \sup \{\kappa _n\} <0 $
. Set
$\bar \kappa = \sup \{\kappa _n\} <0 $
. Set
We have
![]() $\omega <\hat \omega <0$
from the choice of
$\omega <\hat \omega <0$
from the choice of
![]() $\hat \theta < \theta $
in (8).
$\hat \theta < \theta $
in (8).
For the remainder of §3, fix
![]() $0<\delta <1 $
such that for all
$0<\delta <1 $
such that for all
![]() $n\in \mathbb {Z}$
we have
$n\in \mathbb {Z}$
we have
Such a
![]() $\delta>0$
exists since
$\delta>0$
exists since
![]() $\inf \{e^{\alpha (\hat \gamma _n- \gamma _n)}\}>1$
.
$\inf \{e^{\alpha (\hat \gamma _n- \gamma _n)}\}>1$
.
Given
![]() $p,q$
, and n with
$p,q$
, and n with
![]() $q\in W^s_n(p)$
, define
$q\in W^s_n(p)$
, define
Take
![]() $0<\rho _0<1$
such that
$0<\rho _0<1$
such that
where
![]() $C_1\ge 1$
is as in §2.3 and
$C_1\ge 1$
is as in §2.3 and
![]() $C_2\ge 1$
is as above. Fix
$C_2\ge 1$
is as above. Fix
![]() $0<R_0<1$
so that for all
$0<R_0<1$
so that for all
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
![]() $p\in \mathbb {R}^k$
, and
$p\in \mathbb {R}^k$
, and
![]() $q\in W^s_n(p, R_0)$
we have
$q\in W^s_n(p, R_0)$
we have
With this
![]() $R_0$
we establish Theorem 2.4.
$R_0$
we establish Theorem 2.4.
3.1.3 Additional notation
It is enough to prove Theorem 2.4 in the case where
![]() $n=0$
. For the remainder of §3, we fix p and q in
$n=0$
. For the remainder of §3, we fix p and q in
![]() $ \mathbb {R}^k$
with
$ \mathbb {R}^k$
with
![]() $q\in W^s_0(p, R_0)$
as in Theorem 2.4. Write
$q\in W^s_0(p, R_0)$
as in Theorem 2.4. Write
![]() $h:=h_{p,q,0}^s$
.
$h:=h_{p,q,0}^s$
.
Given
![]() $n, j\in \mathbb {Z}$
, write:
$n, j\in \mathbb {Z}$
, write:
-
•
 $f^{(j)}_n:= \mathrm {id}$
,
$f^{(j)}_n:= \mathrm {id}$
,
 $j=0$
;
$j=0$
; -
•
 $f^{(j)}_n:= f_{n+j-1} \circ \cdots \circ f_n$
,
$f^{(j)}_n:= f_{n+j-1} \circ \cdots \circ f_n$
,
 $j>0$
;
$j>0$
; -
•
 $f^{(j)}_n:= f_{n+j}{}^{-1} \circ \cdots \circ f_{n-1}{}^{-1}$
,
$f^{(j)}_n:= f_{n+j}{}^{-1} \circ \cdots \circ f_{n-1}{}^{-1}$
,
 $j<0$
;
$j<0$
; -
• for
 $z\in \mathbb {R}^k$
, write
$z\in \mathbb {R}^k$
, write
 $z_n = f^{(n)}_0(z)$
;
$z_n = f^{(n)}_0(z)$
; -
• write
 $D_n\subset W^c_n(p_n):= f^{(n)}_0(W^c_0(p,1))$
;
$D_n\subset W^c_n(p_n):= f^{(n)}_0(W^c_0(p,1))$
; -
• let
 $\displaystyle \kappa ^{(j)}_n =\begin {cases}\kappa _{n+j-1}+ \cdots + \kappa _n, & j>0,\\ 0, &j= 0,\\ -\kappa _{n+j}- \cdots - \kappa _{n-1}, & j<0; \end {cases}$
$\displaystyle \kappa ^{(j)}_n =\begin {cases}\kappa _{n+j-1}+ \cdots + \kappa _n, & j>0,\\ 0, &j= 0,\\ -\kappa _{n+j}- \cdots - \kappa _{n-1}, & j<0; \end {cases}$
-
• similarly, define
 $\hat \kappa ^{(j)}_n, \gamma ^{(j)}_n,$
and
$\hat \kappa ^{(j)}_n, \gamma ^{(j)}_n,$
and
 $ \hat \gamma ^{(j)}_n $
.
$ \hat \gamma ^{(j)}_n $
.
Note that if
![]() $x\in W^c_0(p,1) = D_0$
and
$x\in W^c_0(p,1) = D_0$
and
![]() $y= h(x)\in W^c_0(q)$
then for all
$y= h(x)\in W^c_0(q)$
then for all
![]() $n\ge 0$
we have
$n\ge 0$
we have
Since
![]() $d(x_n,y_n)<1$
, we obtain initial approximations
$d(x_n,y_n)<1$
, we obtain initial approximations
![]() $\pi _{x_{n},y_{n},n}$
satisfying the properties in §3.1.1. By property (4) of the approximate holonomy maps
$\pi _{x_{n},y_{n},n}$
satisfying the properties in §3.1.1. By property (4) of the approximate holonomy maps
![]() $\pi _{p_{n}, q_{n}, n}$
, it follows that the collection of maps
$\pi _{p_{n}, q_{n}, n}$
, it follows that the collection of maps
![]() $\{\pi _{x_{n},y_{n},n}: x_n\in D_{n}\}$
coincide with the restriction of a single approximation which we denote by
$\{\pi _{x_{n},y_{n},n}: x_n\in D_{n}\}$
coincide with the restriction of a single approximation which we denote by
![]() $\pi _{n} \colon D_{n}\to W^c_{n}(q_{n})$
for the remainder. Note that
$\pi _{n} \colon D_{n}\to W^c_{n}(q_{n})$
for the remainder. Note that
![]() $\pi _{n} \colon D_{n}\to W^c_{n}(q_{n})$
has all the properties enumerated in §3.1.
$\pi _{n} \colon D_{n}\to W^c_{n}(q_{n})$
has all the properties enumerated in §3.1.
3.1.4 Approximate holonomies
For
![]() $n\ge 0$
, we define
$n\ge 0$
, we define
![]() $h_{n}\colon W^c_0(p,1) \to W^c_0(q)$
to be successive approximations to h given by
$h_{n}\colon W^c_0(p,1) \to W^c_0(q)$
to be successive approximations to h given by
Note that each
![]() $h_{n} $
is a
$h_{n} $
is a
![]() $C^{1+\beta '}$
diffeomorphism onto its image. Although the
$C^{1+\beta '}$
diffeomorphism onto its image. Although the
![]() $(1+\beta ')$
-norms of the sequence
$(1+\beta ')$
-norms of the sequence
![]() $h_{n}$
may not be controlled, Theorem 2.2 follows by showing that
$h_{n}$
may not be controlled, Theorem 2.2 follows by showing that
![]() $h_{n} $
converges to
$h_{n} $
converges to
![]() $ h \colon W^c_0(p,1) \to W^c_0(q)$
in the
$ h \colon W^c_0(p,1) \to W^c_0(q)$
in the
![]() $C^1$
topology. We then show
$C^1$
topology. We then show
![]() $Dh\colon SW^c_0(p,1) \to TW^c_0(q)$
is Hölder continuous with uniform estimates for some Hölder exponent
$Dh\colon SW^c_0(p,1) \to TW^c_0(q)$
is Hölder continuous with uniform estimates for some Hölder exponent
![]() $0\,{<}\, \hat \alpha \,{<}\,\beta '$
.
$0\,{<}\, \hat \alpha \,{<}\,\beta '$
.
3.2 An auxiliary lemma
Given
![]() $\xi = (x, v)$
and
$\xi = (x, v)$
and
![]() $\zeta = (y, w)$
in
$\zeta = (y, w)$
in
![]() $S \mathbb {R}^k$
, recall that we write
$S \mathbb {R}^k$
, recall that we write
![]() $d(\xi ,\zeta ) = \sup \{d(x,y), d(v,w)\}$
. Given
$d(\xi ,\zeta ) = \sup \{d(x,y), d(v,w)\}$
. Given
![]() $\xi =(x,v)\in S\mathbb {R}^k $
, we write
$\xi =(x,v)\in S\mathbb {R}^k $
, we write
Similarly, write
![]() $\zeta _{n}:= (y_{n}, w_{n})$
.
$\zeta _{n}:= (y_{n}, w_{n})$
.
Recall the parameters
![]() $0<\delta <1$
satisfying (11) and
$0<\delta <1$
satisfying (11) and
![]() $\alpha $
and
$\alpha $
and
![]() $\hat \beta $
satisfying (8).
$\hat \beta $
satisfying (8).
Lemma 3.1. Given
![]() $x\in \mathbb {R}^k$
,
$x\in \mathbb {R}^k$
,
![]() $\xi =(x,v)$
,
$\xi =(x,v)$
,
![]() $\zeta =(y,w) \in S W^c_0(x) $
,
$\zeta =(y,w) \in S W^c_0(x) $
,
![]() $0\le r\le \delta $
, and
$0\le r\le \delta $
, and
![]() $n\ge 0$
, suppose that
$n\ge 0$
, suppose that
![]() $d(x_{n}, y_{n})\le r e^{\kappa _0^{(n)}}$
,
$d(x_{n}, y_{n})\le r e^{\kappa _0^{(n)}}$
,
![]() $d(\xi _{n}, \zeta _{n})\le r^{\bar \theta }e^{\kappa _0^{(n)} \theta } $
, and for all
$d(\xi _{n}, \zeta _{n})\le r^{\bar \theta }e^{\kappa _0^{(n)} \theta } $
, and for all
![]() $0\le k\le n$
that
$0\le k\le n$
that
Then, for all
![]() $0\le k\le n $
,
$0\le k\le n $
,
In particular,
Proof For the final assertion, note that
follows from inequality (5) as
![]() $ \theta \le (({\kappa _n -\gamma _n})/{\eta _n})\le (({\kappa _n -\gamma _n})/{\kappa _n}) $
holds for all n.
$ \theta \le (({\kappa _n -\gamma _n})/{\eta _n})\le (({\kappa _n -\gamma _n})/{\kappa _n}) $
holds for all n.
We prove the first two assertions by backwards induction on k starting with
![]() $k=n$
. We clearly have
$k=n$
. We clearly have
Moreover, we have
 $$ \begin{align*} d(\xi_{(k-1) }, \zeta_{(k-1)}) &= d((f_{k}^{(-1)})_* (x_{k}, v_{k}) , (f_{k}^{(-1)})_* (y_{k}, w_{k})) \\ &\le d((f_{k}^{(-1)})_* (x_{k}, v_{k}) , (f_{k}^{(-1)})_* (x_{k}, w_{k})) \\ & \quad + d((f_{k}^{(-1)})_* (x_{k}, w_{k}) , (f_{k}^{(-1)})_* (y_{k}, w_{k})) \\ &\le e^{(\hat\gamma_{k-1}-\gamma_{k-1})}d(v_{k}, w_{k}) + C_1d(x_{k} , y_{k})^{\beta} \\ &\le e^{(\hat\gamma_{k-1}-\gamma_{k-1})} (d(v_{k}, w_{k}) + e^{-(\hat\gamma_{k-1}-\gamma_{k-1})}C_1 d(x_{k} , y_{k})^{\beta} )\\ &\le e^{(\hat \gamma_{k-1}-\gamma_{k-1})} (1 + e^{- (\hat \gamma_{k-1}-\gamma_{k-1})}C_1d(x_{k} , y_{k})^{\beta-\hat \beta} ) \\&\quad\cdot \max \{ d(x_{k} , y_{k})^{\hat \beta} ,d(v_{k}, w_{k})\} \\ &\le e^{ (1+\alpha) (\hat\gamma_{k-1}- \gamma_{k-1})} \max \{ r^{\hat \beta} e^{ \hat \beta \kappa _0^{(n)} - \hat \beta \gamma_{k}^{ (n- k)} } , r^{\bar \theta } e^{ \kappa _0^{(n)} \theta + (1+\alpha)(\hat \gamma_{k}^{ (n- k)}- \gamma_{k}^{ (n- k)}) } \}. \notag \end{align*} $$
$$ \begin{align*} d(\xi_{(k-1) }, \zeta_{(k-1)}) &= d((f_{k}^{(-1)})_* (x_{k}, v_{k}) , (f_{k}^{(-1)})_* (y_{k}, w_{k})) \\ &\le d((f_{k}^{(-1)})_* (x_{k}, v_{k}) , (f_{k}^{(-1)})_* (x_{k}, w_{k})) \\ & \quad + d((f_{k}^{(-1)})_* (x_{k}, w_{k}) , (f_{k}^{(-1)})_* (y_{k}, w_{k})) \\ &\le e^{(\hat\gamma_{k-1}-\gamma_{k-1})}d(v_{k}, w_{k}) + C_1d(x_{k} , y_{k})^{\beta} \\ &\le e^{(\hat\gamma_{k-1}-\gamma_{k-1})} (d(v_{k}, w_{k}) + e^{-(\hat\gamma_{k-1}-\gamma_{k-1})}C_1 d(x_{k} , y_{k})^{\beta} )\\ &\le e^{(\hat \gamma_{k-1}-\gamma_{k-1})} (1 + e^{- (\hat \gamma_{k-1}-\gamma_{k-1})}C_1d(x_{k} , y_{k})^{\beta-\hat \beta} ) \\&\quad\cdot \max \{ d(x_{k} , y_{k})^{\hat \beta} ,d(v_{k}, w_{k})\} \\ &\le e^{ (1+\alpha) (\hat\gamma_{k-1}- \gamma_{k-1})} \max \{ r^{\hat \beta} e^{ \hat \beta \kappa _0^{(n)} - \hat \beta \gamma_{k}^{ (n- k)} } , r^{\bar \theta } e^{ \kappa _0^{(n)} \theta + (1+\alpha)(\hat \gamma_{k}^{ (n- k)}- \gamma_{k}^{ (n- k)}) } \}. \notag \end{align*} $$
The last line follows from the induction hypothesis and the choice of
![]() $\delta>0$
in (11).
$\delta>0$
in (11).
From (9) we have
 $$ \begin{align*} \hat \beta \kappa _0^{(n)} - \hat \beta \gamma_{k}^{ (n- k)} & = \hat \beta \kappa_{0}^{(k)} + \hat \beta \kappa_{k}^{(n-k)} - \hat \beta\gamma _{k}^{ (n- k)} \\ &\le \hat \beta \kappa_{0}^{(k)}+ \theta \kappa_{k}^{(n-k)} \\ &\le \theta \kappa_{0}^{(n)} \\ &\le \theta \kappa _0^{(n)} + (1+\alpha)(\hat \gamma_{k}^{ (n- k)}- \gamma_{k}^{ (n- k)}). \end{align*} $$
$$ \begin{align*} \hat \beta \kappa _0^{(n)} - \hat \beta \gamma_{k}^{ (n- k)} & = \hat \beta \kappa_{0}^{(k)} + \hat \beta \kappa_{k}^{(n-k)} - \hat \beta\gamma _{k}^{ (n- k)} \\ &\le \hat \beta \kappa_{0}^{(k)}+ \theta \kappa_{k}^{(n-k)} \\ &\le \theta \kappa_{0}^{(n)} \\ &\le \theta \kappa _0^{(n)} + (1+\alpha)(\hat \gamma_{k}^{ (n- k)}- \gamma_{k}^{ (n- k)}). \end{align*} $$
Hence
and the result follows.
3.3 Step 1:
 $C^0$
convergence
$C^0$
convergence
Recall the ‘true’ holonomies
![]() $h^s_{p,q,n}$
. We fix
$h^s_{p,q,n}$
. We fix
![]() $h= h^s_{p,q,0}$
and let
$h= h^s_{p,q,0}$
and let
![]() $h_n$
be the approximate holonomies in §3.1.4. We have the following lemma.
$h_n$
be the approximate holonomies in §3.1.4. We have the following lemma.
Lemma 3.2.
![]() $h_n \to h$
uniformly on
$h_n \to h$
uniformly on
![]() $W^c_0(p,1)$
.
$W^c_0(p,1)$
.
Proof First (by equivariance of
![]() $W^s_n$
-manifolds) we have
$W^s_n$
-manifolds) we have
![]() $f^{(-n)} _n\circ h^s_{p_{n}, q_{n},n} \circ f^{(n)} _0= h^s_{p,q,0}$
. For
$f^{(-n)} _n\circ h^s_{p_{n}, q_{n},n} \circ f^{(n)} _0= h^s_{p,q,0}$
. For
![]() $x\in W^c_0(p,1)$
we have
$x\in W^c_0(p,1)$
we have
By property (1) of the maps
![]() $\pi _{n}$
,
$\pi _{n}$
,
 $$ \begin{align*} d(h_n(x), h(x)) &= d(f^{(-n)}_0( \pi_{n} (x_{n})), f^{(-n)}_n(h^s_{p_{n}, q_{n},n}(x_{n})))\\ &\le e^{ -\gamma_{0}^{(n)} } d(\pi_{n} (x_{n}), h^s_{p_{n}, q_{n},n}(x_{n}))\\ &\le e^{ -\gamma_{0}^{(n)} } C_2 d(x_n, h^s_{p_{n}, q_{n},n}(x_{n}))\\ &\le C_2 e^{{\kappa_0^{(n)}} -\gamma_{0}^{( n)} } \rho_0.\\[-33pt] \end{align*} $$
$$ \begin{align*} d(h_n(x), h(x)) &= d(f^{(-n)}_0( \pi_{n} (x_{n})), f^{(-n)}_n(h^s_{p_{n}, q_{n},n}(x_{n})))\\ &\le e^{ -\gamma_{0}^{(n)} } d(\pi_{n} (x_{n}), h^s_{p_{n}, q_{n},n}(x_{n}))\\ &\le e^{ -\gamma_{0}^{(n)} } C_2 d(x_n, h^s_{p_{n}, q_{n},n}(x_{n}))\\ &\le C_2 e^{{\kappa_0^{(n)}} -\gamma_{0}^{( n)} } \rho_0.\\[-33pt] \end{align*} $$
3.4 Step 2: Convergence of the projectivized derivative
Consider now the projectivized derivatives
![]() $(h_n)_*\colon S W^c_0(p,1) \to S W^c_0(q).$
We show that the sequence
$(h_n)_*\colon S W^c_0(p,1) \to S W^c_0(q).$
We show that the sequence
![]() $(h_n)_*$
is Cauchy. Set
$(h_n)_*$
is Cauchy. Set
 $$ \begin{align}L_1= C_2 + \sum_{n=0}^{\infty} 3C_2 C_1 e^{\omega n} \end{align} $$
$$ \begin{align}L_1= C_2 + \sum_{n=0}^{\infty} 3C_2 C_1 e^{\omega n} \end{align} $$
where
![]() $\omega <0$
is as in (10).
$\omega <0$
is as in (10).
Lemma 3.3. The sequence of maps
![]() $(h_n)_*\colon S W^c_0(p,1) \to S W^c_0(q) $
is uniformly Cauchy. Moreover, defining
$(h_n)_*\colon S W^c_0(p,1) \to S W^c_0(q) $
is uniformly Cauchy. Moreover, defining
![]() $h_*\colon S W^c_0(p,1) \to S W^c_0(q)$
to be the limit
$h_*\colon S W^c_0(p,1) \to S W^c_0(q)$
to be the limit
![]() $h_*= \lim _{n\to \infty } (h_n)_*$
, for
$h_*= \lim _{n\to \infty } (h_n)_*$
, for
![]() $(x,v)\in SW^c_0(p,1)$
we have
$(x,v)\in SW^c_0(p,1)$
we have
Proof With
![]() $\xi = (x,v)$
, let
$\xi = (x,v)$
, let
![]() $y = h(x)$
and let
$y = h(x)$
and let
![]() $\zeta ^n =(y^n, w^n)= (h_n)_*(\xi )$
.
$\zeta ^n =(y^n, w^n)= (h_n)_*(\xi )$
.
We have
and, using property (1) of the maps
![]() $\pi _{n}$
,
$\pi _{n}$
,
 $$ \begin{align*} d( \pi_{n} (x_{n}), f_{n+1}^{(-1)}( \pi_{n+1}(x_{n+1}))) &\le d( x_{n}, \pi_{n} (x_{n}))+ ( f_{n+1}^{(-1)}(x_{n+1} ), f_{n+1}^{(-1)}(\pi_{n+1}(x_{n+1})))\\ &\le C_2 e^{\kappa _0^{(n)}}d(x,y) + C_1 C_2 e^{\kappa_0^{(n+1)}}d(x,y) \\ &\le 2C_1 C_2 e^{\kappa_0 ^{(n)} }d(x,y). \end{align*} $$
$$ \begin{align*} d( \pi_{n} (x_{n}), f_{n+1}^{(-1)}( \pi_{n+1}(x_{n+1}))) &\le d( x_{n}, \pi_{n} (x_{n}))+ ( f_{n+1}^{(-1)}(x_{n+1} ), f_{n+1}^{(-1)}(\pi_{n+1}(x_{n+1})))\\ &\le C_2 e^{\kappa _0^{(n)}}d(x,y) + C_1 C_2 e^{\kappa_0^{(n+1)}}d(x,y) \\ &\le 2C_1 C_2 e^{\kappa_0 ^{(n)} }d(x,y). \end{align*} $$
Similarly,
and
 $$ \begin{align} &d( (\pi_{n})_* (\xi_{n}), (f^{(-1)}_{n+1})_* (\pi_{n+1})_* (\xi_{n+1})) \notag \\ &\quad\le d( \xi_{n}, (\pi_{n})_* (\xi_{n}) ) + d ((f_{n+1}^{(-1)})_* \xi_{n+1}, ( f_{n+1}^{(-1)})_* (\pi_{n+1})_* (\xi_{n+1})) .\end{align} $$
$$ \begin{align} &d( (\pi_{n})_* (\xi_{n}), (f^{(-1)}_{n+1})_* (\pi_{n+1})_* (\xi_{n+1})) \notag \\ &\quad\le d( \xi_{n}, (\pi_{n})_* (\xi_{n}) ) + d ((f_{n+1}^{(-1)})_* \xi_{n+1}, ( f_{n+1}^{(-1)})_* (\pi_{n+1})_* (\xi_{n+1})) .\end{align} $$
With
![]() $(\pi _{n+1})_* (x_{n+1}, v_{n+1})= (y',w')$
we have
$(\pi _{n+1})_* (x_{n+1}, v_{n+1})= (y',w')$
we have
 $$ \begin{align} &d ((f_{n+1}^{(-1)})_* \xi_{n+1}, ( f_{n+1}^{(-1)})_* (\pi_{n+1})_* (\xi_{n+1}) )\notag\\ &\quad= d ((f_{n+1}^{(-1)})_* (x_{n+1}, v_{n+1}) , ( f_{n+1}^{(-1)})_* ( y',w') ) \notag\\ &\quad\le d ((f_{n+1}^{(-1)})_* (x_{n+1}, v_{n+1}) , ( f_{n+1}^{(-1)})_* ( x_{n+1},w') ) \notag \\ &\qquad+ d ((f_{n+1}^{(-1)})_* (x_{n+1}, w') , ( f_{n+1}^{(-1)})_*( y',w') )\notag\\ &\quad\le C_1 d( v_{n+1}, w') + C_1 d(x_{n+1}, y')^{\beta}\notag\\ &\quad\le C_1 C_2 d( x_{n+1},y_{n+1})^{\bar \theta} + C_1 (C_2 d(x_{n+1}, y_{n+1}))^{\beta} \\ &\quad\le C_1 C_2 e^{\kappa_0 ^{(n+1)} \bar \theta} d(x,y)^{\bar \theta} + C_1 C_2^{\beta} e^{\beta \kappa_0 ^{(n+1)} } d(x,y)^{\beta} \notag\\ &\quad\le 2 C_1 C_2 e^{\bar \theta \kappa_0 ^{(n+1)} }d(x,y)^{\bar \theta }\notag \end{align} $$
$$ \begin{align} &d ((f_{n+1}^{(-1)})_* \xi_{n+1}, ( f_{n+1}^{(-1)})_* (\pi_{n+1})_* (\xi_{n+1}) )\notag\\ &\quad= d ((f_{n+1}^{(-1)})_* (x_{n+1}, v_{n+1}) , ( f_{n+1}^{(-1)})_* ( y',w') ) \notag\\ &\quad\le d ((f_{n+1}^{(-1)})_* (x_{n+1}, v_{n+1}) , ( f_{n+1}^{(-1)})_* ( x_{n+1},w') ) \notag \\ &\qquad+ d ((f_{n+1}^{(-1)})_* (x_{n+1}, w') , ( f_{n+1}^{(-1)})_*( y',w') )\notag\\ &\quad\le C_1 d( v_{n+1}, w') + C_1 d(x_{n+1}, y')^{\beta}\notag\\ &\quad\le C_1 C_2 d( x_{n+1},y_{n+1})^{\bar \theta} + C_1 (C_2 d(x_{n+1}, y_{n+1}))^{\beta} \\ &\quad\le C_1 C_2 e^{\kappa_0 ^{(n+1)} \bar \theta} d(x,y)^{\bar \theta} + C_1 C_2^{\beta} e^{\beta \kappa_0 ^{(n+1)} } d(x,y)^{\beta} \notag\\ &\quad\le 2 C_1 C_2 e^{\bar \theta \kappa_0 ^{(n+1)} }d(x,y)^{\bar \theta }\notag \end{align} $$
where the first term in (16) follows from property (2) of the approximate holonomies in §3.1.1 and the second term in (16) uses property (1) of the approximate holonomies. Combined with (15) and using property (2) of the approximate holonomies
![]() $\pi _n$
, we then have
$\pi _n$
, we then have
 $$ \begin{align*} &d( (\pi_{n})_* (\xi_{n}), (f^{(-1)}_{n+1})_* (\pi_{n+1})_* (\xi_{n+1})) \\ &\quad\le C_2 e^{\bar \theta \kappa_0^{( n)}}d(x,y)^{\bar \theta} + 2C_1 C_2 e^{ \bar \theta \kappa_0^{ (n+1)}} d(x,y)^{\bar \theta}\\ &\quad\le 3C_2 C_1 e^{\bar \theta \kappa _0^{(n)}} d(x,y)^{\bar \theta }. \end{align*} $$
$$ \begin{align*} &d( (\pi_{n})_* (\xi_{n}), (f^{(-1)}_{n+1})_* (\pi_{n+1})_* (\xi_{n+1})) \\ &\quad\le C_2 e^{\bar \theta \kappa_0^{( n)}}d(x,y)^{\bar \theta} + 2C_1 C_2 e^{ \bar \theta \kappa_0^{ (n+1)}} d(x,y)^{\bar \theta}\\ &\quad\le 3C_2 C_1 e^{\bar \theta \kappa _0^{(n)}} d(x,y)^{\bar \theta }. \end{align*} $$
Applying Lemma 3.1 (with
![]() $r= (3C_1C_2)^{\bar \theta ^{-1}}d(x,y) $
) to (14) with the choice of
$r= (3C_1C_2)^{\bar \theta ^{-1}}d(x,y) $
) to (14) with the choice of
![]() $\rho _0$
satisfying (12), it follows that
$\rho _0$
satisfying (12), it follows that
By (10),
and it follows that
![]() $(h_n)_* $
is uniformly Cauchy on
$(h_n)_* $
is uniformly Cauchy on
![]() $SW^c_0(p,1)$
.
$SW^c_0(p,1)$
.
Moreover, for any
![]() $\xi =(x,v)\in SW^c_0(p,1)$
we have
$\xi =(x,v)\in SW^c_0(p,1)$
we have
 $$ \begin{align*} d(\xi, h_* (\xi) ) &\le d(\xi, (\pi_0)_* \xi) + \sum_{n=0}^{\infty} d((h_n)_*\xi, (h_{n+1})_*\xi)\\ &= d(\xi, (\pi_0)_* \xi) + \sum_{n=0}^{\infty} d(\zeta^n, \zeta^{n+1} ) \\ &\le C_2d(x,y)^{\bar \theta } + \sum_{n=0}^{\infty} e^{ \kappa_0^{(n)} \theta + (1+\alpha)(\hat \gamma_0^{(n)}- \gamma_0^{(n)}) } 3C_2 C_1 d(x,y)^{\bar \theta}\\ &\le C_2d(x,y)^{\bar \theta } + \sum_{n=0}^{\infty} e^{ n\omega } 3C_2 C_1 d(x,y)^{\bar \theta} \end{align*} $$
$$ \begin{align*} d(\xi, h_* (\xi) ) &\le d(\xi, (\pi_0)_* \xi) + \sum_{n=0}^{\infty} d((h_n)_*\xi, (h_{n+1})_*\xi)\\ &= d(\xi, (\pi_0)_* \xi) + \sum_{n=0}^{\infty} d(\zeta^n, \zeta^{n+1} ) \\ &\le C_2d(x,y)^{\bar \theta } + \sum_{n=0}^{\infty} e^{ \kappa_0^{(n)} \theta + (1+\alpha)(\hat \gamma_0^{(n)}- \gamma_0^{(n)}) } 3C_2 C_1 d(x,y)^{\bar \theta}\\ &\le C_2d(x,y)^{\bar \theta } + \sum_{n=0}^{\infty} e^{ n\omega } 3C_2 C_1 d(x,y)^{\bar \theta} \end{align*} $$
where we use properties (1) and (2) of the approximate holonomies
![]() $\pi _0$
to bound
$\pi _0$
to bound
![]() $d(\xi , (\pi _0)_* \xi )\le C_2d(x,y)^{\bar \theta } $
. Thus, with
$d(\xi , (\pi _0)_* \xi )\le C_2d(x,y)^{\bar \theta } $
. Thus, with
![]() $L_1$
as above, for any
$L_1$
as above, for any
![]() $\xi = (x,v) \in SW^c_0(p,1)$
and with
$\xi = (x,v) \in SW^c_0(p,1)$
and with
![]() $y= h(x)$
we have
$y= h(x)$
we have
Note that the convergence of the projectivized derivative of the stable holonomies in Lemma 3.3 is independent of the choice of
![]() $p,q\in \mathbb {R}^k$
or
$p,q\in \mathbb {R}^k$
or
![]() $n\in \mathbb {Z}$
in Theorem 2.2. Thus for all
$n\in \mathbb {Z}$
in Theorem 2.2. Thus for all
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
![]() $p'\in \mathbb {R}^k$
, and
$p'\in \mathbb {R}^k$
, and
![]() $q'\in W^s_{n} (p', R_0)$
, let
$q'\in W^s_{n} (p', R_0)$
, let
![]() $(h^s_{p',q',n})_*$
denote the projectivized derivative of stable holonomies constructed as above. We have for all
$(h^s_{p',q',n})_*$
denote the projectivized derivative of stable holonomies constructed as above. We have for all
![]() $\xi '= (x',v')\in SW^c_n(p',1)$
that
$\xi '= (x',v')\in SW^c_n(p',1)$
that
Moreover, from the definition of the limit in Lemma 3.3 defining
![]() $(h^s_{p',q',n})_*$
, we have that
$(h^s_{p',q',n})_*$
, we have that
![]() $(h^s_{p',q',n})_*$
is a holonomy for the projectivized derivative cocycle:
$(h^s_{p',q',n})_*$
is a holonomy for the projectivized derivative cocycle:
Indeed, return to the case
![]() $n=0$
, let
$n=0$
, let
![]() $h = h^s_{p,q, 0}$
, and consider
$h = h^s_{p,q, 0}$
, and consider
![]() $\xi =(x,v)\in SW^c_0(p,1)$
. Then
$\xi =(x,v)\in SW^c_0(p,1)$
. Then
 $$ \begin{align*} (f_0)_* \circ h_* (\xi) &= \lim_{n\to \infty}(f_0)_*\circ (h_n)_*(\xi )\\ &= \lim_{n\to \infty}(f_0)_* (f_n^{(-n)}\circ \pi_n\circ f_0^{(n)})_*(\xi) \\ &= \lim_{n\to \infty} (f_n^{(-(n-1))}\circ \pi_n\circ f_1^{(n-1)})_*(f_0)_*(\xi )\\ &= (h^s_{f_0(p), f_0(q), 1})_*\circ (f_0)_*(\xi). \end{align*} $$
$$ \begin{align*} (f_0)_* \circ h_* (\xi) &= \lim_{n\to \infty}(f_0)_*\circ (h_n)_*(\xi )\\ &= \lim_{n\to \infty}(f_0)_* (f_n^{(-n)}\circ \pi_n\circ f_0^{(n)})_*(\xi) \\ &= \lim_{n\to \infty} (f_n^{(-(n-1))}\circ \pi_n\circ f_1^{(n-1)})_*(f_0)_*(\xi )\\ &= (h^s_{f_0(p), f_0(q), 1})_*\circ (f_0)_*(\xi). \end{align*} $$
To show that the holonomies are
![]() $C^1$
, we next show that each
$C^1$
, we next show that each
![]() $(h^s_{p',q',n})_*$
coincides with the projectivization of a continuous
$(h^s_{p',q',n})_*$
coincides with the projectivization of a continuous
![]() $D h^s_{p',q',n}\colon TW^c_n(p',1)\to TW^c_n(q')$
.
$D h^s_{p',q',n}\colon TW^c_n(p',1)\to TW^c_n(q')$
.
3.5 Step 3: The sequence of maps
 $ Dh_n$
is uniformly Cauchy
$ Dh_n$
is uniformly Cauchy
We return to the notation in Step 2. In particular, we recall our distinguished
![]() $p,q\in \mathbb {R}^k$
and the maps
$p,q\in \mathbb {R}^k$
and the maps
![]() $h_n$
approximating
$h_n$
approximating
![]() $h= h^s_{p,q,0}$
.
$h= h^s_{p,q,0}$
.
We first derive two simple distortion estimates. Fix
![]() $\xi =(x,v)\in S W^c_0(p,1)$
. With
$\xi =(x,v)\in S W^c_0(p,1)$
. With
![]() $\xi _{n}:= (f^{(n)}_0)_*(\xi ) $
, let
$\xi _{n}:= (f^{(n)}_0)_*(\xi ) $
, let
![]() $y=h(x)$
,
$y=h(x)$
,
![]() $\zeta =(y,w) := h_*(\xi )$
,
$\zeta =(y,w) := h_*(\xi )$
,
![]() $\zeta _{n}=(y_{n}, w_{n}) = (f_0 ^{(n)})_* (\zeta ) = (h^s_{p_{n},q_{n}, n})_* (\xi _{n}),$
and
$\zeta _{n}=(y_{n}, w_{n}) = (f_0 ^{(n)})_* (\zeta ) = (h^s_{p_{n},q_{n}, n})_* (\xi _{n}),$
and
![]() $\hat \zeta ^n= (h_n)_*(\xi )= (\hat y^n, \hat w^{n})$
. Write
$\hat \zeta ^n= (h_n)_*(\xi )= (\hat y^n, \hat w^{n})$
. Write
![]() $\hat \zeta ^n_i = (f^{(i)}_0)_*\hat \zeta ^n$
. Then
$\hat \zeta ^n_i = (f^{(i)}_0)_*\hat \zeta ^n$
. Then
From property (1) of the approximate holonomies
![]() $\pi _n$
,
$\pi _n$
,
From Lemma 3.3, we have
By properties (1) and (2) of the approximate holonomies
![]() $\pi _n$
,
$\pi _n$
,
Hence,
Let
![]() $n_0$
be such that
$n_0$
be such that
![]() $(C_2 +L _1) e^{ \bar \theta \kappa _0^{(n_0)}}\le e^{ \theta \kappa _0^{(n_0)}} \delta ^{ \bar \theta }$
so that for
$(C_2 +L _1) e^{ \bar \theta \kappa _0^{(n_0)}}\le e^{ \theta \kappa _0^{(n_0)}} \delta ^{ \bar \theta }$
so that for
![]() $n\ge n_0$
we have
$n\ge n_0$
we have
Given
![]() $\xi = (x,v) \in T\mathbb {R}^k$
, define
$\xi = (x,v) \in T\mathbb {R}^k$
, define
![]() $\|\xi \| = \|v\|$
. For each i, the map
$\|\xi \| = \|v\|$
. For each i, the map
![]() $S \mathbb {R}^k \to \mathbb {R}$
given by
$S \mathbb {R}^k \to \mathbb {R}$
given by
![]() $\zeta \to \log \|Df_i(\zeta )\|$
is
$\zeta \to \log \|Df_i(\zeta )\|$
is
![]() $\beta $
-Hölder on
$\beta $
-Hölder on
![]() $S\mathbb {R}^k$
with uniform Hölder constant
$S\mathbb {R}^k$
with uniform Hölder constant
![]() $C_3$
. Recall
$C_3$
. Recall
![]() $\hat \theta <\theta $
satisfying (8) and
$\hat \theta <\theta $
satisfying (8) and
![]() $\hat \omega $
satisfying (10). Let
$\hat \omega $
satisfying (10). Let
 $$ \begin{align*}K_1:= \sum _{k=0}^{\infty} C_3 (\delta^{\bar \theta} e^{ \hat \omega k } ) ^{\beta} .\end{align*} $$
$$ \begin{align*}K_1:= \sum _{k=0}^{\infty} C_3 (\delta^{\bar \theta} e^{ \hat \omega k } ) ^{\beta} .\end{align*} $$
Lemma 3.4. For all
![]() $n\ge n_0$
,
$n\ge n_0$
,
 $$ \begin{align*}\exp (- K_1e^{ \beta (\theta -\hat \theta ) \kappa_0^{(n)} }) \le \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \hat \zeta^n_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \le \exp(K_1e^{ \beta (\theta -\hat \theta ) \kappa_0^{(n)} }).\end{align*} $$
$$ \begin{align*}\exp (- K_1e^{ \beta (\theta -\hat \theta ) \kappa_0^{(n)} }) \le \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \hat \zeta^n_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \le \exp(K_1e^{ \beta (\theta -\hat \theta ) \kappa_0^{(n)} }).\end{align*} $$
(Note, in particular, that the middle ratio goes to
![]() $1$
as
$1$
as
![]() $n\to \infty $
.)
$n\to \infty $
.)
Proof Recalling Lemma 3.1 (with
![]() $r=\delta $
and estimates (19) and (20)), for
$r=\delta $
and estimates (19) and (20)), for
![]() $n\ge n_0$
we have
$n\ge n_0$
we have
 $$ \begin{align*} \bigg| \log \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \hat \zeta^n_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \bigg| &= \bigg | \sum _{i=0}^{n-1} \log \|Df_{i} \hat \zeta^n_{i}\| - \log \|Df_{i} \zeta_{i}\| \bigg |\\ &\le \sum _{i=0}^{n-1} C_3 d (\hat \zeta^n_{i},\zeta_{i})^{\beta} \\ &\le \sum _{i=0}^{n-1} C_3 (\delta^{\bar \theta} e^{ \kappa_{0}^{(n)} \theta + (1+\alpha)(\hat \gamma_i^{(n-i)}- \gamma_i^{(n-i)})} ) ^{\beta} \\ &\le e^{ \beta \kappa_0^{(n)}(\theta -\hat \theta ) } K_1 \end{align*} $$
$$ \begin{align*} \bigg| \log \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \hat \zeta^n_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \bigg| &= \bigg | \sum _{i=0}^{n-1} \log \|Df_{i} \hat \zeta^n_{i}\| - \log \|Df_{i} \zeta_{i}\| \bigg |\\ &\le \sum _{i=0}^{n-1} C_3 d (\hat \zeta^n_{i},\zeta_{i})^{\beta} \\ &\le \sum _{i=0}^{n-1} C_3 (\delta^{\bar \theta} e^{ \kappa_{0}^{(n)} \theta + (1+\alpha)(\hat \gamma_i^{(n-i)}- \gamma_i^{(n-i)})} ) ^{\beta} \\ &\le e^{ \beta \kappa_0^{(n)}(\theta -\hat \theta ) } K_1 \end{align*} $$
where we use that
 $$ \begin{align*}& \kappa_{0}^{(n)} \theta+ (1+\alpha)(\hat \gamma_i^{(n-i)}- \gamma_i^{(n-i)} ) \\ &\quad\le \kappa_{0}^{(n)} (\theta- \hat \theta) + \kappa_{i}^{(n-i)} \hat \theta + (1+\alpha)(\hat \gamma_i^{(n-i)}- \gamma_i^{(n-i)} )\\ &\quad\le \kappa_{0}^{(n)} (\theta- \hat \theta) + \hat \omega (n-i) \end{align*} $$
$$ \begin{align*}& \kappa_{0}^{(n)} \theta+ (1+\alpha)(\hat \gamma_i^{(n-i)}- \gamma_i^{(n-i)} ) \\ &\quad\le \kappa_{0}^{(n)} (\theta- \hat \theta) + \kappa_{i}^{(n-i)} \hat \theta + (1+\alpha)(\hat \gamma_i^{(n-i)}- \gamma_i^{(n-i)} )\\ &\quad\le \kappa_{0}^{(n)} (\theta- \hat \theta) + \hat \omega (n-i) \end{align*} $$
in the last inequality.
Similarly, letting
 $$ \begin{align*}K_2 = \exp \bigg(\sum _{i=1}^{\infty } C_3 L_1^{\beta} e^{\bar \kappa \bar \theta\beta i} \bigg),\end{align*} $$
$$ \begin{align*}K_2 = \exp \bigg(\sum _{i=1}^{\infty } C_3 L_1^{\beta} e^{\bar \kappa \bar \theta\beta i} \bigg),\end{align*} $$
we have the following lemma.
Lemma 3.5. For all
![]() $n>0$
,
$n>0$
,
 $$ \begin{align*}K_2{}^{-1} \le \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \xi_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \le K _2.\end{align*} $$
$$ \begin{align*}K_2{}^{-1} \le \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \xi_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \le K _2.\end{align*} $$
Proof From Lemma 3.3 we obtain
 $$ \begin{align*} \bigg| \log \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \xi_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \bigg| &= \bigg | \sum _{i=0}^{n-1} \log \|Df_{i} \xi_{i}\| - \log \|Df_{i} \zeta_{i}\| \bigg |\\ &\le \sum _{i=0}^{n-1} C_3 d( \xi_{i},\zeta_{i})^{\beta} \\ &\le \sum _{i=0}^{n-1} C_3 [L_1 d(x_i, y_i)^{\bar \theta } ]^{\beta} \\ &\le \sum _{i=0}^{n-1} C_3 L_1^{\beta} (e^{\kappa_0^{(i)} \bar \theta} ) ^{\beta} d(x,y)^{\beta} \\ &\le \log( K_2). \\[-34pt]\end{align*} $$
$$ \begin{align*} \bigg| \log \dfrac{\prod_{i=0} ^{n-1} \|Df_{i} \xi_{i}\|}{\prod_{i=0} ^{n-1} \|Df_{i} \zeta_{i}\|} \bigg| &= \bigg | \sum _{i=0}^{n-1} \log \|Df_{i} \xi_{i}\| - \log \|Df_{i} \zeta_{i}\| \bigg |\\ &\le \sum _{i=0}^{n-1} C_3 d( \xi_{i},\zeta_{i})^{\beta} \\ &\le \sum _{i=0}^{n-1} C_3 [L_1 d(x_i, y_i)^{\bar \theta } ]^{\beta} \\ &\le \sum _{i=0}^{n-1} C_3 L_1^{\beta} (e^{\kappa_0^{(i)} \bar \theta} ) ^{\beta} d(x,y)^{\beta} \\ &\le \log( K_2). \\[-34pt]\end{align*} $$
We now approximate the derivatives
![]() $D h\colon TW^c_0(p) \to TW^c_0(q)$
by the bundle maps
$D h\colon TW^c_0(p) \to TW^c_0(q)$
by the bundle maps
defined as follows: given
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $(x,v) \in TW^c_0(p,1)$
, let
$(x,v) \in TW^c_0(p,1)$
, let
From (18) the projectivization of each
![]() $\Delta _n$
coincides with
$\Delta _n$
coincides with
![]() $(h^s_{p,q,0})_* = h_*$
. With
$(h^s_{p,q,0})_* = h_*$
. With
![]() $h = h^s_{p,q,0}$
and
$h = h^s_{p,q,0}$
and
![]() $(x,v) \in SW^c_0(0)$
, let
$(x,v) \in SW^c_0(0)$
, let
![]() $h_*(x,v) = (y,w)$
. We have
$h_*(x,v) = (y,w)$
. We have
 $$ \begin{align*}\|\Delta_{n} (x,v) \| = \frac {\|D_xf_0^{(n)}(v)\|}{\|D_yf_0^{(n)}(w)\|}\end{align*} $$
$$ \begin{align*}\|\Delta_{n} (x,v) \| = \frac {\|D_xf_0^{(n)}(v)\|}{\|D_yf_0^{(n)}(w)\|}\end{align*} $$
and
![]() $\Delta _{n} (x,v) = (y, \|\Delta _{n} (x,v) \| w)$
. From Lemma 3.5,
$\Delta _{n} (x,v) = (y, \|\Delta _{n} (x,v) \| w)$
. From Lemma 3.5,
![]() $\|\Delta _{n} \| $
is uniformly bounded over the choice of
$\|\Delta _{n} \| $
is uniformly bounded over the choice of
![]() $(x,v) \in SW^c_0(p,1)$
and n.
$(x,v) \in SW^c_0(p,1)$
and n.
Given
![]() $\xi =(x,v)\in SW^c_0(p)$
, we have
$\xi =(x,v)\in SW^c_0(p)$
, we have
 $$ \begin{align*}\|Dh_n (\xi) \|= \|\Delta_n (\xi)\| \cdot \dfrac{\prod_{i=0} ^{n-1} \|D f_{i} \zeta_{i}\|}{\prod_{i=0} ^{n-1} \|D f_{i} \hat \zeta^n_{i}\|} \cdot \| D\pi_{p_{n},q_{n},n}((f^{(n)}_0)_*(x,v ))\|.\end{align*} $$
$$ \begin{align*}\|Dh_n (\xi) \|= \|\Delta_n (\xi)\| \cdot \dfrac{\prod_{i=0} ^{n-1} \|D f_{i} \zeta_{i}\|}{\prod_{i=0} ^{n-1} \|D f_{i} \hat \zeta^n_{i}\|} \cdot \| D\pi_{p_{n},q_{n},n}((f^{(n)}_0)_*(x,v ))\|.\end{align*} $$
It then follows from Lemma 3.4 and property (3) of the approximate holonomies
![]() $\pi _n$
that
$\pi _n$
that
uniformly in
![]() $ \xi \in SW^c_0(p)$
. Combined with Lemma 3.3, we thus obtain the following
$ \xi \in SW^c_0(p)$
. Combined with Lemma 3.3, we thus obtain the following
Claim 3.6.
![]() $\sup _{\xi \in SW^c_0(p,1) } \{\|Dh_n (\xi ) - \Delta _n(\xi )\|\}\to 0$
as
$\sup _{\xi \in SW^c_0(p,1) } \{\|Dh_n (\xi ) - \Delta _n(\xi )\|\}\to 0$
as
![]() $n\to \infty $
.
$n\to \infty $
.
It follows that the sequence
![]() $D h_n $
converges uniformly if and only if the sequence
$D h_n $
converges uniformly if and only if the sequence
![]() $\Delta _n$
converges uniformly.
$\Delta _n$
converges uniformly.
Lemma 3.7. The sequence of maps
![]() $\Delta _n\colon SW^c_0(p,1) \to TW^c_0(q)$
is uniformly Cauchy.
$\Delta _n\colon SW^c_0(p,1) \to TW^c_0(q)$
is uniformly Cauchy.
Proof Given
![]() $\xi =(x,v) \in SW^c_0(p,1) $
with
$\xi =(x,v) \in SW^c_0(p,1) $
with
![]() $\xi _{n}= (x_{n}, v_{n})\in S D_{n}$
, let
$\xi _{n}= (x_{n}, v_{n})\in S D_{n}$
, let
![]() $\zeta =(y,w) = h_*(\xi )\in SW^c_0(q) $
and
$\zeta =(y,w) = h_*(\xi )\in SW^c_0(q) $
and
![]() $\zeta _{n}=(y_{n}, w_{n})= (h^s_{p_{n},q_{n},{n}})_{*}(\xi _{n}) $
. Observe that both
$\zeta _{n}=(y_{n}, w_{n})= (h^s_{p_{n},q_{n},{n}})_{*}(\xi _{n}) $
. Observe that both
![]() $\Delta _{n} (x,v)$
and
$\Delta _{n} (x,v)$
and
![]() $ \Delta _{n+1} (x, v) $
have footprint y. Then
$ \Delta _{n+1} (x, v) $
have footprint y. Then
 $$ \begin{align} &\| \Delta_{n} (x,v) - \Delta_{n+1} (x, v) \| \notag \\ &\quad= \frac{\| D_x f_0^{(n)} (v)\| }{ \| D_{y}f^{(n)}_0 ( {w})\| } \|D_{y_{n}} f_{n} (w_{n})\|^{-1} \notag \\&\qquad \cdot \vert\kern-0.25ex\vert\kern-0.25ex\vert D_{y_{n}} (f_{n}) (w_{n})\| - \|D_{x_{n}} (f_{n}) (v_{n}) \vert\kern-0.25ex\vert\kern-0.25ex\vert\notag \\ & \quad\le K_2 C_1 ( \vert\kern-0.25ex\vert\kern-0.25ex\vert D_{x_{n}} (f_{n}) (v_{n}) \| - \|D_{x_{n}} (f_{n}) (w_{n})\vert\kern-0.25ex\vert\kern-0.25ex\vert \notag \\ &\qquad + \vert\kern-0.25ex\vert\kern-0.25ex\vert D_{x_{n}} (f_{n}) (w_{n})\| - \|D_{y_{n}} (f_{n}) (w_{n})\vert\kern-0.25ex\vert\kern-0.25ex\vert)\notag \\ & \quad\le K_2 C_1 ( C_1 L _1e^{\bar \theta \kappa _0^{(n)}} + C_0 e^{\kappa _0^{(n)} \beta }) \notag \\ &\quad\le K_2 C_1 2 C_1 L _1 e^{ \bar \theta \kappa _0^{(n)}} \\ &\quad\le K_2 C_1 2 C_1 L _1 e^{\bar \theta \bar \kappa n}\notag \end{align} $$
$$ \begin{align} &\| \Delta_{n} (x,v) - \Delta_{n+1} (x, v) \| \notag \\ &\quad= \frac{\| D_x f_0^{(n)} (v)\| }{ \| D_{y}f^{(n)}_0 ( {w})\| } \|D_{y_{n}} f_{n} (w_{n})\|^{-1} \notag \\&\qquad \cdot \vert\kern-0.25ex\vert\kern-0.25ex\vert D_{y_{n}} (f_{n}) (w_{n})\| - \|D_{x_{n}} (f_{n}) (v_{n}) \vert\kern-0.25ex\vert\kern-0.25ex\vert\notag \\ & \quad\le K_2 C_1 ( \vert\kern-0.25ex\vert\kern-0.25ex\vert D_{x_{n}} (f_{n}) (v_{n}) \| - \|D_{x_{n}} (f_{n}) (w_{n})\vert\kern-0.25ex\vert\kern-0.25ex\vert \notag \\ &\qquad + \vert\kern-0.25ex\vert\kern-0.25ex\vert D_{x_{n}} (f_{n}) (w_{n})\| - \|D_{y_{n}} (f_{n}) (w_{n})\vert\kern-0.25ex\vert\kern-0.25ex\vert)\notag \\ & \quad\le K_2 C_1 ( C_1 L _1e^{\bar \theta \kappa _0^{(n)}} + C_0 e^{\kappa _0^{(n)} \beta }) \notag \\ &\quad\le K_2 C_1 2 C_1 L _1 e^{ \bar \theta \kappa _0^{(n)}} \\ &\quad\le K_2 C_1 2 C_1 L _1 e^{\bar \theta \bar \kappa n}\notag \end{align} $$
where we use Hölder continuity of
![]() $x\mapsto D_xf$
to bound
$x\mapsto D_xf$
to bound
![]() $\|D_{x_{n}} (f_{n}) (w_{n})\| - \|D_{y_{n}} (f_{n}) (w_{n})\|$
and Lemma 3.3 to bound
$\|D_{x_{n}} (f_{n}) (w_{n})\| - \|D_{y_{n}} (f_{n}) (w_{n})\|$
and Lemma 3.3 to bound
From Claim 3.6 and Lemma 3.7 it follows that the sequence of maps
![]() $D h_{ n} $
converges uniformly. As
$D h_{ n} $
converges uniformly. As
![]() $h_{ n}$
converges to h we have that
$h_{ n}$
converges to h we have that
![]() $h = h^s_{p,q,n}$
is differentiable and that
$h = h^s_{p,q,n}$
is differentiable and that
![]() $Dh_{ n}$
converges to
$Dh_{ n}$
converges to
![]() $Dh$
. Furthermore,
$Dh$
. Furthermore,
![]() $\|Dh^s_{p,q,n}\|\le K_2$
. This completes the proof of the
$\|Dh^s_{p,q,n}\|\le K_2$
. This completes the proof of the
![]() $C^1$
properties in Theorem 2.4.
$C^1$
properties in Theorem 2.4.
3.6 Step 4: Hölder continuity of
 $Dh$
$Dh$
We now show that
![]() $Dh$
is Hölder continuous. We begin with the following estimate.
$Dh$
is Hölder continuous. We begin with the following estimate.
Claim 3.8. There is a
![]() $c_0>0$
such that if
$c_0>0$
such that if
![]() $d(x_k,y_k)\le 1$
for all
$d(x_k,y_k)\le 1$
for all
![]() $0\le k\le n-1$
and
$0\le k\le n-1$
and
![]() $d((x,v), (y,w))\le 1$
, then
$d((x,v), (y,w))\le 1$
, then
Proof We have
 $$ \begin{align*} &d((f_0^{(n)})_*(x,v), (f_0^{(n)})_*(y,w)) \\ &\quad\le d((f_0^{(n)})_*(x,v), (f_0^{(n)})_*(x,w))+ d((f_0^{(n)})_*(x,w), (f_0^{(n)})_*(y,w))\\ &\quad\le (C_1)^{2n} d(v,w) + d((f_0^{(n)})_*(x,w), (f_0^{(n)})_*(y,w)). \end{align*} $$
$$ \begin{align*} &d((f_0^{(n)})_*(x,v), (f_0^{(n)})_*(y,w)) \\ &\quad\le d((f_0^{(n)})_*(x,v), (f_0^{(n)})_*(x,w))+ d((f_0^{(n)})_*(x,w), (f_0^{(n)})_*(y,w))\\ &\quad\le (C_1)^{2n} d(v,w) + d((f_0^{(n)})_*(x,w), (f_0^{(n)})_*(y,w)). \end{align*} $$
We have
Proceeding inductively, for
![]() $k\ge 2$
we claim that
$k\ge 2$
we claim that
Indeed,
 $$ \begin{align} &d((f_0^{(k)})_*(x,w), (f_0^{(k)})_*(y,w)) \notag \\ &\quad = d((D_{x_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) , (D_{y_{k-1}}f_{k-1}) _* (D_{y}f_0^{(k-1)})_* (w) ) \notag \\ &\quad\le d((D_{x_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) , (D_{y_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) ) \notag\\ &\qquad + d((D_{y_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) , (D_{y_{k-1}}f_{k-1}) _* (D_{y}f_0^{(k-1)})_* (w) ) \notag\\ & \quad\le C_1 d(x_{k-1}, y_{k-1}) ^{\beta}+ C_1 (k-1) C_1 ^{ (1+\beta)(k-1)} d( x,y)^{\beta} \\ &\quad\le C_1 (C_1)^{k\beta} d(x, y) ^{\beta}+ (k-1) C_1 ^{ (1+\beta)k} d( x,y)^{\beta} \notag \\&\quad \le k C_1 ^{ (1+\beta)k} d( x,y)^{\beta} \notag\end{align} $$
$$ \begin{align} &d((f_0^{(k)})_*(x,w), (f_0^{(k)})_*(y,w)) \notag \\ &\quad = d((D_{x_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) , (D_{y_{k-1}}f_{k-1}) _* (D_{y}f_0^{(k-1)})_* (w) ) \notag \\ &\quad\le d((D_{x_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) , (D_{y_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) ) \notag\\ &\qquad + d((D_{y_{k-1}}f_{k-1}) _* (D_{x}f_0^{(k-1)})_* (w) , (D_{y_{k-1}}f_{k-1}) _* (D_{y}f_0^{(k-1)})_* (w) ) \notag\\ & \quad\le C_1 d(x_{k-1}, y_{k-1}) ^{\beta}+ C_1 (k-1) C_1 ^{ (1+\beta)(k-1)} d( x,y)^{\beta} \\ &\quad\le C_1 (C_1)^{k\beta} d(x, y) ^{\beta}+ (k-1) C_1 ^{ (1+\beta)k} d( x,y)^{\beta} \notag \\&\quad \le k C_1 ^{ (1+\beta)k} d( x,y)^{\beta} \notag\end{align} $$
where the inductive hypothesis is used in (22). Take
![]() $c_0 = 2\log C_1 +1$
.
$c_0 = 2\log C_1 +1$
.
We now show that the maps
![]() $h_*\colon SW^c_0(p,1)\to SW^c_0(q)$
and
$h_*\colon SW^c_0(p,1)\to SW^c_0(q)$
and
![]() $Dh\colon SW^c_0(p,1)\to TW^c_0(q)$
are Hölder continuous.
$Dh\colon SW^c_0(p,1)\to TW^c_0(q)$
are Hölder continuous.
Fix any
![]() $\epsilon _1>0$
(to appear only in the proof of Claim 3.10 below).
$\epsilon _1>0$
(to appear only in the proof of Claim 3.10 below).
-
• Take
 $a_0= \max \{ \sup \{ ({\kappa _n - \hat \gamma _n })/{\kappa _n}\}, \sup \{ ({ { \kappa _n }- \beta \hat \gamma _n -\epsilon _1 })/{\beta \kappa _n}\} ,\sup \{( { { \kappa _n }- c_0 -\epsilon _1})/ { { \beta \kappa _n } }\} \}>0$
. Observe that
$a_0= \max \{ \sup \{ ({\kappa _n - \hat \gamma _n })/{\kappa _n}\}, \sup \{ ({ { \kappa _n }- \beta \hat \gamma _n -\epsilon _1 })/{\beta \kappa _n}\} ,\sup \{( { { \kappa _n }- c_0 -\epsilon _1})/ { { \beta \kappa _n } }\} \}>0$
. Observe that  $$ \begin{align*}a_0 \ge \sup \bigg\{\dfrac { 1- {c_0}( \kappa_n){}^{-1} - {\epsilon_1}({ \kappa_n}){}^{-1} }{ \beta }\bigg\} \ge \beta^{-1}>1.\end{align*} $$
$$ \begin{align*}a_0 \ge \sup \bigg\{\dfrac { 1- {c_0}( \kappa_n){}^{-1} - {\epsilon_1}({ \kappa_n}){}^{-1} }{ \beta }\bigg\} \ge \beta^{-1}>1.\end{align*} $$
-
• Set
 $\bar \alpha = \min \{ \inf \{ ({\kappa _n - \gamma _n })/{a_0 \kappa _n}\}, \inf \{ ({ \theta \kappa _n + (1+\alpha )(\hat \gamma _n - \gamma _n)})/{\kappa _n a_0 } \} , {\bar \theta }/{a_0 } \}.$
We have
$\bar \alpha = \min \{ \inf \{ ({\kappa _n - \gamma _n })/{a_0 \kappa _n}\}, \inf \{ ({ \theta \kappa _n + (1+\alpha )(\hat \gamma _n - \gamma _n)})/{\kappa _n a_0 } \} , {\bar \theta }/{a_0 } \}.$
We have
 $0<\bar \alpha <\bar \theta <1 $
.
$0<\bar \alpha <\bar \theta <1 $
. -
• Recall our fixed
 $0<\rho _0<1 $
satisfying (12) and
$0<\rho _0<1 $
satisfying (12) and
 $R_0>0$
such that
$R_0>0$
such that
 $\rho (p,q,n)\le \rho _0$
for all p and
$\rho (p,q,n)\le \rho _0$
for all p and
 $q\in W^s_n (p, R_0)$
.
$q\in W^s_n (p, R_0)$
. -
• Set
 $\rho _1= \rho _0^{1/\beta } <\rho _0.$
$\rho _1= \rho _0^{1/\beta } <\rho _0.$
Claim 3.9. The function
![]() $(h^s_{p,q,n})_*$
is
$(h^s_{p,q,n})_*$
is
![]() $\bar \alpha $
-Hölder with Hölder constant uniform in all choices of p,
$\bar \alpha $
-Hölder with Hölder constant uniform in all choices of p,
![]() $q\in W^s_n(p, R_0)$
, and
$q\in W^s_n(p, R_0)$
, and
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Proof It is enough to consider the case
![]() $n=0$
. Fix
$n=0$
. Fix
![]() $p\in \mathbb {R}^k$
and
$p\in \mathbb {R}^k$
and
![]() $q\in W^s_0(p, R_0)$
.
$q\in W^s_0(p, R_0)$
.
Given
![]() $n\in \mathbb {N}$
, set
$n\in \mathbb {N}$
, set
Consider any pair
![]() $\xi := (x,v)$
and
$\xi := (x,v)$
and
![]() $ \xi ':= (x',v') $
in
$ \xi ':= (x',v') $
in
![]() $SW^c_0(p, 1)$
. It is enough to consider
$SW^c_0(p, 1)$
. It is enough to consider
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
sufficiently close so that for some
$\xi '$
sufficiently close so that for some
![]() $1\le n$
,
$1\le n$
,
and either
Let
Similarly define
![]() $\zeta '=(y', w') = h_*(\xi ')$
and
$\zeta '=(y', w') = h_*(\xi ')$
and
![]() $\zeta ^{\prime n} = (y^{\prime n}, w^{\prime n}) = (h_n)_*(\xi ')$
. From (17) and (13) we have
$\zeta ^{\prime n} = (y^{\prime n}, w^{\prime n}) = (h_n)_*(\xi ')$
. From (17) and (13) we have
 $$ \begin{align*} d(\zeta, \zeta^n) &\le \sum _{j=n}^{\infty} d(\zeta^{j}, \zeta^{j+1}) \\ &\le \sum _{j=n}^{\infty} e^{ \kappa_0^{(j)} \theta + (1+\alpha)(\hat \gamma_0^{(j)}- \gamma_0^{(j)}) } 3C_2 C_1 d(x,y)^{\bar \theta} \\ &\le e^{ \kappa_0^{(n)} \theta + (1+\alpha)(\hat \gamma_0^{(n)}- \gamma_0^{(n)}) } \sum _{j=0}^{\infty} e^{\omega j} 3C_2 C_1 d(x,y)^{\bar \theta} \\ &\le e^{\kappa_0^{(n)} \theta + (1+\alpha)(\hat \gamma_0^{(n)}- \gamma_0^{(n)})} L_1 d(x,y)^{\bar \theta} \\ &\le e^{\bar \alpha a_0 \kappa_0^{(n)} } L_1 \rho^{\bar \theta}_0\\ & = L_1 \rho_1^{\beta \bar \theta-\alpha} r_n ^{\bar \alpha } \\ & \le L_1 \rho_1^{\beta {\bar \theta} -\bar \alpha} e^{\mu\bar \alpha a_0} r_{n+1}^{ \bar \alpha }, \end{align*} $$
$$ \begin{align*} d(\zeta, \zeta^n) &\le \sum _{j=n}^{\infty} d(\zeta^{j}, \zeta^{j+1}) \\ &\le \sum _{j=n}^{\infty} e^{ \kappa_0^{(j)} \theta + (1+\alpha)(\hat \gamma_0^{(j)}- \gamma_0^{(j)}) } 3C_2 C_1 d(x,y)^{\bar \theta} \\ &\le e^{ \kappa_0^{(n)} \theta + (1+\alpha)(\hat \gamma_0^{(n)}- \gamma_0^{(n)}) } \sum _{j=0}^{\infty} e^{\omega j} 3C_2 C_1 d(x,y)^{\bar \theta} \\ &\le e^{\kappa_0^{(n)} \theta + (1+\alpha)(\hat \gamma_0^{(n)}- \gamma_0^{(n)})} L_1 d(x,y)^{\bar \theta} \\ &\le e^{\bar \alpha a_0 \kappa_0^{(n)} } L_1 \rho^{\bar \theta}_0\\ & = L_1 \rho_1^{\beta \bar \theta-\alpha} r_n ^{\bar \alpha } \\ & \le L_1 \rho_1^{\beta {\bar \theta} -\bar \alpha} e^{\mu\bar \alpha a_0} r_{n+1}^{ \bar \alpha }, \end{align*} $$
and similarly,
Note that for all
![]() $0\le k\le n$
we have
$0\le k\le n$
we have
From Claim 3.8 and the choice of
![]() $a_0$
, for all
$a_0$
, for all
![]() $0\le k\le n$
we have
$0\le k\le n$
we have
From properties (1) and (2) of the maps
![]() $\pi _n$
we have
$\pi _n$
we have
-
•
 $d(x_{n},y^n_{n}) \le C_2 e^{\kappa _0^{(n)}} \rho _0 $
,
$d(x_{n},y^n_{n}) \le C_2 e^{\kappa _0^{(n)}} \rho _0 $
, -
•
 $d(x^{\prime }_{ n},y^{\prime n}_{n}) \le C_2 e^{ \kappa _0^{(n)} } \rho _0 $
,
$d(x^{\prime }_{ n},y^{\prime n}_{n}) \le C_2 e^{ \kappa _0^{(n)} } \rho _0 $
, -
•
 $d (v_{ n}, w^n_ {n}) \le C_2 e^{\kappa _0^{(n)} \bar \theta } \rho ^{\bar \theta }_0 $
, and
$d (v_{ n}, w^n_ {n}) \le C_2 e^{\kappa _0^{(n)} \bar \theta } \rho ^{\bar \theta }_0 $
, and -
•
 $d (v^{\prime }_{n}, w^{\prime n}_{n}) \le C_2 e^{\kappa _0^{(n)} \bar \theta } \rho ^{\bar \theta } _0.$
$d (v^{\prime }_{n}, w^{\prime n}_{n}) \le C_2 e^{\kappa _0^{(n)} \bar \theta } \rho ^{\bar \theta } _0.$
Thus
and
From Lemma 3.1 (with
![]() $r= (1+2C_2) \rho _0$
) we have
$r= (1+2C_2) \rho _0$
) we have
 $$ \begin{align*} d(y^n,y^{\prime n}) & \le (1+2C_2) e^{\kappa_0^{(n)} - \gamma_0^{(n)}}\rho_0\\ & \le (1+2C_2) e^{\bar \alpha a_0 \kappa_0^{(n)} }\rho_0\\ & \le (1+2C_2) e^{\mu\bar \alpha a_0} \rho_1^{\beta-\bar \alpha} (r_{n+1})^{\bar \alpha } \end{align*} $$
$$ \begin{align*} d(y^n,y^{\prime n}) & \le (1+2C_2) e^{\kappa_0^{(n)} - \gamma_0^{(n)}}\rho_0\\ & \le (1+2C_2) e^{\bar \alpha a_0 \kappa_0^{(n)} }\rho_0\\ & \le (1+2C_2) e^{\mu\bar \alpha a_0} \rho_1^{\beta-\bar \alpha} (r_{n+1})^{\bar \alpha } \end{align*} $$
and (from Lemma 3.1 with
![]() $r= (1+2C_2) ^{\bar \theta {}^{-1}} \rho _0<\delta $
)
$r= (1+2C_2) ^{\bar \theta {}^{-1}} \rho _0<\delta $
)
 $$ \begin{align*} d(w^n,w^{\prime n}) &\le (1+2C_2) \rho^{\bar \theta }_0 e^{\kappa_0^{(n)} \theta + (1+\alpha) (\hat \gamma _0^{(n)} - \gamma_0^{(n)}) } \\ & \le (1+2C_2) \rho^{\bar \theta }_0 e^{\bar \alpha a_0 \kappa_0^{(n)} } \\ & \le (1+2C_2) e^{\mu a_0 \bar \alpha} \rho_1^{\bar \theta \beta -\bar \alpha} ( r_{n+1} )^{\bar \alpha}. \end{align*} $$
$$ \begin{align*} d(w^n,w^{\prime n}) &\le (1+2C_2) \rho^{\bar \theta }_0 e^{\kappa_0^{(n)} \theta + (1+\alpha) (\hat \gamma _0^{(n)} - \gamma_0^{(n)}) } \\ & \le (1+2C_2) \rho^{\bar \theta }_0 e^{\bar \alpha a_0 \kappa_0^{(n)} } \\ & \le (1+2C_2) e^{\mu a_0 \bar \alpha} \rho_1^{\bar \theta \beta -\bar \alpha} ( r_{n+1} )^{\bar \alpha}. \end{align*} $$
It follows that there is some uniform
![]() $K_3>0$
so that
$K_3>0$
so that
whence
![]() $d(\zeta , \zeta ') \le K_3 d(\xi , \xi ')^{\bar \alpha }$
.
$d(\zeta , \zeta ') \le K_3 d(\xi , \xi ')^{\bar \alpha }$
.
Claim 3.10. The function
![]() $SW^c_n(p,1)\to SW^c_n(q)$
given by
$SW^c_n(p,1)\to SW^c_n(q)$
given by
is
![]() $ ( \bar \alpha a_0{}^{-1}) $
-Hölder with Hölder constant uniform in all choices of p,
$ ( \bar \alpha a_0{}^{-1}) $
-Hölder with Hölder constant uniform in all choices of p,
![]() $q\in W^s_n(p, R_0)$
, and
$q\in W^s_n(p, R_0)$
, and
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Proof Again, it is enough to consider the case
![]() $n=0$
. Fix
$n=0$
. Fix
![]() $p\in \mathbb {R}^k$
,
$p\in \mathbb {R}^k$
,
![]() $q\in W^s_0(p, R_0)$
, and set
$q\in W^s_0(p, R_0)$
, and set
![]() $h = h^s_{p,q,0}.$
$h = h^s_{p,q,0}.$
We retain the previous notation: given
![]() $n\in \mathbb {N}$
, set
$n\in \mathbb {N}$
, set
and consider
![]() $\xi := (x,v)$
and
$\xi := (x,v)$
and
![]() $ \xi ':= (x',v') $
in
$ \xi ':= (x',v') $
in
![]() $SW^c_0(p, 1)$
with
$SW^c_0(p, 1)$
with
![]() $d(\xi ,\xi ') \le r_n $
and
$d(\xi ,\xi ') \le r_n $
and
![]() $d(\xi ,\xi ') \ge r_{n+1}$
. Write
$d(\xi ,\xi ') \ge r_{n+1}$
. Write
![]() $\zeta = (y, w) = h_*(\xi )$
and
$\zeta = (y, w) = h_*(\xi )$
and
![]() $\zeta '= (y', w') = h_*(\xi ')$
.
$\zeta '= (y', w') = h_*(\xi ')$
.
Recall that for all
![]() $(x,v)\in SW^c_0(p)$
we have
$(x,v)\in SW^c_0(p)$
we have
![]() $\|\Delta _n(x,v)\| - \|D_x h (v) \| \to 0$
as
$\|\Delta _n(x,v)\| - \|D_x h (v) \| \to 0$
as
![]() $n\to \infty $
. Moreover, from (21) and using that
$n\to \infty $
. Moreover, from (21) and using that
![]() $\bar \alpha a_0 \le \bar \theta $
, we have for some uniform
$\bar \alpha a_0 \le \bar \theta $
, we have for some uniform
![]() $ K_4$
and
$ K_4$
and
![]() $K_5$
that
$K_5$
that
We have that
 $$ \begin{align*} \log(\|\Delta_n(x,v) \| ) &= \sum_{j= 0 } ^{n-1} \log \|D_{x_{j}}f_{j} v_{j} \| - \log \|D_{y_{j}}f_{j} w_{j} \|. \end{align*} $$
$$ \begin{align*} \log(\|\Delta_n(x,v) \| ) &= \sum_{j= 0 } ^{n-1} \log \|D_{x_{j}}f_{j} v_{j} \| - \log \|D_{y_{j}}f_{j} w_{j} \|. \end{align*} $$
There exists a uniform choice of
![]() $L_2\ge 1$
with
$L_2\ge 1$
with
Then for all
![]() $0\le j\le n$
we have the following assertions.
$0\le j\le n$
we have the following assertions.
-
•
 $d(x_{j}, x^{\prime }_{j})\le e^{\hat \gamma _0^{(j)}}d(x,x')\le \rho _1 e^{\hat \gamma _0^{(j)} + a_0 \kappa _0 ^{(n)}}$
, whence
$d(x_{j}, x^{\prime }_{j})\le e^{\hat \gamma _0^{(j)}}d(x,x')\le \rho _1 e^{\hat \gamma _0^{(j)} + a_0 \kappa _0 ^{(n)}}$
, whence
 $d(y_j, y^{\prime }_j)\le L_2 \rho _1 e^{\hat \gamma _0^{(j)} + a_0 \kappa _0 ^{(n)}}$
.
$d(y_j, y^{\prime }_j)\le L_2 \rho _1 e^{\hat \gamma _0^{(j)} + a_0 \kappa _0 ^{(n)}}$
. -
• By Claim 3.8,
 $$ \begin{align*} d(v_{j}, v^{\prime}_{j}) \le e^{c_0 j} d ((x,v),(x',v')) ^{\beta} \le e^{c_0 j} \rho_1^{\beta} e^{a_0 \beta \kappa_0^{(n)}}. \end{align*} $$
$$ \begin{align*} d(v_{j}, v^{\prime}_{j}) \le e^{c_0 j} d ((x,v),(x',v')) ^{\beta} \le e^{c_0 j} \rho_1^{\beta} e^{a_0 \beta \kappa_0^{(n)}}. \end{align*} $$
-
 $$ \begin{align*} d(w_{j}, w^{\prime}_{j}) \le K_3 d(\xi_{j}, \xi^{\prime}_{j})^{\bar \alpha} \le K_3 e^{\bar \alpha c_0 j} e^{a_0 \bar \alpha \beta \kappa_0^{(n)}}. \end{align*} $$
$$ \begin{align*} d(w_{j}, w^{\prime}_{j}) \le K_3 d(\xi_{j}, \xi^{\prime}_{j})^{\bar \alpha} \le K_3 e^{\bar \alpha c_0 j} e^{a_0 \bar \alpha \beta \kappa_0^{(n)}}. \end{align*} $$
We remark that
![]() $v\mapsto \log \|D_x f(v)\|$
is
$v\mapsto \log \|D_x f(v)\|$
is
![]() $C_1 ^2$
-Lipschitz for every x. Then for some uniform choice of
$C_1 ^2$
-Lipschitz for every x. Then for some uniform choice of
![]() $K_6$
,
$K_6$
,
![]() $K_7$
, and
$K_7$
, and
![]() $K_8$
we have
$K_8$
we have
 $$ \begin{align} |& \log \| \Delta_n(x,v)\| - \log \|\Delta_n(x',v')\| | \nonumber \\[-1.5pt] &\le \sum_{j= 0 } ^{n-1} | \log\| D_{x_{j}}f_{j} v_{j}\| - \log \|D_{y_{j}}f_{j} w_{j} \| - \log \| D_{x^{\prime}_{j}}f_{j} v^{\prime}_{j} \| +\log \|D_{y^{\prime}_{j}}f_{j} w^{\prime}_{j} \| | \nonumber \\[-1.5pt] &\le \sum_{j= 0 } ^{n-1} | \log \|D_{x_{j}}f_{j} v_{j} \| - \log \| D_{x^{\prime}_{j}}f_{j} v^{\prime}_{j} \| | \nonumber + \sum_{j= 0 } ^{n-1} | \log\| D_{y_{j}}f_{j} w_{j} \| - \log\| D_{y^{\prime}_{j}}f_{j} w^{\prime}_{j} \| | \nonumber \\[-1.5pt] &\le \sum_{j= 0 } ^{n-1} C_1^2 d(v_{j}, v_{j}') + C_3 d(x_{j}, x_{j}') ^{\beta} + C_1^2 d(w_j, w^{\prime}_j) + C_3d(y_{j}, y_{j}')^{\beta} \nonumber \\[-2pt] & \le (K_6 n) \max_{j} \{( e^{\beta \hat \gamma_0^{(j)} + \beta a_0 \kappa_0 ^{(n)}} + e^{c_0 j} e^{a_0 \beta \kappa_0^{(n)}} + e^{\bar \alpha c_0 j} e^{\bar \alpha a_0 \beta \kappa_0^{(n)}} ) \} \nonumber \\[-1.5pt]& \le K_7\max_j\{ ( e^{\epsilon_1 n+ \beta \hat \gamma_0^{(j)} + \beta a_0 \kappa_0 ^{(n)}} + e^{(\epsilon_1 + c_0)n} e^{a_0 \beta \kappa_0^{(n)}} + e^{\bar \alpha ( \epsilon_1 + c_0)n} e^{\bar \alpha a_0 \beta \kappa_0^{(n)}} ) \} \\[-1.5pt] & \le K_7 (e^{ \kappa_0^{(n)} } +e^{ \kappa_0^{(n)} } +e^{\bar \alpha \kappa_0^{(n)} })\nonumber \\[-1.5pt] & \le K_8 (r_{n+1})^{ \bar \alpha a_0{}^{-1}} \nonumber \end{align} $$
$$ \begin{align} |& \log \| \Delta_n(x,v)\| - \log \|\Delta_n(x',v')\| | \nonumber \\[-1.5pt] &\le \sum_{j= 0 } ^{n-1} | \log\| D_{x_{j}}f_{j} v_{j}\| - \log \|D_{y_{j}}f_{j} w_{j} \| - \log \| D_{x^{\prime}_{j}}f_{j} v^{\prime}_{j} \| +\log \|D_{y^{\prime}_{j}}f_{j} w^{\prime}_{j} \| | \nonumber \\[-1.5pt] &\le \sum_{j= 0 } ^{n-1} | \log \|D_{x_{j}}f_{j} v_{j} \| - \log \| D_{x^{\prime}_{j}}f_{j} v^{\prime}_{j} \| | \nonumber + \sum_{j= 0 } ^{n-1} | \log\| D_{y_{j}}f_{j} w_{j} \| - \log\| D_{y^{\prime}_{j}}f_{j} w^{\prime}_{j} \| | \nonumber \\[-1.5pt] &\le \sum_{j= 0 } ^{n-1} C_1^2 d(v_{j}, v_{j}') + C_3 d(x_{j}, x_{j}') ^{\beta} + C_1^2 d(w_j, w^{\prime}_j) + C_3d(y_{j}, y_{j}')^{\beta} \nonumber \\[-2pt] & \le (K_6 n) \max_{j} \{( e^{\beta \hat \gamma_0^{(j)} + \beta a_0 \kappa_0 ^{(n)}} + e^{c_0 j} e^{a_0 \beta \kappa_0^{(n)}} + e^{\bar \alpha c_0 j} e^{\bar \alpha a_0 \beta \kappa_0^{(n)}} ) \} \nonumber \\[-1.5pt]& \le K_7\max_j\{ ( e^{\epsilon_1 n+ \beta \hat \gamma_0^{(j)} + \beta a_0 \kappa_0 ^{(n)}} + e^{(\epsilon_1 + c_0)n} e^{a_0 \beta \kappa_0^{(n)}} + e^{\bar \alpha ( \epsilon_1 + c_0)n} e^{\bar \alpha a_0 \beta \kappa_0^{(n)}} ) \} \\[-1.5pt] & \le K_7 (e^{ \kappa_0^{(n)} } +e^{ \kappa_0^{(n)} } +e^{\bar \alpha \kappa_0^{(n)} })\nonumber \\[-1.5pt] & \le K_8 (r_{n+1})^{ \bar \alpha a_0{}^{-1}} \nonumber \end{align} $$
where we bound the first term of (24) by
when
![]() $ 0\le \ell <j$
and
$ 0\le \ell <j$
and
when
![]() $ j\le \ell <n.$
Combined with (23), it follows that
$ j\le \ell <n.$
Combined with (23), it follows that
is
![]() $ ( \bar \alpha a_0{}^{-1} )$
-Hölder on
$ ( \bar \alpha a_0{}^{-1} )$
-Hölder on
![]() $SW^c(p,1)$
.
$SW^c(p,1)$
.
4 Lyapunov charts and Ledrappier–Young entropy formula
For
![]() $\beta>0$
, let
$\beta>0$
, let
![]() $f\colon M\to M$
be a
$f\colon M\to M$
be a
![]() $C^{1+\beta }$
diffeomorphism of a compact k-dimensional manifold M without boundary. Let
$C^{1+\beta }$
diffeomorphism of a compact k-dimensional manifold M without boundary. Let
![]() $\mu $
be an ergodic, f-invariant Borel probability measure. We briefly discuss the ‘Lipschitz property of unstable manifolds inside center-unstable sets’ discussed in §1.2 and justify Theorems 1.4 and 1.5.
$\mu $
be an ergodic, f-invariant Borel probability measure. We briefly discuss the ‘Lipschitz property of unstable manifolds inside center-unstable sets’ discussed in §1.2 and justify Theorems 1.4 and 1.5.
4.1 Lyapunov charts
Fix M,
![]() $f\colon M\to M$
, and
$f\colon M\to M$
, and
![]() $\mu $
as above. Let
$\mu $
as above. Let
![]() $\Lambda $
denote the set of bi-regular points for
$\Lambda $
denote the set of bi-regular points for
![]() $\mu $
, let
$\mu $
, let
![]() $\lambda _1>\lambda _2 >\cdots >\lambda _p$
denote the Lyapunov exponents, and let
$\lambda _1>\lambda _2 >\cdots >\lambda _p$
denote the Lyapunov exponents, and let
![]() $T_x M = \bigoplus _{i=1}^p E^i(x)$
denote Oseledec’s splitting for
$T_x M = \bigoplus _{i=1}^p E^i(x)$
denote Oseledec’s splitting for
![]() $x\in \Lambda $
. Fix a decomposition
$x\in \Lambda $
. Fix a decomposition
![]() $\mathbb {R}^k = \bigoplus _{i=1}^p \mathbb {R}_i$
where
$\mathbb {R}^k = \bigoplus _{i=1}^p \mathbb {R}_i$
where
![]() $\dim \mathbb {R}_i = m_i$
is the dimension of
$\dim \mathbb {R}_i = m_i$
is the dimension of
![]() $E_i(x)$
for
$E_i(x)$
for
![]() $x\in \Lambda $
. Define the norm
$x\in \Lambda $
. Define the norm
![]() $\|\cdot \|'$
on
$\|\cdot \|'$
on
![]() $\mathbb {R}^k$
as follows: writing
$\mathbb {R}^k$
as follows: writing
![]() $v= \sum _{i=1}^p v_i$
where
$v= \sum _{i=1}^p v_i$
where
![]() $v_i \in \mathbb {R}_i$
for every
$v_i \in \mathbb {R}_i$
for every
![]() $1\le i\le p$
, set
$1\le i\le p$
, set
![]() $\|v\|'= \max \{ \|v_i\|\}$
where
$\|v\|'= \max \{ \|v_i\|\}$
where
![]() $\|v_i\|$
restricts to the standard Euclidean norm on each
$\|v_i\|$
restricts to the standard Euclidean norm on each
![]() $\mathbb {R}_i$
. Let
$\mathbb {R}_i$
. Let
![]() $\lambda _0= \max \{|\lambda _1|, | \lambda _p|\}$
. We denote by
$\lambda _0= \max \{|\lambda _1|, | \lambda _p|\}$
. We denote by
![]() $B(0,r)$
the ball in
$B(0,r)$
the ball in
![]() $\mathbb {R}^k$
of radius r centered at
$\mathbb {R}^k$
of radius r centered at
![]() $0$
in the norm
$0$
in the norm
![]() $\|\cdot \|'$
.
$\|\cdot \|'$
.
Fix a background Riemannian metric and induced distance on M. We have the following standard construction which follows from the construction of a Lyapunov inner product and standard estimates. (See, for example, [Reference Ledrappier and YoungLY1, Appendix] or [Reference Fathi, Herman and YoccozFHY, §2].)
Proposition 4.1. For every sufficiently small
![]() $0<\hat \epsilon <1$
there is a measurable function
$0<\hat \epsilon <1$
there is a measurable function
![]() $\hat \ell \colon \Lambda \to [1,\infty )$
and a measurable family of
$\hat \ell \colon \Lambda \to [1,\infty )$
and a measurable family of
![]() $C^{\infty }$
embeddings
$C^{\infty }$
embeddings
![]() $\{\hat \Phi _x, x\in \Lambda \}$
with the following properties:
$\{\hat \Phi _x, x\in \Lambda \}$
with the following properties:
-
(i)
 $\hat \Phi _x\colon B(0, \hat \ell (x)^{-1})\to M$
is a
$\hat \Phi _x\colon B(0, \hat \ell (x)^{-1})\to M$
is a
 $C^{\infty }$
diffeomorphism onto a neighborhood of x with
$C^{\infty }$
diffeomorphism onto a neighborhood of x with
 $\hat \Phi _x(0) = x$
;
$\hat \Phi _x(0) = x$
; -
(ii)
 $D_0\hat \Phi _x\mathbb {R}_{i}= E^i(x)$
;
$D_0\hat \Phi _x\mathbb {R}_{i}= E^i(x)$
; -
(iii) the map
 $\hat f_x \colon B(0, e^{-\lambda _0 - 3 \hat \epsilon }\hat \ell (x)^{-1}) \to B(0, \hat \ell (f(x))^{-1}) $
given by is well defined;
$\hat f_x \colon B(0, e^{-\lambda _0 - 3 \hat \epsilon }\hat \ell (x)^{-1}) \to B(0, \hat \ell (f(x))^{-1}) $
given by is well defined; $$ \begin{align*} \hat{f}_x(v) =\hat{\Phi}_{f(x) }^{-1} \circ f\circ\hat \Phi_x(v) \end{align*} $$
$$ \begin{align*} \hat{f}_x(v) =\hat{\Phi}_{f(x) }^{-1} \circ f\circ\hat \Phi_x(v) \end{align*} $$
-
(iv)
 $D_0\hat f_x\mathbb {R}_i= \mathbb {R}_i$
, and for
$D_0\hat f_x\mathbb {R}_i= \mathbb {R}_i$
, and for
 $v\in \mathbb {R}_i$
,
$v\in \mathbb {R}_i$
,  $$ \begin{align*} e^{\lambda_i- \hat \epsilon} \|v\|' \le \|D_0\hat f_x v\|'\le e^{\lambda_i + \hat \epsilon}\|v\|'; \end{align*} $$
$$ \begin{align*} e^{\lambda_i- \hat \epsilon} \|v\|' \le \|D_0\hat f_x v\|'\le e^{\lambda_i + \hat \epsilon}\|v\|'; \end{align*} $$
-
(v)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (D\hat f_x)\le \hat \epsilon ( \hat \ell (x))^{\beta }$
whence
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (D\hat f_x)\le \hat \epsilon ( \hat \ell (x))^{\beta }$
whence
 $\operatorname {Lip} (\hat f_x - D_0\hat f_x) \le \hat \epsilon $
;
$\operatorname {Lip} (\hat f_x - D_0\hat f_x) \le \hat \epsilon $
; -
(vi) similar statements to (iii), (iv), and (v) hold for
 $f{}^{-1}$
;
$f{}^{-1}$
; -
(vii) there is a uniform
 $k_0$
so that
$k_0$
so that
 $ \operatorname {Lip}(\hat \Phi _x)\le k_0$
and
$ \operatorname {Lip}(\hat \Phi _x)\le k_0$
and
 $\operatorname {Lip}(\hat \Phi _x^{-1} ) \le \hat \ell (x)$
;
$\operatorname {Lip}(\hat \Phi _x^{-1} ) \le \hat \ell (x)$
; -
(viii)
 $e^{-\hat \epsilon } \le \dfrac {\hat \ell (f(x))}{\hat \ell (x)} \le e^{\hat \epsilon }$
.
$e^{-\hat \epsilon } \le \dfrac {\hat \ell (f(x))}{\hat \ell (x)} \le e^{\hat \epsilon }$
.
Given
![]() $0< \hat \epsilon <1$
and corresponding function
$0< \hat \epsilon <1$
and corresponding function
![]() $\hat \ell \colon \Lambda \to [1, \infty ) $
as in Proposition 4.1, define new charts
$\hat \ell \colon \Lambda \to [1, \infty ) $
as in Proposition 4.1, define new charts
![]() $ \Phi _x \colon B(0, 1) \to M$
by rescaling:
$ \Phi _x \colon B(0, 1) \to M$
by rescaling:
We check that with
![]() $\epsilon = 4\hat \epsilon $
and with
$\epsilon = 4\hat \epsilon $
and with
![]() $\ell (x) = (\hat \ell (x))^2$
, for every
$\ell (x) = (\hat \ell (x))^2$
, for every
![]() $x\in \Lambda $
the following hold:
$x\in \Lambda $
the following hold:
-
(a)
 $\Phi _x\colon B(0, 1)\to M$
is a
$\Phi _x\colon B(0, 1)\to M$
is a
 $C^{\infty }$
diffeomorphism onto a neighborhood of x with
$C^{\infty }$
diffeomorphism onto a neighborhood of x with
 $\Phi _x(0) \,{=}\, x$
;
$\Phi _x(0) \,{=}\, x$
; -
(b)
 $D_0 \Phi _x\mathbb {R}_{i}= E^i(x)$
;
$D_0 \Phi _x\mathbb {R}_{i}= E^i(x)$
; -
(c) the map
 $\tilde f_x \colon B(0, e^{-\lambda _0 - 2 \epsilon } ) \to B(0, 1)$
given by is well defined;
$\tilde f_x \colon B(0, e^{-\lambda _0 - 2 \epsilon } ) \to B(0, 1)$
given by is well defined; $$ \begin{align*} \tilde f_x(v) := \Phi_{f(x) }^{-1} \circ f\circ \Phi_x(v) = \hat \ell(f(x)) (\hat f_x (\hat \ell(x)^{-1} v)) \end{align*} $$
$$ \begin{align*} \tilde f_x(v) := \Phi_{f(x) }^{-1} \circ f\circ \Phi_x(v) = \hat \ell(f(x)) (\hat f_x (\hat \ell(x)^{-1} v)) \end{align*} $$
-
(d)
 $D_0\tilde f_x\mathbb {R}_i= \mathbb {R}_i$
, and for
$D_0\tilde f_x\mathbb {R}_i= \mathbb {R}_i$
, and for
 $v\in \mathbb {R}_i$
,
$v\in \mathbb {R}_i$
,  $$ \begin{align*} e^{\lambda_i- \epsilon} \|v\|' \le \|D_0\tilde f_x v\|'\le e^{\lambda_i + \epsilon}\|v\|'; \end{align*} $$
$$ \begin{align*} e^{\lambda_i- \epsilon} \|v\|' \le \|D_0\tilde f_x v\|'\le e^{\lambda_i + \epsilon}\|v\|'; \end{align*} $$
-
(e)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (D\tilde f_x)\le \epsilon $
, whence
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} (D\tilde f_x)\le \epsilon $
, whence
 $\operatorname {Lip}(\tilde f_x - D_0\tilde f_x) \le \epsilon $
;
$\operatorname {Lip}(\tilde f_x - D_0\tilde f_x) \le \epsilon $
; -
(f) similar statements to (c), (d), and (e) hold for
 $f{}^{-1}$
;
$f{}^{-1}$
; -
(g) there is a uniform
 $k_0$
so that
$k_0$
so that
 $ \operatorname {Lip}( \Phi _x)\le k_0$
and
$ \operatorname {Lip}( \Phi _x)\le k_0$
and
 $\operatorname {Lip}( \Phi _x^{-1} ) \le \ell (x)$
;
$\operatorname {Lip}( \Phi _x^{-1} ) \le \ell (x)$
; -
(h)
 $e^{- \epsilon } \le \dfrac {\ell (f(x))}{\ell (x)}\le e^{ \epsilon }$
.
$e^{- \epsilon } \le \dfrac {\ell (f(x))}{\ell (x)}\le e^{ \epsilon }$
.
Indeed, (a), (b), (c), (g), and (h) follow immediately from construction. For (d) and (e), note that for
![]() $u\in B(0,1)$
and
$u\in B(0,1)$
and
![]() $\xi \in \mathbb {R}^k$
with
$\xi \in \mathbb {R}^k$
with
![]() $\|\xi \|'= 1$
,
$\|\xi \|'= 1$
,
 $$ \begin{align*} D_u\tilde f_x (\xi) = \hat \ell(f(x)) D_{\hat \ell(x)^{-1} u }\hat f_x (\hat \ell (x)^{-1}\xi )= \dfrac{\hat \ell(f(x))}{\hat \ell(x)}D_{\hat \ell(x)^{-1} u }\hat f_x(\xi), \end{align*} $$
$$ \begin{align*} D_u\tilde f_x (\xi) = \hat \ell(f(x)) D_{\hat \ell(x)^{-1} u }\hat f_x (\hat \ell (x)^{-1}\xi )= \dfrac{\hat \ell(f(x))}{\hat \ell(x)}D_{\hat \ell(x)^{-1} u }\hat f_x(\xi), \end{align*} $$
hence
 $$ \begin{align*} D_0\tilde f_x (\xi) = \dfrac{\hat \ell(f(x))}{\hat\ell(x)} D_0 \hat f_x(\xi) \end{align*} $$
$$ \begin{align*} D_0\tilde f_x (\xi) = \dfrac{\hat \ell(f(x))}{\hat\ell(x)} D_0 \hat f_x(\xi) \end{align*} $$
and
 $$ \begin{align*} \|D_u\tilde f_x(\xi) - D_v\tilde f_x(\xi)\|' & = \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\|D_{\hat \ell(x)^{-1} u }\hat f_x (\xi )- D_{\hat \ell(x)^{-1} v }\hat f_x (\xi )\|'\\ & \le \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}}(D\hat f_x ) {\|\hat \ell(x)^{-1} u - \hat \ell(x)^{-1} v\|'}^{\beta} \\ & \le \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\hat \epsilon \hat \ell(x) ^{\beta} (\hat \ell(x)^{-1} )^{\beta} {\| u - v\|'}^{\beta} \\ & = \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\hat \epsilon {\| u - v\|'}^{\beta}. \end{align*} $$
$$ \begin{align*} \|D_u\tilde f_x(\xi) - D_v\tilde f_x(\xi)\|' & = \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\|D_{\hat \ell(x)^{-1} u }\hat f_x (\xi )- D_{\hat \ell(x)^{-1} v }\hat f_x (\xi )\|'\\ & \le \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta}}(D\hat f_x ) {\|\hat \ell(x)^{-1} u - \hat \ell(x)^{-1} v\|'}^{\beta} \\ & \le \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\hat \epsilon \hat \ell(x) ^{\beta} (\hat \ell(x)^{-1} )^{\beta} {\| u - v\|'}^{\beta} \\ & = \dfrac{\hat \ell(f(x))}{\hat \ell(x)}\hat \epsilon {\| u - v\|'}^{\beta}. \end{align*} $$
The family of maps
![]() $\{\Phi _x, x\in \Lambda \}$
is called a family of
$\{\Phi _x, x\in \Lambda \}$
is called a family of
![]() $(\epsilon ,\ell )$
-charts. Fix a suitable bump function
$(\epsilon ,\ell )$
-charts. Fix a suitable bump function
![]() $\Theta \colon \mathbb {R}^k\to [0,1]$
with
$\Theta \colon \mathbb {R}^k\to [0,1]$
with
![]() $\Theta (v) = 0 $
if
$\Theta (v) = 0 $
if
![]() $\|v\|'\ge e^{-\lambda _0 - 2\epsilon } $
and
$\|v\|'\ge e^{-\lambda _0 - 2\epsilon } $
and
![]() $\Theta (v) = 1 $
if
$\Theta (v) = 1 $
if
![]() $\|v\|'\le \tfrac 1 2 e^{-\lambda _0 - 2\epsilon }. $
Let
$\|v\|'\le \tfrac 1 2 e^{-\lambda _0 - 2\epsilon }. $
Let
and write
![]() $\phi _x = \Theta \cdot (\tilde f_x - D_0\tilde f_x)$
. We have
$\phi _x = \Theta \cdot (\tilde f_x - D_0\tilde f_x)$
. We have
![]() $\operatorname {Lip}(\phi _x)\le \operatorname {Lip}(\tilde f_x - D_0\tilde f_x)$
, whence
$\operatorname {Lip}(\phi _x)\le \operatorname {Lip}(\tilde f_x - D_0\tilde f_x)$
, whence
![]() $\|\phi _x\|_{C^1}\le \epsilon .$
Taking
$\|\phi _x\|_{C^1}\le \epsilon .$
Taking
![]() $\epsilon>0$
sufficiently small,
$\epsilon>0$
sufficiently small,
![]() $F_x$
is a diffeomorphism and
$F_x$
is a diffeomorphism and
In particular, given
![]() $\epsilon '>0$
(sufficiently small to apply Proposition 2.1), we may take
$\epsilon '>0$
(sufficiently small to apply Proposition 2.1), we may take
![]() $\epsilon>0$
sufficiently small so that for every
$\epsilon>0$
sufficiently small so that for every
![]() $x\in \Lambda $
:
$x\in \Lambda $
:
-
(1)
 $F_x (u)= \tilde f_x (u)$
and
$F_x (u)= \tilde f_x (u)$
and
 $F_x^{-1} (u)= (\tilde f_x){}^{-1} (u)$
for all u with
$F_x^{-1} (u)= (\tilde f_x){}^{-1} (u)$
for all u with
 $\|u\|\le \tfrac 1 2e^{-2\lambda _0 - 4\epsilon }$
;
$\|u\|\le \tfrac 1 2e^{-2\lambda _0 - 4\epsilon }$
; -
(2)
 $\|F_x- D_0\tilde f_x\|_{C^1}<\epsilon '$
;
$\|F_x- D_0\tilde f_x\|_{C^1}<\epsilon '$
; -
(3)
 $\|F_x{}^{-1} - (D_0\tilde f_x){}^{-1}\|_{C^1}<\epsilon '$
.
$\|F_x{}^{-1} - (D_0\tilde f_x){}^{-1}\|_{C^1}<\epsilon '$
.
Additionally, there is
![]() $C_0>0$
so that:
$C_0>0$
so that:
-
(4)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta }}}_{\|\cdot \|'} (DF_x ) \le C_0$
;
${\mathrm{H}\ddot{\rm o}\mathrm{l}^{{\beta }}}_{\|\cdot \|'} (DF_x ) \le C_0$
; -
(5)
 ${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} _{\|\cdot \|'}(DF_x^{-1} ) \le C_0$
.
${\mathrm{H}\ddot{\rm o}\mathrm{l}}^{{\beta }} _{\|\cdot \|'}(DF_x^{-1} ) \le C_0$
.
Furthermore, taking
![]() $\epsilon>0$
sufficiently small, we can ensure all relevant estimates remain true in the Euclidean norm
$\epsilon>0$
sufficiently small, we can ensure all relevant estimates remain true in the Euclidean norm
![]() $\|\cdot \|$
.
$\|\cdot \|$
.
Given sufficiently small
![]() $\epsilon>0$
, fix a family of
$\epsilon>0$
, fix a family of
![]() $(\epsilon ,\ell )$
-charts
$(\epsilon ,\ell )$
-charts
![]() $\{ \Phi _x : x\in \Lambda \}$
as above. Let
$\{ \Phi _x : x\in \Lambda \}$
as above. Let
![]() $0<\delta <1$
be a reduction factor. (Say
$0<\delta <1$
be a reduction factor. (Say
![]() $\delta <\tfrac 1 4 e^{-3\lambda _0 - 6\epsilon }$
to adapt the arguments in [Reference Ledrappier and YoungLY1, equations (2.2) and (2.3)].) For
$\delta <\tfrac 1 4 e^{-3\lambda _0 - 6\epsilon }$
to adapt the arguments in [Reference Ledrappier and YoungLY1, equations (2.2) and (2.3)].) For
![]() $x\in \Lambda $
, let
$x\in \Lambda $
, let
For
![]() $x\in \Lambda $
,
$x\in \Lambda $
,
![]() $\star \in \{s,u,c,su,cu\}$
, and
$\star \in \{s,u,c,su,cu\}$
, and
![]() $v\in \mathbb {R}^k$
, let
$v\in \mathbb {R}^k$
, let
![]() $\tilde W^{\star }_x(v)$
be the corresponding ‘fake’ manifold through the point v constructed in Proposition 2.1 using the sequence of globalizations
$\tilde W^{\star }_x(v)$
be the corresponding ‘fake’ manifold through the point v constructed in Proposition 2.1 using the sequence of globalizations
![]() $\{F_{f^j(x)}\}$
along the orbit
$\{F_{f^j(x)}\}$
along the orbit
![]() $f^j(x)$
.
$f^j(x)$
.
From the uniformly partially hyperbolic dynamics inside charts we obtain the following claim.
Claim 4.2. For all sufficiently small
![]() $\delta>0$
and almost every x we have
$\delta>0$
and almost every x we have
![]() $S^{cu}_{\delta ,x} \subset \tilde W^{cu}_x (0).$
$S^{cu}_{\delta ,x} \subset \tilde W^{cu}_x (0).$
From Corollary 2.3, it follows (for sufficiently small
![]() $\delta>0$
) that the Lipschitz property of holonomies along unstable manifolds inside the center-unstable sets
$\delta>0$
) that the Lipschitz property of holonomies along unstable manifolds inside the center-unstable sets
![]() $S^{cu}_{\delta ,x}$
derived in [Reference Ledrappier and YoungLY1, equation (4.2)] for
$S^{cu}_{\delta ,x}$
derived in [Reference Ledrappier and YoungLY1, equation (4.2)] for
![]() $C^2$
maps holds for
$C^2$
maps holds for
![]() $C^{1+\beta }$
maps. We similarly obtain that the holonomies along ‘fake’
$C^{1+\beta }$
maps. We similarly obtain that the holonomies along ‘fake’
![]() $W^i$
manifolds is Lipschitz inside
$W^i$
manifolds is Lipschitz inside
![]() $W^{i+1}$
manifolds for
$W^{i+1}$
manifolds for
![]() $\lambda _i>\lambda _{i+1}>0$
; this replaces the Lipschitz estimates [Reference Ledrappier and YoungLY2, Lemma 8.2.5 and equation (8.4)]. Note also that since the coordinate changes intertwining the charts
$\lambda _i>\lambda _{i+1}>0$
; this replaces the Lipschitz estimates [Reference Ledrappier and YoungLY2, Lemma 8.2.5 and equation (8.4)]. Note also that since the coordinate changes intertwining the charts
![]() $\Phi _x$
and
$\Phi _x$
and
![]() $\hat \Phi _x$
are linear we also obtain an analogous Lipschitzness of holonomies relative to the original charts
$\hat \Phi _x$
are linear we also obtain an analogous Lipschitzness of holonomies relative to the original charts
![]() $\hat \Phi _x$
. In particular, [Reference Ledrappier and YoungLY1, Proposition 5.1] and [Reference Ledrappier and YoungLY2, Proposition 11.2] remain valid for
$\hat \Phi _x$
. In particular, [Reference Ledrappier and YoungLY1, Proposition 5.1] and [Reference Ledrappier and YoungLY2, Proposition 11.2] remain valid for
![]() $C^{1+\beta }$
diffeomorphisms. It follows that the results of [Reference Ledrappier and YoungLY1, Reference Ledrappier and YoungLY2] hold for
$C^{1+\beta }$
diffeomorphisms. It follows that the results of [Reference Ledrappier and YoungLY1, Reference Ledrappier and YoungLY2] hold for
![]() $C^{1+\beta }$
diffeomorphisms.
$C^{1+\beta }$
diffeomorphisms.