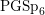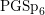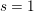1 Introduction
Let  $F$ be a totally real number field, and
$F$ be a totally real number field, and  $\mathbb{A}$ its ring of adèles. Let
$\mathbb{A}$ its ring of adèles. Let  $\unicode[STIX]{x1D70B}\cong \bigotimes _{v}\unicode[STIX]{x1D70B}_{v}$ be an irreducible cuspidal automorphic representation of the group
$\unicode[STIX]{x1D70B}\cong \bigotimes _{v}\unicode[STIX]{x1D70B}_{v}$ be an irreducible cuspidal automorphic representation of the group  $\text{PGSp}_{6}(\mathbb{A})$, which is unramified outside a finite set
$\text{PGSp}_{6}(\mathbb{A})$, which is unramified outside a finite set  $S$ of places (including all real places). Since the Langlands dual group of
$S$ of places (including all real places). Since the Langlands dual group of  $\text{PGSp}_{6}$ is
$\text{PGSp}_{6}$ is  $\text{Spin}_{7}(\mathbb{C})$, there is an associated semisimple conjugacy class
$\text{Spin}_{7}(\mathbb{C})$, there is an associated semisimple conjugacy class  $s_{v}$ in
$s_{v}$ in  $\text{Spin}_{7}(\mathbb{C})$ for
$\text{Spin}_{7}(\mathbb{C})$ for  $v\notin S$; this is the Satake parameter of the local component
$v\notin S$; this is the Satake parameter of the local component  $\unicode[STIX]{x1D70B}_{v}$. If
$\unicode[STIX]{x1D70B}_{v}$. If  $r$ denotes the eight-dimensional spin representation of
$r$ denotes the eight-dimensional spin representation of  $\text{Spin}_{7}(\mathbb{C})$, the partial Spin
$\text{Spin}_{7}(\mathbb{C})$, the partial Spin  $L$-function corresponding to
$L$-function corresponding to  $\unicode[STIX]{x1D70B}$ is defined to be the product
$\unicode[STIX]{x1D70B}$ is defined to be the product
 $$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})=\mathop{\prod }_{v\notin S}\frac{1}{\det (1-r(s_{v})q_{v}^{-s})},\end{eqnarray}$$
$$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})=\mathop{\prod }_{v\notin S}\frac{1}{\det (1-r(s_{v})q_{v}^{-s})},\end{eqnarray}$$ where  $q_{v}$ is the order of the residual field of the local field
$q_{v}$ is the order of the residual field of the local field  $F_{v}$.
$F_{v}$.
It is well known that the stabilizer in  $\text{Spin}_{7}(\mathbb{C})$ of a generic vector in the spin representation is the exceptional group
$\text{Spin}_{7}(\mathbb{C})$ of a generic vector in the spin representation is the exceptional group  $G_{2}(\mathbb{C})$, giving a well-defined conjugacy class of embeddings
$G_{2}(\mathbb{C})$, giving a well-defined conjugacy class of embeddings
 $$\begin{eqnarray}\unicode[STIX]{x1D704}:G_{2}(\mathbb{C})\longrightarrow \text{Spin}_{7}(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}:G_{2}(\mathbb{C})\longrightarrow \text{Spin}_{7}(\mathbb{C}).\end{eqnarray}$$ Therefore, as a special case of the Langlands functoriality principle, if  $L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a simple pole at
$L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a simple pole at  $s=1$, then one expects
$s=1$, then one expects  $\unicode[STIX]{x1D70B}$ to be a functorial lift from an exceptional group of absolute type
$\unicode[STIX]{x1D70B}$ to be a functorial lift from an exceptional group of absolute type  $\mathbf{G}_{2}$ defined over
$\mathbf{G}_{2}$ defined over  $F$. We note that every such group is given as the automorphism group of an octonion algebra
$F$. We note that every such group is given as the automorphism group of an octonion algebra  $\mathbb{O}$ over
$\mathbb{O}$ over  $F$, and by the Hasse principle, the number of isomorphism classes of such groups is
$F$, and by the Hasse principle, the number of isomorphism classes of such groups is  $2^{n}$, where
$2^{n}$, where  $n$ is the number of real places of
$n$ is the number of real places of  $F$.
$F$.
As explained in a recent paper of Chenevier [Reference ChenevierChe19, §6.12], if  $\unicode[STIX]{x1D70B}$ is a tempered cuspidal representation of
$\unicode[STIX]{x1D70B}$ is a tempered cuspidal representation of  $\text{PGSp}_{6}$ such that for almost all places
$\text{PGSp}_{6}$ such that for almost all places  $v$, the Satake parameter
$v$, the Satake parameter  $s_{v}$ of
$s_{v}$ of  $\unicode[STIX]{x1D70B}_{v}$ belongs to
$\unicode[STIX]{x1D70B}_{v}$ belongs to  $\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$ (or more accurately, the conjugacy class
$\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$ (or more accurately, the conjugacy class  $s_{v}$ meets
$s_{v}$ meets  $\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$), then
$\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$), then  $L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ will have a pole at
$L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ will have a pole at  $s=1$ and so one expects such a tempered
$s=1$ and so one expects such a tempered  $\unicode[STIX]{x1D70B}$ to be a functorial lift from
$\unicode[STIX]{x1D70B}$ to be a functorial lift from  $G_{2}$. In this paper we also prove a slightly weaker version of this expectation.
$G_{2}$. In this paper we also prove a slightly weaker version of this expectation.
Theorem 1.1. In the above setting, suppose that  $\unicode[STIX]{x1D70B}$ is a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$ is a cuspidal automorphic representation of  $\text{PGSp}_{6}$ such that
$\text{PGSp}_{6}$ such that  $L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at
$L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at  $s=1$. Then there exist an octonion algebra
$s=1$. Then there exist an octonion algebra  $\mathbb{O}$ over
$\mathbb{O}$ over  $F$ and a cuspidal automorphic representation
$F$ and a cuspidal automorphic representation  $\unicode[STIX]{x1D70B}^{\prime }$ of
$\unicode[STIX]{x1D70B}^{\prime }$ of  $\text{Aut}(\mathbb{O})$ such that the Satake parameters of
$\text{Aut}(\mathbb{O})$ such that the Satake parameters of  $\unicode[STIX]{x1D70B}^{\prime }$ are mapped by
$\unicode[STIX]{x1D70B}^{\prime }$ are mapped by  $\unicode[STIX]{x1D704}$ to those of
$\unicode[STIX]{x1D704}$ to those of  $\unicode[STIX]{x1D70B}$ (i.e.
$\unicode[STIX]{x1D70B}$ (i.e.  $\unicode[STIX]{x1D70B}$ is a weak functorial lift of
$\unicode[STIX]{x1D70B}$ is a weak functorial lift of  $\unicode[STIX]{x1D70B}^{\prime }$).
$\unicode[STIX]{x1D70B}^{\prime }$).
If the cuspidal representation  $\unicode[STIX]{x1D70B}$ of
$\unicode[STIX]{x1D70B}$ of  $\text{PGSp}_{6}$ is tempered, then the following statements are equivalent:
$\text{PGSp}_{6}$ is tempered, then the following statements are equivalent:
(a) for almost all places
 $v$, the Satake parameter
$v$, the Satake parameter  $s_{v}$ of
$s_{v}$ of  $\unicode[STIX]{x1D70B}_{v}$ is contained in
$\unicode[STIX]{x1D70B}_{v}$ is contained in  $\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$;
$\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$;(b) there exist an octonion algebra
 $\mathbb{O}$ over
$\mathbb{O}$ over  $F$ and a cuspidal automorphic representation
$F$ and a cuspidal automorphic representation  $\unicode[STIX]{x1D70B}^{\prime }$ of
$\unicode[STIX]{x1D70B}^{\prime }$ of  $\text{Aut}(\mathbb{O})$ such that
$\text{Aut}(\mathbb{O})$ such that  $\unicode[STIX]{x1D70B}$ is a weak functorial lift of
$\unicode[STIX]{x1D70B}$ is a weak functorial lift of  $\unicode[STIX]{x1D70B}^{\prime }$.
$\unicode[STIX]{x1D70B}^{\prime }$.
Since the local Langlands classification is not known for  $\mathbf{G}_{2}$ or for
$\mathbf{G}_{2}$ or for  $\text{PGSp}_{6}$, this is essentially the best possible result one can expect at the moment. However, if
$\text{PGSp}_{6}$, this is essentially the best possible result one can expect at the moment. However, if  $\unicode[STIX]{x1D70B}$ is unramified everywhere or if it corresponds to a classical Siegel modular form of level one, then
$\unicode[STIX]{x1D70B}$ is unramified everywhere or if it corresponds to a classical Siegel modular form of level one, then  $\unicode[STIX]{x1D70B}$ is a functorial lift. Special cases of this result were previously obtained by Ginzburg and Jiang [Reference Ginzburg and JiangGJ01], Gan and Gurevich [Reference Gan and GurevichGG09] and Pollack and Shah [Reference Pollack and ShahPS18].
$\unicode[STIX]{x1D70B}$ is a functorial lift. Special cases of this result were previously obtained by Ginzburg and Jiang [Reference Ginzburg and JiangGJ01], Gan and Gurevich [Reference Gan and GurevichGG09] and Pollack and Shah [Reference Pollack and ShahPS18].
Our proof of Theorem 1.1 is based on the following three ingredients:
(1) an exceptional theta correspondence for the dual pair
 $\text{Aut}(\mathbb{O})\times \text{PGSp}_{6}$ arising from the minimal representation
$\text{Aut}(\mathbb{O})\times \text{PGSp}_{6}$ arising from the minimal representation  $\unicode[STIX]{x1D6F1}$ of a group of absolute type
$\unicode[STIX]{x1D6F1}$ of a group of absolute type  $\mathbf{E}_{7}$ [Reference Gan and SavinGS05, Reference Hilgert, Kobayashi and MöllersHKM14, Reference SahiSah92];
$\mathbf{E}_{7}$ [Reference Gan and SavinGS05, Reference Hilgert, Kobayashi and MöllersHKM14, Reference SahiSah92];(2) a Siegel–Weil formula proved in this paper (see Theorem 1.2 below);
(3) an integral representation of the Spin
 $L$-function of
$L$-function of  $\unicode[STIX]{x1D70B}$ recently discovered by Pollack [Reference PollackPol17].
$\unicode[STIX]{x1D70B}$ recently discovered by Pollack [Reference PollackPol17].
In greater detail, let  $J$ be the exceptional Jordan algebra of
$J$ be the exceptional Jordan algebra of  $3\times 3$ hermitian symmetric matrices with coefficients in an octonion algebra
$3\times 3$ hermitian symmetric matrices with coefficients in an octonion algebra  $\mathbb{O}$. By the Koecher–Tits construction, the algebra
$\mathbb{O}$. By the Koecher–Tits construction, the algebra  $J$ gives rise to an adjoint group
$J$ gives rise to an adjoint group  $G$ of absolute type
$G$ of absolute type  $\mathbf{E}_{7}$, with a maximal parabolic subgroup
$\mathbf{E}_{7}$, with a maximal parabolic subgroup  $P=MN$, such that the unipotent radical
$P=MN$, such that the unipotent radical  $N$ is commutative and isomorphic to
$N$ is commutative and isomorphic to  $J$. Since
$J$. Since  $G$ is adjoint, the conjugation action of
$G$ is adjoint, the conjugation action of  $M$ on
$M$ on  $N$ is faithful, and
$N$ is faithful, and  $M$ is isomorphic to the similitude group of the natural cubic norm form on
$M$ is isomorphic to the similitude group of the natural cubic norm form on  $J$. Thus the natural action of
$J$. Thus the natural action of  $\text{Aut}(\mathbb{O})$ on
$\text{Aut}(\mathbb{O})$ on  $J$ gives an embedding of
$J$ gives an embedding of  $\text{Aut}(\mathbb{O})$ into
$\text{Aut}(\mathbb{O})$ into  $M$. The centralizer of
$M$. The centralizer of  $\text{Aut}(\mathbb{O})$ is
$\text{Aut}(\mathbb{O})$ is  $\text{PGSp}_{6}$. To see this, observe that the centralizer of
$\text{PGSp}_{6}$. To see this, observe that the centralizer of  $\text{Aut}(\mathbb{O})$ in
$\text{Aut}(\mathbb{O})$ in  $J$ is the Jordan subalgebra
$J$ is the Jordan subalgebra  $J_{F}$ of
$J_{F}$ of  $3\times 3$ symmetric matrices with coefficients in
$3\times 3$ symmetric matrices with coefficients in  $F$. The group
$F$. The group  $\text{PGSp}_{6}$ arises from
$\text{PGSp}_{6}$ arises from  $J_{F}$ by the Koecher–Tits construction. This gives the dual pair
$J_{F}$ by the Koecher–Tits construction. This gives the dual pair
 $$\begin{eqnarray}\text{Aut}(\mathbb{O})\times \text{PGSp}_{6}\subset G\end{eqnarray}$$
$$\begin{eqnarray}\text{Aut}(\mathbb{O})\times \text{PGSp}_{6}\subset G\end{eqnarray}$$alluded to in item (1) above.
We can now describe another dual pair in  $G$. Let
$G$. Let  $D$ be a quaternion algebra over
$D$ be a quaternion algebra over  $F$, and assume that we have an embedding
$F$, and assume that we have an embedding  $i:D\rightarrow \mathbb{O}$. The centralizer of
$i:D\rightarrow \mathbb{O}$. The centralizer of  $D$ in
$D$ in  $\text{Aut}(\mathbb{O})$ is isomorphic to
$\text{Aut}(\mathbb{O})$ is isomorphic to  $D^{1}$, the group of norm-
$D^{1}$, the group of norm- $1$ elements in
$1$ elements in  $D$. Conversely, the centralizer (i.e. the pointwise stabilizer) of
$D$. Conversely, the centralizer (i.e. the pointwise stabilizer) of  $D^{1}$ in
$D^{1}$ in  $\mathbb{O}$ is
$\mathbb{O}$ is  $i(D)\subset \mathbb{O}$. Thus the centralizer of
$i(D)\subset \mathbb{O}$. Thus the centralizer of  $D^{1}$ in
$D^{1}$ in  $J$ is the Jordan subalgebra
$J$ is the Jordan subalgebra  $J_{D}$ of
$J_{D}$ of  $3\times 3$ hermitian symmetric matrices with coefficients in
$3\times 3$ hermitian symmetric matrices with coefficients in  $D$, and the centralizer of
$D$, and the centralizer of  $D^{1}$ in
$D^{1}$ in  $G$ is a group
$G$ is a group  $G_{D}$ of absolute type
$G_{D}$ of absolute type  $\mathbf{D}_{6}$ arising from
$\mathbf{D}_{6}$ arising from  $J_{D}$ by the Koecher–Tits construction. Thus we have a dual pair
$J_{D}$ by the Koecher–Tits construction. Thus we have a dual pair
 $$\begin{eqnarray}D^{1}\times G_{D}\longrightarrow G.\end{eqnarray}$$
$$\begin{eqnarray}D^{1}\times G_{D}\longrightarrow G.\end{eqnarray}$$Indeed, the two dual pairs we have described fit into the following seesaw diagram, where the vertical lines represent inclusions of groups:

The Siegel–Weil formula mentioned in item (2) above concerns the global theta lift  $\unicode[STIX]{x1D6E9}(1)$ of the trivial representation of
$\unicode[STIX]{x1D6E9}(1)$ of the trivial representation of  $D^{1}$ to
$D^{1}$ to  $G_{D}$, obtained by restricting the minimal representation
$G_{D}$, obtained by restricting the minimal representation  $\unicode[STIX]{x1D6F1}$ of
$\unicode[STIX]{x1D6F1}$ of  $G$ to the dual pair
$G$ to the dual pair  $D^{1}\times G_{D}$. Roughly speaking,
$D^{1}\times G_{D}$. Roughly speaking,  $\unicode[STIX]{x1D6E9}(1)$ is the space of automorphic functions on
$\unicode[STIX]{x1D6E9}(1)$ is the space of automorphic functions on  $G_{D}$ obtained by averaging the functions in
$G_{D}$ obtained by averaging the functions in  $\unicode[STIX]{x1D6F1}$ over
$\unicode[STIX]{x1D6F1}$ over  $D^{1}(F)\backslash D^{1}(\mathbb{A})$. We prove that
$D^{1}(F)\backslash D^{1}(\mathbb{A})$. We prove that  $\unicode[STIX]{x1D6E9}(1)$ is an irreducible automorphic representation of
$\unicode[STIX]{x1D6E9}(1)$ is an irreducible automorphic representation of  $G_{D}$ and determine its local components (as abstract representations) by computing the corresponding local theta lifts. We have not computed the local theta lift for complex groups, and this is the source of the restriction in the paper to totally real fields
$G_{D}$ and determine its local components (as abstract representations) by computing the corresponding local theta lifts. We have not computed the local theta lift for complex groups, and this is the source of the restriction in the paper to totally real fields  $F$. The Siegel–Weil formula identifies the functions in
$F$. The Siegel–Weil formula identifies the functions in  $\unicode[STIX]{x1D6E9}(1)$ as residues of certain Siegel–Eisenstein series.
$\unicode[STIX]{x1D6E9}(1)$ as residues of certain Siegel–Eisenstein series.
More precisely, since  $G_{D}$ arises from
$G_{D}$ arises from  $J_{D}$ by the Koecher–Tits construction, it contains a maximal parabolic subgroup with abelian unipotent radical isomorphic to
$J_{D}$ by the Koecher–Tits construction, it contains a maximal parabolic subgroup with abelian unipotent radical isomorphic to  $J_{D}$. Let
$J_{D}$. Let  $E_{D}(s,f)$ be the degenerate Eisenstein series attached to this maximal parabolic subgroup, where
$E_{D}(s,f)$ be the degenerate Eisenstein series attached to this maximal parabolic subgroup, where  $s\in \mathbb{R}$ and
$s\in \mathbb{R}$ and  $f$ varies over all standard sections of the corresponding degenerate principal series representation
$f$ varies over all standard sections of the corresponding degenerate principal series representation  $I_{D}(s)$. In [Reference Hanzer and SavinHS20], it was proved that
$I_{D}(s)$. In [Reference Hanzer and SavinHS20], it was proved that  $E_{D}(s,f)$ has at most a simple pole at
$E_{D}(s,f)$ has at most a simple pole at  $s=1$, and the residual representation
$s=1$, and the residual representation
 $$\begin{eqnarray}{\mathcal{E}}_{D}:=\{\text{Res}_{s=1}E_{D}(s,f):f\in I_{D}(s)\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{D}:=\{\text{Res}_{s=1}E_{D}(s,f):f\in I_{D}(s)\}\end{eqnarray}$$ was completely determined. Our main result is the following Siegel–Weil identity in the space of automorphic forms of  $G_{D}$.
$G_{D}$.
Theorem 1.2. For fixed quaternion  $F$-algebra
$F$-algebra  $D$, we have:
$D$, we have:
 $$\begin{eqnarray}{\mathcal{E}}_{D}=\bigoplus _{i:D\rightarrow \mathbb{O}}\unicode[STIX]{x1D6E9}(1).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{D}=\bigoplus _{i:D\rightarrow \mathbb{O}}\unicode[STIX]{x1D6E9}(1).\end{eqnarray}$$ Here the sum is taken over all isomorphism classes of embeddings  $i:D\rightarrow \mathbb{O}$ into octonion algebras over
$i:D\rightarrow \mathbb{O}$ into octonion algebras over  $F$.
$F$.
We emphasize that  $D$ is fixed here but
$D$ is fixed here but  $\mathbb{O}$ varies. If
$\mathbb{O}$ varies. If  $D$ is split (i.e. a matrix algebra) then
$D$ is split (i.e. a matrix algebra) then  $\mathbb{O}$ is also split, and there is only one term on the right. In general, the number of summands on the right is equal to
$\mathbb{O}$ is also split, and there is only one term on the right. In general, the number of summands on the right is equal to  $2^{m}$, where
$2^{m}$, where  $m$ is the number of real places
$m$ is the number of real places  $v$ of
$v$ of  $F$ such that
$F$ such that  $D_{v}$ is a division algebra.
$D_{v}$ is a division algebra.
At this point, we need the result of Pollack [Reference PollackPol17]: there exists a quaternion algebra  $D$ such that the partial spin-
$D$ such that the partial spin- $L$-function
$L$-function  $L^{S}(\unicode[STIX]{x1D70B},s,\text{Spin})$ is given as an integral, over
$L^{S}(\unicode[STIX]{x1D70B},s,\text{Spin})$ is given as an integral, over  $\text{PGSp}_{6}$, of a function
$\text{PGSp}_{6}$, of a function  $h\in \unicode[STIX]{x1D70B}$ against the Eisenstein series
$h\in \unicode[STIX]{x1D70B}$ against the Eisenstein series  $E_{D}(s,f)$. Thus, if the
$E_{D}(s,f)$. Thus, if the  $L$-function has a pole at
$L$-function has a pole at  $s=1$, then the integral of
$s=1$, then the integral of  $h$ against the elements of
$h$ against the elements of  ${\mathcal{E}}_{D}$ is non-zero. The Siegel–Weil identity (i.e. Theorem 1.2) then implies that
${\mathcal{E}}_{D}$ is non-zero. The Siegel–Weil identity (i.e. Theorem 1.2) then implies that  $\unicode[STIX]{x1D70B}$ appears in the exceptional theta correspondence for the dual pair
$\unicode[STIX]{x1D70B}$ appears in the exceptional theta correspondence for the dual pair  $\text{Aut}(\mathbb{O})\times \text{PGSp}_{6}$, for some
$\text{Aut}(\mathbb{O})\times \text{PGSp}_{6}$, for some  $\mathbb{O}$ containing
$\mathbb{O}$ containing  $D$. Since this exceptional theta correspondence is known to be functorial for spherical representations (see [Reference Loke and SavinLS19] and [Reference Savin and WoodburySW15]), this completes the proof that
$D$. Since this exceptional theta correspondence is known to be functorial for spherical representations (see [Reference Loke and SavinLS19] and [Reference Savin and WoodburySW15]), this completes the proof that  $\unicode[STIX]{x1D70B}$ is a weak lift from a group of absolute type
$\unicode[STIX]{x1D70B}$ is a weak lift from a group of absolute type  $\mathbf{G}_{2}$.
$\mathbf{G}_{2}$.
2 Groups
2.1 Octonion algebra
Let  $F$ be a field of characteristic 0, and
$F$ be a field of characteristic 0, and  $D$ be a quaternion algebra over
$D$ be a quaternion algebra over  $F$. It is a four-dimensional associative and non-commutative algebra over
$F$. It is a four-dimensional associative and non-commutative algebra over  $F$ which comes equipped with a conjugation map
$F$ which comes equipped with a conjugation map  $x\mapsto \overline{x}$ with associated norm
$x\mapsto \overline{x}$ with associated norm  $N(x)=x\overline{x}=\overline{x}x$ and trace
$N(x)=x\overline{x}=\overline{x}x$ and trace  $\text{tr}(x)=x+\overline{x}$. Moreover,
$\text{tr}(x)=x+\overline{x}$. Moreover,  $N:D\rightarrow F$ is a non-degenerate quadratic form.
$N:D\rightarrow F$ is a non-degenerate quadratic form.
An octonion algebra  $\mathbb{O}$ over
$\mathbb{O}$ over  $F$ is obtained by doubling the quaternion algebra
$F$ is obtained by doubling the quaternion algebra  $D$. More precisely, fix a non-zero element
$D$. More precisely, fix a non-zero element  $\unicode[STIX]{x1D706}$ in
$\unicode[STIX]{x1D706}$ in  $F$. As a vector space over
$F$. As a vector space over  $F$,
$F$,  $\mathbb{O}$ is a set of pairs
$\mathbb{O}$ is a set of pairs  $(a,b)$ of elements in
$(a,b)$ of elements in  $D$. The multiplication is defined by the formula
$D$. The multiplication is defined by the formula
 $$\begin{eqnarray}(a,b)\cdot (c,d)=(ac+\unicode[STIX]{x1D706}d\bar{b},\bar{a}d+cb).\end{eqnarray}$$
$$\begin{eqnarray}(a,b)\cdot (c,d)=(ac+\unicode[STIX]{x1D706}d\bar{b},\bar{a}d+cb).\end{eqnarray}$$ If  $x=(a,b)$, then the conjugation map is
$x=(a,b)$, then the conjugation map is  $\bar{x}=(\bar{a},-b)$, so that
$\bar{x}=(\bar{a},-b)$, so that  $N(x)=x\cdot \bar{x}=N(a)-\unicode[STIX]{x1D706}N(b)$ is the norm and
$N(x)=x\cdot \bar{x}=N(a)-\unicode[STIX]{x1D706}N(b)$ is the norm and  $\text{tr}(x)=x+\bar{x}=\text{tr}(a)$ the trace on
$\text{tr}(x)=x+\bar{x}=\text{tr}(a)$ the trace on  $\mathbb{O}$. In particular,
$\mathbb{O}$. In particular,  $\mathbb{O}$ is split if
$\mathbb{O}$ is split if  $\unicode[STIX]{x1D706}$ is a norm of an element in
$\unicode[STIX]{x1D706}$ is a norm of an element in  $D$. Every element
$D$. Every element  $x$ of
$x$ of  $\mathbb{O}$ satisfies its characteristic polynomial
$\mathbb{O}$ satisfies its characteristic polynomial  $t^{2}-\text{tr}(x)t+N(x)$. The automorphism group
$t^{2}-\text{tr}(x)t+N(x)$. The automorphism group  $\text{Aut}(\mathbb{O})$ of the
$\text{Aut}(\mathbb{O})$ of the  $F$-algebra
$F$-algebra  $\mathbb{O}$ is an exceptional group of the Lie type
$\mathbb{O}$ is an exceptional group of the Lie type  $\mathbf{G}_{2}$. It is a simple linear algebraic group of rank 2 which is both simply connected and adjoint. The algebra
$\mathbf{G}_{2}$. It is a simple linear algebraic group of rank 2 which is both simply connected and adjoint. The algebra  $D$ is naturally a subalgebra of
$D$ is naturally a subalgebra of  $\mathbb{O}$, consisting of all
$\mathbb{O}$, consisting of all  $x=(a,0)$. Let
$x=(a,0)$. Let  $D^{1}$ be the group of norm-
$D^{1}$ be the group of norm- $1$ elements in
$1$ elements in  $D$. Then any
$D$. Then any  $g\in D^{1}$ acts as an automorphism of
$g\in D^{1}$ acts as an automorphism of  $\mathbb{O}$ by
$\mathbb{O}$ by  $g\cdot (a,b)=(a,b\bar{g})$ for all
$g\cdot (a,b)=(a,b\bar{g})$ for all  $(a,b)\in \mathbb{O}$. The subgroup
$(a,b)\in \mathbb{O}$. The subgroup  $D^{1}\subset \text{Aut}(\mathbb{O})$ is precisely the pointwise stabilizer of the subalgebra
$D^{1}\subset \text{Aut}(\mathbb{O})$ is precisely the pointwise stabilizer of the subalgebra  $D\subset \mathbb{O}$.
$D\subset \mathbb{O}$.
2.2 Albert algebra
An Albert algebra is an exceptional 27-dimensional Jordan algebra  $J$ over
$J$ over  $F$. It can be realized as the set of matrices
$F$. It can be realized as the set of matrices
 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC} & x & \bar{z}\\ \bar{x} & \unicode[STIX]{x1D6FD} & y\\ z & \bar{y} & \unicode[STIX]{x1D6FE}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC} & x & \bar{z}\\ \bar{x} & \unicode[STIX]{x1D6FD} & y\\ z & \bar{y} & \unicode[STIX]{x1D6FE}\end{array}\right),\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$ and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$ and  $x,y,z\in \mathbb{O}$. The determinant
$x,y,z\in \mathbb{O}$. The determinant  $A\mapsto \det A$ defines a natural cubic form on
$A\mapsto \det A$ defines a natural cubic form on  $J$. Let
$J$. Let  $M$ be the similitude group of this cubic form. It is a reductive group of semisimple type
$M$ be the similitude group of this cubic form. It is a reductive group of semisimple type  $E_{6}$. The
$E_{6}$. The  $M$-orbits in
$M$-orbits in  $J$ are classified by the rank of the matrix
$J$ are classified by the rank of the matrix  $A$. Without going into a general definition of the rank, we say that
$A$. Without going into a general definition of the rank, we say that  $A\neq 0$ has rank
$A\neq 0$ has rank  $1$ if
$1$ if  $A^{2}=\text{tr}(A)\cdot A$. Explicitly, this means that the entries of
$A^{2}=\text{tr}(A)\cdot A$. Explicitly, this means that the entries of  $A$ satisfy the equalities
$A$ satisfy the equalities
 $$\begin{eqnarray}N(x)=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\quad N(y)=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\quad N(z)=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FE}\bar{x}=yz,\quad \unicode[STIX]{x1D6FC}\bar{y}=zx,\quad \unicode[STIX]{x1D6FD}\bar{z}=xy.\end{eqnarray}$$
$$\begin{eqnarray}N(x)=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\quad N(y)=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE},\quad N(z)=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FE}\bar{x}=yz,\quad \unicode[STIX]{x1D6FC}\bar{y}=zx,\quad \unicode[STIX]{x1D6FD}\bar{z}=xy.\end{eqnarray}$$2.3 Dual pairs
Assume that  $G$ is a reductive group over
$G$ is a reductive group over  $F$, adjoint and of absolute type
$F$, adjoint and of absolute type  $E_{7}$, arising from the Albert algebra
$E_{7}$, arising from the Albert algebra  $J$ via the Koecher–Tits construction. For our purposes it will be more convenient to realize
$J$ via the Koecher–Tits construction. For our purposes it will be more convenient to realize  $G$ as a quotient, modulo one-dimensional center
$G$ as a quotient, modulo one-dimensional center  $C\cong F^{\times }$, of a reductive group
$C\cong F^{\times }$, of a reductive group  $\tilde{G}$ acting on the 56-dimensional representation
$\tilde{G}$ acting on the 56-dimensional representation  $W=F+J+J+F$. In particular,
$W=F+J+J+F$. In particular,  $G$ acts on the projective space
$G$ acts on the projective space  $\mathbb{P}(W)$. Let
$\mathbb{P}(W)$. Let  $P$ be a maximal parabolic and
$P$ be a maximal parabolic and  $\bar{P}$ its opposite, defined as fixing the points
$\bar{P}$ its opposite, defined as fixing the points  $(1,0,0,0)$ and
$(1,0,0,0)$ and  $(0,0,0,1)$ in
$(0,0,0,1)$ in  $\mathbb{P}(W)$. Then
$\mathbb{P}(W)$. Then  $P=MN$, where
$P=MN$, where  $N$ is the unipotent radical and
$N$ is the unipotent radical and  $M=P\cap \bar{P}$ a Levi subgroup. Then
$M=P\cap \bar{P}$ a Levi subgroup. Then  $M$ is isomorphic to the similitude group of the cubic form
$M$ is isomorphic to the similitude group of the cubic form  $\det$ on
$\det$ on  $J$, and
$J$, and  $N\cong J$, as
$N\cong J$, as  $M$-modules.
$M$-modules.
Recall that we have constructed  $\mathbb{O}$ by doubling a quaternion subalgebra
$\mathbb{O}$ by doubling a quaternion subalgebra  $D$. Let
$D$. Let  $J_{F}$ and
$J_{F}$ and  $J_{D}$ be the subalgebras consisting of all elements in
$J_{D}$ be the subalgebras consisting of all elements in  $J$ with off-diagonal entries in
$J$ with off-diagonal entries in  $F$ and
$F$ and  $D$, respectively. Let
$D$, respectively. Let  $J_{0}=F$ be the scalar subalgebra of
$J_{0}=F$ be the scalar subalgebra of  $J$. Consider a sequence of simple, simply connected groups
$J$. Consider a sequence of simple, simply connected groups
 $$\begin{eqnarray}D^{1}\subset \text{Aut}(\mathbb{O})\subset \text{Aut}(J),\end{eqnarray}$$
$$\begin{eqnarray}D^{1}\subset \text{Aut}(\mathbb{O})\subset \text{Aut}(J),\end{eqnarray}$$ where an element in  $\text{Aut}(\mathbb{O})$ acts on the off-diagonal entries of elements in
$\text{Aut}(\mathbb{O})$ acts on the off-diagonal entries of elements in  $J$. The pointwise stabilizers in
$J$. The pointwise stabilizers in  $J$ of these three groups are, respectively,
$J$ of these three groups are, respectively,
 $$\begin{eqnarray}J_{D}\supset J_{F}\supset J_{0}=F.\end{eqnarray}$$
$$\begin{eqnarray}J_{D}\supset J_{F}\supset J_{0}=F.\end{eqnarray}$$ Observe that  $\text{Aut}(J)$ naturally acts on
$\text{Aut}(J)$ naturally acts on  $W$, giving an embedding
$W$, giving an embedding  $\text{Aut}(J)\subset \tilde{G}$. The centralizers in
$\text{Aut}(J)\subset \tilde{G}$. The centralizers in  $\tilde{G}$ of the three groups in the sequence are, respectively,
$\tilde{G}$ of the three groups in the sequence are, respectively,
 $$\begin{eqnarray}\tilde{G}_{D}\supset \text{GSp}_{6}(F)\supset \text{GL}_{2}(F).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{G}_{D}\supset \text{GSp}_{6}(F)\supset \text{GL}_{2}(F).\end{eqnarray}$$ These three groups act on the 32-, 14- and four dimensional subspaces of  $W$ obtained by replacing
$W$ obtained by replacing  $J$ by
$J$ by  $J_{D}$,
$J_{D}$,  $J_{F}$ and
$J_{F}$ and  $J_{0}$, respectively. It is worth mentioning that the four-dimensional representation of
$J_{0}$, respectively. It is worth mentioning that the four-dimensional representation of  $\text{GL}_{2}(F)$ is the symmetric cube of the standard two-dimensional representation, twisted by
$\text{GL}_{2}(F)$ is the symmetric cube of the standard two-dimensional representation, twisted by  $\det ^{-1}$. The group
$\det ^{-1}$. The group  $\tilde{G}_{D}$ acts on
$\tilde{G}_{D}$ acts on
 $$\begin{eqnarray}W_{D}=F+J_{D}+J_{D}+F.\end{eqnarray}$$
$$\begin{eqnarray}W_{D}=F+J_{D}+J_{D}+F.\end{eqnarray}$$ It is worth noting that the action of  $\tilde{G}_{D}$ on
$\tilde{G}_{D}$ on  $W_{D}$ is not faithful (it has
$W_{D}$ is not faithful (it has  $\unicode[STIX]{x1D707}_{2}\subset D^{1}$ as its kernel). A detailed description of
$\unicode[STIX]{x1D707}_{2}\subset D^{1}$ as its kernel). A detailed description of  $\tilde{G}_{D}/\unicode[STIX]{x1D707}_{2}$ and its action on
$\tilde{G}_{D}/\unicode[STIX]{x1D707}_{2}$ and its action on  $W_{D}$ can be found in Pollack’s paper [Reference PollackPol17]. Let
$W_{D}$ can be found in Pollack’s paper [Reference PollackPol17]. Let  $G_{D}$ be the quotient of
$G_{D}$ be the quotient of  $\tilde{G}_{D}$ by the center
$\tilde{G}_{D}$ by the center  $C\cong F^{\times }$ of
$C\cong F^{\times }$ of  $\tilde{G}$. Then
$\tilde{G}$. Then  $D^{1}\times G_{D}$ is a dual pair in
$D^{1}\times G_{D}$ is a dual pair in  $G$, as mentioned in the introduction.
$G$, as mentioned in the introduction.
Let  $P_{D}=M_{D}N_{D}=G_{D}\cap P$. With the identification
$P_{D}=M_{D}N_{D}=G_{D}\cap P$. With the identification  $N\cong J$ fixed, we have
$N\cong J$ fixed, we have  $N_{D}\cong J_{D}$. The group
$N_{D}\cong J_{D}$. The group  $P_{D}$ is a maximal parabolic subgroup of type
$P_{D}$ is a maximal parabolic subgroup of type  $\mathbf{A}_{5}$.
$\mathbf{A}_{5}$.
3 Minimal representation
Let  $F$ be a real or
$F$ be a real or  $p$-adic field. Let
$p$-adic field. Let  $I(s)$ be the degenerate principal series representation of
$I(s)$ be the degenerate principal series representation of  $G$ attached to
$G$ attached to  $P$, where
$P$, where  $s\in \mathbb{R}$. We normalize
$s\in \mathbb{R}$. We normalize  $s$ as in [Reference WeissmanWei03] so that the trivial representation is a quotient and a submodule at
$s$ as in [Reference WeissmanWei03] so that the trivial representation is a quotient and a submodule at  $s=9$ and
$s=9$ and  $s=-9$ respectively, whereas the minimal representation
$s=-9$ respectively, whereas the minimal representation  $\unicode[STIX]{x1D6F1}$ is a quotient and a submodule at
$\unicode[STIX]{x1D6F1}$ is a quotient and a submodule at  $s=5$ and
$s=5$ and  $s=-5$, respectively. Note, however, that the group
$s=-5$, respectively. Note, however, that the group  $G$ is simply connected in [Reference WeissmanWei03], whereas our
$G$ is simply connected in [Reference WeissmanWei03], whereas our  $G$ is adjoint here.
$G$ is adjoint here.
3.1 Unitary model
Fix  $\unicode[STIX]{x1D713}:F\rightarrow \mathbb{C}^{\times }$, a non-trivial additive character, unitary if
$\unicode[STIX]{x1D713}:F\rightarrow \mathbb{C}^{\times }$, a non-trivial additive character, unitary if  $F=\mathbb{R}$. After identifying
$F=\mathbb{R}$. After identifying  $N\cong J$ and
$N\cong J$ and  $\bar{N}\cong J$ (note that the resulting actions of
$\bar{N}\cong J$ (note that the resulting actions of  $M$ on
$M$ on  $J$ are dual to each other), any
$J$ are dual to each other), any  $A\in J\cong \bar{N}$ defines a character of
$A\in J\cong \bar{N}$ defines a character of  $N$ given by
$N$ given by
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{A}(B)=\unicode[STIX]{x1D713}(\text{tr}(A\circ B))=\unicode[STIX]{x1D713}_{B}(A)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{A}(B)=\unicode[STIX]{x1D713}(\text{tr}(A\circ B))=\unicode[STIX]{x1D713}_{B}(A)\end{eqnarray}$$ for  $B\in J\cong N$, where
$B\in J\cong N$, where  $A\circ B$ denotes the Jordan multiplication. Every unitary character of
$A\circ B$ denotes the Jordan multiplication. Every unitary character of  $N$ is equal to
$N$ is equal to  $\unicode[STIX]{x1D713}_{A}$ for some
$\unicode[STIX]{x1D713}_{A}$ for some  $A$. Let
$A$. Let  $\unicode[STIX]{x1D6FA}\subseteq J\cong \bar{N}$ be the set of rank-
$\unicode[STIX]{x1D6FA}\subseteq J\cong \bar{N}$ be the set of rank- $1$ elements in
$1$ elements in  $J$. A unitary model of the minimal representation is
$J$. A unitary model of the minimal representation is  ${\mathcal{H}}=L^{2}(\unicode[STIX]{x1D6FA})$ [Reference SahiSah92]. Here only the action of the maximal parabolic
${\mathcal{H}}=L^{2}(\unicode[STIX]{x1D6FA})$ [Reference SahiSah92]. Here only the action of the maximal parabolic  $P=MN$ is obvious: the group
$P=MN$ is obvious: the group  $M$ acts geometrically,
$M$ acts geometrically,
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(m)(f)(A)=\unicode[STIX]{x1D712}(m)f(m^{-1}A),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(m)(f)(A)=\unicode[STIX]{x1D712}(m)f(m^{-1}A),\end{eqnarray}$$ for  $f\in \unicode[STIX]{x1D6F1}$ and for some character
$f\in \unicode[STIX]{x1D6F1}$ and for some character  $\unicode[STIX]{x1D712}:M\rightarrow \mathbb{R}^{\times }$, while
$\unicode[STIX]{x1D712}:M\rightarrow \mathbb{R}^{\times }$, while  $B\in J\cong N$ acts on
$B\in J\cong N$ acts on  $f$ by multiplying it by
$f$ by multiplying it by  $\unicode[STIX]{x1D713}_{B}$.
$\unicode[STIX]{x1D713}_{B}$.
3.2 Smooth model
We have the following theorem [Reference Kobayashi and SavinKS15].
Theorem 3.1. Let  $\unicode[STIX]{x1D6F1}$ be the subspace of
$\unicode[STIX]{x1D6F1}$ be the subspace of  $G$-smooth vectors in the unitary minimal representation
$G$-smooth vectors in the unitary minimal representation  ${\mathcal{H}}$. Then
${\mathcal{H}}$. Then
 $$\begin{eqnarray}C_{c}^{\infty }(\unicode[STIX]{x1D6FA})\subset \unicode[STIX]{x1D6F1}\subset C^{\infty }(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
$$\begin{eqnarray}C_{c}^{\infty }(\unicode[STIX]{x1D6FA})\subset \unicode[STIX]{x1D6F1}\subset C^{\infty }(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$ If  $F$ is
$F$ is  $p$-adic, then
$p$-adic, then
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{N}\cong \unicode[STIX]{x1D6F1}/C_{c}^{\infty }(\unicode[STIX]{x1D6FA})\quad \text{as }M\text{-modules}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{N}\cong \unicode[STIX]{x1D6F1}/C_{c}^{\infty }(\unicode[STIX]{x1D6FA})\quad \text{as }M\text{-modules}.\end{eqnarray}$$ If  $A\in J$ is non-zero, then any continuous functional
$A\in J$ is non-zero, then any continuous functional  $\ell$ on
$\ell$ on  $\unicode[STIX]{x1D6F1}$ such that
$\unicode[STIX]{x1D6F1}$ such that  $\ell (B\cdot f)=\unicode[STIX]{x1D713}_{A}(B)\cdot \ell (f)$ for all
$\ell (B\cdot f)=\unicode[STIX]{x1D713}_{A}(B)\cdot \ell (f)$ for all  $B\in N$ and
$B\in N$ and  $f\in \unicode[STIX]{x1D6F1}$ is equal to a multiple of the evaluation map
$f\in \unicode[STIX]{x1D6F1}$ is equal to a multiple of the evaluation map  $\unicode[STIX]{x1D6FF}_{A}(f)=f(A)$. In particular,
$\unicode[STIX]{x1D6FF}_{A}(f)=f(A)$. In particular,  $\ell =0$ if
$\ell =0$ if  $A$ is not of rank
$A$ is not of rank  $1$.
$1$.
3.3 Spherical vector
It is not so easy to characterize the subspace  $\unicode[STIX]{x1D6F1}\subset C^{\infty }(\unicode[STIX]{x1D6FA})$. However, we can describe a spherical vector in
$\unicode[STIX]{x1D6F1}\subset C^{\infty }(\unicode[STIX]{x1D6FA})$. However, we can describe a spherical vector in  $\unicode[STIX]{x1D6F1}$ in the split case. The algebra
$\unicode[STIX]{x1D6F1}$ in the split case. The algebra  $\mathbb{O}$ is obtained by doubling the matrix algebra
$\mathbb{O}$ is obtained by doubling the matrix algebra  $D=M_{2}(F)$ with
$D=M_{2}(F)$ with  $\unicode[STIX]{x1D706}=1$. Assume firstly that
$\unicode[STIX]{x1D706}=1$. Assume firstly that  $F$ is a
$F$ is a  $p$-adic field. Let
$p$-adic field. Let  $O$ be the ring of integers in
$O$ be the ring of integers in  $F$ and
$F$ and  $\unicode[STIX]{x1D71B}$ a uniformizing element. We have an obvious integral structure on
$\unicode[STIX]{x1D71B}$ a uniformizing element. We have an obvious integral structure on  $D$ (the lattice of integral matrices), and hence on
$D$ (the lattice of integral matrices), and hence on  $\mathbb{O}$, the integral lattice being the set of pairs
$\mathbb{O}$, the integral lattice being the set of pairs  $(a,b)$ where
$(a,b)$ where  $a,b\in M_{2}(O)$. This lattice is a maximal order in
$a,b\in M_{2}(O)$. This lattice is a maximal order in  $\mathbb{O}$. Now we have an integral structure on
$\mathbb{O}$. Now we have an integral structure on  $J$ so that
$J$ so that  $J(O)$ is the set of elements
$J(O)$ is the set of elements  $A\in J$ such that the diagonal entries are integral, and the off-diagonal entries are contained in the maximal order in
$A\in J$ such that the diagonal entries are integral, and the off-diagonal entries are contained in the maximal order in  $\mathbb{O}$. The greatest common divisor (GCD) of entries of
$\mathbb{O}$. The greatest common divisor (GCD) of entries of  $A\in J(O)$ is simply the largest power
$A\in J(O)$ is simply the largest power  $\unicode[STIX]{x1D71B}^{n}$ dividing
$\unicode[STIX]{x1D71B}^{n}$ dividing  $A$, that is, such that
$A$, that is, such that  $A/\unicode[STIX]{x1D71B}^{n}$ is in
$A/\unicode[STIX]{x1D71B}^{n}$ is in  $J(O)$. We have the following theorem [Reference Savin and WoodburySW07].
$J(O)$. We have the following theorem [Reference Savin and WoodburySW07].
Theorem 3.2. Assume that  $G$ is split and
$G$ is split and  $F$ a
$F$ a  $p$-adic field. Assume the conductor of
$p$-adic field. Assume the conductor of  $\unicode[STIX]{x1D713}$ is
$\unicode[STIX]{x1D713}$ is  $O$. Then the spherical vector in
$O$. Then the spherical vector in  $\unicode[STIX]{x1D6F1}$ is a function
$\unicode[STIX]{x1D6F1}$ is a function  $f^{\circ }\in C^{\infty }(\unicode[STIX]{x1D6FA})$ supported in
$f^{\circ }\in C^{\infty }(\unicode[STIX]{x1D6FA})$ supported in  $J(O)$. Its value at
$J(O)$. Its value at  $A\in \unicode[STIX]{x1D6FA}$ depends on the GCD of entries of
$A\in \unicode[STIX]{x1D6FA}$ depends on the GCD of entries of  $A$. More precisely, if the GCD of the entries of
$A$. More precisely, if the GCD of the entries of  $A$ is
$A$ is  $\unicode[STIX]{x1D71B}^{n}$, and
$\unicode[STIX]{x1D71B}^{n}$, and  $q$ is the order of the residual field, then
$q$ is the order of the residual field, then
 $$\begin{eqnarray}f^{\circ }(A)=1+q^{3}+\cdots +q^{3n}.\end{eqnarray}$$
$$\begin{eqnarray}f^{\circ }(A)=1+q^{3}+\cdots +q^{3n}.\end{eqnarray}$$ Since  $\unicode[STIX]{x1D6F1}$ is generated by
$\unicode[STIX]{x1D6F1}$ is generated by  $f^{\circ }$ as a
$f^{\circ }$ as a  $P$-module, and the action of
$P$-module, and the action of  $P$ on
$P$ on  $\unicode[STIX]{x1D6F1}$ is easy to describe, this theorem gives us a good handle on
$\unicode[STIX]{x1D6F1}$ is easy to describe, this theorem gives us a good handle on  $\unicode[STIX]{x1D6F1}$.
$\unicode[STIX]{x1D6F1}$.
Assume now that  $F=\mathbb{R}$; in this case, one has a similar result due to Dvorsky and Sahi [Reference Dvorsky and SahiDS99]. For every
$F=\mathbb{R}$; in this case, one has a similar result due to Dvorsky and Sahi [Reference Dvorsky and SahiDS99]. For every  $a\in M_{2}(\mathbb{R})$, let
$a\in M_{2}(\mathbb{R})$, let  $\Vert a\Vert ^{2}$ be the sum of squares of its entries. For
$\Vert a\Vert ^{2}$ be the sum of squares of its entries. For  $x=(a,b)\in \mathbb{O}$, let
$x=(a,b)\in \mathbb{O}$, let  $\Vert x\Vert ^{2}=\Vert a\Vert ^{2}+\Vert b\Vert ^{2}$. Extend this to
$\Vert x\Vert ^{2}=\Vert a\Vert ^{2}+\Vert b\Vert ^{2}$. Extend this to  $A\in J$ by
$A\in J$ by
 $$\begin{eqnarray}\Vert A\Vert ^{2}=\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}+\unicode[STIX]{x1D6FE}^{2}+\Vert x\Vert ^{2}+\Vert y\Vert ^{2}+\Vert z\Vert ^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert A\Vert ^{2}=\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}+\unicode[STIX]{x1D6FE}^{2}+\Vert x\Vert ^{2}+\Vert y\Vert ^{2}+\Vert z\Vert ^{2}.\end{eqnarray}$$ Let  $K_{3/2}(u)$ denote the modified Bessel function of the second kind. Recall that
$K_{3/2}(u)$ denote the modified Bessel function of the second kind. Recall that  $K_{3/2}(u)$ is greater than 0, for
$K_{3/2}(u)$ is greater than 0, for  $u>0$, and rapidly decreasing as
$u>0$, and rapidly decreasing as  $u\rightarrow +\infty$. Then we have the following result [Reference Dvorsky and SahiDS99, Theorem 0.1].
$u\rightarrow +\infty$. Then we have the following result [Reference Dvorsky and SahiDS99, Theorem 0.1].
Theorem 3.3. Assume that  $G$ is split and
$G$ is split and  $F=\mathbb{R}$. Then the spherical vector in
$F=\mathbb{R}$. Then the spherical vector in  $\unicode[STIX]{x1D6F1}$ is a function
$\unicode[STIX]{x1D6F1}$ is a function  $f^{\circ }\in C^{\infty }(\unicode[STIX]{x1D6FA})$ given by
$f^{\circ }\in C^{\infty }(\unicode[STIX]{x1D6FA})$ given by
 $$\begin{eqnarray}f^{\circ }(A)=\Vert A\Vert ^{-3/2}K_{3/2}(\Vert A\Vert ).\end{eqnarray}$$
$$\begin{eqnarray}f^{\circ }(A)=\Vert A\Vert ^{-3/2}K_{3/2}(\Vert A\Vert ).\end{eqnarray}$$4 Local theta lifts:  $p$-adic case
$p$-adic case
In this section let  $F$ be a
$F$ be a  $p$-adic field, so that the octonion algebra
$p$-adic field, so that the octonion algebra  $\mathbb{O}$ is split. We are interested in understanding the theta lift of the trivial representation of
$\mathbb{O}$ is split. We are interested in understanding the theta lift of the trivial representation of  $D^{1}$ to the group
$D^{1}$ to the group  $G_{D}$.
$G_{D}$.
4.1  $N_{D}$-spectrum
$N_{D}$-spectrum
A crucial step is to understand the  $N_{D}$-spectrum of the minimal representation
$N_{D}$-spectrum of the minimal representation  $\unicode[STIX]{x1D6F1}$. In this case we have an exact sequence of
$\unicode[STIX]{x1D6F1}$. In this case we have an exact sequence of  $P$-modules
$P$-modules
 $$\begin{eqnarray}0\rightarrow C_{c}^{\infty }(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x1D6F1}\rightarrow \unicode[STIX]{x1D6F1}_{N}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow C_{c}^{\infty }(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x1D6F1}\rightarrow \unicode[STIX]{x1D6F1}_{N}\rightarrow 0.\end{eqnarray}$$ The characters of  $N_{D}\cong J_{D}$ are identified with the elements in
$N_{D}\cong J_{D}$ are identified with the elements in  $J_{D}$ using the trace paring, as we did for
$J_{D}$ using the trace paring, as we did for  $J$. We shall only need three characters, denoted by
$J$. We shall only need three characters, denoted by  $\unicode[STIX]{x1D713}_{1}$,
$\unicode[STIX]{x1D713}_{1}$,  $\unicode[STIX]{x1D713}_{2}$ and
$\unicode[STIX]{x1D713}_{2}$ and  $\unicode[STIX]{x1D713}_{3}$, corresponding to the elements
$\unicode[STIX]{x1D713}_{3}$, corresponding to the elements
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\pm 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right),\quad \left(\begin{array}{@{}ccc@{}}\pm 1 & 0 & 0\\ 0 & \pm 1 & 0\\ 0 & 0 & 0\end{array}\right)\quad \text{and}\quad \left(\begin{array}{@{}ccc@{}}\pm 1 & 0 & 0\\ 0 & \pm 1 & 0\\ 0 & 0 & \pm 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\pm 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right),\quad \left(\begin{array}{@{}ccc@{}}\pm 1 & 0 & 0\\ 0 & \pm 1 & 0\\ 0 & 0 & 0\end{array}\right)\quad \text{and}\quad \left(\begin{array}{@{}ccc@{}}\pm 1 & 0 & 0\\ 0 & \pm 1 & 0\\ 0 & 0 & \pm 1\end{array}\right)\end{eqnarray}$$ of rank 1, 2 and 3, respectively. We need to allow signs to capture all possible orbits of rank 1, 2 and 3 in the real case. The following lemma is one of the key ingredients in this paper, and we emphasize that we do not assume that  $D$ is split here.
$D$ is split here.
Lemma 4.1. Let  $\unicode[STIX]{x1D6F1}$ be the minimal representation of
$\unicode[STIX]{x1D6F1}$ be the minimal representation of  $G$. Then:
$G$. Then:
(i)
 $\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{3}}=0$;
$\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{3}}=0$;(ii)
 $\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{2}}\cong C_{c}^{\infty }(D^{1})$, as
$\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{2}}\cong C_{c}^{\infty }(D^{1})$, as  $D^{1}$-modules;
$D^{1}$-modules;(iii) if
 $D$ is a division algebra, then
$D$ is a division algebra, then  $\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{1}}\cong \mathbb{C}$, as
$\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{1}}\cong \mathbb{C}$, as  $D^{1}$-modules.
$D^{1}$-modules.
Proof. Let  $\unicode[STIX]{x1D714}_{i}\subseteq \unicode[STIX]{x1D6FA}$ be the set of all
$\unicode[STIX]{x1D714}_{i}\subseteq \unicode[STIX]{x1D6FA}$ be the set of all  $A\in \unicode[STIX]{x1D6FA}$ such that the restriction of
$A\in \unicode[STIX]{x1D6FA}$ such that the restriction of  $\unicode[STIX]{x1D713}_{A}$ to
$\unicode[STIX]{x1D713}_{A}$ to  $N_{D}$ is equal to
$N_{D}$ is equal to  $\unicode[STIX]{x1D713}_{i}$. Because
$\unicode[STIX]{x1D713}_{i}$. Because  $\unicode[STIX]{x1D713}_{i}$ is not the trivial character, the set
$\unicode[STIX]{x1D713}_{i}$ is not the trivial character, the set  $\unicode[STIX]{x1D714}_{i}$ is (Zariski) closed in
$\unicode[STIX]{x1D714}_{i}$ is (Zariski) closed in  $\unicode[STIX]{x1D6FA}$. Hence,
$\unicode[STIX]{x1D6FA}$. Hence,
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{i}}\cong C_{c}^{\infty }(\unicode[STIX]{x1D714}_{i}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{N_{D},\unicode[STIX]{x1D713}_{i}}\cong C_{c}^{\infty }(\unicode[STIX]{x1D714}_{i}).\end{eqnarray}$$ It remains to determine each  $\unicode[STIX]{x1D714}_{i}$. Let us start with
$\unicode[STIX]{x1D714}_{i}$. Let us start with  $i=3$. Then
$i=3$. Then  $\unicode[STIX]{x1D714}_{3}$ consists of all
$\unicode[STIX]{x1D714}_{3}$ consists of all  $A\in \unicode[STIX]{x1D6FA}$ such that
$A\in \unicode[STIX]{x1D6FA}$ such that
 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}\pm 1 & x & -z\\ -x & \pm 1 & y\\ z & -y & \pm 1\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}\pm 1 & x & -z\\ -x & \pm 1 & y\\ z & -y & \pm 1\end{array}\right),\end{eqnarray}$$ where  $x=(0,a),y=(0,b)$ and
$x=(0,a),y=(0,b)$ and  $z=(0,c)$ for some
$z=(0,c)$ for some  $a,b,c\in D$. Since
$a,b,c\in D$. Since  $A\in \unicode[STIX]{x1D6FA}$, we further have
$A\in \unicode[STIX]{x1D6FA}$, we further have  $A^{2}=\text{tr}(A)A$. Looking at the off-diagonal terms, we get the equations
$A^{2}=\text{tr}(A)A$. Looking at the off-diagonal terms, we get the equations
 $$\begin{eqnarray}yx=\pm z,\quad zy=\pm x\quad \text{and}\quad xz=\pm y.\end{eqnarray}$$
$$\begin{eqnarray}yx=\pm z,\quad zy=\pm x\quad \text{and}\quad xz=\pm y.\end{eqnarray}$$ But the products  $yx$,
$yx$,  $zy$ and
$zy$ and  $xz$ have the second coordinate equal to 0. Hence
$xz$ have the second coordinate equal to 0. Hence  $z=x=y=0$. But then
$z=x=y=0$. But then  $A$ cannot be a rank-
$A$ cannot be a rank- $1$ matrix. Hence
$1$ matrix. Hence  $\unicode[STIX]{x1D714}_{3}$ is empty, and this proves (i).
$\unicode[STIX]{x1D714}_{3}$ is empty, and this proves (i).
For (ii) we see analogously that  $y=z=0$. Now
$y=z=0$. Now  $A$ has rank 1 if and only if the first
$A$ has rank 1 if and only if the first  $2\times 2$ minor is 0. This gives
$2\times 2$ minor is 0. This gives  $x^{2}=\pm 1$. Writing this out, with
$x^{2}=\pm 1$. Writing this out, with  $x=(0,a)$ we see that
$x=(0,a)$ we see that  $\unicode[STIX]{x1D706}a\bar{a}=\pm 1$. Hence
$\unicode[STIX]{x1D706}a\bar{a}=\pm 1$. Hence  $\unicode[STIX]{x1D714}_{2}$ is identified with the set of all elements in
$\unicode[STIX]{x1D714}_{2}$ is identified with the set of all elements in  $D$ with a fixed non-zero norm. This is a principal homogeneous space for
$D$ with a fixed non-zero norm. This is a principal homogeneous space for  $D^{1}$. This establishes (ii). In the last case it is easy to see that
$D^{1}$. This establishes (ii). In the last case it is easy to see that  $x=y=z=0$.◻
$x=y=z=0$.◻
We now derive a consequence. Let  $\unicode[STIX]{x1D6E9}(1)$ be the maximal quotient of
$\unicode[STIX]{x1D6E9}(1)$ be the maximal quotient of  $\unicode[STIX]{x1D6F1}$ on which
$\unicode[STIX]{x1D6F1}$ on which  $D^{1}$ acts trivially; it is naturally a
$D^{1}$ acts trivially; it is naturally a  $G_{D}$-module. Lemma 4.1 implies that
$G_{D}$-module. Lemma 4.1 implies that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(1)_{N_{D},\unicode[STIX]{x1D713}_{3}}=0\quad \text{and}\quad \unicode[STIX]{x1D6E9}(1)_{N_{D},\unicode[STIX]{x1D713}_{2}}=\mathbb{C}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(1)_{N_{D},\unicode[STIX]{x1D713}_{3}}=0\quad \text{and}\quad \unicode[STIX]{x1D6E9}(1)_{N_{D},\unicode[STIX]{x1D713}_{2}}=\mathbb{C}.\end{eqnarray}$$ Let  $I_{D}(s)$ be the degenerate principal series representation of
$I_{D}(s)$ be the degenerate principal series representation of  $G_{D}$ attached to
$G_{D}$ attached to  $P_{D}$ normalized as in [Reference WeissmanWei03]. In particular, the trivial representation is a quotient for
$P_{D}$ normalized as in [Reference WeissmanWei03]. In particular, the trivial representation is a quotient for  $s=5$ and a submodule for
$s=5$ and a submodule for  $s=-5$. The inclusion
$s=-5$. The inclusion  $\unicode[STIX]{x1D6F1}\rightarrow I(-5)$ composed with the restriction of functions from
$\unicode[STIX]{x1D6F1}\rightarrow I(-5)$ composed with the restriction of functions from  $G$ to
$G$ to  $G_{D}$ gives a non-zero
$G_{D}$ gives a non-zero  $D^{1}$-invariant map
$D^{1}$-invariant map  $\unicode[STIX]{x1D6F1}\rightarrow I_{D}(-1)$, which clearly factors through
$\unicode[STIX]{x1D6F1}\rightarrow I_{D}(-1)$, which clearly factors through  $\unicode[STIX]{x1D6E9}(1)$. By [Reference WeissmanWei03] and [Reference Hanzer and SavinHS20],
$\unicode[STIX]{x1D6E9}(1)$. By [Reference WeissmanWei03] and [Reference Hanzer and SavinHS20],  $I_{D}(-1)$ has a composition series of length 2. The unique irreducible submodule
$I_{D}(-1)$ has a composition series of length 2. The unique irreducible submodule  $\unicode[STIX]{x1D6F4}$ has
$\unicode[STIX]{x1D6F4}$ has  $N_{D}$-rank 2. We have the following corollary.
$N_{D}$-rank 2. We have the following corollary.
Corollary 4.2. The above construction gives a surjective  $G_{D}$-equivariant map
$G_{D}$-equivariant map
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(1)\rightarrow \unicode[STIX]{x1D6F4}\subset I_{D}(-1)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(1)\rightarrow \unicode[STIX]{x1D6F4}\subset I_{D}(-1)\end{eqnarray}$$ whose kernel has  $N_{D}$-rank no greater than
$N_{D}$-rank no greater than  $1$. If
$1$. If  $D$ is a division algebra, then
$D$ is a division algebra, then  $\unicode[STIX]{x1D6E9}(1)\cong \unicode[STIX]{x1D6F4}$.
$\unicode[STIX]{x1D6E9}(1)\cong \unicode[STIX]{x1D6F4}$.
Proof. It remains to prove the last statement. The spherical, rank- $2$ representation
$2$ representation  $\unicode[STIX]{x1D6F4}$ is the classical theta lift of the trivial representation of the quaternionic form of
$\unicode[STIX]{x1D6F4}$ is the classical theta lift of the trivial representation of the quaternionic form of  $\text{Sp}(4)$ [Reference YamanaYam11]. Using the theta correspondence, it is easy to check that
$\text{Sp}(4)$ [Reference YamanaYam11]. Using the theta correspondence, it is easy to check that  $\unicode[STIX]{x1D6F4}_{N_{D},\unicode[STIX]{x1D713}_{1}}\cong \mathbb{C}$. Thus, from Lemma 4.1(iii) it follows that the kernel of the map
$\unicode[STIX]{x1D6F4}_{N_{D},\unicode[STIX]{x1D713}_{1}}\cong \mathbb{C}$. Thus, from Lemma 4.1(iii) it follows that the kernel of the map  $\unicode[STIX]{x1D6E9}(1)\rightarrow \unicode[STIX]{x1D6F4}$ has
$\unicode[STIX]{x1D6E9}(1)\rightarrow \unicode[STIX]{x1D6F4}$ has  $N_{D}$-rank 0, that is,
$N_{D}$-rank 0, that is,  $N_{D}$ acts trivially. Since
$N_{D}$ acts trivially. Since  $D^{1}$ is compact,
$D^{1}$ is compact,  $\unicode[STIX]{x1D6E9}(1)$ is a summand of the minimal representation. By the classical result of Howe and Moore the minimal representation cannot contain non-zero vectors fixed by
$\unicode[STIX]{x1D6E9}(1)$ is a summand of the minimal representation. By the classical result of Howe and Moore the minimal representation cannot contain non-zero vectors fixed by  $N_{D}$. Thus the kernel is trivial.◻
$N_{D}$. Thus the kernel is trivial.◻
4.2 Local lifts for split  $D$
$D$
We shall strengthen here the result of Corollary 4.2 by showing that  $\unicode[STIX]{x1D6E9}(1)\cong \unicode[STIX]{x1D6F4}$ even when
$\unicode[STIX]{x1D6E9}(1)\cong \unicode[STIX]{x1D6F4}$ even when  $D$ is split, in which case
$D$ is split, in which case  $G$ is also split.
$G$ is also split.
Let  $T\subset G$ be a maximal split torus, so we have the associated root groups. Furthermore,
$T\subset G$ be a maximal split torus, so we have the associated root groups. Furthermore,  $D^{1}\cong \text{SL}_{2}$ and it is conjugated to a root
$D^{1}\cong \text{SL}_{2}$ and it is conjugated to a root  $\text{SL}_{2}$. Without loss of generality, we can assume that
$\text{SL}_{2}$. Without loss of generality, we can assume that  $\text{SL}_{2}$ corresponds to the highest root for some choice of positive roots. Let
$\text{SL}_{2}$ corresponds to the highest root for some choice of positive roots. Let  $T_{1}=\text{SL}_{2}\cap T$. Then the centralizer of
$T_{1}=\text{SL}_{2}\cap T$. Then the centralizer of  $T_{1}$ in
$T_{1}$ in  $G$ is a Levi subgroup
$G$ is a Levi subgroup  $L$ of semisimple type
$L$ of semisimple type  $\mathbf{D}_{6}$. The Levi subgroup
$\mathbf{D}_{6}$. The Levi subgroup  $L$ is contained in two maximal parabolic subgroups:
$L$ is contained in two maximal parabolic subgroups:  $Q=LU$ and its opposite
$Q=LU$ and its opposite  $\bar{Q}=L\bar{U}$. The unipotent radical
$\bar{Q}=L\bar{U}$. The unipotent radical  $U$ is a two-step unipotent group with the center
$U$ is a two-step unipotent group with the center  $U_{1}$ given by the root group corresponding to the highest root. Similarly, the center of
$U_{1}$ given by the root group corresponding to the highest root. Similarly, the center of  $\bar{U}$ is the root subgroup
$\bar{U}$ is the root subgroup  $\bar{U}_{1}$ corresponding to the lowest root. These two root groups
$\bar{U}_{1}$ corresponding to the lowest root. These two root groups  $U_{1}$ and
$U_{1}$ and  $\bar{U}_{1}$ generate
$\bar{U}_{1}$ generate  $\text{SL}_{2}$. We identify
$\text{SL}_{2}$. We identify  $T_{1}\cong \text{GL}_{1}$ so that
$T_{1}\cong \text{GL}_{1}$ so that  $x\in \text{GL}_{1}$ acts on
$x\in \text{GL}_{1}$ acts on  $U/U_{1}$ as multiplication by
$U/U_{1}$ as multiplication by  $x$.
$x$.
The conjugation action of  $L$ on
$L$ on  $U_{1}$ and
$U_{1}$ and  $\bar{U}_{1}$ is given by a character and its inverse; this character is given by
$\bar{U}_{1}$ is given by a character and its inverse; this character is given by  $x\mapsto x^{2}$ when restricted to
$x\mapsto x^{2}$ when restricted to  $T_{1}\subset L$. Hence
$T_{1}\subset L$. Hence  $G_{D}$ is the kernel of this character, which is the derived group of
$G_{D}$ is the kernel of this character, which is the derived group of  $L$. Since
$L$. Since  $G$ is of adjoint type,
$G$ is of adjoint type,  $G_{D}$ acts faithfully on
$G_{D}$ acts faithfully on  $U/U_{1}$ (a 32-dimensional spin representation). Note that the representation
$U/U_{1}$ (a 32-dimensional spin representation). Note that the representation  $U/U_{1}$ is not
$U/U_{1}$ is not  $W_{D}$, the 32-dimensional representation of
$W_{D}$, the 32-dimensional representation of  $\tilde{G}_{D}$, from § 2.3.
$\tilde{G}_{D}$, from § 2.3.
More precisely, recall that the center of  $\text{Spin}_{12}$ can be identified with
$\text{Spin}_{12}$ can be identified with  $\unicode[STIX]{x1D707}_{2}\times \unicode[STIX]{x1D707}_{2}$ in such a way that the outer automorphism exchanges the two
$\unicode[STIX]{x1D707}_{2}\times \unicode[STIX]{x1D707}_{2}$ in such a way that the outer automorphism exchanges the two  $\unicode[STIX]{x1D707}_{2}$, and fixes the diagonal
$\unicode[STIX]{x1D707}_{2}$, and fixes the diagonal  $\unicode[STIX]{x1D707}_{2}^{\unicode[STIX]{x1D6E5}}$. The quotient of
$\unicode[STIX]{x1D707}_{2}^{\unicode[STIX]{x1D6E5}}$. The quotient of  $\text{Spin}_{12}$ by
$\text{Spin}_{12}$ by  $\unicode[STIX]{x1D707}_{2}^{\unicode[STIX]{x1D6E5}}$ is the special orthogonal group
$\unicode[STIX]{x1D707}_{2}^{\unicode[STIX]{x1D6E5}}$ is the special orthogonal group  $\text{SO}_{12}$. On the other hand, the quotient of
$\text{SO}_{12}$. On the other hand, the quotient of  $\text{Spin}_{12}$ by
$\text{Spin}_{12}$ by  $\unicode[STIX]{x1D707}_{2}=\unicode[STIX]{x1D707}_{2}\times \{1\}$ and that by
$\unicode[STIX]{x1D707}_{2}=\unicode[STIX]{x1D707}_{2}\times \{1\}$ and that by  $\unicode[STIX]{x1D707}_{2}^{\prime }=\{1\}\times \unicode[STIX]{x1D707}_{2}$ are isomorphic (being isomorphic via the outer automorphism). Then one has
$\unicode[STIX]{x1D707}_{2}^{\prime }=\{1\}\times \unicode[STIX]{x1D707}_{2}$ are isomorphic (being isomorphic via the outer automorphism). Then one has
 $$\begin{eqnarray}G_{D}\cong \text{Spin}_{12}/\unicode[STIX]{x1D707}_{2}\quad \text{and}\quad L\cong T_{1}\times _{\unicode[STIX]{x1D707}_{2}}G_{D}\cong \text{GL}_{1}\times _{\unicode[STIX]{x1D707}_{2}^{\prime }}(\text{Spin}_{12}/\unicode[STIX]{x1D707}_{2}),\end{eqnarray}$$
$$\begin{eqnarray}G_{D}\cong \text{Spin}_{12}/\unicode[STIX]{x1D707}_{2}\quad \text{and}\quad L\cong T_{1}\times _{\unicode[STIX]{x1D707}_{2}}G_{D}\cong \text{GL}_{1}\times _{\unicode[STIX]{x1D707}_{2}^{\prime }}(\text{Spin}_{12}/\unicode[STIX]{x1D707}_{2}),\end{eqnarray}$$ so that  $L$ has connected center. On the other hand, the group
$L$ has connected center. On the other hand, the group  $\tilde{G}_{D}$ from § 2.3 is given by
$\tilde{G}_{D}$ from § 2.3 is given by
 $$\begin{eqnarray}\tilde{G}_{D}\cong \text{GL}_{1}\times _{\unicode[STIX]{x1D707}_{2}}\text{Spin}_{12}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{G}_{D}\cong \text{GL}_{1}\times _{\unicode[STIX]{x1D707}_{2}}\text{Spin}_{12}.\end{eqnarray}$$ As we mentioned in § 2.3, the action of  $\tilde{G}_{D}$ on
$\tilde{G}_{D}$ on  $W_{D}$ is not faithful.
$W_{D}$ is not faithful.
We now need a result on the restriction of  $\unicode[STIX]{x1D6F1}$ to the maximal parabolic subgroup
$\unicode[STIX]{x1D6F1}$ to the maximal parabolic subgroup  $Q=LU$. By [Reference Magaard and SavinMS97, Theorem 6.1], the space of
$Q=LU$. By [Reference Magaard and SavinMS97, Theorem 6.1], the space of  $U_{1}$-coinvariants of
$U_{1}$-coinvariants of  $\unicode[STIX]{x1D6F1}$, an
$\unicode[STIX]{x1D6F1}$, an  $L$-module, sits in an exact sequence
$L$-module, sits in an exact sequence
 $$\begin{eqnarray}0\rightarrow C_{c}^{\infty }(\unicode[STIX]{x1D714})\rightarrow \unicode[STIX]{x1D6F1}_{U_{1}}\rightarrow \unicode[STIX]{x1D6F1}_{U}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow C_{c}^{\infty }(\unicode[STIX]{x1D714})\rightarrow \unicode[STIX]{x1D6F1}_{U_{1}}\rightarrow \unicode[STIX]{x1D6F1}_{U}\rightarrow 0,\end{eqnarray}$$ where  $\unicode[STIX]{x1D714}$ is the
$\unicode[STIX]{x1D714}$ is the  $L$-orbit of highest weight vectors in
$L$-orbit of highest weight vectors in  $\bar{U}/\bar{U}_{1}$. The action of
$\bar{U}/\bar{U}_{1}$. The action of  $L$ on
$L$ on  $C_{c}^{\infty }(\unicode[STIX]{x1D714})$ arises from the natural action of
$C_{c}^{\infty }(\unicode[STIX]{x1D714})$ arises from the natural action of  $L$ on
$L$ on  $\unicode[STIX]{x1D714}$ twisted by an unramified character.
$\unicode[STIX]{x1D714}$ twisted by an unramified character.
Let  $Q_{D}=L_{D}U_{D}$ be a maximal parabolic subgroup in
$Q_{D}=L_{D}U_{D}$ be a maximal parabolic subgroup in  $G_{D}$ stabilizing the line through a point
$G_{D}$ stabilizing the line through a point  $v\in \unicode[STIX]{x1D714}$. Note that the Levi factor
$v\in \unicode[STIX]{x1D714}$. Note that the Levi factor  $L_{D}$ of
$L_{D}$ of  $Q_{D}$ is also of type
$Q_{D}$ is also of type  $\mathbf{A}_{5}$ (like that of
$\mathbf{A}_{5}$ (like that of  $P_{D}$). The action of
$P_{D}$). The action of  $Q_{D}$ on the line gives a homomorphism
$Q_{D}$ on the line gives a homomorphism  $\unicode[STIX]{x1D712}:Q_{D}\rightarrow \text{GL}_{1}$. Thus the stabilizer in
$\unicode[STIX]{x1D712}:Q_{D}\rightarrow \text{GL}_{1}$. Thus the stabilizer in  $G_{D}\times \text{GL}_{1}$ of
$G_{D}\times \text{GL}_{1}$ of  $v$ consists of all pairs
$v$ consists of all pairs  $(g,x)$ such that
$(g,x)$ such that  $g\in Q_{D}$ and
$g\in Q_{D}$ and  $\unicode[STIX]{x1D712}(g)=x$. Since
$\unicode[STIX]{x1D712}(g)=x$. Since  $G_{D}\times \text{GL}_{1}$ acts transitively on
$G_{D}\times \text{GL}_{1}$ acts transitively on  $\unicode[STIX]{x1D714}$, it is easy to see that the following theorem holds.
$\unicode[STIX]{x1D714}$, it is easy to see that the following theorem holds.
Theorem 4.3. The normalized Jacquet functor  $\unicode[STIX]{x1D6F1}_{U_{1}}$, as a
$\unicode[STIX]{x1D6F1}_{U_{1}}$, as a  $G_{D}\times \text{GL}_{1}$-module, has a two-step filtration with the following quotient and submodule, respectively:
$G_{D}\times \text{GL}_{1}$-module, has a two-step filtration with the following quotient and submodule, respectively:
∙
 $\unicode[STIX]{x1D6F1}_{U}=\unicode[STIX]{x1D6F1}(G_{D})\otimes |\cdot |^{2}\oplus |\cdot |^{3}$, where
$\unicode[STIX]{x1D6F1}_{U}=\unicode[STIX]{x1D6F1}(G_{D})\otimes |\cdot |^{2}\oplus |\cdot |^{3}$, where  $\unicode[STIX]{x1D6F1}(G_{D})$ is the minimal representation of
$\unicode[STIX]{x1D6F1}(G_{D})$ is the minimal representation of  $G_{D}$, and
$G_{D}$, and  $|\cdot |$ is the absolute value character of
$|\cdot |$ is the absolute value character of  $\text{GL}_{1}$;
$\text{GL}_{1}$;∙
 $\text{Ind}_{Q_{D}}^{G_{D}}C_{c}^{\infty }(\text{GL}_{1})$, where
$\text{Ind}_{Q_{D}}^{G_{D}}C_{c}^{\infty }(\text{GL}_{1})$, where  $C_{c}^{\infty }(\text{GL}_{1})$ is the regular representation of
$C_{c}^{\infty }(\text{GL}_{1})$ is the regular representation of  $\text{GL}_{1}$ (and the induction is normalized).
$\text{GL}_{1}$ (and the induction is normalized).
Now we can prove the following result which strengthens Corollary 4.2 and which is needed later.
Proposition 4.4. Assume that we are in the  $p$-adic case with
$p$-adic case with  $D$ split. Then
$D$ split. Then  $\unicode[STIX]{x1D6E9}(1)$ is irreducible and isomorphic to
$\unicode[STIX]{x1D6E9}(1)$ is irreducible and isomorphic to  $\unicode[STIX]{x1D6F4}$, the representation of
$\unicode[STIX]{x1D6F4}$, the representation of  $G_{D}$ of
$G_{D}$ of  $N_{D}$-rank
$N_{D}$-rank  $2$ that appears as the unique irreducible quotient of
$2$ that appears as the unique irreducible quotient of  $I_{D}(1)$.
$I_{D}(1)$.
Proof. Let  $\unicode[STIX]{x1D70B}$ be an irreducible representation of
$\unicode[STIX]{x1D70B}$ be an irreducible representation of  $\text{SL}_{2}$ and
$\text{SL}_{2}$ and  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ the corresponding big theta lift. We first note that
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ the corresponding big theta lift. We first note that  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ is always non-trivial, as a simple consequence of Lemma 4.1. Moreover,
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ is always non-trivial, as a simple consequence of Lemma 4.1. Moreover,  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is isomorphic to
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is isomorphic to  $\unicode[STIX]{x1D70B}^{\vee }$, so that it is infinite-dimensional if and only if
$\unicode[STIX]{x1D70B}^{\vee }$, so that it is infinite-dimensional if and only if  $\unicode[STIX]{x1D70B}$ is.
$\unicode[STIX]{x1D70B}$ is.
Let  $J(s)$ be the principal series for
$J(s)$ be the principal series for  $\text{SL}_{2}$ normalized so that the trivial representation is a quotient for
$\text{SL}_{2}$ normalized so that the trivial representation is a quotient for  $s=1$ and a submodule for
$s=1$ and a submodule for  $s=-1$. Likewise, let
$s=-1$. Likewise, let  $J_{D}(s)$ denote the degenerate principal series associated to
$J_{D}(s)$ denote the degenerate principal series associated to  $Q_{D}$, normalized so that the trivial representation occurs at
$Q_{D}$, normalized so that the trivial representation occurs at  $J_{D}(\pm 5)$.
$J_{D}(\pm 5)$.
If  $-s\neq 2,3$, then Theorem 4.3 implies by way of the Frobenius reciprocity that
$-s\neq 2,3$, then Theorem 4.3 implies by way of the Frobenius reciprocity that
 $$\begin{eqnarray}\text{Hom}(\unicode[STIX]{x1D6E9}(J(-s)),\mathbb{C})\cong \text{Hom}_{\text{SL}_{2}}(\unicode[STIX]{x1D6F1},J(-s))\cong \text{Hom}(J_{D}(s),\mathbb{C})\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}(\unicode[STIX]{x1D6E9}(J(-s)),\mathbb{C})\cong \text{Hom}_{\text{SL}_{2}}(\unicode[STIX]{x1D6F1},J(-s))\cong \text{Hom}(J_{D}(s),\mathbb{C})\end{eqnarray}$$ as  $G_{D}$-modules. For generic
$G_{D}$-modules. For generic  $s$, both
$s$, both  $J(-s)$ and
$J(-s)$ and  $J_{D}(s)$ are irreducible and the above identity implies that
$J_{D}(s)$ are irreducible and the above identity implies that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(J(-s))\cong J_{D}(s)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(J(-s))\cong J_{D}(s)\end{eqnarray}$$ for such  $s$. It follows from Lemma 4.1 that
$s$. It follows from Lemma 4.1 that  $J_{D}(s)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is infinite-dimensional for such
$J_{D}(s)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is infinite-dimensional for such  $s$. However, since the restriction of
$s$. However, since the restriction of  $J_{D}(s)$ to
$J_{D}(s)$ to  $N_{D}$ is independent of
$N_{D}$ is independent of  $s$, it follows that
$s$, it follows that  $J_{D}(s)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is in fact infinite-dimensional for all
$J_{D}(s)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is in fact infinite-dimensional for all  $s$.
$s$.
Now if  $\unicode[STIX]{x1D70B}$ is a submodule of
$\unicode[STIX]{x1D70B}$ is a submodule of  $J(-s)$ with
$J(-s)$ with  $-s\neq 2,3$, then it follows that
$-s\neq 2,3$, then it follows that
 $$\begin{eqnarray}\text{Hom}(\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B}),\mathbb{C})\cong \text{Hom}_{\text{SL}_{2}}(\unicode[STIX]{x1D6F1},\unicode[STIX]{x1D70B})\subset \text{Hom}_{\text{SL}_{2}}(\unicode[STIX]{x1D6F1},J(-s))\cong \text{Hom}(J_{D}(s),\mathbb{C}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}(\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B}),\mathbb{C})\cong \text{Hom}_{\text{SL}_{2}}(\unicode[STIX]{x1D6F1},\unicode[STIX]{x1D70B})\subset \text{Hom}_{\text{SL}_{2}}(\unicode[STIX]{x1D6F1},J(-s))\cong \text{Hom}(J_{D}(s),\mathbb{C}),\end{eqnarray}$$ so that  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ is a quotient of
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ is a quotient of  $J_{D}(s)$. In particular, for
$J_{D}(s)$. In particular, for  $\unicode[STIX]{x1D70B}=1$ the trivial representation, we may take
$\unicode[STIX]{x1D70B}=1$ the trivial representation, we may take  $s=1$ to deduce that
$s=1$ to deduce that  $\unicode[STIX]{x1D6E9}(1)$ is a quotient of
$\unicode[STIX]{x1D6E9}(1)$ is a quotient of  $J_{D}(1)$. Since we know that
$J_{D}(1)$. Since we know that  $\unicode[STIX]{x1D6E9}(1)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is one-dimensional whereas
$\unicode[STIX]{x1D6E9}(1)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is one-dimensional whereas  $J_{D}(1)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is infinite-dimensional, we conclude that
$J_{D}(1)_{N_{D},\unicode[STIX]{x1D713}_{2}}$ is infinite-dimensional, we conclude that  $\unicode[STIX]{x1D6E9}(1)$ is isomorphic to the unique irreducible quotient of
$\unicode[STIX]{x1D6E9}(1)$ is isomorphic to the unique irreducible quotient of  $J_{D}(1)$ which has
$J_{D}(1)$ which has  $N_{D}$-rank 2. In particular,
$N_{D}$-rank 2. In particular,  $\unicode[STIX]{x1D6E9}(1)$ is irreducible and isomorphic to
$\unicode[STIX]{x1D6E9}(1)$ is irreducible and isomorphic to  $\unicode[STIX]{x1D6F4}$, the unique quotient of
$\unicode[STIX]{x1D6F4}$, the unique quotient of  $I_{D}(1)$.◻
$I_{D}(1)$.◻
As a side remark, the representations  $J_{D}(s)$ have
$J_{D}(s)$ have  $U_{D}$-rank 3. However, since
$U_{D}$-rank 3. However, since  $\unicode[STIX]{x1D6F1}$ has
$\unicode[STIX]{x1D6F1}$ has  $N_{D}$-rank 2, it follows that the two parabolic subgroups
$N_{D}$-rank 2, it follows that the two parabolic subgroups  $P_{D}$ and
$P_{D}$ and  $Q_{D}$ are not conjugate in
$Q_{D}$ are not conjugate in  $G_{D}$. But the two principal series
$G_{D}$. But the two principal series  $I_{D}(s)$ and
$I_{D}(s)$ and  $J_{D}(s)$ share all small-rank subquotients – the trivial representation, the minimal representation and the rank-2 representation
$J_{D}(s)$ share all small-rank subquotients – the trivial representation, the minimal representation and the rank-2 representation  $\unicode[STIX]{x1D6F4}$ – as the above argument shows.
$\unicode[STIX]{x1D6F4}$ – as the above argument shows.
5 Global lifting
Assume now that  $F$ is a global field, with its local completions denoted by
$F$ is a global field, with its local completions denoted by  $F_{v}$, and let
$F_{v}$, and let  $\mathbb{A}$ be the ring of adèles over
$\mathbb{A}$ be the ring of adèles over  $F$.
$F$.
5.1 Global theta lifting
Let  $\unicode[STIX]{x1D6F1}=\otimes \unicode[STIX]{x1D6F1}_{v}$ be the restricted tensor product of minimal representations over all local places
$\unicode[STIX]{x1D6F1}=\otimes \unicode[STIX]{x1D6F1}_{v}$ be the restricted tensor product of minimal representations over all local places  $v$ of
$v$ of  $F$, where
$F$, where  $\unicode[STIX]{x1D6F1}_{v}\subset C^{\infty }(\unicode[STIX]{x1D6FA}_{v})$, as in Theorem 3.1. Every element in
$\unicode[STIX]{x1D6F1}_{v}\subset C^{\infty }(\unicode[STIX]{x1D6FA}_{v})$, as in Theorem 3.1. Every element in  $\unicode[STIX]{x1D6F1}$ is a finite linear combination of pure tensors
$\unicode[STIX]{x1D6F1}$ is a finite linear combination of pure tensors  $f=\otimes f_{v}$, where
$f=\otimes f_{v}$, where  $f_{v}=f_{v}^{\circ }$ for almost all places
$f_{v}=f_{v}^{\circ }$ for almost all places  $v$. There is a unique (up to a non-zero scalar) embedding
$v$. There is a unique (up to a non-zero scalar) embedding  $\unicode[STIX]{x1D703}:\unicode[STIX]{x1D6F1}\rightarrow {\mathcal{A}}(G(F)\backslash G(\mathbb{A}))$ of
$\unicode[STIX]{x1D703}:\unicode[STIX]{x1D6F1}\rightarrow {\mathcal{A}}(G(F)\backslash G(\mathbb{A}))$ of  $\unicode[STIX]{x1D6F1}$ into the space of automorphic functions of uniform moderate growth.
$\unicode[STIX]{x1D6F1}$ into the space of automorphic functions of uniform moderate growth.
We restrict  $\unicode[STIX]{x1D703}(f)$ to the dual pair
$\unicode[STIX]{x1D703}(f)$ to the dual pair  $D^{1}\times G_{D}$ and, for every
$D^{1}\times G_{D}$ and, for every  $h\in {\mathcal{A}}(D^{1}(F)\backslash D^{1}(\mathbb{A}))$, consider the function
$h\in {\mathcal{A}}(D^{1}(F)\backslash D^{1}(\mathbb{A}))$, consider the function  $\unicode[STIX]{x1D6E9}(f,h)$ on
$\unicode[STIX]{x1D6E9}(f,h)$ on  $G_{D}$ defined by
$G_{D}$ defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)(g_{D})=\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(g_{D}g)\cdot \bar{h}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)(g_{D})=\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(g_{D}g)\cdot \bar{h}(g)\,dg.\end{eqnarray}$$ If this is to be of any use, we require the function  $\unicode[STIX]{x1D703}(f)(g_{D}g)\cdot \bar{h}(g)$ to be of rapid decay on
$\unicode[STIX]{x1D703}(f)(g_{D}g)\cdot \bar{h}(g)$ to be of rapid decay on  $D^{1}(F)\backslash D^{1}(\mathbb{A})$ and of moderate growth on
$D^{1}(F)\backslash D^{1}(\mathbb{A})$ and of moderate growth on  $G_{D}(F)\backslash G_{D}(\mathbb{A})$. This condition is clearly satisfied if
$G_{D}(F)\backslash G_{D}(\mathbb{A})$. This condition is clearly satisfied if  $D^{1}$ is anisotropic or if
$D^{1}$ is anisotropic or if  $h$ is a cusp form. It is also satisfied for a regularized theta lift, to be constructed in the next section. Namely, for any finite place
$h$ is a cusp form. It is also satisfied for a regularized theta lift, to be constructed in the next section. Namely, for any finite place  $v$, we will construct an element
$v$, we will construct an element  $z$ in the Bernstein center of
$z$ in the Bernstein center of  $\text{SL}_{2}(F_{v})$, such that for any
$\text{SL}_{2}(F_{v})$, such that for any  $f\in \unicode[STIX]{x1D6F1}$, the function
$f\in \unicode[STIX]{x1D6F1}$, the function  $\unicode[STIX]{x1D703}(z\cdot f)(g_{1}g)$ is of rapid decay on
$\unicode[STIX]{x1D703}(z\cdot f)(g_{1}g)$ is of rapid decay on  $D^{1}(F)\backslash D^{1}(\mathbb{A})$ and of moderate growth on
$D^{1}(F)\backslash D^{1}(\mathbb{A})$ and of moderate growth on  $G_{D}(F)\backslash G_{D}(\mathbb{A})$. (See Proposition 6.1, and the discussion of this particular dual pair thereafter.) In particular, in all these cases, the following integral is convergent:
$G_{D}(F)\backslash G_{D}(\mathbb{A})$. (See Proposition 6.1, and the discussion of this particular dual pair thereafter.) In particular, in all these cases, the following integral is convergent:
 $$\begin{eqnarray}\int _{N_{D}(F)\backslash N_{D}(\mathbb{A})}\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}|\unicode[STIX]{x1D703}(z\cdot f)(ng)\cdot \bar{h}(g)|\,dg\,dn.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{D}(F)\backslash N_{D}(\mathbb{A})}\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}|\unicode[STIX]{x1D703}(z\cdot f)(ng)\cdot \bar{h}(g)|\,dg\,dn.\end{eqnarray}$$5.2 Fourier expansion
Let  $\unicode[STIX]{x1D713}:\mathbb{A}/F\rightarrow \mathbb{C}^{\times }$ be a non-trivial character. Then any
$\unicode[STIX]{x1D713}:\mathbb{A}/F\rightarrow \mathbb{C}^{\times }$ be a non-trivial character. Then any  $A\in J(F)$ defines a character
$A\in J(F)$ defines a character  $\unicode[STIX]{x1D713}_{A}$ of
$\unicode[STIX]{x1D713}_{A}$ of  $N(F)\backslash N(\mathbb{A})$ by
$N(F)\backslash N(\mathbb{A})$ by  $\unicode[STIX]{x1D713}_{A}(B)=\unicode[STIX]{x1D713}(\text{tr}(A\circ B))$ for all
$\unicode[STIX]{x1D713}_{A}(B)=\unicode[STIX]{x1D713}(\text{tr}(A\circ B))$ for all  $B\in N(\mathbb{A})\cong J(\mathbb{A})$. For every
$B\in N(\mathbb{A})\cong J(\mathbb{A})$. For every  $\unicode[STIX]{x1D711}\in {\mathcal{A}}(G(F)\backslash G(\mathbb{A}))$, let
$\unicode[STIX]{x1D711}\in {\mathcal{A}}(G(F)\backslash G(\mathbb{A}))$, let
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{A}(g)=\int _{N(F)\backslash N(\mathbb{A})}\unicode[STIX]{x1D711}(ng)\cdot \overline{\unicode[STIX]{x1D713}_{A}(n)}\,dn\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{A}(g)=\int _{N(F)\backslash N(\mathbb{A})}\unicode[STIX]{x1D711}(ng)\cdot \overline{\unicode[STIX]{x1D713}_{A}(n)}\,dn\end{eqnarray}$$ be the Fourier coefficient corresponding to  $A$. We have a Fourier expansion
$A$. We have a Fourier expansion
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(f)(g)=\unicode[STIX]{x1D703}(f)_{0}(g)+\mathop{\sum }_{A\in \unicode[STIX]{x1D6FA}(F)}\unicode[STIX]{x1D703}(f)_{A}(g).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(f)(g)=\unicode[STIX]{x1D703}(f)_{0}(g)+\mathop{\sum }_{A\in \unicode[STIX]{x1D6FA}(F)}\unicode[STIX]{x1D703}(f)_{A}(g).\end{eqnarray}$$ By uniqueness of local functionals (Theorem 3.1), for every  $A\in \unicode[STIX]{x1D6FA}(F)$ there exists a non-zero scalar
$A\in \unicode[STIX]{x1D6FA}(F)$ there exists a non-zero scalar  $c_{A}$ such that
$c_{A}$ such that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(f)_{A}(g)=c_{A}\mathop{\prod }_{v}(g_{v}\cdot f_{v})(A).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(f)_{A}(g)=c_{A}\mathop{\prod }_{v}(g_{v}\cdot f_{v})(A).\end{eqnarray}$$ This formula is particularly useful if  $g_{v}\in M(F_{v})$, for then
$g_{v}\in M(F_{v})$, for then  $(g_{v}\cdot f_{v})(A)=\unicode[STIX]{x1D712}_{v}(g_{v})\cdot f_{v}(g_{v}^{-1}\cdot A)$ for the character
$(g_{v}\cdot f_{v})(A)=\unicode[STIX]{x1D712}_{v}(g_{v})\cdot f_{v}(g_{v}^{-1}\cdot A)$ for the character  $\unicode[STIX]{x1D712}_{v}$ of
$\unicode[STIX]{x1D712}_{v}$ of  $M(F_{v})$.
$M(F_{v})$.
Let  $\unicode[STIX]{x1D713}_{2}$ and
$\unicode[STIX]{x1D713}_{2}$ and  $\unicode[STIX]{x1D713}_{3}$ be the rank-2 and rank-3 characters of
$\unicode[STIX]{x1D713}_{3}$ be the rank-2 and rank-3 characters of  $N_{D}(\mathbb{A})$, as in the local case. Recall that
$N_{D}(\mathbb{A})$, as in the local case. Recall that  $x\in \mathbb{O}$ is a pair
$x\in \mathbb{O}$ is a pair  $x=(y,z)$ of elements in
$x=(y,z)$ of elements in  $D$, and
$D$, and  $N(x)=N(y)-\unicode[STIX]{x1D706}N(z)$ for some
$N(x)=N(y)-\unicode[STIX]{x1D706}N(z)$ for some  $\unicode[STIX]{x1D706}\in F^{\times }$. Let
$\unicode[STIX]{x1D706}\in F^{\times }$. Let  $\unicode[STIX]{x1D711}_{N_{D},\unicode[STIX]{x1D713}_{i}}$ denote the global Fourier coefficient with respect to these two characters. Let
$\unicode[STIX]{x1D711}_{N_{D},\unicode[STIX]{x1D713}_{i}}$ denote the global Fourier coefficient with respect to these two characters. Let  $\unicode[STIX]{x1D714}_{2}(F)$ be the set of all rank-
$\unicode[STIX]{x1D714}_{2}(F)$ be the set of all rank- $1$ matrices
$1$ matrices
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\pm 1 & x & 0\\ -x & \pm 1 & 0\\ 0 & 0 & 0\end{array}\right)\in J(F)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\pm 1 & x & 0\\ -x & \pm 1 & 0\\ 0 & 0 & 0\end{array}\right)\in J(F)\end{eqnarray}$$ such that  $x=(0,a)$ and
$x=(0,a)$ and  $\unicode[STIX]{x1D706}N(a)=\pm 1$ (for only one choice of sign, depending on
$\unicode[STIX]{x1D706}N(a)=\pm 1$ (for only one choice of sign, depending on  $\unicode[STIX]{x1D713}_{2}$), that is, the
$\unicode[STIX]{x1D713}_{2}$), that is, the  $2\times 2$ minor is 0. Then we have a global version of Lemma 4.1.
$2\times 2$ minor is 0. Then we have a global version of Lemma 4.1.
Lemma 5.1. For every  $f\in \unicode[STIX]{x1D6F1}$,
$f\in \unicode[STIX]{x1D6F1}$,  $\unicode[STIX]{x1D703}(f)_{N_{D},\unicode[STIX]{x1D713}_{3}}=0$ and
$\unicode[STIX]{x1D703}(f)_{N_{D},\unicode[STIX]{x1D713}_{3}}=0$ and
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(f)_{N_{D},\unicode[STIX]{x1D713}_{2}}(g)=\mathop{\sum }_{B\in \unicode[STIX]{x1D714}_{2}(F)}\unicode[STIX]{x1D703}(f)_{B}(g).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(f)_{N_{D},\unicode[STIX]{x1D713}_{2}}(g)=\mathop{\sum }_{B\in \unicode[STIX]{x1D714}_{2}(F)}\unicode[STIX]{x1D703}(f)_{B}(g).\end{eqnarray}$$5.3 Non-vanishing of the theta lift
We shall prove non-vanishing of the (regularized) theta lift by computing the Fourier coefficient
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{N_{D}(F)\backslash N_{D}(\mathbb{A})}\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(ng)\cdot \bar{h}(g)\cdot \bar{\unicode[STIX]{x1D713}}_{2}(n)\,dg\,dn.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{N_{D}(F)\backslash N_{D}(\mathbb{A})}\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(ng)\cdot \bar{h}(g)\cdot \bar{\unicode[STIX]{x1D713}}_{2}(n)\,dg\,dn.\end{eqnarray}$$Since this integral is absolutely convergent, we can reverse the order of integration. Then, using Lemma 5.1, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\mathop{\sum }_{B\in \unicode[STIX]{x1D714}_{2}(F)}\unicode[STIX]{x1D703}(f)_{B}(g)\cdot \bar{h}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\mathop{\sum }_{B\in \unicode[STIX]{x1D714}_{2}(F)}\unicode[STIX]{x1D703}(f)_{B}(g)\cdot \bar{h}(g)\,dg.\end{eqnarray}$$Lemma 5.2. Fix
 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}\pm 1 & x & 0\\ -x & \pm 1 & 0\\ 0 & 0 & 0\end{array}\right)\in \unicode[STIX]{x1D714}_{2}(F),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}\pm 1 & x & 0\\ -x & \pm 1 & 0\\ 0 & 0 & 0\end{array}\right)\in \unicode[STIX]{x1D714}_{2}(F),\end{eqnarray}$$ where  $x=(0,a)$,
$x=(0,a)$,  $a\in D$ satisfies
$a\in D$ satisfies  $\unicode[STIX]{x1D706}N(a)=\pm 1$.
$\unicode[STIX]{x1D706}N(a)=\pm 1$.
For every automorphic form  $h$ and every
$h$ and every  $f\in \unicode[STIX]{x1D6F1}$ we have
$f\in \unicode[STIX]{x1D6F1}$ we have
 $$\begin{eqnarray}\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\mathop{\sum }_{B\in \unicode[STIX]{x1D714}_{2}(F)}\unicode[STIX]{x1D703}(f)_{B}(g)\bar{h}(g)\,dg=c_{A}\int _{D^{1}(\mathbb{A})}f(g^{-1}A)\bar{h}(g)\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\mathop{\sum }_{B\in \unicode[STIX]{x1D714}_{2}(F)}\unicode[STIX]{x1D703}(f)_{B}(g)\bar{h}(g)\,dg=c_{A}\int _{D^{1}(\mathbb{A})}f(g^{-1}A)\bar{h}(g)\,dg,\end{eqnarray}$$where the second integral is absolutely convergent.
Proof. Since  $\unicode[STIX]{x1D714}_{2}(F)$ is a principal homogeneous
$\unicode[STIX]{x1D714}_{2}(F)$ is a principal homogeneous  $D^{1}(F)$-space, the identity formally follows by unfolding the left-hand side and using the formula for
$D^{1}(F)$-space, the identity formally follows by unfolding the left-hand side and using the formula for  $\unicode[STIX]{x1D703}(f)_{A}(g)$ as a product of local functionals given above. Hence it remains to discuss the issue of absolute convergence.
$\unicode[STIX]{x1D703}(f)_{A}(g)$ as a product of local functionals given above. Hence it remains to discuss the issue of absolute convergence.
We may assume that  $f=\bigotimes _{v}f_{v}$ is a pure tensor. For each place
$f=\bigotimes _{v}f_{v}$ is a pure tensor. For each place  $v$, observe that if
$v$, observe that if  $g\in \text{SL}_{2}(F_{v})$, then
$g\in \text{SL}_{2}(F_{v})$, then  $g^{-1}A$ is obtained from
$g^{-1}A$ is obtained from  $A$ by replacing
$A$ by replacing  $x$ by
$x$ by  $xg$. Hence,
$xg$. Hence,  $g\mapsto g^{-1}A$ gives a closed embedding of
$g\mapsto g^{-1}A$ gives a closed embedding of  $\text{SL}_{2}(F_{v})$ into
$\text{SL}_{2}(F_{v})$ into  $J(F_{v})$, with image contained in
$J(F_{v})$, with image contained in  $\unicode[STIX]{x1D6FA}_{v}$. In particular, this image is bounded away from the vertex 0 of the cone
$\unicode[STIX]{x1D6FA}_{v}$. In particular, this image is bounded away from the vertex 0 of the cone  $\unicode[STIX]{x1D6FA}_{v}$. Since
$\unicode[STIX]{x1D6FA}_{v}$. Since  $h$ is of moderate growth on
$h$ is of moderate growth on  $\text{SL}_{2}(F_{v})$, to show that the integral in question is absolutely convergent, we need to show that
$\text{SL}_{2}(F_{v})$, to show that the integral in question is absolutely convergent, we need to show that  $g\mapsto f_{v}(g^{-1}A)$ is a Schwartz function on
$g\mapsto f_{v}(g^{-1}A)$ is a Schwartz function on  $\text{SL}_{2}(F_{v})$. For this, it suffices to show that as a function on the cone
$\text{SL}_{2}(F_{v})$. For this, it suffices to show that as a function on the cone  $\unicode[STIX]{x1D6FA}_{v}$,
$\unicode[STIX]{x1D6FA}_{v}$,  $f_{v}$ is rapidly decreasing toward infinity, as we shall explain below.
$f_{v}$ is rapidly decreasing toward infinity, as we shall explain below.
In greater detail, assume first that  $v$ is a finite place. Due to
$v$ is a finite place. Due to  $N_{v}$-smoothness,
$N_{v}$-smoothness,  $f_{v}\in \unicode[STIX]{x1D6F1}_{v}$ is supported on a lattice in
$f_{v}\in \unicode[STIX]{x1D6F1}_{v}$ is supported on a lattice in  $J_{v}$ (and thus vanishes toward infinity). It follows that
$J_{v}$ (and thus vanishes toward infinity). It follows that  $g\mapsto f_{v}(g^{-1}A)$ is a compactly supported function on
$g\mapsto f_{v}(g^{-1}A)$ is a compactly supported function on  $\text{SL}_{2}(F_{v})$. Moreover, let
$\text{SL}_{2}(F_{v})$. Moreover, let  $S$ be a finite set of places containing all archimedean places such that for
$S$ be a finite set of places containing all archimedean places such that for  $v\notin S$, all data is unramified:
$v\notin S$, all data is unramified:  $D(F_{v})$ is split,
$D(F_{v})$ is split,  $\unicode[STIX]{x1D706}\in O_{v}^{\times }$,
$\unicode[STIX]{x1D706}\in O_{v}^{\times }$,  $a\in \text{GL}_{2}(O_{v})$,
$a\in \text{GL}_{2}(O_{v})$,  $\unicode[STIX]{x1D713}_{v}$ has the conductor
$\unicode[STIX]{x1D713}_{v}$ has the conductor  $O_{v}$,
$O_{v}$,  $f_{v}=f_{v}^{\circ }$, and
$f_{v}=f_{v}^{\circ }$, and  $h$ is right
$h$ is right  $\text{SL}_{2}(O_{v})$-invariant. Here
$\text{SL}_{2}(O_{v})$-invariant. Here  $O_{v}$ is the maximal order in
$O_{v}$ is the maximal order in  $F_{v}$. It follows from Theorem 3.2 that
$F_{v}$. It follows from Theorem 3.2 that  $g\mapsto f_{v}^{\circ }(g^{-1}A)$ is the characteristic function of
$g\mapsto f_{v}^{\circ }(g^{-1}A)$ is the characteristic function of  $\text{SL}_{2}(O_{v})$ for all
$\text{SL}_{2}(O_{v})$ for all  $v\notin S$. Thus if we normalize the local measures so that
$v\notin S$. Thus if we normalize the local measures so that  $\text{vol}(\text{SL}_{2}(O_{v}))=1$ for all
$\text{vol}(\text{SL}_{2}(O_{v}))=1$ for all  $v\notin S$, then
$v\notin S$, then
 $$\begin{eqnarray}\int _{D^{1}(\mathbb{A})}|f(g^{-1}A)\bar{h}(g)|\,dg=\int _{D^{1}(\mathbb{A}_{S})}|f_{S}(g^{-1}A)\bar{h}(g)|\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\int _{D^{1}(\mathbb{A})}|f(g^{-1}A)\bar{h}(g)|\,dg=\int _{D^{1}(\mathbb{A}_{S})}|f_{S}(g^{-1}A)\bar{h}(g)|\,dg,\end{eqnarray}$$ where the subscript  $S$ denotes the product of the local data over all places
$S$ denotes the product of the local data over all places  $v\in S$.
$v\in S$.
Consider now the case where  $v$ is a real place. We need to show that
$v$ is a real place. We need to show that  $C\mapsto f_{v}(C)$ is of rapid decay in
$C\mapsto f_{v}(C)$ is of rapid decay in  $\Vert C\Vert$, where
$\Vert C\Vert$, where  $C\in \unicode[STIX]{x1D6FA}(\mathbb{R})$. To that end, let
$C\in \unicode[STIX]{x1D6FA}(\mathbb{R})$. To that end, let  $m_{v}\in M(\mathbb{R})$ such that
$m_{v}\in M(\mathbb{R})$ such that  $C=m_{v}^{-1}\cdot A$. Then, up to a non-zero constant
$C=m_{v}^{-1}\cdot A$. Then, up to a non-zero constant  $c$, independent of
$c$, independent of  $C$,
$C$,
 $$\begin{eqnarray}f_{v}(C)=c\cdot \unicode[STIX]{x1D712}_{v}(m_{v})^{-1}\cdot \unicode[STIX]{x1D703}(f)_{A}(m_{v})\end{eqnarray}$$
$$\begin{eqnarray}f_{v}(C)=c\cdot \unicode[STIX]{x1D712}_{v}(m_{v})^{-1}\cdot \unicode[STIX]{x1D703}(f)_{A}(m_{v})\end{eqnarray}$$ for the character  $\unicode[STIX]{x1D712}_{v}$ of
$\unicode[STIX]{x1D712}_{v}$ of  $M(\mathbb{R})$. Now observe that
$M(\mathbb{R})$. Now observe that  $m_{v}$ can be taken to be a product of an element
$m_{v}$ can be taken to be a product of an element  $k_{v}$ in a maximal compact subgroup of
$k_{v}$ in a maximal compact subgroup of  $M(\mathbb{R})$ and an element
$M(\mathbb{R})$ and an element  $z_{v}$ in
$z_{v}$ in  $Z_{v}$, the identity component of the center of
$Z_{v}$, the identity component of the center of  $M(\mathbb{R})$. We fix an isomorphism
$M(\mathbb{R})$. We fix an isomorphism  $\unicode[STIX]{x1D708}:Z_{v}\rightarrow \mathbb{R}^{+}$ such that the conjugation action of
$\unicode[STIX]{x1D708}:Z_{v}\rightarrow \mathbb{R}^{+}$ such that the conjugation action of  $z_{v}\in Z_{v}$ on
$z_{v}\in Z_{v}$ on  $N(\mathbb{R})$ is given by multiplication by
$N(\mathbb{R})$ is given by multiplication by  $\unicode[STIX]{x1D708}(z_{v})$. Now, in order to prove that
$\unicode[STIX]{x1D708}(z_{v})$. Now, in order to prove that  $f_{v}$ is rapidly decreasing toward infinity, we shall give a global argument exploiting the automorphic form
$f_{v}$ is rapidly decreasing toward infinity, we shall give a global argument exploiting the automorphic form  $\unicode[STIX]{x1D703}(f)$ (though a local proof is also possible). Namely, it suffices to show that
$\unicode[STIX]{x1D703}(f)$ (though a local proof is also possible). Namely, it suffices to show that  $z_{v}\mapsto \unicode[STIX]{x1D703}(f)_{A}(z_{v}k_{v})$ is rapidly decreasing as
$z_{v}\mapsto \unicode[STIX]{x1D703}(f)_{A}(z_{v}k_{v})$ is rapidly decreasing as  $\unicode[STIX]{x1D708}(z_{v})\rightarrow \infty$, with bounds independent of
$\unicode[STIX]{x1D708}(z_{v})\rightarrow \infty$, with bounds independent of  $k_{v}$. This can be proved using the usual method of integration by parts, as in [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma].
$k_{v}$. This can be proved using the usual method of integration by parts, as in [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma].
More precisely, if  $X\in J\cong \mathfrak{n}$, then the
$X\in J\cong \mathfrak{n}$, then the  $X$-derivative of the character
$X$-derivative of the character  $\unicode[STIX]{x1D713}_{A}$ is a multiple of
$\unicode[STIX]{x1D713}_{A}$ is a multiple of  $\unicode[STIX]{x1D713}_{A}$. Using the definition of the Fourier coefficient and integration by parts, one obtains that
$\unicode[STIX]{x1D713}_{A}$. Using the definition of the Fourier coefficient and integration by parts, one obtains that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(f)_{A}(z_{v}k_{v})\text{ is a multiple of }(R_{Y}\cdot \unicode[STIX]{x1D703}(f))_{A}(z_{v}k_{v})\cdot \unicode[STIX]{x1D708}(z_{v})^{-1},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(f)_{A}(z_{v}k_{v})\text{ is a multiple of }(R_{Y}\cdot \unicode[STIX]{x1D703}(f))_{A}(z_{v}k_{v})\cdot \unicode[STIX]{x1D708}(z_{v})^{-1},\end{eqnarray}$$ where  $Y=k_{v}^{-1}Xk_{v}$ and
$Y=k_{v}^{-1}Xk_{v}$ and  $R_{Y}$ denotes the right
$R_{Y}$ denotes the right  $Y$-derivative of the automorphic form
$Y$-derivative of the automorphic form  $\unicode[STIX]{x1D703}(f)$. We can repeat this procedure to get any negative power of
$\unicode[STIX]{x1D703}(f)$. We can repeat this procedure to get any negative power of  $\unicode[STIX]{x1D708}(z_{v})$. The rapid decay follows from the fact that
$\unicode[STIX]{x1D708}(z_{v})$. The rapid decay follows from the fact that  $\unicode[STIX]{x1D703}(f)$ is of uniform moderate growth, and the fact that
$\unicode[STIX]{x1D703}(f)$ is of uniform moderate growth, and the fact that  $Y=k_{v}^{-1}Xk_{v}$ is a linear combination of vectors in any fixed basis of
$Y=k_{v}^{-1}Xk_{v}$ is a linear combination of vectors in any fixed basis of  $\mathfrak{n}$, with bounded coefficients, as
$\mathfrak{n}$, with bounded coefficients, as  $k_{v}$ runs over the maximal compact subgroup in
$k_{v}$ runs over the maximal compact subgroup in  $M(\mathbb{R})$.
$M(\mathbb{R})$.
Finally, suppose that  $g\in \text{SL}_{2}(\mathbb{R})$ belongs to the double coset of the diagonal matrix
$g\in \text{SL}_{2}(\mathbb{R})$ belongs to the double coset of the diagonal matrix  $(\!\begin{smallmatrix}t & 0\\ 0 & 1/t\end{smallmatrix}\!)$,
$(\!\begin{smallmatrix}t & 0\\ 0 & 1/t\end{smallmatrix}\!)$,  $t>0$, in the Cartan decomposition of
$t>0$, in the Cartan decomposition of  $\text{SL}_{2}(\mathbb{R})$. If we assume for simplicity that
$\text{SL}_{2}(\mathbb{R})$. If we assume for simplicity that  $\unicode[STIX]{x1D706}=1$, so that
$\unicode[STIX]{x1D706}=1$, so that  $a$ in
$a$ in  $x=(0,a)$ can be taken to be the identity matrix, then
$x=(0,a)$ can be taken to be the identity matrix, then  $\Vert xg\Vert ^{2}=t^{2}+1/t^{2}$ (on the nose) and
$\Vert xg\Vert ^{2}=t^{2}+1/t^{2}$ (on the nose) and  $\Vert g^{-1}A\Vert =t+1/t$. In particular,
$\Vert g^{-1}A\Vert =t+1/t$. In particular,  $t<\Vert g^{-1}A\Vert <t+1$ for
$t<\Vert g^{-1}A\Vert <t+1$ for  $t>1$. Hence, the rapid decay toward infinity of
$t>1$. Hence, the rapid decay toward infinity of  $f_{v}$ (as a function on
$f_{v}$ (as a function on  $\unicode[STIX]{x1D6FA}_{v}$) implies that
$\unicode[STIX]{x1D6FA}_{v}$) implies that  $g\mapsto f_{v}(g^{-1}A)$ has rapid decay on
$g\mapsto f_{v}(g^{-1}A)$ has rapid decay on  $\text{SL}_{2}(\mathbb{R})$, as desired.◻
$\text{SL}_{2}(\mathbb{R})$, as desired.◻
We are now ready to prove the non-vanishing of the global theta lift. Assume firstly that  $h$ is a cusp form. Then we have shown that
$h$ is a cusp form. Then we have shown that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{D^{1}(\mathbb{A}_{S})}f_{S}(g^{-1}A)\bar{h}(g)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{D^{1}(\mathbb{A}_{S})}f_{S}(g^{-1}A)\bar{h}(g)\,dg\end{eqnarray}$$ for some large finite set of places. Since for every  $v\in S$ the local
$v\in S$ the local  $f_{v}$ can be an arbitrary compactly supported smooth function on
$f_{v}$ can be an arbitrary compactly supported smooth function on  $\unicode[STIX]{x1D6FA}_{v}$, the integral will not vanish for some choice of data. Now consider the regularized theta integral
$\unicode[STIX]{x1D6FA}_{v}$, the integral will not vanish for some choice of data. Now consider the regularized theta integral  $\unicode[STIX]{x1D6E9}(z\cdot f,h)$, where
$\unicode[STIX]{x1D6E9}(z\cdot f,h)$, where  $h$ is in an automorphic form, not necessarily cuspidal, and
$h$ is in an automorphic form, not necessarily cuspidal, and  $z$ is an element of the Bernstein center of
$z$ is an element of the Bernstein center of  $\text{SL}_{2}(F_{v})$ for a particular fixed finite place
$\text{SL}_{2}(F_{v})$ for a particular fixed finite place  $v$ (see the next section for the construction of
$v$ (see the next section for the construction of  $z$). The corresponding Fourier coefficient is
$z$). The corresponding Fourier coefficient is
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(z\cdot f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{D^{1}(\mathbb{A})}(z\cdot f)(g^{-1}A)\bar{h}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(z\cdot f,h)_{N_{D},\unicode[STIX]{x1D713}_{2}}(1)=\int _{D^{1}(\mathbb{A})}(z\cdot f)(g^{-1}A)\bar{h}(g)\,dg.\end{eqnarray}$$ Let  $K_{v}$ be a sufficiently small open compact subgroup of
$K_{v}$ be a sufficiently small open compact subgroup of  $\text{SL}_{2}(F_{v})$ such that
$\text{SL}_{2}(F_{v})$ such that  $f_{v}$ is
$f_{v}$ is  $K_{v}$-invariant. Then
$K_{v}$-invariant. Then  $z\cdot f_{v}=\unicode[STIX]{x1D6FC}\cdot f_{v}$, where
$z\cdot f_{v}=\unicode[STIX]{x1D6FC}\cdot f_{v}$, where  $\unicode[STIX]{x1D6FC}$ is a
$\unicode[STIX]{x1D6FC}$ is a  $K_{v}$ bi-invariant, compactly supported function on
$K_{v}$ bi-invariant, compactly supported function on  $\text{SL}_{2}(F_{v})$. Let
$\text{SL}_{2}(F_{v})$. Let  $\unicode[STIX]{x1D6FC}^{\vee }(g)=\bar{\unicode[STIX]{x1D6FC}}(g^{-1})$ and define
$\unicode[STIX]{x1D6FC}^{\vee }(g)=\bar{\unicode[STIX]{x1D6FC}}(g^{-1})$ and define  $z^{\vee }\cdot h=\unicode[STIX]{x1D6FC}^{\vee }\cdot h$. Using the convergence guaranteed by Lemma 5.2,
$z^{\vee }\cdot h=\unicode[STIX]{x1D6FC}^{\vee }\cdot h$. Using the convergence guaranteed by Lemma 5.2,
 $$\begin{eqnarray}\int _{D^{1}(\mathbb{A})}(z\cdot f)(g^{-1}A)\bar{h}(g)\,dg=\int _{D^{1}(\mathbb{A})}f(g^{-1}A)(\overline{z^{\vee }\cdot h})(g)\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\int _{D^{1}(\mathbb{A})}(z\cdot f)(g^{-1}A)\bar{h}(g)\,dg=\int _{D^{1}(\mathbb{A})}f(g^{-1}A)(\overline{z^{\vee }\cdot h})(g)\,dg,\end{eqnarray}$$ and this can again be arranged to be non-zero, provided  $z^{\vee }\cdot h\neq 0$. Hence we have proved the following theorem.
$z^{\vee }\cdot h\neq 0$. Hence we have proved the following theorem.
Theorem 5.3. If  $h$ is a non-zero cusp form on
$h$ is a non-zero cusp form on  $D^{1}(\mathbb{A})$, then
$D^{1}(\mathbb{A})$, then  $\unicode[STIX]{x1D6E9}(f,h)\neq 0$ for some
$\unicode[STIX]{x1D6E9}(f,h)\neq 0$ for some  $f\in \unicode[STIX]{x1D6F1}$. If
$f\in \unicode[STIX]{x1D6F1}$. If  $h$ is a (not necessarily cuspidal) automorphic form such that
$h$ is a (not necessarily cuspidal) automorphic form such that  $z^{\vee }\cdot h\neq 0$, then
$z^{\vee }\cdot h\neq 0$, then  $\unicode[STIX]{x1D6E9}(z\cdot f,h)\neq 0$ for some
$\unicode[STIX]{x1D6E9}(z\cdot f,h)\neq 0$ for some  $f\in \unicode[STIX]{x1D6F1}$.
$f\in \unicode[STIX]{x1D6F1}$.
Remark.
The main reason for introduction of the regularized theta lift is to be able to handle the lift of  $h=1$ in the case where
$h=1$ in the case where  $D$ is split. In this case we can take all data to be the simplest possible:
$D$ is split. In this case we can take all data to be the simplest possible:  $\unicode[STIX]{x1D706}=1$, the matrix
$\unicode[STIX]{x1D706}=1$, the matrix  $A$ with
$A$ with  $a=(0,x)$ with
$a=(0,x)$ with  $x$ the identity matrix, etc. Then the non-vanishing of the theta lift is achieved with the spherical vector
$x$ the identity matrix, etc. Then the non-vanishing of the theta lift is achieved with the spherical vector  $f_{\infty }^{\circ }$ at any real place. Indeed, if
$f_{\infty }^{\circ }$ at any real place. Indeed, if  $g\in \text{SL}_{2}(\mathbb{R})$ belongs to the double coset of the diagonal matrix
$g\in \text{SL}_{2}(\mathbb{R})$ belongs to the double coset of the diagonal matrix  $(\!\begin{smallmatrix}t & 0\\ 0 & 1/t\end{smallmatrix}\!)$, with
$(\!\begin{smallmatrix}t & 0\\ 0 & 1/t\end{smallmatrix}\!)$, with  $t>0$, in the Cartan decomposition of
$t>0$, in the Cartan decomposition of  $\text{SL}_{2}(\mathbb{R})$, then
$\text{SL}_{2}(\mathbb{R})$, then  $\Vert xg\Vert ^{2}=t^{2}+1/t^{2}$ and
$\Vert xg\Vert ^{2}=t^{2}+1/t^{2}$ and  $\Vert g^{-1}A\Vert =t+1/t$. Write
$\Vert g^{-1}A\Vert =t+1/t$. Write  $u=t+1/t$ so that
$u=t+1/t$ so that
 $$\begin{eqnarray}du=\biggl(t-\frac{1}{t}\biggr)\frac{dt}{t}.\end{eqnarray}$$
$$\begin{eqnarray}du=\biggl(t-\frac{1}{t}\biggr)\frac{dt}{t}.\end{eqnarray}$$ Using the formula for the spherical vector given by Theorem 3.3 and the formula for the Haar measure on  $\text{SL}_{2}(\mathbb{R})$ with respect to the Cartan decomposition, we have
$\text{SL}_{2}(\mathbb{R})$ with respect to the Cartan decomposition, we have
 $$\begin{eqnarray}\int _{\text{SL}_{2}(\mathbb{R})}f_{\infty }^{\circ }(g^{-1}A)\,dg=\int _{2}^{\infty }\frac{1}{2}\cdot u^{-1/2}K_{3/2}(u)\,du>0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\text{SL}_{2}(\mathbb{R})}f_{\infty }^{\circ }(g^{-1}A)\,dg=\int _{2}^{\infty }\frac{1}{2}\cdot u^{-1/2}K_{3/2}(u)\,du>0.\end{eqnarray}$$It will be interesting to compute the value of this integral.
6 Regularizing Theta
Following some ideas of Kudla and Rallis [Reference Kudla and RallisKR94], the first author introduced in [Reference GanGan11] a regularized theta integral for a particular exceptional dual pair. We simplify the arguments so that regularization is now available for a wider class of examples. The notations used in this largely self-contained section will differ from those of the other sections of this paper. We first recall some basic facts about the notions of uniform moderate growth and rapid decay.
6.1 Moderate growth and rapid decay
Let  $k$ be a number field and let
$k$ be a number field and let  $\mathbb{A}$ denote the corresponding ring of adèles. Let
$\mathbb{A}$ denote the corresponding ring of adèles. Let  $G$ be a reductive group over
$G$ be a reductive group over  $k$. In order to keep the notation simple, we shall assume that
$k$. In order to keep the notation simple, we shall assume that  $G$ is split with a finite center. Fix a maximal split torus
$G$ is split with a finite center. Fix a maximal split torus  $T$ and a minimal parabolic subgroup
$T$ and a minimal parabolic subgroup  $P$ containing
$P$ containing  $T$. Let
$T$. Let  $N$ be the unipotent radical of
$N$ be the unipotent radical of  $P$. We have a root system
$P$. We have a root system  $\unicode[STIX]{x1D6F7}$, obtained by
$\unicode[STIX]{x1D6F7}$, obtained by  $T$ acting on the Lie algebra
$T$ acting on the Lie algebra  $\mathfrak{g}$ of
$\mathfrak{g}$ of  $G$ and a set of simple roots in
$G$ and a set of simple roots in  $\unicode[STIX]{x1D6F7}$ corresponding to the choice of
$\unicode[STIX]{x1D6F7}$ corresponding to the choice of  $P$.
$P$.
If we fix a place  $v$ of
$v$ of  $k$, then
$k$, then  $G_{v}$ will denote the group of
$G_{v}$ will denote the group of  $k_{v}$-points of
$k_{v}$-points of  $G$. Similarly, we shall use the subscript
$G$. Similarly, we shall use the subscript  $v$ to denote various other subgroups of
$v$ to denote various other subgroups of  $G_{v}$. A smooth function
$G_{v}$. A smooth function  $f$ on
$f$ on  $G(\mathbb{A})$ is of uniform moderate growth if there exists an integer
$G(\mathbb{A})$ is of uniform moderate growth if there exists an integer  $m$ such that for every
$m$ such that for every  $X$ in the enveloping algebra of
$X$ in the enveloping algebra of  $\mathfrak{g}$ there exists a constant
$\mathfrak{g}$ there exists a constant  $c_{X}$ such that
$c_{X}$ such that
 $$\begin{eqnarray}|R_{X}f(g)|\leqslant c_{X}\Vert g\Vert ^{m},\end{eqnarray}$$
$$\begin{eqnarray}|R_{X}f(g)|\leqslant c_{X}\Vert g\Vert ^{m},\end{eqnarray}$$ where  $R_{X}$ denotes the action of the enveloping algebra on smooth functions obtained by the differentiation from the right and
$R_{X}$ denotes the action of the enveloping algebra on smooth functions obtained by the differentiation from the right and  $\Vert g\Vert$ is a height function on
$\Vert g\Vert$ is a height function on  $G$ defined in [Reference Moeglin and WaldspurgerMW95, p. 20]. Since there exists a constant
$G$ defined in [Reference Moeglin and WaldspurgerMW95, p. 20]. Since there exists a constant  $c$ such that
$c$ such that  $\Vert gh\Vert \leqslant c\Vert g\Vert \cdot \Vert h\Vert$ for all
$\Vert gh\Vert \leqslant c\Vert g\Vert \cdot \Vert h\Vert$ for all  $g,h\in G(\mathbb{A})$, it is easy to see that the constants
$g,h\in G(\mathbb{A})$, it is easy to see that the constants  $c_{X}$ for the right translates
$c_{X}$ for the right translates  $R_{h}f$ of
$R_{h}f$ of  $f$ are of moderate growth in
$f$ are of moderate growth in  $h$, or more precisely of growth
$h$, or more precisely of growth  $\Vert h\Vert ^{m+d}$ where
$\Vert h\Vert ^{m+d}$ where  $d$ is the degree of
$d$ is the degree of  $X$.
$X$.
Now assume that  $v$ is a real or complex place of
$v$ is a real or complex place of  $k$. Let
$k$. Let  $P_{v}=M_{v}A_{v}N_{v}$ be the Langlands decomposition of
$P_{v}=M_{v}A_{v}N_{v}$ be the Langlands decomposition of  $P_{v}$. For
$P_{v}$. For  $\unicode[STIX]{x1D716}>0$, let
$\unicode[STIX]{x1D716}>0$, let  $A_{v,\unicode[STIX]{x1D716}}$ be a cone in
$A_{v,\unicode[STIX]{x1D716}}$ be a cone in  $A_{v}$ consisting of
$A_{v}$ consisting of  $a\in A_{v}$ such that
$a\in A_{v}$ such that  $\unicode[STIX]{x1D6FC}(a)>\unicode[STIX]{x1D716}$ for all simple roots
$\unicode[STIX]{x1D6FC}(a)>\unicode[STIX]{x1D716}$ for all simple roots  $\unicode[STIX]{x1D6FC}$. Let
$\unicode[STIX]{x1D6FC}$. Let  $A$ be the product of the
$A$ be the product of the  $A_{v}$ and let
$A_{v}$ and let  $A_{\unicode[STIX]{x1D716}}$ be the product of the
$A_{\unicode[STIX]{x1D716}}$ be the product of the  $A_{v,\unicode[STIX]{x1D716}}$ over all real and complex places
$A_{v,\unicode[STIX]{x1D716}}$ over all real and complex places  $v$. Let
$v$. Let  $\unicode[STIX]{x1D714}_{N}$ be a compact set in
$\unicode[STIX]{x1D714}_{N}$ be a compact set in  $N(\mathbb{A})$ containing the identity element. Let
$N(\mathbb{A})$ containing the identity element. Let  $K$ be a product of maximal compact subgroups
$K$ be a product of maximal compact subgroups  $K_{v}$ of
$K_{v}$ of  $G_{v}$, where we have taken
$G_{v}$, where we have taken  $K_{v}$ to be hyperspecial for all
$K_{v}$ to be hyperspecial for all  $p$-adic places. Then
$p$-adic places. Then
 $$\begin{eqnarray}S=\unicode[STIX]{x1D714}_{N}A_{\unicode[STIX]{x1D716}}K\end{eqnarray}$$
$$\begin{eqnarray}S=\unicode[STIX]{x1D714}_{N}A_{\unicode[STIX]{x1D716}}K\end{eqnarray}$$ is a Siegel domain in  $G(\mathbb{A})$. If
$G(\mathbb{A})$. If  $\unicode[STIX]{x1D714}_{N}$ is sufficiently large and
$\unicode[STIX]{x1D714}_{N}$ is sufficiently large and  $\unicode[STIX]{x1D716}$ is sufficiently small, then
$\unicode[STIX]{x1D716}$ is sufficiently small, then  $G(\mathbb{A})=G(k)S$.
$G(\mathbb{A})=G(k)S$.
Let  $\unicode[STIX]{x1D6F1}$ be an automorphic representation of
$\unicode[STIX]{x1D6F1}$ be an automorphic representation of  $G$. Then any smooth
$G$. Then any smooth  $f\in \unicode[STIX]{x1D6F1}$ is of uniform moderate growth. In terms of the Siegel domain
$f\in \unicode[STIX]{x1D6F1}$ is of uniform moderate growth. In terms of the Siegel domain  $S$, this means the following. Let
$S$, this means the following. Let  $\unicode[STIX]{x1D70C}_{P}:A\rightarrow \mathbb{R}^{+}$ be the modular character. There exists an integer
$\unicode[STIX]{x1D70C}_{P}:A\rightarrow \mathbb{R}^{+}$ be the modular character. There exists an integer  $m$ such that for every
$m$ such that for every  $X$ in the enveloping algebra of
$X$ in the enveloping algebra of  $\mathfrak{g}$, there exists a constant
$\mathfrak{g}$, there exists a constant  $c_{X}$ such that
$c_{X}$ such that
 $$\begin{eqnarray}|R_{X}f(nak)|\leqslant c_{X}\cdot \unicode[STIX]{x1D70C}_{P}(a)^{m}\end{eqnarray}$$
$$\begin{eqnarray}|R_{X}f(nak)|\leqslant c_{X}\cdot \unicode[STIX]{x1D70C}_{P}(a)^{m}\end{eqnarray}$$ on  $S$, where the constants
$S$, where the constants  $m$ and
$m$ and  $c_{X}$ are not necessarily the same, but related to those above.
$c_{X}$ are not necessarily the same, but related to those above.
Now let  $Q\supseteq P$ be a maximal parabolic with a unipotent radical
$Q\supseteq P$ be a maximal parabolic with a unipotent radical  $U\subseteq N$, corresponding to a simple root
$U\subseteq N$, corresponding to a simple root  $\unicode[STIX]{x1D6FC}$. We have a standard Levi factor
$\unicode[STIX]{x1D6FC}$. We have a standard Levi factor  $L$ of
$L$ of  $Q$ defined as the centralizer of a fundamental cocharacter
$Q$ defined as the centralizer of a fundamental cocharacter  $\unicode[STIX]{x1D712}:\mathbb{G}_{m}\rightarrow T$ (or a power of it). In any case, any element in
$\unicode[STIX]{x1D712}:\mathbb{G}_{m}\rightarrow T$ (or a power of it). In any case, any element in  $A_{v}$ is uniquely written as a product
$A_{v}$ is uniquely written as a product  $\prod _{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D712}(t_{\unicode[STIX]{x1D712}})$, over all fundamental cocharacters
$\prod _{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D712}(t_{\unicode[STIX]{x1D712}})$, over all fundamental cocharacters  $\unicode[STIX]{x1D712}$, where
$\unicode[STIX]{x1D712}$, where  $t_{\unicode[STIX]{x1D712}}\in \mathbb{R}^{+}$. The element
$t_{\unicode[STIX]{x1D712}}\in \mathbb{R}^{+}$. The element  $\prod _{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D712}(t_{\unicode[STIX]{x1D712}})$ is contained in the cone
$\prod _{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D712}(t_{\unicode[STIX]{x1D712}})$ is contained in the cone  $A_{v,\unicode[STIX]{x1D716}}$ if
$A_{v,\unicode[STIX]{x1D716}}$ if  $t_{\unicode[STIX]{x1D712}}>\unicode[STIX]{x1D716}$ for all
$t_{\unicode[STIX]{x1D712}}>\unicode[STIX]{x1D716}$ for all  $\unicode[STIX]{x1D712}$. Let
$\unicode[STIX]{x1D712}$. Let  $f_{U}$ be the constant term of
$f_{U}$ be the constant term of  $f$ along
$f$ along  $U$. Then, if
$U$. Then, if  $f$ has uniform moderate growth, by [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma] for every positive integer
$f$ has uniform moderate growth, by [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma] for every positive integer  $i$, there is a constant
$i$, there is a constant  $c_{i}$ such that
$c_{i}$ such that
 $$\begin{eqnarray}|(f-f_{U})(nak)|\leqslant c_{i}\cdot \unicode[STIX]{x1D70C}_{P}(a)^{m}\cdot \unicode[STIX]{x1D6FC}^{-i}(a)\end{eqnarray}$$
$$\begin{eqnarray}|(f-f_{U})(nak)|\leqslant c_{i}\cdot \unicode[STIX]{x1D70C}_{P}(a)^{m}\cdot \unicode[STIX]{x1D6FC}^{-i}(a)\end{eqnarray}$$ on  $S$. In particular, if
$S$. In particular, if  $f_{U}=0$, then
$f_{U}=0$, then  $f$ is rapidly decreasing in the variable
$f$ is rapidly decreasing in the variable  $t_{\unicode[STIX]{x1D712}}$. If
$t_{\unicode[STIX]{x1D712}}$. If  $f_{U}=0$ for all maximal parabolic subgroups, then
$f_{U}=0$ for all maximal parabolic subgroups, then  $f$ is rapidly decreasing on
$f$ is rapidly decreasing on  $S$, and that is how the rapid decrease of cusp forms is established. The proof of [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma] involves integration by parts, so it is easy to see that the constants
$S$, and that is how the rapid decrease of cusp forms is established. The proof of [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma] involves integration by parts, so it is easy to see that the constants  $c_{i}$ for the right translates
$c_{i}$ for the right translates  $R_{h}f$ of
$R_{h}f$ of  $f$ are of moderate growth in
$f$ are of moderate growth in  $h$, or more precisely of the growth
$h$, or more precisely of the growth  $\Vert h\Vert ^{m^{\prime }}$ where
$\Vert h\Vert ^{m^{\prime }}$ where  $m^{\prime }$ depends on
$m^{\prime }$ depends on  $i$: a larger
$i$: a larger  $i$ will demand a larger
$i$ will demand a larger  $m^{\prime }$.
$m^{\prime }$.
We highlight another important issue here. Assume that  $f$ belongs to an automorphic representation
$f$ belongs to an automorphic representation  $\unicode[STIX]{x1D70B}$. Then a Frechét space topology on
$\unicode[STIX]{x1D70B}$. Then a Frechét space topology on  $\unicode[STIX]{x1D70B}$ is given by the family of seminorms
$\unicode[STIX]{x1D70B}$ is given by the family of seminorms
 $$\begin{eqnarray}\Vert f\Vert _{X}=\sup _{nak\in S}|R_{X}f(nak)|\cdot \unicode[STIX]{x1D70C}_{P}(a)^{-m},\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{X}=\sup _{nak\in S}|R_{X}f(nak)|\cdot \unicode[STIX]{x1D70C}_{P}(a)^{-m},\end{eqnarray}$$ where  $m$ depends on
$m$ depends on  $\unicode[STIX]{x1D70B}$ and works for all
$\unicode[STIX]{x1D70B}$ and works for all  $X$ in the enveloping algebra. Then [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma] says that convergence in these seminorms implies convergence in the seminorm
$X$ in the enveloping algebra. Then [Reference Moeglin and WaldspurgerMW95, p. 30, Lemma] says that convergence in these seminorms implies convergence in the seminorm
 $$\begin{eqnarray}\sup _{nak\in S}|(f-f_{U})(nak)|\cdot \unicode[STIX]{x1D70C}_{P}(a)^{-m}\cdot \unicode[STIX]{x1D6FC}^{i}(a).\end{eqnarray}$$
$$\begin{eqnarray}\sup _{nak\in S}|(f-f_{U})(nak)|\cdot \unicode[STIX]{x1D70C}_{P}(a)^{-m}\cdot \unicode[STIX]{x1D6FC}^{i}(a).\end{eqnarray}$$This observation will later imply that the regularized theta integral gives a continuous pairing.
6.2 Restricting to a subgroup
Let  $(G_{1},G_{2})$ be a dual pair in
$(G_{1},G_{2})$ be a dual pair in  $G$. Let
$G$. Let  $T_{1}$ be a maximal split torus in
$T_{1}$ be a maximal split torus in  $G_{1}$ and fix a minimal parabolic subgroup
$G_{1}$ and fix a minimal parabolic subgroup  $P_{1}$ containing
$P_{1}$ containing  $T_{1}$. Without loss of generality, we can assume that
$T_{1}$. Without loss of generality, we can assume that  $T_{1}\subseteq T$ and
$T_{1}\subseteq T$ and  $P_{1}\subseteq P$. Let
$P_{1}\subseteq P$. Let  $Q_{1}\supseteq P_{1}$ be a maximal parabolic subgroup of
$Q_{1}\supseteq P_{1}$ be a maximal parabolic subgroup of  $G_{1}$. Let
$G_{1}$. Let  $\unicode[STIX]{x1D712}_{1}:G_{m}\rightarrow T_{1}$ be the corresponding fundamental cocharacter (or a multiple thereof) so that the centralizer of
$\unicode[STIX]{x1D712}_{1}:G_{m}\rightarrow T_{1}$ be the corresponding fundamental cocharacter (or a multiple thereof) so that the centralizer of  $\unicode[STIX]{x1D712}_{1}$ in
$\unicode[STIX]{x1D712}_{1}$ in  $G_{1}$ is a Levi factor
$G_{1}$ is a Levi factor  $L_{1}$ of
$L_{1}$ of  $Q_{1}$. We make the following assumption.
$Q_{1}$. We make the following assumption.
Hypothesis. For every fundamental cocharacter  $\unicode[STIX]{x1D712}_{1}$ of
$\unicode[STIX]{x1D712}_{1}$ of  $G_{1}$, there is a fundamental cocharacter
$G_{1}$, there is a fundamental cocharacter  $\unicode[STIX]{x1D712}$ of
$\unicode[STIX]{x1D712}$ of  $G$ such that
$G$ such that  $\unicode[STIX]{x1D712}_{1}$ is a multiple of
$\unicode[STIX]{x1D712}_{1}$ is a multiple of  $\unicode[STIX]{x1D712}$.
$\unicode[STIX]{x1D712}$.
This hypothesis holds in the following examples:
∙ the dual pair
 $G_{1}\times G_{2}=D^{1}\times G_{D}=\text{SL}_{2}\times G_{D}$ studied in this paper. Here
$G_{1}\times G_{2}=D^{1}\times G_{D}=\text{SL}_{2}\times G_{D}$ studied in this paper. Here  $G_{1}=\text{SL}_{2}$ corresponds to the highest root and the highest weight is also a fundamental weight for
$G_{1}=\text{SL}_{2}$ corresponds to the highest root and the highest weight is also a fundamental weight for  $\mathbf{E}_{7}$ (the ambient group
$\mathbf{E}_{7}$ (the ambient group  $G$).
$G$).∙ the split exceptional dual pairs in
 $G$ of type
$G$ of type  $\mathbf{E}_{n}$ where one member of the dual pair is the type
$\mathbf{E}_{n}$ where one member of the dual pair is the type  $\mathbf{G}_{2}$; see [Reference Loke and SavinLS19]. In particular, this includes the case
$\mathbf{G}_{2}$; see [Reference Loke and SavinLS19]. In particular, this includes the case  $\text{PGL}_{3}\times G_{2}$ treated in [Reference GanGan11].
$\text{PGL}_{3}\times G_{2}$ treated in [Reference GanGan11].
The hypothesis has the following consequences.
∙ It implies that the cone
 $A_{1,\unicode[STIX]{x1D716}}$ sits as a subcone of
$A_{1,\unicode[STIX]{x1D716}}$ sits as a subcone of  $A_{\unicode[STIX]{x1D716}}$; in fact, it is a direct factor in the above cases. In particular, we have an inclusion of Siegel domains
$A_{\unicode[STIX]{x1D716}}$; in fact, it is a direct factor in the above cases. In particular, we have an inclusion of Siegel domains  $S_{1}\subset S$.
$S_{1}\subset S$.∙ Given a fundamental cocharacter
 $\unicode[STIX]{x1D712}_{1}$ of
$\unicode[STIX]{x1D712}_{1}$ of  $G_{1}$, the associated fundamental cocharacter
$G_{1}$, the associated fundamental cocharacter  $\unicode[STIX]{x1D712}$ of
$\unicode[STIX]{x1D712}$ of  $G$ given by the hypothesis corresponds to a simple root and so determines a maximal parabolic subgroup
$G$ given by the hypothesis corresponds to a simple root and so determines a maximal parabolic subgroup  $Q_{\unicode[STIX]{x1D712}_{1}}=L_{\unicode[STIX]{x1D712}_{1}}U_{\unicode[STIX]{x1D712}_{1}}$ of
$Q_{\unicode[STIX]{x1D712}_{1}}=L_{\unicode[STIX]{x1D712}_{1}}U_{\unicode[STIX]{x1D712}_{1}}$ of  $G$. In the following, we will sometimes write
$G$. In the following, we will sometimes write  $U=U_{\unicode[STIX]{x1D712}_{1}}$ to simplify notation.
$U=U_{\unicode[STIX]{x1D712}_{1}}$ to simplify notation.
Now let  $v$ be a
$v$ be a  $p$-adic place and
$p$-adic place and  $z$ an element of the Bernstein center of
$z$ an element of the Bernstein center of  $G_{1}(k_{v})$. Then
$G_{1}(k_{v})$. Then  $z\cdot \unicode[STIX]{x1D6F1}$ is naturally a
$z\cdot \unicode[STIX]{x1D6F1}$ is naturally a  $G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$-submodule of
$G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$-submodule of  $\unicode[STIX]{x1D6F1}$. For a fixed cocharacter
$\unicode[STIX]{x1D6F1}$. For a fixed cocharacter  $\unicode[STIX]{x1D712}_{1}$ of
$\unicode[STIX]{x1D712}_{1}$ of  $G_{1}$, with associated maximal parabolic
$G_{1}$, with associated maximal parabolic  $Q=LU$ of
$Q=LU$ of  $G$, assume that
$G$, assume that
 $$\begin{eqnarray}z\cdot \unicode[STIX]{x1D6F1}_{v}\subset \text{Ker}(\unicode[STIX]{x1D6F1}_{v}\longrightarrow (\unicode[STIX]{x1D6F1}_{v})_{U(k_{v})}).\end{eqnarray}$$
$$\begin{eqnarray}z\cdot \unicode[STIX]{x1D6F1}_{v}\subset \text{Ker}(\unicode[STIX]{x1D6F1}_{v}\longrightarrow (\unicode[STIX]{x1D6F1}_{v})_{U(k_{v})}).\end{eqnarray}$$ We claim that this implies that  $(z\cdot f)_{U}=0$ on
$(z\cdot f)_{U}=0$ on  $G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$. Indeed, if
$G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$. Indeed, if  $g\in G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$, then
$g\in G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$, then
 $$\begin{eqnarray}(z\cdot f)_{U}(g)=(R_{g}(z\cdot f))_{U}(1)=(z\cdot R_{g}(f))_{U}(1)=0,\end{eqnarray}$$
$$\begin{eqnarray}(z\cdot f)_{U}(g)=(R_{g}(z\cdot f))_{U}(1)=(z\cdot R_{g}(f))_{U}(1)=0,\end{eqnarray}$$ where  $R_{g}$ denotes the right translation by
$R_{g}$ denotes the right translation by  $g$. Here, the second equality holds since
$g$. Here, the second equality holds since  $z$ and
$z$ and  $R_{g}$ commute, and the third equality holds since the projection of
$R_{g}$ commute, and the third equality holds since the projection of  $z\cdot \unicode[STIX]{x1D6F1}$ on
$z\cdot \unicode[STIX]{x1D6F1}$ on  $\unicode[STIX]{x1D6F1}_{U}$ vanishes. Write
$\unicode[STIX]{x1D6F1}_{U}$ vanishes. Write  $g=g_{1}\times g_{2}\in G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$ and assume that
$g=g_{1}\times g_{2}\in G_{1}(\mathbb{A})\times G_{2}(\mathbb{A})$ and assume that  $g_{1}\in S_{1}$. Using the hypothesis that
$g_{1}\in S_{1}$. Using the hypothesis that  $S_{1}\subseteq S$ and the estimates for
$S_{1}\subseteq S$ and the estimates for  $|R_{g_{2}}(z\cdot f)-(R_{g_{2}}(z\cdot f))_{U}|$ on
$|R_{g_{2}}(z\cdot f)-(R_{g_{2}}(z\cdot f))_{U}|$ on  $S$ from the last subsection, it follows that
$S$ from the last subsection, it follows that
 $$\begin{eqnarray}(z\cdot f)(g_{1}\times g_{2})=R_{g_{2}}(z\cdot f)(g_{1})\end{eqnarray}$$
$$\begin{eqnarray}(z\cdot f)(g_{1}\times g_{2})=R_{g_{2}}(z\cdot f)(g_{1})\end{eqnarray}$$ is of moderate growth in both variables, and in the variable  $g_{1}\in S_{1}$ it is rapidly decreasing in the direction of the fundamental cocharacter
$g_{1}\in S_{1}$ it is rapidly decreasing in the direction of the fundamental cocharacter  $\unicode[STIX]{x1D712}_{1}$. More precisely, we summarize the discussion in this subsection in the following proposition.
$\unicode[STIX]{x1D712}_{1}$. More precisely, we summarize the discussion in this subsection in the following proposition.
Proposition 6.1. Assume that:
(i) for every fundamental cocharacter
 $\unicode[STIX]{x1D712}_{1}$ of
$\unicode[STIX]{x1D712}_{1}$ of  $G_{1}$, there is a fundamental cocharacter
$G_{1}$, there is a fundamental cocharacter  $\unicode[STIX]{x1D712}$ of
$\unicode[STIX]{x1D712}$ of  $G$ such that
$G$ such that  $\unicode[STIX]{x1D712}_{1}$ is a multiple of
$\unicode[STIX]{x1D712}_{1}$ is a multiple of  $\unicode[STIX]{x1D712}$, which in turn determines a maximal parabolic subgroup
$\unicode[STIX]{x1D712}$, which in turn determines a maximal parabolic subgroup  $Q_{\unicode[STIX]{x1D712}_{1}}=L_{\unicode[STIX]{x1D712}_{1}}U_{\unicode[STIX]{x1D712}_{1}}$;
$Q_{\unicode[STIX]{x1D712}_{1}}=L_{\unicode[STIX]{x1D712}_{1}}U_{\unicode[STIX]{x1D712}_{1}}$;(ii) one can find an element
 $z$ in the Bernstein center of
$z$ in the Bernstein center of  $G_{1}(k_{v})$ such that for every fundamental cocharacter
$G_{1}(k_{v})$ such that for every fundamental cocharacter  $\unicode[STIX]{x1D712}_{1}$ of
$\unicode[STIX]{x1D712}_{1}$ of  $G_{1}$, the natural projection of
$G_{1}$, the natural projection of  $\unicode[STIX]{x1D6F1}_{v}$ to
$\unicode[STIX]{x1D6F1}_{v}$ to  $(\unicode[STIX]{x1D6F1}_{v})_{U_{\unicode[STIX]{x1D712}_{1}}(k_{v})}$ vanishes on
$(\unicode[STIX]{x1D6F1}_{v})_{U_{\unicode[STIX]{x1D712}_{1}}(k_{v})}$ vanishes on  $z\cdot \unicode[STIX]{x1D6F1}_{v}$.
$z\cdot \unicode[STIX]{x1D6F1}_{v}$.
Then for every integer  $n$, there exist an integer
$n$, there exist an integer  $m$ and a constant
$m$ and a constant  $c$ such that
$c$ such that
 $$\begin{eqnarray}|(z\cdot f)(g_{1}\times g_{2})|\leqslant c\Vert g_{1}\Vert ^{-n}\Vert g_{2}\Vert ^{m}\end{eqnarray}$$
$$\begin{eqnarray}|(z\cdot f)(g_{1}\times g_{2})|\leqslant c\Vert g_{1}\Vert ^{-n}\Vert g_{2}\Vert ^{m}\end{eqnarray}$$ for all  $g_{1}\in S_{1}$ and
$g_{1}\in S_{1}$ and  $g_{2}\in G_{2}(\mathbb{A})$.
$g_{2}\in G_{2}(\mathbb{A})$.
In the context of the above proposition, a small tradeoff here is that increasing  $n$ can be obtained only by increasing
$n$ can be obtained only by increasing  $m$ at the same time. But this is still good enough to define a regularized theta lift which produces functions of moderate growth as output. To exploit the proposition, it remains then to construct an appropriate
$m$ at the same time. But this is still good enough to define a regularized theta lift which produces functions of moderate growth as output. To exploit the proposition, it remains then to construct an appropriate  $z$. We also need to ensure that
$z$. We also need to ensure that  $z\cdot \unicode[STIX]{x1D6F1}_{v}\neq 0$, and this may not be always possible, as will be discussed in the next subsection.
$z\cdot \unicode[STIX]{x1D6F1}_{v}\neq 0$, and this may not be always possible, as will be discussed in the next subsection.
6.3 Bernstein’s center
We work here locally over a  $p$-adic field. Thus all our groups are local and we drop the subscript
$p$-adic field. Thus all our groups are local and we drop the subscript  $v$. For simplicity, we shall discuss only the Bernstein center for the Bernstein component containing the trivial representation of
$v$. For simplicity, we shall discuss only the Bernstein center for the Bernstein component containing the trivial representation of  $G_{1}$.
$G_{1}$.
To that end, let  $\hat{T}_{1}$ be the complex torus dual to
$\hat{T}_{1}$ be the complex torus dual to  $T_{1}$, and let
$T_{1}$, and let  $W(G_{1})$ be the Weyl group of
$W(G_{1})$ be the Weyl group of  $G_{1}$. The Bernstein center
$G_{1}$. The Bernstein center  $Z(G_{1})$ of the said component is isomorphic to the algebra of
$Z(G_{1})$ of the said component is isomorphic to the algebra of  $W(G_{1})$-invariant regular functions on
$W(G_{1})$-invariant regular functions on  $\hat{T}_{1}$. Similarly, the Bernstein center
$\hat{T}_{1}$. Similarly, the Bernstein center  $Z(L_{1})$ of the Levi factor
$Z(L_{1})$ of the Levi factor  $L_{1}$ is isomorphic to the algebra of
$L_{1}$ is isomorphic to the algebra of  $W(L_{1})$-invariant regular functions on
$W(L_{1})$-invariant regular functions on  $\hat{T}_{1}$. In particular, we have a natural map
$\hat{T}_{1}$. In particular, we have a natural map  $j:Z(G_{1})\rightarrow Z(L_{1})$. Let
$j:Z(G_{1})\rightarrow Z(L_{1})$. Let  $\unicode[STIX]{x1D70B}$ be a smooth representation of
$\unicode[STIX]{x1D70B}$ be a smooth representation of  $G_{1}$, and let
$G_{1}$, and let  $p:\unicode[STIX]{x1D70B}\rightarrow \unicode[STIX]{x1D70B}_{U_{1}}$ be the natural projection onto the normalized Jacquet module
$p:\unicode[STIX]{x1D70B}\rightarrow \unicode[STIX]{x1D70B}_{U_{1}}$ be the natural projection onto the normalized Jacquet module  $\unicode[STIX]{x1D70B}_{U_{1}}$. Then, for every
$\unicode[STIX]{x1D70B}_{U_{1}}$. Then, for every  $z\in Z(G_{1})$ and
$z\in Z(G_{1})$ and  $v\in \unicode[STIX]{x1D70B}$, we have
$v\in \unicode[STIX]{x1D70B}$, we have
 $$\begin{eqnarray}p(z\cdot v)=j(z)\cdot (p(v)).\end{eqnarray}$$
$$\begin{eqnarray}p(z\cdot v)=j(z)\cdot (p(v)).\end{eqnarray}$$ Now let  $\unicode[STIX]{x1D6F1}$ be a smooth representation of
$\unicode[STIX]{x1D6F1}$ be a smooth representation of  $G$. Recall that we want to find a non-zero
$G$. Recall that we want to find a non-zero  $z\in Z(G_{1})$ such that
$z\in Z(G_{1})$ such that  $z\cdot \unicode[STIX]{x1D6F1}$ is in the kernel of the projection of
$z\cdot \unicode[STIX]{x1D6F1}$ is in the kernel of the projection of  $\unicode[STIX]{x1D6F1}$ onto
$\unicode[STIX]{x1D6F1}$ onto  $\unicode[STIX]{x1D6F1}_{U}$. Since
$\unicode[STIX]{x1D6F1}_{U}$. Since  $\unicode[STIX]{x1D6F1}_{U}$ is an
$\unicode[STIX]{x1D6F1}_{U}$ is an  $L_{1}$-equivariant quotient of
$L_{1}$-equivariant quotient of  $\unicode[STIX]{x1D6F1}_{U_{1}}$,
$\unicode[STIX]{x1D6F1}_{U_{1}}$,  $j(z)\in Z(L_{1})$ acts on
$j(z)\in Z(L_{1})$ acts on  $\unicode[STIX]{x1D6F1}_{U}$ and hence we need to find
$\unicode[STIX]{x1D6F1}_{U}$ and hence we need to find  $z\in Z(G_{1})$ such that
$z\in Z(G_{1})$ such that  $j(z)=0$ on
$j(z)=0$ on  $\unicode[STIX]{x1D6F1}_{U}$. This is always possible if
$\unicode[STIX]{x1D6F1}_{U}$. This is always possible if  $\unicode[STIX]{x1D6F1}$ is a finite-length
$\unicode[STIX]{x1D6F1}$ is a finite-length  $G$-module, in which case
$G$-module, in which case  $\unicode[STIX]{x1D6F1}_{U}$ is a finite-length
$\unicode[STIX]{x1D6F1}_{U}$ is a finite-length  $L$-module. In particular, the center of
$L$-module. In particular, the center of  $L$ acts finitely on
$L$ acts finitely on  $\unicode[STIX]{x1D6F1}_{U}$. Hence, the center of
$\unicode[STIX]{x1D6F1}_{U}$. Hence, the center of  $L_{1}$ (
$L_{1}$ ( $=$ the center of
$=$ the center of  $L$) acts finitely on
$L$) acts finitely on  $\unicode[STIX]{x1D6F1}_{U}$ and the
$\unicode[STIX]{x1D6F1}_{U}$ and the  $Z(L_{1})$-spectrum of
$Z(L_{1})$-spectrum of  $\unicode[STIX]{x1D6F1}_{U}$ is contained in a proper subvariety of
$\unicode[STIX]{x1D6F1}_{U}$ is contained in a proper subvariety of  $\hat{T}_{1}$. In particular, any non-zero
$\hat{T}_{1}$. In particular, any non-zero  $W(G_{1})$-invariant function
$W(G_{1})$-invariant function  $z$ vanishing on the subvariety will have the desired property that
$z$ vanishing on the subvariety will have the desired property that  $j(z)$ vanishes on
$j(z)$ vanishes on  $\unicode[STIX]{x1D6F1}_{U}$. Hence, a non-trivial
$\unicode[STIX]{x1D6F1}_{U}$. Hence, a non-trivial  $z$ with the desired property always exists.
$z$ with the desired property always exists.
A potential problem is that such a  $z$ may kill the whole
$z$ may kill the whole  $\unicode[STIX]{x1D6F1}$. However, if
$\unicode[STIX]{x1D6F1}$. However, if  $G$ is split,
$G$ is split,  $G_{1}$ is the smaller member of the dual pair (also split) and
$G_{1}$ is the smaller member of the dual pair (also split) and  $\unicode[STIX]{x1D6F1}$ the minimal representation, then the spherical matrix coefficient
$\unicode[STIX]{x1D6F1}$ the minimal representation, then the spherical matrix coefficient  $\unicode[STIX]{x1D6F7}$ of
$\unicode[STIX]{x1D6F7}$ of  $\unicode[STIX]{x1D6F1}$, when restricted to
$\unicode[STIX]{x1D6F1}$, when restricted to  $G_{1}$, is typically contained in
$G_{1}$, is typically contained in  $L^{2-\unicode[STIX]{x1D716}}(G_{1})$ for some
$L^{2-\unicode[STIX]{x1D716}}(G_{1})$ for some  $\unicode[STIX]{x1D716}>0$. (This is easy to check in any given situation; see [Reference Loke and SavinLS19]). Thus, in such situations, it makes sense to integrate
$\unicode[STIX]{x1D716}>0$. (This is easy to check in any given situation; see [Reference Loke and SavinLS19]). Thus, in such situations, it makes sense to integrate  $\unicode[STIX]{x1D6F7}$ against spherical tempered functions of
$\unicode[STIX]{x1D6F7}$ against spherical tempered functions of  $G_{1}$, that is, to consider the spherical transform of
$G_{1}$, that is, to consider the spherical transform of  $\unicode[STIX]{x1D6F7}$ on
$\unicode[STIX]{x1D6F7}$ on  $G_{1}(k_{v})$. This integral will be non-zero for almost all tempered spherical functions, hence almost all spherical tempered representations of
$G_{1}(k_{v})$. This integral will be non-zero for almost all tempered spherical functions, hence almost all spherical tempered representations of  $G_{1}(k_{v})$ will appear as a quotient of
$G_{1}(k_{v})$ will appear as a quotient of  $\unicode[STIX]{x1D6F1}$. (This argument for the non-vanishing of the theta lift of almost all irreducible spherical tempered representations holds over archimedean fields as well, as we shall exploit in Lemma 7.6 below.) Hence, if
$\unicode[STIX]{x1D6F1}$. (This argument for the non-vanishing of the theta lift of almost all irreducible spherical tempered representations holds over archimedean fields as well, as we shall exploit in Lemma 7.6 below.) Hence, if  $z$ kills
$z$ kills  $\unicode[STIX]{x1D6F1}$, then
$\unicode[STIX]{x1D6F1}$, then  $z$ kills all spherical tempered representations of
$z$ kills all spherical tempered representations of  $G_{1}(k_{v})$ and hence
$G_{1}(k_{v})$ and hence  $z$ must be equal to 0. Therefore the desired regularization can be carried out in this case.
$z$ must be equal to 0. Therefore the desired regularization can be carried out in this case.
Let us look at our dual pair  $G_{1}\times G_{2}=\text{SL}_{2}\times G_{D}$ in
$G_{1}\times G_{2}=\text{SL}_{2}\times G_{D}$ in  $G$ with
$G$ with  $\unicode[STIX]{x1D6F1}$ the minimal representation. The Bernstein center is
$\unicode[STIX]{x1D6F1}$ the minimal representation. The Bernstein center is
 $$\begin{eqnarray}Z(G_{1})=\mathbb{C}[x^{\pm 1}]^{S_{2}},\end{eqnarray}$$
$$\begin{eqnarray}Z(G_{1})=\mathbb{C}[x^{\pm 1}]^{S_{2}},\end{eqnarray}$$ where  $S_{2}$ acts by permuting
$S_{2}$ acts by permuting  $x$ and
$x$ and  $x^{-1}$. Let
$x^{-1}$. Let
 $$\begin{eqnarray}z=(x-q^{2})(x^{-1}-q^{2})(x-q^{3})(x^{-1}-q^{3}),\end{eqnarray}$$
$$\begin{eqnarray}z=(x-q^{2})(x^{-1}-q^{2})(x-q^{3})(x^{-1}-q^{3}),\end{eqnarray}$$ where  $q$ is the order of the residual field. This element satisfies our requirement, since
$q$ is the order of the residual field. This element satisfies our requirement, since  $j(z)$ vanishes on
$j(z)$ vanishes on  $\unicode[STIX]{x1D6F1}_{U}$ by Theorem 4.3, and the spherical matrix coefficient of
$\unicode[STIX]{x1D6F1}_{U}$ by Theorem 4.3, and the spherical matrix coefficient of  $\unicode[STIX]{x1D6F1}$ is integrable when restricted to
$\unicode[STIX]{x1D6F1}$ is integrable when restricted to  $\text{SL}_{2}$.
$\text{SL}_{2}$.
6.4 Global  $\unicode[STIX]{x1D6E9}(1)$
$\unicode[STIX]{x1D6E9}(1)$
Let  $z$ be the element in the Bernstein center of
$z$ be the element in the Bernstein center of  $G_{1}=\text{SL}_{2}$, as in the previous subsection. We define
$G_{1}=\text{SL}_{2}$, as in the previous subsection. We define  $\unicode[STIX]{x1D6E9}(1)$ as the space of automorphic functions
$\unicode[STIX]{x1D6E9}(1)$ as the space of automorphic functions
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f)(g_{D})=\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(z\cdot f)(g_{D}g)\,dg\quad \text{with }g_{D}\in G_{D}(\mathbb{A}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(f)(g_{D})=\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(z\cdot f)(g_{D}g)\,dg\quad \text{with }g_{D}\in G_{D}(\mathbb{A}),\end{eqnarray}$$ where we assume that  $f_{\infty }$ is
$f_{\infty }$ is  $K_{\infty }$-finite. (We assume this finiteness since in the next section we will determine the local lift at real places in the language of
$K_{\infty }$-finite. (We assume this finiteness since in the next section we will determine the local lift at real places in the language of  $(\mathfrak{g},K)$-modules.) We want to show that
$(\mathfrak{g},K)$-modules.) We want to show that  $\unicode[STIX]{x1D6E9}(1)\neq 0$, using Theorem 5.3. The input in the theta kernel is
$\unicode[STIX]{x1D6E9}(1)\neq 0$, using Theorem 5.3. The input in the theta kernel is  $h=1$, so the first thing is to show that
$h=1$, so the first thing is to show that  $z^{\vee }\cdot 1\neq 0$. In the case at hand,
$z^{\vee }\cdot 1\neq 0$. In the case at hand,  $z^{\vee }$ is obtained from
$z^{\vee }$ is obtained from  $z$ by replacing
$z$ by replacing  $x$ by
$x$ by  $x^{-1}$ in the above expression for
$x^{-1}$ in the above expression for  $z$. In particular,
$z$. In particular,  $z=z^{\vee }$. Moreover,
$z=z^{\vee }$. Moreover,  $z$ acts on the trivial representation by the scalar obtained by substituting
$z$ acts on the trivial representation by the scalar obtained by substituting  $x=q$, and this is non-zero. It remains to argue that we can arrange
$x=q$, and this is non-zero. It remains to argue that we can arrange  $f_{\infty }$ to be
$f_{\infty }$ to be  $K_{\infty }$-finite. This follows by the continuity of the regularized theta integral, which ensures that the non-vanishing for smooth
$K_{\infty }$-finite. This follows by the continuity of the regularized theta integral, which ensures that the non-vanishing for smooth  $f$ implies the non-vanishing for
$f$ implies the non-vanishing for  $K_{\infty }$-finite vectors. Alternatively, by the remark following Theorem 5.3, non-vanishing can be achieved with
$K_{\infty }$-finite vectors. Alternatively, by the remark following Theorem 5.3, non-vanishing can be achieved with  $f_{\infty }=f_{\infty }^{\circ }$ the spherical vector.
$f_{\infty }=f_{\infty }^{\circ }$ the spherical vector.
7 Correspondence for real groups
In this section we work over the field  $\mathbb{R}$ of real numbers. The goal of this section is to determine
$\mathbb{R}$ of real numbers. The goal of this section is to determine  $\unicode[STIX]{x1D6E9}(1)$ explicitly. As in the
$\unicode[STIX]{x1D6E9}(1)$ explicitly. As in the  $p$-adic case, the inclusion of the minimal representation
$p$-adic case, the inclusion of the minimal representation  $\unicode[STIX]{x1D6F1}{\hookrightarrow}I(-5)$ composed with the restriction of functions from
$\unicode[STIX]{x1D6F1}{\hookrightarrow}I(-5)$ composed with the restriction of functions from  $G$ to
$G$ to  $G_{D}$ gives a natural non-zero
$G_{D}$ gives a natural non-zero  $G_{D}$-equivariant map
$G_{D}$-equivariant map  $\unicode[STIX]{x1D6E9}(1)\longrightarrow I_{D}(-1)$. We shall show that this natural map is injective and identify its image as an irreducible submodule of
$\unicode[STIX]{x1D6E9}(1)\longrightarrow I_{D}(-1)$. We shall show that this natural map is injective and identify its image as an irreducible submodule of  $I_{D}(-1)$.
$I_{D}(-1)$.
To determine  $\unicode[STIX]{x1D6E9}(1)$ in the archimedean setting, we need to consider various cases separately. Indeed, recall that the adjoint group
$\unicode[STIX]{x1D6E9}(1)$ in the archimedean setting, we need to consider various cases separately. Indeed, recall that the adjoint group  $G$ arises from an Albert algebra via the Koecher–Tits construction. There are two real forms of octonion algebra, the classical Graves algebra and its split form, and these two algebras can be used to define two Albert algebras of
$G$ arises from an Albert algebra via the Koecher–Tits construction. There are two real forms of octonion algebra, the classical Graves algebra and its split form, and these two algebras can be used to define two Albert algebras of  $3\times 3$ hermitian symmetric matrices with coefficients in the octonion algebra. The group
$3\times 3$ hermitian symmetric matrices with coefficients in the octonion algebra. The group  $G$ is split or of the relative rank 3, depending on whether the octonion algebra is split or not (in the
$G$ is split or of the relative rank 3, depending on whether the octonion algebra is split or not (in the  $p$-adic case,
$p$-adic case,  $G$ is always split since an octonion algebra is necessarily split).
$G$ is always split since an octonion algebra is necessarily split).
We shall study the theta correspondence for real groups in the category of  $(\mathfrak{g},K)$-modules, so that examination of
$(\mathfrak{g},K)$-modules, so that examination of  $K$-types plays a key role. Because of this, it will be convenient to work with the simply connected form
$K$-types plays a key role. Because of this, it will be convenient to work with the simply connected form  $G^{\prime }$ of
$G^{\prime }$ of  $G$ rather than the adjoint form, for the maximal compact subgroup
$G$ rather than the adjoint form, for the maximal compact subgroup  $K^{\prime }$ of
$K^{\prime }$ of  $G^{\prime }$ is then connected (whereas that of
$G^{\prime }$ is then connected (whereas that of  $G$ is not) and its irreducible representations are classified by highest weights. The inclusion
$G$ is not) and its irreducible representations are classified by highest weights. The inclusion  $D^{1}{\hookrightarrow}G$ lifts naturally to
$D^{1}{\hookrightarrow}G$ lifts naturally to  $D^{1}{\hookrightarrow}G^{\prime }$ (since
$D^{1}{\hookrightarrow}G^{\prime }$ (since  $D^{1}$ is simply connected as an algebraic group) and its centralizer in
$D^{1}$ is simply connected as an algebraic group) and its centralizer in  $G^{\prime }$ is the simply connected cover
$G^{\prime }$ is the simply connected cover  $G_{D}^{\prime }$ of
$G_{D}^{\prime }$ of  $G_{D}$. In particular,
$G_{D}$. In particular,  $G_{D}^{\prime }$ is isomorphic to
$G_{D}^{\prime }$ is isomorphic to  $\text{Spin}_{12}$ over
$\text{Spin}_{12}$ over  $\mathbb{C}$ and we have a dual pair
$\mathbb{C}$ and we have a dual pair  $D^{1}\times G_{D}^{\prime }\longrightarrow G^{\prime }$.
$D^{1}\times G_{D}^{\prime }\longrightarrow G^{\prime }$.
Observe that the Lie group  $G_{D}$ (i.e. the Lie group
$G_{D}$ (i.e. the Lie group  $G_{D}(\mathbb{R})$) has two topological connected components and
$G_{D}(\mathbb{R})$) has two topological connected components and  $G_{D}^{\prime }$ is a
$G_{D}^{\prime }$ is a  $2$-fold cover of the identity component of
$2$-fold cover of the identity component of  $G_{D}$. The maximal compact subgroup
$G_{D}$. The maximal compact subgroup  $K_{D}$ has two connected components meeting the connected components of
$K_{D}$ has two connected components meeting the connected components of  $G_{D}$. Hence there is a natural bijection between irreducible spherical representation of
$G_{D}$. Hence there is a natural bijection between irreducible spherical representation of  $G_{D}$ and
$G_{D}$ and  $G_{D}^{\prime }$, via the pullback by the natural map
$G_{D}^{\prime }$, via the pullback by the natural map  $G_{D}^{\prime }\longrightarrow G_{D}$. We shall use this observation to prove, for example, that when
$G_{D}^{\prime }\longrightarrow G_{D}$. We shall use this observation to prove, for example, that when  $G$ is split,
$G$ is split,  $\unicode[STIX]{x1D6E9}(1)$ is an irreducible, spherical
$\unicode[STIX]{x1D6E9}(1)$ is an irreducible, spherical  $(\mathfrak{g}_{D},K_{D})$-module by computing its
$(\mathfrak{g}_{D},K_{D})$-module by computing its  $K_{D}^{\prime }$-types.
$K_{D}^{\prime }$-types.
7.1 Non-split  $\mathbb{O}$
$\mathbb{O}$
Assume firstly that  $\mathbb{O}$ and hence
$\mathbb{O}$ and hence  $G$ is not split. Then the minimal representation of the adjoint group
$G$ is not split. Then the minimal representation of the adjoint group  $G$, when restricted to the simply connected
$G$, when restricted to the simply connected  $G^{\prime }$, breaks up as
$G^{\prime }$, breaks up as  $\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}_{1,0}\oplus \unicode[STIX]{x1D6F1}_{0,1}$, a sum of a holomorphic and an anti-holomorphic irreducible representation. This sum is the socle of the degenerate principal series
$\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}_{1,0}\oplus \unicode[STIX]{x1D6F1}_{0,1}$, a sum of a holomorphic and an anti-holomorphic irreducible representation. This sum is the socle of the degenerate principal series  $I(-5)$ (pulled back to
$I(-5)$ (pulled back to  $G^{\prime }$). The maximal compact subgroup
$G^{\prime }$). The maximal compact subgroup  $K^{\prime }$ is of semisimple type
$K^{\prime }$ is of semisimple type  $E_{6}$, and has one-dimensional center
$E_{6}$, and has one-dimensional center  $\text{U}(1)$ that acts on the Lie algebra
$\text{U}(1)$ that acts on the Lie algebra  $\mathfrak{g}$ with weights
$\mathfrak{g}$ with weights  $-2$,
$-2$,  $0$ and
$0$ and  $2$. The weight-
$2$. The weight- $2$ space is a 27-dimensional representation of
$2$ space is a 27-dimensional representation of  $K^{\prime }$. Let
$K^{\prime }$. Let  $\unicode[STIX]{x1D714}$ be its highest weight. Then
$\unicode[STIX]{x1D714}$ be its highest weight. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{1,0}=\bigoplus _{n\geqslant 0}V_{n\unicode[STIX]{x1D714}}(12),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{1,0}=\bigoplus _{n\geqslant 0}V_{n\unicode[STIX]{x1D714}}(12),\end{eqnarray}$$ where 12 denotes a twist of the irreducible  $K^{\prime }$-module
$K^{\prime }$-module  $V_{n\unicode[STIX]{x1D714}}$ such that
$V_{n\unicode[STIX]{x1D714}}$ such that  $\text{U}(1)$ acts with the weight
$\text{U}(1)$ acts with the weight  $2n+12$ on it.
$2n+12$ on it.
In this case,  $D$ is necessarily non-split. Recalling that
$D$ is necessarily non-split. Recalling that  $G_{D}^{\prime }$ is the simply connected cover of
$G_{D}^{\prime }$ is the simply connected cover of  $G_{D}$, its maximal compact subgroup is
$G_{D}$, its maximal compact subgroup is  $K_{D}^{\prime }\cong \text{U}_{6}$. The socle of
$K_{D}^{\prime }\cong \text{U}_{6}$. The socle of  $I_{D}(-1)$, considered a representation of
$I_{D}(-1)$, considered a representation of  $G_{D}^{\prime }$, is a direct sum of three representations
$G_{D}^{\prime }$, is a direct sum of three representations  $\unicode[STIX]{x1D6F4}_{2,0}\oplus \unicode[STIX]{x1D6F4}_{1,1}\oplus \unicode[STIX]{x1D6F4}_{0,2}$, a holomorphic, spherical and anti-holomorphic representation. respectively [Reference SahiSah93, Theorem C]. The lowest and the highest
$\unicode[STIX]{x1D6F4}_{2,0}\oplus \unicode[STIX]{x1D6F4}_{1,1}\oplus \unicode[STIX]{x1D6F4}_{0,2}$, a holomorphic, spherical and anti-holomorphic representation. respectively [Reference SahiSah93, Theorem C]. The lowest and the highest  $K_{D}^{\prime }$-types of
$K_{D}^{\prime }$-types of  $\unicode[STIX]{x1D6F4}_{2,0}$ and
$\unicode[STIX]{x1D6F4}_{2,0}$ and  $\unicode[STIX]{x1D6F4}_{0,2}$ are one-dimensional with
$\unicode[STIX]{x1D6F4}_{0,2}$ are one-dimensional with  $\text{U}(1)$-weights 12 and
$\text{U}(1)$-weights 12 and  $-12$, respectively. We have the following theorem.
$-12$, respectively. We have the following theorem.
Theorem 7.1. If  $\mathbb{O}$ is non-split (so
$\mathbb{O}$ is non-split (so  $G$ is not split), we have
$G$ is not split), we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}\cong \unicode[STIX]{x1D6F4}_{2,0}\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{0,1}^{D^{1}}\cong \unicode[STIX]{x1D6F4}_{0,2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}\cong \unicode[STIX]{x1D6F4}_{2,0}\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{0,1}^{D^{1}}\cong \unicode[STIX]{x1D6F4}_{0,2}\end{eqnarray}$$ as  $(\mathfrak{g}_{D},K_{D}^{\prime })$-modules. In particular,
$(\mathfrak{g}_{D},K_{D}^{\prime })$-modules. In particular,  $\unicode[STIX]{x1D6E9}(1)\cong \unicode[STIX]{x1D6F4}_{2,0}\oplus \unicode[STIX]{x1D6F4}_{0,2}$ as
$\unicode[STIX]{x1D6E9}(1)\cong \unicode[STIX]{x1D6F4}_{2,0}\oplus \unicode[STIX]{x1D6F4}_{0,2}$ as  $(\mathfrak{g}_{D},K_{D})$-modules.
$(\mathfrak{g}_{D},K_{D})$-modules.
Proof. Since  $\unicode[STIX]{x1D6F1}_{1,0}$ is unitarizable and
$\unicode[STIX]{x1D6F1}_{1,0}$ is unitarizable and  $\text{U}(1)$-admissible, its restriction to
$\text{U}(1)$-admissible, its restriction to  $\mathfrak{g}_{D}$ is a direct sum of irreducible lowest weight representations. The minimal type of
$\mathfrak{g}_{D}$ is a direct sum of irreducible lowest weight representations. The minimal type of  $\unicode[STIX]{x1D6F1}_{1,0}$ generates an irreducible lowest weight
$\unicode[STIX]{x1D6F1}_{1,0}$ generates an irreducible lowest weight  $(\mathfrak{g}_{D},K_{D}^{\prime })$-module, with the minimal
$(\mathfrak{g}_{D},K_{D}^{\prime })$-module, with the minimal  $\text{U}_{6}$-type
$\text{U}_{6}$-type  $\det ^{2}$ (i.e.
$\det ^{2}$ (i.e.  $\text{U}(1)$-weight 12). Thus
$\text{U}(1)$-weight 12). Thus  $\unicode[STIX]{x1D6F4}_{2,0}\subseteq \unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}$. The infinitesimal character of
$\unicode[STIX]{x1D6F4}_{2,0}\subseteq \unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}$. The infinitesimal character of  $\unicode[STIX]{x1D6F4}_{2,0}$ is
$\unicode[STIX]{x1D6F4}_{2,0}$ is  $(3,2,1,0,-1,-2)$, in terms of the standard realization of the
$(3,2,1,0,-1,-2)$, in terms of the standard realization of the  $D_{6}$ root system. If the inclusion
$D_{6}$ root system. If the inclusion  $\unicode[STIX]{x1D6F4}_{2,0}\subseteq \unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}$ is strict, then
$\unicode[STIX]{x1D6F4}_{2,0}\subseteq \unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}$ is strict, then  $\unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}$ contains another lowest weight representation with the same infinitesimal character. There is precisely one other irreducible lowest weight
$\unicode[STIX]{x1D6F1}_{1,0}^{D^{1}}$ contains another lowest weight representation with the same infinitesimal character. There is precisely one other irreducible lowest weight  $(\mathfrak{g}_{D},K_{D}^{\prime })$-module with this infinitesimal character, with the minimal
$(\mathfrak{g}_{D},K_{D}^{\prime })$-module with this infinitesimal character, with the minimal  $\text{U}_{6}$-type
$\text{U}_{6}$-type  $\det ^{3}$ (i.e.
$\det ^{3}$ (i.e.  $\text{U}(1)$-weight 18). Thus the number of irreducible summands in
$\text{U}(1)$-weight 18). Thus the number of irreducible summands in  $\unicode[STIX]{x1D6F1}_{1.0}^{D^{1}}$ is bounded by the dimension of
$\unicode[STIX]{x1D6F1}_{1.0}^{D^{1}}$ is bounded by the dimension of  $\text{SU}_{6}\times D^{1}$-invariants in
$\text{SU}_{6}\times D^{1}$-invariants in  $\unicode[STIX]{x1D6F1}_{1,0}$. By the Cartan–Helgason theorem, a finite-dimensional irreducible representation of
$\unicode[STIX]{x1D6F1}_{1,0}$. By the Cartan–Helgason theorem, a finite-dimensional irreducible representation of  $E_{6}$ has a line fixed by
$E_{6}$ has a line fixed by  $A_{5}\times A_{1}$ if and only if it is self-dual. It follows that the space of
$A_{5}\times A_{1}$ if and only if it is self-dual. It follows that the space of  $\text{SU}_{6}\times D^{1}$-invariants in
$\text{SU}_{6}\times D^{1}$-invariants in  $\unicode[STIX]{x1D6F1}_{1,0}$ is one-dimensional, with the only contribution coming from the trivial type. This proves the theorem.◻
$\unicode[STIX]{x1D6F1}_{1,0}$ is one-dimensional, with the only contribution coming from the trivial type. This proves the theorem.◻
7.2 Split  $\mathbb{O}$ but non-split
$\mathbb{O}$ but non-split  $D$
$D$
We move on to the case where  $\mathbb{O}$ and hence
$\mathbb{O}$ and hence  $G$ is split. Let
$G$ is split. Let  $K^{\prime }$ be a maximal compact subgroup of
$K^{\prime }$ be a maximal compact subgroup of  $G^{\prime }$ (the simply connected form of
$G^{\prime }$ (the simply connected form of  $G$), and
$G$), and  $\mathfrak{g}=\mathfrak{k}\oplus \mathfrak{p}$ the corresponding Cartan decomposition of the complexification of the Lie algebra of
$\mathfrak{g}=\mathfrak{k}\oplus \mathfrak{p}$ the corresponding Cartan decomposition of the complexification of the Lie algebra of  $G$. Then
$G$. Then  $\mathfrak{k}$ is isomorphic to
$\mathfrak{k}$ is isomorphic to  $\mathfrak{sl}_{8}$. Fixing this isomorphism, we see that as a
$\mathfrak{sl}_{8}$. Fixing this isomorphism, we see that as a  $K^{\prime }\cong \text{SU}_{8}/\unicode[STIX]{x1D707}_{2}$-module,
$K^{\prime }\cong \text{SU}_{8}/\unicode[STIX]{x1D707}_{2}$-module,  $\mathfrak{p}$ is isomorphic to
$\mathfrak{p}$ is isomorphic to  $V_{\unicode[STIX]{x1D714}_{4}}$, where
$V_{\unicode[STIX]{x1D714}_{4}}$, where  $\unicode[STIX]{x1D714}_{4}$ is the fourth fundamental weight. The minimal representation
$\unicode[STIX]{x1D714}_{4}$ is the fourth fundamental weight. The minimal representation  $\unicode[STIX]{x1D6F1}$ remains irreducible when pulled back to
$\unicode[STIX]{x1D6F1}$ remains irreducible when pulled back to  $G^{\prime }$ and is a direct sum of
$G^{\prime }$ and is a direct sum of  $K^{\prime }$-types
$K^{\prime }$-types  $V_{n\unicode[STIX]{x1D714}_{4}}$, where
$V_{n\unicode[STIX]{x1D714}_{4}}$, where  $n=0,1,2,\ldots$ .
$n=0,1,2,\ldots$ .
We have two cases depending on  $D$. Assume in this subsection that
$D$. Assume in this subsection that  $D$ is a division algebra. In this case
$D$ is a division algebra. In this case  $D^{1}\cong \text{SU}_{2}$ is compact, and embeds into
$D^{1}\cong \text{SU}_{2}$ is compact, and embeds into  $\text{SU}_{8}$ as a
$\text{SU}_{8}$ as a  $2\times 2$ block. The centralizer of
$2\times 2$ block. The centralizer of  $\text{SU}_{2}$ in
$\text{SU}_{2}$ in  $K^{\prime }=\text{SU}_{8}/\unicode[STIX]{x1D707}_{2}$ is
$K^{\prime }=\text{SU}_{8}/\unicode[STIX]{x1D707}_{2}$ is  $K_{D}^{\prime }\cong \text{U}_{6}$. The minimal representation
$K_{D}^{\prime }\cong \text{U}_{6}$. The minimal representation  $\unicode[STIX]{x1D6F1}$ decomposes discretely when restricted to this dual pair. A simple application of the Gelfand–Zetlin rule shows that the
$\unicode[STIX]{x1D6F1}$ decomposes discretely when restricted to this dual pair. A simple application of the Gelfand–Zetlin rule shows that the  $K_{D}^{\prime }$-types of
$K_{D}^{\prime }$-types of  $\unicode[STIX]{x1D6E9}(1)$ are multiplicity-free and the highest weights of the
$\unicode[STIX]{x1D6E9}(1)$ are multiplicity-free and the highest weights of the  $K_{D}^{\prime }$-types which occur are
$K_{D}^{\prime }$-types which occur are
 $$\begin{eqnarray}(x,x,0,0,y,y),\end{eqnarray}$$
$$\begin{eqnarray}(x,x,0,0,y,y),\end{eqnarray}$$ where  $x\geqslant 0\geqslant y$ are any two integers. Here we are using the standard description of highest weights for
$x\geqslant 0\geqslant y$ are any two integers. Here we are using the standard description of highest weights for  $\text{U}_{6}$ by sextuples of non-increasing integers. But these are precisely the
$\text{U}_{6}$ by sextuples of non-increasing integers. But these are precisely the  $K_{D}^{\prime }$-types of the spherical submodule of
$K_{D}^{\prime }$-types of the spherical submodule of  $I_{D}(-1)$, that is, the
$I_{D}(-1)$, that is, the  $G_{D}^{\prime }$-constituent
$G_{D}^{\prime }$-constituent  $\unicode[STIX]{x1D6F4}_{1,1}$ in [Reference SahiSah93, Theorem C]. In view of the natural non-zero
$\unicode[STIX]{x1D6F4}_{1,1}$ in [Reference SahiSah93, Theorem C]. In view of the natural non-zero  $G_{D}$-equivariant map
$G_{D}$-equivariant map  $\unicode[STIX]{x1D6E9}(1)\rightarrow I_{D}(-1)$, this proves the following theorem.
$\unicode[STIX]{x1D6E9}(1)\rightarrow I_{D}(-1)$, this proves the following theorem.
Theorem 7.2. When  $\mathbb{O}$ is split but
$\mathbb{O}$ is split but  $D$ is non-split, one has
$D$ is non-split, one has
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(1)=\unicode[STIX]{x1D6F1}^{D^{1}}\cong \unicode[STIX]{x1D6F4}_{1,1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(1)=\unicode[STIX]{x1D6F1}^{D^{1}}\cong \unicode[STIX]{x1D6F4}_{1,1}\end{eqnarray}$$ as  $(\mathfrak{g}_{D},K_{D})$-modules.
$(\mathfrak{g}_{D},K_{D})$-modules.
7.3 Split  $\mathbb{O}$ and split
$\mathbb{O}$ and split  $D$
$D$
This is the most involved case. Let  $(e,h,f)$ be an
$(e,h,f)$ be an  $\mathfrak{sl}_{2}$-triple spanning the complexified Lie algebra of
$\mathfrak{sl}_{2}$-triple spanning the complexified Lie algebra of  $D^{1}=\text{SL}_{2}$. After conjugating by
$D^{1}=\text{SL}_{2}$. After conjugating by  $G^{\prime }$, if necessary, we can assume that the triple is stable under the Cartan involution. Then
$G^{\prime }$, if necessary, we can assume that the triple is stable under the Cartan involution. Then  $e\in \mathfrak{p}$ is a highest weight vector for the action of
$e\in \mathfrak{p}$ is a highest weight vector for the action of  $K^{\prime }$, and
$K^{\prime }$, and  $h\in \mathfrak{k}$. Let
$h\in \mathfrak{k}$. Let  $\unicode[STIX]{x1D6E9}(1)$ be the maximal quotient of the
$\unicode[STIX]{x1D6E9}(1)$ be the maximal quotient of the  $(\mathfrak{g},K^{\prime })$-module of the minimal representation such that the
$(\mathfrak{g},K^{\prime })$-module of the minimal representation such that the  $\mathfrak{sl}_{2}$ triple acts trivially.
$\mathfrak{sl}_{2}$ triple acts trivially.
Theorem 7.3. As a  $(\mathfrak{g}_{D},K_{D})$-module,
$(\mathfrak{g}_{D},K_{D})$-module,  $\unicode[STIX]{x1D6E9}(1)$ is irreducible and isomorphic to the unique irreducible submodule
$\unicode[STIX]{x1D6E9}(1)$ is irreducible and isomorphic to the unique irreducible submodule  $\unicode[STIX]{x1D6F4}$ of
$\unicode[STIX]{x1D6F4}$ of  $I_{D}(-1)$, which is a spherical representation.
$I_{D}(-1)$, which is a spherical representation.
The proof of this result will take up the rest of this section. After conjugating by  $K^{\prime }$, if necessary, we can assume that
$K^{\prime }$, if necessary, we can assume that
 $$\begin{eqnarray}h=\frac{1}{2}\left(\begin{array}{@{}cccccccc@{}}1 & & & & & & & \\ & 1 & & & & & & \\ & & 1 & & & & & \\ & & & 1 & & & & \\ & & & & -1 & & & \\ & & & & & -1 & & \\ & & & & & & -1 & \\ & & & & & & & -1\\ \end{array}\right)\in \mathfrak{sl}_{8}.\end{eqnarray}$$
$$\begin{eqnarray}h=\frac{1}{2}\left(\begin{array}{@{}cccccccc@{}}1 & & & & & & & \\ & 1 & & & & & & \\ & & 1 & & & & & \\ & & & 1 & & & & \\ & & & & -1 & & & \\ & & & & & -1 & & \\ & & & & & & -1 & \\ & & & & & & & -1\\ \end{array}\right)\in \mathfrak{sl}_{8}.\end{eqnarray}$$ Then  $G_{D}^{\prime }$ is the centralizer of the
$G_{D}^{\prime }$ is the centralizer of the  $\mathfrak{sl}_{2}$-triple in
$\mathfrak{sl}_{2}$-triple in  $G^{\prime }$ and is isomorphic to
$G^{\prime }$ and is isomorphic to  $\text{Spin}(6,6)$ as an algebraic group. Let
$\text{Spin}(6,6)$ as an algebraic group. Let  $\mathfrak{g}_{D}=\mathfrak{k}_{D}\oplus \mathfrak{p}_{D}$ be the corresponding Cartan decomposition. Then
$\mathfrak{g}_{D}=\mathfrak{k}_{D}\oplus \mathfrak{p}_{D}$ be the corresponding Cartan decomposition. Then  $\mathfrak{k}_{D}\cong \mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}$ sitting block diagonally in
$\mathfrak{k}_{D}\cong \mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}$ sitting block diagonally in  $\mathfrak{sl}_{8}$. The centralizer of
$\mathfrak{sl}_{8}$. The centralizer of  $h$ in
$h$ in  $\text{SU}_{8}/\unicode[STIX]{x1D707}_{2}$ is
$\text{SU}_{8}/\unicode[STIX]{x1D707}_{2}$ is
 $$\begin{eqnarray}K_{D}^{\prime }=\text{SU}_{4}\times \text{SU}_{4}/\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D707}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}K_{D}^{\prime }=\text{SU}_{4}\times \text{SU}_{4}/\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D707}_{2}.\end{eqnarray}$$ Let  $\unicode[STIX]{x1D6F1}$ be the
$\unicode[STIX]{x1D6F1}$ be the  $(\mathfrak{g},K^{\prime })$-module corresponding to the minimal representation of
$(\mathfrak{g},K^{\prime })$-module corresponding to the minimal representation of  $G$. Then, as a
$G$. Then, as a  $K^{\prime }$-module,
$K^{\prime }$-module,
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\bigoplus _{n\geqslant 0}V_{n\unicode[STIX]{x1D714}_{4}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\bigoplus _{n\geqslant 0}V_{n\unicode[STIX]{x1D714}_{4}}.\end{eqnarray}$$ We shall also need the following facts about the action of  $e$ on
$e$ on  $\unicode[STIX]{x1D6F1}$. From the formula for the tensor product
$\unicode[STIX]{x1D6F1}$. From the formula for the tensor product  $V_{\unicode[STIX]{x1D714}_{4}}\otimes V_{\mathbf{n}\unicode[STIX]{x1D714}_{4}}$ it follows that
$V_{\unicode[STIX]{x1D714}_{4}}\otimes V_{\mathbf{n}\unicode[STIX]{x1D714}_{4}}$ it follows that
 $$\begin{eqnarray}e\cdot V_{n\unicode[STIX]{x1D714}_{4}}\subseteq V_{(n-1)\unicode[STIX]{x1D714}_{4}}\oplus V_{(n+1)\unicode[STIX]{x1D714}_{4}}.\end{eqnarray}$$
$$\begin{eqnarray}e\cdot V_{n\unicode[STIX]{x1D714}_{4}}\subseteq V_{(n-1)\unicode[STIX]{x1D714}_{4}}\oplus V_{(n+1)\unicode[STIX]{x1D714}_{4}}.\end{eqnarray}$$ Since  $\unicode[STIX]{x1D6F1}$ is not a highest weight module, by [Reference Vogan, Carmona and VergneVog81, Lemma 3.4],
$\unicode[STIX]{x1D6F1}$ is not a highest weight module, by [Reference Vogan, Carmona and VergneVog81, Lemma 3.4],  $e$ is injective on
$e$ is injective on  $\unicode[STIX]{x1D6F1}$. The same results hold for
$\unicode[STIX]{x1D6F1}$. The same results hold for  $f$.
$f$.
Let  $\unicode[STIX]{x1D70B}$ be an irreducible
$\unicode[STIX]{x1D70B}$ be an irreducible  $\mathfrak{sl}_{2}$-module such that
$\mathfrak{sl}_{2}$-module such that  $h$ acts semisimply and integrally. Let
$h$ acts semisimply and integrally. Let  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ be the big theta lift of
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ be the big theta lift of  $\unicode[STIX]{x1D70B}$; it is a
$\unicode[STIX]{x1D70B}$; it is a  $(\mathfrak{g}_{D},K_{D}^{\prime })$-module. We shall now partially determine the structure of
$(\mathfrak{g}_{D},K_{D}^{\prime })$-module. We shall now partially determine the structure of  $K_{D}^{\prime }$-types of
$K_{D}^{\prime }$-types of  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$. In order to state the result, we need some additional notation. A highest weight
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$. In order to state the result, we need some additional notation. A highest weight  $\unicode[STIX]{x1D707}$ for
$\unicode[STIX]{x1D707}$ for  $\text{SU}_{4}$ is represented by a quadruple
$\text{SU}_{4}$ is represented by a quadruple  $(x,y,z,u)$ of integers, such that
$(x,y,z,u)$ of integers, such that  $x\geqslant y\geqslant z\geqslant u$, and it is determined by the triple
$x\geqslant y\geqslant z\geqslant u$, and it is determined by the triple
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=x-y,\quad \unicode[STIX]{x1D6FD}=y-z,\quad \unicode[STIX]{x1D6FE}=z-u\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=x-y,\quad \unicode[STIX]{x1D6FD}=y-z,\quad \unicode[STIX]{x1D6FE}=z-u\end{eqnarray}$$of non-negative integers.
Proposition 7.4. Let  $V\otimes U$ be a
$V\otimes U$ be a  $K_{D}^{\prime }\cong \text{SU}_{4}\times \text{SU}_{4}/\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D707}_{2}$-type of
$K_{D}^{\prime }\cong \text{SU}_{4}\times \text{SU}_{4}/\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D707}_{2}$-type of  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$. Then
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$. Then  $U\cong V^{\ast }$, the dual representation of
$U\cong V^{\ast }$, the dual representation of  $V$, and the multiplicity of
$V$, and the multiplicity of  $V\otimes V^{\ast }$ in
$V\otimes V^{\ast }$ in  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ is at most
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ is at most  $1$. If
$1$. If  $\unicode[STIX]{x1D70B}=1$, the trivial representation, and
$\unicode[STIX]{x1D70B}=1$, the trivial representation, and  $\unicode[STIX]{x1D707}$ is the highest weight of
$\unicode[STIX]{x1D707}$ is the highest weight of  $V$, then
$V$, then  $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}$.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}$.
Proof. We need the following lemma which can be easily deduced from the Gelfand–Zetlin branching rule.
Lemma 7.5. The restriction of  $V_{n\unicode[STIX]{x1D714}_{4}}$ to
$V_{n\unicode[STIX]{x1D714}_{4}}$ to  $\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}\oplus \mathbb{C}h$ is multiplicity-free and given by
$\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}\oplus \mathbb{C}h$ is multiplicity-free and given by
 $$\begin{eqnarray}V_{n\unicode[STIX]{x1D714}_{4}}=\bigoplus _{n\geqslant x\geqslant y\geqslant z\geqslant u\geqslant 0}V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }\otimes \mathbb{C}(m),\end{eqnarray}$$
$$\begin{eqnarray}V_{n\unicode[STIX]{x1D714}_{4}}=\bigoplus _{n\geqslant x\geqslant y\geqslant z\geqslant u\geqslant 0}V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }\otimes \mathbb{C}(m),\end{eqnarray}$$ where  $\unicode[STIX]{x1D707}$ is represented by the quadruple
$\unicode[STIX]{x1D707}$ is represented by the quadruple  $(x,y,z,u)$ and
$(x,y,z,u)$ and  $h$ acts on
$h$ acts on  $\mathbb{C}(m)$ by the integer
$\mathbb{C}(m)$ by the integer  $m=x+y+z+u-2n$.
$m=x+y+z+u-2n$.
It follows from the lemma that the only  $K_{D}^{\prime }$-types appearing in the restriction of
$K_{D}^{\prime }$-types appearing in the restriction of  $\unicode[STIX]{x1D6F1}$ are isomorphic to
$\unicode[STIX]{x1D6F1}$ are isomorphic to  $V\otimes V^{\ast }$, as claimed. In order to prove multiplicity
$V\otimes V^{\ast }$, as claimed. In order to prove multiplicity  $1$ of
$1$ of  $K_{D}^{\prime }$-types in
$K_{D}^{\prime }$-types in  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$, we proceed as follows.
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$, we proceed as follows.
Let  $m$ be an integer appearing as an
$m$ be an integer appearing as an  $h$-type in
$h$-type in  $\unicode[STIX]{x1D70B}$. Let
$\unicode[STIX]{x1D70B}$. Let  $\unicode[STIX]{x1D6FA}$ be the Casimir element for
$\unicode[STIX]{x1D6FA}$ be the Casimir element for  $\mathfrak{sl}_{2}$ and let
$\mathfrak{sl}_{2}$ and let  $\unicode[STIX]{x1D712}:\mathbb{C}[\unicode[STIX]{x1D6FA}]\rightarrow \mathbb{C}$ be the central character of
$\unicode[STIX]{x1D712}:\mathbb{C}[\unicode[STIX]{x1D6FA}]\rightarrow \mathbb{C}$ be the central character of  $\unicode[STIX]{x1D70B}$. Let
$\unicode[STIX]{x1D70B}$. Let  $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ be the maximal subspace of
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ be the maximal subspace of  $\unicode[STIX]{x1D6F1}$ such that
$\unicode[STIX]{x1D6F1}$ such that  $h$ acts as the integer
$h$ acts as the integer  $m$ and
$m$ and  $\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}$ as a multiple of
$\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}$ as a multiple of  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$. Note that
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$. Note that  $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ is naturally a
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ is naturally a  $\mathbb{C}[\unicode[STIX]{x1D6FA}]$-module, and it suffices to show that the maximal quotient of
$\mathbb{C}[\unicode[STIX]{x1D6FA}]$-module, and it suffices to show that the maximal quotient of  $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ such that
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ such that  $\mathbb{C}[\unicode[STIX]{x1D6FA}]$ acts on it by
$\mathbb{C}[\unicode[STIX]{x1D6FA}]$ acts on it by  $\unicode[STIX]{x1D712}$ is isomorphic to
$\unicode[STIX]{x1D712}$ is isomorphic to  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ as an
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ as an  $\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}$-module. We have a canonical isomorphism
$\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}$-module. We have a canonical isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)\cong (V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast })\otimes \text{Hom}_{\mathfrak{ sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m)),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)\cong (V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast })\otimes \text{Hom}_{\mathfrak{ sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m)),\end{eqnarray}$$ and  $\mathbb{C}[\unicode[STIX]{x1D6FA}]$ acts on
$\mathbb{C}[\unicode[STIX]{x1D6FA}]$ acts on
 $$\begin{eqnarray}\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m))=\bigoplus _{n\geqslant 0}\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{n\unicode[STIX]{x1D714}_{4}}(m)).\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m))=\bigoplus _{n\geqslant 0}\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{n\unicode[STIX]{x1D714}_{4}}(m)).\end{eqnarray}$$ Now notice that, given  $\unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}$ and  $m$,
$m$,  $\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{n\unicode[STIX]{x1D714}_{4}}(m))\neq 0$ for only one parity of
$\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{n\unicode[STIX]{x1D714}_{4}}(m))\neq 0$ for only one parity of  $n$. Furthermore, if this space is non-zero for some
$n$. Furthermore, if this space is non-zero for some  $n$, then it is non-zero for
$n$, then it is non-zero for  $n+2$, as
$n+2$, as  $\unicode[STIX]{x1D707}$ is also represented by
$\unicode[STIX]{x1D707}$ is also represented by  $(x+1,y+1,z+1,u+1)$ and
$(x+1,y+1,z+1,u+1)$ and
 $$\begin{eqnarray}m=x+y+z+u-2n=x+1+y+1+z+1+u+1-2(n+2).\end{eqnarray}$$
$$\begin{eqnarray}m=x+y+z+u-2n=x+1+y+1+z+1+u+1-2(n+2).\end{eqnarray}$$ Let  $n_{0}$ be the first integer such that
$n_{0}$ be the first integer such that  $\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{n_{0}\unicode[STIX]{x1D714}_{4}}(m))\neq 0$ and let
$\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{n_{0}\unicode[STIX]{x1D714}_{4}}(m))\neq 0$ and let  $T_{0}$ be a generator of this one-dimensional space. We then have a natural map
$T_{0}$ be a generator of this one-dimensional space. We then have a natural map
 $$\begin{eqnarray}A:\mathbb{C}[\unicode[STIX]{x1D6FA}]\cdot T_{0}\rightarrow \text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m)).\end{eqnarray}$$
$$\begin{eqnarray}A:\mathbb{C}[\unicode[STIX]{x1D6FA}]\cdot T_{0}\rightarrow \text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m)).\end{eqnarray}$$Lemma 7.6. The map  $A$ is an isomorphism.
$A$ is an isomorphism.
Proof. Let  $i$ be a non-negative integer. Let
$i$ be a non-negative integer. Let  $\mathbb{C}[\unicode[STIX]{x1D6FA}]_{i}$ be the space of polynomials of degree less than or equal to
$\mathbb{C}[\unicode[STIX]{x1D6FA}]_{i}$ be the space of polynomials of degree less than or equal to  $i$, and let
$i$, and let
 $$\begin{eqnarray}\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m))_{i}=\bigoplus _{j=0}^{i}\text{Hom}_{\mathfrak{ sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{(n_{0}+2j)\unicode[STIX]{x1D714}_{4}}(m)).\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m))_{i}=\bigoplus _{j=0}^{i}\text{Hom}_{\mathfrak{ sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },V_{(n_{0}+2j)\unicode[STIX]{x1D714}_{4}}(m)).\end{eqnarray}$$ These two spaces have dimension  $i+1$ and define filtrations of
$i+1$ and define filtrations of  $\mathbb{C}[\unicode[STIX]{x1D6FA}]$ and
$\mathbb{C}[\unicode[STIX]{x1D6FA}]$ and  $\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m))$ as
$\text{Hom}_{\mathfrak{sl}_{4}\oplus \mathfrak{sl}_{4}}(V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast },\unicode[STIX]{x1D6F1}(m))$ as  $i$ increases. Since
$i$ increases. Since  $\unicode[STIX]{x1D6FA}$ has degree 2, as an element of the enveloping algebra of
$\unicode[STIX]{x1D6FA}$ has degree 2, as an element of the enveloping algebra of  $\mathfrak{g}$, the map
$\mathfrak{g}$, the map  $A$ preserves the two filtrations. Thus, in order to prove the claim, it suffices to show that
$A$ preserves the two filtrations. Thus, in order to prove the claim, it suffices to show that  $A$ is injective.
$A$ is injective.
But if it is not, then there would be a polynomial  $p(\unicode[STIX]{x1D6FA})$ acting trivially on
$p(\unicode[STIX]{x1D6FA})$ acting trivially on  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }\subseteq V_{n_{0}\unicode[STIX]{x1D714}_{4}}(m)$. Under the action of
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }\subseteq V_{n_{0}\unicode[STIX]{x1D714}_{4}}(m)$. Under the action of  $\mathfrak{sl}_{2}$, this subspace would generate a finite-length representation
$\mathfrak{sl}_{2}$, this subspace would generate a finite-length representation  $F_{0}\subset \unicode[STIX]{x1D6F1}$ of
$F_{0}\subset \unicode[STIX]{x1D6F1}$ of  $\mathfrak{sl}_{2}$. Let
$\mathfrak{sl}_{2}$. Let  $U(\mathfrak{g})$ be the enveloping algebra of
$U(\mathfrak{g})$ be the enveloping algebra of  $\mathfrak{g}$, and let
$\mathfrak{g}$, and let  $U_{n}(\mathfrak{g})\subset U(\mathfrak{g})$ be the Poincaré–Birkhoff–Witt filtration. We have
$U_{n}(\mathfrak{g})\subset U(\mathfrak{g})$ be the Poincaré–Birkhoff–Witt filtration. We have  $\unicode[STIX]{x1D6F1}=U(\mathfrak{g})\cdot F_{0}$, since
$\unicode[STIX]{x1D6F1}=U(\mathfrak{g})\cdot F_{0}$, since  $\unicode[STIX]{x1D6F1}$ is irreducible
$\unicode[STIX]{x1D6F1}$ is irreducible  $\mathfrak{g}$-module. Hence
$\mathfrak{g}$-module. Hence  $\unicode[STIX]{x1D6F1}$ is a union of
$\unicode[STIX]{x1D6F1}$ is a union of  $F_{n}=U_{n}(\mathfrak{g})\cdot F_{0}$. Now observe that each
$F_{n}=U_{n}(\mathfrak{g})\cdot F_{0}$. Now observe that each  $F_{n}$ is a finite-length
$F_{n}$ is a finite-length  $\mathfrak{sl}_{2}$-module. Hence there could be only countably many irreducible
$\mathfrak{sl}_{2}$-module. Hence there could be only countably many irreducible  $\mathfrak{sl}_{2}$-modules appearing as quotients of
$\mathfrak{sl}_{2}$-modules appearing as quotients of  $\unicode[STIX]{x1D6F1}$. But this contradicts the fact that almost all spherical tempered representations of
$\unicode[STIX]{x1D6F1}$. But this contradicts the fact that almost all spherical tempered representations of  $\mathfrak{sl}_{2}$ are quotients, as discussed in § 6.3. The lemma is proved.◻
$\mathfrak{sl}_{2}$ are quotients, as discussed in § 6.3. The lemma is proved.◻
Lemma 7.6 implies that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)\cong (V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast })\otimes \mathbb{C}[\unicode[STIX]{x1D6FA}]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)\cong (V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast })\otimes \mathbb{C}[\unicode[STIX]{x1D6FA}]\end{eqnarray}$$ as  $\mathbb{C}[\unicode[STIX]{x1D6FA}]$-modules. Hence, if we fix a character
$\mathbb{C}[\unicode[STIX]{x1D6FA}]$-modules. Hence, if we fix a character  $\unicode[STIX]{x1D712}$ of
$\unicode[STIX]{x1D712}$ of  $\mathbb{C}[\unicode[STIX]{x1D6FA}]$, the maximal quotient of
$\mathbb{C}[\unicode[STIX]{x1D6FA}]$, the maximal quotient of  $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ such that
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$ such that  $\mathbb{C}[\unicode[STIX]{x1D6FA}]$ acts by
$\mathbb{C}[\unicode[STIX]{x1D6FA}]$ acts by  $\unicode[STIX]{x1D712}$ is isomorphic to
$\unicode[STIX]{x1D712}$ is isomorphic to  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$. This proves that
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$. This proves that  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ has multiplicity-free
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70B})$ has multiplicity-free  $K_{D}^{\prime }$-types.
$K_{D}^{\prime }$-types.
Finally, we proceed to narrow down the  $K_{D}^{\prime }$-types appearing in
$K_{D}^{\prime }$-types appearing in  $\unicode[STIX]{x1D6E9}(1)$. For every
$\unicode[STIX]{x1D6E9}(1)$. For every  $\unicode[STIX]{x1D707}$, the action of
$\unicode[STIX]{x1D707}$, the action of  $e$ on
$e$ on  $\unicode[STIX]{x1D6F1}$ gives an injective map
$\unicode[STIX]{x1D6F1}$ gives an injective map
 $$\begin{eqnarray}e:\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},-2)\rightarrow \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0).\end{eqnarray}$$
$$\begin{eqnarray}e:\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},-2)\rightarrow \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0).\end{eqnarray}$$Lemma 7.7. If  $e:\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},-2)\rightarrow \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0)$ is bijective, then
$e:\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},-2)\rightarrow \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0)$ is bijective, then  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ is not a
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ is not a  $K_{D}^{\prime }$-type of
$K_{D}^{\prime }$-type of  $\unicode[STIX]{x1D6E9}(1)$.
$\unicode[STIX]{x1D6E9}(1)$.
Proof. The image of  $e$ is necessarily contained in the kernel of the natural surjective map
$e$ is necessarily contained in the kernel of the natural surjective map  $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0)\rightarrow \unicode[STIX]{x1D6E9}(1)(\unicode[STIX]{x1D707})$. Hence the lemma follows.◻
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0)\rightarrow \unicode[STIX]{x1D6E9}(1)(\unicode[STIX]{x1D707})$. Hence the lemma follows.◻
Consider the filtration  $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)_{i}=\bigoplus _{n\leqslant i}V_{n\unicode[STIX]{x1D714}_{4}}(\unicode[STIX]{x1D707},m)$ of
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)_{i}=\bigoplus _{n\leqslant i}V_{n\unicode[STIX]{x1D714}_{4}}(\unicode[STIX]{x1D707},m)$ of  $\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$. Then we have an injective map
$\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},m)$. Then we have an injective map
 $$\begin{eqnarray}e:\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},-2)_{i}\rightarrow \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0)_{i+1}\end{eqnarray}$$
$$\begin{eqnarray}e:\unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},-2)_{i}\rightarrow \unicode[STIX]{x1D6F1}(\unicode[STIX]{x1D707},0)_{i+1}\end{eqnarray}$$ for all  $i$. Hence, if the dimensions of the two spaces are equal for all
$i$. Hence, if the dimensions of the two spaces are equal for all  $i$, then
$i$, then  $e$ is bijective. This will happen precisely when
$e$ is bijective. This will happen precisely when  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ occurs in
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ occurs in  $V_{n\unicode[STIX]{x1D714}_{4}}(-2)$ but not in
$V_{n\unicode[STIX]{x1D714}_{4}}(-2)$ but not in  $V_{(n-1)\unicode[STIX]{x1D714}_{4}}(0)$, for some
$V_{(n-1)\unicode[STIX]{x1D714}_{4}}(0)$, for some  $n$. The occurrence in
$n$. The occurrence in  $V_{n\unicode[STIX]{x1D714}_{4}}(-2)$ implies that there exists a unique quadruple
$V_{n\unicode[STIX]{x1D714}_{4}}(-2)$ implies that there exists a unique quadruple  $(x,y,z,u)$ representing
$(x,y,z,u)$ representing  $\unicode[STIX]{x1D707}$ such that
$\unicode[STIX]{x1D707}$ such that
 $$\begin{eqnarray}n\geqslant x\geqslant y\geqslant z\geqslant u\geqslant 0\quad \text{and}\quad x+y+z+u-2n=-2.\end{eqnarray}$$
$$\begin{eqnarray}n\geqslant x\geqslant y\geqslant z\geqslant u\geqslant 0\quad \text{and}\quad x+y+z+u-2n=-2.\end{eqnarray}$$ Then  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ occurs in
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ occurs in  $V_{(n-1)\unicode[STIX]{x1D714}_{4}}(0)$ if and only if
$V_{(n-1)\unicode[STIX]{x1D714}_{4}}(0)$ if and only if
 $$\begin{eqnarray}n-1\geqslant x\geqslant y\geqslant z\geqslant u\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}n-1\geqslant x\geqslant y\geqslant z\geqslant u\geqslant 0,\end{eqnarray}$$ that is,  $n>x$. Thus, if
$n>x$. Thus, if  $n=x$, then
$n=x$, then  $V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ does not appear in
$V_{\unicode[STIX]{x1D707}}\otimes V_{\unicode[STIX]{x1D707}}^{\ast }$ does not appear in  $\unicode[STIX]{x1D6E9}(1)$.
$\unicode[STIX]{x1D6E9}(1)$.
Let us see what this means in terms of  $\unicode[STIX]{x1D6FC}$,
$\unicode[STIX]{x1D6FC}$,  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FE}$. We have to find
$\unicode[STIX]{x1D6FE}$. We have to find  $n$ such that
$n$ such that  $\unicode[STIX]{x1D707}$ is represented by
$\unicode[STIX]{x1D707}$ is represented by
 $$\begin{eqnarray}(x,y,z,u)=(n,n-\unicode[STIX]{x1D6FC},n-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD},n-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}).\end{eqnarray}$$
$$\begin{eqnarray}(x,y,z,u)=(n,n-\unicode[STIX]{x1D6FC},n-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD},n-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FE}).\end{eqnarray}$$ Since the last entry must be non-negative, we have  $n\geqslant \unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}$. On the other hand,
$n\geqslant \unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}$. On the other hand,  $h$ has to act as
$h$ has to act as  $-2$, hence
$-2$, hence  $x+y+z+u-2n=-2$, and this is equivalent to
$x+y+z+u-2n=-2$, and this is equivalent to  $2n=3\unicode[STIX]{x1D6FC}+2\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}-2$. Combining with the previous inequality, we obtain
$2n=3\unicode[STIX]{x1D6FC}+2\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}-2$. Combining with the previous inequality, we obtain  $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FE}+2$. Hence the types with
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FE}+2$. Hence the types with  $\unicode[STIX]{x1D707}$ such that
$\unicode[STIX]{x1D707}$ such that  $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FE}+2$ do not appear in
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FE}+2$ do not appear in  $\unicode[STIX]{x1D6E9}(1)$. Replacing the role of
$\unicode[STIX]{x1D6E9}(1)$. Replacing the role of  $e$ with
$e$ with  $f$, a similar argument shows that the types such that
$f$, a similar argument shows that the types such that  $\unicode[STIX]{x1D6FE}\geqslant \unicode[STIX]{x1D6FC}+2$ do not appear either. Hence
$\unicode[STIX]{x1D6FE}\geqslant \unicode[STIX]{x1D6FC}+2$ do not appear either. Hence  $|\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FE}|\leqslant 1$ for all types that appear in
$|\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FE}|\leqslant 1$ for all types that appear in  $\unicode[STIX]{x1D6E9}(1)$. Since
$\unicode[STIX]{x1D6E9}(1)$. Since  $\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D6FE}\hspace{0.6em}({\rm mod}\hspace{0.2em}2)$ for any type in
$\unicode[STIX]{x1D6FC}\equiv \unicode[STIX]{x1D6FE}\hspace{0.6em}({\rm mod}\hspace{0.2em}2)$ for any type in  $\unicode[STIX]{x1D6F1}(0)$,
$\unicode[STIX]{x1D6F1}(0)$,  $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}$ for all types that appear in
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}$ for all types that appear in  $\unicode[STIX]{x1D6E9}(1)$. This completes the proof of Proposition 7.4.◻
$\unicode[STIX]{x1D6E9}(1)$. This completes the proof of Proposition 7.4.◻
The  $K_{D}^{\prime }$-types of
$K_{D}^{\prime }$-types of  $\unicode[STIX]{x1D6E9}(1)$, as described in Proposition 7.4, are the same as the
$\unicode[STIX]{x1D6E9}(1)$, as described in Proposition 7.4, are the same as the  $K_{D}^{\prime }$-types of the irreducible spherical rank-2 submodule in
$K_{D}^{\prime }$-types of the irreducible spherical rank-2 submodule in  $I_{D}(-1)$ by [Reference SahiSah95, Theorem 4B]. In view of the natural non-zero
$I_{D}(-1)$ by [Reference SahiSah95, Theorem 4B]. In view of the natural non-zero  $G_{D}$-equivariant map
$G_{D}$-equivariant map  $\unicode[STIX]{x1D6E9}(1)\longrightarrow I_{D}(-1)$, this proves Theorem 7.3.
$\unicode[STIX]{x1D6E9}(1)\longrightarrow I_{D}(-1)$, this proves Theorem 7.3.
8 Siegel–Weil formula
We are now ready to prove the desired Siegel–Weil formula (Theorem 1.2 in the introduction). Assume that  $F$ is a totally real global field and
$F$ is a totally real global field and  $D$ a quaternion algebra over
$D$ a quaternion algebra over  $F$.
$F$.
8.1 The representation  $\unicode[STIX]{x1D6E9}(1)$
$\unicode[STIX]{x1D6E9}(1)$
We have shown that the global (regularized) theta lift  $\unicode[STIX]{x1D6E9}(1)$ is a non-zero automorphic representation of
$\unicode[STIX]{x1D6E9}(1)$ is a non-zero automorphic representation of  $G_{D}(\mathbb{A})$. We have also studied the abstract local theta lift of the trivial representation of
$G_{D}(\mathbb{A})$. We have also studied the abstract local theta lift of the trivial representation of  $D^{1}$ to
$D^{1}$ to  $G_{D}$. The following proposition summarizes what we have shown.
$G_{D}$. The following proposition summarizes what we have shown.
(i) The automorphic representation
 $\unicode[STIX]{x1D6E9}(1)$ is irreducible and occurs with multiplicity
$\unicode[STIX]{x1D6E9}(1)$ is irreducible and occurs with multiplicity  $1$ in the space of automorphic forms of
$1$ in the space of automorphic forms of  $G_{D}$.
$G_{D}$.(ii) For every
 $p$-adic place
$p$-adic place  $v$ of
$v$ of  $F$, the local component
$F$, the local component  $\unicode[STIX]{x1D6E9}(1)_{v}$ is isomorphic to the unique irreducible quotient of the local degenerate principal series
$\unicode[STIX]{x1D6E9}(1)_{v}$ is isomorphic to the unique irreducible quotient of the local degenerate principal series  $I_{D}(1)$.
$I_{D}(1)$.(iii) For every real place
 $v$ of
$v$ of  $F$, the local component
$F$, the local component  $\unicode[STIX]{x1D6E9}(1)_{v}$ is an irreducible quotient of
$\unicode[STIX]{x1D6E9}(1)_{v}$ is an irreducible quotient of  $I_{D}(1)$ as described in Theorems 7.1, 7.2 and 7.3.
$I_{D}(1)$ as described in Theorems 7.1, 7.2 and 7.3.
Proof. Indeed, we have shown that the abstract local theta lift  $\unicode[STIX]{x1D6E9}(1_{v})$ is irreducible. Hence the global
$\unicode[STIX]{x1D6E9}(1_{v})$ is irreducible. Hence the global  $\unicode[STIX]{x1D6E9}(1)$ is an irreducible automorphic representation. The fact that
$\unicode[STIX]{x1D6E9}(1)$ is an irreducible automorphic representation. The fact that  $\unicode[STIX]{x1D6E9}(1)$ has multiplicity
$\unicode[STIX]{x1D6E9}(1)$ has multiplicity  $1$ in the space of automorphic forms follows by [Reference Kobayashi and SavinKS15, Theorem 1.1]. Note that the required conditions, as spelled out in the introduction of [Reference Kobayashi and SavinKS15], are satisfied by the recent work of Möllers and Schwarz [Reference Möllers and SchwarzMS17].◻
$1$ in the space of automorphic forms follows by [Reference Kobayashi and SavinKS15, Theorem 1.1]. Note that the required conditions, as spelled out in the introduction of [Reference Kobayashi and SavinKS15], are satisfied by the recent work of Möllers and Schwarz [Reference Möllers and SchwarzMS17].◻
8.2 A Siegel–Weil formula
For a flat section  $\unicode[STIX]{x1D6F7}\in I_{D}(s)$, let
$\unicode[STIX]{x1D6F7}\in I_{D}(s)$, let  $E_{D}(s,\unicode[STIX]{x1D6F7})$ be the associated Eisenstein series. Then
$E_{D}(s,\unicode[STIX]{x1D6F7})$ be the associated Eisenstein series. Then  $E_{D}(s,\unicode[STIX]{x1D6F7})$ has at most simple poles at
$E_{D}(s,\unicode[STIX]{x1D6F7})$ has at most simple poles at  $s=1,3$ or 5 and the corresponding residual representations are completely described in [Reference Hanzer and SavinHS20, Theorem 6.4]. Set
$s=1,3$ or 5 and the corresponding residual representations are completely described in [Reference Hanzer and SavinHS20, Theorem 6.4]. Set
 $$\begin{eqnarray}{\mathcal{E}}=\{\text{Res}_{s=1}E_{D}(s,\unicode[STIX]{x1D6F7}):\unicode[STIX]{x1D6F7}\in I_{D}(s)\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}=\{\text{Res}_{s=1}E_{D}(s,\unicode[STIX]{x1D6F7}):\unicode[STIX]{x1D6F7}\in I_{D}(s)\}.\end{eqnarray}$$We can now prove Theorem 1.2 in the introduction (which we restate here).
Theorem 8.2. Let  $F$ be a totally real global field and
$F$ be a totally real global field and  $D$ a quaternion algebra over
$D$ a quaternion algebra over  $F$. Then we have the identity
$F$. Then we have the identity
 $$\begin{eqnarray}{\mathcal{E}}=\bigoplus _{i:D\rightarrow \mathbb{O}}\unicode[STIX]{x1D6E9}(1)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}=\bigoplus _{i:D\rightarrow \mathbb{O}}\unicode[STIX]{x1D6E9}(1)\end{eqnarray}$$ in the space of automorphic representations  $G_{D}(\mathbb{A})$, where the sum is taken over all isomorphism classes of embeddings
$G_{D}(\mathbb{A})$, where the sum is taken over all isomorphism classes of embeddings  $i:D\rightarrow \mathbb{O}$ into octonion algebras over
$i:D\rightarrow \mathbb{O}$ into octonion algebras over  $F$.
$F$.
Proof. Comparing Proposition 8.1 with [Reference Hanzer and SavinHS20, Theorem 6.4], one sees that  $\unicode[STIX]{x1D6E9}(1)$ is isomorphic, as an abstract representation, to a summand of
$\unicode[STIX]{x1D6E9}(1)$ is isomorphic, as an abstract representation, to a summand of  ${\mathcal{E}}$. In view of the multiplicity-
${\mathcal{E}}$. In view of the multiplicity- $1$ result in Proposition 8.1(i), it follows that
$1$ result in Proposition 8.1(i), it follows that  $\unicode[STIX]{x1D6E9}(1)$ is equal to that irreducible summand, as a subspace of the space of automorphic forms.
$\unicode[STIX]{x1D6E9}(1)$ is equal to that irreducible summand, as a subspace of the space of automorphic forms.
Now recall that the dual pair  $D^{1}\times G_{D}$ arises from an embedding of
$D^{1}\times G_{D}$ arises from an embedding of  $D$ into an octonion algebra
$D$ into an octonion algebra  $\mathbb{O}$. Every such embedding is unique up to conjugacy by
$\mathbb{O}$. Every such embedding is unique up to conjugacy by  $\text{Aut}(\mathbb{O})$. However, given
$\text{Aut}(\mathbb{O})$. However, given  $D$, there are multiple octonion algebras over
$D$, there are multiple octonion algebras over  $F$ containing
$F$ containing  $D$. An isomorphism class of octonion algebras
$D$. An isomorphism class of octonion algebras  $\mathbb{O}$ over
$\mathbb{O}$ over  $F$ is specified by the isomorphism class of its local completions
$F$ is specified by the isomorphism class of its local completions  $\mathbb{O}_{v}$ for real places
$\mathbb{O}_{v}$ for real places  $v$. At each real place, we have two choices: the classical octonion algebra and its split form. But
$v$. At each real place, we have two choices: the classical octonion algebra and its split form. But  $D_{v}$ embeds into both if and only if it is a quaternion division algebra. Hence the number of octonion algebras over
$D_{v}$ embeds into both if and only if it is a quaternion division algebra. Hence the number of octonion algebras over  $F$ containing
$F$ containing  $D$ is
$D$ is  $2^{m}$, where
$2^{m}$, where  $m$ is the number of real places
$m$ is the number of real places  $v$ such that
$v$ such that  $D_{v}$ is the quaternion algebra. Now, by an easy check left to the reader, non-isomorphic
$D_{v}$ is the quaternion algebra. Now, by an easy check left to the reader, non-isomorphic  $\mathbb{O}$ give non-isomorphic
$\mathbb{O}$ give non-isomorphic  $\unicode[STIX]{x1D6E9}(1)$. Moreover, using our description of
$\unicode[STIX]{x1D6E9}(1)$. Moreover, using our description of  $\unicode[STIX]{x1D6E9}(1)$ in Proposition 8.1 and [Reference Hanzer and SavinHS20, Theorem 6.4], one sees that all those possible
$\unicode[STIX]{x1D6E9}(1)$ in Proposition 8.1 and [Reference Hanzer and SavinHS20, Theorem 6.4], one sees that all those possible  $\unicode[STIX]{x1D6E9}(1)$ sum to
$\unicode[STIX]{x1D6E9}(1)$ sum to  ${\mathcal{E}}$. This proves the theorem.◻
${\mathcal{E}}$. This proves the theorem.◻
9 Spin  $L$-function
$L$-function
To complete the proof of the main result of this paper (Theorem 1.1 in the introduction), the remaining ingredient we need is a Rankin–Selberg integral for the degree-8 Spin L-function for cuspidal representations of  $\text{PGSp}_{6}$ which was discovered by Pollack [Reference PollackPol17]. However, since the paper [Reference PollackPol17] works over
$\text{PGSp}_{6}$ which was discovered by Pollack [Reference PollackPol17]. However, since the paper [Reference PollackPol17] works over  $\mathbb{Q}$ whereas we are working over a general number field
$\mathbb{Q}$ whereas we are working over a general number field  $F$, we recall some details here for the sake of completeness.
$F$, we recall some details here for the sake of completeness.
9.1 Global zeta integrals
Suppose that  $\unicode[STIX]{x1D70B}$ is a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$ is a cuspidal automorphic representation of  $\text{PGSp}_{6}(\mathbb{A})$. Let
$\text{PGSp}_{6}(\mathbb{A})$. Let  $U$ be the unipotent radical of the Siegel maximal parabolic subgroup of
$U$ be the unipotent radical of the Siegel maximal parabolic subgroup of  $\text{PGSp}_{6}(F)$. Let
$\text{PGSp}_{6}(F)$. Let  $J_{F}$ be the Jordan algebra of
$J_{F}$ be the Jordan algebra of  $3\times 3$ symmetric matrices with coefficients in
$3\times 3$ symmetric matrices with coefficients in  $F$. Then
$F$. Then  $U\cong J_{F}$ and any
$U\cong J_{F}$ and any  $T\in J_{F}\cong \bar{U}_{F}$ defines an additive character
$T\in J_{F}\cong \bar{U}_{F}$ defines an additive character  $\unicode[STIX]{x1D719}_{T}:U(\mathbb{A})/U(F)\rightarrow \mathbb{C}^{\times }$. Since
$\unicode[STIX]{x1D719}_{T}:U(\mathbb{A})/U(F)\rightarrow \mathbb{C}^{\times }$. Since  $\unicode[STIX]{x1D70B}$ is cuspidal, there exists a non-degenerate
$\unicode[STIX]{x1D70B}$ is cuspidal, there exists a non-degenerate  $T$ (i.e.
$T$ (i.e.  $\det (T)\neq 0$) such that the global Fourier coefficient
$\det (T)\neq 0$) such that the global Fourier coefficient  $\unicode[STIX]{x1D719}_{T}$ is a non-zero function on
$\unicode[STIX]{x1D719}_{T}$ is a non-zero function on  $\text{PGSp}_{6}(\mathbb{A})$ for any
$\text{PGSp}_{6}(\mathbb{A})$ for any  $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$. We fix such a
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$. We fix such a  $T$ (which depends on
$T$ (which depends on  $\unicode[STIX]{x1D70B}$) in what follows.
$\unicode[STIX]{x1D70B}$) in what follows.
The non-degenerate orbits on  $U(F)\cong J_{F}$, under the action of the Siegel Levi factor in
$U(F)\cong J_{F}$, under the action of the Siegel Levi factor in  $\text{PGSp}_{6}(F)$, are parameterized by quaternion algebras over
$\text{PGSp}_{6}(F)$, are parameterized by quaternion algebras over  $F$. So let
$F$. So let  $D$ be the algebra corresponding to
$D$ be the algebra corresponding to  $T$. Let
$T$. Let  $\tilde{G}_{D}$ be the reductive group of type
$\tilde{G}_{D}$ be the reductive group of type  $\mathbf{D}_{6}$ acting on
$\mathbf{D}_{6}$ acting on  $W_{D}$, as in § 2.3. We shall assume that
$W_{D}$, as in § 2.3. We shall assume that  $\tilde{G}_{D}$ acts from the right on
$\tilde{G}_{D}$ acts from the right on  $W_{D}$. Let
$W_{D}$. Let  $\unicode[STIX]{x1D714}\subset W_{D}$ be the
$\unicode[STIX]{x1D714}\subset W_{D}$ be the  $\tilde{G}_{D}$-orbit of
$\tilde{G}_{D}$-orbit of  $(1,0,0,0)$, that is, the orbit consisting of highest weight vectors. Following Pollack [Reference PollackPol17], for every Schwartz function
$(1,0,0,0)$, that is, the orbit consisting of highest weight vectors. Following Pollack [Reference PollackPol17], for every Schwartz function  $\unicode[STIX]{x1D6F7}=\bigotimes _{v}\unicode[STIX]{x1D6F7}_{v}$ on
$\unicode[STIX]{x1D6F7}=\bigotimes _{v}\unicode[STIX]{x1D6F7}_{v}$ on  $W_{D}(\mathbb{A})$ define an Eisenstein series on
$W_{D}(\mathbb{A})$ define an Eisenstein series on  $\tilde{G}_{D}(\mathbb{A})$ by
$\tilde{G}_{D}(\mathbb{A})$ by
 $$\begin{eqnarray}E_{\unicode[STIX]{x1D6F7}}(g)=\mathop{\sum }_{x\in \unicode[STIX]{x1D714}(F)}\unicode[STIX]{x1D6F7}(xg).\end{eqnarray}$$
$$\begin{eqnarray}E_{\unicode[STIX]{x1D6F7}}(g)=\mathop{\sum }_{x\in \unicode[STIX]{x1D714}(F)}\unicode[STIX]{x1D6F7}(xg).\end{eqnarray}$$ Recall that  $\text{GSp}_{6}\subseteq \tilde{G}_{D}$ and let
$\text{GSp}_{6}\subseteq \tilde{G}_{D}$ and let  $\unicode[STIX]{x1D708}$ be the similitude homomorphism of
$\unicode[STIX]{x1D708}$ be the similitude homomorphism of  $\text{GSp}_{6}$. Define a global zeta integral
$\text{GSp}_{6}$. Define a global zeta integral
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)=\int _{\text{GSp}_{6}(F)\backslash \text{GSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D719}(g)\cdot E_{\unicode[STIX]{x1D6F7}}(g)\cdot |\unicode[STIX]{x1D708}(g)|^{s}\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)=\int _{\text{GSp}_{6}(F)\backslash \text{GSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D719}(g)\cdot E_{\unicode[STIX]{x1D6F7}}(g)\cdot |\unicode[STIX]{x1D708}(g)|^{s}\,dg\end{eqnarray}$$ for  $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$ and
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$ and  $\unicode[STIX]{x1D6F7}$ as above. This integral is absolutely convergent for
$\unicode[STIX]{x1D6F7}$ as above. This integral is absolutely convergent for  $s\in \mathbb{C}$ with sufficiently large real part. After integrating over the center of
$s\in \mathbb{C}$ with sufficiently large real part. After integrating over the center of  $\text{GSp}_{6}(\mathbb{A})$, we see that
$\text{GSp}_{6}(\mathbb{A})$, we see that
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D711},s)=\int _{\text{PGSp}_{6}(F)\backslash P\text{GSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D719}(g)\cdot E(\unicode[STIX]{x1D6F7}_{s},g)\,dg,\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D711},s)=\int _{\text{PGSp}_{6}(F)\backslash P\text{GSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D719}(g)\cdot E(\unicode[STIX]{x1D6F7}_{s},g)\,dg,\end{eqnarray}$$ where  $\unicode[STIX]{x1D6F7}_{s}\in I_{D}(2s-5)$, and
$\unicode[STIX]{x1D6F7}_{s}\in I_{D}(2s-5)$, and  $s\mapsto \unicode[STIX]{x1D6F7}_{s}$ is a holomorphic section for
$s\mapsto \unicode[STIX]{x1D6F7}_{s}$ is a holomorphic section for  $s>0$. Observe that the meromorphic continuation of
$s>0$. Observe that the meromorphic continuation of  $E(\unicode[STIX]{x1D6F7}_{s},g)$ gives a meromorphic continuation of
$E(\unicode[STIX]{x1D6F7}_{s},g)$ gives a meromorphic continuation of  $Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)$.
$Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)$.
9.2 Unfolding
Let  $V\subset U$ be the codimension-
$V\subset U$ be the codimension- $1$ subgroup such that the character
$1$ subgroup such that the character  $\unicode[STIX]{x1D713}_{T}$ is trivial on
$\unicode[STIX]{x1D713}_{T}$ is trivial on  $V(\mathbb{A})$. There is a
$V(\mathbb{A})$. There is a  $w_{T}\in \unicode[STIX]{x1D714}(F)$, contained in the third summand of
$w_{T}\in \unicode[STIX]{x1D714}(F)$, contained in the third summand of  $W_{D}$, such that the stabilizer of
$W_{D}$, such that the stabilizer of  $w_{T}$ in
$w_{T}$ in  $\text{Sp}_{6}$ is
$\text{Sp}_{6}$ is  $V\subset U$; see [Reference PollackPol17, Proposition 5.5]. The integral unfolds into
$V\subset U$; see [Reference PollackPol17, Proposition 5.5]. The integral unfolds into
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)=\int _{V(\mathbb{A})\backslash \text{GSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D719}_{T}(g)\unicode[STIX]{x1D6F7}(w_{T}g)|\unicode[STIX]{x1D708}(g)|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)=\int _{V(\mathbb{A})\backslash \text{GSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D719}_{T}(g)\unicode[STIX]{x1D6F7}(w_{T}g)|\unicode[STIX]{x1D708}(g)|^{s}\,dg.\end{eqnarray}$$ Furthermore, by Theorem 9.4 in the first arXiv version of the paper [Reference PollackPol17] (i.e. in arXiv:1506.03406v1), for a sufficiently large set of places  $S$, including the set
$S$, including the set  $S_{\infty }$ of all real places,
$S_{\infty }$ of all real places,
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D711},s)=L^{S}(s-2,\unicode[STIX]{x1D70B},\text{Spin})\cdot c(s)\cdot \int _{V(\mathbb{A}_{S})\backslash \text{GSp}_{6}(\mathbb{A}_{S})}\unicode[STIX]{x1D719}_{T}(g)\unicode[STIX]{x1D6F7}_{S}(w_{T}g)|\unicode[STIX]{x1D708}(g)|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D711},s)=L^{S}(s-2,\unicode[STIX]{x1D70B},\text{Spin})\cdot c(s)\cdot \int _{V(\mathbb{A}_{S})\backslash \text{GSp}_{6}(\mathbb{A}_{S})}\unicode[STIX]{x1D719}_{T}(g)\unicode[STIX]{x1D6F7}_{S}(w_{T}g)|\unicode[STIX]{x1D708}(g)|^{s}\,dg.\end{eqnarray}$$ Here  $c(s)$ denotes a product of partial Dedekind zeta functions that we have omitted writing down since they do not affect analytic properties of
$c(s)$ denotes a product of partial Dedekind zeta functions that we have omitted writing down since they do not affect analytic properties of  $Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D711},s)$ at our point of interest
$Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D711},s)$ at our point of interest  $s=3$. We note that Pollack works over
$s=3$. We note that Pollack works over  $F=\mathbb{Q}$. However, he has kindly informed us that@
$F=\mathbb{Q}$. However, he has kindly informed us that@
∙ the unfolding of the integral representation works over any number field;
∙ the unramified computation is valid for any non-archimedean place
 $v$ away from 2 such that
$v$ away from 2 such that  $D_{v}$ is split.
$D_{v}$ is split.
The proof of the latter goes through line by line if one makes the following changes of notation: every time  $p$ is used as a uniformizer, replace
$p$ is used as a uniformizer, replace  $p$ with
$p$ with  $\unicode[STIX]{x1D71B}$; every time
$\unicode[STIX]{x1D71B}$; every time  $p$ is used as a magnitude, replace
$p$ is used as a magnitude, replace  $p$ with
$p$ with  $q$. In other words, the above identity holds for
$q$. In other words, the above identity holds for  $S$ containing all real places, places of even residual characteristic and places where
$S$ containing all real places, places of even residual characteristic and places where  $D$ is ramified.
$D$ is ramified.
9.3 Non-vanishing
The following technical result was contained in an earlier version of Pollack’s paper. However, as this particular version is no longer publicly available (even on the arXiv), we reproduce the proof for the sake of completeness (see [Reference Gan and GurevichGG06, Lemma 15.7] for a similar proof).
Lemma 9.1. Let  $s_{0}\in \mathbb{C}$. For some data
$s_{0}\in \mathbb{C}$. For some data  $\unicode[STIX]{x1D719}$ and
$\unicode[STIX]{x1D719}$ and  $\unicode[STIX]{x1D6F7}_{S}$,
$\unicode[STIX]{x1D6F7}_{S}$,
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{S},s)=\int _{V(\mathbb{A}_{S})\backslash \text{GSp}_{6}(\mathbb{A}_{S})}\unicode[STIX]{x1D719}_{T}(g)\unicode[STIX]{x1D6F7}_{S}(w_{T}g)|\unicode[STIX]{x1D708}(g)|^{s}\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{S},s)=\int _{V(\mathbb{A}_{S})\backslash \text{GSp}_{6}(\mathbb{A}_{S})}\unicode[STIX]{x1D719}_{T}(g)\unicode[STIX]{x1D6F7}_{S}(w_{T}g)|\unicode[STIX]{x1D708}(g)|^{s}\,dg\end{eqnarray}$$ extends to a meromorphic function on  $\mathbb{C}$ which is non-vanishing at
$\mathbb{C}$ which is non-vanishing at  $s_{0}$.
$s_{0}$.
Proof. Observe that the meromorphic continuation is clear, since the global zeta integral has a meromorphic continuation, and so does the partial  $L$-function, since it appears in the constant term of an Eisenstein series on the exceptional group
$L$-function, since it appears in the constant term of an Eisenstein series on the exceptional group  $F_{4}$ (à la Langlands–Shahidi theory). All that remains is to deal with non-vanishing.
$F_{4}$ (à la Langlands–Shahidi theory). All that remains is to deal with non-vanishing.
Let  $v\in S$. Consider the local version of the zeta integral:
$v\in S$. Consider the local version of the zeta integral:
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{v},s)=\int _{V_{v}\backslash \text{GSp}_{6}(F_{v})}\unicode[STIX]{x1D719}_{T}(g)\cdot \unicode[STIX]{x1D6F7}_{v}(w_{T}g)\cdot |\unicode[STIX]{x1D708}(g)|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{v},s)=\int _{V_{v}\backslash \text{GSp}_{6}(F_{v})}\unicode[STIX]{x1D719}_{T}(g)\cdot \unicode[STIX]{x1D6F7}_{v}(w_{T}g)\cdot |\unicode[STIX]{x1D708}(g)|^{s}\,dg.\end{eqnarray}$$ The stabilizer of  $w_{T}$ in
$w_{T}$ in  $\text{GSp}_{6}$ is
$\text{GSp}_{6}$ is  $V\rtimes A$, where
$V\rtimes A$, where  $A$ is a one-dimensional torus that we can identify with
$A$ is a one-dimensional torus that we can identify with  $\text{GL}_{1}$ using the similitude character
$\text{GL}_{1}$ using the similitude character  $\unicode[STIX]{x1D708}$. Thus
$\unicode[STIX]{x1D708}$. Thus  $\text{GSp}_{6}$ is a semidirect product of
$\text{GSp}_{6}$ is a semidirect product of  $A$ and
$A$ and  $\text{Sp}_{6}$, and we can write
$\text{Sp}_{6}$, and we can write
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{v},s)=\int _{V_{v}\backslash \text{Sp}_{6}(F_{v})}\unicode[STIX]{x1D6F7}_{v}(w_{T}g)\int _{A_{v}}\unicode[STIX]{x1D719}_{T}(ag)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{v},s)=\int _{V_{v}\backslash \text{Sp}_{6}(F_{v})}\unicode[STIX]{x1D6F7}_{v}(w_{T}g)\int _{A_{v}}\unicode[STIX]{x1D719}_{T}(ag)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da\,dg\end{eqnarray}$$ for an invariant measure  $da$ on
$da$ on  $A_{v}$. Let us set
$A_{v}$. Let us set
 $$\begin{eqnarray}H(\unicode[STIX]{x1D719},s)=\int _{A_{v}}\unicode[STIX]{x1D719}_{T}(a)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da.\end{eqnarray}$$
$$\begin{eqnarray}H(\unicode[STIX]{x1D719},s)=\int _{A_{v}}\unicode[STIX]{x1D719}_{T}(a)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da.\end{eqnarray}$$ If  $h$ is a Schwartz function on
$h$ is a Schwartz function on  $U_{v}$, let
$U_{v}$, let
 $$\begin{eqnarray}{\hat{h}}(a)=\int _{U_{v}}h(u)\unicode[STIX]{x1D713}_{T}(aua^{-1})\,du,\end{eqnarray}$$
$$\begin{eqnarray}{\hat{h}}(a)=\int _{U_{v}}h(u)\unicode[STIX]{x1D713}_{T}(aua^{-1})\,du,\end{eqnarray}$$ where  $a\in A_{v}$. Since
$a\in A_{v}$. Since  $\unicode[STIX]{x1D719}_{T}(aug)=\unicode[STIX]{x1D713}_{T}(aua^{-1})\cdot \unicode[STIX]{x1D719}_{T}(ag)$ for
$\unicode[STIX]{x1D719}_{T}(aug)=\unicode[STIX]{x1D713}_{T}(aua^{-1})\cdot \unicode[STIX]{x1D719}_{T}(ag)$ for  $u\in U_{v}$, it follows that
$u\in U_{v}$, it follows that
 $$\begin{eqnarray}H(h\ast \unicode[STIX]{x1D719},s)=\int _{A_{v}}{\hat{h}}(a)\cdot \unicode[STIX]{x1D719}_{T}(a)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da.\end{eqnarray}$$
$$\begin{eqnarray}H(h\ast \unicode[STIX]{x1D719},s)=\int _{A_{v}}{\hat{h}}(a)\cdot \unicode[STIX]{x1D719}_{T}(a)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da.\end{eqnarray}$$ Since  ${\hat{h}}$ can be any compactly supported function on
${\hat{h}}$ can be any compactly supported function on  $A_{v}$, the integral can be arranged to be non-zero for any
$A_{v}$, the integral can be arranged to be non-zero for any  $s_{0}$. In fact, if
$s_{0}$. In fact, if  $v$ is a finite place, then
$v$ is a finite place, then  ${\hat{h}}$ can be picked so that the integral is 1 for all
${\hat{h}}$ can be picked so that the integral is 1 for all  $s$. Thus, if
$s$. Thus, if  $v$ is a finite place, we can assume that
$v$ is a finite place, we can assume that  $\unicode[STIX]{x1D719}$ has been chosen so that
$\unicode[STIX]{x1D719}$ has been chosen so that  $H(\unicode[STIX]{x1D719},s)=1$, for all
$H(\unicode[STIX]{x1D719},s)=1$, for all  $s$.
$s$.
Next, there exists a compactly supported function  $\unicode[STIX]{x1D711}$ on
$\unicode[STIX]{x1D711}$ on  $\text{Sp}_{6}(F_{v})$ such that
$\text{Sp}_{6}(F_{v})$ such that  $\unicode[STIX]{x1D711}\,\ast \,\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}$. Observe that
$\unicode[STIX]{x1D711}\,\ast \,\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}$. Observe that
 $$\begin{eqnarray}H(\unicode[STIX]{x1D711}\ast \unicode[STIX]{x1D719},s)=\int _{V_{v}\backslash \text{Sp}_{6}(F_{v})}\unicode[STIX]{x1D711}^{\prime }(g)\int _{A_{v}}\unicode[STIX]{x1D719}_{T}(ag)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da\,dg,\end{eqnarray}$$
$$\begin{eqnarray}H(\unicode[STIX]{x1D711}\ast \unicode[STIX]{x1D719},s)=\int _{V_{v}\backslash \text{Sp}_{6}(F_{v})}\unicode[STIX]{x1D711}^{\prime }(g)\int _{A_{v}}\unicode[STIX]{x1D719}_{T}(ag)\cdot |\unicode[STIX]{x1D708}(a)|^{s-5}\,da\,dg,\end{eqnarray}$$ where  $\unicode[STIX]{x1D711}^{\prime }$ is a smooth compactly supported function on
$\unicode[STIX]{x1D711}^{\prime }$ is a smooth compactly supported function on  $V(F_{v})\backslash \text{Sp}_{6}(F_{v})$ defined by
$V(F_{v})\backslash \text{Sp}_{6}(F_{v})$ defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(g)=\int _{V(F_{v})}\unicode[STIX]{x1D711}(ug)\,du.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(g)=\int _{V(F_{v})}\unicode[STIX]{x1D711}(ug)\,du.\end{eqnarray}$$ Using the Iwasawa decomposition of  $\text{Sp}_{6}(F_{v})$, it is not difficult to see that the map
$\text{Sp}_{6}(F_{v})$, it is not difficult to see that the map  $g\mapsto w_{T}g$ gives a locally closed embedding (i.e. an immersion) of
$g\mapsto w_{T}g$ gives a locally closed embedding (i.e. an immersion) of  $V_{v}\backslash \text{Sp}_{6}(F_{v})$ into
$V_{v}\backslash \text{Sp}_{6}(F_{v})$ into  $W_{D}(F_{v})$, with the closure of the image containing the extra point 0. Hence, any smooth compactly supported function on
$W_{D}(F_{v})$, with the closure of the image containing the extra point 0. Hence, any smooth compactly supported function on  $V_{v}\backslash \text{Sp}_{6}(F_{v})$ is the restriction of a smooth compactly supported function on
$V_{v}\backslash \text{Sp}_{6}(F_{v})$ is the restriction of a smooth compactly supported function on  $W_{D}(F_{v})$. In particular, we can pick
$W_{D}(F_{v})$. In particular, we can pick  $\unicode[STIX]{x1D6F7}_{v}$ such that
$\unicode[STIX]{x1D6F7}_{v}$ such that  $\unicode[STIX]{x1D6F7}_{v}(w_{T}g)=\unicode[STIX]{x1D711}^{\prime }(g)$, for all
$\unicode[STIX]{x1D6F7}_{v}(w_{T}g)=\unicode[STIX]{x1D711}^{\prime }(g)$, for all  $g\in \text{Sp}_{6}(F_{v})$. Then, with this choice of
$g\in \text{Sp}_{6}(F_{v})$. Then, with this choice of  $\unicode[STIX]{x1D6F7}_{v}$, one has
$\unicode[STIX]{x1D6F7}_{v}$, one has
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{v},s)=H(\unicode[STIX]{x1D719},s)=1.\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{v},s)=H(\unicode[STIX]{x1D719},s)=1.\end{eqnarray}$$It follows that
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{S},\unicode[STIX]{x1D711},s)=Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{\infty },s)\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{S},\unicode[STIX]{x1D711},s)=Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{\infty },s)\end{eqnarray}$$for some choice of data.
Let  $F_{\infty }=F\otimes _{\mathbb{Q}}\mathbb{R}$. Assume as above that
$F_{\infty }=F\otimes _{\mathbb{Q}}\mathbb{R}$. Assume as above that  $\unicode[STIX]{x1D719}$ has been chosen so that
$\unicode[STIX]{x1D719}$ has been chosen so that  $H(\unicode[STIX]{x1D719},s_{0})\neq 0$. While we perhaps cannot write
$H(\unicode[STIX]{x1D719},s_{0})\neq 0$. While we perhaps cannot write  $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D711}\ast \unicode[STIX]{x1D719}$, for a compactly supported function on
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D711}\ast \unicode[STIX]{x1D719}$, for a compactly supported function on  $\text{Sp}_{6}(F_{\infty })$, by the well-known Dixmier–Malliavin theorem, there exist finitely many compactly supported functions
$\text{Sp}_{6}(F_{\infty })$, by the well-known Dixmier–Malliavin theorem, there exist finitely many compactly supported functions  $\unicode[STIX]{x1D711}_{i}$ on
$\unicode[STIX]{x1D711}_{i}$ on  $\text{Sp}_{6}(F_{\infty })$ such that
$\text{Sp}_{6}(F_{\infty })$ such that  $\unicode[STIX]{x1D719}=\sum _{i}\unicode[STIX]{x1D711}_{i}\ast \unicode[STIX]{x1D719}_{i}$ for some
$\unicode[STIX]{x1D719}=\sum _{i}\unicode[STIX]{x1D711}_{i}\ast \unicode[STIX]{x1D719}_{i}$ for some  $\unicode[STIX]{x1D719}_{i}$. Then, as in the finite-place case, there exist compactly supported
$\unicode[STIX]{x1D719}_{i}$. Then, as in the finite-place case, there exist compactly supported  $\unicode[STIX]{x1D6F7}_{\infty }^{i}$ such that
$\unicode[STIX]{x1D6F7}_{\infty }^{i}$ such that
 $$\begin{eqnarray}\mathop{\sum }_{i}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{\infty }^{i},s)=H(\unicode[STIX]{x1D719},s).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{\infty }^{i},s)=H(\unicode[STIX]{x1D719},s).\end{eqnarray}$$ Since  $H(\unicode[STIX]{x1D719},s_{0})\neq 0$, we see that
$H(\unicode[STIX]{x1D719},s_{0})\neq 0$, we see that  $Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{\infty }^{i},s_{0})\neq 0$ for some
$Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7}_{\infty }^{i},s_{0})\neq 0$ for some  $i$. This completes the proof of the lemma.◻
$i$. This completes the proof of the lemma.◻
10 Applications to Functoriality
Finally, we are ready to assemble the various ingredients and complete the proof of Theorem 1.1 (which we reproduce here).
Theorem 10.1. Suppose that  $\unicode[STIX]{x1D70B}$ is a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$ is a cuspidal automorphic representation of  $\text{PGSp}_{6}$ such that
$\text{PGSp}_{6}$ such that  $L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at
$L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at  $s=1$. Then there exist an octonion algebra
$s=1$. Then there exist an octonion algebra  $\mathbb{O}$ over
$\mathbb{O}$ over  $F$ and a cuspidal automorphic representation
$F$ and a cuspidal automorphic representation  $\unicode[STIX]{x1D70B}^{\prime }$ of
$\unicode[STIX]{x1D70B}^{\prime }$ of  $\text{Aut}(\mathbb{O})$ such that the Satake parameters of
$\text{Aut}(\mathbb{O})$ such that the Satake parameters of  $\unicode[STIX]{x1D70B}^{\prime }$ are mapped by
$\unicode[STIX]{x1D70B}^{\prime }$ are mapped by  $\unicode[STIX]{x1D704}$ to those of
$\unicode[STIX]{x1D704}$ to those of  $\unicode[STIX]{x1D70B}$ (i.e.
$\unicode[STIX]{x1D70B}$ (i.e.  $\unicode[STIX]{x1D70B}$ is a weak functorial lift of
$\unicode[STIX]{x1D70B}$ is a weak functorial lift of  $\unicode[STIX]{x1D70B}^{\prime }$).
$\unicode[STIX]{x1D70B}^{\prime }$).
If the cuspidal representation  $\unicode[STIX]{x1D70B}$ of
$\unicode[STIX]{x1D70B}$ of  $\text{PGSp}_{6}$ is tempered, then the following statements are equivalent.
$\text{PGSp}_{6}$ is tempered, then the following statements are equivalent.
(a) For almost all places
 $v$, the Satake parameter
$v$, the Satake parameter  $s_{v}$ of
$s_{v}$ of  $\unicode[STIX]{x1D70B}_{v}$ is contained in
$\unicode[STIX]{x1D70B}_{v}$ is contained in  $\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$.
$\unicode[STIX]{x1D704}(G_{2}(\mathbb{C}))$.(b) There exist an octonion algebra
 $\mathbb{O}$ over
$\mathbb{O}$ over  $F$ and a cuspidal automorphic representation
$F$ and a cuspidal automorphic representation  $\unicode[STIX]{x1D70B}^{\prime }$ of
$\unicode[STIX]{x1D70B}^{\prime }$ of  $\text{Aut}(\mathbb{O})$ such that
$\text{Aut}(\mathbb{O})$ such that  $\unicode[STIX]{x1D70B}$ is a weak functorial lift of
$\unicode[STIX]{x1D70B}$ is a weak functorial lift of  $\unicode[STIX]{x1D70B}^{\prime }$.
$\unicode[STIX]{x1D70B}^{\prime }$.
Proof. As explained in the introduction, we shall make use of the following seesaw dual pair in  $G$:
$G$:

Let  $\unicode[STIX]{x1D70B}$ be an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$ be an irreducible cuspidal automorphic representation of  $\text{PGSp}_{6}$ and consider its global theta lift
$\text{PGSp}_{6}$ and consider its global theta lift  $\unicode[STIX]{x1D70B}^{\prime }$ on
$\unicode[STIX]{x1D70B}^{\prime }$ on  $\text{Aut}(\mathbb{O})$. It can be shown (by a standard computation of the constant term of the global theta lift) that
$\text{Aut}(\mathbb{O})$. It can be shown (by a standard computation of the constant term of the global theta lift) that  $\unicode[STIX]{x1D70B}^{\prime }$ is contained in the space of cusp forms on
$\unicode[STIX]{x1D70B}^{\prime }$ is contained in the space of cusp forms on  $\text{Aut}(\mathbb{O})$. This was explained in [Reference Ginzburg and JiangGJ01, Theorem 3.1], noting that the genericity assumption on
$\text{Aut}(\mathbb{O})$. This was explained in [Reference Ginzburg and JiangGJ01, Theorem 3.1], noting that the genericity assumption on  $\unicode[STIX]{x1D70B}$ was not needed there. See also [Reference Gan and GurevichGG09, Proposition 5.2] (note, though, that there is a typo in the first paragraph of the proof of [Reference Gan and GurevichGG09, Proposition 5.2]: the word ‘nonzero’ should be ‘zero’).
$\unicode[STIX]{x1D70B}$ was not needed there. See also [Reference Gan and GurevichGG09, Proposition 5.2] (note, though, that there is a typo in the first paragraph of the proof of [Reference Gan and GurevichGG09, Proposition 5.2]: the word ‘nonzero’ should be ‘zero’).
Now suppose that the partial (degree-8) spin  $L$-function
$L$-function  $L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ of
$L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ of  $\unicode[STIX]{x1D70B}$ has a pole at
$\unicode[STIX]{x1D70B}$ has a pole at  $s=1$. Then, by Lemma 9.1, it follows that
$s=1$. Then, by Lemma 9.1, it follows that  $\text{Res}_{s=3}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)$ is non-zero, for some
$\text{Res}_{s=3}Z(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6F7},s)$ is non-zero, for some  $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$ and some
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$ and some  $\unicode[STIX]{x1D6F7}$. At this point we note that Pollack has a slightly different choice of the parameter of the Eisenstein series: his parameter
$\unicode[STIX]{x1D6F7}$. At this point we note that Pollack has a slightly different choice of the parameter of the Eisenstein series: his parameter  $s^{\prime }$ and our
$s^{\prime }$ and our  $s$ are related by
$s$ are related by  $s=2s^{\prime }-5$. Hence the integral of
$s=2s^{\prime }-5$. Hence the integral of  $\unicode[STIX]{x1D719}$ against some residue
$\unicode[STIX]{x1D719}$ against some residue  $\text{Res}_{s=1}E_{D}(s,\unicode[STIX]{x1D6F7})$ is non-zero. Since the space of residues at
$\text{Res}_{s=1}E_{D}(s,\unicode[STIX]{x1D6F7})$ is non-zero. Since the space of residues at  $s=1$ is invariant under the complex conjugation, it follows that the integral of
$s=1$ is invariant under the complex conjugation, it follows that the integral of  $\bar{\unicode[STIX]{x1D719}}$ against some residue
$\bar{\unicode[STIX]{x1D719}}$ against some residue  $\text{Res}_{s=1}E_{D}(s,\unicode[STIX]{x1D6F7})$ is non-zero. Note that the Eisenstein series
$\text{Res}_{s=1}E_{D}(s,\unicode[STIX]{x1D6F7})$ is non-zero. Note that the Eisenstein series  $E_{D}(s,\unicode[STIX]{x1D6F7})$ used in the global zeta integral are associated to smooth sections of the degenerate principals series (holomorphic and non-zero at
$E_{D}(s,\unicode[STIX]{x1D6F7})$ used in the global zeta integral are associated to smooth sections of the degenerate principals series (holomorphic and non-zero at  $s=1$), but the analytic behaviour of these smooth Eisenstein series at
$s=1$), but the analytic behaviour of these smooth Eisenstein series at  $s=1$ is the same as that of
$s=1$ is the same as that of  $K$-finite Eisenstein series by [Reference LapidLap08]. Hence, by the Siegel–Weil formula (Theorem 8.2), it follows that
$K$-finite Eisenstein series by [Reference LapidLap08]. Hence, by the Siegel–Weil formula (Theorem 8.2), it follows that
 $$\begin{eqnarray}\int _{\text{PGSp}_{6}(F)\backslash \text{PGSp}_{6}(\mathbb{A})}\bar{\unicode[STIX]{x1D719}}(g)\cdot \biggl(\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(gh)\,dh\biggr)\,dg\neq 0\end{eqnarray}$$
$$\begin{eqnarray}\int _{\text{PGSp}_{6}(F)\backslash \text{PGSp}_{6}(\mathbb{A})}\bar{\unicode[STIX]{x1D719}}(g)\cdot \biggl(\int _{D^{1}(F)\backslash D^{1}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(gh)\,dh\biggr)\,dg\neq 0\end{eqnarray}$$ for some  $\mathbb{O}\supset D$,
$\mathbb{O}\supset D$,  $f\in \unicode[STIX]{x1D6F1}_{\mathbb{O}}$ and
$f\in \unicode[STIX]{x1D6F1}_{\mathbb{O}}$ and  $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$, where
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D70B}$, where  $\unicode[STIX]{x1D703}(f)$ is rapidly decreasing on
$\unicode[STIX]{x1D703}(f)$ is rapidly decreasing on  $D^{1}(F)\backslash D^{1}(\mathbb{A})$ and of moderate growth on
$D^{1}(F)\backslash D^{1}(\mathbb{A})$ and of moderate growth on  $\text{PGSp}_{6}(\mathbb{A})$. Exchanging the order of integration, we deduce that the global theta lift of
$\text{PGSp}_{6}(\mathbb{A})$. Exchanging the order of integration, we deduce that the global theta lift of  $\unicode[STIX]{x1D70B}$ to
$\unicode[STIX]{x1D70B}$ to  $\text{Aut}(\mathbb{O})$ is non-zero, that is,
$\text{Aut}(\mathbb{O})$ is non-zero, that is,
 $$\begin{eqnarray}\unicode[STIX]{x1D719}^{\prime }(h)=\int _{\text{PGSp}_{6}(F)\backslash \text{PGSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(gh)\bar{\unicode[STIX]{x1D719}}(g)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}^{\prime }(h)=\int _{\text{PGSp}_{6}(F)\backslash \text{PGSp}_{6}(\mathbb{A})}\unicode[STIX]{x1D703}(f)(gh)\bar{\unicode[STIX]{x1D719}}(g)\,dg\end{eqnarray}$$ is a non-zero function of uniform moderate growth on  $\text{Aut}(\mathbb{O})\backslash \text{Aut}(\mathbb{O}\otimes _{F}\mathbb{A})$.
$\text{Aut}(\mathbb{O})\backslash \text{Aut}(\mathbb{O}\otimes _{F}\mathbb{A})$.
It is given that  $\unicode[STIX]{x1D719}$ is an eigenfunction for the center of the enveloping algebra of
$\unicode[STIX]{x1D719}$ is an eigenfunction for the center of the enveloping algebra of  $\text{PGSp}_{6}(F_{v})$ for every real place
$\text{PGSp}_{6}(F_{v})$ for every real place  $v$ of
$v$ of  $F$. By [Reference Huang, Pandžić and SavinHPS96] and [Reference LiLi99], for every element
$F$. By [Reference Huang, Pandžić and SavinHPS96] and [Reference LiLi99], for every element  $z$ in the center of the enveloping algebra of
$z$ in the center of the enveloping algebra of  $\text{PGSp}_{6}(F_{v})$, there exists an element
$\text{PGSp}_{6}(F_{v})$, there exists an element  $z^{\prime }$ in the center of the enveloping algebra of
$z^{\prime }$ in the center of the enveloping algebra of  $\text{Aut}(\mathbb{O}_{v})$ such that
$\text{Aut}(\mathbb{O}_{v})$ such that  $z=z^{\prime }$ when acting on the minimal representation. In particular,
$z=z^{\prime }$ when acting on the minimal representation. In particular,  $z^{\prime }\cdot f=z\cdot f$. Thus
$z^{\prime }\cdot f=z\cdot f$. Thus  $\unicode[STIX]{x1D719}^{\prime }$ is an eigenfunction for the center of the enveloping algebra of
$\unicode[STIX]{x1D719}^{\prime }$ is an eigenfunction for the center of the enveloping algebra of  $\text{Aut}(\mathbb{O}_{v})$ for every real place
$\text{Aut}(\mathbb{O}_{v})$ for every real place  $v$ of
$v$ of  $F$. (At this point we use that
$F$. (At this point we use that  $\unicode[STIX]{x1D719}$ is rapidly decreasing to justify that differentiation of
$\unicode[STIX]{x1D719}$ is rapidly decreasing to justify that differentiation of  $f$ can be carried over to differentiation of
$f$ can be carried over to differentiation of  $\unicode[STIX]{x1D719}$.)
$\unicode[STIX]{x1D719}$.)
Similarly, it is given that  $\unicode[STIX]{x1D719}$ is an eigenfunction for the Hecke algebra for almost all finite places. But so is
$\unicode[STIX]{x1D719}$ is an eigenfunction for the Hecke algebra for almost all finite places. But so is  $\unicode[STIX]{x1D719}^{\prime }$ by matching of Hecke operators under the exceptional theta correspondences [Reference Savin and WoodburySW15]. Moreover, by [Reference Savin and WoodburySW15, Theorem 1.1], if
$\unicode[STIX]{x1D719}^{\prime }$ by matching of Hecke operators under the exceptional theta correspondences [Reference Savin and WoodburySW15]. Moreover, by [Reference Savin and WoodburySW15, Theorem 1.1], if  $s_{v}^{\prime }$ are the Satake conjugacy classes in
$s_{v}^{\prime }$ are the Satake conjugacy classes in  $G_{2}(\mathbb{C})$ corresponding to
$G_{2}(\mathbb{C})$ corresponding to  $\unicode[STIX]{x1D719}^{\prime }$ and
$\unicode[STIX]{x1D719}^{\prime }$ and  $s_{v}$ are the Satake conjugacy classes in
$s_{v}$ are the Satake conjugacy classes in  $\text{Spin}_{7}(\mathbb{C})$ corresponding to
$\text{Spin}_{7}(\mathbb{C})$ corresponding to  $\unicode[STIX]{x1D719}$, then
$\unicode[STIX]{x1D719}$, then  $s_{v}=\unicode[STIX]{x1D704}(s_{v}^{\prime })$, where
$s_{v}=\unicode[STIX]{x1D704}(s_{v}^{\prime })$, where  $\unicode[STIX]{x1D704}:G_{2}(\mathbb{C})\rightarrow \text{Spin}_{7}(\mathbb{C})$ is the natural inclusion. Hence, the submodule generated by all such global theta lifts
$\unicode[STIX]{x1D704}:G_{2}(\mathbb{C})\rightarrow \text{Spin}_{7}(\mathbb{C})$ is the natural inclusion. Hence, the submodule generated by all such global theta lifts  $\unicode[STIX]{x1D719}^{\prime }$ gives an automorphic representation
$\unicode[STIX]{x1D719}^{\prime }$ gives an automorphic representation  $\unicode[STIX]{x1D70B}^{\prime }$ which weakly lifts to
$\unicode[STIX]{x1D70B}^{\prime }$ which weakly lifts to  $\unicode[STIX]{x1D70B}$. This proves the first assertion of the theorem.
$\unicode[STIX]{x1D70B}$. This proves the first assertion of the theorem.
For the second part of the theorem, it is clear that (b) implies (a). Conversely, as observed by Chenevier [Reference ChenevierChe19, Theorem 6.18, equation (6.6)], hypothesis (a) in the theorem implies that
 $$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})=\unicode[STIX]{x1D701}^{S}(s)\cdot L^{S}(s,\unicode[STIX]{x1D70B},\text{Std}),\end{eqnarray}$$
$$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})=\unicode[STIX]{x1D701}^{S}(s)\cdot L^{S}(s,\unicode[STIX]{x1D70B},\text{Std}),\end{eqnarray}$$ where the last L-function on the right is the degree-7 (partial) standard L-function of  $\unicode[STIX]{x1D70B}$. Since we are assuming that
$\unicode[STIX]{x1D70B}$. Since we are assuming that  $\unicode[STIX]{x1D70B}$ is tempered, it follows that
$\unicode[STIX]{x1D70B}$ is tempered, it follows that  $L^{S}(1,\unicode[STIX]{x1D70B},\text{Std})$ is finite and non-zero (by the characterization of the image of the standard functorial lifting of tempered cuspidal representations from
$L^{S}(1,\unicode[STIX]{x1D70B},\text{Std})$ is finite and non-zero (by the characterization of the image of the standard functorial lifting of tempered cuspidal representations from  $\text{Sp}_{6}$ to
$\text{Sp}_{6}$ to  $\text{GL}_{7}$). Hence
$\text{GL}_{7}$). Hence  $L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at
$L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at  $s=1$ and the results we have shown above imply that (b) holds, with
$s=1$ and the results we have shown above imply that (b) holds, with  $\unicode[STIX]{x1D70B}^{\prime }$ the global theta lift of
$\unicode[STIX]{x1D70B}^{\prime }$ the global theta lift of  $\unicode[STIX]{x1D70B}$ to
$\unicode[STIX]{x1D70B}$ to  $\text{Aut}(\mathbb{O})$.
$\text{Aut}(\mathbb{O})$.
This completes the proof of the theorem. ◻
Remark.
Let us comment on the relation of Theorem 10.1 with [Reference ChenevierChe19, Theorem 6.18].
∙ In [Reference ChenevierChe19, Theorem 6.18], Chenevier showed the second part of Theorem 10.1 for globally generic cuspidal representations, by reducing it to the first part of Theorem 10.1, which is a result of Ginzburg and Jiang for globally generic cuspidal representations. As Chenevier remarked in [Reference ChenevierChe19, Remark 6.19], if one has an analog of the endoscopic classification of Arthur for
 $\text{PGSp}_{6}$, one would know that any tempered cuspidal representation of
$\text{PGSp}_{6}$, one would know that any tempered cuspidal representation of  $\text{PGSp}_{6}$ is nearly equivalent to a globally generic cuspidal representation, in which case the second part of the theorem will follow for tempered cuspidal representations by reduction to the globally generic case.
$\text{PGSp}_{6}$ is nearly equivalent to a globally generic cuspidal representation, in which case the second part of the theorem will follow for tempered cuspidal representations by reduction to the globally generic case.∙ In our proof of Theorem 10.1, our argument reducing the second part of the theorem to the first follows Chenevier’s. Thus, the main innovation of Theorem 10.1 is a direct proof of the first part of the theorem for all cuspidal representations, regardless of whether they are globally generic or tempered. In particular, this gives the second part of the theorem without resort to an Arthur-type classification for
 $\text{PGSp}_{6}$.
$\text{PGSp}_{6}$.
We can strengthen our results in the case where  $F=\mathbb{Q}$ and
$F=\mathbb{Q}$ and  $\unicode[STIX]{x1D70B}$ is a cuspidal representation of
$\unicode[STIX]{x1D70B}$ is a cuspidal representation of  $\text{PGSp}_{6}(\mathbb{A})$ that corresponds to a classical Siegel holomorphic form of positive weight. Recall that there are two isomorphism classes of octonion algebras over
$\text{PGSp}_{6}(\mathbb{A})$ that corresponds to a classical Siegel holomorphic form of positive weight. Recall that there are two isomorphism classes of octonion algebras over  $\mathbb{Q}$: the classical octonion algebra
$\mathbb{Q}$: the classical octonion algebra  $\mathbb{O}^{c}$ and its split form
$\mathbb{O}^{c}$ and its split form  $\mathbb{O}^{s}$. Then
$\mathbb{O}^{s}$. Then  $\text{Aut}(\mathbb{O}_{\infty }^{c})$ is an anisotropic group, while
$\text{Aut}(\mathbb{O}_{\infty }^{c})$ is an anisotropic group, while  $\text{Aut}(\mathbb{O}_{\infty }^{s})$ is split.
$\text{Aut}(\mathbb{O}_{\infty }^{s})$ is split.
Theorem 10.2. Let  $F=\mathbb{Q}$, and
$F=\mathbb{Q}$, and  $\unicode[STIX]{x1D70B}$ a cuspidal representation of
$\unicode[STIX]{x1D70B}$ a cuspidal representation of  $\text{PGSp}_{6}(\mathbb{A})$ that corresponds to a classical Siegel holomorphic form
$\text{PGSp}_{6}(\mathbb{A})$ that corresponds to a classical Siegel holomorphic form  $\unicode[STIX]{x1D719}_{2r}$ of weight
$\unicode[STIX]{x1D719}_{2r}$ of weight  $2r>0$. If
$2r>0$. If  $L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at
$L^{S}(s,\unicode[STIX]{x1D70B},\text{Spin})$ has a pole at  $s=1$, then
$s=1$, then  $\unicode[STIX]{x1D70B}$ is a lift from
$\unicode[STIX]{x1D70B}$ is a lift from  $\text{Aut}(\mathbb{O}^{c})$. Moreover, if the level of
$\text{Aut}(\mathbb{O}^{c})$. Moreover, if the level of  $\unicode[STIX]{x1D719}_{2r}$ is
$\unicode[STIX]{x1D719}_{2r}$ is  $1$, then
$1$, then  $\unicode[STIX]{x1D70B}$ is a strong functorial lift from
$\unicode[STIX]{x1D70B}$ is a strong functorial lift from  $\text{Aut}(\mathbb{O}^{c})$.
$\text{Aut}(\mathbb{O}^{c})$.
Proof. Let  $\text{U}_{3}(\mathbb{R})$ be the maximal compact subgroup of
$\text{U}_{3}(\mathbb{R})$ be the maximal compact subgroup of  $\text{Sp}_{6}(\mathbb{R})$. By our assumption,
$\text{Sp}_{6}(\mathbb{R})$. By our assumption,  $\unicode[STIX]{x1D70B}_{\infty }$ is a lowest weight module, with the minimal
$\unicode[STIX]{x1D70B}_{\infty }$ is a lowest weight module, with the minimal  $\text{U}_{3}(\mathbb{R})$-type
$\text{U}_{3}(\mathbb{R})$-type  $\det ^{2r}$,
$\det ^{2r}$,  $r>0$. We need the following lemma.
$r>0$. We need the following lemma.
Lemma 10.3. Let  $\unicode[STIX]{x1D70E}$ is a lowest weight module of
$\unicode[STIX]{x1D70E}$ is a lowest weight module of  $\text{Sp}_{6}(\mathbb{R})$, with the minimal
$\text{Sp}_{6}(\mathbb{R})$, with the minimal  $\text{U}_{3}(\mathbb{R})$-type
$\text{U}_{3}(\mathbb{R})$-type  $\det ^{2r}$,
$\det ^{2r}$,  $r>0$. Then
$r>0$. Then  $\unicode[STIX]{x1D70E}$ does not occur in the exceptional theta correspondence with split
$\unicode[STIX]{x1D70E}$ does not occur in the exceptional theta correspondence with split  $G_{2}(\mathbb{R})$.
$G_{2}(\mathbb{R})$.
Proof. Adopting the notation from [Reference Loke and SavinLS19], let  $G^{\prime }=G_{2}(\mathbb{R})$,
$G^{\prime }=G_{2}(\mathbb{R})$,  $\mathfrak{g}^{\prime }$ the Lie algebra of
$\mathfrak{g}^{\prime }$ the Lie algebra of  $G^{\prime }$,
$G^{\prime }$,  $K^{\prime }$ a maximal compact subgroup of
$K^{\prime }$ a maximal compact subgroup of  $G^{\prime }$, and
$G^{\prime }$, and  $\mathfrak{g}^{\prime }=\mathfrak{k}^{\prime }\oplus \mathfrak{p}^{\prime }$ the corresponding Cartan decomposition. Let
$\mathfrak{g}^{\prime }=\mathfrak{k}^{\prime }\oplus \mathfrak{p}^{\prime }$ the corresponding Cartan decomposition. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\bigoplus _{n=0}^{\infty }V_{n}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\bigoplus _{n=0}^{\infty }V_{n}\end{eqnarray}$$ be the decomposition of the minimal representation of the split real  $E_{7}$ into its
$E_{7}$ into its  $K$-types. Let
$K$-types. Let  $V_{n}^{\det ^{2r}}$ be the maximal subspace of
$V_{n}^{\det ^{2r}}$ be the maximal subspace of  $V_{n}$ on which
$V_{n}$ on which  $\text{U}_{3}(\mathbb{R})$ acts by the character
$\text{U}_{3}(\mathbb{R})$ acts by the character  $\det ^{2r}$. If
$\det ^{2r}$. If  $r=0$, by [Reference Loke and SavinLS19, Proposition 5.2], the dimension of this space is equal to the dimension of
$r=0$, by [Reference Loke and SavinLS19, Proposition 5.2], the dimension of this space is equal to the dimension of  $S_{n}(\mathfrak{p}^{\prime })$, the space of the
$S_{n}(\mathfrak{p}^{\prime })$, the space of the  $n$th symmetric tensor power of
$n$th symmetric tensor power of  $\mathfrak{p}^{\prime }$. But this result can be easily generalized to any
$\mathfrak{p}^{\prime }$. But this result can be easily generalized to any  $r$:
$r$:  $V_{n}^{\det ^{2r}}$ is non-trivial only for
$V_{n}^{\det ^{2r}}$ is non-trivial only for  $n\geqslant 3r$, and the dimension of
$n\geqslant 3r$, and the dimension of  $V_{n+3r}^{\det ^{2r}}$ is equal to the dimension of
$V_{n+3r}^{\det ^{2r}}$ is equal to the dimension of  $S_{n}(\mathfrak{p}^{\prime })$. In particular,
$S_{n}(\mathfrak{p}^{\prime })$. In particular,  $V_{3r}^{\det ^{2r}}$ is one-dimensional. Let
$V_{3r}^{\det ^{2r}}$ is one-dimensional. Let  $v_{r}$ be a vector spanning this line. The group
$v_{r}$ be a vector spanning this line. The group  $K^{\prime }$ acts on this line and the vector
$K^{\prime }$ acts on this line and the vector  $v_{r}$ is fixed by
$v_{r}$ is fixed by  $K^{\prime }$, since
$K^{\prime }$, since  $K^{\prime }$ is semisimple. By [Reference Loke and SavinLS19, Lemma 3.1], the matrix coefficient of
$K^{\prime }$ is semisimple. By [Reference Loke and SavinLS19, Lemma 3.1], the matrix coefficient of  $v_{r}$, when restricted to
$v_{r}$, when restricted to  $G^{\prime }$, is contained in
$G^{\prime }$, is contained in  $L^{3/2+\unicode[STIX]{x1D716}}(G^{\prime })$. This fact, combined with the dimension of
$L^{3/2+\unicode[STIX]{x1D716}}(G^{\prime })$. This fact, combined with the dimension of  $\det ^{2r}$-invariants in the types of
$\det ^{2r}$-invariants in the types of  $\unicode[STIX]{x1D6F1}$, implies that
$\unicode[STIX]{x1D6F1}$, implies that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}^{\det ^{2r}}=U(\mathfrak{g}^{\prime })\cdot v_{r}\cong U(\mathfrak{g}^{\prime })\otimes _{U(k^{\prime })}\mathbb{C}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}^{\det ^{2r}}=U(\mathfrak{g}^{\prime })\cdot v_{r}\cong U(\mathfrak{g}^{\prime })\otimes _{U(k^{\prime })}\mathbb{C}\end{eqnarray}$$ as explained in the introduction of [Reference Loke and SavinLS19], where the case  $r=0$ is discussed. After taking
$r=0$ is discussed. After taking  $\det ^{2r}$-invariants in
$\det ^{2r}$-invariants in  $\unicode[STIX]{x1D6F1}\rightarrow \unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E})\boxtimes \unicode[STIX]{x1D70E}$, it follows that
$\unicode[STIX]{x1D6F1}\rightarrow \unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E})\boxtimes \unicode[STIX]{x1D70E}$, it follows that  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E})$ is a quotient of
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E})$ is a quotient of  $U(\mathfrak{g}^{\prime })\otimes _{U(k^{\prime })}\mathbb{C}$. Thus any irreducible quotient
$U(\mathfrak{g}^{\prime })\otimes _{U(k^{\prime })}\mathbb{C}$. Thus any irreducible quotient  $\unicode[STIX]{x1D70E}^{\prime }$ of
$\unicode[STIX]{x1D70E}^{\prime }$ of  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E})$ is spherical. It was also shown in [Reference Loke and SavinLS19] that
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E})$ is spherical. It was also shown in [Reference Loke and SavinLS19] that  $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E}^{\prime })$ has unique irreducible quotient, and it is spherical. This is a contradiction, since
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D70E}^{\prime })$ has unique irreducible quotient, and it is spherical. This is a contradiction, since  $\unicode[STIX]{x1D70E}$ is not spherical, and hence it cannot appear in this correspondence.◻
$\unicode[STIX]{x1D70E}$ is not spherical, and hence it cannot appear in this correspondence.◻
The correspondence for the dual pair  $\text{Aut}(\mathbb{O}_{\infty }^{c})\times \text{Sp}_{6}(\mathbb{R})$ was completely determined in [Reference Gross and SavinGS98] and is functorial. Thus, if
$\text{Aut}(\mathbb{O}_{\infty }^{c})\times \text{Sp}_{6}(\mathbb{R})$ was completely determined in [Reference Gross and SavinGS98] and is functorial. Thus, if  $\unicode[STIX]{x1D719}_{2r}$ is of level
$\unicode[STIX]{x1D719}_{2r}$ is of level  $1$ (i.e. spherical at all primes), then
$1$ (i.e. spherical at all primes), then  $\unicode[STIX]{x1D70B}$ is indeed a (strong) functorial lift from
$\unicode[STIX]{x1D70B}$ is indeed a (strong) functorial lift from  $\text{Aut}(\mathbb{O}^{c})$.◻
$\text{Aut}(\mathbb{O}^{c})$.◻
Acknowledgements
The authors would like to thank Aaron Pollack for clarifying a few points about his Rankin–Selberg integral for the Spin L-function, especially with regard to the extent the unfolding and unramified computations hold over a more general field. Thanks are also due to the referee for his/her meticulous work, pertinent comments and useful suggestions. W. T. Gan is partially supported by an MOE Tier 2 grant R146-000-233-112. G. Savin is partially supported by Simons Foundation grant 579347, and a grant from the National Science Foundation, DMS-1901745.