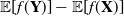1. Introduction
Stochastic orders provide methods of comparing random variables and vectors which are now used in many areas such as statistics and probability [Reference Cal and Carcamo8, Reference Fill and Kahn21, Reference Hazra, Kuiti, Finkelstein and Nanda24, Reference Hu and Zhuang26, Reference Müller and Scarsini41], operations research [Reference Fábián, Mitra and Roman18], actuarial sciences and economic theory [Reference Bäuerle4, Reference López-Díaz, López-Díaz and Martínez-Fernández32], and risk management and other related fields [Reference Bäuerle and Müller5]. For a comprehensive review of the properties and characterizations of stochastic orderings, including a variety of applications, the reader is referred to the monographs of [Reference Müller and Stoyan42], [Reference Denuit, Dhaene, Goovaerts and Kaas15], and [Reference Shaked and Shanthikumar49]. Many of these orders are characterized by the so-called integral stochastic orders which are obtained by comparing expectations of functions in a certain class. A general treatment for these orders has been given in [Reference Whitt52] and [Reference Müller38].
Elliptical distributions are generalizations of the multivariate normal distributions and, therefore, share many of the tractable properties. This class of distributions was introduced by [Reference Kelker29] and was extensively discussed by [Reference Fang, Kotz and Ng20]. This generalization of the normal family seems to provide an attractive tool for statistics, economics, finance, and actuarial science, which can describe fat or light tails and tail dependence among components of a vector. Interested readers are referred to [Reference El Karoui17, Reference Gupta, Varga and Bodnar23, Reference McNeil, Frey and Embrechts34, Reference Sha46, Reference Yin, Wang and Sha55]. Müller [Reference Müller39] studied the stochastic ordering characterizations of multivariate normal random vectors. Arlotto and Scarsini [Reference Arlotto and Scarsini2] unified and generalized several known results on comparisons of multivariate normal random vectors in the sense of different stochastic orders by introducing the so-called Hessian order. Landsman and Tsanakas derived necessary and sufficient conditions for classifying bivariate elliptical distributions through the concordance ordering. Ding and Zhang extended the results in [Reference Müller39] to Kotz-type distributions, which form an important special class of elliptical symmetric distributions. Several stochastic orderings for meta-elliptical bivariate distributions were critically reviewed by [Reference Abdous, Genest and Rémillard1]. Necessary and sufficient conditions for convex order and increasing convex order of general multivariate elliptical random vectors had not been found until the work of [Reference Pan, Qiu and Hu43]. However, few results can be found in the literature that characterize the supermodular order of multivariate elliptical distributions. It is the aim of this paper to fill this gap. We will give some sufficient and necessary conditions for supermodular order of multivariate elliptical random vectors. For the known results, such as on the convex ordering and the increasing convex ordering of multivariate elliptical random vectors, we provide a different simple proof.
The rest of the paper is organized as follows. Section 2 recalls some useful notions that will be used in the what follows, such as certain properties of stochastic orders and elliptical distributions. Section 3 presents necessary and sufficient conditions for several important stochastic orders of multivariate elliptical distributions. Section 4 provides two applications of the main results.
2. Preliminaries
Throughout this paper we use the following notations. We use bold letters to denote vectors or matrices. For example, 
${\bf X}' =(X_1,\ldots, X_n)$ is a row vector and 
${\boldsymbol \Sigma} = (\sigma_{ij})_{n\times n}$ is an 
$n\times n$ matrix. In particular, the symbol 
${\bf 0}_n$ denotes the n-dimensional column vector with all entries equal to 0, 
${\bf 1}_{n}$ denotes the n-dimensional column vector with all components equal to 1, and 
${\bf 1}_{n\times n}$ denotes the 
${n\times n}$ matrix with all entries equal to 1. Denote by 
${\bf O}_{n\times n}$ the 
$n \times n$ matrix with all entries equal to 0, and by 
${\bf I}_n$ the 
$n\times n$ identity matrix. For symmetric matrices A and B of the same size, the notion 
${\bf A} \preceq {\bf B}$ or 
${\bf B} - {\bf A} \succeq {\bf O}$ means that 
${\bf B} - {\bf A}$ is positive semi-definite. Inequality between vectors or matrices denotes componentwise inequalities. Throughout this paper, the terms ‘increasing’ and ‘decreasing’ are used in the weak sense. All integrals and expectations are implicitly assumed to exist whenever they appear.
2.1. Some background on the elliptical distributions
The class of multivariate elliptical distributions is a natural extension of the class of multivariate normal distributions. We follow the notation of [Reference Cambanis, Huang and Simons7] and [Reference Fang, Kotz and Ng20]. An 
$n \times 1$ random vector 
${\bf X} = (X_1, X_2,\ldots, X_n)'$ is said to have an elliptically symmetric distribution if its characteristic function has the form 
$\textrm{e}^{\textrm{i}{\bf t}'{\boldsymbol \mu}}\phi({\bf t}'{\boldsymbol \Sigma}{\bf t})$ for all 
${\bf t}\in \mathbb{R}^n $, denoted 
${\bf{X}}\sim E_n ({\boldsymbol \mu},{\boldsymbol \Sigma},\phi)$, where 
$\phi \in {\boldsymbol \Psi}_n$ is called the characteristic generator satisfying 
$\phi(0)=1$, 
$\boldsymbol{\mu}$ (n-dimensional vector) is its location parameter, and 
$\bf{\Sigma}$ (an 
$n\times n$ matrix with 
$\bf{\Sigma}\succeq {\bf O}$) is its dispersion matrix (or scale matrix). The mean vector 
$\mathbb{E}({\bf X})$ (if it exists) coincides with the location vector and the covariance matrix Cov
$({\bf X})$ (if it exists), and equals 
$-2\phi'(0){\boldsymbol \Sigma}$. Note that in the one-dimensional case, the class of elliptical distributions consists mainly of the class of symmetric distributions, which includes well-known distributions like normal and Student t. A random vector 
$\bf X$ admits the stochastic representation
\begin{equation} {\bf X}={\boldsymbol \mu}+R{\bf A}'{\bf U}^{(n)},\end{equation}
where A is a square matrix such that 
${\bf A}'{\bf A}= {\boldsymbol \Sigma}$, 
${\bf U}^{(n)}$ is uniformly distributed on the unit sphere 
$\mathcal{S}^{n-1}=\{{\bf u}\in \mathbb{R}^n\,{:}\, {\bf u}'{\bf u}=1\} $, 
$R\ge 0$ is a random variable with 
$R \sim F$ in 
$[0, \infty)$ called the generating variate, and F is called the generating distribution function; R and 
${\bf U}^{(n)}$ are independent. The mean vector 
$\mathbb{E}({\bf X})$ exists if and only if 
$\mathbb{E}(R)$ exists; then, 
$\mathbb{E}({\bf X})={\boldsymbol \mu}$. The covariance matrix Cov
$({\bf X})$ exists if and only if 
$\mathbb{E}(R^2)$ exists; then, Cov
$({\bf X})=\frac{1}{n} \mathbb{E}(R^2){\boldsymbol \Sigma}$. In general, an elliptically distributed random vector 
${\bf{X}}\sim E_n ({\boldsymbol \mu},{\boldsymbol \Sigma},\phi)$ does not necessarily possess a density. It is well known that 
${\bf{X}}$ has a density if and only if R has a density and 
${\boldsymbol \Sigma}\succ {\bf O}$. The density has the form
\begin{equation*}f({\bf x})=c_n|{\boldsymbol \Sigma}|^{-\frac{1}{2}}g_n(({\bf x}- {\boldsymbol \mu})'{\boldsymbol \Sigma}^{-1}({\bf x-{\boldsymbol \mu} })), \qquad {\bf x}\in \mathbb{R}^n,\end{equation*}
for some nonnegative function 
$g_n$ called the density generator and for some constant 
$c_n$ called the normalizing constant. We sometimes write 
$X \sim E_n ({\boldsymbol \mu},{\boldsymbol \Sigma},g_n)$ for the n-dimensional elliptical distributions generated from the function 
$g_n$.
The class of elliptical distributions possesses the linearity property. Consider the affine transformations of the form 
${\bf Y = BX+b}$ of a random vector 
${\bf{X}}\sim E_n({\boldsymbol \mu},{\boldsymbol \Sigma},\phi)$, where 
$\bf B$ is an 
$m\times n$ matrix with 
$m<n$ and 
$\textrm{rank}({\bf B})=m$, and 
${\bf b}\in\mathbb{R}^m$. Then, 
${\bf Y} \sim E_n ({\bf B}{\boldsymbol \mu}+{\bf b}, {\bf B}{\boldsymbol \Sigma}{\bf B}',\phi)$. Taking 
$B=(\alpha_1,\ldots,\alpha_n):= {\boldsymbol \alpha}'$ leads to 
${\boldsymbol \alpha}'{\bf X}\sim E_1({\boldsymbol \alpha}'{\boldsymbol \mu}, {\boldsymbol \alpha}'{\boldsymbol \Sigma}{\boldsymbol \alpha},\phi)$. In particular, 
$X_k\sim E_1(\mu_k,\sigma_k^2, \phi), \;\; k=1,2,\cdots, n$, and
\begin{equation*}\sum_{k=1}^n X_k\sim E_1\left(\sum_{k=1}^n\mu_k,\sum_{k=1}^n\sum_{l=1}^n \sigma{_{kl}}, \phi\right).\end{equation*}
2.2. Stochastic orders
In this section we summarize some important definitions and facts about the stochastic orderings of random vectors. The standard references for stochastic orderings are [Reference Denuit, Dhaene, Goovaerts and Kaas15] and [Reference Shaked and Shanthikumar49].
For a function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$, 
${\bf x}\in \mathbb{R}^n$, 
$i\in \{1,\ldots,n\}$, and 
$\delta> 0$, we define the difference operator 
$\Delta_i^{\delta}$ as 
$\Delta_i^{\delta}f({\bf x}) = f({\bf x}+\delta {\bf e}_i)-f ({\bf x})$, where 
${\bf e}_i=(0,\dots, 0, 1, 0,\dots, 0)$ denotes the ith unit vector. In the case 
$n = 1$ we simply write 
$\Delta^{\delta}f( x) = f(x+\delta)-f(x)$. A function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is said to be increasing if 
$\Delta_i^{\delta}f({\bf x})\ge 0$ for all 
${\bf x}\in \mathbb{R}^n$, 
$\delta>0$, and 
$i =1,\ldots,n$. A function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is is said to be supermodular if 
$\Delta_i^{\delta} \Delta_j^{\varepsilon}f({\bf x})\ge 0$ for all 
${\bf x}\in \mathbb{R}^n$, 
$\delta, \varepsilon>0$, and 
$1\le i<j\le n$. Equivalently, a function 
$f\,{:}\, {\mathbb{R}}^n \rightarrow {\Bbb R}$ is said to be supermodular if, for any 
${\bf x, y}\in {\Bbb R}^n$, 
$f({\bf x}) + f({\bf y}) \le f ({\bf x} \wedge {\bf y}) + f ({\bf x} \vee {\bf y})$, where the operators 
$\wedge$ and 
$\vee$ denote coordinatewise minimum and maximum, respectively. A function f is supermodular if and only if 
$-f$ is submodular.
A function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is said to be componentwise convex if f is convex in each argument when the other arguments are held fixed. A function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is said to be directionally convex if 
$\Delta_i^{\delta} \Delta_j^{\varepsilon}f({\bf x})\ge 0$ for all 
${\bf x}\in \mathbb{R}^n$, 
$\delta, \varepsilon>0$, and 
$1\le i, j\le n$. That is, 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is directionally convex if it is supermodular and componentwise convex. Directional convexity neither implies, nor is implied by, conventional convexity.
A function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is said to be a 
$\Delta$-monotone function if, for all 
$1\le k\le n$, 
$\{i_1, \ldots,i_k\}\subset \{1, \ldots, n\}$, and every 
$\delta_1,\ldots,\delta_k>0$, 
$\Delta_{i_1}^{\delta_1}\cdots \Delta_{i_k}^{\delta_{k}}f({\bf x})\ge 0$ for all 
${\bf x}\in \mathbb{R}^n$, 
$\delta, \varepsilon>0$.
We now recall the definitions of stochastic orders that will be used later. Let 
${\mathcal{F}}$ be some class of measurable functions 
$f\,{:}\, {\mathbb{R}}^n \rightarrow {\Bbb R}$. For two random vectors X and Y in 
${\mathbb{R}}^n$, we say that 
${\bf X}\le_\mathcal{F}{\bf Y}$ if 
$\mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ holds for all 
$f\in {\mathcal{F}}$ whenever the expectations are well defined. We list a few important examples below.
Usual stochastic order:
${\bf X}\le_\textrm{st} {\bf Y}$ if $\mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all increasing functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Convex order:
${\bf X}\le_\textrm{cx} {\bf Y}$ if $\mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all convex functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Linear convex order:
${\bf X}\le_\textrm{lcx} {\bf Y}$ if $\mathbb{E}[f({\bf a'X})]\le \mathbb{E}[f({\bf a'Y})]$ for all ${\bf a}\in\mathbb{R}^n$ and for all convex functions $f\,{:}\, \mathbb{R} \rightarrow \mathbb{R}$.Increasing convex order:
${\bf X}\le_\textrm{icx} {\bf Y}$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all increasing convex functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Componentwise convex order:
${\bf X}\le_\textrm{ccx} {\bf Y}$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all componentwise convex functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Increasing componentwise convex order:
${\bf X}\le_\textrm{iccx} {\bf Y}$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all increasing componentwise convex functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Supermodular order:
${\bf X}\le_\textrm{sm} {\bf Y}$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all supermodular functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Increasing supermodular order:
${\bf X}\le_\textrm{ism} {\bf Y}$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all increasing supermodular functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Directionally convex order:
${\bf X}\le_\textrm{dcx} {\bf Y}$ if $\mathbb{E} [f({\bf X})]\le \mathbb{E} [f({\bf Y})]$ for all directionally convex functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.Increasing directionally convex:
${\bf X}\le_\textrm{idcx} {\bf Y}$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ for all increasing directionally convex functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.
The componentwise convex order was introduced by Mosler (1982), the directionally convex order by [Reference Shaked and Shanthikumar49], and the increasing directionally convex order by [Reference Müller and Stoyan42]. The supermodular order compares only the dependence structure of vectors with fixed equal marginals, whereas the increasing directionally convex order also compares both marginal variability and location. However, a univariate function is directionally convex if, and only if, it is convex.
For a random vector 
${\bf X}=(X_1, \ldots, X_n)$, we denote the multivariate distribution function by
\begin{equation*}F_{\bf X} ({\bf t}):= \mathbb{P}({\bf X}\le {\bf t})=\mathbb{P}(X_1\le t_1,\ldots, X_n\le t_n), \qquad{\bf t}=(t_1,\ldots, t_n)\in {\Bbb R}^n,\end{equation*}
and the multivariate survival function by
\begin{equation*}{\overline F}_{\bf X} ({\bf t}):= \mathbb{P}({\bf X}> {\bf t})=\mathbb{P}(X_1> t_1,\ldots, X_n> t_n), \qquad{\bf t}=(t_1,\ldots, t_n)\in {\Bbb R}^n.\end{equation*}
The following definition is taking from [Reference Müller and Scarsini40].
Definition 1. Assume that 
${\bf X, Y}\in {\Bbb R}^n$ are two random vectors.
• X is said to be smaller than Y in the upper orthant order, written
${\bf X}\le_\textrm{uo} {\bf Y}$, if ${\overline F}_{\bf X} ({\bf t})\le {\overline F}_{\bf Y} ({\bf t})$ for all ${\bf t}\in {\Bbb R}^n$.-
• X is said to be smaller than Y in the lower orthant order, written
${\bf X}\le_\textrm{lo} {\bf Y}$, if ${F}_{\bf X} ({\bf t})\le {F}_{\bf Y} ({\bf t})$ for all ${\bf t}\in {\Bbb R}^n$. -
• X is said to be smaller than Y in the concordance order, written
${\bf X}\le_\textrm{c} {\bf Y}$, if both ${\bf X}\le_\textrm{uo} {\bf Y}$ and ${\bf X}\le_\textrm{lo} {\bf Y}$ hold.
The orthant orders were treated by [Reference Shaked and Shanthikumar49] and the concordance order was introduced by [Reference Joe28]. We have the implication 
${\bf X}\le_\textrm{sm} {\bf Y} \Rightarrow {\bf X}\le _\textrm{uo} {\bf Y}$ and 
${\bf X}\le _\textrm{lo} {\bf Y}$, and hence 
${\bf X}\le_\textrm{sm} {\bf Y} \Rightarrow {\bf X}\le _\textrm{c} {\bf Y}$.
The upper orthant order can be defined alternatively by 
$\Delta$-monotone functions. The following lemma can be found in [Reference Rüschendorf44].
Lemma 1. 
${\bf X}\le_\textrm{uo} {\bf Y}$ if and only if 
$ \mathbb{E}[f({\bf X})]\le \mathbb{E} [f({\bf Y})]$ holds for all 
$\Delta$-monotone functions 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$.
The following necessary and sufficient conditions for several important stochastic orders can be found in [Reference Denuit and Müller14] and [Reference Arlotto and Scarsini2].
•
${\bf X}\le_\textrm{sm} {\bf Y}$ if and only if $\mathbb{E} [f({\bf X})]\le \mathbb{E} [f({\bf Y})]$ holds for all twice differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying, for all $1\le i<j\le n$,
(2)
\begin{equation} \frac{\partial^2 }{\partial x_i \partial x_j}f({\bf x})\ge 0, \qquad {\bf x}\in \mathbb{R}^n. \end{equation}
-
•
${\bf X}\le_\textrm{ism} {\bf Y}$ if and only if $\mathbb{E} [f({\bf X})]\le \mathbb{E} [f({\bf Y})]$ holds for all twice differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial }{\partial x_i}f({\bf x})\ge 0$, for ${\bf x}\in \mathbb{R}^n$ and all $1\le i\le n$, and (2) for all $1\le i<j\le n$. -
•
${\bf X}\le_\textrm{dcx} {\bf Y}$ if and only if $ \mathbb{E}[f({\bf X})]\le \mathbb{E} [f({\bf Y})]$ holds for all twice differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying (2) for all $1\le i,j\le n$. -
•
${\bf X}\le_\textrm{idcx} {\bf Y}$ if and only if $ \mathbb{E}[f({\bf X})]\le \mathbb{E} [f({\bf Y})]$ holds for all twice differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial }{\partial x_i}f({\bf x})\ge 0$, for ${\bf x}\in \mathbb{R}^n$ and all $1\le i\le n$, and (2) for all $1\le i, j\le n$. -
•
${\bf X}\le_\textrm{uo} {\bf Y}$ if and only if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ holds for all infinitely differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial^k }{\partial x_{i_1}\cdots \partial x_{i_k}}f({\bf x})\ge 0$ for ${\bf x}\in \mathbb{R}^n$ and all $1\le {i_1}<\cdots< i_k\le n$, $1\le k\le n$. -
•
${\bf X}\le_\textrm{ccx} {\bf Y}$ if and only if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ holds for all twice differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial^2 }{\partial x_i^2}f({\bf x})\ge 0$ for ${\bf x}\in \mathbb{R}^n$ and all $1\le i\le n$. -
•
${\bf X}\le_\textrm{iccx} {\bf Y}$ if and only if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ holds for all twice differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial }{\partial x_i}f({\bf x})\ge 0$ and $\frac{\partial^2 }{\partial x_i^2}f({\bf x})\ge 0$ for ${\bf x}\in \mathbb{R}^n$ and all $1\le i\le n$.
We first list the results of stochastic orderings for univariate elliptical distributions. The case of univariate normal distributions can be found in [Reference Müller39].
Lemma 2. Let 
$X\sim E_1(\mu_x, \sigma_y^2, \phi)$ and 
$Y\sim E_1(\mu_y, \sigma_y^2, \phi)$. Then
(i)
$X \le_\textrm{st} Y$ if and only if $\mu_x\le \mu_y$ and $\sigma_x=\sigma_y$, provided that X and Y are supported on $\mathbb{R}$ [Reference Davidov and Peddada13].-
(ii)
$X \le_\textrm{cx} Y$ if and only if $\mu_x=\mu_y$ and $\sigma_x\le \sigma_y$ [Reference Pan, Qiu and Hu43]. -
(iii)
$X \le_\textrm{icx} Y$ if and only if $\mu_x\le \mu_y$ and $\sigma_x\le \sigma_y$ [Reference Pan, Qiu and Hu43].
Now we list the results of stochastic orderings for multivariate elliptical distributions.
Lemma 3. ([Reference Pan, Qiu and Hu43].) Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. Then the following statements are equivalent:
(i)
${\boldsymbol \mu}^x={\boldsymbol \mu}^y$ and ${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is positive semi-definite.-
(ii)
${\bf X}\le_\textrm{lcx} {\bf Y}$. -
(iii)
${\bf X}\le_\textrm{cx} {\bf Y}$.
For the case of increasing convex order, the sufficient and necessary conditions seem to be unknown. The following sufficient condition for the increasing convex order can be found in [Reference Pan, Qiu and Hu43]. The results for the case of multivariate normal distributions can be found in [Reference Müller39].
Lemma 4. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$.
(i) If
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and ${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is positive semi-definite, then ${\bf X}\le_\textrm{icx} {\bf Y}$.-
(ii) If
${\bf X}\le_\textrm{icx} {\bf Y}$, then ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and ${\bf a}'({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf a}\ge 0$ for all ${\bf a}\ge 0$.
2.3. An identity for multivariate elliptical distributions
If 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is twice continuously differentiable, we write as usual
\begin{equation*}\nabla f({\bf x})=\left(\frac{\partial }{\partial x_1}f({\bf x)}, \ldots, \frac{\partial }{\partial x_n}f({\bf x)}\right)', \qquad {\bf H}_f({\bf x})=\left(\frac{\partial^2}{\partial x_i \partial x_i}f({\bf x)} \right)_{n\times n}\end{equation*}
for the gradient and the Hessian matrix of f. It is well known that f is convex if and only if 
${\bf H}_f({\bf x})$ is positive semidefinite for any 
${\bf x}\in \mathbb{R}^n$; f is strictly convex if and only if 
${\bf H}_f({\bf x})$ is positive definite for any 
${\bf x}\in \mathbb{R}^n$. A function is supermodular if and only if its Hessian has nonnegative off-diagonal elements, i.e. f is supermodular if and only if 
$\frac{\partial^2}{\partial x_i \partial x_i}f({\bf x)}\ge 0$ for every 
$i\neq j$ and 
${\bf x}\in {\mathbb{R}}^n$ (cf. [Reference Carter9, Proposition 4.2]).
The following two results can be found in [Reference Houdré, Pérez-Abreu and Surgailis25], [Reference Müller39], and [Reference Denuit and Müller14] in the multivariate normal case. Ding and Zhang extended the result from multivariate normal distributions to Kotz-type distributions, which form an important class of elliptically symmetric distributions. We develop an identity for multivariate elliptical distributions.
Lemma 5. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^{x},\psi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^{y}, \psi)$, with 
${\boldsymbol \Sigma}^{x}$ and 
${\boldsymbol \Sigma}^{y}$ positive definite. Let 
$\phi_{\lambda}$ be the density function of 
$E_n (\lambda{\boldsymbol \mu}^y+(1-\lambda){\boldsymbol \mu}^x , \lambda{\boldsymbol \Sigma}^{y}+(1-\lambda){\boldsymbol \Sigma}^{x}, \psi)$, 
$0 \le \lambda \le 1$, and 
$\phi_{1\lambda}$ be the density function of 
$E_n (\lambda{\boldsymbol \mu}^y+(1-\lambda){\boldsymbol \mu}^x , \lambda{\boldsymbol \Sigma}^{y}+(1-\lambda){\boldsymbol \Sigma}^{x}, \psi_1)$, 
$0\le \lambda \le 1$, where
\begin{equation*}\psi_1(u)=\frac{1}{ \mathbb{E}(R^2)}\int_0^{\infty} {}_0F_1\left(\frac{n}{2}+1;-\frac{r^2 u}{4}\right)r^2 \mathbb{P}(R\in \textrm{d} r).\end{equation*}
Here,
\begin{equation*}{}_0F_1(\gamma;z)=\sum_{k=0}^{\infty} \frac{\Gamma(\gamma)}{\Gamma(\gamma+k)}\frac{z^k}{k!}\end{equation*}
is the generalized hypergeometric series of order (0, 1), and R is defined by (1) with 
$\mathbb{E}(R^2)<\infty$. Moreover, assume that 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ is twice continuously differentiable and satisfies some polynomial growth conditions at infinity:
\begin{equation} f({\bf x})=O(||{\bf x}||), \qquad \bigtriangledown f({\bf x})=O(||{\bf x}||).\end{equation}
Then
\begin{align*} \mathbb{E}[f({\bf Y})]- \mathbb{E}[f({\bf X})]&=\int_0^1\int_{\mathbb{R}^n}({\boldsymbol \mu}^y-{\boldsymbol \mu}^x)'\nabla f({\bf x})\phi_{\lambda}({\bf x}) \, \textrm{d}{\bf x} \, \textrm{d}\lambda \\[3pt] &\quad +\frac{\mathbb{E}(R^2)}{2n}\int_0^1\int_{\mathbb{R}^n}\textrm{tr}\{({\boldsymbol \Sigma}^{y}-{\boldsymbol \Sigma}^{x}){\bf H}_f({\bf x})\}\phi_{1\lambda}({\bf x}) \, \textrm{d}{\bf x} \, \textrm{d}\lambda,\end{align*}
where 
$\textrm{tr}(A)$ denotes the trace of the matrix A.
For the proof, see the appendix.
Using Lemma 5 and the same argument as the proof of [Reference Müller39, Corollary 3], we have the following corollary.
Corollary 1. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^{x},\psi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^{y},\psi)$, with 
${\boldsymbol \Sigma}^{x}$ and 
${\boldsymbol \Sigma}^{y}$ positive definite or positive semidefinite, and assume that 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfies the conditions of Lemma 5. Then 
$\mathbb{E} [f({\bf X})]\le\mathbb{E}[f({\bf Y})]$ if the following two conditions hold for all 
${\bf x}\in \mathbb{R}^n$:
\begin{equation*}\sum_{i=1}^n({\mu}^{y}_{i}-{ \mu}^{x}_{i})\frac{\partial }{\partial x_i}f({\bf x})\ge 0, \qquad \sum_{i=1}^n\sum_{j=1}^n({\sigma}^y_{ij}-{\sigma}^x_{i j})\frac{\partial^2 }{\partial x_i \partial x_j}f({\bf x})\ge 0.\end{equation*}
3. Main results
The following results can be found in [Reference Davidov and Peddada13]. The multivariate normal case can be found in [Reference Müller39]. Here we provide a different proof.
Theorem 1. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$ be two n-dimensional elliptically distributed random vectors supported on 
${\Bbb R}^n$. Then 
${\bf X}\le_\textrm{st} {\bf Y}$ if and only if 
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and 
${\boldsymbol \Sigma}^y={\boldsymbol \Sigma}^x$.
Proof. For any increasing twice differential function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$, the ‘if’ part follows immediately from Corollary 1, since 
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$, 
${\boldsymbol \Sigma}^y={\boldsymbol \Sigma}^x$, and 
$\nabla f({\bf x})\ge 0$ for all 
${\bf x}\in \mathbb{R}^n$ imply that 
$E[f({\bf Y})]\ge E[f({\bf X})]$. To prove the ‘only if’ part, we choose f to have the forms 
$f({\bf x})=h_1(x_i)$ and 
$f({\bf x})=h_2(x_i+x_j)$, where 
$h_1$ and 
$h_2$ are any two univariate increasing functions. It follows from 
${\bf X}\le_\textrm{st} {\bf Y}$ that 
$X_i\le_\textrm{st} Y_i$ and 
$X_i+X_j\le_\textrm{st} Y_i+Y_j$. Note that 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$ lead to 
$X_i\sim E_1 ({\mu}_i^x,{\sigma}_{ii}^x,\phi)$ and 
$X_i+X_j\sim E_1 ({\mu}_i^x+{\mu}_j^x,{\sigma}_{ii}^x+ {\sigma}_{jj}^x+2\sigma^x_{ij},\phi)$. By the symmetry of elliptical distributions, all 
$X_i$, 
$X_j$, 
$Y_i$, 
$Y_j$, 
$X_i+Y_i$, and 
$X_j+Y_j$ are supported on 
${\mathbb{R}}$. Applying Lemma 2(i), we find that 
${\mu}_i^x\le {\mu}_i^y$ and 
$\sigma^x_{ij}=\sigma^y_{ij}$ for all 
$1\le i,j\le n$. Hence, 
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and 
${\boldsymbol \Sigma}^y={\boldsymbol \Sigma}^x$.
The following result, due to [Reference Pan, Qiu and Hu43], generalizes [Reference Scarsini45, Theorem 4] and [Reference Müller39, Theorem 6] for the multivariate normal case. Here, we provide a different proof.
Theorem 2. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. Then the following statements are equivalent:
(i)
${\boldsymbol \mu}^y={\boldsymbol \mu}^x$ and ${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x \succeq {\bf O}$.-
(ii)
${\bf X}\le_\textrm{cx} {\bf Y}$. -
(iii)
${\bf X}\le_\textrm{lcx} {\bf Y}$.
Proof. (i) 
$\Rightarrow$ (ii): For any twice differential convex function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$, using Lemma 5 we get 
$\mathbb{E}[f({\bf Y})]\ge \mathbb{E}[f({\bf X})]$ since f is convex if and only if its Hessian matrix 
$H_f$ is positive semi-definite. (ii) 
$\Rightarrow$ (iii) is obvious. (iii) 
$\Rightarrow$ (i) is the same as the proof of [Reference Pan, Qiu and Hu43, Theorem 4.1].
The following result, due to [Reference Pan, Qiu and Hu43], generalizes [Reference Müller39, Theorem 7] for the multivariate normal case. Here we provide a different proof.
Theorem 3. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. Then the following statements hold:
(i) If
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and ${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x \succeq {\bf O}$, then ${\bf X}\le_\textrm{icx} {\bf Y}$.-
(ii) If
${\bf X}\le_\textrm{icx} {\bf Y}$, then ${\boldsymbol \mu}^y\ge {\boldsymbol \mu}^x$ and ${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is copositive, i.e. ${\bf a}'({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf a}\ge 0$ for all ${\bf a}\ge 0$.
Proof. (i): For any twice differential increasing convex function 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$, using Lemma 5 together with the conditions 
${\boldsymbol \mu}^y\ge {\boldsymbol \mu}^x$ and 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x \succeq {\bf O}$, we get 
$\mathbb{E}[f({\bf Y})]\ge \mathbb{E}[f({\bf X})]$, and thus we have 
${\bf X}\le_\textrm{icx} {\bf Y}$. The proof of (ii) is the same as the proof of [Reference Pan, Qiu and Hu43, Theorem 4.6(2)].
Remark 1. For the case of increasing convex order, there are no sufficient and necessary conditions in the literature even for normal distributions (see [Reference Müller39] and [Reference Pan, Qiu and Hu43]). We remark that if 
$({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf z}=0$ has a positive solution, then 
${\bf a}'({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf a}\ge 0$ for all 
${\bf a}\ge 0$ if and only if 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x \succeq {\bf O}$ (see Theorem 12). So, we get the following ‘if and only if’ characterization of increasing convex order.
Assume that 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$, 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$, and 
$({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf z}=0$ has a positive solution. Then 
${\bf X}\le_\textrm{icx} {\bf Y}$ if and only if 
${\boldsymbol \mu}^y\ge {\boldsymbol \mu}^x$ and 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x \succeq {\bf O}$.
Remark 2. It is easy to see that 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x \succeq {\bf O}$ implies that 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is copositive, but the converse is not true. We give an example. Let
\begin{equation*}{\boldsymbol \Sigma}^x =\left(\begin{array}{c@{\quad}c} \sigma^2\;& \rho_x\sigma^2 \\ \rho_x\sigma^2\; & \sigma^2\\ \end{array}\right), \qquad {\boldsymbol \Sigma}^y =\left(\begin{array}{c@{\quad}c} \sigma^2\;& \rho_y\sigma^2\\ \rho_y\sigma^2\; & \sigma^2 \\ \end{array}\right),\end{equation*}
where 
$\sigma^2>0$ and 
$-1\le \rho_x<\rho_y\le 1$. Then, for all 
${\bf a}=(a_1,a_2)'\ge 0$, 
${\bf a}'({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf a}=a_1a_2\sigma^2(\rho_y-\rho_x)\ge 0$. But for 
${\bf Z}=(z_1,-z_1)'\in {\Bbb R}^2$, 
${\bf Z}'({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf Z}=-z_1^2\sigma^2(\rho_y-\rho_x)\le 0$.
The following result generalizes [Reference Müller39, Theorem 11], in which the multivariate normal case was considered. Special conditions are given for multivariate normal and elliptically contoured distributions such that 
${\bf X}\le_\textrm{sm} {\bf Y}$ in [Reference Block and Sampson6].
Theorem 4. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. Then the following statements are equivalent:
(i)
${\bf X}\le_\textrm{sm} {\bf Y}$.-
(ii) X and Y have the same marginal and
$\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$.
Proof. (i) 
$\Rightarrow$ (2): If 
${\bf X}\le_\textrm{sm} {\bf Y}$, then X and Y necessarily belong to the same Fréchet space. In particular, X and Y have the same marginal (see, e.g., [Reference Müller and Scarsini41]). Since the function 
$f({\bf x})= x_i x_j$ is supermodular for all 
$1\le i<j\le n$, we see that 
${\bf X}\le_\textrm{sm} {\bf Y}$ implies 
$\sigma^x_{ij}\le \sigma^y_{ij}$ for all 
$1\le i<j\le n$.
Since 
${\bf X}\le_\textrm{sm} {\bf Y}$ if and only if 
$ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ holds for all twice differentiable functions 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying 
$\frac{\partial^2 }{\partial x_i \partial x_j}f({\bf x})\ge 0$ for 
${\bf x}\in \mathbb{R}^n$ and all 
$1\le i<j\le n$, the implication (ii) 
$\Rightarrow$ (i) follows from Corollary 1.
Theorem 5. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$ be two n-dimensional elliptically distributed random vectors supported on 
${\Bbb R}^n$.
(i) If
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$, $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$, and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$, then ${\bf X}\le_\textrm{ism} {\bf Y}$.-
(ii) If
${\bf X}\le_\textrm{ism} {\bf Y}$, then ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$, $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$. -
(iii) If
$({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{ism} ({\bf Y}-{\boldsymbol \mu}^y)$, then $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$.
Proof.
(i): For any twice differentiable functions
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial }{\partial x_i}f({\bf x})\ge 0$ for ${\bf x}\in \mathbb{R}^n$ and all $1\le i\le n$ and $\frac{\partial^2 }{\partial x_i \partial x_j}f({\bf x})\ge 0$ for ${\bf x}\in \mathbb{R}^n$ and all $1\le i<j\le n$, using Corollary 1 together with the conditions ${\boldsymbol \mu}^y\ge {\boldsymbol \mu}^x$, $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$, we get $\mathbb{E}[f({\bf Y})]\ge \mathbb{E}[f({\bf X})]$. Thus, we have ${\bf X}\le_\textrm{ism} {\bf Y}$.-
(ii):
${\bf X}\le_\textrm{ism} {\bf Y}$ implies that $X_i\le_\textrm{st} Y_i$ [Reference Müller and Stoyan42, p. 114]. Applying Lemma 2(i) we find that ${\mu}_i^x\le {\mu}_i^y$ and $\sigma^x_{ii}=\sigma^y_{ii}$ for all $1\le i\le n$. -
(iii):
$({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{ism} ({\bf Y}-{\boldsymbol \mu}^y)$ implies that $(X_i-\mu_i^x)\le_\textrm{st} (Y_i-\mu_i^y)$, and hence $(X_i-\mu_i^x)\stackrel{\textrm{d}}{=}(Y_i-\mu_i^y)$. Thus, $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$. Consequently, $({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{sm} ({\bf Y}-{\boldsymbol \mu}^y)$, which implies that $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$.
Corollary 2. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$ be two n-dimensional elliptically distributed random vectors supported on 
${\Bbb R}^n$. Then the following statements are equivalent:
(i)
$({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{ism} ({\bf Y}-{\boldsymbol \mu}^y)$.-
(ii)
$\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$, and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$.
The following result generalizes [Reference Müller39, Theorem 12] in which the multivariate normal case was considered.
Theorem 6. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. Then the following statements are equivalent:
(i)
${\bf X}\le_\textrm{dcx} {\bf Y}$.-
(ii)
${\boldsymbol \mu}^x={\boldsymbol \mu}^y$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i,j\le n$.
Proof.
(i)
$\Rightarrow$ Note that the functions $f({\bf x})=x_i, -x_i, x_i x_j$ are directionally convex for all $1\le i,j\le n$, and thus ${\boldsymbol \mu}^x={\boldsymbol \mu}^y$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i,j\le n$.
(ii) 
$\Rightarrow$ (i): Since 
${\bf X}\le_\textrm{dcx} {\bf Y}$ if and only if 
$\mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ holds for all twice differentiable functions 
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying 
$\frac{\partial^2 }{\partial x_i \partial x_j}f({\bf x})\ge 0$ for 
${\bf x}\in \mathbb{R}^n$ and all 
$1\le i, j\le n$, the implication follows from Lemma 5.
For increasing directionally convex orders we have the following theorem.
Theorem 7. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$.
(i) If
${\bf X}\le_\textrm{idcx} {\bf Y}$, then ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and $\sigma^x_{ii}\le \sigma^y_{ii}$ for all $1\le i\le n$.-
(ii) If
$({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{idcx} ({\bf Y}-{\boldsymbol \mu}^y)$, then $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i,j\le n$. -
(iii) If
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i,j\le n$, then ${\bf X}\le_\textrm{idcx} {\bf Y}$.
Proof.
(i): Choosing
$f({\bf x})=g(x_i)$ with $g\,{:}\, \mathbb{R} \rightarrow \mathbb{R}$ is increasing and convex. Thus, by Lemma 2(iii), ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and $\sigma^x_{ii}\le \sigma^y_{ii}$ for all $1\le i\le n$.-
(ii):
$({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{idcx} ({\bf Y}-{\boldsymbol \mu}^y)$ implies that $({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{dcx} ({\bf Y}-{\boldsymbol \mu}^y)$ since they have the same mean. The result follows from Theorem 6. -
(iii): For all twice differentiable increasing functions
$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial^2 }{\partial x_i \partial x_j}f({\bf x})\ge 0$ for ${\bf x}\in \mathbb{R}^n$ and all $1\le i, j\le n$, using Corollary 1 together with the conditions ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i, j\le n$, we get $\mathbb{E} [f({\bf Y})]\ge \mathbb{E} [f({\bf X})]$. Thus, we have ${\bf X}\le_\textrm{idcx} {\bf Y}$.
Corollary 3. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x, {\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y, {\boldsymbol \Sigma}^y,\phi)$. Then the following statements are equivalent:
(i)
$({\bf X}-{\boldsymbol \mu}^x)\le_\textrm{idcx} ({\bf Y}-{\boldsymbol \mu}^y)$.-
(ii)
$\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i,j\le n$.
As pointed out by [Reference Müller39], the ‘if and only if’ characterization of the upper orthant order for multinormal distributions has not been found. The following result generalizes and strengthens [Reference Müller39, Theorem 10], in which the multivariate normal case was considered, and [Reference Landsman and Tsanakas30, Theorem 2], in which bivariate elliptical distributions were considered.
Theorem 8. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$ be two n-dimensional elliptically distributed random vectors supported on 
${\Bbb R}^n$.
(i) If
${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$, $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$, then ${\bf X}\le_\textrm{uo} {\bf Y}$.-
(ii) If
${\bf X}\le_\textrm{uo} {\bf Y}$, then ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$, $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$. -
(iii) If X and Y have the same marginal and
${\bf X}\le_\textrm{uo} {\bf Y}$, then $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$.
Proof.
(i): For any
$\Delta$-monotone function $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$, using Lemma 5 together with the conditions ${\boldsymbol \mu}^y\ge {\boldsymbol \mu}^x$, $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$, we get $ \mathbb{E}[f({\bf Y})]\ge \mathbb{E}[f({\bf X})]$, and thus we have ${\bf X}\le_\textrm{uo} {\bf Y}$.-
(ii): Using the fact that
${\bf X}\le_\textrm{uo} {\bf Y}$ implies that $X_i\le_\textrm{st} Y_i$ for all $1\le i\le n$ and Lemma 2(i), we get ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and $\sigma^x_{ii}=\sigma^y_{ii}$ for $i=1,2,\ldots,n$. -
(iii): Using the fact that
${\bf X}\le_\textrm{uo} {\bf Y}$ implies that $(X_i,X_j)'\le_\textrm{uo} (Y_i,Y_j)'$ for any $1\le i<j\le n$ together with X and Y having the same marginal leads to $(X_i,X_j)'\le_\textrm{sm} (Y_i,Y_j)'$ (see [Reference Müller and Scarsini40, Theorem 2.5]). But this implies that $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$.
Corollary 4. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x, {\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y ,{\boldsymbol \Sigma}^y,\phi)$ be two n-dimensional elliptically distributed random vectors with the same marginal. Then the following statements are equivalent:
(i)
${\bf X}\le_\textrm{uo} {\bf Y}$.-
(ii)
$\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i<j\le n$.
The following theorem considers the componentwise convex order. The multivariate normal case can be found in [Reference Müller and Stoyan42]; see also [Reference Arlotto and Scarsini2].
Theorem 9. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. Then the following statements are equivalent:
(i)
${\bf X}\le_\textrm{ccx} {\bf Y}$.-
(ii)
${\boldsymbol \mu}^x= {\boldsymbol \mu}^y$ and $\sigma^x_{ii}\le \sigma^y_{ii}$ for all $1\le i\le n$, and $\sigma^x_{ij}= \sigma^y_{ij}$ for all $1\le i<j\le n$.
Proof.
(i)
$\Rightarrow$ (ii): Note that the functions $f({\bf x})=x_i, -x_i, x_i^2, x_i x_j, - x_i x_j $ are componentwise convex for all $1\le i,j\le n$. Thus, we get ${\boldsymbol \mu}^x={\boldsymbol \mu}^y$, $\sigma^x_{ii}\le \sigma^y_{ii}$ for all $1\le i\le n$ and $\sigma^x_{ij}=\sigma^y_{ij}$ for all $1\le i<j\le n$.-
(ii)
$\Rightarrow$ (i): For any twice differentiable functions $f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfying $\frac{\partial^2 }{\partial x_i^2}f({\bf x})\ge 0$ for ${\bf x}\in \mathbb{R}^n$ and all $1\le i\le n$, using Lemma 5 together with the conditions ${\boldsymbol \mu}^x= {\boldsymbol \mu}^y$, $\sigma^x_{ii}\le \sigma^y_{ii}$ for all $1\le i\le n$, and $\sigma^x_{ij}= \sigma^y_{ij}$ for all $1\le i<j\le n$, we get $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$. Thus, ${\bf X}\le_\textrm{ccx} {\bf Y}$.
Similarly, we establish the result for increasing componentwise convex order as follows.
Theorem 10. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$.
(i) If
${\bf X}\le_\textrm{iccx} {\bf Y}$, then $\mu_i^x\le \mu_i^y$ and $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i, j\le n$.-
(ii) If
$\mu_i^x\le \mu_i^y$ and $\sigma^x_{ii}\le \sigma^y_{ii}$ for all $1\le i\le n$, and $\sigma^x_{ij}= \sigma^y_{ij}$ for all $1\le i<j\le n$, then ${\bf X}\le_\textrm{iccx} {\bf Y}$.
Proof.
(i): Obviously,
${\bf X}\le_\textrm{iccx} {\bf Y}$ implies that ${\bf X}\le_\textrm{icx} {\bf Y}$. Hence, by Lemma 4, ${\boldsymbol \mu}^x\le {\boldsymbol \mu}^y$ and ${\bf a}'({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf a}\ge 0$ for all ${\bf a}\ge 0$. The latter inequality implies that $\sigma^x_{ij}\le \sigma^y_{ij}$ for all $1\le i, j\le n$.-
(ii): The proof is routine and is omitted.
At the end of this section we will consider the copositive and completely positive orders for multivariate elliptical random variables. The multivariate normal case can be found in [Reference Arlotto and Scarsini2]. Before we state Theorem 11, we first give the following definitions.
Definition 2. [Reference Arlotto and Scarsini2]. An 
$n\times n$ matrix A is called copositive if the quadratic form 
${\bf x'Ax} \ge 0$ for all 
${\bf x}\ge 0$, and A is called completely positive if there exists a nonnegative 
$m\times n$ matrix B such that 
${\bf A}={\bf B'B}$.
Denote by 
$\mathcal{C}_\textrm{cop}$ the cone of copositive matrices, and by 
$\mathcal{C}_\textrm{cp}$ the cone of completely positive matrices. Let 
$\mathcal{C}^*_\textrm{cop}$ and 
$\mathcal{C}^*_\textrm{cp}$ be the duals of 
$\mathcal{C}_\textrm{cop}$ and 
$\mathcal{C}_\textrm{cp}$, respectively. It is well known (see [Reference Arlotto and Scarsini2]) that 
$\mathcal{C}^*_\textrm{cop}=\mathcal{C}_\textrm{cp}$ and 
$\mathcal{C}^*_\textrm{cp}=\mathcal{C}_\textrm{cop}$.
The following Hessian orders can be defined (see [Reference Arlotto and Scarsini2]).
•
$X \le _\textrm{cp} Y$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E} [f({\bf Y})]$ holds for all functions f such that ${\bf H}_f({\bf x})\in \mathcal{C}_\textrm{cp}$.-
•
$X \le _\textrm{cop} Y$ if $ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$ holds for all functions f such that ${\bf H}_f({\bf x})\in \mathcal{C}_\textrm{cop}$.
Theorem 11. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. Then
(i)
${\bf X}\le_\textrm{cp} {\bf Y}$ if and only if ${\boldsymbol \mu}^x= {\boldsymbol \mu}^y$ and ${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is copositive.-
(ii)
${\bf X}\le_\textrm{cop} {\bf Y}$ if and only if ${\boldsymbol \mu}^x= {\boldsymbol \mu}^y$ and ${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is completely copositive.
Proof. We prove (i) here; the proof of (ii) is similar.
‘if’: Consider the functions 
$f_i({\bf x})=x_i, -x_i$ 
$(1\le i\le n)$. Observe that 
${\bf H}_{f_i}({\bf x})={\bf O}\in \mathcal{C}_\textrm{cp}$. Thus, 
${\bf X}\le_\textrm{cp} {\bf Y}$ implies 
${\boldsymbol \mu}^x= {\boldsymbol \mu}^y$. Let 
$\mathbb{E} ({\bf X})= \mathbb{E}({\bf Y})={\boldsymbol \mu}$. For any symmetric 
$n\times n$ matrix 
${\bf A}\in \mathcal{C}_\textrm{cp}$, define a function f as 
$f({\bf x})=\frac12 ({\bf x}- {\boldsymbol \mu})'{\bf A}({\bf x-{\boldsymbol \mu} })$. Observe that 
${\bf H}_{f}({\bf x})={\bf A}$ for all x, and thus 
${\bf X}\le_\textrm{cp} {\bf Y}$ implies 
$ \mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$, which is equivalent to 
$\mathbb{E}({\bf X}- {\boldsymbol \mu})'{\bf A}({\bf X-{\boldsymbol \mu} })\le \mathbb{E}({\bf Y}- {\boldsymbol \mu})'{\bf A}({\bf Y-{\boldsymbol \mu} })$. It follows from the above that 
$-2\phi'(0)\textrm{tr}({\boldsymbol \Sigma}^x {\bf A}) \le -2\phi'(0)\textrm{tr}({\boldsymbol \Sigma}^y {\bf A})$. Therefore, 
$\textrm{tr}(({\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x){\bf A})\ge 0$. Since 
${\bf A}\in \mathcal{C}_\textrm{cp}$ is arbitrary, we conclude that 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x\in \mathcal{C}^*_\textrm{cp}$. Hence, 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is copositive, since 
$\mathcal{C}^*_\textrm{cp}=\mathcal{C}_\textrm{cop}$.
‘only if’: For any f such that 
${\bf H}_f({\bf x})\in \mathcal{C}_\textrm{cp}$, using Lemma 5 together with the condition 
${\boldsymbol \mu}^x= {\boldsymbol \mu}^y$ and the fact that 
${\boldsymbol \Sigma}^y-{\boldsymbol \Sigma}^x$ is copositive yields 
$\mathbb{E}[f({\bf X})]\le \mathbb{E}[f({\bf Y})]$, as desired.
The main results in this section are summarized in Table 1.
4. Applications and examples
This section deals with some applications of the previous results. One can obtain a series of probability and expectation inequalities for multivariate elliptical random variables. We will restrict ourselves to applications concerning the supermodular ordering.
Table 1: Comparison criteria for 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$.
4.1. Application 1
Slepian’s theorem for multivariate normal distributions with nonsingular covariance matrix can be found in [Reference Topkis51]. Reference [Reference Das Gupta, Eaton, Olkin, Perlman, Savage and Sobel12] generalized Slepian’s theorem to elliptical distributions with nonsingular covariance matrix, which was later proved in a different way by [Reference Joag-Dev, Perlman and Pitt27]. Reference [Reference Joe28] provided a shorter elementary proof. For its extension to the case of singular covariance matrix the reader is referred to [Reference Fang and Liang19]. Here, we give a simple proof. Further results on the normal comparison inequalities of Slepian type can be found in [Reference Li and Shao31], [Reference Yin54], and [Reference Chernozhukov, Chetverikov and Kato10]. The following result can be found in [Reference Fang and Liang19]. It is an immediate consequence of Theorem 4.
Example 1. Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$. If X and Y have the same marginals and 
$\sigma^x_{ij}\le \sigma^y_{ij}$ for all 
$1\le i<j\le n$, then, for every 
${\bf a}\in {\mathbb{R}}^n$, 
$\mathbb{P}(X_1\le a_1,\ldots,X_n\le a_n)\le \mathbb{P}(Y_1\le a_1,\ldots,Y_n\le a_n)$ and 
$\mathbb{P}(X_1>a_1,\ldots,X_n> a_n)\le \mathbb{P}(Y_1> a_1,\ldots,Y_n> a_n)$. Furthermore, the inequality is strict if 
$\sigma^x_{ij}< \sigma^y_{ij}$ for some i, j and if the supports of 
${\bf X, Y}$ are unbounded.
4.2. Application 2
In this section we list various simple but useful inequalities for certain functions of multivariate elliptical random variables. The proofs are based on the results in Section 3; the most important result is the one on supermodular orders. We remark that supermodular functions play a significant role in applied fields, such as risk management, insurance, queueing, macroeconomic dynamics, optimization, and game theory. The following are some useful results and properties of supermodular functions. The proofs can be found in [Reference Bäuerle3], [Reference Christofides and Vaggelatou11], [Reference Topkis51], and [Reference Marshall and Olkin33, p. 219].
• If f is increasing and supermodular, then
$\max{\{f,c\}}$ is supermodular for all $c\in {\Bbb R}$.-
• If
$f\,{:}\, {\Bbb R}^n\rightarrow {\Bbb R}$ is supermodular then the function $\psi$ defined by $\psi(x_1,x_2,\ldots, x_n)=f(g_1(x_1),\ldots,g_n(x_n)),$ is also supermodular whenever $g_i:{\Bbb R}\rightarrow {\Bbb R}$, $i=1,2,\ldots, n$, are either all increasing or all decreasing. -
• If
$f_i$ is increasing (decreasing) on $\mathbb{R}^1$ for $i=1,2,\ldots,n$, then
is supermodular on
\begin{equation*}f(x)=\min\{f_1(x_1),\ldots, f_n(x_n)\}=-\max\{f_1(x_1),\ldots, f_n(x_n)\}\end{equation*}
$\mathbb{R}^n$.
-
•
$H({\bf x})=\left(\sum_{k=1}^n g_i(x_i)-t\right)^+, \left(\prod_{k=1}^n g_i(x_i)-t\right)^+$ are supermodular for any $t\ge 0$. -
• If f is monotonic supermodular and g is increasing and convex, then
$g\circ f$ is monotonic and supermodular. -
•
$H({\bf x})= \prod_{k=1}^n \phi_i(x_i)$ is supermodular, where $\phi_i:{\Bbb R}\rightarrow {\Bbb R}^+$, $i=1,2,\ldots, n$, are either all increasing or all decreasing. -
• The function
$f(x)=\nu(x_1+\cdots+x_n)$ is supermodular, where $\nu$ is increasing convex. -
•
$H({\bf x})=-\frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X})^2$ is supermodular. -
• The function
$H({\bf x})=\max_{1\le k\le n}\sum_{i=1}^k X_k$ is supermodular and increasing.
The following result is an immediate consequence of Theorem 4 and Lemma 6, and is now used in many areas such as actuarial sciences, economic theory, and statistics and probability (see, e.g., [Reference Chernozhukov, Chetverikov and Kato10, Reference Christofides and Vaggelatou11, Reference Goovaerts and Dhaene22, Reference Müller37]).
Example 2. Assume that 
${\bf{X}}\sim E_n ({\boldsymbol \mu}^x,{\boldsymbol \Sigma}^x,\phi)$, 
${\bf{Y}}\sim E_n ({\boldsymbol \mu}^y,{\boldsymbol \Sigma}^y,\phi)$, that X and Y have the same marginal, and 
$\sigma^x_{ij}\le \sigma^y_{ij}$ for all 
$1\le i<j\le n$.
• Let f be an increasing convex function on
$(-\infty,\infty)$. Then
where
\begin{equation*}\mathbb{E} f(g_1(X_1)+\cdots+g_n(X_n))\le \mathbb{E} f(g_1(Y_1)+\cdots+g_n(Y_n)),\end{equation*}
$g_1, \ldots, g_n$ are monotonic in the same direction.
-
• Assume that
$f\,{:}\, {\Bbb R}^n\rightarrow {\Bbb R}$ is supermodular, and $g_i:{\Bbb R}\rightarrow {\Bbb R}$, $i=1,2,\ldots, n$, are either all increasing or all decreasing. Then
\begin{equation*}\mathbb{E}f(g_1(X_1),\ldots, g_n(X_n))\le \mathbb{E} f(g_1(Y_1),\ldots, g_n(Y_n)).\end{equation*}
-
• If f is increasing and supermodular, then
$\mathbb{E}\max\{f({\bf X}),0\}\le \mathbb{E} \max\{f({\bf Y}),0\}$. -
•
$\mathbb{E}\prod_{k=1}^n \phi_i(X_i)\le \mathbb{E}\prod_{k=1}^n \phi_i(Y_i)$, where $\phi_k: {\Bbb R}\rightarrow {\Bbb R}^+$ are monotonic in the same direction. -
• If
$f_i:{\Bbb R}\rightarrow {\Bbb R}$, $i=1,2,\ldots, n$, are either all increasing or all decreasing, then
\begin{align*} \mathbb{E}\min\{f_1(X_1),\ldots, f_n(X_n)\} & \le \mathbb{E}\min\{f_1(Y_1),\ldots, f_n(Y_n)\} , \\ \mathbb{E}\max\{f_1(X_1),\ldots, f_n(X_n)\} & \ge \mathbb{E}\max\{f_1(Y_1),\ldots, f_n(Y_n)\}. \end{align*}
-
•
$\mathbb{E}S_x^2\ge \mathbb{E}S_y^2$, where
\begin{equation*}S_x^2=\frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X})^2, \qquad S_y^2=\frac{1}{n-1}\sum_{i=1}^n (Y_i-\overline{Y})^2.\end{equation*}
-
• If f is a nondecreasing convex function, then
\begin{equation*}\mathbb{E}f\left(\max_{1\le k\le n}\sum_{i=1}^k X_k\right)\le \mathbb{E}f\left(\max_{1\le k\le n}\sum_{i=1}^k Y_k\right).\end{equation*}
We illustrate special applications of the above result in the following examples.
Example 3. (Equicorrelated elliptical variables.) Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu},{\boldsymbol \Sigma}^x,\phi)$ with 
${\boldsymbol \Sigma}^x=(\sigma^x_{ij})$ such that 
$\sigma^x_{ii}=\sigma^2$, 
$\sigma^x_{ij}=\rho_x\sigma^2$ for 
$1<i<j\le n$, 
$\sigma^2>0$, 
$\rho_x\in [-1,1]$, and let 
${\bf{Y}}\sim E_n ({\boldsymbol \mu},{\boldsymbol \Sigma}^y,\phi)$ with 
${\boldsymbol \Sigma}^y=(\sigma^y_{ij})$ such that 
$\sigma^y_{ii}=\sigma^2$, 
$\sigma^y_{ij}=\rho_y\sigma^2$ for 
$1<i<j\le n$, 
$\rho_y\in [-1,1]$. Then 
${\bf X}\le_\textrm{sm} {\bf Y}$ if and only if 
$\rho_x\le \rho_y$.
Bäuerle [Reference Bäuerle3] obtained the similar result for normal variables and 
$\rho_x, \rho_y\in [0,1]$. For any supermodular function 
$f\,{:}\, {\Bbb R}^n\rightarrow {\Bbb R}$, we deduce that the expectation 
$\mathbb{E}f({\bf X})$ is increasing in 
$\rho_x$. We remark that for this special correlated elliptical variable, the supermodularity of f is not necessary. For example, if 
$f\,{:}\, {\Bbb R}^n\rightarrow {\Bbb R}$ is twice differentiable and satisfies 
$\frac{\partial^2 }{\partial x_i \partial x_j}f({\bf x})\ge 0$ for 
${\bf x}\in \mathbb{R}^n$ and for some 
$1\le i<j\le n$, then [Reference Joag-Dev, Perlman and Pitt27, Proposition 1] and their remarks on p. 454 imply that 
$\mathbb{E}f({\bf X})$ is increasing in 
$\rho_x$. For example, if 
$\rho_x\le \rho_y$, then 
$\mathbb{E}(X_1X_2 X_3^{2})\le \mathbb{E}(Y_1Y_2 Y_3^{2})$ and 
$\mathbb{E}(X_1^3X_2^3 X_3^{4})\le \mathbb{E}(Y_1^3Y_2^3 Y_3^{4})$.
Example 4. (Serial correlated elliptical variables.) Let 
${\bf{X}}\sim E_n ({\boldsymbol \mu},{\boldsymbol \Sigma}^x,\phi)$ and 
${\bf{Y}}\sim E_n ({\boldsymbol \mu},{\boldsymbol \Sigma}^y,\phi)$, with
\begin{align*} {\boldsymbol \Sigma}^x & = \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \sigma^2\;& \rho_x\sigma^2\; &\cdots\; &\rho_x^{n-1}\sigma^2 \\ \\[-7pt] \rho_x\sigma^2\; & \sigma^2\; &\cdots\; &\rho_x^{n-2}\sigma^2 \\ \\[-7pt] \vdots\;&\vdots\;&\ddots\;&\vdots\;\\ \\[-7pt] \rho_x^{n-1}\sigma^2 \; & \rho_x^{n-2}\sigma^2\; &\cdots\; & \sigma^2\\ \\[-7pt] \end{array}\right), \\ {\boldsymbol \Sigma}^y & = \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \sigma^2\;& \rho_y\sigma^2\; &\cdots\; &\rho_y^{n-1}\sigma^2 \\ \\[-7pt] \rho_y\sigma^2\; & \sigma^2\; &\cdots\; &\rho_y^{n-2}\sigma^2 \\ \\[-7pt] \vdots\;&\vdots\;&\ddots\;&\vdots\;\\ \\[-7pt] \rho_y^{n-1}\sigma^2 \; & \rho_y^{n-2}\sigma^2\; &\cdots\; & \sigma^2\\ \\[-7pt] \end{array}\right), \end{align*}
where 
$\sigma^2>0$ and 
$\rho_x, \rho_y\in [-1,1]$. Then 
${\bf X}\le_\textrm{sm} {\bf Y}$ if and only if 
$\rho_x\le \rho_y$.
Appendix A
Theorem 12. Let 
$f({\bf y})={\bf y}'{\bf A}{\bf y}$, 
${\bf y}\in \mathbb{R}^n $, where A is an 
$n\times n$ symmetric matrix. If 
${\bf A z}=0$ has a positive solution, then 
${\bf y}'{\bf A}{\bf y}\ge 0$ for all 
${\bf y}\ge 0$ if and only if 
${\bf y}'{\bf A}{\bf y}\ge 0$ for all 
${\bf y}\in \mathbb{R}^n$.
Proof. We just prove the ‘only if’ part. Since f is quadratic, using Taylor’s expansion we get 
$f({\bf x}+t{\bf y})=f({\bf x})+t{\bf y}'\nabla f({\bf x})+t^2f({\bf y})$, 
${\bf x, y}\in \mathbb{R}^n$, 
$t \in \mathbb{R}$, where 
$\nabla f({\bf x})=2{\bf A}{\bf x}$ is the gradient of f. We choose an 
${\bf x}_0>0$ such that 
${\bf A}{\bf x}_0=0$ and 
$f({\bf x}_0)=0$. Then 
$f({\bf x}_0+t{\bf y})=t^2f({\bf y})$. Since, for any 
${\bf y} \in \mathbb{R}^n$ and 
$t>0$ small enough, we have 
${\bf x}_0+t{\bf y}\ge 0$, we thus get 
$f({\bf y})\ge 0$. 
Proof of Lemma 5. For 
$0\le \lambda\le 1$, define
\begin{equation*} \Psi_{\lambda}({\bf t})=\exp\left(\textrm{i}{\bf t}'\big(\lambda{\boldsymbol \mu}^y+(1-\lambda){\boldsymbol \mu}^x\big)\right)\psi({\bf t}'(\lambda {\boldsymbol \Sigma}^y+(1-\lambda) {\boldsymbol \Sigma}^x){\bf t}), \qquad {\bf t}\in \mathbb{R}^n.\end{equation*}
By using the Fourier inversion theorem,
\begin{equation*}\phi_{\lambda}({\bf x})=\left(\frac{1}{2\pi}\right)^n\int \textrm{e}^{-\textrm{i}{\bf t}'{\bf x}} \Psi_{\lambda}({\bf t}) \, \textrm{d}{\bf t}.\end{equation*}
The derivative of 
$\Psi_{\lambda}$ with respect to 
$\lambda$ is
\begin{align*} \frac{\partial \Psi_{\lambda}({\bf t})}{\partial \lambda}&=\textrm{i}{\bf t}'({\boldsymbol \mu}^y-{\boldsymbol \mu}^x)\exp\left(\textrm{i}{\bf t}'\big(\lambda{\boldsymbol \mu}^y+(1-\lambda){\boldsymbol \mu}^x\big)\right)\psi({\bf t}'(\lambda {\boldsymbol \Sigma}^y+(1-\lambda) {\boldsymbol \Sigma}^x){\bf t})\\[3pt]
&\quad + \ {\bf t}'({\boldsymbol \Sigma}^y- {\boldsymbol \Sigma}^x){\bf t}\exp\left(\textrm{i}{\bf t}'\big(\lambda{\boldsymbol \mu}^y+(1-\lambda){\boldsymbol \mu}^x\big)\right)\psi'({\bf t}'(\lambda {\boldsymbol \Sigma}^y+(1-\lambda) {\boldsymbol \Sigma}^x){\bf t}), \end{align*}
and hence
\begin{align*} \frac{\partial \phi_{\lambda}({\bf x})}{\partial \lambda}&=\left(\frac{1}{2\pi}\right)^n\int \textrm{e}^{-\textrm{i}{\bf t}'{\bf x}}\frac{\partial \Psi_{\lambda}({\bf t})}{\partial \lambda} \, \textrm{d}{\bf t}\\[3pt]
&=\left(\frac{1}{2\pi}\right)^n\int \textrm{e}^{-\textrm{i}{\bf t}'{\bf x}}\Psi_{\lambda}({\bf t})\textrm{i}{\bf t}'({\boldsymbol \mu}^y-{\boldsymbol \mu}^x) \, \textrm{d}{\bf t}\\[3pt]
&\quad +\left(\frac{1}{2\pi}\right)^n\int \textrm{e}^{-\textrm{i}{\bf t}'{\bf x}}{\bf t}'({\boldsymbol \Sigma}^y- {\boldsymbol \Sigma}^x){\bf t}\exp\left(\textrm{i}{\bf t}'\big(\lambda{\boldsymbol \mu}^y+(1-\lambda){\boldsymbol \mu}^x\big)\right)\psi'\\
&\quad \times ({\bf t}'(\lambda {\boldsymbol \Sigma}^y+(1-\lambda) {\boldsymbol \Sigma}^x){\bf t}) \, \textrm{d}{\bf t}\\[3pt]
&=-\sum_{i=1}^n(\mu_i^y-\mu_i^x)\frac{\partial \phi_{\lambda}({\bf x})}{\partial x_i}+\Delta, \end{align*}
where
\begin{equation*}\Delta=\left(\frac{1}{2\pi}\right)^n\int \textrm{e}^{-\textrm{i}{\bf t}'{\bf x}}{\bf t}'({\boldsymbol \Sigma}^y- {\boldsymbol \Sigma}^x){\bf t}\exp\left(\textrm{i}{\bf t}'\big(\lambda{\boldsymbol \mu}^y+(1-\lambda){\boldsymbol \mu}^x\big)\right)\psi'({\bf t}'(\lambda {\boldsymbol \Sigma}^y+(1-\lambda) {\boldsymbol \Sigma}^x){\bf t}) \, \textrm{d}{\bf t}.\end{equation*}
Note that, by (1), there exists a random variable 
$R\ge 0$ such that
\begin{eqnarray*} \psi({\bf t}'{\bf t})=\mathbb{E}\left(\mathbb{E}\big(\textrm{e}^{\textrm{i} R{\bf t}'{\bf U}^{(n)}} \mid R\big)\right)=\int_0^{\infty} {}_0F_1\left(\frac{n}{2};-\frac{r^2 ||{\bf t}||^2}{4}\right)\mathbb{P}(R\in \textrm{d} r), \end{eqnarray*}
where in the second equality we have applied [Reference Fang, Kotz and Ng20, Theorem 3.1] [note that there is a printing error in [Reference Fang, Kotz and Ng20, (3.3)]] and
\begin{equation*}{}_0F_1(\gamma;\ z)=\sum_{k=0}^{\infty}\frac{\Gamma(\gamma)}{\Gamma(\gamma+k)}\frac{z^k}{k!}.\end{equation*}
Thus, for 
$u>0$,
\begin{align*} \psi'(u)&= \frac{\partial}{\partial u}\int_0^{\infty} {}_0F_1\left(\frac{n}{2};-\frac{r^2 u}{4}\right)\mathbb{P}(R\in \textrm{d} r)\\[3pt] &= \int_0^{\infty} \frac{\partial}{\partial u}{}_0F_1\left(\frac{n}{2};-\frac{r^2 u}{4}\right)\mathbb{P}(R\in \textrm{d} r)\\[3pt] &=-\frac{1}{2n}\int_0^{\infty}{}_0F_1\left(\frac{n}{2}+1;-\frac{r^2 u}{4}\right)r^2\mathbb{P}(R\in \textrm{d} r)\\[3pt] &\equiv -\frac{\mathbb{E}\big(R^2\big)}{2n}\psi_1(u), \end{align*}
where
\begin{equation*}\psi_1(u)=\frac{1}{\mathbb{E}\big(R^2\big)}\int_0^{\infty}{}_0F_1\left(\frac{n}{2}+1;-\frac{r^2 u}{4}\right)r^2\mathbb{P}(R\in \textrm{d} r)\end{equation*}
is a characteristic generator. Here,
\begin{equation*}c\big(||{\bf t}||^2\big):= {}_0F_1\left(\frac{n}{2}+1;-\frac{||{\bf t}||^2 }{4}\right)\end{equation*}
is the characteristic function of a uniform distribution in the unit sphere in 
$\mathbb{R}^n$ (see, e.g., [Reference Yin54]). Thus, 
$\Delta$ can be rewritten as
\begin{equation*}\Delta=\frac{\mathbb{E}\big(R^2\big)}{2n}\sum_{i=1}^n\sum_{j=1}^n({\sigma}^y_{ij}-{\sigma}^x_{i j})\frac{\partial^2 \phi_{1\lambda}({\bf x})}{\partial x_i \partial x_j}.\end{equation*}
Define 
$g(\lambda)=\int_{\mathbb{R}^n} f({\bf x})\phi_{\lambda}({\bf x}) \, \textrm{d}{\bf x}$; then, 
$\mathbb{E}[f({\bf Y})]-\mathbb{E}[f({\bf X})]=g(1)-g(0)=\int_0^1 g'(\lambda) \, \textrm{d}\lambda$. The result follows since
\begin{align*} g'(\lambda)&=\int_{\mathbb{R}^n} f({\bf x})\frac{\partial \phi_{\lambda}({\bf x})}{\partial \lambda} \, \textrm{d}{\bf x}\\[3pt]
&=\int_{\mathbb{R}^n}({\boldsymbol \mu}^y-{\boldsymbol \mu}^x)'\nabla f({\bf x})\phi_{\lambda}({\bf x}) \, \textrm{d}{\bf x}\\[3pt]
&\quad + \ \frac{\mathbb{E}\big(R^2\big)}{2n}\int_{\mathbb{R}^n}\textrm{tr}\{({\boldsymbol \Sigma}^{y}-{\boldsymbol \Sigma}^{x}){\bf H}_f({\bf x})\}\phi_{1\lambda}({\bf x}) \, \textrm{d}{\bf x}. \end{align*}
Here, in the last equality we have used the integration by parts formula and the conditions in (3).
Acknowledgements
The author would like to thank Professor Xiaowen Zhou for helpful comments on an earlier draft of the paper. We are deeply grateful to the reviewers and Editor for their comments and suggestions to improve our manuscript. The research was supported by the National Natural Science Foundation of China (Nos. 12071251, 11571198, 11701319).
