2. Electron transfer process in strongly coupled plasmas

Since the resonant electron transfer has no effect on the electronic energy in the reaction system, the interaction between a positive ion $\text{A}^{+}$ with nuclear charge $Z_{A}e$ and a neutral atom B with nuclear charge $Z_{B}e$ is expressed by $\text{A}^{+}+\text{B}\rightarrow \text{A}+\text{B}^{+}$ . The potential energy of an electron in the field of free ions can be found in an excellent work of Fridman & Kennedy (Reference Fridman and Kennedy2011). The physical concept of Debye–Hückel theory (Kleinstreuer Reference Kleinstreuer2010) as a cooperative screening phenomenon is no longer applicable in very dense plasmas since the probability of finding other charged particles in a Debye sphere is quite small and almost vanishes in strongly coupled plasmas. It has been shown that the Debye–Hückel model would not be reliable to represent the interaction potential in strongly coupled plasmas. It has also been shown that the ion-sphere model (Salpeter Reference Salpeter1954; Salzmann Reference Salzmann1998) in strongly coupled plasmas is equivalent to the Wigner–Seitz sphere in condensed matter theory since the ion sphere consists of a single ion and its surrounding negatively charged sphere. The screened Coulomb interaction potential $V_{SC}(r)$ between the electron and the ion with charge $Ze$ in strongly coupled plasmas would be represented by the following ion-sphere model (Jung & Jeong Reference Jung and Jeong1996; Jung Reference Jung2000):

(2.1) $$\begin{eqnarray}V_{SC}(r)=-\frac{Ze^{2}}{r}\left[1-\frac{r}{2R_{I}}\left(3-\frac{r^{2}}{R_{I}^{2}}\right)\right]{\it\theta}(R_{I}-r),\end{eqnarray}$$

where $r$ is the interparticle distance, ${\it\theta}(R_{I}-r)~(=1\text{ for }R_{I}\geqslant r;=0\text{ for }R_{I}<r)$ is the step function and $R_{I}~(=[3(Z-1)/4{\rm\pi}n_{e}]^{1/3})$ is the ion-sphere radius given by the electron density $n_{e}$ and change number $Z$ since the total charge within the ion sphere would be neutral. As shown in (2.1), it is found that the ion-sphere potential $V_{SC}(R_{I})$ and its first derivative $\text{d}V_{SC}(r)/\text{d}r|_{r=R_{I}}$ vanish at the surface of the ion sphere. An improved version of the ion-sphere model has been proposed both in the bound state and in free electron terms taking into account relativistic and exchange effects (Salzmann Reference Salzmann1998). However, the original version of the ion-sphere model has been extensively used to explore various physical processes in high-density and low-temperature plasmas (Fujimoto Reference Fujimoto2004). Hence, the screened potential energy $V_{IS}(r,R_{I})$ of an electron in the field of ions $\text{A}^{+}$ and $\text{B}^{+}$ in strongly coupled plasmas based on the ion-sphere model is represented by

(2.2) $$\begin{eqnarray}\displaystyle V_{IS}(r,R_{I})=-\frac{e^{2}}{r}\left[1-\frac{r}{2R_{I}}\left(3-\frac{r^{2}}{R_{I}^{2}}\right)\right]-\frac{e^{2}}{|r_{AB}-r|}\!\left[1-\frac{|r_{AB}-r|}{2R_{I}}\left(3-\frac{|r_{AB}-r|^{2}}{R_{I}^{2}}\right)\!\right]\!, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

where $r$ is the distance between the electron and the ion $\text{A}^{+}$ and $r_{AB}$ is the interatomic distance. Since the ion-sphere radius $R_{I}$ is usually greater than the interatomic distance $r_{AB}$ in strongly coupled plasmas, the maximum potential energy $V_{IS}^{Max}$ would be obtained by the condition $\partial V_{IS}(r,R_{I})/\partial r=0$ with the constraint of $r<R_{I}$ as

(2.3) $$\begin{eqnarray}V_{IS}^{Max}(r=r_{AB}/2,R_{I})=-\frac{4e^{2}}{r_{AB}}\left[1-\frac{r_{AB}}{4R_{I}}\left(3-\frac{r_{AB}^{2}}{4R_{I}^{2}}\right)\right],\end{eqnarray}$$

where $V_{IS}^{Max}(r=r_{AB}/2,R_{I})$ is the maximum potential value at $r=r_{AB}/2$ . It should be understood that the classical analogy of the electron transfer process would be possible if the maximum potential energy $V_{IS}^{Max}$ were smaller than the initial energy $E_{B}$ as follows:

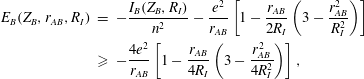(2.4) $$\begin{eqnarray}\displaystyle E_{B}(Z_{B},r_{AB},R_{I}) & = & \displaystyle -\frac{I_{B}(Z_{B},R_{I})}{n^{2}}-\frac{e^{2}}{r_{AB}}\left[1-\frac{r_{AB}}{2R_{I}}\left(3-\frac{r_{AB}^{2}}{R_{I}^{2}}\right)\right]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle -\frac{4e^{2}}{r_{AB}}\left[1-\frac{r_{AB}}{4R_{I}}\left(3-\frac{r_{AB}^{2}}{4R_{I}^{2}}\right)\right],\end{eqnarray}$$

where $I_{B}(Z_{B},R_{I})/n^{2}$ is the ionization energy of the electron in the neutral atom B with principal quantum number $n$ .

3. Atomic states and transfer cross-section

In strongly coupled plasmas, the radial Schrödinger equation (Jung Reference Jung2000) of the neutral atom B with the ion-sphere model and the effective screened charge $Z_{B}-{\it\delta}_{nl}(Z_{B},R_{I})$ is represented by

(3.1) $$\begin{eqnarray}-\frac{\hslash ^{2}}{2m}\left[\frac{1}{r^{2}}\frac{\text{d}}{\text{d}r}\left(r^{2}\frac{\text{d}R_{nl}(r)}{\text{d}r}\right)-\frac{l(l+1)}{r^{2}}R_{nl}(r)\right]-\frac{[Z_{B}-{\it\delta}_{nl}(Z_{B},R_{I})]e^{2}}{r}R_{nl}(r)=E_{nl}R_{nl}(r),\end{eqnarray}$$

where $\hslash$ is the rationalized Planck constant, $m$ is the mass of the electron and $R_{nl}(r)$ and $E_{nl}$ are the screened radial wave function and energy eigenvalue of the $nl$ th state, respectively. The inner screening constant ${\it\delta}_{nl}(Z_{B},R_{I})$ is determined by ${\it\delta}_{nl}(Z_{B},R_{I})=4{\rm\pi}\int _{0}^{n^{2}a_{0}/Z_{nl}}\text{d}r\,r^{2}n_{e}(R_{I})$ , $a_{0}~(=\hslash ^{2}/me^{2})$ is the Bohr radius of the hydrogen atom and $Z_{nl}$ is the effective $Z$ value in the $nl$ th state. For free atoms, the effective $Z$ values for atomic electrons have been introduced by the modified Slater rules (Jung & Gould Reference Jung and Gould1991). Using the $1s$ variation parameter ${\it\xi}_{1s}$ in the ion-sphere model, i.e. the effective Bohr radius in strongly coupled plasmas, the radial part of the screened normalized variational ground state wave function (Jung Reference Jung2000) $R_{1s}(r,{\it\xi}_{1s})$ is assumed to be

(3.2) $$\begin{eqnarray}R_{1s}(r,{\it\xi}_{1s})=\frac{2}{{\it\xi}_{1s}^{3/2}}\exp \left(-\frac{r}{{\it\xi}_{1s}}\right).\end{eqnarray}$$

Using the Rayleigh–Ritz variational technique (Mathews & Walker Reference Mathews and Walker1970) with the ansatz $R_{1s}(r,{\it\xi}_{1s})$ (3.2) and the energy expectation value $\langle E_{1s}(R_{I},{\it\xi}_{1s})\rangle$ for the ground state, the variation parameter (Jung Reference Jung2000) ${\it\xi}_{1s}(Z_{B},R_{I})$ for $a_{Z_{B}}<R_{I}$ would be obtained by the minimization condition $\partial \langle E_{1s}(R_{I},{\it\xi}_{1s})\rangle /\partial {\it\xi}_{1s}=0$ :

(3.3) $$\begin{eqnarray}{\it\xi}_{1s}(Z_{B},R_{I})/a_{Z_{B}}=\frac{1}{1-{\it\delta}_{1s}(Z_{B},R_{I})/Z_{B}},\end{eqnarray}$$

where $a_{Z_{B}}\equiv a_{0}/Z_{B}$ and the $1s$ screening constant ${\it\delta}_{1s}(Z_{B},R_{I})$ is found to be

(3.4) $$\begin{eqnarray}{\it\delta}_{1s}(Z_{B},R_{I})=\frac{(Z_{B}-1)(a_{Z_{B}}/R_{I})^{3}}{1-3(1-1/Z_{B})(a_{Z_{B}}/R_{I})^{3}}.\end{eqnarray}$$

The ionization energy (Jung Reference Jung2000) $I_{B}(Z_{B},R_{I})$ of the electron in the neutral atom B in strongly coupled plasmas is then represented by

(3.5) $$\begin{eqnarray}I_{B}(Z_{B},R_{I})=Z_{B}^{2}Ry[1-{\it\xi}_{1s}(Z_{B},R_{I})/a_{Z_{B}}]^{2},\end{eqnarray}$$

where $Ry~(=me^{4}/2\hslash ^{2}\approx 13.6~\text{eV})$ is the Rydberg constant. In (3.5), it is shown that the ionization limits would come down owing to the pressure ionization (Fujimoto Reference Fujimoto2004). After some mathematical manipulations using (2.3), (2.4), and (3.5), the upper limit of the screened interparticle distance $r_{AB}(Z_{B},R_{I})$ would be obtained by the following relation:

(3.6) $$\begin{eqnarray}r_{AB}(Z_{B},R_{I})\leqslant \frac{3e^{2}}{\displaystyle \frac{Z_{B}^{2}Ry[1-{\it\xi}_{1s}(Z_{B},R_{I})/a_{Z_{B}}]^{2}}{n^{2}}+\frac{3e^{2}}{2R_{I}}}.\end{eqnarray}$$

As seen in (3.6), the term $3e^{2}/2R_{I}$ in the denominator represents the shielding effect on the interparticle distance $r_{AB}(Z_{B},R_{I})$ in strongly coupled plasmas. Since the maximum screened interparticle distance $r_{AB}^{max}(Z_{B},R_{I})$ is represented by $r_{AB}^{max}(Z_{B},R_{I})=3e^{2}/[I_{B}(Z_{B},R_{I})/n^{2}+3e^{2}/2R_{I}]$ , the classical expression of the resonant electron transfer cross-section ${\it\sigma}_{Transf}^{Class}(Z_{B},R_{I})$ between the ion $\text{A}^{+}$ and the neutral atom B in strongly coupled plasmas is then found to be

(3.7) $$\begin{eqnarray}{\it\sigma}_{Transf}^{Class}(Z_{B},R_{I})=\frac{9{\rm\pi}e^{4}n^{4}/Z_{B}^{4}Ry^{2}}{\left[\displaystyle 1+3\frac{n^{2}}{Z_{B}}\left(\frac{a_{Z_{B}}}{R_{I}}\right)-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{a_{Z_{B}}}{R_{I}}\right)^{3}\right]^{2}},\end{eqnarray}$$

where the terms $3(n^{2}/Z_{B})(a_{Z_{B}}/R_{I})-2(1-1/Z_{B})(a_{Z_{B}}/R_{I})^{3}$ in the denominator represent the shielding effects on the classical resonant electron transfer cross-section. Hence, the classical characteristic function $C_{IS}(Z_{B},R_{I})$ for the influence of plasma shielding on the classical expression of the resonant electron transfer cross-section in strongly coupled plasmas based on the ion-sphere model is obtained by

(3.8) $$\begin{eqnarray}C_{IS}(Z_{B},R_{I})=\left[1+3\frac{n^{2}}{Z_{B}}\left(\frac{a_{Z_{B}}}{R_{I}}\right)-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{a_{Z_{B}}}{R_{I}}\right)^{3}\right]^{-2}.\end{eqnarray}$$

As shown in (3.8), it is found that the plasma shielding effect diminishes the classical expression of the resonant electron transfer cross-section in strongly coupled plasmas. When $Z_{B}\gg 1$ , from (3.7) and (3.8), the classical expression of the resonant electron transfer cross-section is found to be ${\it\sigma}_{Transf}^{Class}\propto Z_{B}^{4}$ . In the quantum mechanical charge transfer process, it has been shown that potential barrier penetration or the quantum tunnelling effect (Fridman Reference Fridman2008; Fridman & Kennedy Reference Fridman and Kennedy2011) enhance the resonant electron transfer cross-section for a positive ion and a neutral atom collision case. Using the Wentzel–Kramers–Brillouin (WKB) method (Razavy Reference Razavy2003), the electron tunnelling probability can be represented by the following exponential integral expression: $|T_{Tunnel}^{Q}|^{2}=\exp [-(2/\hslash )\int _{z_{1}}^{z_{2}}\,\text{d}z\sqrt{2m(V(z)-E)}]$ , where $z_{1}$ and $z_{2}$ are the turning points of the potential $V(z)$ . Using the screened potential energy $V_{IS}(r,R_{I})$ (2.2) with (3.3) and (3.5), the quantum tunnelling probability for the resonant electron transfer process between the ion $\text{A}^{+}$ and the neutral atom B in strongly coupled plasmas would be then obtained by

(3.9) $$\begin{eqnarray}|T_{Tunnel}^{Q}(Z_{B},R_{I},d)|^{2}\approx \exp \left[-\frac{2dZ_{B}}{\hslash }\sqrt{2mRy[1-{\it\xi}_{1s}(Z_{B},R_{I})/a_{Z_{B}}]}\right],\end{eqnarray}$$

where $d$ is the width of the potential barrier. Since the maximum width [7] $d_{Max}$ of the potential barrier would be determined when the electron tunnelling frequency exceeds the inverse ion-neutral atom collision time: $I_{B}(Z_{B},R_{I})|T_{Tunnel}^{Q}(Z_{B},R_{I},d)|^{2}/\hslash >v/d$ , where $v$ is the relative collision velocity, the quantum tunnelling resonant electron transfer cross-section can be represented by the geometric relation ${\it\sigma}_{transf}^{Q\text{-}Tunnel}\approx {\rm\pi}\,d_{Max}^{2}$ . Hence, the quantum tunnelling resonant electron transfer cross-section ${\it\sigma}_{transf}^{Q\text{-}Tunnel}(Z_{B},R_{I},\bar{E})$ between the neutral atom B and the ion $\text{A}^{+}$ in strongly coupled plasmas is found to be

(3.10) $$\begin{eqnarray}\displaystyle {\it\sigma}_{transf}^{Q\text{-}Tunnel}(Z_{B},R_{I},\bar{E}) & = & \displaystyle \frac{{\rm\pi}a_{Z_{B}}^{2}}{4\left[\displaystyle 1-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{a_{Z_{B}}}{R_{I}}\right)^{3}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\ln \left[\frac{Z_{B}^{2}}{\sqrt{8\bar{E}}}\left(1-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{a_{Z_{B}}}{R_{I}}\right)^{3}\right)\right]\right\}^{2},\end{eqnarray}$$

where $\bar{E}\equiv (\hslash v/dRy)^{2}/8[=(\tilde{E}/2\bar{d}^{2})(m/{\it\mu})]$ , $\tilde{E}\equiv {\it\mu}v^{2}/2Ry$ , ${\it\mu}$ is the reduced mass of the colliding system $(\text{A}^{+},\text{B})$ and $\bar{d}\equiv d/a_{0}$ . When $Z_{B}\gg 1$ , from (3.10), the quantum tunnelling resonant electron transfer cross-section is found to be ${\it\sigma}_{transf}^{Q\text{-}Tunnel}\propto [\ln Z_{B}^{2}+f(\bar{E})]^{2}$ , where $f(\bar{E})$ is the energy-dependent function. Since the quantum tunnelling process is resolved by the relative collision velocity of the system, the quantum characteristic function $Q_{IS}(Z_{B},\bar{R}_{I},\bar{E})$ for the plasma shielding effect on the quantum tunnelling resonant electron transfer cross-section in strongly coupled plasmas is then determined by

(3.11) $$\begin{eqnarray}Q_{IS}(Z_{B},\bar{R}_{I},\bar{E})=\frac{\ln \left[\displaystyle \frac{Z_{B}^{2}}{\sqrt{8\bar{E}}}\left(1-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{1}{\bar{R}_{I}}\right)^{3}\right)\right]}{\left[\displaystyle 1-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{1}{\bar{R}_{I}}\right)^{3}\right]\ln \left(\displaystyle \frac{Z_{B}^{2}}{\sqrt{8\bar{E}}}\right)},\end{eqnarray}$$

where $\bar{R}_{I}(\equiv R_{I}/a_{Z_{B}})$ is the scaled ion-sphere radius. Using (3.7) and (3.10), the quantum tunnelling effect on the resonant electron transfer cross-section can also be obtained by the following expression of the tunnelling characteristic function $T_{IS}$ :

(3.12) $$\begin{eqnarray}\displaystyle T_{IS}(Z_{B},\bar{R}_{I},\bar{E}) & = & \displaystyle \frac{Z_{B}^{2}}{36n^{4}}\frac{\left[\displaystyle 1+3\frac{n^{2}}{Z_{B}}\left(\frac{a_{Z_{B}}}{R_{I}}\right)-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{a_{Z_{B}}}{R_{I}}\right)^{3}\right]^{2}}{1-2\left(\displaystyle 1-\frac{1}{Z_{B}}\right)\left(\displaystyle \frac{1}{\bar{R}_{I}}\right)^{3}}\nonumber\\ \displaystyle & & \displaystyle \times \,\ln \left[\frac{Z_{B}^{2}}{\sqrt{8\bar{E}}}\left(1-2\left(1-\frac{1}{Z_{B}}\right)\left(\frac{1}{\bar{R}_{I}}\right)^{3}\right)\right].\end{eqnarray}$$

As seen, the influence of quantum tunnelling on the resonant electron transfer process could be explicitly investigated through the logarithmic term in (3.12). Recently, the resonant charge transfer processes in collisions between positive ions have been investigated in strongly coupled plasmas (Jung Reference Jung2005b ) as well as in weakly coupled Lorentzian plasmas (Hong & Jung Reference Hong and Jung2014). However, the quantum tunnelling effect has not been included in the investigation of the resonant electron transfer process in strongly coupled plasmas. Hence, (3.10)–(3.12) are reliable to explore the influence of quantum tunnelling on the resonant electron transfer cross-section in strongly coupled plasmas based on the ion-sphere model. In addition, extensive and excellent investigations for the effective interaction potentials have been carried out in dense semiclassical and quantum plasmas (Deutsch Reference Deutsch1977; Deutsch, Gombert & Minoo Reference Deutsch, Gombert and Minoo1978; Ramazanov, Dzhumagulova & Gabdullin Reference Ramazanov, Dzhumagulova and Gabdullin2010; Ramazanov et al. Reference Ramazanov, Moldabekov, Dzhumagulova and Muratov2011; Shukla & Eliasson Reference Shukla and Eliasson2011; Akbari-Moghanjoughi & Shukla Reference Akbari-Moghanjoughi and Shukla2012; Shukla & Eliasson Reference Shukla and Eliasson2012; Akbari-Moghanjoughi Reference Akbari-Moghanjoughi2013; Dzhumagulova et al. Reference Dzhumagulova, Masheeva, Ramazanov and Donkó2014; Ramazanov et al. Reference Ramazanov, Moldabekov, Gabdullin and Ismagambetova2014). However, quantum tunnelling resonant electron transfer has not been explored as yet in semiclassical or quantum plasmas. Hence, the investigation on the quantum tunnelling and plasma shielding effects on the resonant electron transfer process in dense semiclassical and quantum plasmas will be treated elsewhere. It is important to note that the ion-sphere potential is designed so that potential and its first derivative with respect to $r$ vanish at the ion-sphere radius. In strongly coupled plasmas, plasma screening is better described by this ion-sphere picture, in which the stationary hydrogenic ion of total electric charge $Z-1$ is surrounded by $Z-1$ plasma electrons, uniformly distributed throughout the ion-sphere radius. Hence, the ion-sphere model would be reliable when the ion charge $Z$ is greater than unity since the ion-sphere radius $R_{I}\propto (Z-1)^{1/3}$ . In strongly coupled plasmas (Baimbetov, Nurekenov & Ramazanov Reference Baimbetov, Nurekenov and Ramazanov1996), the temperature $T$ and number density $n$ are shown to be approximately $(1{-}10)\times 10^{4}~\text{K}$ and $10^{19}{-}10^{20}\;\text{cm}^{-3}$ , respectively. Additionally, it has been shown that the physical properties of dense plasmas (Ramazanov et al. Reference Ramazanov, Dzhumagulova and Gabdullin2010) could be expressed by the plasma coupling parameter ${\it\Gamma}~[=(Ze)^{2}/ak_{B}T]$ , degeneracy parameter ${\it\theta}~(=k_{B}T/E_{F})$ and density parameter $r_{s}~(=a/a_{0})$ , where $E_{F}$ is the Fermi energy and $a$ is the average distance between particles in dense plasmas. Recently, the excellent works (Ramazanov et al. Reference Ramazanov, Dzhumagulova, Omarbakiyeva and Röpke2006; Omarbakiyeva, Ramazanov & Röpke Reference Omarbakiyeva, Ramazanov and Röpke2009) have provided the useful effective interaction potentials to describe electron–ion, electron–atom and ion–atom interactions in partially ionized dense plasmas taking into account quantum mechanical effects as well as plasma screening effects. In addition, an excellent investigation has provided the electron–atom interaction, including Pauli blocking and plasma screening in partially ionized hydrogen plasmas, using the Beth–Uhlenbeck approach (Omarbakiyeva et al. Reference Omarbakiyeva, Fortmann, Ramazanov and Röpke2010) to the second-virial coefficient.

Figure 1. The classical characteristic function $C_{IS}$ for the influence of plasma shielding on the classical expression of the resonant electron transfer cross-section in strongly coupled plasmas as a function of the scaled ion-sphere radius $\bar{R}_{I}$ for $n=1$ and $E_{F}/\hslash {\it\omega}_{p}=4$ , where ${\it\omega}_{p}$ is the electron plasma frequency. The solid line is the case of $Z=2$ and ${\it\Gamma}r_{s}{\it\theta}=7.32$ . The dashed line is the case of $Z=6$ and ${\it\Gamma}r_{s}{\it\theta}=65.08$ . The dotted line is the case of $Z=8$ and ${\it\Gamma}r_{s}{\it\theta}=111.12$ .