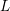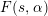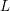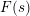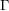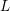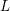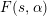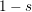1 Introduction
1.1 Motivations
In [Reference Kaczorowski and Perelli9, Reference Kaczorowski and Perelli11] and [Reference Kaczorowski and Perelli14] we introduced and studied the standard twist
of any given function ![]() $F(s)$ from the extended Selberg class
$F(s)$ from the extended Selberg class ![]() ${\mathcal{S}}^{\sharp }$; here
${\mathcal{S}}^{\sharp }$; here ![]() $a(n)$ and
$a(n)$ and ![]() $d>0$ are, respectively, the Dirichlet coefficients and the degree of
$d>0$ are, respectively, the Dirichlet coefficients and the degree of ![]() $F(s)$,
$F(s)$, ![]() $e(x)=e^{2\unicode[STIX]{x1D70B}ix}$ and
$e(x)=e^{2\unicode[STIX]{x1D70B}ix}$ and ![]() $\unicode[STIX]{x1D6FC}>0$. We refer to the next subsection for precise definitions of the quantities we introduce in this subsection; here we recall only that the class
$\unicode[STIX]{x1D6FC}>0$. We refer to the next subsection for precise definitions of the quantities we introduce in this subsection; here we recall only that the class ![]() ${\mathcal{S}}^{\sharp }$ consists, roughly, of the Dirichlet series with analytic continuation to the whole complex plane and satisfying a general functional equation of Riemann type. In particular, essentially all
${\mathcal{S}}^{\sharp }$ consists, roughly, of the Dirichlet series with analytic continuation to the whole complex plane and satisfying a general functional equation of Riemann type. In particular, essentially all ![]() $L$-functions arising from number theory and automorphic forms belong, at least conditionally, to
$L$-functions arising from number theory and automorphic forms belong, at least conditionally, to ![]() ${\mathcal{S}}^{\sharp }$.
${\mathcal{S}}^{\sharp }$.
The main known properties of ![]() $F(s,\unicode[STIX]{x1D6FC})$ are as follows; in order to keep a lighter notation, we shall always assume that
$F(s,\unicode[STIX]{x1D6FC})$ are as follows; in order to keep a lighter notation, we shall always assume that ![]() $F(s)$ is normalized in a way to be explained in Section 1.2; such a normalization is always satisfied by the classical
$F(s)$ is normalized in a way to be explained in Section 1.2; such a normalization is always satisfied by the classical ![]() $L$-functions. For every
$L$-functions. For every ![]() $F\in {\mathcal{S}}^{\sharp }$ and
$F\in {\mathcal{S}}^{\sharp }$ and ![]() $\unicode[STIX]{x1D6FC}>0$, the series in (1.1) converges absolutely for
$\unicode[STIX]{x1D6FC}>0$, the series in (1.1) converges absolutely for ![]() $\unicode[STIX]{x1D70E}>1$ and
$\unicode[STIX]{x1D70E}>1$ and ![]() $F(s,\unicode[STIX]{x1D6FC})$ has meromorphic continuation to
$F(s,\unicode[STIX]{x1D6FC})$ has meromorphic continuation to ![]() $\mathbb{C}$. More precisely, if
$\mathbb{C}$. More precisely, if ![]() $\unicode[STIX]{x1D6FC}$ does not belong to the spectrum Spec
$\unicode[STIX]{x1D6FC}$ does not belong to the spectrum Spec![]() $(F)$ of
$(F)$ of ![]() $F(s)$, an infinite discrete subset of
$F(s)$, an infinite discrete subset of ![]() $\mathbb{R}^{+}$ to be defined in the next subsection, then
$\mathbb{R}^{+}$ to be defined in the next subsection, then ![]() $F(s,\unicode[STIX]{x1D6FC})$ is an entire function of finite order, while if
$F(s,\unicode[STIX]{x1D6FC})$ is an entire function of finite order, while if ![]() $\unicode[STIX]{x1D6FC}\in$ Spec
$\unicode[STIX]{x1D6FC}\in$ Spec![]() $(F)$, then its only singularities are at most simple poles at the points
$(F)$, then its only singularities are at most simple poles at the points
In addition,
hence ![]() $F(s,\unicode[STIX]{x1D6FC})$ has always a simple pole at
$F(s,\unicode[STIX]{x1D6FC})$ has always a simple pole at ![]() $s=s_{0}$ when
$s=s_{0}$ when ![]() $\unicode[STIX]{x1D6FC}\in$ Spec
$\unicode[STIX]{x1D6FC}\in$ Spec![]() $(F)$. Moreover,
$(F)$. Moreover, ![]() $F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on every vertical strip, although the known bounds are weak in general. We refer to our papers [Reference Kaczorowski and Perelli11] and [Reference Kaczorowski and Perelli14] for these and other results.
$F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on every vertical strip, although the known bounds are weak in general. We refer to our papers [Reference Kaczorowski and Perelli11] and [Reference Kaczorowski and Perelli14] for these and other results.
At present, the interest of the standard twist comes mainly from the fact that it plays a central role in the Selberg class theory. The main aim of such a theory is describing the structure of the Selberg class ![]() ${\mathcal{S}}$, roughly the subclass of the functions
${\mathcal{S}}$, roughly the subclass of the functions ![]() $F\in {\mathcal{S}}^{\sharp }$ with a general Euler product and satisfying the Ramanujan conjecture
$F\in {\mathcal{S}}^{\sharp }$ with a general Euler product and satisfying the Ramanujan conjecture ![]() $a(n)\ll n^{\unicode[STIX]{x1D700}}$. It is expected that
$a(n)\ll n^{\unicode[STIX]{x1D700}}$. It is expected that ![]() ${\mathcal{S}}$ coincides with the class of automorphic
${\mathcal{S}}$ coincides with the class of automorphic ![]() $L$-functions and hence, in particular, that the degree
$L$-functions and hence, in particular, that the degree ![]() $d$ is always an integer. The above properties of the standard twist, often coupled with those of other nonlinear twists, have been exploited to verify such an expectation for every degree in the range
$d$ is always an integer. The above properties of the standard twist, often coupled with those of other nonlinear twists, have been exploited to verify such an expectation for every degree in the range ![]() $0<d<2$; see Conrey–Ghosh [Reference Conrey and Ghosh4] and our papers [Reference Kaczorowski and Perelli9] and [Reference Kaczorowski and Perelli12]. A very simple example is the following proof of the nonexistence of functions in
$0<d<2$; see Conrey–Ghosh [Reference Conrey and Ghosh4] and our papers [Reference Kaczorowski and Perelli9] and [Reference Kaczorowski and Perelli12]. A very simple example is the following proof of the nonexistence of functions in ![]() ${\mathcal{S}}^{\sharp }$ with degree
${\mathcal{S}}^{\sharp }$ with degree ![]() $0<d<1$: for
$0<d<1$: for ![]() $d$ in such a range we have that
$d$ in such a range we have that ![]() $s_{0}>1$, see (1.2); hence, choosing
$s_{0}>1$, see (1.2); hence, choosing ![]() $\unicode[STIX]{x1D6FC}\in \text{Spec}(F)$,
$\unicode[STIX]{x1D6FC}\in \text{Spec}(F)$, ![]() $F(s,\unicode[STIX]{x1D6FC})$ would have a pole in the region of absolute convergence.
$F(s,\unicode[STIX]{x1D6FC})$ would have a pole in the region of absolute convergence.
It is therefore natural to ask for a description of the finer analytic properties of ![]() $F(s,\unicode[STIX]{x1D6FC})$, and in particular to raise the following problems.
$F(s,\unicode[STIX]{x1D6FC})$, and in particular to raise the following problems.
(i) Does
 $F(s,\unicode[STIX]{x1D6FC})$ satisfy a functional equation relating
$F(s,\unicode[STIX]{x1D6FC})$ satisfy a functional equation relating  $s$ to
$s$ to  $1-s$? We refer to the discussion at the end of Section 1.3 for additional information related to this problem.
$1-s$? We refer to the discussion at the end of Section 1.3 for additional information related to this problem.(ii) Study of the finer polar structure of
 $F(s,\unicode[STIX]{x1D6FC})$, in particular the existence of finitely or infinitely many poles at the points (1.2); examples of both type exist, see Remark 3.
$F(s,\unicode[STIX]{x1D6FC})$, in particular the existence of finitely or infinitely many poles at the points (1.2); examples of both type exist, see Remark 3.(iii) Give precise convexity bounds for the Lindelöf
 $\unicode[STIX]{x1D707}$-function of
$\unicode[STIX]{x1D707}$-function of  $F(s,\unicode[STIX]{x1D6FC})$(1.3)
$F(s,\unicode[STIX]{x1D6FC})$(1.3) $$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D707}_{F}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FC})=\inf \{\unicode[STIX]{x1D709}:F(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D6FC})\ll (1+|t|)^{\unicode[STIX]{x1D709}}\text{ as }|t|\rightarrow \infty \}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D707}_{F}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FC})=\inf \{\unicode[STIX]{x1D709}:F(\unicode[STIX]{x1D70E}+it,\unicode[STIX]{x1D6FC})\ll (1+|t|)^{\unicode[STIX]{x1D709}}\text{ as }|t|\rightarrow \infty \}.\end{eqnarray}$$(iv) Determine location and counting of the zeros of
 $F(s,\unicode[STIX]{x1D6FC})$, distinguishing between trivial and nontrivial zeros.
$F(s,\unicode[STIX]{x1D6FC})$, distinguishing between trivial and nontrivial zeros.(v) Other analytic problems on
 $F(s,\unicode[STIX]{x1D6FC})$ like bounds for moments, sharp uniform bounds in
$F(s,\unicode[STIX]{x1D6FC})$ like bounds for moments, sharp uniform bounds in  $\unicode[STIX]{x1D6FC}$, etc.
$\unicode[STIX]{x1D6FC}$, etc.
None of these problems is solved at present when the degree ![]() $d$ of
$d$ of ![]() $F(s)$ is
$F(s)$ is ![]() ${\geqslant}2$; in this paper we give a first contribution, in the framework of a special family of degree 2
${\geqslant}2$; in this paper we give a first contribution, in the framework of a special family of degree 2 ![]() $L$-functions.
$L$-functions.
1.2 Definitions and notation
The extended Selberg class ![]() ${\mathcal{S}}^{\sharp }$ consists of nonidentically vanishing Dirichlet series
${\mathcal{S}}^{\sharp }$ consists of nonidentically vanishing Dirichlet series ![]() $F(s)$, absolutely convergent for
$F(s)$, absolutely convergent for ![]() $\unicode[STIX]{x1D70E}>1$, such that
$\unicode[STIX]{x1D70E}>1$, such that ![]() $(s-1)^{m}F(s)$ is entire of finite order for some integer
$(s-1)^{m}F(s)$ is entire of finite order for some integer ![]() $m$ and satisfying a functional equation of type
$m$ and satisfying a functional equation of type
with ![]() $|\unicode[STIX]{x1D714}|=1$,
$|\unicode[STIX]{x1D714}|=1$, ![]() $Q>0$,
$Q>0$, ![]() $\unicode[STIX]{x1D706}_{j}>0$ and
$\unicode[STIX]{x1D706}_{j}>0$ and ![]() $\Re \unicode[STIX]{x1D707}_{j}\geqslant 0$. We refer to Selberg [Reference Selberg and Bombieri25], Conrey–Ghosh [Reference Conrey and Ghosh4], to our survey papers [Reference Kaczorowski, Perelli and Viola7, Reference Kaczorowski, Perelli and Györy10, Reference Perelli21–Reference Perelli24] and to the forthcoming book [Reference Kaczorowski and Perelli17] for definitions, examples and the basic theory of the class
$\Re \unicode[STIX]{x1D707}_{j}\geqslant 0$. We refer to Selberg [Reference Selberg and Bombieri25], Conrey–Ghosh [Reference Conrey and Ghosh4], to our survey papers [Reference Kaczorowski, Perelli and Viola7, Reference Kaczorowski, Perelli and Györy10, Reference Perelli21–Reference Perelli24] and to the forthcoming book [Reference Kaczorowski and Perelli17] for definitions, examples and the basic theory of the class ![]() ${\mathcal{S}}^{\sharp }$. We recall that degree
${\mathcal{S}}^{\sharp }$. We recall that degree ![]() $d$, conductor
$d$, conductor ![]() $q$ and
$q$ and ![]() $\unicode[STIX]{x1D709}$-invariant of
$\unicode[STIX]{x1D709}$-invariant of ![]() $F(s)$ are defined, respectively, by
$F(s)$ are defined, respectively, by
with ![]() $\unicode[STIX]{x1D702},\unicode[STIX]{x1D703}\in \mathbb{R}$. Throughout the paper we always assume that
$\unicode[STIX]{x1D702},\unicode[STIX]{x1D703}\in \mathbb{R}$. Throughout the paper we always assume that ![]() $F(s)$ is normalized by the condition
$F(s)$ is normalized by the condition ![]() $\unicode[STIX]{x1D703}=0$. Moreover, we write
$\unicode[STIX]{x1D703}=0$. Moreover, we write ![]() $n_{\unicode[STIX]{x1D6FC}}=qd^{-d}\unicode[STIX]{x1D6FC}^{d}$ and the spectrum of
$n_{\unicode[STIX]{x1D6FC}}=qd^{-d}\unicode[STIX]{x1D6FC}^{d}$ and the spectrum of ![]() $F(s)$ is defined as
$F(s)$ is defined as
1.3 Setup of the problem
As already pointed out, to gain experience on the problems listed in Section 1.1 we consider the following special case related to half-integral weight modular forms. Their Hecke ![]() $L$-functions satisfy a special functional equation, and by a lucky coincidence we can apply certain methods developed after Linnik in our papers, and in particular in [Reference Kaczorowski and Perelli16].
$L$-functions satisfy a special functional equation, and by a lucky coincidence we can apply certain methods developed after Linnik in our papers, and in particular in [Reference Kaczorowski and Perelli16].
Let ![]() $f$ be a cusp form of half-integral weight
$f$ be a cusp form of half-integral weight ![]() $\unicode[STIX]{x1D705}=k/2$ and level
$\unicode[STIX]{x1D705}=k/2$ and level ![]() $N$, where
$N$, where ![]() $k>0$ is an odd integer and
$k>0$ is an odd integer and ![]() $4\mid N$, and
$4\mid N$, and ![]() $L_{f}(s)$ be the associated Hecke
$L_{f}(s)$ be the associated Hecke ![]() $L$-function. Then
$L$-function. Then ![]() $L_{f}(s)$ is entire and satisfies the functional equation
$L_{f}(s)$ is entire and satisfies the functional equation
![]() $\unicode[STIX]{x1D714}=i^{-\unicode[STIX]{x1D705}}$ and
$\unicode[STIX]{x1D714}=i^{-\unicode[STIX]{x1D705}}$ and ![]() $f^{\ast }$ is related to
$f^{\ast }$ is related to ![]() $f$ by
$f$ by ![]() $f^{\ast }(z)=(\sqrt{N}z)^{-\unicode[STIX]{x1D705}}f(-1/Nz)$. Note that
$f^{\ast }(z)=(\sqrt{N}z)^{-\unicode[STIX]{x1D705}}f(-1/Nz)$. Note that ![]() $L_{f^{\ast }}(s)$ is also entire and has properties similar to
$L_{f^{\ast }}(s)$ is also entire and has properties similar to ![]() $L_{f}(s)$. We refer to Ogg [Reference Ogg19] and to Miyake [Reference Miyake18, Section 4.3] for the basic analytic theory of modular forms, and to Bruinier [Reference Bruinier2] for a detailed exposition of the half-integral weight case.
$L_{f}(s)$. We refer to Ogg [Reference Ogg19] and to Miyake [Reference Miyake18, Section 4.3] for the basic analytic theory of modular forms, and to Bruinier [Reference Bruinier2] for a detailed exposition of the half-integral weight case.
Comparing functional equations (1.4) and (1.6), it is clear that the function ![]() $L_{f}(s)$ does not belong to the extended Selberg class
$L_{f}(s)$ does not belong to the extended Selberg class ![]() ${\mathcal{S}}^{\sharp }$. However, it comes close after the normalization
${\mathcal{S}}^{\sharp }$. However, it comes close after the normalization ![]() $s\mapsto s+(\unicode[STIX]{x1D705}-1)/2$. Indeed, writing
$s\mapsto s+(\unicode[STIX]{x1D705}-1)/2$. Indeed, writing
the functional equation (1.6) becomes
Although this is not exactly of the form (1.4) (indeed ![]() $F^{\ast }(s)$ is not necessarily equal to
$F^{\ast }(s)$ is not necessarily equal to ![]() $\overline{F(\overline{s})}$, and for
$\overline{F(\overline{s})}$, and for ![]() $k=1$ we have
$k=1$ we have ![]() $(\unicode[STIX]{x1D705}-1)/2=(k-2)/4<0$), most results in the Selberg class theory hold in this case as well. Note that the other requirements of
$(\unicode[STIX]{x1D705}-1)/2=(k-2)/4<0$), most results in the Selberg class theory hold in this case as well. Note that the other requirements of ![]() ${\mathcal{S}}^{\sharp }$ are satisfied by
${\mathcal{S}}^{\sharp }$ are satisfied by ![]() $F(s)$, as it can be checked by the argument in Iwaniec [Reference Iwaniec5, proof of Theorem 5.1 and Corollary 5.2] (see also Kaczorowski et al. [Reference Kaczorowski, Molteni, Perelli, Steuding and Wolfart8, proof of the Theorem] and Carletti et al. [Reference Carletti, Monti Bragadin and Perelli3, pp. 217–218]). In particular, both
$F(s)$, as it can be checked by the argument in Iwaniec [Reference Iwaniec5, proof of Theorem 5.1 and Corollary 5.2] (see also Kaczorowski et al. [Reference Kaczorowski, Molteni, Perelli, Steuding and Wolfart8, proof of the Theorem] and Carletti et al. [Reference Carletti, Monti Bragadin and Perelli3, pp. 217–218]). In particular, both ![]() $F(s)$ and
$F(s)$ and ![]() $F^{\ast }(s)$ are absolutely convergent for
$F^{\ast }(s)$ are absolutely convergent for ![]() $\unicode[STIX]{x1D70E}>1$. Note also that, in view of (1.8),
$\unicode[STIX]{x1D70E}>1$. Note also that, in view of (1.8), ![]() $F(s)$ has degree
$F(s)$ has degree ![]() $d=2$ and conductor
$d=2$ and conductor ![]() $q=N$.
$q=N$.
From now on we consider cusp forms ![]() $f$ of weight
$f$ of weight ![]() $\unicode[STIX]{x1D705}$ and level
$\unicode[STIX]{x1D705}$ and level ![]() $N$ as above, and the normalized Hecke
$N$ as above, and the normalized Hecke ![]() $L$-functions
$L$-functions ![]() $F(s)$ and
$F(s)$ and ![]() $F^{\ast }(s)$ as in (1.7). We denote by
$F^{\ast }(s)$ as in (1.7). We denote by ![]() $a(n)$ and
$a(n)$ and ![]() $a^{\ast }(n)$ their Dirichlet coefficients, respectively, and let
$a^{\ast }(n)$ their Dirichlet coefficients, respectively, and let ![]() $F(s,\unicode[STIX]{x1D6FC})$ be the standard twist of
$F(s,\unicode[STIX]{x1D6FC})$ be the standard twist of ![]() $F(s)$, defined by (1.1) with
$F(s)$, defined by (1.1) with ![]() $d=2$ in this case. Then, minor formal modifications to [Reference Kaczorowski and Perelli11, proof of Theorem 1], or [Reference Kaczorowski and Perelli14, Theorems 1 and 2], give the following properties of
$d=2$ in this case. Then, minor formal modifications to [Reference Kaczorowski and Perelli11, proof of Theorem 1], or [Reference Kaczorowski and Perelli14, Theorems 1 and 2], give the following properties of ![]() $F(s,\unicode[STIX]{x1D6FC})$. Writing in this special case
$F(s,\unicode[STIX]{x1D6FC})$. Writing in this special case
where ![]() $a^{\ast }(n_{\unicode[STIX]{x1D6FC}})=0$ if
$a^{\ast }(n_{\unicode[STIX]{x1D6FC}})=0$ if ![]() $n_{\unicode[STIX]{x1D6FC}}\not \in \mathbb{N}$, we have that
$n_{\unicode[STIX]{x1D6FC}}\not \in \mathbb{N}$, we have that ![]() $F(s,\unicode[STIX]{x1D6FC})$ is entire if
$F(s,\unicode[STIX]{x1D6FC})$ is entire if ![]() $\unicode[STIX]{x1D6FC}\not \in$ Spec
$\unicode[STIX]{x1D6FC}\not \in$ Spec![]() $^{\ast }(F)$. If
$^{\ast }(F)$. If ![]() $\unicode[STIX]{x1D6FC}\in$ Spec
$\unicode[STIX]{x1D6FC}\in$ Spec![]() $^{\ast }(F)$, then
$^{\ast }(F)$, then ![]() $F(s,\unicode[STIX]{x1D6FC})$ is meromorphic over
$F(s,\unicode[STIX]{x1D6FC})$ is meromorphic over ![]() $\mathbb{C}$ with at most simple poles at
$\mathbb{C}$ with at most simple poles at
(in this case the condition ![]() $\unicode[STIX]{x1D703}=0$ is satisfied) and
$\unicode[STIX]{x1D703}=0$ is satisfied) and
Moreover, in all cases ![]() $F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on vertical strips.
$F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on vertical strips.
The main result of this paper is the affirmative answer to problem (i) in Section 1.1 in this special case, that is, ![]() $F(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation relating
$F(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation relating ![]() $s$ to
$s$ to ![]() $1-s$ by means of the
$1-s$ by means of the ![]() $\unicode[STIX]{x1D6E4}$ function. Once this is obtained, more or less standard techniques allow to solve some of the other problems in the list, in particular (ii)–(iv). However, the output is somehow unconventional in some cases, for example, for the trivial zeros. Of course, the functional equation of
$\unicode[STIX]{x1D6E4}$ function. Once this is obtained, more or less standard techniques allow to solve some of the other problems in the list, in particular (ii)–(iv). However, the output is somehow unconventional in some cases, for example, for the trivial zeros. Of course, the functional equation of ![]() $F(s,\unicode[STIX]{x1D6FC})$ may be of independent interest inside the modular forms theory, as it provides new information about the associated
$F(s,\unicode[STIX]{x1D6FC})$ may be of independent interest inside the modular forms theory, as it provides new information about the associated ![]() $L$-functions.
$L$-functions.
Before stating the main theorem, we recall that in [Reference Kaczorowski, Perelli and Pintz13] we proved that if a function ![]() $F\in {\mathcal{S}}^{\sharp }$ has degree
$F\in {\mathcal{S}}^{\sharp }$ has degree ![]() ${\geqslant}2$ and satisfies the Ramanujan conjecture (i.e.,
${\geqslant}2$ and satisfies the Ramanujan conjecture (i.e., ![]() $a(n)\ll n^{\unicode[STIX]{x1D700}}$), then the standard twist
$a(n)\ll n^{\unicode[STIX]{x1D700}}$), then the standard twist ![]() $F(s,\unicode[STIX]{x1D6FC})$ does not belong to
$F(s,\unicode[STIX]{x1D6FC})$ does not belong to ![]() ${\mathcal{S}}^{\sharp }$. Actually, a variant of the arguments in [Reference Kaczorowski, Perelli and Pintz13], which we sketch in the Appendix, proves under the same assumptions the stronger assertion that
${\mathcal{S}}^{\sharp }$. Actually, a variant of the arguments in [Reference Kaczorowski, Perelli and Pintz13], which we sketch in the Appendix, proves under the same assumptions the stronger assertion that ![]() $F(s,\unicode[STIX]{x1D6FC})$ does not satisfy a functional equation of type (1.4). Nevertheless, in the case of half-integral weight modular forms,
$F(s,\unicode[STIX]{x1D6FC})$ does not satisfy a functional equation of type (1.4). Nevertheless, in the case of half-integral weight modular forms, ![]() $F(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation reflecting
$F(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation reflecting ![]() $s$ into
$s$ into ![]() $1-s$ via suitable
$1-s$ via suitable ![]() $\unicode[STIX]{x1D6E4}$-factors.
$\unicode[STIX]{x1D6E4}$-factors.
Remark 1. The Ramanujan conjecture is crucial for our results in [Reference Kaczorowski, Perelli and Pintz13]. Indeed, for certain Dirichlet ![]() $L$-functions, say
$L$-functions, say ![]() $L_{1}(s)$, the standard twists
$L_{1}(s)$, the standard twists ![]() $L_{1}(s,\unicode[STIX]{x1D6FC})$ are still degree 1 functions of
$L_{1}(s,\unicode[STIX]{x1D6FC})$ are still degree 1 functions of ![]() ${\mathcal{S}}^{\sharp }$ for suitable values of
${\mathcal{S}}^{\sharp }$ for suitable values of ![]() $\unicode[STIX]{x1D6FC}$. But such
$\unicode[STIX]{x1D6FC}$. But such ![]() $L_{1}(s)$ can be lifted to degree 2 functions
$L_{1}(s)$ can be lifted to degree 2 functions ![]() $L_{2}(s)$ by letting
$L_{2}(s)$ by letting ![]() $s\mapsto 2s-1/2$, and for the same values of
$s\mapsto 2s-1/2$, and for the same values of ![]() $\unicode[STIX]{x1D6FC}$ their standard twists
$\unicode[STIX]{x1D6FC}$ their standard twists ![]() $L_{2}(s,\unicode[STIX]{x1D6FC})$ satisfy a degree 2 functional equation of type (1.8), with
$L_{2}(s,\unicode[STIX]{x1D6FC})$ satisfy a degree 2 functional equation of type (1.8), with ![]() $\unicode[STIX]{x1D705}=1/2$ or
$\unicode[STIX]{x1D705}=1/2$ or ![]() $\unicode[STIX]{x1D705}=3/2$. Moreover, when
$\unicode[STIX]{x1D705}=3/2$. Moreover, when ![]() $\unicode[STIX]{x1D705}=3/2$ both
$\unicode[STIX]{x1D705}=3/2$ both ![]() $L_{2}(s)$ and
$L_{2}(s)$ and ![]() $L_{2}(s,\unicode[STIX]{x1D6FC})$ belong to
$L_{2}(s,\unicode[STIX]{x1D6FC})$ belong to ![]() ${\mathcal{S}}^{\sharp }$. However, such
${\mathcal{S}}^{\sharp }$. However, such ![]() $L_{2}(s)$’s do not satisfy the Ramanujan conjecture, thus showing that this hypothesis is crucial in [Reference Kaczorowski, Perelli and Pintz13]; also, it turns out that such
$L_{2}(s)$’s do not satisfy the Ramanujan conjecture, thus showing that this hypothesis is crucial in [Reference Kaczorowski, Perelli and Pintz13]; also, it turns out that such ![]() $L$-functions are related with half-integral weight modular forms. We refer to [Reference Kaczorowski and Perelli15, Section 2] for the basic properties of lifts in
$L$-functions are related with half-integral weight modular forms. We refer to [Reference Kaczorowski and Perelli15, Section 2] for the basic properties of lifts in ![]() ${\mathcal{S}}^{\sharp }$. Apart from these special cases, we do not know examples of functions
${\mathcal{S}}^{\sharp }$. Apart from these special cases, we do not know examples of functions ![]() $F(s)$, satisfying a functional equation of type (1.4) with degree
$F(s)$, satisfying a functional equation of type (1.4) with degree ![]() $d\geqslant 2$ but not the Ramanujan conjecture, with standard twist
$d\geqslant 2$ but not the Ramanujan conjecture, with standard twist ![]() $F(s,\unicode[STIX]{x1D6FC})$ also satisfying a functional equation of type (1.4).◻
$F(s,\unicode[STIX]{x1D6FC})$ also satisfying a functional equation of type (1.4).◻
1.4 Functional equation
Let ![]() $f$ be a cusp form of half-integral weight
$f$ be a cusp form of half-integral weight ![]() $\unicode[STIX]{x1D705}=k/2$ and level
$\unicode[STIX]{x1D705}=k/2$ and level ![]() $N$,
$N$, ![]() $F(s)$ and
$F(s)$ and ![]() $F^{\ast }(s)$ be as in (1.7),
$F^{\ast }(s)$ be as in (1.7), ![]() $F(s,\unicode[STIX]{x1D6FC})$ be the standard twist of
$F(s,\unicode[STIX]{x1D6FC})$ be the standard twist of ![]() $F(s)$, and
$F(s)$, and ![]() $a^{\ast }(n)$ be the coefficients of
$a^{\ast }(n)$ be the coefficients of ![]() $F^{\ast }(s)$. We write
$F^{\ast }(s)$. We write
Moreover, for ![]() $\ell =0,\ldots ,h^{\ast }$ we also write
$\ell =0,\ldots ,h^{\ast }$ we also write
where, putting
 $$\begin{eqnarray}c^{\ast }(\unicode[STIX]{x1D708}^{2})=c_{\ell }^{\ast }(\unicode[STIX]{x1D708}^{2})=\left\{\begin{array}{@{}ll@{}}-e^{i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}a^{\ast }(\unicode[STIX]{x1D708}^{2})\quad & \text{if }\unicode[STIX]{x1D708}\geqslant 1,\\ e^{i\unicode[STIX]{x1D70B}(1/2+\ell -\unicode[STIX]{x1D707})}a^{\ast }(\unicode[STIX]{x1D708}^{2})\quad & \text{if }-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D708}\leqslant -1,\\ e^{-i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}a^{\ast }(\unicode[STIX]{x1D708}^{2})\quad & \text{if }\unicode[STIX]{x1D708}<-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}c^{\ast }(\unicode[STIX]{x1D708}^{2})=c_{\ell }^{\ast }(\unicode[STIX]{x1D708}^{2})=\left\{\begin{array}{@{}ll@{}}-e^{i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}a^{\ast }(\unicode[STIX]{x1D708}^{2})\quad & \text{if }\unicode[STIX]{x1D708}\geqslant 1,\\ e^{i\unicode[STIX]{x1D70B}(1/2+\ell -\unicode[STIX]{x1D707})}a^{\ast }(\unicode[STIX]{x1D708}^{2})\quad & \text{if }-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D708}\leqslant -1,\\ e^{-i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}a^{\ast }(\unicode[STIX]{x1D708}^{2})\quad & \text{if }\unicode[STIX]{x1D708}<-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}},\end{array}\right.\end{eqnarray}$$ the generalized Dirichlet series ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are defined by
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are defined by
 $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}F_{\ell }^{+}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D708}>-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{c^{\ast }(\unicode[STIX]{x1D708}^{2})}{|\unicode[STIX]{x1D708}|^{1/2+\ell }|\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|^{2s-1/2-\ell }}},\\ F_{\ell }^{-}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D708}<-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{c^{\ast }(\unicode[STIX]{x1D708}^{2})}{|\unicode[STIX]{x1D708}|^{1/2+\ell }|\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|^{2s-1/2-\ell }}};\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}F_{\ell }^{+}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D708}>-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{c^{\ast }(\unicode[STIX]{x1D708}^{2})}{|\unicode[STIX]{x1D708}|^{1/2+\ell }|\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|^{2s-1/2-\ell }}},\\ F_{\ell }^{-}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D708}<-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{c^{\ast }(\unicode[STIX]{x1D708}^{2})}{|\unicode[STIX]{x1D708}|^{1/2+\ell }|\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|^{2s-1/2-\ell }}};\end{array}\right.\end{eqnarray}$$ see also (2.27) for more information on the shape of (1.16). Note that, thanks to the convergence properties of ![]() $F^{\ast }(s)$, such generalized Dirichlet series are absolutely convergent for
$F^{\ast }(s)$, such generalized Dirichlet series are absolutely convergent for ![]() $\unicode[STIX]{x1D70E}>1$. Note also that the second range in (1.15) is empty if
$\unicode[STIX]{x1D70E}>1$. Note also that the second range in (1.15) is empty if ![]() $0\leqslant n_{\unicode[STIX]{x1D6FC}}\leqslant 1$. Finally we define the coefficients
$0\leqslant n_{\unicode[STIX]{x1D6FC}}\leqslant 1$. Finally we define the coefficients ![]() $a_{\ell }=a_{\ell }(h^{\ast })$ by means of the following polynomial identity
$a_{\ell }=a_{\ell }(h^{\ast })$ by means of the following polynomial identity
where, throughout the paper, an empty product equals 1; note that ![]() $a_{0}=1$ for every
$a_{0}=1$ for every ![]() $h^{\ast }\geqslant 0$. With the above notation we have
$h^{\ast }\geqslant 0$. With the above notation we have
Theorem. Let ![]() $\unicode[STIX]{x1D6FC}>0$ and
$\unicode[STIX]{x1D6FC}>0$ and ![]() $\ell =0,\ldots ,h^{\ast }$. Then the functions
$\ell =0,\ldots ,h^{\ast }$. Then the functions ![]() $F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ are entire and
$F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ are entire and ![]() $F(s,\unicode[STIX]{x1D6FC})$ satisfies the functional equation
$F(s,\unicode[STIX]{x1D6FC})$ satisfies the functional equation
Note that functional equation (1.18) is not exactly of Riemann type, but not far from it. Indeed, one can see from the proofs of Lemma 2.1 and Corollary 1 that the functions ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ can be expressed as a kind of stratification of
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ can be expressed as a kind of stratification of ![]() $F^{\ast }(s)$; by this we mean that each
$F^{\ast }(s)$; by this we mean that each ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ is related to a combination of shifts of
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ is related to a combination of shifts of ![]() $F^{\ast }(s)$, see (2.29), (2.32) and (2.34). Therefore, (1.18) resembles the asymmetric form of the functional equation of
$F^{\ast }(s)$, see (2.29), (2.32) and (2.34). Therefore, (1.18) resembles the asymmetric form of the functional equation of ![]() $F(s)$, and hence
$F(s)$, and hence ![]() $F(s,\unicode[STIX]{x1D6FC})$ is expected to behave essentially as a degree 2 function in the extended Selberg class
$F(s,\unicode[STIX]{x1D6FC})$ is expected to behave essentially as a degree 2 function in the extended Selberg class ![]() ${\mathcal{S}}^{\sharp }$; this is confirmed by the results below. Note also that letting
${\mathcal{S}}^{\sharp }$; this is confirmed by the results below. Note also that letting ![]() $\unicode[STIX]{x1D6FC}=0$ in (1.18) one obtains the asymmetric form of the functional equation of
$\unicode[STIX]{x1D6FC}=0$ in (1.18) one obtains the asymmetric form of the functional equation of ![]() $F(s)$. Indeed, for every
$F(s)$. Indeed, for every ![]() $\ell =0,\ldots ,h^{\ast }$ we have
$\ell =0,\ldots ,h^{\ast }$ we have
and following the initial steps of the proof of the Theorem one can easily rebuild the ![]() $\unicode[STIX]{x1D6E4}$-factor of
$\unicode[STIX]{x1D6E4}$-factor of ![]() $F(s)$ from the
$F(s)$ from the ![]() $\unicode[STIX]{x1D6E4}$-factors in (1.18).
$\unicode[STIX]{x1D6E4}$-factors in (1.18).
Remark 2. We obtain the functional equation in the theorem thanks to the special form of the ![]() $\unicode[STIX]{x1D6E4}$-factor in (1.8), which enables the explicit computation of a certain hypergeometric function arising in the proof, see (2.12) and (2.13). Obviously, we can get the same result for any
$\unicode[STIX]{x1D6E4}$-factor in (1.8), which enables the explicit computation of a certain hypergeometric function arising in the proof, see (2.12) and (2.13). Obviously, we can get the same result for any ![]() $F\in {\mathcal{S}}^{\sharp }$ with the same
$F\in {\mathcal{S}}^{\sharp }$ with the same ![]() $\unicode[STIX]{x1D6E4}$-factor in its functional equation. Moreover, similar arguments can be carried over for a certain class of
$\unicode[STIX]{x1D6E4}$-factor in its functional equation. Moreover, similar arguments can be carried over for a certain class of ![]() $\unicode[STIX]{x1D6E4}$-factors, for example of type
$\unicode[STIX]{x1D6E4}$-factors, for example of type ![]() $\unicode[STIX]{x1D6E4}(ds/2+\unicode[STIX]{x1D707})$ with any
$\unicode[STIX]{x1D6E4}(ds/2+\unicode[STIX]{x1D707})$ with any ![]() $d\geqslant 1$ and suitable real values of
$d\geqslant 1$ and suitable real values of ![]() $\unicode[STIX]{x1D707}$, thus producing analogous functional equations for the standard twists of the corresponding
$\unicode[STIX]{x1D707}$, thus producing analogous functional equations for the standard twists of the corresponding ![]() $L$-functions. Here we restrict ourselves to the case of (1.7) for simplicity, since it already covers an interesting classical case. We also remark that, as it is, our method does not apply to the case of classical modular forms of integral weight, nor to the Maass forms. Actually, we do not even expect a functional equation as in the theorem in such cases. For example, we know from [Reference Kaczorowski6] that there are integral weight modular forms whose associated standard twist has infinitely many poles at the points
$L$-functions. Here we restrict ourselves to the case of (1.7) for simplicity, since it already covers an interesting classical case. We also remark that, as it is, our method does not apply to the case of classical modular forms of integral weight, nor to the Maass forms. Actually, we do not even expect a functional equation as in the theorem in such cases. For example, we know from [Reference Kaczorowski6] that there are integral weight modular forms whose associated standard twist has infinitely many poles at the points ![]() $s_{\ell }$ in (1.2) when
$s_{\ell }$ in (1.2) when ![]() $\unicode[STIX]{x1D6FC}$ is in the spectrum, and this is not coherent with a functional equation of type (1.18).◻
$\unicode[STIX]{x1D6FC}$ is in the spectrum, and this is not coherent with a functional equation of type (1.18).◻
Remark 3. Let ![]() $F\in {\mathcal{S}}^{\sharp }$ and
$F\in {\mathcal{S}}^{\sharp }$ and ![]() $\unicode[STIX]{x1D6FC}\in$ Spec
$\unicode[STIX]{x1D6FC}\in$ Spec![]() $(F)$. We already pointed out in Section 1.1 that
$(F)$. We already pointed out in Section 1.1 that ![]() $F(s,\unicode[STIX]{x1D6FC})$ has at most simple poles at the points
$F(s,\unicode[STIX]{x1D6FC})$ has at most simple poles at the points ![]() $s=s_{\ell }$ in (1.2), and from Remark 2 we see that there are cases where
$s=s_{\ell }$ in (1.2), and from Remark 2 we see that there are cases where ![]() $s=s_{\ell }$ is actually a pole for infinitely many
$s=s_{\ell }$ is actually a pole for infinitely many ![]() $\ell$’s. On the other hand, only
$\ell$’s. On the other hand, only ![]() $s=s_{0}$ is a pole in the case
$s=s_{0}$ is a pole in the case ![]() $F(s)=\unicode[STIX]{x1D701}(s)$. The existence of infinitely or finitely many poles at the points
$F(s)=\unicode[STIX]{x1D701}(s)$. The existence of infinitely or finitely many poles at the points ![]() $s=s_{\ell }$ depends on the structure of certain quotients of
$s=s_{\ell }$ depends on the structure of certain quotients of ![]() $\unicode[STIX]{x1D6E4}$ functions related to the hypergeometric function arising as Mellin transform of the
$\unicode[STIX]{x1D6E4}$ functions related to the hypergeometric function arising as Mellin transform of the ![]() $\unicode[STIX]{x1D6E4}$-factors in the functional equation of
$\unicode[STIX]{x1D6E4}$-factors in the functional equation of ![]() $F(s)$. In the case treated in the theorem, it follows directly from the functional equation (1.18) that
$F(s)$. In the case treated in the theorem, it follows directly from the functional equation (1.18) that ![]() $F(s,\unicode[STIX]{x1D6FC})$ is holomorphic apart possibly at
$F(s,\unicode[STIX]{x1D6FC})$ is holomorphic apart possibly at ![]() $s=s_{\ell }$ with
$s=s_{\ell }$ with ![]() $\ell =0,\ldots ,h^{\ast }$, since the functions
$\ell =0,\ldots ,h^{\ast }$, since the functions ![]() $F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ are entire. An explicit expression for the residue
$F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ are entire. An explicit expression for the residue ![]() $\unicode[STIX]{x1D705}_{\ell }(\unicode[STIX]{x1D6FC})$ of
$\unicode[STIX]{x1D705}_{\ell }(\unicode[STIX]{x1D6FC})$ of ![]() $F(s,\unicode[STIX]{x1D6FC})$ at
$F(s,\unicode[STIX]{x1D6FC})$ at ![]() $s=s_{\ell }$,
$s=s_{\ell }$, ![]() $\ell =0,\ldots ,h^{\ast }$, is given in (2.23). Moreover, (1.18) provides an alternative expression for such residues. We also note that, whatever the value of
$\ell =0,\ldots ,h^{\ast }$, is given in (2.23). Moreover, (1.18) provides an alternative expression for such residues. We also note that, whatever the value of ![]() $\unicode[STIX]{x1D6FC}$ is, the coefficient
$\unicode[STIX]{x1D6FC}$ is, the coefficient ![]() $a^{\ast }(n_{\unicode[STIX]{x1D6FC}})$ never appears on the right hand side of (1.18) (see (1.14) and (1.16)), but it pops up on the left hand side of (1.18) when
$a^{\ast }(n_{\unicode[STIX]{x1D6FC}})$ never appears on the right hand side of (1.18) (see (1.14) and (1.16)), but it pops up on the left hand side of (1.18) when ![]() $\unicode[STIX]{x1D6FC}\in$ Spec
$\unicode[STIX]{x1D6FC}\in$ Spec![]() $^{\ast }(F)$, inside the residue at
$^{\ast }(F)$, inside the residue at ![]() $s=s_{0}$ (see (1.11)).◻
$s=s_{0}$ (see (1.11)).◻
In the next three subsections we prove some corollaries of our main result; hence ![]() $F(s)$ is as in (1.7) and
$F(s)$ is as in (1.7) and ![]() $F(s,\unicode[STIX]{x1D6FC})$ is its standard twist in such corollaries. We also introduce several constants, sometimes explicitly depending on
$F(s,\unicode[STIX]{x1D6FC})$ is its standard twist in such corollaries. We also introduce several constants, sometimes explicitly depending on ![]() $\unicode[STIX]{x1D6FC}$; it is however clear that in general all such constants may depend on
$\unicode[STIX]{x1D6FC}$; it is however clear that in general all such constants may depend on ![]() $f$ and
$f$ and ![]() $\unicode[STIX]{x1D6FC}$.
$\unicode[STIX]{x1D6FC}$.
1.5 Order of growth
Functional equation (1.18) and the properties of the functions ![]() $F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ open the possibility of a further study of the standard twist
$F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ open the possibility of a further study of the standard twist ![]() $F(s,\unicode[STIX]{x1D6FC})$. We already know that
$F(s,\unicode[STIX]{x1D6FC})$. We already know that ![]() $F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on vertical strips, see [Reference Kaczorowski and Perelli11, Theorem 2], but the bounds there are definitely weak from a quantitative viewpoint. The functions
$F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on vertical strips, see [Reference Kaczorowski and Perelli11, Theorem 2], but the bounds there are definitely weak from a quantitative viewpoint. The functions ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ have polynomial growth on vertical strips as well, see Lemma 2.1, and for each choice of
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ have polynomial growth on vertical strips as well, see Lemma 2.1, and for each choice of ![]() $\pm$ we denote by
$\pm$ we denote by
the one-sided Lindelöf ![]() $\unicode[STIX]{x1D707}$-function of
$\unicode[STIX]{x1D707}$-function of ![]() $F_{0}^{\pm }(s,\unicode[STIX]{x1D6FC})$. One checks by standard arguments (see Titchmarsh [Reference Titchmarsh26, Section 9.41]) that the main properties of the Lindelöf
$F_{0}^{\pm }(s,\unicode[STIX]{x1D6FC})$. One checks by standard arguments (see Titchmarsh [Reference Titchmarsh26, Section 9.41]) that the main properties of the Lindelöf ![]() $\unicode[STIX]{x1D707}$-function of Dirichlet series are satisfied by
$\unicode[STIX]{x1D707}$-function of Dirichlet series are satisfied by ![]() $\unicode[STIX]{x1D707}^{\pm }(\unicode[STIX]{x1D70E})$ as well, namely
$\unicode[STIX]{x1D707}^{\pm }(\unicode[STIX]{x1D70E})$ as well, namely ![]() $\unicode[STIX]{x1D707}^{\pm }(\unicode[STIX]{x1D70E})$ is continuous, convex, nonnegative and strictly decreasing until it becomes identically vanishing. Moreover, let
$\unicode[STIX]{x1D707}^{\pm }(\unicode[STIX]{x1D70E})$ is continuous, convex, nonnegative and strictly decreasing until it becomes identically vanishing. Moreover, let
Under the same assumptions of the previous subsection, with the above notation and recalling (1.3) we have the following degree 2 convexity bound for ![]() $F(s,\unicode[STIX]{x1D6FC})$.
$F(s,\unicode[STIX]{x1D6FC})$.
Corollary 1. Let ![]() $\unicode[STIX]{x1D6FC}>0$ and
$\unicode[STIX]{x1D6FC}>0$ and ![]() $\ell =0,\ldots ,h^{\ast }$. Then the functions
$\ell =0,\ldots ,h^{\ast }$. Then the functions ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are entire with polynomial growth on vertical strips, and
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are entire with polynomial growth on vertical strips, and
Hence
and the same holds for ![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E})$. Comparing with the bounds for the general standard twist in [Reference Kaczorowski and Perelli11, Theorem 2], we see that Corollary 1 is definitely sharper, of course in the special case under consideration.
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E})$. Comparing with the bounds for the general standard twist in [Reference Kaczorowski and Perelli11, Theorem 2], we see that Corollary 1 is definitely sharper, of course in the special case under consideration.
1.6 Trivial zeros
Our next two results study the zeros of ![]() $F(s,\unicode[STIX]{x1D6FC})$, denoted as usual by
$F(s,\unicode[STIX]{x1D6FC})$, denoted as usual by ![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6FD}+i\unicode[STIX]{x1D6FE}$. We first study the trivial zeros, although distinguishing between trivial and nontrivial zeros is more delicate and unconventional in this case. Indeed, due to the shape of
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6FD}+i\unicode[STIX]{x1D6FE}$. We first study the trivial zeros, although distinguishing between trivial and nontrivial zeros is more delicate and unconventional in this case. Indeed, due to the shape of ![]() $F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ and to the lack of Euler product, trivial zeros come from the interferences between the two terms on the right hand side of (1.14), rather than from the poles of the
$F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ and to the lack of Euler product, trivial zeros come from the interferences between the two terms on the right hand side of (1.14), rather than from the poles of the ![]() $\unicode[STIX]{x1D6E4}$-factors as in the classical cases. As it will be clear in a moment, in this paper we restrict ourselves to a rough definition of trivial zeros, which in principle does not locate them uniquely. Recalling (1.12)–(1.15) let
$\unicode[STIX]{x1D6E4}$-factors as in the classical cases. As it will be clear in a moment, in this paper we restrict ourselves to a rough definition of trivial zeros, which in principle does not locate them uniquely. Recalling (1.12)–(1.15) let
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{+} & = & \displaystyle \unicode[STIX]{x1D708}_{+}(\unicode[STIX]{x1D6FC})\text{ be the value }\unicode[STIX]{x1D708}>-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}\text{for which }c^{\ast }(\unicode[STIX]{x1D708}^{2})\neq 0\qquad \text{and}\qquad \nonumber\\ \displaystyle & & \displaystyle |\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|\text{is minimum},\nonumber\\ \displaystyle \unicode[STIX]{x1D708}_{-} & = & \displaystyle \unicode[STIX]{x1D708}_{-}(\unicode[STIX]{x1D6FC})\text{ be the value }\unicode[STIX]{x1D708}<-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}\text{for which }c^{\ast }(\unicode[STIX]{x1D708}^{2})\neq 0\qquad \text{and}\qquad \nonumber\\ \displaystyle & & \displaystyle |\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|\text{is minimum}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{+} & = & \displaystyle \unicode[STIX]{x1D708}_{+}(\unicode[STIX]{x1D6FC})\text{ be the value }\unicode[STIX]{x1D708}>-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}\text{for which }c^{\ast }(\unicode[STIX]{x1D708}^{2})\neq 0\qquad \text{and}\qquad \nonumber\\ \displaystyle & & \displaystyle |\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|\text{is minimum},\nonumber\\ \displaystyle \unicode[STIX]{x1D708}_{-} & = & \displaystyle \unicode[STIX]{x1D708}_{-}(\unicode[STIX]{x1D6FC})\text{ be the value }\unicode[STIX]{x1D708}<-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}\text{for which }c^{\ast }(\unicode[STIX]{x1D708}^{2})\neq 0\qquad \text{and}\qquad \nonumber\\ \displaystyle & & \displaystyle |\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|\text{is minimum}\nonumber\end{eqnarray}$$and write
clearly, ![]() $m_{\pm },\unicode[STIX]{x1D70C}_{\pm }>0$,
$m_{\pm },\unicode[STIX]{x1D70C}_{\pm }>0$, ![]() $\unicode[STIX]{x1D703}_{\pm }\in [0,2\unicode[STIX]{x1D70B})$ and
$\unicode[STIX]{x1D703}_{\pm }\in [0,2\unicode[STIX]{x1D70B})$ and ![]() $\unicode[STIX]{x1D70C}_{\pm },\unicode[STIX]{x1D703}_{\pm }$ depend on
$\unicode[STIX]{x1D70C}_{\pm },\unicode[STIX]{x1D703}_{\pm }$ depend on ![]() $\unicode[STIX]{x1D6FC}$. Further, writing as usual
$\unicode[STIX]{x1D6FC}$. Further, writing as usual ![]() $s=\unicode[STIX]{x1D70E}+it$, let
$s=\unicode[STIX]{x1D70E}+it$, let ![]() $\ell (\unicode[STIX]{x1D6FC})$ be the line of equation
$\ell (\unicode[STIX]{x1D6FC})$ be the line of equation
and for ![]() $\unicode[STIX]{x1D700}>0$ let
$\unicode[STIX]{x1D700}>0$ let
Then the trivial zeros of ![]() $F(s,\unicode[STIX]{x1D6FC})$ may be defined as the zeros contained in the part of the tubular region
$F(s,\unicode[STIX]{x1D6FC})$ may be defined as the zeros contained in the part of the tubular region ![]() ${\mathcal{L}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D6FC})$ with
${\mathcal{L}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D6FC})$ with ![]() $\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}^{-}$, with suitable
$\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}^{-}$, with suitable ![]() $\unicode[STIX]{x1D6FF}>0$ and
$\unicode[STIX]{x1D6FF}>0$ and ![]() $\unicode[STIX]{x1D70E}^{-}\geqslant 0$. Indeed, under the same assumptions of Section 1.4 we have
$\unicode[STIX]{x1D70E}^{-}\geqslant 0$. Indeed, under the same assumptions of Section 1.4 we have
Corollary 2. Let ![]() $\unicode[STIX]{x1D6FC}>0$. Then there exist
$\unicode[STIX]{x1D6FC}>0$. Then there exist ![]() $\unicode[STIX]{x1D6FF}>0$ and
$\unicode[STIX]{x1D6FF}>0$ and ![]() $\unicode[STIX]{x1D70E}^{-}\geqslant 0$ such that
$\unicode[STIX]{x1D70E}^{-}\geqslant 0$ such that ![]() $F(s,\unicode[STIX]{x1D6FC})\neq 0$ for
$F(s,\unicode[STIX]{x1D6FC})\neq 0$ for ![]() $\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}^{-}$ unless
$\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}^{-}$ unless ![]() $s\in {\mathcal{L}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D6FC})$. More precisely, there exists
$s\in {\mathcal{L}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D6FC})$. More precisely, there exists ![]() $c_{1}(\unicode[STIX]{x1D6FC})>0$ with the property that for every
$c_{1}(\unicode[STIX]{x1D6FC})>0$ with the property that for every ![]() $0<\unicode[STIX]{x1D700}<c_{1}(\unicode[STIX]{x1D6FC})$ there exists
$0<\unicode[STIX]{x1D700}<c_{1}(\unicode[STIX]{x1D6FC})$ there exists ![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}\geqslant 0$ such that
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}\geqslant 0$ such that
(i)
 $F(s,\unicode[STIX]{x1D6FC})\neq 0$ for
$F(s,\unicode[STIX]{x1D6FC})\neq 0$ for  $\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$ unless
$\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$ unless  $s\in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$,
$s\in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$,(ii) there exist infinitely many zeros of
 $F(s,\unicode[STIX]{x1D6FC})$ in
$F(s,\unicode[STIX]{x1D6FC})$ in  ${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with
${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with  $\unicode[STIX]{x1D6FD}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$.
$\unicode[STIX]{x1D6FD}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$.
Hence we may choose as ![]() $\unicode[STIX]{x1D70E}^{-}$ any fixed value larger than the infimum of the
$\unicode[STIX]{x1D70E}^{-}$ any fixed value larger than the infimum of the ![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$’s, and
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$’s, and ![]() $\unicode[STIX]{x1D6FF}$ accordingly, although in principle this does not define uniquely the trivial zeros. However, denoting by
$\unicode[STIX]{x1D6FF}$ accordingly, although in principle this does not define uniquely the trivial zeros. However, denoting by ![]() $T_{\unicode[STIX]{x1D700}}(R,\unicode[STIX]{x1D6FC})$ the number of the zeros in
$T_{\unicode[STIX]{x1D700}}(R,\unicode[STIX]{x1D6FC})$ the number of the zeros in ![]() ${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with
${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with ![]() $-R\leqslant \unicode[STIX]{x1D6FD}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$, it is clear from the proof of Corollary 2 that as
$-R\leqslant \unicode[STIX]{x1D6FD}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$, it is clear from the proof of Corollary 2 that as ![]() $R\rightarrow +\infty$
$R\rightarrow +\infty$
for any given ![]() $\unicode[STIX]{x1D6FC}>0$, with some
$\unicode[STIX]{x1D6FC}>0$, with some ![]() $c_{2}(\unicode[STIX]{x1D6FC})\neq 0$ (see in particular (3.8)). Hence trivial zeros are well defined by the above choice, apart from a finite number of them. Note that letting
$c_{2}(\unicode[STIX]{x1D6FC})\neq 0$ (see in particular (3.8)). Hence trivial zeros are well defined by the above choice, apart from a finite number of them. Note that letting ![]() $\unicode[STIX]{x1D6FC}=0$ we obtain that the line in (1.22) becomes the real axis, since
$\unicode[STIX]{x1D6FC}=0$ we obtain that the line in (1.22) becomes the real axis, since ![]() $\unicode[STIX]{x1D708}_{-}=-\unicode[STIX]{x1D708}_{+}$ and hence
$\unicode[STIX]{x1D708}_{-}=-\unicode[STIX]{x1D708}_{+}$ and hence ![]() $m_{-}=m_{+}$ and
$m_{-}=m_{+}$ and ![]() $\unicode[STIX]{x1D70C}_{-}=\unicode[STIX]{x1D70C}_{+}$ in this case. Of course, this is consistent with the trivial zeros of
$\unicode[STIX]{x1D70C}_{-}=\unicode[STIX]{x1D70C}_{+}$ in this case. Of course, this is consistent with the trivial zeros of ![]() $F(s)$, which lie on the real axis thanks to the special form of (1.8), and with asymptotic formula (1.23).
$F(s)$, which lie on the real axis thanks to the special form of (1.8), and with asymptotic formula (1.23).
Remark 4. Note that when ![]() $\unicode[STIX]{x1D6FC}$ varies in such a way that
$\unicode[STIX]{x1D6FC}$ varies in such a way that ![]() $\sqrt{n}<\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}<\sqrt{n+1}$ with some
$\sqrt{n}<\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}<\sqrt{n+1}$ with some ![]() $n\in \mathbb{N}$, the coefficients of the line in (1.22) may in principle continuously vary between
$n\in \mathbb{N}$, the coefficients of the line in (1.22) may in principle continuously vary between ![]() $-\infty$ and
$-\infty$ and ![]() $+\infty$. But when
$+\infty$. But when ![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}$ hits the square root of an integer, the position of such a line may change suddenly. This shows an interesting discontinuity in the
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}$ hits the square root of an integer, the position of such a line may change suddenly. This shows an interesting discontinuity in the ![]() $\unicode[STIX]{x1D6FC}$-behavior of
$\unicode[STIX]{x1D6FC}$-behavior of ![]() $F(s,\unicode[STIX]{x1D6FC})$.◻
$F(s,\unicode[STIX]{x1D6FC})$.◻
1.7 Nontrivial zeros
Now we turn to the nontrivial zeros of ![]() $F(s,\unicode[STIX]{x1D6FC})$. Let
$F(s,\unicode[STIX]{x1D6FC})$. Let ![]() $\unicode[STIX]{x1D70E}^{+}$ be the upper bound of the real parts of the zeros of
$\unicode[STIX]{x1D70E}^{+}$ be the upper bound of the real parts of the zeros of ![]() $F(s,\unicode[STIX]{x1D6FC})$ and
$F(s,\unicode[STIX]{x1D6FC})$ and ![]() $\unicode[STIX]{x1D70E}^{-}$ be as in the previous subsection. The nontrivial zeros of
$\unicode[STIX]{x1D70E}^{-}$ be as in the previous subsection. The nontrivial zeros of ![]() $F(s,\unicode[STIX]{x1D6FC})$ are those in the vertical strip
$F(s,\unicode[STIX]{x1D6FC})$ are those in the vertical strip ![]() $-\unicode[STIX]{x1D70E}^{-}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}^{+}$, thus the zeros of
$-\unicode[STIX]{x1D70E}^{-}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}^{+}$, thus the zeros of ![]() $F(s,\unicode[STIX]{x1D6FC})$ are the disjoint union of trivial and nontrivial zeros. Let
$F(s,\unicode[STIX]{x1D6FC})$ are the disjoint union of trivial and nontrivial zeros. Let
be the counting function of the nontrivial zeros, and let ![]() $\overline{n}$ be the smallest
$\overline{n}$ be the smallest ![]() $n$ with
$n$ with ![]() $a(n)\neq 0$. A suitable application of the argument principle gives the following analog of the Riemann–von Mangoldt formula.
$a(n)\neq 0$. A suitable application of the argument principle gives the following analog of the Riemann–von Mangoldt formula.
Corollary 3. Let ![]() $\unicode[STIX]{x1D6FC}>0$. Then as
$\unicode[STIX]{x1D6FC}>0$. Then as ![]() $T\rightarrow \infty$ we have
$T\rightarrow \infty$ we have
Again, note that letting ![]() $\unicode[STIX]{x1D6FC}=0$ in Corollary 3 we get the well known asymptotic formula for the counting function of the nontrivial zeros of
$\unicode[STIX]{x1D6FC}=0$ in Corollary 3 we get the well known asymptotic formula for the counting function of the nontrivial zeros of ![]() $F(s)$, obtained substituting
$F(s)$, obtained substituting ![]() $m_{+}m_{-}$ by
$m_{+}m_{-}$ by ![]() $\overline{n}$ in (1.25), since indeed
$\overline{n}$ in (1.25), since indeed ![]() $m_{+}m_{-}=\overline{n}$ in this case. Also, thanks to the constant 2 in the main term of (1.25), Corollary 3 shows once more the degree 2 behavior of
$m_{+}m_{-}=\overline{n}$ in this case. Also, thanks to the constant 2 in the main term of (1.25), Corollary 3 shows once more the degree 2 behavior of ![]() $F(s,\unicode[STIX]{x1D6FC})$. Further, when
$F(s,\unicode[STIX]{x1D6FC})$. Further, when ![]() $\unicode[STIX]{x1D6FC}$ varies we can observe a similar phenomenon as in Remark 4 in the behavior of the coefficient of
$\unicode[STIX]{x1D6FC}$ varies we can observe a similar phenomenon as in Remark 4 in the behavior of the coefficient of ![]() $T$ in (1.25).
$T$ in (1.25).
We conclude remarking that several other problems can be studied once the functional equation is established, for example Voronoi type formulas and related estimates for nonlinear exponential sums, with modular coefficients in the case treated in this paper. We shall return on these and other questions in a future paper. Anyway, already the above theorem shows that the standard twist ![]() $F(s,\unicode[STIX]{x1D6FC})$ is a respectable object from the
$F(s,\unicode[STIX]{x1D6FC})$ is a respectable object from the ![]() $L$-functions point of view, at least in the case of half-integral weight modular forms. Moreover, although the arguments in this paper are not sufficient to prove the functional equation of
$L$-functions point of view, at least in the case of half-integral weight modular forms. Moreover, although the arguments in this paper are not sufficient to prove the functional equation of ![]() $F(s,\unicode[STIX]{x1D6FC})$ for general
$F(s,\unicode[STIX]{x1D6FC})$ for general ![]() $F\in {\mathcal{S}}^{\sharp }$, we believe that indeed
$F\in {\mathcal{S}}^{\sharp }$, we believe that indeed ![]() $F(s,\unicode[STIX]{x1D6FC})$ satisfies a suitable functional equation in such a general case. Again, we shall return on this question in a future paper, but here we add a final remark.
$F(s,\unicode[STIX]{x1D6FC})$ satisfies a suitable functional equation in such a general case. Again, we shall return on this question in a future paper, but here we add a final remark.
Remark 5. Thanks to the characterization in [Reference Kaczorowski and Perelli9] of the degree 1 functions of ![]() ${\mathcal{S}}^{\sharp }$ as linear combinations of Dirichlet
${\mathcal{S}}^{\sharp }$ as linear combinations of Dirichlet ![]() $L$-functions over Dirichlet polynomials from
$L$-functions over Dirichlet polynomials from ![]() ${\mathcal{S}}^{\sharp }$, the standard twists of degree 1 functions in
${\mathcal{S}}^{\sharp }$, the standard twists of degree 1 functions in ![]() ${\mathcal{S}}^{\sharp }$ are closely related to the Hurwitz–Lerch zeta function
${\mathcal{S}}^{\sharp }$ are closely related to the Hurwitz–Lerch zeta function
Since such zeta functions satisfy a functional equation, see for example, Berndt [Reference Berndt1], one certainly expects that the standard twits of degree 1 functions satisfy a functional equation of Hurwitz–Lerch type. Since (1.18) may clearly be regarded as a degree 2 analog of the Hurwitz–Lerch functional equation, and the same holds in the higher degree cases mentioned in Remark 2, it is not unreasonable to expect that, in general, standard twists satisfy a kind of general functional equation of Hurwitz–Lerch type. ◻
2 Proof of the Theorem and Corollary 1
2.1 Basic formula
For convenience we write
thus, recalling (1.12), functional equation (1.8) becomes
By the reflection formula ![]() $\unicode[STIX]{x1D6E4}(z)^{-1}=\unicode[STIX]{x1D6E4}(1-z)\sin (\unicode[STIX]{x1D70B}z)/\unicode[STIX]{x1D70B}$ with
$\unicode[STIX]{x1D6E4}(z)^{-1}=\unicode[STIX]{x1D6E4}(1-z)\sin (\unicode[STIX]{x1D70B}z)/\unicode[STIX]{x1D70B}$ with ![]() $z=s+\unicode[STIX]{x1D707}$, we transform (2.2) in the asymmetric form
$z=s+\unicode[STIX]{x1D707}$, we transform (2.2) in the asymmetric form
Therefore, writing for ![]() $h^{\ast }$ as in (1.12)
$h^{\ast }$ as in (1.12)
and observing that ![]() $\unicode[STIX]{x1D707}=\pm \unicode[STIX]{x1D707}^{\ast }$ if
$\unicode[STIX]{x1D707}=\pm \unicode[STIX]{x1D707}^{\ast }$ if ![]() $h^{\ast }=0$ and
$h^{\ast }=0$ and ![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}^{\ast }$ if
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}^{\ast }$ if ![]() $h^{\ast }\geqslant 1$, for every
$h^{\ast }\geqslant 1$, for every ![]() $h^{\ast }\geqslant 0$ we rewrite the above functional equation as
$h^{\ast }\geqslant 0$ we rewrite the above functional equation as
Thanks to the special value of ![]() $\unicode[STIX]{x1D707}$ (and hence of
$\unicode[STIX]{x1D707}$ (and hence of ![]() $\unicode[STIX]{x1D707}^{\ast }$) in (1.12) we may suitably transform the two
$\unicode[STIX]{x1D707}^{\ast }$) in (1.12) we may suitably transform the two ![]() $\unicode[STIX]{x1D6E4}$-factors in (2.4). To this and, since
$\unicode[STIX]{x1D6E4}$-factors in (2.4). To this and, since ![]() $\unicode[STIX]{x1D707}^{\ast }-h^{\ast }=-\unicode[STIX]{x1D707}^{\ast }+1/2$, we first apply
$\unicode[STIX]{x1D707}^{\ast }-h^{\ast }=-\unicode[STIX]{x1D707}^{\ast }+1/2$, we first apply ![]() $h^{\ast }$-times the factorial formula to the first
$h^{\ast }$-times the factorial formula to the first ![]() $\unicode[STIX]{x1D6E4}$-factor in (2.4) to get (recall that an empty product equals 1)
$\unicode[STIX]{x1D6E4}$-factor in (2.4) to get (recall that an empty product equals 1)
Then we apply the duplication formula ![]() $\unicode[STIX]{x1D6E4}(z)\unicode[STIX]{x1D6E4}(z+1/2)=\unicode[STIX]{x1D70B}^{1/2}2^{1-2z}\unicode[STIX]{x1D6E4}(2z)$ with
$\unicode[STIX]{x1D6E4}(z)\unicode[STIX]{x1D6E4}(z+1/2)=\unicode[STIX]{x1D70B}^{1/2}2^{1-2z}\unicode[STIX]{x1D6E4}(2z)$ with ![]() $z=1-s-\unicode[STIX]{x1D707}^{\ast }$. In view of (2.3), a simple computation shows that (2.4) becomes
$z=1-s-\unicode[STIX]{x1D707}^{\ast }$. In view of (2.3), a simple computation shows that (2.4) becomes
 $$\begin{eqnarray}\displaystyle F(s) & = & \displaystyle \frac{2\unicode[STIX]{x1D714}}{\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\unicode[STIX]{x1D6E4}(2(1-s)-1/2-h^{\ast })\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{1\leqslant j\leqslant h^{\ast }}(2(1-s)-1/2-h^{\ast }+2j-1)\biggr)\sin \unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})F^{\ast }(1-s).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(s) & = & \displaystyle \frac{2\unicode[STIX]{x1D714}}{\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\unicode[STIX]{x1D6E4}(2(1-s)-1/2-h^{\ast })\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{1\leqslant j\leqslant h^{\ast }}(2(1-s)-1/2-h^{\ast }+2j-1)\biggr)\sin \unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})F^{\ast }(1-s).\end{eqnarray}$$ Applying identity (1.17) with ![]() $X=2(1-s)-1/2-h^{\ast }$ we see that (2.5) can be written as
$X=2(1-s)-1/2-h^{\ast }$ we see that (2.5) can be written as
Let now
and
clearly, ![]() $F_{X}(s,\unicode[STIX]{x1D6FC})$ converges for every
$F_{X}(s,\unicode[STIX]{x1D6FC})$ converges for every ![]() $s\in \mathbb{C}$. Given
$s\in \mathbb{C}$. Given ![]() $K>0$, for
$K>0$, for ![]() $-K<\unicode[STIX]{x1D70E}<0$ by Mellin’s transform we have
$-K<\unicode[STIX]{x1D70E}<0$ by Mellin’s transform we have
then we shift the line of integration to ![]() $\Re w=\unicode[STIX]{x1D6FF}$; here and later,
$\Re w=\unicode[STIX]{x1D6FF}$; here and later, ![]() $\unicode[STIX]{x1D6FF}>0$ is a sufficiently small constant, not necessarily the same at each occurrence. Since
$\unicode[STIX]{x1D6FF}>0$ is a sufficiently small constant, not necessarily the same at each occurrence. Since ![]() $F(s)$ is entire, for
$F(s)$ is entire, for ![]() $-K<\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D6FF}$ we may use functional equation (2.6) and expand
$-K<\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D6FF}$ we may use functional equation (2.6) and expand ![]() $F^{\ast }(1-s-w/2)$ to obtain
$F^{\ast }(1-s-w/2)$ to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{X}(s,\unicode[STIX]{x1D6FC})=\frac{2\unicode[STIX]{x1D714}}{\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(\unicode[STIX]{x1D6FF})}\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell -w)\unicode[STIX]{x1D6E4}(w)\sin \unicode[STIX]{x1D70B}\biggl(s+\frac{w}{2}+\unicode[STIX]{x1D707}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl(\frac{Qz_{X}}{2\sqrt{n}}\biggr)^{-w}\,\text{d}w.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{X}(s,\unicode[STIX]{x1D6FC})=\frac{2\unicode[STIX]{x1D714}}{\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(\unicode[STIX]{x1D6FF})}\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell -w)\unicode[STIX]{x1D6E4}(w)\sin \unicode[STIX]{x1D70B}\biggl(s+\frac{w}{2}+\unicode[STIX]{x1D707}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl(\frac{Qz_{X}}{2\sqrt{n}}\biggr)^{-w}\,\text{d}w.\end{eqnarray}$$ Using the expression ![]() $\sin \unicode[STIX]{x1D70B}z=(e^{i\unicode[STIX]{x1D70B}z}-e^{-i\unicode[STIX]{x1D70B}z})/2i$ we rewrite (2.9) as
$\sin \unicode[STIX]{x1D70B}z=(e^{i\unicode[STIX]{x1D70B}z}-e^{-i\unicode[STIX]{x1D70B}z})/2i$ we rewrite (2.9) as
 $$\begin{eqnarray}\displaystyle F_{X}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\nonumber\\ \displaystyle & & \displaystyle \times \,(e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}H(s+\ell /2,z_{X}(n,\unicode[STIX]{x1D6FC}))\nonumber\\ \displaystyle & & \displaystyle -\,e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}H(s+\ell /2,-z_{X}(n,\unicode[STIX]{x1D6FC}))),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{X}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\nonumber\\ \displaystyle & & \displaystyle \times \,(e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}H(s+\ell /2,z_{X}(n,\unicode[STIX]{x1D6FC}))\nonumber\\ \displaystyle & & \displaystyle -\,e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}H(s+\ell /2,-z_{X}(n,\unicode[STIX]{x1D6FC}))),\end{eqnarray}$$where
in view of (2.7), and
An explicit expression for the function ![]() $H(s,z)$ can be obtained from the formula for the Mellin–Barnes integral in (3.3.9) of Paris–Kaminski [Reference Paris and Kaminski20, Ch. 3], namely
$H(s,z)$ can be obtained from the formula for the Mellin–Barnes integral in (3.3.9) of Paris–Kaminski [Reference Paris and Kaminski20, Ch. 3], namely
provided ![]() $0<c<\Re \unicode[STIX]{x1D709}$ and
$0<c<\Re \unicode[STIX]{x1D709}$ and ![]() $|\text{arg}\,z|<\unicode[STIX]{x1D70B}$. To evaluate
$|\text{arg}\,z|<\unicode[STIX]{x1D70B}$. To evaluate ![]() $H(s+\ell /2,\pm z_{X}(n,\unicode[STIX]{x1D6FC}))$ we have to check the first condition, the second one being certainly satisfied in our case. Recalling that we already have the condition
$H(s+\ell /2,\pm z_{X}(n,\unicode[STIX]{x1D6FC}))$ we have to check the first condition, the second one being certainly satisfied in our case. Recalling that we already have the condition ![]() $-K<\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D6FF}$, we choose
$-K<\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D6FF}$, we choose ![]() $K=h^{\ast }+10$ and
$K=h^{\ast }+10$ and
so in view of (1.10) the first condition required by (2.13) is also satisfied for every ![]() $0\leqslant \ell \leqslant h^{\ast }$. Therefore, from (2.12) and (2.13) we get
$0\leqslant \ell \leqslant h^{\ast }$. Therefore, from (2.12) and (2.13) we get
and inserting (2.15) into (2.10) we obtain, for ![]() $\unicode[STIX]{x1D70E}$ as in (2.14), the basic formula
$\unicode[STIX]{x1D70E}$ as in (2.14), the basic formula
 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{X}(s,\unicode[STIX]{x1D6FC})=\frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\{e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}(1+z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}-e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}(1-z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{X}(s,\unicode[STIX]{x1D6FC})=\frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\{e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}(1+z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}-e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}(1-z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\},\end{eqnarray}$$ where ![]() $\unicode[STIX]{x1D714}$,
$\unicode[STIX]{x1D714}$, ![]() $a_{\ell }$,
$a_{\ell }$, ![]() $z_{X}(n,\unicode[STIX]{x1D6FC})$ and
$z_{X}(n,\unicode[STIX]{x1D6FC})$ and ![]() $s_{\ell }$ are given by (1.8), (1.17), (2.11) and (1.10), respectively. Note that the series in (2.16) is absolutely convergent since
$s_{\ell }$ are given by (1.8), (1.17), (2.11) and (1.10), respectively. Note that the series in (2.16) is absolutely convergent since ![]() $\unicode[STIX]{x1D70E}<0$ and
$\unicode[STIX]{x1D70E}<0$ and ![]() $|(1\pm z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}|\rightarrow 1$ as
$|(1\pm z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}|\rightarrow 1$ as ![]() $n\rightarrow \infty$.
$n\rightarrow \infty$.
2.2 Limit as  $X\rightarrow \infty$
$X\rightarrow \infty$
Letting ![]() $X\rightarrow \infty$ in (2.16) requires some care. Indeed, the limit of
$X\rightarrow \infty$ in (2.16) requires some care. Indeed, the limit of ![]() $F_{X}(s,\unicode[STIX]{x1D6FC})$ is clearly
$F_{X}(s,\unicode[STIX]{x1D6FC})$ is clearly ![]() $F(s,\unicode[STIX]{x1D6FC})$ for every
$F(s,\unicode[STIX]{x1D6FC})$ for every ![]() $\unicode[STIX]{x1D6FC}>0$ when
$\unicode[STIX]{x1D6FC}>0$ when ![]() $\unicode[STIX]{x1D70E}>1$, but (2.16) holds in a different range, namely for
$\unicode[STIX]{x1D70E}>1$, but (2.16) holds in a different range, namely for ![]() $s$ as in (2.14). Moreover, the limit of the term
$s$ as in (2.14). Moreover, the limit of the term ![]() $(1-z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}$ is not always well defined, since as
$(1-z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}$ is not always well defined, since as ![]() $X\rightarrow \infty$ we have
$X\rightarrow \infty$ we have ![]() $1-z_{X}(n,\unicode[STIX]{x1D6FC})\rightarrow 1-\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}Q/\sqrt{n}$, which may vanish for suitable values of
$1-z_{X}(n,\unicode[STIX]{x1D6FC})\rightarrow 1-\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}Q/\sqrt{n}$, which may vanish for suitable values of ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $n$. Actually, in view of (2.1) and of the definition of
$n$. Actually, in view of (2.1) and of the definition of ![]() $n_{\unicode[STIX]{x1D6FC}}$ and Spec
$n_{\unicode[STIX]{x1D6FC}}$ and Spec![]() $^{\ast }(F)$ in (1.9), such critical values of
$^{\ast }(F)$ in (1.9), such critical values of ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $n$ arise when
$n$ arise when ![]() $\unicode[STIX]{x1D6FC}\in$ Spec
$\unicode[STIX]{x1D6FC}\in$ Spec![]() $^{\ast }(F)$ and
$^{\ast }(F)$ and ![]() $n=n_{\unicode[STIX]{x1D6FC}}$. Therefore, before letting
$n=n_{\unicode[STIX]{x1D6FC}}$. Therefore, before letting ![]() $X\rightarrow \infty$ we derive a different expression for
$X\rightarrow \infty$ we derive a different expression for ![]() $F_{X}(s,\unicode[STIX]{x1D6FC})$.
$F_{X}(s,\unicode[STIX]{x1D6FC})$.
Since we already have information on the analytic properties of ![]() $F(s,\unicode[STIX]{x1D6FC})$, see Section 1.1 or [Reference Kaczorowski and Perelli11] and [Reference Kaczorowski and Perelli14], we now consider
$F(s,\unicode[STIX]{x1D6FC})$, see Section 1.1 or [Reference Kaczorowski and Perelli11] and [Reference Kaczorowski and Perelli14], we now consider ![]() $F_{X}(s,\unicode[STIX]{x1D6FC})$ as the twist of
$F_{X}(s,\unicode[STIX]{x1D6FC})$ as the twist of ![]() $F(s,\unicode[STIX]{x1D6FC})$ by
$F(s,\unicode[STIX]{x1D6FC})$ by ![]() $e^{-\sqrt{n}/X}$, see (2.8). Hence, by Mellin’s transform, for
$e^{-\sqrt{n}/X}$, see (2.8). Hence, by Mellin’s transform, for ![]() $s$ as in (2.14),
$s$ as in (2.14), ![]() $X>1$ and
$X>1$ and ![]() $K=h^{\ast }+10$ we have
$K=h^{\ast }+10$ we have
The integrand has simple poles at ![]() $w=-r$,
$w=-r$, ![]() $r=0,1,\ldots$ and, as already mentioned in the Introduction, at most simple poles at
$r=0,1,\ldots$ and, as already mentioned in the Introduction, at most simple poles at ![]() $w=2(s_{\ell }-s)$, where
$w=2(s_{\ell }-s)$, where ![]() $s_{\ell }$ are defined by (1.10). We denote by
$s_{\ell }$ are defined by (1.10). We denote by ![]() $\unicode[STIX]{x1D70C}_{\ell }(\unicode[STIX]{x1D6FC})$ the residue of
$\unicode[STIX]{x1D70C}_{\ell }(\unicode[STIX]{x1D6FC})$ the residue of ![]() $F(s+w/2,\unicode[STIX]{x1D6FC})$ at
$F(s+w/2,\unicode[STIX]{x1D6FC})$ at ![]() $w=2(s_{\ell }-s)$; clearly
$w=2(s_{\ell }-s)$; clearly
where ![]() $\unicode[STIX]{x1D705}_{\ell }(\unicode[STIX]{x1D6FC})$ is the residue of
$\unicode[STIX]{x1D705}_{\ell }(\unicode[STIX]{x1D6FC})$ is the residue of ![]() $F(s,\unicode[STIX]{x1D6FC})$ at
$F(s,\unicode[STIX]{x1D6FC})$ at ![]() $s_{\ell }$. We shift the line of integration to
$s_{\ell }$. We shift the line of integration to ![]() $\Re w=-\unicode[STIX]{x1D6FF}$ (once more, with a sufficiently small
$\Re w=-\unicode[STIX]{x1D6FF}$ (once more, with a sufficiently small ![]() $\unicode[STIX]{x1D6FF}>0$, not necessarily the same as at previous places), thus collecting residues of the poles at
$\unicode[STIX]{x1D6FF}>0$, not necessarily the same as at previous places), thus collecting residues of the poles at ![]() $w=0$ and, recalling that
$w=0$ and, recalling that ![]() $s$ is as in (2.14), also at
$s$ is as in (2.14), also at ![]() $w=2(s_{\ell }-s)$ with
$w=2(s_{\ell }-s)$ with ![]() $0\leqslant \ell \leqslant h^{\ast }$. Therefore, still for
$0\leqslant \ell \leqslant h^{\ast }$. Therefore, still for ![]() $s$ as in (2.14), we get
$s$ as in (2.14), we get
 $$\begin{eqnarray}\displaystyle F_{X}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle F(s,\unicode[STIX]{x1D6FC})+\mathop{\sum }_{\ell =0}^{h^{\ast }}\unicode[STIX]{x1D70C}_{\ell }(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6E4}(2(s_{\ell }-s))X^{2(s_{\ell }-s)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(-\unicode[STIX]{x1D6FF})}F\biggl(s+\frac{w}{2},\unicode[STIX]{x1D6FC}\biggr)\unicode[STIX]{x1D6E4}(w)X^{w}\,\text{d}w\nonumber\\ \displaystyle & = & \displaystyle F(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})+I_{X}(s,\unicode[STIX]{x1D6FC}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{X}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle F(s,\unicode[STIX]{x1D6FC})+\mathop{\sum }_{\ell =0}^{h^{\ast }}\unicode[STIX]{x1D70C}_{\ell }(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6E4}(2(s_{\ell }-s))X^{2(s_{\ell }-s)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(-\unicode[STIX]{x1D6FF})}F\biggl(s+\frac{w}{2},\unicode[STIX]{x1D6FC}\biggr)\unicode[STIX]{x1D6E4}(w)X^{w}\,\text{d}w\nonumber\\ \displaystyle & = & \displaystyle F(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})+I_{X}(s,\unicode[STIX]{x1D6FC}),\end{eqnarray}$$ say. Moreover, since ![]() $F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth, see [Reference Kaczorowski and Perelli11, Reference Kaczorowski and Perelli14] or the Introduction, as
$F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth, see [Reference Kaczorowski and Perelli11, Reference Kaczorowski and Perelli14] or the Introduction, as ![]() $X\rightarrow \infty$ we have
$X\rightarrow \infty$ we have
On the other hand, rewriting (2.16) as (recall that ![]() $a^{\ast }(n_{\unicode[STIX]{x1D6FC}})=0$ if
$a^{\ast }(n_{\unicode[STIX]{x1D6FC}})=0$ if ![]() $n_{\unicode[STIX]{x1D6FC}}\not \in \mathbb{N}$)
$n_{\unicode[STIX]{x1D6FC}}\not \in \mathbb{N}$)
 $$\begin{eqnarray}\displaystyle F_{X}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}(1+z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\right.\nonumber\\ \displaystyle & & \displaystyle -\,e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\mathop{\sum }_{\substack{ n=1 \\ n\neq n_{\unicode[STIX]{x1D6FC}}}}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}(1-z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\nonumber\\ \displaystyle & & \displaystyle -\left.e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\frac{a^{\ast }(n_{\unicode[STIX]{x1D6FC}})}{n_{\unicode[STIX]{x1D6FC}}^{1-s}}(1-z_{X}(n_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\vphantom{\mathop{\sum }_{n=1}^{\infty }}\right\}\nonumber\\ \displaystyle & = & \displaystyle A_{X}(s,\unicode[STIX]{x1D6FC})-B_{X}(s,\unicode[STIX]{x1D6FC})-C_{X}(s,\unicode[STIX]{x1D6FC})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{X}(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}(1+z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\right.\nonumber\\ \displaystyle & & \displaystyle -\,e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\mathop{\sum }_{\substack{ n=1 \\ n\neq n_{\unicode[STIX]{x1D6FC}}}}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}(1-z_{X}(n,\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\nonumber\\ \displaystyle & & \displaystyle -\left.e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\frac{a^{\ast }(n_{\unicode[STIX]{x1D6FC}})}{n_{\unicode[STIX]{x1D6FC}}^{1-s}}(1-z_{X}(n_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}))^{2(s-s_{\ell })}\vphantom{\mathop{\sum }_{n=1}^{\infty }}\right\}\nonumber\\ \displaystyle & = & \displaystyle A_{X}(s,\unicode[STIX]{x1D6FC})-B_{X}(s,\unicode[STIX]{x1D6FC})-C_{X}(s,\unicode[STIX]{x1D6FC})\end{eqnarray}$$ say, from (2.18) and (2.20) we get, for ![]() $X>1$ and
$X>1$ and ![]() $s$ as in (2.14), that
$s$ as in (2.14), that
From (2.19) and (2.20) it is clear that, as ![]() $X\rightarrow \infty$,
$X\rightarrow \infty$, ![]() $I_{X}(s,\unicode[STIX]{x1D6FC})$,
$I_{X}(s,\unicode[STIX]{x1D6FC})$, ![]() $A_{X}(s,\unicode[STIX]{x1D6FC})$ and
$A_{X}(s,\unicode[STIX]{x1D6FC})$ and ![]() $B_{X}(s,\unicode[STIX]{x1D6FC})$ tend, respectively, to
$B_{X}(s,\unicode[STIX]{x1D6FC})$ tend, respectively, to ![]() $0$ and to well defined functions
$0$ and to well defined functions ![]() $A(s,\unicode[STIX]{x1D6FC})$ and
$A(s,\unicode[STIX]{x1D6FC})$ and ![]() $B(s,\unicode[STIX]{x1D6FC})$, say, in the range (2.14). Later on we shall compute explicitly such functions, but first we treat the critical term
$B(s,\unicode[STIX]{x1D6FC})$, say, in the range (2.14). Later on we shall compute explicitly such functions, but first we treat the critical term ![]() $C_{X}(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$, depending on
$C_{X}(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$, depending on ![]() $\unicode[STIX]{x1D6FC}$ belonging to Spec
$\unicode[STIX]{x1D6FC}$ belonging to Spec![]() $^{\ast }(F)$ or not. Actually, we show that in both cases
$^{\ast }(F)$ or not. Actually, we show that in both cases ![]() $C_{X}(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ vanishes identically.
$C_{X}(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ vanishes identically.
Suppose first that ![]() $\unicode[STIX]{x1D6FC}\not \in$ Spec
$\unicode[STIX]{x1D6FC}\not \in$ Spec![]() $^{\ast }(F)$. Then
$^{\ast }(F)$. Then ![]() $F(s,\unicode[STIX]{x1D6FC})$ is entire and
$F(s,\unicode[STIX]{x1D6FC})$ is entire and ![]() $a^{\ast }(n_{\unicode[STIX]{x1D6FC}})=0$; hence both
$a^{\ast }(n_{\unicode[STIX]{x1D6FC}})=0$; hence both ![]() $C_{X}(s,\unicode[STIX]{x1D6FC})$ and
$C_{X}(s,\unicode[STIX]{x1D6FC})$ and ![]() $\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ vanish identically. Suppose now
$\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ vanish identically. Suppose now ![]() $\unicode[STIX]{x1D6FC}\in$ Spec
$\unicode[STIX]{x1D6FC}\in$ Spec![]() $^{\ast }(F)$. Then from (1.9), (2.1) and (2.11) we have
$^{\ast }(F)$. Then from (1.9), (2.1) and (2.11) we have
Since in view of (1.10) we have ![]() $2(s_{\ell }-s)=2(1-s)-1/2-\ell$, and recalling the definition of conductor
$2(s_{\ell }-s)=2(1-s)-1/2-\ell$, and recalling the definition of conductor ![]() $q$ of
$q$ of ![]() $F(s)$ in (1.5), by a simple computation we obtain
$F(s)$ in (1.5), by a simple computation we obtain
with
Since ![]() $\Re (s_{\ell }-s)>0$ for
$\Re (s_{\ell }-s)>0$ for ![]() $s$ as in (2.14), comparing
$s$ as in (2.14), comparing ![]() $\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ in (2.18) with the above expression for
$\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ in (2.18) with the above expression for ![]() $C_{X}(s,\unicode[STIX]{x1D6FC})$ and observing that all other terms in (2.21) remain bounded as
$C_{X}(s,\unicode[STIX]{x1D6FC})$ and observing that all other terms in (2.21) remain bounded as ![]() $X\rightarrow \infty$, we deduce that
$X\rightarrow \infty$, we deduce that ![]() $C_{X}(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ must vanish identically. In particular, thanks to (2.17) and (2.22) the residue
$C_{X}(s,\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6F4}_{X}(s,\unicode[STIX]{x1D6FC})$ must vanish identically. In particular, thanks to (2.17) and (2.22) the residue ![]() $\unicode[STIX]{x1D705}_{\ell }(\unicode[STIX]{x1D6FC})$ of
$\unicode[STIX]{x1D705}_{\ell }(\unicode[STIX]{x1D6FC})$ of ![]() $F(s,\unicode[STIX]{x1D6FC})$ at
$F(s,\unicode[STIX]{x1D6FC})$ at ![]() $s=s_{\ell }$ is explicitly given by
$s=s_{\ell }$ is explicitly given by
where ![]() $\unicode[STIX]{x1D714}$,
$\unicode[STIX]{x1D714}$, ![]() $a_{\ell }$ and
$a_{\ell }$ and ![]() $\unicode[STIX]{x1D707}$ are defined by (1.6), (1.17) and (1.12), respectively.
$\unicode[STIX]{x1D707}$ are defined by (1.6), (1.17) and (1.12), respectively.
Finally we may let ![]() $X\rightarrow \infty$ in (2.21) thus getting, for every
$X\rightarrow \infty$ in (2.21) thus getting, for every ![]() $\unicode[STIX]{x1D6FC}>0$ and
$\unicode[STIX]{x1D6FC}>0$ and ![]() $s$ as in (2.14), that
$s$ as in (2.14), that
2.3 Functional equation
We first compute ![]() $A(s,\unicode[STIX]{x1D6FC})$ and
$A(s,\unicode[STIX]{x1D6FC})$ and ![]() $B(s,\unicode[STIX]{x1D6FC})$. Note that by (1.9), (1.13) and (2.1)
$B(s,\unicode[STIX]{x1D6FC})$. Note that by (1.9), (1.13) and (2.1)
Hence, letting ![]() $X\rightarrow \infty$, from (2.11) and (2.20) we obtain at once that
$X\rightarrow \infty$, from (2.11) and (2.20) we obtain at once that
 $$\begin{eqnarray}\displaystyle A(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\biggl(1+\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\biggr)^{2(s-s_{\ell })}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )e^{i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n=1}^{\infty }\frac{a^{\ast }(n)}{n^{1-s}}\biggl(1+\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\biggr)^{2(s-s_{\ell })}.\end{eqnarray}$$ From (1.9) and (2.11) we see that for ![]() $n<n_{\unicode[STIX]{x1D6FC}}$ the real part of
$n<n_{\unicode[STIX]{x1D6FC}}$ the real part of ![]() $1-z_{X}(n,\unicode[STIX]{x1D6FC})$ is negative; hence for such
$1-z_{X}(n,\unicode[STIX]{x1D6FC})$ is negative; hence for such ![]() $n$’s we have
$n$’s we have
Therefore, arguing as for ![]() $A(s,\unicode[STIX]{x1D6FC})$ and recalling that an empty sum equals 0, we get
$A(s,\unicode[STIX]{x1D6FC})$ and recalling that an empty sum equals 0, we get
 $$\begin{eqnarray}\displaystyle B(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{e^{i\unicode[STIX]{x1D70B}2(s-s_{\ell })}\mathop{\sum }_{1\leqslant n<n_{\unicode[STIX]{x1D6FC}}}\frac{a^{\ast }(n)}{n^{1-s}}\left|1-\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\right|^{2(s-s_{\ell })}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{n>n_{\unicode[STIX]{x1D6FC}}}\frac{a^{\ast }(n)}{n^{1-s}}\left|1-\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\right|^{2(s-s_{\ell })}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{\unicode[STIX]{x1D714}}{i\sqrt{2\unicode[STIX]{x1D70B}}}\biggl(\frac{Q}{2}\biggr)^{1-2s}\mathop{\sum }_{\ell =0}^{h^{\ast }}a_{\ell }\unicode[STIX]{x1D6E4}(2(1-s)-1/2-\ell )e^{-i\unicode[STIX]{x1D70B}(s+\unicode[STIX]{x1D707})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{e^{i\unicode[STIX]{x1D70B}2(s-s_{\ell })}\mathop{\sum }_{1\leqslant n<n_{\unicode[STIX]{x1D6FC}}}\frac{a^{\ast }(n)}{n^{1-s}}\left|1-\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\right|^{2(s-s_{\ell })}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{n>n_{\unicode[STIX]{x1D6FC}}}\frac{a^{\ast }(n)}{n^{1-s}}\left|1-\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\right|^{2(s-s_{\ell })}\right\}.\end{eqnarray}$$ Note, as after (2.16), that the series in (2.25) and (2.26) are absolutely convergent since ![]() $\unicode[STIX]{x1D70E}<0$.
$\unicode[STIX]{x1D70E}<0$.
Next we give a uniform shape to the generalized Dirichlet series in ![]() $A(s,\unicode[STIX]{x1D6FC})$ and
$A(s,\unicode[STIX]{x1D6FC})$ and ![]() $B(s,\unicode[STIX]{x1D6FC})$. To accomplish this we recall that
$B(s,\unicode[STIX]{x1D6FC})$. To accomplish this we recall that ![]() $\unicode[STIX]{x1D708}=\pm \sqrt{n}$ with
$\unicode[STIX]{x1D708}=\pm \sqrt{n}$ with ![]() $n=1,2\ldots \,$; hence for
$n=1,2\ldots \,$; hence for ![]() $\unicode[STIX]{x1D708}\neq -\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}$ we have
$\unicode[STIX]{x1D708}\neq -\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}$ we have
 $$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D708}|^{2(1-s_{\ell })}|\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|^{2(s_{\ell }-s)}}=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{n^{1-s}}}\biggl(1+{\displaystyle \frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}}\biggr)^{2(s-s_{\ell })}\quad & \text{if }\unicode[STIX]{x1D708}\geqslant 1,\\ {\displaystyle \frac{1}{n^{1-s}}}\left|1-{\displaystyle \frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}}\right|^{2(s-s_{\ell })}\quad & \text{if }\unicode[STIX]{x1D708}\leqslant -1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D708}|^{2(1-s_{\ell })}|\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|^{2(s_{\ell }-s)}}=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{n^{1-s}}}\biggl(1+{\displaystyle \frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}}\biggr)^{2(s-s_{\ell })}\quad & \text{if }\unicode[STIX]{x1D708}\geqslant 1,\\ {\displaystyle \frac{1}{n^{1-s}}}\left|1-{\displaystyle \frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}}\right|^{2(s-s_{\ell })}\quad & \text{if }\unicode[STIX]{x1D708}\leqslant -1.\end{array}\right.\end{eqnarray}$$ Therefore, a simple computation based on (2.24)–(2.27) and (1.10) shows that for ![]() $s$ as in (2.14) we have
$s$ as in (2.14) we have
with ![]() $F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ as in (1.14). The Theorem now follows by analytic continuation from (2.1), (2.28) and the following lemma.
$F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ as in (1.14). The Theorem now follows by analytic continuation from (2.1), (2.28) and the following lemma.
Lemma 2.1. Let ![]() $\unicode[STIX]{x1D6FC}>0$ and
$\unicode[STIX]{x1D6FC}>0$ and ![]() $\ell =0,\ldots ,h^{\ast }$. Then the functions
$\ell =0,\ldots ,h^{\ast }$. Then the functions ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are entire with polynomial growth on vertical strips.
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are entire with polynomial growth on vertical strips.
Proof. We prove the lemma by showing that the ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$’s are close to certain stratifications of
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$’s are close to certain stratifications of ![]() $F^{\ast }(s)$. Let
$F^{\ast }(s)$. Let ![]() $H>\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}^{2}+1$ be an integer to be chosen later on. From (2.27) and the definition of
$H>\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}^{2}+1$ be an integer to be chosen later on. From (2.27) and the definition of ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$, see (1.16), for
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$, see (1.16), for ![]() $\unicode[STIX]{x1D70E}>1$ we have
$\unicode[STIX]{x1D70E}>1$ we have
with certain generalized Dirichlet polynomials ![]() $G_{\ell }^{\pm }(s)=G_{\ell ,H}^{\pm }(s,\unicode[STIX]{x1D6FC})$, which are entire. Writing
$G_{\ell }^{\pm }(s)=G_{\ell ,H}^{\pm }(s,\unicode[STIX]{x1D6FC})$, which are entire. Writing
we have
where ![]() $\unicode[STIX]{x1D6F4}_{1}$ is the sum over
$\unicode[STIX]{x1D6F4}_{1}$ is the sum over ![]() $r\leqslant R$ and
$r\leqslant R$ and ![]() $\unicode[STIX]{x1D6F4}_{2}$ over
$\unicode[STIX]{x1D6F4}_{2}$ over ![]() $r\geqslant R+1$,
$r\geqslant R+1$, ![]() $R$ being an arbitrarily large positive integer. Clearly
$R$ being an arbitrarily large positive integer. Clearly
therefore, writing
and choosing ![]() $H\geqslant 2K^{2}$, for
$H\geqslant 2K^{2}$, for ![]() $n\geqslant H$ we obtain
$n\geqslant H$ we obtain
Consequently we have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{n\geqslant H}\frac{c^{\ast }(n)}{n^{s}}\biggl(1\pm \frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\biggr)^{\unicode[STIX]{x1D70C}} & = & \displaystyle \mathop{\sum }_{n\geqslant H}\frac{c^{\ast }(n)}{n^{s}}\mathop{\sum }_{r\leqslant R}(\pm 1)^{r}\binom{\unicode[STIX]{x1D70C}}{r}\biggl(\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\biggr)^{r}\nonumber\\ \displaystyle & & \displaystyle +\,O\biggl(K^{R+1}\mathop{\sum }_{n\geqslant H}\frac{|c^{\ast }(n)|}{n^{\unicode[STIX]{x1D70E}+(R+1)/2}}\biggr)=E_{1}^{\pm }(s)+E_{2}^{\pm }(s),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n\geqslant H}\frac{c^{\ast }(n)}{n^{s}}\biggl(1\pm \frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\biggr)^{\unicode[STIX]{x1D70C}} & = & \displaystyle \mathop{\sum }_{n\geqslant H}\frac{c^{\ast }(n)}{n^{s}}\mathop{\sum }_{r\leqslant R}(\pm 1)^{r}\binom{\unicode[STIX]{x1D70C}}{r}\biggl(\frac{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}}{\sqrt{n}}\biggr)^{r}\nonumber\\ \displaystyle & & \displaystyle +\,O\biggl(K^{R+1}\mathop{\sum }_{n\geqslant H}\frac{|c^{\ast }(n)|}{n^{\unicode[STIX]{x1D70E}+(R+1)/2}}\biggr)=E_{1}^{\pm }(s)+E_{2}^{\pm }(s),\end{eqnarray}$$ say, where ![]() $E_{j}^{\pm }(s)=E_{j,\ell ,H,R}^{\pm }(s,\unicode[STIX]{x1D6FC})$.
$E_{j}^{\pm }(s)=E_{j,\ell ,H,R}^{\pm }(s,\unicode[STIX]{x1D6FC})$.
Let ![]() ${\mathcal{K}}$ be any compact subset of
${\mathcal{K}}$ be any compact subset of ![]() $\mathbb{C}$ intersecting the half-plane
$\mathbb{C}$ intersecting the half-plane ![]() $\unicode[STIX]{x1D70E}>1$ and choose
$\unicode[STIX]{x1D70E}>1$ and choose
Then ![]() $E_{2}^{\pm }(s)$ is a double series of holomorphic functions, absolutely and uniformly convergent in
$E_{2}^{\pm }(s)$ is a double series of holomorphic functions, absolutely and uniformly convergent in ![]() $\{\unicode[STIX]{x1D70E}>-(R-1)/2\}\cap {\mathcal{K}}$. Now observe that, in view of (1.15), for
$\{\unicode[STIX]{x1D70E}>-(R-1)/2\}\cap {\mathcal{K}}$. Now observe that, in view of (1.15), for ![]() $n\geqslant H$ we have, depending on the choice of
$n\geqslant H$ we have, depending on the choice of ![]() $\pm$ in
$\pm$ in ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$,
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$,
Therefore, rearranging terms we obtain
 $$\begin{eqnarray}\displaystyle E_{1}^{\pm }(s) & = & \displaystyle \mp e^{\pm i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}\mathop{\sum }_{r\leqslant R}(\pm 1)^{r}\binom{\unicode[STIX]{x1D70C}}{r}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}^{r}\mathop{\sum }_{n\geqslant H}\frac{a^{\ast }(n)}{n^{s+r/2}}\nonumber\\ \displaystyle & = & \displaystyle \mp e^{\pm i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}\mathop{\sum }_{r\leqslant R}(\pm 1)^{r}\binom{\unicode[STIX]{x1D70C}}{r}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}^{r}(F^{\ast }(s+r/2)-D^{\ast }(s+r/2))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r\leqslant R}Q_{r}^{\pm }(s)F^{\ast }(s+r/2)+E_{3}^{\pm }(s),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}^{\pm }(s) & = & \displaystyle \mp e^{\pm i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}\mathop{\sum }_{r\leqslant R}(\pm 1)^{r}\binom{\unicode[STIX]{x1D70C}}{r}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}^{r}\mathop{\sum }_{n\geqslant H}\frac{a^{\ast }(n)}{n^{s+r/2}}\nonumber\\ \displaystyle & = & \displaystyle \mp e^{\pm i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}}\mathop{\sum }_{r\leqslant R}(\pm 1)^{r}\binom{\unicode[STIX]{x1D70C}}{r}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}^{r}(F^{\ast }(s+r/2)-D^{\ast }(s+r/2))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r\leqslant R}Q_{r}^{\pm }(s)F^{\ast }(s+r/2)+E_{3}^{\pm }(s),\end{eqnarray}$$ where ![]() $D^{\ast }(s)=D_{H}^{\ast }(s)$ is a Dirichlet polynomial, the
$D^{\ast }(s)=D_{H}^{\ast }(s)$ is a Dirichlet polynomial, the ![]() $Q_{r}^{\pm }(s)=Q_{r,\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are polynomials and
$Q_{r}^{\pm }(s)=Q_{r,\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are polynomials and ![]() $E_{3}^{\pm }(s)=E_{3,\ell ,H,R}^{\pm }(s,\unicode[STIX]{x1D6FC})$ is an entire function. Thus
$E_{3}^{\pm }(s)=E_{3,\ell ,H,R}^{\pm }(s,\unicode[STIX]{x1D6FC})$ is an entire function. Thus ![]() $E_{1}^{\pm }(s)$ is also entire thanks to the properties of
$E_{1}^{\pm }(s)$ is also entire thanks to the properties of ![]() $F^{\ast }(s)$, and hence from (2.29)–(2.34) we deduce that the generalized Dirichlet series
$F^{\ast }(s)$, and hence from (2.29)–(2.34) we deduce that the generalized Dirichlet series ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$, absolutely convergent for
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$, absolutely convergent for ![]() $\unicode[STIX]{x1D70E}>1$, are actually entire functions since
$\unicode[STIX]{x1D70E}>1$, are actually entire functions since ![]() $R$ and
$R$ and ![]() ${\mathcal{K}}$ are arbitrary.
${\mathcal{K}}$ are arbitrary.
To prove that ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ have polynomial growth on vertical strips we write, in view of (2.29), (2.30) and (2.32),
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ have polynomial growth on vertical strips we write, in view of (2.29), (2.30) and (2.32),
and recall that the functions on the right hand side depend on ![]() $H$. Moreover, from (2.30), (2.31), (2.33) and choosing
$H$. Moreover, from (2.30), (2.31), (2.33) and choosing ![]() ${\mathcal{K}}$ to be the rectangle
${\mathcal{K}}$ to be the rectangle ![]() $[-(R-2)/2,2]\times [-|t|,|t|]$, we have that
$[-(R-2)/2,2]\times [-|t|,|t|]$, we have that
uniformly for ![]() $-(R-2)/2\leqslant \unicode[STIX]{x1D70E}\leqslant 2$. Since the (generalized) Dirichlet polynomials involved in (2.35) have length
$-(R-2)/2\leqslant \unicode[STIX]{x1D70E}\leqslant 2$. Since the (generalized) Dirichlet polynomials involved in (2.35) have length ![]() $\ll H$ and coefficients closely related with
$\ll H$ and coefficients closely related with ![]() $a^{\ast }(n)$, recalling that
$a^{\ast }(n)$, recalling that ![]() $F^{\ast }(s)$ has polynomial growth on vertical strips we see from (2.32), (2.34) and (2.35) that
$F^{\ast }(s)$ has polynomial growth on vertical strips we see from (2.32), (2.34) and (2.35) that
with some ![]() $c(R)>0$, uniformly for
$c(R)>0$, uniformly for ![]() $-(R-2)/2\leqslant \unicode[STIX]{x1D70E}\leqslant 2$ with an arbitrarily large
$-(R-2)/2\leqslant \unicode[STIX]{x1D70E}\leqslant 2$ with an arbitrarily large ![]() $R>0$.◻
$R>0$.◻
2.4 Proof of Corollary 1
The first assertion is already proved in Lemma 2.1. We note preliminarily that from (1.14) we have
for every ![]() $\unicode[STIX]{x1D70E}$, since
$\unicode[STIX]{x1D70E}$, since ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are generalized Dirichlet series with polynomial growth on vertical strips. Hence Stirling’s formula coupled with (1.18) shows that
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are generalized Dirichlet series with polynomial growth on vertical strips. Hence Stirling’s formula coupled with (1.18) shows that
since the factorial formula of the ![]() $\unicode[STIX]{x1D6E4}$ function implies that for
$\unicode[STIX]{x1D6E4}$ function implies that for ![]() $\ell =0,\ldots ,h^{\ast }$
$\ell =0,\ldots ,h^{\ast }$
with certain polynomials ![]() $P_{\ell }(s)$ of degree
$P_{\ell }(s)$ of degree ![]() $\ell$ and
$\ell$ and ![]() $P_{0}(s)\equiv 1$. Now we proceed in a similar way as in Lemma 2.1 to show that
$P_{0}(s)\equiv 1$. Now we proceed in a similar way as in Lemma 2.1 to show that ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are a kind of stratification of
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are a kind of stratification of ![]() $F_{0}^{\pm }(s,\unicode[STIX]{x1D6FC})$. Clearly we may write
$F_{0}^{\pm }(s,\unicode[STIX]{x1D6FC})$. Clearly we may write ![]() $|\unicode[STIX]{x1D708}||\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|$, with
$|\unicode[STIX]{x1D708}||\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}|$, with ![]() $\unicode[STIX]{x1D708}=\pm \sqrt{n}$ and
$\unicode[STIX]{x1D708}=\pm \sqrt{n}$ and ![]() $n$ large enough, as
$n$ large enough, as ![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D708}\pm \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})$ with
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D708}\pm \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})$ with ![]() $\unicode[STIX]{x1D708}=\sqrt{n}$. Hence, choosing
$\unicode[STIX]{x1D708}=\sqrt{n}$. Hence, choosing ![]() $V>0$ sufficiently large, for
$V>0$ sufficiently large, for ![]() $\ell =0,\ldots ,h^{\ast }$ we write
$\ell =0,\ldots ,h^{\ast }$ we write
 $$\begin{eqnarray}\displaystyle F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D708}\geqslant V}\frac{c^{\ast }(\unicode[STIX]{x1D708}^{2})}{\unicode[STIX]{x1D708}^{1/2+\ell }(\unicode[STIX]{x1D708}\pm \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})^{2s-1/2-\ell }}+D_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & = & \displaystyle G_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})+D_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D708}\geqslant V}\frac{c^{\ast }(\unicode[STIX]{x1D708}^{2})}{\unicode[STIX]{x1D708}^{1/2+\ell }(\unicode[STIX]{x1D708}\pm \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})^{2s-1/2-\ell }}+D_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & = & \displaystyle G_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})+D_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC}),\end{eqnarray}$$ say, where ![]() $D_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are generalized Dirichlet polynomials. Moreover, since
$D_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ are generalized Dirichlet polynomials. Moreover, since
we have
and therefore by (2.38)
Hence, since the generalized Dirichlet series are bounded in the half-plane of absolute convergence, for every ![]() $\unicode[STIX]{x1D70E}$ there exists
$\unicode[STIX]{x1D70E}$ there exists ![]() $K=K(\unicode[STIX]{x1D70E})$ such that as
$K=K(\unicode[STIX]{x1D70E})$ such that as ![]() $|t|\rightarrow \infty$
$|t|\rightarrow \infty$
From (1.14), (1.18) and (2.39) we therefore have
with suitable ![]() $a\in \mathbb{R}$,
$a\in \mathbb{R}$, ![]() $b\in \mathbb{C}$ and
$b\in \mathbb{C}$ and
 $$\begin{eqnarray}\displaystyle H_{\ell }(1-s,\unicode[STIX]{x1D6FC}) & = & \displaystyle e^{-i\unicode[STIX]{x1D70B}(1-s)}\mathop{\sum }_{r=0}^{K}(-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})^{r}\binom{-\ell }{r}F_{0}^{+}(1-s+r/2,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & & \displaystyle +\,e^{i\unicode[STIX]{x1D70B}(1-s)}\mathop{\sum }_{r=0}^{K}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})^{r}\binom{-\ell }{r}F_{0}^{-}(1-s+r/2,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & = & \displaystyle H_{\ell }^{+}(1-s,\unicode[STIX]{x1D6FC})+H_{\ell }^{-}(1-s,\unicode[STIX]{x1D6FC}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\ell }(1-s,\unicode[STIX]{x1D6FC}) & = & \displaystyle e^{-i\unicode[STIX]{x1D70B}(1-s)}\mathop{\sum }_{r=0}^{K}(-\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})^{r}\binom{-\ell }{r}F_{0}^{+}(1-s+r/2,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & & \displaystyle +\,e^{i\unicode[STIX]{x1D70B}(1-s)}\mathop{\sum }_{r=0}^{K}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}})^{r}\binom{-\ell }{r}F_{0}^{-}(1-s+r/2,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & = & \displaystyle H_{\ell }^{+}(1-s,\unicode[STIX]{x1D6FC})+H_{\ell }^{-}(1-s,\unicode[STIX]{x1D6FC}),\nonumber\end{eqnarray}$$ say. Note that if ![]() $t\rightarrow +\infty$, then
$t\rightarrow +\infty$, then ![]() $H_{\ell }^{+}(1-s,\unicode[STIX]{x1D6FC})$ has exponential decay since
$H_{\ell }^{+}(1-s,\unicode[STIX]{x1D6FC})$ has exponential decay since ![]() $F_{0}^{+}(s,\unicode[STIX]{x1D6FC})$ has polynomial growth, and similarly for
$F_{0}^{+}(s,\unicode[STIX]{x1D6FC})$ has polynomial growth, and similarly for ![]() $H_{\ell }^{-}(1-s,\unicode[STIX]{x1D6FC})$ if
$H_{\ell }^{-}(1-s,\unicode[STIX]{x1D6FC})$ if ![]() $t\rightarrow -\infty$. Suppose that
$t\rightarrow -\infty$. Suppose that ![]() $\unicode[STIX]{x1D707}^{\ast }(1-\unicode[STIX]{x1D70E})=0$, and hence by (1.20) also
$\unicode[STIX]{x1D707}^{\ast }(1-\unicode[STIX]{x1D70E})=0$, and hence by (1.20) also ![]() $\unicode[STIX]{x1D707}^{\pm }(1-\unicode[STIX]{x1D70E})=0$. Then, again by Stirling’s formula and (2.37), from (2.40) we get that
$\unicode[STIX]{x1D707}^{\pm }(1-\unicode[STIX]{x1D70E})=0$. Then, again by Stirling’s formula and (2.37), from (2.40) we get that ![]() $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D70E})\leqslant 1-2\unicode[STIX]{x1D70E}$ and therefore by (2.36)
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D70E})\leqslant 1-2\unicode[STIX]{x1D70E}$ and therefore by (2.36)
in this case. Suppose now that ![]() $\unicode[STIX]{x1D707}^{\ast }(1-\unicode[STIX]{x1D70E})>0$. Then, thanks to definitions (1.19) and (1.20), the error term in (2.40) is negligible and, still by Stirling’s formula and (2.37), from (2.40) we get
$\unicode[STIX]{x1D707}^{\ast }(1-\unicode[STIX]{x1D70E})>0$. Then, thanks to definitions (1.19) and (1.20), the error term in (2.40) is negligible and, still by Stirling’s formula and (2.37), from (2.40) we get
The proof of the corollary is now complete.
3 Proof of Corollaries 2 and 3
3.1 Proof of Corollary 2
We start recalling the notation of Section 1.6 and writing
note that by (1.18) the zeros of ![]() $F(s,\unicode[STIX]{x1D6FC})$ coincide with those of
$F(s,\unicode[STIX]{x1D6FC})$ coincide with those of ![]() $\unicode[STIX]{x1D6F4}(1-s)$. By (2.37) we write, again with obvious polynomials
$\unicode[STIX]{x1D6F4}(1-s)$. By (2.37) we write, again with obvious polynomials ![]() $Q_{\ell }(s)$ of degree
$Q_{\ell }(s)$ of degree ![]() $\ell$,
$\ell$,
say. Moreover, thanks to the definition of ![]() $F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ and of
$F_{\ell }^{\pm }(s,\unicode[STIX]{x1D6FC})$ and of ![]() $\unicode[STIX]{x1D708}_{\pm }$, we have
$\unicode[STIX]{x1D708}_{\pm }$, we have
where ![]() $h_{\ell }^{\pm }(s)$ are holomorphic and satisfy, uniformly for
$h_{\ell }^{\pm }(s)$ are holomorphic and satisfy, uniformly for ![]() $t\in \mathbb{R}$ and
$t\in \mathbb{R}$ and ![]() $\ell =0,\ldots ,h^{\ast }$ as
$\ell =0,\ldots ,h^{\ast }$ as ![]() $\unicode[STIX]{x1D70E}\rightarrow +\infty$,
$\unicode[STIX]{x1D70E}\rightarrow +\infty$,
Hence, recalling the definition of ![]() $m_{\pm }$ and
$m_{\pm }$ and ![]() $c_{\pm }^{\ast }$ in (1.21), and that
$c_{\pm }^{\ast }$ in (1.21), and that ![]() $\deg Q_{\ell }\geqslant 1$ for
$\deg Q_{\ell }\geqslant 1$ for ![]() $\ell \geqslant 1$, from (1.14), (3.1) and (3.2) we obtain
$\ell \geqslant 1$, from (1.14), (3.1) and (3.2) we obtain
where ![]() $h^{\pm }(s)$ are holomorphic and satisfy, uniformly for
$h^{\pm }(s)$ are holomorphic and satisfy, uniformly for ![]() $t\in \mathbb{R}$ as
$t\in \mathbb{R}$ as ![]() $\unicode[STIX]{x1D70E}\rightarrow +\infty$,
$\unicode[STIX]{x1D70E}\rightarrow +\infty$,
In order to detect the zeros of ![]() $\unicode[STIX]{x1D6F4}(1-s)$ with
$\unicode[STIX]{x1D6F4}(1-s)$ with ![]() $\unicode[STIX]{x1D70E}<0$ we write
$\unicode[STIX]{x1D70E}<0$ we write
and study the zeros of ![]() $W(1-s)$; an application of Rouché’s theorem will then allow to get corresponding results for
$W(1-s)$; an application of Rouché’s theorem will then allow to get corresponding results for ![]() $\unicode[STIX]{x1D6F4}(1-s)$. Since
$\unicode[STIX]{x1D6F4}(1-s)$. Since ![]() $-1=e^{i\unicode[STIX]{x1D70B}}$, in view of (1.21) we have that
$-1=e^{i\unicode[STIX]{x1D70B}}$, in view of (1.21) we have that ![]() $W(1-s)=0$ if and only if
$W(1-s)=0$ if and only if
that is,
Hence the moduli of the two sides of (3.5) are equal provided
while the arguments are equal provided for some ![]() $k\in \mathbb{Z}$
$k\in \mathbb{Z}$
Since the lines in (3.6) and (3.7) are orthogonal, as ![]() $k$ varies over
$k$ varies over ![]() $\mathbb{Z}$ they have infinitely many intersections in the half-plane
$\mathbb{Z}$ they have infinitely many intersections in the half-plane ![]() $\unicode[STIX]{x1D70E}<0$. Hence
$\unicode[STIX]{x1D70E}<0$. Hence ![]() $W(1-s)$ has infinitely many zeros on the part of the line (3.6) with
$W(1-s)$ has infinitely many zeros on the part of the line (3.6) with ![]() $\unicode[STIX]{x1D70E}<0$, and the line (3.6) is exactly the same line in the definition of
$\unicode[STIX]{x1D70E}<0$, and the line (3.6) is exactly the same line in the definition of ![]() ${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$, see (1.22). Moreover, the number of such zeros in
${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$, see (1.22). Moreover, the number of such zeros in ![]() $-R\leqslant \unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}_{0}$ clearly equals
$-R\leqslant \unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}_{0}$ clearly equals
with a certain ![]() $c_{2}(\unicode[STIX]{x1D6FC})\neq 0$, for any
$c_{2}(\unicode[STIX]{x1D6FC})\neq 0$, for any ![]() $\unicode[STIX]{x1D70E}_{0}>0$.
$\unicode[STIX]{x1D70E}_{0}>0$.
Now we write
In view of the above argument, Corollary 2 will follow if we show that there exists ![]() $c>0$ such that for every sufficiently small
$c>0$ such that for every sufficiently small ![]() $\unicode[STIX]{x1D700}>0$
$\unicode[STIX]{x1D700}>0$
 $$\begin{eqnarray}\displaystyle |W(1-s)| & {\geqslant} & \displaystyle c\unicode[STIX]{x1D700}\max \left(\left|e^{-i\unicode[STIX]{x1D70B}(1-s)}\frac{c_{+}^{\ast }}{m_{+}^{2(1-s)}}\right|,\left|e^{i\unicode[STIX]{x1D70B}(1-s)}\frac{c_{-}^{\ast }}{m_{-}^{2(1-s)}}\right|\right)\nonumber\\ \displaystyle & = & \displaystyle c\unicode[STIX]{x1D700}\unicode[STIX]{x1D70C}(1-s),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |W(1-s)| & {\geqslant} & \displaystyle c\unicode[STIX]{x1D700}\max \left(\left|e^{-i\unicode[STIX]{x1D70B}(1-s)}\frac{c_{+}^{\ast }}{m_{+}^{2(1-s)}}\right|,\left|e^{i\unicode[STIX]{x1D70B}(1-s)}\frac{c_{-}^{\ast }}{m_{-}^{2(1-s)}}\right|\right)\nonumber\\ \displaystyle & = & \displaystyle c\unicode[STIX]{x1D700}\unicode[STIX]{x1D70C}(1-s),\end{eqnarray}$$ say, for ![]() $s\not \in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with
$s\not \in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with ![]() $\unicode[STIX]{x1D70E}<0$ and for
$\unicode[STIX]{x1D70E}<0$ and for ![]() $s$ on the vertical segments
$s$ on the vertical segments ![]() ${\mathcal{R}}_{n}={\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})\cap \{\unicode[STIX]{x1D70E}=-R_{n}\}$, where
${\mathcal{R}}_{n}={\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})\cap \{\unicode[STIX]{x1D70E}=-R_{n}\}$, where ![]() $R_{n}\geqslant 0$,
$R_{n}\geqslant 0$, ![]() $n\geqslant 1$, is a suitable increasing sequence tending to
$n\geqslant 1$, is a suitable increasing sequence tending to ![]() $+\infty$. Indeed, by (3.4), for
$+\infty$. Indeed, by (3.4), for ![]() $\unicode[STIX]{x1D70E}\rightarrow -\infty$ we have
$\unicode[STIX]{x1D70E}\rightarrow -\infty$ we have
uniformly for ![]() $t\in \mathbb{R}$; hence (3.9)–(3.11) imply that
$t\in \mathbb{R}$; hence (3.9)–(3.11) imply that ![]() $H(1-s)\neq 0$ for
$H(1-s)\neq 0$ for ![]() $s\not \in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ and
$s\not \in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ and ![]() $\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$ for some
$\unicode[STIX]{x1D70E}<-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$ for some ![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}\geqslant 0$. Therefore, Corollary 2(i) follows from (1.18) and (3.1). Moreover, given
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}\geqslant 0$. Therefore, Corollary 2(i) follows from (1.18) and (3.1). Moreover, given ![]() $n_{0}$ with
$n_{0}$ with ![]() $R_{n_{0}}>\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$, let
$R_{n_{0}}>\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}}$, let ![]() ${\mathcal{P}}_{\unicode[STIX]{x1D700}}$ be the parallelogram with sides
${\mathcal{P}}_{\unicode[STIX]{x1D700}}$ be the parallelogram with sides ![]() ${\mathcal{R}}_{n_{0}}$,
${\mathcal{R}}_{n_{0}}$, ![]() ${\mathcal{R}}_{n}$ with
${\mathcal{R}}_{n}$ with ![]() $n>n_{0}$ and the two segments of boundary of
$n>n_{0}$ and the two segments of boundary of ![]() ${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with real part between
${\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with real part between ![]() $-R_{n}$ and
$-R_{n}$ and ![]() $-R_{n_{0}}$. Then by the same reason as before, for
$-R_{n_{0}}$. Then by the same reason as before, for ![]() $s\in {\mathcal{P}}_{\unicode[STIX]{x1D700}}$ we have
$s\in {\mathcal{P}}_{\unicode[STIX]{x1D700}}$ we have
hence by Rouché’s theorem ![]() $H(1-s)$ has inside
$H(1-s)$ has inside ![]() ${\mathcal{P}}_{\unicode[STIX]{x1D700}}$ the same number of zeros as
${\mathcal{P}}_{\unicode[STIX]{x1D700}}$ the same number of zeros as ![]() $W(1-s)$. Therefore, Corollary 2(ii) follows by letting
$W(1-s)$. Therefore, Corollary 2(ii) follows by letting ![]() $n\rightarrow \infty$, since we already detected the zeros of
$n\rightarrow \infty$, since we already detected the zeros of ![]() $W(1-s)$, and the poles of
$W(1-s)$, and the poles of ![]() $\unicode[STIX]{x1D6E4}(2(1-s)-1/2)$ cannot cancel such zeros.
$\unicode[STIX]{x1D6E4}(2(1-s)-1/2)$ cannot cancel such zeros.
It remains to prove (3.10). We already know that
say, when ![]() $s$ is on the line (3.6). Writing such a line as
$s$ is on the line (3.6). Writing such a line as ![]() $t=t(\unicode[STIX]{x1D70E})$, we denote the points
$t=t(\unicode[STIX]{x1D70E})$, we denote the points ![]() $s\not \in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with
$s\not \in {\mathcal{L}}_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FC})$ with ![]() $\unicode[STIX]{x1D70E}<0$ as
$\unicode[STIX]{x1D70E}<0$ as ![]() $s=\unicode[STIX]{x1D70E}+i(t(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D6FF})$ with
$s=\unicode[STIX]{x1D70E}+i(t(\unicode[STIX]{x1D70E})+\unicode[STIX]{x1D6FF})$ with ![]() $|\unicode[STIX]{x1D6FF}|\geqslant \unicode[STIX]{x1D700}$. Then in view of (3.5) we have
$|\unicode[STIX]{x1D6FF}|\geqslant \unicode[STIX]{x1D700}$. Then in view of (3.5) we have
with certain ![]() $\unicode[STIX]{x1D703}_{j}(s)\in \mathbb{R}$. Hence with a certain
$\unicode[STIX]{x1D703}_{j}(s)\in \mathbb{R}$. Hence with a certain ![]() $c>0$ we have
$c>0$ we have
as it is easy to check analysing the two cases ![]() $\unicode[STIX]{x1D700}\leqslant |\unicode[STIX]{x1D6FF}|\leqslant 1$ and
$\unicode[STIX]{x1D700}\leqslant |\unicode[STIX]{x1D6FF}|\leqslant 1$ and ![]() $|\unicode[STIX]{x1D6FF}|\geqslant 1$. A similar lower bound can be obtained for
$|\unicode[STIX]{x1D6FF}|\geqslant 1$. A similar lower bound can be obtained for ![]() $s\in {\mathcal{R}}_{n}$ as follows. By continuity, between two consecutive intersections of the lines (3.6) and (3.7) in the half-plane
$s\in {\mathcal{R}}_{n}$ as follows. By continuity, between two consecutive intersections of the lines (3.6) and (3.7) in the half-plane ![]() $\unicode[STIX]{x1D70E}<0$, there is a value of
$\unicode[STIX]{x1D70E}<0$, there is a value of ![]() $\unicode[STIX]{x1D70E}$ such that the two terms in
$\unicode[STIX]{x1D70E}$ such that the two terms in ![]() $W(1-s)$ have the same argument when
$W(1-s)$ have the same argument when ![]() $s=\unicode[STIX]{x1D70E}+it(\unicode[STIX]{x1D70E})$. Then we choose the
$s=\unicode[STIX]{x1D70E}+it(\unicode[STIX]{x1D70E})$. Then we choose the ![]() $R_{n}$ to be these values of
$R_{n}$ to be these values of ![]() $\unicode[STIX]{x1D70E}$, thus
$\unicode[STIX]{x1D70E}$, thus
Due to the shape of such arguments, see (3.5), and since ![]() $0<\unicode[STIX]{x1D700}<c_{1}(\unicode[STIX]{x1D6FC})$ and
$0<\unicode[STIX]{x1D700}<c_{1}(\unicode[STIX]{x1D6FC})$ and ![]() $c_{1}(\unicode[STIX]{x1D6FC})$ can be chosen sufficiently small depending on
$c_{1}(\unicode[STIX]{x1D6FC})$ can be chosen sufficiently small depending on ![]() $F(s)$ and
$F(s)$ and ![]() $\unicode[STIX]{x1D6FC}$, the absolute value of the difference between the above arguments when
$\unicode[STIX]{x1D6FC}$, the absolute value of the difference between the above arguments when ![]() $s$ runs over
$s$ runs over ![]() ${\mathcal{R}}_{n}$ is bounded by
${\mathcal{R}}_{n}$ is bounded by ![]() $\unicode[STIX]{x1D70B}/100$, say. Hence
$\unicode[STIX]{x1D70B}/100$, say. Hence
for ![]() $s\in {\mathcal{R}}_{n}$, and (3.10) follows. Corollary 2 is therefore proved.
$s\in {\mathcal{R}}_{n}$, and (3.10) follows. Corollary 2 is therefore proved.
3.2 Proof of Corollary 3
Let ![]() $N_{F}(T,\unicode[STIX]{x1D6FC})$ be as in (1.24),
$N_{F}(T,\unicode[STIX]{x1D6FC})$ be as in (1.24), ![]() $T_{0}>0,a>\unicode[STIX]{x1D70E}^{-}$ and
$T_{0}>0,a>\unicode[STIX]{x1D70E}^{-}$ and ![]() $b>\unicode[STIX]{x1D70E}^{+}$ be sufficiently large,
$b>\unicode[STIX]{x1D70E}^{+}$ be sufficiently large,
and similarly for ![]() $N^{-}(T)$, with
$N^{-}(T)$, with ![]() $-T\leqslant \unicode[STIX]{x1D6FE}<-T_{0}$. Then in view of the results in Section 1.6, see in particular (1.23), we have
$-T\leqslant \unicode[STIX]{x1D6FE}<-T_{0}$. Then in view of the results in Section 1.6, see in particular (1.23), we have
Corollary 3 will follow from a suitable application to ![]() $N^{\pm }(T)$ of the classical technique for the Riemann–von Mangoldt formula based on the argument principle; we give only a sketch of the proof, mainly in order to compute the slightly nonstandard coefficient of
$N^{\pm }(T)$ of the classical technique for the Riemann–von Mangoldt formula based on the argument principle; we give only a sketch of the proof, mainly in order to compute the slightly nonstandard coefficient of ![]() $T$ in (1.25).
$T$ in (1.25).
Let ![]() ${\mathcal{R}}^{+}$ be the rectangle joining the points
${\mathcal{R}}^{+}$ be the rectangle joining the points ![]() $-a+iT_{0}$,
$-a+iT_{0}$, ![]() $b+iT_{0}$,
$b+iT_{0}$, ![]() $b+iT$ and
$b+iT$ and ![]() $-a+iT$ with positive orientation, and denote by
$-a+iT$ with positive orientation, and denote by ![]() ${\mathcal{L}}_{j}$,
${\mathcal{L}}_{j}$, ![]() $j=1,\ldots ,4$, its sides, starting with the lower horizontal side. Hence
$j=1,\ldots ,4$, its sides, starting with the lower horizontal side. Hence
say, and clearly
Recalling the definition of ![]() $\overline{n}$ in Section 1.7 we have
$\overline{n}$ in Section 1.7 we have
 $$\begin{eqnarray}\displaystyle F(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{1}{\overline{n}^{s}}\left(a(\overline{n})e(-\unicode[STIX]{x1D6FC}\sqrt{\overline{n}})+\mathop{\sum }_{n>\overline{n}}\frac{a(n)e(-\unicode[STIX]{x1D6FC}\sqrt{n})}{(n/\overline{n})^{s}}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\overline{n}^{s}}(a(\overline{n})e(-\unicode[STIX]{x1D6FC}\sqrt{\overline{n}})+o(1))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(s,\unicode[STIX]{x1D6FC}) & = & \displaystyle \frac{1}{\overline{n}^{s}}\left(a(\overline{n})e(-\unicode[STIX]{x1D6FC}\sqrt{\overline{n}})+\mathop{\sum }_{n>\overline{n}}\frac{a(n)e(-\unicode[STIX]{x1D6FC}\sqrt{n})}{(n/\overline{n})^{s}}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\overline{n}^{s}}(a(\overline{n})e(-\unicode[STIX]{x1D6FC}\sqrt{\overline{n}})+o(1))\nonumber\end{eqnarray}$$ uniformly for ![]() $s\in {\mathcal{L}}_{2}$ as
$s\in {\mathcal{L}}_{2}$ as ![]() $b\rightarrow \infty$; hence for
$b\rightarrow \infty$; hence for ![]() $b$ sufficiently large
$b$ sufficiently large
For the treatment of ![]() ${\mathcal{L}}_{3}$ we consider the conjugate function
${\mathcal{L}}_{3}$ we consider the conjugate function
so that
say. We follow the standard approach of bounding the variation of the argument of ![]() $F(s,\unicode[STIX]{x1D6FC})$ on
$F(s,\unicode[STIX]{x1D6FC})$ on ![]() ${\mathcal{L}}_{3}$ by means of the number of zeros of
${\mathcal{L}}_{3}$ by means of the number of zeros of ![]() $\Re F(\unicode[STIX]{x1D70E}+iT,\unicode[STIX]{x1D6FC})$ on the segment
$\Re F(\unicode[STIX]{x1D70E}+iT,\unicode[STIX]{x1D6FC})$ on the segment ![]() $-a\leqslant \unicode[STIX]{x1D70E}\leqslant b$. In turn, such number is bounded via Jensen’s inequality by the number of zeros of the holomorphic function
$-a\leqslant \unicode[STIX]{x1D70E}\leqslant b$. In turn, such number is bounded via Jensen’s inequality by the number of zeros of the holomorphic function ![]() $f(s)$ on the circle of radius
$f(s)$ on the circle of radius ![]() $r=(a+b)/2$ and center
$r=(a+b)/2$ and center ![]() $s_{0}=(b-a)/2$. Since
$s_{0}=(b-a)/2$. Since ![]() $F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on vertical strips we obtain
$F(s,\unicode[STIX]{x1D6FC})$ has polynomial growth on vertical strips we obtain
On ![]() ${\mathcal{L}}_{4}$ we use functional equation (1.18). Using once again the factorial formula for the
${\mathcal{L}}_{4}$ we use functional equation (1.18). Using once again the factorial formula for the ![]() $\unicode[STIX]{x1D6E4}$ function as in (2.37) and (3.1), in view of the definition of
$\unicode[STIX]{x1D6E4}$ function as in (2.37) and (3.1), in view of the definition of ![]() $F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ in (1.14) and of
$F_{\ell }^{\ast }(s,\unicode[STIX]{x1D6FC})$ in (1.14) and of ![]() $m_{\pm }$ in (1.21) we get, uniformly for
$m_{\pm }$ in (1.21) we get, uniformly for ![]() $s\in {\mathcal{L}}_{4}$ as
$s\in {\mathcal{L}}_{4}$ as ![]() $a\rightarrow \infty$, that
$a\rightarrow \infty$, that
with a certain constant ![]() $c\in \mathbb{C}$,
$c\in \mathbb{C}$, ![]() $c\neq 0$. Hence for
$c\neq 0$. Hence for ![]() $a$ sufficiently large, from Stirling’s formula we obtain
$a$ sufficiently large, from Stirling’s formula we obtain
therefore from (3.13)–(3.17) we finally deduce that
A completely analogous argument, applied to the rectangle ![]() ${\mathcal{R}}^{-}$ joining the points
${\mathcal{R}}^{-}$ joining the points ![]() $-a-iT$,
$-a-iT$, ![]() $b-iT$,
$b-iT$, ![]() $b-iT_{0}$ and
$b-iT_{0}$ and ![]() $-a-iT_{0}$, with positive orientation, shows that
$-a-iT_{0}$, with positive orientation, shows that
Acknowledgments
We wish to thank Jan Hendrik Bruinier and Winfried Kohnen for their advice concerning half-integral weight modular forms. This research was partially supported by the Istituto Nazionale di Alta Matematica, by the MIUR grant PRIN-2015 “Number Theory and Arithmetic Geometry” and by grant 2017/25/B/ST1/00208 “Analytic methods in number theory” from the National Science Centre, Poland.
Appendix
Here we prove an assertion made in Section 1.3, namely that if a function ![]() $F\in {\mathcal{S}}^{\sharp }$ has degree
$F\in {\mathcal{S}}^{\sharp }$ has degree ![]() ${\geqslant}2$ and satisfies the Ramanujan conjecture, then its standard twist
${\geqslant}2$ and satisfies the Ramanujan conjecture, then its standard twist ![]() $F(s,\unicode[STIX]{x1D6FC})$ does not satisfy a functional equation of type (1.4). Since the argument is similar to [Reference Kaczorowski, Perelli and Pintz13, proof of Theorem 1], which asserts the slightly weaker statement that
$F(s,\unicode[STIX]{x1D6FC})$ does not satisfy a functional equation of type (1.4). Since the argument is similar to [Reference Kaczorowski, Perelli and Pintz13, proof of Theorem 1], which asserts the slightly weaker statement that ![]() $F(s,\unicode[STIX]{x1D6FC})$ does not belong to
$F(s,\unicode[STIX]{x1D6FC})$ does not belong to ![]() ${\mathcal{S}}^{\sharp }$ under the same hypotheses on
${\mathcal{S}}^{\sharp }$ under the same hypotheses on ![]() $F(s)$, we only give a sketch of the proof.
$F(s)$, we only give a sketch of the proof.
Fact 1. The standard twist ![]() $L(s,\unicode[STIX]{x1D6FD})$ of
$L(s,\unicode[STIX]{x1D6FD})$ of ![]() $L(s)$ is meromorphic on
$L(s)$ is meromorphic on ![]() $\mathbb{C}$ with all poles (if any) on a certain horizontal left half-line, and away from its poles is
$\mathbb{C}$ with all poles (if any) on a certain horizontal left half-line, and away from its poles is ![]() $\ll e^{|s|^{c}}$ for some
$\ll e^{|s|^{c}}$ for some ![]() $c>0$ as
$c>0$ as ![]() $|s|\rightarrow \infty$. Moreover, if
$|s|\rightarrow \infty$. Moreover, if ![]() $\unicode[STIX]{x1D6FD}\in \text{Spec}(L)$ then
$\unicode[STIX]{x1D6FD}\in \text{Spec}(L)$ then ![]() $L(s,\unicode[STIX]{x1D6FD})$ has a pole at the right end of such half-line. Further, all nonlinear twists of
$L(s,\unicode[STIX]{x1D6FD})$ has a pole at the right end of such half-line. Further, all nonlinear twists of ![]() $L(s)$ of type
$L(s)$ of type
where ![]() $\unicode[STIX]{x1D6FC}_{0}\geqslant 0$,
$\unicode[STIX]{x1D6FC}_{0}\geqslant 0$, ![]() $\unicode[STIX]{x1D6FC}_{1}>0$ and
$\unicode[STIX]{x1D6FC}_{1}>0$ and ![]() $0<\unicode[STIX]{x1D706}<1/d$, are entire.
$0<\unicode[STIX]{x1D706}<1/d$, are entire.
Fact 1 follows as a special case from [Reference Kaczorowski and Perelli14, Theorems 1–3].
Fact 2. If the standard twist ![]() $L(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation of type (1.4), then the results in Fact
$L(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation of type (1.4), then the results in Fact ![]() $1$ hold also with
$1$ hold also with ![]() $L(s,\unicode[STIX]{x1D6FC})$ in place of
$L(s,\unicode[STIX]{x1D6FC})$ in place of ![]() $L(s)$.
$L(s)$.
Indeed, [Reference Kaczorowski and Perelli14, Theorems 1–3] are proved for functions belonging to ![]() ${\mathcal{S}}^{\sharp }$, but under the assumption in Fact 2 we have:
${\mathcal{S}}^{\sharp }$, but under the assumption in Fact 2 we have:
(i)
 $L(s,\unicode[STIX]{x1D6FC})$ is absolutely convergent for
$L(s,\unicode[STIX]{x1D6FC})$ is absolutely convergent for  $\unicode[STIX]{x1D70E}>1$;
$\unicode[STIX]{x1D70E}>1$;(ii)
 $L(s,\unicode[STIX]{x1D6FC})$ has the meromorphic structure described in Fact 1;
$L(s,\unicode[STIX]{x1D6FC})$ has the meromorphic structure described in Fact 1;(iii)
 $L(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation of type (1.4).
$L(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation of type (1.4).
Fact 2 now follows observing that (i)–(iii) differ from the definition of ![]() ${\mathcal{S}}^{\sharp }$ only by condition (ii); moreover, one can check that the arguments leading to the above quoted theorems do not depend on the presence of a pole at
${\mathcal{S}}^{\sharp }$ only by condition (ii); moreover, one can check that the arguments leading to the above quoted theorems do not depend on the presence of a pole at ![]() $s=1$ only, as in the case of
$s=1$ only, as in the case of ![]() ${\mathcal{S}}^{\sharp }$, and still work if the function under consideration satisfies (ii). From Facts 1 and 2, and the arguments in [Reference Kaczorowski, Perelli and Pintz13, Theorem 1], we now derive the following result, thus justifying the assertion made in Section 1.3.
${\mathcal{S}}^{\sharp }$, and still work if the function under consideration satisfies (ii). From Facts 1 and 2, and the arguments in [Reference Kaczorowski, Perelli and Pintz13, Theorem 1], we now derive the following result, thus justifying the assertion made in Section 1.3.
Proposition A.1. If ![]() $F\in {\mathcal{S}}^{\sharp }$ has degree
$F\in {\mathcal{S}}^{\sharp }$ has degree ![]() ${\geqslant}2$ and satisfies the Ramanujan conjecture, then the standard twist
${\geqslant}2$ and satisfies the Ramanujan conjecture, then the standard twist ![]() $F(s,\unicode[STIX]{x1D6FC})$ does not satisfy a functional equation of type (1.4).
$F(s,\unicode[STIX]{x1D6FC})$ does not satisfy a functional equation of type (1.4).
Note that Proposition A.1 in the case ![]() $\unicode[STIX]{x1D6FC}\not \in$ Spec
$\unicode[STIX]{x1D6FC}\not \in$ Spec![]() $(F)$ is an immediate consequence of the above mentioned [Reference Kaczorowski, Perelli and Pintz13, Theorem 1]. Indeed, in this case
$(F)$ is an immediate consequence of the above mentioned [Reference Kaczorowski, Perelli and Pintz13, Theorem 1]. Indeed, in this case ![]() $F(s,\unicode[STIX]{x1D6FC})$ satisfies the first two conditions in the definition of
$F(s,\unicode[STIX]{x1D6FC})$ satisfies the first two conditions in the definition of ![]() ${\mathcal{S}}^{\sharp }$; hence the fact that
${\mathcal{S}}^{\sharp }$; hence the fact that ![]() $F(s,\unicode[STIX]{x1D6FC})$ does not belong to
$F(s,\unicode[STIX]{x1D6FC})$ does not belong to ![]() ${\mathcal{S}}^{\sharp }$ means simply that
${\mathcal{S}}^{\sharp }$ means simply that ![]() $F(s,\unicode[STIX]{x1D6FC})$ does not satisfy functional equation (1.4).
$F(s,\unicode[STIX]{x1D6FC})$ does not satisfy functional equation (1.4).
Proof of Proposition A.1.
Let ![]() $d_{F}$ and
$d_{F}$ and ![]() $a(n)$ denote, respectively, degree and Dirichlet coefficients of
$a(n)$ denote, respectively, degree and Dirichlet coefficients of ![]() $F(s)$, write
$F(s)$, write
and assume that ![]() $G(s)$ satisfies (1.4). Then we can define degree
$G(s)$ satisfies (1.4). Then we can define degree ![]() $d_{G}$ and spectrum Spec
$d_{G}$ and spectrum Spec![]() $(G)$ of
$(G)$ of ![]() $G(s)$ and, thanks to Fact 2,
$G(s)$ and, thanks to Fact 2, ![]() $G(s)$ has the properties described in Fact 1 for
$G(s)$ has the properties described in Fact 1 for ![]() $L(s)$.
$L(s)$.
We may assume that ![]() $d_{G}\geqslant d_{F}$, otherwise we replace
$d_{G}\geqslant d_{F}$, otherwise we replace ![]() $F(s)$ by
$F(s)$ by ![]() $\overline{G}(s)$ in what follows. If
$\overline{G}(s)$ in what follows. If ![]() $d_{G}>d_{F}$ we choose
$d_{G}>d_{F}$ we choose ![]() $\unicode[STIX]{x1D6FD}\in$ Spec
$\unicode[STIX]{x1D6FD}\in$ Spec![]() $(G)$ and note from Fact 1, applied to
$(G)$ and note from Fact 1, applied to ![]() $G(s)$, that the standard twist
$G(s)$, that the standard twist ![]() $G(s,\unicode[STIX]{x1D6FD})$ is not entire. Moreover, it can be written as
$G(s,\unicode[STIX]{x1D6FD})$ is not entire. Moreover, it can be written as
But, since ![]() $\unicode[STIX]{x1D6FD}>0$ and
$\unicode[STIX]{x1D6FD}>0$ and ![]() $0<1/\text{d}_{G}<1/d_{F}$, from Fact 1 applied to
$0<1/\text{d}_{G}<1/d_{F}$, from Fact 1 applied to ![]() $F(s)$ we have that
$F(s)$ we have that ![]() $G(s,\unicode[STIX]{x1D6FD})$ is entire, a contradiction.
$G(s,\unicode[STIX]{x1D6FD})$ is entire, a contradiction.
Thus we have that ![]() $d_{F}=d_{G}=d\geqslant 2$, say. Now we follow [Reference Kaczorowski, Perelli and Pintz13, proof of Theorem 1] (see p. 150, after (2.1) there) and obtain that the Dirichlet series of
$d_{F}=d_{G}=d\geqslant 2$, say. Now we follow [Reference Kaczorowski, Perelli and Pintz13, proof of Theorem 1] (see p. 150, after (2.1) there) and obtain that the Dirichlet series of ![]() $G(s)$, and hence of
$G(s)$, and hence of ![]() $F(s)$ as well, is absolutely convergent for
$F(s)$ as well, is absolutely convergent for ![]() $\unicode[STIX]{x1D70E}>1/d$. This gives a contradiction, since [Reference Kaczorowski and Perelli11, Corollary 3] states that the abscissa of absolute convergence of
$\unicode[STIX]{x1D70E}>1/d$. This gives a contradiction, since [Reference Kaczorowski and Perelli11, Corollary 3] states that the abscissa of absolute convergence of ![]() $F(s)$ is
$F(s)$ is ![]() ${\geqslant}(d+1)/2d$.◻
${\geqslant}(d+1)/2d$.◻
We finally remark that the Ramanujan conjecture enters the part of [Reference Kaczorowski, Perelli and Pintz13, proof of Theorem] which we followed without giving details, and is used to show the absolute convergence for ![]() $\unicode[STIX]{x1D70E}>1/d$.
$\unicode[STIX]{x1D70E}>1/d$.