Introduction
We consider a system composed of an electron which interacts with electromagnetic (EM) field. The analysis of the experiments from literature (Bula et al., Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996; Burke et al., Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997; Bamber et al., Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999; Kirsebom et al., Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001) shows that the quantum electrodynamics (QED) effects, including the strong interactions between electron spin magnetic momentum and EM field, occur for electron energies of the order of few tens of GeV or higher, for typical laser beam intensities comprised between 1018 and 1019 W/cm2 (Bula et al., Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996; Burke et al., Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997; Bamber et al., Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999), or for amplitude of the electric field intensity of the order of 1013 V/m (Kirsebom et al., Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001). The solution of the Dirac equation, for this system, is a column matrix having four elements (Dirac, Reference Dirac1958). In this paper, we prove that the system of four partial differential equations, which is equivalent to the Dirac equation, leads to a simple solution, which reveals directly the conditions of the generation of the quantum effects, in good agreement with the above experimental results. Our solution is different of the solutions from literature, for similar interactions (Volkov, Reference Volkov1935; Brown and Kibble, Reference Brown and Kibble1964; Panek et al., Reference Panek, Kaminski and Ehlotzki2002; Boca and Florescu, Reference Boca and Florescu2009; Harvey et al., Reference Harvey, Heinzl and Ilderton2009; Krajewska and Kaminski, Reference Kirsebom and Kaminski2012), the list not being exhaustive.
Our calculation is performed with the aid of a periodicity property of the system composed of an electron in EM field (Popa, Reference Popa2011), which is validated by numerous published experimental data. We have used this periodicity property to simplify the modeling of many applications involving the interaction between electrons and laser beams. For instance, we proved that this property leads to new polarization effects of the radiation generated by the collision between laser beams at arbitrary angles and relativistic electron beams (REBs) (Popa, Reference Popa2012). This property can be used to calculate the radiation damping parameters in the interaction between very intense laser beams and REBs (Popa, Reference Popa2014a). We have presented a lot of other applications of this property in the books Popa (Reference Popa2014b and Reference Popa2014c).
The paper is structured as follows. The section Initial data presents initial data necessary for our analysis, namely initial hypotheses related to the system composed of electron in an EM field and the Dirac equation, written for this system. In the section Solution of the system equivalent to the Dirac equation and its verification, we solve the system of equations equivalent to the Dirac equation in the laboratory frame of reference and give a verification of its solution. The section Solution of the system of equations in the rest frame of the relativistic electron presents the solution of the system of equations in the rest frame of reference of relativistic electrons, for interactions between laser beams and REBs. In the section Discussion of our solution in the light of experimental data from literature, we discuss our theoretical results in the light of experimental data from literature.
The equations are written in the International System (IS).
Initial data
Initial hypotheses
We analyze a system composed of a very intense EM field that interacts with an electron. We consider the following initial hypotheses:
(h1) We consider that the EM field is plane, elliptically polarized. In a Cartesian system of coordinates, the intensity of the electric field and of the magnetic induction vector, denoted, respectively, by 
$\overline E _{\rm L}$ and 
$\overline B _{\rm L}$, are polarized in the plane xy, while the wave vector, denoted by 
$\overline k _{\rm L}$, is parallel to the axis oz. The expression of the electric field is
$$\overline E _{\rm L} = E_{{\rm M1}}\cos \,{\rm \eta} \overline i + E_{{\rm M2}}\sin \,{\rm \eta} \overline j $$with
$${\rm \eta} = {\rm \omega} _{\rm L}t - \vert {{\overline k}_{\rm L}} \vert z + {\rm \eta} _i\;\hbox{and}\;\vert {{\overline k}_{\rm L}} \vert c = {\rm \omega} _{\rm L}$$where 
$\overline i $, 
$\overline j $, and 
$\overline k $ are versors of the ox, oy, and oz-axes, E M1, E M2 are the amplitudes of the electric field oscillations in the ox and oy directions, ωL is the angular frequency of the laser EM field, c is the light velocity, ηi is an arbitrary initial phase and t is the time in the xyz system in which the motion of the electron is studied.
From the properties of the EM field, it follows that the corresponding magnetic induction vector is
$$\overline B _{\rm L} = - B_{{\rm M2}}\sin \,{\rm \eta} \overline i + B_{{\rm M1}}\cos \,{\rm \eta} \overline j $$with
$$E_{{\rm M1}} = cB_{{\rm M1}},\;E_{{\rm M2}} = cB_{{\rm M2}}\;\hbox{and}\;c\overline B _{\rm L} = \overline k \times \overline E _{\rm L}$$where B M1 and B M2 are the amplitudes of the magnetic field oscillations in the oy and ox directions.
(h2) The electric potential of the field is constant. Since the magnetic potential vector of the field, denoted by 
$\overline A _{\rm L}$, results from the relation 
$\overline E _{\rm L} = - \partial \overline A _{\rm L}/\partial t$, we obtain from (1)
$$\overline A _{\rm L} = - A_{{\rm M1}}\sin \,{\rm \eta} \overline i + A_{{\rm M2}}\cos \,{\rm \eta} \overline {\rm j} $$with
$$A_{{\rm M1}} = \displaystyle{{E_{{\rm M1}}} \over {{\rm \omega} _{\rm L}}}\;\hbox{and}\;A_{{\rm M2}} = \displaystyle{{E_{{\rm M2}}} \over {{\rm \omega} _{\rm L}}}$$where A M1 and A M2 are the amplitudes of the magnetic potential vector oscillations in the ox and oy directions.
We note by a 1 and a 2 the relativistic parameters and have:
$$a_1 = \displaystyle{{eE_{{\rm M1}}} \over {mc{\rm \omega} _{\rm L}}}\;\hbox{and}\;a_2 = \displaystyle{{eE_{{\rm M2}}} \over {mc{\rm \omega} _{\rm L}}}$$Dirac equation, written in the laboratory frame system
We write the Dirac equation when the EM field is described by Eqs. (1)–(6). In virtue of hypothesis (h2), we write the Dirac equation [see Dirac (Reference Dirac1958), page 257] using our notations, in IS, as follows:
$$\lsqb {{\widehat{\,p}}_0 - {\rm \rho}_1({\rm \sigma}, \widehat{\,p} + e{\overline A}_{\rm L}) - {\rm \rho}_3mc} \rsqb {\rm \psi} = 0$$where
$$\eqalign{ & \widehat{\,p}_0 = \displaystyle{{i\hbar} \over c}\displaystyle{\partial \over {\partial t}},\;\widehat{\,p}_x = - i\hbar \displaystyle{\partial \over {\partial x}},\;\widehat{\,p}_y = - i\hbar \displaystyle{\partial \over {\partial y}}\ \ \hbox{and}\; \cr & \widehat{\,p}_z = - i\hbar \displaystyle{\partial \over {\partial z}}$$e is the absolute value of the electron charge, ψ is the column matrix of the wave function, having four elements, and σ 1, σ 2, σ 3, ρ1, ρ2, and ρ3 are the matrix operators which were been used by Dirac in his equation. These matrices are as follows:
$$\eqalign{& {\rm \sigma} _1 = \left( {\matrix{ 0 & 1 & 0 & 0 \cr 1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 1 \cr 0 & 0 & 1 & 0 \cr}} \right), \quad {\rm \sigma} _2 = \left( {\matrix{ 0 & { - i} & 0 & 0 \cr i & 0 & 0 & 0 \cr 0 & 0 & 0 & { - i} \cr 0 & 0 & i & 0 \cr}} \right), \cr & \quad {\rm \sigma} _3 = \left( {\matrix{ 1 & 0 & 0 & 0 \cr 0 & { - 1} & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & { - 1} \cr}} \right)} $$and
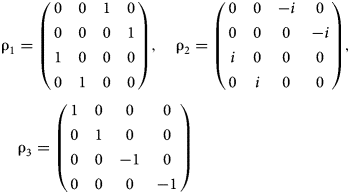$$\eqalign{& {\rm \rho} _1 = \left( {\matrix{ 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \cr 1 & 0 & 0 & 0 \cr 0 & 1 & 0 & 0 \cr}} \right), \quad {\rm \rho} _2 = \left( {\matrix{ 0 & 0 & { - i} & 0 \cr 0 & 0 & 0 & { - i} \cr i & 0 & 0 & 0 \cr 0 & i & 0 & 0 \cr}} \right), \cr & \quad {\rm \rho} _3 = \left( {\matrix{ 1 & 0 & 0 & 0 \cr 0 & 1 & 0 & 0 \cr 0 & 0 & { - 1} & 0 \cr 0 & 0 & 0 & { - 1} \cr}} \right)} $$In agreement with the Dirac's notations, we have
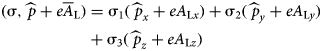$$\eqalignb{& ({\rm \sigma}, \widehat{\,p} + e\overline A _{\rm L}) = {\rm \sigma} _1 (\hskip1pt \widehat{\,p}_x + eA_{{\rm L}x}) + {\rm \sigma} _2(\hskip1pt \widehat{\,p}_y + eA_{{\rm L}y}) \cr & \qquad \qquad \quad \, + {\rm \sigma} _3(\hskip1pt \widehat{\,p}_z + eA_{{\rm L}z})} $$Dirac has multiplied the relation (8) by the following factor
$$\widehat{\,p}_0 + {\rm \rho} _1({\rm \sigma}, \widehat{\,p} + e\overline A _{\rm L}) + {\rm \rho} _3mc$$on the left, and obtained, after a mathematical processing, the following relation [see Dirac (Reference Dirac1958), page 265]:
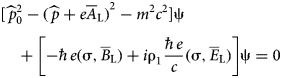$$\eqalign{& \lsqb {\widehat{\,p}_0^2 - {(\widehat{\,p} + e{\overline A}_{\rm L})}^2 - m^2c^2} \rsqb {\rm \psi} \cr & \quad + \left[ { - \hbar e({\rm \sigma}, {\overline B}_{\rm L}) + i{\rm \rho}_1\displaystyle{{\hbar e} \over c}({\rm \sigma}, {\overline E}_{\rm L})} \right]{\rm \psi} = 0} $$Taking into account the relations (1), (3), and (9), Eq. (12) becomes
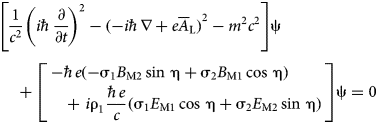$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]{\rm \psi} \cr & \quad + \left[ \matrix{ - \hbar e( - {\rm \sigma}_1B_{{\rm M2}}\sin \,{\rm \eta} + {\rm \sigma}_2B_{{\rm M1}}\cos \,{\rm \eta} ) \hfill \cr \quad + \ i{\rm \rho}_1\displaystyle{{\hbar e} \over c}({\rm \sigma}_1E_{{\rm M1}}\cos \,{\rm \eta} + {\rm \sigma}_2E_{{\rm M2}}\sin \,{\rm \eta} ) \hfill} \right]{\rm \psi} = 0} $$which can be written, with the aid of (4), as follows:
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]{\rm \psi} \cr & \quad + \displaystyle{{\hbar e} \over c}( - {\rm \sigma} _2 + i{\rm \rho} _1{\rm \sigma} _1)E_{{\rm M1}}\cos \,{\rm \eta} \cdot {\rm \psi} \cr & \quad + \displaystyle{{\hbar e} \over c}({\rm \sigma} _1 + i{\rm \rho} _1{\rm \sigma} _2)E_{{\rm M2}}\sin \,{\rm \eta} \cdot {\rm \psi} = 0} $$We consider the above matrices σ 1, σ 2, and ρ1. A simple calculation leads to the expressions of the matrices which enter in Eq. (14):
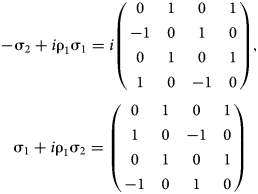$$\eqalign{& - \! {\rm \sigma} _2 + i{\rm \rho} _1{\rm \sigma} _1 = i\left( {\matrix{ 0 & 1 & 0 & 1 \cr { - 1} & 0 & 1 & 0 \cr 0 & 1 & 0 & 1 \cr 1 & 0 & { - 1} & 0 \cr}} \right), \cr & \quad {\rm \sigma} _1 + i{\rm \rho} _1{\rm \sigma} _2 = \left( {\matrix{ 0 & 1 & 0 & 1 \cr 1 & 0 & { - 1} & 0 \cr 0 & 1 & 0 & 1 \cr { - 1} & 0 & 1 & 0 \cr}} \right)} $$By introducing the expressions from Eq. (15) into Eq. (14), we obtain the following form of the Dirac equation
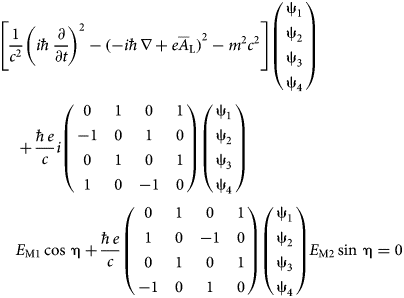$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]\left( {\matrix{ {{\rm \psi}_1} \cr {{\rm \psi}_2} \cr {{\rm \psi}_3} \cr {{\rm \psi}_4} \cr}} \right) \cr & \quad + \displaystyle{{\hbar e} \over c}i\left( {\matrix{ 0 & 1 & 0 & 1 \cr { - 1} & 0 & 1 & 0 \cr 0 & 1 & 0 & 1 \cr 1 & 0 & { - 1} & 0 \cr}} \right)\left( {\matrix{ {{\rm \psi}_1} \cr {{\rm \psi}_2} \cr {{\rm \psi}_3} \cr {{\rm \psi}_4} \cr}} \right) \cr & \quad E_{{\rm M1}}\cos \,{\rm \eta} + \displaystyle{{\hbar e} \over c}\left( {\matrix{ 0 & 1 & 0 & 1 \cr 1 & 0 & { - 1} & 0 \cr 0 & 1 & 0 & 1 \cr { - 1} & 0 & 1 & 0 \cr}} \right)\left( {\matrix{ {{\rm \psi}_1} \cr {{\rm \psi}_2} \cr {{\rm \psi}_3} \cr {{\rm \psi}_4} \cr}} \right)E_{{\rm M2}}\sin \,{\rm \eta} = 0} $$which can be written as follows:
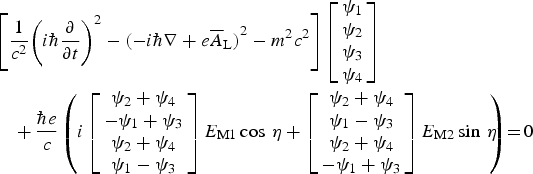$$\! \!\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]\left[ {\matrix{ {{\rm \psi}_1} \cr {{\rm \psi}_2} \cr {{\rm \psi}_3} \cr {{\rm \psi}_4} \cr}} \right] \cr & \quad + \displaystyle{{\hbar e} \over c}\left( {i\left[ {\matrix{ {{\rm \psi}_2 + {\rm \psi}_4} \cr { - {\rm \psi}_1 + {\rm \psi}_3} \cr {{\rm \psi}_2 + {\rm \psi}_4} \cr {{\rm \psi}_1 - {\rm \psi}_3} \cr}} \right]E_{{\rm M1}}\cos \,{\rm \eta} + \left[ {\matrix{ {{\rm \psi}_2 + {\rm \psi}_4} \cr {{\rm \psi}_1 - {\rm \psi}_3} \cr {{\rm \psi}_2 + {\rm \psi}_4} \cr { - {\rm \psi}_1 + {\rm \psi}_3} \cr}} \right]E_{{\rm M2}}\sin \,{\rm \eta}} \!\! \right ) \! = \! 0} $$Solution of the system equivalent to the Dirac equation and its verification
Solution of the system
Written in terms of the components ψ 1, …, ψ 4 of ψ, the Dirac equation, given by (16), is equivalent to the following system of four equations with four unknown:
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]{\rm \psi} _1 \cr & \quad + \displaystyle{{\hbar e} \over c}({\rm \psi} _2 + {\rm \psi} _4)(iE_{{\rm M1}}\cos \,{\rm \eta} + E_{{\rm M2}}\sin \,{\rm \eta} ) = 0} $$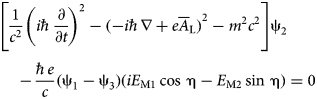
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]{\rm \psi} _2 \cr & \quad - \displaystyle{{\hbar e} \over c}({\rm \psi} _1 - {\rm \psi} _3)(iE_{{\rm M1}}\cos \,{\rm \eta} - E_{{\rm M2}}\sin \,{\rm \eta} ) = 0} $$
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]{\rm \psi} _3 \cr & \quad + \displaystyle{{\hbar e} \over c}({\rm \psi} _2 + {\rm \psi} _4)(iE_{{\rm M1}}\cos \,{\rm \eta} + E_{{\rm M2}}\sin \,{\rm \eta} ) = 0} $$
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {\lpar { - i\hbar \nabla + e{\overline A}_{\rm L}} \rpar }^2 - m^2c^2} \right]{\rm \psi} _4 \cr & \quad + \displaystyle{{\hbar e} \over c}\lpar {{\rm \psi}_1 - {\rm \psi}_3} \rpar \lpar {iE_{{\rm M1}}\cos \,{\rm \eta} - E_{{\rm M2}}\sin \,{\rm \eta}} \rpar = 0} $$We observe that the expressions from square brackets in Eqs. (17)–(20) are identical to the operator from the Klein–Gordon equation, divided by − c 2 (Messiah, Reference Messiah1962), and we have:
$$\left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]{\rm \psi} _{{\rm KG}} = 0$$where ψ KG is the solution of the Klein–Gordon equation.
Supposing that F j(η), with j = 1, 2, 3, 4, are functions of η, and taking into account the relations (2), (5), and 
$\vert {{\overline k}_{\rm L}} \vert c = {\rm \omega} _{\rm L}$, we can easily obtain 
$\nabla \lsqb {e{\overline A}_{\rm L}F_j({\rm \eta} )} \rsqb = 0$, 
$e\overline A _{\rm L}\nabla F_j({\rm \eta} ) = 0$ and 
$[(1/c^2){\rm }(i\hbar \partial /\partial t)^2 - ( - i\hbar \nabla )^2]F_j(\eta ) = 0$. Taking into account these relations, together with (7) and (21), we obtain the following relation:
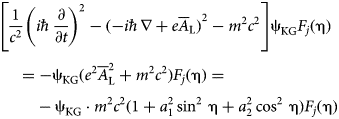$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 - {( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - m^2c^2} \right]{\rm \psi} _{{\rm KG}}F_j({\rm \eta} ) \cr & {\kern 1pt} \quad = - {\rm \psi} _{{\rm KG}}(e^2\overline A _{\rm L}^2 + m^2c^2)F_j({\rm \eta} ) = \cr & \qquad \, - {\rm \psi} _{{\rm KG}} \cdot m^2c^2(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )F_j({\rm \eta} )} $$In virtue of Eq. (22) we can see easily that the solution of the system (17)–(20) is of the form:
$${\rm \psi} _1 = C{\rm \psi} _{{\rm KG}}\lsqb {1 + F_1({\rm \eta} )} \rsqb $$
$${\rm \psi} _2 = C{\rm \psi} _{{\rm KG}}\lsqb {1 + F_2({\rm \eta} )} \rsqb $$
$${\rm \psi} _3 = C{\rm \psi} _{{\rm KG}}\lsqb { - 1 + F_1({\rm \eta} )} \rsqb $$
$${\rm \psi} _4 = C{\rm \psi} _{{\rm KG}}\lsqb {1 - F_2({\rm \eta} )} \rsqb $$where c is a constant of normalization. This solution corresponds to F 1 = F 3 and F 2 = F 4.
We introduce the functions from Eqs. (23) to (26) in Eqs. (17)–(20) and, with the aid of Eq. (22), we have:
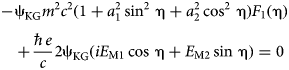$$\eqalign{& - \! {\rm \psi} _{{\rm KG}}m^2c^2(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )F_1({\rm \eta} ) \cr & \quad + \displaystyle{{\hbar e} \over c}2{\rm \psi} _{{\rm KG}}(iE_{{\rm M1}}\cos \,{\rm \eta} + E_{{\rm M2}}\sin \,{\rm \eta} ) = 0} $$
$$\eqalign{& - \! {\rm \psi} _{{\rm KG}}m^2c^2(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )F_2({\rm \eta} ) \cr & \quad - \displaystyle{{\hbar e} \over c}2{\rm \psi} _{{\rm KG}}\lpar {iE_{{\rm M1}}\cos \,{\rm \eta} - E_{{\rm M2}}\sin \,{\rm \eta}} \rpar = 0} $$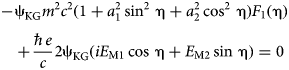
$$\eqalign{& - \! {\rm \psi} _{{\rm KG}}m^2c^2(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )F_1({\rm \eta} ) \cr & \quad + \displaystyle{{\hbar e} \over c}2{\rm \psi} _{{\rm KG}}(iE_{{\rm M1}}\cos \,{\rm \eta} + E_{{\rm M2}}\sin \,{\rm \eta} ) = 0} $$
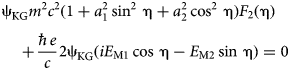$$\eqalign{& {\rm \psi} _{{\rm KG}}m^2c^2(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )F_2({\rm \eta} ) \cr & \quad + \displaystyle{{\hbar e} \over c}2{\rm \psi} _{{\rm KG}}(iE_{{\rm M1}}\cos \,{\rm \eta} - E_{{\rm M2}}\sin \,{\rm \eta} ) = 0} $$We consider also the following relations
$$E_{{\rm 1rms}} = \displaystyle{1 \over {\sqrt 2}} E_{{\rm M1}},\;E_{{\rm 2rms}} = \displaystyle{1 \over {\sqrt 2}} E_{{\rm M2}}$$
$$E_{\rm S} = \displaystyle{{m^2c^3} \over {e\hbar}}, \;Y_{{\rm 1e}} = \displaystyle{{E_{{\rm 1rms}}} \over {E_{\rm S}}}\;\hbox{and}\;Y_{{\rm 2e}} = \displaystyle{{E_{{\rm 2rms}}} \over {E_{\rm S}}}$$where E 1rms and E 2rms are the root mean squares of the components E Lx and E Ly of the electric field, E S is the Schwinger electric field, while Y 1e and Y 2e are parameters entering in QED calculations (Bamber et al., Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999).
The system (27)–(30), together with (31) and (32) lead to the following expressions of the functions F 1 and F 2:
$$F_1 = \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}} $$
$$F_2 = - \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}} $$Introducing the expressions from (33) and (34) into (23)–(26), we obtain:
$${\rm \psi} _1 = C{\rm \psi} _{{\rm KG}}\left[ {1 + \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${\rm \psi} _2 = C{\rm \psi} _{{\rm KG}}\left[ {1 - \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${\rm \psi} _3 = C{\rm \psi} _{{\rm KG}}\left[ { - 1 + \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${\rm \psi} _4 = C{\rm \psi} _{{\rm KG}}\left[ {1 + \displaystyle{{2\sqrt 2 (iY_{1{\rm e}}\cos \,{\rm \eta} - Y_{2{\rm e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$In the paper Popa (Reference Popa2011), at pages 023824–13, and in the book Popa (Reference Popa2014b), at page 26, we proved, without any approximation, that the Klein–Gordon equation is verified by the function
$${\rm \psi} _{{\rm KG}} = \exp \left( {\displaystyle{{iS} \over \hbar}} \right)$$where S is the action function, which is the solution of the relativistic Hamilton–Jacobi equation (Landau and Lifshitz, Reference Landau and Lifshitz1959; Jackson, Reference Jackson1999):
$$c^2(\nabla S + e\overline A _{\rm L})^2 - \left( {\displaystyle{{\partial S} \over {\partial t}}} \right)^2 + \; (mc^2)^2 = 0.$$In Appendix A we give a brief proof that the function ψKG, given by Eq. (39), verifies the Klein–Gordon equation and in Appendix B we calculate the expression of the S function.
With the aid of Eq. (39), the solution of the Dirac equation becomes:
$${\rm \psi} _1 = C\,\exp \left( {\displaystyle{{iS} \over \hbar}} \right)\left[ {1 + \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${\rm \psi} _2 = C\,\exp \left( {\displaystyle{{iS} \over \hbar}} \right)\left[ {1 - \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${\rm \psi} _3 = C\,\exp \left( {\displaystyle{{iS} \over \hbar}} \right)\left[ { - 1 + \displaystyle{{2\sqrt 2 (iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${\rm \psi} _4 = C\,\exp \left( {\displaystyle{{iS} \over \hbar}} \right)\left[ {1 + \displaystyle{{2\sqrt 2 (iY_{1{\rm e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$Verification of the solution
We prove now that the solution represented by Eqs. (41)–(44) verifies the continuity equation from QED. According to Eqs. (1.1.28) and (1.1.29) from Weinberg (Reference Weinberg1995), the continuity equation is given by the following relations:
$$\displaystyle{{\partial {\rm \rho}} \over {\partial t}} + \nabla \cdot \overline J = 0$$with
$${\rm \rho} = \vert {\rm \psi} \vert ^2,\;\overline J = c{\rm \psi} ^ + {\rm \alpha} {\rm \psi} $$where ρ is the probability density, 
$\overline j $ is the probability current density and the components of the matrix α are as follows:
$$\eqalign{& {\rm \alpha} _1 = \left( {\matrix{ 0 & 0 & 0 & 1 \cr 0 & 0 & 1 & 0 \cr 0 & 1 & 0 & 0 \cr 1 & 0 & 0 & 0 \cr}} \right), \quad {\rm \alpha} _2 = \left( {\matrix{ 0 & 0 & 0 & { - i} \cr 0 & 0 & i & 0 \cr 0 & { - i} & 0 & 0 \cr i & 0 & 0 & 0 \cr}} \right), \cr & \quad {\rm \alpha} _3 = \left( {\matrix{ 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & { - 1} \cr 1 & 0 & 0 & 0 \cr 0 & { - 1} & 0 & 0 \cr}} \right)} $$Using the above relations, we calculate the expressions of the probability density ρ, and of the components of the current probability, J x, J y, and J z and obtain:
$$\eqalign{{\rm \rho} & = \left( {\matrix{ {{\rm \psi}_1^{^\ast}} & {{\rm \psi}_2^{^\ast}} & {{\rm \psi}_3^{^\ast}} & {{\rm \psi}_4^{^\ast}} \cr}} \right)\left( {\matrix{ {{\rm \psi}_1} \cr {{\rm \psi}_2} \cr {{\rm \psi}_3} \cr {{\rm \psi}_4} \cr}} \right) \cr & = {\rm \psi} _1^{^\ast} {\rm \psi} _1 + {\rm \psi} _2^{^\ast} {\rm \psi} _2 + {\rm \psi} _3^{^\ast} {\rm \psi} _3 + {\rm \psi} _4^{^\ast} {\rm \psi} _4} $$
$$\eqalignb{ J_x = c{\rm \psi} ^ + {\rm \alpha} _1{\rm \psi} \cr & \ \ = c\left( {\matrix{ {{\rm \psi}_1^{^\ast}} {{\rm \psi}_2^{^\ast}} & {{\rm \psi}_3^{^\ast}} & {{\rm \psi}_4^{^\ast}} \cr}} \right) \left( {\matrix{ 0 & 0 & 0 & 1 \cr 0 & 0 & 1 & 0 \cr 0 & 1 & 0 & 0 \cr 1 & 0 & 0 & 0 \cr}} \right)\left( {\matrix{ {{\rm \psi}_1} \cr {{\rm \psi}_2} \cr {{\rm \psi}_3} \cr {{\rm \psi}_4} \cr}} \right) \cr & \ \ = c\lpar {{\rm \psi}_1^{^\ast} {\rm \psi}_4 + {\rm \psi}_2^{^\ast} {\rm \psi}_3 + {\rm \psi}_3^{^\ast} {\rm \psi}_2 + {\rm \psi}_4^{^\ast} {\rm \psi}_1} \rpar } $$In a similar manner, we obtain
$$J_y = c{\rm \psi} ^ + {\rm \alpha} _2{\rm \psi} = ci( - {\rm \psi} _1^{^\ast} {\rm \psi} _4 + {\rm \psi} _2^{^\ast} {\rm \psi} _3 - {\rm \psi} _3^{^\ast} {\rm \psi} _2 + {\rm \psi} _4^{^\ast} {\rm \psi} _1)$$
$$J_z = c{\rm \psi} ^ + {\rm \alpha} _3{\rm \psi} = c({\rm \psi} _1^{\ast} {\rm \psi} _3 - {\rm \psi} _2^{\ast} {\rm \psi} _4 + {\rm \psi} _3^{\ast} {\rm \psi} _1 - {\rm \psi} _4^{\ast} {\rm \psi} _2)$$Noting
$$K = \displaystyle{{2\sqrt 2} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}} $$we introduce the components of the wave function, given by Eqs. (41)–(44) in Eq. (47) and obtain:
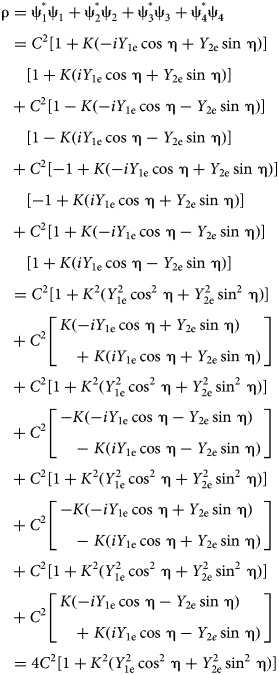$$\openup4pt\eqalign{{\rm \rho} & = {\rm \psi} _1^{^\ast} {\rm \psi} _1 + {\rm \psi} _2^{^\ast} {\rm \psi} _2 + {\rm \psi} _3^{^\ast} {\rm \psi} _3 + {\rm \psi} _4^{^\ast} {\rm \psi} _4 \cr & = C^2\lsqb {1 + K( - iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & \quad \lsqb {1 + K(iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & + C^2\lsqb {1 - K( - iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & \quad \lsqb {1 - K(iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & + C^2\lsqb { - 1 + K( - iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & \quad \lsqb { - 1 + K(iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & + C^2\lsqb {1 + K( - iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & \quad \lsqb {1 + K(iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} )} \rsqb \cr & = C^2\lsqb {1 + K^2(Y_{{\rm 1e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{{\rm 2e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} )} \rsqb \cr & + C^2\left[ \matrix{K( - iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} ) \hfill \cr \quad + \; K(iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{{\rm 2e}}\sin \,{\rm \eta} ) \hfill} \right] \cr & + C^2\lsqb {1 + K^2(Y_{{\rm 1e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{{\rm 2e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} )} \rsqb \cr & + C^2\left[ \matrix{ - K( - iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} ) \hfill \cr \quad - \; K(iY_{{\rm 1e}}\cos \,{\rm \eta} - Y_{{\rm 2e}}\sin \,{\rm \eta} ) \hfill} \right] \cr & + C^2\lsqb {1 + K^2(Y_{{\rm 1e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{{\rm 2e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} )} \rsqb \cr & + C^2\left[ \matrix{ - K( - iY_{{\rm 1e}}\cos \,{\rm \eta} + Y_{2{\rm e}}\sin \,{\rm \eta} ) \hfill \cr \quad - \; K(iY_{1{\rm e}}\cos \,{\rm \eta} + Y_{2{\rm e}}\sin \,{\rm \eta} ) \hfill} \right] \cr & + C^2\lsqb {1 + K^2(Y_{1{\rm e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{2{\rm e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} )} \rsqb \cr & + C^2\left[ \matrix{K( - iY_{1{\rm e}}\cos \,{\rm \eta} - Y_{2{\rm e}}\sin \,{\rm \eta} ) \hfill \cr \quad + \; K(iY_{1{\rm e}}\cos \,{\rm \eta} - Y_{2e}\sin \,{\rm \eta} ) \hfill} \right] \cr & = 4C^2\lsqb {1 + K^2(Y_{1{\rm e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{2{\rm e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} )} \rsqb } $$which can be written as
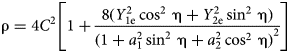$${\rm \rho} = 4C^2\left[ {1 + \displaystyle{{8(Y_{1{\rm e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{2{\rm e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} )} \over {{(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )}^2}}} \right]$$Similarly, we introduce the expressions of the components of the wave function given by Eqs. (41)–(44) in Eqs. (48)–(50) and, by simple calculations, obtain
$$J_x = 0,\quad J_y = 0$$
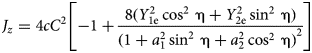$$J_z = 4cC^2\left[ { - 1 + \displaystyle{{8(Y_{1{\rm e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{2{\rm e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} )} \over {{(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )}^2}}} \right]$$We observe that ρ and J z are periodic functions of only one variable, which is η. From Eqs. (53)–(55) we have:
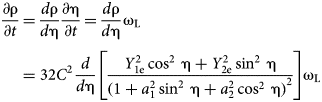$$\eqalign{ \displaystyle{{\partial {\rm \rho}} \over {\partial t}} & = \displaystyle{{d{\rm \rho}} \over {d{\rm \eta}}} \displaystyle{{\partial {\rm \eta}} \over {\partial t}} = \displaystyle{{d{\rm \rho}} \over {d{\rm \eta}}} {\rm \omega} _{\rm L} \cr & = 32C^2\displaystyle{d \over {d{\rm \eta}}} \left[ {\displaystyle{{Y_{1{\rm e}}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{2{\rm e}}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta}} \over {{(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )}^2}}} \right]{\rm \omega} _{\rm L}} $$
$$\eqalign{& \nabla \overline J = \displaystyle{{\partial J_z} \over {\partial z}} = \displaystyle{{dJ_z} \over {d{\rm \eta}}} \displaystyle{{\partial {\rm \eta}} \over {\partial z}} = \displaystyle{{dJ_z} \over {d{\rm \eta}}} \lpar { - \vert {{\overline k}_{\rm L}} \vert } \rpar \cr & \quad = 32cC^2\displaystyle{d \over {d{\rm \eta}}} \left[ {\displaystyle{{Y_{1e}^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} + Y_{2e}^2 \mathop {\sin} \nolimits^2 \,{\rm \eta}} \over {{(1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta} )}^2}}} \right]\lpar { - \vert {{\overline k}_{\rm L}} \vert } \rpar } $$ We see that, in virtue of relations (56), (57), and 
$\vert {{\overline k}_{\rm L}} \vert c = {\rm \omega} _{\rm L}$, the continuity Eq. (45) is verified.
Solution of the system of equations in the rest frame of the relativistic electron
The analysis of the experimental data from literature shows that the quantum effects are significant in interactions between very intense laser beams and REBs having energies of the order of few tens of GeV (Bula et al., Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996; Burke et al., Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997; Bamber et al., Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999; Kirsebom et al., Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001). For this regime, it is convenient to study the interaction between EM field and electron in the rest reference frame of the electron.
We consider an interaction between the laser beam and a REB which collide head-on with each other. The initial conditions, written in the laboratory reference system, denoted by S(t, x, y, z), are as follows:
$$ \eqalign{ t = 0,\;\;x = y = z = 0,\;\;v_x = v_y = 0,\;\;v_z = - \vert V_0 \vert \;\hbox{and}\;{\rm \eta} = {\rm \eta} _i$$where v x, v y, and v z are the components of the electron velocity in the system S.
The relations (1)–(6) remain valid in the S system, and they are used to calculate the components of the EM field in the inertial system of reference denoted by S′(t′, x′, y′, z′), in which the initial velocity of the electron is zero. The Cartesian axes in the systems S(t, x, y, z) and S′(t′, x′, y′, z′) are parallel. In our case, the S′ system moves with velocity −|V 0| along the oz-axis.
Since the phase of the EM field is a relativistic invariant (Jackson, Reference Jackson1999), the initial conditions in the inertial system S′ are as follows:
$$\eqalign{\! {t}^{\prime} = 0,\;\;{x}^{\prime} = {y}^{\prime} = {z}^{\prime} = 0,\;\;{v}^{\prime}_{{x}^{\prime}} = {v}^{\prime}_{{y}^{\prime}} = {v}^{\prime}_{{z}^{\prime}} = 0\;\;\hbox{and}\;\;{\rm \eta} = {{\rm \eta}} ^{\prime} = {\rm \eta} _i$$where 
${v}^{\prime}_{{x}^{\prime}}$, 
${v}^{\prime}_{{y}^{\prime}}$ and 
${v}^{\prime}_{{z}^{\prime}}$ are the components of the electron velocity in S′.
We calculate now the parameters of the laser field, denoted by 
$\overline {E{\rm ^{\prime}}} _{\rm L}$, 
$\overline B {\rm ^{\prime}}_{\rm L}$, 
$\overline k {\rm ^{\prime}}_{\rm L}$, and 
${{\rm \omega}} ^{\prime}_{\rm L}$, in the S′ system. We denote the four-dimensional wave vectors by (ωL/c, k Lx, k Ly, k Lz) and 
$({{\rm \omega}} ^{\prime}_{\rm L}/c,{k}^{\prime}_{{\rm L}{x}^{\prime}},{k}^{\prime}_{{\rm L}{y}^{\prime}},{k}^{\prime}_{{\rm L}{z}^{\prime}})$ in the systems S and S′, respectively.
In virtue of the Lorentz transformation, given by relations (11.22) of Jackson (Reference Jackson1999), we have
$$\displaystyle{{{{{\rm \omega}} ^{\prime}}_{\rm L}} \over c} = \displaystyle{{{\rm \omega} _{\rm L}} \over c}{\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar $$
$${k}^{\prime}_{{\rm L}{z}^{\prime}} = \vert {{\overline {k{\rm^{\prime}}}}_{\rm L}} \vert = \vert {{\overline k}_{\rm L}} \vert {\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar $$
$${k}^{\prime}_{{\rm L}{x}^{\prime}} = k_{{\rm L}x} = {k}^{\prime}_{{\rm L}{y}^{\prime}} = k_{{\rm L}y} = 0$$where
$$\overline {\rm \beta} _0 = - \displaystyle{{ \vert {\overline V} _0 \vert} \over c}\overline k \;\hbox{and}\;{\rm \gamma} _0 = \lpar {1 - \overline {\rm \beta}_0^2} \rpar ^{ - \textstyle{1 \over 2}}$$The phase of the EM wave is
$${\rm \eta} = {\rm \omega} _{\rm L}t - \overline k _{\rm L} \cdot \overline r + {\rm \eta} _i = {{\rm \omega}} ^{\prime}_{\rm L}{t}^{\prime} - \overline k {\rm ^{\prime}}_L \cdot \overline r {\rm ^{\prime}} + {\rm \eta} _i = {{\rm \eta}} ^{\prime}$$where 
$\overline r $ and 
$\overline r {\rm ^{\prime}}$ are the positions vectors of the electron in the two systems.
We write equations (11.149) from Jackson (Reference Jackson1999) in IS and with the aid of Eqs. (4) and (63), we obtain the following expressions for the components of the EM field in the S′ system:
$$\overline {E{\rm ^{\prime}}} _{\rm L} = {\rm \gamma} _0\lpar {{\overline E}_{\rm L} + {\overline {\rm \beta}}_0 \times c{\overline B}_{\rm L}} \rpar = {\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar \overline E _{\rm L}$$
$$\overline B {\rm ^{\prime}}_{\rm L} = {\rm \gamma} _0\lpar {{\overline B}_{\rm L} - {\overline {\rm \beta}}_0 \times {\overline E}_{\rm L}/c} \rpar = {\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar \overline B _{\rm L}$$where the relations between the amplitudes of the components of the electric field, in the systems S and S′, are as follows
$${E}^{\prime}_{{\rm M1}} = {\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar E_{{\rm M1}}\;\hbox{and}\;{E}^{\prime}_{{\rm M2}} = {\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar E_{{\rm M2}}$$In virtue of the relations (60) and (67), it follows that the relativistic parameters are relativistic invariants because we have
$${a}^{\prime}_1 = \displaystyle{{e{{E}^{\prime}}_{{\rm M1}}} \over {mc{{{\rm \omega}} ^{\prime}}_{\rm L}}} = \displaystyle{{eE_{{\rm M1}}} \over {mc{\rm \omega} _{\rm L}}} = a_1\;\hbox{and}\;{a}^{\prime}_2 = \displaystyle{{e{{E}^{\prime}}_{{\rm M2}}} \over {mc{{{\rm \omega}} ^{\prime}}_{\rm L}}} = \displaystyle{{eE_{{\rm M2}}} \over {mc{\rm \omega} _{\rm L}}} = a_2$$According to the theory presented in Section 68 from Dirac (Reference Dirac1958), the Dirac equation has the same form in the inertial systems S and S′, and the Eqs. (8) and (12) from pages 257 and 265 of Dirac (Reference Dirac1958), can be written in the system S′, as follows:
$$\lsqb {{\widehat{{{\,p}^{\prime}}}}_{{0}^{\prime}} - {\rm \rho}_1\lpar {{\rm \sigma}, \widehat{{{\,p}^{\prime}}} + e{\overline A}^{\prime}_{\rm L}} \rpar - {\rm \rho}_3mc} \rsqb {{\rm \psi}} ^{\prime} = 0$$and
$$\eqalign{& \lsqb {{\lpar {\widehat{\,p}{\rm^{\prime}}_{{0}^{\prime}}} \rpar }^2 - {\lpar {{\rm \sigma}, \widehat{\,p}{\rm^{\prime}} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar }^2 - m^2c^2} \rsqb {{\rm \psi}} ^{\prime} \cr & \quad + \left[ { - \hbar e\lpar {{\rm \sigma}, \overline B {\rm^{\prime}}_{\rm L}} \rpar + i{\rm \rho}_1\displaystyle{{\hbar e} \over c}\lpar {{\rm \sigma}, \overline E {\rm^{\prime}}_{\rm L}} \rpar } \right]{{\rm \psi}} ^{\prime} = 0} $$where
$$\eqalign{& \lpar {{\rm \sigma}, \widehat{\,p}{\rm^{\prime}} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar = {\rm \sigma} _1\lpar {\widehat{\,p}{\rm^{\prime}}_{{x}^{\prime}} + e{{A}^{\prime}}_{{\rm L}{x}^{\prime}}} \rpar \cr & \quad + {\rm \sigma} _2\lpar {\widehat{\,p}{\rm^{\prime}}_{{y}^{\prime}} + e{{A}^{\prime}}_{{\rm L}{y}^{\prime}}} \rpar + {\rm \sigma} _3\lpar {\widehat{\,p}{\rm^{\prime}}_{{z}^{\prime}} + e{{A}^{\prime}}_{{\rm L}{z}^{\prime}}} \rpar } $$
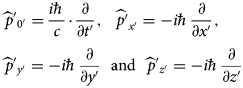$$\eqalign{& \widehat{\,p}{\rm ^{\prime}}_{{0}^{\prime}} = \displaystyle{{i\hbar} \over c} \cdot \displaystyle{\partial \over {\partial {t}^{\prime}}},\;\;\widehat{{\,p{\rm ^{\prime}}}}_{{x}^{\prime}} = - i\hbar \displaystyle{\partial \over {\partial {x}^{\prime}}}, \cr & \widehat{\,p}{\rm ^{\prime}}_{{y}^{\prime}} = - i\hbar \displaystyle{\partial \over {\partial {y}^{\prime}}}\;\;\hbox{and}\;\;\widehat{\,p}{\rm ^{\prime}}_{{z}^{\prime}} = - i\hbar \displaystyle{\partial \over {\partial {z}^{\prime}}}} $$and the matrices ρ and σ have the same form in the systems S and S′.
An identical treatment, as that presented in the subsection Solution of the system, leads to the following system, which is equivalent to the Dirac equation:
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial {t}^{\prime}}}} \right)}^2 - {\lpar { - i\hbar {\nabla}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar }^2 - m^2c^2} \right]{{{\rm \psi}} ^{\prime}}_1 \cr & \quad + \displaystyle{{\hbar e} \over c}({{{\rm \psi}} ^{\prime}}_2 + {{{\rm \psi}} ^{\prime}}_4)(i{{E}^{\prime}}_{{\rm M1}}\cos \,{{\rm \eta}} ^{\prime} + {{E}^{\prime}}_{{\rm M2}}\sin \,{{\rm \eta}} ^{\prime}) = 0} $$
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial {t}^{\prime}}}} \right)}^2 - {\lpar { - i\hbar {\nabla}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar }^2 - m^2c^2} \right]{{{\rm \psi}} ^{\prime}}_2 \cr & \quad - \displaystyle{{\hbar e} \over c}({{{\rm \psi}} ^{\prime}}_1 - {{{\rm \psi}} ^{\prime}}_3)(i{{E}^{\prime}}_{{\rm M1}}\cos {{\rm \eta}} ^{\prime} - {{E}^{\prime}}_{{\rm M2}}\sin {{\rm \eta}} ^{\prime}) = 0} $$
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial {t}^{\prime}}}} \right)}^2 - {\lpar { - i\hbar {\nabla}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar }^2 - m^2c^2} \right]{{{\rm \psi}} ^{\prime}}_3 \cr & \quad + \displaystyle{{\hbar e} \over c}({{{\rm \psi}} ^{\prime}}_2 + {{{\rm \psi}} ^{\prime}}_4)(i{{E}^{\prime}}_{{\rm M1}}\cos \,{{\rm \eta}} ^{\prime} + {{E}^{\prime}}_{{\rm M2}}\sin \,{{\rm \eta}} ^{\prime}) = 0} $$
$$\eqalign{& \left[ {\displaystyle{1 \over {c^2}}{\left( {i\hbar \displaystyle{\partial \over {\partial {t}^{\prime}}}} \right)}^2 - {\lpar { - i\hbar {\nabla}^{\prime} + e\overline A^{\prime}_{\rm L}} \rpar }^2 - m^2c^2} \right]{{{\rm \psi}} ^{\prime}}_4 \cr & \quad + \displaystyle{{\hbar e} \over c}({{{\rm \psi}} ^{\prime}}_1 - {{{\rm \psi}} ^{\prime}}_3)(i{{E}^{\prime}}_{{\rm M1}}\cos \,{\rm \eta} - {{E}^{\prime}}_{{\rm M2}}\sin \,{\rm \eta} ) = 0} $$where 
${{\rm \psi}} ^{\prime}_1, \ldots, {{\rm \psi}} ^{\prime}_4$ of ψ′ are the four unknown and the expressions from square brackets in Eqs. (73)–(76) are identical to the operator from the Klein–Gordon equation, divided by − c 2 (Messiah, Reference Messiah1962).
An identical procedure, as that presented in the subsection Solution of the system, leads to the following solution of this system:
$${{\rm \psi}} ^{\prime}_1 = {C}^{\prime}{{\rm \psi}} ^{\prime}_{{\rm KG}}\left[ {1 + \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{1{\rm e}}\cos \,{\rm \eta} + {{Y}^{\prime}}_{2{\rm e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${{\rm \psi}} ^{\prime}_2 = {C}^{\prime}{{\rm \psi}} ^{\prime}_{{\rm KG}}\left[ {1 - \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{{\rm 1e}}\cos \,{\rm \eta} - {{Y}^{\prime}}_{2{\rm e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${{\rm \psi}} ^{\prime}_3 = {C}^{\prime}{{\rm \psi}} ^{\prime}_{{\rm KG}}\left[ { - 1 + \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{{\rm 1e}}\cos \,{\rm \eta} + {{Y}^{\prime}}_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${{\rm \psi}} ^{\prime}_4 = {C}^{\prime}{{\rm \psi}} ^{\prime}_{{\rm KG}}\left[ {1 + \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{{\rm 1e}}\cos \,{\rm \eta} - {{Y}^{\prime}}_{2{\rm e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$where 
${{\rm \psi}} ^{\prime}_{{\rm KG}}$ is the solution of the Klein–Gordon equation, written in the S′ system, C′ is the constant of normalization, and 
${Y}^{\prime}_{{\rm 1e}}$ and 
${Y}^{\prime}_{{\rm 2e}}$ are given by the following relations:
$${Y}^{\prime}_{1{\rm e}} = \displaystyle{{{{E}^{\prime}}_{{\rm 1rms}}} \over {E_{\rm S}}} = \displaystyle{1 \over {\sqrt 2}} \cdot \displaystyle{{{{E}^{\prime}}_{{\rm M1}}} \over {E_{\rm S}}} = \displaystyle{1 \over {\sqrt 2}} \cdot \displaystyle{{{\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar E_{{\rm M1}}} \over {E_{\rm S}}}$$
$${Y}^{\prime}_{{\rm 2e}} = \displaystyle{{{{E}^{\prime}}_{{\rm 2rms}}} \over {E_{\rm S}}} = \displaystyle{1 \over {\sqrt 2}} \cdot \displaystyle{{{{E}^{\prime}}_{{\rm M2}}} \over {E_{\rm S}}} = \displaystyle{1 \over {\sqrt 2}} \cdot \displaystyle{{{\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar E_{{\rm M2}}} \over {E_{\rm S}}}$$In Appendix A we prove that
$${{\rm \psi}} ^{\prime}_{{\rm KG}} = \exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)$$where S′ is the action function, written in the inertial system S′. Introducing this expression in Eqs. (77)–(80), we obtain the following solution of the system of equations in the inertial system S′.
$${{\rm \psi}} ^{\prime}_1 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left[ {1 + \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{{\rm 1e}}\cos \,{\rm \eta} + {{Y}^{\prime}}_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${{\rm \psi}} ^{\prime}_2 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left[ {1 - \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{1{\rm e}}\cos \,{\rm \eta} - {{Y}^{\prime}}_{2{\rm e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${{\rm \psi}} ^{\prime}_3 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left[ { - 1 + \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{{\rm 1e}}\cos \,{\rm \eta} + {{Y}^{\prime}}_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$
$${{\rm \psi}} ^{\prime}_4 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left[ {1 + \displaystyle{{2\sqrt 2 (i{{Y}^{\prime}}_{{\rm 1e}}\cos \,{\rm \eta} - {{Y}^{\prime}}_{{\rm 2e}}\sin \,{\rm \eta} )} \over {1 + a_1^2 \mathop {\sin} \nolimits^2 \,{\rm \eta} + a_2^2 \mathop {\cos} \nolimits^2 \,{\rm \eta}}}} \right]$$We observe that both, the system of equations which is equivalent to Dirac equation, and its solutions, have the same form if they wrote in the S and S′ systems.
Discussion of our solution in the light of experimental data from the literature
In order to simplify the analysis, without loss of generality, we assume in this section that the incident laser field is linearly polarized. That is, its components are
$$\overline E _{\rm L} = E_{\rm M}\cos \,{\rm \eta} \overline i, \;\;\overline B _{\rm L} = B_{\rm M}\cos \,{\rm \eta} \overline j \;\hbox{and}\;\overline A _{\rm L} = - A_{\rm M}\sin \,{\rm \eta} \overline i $$where
$$E_{\rm M} = cB_{\rm M}\;\;\hbox{and}\;\;A_{\rm M} = \displaystyle{{E_{\rm M}} \over {{\rm \omega} _{\rm L}}}$$In this case, the components of the wave function in the system S′ become
$${{\rm \psi}} ^{\prime}_1 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left( {1 + 2\sqrt 2 \cdot i{{Y}^{\prime}}_{\rm e} \cdot \displaystyle{{\cos \,{{\rm \eta}}^{\prime}} \over {1 + a^2\mathop {\sin} \nolimits^2 \,{{\rm \eta}}^{\prime}}}} \right)$$
$${{\rm \psi}} ^{\prime}_2 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left( {1 - 2\sqrt 2 \cdot i{{Y}^{\prime}}_{\rm e} \cdot \displaystyle{{\cos \,{{\rm \eta}}^{\prime}} \over {1 + a^2\mathop {\sin} \nolimits^2 \,{{\rm \eta}}^{\prime}}}} \right)$$
$${{\rm \psi}} ^{\prime}_3 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left( { - 1 + 2\sqrt 2 \cdot i{{Y}^{\prime}}_{\rm e} \cdot \displaystyle{{\cos \,{{\rm \eta}}^{\prime}} \over {1 + a^2\mathop {\sin} \nolimits^2 \,{{\rm \eta}}^{\prime}}}} \right)$$
$${{\rm \psi}} ^{\prime}_4 = {C}^{\prime}\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)\left( {1 + 2\sqrt 2 \cdot i{{Y}^{\prime}}_{\rm e} \cdot \displaystyle{{\cos \,{{\rm \eta}}^{\prime}} \over {1 + a^2\mathop {\sin} \nolimits^2 \,{{\rm \eta}}^{\prime}}}} \right)$$where
$$a = \displaystyle{{eE_{\rm M}} \over {mc{\rm \omega} _{\rm L}}}$$and
$${Y}^{\prime}_{\rm e} = \displaystyle{{{{E}^{\prime}}_{{\rm rms}}} \over {E_{\rm S}}} = \displaystyle{1 \over {\sqrt 2}} \displaystyle{{{{E}^{\prime}}_{\rm M}} \over {E_{\rm S}}} = \displaystyle{1 \over {\sqrt 2}} \displaystyle{{{\rm \gamma} _0\lpar {1 + \vert {{\overline {\rm \beta}}_0} \vert } \rpar E_{\rm M}} \over {E_{\rm S}}}$$To our knowledge, the only experiments showing QED effects in the literature involve interactions between very intense EM beams and REB. In this respect, we confine ourselves to discussing the experimental data from Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996); Burke et al. (Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997); Bamber et al. (Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999); and Kirsebom et al. (Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001). In all these cases the calculations are made in the rest frame of the electron.
Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996) and Bamber et al. (Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999) present experimental data for nonlinear Compton scattering of Nd:glass laser beams at 1.054 and 0.527 μm wavelengths on relativistic electron bunches. The peak laser intensities and electron energies are I p = 1018 W/cm2 and E e = 46.6 GeV in Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996) and I p = 0.5 × 1018 W/cm2 and E e = 46.6 and 49.1 GeV in Bamber et al. (Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999). The values of the QED parameter 
${Y}^{\prime}_{\rm e}$ for which the nonlinear Compton scattering effect takes place, are, respectively, 0.17 for λL = 1.054 μm and 0.27 for λL = 0.527 μm (Bamber et al., Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999). In other words, the quantum effects are evidenced experimentally when the parameter 
${Y}^{\prime}_{\rm e}$, given by Eq. (95), has values of the order of few tenths. This happens when the root mean square of the electric field in the system S′ is of the order of few tenths of Schwinger field.
Burke et al. (Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997) present an experiment in which electron–positron pairs are produced at the interaction between a Nd:glass laser beam having I p = 1019 W/cm2 at a wavelength of 0.527 μm, and a 46.6 GeV electron energy. The conditions of generation of quantum effects are roughly similar to those from Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996); Bamber et al. (Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999).
In Kirsebom et al. (Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001) the influence of the electron spin on the energy loss of ultra-relativistic electrons in huge EM fields is shown experimentally. According to Fig. 2 from that paper, the minimum value of the electron energy at which this effect takes place is E e = 35 GeV, when the amplitude of the intensity of the electric field is E M = 1013 V/m. With the aid of the relations γ 0 = E e/(mc 2), 
$\vert {{\overline {\rm \beta} }_0} \vert = (1 - 1/{\rm \gamma} _0^2 )^{1/2} \cong 1$ and 
$Y_{\rm e}^^{\prime} = (2\gamma _0E_{\rm M})/(\sqrt 2 E_{\rm S})$, we obtain γ 0 = 6.85 × 104, and 
${Y}^{\prime}_{\rm e} = 0.734$.
On the other hand, the term 
${Y}^{\prime}_{\rm e}$ can be written as follows:
$${Y}^{\prime}_{\rm e} = \displaystyle{{{{E}^{\prime}}_{{\rm rms}}} \over {E_{\rm S}}} = \displaystyle{{e\hbar c{{B}^{\prime}}_{{\rm rms}}} \over {m^2c^3}} = 2\left( {\displaystyle{{e\hbar} \over {2m}}{{B}^{\prime}}_{{\rm rms}}} \right)\displaystyle{1 \over {mc^2}}$$where the expression in parenthesis is the energy of interaction between electron spin and a magnetic field having an intensity equal to 
${B}^{\prime}_{{\rm rms}}$. In virtue of the experimental data presented in Kirsebom et al. (Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001), the interactions between the electron spin and magnetic field are significant when E e > 35 GeV and 
${Y}^{\prime}_{\rm e}$ has values of the order of a few tenths of unity. This happens when the value of the energy of interaction between the electron spin and magnetic field is of the order of a few tenths of the value of the rest energy of the electron.
In conclusion, according to the experiments from Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996); Burke et al. (Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997); Bamber et al. (Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999); Kirsebom et al. (Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001), the QED effects are evidenced when the electron energy, laser beam intensity and the amplitude of the intensity of the electric field have, respectively, values of the order E e = 40 GeV, I p = 1018…1019 W/cm2 and E M = 1013 V/m, while the parameter 
${Y}^{\prime}_{\rm e}$ has values of a few tenths of unity.
We call “quantum terms” the terms appearing in the expressions of the components of the wave function, which contain the parameter 
${Y}^{\prime}_{\rm e}$. We observe that when the quantum terms are negligible, the components of the wave function in Eqs. (90)–(93) reduce to the wave function associated with classical motion, namely 
${C}^{\prime}\exp \,i{S}^{\prime}/\hbar $.
The factor 
$2\sqrt 2 \cos \,{{\rm \eta}} ^{\prime}/(1 + a^2\mathop {\sin} \nolimits^2 \,{{\rm \eta}} ^{\prime})$ from the equations of the components of wave functions, namely Eqs. (90)–(93), takes values between 
$ - 2\sqrt 2 $ and 
$2\sqrt 2 $. A simple calculation shows that the quantum terms from these equations have significant values, of the order of unity, for the values of 
${Y}^{\prime}_{\rm e}$ at which quantum effects are evidenced experimentally. These values are shown in Table 1. It follows that the quantum terms are significant when they correspond to parameters at which quantum effects are evidenced experimentally.
Table 1. Typical values of parameters a and 
${Y}^{\prime}_{\rm e}$, in the rest frame of the electron, in interactions between very intense laser beams and relativistic electron beams, when quantum effects are significant. Calculations are made for the electron energy E e = 40 GeV, when λL = 1.054 and 0.527 μm, for two peak values of laser intensity, I p = 1018 W/cm2 and I p = 1019 W/cm2
It is easy to show that when the electron energy, E e, is strongly diminished, the quantum terms are much smaller than unity, and the system can be treated classically. It follows that the interaction of electrons with laser beams could be modeled using classical approaches, regardless of the laser beam intensity, as long as the relation E e ≪ 40 GeV is valid. This property is also valid in the case of the interactions between non-relativistic electrons and laser beams. In the books Popa (Reference Popa2014b and Reference Popa2014c), we presented a synthesis of our papers referring to classical approaches of these interactions, when E e ≪ 40 GeV. All these approaches lead to results which are in good agreement with the experimental data from the literature.
We show now that our results are in agreement with the Compton relation. The coefficient which enters in the Compton relation, and reflects the quantum behavior of the system, written in the inertial system S′, is 
${Y}^{\prime}_{\rm C} = \hbar {{\rm \omega}} ^{\prime}_{\rm L}/(mc^2)$. When the coefficient 
${Y}^{\prime}_{\rm C}$ has values of the order of unity, the quantum effects are significant, while when Y C ≪ 1, the system is at the classical limit. We consider a typical value of the electron energy, E e = 40 GeV, at which, according to our calculations, the quantum effects become significant, and two values of the wavelength of the EM field, namely λL = 1.054 × 10−6 m and λL = 0.527 × 10−6 m. We use the relations γ 0 = E e/(mc 2), 
$\vert {{\overline {\rm \beta} }_0} \vert = (1 - 1/{\rm \gamma} _0^2 )^{1/2} \cong 1$, ωL = 2πc/λL, and 
${{\rm \omega}} ^{\prime}_{\rm L} = 2{\rm \gamma} _0{\rm \omega} _{\rm L}$ and obtain, respectively, the values 0.7208 and 0.3604 for 
${Y}^{\prime}_{\rm C}$. In virtue of the Compton relation, these values correspond to significant quantum effects. It follows that there is a concordance between our calculations and the Compton relation. Our treatment is self-consistent, because all our classical approaches presented in Popa (Reference Popa2014b and Reference Popa2014c) correspond to the conditions 
$\hbar {\rm \omega} _{\rm L}/mc^2 \ll 1$ or 
$\hbar {{\rm \omega}} ^{\prime}_{\rm L}/mc^2 \ll 1$, which are valid when the Compton relation is at the classical limit.
The property that the quantum effects are evidenced when the initial electron energies are of the order of few tents of GeV is reflected by the fact that the references “Bamber, Bula and Burke” refer to similar experiments which need very energetic electron accelerators and laser beams having intensities of the order I p = 1018…1019 W/cm2.
We note that the experimental data from Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg, Burke, Field, Horton-Smith, Odian, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1996); Burke et al. (Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg1997); Bamber et al. (Reference Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis, Ragg, Bula, McDonald, Prebys, Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov and Weidemann1999); Kirsebom et al. (Reference Kirsebom, Mikkelsen, Uggerhoj, Elsener, Ballestrero, Sona and Vilakazi2001), for nonlinear Compton scattering, electron–positron pairs production, or for the interaction between electron spin and huge EM fields, correspond to values of the parameter 
${Y}^{\prime}_{\rm e}$ of the order of few tenths of unity. For these values, the quantum terms in our relations begin to be significant.
We conclude that our relations are in agreement with the experimental data from the literature, as the quantum terms from the wave functions have significant values for electron energies and laser beam intensities at which quantum effects are evidenced experimentally.
Conclusions
We presented a solution of the system of equations which is equivalent to the Dirac equation, written for the system composed of an electron in EM field, which depends on the phase of the field and on the QED parameter Y e. This solution predicts significant quantum effects in the case of interactions between very intense laser fields and relativistic electrons, for electron energy and laser beam intensity, having values, respectively, of the orders E e = 40 GeV and I p = 1018…1019 V/cm2, in agreement with experiments reported in the literature. The classical models are valid for interactions between very intense laser fields and nonrelativistic electrons, regardless of the laser beam intensity, in agreement with numerous classical approaches from literature.
Appendix A Solution of the Klein–Gordon equation
We prove briefly that the function 
$\exp (iS/\hbar )$ verifies the Klein–Gordon equation [see pages 023824–13 from Popa (Reference Popa2011) or page 26 from the book Popa (Reference Popa2014b)]. We need to present this demonstration to show that it is valid also in the inertial system S′. We solve first the relativistic system of the equations of the motion of the electron: Taking into account (1) and (3), the equations of motion of the electron are
$$m\displaystyle{d \over {dt}}({\rm \gamma} v_x) = - eE_{{\rm M1}}\cos \,{\rm \eta} + ev_zB_{{\rm M1}}\cos \,{\rm \eta}$$
$$m\displaystyle{d \over {dt}}({\rm \gamma} v_y) = - eE_{{\rm M2}}\sin \,{\rm \eta} + ev_zB_{{\rm M2}}\sin \,{\rm \eta}$$
$$m\displaystyle{d \over {dt}}({\rm \gamma} v_z) = - ev_xB_{{\rm M1}}\cos \,{\rm \eta} - ev_yB_{{\rm M2}}\sin \,{\rm \eta}$$where v x, v y, and v z are the components of the electron velocities and
$${\rm \gamma} = (1 - {\rm \beta} _x^2 - {\rm \beta} _y^2 - {\rm \beta} _z^2 )^{ - \textstyle{1 \over 2}}$$with βx = v x/c, βy = v y/c and βz = v z/c. In our relations e is the absolute value of the electron charge and m is the electron mass.
We consider the following initial conditions
$$\eqalign{& t = 0,\;\;x = y = z = 0,\;\;v_x = v_{xi},\; \cr & \quad \;v_y = v_{yi},\;\;v_z = v_{zi}\;\;\hbox{and}\;\;{\rm \eta} = {\rm \eta} _i}$$Using (4), the equations of motion become
$$\displaystyle{d \over {dt}}({\rm \gamma} {\rm \beta} _x) = - a_1{\rm \omega} _{\rm L}(1 - {\rm \beta} _z)\cos \,{\rm \eta}$$
$$\displaystyle{d \over {dt}}({\rm \gamma} {\rm \beta} _y) = - a_2{\rm \omega} _{\rm L}(1 - {\rm \beta} _z)\sin \,{\rm \eta}$$
$$\displaystyle{d \over {dt}}({\rm \gamma} {\rm \beta} _z) = - {\rm \omega} _{\rm L}(a_1{\rm \beta} _x\cos \,{\rm \eta} + a_2{\rm \beta} _y\sin \,{\rm \eta} )$$where a 1 and a 2 are the relativistic parameters, which are given by Eq. (7).
We presented an exact solution of the system (A6)–(A8) in the paper Popa (Reference Popa2011). We will present now briefly this solution, as follows.
We multiply (A6), (A7), and (A8), respectively, by βx, βy, and βz. Since 
${\rm \beta} _x^2 + {\rm \beta} _y^2 + {\rm \beta} _z^2 = 1 - 1/{\rm \gamma} ^2$ their sum leads to
$$\displaystyle{{d{\rm \gamma}} \over {dt}} = - {\rm \omega} _{\rm L}(a_1{\rm \beta} _x\cos \,{\rm \eta} + a_2{\rm \beta} _y\sin \,{\rm \eta} )$$Taking into account (A8) and (A9) we obtain d(γβ z)/dt = dγ/dt. We integrate this relation with respect to time between 0 and t, using the initial conditions (5), and obtain γ − γ i = γβ z − γ iβzi. From (2) we have dη/dt = ωL(1 − βz). From the last two relations, we obtain:
$$1 - {\rm \beta} _z = \displaystyle{1 \over {{\rm \omega} _{\rm L}}}\displaystyle{{d{\rm \eta}} \over {dt}} = \displaystyle{{\,f_0} \over {\rm \gamma}} \;\;\hbox{where}\;f_0 = {\rm \gamma} _i(1 - {\rm \beta} _{zi})$$with βxi = v xi/c, βyi = v yi/c, βzi = v zi/c and 
${\rm \gamma} _i = 1/\sqrt {1 - {\rm \beta} _{xi}^2 - {\rm \beta} _{yi}^2 - {\rm \beta} _{zi}^2} $.
We integrate (A6) with respect to time between 0 and t, and to phase between ηi and η, taking into account the initial conditions (A5), and, changing the variables t and η in agreement with (A10), we obtain
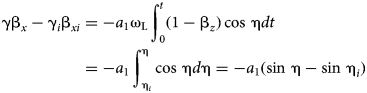$$\eqalignb{ {\rm \gamma} {\rm \beta} _x - {\rm \gamma} _i{\rm \beta} _{xi} & = - a_1{\rm \omega} _{\rm L}\int_0^t (1 - {\rm \beta} _z)\cos \,{\rm \eta} dt \cr & = - a_1\int_{{\rm \eta} _i}^{\rm \eta} \cos \,{\rm \eta} d{\rm \eta} = - a_1(\sin \,{\rm \eta} - \sin \,{\rm \eta} _i)}$$or
$${\rm \beta} _x = \displaystyle{{\,f_1} \over {\rm \gamma}} \;\;\hbox{where}\;f_1 = - a_1(\sin \,{\rm \eta} - \sin \,{\rm \eta} _i) + {\rm \gamma} _i{\rm \beta} _{xi}$$Similarly, integrating (A7) and taking into account (A5) and (A10), we obtain
$${\rm \beta} _y = \displaystyle{{\,f_2} \over {\rm \gamma}} \;\;\hbox{where}\;f_2 = - a_2(\cos {\rm \eta} _i - \cos {\rm \eta} ) + {\rm \gamma} _i{\rm \beta} _{yi}$$From (A10) we obtain
$${\rm \beta} _z = \displaystyle{{\,f_3} \over {\rm \gamma}} \;\;\hbox{where}\;f_3 = {\rm \gamma} - f_0$$We substitute the expressions of βx, βy, and βz, respectively, from (A12), (A13), and (A14) into (A4) and obtain:
$${\rm \gamma} = \displaystyle{1 \over {2f_0}}\lpar {1 + f_0^2 + f_1^2 + f_2^2} \rpar$$Using the same procedure, in Appendix B we calculate the expressions of the electron coordinates and of the action.
The analysis of the relations (A12)–(A15) shows that the functions βx, βy, and βz are periodic functions of only one variable, that is η.
We consider now the following relations (Landau and Lifshitz, Reference Landau and Lifshitz1959; Jackson, Reference Jackson1999):
$$\overline p = {\rm \gamma} m\overline v, \;\;H = {\rm \gamma} mc^2$$
$$\nabla S = \overline p - e\overline A _{\rm L}\;\hbox{and}\;H = - \displaystyle{{\partial S} \over {\partial t}}$$With the aid of these relations, together with (A12)–(A15), we need to calculate the following expression:
$$\openup15pt \eqalign{& \left[ {\nabla \lpar {\nabla S + e{\overline A}_{\rm L}} \rpar - \displaystyle{{\partial^2S} \over {c^2\partial t^2}}} \right] = \nabla \overline p + \displaystyle{1 \over {c^2}}\displaystyle{{\partial H} \over {\partial t}} \cr & \quad = \displaystyle{\partial \over {\partial x}}(mc{\rm \gamma} {\rm \beta} _x) + \displaystyle{\partial \over {\partial y}}(mc{\rm \gamma} {\rm \beta} _y) \cr & \quad \quad + \displaystyle{\partial \over {\partial z}}(mc{\rm \gamma} {\rm \beta} _z) + \displaystyle{1 \over {c^2}}\displaystyle{\partial \over {\partial t}}(mc^2{\rm \gamma} ) \cr & \quad = mc\displaystyle{{df_1} \over {d{\rm \eta}}} \displaystyle{{\partial {\rm \eta}} \over {\partial x}} + mc\displaystyle{{df_2} \over {d{\rm \eta}}} \displaystyle{{\partial {\rm \eta}} \over {\partial y}} + mc\displaystyle{{df_3} \over {d{\rm \eta}}} \displaystyle{{\partial {\rm \eta}} \over {\partial z}} \cr & \quad \quad + m\displaystyle{{d{\rm \gamma}} \over {d{\rm \eta}}} \displaystyle{{\partial {\rm \eta}} \over {\partial t}} = - mc\displaystyle{{df_3} \over {d{\rm \eta}}} \vert {{\overline k}_{\rm L}} \vert + m\displaystyle{{d{\rm \gamma}} \over {d{\rm \eta}}} {\rm \omega} _{\rm L}}$$From (2) and (A14) we have, respectively, c|k L| = ωL and df 3/dη = dγ/dη, so (A18) becomes:
$$\left[ {\nabla (\nabla S + e{\overline A}_{\rm L}) - \displaystyle{{\partial^2S} \over {c^2\partial t^2}}} \right] = 0$$We observe that the expression from the first member of the above relation is the divergence of the energy-momentum four vector.
The relativistic Hamilton–Jacobi and Klein–Gordon equations are given by the following relations (Landau and Lifshitz, Reference Landau and Lifshitz1959; Messiah, Reference Messiah1962; Jackson, Reference Jackson1999):
$$c^2(\nabla S + e\overline A _{\rm L})^2 - \left( {\displaystyle{{\partial S} \over {\partial t}}} \right)^2 + \; (mc^2)^2 = 0.$$
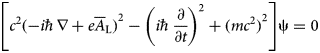$$\left[ {c^2{( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - {\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 + {(mc^2)}^2} \right]{\rm \psi} = 0$$where ψ is the wave function. Recall that e is the absolute value of the electron charge.
In the paper Popa (Reference Popa2011), at pages 023824–13, we proved that the Klein–Gordon equation is verified by the function 
$\exp (iS/\hbar )$. In order to check this, we substitute 
${\rm \psi} = \exp (iS/\hbar )$ in Eq. (A21), and obtain
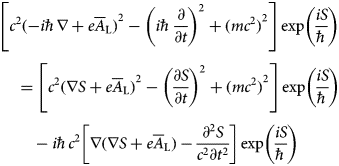$$\eqalign{& \left[ {c^2{( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - {\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 + {(mc^2)}^2} \right]\exp \left( {\displaystyle{{iS} \over \hbar}} \right) \cr & \quad = \left[ {c^2{(\nabla S + e{\overline A}_{\rm L})}^2 - {\left( {\displaystyle{{\partial S} \over {\partial t}}} \right)}^2 + {(mc^2)}^2} \right]\exp \left( {\displaystyle{{iS} \over \hbar}} \right) \cr & \qquad - i\hbar c^2\left[ {\nabla (\nabla S + e{\overline A}_{\rm L}) - \displaystyle{{\partial^2S} \over {c^2\partial t^2}}} \right]\exp \left( {\displaystyle{{iS} \over \hbar}} \right)}$$Taking into account Eqs. (A19) and (A20), the relation (A22) becomes
$$\left[ {c^2{( - i\hbar \nabla + e{\overline A}_{\rm L})}^2 - {\left( {i\hbar \displaystyle{\partial \over {\partial t}}} \right)}^2 + {(mc^2)}^2} \right]\exp \left( {\displaystyle{{iS} \over \hbar}} \right) = 0$$and the solution of the Klein–Gordon equation is verified.
We write now the above equations in the inertial system S′, which is described in the section Solution of the system of equations in the rest frame of the relativistic electron. It is easy to prove that the relativistic system of equations of motion of the electron, (A6)–(A8), has the same form in the inertial systems S and S′ [see (Popa, Reference Popa2011), pages 023824–9], and we can write
$$\displaystyle{d \over {d{t}^{\prime}}}({{\rm \gamma}} ^{\prime}{{\rm \beta}} ^{\prime}_{{x}^{\prime}}) = - {a}^{\prime}_1{{\rm \omega}} ^{\prime}_{\rm L}(1 - {{\rm \beta}} ^{\prime}_{{z}^{\prime}})\cos \,{{\rm \eta}} ^{\prime}$$
$$\displaystyle{d \over {d{t}^{\prime}}}({{\rm \gamma}} ^{\prime}{{\rm \beta}} ^{\prime}_{{y}^{\prime}}) = - {a}^{\prime}_2{{\rm \omega}} ^{\prime}_{\rm L}(1 - {{\rm \beta}} ^{\prime}_{{z}^{\prime}})\sin {{\rm \eta}} ^{\prime}$$
$$\displaystyle{d \over {d{t}^{\prime}}}({{\rm \gamma}} ^{\prime}{{\rm \beta}} ^{\prime}_{{z}^{\prime}}) = - {{\rm \omega}} ^{\prime}_{\rm L}({a}^{\prime}_1{{\rm \beta}} ^{\prime}_{{x}^{\prime}}\cos \,{{\rm \eta}} ^{\prime} + {a}^{\prime}_2{{\rm \beta}} ^{\prime}_{{y}^{\prime}}\sin \,{{\rm \eta}} ^{\prime})$$where 
${a}^{\prime}_1 = a_1$ and 
${a}^{\prime}_2 = a_2$ are given by Eq. (68) and the initial conditions in the systems S and S′ are given, respectively, by Eqs. (58) and (59).
An identical solution, as that for Eqs. (A6)–(A8), leads to
$${{\rm \beta}} ^{\prime}_{{x}^{\prime}} = \displaystyle{{{{\,f}^{\prime}}_{\hskip-3.5pt 1}} \over {{{\rm \gamma}} ^{\prime}}}\;\;\hbox{where}\;{\,f}^{\prime}_1 = - a_1(\sin \,{{\rm \eta}} ^{\prime} - \sin \,{\rm \eta} _i)$$
$${{\rm \beta}} ^{\prime}_{{y}^{\prime}} = \displaystyle{{{{\,f}^{\prime}}_{\hskip-3.5pt 2}} \over {{{\rm \gamma}} ^{\prime}}}\;\;\hbox{where}\;{\,f}^{\prime}_2 = - a_2(\cos \,{\rm \eta} _i - \cos \,{{\rm \eta}} ^{\prime})$$
$${{\rm \beta}} ^{\prime}_{{z}^{\prime}} = \displaystyle{{{{\,f}^{\prime}}_{\hskip-3.5pt 3}} \over {{{\rm \gamma}} ^{\prime}}}\;\;{\rm where}\;{\,f}^{\prime}_3 = {{\rm \gamma}} ^{\prime} - 1$$where
$${{\rm \gamma}} ^{\prime} = {\displaystyle{1 \over 2}}(2 + {\,f^{\prime}}_1^2 + {\,f^{\prime}}_2^2 )$$ Since the relativistic relations (A16) and (A17) have the same form in the inertial systems S and S′, we have 
$\overline p {\rm ^{\prime}} = {{\rm \gamma}} ^{\prime}m\overline v {\rm ^{\prime}}$, H′ = γ′mc 2, 
${\nabla} ^{\prime}{S}^{\prime} = \overline p {\rm ^{\prime}} - e\overline A {\rm ^{\prime}}_{\rm L}$ and H′ = −∂S′/∂t′. According to these relations, together with (A27)–(A30), an identical calculation, as that from Eq. (A18), leads to the following relation:
$$\left[ {{\nabla}^{\prime}\lpar {{\nabla}^{\prime}{S}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar - \displaystyle{{\partial^2{S}^{\prime}} \over {c^2\partial {{t}^{\prime}}^2}}} \right] = 0$$It follows that the divergence of the energy-momentum four vector is also equal to zero in the system S′.
The relativistic Hamilton–Jacobi and Klein–Gordon equations can be written in the system S′, as follows:
$$c^2\lpar {{\nabla}^{\prime}{S}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar ^2 - \left( {\displaystyle{{\partial {S}^{\prime}} \over {\partial {t}^{\prime}}}} \right)^2 + \; (mc^2)^2 = 0.$$
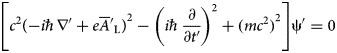$$\left[ {c^2{\lpar { - i\hbar {\nabla}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar }^2 - {\left( {i\hbar \displaystyle{\partial \over {\partial {t}^{\prime}}}} \right)}^2 + {(mc^2)}^2} \right]{{\rm \psi}} ^{\prime} = 0$$ We substitute 
${{\rm \psi}} ^{\prime} = \exp (i{S}^{\prime}/\hbar )$ in Eq. (A33), and obtain
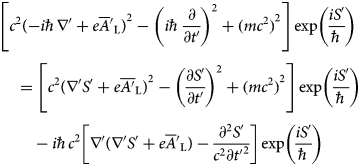$$\eqalign{& \left[ {c^2{\lpar { - i\hbar {\nabla}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar }^2 - {\left( {i\hbar \displaystyle{\partial \over {\partial {t}^{\prime}}}} \right)}^2 + {(mc^2)}^2} \right]\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right) \cr & \quad = \left[ {c^2{\lpar {{\nabla}^{\prime}{S}^{\prime} + e{\overline {A{\rm^{\prime}}}}_{\rm L}} \rpar }^2 - {\left( {\displaystyle{{\partial {S}^{\prime}} \over {\partial {t}^{\prime}}}} \right)}^2 + {(mc^2)}^2} \right]\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right) \cr & \qquad - i\hbar c^2\left[ {{\nabla}^{\prime}\lpar {{\nabla}^{\prime}{S}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar - \displaystyle{{\partial^2{S}^{\prime}} \over {c^2\partial {{t}^{\prime}}^2}}} \right]\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right)}$$Taking into account the Eqs. (A31) and (A32), the relation (A34) becomes
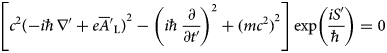$$\left[ {c^2{\lpar { - i\hbar {\nabla}^{\prime} + e\overline A {\rm^{\prime}}_{\rm L}} \rpar }^2 - {\left( {i\hbar \displaystyle{\partial \over {\partial {t}^{\prime}}}} \right)}^2 + {(mc^2)}^2} \right]\exp \left( {\displaystyle{{i{S}^{\prime}} \over \hbar}} \right) = 0$$and the solution of the Klein–Gordon equation, in the S′ system, is verified.
Appendix B Calculations of electron coordinates and action
We obtain the expressions of the electron coordinates using the procedure presented in Appendix A. Thus, to calculate x, we integrate the expression of βx, given by Eq. (A12), between 0 and t, taking into account (A10) and the initial conditions (A5). From (A10) we have dt = [γ/(ωLf 0)]dη and obtain
$$\eqalign{x = & \; c\int_0^t {\rm \beta} _xdt = \displaystyle{c \over {{\rm \omega} _{\rm L}f_0}}\int_{{\rm \eta} _i}^{\rm \eta} \lsqb { - a_1(\sin \,{\rm \eta} - \sin \,{\rm \eta}_i) + {\rm \gamma}_i{\rm \beta}_{xi}} \rsqb d{\rm \eta} \cr = & \displaystyle{c \over {{\rm \omega} _Lf_0}}\lsqb {a_1(\cos \,{\rm \eta} - \cos \,{\rm \eta}_i) + c_1({\rm \eta} - {\rm \eta}_i)} \rsqb }$$Similarly, integrating the expressions of βy and βz, given by Eqs. (A13) and (A14), we obtain
$$y = \displaystyle{c \over {{\rm \omega} _{\rm L}f_0}}\lsqb {a_2(\sin \,{\rm \eta} - \sin \,{\rm \eta}_i) + c_2({\rm \eta} - {\rm \eta}_i)} \rsqb$$
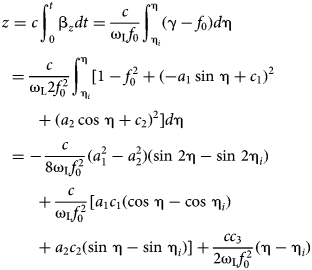$$\eqalign{& z = c\int_0^t {\rm \beta} _zdt = \displaystyle{c \over {{\rm \omega} _{\rm L}f_0}}\int_{{\rm \eta} _i}^{\rm \eta} ({\rm \gamma} - f_0)d{\rm \eta} \cr & \quad \!\!\!\! = \displaystyle{c \over {{\rm \omega} _{\rm L}2f_0^2}} \int_{{\rm \eta} _i}^{\rm \eta} [1 - f_0^2 + ( - a_1\sin \,{\rm \eta} + c_1)^2 \cr & \qquad + (a_2\cos \,{\rm \eta} + c_2)^2]d{\rm \eta} \cr & \quad \!\!\! \! = - \displaystyle{c \over {8{\rm \omega} _{\rm L}f_0^2}} (a_1^2 - a_2^2 )(\sin \,2{\rm \eta} - \sin \,2{\rm \eta} _i) \cr & \qquad + \displaystyle{c \over {{\rm \omega} _{\rm L}f_0^2}} [a_1c_1(\cos \,{\rm \eta} - \cos \,{\rm \eta} _i) \cr & \qquad + a_2c_2(\sin \,{\rm \eta} - \sin \,{\rm \eta} _i)] + \displaystyle{{cc_3} \over {2{\rm \omega} _{\rm L}f_0^2}} ({\rm \eta} - {\rm \eta} _i)}$$The constants c 1, c 2, and c 3 from Eqs. (B1)–(B3) are given by the following relations:
$$c_1 = a_1\sin \,{\rm \eta} _i + {\rm \gamma} _i{\rm \beta} _{xi}$$
$$c_2 = - a_2\cos \,{\rm \eta} _i + {\rm \gamma} _i{\rm \beta} _{yi}$$
$$c_3 = 1 - f_0^2 + \displaystyle{1 \over 2}(a_1^2 + a_2^2 ) + c_1^2 + c_2^2$$The analysis of the relations (B1)–(B3) shows that the coordinates x, y, and z are functions of only one variable, which is η.
We calculate now the S action. In virtue of the relations (5), (A16), and (A17), the variation of the action can be written
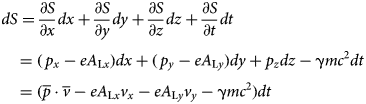$$\eqalign{ dS = \displaystyle{{\partial S} \over {\partial x}}dx + \displaystyle{{\partial S} \over {\partial y}}dy + \displaystyle{{\partial S} \over {\partial z}}dz + \displaystyle{{\partial S} \over {\partial t}}dt \cr & \quad \! = (\,p_x - eA_{{\rm L}x})dx + (\,p_y - eA_{{\rm L}y})dy + p_zdz - {\rm \gamma} mc^2dt \cr & \quad \! = (\overline p \cdot \overline v - eA_{{\rm L}x}v_x - eA_{{\rm L}y}v_y - {\rm \gamma} mc^2)dt}$$where A Lx = −A M1sin η and A Ly = A M2cos η.
We calculate the terms of this relation, as follows. From (A4) and (A16) we have:
$$\overline p \cdot \overline v - {\rm \gamma} mc^2 = - mc^2{\rm \gamma} \lpar {1 - {\overline {\rm \beta}}^2} \rpar = - \displaystyle{{mc^2} \over {\rm \gamma}}$$From (6), (7), (A12), (A13), (B4), and (B5) we obtain
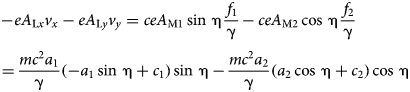$$\eqalign{& - \! eA_{{\rm L}x}v_x - eA_{{\rm L}y}v_y = ceA_{{\rm M}1}\sin \,{\rm \eta} \displaystyle{{\,f_1} \over {\rm \gamma}} - ceA_{{\rm M2}}\cos \,{\rm \eta} \displaystyle{{\,f_2} \over {\rm \gamma}} \cr & = \displaystyle{{mc^2a_1} \over {\rm \gamma}} ( - a_1\sin \,{\rm \eta} + c_1)\sin \,{\rm \eta} - \displaystyle{{mc^2a_2} \over {\rm \gamma}} (a_2\cos \,{\rm \eta} + c_2)\cos \,{\rm \eta}}$$From Eq. (A10) we have dt = [γ/(ωLf 0)]dη. We use this relation together with Eqs. (B7)–(B9) and obtain:
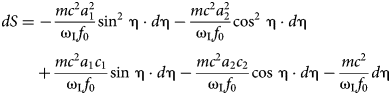$$\eqalign{& dS = - \displaystyle{{mc^2a_1^2} \over {{\rm \omega} _{\rm L}f_0}}\mathop {\sin} \nolimits^2 \,{\rm \eta} \cdot d{\rm \eta} - \displaystyle{{mc^2a_2^2} \over {{\rm \omega} _{\rm L}f_0}}\mathop {\cos} \nolimits^2 \,{\rm \eta} \cdot d{\rm \eta} \cr & \qquad + \displaystyle{{mc^2a_1c_1} \over {{\rm \omega} _{\rm L}f_0}}\sin \,{\rm \eta} \cdot d{\rm \eta} - \displaystyle{{mc^2a_2c_2} \over {{\rm \omega} _{\rm L}f_0}}\cos \,{\rm \eta} \cdot d{\rm \eta} - \displaystyle{{mc^2} \over {{\rm \omega} _{\rm L}f_0}}d{\rm \eta}}$$We integrate (B10) with respect to phase between ηi and η and have
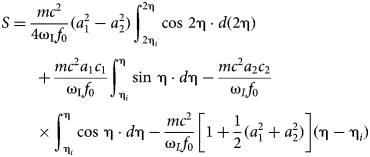$$\eqalign{& S = \displaystyle{{mc^2} \over {4{\rm \omega} _{\rm L}f_0}}(a_1^2 - a_2^2 )\int_{2{\rm \eta} _i}^{2{\rm \eta}} \cos \,2{\rm \eta} \cdot d(2{\rm \eta} ) \cr & \qquad + \displaystyle{{mc^2a_1c_1} \over {{\rm \omega} _{\rm L}f_0}}\int_{{\rm \eta} _i}^{\rm \eta} \sin \,{\rm \eta} \cdot d{\rm \eta} - \displaystyle{{mc^2a_2c_2} \over {{\rm \omega} _Lf_0}} \cr & \qquad \times \int_{{\rm \eta} _i}^{\rm \eta} \cos \,{\rm \eta} \cdot d{\rm \eta} - \displaystyle{{mc^2} \over {{\rm \omega} _Lf_0}}\left[ {1 + \displaystyle{1 \over 2}(a_1^2 + a_2^2 )} \right]({\rm \eta} - {\rm \eta} _i)}$$or
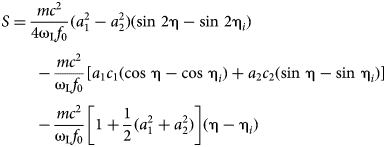$$\eqalign{& S = \displaystyle{{mc^2} \over {4{\rm \omega} _{\rm L}f_0}}(a_1^2 - a_2^2 )(\sin \,2{\rm \eta} - \sin \,2{\rm \eta} _i) \cr & \qquad - \displaystyle{{mc^2} \over {{\rm \omega} _{\rm L}f_0}}\lsqb {a_1c_1(\cos \,{\rm \eta} - \cos \,{\rm \eta}_i) + a_2c_2(\sin \,{\rm \eta} - \sin \,{\rm \eta}_i)} \rsqb \cr & \qquad - \displaystyle{{mc^2} \over {{\rm \omega} _{\rm L}f_0}}\left[ {1 + \displaystyle{1 \over 2}(a_1^2 + a_2^2 )} \right]({\rm \eta} - {\rm \eta} _i)}$$It follows that S is written in the form of a function of only one variable, which is η.
