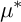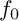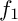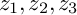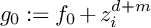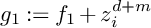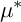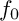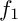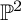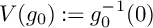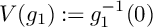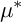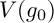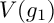1 Introduction and statement of the result
Let
$g_0$
and
$g_1$
be two polynomials in three complex variables
$z_1,z_2,z_3$
. We assume that they vanish at the origin
$\mathbf {0}\in \mathbb {C}^3$
and that the corresponding germs of surfaces,
$V(g_0):=g_0^{-1}(0)$
and
$V(g_1):=g_1^{-1}(0)$
, have an isolated singularity at
$\mathbf {0}$
. It is well known that if
$V(g_0)$
and
$V(g_1)$
have the same embedded topology (i.e., if the pairs
$(\mathbb {C}^3,V(g_0))$
and
$(\mathbb {C}^3,V(g_1))$
are homeomorphic in a neighborhood of the origin, or equivalently, by [Reference Saeki28], if the pairs
$(\mathbb {S}_\varepsilon ^5,K_{g_0})$
and
$(\mathbb {S}_\varepsilon ^5,K_{g_1})$
are diffeomorphic for any
$\varepsilon $
small enough), then they have the same Milnor number (see [Reference Lê18], [Reference Milnor23], [Reference Teissier33]). Here,
$K_{g_l}$
denotes the link of
$g_l$
(
$l\in \{0,1\}$
), that is,
$K_{g_l}:=\mathbb {S}^5_\varepsilon \cap V(g_l)$
for
$\varepsilon $
small enough, where
$\mathbb {S}_\varepsilon ^5$
is the sphere with radius
$\varepsilon $
centered at
$\mathbf {0}\in \mathbb {C}^3$
. (Note that the diffeomorphism type of the embedded link
$(\mathbb {S}_\varepsilon ^5,K_{g_l})$
is independent of
$\varepsilon $
, provided that
$\varepsilon $
is small enough.) On the other hand, it is quite possible for two isolated surface singularities
$V(g_0)$
and
$V(g_1)$
to have the same Milnor number and non-diffeomorphic embedded links. In [Reference Artal-Bartolo3], [Reference Artal-Bartolo4], using Luengo’s theory of superisolated singularities [Reference Luengo20], Artal-Bartolo even showed that the embedded topology of the link of a superisolated surface singularity is not determined by the topology of the abstract link and the characteristic polynomial of the monodromy. However, in practice, given
$g_0$
and
$g_1$
with the same characteristic polynomial (or equivalently, the same monodromy zeta-function), the same abstract topology, and even with the same Teissier
$\mu ^*$
-invariant, it is extremely difficult to determine whether
$(\mathbb {S}_\varepsilon ^5,K_{g_0})$
and
$(\mathbb {S}_\varepsilon ^5,K_{g_1})$
are diffeomorphic or not. The goal of this paper is to investigate a special class of Lê–Yomdin surface singularities which are “likely to systematically produce” pairs of germs sharing all these invariants but having non-diffeomorphic embedded links. Such pairs are called
$\mu ^*$
-Zariski pairs of surface singularities and are defined as follows.
Consider a classical Zariski pair of (reduced) projective curves
$C_0=\{f_0=0\}$
and
$C_1=\{f_1=0\}$
of degree d in the complex projective plane
$\mathbb {P}^2$
, that is, there are regular neighborhoods
$N_0$
and
$N_1$
of
$C_0$
and
$C_1$
, respectively, such that
$(N_0,C_0)$
and
$(N_1,C_1)$
are homeomorphic, while
$(\mathbb {P}^2,C_0)$
and
$(\mathbb {P}^2,C_1)$
are not. The first example of such a pair was found by Zariski [Reference Zariski36] in the early 1930s, and their systematic study was initiated by Artal-Bartolo [Reference Artal-Bartolo5] in the mid-1990s (for a detailed survey on this topic, see [Reference Artal-Bartolo, Cogolludo and Tokunaga6], [Reference Oka25]). By a linear change of the coordinates
$z_1,z_2,z_3$
, we may assume that the singularities of the curves
$C_0$
and
$C_1$
are not located on the coordinate lines
$z_i=0$
(
$1\leq i\leq 3$
) and that their defining polynomials
$f_0$
and
$f_1$
are convenientFootnote
1
and Newton non-degenerate on any face
$\Delta $
of their (common) Newton diagram if
$\Delta $
is not top-dimensional. The fact that the singularities of the curves do not sit on the coordinate lines implies that for any integers
$m\geq 1$
and
$1\leq i\leq 3$
, the polynomials
$$ \begin{align*} g_0:=f_0+z_i^{d+m} \quad\mbox{and}\quad g_1:=f_1+z_i^{d+m} \end{align*} $$
define an isolated surface singularity at
$\mathbf {0}$
(see [Reference Luengo and Melle21, Th. 2]). Such singularities are called m-Lê–Yomdin singularities and were first investigated by Yomdin and Lê in [Reference Lê19], [Reference Iomdin13], respectively. The monodromy zeta-function (or the characteristic polynomial) of such a singularity was computed by Siersma [Reference Siersma29], [Reference Siersma30], Stevens [Reference Stevens31], and Gusein-Zade, Luengo, and Melle-Hernández [Reference Gusein-Zade, Luengo and Melle-Hernández11] (see also [Reference Oka and Papadopoulos26]). (The Milnor number was already known from [Reference Luengo and Melle21].) In [Reference Artal-Bartolo, Cogolludo-Agustín and Martín-Morales7], Artal-Bartolo, Cogolludo-Agustín, and Martín-Morales gave a characterization for the abstract link of a Lê–Yomdin singularity to be a rational homology sphere.
In the special case where
$m=1$
, a
$1$
-Lê–Yomdin singularity is called a superisolated singularity. Superisolated singularities were introduced by Luengo [Reference Luengo20] to answer important questions and conjectures. For example, in [Reference Luengo20], Luengo gave examples of superisolated surface singularities for which the
$\mu $
-constant stratum in the miniversal deformation is not smooth.
Now, let us make precise the notion of Zariski pair of surface singularities. Let
$g_0=f_0+z_i^{d+m}$
and
$g_1=f_1+z_i^{d+m}$
be two Lê–Yomdin surface singularities obtained from a Zariski pair of curves
$f_0$
and
$f_1$
as above.
-
• We say that
$(V(g_0),V(g_1))$
is a weak
$\zeta $
-Zariski pair of surface singularities if
$g_0$
and
$g_1$
have the same monodromy zeta-function (in particular, the same Milnor number). -
• A weak
$\zeta $
-Zariski pair for which the germs
$V(g_0)$
and
$V(g_1)$
(or equivalently, the links
$K_{g_0}$
and
$K_{g_1}$
) have the same abstract topology is called a
$\zeta $
-Zariski pair (without the adjective “weak”). -
• A (weak)
$\zeta $
-Zariski pair is said to be a (weak)
$\mu ^*$
-Zariski pair if
$g_0$
and
$g_1$
have the same
$\mu ^*$
-invariant while belonging to distinct path-connected components of the
$\mu ^*$
-constant stratum. -
• A (weak)
$\mu ^*$
-Zariski pair is called a (weak)
$\mu $
-Zariski pair if furthermore
$g_0$
and
$g_1$
lie in different path-connected components of the
$\mu $
-constant stratum. -
• Finally, a (weak)
$\zeta $
-Zariski pair is called a (weak) Zariski pair if the germs
$V(g_0)$
and
$V(g_1)$
(or equivalently,
$K_{g_0}$
and
$K_{g_1}$
) have distinct embedded topologies.
Note that a (weak) Zariski pair of surface singularities
$V(g_0)$
and
$V(g_1)$
sharing the same
$\mu ^*$
-invariant is always a (weak)
$\mu $
-Zariski pair, and hence a (weak)
$\mu ^*$
-Zariski pair. That is, being a (weak)
$\mu ^*$
-Zariski pair is a necessary condition for being a (weak) Zariski pair. Indeed, by [Reference Eyral and Oka10, Th. 5.3], if
$g_0$
and
$g_1$
lie in the same path-connected component of the
$\mu ^*$
-constant stratum, then they can always be joined by a piecewise complex-analytic path (defined in the relevant natural way), and by a well-known theorem of Teissier [Reference Teissier32, théorème 3.9], this in turn implies that the diffeomorphism type of the pairs
$(\mathbb {S}_\varepsilon ^5,K_{g_0})$
and
$(\mathbb {S}_\varepsilon ^5,K_{g_1})$
is identical.
In [Reference Luengo20], Luengo proved that for superisolated singularities (i.e., for
$m=1$
), the abstract links
$K_{g_0}$
and
$K_{g_1}$
are homeomorphic. The second-named author showed a similar property for
$m\geq 1$
if the singularities of the corresponding curves
$C_0$
and
$C_1$
are Newton non-degenerate (see [Reference Oka27, Th. 24 and Rem. 25]). In [Reference Artal-Bartolo3, théorème 4.4] and [Reference Artal-Bartolo4, théorème 1.6, §1.7, and corollaire 5.6.6], Artal-Bartolo proved that if
$m=1$
, then
$V(g_0)$
and
$V(g_1)$
also share the same characteristic polynomial of the monodromy, and if furthermore the Alexander polynomials of the curves
$C_0$
and
$C_1$
do not coincide, then
$V(g_0)$
and
$V(g_1)$
do not have the same embedded topology. In particular, combined with Luengo’s result, this shows that, in this latter case,
$(V(g_0),V(g_1))$
is a Zariski pair of surface singularities.
In this paper, we prove the following theorem.
Theorem 1.1. If the singularities of the curves
$C_0$
and
$C_1$
are Newton non-degenerate in some suitable local coordinates,Footnote
2
then the pair made up of the m-Lê–Yomdin singularities
$V(g_0)$
and
$V(g_1)$
is a
$\mu ^*$
-Zariski pair of surface singularities.
Again, we emphasize that being a
$\mu ^*$
-Zariski pair is a necessary condition for being a Zariski pair of surface singularities. We also highlight that in the above theorem, the Alexander polynomials of the curves
$C_0$
and
$C_1$
may coincide.
We expect that with the assumption of the theorem,
$(V(g_0),V(g_1))$
is a
$\mu $
-Zariski pair, and in fact, a Zariski pair of surface singularities. As mentioned above, in the special case of superisolated singularities (i.e.,
$m=1$
), and provided that the curves have distinct Alexander polynomials (but not necessarily Newton non-degenerate singularities), this is already proved by combining Artal-Bartolo’s [Reference Artal-Bartolo3], [Reference Artal-Bartolo4] and Luengo’s [Reference Luengo20] results.
2 Proof of Theorem 1.1
First, we show that
$(V(g_0),V(g_1))$
is a
$\zeta $
-Zariski pair of surface singularities, and then we prove that it is in fact a
$\mu ^*$
-Zariski pair. To simplify, we assume that
$i=1$
, that is,
$g_l=f_l+z_1^{d+m}$
(
$l\in \{0,1\}$
).
To compute the monodromy zeta-function
$\zeta _{g_l,\mathbf {0}}(t)$
of
$g_l$
, we use the classical formula of Siersma (see [Reference Siersma29, Main theorem, p. 183] and [Reference Siersma30, Th. 3.4 and Rem. 3.6]), Stevens (see [Reference Stevens31, p. 140]), and Gusein-Zade, Luengo, and Melle-Hernández (see [Reference Gusein-Zade, Luengo and Melle-Hernández11, p. 250]) (see also [Reference Oka and Papadopoulos26, Lem. 3.2 and Th. 3.7]). More precisely, the ordinary point blowing up at
$\mathbf {0}\in \mathbb {C}^3$
, denoted by
$\pi \colon X\to \mathbb {C}^3$
, being a biholomorphism over
$\mathbb {C}^3\setminus V(g_l)$
, the tubular Milnor fibration of
$g_l$
at
$\mathbf {0}$
can be lifted to X, so that the pullback
$\pi ^* g_l\equiv g_l\circ \pi $
is a locally trivial fibration which is isomorphic to it. Let
$U_1:=\mathbb {P}^2\setminus \{z_1=0\}$
be the standard affine chart of
$\mathbb {P}^2$
with coordinates
$(z_2/z_1,z_3/z_1)$
. In the corresponding chart
$X\cap (\mathbb {C}^3\times U_1)$
of X, with coordinates
$\mathbf {y}\equiv (y_1,y_2,y_3):=(z_1,z_2/z_1,z_3/z_1)$
, the pullback
$\pi ^*g_l$
is written as
$$ \begin{align*} \pi^*g_l (\mathbf{y}) = y_1^d(f_l(1,y_2,y_3)+y_1^m). \end{align*} $$
The first factor,
$y_1^d$
, corresponds to the exceptional divisor
$E\simeq \mathbb {P}^2$
, while the second one represents the strict transform
$\tilde V(g_l)$
of
$V(g_l)$
. Outside of the exceptional divisor,
$\tilde V(g_l)$
has no singularities. On the exceptional divisor, it has a finite number of isolated singularities, which are given by the singular points
$\mathbf {p}\in \Sigma (C_l)$
of the reduced curve
$C_l$
. Then the formula for the zeta-function mentioned above is written as
$$ \begin{align} \zeta_{g_l,\mathbf{0}}(t)=\zeta_d(t)\times (1-t^{d})^{\mu^{\scriptscriptstyle{\text{tot}}}(C_l)} \times \prod_{\substack{\mathbf{p}\in\Sigma(C_l)}} \zeta_{\pi^*g_l,\mathbf{p}}(t), \end{align} $$
where
$\zeta _d(t)$
is the zeta-function of a Newton non-degenerate homogeneous polynomial of degree d (i.e.,
$\zeta _d(t)=(1-t^{d})^{-d^2+3d-3}$
),
$\Sigma (C_l)$
is the set of singular points of
$C_l$
, and
$\mu ^{\scriptscriptstyle{\text{tot}}}(C_l)$
is the total Milnor number of
$C_l$
(i.e., the sum of the local Milnor numbers at the singular points of
$C_l$
).
By our assumption, there exist local coordinates
$\mathbf {x}=(x_1,x_2,x_3)$
and
$\mathbf {u}=(u_1,u_2,u_3)$
near
$\mathbf {p}_0\in \Sigma (C_0)$
and
$\mathbf {p}_1\in \Sigma (C_1)$
, respectively, where
$x_1=u_1=y_1$
and
$(x_2,x_3)$
and
$(u_2,u_3)$
are analytic coordinate changes of
$(y_2,y_3)$
,Footnote
3
such that
$$ \begin{align*} \pi^* g_0 (\mathbf{x}) = x_1^d(h_0(x_2,x_3)+x_1^m) \quad\mbox{and}\quad \pi^* g_1 (\mathbf{u}) = u_1^d(h_1(u_2,u_3)+u_1^m), \end{align*} $$
where
$h_0$
and
$h_1$
are Newton non-degenerate. Moreover, if the singularities
$(C_1,\mathbf {p}_1)$
and
$(C_0,\mathbf {p}_0)$
are topologically equivalent, then we may assume that the Newton diagrams,
$\Gamma (h_0)$
and
$\Gamma (h_1)$
, of
$h_0$
and
$h_1$
coincide. It follows that
$\pi ^* g_0$
and
$\pi ^* g_1$
are Newton non-degenerate with the same Newton diagram, and hence, by Varchenko’s formula (see [Reference Varchenko34, Th. (4.1)]), we have
$$ \begin{align*} \zeta_{\pi^*\!g_0,\mathbf{p}_0}(t)=\zeta_{\pi^*\!g_1,\mathbf{p}_1}(t). \end{align*} $$
Since
$(C_0,C_1)$
is a Zariski pair of projective curves, the total Milnor numbers
$\mu ^{\scriptscriptstyle{\text{tot}}}(C_0)$
and
$\mu ^{\scriptscriptstyle{\text{tot}}}(C_1)$
coincide, and the equality
$\zeta _{g_0,\mathbf {0}}(t)=\zeta _{g_1,\mathbf {0}}(t)$
follows immediately from (2.1).
To conclude that
$(V(g_0),V(g_1))$
is a
$\zeta $
-Zariski pair, it remains to observe that the links
$K_{g_0}$
and
$K_{g_1}$
have the same abstract topology; this is proved in [Reference Oka27, Th. 24 and Rem. 25].
Now, let us show that
$(V(g_0),V(g_1))$
is a
$\mu ^*$
-Zariski pair of surface singularities. For that, we must first show that
$g_0$
and
$g_1$
have the same
$\mu ^*$
-invariant at
$\mathbf {0}$
. We recall that the
$\mu ^*$
-invariant of
$g_l$
at
$\mathbf {0}$
, introduced by Teissier in [Reference Teissier32], is the triple
$$ \begin{align*} \mu^*_{\mathbf{0}}(g_l):=(\mu_{\mathbf{0}}(g_l),\mu_{\mathbf{0}}({g_l}\vert_{H}),\mbox{mult}_{\mathbf{0}}(g_l)-1), \end{align*} $$
where
$\mu _{\mathbf {0}}(g_l)$
is the Milnor number of
$g_l$
at
$\mathbf {0}$
,
$\mu _{\mathbf {0}}({g_l}\vert _{H})$
is the Milnor number at
$\mathbf {0}$
of the restriction of
$g_l$
to a generic plane H of
$\mathbb {C}^3$
through the origin (this number is usually denoted by
$\mu _{\mathbf {0}}^{(2)}({g_l})$
), and
$\mbox {mult}_{\mathbf {0}}(g_l)$
is the multiplicity of
$g_l$
at
$\mathbf {0}$
.
By [Reference Luengo and Melle21, Th. 2], for any
$l\in \{0,1\}$
, the Milnor number
$\mu _{\mathbf {0}}(g_l)$
is given by
$$ \begin{align*} \mu_{\mathbf{0}}(g_l)=(d-1)^3+m \mu^{\scriptscriptstyle{\text{tot}}}, \end{align*} $$
where
$\mu ^{\scriptscriptstyle{\text{tot}}}$
is the (common) total Milnor number of
$C_0$
and
$C_1$
.
For a generic plane H of
$\mathbb {C}^3$
through the origin, the restriction
$f_l\vert _{H}$
is a homogeneous polynomial of degree d with an isolated singularity at
$\mathbf {0}$
, so that its Milnor number at
$\mathbf {0}$
is
$\mu _{\mathbf {0}}(f_l\vert _{H})=(d-1)^2$
. Since
$f_l\vert _{H}$
is Newton non-degenerate and the term
$z_1^{d+m}$
is above the Newton diagram
$\Gamma (g_l\vert _{H})=\Gamma (f_l\vert _{H})$
, the restriction
$g_l\vert _{H}$
is Newton non-degenerate too. Thus, its Milnor number at
$\mathbf {0}$
is determined by
$\Gamma (g_l\vert _{H})$
, and hence we have
$$ \begin{align*} \mu_{\mathbf{0}}^{(2)}({g_l}):=\mu_{\mathbf{0}}(g_l\vert_{H})=\mu_{\mathbf{0}}(f_l\vert_{H})=(d-1)^2. \end{align*} $$
Lastly, since the multiplicities of
$g_0$
and
$g_1$
at
$\mathbf {0}$
are equal to d, it follows that
$g_0$
and
$g_1$
have the same
$\mu ^*$
-invariant at
$\mathbf {0}$
, namely, for any
$l\in \{0,1\}$
, we have
$$ \begin{align*} \mu_{\mathbf{0}}^*(g_l)=((d-1)^3+m \mu^{\scriptscriptstyle{\text{tot}}},(d-1)^2,d-1). \end{align*} $$
Finally, and this is the heart of the proof, we must now show that
$g_0$
and
$g_1$
lie in different path-connected components of the
$\mu ^*$
-constant stratum. To this end, we argue by contradiction. Suppose that
$g_0$
and
$g_1$
belong to the same component. Then, by [Reference Eyral and Oka10, Th. 5.3], there exists a
$\mu ^*$
-constant piecewise complex-analytic family
$\{g_s\}_{0\leq s\leq 1}$
connecting
$g_0$
and
$g_1$
. In particular, the multiplicity
$\mbox {mult}_{\mathbf {0}}(g_s)$
of
$g_s$
at
$\mathbf {0}$
is independent of
$s\in [0,1]$
, and the initial polynomial
$\mbox {in}(g_s)$
of
$g_s$
(i.e., the sum of the monomials of
$g_s$
of lowest degree) has degree d.
Lemma 2.1. For each
$s\in [0,1]$
, the homogeneous polynomial
${\mathrm{in}}(g_s)$
is reduced, so that the projective curve
$C_{s}\subseteq \mathbb {P}^2$
defined by
${\mathrm{in}}(g_s)$
has only isolated singularities.
Proof. We argue by contradiction. Suppose there exists
$s_0\in [0,1]$
such that
$\mbox {in}(g_{s_0})$
is not reduced (i.e.,
$C_{s_0}$
has non-isolated singularities). Then, for a generic linear plane H of
$\mathbb {C}^3$
, there are coordinates
$(x,y)$
for H and linear forms
$\ell _1(x,y),\ldots ,\ell _q(x,y)$
such that
$$ \begin{align*} \mbox{in}(g_{s_0})\vert_H(x,y)=\ell_1(x,y)^{p_1}\cdots\ell_q(x,y)^{p_q} \end{align*} $$
with
$p_1\geq \cdots \geq p_q$
and
$p_1\geq 2$
. By a linear change of coordinates, we may assume that
$\ell _1(x,y)\equiv x$
, so that
$$ \begin{align*} \mbox{in}(g_{s_0})\vert_H(x,y)=x^{p_1}h(x,y), \end{align*} $$
where h is a homogeneous polynomial of degree
$d-p_1$
(in particular,
$\mbox {in}(g_{s_0})\vert _H$
is not convenient with respect to the coordinates
$(x,y)$
). By adding monomials of the form
$x^{\alpha }$
and
$y^{\beta }$
for
$\alpha ,\, \beta $
large enough, we may also assume that
$g_{s_0}\vert _H$
is convenient. Now, since the integral point
$(1,d-1)$
is not on the Newton diagram
$\Gamma (\mbox {in}(g_{s_0})\vert _H)$
of
$\mbox {in}(g_{s_0})\vert _H$
with respect to the coordinates
$(x,y)$
, it followsFootnote
4
that
$$ \begin{align*} \nu(\Gamma_{\!-}(g_{s_0}\vert_H))>\nu(\Gamma_{\!-}(g_{0}\vert_H)) \end{align*} $$
(see Figure 1, where
$\Gamma _{\!+}(\mbox {in}(g_{s_0})\vert _H)$
is the Newton polyhedron of
$\mbox {in}(g_{s_0})\vert _H$
in the coordinates
$(x,y)$
). Here,
$\nu (\cdot )$
denotes the Newton number (see [Reference Kouchnirenko14] for the definition) and
$\Gamma _{\!-}(g_{s_0}\vert _H)$
stands for the cone over
$\Gamma (g_{s_0}\vert _H)$
with the origin as vertex. (Again,
$\Gamma (g_{s_0}\vert _H)$
denotes the Newton diagram of
$g_{s_0}\vert _H$
with respect to the coordinates
$(x,y)$
.) The polyhedron
$\Gamma _{\!-}(g_{0}\vert _H)$
is defined similarly. Since
$$ \begin{align*} \mu_{\mathbf{0}}(g_{s_0}\vert_H)\geq \nu(\Gamma_{\!-}(g_{s_0}\vert_H)) \end{align*} $$
(see [Reference Kouchnirenko14, théorème 1.10]), altogether we have
$$ \begin{align*} \mu^{(2)}_{\mathbf{0}}(g_{s_0})=\mu_{\mathbf{0}}(g_{s_0}\vert_H)\geq \nu(\Gamma_{\!-}(g_{s_0}\vert_H))>\nu(\Gamma_{\!-}(g_{0}\vert_H))=(d-1)^2=\mu^{(2)}_{\mathbf{0}}(g_{0}), \end{align*} $$
which is a contradiction to the
$\mu ^*$
-constancy.
Lemma 2.2. The zeta-function
$\zeta _{g_s,\mathbf {0}}(t)$
is independent of
$s\in [0,1]$
.
Figure 1 Newton diagrams.
Proof. It is well known that in a
$\mu ^*$
-constant piecewise complex-analytic family
$\{g_s\}$
, the diffeomorphism type of the embedded link
$(\mathbb {S}_\varepsilon ^5,K_{g_s})$
is independent of s (see [Reference Teissier32, théorème 3.9 and remarque 3.12]). Alternatively, we may use [Reference Oka27, Lem. 12], which asserts that in a
$\mu $
-constant (a fortiori in a
$\mu ^*$
-constant) piecewise complex-analytic family
$\{g_s\}$
, the zeta-function
$\zeta _{g_s,\mathbf {0}}(t)$
is independent of s.
Now, by the A’Campo formula (see [Reference A’Campo1, théorème 3]), we know that the zeta-function
$\zeta _{g_s,\mathbf {0}}(t)$
is uniquely written as
$$ \begin{align} \zeta_{g_s,\mathbf{0}}(t)=\prod_{i=1}^{\ell} (1-t^{d_i})^{\nu_i}, \end{align} $$
where
$d_1,\ldots ,d_{\ell }$
are mutually disjoint and
$\nu _1,\ldots ,\nu _{\ell }$
are nonzero integers. The smallest integer
$d_{i_0}$
among
$d_1,\ldots ,d_\ell $
is called the zeta-multiplicity of
$g_s$
and is denoted by
$m_\zeta (g_s)$
. We define the zeta-multiplicity factor of
$\zeta _{g_s,\mathbf {0}}(t)$
as the factor
$(1-t^{d_{i_0}})^{\nu _{i_0}}$
of (2.2) corresponding to the zeta-multiplicity
$d_{i_0}\equiv m_\zeta (g_s)$
. Note that, by Lemma 2.2, the zeta-multiplicity of
$g_s$
and the zeta-multiplicity factor of
$\zeta _{g_s,\mathbf {0}}(t)$
are independent of s. Moreover, by [Reference Oka27, Prop. 11], we know that
$m_\zeta (g_s)\geq \mbox {mult}_{\mathbf {0}}(g_s)=d$
, and the formula (2.1) shows that for
$s=0$
we have
$m_{\zeta }(g_0)\leq d$
. So, altogether,
$m_{\zeta }(g_s)=d$
for any
$s\in [0,1]$
.
Lemma 2.3. For any
$s\in [0,1]$
, the zeta-multiplicity factor of
$\zeta _{g_s,\mathbf {0}}(t)$
is given by
$$ \begin{align*} (1-t^d)^{-d^2+3d-3+\mu^{\scriptscriptstyle{\mathrm{tot}}}(C_{s})}, \end{align*} $$
and since the latter is independent of s, so is the total Milnor number
$\mu ^{\scriptscriptstyle{\mathrm{tot}}}(C_{s})$
.
Proof. Here, to compute
$\zeta _{g_s,\mathbf {0}}(t)$
, we apply a method developed by the second-named author in [Reference Oka24]. This method, inspired by an approach of Clemens [Reference Clemens8], was used in [Reference Oka24, Chap. I, Proof of Th. 5.2] to generalize the classical zeta-function formula of A’Campo [Reference A’Campo1]. Roughly, the idea is to decompose the lifted Milnor fibration
$\pi ^*g_s$
(which is isomorphic to the original Milnor fibration of
$g_s$
at
$\mathbf {0}$
) into its restrictions along “controlled” tubular neighborhoods of the strata in a canonical regular stratification of
$\pi ^{-1}(V(g_s))$
. Then, by the multiplicativeness of the zeta-function, it suffices to compute the zeta-functions of the induced restricted fibrations. More precisely, let
$\mathbf {p}_1,\ldots ,\mathbf {p}_{k_0}$
be the points of the singular set
$\Sigma (C_s)$
of
$C_s$
, and for each
$\mathbf {p}_k$
, let
$B_\varepsilon (\mathbf {p}_k)$
be a small ball centered at
$\mathbf {p}_k$
. Put
$$ \begin{align*} B:=\bigcup_{k=1}^{k_0}B_\varepsilon(\mathbf{p}_k), \end{align*} $$
and consider tubular neighborhoods
$N(C_s)$
and
$N(E)$
of
$C_s\setminus B$
and
$E\setminus (N(C_s)\cup B)$
, respectively. As in [Reference Oka24, Chap. I, p. 56], we assume that the triple
$$ \begin{align} \{B,N(C_s),N(E)\}, \end{align} $$
together with its natural associated projections and distance functions, makes a family of “control data” in the sense of Mather [Reference Mather22, §7]. Consider the restrictions of
$\hat g_s:=\pi ^*g_s$
to
$N(E)$
,
$N(C_s)$
and the balls
$B_\varepsilon (\mathbf {p}_k)$
, respectively. The relations (5.2.4) and (5.2.5), together with Lemmas (5.3) and (5.4), of [Reference Oka24, Chap. I] say that
$$ \begin{align} \zeta_{g_s,\mathbf{0}}(t)\equiv \zeta_{\hat g_s}(t) = \zeta_{\hat g_s\vert_{N(E)}}(t)\cdot \zeta_{\hat g_s\vert_{N(C_s)}}(t)\cdot \prod_{k=1}^{k_0} \zeta_{\hat g_s\vert_{B_\varepsilon(\mathbf{p}_k)}}(t). \end{align} $$
Thus, it suffices to compute each piece
$\zeta _{\hat g_s\vert _{N(E)}}(t)$
,
$\zeta _{\hat g_s\vert _{N(C_s)}}(t)$
, and
$\zeta _{\hat g_s\vert _{B_\varepsilon (\mathbf {p}_k)}}(t)$
separately.
We start with the calculation of the zeta-function
$\zeta _{\hat g_s\vert _{N(E)}}(t)$
of the fibration
$\hat g_s\vert _{N(E)}$
. For admissible coordinates
$\mathbf {x}=(x_1,x_2,x_3)$
in a neighborhood
$U_{\mathbf {p}}$
of a point
$\mathbf {p}\in E':=E\setminus (N(C_s)\cup B)$
, we may assume that the projection
$$ \begin{align*} p\colon U_{\mathbf{p}}\cap N(E)\to E' \end{align*} $$
associated with the family of control data (2.3) is given by
$\mathbf {x}\mapsto (0,x_2,x_3)$
, so that
$E'$
is defined by
$x_1=0$
and the restriction of
$\hat g_s$
to
$p^{-1}(\mathbf {p})$
is given by
$x_1^d$
. Then, by the relation (5.2.5) of [Reference Oka24, Chap. I], the normal zeta-function
$\zeta _{E'}^\bot (t)$
of
$\hat g_s$
along
$E'$
(see [Reference Oka24, Chap. I, p. 59] for the definition) is given by
$$ \begin{align*} \zeta_{E'}^\bot(t)=(1-t^d)^{-1}. \end{align*} $$
Thus, by [Reference Oka24, Chap. I, Lems. (5.3) and (5.4)], we get
$$ \begin{align*} \zeta_{\hat g_s\vert_{N(E)}}(t) & =(\zeta_{E'}^\bot(t))^{\chi(E\setminus \tilde V(g_s))}=(\zeta_{E'}^\bot(t))^{\chi(\mathbb{P}^2\setminus C_s)}=(\zeta_{E'}^\bot(t))^{\chi(\mathbb{P}^2)-\chi(C_s)}\\ &=(1-t^d)^{-\chi(\mathbb{P}^2)+\chi(C_s)}=(1-t^d)^{-3+\chi(C_s)} =(1-t^d)^{-3+3d-d^2+\mu^{\scriptscriptstyle{\text{tot}}}(C_s)}. \end{align*} $$
Here,
$\chi (\cdot )$
denotes the Euler–Poincaré characteristic, and we recall that for a reduced curve
$C_s$
of degree d, we have
$\chi (C_s)=3d-d^2+\mu ^{\scriptscriptstyle{\text{tot}}}(C_s)$
(see, e.g., [Reference Wall35, Cor. 7.1.4]).
Next, we look at the zeta-function
$\zeta _{\hat g_s\vert _{N(C_s)}}(t)$
. This time, for admissible coordinates
$\mathbf {x}=(x_1,x_2,x_3)$
in a neighborhood
$U_{\mathbf {p}}$
of a point
$\mathbf {p}\in C^{\prime }_s:=C_s\setminus B$
, we may assume that the projection
$$ \begin{align*} p'\colon U_{\mathbf{p}}\cap N(C_s)\to C^{\prime}_s \end{align*} $$
associated with the family of control data (2.3) is given by
$\mathbf {x}\mapsto (0,x_2,0)$
, so that
$C^{\prime }_s$
is defined by
$x_1=x_3=0$
and the restriction of
$\hat g_s$
to
$p^{\prime -1}(\mathbf {p})$
is given by
$x_1^dx_3$
. Then, by the relation (5.2.5) of [Reference Oka24, Chap. I], the normal zeta-function of
$\hat g_s$
along
$C^{\prime }_s$
is given by
$\zeta _{C^{\prime }_s}^\bot (t)=1$
, and hence, by [Reference Oka24, Chap. I, Lems. (5.3) and (5.4)] again, we get
$$ \begin{align*} \zeta_{\hat g_s\vert_{N(C_s)}}(t)=1. \end{align*} $$
As for the zeta-function
$\zeta _{\hat g_s\vert _{B_\varepsilon (\mathbf {p}_k)}}(t)$
, since the zeta-multiplicity of
$g_s$
is d and the (usual) multiplicity of
$\hat g_s$
at
$\mathbf {p}_{k}$
is greater than or equal to
$d+1$
, it follows from [Reference Oka27, Prop. 11] that
$\zeta _{\hat g_s\vert _{B_\varepsilon (\mathbf {p}_k)}}(t)$
does not contribute to the zeta-multiplicity factor of
$\zeta _{\hat g_s}(t)$
.
So, altogether, the unique contribution to the zeta-multiplicity factor of
$\zeta _{\hat g_s}(t)$
comes from the zeta-function
$\zeta _{\hat g_s\vert _{N(E)}}(t)$
and is given by
$(1-t^d)^{-3+3d-d^2+\mu ^{\scriptscriptstyle{\text{tot}}}(C_s)}$
.
We can now easily complete the proof of Theorem 1.1 thanks to two theorems of Lê. Indeed, we first observe that if there exists
$s_0\in [0,1]$
such that the family
$\{\mbox {in}(g_s)\}$
has a bifurcation of the singularities in a small ball B centered at a singular point
$\mathbf {p}_0$
of
$C_{s_0}$
,Footnote
5
then, by [Reference Lê17, théorème B] (see also [Reference Haş Bey12], [Reference Lazzeri15]), for
$s\not =s_0$
near
$s_0$
, we have
$$ \begin{align*} \sum_{\mathbf{p}\in B\cap \Sigma(C_s)}\mu_{\mathbf{p}}(\mbox{in}(g_s)) < \mu_{\mathbf{p}_0}(\mbox{in}(g_{s_0})), \end{align*} $$
and hence
$\mu ^{\scriptscriptstyle{\text{tot}}}(C_{s})<\mu ^{\scriptscriptstyle{\text{tot}}}(C_{s_0})$
, which contradicts Lemma 2.3. Therefore, there is no such an
$s_0$
. But in this case it follows from [Reference Lê16] and the discussion in [Reference Dimca9, pp. 17–18, 121] that the topological type of the pair
$(\mathbb {P}^2,C_s)$
is independent of s, so that
$(C_0,C_1)$
is not a Zariski pair—again a contradiction.
Figure 2 Bifurcation of singularities.
