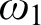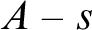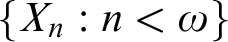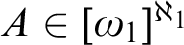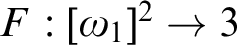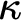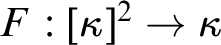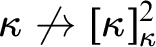In this note we consider three problems of the Erdős–Hajnal collection of unsolved problems in set theory Reference Erdős and Hajnal[1].
The first problem is the following.
Problem 69. Let X be a graph on
![]() $\omega _1$
. Assume that for every
$\omega _1$
. Assume that for every
![]() $A\in [\omega _1]^{\aleph _1}$
there is a finite
$A\in [\omega _1]^{\aleph _1}$
there is a finite
![]() $s\subseteq A$
such that each element of
$s\subseteq A$
such that each element of
![]() $A-s$
is joined to some element of s. Does X necessarily contain an uncountable clique?
$A-s$
is joined to some element of s. Does X necessarily contain an uncountable clique?
I slightly modified the formulation by requiring
![]() $|A|=\aleph _1$
, originally the authors only assumed
$|A|=\aleph _1$
, originally the authors only assumed
![]() $A\subseteq \omega _1$
. This is, however, problematic, as if there is no uncountable clique, then there is an infinite independent vertex set by the Erdős–Dushnik–Miller theorem, so the statement trivially holds.
$A\subseteq \omega _1$
. This is, however, problematic, as if there is no uncountable clique, then there is an infinite independent vertex set by the Erdős–Dushnik–Miller theorem, so the statement trivially holds.
For technical reasons we reformulate the problem for the complement of X.
Problem 69. Let X be a graph on
![]() $\omega _1$
. Assume that for every
$\omega _1$
. Assume that for every
![]() $A\in [\omega _1]^{\aleph _1}$
there is a finite
$A\in [\omega _1]^{\aleph _1}$
there is a finite
![]() $s\subseteq A$
such that no element of
$s\subseteq A$
such that no element of
![]() $A-s$
is joined to every element of s. Does X necessarily contain an uncountable independent set?
$A-s$
is joined to every element of s. Does X necessarily contain an uncountable independent set?
In this note I prove the consistency of both the statement and its negation (Corollary 2, Theorem 3).
The second problem is the following.
Problem 61. Do there exist circuitfree graphs
![]() $\{X_n:n<\omega \}$
on
$\{X_n:n<\omega \}$
on
![]() $\omega _1$
such that if
$\omega _1$
such that if
![]() $A\in [\omega _1]^{\aleph _1}$
, then
$A\in [\omega _1]^{\aleph _1}$
, then
![]() $\{n<\omega :X_n\cap [A]^2=\emptyset \}$
is finite?
$\{n<\omega :X_n\cap [A]^2=\emptyset \}$
is finite?
Erdős and Hajnal remarked in Reference Erdős and Hajnal[2], CH implies a ‘yes’ answer. As it remained unpublished, we reprove this result here (Theorem 4).
For the other direction, we show that a ‘no’ answer follows from
![]() $\mathrm {MA}_{\omega _1}$
(Theorem 5).
$\mathrm {MA}_{\omega _1}$
(Theorem 5).
The third problem we address from the Erdős–Hajnal list is the following.
Problem 68. (GCH)
Assume that
![]() $F:[\omega _1]^2\to 3$
is such that F assumes all values on any uncountable subset of
$F:[\omega _1]^2\to 3$
is such that F assumes all values on any uncountable subset of
![]() $\omega _1$
. Do there exist
$\omega _1$
. Do there exist
![]() $\alpha <\beta <\gamma <\omega _1$
with
$\alpha <\beta <\gamma <\omega _1$
with
![]() $\{F(\alpha ,\beta ),F(\alpha ,\gamma ),F(\beta ,\gamma )\}=\{0,1,2\}$
?
$\{F(\alpha ,\beta ),F(\alpha ,\gamma ),F(\beta ,\gamma )\}=\{0,1,2\}$
?
In what follows we call a triangle
![]() $\{x,y,z\}$
three-colored, if
$\{x,y,z\}$
three-colored, if
![]() $F(x,y)$
,
$F(x,y)$
,
![]() $F(x,z)$
, and
$F(x,z)$
, and
![]() $F(y,z)$
are distinct. A function
$F(y,z)$
are distinct. A function
![]() $F:[\kappa ]^2\to \gamma $
is said to establish
$F:[\kappa ]^2\to \gamma $
is said to establish
 $\kappa \not \to [\kappa ]^2_{\gamma }$
if F assumes all values on every
$\kappa \not \to [\kappa ]^2_{\gamma }$
if F assumes all values on every
![]() $A\in [\kappa ]^{\kappa }$
. In [Reference Shelah3], Shelah proved that
$A\in [\kappa ]^{\kappa }$
. In [Reference Shelah3], Shelah proved that
![]() $2^{\kappa }=\kappa ^+$
implies the existence of a function establishing
$2^{\kappa }=\kappa ^+$
implies the existence of a function establishing
![]() $\kappa ^+\not \to [\kappa ^+]^2_{\kappa }$
with no three-colored triangles. We include his proof as it can be considerably simplified using a well known consequence of CH (Theorem 8).
$\kappa ^+\not \to [\kappa ^+]^2_{\kappa }$
with no three-colored triangles. We include his proof as it can be considerably simplified using a well known consequence of CH (Theorem 8).
Shelah also proved, that if V=L, then for every regular cardinal
![]() $\lambda $
, there is a function
$\lambda $
, there is a function
![]() $F:[\lambda ^+]^2\to \lambda ^+$
witnessing
$F:[\lambda ^+]^2\to \lambda ^+$
witnessing
 $\lambda ^+\not \to [\lambda ^+]^2_{\lambda ^+}$
with no triangles of three colors. Todorcevic in [Reference Todorcevic5] proved the stronger result that a similar function exists on a cardinal
$\lambda ^+\not \to [\lambda ^+]^2_{\lambda ^+}$
with no triangles of three colors. Todorcevic in [Reference Todorcevic5] proved the stronger result that a similar function exists on a cardinal
![]() $\kappa $
for which a
$\kappa $
for which a
![]() $\kappa $
-Suslin tree exists. We give a different proof to his result (Theorem 10). Following the referee’s suggestion, we show that if
$\kappa $
-Suslin tree exists. We give a different proof to his result (Theorem 10). Following the referee’s suggestion, we show that if
![]() $\kappa ^{<\kappa }=\kappa $
holds then forcing with
$\kappa ^{<\kappa }=\kappa $
holds then forcing with
![]() $\mathrm {Add}(\kappa ,1)$
adds such an example on
$\mathrm {Add}(\kappa ,1)$
adds such an example on
![]() $\kappa ^+$
(Theorem 11). Finally, we show that the existence of
$\kappa ^+$
(Theorem 11). Finally, we show that the existence of
![]() $F:[\kappa ]^2\to \kappa $
establishing
$F:[\kappa ]^2\to \kappa $
establishing
![]() $\kappa \not \to [\kappa ]^2_{\kappa }$
with no three-colored triangles which in turn implies the existence of a
$\kappa \not \to [\kappa ]^2_{\kappa }$
with no three-colored triangles which in turn implies the existence of a
![]() $\kappa $
-Aronszajn tree. By result of Mitchell [Reference William7, Theorem 4], this gives that it is consistent (relative to the consistency of a weakly compact) that there is no
$\kappa $
-Aronszajn tree. By result of Mitchell [Reference William7, Theorem 4], this gives that it is consistent (relative to the consistency of a weakly compact) that there is no
![]() $F:[\omega _2]^2\to \omega _2$
establishing
$F:[\omega _2]^2\to \omega _2$
establishing
 $\aleph _2\not \to [\aleph _2]^2_{\aleph _2}$
with no three-colored triangles.
$\aleph _2\not \to [\aleph _2]^2_{\aleph _2}$
with no three-colored triangles.
Notation and Definitions. We use the notions and definitions of axiomatic set theory. In particular, each ordinal is a von Neumann ordinal, each cardinal is identified with the least ordinal of that cardinality. If f is a function, A a set, then
![]() $f[A]=\{f(x):x\in A\}$
. If
$f[A]=\{f(x):x\in A\}$
. If
![]() $\kappa $
is an infinite cardinal, then
$\kappa $
is an infinite cardinal, then
![]() $\kappa ^+$
is its successor cardinal. If
$\kappa ^+$
is its successor cardinal. If
![]() $(A,<)$
is an ordered set, then
$(A,<)$
is an ordered set, then
![]() $\mathrm {tp}(A,<)$
or just
$\mathrm {tp}(A,<)$
or just
![]() $\mathrm {tp}(A)$
denotes its order type. If A, B are subsets of the same ordered set, then
$\mathrm {tp}(A)$
denotes its order type. If A, B are subsets of the same ordered set, then
![]() $A<B$
denotes that
$A<B$
denotes that
![]() $x<y$
holds for any
$x<y$
holds for any
![]() $x\in A$
,
$x\in A$
,
![]() $y\in B$
. If A or B is a singleton, we write
$y\in B$
. If A or B is a singleton, we write
![]() $a<B$
instead of
$a<B$
instead of
![]() $\{a\}<B$
, etc. If S is a set,
$\{a\}<B$
, etc. If S is a set,
![]() $\kappa $
a cardinal, then
$\kappa $
a cardinal, then
![]() $[S]^{\kappa }=\{x\subseteq S:|x|=\kappa \}$
,
$[S]^{\kappa }=\{x\subseteq S:|x|=\kappa \}$
,
![]() $[S]^{<\kappa }=\{x\subseteq S:|x|<\kappa \}$
,
$[S]^{<\kappa }=\{x\subseteq S:|x|<\kappa \}$
,
![]() $[S]^{\leq \kappa }=\{x\subseteq S:|x|\leq \kappa \}$
.
$[S]^{\leq \kappa }=\{x\subseteq S:|x|\leq \kappa \}$
.
A tree is a partially ordered set
![]() $(T,\leq )$
, such that
$(T,\leq )$
, such that
![]() $t\!\downarrow =\{t'\in T:t'<t\}$
is well ordered for each element (or node)
$t\!\downarrow =\{t'\in T:t'<t\}$
is well ordered for each element (or node)
![]() $t\in T$
. If
$t\in T$
. If
![]() $(T,\leq )$
is a tree,
$(T,\leq )$
is a tree,
![]() $t\in T$
, then
$t\in T$
, then
![]() $\mathrm {ht}(t)=\mathrm {tp}((t\!\downarrow ))$
is the height of t. We also use the piece of notation
$\mathrm {ht}(t)=\mathrm {tp}((t\!\downarrow ))$
is the height of t. We also use the piece of notation
![]() $t\!\uparrow =\{t'\in T:t<t'\}$
.
$t\!\uparrow =\{t'\in T:t<t'\}$
.
![]() $T_{\alpha }=\{t\in T:\mathrm {ht}(t)=\alpha \}$
for any ordinal
$T_{\alpha }=\{t\in T:\mathrm {ht}(t)=\alpha \}$
for any ordinal
![]() $\alpha $
. The height of a tree
$\alpha $
. The height of a tree
![]() $(T,\leq )$
,
$(T,\leq )$
,
![]() $\mathrm {ht}(T,\leq )$
is the least ordinal such that
$\mathrm {ht}(T,\leq )$
is the least ordinal such that
![]() $T_{\alpha }=\emptyset $
.
$T_{\alpha }=\emptyset $
.
A chain in a tree
![]() $(T,\leq )$
is a set of pairwise comparable nodes. A
$(T,\leq )$
is a set of pairwise comparable nodes. A
![]() $\kappa $
-branch is a chain
$\kappa $
-branch is a chain
![]() $B\subseteq T$
, such that
$B\subseteq T$
, such that
![]() $b\cap T_{\alpha }\neq \emptyset $
(
$b\cap T_{\alpha }\neq \emptyset $
(
![]() $\alpha <\kappa $
). An antichain in a tree
$\alpha <\kappa $
). An antichain in a tree
![]() $(T,\leq )$
is a set of pairwise incomparable nodes.
$(T,\leq )$
is a set of pairwise incomparable nodes.
A tree is normal, if
-
(1)
 $|T_0|=1$
,
$|T_0|=1$
, -
(2) each
 $t\in T_{\alpha }$
has at least two successors in
$t\in T_{\alpha }$
has at least two successors in
 $T_{\alpha +1}$
(
$T_{\alpha +1}$
(
 $\alpha +1<\mathrm {ht}(T,\leq )$
),
$\alpha +1<\mathrm {ht}(T,\leq )$
), -
(3) if
 $\alpha <\beta <\mathrm {ht}(T)$
,
$\alpha <\beta <\mathrm {ht}(T)$
,
 $x\in T_{\alpha }$
, then there is
$x\in T_{\alpha }$
, then there is
 $x<y\in T_{\beta }$
, and
$x<y\in T_{\beta }$
, and -
(4) if
 $\alpha <\mathrm {ht}(T)$
is a limit ordinal, x, y are distinct elements of
$\alpha <\mathrm {ht}(T)$
is a limit ordinal, x, y are distinct elements of
 $T_{\alpha }$
, then
$T_{\alpha }$
, then
 $x\!\downarrow \neq y\!\downarrow $
.
$x\!\downarrow \neq y\!\downarrow $
.
If
![]() $(T,\leq )$
is normal, then for each
$(T,\leq )$
is normal, then for each
![]() $x,y\in T$
there is a largest lower bound denoted by
$x,y\in T$
there is a largest lower bound denoted by
![]() $x\land y$
.
$x\land y$
.
A tree
![]() $(T,\leq )$
of height
$(T,\leq )$
of height
![]() $\kappa $
is a
$\kappa $
is a
![]() $\kappa $
-Suslin tree if there are no chains or antichains of size
$\kappa $
-Suslin tree if there are no chains or antichains of size
![]() $\kappa $
in it. We freely use the facts that if there is a
$\kappa $
in it. We freely use the facts that if there is a
![]() $\kappa $
-Suslin tree, then there is a normal
$\kappa $
-Suslin tree, then there is a normal
![]() $\kappa $
-Suslin tree, and that for a normal tree to be
$\kappa $
-Suslin tree, and that for a normal tree to be
![]() $\kappa $
-Suslin it suffices to assume that it does not contain antichains of cardinality
$\kappa $
-Suslin it suffices to assume that it does not contain antichains of cardinality
![]() $\kappa $
. An
$\kappa $
. An
![]() $\omega _1$
-Suslin tree is simply called a Suslin-tree.
$\omega _1$
-Suslin tree is simply called a Suslin-tree.
A graph is any pair
![]() $(V,X)$
where
$(V,X)$
where
![]() $X\subseteq [V]^2$
. If
$X\subseteq [V]^2$
. If
![]() $\kappa ,\lambda $
are cardinals, then
$\kappa ,\lambda $
are cardinals, then
![]() $K_{\kappa ,\lambda }$
is the complete bipartite graph with bipartition classes of size
$K_{\kappa ,\lambda }$
is the complete bipartite graph with bipartition classes of size
![]() $\kappa ,\lambda $
.
$\kappa ,\lambda $
.
If
![]() $(T,\leq )$
is a tree, then a graph
$(T,\leq )$
is a tree, then a graph
![]() $X\subseteq [T]^2$
obeys
$X\subseteq [T]^2$
obeys
![]() $(T,\leq )$
, if
$(T,\leq )$
, if
![]() $\{t,t'\}\in X$
implies
$\{t,t'\}\in X$
implies
![]() $t'$
or
$t'$
or
![]() $t'<t$
.
$t'<t$
.
Theorem 1. It is consistent that there exist a Suslin tree
![]() $(T,\leq )$
and a graph X on T such that
$(T,\leq )$
and a graph X on T such that
-
(1) X obeys
 $(T,\leq )$
,
$(T,\leq )$
, -
(2) there is no uncountable independent set in X, and
-
(3) if
 $t_0,t_1\in T$
are incomparable, then is finite.
$t_0,t_1\in T$
are incomparable, then is finite. $$ \begin{align*} N(t_0,t_1)=\left\{t\in T:\{t,t_0\},\{t,t_1\}\in X\right\} \end{align*} $$
$$ \begin{align*} N(t_0,t_1)=\left\{t\in T:\{t,t_0\},\{t,t_1\}\in X\right\} \end{align*} $$
Notice that if
![]() $t_0,t_1$
are as in (3),
$t_0,t_1$
are as in (3),
![]() $t\in N(t_0,t_1)$
, then
$t\in N(t_0,t_1)$
, then
![]() $t<t_0,t_1$
. Indeed, both
$t<t_0,t_1$
. Indeed, both
![]() $t_0<t<t_1$
and
$t_0<t<t_1$
and
![]() $t_0,t_1<t$
are ruled out as they would imply that
$t_0,t_1<t$
are ruled out as they would imply that
![]() $t_0,t_1$
are comparable.
$t_0,t_1$
are comparable.
Proof. Let
![]() $(T,\leq )$
be a Suslin tree.
$(T,\leq )$
be a Suslin tree.
Define the notion of forcing
![]() $(P,\leq )$
as follows.
$(P,\leq )$
as follows.
![]() $p\in P$
if
$p\in P$
if
![]() $p=(s,g)$
where
$p=(s,g)$
where
![]() $s\in [T]^{<\omega }$
,
$s\in [T]^{<\omega }$
,
![]() $g\subseteq [s]^2$
, g obeys
$g\subseteq [s]^2$
, g obeys
![]() $(T,\leq )$
.
$(T,\leq )$
.
![]() $(s',g')\leq (s,g)$
iff
$(s',g')\leq (s,g)$
iff
![]() $s'\supseteq s$
,
$s'\supseteq s$
,
![]() $g=g'\cap [s]^2$
, and there are no
$g=g'\cap [s]^2$
, and there are no
![]() $t_0,t_1\in s$
incomparable,
$t_0,t_1\in s$
incomparable,
![]() $t\in s'-s$
such that
$t\in s'-s$
such that
![]() $\{t,t_0\},\{t,t_1\}\in g'$
.⊣
$\{t,t_0\},\{t,t_1\}\in g'$
.⊣
Claim 1.
![]() $\leq $
is transitive.
$\leq $
is transitive.
Proof. Straightforward.⊣
Claim 2. If
![]() $t\in T$
, then
$t\in T$
, then
![]() $D_t=\{(s,g):t\in s\}$
is dense.
$D_t=\{(s,g):t\in s\}$
is dense.
Proof. If
![]() $t\in T$
,
$t\in T$
,
![]() $(s,g)\in P$
, then
$(s,g)\in P$
, then
![]() $(s\cup \{t\},g)$
is a condition and
$(s\cup \{t\},g)$
is a condition and
![]() $(s\cup \{t\},g)\leq (s,g)$
.⊣
$(s\cup \{t\},g)\leq (s,g)$
.⊣
Claim 3.
![]() $(P,\leq )$
has the Knaster property.
$(P,\leq )$
has the Knaster property.
Proof. Assume that
![]() $p_{\xi }\in P$
(
$p_{\xi }\in P$
(
![]() $\xi <\omega _1$
). Using the pigeon hole principle and the
$\xi <\omega _1$
). Using the pigeon hole principle and the
![]() ${\Delta }$
-system lemma, we can assume that
${\Delta }$
-system lemma, we can assume that
![]() $p_{\xi }=(s\cup s_{\xi },g_{\xi })$
with
$p_{\xi }=(s\cup s_{\xi },g_{\xi })$
with
![]() $g_{\xi }\cap [s]^2=g$
. If now
$g_{\xi }\cap [s]^2=g$
. If now
![]() $\xi <\eta $
, then
$\xi <\eta $
, then
![]() $p'=(s',g')$
is a condition where
$p'=(s',g')$
is a condition where
![]() $s'=s\cup s_{\xi }\cup s_{\eta }$
,
$s'=s\cup s_{\xi }\cup s_{\eta }$
,
![]() $g'=g_{\xi }\cup g_{\eta }$
. The only possibility that
$g'=g_{\xi }\cup g_{\eta }$
. The only possibility that
![]() $p'\leq p_{\xi },p_{\eta }$
does not hold is that there are incomparable
$p'\leq p_{\xi },p_{\eta }$
does not hold is that there are incomparable
![]() $t_0,t_1 \in s_{\eta }$
,
$t_0,t_1 \in s_{\eta }$
,
![]() $t\in s_{\xi }$
, with
$t\in s_{\xi }$
, with
![]() $\{t,t_0\},\{t,t_1\}\in g'$
, which is not the case.⊣
$\{t,t_0\},\{t,t_1\}\in g'$
, which is not the case.⊣
Let
![]() $G\subseteq P$
be generic.
$G\subseteq P$
be generic.
Claim 4.
![]() $(T,\leq )$
remains Suslin in
$(T,\leq )$
remains Suslin in
![]() $V[G]$
.
$V[G]$
.
Proof. Immediate from Claim 3.⊣
In
![]() $V[G]$
, define
$V[G]$
, define
![]() $X=\bigcup \{g:(s,g)\in G\}$
.
$X=\bigcup \{g:(s,g)\in G\}$
.
Claim 5. If
![]() $t_0,t_1\in T$
are incomparable, then
$t_0,t_1\in T$
are incomparable, then
![]() $N(t_0,t_1)$
is finite.
$N(t_0,t_1)$
is finite.
Proof. Assume that
![]() $t_0,t_1\in T$
are incomparable. By Claim 2, there is
$t_0,t_1\in T$
are incomparable. By Claim 2, there is
![]() $p=(s,g)\in G$
with
$p=(s,g)\in G$
with
![]() $t_0,t_1\in s$
. By the definition of extension of conditions,
$t_0,t_1\in s$
. By the definition of extension of conditions,
holds for every
![]() $p'=(s',g')\leq p$
. But then,
$p'=(s',g')\leq p$
. But then,
![]() $N(t_0,t_1)\subseteq s$
, therefore
$N(t_0,t_1)\subseteq s$
, therefore
![]() $N(t_0,t_1)$
is finite.⊣
$N(t_0,t_1)$
is finite.⊣
Claim 6. X has no uncountable independent subset.
Proof. Assume that p forces that
![]() $A\subseteq T$
is an uncountable independent set of X. For an uncountable set
$A\subseteq T$
is an uncountable independent set of X. For an uncountable set
![]() $B\subseteq T$
there are
$B\subseteq T$
there are
![]() . Using again the pigeon hole principle and the
. Using again the pigeon hole principle and the
![]() ${\Delta }$
-system lemma, there is an uncountable
${\Delta }$
-system lemma, there is an uncountable
![]() $B'\subseteq B$
, such that
$B'\subseteq B$
, such that
![]() $p_t=(s\cup s_t,g_t)$
where
$p_t=(s\cup s_t,g_t)$
where
![]() $g_t\cap [s]^2=g$
,
$g_t\cap [s]^2=g$
,
![]() $t\in s_t$
, if
$t\in s_t$
, if
![]() $t',t''\in B'$
then
$t',t''\in B'$
then
![]() $\mathrm {ht}(t')\neq \mathrm {ht}(t'')$
and if
$\mathrm {ht}(t')\neq \mathrm {ht}(t'')$
and if
![]() $\mathrm {ht}(t')<\mathrm {ht}(t'')$
, then
$\mathrm {ht}(t')<\mathrm {ht}(t'')$
, then
![]() $\mathrm {ht}[s]<\mathrm {ht}[s_{t'}]<\mathrm {ht}[s_{t''}]$
.
$\mathrm {ht}[s]<\mathrm {ht}[s_{t'}]<\mathrm {ht}[s_{t''}]$
.
As
![]() $(T,\leq )$
is a Suslin tree, there are
$(T,\leq )$
is a Suslin tree, there are
![]() $t',t''\in B'$
with
$t',t''\in B'$
with
![]() $t'<t''$
. Define
$t'<t''$
. Define
![]() $p^*=(s^*,g^*)$
where
$p^*=(s^*,g^*)$
where
and
It is clear that
![]() $p^*$
is a condition. The only trouble with
$p^*$
is a condition. The only trouble with
![]() $p^*\leq p_{t'},p_{t''}$
could be that there are incomparable
$p^*\leq p_{t'},p_{t''}$
could be that there are incomparable
![]() $t_0,t_1\in s_{t''}$
,
$t_0,t_1\in s_{t''}$
,
![]() $t\in s_{t'}$
with
$t\in s_{t'}$
with
![]() $\{t,t_0\},\{t,t_1\}\in g^*$
. As there are no such elements, we have
$\{t,t_0\},\{t,t_1\}\in g^*$
. As there are no such elements, we have
![]() $p^*\leq p_{t'},p_{t''}$
and so
$p^*\leq p_{t'},p_{t''}$
and so
a contradiction.
Corollary 2. It is consistent that there is a graph X on
![]() $\omega _1$
such that
$\omega _1$
such that
-
(A) if
 $A\in [\omega _1]^{\aleph _1}$
, then there is some
$A\in [\omega _1]^{\aleph _1}$
, then there is some
 $\emptyset \neq s\in [A]^{<\omega }$
, such that no
$\emptyset \neq s\in [A]^{<\omega }$
, such that no
 $x\in A-s$
is joined to every element of s, and
$x\in A-s$
is joined to every element of s, and -
(B) there is no uncountable independent set in X.
Proof. Let
![]() $(T,\leq )$
be a Suslin tree and X be a graph on T, as in Theorem 1. We claim that X is as required.
$(T,\leq )$
be a Suslin tree and X be a graph on T, as in Theorem 1. We claim that X is as required.
Assume that A is an uncountable subset of T. As
![]() $(T,\leq )$
is Suslin, there are incomparable
$(T,\leq )$
is Suslin, there are incomparable
![]() $t_0,t_1\in A$
. Let
$t_0,t_1\in A$
. Let
The finite set s satisfies the above property (A): if
![]() $t\in A-s$
,
$t\in A-s$
,
![]() $\{t_0,t\},\{t_1,t\}\in X$
, then
$\{t_0,t\},\{t_1,t\}\in X$
, then
![]() $t\in N(t_0,t_1)\cap A\subseteq s$
, a contradiction. As property (B) obviously holds, we are done.⊣
$t\in N(t_0,t_1)\cap A\subseteq s$
, a contradiction. As property (B) obviously holds, we are done.⊣
We will apply the following result of Todorcevic.
Theorem A (Todorcevic, [Reference William6])
It is consistent that
![]() $\mathfrak {c}=\aleph _2$
,
$\mathfrak {c}=\aleph _2$
,
![]() $\mathrm {MA}_{\omega _1}$
holds, and if X is a graph on
$\mathrm {MA}_{\omega _1}$
holds, and if X is a graph on
![]() $\omega _1$
then either X contains an uncountable independent set or it has two sets,
$\omega _1$
then either X contains an uncountable independent set or it has two sets,
![]() $A,B\subseteq \omega _1$
,
$A,B\subseteq \omega _1$
,
![]() $|A|=\aleph _0$
,
$|A|=\aleph _0$
,
![]() $|B|=\aleph _1$
, such that
$|B|=\aleph _1$
, such that
![]() $[A]^2\subseteq X$
and each vertex of A is joined to each vertex in B.
$[A]^2\subseteq X$
and each vertex of A is joined to each vertex in B.
In fact, the result follows from PFA.
Theorem 3. It is consistent that if X is a graph on
![]() $\omega _1$
such that for every
$\omega _1$
such that for every
![]() $A\in [\omega _1]^{\aleph _1}$
there is
$A\in [\omega _1]^{\aleph _1}$
there is
![]() $\emptyset \neq s\in [A]^{<\omega }$
with the property that every
$\emptyset \neq s\in [A]^{<\omega }$
with the property that every
![]() $x\in A-s$
is not joined to at least one
$x\in A-s$
is not joined to at least one
![]() $y\in s$
, then X has an uncountable independent vertex set.
$y\in s$
, then X has an uncountable independent vertex set.
Proof. We refer to a model of Theorem A. In that model, if X is a graph on
![]() $\omega _1$
not containing an uncountable independent set, then there are
$\omega _1$
not containing an uncountable independent set, then there are
![]() $A\in [\omega _1]^{\omega }$
,
$A\in [\omega _1]^{\omega }$
,
![]() $B\in [\omega _1]^{\omega _1}$
with
$B\in [\omega _1]^{\omega _1}$
with
![]() $[A]^2\subseteq X$
and
$[A]^2\subseteq X$
and
We claim that
![]() $A\cup B$
does not satisfy the condition in the Problem. For that, let
$A\cup B$
does not satisfy the condition in the Problem. For that, let
![]() $s\in [A\cup B]^{<\omega }$
. If now
$s\in [A\cup B]^{<\omega }$
. If now
![]() $x\in A-s$
, then x is joined to each element of s.⊣
$x\in A-s$
, then x is joined to each element of s.⊣
Theorem 4. (Erdős–Hajnal)
If CH holds, then there are disjoint circuitfree graphs
![]() $\{X_n:n<\omega \}$
such that if
$\{X_n:n<\omega \}$
such that if
![]() $A\in [\omega _1]^{\aleph _1}$
, then
$A\in [\omega _1]^{\aleph _1}$
, then
![]() $\{n<\omega :X_n\cap [A]^2=\emptyset \}$
is finite.
$\{n<\omega :X_n\cap [A]^2=\emptyset \}$
is finite.
Proof. Enumerate
![]() $[\omega _1]^{\omega }\times [\omega ]^{\omega }$
as
$[\omega _1]^{\omega }\times [\omega ]^{\omega }$
as
![]() $\{\langle A_{\alpha },B_{\alpha }\rangle :\alpha <\omega _1\}$
. Then define the partial function F with
$\{\langle A_{\alpha },B_{\alpha }\rangle :\alpha <\omega _1\}$
. Then define the partial function F with
![]() ${\mathrm {Dom}}(F)\subseteq [\omega _1]^2$
,
${\mathrm {Dom}}(F)\subseteq [\omega _1]^2$
,
![]() $\mathrm {Ran}(F)\subseteq \omega $
such that
$\mathrm {Ran}(F)\subseteq \omega $
such that
-
(a)
 $F(\beta ,\alpha )\neq F(\beta ',\alpha )$
(
$F(\beta ,\alpha )\neq F(\beta ',\alpha )$
(
 $\beta <\beta '<\alpha $
) and
$\beta <\beta '<\alpha $
) and -
(b) if
 $\beta <\alpha $
is such that
$\beta <\alpha $
is such that
 $A_{\beta }\subseteq \alpha $
, then there are
$A_{\beta }\subseteq \alpha $
, then there are
 $\gamma \in A_{\beta }$
,
$\gamma \in A_{\beta }$
,
 $n\in B_{\beta }$
with
$n\in B_{\beta }$
with
 $F(\gamma ,\alpha )=n$
.
$F(\gamma ,\alpha )=n$
.
One can immediately see that
![]() $X_n=F^{-1}(n)$
(
$X_n=F^{-1}(n)$
(
![]() $n<\omega $
) are as required.⊣
$n<\omega $
) are as required.⊣
One cannot change “finite” to “empty” in the Theorem, as for every
![]() $n<\omega $
there is
$n<\omega $
there is
![]() $A\in [\omega _1]^{\omega _1}$
such that
$A\in [\omega _1]^{\omega _1}$
such that
![]() $X_n\cap [A]^2=\emptyset $
. Namely, any uncountable color class in the two-coloring of the graph
$X_n\cap [A]^2=\emptyset $
. Namely, any uncountable color class in the two-coloring of the graph
![]() $X_n$
.
$X_n$
.
Forcing with
![]() $P=\mathrm {Add}(\omega ,\kappa )$
over a model of CH gives a model of the statement in the Theorem with large continuum. In fact, the ground model construction retains its property via forcing with any P with the Knaster property.
$P=\mathrm {Add}(\omega ,\kappa )$
over a model of CH gives a model of the statement in the Theorem with large continuum. In fact, the ground model construction retains its property via forcing with any P with the Knaster property.
Theorem 5. (
 $\mathrm {MA}_{\omega _1}$
)
$\mathrm {MA}_{\omega _1}$
)
There are no graphs
![]() $\{X_n:n<\omega \}$
on
$\{X_n:n<\omega \}$
on
![]() $\omega _1$
such that if
$\omega _1$
such that if
![]() $A\in [\omega _1]^{\aleph _1}$
, then
$A\in [\omega _1]^{\aleph _1}$
, then
![]() $\{n<\omega :X_n\cap [A]^2=\emptyset \}$
is finite.
$\{n<\omega :X_n\cap [A]^2=\emptyset \}$
is finite.
Proof. Assume that
![]() $X_0,X_1,\dots $
are circuitfree graphs on
$X_0,X_1,\dots $
are circuitfree graphs on
![]() $\omega _1$
. Let D be a nonprincipal ultrafilter on
$\omega _1$
. Let D be a nonprincipal ultrafilter on
![]() $\omega $
. Set
$\omega $
. Set
![]() $e\in X$
iff
$e\in X$
iff
![]() $\{n<\omega :e\in X_n\}\in D$
. X is circuitfree: should
$\{n<\omega :e\in X_n\}\in D$
. X is circuitfree: should
![]() $\{e_0,\dots ,e_k\}$
be a circuit, then we had
$\{e_0,\dots ,e_k\}$
be a circuit, then we had
![]() $e_0,\dots ,e_k\in X_n$
for some n, a contradiction. X is a bipartite graph on
$e_0,\dots ,e_k\in X_n$
for some n, a contradiction. X is a bipartite graph on
![]() $\omega _1$
, let V be one of the uncountable bipartition classes.
$\omega _1$
, let V be one of the uncountable bipartition classes.
If we now restrict to V and redefine it to
![]() $\omega _1$
, then we obtain that
$\omega _1$
, then we obtain that
![]() $X_0,\dots $
are circuitfree graphs on
$X_0,\dots $
are circuitfree graphs on
![]() $\omega _1$
and
$\omega _1$
and
(*)
![]() $\{n:e\in X_n\}\notin D$
for every
$\{n:e\in X_n\}\notin D$
for every
![]() $e\in [\omega _1]^2$
.
$e\in [\omega _1]^2$
.
Define
![]() $(s,t)\in P$
if
$(s,t)\in P$
if
![]() $s\in [\omega _1]^{<\omega }$
,
$s\in [\omega _1]^{<\omega }$
,
![]() $t\in [\omega ]^{<\omega }$
, and s is independent in
$t\in [\omega ]^{<\omega }$
, and s is independent in
![]() $X_n$
(
$X_n$
(
![]() $n\in t$
).
$n\in t$
).
![]() $(s',t')\leq (s,t)$
if
$(s',t')\leq (s,t)$
if
![]() $s'\supseteq s$
,
$s'\supseteq s$
,
![]() $t'\supseteq t$
.
$t'\supseteq t$
.
By (*), for each
![]() $n<\omega $
, the set
$n<\omega $
, the set
![]() $D_n=\{(s,t):|t|>n\}$
is dense.
$D_n=\{(s,t):|t|>n\}$
is dense.
In order to show ccc, assume that
![]() $p_{\alpha }\in P$
(
$p_{\alpha }\in P$
(
![]() $\alpha <\omega _1$
). Without loss of generality,
$\alpha <\omega _1$
). Without loss of generality,
![]() $p_{\alpha }=(s\cup s_{\alpha },t)$
where
$p_{\alpha }=(s\cup s_{\alpha },t)$
where
![]() $\{s,s_{\alpha }:\alpha <\omega _1\}$
are disjoint. If
$\{s,s_{\alpha }:\alpha <\omega _1\}$
are disjoint. If
![]() $(s\cup s_{\alpha },t)$
,
$(s\cup s_{\alpha },t)$
,
![]() $(s\cup s_{\beta },t)$
are incompatible, then there is an edge of
$(s\cup s_{\beta },t)$
are incompatible, then there is an edge of
![]() $Y=\bigcup \{X_k:k\in t\}$
between
$Y=\bigcup \{X_k:k\in t\}$
between
![]() $s_{\alpha }$
and
$s_{\alpha }$
and
![]() $s_{\beta }$
. Using this, one obtains that Y contains a
$s_{\beta }$
. Using this, one obtains that Y contains a
![]() $K_{n+1,n^2}$
where
$K_{n+1,n^2}$
where
![]() $n=|t|$
. If the edges of this
$n=|t|$
. If the edges of this
![]() $K_{n+1,n^2}$
are colored with n colors, then there is a monocolored
$K_{n+1,n^2}$
are colored with n colors, then there is a monocolored
![]() $C_4$
, i.e., some
$C_4$
, i.e., some
![]() $X_i$
contains a
$X_i$
contains a
![]() $C_4$
, a contradiction.
$C_4$
, a contradiction.
By ccc, there is
![]() $\gamma <\omega _1$
, such that if
$\gamma <\omega _1$
, such that if
![]() $(s,t)\in P$
,
$(s,t)\in P$
,
![]() $s\cap \gamma =\emptyset $
, then for every
$s\cap \gamma =\emptyset $
, then for every
![]() $\gamma <\alpha <\omega _1$
there is
$\gamma <\alpha <\omega _1$
there is
![]() $(s',t')\leq (s,t)$
,
$(s',t')\leq (s,t)$
,
![]() $s'\cap \gamma =\emptyset $
,
$s'\cap \gamma =\emptyset $
,
![]() $s'\not \subseteq \alpha $
. We can now redefine P by adding the condition
$s'\not \subseteq \alpha $
. We can now redefine P by adding the condition
![]() $s\cap \gamma =\emptyset $
to the definition of
$s\cap \gamma =\emptyset $
to the definition of
![]() $(s,t)\in P$
.
$(s,t)\in P$
.
Finally, a standard application of
![]() $\mathrm {MA}_{\omega _1}$
gives the result.⊣
$\mathrm {MA}_{\omega _1}$
gives the result.⊣
Lemma 6. If
![]() $f:[\kappa ]^2\to \lambda $
is a coloring with no three-colored triangle,
$f:[\kappa ]^2\to \lambda $
is a coloring with no three-colored triangle,
![]() $g:\lambda \to \mu $
is arbitrary, then
$g:\lambda \to \mu $
is arbitrary, then
![]() $g\circ f:[\kappa ]^2\to \mu $
is a coloring with no three-colored triangle.
$g\circ f:[\kappa ]^2\to \mu $
is a coloring with no three-colored triangle.
Proof. Immediate.⊣
Theorem 7. (Shelah [Reference Shelah3])
If
![]() $\kappa ^{<\kappa }=\kappa $
and
$\kappa ^{<\kappa }=\kappa $
and
![]() $2^{\kappa }=\kappa ^+$
, then there is a coloring
$2^{\kappa }=\kappa ^+$
, then there is a coloring
![]() $F:[\kappa ^+]^2\to \kappa $
establishing
$F:[\kappa ^+]^2\to \kappa $
establishing
![]() $\kappa ^+\not \to [\kappa ^+]^2_{\kappa }$
with no three-colored triangle.
$\kappa ^+\not \to [\kappa ^+]^2_{\kappa }$
with no three-colored triangle.
Proof. Let
![]() $A\subseteq {}^{\kappa }2$
be a Lusin set, i.e.,
$A\subseteq {}^{\kappa }2$
be a Lusin set, i.e.,
![]() $|A|=\kappa ^+$
and every
$|A|=\kappa ^+$
and every
 $B\subseteq [A]^{\kappa ^+}$
is somewhere dense in the lexicographically ordered
$B\subseteq [A]^{\kappa ^+}$
is somewhere dense in the lexicographically ordered
![]() ${}^{\kappa }2$
. Define
${}^{\kappa }2$
. Define
![]() $H(f,g)<\kappa $
as the place of the least difference of
$H(f,g)<\kappa $
as the place of the least difference of
![]() $f,g\in A$
. If
$f,g\in A$
. If
 $B\in [A]^{\kappa ^+}$
, then the range of H on
$B\in [A]^{\kappa ^+}$
, then the range of H on
![]() $[B]^2$
contains an end-segment of
$[B]^2$
contains an end-segment of
![]() $\kappa $
, by the Lusin property. If
$\kappa $
, by the Lusin property. If
![]() $g:\kappa \to \kappa $
is such that
$g:\kappa \to \kappa $
is such that
![]() $g^{-1}(\alpha )$
is cofinal in
$g^{-1}(\alpha )$
is cofinal in
![]() $\kappa $
for each
$\kappa $
for each
![]() $\alpha <\kappa $
, then
$\alpha <\kappa $
, then
![]() $F=g\circ H$
is as required by Lemma 6 and the above observation.⊣
$F=g\circ H$
is as required by Lemma 6 and the above observation.⊣
Lemma 8. If
![]() $(T,\leq )$
is a normal tree,
$(T,\leq )$
is a normal tree,
![]() $\mathrm {ht}(T)=\kappa $
,
$\mathrm {ht}(T)=\kappa $
,
![]() $F(t_0,t_1)=\mathrm {ht}(t_0\land t_1)$
, then
$F(t_0,t_1)=\mathrm {ht}(t_0\land t_1)$
, then
![]() $F:[T]^2\to \kappa $
is a coloring with no three-colored triangle.
$F:[T]^2\to \kappa $
is a coloring with no three-colored triangle.
Proof. Let
![]() $t_0,t_1$
, and
$t_0,t_1$
, and
![]() $t_2$
be three distinct elements of T. It suffices to show that some two of
$t_2$
be three distinct elements of T. It suffices to show that some two of
![]() $t_0\land t_1,t_0\land t_2,t_1\land t_2$
are equal. As we have
$t_0\land t_1,t_0\land t_2,t_1\land t_2$
are equal. As we have
![]() $t_0\land t_1,t_0\land t_2\leq t_0$
, the nodes
$t_0\land t_1,t_0\land t_2\leq t_0$
, the nodes
![]() $t_0\land t_1$
and
$t_0\land t_1$
and
![]() $t_0\land t_2$
are comparable. As we are done if they are equal, we can assume that
$t_0\land t_2$
are comparable. As we are done if they are equal, we can assume that
![]() $t_0\land t_1<t_0\land t_2$
. If
$t_0\land t_1<t_0\land t_2$
. If
![]() $t'=t_0\land t_1$
, then
$t'=t_0\land t_1$
, then
![]() $t'\leq t_1$
,
$t'\leq t_1$
,
![]() $t'<t_0\land t_2\leq t_2$
. If
$t'<t_0\land t_2\leq t_2$
. If
![]() $x,y$
are the immediate successors of
$x,y$
are the immediate successors of
![]() $t'$
with
$t'$
with
![]() $x\leq t_0$
,
$x\leq t_0$
,
![]() $y\leq t_1$
, then
$y\leq t_1$
, then
![]() $t_1\land t_2=t'$
, and we are finished.⊣
$t_1\land t_2=t'$
, and we are finished.⊣
Lemma 9. If
![]() $(T,\leq )$
is a
$(T,\leq )$
is a
![]() $\kappa $
-Suslin tree and
$\kappa $
-Suslin tree and
![]() $H\in [T]^{\kappa }$
, then H is somewhere dense in
$H\in [T]^{\kappa }$
, then H is somewhere dense in
![]() $(T,\leq )$
.
$(T,\leq )$
.
Proof. Assume indirectly that H is nowhere dense. Let
![]() $A\subseteq T$
be a maximal antichain consisting of elements
$A\subseteq T$
be a maximal antichain consisting of elements
![]() $t\in T$
such that
$t\in T$
such that
![]() $t\!\uparrow \cap H=\emptyset $
. As
$t\!\uparrow \cap H=\emptyset $
. As
![]() $(T,\leq )$
is
$(T,\leq )$
is
![]() $\kappa $
-Suslin,
$\kappa $
-Suslin,
![]() $|A|<\kappa $
, consequently,
$|A|<\kappa $
, consequently,
![]() $A\subseteq T_{<\alpha }$
for some
$A\subseteq T_{<\alpha }$
for some
![]() $\alpha <\kappa $
.⊣
$\alpha <\kappa $
.⊣
Claim.
![]() $H\subseteq T_{<\alpha }$
.
$H\subseteq T_{<\alpha }$
.
Proof. Assume not, and so
![]() $s\in H\cap T_{\geq \alpha }$
. As
$s\in H\cap T_{\geq \alpha }$
. As
![]() $s\in H$
, we cannot have
$s\in H$
, we cannot have
![]() $t<s$
for some
$t<s$
for some
![]() $t\in A$
. Also,
$t\in A$
. Also,
![]() $s<t$
is impossible by height considerations. Let
$s<t$
is impossible by height considerations. Let
![]() $s'>s$
be such that
$s'>s$
be such that
![]() $(s'\!\uparrow )\cap H=\emptyset $
(exists by the indirect assumption). As
$(s'\!\uparrow )\cap H=\emptyset $
(exists by the indirect assumption). As
![]() $s'$
is incomparable by any element of A,
$s'$
is incomparable by any element of A,
![]() $A\cup \{s'\}$
would properly extend A, a contradiction.
$A\cup \{s'\}$
would properly extend A, a contradiction.
As by the Claim
![]() $|H|<\kappa $
holds, we have reached the desired contradiction.⊣
$|H|<\kappa $
holds, we have reached the desired contradiction.⊣
A different argument is the following. Let G be generic for
![]() $(T,\leq )$
. As we force with a
$(T,\leq )$
. As we force with a
![]() $\kappa $
-cc forcing, some
$\kappa $
-cc forcing, some
![]() $t\in T$
forces that
$t\in T$
forces that
![]() $|H\cap G|=\kappa $
. Obviously, H is dense above t.
$|H\cap G|=\kappa $
. Obviously, H is dense above t.
Theorem 10. (Todorcevic [Reference Todorcevic5])
If there is a
![]() $\kappa $
-Suslin tree, then there is a coloring
$\kappa $
-Suslin tree, then there is a coloring
![]() $F:[\kappa ]^2\to \kappa $
establishing
$F:[\kappa ]^2\to \kappa $
establishing
![]() $\kappa \not \to [\kappa ]^2_{\kappa }$
with no three-colored triangles.
$\kappa \not \to [\kappa ]^2_{\kappa }$
with no three-colored triangles.
Proof. Let
![]() $(T,\leq )$
be a normal
$(T,\leq )$
be a normal
![]() $\kappa $
-Suslin tree. Set
$\kappa $
-Suslin tree. Set
![]() $F_0(t_0,t_1)=\mathrm {ht}(t_0\land t_1)$
. Let
$F_0(t_0,t_1)=\mathrm {ht}(t_0\land t_1)$
. Let
![]() $g:\kappa \to \kappa $
be such that
$g:\kappa \to \kappa $
be such that
![]() $|g^{-1}(\alpha )|=\kappa $
(
$|g^{-1}(\alpha )|=\kappa $
(
![]() $\alpha <\kappa $
). We claim the
$\alpha <\kappa $
). We claim the
![]() $F=g\circ F_0$
is as required. F has no three-colored triangle by Lemmas 6 and 8.
$F=g\circ F_0$
is as required. F has no three-colored triangle by Lemmas 6 and 8.
In order to prove that F establishes
![]() $T\not \to [\kappa ]^2_{\kappa }$
, let
$T\not \to [\kappa ]^2_{\kappa }$
, let
![]() $H\in [T]^{\kappa }$
.⊣
$H\in [T]^{\kappa }$
.⊣
Claim.
![]() $\mathrm {Ran}(F_0|[H]^2)$
contains an end segment of
$\mathrm {Ran}(F_0|[H]^2)$
contains an end segment of
![]() $\kappa $
.
$\kappa $
.
Proof. By Lemma 9, H is somewhere dense, say, above
![]() $t\in T$
. Set
$t\in T$
. Set
![]() $\alpha =\mathrm {ht}(t)$
. As T is normal, if
$\alpha =\mathrm {ht}(t)$
. As T is normal, if
![]() $\gamma>\alpha $
, there is
$\gamma>\alpha $
, there is
![]() $t'>t$
,
$t'>t$
,
![]() $\mathrm {ht}(t')=\gamma $
. Let
$\mathrm {ht}(t')=\gamma $
. Let
![]() $t_0,t_1$
be two immediate successors of
$t_0,t_1$
be two immediate successors of
![]() $t'$
(exist, as T is normal). As H is dense above t, there are
$t'$
(exist, as T is normal). As H is dense above t, there are
![]() $x_0>t_0$
,
$x_0>t_0$
,
![]() $x_1>t_1$
,
$x_1>t_1$
,
![]() $x_0,x_1\in H$
. Now
$x_0,x_1\in H$
. Now
![]() $F_0(x_0,x_1)=\mathrm {ht}(x_0\land x_1)=\mathrm {ht}(t')=\gamma $
.
$F_0(x_0,x_1)=\mathrm {ht}(x_0\land x_1)=\mathrm {ht}(t')=\gamma $
.
As we proved that
![]() $(\alpha ,\kappa )\subseteq \mathrm {Ran}(F_0|[H]^2)$
, we are done.
$(\alpha ,\kappa )\subseteq \mathrm {Ran}(F_0|[H]^2)$
, we are done.
By the definition of g, g assumes every value of
![]() $(\alpha ,\kappa )$
, we are finished.⊣
$(\alpha ,\kappa )$
, we are finished.⊣
Theorem 11. (
 $\kappa ^{<\kappa }=\kappa $
)
$\kappa ^{<\kappa }=\kappa $
)
After forcing with
![]() $\mathrm {Add}(\kappa ,1)$
, there is a three-colored triangle free coloring
$\mathrm {Add}(\kappa ,1)$
, there is a three-colored triangle free coloring
![]() $F:[\kappa ^+]^2\to \kappa ^+$
establishing
$F:[\kappa ^+]^2\to \kappa ^+$
establishing
 $\kappa ^+\not \to [\kappa ^+]^2_{\kappa ^+}$
.
$\kappa ^+\not \to [\kappa ^+]^2_{\kappa ^+}$
.
Proof. By Shelah’s theorem [Reference Todorcevic4], in the forced model there is a
![]() $\kappa ^+$
-Suslin tree and so we can apply Theorem 10.⊣
$\kappa ^+$
-Suslin tree and so we can apply Theorem 10.⊣
Theorem 12. If
![]() $\kappa>\omega $
is regular, there is a coloring
$\kappa>\omega $
is regular, there is a coloring
![]() $F:[\kappa ]^2\to \kappa $
establishing
$F:[\kappa ]^2\to \kappa $
establishing
![]() $\kappa \not \to [\kappa ]^2_{\kappa }$
with no three-colored triangles, then there is a
$\kappa \not \to [\kappa ]^2_{\kappa }$
with no three-colored triangles, then there is a
![]() $\kappa $
-Aronszajn tree.
$\kappa $
-Aronszajn tree.
Proof. Let F be as in the Theorem. Set
![]() $h(\alpha )=\{F(\alpha ,\beta ):\alpha <\beta <\kappa \}$
for
$h(\alpha )=\{F(\alpha ,\beta ):\alpha <\beta <\kappa \}$
for
![]() $\alpha <\kappa $
.⊣
$\alpha <\kappa $
.⊣
Claim 1.
![]() $|h(\alpha )|<\kappa (\alpha <\kappa )$
.
$|h(\alpha )|<\kappa (\alpha <\kappa )$
.
Proof. Otherwise pick
![]() $\alpha <\beta _i$
for
$\alpha <\beta _i$
for
![]() $0<i\in h(\alpha )$
such that
$0<i\in h(\alpha )$
such that
![]() $F(\alpha ,\beta _i)=i$
. If
$F(\alpha ,\beta _i)=i$
. If
![]() $i\neq j$
, then, as
$i\neq j$
, then, as
![]() $F(\alpha ,\beta _i)=i$
and
$F(\alpha ,\beta _i)=i$
and
![]() $F(\alpha ,\beta _j)=j$
, necessarily
$F(\alpha ,\beta _j)=j$
, necessarily
![]() $F(\beta _i,\beta _j)\in \{i,j\}$
(as otherwise
$F(\beta _i,\beta _j)\in \{i,j\}$
(as otherwise
![]() $\{\alpha ,\beta _i,\beta _j\}$
formed a three-colored triangle). This implies that F restricted to
$\{\alpha ,\beta _i,\beta _j\}$
formed a three-colored triangle). This implies that F restricted to
![]() $\{\beta _i:i\in h(\alpha )-\{0\}\}$
misses color 0, a contradiction.⊣
$\{\beta _i:i\in h(\alpha )-\{0\}\}$
misses color 0, a contradiction.⊣
We now describe the tree
![]() $(T,\leq )$
. Its elements are of the form
$(T,\leq )$
. Its elements are of the form
![]() $t\in {}^{<\kappa }\kappa $
with
$t\in {}^{<\kappa }\kappa $
with
![]() $t<t'$
iff
$t<t'$
iff
![]() $t'$
extends t. If
$t'$
extends t. If
![]() $t\in {}^{\alpha }\kappa $
is in T and
$t\in {}^{\alpha }\kappa $
is in T and
![]() $\beta <\alpha $
, then
$\beta <\alpha $
, then
![]() $t|\beta \in T$
, i.e.,
$t|\beta \in T$
, i.e.,
![]() $(T,\leq )$
is a subtree of
$(T,\leq )$
is a subtree of
![]() ${}^{<\kappa }\kappa $
.
${}^{<\kappa }\kappa $
.
For each
![]() $t\in T$
we define
$t\in T$
we define
![]() $V(t)\subseteq \kappa $
and
$V(t)\subseteq \kappa $
and
![]() $p(t)<\kappa $
.
$p(t)<\kappa $
.
Set
![]() $T_0=\{\emptyset \}$
,
$T_0=\{\emptyset \}$
,
![]() $V(\emptyset )=\kappa $
,
$V(\emptyset )=\kappa $
,
![]() $p(\emptyset )=0$
. If
$p(\emptyset )=0$
. If
![]() $t\in T_{\alpha }$
, define
$t\in T_{\alpha }$
, define
for
![]() $i\in h(p(t))$
and put
$i\in h(p(t))$
and put
![]() $t{}^{\smallfrown } i$
into T if
$t{}^{\smallfrown } i$
into T if
![]() $V(t{}^{\smallfrown } i)\neq \emptyset $
. In this case, define
$V(t{}^{\smallfrown } i)\neq \emptyset $
. In this case, define
![]() $p(t{}^{\smallfrown } i)=\min (V(t{}^{\smallfrown } i))$
.
$p(t{}^{\smallfrown } i)=\min (V(t{}^{\smallfrown } i))$
.
If
![]() $\alpha <\kappa $
is limit,
$\alpha <\kappa $
is limit,
![]() $t\in {}^{\alpha } \kappa $
, define
$t\in {}^{\alpha } \kappa $
, define
![]() $t\in T_{\alpha }$
if
$t\in T_{\alpha }$
if
![]() $V(t)=\bigcap \{V(t|\beta ):\beta <\alpha \}\neq \emptyset $
. In this case set
$V(t)=\bigcap \{V(t|\beta ):\beta <\alpha \}\neq \emptyset $
. In this case set
![]() $p(t)=\min (V(t))$
.
$p(t)=\min (V(t))$
.
Claim 2.
![]() $\bigcup \{V(t):t\in T_{\alpha }\}=\kappa -\{p(t):t\in T_{<\alpha }\}$
.
$\bigcup \{V(t):t\in T_{\alpha }\}=\kappa -\{p(t):t\in T_{<\alpha }\}$
.
Proof. By induction on
![]() $\alpha $
, immediately from the definition.⊣
$\alpha $
, immediately from the definition.⊣
Claim 3. If
![]() $t\in T_{\alpha }$
, then
$t\in T_{\alpha }$
, then
![]() $|\{t'<T_{\alpha +1}:t<t'\}|<\kappa $
.
$|\{t'<T_{\alpha +1}:t<t'\}|<\kappa $
.
Proof. As
![]() $|h(p(t))|<\kappa $
.⊣
$|h(p(t))|<\kappa $
.⊣
Claim 4.
![]() $|T_{\alpha }|<\kappa $
(
$|T_{\alpha }|<\kappa $
(
![]() $\alpha <\kappa $
).
$\alpha <\kappa $
).
Proof. By induction on
![]() $\alpha $
. If this holds for
$\alpha $
. If this holds for
![]() $\alpha $
, then
$\alpha $
, then
![]() $T_{\alpha +1}$
is the union of
$T_{\alpha +1}$
is the union of
![]() $<\kappa $
sets each of size
$<\kappa $
sets each of size
![]() $<\kappa $
by Claim 3 and we are finished as
$<\kappa $
by Claim 3 and we are finished as
![]() $\kappa $
is regular.
$\kappa $
is regular.
Assume that
![]() $\alpha <\kappa $
is limit and we have the Claim for all
$\alpha <\kappa $
is limit and we have the Claim for all
![]() $\beta <\alpha $
. Then
$\beta <\alpha $
. Then
![]() $|T_{<\alpha }|<\kappa $
as
$|T_{<\alpha }|<\kappa $
as
![]() $\kappa $
is regular. Assume indirectly that
$\kappa $
is regular. Assume indirectly that
![]() $|T_{\alpha }|=\kappa $
. Consider the set
$|T_{\alpha }|=\kappa $
. Consider the set
![]() $P=\{p(t):t\in T_{\alpha }\}$
. If
$P=\{p(t):t\in T_{\alpha }\}$
. If
![]() $t_0,t_1\in T_{\alpha }$
, then there are a
$t_0,t_1\in T_{\alpha }$
, then there are a
![]() $\beta <\alpha $
and
$\beta <\alpha $
and
![]() $t\in T_{\beta }$
and there are
$t\in T_{\beta }$
and there are
![]() $t^{\prime }_0,t^{\prime }_1\in T_{\beta +1}$
such that
$t^{\prime }_0,t^{\prime }_1\in T_{\beta +1}$
such that
![]() $t<t^{\prime }_0<t_0$
,
$t<t^{\prime }_0<t_0$
,
![]() $t<t^{\prime }_1<t_1$
and so by the construction
$t<t^{\prime }_1<t_1$
and so by the construction
Consequently, the values of F on
![]() $[P]^2$
are of the form
$[P]^2$
are of the form
![]() $F(p(t),p(t'))$
for some
$F(p(t),p(t'))$
for some
![]() $t<t'\in T_{<\alpha }$
and there are
$t<t'\in T_{<\alpha }$
and there are
![]() $<\kappa $
such possibilities by the inductive hypothesis, i.e., F misses some values on
$<\kappa $
such possibilities by the inductive hypothesis, i.e., F misses some values on
![]() $[P]^2$
, contradicting our condition on F.⊣
$[P]^2$
, contradicting our condition on F.⊣
Claim 5.
![]() $(T,\leq )$
has no
$(T,\leq )$
has no
![]() $\kappa $
-branch.
$\kappa $
-branch.
Proof. Assume indirectly that
![]() $b=\{t_{\alpha }:\alpha <\kappa \}$
is a
$b=\{t_{\alpha }:\alpha <\kappa \}$
is a
![]() $\kappa $
-branch with
$\kappa $
-branch with
![]() $t_{\alpha }\in T_{\alpha }$
(
$t_{\alpha }\in T_{\alpha }$
(
![]() $\alpha <\kappa $
). By the way we constructed T, we have
$\alpha <\kappa $
). By the way we constructed T, we have
![]() $t_{\alpha }=g|\alpha $
for some function
$t_{\alpha }=g|\alpha $
for some function
![]() $g:\kappa \to \kappa $
. Further,
$g:\kappa \to \kappa $
. Further,
![]() $F(p(t_{\beta }),p(t_{\alpha }))=g(\beta )$
for
$F(p(t_{\beta }),p(t_{\alpha }))=g(\beta )$
for
![]() $\beta <\alpha $
, i.e., the branch is end-homogeneous. There is some
$\beta <\alpha $
, i.e., the branch is end-homogeneous. There is some
![]() $i<\kappa $
such that
$i<\kappa $
such that
![]() $|\kappa -g^{-1}(i)|=\kappa $
and then the set
$|\kappa -g^{-1}(i)|=\kappa $
and then the set
![]() $\{p(t_{\alpha }):g(\alpha )\neq i\}$
has cardinality
$\{p(t_{\alpha }):g(\alpha )\neq i\}$
has cardinality
![]() $\kappa $
and it misses color i, a contradiction.
$\kappa $
and it misses color i, a contradiction.
As by Claims 2, 4, and 5
![]() $(T,\leq )$
is a
$(T,\leq )$
is a
![]() $\kappa $
-Aronszajn tree, the proof is complete.⊣
$\kappa $
-Aronszajn tree, the proof is complete.⊣
Acknowledgments
The author is thankful to the referee for his kind suggestions which considerably improved the exposition. This work is partially supported by Hungarian National Research Grant OTKA K 131842.