Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T08:07:43.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy exchange between the lattice and electrons in a metal under femtosecond laser irradiation

Published online by Cambridge University Press:  30 August 2005

YU.V. PETROV
YU.V. PETROV
Affiliation:
L.D. Landau Institute for Theoretical Physics, Chernogolovka, Russia
Rights & Permissions [Opens in a new window]

Abstract

The energy transfer rate between the lattice and electrons in strongly nonequilibrium electron-phonon system of crystalline aluminum created by ultrashort femtosecond laser pulse is calculated in the frame of two-temperature model for a wide range of electron temperature. It is shown that the energy, transmitted from electrons to the lattice per unit volume of the crystal per unut time strongly increases when taking into account the umklapp processes in the electron-phonon scattering.

Keywords

Electron-lattice energy transferFemtosecond laser pulseUmklapp processes
Type
Research Article
Information
Laser and Particle Beams , Volume 23 , Issue 3 , September 2005 , pp. 283 - 289
Copyright
© 2005 Cambridge University Press

1. INTRODUCTION

Interaction of ultrashort laser pulses with solids leads to a strong increase in the temperature of electrons, absorbing the laser radiation (Anisimov et al., 1974). Electrons in this case are not in the thermodynamic equilibrium with the lattice. Strongly nonequilibrium electron-ion system as a consequence of the short laser pulse duration can be produced in semiconductors (Stampfli & Bennemann, 1990; Ashitkov et al., 2002), as well as in metals (Anisimov et al., 1977; Schoenlein et al., 1992; Fal'kovskii & Mishchenko, 1997), and also in plasmas (Alouani Bibi et al., 2004a, 2004b). Heat balance in such electron-phonon system depends to a great extent on the energy transfer rate between the electrons and phonons. The energy relaxation between the electrons and crystalline lattice was considered by Kaganov et al. (1957), Allen (1987), and Rethfeld et al. (2002). Since the electron-electron and phonon-phonon relaxation times are significantly shorter than the electron-phonon relaxation time, electrons and the lattice can be characterized by their own temperatures Te and Ti. When considering the electron-phonon scattering in the above cited works, it is proposed that it takes place within one Brillouine zone. An important role of the umklapp electron-phonon processes during the photon absorption in metals was emphasized by Lugovskoy and Bray (1999). But at this stage of the laser-metal interaction, the electron-phonon scattering in their work was considered in quasielastic approximation. In our work, we consider the influence of the umklapp processes in the electron-phonon interaction onto the electron-lattice energy transfer rate.

2. MODEL

In a similar way as in the classical work by Kaganov et al. (1957), we consider the local pseudopotential interaction between the electron and crystalline lattice

Here a is the vectors of an ideal crystalline lattice (face-centered cubic (fcc) for crystalline aluminum), u(a) is the ion displacement from the site a due to the lattice vibration. For a small deviations from the equilibrium positions

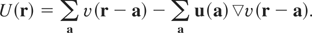
The perturbation potential, due to the ion oscillations,

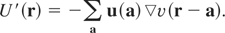
By expanding the ion displacements in terms of the normal coordinates Q(q,ν) with the unit polarization vector of the corresponding plane wave ξ(q,ν), where q is the phonon wave vector, lying within the Brillouine zone, and ν = 1,2,3 corresponds to three acoustic phonons of the fcc lattice, we obtain

Here M is the single atom mass in a monatomic crystal, Nc is a number of unit cells. Then

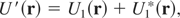
where

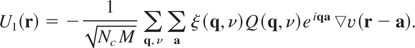
We choose the wave functions of the electron with momentum k as

with the energy eigenvalues ε(k) = ħ2k2/2m (V is the crystal volume, m is the electron effective mass, which we consider to be equal to the mass of a free electron). The phonon states are denoted as Φ. Pseudopotential function v(r) is expressed in the form

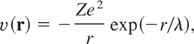
corresponding to the screened Coulomb interaction between the electron and ion with the charge Z and the screening length λ. Then the matrix element for the potential energy perturbation U1 for two electron-phonon states, |k,Φ〉 and |k′,Φ′〉, equals

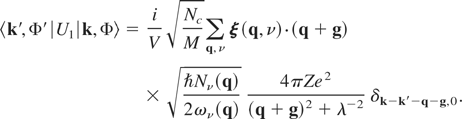
Analogously, for U1*

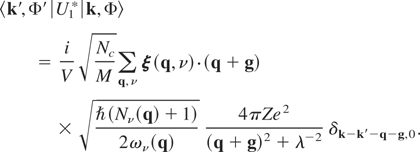
Here g is the reciprocal lattice vector.

Energy transfer from the electrons to lattice per unit volume and unit time can be presented as a sum of energies, transmitted to phonons of different branches:

Integration in (11) is performed within the Brillouine zone (BZ) and

is the change in number of phonons of ν-branch per unit volume and unit time due to the process k′ → k − q − g. Assuming, as in the works by Kaganov et al. (1957) and Allen (1987), that electron-electron and phonon-phonon collisions lead to the fast equilibrium establishment separately in the electron and phonon subsystems with the temperatures Te and Ti respectively, we have for the equilibrium distribution functions f (k) for electrons and Nν(q) for phonons:

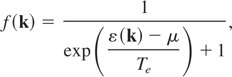
Here μ is the electron chemical potential.

For the phonons in the fcc lattice with one atom per unit cell, having only acoustical modes, we suppose the Debye dispersion law, ων(q) = sν q, where s1 = sL is the speed of longitudinal acoustical phonons, s2,3 = sT is the speed of transverse acoustical phonons. For aluminum at Te = Ti = 0 K sound speeds are connected by the relation sL = γsT with γ ≃ 2.

The quantity wν(k,k′,g) in (12) is equal to

where n is the atom number density, n = 4/a3, with a being the size of the cubic cell of the fcc crystal, ρ is the mass density (ρ = Mn).

Taking into account only eight nearest-neighbor to the Brillouine zone g = 0 reciprocal lattice vectors and introducing in the Debye approach longitudinal (L) phonons with ν = 1 and transversal (T) phonons with ν = 2,3, we obtain:

Here g1 = 2π/a(−1;1;1) is the nearest-neighbor reciprocal lattice vector. Taking into account (13) and (14), we can write

The Debye approach corresponds to the change of the Brillouine zone of fcc lattice to the Debye sphere of radius kD = (24π2)1/3/a. The sound speed s0 at Te = 0 K, averaged as

is equal to s0 = sL0(3/(2γ3 + 1))1/3 and defines the Debye temperature ΘD0 at Te = 0 K

For aluminum, longitudinal phonon frequencies ωL(q) can be well found from the “jellium” model. Taking into account the screened electron-ion interaction, we have

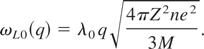
Here λ0 is the screening length at Te = 0 K. Then the Debye temperature at Te = 0 K is given by:

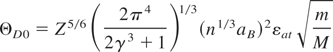
(aB = ħ2/me2 is the Bohr radius, εat = e2/aB = 27.2 eV is the atomic unit of energy). For aluminum with Z = 3 it gives ΘD0 = 350 K (experimental value corresponds to ΘD0 = 380 − 400 K (Girifalco, 1973; Landau & Lifshits, 1980)). As it is shown by Medvedev and Petrov (1999), when the electron temperature increases up to Te ∼ TF (TF is the Fermi temperature), longitudinal phonon frequencies increase up to several times, whereas transverse phonon frequencies do not depend practically on the electron temperature. Dependence of the longitudinal vibrational frequencies on the electron temperature is determined by the increase of screening length:

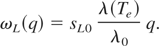
At the same time independent on the electron temperature transverse phonon frequencies are

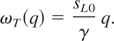
We calculate the screening length λ(Te) in Thomas-Fermi approach as

The electron chemical potential is equal to

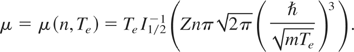
Here I1/2−1(x) is a function, inverse to the Fermi integral

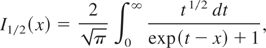
so that I1/2−1(I1/2(x)) = x.

At Te = 0 K the screening length is

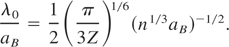
Then the quantities in (16) are:

Only longitudinal phonons contribute to the electron-phonon collisions when g = 0 (Eq. (28)).

For collisions with g ≠ 0 (eqs. (29) and (30)) transverse phonons as well as longitudinal phonons are taken into account. Equations (28)–(30) contain the following functions of the modulus of the phonon wave number q normalized by the Debye wave number (x = q/qD):

longitudinal phonon frequencies at the electron temperature Te

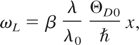
transverse phonon frequencies

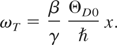
In addition,

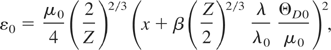
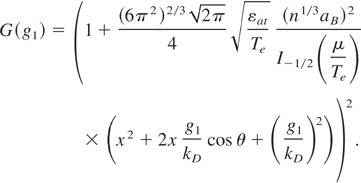
The coefficient A(n,Te) in Eqs. (28)–(30), having the dimension of the energy per unit volume per unit time, is equal to

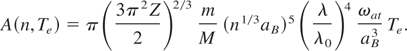
Here ωat = εat /ħ = 4.1 * 1016s−1 is the atomic frequency unit, β = ((2γ3 + 1)/3)1/3, μ0 = (εat /2)(3π2Z)2/3(n1/3aB)2 is the electron chemical potential at Te = 0 K.

The change of the screening length can be performed as

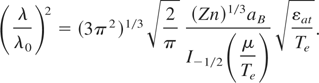
The Debye temperature and the electron chemical potential at T = 0 K ratio in Eqs. (33)–(35) is equal to

3. RESULTS

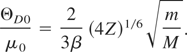
In Fig. 1 the results of the calculation of the energy transfer from the electrons to the crystalline lattice per unit volume and unit time, as a function of the electron temperature for aluminum are presented within a wide range of electron temperatures. All quantities under consideration are measured in atomic units: vat = aB−3, tat = ħ3/me4 = 2.4 * 10−17s. The lattice temperature in Figure 1 is taken to be Ti = 300 K. Curve 1 shows the energy transfer in the absence of the umklapp processes (g = 0) in the electron-phonon scattering. In this case only the longitudinal phonons take part in the energy transfer. Even the longitudinal phonons with g ≠ 0 only in addition to the longitudinal phonons with g = 0 nearly redouble the energy transfer rate when taking into account umklapp processes (curve 2). Curve 3 shows the contribution of the transverse phonons to the electron-lattice energy transfer. It takes place only for g ≠ 0 and exceeds the contribution of longitudinal phonons (curve 2) even when the number of the transverse vibrational modes is greater than the number of longitudinal modes. Curve 4 is obtained when all contributions with g = 0 and g ≠ 0, including longitudinal and transverse phonons, are taken into account and presents in our approximation, the total energy transfer from the electrons to the lattice per unit volume and unit time when the lattice is at room temperature. Total energy transfer is several times greater than that in the case when only longitudinal phonons with g = 0 (curve 1) are taken into account.

Energy transferred from electrons to the lattice in aluminum crystal per unit volume per unit time as a function of the electron temperature. Lattice temperature is chosen to be Ti = 300 K. 1—in the absence of the umklapp processes in the electron-phonon scattering when considering only longitudinal phonons and reciprocal lattice vector g = 0; 2—contribution of longitudinal phonons with g ≠ 0; 3—contribution of the transversal phonons (for them g ≠ 0) into the electron-lattice energy relaxation; 4—electron-lattice energy transfer when all umklapp processes are taken into account.

Then we can obtain the electron-lattice energy transfer rate α, defined by the equation

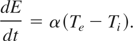
Energy transfer rate α as a function of the electron temperature is presented in Figure 2. Curve 1 corresponds to the energy transfer in the absence of the umklapp processes and curve 2 takes into account the electron-phonon scattering with g ≠ 0.

Electron-lattice energy transfer rate α as a function of the electron temperature. 1—electron-phonon scattering with g = 0 only; 2—the umklapp processes are taken into account.

When the energy transfer between the electrons and crystalline lattice is known, the system of equations governing the change of electron and lattice temperatures can be written. Neglecting the spatial change of crystal during the short time of the electron-lattice energy exchange, for the electron temperatures not exceeding the Fermi temperature, this system of equations can be written as

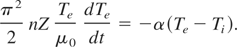
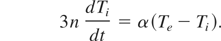
Introducing the designation

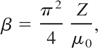
these equations can be written in the form

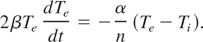
As it is shown in Figure 2, α can be considered as a constant value. Combining Eqs. (44) and (45) we obtain the energy integral

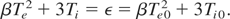
Here ε is the thermal part of initial crystal energy after the laser pulse, when the electron temperature is equal to Te0 and the lattice temperature stays at the room value, Ti0 = 300 K. Substituting Ti from (46) to (44) and integrating equation obtained, we can write temporal dependence of the electron temperature Te and lattice temperature Ti in the form of equations:

Here we denote

. Now we can obtain from Eqs. (47) and (48) the time τ needed to heat the crystalline lattice from the initial room temperature Ti0 to the melting temperature Tm (for aluminum Tm = 933 K). This time interval τ as a function of the initial electron temperature just after the laser pulse, Te0, is presented in Figure 3 for the case when umklapp processes in the electron-phonon scattering are excluded (curve 1) as well as for the case when they are taken into account (curve 2). While taking into consideration umklapp processes, τ become significantly shorter.

Time interval τ for heating the lattice from the room temperature to the melting temperature. 1—in the absence of the umklapp processes; 2—the umklapp processes are taken into account.

Assuming in Eqs. (47) and (48), Te = Ti = Tm at t → ∞, we obtain the threshold value of the initial electron temperature Te* for the heating the lattice up to the melting temperature Tm:

For aluminum Te* is equal to 0.01885 a.u. = 5950 K.

To estimate a threshold value of laser fluence J*, which is necessary to heat the lattice up to the melting temperature, suppose that the energy of laser pulse is absorbed by electrons within a thin layer h. Thus we can write the equation:

Here R ≃ 0.3 is a reflectivity of aluminum if the laser wavelength is equal to 620 nm. Assuming h = 10 nm, we obtain J* = 5 mJ/cm2.

ACKNOWLEDGMENTS

The author gratefully acknowledges Prof.S.I.Anisimov for helpful discussions. This work is supported by Grants of Russian Fund for Fundamental Research.

References

REFERENCES

Allen, P.B. (1987). Theory of thermal relaxation of electrons in metals. Phys. Rev. Lett. 59, 1460–1462.CrossRefGoogle Scholar
Alouani Bibi, F., Matte, J.-P. & Kieffer, J.-C. (2004a). Fokker-Planck simulations of hot electron transport in solid density plasma. Laser Part. Beams 22, 97–102.Google Scholar
Alouani Bibi, F. & Matte, J.-P. (2004b). Nonlocal electron heat transport and election-ion energy transfer in the presence of strong collisional heating. Laser Part. Beams 22, 103–108.Google Scholar
Anisimov, S.I., Kapeliovich, B.L. & Perel'man, T.L. (1974). Electron emission from metal surfaces exposed to ultrashort laser pulses. Zh. Eksp. Teor. Fix. 66, 776–781; Sov. Phys. JETP 39, 375–377.Google Scholar
Anisimov, S.I., Benderskii, V.A. & Farkas, Gy. (1977). Non-linear photoelectric effect in metals produced by a laser radiation. Usp. Fiz. Nauk. 122, 185–222; Sov. Phys.-Uspekhi 20, 467–488.Google Scholar
Ashitkov, S.I., Agranat, M.B., Kondratenko, P.S., Anisimov, S.I., Fortov, V.E., Temnov, V.V., Sokolovski-Tinten, K., Rethfeld, B., Zhou, P. & von der Linde, D. (2002). Ultrafast laser-induced phase transitions in tellurium. Pis'ma v ZhETF 76, 538–541.CrossRefGoogle Scholar
Fal'kovskii, L.A. & Mishchenko, E.G. (1997). Lattice deformation from interaction with electrons heated by an untrashort laser pulse. Pis'ma v ZhETF 66, 195–199; JETP Lett. 66, 208–213.Google Scholar
Girifalco, L.A. (1973). Statistical Physics of Materials. New York: John Wiley & Sons.
Kaganov, M.I., Lifshits, I.M. & Tanatarov, L.V. (1957). Relaxation between electrons and a lattice. Zh. Eksp. Teor. Fiz. 31, 232–237; Sov. Phys. JETP 4, 173–178.Google Scholar
Landau, L.D. & Lifshits, E.M. (1980). Statistical Physics. Oxford: Pergamon.
Lugovskoy, A.V. & Bray, I. (1999). Ultrafast electron dynamics in metals under laser irradiation. Phys. Rev. B 60, 3279–3288.CrossRefGoogle Scholar
Medvedev, D.M. & Petrov, Yu.V. (1999). Dependence of the phonon spectrum of a metal on electron temperature in a nonequilibrium electron-phonon system. Zh. Eksp. Teor. Fiz. 115, 231–242; JETP 88, 128–134.Google Scholar
Rethfeld, B., Kaiser, A., Vicanek, M. & Simon, G. (2002). Ultrafast dynamics of nonequilibrium electrons in metals under femtosecond laser irradiation. Phys. Rev. B 65, 214303 (1–11).Google Scholar
Schoenlein, R.W., Lin, W.Z., Fujimoto, J.G. & Eesley, G.L. (1992). Femtosecond studies of nonequilibrium electronic processes in metals. Phys. Rev. Lett. 58, 1680–1683.Google Scholar
Stampfli, P. & Bennemann, K.H. (1990). Theory for the instability of the diamond structure of Si, Ge and C induced by a dense electron-hole plasma. Phys. Rev. B 42, 7163–7173.CrossRefGoogle Scholar
Figure 0

Energy transferred from electrons to the lattice in aluminum crystal per unit volume per unit time as a function of the electron temperature. Lattice temperature is chosen to be Ti = 300 K. 1—in the absence of the umklapp processes in the electron-phonon scattering when considering only longitudinal phonons and reciprocal lattice vector g = 0; 2—contribution of longitudinal phonons with g ≠ 0; 3—contribution of the transversal phonons (for them g ≠ 0) into the electron-lattice energy relaxation; 4—electron-lattice energy transfer when all umklapp processes are taken into account.

Figure 1

Electron-lattice energy transfer rate α as a function of the electron temperature. 1—electron-phonon scattering with g = 0 only; 2—the umklapp processes are taken into account.

Figure 2

Time interval τ for heating the lattice from the room temperature to the melting temperature. 1—in the absence of the umklapp processes; 2—the umklapp processes are taken into account.