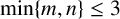1 Introduction
An oriented graph D is obtained from an undirected graph by assigning a direction to each edge. The adjacency matrix of D is the matrix
$A(D)=(a_{ij})$
such that
$a_{ij}=1$
if there is an arc from i to j or from j to i, and
$a_{ij}=0$
otherwise. The rank of D, denoted by
$r(D)$
, is the rank of its adjacency matrix
$A(D)$
. Thus D is nonsingular if and only if
$r(D)$
is equal to the order of D.
The chemical importance of the singularity of undirected graphs arises from the Hückel molecular orbital model. If the molecular graph is singular, then the corresponding chemical compound is highly reactive and unstable, or nonexistent (see [Reference Cvetković, Gutman and Trinajstíc6, Reference Hückel11]). In 1957, Collatz and Sinogowitz [Reference Collatz and Sinogowitz3] posed the problem of characterising all singular graphs. The eigenvalues of paths, cycles and complete graphs have been determined explicitly (see [Reference Cvetković, Doob and Sachs4]), and so the singular cases can be determined. Cvetković and Gutman [Reference Cvetković and Gutman5, Reference Cvetković, Gutman and Trinajstíc6] proved that if B is bipartite and has no cycles with length
$0\pmod 4$
, then
$r(B)=2m(B)$
, where
$m(B)$
is the matching number of B. This implies that B is nonsingular if and only if it has a perfect matching. Guo et al. [Reference Guo, Yan and Yeh8] determined all nonsingular unicyclic graphs. Li et al. [Reference Li, Fan and Su12] characterised the singularity of line graphs of unicyclic graphs with depth one. Gutman and Sciriha [Reference Gutman and Sciriha9] presented a beautiful result showing that the line graph
$L(T)$
of a tree T is either nonsingular or has exactly one zero eigenvalue. For bipartite graphs [Reference Fan and Qian7], bicyclic graphs [Reference Hu, Tan and Liu10] and tricyclic graphs [Reference Cheng and Liu2]), the rank sets of each type have been determined, but the characterisations of nonsingular graphs remain open. A quasi-tree is a connected graph such that removal of a vertex along with all its incident edges results in a tree. The problem of determining the singularity of a quasi-tree seems hard and remains open.
There have been only a few investigations on the singularity of oriented graphs. Monsalve and Rada [Reference Monsalve and Rada13] proposed the sink-source orientations, which preserve the rank for an oriented graph, and thus are very useful in singularity problems. Based on this, Zhang et al. [Reference Zhang, Xu and Wong14] characterised the oriented graphs with rank no larger than two. Chen et al. [Reference Chen, Yang, Geng and Wang1] determined the singularities of oriented graphs from three classes: graphs in which cycles are vertex disjoint, graphs in which all cycles share exactly one common vertex and graphs formed by cycles sharing a common path. In this note, we propose a new approach by using characteristic polynomials and, as an application, the singularity of an oriented quasi-tree is determined in Section 3. All the main results in [Reference Chen, Yang, Geng and Wang1] follow as corollaries. In Section 4, we first give a necessary condition for an oriented bipartite graph
$B_{m,n}$
to be nonsingular, then characterise all nonsingular cases when
$\min \{m,n\}\leq 3$
.
2 Preliminaries
In this section, we make preparations for the main results. An oriented graph D is connected if its underlying graph is connected. Two vertices are adjacent if they are connected by an arc. We indicate an arc from u to v by writing
$uv$
. For a vertex v of D, we denote by
$N^+(v)$
(respectively,
$N^-(v))$
the set of vertices u such that
$vu$
(respectively,
$uv$
) is an arc of D and write
$N(v)=N^+(v)\cup N^-(v)$
. The out-degree (respectively, in-degree) of v is
$d_+(v)=|N_+(v)|$
(respectively,
$d_-(v)=|N_-(v)|$
). The degree of v in D is
$d(v)=d_+(v)+d_-(v)$
. If
$d(v) =1$
, we call v a pendant vertex. We call v a sink (respectively, source) vertex if
$d_+(v)=0$
(respectively,
$d_-(v)=0$
) and a sink-source vertex if
$d_+(v)d_-(v)=0$
. Let
$D=(V(D), E(D))$
be an oriented graph. An oriented graph
$H= (V(H), E(H)$
) is called a subgraph of D if
$V(H)\subseteq V(D)$
and
$E(H)\subseteq E(D)$
.
An oriented cycle is called directed if it contains no sink-source vertex. For an oriented cycle C in D, if
$u, v\in V(C)$
and either
$uv\in E(D)\backslash E(C)$
or
$vu\in E(D)\backslash E(C)$
, then we say that
$uv$
is a chord of C. A cycle cover of an oriented graph D is a set of pairwise vertex disjoint directed cycles which are subgraphs of D and contain all vertices of D. Obviously there may exist no cycle cover for some oriented graphs.
Let D be an oriented graph of order n and
$A(D)$
be its adjacency matrix. Denote by
$f(\lambda )=\sum _{i=0}^{n}a_i\lambda ^{i}$
the characteristic polynomial of
$A(D)$
. The following lemma is our main idea and will be used repeatedly throughout this note.
Lemma 2.1. Let D be an oriented graph.
-
(i) If D has no cycle cover, then D is singular.
-
(ii) If D has a unique cycle cover, then D is nonsingular.
Proof. Clearly, D is nonsingular if and only if
$A(D)$
has no
$0$
eigenvalue, that is, if and only if the coefficient
$a_0$
in its characteristic polynomial is nonzero. Actually,
$a_0$
is the summation of
$\pm 1$
s and
$0$
s, and each
$\pm 1$
is the product of
$1$
s (along with a sign) from n pairwise distinct rows and columns, where n is the order of D. Recall that
$a_{ij}=1$
in
$A(D)$
represents an arc between vertices i and j. It is clear that each
$\pm 1$
corresponds to a cycle cover of D. If D has no cycle cover, then
$a_0=0$
. However, if D has a unique cycle cover, then
$a_0$
is either
$1$
or
$-1$
.
The following lemma can be found in [Reference Chen, Yang, Geng and Wang1], but it can also be viewed as a corollary of Lemma 2.1, since an oriented graph containing sink-source vertices has no cycle cover.
Lemma 2.2 [Reference Chen, Yang, Geng and Wang1]
Let D be an oriented graph. If D has a sink-source vertex, then D is singular. In particular, if D has a pendant vertex, then D is singular.
3 Oriented quasi-trees
Since the singularities of undirected trees and oriented trees have been determined, it is natural to ask for the (oriented) graphs obtained from trees by adding one vertex along with some incident edges or arcs. For undirected quasi-trees, the problem seems hard and there is no general answer yet. We determine the singularity of oriented quasi-trees. An example of a nonsingular oriented quasi-tree is depicted in Figure 1.
Theorem 3.1. Let T be an oriented tree. If D is an oriented quasi-tree obtained from T by adding a vertex x along with some incident arcs, then D is nonsingular if and only if the following three conditions hold:
-
(i)
$T=v_1v_2\cdots v_n$
is an oriented path; -
(ii)
$\{v_1, v_n\}\subseteq N(x)$
; -
(iii)
$xv_1v_2\cdots v_n x$
is a directed cycle.
Proof.
Sufficiency. Assume the three conditions hold for D. Observe that x lies in each possible directed cycle of D, so it is easy to see that
$xv_1v_2\cdots v_nx$
is a unique cycle cover of D. Thus D is nonsingular by Lemma 2.1(ii).
Necessity. By Lemma 2.2, if T has at least three pendant vertices, then they are adjacent to x. However, D has no cycle cover in such a case. Thus T has exactly two pendant vertices, that is, it is an oriented path, say
$T=v_1v_2\cdots v_n$
, such that
$\{v_1, v_n\}\subseteq N(x)$
. Now it is easy to see that
$xv_1v_2\cdots v_n x$
is the only possible cycle cover for D. Since D must have at least one cycle cover by Lemma 2.1(i),
$xv_1v_2\cdots v_nx$
must be a directed cycle. This completes the proof.
In [Reference Chen, Yang, Geng and Wang1], the authors considered three types of oriented graphs and determined their singularities. Obviously, if D is an oriented graph such that all cycles share exactly one common vertex or is formed by cycles sharing one common path, then D is an oriented quasi-tree. By Theorem 3.1, the following two corollaries follow immediately.
Figure 1 A nonsingular oriented quasi-tree, in which the arc
$v_2x$
can be removed or the direction of
$v_2x$
can be reversed.
Corollary 3.2 [Reference Chen, Yang, Geng and Wang1, Theorem 4.1]
Let D be an oriented connected graph in which all (
$\geq 2$
) cycles share exactly one common vertex. Then D is singular.
Corollary 3.3 [Reference Chen, Yang, Geng and Wang1, Theorem 5.1]
Let D be an oriented connected graph formed by (
$\geq 2$
) cycles sharing a path. Then D is nonsingular if and only if it is obtained from a directed cycle by adding a chord.
Chen et al. also considered oriented graphs in which cycles are pairwise vertex disjoint. For an oriented graph D belonging to this class, we call two cycles adjacent if there is a path connecting them using only vertices outside the cycles. By applying Lemma 2.1, the singularity can also be determined easily.
Corollary 3.4 [Reference Chen, Yang, Geng and Wang1, Theorem 3.1]
Let D be an oriented connected graph in which cycles are vertex disjoint. Then D is nonsingular if and only if it satisfies all the following conditions:
-
(i) D has no pendant vertices;
-
(ii) each oriented cycle in D is directed;
-
(iii) two oriented cycles are adjacent in D if and only if they are connected by an arc.
Proof. The sufficiency is confirmed by Lemma 2.1(ii) immediately since all the directed cycles form a unique cycle cover for D. For the necessity, each vertex must be in some oriented cycle by Lemma 2.1(i). Thus D has no pendant vertices, and two oriented cycles are adjacent in D if and only if they are connected by an arc. Now all the oriented cycles form the only possible cycle cover for D. They must be directed since D must have at least one cycle cover.
4 Oriented bipartite graphs
As noted in Section 1, an undirected bipartite graph having no cycles with length
$0\pmod 4$
is nonsingular if and only if it has a perfect matching. However, the singularity of a general bipartite graph has not been determined. In this section, we give a necessary condition for an oriented bipartite graph to be nonsingular. By applying this result, we characterise all the nonsingular oriented graphs
$B_{m,n}$
when
$\min \{m,n\}\leq 3$
.
Lemma 4.1. Let
$B_{m,n}$
be an oriented bipartite graph. If
$B_{m,n}$
is nonsingular, then
$m=n$
.
Proof. Let X and Y be the two bipartite sets of
$B_{m,n}$
with
$|X|=m$
and
$|Y|=n$
. By Lemma 2.1(i),
$B_{m,n}$
has at least one cycle cover. Let
$\mathbf {C}=\{C^1, C^2, \ldots , C^k\}$
be such a cycle cover. Then for each
$i\in \{1,2 ,\ldots , k\}$
,
$C^i$
is an even cycle since
$B_{m,n}$
is a bipartite graph. Thus
$C^i$
covers the same number of vertices from X and Y. Since
$\mathbf {C}$
is a set of vertex disjoint directed cycles covering all the vertices, it follows that
$|X|=|Y|$
and the proof is done.
Corollary 4.2. Let
$B_{m,n}$
be an oriented bipartite graph.
-
(i) If
$\min \{m,n\}=1$
, then
$B_{m,n}$
is singular. -
(ii) If
$\min \{m,n\}=2$
, then
$B_{m,n}$
is nonsingular if and only if it is a directed cycle
$C_4$
.
Proof. For (i), we can also use Lemma 2.2 since
$B_{m,n}$
is actually an oriented tree. For (ii), the sufficiency is obvious since
$C_4$
itself is the unique cycle cover.
For the necessity, if
$B_{m,n}$
is nonsingular, then
$m=n=2$
by Lemma 4.1. Thus
$B_{m,n}$
must be a directed cycle
$C_4$
since it must have at least one directed cycle by Lemma 2.1(i).
Finally, we characterise all the nonsingular oriented bipartite graphs
$B_{n,m}$
with
$\min \{m,n\}=3$
.
Theorem 4.3. Let
$B_{m,n}$
be an oriented bipartite graph. If
$\min \{m,n\}=3$
, then
$B_{m,n}$
is nonsingular if and only if
$m=n=3$
and it contains a directed cycle
$C_6$
.
Proof.
Necessity. We have
$m=n=3$
by Lemma 4.1. Further by Lemma 2.1(i),
$B_{3,3}$
contains a cycle cover
$\mathbf {C}$
. Recall that the directed cycles in
$\mathbf {C}$
are vertex disjoint. Since the length of a cycle is at least
$4$
in a bipartite graph, we know that a cycle cover of
$B_{3,3}$
contains only a directed cycle
$C_6$
, that is,
$\mathbf {C}=\{C_6\}$
for each cycle cover of
$B_{3,3}$
.
Sufficiency. Denote
$X=\{x_1, x_2, x_3\}$
,
$Y=\{y_1,y_2,y_3\}$
and let
$C_6=x_1y_1x_2y_2x_3y_3x_1$
be a directed cycle. Let
$C_6'$
be any other directed cycle with length
$6$
distinct with
$C_6$
. Since
$B_{3,3}$
contains at most
$9$
arcs,
$C_6'$
and
$C_6$
share at least
$3$
common arcs. We consider the following two cases.
Case 1:
$3$
arcs in
$E(C_6)\cap E(C_6')$
form a directed path of order 4. Then it is easy to check that
$C_6'$
is exactly the same directed cycle as
$C_6$
.
Case 2:
$E(C_6)\cap E(C_6')$
is a disjoint union of
$3$
arcs. Assume without loss of generality that
$E(C_6)\cap E(C_6')=\{x_1y_1, x_2y_2, x_3y_3\}$
. Since
$C_6'$
is distinct from
$C_6$
, it is easy to see that
$x_1y_1x_3y_3x_2y_2x_1$
is the only possible choice for
$C_6'$
. As
$C_6'$
can be obtained from
$C_6$
by applying two interchanges (
$x_2\leftrightarrow x_3$
and
$y_2\leftrightarrow y_3$
), their corresponding terms in the determinant of
$A(B_{3,3})$
have the same sign. That is,
$a_0=\pm 2$
in the characteristic polynomial. Thus
$B_{3,3}$
is nonsingular.
