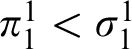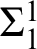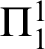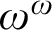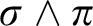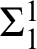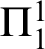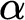1 Introduction
Let
![]() $L_{\alpha }$
denote the
$L_{\alpha }$
denote the
![]() $\alpha $
th level of Gödel’s constructible hierarchy, given by
$\alpha $
th level of Gödel’s constructible hierarchy, given by
![]() $L_{0} = \varnothing $
,
$L_{0} = \varnothing $
,
![]() $L_{\alpha +1} =$
all sets definable over
$L_{\alpha +1} =$
all sets definable over
![]() $L_{\alpha }$
with parameters, and
$L_{\alpha }$
with parameters, and
 $L_{\eta } = \bigcup _{\alpha <\eta } L_{\alpha }$
at limit stages. In
$L_{\eta } = \bigcup _{\alpha <\eta } L_{\alpha }$
at limit stages. In
![]() $\alpha $
-recursion theory, one lifts the usual notion of “computation” over the natural numbers (or, equivalently, over
$\alpha $
-recursion theory, one lifts the usual notion of “computation” over the natural numbers (or, equivalently, over
![]() $L_{\omega }$
) to
$L_{\omega }$
) to
![]() $L_{\alpha }$
, for sufficiently closed
$L_{\alpha }$
, for sufficiently closed
![]() $\alpha $
. As became evident from early work by Kreisel, Kripke, Platek, Sacks, Takeuti, and others (see e.g., Simpson [Reference Simpson11]), facts about recursion on
$\alpha $
. As became evident from early work by Kreisel, Kripke, Platek, Sacks, Takeuti, and others (see e.g., Simpson [Reference Simpson11]), facts about recursion on
![]() $L_{\alpha }$
can be translated into facts about recursion on
$L_{\alpha }$
can be translated into facts about recursion on
![]() $L_{\omega }$
in various ways. In particular, the termination of simple inductive definitions of sets of natural numbers is deeply connected with the reflecting structure of L (see e.g., Cenzer [Reference Cenzer7] or Aczel and Richter [Reference Aczel and Richter3]). The purpose of this article is to study the order in which various reflecting properties given in terms of iterated
$L_{\omega }$
in various ways. In particular, the termination of simple inductive definitions of sets of natural numbers is deeply connected with the reflecting structure of L (see e.g., Cenzer [Reference Cenzer7] or Aczel and Richter [Reference Aczel and Richter3]). The purpose of this article is to study the order in which various reflecting properties given in terms of iterated
![]() $\Sigma ^{1}_{1}$
- and
$\Sigma ^{1}_{1}$
- and
![]() $\Pi ^{1}_{1}$
-reflection first occur in the constructible hierarchy.
$\Pi ^{1}_{1}$
-reflection first occur in the constructible hierarchy.
A formula in the language of set theory is
![]() $\Sigma ^{1}_{1}$
if it contains only existential second-order quantifiers (i.e., ranging over classes) followed by arbitrary first-order quantifiers. An ordinal
$\Sigma ^{1}_{1}$
if it contains only existential second-order quantifiers (i.e., ranging over classes) followed by arbitrary first-order quantifiers. An ordinal
![]() $\alpha $
is said to be
$\alpha $
is said to be
![]() $\Sigma ^{1}_{1}$
-reflecting if whenever
$\Sigma ^{1}_{1}$
-reflecting if whenever
![]() $\phi $
is a
$\phi $
is a
![]() $\Sigma ^{1}_{1}$
formula in the language of set theory and
$\Sigma ^{1}_{1}$
formula in the language of set theory and
![]() $a_{1},\ldots , a_{n}$
are finitely many elements of
$a_{1},\ldots , a_{n}$
are finitely many elements of
![]() $L_{\alpha }$
, then
$L_{\alpha }$
, then
Given a class of ordinals X, an ordinal
![]() $\alpha $
is said to be
$\alpha $
is said to be
![]() $\Sigma ^{1}_{1}$
-reflecting on X if one can additionally demand that the ordinal
$\Sigma ^{1}_{1}$
-reflecting on X if one can additionally demand that the ordinal
![]() $\beta $
above belong to X. The least
$\beta $
above belong to X. The least
![]() $\Sigma ^{1}_{1}$
-reflecting ordinal is denoted by
$\Sigma ^{1}_{1}$
-reflecting ordinal is denoted by
![]() $\sigma ^{1}_{1}$
, and
$\sigma ^{1}_{1}$
, and
![]() $\pi ^{1}_{1}$
is defined dually.
$\pi ^{1}_{1}$
is defined dually.
An ordinal
![]() $\alpha $
is said to be
$\alpha $
is said to be
![]() $\beta $
-stable if
$\beta $
-stable if
![]() $L_{\alpha }$
is a
$L_{\alpha }$
is a
![]() $\Sigma _{1}$
-elementary substructure of
$\Sigma _{1}$
-elementary substructure of
![]() $L_{\beta }$
; in symbols:
$L_{\beta }$
; in symbols:
Given an ordinal
![]() $\alpha $
, write
$\alpha $
, write
![]() $\alpha ^+$
for the smallest admissible ordinal greater than
$\alpha ^+$
for the smallest admissible ordinal greater than
![]() $\alpha $
. Aczel and Richter [Reference Aczel and Richter3] showed that
$\alpha $
. Aczel and Richter [Reference Aczel and Richter3] showed that
![]() $\pi ^{1}_{1} \neq \sigma ^{1}_{1}$
and that a countable ordinal
$\pi ^{1}_{1} \neq \sigma ^{1}_{1}$
and that a countable ordinal
![]() $\alpha $
is
$\alpha $
is
![]() $\Pi ^{1}_{1}$
-reflecting if, and only if, it is
$\Pi ^{1}_{1}$
-reflecting if, and only if, it is
![]() $\alpha ^+$
-stable. Afterwards, Aanderaa [Reference Aanderaa1] showed that
$\alpha ^+$
-stable. Afterwards, Aanderaa [Reference Aanderaa1] showed that
![]() $\pi ^{1}_{1} < \sigma ^{1}_{1}$
. Gostanian [Reference Gostanian8] showed that
$\pi ^{1}_{1} < \sigma ^{1}_{1}$
. Gostanian [Reference Gostanian8] showed that
![]() $\sigma ^{1}_{1}$
is smaller than the least
$\sigma ^{1}_{1}$
is smaller than the least
![]() $\alpha $
which is
$\alpha $
which is
![]() $(\alpha ^++1)$
-stable; moreover, he showed that any
$(\alpha ^++1)$
-stable; moreover, he showed that any
![]() $\alpha $
which is both
$\alpha $
which is both
![]() $(\alpha ^++1)$
-stable and locally countable is also
$(\alpha ^++1)$
-stable and locally countable is also
![]() $\Sigma ^{1}_{1}$
-reflecting. Later Gostanian and Hrbacek [Reference Gostanian and Hrbacek9] employed Gostanian’s method to give a new proof of Aanderaa’s theorem. A third, apparently folklore proof appears in Simpson [Reference Simpson11]. Aanderaa’s theorem is also an immediate consequence of Proposition 16 below.
$\Sigma ^{1}_{1}$
-reflecting. Later Gostanian and Hrbacek [Reference Gostanian and Hrbacek9] employed Gostanian’s method to give a new proof of Aanderaa’s theorem. A third, apparently folklore proof appears in Simpson [Reference Simpson11]. Aanderaa’s theorem is also an immediate consequence of Proposition 16 below.
Let us now generalize the definitions of
![]() $\sigma ^{1}_{1}$
and
$\sigma ^{1}_{1}$
and
![]() $\pi ^{1}_{1}$
as follows:
$\pi ^{1}_{1}$
as follows:
Definition 1. The notion of a reflection pattern is given inductively: the empty set is a reflection pattern; if s and t are reflection patterns, then so too are
![]() $s\wedge t$
,
$s\wedge t$
,
![]() $\sigma s$
, and
$\sigma s$
, and
![]() $\pi s$
.
$\pi s$
.
Most of the time, we omit writing
![]() $\varnothing $
and instead write e.g.,
$\varnothing $
and instead write e.g.,
![]() $\sigma $
for
$\sigma $
for
![]() $\sigma \varnothing $
and
$\sigma \varnothing $
and
![]() $\pi $
for
$\pi $
for
![]() $\pi \varnothing $
.
$\pi \varnothing $
.
Definition 2. A reflection pattern is linear if it contains no conjunctions, and non-linear otherwise.
Definition 3. An ordinal is said to be
![]() $\varnothing $
-reflecting if it is admissible. Let s and t be reflection patterns. Inductively, an ordinal
$\varnothing $
-reflecting if it is admissible. Let s and t be reflection patterns. Inductively, an ordinal
![]() $\alpha $
is said to be
$\alpha $
is said to be
![]() $\sigma s$
-reflecting if it reflects
$\sigma s$
-reflecting if it reflects
![]() $\Sigma ^{1}_{1}$
statements on s-reflecting ordinals; it is said to be
$\Sigma ^{1}_{1}$
statements on s-reflecting ordinals; it is said to be
![]() $\pi s$
-reflecting if it reflects
$\pi s$
-reflecting if it reflects
![]() $\Pi ^{1}_{1}$
statements on s-reflecting ordinals; it is said to be
$\Pi ^{1}_{1}$
statements on s-reflecting ordinals; it is said to be
![]() $s\wedge t$
-reflecting if it is both s-reflecting and t-reflecting.
$s\wedge t$
-reflecting if it is both s-reflecting and t-reflecting.
Thus, being
![]() $\sigma $
-reflecting is the same as being
$\sigma $
-reflecting is the same as being
![]() $\Sigma ^{1}_{1}$
-reflecting, and we might use these two terms interchangeably; however, the reader will soon realize that the shorthand notation just introduced is immensely more convenient for longer reflection patterns.
$\Sigma ^{1}_{1}$
-reflecting, and we might use these two terms interchangeably; however, the reader will soon realize that the shorthand notation just introduced is immensely more convenient for longer reflection patterns.
The main problem of concern in this article is the ordering problem: given two reflection patterns s and t, determine whether the least s-reflecting ordinal is smaller than the least t-reflecting ordinal.
Definition 4. Let s and t be reflection patterns. We write
![]() $s<t$
if the least s-reflecting ordinal is smaller than the least t-reflecting ordinal. We write
$s<t$
if the least s-reflecting ordinal is smaller than the least t-reflecting ordinal. We write
![]() $s\leq t$
if the least s-reflecting ordinal is smaller than or equal to the least t-reflecting ordinal.
$s\leq t$
if the least s-reflecting ordinal is smaller than or equal to the least t-reflecting ordinal.
Thus, instances of the ordering problem are e.g., determining whether
or whether
Other related problems emerge. For instance, one may ask whether the least
![]() $\sigma \sigma $
-reflecting ordinal is the least
$\sigma \sigma $
-reflecting ordinal is the least
![]() $\sigma $
-reflecting ordinal which is also a limit of
$\sigma $
-reflecting ordinal which is also a limit of
![]() $\sigma $
-reflecting ordinals. (Incidentally, the answer to all three questions is “no.”)
$\sigma $
-reflecting ordinals. (Incidentally, the answer to all three questions is “no.”)
Definition 5. The order of reflection is the set of all reflection patterns, prewellordered by
![]() $\leq $
. The order of linear reflection is the subordering of the order of reflection comprised of linear reflection patterns.
$\leq $
. The order of linear reflection is the subordering of the order of reflection comprised of linear reflection patterns.
In this article, we solve the ordering problem for linear reflection patterns: we exhibit a way of assigning ordinals to linear patterns in a way that respects their ordering; in particular, we show:
Theorem 6. The order of linear reflection is a prewellordering of length
![]() $\omega ^{\omega }$
.
$\omega ^{\omega }$
.
The proof requires analyzing the structure of the (full) order of reflection to a certain extent. We shall see that all reflection patterns are witnessed for the first time by ordinals between the least
![]() $\alpha $
which is
$\alpha $
which is
![]() $\alpha ^+$
-stable and the least
$\alpha ^+$
-stable and the least
![]() $\alpha $
which is
$\alpha $
which is
![]() $(\alpha ^++1)$
-stable. In addition, we show:
$(\alpha ^++1)$
-stable. In addition, we show:
Theorem 7. The order of linear reflection is cofinal in the order of reflection.
This raises the question of whether the (full) order of reflection also has length
![]() $\omega ^{\omega }$
. This turns out to be false:
$\omega ^{\omega }$
. This turns out to be false:
Theorem 8. The pattern
![]() $\sigma \sigma $
has rank
$\sigma \sigma $
has rank
![]() $\omega ^{\omega }$
in the order of reflection.
$\omega ^{\omega }$
in the order of reflection.
As part of the proof of Theorem 8, we compute the rank of every pattern below
![]() $\sigma \sigma $
in the order of reflection.
$\sigma \sigma $
in the order of reflection.
In the course of proving these theorems, we find various easier results which we believe to be of independent interest; these are labelled “propositions.”
Convention. Even if not mentioned explicitly, every ordinal in this article is assumed to be both countable and locally countable (i.e., for all
![]() $\beta <\alpha $
, there is a surjection from
$\beta <\alpha $
, there is a surjection from
![]() $\omega $
to
$\omega $
to
![]() $\beta $
in
$\beta $
in
![]() $L_{\alpha }$
). These are the hypotheses for the theorems of Gostanian and Aczel–Richter mentioned above, respectively.
$L_{\alpha }$
). These are the hypotheses for the theorems of Gostanian and Aczel–Richter mentioned above, respectively.
2 Stability and Gandy ordinals
For an admissible ordinal
![]() $\alpha $
, write
$\alpha $
, write
 $$ \begin{align*}\delta_{\alpha} = \mathrm{sup}\big\{\delta: \delta \text{ is the length of an }\alpha\text{-recursive wellordering of a subset of }\alpha \big\},\end{align*} $$
$$ \begin{align*}\delta_{\alpha} = \mathrm{sup}\big\{\delta: \delta \text{ is the length of an }\alpha\text{-recursive wellordering of a subset of }\alpha \big\},\end{align*} $$
where a subset of
![]() $\alpha $
is said to be
$\alpha $
is said to be
![]() $\alpha $
-recursive if it is
$\alpha $
-recursive if it is
![]() $\Delta _{1}$
-definable over
$\Delta _{1}$
-definable over
![]() $L_{\alpha }$
with parameters. The value of
$L_{\alpha }$
with parameters. The value of
![]() $\delta _{\alpha }$
remains unchanged if one replaces “
$\delta _{\alpha }$
remains unchanged if one replaces “
![]() $\alpha $
-recursive” by “
$\alpha $
-recursive” by “
![]() $\alpha $
-r.e.” in the definition. For every admissible
$\alpha $
-r.e.” in the definition. For every admissible
![]() $\alpha $
,
$\alpha $
,
![]() $\delta _{\alpha }$
is easily seen to be a limit and e.g., additively indecomposable. We always have
$\delta _{\alpha }$
is easily seen to be a limit and e.g., additively indecomposable. We always have
![]() $\delta _{\alpha }\leq \alpha ^+$
; an ordinal
$\delta _{\alpha }\leq \alpha ^+$
; an ordinal
![]() $\alpha $
is Gandy if
$\alpha $
is Gandy if
![]() $\delta _{\alpha } = \alpha ^+$
. Gostanian [Reference Gostanian8] showed that
$\delta _{\alpha } = \alpha ^+$
. Gostanian [Reference Gostanian8] showed that
![]() $\sigma ^{1}_{1}$
is the smallest ordinal which is not Gandy. In fact, he showed that a locally countable ordinal is not Gandy if, and only if, it is
$\sigma ^{1}_{1}$
is the smallest ordinal which is not Gandy. In fact, he showed that a locally countable ordinal is not Gandy if, and only if, it is
![]() $\Sigma ^{1}_{1}$
-reflecting. Abramson and Sacks [Reference Abramson and Sacks2] showed that
$\Sigma ^{1}_{1}$
-reflecting. Abramson and Sacks [Reference Abramson and Sacks2] showed that
![]() $(\aleph _{\omega }^{L})^+$
is Gandy, so not every Gandy ordinal is locally countable.
$(\aleph _{\omega }^{L})^+$
is Gandy, so not every Gandy ordinal is locally countable.
The purpose of this section is to derive connections between reflecting properties of ordinals and their degrees of stability. We begin with the following elementary fact:
Lemma 9. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $(\delta _{\alpha }+1)$
-stable. Then
$(\delta _{\alpha }+1)$
-stable. Then
![]() $\alpha $
is
$\alpha $
is
![]() $\Sigma ^{1}_{1}$
-reflecting.
$\Sigma ^{1}_{1}$
-reflecting.
Proof. Otherwise,
![]() $\delta _{\alpha } = \alpha ^+$
by Gostanian’s characterization of
$\delta _{\alpha } = \alpha ^+$
by Gostanian’s characterization of
![]() $\Sigma ^{1}_{1}$
-reflection, so
$\Sigma ^{1}_{1}$
-reflection, so
![]() $\alpha $
is
$\alpha $
is
![]() $(\alpha ^++1)$
-stable. By Gostanian’s result mentioned in the introduction, if
$(\alpha ^++1)$
-stable. By Gostanian’s result mentioned in the introduction, if
![]() $\alpha $
is
$\alpha $
is
![]() $(\alpha ^++1)$
-stable, then it is
$(\alpha ^++1)$
-stable, then it is
![]() $\Sigma ^{1}_{1}$
-reflecting. ⊣
$\Sigma ^{1}_{1}$
-reflecting. ⊣
Since we know what the degree of stability of
![]() $\pi ^{1}_{1}$
is, viz.
$\pi ^{1}_{1}$
is, viz.
![]() $(\pi ^{1}_{1})^+$
, a possible first question is that of the degree of stability of
$(\pi ^{1}_{1})^+$
, a possible first question is that of the degree of stability of
![]() $\sigma ^{1}_{1}$
.
$\sigma ^{1}_{1}$
.
Proposition 10.
![]() $\sigma ^{1}_{1}$
is not
$\sigma ^{1}_{1}$
is not
 $(\delta _{\sigma ^{1}_{1}}+1)$
-stable.
$(\delta _{\sigma ^{1}_{1}}+1)$
-stable.
Proof. Let
 $\delta = \delta _{\sigma ^{1}_{1}}$
. Since
$\delta = \delta _{\sigma ^{1}_{1}}$
. Since
![]() $\delta <(\sigma ^{1}_{1})^+$
, it is not admissible. As we observed before,
$\delta <(\sigma ^{1}_{1})^+$
, it is not admissible. As we observed before,
![]() $\delta $
is a limit ordinal; thus, the failure of admissibility must be due to an instance of collection. Choose some
$\delta $
is a limit ordinal; thus, the failure of admissibility must be due to an instance of collection. Choose some
![]() $\Delta _{0}$
formula
$\Delta _{0}$
formula
![]() $\psi $
such that for some
$\psi $
such that for some
![]() $\vec a \in L_{\delta }$
,
$\vec a \in L_{\delta }$
,
![]() $L_{\delta }\not \models \psi (\vec a)\text {-collection}.$
To see that
$L_{\delta }\not \models \psi (\vec a)\text {-collection}.$
To see that
![]() $\sigma ^{1}_{1}$
is not
$\sigma ^{1}_{1}$
is not
![]() $(\delta +1)$
-stable, consider the formula
$(\delta +1)$
-stable, consider the formula
![]() $\phi $
in the language of set theory asserting that there are sets A and B such that:
$\phi $
in the language of set theory asserting that there are sets A and B such that:
-
1. A and B are transitive sets satisfying
 $V=L$
, A is admissible,
$V=L$
, A is admissible,
 $A \in B$
, and there is
$A \in B$
, and there is
 $\vec a \in B$
such that B does not satisfy
$\vec a \in B$
such that B does not satisfy
 $\psi (\vec a)\text {-collection}$
;
$\psi (\vec a)\text {-collection}$
; -
2. for each
 $({\mathsf {Ord}}\cap A)$
-recursive linear ordering
$({\mathsf {Ord}}\cap A)$
-recursive linear ordering
 $R \in B$
, either there is an infinite descending sequence b through R with
$R \in B$
, either there is an infinite descending sequence b through R with
 $b\in A$
, or there is an ordinal
$b\in A$
, or there is an ordinal
 $\beta \in B$
and an isomorphism
$\beta \in B$
and an isomorphism
 $f \in B$
from R to
$f \in B$
from R to
 $\beta $
;
$\beta $
; -
3. for each
 $\beta \in B$
, there is an
$\beta \in B$
, there is an
 $({\mathsf {Ord}} \cap A)$
-recursive linear ordering
$({\mathsf {Ord}} \cap A)$
-recursive linear ordering
 $R \in B$
and an isomorphism
$R \in B$
and an isomorphism
 $f \in B$
from R to
$f \in B$
from R to
 $\beta $
.
$\beta $
.
Notice that
![]() $\phi $
is a
$\phi $
is a
![]() $\Sigma _{1}$
formula, since the only unbounded quantifier is the one on B. Moreover, it does not hold in
$\Sigma _{1}$
formula, since the only unbounded quantifier is the one on B. Moreover, it does not hold in
 $L_{\sigma ^{1}_{1}}$
, for the sets A and B would need to be of the form
$L_{\sigma ^{1}_{1}}$
, for the sets A and B would need to be of the form
![]() $L_{\alpha }$
and
$L_{\alpha }$
and
![]() $L_{\beta }$
, with
$L_{\beta }$
, with
![]() $\alpha <\beta <\sigma ^{1}_{1}$
. Conditions (2) and (3) together imply that
$\alpha <\beta <\sigma ^{1}_{1}$
. Conditions (2) and (3) together imply that
![]() $\beta = \delta _{\alpha }$
, but Gostanian’s characterization of
$\beta = \delta _{\alpha }$
, but Gostanian’s characterization of
![]() $\sigma ^{1}_{1}$
then implies
$\sigma ^{1}_{1}$
then implies
![]() $\beta = \alpha ^+$
, contradicting condition (1). Finally, it does hold in
$\beta = \alpha ^+$
, contradicting condition (1). Finally, it does hold in
![]() $L_{\delta +1}$
, as witnessed by
$L_{\delta +1}$
, as witnessed by
 $A = L_{\sigma ^{1}_{1}}$
and
$A = L_{\sigma ^{1}_{1}}$
and
![]() $B = L_{\delta }$
. To see that (2) holds, recall a theorem of Gostanian [Reference Gostanian8, Theorem 3.2] by which if
$B = L_{\delta }$
. To see that (2) holds, recall a theorem of Gostanian [Reference Gostanian8, Theorem 3.2] by which if
![]() $\alpha $
is
$\alpha $
is
![]() $\Sigma ^{1}_{1}$
-reflecting, then every
$\Sigma ^{1}_{1}$
-reflecting, then every
![]() $\alpha $
-recursive linear ordering which is not a wellordering has an infinite descending sequence in
$\alpha $
-recursive linear ordering which is not a wellordering has an infinite descending sequence in
![]() $L_{\alpha }$
. Thus, every
$L_{\alpha }$
. Thus, every
![]() $\sigma ^{1}_{1}$
-recursive linear ordering R either has an infinite descending sequence in
$\sigma ^{1}_{1}$
-recursive linear ordering R either has an infinite descending sequence in
 $L_{\sigma ^{1}_{1}}$
, or else is isomorphic to some ordinal
$L_{\sigma ^{1}_{1}}$
, or else is isomorphic to some ordinal
![]() $\beta <\delta $
. One can construct an isomorphism witnessing this by transfinite recursion: at stage
$\beta <\delta $
. One can construct an isomorphism witnessing this by transfinite recursion: at stage
![]() $\gamma <\beta $
, one has defined
$\gamma <\beta $
, one has defined
![]() $f\upharpoonright \gamma $
and sets
$f\upharpoonright \gamma $
and sets
![]() $f(\gamma )$
equal to the R-least element not in the range of
$f(\gamma )$
equal to the R-least element not in the range of
![]() $f\upharpoonright \gamma $
. Since this process takes
$f\upharpoonright \gamma $
. Since this process takes
![]() $\beta $
-many stages and
$\beta $
-many stages and
 $R \in L_{\sigma ^{1}_{1}+1}$
, such an isomorphism belongs to
$R \in L_{\sigma ^{1}_{1}+1}$
, such an isomorphism belongs to
 $L_{\sigma ^{1}_{1} + \delta }$
. Since
$L_{\sigma ^{1}_{1} + \delta }$
. Since
![]() $\delta $
is additively indecomposable, it belongs to
$\delta $
is additively indecomposable, it belongs to
![]() $L_{\delta }$
. The proof that (3) holds is similar. ⊣
$L_{\delta }$
. The proof that (3) holds is similar. ⊣
In the proof of Proposition 10, one could also extend conditions (1) (3) by demanding that the set A satisfy any first-order property. This shows:
Proposition 11. Suppose
![]() $\alpha $
is the least
$\alpha $
is the least
![]() $\Sigma ^{1}_{1}$
-reflecting ordinal satisfying some first-order property
$\Sigma ^{1}_{1}$
-reflecting ordinal satisfying some first-order property
![]() $\phi $
with parameters in
$\phi $
with parameters in
![]() $\alpha $
. Then,
$\alpha $
. Then,
![]() $\alpha $
is not
$\alpha $
is not
![]() $(\delta _{\alpha }+1)$
-stable.
$(\delta _{\alpha }+1)$
-stable.
The proof of the proposition concludes by arriving at the contradiction that there is a smaller
![]() $\Sigma ^{1}_{1}$
-reflecting ordinal satisfying the property
$\Sigma ^{1}_{1}$
-reflecting ordinal satisfying the property
![]() $\phi $
. Thus, one can rephrase the result as:
$\phi $
. Thus, one can rephrase the result as:
Proposition 12. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $(\delta _{\alpha }+1)$
-stable and satisfies some first-order property
$(\delta _{\alpha }+1)$
-stable and satisfies some first-order property
![]() $\phi $
. Then,
$\phi $
. Then,
![]() $\alpha $
is a limit of
$\alpha $
is a limit of
![]() $\Sigma ^{1}_{1}$
-reflecting ordinals satisfying
$\Sigma ^{1}_{1}$
-reflecting ordinals satisfying
![]() $\phi $
.
$\phi $
.
Proof. The proof of the proposition is as in the comment directly preceding its statement. The only additional observation needed is that the hypothesis implies that
![]() $\alpha $
is
$\alpha $
is
![]() $\Sigma ^{1}_{1}$
-reflecting, by Lemma 9. ⊣
$\Sigma ^{1}_{1}$
-reflecting, by Lemma 9. ⊣
Definition 13. We denote by
 $\sigma ^{1,\ell }_{1}$
the least
$\sigma ^{1,\ell }_{1}$
the least
![]() $\Sigma ^{1}_{1}$
-reflecting ordinal which is a limit of
$\Sigma ^{1}_{1}$
-reflecting ordinal which is a limit of
![]() $\Sigma ^{1}_{1}$
-reflecting ordinals.
$\Sigma ^{1}_{1}$
-reflecting ordinals.
Proposition 14.
 $\sigma ^{1,\ell }_{1}$
is smaller than the least
$\sigma ^{1,\ell }_{1}$
is smaller than the least
![]() $\alpha $
which is
$\alpha $
which is
![]() $(\delta _{\alpha }+1)$
-stable.
$(\delta _{\alpha }+1)$
-stable.
Proof. Let
![]() $\alpha $
be as in the statement. By Proposition 12, it is a limit of
$\alpha $
be as in the statement. By Proposition 12, it is a limit of
![]() $\Sigma ^{1}_{1}$
-reflecting ordinals. This fact is first-order expressible over
$\Sigma ^{1}_{1}$
-reflecting ordinals. This fact is first-order expressible over
![]() $\alpha $
, since it is recursively inaccessible (and thus
$\alpha $
, since it is recursively inaccessible (and thus
![]() $\Sigma ^{1}_{1}$
-correct). By Proposition 12 again,
$\Sigma ^{1}_{1}$
-correct). By Proposition 12 again,
![]() $\alpha $
is a limit of
$\alpha $
is a limit of
![]() $\Sigma ^{1}_{1}$
-reflecting ordinals which are limits of
$\Sigma ^{1}_{1}$
-reflecting ordinals which are limits of
![]() $\Sigma _{1}^{1}$
-reflecting ordinals. ⊣
$\Sigma _{1}^{1}$
-reflecting ordinals. ⊣
One cannot improve the conclusion of Proposition 10 by replacing
 $\delta _{\sigma ^{1}_{1}}+1$
by
$\delta _{\sigma ^{1}_{1}}+1$
by
![]() $\delta _{\sigma ^{1}_{1}}$
—every
$\delta _{\sigma ^{1}_{1}}$
—every
![]() $\Sigma ^{1}_{1}$
-reflecting ordinal is stable to the supremum of its recursive wellorderings:
$\Sigma ^{1}_{1}$
-reflecting ordinal is stable to the supremum of its recursive wellorderings:
Proposition 15. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\Sigma ^{1}_{1}$
-reflecting. Then
$\Sigma ^{1}_{1}$
-reflecting. Then
![]() $\alpha $
is
$\alpha $
is
![]() $\delta _{\alpha }$
-stable.
$\delta _{\alpha }$
-stable.
Proof. Write
![]() $\delta = \delta _{\alpha }$
. Since
$\delta = \delta _{\alpha }$
. Since
![]() $\delta $
is a limit ordinal, it suffices to consider arbitrary
$\delta $
is a limit ordinal, it suffices to consider arbitrary
![]() $\gamma <\delta $
and show that
$\gamma <\delta $
and show that
Let
![]() $a \in L_{\alpha }$
and
$a \in L_{\alpha }$
and
![]() $\phi $
be a
$\phi $
be a
![]() $\Sigma _{1}$
-formula such that
$\Sigma _{1}$
-formula such that
![]() $L_{\gamma }\models \phi (a)$
. Without loss of generality, assume that a is an ordinal. Let R be a
$L_{\gamma }\models \phi (a)$
. Without loss of generality, assume that a is an ordinal. Let R be a
![]() $\alpha $
-recursive wellordering of length
$\alpha $
-recursive wellordering of length
![]() $\gamma $
. In particular, R is
$\gamma $
. In particular, R is
![]() $\alpha $
-r.e., so there is a
$\alpha $
-r.e., so there is a
![]() $\Sigma _{1}$
formula
$\Sigma _{1}$
formula
![]() $\psi $
, such that for all
$\psi $
, such that for all
![]() $x,y \in L_{\alpha }$
,
$x,y \in L_{\alpha }$
,
Let us assume for notational simplicity that
![]() $\psi $
is defined without parameters. Given an ordinal
$\psi $
is defined without parameters. Given an ordinal
![]() ${\alpha ^{\prime }}$
, let
${\alpha ^{\prime }}$
, let
![]() $R_{\alpha ^{\prime }}$
be the binary relation given by
$R_{\alpha ^{\prime }}$
be the binary relation given by
Since
![]() $\psi $
is
$\psi $
is
![]() $\Sigma _{1}$
, we have
$\Sigma _{1}$
, we have
![]() $R_{\alpha ^{\prime }}\subset R_{\tau }$
whenever
$R_{\alpha ^{\prime }}\subset R_{\tau }$
whenever
![]() ${\alpha ^{\prime }}\leq \tau \leq \alpha $
. In particular,
${\alpha ^{\prime }}\leq \tau \leq \alpha $
. In particular,
![]() $R_{\alpha ^{\prime }}$
is wellfounded for all
$R_{\alpha ^{\prime }}$
is wellfounded for all
![]() $\alpha ^{\prime }<\alpha $
.
$\alpha ^{\prime }<\alpha $
.
Because
![]() $L_{\gamma }\models \phi (a)$
, there is a subset A of
$L_{\gamma }\models \phi (a)$
, there is a subset A of
![]() $L_{\alpha }$
such that
$L_{\alpha }$
such that
-
1. A codes a model
 $(M, E)$
of
$(M, E)$
of
 ${\mathsf {KP}} + V = L$
;
${\mathsf {KP}} + V = L$
; -
2. M has a largest admissible ordinal
 $\tau $
and
$\tau $
and
 $(\tau , E)$
is isomorphic to
$(\tau , E)$
is isomorphic to
 $(\alpha , \in )$
;
$(\alpha , \in )$
; -
3. there is an ordinal
 $\beta $
of M and a function
$\beta $
of M and a function
 $f \in M$
which is an isomorphism between
$f \in M$
which is an isomorphism between
 $R_{\tau }^{M}$
(i.e.,
$R_{\tau }^{M}$
(i.e.,
 $R_{\tau }$
computed within M) and
$R_{\tau }$
computed within M) and
 $\beta $
, and
$\beta $
, and
 $L_{\beta }^{M}\models \phi (a)$
.
$L_{\beta }^{M}\models \phi (a)$
.
The existence of such an A can be expressed by a set-theoretic
![]() $\Sigma ^{1}_{1}$
formula over
$\Sigma ^{1}_{1}$
formula over
![]() $L_{\alpha }$
with parameter a (as well as any other parameters involved in the definition of R). In particular, reference to
$L_{\alpha }$
with parameter a (as well as any other parameters involved in the definition of R). In particular, reference to
![]() $\alpha $
can be made over
$\alpha $
can be made over
![]() $L_{\alpha }$
, since
$L_{\alpha }$
, since
![]() $\alpha = {\mathsf {Ord}}^{L_{\alpha }}$
. Thus, clause (2) can be expressed in a
$\alpha = {\mathsf {Ord}}^{L_{\alpha }}$
. Thus, clause (2) can be expressed in a
![]() $\Sigma ^{1}_{1}$
way over
$\Sigma ^{1}_{1}$
way over
![]() $L_{\alpha }$
by asserting the existence of a bijection h with domain
$L_{\alpha }$
by asserting the existence of a bijection h with domain
![]() $\alpha $
and range (the set of codes of elements of)
$\alpha $
and range (the set of codes of elements of)
![]() $\tau $
such that for all
$\tau $
such that for all
![]() $\beta _{0},\beta _{1}<\alpha $
,
$\beta _{0},\beta _{1}<\alpha $
,
![]() $\beta _{0} \in \beta _{1}$
if, and only if,
$\beta _{0} \in \beta _{1}$
if, and only if,
![]() $h(\beta _{0})Eh(\beta _{1})$
. Note that quantification over
$h(\beta _{0})Eh(\beta _{1})$
. Note that quantification over
![]() $\alpha $
is first-order over
$\alpha $
is first-order over
![]() $L_{\alpha }$
.
$L_{\alpha }$
.
By
![]() $\Sigma ^{1}_{1}$
-reflection, there is some
$\Sigma ^{1}_{1}$
-reflection, there is some
![]() ${\alpha ^{\prime }}<\alpha $
and some
${\alpha ^{\prime }}<\alpha $
and some
![]() $A_{\alpha ^{\prime }}\subset L_{\alpha ^{\prime }}$
such that
$A_{\alpha ^{\prime }}\subset L_{\alpha ^{\prime }}$
such that
![]() $a \in L_{\alpha ^{\prime }}$
and
$a \in L_{\alpha ^{\prime }}$
and
-
4.
 $A_{\alpha ^{\prime }}$
codes a model
$A_{\alpha ^{\prime }}$
codes a model
 $(N, F)$
of
$(N, F)$
of
 ${\mathsf {KP}} + V = L$
;
${\mathsf {KP}} + V = L$
; -
5. N has a largest admissible ordinal
 $\eta $
and
$\eta $
and
 $(\eta , F)$
is isomorphic to
$(\eta , F)$
is isomorphic to
 $({\alpha ^{\prime }},\in )$
;
$({\alpha ^{\prime }},\in )$
; -
6. there is an ordinal b of N and a function
 $g \in N$
which is an isomorphism between
$g \in N$
which is an isomorphism between
 $R_{\eta }^{N}$
and b, and
$R_{\eta }^{N}$
and b, and
 $L_{b}^{N}\models \phi (a)$
.
$L_{b}^{N}\models \phi (a)$
.
Here and for the rest of our lives, let us identify the wellfounded part of N with its transitive collapse. Condition (5) implies that
![]() $L_{\alpha ^{\prime }} \in N$
. By (6), there is an ordinal b of N and an isomorphism
$L_{\alpha ^{\prime }} \in N$
. By (6), there is an ordinal b of N and an isomorphism
![]() $g \in N$
from
$g \in N$
from
![]() $R_{\alpha ^{\prime }}$
to b. Because
$R_{\alpha ^{\prime }}$
to b. Because
![]() $R_{\alpha ^{\prime }} \subset R$
, it is wellfounded, and so b really is an ordinal. Now,
$R_{\alpha ^{\prime }} \subset R$
, it is wellfounded, and so b really is an ordinal. Now,
![]() $L_{b}\models \phi (a)$
, and N has no admissible ordinals above
$L_{b}\models \phi (a)$
, and N has no admissible ordinals above
![]() ${\alpha ^{\prime }}$
, so
${\alpha ^{\prime }}$
, so
![]() $b<({\alpha ^{\prime }})^+<\alpha $
. Since
$b<({\alpha ^{\prime }})^+<\alpha $
. Since
![]() $\phi $
is
$\phi $
is
![]() $\Sigma _{1}$
, we conclude that
$\Sigma _{1}$
, we conclude that
![]() $L_{\alpha }\models \phi (a)$
, as was to be shown. ⊣
$L_{\alpha }\models \phi (a)$
, as was to be shown. ⊣
We have shown that
![]() $\sigma ^{1}_{1}$
is
$\sigma ^{1}_{1}$
is
![]() $\delta _{\sigma ^{1}_{1}}$
-stable and not
$\delta _{\sigma ^{1}_{1}}$
-stable and not
 $(\delta _{\sigma ^{1}_{1}}+1)$
-stable. The proof of Proposition 15 illustrates how one derives consequences of an ordinal being
$(\delta _{\sigma ^{1}_{1}}+1)$
-stable. The proof of Proposition 15 illustrates how one derives consequences of an ordinal being
![]() $\Sigma ^{1}_{1}$
-reflecting. We shall carry out many similar arguments in the future, perhaps omitting some of the details that show up repeatedly. We note the following consequence of Proposition 15:
$\Sigma ^{1}_{1}$
-reflecting. We shall carry out many similar arguments in the future, perhaps omitting some of the details that show up repeatedly. We note the following consequence of Proposition 15:
Proposition 16. There is a
![]() $\Sigma ^{1}_{1}$
-sentence
$\Sigma ^{1}_{1}$
-sentence
![]() $\phi $
such that
$\phi $
such that
![]() $L_{\alpha }\models \phi $
if, and only if,
$L_{\alpha }\models \phi $
if, and only if,
![]() $\alpha $
is
$\alpha $
is
![]() $\Sigma ^{1}_{1}$
-reflecting or
$\Sigma ^{1}_{1}$
-reflecting or
![]() $\Pi ^{1}_{1}$
-reflecting.
$\Pi ^{1}_{1}$
-reflecting.
Proof. Let
![]() $\phi $
be the sentence that asserts the existence of some
$\phi $
be the sentence that asserts the existence of some
![]() $A\subset L_{\alpha }$
coding a model
$A\subset L_{\alpha }$
coding a model
![]() $(M,E)$
of
$(M,E)$
of
![]() ${\mathsf {KP}} + V = L$
containing
${\mathsf {KP}} + V = L$
containing
![]() $\alpha $
and such that
$\alpha $
and such that
Clearly, every
![]() $\Pi ^{1}_{1}$
-reflecting ordinal satisfies this sentence, as does every
$\Pi ^{1}_{1}$
-reflecting ordinal satisfies this sentence, as does every
![]() $\Sigma ^{1}_{1}$
-reflecting ordinal, by Proposition 15.
$\Sigma ^{1}_{1}$
-reflecting ordinal, by Proposition 15.
Suppose that
![]() $L_{\alpha } \models \phi $
, as witnessed by
$L_{\alpha } \models \phi $
, as witnessed by
![]() $(M,E)$
. Suppose moreover that
$(M,E)$
. Suppose moreover that
![]() $\alpha $
is not
$\alpha $
is not
![]() $\Sigma ^{1}_{1}$
-reflecting, so that
$\Sigma ^{1}_{1}$
-reflecting, so that
![]() $\delta _{\alpha } = \alpha ^+$
by Gostanian’s characterization. Since
$\delta _{\alpha } = \alpha ^+$
by Gostanian’s characterization. Since
![]() $\alpha \in M$
, a well-known theorem of F. Ville (see e.g., Barwise [Reference Barwise5] for a proof) implies that
$\alpha \in M$
, a well-known theorem of F. Ville (see e.g., Barwise [Reference Barwise5] for a proof) implies that
![]() $L_{\alpha ^+}\subset M$
. Given an arbitrary
$L_{\alpha ^+}\subset M$
. Given an arbitrary
![]() $\beta <\alpha ^+$
, we then have
$\beta <\alpha ^+$
, we then have
![]() $\beta \in M$
and
$\beta \in M$
and
![]() $\beta < \delta _{\alpha }^{M}$
, for otherwise
$\beta < \delta _{\alpha }^{M}$
, for otherwise
![]() $\delta _{\alpha }^{M}<\alpha ^+$
, which is impossible, since any
$\delta _{\alpha }^{M}<\alpha ^+$
, which is impossible, since any
![]() $\alpha $
-recursive wellordering of a subset of
$\alpha $
-recursive wellordering of a subset of
![]() $\alpha $
of length
$\alpha $
of length
![]() $\delta _{\alpha }^{M}$
would belong to M. By choice of M,
$\delta _{\alpha }^{M}$
would belong to M. By choice of M,
and so
![]() $M\models L_{\alpha }\prec _{1} L_{\beta }$
. However, being
$M\models L_{\alpha }\prec _{1} L_{\beta }$
. However, being
![]() $\Sigma _{1}$
-elementary is absolute, so we really do have
$\Sigma _{1}$
-elementary is absolute, so we really do have
![]() $L_{\alpha }\prec _{1} L_{\beta }$
and, since
$L_{\alpha }\prec _{1} L_{\beta }$
and, since
![]() $\beta $
was arbitrary, we have
$\beta $
was arbitrary, we have
![]() $L_{\alpha } \prec _{1} L_{\alpha ^+}$
, so
$L_{\alpha } \prec _{1} L_{\alpha ^+}$
, so
![]() $\alpha $
is
$\alpha $
is
![]() $\Pi ^{1}_{1}$
-reflecting.⊣
$\Pi ^{1}_{1}$
-reflecting.⊣
An immediate consequence is Aanderaa’s classical result:
Corollary 17 (Aanderaa)
![]() $\pi ^{1}_{1}<\sigma ^{1}_{1}$
.
$\pi ^{1}_{1}<\sigma ^{1}_{1}$
.
Corollary 17 holds in a strong form:
Corollary 18.
![]() $\sigma ^{1}_{1}$
reflects
$\sigma ^{1}_{1}$
reflects
![]() $\Sigma ^{1}_{1}$
sentences on
$\Sigma ^{1}_{1}$
sentences on
![]() $\Pi ^{1}_{1}$
-reflecting ordinals.
$\Pi ^{1}_{1}$
-reflecting ordinals.
Proof. Let
![]() $\phi $
be the sentence from Proposition 16. Then, if
$\phi $
be the sentence from Proposition 16. Then, if
![]() $\psi $
is another
$\psi $
is another
![]() $\Sigma ^{1}_{1}$
sentence, so is the conjunction
$\Sigma ^{1}_{1}$
sentence, so is the conjunction
![]() $\phi \wedge \psi $
. ⊣
$\phi \wedge \psi $
. ⊣
Corollary 18 is not new; it also follows from the proof of Corollary 17 written down in Simpson [Reference Simpson11]. Our method for analyzing the order of reflection is to prove results akin to Corollary 18. Now that we know the degree of stability of
![]() $\sigma ^{1}_{1}$
, it is natural to ask what the least ordinal
$\sigma ^{1}_{1}$
, it is natural to ask what the least ordinal
![]() $\alpha $
which is
$\alpha $
which is
![]() $(\delta _{\alpha }+1)$
-stable is. We shall eventually see that it is rather small and in fact smaller than the successor of
$(\delta _{\alpha }+1)$
-stable is. We shall eventually see that it is rather small and in fact smaller than the successor of
![]() $\sigma ^{1}_{1}$
in the order of reflection. We finish this section with some related results that will not be used in future sections.
$\sigma ^{1}_{1}$
in the order of reflection. We finish this section with some related results that will not be used in future sections.
Proposition 19. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma \sigma $
-reflecting. Then
$\sigma \sigma $
-reflecting. Then
![]() $\alpha $
is
$\alpha $
is
![]() $(\delta _{\alpha }+1)$
-stable.
$(\delta _{\alpha }+1)$
-stable.
Proof. This is similar to the proof of Proposition 15. Again, it is easy to see that
![]() $\delta _{\alpha }$
is a limit. Let
$\delta _{\alpha }$
is a limit. Let
![]() $\gamma = \delta _{\alpha }+1$
and
$\gamma = \delta _{\alpha }+1$
and
![]() $a \in L_{\alpha }$
be such that
$a \in L_{\alpha }$
be such that
![]() $L_{\gamma }\models \phi (a)$
, for some
$L_{\gamma }\models \phi (a)$
, for some
![]() $\Sigma _{1}$
formula
$\Sigma _{1}$
formula
![]() $\phi $
. Let
$\phi $
. Let
![]() $\psi $
be the
$\psi $
be the
![]() $\Sigma ^{1}_{1}$
formula expressing that
$\Sigma ^{1}_{1}$
formula expressing that
![]() $\alpha $
is locally countable and there is a set
$\alpha $
is locally countable and there is a set
![]() $A\subset L_{\alpha }$
coding a model
$A\subset L_{\alpha }$
coding a model
![]() $(M,E)$
of
$(M,E)$
of
![]() ${\mathsf {KP}} + V = L$
with
${\mathsf {KP}} + V = L$
with
![]() $\alpha \in M$
and such that
$\alpha \in M$
and such that
Then
![]() $L_{\alpha }\models \psi $
. By hypothesis, there is a
$L_{\alpha }\models \psi $
. By hypothesis, there is a
![]() $\Sigma ^{1}_{1}$
-reflecting
$\Sigma ^{1}_{1}$
-reflecting
![]() $\tau <\alpha $
such that
$\tau <\alpha $
such that
![]() $L_{\tau }\models \psi $
. Thus,
$L_{\tau }\models \psi $
. Thus,
![]() $\tau $
is locally countable and there is a model
$\tau $
is locally countable and there is a model
![]() $(M,E)$
of
$(M,E)$
of
![]() ${\mathsf {KP}} + V = L$
with
${\mathsf {KP}} + V = L$
with
![]() $\tau \in M$
and such that
$\tau \in M$
and such that
By Ville’s theorem,
![]() $L_{\tau ^+}\subset M$
and, since
$L_{\tau ^+}\subset M$
and, since
![]() $\tau $
is
$\tau $
is
![]() $\Sigma ^{1}_{1}$
-reflecting,
$\Sigma ^{1}_{1}$
-reflecting,
![]() $\delta _{\tau } < \tau ^+$
. Hence, M computes
$\delta _{\tau } < \tau ^+$
. Hence, M computes
![]() $\delta _{\tau }$
and
$\delta _{\tau }$
and
![]() $\delta _{\tau }+1$
correctly and so we really have
$\delta _{\tau }+1$
correctly and so we really have
![]() $L_{\delta _{\tau }+1}\models \phi (a)$
. Since
$L_{\delta _{\tau }+1}\models \phi (a)$
. Since
![]() $\phi $
is
$\phi $
is
![]() $\Sigma _{1}$
, we conclude
$\Sigma _{1}$
, we conclude
![]() $L_{\alpha }\models \phi (a)$
, as desired. ⊣
$L_{\alpha }\models \phi (a)$
, as desired. ⊣
The preceding proof shows that if
![]() $\alpha $
is as in Proposition 19, then
$\alpha $
is as in Proposition 19, then
![]() $\alpha $
is
$\alpha $
is
![]() $(\delta _{\alpha }+2)$
-stable,
$(\delta _{\alpha }+2)$
-stable,
![]() $(\delta _{\alpha })^{\omega }$
-stable, etc. It shows that if f is a function on ordinals which is uniformly
$(\delta _{\alpha })^{\omega }$
-stable, etc. It shows that if f is a function on ordinals which is uniformly
![]() $\Sigma _{1}$
-definable (with parameters in
$\Sigma _{1}$
-definable (with parameters in
![]() $L_{\alpha }$
) on e.g., multiplicatively indecomposable levels of L containing all parameters, then
$L_{\alpha }$
) on e.g., multiplicatively indecomposable levels of L containing all parameters, then
![]() $\alpha $
is
$\alpha $
is
![]() $f(\delta _{\alpha })$
-stable.
$f(\delta _{\alpha })$
-stable.
As a consequence of Propositions 14 and 19, we obtain a negative answer to one of the questions posed in the introduction.
Corollary 20.
 $\sigma ^{1,\ell }_{1}$
is not
$\sigma ^{1,\ell }_{1}$
is not
![]() $\sigma \sigma $
-reflecting.
$\sigma \sigma $
-reflecting.
We state without proof a result implying that
 $\sigma ^{1,\ell }_{1}$
is smaller than the least
$\sigma ^{1,\ell }_{1}$
is smaller than the least
![]() $\pi \sigma $
-reflecting ordinal. Its proof is similar to that of Theorem 32 below.
$\pi \sigma $
-reflecting ordinal. Its proof is similar to that of Theorem 32 below.
Proposition 21. Let
![]() $\tau $
denote the least
$\tau $
denote the least
![]() $\pi \sigma $
-reflecting ordinal. For every
$\pi \sigma $
-reflecting ordinal. For every
![]() $\beta <\tau $
, there is some
$\beta <\tau $
, there is some
![]() $\alpha <\tau $
which is both
$\alpha <\tau $
which is both
![]() $\Sigma ^{1}_{1}$
-reflecting and
$\Sigma ^{1}_{1}$
-reflecting and
![]() $(\delta _{\alpha }+\beta )$
-stable.
$(\delta _{\alpha }+\beta )$
-stable.
Figure 1 summarizes the relationships between the ordinals considered so far. We shall also see that

Figure 1 Ordinals below the least
![]() $\pi \sigma $
-reflecting ordinal. The arrow from left to right represents the “less than” relation.
$\pi \sigma $
-reflecting ordinal. The arrow from left to right represents the “less than” relation.
3 Reflection transfer theorems
Definition 22. Let s and t be reflection patterns. We write
![]() $s \to t$
if every (countable and locally countable) s-reflecting ordinal is t-reflecting. We write
$s \to t$
if every (countable and locally countable) s-reflecting ordinal is t-reflecting. We write
![]() $s\equiv t$
if
$s\equiv t$
if
![]() $s\to t$
and
$s\to t$
and
![]() $t\to s$
.
$t\to s$
.
In this section, we will present some results on the transfer of reflection properties, i.e., results of the form
where s and t are reflection patterns. Some properties of the relation
![]() $\to $
follow trivially from simple propositional reasoning. For instance,
$\to $
follow trivially from simple propositional reasoning. For instance,
 $$ \begin{align*} \sigma s &\to \sigma,\\ \pi s &\to \pi, \\ s &\to s\wedge s, \text{ and}\\ s\wedge t &\to s. \end{align*} $$
$$ \begin{align*} \sigma s &\to \sigma,\\ \pi s &\to \pi, \\ s &\to s\wedge s, \text{ and}\\ s\wedge t &\to s. \end{align*} $$
It is also obvious that the collection of reflection patterns forms a directed preorder under the relation
![]() $\to $
. Moreover, if
$\to $
. Moreover, if
![]() $s\to t$
, then
$s\to t$
, then
![]() $\sigma s \to \sigma t$
and
$\sigma s \to \sigma t$
and
![]() $\pi s\to \pi t$
. These facts, as well as generalizations thereof obtained by straightforward propositional reasoning we shall use in the future without mention.
$\pi s\to \pi t$
. These facts, as well as generalizations thereof obtained by straightforward propositional reasoning we shall use in the future without mention.
In the next lemmata we present a few reflection transfer results whose proofs, although possibly not straightforward propositional reasoning, are still rather elementary:
Lemma 23. Let s be a reflection pattern.
-
1.
 $\sigma \sigma s\to \sigma s;$
$\sigma \sigma s\to \sigma s;$
-
2.
 $\pi \pi s\to \pi s$
.
$\pi \pi s\to \pi s$
.
Proof. If
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma \sigma s$
-reflecting and
$\sigma \sigma s$
-reflecting and
![]() $L_{\alpha }$
satisfies a
$L_{\alpha }$
satisfies a
![]() $\Sigma ^{1}_{1}$
sentence
$\Sigma ^{1}_{1}$
sentence
![]() $\phi $
, then, by definition, there is a
$\phi $
, then, by definition, there is a
![]() $\sigma s$
-reflecting
$\sigma s$
-reflecting
![]() $\tau <\alpha $
such that
$\tau <\alpha $
such that
![]() $L_{\tau } \models \phi $
. By
$L_{\tau } \models \phi $
. By
![]() $\sigma s$
-reflection, there is an s-reflecting
$\sigma s$
-reflection, there is an s-reflecting
![]() $\eta <\tau $
such that
$\eta <\tau $
such that
![]() $L_{\tau }\models \phi $
. Hence,
$L_{\tau }\models \phi $
. Hence,
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma s$
-reflecting. The argument for
$\sigma s$
-reflecting. The argument for
![]() $\pi \pi s$
-reflection is similar. ⊣
$\pi \pi s$
-reflection is similar. ⊣
For the next reflection transfer results, we need the following observation on the definability of reflection patterns.
Lemma 24. Let s be a reflection pattern. Then, the property
is
![]() $\Sigma ^{1}_{1}$
-definable over
$\Sigma ^{1}_{1}$
-definable over
![]() $L_{\alpha }$
. Similarly, the property
$L_{\alpha }$
. Similarly, the property
is
![]() $\Pi ^{1}_{1}$
-definable over
$\Pi ^{1}_{1}$
-definable over
![]() $L_{\alpha }$
.
$L_{\alpha }$
.
Proof. We prove the first claim; the second one is similar. An admissible
![]() $\alpha $
being
$\alpha $
being
![]() $\pi s$
-reflecting means that for every
$\pi s$
-reflecting means that for every
![]() $\Pi ^{1}_{1}$
sentence
$\Pi ^{1}_{1}$
sentence
![]() $\phi $
with a parameter
$\phi $
with a parameter
![]() $\gamma <\alpha $
, if
$\gamma <\alpha $
, if
![]() $L_{\alpha }\models \phi (\gamma )$
, then there is
$L_{\alpha }\models \phi (\gamma )$
, then there is
![]() $\beta $
with
$\beta $
with
![]() $\gamma <\beta <\alpha $
such that
$\gamma <\beta <\alpha $
such that
![]() $\beta $
is s-reflecting and
$\beta $
is s-reflecting and
![]() $L_{\beta }\models \phi (\gamma )$
. By choosing a suitably universal
$L_{\beta }\models \phi (\gamma )$
. By choosing a suitably universal
![]() $\Pi ^{1}_{1}$
formula, we can reduce
$\Pi ^{1}_{1}$
formula, we can reduce
![]() $\pi s$
-reflection to a single sentence: it suffices to show that for a fixed
$\pi s$
-reflection to a single sentence: it suffices to show that for a fixed
![]() $\Pi ^{1}_{1}$
sentence
$\Pi ^{1}_{1}$
sentence
![]() $\phi $
and a fixed parameter
$\phi $
and a fixed parameter
![]() $\gamma $
, the sentence
$\gamma $
, the sentence

is uniformly equivalent to a
![]() $\Sigma ^{1}_{1}$
sentence, for then we can quantify over all
$\Sigma ^{1}_{1}$
sentence, for then we can quantify over all
![]() $\gamma <\alpha $
and the resulting sentence is still
$\gamma <\alpha $
and the resulting sentence is still
![]() $\Sigma ^{1}_{1}$
.
$\Sigma ^{1}_{1}$
.
The key observation for this is the fact that
![]() $\Pi ^{1}_{1}$
(and thus also
$\Pi ^{1}_{1}$
(and thus also
![]() $\Sigma ^{1}_{1}$
) sentences with parameters
$\Sigma ^{1}_{1}$
) sentences with parameters
![]() $a_{0},\ldots , a_{n}$
about a structure of the form
$a_{0},\ldots , a_{n}$
about a structure of the form
![]() $L_{\xi }$
are equivalent to first-order sentences with parameters
$L_{\xi }$
are equivalent to first-order sentences with parameters
![]() $a_{0},\ldots , a_{n},\xi $
over any admissible
$a_{0},\ldots , a_{n},\xi $
over any admissible
![]() $L_{\zeta }$
, with
$L_{\zeta }$
, with
![]() $\xi <\zeta $
, and the equivalence is uniform (see Aczel–Richter [Reference Aczel and Richter3, Theorem 6.2] for a proof of this fact). Hence, every recursively inaccessible ordinal is
$\xi <\zeta $
, and the equivalence is uniform (see Aczel–Richter [Reference Aczel and Richter3, Theorem 6.2] for a proof of this fact). Hence, every recursively inaccessible ordinal is
![]() $\Sigma ^{1}_{1}$
-correct and a straightforward induction shows that whether an ordinal
$\Sigma ^{1}_{1}$
-correct and a straightforward induction shows that whether an ordinal
![]() $\xi $
is t-reflecting is computed correctly by any
$\xi $
is t-reflecting is computed correctly by any
![]() $L_{\zeta }$
whenever
$L_{\zeta }$
whenever
![]() $\xi <\zeta $
and
$\xi <\zeta $
and
![]() $\zeta $
is recursively inaccessible, for any reflection pattern t. Since every
$\zeta $
is recursively inaccessible, for any reflection pattern t. Since every
![]() $\Sigma ^{1}_{1}$
- or
$\Sigma ^{1}_{1}$
- or
![]() $\Pi ^{1}_{1}$
-reflecting ordinal is recursively inaccessible, (1) is equivalent to the conjunction of
$\Pi ^{1}_{1}$
-reflecting ordinal is recursively inaccessible, (1) is equivalent to the conjunction of
-
2.
 $\alpha $
is recursively inaccessible, and
$\alpha $
is recursively inaccessible, and -
3.
 $\big (L_{\alpha }\models \phi (\gamma )\big ) \to \exists \beta \, \big (\gamma <\beta <\alpha \wedge L_{\alpha }\models $
“
$\big (L_{\alpha }\models \phi (\gamma )\big ) \to \exists \beta \, \big (\gamma <\beta <\alpha \wedge L_{\alpha }\models $
“
 $\beta $
is s-reflecting and
$\beta $
is s-reflecting and
 $L_{\beta }\models \phi (\gamma )$
”
$L_{\beta }\models \phi (\gamma )$
”
 $\big )$
,
$\big )$
,
and both of these conjuncts are easily seen to be
![]() $\Sigma ^{1}_{1}$
.⊣
$\Sigma ^{1}_{1}$
.⊣
Lemma 25. Let s and t be reflection patterns.
-
1.
 $\sigma s\wedge \pi t\to \pi (\sigma s\wedge t);$
$\sigma s\wedge \pi t\to \pi (\sigma s\wedge t);$
-
2.
 $\sigma s \wedge \pi t\to \sigma (s\wedge \pi t);$
$\sigma s \wedge \pi t\to \sigma (s\wedge \pi t);$
-
3.
 $\sigma s\to \sigma (s \wedge \pi )$
.
$\sigma s\to \sigma (s \wedge \pi )$
.
Proof. Recall that if an ordinal
![]() $\alpha $
is s-reflecting, for any nontrivial reflection pattern s, then it is recursively inaccessible and, in fact, a limit of recursively inaccessible ordinals. (1) then follows from the fact that being
$\alpha $
is s-reflecting, for any nontrivial reflection pattern s, then it is recursively inaccessible and, in fact, a limit of recursively inaccessible ordinals. (1) then follows from the fact that being
![]() $\sigma s$
-reflecting is expressible by a
$\sigma s$
-reflecting is expressible by a
![]() $\Pi ^{1}_{1}$
sentence
$\Pi ^{1}_{1}$
sentence
![]() $\psi $
. Thus, if
$\psi $
. Thus, if
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma s \wedge \pi t$
-reflecting and satisfies some
$\sigma s \wedge \pi t$
-reflecting and satisfies some
![]() $\Pi ^{1}_{1}$
-sentence
$\Pi ^{1}_{1}$
-sentence
![]() $\phi $
, then the conjunction
$\phi $
, then the conjunction
![]() $\phi \wedge \psi $
is also
$\phi \wedge \psi $
is also
![]() $\Pi ^{1}_{1}$
, and any ordinal satisfying it must be
$\Pi ^{1}_{1}$
, and any ordinal satisfying it must be
![]() $\sigma s$
-reflecting.
$\sigma s$
-reflecting.
(2) is similar. For (3), there are two cases: if
![]() $\alpha $
is
$\alpha $
is
![]() $\pi $
-reflecting, then the result follows from (2). If
$\pi $
-reflecting, then the result follows from (2). If
![]() $\alpha $
is not
$\alpha $
is not
![]() $\pi $
-reflecting, it is not
$\pi $
-reflecting, it is not
![]() $\alpha ^+$
-stable. Hence, there is a least
$\alpha ^+$
-stable. Hence, there is a least
![]() $\gamma <\alpha ^+$
such that
$\gamma <\alpha ^+$
such that
![]() $\alpha $
is not
$\alpha $
is not
![]() $\gamma $
-stable, i.e., there is a
$\gamma $
-stable, i.e., there is a
![]() $\Sigma _{1}$
-formula
$\Sigma _{1}$
-formula
![]() $\psi $
and some parameter
$\psi $
and some parameter
![]() $\beta <\alpha $
such that
$\beta <\alpha $
such that
![]() $L_{\gamma }\models \psi (\beta )$
, but
$L_{\gamma }\models \psi (\beta )$
, but
![]() $L_{\alpha }\not \models \psi (\beta )$
. The remainder of the proof is an adaptation of the proof of Corollary 17 presented in Simpson [Reference Simpson11]:
$L_{\alpha }\not \models \psi (\beta )$
. The remainder of the proof is an adaptation of the proof of Corollary 17 presented in Simpson [Reference Simpson11]:
Let
![]() $\phi $
be the
$\phi $
be the
![]() $\Sigma ^{1}_{1}$
statement expressing that there is a model
$\Sigma ^{1}_{1}$
statement expressing that there is a model
![]() $(M,E)$
of
$(M,E)$
of
![]() ${\mathsf {KP}} + V = L$
end-extending
${\mathsf {KP}} + V = L$
end-extending
![]() $L_{\alpha +1}$
such that for some
$L_{\alpha +1}$
such that for some
![]() $\gamma ^{\prime } \in M$
with
$\gamma ^{\prime } \in M$
with
![]() $\gamma ^{\prime }<\alpha ^{+M}$
,
$\gamma ^{\prime }<\alpha ^{+M}$
,
 $L_{\gamma ^{\prime }}^{M}\models \psi (\beta )$
and, moreover, if
$L_{\gamma ^{\prime }}^{M}\models \psi (\beta )$
and, moreover, if
![]() $\gamma ^{\prime }$
is least such, then
$\gamma ^{\prime }$
is least such, then
![]() $M\models $
“
$M\models $
“
![]() $\alpha $
is
$\alpha $
is
![]() $({<}\gamma ^{\prime })$
-stable.” Then
$({<}\gamma ^{\prime })$
-stable.” Then
![]() $L_{\alpha }\models \phi $
. By choice of
$L_{\alpha }\models \phi $
. By choice of
![]() $\alpha $
, there is an s-reflecting ordinal
$\alpha $
, there is an s-reflecting ordinal
![]() $\tau <\alpha $
such that
$\tau <\alpha $
such that
![]() $L_{\tau }\models \phi $
. This means that there is a model
$L_{\tau }\models \phi $
. This means that there is a model
![]() $(M,E)$
of
$(M,E)$
of
![]() ${\mathsf {KP}} + V = L$
end-extending
${\mathsf {KP}} + V = L$
end-extending
![]() $L_{\tau +1}$
such that for some
$L_{\tau +1}$
such that for some
![]() $\gamma ^{\prime }\in M$
with
$\gamma ^{\prime }\in M$
with
![]() $\gamma ^{\prime } < \tau ^{+M}$
,
$\gamma ^{\prime } < \tau ^{+M}$
,
 $L^{M}_{\gamma ^{\prime }}\models \psi (\beta )$
and, for the least such
$L^{M}_{\gamma ^{\prime }}\models \psi (\beta )$
and, for the least such
![]() $\gamma ^{\prime }$
, we have
$\gamma ^{\prime }$
, we have
![]() $M\models $
“
$M\models $
“
![]() $\tau $
is
$\tau $
is
![]() $({<}\gamma ^{\prime })$
-stable.” Since
$({<}\gamma ^{\prime })$
-stable.” Since
![]() $\psi $
is
$\psi $
is
![]() $\Sigma _{1}$
and
$\Sigma _{1}$
and
![]() $L_{\alpha }\not \models \psi (\beta )$
,
$L_{\alpha }\not \models \psi (\beta )$
,
![]() $\gamma ^{\prime }$
must belong to the illfounded part of M. So
$\gamma ^{\prime }$
must belong to the illfounded part of M. So
![]() $\tau $
is s-reflecting and, as in the proof of Proposition 16,
$\tau $
is s-reflecting and, as in the proof of Proposition 16,
![]() $\tau $
is
$\tau $
is
![]() $\pi $
-reflecting. By taking conjunctions as before, one sees that every
$\pi $
-reflecting. By taking conjunctions as before, one sees that every
![]() $\Sigma ^{1}_{1}$
sentence satisfied by
$\Sigma ^{1}_{1}$
sentence satisfied by
![]() $L_{\alpha }$
is satisfied by some
$L_{\alpha }$
is satisfied by some
![]() $(s\wedge \pi )$
-reflecting
$(s\wedge \pi )$
-reflecting
![]() $\tau <\alpha $
, as was to be shown. ⊣
$\tau <\alpha $
, as was to be shown. ⊣
Example 26. We claim that
To see this, notice that Lemma 25(1) and (2) implies that
and thus that
On the other hand, Lemma 25(3) implies that
and so
as claimed.
A natural question is whether one can strengthen
![]() $\pi $
in the statement of Lemma 25(3) and, in particular, whether
$\pi $
in the statement of Lemma 25(3) and, in particular, whether
![]() $\sigma ^{1}_{1}$
is
$\sigma ^{1}_{1}$
is
![]() $\sigma \pi \pi $
-reflecting. By generalizing the proof of Lemma 25(3), we will soon see that the answer is “yes.”
$\sigma \pi \pi $
-reflecting. By generalizing the proof of Lemma 25(3), we will soon see that the answer is “yes.”
Definition 27. Let s be a reflection pattern. An ordinal
![]() $\alpha $
is
$\alpha $
is
![]() $\beta $
-stable on s if whenever
$\beta $
-stable on s if whenever
![]() $L_{\beta }$
satisfies a
$L_{\beta }$
satisfies a
![]() $\Sigma _{1}$
sentence
$\Sigma _{1}$
sentence
![]() $\phi (L_{\alpha })$
with additional parameters in
$\phi (L_{\alpha })$
with additional parameters in
![]() $L_{\alpha } $
, there is an s-reflecting
$L_{\alpha } $
, there is an s-reflecting
![]() $\gamma <\alpha $
such that
$\gamma <\alpha $
such that
 $L_{\gamma ^+}\models \phi (L_{\gamma })$
.
$L_{\gamma ^+}\models \phi (L_{\gamma })$
.
Stability to the next admissible on a reflection pattern can be characterized in terms of reflection as follows:
Lemma 28. Let s be a reflection pattern. The following are equivalent:
-
1.
 $\alpha $
is
$\alpha $
is
 $\alpha ^+$
-stable on
$\alpha ^+$
-stable on
 $s;$
$s;$
-
2.
 $\alpha $
is
$\alpha $
is
 $\pi s$
-reflecting.
$\pi s$
-reflecting.
We omit the proof of Lemma 28, which is a simple adaptation of Aczel and Richter’s characterization of
![]() $\pi $
-reflection (see Aczel–Richter [Reference Aczel and Richter3, Theorem 6.2]).
$\pi $
-reflection (see Aczel–Richter [Reference Aczel and Richter3, Theorem 6.2]).
Theorem 29. Let s be a reflection pattern. Then
![]() $\sigma s\to \sigma (s\wedge \pi s)$
.
$\sigma s\to \sigma (s\wedge \pi s)$
.
Proof. The conclusion of the theorem follows from Lemma 25 if
![]() $\alpha $
is
$\alpha $
is
![]() $\pi s$
-reflecting, so we may assume that it is not.
$\pi s$
-reflecting, so we may assume that it is not.
Since
![]() $\alpha $
is not
$\alpha $
is not
![]() $\pi s$
-reflecting, it is not
$\pi s$
-reflecting, it is not
![]() $\alpha ^+$
-stable on s, so there is a least
$\alpha ^+$
-stable on s, so there is a least
![]() $\beta <\alpha ^+$
and a
$\beta <\alpha ^+$
and a
![]() $\Sigma _{1}$
-formula
$\Sigma _{1}$
-formula
![]() $\exists x\,\phi (y,x)$
such that
$\exists x\,\phi (y,x)$
such that
![]() $L_{\beta }\models \exists x\,\phi (L_{\alpha },x)$
and whenever
$L_{\beta }\models \exists x\,\phi (L_{\alpha },x)$
and whenever
![]() $\gamma <\alpha $
and
$\gamma <\alpha $
and
![]() $\gamma $
is s-reflecting, then
$\gamma $
is s-reflecting, then
 $L_{\gamma ^+} \not \models \exists x\,\phi (L_{\gamma },x)$
. Let
$L_{\gamma ^+} \not \models \exists x\,\phi (L_{\gamma },x)$
. Let
![]() $\psi $
be the formula expressing that there is a model M of
$\psi $
be the formula expressing that there is a model M of
![]() ${\mathsf {KP}} + V = L$
such that
${\mathsf {KP}} + V = L$
such that
-
1. M contains
 $\alpha $
.
$\alpha $
. -
2.
 $M\models $
“
$M\models $
“
 $\exists x\, \phi (L_{\alpha },x)$
and, letting
$\exists x\, \phi (L_{\alpha },x)$
and, letting
 $\beta $
be least such that
$\beta $
be least such that
 $M\models \phi (L_{\alpha },a)$
for some
$M\models \phi (L_{\alpha },a)$
for some
 $a \in L_{\gamma }$
,
$a \in L_{\gamma }$
,
 $\alpha $
is
$\alpha $
is
 ${<}\beta $
-stable on s.”
${<}\beta $
-stable on s.”
Since
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma s$
-reflecting, there is an s-reflecting
$\sigma s$
-reflecting, there is an s-reflecting
![]() $\tau <\alpha $
with
$\tau <\alpha $
with
![]() $L_{\tau }\models \psi $
, as witnessed by some model N which end-extends
$L_{\tau }\models \psi $
, as witnessed by some model N which end-extends
![]() $L_{\tau ^+}$
. Let
$L_{\tau ^+}$
. Let
![]() $\gamma $
be N-least such that
$\gamma $
be N-least such that
![]() $N\models \exists x\in L_{\gamma }\, \phi (L_{\tau },x)$
. Then, we cannot have
$N\models \exists x\in L_{\gamma }\, \phi (L_{\tau },x)$
. Then, we cannot have
![]() $\gamma < \tau ^+$
, for otherwise
$\gamma < \tau ^+$
, for otherwise
![]() $\tau $
is an s-reflecting ordinal such that
$\tau $
is an s-reflecting ordinal such that
![]() $L_{\tau ^+}\models \exists x\, \phi (L_{\tau },x)$
, contradicting the choice of
$L_{\tau ^+}\models \exists x\, \phi (L_{\tau },x)$
, contradicting the choice of
![]() $\phi $
. Thus,
$\phi $
. Thus,
![]() $\gamma $
belongs to the illfounded part of N and, in N,
$\gamma $
belongs to the illfounded part of N and, in N,
![]() $\tau $
is
$\tau $
is
![]() ${<}\gamma $
-stable on s. Since
${<}\gamma $
-stable on s. Since
![]() $\tau $
is recursively inaccessible (this can be assumed also if
$\tau $
is recursively inaccessible (this can be assumed also if
![]() $s = \varnothing $
), N is correct about s-reflection below
$s = \varnothing $
), N is correct about s-reflection below
![]() $\tau $
, so an argument as before shows that
$\tau $
, so an argument as before shows that
![]() $\tau $
is
$\tau $
is
![]() $\tau ^+$
-stable on s and thus
$\tau ^+$
-stable on s and thus
![]() $\pi s$
-reflecting.⊣
$\pi s$
-reflecting.⊣
Example 30. By repeatedly applying Theorem 29, we obtain
This implies the inequality
for every
![]() $n\in \mathbb {N}$
, which strengthens Corollary 17.
$n\in \mathbb {N}$
, which strengthens Corollary 17.
The following strengthening of Proposition 15 is proved similarly:
Lemma 31. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma s$
-reflecting. Then, it is
$\sigma s$
-reflecting. Then, it is
![]() $\delta _{\alpha }$
-stable on s.
$\delta _{\alpha }$
-stable on s.
Proof. Let
![]() $\theta (L_{\alpha })$
be a
$\theta (L_{\alpha })$
be a
![]() $\Sigma _{1}$
sentence with parameters in
$\Sigma _{1}$
sentence with parameters in
![]() $L_{\alpha }$
, say, of the form
$L_{\alpha }$
, say, of the form
![]() $\exists x\,\theta _{0}(x,L_{\alpha })$
. Let
$\exists x\,\theta _{0}(x,L_{\alpha })$
. Let
![]() $\eta <\delta _{\alpha }$
and
$\eta <\delta _{\alpha }$
and
![]() $b \in L_{\eta }$
be such that
$b \in L_{\eta }$
be such that
![]() $L_{\delta _{\alpha }}\models \theta _{0}(b,L_{\alpha })$
. Since
$L_{\delta _{\alpha }}\models \theta _{0}(b,L_{\alpha })$
. Since
![]() $\eta <\delta _{\alpha }$
, there is an
$\eta <\delta _{\alpha }$
, there is an
![]() $\alpha $
-recursive wellorder R of length
$\alpha $
-recursive wellorder R of length
![]() $\eta $
. Let
$\eta $
. Let
![]() $\psi $
be the sentence asserting the existence of a model M of
$\psi $
be the sentence asserting the existence of a model M of
![]() ${\mathsf {KP}}$
such that
${\mathsf {KP}}$
such that
-
1. M end-extends
 $L_{\alpha +1}$
and
$L_{\alpha +1}$
and
 $M\models $
“
$M\models $
“
 $\alpha ^+$
exists”;
$\alpha ^+$
exists”; -
2. in M, R is isomorphic to an ordinal
 $\eta _{0}$
and there is
$\eta _{0}$
and there is
 $b_{0} \in L_{\eta _{0}}^{M}$
such that
$b_{0} \in L_{\eta _{0}}^{M}$
such that
 $L_{\eta _{0}}^{M} \models \theta _{0}(b_{0},L_{\alpha })$
.
$L_{\eta _{0}}^{M} \models \theta _{0}(b_{0},L_{\alpha })$
.
Then
![]() $L_{\alpha }\models \psi $
. Moreover,
$L_{\alpha }\models \psi $
. Moreover,
![]() $\psi $
is
$\psi $
is
![]() $\Sigma ^{1}_{1}$
so, by reflection, there is an s-reflecting
$\Sigma ^{1}_{1}$
so, by reflection, there is an s-reflecting
![]() $\tau <\alpha $
such that
$\tau <\alpha $
such that
![]() $L_{\tau }\models \psi $
, as witnessed by some model N which end-extends
$L_{\tau }\models \psi $
, as witnessed by some model N which end-extends
![]() $L_{\tau ^+}$
. Now, in N,
$L_{\tau ^+}$
. Now, in N,
 $L_{\tau ^+}^{N}\models \theta _{0}(b_{0}, L_{\tau })$
for some
$L_{\tau ^+}^{N}\models \theta _{0}(b_{0}, L_{\tau })$
for some
 $b_{0} \in L^{N}_{\eta _{0}}$
, where
$b_{0} \in L^{N}_{\eta _{0}}$
, where
![]() $\eta _{0}$
is some N-ordinal isomorphic to
$\eta _{0}$
is some N-ordinal isomorphic to
![]() $R_{\tau }$
. However,
$R_{\tau }$
. However,
![]() $R_{\tau }\subset R$
, since R is
$R_{\tau }\subset R$
, since R is
![]() $\alpha $
-recursive, and
$\alpha $
-recursive, and
![]() $\theta _{0}$
is
$\theta _{0}$
is
![]() $\Sigma _{0}$
, so we really have
$\Sigma _{0}$
, so we really have
![]() $L_{\tau ^+}\models \theta (L_{\tau })$
, as desired. ⊣
$L_{\tau ^+}\models \theta (L_{\tau })$
, as desired. ⊣
The following theorem, although perhaps odd-looking at first, is crucial for our analysis of the order of reflection.
Theorem 32. Let s be a reflection pattern. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\pi \sigma s$
-reflecting but not
$\pi \sigma s$
-reflecting but not
![]() $\sigma $
-reflecting. Then
$\sigma $
-reflecting. Then
![]() $\alpha $
is
$\alpha $
is
![]() $\pi s$
-reflecting.
$\pi s$
-reflecting.
Proof. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\pi $
-reflecting on
$\pi $
-reflecting on
![]() $\sigma s$
-reflecting ordinals but not
$\sigma s$
-reflecting ordinals but not
![]() $\sigma $
-reflecting. Let
$\sigma $
-reflecting. Let
![]() $\psi $
be the statement expressing that whenever
$\psi $
be the statement expressing that whenever
![]() $(M,E)$
is an end-extension of
$(M,E)$
is an end-extension of
![]() $L_{\alpha +1}$
satisfying
$L_{\alpha +1}$
satisfying
![]() ${\mathsf {KPi}}$
,Footnote
1
then
${\mathsf {KPi}}$
,Footnote
1
then
![]() $M\models $
“
$M\models $
“
![]() $\alpha $
is not
$\alpha $
is not
![]() $\sigma s$
-reflecting.” This sentence is
$\sigma s$
-reflecting.” This sentence is
![]() $\Pi ^{1}_{1}$
and thus cannot be satisfied by
$\Pi ^{1}_{1}$
and thus cannot be satisfied by
![]() $L_{\alpha }$
, for otherwise it would be reflected to a
$L_{\alpha }$
, for otherwise it would be reflected to a
![]() $\sigma s$
-reflecting ordinal. But clearly
$\sigma s$
-reflecting ordinal. But clearly
![]() $L_{\beta }$
cannot satisfy
$L_{\beta }$
cannot satisfy
![]() $\psi $
if
$\psi $
if
![]() $\beta $
is
$\beta $
is
![]() $\sigma s$
-reflecting.
$\sigma s$
-reflecting.
Thus,
![]() $L_{\alpha }\not \models \psi $
, so there is a model M of
$L_{\alpha }\not \models \psi $
, so there is a model M of
![]() ${\mathsf {KPi}}$
end-extending
${\mathsf {KPi}}$
end-extending
![]() $L_{\alpha +1}$
such that
$L_{\alpha +1}$
such that
For ordinals
![]() $\tau <\alpha $
, whether
$\tau <\alpha $
, whether
![]() $\tau $
is t-reflecting is computed correctly by M, for any reflection pattern t. By Lemma 31 applied within M,
$\tau $
is t-reflecting is computed correctly by M, for any reflection pattern t. By Lemma 31 applied within M,
Let
![]() $\phi $
be a
$\phi $
be a
![]() $\Pi ^{1}_{1}$
statement, and
$\Pi ^{1}_{1}$
statement, and
![]() $a \in L_{\alpha }$
be a parameter such that
$a \in L_{\alpha }$
be a parameter such that
![]() $L_{\alpha } \models \phi (a)$
. By Barwise–Gandy–Moschovakis [Reference Barwise, Gandy and Moschovakis6], there is a
$L_{\alpha } \models \phi (a)$
. By Barwise–Gandy–Moschovakis [Reference Barwise, Gandy and Moschovakis6], there is a
![]() $\Sigma _{1}$
formula
$\Sigma _{1}$
formula
![]() $\phi ^{*}$
such that for all admissible
$\phi ^{*}$
such that for all admissible
![]() $\beta $
with
$\beta $
with
![]() $a \in L_{\beta }$
,
$a \in L_{\beta }$
,
![]() $L_{\beta }\models \phi (a)$
if, and only if,
$L_{\beta }\models \phi (a)$
if, and only if,
 $L_{\beta ^+}\models \phi ^{*}(a,L_{\beta })$
; thus,
$L_{\beta ^+}\models \phi ^{*}(a,L_{\beta })$
; thus,
![]() $L_{\alpha ^+} \models \phi ^{*}(a,L_{\alpha })$
. Let
$L_{\alpha ^+} \models \phi ^{*}(a,L_{\alpha })$
. Let
![]() $b \in L_{\alpha ^+}$
be a witness for
$b \in L_{\alpha ^+}$
be a witness for
![]() $\phi ^{*}$
and let
$\phi ^{*}$
and let
![]() $\gamma <\alpha ^+$
be large enough so that
$\gamma <\alpha ^+$
be large enough so that
![]() $b \in L_{\gamma }$
. Since
$b \in L_{\gamma }$
. Since
![]() $\alpha $
is not
$\alpha $
is not
![]() $\sigma ^{1}_{1}$
-reflecting (in the real world),
$\sigma ^{1}_{1}$
-reflecting (in the real world),
![]() $\delta _{\alpha } = \alpha ^+$
, and thus
$\delta _{\alpha } = \alpha ^+$
, and thus
Since
![]() $\phi ^{*}$
is
$\phi ^{*}$
is
![]() $\Sigma _{1}$
,
$\Sigma _{1}$
,
so by the
![]() $\delta _{\alpha }$
-stability of
$\delta _{\alpha }$
-stability of
![]() $\alpha $
on s within M, there is an s-reflecting
$\alpha $
on s within M, there is an s-reflecting
![]() $\tau <\alpha $
such that
$\tau <\alpha $
such that
Since
![]() $\tau ^+ < \alpha $
, we really do have
$\tau ^+ < \alpha $
, we really do have
and so
![]() $L_{\tau }\models \phi (a)$
. This completes the proof of the theorem. ⊣
$L_{\tau }\models \phi (a)$
. This completes the proof of the theorem. ⊣
Remark 33. Theorem 32 essentially states that
Indeed, this is how we would have stated it had we included disjunctions in the recursive definition of “reflection pattern.” We have chosen not to do so, however.
Remark 34. The assumption that
![]() $\alpha $
is not
$\alpha $
is not
![]() $\sigma $
-reflecting cannot be removed from the statement of Theorem 32. To see this, let s be the pattern
$\sigma $
-reflecting cannot be removed from the statement of Theorem 32. To see this, let s be the pattern
![]() $\pi $
. By Lemma 25(1),
$\pi $
. By Lemma 25(1),
![]() $\sigma \wedge \pi \to \pi \sigma \pi $
. However, the least
$\sigma \wedge \pi \to \pi \sigma \pi $
. However, the least
![]() $\sigma \wedge \pi $
-reflecting ordinal is not
$\sigma \wedge \pi $
-reflecting ordinal is not
![]() $\pi \pi $
-reflecting, for
$\pi \pi $
-reflecting, for
Remark 35. By analogy with Theorem 29, one might expect that Theorem 32 can be improved to conclude, under the same assumptions, that
![]() $\alpha $
is
$\alpha $
is
![]() $\pi (\sigma s\wedge s)$
-reflecting. However, this is not the case, for let
$\pi (\sigma s\wedge s)$
-reflecting. However, this is not the case, for let
![]() $s = \pi $
, so the hypothesis yields that
$s = \pi $
, so the hypothesis yields that
![]() $\alpha $
is
$\alpha $
is
![]() $\pi \sigma \pi $
-reflecting. However, by Lemma 25(3),
$\pi \sigma \pi $
-reflecting. However, by Lemma 25(3),
and we have seen in Example 26 that
so we cannot conclude that
![]() $\alpha $
is
$\alpha $
is
![]() $\pi (\sigma \wedge \pi )$
-reflecting.
$\pi (\sigma \wedge \pi )$
-reflecting.
Example 36. By Lemma 25(1), the least
![]() $\pi \sigma $
reflecting ordinal is not
$\pi \sigma $
reflecting ordinal is not
![]() $\sigma $
-reflecting. Hence, by combining Theorems 29 and 32, one sees that the least
$\sigma $
-reflecting. Hence, by combining Theorems 29 and 32, one sees that the least
![]() $\pi \sigma $
reflecting ordinal is
$\pi \sigma $
reflecting ordinal is
![]() $\pi \sigma \wedge \pi \pi $
-reflecting,
$\pi \sigma \wedge \pi \pi $
-reflecting,
![]() $\pi \sigma \wedge \pi \pi \pi $
-reflecting, and so on. As a useful exercise, the reader might want to verify that
$\pi \sigma \wedge \pi \pi \pi $
-reflecting, and so on. As a useful exercise, the reader might want to verify that
![]() $\pi \sigma $
is smaller than both
$\pi \sigma $
is smaller than both
![]() $\sigma \sigma $
and
$\sigma \sigma $
and
![]() $\sigma \wedge \pi $
and conclude that
$\sigma \wedge \pi $
and conclude that
![]() $\sigma $
and
$\sigma $
and
![]() $\pi \sigma $
have order-types
$\pi \sigma $
have order-types
![]() $\omega $
and
$\omega $
and
![]() $\omega +1$
in the order of reflection.
$\omega +1$
in the order of reflection.
Example 37. Let us present a proof of the inequality
We apply Theorem 29 three times:
 $$ \begin{align*} \sigma\sigma &\equiv \sigma(\sigma\wedge\pi)\\ &\equiv \sigma(\sigma\wedge\pi(\sigma\wedge\pi))\\ &\equiv \sigma (\sigma\wedge\pi(\sigma\wedge\pi)\wedge\pi(\sigma\wedge\pi(\sigma\wedge\pi))), \end{align*} $$
$$ \begin{align*} \sigma\sigma &\equiv \sigma(\sigma\wedge\pi)\\ &\equiv \sigma(\sigma\wedge\pi(\sigma\wedge\pi))\\ &\equiv \sigma (\sigma\wedge\pi(\sigma\wedge\pi)\wedge\pi(\sigma\wedge\pi(\sigma\wedge\pi))), \end{align*} $$
so
![]() $\sigma \sigma $
is a limit of
$\sigma \sigma $
is a limit of
![]() $\pi (\sigma \wedge \pi (\sigma \wedge \pi ))$
-reflecting ordinals.
$\pi (\sigma \wedge \pi (\sigma \wedge \pi ))$
-reflecting ordinals.
The preceding example involved an equivalence of reflection patterns obtained by applying Theorem 29 multiple times. This type of computation will occur frequently in latter sections.
We finish this section with a final reflection transfer theorem. It is a strengthening of Theorem 32 which clarifies the hypothesis on
![]() $\alpha $
not being
$\alpha $
not being
![]() $\sigma $
-reflecting. We state it separately, however, since the proof is longer and the result is not used afterwards.
$\sigma $
-reflecting. We state it separately, however, since the proof is longer and the result is not used afterwards.
Theorem 38. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\pi \sigma (t\wedge \pi s)$
-reflecting. Then, one of the following holds:
$\pi \sigma (t\wedge \pi s)$
-reflecting. Then, one of the following holds:
-
1.
 $\alpha $
is
$\alpha $
is
 $\pi s$
-reflecting; or
$\pi s$
-reflecting; or -
2.
 $\alpha $
is
$\alpha $
is
 $\sigma (t\wedge \pi s)$
-reflecting.
$\sigma (t\wedge \pi s)$
-reflecting.
Proof. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\pi \sigma (t\wedge \pi s)$
-reflecting but not
$\pi \sigma (t\wedge \pi s)$
-reflecting but not
![]() $\pi s$
-reflecting. Let
$\pi s$
-reflecting. Let
![]() $\theta $
be a
$\theta $
be a
![]() $\Sigma ^{1}_{1}$
sentence with parameters in
$\Sigma ^{1}_{1}$
sentence with parameters in
![]() $L_{\alpha }$
such that
$L_{\alpha }$
such that
we need to find a
![]() $(t\wedge \pi s)$
-reflecting
$(t\wedge \pi s)$
-reflecting
![]() $\tau <\alpha $
such that
$\tau <\alpha $
such that
By Barwise–Gandy–Moschovakis [Reference Barwise, Gandy and Moschovakis6], there is a
![]() $\Pi _{1}$
formula
$\Pi _{1}$
formula
![]() $\theta ^{*}(a)$
such that for every admissible
$\theta ^{*}(a)$
such that for every admissible
![]() $\beta $
containing the parameters of
$\beta $
containing the parameters of
![]() $\theta $
,
$\theta $
,
![]() $L_{\beta }\models \theta $
if, and only if,
$L_{\beta }\models \theta $
if, and only if,
 $L_{\beta ^+}\models \theta ^{*}(L_{\beta }).$
In particular,
$L_{\beta ^+}\models \theta ^{*}(L_{\beta }).$
In particular,
Since
![]() $\alpha $
is not
$\alpha $
is not
![]() $\pi s$
-reflecting, there is a least
$\pi s$
-reflecting, there is a least
![]() $\gamma <\alpha ^+$
such that
$\gamma <\alpha ^+$
such that
![]() $\alpha $
is not
$\alpha $
is not
![]() $\gamma $
-stable on s. Because
$\gamma $
-stable on s. Because
![]() $\theta ^{*}$
is
$\theta ^{*}$
is
![]() $\Pi _{1}$
,
$\Pi _{1}$
,
Let
![]() $\phi $
be the sentence asserting the non-existence of a model M of
$\phi $
be the sentence asserting the non-existence of a model M of
![]() ${\mathsf {KPi}} + V = L$
end-extending
${\mathsf {KPi}} + V = L$
end-extending
![]() $L_{\alpha +1}$
in which
$L_{\alpha +1}$
in which
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma (t\wedge \pi s)$
-reflecting. This is a
$\sigma (t\wedge \pi s)$
-reflecting. This is a
![]() $\Pi ^{1}_{1}$
sentence and thus cannot be satisfied by any
$\Pi ^{1}_{1}$
sentence and thus cannot be satisfied by any
![]() $\pi \sigma (t\wedge \pi s)$
-reflecting ordinal and, in particular, by
$\pi \sigma (t\wedge \pi s)$
-reflecting ordinal and, in particular, by
![]() $\alpha $
. Thus, there is a model M of
$\alpha $
. Thus, there is a model M of
![]() ${\mathsf {KPi}} + V = L$
end-extending
${\mathsf {KPi}} + V = L$
end-extending
![]() $L_{\alpha +1}$
and such that
$L_{\alpha +1}$
and such that
Let
![]() $\chi $
be the sentence asserting the existence of a model N of
$\chi $
be the sentence asserting the existence of a model N of
![]() ${\mathsf {KP}} + V = L$
such that
${\mathsf {KP}} + V = L$
such that
-
1. N contains
 $\alpha $
;
$\alpha $
; -
2. in N, letting
 $\gamma $
be least such that
$\gamma $
be least such that
 $\alpha $
is not
$\alpha $
is not
 $\gamma $
-stable on s, we have
$\gamma $
-stable on s, we have 
Since
![]() $\gamma <\alpha ^+$
and M must end-extend
$\gamma <\alpha ^+$
and M must end-extend
![]() $L_{\alpha ^+}$
,
$L_{\alpha ^+}$
,
![]() $\gamma \in M$
and M is correct about
$\gamma \in M$
and M is correct about
![]() $\gamma $
being the least ordinal at which
$\gamma $
being the least ordinal at which
![]() $\alpha $
fails to be stable on s. Thus, we have
$\alpha $
fails to be stable on s. Thus, we have
as witnessed, say, by
 $L^{M}_{\alpha ^+}$
. Within M,
$L^{M}_{\alpha ^+}$
. Within M,
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma (t\wedge \pi s)$
-reflecting and thus there is some
$\sigma (t\wedge \pi s)$
-reflecting and thus there is some
![]() $\tau <\alpha $
such that
$\tau <\alpha $
such that
and so we really do have
Moreover, M is correct about reflection below
![]() $\alpha $
, so we may assume that
$\alpha $
, so we may assume that
![]() $\tau $
is
$\tau $
is
![]() $(t\wedge \pi s)$
-reflecting. By the definition of
$(t\wedge \pi s)$
-reflecting. By the definition of
![]() $\chi $
, there is a model N of
$\chi $
, there is a model N of
![]() ${\mathsf {KP}} + V = L$
such that
${\mathsf {KP}} + V = L$
such that
-
1. N contains
 $\tau $
;
$\tau $
; -
2. in N, letting
 $\gamma $
be least such that
$\gamma $
be least such that
 $\tau $
is not
$\tau $
is not
 $\gamma $
-stable on s, we have
$\gamma $
-stable on s, we have 
Since
![]() $\tau $
is
$\tau $
is
![]() $\pi s$
-reflecting, it is
$\pi s$
-reflecting, it is
![]() $\tau ^+$
-stable on s, and thus
$\tau ^+$
-stable on s, and thus
![]() $\gamma $
cannot be a true ordinal smaller than
$\gamma $
cannot be a true ordinal smaller than
![]() $\tau ^+$
. By Ville’s Theorem, N must end-extend
$\tau ^+$
. By Ville’s Theorem, N must end-extend
![]() $L_{\tau ^+}$
. Because
$L_{\tau ^+}$
. Because
![]() $\theta ^{*}$
is
$\theta ^{*}$
is
![]() $\Pi _{1}$
, it follows that
$\Pi _{1}$
, it follows that
and thus, that
as was to be shown. ⊣
Remark 39. Theorem 38 could alternatively be stated as
4 Linear patterns
The purpose of this section is to prove some results concerning the order of linear reflection. Let us begin with the following “contraction” lemma, which will be crucial. It will be used frequently throughout the remainder of the article, sometimes without mention.
Lemma 40 (Contraction)
Suppose s is a reflection pattern. Then,
Proof. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma \pi \sigma \pi s$
-reflecting. For every
$\sigma \pi \sigma \pi s$
-reflecting. For every
![]() $\Sigma ^{1}_{1}$
-sentence
$\Sigma ^{1}_{1}$
-sentence
![]() $\phi $
satisfied by
$\phi $
satisfied by
![]() $L_{\alpha }$
, one can find some
$L_{\alpha }$
, one can find some
![]() $\pi \sigma \pi s$
-reflecting
$\pi \sigma \pi s$
-reflecting
![]() $\beta <\alpha $
such that
$\beta <\alpha $
such that
![]() $L_{\beta }\models \phi $
and
$L_{\beta }\models \phi $
and
![]() $\beta $
is not
$\beta $
is not
![]() $\sigma $
-reflecting. (To see this, use
$\sigma $
-reflecting. (To see this, use
![]() $\sigma \pi \sigma s$
-reflection to find some
$\sigma \pi \sigma s$
-reflection to find some
![]() $\pi \sigma \pi s$
-reflecting ordinal
$\pi \sigma \pi s$
-reflecting ordinal
![]() $\beta _{0}$
such that
$\beta _{0}$
such that
![]() $L_{\beta _{0}}\models \phi $
. If
$L_{\beta _{0}}\models \phi $
. If
![]() $\beta _{0}$
is not
$\beta _{0}$
is not
![]() $\sigma $
-reflecting, then we are done. Otherwise,
$\sigma $
-reflecting, then we are done. Otherwise,
![]() $\beta _{0}$
is
$\beta _{0}$
is
![]() $\sigma $
-reflecting and
$\sigma $
-reflecting and
![]() $\pi \sigma \pi s$
-reflecting, thus
$\pi \sigma \pi s$
-reflecting, thus
![]() $\sigma \pi \sigma \pi s$
-reflecting by Lemma 25. Hence, there is some
$\sigma \pi \sigma \pi s$
-reflecting by Lemma 25. Hence, there is some
![]() $\pi \sigma \pi s$
-reflecting
$\pi \sigma \pi s$
-reflecting
![]() $\beta _{1}<\beta _{0}$
such that
$\beta _{1}<\beta _{0}$
such that
![]() $L_{\beta _{1}}\models \phi $
. Proceeding this way, one eventually finds some
$L_{\beta _{1}}\models \phi $
. Proceeding this way, one eventually finds some
![]() $\pi \sigma \pi s$
-reflecting
$\pi \sigma \pi s$
-reflecting
![]() $\beta _{n}$
such that
$\beta _{n}$
such that
![]() $L_{\beta _{n}}\models \phi $
and
$L_{\beta _{n}}\models \phi $
and
![]() $\beta _{n}$
is not
$\beta _{n}$
is not
![]() $\sigma $
-reflecting. Then
$\sigma $
-reflecting. Then
![]() $\beta = \beta _{n}$
is as desired.) By Theorem 32,
$\beta = \beta _{n}$
is as desired.) By Theorem 32,
![]() $\beta $
is
$\beta $
is
![]() $\pi \pi s$
-reflecting. By Lemma 23,
$\pi \pi s$
-reflecting. By Lemma 23,
![]() $\beta $
is
$\beta $
is
![]() $\pi s$
-reflecting, as desired. ⊣
$\pi s$
-reflecting, as desired. ⊣
Remark 41. Although this issue shall not arise again in this article, we caution the reader that, in contrast to Lemma 40, in general not every
![]() $\pi \sigma \pi \sigma s$
-reflecting ordinal is
$\pi \sigma \pi \sigma s$
-reflecting ordinal is
![]() $\pi \sigma s$
-reflecting. For example, the least ordinal which is
$\pi \sigma s$
-reflecting. For example, the least ordinal which is
is not
![]() $\pi \sigma \sigma $
-reflecting. A proof of this fact would require digressing significantly, so we omit it.
$\pi \sigma \sigma $
-reflecting. A proof of this fact would require digressing significantly, so we omit it.
Our first result in this section concerns the length of the order of linear reflection.
Theorem 42. The length of the order of linear reflection is
![]() $\omega ^{\omega }$
.
$\omega ^{\omega }$
.
Proof. Recursively, we assign ordinals to reflection patterns without conjunction: we assign the ordinal
![]() $\omega ^{n}$
to the pattern
$\omega ^{n}$
to the pattern
In particular, the ordinal
![]() $1$
is assigned to the empty pattern. If s and t are (possibly empty) patterns to which ordinals
$1$
is assigned to the empty pattern. If s and t are (possibly empty) patterns to which ordinals
![]() $o(s)$
and
$o(s)$
and
![]() $o(t)$
have been assigned, we assign the ordinal
$o(t)$
have been assigned, we assign the ordinal
to the pattern
We have to check that this assignment is well defined, in the sense that
![]() $s\equiv t$
if and only if
$s\equiv t$
if and only if
![]() $o(s) = o(t)$
. Note that if
$o(s) = o(t)$
. Note that if
![]() $0< n < m$
, then, on the one hand,
$0< n < m$
, then, on the one hand,
while, on the other,
 $$ \begin{align*} \sigma^{m} \pi s &\to \sigma^{m-n}\sigma^{n} \pi s\\ &\to \sigma^{m-n}(\sigma^{n} \pi s \wedge \pi) & \text{by Lemma 25(3)}\\ &\to \sigma^{m-n}(\sigma^{n}\pi s \wedge \pi\sigma^{n} \pi s) & \text{by Lemma 25(1)}\\ &\to \sigma^{m-n}(\sigma^{n}(\pi s \wedge \pi\sigma^{n} \pi s) \wedge \pi\sigma^{n}\pi s) & \text{by Lemma 25(2)}\\ &\to \sigma^{m}(\pi s \wedge \pi\sigma^{n} \pi s) \\ &\to \sigma^{m} \pi s \wedge \sigma^{m}\pi\sigma^{n} \pi s\\ &\to \sigma^{m} \pi s. \end{align*} $$
$$ \begin{align*} \sigma^{m} \pi s &\to \sigma^{m-n}\sigma^{n} \pi s\\ &\to \sigma^{m-n}(\sigma^{n} \pi s \wedge \pi) & \text{by Lemma 25(3)}\\ &\to \sigma^{m-n}(\sigma^{n}\pi s \wedge \pi\sigma^{n} \pi s) & \text{by Lemma 25(1)}\\ &\to \sigma^{m-n}(\sigma^{n}(\pi s \wedge \pi\sigma^{n} \pi s) \wedge \pi\sigma^{n}\pi s) & \text{by Lemma 25(2)}\\ &\to \sigma^{m}(\pi s \wedge \pi\sigma^{n} \pi s) \\ &\to \sigma^{m} \pi s \wedge \sigma^{m}\pi\sigma^{n} \pi s\\ &\to \sigma^{m} \pi s. \end{align*} $$
Thus, every
![]() $\sigma ^{m} \pi s$
-reflecting ordinal is also
$\sigma ^{m} \pi s$
-reflecting ordinal is also
![]() $\sigma ^{m} \pi \sigma ^{n} \pi s$
-reflecting when
$\sigma ^{m} \pi \sigma ^{n} \pi s$
-reflecting when
![]() $n < m$
; the converse is also true, by Lemmas 23 and 40. By Lemma 23 and Theorem 29, we have
$n < m$
; the converse is also true, by Lemmas 23 and 40. By Lemma 23 and Theorem 29, we have
for any pair of nonzero numbers n and m. It follows that every linear pattern of reflection is equivalent to one of the form
with
![]() $0 < k_{0} \leq k_{1} \leq \cdots \leq k_{l}$
, and moreover there is a unique choice of such
$0 < k_{0} \leq k_{1} \leq \cdots \leq k_{l}$
, and moreover there is a unique choice of such
![]() $m,l, k_{0}, \dots , k_{l}$
. Observe that transforming a linear reflection pattern into one of the form (2) preserves the assigned ordinal. We conclude that if s and t are two linear patterns of reflection and
$m,l, k_{0}, \dots , k_{l}$
. Observe that transforming a linear reflection pattern into one of the form (2) preserves the assigned ordinal. We conclude that if s and t are two linear patterns of reflection and
![]() $s \equiv t$
, then
$s \equiv t$
, then
![]() $o(s) = o(t)$
. Similarly, if
$o(s) = o(t)$
. Similarly, if
![]() $o(s) = o(t)$
, then s and t are each equivalent to the same pattern of the form (2) and hence to each other, thus proving the claim that the assignment of ordinals is well defined.
$o(s) = o(t)$
, then s and t are each equivalent to the same pattern of the form (2) and hence to each other, thus proving the claim that the assignment of ordinals is well defined.
Now that we know that the assignment is well defined, we can prove that for all linear patterns s and t, we have
![]() $s < t$
if, and only if,
$s < t$
if, and only if,
![]() $o(s) < o(t)$
. If
$o(s) < o(t)$
. If
![]() $o(s) < o(t)$
, let
$o(s) < o(t)$
, let
![]() $\gamma $
be so that
$\gamma $
be so that
![]() $o(s) + \gamma = o(t)$
and let r be a pattern so that
$o(s) + \gamma = o(t)$
and let r be a pattern so that
![]() $o(r) = \gamma $
. Then,
$o(r) = \gamma $
. Then,
![]() $o(r\pi s) = o(t)$
, so that
$o(r\pi s) = o(t)$
, so that
![]() $r \pi s\equiv t$
. It follows that every t-reflecting ordinal is a limit of s-reflecting ordinals.
$r \pi s\equiv t$
. It follows that every t-reflecting ordinal is a limit of s-reflecting ordinals.
Conversely, suppose that
![]() $s< t$
. We cannot have
$s< t$
. We cannot have
![]() $o(s) = o(t)$
, as this would contradict well-definedness; we cannot have
$o(s) = o(t)$
, as this would contradict well-definedness; we cannot have
![]() $o(t) < o(s)$
, as this would contradict the conclusion of the previous paragraph. Therefore, we must have
$o(t) < o(s)$
, as this would contradict the conclusion of the previous paragraph. Therefore, we must have
![]() $o(s) < o(t)$
.⊣
$o(s) < o(t)$
.⊣
By comparing the ordinals associated to linear reflection patterns in the proof of Theorem 42, we can determine which one is greater.
Example 43. Let
 $$ \begin{align*} s &= \sigma^{4}\pi^{2}\sigma\pi^{2} = \sigma^{4}\pi\sigma^{0}\pi\sigma^{1}\pi\sigma^{0}\pi\sigma^{0},\\ t &= \pi^{3}\sigma\pi^{3}\sigma^{5} = \sigma^{0}\pi\sigma^{0}\pi\sigma^{0}\pi\sigma^{1}\pi\sigma^{0}\pi\sigma^{0}\pi\sigma^{5},\\ r &= \sigma^{4} \pi \sigma^{3}. \end{align*} $$
$$ \begin{align*} s &= \sigma^{4}\pi^{2}\sigma\pi^{2} = \sigma^{4}\pi\sigma^{0}\pi\sigma^{1}\pi\sigma^{0}\pi\sigma^{0},\\ t &= \pi^{3}\sigma\pi^{3}\sigma^{5} = \sigma^{0}\pi\sigma^{0}\pi\sigma^{0}\pi\sigma^{1}\pi\sigma^{0}\pi\sigma^{0}\pi\sigma^{5},\\ r &= \sigma^{4} \pi \sigma^{3}. \end{align*} $$
Then
 $$ \begin{align*} o(s) &= 1 + 1 + \omega + 1 + \omega^{4} = \omega^{4},\\ o(t) &= \omega^{5} + 1 + 1 + \omega + 1 + 1 + 1 = \omega^{5} + \omega + 3,\\ o(r) &= \omega^{3} + \omega^{4} = \omega^{4}, \end{align*} $$
$$ \begin{align*} o(s) &= 1 + 1 + \omega + 1 + \omega^{4} = \omega^{4},\\ o(t) &= \omega^{5} + 1 + 1 + \omega + 1 + 1 + 1 = \omega^{5} + \omega + 3,\\ o(r) &= \omega^{3} + \omega^{4} = \omega^{4}, \end{align*} $$
so
![]() $s < t$
and
$s < t$
and
![]() $s \equiv r$
.
$s \equiv r$
.
The second result of this section is that the linear patterns are cofinal in the order of reflection.
Theorem 44. The sequence
![]() $\{\sigma ^{n}:n\in \mathbb {N}\}$
is cofinal in the order of reflection.
$\{\sigma ^{n}:n\in \mathbb {N}\}$
is cofinal in the order of reflection.
Proof. To prove the theorem, we shall prove that for every reflection pattern s there is some
![]() $n\in \mathbb {N}$
such that whenever
$n\in \mathbb {N}$
such that whenever
![]() $n\leq k$
, for every reflection pattern t, every
$n\leq k$
, for every reflection pattern t, every
![]() $\sigma (\sigma ^{k} \wedge t)$
-reflecting ordinal is also
$\sigma (\sigma ^{k} \wedge t)$
-reflecting ordinal is also
![]() $\sigma (\sigma ^{k}\wedge t \wedge s)$
-reflecting. If s is a reflection pattern, then for such an n we have
$\sigma (\sigma ^{k}\wedge t \wedge s)$
-reflecting. If s is a reflection pattern, then for such an n we have
![]() $s < \sigma ^{n+1}$
(this follows by taking t to be trivial), so the theorem will follow.
$s < \sigma ^{n+1}$
(this follows by taking t to be trivial), so the theorem will follow.
This is done by induction on the construction of s. The case that s is of the form
![]() $\pi s^{\prime }$
is immediate from Theorem 29. Suppose s is of the form
$\pi s^{\prime }$
is immediate from Theorem 29. Suppose s is of the form
![]() $s_{1} \wedge s_{2}$
. Use the induction hypothesis to find
$s_{1} \wedge s_{2}$
. Use the induction hypothesis to find
![]() $n_{1},n_{2}\in \mathbb {N}$
such that whenever
$n_{1},n_{2}\in \mathbb {N}$
such that whenever
![]() $n_{1}\leq k_{1}$
and
$n_{1}\leq k_{1}$
and
![]() $n_{2}\leq k_{2}$
, for every reflection pattern t,
$n_{2}\leq k_{2}$
, for every reflection pattern t,
and
Let
![]() $n = \max \{n_{1},n_{2}\}$
and
$n = \max \{n_{1},n_{2}\}$
and
![]() $n\leq k$
. Then, we have
$n\leq k$
. Then, we have
Finally, suppose that
![]() $s = \sigma s^{\prime }$
. Use the induction hypothesis to find
$s = \sigma s^{\prime }$
. Use the induction hypothesis to find
![]() $n\in \mathbb {N}$
such that whenever
$n\in \mathbb {N}$
such that whenever
![]() $n\leq k$
, for every reflection pattern t, every
$n\leq k$
, for every reflection pattern t, every
![]() $\sigma (\sigma ^{k} \wedge t)$
-reflecting ordinal is also
$\sigma (\sigma ^{k} \wedge t)$
-reflecting ordinal is also
![]() $\sigma (\sigma ^{k}\wedge t \wedge s^{\prime })$
-reflecting. Then,
$\sigma (\sigma ^{k}\wedge t \wedge s^{\prime })$
-reflecting. Then,
 $$ \begin{align*}\sigma(\sigma^{k+1} \kern1.4pt{\wedge}\kern1.4pt t) \equiv \sigma(\sigma\sigma^{k}\kern1.4pt{\wedge}\kern1.4pt t\kern-0.5pt) \equiv \sigma\big(\sigma(\sigma^{k} \kern1.4pt{\wedge}\kern1.4pt s^{\prime})\kern1.4pt{\wedge}\kern1.4pt t\kern-0.5pt\big) \equiv \sigma(\sigma^{k+1} \kern1.4pt{\wedge}\kern1.4pt \sigma s^{\prime} \kern1.4pt{\wedge}\kern1.4pt t\kern-0.5pt) \equiv \sigma(\sigma^{k+1}\kern1.4pt{\wedge}\kern1.4pt t\kern1.4pt{\wedge}\kern1.4pt s\kern-0.5pt),\end{align*} $$
$$ \begin{align*}\sigma(\sigma^{k+1} \kern1.4pt{\wedge}\kern1.4pt t) \equiv \sigma(\sigma\sigma^{k}\kern1.4pt{\wedge}\kern1.4pt t\kern-0.5pt) \equiv \sigma\big(\sigma(\sigma^{k} \kern1.4pt{\wedge}\kern1.4pt s^{\prime})\kern1.4pt{\wedge}\kern1.4pt t\kern-0.5pt\big) \equiv \sigma(\sigma^{k+1} \kern1.4pt{\wedge}\kern1.4pt \sigma s^{\prime} \kern1.4pt{\wedge}\kern1.4pt t\kern-0.5pt) \equiv \sigma(\sigma^{k+1}\kern1.4pt{\wedge}\kern1.4pt t\kern1.4pt{\wedge}\kern1.4pt s\kern-0.5pt),\end{align*} $$
as desired. ⊣
5 The reflection order below
 $\sigma ^{2}$
$\sigma ^{2}$
In this section, we describe the order of reflection below
![]() $\sigma ^{2}$
. Below, we express concatenation of patterns by direct juxtaposition, so that e.g., if
$\sigma ^{2}$
. Below, we express concatenation of patterns by direct juxtaposition, so that e.g., if
![]() $s = \sigma \wedge \pi $
, then
$s = \sigma \wedge \pi $
, then
(We emphasize that
![]() $ss$
does not mean
$ss$
does not mean
![]() $(\sigma \wedge \pi )(\sigma \wedge \pi )$
, among other reasons, because this expression has not been defined.) Clearly, if
$(\sigma \wedge \pi )(\sigma \wedge \pi )$
, among other reasons, because this expression has not been defined.) Clearly, if
![]() $t_{0}\to t_{1}$
, then
$t_{0}\to t_{1}$
, then
![]() $st_{0}\to st_{1}$
for any s.
$st_{0}\to st_{1}$
for any s.
Definition 45. Let
![]() $k \in \mathbb {N}$
and s be a reflection pattern. We write
$k \in \mathbb {N}$
and s be a reflection pattern. We write
 $c^{k}_{0}s = s$
; inductively,
$c^{k}_{0}s = s$
; inductively,
 $$ \begin{align*}c_{n+1}^{k}s = \sigma\wedge\pi^{k}\sigma\pi c^{k}_{n}s.\end{align*} $$
$$ \begin{align*}c_{n+1}^{k}s = \sigma\wedge\pi^{k}\sigma\pi c^{k}_{n}s.\end{align*} $$
We write
![]() $c^{k}_{n}$
for
$c^{k}_{n}$
for
![]() $c^{k}_{n}s$
, where s is the empty pattern.
$c^{k}_{n}s$
, where s is the empty pattern.
We remark that, in particular,
![]() $c^{0}_{n} = (\sigma \pi )^{n}$
.
$c^{0}_{n} = (\sigma \pi )^{n}$
.
Lemma 46. For every
![]() $n,k \in \mathbb {N}$
and every reflection pattern s, we have
$n,k \in \mathbb {N}$
and every reflection pattern s, we have
 $$ \begin{align*}\sigma\wedge \pi^{k+1}s\to \pi c^{k}_{n}s.\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi^{k+1}s\to \pi c^{k}_{n}s.\end{align*} $$
Proof. By Lemma 25,
We show by induction on n that
 $$ \begin{align*}\sigma\wedge \pi c^{k}_{1} s \equiv \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s.\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi c^{k}_{1} s \equiv \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s.\end{align*} $$
Suppose that
 $$ \begin{align*}\sigma\wedge \pi c^{k}_{1} s \equiv \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s.\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi c^{k}_{1} s \equiv \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s.\end{align*} $$
After some applications of Lemma 25, we have
 $$ \begin{align*} \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s &\equiv\sigma\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\\ &\equiv\sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\\ &\equiv\sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s))\\ &\equiv\sigma \wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s))\\ &\equiv\sigma \wedge \pi (\sigma\wedge\pi^{k}(\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s))). \end{align*} $$
$$ \begin{align*} \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s &\equiv\sigma\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\\ &\equiv\sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\\ &\equiv\sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s))\\ &\equiv\sigma \wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s))\\ &\equiv\sigma \wedge \pi (\sigma\wedge\pi^{k}(\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s))). \end{align*} $$
After some additional manipulations, we have
 $$ \begin{align*} \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) &\equiv \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) \wedge \sigma\pi (\pi^{k}\sigma\pi c^{k}_{n} s)\\ &\equiv \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) \wedge \sigma\pi \sigma\pi c^{k}_{n} s\\ &\equiv \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) \wedge \sigma\pi c^{k}_{n} s\\ &\equiv \sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s), \end{align*} $$
$$ \begin{align*} \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) &\equiv \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) \wedge \sigma\pi (\pi^{k}\sigma\pi c^{k}_{n} s)\\ &\equiv \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) \wedge \sigma\pi \sigma\pi c^{k}_{n} s\\ &\equiv \sigma\pi (\sigma\wedge \pi^{k}\sigma\pi c^{k}_{n} s) \wedge \sigma\pi c^{k}_{n} s\\ &\equiv \sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s), \end{align*} $$
where the second equivalence follows from Lemma 23 and the third follows from Lemma 40. Putting this together with the previous computation,
 $$ \begin{align*} \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s &\equiv \sigma \wedge \pi (\sigma\wedge\pi^{k}(\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)))\\ &\equiv \sigma\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi (\sigma\wedge\pi^{k} \sigma\pi c^{k}_{n} s))\\ &\equiv \sigma\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n+1} s)\\ &\equiv \sigma\wedge \pi (c^{k}_{1} c^{k}_{n+1} s), \end{align*} $$
$$ \begin{align*} \sigma\wedge \pi c^{k}_{1} c^{k}_{n} s &\equiv \sigma \wedge \pi (\sigma\wedge\pi^{k}(\sigma\pi c^{k}_{n} s \wedge \sigma\pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s)))\\ &\equiv \sigma\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi (\sigma\wedge\pi^{k} \sigma\pi c^{k}_{n} s))\\ &\equiv \sigma\wedge \pi (\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n+1} s)\\ &\equiv \sigma\wedge \pi (c^{k}_{1} c^{k}_{n+1} s), \end{align*} $$
as desired. The chain of equivalences at the beginning of the proof shows that every
![]() $\sigma \wedge \pi ^{k+1}s$
-reflecting ordinal is also
$\sigma \wedge \pi ^{k+1}s$
-reflecting ordinal is also
![]() $\pi c^{k}_{1} s$
-reflecting (the converse is not true in general), and the equivalence just proved by induction shows that it is therefore
$\pi c^{k}_{1} s$
-reflecting (the converse is not true in general), and the equivalence just proved by induction shows that it is therefore
![]() $\pi c^{k}_{n} s$
-reflecting for any n, as desired. ⊣
$\pi c^{k}_{n} s$
-reflecting for any n, as desired. ⊣
Corollary 47. For every
![]() $n,k \in \mathbb {N}$
, every
$n,k \in \mathbb {N}$
, every
![]() $l\leq k$
, and every reflection pattern s, we have
$l\leq k$
, and every reflection pattern s, we have
 $$ \begin{align*}\sigma\wedge \pi^{k+1}s\to\pi^{k+1}\sigma\pi c^{l}_{n}s.\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi^{k+1}s\to\pi^{k+1}\sigma\pi c^{l}_{n}s.\end{align*} $$
Proof. By Lemma 46,
 $$ \begin{align*}\sigma\wedge \pi^{k+1}s \to \pi c^{k}_{n+1}s.\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi^{k+1}s \to \pi c^{k}_{n+1}s.\end{align*} $$
By definition,
 $$ \begin{align*}\pi c^{k}_{n+1}s \equiv \pi(\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s);\end{align*} $$
$$ \begin{align*}\pi c^{k}_{n+1}s \equiv \pi(\sigma\wedge\pi^{k}\sigma\pi c^{k}_{n} s);\end{align*} $$
in particular,
 $$ \begin{align*}\sigma\wedge \pi^{k+1}s\to\pi^{k+1}\sigma\pi c^{k}_{n}s.\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi^{k+1}s\to\pi^{k+1}\sigma\pi c^{k}_{n}s.\end{align*} $$
Applying Lemma 23 n times to see that
 $$ \begin{align*}c^{k}_{n} s\to c^{l}_{n} s,\end{align*} $$
$$ \begin{align*}c^{k}_{n} s\to c^{l}_{n} s,\end{align*} $$
from which the result follows. ⊣
Lemma 48. For every
![]() $k \in \mathbb {N}$
, every
$k \in \mathbb {N}$
, every
![]() $n_{0},\ldots , n_{k} \in \mathbb {N}$
, and every reflection pattern s, we have
$n_{0},\ldots , n_{k} \in \mathbb {N}$
, and every reflection pattern s, we have
 $$ \begin{align*}\sigma\wedge \pi^{k+1}s\to\pi^{k+1} \sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}s.\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi^{k+1}s\to\pi^{k+1} \sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}s.\end{align*} $$
Proof. Observe that every reflection pattern of the form
![]() $\sigma \pi c^{l}_{m}$
, for
$\sigma \pi c^{l}_{m}$
, for
![]() $l,m\in \mathbb {N}$
, is of the form
$l,m\in \mathbb {N}$
, is of the form
![]() $t^{\prime } \sigma \pi $
. Thus, Lemma 40 implies that
$t^{\prime } \sigma \pi $
. Thus, Lemma 40 implies that
 $$ \begin{align*}\sigma\pi c^{l}_{m} \sigma \pi s \equiv \sigma\pi c^{l}_{m} s.\end{align*} $$
$$ \begin{align*}\sigma\pi c^{l}_{m} \sigma \pi s \equiv \sigma\pi c^{l}_{m} s.\end{align*} $$
The result then follows from applying Corollary 47 repeatedly. ⊣
Definition 49. A reflection pattern is
![]() $2$
-normal or simply normal Footnote
2
if it is of the form
$2$
-normal or simply normal Footnote
2
if it is of the form
 $$ \begin{align*}\pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}},\end{align*} $$
$$ \begin{align*}\pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}},\end{align*} $$
for some natural numbers k, n,
![]() $n_{0},n_{1},\ldots , n_{k}$
. If w is the reflection pattern above, we define
$n_{0},n_{1},\ldots , n_{k}$
. If w is the reflection pattern above, we define
We shall see that normal patterns have very nice properties.
Lemma 50. Suppose s is a normal reflection pattern. Then,
Proof. Let
 $$ \begin{align*}s=\pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}.\end{align*} $$
$$ \begin{align*}s=\pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}.\end{align*} $$
Suppose first
![]() $n_{0} \neq 0$
. By Theorem 29,
$n_{0} \neq 0$
. By Theorem 29,
 $$ \begin{align*}\sigma(\sigma\wedge \pi^{\max\{n,k+1\}})\to \sigma(\sigma\wedge \pi^{n} \sigma\pi c^{0}_{n_{0}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}),\end{align*} $$
$$ \begin{align*}\sigma(\sigma\wedge \pi^{\max\{n,k+1\}})\to \sigma(\sigma\wedge \pi^{n} \sigma\pi c^{0}_{n_{0}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}),\end{align*} $$
as desired. Suppose now that
![]() $n_{0} = 0$
and let l be least such that
$n_{0} = 0$
and let l be least such that
![]() $n_{l} \neq 0$
(if there is no such l, the lemma follows from Theorem 29). Thus,
$n_{l} \neq 0$
(if there is no such l, the lemma follows from Theorem 29). Thus,
 $$ \begin{align*}s=\pi^{n}c^{l}_{n_{l}}\dots c^{k}_{n_{k}} = \pi^{n}(\sigma\wedge \pi^{l}\sigma\pi c^{l}_{n_{l}-1}\dots c^{k}_{n_{k}}).\end{align*} $$
$$ \begin{align*}s=\pi^{n}c^{l}_{n_{l}}\dots c^{k}_{n_{k}} = \pi^{n}(\sigma\wedge \pi^{l}\sigma\pi c^{l}_{n_{l}-1}\dots c^{k}_{n_{k}}).\end{align*} $$
As before,
 $$ \begin{align*}\sigma\sigma\to\sigma(\sigma\wedge \pi^{l} \sigma\pi c^{l}_{n_{l}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}).\end{align*} $$
$$ \begin{align*}\sigma\sigma\to\sigma(\sigma\wedge \pi^{l} \sigma\pi c^{l}_{n_{l}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}).\end{align*} $$
By Theorem 29,
 $$ \begin{align*}\sigma(\sigma\wedge \pi^{l} \sigma\pi c^{l}_{n_{l}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\to \sigma\pi^{n}(\sigma\wedge \pi^{l} \sigma\pi c^{l}_{n_{l}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}).\end{align*} $$
$$ \begin{align*}\sigma(\sigma\wedge \pi^{l} \sigma\pi c^{l}_{n_{l}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\to \sigma\pi^{n}(\sigma\wedge \pi^{l} \sigma\pi c^{l}_{n_{l}-1}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}).\end{align*} $$
as desired. ⊣
Lemma 51. Suppose
![]() $\pi t$
and
$\pi t$
and
![]() $\pi s$
are normal reflection patterns such that
$\pi s$
are normal reflection patterns such that
![]() $o(\pi t) \leq o(\pi s)$
. Then, every
$o(\pi t) \leq o(\pi s)$
. Then, every
![]() $\pi s$
-reflecting ordinal is either
$\pi s$
-reflecting ordinal is either
![]() $\pi t$
-reflecting or
$\pi t$
-reflecting or
![]() $\sigma $
-reflecting.
$\sigma $
-reflecting.
Proof. Let
 $$ \begin{align*}\pi t = \pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}},\end{align*} $$
$$ \begin{align*}\pi t = \pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}},\end{align*} $$
and
 $$ \begin{align*}\pi s = \pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}},\end{align*} $$
$$ \begin{align*}\pi s = \pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}},\end{align*} $$
where n and m are nonzero. Without loss of generality, we assume that
![]() $n_{k}$
and
$n_{k}$
and
![]() $m_{l}$
are also nonzero. It follows that
$m_{l}$
are also nonzero. It follows that
![]() $k \leq l$
. Suppose that
$k \leq l$
. Suppose that
![]() $o(\pi t) < o(\pi s)$
. It will be convenient, for illustrative purposes, to consider the case that
$o(\pi t) < o(\pi s)$
. It will be convenient, for illustrative purposes, to consider the case that
![]() $k < l$
first. If so, it suffices to show that every
$k < l$
first. If so, it suffices to show that every
![]() $\pi (\sigma \wedge \pi ^{l})$
-reflecting ordinal which is not
$\pi (\sigma \wedge \pi ^{l})$
-reflecting ordinal which is not
![]() $\sigma $
-reflecting is
$\sigma $
-reflecting is
![]() $(\pi t)$
-reflecting, for then the result follows from Theorem 32 and contraction. By Lemma 48,
$(\pi t)$
-reflecting, for then the result follows from Theorem 32 and contraction. By Lemma 48,
 $$ \begin{align*} \pi(\sigma\wedge\pi^{l}) \to \pi(\sigma\wedge \pi^{l} \sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}). \end{align*} $$
$$ \begin{align*} \pi(\sigma\wedge\pi^{l}) \to \pi(\sigma\wedge \pi^{l} \sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}). \end{align*} $$
By Lemma 25,
 $$ \begin{align*}\pi(\sigma\wedge \pi^{l} \sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\to \pi(\sigma \pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}),\end{align*} $$
$$ \begin{align*}\pi(\sigma\wedge \pi^{l} \sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\to \pi(\sigma \pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}),\end{align*} $$
and, by Theorem 29,
 $$ \begin{align*}\pi(\sigma \pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\to \pi(\sigma \pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}),\end{align*} $$
$$ \begin{align*}\pi(\sigma \pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\to \pi(\sigma \pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}),\end{align*} $$
so that, if a
![]() $\pi (\sigma \wedge \pi ^{l})$
-reflecting ordinal is not
$\pi (\sigma \wedge \pi ^{l})$
-reflecting ordinal is not
![]() $\sigma $
-reflecting, then it is
$\sigma $
-reflecting, then it is
 $$ \begin{align*}\pi(\pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\text{-reflecting,}\end{align*} $$
$$ \begin{align*}\pi(\pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}})\text{-reflecting,}\end{align*} $$
by Theorem 32, i.e.,
![]() $\pi t$
-reflecting.
$\pi t$
-reflecting.
The case
![]() $k = l$
is not very different: let
$k = l$
is not very different: let
![]() $i\leq k$
be greatest such that
$i\leq k$
be greatest such that
![]() $n_{i} < m_{i}$
and notice that
$n_{i} < m_{i}$
and notice that
 $$ \begin{align*}c_{m_{i}}^{i} = c_{m_{i}-n_{i}}^{i}c_{n_{i}}^{i}.\end{align*} $$
$$ \begin{align*}c_{m_{i}}^{i} = c_{m_{i}-n_{i}}^{i}c_{n_{i}}^{i}.\end{align*} $$
Thus,
 $$ \begin{align*}\pi t = \pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime},\end{align*} $$
$$ \begin{align*}\pi t = \pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime},\end{align*} $$
where
 $t^{\prime } = c^{i}_{n_{i}}\dots c^{k}_{n_{k}}$
; and
$t^{\prime } = c^{i}_{n_{i}}\dots c^{k}_{n_{k}}$
; and
 $$ \begin{align*}\pi s = \pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c_{m_{i}-n_{i}}^{i}t^{\prime}.\end{align*} $$
$$ \begin{align*}\pi s = \pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c_{m_{i}-n_{i}}^{i}t^{\prime}.\end{align*} $$
It suffices to show that every
![]() $\pi (\sigma \wedge \pi ^{i}\sigma \pi t^{\prime })$
-reflecting ordinal which is not
$\pi (\sigma \wedge \pi ^{i}\sigma \pi t^{\prime })$
-reflecting ordinal which is not
![]() $\sigma $
-reflecting is
$\sigma $
-reflecting is
![]() $\pi t$
-reflecting, for then the result follows from Theorem 32 and contraction. Lemma 48 (with
$\pi t$
-reflecting, for then the result follows from Theorem 32 and contraction. Lemma 48 (with
![]() $\sigma \pi t^{\prime }$
being the s in the statement) shows that
$\sigma \pi t^{\prime }$
being the s in the statement) shows that
 $$ \begin{align*} \pi(\sigma\wedge\pi^{i}\sigma\pi t^{\prime})\to \pi(\sigma\wedge \pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime}). \end{align*} $$
$$ \begin{align*} \pi(\sigma\wedge\pi^{i}\sigma\pi t^{\prime})\to \pi(\sigma\wedge \pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime}). \end{align*} $$
By Lemma 25,
 $$ \begin{align*} \pi(\sigma\wedge \pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime})\to \pi(\sigma\pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime}). \end{align*} $$
$$ \begin{align*} \pi(\sigma\wedge \pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime})\to \pi(\sigma\pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime}). \end{align*} $$
By contraction,
 $$ \begin{align*} \pi(\sigma\pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime}) &\to \pi(\sigma\pi\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime})\\ &\to \pi(\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime})\\ &\to \pi(\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime}). \end{align*} $$
$$ \begin{align*} \pi(\sigma\pi^{i}\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime}) &\to \pi(\sigma\pi\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime})\\ &\to \pi(\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}\sigma\pi t^{\prime})\\ &\to \pi(\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime}). \end{align*} $$
By Theorem 29,
 $$ \begin{align*} \pi(\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime})\to \pi(\sigma\pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime}), \end{align*} $$
$$ \begin{align*} \pi(\sigma\pi c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime})\to \pi(\sigma\pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime}), \end{align*} $$
so that if a
![]() $\pi (\sigma \wedge \pi ^{i}\sigma \pi t^{\prime })$
-reflecting ordinal is not
$\pi (\sigma \wedge \pi ^{i}\sigma \pi t^{\prime })$
-reflecting ordinal is not
![]() $\sigma $
-reflecting, then it is
$\sigma $
-reflecting, then it is
 $$ \begin{align*} \pi(\pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime})\text{-reflecting,} \end{align*} $$
$$ \begin{align*} \pi(\pi^{n} c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{i-1}_{n_{i-1}}t^{\prime})\text{-reflecting,} \end{align*} $$
by Theorem 32, as desired. ⊣
Although Lemma 51 does not directly provide any equivalences between reflection patterns, it leads to some when coupled with previous techniques.
Lemma 52. Suppose
![]() $s_{0}$
,
$s_{0}$
,
![]() $s_{1}, \ldots , s_{n}$
are normal reflection patterns, all of the form
$s_{1}, \ldots , s_{n}$
are normal reflection patterns, all of the form
![]() $\pi v$
. Suppose moreover that
$\pi v$
. Suppose moreover that
![]() $o(s_{i}) \leq o(s_{n})$
for all
$o(s_{i}) \leq o(s_{n})$
for all
![]() $i\leq n$
. Then,
$i\leq n$
. Then,
Proof. We restrict to the case
![]() $n = 1$
and let
$n = 1$
and let
![]() $s_{0} = t$
and
$s_{0} = t$
and
![]() $s_{1} = s$
, since the general case is similar. We prove
$s_{1} = s$
, since the general case is similar. We prove
![]() $\sigma s\equiv \sigma (s\wedge t)$
, since clearly every
$\sigma s\equiv \sigma (s\wedge t)$
, since clearly every
![]() $\sigma (s\wedge t)$
-reflecting ordinal is
$\sigma (s\wedge t)$
-reflecting ordinal is
![]() $(\sigma s\wedge \sigma t)$
-reflecting, and every
$(\sigma s\wedge \sigma t)$
-reflecting, and every
![]() $(\sigma s\wedge \sigma t)$
-reflecting ordinal is
$(\sigma s\wedge \sigma t)$
-reflecting ordinal is
![]() $\sigma s$
-reflecting. Suppose
$\sigma s$
-reflecting. Suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma s$
-reflecting and let
$\sigma s$
-reflecting and let
![]() $\phi $
be a
$\phi $
be a
![]() $\Sigma ^{1}_{1}$
-sentence satisfied by
$\Sigma ^{1}_{1}$
-sentence satisfied by
![]() $L_{\alpha }$
. We must find some
$L_{\alpha }$
. We must find some
![]() $(s\wedge t)$
-reflecting
$(s\wedge t)$
-reflecting
![]() $\beta <\alpha $
such that
$\beta <\alpha $
such that
![]() $L_{\beta }\models \phi $
. By Lemma 51, it suffices that
$L_{\beta }\models \phi $
. By Lemma 51, it suffices that
![]() $\beta $
be s-reflecting and not
$\beta $
be s-reflecting and not
![]() $\sigma $
-reflecting.
$\sigma $
-reflecting.
![]() $\beta $
is found as in the proof of Lemma 40:
$\beta $
is found as in the proof of Lemma 40:
By
![]() $\sigma s$
-reflection, there is some s-reflecting ordinal
$\sigma s$
-reflection, there is some s-reflecting ordinal
![]() $\beta _{0}$
such that
$\beta _{0}$
such that
![]() $L_{\beta _{0}}\models \phi $
. If
$L_{\beta _{0}}\models \phi $
. If
![]() $\beta _{0}$
is not
$\beta _{0}$
is not
![]() $\sigma $
-reflecting, then we are done. Otherwise,
$\sigma $
-reflecting, then we are done. Otherwise,
![]() $\beta _{0}$
is
$\beta _{0}$
is
![]() $\sigma $
-reflecting and s-reflecting, thus (because s is of the form
$\sigma $
-reflecting and s-reflecting, thus (because s is of the form
![]() $\pi v$
)
$\pi v$
)
![]() $\sigma s$
-reflecting by Lemma 25. Hence, there is some s-reflecting
$\sigma s$
-reflecting by Lemma 25. Hence, there is some s-reflecting
![]() $\beta _{1}<\beta _{0}$
such that
$\beta _{1}<\beta _{0}$
such that
![]() $L_{\beta _{1}}\models \phi $
. Proceeding this way, one eventually finds some s-reflecting
$L_{\beta _{1}}\models \phi $
. Proceeding this way, one eventually finds some s-reflecting
![]() $\beta _{n}$
such that
$\beta _{n}$
such that
![]() $L_{\beta _{n}}\models \phi $
and
$L_{\beta _{n}}\models \phi $
and
![]() $\beta _{n}$
is not
$\beta _{n}$
is not
![]() $\sigma $
-reflecting. Then
$\sigma $
-reflecting. Then
![]() $\beta = \beta _{n}$
is as desired. ⊣
$\beta = \beta _{n}$
is as desired. ⊣
Lemma 53. Suppose t is a normal reflection pattern. Then
![]() $\sigma \wedge t$
is equivalent to a normal reflection pattern.
$\sigma \wedge t$
is equivalent to a normal reflection pattern.
Proof. Put
 $t = \pi ^{k}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}$
. The lemma is immediate unless
$t = \pi ^{k}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}$
. The lemma is immediate unless
![]() $k \neq 0$
and there is some least
$k \neq 0$
and there is some least
![]() $i \leq l$
such that
$i \leq l$
such that
![]() $m_{i} \neq 0$
. Thus,
$m_{i} \neq 0$
. Thus,
 $$ \begin{align*} t &= \pi^{k}c^{i}_{m_{i}}c^{i+1}_{m_{i+1}}\dots c^{l}_{m_{l}}\\ &= \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{l}_{m_{l}}). \end{align*} $$
$$ \begin{align*} t &= \pi^{k}c^{i}_{m_{i}}c^{i+1}_{m_{i+1}}\dots c^{l}_{m_{l}}\\ &= \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{l}_{m_{l}}). \end{align*} $$
Let
 $$ \begin{align*}s = c^{k+i}_{m_{k+i}}c^{k+ i+1}_{m_{k+i+1}}\dots c^{l}_{m_{l}},\end{align*} $$
$$ \begin{align*}s = c^{k+i}_{m_{k+i}}c^{k+ i+1}_{m_{k+i+1}}\dots c^{l}_{m_{l}},\end{align*} $$
so that
 $$ \begin{align*}t = \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k + i-1}}s).\end{align*} $$
$$ \begin{align*}t = \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k + i-1}}s).\end{align*} $$
If all the displayed
![]() $m_{j}$
are zero, then the result follows easily; otherwise, by Lemma 25 and contraction,
$m_{j}$
are zero, then the result follows easily; otherwise, by Lemma 25 and contraction,
 $$ \begin{align*}t \equiv \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k + i-1}_{m_{k + i-1}}\sigma\pi s).\end{align*} $$
$$ \begin{align*}t \equiv \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k + i-1}_{m_{k + i-1}}\sigma\pi s).\end{align*} $$
By Lemma 25,
 $$ \begin{align*} \sigma\wedge t &\equiv \sigma \wedge \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k+i-1}}\sigma\pi s)\\ &\equiv \sigma \wedge \pi^{k}(\pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k+i-1}}\sigma\pi s)\\ &\equiv \sigma \wedge \pi^{k+i}\sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k+i-1}}\sigma\pi s). \end{align*} $$
$$ \begin{align*} \sigma\wedge t &\equiv \sigma \wedge \pi^{k}(\sigma \wedge \pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k+i-1}}\sigma\pi s)\\ &\equiv \sigma \wedge \pi^{k}(\pi^{i} \sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k+i-1}}\sigma\pi s)\\ &\equiv \sigma \wedge \pi^{k+i}\sigma\pi c^{i}_{m_{i}-1}c^{i+1}_{m_{i+1}}\dots c^{k+i-1}_{m_{k+i-1}}\sigma\pi s). \end{align*} $$
By Lemma 48 on the one hand and Lemma 23 and contraction on the other,
but the reflection pattern on the left-hand side is readily seen to be equivalent to a normal one. ⊣
Theorem 55 below is our main technical result. Before stating it, we introduce the notion of a pattern being quasi-normal.
Definition 54. The notion of a reflection pattern being quasi-normal is defined recursively: every normal reflection pattern is quasi-normal. Suppose that
-
1. s is a quasi-normal reflection pattern which is not normal, or s is a normal reflection pattern of the form
 $\pi s^{\prime }$
, and
$\pi s^{\prime }$
, and -
2. t is a quasi-normal reflection pattern which is not normal, or t is a normal reflection pattern of the form
 $\pi t^{\prime }$
.
$\pi t^{\prime }$
.
Then
![]() $s \wedge t$
and
$s \wedge t$
and
![]() $\pi t$
are quasi-normal reflection patterns.
$\pi t$
are quasi-normal reflection patterns.
Theorem 55. Let s be a reflection pattern in which the string
![]() $\sigma \sigma $
does not occur. Then, s is equivalent to a quasi-normal reflection pattern.
$\sigma \sigma $
does not occur. Then, s is equivalent to a quasi-normal reflection pattern.
Proof. We shall prove the following claims:
-
1. If s is a normal reflection pattern, then so too is
 $\pi s$
and, if s is of the form
$\pi s$
and, if s is of the form
 $\pi s^{\prime }$
,
$\pi s^{\prime }$
,
 $\sigma s$
is also equivalent to a normal reflection pattern.
$\sigma s$
is also equivalent to a normal reflection pattern. -
2. If s and t are normal reflection patterns, and at least one of them is not of the form
 $\pi v$
, then
$\pi v$
, then
 $s\wedge t$
is equivalent to a normal reflection pattern.
$s\wedge t$
is equivalent to a normal reflection pattern. -
3. If s is a quasi-normal reflection pattern which is not normal, then
 $\sigma s$
and
$\sigma s$
and
 $\sigma \wedge s$
are equivalent to normal reflection patterns, provided the string
$\sigma \wedge s$
are equivalent to normal reflection patterns, provided the string
 $\sigma \sigma $
does not occur in them.
$\sigma \sigma $
does not occur in them.
Let us derive the conclusion of the theorem from (1) (3) by induction on the construction of s. Suppose s is quasi-normal. Then so too is
![]() $\pi s$
by definition. Suppose s is quasi-normal and the string
$\pi s$
by definition. Suppose s is quasi-normal and the string
![]() $\sigma \sigma $
does not occur in
$\sigma \sigma $
does not occur in
![]() $\sigma s$
. If s is not normal, then
$\sigma s$
. If s is not normal, then
![]() $\sigma s$
is normal by (3). Otherwise, if s is normal, then, since
$\sigma s$
is normal by (3). Otherwise, if s is normal, then, since
![]() $\sigma \sigma $
does not occur in s, s must be of the form
$\sigma \sigma $
does not occur in s, s must be of the form
![]() $\pi s^{\prime }$
, and thus
$\pi s^{\prime }$
, and thus
![]() $\sigma s$
is normal by (1). Lastly, suppose that s and t are quasi-normal reflection patterns. If none of them is normal, then
$\sigma s$
is normal by (1). Lastly, suppose that s and t are quasi-normal reflection patterns. If none of them is normal, then
![]() $s\wedge t$
is quasi-normal by definition. Otherwise, say t is normal and s is not. If t is of the form
$s\wedge t$
is quasi-normal by definition. Otherwise, say t is normal and s is not. If t is of the form
![]() $\pi t^{\prime }$
, then
$\pi t^{\prime }$
, then
![]() $s\wedge t$
is quasi-normal by definition. Otherwise,
$s\wedge t$
is quasi-normal by definition. Otherwise,
![]() $t \equiv \sigma \wedge t$
, so that
$t \equiv \sigma \wedge t$
, so that
![]() $\sigma \wedge s$
is normal by (3) and thus
$\sigma \wedge s$
is normal by (3) and thus
![]() $s\wedge t$
is normal by (2). Finally, if both s and t are normal, then either they are both of the form
$s\wedge t$
is normal by (2). Finally, if both s and t are normal, then either they are both of the form
![]() $\pi u$
, so that
$\pi u$
, so that
![]() $s\wedge t$
is quasi-normal by definition, or
$s\wedge t$
is quasi-normal by definition, or
![]() $s\wedge t\equiv \sigma \wedge s\wedge t$
is normal by (2).
$s\wedge t\equiv \sigma \wedge s\wedge t$
is normal by (2).
We begin with the proof of (1). Clearly, if s is equivalent to a normal reflection pattern, then so too is
![]() $\pi s$
. We only need to consider the string
$\pi s$
. We only need to consider the string
![]() $\sigma s$
in the case that s is of the form
$\sigma s$
in the case that s is of the form
 $$ \begin{align*}\pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}},\end{align*} $$
$$ \begin{align*}\pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}},\end{align*} $$
where m is nonzero. Then, it is easy to see that
 $$ \begin{align*} \sigma\pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}} &\equiv \sigma\pi c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}\\ &\equiv c^{0}_{m_{0}+1}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}. \end{align*} $$
$$ \begin{align*} \sigma\pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}} &\equiv \sigma\pi c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}\\ &\equiv c^{0}_{m_{0}+1}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}. \end{align*} $$
This proves (1).
To prove (2), let
 $$ \begin{align*}s = \pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}\end{align*} $$
$$ \begin{align*}s = \pi^{m}c^{0}_{m_{0}}c^{1}_{m_{1}}\dots c^{l}_{m_{l}}\end{align*} $$
be as above, and let
 $$ \begin{align*}t = \pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}.\end{align*} $$
$$ \begin{align*}t = \pi^{n}c^{0}_{n_{0}}c^{1}_{n_{1}}\dots c^{k}_{n_{k}}.\end{align*} $$
We need to show that
![]() $s\wedge t$
is equivalent to a normal reflection pattern. By the case hypothesis, at least one of m and n is zero, so that
$s\wedge t$
is equivalent to a normal reflection pattern. By the case hypothesis, at least one of m and n is zero, so that
Write
![]() $n = n_{-1}$
and
$n = n_{-1}$
and
![]() $m = m_{-1}$
and let i and j be least such that
$m = m_{-1}$
and let i and j be least such that
![]() $n_{i}$
and
$n_{i}$
and
![]() $m_{j}$
are nonzero, respectively. There are four cases to consider. The first one is that in which both i and j are equal to
$m_{j}$
are nonzero, respectively. There are four cases to consider. The first one is that in which both i and j are equal to
![]() $0$
. Then, there are reflection patterns u and v, both normal, such that
$0$
. Then, there are reflection patterns u and v, both normal, such that
and
The conclusion then follows from Lemma 52.
We now consider the case that both i and j are nonzero. The remaining cases, in which one of them is
![]() $0$
and the other one is not, are treated similarly, and we leave them to the reader. We need to show that the pattern
$0$
and the other one is not, are treated similarly, and we leave them to the reader. We need to show that the pattern
is normal. It was shown as part of Lemma 53 (see Equation (3)) that if s is normal, then
![]() $\sigma \wedge s$
has the form
$\sigma \wedge s$
has the form
 $$ \begin{align*}\sigma\wedge \pi^{p}\sigma\pi c^{p}_{m_{p}-1}\dots c^{l}_{m_{l}},\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi^{p}\sigma\pi c^{p}_{m_{p}-1}\dots c^{l}_{m_{l}},\end{align*} $$
for some suitably chosen
![]() $p\in \mathbb {N}$
. Similarly,
$p\in \mathbb {N}$
. Similarly,
![]() $\sigma \wedge t$
has the form
$\sigma \wedge t$
has the form
 $$ \begin{align*}\sigma\wedge \pi^{q}\sigma\pi c^{q}_{n_{q}-1}\dots c^{k}_{n_{k}},\end{align*} $$
$$ \begin{align*}\sigma\wedge \pi^{q}\sigma\pi c^{q}_{n_{q}-1}\dots c^{k}_{n_{k}},\end{align*} $$
for some suitably chosen
![]() $q\in \mathbb {N}$
. Put
$q\in \mathbb {N}$
. Put
 $u = c^{p}_{m_{p}-1}\dots c^{l}_{m_{l}}$
and
$u = c^{p}_{m_{p}-1}\dots c^{l}_{m_{l}}$
and
 $v = c^{q}_{n_{q}-1}\dots c^{k}_{n_{k}}$
, so
$v = c^{q}_{n_{q}-1}\dots c^{k}_{n_{k}}$
, so
and
By Lemma 52 one of u and v, say w, has the property that
Let
![]() $r = \max \{p,q\}$
.⊣
$r = \max \{p,q\}$
.⊣
Claim 56.
![]() $\sigma \wedge \pi ^{r} \sigma \pi w \equiv s\wedge t$
.
$\sigma \wedge \pi ^{r} \sigma \pi w \equiv s\wedge t$
.
Proof. We have to show that
By direct computation, using the usual tools:
 $$ \begin{align*} \sigma \wedge \pi^{r} \sigma\pi w &\equiv \sigma \pi^{r} \sigma\pi w \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma \pi \sigma\pi w \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma\pi w \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma(\pi u \wedge \pi v) \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma \wedge \pi^{r} (\sigma\pi w\wedge \sigma(\pi u \wedge \pi v))\\ &\equiv \sigma \wedge \pi^{r} \sigma\pi w\wedge \pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v. \end{align*} $$
$$ \begin{align*} \sigma \wedge \pi^{r} \sigma\pi w &\equiv \sigma \pi^{r} \sigma\pi w \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma \pi \sigma\pi w \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma\pi w \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma(\pi u \wedge \pi v) \wedge \pi^{r} \sigma\pi w\\ &\equiv \sigma \wedge \pi^{r} (\sigma\pi w\wedge \sigma(\pi u \wedge \pi v))\\ &\equiv \sigma \wedge \pi^{r} \sigma\pi w\wedge \pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v. \end{align*} $$
Since w is either u or v, we have
Now, on the one hand,
![]() $r = \max \{p,q\}$
and this implies that
$r = \max \{p,q\}$
and this implies that
On the other hand,
 $$ \begin{align*} \sigma \wedge \pi^{p} \sigma \pi u \wedge \pi^{q}\sigma \pi v &\to \sigma (\pi^{p} \sigma \pi u \wedge \pi^{q}\sigma \pi v)\\ &\to \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v), \end{align*} $$
$$ \begin{align*} \sigma \wedge \pi^{p} \sigma \pi u \wedge \pi^{q}\sigma \pi v &\to \sigma (\pi^{p} \sigma \pi u \wedge \pi^{q}\sigma \pi v)\\ &\to \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v), \end{align*} $$
where the last implication follows by Theorem 29. Since r is one of p and q, we have
With one last computation, we obtain:
 $$ \begin{align*} \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v) \wedge \pi^{r} &\to \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v) \wedge \pi^{r} \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v)\\ &\to \sigma \wedge \pi^{r} \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v)\\ &\to \sigma \wedge \pi^{r} \sigma \pi^{r} \sigma \pi u \wedge \pi^{r} \sigma \pi^{r}\sigma \pi v\\ &\to \sigma \wedge \pi^{r} \sigma \pi u \wedge \pi^{r} \sigma \pi v\\ &\to \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v) \wedge \pi^{r}, \end{align*} $$
$$ \begin{align*} \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v) \wedge \pi^{r} &\to \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v) \wedge \pi^{r} \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v)\\ &\to \sigma \wedge \pi^{r} \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v)\\ &\to \sigma \wedge \pi^{r} \sigma \pi^{r} \sigma \pi u \wedge \pi^{r} \sigma \pi^{r}\sigma \pi v\\ &\to \sigma \wedge \pi^{r} \sigma \pi u \wedge \pi^{r} \sigma \pi v\\ &\to \sigma (\pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v) \wedge \pi^{r}, \end{align*} $$
so that
We have shown that
 $$ \begin{align*} \sigma\wedge \pi^{r} \sigma \pi w &\equiv \sigma \wedge \pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v\\ &\equiv \sigma \wedge \pi^{p} \sigma \pi u \wedge \pi^{q}\sigma \pi v, \end{align*} $$
$$ \begin{align*} \sigma\wedge \pi^{r} \sigma \pi w &\equiv \sigma \wedge \pi^{r} \sigma \pi u \wedge \pi^{r}\sigma \pi v\\ &\equiv \sigma \wedge \pi^{p} \sigma \pi u \wedge \pi^{q}\sigma \pi v, \end{align*} $$
as had been claimed. ⊣
Since w is a normal reflection pattern by assumption, Lemma 53 implies that
![]() $\sigma \wedge \pi ^{r}\sigma \pi w$
is equivalent to a normal reflection pattern. This proves (2).
$\sigma \wedge \pi ^{r}\sigma \pi w$
is equivalent to a normal reflection pattern. This proves (2).
It remains to prove claim (3). Let s be a quasi-normal reflection pattern which is not normal. We prove that
![]() $\sigma \wedge s$
is equivalent to a normal reflection pattern by induction on the construction on s. Suppose that
$\sigma \wedge s$
is equivalent to a normal reflection pattern by induction on the construction on s. Suppose that
![]() $s = \pi t$
and
$s = \pi t$
and
![]() $\sigma \wedge t$
is equivalent to a normal reflection pattern. Since
$\sigma \wedge t$
is equivalent to a normal reflection pattern. Since
and
![]() $\sigma \wedge t$
is equivalent to a normal reflection pattern,
$\sigma \wedge t$
is equivalent to a normal reflection pattern,
![]() $\pi (\sigma \wedge s)$
is too, so the result follows from (2). Suppose that
$\pi (\sigma \wedge s)$
is too, so the result follows from (2). Suppose that
![]() $s = t_{0} \wedge t_{1}$
, and that
$s = t_{0} \wedge t_{1}$
, and that
![]() $\sigma \wedge t_{0}$
and
$\sigma \wedge t_{0}$
and
![]() $\sigma \wedge t_{1}$
are equivalent to normal reflection pattern. Then
$\sigma \wedge t_{1}$
are equivalent to normal reflection pattern. Then
so the result follows again from (2).
The proof that
![]() $\sigma s$
is equivalent to a normal reflection pattern is not quite by induction, but it is similar. By the definition of “quasi-normal,” s is of the form
$\sigma s$
is equivalent to a normal reflection pattern is not quite by induction, but it is similar. By the definition of “quasi-normal,” s is of the form
for some k (possibly zero) and some
![]() $s_{0}$
,
$s_{0}$
,
![]() $s_{1}$
,
$s_{1}$
,
![]() $\ldots , s_{n}$
, each of which is either normal or quasi-normal but not normal. We may assume without loss of generality that none of the
$\ldots , s_{n}$
, each of which is either normal or quasi-normal but not normal. We may assume without loss of generality that none of the
![]() $s_{i}$
is a conjunction (otherwise we could have split it into
$s_{i}$
is a conjunction (otherwise we could have split it into
![]() $s_{i}^{0}$
and
$s_{i}^{0}$
and
![]() $s_{i}^{1}$
). None of the
$s_{i}^{1}$
). None of the
![]() $s_{i}$
can be of the form
$s_{i}$
can be of the form
![]() $\sigma s_{i}^{\prime }$
, because the definition of “quasi-normal pattern,” does not allow taking conjunctions of patterns of the form
$\sigma s_{i}^{\prime }$
, because the definition of “quasi-normal pattern,” does not allow taking conjunctions of patterns of the form
![]() $\sigma s^{\prime }$
, so if
$\sigma s^{\prime }$
, so if
![]() $s_{i}$
were of the form
$s_{i}$
were of the form
![]() $\sigma s_{i}^{\prime }$
, then the conjunction
$\sigma s_{i}^{\prime }$
, then the conjunction
would have to be trivial, and thus we would have
contradicting the hypothesis that s is not normal. We conclude that each
![]() $s_{i}$
is necessarily of the form
$s_{i}$
is necessarily of the form
![]() $\pi s_{i}^{\prime }$
.
$\pi s_{i}^{\prime }$
.
With an application of Theorem 29, we see that
 $$ \begin{align*} \sigma(s_{0}\wedge s_{1} \wedge \cdots \wedge s_{n}) &\to \sigma s\\ &\to \sigma(\pi^{k} s_{0}\wedge \pi^{k} s_{1} \wedge \cdots \wedge \pi^{k} s_{n})\\ &\to \sigma(s_{0}\wedge s_{1} \wedge \cdots \wedge s_{n}), \end{align*} $$
$$ \begin{align*} \sigma(s_{0}\wedge s_{1} \wedge \cdots \wedge s_{n}) &\to \sigma s\\ &\to \sigma(\pi^{k} s_{0}\wedge \pi^{k} s_{1} \wedge \cdots \wedge \pi^{k} s_{n})\\ &\to \sigma(s_{0}\wedge s_{1} \wedge \cdots \wedge s_{n}), \end{align*} $$
where the last implication follows from the fact that each
![]() $s_{i}$
is of the form
$s_{i}$
is of the form
![]() $\pi s_{i}^{\prime }$
. Hence,
$\pi s_{i}^{\prime }$
. Hence,
If each
![]() $s_{i}$
is normal, then
$s_{i}$
is normal, then
![]() $\sigma s$
is equivalent to a normal reflection pattern by Lemma 52. Otherwise, say
$\sigma s$
is equivalent to a normal reflection pattern by Lemma 52. Otherwise, say
![]() $s_{i}$
is not normal. Certainly it is quasi-normal, so—by the same argument—it must be of the form
$s_{i}$
is not normal. Certainly it is quasi-normal, so—by the same argument—it must be of the form
![]() $\pi ^{k_{i}}(s_{i}^{0} \wedge s_{i}^{1} \ldots s_{i}^{n_{i}})$
for some
$\pi ^{k_{i}}(s_{i}^{0} \wedge s_{i}^{1} \ldots s_{i}^{n_{i}})$
for some
![]() $k_{i}$
and some patterns
$k_{i}$
and some patterns
 $s_{i}^{0}, s_{i}^{1}, \ldots , s_{i}^{n_{i}}$
, all of the form
$s_{i}^{0}, s_{i}^{1}, \ldots , s_{i}^{n_{i}}$
, all of the form
![]() $\pi s^{\prime }$
. As before, we obtain
$\pi s^{\prime }$
. As before, we obtain
 $$ \begin{align*}\sigma s \equiv \sigma(s_{0}\wedge \cdots \wedge s_{i-1} \wedge s_{i}^{0} \wedge s_{i}^{1} \wedge \cdots \wedge s_{i}^{n_{i}} \wedge s_{i+1} \wedge\cdots \wedge s_{n}).\end{align*} $$
$$ \begin{align*}\sigma s \equiv \sigma(s_{0}\wedge \cdots \wedge s_{i-1} \wedge s_{i}^{0} \wedge s_{i}^{1} \wedge \cdots \wedge s_{i}^{n_{i}} \wedge s_{i+1} \wedge\cdots \wedge s_{n}).\end{align*} $$
Continuing this way, we eventually see that
![]() $\sigma s$
is equivalent to a reflection pattern of the form
$\sigma s$
is equivalent to a reflection pattern of the form
![]() $\sigma (t_{0}\wedge t_{1}\wedge \cdots \wedge t_{n})$
for some n, where each
$\sigma (t_{0}\wedge t_{1}\wedge \cdots \wedge t_{n})$
for some n, where each
![]() $t_{i}$
is a normal reflection pattern of the form
$t_{i}$
is a normal reflection pattern of the form
![]() $\pi t^{\prime }$
, so that the result follows from Lemma 52. This proves (3) and completes the proof of the theorem.
$\pi t^{\prime }$
, so that the result follows from Lemma 52. This proves (3) and completes the proof of the theorem.
With little more work, we can show that quasi-normal patterns which are not normal play no role in computing the rank of a normal pattern in the order of reflection. To do this, we assign ordinals to these patterns:
Definition 57. Recursively, we extend
![]() $o(\cdot )$
to quasi-normal reflection patterns which are not normal.
$o(\cdot )$
to quasi-normal reflection patterns which are not normal.
-
1. Let s and t be normal patterns, both of the form
 $\pi u$
. Then
$\pi u$
. Then
 $o(s\wedge t)$
is defined to be
$o(s\wedge t)$
is defined to be
 $\max \{ o(s), o(t)\}$
.
$\max \{ o(s), o(t)\}$
. -
2. Suppose s is quasi-normal but not normal. Then
 $o(\pi s) = o(s) + 1$
.
$o(\pi s) = o(s) + 1$
. -
3. Suppose t is quasi-normal but not normal and s is quasi-normal and of the form
 $\pi s^{\prime }$
. Then
$\pi s^{\prime }$
. Then
 $o(s \wedge t) = \max \{ o(s), o(t)\}$
.
$o(s \wedge t) = \max \{ o(s), o(t)\}$
.
Lemma 58. Suppose s is a quasi-normal reflection pattern which is not normal. Then,
![]() $o(s)$
is a successor ordinal.
$o(s)$
is a successor ordinal.
Proof. This is immediate from the definition. ⊣
Lemma 59. Suppose s is a quasi-normal reflection pattern and t is a normal reflection pattern such that
![]() $o(s) = o(t)$
. Then, every t-reflecting ordinal is either
$o(s) = o(t)$
. Then, every t-reflecting ordinal is either
![]() $\sigma $
-reflecting or s-reflecting.
$\sigma $
-reflecting or s-reflecting.
Proof. This is proved by induction on the construction of s. If s is a conjunction of two normal reflection patterns, both of the form
![]() $\pi u$
, then the lemma follows from Lemma 51. If s is of the form
$\pi u$
, then the lemma follows from Lemma 51. If s is of the form
![]() $s_{0}\wedge s_{1}$
, where, say,
$s_{0}\wedge s_{1}$
, where, say,
![]() $s_{1}$
is not normal, then
$s_{1}$
is not normal, then
![]() $o(s) = \max \{o(s_{0}),o(s_{1})\}$
. Both
$o(s) = \max \{o(s_{0}),o(s_{1})\}$
. Both
![]() $o(s_{0})$
and
$o(s_{0})$
and
![]() $o(s_{1})$
are successor ordinals, so the normal reflection patterns
$o(s_{1})$
are successor ordinals, so the normal reflection patterns
![]() $t_{0}$
and
$t_{0}$
and
![]() $t_{1}$
such that
$t_{1}$
such that
![]() $o(t_{0}) = o(s_{0})$
and
$o(t_{0}) = o(s_{0})$
and
![]() $o(t_{1}) = o(s_{1})$
are both of the form
$o(t_{1}) = o(s_{1})$
are both of the form
![]() $\pi t^{\prime }$
. Assume without loss of generality that
$\pi t^{\prime }$
. Assume without loss of generality that
![]() $o(s_{0}) < o(s_{1})$
. By Lemma 51, every
$o(s_{0}) < o(s_{1})$
. By Lemma 51, every
![]() $t_{1}$
-reflecting ordinal is either
$t_{1}$
-reflecting ordinal is either
![]() $\sigma $
-reflecting or
$\sigma $
-reflecting or
![]() $t_{0}$
-reflecting. By the induction hypothesis applied to each of
$t_{0}$
-reflecting. By the induction hypothesis applied to each of
![]() $s_{0}$
and
$s_{0}$
and
![]() $s_{1}$
, every
$s_{1}$
, every
![]() $t_{1}$
-reflecting ordinal is either
$t_{1}$
-reflecting ordinal is either
![]() $\sigma $
-reflecting or both
$\sigma $
-reflecting or both
![]() $s_{0}$
-reflecting and
$s_{0}$
-reflecting and
![]() $s_{1}$
-reflecting.
$s_{1}$
-reflecting.
Finally, if s is of the form
![]() $\pi s^{\prime }$
, for some
$\pi s^{\prime }$
, for some
![]() $s^{\prime }$
which is quasi-normal but not normal, then t is of the form
$s^{\prime }$
which is quasi-normal but not normal, then t is of the form
![]() $\pi t^{\prime }$
, for some
$\pi t^{\prime }$
, for some
![]() $t^{\prime }$
. By induction hypothesis, every
$t^{\prime }$
. By induction hypothesis, every
![]() $t^{\prime }$
-reflecting ordinal is either
$t^{\prime }$
-reflecting ordinal is either
![]() $\sigma $
-reflecting or
$\sigma $
-reflecting or
![]() $s^{\prime }$
-reflecting. Suppose
$s^{\prime }$
-reflecting. Suppose
![]() $\alpha $
is t-reflecting but not
$\alpha $
is t-reflecting but not
![]() $\sigma $
-reflecting. There are two cases: if
$\sigma $
-reflecting. There are two cases: if
![]() $\alpha $
is
$\alpha $
is
![]() $\pi $
-reflecting on ordinals which are
$\pi $
-reflecting on ordinals which are
![]() $t^{\prime }$
-reflecting but not
$t^{\prime }$
-reflecting but not
![]() $\sigma $
-reflecting, then
$\sigma $
-reflecting, then
![]() $\alpha $
is
$\alpha $
is
![]() $\pi $
-reflecting on ordinals which are
$\pi $
-reflecting on ordinals which are
![]() $s^{\prime }$
-reflecting, by induction hypothesis, so
$s^{\prime }$
-reflecting, by induction hypothesis, so
![]() $\alpha $
is
$\alpha $
is
![]() $\pi s^{\prime }$
-reflecting.
$\pi s^{\prime }$
-reflecting.
The other case is a bit subtler: suppose
![]() $\alpha $
is
$\alpha $
is
![]() $\pi (\sigma \wedge t^{\prime })$
-reflecting.
$\pi (\sigma \wedge t^{\prime })$
-reflecting.
![]() $s^{\prime }$
is quasi-normal but not normal, so
$s^{\prime }$
is quasi-normal but not normal, so
![]() $o(s^{\prime })$
is a successor ordinal, and thus
$o(s^{\prime })$
is a successor ordinal, and thus
![]() $t^{\prime }$
is of the form
$t^{\prime }$
is of the form
![]() $\pi t^{\prime \prime }$
. It follows that
$\pi t^{\prime \prime }$
. It follows that
![]() $\alpha $
is
$\alpha $
is
![]() $\pi (\sigma t^{\prime } \wedge t^{\prime })$
-reflecting and in particular
$\pi (\sigma t^{\prime } \wedge t^{\prime })$
-reflecting and in particular
![]() $\pi \sigma t^{\prime }$
-reflecting. We claim that
$\pi \sigma t^{\prime }$
-reflecting. We claim that
![]() $\alpha $
is
$\alpha $
is
![]() $\pi $
-reflecting on ordinals which are
$\pi $
-reflecting on ordinals which are
![]() $\sigma $
-reflecting on ordinals which are
$\sigma $
-reflecting on ordinals which are
![]() $t^{\prime }$
-reflecting but not
$t^{\prime }$
-reflecting but not
![]() $\sigma $
-reflecting. To see this, let
$\sigma $
-reflecting. To see this, let
![]() $\phi $
be any
$\phi $
be any
![]() $\Pi ^{1}_{1}$
sentence satisfied by
$\Pi ^{1}_{1}$
sentence satisfied by
![]() $L_{\alpha }$
and find a
$L_{\alpha }$
and find a
![]() $\sigma t^{\prime }$
-reflecting ordinal
$\sigma t^{\prime }$
-reflecting ordinal
![]() $\beta <\alpha $
such that
$\beta <\alpha $
such that
![]() $L_{\beta }$
satisfies
$L_{\beta }$
satisfies
![]() $\phi $
. Now, let
$\phi $
. Now, let
![]() $\psi $
be a
$\psi $
be a
![]() $\Sigma ^{1}_{1}$
sentence satisfied by
$\Sigma ^{1}_{1}$
sentence satisfied by
![]() $L_{\beta }$
. We must find some
$L_{\beta }$
. We must find some
![]() $\gamma <\beta $
which is
$\gamma <\beta $
which is
![]() $t^{\prime }$
-reflecting and not
$t^{\prime }$
-reflecting and not
![]() $\sigma $
-reflecting and such that
$\sigma $
-reflecting and such that
![]() $L_{\gamma }\models \psi $
. By
$L_{\gamma }\models \psi $
. By
![]() $\sigma t^{\prime }$
-reflection, there is some
$\sigma t^{\prime }$
-reflection, there is some
![]() $\gamma _{0}<\beta $
which is
$\gamma _{0}<\beta $
which is
![]() $t^{\prime }$
-reflecting and such that
$t^{\prime }$
-reflecting and such that
![]() $L_{\gamma _{0}}\models \psi $
. If
$L_{\gamma _{0}}\models \psi $
. If
![]() $\gamma _{0}$
is not
$\gamma _{0}$
is not
![]() $\sigma $
-reflecting, then we are done. Otherwise,
$\sigma $
-reflecting, then we are done. Otherwise,
![]() $\gamma _{0}$
is
$\gamma _{0}$
is
![]() $\sigma $
-reflecting and
$\sigma $
-reflecting and
![]() $t^{\prime }$
-reflecting, thus
$t^{\prime }$
-reflecting, thus
![]() $\sigma t^{\prime }$
-reflecting. Hence, there is
$\sigma t^{\prime }$
-reflecting. Hence, there is
![]() $\gamma _{1}<\gamma _{0}$
which is
$\gamma _{1}<\gamma _{0}$
which is
![]() $t^{\prime }$
-reflecting and such that
$t^{\prime }$
-reflecting and such that
![]() $L_{\gamma _{1}}\models \psi $
. Since there cannot be an infinite descending sequence of ordinals, this procedure eventually produces a
$L_{\gamma _{1}}\models \psi $
. Since there cannot be an infinite descending sequence of ordinals, this procedure eventually produces a
![]() $\gamma $
as desired. Thus,
$\gamma $
as desired. Thus,
![]() $\alpha $
is
$\alpha $
is
![]() $\pi $
-reflecting on ordinals which are
$\pi $
-reflecting on ordinals which are
![]() $\sigma $
-reflecting on ordinals which are
$\sigma $
-reflecting on ordinals which are
![]() $s^{\prime }$
-reflecting (by induction hypothesis), i.e.,
$s^{\prime }$
-reflecting (by induction hypothesis), i.e.,
![]() $\alpha $
is
$\alpha $
is
![]() $\pi \sigma s^{\prime }$
-reflecting. Since
$\pi \sigma s^{\prime }$
-reflecting. Since
![]() $\alpha $
is not
$\alpha $
is not
![]() $\sigma $
-reflecting (by assumption), it is
$\sigma $
-reflecting (by assumption), it is
![]() $\pi s^{\prime }$
-reflecting, by Theorem 32, as desired. ⊣
$\pi s^{\prime }$
-reflecting, by Theorem 32, as desired. ⊣
Corollary 60. Suppose s is a quasi-normal reflection pattern and t is a normal reflection pattern such that
![]() $o(s) = o(t)$
. Then, the least s-reflecting ordinal is the least t-reflecting ordinal.
$o(s) = o(t)$
. Then, the least s-reflecting ordinal is the least t-reflecting ordinal.
Proof. Let us assume that s is not normal, for otherwise the result is trivial. That the least t-reflecting ordinal is s-reflecting follows from Lemma 59 and the observation that the least t-reflecting ordinal is not
![]() $\sigma $
-reflecting, by Lemmas 25 and 58. That the least s-reflecting ordinal is t-reflecting is immediate from the definition of
$\sigma $
-reflecting, by Lemmas 25 and 58. That the least s-reflecting ordinal is t-reflecting is immediate from the definition of
![]() $o(s)$
. ⊣
$o(s)$
. ⊣
Theorem 61.
![]() $\sigma \sigma $
has order-type
$\sigma \sigma $
has order-type
![]() $\omega ^{\omega }$
in the order of reflection.
$\omega ^{\omega }$
in the order of reflection.
Proof. If a reflection pattern contains the string
![]() $\sigma \sigma $
, then naturally, it cannot be strictly smaller than
$\sigma \sigma $
, then naturally, it cannot be strictly smaller than
![]() $\sigma \sigma $
. If it does not contain the string
$\sigma \sigma $
. If it does not contain the string
![]() $\sigma \sigma $
, then it is equivalent to a quasi-normal reflection pattern by Theorem 55. By Corollary 60, the least ordinal which reflects according to a quasi-normal reflection pattern is the least ordinal which reflects according to some normal reflection pattern, and these ordinals are all smaller than the least
$\sigma \sigma $
, then it is equivalent to a quasi-normal reflection pattern by Theorem 55. By Corollary 60, the least ordinal which reflects according to a quasi-normal reflection pattern is the least ordinal which reflects according to some normal reflection pattern, and these ordinals are all smaller than the least
![]() $\sigma \sigma $
-reflecting ordinal, by Lemma 50. Thus, the rank of
$\sigma \sigma $
-reflecting ordinal, by Lemma 50. Thus, the rank of
![]() $\sigma \sigma $
in the order of reflection is the order-type of the set of normal reflection patterns. An easy induction using Lemma 48 shows that, for normal reflection patterns u and v,
$\sigma \sigma $
in the order of reflection is the order-type of the set of normal reflection patterns. An easy induction using Lemma 48 shows that, for normal reflection patterns u and v,
![]() $u < v$
if, and only if,
$u < v$
if, and only if,
![]() $o(u) < o(v)$
, so the result follows. ⊣
$o(u) < o(v)$
, so the result follows. ⊣
6 Concluding remarks and questions
The most obvious open problem is that of the length of the order of reflection:
Question 62. What is the length of the order of reflection?
While we do not have an answer, the following proposition, which contrasts with the fact that
![]() $\pi ^{1}_{1}$
is the least ordinal
$\pi ^{1}_{1}$
is the least ordinal
![]() $\alpha $
which is
$\alpha $
which is
![]() $\alpha ^+$
-stable, provides a (non-recursive) upper bound:
$\alpha ^+$
-stable, provides a (non-recursive) upper bound:
Proposition 63. Let s be a reflection pattern and suppose
![]() $\alpha $
is an ordinal such that
$\alpha $
is an ordinal such that
Then,
![]() $\alpha $
is s-reflecting.
$\alpha $
is s-reflecting.
Proof. Since
it follows that
![]() $\alpha $
is
$\alpha $
is
![]() $\pi $
-reflecting. By Gostanian’s theorem [Reference Gostanian8] mentioned in the introduction,
$\pi $
-reflecting. By Gostanian’s theorem [Reference Gostanian8] mentioned in the introduction,
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma $
-reflecting. Inductively, suppose
$\sigma $
-reflecting. Inductively, suppose
![]() $\alpha $
is s-reflecting and let
$\alpha $
is s-reflecting and let
![]() $\psi $
be a
$\psi $
be a
![]() $\Sigma ^{1}_{1}$
sentence such that
$\Sigma ^{1}_{1}$
sentence such that
Choose a
![]() $\Pi _{1}$
sentence
$\Pi _{1}$
sentence
![]() $\psi ^{*}$
such that for all admissible
$\psi ^{*}$
such that for all admissible
![]() $\beta $
containing all relevant parameters,
$\beta $
containing all relevant parameters,
if, and only if,
so that, in particular,
Then, from the point of view of
![]() $L_{\alpha ^++1}$
, there are admissible sets
$L_{\alpha ^++1}$
, there are admissible sets
![]() $L_{\alpha }$
and
$L_{\alpha }$
and
![]() $L_{\alpha ^+}$
such that
$L_{\alpha ^+}$
such that
-
1.
 $\alpha $
is s-reflecting (this is a first-order statement about
$\alpha $
is s-reflecting (this is a first-order statement about
 $L_{\alpha ^+}$
),
$L_{\alpha ^+}$
), -
2.
 $L_{\alpha ^+}\models \psi ^{*}(L_{\alpha })$
.
$L_{\alpha ^+}\models \psi ^{*}(L_{\alpha })$
.
Thus, by stability, there are admissible sets
![]() $L_{\beta }$
and
$L_{\beta }$
and
![]() $L_{\beta ^+}$
in
$L_{\beta ^+}$
in
![]() $L_{\alpha }$
such that
$L_{\alpha }$
such that
![]() $\beta $
is s-reflecting and
$\beta $
is s-reflecting and
 $L_{\beta ^+}\models \psi ^{*}(L_{\beta })$
. Hence,
$L_{\beta ^+}\models \psi ^{*}(L_{\beta })$
. Hence,
![]() $\alpha $
is
$\alpha $
is
![]() $\sigma s$
-reflecting. A similar argument shows that
$\sigma s$
-reflecting. A similar argument shows that
![]() $\alpha $
is
$\alpha $
is
![]() $\pi s$
-reflecting. A simple induction thus shows that
$\pi s$
-reflecting. A simple induction thus shows that
![]() $\alpha $
is s-reflecting for every reflection pattern. ⊣
$\alpha $
is s-reflecting for every reflection pattern. ⊣
The length of the order of reflection is thus at most the least ordinal
![]() $\alpha $
such that
$\alpha $
such that
Moreover, surely each inequality between reflection patterns is provable in any theory that proves the existence of the corresponding ordinals. This suggests strongly that the length of the order of reflection is smaller than the proof-theoretic ordinal of the subsystem
![]() ${\boldsymbol \Pi }^{1}_{2}$
-CA
${\boldsymbol \Pi }^{1}_{2}$
-CA
![]() $_{0}$
of analysis and in fact smaller than the ordinal described in Rathjen [Reference Rathjen10], though we do not have a proof of this.
$_{0}$
of analysis and in fact smaller than the ordinal described in Rathjen [Reference Rathjen10], though we do not have a proof of this.
In regard to lower bounds, the reader may consult [Reference Aguilera4] for an example of a chain of length
![]() $\varepsilon _{0}$
in the order of reflection. The construction in [Reference Aguilera4] uses Theorem 38. The facts that
$\varepsilon _{0}$
in the order of reflection. The construction in [Reference Aguilera4] uses Theorem 38. The facts that
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma ^{2}$
have ranks
$\sigma ^{2}$
have ranks
![]() $\omega $
and
$\omega $
and
![]() $\omega ^{\omega }$
in the order of reflection suggest that perhaps the bound is optimal.
$\omega ^{\omega }$
in the order of reflection suggest that perhaps the bound is optimal.
Question 64. Is the rank of
![]() $\sigma ^{3}$
in the order of reflection
$\sigma ^{3}$
in the order of reflection
![]() $\omega ^{\omega ^{\omega }}$
?
$\omega ^{\omega ^{\omega }}$
?
It was shown in [Reference Aguilera4] that the rank of
![]() $\sigma ^{3}$
is at least
$\sigma ^{3}$
is at least
![]() $\omega ^{\omega ^{\omega }}$
. A related project concerns studying reflection patterns with focus on the implication ordering:
$\omega ^{\omega ^{\omega }}$
. A related project concerns studying reflection patterns with focus on the implication ordering:
Question 65. What is the structure of the set of reflection patterns under the ordering
![]() $\to $
?
$\to $
?
Acknowledgments
We would like to thank David Schrittesser and Lev Beklemishev for fruitful conversations during the 2019 Arctic Set Theory meeting and the 2019 Barcelona Wormshop, respectively. This work was partially supported by FWO grant 3E017319, by FWF-FWO grant I-4513, and by FWF-RSF grant I-4427.