2.1. Non-dimensional parameters and equations

Fluid flow and solute transport in the gap are governed by the incompressible continuity, Navier–Stokes and advection–diffusion equations. These are non-dimensionalized using the gap width $d = r_{2} - r_{1}$ for the characteristic length, $\nu /d$ for the characteristic velocity, $d^2/\nu$ for the characteristic time, $\rho {\nu ^2}/d^2$ for the characteristic pressure and the average concentration $C_{0}$ for the characteristic concentration, where $\rho$ is the fluid density and $\nu$ its kinematic viscosity. Hereinafter, all expressions are non-dimensional, unless otherwise stated. The governing equations may be expressed as

(2.7)\begin{equation} \left. \begin{aligned} & \displaystyle \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{V}={0} ,\\ & \displaystyle \frac{\partial \boldsymbol{V}}{\partial t} +\left(\boldsymbol{V}\boldsymbol{\cdot}\boldsymbol{\nabla}\right)\boldsymbol{V}={-}\boldsymbol{\nabla}{P}+\nabla^2\boldsymbol{V} ,\\ & \displaystyle \frac{\partial {C}}{\partial t}+\boldsymbol{V}\boldsymbol{\cdot}\boldsymbol{\nabla}{C}= \frac{1}{{Sc}}\nabla^2{C} , \end{aligned} \right\} \end{equation}

where ${Sc} = {\nu }/{\mathcal {D}}$ is the Schmidt number. Boundary conditions are now expressed at the non-dimensional inner and outer radii $r_{1}=\eta /(1-\eta )$ and $r_{2}=1/(1-\eta )$, respectively. The boundary conditions for the tangential velocity components can be expressed as

(2.8a,b)\begin{equation} \left. V\right|_{r=r_{1}} = {Ta}, \quad \left.W\right|_{r=r_{1}} = \left.V\right|_{r=r_{2}} = \left.W\right|_{r=r_{2}} = 0, \end{equation}

where ${Ta} = r_{1} \varOmega d/\nu$ is the Taylor number. The boundary conditions for $U$ and $C$ at the cylinder are written as

(2.9a)\begin{equation} \left. \begin{aligned} \displaystyle \left.U\right|_{r=r_{1}}=\sigma \left(P_{{in}}-\left.P\right|_{r=r_{1}}\right)+\chi \left.C\right|_{r=r_{1}},\\ \displaystyle \left. U\right|_{r=r_{2}}={-}\sigma \left(P_{{out}}-\left. P\right|_{r=r_{2}}\right)-\chi \left.C\right|_{r=r_{2}}, \end{aligned} \right\} \end{equation}

(2.9b)\begin{equation} \left[{Sc} \,UC - \frac{\partial C} {\partial r} \right]_{r=r_{1}}= \left[ {Sc} \,UC - \frac{\partial C} {\partial r} \right]_{r=r_{2}}=0. \end{equation}

The semi-permeable nature of the membrane and its permeance $K$ manifest through two independent non-dimensional coefficients in boundary conditions (2.9a): the velocity–pressure coupling coefficient $\sigma = K\rho \nu /d$ and the velocity–concentration coupling coefficient $\chi = {K R T d\,C_{0}}/{\nu }$. Lastly, the averaged transmembrane velocities are expressed in terms of the Reynolds number

(2.10)\begin{equation} {Re} = \frac{r_{1}\left\langle U\right\rangle_{r_{1}}}{\nu} = \frac{r_{2}\left\langle U\right\rangle_{r_{2}}}{\nu}. \end{equation}

Although this set-up is not commonly used in industrial RO or nanofiltration devices, we nonetheless establish the ranges of the non-dimensional parameters that would prevail in a RO Taylor–Couette cell with semi-permeable cylinders and filled with seawater. In typical seawater plate-and-frame RO systems, the transmembrane velocity is of order $10^{-6}\,\textrm {m}\,\textrm {s}^{-1}$ for operating pressure ranging from $5$ to $8$ MPa, with the osmotic pressure being around $3$ MPa. The permeance $K$ of these membranes is of order $10^{-13}$ to $10^{-12}\,\textrm {m}\,\textrm {s}^{-1}\,\textrm {Pa}^{-1}$ (see table 1 in van Wagner et al. Reference van Wagner, Sagle, Sharma and Freeman2009, for examples of commercial RO membranes). Assuming arbitrarily the radii $r_{1}$ and $r_{2}$ are of order $10^{-2}$ to $10^{-1}$ m, and the gap width $d$ is of order $10^{-3}$ to $10^{-2}$ m, produces velocity–pressure coupling coefficients and Reynolds numbers ranging between $10^{-14}<\sigma <10^{-12}$ and $10^{-2}<{Re}<10^{-1}$, respectively. Assuming seawater at $25\,^{\circ }\textrm {C}$, with an average salt concentration $C_0\approx 10^{3}\,\textrm {mol}\,\textrm {m}^{-3}$, produces velocity–concentration coupling coefficients ranging between $10^{-3}<\chi <10^{-1}$. Considering that ${\mathcal {D}}$ for monovalent ions such as Na$^{+}$ and Cl$^{-}$ is of order $10^{-9}\,\textrm {m}^2\,\textrm {s}^{-1}$, the Schmidt number is of order $10^{3}$. Typical transitional Taylor numbers ${Ta}\sim 100$ then correspond to rotation rates $\varOmega$ ranging from $10^{-1}$ to $10\,\textrm {rad}\,\textrm {s}^{-1}$.

2.2. Steady base state

Equations (2.7)–(2.9) admit a steady, axially and azimuthally invariant base state $[\boldsymbol {V}_b(r),\,P_b(r),\,C_b(r)]$, the expression of which is given in Appendix A. These velocity and pressure fields are parameterized by ${Ta}$ and ${Re}$ solely. Positive values of ${Re}$ produce a radial velocity $U_b>0$ flowing outwards, while ${Re}<0$ produces radial velocities $U_b<0$ flowing inwards, as seen in figure 3(a) for ${Re}=-0.1$. By writing the base state in this form, we apply the Reynolds number ${Re}$ directly, and then compute the necessary operating pressure (2.1) from boundary conditions (2.9a),

(2.11)\begin{equation} \Delta P=P_b(r_{1})-P_b(r_{2}) + \frac{\chi}{\sigma}\left[ C_b(r_{2})- C_b(r_{1})\right] + \frac{1}{\sigma}\left[ U_b(r_{2}) + U_b(r_{1})\right]. \end{equation}

Figure 3. (a) Radial velocity of the base state $U_b(r)$ for radius ratio $\eta =0.85$ and radial inflow ${Re}=-0.1$. (b) Concentration field of the base state $C_b(r)$ for radius ratio $\eta =0.85$ a radial inflow with Péclet number ${Pe}={Re}\,{Sc}=-20$ (light grey, green online) and ${Pe}={Re}\,{Sc}=-100$ (dark grey, blue online). The vertical dashed (blue online) line materializes the polarization layer thickness $\delta$ as computed from (2.15) for ${Pe}=-100$.

To further interpret the concentration boundary layer, the base state $C_b$ in (A4) can be re-expressed in terms of the radius ratio $\eta =r_{1}/r_{2}$ and the Péclet number associated with the radial transmembrane flow ${Pe}={Re}\,{Sc}$

(2.12)\begin{equation} C_b(r)=\frac{{Pe}+2}{2}\frac{1-\eta^2}{1-\eta^{{Pe}+2}}\left(1-\eta\right)^{{Pe}}r^{{Pe}}\quad\text{for}\ {Pe}\neq{-}2. \end{equation}

Figure 3(b) shows two examples of $C_b$ when $\eta =0.85$ with Péclet numbers ${Pe}=-20$ (light grey, green online) and ${Pe}=-100$ (dark grey, blue online). As ${Pe}$ increases in absolute value, whether by increasing the Reynolds or the Schmidt numbers, the solute accumulates in an increasingly thin boundary layer near the inner membrane. Simultaneously, pure solvent entering through the outer cylinder depletes the solute concentration outside the polarization layer. To characterize the base-state polarization layer, we first compute the maximum concentration $C_{b,{max}}$ (shown as dots in figure 3), which occurs on the membrane surface. We then define the polarization layer thickness $\delta$ as the radial distance from the membrane where the concentration is $0.05C_{b,{max}}$. Depending on the direction of the radial flow, $C_{b,{max}}$ is obtained from (2.12) as

(2.13)\begin{equation} C_{b,{max}} = \left\{ \begin{array}{@{}ll} \displaystyle C_b(r_{1}) = \dfrac{-({Pe}+2)}{2} \, \dfrac{1-\eta^{2}}{1-\eta^{-({Pe} + 2)}}\dfrac{1}{\eta^2}, & \text{for} \ {Pe} < 0,\\ \displaystyle C_b(r_{2}) = \dfrac{{Pe}+2}{2} \, \dfrac{1 - \eta^{2}}{1-\eta^{{Pe} + 2}}, & \text{for} \ {Pe} > 0, \end{array} \right. \end{equation}

and, combined with (2.12), leads to

(2.14)\begin{equation} \delta = \left\{ \begin{array}{@{}ll} \displaystyle(0.05^{1/{Pe}}-1)\dfrac{\eta}{1-\eta}, & \text{for} \ {Pe} < 0,\\ \displaystyle(1-0.05^{1/{Pe}})\dfrac{1}{1-\eta}, & \text{for} \ {Pe} > 0. \end{array}\right. \end{equation}

For large Péclet numbers (in absolute value), the boundary layer thickness can be approximated by

(2.15)\begin{equation} \delta\approx \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{\log(20)}{-{Pe}}\dfrac{\eta}{1-\eta}, & \text{for} \ {Pe} < 0,\\ \displaystyle \dfrac{\log(20)}{{Pe}}\dfrac{1}{1-\eta}, & \text{for} \ {Pe} > 0, \end{array} \right. \end{equation}

and is inversely proportional to the Péclet number. Figure 4 shows $C_{b,{max}}$ and $\delta$ as functions of the radius ratio $\eta$ and Péclet number ${Pe}$, where ${Pe}<0$ represents radial inflow and ${Pe}>0$ represents radial outflow. Maximum non-dimensional concentrations beyond $10^3$ are not depicted, because these would likely trigger solute precipitation and call the governing equations into question. Non-dimensional boundary layer thicknesses above $1$ are not shown because this would correspond to layers larger than the gap. For $\delta >1$, one can assume that no boundary layer forms. As expected, increasing the magnitude of the Péclet number reduces the boundary layer thickness $\delta$ and increases the maximum concentration $C_{b,{max}}$. Decreasing the radius ratio $\eta$, by reducing the radii $r_{1}$ and $r_{2}$, increases the magnitude of the velocities $U_b(r_{1})$ and $U_b(r_{2})$ for a prescribed Péclet number. It thus reduces the boundary layer thickness $\delta$ and increases the maximum concentration $C_{b,{max}}$. Note that for a given Péclet number, the magnitude of the radial velocity through the inner cylinder always exceeds that through the outer, because $U_b(r_{1}) = U_b(r_{2})/\eta$. Consequently, in figure 4(a), the solute concentration on the inner cylinder is greater than that on the outer cylinder. Accordingly, in figure 4(b), the boundary layer at the inner cylinder is thinner than that on the outer cylinder.

Figure 4. (a) Maximum of the concentration field $C_{b,{max}}$ (in log scale) as a function of the radius ratio $\eta$ and Péclet number ${Pe}={Re}\,{Sc}$ (in log scale). (b) Boundary layer thickness $\delta$ (in log scale) as a function of the radius ratio $\eta$ and Péclet number ${Pe}={Re}\,{Sc}$ (in log scale). Note the uncommon ${Pe}$-axis merging negative and positive values of this parameter to account for radial in- and outflows, and the resulting discontinuities of the surfaces. Note also the reversed $\eta$-axes in both figures.

The base state ((A1a,b)–(A4)) does not present any dependence on the velocity– concentration coupling coefficient $\chi$ and velocity–pressure coupling coefficient $\sigma$, as these parameters only affect the operating pressure (2.11). This operating pressure is of major practical importance because it imposes the non-dimensional power per unit axial length needed to drive the fluid across the Taylor–Couette cell: ${\mathcal {P}}=2{\rm \pi} {Re}\Delta P$. The impact of system design and operating conditions on $\Delta P$ can be understood by investigating each term in expression (2.11), repeated below for convenience

(2.16)\begin{equation} \Delta P=P_b(r_{1})-P_b(r_{2}) + \frac{\chi}{\sigma}[ C_b(r_{2})- C_b(r_{1})] + \frac{1}{\sigma}[ U_b(r_{2}) + U_b(r_{1})]. \end{equation}

The first term $P_b(r_{1})-P_b(r_{2})$ is due to hydrodynamics and combines a contribution due to the curvature of the azimuthal flow, scaling with ${Ta}^2$, and a contribution due to the radial flow, scaling with ${Re}^2$, both up to multiplicative functions of $\eta$. The next term

(2.17)\begin{equation} \frac{\chi}{\sigma}\left[C_b(r_{2})-C_b(r_{1})\right]=\frac{\chi\left({Pe}+2\right)}{2\sigma}\frac{1-\eta^2}{1-\eta^{{Pe}+2}}(1-\eta^{{Pe}}), \end{equation}

is due to the osmotic pressure. For large Péclet numbers (in absolute value), it mostly scales with $\chi {Pe}\,\sigma ^{-1}=\chi {Re}\,{Sc}\,\sigma ^{-1}$, up to a multiplicative function of $\eta$. The last term

(2.18)\begin{equation} \frac{1}{\sigma}\left[U_b(r_{2})+U_b(r_{1})\right]=\frac{{Re}}{\sigma}\frac{1-\eta^2}{\eta}, \end{equation}

is due to the transmembrane flow of solvent and scales with ${Re}\,\sigma ^{-1}$, up to a multiplicative function of $\eta$. Typical membrane filtration conditions present very small $\sigma$, such that the hydrodynamic term in the operating pressure (2.11) is negligible compared with the two next terms, i.e. the operating pressure is mostly imposed by the membrane permeance and osmotic pressure. Neglecting the hydrodynamic terms leads to the approximation

(2.19)\begin{equation} \frac{\sigma\Delta P}{{Re}}\approx\frac{1-\eta^2}{\eta}\left(1+\frac{\chi\, {Sc}\left({Pe}+2\right)}{2{Pe}}\eta\frac{1-\eta^{{Pe}}}{1-\eta^{{Pe}+2}}\right), \end{equation}

depicted in figure 5 for narrow ($\eta =0.85$) and wide ($\eta =0.25$) gaps. For narrow gaps, this operating pressure is almost independent of the Péclet number. For wide gaps, the operating pressure becomes substantially stronger for inflows than for outflows, due to the strong discrepancy between the transmembrane velocities at the inner and outer cylinders.

Figure 5. Reduced operating pressure $\sigma \Delta P/{Re}$ as a function of $\chi \,{Sc}$ and ${Pe}={Re}\,{Sc}$, for (a) $\eta =0.85$ and (b) $\eta =0.25$. All quantities are in log scale and note the uncommon ${Pe}$-axis merging positive and negative values of this parameter to account for out- and inflows and the resulting discontinuities of the surfaces.

3.1. Linear stability analysis

The stability analysis decomposes the flow fields into the sum of the base state $[\boldsymbol {V}_{b},\,{P}_{b},\,{C}_{b}]$ and small perturbations $[\boldsymbol {V}_{p}(\boldsymbol {x},t),\,{P}_{p}(\boldsymbol {x},t),\,{C}_{p}(\boldsymbol {x},t)]$. Linearizing equations (2.7) about the base state produces the following evolution equations for the small perturbation,

(3.1)\begin{equation} \left. \begin{aligned} & \displaystyle \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{V}_{p}={0}\, ,\\ & \displaystyle \frac{\partial \boldsymbol{V}_{p}}{\partial t}+\boldsymbol{V}_{b}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{V}_{p} + \boldsymbol{V}_{p}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{V}_{b} ={-}\boldsymbol{\nabla}{P_{p}}+\nabla^2\boldsymbol{V}_{p} ,\\ & \displaystyle \frac{\partial {C_{p}}}{\partial t}+\,\boldsymbol{V}_{b}\boldsymbol{\cdot}\boldsymbol{\nabla}{C_{p}} +\boldsymbol{V}_{p}\boldsymbol{\cdot}\boldsymbol{\nabla}{C_{b}}= \frac{1}{{Sc}}\nabla^2{C_{p}}. \end{aligned} \right\} \end{equation}

The linearization of boundary conditions (2.9) produces

(3.2a)\begin{equation} \left.V_{p}\right|_{r=r_{i}} = \left.W_{p}\right|_{r=r_{i}} = 0, \end{equation}

(3.2b)\begin{equation} \displaystyle\left. U_{p}\right|_{r=r_{i}}={\mp} \left[\sigma P_{p}-\chi C_{p}\right]_{r=r_{i}}, \end{equation}

(3.2c)\begin{equation} \left[ U_{p} C_{b} + U_{b} C_{p} -\frac{1}{{Sc}}\frac{\partial C_{p}} {\partial r} \right]_{r=r_i}= 0, \end{equation}

where $r_i=r_{1}$ or $r_{2}$, and the negative (positive) sign in condition (3.2b) is used when $r=r_{1}$ ($r=r_{2}$). Note that the terms $U_pC_b$ and $U_bC_p$ in the no-flux condition (3.2c) arise from the linearization of the solute advection term $UC$ in condition (2.5).

Our stability analysis considers perturbations of the form

(3.3)\begin{equation} \left[\boldsymbol{V}_{p}(\boldsymbol{x},t),\,{P}_{p}(\boldsymbol{x},t),\,{C}_{p}(\boldsymbol{x},t)\right] = [\boldsymbol{v}_{p}(r),\,p_{p}(r),\,c_{p}(r)] \exp (\mathrm{i} k z + \mathrm{i} n \theta + st), \end{equation}

where $k$ and $n$ are the axial and azimuthal wavenumbers, respectively, $s$ is the growth rate and $[\boldsymbol {v}_{p}(r),\,p_{p}(r),\,c_{p}(r)]$ are radial profiles, describing the variation of the perturbation structures in the radial direction. Substituting form (3.3) into the linearized equations (3.1)–(3.2) produces a generalized eigenvalue problem

(3.4)\begin{equation} {\mathcal{A}}[\boldsymbol{v}_{p},\,p_{p},\,c_{p}] ={-} s {\mathcal{B}} [\boldsymbol{v}_{p},\,p_{p},\,c_{p}], \end{equation}

for which $s$ and $[\boldsymbol {v}_{p},\,p_{p},\,c_{p}]$ are the eigenvalues and eigenvectors, respectively. The differential operators ${\mathcal {A}}$ and ${\mathcal {B}}$ are given in Appendix B. The radial profiles satisfy the boundary conditions

(3.5a)\begin{equation} v_{p}(r_{i}) =w_{p}(r_{i}) = 0, \end{equation}

(3.5b)\begin{equation} u_{p}(r_{i})={\mp} \left[\sigma p_{p}\left(r_{i}\right) - \chi c_{p}\left(r_{i}\right)\right], \end{equation}

(3.5c)\begin{equation} u_{p}(r_{i}) C_{b}(r_{i}) + U_{b}(r_{i}) c_{p}(r_{i}) - \frac{1}{{Sc}}\frac{d c_{p}} {d r}(r_{i}) = 0, \end{equation}

where, again, $r_i=r_{1}$ or $r_{2}$, and the negative sign in condition (3.5b) is used when $r=r_{1}$.

The eigenvalue problem is solved using a standard spectral collocation method with a typical resolution of $72$ Chebyshev polynomials in the radial direction. Newton–Raphson methods previously explained in Martinand, Serre & Lueptow (Reference Martinand, Serre and Lueptow2009) are used to determine the critical conditions of the most unstable mode. This yields the critical Taylor number $Ta^{{crit}}$ above which the real part of a first eigenvalue $s$, associated with the eigenmode $[\boldsymbol {v}_{p}^{{crit}},\,p_{p}^{{crit}},\,c_{p}^{{crit}}]$ with axial wavenumber $k^{{crit}}$ and azimuthal wavenumber $n^{{crit}}$, becomes positive.

3.2. Direct numerical simulations

We perform axisymmetric direct numerical simulations (DNS) of (2.7)–(2.9) using an in-house pseudo-spectral code previously detailed in Tilton et al. (Reference Tilton, Serre, Martinand and Lueptow2014). The code has been successfully used to simulate tubular membrane filtration systems (Tilton et al. Reference Tilton, Martinand, Serre and Lueptow2012), and steady (Tilton et al. Reference Tilton, Martinand, Serre and Lueptow2010) and unsteady (Tilton & Martinand Reference Tilton and Martinand2018) flows in Taylor–Couette–Poiseuille cells with permeable inner cylinders and pure solvent, and has been modified to include the resolution of the scalar equation and boundary conditions (2.9). The code discretizes the radial and axial directions using Chebyshev polynomials, and uses a second-order semi-implicit temporal scheme suggested by Vanel, Peyret & Bontoux (Reference Vanel, Peyret and Bontoux1986). The pressure solver is based on the projection method introduced in Raspo et al. (Reference Raspo, Hughes, Serre, Randriamampianina and Bontoux2002) and extended in Tilton et al. (Reference Tilton, Serre, Martinand and Lueptow2014) to satisfy the velocity–pressure and velocity–concentration couplings on the semi-permeable membranes. We simulate a domain of non-dimensional axial length $L=20$ with $36$ and $148$ collocation points in the radial and axial directions, respectively. Spatial convergence is confirmed by monitoring the Chebyshev expansion coefficients. The base flow $\boldsymbol {V}_b(r)$ in Appendix A is imposed at both axial ends of the domain, so that no net axial flow exists and the conservation of the total radial flux (2.10) is satisfied. Moreover, the concentration field satisfies vanishing Neumann boundary conditions at those two axial ends, so that the average concentration in the domain is conserved. The initial conditions are composed of a small disturbance added to the analytical base state ((A1a,b)–(A4)). To reduce the simulation time, the initial disturbance takes the form of the analytically computed marginal mode $[\boldsymbol {V}_{p}^{{crit}},\,P_{p}^{{crit}},\,C_{p}^{{crit}}]$ with an arbitrarily small amplitude. This was implemented after first verifying that disturbances in this form or in the form of white noise on the axial velocity led to the same final flow. For the supercritical Taylor numbers considered, we found that perturbation growth eventually saturated such that all simulations settled to steady states.

4.1. Numerical and analytical results at $\eta =0.85$, ${Pe}=100$ and $\chi =10^{-3}$

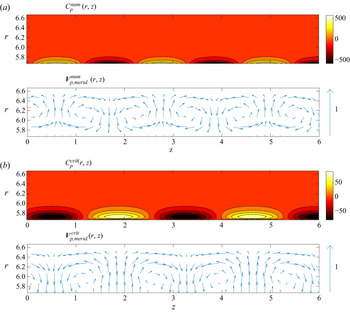
Figure 6 shows the steady radial velocity $U(r,z)$ and concentration field $C(r,z)$ obtained by DNS for a radial inflow of ${Re}=-0.1$, velocity–pressure coupling coefficient $\sigma =10^{-10}$, Schmidt number ${Sc}=1000$ and velocity–concentration coupling coefficient $\chi = 10^{-3}$, in a narrow-gap cell with $\eta =0.85$ at ${Ta}=90$. A full analysis of the numerical flow fields $[\boldsymbol {V}^{{num}},\, P^{{num}},\,C^{{num}}]$ shows that these fields are composed of the base state and a perturbation in the form of toroidal counter-rotating vortices with an axial wavelength $\lambda \approx 2.5$. These vortices present a non-zero radial velocity at the inner cylinder. The order of magnitude of this transmembrane velocity is comparable to the order of magnitude of the radial velocity of the vortices observed in the bulk of the flow. Together with these vortices, the concentration field exhibits substantial fluctuations with the same aforementioned axial wavelength. These fluctuations are mostly observed within the polarization layer, whose width $\delta =0.171$ is computed from (2.15), and located between the inner cylinder and the superimposed dashed curve in figure 6(b). A similar DNS at Taylor number ${Ta}=78$ (not shown here) retrieved the base state, free of any vortex. For this set of parameters ($\eta =0.85$, ${Re}=-0.1$, $\sigma =10^{-10}$, $\chi = 10^{-3}$), the linear stability analysis predicts ${Ta}^{{crit}}=79.1$ and $\lambda ^{{crit}}=2.26$, in good agreement with the DNS. The non-zero critical Taylor number means that the centrifugal force remains the necessary ingredient to the development of the vortices. If we remove osmotic pressure effects by setting $\chi =0$ (by assuming, for instance, that the reference physical concentration $C_0$ tends to $0$), the stability analysis predicts for Taylor vortices slightly modified by the radial inflow ${Ta}^{{crit}}=106.9$ and $\lambda ^{{crit}}=2.04$: the presence of osmotic pressure dramatically decreases the critical Taylor number, together with increasing the wavelength of the vortices.

Figure 6. (a) Radial velocity field $U^{{num}}$ and (b) concentration field $C^{{num}}$ as functions of $r$ and $z$, obtained by DNS for $\eta =0.85$, ${Re}=-0.1$, $\sigma =10^{-10}$, ${Sc}=1000$ and $\chi = 10^{-3}$, at ${Ta}=90$. The black superimposed curves highlight the fluctuations of radial velocity and concentration at the membrane. The dark grey (blue online) frames on both surfaces are a reminder of the base state $U_b$ and $C_b$ and the dark grey (blue online) dashed curve superimposed on the concentration field bounds the polarization layer, the thickness of which $\delta$ is given by (2.15). Note that for the sake of clarity, the $r$-axis has been reversed between both surfaces.

To compare the numerical and analytical results for the perturbation velocity and concentration, the DNS hereinafter is performed closer to critical conditions at ${Ta}=80$, and considered at a time before the steady state, shown in figure 6, is reached, so that the growth of the instability is still in its linear dynamic. Figure 7 first shows the velocity and concentration fields of the perturbation in a meridional plane, in the form of the numerical velocity and concentration fields, $(U^{{num}}_p(r,z),W^{{num}}_p(r,z))$ and $C_p^{{num}}(r,z)$, obtained by removing the base state $[\boldsymbol {V}_b,\, P_b,\,C_b]$ from the complete DNS fields $[\boldsymbol {V}^{{num}},\, P^{{num}},\,C^{{num}}]$ (panel a), together with the analytical fields, $(U^{{crit}}_p(r,z),W^{{crit}}_p(r,z))$ and $C_p^{{crit}}(r,z)$ (panel b). The focus being on the linear dynamic of the instabilities, the amplitudes of the perturbations are reset so that the maxima of the analytical and numerical azimuthal velocity components are both normalized to $1$.

Figure 7. Velocity fields of the vortices $\boldsymbol {V}_{p,{merid{.}}}=(U_{p},W_{p})$ and concentration perturbation $C_{p}$ in a meridional plane $(r,z)$, for $\eta =0.85$, ${Re}=-0.1$, ${Sc}=1000$, $\sigma =10^{-10}$ and $\chi =10^{-3}$, obtained numerically at ${Ta}=80$ (a) and analytically at critical conditions ${Ta}^{{crit}}=78.4$ (b). Corresponding radial profiles of the radial (c), azimuthal (d) and axial (e) components of the velocity and concentration ( f) perturbations, obtained by linear stability analysis (light grey, green online, solid curves) and DNS (dark grey, blue online, dashed curves).

The numerical and analytical fields compare favourably and further ascertain the validity of both approaches. Figure 7 also sheds light on the coupling between the vortices, concentration boundary layer, and osmotic pressure. The non-zero boundary condition at the inner cylinder for the radial velocity of the perturbation is obvious, and extra extraction of fluid at the inner cylinder (related to the perturbation, in addition to the radial mean flow) is found to coincide with the inward jets of the vortices in the bulk. Symmetrically, extra injection of fluid at the inner cylinder is found to coincide with the outward jets of the vortices in the bulk. Moreover, it can be seen that injections/outward jets occur at the axial locations where the perturbation develops an excess of solute, whereas extractions/inward jets occur at the axial locations where the perturbation depletes the solute. From these observations, a mechanism by which osmotic pressure retroacts on the vortices can be proposed. The regions of excess of solute act via osmotic pressure to add extra injection of pure solvent in the bulk through the inner cylinder, thus reinforcing the outward jets of the vortices. Similarly, regions of depleted solute add extra extraction of pure solvent from the bulk, thus reinforcing the inward jets of the vortices. As far as the perturbation $[\boldsymbol {V}_p,\, P_p,\,C_p]$ is concerned, vortices and osmosis are found to work in a cooperative fashion, and osmotic pressure hence reduces the critical conditions for centrifugal instabilities. Moreover, owing to the non-zero boundary condition for the radial velocity, the vortices ‘penetrate’ into the inner cylinder, and the increased perceived radial characteristic size of a vortex induces an increased axial one to conserve a ‘round’ cross-section, explaining the observed increase of the axial wavelength.

A finer comparison between our numerical and analytical results is obtained by assessing the radial profiles of the perturbation structures. The solid curves (green online) in figure 7(c–f) shows the analytical results for the critical eigenmode $[\boldsymbol {v}_p^{{crit}},\,c_p^{{crit}}]$. The dashed curves (blue online) show the corresponding DNS results for $[\boldsymbol {V}^{{num}}-\boldsymbol {V}_b,\,C^{{num}}-C_b]$, at ${Ta}=80$ and the axial location $z_{{outward}}$ of an outward jet (and between two neighbouring outward and inward jets for the axial component $w_p(r)$). Beyond the nearly identical radial profiles, the membrane boundary conditions (3.2b) and (3.2c) are accurately captured by both the DNS and linear analysis, but a minute discrepancy, that could not be explained so far, is observed between the two approaches.

4.2. Parametric study by linear stability analysis

The case shown in § 4.1 demonstrates that transmembrane flow, concentration polarization and osmotic pressure can substantially decrease the critical Taylor number for the appearance of vortices. The next question is to evaluate whether these phenomena always favour the development of the centrifugal instabilities, and to what extent they impact the critical Taylor number. For that purpose, we use the analytic approach presented in § 3.1 to perform a parametric study considering wide to narrow-gap cases with radius ratios varying in the range $0.25\le \eta \le 0.95$, radial Reynolds numbers varying in the range $-1\le {Re}\le 1$, Schmidt numbers varying in the range $0\le {Sc}\le 20\,000$ and velocity–concentration coupling coefficients (scaling the magnitude of the osmotic pressure) varying in the range $10^{-6}\le \chi \le 1$. In addition to tracking the critical Taylor number, we explore the effects of osmotic pressure on the geometrical features of the vortices, in terms of wavenumber and radial profiles.

It might be surprising that the velocity–pressure coupling coefficient $\sigma$ is disregarded in the parametric study. Recall, however, that the base state $[\boldsymbol {V}_b,\,P_b,\,C_b]$ computed in § 2.2 does not depend on $\sigma$, because this latter only affects the operating pressure $\Delta P$. In the linear stability problem, $\sigma$ thus only appears in boundary conditions (3.2b). Figure 8 shows that, for ${Re}=-0.1, {Sc}=10^{3}, \chi = 10^{-1}$ and $\eta =0.85$, the critical Taylor number ${Ta}^{{crit}}$ and axial wavenumber $k^{{crit}}$ together with the radial profiles of the critical perturbation $u_p^{{crit}}(r)$ and $c_p^{{crit}}(r)$ are barely affected by a non-zero velocity–pressure coupling coefficient, up to $\sigma \sim 10^{-3}$. More specifically in figure 8(a,b), removing the pressure term in boundary conditions (3.5b), i.e. setting $\sigma =0$, leads to ${Ta}^{{crit}} = 79.1$ and $k^{{crit}}=2.26$ (the asymptotic dashed lines), whereas $\sigma =10^{-3}$ (the light grey, green online, circles) leads to ${Ta}^{{crit}}=78.4$ and $k^{{crit}}=2.24$. In figure 8(c,d), the radial profiles of the radial velocity component and concentration of the perturbation (the dark grey, blue online, dashed curves for $\sigma =0$ and the light grey, green online, solid curves for $\sigma =10^{-3}$) are barely distinguishable. Beyond $10^{-3}$, $\sigma$ noticeably impacts the critical conditions and perturbation. With $\sigma = 10^{-2}$ (the dark grey, red online, circles in figure 8a,b), ${Ta}^{{crit}}=73.0$, $k^{{crit}}=2.02$ and the velocity–pressure coupling at the membranes also clearly affects the radial profiles (the dark grey, red online, solid curves in figure 8c,d). For very weak values of $\sigma$ typical of RO, the pressure term in boundary conditions (3.2b) can be ignored. As its boundary condition (3.5b) reduces then to

(4.1)\begin{equation} u_{p}(r_{i})={\pm} \chi c_{p}(r_{i}), \end{equation}

the stability analysis is now completely independent of $\sigma$. We stress, however, that the membrane permeance $K$ also enters the velocity–concentration coupling coefficient $\chi$. Our approximation consequently amounts to neglecting the hydrodynamic pressure compared with the osmotic pressure in the transmembrane flow of the perturbation. Our DNS, however, implements the complete boundary conditions (2.9a).

Figure 8. Analytically obtained critical Taylor number ${Ta}^{{crit}}$ (a) and axial wavenumber $k^{{crit}}$ (b), in the presence of radial inflow with ${Re}=-0.1$, for $\eta =0.85$, ${Sc}=10^3$ and $\chi =10^{-3}$, as functions of the velocity–pressure coupling coefficient $\sigma$, in log scale. The dashed horizontal lines correspond to the case where $\sigma =0$ in boundary conditions (3.2b). Analytically obtained radial profiles of the radial component of the velocity (c) and concentration (d) for ${Re}=-0.1$, $\eta =0.85$, ${Sc}=10^3$ $\chi =10^{-3}$ and $\sigma =0$ (dashed, blue online, curve), $\sigma =10^{-3}$ (light grey, green online, solid curve) and $\sigma =10^{-2}$ (dark grey, red online, solid curve).

For the full range of parameters considered, the linear critical modes of instability were always in the form of counter-rotating toroidal vortices, i.e. $n^{{crit}}\equiv 0$, as depicted in figure 6. To reduce the CPU time, we consequently limit our DNS to axisymmetric computations.

To explore the effect of the osmotic pressure induced by concentration polarization, we begin by considering the impact of the Schmidt number ${Sc}$ and the coupling coefficient $\chi$, at fixed values of the radius ratio $\eta$ and radial Reynolds number ${Re}$. The salient features are summarized in figure 9, showing ${Ta}^{{crit}}$ as a function of the ${Sc}$ and $\chi$ for $\eta =0.85$ and ${Re}=-0.1$ (panel a) and ${Re}=0.1$ (panel b). As ${Sc}$ and/or $\chi$ are increased, the critical Taylor number ${Ta}^{{crit}}$ first substantially decreases, before eventually levelling off. Starting from its value obtained in the case of pure solvent ${Ta}^{{crit}}_{{pure}}$, the critical Taylor number tends towards a limit value in conditions where osmosis performs its maximum effect to favour the instabilities. This smooth decrease of ${Ta}^{{crit}}$, and the fact that it never vanishes, support the fact that these instabilities remain driven by the centrifugal force and take the form of altered Taylor vortices, favoured by osmotic pressure.

Figure 9. Critical Taylor number as a function of the Schmidt number ${Sc}$ and coupling coefficient $\chi$, in log scale, for $\eta =0.85$ and ${Re}=-0.1$ (a) and ${Re}=0.1$ (b). The dark grey (blue online) solid curves correspond to the locus of the boundary condition criterion on the inner cylinder $\chi _1$ (5.7) and the light grey (green online) ones to the boundary condition criterion on the outer cylinder $\chi _2$ (5.11).

This reinforcement is observed when polarization occurs at the inner cylinder (${Re}=-0.1$ in panel a), or at the outer cylinder (${Re}=0.1$ in panel b), but it is more pronounced in the former. Although the critical Taylor number asymptotically tends towards a limit value, we will assume that this limit is almost reached at the minimum of the critical Taylor number ${Ta}^{{crit}}_{{min}}$ in the parameter range of this study, i.e. for ${Sc}<2000$ and $\chi <1$. The overall decrease of ${Ta}^{{crit}}$ can be quantified by introducing the ratio $\epsilon$

(4.2)\begin{equation} \displaystyle\epsilon= 1-\frac{Ta^{{crit}}_{min}}{Ta^{{crit}}_{{pure}}}. \end{equation}

Quantitatively, for $\eta =0.85$ and radial inflow ${Re}=-0.1$, the critical Taylor number decreases up to ${Ta}^{{crit}}_{min}=\left.{Ta}^{{crit}}\right |_{{Sc}=2000,\chi = 1}=67.6$, compared with ${Ta}^{{crit}}_{{pure}}=108.4$, corresponding to $\epsilon \approx 0.37$. For $\eta =0.85$ and radial outflow ${Re}=0.1$, the critical Taylor number decreases up to ${Ta}^{{crit}}_{min}=\left.{Ta}^{{crit}}\right |_{{Sc}=2000,\chi = 1}=79.0$, compared with ${Ta}^{{crit}}_{{pure}}=108.2$, corresponding to $\epsilon = 0.27$. Section 5 elaborates further on the mechanism by which osmotic pressure, molecular diffusion and Taylor vortices couple and explain in a more detailed fashion the variations of ${Ta}^{{crit}}$ with $\chi$.

Figure 10 demonstrates the impact of the magnitude of the imposed radial flow, quantified by the radial Reynolds number ${Re}$. Panel (a) shows the critical Taylor number obtained for $\eta =0.85$ and a strong radial inflow ${Re}=-1$. The Schmidt number ranges from $0$ to $200$ and the coupling coefficient $\chi$ ranges from $10^{-4}$ to $10$. Panel (b) shows the corresponding results for a weak radial inflow ${Re}=-0.01$, with Schmidt number ranging from $0$ to $20\,000$ and coupling coefficient $\chi$ ranging from $10^{-6}$ to $10^{-1}$. The surfaces shown in figures 9(a), 10(a) and 10(b) clearly collapse under the rescaling $({Re},{Sc},\chi )\rightarrow (a^{-1}\,{Re},a\,{Sc},a^{-1}\,\chi )$, with $a$ an arbitrary constant. The critical conditions thus depend on combinations $({Re}\,{Sc},\chi \,{Sc})$ rather than parameters $({Re},{Sc},\chi )$.

Figure 10. Critical Taylor number as a function of the Schmidt number ${Sc}$ and coupling coefficient $\chi$, in log scale, for $\eta =0.85$ and ${Re}=-1$ (a) and ${Re}=-0.01$ (b). The dark grey (blue online) solid curves correspond to the locus of the boundary condition criterion on the inner cylinder $\chi _1$ (5.7) and the light grey (green online) ones to the boundary condition criterion on the outer cylinder $\chi _2$ (5.11).

Figure 11 demonstrates the influence of the radius ratio $\eta$ on the critical conditions of the vortices. Figure 11(a) shows ${Ta}^{{crit}}$ as a function of the Schmidt number $Sc$ and coupling coefficient $\chi$, for a radial inflow ${Re}=-0.1$, in a narrow gap $\eta =0.95$. Figure 11(b) shows the corresponding results in a medium gap $\eta =0.55$. Variations of $\eta$ are known to induce large changes in the critical Taylor number in the case of pure solvent. We see these changes are also observed as solute and osmosis are present. In the medium gap ($\eta =0.55$ in panel b), Taylor vortices appear above ${Ta}^{{crit}} = 40.1$ for ${Sc}=2000$ and $\chi =1$, compared with ${Ta}^{{crit}}_{{pure}} = 69.6$ for pure solvent, corresponding to $\epsilon = 0.42$. In the narrow gap ($\eta =0.95$ in panel a), the critical Taylor number exhibits a novel feature. At fixed Schmidt number, as the coupling coefficient $\chi$ is increased, ${Ta}^{{crit}}$ first decreases under the effect of osmotic pressure, but eventually increases to recover the value obtained for pure solvent. In this narrow gap, the minimum critical Taylor number is reached for $\chi =0.023$ instead of $\chi =1$ for the other cases. The critical Taylor number decreased up to ${Ta}^{{crit}}_{min}=131.0$, compared with ${Ta}^{{crit}}_{{pure}}=185.1$, corresponding to $\epsilon = 0.29$.

Figure 11. Critical Taylor number as a function of the Schmidt number ${Sc}$ and coupling coefficient $\chi$, in log scale, for ${Re}=-0.1$ and $\eta =0.95$ (a) and $\eta =0.55$ (b). The dark grey (blue online) solid curves correspond to the locus of the boundary condition criterion on the inner cylinder $\chi _1$ (5.7) and the light grey (green online) ones to the boundary condition criterion on the outer cylinder $\chi _2$ (5.11).

4.3. Velocity and concentration fields of the centrifugal instabilities

Above ${Ta}^{{crit}}$, the centrifugal instabilities take the form of counter-rotating toroidal vortices, with $n^{{crit}}=0$. To investigate how osmotic pressure modifies the structure of these centrifugal instabilities, figure 12 shows the critical axial wavelength $\lambda ^{{crit}}=2{\rm \pi} /k^{{crit}}$, as a function of ${Sc}$ and $\chi$ for $\eta =0.95$ (panel a) and $\eta =0.55$ (panel b). By comparing figures 11 and 12, conditions for which the critical Taylor number is affected by osmosis are readily found to also increase the characteristic size of the vortices along the axial direction. Similarly, when the effect of osmosis plateaus and the critical Taylor number tends to its limit ${Ta}^{{crit}}_{{osm}}$, so does the axial wavelength. At its maximum, the axial wavelength $\lambda ^{{crit}}$ is increased by almost $50\,\%$, in relation with a decreasing critical axial wavenumber $k^{{crit}}$.

Figure 12. Wavelength at critical conditions $\lambda ^{{crit}}$, as a function of the Schmidt number ${Sc}$ and coupling coefficient $\chi$ in log scale, for $Re=-0.1$ and $\eta =0.95$ (a) and $\eta =0.55$ (b). Note the axes orientation differs from figure 11.

We further explore the structure of the vortices by considering the perturbation fields $\boldsymbol {V}^{{crit}}_{p}$ and $C^{{crit}}_{p}$, obtained analytically at ${Ta}^{{crit}}$. In addition to figure 7(b) showing those fields in a meridional plane for $\eta =0.85$, $\alpha =-0.1$, $\chi =10^{-2}$ and ${Sc}=1000$, figure 13 shows them for ${Sc}=500$ (panel a) and ${Sc}=2000$ (panel b). Whereas the vortices are only marginally impacted as molecular diffusion is decreased, the patches of solute accumulation and depletion are found to get thinner along the radial direction, following the similar evolution of the boundary layer thickness $\delta$, as shown in figure 4.

Figure 13. Velocity fields of the vortices $\boldsymbol {V}_{p,{merid{.}}}=(U_{p},W_{p})$ and concentration perturbation $C_{p}$ in a meridional plane $(r,z)$, for $\eta =0.85$, ${Re}=-0.1$, $\chi =10^{-3}$ and ${Sc}=500$ (a) and ${Sc}=2000$ (b), obtained analytically at critical conditions. The dark grey (blue online) dashed lines above the inner cylinder bound the polarization layer, the thickness of which is given by (2.15).

Figure 14 shows the perturbation for $\eta =0.85$, $\alpha =-0.1$ and ${Sc}=1000$, at $\chi =5\times 10^{-5}$ (panel a) and $\chi =10^{-1}$ (panel b). As osmosis is weak in figure 14(a), the vortices are almost identical to Taylor vortices, and the radial transmembrane flow associated with boundary condition (3.2c) is barely observed. The advection of the concentration boundary layer by the vortices generates patches of solute depletion and accumulation, but these only weakly retro-act on the vortices. As osmosis kicks in in figure 7(b), boundary condition (2.9a) now drives a noticeable extra radial transmembrane flow. This causes the axial wavelength of the vortices to increase. Although five full vortices are observed in figure 14(a), only four are observed along the same axial length in figures 7(b) and 14(b). As the effect of osmosis is further increased between figures 7(b) and 14(b), we also observe a modification of the patches of solute depletion and accumulation, such that the local extrema of these patches detach from the inner cylinder. Together with these detached extrema, the radial transmembrane flow does not further increase. The evolution of the perturbation of concentration and radial velocity fields is further addressed in the next section.

Figure 14. Velocity fields of the vortices ($U_{p},W_{p}$) and concentration perturbation $C_{p}$ in a meridional plane for $\eta =0.85$, ${Re}=-0.1$, ${Sc}=1000$ and $\chi =5\times 10^{-5}$ (a) and $\chi =10^{-1}$ (b), obtained analytically at critical conditions.

5.1. Coupling in the polarization layer

Figure 15 shows how the increase of the coupling coefficient $\chi$ affects the Taylor vortices, the concentration perturbation and its dynamics. To compare the perturbations $[\boldsymbol {v}_p(r),\,c_p(r)]$ at different $\chi$, they are normalized by the maximum of their azimuthal velocity component $v_p(r)$, which is found to be barely affected by osmosis. First, figure 15(a) is a reminder that ${Ta}^{{crit}}$ decreases as $\chi$ increases, at specific conditions ${Sc}=1000$ and ${Re}=-0.1$, in the case of a narrow gap ($\eta =0.85$). In these conditions, the thickness of the base-state polarization layer is $\delta \approx 0.171$. Figure 15(b,c) shows how the increase of the coupling coefficient impacts the radial velocity perturbation $u_p(r)$ and concentration perturbation $c_p(r)$, respectively. Figure 15(d,e) shows how advection terms in the scalar transport equation (5.2), $-{Sc}\,u_p(r)d_r C_b$ and $-{Sc}\,U_b(r)d_r c_p$, respectively, evolve with the coupling coefficient.

Figure 15. (a) Critical Taylor number $Ta^{{crit}}$ as a function of the coupling coefficient $\chi$ in log scale, for $\eta =0.85$, ${Re}=-0.1$ and ${Sc}=1000$. (b) Radial velocity perturbation $u_p$, (c) concentration perturbation $c_p$, the dashed black vertical line bounding the polarization layer, the thickness of which $\delta$ is given by (2.15), (d) advection of the bases-state concentration by the radial velocity perturbation (term ${\bigcirc{\kern-6pt 3}}$ of (5.2)) and (e) advection of the concentration perturbation by the base-state radial flow (term ${\bigcirc{\kern-6pt 1}}$ of (5.2)), as functions of $r$, obtained analytically at $\chi =0$ (solid black curves), $10^{-4}$ (dotted curves, magenta online), $10^{-3}$ (dashed curves, blue online), $10^{-2}$ (dashed-dotted curves, red online) and $10^{-1}$ (solid light grey curves, green online), the circles in (a) correspond to the four last cases, whilst the black horizontal dashed line corresponds to the osmosis-free $\chi =0$ case. The dashed vertical (blue online) line in (a) corresponds to the limit value $\chi _1$ inferred from (5.7).

In the case of no osmotic pressure, $\chi =0$ (the dashed horizontal black line in figure 15(a) and black solid curves in figure 15b–e), the solute has no impact on the centrifugal instabilities, which take the form of the classical Taylor vortices, with no velocity at the inner cylinder $u_{p}(r_{1})=0$. More specifically, figure 15(b) shows that the radial velocity of these vortices vanishes at the inner cylinder. Due to this boundary condition, the base-state polarization layer and the radial velocity of the vortices barely overlap, such that the source term ${\bigcirc{\kern-6pt 3}}$ in (5.2), shown as a black curve in figure 15(d), is nearly zero. The transport of the concentration perturbation is thus mostly a balance between its advection by the base-flow $U_b(r)$ and molecular diffusion. For $\chi =0$, the solute rejection condition (5.3) further reduces to

(5.4)\begin{equation} \frac{{\rm d}c_p}{{\rm d}r}\left(r_{1}\right)={Sc}\,U_{b}\left(r_{1}\right)c_{p}\left(r_{1}\right). \end{equation}

Axial diffusion being much weaker than radial diffusion in term ${\bigcirc{\kern-6pt 2}}$, the concentration perturbation satisfies the same equation and boundary conditions as the base-state concentration, and $c_p(r)$ is similar, up to a scaling factor, to $C_b(r)$. This can be seen in figure 15(c). Although weak, the positive source term $-{Sc}\,u_p\,d_r C_b$ triggers the coincidence of the radial outward jet with an excess of concentration, or equivalently, a positive radial perturbation velocity $u_p(r)$ (the black curve in figure 15b) corresponds to a positive concentration perturbation $c_p(r)$ (the black curve in figure 15c).

As $\chi$ departs from zero, the radial velocity perturbation no longer vanishes at the inner cylinder and boundary condition (5.1) implies $u_p(r_{1})>0$. This is illustrated in figure 15(b), where the dotted (magenta online) curve is obtained at $\chi =10^{-4}$. Osmosis, via this injection of fluid at the inner cylinder, fosters the Taylor vortices and the critical Taylor number decreases accordingly, as recalled in figure 15(a). As the radial velocity perturbation $u_p(r)$ and the base-state concentration $C_b(r)$ now overlap, source term ${\bigcirc{\kern-6pt 3}}$ acts in the polarization layer (the dotted, magenta online, curve in figure 15d). The concentration perturbation in the polarization layer is also affected by the modification of the solute rejection condition (5.3), where the negative effective transmembrane flow $[U_{b}(r_{1}) + \chi \, C_{b}(r_{1})]$ increases. Outside the polarization layer, the concentration perturbation remains unaffected by osmosis, and similar to the case with $\chi =0$. Matching the concentration perturbation inside and outside the polarization layer forces $c_p(r_{1})$ to decrease and $d_r c_p(r_{1})$ to increase as $\chi$ increases, as seen in figure 15(c).

For large values of $\chi$, the perturbation tends to a limit solution for which the radial profiles and the critical Taylor number are no longer $\chi$-dependent. This is demonstrated by the asymptotic regime for large values of $\chi$ in figure 15(a), and the dash-dotted (red online) and solid light grey (green online) curves in figure 15(b,c), obtained at $\chi =10^{-2}$ and $\chi =10^{-1}$, respectively. As $\chi$ increases, figure 15(b) shows that $u_p(r_{1})$ tends to a limit value $u_p^{\infty }(r_{1})$, and figure 15(c) shows that $c_p(r)$ now presents a maximum concentration detached from the inner cylinder, while $c_p(r_{1})$ tends to $0$. Outside the polarization layer, $c_p(r)$ remains unaffected by osmosis.

To explain this limit regime, first note that at large $\chi$, the solute rejection condition at the inner cylinder (5.3) simplifies to

(5.5)\begin{equation} \frac{{\rm d}c_p}{{\rm d}r}\left(r_{1}\right)\approx \chi\,{Sc}\,C_b(r_{1})\,c_p(r_{1}), \end{equation}

and $d_r c_p(r_{1})$ is now positive. Matching boundary condition (5.5) to the concentration perturbation outside the polarization layer forces $c_p(r)$ to reach its maximum in the polarization layer instead of at the inner cylinder. Furthermore, as $\chi$ increases, the solute rejection condition (5.5) forces the concentration perturbation at the inner cylinder $c_p(r_{1})$ to decrease and tend to $0$, to avoid $u_p(r_{1})$ diverging. The concentration perturbation $c_p(r)$ is now a solution of the transport equation (5.2) with boundary conditions (5.1) and (5.3) rewritten as

(5.6a,b)\begin{equation} c_p(r_{1})=\frac{1}{\chi}u_p^{\infty}(r_{1})\quad\text{and}\quad\frac{{\rm d}c_p}{{\rm d}r}(r_{1})={Sc}\,C_b(r_{1})u_p^{\infty}(r_{1}), \end{equation}

respectively. The small value of $c_p(r_{1})$ excepted, these solutions are independent of $\chi$. The extra injection of pure solvent at the inner cylinder $u_p(r_{1})$ levels off, and no further decrease of ${Ta}^{{crit}}$ is observed as $\chi$ increases, as seen in figure 15(a).

Figure 15 thus highlights two obvious regimes of coupling between osmosis and Taylor vortices. For small $\chi$, $d_r c_p(r_{1})$ is negative, $c_p(r_{1})$ is large and $u_p(r_{1})$ increases with $\chi$. For large $\chi$, $d_r c_p(r_{1})$ is positive, $c_p(r_{1})$ is almost zero and $u_p(r_{1})$ is independent of $\chi$. The distinction between these two regimes is imposed by the sign of the effective transmembrane velocity $U_b(r_{1})+\chi \,C_b(r_{1})$ in the solute rejection boundary condition (5.3). This velocity is negative for small values of $\chi$, and becomes positive when $\chi >\chi _1$, where

(5.7)\begin{equation} \chi_1=\left|\frac{U_b(r_{1})}{C_b(r_{1})}\right|=\left|\frac{2{Re}\left(1-\eta\right)\left(1-\eta^{-{Re}\,{Sc}-2}\right)}{\left({Re}\,{Sc}+2\right)\left(\eta^{{-}2}-1\right)\eta}\right|. \end{equation}

This limit value $\chi _1$ is inferred from the base state alone. It is shown as a dashed vertical (blue online) line at $\chi _1\approx 9.38\times 10^{-4}$ in figure 15(a) for $\eta =0.85$, ${Re}=-0.1$ and ${Sc}=1000$. This limit almost corresponds to the dashed, blue online, curves in figure 15(b–e) at $\chi =10^{-3}$. For $\chi <\chi _1$, osmosis favours vortices by injecting pure solvent in the outward jets and extracting pure solvent from the inward jets. In this regime, ${Ta}^{{crit}}$ decreases as $\chi$ increases. For $\chi >\chi _1$, this mechanism subsides, such that ${Ta}^{{crit}}$ plateaus to its limit minimal value. The limit value $\chi _1$ has been added as dark grey (blue online) curves on figures 9–11. For sufficiently large Péclet numbers, it indeed coincides, for cases with a radial inflow base-state, to the value of $\chi$ beyond which ${Ta}^{{crit}}$ is no longer affected by increasing the coupling coefficient.

5.2. Coupling on the depleted side

The solute rejection boundary condition explains another feature of the impact of $\chi$ on ${Ta}^{{crit}}$, observed in figures 11(a) and 16(a). For $\eta =0.95$, ${Re}=-0.1$ and ${Sc}=1000$, ${Ta}^{{crit}}$ is found to be a decreasing then increasing function of $\chi$. Concerning the base state, $\eta =0.95$ yields a thicker polarization layer $\delta \approx 0.57$ than for $\eta =0.85$. Accordingly, the solute is less depleted at the outer cylinder for $\eta =0.95$ than for $\eta =0.85$. As explained above, in the case of no osmotic pressure, $c_p(r)$ recovers the base-state concentration $C_b(r)$ up to a multiplicative constant and $c_p(r_{2})$ noticeably departs from zero for cases with thick polarization layers.

Figure 16. (a) Critical Taylor number ${Ta}^{{crit}}$ as a function of the coupling coefficient $\chi$, in log scale, for $\eta =0.95$, ${Re}=-0.1$ and ${Sc}=1000$. (b) Radial velocity perturbation $u_p(r)$ and (c) concentration perturbation $c_p(r)$ , obtained analytically at $\chi =10^{-4}$ (solid curves, green online), $10^{-2}$ (dashed curves, blue online) and $5\times 10^{-1}$ (dashed-dotted curves, red online), the circles in (a) correspond to these three cases.

As $\chi$ remains limited, the radial velocity perturbation $u_p(r)$ and concentration perturbation $c_p(r)$ and their evolution with $\chi$ at $\eta =0.95$ are similar to the case $\eta =0.85$, and governed by osmosis and the advection of the polarization layer at the inner cylinder. This is demonstrated in figure 16(b,c), where the solid (green online) curves are obtained at $\chi =10^{-4}$ and dashed (blue online) curves at $\chi =10^{-2}$. As $\chi$ is further increased, the radial velocity perturbation at the outer cylinder, $u_p(r_{2})$, substantially departs from $0$, to be negative. This is illustrated in figure 16(b) where the dash-dotted (red online) curve is obtained at $\chi =5\times 10^{-1}$. This counter-flow acts against the outward jet and explains the increase of the critical Taylor number, as recalled in figure 16(a). This counter-flow is induced by the boundary condition for $u_p(r)$ at the outer cylinder

(5.8)\begin{equation} \displaystyle u_{p}\left(r_{2}\right)={-} \chi c_{p}\left(r_{2}\right). \end{equation}

Moreover, as the source term ${\bigcirc{\kern-6pt 3}}$ in the transport equation (5.2) vanishes outside the polarization layer, $d_r c_p(r_{2})$ must be independent of $\chi$. In the solute rejection condition at the outer cylinder

(5.9)\begin{equation} \displaystyle {Sc}\left[U_{b}\left(r_{2}\right) - \chi\,C_{b}\left(r_{2}\right)\right] c_{p}\left(r_{2}\right)- \frac{{\rm d} c_{p}}{{\rm d} r} \left(r_{2}\right) = 0, \end{equation}

the (negative) effective transmembrane velocity $U_{b}(r_{2}) -\chi \,C_b(r_{2})$ decreases with $\chi$, and forces $c_p(r_{2})$ to tend to zero as $\chi$ increases.

For large values of $\chi$, the solute rejection condition further reduces to

(5.10)\begin{equation} \frac{{\rm d} c_{p}}{{\rm d} r}\left(r_{2}\right)\approx{-}\chi\,{Sc}\,C_{b}\left(r_{2}\right)\,c_p(r_{2}), \end{equation}

and forces $u_p(r_{2})=-\chi \,c_p(r_{2})$ to tend to a negative limit value $u_p^{\infty }(r_{2})$. The limit regime at the outer cylinder occurs as $\chi$ exceeds

(5.11)\begin{equation} \chi_2=\left|\frac{U_b(r_{2})}{C_b(r_{2})}\right| =\left|\frac{2{Re}\left(1-\eta\right)\left(1-\eta^{{Re}\,{Sc}+2}\right)}{\left({Re}\,{Sc} +2\right)\left(\eta^{2}-1\right)}\right|, \end{equation}

and $-\chi \,C_{b}(r_{2})$ becomes dominant over $U_{b}(r_{2})$ in boundary condition (5.9). The limit value (5.11) has been added as light grey (green online) curves in figures 9–11. It roughly coincides, for cases with a radial inflow base state, to the value of $\chi$ beyond which the decrease of ${Ta}^{{crit}}$ due to osmosis at the inner cylinder is no longer observed.