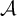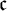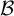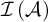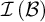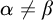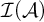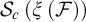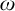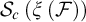1 Introduction
FiltersFootnote
1
on countable sets play a fundamental role in set theory, topology, model theory, and many other branches of mathematics. Given a filter
$\mathcal {F}$
on
$\omega ,$
we may define the topological space
$\xi (\mathcal {F})$
as follows: its underlying set is
$\omega \cup \{\mathcal {F}\}$
, the elements of
$\omega $
are isolated points and the open neighborhoods of
$\mathcal {F}$
are of the form
$\{\mathcal {F}\}\cup F$
where
$F\in \mathcal {F}.$
This is a very interesting space since the combinatorial properties of
$\mathcal {F}$
nicely translate into topological properties of
$\xi (\mathcal {F}).$
For example, it is easy to see that given
$A\subseteq \omega ,$
the following holds:
$$ \begin{align*} \begin{array}{clc} A\cup\left\{ \mathcal{F}\right\} \text{ is an open set of } \xi(\mathcal{F}) & \text{if and only if} &A\in\mathcal{F},\\ \mathcal{F}\in\overline{A} & \text{if and only if } &A\in\mathcal{F}^{+},\\ A\text{ converges to } \mathcal{F} &\text{if and only if} &A\text{ is a pseudointersection}\\ & & \text{of } \mathcal{F}. \end{array} \end{align*} $$
In this paper, we will be mainly interested the filters
$\mathcal {F}$
whose
$\xi (\mathcal {F})$
is Fréchet–Urysohn. Recall that a topological space X is Fréchet–Urysohn if for every
$x\in X$
and
$Y\subseteq X,$
if
$\ x\in \overline {Y},$
then there is a sequence
$(x_{n})_{n<\omega }$
in Y that converges to
$x.$
It is easy to see that metric spaces are Fréchet–Urysohn, but there are many examples of Fréchet–Urysohn spaces that are not metric. We say that a filter
$\mathcal {F}$
is Fréchet–Urysohn (of
$\mathcal {F}$
is a FU
-filter) if the space
$\xi (\mathcal {F})$
is Fréchet–Urysohn. Using the translation above, it is easy to see that
$\mathcal {F}$
is a FU-filter if and only if for every
$A\subseteq \omega $
such that
$F\cap A\neq \emptyset $
, for all
$F\in \mathcal {F}$
, there is
$B\in \lbrack A]^{\omega }$
such that
$B\subseteq ^{\ast }F$
for all
$F\in \mathcal {F}$
. An example of a FU-filter is the Fréchet filter
$\mathcal {F}_{r}$
which consists of all the coinfinite subsets of
$\omega .$
In [Reference Garcia-Ferreira and Uzcátegui9] it was proved that there are
$2^{\mathfrak {c}}$
-many pairwise non-equivalent FU-filters (where
$\mathfrak {c}$
denotes the size of the continuum). In this paper, we continue studying the Fréchet–Urysohn filters by solving three problems posed in the papers [Reference Garcia-Ferreira and Rivera-Gómez5] and [Reference Garcia-Ferreira and Rivera-Gómez6].
For us, it will be more convenient to work with ideals instead of filters. Thus, an ideal
$\mathcal {I}$
is called a FU-ideal (or nowhere tall) if the filter
$\mathcal {I}^{\ast }$
is a FU-filter. In other words,
$\mathcal {I}$
is a FU-ideal, if for every
$A\in \mathcal {I}^{+}$
there is
$B\in \left [ A\right ] ^{\omega }$
such that
$B\cap I$
is finite for every
$I\in \mathcal {I}$
.
Since filters and ideals are very important in infinite combinatorics and topology, it is desirable to develop tools in order to classify them so that we can achieve a better understanding of their nature. A way to classify filters and ideals that has proven to be very useful is the Rudin–Keisler pre-order:
Definition 1.1 (Rudin–Keisler pre-order)
Let
$\mathcal {I}$
be an ideal on X and
$\mathcal {J}$
an ideal on Y.
-
1. We say
$f:X\longrightarrow Y$
is a Rudin–Keisler morphism
$($
or Rudin–Keisler function) if for every
$A\subseteq Y$
the following holds:In this case, we say f is a Rudin–Keisler morphism from
$$ \begin{align*} \begin{array}{c} A\in\mathcal{J} \textit{ if and only if } f^{-1}\left( A\right) \in\mathcal{I}. \end{array} \end{align*} $$
$\left ( X,\mathcal {I}\right ) $
to
$\left ( Y,\mathcal {J}\right ) .$
-
2. We say
$\mathcal {J\leq }_{{\textsf {RK}}} \ \mathcal {I}$
if there is a Rudin–Keisler morphism from
$\left ( X,\mathcal {I}\right ) $
to
$\left ( Y,\mathcal {J}\right ) .$
-
3. We say that
$\mathcal {I}$
and
$\mathcal {J}$
are RK-equivalent if
$\mathcal {J\leq }_{{\textsf {RK}}}\ \mathcal {I}$
and
$\mathcal {I\leq }_{{\textsf {RK}}}\ \mathcal {J}$
. -
4. By
$\mathcal {J}<_{{\textsf {RK}}}\mathcal {I}$
we mean that
$\mathcal {J}\leq _{{\textsf {RK}}}\mathcal {I}$
but
$\mathcal {J}$
and
$\mathcal {I}$
are not RK-equivalent.
In the articles [Reference Garcia-Ferreira and Rivera-Gómez5] and [Reference Garcia-Ferreira and Rivera-Gómez6] the Rudin–Keisler pre-order was successfully applied in the study and classification of the FU-filters (hence, the FU-ideals). We continue this line of research and solve three problems posed in those papers, providing a clearer picture of the structure of the class of FU-filters with the Rudin–Keisler pre-order. After that, we study the hyperspace of nontrivial convergent sequences of the space
$\xi (\mathcal {F})$
(for
$\mathcal {F}$
a FU-filter). Before stating our results on this topic, we will first explain the context of the problem:
The systematic study of the hyperspace of nontrivial convergent sequences
$\mathcal {S}_{c}(X)$
of a Fréchet–Urysohn nondiscrete space X was initiated in [Reference Garcia-Ferreira and Ortiz-Castillo4], where
$\mathcal {S}_{c}(X)$
is equipped with the Vietoris topology. The categorical properties on
$\mathcal {S}_{c}(X)$
, together with other topological properties, were considered in [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7]. Indeed, in that paper, it was proved that
$\mathcal {S}_{c}(X)$
is never a Baire space when the space X is crowded, and this result was improved in [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7] by showing that
$\mathcal {S}_{c}(X)$
is meager whenever X is crowded (this assertion was also proved independently in [Reference Poplawski18]). Hence, if
$\mathcal {S}_{c}(X)$
is Baire, then X has a dense subset of isolated points. Nontrivial examples of spaces X for which
$\mathcal {S} _{c}(X)$
is Baire were given in [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7]. The authors of [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7, Proposition 2.8] proposed the following problem:
Problem 1.2. Determine the FU-filters
$\mathcal {F}$
on
$\omega $
for which the space
$\mathcal {S}_{c}\left ( \xi \left ( \mathcal {F}\right ) \right ) $
is Baire.
In this paper we will prove that if
$\mathcal {F}$
is a FU-filter, then the space
$\mathcal {S}_{c}\left ( \xi \left ( \mathcal {F}\right ) \right ) $
is Baire if and only if
$\mathcal {F}$
is a FUF-filter, providing a complete solution to Problem 1.2 (the notion of FUF-filter will be reviewed in Section 4).
The paper is organized as follows: In Section 2 we introduce some definitions and notation that will be used throughout the paper. In Section 3 we study the Rudin–Keisler pre-order restricted to FU-filters, providing answers to problems from [Reference Garcia-Ferreira and Rivera-Gómez5] and [Reference Garcia-Ferreira and Rivera-Gómez6]. The three questions mentioned in the abstract and their respective solutions will be explicitly stated in that section. In Section 4 we study the hyperspace of nontrivial convergent sequences of spaces of the form
$\xi (\mathcal {F}).$
We answer Problem 1.2 and obtain more results.
2 Preliminaries and notation
Most of our definitions and notation are standard, but for the convenience of the reader, in this section we will review some notions that will be used throughout the paper.
Let
$A,B$
be two sets. We write
$A\subseteq ^{\ast }B$
(A is an almost subset of B) if
$A\setminus B$
is finite. Let
$\mathcal {X}\subseteq \wp \left ( \omega \right ) $
(If X is any set, by
$\wp \left ( X\right ) $
we denote the power set of X) and
$A\in \left [ \omega \right ] ^{\omega },$
we say that
$A$
is a pseudointersection of
$\mathcal {X}$
if A is almost included in every element of
$\mathcal {X}.$
Let X be a non-empty set. Informally, we can think of filters on X as being a collection of “big” subsets of X while ideals are collections of “small” subsets of
$X.$
The formal definitions are the following (for us, all ideals contain all finite sets).
Definition 2.1. Let X be a set.
-
1. We say that
$\mathcal {F\subseteq }\ \wp \left ( X\right ) $
is a filter on X if the following conditions hold:-
(a)
$X\in \mathcal {F}$
and
$\emptyset \notin \mathcal {F}.$
-
(b) If
$A\in \mathcal {F}$
and
$A\subseteq ^{\ast }B$
then
$B\in \mathcal {F}.$
-
(c) If
$A,B\in \mathcal {F}$
then
$A\cap B\in \mathcal {F}.$
-
-
2. We say that
$\mathcal {I\subseteq }\ \wp \left ( X\right ) $
is an ideal on X if the following conditions hold:-
(a)
$X\notin \mathcal {I}$
and
$\emptyset \in \mathcal {I}.$
-
(b) If
$A\in \mathcal {I}$
and
$B\subseteq ^{\ast }A$
then
$B\in \mathcal {I}.$
-
(c) If
$A,B\in \mathcal {I}$
then
$A\cup B\in \mathcal {I}.$
-
Given an ideal
$\mathcal {I}$
on
$\omega ,$
we define
$\mathcal {I}^{+} =\wp \left ( \omega \right ) \setminus \mathcal {I}$
. If
$\mathcal {X}$
is a collection of subsets of
$\omega ,$
we define
$\mathcal {X}^{\ast }=\left \{ \omega \setminus A\mid A\in \mathcal {X}\right \} $
. The dual filter of an ideal
$\mathcal {I}$
is the filter
$\mathcal {I}^{\ast }$
. If
$\mathcal {F}$
is a filter, define
$\mathcal {F}^{+}=(\mathcal {F}^{\ast })^{+}.$
Note that
$F\in \mathcal {F}^{+}$
if and only if
$\omega \setminus F\notin \mathcal {F}$
.
We say that two sets
$A,B\subseteq \omega $
are almost disjoint if
$A\cap B$
is finite. A family
$\mathcal {A}\subseteq \left [ \omega \right ] ^{\omega }$
is an AD family if it is infinite and any two of its elements are almost disjoint. We say that
$\mathcal {A}$
is a MAD family if it is a maximal AD family. For an AD family
$\mathcal {A},$
the orthogonal of
$\mathcal {A}$
(denoted by
$\mathcal {A}^{\perp }$
) is defined as the set of all
$X\subseteq \omega $
such that
$X\cap A$
is finite for every
$A\in \mathcal {A}.$
It is easy to see that
$\mathcal {A}^{\perp }$
is an ideal and that
$\mathcal {A}$
is a MAD family if and only if
$\mathcal {A}^{\perp }$
is the collection of all finite subsets of
$\omega .$
Given an AD family
$\mathcal {A}$
, we denote by
$\mathcal {I(A)}$
the ideal generated by
$\mathcal {A}.$
In this way, if
$X\subseteq \omega ,$
then
$X\in \mathcal {I}\left ( \mathcal {A}\right ) $
if and only if there are
$A_{0},...,A_{n}\in \mathcal {A}$
such that
$X\subseteq ^{\ast }A_{0}\cup ...\cup A_{n}$
. We will say that
$\mathcal {A}$
is nowhere MAD if for every
$X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+},$
we have that
$\left [ X\right ] ^{\omega }\cap \mathcal {A}^{\perp }\neq \emptyset $
. For convenience, the expression “
$\mathcal {A}$
is nowhere MAD” will actually mean “
$\mathcal {A}$
is an AD family and it is nowhere MAD.” It is not hard to prove that an AD family
$\mathcal {A}$
is nowhere MAD if and only if
$\mathcal {I}\left ( \mathcal {A}\right ) $
is a FU-ideal.
3 The Rudin–Keisler pre-order on Fréchet ideals
We are interested in studying the Rudin–Keisler pre-order on Fréchet filters and on nowhere MAD families. As mentioned in the abstract, this project was initiated in the articles [Reference Garcia-Ferreira and Rivera-Gómez5] and [Reference Garcia-Ferreira and Rivera-Gómez6]. We will answer some questions that were left open. The first question that we will address and solve was formulated in [Reference Garcia-Ferreira and Rivera-Gómez5, Question 5.7]:
Problem 3.1. Given an AD family
$\mathcal {A}$
, is there an AD family
$\mathcal {B}$
such that
$\mathcal {A}^{\perp }<_{{\textsf {RK}}} \mathcal {B}^{\perp }$
?
We will require several concepts, facts, and lemmas before answering the problem.
Definition 3.2. Let
$\mathcal {A}$
be an AD family on
$\omega .$
-
1. We define
$\mathcal {I}\left ( \mathcal {A}\right ) ^{++}$
as the set of all
$X\in \left [ \omega \right ] ^{\omega }$
for which there is
$\mathcal {B} \in \left [ \mathcal {A}\right ] ^{\omega }$
such that
$\left \vert X\cap A\right \vert =\omega $
for every
$A\in \mathcal {B}.$
-
2.
$\mathcal {A}$
is completely separable if for every
$X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{++}$
there is
$A\in \mathcal {A}$
such that
$A\subseteq X.$
Given an AD family
$\mathcal {A},$
it is always the case that
$\mathcal {I(A)}^{++}\subseteq \mathcal {I(A)}^{+},$
while equality holds if and only if
$\mathcal {A}$
is MAD. The existence of a completely separable MAD family is an old question of P. Erdös and S. Shelah (see [Reference Erdös and Shelah2]); nevertheless, significant progress has been made on this problem (see [Reference Hrušák14, Reference Mildenberger, Raghavan and Steprans16, Reference Shelah20]). On the other hand, the following is an impressive result of P. Simon:
Proposition 3.3 (Simon [Reference Galvin and Simon3])
There is a nowhere MAD completely separable AD family.
The following lemma is well-known, but we provide a proof of it for the sake of completeness.
Lemma 3.4. Let
$\mathcal {A}$
be a completely separable AD family. If
$X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{++}$
, then the set
$\left \{ A\in \mathcal {A}\mid A\subseteq X\right \} $
has size
$\mathfrak {c}.$
Proof. Since
$X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{++},$
we know there is a family
$\left \{ A_{n}\mid n\in \omega \right \} \subseteq \mathcal {A}$
such that
$A_{n}\neq A_{m}$
whenever
$n\neq m$
and
$A_{n}\cap X$
is infinite for every
$n\in \omega .$
We can now find an almost disjoint family
$\mathcal {B} \subseteq \left [ X\right ] ^{\omega }$
of size
$\mathfrak {c}$
such that
$B\cap A_{n}$
is infinite for every
$n\in \omega $
and
$B\in \mathcal {B}.$
Since
$\mathcal {A}$
is completely separable, for every
$B\in \mathcal {B},$
there is
$A_{B}\in \mathcal {A}$
such that
$A_{B}\subseteq B.$
Finally, note that if
$B,C\in \mathcal {B}$
and
$B\neq C,$
then
$A_{B}\neq A_{C}$
since B and C are almost disjoint.⊣
In particular, it follows that every completely separable AD family has size
$\mathfrak {c}.$
We are ready to answer positively Question 3.1:
Theorem 3.5. If
$\mathcal {D}$
is an AD family, then there is an AD family
$\mathcal {A}$
such that
$\mathcal {D}^{\perp } <_{{\textsf {RK}}}\mathcal {A}^{\perp }.$
Proof. Let
$\mathcal {D}$
be and AD family in
$\omega .$
Let
$C_{n}=\left \{ n\right \} \times \omega $
and define
$\pi :\omega \times \omega \longrightarrow \omega $
where
$\pi \left ( n,m\right ) =n.$
Fix two disjoint sets
$W_{0},W_{1}$
such that
$\mathfrak {c}\setminus \omega =W_{0}\cup W_{1}$
and
$\left \vert W_{i}\right \vert =\mathfrak {c}$
for each
$i<2.$
We also fix an enumeration
$\mathcal {I}\left ( \mathcal {D}\right ) \cap \left [ \omega \right ] ^{\omega }=\left \{ X_{\alpha }\mid \alpha \in W_{0}\right \} .$
By Proposition 3.3, there is
$\mathcal {B}\subseteq \wp \left ( \omega \times \omega \right ) $
a completely separable AD family such that
$\left \{ C_{n}\mid n\in \omega \right \} \subseteq \mathcal {B}.$
It is easy to see that
$\mathcal {B}$
has the following properties:
-
1. If
$B\in \mathcal {B}$
and
$B\notin \left \{ C_{n}\mid n\in \omega \right \} $
then
$B\cap C_{n}$
is finite for every
$n\in \omega .$
-
2. If
$X\in \left [ \omega \right ] ^{\omega }$
then
$\pi ^{-1}\left ( X\right ) \in \mathcal {I}\left ( \mathcal {B}\right ) ^{++}$
(this holds since
$\left \{ C_{n}\mid n\in \omega \right \} \subseteq \mathcal {B}$
).
Now, we recursively construct an AD family
$\mathcal {P=}\ \left \{ p_{\alpha }\mid \alpha <\mathfrak {c}\right \} $
with the following properties:
-
1.
$p_{n}=C_{n}$
for every
$n\in \omega .$
-
2. For every
$\alpha <\mathfrak {c}$
there is
$B\left ( p_{\alpha }\right ) \in \mathcal {B}$
such that
$p_{\alpha }\subseteq B\left ( p_{\alpha }\right ) .$
-
3. If
$\alpha \neq \beta $
then
$B\left ( p_{\alpha }\right ) \neq B\left ( p_{\beta }\right ) .$
-
4. If
$\alpha \geq \omega $
then
$p_{\alpha }\subseteq \omega \times \omega $
is a partial infinite function such that
$dom\left ( p_{\alpha }\right ) =\pi \left ( p_{\alpha }\right ) \in \mathcal {I}\left ( \mathcal {D}\right ) .$
-
5. If
$\alpha \ \in W_{0}$
then
$p_{\alpha }\subseteq \pi ^{-1}\left ( X_{\alpha }\right ) .$
The construction is straightforward (but note that we need that
$\mathcal {C}$
is completely separable in order to satisfy points 2 and 5 above). Fix an enumeration
$\left ( \omega \times \omega \right ) ^{\omega }=\left \{ f_{\alpha }\mid \alpha \in W_{1}\right \} $
we now define the family
$\mathcal {A=}\left \{ p_{\alpha }\mid \alpha \in W_{0}\right \} \cup \left \{ p_{\alpha }\mid \alpha \in W_{1}\wedge \left ( f_{\alpha }^{-1}\left ( p_{\alpha }\right ) \in \mathcal {D}^{\bot }\right ) \right \} .$
Clearly
$\mathcal {A}$
is an AD family. We will now prove that
$\pi $
is a Rudin–Keisler morphism from
$\left ( \omega \times \omega ,\mathcal {A}^{\perp }\right ) $
to
$\left ( \omega ,\mathcal {D}^{\perp }\right ) .$
Let
$X\subseteq \omega .$
If
$X\in \mathcal {D}^{\perp },$
then
$\pi ^{-1}\left ( X\right ) \in \mathcal {A} ^{\perp }$
because each
$p_{\alpha }\in \mathcal {A}$
is a partial function whose domain is in
$\mathcal {I}\left ( \mathcal {D}\right ) .$
In case
$X\notin \mathcal {D}^{\perp },$
we find
$D\in \mathcal {D}$
such that
$X\cap D$
is infinite. Let
$\alpha \in W_{0}$
such that
$X_{\alpha }=X\cap D.$
By definition,
$p_{\alpha }\in \mathcal {A}$
and
$p_{\alpha }\subseteq \pi ^{-1}\left ( X_{\alpha }\right ) \subseteq \pi ^{-1}\left ( X\right ) ,$
so
$\pi ^{-1}\left ( X\right ) \notin \mathcal {A}^{\perp }.$
We conclude that
$\mathcal {D}^{\perp } \leq _{{\textsf {RK}}}\mathcal {A}^{\perp }.$
We will now show that there is no Rudin–Keisler morphism from
$\left ( \omega ,\mathcal {D}^{\perp }\right ) $
to
$\left ( \omega \times \omega ,\mathcal {A}^{\perp }\right ) .$
Obviously, it is enough to see that
$f_{\alpha }$
is not a Rudin–Keisler morphism for every
$\alpha \in W_{1}.$
There are two cases to consider: First assume that
$p_{\alpha }\in \mathcal {A},$
this means that
$f_{\alpha }^{-1}\left ( p_{\alpha }\right ) \in \mathcal {D} ^{\bot }$
but obviously
$p_{\alpha }\notin \mathcal {A}^{\perp }.$
In case
$p_{\alpha }\notin \mathcal {A}$
, we may conclude that
$f_{\alpha }^{-1}\left ( p_{\alpha }\right ) \notin \mathcal {D}^{\bot }.$
Furthermore, since
$p_{\alpha }\in \mathcal {P}$
it follows that
$p_{\alpha }\in \mathcal {A}^{\perp }$
(recall that
$\mathcal {P}$
is an AD family). Hence
$p_{\alpha }\in \mathcal {A}^{\perp }$
but
$f_{\alpha }^{-1}\left ( p_{\alpha }\right ) \notin \mathcal {D}^{\bot },$
so
$f_{\alpha }$
is not a Rudin–Keisler morphism.
We will now show that
$f_{\alpha }(\mathcal {A}^{\perp })\neq \mathcal {B}^{\perp }$
for every
$\alpha \in W_{1}.$
There are two cases to be considered for a fixed
$\alpha \in W_{1}$
: First assume that
$D_{\alpha }\in \mathcal {B},$
this means that
$f_{\alpha }^{-1}\left ( D_{\alpha }\right ) \in \mathcal {A}^{\bot }$
but obviously
$D_{\alpha }\notin \mathcal {B}^{\perp }.$
In the second case, assume that
$D_{\alpha }\notin \mathcal {B}$
. So, by definition, we obtain that
$f_{\alpha }^{-1}\left ( D_{\alpha }\right ) \notin \mathcal {A}^{\bot }.$
Furthermore, since
$D_{\alpha }\in \mathcal {D}$
, then
$D_{\alpha }\in \mathcal {B}^{\perp }$
(recall that
$\mathcal {D}$
is an AD family). Hence,
$D_{\alpha }\in \mathcal {B}^{\perp }$
but
$f_{\alpha }^{-1}\left ( D_{\alpha }\right ) \notin \mathcal {A}^{\bot }$
. Therefore,
$f_{\alpha }(\mathcal {A}^{\perp })\neq \mathcal {B}^{\perp }$
for every
$\alpha \in W_{1}$
.⊣
We will now consider FU-ideals of the form
$\mathcal {I}\left (\mathcal {A}\right ) $
where
$\mathcal {A}$
is a nowhere
$\mathsf {MAD}$
family. The following is another open question from [Reference Garcia-Ferreira and Rivera-Gómez5, Question 4.6]:
Problem 3.6. Given a nowhere MAD family
$\mathcal {A}$
of size
$\mathfrak {c}$
, is there a FU-ideal that is RK-incomparable with
$\mathcal {I} \left ( \mathcal {A}\right ) $
?
To provide a positive answer to the previous question, we shall need the following concepts and four lemmas:
Definition 3.7. Let
$\mathcal {A}$
be an AD family of size
$\mathfrak {c}.$
-
1. We say an AD family
$\mathcal {B}\subseteq \left [ \omega \right ] ^{\omega }$
is a shrinking of
$\mathcal {A}$
if the following holds:-
(a) For every
$B\in \mathcal {B}$
there is
$A\in \mathcal {A}$
such that
$B\subseteq A.$
-
(b) Every element of
$\mathcal {A}$
contains at most one element of
$\mathcal {B}.$
-
-
2. Define
$\mathbb {S}\left ( \mathcal {A}\right ) $
as the set of all infinite shrinkings
$\mathcal {B}$
of
$\mathcal {A}$
such that
$\left \vert \mathcal {B}\right \vert <\mathfrak {c}$
. -
3. For
$\mathcal {B\in }\ \mathbb {S}\left ( \mathcal {A}\right ) $
, we define
$$ \begin{align*} \mathcal{I}_{\mathcal{A}}\left( \mathcal{B}\right) ^{+++}=\{X\subseteq \omega\mid\forall\mathcal{C}\in\mathbb{S}\left( \mathcal{A}\right) (\mathcal{B\subseteq C\longrightarrow} X\in\mathcal{I}\left( \mathcal{C}\right) ^{+})\}. \end{align*} $$
We will now prove the first lemma.
Lemma 3.8. Let
$\mathcal {A}$
be an AD family of size
$\mathfrak {c}\mathbf {\ }$
and
$\mathcal {B}\in \mathbb {S}\left ( \mathcal {A}\right ).$
-
1. If
$A\in \mathcal {A}$
is such that A does not contain an element of
$\mathcal {B}$
and
$X\in \left [ A\right ] ^{\omega }$
, then there is
$\mathcal {D}\in \mathbb {S}\left ( \mathcal {A}\right ) $
such that
$\mathcal {B\subseteq D}$
,
$\left \vert \mathcal {B}\right \vert =\left \vert \mathcal {D}\right \vert $
, and
$X\in \mathcal {I}_{\mathcal {A}}\left (\mathcal {D}\right ) ^{+++}.$
-
2. If
$X\in \mathcal {I}\left ( \mathcal {B}\right ) ^{+}$
, then there is
$\mathcal {D}\in \mathbb {S}\left ( \mathcal {A}\right ) $
such that
$\mathcal {B\subseteq D}$
,
$\left \vert \mathcal {B}\right \vert =\left \vert \mathcal {D}\right \vert $
, and
$X\in \mathcal {I}_{\mathcal {A}}\left (\mathcal {D}\right ) ^{+++}.$
Proof. For the first assertion, let
$D\in \left [ A\right ] ^{\omega }$
be such that
$X\diagdown D$
is infinite, then define
$\mathcal {D}=\mathcal {B}\cup \left \{ D\right \} .$
To prove (2) we consider two cases: First, assume that there is
$A\in \mathcal {A}$
such that
$A\cap X$
is infinite and A does not contain any element of
$\mathcal {B}$
and apply (1) to
$A\cap X.$
If
$A\cap X$
is finite for all
$A\in \mathcal {A}$
which do not contain any element of
$\mathcal {B}$
, then we have that
$X\in \mathcal {I}_{\mathcal {A}}\left ( \mathcal {B}\right ) ^{+++}$
.⊣
Our second lemma is the following.
Lemma 3.9. Let
$\mathcal {A}$
be an AD family of size
$\mathfrak {c}$
and
$\mathcal {B}\in \mathbb {S}\left ( \mathcal {A}\right ) .$
If
$\mathcal {C}$
is an AD family,
$f:\omega \longrightarrow \omega $
is a function, and
$A\in \mathcal {A}$
does not contain any element of
$\mathcal {B}$
, then there is
$\mathcal {D} \in \mathbb {S}\left ( \mathcal {A}\right ) $
such that
$\mathcal {B\subseteq D}$
,
$\left \vert \mathcal {B}\right \vert =\left \vert \mathcal {D}\right \vert $
, and one of the following conditions holds:
-
1.
$f^{-1}\left ( A\right ) \in \mathcal {I}\left ( \mathcal {C}\right ) $
and
$A\in \mathcal {I}_{\mathcal {A}}\left ( \mathcal {D}\right ) ^{+++}$
, or -
2.
$f^{-1}\left ( A\right ) \in \mathcal {I}\left ( \mathcal {C}\right ) ^{+} $
and
$A\in \mathcal {I}\left ( \mathcal {D}\right ) $
.
Proof. For point 1, suppose that
$f^{-1}\left ( A\right ) \in \mathcal {I}\left ( \mathcal {C}\right ) $
. According to Lemma 3.8(1), there is
$\mathcal {D} \in \mathbb {S}\left ( \mathcal {A}\right ) $
such that
$\mathcal {B\subseteq D}$
,
$\left \vert \mathcal {B}\right \vert =\left \vert \mathcal {D}\right \vert $
, and
$A\in \mathcal {I}_{\mathcal {A}}\left ( \mathcal {D}\right ) ^{+++}.$
For point 2, if
$f^{-1}\left ( A\right ) \in \mathcal {I}\left ( \mathcal {C}\right ) ^{+} $
, then define
$\mathcal {D}=\mathcal {B}\cup \left \{ A\right \} $
.⊣
The third lemma is the following:
Lemma 3.10. Let
$\mathcal {A}$
be an AD family of size
$\mathfrak {c}$
and
$\mathcal {B}\in \mathbb {S}\left ( \mathcal {A}\right ) $
. For every AD family
$\mathcal {C}$
of size
$\mathfrak {c}$
and for every function
$f:\omega \longrightarrow \omega $
there is
$\mathcal {D}\in \mathbb {S}\left ( \mathcal {A}\right ) $
such that
$\mathcal {B\subseteq D}$
,
$\left \vert \mathcal {B}\right \vert =\left \vert \mathcal {D}\right \vert $
, and one of the following conditions holds:
-
1. either there is
$X\in \mathcal {I}\left ( \mathcal {C}\right ) $
such that
$f^{-1}\left ( X\right ) \ \in \mathcal {I}_{\mathcal {A}}\left ( \mathcal {D} \right ) ^{+++} $
, or -
2. there is
$X\in \mathcal {I}\left ( \mathcal {C}\right ) ^{+}$
such that
$f^{-1}\left ( X\right ) \in \mathcal {I}\left ( \mathcal {D}\right ) .$
Proof. We start with point 1. In case that there is
$X\in \mathcal {C}$
such that
$f^{-1}\left ( X\right ) \in \mathcal {I}\left ( \mathcal {B}\right ) ^{+}$
, by Lemma 3.8 we find
$\mathcal {D}\in \mathbb {S}\left (\mathcal {A}\right ) $
such that
$\mathcal {B\subseteq D}$
,
$\left \vert \mathcal {B}\right \vert =\left \vert \mathcal {D}\right \vert $
, and
$f^{-1}\left (X\right ) \in \mathcal {I}_{\mathcal {A}}\left ( \mathcal {D}\right ) ^{+++}.$
For point 2, assume
$f^{-1}\left ( C\right ) \in \mathcal {I}\left ( \mathcal {B}\right ) $
for every
$C\in \mathcal {C}$
. We claim that we can define
$\mathcal {D=B}$
. For every
$C\in \mathcal {C}$
let
$F_{C}\in \left [ \mathcal {B}\right ] ^{<\omega }$
and
$s_{C}\in \left [ \omega \right ] ^{<\omega }$
such that
$f^{-1}\left ( C\right ) \subseteq {\textstyle \bigcup } F_{C}\cup s_{C}.$
Since
$\left \vert B\right \vert <\mathfrak {c}$
and
$\left \vert \mathcal {C}\right \vert =\mathfrak {c}$
there are
$F\in \left [ \mathcal {B}\right ] ^{<\omega }$
,
$s\in \left [ \omega \right ] ^{<\omega }$
, and
$\left \{ C_{n}\mid n<\omega \right \} \subseteq \mathcal {C}$
such that
$F=F_{C_{n}}$
,
$s=s_{C_{n}}$
for every
$n<\omega $
, and
$C_{n}\neq C_{m}$
whenever
$n\neq m.$
Note that if
$X= {\textstyle \bigcup } C_{n}$
then
$X\in \mathcal {I}\left ( \mathcal {C}\right ) ^{+}$
while
$f^{-1}\left ( X\right ) \in \ \mathcal {I}\left ( \mathcal {B}\right ) .$
⊣
The next lemma will be used in the proof of the two upcoming theorems.
Lemma 3.11. Let
$\mathcal {A}$
be a nowhere MAD family and
$\{\mathcal {B}_{\alpha }:\alpha <\mathfrak {c}\}$
a collection of AD families such that:
-
1.
$\mathcal {B}_{\alpha }\in \mathbb {S}(\mathcal {A})$
for each
$\alpha < \mathfrak {c}$
, and -
2.
$\mathcal {B}_{\alpha }\subseteq \mathcal {B}_{\beta }$
provided that
$\alpha < \beta < \mathfrak {c}$
.
Then,
$\bigcup _{\alpha <\mathfrak {c}}\mathcal {B}_{\alpha }$
is a nowhere MAD family.
Proof. Put
$\mathcal {B}:=\bigcup _{\alpha <\mathfrak {c}}\mathcal {B}_{\alpha }$
. It is evident that
$\mathcal {B}$
is an AD family. Now, fix
$X\in \mathcal {I}(\mathcal {B})^{+}$
. If
$X\in \mathcal {I}(\mathcal {A})^{+}$
, then there is
$Y\in \lbrack X]^{\omega }\cap \mathcal {A}^{\perp }$
and it is evident from (1) that
$Y\in \mathcal {B}^{\perp }$
. Suppose that
$X\in \mathcal {I} (\mathcal {A})$
. Then there is
$\{A_{0}.\ldots ,A_{l}\}\subseteq \mathcal {A}$
and
$F\in \lbrack \omega ]^{<\omega }$
such that
$X\subseteq F\cup \big (\bigcup _{i\leq l}A_{i}\big )$
. Since the set
$\mathcal {E}=\{B\in \mathcal {B}:\exists i\leq l\big (B\subseteq A_{i}\big )\}$
has size at most l, there exists
$\alpha <\mathfrak {c}$
such that
$\mathcal {E}\subseteq \mathcal {B}_{\alpha }$
and since
$\mathcal {B}_{\alpha }\in \mathbb {S}(\mathcal {A})$
and
$Y:=X\setminus \big (\bigcup _{B\in \mathcal {E}}B)$
is infinite, we must have that
$Y\in \lbrack X]^{\omega }\cap \mathcal {B}^{\perp }$
.⊣
We can now answer Question 3.6:
Theorem 3.12. If
$\mathcal {A}$
is a nowhere MAD family of size
$\mathfrak {c}$
, then there is a nowhere MAD family
$\mathcal {B}$
such that
$\mathcal {I} \left ( \mathcal {A}\right ) $
and
$\mathcal {I}\left ( \mathcal {B}\right ) $
are RK-incomparable.
Proof. Let
$\mathcal {A}$
be a nowhere MAD family of size
$\mathfrak {c}$
. Enumerate the set of all functions from
$\omega $
to
$\omega $
as
$\{ f_{\alpha }: \alpha < \mathfrak {c} \}$
. By using alternatively Lemmas 3.9 and 3.10, we inductively define a set
$\{ \mathcal {D}_{\alpha }^{i} : i < 2 \ \text {and} \ \alpha < \mathfrak {c} \}$
of AD families such that:
-
1.
$\mathcal {D}_{\alpha }^{i} \in \mathbb {S}\left ( \mathcal {A}\right ) $
for every
$i < 2$
and
$\alpha < \mathfrak {c}$
. -
2.
$\mathcal {D}_{\alpha }^{0}\subseteq \mathcal {D}_{\alpha }^{1}$
for every
$\alpha <\mathfrak {c}$
. -
3.
$\mathcal {D}_{\beta }^{i} \subseteq \mathcal {D}_{\alpha }^{0} $
provided that
$i < 2$
and
$\beta < \alpha < \mathfrak {c}$
. -
4.
$|\mathcal {D}_{\alpha }^{0}| < \mathfrak {c}$
for every
$\alpha < \mathfrak {c}$
. -
5. For every
$\alpha < \mathfrak {c}$
one of the following conditions holds:-
5.i) either there is
$X\in \mathcal {I}\left ( \mathcal {A}\right ) $
such that
$f_{\alpha }^{-1}\left ( X\right ) \ \in \mathcal {I}_{\mathcal {A}}\left ( \mathcal {D}_{\alpha }^{0}\right ) ^{+++} $
, or -
5.ii) there is
$X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+}$
such that
$f_{\alpha }^{-1}\left ( X\right ) \in \mathcal {I}\left ( \mathcal {D} _{\alpha }^{0}\right ) .$
-
-
6. For every
$\alpha < \mathfrak {c}$
one of the following conditions is satisfied:-
6.i) either there is
$X\in \mathcal {I}_{\mathcal {A}}\left ( \mathcal {D}_{\alpha }^{1}\right ) ^{+++}$
such that
$f_{\alpha }^{-1}\left ( X\right ) \in \mathcal {I(A)}$
, or -
6.ii) there is
$X\in \mathcal {I}\left ( \mathcal {D}_{\alpha }^{1}\right ) $
such that
$f_{\alpha }^{-1}\left ( X\right ) \in \mathcal {I(A)}^{+}.$
-
Finally, define
$\mathcal {B}=\bigcup _{\alpha <\mathfrak {c}}\mathcal {D}_{\alpha }^{1}$
. It follows from Lemma 3.11 that
$\mathcal {B}$
is a nowhere MAD family. By clauses 5.i) and 5.ii) we deduce that
$\mathcal {I} \left ( \mathcal {A}\right ) \not \leq _{{\textsf {RK}}}\mathcal {I}\left ( \mathcal {B}\right ) $
. Clauses 6.i) and 6.ii) guarantee that
$\mathcal {I} \left ( \mathcal {B}\right ) \not \leq _{{\textsf {RK}}}\mathcal {I}\left ( \mathcal {A}\right ) $
. It follows that
$\mathcal {I}\left ( \mathcal {A}\right ) $
and
$\mathcal {I}\left ( \mathcal {B}\right ) $
are RK incomparable.⊣
The following is another problem from [Reference Garcia-Ferreira and Rivera-Gómez6, Question 6.10]:
Problem 3.13. Is there an RK-antichain of size
$\mathfrak {c}$
consisting of FU-ideals?
This problem is answered as follows:
Theorem 3.14. There is a family
$\left \{ \mathcal {B}_{\alpha }\mid \alpha \in \mathfrak {c} \right \} $
of nowhere MAD families such that if
$\alpha ,\beta <\mathfrak {c}$
and
$\alpha \neq \beta $
, then
$\mathcal {I}\left (\mathcal {B}_{\alpha }\right ) $
and
$\mathcal {I}\left ( \mathcal {B}_{\beta }\right ) $
are RK-incomparable.
Proof. Let
$\{\mathcal {A}_{\alpha }\mid \alpha \in \mathfrak {c}\}$
be a familyFootnote
2
of nowhere MAD families, each one of size
$\mathfrak {c}.$
Let
$\mathcal {A}_{\alpha }=\{A_{\alpha }\left ( \xi \right ) \mid \xi \in \mathfrak {c}\}.$
We now define
$\mathbb {P}$
as the set of all p such that there is
$\beta _{p}<\mathfrak {c}$
with the following properties:
-
1. p is a function with domain contained in
$\beta _{p}.$
-
2. If
$\alpha \in dom\left ( p\right ) ,$
then
$p\left ( \alpha \right ) \in \mathbb {S}(\mathcal {A}_{\alpha })$
and
$\left \vert p\left ( \alpha \right ) \right \vert \leq \beta _{p}+\omega .$
Given
$p,q\in \mathbb {P},$
define
$p\leq q$
if the following conditions hold:
-
1.
$dom\left ( q\right ) \subseteq dom\left ( p\right ) .$
-
2. If
$\alpha \in dom\left ( q\right ) ,$
then
$q\left ( \alpha \right ) \subseteq p\left ( \alpha \right ) .$
We need the following notions:
-
1. Let
$\alpha ,\xi \in \mathfrak {c}.$
Define
$D_{\alpha }\left ( \xi \right ) $
as the set of all
$p\in \mathbb {P}$
such that:-
(a)
$\alpha \in dom\left ( p\right ) .$
-
(b) There is
$B\in p\left ( \alpha \right ) $
such that
$B\subseteq A_{\alpha }\left ( \xi \right ) .$
-
-
2. Let
$\alpha ,\gamma \in \mathfrak {c}$
with
$\alpha \neq \gamma $
and
$f\in \omega ^{\omega }.$
Define
$E\left ( \alpha ,\gamma ,f\right ) $
as the set of all
$p\in \mathbb {P}$
such that
$\alpha ,\gamma \in dom\left ( p\right ) $
and there is
$A\in \mathcal {A}_{\alpha }$
that satisfies one of the following conditions:-
(a)
$f^{-1}\left ( A\right ) \in \mathcal {I(}p(\gamma )\mathcal {)}$
and
$A\in \mathcal {I}_{\mathcal {A}_{\alpha }}(p\left ( \alpha \right ) )^{+++}$
, or -
(b)
$f^{-1}\left ( A\right ) \in \mathcal {I}_{\mathcal {A}_{\gamma }}(p\left ( \gamma \right ) )^{+++}$
and
$A\in \mathcal {I(}p\left ( \alpha \right ) \mathcal {)}.$
-
We now have the following:
Claim 3.15. Let
$q\in \mathbb {P}$
and W such that either
$W=D_{\alpha }\left ( \xi \right ) \ ($
for some
$\alpha ,\xi <\mathfrak {c})$
or
$W=E\left ( \alpha ,\gamma ,f\right )\ ($
for some
$\alpha ,\gamma <\mathfrak {c}$
and
$f\in \omega ^{\omega })$
. There is
$p\in \mathbb {P}$
with the following properties:
-
1.
$p\leq q.$
-
2.
$p\in W.$
-
3.
$\left \vert dom\left ( p\right ) \right \vert \leq \left \vert dom\left ( q\right ) \right \vert +\omega .$
-
4. If
$\eta \in dom\left ( q\right ) ,$
then
$\left \vert p\left (\eta \right ) \right \vert \leq \left \vert q\left ( \eta \right ) \right \vert +\omega .$
The claim is trivial in case
$W=D_{\alpha }\left ( \xi \right ) ,$
so we will focus on the case that
$W=E\left ( \alpha ,\gamma ,f\right ) .$
Let
$q\in \mathbb {P},$
we want to extend q to an element of
$E\left ( \alpha ,\gamma ,f\right ) .$
Without loss of generality, we may assume that
$\alpha ,\gamma \in dom\left ( q\right ) .$
Let
$A\in \mathcal {A}_{\alpha }$
such that A does not contain an element of
$q\left ( \alpha \right ) $
(such A exists since
$\left \vert \mathcal {A}_{\alpha }\right \vert =\mathfrak {c}$
, while
$\left \vert q\left ( \alpha \right ) \right \vert <\mathfrak {c}$
). We now apply Lemma 3.9 (with
$\mathcal {A=A}_{\alpha }$
,
$\mathcal {B}=q\left ( \alpha \right ) $
,
$\mathcal {C}=q\left ( \gamma \right ) $
,
$f=f$
, and
$A=A$
) in order to find
$\mathcal {D}\in \mathbb {S(}\mathcal {A}_{\alpha })$
such that
$q\left ( \alpha \right ) \subseteq \mathcal {D}$
,
$\left \vert \mathcal {D} \right \vert =\left \vert q\left ( \alpha \right ) \right \vert $
, and one of the following conditions holds:
-
1.
$f^{-1}\left ( A\right ) \in \mathcal {I(}q\left ( \gamma \right ) \mathcal {)}$
and
$A\in \mathcal {I}_{\mathcal {A}_{\alpha }}(\mathcal {D})^{+++}$
, or -
2.
$f^{-1}\left ( A\right ) \in \mathcal {I(}q\left ( \gamma \right ) \mathcal {)}^{+}$
and
$A\in \mathcal {I(D)}.$
Define
$p_{1}$
as follows:
-
1.
$dom\left ( p_{1}\right ) =dom\left ( q\right ) .$
-
2.
$p_{1}\left ( \alpha \right ) =\mathcal {D}$
. -
3. If
$\xi \in dom\left ( p_{1}\right ) $
and
$\xi \neq \alpha ,$
then
$p_{1}\left ( \xi \right ) =q\left ( \xi \right ) .$
It is clear that
$p_{1}\in \mathbb {P}$
and
$p_{1}\leq p.$
We have the following:
-
1.
$f^{-1}\left ( A\right ) \in \mathcal {I(}p_{1}\left ( \gamma \right ) \mathcal {)}$
and
$A\in \mathcal {I}_{\mathcal {A}_{\alpha }}(p_{1}\left ( \alpha \right ) )^{+++}$
, or -
2.
$f^{-1}\left ( A\right ) \in \mathcal {I(}p_{1}\left ( \gamma \right ) \mathcal {)}^{+}$
and
$A\in \mathcal {I(}p_{1}\left ( \alpha \right ) \mathcal {)}.$
If case 1 above holds, then
$p_{1}\in E\left ( \alpha ,\gamma ,f\right ) $
and we are done, so we will now assume that case 2 is the one that is true. We now apply the second point of Lemma 3.8 (with
$\mathcal {A=A}_{\gamma }$
,
$\mathcal {B}=p_{1}\left ( \gamma \right ) $
, and
$X=f^{-1}\left ( A\right ) $
) and find
$\mathcal {D}_{1}\in \mathbb {S(\mathcal {A}}_{\gamma }\mathbb {)}$
such that
$p_{1}\left ( \gamma \right ) \subseteq \mathcal {D}_{1}$
,
$\left \vert \mathcal {D}\right \vert =\left \vert p_{1}\left ( \gamma \right ) \right \vert $
, and
$f^{-1}\left ( A\right ) \in \mathcal {I}_{\mathcal {A}_{\gamma }} (\mathcal {D}_{1})^{+++}.$
Define
$p_{2}$
as follows:
-
1.
$dom\left ( p_{2}\right ) =dom\left ( p_{1}\right ) .$
-
2.
$p_{2}\left ( \gamma \right ) =\mathcal {D}_{1}$
. -
3. If
$\xi \in dom\left ( p_{2}\right ) $
and
$\xi \neq \gamma ,$
then
$p_{2}\left ( \xi \right ) =p_{1}\left ( \xi \right ) .$
It follows that
$f^{-1}\left ( A\right ) \in \mathcal {I}_{\mathcal {A}_{\gamma } }(p_{2}\left ( \gamma \right ) )^{+++}$
and
$A\in \mathcal {I(}p_{2}\left ( \alpha \right ) \mathcal {)},$
so
$p_{2}\in E\left ( \alpha ,\gamma ,f\right ) .$
This finishes the proof of the claim.
Now, with a careful bookkeeping, we can recursively build
$G=\{p_{\alpha } \mid \alpha <\mathfrak {c\}}\subseteq \mathbb {P}$
with the following properties:
-
1.
$p_{\alpha }\leq p_{\beta }$
whenever
$\beta <\alpha .$
-
2.
$G\cap D_{\alpha }\left ( \xi \right ) \neq \emptyset $
for every
$\alpha ,\xi <\mathfrak {c}.$
-
3.
$G\cap E\left ( \alpha ,\gamma ,f\right ) \neq \emptyset $
for every
$\alpha ,\gamma <\mathfrak {c}$
with
$\alpha \neq \gamma $
and
$f\in \omega ^{\omega }.$
For every
$\alpha <\mathfrak {c},$
define
$\mathcal {B}_{\alpha }= {\textstyle \bigcup } \{p\left ( \alpha \right ) \mid p\in G\}.$
Using Lemma 3.11, one sees that
$\{\mathcal {B}_{\alpha }\mid \alpha <\mathfrak {c}\}$
is a family of nowhere MAD families. Moreover,
$\mathcal {I}\left ( \mathcal {B}_{\alpha }\right ) $
and
$\mathcal {I}\left ( \mathcal {B}_{\beta }\right ) $
are RK-incomparable whenever
$\alpha \neq \beta .$
⊣
Now that we know that there is an RK-antichain of size
$\mathfrak {c}$
, it is natural to ask the following questions:
Problem 3.16. Is there an RK-antichain of size
$\mathfrak {c}^{+}$
consisting of FU ideals?
Problem 3.17. Is there a strictly increasing RK-chain of size
$\mathfrak {c}$
consisting of FU ideals?
The last question is related to Theorem 3.5:
Problem 3.18. Given two AD families
$\mathcal {A\ }$
and
$\mathcal {B},$
is there an AD family
$\mathcal {C}$
such that
$\mathcal {A}^{\perp } <_{{\textsf {RK}}}\mathcal {C}^{\perp }$
and
$\mathcal {B}^{\perp }<_{{\textsf {RK}}}\mathcal {C}^{\perp }$
?
4 The hyperspace of convergent sequences
If X is a Fréchet–Urysohn space, the nontrivial convergentFootnote
3
sequences in X carry a lot of information on the topological properties of X. Obviously a nontrivial convergent sequence is a closed subspace of
$X,$
so we can view the set of nontrivial convergent sequences of X as a subspace of its hyperspace of compact sets (equipped with the Vietoris topology).
For the convenience of the reader, we will review the basics of hyperspaces and the Vietoris topology. Let X be a topological space; by
$\mathcal {K} \left ( X\right ) $
we denote the set of all non-empty compact subspaces of
$X.$
Let
$U\subseteq X$
be a non-empty open set. Define:
$$ \begin{align*} \begin{array}{c} U^{+}=\{K\in\mathcal{K}(X)\mid K\subseteq U\},\\ U^{-}=\{K\in\mathcal{K}(X)\mid K\cap U\neq\emptyset\}.\\ \end{array} \end{align*} $$
The Vietoris topology is the topology on
$\mathcal {K}(X)$
generated by the sets of the form
$U^{+}$
and
$U^{-}$
(where U is a non-empty open set). We now introduce the most important notion of the section:
Definition 4.1. Let X be a topological space. By
$\mathcal {S}_{c}\left ( X\right ) $
we denote the set of all nontrivial sequences of
$X.$
Since
$\mathcal {S}_{c}\left ( X\right ) $
is a subset of
$\mathcal {K(} X\mathcal {)},$
we endow
$\mathcal {S}_{c}\left ( X\right ) $
with the subspace topology inherited by
$\mathcal {K}\left ( X\right ) .$
The reader wishing to know more about subspaces of convergent sequences may consult [Reference Garcia-Ferreira and Ortiz-Castillo4], [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7], and [Reference Poplawski18]. In this section, we will characterize the Fréchet filters for which the subspace of nontrivial convergent sequences is Baire, answering a question asked in [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7].
Let X be a Fréchet–Urysohn space that has a dense set D of isolated points. The topological game
$GS(X,\beta ,\alpha )$
introduced in [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7] is defined as follows:
Players
$\alpha $
and
$\beta $
will take turns choosing a pair
$(E,W)$
consisting of a non-empty finite subset E of D and a nondiscrete open subset W disjoint from E as follows: Player
$\beta $
goes first by choosing a pair
$(F_{0},U_{0})$
consisting of a non-empty finite subset
$F_{0}$
of D and a nondiscrete open subset
$U_{0}$
disjoint from
$F_{0}$
. Then player
$\alpha $
chooses a pair
$(G_{0},V_{0})$
such that
$G_{0}$
is a non-empty finite subset
$G_{0}\subseteq U_{0}\cap D$
and a nondiscrete open subset
$V_{0}$
contained in
$U_{0}$
and missing
$G_{0}$
and so on as it is shown in the diagram
where the following holds for every
$n\in \omega $
:
-
1.
$F_{n},G_{n}\in \left [ D\right ] ^{<\omega }$
and
$F_{n}\neq \emptyset \neq G_{n}.$
-
2.
$U_{n},V_{n}\subseteq X$
are nondiscrete open sets. -
3.
$F_{n}\cap U_{n}=\emptyset = G_{n}\cap V_{n}.$
-
4.
$G_{n}\cup V_{n}\subseteq U_{n}.$
-
5.
$F_{n+1}\cup U_{n+1}\subseteq V_{n}.$
We declare that player
$\alpha $
wins the match if the countable set
$\bigcup _{n<\omega }(F_{n}\cup G_{n})$
converges to some point of X. Otherwise, we say that player
$\beta $
wins. We will use the following Theorem:
Theorem 4.2 (García-Ferreira and Rojas-Hernández [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo8])
If X is a Fréchet–Urysohn nondiscrete space, then the hyperspace
$\mathcal {S}_{c}(X)$
is Baire if and only if X has a dense set of isolated points D and the space X does not admit a winning strategy for player
$\beta $
in the game
$GS(X,\beta ,\alpha )$
.
Let
$\mathcal {F}$
be a filter on
$\omega .$
To simplify our combinatorial arguments, we redefine the game
$GS(\xi (\mathcal {F}),\beta ,\alpha )$
as follows:
where the following holds for every
$n\in \omega $
:
-
1.
$s_{n},t_{n}\in \left [ \omega \right ] ^{<\omega }$
and
$s_{n} \neq \emptyset \neq t_{n}.$
-
2.
$F_{n},G_{n}\in \mathcal {F}.$
-
3.
$s_{n}\cap F_{n}=\emptyset = t_{n}\cap G_{n}$
. -
4.
$t_{n}\cup G_{n}\subseteq F_{n}.$
-
5.
$s_{n+1}\cup F_{n+1}\subseteq G_{n}.$
We will say that player
$\alpha $
wins the match if
$\bigcup _{n<\omega }\left ( s_{n}\cup t_{n}\right ) $
is a pseudointersection of
$\mathcal {F}.$
For convenience, the game
$GS(\xi (\mathcal {F}),\beta ,\alpha )$
will be simply denoted by
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
. We get the following corollary from Theorem 4.2.
Corollary 4.3. Let
$\mathcal {F}$
be a Fréchet filter on
$\omega .$
The following are equivalent:
-
1.
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $
is Baire. -
2. Player
$\beta $
does not have a winning strategy in the game
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
In order to study the categorical properties of the space
$\mathcal {\xi }\left ( \mathcal {F}\right ) $
, we will need the following notion:
Definition 4.4. Given
$A\in \wp \left ( \omega \right ) ,$
define
$\left [ A\right ] _{+}^{<\omega }=\left [ A\right ] ^{<\omega }\setminus \left \{ \emptyset \right \} .$
For a filter
$\mathcal {F}$
on
$\omega $
, we define the filter
$\mathcal {F}^{<\omega }$
on
$\left [ \omega \right ] _{+}^{<\omega }$
as the filter generated by
$\left \{ \left [ A\right ] _{+}^{<\omega }:A\in \mathcal {F}\right \} .$
It is easy to see that
$X\in \left ( \mathcal {F}^{<\omega }\right ) ^{+}$
if and only if for every
$A\in \mathcal {F}$
, there is
$s\in X$
such that
$s\subseteq A.$
In the same way as with
$\mathcal {F},$
we define the topological space
$\xi (\mathcal {F}^{<\omega })$
(whose underlying set is
$\left [ \omega \right ] _{+}^{<\omega }\cup \left \{ \mathcal {F}^{<\omega }\right \} $
). We also have the following simple remark:
Lemma 4.5. Let
$\mathcal {F}$
be a filter on
$\omega $
and
$Y=\left \{ s_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] _{+}^{<\omega }$
a family of pairwise disjoint sets. The following are equivalent:
-
1. Y is a pseudointersection of
$\mathcal {F}^{<\omega }.$
-
2.
$\bigcup Y$
is a pseudointersection of
$\mathcal {F}.$
Proof.
$(1)\Rightarrow (2)$
. Assume that Y is a pseudointersection of
$\mathcal {F} ^{<\omega }$
and fix
$A\in \mathcal {F}$
. Since
$\left [ A\right ] _{+}^{<\omega }\in \mathcal {F}^{<\omega },$
we know that
$Y\subseteq ^{\ast }\left [ A\right ] ^{<\omega }.$
Let
$n<\omega $
such that
$s_{m}\subseteq A$
for every
$m>n.$
It follows that
$\bigcup \limits _{n<m<\omega }s_{m}\subseteq A,$
so
$\bigcup Y$
is almost contained in
$A.$
$(2) \Rightarrow (1)$
. Suppose that
$\bigcup Y$
is a pseudointersection of
$\mathcal {F}$
and fix
$A\in \mathcal {F}.$
Since
$\bigcup Y$
is a pseudointersection of
$\mathcal {F},$
we know that
$\bigcup Y\subseteq ^{\ast }A $
and since Y consists of pairwise disjoint sets, it follows that there is
$n < \omega $
such that
$s_{m}\subseteq B$
for every
$m>n,$
which implies that
$Y\subseteq ^{\ast }\left [ A\right ] ^{<\omega }.$
⊣
It turns out, that in the case for filters, the previously defined game can be greatly simplified. Let
$\mathcal {F}$
be a filter on
$\omega ;$
the game
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
is defined as follows:
where the following conditions hold for every
$n<\omega $
:
-
1.
$s_{0}$
is a finite subset of
$\omega .$
-
2.
$\emptyset \neq s_{n+1}\in \left [ G_{n}\right ] ^{<\omega }$
. -
3.
$G_{n}\in \mathcal {F}.$
-
4.
$G_{n+1}\subseteq G_{n}.$
-
5.
$s_{n}\cap G_{n}=\emptyset .$
We will say that player
$\alpha $
wins the match if
$ {\textstyle \bigcup \limits _{n\in \omega }} s_{n}$
is a pseudointersection of
$\mathcal {F}.$
Note that
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
is a simplified version of the game
$GS\left ( \mathcal {F},\beta ,\alpha \right ) ;$
player
$\beta $
does not need to play filter sets and player
$\alpha $
no longer needs to play finite sets.
We will need another game, which was introduced by G. Gruenhage in his dissertation (see [Reference Gruenhage10, Reference Gruenhage11]). Let X be a topological space and
$a\in X.$
The Gruenhage game
$\mathcal {H}\left ( X,a\right ) $
is played between the players Open and Point as follows:
where
$U_{n}\subseteq X$
is an open neighborhood of a and
$b_{n}\in U_{n}$
for every
$n\in \omega $
. We will say that the Open player wins the game if the sequence
$\left \langle b_{n}\right \rangle _{n<\omega }$
converges to
$a.$
We shall prove that, in a natural sense, the games
$GS\left ( \mathcal {F},\beta ,\alpha ,\right ) $
,
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha ,\right ) $
, and
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })$
are equivalent.
Theorem 4.6. Let
$\mathcal {F}$
be a FU-filter on
$\omega .$
-
1. The following are equivalent:
-
(a) Player
$\beta $
has a winning strategy in
$GS\left ( \mathcal {F} ,\beta ,\alpha ,\right ) .$
-
(b) Player
$\beta $
has a winning strategy in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
(c) The Point player has a winning strategy in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
-
-
2. The following are equivalent:
-
(a) Player
$\alpha $
has a winning strategy in
$GS\left ( \mathcal {F} ,\beta ,\alpha \right ) .$
-
(b) Player
$\alpha $
has a winning strategy in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
(c) The Open player has a winning strategy in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
-
Proof. (1) (a)
$\Rightarrow $
(b). First, assume that
$\sigma $
is a winning strategy for player
$\beta $
in the game
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
. We shall define a winning strategy
$\pi $
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
. Since
$\mathcal {F}$
is a FU-filter, we may fix a pseudointersection A of
$\mathcal {F}$
and for every
$F\in \mathcal {F}$
we let
$a^{F}$
be the first element of
$F\cap A.$
Let us define the strategy
$\pi $
for player
$\beta $
in the game
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
While playing a match in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) ,$
player
$\beta $
will be secretly imagining a match of
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
in which he is using his strategy
$\sigma .$
The match in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
is played as follows:
-
• Let
$\sigma \left ( \emptyset \right ) =\left ( s_{0} ,F_{0}\right ) $
be the first move of player
$\beta $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
(according to
$\sigma $
). Player
$\beta $
will play
$s_{0}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
• Assume that player
$\alpha $
plays
$G_{0}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
Let
$H_{0}=G_{0}\cap F_{0}$
and player
$\beta $
pretends that player
$\alpha $
played
$\left ( a^{H_{0} },H_{0}\right ) ;$
let
$\left ( s_{1},F_{1}\right ) $
be his response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
(following
$\sigma $
). Now, player
$\beta $
plays
$s_{1}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
• Suppose that player
$\alpha $
plays
$G_{1}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
Let
$H_{1}=G_{1}\cap F_{1}$
and player
$\beta $
pretends that player
$\alpha $
played
$\left ( a^{H_{1} },H_{1}\right ) ;$
let
$\left ( s_{2},F_{2}\right ) $
be his response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
. Now, player
$\beta $
plays
$s_{2}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
⋮
$\ \ \vdots $
$GS\left ( \mathcal {F},\beta ,\alpha \right ) :$
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ):$
We claim that player
$\beta $
won the match in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
In other words, we need to show that
$Y=\bigcup s_{n}$
is not a pseudointersection of
$\mathcal {F}.$
Indeed, set
$Z=Y\cup \left \{ a^{H_{n}}\mid n<\omega \right \} $
and note that Z is the outcome of the match in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
simulated by player
$\beta $
. Since
$\sigma $
is a winning strategy, it follows that Z is not a pseudointersection of
$\mathcal {F}.$
Since
$Z\subseteq Y\cup A$
and the union of two pseudointersections is a pseudointersection, it follows that Y is not a pseudointersection of
$\mathcal {F},$
so player
$\beta $
won the match.
(1) (b)
$\Rightarrow $
(c). Assume that player
$\beta $
has a winning strategy in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
. We shall show that the Point player has a winning strategy in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
In fact, the proof is very simple, the idea is that the points in
$\xi (\mathcal {F}^{<\omega })\setminus \{\mathcal {F}^{<\omega }\}$
are precisely the non-empty finite subsets of
$\omega .$
Let
$\sigma $
be a winning strategy for player
$\beta $
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
We shall define a strategy
$\pi $
for the Point player in the game
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
While playing a match in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }),$
the Point player will be secretly simulating a match of
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
in which he is playing as player
$\beta $
using the strategy
$\sigma .$
The match in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })$
is played as follows:
-
• Assume the Open player plays
$\left [ G_{0}\right ] _{+}^{<\omega }$
as its first move in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
Let
$s_{0}$
be the first move of player
$\beta $
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
(according to
$\sigma $
). The Point player imagines player
$\alpha $
played
$G_{0}\setminus s_{0}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) ;$
let
$s_{1}$
be the response of player
$\beta $
. The Point player plays
$s_{1}$
in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
-
• Assume the Open player now plays
$\left [ G_{1}\right ] _{+}^{<\omega }$
as its response
$.$
The Point player imagines player
$\alpha $
played
$G_{1}\setminus s_{1}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) ;$
let
$s_{2}$
be the response of player
$\beta $
. The Point player plays
$s_{2}$
in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
-
⋮
$\ \ \vdots $
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }):$
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) :$
We claim that the Point player won the match in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
In other words, we need to show that
$Y=\left \{ s_{n}\mid n < \omega \right \} $
is not a pseudointersection of
$\left [ \mathcal {F}\right ] ^{<\omega }.$
Indeed, since
$\sigma $
is a winning strategy, it follows that player
$\beta $
won the simulated game of
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) ,$
which means that
$\bigcup \limits _{n < \omega }s_{n}$
is not a pseudointersection of
$\mathcal {F}.$
By Lemma 4.5, it follows that Y is not a pseudointersection of
$\left [ \mathcal {F}\right ] ^{<\omega }$
.
(1) (c)
$\Rightarrow $
(a). Now, assume that
$\sigma $
is a winning strategy for the Point player in the game
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })$
. We have to prove that player
$\beta $
has a winning strategy in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
We will define a strategy
$\pi $
for player
$\beta $
in the game
$GS\left ( \mathcal {F} ,\beta ,\alpha \right ) .$
While playing a match in
$GS\left ( \mathcal {F} ,\beta ,\alpha \right ) ,$
player
$\beta $
will be secretly simulating a match of
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })$
in which it is playing as the Point player using the strategy
$\sigma .$
The match in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
is played as follows:
-
• Player
$\beta $
starts by imagining that the Open player plays
$\left [ \omega \right ] _{+}^{<\omega }$
as its first move in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
Let
$s_{0}$
be the first move of the Point player in
$\mathcal {H}(\xi (\mathcal {F} ^{<\omega }),\mathcal {F}^{<\omega })$
(according to
$\sigma $
). Now, player
$\beta $
plays
$\left ( s_{0},\omega \setminus s_{0}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
• Assume player
$\alpha $
plays
$\left ( t_{0},G_{0}\right ) $
as its response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
. Player
$\beta $
imagines that the Open player played
$\left [ G_{0}\right ] _{+}^{<\omega }$
in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F} ^{<\omega })\mathsf {.}$
Let
$s_{1}$
be the response of the Point player in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })\mathsf {.}$
Then player
$\beta $
plays
$\left ( s_{1},G_{0}\setminus s_{1}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
• Assume player
$\alpha $
plays
$\left ( t_{1},G_{1}\right ) $
as its response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
Player
$\beta $
imagines that the Open player played
$\left [ G_{1}\right ] _{+}^{<\omega }$
in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F} ^{<\omega })\mathsf {.}$
Let
$s_{2}$
be the response of the Point player in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })\mathsf {.}$
Then player
$\beta $
plays
$\left ( s_{2},G_{1}\setminus s_{2}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
⋮
$\ \ \vdots $
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }):$
$GS\left ( \mathcal {F},\beta ,\alpha \right ) :$
We claim that player
$\beta $
won the match in
$GS\left ( \mathcal {F} ,\beta ,\alpha \right ) $
. In other words, we need to show that
$\bigcup \limits _{n< \omega }\left ( s_{n}\cup t_{n}\right ) $
is not a pseudointersection of
$\mathcal {F}. $
Since
$\sigma $
is a winning strategy, it follows that the Point player won the simulated game of
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }),$
which means that
$Y=\left \{ s_{n}\mid n < \omega \right \} $
is not a converging sequence to
$\mathcal {F}^{<\omega }.$
This means that Y is not a pseudointersection of
$\mathcal {F} ^{<\omega }.$
By Lemma 4.5, it follows that
$\bigcup Y$
is not a pseudointersection of
$\mathcal {F}$
; in particular,
$\bigcup \limits _{n < \omega }\left ( s_{n}\cup t_{n}\right ) $
is not a pseudointersection of
$\mathcal {F}.$
This finishes the proof of the first part of the proposition.
(2) (a)
$\Rightarrow $
(b). Now, suppose that
$\sigma $
is a winning strategy for player
$\alpha $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
. We need to define a strategy
$\pi $
for player
$\alpha $
in the game
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
While playing a match in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) ,$
player
$\alpha $
will secretly imagine a match of
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
in which it is using its strategy
$\sigma .$
The match in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
is played as follows:
-
• Let
$s_{0}$
be the first move of player
$\beta $
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
. Player
$\alpha $
imagines that player
$\beta $
played
$\left ( s_{0},\omega \setminus s_{0}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
Let
$\left ( t_{0},G_{0}\right ) $
be its response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
(according to
$\sigma $
). Now, player
$\alpha $
plays
$G_{0}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
• Let
$s_{1}$
be the next move of player
$\beta $
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
. Player
$\alpha $
imagines that player
$\beta $
played
$\left ( s_{1},G_{0}\setminus s_{1}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
Let
$\left ( t_{1},G_{1}\right ) $
be its response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
. Now, player
$\alpha $
plays
$G_{1}$
in
$\overline {GS}(\mathcal {F},\beta ,\alpha ).$
-
⋮
$\ \ \vdots $
$GS\left ( \mathcal {F},\beta ,\alpha \right ) :$
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) :$
We claim that player
$\alpha $
won the match in
$\overline {GS} (\mathcal {F},\beta ,\alpha ).$
We need to show that
$Y=\bigcup s_{n}$
is a pseudointersection of
$\mathcal {F}.$
Since
$\sigma $
is a winning strategy, it follows that
$\bigcup \limits _{n<\omega }\left ( s_{n}\cup t_{n}\right ) $
is a pseudointersection of
$\mathcal {F},$
so clearly Y is also a pseudointersection.
2. (b)
$\Rightarrow $
(c). Assume that
$\sigma $
is a winning strategy for player
$\alpha $
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
We shall show that the Open player has a winning strategy in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
We will define a strategy
$\pi $
for the Open player in the game
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
While playing a match in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }),$
the Open player will be secretly playing a match of
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
in which it is playing as player
$\alpha $
using the strategy
$\sigma .$
The match in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })$
is played as follows:
-
• The Open player imagines that player
$\beta $
played
$s_{0}=\left \{ 0\right \} $
as its first move in
$\overline {GS} (\mathcal {F},\beta ,\alpha ).$
Let
$s_{0}$
be the first move of player
$\beta $
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) $
. Let
$G_{0}$
be the response of player
$\alpha $
in
$\overline {GS}(\mathcal {F},\beta ,\alpha )$
(following
$\sigma $
). The Open player plays
$\left [ G_{0}\right ] _{+}^{<\omega }$
in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F} ^{<\omega }).$
-
• Assume the Point player plays
$s_{1}$
as its response
$.$
Then the Open player imagines that player
$\beta $
played
$s_{1}$
in
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
Let
$G_{1}$
be the response of player
$\alpha $
. The Open player plays
$\left [ G_{1}\right ] ^{<\omega }$
in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
-
⋮
$\ \ \vdots $
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }):$
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) :$
We claim that the Open player won the match in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
We will show that
$Y = \left \{ s_{n}\mid n < \omega \right \} $
is a pseudointersection of
$\mathcal {F}^{<\omega }.$
Since
$\sigma $
is a winning strategy, we know that player
$\alpha $
won the simulated game of
$\overline {GS}\left ( \mathcal {F} ,\beta ,\alpha \right ) ,$
which means that
$\bigcup \limits _{n < \omega }s_{n}$
is a pseudointersection of
$\mathcal {F}.$
By Lemma 4.5, it follows that Y is a pseudointersection of
$\left [ \mathcal {F}\right ] ^{<\omega }$
.
2. (c)
$\Rightarrow $
(a). Finally, assume that
$\sigma $
is a winning strategy for the Open player in the game
$\mathcal {H}(\xi (\mathcal {F} ^{<\omega }),\mathcal {F}^{<\omega })$
. We shall define a winning strategy
$\pi $
for player
$\alpha $
in the game
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
While playing a match in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) ,$
player
$\alpha $
will be secretly simulating a match of
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })$
in which it is playing as the Open player using the strategy
$\sigma .$
Since
$\mathcal {F}$
is a FU-filter, we can find A a pseudointersection of
$\mathcal {F}.$
Given
$F\in \mathcal {F},$
let
$t^{F}=\left \{ \min \left ( F\cap A\right ) \right \} .$
The match in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
is played as follows:
-
• Assume player
$\beta $
plays
$\left ( s_{0},F_{0}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
Let
$\left [ K_{0}\right ] _{+}^{<\omega }$
be the first move of the Open player in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
Let
$b_{0}=\left \{ \min \left ( K_{0}\right ) \right \} ;$
now, player
$\alpha $
imagines that the Point player plays
$b_{0}$
as its first move in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
Let
$\left [ K_{1}\right ] _{+}^{<\omega }$
be the next move of the Open player in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })$
. Let
$G_{0}=\left ( F_{0}\cap K_{1}\right ) \setminus s_{0}.$
Player
$\alpha $
plays
$\left ( t^{G_{0}},G_{0}\right ) $
as its first move in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
• Assume player
$\beta $
plays
$\left ( s_{1},F_{1}\right ) $
as his response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
Player
$\alpha $
imagines that the Point player played
$s_{1}$
in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
Let
$\left [ K_{2}\right ] _{+}^{<\omega }$
be the response of the Open player in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })\mathsf {.}$
Let
$G_{1}=\left ( F_{1}\cap K_{2}\right ) \setminus s_{1}.$
Player
$\alpha $
plays
$\left ( t^{G_{1}},G_{1}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ). $
-
• Assume player
$\beta $
plays
$\left ( s_{2},F_{2}\right ) $
as its response in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) $
. Player
$\alpha $
imagines that the Point player played
$s_{2}$
in
$\mathcal {H} (\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }).$
Let
$\left [ K_{3}\right ] _{+}^{<\omega }$
be the response of the Open player in
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega })\mathsf {.}$
Let
$G_{2}=\left ( F_{2}\cap K_{3}\right ) \setminus s_{2}.$
Player
$\alpha $
plays
$\left ( t^{G_{2}},G_{2}\right ) $
in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
-
⋮
$\ \ \vdots $
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }):$
$GS\left ( \mathcal {F},\beta ,\alpha \right ):$
We claim that player
$\alpha $
won the match in
$GS\left ( \mathcal {F} ,\beta ,\alpha \right ) .$
We need to show that
$\bigcup \limits _{n < \omega }\left ( s_{n}\cup t^{G_{n}}\right ) $
is a pseudointersection of
$\mathcal {F}.$
By definition, we know that
$\bigcup \limits _{n < \omega }t^{G_{n}}$
is a pseudointersection of
$\mathcal {F},$
so we only need to show that
$\bigcup \limits _{n < \omega }s_{n}$
is also a pseudointersection. Since
$\sigma $
is a winning strategy, it follows that the Open player won the simulated game of
$\mathcal {H}(\xi (\mathcal {F}^{<\omega }),\mathcal {F} ^{<\omega }),$
which means that
$Y=\left \{ s_{n}\mid n < \omega \right \} $
is a converging sequence to
$\mathcal {F}^{<\omega }.$
Hence, we have that Y is a pseudointersection of
$\left [ \mathcal {F}\right ] ^{<\omega }.$
By Lemma 4.5, it follows that
$\bigcup Y=\bigcup \limits _{n < \omega }s_{n}$
is a pseudointersection of
$\mathcal {F}$
and we are done.⊣
The following definition is due to G. Gruenhage [Reference Gruenhage10]:
Definition 4.7. Let X be a topological space. We say that X is a W-space if for every
$a\in X,$
the Open player has a winning strategy in the game
$\mathcal {H}\left ( X,a\right ).$
Regarding this important class of spaces, the following facts are known:
Proposition 4.8 (Gruenhage [Reference Gruenhage10]; see also [Reference Gruenhage11])
Let X be a topological space.
-
1. If X is first countable, then X is a W-space.
-
2. If X is a separable W-space, then X is first countable. Therefore, the notions of first countable and W-space coincide in the realm of separable spaces.
The reader may consult [Reference Gruenhage10] and [Reference Gruenhage11] to learn more about W-spaces and other topological games.
Definition 4.9. Let
$\mathcal {F}$
be a filter on
$\omega .$
We say that
$\mathcal {F}$
is countably generated if it has a countable base. That is, there is a countable family
$\mathcal {B}=\left \{ B_{n}\mid n\in \omega \right \} \subseteq \mathcal {F}$
such that for every
$F\in \mathcal {F},$
there is
$n < \omega $
such that
$B_{n}\subseteq F.$
Notice that
$\mathcal {F}$
is countably generated if and only if the space
$\xi \left ( \mathcal {F}\right ) $
is first countable.
Lemma 4.10. Let
$\mathcal {F}$
be a filter on
$\omega .$
The following are equivalent:
-
1.
$\mathcal {F}$
is countably generated. -
2.
$\mathcal {F}^{<\omega }$
is countably generated.
Proof. Let
$\mathcal {B}$
be a subfamily of
$\mathcal {F}.$
It is easy to see that
$\mathcal {B}$
is a base of
$\mathcal {F}$
if and only if
$\left \{ \left [ B\right ] _{+}^{<\omega }\mid B\in \mathcal {B}\right \} $
is a base of
$\mathcal {F}^{<\omega }.$
It follows that if
$\mathcal {F}$
is countably generated, then
$\mathcal {F}^{<\omega }$
is countably generated.
For the other implication, assume that
$\mathcal {F}^{<\omega }$
is countably generated. Let
$\left \{ X_{n}\mid n\in \omega \right \} $
be a base for
$\mathcal {F}^{<\omega }.$
Since
$\mathcal {F}^{<\omega }$
is generated by
$\left \{ \left [ A\right ] _{+}^{<\omega }:A\in \mathcal {F}\right \} ,$
for every
$n\in \omega $
we can find
$A_{n}\in \mathcal {F}$
such that
$\left [ A_{n}\right ] _{+}^{<\omega }\subseteq X_{n}.$
In this way,
$\{\left [ A_{n}\right ] _{+}^{<\omega }\mid n\in \omega \}$
is a base of
$\mathcal {F} ^{<\omega },$
which implies that
$\left \{ A_{n}\mid n\in \omega \right \} $
is a base of
$\mathcal {F}$
.⊣
We can now prove the following:
Theorem 4.11. For a FU-filter
$\mathcal {F}$
on
$\omega $
the following are equivalent:
-
1.
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $
is homeomorphic to
$\omega ^{\omega }.$
-
2.
$\mathcal {F}$
is countably generated. -
3.
$\xi \left ( \mathcal {F}^{<\omega }\right ) $
is a W-space. -
4. Player
$\alpha $
has a winning strategy for the game
$GS\left (\mathcal {F},\beta ,\alpha \right ) .$
Proof. The equivalence between (1) and (2) was proved in Theorem 2.2 of [Reference Garcia-Ferreira, Rojas-Hernández and Ortiz-Castillo7]. Note that
$\xi \left ( \mathcal {F}^{<\omega }\right ) $
is a W-space if and only if the Open player has a winning strategy in
$\mathcal {H(}\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }\mathcal {)}$
(this is because any other point in
$\xi (\mathcal {F}^{<\omega })$
is isolated). From this remark and Theorem 4.6(2) it follows that clauses (3) and (4) are equivalent. In order to prove that (2) is equivalent to (3), by Lemma 4.10, we know that
$\mathcal {F}$
is countably generated if and only if is
$\mathcal {F}^{<\omega }$
countably generated and by Proposition 4.8, this holds if and only if
$\xi \left ( \mathcal {F}^{<\omega }\right ) $
is a W-space.⊣
The previous results provide more characterizations of the filters in which player
$\alpha $
has a winning strategy in the game
$GS\left ( \mathcal {F},\beta ,\alpha \right )$
. In the sequel, we will provide a characterization of the filters for which the hyperspace
$\mathcal {S}_{c}\left ( \xi \left (\mathcal {F}\right ) \right ) $
is Baire (Problem 1.2). We shall need the following kinds of filters:
Definition 4.12. A filter
$\mathcal {F}$
on
$\omega $
is said to be a FUF
-filterif for every
$X\in \left ( \mathcal {F}^{<\omega }\right ) ^{+},$
there is
$\left \{ s_{n}\mid n\in \omega \right \} \subseteq X$
such that whenever
$F\in \mathcal {F},$
there is
$n < \omega $
such that
$s_{m}\subseteq F$
for every
$m\geq n.$
It is easy to see that every countably generated filter is a FUF-filter and every FUF-filter is a FU-filter. We deduce from the definition that a filter
$\mathcal {F}$
is a FUF-filter if and only if
$\mathcal {F}^{<\omega }$
is a FU-filter. For convenience, we will denote by
$P\left ( \mathcal {F}\right ) $
the set of all
$Y=\left \{ s_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] _{+}^{<\omega }$
such that whenever
$F\in \mathcal {F},$
there is
$n<\omega $
such that
$s_{m}\subseteq F$
for every
$m\geq n.$
The elements of
$P(\mathcal {F})$
are the pseudointersections of
$\mathcal {F}^{<\omega }$
or equivalently the sequences in
$\left [ \omega \right ] _{+}^{<\omega }$
that converge to
$\mathcal {F}^{<\omega }$
in the space
$\xi (\mathcal {F}^{<\omega }).$
When
$Y=\left \langle s_{n}\right \rangle _{n\in \omega }$
is a sequence of elements of
$\left [ \omega \right ] _{+}^{<\omega },$
we will often abuse notation and write
$Y\in P(\mathcal {F})$
to mean
$\left \{ s_{n}\mid n\in \omega \right \} \in P(\mathcal {F}).$
We need the following result, which is a particular of a theorem of G. Gruenhage and P. J. Szeptycki [Reference Gruenhage and Szeptycki12, Theorem 17].
Theorem 4.13 (Gruenhage and Szeptycki [Reference Gruenhage and Szeptycki12])
Let
$\mathcal {F}$
be a FU-filterFootnote
4
on
$\omega .$
The following are equivalent:
-
1.
$\mathcal {F}$
is a FUF-filter. -
2. For every family
$\left \{ X_{n}\mid n < \omega \right \} \subseteq \left ( \mathcal {F}^{<\omega }\right ) ^{+},$
there is
$s_{n}\in X_{n}$
such that
$\left \{ s_{n}\mid n\in \omega \right \} \in P\left ( \mathcal {F} \right ). $
The reader may note that the statements of [Reference Gruenhage and Szeptycki12, Theorem 17] and of Theorem 4.13 look quite different. For the convenience of the reader, we will explain how to derive the latter from the former. We need the following notions:
Definition 4.14. Let X be a topological space,
$A\subseteq \left [ X\right ] ^{<\omega }$
, and
$a\in X.$
-
1. We say that A converges to
$a \ ($
denoted by
$A\longrightarrow a)$
if for every
$U\subseteq X$
open neighborhood of
$a,$
the set
$\left \{ s\in A\mid s\nsubseteq U\right \} $
is finite. -
2. We say that A is a
$\pi $
-network at
$a \ ($
or
$\pi $
-net at
$a)$
if for every
$U\subseteq X$
open neighborhood of
$a,$
there is
$s\in A$
such that
$s\subseteq U.$
-
3. X is Fréchet–Urysohn for finite sets at
$a \ ($
or X is FU
$_{{\textsf {fin}}}$
at a for short) if for every
$B\subseteq \left [ X\right ] ^{<\omega },$
if B is a
$\pi $
-network at
$a,$
then there is
$C\in \left [ B\right ] ^{\leq \omega }$
such that
$C\longrightarrow a.$
-
4. X is Fréchet–Urysohn for finite sets
$($
or X is FU
$_{{\textsf {fin}}}$
for short
$)$
if X is FU
$_{{\textsf {fin}}}$
at all of its points.
It is straightforward to check the following:
Lemma 4.15. Let
$\mathcal {F}$
be a filter on
$\omega $
and
$X\subseteq \left [ \omega \right ] _{+}^{<\omega }.$
In the space
$\xi (\mathcal {F}),$
the following holds:
-
1. X is a
$\pi $
-network at
$\mathcal {F}$
if and only if
$X\in (\mathcal {F}^{<\omega })^{+}.$
-
2. X converges to
$\mathcal {F}$
if and only if
$X\in P(\mathcal {F}).$
-
3.
$\xi (\mathcal {F})$
is FU
$_{{\textsf {fin}}}$
if and only if
$\xi (\mathcal {F})$
is FU
$_{{\textsf {fin}}}$
at
$\mathcal {F}.$
-
4.
$\xi (\mathcal {F})$
is FU
$_{{\textsf {fin}}}$
if and only if
$\mathcal {F}$
is a FUF-filter.
The following is the theorem of G. Gruenhage and P. J. Szeptycki mentioned before [Reference Gruenhage and Szeptycki12, Theorem 17]:
Theorem 4.16 (Gruenhage and Szeptycki)
Let X be a topological space and
$x\in X.$
The following are equivalent:
-
1. X is FU
$_{{\textsf {fin}}}$
at
$x.$
-
2. For every sequence
$\left \langle P_{n}\right \rangle _{n\in \omega }$
of
$\pi $
-networks at x consisting of finite sets, for infinitely many
$n\in \omega $
there are
$F_{n}\in P_{n}$
such that
$\{F_{n}\mid n\in \omega \}\longrightarrow x.$
-
3. For every sequence
$\left \langle P_{n}\right \rangle _{n\in \omega }$
of
$\pi $
-networks at x consisting of finite sets, for every
$n\in \omega $
there are
$F_{n}\in P_{n}$
such that
$\{F_{n}\mid n\in \omega \}\longrightarrow x.$
-
4. P has no winning strategy in the game
$G_{O,P}^{fin}(X,x).$
Footnote
5
In particular using the equivalence of (1) and (3) in the above theorem and Lemma 4.15, we obtain Theorem 4.13.
We require the introduction of some additional terminology:
Let T be a tree inside of
$\left ( \left [ \omega \right ] ^{<\omega }\right ) ^{<\omega }$
and let
$\mathcal {F}$
be a filter on
$\omega .$
For
$p\in T,$
we define
$suc_{T}\left ( p\right ) =\left \{ s\in \left [ \omega \right ] ^{<\omega } : p^{\frown }\left \langle s\right \rangle \in T\right \} $
(where
$p^{\frown }\left \langle s\right \rangle $
denotes the concatenation of p and the sequence
$\left \langle s\right \rangle $
). By
$\left [ T\right ] $
we denote the set of all branches (maximal paths) through
$T.$
Given
$n < \omega ,$
define
$T_{n}$
as the set of sequences of T of length
$n.$
We will say that T is
$\left ( \mathcal {F}^{<\omega }\right ) ^{+}$
-branchingif
$suc_{T}\left ( p\right ) \in \left ( \mathcal {F}^{<\omega }\right ) ^{+}$
for every
$p\in T.$
Lemma 4.17. Let
$\mathcal {F}$
be a filter on
$\omega .$
The following are equivalent:
-
1.
$\mathcal {F}$
is a FUF-filter. -
2. For every
$\left ( \mathcal {F}^{<\omega }\right ) ^{+}$
-branching tree
$T, $
there is
$Y \in \left [ T\right ] $
such that
$Y\in P\left ( \mathcal {F}\right ) .$
Proof.
$(1)\Rightarrow (2)$
. Assume that T is a
$\left ( \mathcal {F}^{<\omega }\right ) ^{+}$
-branching tree. Since the set
$\left \{ suc_{T}\left ( p\right ) \mid p\in T\right \} $
is included in
$\left ( \mathcal {F}^{<\omega }\right ) ^{+},$
by Theorem 4.13, for every
$p\in T,$
there is
$s_{p}\in suc_{T}\left ( p\right ) $
such that
$S=\left \{ s_{p}\mid p\in T\right \} \in P\left ( \mathcal {F}\right ) .$
We can now recursively find a branch Y (whose image) is contained in
$S.$
Since
$S\in P\left ( \mathcal {F}\right ) ,$
it follows that
$Y\in P\left ( \mathcal {F}\right ). $
$(2)\Rightarrow (1)$
. Fix
$X\in \left ( \mathcal {F}^{<\omega }\right ) ^{+}$
and consider the tree
$T=\{\emptyset \}\cup \{t_{0}^{\frown }\ldots {}^{\frown } t_{n}:n<\omega \ \text {and}\ \forall i\leq n(t_{i}\in X)\}$
. It is clear that T is
$\left ( \mathcal {F}^{<\omega }\right ) ^{+}$
-branching and, by assumption, there is
$Y\in \left [ T\right ] $
so that
$Y\in P\left ( \mathcal {F}\right ) .$
If
$\{s_{n}:n<\omega \}\subseteq \lbrack \omega ]^{<\omega }$
satisfies that
$Y=\left \langle s_{n}\right \rangle _{n\in \omega }$
, then for every
$F\in \mathcal {F},$
there is
$n<\omega $
such that
$s_{m}\subseteq F$
for every
$m\geq n.$
⊣
We are ready to provide a solution to Problem 1.2.
Theorem 4.18. For a FU-filter
$\mathcal {F}$
the following are equivalent:
-
1.
$\mathcal {F}$
is a FUF-filter. -
2.
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $
is Baire.
Proof. Recall that
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $
is Baire if and only if player
$\beta $
does not have a winning strategy in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) .$
We will first prove that if
$\mathcal {F}$
is not a FUF-filter, then player
$\beta $
has a winning strategy in
$GS\left ( \mathcal {F},\beta ,\alpha \right ) ,$
or equivalently (by Theorem 4.6(1)), that the Point player has a winning strategy in
$\mathcal {H(}\xi (\mathcal {F}^{<\omega }),\mathcal {F}^{<\omega }\mathcal {)}.$
Since
$\mathcal {F}$
is not a FUF-filter, there is
$X\in \left ( \mathcal {F}^{<\omega }\right ) ^{+}$
such that X does not contain sequences converging to
$\mathcal {F}^{<\omega }.$
The strategy for the Point player is as follows: At step
$n,$
if the Open player plays
$\left [ K_{n}\right ] _{+}^{<\omega },$
then the Point player picks
$w_{n}\in X\cap \left [K_{n}\right ] _{+}^{<\omega }$
(with the requirement that
$w_{n}\neq w_{m}$
whenever
$n\neq m$
). The outcome of the game will be an infinite subset of
$X,$
which we already know cannot be a convergent sequence, so the Point player wins the match.
Now, assume that
$\mathcal {F}$
is a FUF-filter; it suffices to prove that player
$\beta $
does not have a winning strategy in
$\overline {GS}\left (\mathcal {F},\beta ,\alpha \right ) $
(see Theorem 4.6(1)). Assume that
$\pi $
is a winning strategy for player
$\beta $
. Based on the strategy
$\pi $
we inductively build a suitable tree T inside of
$\left (\left [ \omega \right ] ^{<\omega }\right ) ^{<\omega }$
and a family
$\left \{G_{p}\mid p\in T\right \} ,$
with the following properties:
-
1.
$\emptyset \in T$
. -
2.
$G_{p}\in \mathcal {F}$
for every
$p\in T$
. -
3. If
$p=\left \langle s_{0},s_{1},...,s_{n}\right \rangle \in T$
then
$J\left ( p\right ) =\left \langle \sigma \left ( \emptyset \right ) ,G_{\left \langle s_{0}\right \rangle },s_{0},G_{\left \langle s_{0} ,s_{1}\right \rangle },...,G_{p}\right \rangle $
is a legal partial play of
$\overline {GS}(\mathcal {F},\beta ,\alpha )$
in which player
$\beta $
is using his strategy
$\pi .$
Footnote
6
-
4.
$T_{1}$
is the set of all
$\left \langle s\right \rangle $
such that
$s\in \left [ \omega \right ] ^{<\omega }$
and there is
$G\in \mathcal {F}$
such that
$\left \langle \sigma \left ( \emptyset \right ) ,G,s\right \rangle $
is a legal partial play of
$\overline {GS}(\mathcal {F},\beta ,\alpha )$
in which player
$\beta $
is using his strategy
$\pi .$
-
5. For every s such that
$\left \langle s\right \rangle \in T_{1},$
we choose and fix
$G_{\left \langle s\right \rangle }$
as above. -
6. Given a node
$p=\left \langle s_{0},s_{1},...,s_{n}\right \rangle \in T$
, let
$suc_{T}\left ( p\right ) $
be the set of all
$z\in \left [ \omega \right ] ^{<\omega }$
for which there is
$G\in \mathcal {F}$
such that
$J\left ( p\right ) ^{\frown }\left \langle G,z\right \rangle $
is a legal partial play (in which player
$\beta $
is using his strategy
$\pi $
). We choose and fix
$G_{z}$
with this properties.
We claim that T is
$\left ( \mathcal {F}^{<\omega }\right ) ^{+}$
-branching. Indeed, fix
$p=\left \langle s_{0},s_{1},...,s_{n}\right \rangle \in T$
and an arbitrary
$G\in \mathcal {F}$
. Since
$\pi $
is a winning strategy for
$\beta $
, when
$\alpha $
chooses G then
$J\left ( p\right ) ^{\frown }\left \langle G\right \rangle $
is a legal play, and so there must be
$s\in suc_{T}\left ( p\right ) $
such that
$s\subseteq G$
. Since
$\mathcal {F}$
is a FUF-filter, by Lemma 4.17, there is
$Y=\left \langle s_{n}\right \rangle _{n\in \omega }\in \left [ T\right ] $
such that
$Y\in P\left ( \mathcal {F} \right ) .$
Note that T induces a run of the game
$\overline {GS}\left ( \mathcal {F},\beta ,\alpha \right ) .$
Since Y is a pseudointersection of
$\mathcal {F}^{<\omega },$
it follows from Lemma 4.5 that
$ {\textstyle \bigcup \limits _{n\in \omega }} s_{n}$
is a pseudointersection of
$\mathcal {F},$
so player
$\alpha $
won the match.⊣
After having obtained Theorems 4.11 and 4.18, it is then natural to ask the following question:
$$ \begin{align*} \begin{array}{c} \textit{Is}\ \textit{there}\ \textit{a} \ \textsf{FU}\textit{-filter} \ \mathcal{F}\ \textit{on}\ \omega \ \textit{such}\ \textit{that} \ S_{c}\left(\mathcal{F}\right) \ \textit{is}\ \textit{Baire},\ \textit{but}\ \textit{not}\\ \textit{homeomorphic}\ \textit{to}\ \omega^{\omega}\ (\textit{i.e.,} GS\left(\mathcal{F},\beta,\alpha\right)\ \textit{is}\ \textit{not} \textit{determined})? \end{array} \end{align*} $$
This is the same as asking if there is an uncountably generated FUF-filter. Many (consistent) examples of such filters have been constructed by using some set-theoretical assumptions:
Proposition 4.19. There is an uncountably generated FUF-filter under the following hypotheses:
-
1. ([Reference Nyikos17])
$\mathfrak {p}>\omega _{1}$
. -
2. ([Reference Nyikos17])
$\mathfrak {b=p}.$
-
3. ([Reference Hrušák and Ramos-García15])
$\Diamond \left ( 2,=\right ) .$
In what follows, we will describe a connection between the uncountably generated FUF-filters and some Fréchet–Urysohn groups.
Consider the Boolean group
$\left ( \left [ \omega \right ] ^{<\omega },\triangle \right ) $
, where
$\triangle $
is the symmetric difference. We know that every filter
$\mathcal {F}$
on
$\omega $
induces a topological group topology on
$\left [ \omega \right ] ^{<\omega }$
by declaring that
$\mathcal {F}^{<\omega }$
is an open local base for
$\emptyset .$
Denote this topology by
$\tau _{\mathcal {F}}$
and the topological group by
$G_{\mathcal {F} }$
. Clauses
$(1)$
and
$(2)$
of the following theorem were proved equivalent by E. A. Reznichenko and O. V. Sipacheva in their article [Reference Reznichenko and Sipacheva19] and the equivalence with
$(3)$
follows from Theorem 4.18:
Theorem 4.20. Let
$\mathcal {F}$
be a filter on
$\omega .$
The following are equivalent:
-
1.
$\mathcal {F}$
is an uncountably generated FUF-filter. -
2.
$G_{\mathcal {F}}$
is a non-first countable Fréchet–Urysohn group. -
3.
$\mathcal {F}$
is uncountably generated and
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $
is Baire.
In connection with this last result, we mention that a famous problem of V. I. Malykhin asked if there is a Fréchet–Urysohn group that is not first countable.Footnote 7 Based on a previous theorem of J. Brendle and M. Hrušák (see [Reference Brendle and Hrušák1]), this important problem was finally solved by M. Hrušák and U. A. Ramos-Garcia:
Theorem 4.21 (Hrušák and Ramos-Garcia [Reference Hrušák and Ramos-García15])
It is consistent that every Fréchet–Urysohn group is first countable.
It follows from the previous theorem that it is consistent that every FUF-filter is countably generated. Hence, we have the next corollary:
Corollary 4.22. It is consistent that for every filter
$\mathcal {F}$
on
$\ \omega $
, the space
$\mathcal {S}_{c}\left ( \mathcal {F}\right ) $
is Baire if and only if
$\mathcal {S}_{c}\left ( \mathcal {F}\right ) $
is homeomorphic to
$\omega ^{\omega } \ ($
i.e., the game
$GS\left ( \mathcal {F} ,\beta ,\alpha \right ) $
is always determined
$)$
.
In this way, in the model defined in [Reference Hrušák and Ramos-García15], we have that the game
$\mathcal {H(\xi (F}^{<\omega }\mathcal {)},\mathcal {F}^{<\omega }\mathcal {)}$
is determined for every filter
$\mathcal {F}$
on
$\omega $
. On the other hand, there are ZFC examples of filters
$\mathcal {G}$
on
$\omega $
for which the game
$\mathcal {H(\xi (G)},\mathcal {G)}$
is undetermined (see [Reference Gruenhage11, Reference Nyikos17]). By virtue of Corollary 4.22, we know that those examples cannot be of the form
$\mathcal {F}^{<\omega }$
(this remark was pointed out to us by M. Hrušák).
S. Todorcevic and C. E. Uzcategui initiated the study of analytic topologies over the natural numbers. Since we can identify every subset of
$\omega $
with its characteristic function, we can define a topology on
$\wp \left ( \omega \right ) $
that is homeomorphic to
$2^{\omega }$
. Since every topology over
$\omega $
is a subset of
$\wp \left ( \omega \right ) $
, we can say when a topology is Borel or analytic. Regarding Malykhin’s Problem in the definable setting, S. Todorcevic and C. E. Uzcategui established the next result (see Theorem 7.3 of [Reference Todorčević and Uzcátegui22]):
Theorem 4.23 (Todorcevic and Uzcategui [Reference Todorčević and Uzcátegui22])
Every Fréchet–Urysohn analytic group is first countable.Footnote 8
In particular, it follows that there are no uncountably generated analytic FUF-filters. We will conclude this article by providing an alternative proof of this particular case of Theorem 4.23. We will use a separation theorem due to S. Todorcevic. In order to do this, we need the following definitions:
Definition 4.24. Let
$\mathcal {A},\mathcal {B} \subseteq \left [ \omega \right ] ^{\omega }.$
-
1.
$\mathcal {A}$
is called countably generated in
$\mathcal {B} $
if there is a family
$\left \{ B_{n}\mid n < \omega \right \} \subseteq \mathcal {B}$
such that for every
$A\in \mathcal {A},$
there is
$n < \omega $
such that
$A\subseteq B_{n}.$
-
2. We say that
$\mathcal {A\ }$
and
$\mathcal {B}$
are orthogonalif
$A\cap B$
is finite for every
$A\in \mathcal {A}$
and
$B\in \mathcal {B}.$
For a tree
$T\subseteq \left [ \omega \right ] ^{<\omega }$
and an ideal
$\mathcal {I}$
on
$\omega ,$
we will say that T is
$\mathcal {I}$
-branching if
$suc_{T}\left ( p\right ) =\{n\mid p^{\frown }\left \langle n\right \rangle \in T\}$
is an infinite element of
$\mathcal {I}$
for every
$p\in T$
(in the terminology of [Reference Todorčević21] this would be called an
$\mathcal {I}$
-tree). In the paper [Reference Todorčević21], S. Todorcevic proved the following interesting dichotomy:
Theorem 4.25 (Todorcevic [Reference Todorčević21])
Let
$\mathcal {I}$
and
$\mathcal {J}$
be two orthogonal ideals on
$\omega $
such that
$\mathcal {I}$
is analytic. One of the following holds:
-
1.
$\mathcal {I}$
is countably generated in
$\mathcal {J}^{\perp }.$
-
2. There is a
$\mathcal {J}$
-branching tree
$T\subseteq \left [ \omega \right ] ^{<\omega }$
such that
$\left [ T\right ] \subseteq \mathcal {I}.$
The following corollary is a direct consequence of the previous dichotomy:
Corollary 4.26. Let
$\mathcal {I}$
be an analytic FU-ideal on
$\omega .$
Then one of the following statement holds:
-
1.
$\mathcal {I}$
is countably generated. -
2. There is an
$\mathcal {I}^{\perp }$
-branching tree
$T\subseteq \left [ \omega \right ] ^{<\omega }$
such that
$\left [ T\right ] \subseteq \mathcal {I}.$
Proof. Since
$\mathcal {I}$
is a FU-ideal, it follows that
$\mathcal {I=I} ^{\perp \perp }.$
The result follows by applying Theorem 4.25 to
$\mathcal {I}$
and
$\mathcal {I}^{\perp }.$
⊣
We are ready to prove the following particular case of Theorem 4.23:
Proposition 4.27. There are no uncountably generated analytic FUF-filters.
Proof. Let
$\mathcal {F}$
be an uncountably generated analytic FU-filter. By Corollary 4.26, we get that there is an
$\left ( \mathcal {F}^{\ast }\right ) ^{\perp }$
-branching tree
$T\subseteq \left [ \omega \right ] ^{<\omega }$
such that
$\left [ T\right ] \subseteq \mathcal {F}^{\ast }.$
For every
$p=\left \langle m_{0},...,m_{n}\right \rangle \in T,$
define
$\widehat {p}=\left \langle \left \{ m_{0}\right \} ,...,\left \{ m_{n}\right \} \right \rangle .$
Let
$S=\left \{ \widehat {p}\mid p\in T\right \} $
and note that
$S\subseteq \left ( \left [ \omega \right ] ^{<\omega }\right ) ^{<\omega }$
is a tree. Furthermore, S is an
$\left ( \mathcal {F}^{<\omega }\right ) ^{+}\,$
-branching tree because T is an
$\left ( \mathcal {F}^{\ast }\right ) ^{\perp }$
-branching tree. Since
$\left [ T\right ] \subseteq \mathcal {F}^{\ast },$
we get that
$\left [ S\right ] \cap P\left ( \mathcal {F}\right ) =\emptyset .$
By Proposition 4.17, we conclude that
$\mathcal {F}$
is not a FUF-filter.⊣
Acknowledgments
We would like to thank M. Hrušák for his valuable comments and for pointing them to the paper [Reference Gruenhage10]. We would also like to thank R. Rojas-Hernández for his valuable suggestions and comments. We would also like to thank the referee for his/her amazing job and the valuable comments that greatly improved the paper. The research of the first-named author was supported by the PAPIIT grant no. IN-105318. The second author was partially supported by a CONACyT grant A1-S-16164 and a PAPIIT grant IN104220.
