INTRODUCTION
Population aging and its macroeconomic effects have emerged over the last decade as a key issue on the policy agendas of most industrialized countries. During the postwar period, the population share of elderly people has increased dramatically. Following the postwar “baby boom”—during which population growth rates temporarily accelerated—fertility rates have declined substantially, commonly known as the “baby bust.” At the same time, mortality rates have decreased in most industrialized nations, owing to healthier lifestyles and medical advances.1
Birth rates (per 100 of the population) in the United States came down from 2.43 in 1950 to 1.45 in 2000. The drop in death rates (per 100 of the population) was less spectacular, declining from 0.95 in 1950 to 0.83 in 2000 (United Nations, 2003).
The effects of the postwar demographic transition on old-age dependency ratios (that is, the ratio of the population aged 65 years and older to the population aged 15–64 years) for selected OECD countries are presented in Table 1. The evolution of the old-age dependency ratio shows pronounced population aging for all countries, where it is apparent that populations in European countries and Japan are older than elsewhere. Japan stands out as having an old-age dependency ratio of only 10 percent in 1970, and a projected ratio of more than 70 percent in 2050, a large increase unparalleled across OECD countries. The youth dependency ratio2
The youth dependency ratio is defined as the ratio of the population aged 0–14 years to the population aged 15–64 years.

Demographic changes have profound economic effects, which may span many generations. Particularly, the impending retirement of the baby boom generation is raising a great deal of concern. If a large fraction of the population retires (or passes away), society is expected to save less, leading to a lower rate of capital accumulation and lower living standards.3
Bloom et al. (2003) provide econometric evidence on the positive relationship between life expectancy and the savings rate.
The informal literature on population aging, for example, Group of Ten (1998) and McMorrow and Röger (2003), is voluminous. Although not as large yet, the theoretical literature is developing. Many formal contributions employ calibrated life-cycle models—in the tradition of Samuelson (1958), Diamond (1965),4
Diamond (1965) assumes that individuals live for two discrete time periods, in which they work and save in the first period and consume out of savings in the second period.
Auerbach et al. (1989), Auerbach et al. (1991), Rí os-Rull (2001), and Brooks (2002) employ a Diamond-Samuelson overlapping generations model, which is generalized to many periods. Cutler et al. (1990) use a representative-agent model.
Momota and Futagami (2000), however, study demographic transition in a small open economy using endogenous fertility theory (see Becker and Barro, 1988).
Weil (1989) also allows for population growth, but he assumes infinitely lived overlapping generations and thus differs from the uncertain lifetimes approach of Yaari-Blanchard.
Bovenberg (1993) has employed the Yaari-Blanchard-Buiter framework to study the effects of a permanent rise in the capital tax in an open economy. Bovenberg and Heijdra (1998) consider a closed economy, but they do not allow for net population growth or endogenous labour supply.
A simple graphical apparatus is developed to provide an intuitive account of the long-run and dynamic effects of various demographic changes. The model is versatile because it encompasses results of various seminal works—that of Blanchard (1985), Buiter (1988), and Weil (1989)—by varying the assumptions made on demography and the intertemporal substitution elasticity in labor supply. Moreover, it can be employed to get insight into and extend the results from the population aging literature. Our approach differs from previous theoretical analyses on population dynamics by being able to trace out impulse-responses at business cycle frequencies.9
The Laplace transform technique of Judd (1982) is used to solve for the entire transition path of the demographic change.
Three demographic scenarios are analyzed analytically. The first shock concerns an unexpected and permanent decrease in the (exogenous) fertility rate (that is, a pure “baby bust”). It is shown that the optimal savings response to declining fertility entails either a decrease or an increase in per capita savings depending on the assumptions made on the elasticity of labor supply and the generational turnover effect, thereby generalizing the results of Elmendorf and Sheiner (2000). Second, a proportionate fall in the fertility and death rates so as to yield a stationary population growth rate is studied. Under this scenario, the qualitative results are identical to those of a subsidy on capital; both the per capita capital stock and per capita consumption rise in the new steady state. The final scenario—studying a drop in the fertility rate and a compensating increase in the death rate so as to maintain the rate of generational turnover constant—gives rise to a rise in long-run per capita consumption, although the per capita capital stock falls.
The remainder of the paper is organized as follows. Section 2 sets out the Yaari-Blanchard overlapping generations model extended for endogenous labor supply and exogenous population dynamics. Section 3 solves the model graphically and analyzes the dynamics around the long-run equilibrium. Section 4 employes the graphical framework of Section 3 to qualitatively study various demographic shocks. Section 5 concludes.
A MODEL OF OVERLAPPING GENERATIONS
Individual Households and Demographics
As in Blanchard (1985), individual households face an age-invariant probability of death (β [ges ] 0). Each household has a time endowment of unity, which is allocated optimally over labor supply and leisure. The utility functional at time t of the representative agent born at time v is denoted by Λ(v, t):
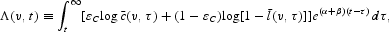
where
and
are, respectively, private consumption and labor supply in period t by an agent born in period v, α is the pure rate of time preference (α > 0) that applies across generations and εC is the share of consumption in utility.10
We use the notation introduced by Buiter (1988) by letting lowercase barred variables denote values at the individual household level.
. The representative agent's dynamic budget identity can be expressed as:
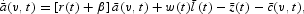
where
,
are real financial assets, r(t) is the real rate of interest, w(t) is the real wage rate (assumed age-independent for convenience), and
are real net lump-sum taxes. The return on financial assets exceeds the rate of interest because, with lifetime uncertainty and in the absence of bequest motives, agents conclude actuarially fair contracts with life insurance companies.11
In particular, agents receive an annuity payment from the insurance company proportional to their financial wealth (
) in exchange for transferring their entire estate to the insurance company upon death. Because the contracts are actuarially fair, the annuity rate equals the death rate β.
The individual household chooses time profiles for
and
in order to maximize Λ(v, t) subject to the budget identity (2) and a No-Ponzi-Game solvency condition,
. The optimal solutions for private consumption and labor supply on the interval
are fully characterized by:12
Details of the solution methods and all mathematical derivations can be found in a technical appendix (Heijdra and Ligthart, 2004), which can be downloaded from the authors' Web site.
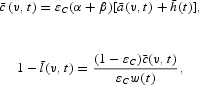
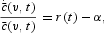
where
is expected lifetime human wealth:
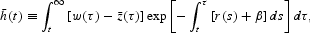
which is age-independent. According to (3), goods consumption in the planning period t is proportional to total wealth, comprising the sum of financial and human wealth. Equation (4) shows that in each period, the marginal rate of substitution between leisure and private consumption is equated to the real wage rate. Note that labor supply is a negative function of individual consumption. This wealth effect causes wealthier agents to consume more leisure and thus allows for the proportion of agents opting for “voluntary retirement” to increase with age.13
Because there is no upper limit on an agent's age, there exist some old (and wealthy) agents who consume more leisure than their unit time endowment allows for (that is, l(v, t) < 0 for v → −∞). Such agents no longer work themselves but, rather, are net demanders of labor.
To allow for net population growth or decline, we draw on Buiter (1988) and distinguish between the probability of death β ([ges ]0) and the birth rate η ([ges ]0). An attractive feature of modeling demographics this way is that it nests two seminal overlapping generations models as special cases. By setting η = β Blanchard's (1985) model14
Furthermore, the intertemporal labor supply elasticity should equal unity because labor supply is exogenous in Blanchard's model. See Appendix A.1 for further details.
Bovenberg (1993) interprets the special case of η = 0 and β < 0 as a Ramsey model with intra-dynasty population growth, implying that the Ricardian equivalence proposition still holds. If η > 0 and β = 0, there is extra-dynasty growth. Because of the birth of disconnected generations (or dynasties) Ricardian equivalence would not hold.
By solving (7) subject to the initial condition N(0) = 1, the path for the aggregate population is obtained:
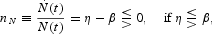
where the population size at time t is denoted by N(t). The size of a newborn generation is proportional to the current population N(v, v) = ηN(v), where N(v, t) is the size at time t of the cohort born at some time v(t [ges ] v). Because the death rate is constant and cohorts are assumed to be large, the size of each existing generation falls exponentially according to:
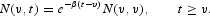
Aggregate Household Sector
Given the simple demographic structure, aggregate variables can be calculated as the weighted integral of the values for the different generations. Aggregate financial wealth is, for example, defined as
, where N(v, t) = ηeηve−βt (and aggregate values for C(t) and L(t) are derived in a similar fashion). The main equations describing optimal behavior of the aggregate household sector can be written as:
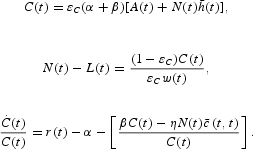
Equations (9) and (10) are aggregate versions of (3) and (4), respectively. Equation (11) is the Keynes-Ramsey rule modified for the existence of overlapping generations of finitely lived agents. It says that aggregate consumption growth differs from individual consumption growth [equation (5)], because of the distributional effects caused by the turnover of generations. This so-called generational turnover effect (see Heijdra and Ligthart, 2000)—represented by the second term between brackets of (11)—is comprised of two opposing forces. On the one hand, aggregate growth exceeds individual growth because of the birth of new generations, who start consuming out of human wealth immediately (represented by
). On the other hand, aggregate consumption growth falls short of individual growth, reflecting that at each instant of time a cross section of the population dies and consequently ceases to consume (represented by βC(t)). For future reference, equation (11) can be rewritten in terms of aggregate variables:17
Using equations (3), (7), and (9), and noting that, in the absence of bequests, newborns possess no financial wealth (so that
).
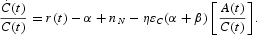
Firms
Firms in the final goods sector18
There are many identical firms and, for convenience, their number is normalized to unity.
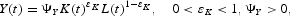
where ΨY is a general technology index, which is assumed to be constant. Real profits of the representative firm are defined in the usual way:
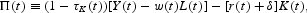
where r(t) + δ is the effective rental rate of capital, δ is the rate of capital depreciation, and τK(t) is a capital income tax (or capital subsidy if τK(t) < 0). The representative producer chooses K(t) and L(t) in order to maximize Π(t), taking factor prices as given. The first-order conditions for this static optimization problem are:
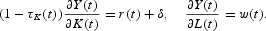
Because technology features constant returns to scale and markets are perfectly competitive, excess profits are zero (that is, Π(t) = 0). Furthermore, because there are no adjustment costs associated with investment, the value of household share holdings equals the capital stock, that is, V(t) = K(t).
Government and Market Equilibrium
The government consumes a fixed share of the final good. Abstracting from public debt and labor taxes, the periodic budget restriction of the government can be written as:
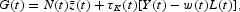
where G(t) denotes public consumption and
are total net lump-sum taxes.
Because of the assumption of perfect foresight, agents' behavior depends on current and future prices. Flexible factor prices cause factor markets to clear instantaneously. Financial market equilibrium implies that households' claims on capital equal the physical capital stock (that is, A(t) = K(t)). Equilibrium on the goods market implies that:
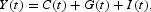
where I(t) denotes gross investment:
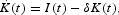
where
is net capital accumulation.
Model Summary
In the presence of population growth, the model will give rise to ongoing economic growth also in the steady state.19
Growth is exogenous in the steady state, but endogenous during transition. See Sections 3 and 4.
This follows from noting that the steady-state aggregate stock of financial assets (or capital stock per capita) is positive (k(t) > 0). If the birth rate is zero (that is, η = 0), then (T1.2) implies the familiar Ramsey result of r = α in the steady state.

Equations (T1.3)–(T1.7) are essentially static equations. Equation (T1.3) is the intensive-form production function, obtained from (13). The factor demand equations (T1.4)–(T1.5) are derived by rewriting the expressions in (15) in intensive form. Equation (T1.4) represents a downward-sloping labor demand curve in the (w, l) space. The per capita labor supply expression (T1.6) results on rewriting (10), and is referred to as the macroeconomic participation rate. Population growth affects the participation rate both through its effect on the population size and through its effect on aggregate labor supply. Note that the participation rate is a negative function of per capita consumption. The short-run per capita capital supply curve is a vertical schedule—representing a given capital stock—whereas the short-run demand for capital (T1.5) is a standard downward-sloping demand curve, because of diminishing returns to capital accumulation. Finally, the government budget restriction (T1.7) is a reworked version of (16).
GRAPHICAL SOLUTION
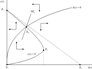
As was shown in the previous section, the dynamic part of the model can be analytically reduced to two variables: the per capita capital stock (a predetermined variable) and per capita consumption (a forward-looking or jump variable). The model can be graphically summarized by a phase diagram as shown in Figure 1.21
Details of the derivation of the phase diagram are found in Heijdra and Ligthart (2004).
line represents all combinations of c and k for which the per capita stock of capital is constant over time. It passes though the origin and is upward-sloping provided k falls short of its golden-rule level. For points above (below) the
line, employment22
In deriving the equilibrium loci, we take into account that equilibrium employment depends on both c and k. Indeed, by combining labor demand (T1.4), labor supply (T1.6), and the production function (T1.3) we find that the labor market equilibrium condition can be written as:

where ω0 is a positive constant, f′(·) < 0, and f′′(·) > 0 (for l ∈ [0, 1]). Given k, an increase in c reduces labor supply and thus lowers equilibrium employment.

Phase diagram.
The
line denotes all (c, k)-combinations for which per capita consumption is constant over time. The dashed line connecting points P3 and P4 in Figure 1 is the
line for the special case of a zero birth and mortality rate (that is, η = β = 0), known in the literature as the infinite-horizon Ramsey (1928) model.23
Strictly speaking, β = 0 is not needed to generate r = α in steady state. See (T.1.2) in Table 2 and the discussion in footnote 15.
line is linear and negatively sloped.
For a positive birth rate, the
curve is given by the solid line connecting points P1, P2, and P3. The position and slope of the
line is determined by two effects working in opposite directions: (i) the generational turnover effect; and (ii) the aggregate labor supply effect. The
line is almost horizontal near the origin, where labor supply is close to unity and thus approaches full exogeneity [corresponding to the Blanchard (1985), Buiter (1988), and Weil (1989) models].24
The
line can only be described parametrically, that is, by varying l in the feasible interval [0, 1]. In moving from point P1 to P3, l falls from 1 to 0; it follows that in P1, l = 1 and the labor-leisure ratio (ωLL) equals zero, while in P3, l → 0 and ωLL → ∞.
line is upward-sloping on the line segment P1P2, reflecting the dominant generational turnover effect. In contrast, on the line segment P2P3, labor supply is fairly elastic, yielding a downward-sloping
curve that is steeper than the Ramsey
line (which is given by the dashed line going through points P3 and P4). If the elasticity of intertemporal labor supply approaches infinity (near P3), the two curves coincide.
The consumption dynamics—illustrated by the vertical arrows in Figure 1—are as follows. For points to the left (right) of the
line, consumption rises (falls) over time. To see why, note the following that the interest rate depends on both c and k according to r(c, k), where ∂r/∂k < 0 and ∂r/∂c < 0. The
line can thus be written in shorthand notation as r(c, k) − α = η(α + β)εC(k/c). Given c, a fall (rise) in k leads to an increase (decrease) in the rate of interest and a decrease (increase) in the k/c ratio—representing the generational turnover term—yielding an increase (decrease) in consumption growth.
There is a unique equilibrium at point E0 and the configuration of arrows in Figure 1 confirms that this equilibrium is a saddle point. (See the Appendix for a formal proof.) The saddle path associated with E0 is denoted by SP0. Although Figure 1 has been drawn under the assumption that the equilibrium occurs along the downward-sloping segment P2P3 of the
line, it cannot be ruled out a priori that the intersection occurs somewhere along the upward-sloping segment P1P2. In Section 5, however, we shall argue that the case illustrated in Figure 1 is empirically the most relevant one.
QUALITATIVE ANALYSIS OF SMALL DEMOGRAPHIC SHOCKS
This section studies the effect of demographic shocks on the optimal savings-labor supply response of the household sector and on the investment decisions of firms. Specifically, we analyze the short-run, transition, and long-run macroeconomic effects of stylized demographic scenarios, employing the graphical apparatus developed in the previous section. To keep matters simple, attention is paid to unanticipated and permanent changes in demographics. The formal proofs underlying the qualitative analysis—obtained by log-linearizing the model around an initial steady state and subsequently perturbing the system—can be found in the Appendix.
Three demographic shocks are considered. The first shock concerns an exogenous drop in fertility, taking as given the mortality rate, which we shall refer to as the pure baby-bust scenario. Here, the focus is on a drop in the fertility rate rather than a drop in the death rate, because the former is in many industrialized countries the more important factor quantitatively. The next two shocks pertain to composite changes as both the fertility and death rates are changed simultaneously. It is of interest to analyze these cases because it is not a priori evident whether the macroeconomy would be affected at all. One scenario is an exogenous decrease in fertility exactly matched by an increase in longevity (that is, a fall in the death rate), so as to maintain a constant population growth rate. Although it is a stylized case, some industrialized countries may at times be experiencing this type of demographic change. Another scenario concerns an exogenous decrease in the birth rate while adjusting the death rate endogenously so as to offset the generational turnover effect of a lower birth rate. This scenario could be of practical relevance to developing countries at war or to postconflict economies, where drops in birth rates and rises in death rates often occur simultaneously. It will be shown that the latter two scenarios have qualitatively different macroeconomic results, because of the generational turnover effect.
Pure Baby Bust
A permanent and unexpected decrease in the fertility rate (that is, dη < 0), given a constant mortality rate, decreases the population growth rate (that is, dnN = dη < 0). As a result, generational turnover decreases, reflecting that deceased generations are replaced by newly born agents at a slower pace.25
The model features a constant probability of death, implying that a young person has the same expected remaining lifetime—that is, the inverse of the probability of death—as a very old person.
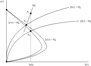
line up and moves the
line to the right, shifting the long-run equilibrium from point E0 to E1, where per capita consumption has increased. The lines labeled [ · ]0 represent the equilibrium loci before the demographic shock, whereas the ones labeled [ · ]1 indicate the loci after the shock. Figure 2 depicts the situation in which the shift in the
line is sufficiently large to generate a new equilibrium to the left of the old equilibrium (see the discussion later).

Baby bust.
On impact, consumption jumps up to point A on the new saddle path, reflecting the drop in the short-run interest rate, making present consumption more attractive than future consumption. As a result, per capita labor supply (that is, the macroeconomic participation rate) falls, pushing up short-run wages, and thus benefiting young generations—who mainly consume out of wage income—while depressing interest income of the elderly. During transition, consumption gradually falls, mirroring the smooth rise in the interest rate, which, however, remains below its old steady state value.
Per capita consumption is higher26
This partly reflects what Cutler et al. (1990) have labeled the “Solow effect.” Because of the reduction in the population growth rate a lower amount of savings is required to maintain a given per capita capital stock.
This requires that the initial birth and death rates are small so that the rightward shift in the
line is sufficiently small. With initial birth and death rates close zero—that is, r [thkap ] α, thereby approximating the case of infinitely lived households—the per capita capital stock would unambiguously fall.

If individual consumption growth profiles are relatively steep, the per capita capital stock may even increase. Intuitively, the positive savings effect associated with the reduction in generational turnover attenuates the fall in aggregate savings induced by the lower rate of interest. Overlapping generations may thus give rise to diametrically different results than those derived in the infinite-horizon Ramsey model. The assumptions made on the elasticity of labor supply are crucial in this respect.28
In the following, it is assumed that the labor supply effect is sufficiently strong to generate a stable equilibrium on the downward-sloping section of the consumption equilibrium locus (Figure 1). It can easily be shown by a plausible calibration of the model that this is indeed the case. The labor supply effect dominates even for quite high values of the birth rate. The derivations in the Appendix cover the general case.
Elmendorf and Sheiner (2000) employ a Diamond model with exogenous population growth, but they do not work out the comparative statics analytically.
Appendix A.2.1 shows that the results of Cutler et al. (1990), who assume infinitely lived agents, exogenous population growth, and exogenous labor supply, are a special case of our model. In their framework, a fertility drop yields a reduction in aggregate steady-state savings, whereas the optimal capital intensity remains—in contrast to our results—unaffected.30
Cutler et al. (1990) thus effectively set β < 0 and η = 0 (see footnote 15), so that r(k) = α, explaining why the optimal capital intensity remains unaffected in the steady state.
Stationary Population Growth
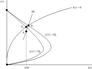
Consider a demographic change that involves simultaneously decreasing the birth rate and mortality rate (that is, dη = dβ < 0 and thus dnN = 0) so as to yield a stationary population growth rate. Generational turnover falls, but by less than in the pure baby-bust scenario. Figure 3 shows that this type of demographic shock leaves the
line unaffected but shifts the
line to the right, yielding a higher capital intensity. Equiproportionate changes in the birth and death rates thus have a nonneutral effect on the economy.

Stationary population growth.
On impact, the rate of interest rises, making current consumption less attractive compared to future consumption. The latter is represented by a downward jump in consumption from point E0 to point A on the new saddle path SP1. The fall in consumption per capita shifts the short-run labor supply curve to the right, so that for a given level of labor demand, per capita employment and per capita output rise and wages fall. The simultaneous decrease in per capita consumption and increase in per capita output crowds in investment during transition.
Consumption gradually increases along the transition path to the new steady state, where per capita capital accumulation and per capita consumption are higher than in the old steady state. Given the stationarity of the population growth rate, the aggregate stock of capital and aggregate consumption have increased as well (that is, they are both on a higher path exhibiting the same rate of exponential growth). The rise in the capital stock increases labor demand, but the rise in consumption induces households to supply less labor. On a net basis, equilibrium employment rises. The steady-state interest rate falls and the wage rate rises, reflecting an increase in the long-run capital-labor ratio.
The qualitative effects of a decline in population turnover are identical to those of a capital income subsidy (Appendix A.2).31
See Heijdra and Ligthart (2000) for an overview of the macroeconomic effects of capital income taxes.
Constant Generational Turnover
Rather than keeping the population growth rate constant, one also could consider a demographic change that leaves unaffected the rate of generational turnover [that is, the second term in (T1.2)]. This requires that the death rate has to rise at impact by dβ = −(α + β)(dη/η) > 0 to compensate for the fall in population turnover induced by the reduced rate at which new generations are born (that is, dη < 0). Accordingly, dnN = (α + β + η)(dη/η) < 0, implying a reduction in net population growth, which is larger than under a pure baby-bust scenario.
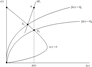
The effects of the shock can be analyzed with the aid of Figure 4. The
line remains unaffected, but the
shifts up. The short-run and long-run qualitative effects are equivalent to those of a pure baby bust, although generational turnover is left unaffected. In the new steady state, per capita consumption has increased while the per capita capital stock has fallen. Quantitatively, the two demographic shocks do differ, however, which is not surprising given that the generational turnover effect is a drag on aggregate consumption growth.32
Using numerical simulations, it can be easily shown that the fall in the per capita capital stock is larger under constant generational turnover for reasonable values of the parameters.

Constant generational turnover.
As is shown in Appendix A.2, the demographic scenario of constant generational turnover yields macroeconomic results qualitatively similar to that of a fall in per capita public spending. Intuitively, both decrease labor market participation via the wealth effect in aggregate labor supply, thereby raising wages and reducing the long-run rate of interest. The latter discourages household savings.
CONCLUDING REMARKS
The paper studies the dynamic macroeconomic effects of demographic shocks employing a Yaari-Blanchard overlapping generations framework extended for endogenous labor supply while allowing for a richer demography. Our theory model provides for a flexible framework, enabling us to reproduce key results from seminal articles and to provide new insights on the role of demographics in macroeconomics.
The main results are summarized as follows. With overlapping generations, a drop in fertility does not necessarily lead to a reduction in per capita savings and output as is derived in the standard infinitely lived household model. Per capita savings may increase if the effect of generational turnover is sufficiently strong to dominate the aggregate labor supply effect, but this is not the empirically relevant case.
Endogenizing labor supply in a model with exogenous population growth and infinitely-lived households reinforces the negative aggregate savings effect found by Cutler et al. (1990). With endogenous labor supply, aggregate savings fall by more than under exogenous labor supply, giving rise to a fall in per capita savings and per capita output. With exogenous labor supply, however, the capital intensity is left unaffected by the shock.
Depending on the nature of the demographic change, the steady state effects on the macroeconomy differ. A pure baby bust gives rise to a fall in steady-state output but a rise in per capita consumption. A drop in fertility while keeping generational turnover constant by adjusting the death rate yields results qualitatively similar to those of a pure baby bust. The qualitative effects of a decline in generational turnover at constant population growth are diametrically different. Output per capita increases, but steady-state consumption per capita declines. Policy makers should therefore carefully analyze what changes in demography give rise to observed population dynamics before prescribing a suitable long-run fiscal policy response.
The short-run effects of demographic changes can differ markedly from the long-run effects, not only quantitatively but also qualitatively. For example, an equiproportionate decline in death and fertility rates yields a decline in per capita consumption on impact but increases per capita consumption in the new steady state. A pure baby-bust scenario, however, gives rise to overshooting in per capita consumption while yielding a higher per capita consumption in the new steady state. Notice that long-run wages are pushed up in all three scenarios, and generally rise in the short run, too, except in a demographic scenario that keeps the population growth rate constant.
The analysis has abstracted from a pension sector. Furthermore, we have not looked at the welfare effects of demographic changes. This would be particularly relevant in the study of the design of optimal policies to address population aging. These extensions are left for further research.
APPENDIX: MODEL SOLUTION
In this appendix, we show how the main results mentioned in the text were derived. First, the model is solved. Second, the comparative statics are derived.
GENERAL SOLUTION APPROACH
We log-linearize the model of Table 1 around an initial steady state, using the notational conventions mentioned at the beginning of Section 2. After some simplifications, the following quasi-reduced form equations can be derived:
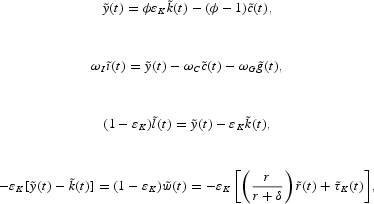
where a tilde (~) denotes a relative change (for example,
, except for
), ωC ≡ c/y denotes the share of private consumption in real output, ωI ≡ i/y is the share of investment in real output, and ωG ≡ g/y denotes the share of government consumption in real output.
The parameter ϕ represents the intertemporal labor supply effect, which is defined as:
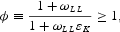
where ωLL (≡(1 − l)/l = (N − L)/L [ges ] 0) is the ratio of leisure to labor, which also represents the aggregate intertemporal substitution elasticity of labor supply. Notice that ϕ = 1 if labor supply is exogenous (because l = 1 or N = L implies that ωLL = 0). Since ωLL [ges ] 0 the sign restriction on ϕ is automatically satisfied if εK [ges ] 0. If εK > 0, ϕ is a concave function of ωLL with a positive asymptote of 1/εK as ωLL → ∞, and if εK = 0, we arrive at ϕ = 1 + ωLL [ges ] 1.
The dynamics of the per capita capital stock and per capita consumption are given by:
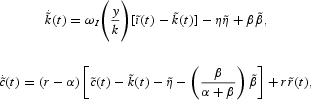
where a variable with a tilde and a dot is the time rate of change (relative to the initial steady state) and y/k = (r + δ)/(εK(1 − τK)). Using equations (A.1)–(A.4) and (A.6)–(A.7) the model can be reduced to a two-dimensional system of first-order differential equations in the per capita capital stock,
, and per capita private consumption,
. In its most general form, the dynamic system can be written as:
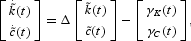
where Δ denotes the Jacobian matrix (with typical element δij evaluated at steady state:
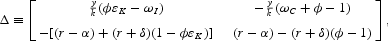
and γK(t) and γC(t) are shock terms:
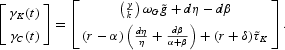
It can be shown that the determinant of the Jacobian matrix is negative, that is,
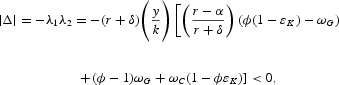
where ϕ(1 − εK) − ωG > 0, −λ1 < 0 is the stable characteristic root, and λ2 > 0 is the unstable root. The latter satisfies the inequality λ2 > r − α + ωC(r + δ), which we employ to sign the short run consumption change. Thus, there exists a unique steady state.
The Laplace transform33
The Laplace transform of x(t) is denoted by
. Intuitively,
represents the present value of x(t) using s as the discount rate.
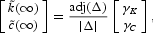
where t = ∞ identifies the new steady state that materializes after the demographic shock and adj(Δ) is the adjoint matrix of Δ.
COMPARATIVE STATICS
Pure Baby Bust
Let us first consider the pure baby-bust scenario. Using (A.10) and (A.12) we can derive the long-run effects of an exogenous decrease in the fertility rate (that is, dη < 0) while keeping the death rate constant (that is, dβ = 0). The effect on the steady-state per capita capital stock is ambiguous:
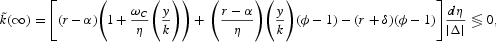
where r > α because of the overlapping generations structure of the model and |Δ|−1dη > 0. If the initial death rate is small—and thus individual consumption growth profiles are fairly flat—and intertemporal labor supply is sufficiently elastic, a drop in fertility depresses the per capita capital stock.
In the infinite horizon Ramsey model, featuring r = α in steady state, the first and second term of (A.13) drop out,34
Note that r = α for η = 0 because there is no extra-dynasty growth.
With overlapping generations (that is, r > α) and exogenous labor supply (that is, ϕ = 1, so that the second and third term of (A.13) drop out), the per capita capital stock unambiguously rises:
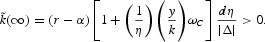
Making use of (A.10) and (A.12) again, we can derive the long-run effect of a pure baby bust on per capita consumption:
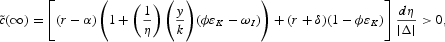
which is unambiguously positive. Initial per capita consumption changes according to:
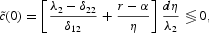
where λ2 − δ22 > 0 and t = 0 identifies the time of the shock. The first term of (A.16) is negative and the second term positive, giving rise to an ambiguous effect. The initial effect on consumption is positive if the labor supply effect dominates the generational turnover effect. Using equations (A.1)–(A.4) together with (A.12) and (A.15), the steady-state and impact effects on l, i, r, and w can be derived as well.35
See Heijdra and Ligthart (2004) for a formal derivation.
Stationary Population Growth Rate
The stationary population growth rate scenario implies an equiproportionate fall in the birth and death rate (that is, dη = dβ < 0, so that dnN = 0). The per capita capital stock rises in the new steady state:
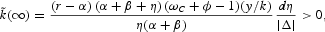
and the change in steady-state per capita consumption is given by:
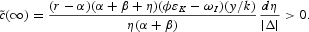
The impact effect on private consumption is unambiguously negative:
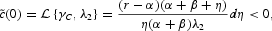
where use is made of
Constant Generational Turnover
If generational turnover is kept constant, the birth rate falls by less than the death rate, that is, dη = −ηdβ/(α + β) < 0, where dβ > 0, so that dnN = (α + β + η)(dη/η) < 0. The long-run effect on the per capita capital stock is negative if the labor supply effect dominates the generational turnover effect:
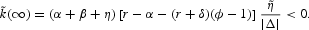
The long-run change in per capita consumption is given by:
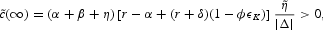
and private consumption jumps up on impact:
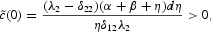
as δ12 < 0 and dη < 0.
A Fall in Public Spending
A fall in public spending (that is,
) has qualitatively similar effects to a fall in the birth rate while keeping the rate of generational turnover constant. The steady state effect on the per capita capital stock is negative and is given by:
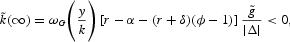
if the labor supply effect is sufficiently strong. The steady-state effect on private consumption is given by
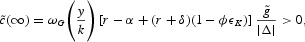
and per capita private consumption rises initially:
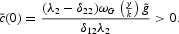
A Rise in Capital Income Subsidies
A rise in the capital income subsidy (which is represented by
and τK < 0) yields an increase in the per capita capital stock:
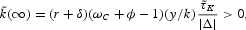
and a rise in per capita consumption in the new steady state:
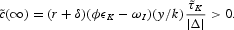
while per capita private consumption falls initially:
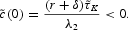
The authors would like to thank Leon Bettendorf, Peter Broer, Seppo Kari, and Hans-Werner Sinn for helpful comments. Ligthart gratefully acknowledges financial support from the Dutch Ministry of Finance. The paper was partly written when Heijdra was associated with OCFEB.