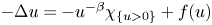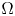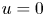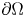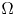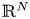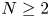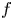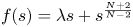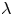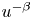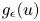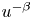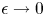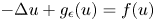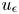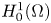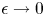1. Introduction
In this paper, we show that the problem

has a non-negative solution when $f$![]() has subcritical growth. The expression $\chi _{\{u>0\}}$
has subcritical growth. The expression $\chi _{\{u>0\}}$![]() denotes the characteristic function corresponding to the set $\{x \in \Omega : u(x)>0\}$
denotes the characteristic function corresponding to the set $\{x \in \Omega : u(x)>0\}$![]() and by convention $u^{-\beta }\chi _{\{u>0\}}=0$
and by convention $u^{-\beta }\chi _{\{u>0\}}=0$![]() if $u=0$
if $u=0$![]() . Hereafter, $\Omega \subset \mathbb {R}^{N}$
. Hereafter, $\Omega \subset \mathbb {R}^{N}$![]() , $N\geq 2$
, $N\geq 2$![]() , is a bounded smooth domain, $0<\beta <1$
, is a bounded smooth domain, $0<\beta <1$![]() and $2^{*}=\frac {2N}{N-2}$
and $2^{*}=\frac {2N}{N-2}$![]() for $N\geq 3$
for $N\geq 3$![]() .
.
By a solution of problem (1), we mean a function $u \in H_0^{1}(\Omega )$![]() such that
such that
and
Here, $C_{c}^{1}(\Omega )$![]() stands for the functions belonging to $C^{1}(\Omega )$
stands for the functions belonging to $C^{1}(\Omega )$![]() with compact support.
with compact support.
We consider the perturbed problem

where the perturbation $g_{\epsilon }$![]() is given by
is given by

and $0< q<\frac {1}{2}$![]() . We say that $u_{\epsilon }\in H_{0}^{1}(\Omega )$
. We say that $u_{\epsilon }\in H_{0}^{1}(\Omega )$![]() is a weak solution of problem (2) if
is a weak solution of problem (2) if
We define the functional $I_{\epsilon }: H_{0}^{1}(\Omega )\to \mathbb {R}$![]() associated to problem (2) by
associated to problem (2) by
where $G_{\epsilon }(s)=\int _{0}^{s}g_{\epsilon }(t)\,{\rm d}t$![]() and $F(s)=\int _{0}^{s}f(t)\,{\rm d}t$
and $F(s)=\int _{0}^{s}f(t)\,{\rm d}t$![]() . It turns out that certain solutions of problem (2) converge to a solution of problem (1). Initially, we make the following assumptions on $f$
. It turns out that certain solutions of problem (2) converge to a solution of problem (1). Initially, we make the following assumptions on $f$![]() .
.
for some $0<\nu <1$![]() and $0< q_{1}<1$
and $0< q_{1}<1$![]() , and
, and
We also assume that there exist constants $0<\epsilon _{0},\, \delta <1$![]() such that
such that
and that there exists a constant $C>0$![]() such that
such that
where $0< p<2^{*}-1$![]() ($0< p<\infty$
($0< p<\infty$![]() when $N=2$
when $N=2$![]() ). We also assume that there exists constants $0<\theta <1/2$
). We also assume that there exists constants $0<\theta <1/2$![]() , $R>0$
, $R>0$![]() and $c>0$
and $c>0$![]() such that
such that
and that there exists $\phi _{0}\in H_{0}^{1}(\Omega )\cap L^{\infty }(\Omega )$![]() such that
such that
Condition (11) holds provided
Assumptions (6) and (9) imply that $I_{\epsilon }$![]() is of class $C^{1}$
is of class $C^{1}$![]() and
and
Our first result is as the following
Examples: Let $\lambda >0$![]() and $\mu \geq 0$
and $\mu \geq 0$![]() be constants. Conditions (6)–(11) hold for the following examples of $f$
be constants. Conditions (6)–(11) hold for the following examples of $f$![]() .
.

Indeed, condition (10) will hold for $\frac {1}{1+p}<\theta <1/2$![]() and condition (8) will hold because for each $\lambda >0$
and condition (8) will hold because for each $\lambda >0$![]() and $0<\tau <1$
and $0<\tau <1$![]() there exists $0<\delta _{\tau,\lambda }<1$
there exists $0<\delta _{\tau,\lambda }<1$![]() and $0<\epsilon _{\tau,\lambda }<1$
and $0<\epsilon _{\tau,\lambda }<1$![]() such that
such that
provided $0< q<\tau$![]() in (3).
in (3).
Next, we study problem (1) with $N\geq 3$![]() and $f(s)=\lambda s+s^{2^{*}-1}$
and $f(s)=\lambda s+s^{2^{*}-1}$![]() , where $\lambda >0$
, where $\lambda >0$![]() . We prove
. We prove
Theorem 1.2 Assume that $N\geq 3$![]() and $f(s)=\lambda s+s^{2^{*}-1}$
and $f(s)=\lambda s+s^{2^{*}-1}$![]() . Then, there exists $\lambda _{0}>0$
. Then, there exists $\lambda _{0}>0$![]() such that problem (1) has a non-trivial non-negative solution for all $\lambda >\lambda _{0}$
such that problem (1) has a non-trivial non-negative solution for all $\lambda >\lambda _{0}$![]() .
.
We recall the works of [Reference Ambrosetti, Brezis and Cerami1, Reference Brezis and Nirenberg5], where the authors studied the problem

In [Reference Brezis and Nirenberg5], it was assumed that $1< p<2^{*}-1$![]() in (13). They proved that problem (13) has a positive solution for every $\lambda >0$
in (13). They proved that problem (13) has a positive solution for every $\lambda >0$![]() provided $N\geq 4$
provided $N\geq 4$![]() . The same result holds if $N=3$
. The same result holds if $N=3$![]() and $3< p<5$
and $3< p<5$![]() . In the case $N=3$
. In the case $N=3$![]() and $1< p\leq 3$
and $1< p\leq 3$![]() , the authors proved in [Reference Brezis and Nirenberg5] that (13) possesses a positive solution provided $\lambda >0$
, the authors proved in [Reference Brezis and Nirenberg5] that (13) possesses a positive solution provided $\lambda >0$![]() is sufficiently large. In [Reference Ambrosetti, Brezis and Cerami1], the authors studied problem (13) when $0< p<1$
is sufficiently large. In [Reference Ambrosetti, Brezis and Cerami1], the authors studied problem (13) when $0< p<1$![]() . They showed that there exists a constant $\Lambda _{1}>0$
. They showed that there exists a constant $\Lambda _{1}>0$![]() such that problem (13) has at least two solutions if $0<\lambda <\Lambda _{1}$
such that problem (13) has at least two solutions if $0<\lambda <\Lambda _{1}$![]() and has no solution for $\lambda >\Lambda _{1}$
and has no solution for $\lambda >\Lambda _{1}$![]() . In [Reference Diaz, Morel and Oswald12], the authors studied the problem $-\Delta u=-u^{-\beta }+f(x)$
. In [Reference Diaz, Morel and Oswald12], the authors studied the problem $-\Delta u=-u^{-\beta }+f(x)$![]() in $\Omega$
in $\Omega$![]() , $u=0$
, $u=0$![]() in $\partial \Omega$
in $\partial \Omega$![]() , the sub-supersolution method was used and positive solutions were obtained. Equation $-\Delta u+K(x)u^{-\beta }=\lambda u^{p}$
, the sub-supersolution method was used and positive solutions were obtained. Equation $-\Delta u+K(x)u^{-\beta }=\lambda u^{p}$![]() with $0< p<1$
with $0< p<1$![]() and zero boundary condition was studied in [Reference Shi and Yao27], where $K$
and zero boundary condition was studied in [Reference Shi and Yao27], where $K$![]() was assumed to be of class $C^{2,\alpha }(\overline {\Omega })$
was assumed to be of class $C^{2,\alpha }(\overline {\Omega })$![]() . For more on singular problems with sublinear nonlinearities, see [Reference Papageorgiou and Rădulescu23, Reference Zhang30]. Theorem 1.1 asserts that the problem
. For more on singular problems with sublinear nonlinearities, see [Reference Papageorgiou and Rădulescu23, Reference Zhang30]. Theorem 1.1 asserts that the problem

is solvable for each $\lambda >0$![]() and $\mu \geq 0$
and $\mu \geq 0$![]() , provided $0< q< p<2^{*}-1$
, provided $0< q< p<2^{*}-1$![]() and $p>1$
and $p>1$![]() . Problems (13) and (14) are similar in essence, the latter being a singular version of the former. Theorem 1.1 should also be compared with the results of [Reference Dávila and Montenegro10, Reference Montenegro and Silva22], where the authors studied the problem
. Problems (13) and (14) are similar in essence, the latter being a singular version of the former. Theorem 1.1 should also be compared with the results of [Reference Dávila and Montenegro10, Reference Montenegro and Silva22], where the authors studied the problem

with $\lambda >0$![]() . In [Reference Dávila and Montenegro10], the authors assumed that $p>1$
. In [Reference Dávila and Montenegro10], the authors assumed that $p>1$![]() and they obtained one solution of (15) for each $\lambda >0$
and they obtained one solution of (15) for each $\lambda >0$![]() . The case $p=1$
. The case $p=1$![]() was also studied in [Reference Dávila and Montenegro10], and they obtained one solution for $\lambda >\lambda _{1}$
was also studied in [Reference Dávila and Montenegro10], and they obtained one solution for $\lambda >\lambda _{1}$![]() , where $\lambda _{1}$
, where $\lambda _{1}$![]() is the first eigenvalue of $-\Delta$
is the first eigenvalue of $-\Delta$![]() . In [Reference Montenegro and Silva22], the authors assumed that $0< p<1$
. In [Reference Montenegro and Silva22], the authors assumed that $0< p<1$![]() and they obtained two distinct solutions of (15) for large values of $\lambda$
and they obtained two distinct solutions of (15) for large values of $\lambda$![]() . See also [Reference Dávila and Montenegro9], where the authors obtained sharper regularity results for solutions $u_{\lambda }$
. See also [Reference Dávila and Montenegro9], where the authors obtained sharper regularity results for solutions $u_{\lambda }$![]() of problem (15) with $0< p<1$
of problem (15) with $0< p<1$![]() . In this work, we consider general nonlinearities $f$
. In this work, we consider general nonlinearities $f$![]() with subcritical growth, and we do not make use of parameters. Observe also that in Theorem 1.1, we make no assumptions on the sign of $f$
with subcritical growth, and we do not make use of parameters. Observe also that in Theorem 1.1, we make no assumptions on the sign of $f$![]() .
.
Theorem 1.2 should be compared with the results of [Reference Figueiredo and Montenegro14], where the authors studied the problem

When $0< p<1$![]() in (16), the authors obtained a constant $\Lambda _{0}>0$
in (16), the authors obtained a constant $\Lambda _{0}>0$![]() such that problem (16) has two distinct non-trivial and non-negative solutions for $0<\lambda <\Lambda _{0}$
such that problem (16) has two distinct non-trivial and non-negative solutions for $0<\lambda <\Lambda _{0}$![]() . If $1< p<\frac {N+2}{N-2}$
. If $1< p<\frac {N+2}{N-2}$![]() , the authors obtained a constant $\Lambda _{0}^{*}>0$
, the authors obtained a constant $\Lambda _{0}^{*}>0$![]() such that problem (16) admits a solution provided $\lambda >\Lambda _{0}^{*}$
such that problem (16) admits a solution provided $\lambda >\Lambda _{0}^{*}$![]() . Theorem 1.2 addresses the case $p=1$
. Theorem 1.2 addresses the case $p=1$![]() in (16).
in (16).
Problems similar to (1) and (2) arise in the context of heterogeneous catalysis. Consider a reaction $R$![]() which converts a given gas to useful products, and suppose that $R$
which converts a given gas to useful products, and suppose that $R$![]() occurs only in the presence of a catalyst that comes in the form of a porous pellet $\Omega$
occurs only in the presence of a catalyst that comes in the form of a porous pellet $\Omega$![]() . For the pellet to be useful, the gas must diffuse inside it. In this context, two entities arise: the rate of reaction $k_{R}$
. For the pellet to be useful, the gas must diffuse inside it. In this context, two entities arise: the rate of reaction $k_{R}$![]() and the rate of diffusion $k_{D}$
and the rate of diffusion $k_{D}$![]() of the gas in regions of $\Omega$
of the gas in regions of $\Omega$![]() . If $k_{D}$
. If $k_{D}$![]() is large compared to $k_{R}$
is large compared to $k_{R}$![]() , then the reaction occurs throughout $\Omega$
, then the reaction occurs throughout $\Omega$![]() and no free boundary arises. However, when $k_{D}$
and no free boundary arises. However, when $k_{D}$![]() is small compared to $k_{R}$
is small compared to $k_{R}$![]() , then there are zones within $\Omega$
, then there are zones within $\Omega$![]() in which no reaction takes place, these are known as dead cores. The rates of adsorption $k_{a}$
in which no reaction takes place, these are known as dead cores. The rates of adsorption $k_{a}$![]() and desorption $k_{d}$
and desorption $k_{d}$![]() of gas in the surface of the pellet must also be considered, for the equilibrium is reached when $k_{a}$
of gas in the surface of the pellet must also be considered, for the equilibrium is reached when $k_{a}$![]() equals $k_{d}$
equals $k_{d}$![]() . Let $A_{1},\, A_{2},\,\ldots A_{S}$
. Let $A_{1},\, A_{2},\,\ldots A_{S}$![]() be chemical species involved in the reaction
be chemical species involved in the reaction

where $\alpha _{j}$![]() denote the number of molecules of $A_{j}$
denote the number of molecules of $A_{j}$![]() being formed ($\alpha _{j}>0$
being formed ($\alpha _{j}>0$![]() ) or consumed ($\alpha _{j}<0$
) or consumed ($\alpha _{j}<0$![]() ) in $\Omega$
) in $\Omega$![]() . Then, under certain assumptions about the mechanism of the reaction, the concentration $c_{j}=c_{j}(x)$
. Then, under certain assumptions about the mechanism of the reaction, the concentration $c_{j}=c_{j}(x)$![]() of $A_{j}$
of $A_{j}$![]() at $x\in \Omega$
at $x\in \Omega$![]() satisfies the following elliptic equation
satisfies the following elliptic equation
for each $j\in \{1,\,2,\,\ldots,\,S\}$![]() . Here, $D_{j}$
. Here, $D_{j}$![]() denotes the diffusion coefficient of $A_{j}$
denotes the diffusion coefficient of $A_{j}$![]() and $\pi _{S}$
and $\pi _{S}$![]() the catalytic area per unit volume. At equilibrium, the reaction rate $k_{R}$
the catalytic area per unit volume. At equilibrium, the reaction rate $k_{R}$![]() can be calculated as a function of the concentrations $c_{j}$
can be calculated as a function of the concentrations $c_{j}$![]() . Using a suitable change of variables (see [Reference Aris3], p.168), we get an equation of the form
. Using a suitable change of variables (see [Reference Aris3], p.168), we get an equation of the form
where $\lambda >0$![]() is a constant called Thiele Modulus, $R:\mathbb {R}\to \mathbb {R}$
is a constant called Thiele Modulus, $R:\mathbb {R}\to \mathbb {R}$![]() is a rational function and $0\leq u\leq 1$
is a rational function and $0\leq u\leq 1$![]() represents a ‘normalized dimensionless concentration’. We see that equations (2) and (17) are similar in essence.
represents a ‘normalized dimensionless concentration’. We see that equations (2) and (17) are similar in essence.
For more applications in catalysis and in other fields of research, such as biochemistry, see [Reference Aris3, Reference Diaz11]. See [Reference Friedman and Phillips15, Reference Phillips26] for studies of the free boundary of solutions of some elliptic equations.
Singular equations are related to phase field models, see [Reference Copetti and Elliott6, Reference Dal Passo, Giacomelli and Novick-Cohen8, Reference Elliot and Garcke13, Reference Gilardi and Rocca16]. For more results on singular elliptic equations, see [Reference Anello and Faraci2, Reference Bai, Gasiński and Papageorgiou4, Reference Hirano, Saccon and Shioji17, Reference Long, Sun and Wu19, Reference Montenegro and Queiroz21, Reference Papageorgiou and Smyrlis24, Reference Perera and Silva25, Reference Wang, Qin and Hu28].
Our paper is organized as follows. In § 2, we give some preliminary results. Next, we study problem (2) by considering two different scenarios; in § 3, we consider the subcritical case and in § 4, we study problem (2) with $f(s)=\lambda s+s^{\frac {N+2}{N-2}}$![]() . In both cases, we show that the associated functional satisfy the assumptions of the Mountain Pass Theorem. We thus obtain solutions of problem (2). These solutions will be shown to be bounded in $H_{0}^{1}(\Omega )$
. In both cases, we show that the associated functional satisfy the assumptions of the Mountain Pass Theorem. We thus obtain solutions of problem (2). These solutions will be shown to be bounded in $H_{0}^{1}(\Omega )$![]() by a constant that does not depend on $\epsilon$
by a constant that does not depend on $\epsilon$![]() . Such an estimate will be crucial in § 5, where we will establish regularity results for the solutions of problem (2) obtained in § 3 and § 4. In § 6, we prove Theorems 1.1 and 1.2.
. Such an estimate will be crucial in § 5, where we will establish regularity results for the solutions of problem (2) obtained in § 3 and § 4. In § 6, we prove Theorems 1.1 and 1.2.
2. Preliminary results
First, we show that critical points of the functional $I_{\epsilon }$![]() defined in (5) must be non-negative.
defined in (5) must be non-negative.
Lemma 2.1 Assume that (6), (7) and (9) hold. Let $u_{\epsilon }$![]() be a critical point of the functional $I_{\epsilon }$
be a critical point of the functional $I_{\epsilon }$![]() defined by (5). Then $u_{\epsilon }\geq 0$
defined by (5). Then $u_{\epsilon }\geq 0$![]() and $u_{\epsilon }$
and $u_{\epsilon }$![]() is a weak solution of problem (2).
is a weak solution of problem (2).
Proof of Lemma 2.1 Let $u_{\epsilon }^{-}=\max \{-u_{\epsilon },\,0\}$![]() . Taking $v=u_{\epsilon }^{-}$
. Taking $v=u_{\epsilon }^{-}$![]() in (12) and using (7), we obtain
in (12) and using (7), we obtain
Hence, $u_{\epsilon }\geq 0$![]() and
and
We will need estimates of the perturbation $g_{\epsilon }$![]() defined in (3). Note that
defined in (3). Note that
Hence,
Therefore, from the fact that $0< q<\frac {1}{2}$![]() , it follows that, for each $M>0$
, it follows that, for each $M>0$![]() , there exists $\overline {\delta }=\overline {\delta }(M)<1$
, there exists $\overline {\delta }=\overline {\delta }(M)<1$![]() such that
such that
We thus obtain
Observe that
Hence,
The following lemma will play a crucial role in § 4.
Lemma 2.2
Proof of Lemma 2.2 Indeed, let $\widetilde {B}_{\epsilon }(s)=G_{\epsilon }(s)-\frac {1}{2}g_{\epsilon }(s)s$![]() . We have that $B_{\epsilon }(0)=0$
. We have that $B_{\epsilon }(0)=0$![]() and
and
Therefore, $\widetilde {B}_{\epsilon }'(s)\geq 0$![]() if and only if
if and only if
From (19), this inequality will be true if
Since $q<1/2$![]() , (20) holds for each $s\geq 0$
, (20) holds for each $s\geq 0$![]() . This proves Lemma 2.2.
. This proves Lemma 2.2.
Now, we show that a version of the Ambrosetti–Rabinowitz condition holds. We define
Consequently,
where $J_{\epsilon }(s)=\int _{0}^{s}j_{\epsilon }(t)\,{\rm d}t$![]() . For simplicity of notation, we denote $J_{\epsilon }$
. For simplicity of notation, we denote $J_{\epsilon }$![]() and $j_{\epsilon }$
and $j_{\epsilon }$![]() merely by $J$
merely by $J$![]() and $j$
and $j$![]() respectively.
respectively.
Lemma 2.3 Suppose that (6) and (10) hold. Let $0<\theta <1/2$![]() be given by (10). There exists a constant $\overline {R}>0$
be given by (10). There exists a constant $\overline {R}>0$![]() such that
such that
Proof of Lemma 2.3 Let $B_{\epsilon }(s)=J(s)-\theta s j(s)$![]() . We have
. We have
Hence,
From (19) we obtain
It is also clear that
Hence, for each $0<\tau <1$![]() there exists $R_{\tau }>0$
there exists $R_{\tau }>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Therefore,
Consequently, from (10), we get
where $c>0$![]() and $R>0$
and $R>0$![]() are given by (10). Choosing $\tau =c/2$
are given by (10). Choosing $\tau =c/2$![]() , we get
, we get
where
Note that
where
Therefore, (21) implies that there exists a constant $T>0$![]() such that
such that
Hence, $B_{\epsilon }(s)\leq 0$![]() for $s\geq \max \{R_{2},\,2T/c\}$
for $s\geq \max \{R_{2},\,2T/c\}$![]() . This proves Lemma 2.3.
. This proves Lemma 2.3.
Let $\phi _0 \in H^{1}_{0}(\Omega )\cap L^{\infty }(\Omega )$![]() be given by (11). We have
be given by (11). We have
Lemma 2.4 Assume that (6), (9) and (11) hold. There exist a constant $a_{2}>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Proof of Lemma 2.4 We have
Consequently, we get
We conclude that
where

3. Existence of solution of the perturbed subcritical problem
Throughout this section, we will assume that $f$![]() satisfies (9) with $0< p<2^{*}-1$
satisfies (9) with $0< p<2^{*}-1$![]() . Our aim is to show that problem (2) has a non-negative non-trivial solution. We recall that given a Banach space $E$
. Our aim is to show that problem (2) has a non-negative non-trivial solution. We recall that given a Banach space $E$![]() and a functional $\Psi \in C^{1}(E;\mathbb {R})$
and a functional $\Psi \in C^{1}(E;\mathbb {R})$![]() , we say that a sequence $(u_n)$
, we say that a sequence $(u_n)$![]() in $E$
in $E$![]() is a Palais–Smale sequence of $\Psi$
is a Palais–Smale sequence of $\Psi$![]() if there exists $c\in \mathbb {R}$
if there exists $c\in \mathbb {R}$![]() such that $\Psi (u_n)\to c$
such that $\Psi (u_n)\to c$![]() and $\|\Psi '(u_{n})\|\to 0$
and $\|\Psi '(u_{n})\|\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . We say that $\Psi$
. We say that $\Psi$![]() satisfies the Palais–Smale condition if every Palais–Smale sequence of $\Psi$
satisfies the Palais–Smale condition if every Palais–Smale sequence of $\Psi$![]() has a convergent subsequence.
has a convergent subsequence.
Lemma 3.1 Assume that (6)–(10) hold. Fix $0<\epsilon <1$![]() and let $(u_{n}^{\epsilon })$
and let $(u_{n}^{\epsilon })$![]() be a Palais–Smale sequence for $I_{\epsilon }$
be a Palais–Smale sequence for $I_{\epsilon }$![]() in $H_{0}^{1}(\Omega )$
in $H_{0}^{1}(\Omega )$![]() . Assume that there exists a constant $C>0$
. Assume that there exists a constant $C>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Then, there exists $D>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Furthermore, there exists $u_{\epsilon }\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence, $u_{n}^{\epsilon }\to u_{\epsilon }$
such that, up to a subsequence, $u_{n}^{\epsilon }\to u_{\epsilon }$![]() strongly in $H_{0}^{1}(\Omega )$
strongly in $H_{0}^{1}(\Omega )$![]() . Consequently, $u_{\epsilon }$
. Consequently, $u_{\epsilon }$![]() is a critical point of $I_{\epsilon }$
is a critical point of $I_{\epsilon }$![]() .
.
Proof of Lemma 3.1 Throughout this proof, we denote $\|\cdot \|_{H_{0}^{1}(\Omega )}$![]() by $\|\cdot \|$
by $\|\cdot \|$![]() . Let $(u_{n}^{\epsilon })_{n\in \mathbb {N}}$
. Let $(u_{n}^{\epsilon })_{n\in \mathbb {N}}$![]() be a Palais–Smale sequence for $I_{\epsilon }$
be a Palais–Smale sequence for $I_{\epsilon }$![]() satisfying (23). Consequently,
satisfying (23). Consequently,
and there is a sequence $\tau _{n}\rightarrow 0$![]() such that
such that
Let $0<\theta <1/2$![]() be given by (10). From Lemma 2.3, there is a constant $\overline {R}>0$
be given by (10). From Lemma 2.3, there is a constant $\overline {R}>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Since there exists $D_{1}>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
we may find a constant $D_{2}>0$![]() such that
such that
We know from (25) that there is a constant $D_{3}>0$![]() such that
such that
Taking $w=u_{n}^{\epsilon }$![]() in (26), we also conclude that
in (26), we also conclude that
Hence,
Since $0<\theta <\frac {1}{2}$![]() , (24) follows. Consequently, there exists $u_{\epsilon }\in H_{0}^{1}(\Omega )$
, (24) follows. Consequently, there exists $u_{\epsilon }\in H_{0}^{1}(\Omega )$![]() such that $u_{n}^{\epsilon }\rightharpoonup u_{\epsilon }$
such that $u_{n}^{\epsilon }\rightharpoonup u_{\epsilon }$![]() weakly in $H_{0}^{1}(\Omega )$
weakly in $H_{0}^{1}(\Omega )$![]() . Since $J_{\epsilon }$
. Since $J_{\epsilon }$![]() has subcritical growth at infinity (see [Reference Costa7], Theorem 3.4 and Remark 2.2.1), we conclude that, up to a subsequence, $u_{n}^{\epsilon }\to u_{\epsilon }$
has subcritical growth at infinity (see [Reference Costa7], Theorem 3.4 and Remark 2.2.1), we conclude that, up to a subsequence, $u_{n}^{\epsilon }\to u_{\epsilon }$![]() strongly in $H_{0}^{1}(\Omega )$
strongly in $H_{0}^{1}(\Omega )$![]() . Since $I_{\epsilon }'(u_{n}^{\epsilon })\to 0$
. Since $I_{\epsilon }'(u_{n}^{\epsilon })\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() and $I_{\epsilon }$
and $I_{\epsilon }$![]() is of class $C^{1}$
is of class $C^{1}$![]() , we conclude that $I_{\epsilon }'(u_{\epsilon })=0$
, we conclude that $I_{\epsilon }'(u_{\epsilon })=0$![]() . This proves the result.
. This proves the result.
Now, we obtain one solution for problem (2).
Proposition 3.2 Assume that (6)–(11) hold and let $a_{2}>0$![]() be given by Lemma 2.4. Then, there is a non-negative solution $u_{\epsilon }$
be given by Lemma 2.4. Then, there is a non-negative solution $u_{\epsilon }$![]() of problem (2) and there exist constants $a_{1}>0$
of problem (2) and there exist constants $a_{1}>0$![]() and $D>0$
and $D>0$![]() that do not depend on $\epsilon$
that do not depend on $\epsilon$![]() such that
such that
and
Proof of Proposition 3.2 Let $\delta >0$![]() and $\epsilon _{0}$
and $\epsilon _{0}$![]() be given by (8). Note that
be given by (8). Note that

The fact that $g_{\epsilon }$![]() is monotone in $\epsilon$
is monotone in $\epsilon$![]() implies that
implies that
Using the fact that $G_{\epsilon }\geq 0$![]() , we get
, we get
From (9), we have
Consequently,
We conclude that there exists $\widetilde {C}>0$![]() such that
such that
where $\sigma >2$![]() is chosen such that $1+p<\sigma <2^{*}$
is chosen such that $1+p<\sigma <2^{*}$![]() . The Sobolev embedding implies that there is a constant $C_{3}>0$
. The Sobolev embedding implies that there is a constant $C_{3}>0$![]() such that
such that
Therefore,
where

Also,
where
Let $\phi _{0}$![]() be given by (11) and $\Gamma =\{\gamma \in C([0,\,1],\, H_{0}^{1}(\Omega )):\gamma (0)=0,\, \gamma (1)=\phi _{0}\}$
be given by (11) and $\Gamma =\{\gamma \in C([0,\,1],\, H_{0}^{1}(\Omega )):\gamma (0)=0,\, \gamma (1)=\phi _{0}\}$![]() . We know from (23) that $I_{\epsilon }(\phi _{0})<0$
. We know from (23) that $I_{\epsilon }(\phi _{0})<0$![]() . Consequently, we may apply the Mountain Pass Theorem [Reference Willem29], page 12) to conclude that there is a Palais–Smale sequence $(u_{n}^{\epsilon }$
. Consequently, we may apply the Mountain Pass Theorem [Reference Willem29], page 12) to conclude that there is a Palais–Smale sequence $(u_{n}^{\epsilon }$![]() for $I_{\epsilon }$
for $I_{\epsilon }$![]() in $H_{0}^{1}(\Omega )$
in $H_{0}^{1}(\Omega )$![]() and a number
and a number
such that
From Lemma 2.4, we know that $a_{1}\leq c_{\epsilon }\leq a_{2}$![]() . From Lemma 3.1, we conclude that there exist $D>0$
. From Lemma 3.1, we conclude that there exist $D>0$![]() (that does not depend on $\epsilon$
(that does not depend on $\epsilon$![]() ) and $u_{\epsilon }\in H_{0}^{1}(\Omega )$
) and $u_{\epsilon }\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence, $u_{n}^{\epsilon }\to u_{\epsilon }$
such that, up to a subsequence, $u_{n}^{\epsilon }\to u_{\epsilon }$![]() strongly in $H_{0}^{1}(\Omega )$
strongly in $H_{0}^{1}(\Omega )$![]() and
and
Consequently, $I_{\epsilon }'(u_{\epsilon })=0$![]() and
and
This proves the result.
4. Existence of solution of the perturbed problem when $p=2^{*}-1$
In this section, we study problem (2) with $f(s)=\lambda s+s^{2^{*}-1}$![]() for $s\geq 0$
for $s\geq 0$![]() . We assume that $f(s)=0$
. We assume that $f(s)=0$![]() for $s\leq 0$
for $s\leq 0$![]() . This function satisfies (6), (7), (8) and (10). The difficulty here is that $f$
. This function satisfies (6), (7), (8) and (10). The difficulty here is that $f$![]() no longer satisfies (9), so that Lemma 3.1 does not hold. The associated functional then becomes
no longer satisfies (9), so that Lemma 3.1 does not hold. The associated functional then becomes
where $u^{+}=\max \{u,\,0\}$![]() . The functional $I_{\epsilon,\lambda }$
. The functional $I_{\epsilon,\lambda }$![]() is of class $C^{1}$
is of class $C^{1}$![]() and
and

The same argument given by Lemma 2.1 implies that critical points of $I_{\epsilon,\lambda }$![]() are non-negative solutions of problem (2). Observe also that zero is a local minimum of the functional $I_{\epsilon,\lambda }$
are non-negative solutions of problem (2). Observe also that zero is a local minimum of the functional $I_{\epsilon,\lambda }$![]() . Indeed, let $0<\overline {\delta }<1$
. Indeed, let $0<\overline {\delta }<1$![]() be given by (18). Note that
be given by (18). Note that
Choosing $M=\lambda$![]() in (18), we obtain
in (18), we obtain
Observe that there exists a constant $C_{1}>0$![]() such that
such that
Hence, there exists a constant $C_{2}>0$![]() such that
such that
Consequently, the Sobolev embedding implies that
We conclude that
where

Also,
where
We now show that there exists $\phi \in H_{0}^{1}(\Omega )\cap L^{\infty }(\Omega )$![]() such that
such that
Indeed, let $\phi _1 \in H^{1}_{0}(\Omega )$![]() be the first eigenfunction of the operator $-\Delta$
be the first eigenfunction of the operator $-\Delta$![]() with $\|\phi _1\|_{H^{1}_{0}(\Omega )}= 1$
with $\|\phi _1\|_{H^{1}_{0}(\Omega )}= 1$![]() . We have
. We have
Lemma 4.1 There exist constants $N_{0}>0,$![]() $a_{2}>0$
$a_{2}>0$![]() and $b_{1}>0$
and $b_{1}>0$![]() such that
such that
and
Moreover, these constants do not depend on $\lambda$![]() .
.
Proof of Lemma 2.4 For each $t>0$![]() , we have
, we have
From the fact that $G_{\epsilon }(s)\leq \frac {s^{1-\beta }}{1-\beta }$![]() for all $s\geq 0$
for all $s\geq 0$![]() , we get
, we get
Since $2^{*}>2>1-\beta$![]() , inequality (30) then follows by taking $t$
, inequality (30) then follows by taking $t$![]() large enough in (32). We also have
large enough in (32). We also have
Consequently, we get
We conclude that
where
Lemma 4.1, (29) and the Mountain Pass Theorem imply that there is a sequence $(u_{n}^{\epsilon })$![]() in $H_{0}^{1}(\Omega )$
in $H_{0}^{1}(\Omega )$![]() and a number
and a number
such that
where $\Gamma =\{\gamma \in C([0,\,1],\, H_{0}^{1}(\Omega )):\gamma (0)=0,\, \gamma (1)=N_{0}\phi _{1}\}$![]() . It is clear that the function $f(s)=\lambda s+s^{2^{*}-1}$
. It is clear that the function $f(s)=\lambda s+s^{2^{*}-1}$![]() satisfies (10). Consequently, the same computations developed in the proof of Lemma 2.3 imply that there exists $0<\theta <1/2$
satisfies (10). Consequently, the same computations developed in the proof of Lemma 2.3 imply that there exists $0<\theta <1/2$![]() such that
such that
where $j(s)=\lambda s+s^{2^{*}-1}-g_{\epsilon }(s)$![]() and $J(s)=\int _{0}^{s}j(t)\,{\rm d}t$
and $J(s)=\int _{0}^{s}j(t)\,{\rm d}t$![]() . Consequently, by a similar argument given in the proof of Lemma 3.1, we obtain a constant $D>0$
. Consequently, by a similar argument given in the proof of Lemma 3.1, we obtain a constant $D>0$![]() such that
such that
Furthermore, we have
Lemma 4.2 Let $c_{\lambda,\epsilon }$![]() be given by (33). Then
be given by (33). Then
Proof of Lemma 4.2 Fix $0<\epsilon <1$![]() and let $t_{\lambda,\epsilon }\geq 0$
and let $t_{\lambda,\epsilon }\geq 0$![]() be such that
be such that
From Lemmas 2.4 and (29), we get
Hence, $0< t_{\lambda,\epsilon }<1$![]() . Consequently,
. Consequently,

Equivalently, from (28),

Fix a sequence $(\lambda _{n})$![]() in $\mathbb {R}$
in $\mathbb {R}$![]() such that $\lambda _{n}\to \infty$
such that $\lambda _{n}\to \infty$![]() . Since $0< t_{\lambda _{n},\,\epsilon }<1$
. Since $0< t_{\lambda _{n},\,\epsilon }<1$![]() , we know that for each $0<\epsilon <1$
, we know that for each $0<\epsilon <1$![]() there exists an element $0\leq t_{0,\epsilon }\leq 1$
there exists an element $0\leq t_{0,\epsilon }\leq 1$![]() such that
such that
We will show that $t_{0,\epsilon }=0$![]() . Indeed, from (37) there exists a constant $M_{0}>0$
. Indeed, from (37) there exists a constant $M_{0}>0$![]() that does not depend on $\lambda$
that does not depend on $\lambda$![]() nor on $\epsilon$
nor on $\epsilon$![]() such that
such that
Letting $n\to \infty$![]() in (38), it follows that $t_{\lambda _{n},\,\epsilon }\to 0$
in (38), it follows that $t_{\lambda _{n},\,\epsilon }\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() uniformly on $\epsilon$
uniformly on $\epsilon$![]() . Hence, $t_{0,\epsilon }=0$
. Hence, $t_{0,\epsilon }=0$![]() . Consequently,
. Consequently,
Letting $n\to \infty$![]() , we obtain
, we obtain
Since the sequence $(\lambda _{n})$![]() was arbitrarily chosen, (36) follows.
was arbitrarily chosen, (36) follows.
Consequently, there exist $\lambda _{0}>0$![]() and $0<\epsilon _{0}<1$
and $0<\epsilon _{0}<1$![]() such that
such that
where

We now obtain the main result of this section.
Proposition 4.3 Let $a_{1}>0,$![]() $a_{2}>0$
$a_{2}>0$![]() and $\lambda _{0}>0$
and $\lambda _{0}>0$![]() be given by (29), Lemmas 4.1 and (39), respectively. If $\lambda >\lambda _{0},$
be given by (29), Lemmas 4.1 and (39), respectively. If $\lambda >\lambda _{0},$![]() then problem (2) has a non-negative solution $u_{\epsilon }$
then problem (2) has a non-negative solution $u_{\epsilon }$![]() such that
such that
where $c_{\lambda,\epsilon }$![]() is given by (33). Furthermore, there exists a constant $D>0$
is given by (33). Furthermore, there exists a constant $D>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Proof of Proposition 4.3 Inequality (35) implies that there is $u_{\epsilon }\in H_{0}^{1}(\Omega )$![]() with $\|u_{\epsilon }\|_{H^{1}_{0}(\Omega )}< D$
with $\|u_{\epsilon }\|_{H^{1}_{0}(\Omega )}< D$![]() such that, up to a subsequence,
such that, up to a subsequence,
We claim that
To do this, we use the ideas given in [Reference Figueiredo and Montenegro14]. Note that there exist positive measures $\mu,\,\nu$![]() in $\Omega$
in $\Omega$![]() such that
such that
Using the concentration-compactness principle due to Lions (cf. [Reference Lions18], Lemma 1.1), we obtain at most a countable set of indexes denoted by $\Lambda$![]() , sequences $x_{i}\in \overline {\Omega }$
, sequences $x_{i}\in \overline {\Omega }$![]() , $\mu _{i},\,\nu _{i}\in (0,\,\infty )$
, $\mu _{i},\,\nu _{i}\in (0,\,\infty )$![]() such that
such that
for every $i\in \Lambda$![]() , where $S$
, where $S$![]() is given by (40). Now, for every $\sigma >0$
is given by (40). Now, for every $\sigma >0$![]() and $i\in \Lambda$
and $i\in \Lambda$![]() , we define
, we define
where $\psi \in C_{c}^{\infty }(\mathbb {R}^{n})$![]() is a function satisfying
is a function satisfying
Since the function $\psi _{\sigma,i}(u_{n}^{\epsilon })^{+}$![]() is bounded in $H_{0}^{1}(\Omega )$
is bounded in $H_{0}^{1}(\Omega )$![]() , we know that $I_{\lambda,\epsilon }'(u_{n})(\psi _{\sigma,i}(u_{n}^{\epsilon })^{+})\to 0$
, we know that $I_{\lambda,\epsilon }'(u_{n})(\psi _{\sigma,i}(u_{n}^{\epsilon })^{+})\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . Hence,
. Hence,

Consequently,
Note that
Hence,
It is also clear that
and
We claim that
Indeed,
Therefore,
where
Using the Lebesgue Differentiation Theorem and the bound on $\nabla \psi$![]() , we obtain
, we obtain
where $V(B_{2\sigma }(x_{i}))$![]() denotes the volume of the ball $B_{2\sigma }(x_{i})$
denotes the volume of the ball $B_{2\sigma }(x_{i})$![]() . Hence, $\lim _{\sigma \to 0}J_{1,\sigma }=0$
. Hence, $\lim _{\sigma \to 0}J_{1,\sigma }=0$![]() . It is also clear that $\lim _{\sigma \to 0}J_{2,\sigma }=0$
. It is also clear that $\lim _{\sigma \to 0}J_{2,\sigma }=0$![]() . This proves (44). Letting $n\to \infty$
. This proves (44). Letting $n\to \infty$![]() and $\sigma \to 0$
and $\sigma \to 0$![]() in (43), we get
in (43), we get
Hence,
Since
and
it follows that
From Lemmas 2.2, (34) and from the definition of $\psi _{\sigma,i}$![]() , we obtain
, we obtain
Note that
Hence, letting $n\to \infty$![]() in (45), we obtain
in (45), we obtain
This contradicts (39). This proves that $\Lambda =\emptyset$![]() and therefore (42) holds. We will now show that $u_{n}^{\epsilon }\to u_{\epsilon }$
and therefore (42) holds. We will now show that $u_{n}^{\epsilon }\to u_{\epsilon }$![]() in $H_{0}^{1}(\Omega )$
in $H_{0}^{1}(\Omega )$![]() . Indeed
. Indeed

where

and
Using the Dominated Convergence Theorem, (41) and (42), we obtain that
Therefore, it follows from (34) that
Therefore, $u_{n}^{\epsilon }\to u_{\epsilon }$![]() strongly in $H_{0}^{1}(\Omega )$
strongly in $H_{0}^{1}(\Omega )$![]() . From (34), it follows that $u_{\epsilon }$
. From (34), it follows that $u_{\epsilon }$![]() is a critical point of $I_{\epsilon,\lambda }$
is a critical point of $I_{\epsilon,\lambda }$![]() with
with
In particular, we know that $u_{\epsilon }\geq 0$![]() . This proves Proposition 4.3.
. This proves Proposition 4.3.
5. Regularity results and gradient estimates
We will need the following a priori bound in $L^{\infty }(\Omega )$![]() .
.
Lemma 5.1 Let $u_{\epsilon,\lambda }\in H_{0}^{1}(\Omega )$![]() be a non-negative solution of problem (2) with $f(s)=\lambda s+s^{p}$
be a non-negative solution of problem (2) with $f(s)=\lambda s+s^{p}$![]() and assume that there exists a constant $D>0$
and assume that there exists a constant $D>0$![]() independent of $\epsilon$
independent of $\epsilon$![]() such that
such that
Then the following assertions hold
${\rm (i)}$![]() If $1< p<2^{*}-1$
If $1< p<2^{*}-1$![]() then $u_{\epsilon,\lambda }\in L^{\infty }(\Omega )$
then $u_{\epsilon,\lambda }\in L^{\infty }(\Omega )$![]() and there exists a constant $K_{1}>0$
and there exists a constant $K_{1}>0$![]() such that
such that
${\rm (ii)}$![]() If $p=2^{*}-1$
If $p=2^{*}-1$![]() and
and
then there exists $\widehat {\lambda _{0}}>0$![]() such that $u_{\epsilon,\lambda }\in L^{\infty }(\Omega )$
such that $u_{\epsilon,\lambda }\in L^{\infty }(\Omega )$![]() for each $\lambda >\widehat {\lambda _{0}}$
for each $\lambda >\widehat {\lambda _{0}}$![]() and (47) holds.
and (47) holds.
Proof of Lemma 5.1 For simplicity, we denote $u_{\epsilon,\lambda }$![]() by $u_{\epsilon }$
by $u_{\epsilon }$![]() . For $s\geq 0$
. For $s\geq 0$![]() , define $h(s)=\lambda s+s^{p}$
, define $h(s)=\lambda s+s^{p}$![]() . From (4), we get
. From (4), we get
Note that
Hence, the exists $0<\delta _{\lambda }<1$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Also,
Therefore, we conclude that
where
It is also clear that
Using (50), (51) and (52), we obtain
Hence, from (70), we get
We will now prove assertions $(i)$![]() and $(ii)$
and $(ii)$![]() separately. The proof of $(ii)$
separately. The proof of $(ii)$![]() is more intricate, because we need to study the dependence of certain constants on $\lambda$
is more intricate, because we need to study the dependence of certain constants on $\lambda$![]() , so that we can let $\lambda \to \infty$
, so that we can let $\lambda \to \infty$![]() .
.
Proof of (i): From (53), we obtain a constant $C_{\delta,\lambda }>0$![]() such that
such that
For $L > 1$![]() , we define,
, we define,

with $\sigma > 1$![]() to be determined later. Note that $z_{L,\epsilon }\in H_{0}^{1}(\Omega )$
to be determined later. Note that $z_{L,\epsilon }\in H_{0}^{1}(\Omega )$![]() , $z_{L,\epsilon }\geq 0$
, $z_{L,\epsilon }\geq 0$![]() and
and
Taking $v=z_{L,\epsilon }$![]() in (54) we obtain
in (54) we obtain
Since $\sigma >1$![]() and
and
we conclude that
On the other hand, from the Sobolev embedding, we know that there is a constant $C_{1}>0$![]() such that
such that

Since
it follows that

From the definition of $u_{L,\epsilon }$![]() , we conclude that
, we conclude that

Using (55), we obtain

Now, observe that

Hence, there is a constant $\widetilde {C_{\delta,\lambda }}>0$![]() such that
such that

Let $\alpha _{1},\,\alpha _{2}>1$![]() be constants such that $\frac {1}{\alpha _{1}}+\frac {1}{\alpha _{2}}=1$
be constants such that $\frac {1}{\alpha _{1}}+\frac {1}{\alpha _{2}}=1$![]() and $p+1<\alpha _{1}(p-1)<2^{*}$
and $p+1<\alpha _{1}(p-1)<2^{*}$![]() . From (57) and Hölder's inequality it follows that
. From (57) and Hölder's inequality it follows that

Using (46) and the Sobolev Embedding, we obtain a constant $\widetilde {C}>0$![]() such that
such that
Hence, there exists a constant $\widehat {C}>0$![]() that does not depend on $\sigma$
that does not depend on $\sigma$![]() nor on $\epsilon$
nor on $\epsilon$![]() such that
such that

Letting $L\to \infty$![]() in (58) and using Fatou's Lemma, we conclude that
in (58) and using Fatou's Lemma, we conclude that

provided $u_{\epsilon }\in L^{2\sigma \alpha _{2}}(\Omega )$![]() . Equivalently,
. Equivalently,
where $C=\sqrt {\widehat {C}}$![]() . Observe that the choices of $\alpha _{1}$
. Observe that the choices of $\alpha _{1}$![]() and $\alpha _{2}$
and $\alpha _{2}$![]() imply that $\sigma (p+1)>2\sigma \alpha _{2}$
imply that $\sigma (p+1)>2\sigma \alpha _{2}$![]() . The result now follows from an iterative argument. Indeed, take
. The result now follows from an iterative argument. Indeed, take
Using the Sobolev embedding and (46), we obtain a constant $\widetilde {D}>0$![]() such that
such that
Now, take $\sigma _{2}=\sigma _{1}^{2}$![]() in (59). We get
in (59). We get
Taking $\sigma _{k}=\sigma _{1}^{k}$![]() in (59), we get
in (59), we get
It is clear that
Letting $k\rightarrow \infty$![]() in (60), it follows that $u_{\epsilon }\in L^{\infty }(\Omega )$
in (60), it follows that $u_{\epsilon }\in L^{\infty }(\Omega )$![]() and we obtain a constant $K_{1}>0$
and we obtain a constant $K_{1}>0$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
This proves (47).
Proof of (ii). Suppose that $p=2^{*}-1$![]() . This case is much more complicated. We have
. This case is much more complicated. We have
Consequently, since $g_{\epsilon }\geq 0$![]() , we know that
, we know that
For each $0<\epsilon <1$![]() , we define
, we define
Observe that

where $C(N)$![]() is a constant that depends only on $N$
is a constant that depends only on $N$![]() . From (46) and the Sobolev embedding, we get a constant $C>0$
. From (46) and the Sobolev embedding, we get a constant $C>0$![]() such that
such that
Let $\sigma \geq 0$![]() be a constant to be fixed later and consider the function $z_{L,\epsilon }=u_{\epsilon }\min \{u_{\epsilon }^{2\sigma },\, L^{2}\}\in H_{0}^{1}(\Omega )$
be a constant to be fixed later and consider the function $z_{L,\epsilon }=u_{\epsilon }\min \{u_{\epsilon }^{2\sigma },\, L^{2}\}\in H_{0}^{1}(\Omega )$![]() , with $L>0$
, with $L>0$![]() . Observe that
. Observe that
Taking $v=z_{L,\epsilon }$![]() in (61), we get
in (61), we get
Define $w_{L,\epsilon }$![]() by $w_{L,\epsilon }=u_{\epsilon }\min \{u_{\epsilon }^{\sigma },\,L\}\in H_{0}^{1}(\Omega )$
by $w_{L,\epsilon }=u_{\epsilon }\min \{u_{\epsilon }^{\sigma },\,L\}\in H_{0}^{1}(\Omega )$![]() . We have
. We have
We thus get
Hence,
and
We conclude that
where $c(\sigma )=1+\sigma (\sigma +1)$![]() . From (62), we get
. From (62), we get
Now, fix $K>0$![]() . We have
. We have
Hence,

Consequently,

From the Sobolev embedding Theorem, we get

Choose $K>0$![]() such that
such that

Claim 1: $K$![]() can be chosen independently of $\epsilon$
can be chosen independently of $\epsilon$![]() , provided $\lambda$
, provided $\lambda$![]() is sufficiently large.
is sufficiently large.
Assuming the claim to be true, we obtain
Consequently,
Suppose that $u_{\epsilon }\in L^{2\sigma +2}(\Omega )$![]() and let $u_{L,\epsilon }=(u_{\epsilon }\min \{u_{\epsilon }^{\sigma },\,L\})^{2}$
and let $u_{L,\epsilon }=(u_{\epsilon }\min \{u_{\epsilon }^{\sigma },\,L\})^{2}$![]() . Observe that
. Observe that
Furthermore,
The Monotone Convergence Theorem implies that
From Fatou's Lemma, we get
Consequently, $u_{\epsilon }^{\sigma +1}\in H_{0}^{1}(\Omega )$![]() and $u_{\epsilon }\in L^{\frac {(2+2\sigma )N}{N-2}}(\Omega )$
and $u_{\epsilon }\in L^{\frac {(2+2\sigma )N}{N-2}}(\Omega )$![]() . Now let $q>1$
. Now let $q>1$![]() . We will show that
. We will show that
Indeed, this follows by choosing adequate values for $\sigma$![]() in (64). Let $\sigma _{0}=0$
in (64). Let $\sigma _{0}=0$![]() . From (64), we get
. From (64), we get
Let $\sigma _{1}=\frac {N}{N-2}-1$![]() . From (64), we get
. From (64), we get
Consequently, $u_{\epsilon }^{\frac {N}{N-2}}\in H_{0}^{1}(\Omega )$![]() and
and
Let $\sigma _{2}=\frac {4N-4}{(N-2)^{2}}$![]() . From (64), we get
. From (64), we get
Consequently, $u_{\epsilon }^{\frac {N^{2}}{(N-2)^{2}}}\in H_{0}^{1}(\Omega )$![]() and
and
Assertion (65) then follows by choosing
and iterating up until $s_{M}>q$![]() for some $M\in \mathbb {N}$
for some $M\in \mathbb {N}$![]() . Now let $w_{\epsilon }$
. Now let $w_{\epsilon }$![]() be the solution of the non-singular problem
be the solution of the non-singular problem
Assertion (65) and elliptic regularity theory implies that $w_{\epsilon }\in W^{2,q}(\Omega )$![]() and
and
where $C_{q}$![]() does not depend on $\epsilon$
does not depend on $\epsilon$![]() . Consequently, the Sobolev embedding assures that $w_{\epsilon }\in C^{1}(\overline {\Omega })$
. Consequently, the Sobolev embedding assures that $w_{\epsilon }\in C^{1}(\overline {\Omega })$![]() and
and
Observe that
Consequently,
The weak maximum principle implies
Hence,
Consequently,
This proves the result. We need to only show that the claim holds. Indeed, from (46), there exists an element $u\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence,
such that, up to a subsequence,

We first show that
Again using the Concentration-compactness principle of Lions, we get positive measures $\mu,\,\nu$![]() in $\Omega$
in $\Omega$![]() such that
such that
Furthermore, there is at most a countable set of indexes denoted by $\Lambda$![]() , sequences $x_{i}\in \overline {\Omega }$
, sequences $x_{i}\in \overline {\Omega }$![]() , $\mu _{i},\,\nu _{i}\in (0,\,\infty )$
, $\mu _{i},\,\nu _{i}\in (0,\,\infty )$![]() such that
such that
for every $i\in \Lambda$![]() , where $S$
, where $S$![]() is given by (40). Now, for every $\sigma >0$
is given by (40). Now, for every $\sigma >0$![]() and $i\in \Lambda$
and $i\in \Lambda$![]() , we define
, we define
where $\psi \in C_{c}^{\infty }(\mathbb {R}^{n})$![]() is a function satisfying
is a function satisfying
Proceeding as in the proof of Proposition 4.3 and using the hypothesis $\lim _{\lambda \to \infty }I_{\epsilon }(u_{\epsilon,\lambda })=0$![]() , we conclude that $\Lambda =\emptyset$
, we conclude that $\Lambda =\emptyset$![]() , provided $\lambda >0$
, provided $\lambda >0$![]() is sufficiently large, thus proving (68). Consequently, $a_{\epsilon }^{\frac {N}{2}}$
is sufficiently large, thus proving (68). Consequently, $a_{\epsilon }^{\frac {N}{2}}$![]() converges in $L^{1}(\Omega )$
converges in $L^{1}(\Omega )$![]() to $a$
to $a$![]() , where
, where
We now show that for each $\delta ^{*}>0$![]() there exists $\eta >0$
there exists $\eta >0$![]() and $\epsilon _{0}>0$
and $\epsilon _{0}>0$![]() such that
such that
Since $a\in L^{1}(\Omega )$![]() , there exists $\eta >0$
, there exists $\eta >0$![]() such that
such that
We write
and we choose $\epsilon _{0}>0$![]() such that
such that
Consequently,
This proves (69). We now finally prove Claim 1. Indeed, we choose

and we choose $K>0$![]() such that
such that

Observe that
The choice of $K$![]() implies that
implies that

Consequently, from (69) and the choice of $\delta ^{*}$![]() , we get
, we get

This proves Claim 1 and the result.
We also have
Lemma 5.2 Let $u_{\epsilon }\in H_{0}^{1}(\Omega )$![]() be a non-negative solution of problem (2) and assume that there exists a constant $D>0$
be a non-negative solution of problem (2) and assume that there exists a constant $D>0$![]() independent of $\epsilon$
independent of $\epsilon$![]() such that
such that
If $f$![]() satisfies (8) and (9) for $0< p<\frac {N+2}{N-2}$
satisfies (8) and (9) for $0< p<\frac {N+2}{N-2}$![]() , then $u_{\epsilon }\in L^{\infty }(\Omega )$
, then $u_{\epsilon }\in L^{\infty }(\Omega )$![]() and there exists a constant $K_{2}>0$
and there exists a constant $K_{2}>0$![]() such that
such that
Proof of Lemma 5.2 From (4), we get
From (8), we get
Consequently,
From (9), we get
Consequently,
Consequently, there exists $\widetilde {C}>0$![]() and $1<\widetilde {p}<2^{*}-1$
and $1<\widetilde {p}<2^{*}-1$![]() such that
such that
The proof then follows as in item $(i)$![]() of Lemma 5.1.
of Lemma 5.1.
Now, we obtain gradient estimates for solutions $u_{\epsilon }$![]() of problem (2).
of problem (2).
Lemma 5.3 Assume that $f$![]() satisfies (6). For each $0<\epsilon <1$
satisfies (6). For each $0<\epsilon <1$![]() , let $u_\epsilon \in H_{0}^{1}(\Omega )\cap L^{\infty }(\Omega )$
, let $u_\epsilon \in H_{0}^{1}(\Omega )\cap L^{\infty }(\Omega )$![]() be a non-negative solution of problem (2) and assume that there exists a constant $T>0$
be a non-negative solution of problem (2) and assume that there exists a constant $T>0$![]() such that
such that
Let $\psi$![]() be such that
be such that
Then, there exist constants $M>0$![]() and $\epsilon _{0}>0$
and $\epsilon _{0}>0$![]() such that
such that
Proof of Lemma 5.3 From (6), we obtain constants $C_{1}>0$![]() and $0< t_{0}<1$
and $0< t_{0}<1$![]() such that
such that
From (71) we obtain that $\Delta u_\epsilon$![]() is bounded in $L^{\infty }(\Omega )$
is bounded in $L^{\infty }(\Omega )$![]() . Thus, by standard elliptic regularity, $u_\epsilon$
. Thus, by standard elliptic regularity, $u_\epsilon$![]() belongs to $C^{1,\nu }(\overline \Omega )$
belongs to $C^{1,\nu }(\overline \Omega )$![]() . We define
. We define
We shall denote $u_\epsilon$![]() simply by $u$
simply by $u$![]() . Define the functions
. Define the functions
where $a>0$![]() is small. Note that $v$
is small. Note that $v$![]() is $C^{2}$
is $C^{2}$![]() at all points $x\in \Omega$
at all points $x\in \Omega$![]() such that $u(x)>0$
such that $u(x)>0$![]() . Indeed, let $x\in \Omega$
. Indeed, let $x\in \Omega$![]() be one such point. By continuity, there must exist an open ball $B\subset \Omega$
be one such point. By continuity, there must exist an open ball $B\subset \Omega$![]() centred at $x$
centred at $x$![]() such that $u>0$
such that $u>0$![]() in $\overline {B}$
in $\overline {B}$![]() . Consequently, we know that $g_{\epsilon }(u)\in C^{1,\nu }(B)$
. Consequently, we know that $g_{\epsilon }(u)\in C^{1,\nu }(B)$![]() and $f(u)\in C^{1,\nu }(B)$
and $f(u)\in C^{1,\nu }(B)$![]() . Hence, $\overline {h}_{\epsilon }(u)\in C^{1,\nu }(B)$
. Hence, $\overline {h}_{\epsilon }(u)\in C^{1,\nu }(B)$![]() . Since $u$
. Since $u$![]() satisfies the equation $-\Delta u+\overline {h}_{\epsilon }(u)=0$
satisfies the equation $-\Delta u+\overline {h}_{\epsilon }(u)=0$![]() in $B$
in $B$![]() , we conclude that $u\in C^{3}(B)$
, we conclude that $u\in C^{3}(B)$![]() , implying that $Z(u)$
, implying that $Z(u)$![]() and $w$
and $w$![]() are $C^{2}$
are $C^{2}$![]() in $B$
in $B$![]() .
.
The function $v$![]() is continuous in $\overline \Omega$
is continuous in $\overline \Omega$![]() , hence it attains its maximum at some point $x_0 \in \overline \Omega$
, hence it attains its maximum at some point $x_0 \in \overline \Omega$![]() . Thus, we obtain
. Thus, we obtain
Note that $x_0 \in \Omega$![]() , because $v=0$
, because $v=0$![]() on $\partial \Omega$
on $\partial \Omega$![]() . Furthermore, $u(x_{0})>0$
. Furthermore, $u(x_{0})>0$![]() , since otherwise $x_{0}$
, since otherwise $x_{0}$![]() would be a critical point of $u$
would be a critical point of $u$![]() and $w(x_{0})=0$
and $w(x_{0})=0$![]() . Hence,
. Hence,
and
The computations already carried out in [Reference Lorca and Montenegro20, Reference Montenegro and Silva22] lead to the following expression evaluated at $x_0$![]()

where
We will show that if $v(x_0)$![]() is large enough then the right-hand side of (74) must be positive, which would contradict (73).
is large enough then the right-hand side of (74) must be positive, which would contradict (73).
We will establish the following estimates uniformly for every $\epsilon$![]() sufficiently small.
sufficiently small.
for every $0 \leq u \leq T$![]() . The constant $C$
. The constant $C$![]() depends only on $T$
depends only on $T$![]() , but not on $\epsilon$
, but not on $\epsilon$![]() nor on $a$
nor on $a$![]() .
.
Assuming for a moment that (75)–(78) are true. Inequality (74) implies that

Since $\Delta v(x_{0})\leq 0$![]() and
and
we conclude that
Consequently, there exists $M>0$![]() that does not depend on $a$
that does not depend on $a$![]() such that
such that
Consequently,
The result then follows by letting $a\to 0$![]() .
.
We prove now the relations (75)–(78). In the course of this proof, $C$![]() , $\widetilde {C}$
, $\widetilde {C}$![]() , $C_{i}$
, $C_{i}$![]() , $i\in \{1,\,2,\,3,\,\ldots \}$
, $i\in \{1,\,2,\,3,\,\ldots \}$![]() denote various positive constants independent of $\epsilon$
denote various positive constants independent of $\epsilon$![]() and $a$
and $a$![]() , we obtain gradient
, we obtain gradient
Hence,
We first prove (78). Indeed, there is a constant $C>0$![]() such that
such that
Hence, (78) follows from (79).
We now prove (77). Note that there exists a constant $\widetilde {C}>0$![]() such that
such that

Inequality (77) then follows from (79).
Now, we prove (76). Note that
We split the proof of (76) in three cases.
Case I. Suppose that $0< u<\min \{\tfrac {q\epsilon }{2\beta },\,t_{0}\}$![]() , where $0< t_{0}<1$
, where $0< t_{0}<1$![]() is given by (72). We define
is given by (72). We define
where $C_{1}>0$![]() is given by (72). We claim that there exists $\epsilon _{0}>0$
is given by (72). We claim that there exists $\epsilon _{0}>0$![]() such that $\omega _{\epsilon }(u)>0$
such that $\omega _{\epsilon }(u)>0$![]() for each $0<\epsilon <\epsilon _{0}$
for each $0<\epsilon <\epsilon _{0}$![]() . Indeed, assume by contradiction that $\omega _{\epsilon }(u)<0$
. Indeed, assume by contradiction that $\omega _{\epsilon }(u)<0$![]() for some $0< u<\frac {q\epsilon }{2\beta }$
for some $0< u<\frac {q\epsilon }{2\beta }$![]() . We then have
. We then have

Now take $\epsilon _{0}>0$![]() such that
such that
We may assume that $0< q< q_{1}$![]() . Consequently,
. Consequently,
Hence,
which implies that
This contradicts our initial assumption. The claim is proven. Since
we obtain
Hence,
where $t_{1}>0$![]() is chosen such that
is chosen such that
Therefore,
Comparing with (79), it follows that there exists a constant $C>0$![]() that does not depend on $a$
that does not depend on $a$![]() such that
such that
Case II. Suppose that $\frac {\epsilon q}{2\beta }\leq u\leq \min \{t_{0},\,t_{1}\}$![]() . We have
. We have
Note that $|q\epsilon -\beta u|\leq \beta u$![]() if $2\beta u\geq q\epsilon$
if $2\beta u\geq q\epsilon$![]() . We then obtain
. We then obtain

Now, observe that there exists $0< t_{2}<\min \{t_{0},\,t_{1}\}$![]() that does not depend on $\epsilon$
that does not depend on $\epsilon$![]() such that
such that
Therefore,
Comparing with (79), we obtain
Case III. Assume that $t_{2}\leq u\leq T$![]() . Since there exists a constant $C>0$
. Since there exists a constant $C>0$![]() such that $|\overline {h}_{\epsilon }'(u)|\leq C$
such that $|\overline {h}_{\epsilon }'(u)|\leq C$![]() for $t_{2}\leq u\leq T$
for $t_{2}\leq u\leq T$![]() , it follows from (78) that
, it follows from (78) that
Hence, (76) follows from (80), (81) and (82).
We now prove (75). Observe that
Hence,
When $0\leq u\leq 1$![]() we know that $u^{2}\leq u$
we know that $u^{2}\leq u$![]() . Hence $u^{-\beta }\leq u^{-2\beta }$
. Hence $u^{-\beta }\leq u^{-2\beta }$![]() . Therefore, from (79), there exist constants $C_{3}>0$
. Therefore, from (79), there exist constants $C_{3}>0$![]() and $C_{4}>C_{3}$
and $C_{4}>C_{3}$![]() such that
such that
If $1\leq u\leq T$![]() , we know that there exists a constant $C_{5}>0$
, we know that there exists a constant $C_{5}>0$![]() such that $Z'(u) Z(u)^{1/2}\leq C_{5}$
such that $Z'(u) Z(u)^{1/2}\leq C_{5}$![]() . Hence, from (79), there exists a constant $C_{6}>0$
. Hence, from (79), there exists a constant $C_{6}>0$![]() such that
such that
Inequality (75) then follows from (83) and (84). We have proved Lemma 5.3.
Consequently, we obtain
Corollary 5.4 For each $0<\epsilon <1,$![]() let $u_\epsilon$
let $u_\epsilon$![]() be the solution of problem (2) obtained in Propositions 3.2 and 4.3. Let $\psi$
be the solution of problem (2) obtained in Propositions 3.2 and 4.3. Let $\psi$![]() be as in the hypothesis of Lemma 5.3. Then there exist constants $M>0$
be as in the hypothesis of Lemma 5.3. Then there exist constants $M>0$![]() and $\epsilon _{0}>0$
and $\epsilon _{0}>0$![]() such that
such that
Proof of Corollary 5.4 From Propositions 3.2 and 4.3, we know that there is a constant $D>0$![]() such that
such that
From Lemmas 4.2, 5.1 and 5.2 we conclude that the solutions $u_{\epsilon }$![]() of (2) are bounded in $L^{\infty }(\Omega )$
of (2) are bounded in $L^{\infty }(\Omega )$![]() by constant $K_{1}>0$
by constant $K_{1}>0$![]() and $K_{2}>0$
and $K_{2}>0$![]() independent of $\epsilon$
independent of $\epsilon$![]() . Corollary 5.4 then follows by Lemma 5.3.
. Corollary 5.4 then follows by Lemma 5.3.
6. The limit of approximate solutions
Now we will study the convergence as $\epsilon \to 0$![]() of the solutions $u_{\epsilon }$
of the solutions $u_{\epsilon }$![]() of problem (2) obtained in Propositions 3.2 and 4.3. First, we obtain the existence of a non-trivial limit $u$
of problem (2) obtained in Propositions 3.2 and 4.3. First, we obtain the existence of a non-trivial limit $u$![]() . Next, we prove that $u$
. Next, we prove that $u$![]() is a solution of problem (1).
is a solution of problem (1).
Lemma 6.1 Let $(\epsilon _{n})$![]() be a sequence in $(0,\,1)$
be a sequence in $(0,\,1)$![]() such that $\epsilon _{n}\to 0$
such that $\epsilon _{n}\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . Let $(u_{\epsilon _{n}}^{1})$
. Let $(u_{\epsilon _{n}}^{1})$![]() and $(u_{\epsilon _{n}}^{2})$
and $(u_{\epsilon _{n}}^{2})$![]() be the sequences of solutions obtained in Propositions 3.2 and 4.3 respectively. Then there exist non-trivial functions $u_{1}\in H_{0}^{1}(\Omega )$
be the sequences of solutions obtained in Propositions 3.2 and 4.3 respectively. Then there exist non-trivial functions $u_{1}\in H_{0}^{1}(\Omega )$![]() and $u_{2}\in H_{0}^{1}(\Omega )$
and $u_{2}\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence, $u_{\epsilon _{n}}^{i}\rightharpoonup u_{i}$
such that, up to a subsequence, $u_{\epsilon _{n}}^{i}\rightharpoonup u_{i}$![]() weakly in $H_{0}^{1}(\Omega ),$
weakly in $H_{0}^{1}(\Omega ),$![]() where $i\in \{1,\,2\}$
where $i\in \{1,\,2\}$![]() .
.
Proof of Lemma 6.1 From Propositions 3.2 and 4.3, we know that there exist constants $D_{i}>0$![]() such that
such that
Hence, there exist functions $u_{i}\in H_{0}^{1}(\Omega )$![]() such that
such that

Lemmas 5.1 and 5.2 imply that $u_{\epsilon _{n}}^{i}\in L^{\infty }(\Omega )$![]() with $\|u_{\epsilon _{n}}^{i}\|_{L^{\infty }(\Omega )}< K_{i}$
with $\|u_{\epsilon _{n}}^{i}\|_{L^{\infty }(\Omega )}< K_{i}$![]() for all $n\in \mathbb {N}$
for all $n\in \mathbb {N}$![]() . Consequently, the Dominated Convergence Theorem implies that
. Consequently, the Dominated Convergence Theorem implies that
We prove the result for $i=1$![]() and denote $(u_{\epsilon _{n}}^{1})$
and denote $(u_{\epsilon _{n}}^{1})$![]() and $u_{1}$
and $u_{1}$![]() merely by $(u_{\epsilon _{n}})$
merely by $(u_{\epsilon _{n}})$![]() and $u$
and $u$![]() respectively. From Proposition 3.2, we have
respectively. From Proposition 3.2, we have
Since $u_{\epsilon _{n}}$![]() is a non-negative critical point of $I_{\epsilon _{n}}$
is a non-negative critical point of $I_{\epsilon _{n}}$![]() , we have
, we have
Hence,
The Dominated Convergence Theorem implies that

and
Taking the above claims into account and letting $n\rightarrow \infty$![]() in (86), we obtain
in (86), we obtain
We proved that $u$![]() is non-trivial. The proof for $i=2$
is non-trivial. The proof for $i=2$![]() is analogous.
is analogous.
We now show that the functions $u_{1}$![]() and $u_{2}$
and $u_{2}$![]() defined in Lemma 6.1 satisfy the following property.
defined in Lemma 6.1 satisfy the following property.
Lemma 6.2 Let $u_{1}$![]() and $u_{2}$
and $u_{2}$![]() be the functions given by Lemma 6.1. The function $u_{i}^{-\beta }\chi _{\{u_{i}>0\}}$
be the functions given by Lemma 6.1. The function $u_{i}^{-\beta }\chi _{\{u_{i}>0\}}$![]() belongs to $L^{1}_{loc}(\Omega )$
belongs to $L^{1}_{loc}(\Omega )$![]() for $i\in \{1,\,2\}$
for $i\in \{1,\,2\}$![]() .
.
Proof of Lemma 6.2 We again prove the result for $i=1$![]() . The proof for $i=2$
. The proof for $i=2$![]() is analogous. Let $(u_{\epsilon _{n}})$
is analogous. Let $(u_{\epsilon _{n}})$![]() and $u$
and $u$![]() be given by (85) with $i=1$
be given by (85) with $i=1$![]() . Let $V \subset \Omega$
. Let $V \subset \Omega$![]() be a open set such that $\overline {V}\subset \Omega$
be a open set such that $\overline {V}\subset \Omega$![]() . Take $\zeta \in C^{1}_c(\Omega )$
. Take $\zeta \in C^{1}_c(\Omega )$![]() such that $0 \leq \zeta \leq 1$
such that $0 \leq \zeta \leq 1$![]() and $\zeta \equiv 1$
and $\zeta \equiv 1$![]() in $V$
in $V$![]() . Since $u_{\epsilon _{n}}$
. Since $u_{\epsilon _{n}}$![]() is a critical point of $I_{\epsilon _{n}},$
is a critical point of $I_{\epsilon _{n}},$![]() we obtain
we obtain
Corollary 5.4 implies that $u_{\epsilon _{n}}\to u$![]() uniformly in compact subsets of $\Omega$
uniformly in compact subsets of $\Omega$![]() . Since $u_{\epsilon _{n}}\rightharpoonup u$
. Since $u_{\epsilon _{n}}\rightharpoonup u$![]() weakly in $H_{0}^{1}(\Omega )$
weakly in $H_{0}^{1}(\Omega )$![]() , we get
, we get
Define the set $\Omega _\rho = \{ x \in \Omega : u(x) \geq \rho \}$![]() for $\rho >0$
for $\rho >0$![]() . It follows from (87) that there exists a constant $C>0$
. It follows from (87) that there exists a constant $C>0$![]() that does not depend on $n$
that does not depend on $n$![]() nor on $\rho$
nor on $\rho$![]() such that
such that
Letting $n\to \infty$![]() and using Fatou's Lemma, we then get
and using Fatou's Lemma, we then get
Letting $\rho \rightarrow 0$![]() and applying Fatou's Lemma again, we conclude that
and applying Fatou's Lemma again, we conclude that
Since $V$![]() was arbitrarily chosen, Lemma 6.2 is proved.
was arbitrarily chosen, Lemma 6.2 is proved.
Proof of Theorem 1.1 The proof of this result is very similar to the one given in [Reference Figueiredo and Montenegro14], but for the sake of completeness, we give the proof with details. We will show that the sequences $(u_{\epsilon _{n}}^{1})$![]() given by Lemma 6.1 converge to a solution $u_{1}$
given by Lemma 6.1 converge to a solution $u_{1}$![]() of (1) as $n\to \infty$
of (1) as $n\to \infty$![]() . In doing so, we obtain a solution $u_{1}$
. In doing so, we obtain a solution $u_{1}$![]() of (1) which is non-trivial. The non-triviality of $u_{1}$
of (1) which is non-trivial. The non-triviality of $u_{1}$![]() is guaranteed by Lemma 6.1. From now on, we denote $u_{\epsilon _{n}}$
is guaranteed by Lemma 6.1. From now on, we denote $u_{\epsilon _{n}}$![]() and $u_{1}$
and $u_{1}$![]() merely by $u_{\epsilon }$
merely by $u_{\epsilon }$![]() and $u$
and $u$![]() respectively. Let $\varphi \in C_c^{1}(\Omega )$
respectively. Let $\varphi \in C_c^{1}(\Omega )$![]() . From Proposition 3.2, we have
. From Proposition 3.2, we have
Let $\eta \in C^{\infty }(\mathbb {R})$![]() , $0 \leq \eta \leq 1$
, $0 \leq \eta \leq 1$![]() , $\eta (s)=0$
, $\eta (s)=0$![]() for $s \leq 1/2$
for $s \leq 1/2$![]() , $\eta (s)=1$
, $\eta (s)=1$![]() for $s \geq 1$
for $s \geq 1$![]() . For $m >0$
. For $m >0$![]() the function $\varrho := \varphi \eta (u_\epsilon /m)$
the function $\varrho := \varphi \eta (u_\epsilon /m)$![]() belongs to $C_c^{1}(\Omega )$
belongs to $C_c^{1}(\Omega )$![]() .
.
From Corollary 5.4, we know that $|\nabla u_\epsilon |$![]() is locally bounded independent on $0<\epsilon <\epsilon _{0}$
is locally bounded independent on $0<\epsilon <\epsilon _{0}$![]() . It then follows from (47) and the Arzelà-Ascoli Theorem that $u_\epsilon \to u$
. It then follows from (47) and the Arzelà-Ascoli Theorem that $u_\epsilon \to u$![]() in $C^{0}_{loc}(\Omega )$
in $C^{0}_{loc}(\Omega )$![]() , and the set $\Omega _+ = \{ x \in \Omega : u(x) > 0 \}$
, and the set $\Omega _+ = \{ x \in \Omega : u(x) > 0 \}$![]() is open. Let $\tilde \Omega$
is open. Let $\tilde \Omega$![]() be an open set such that $\overline {support ( \varphi ) } \subset \tilde \Omega$
be an open set such that $\overline {support ( \varphi ) } \subset \tilde \Omega$![]() and $\overline {\tilde \Omega } \subset \Omega$
and $\overline {\tilde \Omega } \subset \Omega$![]() . Let $\Omega _0 = \Omega _+ \cap \tilde \Omega$
. Let $\Omega _0 = \Omega _+ \cap \tilde \Omega$![]() . For every $m >0$
. For every $m >0$![]() , there is an $\epsilon _1 > 0$
, there is an $\epsilon _1 > 0$![]() such that
such that
Replacing $\varphi$![]() by $\varrho$
by $\varrho$![]() in (88), we obtain
in (88), we obtain
We break the previous integral as
and
Clearly, $Y_\epsilon =0$![]() , whenever $0<\epsilon \leq \epsilon _1$
, whenever $0<\epsilon \leq \epsilon _1$![]() by (89) and the definition of $\eta$
by (89) and the definition of $\eta$![]() . From (47), the Dominated Convergence Theorem and from the fact that $u_{\epsilon }\to u$
. From (47), the Dominated Convergence Theorem and from the fact that $u_{\epsilon }\to u$![]() uniformly in $\Omega _0$
uniformly in $\Omega _0$![]() , we get
, we get
We take the limit in $m$![]() to conclude that
to conclude that
since $\eta (u/m) \leq 1$![]() and $u^{-\beta }\chi _{\Omega ^{+}} + f(u) \in L^{1}(\tilde \Omega )$
and $u^{-\beta }\chi _{\Omega ^{+}} + f(u) \in L^{1}(\tilde \Omega )$![]() , according to Lemma 6.2.
, according to Lemma 6.2.
What follows next is identical to [Reference Lorca and Montenegro20]. We proceed with the integral on the left side of (90). We have
where
Consequently,
since $u_\epsilon \rightharpoonup u$![]() weakly in $H_0^{1}(\Omega )$
weakly in $H_0^{1}(\Omega )$![]() and $u_\epsilon \to u$
and $u_\epsilon \to u$![]() uniformly in $\tilde \Omega$
uniformly in $\tilde \Omega$![]() . Hence, by the Dominated Convergence Theorem,
. Hence, by the Dominated Convergence Theorem,
Now we only need to show that
Let $Z_{0}(u_{\epsilon })=u_{\epsilon }^{1-\beta }+u_{\epsilon }$![]() . The estimate $|\nabla u_\epsilon |^{2} \leq M Z_{0}(u_\epsilon )$
. The estimate $|\nabla u_\epsilon |^{2} \leq M Z_{0}(u_\epsilon )$![]() in $\tilde \Omega$
in $\tilde \Omega$![]() provided by Corollary 5.4 yields
provided by Corollary 5.4 yields

Consequently

for every $m>0$![]() .
.
The claim follows by letting $m\to 0$![]() and by using Lemma 6.2.
and by using Lemma 6.2.
As a immediate consequence of (90), (91),(92), (93) and (94), we have
for every $\varphi \in C_c^{1}(\Omega )$![]() . This concludes the proof of Theorem 1.1.
. This concludes the proof of Theorem 1.1.
Acknowledgements
M.F.S.has been partially supported by CAPES. The author thanks the anonymous referees for their valuable suggestions.
Competing interest declaration
The author declares none.