II. CONCEPTS USED

A. Symmetry-breaking spontaneous strain

In order to be able to analyze the line broadening effects because of reflection splitting in the following sections, a treatment of symmetry-breaking strain according to Aizu (Reference Aizu1970) introduced in the context of analysis of ferroelastic phase transitions will be adapted for the present purposes. Aizu, in particular, dealt with the problem that, in the existence regime of a low-symmetry (often low-temperature) phase, frequently the high-symmetry phase is not stable and cannot be studied. This obstructs precise determination of the strain describing the distortion of the low-symmetry phase with respect to the high-symmetry phase at a specific temperature and pressure, which is needed for detailed analysis of strains, e.g. by means of Landau theory (Carpenter et al., Reference Carpenter, Salje and Grame-Barber1998). Aizu proposed to refer the strain associated with the low-symmetry state relative to some specific hypothetical high-symmetry state, which has a lattice metric purely derived from the metric of the low-temperature state. For that Aizu required the sum over the strain tensors ^m ε _S pertaining to the n different domain states amounts 0:

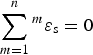(1) $$\sum\limits_{m = 1}^n {{}^m{\bi \varepsilon} _{\rm s}} = 0$$

whereby the tensors had originally been denoted as x _s by Aizu (Reference Aizu1970). Equation (1) implies that the metric of the high-symmetry phase is some averaged metric of the low-symmetry phase. Note, moreover, that because of their definition, the tensors ^m ε have a trace of 0. Note, moreover, that the n tensors ^m ε _s are inter-related with each other by tensor transformations using the symmetry operators R , which get lost upon reducing the symmetry from the high- to the low-symmetry phase:

(2) $${\bi R}{}^m{\bi \varepsilon} _{\rm s}{\bi R}^T = {}^{m^{\prime}} \! {\bi \varepsilon} _{\rm s}$$

In order to quantify the symmetry-breaking strain exerted by ^m ε _s, Aizu (Reference Aizu1970) suggested use of a scalar magnitude ε _s called the spontaneous strain ε _s (originally called x _s) defined as

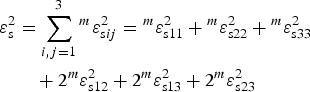(3) $$\eqalign{ \varepsilon _{\rm s}^2 & = \sum\limits_{i,j = 1}^3 {{}^m\varepsilon _{{\rm s}ij}^2} = {}^m\varepsilon _{{\rm s}11}^2 + {}^m\varepsilon _{{\rm s}22}^2 + {}^m\varepsilon _{{\rm s}33}^2 \cr & \quad + 2{}^m\varepsilon _{{\rm s}12}^2 + 2{}^m\varepsilon _{{\rm s}13}^2 + 2{}^m\varepsilon _{{\rm s}23}^2} $$

ε _s does not change upon transformation of ^m ε _s, which means that its value is independent of m.

Aizu indicated that the (then ferroelastic) symmetry distortion increases upon increase of ε _s . A more explicit meaning of the value of ε _s can be derived by analyzing how ε _s is related with the variation of the strain ^m ε _s( x ) measured along a unit vector x in the crystal frame of reference:

(4) $$^m \varepsilon _{\rm s}({\bi x}) = ^{m}\!\!\!\varepsilon _{{\rm s}ij}x_ix_j $$

applying here and henceforth the Einstein summation convention. The direction average of this and other scalar quantities can be obtained by expressing the components of x in polar coordinates (x ₁ = cosφsinϑ, x ₂ = sinφsinϑ, x ₃ = cosϑ) and integrating over sinϑ/(4π)d ϑd φ from 0 to π for ϑ and 0 to 2π for φ. Equation (4) yields after integration

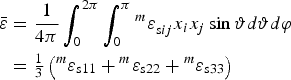(5) $$\eqalign{\bar \varepsilon & = \displaystyle{1 \over {4\pi}} \int_0^{2\pi} {\int_0^\pi {{}^m\varepsilon _{{\rm s}ij}^{} x_ix_j\sin \vartheta d\vartheta d\varphi}} \cr & = {\textstyle{1 \over 3}}\left( {{}^m\varepsilon _{{\rm s}11} + {}^m\varepsilon _{{\rm s}22} + {}^m\varepsilon _{{\rm s}33}} \right)} $$

Equation (5) is, like Eq. (3), invariant with respect to tensor transformation of ^m ε _s and is, therefore, m-independent and amounts 0 in line with the definition of this strain tensor (see above). Note that, here and henceforth, the overbar will be used to indicate an average over all directions of x (see Leineweber, Reference Leineweber2016). The anisotropy of the direction-dependent strain can be quantified by its variance, $\overline {{(\varepsilon - \bar \varepsilon )}^2} = \overline {\varepsilon ^2} $ , which then is obtained in view of Eq. (5) as

(6a) $$\eqalign{\overline {{(\varepsilon - \bar \varepsilon )}^2} = \overline {\varepsilon ^2} & = \displaystyle{1 \over {4\pi}} \int_0^{2\pi} {\int_0^\pi {{\left( {{}^m\varepsilon _{{\rm s}ij}x_ix_j} \right)}^2\sin \vartheta d\vartheta d\varphi}}, \cr & = \displaystyle{1 \over {15}}\left( {3{}^m\varepsilon _{{\rm s}11}^2 + 3{}^m\varepsilon _{{\rm s}22}^2 + 3{}^m\varepsilon _{{\rm s}33}^2 + 2{}^m\varepsilon _{{\rm s}11}{}^m\varepsilon _{{\rm s}22}} \right. \cr & \quad + \!2{}^m\varepsilon _{{\rm s}11}{}^m\varepsilon _{{\rm s}33} + 2{}^m\varepsilon _{{\rm s}22}{}^m\varepsilon _{{\rm s}33} \cr & \quad \left. { \;\hskip -.5pt+ \,4{}^m\varepsilon _{{\rm s}12}^2 + 4{}^m\varepsilon _{{\rm s}13}^2 + 4{}^m\varepsilon _{{\rm s}23}^2} \right)} $$

whereby the upper left index of m is omitted for the variances because the result is, again, m-independent.

Subtraction of 0 = 1/15( ^m ε_s11 +  ^m ε_s22 +  ^m ε_s33)² from Eq. (6a) gives

(6b) $$\overline {\varepsilon ^2} = \displaystyle{2 \over {15}}\left( {{}^m\varepsilon _{{\rm s}11}^2 + {}^m\varepsilon _{{\rm s}22}^2 + {}^m\varepsilon _{{\rm s}33}^2 + 2{}^m\varepsilon _{{\rm s}12}^2 + 2{}^m\varepsilon _{{\rm s}13}^2 + 2{}^m\varepsilon _{{\rm s}23}^2} \right)$$

which is again independent of m. Comparison of Eq. (6b) with Eq. (3) shows, that the spontaneous strain ε _S introduced by Aizu (Reference Aizu1970) is proportional to the variance of the direction-dependent strain caused by ^m ε _s.

B. General description of microstrain broadening

Microstrain in an untextured crystalline material implies, in the crystal frame of direction, a distribution of strain around its average, defined as strain 〈 ε 〉 = 0 in the present work. At this zero strain, the material exhibits its average lattice parameters. The microstrain can then be understood as a correlated distribution of the components of the strain tensor ε around zero strain. That distribution is usually regarded as unimodal, and if it is symmetric, it has its maximum at 〈 ε 〉 = 0. Typical origin of such microstrain is sufficiently long-range distortions of the crystal lattice (i.e. strains) randomly occurring over the diffracting material because of some microstructural inhomogeneities, like composition variations, temperature variations, and, most prominently, locally varying stresses (microstress) caused by dislocations but also by pure elastically accommodated misfit between grains within a polycrystal.

By means of powder diffraction, this microstrain can be characterized by analyzing the microstrain measured in the direction of reciprocal lattice vectors (i.e. the broadening for different hkl) and making conclusions about the overall microstrain distribution).

The correlated distribution of the components of the strain tensor around their average values is conveniently done by means of the tensors quantifying the joint central moments (or cumulants) of second and higher order (Leineweber, Reference Leineweber2009, Reference Leineweber2011). In most cases, only the second moments are considered, i.e. the variances and covariances of the strain tensor's components, which are (for averages = 0) given as the at maximum 81 components E _ijpq  = 〈ε _ij ε _pq 〉 of a fourth rank tensor E . At maximum 21 of these components are independent; that number can be further reduced by crystal symmetry. The variance of the microstrain broadening measurable in a direction x is then given by the polynomial

(7) $$\left\langle {\varepsilon _{hkl}^2} \right\rangle = \left\langle {\varepsilon _{}^2 \left( x \right)} \right\rangle = \left\langle {\varepsilon _{ij}\varepsilon _{\,pq}} \right\rangle x_ix_jx_px_q$$

Thereby, the hkl dependence of $\langle \varepsilon _{hkl}^2 \rangle = \langle \varepsilon ^2(\bi x)\rangle $ is contained in the components of x ₁, x ₂, and x ₃, which are linearly related with h, k, and l. Note that now the 〈〉 indicates averaging over the different strain values over the ensemble of crystallites/domains, now not involving direction averaging indicated by the overbar (see above). In the course of Rietveld refinement, $\langle \varepsilon _{hkl}^2 \rangle $ is typically associated with a certain shape for the line broadening, most frequently with a Gaussian. (In the case that the line broadening is/appears to be of Lorentzian or pseudo-Voigt shape (Stephens, Reference Stephens1999), alternative width parameters have to be used, since the variance does not exist for these shapes, as long as the pseudo-Voigt does not correspond to a pure Gaussian. See also Leineweber (Reference Leineweber2011).) Thereby, fitting on the basis of experimental data is done with only 15 independent fitting parameters, the number of which can be further reduced by the crystal symmetry, which are given by

(8) $$Z_{ijpq} = {\textstyle{1 \over 3}}\left( {\left\langle {\varepsilon _{ij}\varepsilon _{\,pq}} \right\rangle + \left\langle {\varepsilon _{ip}\varepsilon _{\,jq}} \right\rangle + \left\langle {\varepsilon _{iq}\varepsilon _{\,jp}} \right\rangle} \right)$$

These Z _ijpq parameters can be used to analyze the above mentioned microstructural characteristics provided that a model exists relating strain and inhomogeneously distributed quantities causing the microstrain (composition, temperature, stress).

III. REFLECTION SPLITTING-INDUCED MICROSTRAIN BROADENING

Upon reducing the symmetry of the crystal family of a high-symmetry structure, the accompanying symmetry-breaking strain will, in a powder-diffraction pattern, lead to some reflection splitting for some or all hkl pertaining to the high-symmetry phase. This is because of a probability density function of strain along the diffraction vector, which is a superposition of n delta functions located at the values ^m ε _s( x ) according to Eq. (4) with m = 1…n, where x is the unit vector parallel to the diffraction vector of any of the hkl reflections of the high-symmetry structure. Averaging over these strain values yields with use of Eq. (1):

(9) $$\left\langle \varepsilon \right\rangle \left( x \right) = {\textstyle{1 \over n}}\sum\limits_{m = 1}^n {\left( {{}^m\varepsilon _{{\rm s}ij}x_ix_j} \right)} = {\textstyle{1 \over n}}\left( {\sum\limits_{m = 1}^n {{}^m\varepsilon _{{\rm s}ij}}} \right)x_ix_j = 0$$

Equation (9) indicates that the average of the reflection positions corresponds to the reflection position of the hypothetical high-symmetry state according to Aizu (Reference Aizu1970). The component reflections then can be indexed in accordance with the low-symmetry structure.

If the magnitude of reflection splitting is so small that it is largely masked by instrumental and other broadening contributions, the splitting might also get interpreted as line broadening of a single, unimodally broadened peak located at a position of ε( x ) = 0. It is reasonable to assume that in the course of a full-profile-based refinement based on such broadened diffraction data, the actual bi- or multimodal shape of the reflection splitting can reasonably be approximated by such a single unimodal peak with a variance determined by the magnitude of the reflection splitting. A bimodal delta-shaped discrete strain distribution which can be because of reflection splitting and a (unimodal) Gaussian having the same variance are illustrated in Figure 1.

Figure 1. Probability density functions (pdfs) of a scaled strain around an average of zero and the same variances with (i) a Gaussian shape and a bimodal-delta shape represented by the two vertical lines assumed to have together the same area as the Gaussian. In a powder diffraction pattern, these pdfs may correspond to the strain distributions along the diffraction vector of a reflection hkl and have to be convoluted with other line broadening contributions (instrumental, size…) to yield the total measurable line profile. If these other contributions are sufficiently broad, the actual structure of the two pdfs gets masked by these, so that both pdfs will lead to a similar measurable peak profiles both located at a position corresponding to ε = 0.

It will turn out that the x -dependent reflection splitting-induced line broadening because of the symmetry breaking strains ^m ε _s is of microstrain-like character compatible with Eq. (7). The required values of 〈ε _ij ε _pq 〉 can be calculated by averaging the over the strains ^m ε _sij of the different domain states:

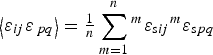(10) $$\left\langle {\varepsilon _{ij}\varepsilon _{\,pq}} \right\rangle = {\textstyle{1 \over n}}\sum\limits_{m = 1}^n {{}^m\varepsilon _{{\rm s}ij}{}^m\varepsilon _{{\rm s}pq}} $$

Note that requirement for use of the 〈ε _ij ε _pq 〉 values from Eq. (10) is validity of Eq. (1) ensuring that 〈ε _ij ε _pq 〉 are truly variances and covariances (which would not be the case if Eq. (1) would not hold, i.e. Σε _sij  ≠ 0). The averaging resulting from Eq. (10) can easily be performed on the basis of the strain matrices for the different ferroelastic species listed by Aizu (Reference Aizu1970). Since ^m ε _s is invariant with respect to the symmetry operations of the low-symmetry phase's crystal class, and since the symmetry elements, which are lost in the course of symmetry reduction, act on each ^m ε _s to form a complete set of strain tensors pertaining to all domain states, the tensor 〈ε _ij ε _pq 〉 is symmetry invariant with respect to the point group (Laue class) of the high-symmetry phase. Hence, also the polynomial (7) is symmetry invariant with respect to the high-symmetry phase, as it is typically assumed to be the case (Popa, Reference Popa1998; Stephens, Reference Stephens1999; Leineweber, Reference Leineweber2006, Reference Leineweber2011).

It may be interesting to analyze the direction-averaged extent of the reflection splitting-induced microstrain broadening using a measure introduced by Leineweber (Reference Leineweber2011) and a modified notation from Leineweber (Reference Leineweber2016). This measure amounts the direction average of $\langle \varepsilon _{hkl}^2 \rangle $ :

(11) $$\overline {\left\langle {\varepsilon _{hkl}^2} \right\rangle} = {\textstyle{1 \over 5}}\left( {Z_{1111} + Z_{2222} + Z_{3333} + 2Z_{1122} + 2Z_{1133} + 2Z_{2233}} \right)$$

which becomes upon use of Eqs (8) and (10):

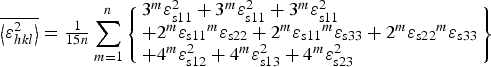(12) $$\overline {\left\langle {\varepsilon _{hkl}^2} \right\rangle} = {\textstyle{1 \over {15n}}}\sum\limits_{m = 1}^n {\left\{ \matrix{3{}^m\varepsilon _{{\rm s}11}^2 + 3{}^m\varepsilon _{{\rm s}11}^2 + 3{}^m\varepsilon _{{\rm s}11}^2 \hfill \cr + 2{}^m\varepsilon _{{\rm s}11}{}^m\varepsilon _{{\rm s}22} + 2{}^m\varepsilon _{{\rm s}11}{}^m\varepsilon _{{\rm s}33} + 2{}^m\varepsilon _{{\rm s}22}{}^m\varepsilon _{{\rm s}33} \hfill \cr + 4{}^m\varepsilon _{{\rm s}12}^2 + 4{}^m\varepsilon _{{\rm s}13}^2 + 4{}^m\varepsilon _{{\rm s}23}^2 \hfill} \right\}} $$

Addition of 0 = −( ^m ε_s11 +  ^m ε_s22 +  ^m ε_s33)² in the bracket yields

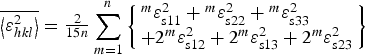(13) $$\overline {\left\langle {\varepsilon _{hkl}^2} \right\rangle} = {\textstyle{2 \over {15n}}}\sum\limits_{m = 1}^n {\left\{ \matrix{{}^m\varepsilon _{{\rm s}11}^2 + {}^m\varepsilon _{{\rm s}22}^2 + {}^m\varepsilon _{{\rm s33}}^2 \hfill \cr + 2{}^m\varepsilon _{{\rm s}12}^2 + 2{}^m\varepsilon _{{\rm s}13}^2 + 2{}^m\varepsilon _{{\rm s}23}^2 \hfill} \right\}} $$

Comparison of Eq. (13) with Eq. (6b) reveals each addend in Eq. (13) is equal, i.e. independent of m. Moreover, this comparison indicates that the

(14) $$\overline {\left\langle {\varepsilon _{hkl}^2} \right\rangle} = \overline {\varepsilon ^2} $$

holds. Hence, if microstrain broadening is induced by a slight distortion with respect to the unit cell of the high-symmetry state, the direction average of the variance of the microstrain broadening equals the direction average of the variance of the strain and is thus proportional to the squared Aizu's spontaneous strain.

IV. EXAMPLE: APPLICATION TO THE CASE TETRAGONALLY DISTORTED CUBIC MATERIALS

The case of a cubic-to-tetragonal phase transition is treated here because the line broadening associated with the corresponding reflection splitting has been considered very recently (Fabrykiewicz and Przenioslo, Reference Fabrykiewicz and Przenioslo2016) by describing the broadening within Stephens’ (Reference Stephens1999) description for anisotropic microstrain broadening. That description is based on the coefficients of a fourth-order polynomial in h, k, and l instead of the coefficients of the fourth-order polynomial in x ₁, x ₂, and x ₃ as used in Eq. (7) in connection with Eq. (8), as employed here. Unfortunately, in that work, the analysis of the experimentally determined independent coefficients S ₄₀₀ and S ₂₂₀ of these polynomials remains on a qualitative basis and does not translate magnitudes of tetragonal distortion into values of S ₄₀₀ and S ₂₂₀. This is done here within the formalism of Eqs (7) and (8), which appears to be simpler than doing so in the S _hkl formalism (an advantage which is even more relevant for even lower symmetries).

Assuming that the symmetry reduces from m $\bar 3$ m to 4/mmm point group (corresponding to the “ferroelastic species” m $\bar 3$ mF4/mmm; Aizu, Reference Aizu1970), having group orders of 48 and 16, the number of domain states amounts n = 3 = 48/16. The strains ^m ε _s pertaining to these domain states are:

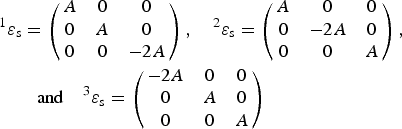(15) $$\eqalign{& {}^1{\bi \varepsilon}_{\rm s} = \left( {\matrix{ A & 0 & 0 \cr 0 & A & 0 \cr 0 & 0 & { - 2A} \cr}} \right),\quad {}^2{\bi \varepsilon} _{\rm s} = \left( {\matrix{ A & 0 & 0 \cr 0 & { - 2A} & 0 \cr 0 & 0 & A \cr}} \right), \cr & \quad \quad {\rm and}\quad {}^3{\bi \varepsilon}_{\rm s} = \left( {\matrix{ { - 2A} & 0 & 0 \cr 0 & A & 0 \cr 0 & 0 & A \cr}} \right)} $$

Considering the distortions because of these tensors, one can calculate the distributions of strain because of the different strain states measurable in the directions x  = (1, 0, 0), x  = (1, 1, 0)/2^1/2, and x  = (1, 1, 1)/3^1/2, where the occurring strains have been calculated by means of Eq. (4). The corresponding strains relative to a cubic average are shown in Figure 2 and correspond to the typical tetragonal reflection splitting in a powder diffraction pattern if this splitting is not masked by other line broadening contributions.

Figure 2. Distribution of strains for three different crystallographic directions for a tetragonally distorting cubic structure if all three domain states with the strains given in Eq. (15) occur with equal probability. The variances $\langle \varepsilon _{hkl}^2 \rangle = \langle \varepsilon ^2(\bi x)\rangle $ of the strains according to Eq. (14) are (a) 2A ², (b) A ², (c) 0 and will show up as microstrain broadening instead of reflection splitting, if the reflection splitting is sufficiently masked by other line broadening contributions.

If that masking occurs, the coefficients of Eq. (7) describing the microstrain broadening can be calculated by use of Eqs (10) and (15) giving

(16) $$\eqalign{&\quad \quad \left\langle {\varepsilon _{11}^2} \right\rangle = \left\langle {\varepsilon _{22}^2} \right\rangle = \left\langle {\varepsilon _{33}^2} \right\rangle = 2A^2 \cr & \left\langle {\varepsilon _{11}\varepsilon _{22}} \right\rangle = \left\langle {\varepsilon _{11}\varepsilon _{33}} \right\rangle = \left\langle {\varepsilon _{22}\varepsilon _{33}} \right\rangle = - A^2 \cr & \quad \quad \hbox{and all other}\;\left\langle {\varepsilon _{ij}\varepsilon _{\,pq}} \right\rangle = 0 }$$

These results indicate that the microstrain distribution is symmetry invariant with respect to the high-symmetry m $\bar 3$ m point group.

Upon use of Eq. (16) in Eq. (7) one obtains the formula for the direction-dependent microstrain:

(17) $$\left\langle {\varepsilon _{hkl}^2} \right\rangle = 2A^2\left( {x_1^4 + x_2^4 + x_3^4 - x_1^2 x_2^2 - x_1^2 x_3^2 - x_2^2 x_3^2} \right)$$

Addition and subtraction of $ + 2x_1^2 x_2^2 + 2x_1^2 x_3^2 + 2x_2^2 x_3^2 $ on the right side of Eq. (17) and using $x_1^4 + x_2^4 + x_3^4 + 2x_1^2 x_2^2 + 2x_1^2 x_3^2 + 2x_2^2 x_3^2 = 1$ yields:

(18) $$\left\langle {\varepsilon _{hkl}^2} \right\rangle = 2A^2\left( {1 - 3 {\it \Gamma}} \,\right)$$

with ${\it \Gamma} = x_1^2 x_2^2 + x_1^2 x_3^2 + x_2^2 x_3^2 $  = (h ² k ² + h ² l ² + k ² l ²)/(h ² + k ² + l ²)². Thereby, the maximum value of 〈 $\varepsilon _{hkl}^2 $ 〉 is present for Γ = 0, i.e. x  = (±1,0,0), (0, ±1,0), and (0,0, ±1) [Figure 2(a)] with $\langle \varepsilon _{hkl}^2 \rangle = 2A^2$ . This corresponds to the splitting pattern for {h00} reflections. The minimum (zero) microstrain occurs for Γ = 1/3, i.e. x  = (±1, ±1, ±1) with $\langle \varepsilon _{hkl}^2 \rangle = 0$ , which is the minimum possible value for a variance. This corresponds to the absent splitting of {hhh} reflections for a symmetry reduction from cubic to tetragonal.

Note that the cubic-to-tetragonal case considered here is associated with an asymmetric distribution of the strains for all directions where the variance $\langle \varepsilon _{hkl}^2 \rangle \gt 0$ , whereas many other cases are associated with a symmetric 1:1 splitting. This direction/hkl dependence of this asymmetry can be considered by calculation of the third (central) moments of the microstrain distribution, on the basis of which the skewness can be calculated (Leineweber, Reference Leineweber2009).