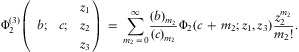1 Introduction
Consider a classical risk model in which the surplus process ![]() $$$ \{ U(t);t\:\geq \:0\} $$$
with initial surplus u ≥ 0 is given by
$$$ \{ U(t);t\:\geq \:0\} $$$
with initial surplus u ≥ 0 is given by
where c is the constant premium rate and ![]() $$$ {{\{ {{X}_i}\} }_{i\,\geq \,1}} $$$
are i.i.d. random variables representing the individual claim amounts, with common probability distribution function (d.f.) P, density function p, mean μ and Laplace transform (LT)
$$$ {{\{ {{X}_i}\} }_{i\,\geq \,1}} $$$
are i.i.d. random variables representing the individual claim amounts, with common probability distribution function (d.f.) P, density function p, mean μ and Laplace transform (LT) ![]() $$$ \hat{p} $$$
. The counting process
$$$ \hat{p} $$$
. The counting process ![]() $$$ \{ N(t);\:t\geq 0\} $$$
denotes the number of claims up to time t and is defined as
$$$ \{ N(t);\:t\geq 0\} $$$
denotes the number of claims up to time t and is defined as ![]() $$$ N(t)\, = \,\max \{ k\!:\!{{W}_1}+ {{W}_2} + \cdots + {{W}_k}\leq t\}, $$$
where the inter-claim times,
$$$ N(t)\, = \,\max \{ k\!:\!{{W}_1}+ {{W}_2} + \cdots + {{W}_k}\leq t\}, $$$
where the inter-claim times, ![]() $$$ {{\{ {{W}_i}\} }_{i\,\geq \,1}}, $$$
are assumed to be independent and exponentially distributed random variables with mean 1/λ. That is,
$$$ {{\{ {{W}_i}\} }_{i\,\geq \,1}}, $$$
are assumed to be independent and exponentially distributed random variables with mean 1/λ. That is, ![]() $$$ \{ N(t);\:t\geq 0\} $$$
is a Poisson process with parameter λ > 0. We further assume that
$$$ \{ N(t);\:t\geq 0\} $$$
is a Poisson process with parameter λ > 0. We further assume that ![]() $$$ {{\{ {{W}_i}\} }_{i\,\geq \,1}} $$$
and
$$$ {{\{ {{W}_i}\} }_{i\,\geq \,1}} $$$
and ![]() $$$ {{\{ {{X}_i}\} }_{i\,\geq \,1}} $$$
are independent and c >λμ so that the loading factor is positive.
$$$ {{\{ {{X}_i}\} }_{i\,\geq \,1}} $$$
are independent and c >λμ so that the loading factor is positive.
Define ![]() $$$ T\, = \,\inf \{ t\geq 0\,:\,U(t)\, \lt \,0\} $$$
to be the time of ruin, with
$$$ T\, = \,\inf \{ t\geq 0\,:\,U(t)\, \lt \,0\} $$$
to be the time of ruin, with ![]() $$$ T\, = \,\infty, $$$
if
$$$ T\, = \,\infty, $$$
if ![]() $$$ U(t)\geq 0 $$$
for all t ≥ 0. Further we define
$$$ U(t)\geq 0 $$$
for all t ≥ 0. Further we define
to be the Laplace transform of the time of ruin. In particular, when δ = 0, ![]() $$$ {{\phi }_\delta }(u) $$$
simplifies to the probability of the time of ruin, denoted by
$$$ {{\phi }_\delta }(u) $$$
simplifies to the probability of the time of ruin, denoted by ![]() $$$ \psi (u). $$$
$$$ \psi (u). $$$
In recent years, there has been considerable interest in finding the density of the time of ruin in the classical risk model by inverting its Laplace transform; see Drekic and Willmot (Reference Drekic and Willmot2003), Garcia (Reference Garcia2005), Dickson and Willmot (Reference Dickson and Willmot2005), and Dickson (Reference Dickson2007). By inverting the bivariate Laplace transform of the time of ruin and the deficit at ruin in the classical risk model, Dickson (Reference Dickson2008) gives some explicit expressions for their joint distribution. Landriault and Willmot (Reference Landriault and Willmot2009) derive an explicit expression for the joint distribution of the time of ruin, the surplus prior to ruin, and the deficit at ruin. The joint distribution of the time to ruin and the number of claims until ruin for the classical risk model has been investigated by Landriault et al. (Reference Landriault, Shi and Willmot2011) and Dickson (Reference Dickson2012).
In this paper, a classical risk model with a constant dividend barrier is considered. We apply the approach developed by Dickson and Willmot (Reference Dickson and Willmot2005) to find explicit expressions for the density function of the time of ruin and its two components: [1] the density function of the time of ruin without paying dividends (without the surplus reaching b); [2] the density of the time of ruin with dividend payments. We give explicit expressions through special functions for the density functions of the time of ruin in a classical risk model with a constant dividend barrier and exponential claims. It is worth mentioning that Perry et al. (Reference Perry, Stadje and Zacks2005) give an (integral) expression for the density of a general two-sided first exit time in the compound Poisson process with general claim amount distributions; their results can be used to derive the density of the time of ruin without dividend payments mentioned above. For more results and developments on the two-sided first exit time problems appeared in the applied probability literature, see Perry et al. (Reference Perry, Stadje and Zacks2005) and the references therein.
2 Preliminary results
In this section, we review some results that are used for deriving the density functions of quantities mentioned above under exponential claims.
Gerber and Shiu (Reference Gerber and Shiu1998) show that the following Lundberg's fundamental equation
has a unique positive solution, denoted as ρ(δ). Further if ![]() $$$ p(x) $$$
is sufficiently regular, Eq. (2.1) has a negative solution, denoted as −R(δ). In the rest of the paper, we write ρ(δ) as ρ and write R(δ) as R. Dickson and Willmot (Reference Dickson and Willmot2005, p.45) show that if
$$$ p(x) $$$
is sufficiently regular, Eq. (2.1) has a negative solution, denoted as −R(δ). In the rest of the paper, we write ρ(δ) as ρ and write R(δ) as R. Dickson and Willmot (Reference Dickson and Willmot2005, p.45) show that if
then function g can be obtained as
 $${ g(t)\, & = \, c{{e}^{{\rm{ - }}\lambda t}} f(ct)\, + \,\mathop{\sum}\limits_{n\, = \,1}^\infty \frac{{{{\lambda }^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\lambda t}} }}{{n!}}{\int}_{\!\!\!\!0}^{{ct}} y{{p}^{n\ast}} (ct\,{\rm{ - }}\,y)f(y)dy\: \cr & = \,\mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{\lambda }^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\lambda t}} }}{{n!}}{\int}_{\!\!\!\!0}^{{ct}} y{{p}^{n\ast}} (ct\,{\rm{ - }}\,y)f(y)dy, \cr}$$
$${ g(t)\, & = \, c{{e}^{{\rm{ - }}\lambda t}} f(ct)\, + \,\mathop{\sum}\limits_{n\, = \,1}^\infty \frac{{{{\lambda }^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\lambda t}} }}{{n!}}{\int}_{\!\!\!\!0}^{{ct}} y{{p}^{n\ast}} (ct\,{\rm{ - }}\,y)f(y)dy\: \cr & = \,\mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{\lambda }^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\lambda t}} }}{{n!}}{\int}_{\!\!\!\!0}^{{ct}} y{{p}^{n\ast}} (ct\,{\rm{ - }}\,y)f(y)dy, \cr}$$
as ![]() $$$ {{p}^{0\ast}} (y)\, = \,I(y\, = \,0) $$$
and
$$$ {{p}^{0\ast}} (y)\, = \,I(y\, = \,0) $$$
and ![]() $$$ {\int}_{\!\!0}^{{ct}} y{{p}^{0\ast}} (ct\,{\rm{ - }}\,y)f(y)dy\, = \,ctf(ct) $$$
. In the following sections, we first derive the Laplace inversion with respect to ρ (function f), and then obtain the corresponding Laplace inversion with respect to δ (function g) using (2.2).
$$$ {\int}_{\!\!0}^{{ct}} y{{p}^{0\ast}} (ct\,{\rm{ - }}\,y)f(y)dy\, = \,ctf(ct) $$$
. In the following sections, we first derive the Laplace inversion with respect to ρ (function f), and then obtain the corresponding Laplace inversion with respect to δ (function g) using (2.2).
Three special functions are used in this paper which are given below.
1. The generalized hypergeometric function with definition
where $$)(--><$$> _{p} {{F}_q}({{a}_1},{{a}_2}, \ldots, {{a}_p};{{b}_1},{{b}_2}, \ldots, {{b}_q};z)\, = \,\mathop{\sum}\limits_{m\, = \,0}^\infty \frac{{{{{({{a}_1})}}_m}{{{({{a}_2})}}_m} \ldots {{{({{a}_p})}}_m}}}{{{{{({{b}_1})}}_m}{{{({{b}_2})}}_m} \ldots {{{({{b}_q})}}_m}}}\frac{{{{z}^m} }}{{m!}}\:, <$$><!--$$
$$)(--><$$> _{p} {{F}_q}({{a}_1},{{a}_2}, \ldots, {{a}_p};{{b}_1},{{b}_2}, \ldots, {{b}_q};z)\, = \,\mathop{\sum}\limits_{m\, = \,0}^\infty \frac{{{{{({{a}_1})}}_m}{{{({{a}_2})}}_m} \ldots {{{({{a}_p})}}_m}}}{{{{{({{b}_1})}}_m}{{{({{b}_2})}}_m} \ldots {{{({{b}_q})}}_m}}}\frac{{{{z}^m} }}{{m!}}\:, <$$><!--$$
 $$$ {{(a)}_m}\, = \,{\rm{\rGamma }}(a\, + \,m)/{\rm{\rGamma }}(a) $$$
.
$$$ {{(a)}_m}\, = \,{\rm{\rGamma }}(a\, + \,m)/{\rm{\rGamma }}(a) $$$
.2. A special confluent hypergeometric series in two variables (see, for example, Srivastava and Karisson, 1985, p.25, (17)) with definition:
 $$)(--><$$> {{{\rm{\rPhi }}}_2}(c;\ {{z}_1},{{z}_2})\, = \,\mathop{\sum}\limits_{{{m}_1},{{m}_2}\, = \,0}^\infty \frac{1}{{{{{(c)}}_{{{m}_1}\, + \,{{m}_2}}}}}\frac{{z_{1}^{{{{m}_1}}} z_{2}^{{{{m}_2}}} }}{{{{m}_1}!{{m}_2}!}}\:. \eqno<$$><!--$$
$$)(--><$$> {{{\rm{\rPhi }}}_2}(c;\ {{z}_1},{{z}_2})\, = \,\mathop{\sum}\limits_{{{m}_1},{{m}_2}\, = \,0}^\infty \frac{1}{{{{{(c)}}_{{{m}_1}\, + \,{{m}_2}}}}}\frac{{z_{1}^{{{{m}_1}}} z_{2}^{{{{m}_2}}} }}{{{{m}_1}!{{m}_2}!}}\:. \eqno<$$><!--$$
3. A special confluent form of Lauricella series
 $$$ {\rm{\rPhi }}_{2}^{{(3)}} $$$
(see, Erdélyi Reference Erdélyi1937, p.446) with definition:
$$$ {\rm{\rPhi }}_{2}^{{(3)}} $$$
(see, Erdélyi Reference Erdélyi1937, p.446) with definition:  $$)(--><$$> {\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026; {{{z}_1}} \hfill \cr\ {b;} \hfill &#x0026; {c;} \hfill &#x0026; {{{z}_2}} \hfill \cr\ {} \hfill &#x0026; {} \hfill &#x0026; {{{z}_3}} \hfill \\\end{}} \right)\, = \,\mathop{\sum}\limits_{{{m}_1},{{m}_2},{{m}_3}\, = \,0}^\infty \frac{{{{{(b)}}_{{{m}_2}}}}}{{{{{(c)}}_{{{m}_1}\, + \,{{m}_2}\, + \,{{m}_3}}}}}\frac{{z_{1}^{{{{m}_1}}} z_{2}^{{{{m}_2}}} z_{3}^{{{{m}_3}}} }}{{{{m}_1}!{{m}_2}!{{m}_3}!}}\:.\eqno<$$><!--$$
$$)(--><$$> {\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026; {{{z}_1}} \hfill \cr\ {b;} \hfill &#x0026; {c;} \hfill &#x0026; {{{z}_2}} \hfill \cr\ {} \hfill &#x0026; {} \hfill &#x0026; {{{z}_3}} \hfill \\\end{}} \right)\, = \,\mathop{\sum}\limits_{{{m}_1},{{m}_2},{{m}_3}\, = \,0}^\infty \frac{{{{{(b)}}_{{{m}_2}}}}}{{{{{(c)}}_{{{m}_1}\, + \,{{m}_2}\, + \,{{m}_3}}}}}\frac{{z_{1}^{{{{m}_1}}} z_{2}^{{{{m}_2}}} z_{3}^{{{{m}_3}}} }}{{{{m}_1}!{{m}_2}!{{m}_3}!}}\:.\eqno<$$><!--$$
Remarks:
1. As
 $$$ {{(c)}_{{{m}_1}\, + \,{{m}_2}}}\, = \,{{(c\, + \,{{m}_1})}_{{{m}_2}}}{{(c)}_{{{m}_1}}} $$$
, Φ2 in (2.3) can be rewritten as
$$$ {{(c)}_{{{m}_1}\, + \,{{m}_2}}}\, = \,{{(c\, + \,{{m}_1})}_{{{m}_2}}}{{(c)}_{{{m}_1}}} $$$
, Φ2 in (2.3) can be rewritten as  $$)(--><$$>\quad\quad\quad\quad\quad\quad\quad\quad\quad{{{\rm{\rPhi }}}_2}(c;\ {{z}_1},{{z}_2})\, = \,\mathop{\sum}\limits_{{{m}_1}\, = \,0}^\infty \frac{1}{{{{{(c)}}_{{{m}_1}}}}}{{\;}_0}{{F}_1}(;c\, + \,{{m}_1};{{z}_2})\frac{{z_{1}^{{{{m}_1}}} }}{{{{m}_1}!}}\:.\eqno<$$><!--$$
$$)(--><$$>\quad\quad\quad\quad\quad\quad\quad\quad\quad{{{\rm{\rPhi }}}_2}(c;\ {{z}_1},{{z}_2})\, = \,\mathop{\sum}\limits_{{{m}_1}\, = \,0}^\infty \frac{1}{{{{{(c)}}_{{{m}_1}}}}}{{\;}_0}{{F}_1}(;c\, + \,{{m}_1};{{z}_2})\frac{{z_{1}^{{{{m}_1}}} }}{{{{m}_1}!}}\:.\eqno<$$><!--$$
2. Similarly,
 $$$ {\rm{\rPhi }}_{2}^{{(3)}} $$$
in (2.4) can be expressed as
$$$ {\rm{\rPhi }}_{2}^{{(3)}} $$$
in (2.4) can be expressed as  $$)(--><$$>\quad\quad\quad\quad\quad\quad\quad\quad\quad {\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix {&#x0026; &#x0026;{{{z}_1}} \hfill \cr\ {b;} \hfill &#x0026; {c;} \hfill &#x0026; {{{z}_2}} \hfill \cr\ {} \hfill &#x0026; {} \hfill &#x0026; {{{z}_3}} \hfill \\\end{}} \right)\, = \,\mathop{\sum}\limits_{{{m}_2}\, = \,0}^\infty \frac{{{{{(b)}}_{{{m}_2}}}}}{{{{{(c)}}_{{{m}_2}}}}}{{{\rm{\rPhi }}}_2}(c\, + \,{{m}_2};{{z}_1},{{z}_3})\:\frac{{z_{2}^{{{{m}_2}}} }}{{{{m}_2}!}}\:.\eqno <$$><!--$$
$$)(--><$$>\quad\quad\quad\quad\quad\quad\quad\quad\quad {\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix {&#x0026; &#x0026;{{{z}_1}} \hfill \cr\ {b;} \hfill &#x0026; {c;} \hfill &#x0026; {{{z}_2}} \hfill \cr\ {} \hfill &#x0026; {} \hfill &#x0026; {{{z}_3}} \hfill \\\end{}} \right)\, = \,\mathop{\sum}\limits_{{{m}_2}\, = \,0}^\infty \frac{{{{{(b)}}_{{{m}_2}}}}}{{{{{(c)}}_{{{m}_2}}}}}{{{\rm{\rPhi }}}_2}(c\, + \,{{m}_2};{{z}_1},{{z}_3})\:\frac{{z_{2}^{{{{m}_2}}} }}{{{{m}_2}!}}\:.\eqno <$$><!--$$
Consider that claim amounts are exponentially distributed with ![]() $$$ p(x)\, = \,\beta {{e}^{{\rm{ - }}\beta x}}, x\, \gt \,0 $$$
. It is shown in Gerber and Shiu (Reference Gerber and Shiu1998, p.63, (5.38)) that
$$$ p(x)\, = \,\beta {{e}^{{\rm{ - }}\beta x}}, x\, \gt \,0 $$$
. It is shown in Gerber and Shiu (Reference Gerber and Shiu1998, p.63, (5.38)) that
where −R is the negative root of the Lundberg's fundamental equation
Both ρ and −R play important roles in studying the ruin-related quantities for the classical risk model in the ruin theory, especially in finding the probability density functions in this paper.
Note that (2.6) implies
Since ρ satisfies (2.6), it is not difficult to obtain the following two equations which are crucial in our derivations:
A particular form of ![]() $$$ \hat{f}(\rho ) $$$
is seen frequently throughout this paper when claims are exponentially distributed with paraneter β, and hence we present its corresponding expressions of f(t) and g(t) below as a lemma.
$$$ \hat{f}(\rho ) $$$
is seen frequently throughout this paper when claims are exponentially distributed with paraneter β, and hence we present its corresponding expressions of f(t) and g(t) below as a lemma.
Lemma 1 If ![]() $$$ \hat{f}(\rho ) $$$
is of the form
$$$ \hat{f}(\rho ) $$$
is of the form
then
and
 $$\openup 3pt{ g(t)\, = &#x0026; \,{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} \frac{{{{{(ct\,{\rm{ - }}\,\theta )}}^{\nu \, + \,\kappa \,{\rm{ - }}\,1}} }}{{{\rm{\rGamma }}(\nu \, + \,\kappa )}}\left[ {c\thinsp\, {\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026;{\lambda \beta t(ct\,{\rm{ - }}\,\theta )} \cr\ {\kappa ;} &#x0026; {\nu \, + \,\kappa ;} &#x0026; \!\!\!\!\! {\beta (ct\,{\rm{ - }}\,\theta )} \cr\ {} &#x0026; {} &#x0026; \!\!\!\!\!{\mu (ct\,{\rm{ - }}\,\theta )} \\\end{}} \right)} \right. \cr &#x0026; \; \; \left. {{\rm{ - }}\frac{{\lambda \beta {{{(ct\,{\rm{ - }}\,\theta )}}^2} }}{{(\nu \, + \,\kappa )(\nu \, + \,\kappa \, + \,1)}}{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026;{\lambda \beta t(ct\,{\rm{ - }}\,\theta )} \cr\ {\kappa ;} &#x0026; {\nu \, + \,\kappa \, + \,2;} &#x0026; \!\!\!\!\!{\beta (ct\,{\rm{ - }}\,\theta )} \cr\ {} &#x0026; {} &#x0026; \!\!\!\!\!{\mu (ct\,{\rm{ - }}\,\theta )} \\\end{}} \right)} \right]\:,\; \; t\, \gt \,\frac{\theta }{c}\thinsp, }\eqno $$
$$\openup 3pt{ g(t)\, = &#x0026; \,{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} \frac{{{{{(ct\,{\rm{ - }}\,\theta )}}^{\nu \, + \,\kappa \,{\rm{ - }}\,1}} }}{{{\rm{\rGamma }}(\nu \, + \,\kappa )}}\left[ {c\thinsp\, {\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026;{\lambda \beta t(ct\,{\rm{ - }}\,\theta )} \cr\ {\kappa ;} &#x0026; {\nu \, + \,\kappa ;} &#x0026; \!\!\!\!\! {\beta (ct\,{\rm{ - }}\,\theta )} \cr\ {} &#x0026; {} &#x0026; \!\!\!\!\!{\mu (ct\,{\rm{ - }}\,\theta )} \\\end{}} \right)} \right. \cr &#x0026; \; \; \left. {{\rm{ - }}\frac{{\lambda \beta {{{(ct\,{\rm{ - }}\,\theta )}}^2} }}{{(\nu \, + \,\kappa )(\nu \, + \,\kappa \, + \,1)}}{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026;{\lambda \beta t(ct\,{\rm{ - }}\,\theta )} \cr\ {\kappa ;} &#x0026; {\nu \, + \,\kappa \, + \,2;} &#x0026; \!\!\!\!\!{\beta (ct\,{\rm{ - }}\,\theta )} \cr\ {} &#x0026; {} &#x0026; \!\!\!\!\!{\mu (ct\,{\rm{ - }}\,\theta )} \\\end{}} \right)} \right]\:,\; \; t\, \gt \,\frac{\theta }{c}\thinsp, }\eqno $$
where function ![]() $$$ {\rm{\rPhi }}_{2}^{{(3)}} $$$
is defined in (2.4).
$$$ {\rm{\rPhi }}_{2}^{{(3)}} $$$
is defined in (2.4).
Proof. First note the Laplace transform formula below (see, Abramowitz and Stegun (Reference Abramowitz and Stegun1972, page 1026, 29.3.81))
 $${ &#x0026; \frac{{{{e}^{\frac{\mu }{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^\nu } }}\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \left( {{{e}^{{\rm{ - }}\beta t}} {{t}^{\nu \,{\rm{ - }}\,1}} \mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{\left( {\mu t} \right)}}^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu )}}} \right)dt\:,\; \; \; \; \mu \,\geq \,0,\nu \, \gt \,0\:, \cr &#x0026; \quad\quad\!\frac{{{{e}^{{\rm{ - }}\theta \rho }} }}{{{{\rho }^\kappa } }}\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \left( {\frac{{{{{(t\,{\rm{ - }}\,\theta )}}^{\kappa \,{\rm{ - }}\,1}} }}{{{\rm{\rGamma }}(\kappa )}}I(t\, \gt \,\theta )} \right)dt\:,\; \; \; \; \theta \,\geq \,0,\kappa \, \gt \,0\thinsp. }$$
$${ &#x0026; \frac{{{{e}^{\frac{\mu }{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^\nu } }}\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \left( {{{e}^{{\rm{ - }}\beta t}} {{t}^{\nu \,{\rm{ - }}\,1}} \mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{\left( {\mu t} \right)}}^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu )}}} \right)dt\:,\; \; \; \; \mu \,\geq \,0,\nu \, \gt \,0\:, \cr &#x0026; \quad\quad\!\frac{{{{e}^{{\rm{ - }}\theta \rho }} }}{{{{\rho }^\kappa } }}\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \left( {\frac{{{{{(t\,{\rm{ - }}\,\theta )}}^{\kappa \,{\rm{ - }}\,1}} }}{{{\rm{\rGamma }}(\kappa )}}I(t\, \gt \,\theta )} \right)dt\:,\; \; \; \; \theta \,\geq \,0,\kappa \, \gt \,0\thinsp. }$$
Then the Laplace inversion of ![]() $$$ \hat{f}(\rho ) $$$
with respect to ρ is obtained in terms of the convolution as
$$$ \hat{f}(\rho ) $$$
with respect to ρ is obtained in terms of the convolution as
 $${ f(t)\, = &#x0026; \,{\int}_{\!\!\!\!0}^{t} \left( {\frac{{{{{(t\,{\rm{ - }}\,x\,{\rm{ - }}\,\theta )}}^{\kappa \,{\rm{ - }}\,1}} }}{{\rGamma (\kappa )}}I(t\,{\rm{ - }}\,x\, \gt \,\theta )} \right)\left( {{{e}^{{\rm{ - }}\beta x}} {{x}^{\nu \,{\rm{ - }}\,1}} \mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{\left( {\mu x} \right)}}^i} }}{{i!\rGamma (i\, + \,\nu )}}} \right)dx \cr = &#x0026; \,\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!\rGamma (i\, + \,\nu )\rGamma (\kappa )}}{\int}_{\!\!\!\!0}^{{t\,{\rm{ - }}\,\theta }} {{e}^{{\rm{ - }}\beta x}} {{(t\,{\rm{ - }}\,x\,{\rm{ - }}\,\theta )}^{\kappa \,{\rm{ - }}\,1}} {{x}^{i\, + \,\nu \,{\rm{ - }}\,1}} dx\:,\; \; \; \; t\, \gt \,\theta \:. \cr}$$
$${ f(t)\, = &#x0026; \,{\int}_{\!\!\!\!0}^{t} \left( {\frac{{{{{(t\,{\rm{ - }}\,x\,{\rm{ - }}\,\theta )}}^{\kappa \,{\rm{ - }}\,1}} }}{{\rGamma (\kappa )}}I(t\,{\rm{ - }}\,x\, \gt \,\theta )} \right)\left( {{{e}^{{\rm{ - }}\beta x}} {{x}^{\nu \,{\rm{ - }}\,1}} \mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{\left( {\mu x} \right)}}^i} }}{{i!\rGamma (i\, + \,\nu )}}} \right)dx \cr = &#x0026; \,\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!\rGamma (i\, + \,\nu )\rGamma (\kappa )}}{\int}_{\!\!\!\!0}^{{t\,{\rm{ - }}\,\theta }} {{e}^{{\rm{ - }}\beta x}} {{(t\,{\rm{ - }}\,x\,{\rm{ - }}\,\theta )}^{\kappa \,{\rm{ - }}\,1}} {{x}^{i\, + \,\nu \,{\rm{ - }}\,1}} dx\:,\; \; \; \; t\, \gt \,\theta \:. \cr}$$
With the variable change ![]() $$$ x\, = \,(t\,{\rm{ - }}\,\theta )y $$$
, we obtain (2.10).
$$$ x\, = \,(t\,{\rm{ - }}\,\theta )y $$$
, we obtain (2.10).
Note that the n-fold convolution of p(x), ![]() $$$ {{p}^{n\ast}} (x) $$$
, is the density function of Erlang (n) distribution with scale parameter β, given by
$$$ {{p}^{n\ast}} (x) $$$
, is the density function of Erlang (n) distribution with scale parameter β, given by
Then by (2.2) and (2.13), we have, for ![]() $$$ t\, \gt \,\theta /c $$$
,
$$$ t\, \gt \,\theta /c $$$
,
 $${ g(t)\, = &#x0026; \,\mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\lambda t}} }}{{n!}}{\int}_{\!\!\!\!0}^{{ct}} y\frac{{{{{(ct\,{\rm{ - }}\,y)}}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\beta (ct\,{\rm{ - }}\,y)}} }}{{{\rm{\rGamma }}(n)}}f(y)dy \cr = &#x0026; \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t}} }}{{n!{\rm{\rGamma }}(n)}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu )\rGamma (\kappa )}} \cr &#x0026; \,\,\; \; \times \,{\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{e}^{\beta y}} \left( {{\int}_{\!\!\!\!0}^{{y\,{\rm{ - }}\,\theta }} {{e}^{{\rm{ - }}\beta x}} {{{(y\,{\rm{ - }}\,x\,{\rm{ - }}\,\theta )}}^{\kappa \,{\rm{ - }}\,1}} {{x}^{i\, + \,\nu \,{\rm{ - }}\,1}} dx} \right)dy \cr = &#x0026; \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} }}{{n!{\rm{\rGamma }}(n)}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu ){\rm{\rGamma }}(\kappa )}} \cr &#x0026; \; \; \; \; \times \,{\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} \left( {{\int}_{\!\!\!\!0}^{1} {{e}^{\beta (y\,{\rm{ - }}\,\theta )x}} {{x}^{\kappa \,{\rm{ - }}\,1}} {{{(1\,{\rm{ - }}\,x)}}^{i\, + \,\nu \,{\rm{ - }}\,1}} dx} \right)dy\:. \cr}$$
$${ g(t)\, = &#x0026; \,\mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\lambda t}} }}{{n!}}{\int}_{\!\!\!\!0}^{{ct}} y\frac{{{{{(ct\,{\rm{ - }}\,y)}}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}\beta (ct\,{\rm{ - }}\,y)}} }}{{{\rm{\rGamma }}(n)}}f(y)dy \cr = &#x0026; \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t}} }}{{n!{\rm{\rGamma }}(n)}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu )\rGamma (\kappa )}} \cr &#x0026; \,\,\; \; \times \,{\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{e}^{\beta y}} \left( {{\int}_{\!\!\!\!0}^{{y\,{\rm{ - }}\,\theta }} {{e}^{{\rm{ - }}\beta x}} {{{(y\,{\rm{ - }}\,x\,{\rm{ - }}\,\theta )}}^{\kappa \,{\rm{ - }}\,1}} {{x}^{i\, + \,\nu \,{\rm{ - }}\,1}} dx} \right)dy \cr = &#x0026; \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} }}{{n!{\rm{\rGamma }}(n)}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu ){\rm{\rGamma }}(\kappa )}} \cr &#x0026; \; \; \; \; \times \,{\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} \left( {{\int}_{\!\!\!\!0}^{1} {{e}^{\beta (y\,{\rm{ - }}\,\theta )x}} {{x}^{\kappa \,{\rm{ - }}\,1}} {{{(1\,{\rm{ - }}\,x)}}^{i\, + \,\nu \,{\rm{ - }}\,1}} dx} \right)dy\:. \cr}$$
Now using
we can further write g(t) as
 $${ g(t)\, = &#x0026; \,\mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} }}{{n!{\rm{\rGamma }}(n)}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu \, + \,\kappa )}} \cr &#x0026; \; \; \; \; \times {\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} _{1} {{F}_1}(\kappa, i\, + \,\nu \, + \,\kappa ;\beta (y\,{\rm{ - }}\,\theta ))dy \cr = &#x0026; \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} }}{{n!{\rm{\rGamma }}(n){\rm{\rGamma }}(\kappa )}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!}}\mathop{\sum}\limits_{m\, = \,0}^\infty \frac{{{{\beta }^m} {\rm{\rGamma }}(m\, + \,\kappa )}}{{m!{\rm{\rGamma }}(m\, + \,i\, + \,\nu \, + \,\kappa )}} \cr &#x0026; \; \; \; \; \times {\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{m\, + \,i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} dy\:. \cr}$$
$${ g(t)\, = &#x0026; \,\mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} }}{{n!{\rm{\rGamma }}(n)}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!{\rm{\rGamma }}(i\, + \,\nu \, + \,\kappa )}} \cr &#x0026; \; \; \; \; \times {\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} _{1} {{F}_1}(\kappa, i\, + \,\nu \, + \,\kappa ;\beta (y\,{\rm{ - }}\,\theta ))dy \cr = &#x0026; \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{(\lambda \beta )}}^n} {{t}^{n\,{\rm{ - }}\,1}} {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} }}{{n!{\rm{\rGamma }}(n){\rm{\rGamma }}(\kappa )}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{\mu }^i} }}{{i!}}\mathop{\sum}\limits_{m\, = \,0}^\infty \frac{{{{\beta }^m} {\rm{\rGamma }}(m\, + \,\kappa )}}{{m!{\rm{\rGamma }}(m\, + \,i\, + \,\nu \, + \,\kappa )}} \cr &#x0026; \; \; \; \; \times {\int}_{\!\!\!\!\theta }^{{ct}} y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{m\, + \,i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} dy\:. \cr}$$
With the help of
it is not difficult to obtain the following expression for the integral in (2.14) as
 $${ {\int}_{\!\!\!\!\theta }^{{ct}} &#x0026; y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{m\, + \,i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} dy \cr &#x0026; \; \; = \,{{(ct\,{\rm{ - }}\,\theta )}^{n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} \frac{{{\rm{\rGamma }}(n){\rm{\rGamma }}(m\, + \,i\, + \,\nu \, + \,\kappa )}}{{{\rm{\rGamma }}(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa \, + \,1)}}[ct(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa )\,{\rm{ - }}\,n(ct\,{\rm{ - }}\,\theta )]\:, \cr}$$
$${ {\int}_{\!\!\!\!\theta }^{{ct}} &#x0026; y{{(ct\,{\rm{ - }}\,y)}^{n\,{\rm{ - }}\,1}} {{(y\,{\rm{ - }}\,\theta )}^{m\, + \,i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} dy \cr &#x0026; \; \; = \,{{(ct\,{\rm{ - }}\,\theta )}^{n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa \,{\rm{ - }}\,1}} \frac{{{\rm{\rGamma }}(n){\rm{\rGamma }}(m\, + \,i\, + \,\nu \, + \,\kappa )}}{{{\rm{\rGamma }}(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa \, + \,1)}}[ct(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa )\,{\rm{ - }}\,n(ct\,{\rm{ - }}\,\theta )]\:, \cr}$$
and hence g(t) can be written as
 $${ g(t)\, = \, &#x0026; {{e}^{ - (\lambda \, + \,\beta c)t\, + \,\beta \theta }} {{(ct\, - \,\theta )}^{\nu \, + \,\kappa \, - \,1}} \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{[\lambda \beta t(ct\, - \,\theta )]}}^n} }}{{n!}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{[\mu (ct\, - \,\theta )]}}^i} }}{{i!}} \cr &#x0026; \; \; \; \; \times \,\mathop{\sum}\limits_{m\, = \,0}^\infty \left( {\frac{{c{{{(\kappa )}}_m}}}{{{\rm{\rGamma }}(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa )}}\, - \,\frac{{\lambda \beta {{{(ct\, - \,\theta )}}^2} {{{(\kappa )}}_m}}}{{{\rm{\rGamma }}(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa \, + \,2)}}} \right)\frac{{{{{[\beta (ct\, - \,\theta )]}}^m} }}{{m!}} \cr = &#x0026;\, {{e}^{ - (\lambda \, + \,\beta c)t\, + \,\beta \theta }} \frac{{{{{(ct\, - \,\theta )}}^{\nu \, + \,\kappa \, - \,1}} }}{{{\rm{\rGamma }}(\nu \, + \,\kappa )}} \cr &#x0026; \; \; \times \left( {c\mathop{\sum}\limits_{n,m,i\, = \,0}^\infty \frac{{{{{(\kappa )}}_m}}}{{{{{(\nu \, + \,\kappa )}}_{n\, + \,i\, + \,m}}}}\frac{{{{{[\lambda \beta t(ct\,{\rm{ - }}\,\theta )]}}^n} }}{{n!}}\frac{{{{{[\beta (ct\,{\rm{ - }}\,\theta )]}}^m} }}{{m!}}\frac{{{{{[\mu (ct\,{\rm{ - }}\,\theta )]}}^i} }}{{i!}}} \right. \cr &#x0026; \; \; \; \left. {{\rm{ - }}\,\frac{{\lambda \beta {{{(ct\,{\rm{ - }}\,\theta )}}^2} }}{{(\nu \, + \,\kappa )(\nu \, + \,\kappa \, + \,1)}}\mathop{\sum}\limits_{n,m,i\, = \,0}^\infty \frac{{{{{(\kappa )}}_m}}}{{{{{(\nu \, + \,\kappa \, + \,2)}}_{n\, + \,i\, + \,m}}}}\frac{{{{{[\lambda \beta t(ct\,{\rm{ - }}\,\theta )]}}^n} }}{{n!}}\frac{{{{{[\beta (ct\,{\rm{ - }}\,\theta )]}}^m} }}{{m!}}\frac{{{{{[\mu (ct\,{\rm{ - }}\,\theta )]}}^i} }}{{i!}}} \right)\:. \cr}$$
$${ g(t)\, = \, &#x0026; {{e}^{ - (\lambda \, + \,\beta c)t\, + \,\beta \theta }} {{(ct\, - \,\theta )}^{\nu \, + \,\kappa \, - \,1}} \mathop{\sum}\limits_{n\, = \,0}^\infty \frac{{{{{[\lambda \beta t(ct\, - \,\theta )]}}^n} }}{{n!}}\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{[\mu (ct\, - \,\theta )]}}^i} }}{{i!}} \cr &#x0026; \; \; \; \; \times \,\mathop{\sum}\limits_{m\, = \,0}^\infty \left( {\frac{{c{{{(\kappa )}}_m}}}{{{\rm{\rGamma }}(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa )}}\, - \,\frac{{\lambda \beta {{{(ct\, - \,\theta )}}^2} {{{(\kappa )}}_m}}}{{{\rm{\rGamma }}(n\, + \,m\, + \,i\, + \,\nu \, + \,\kappa \, + \,2)}}} \right)\frac{{{{{[\beta (ct\, - \,\theta )]}}^m} }}{{m!}} \cr = &#x0026;\, {{e}^{ - (\lambda \, + \,\beta c)t\, + \,\beta \theta }} \frac{{{{{(ct\, - \,\theta )}}^{\nu \, + \,\kappa \, - \,1}} }}{{{\rm{\rGamma }}(\nu \, + \,\kappa )}} \cr &#x0026; \; \; \times \left( {c\mathop{\sum}\limits_{n,m,i\, = \,0}^\infty \frac{{{{{(\kappa )}}_m}}}{{{{{(\nu \, + \,\kappa )}}_{n\, + \,i\, + \,m}}}}\frac{{{{{[\lambda \beta t(ct\,{\rm{ - }}\,\theta )]}}^n} }}{{n!}}\frac{{{{{[\beta (ct\,{\rm{ - }}\,\theta )]}}^m} }}{{m!}}\frac{{{{{[\mu (ct\,{\rm{ - }}\,\theta )]}}^i} }}{{i!}}} \right. \cr &#x0026; \; \; \; \left. {{\rm{ - }}\,\frac{{\lambda \beta {{{(ct\,{\rm{ - }}\,\theta )}}^2} }}{{(\nu \, + \,\kappa )(\nu \, + \,\kappa \, + \,1)}}\mathop{\sum}\limits_{n,m,i\, = \,0}^\infty \frac{{{{{(\kappa )}}_m}}}{{{{{(\nu \, + \,\kappa \, + \,2)}}_{n\, + \,i\, + \,m}}}}\frac{{{{{[\lambda \beta t(ct\,{\rm{ - }}\,\theta )]}}^n} }}{{n!}}\frac{{{{{[\beta (ct\,{\rm{ - }}\,\theta )]}}^m} }}{{m!}}\frac{{{{{[\mu (ct\,{\rm{ - }}\,\theta )]}}^i} }}{{i!}}} \right)\:. \cr}$$
We then immediately obtain (2.11) in terms of function ![]() $$${\rm{\rPhi }}_{2}^{{(3)}} $$$
. □
$$${\rm{\rPhi }}_{2}^{{(3)}} $$$
. □
Corollary 1 Two particular results of Lemma 1:
1. If ![]() $$$ \theta \, = \,\kappa \, = \,0 $$$
in (2.9), then, for t > 0,
$$$ \theta \, = \,\kappa \, = \,0 $$$
in (2.9), then, for t > 0,
2. If κ = 0 in (2.9), then,
 $${ g(t)\, = \, &#x0026; {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} \frac{{{{{(ct\,{\rm{ - }}\,\theta )}}^{\nu \,{\rm{ - }}\,1}} }}{{{\rm{\rGamma }}(\nu )}}\bigg(c\:{{{\rm{\rPhi }}}_2}(\nu ;\lambda \beta t(ct\,{\rm{ - }}\,\theta ),\mu (ct\,{\rm{ - }}\,\theta )) \cr &#x0026; \; \; \left. {{\rm{ - }}\frac{{\lambda \beta {{{(ct\,{\rm{ - }}\,\theta )}}^2} }}{{\nu (\nu \, + \,1)}}{{{\rm{\rPhi }}}_2}(\nu \, + \,2;\lambda \beta t(ct\,{\rm{ - }}\,\theta ),\mu (ct\,{\rm{ - }}\,\theta ))} \right)\:,\; \; \; \; t\, \gt \,\frac{\theta }{c}\:, \cr}$$
$${ g(t)\, = \, &#x0026; {{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\, + \,\beta \theta }} \frac{{{{{(ct\,{\rm{ - }}\,\theta )}}^{\nu \,{\rm{ - }}\,1}} }}{{{\rm{\rGamma }}(\nu )}}\bigg(c\:{{{\rm{\rPhi }}}_2}(\nu ;\lambda \beta t(ct\,{\rm{ - }}\,\theta ),\mu (ct\,{\rm{ - }}\,\theta )) \cr &#x0026; \; \; \left. {{\rm{ - }}\frac{{\lambda \beta {{{(ct\,{\rm{ - }}\,\theta )}}^2} }}{{\nu (\nu \, + \,1)}}{{{\rm{\rPhi }}}_2}(\nu \, + \,2;\lambda \beta t(ct\,{\rm{ - }}\,\theta ),\mu (ct\,{\rm{ - }}\,\theta ))} \right)\:,\; \; \; \; t\, \gt \,\frac{\theta }{c}\:, \cr}$$
where Φ2 is defined in (2.3).
Proof. Note that since (2.12) is valid only when κ > 0, results in Lemma 1 can not be reduced directly to the corresponding ones in this corollary. However, the proof is straightforward and similar to the proof of Lemma 1. We hence do not show details here. □
Note that by the property in Srivastava and Karlsson (1985, p.28, 30), we may further write g(t) in Corollary 1 in terms of function ![]() $$$ _{0} {{F}_1} $$$
; for example, (2.16) can be rewritten as
$$$ _{0} {{F}_1} $$$
; for example, (2.16) can be rewritten as
3 Density functions of the time of ruin in presence of a constant dividend barrier
In this section, we introduce a constant dividend barrier to the classical risk model, that is, whenever the surplus reaches the level b, the premium is paid as dividends so that the surplus stays at level b until a claim makes it drop below b.
Let ![]() $$$ \{ {{U}_b}(t);t\,\geq \,0\} $$$
be the corresponding surplus process with initial surplus
$$$ \{ {{U}_b}(t);t\,\geq \,0\} $$$
be the corresponding surplus process with initial surplus ![]() $$$ {{U}_b}(0)\, = \,u $$$
under a constant barrier (level b) dividend strategy. Then
$$$ {{U}_b}(0)\, = \,u $$$
under a constant barrier (level b) dividend strategy. Then ![]() $$$ \{ {{U}_b}(t);t\geq 0\} $$$
can be expressed as
$$$ \{ {{U}_b}(t);t\geq 0\} $$$
can be expressed as
Let ![]() $$$ {{T}_b}\, = \,\inf \{ t\,:\,{{U}_b}(t)\, \lt \,0\} $$$
be the time of ruin (with
$$$ {{T}_b}\, = \,\inf \{ t\,:\,{{U}_b}(t)\, \lt \,0\} $$$
be the time of ruin (with ![]() $$$ {{T}_b}\, = \,\infty $$$
if ruin does not occur) for the modified surplus process in (3.1). It is well-known that ruin is certain for this model and we are interested in finding the probability density function of the time of ruin Tb.
$$$ {{T}_b}\, = \,\infty $$$
if ruin does not occur) for the modified surplus process in (3.1). It is well-known that ruin is certain for this model and we are interested in finding the probability density function of the time of ruin Tb.
Define
to be the Laplace transform of Tb with ![]() $$$ {{\phi }_{\infty, \delta }}(u)\, = \,{{\phi }_\delta }(u) $$$
. In the first subsection, we aim to find an explicit expression for the density function of the time of ruin by inverting
$$$ {{\phi }_{\infty, \delta }}(u)\, = \,{{\phi }_\delta }(u) $$$
. In the first subsection, we aim to find an explicit expression for the density function of the time of ruin by inverting ![]() $$$ {{\phi }_{b,\delta }}(u) $$$
. By a similar approach, we derive the density function of the time of ruin without dividend payments. We then numerically compare these two sets of probability density functions in Section 4.
$$$ {{\phi }_{b,\delta }}(u) $$$
. By a similar approach, we derive the density function of the time of ruin without dividend payments. We then numerically compare these two sets of probability density functions in Section 4.
3.1 The density function of the time of ruin
If claim amounts are exponentially distributed with mean 1/β, Lin et al. (Reference Lin, Willmot and Drekic2003, Eq. (6.3)) show that
First, we derive the density function of ![]() $$$ {{\phi }_\delta }(u) $$$
given in (2.5). Using the expressions (2.7) and (2.8) we can rewrite
$$$ {{\phi }_\delta }(u) $$$
given in (2.5). Using the expressions (2.7) and (2.8) we can rewrite ![]() $$$ {{\phi }_\delta }(u) $$$
as
$$$ {{\phi }_\delta }(u) $$$
as
Let ![]() $$$ \zeta (t;u) $$$
be the density of the time of ruin for the classical risk model and
$$$ \zeta (t;u) $$$
be the density of the time of ruin for the classical risk model and ![]() $$$ \bar{\zeta }(t;u) $$$
be a function such that
$$$ \bar{\zeta }(t;u) $$$
be a function such that
Following (2.15) and (2.16) in Corollary 1 with ![]() $$$ \mu \, = \,\frac{{\lambda \beta }}{c}u $$$
and
$$$ \mu \, = \,\frac{{\lambda \beta }}{c}u $$$
and ![]() $$$ \nu \, = \,1 $$$
, we can easily get for t > 0 that
$$$ \nu \, = \,1 $$$
, we can easily get for t > 0 that
 $${ &#x0026; \bar{\zeta }(t;u)\, = \,\frac{{{{e}^{{\rm{ - }}\beta (u\, + \,t)}} }}{\beta }\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{i\, + \,1}} {{{(ut)}}^i} }}{{i!{\rm{\rGamma }}(i\, + \,1)}}\:, \cr &#x0026; \zeta (t;u)\, = \,\lambda {{e}^{ - (\lambda \, + \,\beta c)t\, - \,\beta u}} \left( {{{{\rm{\rPhi }}}_2}(1;\lambda \beta c{{t}^2}, \lambda \beta ut)\, - \,\frac{{\lambda \beta c{{t}^2} }}{2}{{{\rm{\rPhi }}}_2}(3;\lambda \beta c{{t}^2}, \lambda \beta ut)} \right)\:. \cr}$$
$${ &#x0026; \bar{\zeta }(t;u)\, = \,\frac{{{{e}^{{\rm{ - }}\beta (u\, + \,t)}} }}{\beta }\mathop{\sum}\limits_{i\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{i\, + \,1}} {{{(ut)}}^i} }}{{i!{\rm{\rGamma }}(i\, + \,1)}}\:, \cr &#x0026; \zeta (t;u)\, = \,\lambda {{e}^{ - (\lambda \, + \,\beta c)t\, - \,\beta u}} \left( {{{{\rm{\rPhi }}}_2}(1;\lambda \beta c{{t}^2}, \lambda \beta ut)\, - \,\frac{{\lambda \beta c{{t}^2} }}{2}{{{\rm{\rPhi }}}_2}(3;\lambda \beta c{{t}^2}, \lambda \beta ut)} \right)\:. \cr}$$
Note that equation (3.3) in another format is given in Drekic and Willmot (Reference Drekic and Willmot2003).
Now let ![]() $$$ \zeta (t;u,b) $$$
be the density of the time of ruin for the classical risk model with a constant dividend barrier b, and
$$$ \zeta (t;u,b) $$$
be the density of the time of ruin for the classical risk model with a constant dividend barrier b, and ![]() $$$ \bar{\zeta }(t;u,b) $$$
be a function such that
$$$ \bar{\zeta }(t;u,b) $$$
be a function such that
Note that the inverse of the first term of ![]() $$$ {{\phi }_{b,\delta }}(u) $$$
in (3.2) with respect to δ is given by (3.3). Hence, we only consider below the second term in (3.2), denoted by (II). We write
$$$ {{\phi }_{b,\delta }}(u) $$$
in (3.2) with respect to δ is given by (3.3). Hence, we only consider below the second term in (3.2), denoted by (II). We write
 $${ ({\rm{II}})\, = &#x0026; \,\frac{1}{\beta }\frac{{(\beta \,{\rm{ - }}\,R)R{{e}^{{\rm{ - }}Rb}} }}{{(\rho \, + \,\beta )\rho {{e}^{\rho b}} }}\frac{{(\rho \, + \,\beta ){{e}^{\rho u}} \,{\rm{ - }}\,(\beta \,{\rm{ - }}\,R){{e}^{{\rm{ - }}Ru}} }}{{1\, + \,\frac{{(\beta \,{\rm{ - }}\,R)R{{e}^{{\rm{ - }}Rb}} }}{{(\rho \, + \,\beta )\rho {{e}^{\rho b}} }}}} \cr = &#x0026; \,\frac{1}{\beta }\left[ {(\rho \, + \,\beta ){{e}^{\rho u}} \,{\rm{ - }}\,(\beta \,{\rm{ - }}\,R){{e}^{{\rm{ - }}Ru}} } \right]\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{({\rm{ - }}1)}}^k} }}{{k!}}{{\left[ {\frac{{(\beta \,{\rm{ - }}\,R)R}}{{(\rho \, + \,\beta )\rho }}} \right]}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)(R\, + \,\rho )b}} \:. \cr}$$
$${ ({\rm{II}})\, = &#x0026; \,\frac{1}{\beta }\frac{{(\beta \,{\rm{ - }}\,R)R{{e}^{{\rm{ - }}Rb}} }}{{(\rho \, + \,\beta )\rho {{e}^{\rho b}} }}\frac{{(\rho \, + \,\beta ){{e}^{\rho u}} \,{\rm{ - }}\,(\beta \,{\rm{ - }}\,R){{e}^{{\rm{ - }}Ru}} }}{{1\, + \,\frac{{(\beta \,{\rm{ - }}\,R)R{{e}^{{\rm{ - }}Rb}} }}{{(\rho \, + \,\beta )\rho {{e}^{\rho b}} }}}} \cr = &#x0026; \,\frac{1}{\beta }\left[ {(\rho \, + \,\beta ){{e}^{\rho u}} \,{\rm{ - }}\,(\beta \,{\rm{ - }}\,R){{e}^{{\rm{ - }}Ru}} } \right]\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{({\rm{ - }}1)}}^k} }}{{k!}}{{\left[ {\frac{{(\beta \,{\rm{ - }}\,R)R}}{{(\rho \, + \,\beta )\rho }}} \right]}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)(R\, + \,\rho )b}} \:. \cr}$$
As both ρ and −R are roots of equation (2.6), and by (2.8), we further have
and thus
Now by (2.8) and (3.5), (3.4) becomes
 $${ ({\rm{II}})\, = &#x0026; \,\frac{1}{\beta }\left[ {(\rho \, + \,\beta ){{e}^{\rho u}} \,{\rm{ - }}\,\frac{{\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}{{e}^{{\rm{ - }}\left( {\beta \,{\rm{ - }}\,\frac{{\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}} \right)u}} } \right] \cr &#x0026; \; \; \times \,\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{({\rm{ - }}1)}}^k} }}{{k!}}\frac{{{{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,1}} }}{{{{\rho }^{k\, + \,1}} {{{(\rho + \beta )}}^{2(k\, + \,1)}} }}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix {{k\, + \,1} \cr\ i \\\end{}} \right)\frac{{{{{\left( {{\rm{ - }}\,\frac{\lambda }{c}} \right)}}^i} }}{{{{{(\rho \, + \,\beta )}}^i} }}{{e}^{{\rm{ - }}(k\, + \,1)\left( {\rho \, + \,\beta \,{\rm{ - }}\,\frac{{\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}} \right)b}} \cr = &#x0026; \ {\frac{1}{\beta }\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{({\rm{ - }}1)}}^k} }}{{k!}}{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} \mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix {{k\, + \,1} \cr\ i \\\end{}} \right){{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}^i}} \cr &#x0026;\; \; \times \left[ {\frac{{{{e}^{{\rm{ - }}[(k\, + \,1)b\,{\rm{ - }}\,u]\rho }} }}{{{{\rho }^{k\, + \,1}} }}\frac{{{{e}^{\frac{{(k\, + \,1)b\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,i\, + \,1}} }}\,{\rm{ - }}\,\frac{{\lambda \beta }}{c}{{e}^{{\rm{ - }}\beta u}} \frac{{{{e}^{{\rm{ - }}(k\, + \,1)b\rho }} }}{{{{\rho }^{k\, + \,1}} }}\frac{{{{e}^{\frac{{[u\, + \,(k\, + \,1)b]\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,i\, + \,3}} }}} \right]\:. \cr}\eqno$$
$${ ({\rm{II}})\, = &#x0026; \,\frac{1}{\beta }\left[ {(\rho \, + \,\beta ){{e}^{\rho u}} \,{\rm{ - }}\,\frac{{\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}{{e}^{{\rm{ - }}\left( {\beta \,{\rm{ - }}\,\frac{{\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}} \right)u}} } \right] \cr &#x0026; \; \; \times \,\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{({\rm{ - }}1)}}^k} }}{{k!}}\frac{{{{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,1}} }}{{{{\rho }^{k\, + \,1}} {{{(\rho + \beta )}}^{2(k\, + \,1)}} }}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix {{k\, + \,1} \cr\ i \\\end{}} \right)\frac{{{{{\left( {{\rm{ - }}\,\frac{\lambda }{c}} \right)}}^i} }}{{{{{(\rho \, + \,\beta )}}^i} }}{{e}^{{\rm{ - }}(k\, + \,1)\left( {\rho \, + \,\beta \,{\rm{ - }}\,\frac{{\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}} \right)b}} \cr = &#x0026; \ {\frac{1}{\beta }\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{({\rm{ - }}1)}}^k} }}{{k!}}{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} \mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix {{k\, + \,1} \cr\ i \\\end{}} \right){{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}^i}} \cr &#x0026;\; \; \times \left[ {\frac{{{{e}^{{\rm{ - }}[(k\, + \,1)b\,{\rm{ - }}\,u]\rho }} }}{{{{\rho }^{k\, + \,1}} }}\frac{{{{e}^{\frac{{(k\, + \,1)b\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,i\, + \,1}} }}\,{\rm{ - }}\,\frac{{\lambda \beta }}{c}{{e}^{{\rm{ - }}\beta u}} \frac{{{{e}^{{\rm{ - }}(k\, + \,1)b\rho }} }}{{{{\rho }^{k\, + \,1}} }}\frac{{{{e}^{\frac{{[u\, + \,(k\, + \,1)b]\frac{{\lambda \beta }}{c}}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,i\, + \,3}} }}} \right]\:. \cr}\eqno$$
Define
Then
Furthermore, we let
 $${ &#x0026; Y(\rho ;u,b)\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \bar{y}(t;u,b)dt\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\delta t}} y(t;u,b)dt\:, \cr &#x0026; Z(\rho ;u,b)\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \bar{z}(t;u,b)dt\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\delta t}} z(t;u,b)dt\:. \cr}$$
$${ &#x0026; Y(\rho ;u,b)\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \bar{y}(t;u,b)dt\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\delta t}} y(t;u,b)dt\:, \cr &#x0026; Z(\rho ;u,b)\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\rho t}} \bar{z}(t;u,b)dt\, = \,{\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{ - }}\delta t}} z(t;u,b)dt\:. \cr}$$
Recognizing the parameters for terms in ![]() $$$ Y(\rho ;u,b) $$$
are
$$$ Y(\rho ;u,b) $$$
are ![]() $$$ \mu \, = \,\frac{{\lambda \beta }}{c}(k\, + \,1)b $$$
,
$$$ \mu \, = \,\frac{{\lambda \beta }}{c}(k\, + \,1)b $$$
, ![]() $$$ \nu \, = \,2k\, + \,i\, + \,1 $$$
,
$$$ \nu \, = \,2k\, + \,i\, + \,1 $$$
, ![]() $$$ \theta \, = \,(k\, + \,1)b\,{\rm{ - }}\,u $$$
,
$$$ \theta \, = \,(k\, + \,1)b\,{\rm{ - }}\,u $$$
, ![]() $$$ \kappa \, = \,k\, + \,1 $$$
, and for terms in
$$$ \kappa \, = \,k\, + \,1 $$$
, and for terms in ![]() $$$ Z(\rho ;u,b) $$$
are
$$$ Z(\rho ;u,b) $$$
are ![]() $$$ \mu \, = \,\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b] $$$
,
$$$ \mu \, = \,\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b] $$$
, ![]() $$$ \nu \, = \,2k\, + \,i\, + \,3 $$$
,
$$$ \nu \, = \,2k\, + \,i\, + \,3 $$$
, ![]() $$$ \theta \, = \,(k\, + \,1)b $$$
, and
$$$ \theta \, = \,(k\, + \,1)b $$$
, and ![]() $$$ \kappa \, = \,k\, + \,1 $$$
, and using (2.10), we get
$$$ \kappa \, = \,k\, + \,1 $$$
, and using (2.10), we get
 $$ { \bar{y}(t;u,b)\, = &#x0026; \,\frac{1}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{t\, + \,u}}{b}{\rm{ - }}1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} }}{{k!}}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix {{k\, + \,1} \cr\ i \\\end{}} \right){{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}^i} \cr &#x0026; \; \; \times \,\mathop{\sum}\limits_{j\, = \,0}^\infty \frac{{{{{\left[ {\frac{{\lambda \beta }}{c}(k\, + \,1)b} \right]}}^j} {{{\left[ {t\, + \,u\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{j\, + \,3k\, + \,i\, + \,3}} }}{{j!{\rm{\rGamma }}(j\, + \,2k\, + \,i\, + \,1){\rm{\rGamma }}(k\, + \,1)}} \cr &#x0026; \; \; \times {\int}_{\!\!\!0}^{1} {{e}^{{\rm{ - }}\beta \left[ {t\, + \,u\,{\rm{ - }}\,(k\, + \,1)b} \right]y}} {{(1\,{\rm{ - }}\,y)}^k} {{y}^{j\, + \,2k\, + \,i}} dy\:,\; \; \; \; t\, \gt \,b\,{\rm{ - }}\,u\:, \cr} $$
$$ { \bar{y}(t;u,b)\, = &#x0026; \,\frac{1}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{t\, + \,u}}{b}{\rm{ - }}1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} }}{{k!}}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix {{k\, + \,1} \cr\ i \\\end{}} \right){{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}^i} \cr &#x0026; \; \; \times \,\mathop{\sum}\limits_{j\, = \,0}^\infty \frac{{{{{\left[ {\frac{{\lambda \beta }}{c}(k\, + \,1)b} \right]}}^j} {{{\left[ {t\, + \,u\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{j\, + \,3k\, + \,i\, + \,3}} }}{{j!{\rm{\rGamma }}(j\, + \,2k\, + \,i\, + \,1){\rm{\rGamma }}(k\, + \,1)}} \cr &#x0026; \; \; \times {\int}_{\!\!\!0}^{1} {{e}^{{\rm{ - }}\beta \left[ {t\, + \,u\,{\rm{ - }}\,(k\, + \,1)b} \right]y}} {{(1\,{\rm{ - }}\,y)}^k} {{y}^{j\, + \,2k\, + \,i}} dy\:,\; \; \; \; t\, \gt \,b\,{\rm{ - }}\,u\:, \cr} $$
 $$ { \bar{z}(t;u,b)\, = &#x0026; \,\frac{1}{{{{\beta }^2} }}\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{t}{b}{\rm{ - }}1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,2}} {{e}^{{\rm{ - }}[u\, + \,(k\, + \,1)b]\beta }} }}{{k!}}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix{{k\, + \,1} \cr\ i \\\end{}} \right){{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}^i} \cr &#x0026; \; \; \,\times \,\mathop{\sum}\limits_{j\, = \,0}^\infty \frac{{{{{\left[ {\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b]} \right]}}^j} {{{\left[ {t\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{j\, + \,3k\, + \,i\, + \,5}} }}{{j!\rGamma (j\, + \,2k\, + \,i\, + \,3)\rGamma (k\, + \,1)}} \cr &#x0026; \; \; \,\times \,{\int}_{\!\!\!\!0}^{1} {{e}^{{\rm{ - }}\beta \left[ {t\,{\rm{ - }}\,(k\, + \,1)b} \right]y}} {{(1\,{\rm{ - }}\,y)}^k} {{y}^{j\, + \,2k\, + \,i\, + \,2}} dy\:,\; \; \; \; t\, \gt \,b\:, \cr} $$
$$ { \bar{z}(t;u,b)\, = &#x0026; \,\frac{1}{{{{\beta }^2} }}\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{t}{b}{\rm{ - }}1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,2}} {{e}^{{\rm{ - }}[u\, + \,(k\, + \,1)b]\beta }} }}{{k!}}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix{{k\, + \,1} \cr\ i \\\end{}} \right){{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}^i} \cr &#x0026; \; \; \,\times \,\mathop{\sum}\limits_{j\, = \,0}^\infty \frac{{{{{\left[ {\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b]} \right]}}^j} {{{\left[ {t\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{j\, + \,3k\, + \,i\, + \,5}} }}{{j!\rGamma (j\, + \,2k\, + \,i\, + \,3)\rGamma (k\, + \,1)}} \cr &#x0026; \; \; \,\times \,{\int}_{\!\!\!\!0}^{1} {{e}^{{\rm{ - }}\beta \left[ {t\,{\rm{ - }}\,(k\, + \,1)b} \right]y}} {{(1\,{\rm{ - }}\,y)}^k} {{y}^{j\, + \,2k\, + \,i\, + \,2}} dy\:,\; \; \; \; t\, \gt \,b\:, \cr} $$
where ![]() $$$ {\lfloor}x{\rfloor} $$$
is the integer part of real number x.
$$$ {\lfloor}x{\rfloor} $$$
is the integer part of real number x.
Then using (2.11), we further get for ![]() $$$ t\, \gt \,\frac{{b\,{\rm{ - }}\,u}}{c} $$$
that
$$$ t\, \gt \,\frac{{b\,{\rm{ - }}\,u}}{c} $$$
that
 $${ y(t;u,b)\, = \, &#x0026; \frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct\, + \,u}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,1}} }}{{k!}} \cr &#x0026; \mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left(\matrix {{k\, + \,1} \cr { i}}\right) \frac{{{{{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}}^i} {{{\left[ {ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{3k\, + \,i\, + \,1}} }}{{{\rm{\rGamma }}(3k\, + \,i\, + \,2)}} \cr &#x0026;\times \left[ {c\:{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026;&#x0026;{\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}\hfill \cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,2;} &#x0026; {\beta [ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \hfill \cr\ &#x0026; &#x0026; {\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right. \cr &#x0026;\quad\ \ {\rm{ - }}\,\frac{{\lambda \beta {{{[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(3k\, + \,i\, + \,2)(3k\, + \,i\, + \,3)}} \cr &#x0026;\times \left. {{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026;&#x0026;{\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,4;} &#x0026; {\beta [ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ &#x0026;&#x0026;{\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right]\:, \cr}$$
$${ y(t;u,b)\, = \, &#x0026; \frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct\, + \,u}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,1}} }}{{k!}} \cr &#x0026; \mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left(\matrix {{k\, + \,1} \cr { i}}\right) \frac{{{{{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}}^i} {{{\left[ {ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{3k\, + \,i\, + \,1}} }}{{{\rm{\rGamma }}(3k\, + \,i\, + \,2)}} \cr &#x0026;\times \left[ {c\:{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026;&#x0026;{\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}\hfill \cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,2;} &#x0026; {\beta [ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \hfill \cr\ &#x0026; &#x0026; {\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right. \cr &#x0026;\quad\ \ {\rm{ - }}\,\frac{{\lambda \beta {{{[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(3k\, + \,i\, + \,2)(3k\, + \,i\, + \,3)}} \cr &#x0026;\times \left. {{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026;&#x0026;{\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,4;} &#x0026; {\beta [ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ &#x0026;&#x0026;{\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right]\:, \cr}$$
and for ![]() $$$ t\, \gt \,\frac{b}{c} $$$
that
$$$ t\, \gt \,\frac{b}{c} $$$
that
 $${ z(t;u,b)\, = \, &#x0026; \frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{{{{\beta }^2} }}\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,2}} }}{{k!}}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix { {k\, + \,1} \cr i \\\end{}} \right)\frac{{{{{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}}^i} {{{\left[ {ct\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{3k\, + \,i\, + \,3}} }}{{{\rm{\rGamma }}(3k\, + \,i\, + \,4)}} \cr &#x0026; \times \left[ {c\:{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix {&#x0026; &#x0026; {\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,4;} &#x0026; {\beta [ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {} &#x0026; {} &#x0026; {\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right. \cr &#x0026; \quad\ \ {\rm{ - }}\frac{{\lambda \beta {{{[ct\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(3k\, + \,i\, + \,4)(3k\, + \,i\, + \,5)}} \cr &#x0026; \times \left. {{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026; {\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,6;} &#x0026; {\beta [ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {} &#x0026; {} &#x0026; {\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right]\:. \cr}$$
$${ z(t;u,b)\, = \, &#x0026; \frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{{{{\beta }^2} }}\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{({\rm{ - }}1)}}^k} {{{\left( {\frac{{\lambda {{\beta }^2} }}{c}} \right)}}^{k\, + \,2}} }}{{k!}}\mathop{\sum}\limits_{i\, = \,0}^{k\, + \,1} \left( \matrix { {k\, + \,1} \cr i \\\end{}} \right)\frac{{{{{\left( {{\rm{ - }}\frac{\lambda }{c}} \right)}}^i} {{{\left[ {ct\,{\rm{ - }}\,(k\, + \,1)b} \right]}}^{3k\, + \,i\, + \,3}} }}{{{\rm{\rGamma }}(3k\, + \,i\, + \,4)}} \cr &#x0026; \times \left[ {c\:{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix {&#x0026; &#x0026; {\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,4;} &#x0026; {\beta [ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {} &#x0026; {} &#x0026; {\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right. \cr &#x0026; \quad\ \ {\rm{ - }}\frac{{\lambda \beta {{{[ct\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(3k\, + \,i\, + \,4)(3k\, + \,i\, + \,5)}} \cr &#x0026; \times \left. {{\rm{\rPhi }}_{2}^{{(3)}} \left( \matrix { &#x0026; &#x0026; {\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {k\, + \,1;} &#x0026; {3k\, + \,i\, + \,6;} &#x0026; {\beta [ct\,{\rm{ - }}\,(k\, + \,1)b]} \hfill\cr\ {} &#x0026; {} &#x0026; {\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\,{\rm{ - }}\,(k\, + \,1)b]} \\\end{}} \right)} \right]\:. \cr}$$
Finally, we obtain the density of the time of ruin for the classical risk model with a constant dividend barrier b as
 $$\zeta (t;u,b)\, = \,\left\{ \matrix { {\zeta (t;u),} \hfill &#x0026; {0\,\leq \,t\,\leq \,\frac{{b\,{\rm{ - }}\,u}}{c},} \cr {\zeta (t;u)\, + \,y(t;u,b),} \hfill &#x0026; {\frac{{b\,{\rm{ - }}\,u}}{c}\, \lt \,t\,\leq \,\frac{b}{c},} \cr {\zeta (t;u)\, + \,y(t;u,b)\,{\rm{ - }}\,z(t;u,b),} \hfill &#x0026; {t\, \gt \,\frac{b}{c},} \hfill \\\end{}} \right.$$
$$\zeta (t;u,b)\, = \,\left\{ \matrix { {\zeta (t;u),} \hfill &#x0026; {0\,\leq \,t\,\leq \,\frac{{b\,{\rm{ - }}\,u}}{c},} \cr {\zeta (t;u)\, + \,y(t;u,b),} \hfill &#x0026; {\frac{{b\,{\rm{ - }}\,u}}{c}\, \lt \,t\,\leq \,\frac{b}{c},} \cr {\zeta (t;u)\, + \,y(t;u,b)\,{\rm{ - }}\,z(t;u,b),} \hfill &#x0026; {t\, \gt \,\frac{b}{c},} \hfill \\\end{}} \right.$$
where ![]() $$$ \zeta (t;u) $$$
,
$$$ \zeta (t;u) $$$
, ![]() $$$ y(t;u,b) $$$
and
$$$ y(t;u,b) $$$
and ![]() $$$ z(t;u,b) $$$
are given by (3.3), (3.6) and (3.7), respectively.
$$$ z(t;u,b) $$$
are given by (3.3), (3.6) and (3.7), respectively.
3.2 The decompositions of the density of the time of ruin
For the risk model with a constant dividend barrier, there are two possibilities for ruin occurring: [1] ruin occurs without dividend payments (without the surplus reaching the dividend barrier); [2] ruin occurs with dividend payments. Therefore, the density obtained in Section 3.1 can be decomposed into two parts: [1] density of the time of ruin without dividend payments, denoted as ![]() $$$ \xi (t;u,b) $$$
; [2] density of the time of ruin with dividend payments. In what follows, we derive
$$$ \xi (t;u,b) $$$
; [2] density of the time of ruin with dividend payments. In what follows, we derive ![]() $$$ \xi (t;u,b) $$$
, and the density of the time of ruin with dividend payments is
$$$ \xi (t;u,b) $$$
, and the density of the time of ruin with dividend payments is ![]() $$$ \zeta (t;u,b)\,{\rm{ - }}\,\xi (t;u,b) $$$
.
$$$ \zeta (t;u,b)\,{\rm{ - }}\,\xi (t;u,b) $$$
.
For ![]() $$$ 0\,\leq \,u\,\leq \,b, $$$
define
$$$ 0\,\leq \,u\,\leq \,b, $$$
define
to be the first time that the surplus process reaches b from u. Let H(u; b) be the Laplace transform of the first time of hitting b without ruin occurring, and L(u; b) be the Laplace transform of the time of ruin without surplus reaching b, namely,
For the classical risk model, by distinguishing whether or not the surplus hitting level b before the time of ruin, we have
where ![]() $$$ {{\phi }_\delta }(u) $$$
is defined in (1.1), representing the Laplace transform of the time of ruin T with respect to δ. It follows that
$$$ {{\phi }_\delta }(u) $$$
is defined in (1.1), representing the Laplace transform of the time of ruin T with respect to δ. It follows that
Let ![]() $$$ \xi (t;u,b) $$$
and
$$$ \xi (t;u,b) $$$
and ![]() $$$ \bar{\xi }(t;u,b) $$$
be two functions such that
$$$ \bar{\xi }(t;u,b) $$$
be two functions such that
We aim to find an explicit expression of ![]() $$$ \xi (t;u,b) $$$
by the similar inversion technique used in previous subsection.
$$$ \xi (t;u,b) $$$
by the similar inversion technique used in previous subsection.
Remark: When ![]() $$$ \delta \, = \,0 $$$
, it follows from Dickson and Gray (1984) that
$$$ \delta \, = \,0 $$$
, it follows from Dickson and Gray (1984) that
implying that ![]() $$$ \xi (t;u,b) $$$
is a defective density function.
$$$ \xi (t;u,b) $$$
is a defective density function.
Gerber and Shiu (Reference Gerber and Shiu1998) show that
where ![]() $$$ {{\psi }_1}(u) $$$
is the Laplace transform of the time of recovery with respect to δ, and the time of recovery refers to the first time that the surplus reaches zero after ruin. Further when claims are exponentially distributed with parameter β using expressions (2.7) and (2.8) we have
$$$ {{\psi }_1}(u) $$$
is the Laplace transform of the time of recovery with respect to δ, and the time of recovery refers to the first time that the surplus reaches zero after ruin. Further when claims are exponentially distributed with parameter β using expressions (2.7) and (2.8) we have
where ρ and −R are positive and negative solutions to equation (2.6).
Now by the Taylor expansion and (3.14), H(u; b) in (3.13) can be re-expressed as
 $${ H(u;b)\, = \, &#x0026; {{e}^{\rho (u\,{\rm{ - }}\,b)}} \frac{{1\,{\rm{ - }}\,{{\psi }_1}(u){{e}^{{\rm{ - }}\rho u}} }}{{1\,{\rm{ - }}\,{{\psi }_1}(b){{e}^{{\rm{ - }}\rho b}} }} \cr = &#x0026; {{e}^{\rho (u\,{\rm{ - }}\,b)}} \left[ {1\,{\rm{ - }}\,{{\psi }_1}(u){{e}^{{\rm{ - }}\rho u}} } \right]\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{[{{\psi }_1}(b)]}}^k} }}{{k!}}{{e}^{{\rm{ - }}kb\rho }} \cr = &#x0026; {{e}^{{\rm{ - }}\rho (b\,{\rm{ - }}\,u)}} \, + \,\mathop{\sum}\limits_{k\, = \,1}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^k} {{e}^{{\rm{ - }}k\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}kb}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k}} }}{{e}^{{\rm{ - }}[(k\, + \,1)b\,{\rm{ - }}\,u]\rho }} \cr &#x0026; {\rm{ - }}{{e}^{{\rm{ - }}\beta u}} \mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,1}} {{e}^{{\rm{ - }}k\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}(u\, + \,kb)}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,2}} }}{{e}^{{\rm{ - }}(k\, + \,1)b\rho }} \:. \cr}$$
$${ H(u;b)\, = \, &#x0026; {{e}^{\rho (u\,{\rm{ - }}\,b)}} \frac{{1\,{\rm{ - }}\,{{\psi }_1}(u){{e}^{{\rm{ - }}\rho u}} }}{{1\,{\rm{ - }}\,{{\psi }_1}(b){{e}^{{\rm{ - }}\rho b}} }} \cr = &#x0026; {{e}^{\rho (u\,{\rm{ - }}\,b)}} \left[ {1\,{\rm{ - }}\,{{\psi }_1}(u){{e}^{{\rm{ - }}\rho u}} } \right]\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{[{{\psi }_1}(b)]}}^k} }}{{k!}}{{e}^{{\rm{ - }}kb\rho }} \cr = &#x0026; {{e}^{{\rm{ - }}\rho (b\,{\rm{ - }}\,u)}} \, + \,\mathop{\sum}\limits_{k\, = \,1}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^k} {{e}^{{\rm{ - }}k\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}kb}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k}} }}{{e}^{{\rm{ - }}[(k\, + \,1)b\,{\rm{ - }}\,u]\rho }} \cr &#x0026; {\rm{ - }}{{e}^{{\rm{ - }}\beta u}} \mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,1}} {{e}^{{\rm{ - }}k\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}(u\, + \,kb)}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,2}} }}{{e}^{{\rm{ - }}(k\, + \,1)b\rho }} \:. \cr}$$
Using (3.15) and (2.5), we can write the second term in (3.12) as
 $${ H(u;b){{\phi }_\delta }(b)\, = &#x0026; \,\frac{1}{\beta }\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}(k\, + \,1)b}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,1}} }}{{e}^{{\rm{ - }}[(k\, + \,1)b\,{\rm{ - }}\,u]\rho }} \cr &#x0026; {\rm{ - }}\frac{{{{e}^{{\rm{ - }}\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,2}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b]}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,3}} }}{{e}^{{\rm{ - }}(k\, + \,1)b\rho }} \:, \cr = &#x0026; \,V(\rho ;u,b)\,{\rm{ - }}\,W(\rho ;u,b)\:. \cr}$$
$${ H(u;b){{\phi }_\delta }(b)\, = &#x0026; \,\frac{1}{\beta }\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,1}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}(k\, + \,1)b}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,1}} }}{{e}^{{\rm{ - }}[(k\, + \,1)b\,{\rm{ - }}\,u]\rho }} \cr &#x0026; {\rm{ - }}\frac{{{{e}^{{\rm{ - }}\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^\infty \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,2}} {{e}^{{\rm{ - }}(k\, + \,1)\beta b}} }}{{k!}}\frac{{{{e}^{\frac{{\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b]}}{{\rho \, + \,\beta }}}} }}{{{{{(\rho \, + \,\beta )}}^{2k\, + \,3}} }}{{e}^{{\rm{ - }}(k\, + \,1)b\rho }} \:, \cr = &#x0026; \,V(\rho ;u,b)\,{\rm{ - }}\,W(\rho ;u,b)\:. \cr}$$
Let
Noticing the parameters for ![]() $$$ V(\rho ;u,b) $$$
are
$$$ V(\rho ;u,b) $$$
are ![]() $$$ \mu \, = \,\frac{{\lambda \beta }}{c}(k\, + \,1)b $$$
,
$$$ \mu \, = \,\frac{{\lambda \beta }}{c}(k\, + \,1)b $$$
, ![]() $$$ \nu \, = \,2k\, + \,1 $$$
,
$$$ \nu \, = \,2k\, + \,1 $$$
, ![]() $$$ \theta \, = \,(k\, + \,1)b\,{\rm{ - }}\,u $$$
, κ = 0, and for
$$$ \theta \, = \,(k\, + \,1)b\,{\rm{ - }}\,u $$$
, κ = 0, and for ![]() $$$ W(\rho ;u,b) $$$
are
$$$ W(\rho ;u,b) $$$
are ![]() $$$ \mu \, = \,\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b] $$$
,
$$$ \mu \, = \,\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b] $$$
, ![]() $$$ \nu \, = \,2k\, + \,3 $$$
,
$$$ \nu \, = \,2k\, + \,3 $$$
, ![]() $$$ \theta \, = \,(k\, + \,1)b $$$
, and κ = 0, and using (2.18), we get for
$$$ \theta \, = \,(k\, + \,1)b $$$
, and κ = 0, and using (2.18), we get for ![]() $$$ t\, \gt \,\frac{{b\,{\rm{ - }}\,u}}{c} $$$
that
$$$ t\, \gt \,\frac{{b\,{\rm{ - }}\,u}}{c} $$$
that
 $${ v(t;u,b)\, = \, &#x0026; \frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct\, + \,u}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,1}} }}{{k!}}\frac{{{{{[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}}^{2k}} }}{{{\rm{\rGamma }}(2k\, + \,1)}} \cr &#x0026;\times \,\bigg[c\:{{{\rm{\rPhi }}}_2}\left( {2k\, + \,1;\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \right) \cr &#x0026; \quad\quad{\rm{ - }}\frac{{\lambda \beta {{{[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(2k\, + \,1)(2k\, + \,2)}} \cr &#x0026; \times \left. {{{{\rm{\rPhi }}}_2}\left( {2k\, + \,3;\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \right)} \right]\:, \cr}$$
$${ v(t;u,b)\, = \, &#x0026; \frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct\, + \,u}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,1}} }}{{k!}}\frac{{{{{[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}}^{2k}} }}{{{\rm{\rGamma }}(2k\, + \,1)}} \cr &#x0026;\times \,\bigg[c\:{{{\rm{\rPhi }}}_2}\left( {2k\, + \,1;\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \right) \cr &#x0026; \quad\quad{\rm{ - }}\frac{{\lambda \beta {{{[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(2k\, + \,1)(2k\, + \,2)}} \cr &#x0026; \times \left. {{{{\rm{\rPhi }}}_2}\left( {2k\, + \,3;\lambda \beta t[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}(k\, + \,1)b[ct\, + \,u\,{\rm{ - }}\,(k\, + \,1)b]} \right)} \right]\:, \cr}$$
and for ![]() $$$ t\, \gt \,\frac{b}{c} $$$
that
$$$ t\, \gt \,\frac{b}{c} $$$
that
 $${ w(t;u,b)\, = &#x0026; \,\frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,2}} }}{{k!}}\frac{{{{{[ct\,{\rm{ - }}\,(k\, + \,1)b]}}^{2k\, + \,2}} }}{{{\rm{\rGamma }}(2k\, + \,3)}} \cr &#x0026;\times \bigg[c\:{{{\rm{\rPhi }}}_2}\left( {2k\, + \,3;\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b][ct\,{\rm{ - }}\,(k\, + \,1)b]} \right) \cr &#x0026; \quad \quad{\rm{ - }}\frac{{\lambda \beta {{{[ct\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(2k\, + \,3)(2k\, + \,4)}} \cr &#x0026; \ \left {\times \,{{{\rm{\rPhi }}}_2}\left( {2k\, + \,5;\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b][ct\,{\rm{ - }}\,(k\, + \,1)b]} \right)} \right]\:. \cr}$$
$${ w(t;u,b)\, = &#x0026; \,\frac{{{{e}^{{\rm{ - }}(\lambda \, + \,\beta c)t\,{\rm{ - }}\,\beta u}} }}{\beta }\mathop{\sum}\limits_{k\, = \,0}^{\left\lfloor {\frac{{ct}}{b}\,{\rm{ - }}\,1} \right\rfloor } \frac{{{{{\left( {\frac{{\lambda \beta }}{c}} \right)}}^{k\, + \,2}} }}{{k!}}\frac{{{{{[ct\,{\rm{ - }}\,(k\, + \,1)b]}}^{2k\, + \,2}} }}{{{\rm{\rGamma }}(2k\, + \,3)}} \cr &#x0026;\times \bigg[c\:{{{\rm{\rPhi }}}_2}\left( {2k\, + \,3;\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b][ct\,{\rm{ - }}\,(k\, + \,1)b]} \right) \cr &#x0026; \quad \quad{\rm{ - }}\frac{{\lambda \beta {{{[ct\,{\rm{ - }}\,(k\, + \,1)b]}}^2} }}{{(2k\, + \,3)(2k\, + \,4)}} \cr &#x0026; \ \left {\times \,{{{\rm{\rPhi }}}_2}\left( {2k\, + \,5;\lambda \beta t[ct\,{\rm{ - }}\,(k\, + \,1)b],\frac{{\lambda \beta }}{c}[u\, + \,(k\, + \,1)b][ct\,{\rm{ - }}\,(k\, + \,1)b]} \right)} \right]\:. \cr}$$
Finally, we have the density function for the time of ruin without paying dividends as
 $$\xi (t;u,b)\, = \,\left\{ \matrix { {\zeta (t;u),} \hfill &#x0026; {0\,\leq \,t\,\leq \frac{{b\,{\rm{ - }}\,u}}{c},} \cr {\zeta (t;u)\,{\rm{ - }}\,v(t;u,b),} \hfill &#x0026; {\frac{{b\,{\rm{ - }}\,u}}{c}\, \lt \,t\,\leq \,\frac{b}{c},} \hfill \cr {\zeta (t;u)\,{\rm{ - }}\,v(t;u,b)\, + \,w(t;u,b),} \hfill &#x0026; {t\, \gt \,\frac{b}{c},} \hfill \\\end{}} \right.$$
$$\xi (t;u,b)\, = \,\left\{ \matrix { {\zeta (t;u),} \hfill &#x0026; {0\,\leq \,t\,\leq \frac{{b\,{\rm{ - }}\,u}}{c},} \cr {\zeta (t;u)\,{\rm{ - }}\,v(t;u,b),} \hfill &#x0026; {\frac{{b\,{\rm{ - }}\,u}}{c}\, \lt \,t\,\leq \,\frac{b}{c},} \hfill \cr {\zeta (t;u)\,{\rm{ - }}\,v(t;u,b)\, + \,w(t;u,b),} \hfill &#x0026; {t\, \gt \,\frac{b}{c},} \hfill \\\end{}} \right.$$
where ![]() $$$ \zeta (t;u) $$$
, v(t; u; b) and w(t; u; b) are given by (3.3), (3.16) and (3.17), respectively.
$$$ \zeta (t;u) $$$
, v(t; u; b) and w(t; u; b) are given by (3.3), (3.16) and (3.17), respectively.
4 Numerical illustrations
In this section, we illustrate some results derived in previous sections numerically. The probability density function of the time of ruin and its two components are evaluated and compared. The probabilities of ruin in finite time in the classical risk model with and without a constant dividend barrier are calculated and compared for exponential claims.
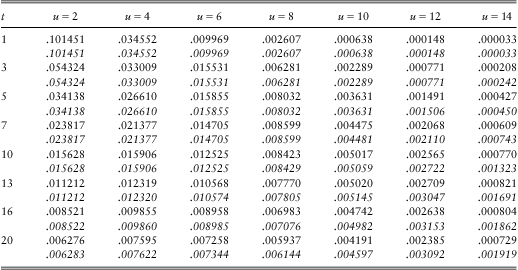
Example 1 We set c = 1.1, λ = 1, β = 1 and b = 15. In Table 1, ![]() $$$ \xi (t;u,15) $$$
(upper rows, Roman font) and
$$$ \xi (t;u,15) $$$
(upper rows, Roman font) and ![]() $$$ \zeta (t;u,15) $$$
(lower rows, Italic font) are calculated and tabulated for u = 2, 4, … ,14 and some t values (1 ≤ t ≤ 20).
$$$ \zeta (t;u,15) $$$
(lower rows, Italic font) are calculated and tabulated for u = 2, 4, … ,14 and some t values (1 ≤ t ≤ 20).
Table 1 Probability density function ![]() $$$\xi (t;u,15)$$$
and
$$$\xi (t;u,15)$$$
and ![]() $$$\zeta (t;u,15)$$$
values for u = 2,4,…,14 and some t values (1 ≤ t ≤ 20) with c = 1.1, λ = β = 1Footnote *
$$$\zeta (t;u,15)$$$
values for u = 2,4,…,14 and some t values (1 ≤ t ≤ 20) with c = 1.1, λ = β = 1Footnote *

* Roman font for ![]() $$$\xi (t;u,15)$$$
and Italic font for
$$$\xi (t;u,15)$$$
and Italic font for ![]() $$$\zeta (t;u,15)$$$
$$$\zeta (t;u,15)$$$
Figure 1 graphically compares ![]() $$$ \xi (t;u,15) $$$
(solid lines) and
$$$ \xi (t;u,15) $$$
(solid lines) and ![]() $$$ \zeta (t;u,15) $$$
(dashed lines) for u = 8,10,12,14 (from top to bottom). It can be observed that when both u and t are small, values of both density functions
$$$ \zeta (t;u,15) $$$
(dashed lines) for u = 8,10,12,14 (from top to bottom). It can be observed that when both u and t are small, values of both density functions ![]() $$$ \xi (t;u,15) $$$
and
$$$ \xi (t;u,15) $$$
and ![]() $$$ \zeta (t;u,15) $$$
are very close to each other (same the first six decimals), that is to say, the density of time of ruin with dividend payments is very small. When u or t becomes large,
$$$ \zeta (t;u,15) $$$
are very close to each other (same the first six decimals), that is to say, the density of time of ruin with dividend payments is very small. When u or t becomes large, ![]() $$$ \zeta (t;u,15)\,{\rm{ - }}\,\xi (t;u,15), $$$
the density of the time of ruin with dividend payments are significantly larger than zero, implying the dividend barrier affects the ruin probability significantly. Furthermore, all densities are decreasing in u.
$$$ \zeta (t;u,15)\,{\rm{ - }}\,\xi (t;u,15), $$$
the density of the time of ruin with dividend payments are significantly larger than zero, implying the dividend barrier affects the ruin probability significantly. Furthermore, all densities are decreasing in u.

Figure 1 Density functions of the time of ruin without dividend payments (solid lines) and density of the time of ruin with b = 15 (dashed lines) for u = 8,10,12,14 (from top to bottom) with c = 1.1, λ = β = 1.
Example 2 We set u = 10, λ = 10/11, β = 1, c = 1 so that the loading factor is 10%. In this example, we compute some finite-time ruin probabilities for the classical risk model with a constant dividend barrier, denoted by ![]() $$$ \psi (t;u,b) $$$
. They can be calculated by
$$$ \psi (t;u,b) $$$
. They can be calculated by
where ![]() $$$ \zeta (s;u,b) $$$
is given by (3.8).
$$$ \zeta (s;u,b) $$$
is given by (3.8).
Table 2 displays values of ![]() $$$ \psi (t;10,b) $$$
for some t (5 ≤ t ≤ 100) and b = 15,25,40, as well as values when b = ∞, where
$$$ \psi (t;10,b) $$$
for some t (5 ≤ t ≤ 100) and b = 15,25,40, as well as values when b = ∞, where ![]() $$$ \psi (t;10,\infty ) $$$
are the probabilities of ruin in finite time in the classical risk model with exponential claims; see for example formula (1.6) in Asmussen and Albrecher (Reference Asmussen and Albrecher2010, Chapter V, Proposition 1.3 on page 118). Values of
$$$ \psi (t;10,\infty ) $$$
are the probabilities of ruin in finite time in the classical risk model with exponential claims; see for example formula (1.6) in Asmussen and Albrecher (Reference Asmussen and Albrecher2010, Chapter V, Proposition 1.3 on page 118). Values of ![]() $$$ \psi (t;10,\infty ) $$$
are calculated using the mathematical computing software Maple. The values of
$$$ \psi (t;10,\infty ) $$$
are calculated using the mathematical computing software Maple. The values of ![]() $$$ \psi (t;10,b) $$$
in the table are calculated numerically by the composite Simpson's rule with a step length h = t‰ using R. To show that the accuracy of the numerical integration depends on h, we also provide approximated values of
$$$ \psi (t;10,b) $$$
in the table are calculated numerically by the composite Simpson's rule with a step length h = t‰ using R. To show that the accuracy of the numerical integration depends on h, we also provide approximated values of ![]() $$$ \psi (t;10,b) $$$
for b = 50 and h = (t/2)‰.
$$$ \psi (t;10,b) $$$
for b = 50 and h = (t/2)‰.
Table 2 Probability of ruin in finite time ![]() $$$\psi (t;u,b)$$$
for finite b(> u) vs
$$$\psi (t;u,b)$$$
for finite b(> u) vs ![]() $$$\psi (t;u,\infty)$$$
when u = 10, c = 1,
$$$\psi (t;u,\infty)$$$
when u = 10, c = 1, ![]() $$$\lambda=10/11$$$
, β = 1
$$$\lambda=10/11$$$
, β = 1
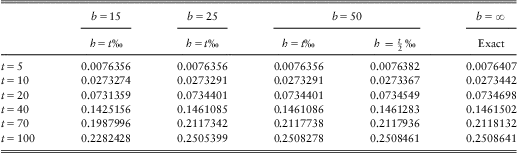
We observe from Table 2 that for fixed b, these probabilities of ruin in finite time increase as t increases. While for fixed t, these values increase as b increases and very close to the corresponding ones without a constant dividend barrier (b = ∞ case) as expected. For b = 50 case, the set of probabilities with h = (t/2)‰ are more closer than those with h = t‰ to the set of probabilities when b = ∞. Furthermore, it is confirmed that ![]() $$$ \psi (5000;10,\infty )\, = \,0.3662639 $$$
, which is the same as
$$$ \psi (5000;10,\infty )\, = \,0.3662639 $$$
, which is the same as ![]() $$$ \psi (10)\, = \,\psi (\infty ;10,\infty ) $$$
in first seven decimals, here
$$$ \psi (10)\, = \,\psi (\infty ;10,\infty ) $$$
in first seven decimals, here ![]() $$$ \psi (10) $$$
is the ultimate ruin probability in the classical risk model with initial surplus u = 10 and exponentially distributed claim amounts with mean 1, and
$$$ \psi (10) $$$
is the ultimate ruin probability in the classical risk model with initial surplus u = 10 and exponentially distributed claim amounts with mean 1, and ![]() $$$ \psi (10)\, = \,(10/11){{e}^{{\rm{ - }}(10/11)}} $$$
for this example.
$$$ \psi (10)\, = \,(10/11){{e}^{{\rm{ - }}(10/11)}} $$$
for this example.
5 Concluding remarks
In this paper, we give an explicit formula for the density function of the time of ruin and its decompositions in the classical risk model with a constant dividend barrier and exponential claims. Our techniques and results can stimulate further research such as obtaining the density function of the time of ruin for the classical risk model with a threshold dividend payment strategy. Our expressions for the densities are computationally tractable as they are expressed in terms of special functions that are readily available in most computational software packages. It seems that it is unlikely to obtain the densities for these quantities under other distributions for claim sizes. However, our results may be used to approximate these densities under other claim size distributions by using the De Vylder's approximations (De Vylder, Reference De Vylder1978).
Acknowledgments
The authors would like to thank two anonymous referees for their constructive comments and suggestions which lead to the significant improvement of the paper. The authors would also like to thank Ms. Yu Xia for her help on the numerical calculation of examples in Section 4. This research for Dr. Yi Lu was supported by the Natural Science and Engineering Research Council of Canada.