Introduction
Rutile (tetragonal, space group P42/mnm) is one of the polymorphs of TiO2. It is a common accessory mineral in metamorphic rocks such as gneisses and schists and it is the primary titanium-bearing phase in eclogites (e.g. Meinhold, Reference Meinhold2010). Mei et al. (Reference Mei, Wang, Shang and Liu2014) summarised all of the density functional theory (DFT) studies of the TiO2 polymorphs and provided an equilibrium phase diagram that appears to be fairly consistent with experimental data available in the literature. This suggests that anatase is the thermodynamically stable phase at room conditions, whereas rutile becomes the thermodynamically stable phase above 1200 K and therefore it is metastable up to 1200 K at atmospheric pressure. The occurrence of rutile inclusions in metamorphic rocks indicates that rutile is the thermodynamically stable phase at metamorphic conditions. The high-pressure polymorphs of rutile were studied extensively with X-ray diffraction (XRD) experiments in diamond-anvil cells (e.g. Dubrovinskaia et al., Reference Dubrovinskaia, Dubrovinsky, Ahuja, Prokopenko, Dmitriev, Weber, Osorio-Guillen and Johansson2001; Al-Khatatbeh et al., Reference Al-Khatatbeh, Lee and Kiefer2009). The first transition of rutile upon compression is to a phase with an α-PbO2 type structure called TiO2 II. The pressure for this transition ranges from 2.6 GPa to 34 GPa (McQueen et al., Reference McQueen, Jamieson and Marsh1967; Nicol and Fong, Reference Nicol and Fong1971; Al'tshuler et al., Reference Al'tshuler, Podurets, Simakov and Trunin1973; Mammone et al., Reference Mammone, Sharma and Nicol1980; Syono et al., Reference Syono, Kusaba, Kikuchi, Fukuoka, Goto, Manghnani and Syono1987; Arashi, Reference Arashi1992). XRD experiments (Sato, Reference Sato, Manghnani and Akimoto1977; Ming and Manghnani, Reference Ming and Manghnani1979; Hazen and Finger, Reference Hazen and Finger1981; Kudoh and Takeda, Reference Kudoh and Takeda1986; Gerward and Staun Olsen, Reference Gerward and Staun Olsen1997) are however in agreement with each other in demonstrating that rutile shows no transition below 12 GPa at room temperature. However, Kojitani et al. (Reference Kojitani, Yamazaki, Kojima, Inaguma, Mori and Akaogi2018) calculated from thermodynamic properties that the equilibrium phase boundary between rutile and TiO2 II passes through room conditions, which implies that rutile is metastable at any pressure at room temperature. Therefore, the thermodynamic stability of rutile remains unclear and we restrict our analysis to pressures of less than 7.3 GPa, and temperatures less than 1100 K, under which conditions rutile at least appears to be kinetically stable and does not normally transform to other TiO2 polymorphs.
Rutile is commonly formed during prograde metamorphism by reactions that also generate garnet, for example (e.g. Meinhold, Reference Meinhold2010; Zack and Kooijman, Reference Zack, Kooijman, Kohn, Engi and Lanari2017):
$$\displaylines{{\rm anorthite} + {\rm quartz} + 2\;{\rm ilmenite} = {\rm garnet} \lpar {{\rm Gr1Alm}2} \rpar + 2\;{\rm rutile} \cr {\rm Al}_2{\rm Si}{\rm O}_5 + 2\;{\rm quartz} + 3\;{\rm ilmenite} = {\rm almandine} + 3\;{\rm rutile}} $$When rutile is formed together with garnet, or when it is already present in the protolith, it can be trapped as inclusions in garnet. Whereas the distribution of Ti between rutile and other minerals, such as quartz, is commonly used as a geothermometer for metamorphic rocks (e.g. Zack and Kooijman, Reference Zack, Kooijman, Kohn, Engi and Lanari2017), the potential for using rutile inclusions in garnets as an elastic geobarometer has not yet been evaluated. Elastic geobarometry is based on the evidence that minerals trapped as inclusions within other host minerals can develop non-lithostatic pressures on exhumation as a result of the differences between the thermo-elastic properties of the host and inclusion phases (e.g. Angel et al., Reference Angel, Nimis, Mazzucchelli, Alvaro and Nestola2015). With modern Equations of State (EoS) and elasticity data of the mineral phases, the entrapment conditions of host-inclusion systems can be derived from the residual pressure measured in the inclusions at room conditions (e.g. Zhang, Reference Zhang1998; Kohn, Reference Kohn2014; Angel et al., Reference Angel, Mazzucchelli, Alvaro and Nestola2017). In this study, we evaluate for the first time whether rutile inclusions in garnets can be used for host-inclusion geobarometry by critically examining its EoS. The difficulty is that rutile is a very stiff material and the changes in its unit-cell volume and cell parameters are small over its P –T range of stability. Thus, it is not possible to determine reliable EoS parameters simply by performing conventional refinements to individual P –V or P –V –T datasets. Therefore, we make use of the fact that the variation with P and T of the bulk modulus of a crystal is determined by the same EoS parameters that define the variation of the unit-cell volume. We re-analyse all of the available literature for the variation of unit-cell parameters and elastic moduli of rutile with P and T, to obtain an internally-consistent dataset. We then determine the EoS parameters by a simultaneous fit to the compression, expansion and elasticity data. In doing so we discuss the criteria for obtaining self-consistency between the fits to the volumes and the cell parameters, which provide further constraints on the EoS parameters and also a ‘recipe book’ for the refinement of the EoS of other anisotropic stiff materials.
Data
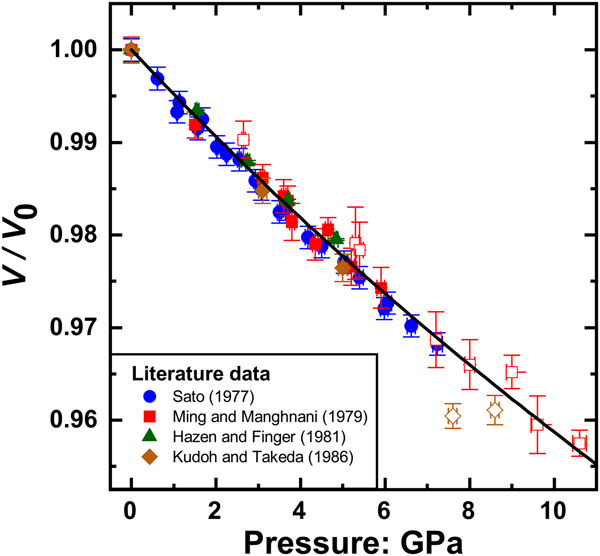
The elastic properties of rutile have been studied extensively as a function of both pressure and temperature by means of different experimental techniques and computational studies. Mei et al. (Reference Mei, Wang, Shang and Liu2014) demonstrated that the elastic properties of rutile from DFT simulations are strongly dependent upon the choice of exchange–correlation functional used, with their own calculations showing a total spread of 60 GPa in the value of the isothermal Reuss bulk modulus, 
$K_{TR} = -V\left( {\displaystyle{{\partial P} \over {\partial V}}} \right)_T$. Given the difficulties of extending computer simulations to finite temperatures, in part because of the limitations of the quasi-harmonic approximation that we discuss below, we therefore only include experimental data in this analysis. Compressional data available in the literature obtained by various diffraction methods at room temperature extend to 10.6 GPa but exhibit considerable data scatter in the volume measurements above 7.3 GPa (Fig. 1), and similar behaviour in the values of the unit-cell parameters. We therefore restricted our dataset to the more consistent studies below 7.3 GPa (Table 1). Because the excluded data are not inconsistent (within their large uncertainties) with the data used in the reported EoS fits, their inclusion in the fits makes no significant difference to the refined parameters but only increases their estimated uncertainties.
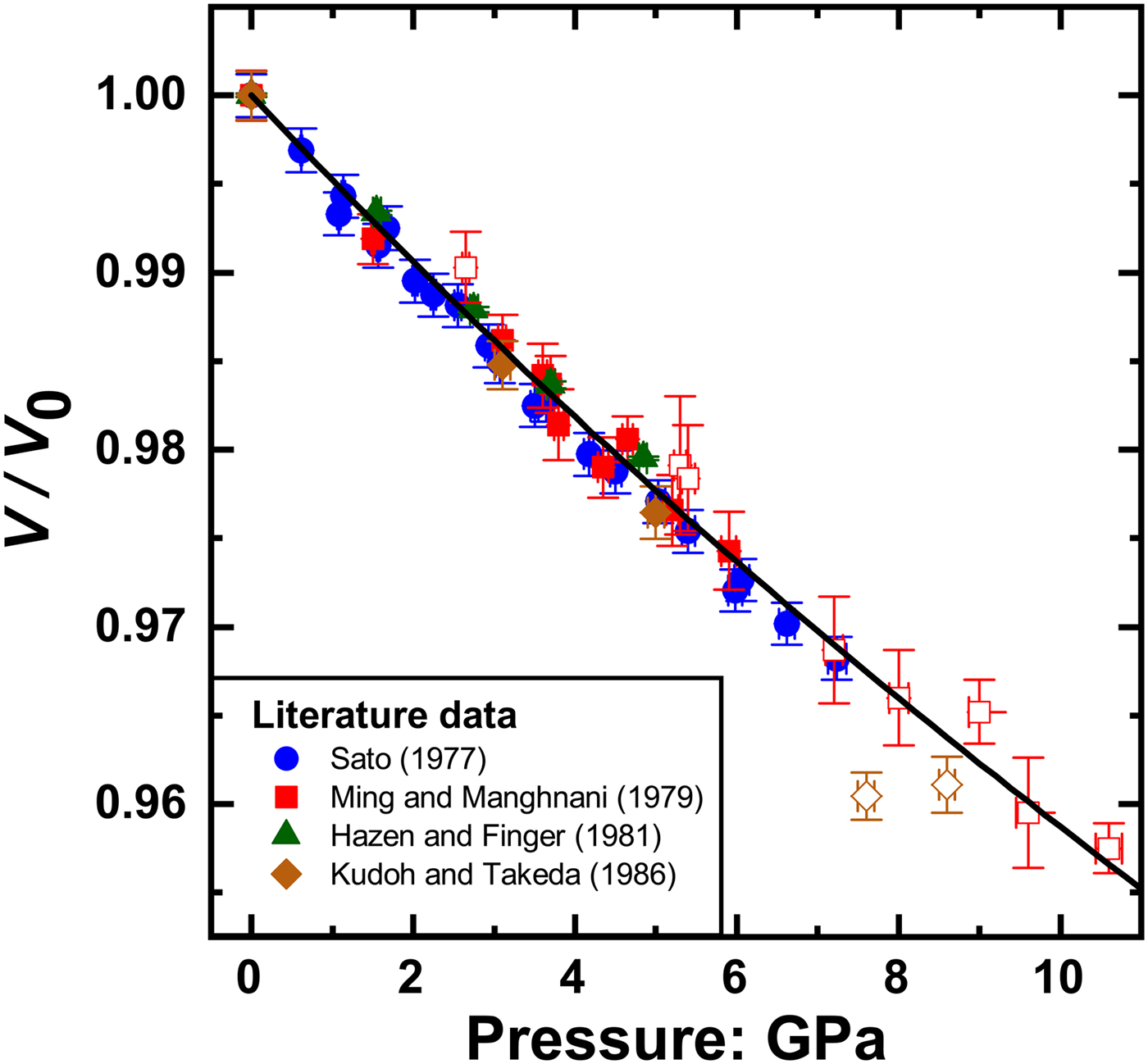
Fig. 1. P–V data of rutile taken from the literature. The open symbols are the data excluded from the current analysis. The full symbols are the selected data fitted with the final EoS (solid line) with the parameters given in Table 2.
Table 1. Data used to determine elastic parameters for rutile.
‘Ndata’ is the number of data from each source used in the refinement of EoS parameters. This data is available in the Supplementary materials and at http://www.rossangel.net as .dat text files that can be read by the EosFit suite of programs.
Table 2. Best-fit elastic parameters for rutile.
Parameters for a Birch–Murnaghan 3rd-order EoS, combined with the Holland and Powell (Reference Holland and Powell2011) thermal expansion model as modified following Kroll et al. (Reference Kroll, Kirfel, Heinemann and Barbier2012) and the temperature variation of bulk modulus after Hellfrich and Connolly (Reference Hellfrich and Connolly2009). For a full definition of these parameters, see Angel et al. (Reference Angel, Alvaro and Nestola2018). ‘Ndata’ is the number of data used in the refinement of EoS parameters. These parameters are available in the Supplementary materials and at http://www.rossangel.net as .eos files that can be used in the EosFit suite of programs.
The available data for volume (and cell parameter) variation with temperature at room pressure is much more consistent (Fig. 2a), with the exception of the data of Wang et al. (Reference Wang, Wang and Li2013) and the data point of Meagher and Lager (Reference Meagher and Lager1979) at 1173 K which were excluded from the current analysis because they are inconsistent with the remaining data (Fig 2a). The reasons for these inconsistencies are not obvious from the published information. Of special importance for constraining both the appropriate thermal expansion model and its coefficients are the precise data collected below room temperature by optical interferometry (Kirby, Reference Kirby1967) and by neutron powder diffraction (Burdett et al., Reference Burdett, Hughbanks, Miller, Richardson and Smith1987). To the best of our knowledge there are no measurements of the volume of rutile at simultaneous high P and T.
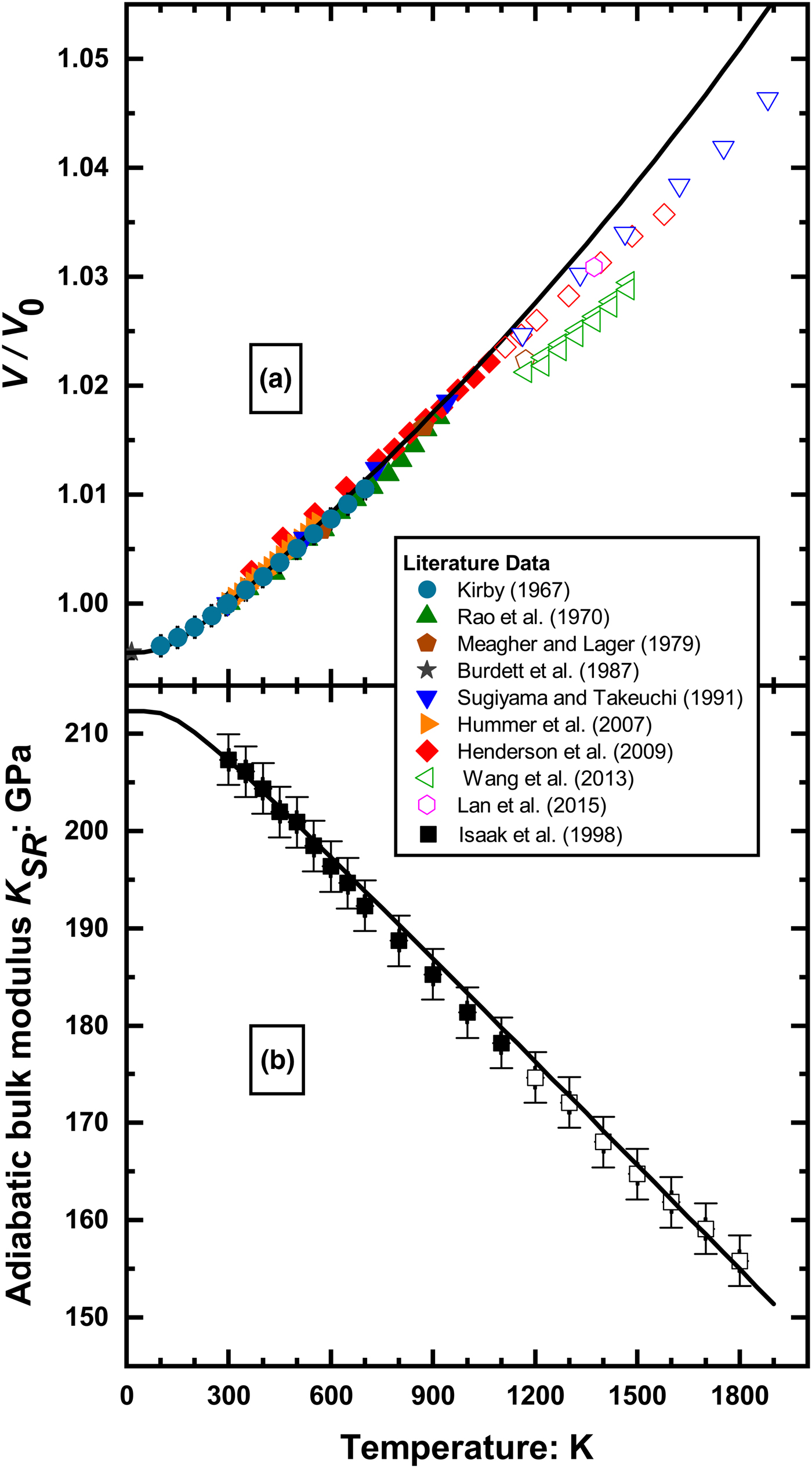
Fig. 2. (a) T–V data of rutile taken from the literature; (b) the variation of the adiabatic Reuss bulk modulus determined by Isaak et al. (Reference Isaak, Carnes, Anderson, Cynn and Hake1998), showing the decrease in the temperature variation of the bulk modulus above 1100 K. The open symbols are the data excluded from the current analysis. The full symbols are the selected data fitted with the final EoS (solid lines) with the parameters given in Table 2.
The full elastic tensor of rutile as a function of temperature up to 1800 K was determined by Isaak et al. (Reference Isaak, Carnes, Anderson, Cynn and Hake1998) using the rectangular parallelepiped resonance (RPR) method, from which the variation of the adiabatic Reuss bulk 
$K_{SR} = -V\left( {\displaystyle{{\partial P} \over {\partial V}}} \right)_S$ and linear moduli 
$M_{1SR} = M_{2SR} = -a\left( {\displaystyle{{\partial P} \over {\partial a}}} \right)_S$ and 
$M_{3SR} = -c\left( {\displaystyle{{\partial P} \over {\partial c}}} \right)_S$ can be obtained. Unfortunately, the low-temperature determinations of the elastic tensor of rutile by Manghnani et al. (Reference Manghnani, Fisher and Brower1972) are incomplete and no moduli can be obtained from them, and the results of Fritz (Reference Fritz1974) are only reported as pressure and temperature derivatives. We are therefore only able to use the interpolated values for the elastic tensor components up to 0.75 GPa that are reported in Manghnani (Reference Manghnani1969) in addition to data from Isaak et al. (Reference Isaak, Carnes, Anderson, Cynn and Hake1998). Fritz (Reference Fritz1974) shows that all of these earlier studies are in reasonable agreement with each other with the exception of the first derivative of M 3S. We use the pressure derivatives reported by Fritz (Reference Fritz1974), as an additional constraint when fitting the unit-cell parameters because his values for the pressure derivatives of the linear moduli are in better agreement with the XRD data reported in the literature than the linear moduli that can be obtained from the elastic moduli reported by Manghnani (Reference Manghnani1969).
In most solids, the thermal expansion coefficient increases or remains constant at high temperatures (e.g. Anderson, Reference Anderson1995). However, at high temperatures above ~1100 K, the measured unit-cell volumes of rutile deviate towards smaller values than would be expected by extrapolation from lower temperatures, implying that rutile is denser than expected (Fig. 2a). In agreement with this observation, 
$\left( {\displaystyle{{\partial K_{SR}} \over {\partial T}}} \right)_{P = 0}$ becomes less negative above 1100 K than at lower temperatures (Fig. 2b and Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) meaning that rutile is stiffer than expected at high temperatures. This behaviour is in part due to the anomalous stiffening of the acoustic phonons driven by hybridisation of electrons between the Ti and O atoms (Lan et al., Reference Lan, Li, Hellman, Kim, Munoz, Smith, Abernathy and Fultz2015) and causes a change in the atomic-scale expansion mechanism within the rutile structure at high temperatures (see Sugiyama and Takeuchi, Reference Sugiyama and Takeuchi1991). The effects of partial oxidation in some experiments cannot be excluded. This deviation of properties cannot be described by a simple EoS, and therefore we only used data up to 1100 K in our analysis. The dataset used to determine the elastic parameters of rutile therefore consists of 111 data (Table 1), made up of 17 direct measurements of elastic moduli, 12 direct measurements of dimensional changes with temperature by interferometry and 82 determinations of unit-cell parameters by diffraction.
Equation of State analysis
All fits of elastic parameters were performed with the EosFit7c program (Angel et al., Reference Angel, Gonzalez-Platas and Alvaro2014) following the approach of Milani et al. (Reference Milani, Angel, Scandolo, Mazzucchelli, Boffa-Ballaran, Klemme, Domeneghetti, Miletich, Scheidl, Derzsi, Tokar, Prencipe, Alvaro and Nestola2017) to perform simultaneous fits of elastic moduli and cell parameters. Initial fits of the cell parameters with temperature yield values of the linear thermal expansion coefficients of 
${\rm \alpha} _1 = {\rm \alpha} _2 \sim 0.77 \times 10^{-5}{\rm K}^{-1}$ and 
${\rm \alpha} _3 \sim 0.99 \times 10^{-5}{\rm K}^{-1}$. The room-temperature elastic moduli (e.g. Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) give values of the adiabatic linear moduli of 
$M_{1SR} = M_{2SR} \sim 506\; {\rm GPa}$ and 
$M_{3SR} \sim 1149\; {\rm GPa}$. The c axis is therefore more than twice as stiff as the a axis, but it also has a significantly higher thermal expansion coefficient. This has an important consequence for the types of EoS that can be used to fit the data for rutile. The gradient of a line of constant unit-cell parameter a in P –T space is defined by 
$\left( {\displaystyle{{\partial P} \over {\partial T}}} \right)_a = {\rm \alpha} _1M_{1TR}$. An equivalent expression applies for c. We do not have direct measurements of the isothermal moduli M 1TR and M 3TR but they do not differ by more than 2% from the adiabatic values, as we confirm in our analysis described later. Therefore, for initial analysis we can determine the approximate slopes of lines of constant a and c cell parameters at room conditions from the adiabatic moduli as 
$\left( {\displaystyle{{\partial P} \over {\partial T}}} \right)_a \sim \; 3.9\; {\rm MPa}\; {\rm K}^{-1}$ and 
$\left( {\displaystyle{{\partial P} \over {\partial T}}} \right)_c \sim \; 11.3\; {\rm MPa\;} {\rm K}^{-1}$. These values differ by a factor of 3, implying that lines of constant a and c diverge rapidly in P –T space (Fig. 3a). Neither do these lines follow the isochor through room conditions, whose slope is given by the product of the volume thermal expansion coefficient and the isothermal Reuss bulk modulus, 
$\left( {\displaystyle{{\partial P} \over {\partial T}}} \right)_V = {\rm \alpha} _VK_{TR}$. Therefore, while along an isochor of rutile the volume does not change, the a and c cell parameters change significantly (Fig. 3b), generating significant unit cell strains (in Voigt notation) 
${\rm \varepsilon} _1 = {{\Delta a} \over a} = {\rm \varepsilon} _2 = {{\Delta b} \over b}$ and 
${\rm \varepsilon} _3 = {{\Delta c} \over c}$. Along an isochor the linear strains sum to zero because:
$${\rm \varepsilon} _V = \displaystyle{{\Delta V} \over V} = {\rm \varepsilon} _1 + {\rm \varepsilon} _2 + {\rm \varepsilon} _3$$The frequencies of vibrational modes are primarily dependent upon the strains applied to the unit cell (e.g. Grüneisen, Reference Grüneisen1926; Barron et al., Reference Barron, Collins and White1980; Angel et al., Reference Angel, Murri, Mihailova and Alvaro2019). Therefore, in rutile the phonon mode frequencies must change along isochors. This violates the fundamental assumption of the quasi-harmonic approximation (QHA) to the thermodynamics of solids (e.g. Anderson, Reference Anderson1995) which underlies the derivation of thermal-pressure EoS such as Mie-Grüneisen-Debye (MGD) or the simplified thermal-pressure model of Holland and Powell (Reference Holland and Powell2011).
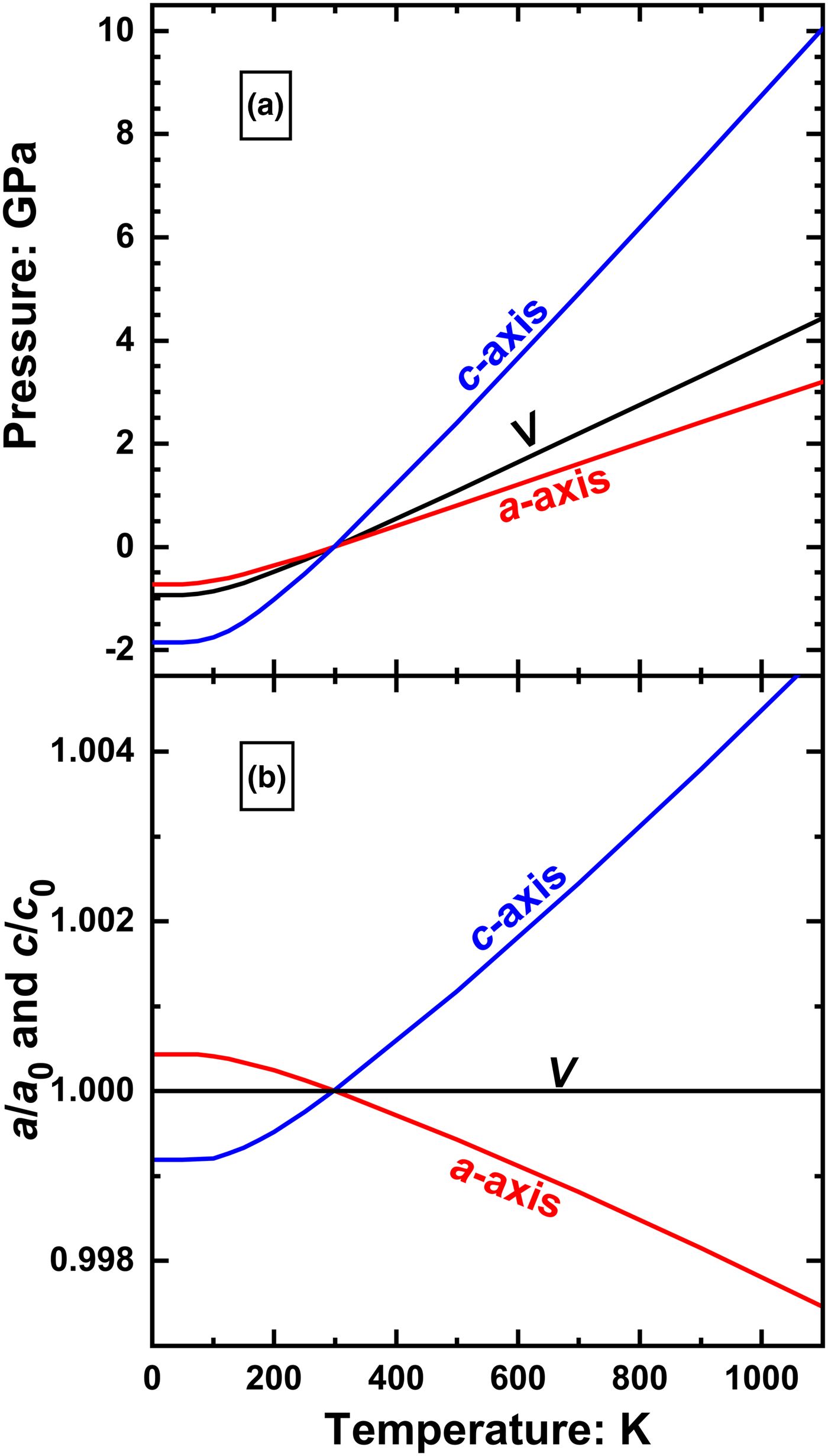
Fig. 3. (a) The lines of constant a and c of rutile in P–T space calculated from the final refined elastic parameters (Table 2) deviate significantly from the isochor that passes through room conditions; (b) as a consequence, the unit cell parameters of rutile change significantly along the isochor.
A simple consequence is that such QHA-based EoS cannot simultaneously fit all of the volume and elasticity data of rutile. For example, if the pressure derivative of the bulk modulus 
$\left( {\displaystyle{{\partial K} \over {\partial P}}} \right)_{T = 298{\rm K}} = K_0^{\prime} $ is held to the value of 6.92 (average of values from Manghnani, Reference Manghnani1969; Fritz, Reference Fritz1974) determined by direct measurements of the elasticity of rutile, then refinement of the other parameters of an MGD EoS to the selected data for rutile do not allow the measured variation of K SR with temperature (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) to be fit (Fig. 4). Instead, a value of 
$K_0^{\prime} \approx 9$ is required to fit the variation of K SR with temperature, but such a high value is incompatible with the high-pressure measurements of the volume and elasticity (Manghnani, Reference Manghnani1969; Fritz, Reference Fritz1974). This confirms the conclusion of Lan et al. (Reference Lan, Li, Hellman, Kim, Munoz, Smith, Abernathy and Fultz2015) that the QHA does not apply to rutile. Therefore, to fit the data of rutile we have used an ‘isothermal’ type of EoS in which there are no underlying assumptions of quasi-harmonic behaviour (Angel et al., Reference Angel, Alvaro and Nestola2018). In an ‘isothermal’ EoS, the volume at P and T is obtained by first calculating the volume thermal expansion at room pressure to the T of interest. Then an isothermal EoS is used to calculate the isothermal compression at the temperature T from room pressure to the final pressure. This requires that the temperature variation of K TR and 
$K_{TR}^{\prime} $ must be described by additional parameters (Angel et al., Reference Angel, Alvaro and Nestola2018). The disadvantage of this approach compared to thermal-pressure EoS based on QHA is that it requires more parameters, and therefore other constraints or restraints on the EoS parameters must be introduced when, as is the case for rutile, the available data are insufficient to determine all of the parameter values independently. We discuss the appropriate constraints as we present the results of our analysis below.
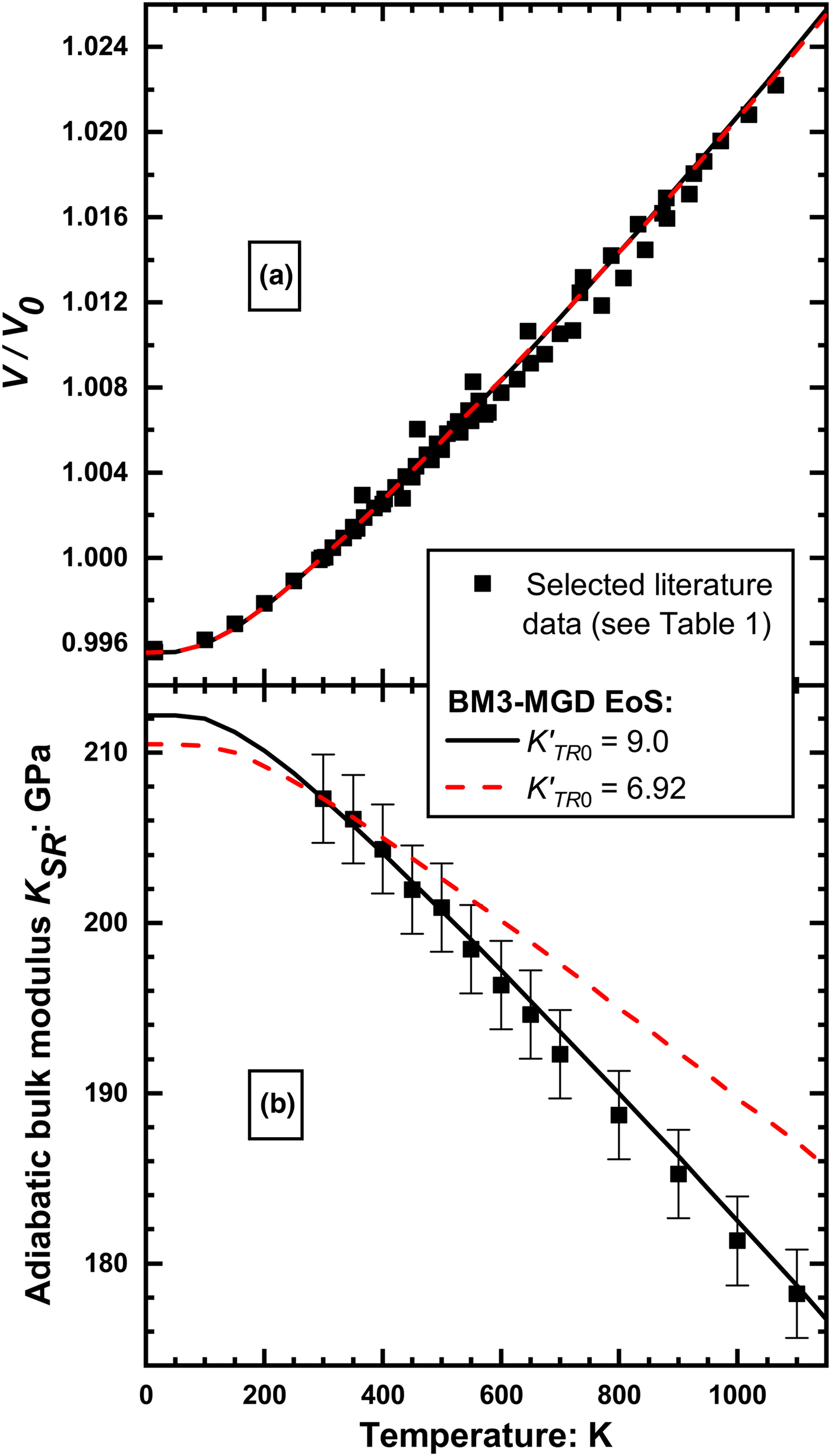
Fig. 4. The variation with temperature of (a) volume and (b) adiabatic Reuss bulk modulus of rutile. The volume variation is well-reproduced by an MGD thermal-pressure EoS with a wide range of 
$K_{TR0}^{\prime} $. The bulk modulus data can only be modelled with 
$K_{TR0}^{\prime} \approx 9$ , a value that is incompatible with the high-pressure volume and elasticity data.
Volume Equation of State
As noted above, the direct measurements of the elastic moduli of rutile at high pressures show that 
$K_0^{\prime} $ is significantly higher than 4, so we use a Birch-Murnaghan 3rd-order EoS (Birch, Reference Birch1947) to describe the compressional behaviour in which K TR0 and 
$K_{TR0}^{\prime} $ are the parameters to be determined. For thermal expansion at room pressure we use the equation developed by Kroll et al. (Reference Kroll, Kirfel, Heinemann and Barbier2012) as a version of the Holland and Powell (Reference Holland and Powell2011) model, which describes the thermal expansion in terms of an Einstein oscillator. But we explicitly use the Anderson-Grüneisen parameter δT (Anderson Reference Anderson1995) in place of 
$\lpar {1 + K_T^{\prime}} \rpar $. This approach separates the thermal and baric parts of the EoS (Angel et al., Reference Angel, Alvaro and Nestola2018) while maintaining a reasonable physical basis in the Einstein oscillator model behind the thermal expansion model. The separation of variables (Angel et al., Reference Angel, Alvaro and Nestola2018) allows both the room-T high-pressure data and the variation of the bulk modulus with temperature to be fitted. We also use δT to define the temperature variation of the bulk modulus in a way (Anderson, Reference Anderson1995; Hellfrich and Connolly, Reference Hellfrich and Connolly2009; Angel et al., Reference Angel, Alvaro and Nestola2018) that is thermodynamically valid:
$$K_{TR}\lpar {T,P = 0} \rpar = K_{TR0}\left( {\displaystyle{{V_0} \over {V\lpar T \rpar }}} \right)^{{\rm \delta} _T}$$There are no data available for rutile to constrain the temperature variation of K ′, so we have to assume that 
$\lpar {\partial K_{TR}^{\prime} /\partial T} \rpar _P = 0$. The thermal effects in the EoS are therefore described by the thermal expansion coefficient at room conditions αV0, the Einstein temperature θE (Holland and Powell, Reference Holland and Powell2011) and the Anderson-Grüneisen parameter δT. The isotropic thermal Grüneisen parameter γV (Anderson, Reference Anderson1995) is needed to relate the isothermal bulk moduli used to describe the volume variation with pressure, to the adiabatic bulk moduli measured in ultrasonic resonance (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) and wave velocity experiments (Manghnani, Reference Manghnani1969):
$$K_S = \lpar {1 + {\rm \alpha}_V{\rm \gamma}_VT} \rpar K_T$$The value of γV for rutile is not known exactly but appears to lie in the range of 1.2 to 1.6 at room conditions, and to either increase or decrease to 1.6 or 1.4 at 1100 K (see Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998, fig. 9). Test fits of isothermal-type EoS to the selected data for rutile indicate that the particular value chosen for γV within this range has no significant influence on the refined parameters of the EoS or the quality of fit to the data. We therefore used an average value of γV = 1.4 and assumed that it does not vary over the temperature interval 0–1100 K. Because rutile is so stiff, it is also necessary to over-weight (by artificially reducing its uncertainty) the experimental datum for K SR at room conditions in order to stabilise the refinement. With these constraints the final refined EoS parameters reported in Table 2 are obtained, which clearly fit all of the selected experimental data within the experimental uncertainties (Figs 1, 2). But whether these EoS parameters correctly predict the volume of rutile outside the range of the underlying data (to 7.3 GPa and 1100 K) is not known. The values of δT and 
$K_{TR}^{\prime} $ are significantly different from one another, which indicates that the bulk modulus variation along an isochor, 
$\left( {\displaystyle{{\partial K_{TR}} \over {\partial T}}} \right)_V = {\rm \alpha} _VK_{TR}\lpar {K_{TR}^{\prime} -{\rm \delta}_T} \rpar $, is –0.004(3) GPa K–1, a value similar to that estimated for olivine (e.g. Anderson et al., Reference Anderson, Isaak and Oda1992; Angel et al., Reference Angel, Alvaro and Nestola2018).
Cell parameters
As for the volume, the values of the anisotropic thermal Grüneisen parameters cannot be refined and must be fixed to values determined independently. For the principal axes of compression the thermodynamically-correct expression that relates the corresponding adiabatic and isothermal linear moduli M iS and M iT can be derived (Nye, Reference Nye1957; Barron et al., Reference Barron, Collins and White1980; Milani et al., Reference Milani, Angel, Scandolo, Mazzucchelli, Boffa-Ballaran, Klemme, Domeneghetti, Miletich, Scheidl, Derzsi, Tokar, Prencipe, Alvaro and Nestola2017) from the relationship between the adiabatic and isothermal elastic compliance tensors as:
$$M_{iS} = \left( {1 + {\rm \alpha}_i{\rm \gamma}_VT\displaystyle{{M_{iS}} \over {K_S}}} \right)M_{iT}$$However, the bulk modulus K S required for this conversion of the linear moduli is not always available when fits of unit-cell parameters are performed. Within the EosFit7c program anisotropic thermal Grüneisen parameters γi are therefore used in an equation analogous to (3):
$$M_{iS} = \lpar {1 + 3{\rm \alpha}_i{\rm \gamma}_iT} \rpar M_{iT}$$The values of the anisotropic thermal Grüneisen parameters used in EosFit7c are then given by:
$${\rm \gamma} _i = \displaystyle{1 \over 3}\displaystyle{{M_{iS}} \over {K_S}}{\rm \gamma} _V$$Note that for materials such as rutile with significant elastic anisotropy, γi ≠ γV. The other EoS parameters are not especially sensitive to the values of γi, which were therefore obtained (Table 2) from γV by using the values of the elastic moduli determined at room temperature (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998).
The variation of the unit-cell parameters of a crystal with pressure is always proportionally smaller than that of the volume. For a stiff material such as rutile there is too little variation of the a and c unit-cell parameters over the accessible pressure range to allow simultaneous refinement of both the linear moduli M iTR and their pressure derivatives 
$M_{iTR}^{\prime} $. We therefore constrained some of these parameters to values that are consistent with both the data for the a and c axes and the corresponding parameters for the volume, and we confirmed after fitting that the remaining refined parameters for the a and c unit-cell parameters were consistent with the volume parameters. Because the volume strain of the crystal induced by a change in T or P is given by the sum of the linear strains of the unit-cell parameters (equation 1), it follows that the axial thermal expansion and compressibilities sum to the corresponding quantities for the volume:
$$\eqalign{& {\rm \alpha} _V = \displaystyle{1 \over V}\left( {\displaystyle{{\partial V} \over {\partial T}}} \right)_P = {\rm \alpha} _1 + {\rm \alpha} _2 + {\rm \alpha} _3 \cr & {\rm \beta} _V = \displaystyle{1 \over V}\left( {\displaystyle{{\partial V} \over {\partial P}}} \right)_T = {\rm \beta} _1 + {\rm \beta} _2 + {\rm \beta} _3.} $$Because the volume compressibility is the inverse of the isothermal Reuss bulk modulus, 
$K_{TR} = -V\left( {\displaystyle{{\partial P} \over {\partial V}}} \right)_T$, and the linear compressibilities are the inverse of the corresponding isothermal Reuss linear moduli, 
$M_{iTR} = -l_i\left( {\displaystyle{{\partial P} \over {\partial l_i}}} \right)_T$, the relationship between these moduli must always be:
$$K_{TR} = \lpar {M_{1TR}^{-1} + M_{2TR}^{-1} + M_{3TR}^{-1}} \rpar ^{-1}$$Differentiation of (8) gives the relationship between the first pressure derivatives of the moduli:
$$K_{TR}^{\prime} = K_{TR}^2 \mathop \sum \limits_{i = 1}^3 \displaystyle{{M_{iTR}^{\prime}} \over {M_{iTR}^2}} $$In the fits to the data, the values of 
$M_{iTR}^{\prime} $ (Table 2) were taken from Fritz (Reference Fritz1974) with a slight adjustment within the reported experimental uncertainties to ensure that they conform to equation 9. In addition, the linear modulus of the c axis, M 3TR0, cannot be refined simultaneously with the value of δT and it was therefore fixed to a value consistent with the experimental determinations of M 3SR at room temperature (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) and the calculated value of γ3. The values of the remaining parameters obtained by refinement are reported in Table 2. They fulfil the consistency requirements given in equations 7, 8, and 9, and reproduce the experimental data within their uncertainties.
Conclusions
We have demonstrated that for stiff minerals it is possible to obtain more reliable EoS parameters by fitting experimental elastic moduli and cell parameter data simultaneously. Of particular importance, in the absence of data collected at simultaneous high T and P, is the use of high-temperature measurements of the elastic moduli to constrain the P –T ‘cross-terms’ in the EoS. Without such data, it is not possible to determine whether the quasi-harmonic approximation is valid or not for the mineral, as we have done in Fig. 4. For materials such as rutile in which αiM iTR varies strongly with direction in the crystal, EoS based on QHA are not only theoretically invalid but also cannot fit all of the available experimental data. The isothermal types of EoS do not suffer from this theoretical problem, but they involve more parameters than can be determined independently from the experimental data for stiff materials such as rutile. Applying the requirements for consistency between linear and volume parameters of the EoS can help overcome this issue in a thermodynamically-consistent manner. The resulting elastic parameters for the volume and unit-cell parameters of rutile (Table 2) are also available as .eos files in the Supplementary materials (see below) for this paper and from the website http://www.rossangel.net for use in the EosFit7 suite of programs.
As noted above, rutile is a very common inclusion in metamorphic garnets. Minerals trapped as inclusions within other host minerals can exhibit residual pressures when measured at room conditions because of the differences between the thermoelastic properties of the host and inclusion phases. This residual or remnant pressure can be measured by a variety of techniques such as diffraction or spectroscopy (e.g. Kohn, Reference Kohn2014; Murri et al., Reference Murri, Mazzucchelli, Campomenosi, Korsakov, Prencipe, Mihailova, Scambelluri, Angel and Alvaro2018; Angel et al., Reference Angel, Murri, Mihailova and Alvaro2019), and with knowledge of the EoS of both the host and inclusion phases the P and T of inclusion entrapment can be inferred (Rosenfeld and Chase, Reference Rosenfeld and Chase1961). To understand the development of inclusion pressures Rosenfeld and Chase (Reference Rosenfeld and Chase1961) introduced the thermodynamic concept of an ‘isomeke’ (first named as such by Adams et al., Reference Adams, Cohen and Rosenfeld1975). The isomeke is the only path in P–T space along which no residual pressures would be developed in the inclusion after entrapment. The slope of an isomeke is 
$\left( {\displaystyle{{\partial P} \over {\matrix{ {\partial T} \cr}}}} \right)_{V_I-V_H} = \displaystyle{{\matrix{ {{\rm \alpha} _I} \cr} -\matrix{ {{\rm \alpha} _H} \cr}} \over {\matrix{ {{\rm \beta} _I} \cr} -\matrix{ {{\rm \beta} _H} \cr}}} $ where the subscript ‘I’ indicates the inclusion and the subscript ‘H’ the host mineral, α is the volume thermal expansion coefficient and β is the volume compressibility (e.g. Rosenfeld and Chase, Reference Rosenfeld and Chase1961; Angel et al., Reference Angel, Nimis, Mazzucchelli, Alvaro and Nestola2015). Rutile (Table 2) is stiffer than pyrope and has a similar thermal expansion coefficient to that of pyrope (Milani et al. Reference Milani, Nestola, Alvaro, Pasqual, Mazzucchelli, Domeneghetti and Geiger2015), which means that βI < βH and αI ≃ αH. Therefore, the isomekes of rutile trapped in pyrope are almost flat, as shown in Fig. 5a; in particular, the isomeke passing through room conditions has ∂P/∂T ≃ 0 at temperatures below ~600 K and a negative ∂P/∂T at higher temperatures. In fact, βI – βH is always negative over the P–T range shown in Fig. 5 but αI becomes larger than αH at higher temperatures leading to a negative ∂P/∂T.
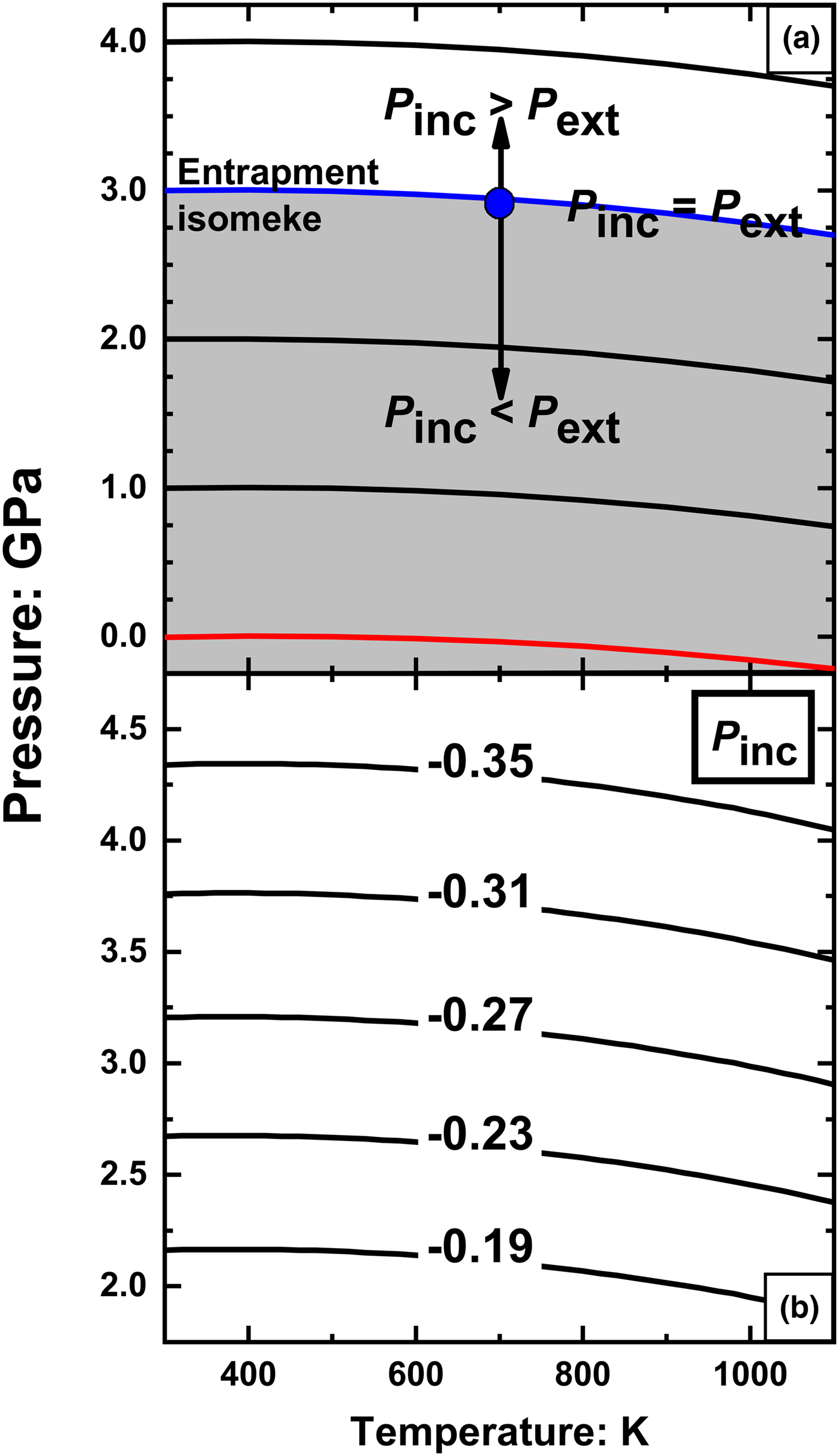
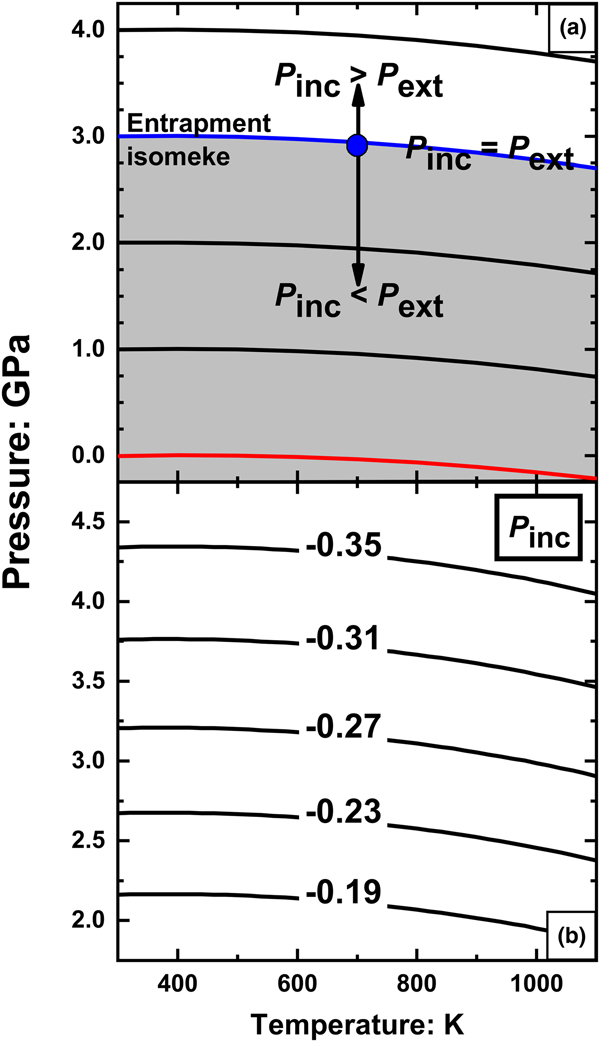
Fig. 5. (a) Isomekes for rutile and pyrope. Consider a rutile inclusion trapped in pyrope at 700 K and 2.95 GPa (blue spot). If the external pressure is raised above the entrapment isomeke (blue line) the inclusion will have a higher pressure than the external pressure. At external pressures below the entrapment isomeke, the inclusion pressure is lower than the external pressure. The red line is the isomeke passing through room conditions; in order for an inclusion measured at room conditions to exhibit a positive residual inclusion pressure it must be trapped below the red isomeke; (b) Entrapment isomekes showing the residual pressures P inc (GPa) in an inclusion measured at room conditions as a function of the entrapment P and T.
When the host-inclusion system leaves the isomeke, a residual pressure is developed in the inclusion. This can be most easily understood for a small isothermal change in the external pressure, P ext, applied to the host. By definition of the isothermal bulk modulus of the host, the change in volume of the inclusion cavity will be 
$\displaystyle{{\Delta V} \over V} = \displaystyle{{-\Delta P_{ext}} \over {K_H}}$. This volume change applied to the inclusion changes its pressure by 
$\Delta P_{inc} = \displaystyle{{K_I} \over {K_H}}\Delta P_{ext}$ (Angel et al., Reference Angel, Mazzucchelli, Alvaro and Nestola2017; Ferrero and Angel, Reference Ferrero and Angel2018). For a stiff inclusion trapped in a softer host mineral, like the case of rutile trapped in pyrope, the change in the inclusion pressure ΔP inc will always be greater than the change in external pressure ΔP ext. Therefore, when the system is taken to a P and T above the entrapment isomeke, the residual pressure (P inc) will be higher than the external pressure (P ext). On the contrary, when the system is taken to lower external P than the entrapment isomeke, P inc will be less than P ext (Fig. 5a). Therefore, rutile inclusions will exhibit positive P inc at room conditions only if room conditions lie above the entrapment isomeke. The isomeke through room conditions (Fig. 5a) thus divides P–T space in two areas: rutile inclusions trapped below this isomeke will exhibit positive P inc when measured at room conditions, whereas rutile inclusions trapped above this isomeke will exhibit negative P inc. This means that rutile inclusions trapped in pyrope from ultra-high-pressure metamorphic rocks should always exhibit negative residual pressures. The calculated P inc as a function of entrapment conditions are shown as contours in Fig. 5b. A negative value of P inc represents an expansion of the inclusion crystal relative to a free crystal of rutile at room conditions. Such expansion could only occur if rutile inclusion crystals are strongly bonded to the garnet host at the host/inclusion interface. If such bonding does not occur, then rutile inclusions will be free to contract back to the volume of a free crystal at room conditions, leaving a void space between the inclusion crystal and the host crystal. If that occurs, the inclusions will exhibit a pressure equal to ambient P, independent of the conditions of entrapment. Rutile inclusions in pyrope garnets from Dora Maira massif measured with Raman spectroscopy (N. Campomenosi, 2018, pers. comm.) exhibit zero residual pressure (within the measurement uncertainties), thus confirming this analysis and that the rutile inclusion crystals become mechanically detached from the garnet host. The same conclusion is obtained even if the EoS for rutile of Holland and Powell (Reference Holland and Powell2011) is used. It has a much lower volume thermal expansion coefficient and a stiffer bulk modulus that do not reproduce the experimental data (Tables 1) as well as the EoS given in Table 2. The rutile-pyrope isomekes calculated with it therefore have slopes more positive than those shown in Fig. 5a, but the bulk modulus contrast between rutile and garnet ensures that it still predicts that the final P inc will be negative for rutile inclusions entrapped at metamorphic conditions. Rutile trapped in other garnet compositions should also show negative or zero residual pressures because all garnets in metamorphic rocks are significantly less stiff than rutile (Milani et al., Reference Milani, Nestola, Alvaro, Pasqual, Mazzucchelli, Domeneghetti and Geiger2015; Milani et al., Reference Milani, Angel, Scandolo, Mazzucchelli, Boffa-Ballaran, Klemme, Domeneghetti, Miletich, Scheidl, Derzsi, Tokar, Prencipe, Alvaro and Nestola2017).
The determination of the variation of the unit-cell parameters of rutile (Table 2) also allows us to calculate the residual unit-cell strains expected for rutile inclusions in garnets. These calculations show that at room conditions the c axis of a rutile inclusion will be stretched compared to the c axis of a free crystal of rutile (i.e. positive strain) whereas the a axis will exhibit a compressive strain (i.e. negative strain) but these strains always result in a positive volume strain and thus negative P inc. All of these observations lead to the conclusion that rutile is not suitable for elastic geobarometry when it is trapped in garnet. This contrasts with the behaviour of zircon inclusions trapped in garnet which exhibit positive P inc when measured at room conditions (Campomenosi et al., Reference Campomenosi, Mazzucchelli, Mihailova, Scambelluri, Angel, Nestola, Reali and Alvaro2018; Stangarone et al., Reference Stangarone, Alvaro, Angel, Prencipe and Mihailova2019) even though zircon (e.g. Van Westrenen et al., Reference Van Westrenen, Frank, Hanchar, Fei, Finch and Zha2004; Zaffiro et al., Reference Zaffiro, Angel, Alvaro, Prencipe and Stangarone2018), like rutile, is stiffer than garnet. In the case of zircon however, the contrast in bulk modulus with the garnets is compensated by the substantially lower thermal expansion coefficient of zircon. Therefore, stiff inclusions trapped in softer host minerals are suitable for elastic geobarometry only when αV of the inclusion is significantly lower than the α V of the host, which is not the case of rutile inclusions trapped in garnet hosts.
Author ORCIDs
Ross J. Angel, 0000-0003-0861-398X
Acknowledgements
This work was supported by ERC starting grant 714936 ‘True Depths’ to Matteo Alvaro. We thank Mattia Mazzucchelli for help with the calculations of remnant inclusion strains. We also thank our colleagues Kira Musiyachenko, Nicola Campomenosi and Hugo van Schrojenstein Lantman for discussions, and two anonymous reviewers whose comments helped improve the manuscript.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2019.24
Target article
Constraints on the Equations of State of stiff anisotropic minerals: rutile, and the implications for rutile elastic barometry
Related commentaries (1)
Commentary on “Constraints on the Equations of State of stiff anisotropic minerals: rutile, and the implications for rutile elastic barometry” [Miner. Mag. 83 (2019) pp. 339–347]