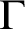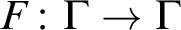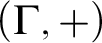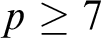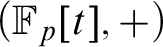1 Introduction
A set S of natural numbers is said to be p-automatic if the set of representations base p of the elements of S forms a regular language—meaning that it is recognized by a finite automaton. Motivated by the isotrivial Mordell–Lang problem, Bell and Moosa were led in [Reference Bell and Moosa2] to extend this notion to the context where the natural numbers are replaced by an abelian group
![]() $\Gamma $
and multiplication by p is replaced by a fixed injective endomorphism F of
$\Gamma $
and multiplication by p is replaced by a fixed injective endomorphism F of
![]() $\Gamma $
. The intended examples were when
$\Gamma $
. The intended examples were when
![]() $\Gamma $
is a finitely generated subgroup of a semiabelian variety G over a finite field
$\Gamma $
is a finitely generated subgroup of a semiabelian variety G over a finite field
![]() $\mathbb {F}_q$
, with
$\mathbb {F}_q$
, with
![]() $\Gamma $
preserved by the q-power Frobenius endomorphism F of G. In that setting, Bell and Moosa show in [Reference Bell and Moosa2] that if X is a closed subvariety of G then
$\Gamma $
preserved by the q-power Frobenius endomorphism F of G. In that setting, Bell and Moosa show in [Reference Bell and Moosa2] that if X is a closed subvariety of G then
![]() $X\cap \Gamma $
is F-automatic; they do so using the isotrivial Mordell–Lang theorem of Moosa and Scanlon in [Reference Moosa and Scanlon6], which describes
$X\cap \Gamma $
is F-automatic; they do so using the isotrivial Mordell–Lang theorem of Moosa and Scanlon in [Reference Moosa and Scanlon6], which describes
![]() $X\cap \Gamma $
. These results have recently been made effective and generalized to arbitrary commutative algebraic groups by Bell, Ghioca, and Moosa in [Reference Bell, Ghioca and Moosa1].
$X\cap \Gamma $
. These results have recently been made effective and generalized to arbitrary commutative algebraic groups by Bell, Ghioca, and Moosa in [Reference Bell, Ghioca and Moosa1].
Our interest here is in the general theory of F-automata. The precise definition of an F-automatic subset of
![]() $\Gamma $
is recalled in Section 2, but let us give an informal explanation now. First one needs to know that
$\Gamma $
is recalled in Section 2, but let us give an informal explanation now. First one needs to know that
![]() $(\Gamma ,F)$
admits a “spanning set”: this is a finite subset
$(\Gamma ,F)$
admits a “spanning set”: this is a finite subset
![]() $\Sigma $
such that every element of
$\Sigma $
such that every element of
![]() $\Gamma $
can be expressed as
$\Gamma $
can be expressed as
![]() $s_0+Fs_1+\cdots + F^ns_n$
for some
$s_0+Fs_1+\cdots + F^ns_n$
for some
![]() $s_0,\ldots ,s_n\in \Sigma $
. Then a subset S of
$s_0,\ldots ,s_n\in \Sigma $
. Then a subset S of
![]() $\Gamma $
is said to be F-automatic if the set of words
$\Gamma $
is said to be F-automatic if the set of words
![]() $s_0s_1\cdots s_n$
such that
$s_0s_1\cdots s_n$
such that
![]() $s_0+Fs_1+\cdots +F^ns_n\in S$
forms a regular language on the alphabet
$s_0+Fs_1+\cdots +F^ns_n\in S$
forms a regular language on the alphabet
![]() $\Sigma $
.
$\Sigma $
.
Our goals in this paper are twofold: (1) to clarify and further develop the foundations of this theory, and (2) to investigate the model-theoretic properties of F-automatic sets, in particular with respect to the stability-theoretic hierarchy.
Regarding foundations, our main results are:
-
• A characterization of when
 $(\Gamma ,F)$
admits a spanning set in terms of the existence of a height function on
$(\Gamma ,F)$
admits a spanning set in terms of the existence of a height function on
 $\Gamma $
(Theorem 3.10) and, in the finitely generated case, in terms of the eigenvalues of
$\Gamma $
(Theorem 3.10) and, in the finitely generated case, in terms of the eigenvalues of
 $F \otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}}$
(Theorem 3.12).
$F \otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}}$
(Theorem 3.12). -
• A characterization of F-automaticity in terms of kernels; this is Theorem 4.2 below. This result brings the basic theory of F-automatic sets closer to the classical case of p-automaticity.
-
• A characterization of F-sparsity. In the theory of regular languages there is a natural sparse/non-sparse dichotomy in terms of the growth of the number of accepted words of bounded length. This was extended and investigated in [Reference Bell and Moosa2]; see Definition 5.1 below for details. We clarify some properties of F-sparse sets (answering a question in [Reference Bell and Moosa2] along the way) and characterize them in terms of length functions (Theorem 5.10). As a consequence, we obtain in Corollary 5.12 a useful criterion for verifying F-sparsity; this criterion is used by Bell–Ghioca–Moosa in the recent preprint [Reference Bell, Ghioca and Moosa1] on effective isotrivial Mordell–Lang.
We next turn to the model-theoretic analysis. Here our main results are:
-
• An explicit characterization of stable F-sparse sets as finite Boolean combinations of translates of finite sums of sets of the form
 $\{a+Fa+\cdots +F^na : {n <\omega}\}$
—these are the “groupless F-sets” of [Reference Moosa and Scanlon6]. That the groupless F-sets are stable is from [Reference Moosa and Scanlon6]; the converse is Theorem 6.3 below.
$\{a+Fa+\cdots +F^na : {n <\omega}\}$
—these are the “groupless F-sets” of [Reference Moosa and Scanlon6]. That the groupless F-sets are stable is from [Reference Moosa and Scanlon6]; the converse is Theorem 6.3 below. -
• The production of some new NIP expansions of
 $(\Gamma ,+)$
; see Theorem 7.7. This includes
$(\Gamma ,+)$
; see Theorem 7.7. This includes
 $(\Gamma ,+,A)$
for any F-sparse
$(\Gamma ,+,A)$
for any F-sparse
 $A\subseteq \Gamma $
, but it also includes some examples that are not even F-automatic, most notably the expansion of
$A\subseteq \Gamma $
, but it also includes some examples that are not even F-automatic, most notably the expansion of
 $(\mathbb {F}_p[t],+)$
by the graph of multiplication restricted to
$(\mathbb {F}_p[t],+)$
by the graph of multiplication restricted to
 $t^{\mathbb {N}}$
, when
$t^{\mathbb {N}}$
, when
 $p\ge 7$
. This last example is Theorem 7.8 below.
$p\ge 7$
. This last example is Theorem 7.8 below.
2 Preliminaries
We first recall the relevant theory of regular languages; the interested reader is directed to [Reference Yu7] for further details. Fix a finite set
![]() $\Lambda $
, which we will use as an alphabet. We use
$\Lambda $
, which we will use as an alphabet. We use
![]() $\Lambda ^*$
to denote the set of strings of elements of
$\Lambda ^*$
to denote the set of strings of elements of
![]() $\Lambda $
. A language is any subset
$\Lambda $
. A language is any subset
![]() $L\subseteq \Lambda ^*$
. We use
$L\subseteq \Lambda ^*$
. We use
![]() $\epsilon $
to denote the empty string. Given
$\epsilon $
to denote the empty string. Given
![]() $\sigma \in \Lambda ^*$
,
$\sigma \in \Lambda ^*$
,
![]() ${\lvert \sigma \rvert }$
denotes the length of
${\lvert \sigma \rvert }$
denotes the length of
![]() $\sigma $
.
$\sigma $
.
Definition 2.1. The set of regular languages over
![]() $\Lambda $
is the smallest set of languages that contains the finite languages and is such that if
$\Lambda $
is the smallest set of languages that contains the finite languages and is such that if
![]() $L_1,L_2\subseteq \Lambda ^*$
are regular then so are
$L_1,L_2\subseteq \Lambda ^*$
are regular then so are
![]() $L_1\cup L_2$
,
$L_1\cup L_2$
,
![]() $L_1L_2 = \{\sigma \tau :\sigma \in L_1,\tau \in L_2\}$
, and
$L_1L_2 = \{\sigma \tau :\sigma \in L_1,\tau \in L_2\}$
, and
![]() $L_1^* = \{\sigma _1\cdots \sigma _n : \sigma _1,\ldots ,\sigma _n\in L_1\}$
.
$L_1^* = \{\sigma _1\cdots \sigma _n : \sigma _1,\ldots ,\sigma _n\in L_1\}$
.
Regular languages can be characterized as those recognized by machines of a certain form:
Definition 2.2. A non-deterministic finite automaton (or NFA) is a
![]() $5$
-tuple
$5$
-tuple
![]() $M = (\Lambda , Q,q_0,\Omega ,\delta )$
, where:
$M = (\Lambda , Q,q_0,\Omega ,\delta )$
, where:
-
•
 $\Lambda $
is a finite alphabet.
$\Lambda $
is a finite alphabet. -
• Q is a finite set of states.
-
•
 $q_0\in Q$
is the initial state.
$q_0\in Q$
is the initial state. -
•
 $\Omega \subseteq Q$
is the set of finish states.
$\Omega \subseteq Q$
is the set of finish states. -
•
 $\delta \colon Q\times \Lambda \to 2^Q$
is the transition function: given
$\delta \colon Q\times \Lambda \to 2^Q$
is the transition function: given
 $(q,a)\in Q\times \Lambda $
it outputs the set of states the machine could transition to if it is in state q and reads input a.
$(q,a)\in Q\times \Lambda $
it outputs the set of states the machine could transition to if it is in state q and reads input a.
We identify
![]() $\delta $
with its natural extension
$\delta $
with its natural extension
![]() $Q\times \Lambda ^*\to 2^Q$
given by
$Q\times \Lambda ^*\to 2^Q$
given by
![]() $\delta (q,\sigma a) = \bigcup \{\delta (q',a) : q'\in \delta (q,\sigma )\}$
. If
$\delta (q,\sigma a) = \bigcup \{\delta (q',a) : q'\in \delta (q,\sigma )\}$
. If
![]() $\sigma \in \Lambda ^*$
we say M accepts
$\sigma \in \Lambda ^*$
we say M accepts
![]() $\sigma $
if
$\sigma $
if
![]() $\delta (q_0,\sigma )\cap \Omega \ne \emptyset $
; the set of such
$\delta (q_0,\sigma )\cap \Omega \ne \emptyset $
; the set of such
![]() $\sigma $
is the language recognized by M. If
$\sigma $
is the language recognized by M. If
![]() ${\lvert {\delta (q,a)} \rvert } = 1$
for all
${\lvert {\delta (q,a)} \rvert } = 1$
for all
![]() $q\in Q$
and
$q\in Q$
and
![]() $a\in \Lambda $
we say M is a deterministic finite automaton (or DFA). In this case we regard
$a\in \Lambda $
we say M is a deterministic finite automaton (or DFA). In this case we regard
![]() $\delta $
as having codomain Q, rather than
$\delta $
as having codomain Q, rather than
![]() $2^Q$
.
$2^Q$
.
Fact 2.3 [Reference Yu7, Lemma 2.2 and Sections 3.2 and 3.3]
If
![]() $L\subseteq \Lambda ^*$
then the following are equivalent:
$L\subseteq \Lambda ^*$
then the following are equivalent:
-
• L is regular.
-
• L is recognized by some DFA.
-
• L is recognized by some NFA.
A note on exponential notation: we use
![]() $\Lambda ^r$
to denote the alphabet of r-tuples of elements of
$\Lambda ^r$
to denote the alphabet of r-tuples of elements of
![]() $\Lambda $
, and we use
$\Lambda $
, and we use
![]() $\Lambda ^{(r)}$
to denote the language
$\Lambda ^{(r)}$
to denote the language
![]() $\{\sigma \in \Lambda ^* : {\lvert \sigma \rvert } =r\}$
.
$\{\sigma \in \Lambda ^* : {\lvert \sigma \rvert } =r\}$
.
Throughout the paper, we fix an infinite abelian group
![]() $\Gamma $
equipped with some injective endomorphism
$\Gamma $
equipped with some injective endomorphism
![]() $F\colon \Gamma \to \Gamma $
. We let
$F\colon \Gamma \to \Gamma $
. We let
![]() $\mathbb {Z}[F]$
denote the subring of
$\mathbb {Z}[F]$
denote the subring of
![]() $\operatorname {\mathrm {End}}(\Gamma )$
generated by F, and consider
$\operatorname {\mathrm {End}}(\Gamma )$
generated by F, and consider
![]() $\Gamma $
as a
$\Gamma $
as a
![]() $\mathbb {Z}[F]$
-module. Our context is slightly more general than that of [Reference Bell and Moosa2]: they require that
$\mathbb {Z}[F]$
-module. Our context is slightly more general than that of [Reference Bell and Moosa2]: they require that
![]() $\Gamma $
be a finitely generated abelian group, which we do not. Most of the results of [Reference Bell and Moosa2] go through in this context with no additional effort.
$\Gamma $
be a finitely generated abelian group, which we do not. Most of the results of [Reference Bell and Moosa2] go through in this context with no additional effort.
Following [Reference Bell and Moosa2], given a string
![]() $s_0\cdots s_n$
of elements in
$s_0\cdots s_n$
of elements in
![]() $\Gamma $
we let
$\Gamma $
we let
Note that when
![]() $(\Gamma ,F) = (\mathbb {Z},d)$
and
$(\Gamma ,F) = (\mathbb {Z},d)$
and
![]() $s_i\in \{0,\ldots ,d-1\}$
this is just computing the number represented by
$s_i\in \{0,\ldots ,d-1\}$
this is just computing the number represented by
![]() $s_0\cdots s_n$
base d. Given a set L of strings of elements of
$s_0\cdots s_n$
base d. Given a set L of strings of elements of
![]() $\Gamma $
, we let
$\Gamma $
, we let
Definition 2.4. If
![]() $\Sigma $
is a finite subset of
$\Sigma $
is a finite subset of
![]() $\Gamma $
we say
$\Gamma $
we say
![]() $\Sigma $
is an F-spanning set (for
$\Sigma $
is an F-spanning set (for
![]() $\Gamma $
) if it satisfies the following axioms:
$\Gamma $
) if it satisfies the following axioms:
-
(i) For all
 $a\in \Gamma $
there is
$a\in \Gamma $
there is
 $\sigma \in \Sigma ^* $
such that
$\sigma \in \Sigma ^* $
such that
 $a = [\sigma ]_F$
.
$a = [\sigma ]_F$
. -
(ii)
 $0\in \Sigma $
, and if
$0\in \Sigma $
, and if
 $a\in \Sigma $
then
$a\in \Sigma $
then
 $-a\in \Sigma $
.
$-a\in \Sigma $
. -
(iii) If
 $a_1,\ldots ,a_5\in \Sigma $
then
$a_1,\ldots ,a_5\in \Sigma $
then
 $a_1+\cdots +a_5\in \Sigma +F\Sigma $
.
$a_1+\cdots +a_5\in \Sigma +F\Sigma $
. -
(iv) If
 $a_1,a_2,a_3\in \Sigma $
and
$a_1,a_2,a_3\in \Sigma $
and
 $a_1+a_2+a_3\in F\Gamma $
then
$a_1+a_2+a_3\in F\Gamma $
then
 $a_1+a_2+a_3\in F\Sigma $
.
$a_1+a_2+a_3\in F\Sigma $
.
Condition (i) is what allows us to make a sensible definition of F-automaticity: it says that every element of
![]() $\Gamma $
has an “F-expansion with digits in
$\Gamma $
has an “F-expansion with digits in
![]() $\Sigma $
.” Conditions (iii) and (iv) are somewhat technical. Roughly speaking, their main use is to constrain how addition and application of powers of F can affect the length of the shortest F-expansion of a given group element; see for example [Reference Bell and Moosa2, Lemma 5.3] and the proof of Proposition 3.8. The latter is the only place we will directly make use of condition (iii) or (iv); for more details on how they are used in establishing the basic properties of F-automatic sets, see [Reference Bell and Moosa2, Sections 5 and 6].
$\Sigma $
.” Conditions (iii) and (iv) are somewhat technical. Roughly speaking, their main use is to constrain how addition and application of powers of F can affect the length of the shortest F-expansion of a given group element; see for example [Reference Bell and Moosa2, Lemma 5.3] and the proof of Proposition 3.8. The latter is the only place we will directly make use of condition (iii) or (iv); for more details on how they are used in establishing the basic properties of F-automatic sets, see [Reference Bell and Moosa2, Sections 5 and 6].
Note that the existence of an F-spanning set will imply that
![]() $\Gamma $
is finitely generated as a
$\Gamma $
is finitely generated as a
![]() $\mathbb {Z}[F]$
-module, and that
$\mathbb {Z}[F]$
-module, and that
![]() $\Gamma /F\Gamma $
is finite.
$\Gamma /F\Gamma $
is finite.
It is pointed out in [Reference Bell and Moosa2, Lemmas 5.6 and 5.7] that for
![]() $r>0$
if
$r>0$
if
![]() $\Sigma $
is an F-spanning set then
$\Sigma $
is an F-spanning set then
![]() $[\Sigma ^{(r)}]_F$
is both an F-spanning set and an
$[\Sigma ^{(r)}]_F$
is both an F-spanning set and an
![]() $F^r$
-spanning set.Footnote
1
$F^r$
-spanning set.Footnote
1
Definition 2.5. We say
![]() $A\subseteq \Gamma $
is F-automatic if there is an
$A\subseteq \Gamma $
is F-automatic if there is an
![]() $F^r$
-spanning set
$F^r$
-spanning set
![]() $\Sigma $
for some
$\Sigma $
for some
![]() $r>0$
such that
$r>0$
such that
![]() $\{\sigma \in \Sigma ^* : [\sigma ]_{F^r} \in A\}$
is regular.
$\{\sigma \in \Sigma ^* : [\sigma ]_{F^r} \in A\}$
is regular.
The following is a useful strengthening of [Reference Bell and Moosa2, Proposition 6.3]:
Proposition 2.6. Suppose
![]() $A\subseteq \Gamma $
is F-automatic. Then for any
$A\subseteq \Gamma $
is F-automatic. Then for any
![]() $r>0$
and any
$r>0$
and any
![]() $F^r$
-spanning set
$F^r$
-spanning set
![]() $\Sigma $
,
$\Sigma $
,
![]() $\{\sigma \in \Sigma ^*:[\sigma ]_{F^r}\in A\}$
is regular.
$\{\sigma \in \Sigma ^*:[\sigma ]_{F^r}\in A\}$
is regular.
Proof By F-automaticity there is
![]() $r_0>0$
and an
$r_0>0$
and an
![]() $F^{r_0}$
-spanning set
$F^{r_0}$
-spanning set
![]() $\Sigma _0$
such that
$\Sigma _0$
such that
![]() $\{\sigma \in \Sigma _0^* : [\sigma ]_{F^{r_0}}\in A\}$
is regular. Now
$\{\sigma \in \Sigma _0^* : [\sigma ]_{F^{r_0}}\in A\}$
is regular. Now
![]() $\Theta := [\Sigma ^{(r_0)}]_{F^r}$
is an
$\Theta := [\Sigma ^{(r_0)}]_{F^r}$
is an
![]() $F^{rr_0}$
-spanning set, and by [Reference Bell and Moosa2, Proposition 6.3] we have that
$F^{rr_0}$
-spanning set, and by [Reference Bell and Moosa2, Proposition 6.3] we have that
![]() $\{\sigma \in \Theta ^* : [\sigma ]_{F^{rr_0}}\in A\}$
is regular. Suppose it is recognized by the automaton
$\{\sigma \in \Theta ^* : [\sigma ]_{F^{rr_0}}\in A\}$
is regular. Suppose it is recognized by the automaton
![]() $M=(\Theta ,Q,q_0,\Omega ,\delta )$
. Now define a new automaton
$M=(\Theta ,Q,q_0,\Omega ,\delta )$
. Now define a new automaton
![]() $M' = (\Sigma ,Q\times \Sigma ^{(<r_0)},(q_0,\epsilon ),\Omega ',\delta ')$
by
$M' = (\Sigma ,Q\times \Sigma ^{(<r_0)},(q_0,\epsilon ),\Omega ',\delta ')$
by
 $$ \begin{align*} \delta '((q,\sigma ), a) &= \begin{cases} (\delta (q,[\sigma a]_{F^r}),\epsilon ) &{\text{if }} {\lvert{\sigma } \rvert} = r_0-1, \\ (q,\sigma a) &{\text{if }} {\lvert{\sigma}\rvert}<r_0-1, \end{cases} \\ \Omega ' &= \{(q,\sigma ) : \delta (q,[\sigma ]_{F^r}) \in \Omega\}. \end{align*} $$
$$ \begin{align*} \delta '((q,\sigma ), a) &= \begin{cases} (\delta (q,[\sigma a]_{F^r}),\epsilon ) &{\text{if }} {\lvert{\sigma } \rvert} = r_0-1, \\ (q,\sigma a) &{\text{if }} {\lvert{\sigma}\rvert}<r_0-1, \end{cases} \\ \Omega ' &= \{(q,\sigma ) : \delta (q,[\sigma ]_{F^r}) \in \Omega\}. \end{align*} $$
(Note if
![]() ${\lvert \sigma \rvert } <r_0$
that
${\lvert \sigma \rvert } <r_0$
that
![]() $[\sigma ]_{F^r} = [\sigma 0^{r_0-{\lvert \sigma \rvert }}]_{F^r} \in \Theta $
, so
$[\sigma ]_{F^r} = [\sigma 0^{r_0-{\lvert \sigma \rvert }}]_{F^r} \in \Theta $
, so
![]() $\delta (q,[\sigma ]_{F^r})$
is defined.) Given
$\delta (q,[\sigma ]_{F^r})$
is defined.) Given
![]() $\sigma \in \Sigma ^*$
we can write
$\sigma \in \Sigma ^*$
we can write
![]() $\sigma =\sigma _1\cdots \sigma _{n+1}$
where
$\sigma =\sigma _1\cdots \sigma _{n+1}$
where
![]() ${\lvert {\sigma _1} \rvert }=\cdots ={\lvert {\sigma _n}\rvert } = r_0$
and
${\lvert {\sigma _1} \rvert }=\cdots ={\lvert {\sigma _n}\rvert } = r_0$
and
![]() ${\lvert {\sigma _{n+1}} \rvert }< r_0$
. Now,
${\lvert {\sigma _{n+1}} \rvert }< r_0$
. Now,
![]() $M'$
accepts
$M'$
accepts
![]() $\sigma $
if and only if M accepts
$\sigma $
if and only if M accepts
![]() $[\sigma _1]_{F^r}\cdots [\sigma _{n+1}]_{F^r}$
(where again
$[\sigma _1]_{F^r}\cdots [\sigma _{n+1}]_{F^r}$
(where again
![]() $[\sigma _{n+1}]_{F^r} = [\sigma _{n+1}0^{r_0-{\lvert {\sigma _{n+1}} \rvert }}]_{F^r}\in \Theta $
), which is in turn equivalent to
$[\sigma _{n+1}]_{F^r} = [\sigma _{n+1}0^{r_0-{\lvert {\sigma _{n+1}} \rvert }}]_{F^r}\in \Theta $
), which is in turn equivalent to
![]() $[\sigma ]_{F^r} = [[\sigma _1]_{F^r}\cdots [\sigma _{n+1}]_{F^r}]_{F^{rr_0}}\in A$
. So
$[\sigma ]_{F^r} = [[\sigma _1]_{F^r}\cdots [\sigma _{n+1}]_{F^r}]_{F^{rr_0}}\in A$
. So
![]() $M'$
recognizes
$M'$
recognizes
![]() $\{\sigma \in \Sigma ^*:[\sigma ]_{F^r}\in A\}$
, as desired.
$\{\sigma \in \Sigma ^*:[\sigma ]_{F^r}\in A\}$
, as desired.
3 Existence of spanning sets
We first study what it means for
![]() $\Gamma $
to admit an F-spanning set. It is clear in [Reference Bell and Moosa2] that the authors do not expect all finitely generated abelian groups to admit spanning sets, but no example was given. Here is one:
$\Gamma $
to admit an F-spanning set. It is clear in [Reference Bell and Moosa2] that the authors do not expect all finitely generated abelian groups to admit spanning sets, but no example was given. Here is one:
Example 3.1. Consider
![]() $\Gamma =\mathbb {Z}^2$
. Fix
$\Gamma =\mathbb {Z}^2$
. Fix
![]() $T\in M_2(\mathbb {Z})$
invertible and diagonalizable over
$T\in M_2(\mathbb {Z})$
invertible and diagonalizable over
![]() $\mathbb {C}$
, and with an eigenvalue
$\mathbb {C}$
, and with an eigenvalue
![]() $\mu $
with
$\mu $
with
![]() ${\lvert \mu \rvert } <1$
; for example
${\lvert \mu \rvert } <1$
; for example
 $T = \begin {pmatrix} 1 & 1 \\ 1 & 0 \end {pmatrix}$
. Let
$T = \begin {pmatrix} 1 & 1 \\ 1 & 0 \end {pmatrix}$
. Let
![]() $F\colon \mathbb {Z}^2\to \mathbb {Z}^2$
be the associated linear map on
$F\colon \mathbb {Z}^2\to \mathbb {Z}^2$
be the associated linear map on
![]() $\mathbb {Z}^2$
. Suppose for contradiction that there were an F-spanning set
$\mathbb {Z}^2$
. Suppose for contradiction that there were an F-spanning set
![]() $\Sigma $
for
$\Sigma $
for
![]() $\mathbb {Z}^2 $
. Let
$\mathbb {Z}^2 $
. Let
![]() $\{v,w\}\subseteq \mathbb {C}^2$
be an eigenbasis for T, say with
$\{v,w\}\subseteq \mathbb {C}^2$
be an eigenbasis for T, say with
![]() $Tv = \mu v$
and
$Tv = \mu v$
and
![]() $Tw = \nu w$
. Write each element of
$Tw = \nu w$
. Write each element of
![]() $\Sigma $
(uniquely) in the form
$\Sigma $
(uniquely) in the form
![]() $av+bw$
for
$av+bw$
for
![]() $a,b\in \mathbb {C}$
, and let M be the largest
$a,b\in \mathbb {C}$
, and let M be the largest
![]() ${\lvert a\rvert } $
obtained in this way. Given
${\lvert a\rvert } $
obtained in this way. Given
![]() $x\in \mathbb {Z}^2$
we can write
$x\in \mathbb {Z}^2$
we can write
 $$ \begin{align*}x = [s_0\cdots s_n]_F = \sum_{i=0}^n T^i(a_iv + b_iw) = \bigg( {\sum_{i=0}^n a_i\mu ^i}\bigg)v + \bigg( {\sum_{i=0}^n b_i\nu ^i}\bigg)w, \end{align*} $$
$$ \begin{align*}x = [s_0\cdots s_n]_F = \sum_{i=0}^n T^i(a_iv + b_iw) = \bigg( {\sum_{i=0}^n a_i\mu ^i}\bigg)v + \bigg( {\sum_{i=0}^n b_i\nu ^i}\bigg)w, \end{align*} $$
where
![]() $s_i = a_i v+ b_iw\in \Sigma $
. So by independence of
$s_i = a_i v+ b_iw\in \Sigma $
. So by independence of
![]() $\{v,w\}$
if we write
$\{v,w\}$
if we write
![]() $x = av + bw$
then
$x = av + bw$
then
 $$ \begin{align*}{\lvert a\rvert} = {\bigg\lvert{\sum_{i=0}^n a_i\mu ^i} \bigg\rvert} \le \sum_{i=0}^n {\lvert{a_i} \rvert} {\lvert\mu \rvert}^i \le M\sum_{i=0}^{\infty} {\lvert\mu \rvert}^i \le M(1-{\lvert\mu \rvert})^{-1}. \end{align*} $$
$$ \begin{align*}{\lvert a\rvert} = {\bigg\lvert{\sum_{i=0}^n a_i\mu ^i} \bigg\rvert} \le \sum_{i=0}^n {\lvert{a_i} \rvert} {\lvert\mu \rvert}^i \le M\sum_{i=0}^{\infty} {\lvert\mu \rvert}^i \le M(1-{\lvert\mu \rvert})^{-1}. \end{align*} $$
On the other hand, if we had
![]() $a\ne 0$
then since
$a\ne 0$
then since
![]() $\mathbb {Z}^2$
is closed under integer scaling there would be some
$\mathbb {Z}^2$
is closed under integer scaling there would be some
![]() $x\in \mathbb {Z}^2$
such that the corresponding a did not satisfy
$x\in \mathbb {Z}^2$
such that the corresponding a did not satisfy
![]() ${\lvert {a}\rvert } \le M(1-{\lvert {\mu }\rvert })^{-1}$
, a contradiction. So
${\lvert {a}\rvert } \le M(1-{\lvert {\mu }\rvert })^{-1}$
, a contradiction. So
![]() $a = 0$
, and
$a = 0$
, and
![]() $\mathbb {Z}^2\subseteq \mathbb {C}w$
, contradicting the fact that the
$\mathbb {Z}^2\subseteq \mathbb {C}w$
, contradicting the fact that the
![]() $\mathbb {C}$
-linear span of
$\mathbb {C}$
-linear span of
![]() $\mathbb {Z}^2$
is all of
$\mathbb {Z}^2$
is all of
![]() $\mathbb {C}^2$
. So no F-spanning set exists for
$\mathbb {C}^2$
. So no F-spanning set exists for
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Bell and Moosa [Reference Bell and Moosa2] give a sufficient condition for
![]() $\Gamma $
to admit an
$\Gamma $
to admit an
![]() $F^r$
-spanning set for some r (under the assumption that
$F^r$
-spanning set for some r (under the assumption that
![]() $\Gamma /F\Gamma $
is finite) in terms of the existence of what they call a height function on
$\Gamma /F\Gamma $
is finite) in terms of the existence of what they call a height function on
![]() $\Gamma $
. Our first goal is to show that this is also necessary.
$\Gamma $
. Our first goal is to show that this is also necessary.
Definition 3.2. A height function for
![]() $(\Gamma ,F) $
is a map
$(\Gamma ,F) $
is a map
![]() $h\colon \Gamma \to \mathbb {R}_{\ge 0}$
satisfying the following:
$h\colon \Gamma \to \mathbb {R}_{\ge 0}$
satisfying the following:
-
(Symmetry and triangle inequality) There are
 $\alpha ,\kappa {{\kern-1.5pt}\in{\kern-1.5pt}} \mathbb {R}$
with
$\alpha ,\kappa {{\kern-1.5pt}\in{\kern-1.5pt}} \mathbb {R}$
with
 $\alpha{{\kern-1.5pt}>{\kern-1.5pt}}1$
and
$\alpha{{\kern-1.5pt}>{\kern-1.5pt}}1$
and
 $\kappa{{\kern-1.5pt}>{\kern-1.5pt}}0$
such that
$\kappa{{\kern-1.5pt}>{\kern-1.5pt}}0$
such that
 $h(-a){{\kern-1.5pt}\le{\kern-1.5pt}} \alpha h(a)+\kappa $
and
$h(-a){{\kern-1.5pt}\le{\kern-1.5pt}} \alpha h(a)+\kappa $
and
 $h(a+b){{\kern-1.5pt}\le{\kern-1.5pt}} \alpha (h(a)+h(b))+\kappa $
for all
$h(a+b){{\kern-1.5pt}\le{\kern-1.5pt}} \alpha (h(a)+h(b))+\kappa $
for all
 $a,b{{\kern-1.5pt}\in{\kern-1.5pt}} \Gamma $
.
$a,b{{\kern-1.5pt}\in{\kern-1.5pt}} \Gamma $
. -
(Northcott property) For all
 $N\in \mathbb {N}$
there are finitely many
$N\in \mathbb {N}$
there are finitely many
 $a{{\kern-1.5pt}\in{\kern-1.5pt}} \Gamma $
with
$a{{\kern-1.5pt}\in{\kern-1.5pt}} \Gamma $
with
 $h(a){{\kern-1.5pt}\le{\kern-1.5pt}} N$
.
$h(a){{\kern-1.5pt}\le{\kern-1.5pt}} N$
. -
(Canonicity) There is
 $\beta \in \mathbb {R}$
with
$\beta \in \mathbb {R}$
with
 $\beta>1$
such that
$\beta>1$
such that
 $h(Fa)\ge \beta h(a)$
for cofinitely many
$h(Fa)\ge \beta h(a)$
for cofinitely many
 $a\in \Gamma $
.
$a\in \Gamma $
.
We will find it useful to work with a different class of functions on
![]() $\Gamma $
:
$\Gamma $
:
Definition 3.3. A length function for
![]() $(\Gamma ,F) $
is a map
$(\Gamma ,F) $
is a map
![]() $\lambda \colon \Gamma \to \mathbb {R}_{\ge 0}$
satisfying the following:
$\lambda \colon \Gamma \to \mathbb {R}_{\ge 0}$
satisfying the following:
-
(Symmetry)
 $\lambda (a) = \lambda (-a)$
for all
$\lambda (a) = \lambda (-a)$
for all
 $a\in \Gamma $
.
$a\in \Gamma $
. -
(Ultrametric inequality) There is
 $D\in \mathbb {R}$
with
$D\in \mathbb {R}$
with
 $D\ge 0$
such that
$D\ge 0$
such that
 $\lambda (a+b)\le \max (\lambda (a),\lambda (b))+D$
for all
$\lambda (a+b)\le \max (\lambda (a),\lambda (b))+D$
for all
 $a,b\in \Gamma $
.
$a,b\in \Gamma $
. -
(Northcott property) For all
 $N{{\kern-1.5pt}\in{\kern-1.5pt}} \mathbb {N}$
there are finitely many
$N{{\kern-1.5pt}\in{\kern-1.5pt}} \mathbb {N}$
there are finitely many
 $a{{\kern-1.5pt}\in{\kern-1.5pt}} \Gamma $
with
$a{{\kern-1.5pt}\in{\kern-1.5pt}} \Gamma $
with
 $\lambda (a)\le N$
.
$\lambda (a)\le N$
. -
(Logarithmic property) There is a finite exceptional set A and
 $C,E\in \mathbb {R}$
with
$C,E\in \mathbb {R}$
with
 $C>0$
and
$C>0$
and
 $E\ge 0$
such that
$E\ge 0$
such that-
•
 $\lambda (Fa)\le \lambda (a)+C$
for all
$\lambda (Fa)\le \lambda (a)+C$
for all
 $a\in \Gamma $
, and
$a\in \Gamma $
, and -
•
 $\lambda (F^na)\ge \lambda (a)+nC - E$
for all
$\lambda (F^na)\ge \lambda (a)+nC - E$
for all
 $a\in \Gamma \setminus A$
and
$a\in \Gamma \setminus A$
and
 $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
-
Note that if
![]() $\lambda $
satisfies all the axioms of being a length function besides symmetry, then
$\lambda $
satisfies all the axioms of being a length function besides symmetry, then
![]() $\lambda '(a) := \max (\lambda (a) , \lambda (-a))$
will be a length function.
$\lambda '(a) := \max (\lambda (a) , \lambda (-a))$
will be a length function.
There is an immediate connection between length functions and height functions. Suppose
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F)$
with exceptional set A and associated constants
$(\Gamma ,F)$
with exceptional set A and associated constants
![]() $C,D,E$
. Pick r so that
$C,D,E$
. Pick r so that
![]() $rC>E$
. It is then straightforward to check that
$rC>E$
. It is then straightforward to check that
![]() $h(a) := 2^{\lambda (a)} $
is a height function for
$h(a) := 2^{\lambda (a)} $
is a height function for
![]() $(\Gamma ,F^r)$
with exceptional set A and associated constants
$(\Gamma ,F^r)$
with exceptional set A and associated constants
![]() $\alpha =2^D$
,
$\alpha =2^D$
,
![]() $\beta = 2^{rC-E}$
, and
$\beta = 2^{rC-E}$
, and
![]() $\kappa =1$
. It is harder to derive a length function from a height function. One might attempt to reverse the above, and given a height function h ask whether
$\kappa =1$
. It is harder to derive a length function from a height function. One might attempt to reverse the above, and given a height function h ask whether
![]() $\lambda (a):= \log (h(a))$
is a length function. A first obstacle is that we might have
$\lambda (a):= \log (h(a))$
is a length function. A first obstacle is that we might have
![]() $h(a)<1$
, though this could be dealt with by setting
$h(a)<1$
, though this could be dealt with by setting
![]() $\lambda (a) = 0$
for such a. A more fundamental problem is that the axioms of height functions place no upper bound on
$\lambda (a) = 0$
for such a. A more fundamental problem is that the axioms of height functions place no upper bound on
![]() $h(Fa)$
in terms of
$h(Fa)$
in terms of
![]() $h(a)$
, whereas the axioms of length functions demand such a bound on
$h(a)$
, whereas the axioms of length functions demand such a bound on
![]() $\lambda (Fa)$
. We will see in Theorem 3.10, however, that the existence of a height function indeed implies the existence of a length function, and moreover that both are equivalent to the existence of a spanning set.
$\lambda (Fa)$
. We will see in Theorem 3.10, however, that the existence of a height function indeed implies the existence of a length function, and moreover that both are equivalent to the existence of a spanning set.
Remark 3.4. It will sometimes be convenient to assume that C is large compared to some function of D and E (and possibly other constants). If we are willing to pass from F to a power thereof, this can always be assumed: if
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F)$
with associated constants
$(\Gamma ,F)$
with associated constants
![]() $C,D,E$
, we can take r such that
$C,D,E$
, we can take r such that
![]() $rC$
satisfied the desired inequalities. Then
$rC$
satisfied the desired inequalities. Then
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F^r)$
with associated constants
$(\Gamma ,F^r)$
with associated constants
![]() $rC,D,E$
.
$rC,D,E$
.
Lemma 3.5. Suppose
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F)$
with exceptional set A and associated constants
$(\Gamma ,F)$
with exceptional set A and associated constants
![]() $C,D,E$
. By increasing E we can assume that every element of the exceptional set A has finite F-orbit.
$C,D,E$
. By increasing E we can assume that every element of the exceptional set A has finite F-orbit.
Proof Suppose the F-orbit of
![]() $a\in A$
is infinite; so there is
$a\in A$
is infinite; so there is
![]() $i_a$
such that
$i_a$
such that
![]() $F^{i_a}a\notin A$
. Now, for all
$F^{i_a}a\notin A$
. Now, for all
![]() $n\ge i_a$
we have
$n\ge i_a$
we have
 $$ \begin{align*}\lambda (F^na) &= \lambda (F^{n-i_a}F^{i_a}a) \ge \lambda (F^{i_a}a) + (n-i_a)C - E\\ &= \lambda (a) + nC - (\underbrace{E+ i_aC + \lambda (a)-\lambda (F^{i_a}a)}_*), \end{align*} $$
$$ \begin{align*}\lambda (F^na) &= \lambda (F^{n-i_a}F^{i_a}a) \ge \lambda (F^{i_a}a) + (n-i_a)C - E\\ &= \lambda (a) + nC - (\underbrace{E+ i_aC + \lambda (a)-\lambda (F^{i_a}a)}_*), \end{align*} $$
and for
![]() $n< i_a$
we have
$n< i_a$
we have
 $$ \begin{align*}\lambda (F^na) = \lambda (a) + nC - (\underbrace{nC + \lambda (a) - \lambda (F^na)}_*). \end{align*} $$
$$ \begin{align*}\lambda (F^na) = \lambda (a) + nC - (\underbrace{nC + \lambda (a) - \lambda (F^na)}_*). \end{align*} $$
Hence taking
![]() $E'$
to be the maximum of E and all the quantities marked
$E'$
to be the maximum of E and all the quantities marked
![]() $*$
, we get that
$*$
, we get that
![]() $\lambda (F^na)\ge \lambda (a)+ nC-E'$
so that a is no longer exceptional with respect to this new
$\lambda (F^na)\ge \lambda (a)+ nC-E'$
so that a is no longer exceptional with respect to this new
![]() $E'$
. Iterating this procedure for each
$E'$
. Iterating this procedure for each
![]() $a\in A$
with infinite F-orbit, we eventually produce a new
$a\in A$
with infinite F-orbit, we eventually produce a new
![]() $\widetilde {E}\ge E$
such that only the elements of A of finite F-orbit remain exceptional.
$\widetilde {E}\ge E$
such that only the elements of A of finite F-orbit remain exceptional.
Remark 3.6. If there is a length function for
![]() $(\Gamma ,F)$
and
$(\Gamma ,F)$
and
![]() $a\in \Gamma $
has finite F-orbit, then a must have finite order. Indeed, the F-orbit of
$a\in \Gamma $
has finite F-orbit, then a must have finite order. Indeed, the F-orbit of
![]() $ka$
is finite for all
$ka$
is finite for all
![]() $k\in \mathbb {N}$
; but the logarithmic property then implies that all
$k\in \mathbb {N}$
; but the logarithmic property then implies that all
![]() $ka$
lie in the finite exceptional set.
$ka$
lie in the finite exceptional set.
Combining Lemma 3.5 and Remark 3.6 we may assume the logarithmic property applies to all elements of infinite order.
Here is the motivating example of a length function.
Definition 3.7. If
![]() $\Sigma $
is an F-spanning set for
$\Sigma $
is an F-spanning set for
![]() $\Gamma $
, we define
$\Gamma $
, we define
![]() $\lambda _{\Sigma } \colon \Gamma \to \mathbb {R}_{\ge 0}$
by setting
$\lambda _{\Sigma } \colon \Gamma \to \mathbb {R}_{\ge 0}$
by setting
![]() $\lambda _{\Sigma } (a)$
to be the length of the shortest
$\lambda _{\Sigma } (a)$
to be the length of the shortest
![]() $\sigma \in \Sigma ^*$
such that
$\sigma \in \Sigma ^*$
such that
![]() $[\sigma ]_F = a$
.
$[\sigma ]_F = a$
.
Proposition 3.8. If
![]() $\Sigma $
is an F-spanning set for
$\Sigma $
is an F-spanning set for
![]() $\Gamma $
then
$\Gamma $
then
![]() $\lambda _{\Sigma } $
is a length function for
$\lambda _{\Sigma } $
is a length function for
![]() $(\Gamma ,F)$
with associated constants
$(\Gamma ,F)$
with associated constants
![]() $C=D=E=1$
and exceptional set
$C=D=E=1$
and exceptional set
![]() $\Sigma $
.
$\Sigma $
.
Proof We verify the axioms. Symmetry of
![]() $\lambda _{\Sigma } $
is simply by symmetry of
$\lambda _{\Sigma } $
is simply by symmetry of
![]() $\Sigma $
. Lemma 5.3 of [Reference Bell and Moosa2] implies that the ultrametric inequality holds of
$\Sigma $
. Lemma 5.3 of [Reference Bell and Moosa2] implies that the ultrametric inequality holds of
![]() $\lambda _{\Sigma } $
with
$\lambda _{\Sigma } $
with
![]() $D=1$
. Since
$D=1$
. Since
![]() $\Sigma $
is finite there are finitely many
$\Sigma $
is finite there are finitely many
![]() $\sigma \in \Sigma ^*$
of length
$\sigma \in \Sigma ^*$
of length
![]() $\le N$
, and hence
$\le N$
, and hence
![]() $\lambda _{\Sigma } $
satisfies the Northcott property. Finally, we prove that
$\lambda _{\Sigma } $
satisfies the Northcott property. Finally, we prove that
![]() $\lambda _{\Sigma } $
satisfies the logarithmic property with
$\lambda _{\Sigma } $
satisfies the logarithmic property with
![]() $C=E=1$
and exceptional set
$C=E=1$
and exceptional set
![]() $\Sigma $
. For the upper bound, note that if
$\Sigma $
. For the upper bound, note that if
![]() $a = [s_0\cdots s_{\ell } ]_F$
with
$a = [s_0\cdots s_{\ell } ]_F$
with
![]() $s_0,\ldots ,s_{\ell } \in \Sigma $
then
$s_0,\ldots ,s_{\ell } \in \Sigma $
then
![]() $Fa = [0s_0\cdots s_{\ell } ]_F$
; so
$Fa = [0s_0\cdots s_{\ell } ]_F$
; so
![]() $\lambda _{\Sigma } (Fa)\le \lambda _{\Sigma } (a)+1$
. It remains to show the lower bound.
$\lambda _{\Sigma } (Fa)\le \lambda _{\Sigma } (a)+1$
. It remains to show the lower bound.
Suppose
![]() $a\notin \Sigma $
. Write
$a\notin \Sigma $
. Write
![]() $\lambda _{\Sigma } (a) = \ell $
for some
$\lambda _{\Sigma } (a) = \ell $
for some
![]() $\ell>1$
; say
$\ell>1$
; say
![]() $a = [s_0\cdots s_{\ell -1}]_F$
. Suppose for contradiction that
$a = [s_0\cdots s_{\ell -1}]_F$
. Suppose for contradiction that
![]() $\lambda _{\Sigma } (F^ma) < m+\ell -1 $
; so we can write
$\lambda _{\Sigma } (F^ma) < m+\ell -1 $
; so we can write
![]() $F^ma = [t_0\cdots t_{m+\ell -3}]_F$
. Then
$F^ma = [t_0\cdots t_{m+\ell -3}]_F$
. Then
Then
![]() $t_0\in F\Gamma $
, so by axiom (iv) we get that
$t_0\in F\Gamma $
, so by axiom (iv) we get that
![]() $t_0 = Ft_0^{\prime }$
for some
$t_0 = Ft_0^{\prime }$
for some
![]() $t_0^{\prime }\in \Sigma $
. Inductively suppose for some
$t_0^{\prime }\in \Sigma $
. Inductively suppose for some
![]() $i<m-1$
we can write
$i<m-1$
we can write
![]() $t_0 + \cdots + F^it_i = F^{i+1}t_i^{\prime }$
for some
$t_0 + \cdots + F^it_i = F^{i+1}t_i^{\prime }$
for some
![]() $t_i^{\prime }\in \Sigma $
. Then
$t_i^{\prime }\in \Sigma $
. Then
![]() $F^{i+1}(t_i^{\prime }+t_{i+1}) = t_0 + \cdots + F^{i+1}t_{i+1}$
which can be seen to be in
$F^{i+1}(t_i^{\prime }+t_{i+1}) = t_0 + \cdots + F^{i+1}t_{i+1}$
which can be seen to be in
![]() $ F^{i+2}\Gamma $
using Equation (1) and the fact that
$ F^{i+2}\Gamma $
using Equation (1) and the fact that
![]() $m\ge i+2$
. Hence
$m\ge i+2$
. Hence
![]() $t_i^{\prime }+t_{i+1}\in F\Gamma $
by injectivity of F, and again by axiom (iv) we can write
$t_i^{\prime }+t_{i+1}\in F\Gamma $
by injectivity of F, and again by axiom (iv) we can write
![]() $t_i^{\prime }+t_{i+1} = Ft_{i+1}^{\prime }$
for some
$t_i^{\prime }+t_{i+1} = Ft_{i+1}^{\prime }$
for some
![]() $t_{i+1}\in \Sigma $
. So
$t_{i+1}\in \Sigma $
. So
 $t_0 + \cdots + F^{i+1}t_{i+1} = F^{i+2}t_{i+1}^{\prime }$
. It follows that
$t_0 + \cdots + F^{i+1}t_{i+1} = F^{i+2}t_{i+1}^{\prime }$
. It follows that
 $t_0+\cdots +F^{m-1}t_{m-1} = F^mt_{m-1}^{\prime }$
for some
$t_0+\cdots +F^{m-1}t_{m-1} = F^mt_{m-1}^{\prime }$
for some
![]() $t_{m-1}^{\prime }\in \Sigma $
. (Note
$t_{m-1}^{\prime }\in \Sigma $
. (Note
![]() $t_{m-1}$
is defined since
$t_{m-1}$
is defined since
![]() $\ell \ge 2$
.) So
$\ell \ge 2$
.) So
 $F^ma = F^mt_{m-1}^{\prime } + F^mt_m + \cdots + F^{m+\ell -3}t_{m+\ell -3}$
, and thus
$F^ma = F^mt_{m-1}^{\prime } + F^mt_m + \cdots + F^{m+\ell -3}t_{m+\ell -3}$
, and thus
 $$ \begin{align*}a = t_{m-1}^{\prime} + (t_m + \cdots + F^{\ell -3}t_{m+\ell -3}). \end{align*} $$
$$ \begin{align*}a = t_{m-1}^{\prime} + (t_m + \cdots + F^{\ell -3}t_{m+\ell -3}). \end{align*} $$
Hence by [Reference Bell and Moosa2, Lemma 5.3] we get that a can be represented by a string of length
![]() $\le \ell -1$
, contradicting our assumption that
$\le \ell -1$
, contradicting our assumption that
![]() $\lambda _{\Sigma } (a) = \ell $
.
$\lambda _{\Sigma } (a) = \ell $
.
We will want to use a result of [Reference Bell and Moosa2] to deduce that the existence of a height function implies the existence of a spanning set. To do so we will need to know that
![]() $\Gamma /F^r\Gamma $
is finite for all r.
$\Gamma /F^r\Gamma $
is finite for all r.
Lemma 3.9. Suppose
![]() $S\subseteq \Gamma $
contains a representative of each coset of
$S\subseteq \Gamma $
contains a representative of each coset of
![]() $F\Gamma $
. Then
$F\Gamma $
. Then
 $$ \begin{align*}[S^{(r)}]_F = \{s_0+\cdots +F^{r-1}s_{r-1} : s_0,\ldots ,s_{r-1}\in S\} \end{align*} $$
$$ \begin{align*}[S^{(r)}]_F = \{s_0+\cdots +F^{r-1}s_{r-1} : s_0,\ldots ,s_{r-1}\in S\} \end{align*} $$
contains a representative of each coset of
![]() $F^r\Gamma $
. In particular, if
$F^r\Gamma $
. In particular, if
![]() $\Gamma /F\Gamma $
is finite then so too is
$\Gamma /F\Gamma $
is finite then so too is
![]() $\Gamma /F^r\Gamma $
for all
$\Gamma /F^r\Gamma $
for all
![]() $r>0$
.
$r>0$
.
Proof Given
![]() $a\in \Gamma $
we can find
$a\in \Gamma $
we can find
![]() $s_0\in S$
such that
$s_0\in S$
such that
![]() $a\equiv s_0{\pmod {F\Gamma }}$
. Then inductively we can find
$a\equiv s_0{\pmod {F\Gamma }}$
. Then inductively we can find
![]() $s_1,\ldots ,s_{r-1}\in S$
such that
$s_1,\ldots ,s_{r-1}\in S$
such that
![]() $F^{-1}(a-s_0)\equiv s_1+\cdots +F^{r-2}s_{r-1}{\pmod {F^{r-1}\Gamma }}$
, at which point it follows that
$F^{-1}(a-s_0)\equiv s_1+\cdots +F^{r-2}s_{r-1}{\pmod {F^{r-1}\Gamma }}$
, at which point it follows that
![]() $a\equiv s_0+\cdots + F^{r-1}s_{r-1}{\pmod {F^r\Gamma }}$
.
$a\equiv s_0+\cdots + F^{r-1}s_{r-1}{\pmod {F^r\Gamma }}$
.
Putting all this together, we deduce the following characterization for the existence of spanning sets, which in particular provides a converse to [Reference Bell and Moosa2, Proposition 5.8].
Theorem 3.10. Suppose
![]() $\Gamma /F\Gamma $
is finite. The following are equivalent
$\Gamma /F\Gamma $
is finite. The following are equivalent
![]() $:$
$:$
-
1.
 $\Gamma $
admits an
$\Gamma $
admits an
 $F^r$
-spanning set for some
$F^r$
-spanning set for some
 $r>0$
.
$r>0$
. -
2. There is a length function for some
 $(\Gamma ,F^r)$
.
$(\Gamma ,F^r)$
. -
3. There is a height function for some
 $(\Gamma ,F^r)$
.
$(\Gamma ,F^r)$
.
Proof (1)
![]() $\implies $
(2) is Proposition 3.8, and we noted (2)
$\implies $
(2) is Proposition 3.8, and we noted (2)
![]() $\implies $
(3) after the definition of length functions. For (3)
$\implies $
(3) after the definition of length functions. For (3)
![]() $\implies $
(1), we appeal to [Reference Bell and Moosa2, Proposition 5.8]. Formally they require that
$\implies $
(1), we appeal to [Reference Bell and Moosa2, Proposition 5.8]. Formally they require that
![]() $\Gamma $
be finitely generated as a group, but this is only used to deduce that
$\Gamma $
be finitely generated as a group, but this is only used to deduce that
![]() $\Gamma /F^r\Gamma $
is finite for all r; by Lemma 3.9 we can assume as much from the fact that
$\Gamma /F^r\Gamma $
is finite for all r; by Lemma 3.9 we can assume as much from the fact that
![]() $\Gamma /F\Gamma $
is finite.
$\Gamma /F\Gamma $
is finite.
Corollary 3.11. Suppose there is an
![]() $F^r$
-spanning set for
$F^r$
-spanning set for
![]() $\Gamma $
for some
$\Gamma $
for some
![]() $r>0$
and
$r>0$
and
![]() $H\le \Gamma $
is F-invariant. Then there is an
$H\le \Gamma $
is F-invariant. Then there is an
![]() $F^s$
-spanning set for H for some
$F^s$
-spanning set for H for some
![]() $s>0$
. Furthermore if
$s>0$
. Furthermore if
![]() $A\subseteq H$
then A is F-automatic in
$A\subseteq H$
then A is F-automatic in
![]() $\Gamma $
if and only A is F-automatic in H.
$\Gamma $
if and only A is F-automatic in H.
Proof By Theorem 3.10 there is a length function
![]() $\lambda $
for some
$\lambda $
for some
![]() $(\Gamma ,F^r)$
. One can check that
$(\Gamma ,F^r)$
. One can check that
![]() $\lambda \restriction H$
is a length function for
$\lambda \restriction H$
is a length function for
![]() $(H,(F\restriction H)^r)$
. So again by Theorem 3.10 there is an
$(H,(F\restriction H)^r)$
. So again by Theorem 3.10 there is an
![]() $F^s$
-spanning set for H for some
$F^s$
-spanning set for H for some
![]() $s>0$
.
$s>0$
.
For the “furthermore,” note by the above and [Reference Bell and Moosa2, Lemmas 5.6 and 5.7] there is s such that there is an
![]() $F^s$
-spanning set
$F^s$
-spanning set
![]() $\Sigma $
for
$\Sigma $
for
![]() $H $
that is contained in an
$H $
that is contained in an
![]() $F^s$
-spanning set
$F^s$
-spanning set
![]() $\Sigma '$
for
$\Sigma '$
for
![]() $\Gamma $
. The right-to-left direction then follows from [Reference Bell and Moosa2, Proposition 6.8(b)]. For the left-to-right, note that
$\Gamma $
. The right-to-left direction then follows from [Reference Bell and Moosa2, Proposition 6.8(b)]. For the left-to-right, note that
![]() $\{\sigma \in \Sigma ^* : [\sigma ]_{F^s}\in A\} = \{\sigma \in (\Sigma ')^* : [\sigma ]_{F^s}\in A\}\cap \Sigma ^*$
is the intersection of two regular languages, and is thus regular (see [Reference Yu7, Theorem 2.1]); so A is F-automatic in H.
$\{\sigma \in \Sigma ^* : [\sigma ]_{F^s}\in A\} = \{\sigma \in (\Sigma ')^* : [\sigma ]_{F^s}\in A\}\cap \Sigma ^*$
is the intersection of two regular languages, and is thus regular (see [Reference Yu7, Theorem 2.1]); so A is F-automatic in H.
In fact when
![]() $\Gamma $
is a finitely generated abelian group, we can use the above to deduce a concrete and verifiable characterization of the existence of spanning sets.
$\Gamma $
is a finitely generated abelian group, we can use the above to deduce a concrete and verifiable characterization of the existence of spanning sets.
Theorem 3.12. Suppose
![]() $\Gamma $
is a finitely generated abelian group. Then
$\Gamma $
is a finitely generated abelian group. Then
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
if and only if the eigenvalues of
$r>0$
if and only if the eigenvalues of
![]() $F\otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}}$
(viewed as a linear map on the
$F\otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}}$
(viewed as a linear map on the
![]() $\mathbb {C}$
-vector space
$\mathbb {C}$
-vector space
![]() $\Gamma \otimes _{\mathbb {Z}}\mathbb {C})$
all have modulus
$\Gamma \otimes _{\mathbb {Z}}\mathbb {C})$
all have modulus
![]() $>1$
.
$>1$
.
We will want to restrict our attention to the torsion-free case; the following lemma tells us that the torsion subgroup can be ignored for the purposes of determining whether there is a spanning set.
Lemma 3.13. Suppose
![]() $\Gamma $
is a finitely generated abelian group
$\Gamma $
is a finitely generated abelian group
![]() $;$
write
$;$
write
![]() $\Gamma =\Gamma _0\times H$
where
$\Gamma =\Gamma _0\times H$
where
![]() $\Gamma _0$
is torsion-free and H is finite. Let
$\Gamma _0$
is torsion-free and H is finite. Let
![]() $\pi \colon \Gamma \to \Gamma _0$
be the projection, and let
$\pi \colon \Gamma \to \Gamma _0$
be the projection, and let
![]() $F_0\colon \Gamma _0\to \Gamma _0$
be the map induced by F. Then
$F_0\colon \Gamma _0\to \Gamma _0$
be the map induced by F. Then
-
1.
 $\pi ([s_0\cdots s_n]_F) = [(\pi (s_0))\cdots (\pi (s_n))]_{F_0}$
for
$\pi ([s_0\cdots s_n]_F) = [(\pi (s_0))\cdots (\pi (s_n))]_{F_0}$
for
 $s_0,\ldots ,s_n\in \Gamma $
.
$s_0,\ldots ,s_n\in \Gamma $
. -
2. If
 $\Sigma $
is an F-spanning set for
$\Sigma $
is an F-spanning set for
 $\Gamma $
then
$\Gamma $
then
 $\pi (\Sigma )$
is an
$\pi (\Sigma )$
is an
 $F_0$
-spanning set for
$F_0$
-spanning set for
 $\Gamma _0$
.
$\Gamma _0$
. -
3. If
 $\Sigma _0 $
is an
$\Sigma _0 $
is an
 $F_0$
-spanning set for
$F_0$
-spanning set for
 $\Gamma _0$
then
$\Gamma _0$
then
 $\pi ^{-1}(\Sigma _0 )$
is an F-spanning set for
$\pi ^{-1}(\Sigma _0 )$
is an F-spanning set for
 $\Gamma $
.
$\Gamma $
.
Proof Note first that since F is injective and H is finite we get that
![]() $FH = H$
; so there is indeed a well-defined and injective
$FH = H$
; so there is indeed a well-defined and injective
![]() $F_0\colon \Gamma _0\to \Gamma _0$
that satisfies
$F_0\colon \Gamma _0\to \Gamma _0$
that satisfies
![]() $\pi \circ F=F_0\circ \pi $
.
$\pi \circ F=F_0\circ \pi $
.
-
1. Note that
 $\pi ([s_0\cdots s_n]_F) {{\kern-1.5pt}={\kern-1.5pt}} \pi (s_0) + \pi (Fs_1) + \cdots + \pi (F^ns_n) {{\kern-1.5pt}={\kern-1.5pt}} \pi (s_0) + F_0(\pi (s_1)) + \cdots + F_0^n(\pi (s_n)) {{\kern-1.5pt}={\kern-1.5pt}} [(\pi (s_0))\cdots (\pi (s_n))]_{F_0}$
.
$\pi ([s_0\cdots s_n]_F) {{\kern-1.5pt}={\kern-1.5pt}} \pi (s_0) + \pi (Fs_1) + \cdots + \pi (F^ns_n) {{\kern-1.5pt}={\kern-1.5pt}} \pi (s_0) + F_0(\pi (s_1)) + \cdots + F_0^n(\pi (s_n)) {{\kern-1.5pt}={\kern-1.5pt}} [(\pi (s_0))\cdots (\pi (s_n))]_{F_0}$
. -
2. Suppose
 $\Sigma $
is an F-spanning set for
$\Sigma $
is an F-spanning set for
 $\Gamma $
; we verify that
$\Gamma $
; we verify that
 $\pi (\Sigma )$
satisfies the axioms.
$\pi (\Sigma )$
satisfies the axioms.-
(i) Suppose
 $a\in \Gamma _0$
. Since
$a\in \Gamma _0$
. Since
 $\Sigma $
satisfies axiom (i) there is
$\Sigma $
satisfies axiom (i) there is
 $s_0\cdots s_n \in \Sigma ^*$
such that
$s_0\cdots s_n \in \Sigma ^*$
such that
 $[s_0\cdots s_n]_F = a$
. Then by part (1) we get that
$[s_0\cdots s_n]_F = a$
. Then by part (1) we get that
 $a = \pi (a) = [(\pi (s_0))\cdots (\pi (s_n))]_{F_0}$
.
$a = \pi (a) = [(\pi (s_0))\cdots (\pi (s_n))]_{F_0}$
. -
(ii) Since
 $0\in \Sigma $
we get that
$0\in \Sigma $
we get that
 $0=\pi (0)\in \pi (\Sigma )$
. If
$0=\pi (0)\in \pi (\Sigma )$
. If
 $\pi (a)\in \pi (\Sigma )$
then since
$\pi (a)\in \pi (\Sigma )$
then since
 $\Sigma $
satisfies axiom (ii) we get that
$\Sigma $
satisfies axiom (ii) we get that
 $-a\in \Sigma $
, and hence
$-a\in \Sigma $
, and hence
 $-\pi (a)\in \pi (\Sigma )$
.
$-\pi (a)\in \pi (\Sigma )$
. -
(iii) Suppose
 $\pi (a_1),\ldots ,\pi (a_5)\in \pi (\Sigma )$
. Since
$\pi (a_1),\ldots ,\pi (a_5)\in \pi (\Sigma )$
. Since
 $\Sigma $
satisfies axiom (iii) there are
$\Sigma $
satisfies axiom (iii) there are
 $b_0,b_1\in \Sigma $
such that
$b_0,b_1\in \Sigma $
such that
 $a_1+\cdots +a_5 = b_0 + Fb_1$
. Then
$a_1+\cdots +a_5 = b_0 + Fb_1$
. Then
 $\pi (a_1)+\cdots +\pi (a_5) = \pi (b_0) + \pi (Fb_1) = \pi (b_0) + F_0(\pi (b_1))\in \pi (\Sigma ) + F_0(\pi (\Sigma ))$
, as desired.
$\pi (a_1)+\cdots +\pi (a_5) = \pi (b_0) + \pi (Fb_1) = \pi (b_0) + F_0(\pi (b_1))\in \pi (\Sigma ) + F_0(\pi (\Sigma ))$
, as desired. -
(iv) Suppose
 $\pi (a_1),\pi (a_2),\pi (a_3)\in \pi (\Sigma )$
and
$\pi (a_1),\pi (a_2),\pi (a_3)\in \pi (\Sigma )$
and
 $\pi (a_1)+ \pi (a_2) + \pi (a_3) = F_0b$
for some
$\pi (a_1)+ \pi (a_2) + \pi (a_3) = F_0b$
for some
 $b\in \Gamma _0$
. Then
$b\in \Gamma _0$
. Then
 $\pi (a_1+a_2+a_3) = F_0(\pi (b)) = \pi (Fb)$
, so there is
$\pi (a_1+a_2+a_3) = F_0(\pi (b)) = \pi (Fb)$
, so there is
 $h\in H$
such that
$h\in H$
such that
 $a_1+a_2+a_3 = Fb + h$
. Since F is bijective on H, there is
$a_1+a_2+a_3 = Fb + h$
. Since F is bijective on H, there is
 $h_0\in H$
such that
$h_0\in H$
such that
 $Fh_0 = h$
. So
$Fh_0 = h$
. So
 $a_1+a_2+a_3 = F(b+h_0)$
; thus since
$a_1+a_2+a_3 = F(b+h_0)$
; thus since
 $\Sigma $
satisfies axiom (iv) we get that
$\Sigma $
satisfies axiom (iv) we get that
 $b+h_0\in \Sigma $
, and hence that
$b+h_0\in \Sigma $
, and hence that
 $b=\pi (b+h_0) \in \pi (\Sigma )$
.
$b=\pi (b+h_0) \in \pi (\Sigma )$
.
-
-
3. Suppose
 $\Sigma _0 $
is an
$\Sigma _0 $
is an
 $F_0$
-spanning set for
$F_0$
-spanning set for
 $\Gamma _0 $
; we verify that
$\Gamma _0 $
; we verify that
 $\pi ^{-1}(\Sigma _0 )$
satisfies the axioms.
$\pi ^{-1}(\Sigma _0 )$
satisfies the axioms.-
(i) Suppose
 $a\in \Gamma $
. Since
$a\in \Gamma $
. Since
 $\Sigma _0 $
satisfies axiom (i) there is
$\Sigma _0 $
satisfies axiom (i) there is
 $s_0\cdots s_n\in \Sigma _0^*$
such that
$s_0\cdots s_n\in \Sigma _0^*$
such that
 $\pi (a) = [s_0\cdots s_n]_{F_0} = [(\pi (s_0))\cdots (\pi (s_n))]_{F_0} = \pi ([s_0\cdots s_n]_F)$
(since each
$\pi (a) = [s_0\cdots s_n]_{F_0} = [(\pi (s_0))\cdots (\pi (s_n))]_{F_0} = \pi ([s_0\cdots s_n]_F)$
(since each
 $s_i\in \Sigma _0\subseteq \Gamma _0$
). Let
$s_i\in \Sigma _0\subseteq \Gamma _0$
). Let
 $h=a-[s_0\cdots s_n]_F\in H$
. Then
$h=a-[s_0\cdots s_n]_F\in H$
. Then
 $a = h + [s_0\cdots s_n]_F = [(s_0+h)s_1\cdots s_n]_F$
and
$a = h + [s_0\cdots s_n]_F = [(s_0+h)s_1\cdots s_n]_F$
and
 $s_0+h,s_1,\ldots ,s_n\in \pi ^{-1}(\Sigma _0)$
, as desired.
$s_0+h,s_1,\ldots ,s_n\in \pi ^{-1}(\Sigma _0)$
, as desired. -
(ii) Since
 $0\in \Sigma _0$
we get that
$0\in \Sigma _0$
we get that
 $0 \in \pi ^{-1}(0)\subseteq \pi ^{-1}(\Sigma _0)$
. If
$0 \in \pi ^{-1}(0)\subseteq \pi ^{-1}(\Sigma _0)$
. If
 $a+h\in \pi ^{-1}(\Sigma _0)$
with
$a+h\in \pi ^{-1}(\Sigma _0)$
with
 $a\in \Sigma _0$
and
$a\in \Sigma _0$
and
 $h\in H$
, then since
$h\in H$
, then since
 $\Sigma _0$
satisfies axiom (ii) we get that
$\Sigma _0$
satisfies axiom (ii) we get that
 $-a\in \Sigma _0$
, and hence
$-a\in \Sigma _0$
, and hence
 $-(a+h)\in \pi ^{-1}(\Sigma _0)$
.
$-(a+h)\in \pi ^{-1}(\Sigma _0)$
. -
(iii) Suppose
 $a_1+h_1,\ldots ,a_5+h_5\in \pi ^{-1}(\Sigma _0)$
with each
$a_1+h_1,\ldots ,a_5+h_5\in \pi ^{-1}(\Sigma _0)$
with each
 $a_i\in \Sigma _0$
and each
$a_i\in \Sigma _0$
and each
 $h_i\in H$
. Since
$h_i\in H$
. Since
 $\Sigma _0$
satisfies axiom (iii) there are
$\Sigma _0$
satisfies axiom (iii) there are
 $b_0,b_1\in \Sigma _0$
such that for some
$b_0,b_1\in \Sigma _0$
such that for some $$ \begin{align*}a_1+\cdots +a_5 {{\kern-1pt}={\kern-1pt}} b_0 + F_0b_1 {{\kern-1pt}={\kern-1pt}} b_0 + F_0(\pi (b_1)) {{\kern-1pt}={\kern-1pt}} b_0 + \pi (Fb_1) {{\kern-1pt}={\kern-1pt}} b_0 + Fb_1 + h, \end{align*} $$
$$ \begin{align*}a_1+\cdots +a_5 {{\kern-1pt}={\kern-1pt}} b_0 + F_0b_1 {{\kern-1pt}={\kern-1pt}} b_0 + F_0(\pi (b_1)) {{\kern-1pt}={\kern-1pt}} b_0 + \pi (Fb_1) {{\kern-1pt}={\kern-1pt}} b_0 + Fb_1 + h, \end{align*} $$
 $h\in H$
. Then and
$h\in H$
. Then and $$ \begin{align*}(a_1+h_1)+\cdots +(a_5+h_5) = (b_0+ h_1+h_2+\cdots +h_5+h) + Fb_1 \end{align*} $$
$$ \begin{align*}(a_1+h_1)+\cdots +(a_5+h_5) = (b_0+ h_1+h_2+\cdots +h_5+h) + Fb_1 \end{align*} $$
 $b_0+h_1+h_2+\cdots +h_5+h, b_1\in \pi ^{-1}(\Sigma _0)$
.
$b_0+h_1+h_2+\cdots +h_5+h, b_1\in \pi ^{-1}(\Sigma _0)$
.
-
(iv) Suppose
 $a_1+h_1,a_2+h_2,a_3+h_3\in \pi ^{-1}(\Sigma _0)$
with each
$a_1+h_1,a_2+h_2,a_3+h_3\in \pi ^{-1}(\Sigma _0)$
with each
 $a_i\in \Sigma _0$
and each
$a_i\in \Sigma _0$
and each
 $h_i\in H$
; suppose further that
$h_i\in H$
; suppose further that
 $(a_1+h_1) + (a_2+h_2) + (a_3+h_3) = Fb$
for some
$(a_1+h_1) + (a_2+h_2) + (a_3+h_3) = Fb$
for some
 $b\in \Gamma $
. Then
$b\in \Gamma $
. Then
 $a_1+a_2+a_3 = \pi (Fb) = F_0(\pi (b))$
; thus since
$a_1+a_2+a_3 = \pi (Fb) = F_0(\pi (b))$
; thus since
 $\Sigma _0$
satisfies axiom (iv) we get that
$\Sigma _0$
satisfies axiom (iv) we get that
 $\pi (b)\in \Sigma _0$
, and
$\pi (b)\in \Sigma _0$
, and
 $b\in \pi ^{-1}(\Sigma _0)$
.
$b\in \pi ^{-1}(\Sigma _0)$
.
-
Proof of Theorem 3.12 We first reduce to the torsion-free case. By the fundamental theorem of finitely generated abelian groups we may assume
![]() $\Gamma =\mathbb {Z}^m \times H$
where H is a finite group; let
$\Gamma =\mathbb {Z}^m \times H$
where H is a finite group; let
![]() $\pi \colon \Gamma \to \mathbb {Z}^m$
be the projection. Let
$\pi \colon \Gamma \to \mathbb {Z}^m$
be the projection. Let
![]() $F_0$
be the endomorphism of
$F_0$
be the endomorphism of
![]() $\mathbb {Z}^m$
induced by F; note then that
$\mathbb {Z}^m$
induced by F; note then that
![]() $F_0^r$
is the endomorphism of
$F_0^r$
is the endomorphism of
![]() $\mathbb {Z}^m$
induced by
$\mathbb {Z}^m$
induced by
![]() $F^r$
. So by Lemma 3.13
$F^r$
. So by Lemma 3.13
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
if and only if
$r>0$
if and only if
![]() $\mathbb {Z}^m$
admits an
$\mathbb {Z}^m$
admits an
![]() $F_0^r$
-spanning set for some
$F_0^r$
-spanning set for some
![]() $r>0$
. Moreover under the identification
$r>0$
. Moreover under the identification
![]() $\Gamma \otimes _{\mathbb {Z}}\mathbb {C}=\mathbb {Z}^m\otimes _{\mathbb {Z}}\mathbb {C}$
we have that
$\Gamma \otimes _{\mathbb {Z}}\mathbb {C}=\mathbb {Z}^m\otimes _{\mathbb {Z}}\mathbb {C}$
we have that
![]() $F\otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}} \sim F_0\otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}}$
, and in particular they have the same eigenvalues.
$F\otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}} \sim F_0\otimes _{\mathbb {Z}}\operatorname {\mathrm {id}}_{\mathbb {C}}$
, and in particular they have the same eigenvalues.
We may therefore assume
![]() $\Gamma =\mathbb {Z}^m$
for some m and
$\Gamma =\mathbb {Z}^m$
for some m and
![]() $F\in M_m(\mathbb {Z})$
.
$F\in M_m(\mathbb {Z})$
.
-
 $(\impliedby )$
By replacing F with a power, we may assume
$(\impliedby )$
By replacing F with a power, we may assume
 ${\lvert \mu \rvert }>2$
for all
${\lvert \mu \rvert }>2$
for all
 $\mu \in \sigma (F)$
. We show there exists a height function for
$\mu \in \sigma (F)$
. We show there exists a height function for
 $(\Gamma ,F)$
. Pick a basis
$(\Gamma ,F)$
. Pick a basis
 $\{e_1,\ldots ,e_m \}$
for
$\{e_1,\ldots ,e_m \}$
for
 $\mathbb {C}^m$
that puts F in Jordan canonical form. Let
$\mathbb {C}^m$
that puts F in Jordan canonical form. Let
 $h\colon \mathbb {C}^m\to \mathbb {R}_{\ge 0}$
be the infinity norm associated with
$h\colon \mathbb {C}^m\to \mathbb {R}_{\ge 0}$
be the infinity norm associated with
 $\{e_1,\ldots ,e_m\}$
: so
$\{e_1,\ldots ,e_m\}$
: so
 $h(a_1e_1+\cdots +a_me_m) = \max _i {\lvert {a_i}\rvert }$
. We show that
$h(a_1e_1+\cdots +a_me_m) = \max _i {\lvert {a_i}\rvert }$
. We show that
 $h\restriction \mathbb {Z}^m$
is a height function for
$h\restriction \mathbb {Z}^m$
is a height function for
 $(\Gamma ,F)$
. Triangle inequality and symmetry are clear. For the Northcott property, recall that two norms
$(\Gamma ,F)$
. Triangle inequality and symmetry are clear. For the Northcott property, recall that two norms
 $\lVert {\cdot }\rVert _1$
and
$\lVert {\cdot }\rVert _1$
and
 $\lVert {\cdot }\rVert _2$
on a vector space V are equivalent if there are
$\lVert {\cdot }\rVert _2$
on a vector space V are equivalent if there are
 $c_1,c_2>0$
such that
$c_1,c_2>0$
such that
 $c_1\lVert {v}\rVert _1\le \lVert {v}\rVert _2 \le c_2\lVert {v}\rVert _1$
for all
$c_1\lVert {v}\rVert _1\le \lVert {v}\rVert _2 \le c_2\lVert {v}\rVert _1$
for all
 $v\in V$
; recall further that all norms on a finite-dimensional space are equivalent. In particular, our infinity norm is equivalent to the usual infinity norm
$v\in V$
; recall further that all norms on a finite-dimensional space are equivalent. In particular, our infinity norm is equivalent to the usual infinity norm
 $\lVert {\cdot }\rVert _{\infty } $
on
$\lVert {\cdot }\rVert _{\infty } $
on
 $\mathbb {C}^m$
, and there is
$\mathbb {C}^m$
, and there is
 $c>0$
such that
$c>0$
such that
 $\lVert {v}\rVert _{\infty } \le ch(v)$
for all
$\lVert {v}\rVert _{\infty } \le ch(v)$
for all
 $v\in \mathbb {C}^m$
. So if
$v\in \mathbb {C}^m$
. So if
 $h(v)\le N$
then
$h(v)\le N$
then
 $\lVert {v}\rVert _{\infty } \le cN$
, and there can only be finitely many such
$\lVert {v}\rVert _{\infty } \le cN$
, and there can only be finitely many such
 $v\in \mathbb {Z}^m$
.
$v\in \mathbb {Z}^m$
.It remains to check canonicity. Fix some
 $\beta>1$
such that
$\beta>1$
such that
 $\beta +1<{\lvert \mu \rvert }$
for all
$\beta +1<{\lvert \mu \rvert }$
for all
 $\mu \in \sigma (F)$
. Suppose
$\mu \in \sigma (F)$
. Suppose
 $v = v_1e_1+\cdots +v_me_m\in \mathbb {C}^m\setminus \{0\}$
; write
$v = v_1e_1+\cdots +v_me_m\in \mathbb {C}^m\setminus \{0\}$
; write
 $Fv = w_1e_1+\cdots +w_me_m$
. Fix i such that
$Fv = w_1e_1+\cdots +w_me_m$
. Fix i such that
 ${\lvert {v_i}\rvert } = h(v)$
. Depending on the structure of the Jordan blocks, we get that
${\lvert {v_i}\rvert } = h(v)$
. Depending on the structure of the Jordan blocks, we get that
 $w_i$
is either
$w_i$
is either
 $\mu v_i + v_{i+1}$
or
$\mu v_i + v_{i+1}$
or
 $\mu v_i$
(for
$\mu v_i$
(for
 $\mu \in \sigma (F)$
corresponding to
$\mu \in \sigma (F)$
corresponding to
 $v_i$
). In the first case, reverse triangle inequality yields and in the second case we get
$v_i$
). In the first case, reverse triangle inequality yields and in the second case we get $$ \begin{align*}h(Fv)\ge {\lvert{w_i} \rvert}\ge {\lvert {\mu }\rvert}{\lvert{v_i}\rvert} - {\lvert{v_{i+1}\rvert}} \ge ({\lvert\mu -1 \rvert}){\lvert{v_i} \rvert}> \beta {\lvert {v_i}\rvert} = \beta h(v), \end{align*} $$
So h satisfies canonicity, as desired.
$$ \begin{align*}h(Fv)\ge {\lvert{w_i} \rvert}\ge {\lvert {\mu }\rvert}{\lvert{v_i}\rvert} - {\lvert{v_{i+1}\rvert}} \ge ({\lvert\mu -1 \rvert}){\lvert{v_i} \rvert}> \beta {\lvert {v_i}\rvert} = \beta h(v), \end{align*} $$
So h satisfies canonicity, as desired. $$ \begin{align*}h(Fv)\ge {\lvert{w_i} \rvert} = {\lvert\mu \rvert}{\lvert{v_i} \rvert}> \beta {\lvert{v_i} \rvert} = \beta h(v). \end{align*} $$
$$ \begin{align*}h(Fv)\ge {\lvert{w_i} \rvert} = {\lvert\mu \rvert}{\lvert{v_i} \rvert}> \beta {\lvert{v_i} \rvert} = \beta h(v). \end{align*} $$
-
 $(\implies )$
Suppose there is
$(\implies )$
Suppose there is
 $\mu \in \sigma (F)$
with
$\mu \in \sigma (F)$
with
 ${\lvert \mu \rvert } \le 1$
. There are two cases:
${\lvert \mu \rvert } \le 1$
. There are two cases:-
Case 1. Suppose there is
 $\mu \in \sigma (F)$
with
$\mu \in \sigma (F)$
with
 ${\lvert \mu \rvert } <1$
; the argument in this case is similar to Example 3.1. Since the same is true for all powers of F it suffices to show that there is no F-spanning set. Pick a basis
${\lvert \mu \rvert } <1$
; the argument in this case is similar to Example 3.1. Since the same is true for all powers of F it suffices to show that there is no F-spanning set. Pick a basis
 $\{e_1,\ldots ,e_m\}$
for
$\{e_1,\ldots ,e_m\}$
for
 $\mathbb {C}^m$
that puts F into Jordan canonical form; for
$\mathbb {C}^m$
that puts F into Jordan canonical form; for
 $x\in \mathbb {C}^m$
we write so each
$x\in \mathbb {C}^m$
we write so each $$ \begin{align*}x = \sum_{i=1}^m f_i(x)e_i; \end{align*} $$
$$ \begin{align*}x = \sum_{i=1}^m f_i(x)e_i; \end{align*} $$
 $f_i\colon \mathbb {C}^m\to \mathbb {C}$
is linear. Pick some
$f_i\colon \mathbb {C}^m\to \mathbb {C}$
is linear. Pick some
 $e_k$
corresponding to the bottom-right of some Jordan block for
$e_k$
corresponding to the bottom-right of some Jordan block for
 $\mu $
; so
$\mu $
; so
 $f_k(Fx) = \mu f_k(x)$
for
$f_k(Fx) = \mu f_k(x)$
for
 $x\in \mathbb {C}^m$
.
$x\in \mathbb {C}^m$
.
Suppose for contradiction we had an F-spanning set
 $\Sigma $
. Let
$\Sigma $
. Let
 $M = \max \{{\lvert {f_k(a)} \rvert }:a\in \Sigma \}$
. Then if for
$M = \max \{{\lvert {f_k(a)} \rvert }:a\in \Sigma \}$
. Then if for $$ \begin{align*}y = \sum_{i=0}^{\ell} F^ia_i \end{align*} $$
$$ \begin{align*}y = \sum_{i=0}^{\ell} F^ia_i \end{align*} $$
 $a_i\in \Sigma $
then So every
$a_i\in \Sigma $
then So every $$ \begin{align*}{\lvert{f_k(y)} \rvert} &= {\bigg\lvert {\sum_{i=0}^{\ell} \mu ^if_k(a_i)}\bigg\rvert} \le \sum_{i=0}^{\ell} {\lvert{\mu ^if_k(a_i)} \rvert} \\ &= \sum_{i=0}^{\ell} {\lvert \mu \rvert}^i{\lvert{f_k(a_i)} \rvert} \le M\sum_{i<\omega }{\lvert \mu \rvert}^i = M\frac1{1-{\lvert\mu \rvert} }. \end{align*} $$
$$ \begin{align*}{\lvert{f_k(y)} \rvert} &= {\bigg\lvert {\sum_{i=0}^{\ell} \mu ^if_k(a_i)}\bigg\rvert} \le \sum_{i=0}^{\ell} {\lvert{\mu ^if_k(a_i)} \rvert} \\ &= \sum_{i=0}^{\ell} {\lvert \mu \rvert}^i{\lvert{f_k(a_i)} \rvert} \le M\sum_{i<\omega }{\lvert \mu \rvert}^i = M\frac1{1-{\lvert\mu \rvert} }. \end{align*} $$
 $y{{\kern-1.2pt}\in{\kern-1.2pt}} \mathbb {Z}^m$
satisfies
$y{{\kern-1.2pt}\in{\kern-1.2pt}} \mathbb {Z}^m$
satisfies
 ${\lvert {f_k(y)}\rvert }{{\kern-1.2pt}\le{\kern-1.2pt}} M\frac 1{1-{\lvert \mu \rvert } }$
. So since the integers are closed under doubling and
${\lvert {f_k(y)}\rvert }{{\kern-1.2pt}\le{\kern-1.2pt}} M\frac 1{1-{\lvert \mu \rvert } }$
. So since the integers are closed under doubling and
 $f_k$
is linear, we get that
$f_k$
is linear, we get that
 $f_k(y) = 0$
for each
$f_k(y) = 0$
for each
 $y\in \mathbb {Z}^m$
. So
$y\in \mathbb {Z}^m$
. So
 $\mathbb {C}^m = \operatorname {\mathrm {span}}_{\mathbb {C}}\mathbb {Z}^m$
is spanned by
$\mathbb {C}^m = \operatorname {\mathrm {span}}_{\mathbb {C}}\mathbb {Z}^m$
is spanned by
 $\{e_1,\ldots ,e_m\}\setminus \{e_k\}$
, a contradiction.
$\{e_1,\ldots ,e_m\}\setminus \{e_k\}$
, a contradiction.
-
Case 2. Suppose
 ${\lvert \mu \rvert } \ge 1$
for all
${\lvert \mu \rvert } \ge 1$
for all
 $\mu \in \sigma (F)$
; pick some
$\mu \in \sigma (F)$
; pick some
 $\mu \in \sigma (F)$
with
$\mu \in \sigma (F)$
with
 ${\lvert \mu \rvert } =1$
. We show that there is non-zero
${\lvert \mu \rvert } =1$
. We show that there is non-zero
 $a\in \mathbb {Z}^m$
such that
$a\in \mathbb {Z}^m$
such that
 $F^ia=F^ja$
for some
$F^ia=F^ja$
for some
 $i\ne j$
, and deduce that no power of F admits a length function.
$i\ne j$
, and deduce that no power of F admits a length function.Let
 $p_{\mu } (x)$
be the minimal polynomial for
$p_{\mu } (x)$
be the minimal polynomial for
 $\mu $
over
$\mu $
over
 $\mathbb {Q}$
. Note that if
$\mathbb {Q}$
. Note that if
 $\nu \in \mathbb {C}$
is a root of
$\nu \in \mathbb {C}$
is a root of
 $p_{\mu } $
then so is
$p_{\mu } $
then so is
 $\nu ^{-1}$
. Indeed, this is true of
$\nu ^{-1}$
. Indeed, this is true of
 $\mu $
since
$\mu $
since
 $\mu ^{-1}=\overline {\mu }$
and
$\mu ^{-1}=\overline {\mu }$
and
 $p_{\mu } \in \mathbb {Q}[x]$
, and hence is true of all
$p_{\mu } \in \mathbb {Q}[x]$
, and hence is true of all
 $\operatorname {\mathrm {Aut}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-conjugates of
$\operatorname {\mathrm {Aut}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-conjugates of
 $\mu $
. But
$\mu $
. But
 $p_{\mu } $
divides the characteristic polynomial of F, and hence
$p_{\mu } $
divides the characteristic polynomial of F, and hence
 $p_{\mu } $
has no roots of modulus
$p_{\mu } $
has no roots of modulus
 $<1$
by hypothesis. It follows that
$<1$
by hypothesis. It follows that
 $p_{\mu } $
has no roots of modulus
$p_{\mu } $
has no roots of modulus
 $>1$
either. That is, the roots of
$>1$
either. That is, the roots of
 $p_{\mu } $
lie on the unit circle.
$p_{\mu } $
lie on the unit circle.Now,
 $p_{\mu } (F)$
isn’t invertible over
$p_{\mu } (F)$
isn’t invertible over
 $\mathbb {C}$
, since
$\mathbb {C}$
, since
 $p_{\mu } (F)v= p_{\mu } (\mu )v = 0$
for any eigenvector v of F with eigenvalue
$p_{\mu } (F)v= p_{\mu } (\mu )v = 0$
for any eigenvector v of F with eigenvalue
 $\mu $
. So
$\mu $
. So
 $p_{\mu } (F)$
isn’t invertible over
$p_{\mu } (F)$
isn’t invertible over
 $\mathbb {Q}$
, and thus
$\mathbb {Q}$
, and thus
 $V:=\ker _{\mathbb {Q}}(p_{\mu } (F))$
is a non-trivial F-invariant subspace of
$V:=\ker _{\mathbb {Q}}(p_{\mu } (F))$
is a non-trivial F-invariant subspace of
 $\mathbb {Q}^m$
. Furthermore
$\mathbb {Q}^m$
. Furthermore
 $p_{\mu } (F\restriction V) = 0$
, so the minimal polynomial of
$p_{\mu } (F\restriction V) = 0$
, so the minimal polynomial of
 $F\restriction V$
is separable (since
$F\restriction V$
is separable (since
 $p_{\mu } $
is); so
$p_{\mu } $
is); so
 $F\restriction V$
is diagonalizable (over
$F\restriction V$
is diagonalizable (over
 $\mathbb {C}$
) with eigenvalues that are roots of
$\mathbb {C}$
) with eigenvalues that are roots of
 $p_{\mu } $
, and hence lie on the unit circle. In particular in the inner product induced by the eigenbasis for
$p_{\mu } $
, and hence lie on the unit circle. In particular in the inner product induced by the eigenbasis for
 $F\restriction V$
we get that
$F\restriction V$
we get that
 $F\restriction V$
is unitary.
$F\restriction V$
is unitary.Since V is a non-trivial subspace of
 $\mathbb {Q}^m$
it contains a non-zero
$\mathbb {Q}^m$
it contains a non-zero
 $a\in \mathbb {Z}^m$
. So
$a\in \mathbb {Z}^m$
. So
 $Fa\in V\cap \mathbb {Z}^m$
as well and
$Fa\in V\cap \mathbb {Z}^m$
as well and
 $\lVert {Fa}\rVert = \lVert {a}\rVert $
(where the norm is induced by the aforementioned inner product); inductively we get
$\lVert {Fa}\rVert = \lVert {a}\rVert $
(where the norm is induced by the aforementioned inner product); inductively we get
 $\lVert {F^na}\rVert = \lVert {a} \rVert $
and
$\lVert {F^na}\rVert = \lVert {a} \rVert $
and
 $F^na\in \mathbb {Z}^m$
for all n. But
$F^na\in \mathbb {Z}^m$
for all n. But
 $\lVert {\cdot }\rVert $
is equivalent to the Euclidean norm (since both are norms on a finite-dimensional space); so there are finitely many
$\lVert {\cdot }\rVert $
is equivalent to the Euclidean norm (since both are norms on a finite-dimensional space); so there are finitely many
 $b\in \mathbb {Z}^m$
with
$b\in \mathbb {Z}^m$
with
 $\lVert {b}\rVert = \lVert {a}\rVert $
. So
$\lVert {b}\rVert = \lVert {a}\rVert $
. So
 $F^i a = F^ja$
for some
$F^i a = F^ja$
for some
 $i\ne j$
. By injectivity of F we get
$i\ne j$
. By injectivity of F we get
 $F^{i-j}a = a$
, and hence that
$F^{i-j}a = a$
, and hence that
 $(F^n)^{i-j} a = a$
for all n. It follows that the
$(F^n)^{i-j} a = a$
for all n. It follows that the
 $F^n$
-orbit of a is finite for all
$F^n$
-orbit of a is finite for all
 $n>0$
. Since a has infinite order, Remark 3.6 yields that no power of F admits a length function. Hence by Theorem 3.10
$n>0$
. Since a has infinite order, Remark 3.6 yields that no power of F admits a length function. Hence by Theorem 3.10
 $\Gamma $
does not admit an
$\Gamma $
does not admit an
 $F^r$
-spanning set for any
$F^r$
-spanning set for any
 $r>0$
.
$r>0$
.
-
4 A characterization of F-automaticity
A useful characterization of classical automaticity is in terms of “finiteness of kernels.” A version of this for F-automaticity is given in [Reference Bell and Moosa2, Lemma 6.2]. Using length functions we are able to improve this result. First, here is what kernels mean in our setting, as introduced in Definition 6.1 of [Reference Bell and Moosa2]. As before, we fix an abelian group
![]() $\Gamma $
with an injective endomorphism F.
$\Gamma $
with an injective endomorphism F.
Definition 4.1. Suppose
![]() $A\subseteq \Gamma $
. Given
$A\subseteq \Gamma $
. Given
![]() $s_0,\ldots ,s_{n-1}\in \Gamma $
we set
$s_0,\ldots ,s_{n-1}\in \Gamma $
we set
 $$ \begin{align*}A_{s_0\cdots s_{n-1}}(x) = \{x\in\Gamma : s_0 + \cdots + F^{n-1}s_{n-1}+F^n x\in A\} \end{align*} $$
$$ \begin{align*}A_{s_0\cdots s_{n-1}}(x) = \{x\in\Gamma : s_0 + \cdots + F^{n-1}s_{n-1}+F^n x\in A\} \end{align*} $$
(so
![]() $A_{\epsilon } = A$
). Given
$A_{\epsilon } = A$
). Given
![]() $S\subseteq \Gamma $
, by the
$S\subseteq \Gamma $
, by the
![]() $(S,F)$
-kernel of A we mean the set
$(S,F)$
-kernel of A we mean the set
![]() $\{A_{\sigma } :\sigma \in S^*\} $
.
$\{A_{\sigma } :\sigma \in S^*\} $
.
Theorem 4.2. Suppose
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
(and so in particular that
$r>0$
(and so in particular that
![]() $\Gamma /F\Gamma $
is finite). Fix finite
$\Gamma /F\Gamma $
is finite). Fix finite
![]() $S\subseteq \Gamma $
containing a representative of each coset of
$S\subseteq \Gamma $
containing a representative of each coset of
![]() $F\Gamma $
in
$F\Gamma $
in
![]() $\Gamma $
. Then
$\Gamma $
. Then
![]() $A\subseteq \Gamma $
is F-automatic if and only if the
$A\subseteq \Gamma $
is F-automatic if and only if the
![]() $(S,F)$
-kernel of A is finite.
$(S,F)$
-kernel of A is finite.
The big improvement here is that S need not be a spanning set—being a complete set of representatives for
![]() $\Gamma /F\Gamma $
is a much weaker condition. A nice feature of this characterization is that, apart from the hypothesis on existence of a spanning set, F-automaticity of a set A can be checked without references to higher powers of F.
$\Gamma /F\Gamma $
is a much weaker condition. A nice feature of this characterization is that, apart from the hypothesis on existence of a spanning set, F-automaticity of a set A can be checked without references to higher powers of F.
Lemma 4.3. Let
![]() $\Gamma $
, F, and S be as in Theorem 4.2. Suppose
$\Gamma $
, F, and S be as in Theorem 4.2. Suppose
![]() $n>0$
. The
$n>0$
. The
![]() $(S,F)$
-kernel of A is finite if and only if the
$(S,F)$
-kernel of A is finite if and only if the
![]() $(S^{(n)},F^n)$
-kernel of
$(S^{(n)},F^n)$
-kernel of
![]() $A $
is finite.
$A $
is finite.
Proof The
![]() $(S^{(n)},F^n)$
-kernel is clearly contained in the
$(S^{(n)},F^n)$
-kernel is clearly contained in the
![]() $(S,F)$
-kernel. Suppose the
$(S,F)$
-kernel. Suppose the
![]() $(S,F)$
-kernel is infinite.
$(S,F)$
-kernel is infinite.
Note that if
![]() $\sigma =s_0\cdots s_{k-1},\tau =t_0\cdots t_{\ell -1}\in S^*$
, and
$\sigma =s_0\cdots s_{k-1},\tau =t_0\cdots t_{\ell -1}\in S^*$
, and
![]() $a\in \Gamma $
then
$a\in \Gamma $
then
 $$ \begin{align*} a\in (A_{\sigma} )_{\tau} &\iff t_0+\cdots +F^{\ell -1}t_{\ell -1}+F^{\ell} a\in A_{\sigma} \\ &\iff s_0 + \cdots + F^{k-1}s_{k-1} + F^k(t_0+\cdots +F^{\ell -1}t_{\ell -1}+F^{\ell} a) \in A \\ &\iff s_0 + \cdots + F^{k-1}s_{k-1} + F^kt_0 + \cdots + F^{k+\ell -1}t_{\ell -1} + F^{k+\ell }a \in A \\ &\iff a\in A_{\sigma \tau}. \end{align*} $$
$$ \begin{align*} a\in (A_{\sigma} )_{\tau} &\iff t_0+\cdots +F^{\ell -1}t_{\ell -1}+F^{\ell} a\in A_{\sigma} \\ &\iff s_0 + \cdots + F^{k-1}s_{k-1} + F^k(t_0+\cdots +F^{\ell -1}t_{\ell -1}+F^{\ell} a) \in A \\ &\iff s_0 + \cdots + F^{k-1}s_{k-1} + F^kt_0 + \cdots + F^{k+\ell -1}t_{\ell -1} + F^{k+\ell }a \in A \\ &\iff a\in A_{\sigma \tau}. \end{align*} $$
So
![]() $(A_{\sigma } )_{\tau } = A_{\sigma \tau }$
; in particular, if
$(A_{\sigma } )_{\tau } = A_{\sigma \tau }$
; in particular, if
![]() $A _{\sigma \tau }\ne A _{\sigma '\tau }$
then
$A _{\sigma \tau }\ne A _{\sigma '\tau }$
then
![]() $A _{\sigma } \ne A _{\sigma '}$
.
$A _{\sigma } \ne A _{\sigma '}$
.
Since the set of all
![]() $A_{\sigma } $
is infinite, there is
$A_{\sigma } $
is infinite, there is
![]() $0\le i<n$
such that the set of
$0\le i<n$
such that the set of
![]() $A_{\sigma } $
with
$A_{\sigma } $
with
![]() ${\lvert \sigma \rvert } \equiv i{\pmod {n}}$
is infinite. Now, as S is finite, this means there is
${\lvert \sigma \rvert } \equiv i{\pmod {n}}$
is infinite. Now, as S is finite, this means there is
![]() $\tau \in S^*$
of length i such that
$\tau \in S^*$
of length i such that
![]() $\{A _{\rho \tau } : \rho \in S^*,{\lvert \rho \rvert } \in n\mathbb {Z}\} $
is infinite. It follows by the above observation that
$\{A _{\rho \tau } : \rho \in S^*,{\lvert \rho \rvert } \in n\mathbb {Z}\} $
is infinite. It follows by the above observation that
![]() $\{A _{\rho } :\rho \in S^*,{\lvert \rho \rvert } \in n\mathbb {Z}\}$
is infinite, and so the
$\{A _{\rho } :\rho \in S^*,{\lvert \rho \rvert } \in n\mathbb {Z}\}$
is infinite, and so the
![]() $(S^{(n)}, F^n)$
-kernel is infinite.
$(S^{(n)}, F^n)$
-kernel is infinite.
Lemma 4.4. Suppose
![]() $\Gamma $
admits a length function
$\Gamma $
admits a length function
![]() $\lambda $
for
$\lambda $
for
![]() $(\Gamma ,F)$
with associated constants
$(\Gamma ,F)$
with associated constants
![]() $C,D,E$
such that
$C,D,E$
such that
![]() $C\ge D$
. Suppose
$C\ge D$
. Suppose
![]() $S,T\subseteq \Gamma $
are finite sets both containing a representative of each coset of
$S,T\subseteq \Gamma $
are finite sets both containing a representative of each coset of
![]() $F\Gamma $
. Then A has finite
$F\Gamma $
. Then A has finite
![]() $(S,F)$
-kernel if and only if it has finite
$(S,F)$
-kernel if and only if it has finite
![]() $(T,F)$
-kernel.
$(T,F)$
-kernel.
Proof Let
![]() $N = \max \{\lambda (s-t) : s\in S,t\in T\}$
. Suppose the
$N = \max \{\lambda (s-t) : s\in S,t\in T\}$
. Suppose the
![]() $(T,F)$
-kernel of A is finite.
$(T,F)$
-kernel of A is finite.
Take an element
![]() $A _{\sigma } $
of the
$A _{\sigma } $
of the
![]() $(S,F)$
-kernel of
$(S,F)$
-kernel of
![]() $A $
, say with
$A $
, say with
![]() $\sigma = s_0\cdots s_{n-1}\in S^*$
. By Lemma 3.9 there is
$\sigma = s_0\cdots s_{n-1}\in S^*$
. By Lemma 3.9 there is
![]() $\tau = t_0\ldots t_{n-1}\in T^*$
such that
$\tau = t_0\ldots t_{n-1}\in T^*$
such that
So
![]() $A_{\tau } $
lies in the
$A_{\tau } $
lies in the
![]() $(T,F)$
-kernel of
$(T,F)$
-kernel of
![]() $A $
. Let
$A $
. Let
so for
![]() $a\in \Gamma $
we have
$a\in \Gamma $
we have
 $$ \begin{align*} a+\delta \in A_{\tau} &\iff t_0 + \cdots +F^{n-1}t_{n-1} + F^n (a+\delta )\in A\\ &\iff t_0 + \cdots +F^{n-1}t_{n-1} + F^n a + (s_0-t_0)+\cdots +F^{n-1}(s_{n-1}-t_{n-1}) \in A\\ &\iff s_0 + \cdots F^{n-1}s_{n-1} + F^na \in A\\ &\iff a\in A_{\sigma}. \end{align*} $$
$$ \begin{align*} a+\delta \in A_{\tau} &\iff t_0 + \cdots +F^{n-1}t_{n-1} + F^n (a+\delta )\in A\\ &\iff t_0 + \cdots +F^{n-1}t_{n-1} + F^n a + (s_0-t_0)+\cdots +F^{n-1}(s_{n-1}-t_{n-1}) \in A\\ &\iff s_0 + \cdots F^{n-1}s_{n-1} + F^na \in A\\ &\iff a\in A_{\sigma}. \end{align*} $$
So
![]() $A_{\sigma } = A_{\tau } -\delta $
. Hence to show that the
$A_{\sigma } = A_{\tau } -\delta $
. Hence to show that the
![]() $(S,F)$
-kernel of A is finite it suffices to show that
$(S,F)$
-kernel of A is finite it suffices to show that
![]() $\delta $
can take on one of only finitely many values (as
$\delta $
can take on one of only finitely many values (as
![]() $\sigma ,\tau $
vary). We show that
$\sigma ,\tau $
vary). We show that
![]() $\lambda (\delta )$
is bounded in terms of
$\lambda (\delta )$
is bounded in terms of
![]() $S,T$
, which suffices by the Northcott property.
$S,T$
, which suffices by the Northcott property.
We first bound
![]() $\lambda (F^n\delta ) = \lambda ((s_0-t_0) + \cdots + F^{n-1}(s_{n-1}-t_{n-1})) $
. Since
$\lambda (F^n\delta ) = \lambda ((s_0-t_0) + \cdots + F^{n-1}(s_{n-1}-t_{n-1})) $
. Since
![]() $\lambda (s_0-t_0)\le N$
and
$\lambda (s_0-t_0)\le N$
and
![]() $\lambda (F(s_1-t_1))\le N+C$
, the ultrametric inequality yields
$\lambda (F(s_1-t_1))\le N+C$
, the ultrametric inequality yields
Since
![]() $\lambda (F^2(s_2-t_2))\le N+2C$
, another application of ultrametric inequality yields
$\lambda (F^2(s_2-t_2))\le N+2C$
, another application of ultrametric inequality yields
(since by hypothesis
![]() $C\ge D$
). Continuing inductively, we find that
$C\ge D$
). Continuing inductively, we find that
![]() $\lambda (F^n\delta )\le N+(n-1)C+D$
. Hence by the logarithmic property we get that
$\lambda (F^n\delta )\le N+(n-1)C+D$
. Hence by the logarithmic property we get that
![]() $\lambda (\delta )\le N-C+D+E$
.
$\lambda (\delta )\le N-C+D+E$
.
Proof of Theorem 4.2 Suppose
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^n$
-spanning set
$F^n$
-spanning set
![]() $\Sigma $
for some
$\Sigma $
for some
![]() $n>0$
. By Proposition 3.8
$n>0$
. By Proposition 3.8
![]() $\lambda _{\Sigma } $
is a length function for
$\lambda _{\Sigma } $
is a length function for
![]() $(\Gamma ,F^n)$
with associated constants
$(\Gamma ,F^n)$
with associated constants
![]() $C,D,E$
such that
$C,D,E$
such that
![]() $C\ge D$
. Suppose
$C\ge D$
. Suppose
![]() $A\subseteq \Gamma $
. Then by the previous two lemmas, the
$A\subseteq \Gamma $
. Then by the previous two lemmas, the
![]() $(S,F)$
-kernel of A is finite if and only if the
$(S,F)$
-kernel of A is finite if and only if the
![]() $(S^{(n)},F^n)$
-kernel of A is, which occurs if and only if the
$(S^{(n)},F^n)$
-kernel of A is, which occurs if and only if the
![]() $(\Sigma ,F^n)$
-kernel of A is. (Note that an
$(\Sigma ,F^n)$
-kernel of A is. (Note that an
![]() $F^n$
-spanning set must contain a representative of every coset of
$F^n$
-spanning set must contain a representative of every coset of
![]() $F\Gamma $
.) But by [Reference Bell and Moosa2, Lemma 6.2] this is equivalent to A being F-automatic, as desired.
$F\Gamma $
.) But by [Reference Bell and Moosa2, Lemma 6.2] this is equivalent to A being F-automatic, as desired.
As an illustration of the usefulness of this characterization we give quick proof of [Reference Bell and Moosa2, Lemma 6.7(a)]: that if a spanning set exists then the equivalence relation of “representing the same element” on strings is characterized by a finite automaton.
Corollary 4.5. Suppose
![]() $\Sigma $
is an F-spanning set. Then
$\Sigma $
is an F-spanning set. Then
![]() $\{(\sigma ,\tau )\in (\Sigma ^2)^* : [\sigma ]_F = [\tau ]_F\}$
is a regular language over
$\{(\sigma ,\tau )\in (\Sigma ^2)^* : [\sigma ]_F = [\tau ]_F\}$
is a regular language over
![]() $(\Sigma ^2)^*$
.
$(\Sigma ^2)^*$
.
Here we are conflating
![]() $(\Sigma ^2)^*$
with the subset of
$(\Sigma ^2)^*$
with the subset of
![]() $(\Sigma ^*)^2$
consisting of the
$(\Sigma ^*)^2$
consisting of the
![]() $(\sigma ,\tau )$
such that
$(\sigma ,\tau )$
such that
![]() ${\lvert \sigma \rvert } ={\lvert \tau \rvert } $
.
${\lvert \sigma \rvert } ={\lvert \tau \rvert } $
.
Proof By Proposition 2.6 this is equivalent to
![]() $\Delta = \{(a,a) : a\in \Gamma \}\subseteq \Gamma ^2$
being F-automatic. Fix a set S containing exactly one representative of each coset of
$\Delta = \{(a,a) : a\in \Gamma \}\subseteq \Gamma ^2$
being F-automatic. Fix a set S containing exactly one representative of each coset of
![]() $F\Gamma $
in
$F\Gamma $
in
![]() $\Gamma $
; we will show that the
$\Gamma $
; we will show that the
![]() $(S^2,F)$
-kernel of
$(S^2,F)$
-kernel of
![]() $\Delta $
is finite. Note that if
$\Delta $
is finite. Note that if
![]() $s_0\cdots s_{n-1},t_0\cdots t_{n-1}\in S^{(n)}$
are unequal, say with i minimal such that
$s_0\cdots s_{n-1},t_0\cdots t_{n-1}\in S^{(n)}$
are unequal, say with i minimal such that
![]() $s_i\ne t_i$
, then since
$s_i\ne t_i$
, then since
![]() $s_{i} \not \equiv t_{i}{\pmod {F\Gamma }}$
and F is injective we get that
$s_{i} \not \equiv t_{i}{\pmod {F\Gamma }}$
and F is injective we get that
![]() $s_0+\cdots +F^{n-1}s_{n-1}{\not \equiv } t_0+\cdots + F^{n-1}t_{n-1}{\pmod {F^{i+1}\Gamma }}$
. So
$s_0+\cdots +F^{n-1}s_{n-1}{\not \equiv } t_0+\cdots + F^{n-1}t_{n-1}{\pmod {F^{i+1}\Gamma }}$
. So
![]() $s_0+\cdots +F^{n-1}s_{n-1}{\not \equiv } t_0+\cdots +F^{n-1}t_{n-1}{\pmod {F^n\Gamma }}$
, and thus
$s_0+\cdots +F^{n-1}s_{n-1}{\not \equiv } t_0+\cdots +F^{n-1}t_{n-1}{\pmod {F^n\Gamma }}$
, and thus
![]() $s_0 + \cdots + F^{n-1}s_{n-1} + F^na \ne t_0 + \cdots + F^{n-1}t_{n-1} + F^nb$
for any
$s_0 + \cdots + F^{n-1}s_{n-1} + F^na \ne t_0 + \cdots + F^{n-1}t_{n-1} + F^nb$
for any
![]() $a,b\in \Gamma $
. So
$a,b\in \Gamma $
. So
![]() $\Delta _{(\sigma ,\tau ) }$
is empty if
$\Delta _{(\sigma ,\tau ) }$
is empty if
![]() $(\sigma , \tau ) \in (S^2)^*$
and
$(\sigma , \tau ) \in (S^2)^*$
and
![]() $\sigma \ne \tau $
. Furthermore if
$\sigma \ne \tau $
. Furthermore if
![]() $\sigma =\tau $
then by injectivity of F we get
$\sigma =\tau $
then by injectivity of F we get
![]() $\Delta _{(\sigma ,\tau )} = \Delta $
. So the
$\Delta _{(\sigma ,\tau )} = \Delta $
. So the
![]() $(S^2,F)$
-kernel of
$(S^2,F)$
-kernel of
![]() $\Delta $
contains two elements.
$\Delta $
contains two elements.
5 A characterization of F-sparsity
Recall that a language
![]() $L\subseteq \Sigma ^*$
is sparse if it is regular and
$L\subseteq \Sigma ^*$
is sparse if it is regular and
![]() ${\lvert {\{\sigma \in L : {\lvert \sigma \rvert } \le x\}}\rvert }$
grows polynomially in x. See the beginning of [Reference Bell and Moosa2, Section 7] for a brief overview of sparsity.
${\lvert {\{\sigma \in L : {\lvert \sigma \rvert } \le x\}}\rvert }$
grows polynomially in x. See the beginning of [Reference Bell and Moosa2, Section 7] for a brief overview of sparsity.
Fix
![]() $(\Gamma ,F)$
an abelian group equipped with an injective endomorphism. In [Reference Bell and Moosa2] Bell and Moosa adapt the notion of sparsity to the setting of F-automatic sets.
$(\Gamma ,F)$
an abelian group equipped with an injective endomorphism. In [Reference Bell and Moosa2] Bell and Moosa adapt the notion of sparsity to the setting of F-automatic sets.
Definition 5.1. A subset
![]() $A\subseteq \Gamma $
is F-sparse if there is an
$A\subseteq \Gamma $
is F-sparse if there is an
![]() $F^r$
-spanning set
$F^r$
-spanning set
![]() $\Sigma $
for some
$\Sigma $
for some
![]() $r>0$
and a sparse
$r>0$
and a sparse
![]() $L\subseteq \Sigma ^*$
such that
$L\subseteq \Sigma ^*$
such that
![]() $A = [L]_{F^r}$
.
$A = [L]_{F^r}$
.
While the definition of F-sparsity is sufficient for the purposes of [Reference Bell and Moosa2], it is cumbersome in some contexts. In particular, in order to show a set is not sparse one needs to check every possible set of representatives in every possible spanning set for every possible power of F. For example, it is not immediate from the definition that
![]() $\Gamma $
itself isn’t F-sparse.
$\Gamma $
itself isn’t F-sparse.
In this section we will give a characterization of F-sparsity in terms of length functions, and deduce from that some natural properties of F-sparsity. We will use the following characterization of sparsity:
Fact 5.2 [Reference Bell and Moosa2, Proposition 7.1]
![]() $L\subseteq \Sigma ^*$
is sparse if and only if it is a finite union of sets of the form
$L\subseteq \Sigma ^*$
is sparse if and only if it is a finite union of sets of the form
![]() $v_0w_1^*v_1\cdots v_{n-1}w_n^*v_n$
where
$v_0w_1^*v_1\cdots v_{n-1}w_n^*v_n$
where
![]() $v_0,\ldots ,v_n,w_1,\ldots ,w_n\in \Sigma ^*$
.
$v_0,\ldots ,v_n,w_1,\ldots ,w_n\in \Sigma ^*$
.
We call languages of the form
![]() $v_0w_1^*v_1\cdots v_{n-1}w_n^*v_n$
simple sparse. By Fact 5.2 an F-sparse set is a finite union of sets of the form
$v_0w_1^*v_1\cdots v_{n-1}w_n^*v_n$
simple sparse. By Fact 5.2 an F-sparse set is a finite union of sets of the form
![]() $[L]_{F^r}$
where L is a simple sparse language. The following further simplification in the structure of F-sparse sets will be useful both for proving basic closure properties below, and for studying stability in the next section.
$[L]_{F^r}$
where L is a simple sparse language. The following further simplification in the structure of F-sparse sets will be useful both for proving basic closure properties below, and for studying stability in the next section.
Proposition 5.3. Suppose
![]() $A\subseteq \Gamma $
is F-sparse. There is
$A\subseteq \Gamma $
is F-sparse. There is
![]() $s_0\in \mathbb {N}$
such that for all
$s_0\in \mathbb {N}$
such that for all
![]() $s\in s_0\mathbb {N}$
we can write A as a finite union of translates of sets of the form
$s\in s_0\mathbb {N}$
we can write A as a finite union of translates of sets of the form
![]() $[a _1^*\cdots a _n^*]_{F^s}$
where
$[a _1^*\cdots a _n^*]_{F^s}$
where
![]() $a_1,\ldots ,a_n\in \Gamma $
.
$a_1,\ldots ,a_n\in \Gamma $
.
Proof By Fact 5.2 we can write A as a finite union of sets of the form
![]() $[v_0w_1^*v_1\cdots w_n^*v_n]_{F^r}$
for some strings
$[v_0w_1^*v_1\cdots w_n^*v_n]_{F^r}$
for some strings
![]() $v_i,w_i\in \Gamma ^*$
. By replacing F with
$v_i,w_i\in \Gamma ^*$
. By replacing F with
![]() $F^r$
we may assume
$F^r$
we may assume
![]() $r=1$
. Let
$r=1$
. Let
![]() $s_0$
be the least common multiple of all the
$s_0$
be the least common multiple of all the
![]() ${\lvert {w_i}\rvert }$
.
${\lvert {w_i}\rvert }$
.
In the case where
![]() $\Gamma =\mathbb {Z}^m$
and F is multiplication by some
$\Gamma =\mathbb {Z}^m$
and F is multiplication by some
![]() $d>0$
, an intermediate result in the proof of [Reference Hawthorne5, Lemma 3.4] is that we can write A as a finite union of translates of sets of the form
$d>0$
, an intermediate result in the proof of [Reference Hawthorne5, Lemma 3.4] is that we can write A as a finite union of translates of sets of the form
![]() $[\tau _1^*\cdots \tau _n^*]_F$
where
$[\tau _1^*\cdots \tau _n^*]_F$
where
![]() $\tau _1,\ldots ,\tau _n\in \Gamma ^*$
all have length
$\tau _1,\ldots ,\tau _n\in \Gamma ^*$
all have length
![]() $s_0$
. In fact with little additional effort the proof of this generalizes to our setting, and can be made to show that if
$s_0$
. In fact with little additional effort the proof of this generalizes to our setting, and can be made to show that if
![]() $s\in s_0\mathbb {N}$
then we may take all
$s\in s_0\mathbb {N}$
then we may take all
![]() $\tau _i$
to have length s rather than
$\tau _i$
to have length s rather than
![]() $s_0$
. But if we let
$s_0$
. But if we let
![]() $a_i = [\tau _i]_F$
then
$a_i = [\tau _i]_F$
then
![]() $[\tau _1^*\cdots \tau _n^*]_F = [a_1^*\cdots a_n^*]_{F^s}$
; so we have written A in the desired form.
$[\tau _1^*\cdots \tau _n^*]_F = [a_1^*\cdots a_n^*]_{F^s}$
; so we have written A in the desired form.
We note some closure properties:
Proposition 5.4.
-
1. For any
 $A\subseteq \Gamma $
and
$A\subseteq \Gamma $
and
 $s>0$
, A is F-sparse if and only if it is
$s>0$
, A is F-sparse if and only if it is
 $F^s$
-sparse.
$F^s$
-sparse. -
2. If
 $A,B\subseteq \Gamma $
are F-sparse then so is
$A,B\subseteq \Gamma $
are F-sparse then so is
 $A\cup B$
.
$A\cup B$
. -
3. If
 $A\subseteq \Gamma $
is F-sparse and
$A\subseteq \Gamma $
is F-sparse and
 $X\subseteq \Gamma $
is F-automatic then
$X\subseteq \Gamma $
is F-automatic then
 $A\cap X$
is F-sparse.
$A\cap X$
is F-sparse. -
4. If
 $A,B\subseteq \Gamma $
are F-sparse then so is
$A,B\subseteq \Gamma $
are F-sparse then so is
 $A+B$
.
$A+B$
.
Proof
-
1. The right-to-left is by definition; for the left-to-right, take an
 $F^r$
-spanning set
$F^r$
-spanning set
 $\Sigma $
for some
$\Sigma $
for some
 $r{{\kern-1pt}>{\kern-1pt}}0$
and a sparse language
$r{{\kern-1pt}>{\kern-1pt}}0$
and a sparse language
 $L{{\kern-1pt}\subseteq{\kern-1pt}} \Sigma ^*$
such that
$L{{\kern-1pt}\subseteq{\kern-1pt}} \Sigma ^*$
such that
 $A = [L]_{F^r}$
. Recall by [Reference Bell and Moosa2, Lemma 5.7] that
$A = [L]_{F^r}$
. Recall by [Reference Bell and Moosa2, Lemma 5.7] that
 $\Sigma ' = [\Sigma ^{(s)}]_{F^r}$
is an
$\Sigma ' = [\Sigma ^{(s)}]_{F^r}$
is an
 $F^{rs}$
-spanning set. Given
$F^{rs}$
-spanning set. Given
 $\sigma \in \Sigma ^*$
with
$\sigma \in \Sigma ^*$
with
 $s\mid {\lvert \sigma \rvert } $
we can associate
$s\mid {\lvert \sigma \rvert } $
we can associate
 $\sigma '\in (\Sigma ')^*$
as follows: write
$\sigma '\in (\Sigma ')^*$
as follows: write
 $\sigma = \sigma _1\cdots \sigma _{\frac {{\lvert \sigma \rvert } }s}$
with each
$\sigma = \sigma _1\cdots \sigma _{\frac {{\lvert \sigma \rvert } }s}$
with each
 $\sigma _i\in \Sigma ^{(s)}$
, and set
$\sigma _i\in \Sigma ^{(s)}$
, and set
 $\sigma ' = [\sigma _1]_{F^r}\cdots [\sigma _{\frac {{\lvert \sigma \rvert } }s}]_{F^r}$
. So
$\sigma ' = [\sigma _1]_{F^r}\cdots [\sigma _{\frac {{\lvert \sigma \rvert } }s}]_{F^r}$
. So
 $[\sigma ]_{F^r} = [\sigma ']_{F^{rs}}$
, and
$[\sigma ]_{F^r} = [\sigma ']_{F^{rs}}$
, and
 ${\lvert {\sigma '} \rvert } = \frac {{\lvert \sigma \rvert } }s$
.
${\lvert {\sigma '} \rvert } = \frac {{\lvert \sigma \rvert } }s$
.Note now that
Since regular languages are closed under intersection (see [Reference Yu7, Theorem 2.1]), we get that $$ \begin{align*}A = [L]_{F^r} = [L0^*\cap (\Sigma ^{(s)})^*]_{F^r} = [\underbrace{\{\sigma ' : \sigma \in L0^*\cap \Sigma ^{(s\mathbb{N})}\}}_{L'}]_{F^{rs}}. \end{align*} $$
$$ \begin{align*}A = [L]_{F^r} = [L0^*\cap (\Sigma ^{(s)})^*]_{F^r} = [\underbrace{\{\sigma ' : \sigma \in L0^*\cap \Sigma ^{(s\mathbb{N})}\}}_{L'}]_{F^{rs}}. \end{align*} $$
 $L0^*\cap (\Sigma ^s)^*$
is regular; one can then use a DFA that recognizes
$L0^*\cap (\Sigma ^s)^*$
is regular; one can then use a DFA that recognizes
 $L0^*\cap (\Sigma ^s)^*$
to construct an NFA that recognizes
$L0^*\cap (\Sigma ^s)^*$
to construct an NFA that recognizes
 $L'$
. By Fact 5.2
$L'$
. By Fact 5.2
 $L0^*$
, and hence
$L0^*$
, and hence
 $L0^*\cap (\Sigma ^s)^*$
, is a sparse language; thus since
$L0^*\cap (\Sigma ^s)^*$
, is a sparse language; thus since
 ${\lvert {\sigma '} \rvert }= \frac {{\lvert \sigma \rvert } }s$
we get that
${\lvert {\sigma '} \rvert }= \frac {{\lvert \sigma \rvert } }s$
we get that
 $L'$
is sparse. So
$L'$
is sparse. So
 $A = [L']_{F^{rs}}$
is
$A = [L']_{F^{rs}}$
is
 $F^s$
-sparse.
$F^s$
-sparse.
-
2. Take an
 $F^r$
-spanning set
$F^r$
-spanning set
 $\Sigma $
and an
$\Sigma $
and an
 $F^s$
-spanning set
$F^s$
-spanning set
 $\Theta $
with sparse languages
$\Theta $
with sparse languages
 $L_1\subseteq \Sigma ^*$
and
$L_1\subseteq \Sigma ^*$
and
 $L_2\subseteq \Theta ^*$
such that
$L_2\subseteq \Theta ^*$
such that
 $A = [L_1]_{F^r}$
and
$A = [L_1]_{F^r}$
and
 $B = [L_2]_{F^s}$
. By the argument given in the proof of (1), we may assume
$B = [L_2]_{F^s}$
. By the argument given in the proof of (1), we may assume
 $r=s$
. By [Reference Bell and Moosa2, Lemma 5.6], there is an
$r=s$
. By [Reference Bell and Moosa2, Lemma 5.6], there is an
 $F^r$
-spanning set
$F^r$
-spanning set
 $\Omega $
containing
$\Omega $
containing
 $\Sigma \cup \Theta $
. Then
$\Sigma \cup \Theta $
. Then
 $L_1\cup L_2$
is a sparse language in
$L_1\cup L_2$
is a sparse language in
 $\Omega ^*$
, and
$\Omega ^*$
, and
 $A\cup B = [L_1\cup L_2]_{F^r}$
. So
$A\cup B = [L_1\cup L_2]_{F^r}$
. So
 $A\cup B$
is F-sparse.
$A\cup B$
is F-sparse. -
3. Take an
 $F^r$
-spanning set
$F^r$
-spanning set
 $\Sigma $
for some
$\Sigma $
for some
 $r>0$
and a sparse language
$r>0$
and a sparse language
 $L\subseteq \Sigma ^*$
such that
$L\subseteq \Sigma ^*$
such that
 $A = [L]_{F^r}$
. By Proposition 2.6
$A = [L]_{F^r}$
. By Proposition 2.6
 $\{\sigma \in \Sigma ^*:[\sigma ]_{F^r}\in X\}$
is regular. So if
$\{\sigma \in \Sigma ^*:[\sigma ]_{F^r}\in X\}$
is regular. So if
 $L' = \{\sigma \in L : [\sigma ]_{F^r}\in X\}$
then
$L' = \{\sigma \in L : [\sigma ]_{F^r}\in X\}$
then
 $L'$
is regular (as the intersection of two regular languages; see [Reference Yu7, Theorem 2.1]) and thus sparse (as it’s contained in L). But
$L'$
is regular (as the intersection of two regular languages; see [Reference Yu7, Theorem 2.1]) and thus sparse (as it’s contained in L). But
 $[L']_{F^r} = A\cap X$
; so
$[L']_{F^r} = A\cap X$
; so
 $A\cap X$
is F-sparse.
$A\cap X$
is F-sparse. -
4. We first check the case where
 $B = \{\gamma \}$
is a singleton. Take an
$B = \{\gamma \}$
is a singleton. Take an
 $F^r$
-spanning set
$F^r$
-spanning set
 $\Sigma $
for some
$\Sigma $
for some
 $r>0$
and a sparse language
$r>0$
and a sparse language
 $L\subseteq \Sigma ^*$
such that
$L\subseteq \Sigma ^*$
such that
 $A = [L]_{F^r}$
. By [Reference Bell and Moosa2, Lemma 5.6] there is an
$A = [L]_{F^r}$
. By [Reference Bell and Moosa2, Lemma 5.6] there is an
 $F^r$
-spanning set
$F^r$
-spanning set
 $\Sigma '\supseteq \Sigma $
that contains
$\Sigma '\supseteq \Sigma $
that contains
 $a+\gamma $
for every
$a+\gamma $
for every
 $a\in \Sigma $
. Given
$a\in \Sigma $
. Given
 $\sigma = a_1\cdots a_{{\lvert \sigma \rvert } } \in \Sigma ^*$
non-empty let
$\sigma = a_1\cdots a_{{\lvert \sigma \rvert } } \in \Sigma ^*$
non-empty let
 $\sigma _{\gamma } = (a_1+\gamma )a_2\cdots a_{{\lvert \sigma \rvert } }\in (\Sigma ')^*$
; so
$\sigma _{\gamma } = (a_1+\gamma )a_2\cdots a_{{\lvert \sigma \rvert } }\in (\Sigma ')^*$
; so
 $[\sigma _{\gamma } ]_{F^r} = [\sigma ]_{F^r}+\gamma $
. It is routine to check that sparsity of L implies sparsity of
$[\sigma _{\gamma } ]_{F^r} = [\sigma ]_{F^r}+\gamma $
. It is routine to check that sparsity of L implies sparsity of
 $L_{\gamma } := \{\sigma _{\gamma } : \sigma \in L\} \subseteq (\Sigma ')^*$
. So
$L_{\gamma } := \{\sigma _{\gamma } : \sigma \in L\} \subseteq (\Sigma ')^*$
. So
 $A+\gamma = [L_{\gamma } ]_{F^r}$
is F-sparse.
$A+\gamma = [L_{\gamma } ]_{F^r}$
is F-sparse.We now do the general case. By Proposition 5.3 there is s such that there is an
 $F^s$
-spanning set and such that both A and B can be written as a finite union of translates of sets of the form
$F^s$
-spanning set and such that both A and B can be written as a finite union of translates of sets of the form
 $[a_1^*\cdots a_n^*]_{F^s}$
. Distributing, it suffices to check the case
$[a_1^*\cdots a_n^*]_{F^s}$
. Distributing, it suffices to check the case
 $A = \gamma + [a_1^*\cdots a_n^*]_{F^s}$
and
$A = \gamma + [a_1^*\cdots a_n^*]_{F^s}$
and
 $B = \gamma '+[b_1^*\cdots b_{n'}^*]_{F^s}$
. By the first case, we may assume
$B = \gamma '+[b_1^*\cdots b_{n'}^*]_{F^s}$
. By the first case, we may assume
 $\gamma =\gamma '=0$
. Given
$\gamma =\gamma '=0$
. Given
 $\sigma \in a_1^*\cdots a_n^*$
and
$\sigma \in a_1^*\cdots a_n^*$
and
 $\tau \in b_1^*\cdots b_{n'}^*$
we let
$\tau \in b_1^*\cdots b_{n'}^*$
we let
 $\sigma \oplus \tau \in \Gamma ^*$
denote the string obtained by characterwise addition; so
$\sigma \oplus \tau \in \Gamma ^*$
denote the string obtained by characterwise addition; so
 $[\sigma \oplus \tau ]_{F^s} = [\sigma ]_{F^s}+[\tau ]_{F^s}$
. Then and is thus sparse by an inductive argument on
$[\sigma \oplus \tau ]_{F^s} = [\sigma ]_{F^s}+[\tau ]_{F^s}$
. Then and is thus sparse by an inductive argument on $$ \begin{align*}a_1^*\cdots a_n^*\oplus b_1^*\cdots b_{n'}^* &= (a_1+b_1)^*(a_2^*\cdots a_n^*\oplus b_1^*\cdots b_{n'}^*)\\ &\quad\cup (a_1+b_1)^* (a_1^*\cdots a_n^* \oplus b_2^*\cdots b_{n'}^*) \end{align*} $$
$$ \begin{align*}a_1^*\cdots a_n^*\oplus b_1^*\cdots b_{n'}^* &= (a_1+b_1)^*(a_2^*\cdots a_n^*\oplus b_1^*\cdots b_{n'}^*)\\ &\quad\cup (a_1+b_1)^* (a_1^*\cdots a_n^* \oplus b_2^*\cdots b_{n'}^*) \end{align*} $$
 $(n,n')$
. So
$(n,n')$
. So
 $A+B = [a_1^*\cdots a_n^*\oplus b_1^*\cdots b_{n'}^*]_{F^s}$
is F-sparse.
$A+B = [a_1^*\cdots a_n^*\oplus b_1^*\cdots b_{n'}^*]_{F^s}$
is F-sparse.
Remark 5.5. A special case of Proposition 5.4(4) is that the F-sparse sets are closed under translation. This answers a question posed in [Reference Bell and Moosa2, Remark 7.3].
We now work towards a characterization of F-sparsity using length functions.
Definition 5.6. Suppose
![]() $A\subseteq \Gamma $
and
$A\subseteq \Gamma $
and
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F)$
. We let
$(\Gamma ,F)$
. We let
![]() $f_{A,\lambda }(x) = {\lvert {\{a\in A : \lambda (a)\le x\}}\rvert }$
, and we say A is
$f_{A,\lambda }(x) = {\lvert {\{a\in A : \lambda (a)\le x\}}\rvert }$
, and we say A is
![]() $\lambda $
-sparse if
$\lambda $
-sparse if
![]() $f_{A,\lambda }(x)\in O(x^d)$
for some
$f_{A,\lambda }(x)\in O(x^d)$
for some
![]() $d\in \mathbb {N}$
.
$d\in \mathbb {N}$
.
For our characterization of F-sparsity we will need the following reverse ultrametric inequality:
Lemma 5.7. If
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F)$
with associated constants
$(\Gamma ,F)$
with associated constants
![]() $C,D,E$
and
$C,D,E$
and
![]() $a,b\in \Gamma $
satisfy
$a,b\in \Gamma $
satisfy
![]() $\lambda (b) < \lambda (a)-D$
then
$\lambda (b) < \lambda (a)-D$
then
![]() $\lambda (a+b)\ge \lambda (a)-D$
.
$\lambda (a+b)\ge \lambda (a)-D$
.
Proof Otherwise
![]() $\lambda (a)> \max (\lambda (b), \lambda (a+b))+D= \max (\lambda (-b),\lambda (a+b))+D\ge \lambda (a)$
.
$\lambda (a)> \max (\lambda (b), \lambda (a+b))+D= \max (\lambda (-b),\lambda (a+b))+D\ge \lambda (a)$
.
We will also require the following observation relating the length of a string to the length of the group element it represents:
Lemma 5.8. Suppose
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F)$
with associated constants
$(\Gamma ,F)$
with associated constants
![]() $C,D,E;$
suppose
$C,D,E;$
suppose
![]() $S $
is a finite subset of
$S $
is a finite subset of
![]() $\Gamma $
. Then there is
$\Gamma $
. Then there is
![]() $M\ge 0$
such that
$M\ge 0$
such that
![]() $\lambda ([\sigma ]_F)\le {\lvert \sigma \rvert } C+M$
for all
$\lambda ([\sigma ]_F)\le {\lvert \sigma \rvert } C+M$
for all
![]() $\sigma \in S ^*$
.
$\sigma \in S ^*$
.
Proof Pick
![]() $r\in \mathbb {N}$
such that
$r\in \mathbb {N}$
such that
![]() $rC\ge D$
, and let
$rC\ge D$
, and let
 $K = \max \{\lambda ([\sigma ]_F) : \sigma \in S ^{(r)}\}$
.
$K = \max \{\lambda ([\sigma ]_F) : \sigma \in S ^{(r)}\}$
.
We show by induction on
![]() $k\ge 1$
that if
$k\ge 1$
that if
![]() $\sigma \in S ^{(kr)}$
then
$\sigma \in S ^{(kr)}$
then
![]() $\lambda ([\sigma ]_F)\le (k-1)rC + D + K$
. The base case is just the definition of K. For the induction step, write
$\lambda ([\sigma ]_F)\le (k-1)rC + D + K$
. The base case is just the definition of K. For the induction step, write
![]() $\sigma = \sigma _1\sigma _2$
where
$\sigma = \sigma _1\sigma _2$
where
![]() ${\lvert {\sigma _2} \rvert } =r$
. Then by the induction hypothesis
${\lvert {\sigma _2} \rvert } =r$
. Then by the induction hypothesis
![]() $\lambda ([\sigma _1]_F)\le (k-2)rC + D + K$
, and by the logarithmic property we get that
$\lambda ([\sigma _1]_F)\le (k-2)rC + D + K$
, and by the logarithmic property we get that
![]() $\lambda (F^{(k-1)r}[\sigma _2]_F) \le \lambda ([\sigma _2]_F)+ (k-1)rC \le {(k-1)rC + K}$
. So by the ultrametric inequality we get that
$\lambda (F^{(k-1)r}[\sigma _2]_F) \le \lambda ([\sigma _2]_F)+ (k-1)rC \le {(k-1)rC + K}$
. So by the ultrametric inequality we get that
 $$ \begin{align*}\lambda ([\sigma ]_F) &= \lambda ([\sigma _1]_F + F^{(k-1)r}[\sigma _2]_F) \le \max((k-2)rC+D+K,(k-1)rC+K)+D\\ &= (k-1)rC+D+K \end{align*} $$
$$ \begin{align*}\lambda ([\sigma ]_F) &= \lambda ([\sigma _1]_F + F^{(k-1)r}[\sigma _2]_F) \le \max((k-2)rC+D+K,(k-1)rC+K)+D\\ &= (k-1)rC+D+K \end{align*} $$
(since
![]() $rC\ge D$
).
$rC\ge D$
).
Now, for any
![]() $\sigma \in S ^*$
we can pad by some string of zeroes
$\sigma \in S ^*$
we can pad by some string of zeroes
![]() $\tau $
of length
$\tau $
of length
![]() $<r$
to get that
$<r$
to get that
![]() ${\lvert {\sigma \tau } \rvert }\in r\mathbb {Z}$
, at which point we get
${\lvert {\sigma \tau } \rvert }\in r\mathbb {Z}$
, at which point we get
![]() $\lambda ([\sigma ]_F) = \lambda ([\sigma \tau ]_F) \le ({\lvert {\sigma \tau } \rvert }-r)C+ D+ K\le C{\lvert \sigma \rvert } + D+K$
.
$\lambda ([\sigma ]_F) = \lambda ([\sigma \tau ]_F) \le ({\lvert {\sigma \tau } \rvert }-r)C+ D+ K\le C{\lvert \sigma \rvert } + D+K$
.
Lemma 5.9. Suppose
![]() $\Sigma $
is an
$\Sigma $
is an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
. Suppose
$r>0$
. Suppose
![]() $L\subseteq \Sigma ^*$
is regular and
$L\subseteq \Sigma ^*$
is regular and
![]() $\preceq $
is a linear ordering on
$\preceq $
is a linear ordering on
![]() $\Sigma$
(which induces a length-lexicographicalFootnote
2
ordering on
$\Sigma$
(which induces a length-lexicographicalFootnote
2
ordering on
![]() $\Sigma ^*$
which we also denote by
$\Sigma ^*$
which we also denote by
![]() $\preceq )$
. Let
$\preceq )$
. Let
 $$ \begin{align*}\widetilde{L} = \{\sigma \in L : \sigma \preceq \tau \text{ for all }\tau \in L\text{ such that }[\sigma ]_{F^r} = [\tau ]_{F^r}\}. \end{align*} $$
$$ \begin{align*}\widetilde{L} = \{\sigma \in L : \sigma \preceq \tau \text{ for all }\tau \in L\text{ such that }[\sigma ]_{F^r} = [\tau ]_{F^r}\}. \end{align*} $$
Then
![]() $\widetilde {L}$
is regular. Moreover if
$\widetilde {L}$
is regular. Moreover if
![]() $[L]_{F^r}$
is
$[L]_{F^r}$
is
![]() $\lambda _{\Sigma } $
-sparse then
$\lambda _{\Sigma } $
-sparse then
![]() $\widetilde {L}$
is sparse.
$\widetilde {L}$
is sparse.
Proof Be replacing F with
![]() $F^r$
we may assume
$F^r$
we may assume
![]() $r=1$
. Let
$r=1$
. Let
![]() $K\subseteq (\Sigma ^2)^*$
be the set of
$K\subseteq (\Sigma ^2)^*$
be the set of
 $\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}$
such that
$\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}$
such that
-
•
 $\sigma \in L$
;
$\sigma \in L$
; -
•
 $[\sigma ]_F = [\tau ]_F$
; and
$[\sigma ]_F = [\tau ]_F$
; and -
•
 $\tau \in L\ \mathrm{and}\ \tau \prec \sigma,\ \mathrm{or}\ \tau \in L00^*$
.
$\tau \in L\ \mathrm{and}\ \tau \prec \sigma,\ \mathrm{or}\ \tau \in L00^*$
.
So if
![]() $\sigma \in L$
then
$\sigma \in L$
then
 ${\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}} \in K$
if and only if
${\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}} \in K$
if and only if
![]() $\tau $
(with possibly the trailing
$\tau $
(with possibly the trailing
![]() $0$
removed) witnesses that
$0$
removed) witnesses that
 $\sigma \notin \widetilde {L}$
; so
$\sigma \notin \widetilde {L}$
; so
 $\widetilde {L} = L\setminus \pi (K)$
, where
$\widetilde {L} = L\setminus \pi (K)$
, where
![]() $\pi \colon (\Sigma ^2)^*\to \Sigma ^*$
is projection to the first coordinate. So since L is regular it suffices to show that
$\pi \colon (\Sigma ^2)^*\to \Sigma ^*$
is projection to the first coordinate. So since L is regular it suffices to show that
![]() $\pi (K)$
is regular (since by [Reference Yu7, Theorems 2.1 and 2.2] regular languages are closed under Boolean combinations).
$\pi (K)$
is regular (since by [Reference Yu7, Theorems 2.1 and 2.2] regular languages are closed under Boolean combinations).
Note that K is regular: this is because
![]() $L\times L$
, equality (see Corollary 4.5), ending in
$L\times L$
, equality (see Corollary 4.5), ending in
![]() $0$
, and
$0$
, and
![]() $\prec $
are regular, and so K is a Boolean combination of regular languages. Fix a DFA
$\prec $
are regular, and so K is a Boolean combination of regular languages. Fix a DFA
![]() $(\Sigma ^2, Q, q_0,\Omega ,\delta )$
for K; we use this to construct an NFA
$(\Sigma ^2, Q, q_0,\Omega ,\delta )$
for K; we use this to construct an NFA
![]() $(\Sigma ,Q',q_0^{\prime },\Omega ',\delta ')$
recognizing
$(\Sigma ,Q',q_0^{\prime },\Omega ',\delta ')$
recognizing
![]() $\pi (K)$
. We let
$\pi (K)$
. We let
![]() $Q' = Q$
,
$Q' = Q$
,
![]() $q_0^{\prime } = q_0$
, and
$q_0^{\prime } = q_0$
, and
![]() $\Omega ' = \Omega $
. For the transition function we set
$\Omega ' = \Omega $
. For the transition function we set
 $$ \begin{align*} \delta' (q, a) =\bigg\{\delta \bigg( {q, \begin{pmatrix}{a}\\{b}\end{pmatrix}}\bigg) : b\in \Sigma\bigg\}. \end{align*} $$
$$ \begin{align*} \delta' (q, a) =\bigg\{\delta \bigg( {q, \begin{pmatrix}{a}\\{b}\end{pmatrix}}\bigg) : b\in \Sigma\bigg\}. \end{align*} $$
Then
![]() $\sigma $
is accepted by our NFA if and only if there is
$\sigma $
is accepted by our NFA if and only if there is
![]() $\tau \in \Sigma ^*$
with
$\tau \in \Sigma ^*$
with
![]() ${\lvert \tau \rvert } ={\lvert \sigma \rvert } $
such that
${\lvert \tau \rvert } ={\lvert \sigma \rvert } $
such that
 $\delta \left ( {q_0,{\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}} }\right )\in \Omega $
; i.e., such that
$\delta \left ( {q_0,{\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}} }\right )\in \Omega $
; i.e., such that
 ${\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}} \in K$
. So our NFA recognizes
${\begin {pmatrix}{\sigma }\\{\tau }\end {pmatrix}} \in K$
. So our NFA recognizes
![]() $\pi (K)$
, and
$\pi (K)$
, and
![]() $\pi (K)$
is regular. So
$\pi (K)$
is regular. So
![]() $\widetilde {L}$
is regular.
$\widetilde {L}$
is regular.
For the “moreover” clause, suppose
![]() $[L]_F$
is
$[L]_F$
is
![]() $\lambda _{\Sigma } $
-sparse. Note that
$\lambda _{\Sigma } $
-sparse. Note that
![]() $[\cdot ]_F$
is a bijection
$[\cdot ]_F$
is a bijection
 $ \widetilde {L}\to [L]_F $
; furthermore by definition of
$ \widetilde {L}\to [L]_F $
; furthermore by definition of
![]() $\lambda _{\Sigma } $
we have that
$\lambda _{\Sigma } $
we have that
![]() $\lambda _{\Sigma } ([\sigma ]_F)\le {\lvert \sigma \rvert } $
. It follows that
$\lambda _{\Sigma } ([\sigma ]_F)\le {\lvert \sigma \rvert } $
. It follows that
![]() $\widetilde {L}$
is sparse: since
$\widetilde {L}$
is sparse: since
![]() $[L]_F$
is
$[L]_F$
is
![]() $\lambda _{\Sigma } $
-sparse, we get that
$\lambda _{\Sigma } $
-sparse, we get that
 $$ \begin{align*}{\lvert{\{\sigma \in \widetilde{L} : {\lvert \sigma\rvert} \le x\}}\rvert} \le {\lvert{\{a\in [L]_F: \lambda _{\Sigma} (a)\le x\}} \rvert} = f_{[L]_F,\lambda_{\Sigma} }(x)\in O(x^d), \end{align*} $$
$$ \begin{align*}{\lvert{\{\sigma \in \widetilde{L} : {\lvert \sigma\rvert} \le x\}}\rvert} \le {\lvert{\{a\in [L]_F: \lambda _{\Sigma} (a)\le x\}} \rvert} = f_{[L]_F,\lambda_{\Sigma} }(x)\in O(x^d), \end{align*} $$
for some d.
The construction of the NFA in the above proof can be generalized to show that the projection away from some coordinate of a regular language over
![]() $\Sigma ^{m+1}$
is regular over
$\Sigma ^{m+1}$
is regular over
![]() $\Sigma ^m$
. We also used the fact that Boolean combinations of regular languages are regular; combining these two facts gives us a sense in which regular languages interact nicely with first-order logic.
$\Sigma ^m$
. We also used the fact that Boolean combinations of regular languages are regular; combining these two facts gives us a sense in which regular languages interact nicely with first-order logic.
Theorem 5.10. Suppose
![]() $\lambda $
is a length function for some
$\lambda $
is a length function for some
![]() $(\Gamma ,F^r)$
. Then
$(\Gamma ,F^r)$
. Then
![]() $A\subseteq \Gamma $
is F-sparse if and only if it is F-automatic and
$A\subseteq \Gamma $
is F-sparse if and only if it is F-automatic and
![]() $\lambda $
-sparse.
$\lambda $
-sparse.
Proof By Proposition 5.4-(1) it suffices to check the case
![]() $r=1$
; so assume
$r=1$
; so assume
![]() $\lambda $
is a length function for
$\lambda $
is a length function for
![]() $(\Gamma ,F)$
. Let
$(\Gamma ,F)$
. Let
![]() $C,D,E$
be the constants associated with
$C,D,E$
be the constants associated with
![]() $\lambda $
.
$\lambda $
.
-
 $(\implies )$
Suppose A is F-sparse; so there is some
$(\implies )$
Suppose A is F-sparse; so there is some
 $F^s$
-spanning set
$F^s$
-spanning set
 $\Sigma $
and some sparse
$\Sigma $
and some sparse
 $L\subseteq \Sigma ^*$
such that
$L\subseteq \Sigma ^*$
such that
 $A = [L]_{F^s}$
. We get by [Reference Bell and Moosa2, Proposition 6.8(b)] that A is F-automatic; it remains to show that A is
$A = [L]_{F^s}$
. We get by [Reference Bell and Moosa2, Proposition 6.8(b)] that A is F-automatic; it remains to show that A is
 $\lambda $
-sparse. Since
$\lambda $
-sparse. Since
 $\lambda $
is also a length function for
$\lambda $
is also a length function for
 $(\Gamma ,F^s)$
(see Remark 3.4), we can replace F with
$(\Gamma ,F^s)$
(see Remark 3.4), we can replace F with
 $F^s$
and thus assume that
$F^s$
and thus assume that
 $s=1$
. By Fact 5.2 L is a finite union of simple sparse languages. One can verify that a finite union of
$s=1$
. By Fact 5.2 L is a finite union of simple sparse languages. One can verify that a finite union of
 $\lambda $
-sparse sets is
$\lambda $
-sparse sets is
 $\lambda $
-sparse; it thus suffices to check the case where L is simple sparse, say
$\lambda $
-sparse; it thus suffices to check the case where L is simple sparse, say
 $L = v_0w_1^*\cdots v_{n-1}w_n^*v_n$
with
$L = v_0w_1^*\cdots v_{n-1}w_n^*v_n$
with
 $u_i,v_i\in \Sigma ^*$
. We apply induction on n; the base case
$u_i,v_i\in \Sigma ^*$
. We apply induction on n; the base case
 $n=0$
is trivial.
$n=0$
is trivial.For the induction step, we have two cases.
-
Case 1. Suppose
 $[w_n^*v_n]_F$
is finite. Then and by the induction hypothesis each
$[w_n^*v_n]_F$
is finite. Then and by the induction hypothesis each $$ \begin{align*}A = \bigcup _{a \in [w_n^*v_n]_F} [v_0w_1^*\cdots w_{n-1}^*v_{n-1}a ]_F, \end{align*} $$
$$ \begin{align*}A = \bigcup _{a \in [w_n^*v_n]_F} [v_0w_1^*\cdots w_{n-1}^*v_{n-1}a ]_F, \end{align*} $$
 $[v_0w_1^*\cdots w_{n-1}^*v_{n-1}a ]_F$
is
$[v_0w_1^*\cdots w_{n-1}^*v_{n-1}a ]_F$
is
 $\lambda $
-sparse. So A is
$\lambda $
-sparse. So A is
 $\lambda $
-sparse.
$\lambda $
-sparse.
-
Case 2. Suppose
 $[w_n^*v_n]_F$
is infinite.
$[w_n^*v_n]_F$
is infinite.Claim 5.11. There is
 $M\in \mathbb {R}$
and
$M\in \mathbb {R}$
and
 $i\in \mathbb {N}$
such that if
$i\in \mathbb {N}$
such that if
 $k_n\ge i$
then
$k_n\ge i$
then
 $\lambda ([v_0w_1^{k_1}\cdots w_n^{k_n}v_n]_F)\ge C{\lvert {v_0w_1^{k_1}\cdots w_n^{k_n}v_n} \rvert }+M $
.Now, we can write
$\lambda ([v_0w_1^{k_1}\cdots w_n^{k_n}v_n]_F)\ge C{\lvert {v_0w_1^{k_1}\cdots w_n^{k_n}v_n} \rvert }+M $
.Now, we can writeProof Our strategy will be to write
 $$ \begin{align*}\underbrace{[v_0w_1^{k_1}\cdots w_n^{k_n}v_n]_F}_a &= [v_0w_1^{k_1}\cdots w_{n-1}^{k_{n-1}}v_{n-1}w_n^{k_n-i}]_F\\[-3pt] &\quad+ \underbrace{F^{{\lvert {v_0w_1^{k_1}\cdots w_{n-1}^{k_{n-1}}v_{n-1}w_n^{k_n-i}}\rvert}}[w_n^iv_n]_F}_b \end{align*} $$
$$ \begin{align*}\underbrace{[v_0w_1^{k_1}\cdots w_n^{k_n}v_n]_F}_a &= [v_0w_1^{k_1}\cdots w_{n-1}^{k_{n-1}}v_{n-1}w_n^{k_n-i}]_F\\[-3pt] &\quad+ \underbrace{F^{{\lvert {v_0w_1^{k_1}\cdots w_{n-1}^{k_{n-1}}v_{n-1}w_n^{k_n-i}}\rvert}}[w_n^iv_n]_F}_b \end{align*} $$
and then use the reverse ultrametric inequality to show that
 $\lambda (a)$
is not much less than
$\lambda (a)$
is not much less than
 $\lambda (b)$
.
$\lambda (b)$
.Applying Lemma 5.8 with
 $S=\Sigma $
, we find that there is
$S=\Sigma $
, we find that there is
 $M_0\ge 0$
such that
$M_0\ge 0$
such that
 $\lambda ([\sigma ]_F)\le C{\lvert \sigma \rvert } +M_0$
for all
$\lambda ([\sigma ]_F)\le C{\lvert \sigma \rvert } +M_0$
for all
 $\sigma \in \Sigma ^*$
. Then by Northcott property there is some i such that
$\sigma \in \Sigma ^*$
. Then by Northcott property there is some i such that
 $\lambda ([w_n^iv_n]_F)> M_0+D+E$
. Suppose
$\lambda ([w_n^iv_n]_F)> M_0+D+E$
. Suppose
 $k_1,\ldots ,k_n\in \mathbb {N}$
with
$k_1,\ldots ,k_n\in \mathbb {N}$
with
 $k_n\ge i$
; to avoid notational clutter we abbreviate
$k_n\ge i$
; to avoid notational clutter we abbreviate
 $\sigma = v_0w_1^{k_1}\cdots w_{n-1}^{k_{n-1}}v_{n-1}w_n^{k_n-i}$
. We then wish to show that
$\sigma = v_0w_1^{k_1}\cdots w_{n-1}^{k_{n-1}}v_{n-1}w_n^{k_n-i}$
. We then wish to show that
 $\lambda ([\sigma w_n^iv_n]_F)$
is not much less than
$\lambda ([\sigma w_n^iv_n]_F)$
is not much less than
 $\lambda (F^{{\lvert \sigma \rvert } }[w_n^iv_n]_F)$
.
$\lambda (F^{{\lvert \sigma \rvert } }[w_n^iv_n]_F)$
.Note that
 $$ \begin{align*}\lambda (F^{{\lvert \sigma\rvert} }[w_n^iv_n]_F) {{\kern-1pt}\ge{\kern-1pt}} \lambda ([w_n^iv_n]_F){{\kern-1pt}+{\kern-1pt}}{\lvert \sigma\rvert} C -E{{\kern-1pt}>{\kern-1pt}} C{\lvert \sigma\rvert} {{\kern-1pt}+{\kern-1pt}}D{{\kern-1pt}+{\kern-1pt}}M_0 {{\kern-1pt}\ge{\kern-1pt}} \lambda ([\sigma ]_F){{\kern-1pt}+{\kern-1pt}}D \end{align*} $$
$$ \begin{align*}\lambda (F^{{\lvert \sigma\rvert} }[w_n^iv_n]_F) {{\kern-1pt}\ge{\kern-1pt}} \lambda ([w_n^iv_n]_F){{\kern-1pt}+{\kern-1pt}}{\lvert \sigma\rvert} C -E{{\kern-1pt}>{\kern-1pt}} C{\lvert \sigma\rvert} {{\kern-1pt}+{\kern-1pt}}D{{\kern-1pt}+{\kern-1pt}}M_0 {{\kern-1pt}\ge{\kern-1pt}} \lambda ([\sigma ]_F){{\kern-1pt}+{\kern-1pt}}D \end{align*} $$
by hypothesis on
 $M_0$
. So by the reverse ultrametric inequality we get that
$M_0$
. So by the reverse ultrametric inequality we get that  $$ \begin{align*}\lambda ([\sigma w_n^iv_n]_F) &= \lambda ([\sigma ]_F + F^{{\lvert \sigma\rvert} }[w_n^iv_n]_F) \ge \lambda (F^{{\lvert \sigma\rvert} }[w_n^iv_n]_F)-D\\ &\ge \lambda ([w_n^iv_n]_F)+{\lvert \sigma\rvert} C - D - E. \end{align*} $$
$$ \begin{align*}\lambda ([\sigma w_n^iv_n]_F) &= \lambda ([\sigma ]_F + F^{{\lvert \sigma\rvert} }[w_n^iv_n]_F) \ge \lambda (F^{{\lvert \sigma\rvert} }[w_n^iv_n]_F)-D\\ &\ge \lambda ([w_n^iv_n]_F)+{\lvert \sigma\rvert} C - D - E. \end{align*} $$
Let
 $M = \lambda ([w_n^iv_n]_F)- {\lvert {w_n^iv_n} \rvert }C -D -E$
. Then if
$M = \lambda ([w_n^iv_n]_F)- {\lvert {w_n^iv_n} \rvert }C -D -E$
. Then if
 $k_n\ge i$
then
$k_n\ge i$
then
 $\lambda ([v_0w_1^{k_1}\cdots w_n^{k_n}v_n]_F)\ge {\lvert {v_0w_1^{k_1}\cdots w_n^{k_n}v_n} \rvert } C +M$
, as desired.By the induction hypothesis each
$\lambda ([v_0w_1^{k_1}\cdots w_n^{k_n}v_n]_F)\ge {\lvert {v_0w_1^{k_1}\cdots w_n^{k_n}v_n} \rvert } C +M$
, as desired.By the induction hypothesis each $$ \begin{align*}L {{\kern-1pt}={\kern-1pt}} \{v_0w_1^{k_1}\cdots w_n^{k_n}v_n : k_1,\ldots ,k_n\in\mathbb{N},\ k_n\ge i\}{{\kern-1pt}\cup{\kern-1pt}}\bigcup _{j<i} v_0w_1^*\cdots w_{n-1}^*v_{n-1}w_n^jv_n. \end{align*} $$
$$ \begin{align*}L {{\kern-1pt}={\kern-1pt}} \{v_0w_1^{k_1}\cdots w_n^{k_n}v_n : k_1,\ldots ,k_n\in\mathbb{N},\ k_n\ge i\}{{\kern-1pt}\cup{\kern-1pt}}\bigcup _{j<i} v_0w_1^*\cdots w_{n-1}^*v_{n-1}w_n^jv_n. \end{align*} $$
 $[v_0w_1^*\cdots w_{n-1}^*v_{n-1}w_n^jv_n]_F$
is
$[v_0w_1^*\cdots w_{n-1}^*v_{n-1}w_n^jv_n]_F$
is
 $\lambda $
-sparse; it remains to check the case
$\lambda $
-sparse; it remains to check the case
 $k_n\ge i$
.
$k_n\ge i$
.
If
 $\tau =v_0w_1^{k_1}\cdots w_n^{k_n}v_n$
with
$\tau =v_0w_1^{k_1}\cdots w_n^{k_n}v_n$
with
 $k_n\ge i$
and
$k_n\ge i$
and
 $\tau $
satisfies
$\tau $
satisfies
 $\lambda ([\tau ]_F)\le x$
then by the claim
$\lambda ([\tau ]_F)\le x$
then by the claim
 ${\lvert \tau \rvert } C+M\le x$
, and thus
${\lvert \tau \rvert } C+M\le x$
, and thus
 ${\lvert \tau \rvert } \le C^{-1}( x-M)$
. But by hypothesis there are
${\lvert \tau \rvert } \le C^{-1}( x-M)$
. But by hypothesis there are
 $d,K$
such that eventually
$d,K$
such that eventually
 ${{\lvert {\{\tau \in L :{\lvert \tau \rvert } \le y\,\}} \rvert } \le Ky^d}$
. So if x is sufficiently large there are at most
${{\lvert {\{\tau \in L :{\lvert \tau \rvert } \le y\,\}} \rvert } \le Ky^d}$
. So if x is sufficiently large there are at most
 $K(C^{-1}(x-M))^d\in O(x^d)$
strings
$K(C^{-1}(x-M))^d\in O(x^d)$
strings
 $\tau \in L$
satisfying
$\tau \in L$
satisfying
 $\lambda ([\tau ]_F)\le x$
; so A is
$\lambda ([\tau ]_F)\le x$
; so A is
 $\lambda $
-sparse.
$\lambda $
-sparse.
-
-
 $(\impliedby )$
Let
$(\impliedby )$
Let
 $\Sigma $
be an
$\Sigma $
be an
 $F^s$
-spanning set for some
$F^s$
-spanning set for some
 $s>0$
. Note first that A is
$s>0$
. Note first that A is
 $\lambda _{\Sigma } $
-sparse. Indeed, by Lemma 5.8 (applied to
$\lambda _{\Sigma } $
-sparse. Indeed, by Lemma 5.8 (applied to
 $(\Gamma ,F^s)$
with
$(\Gamma ,F^s)$
with
 $S=\Sigma $
) there is
$S=\Sigma $
) there is
 $M\in \mathbb {R}$
such that
$M\in \mathbb {R}$
such that
 $\lambda ([\sigma ]_{F^s}) \le {\lvert \sigma \rvert } C+M$
for all
$\lambda ([\sigma ]_{F^s}) \le {\lvert \sigma \rvert } C+M$
for all
 $\sigma \in \Sigma ^*$
. So if
$\sigma \in \Sigma ^*$
. So if
 $\lambda _{\Sigma } (a)\le x$
then
$\lambda _{\Sigma } (a)\le x$
then
 $\lambda (a)\le xC+M $
; thus
$\lambda (a)\le xC+M $
; thus
 $f_{A,\lambda _{\Sigma } }(x)\le f_{A,\lambda }(xC+M)\in O(x^d)$
for some d, and A is
$f_{A,\lambda _{\Sigma } }(x)\le f_{A,\lambda }(xC+M)\in O(x^d)$
for some d, and A is
 $\lambda _{\Sigma } $
-sparse.
$\lambda _{\Sigma } $
-sparse.Let
 $L = \{\sigma \in \Sigma ^* : [\sigma ]_{F^s}\in A\}$
; so L is regular by Proposition 2.6. Fix any total order
$L = \{\sigma \in \Sigma ^* : [\sigma ]_{F^s}\in A\}$
; so L is regular by Proposition 2.6. Fix any total order
 $\preceq $
on
$\preceq $
on
 $\Sigma $
, and let
$\Sigma $
, and let
 $\widetilde {L}$
be as in Lemma 5.9; so
$\widetilde {L}$
be as in Lemma 5.9; so
 $\widetilde {L}$
is sparse, since
$\widetilde {L}$
is sparse, since
 $[L]_{F^s} = A$
is
$[L]_{F^s} = A$
is
 $\lambda _{\Sigma } $
-sparse. So
$\lambda _{\Sigma } $
-sparse. So
 $A = [\widetilde {L}]_{F^s}$
is F-sparse.
$A = [\widetilde {L}]_{F^s}$
is F-sparse.
It follows from Lemma 5.9 and Theorem 5.10 that F-sparsity can be checked in any spanning set by looking at a set of “minimal” representations of elements of A.
Corollary 5.12. Suppose
![]() $\Sigma $
is an
$\Sigma $
is an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
. Suppose
$r>0$
. Suppose
![]() $L\subseteq \Sigma ^*$
is regular and
$L\subseteq \Sigma ^*$
is regular and
![]() $\preceq $
is a linear ordering on
$\preceq $
is a linear ordering on
![]() $\Sigma$
(which we again identify with the induced length-lexicographic ordering on
$\Sigma$
(which we again identify with the induced length-lexicographic ordering on
![]() $\Sigma ^*)$
. Let
$\Sigma ^*)$
. Let
 $$ \begin{align*}\widetilde{L} = \{\sigma \in L : \sigma \preceq \tau \text{ for all }\tau \in L\text{ such that }[\sigma ]_{F^r} = [\tau ]_{F^r}\}. \end{align*} $$
$$ \begin{align*}\widetilde{L} = \{\sigma \in L : \sigma \preceq \tau \text{ for all }\tau \in L\text{ such that }[\sigma ]_{F^r} = [\tau ]_{F^r}\}. \end{align*} $$
Then
![]() $[L]_{F^r}$
is F-sparse if and only if
$[L]_{F^r}$
is F-sparse if and only if
![]() $\widetilde {L}$
is sparse.
$\widetilde {L}$
is sparse.
Proof The right-to-left direction is by definition of F-sparsity. For the left-to-right direction, we use Theorem 5.10 to deduce that
![]() $[L]_{F^r}$
is
$[L]_{F^r}$
is
![]() $\lambda _{\Sigma } $
-sparse, at which point it follows from Lemma 5.9 that
$\lambda _{\Sigma } $
-sparse, at which point it follows from Lemma 5.9 that
![]() $\widetilde {L}$
is sparse.
$\widetilde {L}$
is sparse.
Another consequence is that if A is contained in an F-invariant subgroup H then sparsity of A can be checked in H:
Corollary 5.13. Suppose there is an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
. Suppose
$r>0$
. Suppose
![]() $H\le \Gamma $
is F-invariant and
$H\le \Gamma $
is F-invariant and
![]() $A\subseteq H$
. Then A is F-sparse in
$A\subseteq H$
. Then A is F-sparse in
![]() $\Gamma $
if and only if A is F-sparse in H.
$\Gamma $
if and only if A is F-sparse in H.
Proof For the right-to-left direction, note by Proposition 5.4(1) that A is
![]() $F^r$
-sparse. So there is
$F^r$
-sparse. So there is
![]() $s>0$
with an
$s>0$
with an
![]() $F^{rs}$
-spanning set
$F^{rs}$
-spanning set
![]() $\Sigma $
for H and
$\Sigma $
for H and
![]() $L\subseteq \Sigma ^*$
sparse such that
$L\subseteq \Sigma ^*$
sparse such that
![]() $A = [L]_{F^{rs}}$
. Then using [Reference Bell and Moosa2, Lemmas 5.6 and 5.7], since there is an
$A = [L]_{F^{rs}}$
. Then using [Reference Bell and Moosa2, Lemmas 5.6 and 5.7], since there is an
![]() $F^r$
-spanning set for
$F^r$
-spanning set for
![]() $\Gamma $
we may assume there is an
$\Gamma $
we may assume there is an
![]() $F^{rs}$
-spanning set
$F^{rs}$
-spanning set
![]() $\Sigma '$
for
$\Sigma '$
for
![]() $\Gamma $
containing
$\Gamma $
containing
![]() $\Sigma $
. Then
$\Sigma $
. Then
![]() $L\subseteq (\Sigma ')^*$
witnesses that A is F-sparse in
$L\subseteq (\Sigma ')^*$
witnesses that A is F-sparse in
![]() $\Gamma $
.
$\Gamma $
.
For the left-to-right direction, fix any length function
![]() $\lambda $
for some
$\lambda $
for some
![]() $(\Gamma ,F^s)$
(using Theorem 3.10). One can check that
$(\Gamma ,F^s)$
(using Theorem 3.10). One can check that
![]() $\lambda $
is a length function for H; so by Theorem 5.10 applied to H it suffices to show that A is F-automatic in
$\lambda $
is a length function for H; so by Theorem 5.10 applied to H it suffices to show that A is F-automatic in
![]() $H $
and
$H $
and
![]() $\lambda $
-sparse. By Theorem 5.10 applied to
$\lambda $
-sparse. By Theorem 5.10 applied to
![]() $\Gamma $
we get that A is F-automatic in
$\Gamma $
we get that A is F-automatic in
![]() $\Gamma $
and
$\Gamma $
and
![]() $\lambda $
-sparse. Then Corollary 3.11 yields that A is F-automatic in H, and since
$\lambda $
-sparse. Then Corollary 3.11 yields that A is F-automatic in H, and since
![]() $A\subseteq H$
we get that
$A\subseteq H$
we get that
![]() $\lambda $
-sparsity in
$\lambda $
-sparsity in
![]() $\Gamma $
agrees with
$\Gamma $
agrees with
![]() $\lambda $
-sparsity in H. So A is F-sparse in H.
$\lambda $
-sparsity in H. So A is F-sparse in H.
We can now see that
![]() $\Gamma $
(and more generally any set containing an infinite F-invariant subgroup of
$\Gamma $
(and more generally any set containing an infinite F-invariant subgroup of
![]() $\Gamma $
) is not F-sparse.
$\Gamma $
) is not F-sparse.
Corollary 5.14. Suppose
![]() $A\subseteq \Gamma $
is F-sparse.
$A\subseteq \Gamma $
is F-sparse.
-
1. A does not contain any coset of any infinite F-invariant subgroup.
-
2. If
 $\;\Gamma $
is finitely generated then A does not contain any coset of any infinite subgroup.
$\;\Gamma $
is finitely generated then A does not contain any coset of any infinite subgroup.
Proof
-
1. We first show that
 $\Gamma $
itself is not F-sparse. Since F-sparse implies
$\Gamma $
itself is not F-sparse. Since F-sparse implies
 $F^r$
-sparse (Proposition 5.4 (1)) and F-invariant implies
$F^r$
-sparse (Proposition 5.4 (1)) and F-invariant implies
 $F^r$
-invariant, we may assume there is an F-spanning set
$F^r$
-invariant, we may assume there is an F-spanning set
 $\Sigma $
. By Lemma 3.5 we may assume the exceptional set of
$\Sigma $
. By Lemma 3.5 we may assume the exceptional set of
 $\lambda _{\Sigma } $
contains only elements of finite F-orbit; say the new associated constants are
$\lambda _{\Sigma } $
contains only elements of finite F-orbit; say the new associated constants are
 $C,D,E$
. Note that we can take
$C,D,E$
. Note that we can take
 $C=1$
: the constants obtained from Proposition 3.8 are
$C=1$
: the constants obtained from Proposition 3.8 are
 $C=D=E=1$
, and Lemma 3.5 doesn’t require changing C. Note that there is
$C=D=E=1$
, and Lemma 3.5 doesn’t require changing C. Note that there is
 $a\in \Sigma $
of infinite F-orbit: otherwise by Remark 3.6 all
$a\in \Sigma $
of infinite F-orbit: otherwise by Remark 3.6 all
 $a\in \Sigma $
would be of finite order as well, and thus would be finite, and
$a\in \Sigma $
would be of finite order as well, and thus would be finite, and $$ \begin{align*}\mathbb{Z}[F]a= \left\{\sum_{i<{\lvert{\{a,Fa,\ldots \}}\rvert} } k_iF^ia : \text{ each } k_i < {\lvert {a} \rvert}\right\} \end{align*} $$
$$ \begin{align*}\mathbb{Z}[F]a= \left\{\sum_{i<{\lvert{\{a,Fa,\ldots \}}\rvert} } k_iF^ia : \text{ each } k_i < {\lvert {a} \rvert}\right\} \end{align*} $$
 $\Gamma = \mathbb {Z}[F]\Sigma $
would be finite, a contradiction.
$\Gamma = \mathbb {Z}[F]\Sigma $
would be finite, a contradiction.
Fix
 $a\in \Sigma $
of infinite F-orbit; fix
$a\in \Sigma $
of infinite F-orbit; fix
 $s>D+E$
.
$s>D+E$
.Claim 5.15. Suppose
 $\sigma \in \{- a,0,a\}^*\setminus \{0\}^* $
. Then
$\sigma \in \{- a,0,a\}^*\setminus \{0\}^* $
. Then
 $[\sigma ]_{F^s}\ne 0$
.It follows that
$[\sigma ]_{F^s}\ne 0$
.It follows thatProof We show that
 $\lambda _{\Sigma } ([\sigma ]_{F^s})\ne 0$
, which will suffice.
$\lambda _{\Sigma } ([\sigma ]_{F^s})\ne 0$
, which will suffice.Let
 $\ell ={\lvert \sigma \rvert }>0$
. The claim is clear when
$\ell ={\lvert \sigma \rvert }>0$
. The claim is clear when
 $\ell =1$
; assume then that
$\ell =1$
; assume then that
 $\ell \ge 2$
. We may assume
$\ell \ge 2$
. We may assume
 $\sigma $
has no trailing zeroes and, by possibly negating, that
$\sigma $
has no trailing zeroes and, by possibly negating, that
 $\sigma _{\ell -1}=a$
; so
$\sigma _{\ell -1}=a$
; so  $$ \begin{align*}\lambda _{\Sigma} ([\sigma ]_{F^s}) = \lambda_{\Sigma} ([\sigma _0\cdots \sigma _{\ell -2}]_{F^s} + F^{s(\ell -1)}a). \end{align*} $$
$$ \begin{align*}\lambda _{\Sigma} ([\sigma ]_{F^s}) = \lambda_{\Sigma} ([\sigma _0\cdots \sigma _{\ell -2}]_{F^s} + F^{s(\ell -1)}a). \end{align*} $$
We look to apply the reverse ultrametric inequality. Note that
 $\lambda _{\Sigma } ([\sigma _0\cdots \sigma _{\ell -2}]_{F^s})\le s(\ell -2)+1 $
by definition of
$\lambda _{\Sigma } ([\sigma _0\cdots \sigma _{\ell -2}]_{F^s})\le s(\ell -2)+1 $
by definition of
 $\lambda _{\Sigma } $
. Thus
$\lambda _{\Sigma } $
. Thus  $$ \begin{align*}\lambda _{\Sigma} (F^{s(\ell -1)}a)\ge 1+s(\ell -1)-E> 1+s(\ell -2)+D \ge \lambda_{\Sigma} ([\sigma _0\cdots \sigma _{\ell -2}]_{F^s})+D \end{align*} $$
$$ \begin{align*}\lambda _{\Sigma} (F^{s(\ell -1)}a)\ge 1+s(\ell -1)-E> 1+s(\ell -2)+D \ge \lambda_{\Sigma} ([\sigma _0\cdots \sigma _{\ell -2}]_{F^s})+D \end{align*} $$
by the logarithmic property (recalling that
 $C=1$
) and since
$C=1$
) and since
 $s>D+E$
; note that the logarithmic property applies since a has infinite F-orbit. So by the reverse ultrametric inequality
$s>D+E$
; note that the logarithmic property applies since a has infinite F-orbit. So by the reverse ultrametric inequality  $$ \begin{align*}\lambda _{\Sigma} ([\sigma ]_{F^s})\ge \lambda_{\Sigma} (F^{s(\ell -1)}a) -D\ge 1+s(\ell -1)-E -D \ge 1+s-E-D> 0, \end{align*} $$
$$ \begin{align*}\lambda _{\Sigma} ([\sigma ]_{F^s})\ge \lambda_{\Sigma} (F^{s(\ell -1)}a) -D\ge 1+s(\ell -1)-E -D \ge 1+s-E-D> 0, \end{align*} $$
since
 $\ell \ge 2$
and
$\ell \ge 2$
and
 $s>D+E$
. So in particular
$s>D+E$
. So in particular
 $[\sigma ]_{F^s}\ne 0$
.
$[\sigma ]_{F^s}\ne 0$
. $[\cdot ]_{F^s} \restriction \{0,a\}^*a$
is injective. Indeed, suppose
$[\cdot ]_{F^s} \restriction \{0,a\}^*a$
is injective. Indeed, suppose
 $\sigma ,\tau \in \{0,a\}^*a$
are distinct; then we can write
$\sigma ,\tau \in \{0,a\}^*a$
are distinct; then we can write
 $[\sigma ]_{F^s}-[\tau ]_{F^s}= [\nu ]_{F^s}$
for some
$[\sigma ]_{F^s}-[\tau ]_{F^s}= [\nu ]_{F^s}$
for some
 $\nu \in \{-a,0,a\}^*\setminus \{0\}^*$
. Hence by the claim
$\nu \in \{-a,0,a\}^*\setminus \{0\}^*$
. Hence by the claim
 $[\sigma ]_{F^s}-[\tau ]_{F^s}\ne 0$
.
$[\sigma ]_{F^s}-[\tau ]_{F^s}\ne 0$
.
But then
So $$ \begin{align*}f_{\Gamma ,\lambda _{\Sigma} }(s\ell +1) &= {\lvert{\{[\sigma ]_F : \sigma \in\Sigma ^*, {\lvert \sigma\rvert} \le s\ell +1\}} \rvert} \ge {\lvert{\{ [\sigma ]_{F^s} : \sigma \in\{0,a\}^{(\ell )}a\}} \rvert}\\ &= {\lvert{\{0,a\}^{(\ell )}a} \rvert} = 2^{\ell}. \end{align*} $$
$$ \begin{align*}f_{\Gamma ,\lambda _{\Sigma} }(s\ell +1) &= {\lvert{\{[\sigma ]_F : \sigma \in\Sigma ^*, {\lvert \sigma\rvert} \le s\ell +1\}} \rvert} \ge {\lvert{\{ [\sigma ]_{F^s} : \sigma \in\{0,a\}^{(\ell )}a\}} \rvert}\\ &= {\lvert{\{0,a\}^{(\ell )}a} \rvert} = 2^{\ell}. \end{align*} $$
 $f_{\Gamma ,\lambda _{\Sigma } }\notin O(x^d)$
for any d; so
$f_{\Gamma ,\lambda _{\Sigma } }\notin O(x^d)$
for any d; so
 $\Gamma $
is not
$\Gamma $
is not
 $\lambda _{\Sigma } $
-sparse, and hence by Theorem 5.10
$\lambda _{\Sigma } $
-sparse, and hence by Theorem 5.10
 $\Gamma $
is not F-sparse.
$\Gamma $
is not F-sparse.
Suppose now that H is an infinite F-invariant subgroup of
 $\Gamma $
; we show that A contains no coset of H. Replacing A by a translate (which is harmless by Proposition 5.4(4)), it suffices to show that A doesn’t contain H. By the above special case we get that H isn’t F-sparse in H; so Corollary 5.13 yields that H isn’t F-sparse in
$\Gamma $
; we show that A contains no coset of H. Replacing A by a translate (which is harmless by Proposition 5.4(4)), it suffices to show that A doesn’t contain H. By the above special case we get that H isn’t F-sparse in H; so Corollary 5.13 yields that H isn’t F-sparse in
 $\Gamma $
. Since H is F-invariant, it is F-automatic in
$\Gamma $
. Since H is F-invariant, it is F-automatic in
 $\Gamma $
; this follows from Corollary 3.11. So if we had
$\Gamma $
; this follows from Corollary 3.11. So if we had
 $A\supseteq H$
then by Proposition 5.4(3) H would be F-sparse in
$A\supseteq H$
then by Proposition 5.4(3) H would be F-sparse in
 $\Gamma $
, a contradiction. So
$\Gamma $
, a contradiction. So
 $A\not \supseteq H$
, as desired.
$A\not \supseteq H$
, as desired. -
2. Again using Proposition 5.4(1) we may assume there is a length function
 $\lambda $
for
$\lambda $
for
 $(\Gamma ,F)$
. Since F-sparsity is closed under translation (Proposition 5.4(4)), it suffices to show that A does not contain any infinite
$(\Gamma ,F)$
. Since F-sparsity is closed under translation (Proposition 5.4(4)), it suffices to show that A does not contain any infinite
 $H\le \Gamma $
; suppose for contradiction there is such an H. Since
$H\le \Gamma $
; suppose for contradiction there is such an H. Since
 $\Gamma $
is finitely generated and H is infinite there is some
$\Gamma $
is finitely generated and H is infinite there is some
 $a\in H$
of infinite order; we will show that
$a\in H$
of infinite order; we will show that
 $\mathbb {Z}a$
isn’t
$\mathbb {Z}a$
isn’t
 $\lambda $
-sparse. We show by induction on k that if
$\lambda $
-sparse. We show by induction on k that if
 $1\le n\le 2^k$
then
$1\le n\le 2^k$
then
 $\lambda (na)\le \lambda (a)+kD$
. The base case
$\lambda (na)\le \lambda (a)+kD$
. The base case
 $k=0$
is immediate. For the induction step, suppose the claim holds of k; suppose
$k=0$
is immediate. For the induction step, suppose the claim holds of k; suppose
 $2^k < n\le 2^{k+1}$
. Then by the induction hypothesis.
$2^k < n\le 2^{k+1}$
. Then by the induction hypothesis. $$ \begin{align*}\lambda (na) &= \lambda (2^ka + (n-2^k)a) \le \max(\lambda (2^ka),\lambda ((n-2^k)a))+D\\ &\le (\lambda (a)+kD)+D\le \lambda (a)+(k+1)D \end{align*} $$
$$ \begin{align*}\lambda (na) &= \lambda (2^ka + (n-2^k)a) \le \max(\lambda (2^ka),\lambda ((n-2^k)a))+D\\ &\le (\lambda (a)+kD)+D\le \lambda (a)+(k+1)D \end{align*} $$
Then
 $\{na : n\in \mathbb {Z},\lambda (na)\le \lambda (a)+kD\}\supseteq \{na: 1\le n\le 2^k\}$
contains at least
$\{na : n\in \mathbb {Z},\lambda (na)\le \lambda (a)+kD\}\supseteq \{na: 1\le n\le 2^k\}$
contains at least
 $2^k$
elements. So
$2^k$
elements. So
 $f_{\mathbb {Z}a,\lambda }(x)\notin O(x^d)$
for any d, and
$f_{\mathbb {Z}a,\lambda }(x)\notin O(x^d)$
for any d, and
 $\mathbb {Z}a$
isn’t
$\mathbb {Z}a$
isn’t
 $\lambda $
-sparse. But
$\lambda $
-sparse. But
 $A\supseteq H\supseteq \mathbb {Z}a$
; so
$A\supseteq H\supseteq \mathbb {Z}a$
; so
 $f_{A,\lambda }(x)\ge f_{\mathbb {Z}a,\lambda }(x)$
, and A isn’t
$f_{A,\lambda }(x)\ge f_{\mathbb {Z}a,\lambda }(x)$
, and A isn’t
 $\lambda $
-sparse. So A isn’t F-sparse by Theorem 5.10, a contradiction.
$\lambda $
-sparse. So A isn’t F-sparse by Theorem 5.10, a contradiction.
6 F-sparse sets and stable expansions of finitely generated abelian groups
Fix an infinite abelian group
![]() $\Gamma $
and a subset
$\Gamma $
and a subset
![]() $A\subseteq \Gamma $
. We say that A is stable in
$A\subseteq \Gamma $
. We say that A is stable in
![]() $\Gamma $
if there do not exist arbitrarily long tuples
$\Gamma $
if there do not exist arbitrarily long tuples
![]() $(a_1,\ldots ,a_N; b_1,\ldots ,b_N)$
of elements of
$(a_1,\ldots ,a_N; b_1,\ldots ,b_N)$
of elements of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $a_i + b_j\in A$
if and only if
$a_i + b_j\in A$
if and only if
![]() $i\le j$
. This can be expressed model-theoretically by requiring that in
$i\le j$
. This can be expressed model-theoretically by requiring that in
![]() $\operatorname {\mathrm {Th}}(\Gamma ,0,+,A)$
the formula
$\operatorname {\mathrm {Th}}(\Gamma ,0,+,A)$
the formula
![]() $x+y\in A$
be a stable formula. The question of which subsets of
$x+y\in A$
be a stable formula. The question of which subsets of
![]() $\Gamma $
are stable has been of significant interest to model theorists for some time. We refine the question here as follows:
$\Gamma $
are stable has been of significant interest to model theorists for some time. We refine the question here as follows:
Question 6.1. Suppose
![]() $\Gamma $
is a finitely generated abelian group and
$\Gamma $
is a finitely generated abelian group and
![]() $F\colon \Gamma \to \Gamma $
is an injective endomorphism, such that
$F\colon \Gamma \to \Gamma $
is an injective endomorphism, such that
![]() $(\Gamma ,F)$
admits a spanning set for some
$(\Gamma ,F)$
admits a spanning set for some
![]() $r>0$
. Which F-automatic sets of
$r>0$
. Which F-automatic sets of
![]() $\Gamma $
are stable?
$\Gamma $
are stable?
In [Reference Hawthorne5] I answered this question in the classical case where
![]() $\Gamma =\mathbb {Z}$
and F is multiplication by a positive integer. Here, we generalize the methods of [Reference Hawthorne5] to answer the above question for F-sparse sets. This is Theorem 6.3 below. There are some issues that arise in generalizing; we focus our exposition on what needs to be done beyond what was done in [Reference Hawthorne5].
$\Gamma =\mathbb {Z}$
and F is multiplication by a positive integer. Here, we generalize the methods of [Reference Hawthorne5] to answer the above question for F-sparse sets. This is Theorem 6.3 below. There are some issues that arise in generalizing; we focus our exposition on what needs to be done beyond what was done in [Reference Hawthorne5].
Our answer will be in terms of the “F-cycles” introduced in [Reference Moosa and Scanlon6]:
Definition 6.2. Suppose
![]() $\Gamma $
is an abelian group and F is an injective endomorphism. An F-cycle is a set of the form
$\Gamma $
is an abelian group and F is an injective endomorphism. An F-cycle is a set of the form
![]() $C(a;F^{\delta } ) := \{a + F^{\delta } a + \cdots + F^{\delta n}a : n<\omega \}$
. An F-set of
$C(a;F^{\delta } ) := \{a + F^{\delta } a + \cdots + F^{\delta n}a : n<\omega \}$
. An F-set of
![]() $\Gamma ^m$
is a finite union of sets of the form
$\Gamma ^m$
is a finite union of sets of the form
![]() $\gamma + H+ C(a_1;F^{r_1})+\cdots + C(a_n; F^{r_n})$
where
$\gamma + H+ C(a_1;F^{r_1})+\cdots + C(a_n; F^{r_n})$
where
![]() $\gamma \in \Gamma ^m$
,
$\gamma \in \Gamma ^m$
,
![]() $H\le \Gamma ^m$
is F-invariant, each
$H\le \Gamma ^m$
is F-invariant, each
![]() $a_i\in \Gamma ^m$
, and each
$a_i\in \Gamma ^m$
, and each
![]() $r_i>0$
. A groupless F-set is a finite union of sets of the form
$r_i>0$
. A groupless F-set is a finite union of sets of the form
![]() $\gamma +C(a_1;F^{r_1})+\cdots + C(a_n; F^{r_n})$
with
$\gamma +C(a_1;F^{r_1})+\cdots + C(a_n; F^{r_n})$
with
![]() $\gamma ,a_i,r_i$
as above. The F-structure
$\gamma ,a_i,r_i$
as above. The F-structure
![]() $(\Gamma ,\mathcal {F})$
on
$(\Gamma ,\mathcal {F})$
on
![]() $\Gamma $
has domain
$\Gamma $
has domain
![]() $\Gamma $
and a predicate for every F-set of every
$\Gamma $
and a predicate for every F-set of every
![]() $\Gamma ^m$
.
$\Gamma ^m$
.
Note in particular that the graph of addition is an F-invariant subgroup of
![]() $\Gamma ^3$
, and is thus an F-set; so
$\Gamma ^3$
, and is thus an F-set; so
![]() $(\Gamma ,\mathcal {F})$
expands
$(\Gamma ,\mathcal {F})$
expands
![]() $(\Gamma ,+)$
.
$(\Gamma ,+)$
.
In [Reference Moosa and Scanlon6] it was shown that if
![]() $\Gamma $
is finitely generated and
$\Gamma $
is finitely generated and
 $$ \begin{align} \bigcap_{i\in \mathbb{N}} (F^i) = \{0\} \end{align} $$
$$ \begin{align} \bigcap_{i\in \mathbb{N}} (F^i) = \{0\} \end{align} $$
holds in
![]() $\mathbb {Z}[F]$
then the F-structure
$\mathbb {Z}[F]$
then the F-structure
![]() $(\Gamma ,\mathcal {F})$
is stable. (Here
$(\Gamma ,\mathcal {F})$
is stable. (Here
![]() $(F^i)$
is the ideal generated by
$(F^i)$
is the ideal generated by
![]() $F^i$
in
$F^i$
in
![]() $\mathbb {Z}[F]$
.) In particular, all F-sets are stable in
$\mathbb {Z}[F]$
.) In particular, all F-sets are stable in
![]() $\Gamma $
. Here we prove a converse for F-sparse sets.
$\Gamma $
. Here we prove a converse for F-sparse sets.
Theorem 6.3. Suppose
![]() $\Gamma $
is a finitely generated abelian group and F is an injective endomorphism of
$\Gamma $
is a finitely generated abelian group and F is an injective endomorphism of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
. If
$r>0$
. If
![]() $A\subseteq \Gamma $
is F-sparse and stable in
$A\subseteq \Gamma $
is F-sparse and stable in
![]() $\Gamma $
then A is a finite Boolean combination of groupless F-sets.
$\Gamma $
then A is a finite Boolean combination of groupless F-sets.
We would like to use the results of [Reference Moosa and Scanlon6] to deduce quantifier elimination of
![]() $(\Gamma ,\mathcal {F})$
; unfortunately, this requires that
$(\Gamma ,\mathcal {F})$
; unfortunately, this requires that
![]() $\mathbb {Z}[F]$
satisfy (†), which doesn’t follow from the existence of a spanning set. Consider for example
$\mathbb {Z}[F]$
satisfy (†), which doesn’t follow from the existence of a spanning set. Consider for example
![]() $\Gamma {{\kern-1pt}={\kern-1pt}} \mathbb {Z}{{\kern-1pt}\times{\kern-1pt}} (\mathbb {Z}/2\mathbb {Z})$
with the endomorphism
$\Gamma {{\kern-1pt}={\kern-1pt}} \mathbb {Z}{{\kern-1pt}\times{\kern-1pt}} (\mathbb {Z}/2\mathbb {Z})$
with the endomorphism
![]() $F(a,b) = (2a,b)$
. One can check using, e.g., Theorem 3.12 that
$F(a,b) = (2a,b)$
. One can check using, e.g., Theorem 3.12 that
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r{{\kern-1pt}>{\kern-1pt}}0$
, but
$r{{\kern-1pt}>{\kern-1pt}}0$
, but
![]() $F-2 {{\kern-1pt}={\kern-1pt}} F^i(F-2){{\kern-1pt}\in{\kern-1pt}} (F^i)$
for all
$F-2 {{\kern-1pt}={\kern-1pt}} F^i(F-2){{\kern-1pt}\in{\kern-1pt}} (F^i)$
for all
![]() $i{{\kern-1pt}\in{\kern-1pt}} \mathbb {N}$
.
$i{{\kern-1pt}\in{\kern-1pt}} \mathbb {N}$
.
We give a sufficient condition for (†) to hold, and then reduce Theorem 6.3 to the case where this condition holds.
Lemma 6.4. If
![]() $\Gamma $
is torsion-free and admits an
$\Gamma $
is torsion-free and admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
then
$r>0$
then
![]() $\mathbb {Z}[F]$
satisfies (†).
$\mathbb {Z}[F]$
satisfies (†).
Proof Fix
![]() $r>0$
for which there is a length function
$r>0$
for which there is a length function
![]() $\lambda $
for
$\lambda $
for
![]() $(\Gamma ,F^r)$
, say with associated constants
$(\Gamma ,F^r)$
, say with associated constants
![]() $C,D,E$
. By Lemma 3.5 and Remark 3.6 we may assume the logarithmic property applies to all non-zero elements.
$C,D,E$
. By Lemma 3.5 and Remark 3.6 we may assume the logarithmic property applies to all non-zero elements.
Suppose
 $G\in \bigcap _{i\in \mathbb {N}}(F^i)$
, and suppose
$G\in \bigcap _{i\in \mathbb {N}}(F^i)$
, and suppose
![]() $a\in \Gamma $
; suppose for contradiction that
$a\in \Gamma $
; suppose for contradiction that
![]() $Ga\ne 0$
. For
$Ga\ne 0$
. For
![]() $n\in \mathbb {N}$
since
$n\in \mathbb {N}$
since
![]() $G\in (F^{rn})$
there is
$G\in (F^{rn})$
there is
![]() $G_n\in \mathbb {Z}[F]$
such that
$G_n\in \mathbb {Z}[F]$
such that
![]() $G = F^{rn}G_n$
. Since
$G = F^{rn}G_n$
. Since
![]() $Ga\ne 0$
we get that
$Ga\ne 0$
we get that
![]() $G_na\ne 0$
, and thus the logarithmic property applies to
$G_na\ne 0$
, and thus the logarithmic property applies to
![]() $G_na$
. So
$G_na$
. So
![]() $\lambda (Ga) = \lambda (F^{rn}G_na) \ge \lambda (G_na)+nC-E\ge nC-E$
. But this grows without bound, a contradiction. So
$\lambda (Ga) = \lambda (F^{rn}G_na) \ge \lambda (G_na)+nC-E\ge nC-E$
. But this grows without bound, a contradiction. So
![]() $Ga = 0$
for all
$Ga = 0$
for all
![]() $a\in \Gamma $
, and
$a\in \Gamma $
, and
![]() $G=0$
.
$G=0$
.
We can now show Theorem 6.3 under the assumption that
![]() $\Gamma $
is torsion-free.
$\Gamma $
is torsion-free.
Proposition 6.5. Suppose
![]() $\Gamma $
is torsion-free and finitely generated, and admits an
$\Gamma $
is torsion-free and finitely generated, and admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
. If
$r>0$
. If
![]() $A\subseteq \Gamma $
is stable and F-sparse then A is a finite Boolean combination of groupless F-sets.
$A\subseteq \Gamma $
is stable and F-sparse then A is a finite Boolean combination of groupless F-sets.
Proof By replacing F with a power thereof we may assume
![]() $\Gamma $
admits an F-spanning set (since A is also
$\Gamma $
admits an F-spanning set (since A is also
![]() $F^r$
-sparse by Proposition 5.4(1)). By Proposition 5.3 we can write A as a finite union of sets of the form
$F^r$
-sparse by Proposition 5.4(1)). By Proposition 5.3 we can write A as a finite union of sets of the form
![]() $\gamma +[a_1^*\cdots a_n^*]_{F^s} $
for some
$\gamma +[a_1^*\cdots a_n^*]_{F^s} $
for some
![]() $s>0$
and
$s>0$
and
![]() $\gamma ,a_1,\ldots ,a_n\in \Gamma $
. If we let
$\gamma ,a_1,\ldots ,a_n\in \Gamma $
. If we let
![]() $b_1,\ldots ,b_n\in \Gamma $
be such that
$b_1,\ldots ,b_n\in \Gamma $
be such that
 $a_i = \sum _{j\ge i} b_i$
then we can rewrite
$a_i = \sum _{j\ge i} b_i$
then we can rewrite
and thus write A as a finite union of sets of this form. Fix one such
![]() $\gamma +\{[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s} : e_1\le \cdots \le e_n\}$
in the union; we show it is contained in some B of the desired form that is itself contained in A.
$\gamma +\{[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s} : e_1\le \cdots \le e_n\}$
in the union; we show it is contained in some B of the desired form that is itself contained in A.
We will proceed by examining the
![]() $e_i$
such that
$e_i$
such that
![]() $[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s}\in A$
.
$[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s}\in A$
.
Claim 6.6.
![]() $X:=\{(e_1,\ldots ,e_n)\in \mathbb {N}^n : [b_1^{e_1}]_{F^s}+\cdots + [b_n^{e_n}]_{F^s}\in A-\gamma \}$
is quantifier-free definable in
$X:=\{(e_1,\ldots ,e_n)\in \mathbb {N}^n : [b_1^{e_1}]_{F^s}+\cdots + [b_n^{e_n}]_{F^s}\in A-\gamma \}$
is quantifier-free definable in
![]() $(\mathbb {N},0,S,\delta \mathbb {N})$
for some
$(\mathbb {N},0,S,\delta \mathbb {N})$
for some
![]() $\delta \in \mathbb {N}\setminus \{0\}$
, where S is the successor function.
$\delta \in \mathbb {N}\setminus \{0\}$
, where S is the successor function.
Proof Fix
![]() $\sigma \in S_n$
, and suppose
$\sigma \in S_n$
, and suppose
![]() $e_{\sigma (1)}\le \cdots \le e_{\sigma (n)}$
. Let
$e_{\sigma (1)}\le \cdots \le e_{\sigma (n)}$
. Let
 $c_i = \sum _{j\ge i}b_{\sigma (i)}$
; so
$c_i = \sum _{j\ge i}b_{\sigma (i)}$
; so
By [Reference Bell and Moosa2, Lemmas 5.6 and 5.7] there is an
![]() $F^s$
-spanning set
$F^s$
-spanning set
![]() $\Sigma $
containing all the
$\Sigma $
containing all the
![]() $c_i$
; so by Proposition 2.6
$c_i$
; so by Proposition 2.6
![]() $\{\sigma \in \Sigma ^* : [\sigma ]_{F^s}\in A-\gamma \}$
is regular. Then as argued in the proof of [Reference Hawthorne5, Proposition 2.2] there is some Boolean combination
$\{\sigma \in \Sigma ^* : [\sigma ]_{F^s}\in A-\gamma \}$
is regular. Then as argued in the proof of [Reference Hawthorne5, Proposition 2.2] there is some Boolean combination
![]() $\phi (x_1,\ldots ,x_n)$
of congruences and equalities between one variable and one constant such that
$\phi (x_1,\ldots ,x_n)$
of congruences and equalities between one variable and one constant such that
 $$ \begin{align*}(e_1,\ldots ,e_n)\in X &\iff [c_1^{e_1}c_2^{e_2-e_1}\cdots c_n^{e_n-e_{n-1}}]_{F^s}\\ &\iff (\mathbb{N},0,S,\delta \mathbb{N})\models \phi (e_1,e_2-e_1,\ldots ,e_n-e_{n-1}) \end{align*} $$
$$ \begin{align*}(e_1,\ldots ,e_n)\in X &\iff [c_1^{e_1}c_2^{e_2-e_1}\cdots c_n^{e_n-e_{n-1}}]_{F^s}\\ &\iff (\mathbb{N},0,S,\delta \mathbb{N})\models \phi (e_1,e_2-e_1,\ldots ,e_n-e_{n-1}) \end{align*} $$
(again, under the assumption that
![]() $e_{\sigma (1)}\le \cdots \le e_{\sigma (n)}$
). But a congruence or equality between a constant
$e_{\sigma (1)}\le \cdots \le e_{\sigma (n)}$
). But a congruence or equality between a constant
![]() $N\in \mathbb {N}$
and either
$N\in \mathbb {N}$
and either
![]() $e_1$
or
$e_1$
or
![]() $e_{i+1}-e_i$
can be expressed as a formula in
$e_{i+1}-e_i$
can be expressed as a formula in
![]() $(\mathbb {N},0,S,\delta \mathbb {N})$
, for some sufficiently large
$(\mathbb {N},0,S,\delta \mathbb {N})$
, for some sufficiently large
![]() $\delta $
. So this is in turn equivalent to
$\delta $
. So this is in turn equivalent to
![]() $(\mathbb {N},0,S,\delta \mathbb {N})\models \psi (e_1,\ldots ,e_n)$
for some quantifier-free
$(\mathbb {N},0,S,\delta \mathbb {N})\models \psi (e_1,\ldots ,e_n)$
for some quantifier-free
![]() $\psi $
.
$\psi $
.
Doing this for all
![]() $\sigma $
and taking LCMs of the
$\sigma $
and taking LCMs of the
![]() $\delta $
and disjunctions over the possible orderings of the
$\delta $
and disjunctions over the possible orderings of the
![]() $e_i$
, we find that there is a single quantifier-free formula
$e_i$
, we find that there is a single quantifier-free formula
![]() $\phi $
in
$\phi $
in
![]() $(\mathbb {N},0,S,\delta \mathbb {N},<)$
such that
$(\mathbb {N},0,S,\delta \mathbb {N},<)$
such that
![]() $X = \phi (\mathbb {N}^n)$
. Then
$X = \phi (\mathbb {N}^n)$
. Then
![]() $\phi $
is a stable formula under any partitioning of its variables: large ladders for
$\phi $
is a stable formula under any partitioning of its variables: large ladders for
![]() $\phi $
would yield large ladders for the corresponding partitioning of
$\phi $
would yield large ladders for the corresponding partitioning of
and the latter is stable under any partitioning of the variables as A is stable (and addition is commutative and associative).
But the stable quantifier-free formulas in
![]() $(\mathbb {N},0,S,\delta \mathbb {N},<)$
are known to be quantifier-free formulas in
$(\mathbb {N},0,S,\delta \mathbb {N},<)$
are known to be quantifier-free formulas in
![]() $(\mathbb {N},0,S,\delta \mathbb {N})$
; this is [Reference Hawthorne5, Proposition 3.3]. So X is quantifier-free definable in
$(\mathbb {N},0,S,\delta \mathbb {N})$
; this is [Reference Hawthorne5, Proposition 3.3]. So X is quantifier-free definable in
![]() $(\mathbb {N},0,S,\delta \mathbb {N})$
.
$(\mathbb {N},0,S,\delta \mathbb {N})$
.
Claim 6.7.
![]() $Y := \{[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s} : (e_1,\ldots ,e_n)\in X\}$
is definable in
$Y := \{[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s} : (e_1,\ldots ,e_n)\in X\}$
is definable in
![]() $(\Gamma ,\mathcal {F})$
.
$(\Gamma ,\mathcal {F})$
.
Proof Fix
![]() $a\in \Gamma $
such that
$a\in \Gamma $
such that
![]() $F^ia\ne F^ja$
for
$F^ia\ne F^ja$
for
![]() $i\ne j$
; the logarithmic property of any length function for any
$i\ne j$
; the logarithmic property of any length function for any
![]() $(\Gamma ,F^t)$
shows such a must exist. Then
$(\Gamma ,F^t)$
shows such a must exist. Then
![]() $[a^i]_{F^s}\ne [a^j]_{F^s}$
for
$[a^i]_{F^s}\ne [a^j]_{F^s}$
for
![]() $i\ne j$
; indeed, otherwise applying
$i\ne j$
; indeed, otherwise applying
![]() $F^s-1$
to both sides we would have
$F^s-1$
to both sides we would have
![]() $F^{si}a= F^{sj}a$
, a contradiction.
$F^{si}a= F^{sj}a$
, a contradiction.
Consider
![]() $\Phi \colon \mathbb {N}\to \Gamma $
given by
$\Phi \colon \mathbb {N}\to \Gamma $
given by
![]() $i\mapsto [a^i]_{F^s}$
. By a similar argument to the one given in the proof of [Reference Hawthorne5, Lemma 3.6] we get that
$i\mapsto [a^i]_{F^s}$
. By a similar argument to the one given in the proof of [Reference Hawthorne5, Lemma 3.6] we get that
![]() $\Phi $
is an interpretation of
$\Phi $
is an interpretation of
![]() $(\mathbb {N},0,S,\delta \mathbb {N})$
in
$(\mathbb {N},0,S,\delta \mathbb {N})$
in
![]() $(\Gamma ,\mathcal {F})$
. Furthermore each map
$(\Gamma ,\mathcal {F})$
. Furthermore each map
![]() $[a^i]_{F^s}\mapsto [b^i]_{F^s}$
is definable in
$[a^i]_{F^s}\mapsto [b^i]_{F^s}$
is definable in
![]() $(\Gamma ,\mathcal {F})$
, as is addition. So
$(\Gamma ,\mathcal {F})$
, as is addition. So
![]() $Y = \{[b_1^{e_1}]_{F^s}+\cdots + [b_n^{e_n}]_{F^s} : ([a^{e_1}]_{F^s},\ldots ,[a^{e_n}]_{F^s})\in \Phi (X)\}$
is definable in
$Y = \{[b_1^{e_1}]_{F^s}+\cdots + [b_n^{e_n}]_{F^s} : ([a^{e_1}]_{F^s},\ldots ,[a^{e_n}]_{F^s})\in \Phi (X)\}$
is definable in
![]() $(\Gamma ,\mathcal {F})$
, as desired.
$(\Gamma ,\mathcal {F})$
, as desired.
We get by Lemma 6.4 that
![]() $(\Gamma ,F)$
satisfies (†). Moreover the fact that
$(\Gamma ,F)$
satisfies (†). Moreover the fact that
![]() $\Gamma $
is infinite and finitely generated and that F is injective implies that
$\Gamma $
is infinite and finitely generated and that F is injective implies that
![]() $\mathbb {Z}[F]$
satisfies the other conditions assumed by [Reference Moosa and Scanlon6]: namely that
$\mathbb {Z}[F]$
satisfies the other conditions assumed by [Reference Moosa and Scanlon6]: namely that
![]() $\mathbb {Z}[F]$
is a finite extension of
$\mathbb {Z}[F]$
is a finite extension of
![]() $\mathbb {Z}$
generated by F and that F is not a zero divisor in
$\mathbb {Z}$
generated by F and that F is not a zero divisor in
![]() $\mathbb {Z}[F]$
. So by [Reference Moosa and Scanlon6, Theorem A]
$\mathbb {Z}[F]$
. So by [Reference Moosa and Scanlon6, Theorem A]
![]() $(\Gamma ,\mathcal {F})$
admits quantifier elimination; so Y (and hence
$(\Gamma ,\mathcal {F})$
admits quantifier elimination; so Y (and hence
![]() $\gamma +Y$
) is a Boolean combination of F-sets. At this point the argument given in the proof of [Reference Hawthorne5, Theorem 3.1] shows that
$\gamma +Y$
) is a Boolean combination of F-sets. At this point the argument given in the proof of [Reference Hawthorne5, Theorem 3.1] shows that
![]() $\gamma +Y$
is a Boolean combination of F-sparse F-sets. Now by Corollary 5.14 an F-sparse F-set must be groupless; so
$\gamma +Y$
is a Boolean combination of F-sparse F-sets. Now by Corollary 5.14 an F-sparse F-set must be groupless; so
![]() $\gamma +Y$
is a Boolean combination of groupless F-sets. But
$\gamma +Y$
is a Boolean combination of groupless F-sets. But
So we can replace
![]() $\gamma +\{[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s}: e_1\le \cdots \le e_n\}$
with
$\gamma +\{[b_1^{e_1}]_{F^s} + \cdots + [b_n^{e_n}]_{F^s}: e_1\le \cdots \le e_n\}$
with
![]() $\gamma +Y$
in the union defining A without changing the union. Applying this to all sets in the union, we have written A as a Boolean combination of groupless F-sets.
$\gamma +Y$
in the union defining A without changing the union. Applying this to all sets in the union, we have written A as a Boolean combination of groupless F-sets.
Proof of Theorem 6.3 By Proposition 5.4(1) we may replace F with
![]() $F^r$
, and thus assume that
$F^r$
, and thus assume that
![]() $\Gamma $
admits an F-spanning set
$\Gamma $
admits an F-spanning set
![]() $\Sigma $
. Using the fundamental theorem of finitely generated abelian groups we can write
$\Sigma $
. Using the fundamental theorem of finitely generated abelian groups we can write
![]() $\Gamma =\Gamma _0\oplus H$
where H is the torsion subgroup of
$\Gamma =\Gamma _0\oplus H$
where H is the torsion subgroup of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma _0$
is torsion-free. Let
$\Gamma _0$
is torsion-free. Let
![]() $F_0\colon \Gamma _0\to \Gamma _0$
be the endomorphism of
$F_0\colon \Gamma _0\to \Gamma _0$
be the endomorphism of
![]() $\Gamma _0$
induced by F, as in Lemma 3.13, and let
$\Gamma _0$
induced by F, as in Lemma 3.13, and let
![]() $\pi _0\colon \Gamma \to \Gamma _0$
be the projection. Then Lemma 3.13 yields that
$\pi _0\colon \Gamma \to \Gamma _0$
be the projection. Then Lemma 3.13 yields that
![]() $\pi _0(\Sigma )$
is an
$\pi _0(\Sigma )$
is an
![]() $F_0$
-spanning set for
$F_0$
-spanning set for
![]() $\Gamma _0$
. Moreover if
$\Gamma _0$
. Moreover if
![]() $v_i,w_i\in \Sigma ^*$
then Lemma 3.13 also yields that
$v_i,w_i\in \Sigma ^*$
then Lemma 3.13 also yields that
 $\pi _0([v_0w_1^{k_1}v_1\cdots w_n^{k_n}v_n]_{F^r}) = [\pi _0(v_0)\pi _0(w_1)^{k_1}\pi _0(v_1)\cdots \pi _0(w_n)^{k_n}\pi _0(w_n)]_{F_0^r}$
, where for
$\pi _0([v_0w_1^{k_1}v_1\cdots w_n^{k_n}v_n]_{F^r}) = [\pi _0(v_0)\pi _0(w_1)^{k_1}\pi _0(v_1)\cdots \pi _0(w_n)^{k_n}\pi _0(w_n)]_{F_0^r}$
, where for
![]() $\sigma \in \Sigma ^*$
we obtain
$\sigma \in \Sigma ^*$
we obtain
![]() $\pi _0(\sigma )\in (\pi _0(\Sigma ))^*$
by applying
$\pi _0(\sigma )\in (\pi _0(\Sigma ))^*$
by applying
![]() $\pi _0$
to each letter of
$\pi _0$
to each letter of
![]() $\sigma $
. So if
$\sigma $
. So if
![]() $B\subseteq \Gamma $
is F-sparse then
$B\subseteq \Gamma $
is F-sparse then
![]() $\pi _0(B)\subseteq \Gamma _0$
is
$\pi _0(B)\subseteq \Gamma _0$
is
![]() $F_0$
-sparse.
$F_0$
-sparse.
For
![]() $b\in H$
let
$b\in H$
let
![]() $A_b = \{a\in \Gamma _0 : a\oplus b\in A\}$
. Note that
$A_b = \{a\in \Gamma _0 : a\oplus b\in A\}$
. Note that
![]() $x+y\in A_b$
is stable in
$x+y\in A_b$
is stable in
![]() $\Gamma _0$
: if we had arbitrarily long tuples
$\Gamma _0$
: if we had arbitrarily long tuples
![]() $(a_1,\ldots ,a_N; b_1,\ldots ,b_N)$
in
$(a_1,\ldots ,a_N; b_1,\ldots ,b_N)$
in
![]() $\Gamma _0$
witnessing the contrary, then the tuples
$\Gamma _0$
witnessing the contrary, then the tuples
![]() $(a_1,\ldots ,a_N; b_1+b,\ldots ,b_N+b)$
would witness the instability of A in
$(a_1,\ldots ,a_N; b_1+b,\ldots ,b_N+b)$
would witness the instability of A in
![]() $\Gamma $
, a contradiction. We wish to show that
$\Gamma $
, a contradiction. We wish to show that
![]() $A_b$
is F-automatic in
$A_b$
is F-automatic in
![]() $\Gamma $
; since regular languages are closed under intersection and
$\Gamma $
; since regular languages are closed under intersection and
![]() $A-b$
is F-automatic it suffices to show that
$A-b$
is F-automatic it suffices to show that
![]() $\Gamma _0$
is. Fix a generating set
$\Gamma _0$
is. Fix a generating set
![]() $\{\gamma _1,\ldots ,\gamma _{\ell }\}$
for
$\{\gamma _1,\ldots ,\gamma _{\ell }\}$
for
![]() $\Gamma $
, and write
$\Gamma $
, and write
 $$ \begin{align*}F\gamma _i = \sum_{j=1}^{\ell} a_{ij}\gamma _j, \end{align*} $$
$$ \begin{align*}F\gamma _i = \sum_{j=1}^{\ell} a_{ij}\gamma _j, \end{align*} $$
for
![]() $a_{ij}\in \mathbb {Z}$
; let
$a_{ij}\in \mathbb {Z}$
; let
 $X = (a_{ij} + {\lvert {H}\rvert } \mathbb {Z})_{i,j=1}^{\ell } \in M_{\ell } (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})$
. We construct a DFA recognizing
$X = (a_{ij} + {\lvert {H}\rvert } \mathbb {Z})_{i,j=1}^{\ell } \in M_{\ell } (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})$
. We construct a DFA recognizing
![]() $\Gamma _0$
. Let
$\Gamma _0$
. Let
![]() $\pi _H\colon \Gamma \to H$
be the projection. The idea is to observe that if
$\pi _H\colon \Gamma \to H$
be the projection. The idea is to observe that if
![]() $c = c_1\gamma _1+\cdots +c_{\ell } \gamma _{\ell } \in \Gamma $
then to compute
$c = c_1\gamma _1+\cdots +c_{\ell } \gamma _{\ell } \in \Gamma $
then to compute
![]() $\pi _H(F^nc)$
it suffices to know
$\pi _H(F^nc)$
it suffices to know
 $X^n(c_i+{\lvert {H}\rvert } \mathbb {Z} )_{i=1}^{\ell } $
, and since X is a matrix over a finite ring, its powers can be tracked using a finite automaton. Using this we can determine
$X^n(c_i+{\lvert {H}\rvert } \mathbb {Z} )_{i=1}^{\ell } $
, and since X is a matrix over a finite ring, its powers can be tracked using a finite automaton. Using this we can determine
![]() $\pi _H([\sigma c]_F)$
from
$\pi _H([\sigma c]_F)$
from
![]() $\pi _H([\sigma ]_F)$
and
$\pi _H([\sigma ]_F)$
and
 $X^n(c_i+{\lvert {H}\rvert } \mathbb {Z})_{i=1}^{\ell } $
, which are finitary objects.
$X^n(c_i+{\lvert {H}\rvert } \mathbb {Z})_{i=1}^{\ell } $
, which are finitary objects.
The set of states is
![]() $Q = \{(h,Y ) : h\in H,Y\in M_{\ell } (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})\}$
. The initial state is
$Q = \{(h,Y ) : h\in H,Y\in M_{\ell } (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})\}$
. The initial state is
![]() $q_0 = (0, I)$
, and the finish states are
$q_0 = (0, I)$
, and the finish states are
![]() $\Omega = \{(0,Y) : Y\in M_{\ell } (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})\}$
. For the transition map, suppose we are in state
$\Omega = \{(0,Y) : Y\in M_{\ell } (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})\}$
. For the transition map, suppose we are in state
![]() $(h, Y)$
and receive input
$(h, Y)$
and receive input
![]() $c\in \Sigma $
. Let
$c\in \Sigma $
. Let
![]() $Y' = XY$
. Write
$Y' = XY$
. Write
![]() $c = c_1\gamma _1+\cdots +c_{\ell } \gamma _{\ell } $
for
$c = c_1\gamma _1+\cdots +c_{\ell } \gamma _{\ell } $
for
![]() $c_i\in \mathbb {Z}$
, and let
$c_i\in \mathbb {Z}$
, and let
 $v = (c_i + {\lvert {H}\rvert } \mathbb {Z})_{i=1}^{\ell } \in (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})^{\ell } $
. Let
$v = (c_i + {\lvert {H}\rvert } \mathbb {Z})_{i=1}^{\ell } \in (\mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z})^{\ell } $
. Let
 $$ \begin{align*}h' = h + \sum_{i=1}^{\ell} \pi _H((Yv)_i\gamma _i), \end{align*} $$
$$ \begin{align*}h' = h + \sum_{i=1}^{\ell} \pi _H((Yv)_i\gamma _i), \end{align*} $$
where
![]() $(Yv)_i\in \mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z}$
is the ith entry of
$(Yv)_i\in \mathbb {Z}/{\lvert {H}\rvert } \mathbb {Z}$
is the ith entry of
![]() $Yv$
. Note that this is well-defined since
$Yv$
. Note that this is well-defined since
![]() $\pi _H({\lvert {H}\rvert } \Gamma ) = 0$
. Our machine then transitions to
$\pi _H({\lvert {H}\rvert } \Gamma ) = 0$
. Our machine then transitions to
![]() $(h',Y')$
. One can check by induction on
$(h',Y')$
. One can check by induction on
![]() ${\lvert \sigma \rvert } $
that
${\lvert \sigma \rvert } $
that
![]() $\delta (q_0,\sigma ) = (\pi _H([\sigma ]_F), X^{{\lvert \sigma \rvert } })$
. So our machine recognizes the representations over
$\delta (q_0,\sigma ) = (\pi _H([\sigma ]_F), X^{{\lvert \sigma \rvert } })$
. So our machine recognizes the representations over
![]() $\Sigma $
of
$\Sigma $
of
![]() $\pi _H^{-1}(0)=\Gamma _0$
; thus
$\pi _H^{-1}(0)=\Gamma _0$
; thus
![]() $\Gamma _0$
(and hence
$\Gamma _0$
(and hence
![]() $A_b$
) is F-automatic in
$A_b$
) is F-automatic in
![]() $\Gamma $
.
$\Gamma $
.
Furthermore
![]() $A_b\subseteq A-b$
, and A is F-sparse; so by Proposition 5.4(3) and (4)
$A_b\subseteq A-b$
, and A is F-sparse; so by Proposition 5.4(3) and (4)
![]() $A_b$
is F-sparse in
$A_b$
is F-sparse in
![]() $\Gamma $
. So as remarked above we get that
$\Gamma $
. So as remarked above we get that
![]() $A_b$
is
$A_b$
is
![]() $F_0$
-sparse in
$F_0$
-sparse in
![]() $\Gamma _0$
. So by Proposition 6.5 each
$\Gamma _0$
. So by Proposition 6.5 each
![]() $A_b$
is a Boolean combination of groupless
$A_b$
is a Boolean combination of groupless
![]() $F_0$
-sets. So since
$F_0$
-sets. So since
 $$ \begin{align*}A = \bigcup _{b\in H} (A_b+b), \end{align*} $$
$$ \begin{align*}A = \bigcup _{b\in H} (A_b+b), \end{align*} $$
it suffices to show that we can write
![]() $C(a;F_0^s)$
as a union of translates of sets of the form
$C(a;F_0^s)$
as a union of translates of sets of the form
![]() $C(b;F^t)$
. Let
$C(b;F^t)$
. Let
 $\sigma = a0^{s-1}\in \Gamma _0^*$
. We would like to use the above automaton to compute
$\sigma = a0^{s-1}\in \Gamma _0^*$
. We would like to use the above automaton to compute
![]() $\pi _H([\sigma ^i]_F)$
; unfortunately, there’s no guarantee that
$\pi _H([\sigma ^i]_F)$
; unfortunately, there’s no guarantee that
![]() $a\in \Sigma $
, so we may not have that
$a\in \Sigma $
, so we may not have that
![]() $\sigma \in \Sigma ^*$
. However, by [Reference Bell and Moosa2, Lemma 5.6] there is an F-spanning set
$\sigma \in \Sigma ^*$
. However, by [Reference Bell and Moosa2, Lemma 5.6] there is an F-spanning set
![]() $\Sigma '$
containing a; running through the argument given above, we can assume the automaton accepts inputs from
$\Sigma '$
containing a; running through the argument given above, we can assume the automaton accepts inputs from
![]() $(\Sigma ')^*$
. Since there are only finitely many states, we see that
$(\Sigma ')^*$
. Since there are only finitely many states, we see that
![]() $\delta (q_0,\sigma ^i)$
, and hence
$\delta (q_0,\sigma ^i)$
, and hence
![]() $\pi _H([\sigma ^i]_F)$
is ultimately periodic in i; say
$\pi _H([\sigma ^i]_F)$
is ultimately periodic in i; say
![]() $\pi _H([\sigma ^{i+\mu }]_F) = \pi _H([\sigma ^i]_F)$
for
$\pi _H([\sigma ^{i+\mu }]_F) = \pi _H([\sigma ^i]_F)$
for
![]() $i\ge N$
. Then
$i\ge N$
. Then
 $$ \begin{align*}C(a;F_0^s) &= \{ [\sigma ^i]_{F_0} : i>0\}\\ &= \{ [\sigma ^i]_{F_0} : 0< i < N+\mu\} \cup\bigcup _{j<\mu }\{ [\sigma ^{N+j+i\mu }]_{F_0} : i\in\mathbb{N}\setminus \{0\}\}. \end{align*} $$
$$ \begin{align*}C(a;F_0^s) &= \{ [\sigma ^i]_{F_0} : i>0\}\\ &= \{ [\sigma ^i]_{F_0} : 0< i < N+\mu\} \cup\bigcup _{j<\mu }\{ [\sigma ^{N+j+i\mu }]_{F_0} : i\in\mathbb{N}\setminus \{0\}\}. \end{align*} $$
But
![]() $[\sigma ^{N+j+i\mu }]_F = \pi _H([\sigma ^{N+j+i\mu }]_F) + \pi _0([\sigma ^{N+j+i\mu }]_F) = \pi _H([\sigma ^{N+j}]_F) + [\sigma ^{N+j+i\mu }]_{F_0}$
(by Lemma 3.13). So
$[\sigma ^{N+j+i\mu }]_F = \pi _H([\sigma ^{N+j+i\mu }]_F) + \pi _0([\sigma ^{N+j+i\mu }]_F) = \pi _H([\sigma ^{N+j}]_F) + [\sigma ^{N+j+i\mu }]_{F_0}$
(by Lemma 3.13). So
 $$ \begin{align*} \{[\sigma ^{N+j+i\mu }]_{F_0} : i\in\mathbb{N}\setminus \{0\}\} &= -\pi _H([\sigma ^{N+j}]_F)+\{ [\sigma ^{N+j+i\mu }]_F : i\in\mathbb{N}\setminus \{0\}\} \\ &= -\pi _H([\sigma ^{N+j}]_F)+[\sigma ^{N+j}]_F+ C(F^{(N+j)s}[\sigma ^{\mu} ]_F;F^{\mu s}). \end{align*} $$
$$ \begin{align*} \{[\sigma ^{N+j+i\mu }]_{F_0} : i\in\mathbb{N}\setminus \{0\}\} &= -\pi _H([\sigma ^{N+j}]_F)+\{ [\sigma ^{N+j+i\mu }]_F : i\in\mathbb{N}\setminus \{0\}\} \\ &= -\pi _H([\sigma ^{N+j}]_F)+[\sigma ^{N+j}]_F+ C(F^{(N+j)s}[\sigma ^{\mu} ]_F;F^{\mu s}). \end{align*} $$
Substituting this into the above expression for
![]() $C(a;F_0^s)$
, we have written
$C(a;F_0^s)$
, we have written
![]() $C(a;F_0^s)$
as a union of translates of
$C(a;F_0^s)$
as a union of translates of
![]() $C(b; F^{\mu s})$
, as desired.
$C(b; F^{\mu s})$
, as desired.
It is worth pointing out that, assuming the existence of spanning sets, there are always F-sparse sets that aren’t F-sets. Indeed, fix any
![]() $a\in \Gamma $
of infinite F-orbit. One can check that
$a\in \Gamma $
of infinite F-orbit. One can check that
 $A = \bigg \{\begin {pmatrix}{F^ia}\\{F^ja}\end {pmatrix} : i\le j\bigg \}\subseteq \Gamma ^2$
is F-sparse. If A were an F-set then by [Reference Moosa and Scanlon6] it would be stable, contradicting the fact that
$A = \bigg \{\begin {pmatrix}{F^ia}\\{F^ja}\end {pmatrix} : i\le j\bigg \}\subseteq \Gamma ^2$
is F-sparse. If A were an F-set then by [Reference Moosa and Scanlon6] it would be stable, contradicting the fact that
 $\begin {pmatrix}{F^ia}\\{0}\end {pmatrix} + \begin {pmatrix}{0}\\{F^ja}\end {pmatrix}\in A$
if and only if
$\begin {pmatrix}{F^ia}\\{0}\end {pmatrix} + \begin {pmatrix}{0}\\{F^ja}\end {pmatrix}\in A$
if and only if
![]() $i\le j$
. With some effort one can encode sets like this into subsets of
$i\le j$
. With some effort one can encode sets like this into subsets of
![]() $\Gamma $
itself.
$\Gamma $
itself.
7 NIP expansions of
 $(\Gamma ,+)$
$(\Gamma ,+)$
We now turn our attention to NIP expansions of
![]() $(\Gamma ,+)$
. We produce a class of subsets
$(\Gamma ,+)$
. We produce a class of subsets
![]() $A\subseteq \Gamma $
, which we call the F-EDP sets, that contains the F-sparse sets; we show that if A is F-EDP then
$A\subseteq \Gamma $
, which we call the F-EDP sets, that contains the F-sparse sets; we show that if A is F-EDP then
![]() $(\Gamma ,+,A)$
is NIP. Our argument generalizes that of [Reference Hawthorne5, Section 6.2], which deals with the case when
$(\Gamma ,+,A)$
is NIP. Our argument generalizes that of [Reference Hawthorne5, Section 6.2], which deals with the case when
![]() $\Gamma =\mathbb {Z}$
and F is multiplication by some
$\Gamma =\mathbb {Z}$
and F is multiplication by some
![]() $d>1$
. As an application of our general result, we will see that
$d>1$
. As an application of our general result, we will see that
![]() $(\mathbb {F}_p[t],+,{\times \mathord \restriction t^{\mathbb {N}}})$
is NIP, where
$(\mathbb {F}_p[t],+,{\times \mathord \restriction t^{\mathbb {N}}})$
is NIP, where
![]() ${\times \mathord \restriction t^{\mathbb {N}}}$
is the graph of multiplication on
${\times \mathord \restriction t^{\mathbb {N}}}$
is the graph of multiplication on
![]() $t^{\mathbb {N}}$
.
$t^{\mathbb {N}}$
.
We introduce some convenient multi-index notation. Suppose
![]() $\textbf{s} = (\sigma _1,\ldots ,\sigma _n)$
with
$\textbf{s} = (\sigma _1,\ldots ,\sigma _n)$
with
![]() $\sigma _1,\ldots ,\sigma _n\in \Gamma ^*$
and
$\sigma _1,\ldots ,\sigma _n\in \Gamma ^*$
and
![]() $\textbf{k} = (k _1,\ldots ,k _n)\in \mathbb {N}^n$
. Then by
$\textbf{k} = (k _1,\ldots ,k _n)\in \mathbb {N}^n$
. Then by
![]() $\textbf{s}^{\textbf{k}}$
we mean the string
$\textbf{s}^{\textbf{k}}$
we mean the string
 $\sigma _1^{k_1}\cdots \sigma _n^{k_n}$
. Note that if
$\sigma _1^{k_1}\cdots \sigma _n^{k_n}$
. Note that if
![]() $\textbf{0} = (0,\ldots ,0)$
then
$\textbf{0} = (0,\ldots ,0)$
then
![]() $\textbf{s}^{\textbf{0}} = \epsilon $
, the empty word.
$\textbf{s}^{\textbf{0}} = \epsilon $
, the empty word.
Definition 7.1. By an F-exponentially definable in Presburger (F-EDP) subset of
![]() $\Gamma $
we mean a set of the form
$\Gamma $
we mean a set of the form
 $[\textbf{s}^{\phi (\mathbb {N})} ]_F := \{ [\textbf{s}^{\textbf{k}}]_F : (\mathbb {N},+)\models \phi (\textbf{k})\} $
for some tuple
$[\textbf{s}^{\phi (\mathbb {N})} ]_F := \{ [\textbf{s}^{\textbf{k}}]_F : (\mathbb {N},+)\models \phi (\textbf{k})\} $
for some tuple
![]() $\textbf{s}$
of strings over
$\textbf{s}$
of strings over
![]() $\Gamma $
and some formula
$\Gamma $
and some formula
![]() $\phi (\textbf {x})$
with
$\phi (\textbf {x})$
with
![]() $|{\textbf {x}}| = |{\textbf {s}}|$
.
$|{\textbf {x}}| = |{\textbf {s}}|$
.
Lemma 7.2.
-
1. F-EDP sets are closed under finite union.
-
2. F-sparse sets are F-EDP.
Proof
-
1. It suffices to check pairwise unions. Suppose we are given F-EDP sets
 $[\textbf{s}_1^{\phi (\mathbb {N})}]_F$
and
$[\textbf{s}_1^{\phi (\mathbb {N})}]_F$
and
 $[\textbf{s}_2^{\psi (\mathbb {N})}]_F$
. Then their union can be written as
$[\textbf{s}_2^{\psi (\mathbb {N})}]_F$
. Then their union can be written as
 $[(\textbf{s}_1\textbf{s}_2)^{\chi (\mathbb {N})}]_F$
where
$[(\textbf{s}_1\textbf{s}_2)^{\chi (\mathbb {N})}]_F$
where
 $\chi (\textbf{x},\textbf{y})$
is
$\chi (\textbf{x},\textbf{y})$
is
 $ (\phi (\textbf{x})\wedge \textbf{y}=\textbf{0})\vee (\psi (\textbf{y})\wedge \textbf{x}=\textbf{0})$
, and is thus F-EDP.
$ (\phi (\textbf{x})\wedge \textbf{y}=\textbf{0})\vee (\psi (\textbf{y})\wedge \textbf{x}=\textbf{0})$
, and is thus F-EDP. -
2. Suppose we are given an
 $F^r$
-spanning set
$F^r$
-spanning set
 $\Sigma $
for some
$\Sigma $
for some
 $r>0$
and a sparse
$r>0$
and a sparse
 $L\subseteq \Sigma ^*$
. By Fact 5.2 we may assume L is a finite union of simple sparse languages; by part (1) we may assume L itself is simple sparse, say
$L\subseteq \Sigma ^*$
. By Fact 5.2 we may assume L is a finite union of simple sparse languages; by part (1) we may assume L itself is simple sparse, say
 $L = v_0w_1^*v_1\cdots w_n^*v_n$
for
$L = v_0w_1^*v_1\cdots w_n^*v_n$
for
 $v_i,w_i\in \Sigma ^*$
. Given
$v_i,w_i\in \Sigma ^*$
. Given
 $\sigma = s_0\cdots s_{{\lvert \sigma \rvert }-1}\in \Sigma ^*$
let
$\sigma = s_0\cdots s_{{\lvert \sigma \rvert }-1}\in \Sigma ^*$
let
 $\sigma ' = s_00^{r-1}s_10^{r-1}\cdots s_{{\lvert \sigma \rvert } -1}0^{r-1}$
. Then
$\sigma ' = s_00^{r-1}s_10^{r-1}\cdots s_{{\lvert \sigma \rvert } -1}0^{r-1}$
. Then
 $(\sigma \tau )' = \sigma '\tau '$
and
$(\sigma \tau )' = \sigma '\tau '$
and
 $[\sigma ']_F = [\sigma ]_{F^r}$
. So is F-EDP.
$[\sigma ']_F = [\sigma ]_{F^r}$
. So is F-EDP. $$ \begin{align*}[L]_{F^r} &= \{[(v_0^{\prime})^{\ell _0}(w_1^{\prime})^{k_1}(v_1^{\prime})^{\ell _1}\cdots (w_n^{\prime})^{k_n}(v_n^{\prime})^{\ell _n}]_F : k_1,\ldots ,k_n,\ell _0,\ldots ,\ell _n\in\mathbb{N},\\ &\qquad\ell _0 = \cdots = \ell _n = 1\} \end{align*} $$
$$ \begin{align*}[L]_{F^r} &= \{[(v_0^{\prime})^{\ell _0}(w_1^{\prime})^{k_1}(v_1^{\prime})^{\ell _1}\cdots (w_n^{\prime})^{k_n}(v_n^{\prime})^{\ell _n}]_F : k_1,\ldots ,k_n,\ell _0,\ldots ,\ell _n\in\mathbb{N},\\ &\qquad\ell _0 = \cdots = \ell _n = 1\} \end{align*} $$
The F-EDP sets contain significantly more than just the F-sparse sets. For instance, if
![]() $a,b,c\in \Gamma $
then
$a,b,c\in \Gamma $
then
![]() $\{[a^ib^i]_F : i \in \mathbb {N}\}$
and
$\{[a^ib^i]_F : i \in \mathbb {N}\}$
and
![]() $\{[a^ib^jc^{i+j}]_F : i,j\in \mathbb {N}\}$
are F-EDP, but are not typically F-automatic, and hence not F-sparse.
$\{[a^ib^jc^{i+j}]_F : i,j\in \mathbb {N}\}$
are F-EDP, but are not typically F-automatic, and hence not F-sparse.
Our goal is to prove that if we start with a weakly minimal abelian group
![]() $(\Gamma ,+) $
, and if
$(\Gamma ,+) $
, and if
![]() $A\subseteq \Gamma $
is F-EDP, then
$A\subseteq \Gamma $
is F-EDP, then
![]() $(\Gamma ,+,A)$
is an NIP structure. Recall that
$(\Gamma ,+,A)$
is an NIP structure. Recall that
![]() $\Gamma $
being weakly minimal means that
$\Gamma $
being weakly minimal means that
![]() $\operatorname {\mathrm {Th}}(\Gamma ,+)$
is superstable and of U-rank
$\operatorname {\mathrm {Th}}(\Gamma ,+)$
is superstable and of U-rank
![]() $1$
. Equivalently, for all
$1$
. Equivalently, for all
![]() $n>0$
,
$n>0$
,
![]() $n\Gamma $
and the subgroup of n-torsion are either finite or of finite index in
$n\Gamma $
and the subgroup of n-torsion are either finite or of finite index in
![]() $\Gamma $
—see for example [Reference Conant and Laskowski4, Proposition 3.1]. So, for example, all finitely generated abelian groups are weakly minimal.
$\Gamma $
—see for example [Reference Conant and Laskowski4, Proposition 3.1]. So, for example, all finitely generated abelian groups are weakly minimal.
We begin by adapting Proposition 5.3 to EDP sets.
Lemma 7.3. If A is F-EDP then there is
![]() $s_0$
such that for all
$s_0$
such that for all
![]() $s\in s_0\mathbb {N}$
we can write A in the form
$s\in s_0\mathbb {N}$
we can write A in the form
![]() $[\textbf{a}^{\phi (\mathbb {N})}]_{F^s}$
for some formula
$[\textbf{a}^{\phi (\mathbb {N})}]_{F^s}$
for some formula
![]() $\phi $
in Presburger arithmetic and some tuple
$\phi $
in Presburger arithmetic and some tuple
![]() $\textbf{a}$
of elements of
$\textbf{a}$
of elements of
![]() $\Gamma $
(i.e., strings of length
$\Gamma $
(i.e., strings of length
![]() $1)$
.
$1)$
.
Proof Write
![]() $A = \{[\textbf{s}^{\textbf{k}}]_F:(\mathbb {N},+)\models \phi (\textbf{k})\}$
where
$A = \{[\textbf{s}^{\textbf{k}}]_F:(\mathbb {N},+)\models \phi (\textbf{k})\}$
where
![]() $\textbf{s}= (\sigma _1,\ldots ,\sigma _n)$
. Let
$\textbf{s}= (\sigma _1,\ldots ,\sigma _n)$
. Let
![]() $s_0 = \operatorname {\mathrm {lcm}}({\lvert {\sigma _1}\rvert },\ldots ,{\lvert {\sigma _n}\rvert })$
, and suppose
$s_0 = \operatorname {\mathrm {lcm}}({\lvert {\sigma _1}\rvert },\ldots ,{\lvert {\sigma _n}\rvert })$
, and suppose
![]() $s\in s_0\mathbb {N}$
. If
$s\in s_0\mathbb {N}$
. If
 $\sigma _i^{\prime } = \sigma _i^{\frac s{{\lvert {\sigma _i}\rvert }}}$
then
$\sigma _i^{\prime } = \sigma _i^{\frac s{{\lvert {\sigma _i}\rvert }}}$
then
 $$ \begin{align*} A &= \bigcup _{i_1 < \frac s{{\lvert{\sigma _1} \rvert}}}\cdots \bigcup _{i_n < \frac s{{\lvert{\sigma _n} \rvert}}} \bigg\{[(\sigma _1^{\prime})^{k_1^{\prime}}\sigma _1^{i_1}\cdots (\sigma _n^{\prime}) ^{k_n^{\prime}}\sigma _n ^{i_n }]_F :\\ &\qquad\qquad\qquad\quad(\mathbb{N},+)\models \phi \bigg( {\frac s{{\lvert{\sigma _1} \rvert}} k_1^{\prime}+i_1,\ldots ,\frac s{{\lvert{\sigma_n}\rvert}}k_n '+i_n }\bigg)\bigg\}. \end{align*} $$
$$ \begin{align*} A &= \bigcup _{i_1 < \frac s{{\lvert{\sigma _1} \rvert}}}\cdots \bigcup _{i_n < \frac s{{\lvert{\sigma _n} \rvert}}} \bigg\{[(\sigma _1^{\prime})^{k_1^{\prime}}\sigma _1^{i_1}\cdots (\sigma _n^{\prime}) ^{k_n^{\prime}}\sigma _n ^{i_n }]_F :\\ &\qquad\qquad\qquad\quad(\mathbb{N},+)\models \phi \bigg( {\frac s{{\lvert{\sigma _1} \rvert}} k_1^{\prime}+i_1,\ldots ,\frac s{{\lvert{\sigma_n}\rvert}}k_n '+i_n }\bigg)\bigg\}. \end{align*} $$
Since sets of the desired form are closed under union (as in Lemma 7.2(1)) it thus suffices to check the case
 $$ \begin{align*}A = \{[v _0w_1^{k_1}\cdots w _n ^{k_n }v _n]_F : (\mathbb{N},+)\models \phi (k_1,\ldots ,k_n )\}, \end{align*} $$
$$ \begin{align*}A = \{[v _0w_1^{k_1}\cdots w _n ^{k_n }v _n]_F : (\mathbb{N},+)\models \phi (k_1,\ldots ,k_n )\}, \end{align*} $$
where the
![]() $w _i$
all have the same length s. But by the argument given in [Reference Hawthorne5, Lemma 3.4] (which generalizes to our context, as we noted in the proof of Proposition 5.3) there are
$w _i$
all have the same length s. But by the argument given in [Reference Hawthorne5, Lemma 3.4] (which generalizes to our context, as we noted in the proof of Proposition 5.3) there are
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $\tau _1,\ldots ,\tau _n \in \Gamma ^* $
of length s such that if each
$\tau _1,\ldots ,\tau _n \in \Gamma ^* $
of length s such that if each
![]() $k_j>0$
then we can write
$k_j>0$
then we can write
 $$ \begin{align*}[v_0w _1^{k_1}\cdots w _n ^{k_n }v _n ]_F = \gamma + [\tau _1^{k_1-1}\cdots \tau _n ^{k_n -1}]_F =\gamma + [a_1^{k_1-1}\cdots a_n^{k_n-1}]_{F^s}, \end{align*} $$
$$ \begin{align*}[v_0w _1^{k_1}\cdots w _n ^{k_n }v _n ]_F = \gamma + [\tau _1^{k_1-1}\cdots \tau _n ^{k_n -1}]_F =\gamma + [a_1^{k_1-1}\cdots a_n^{k_n-1}]_{F^s}, \end{align*} $$
where
![]() $a_i = [\tau _i]_F$
. The case where some
$a_i = [\tau _i]_F$
. The case where some
![]() $k_j=0$
can be dealt with inductively, again using closure under union; so it suffices to check the case
$k_j=0$
can be dealt with inductively, again using closure under union; so it suffices to check the case
 $\gamma + \{[a_1^{k_1}\cdots a_n^{k_n}]_{F^s} : (\mathbb {N},+)\models \phi (k_1,\ldots ,k_n)\}$
. But we can rewrite this as
$\gamma + \{[a_1^{k_1}\cdots a_n^{k_n}]_{F^s} : (\mathbb {N},+)\models \phi (k_1,\ldots ,k_n)\}$
. But we can rewrite this as
 $$ \begin{align*}\bigcup _{i=1}^n \{[(\gamma +a_i)a_i^{k_i}\cdots a_n^{k_n}]_{F^s} : (\mathbb{N},+)\models \phi (0,\ldots ,0,k_i+1,k_{i+1},\ldots ,k_n)\}, \end{align*} $$
$$ \begin{align*}\bigcup _{i=1}^n \{[(\gamma +a_i)a_i^{k_i}\cdots a_n^{k_n}]_{F^s} : (\mathbb{N},+)\models \phi (0,\ldots ,0,k_i+1,k_{i+1},\ldots ,k_n)\}, \end{align*} $$
which takes the desired form by closure under union.
The source of NIP in Theorem 7.7 will be that
![]() $(\mathbb {N},+)$
is NIP. The following lemma and corollary relate automatic and F-EDP sets to sets definable in
$(\mathbb {N},+)$
is NIP. The following lemma and corollary relate automatic and F-EDP sets to sets definable in
![]() $(\mathbb {N},+)$
.
$(\mathbb {N},+)$
.
Lemma 7.4. Suppose
![]() $\Lambda $
is a finite alphabet and
$\Lambda $
is a finite alphabet and
![]() $L\subseteq (\Lambda ^m) ^*$
is regular. Suppose
$L\subseteq (\Lambda ^m) ^*$
is regular. Suppose
![]() $ \textbf{a}_1,\ldots ,\textbf{a}_m$
are tuples from
$ \textbf{a}_1,\ldots ,\textbf{a}_m$
are tuples from
![]() $\Lambda $
. Then the relation
$\Lambda $
. Then the relation
 $$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m) : {\lvert{\textbf{a}_1^{\textbf{k}_1}} \rvert} = \cdots = {\lvert{\textbf{a}_m^{\textbf{k}_m}} \rvert}, \begin{pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots\\ {\textbf{a}_m^{\textbf{k}_m}}\end{pmatrix}\in L\right\} \subseteq \mathbb{N}^{{|{\textbf{a}_1}} |}\times \cdots \times \mathbb{N}^{{|{\textbf{a}_m}} |} \end{align*} $$
$$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m) : {\lvert{\textbf{a}_1^{\textbf{k}_1}} \rvert} = \cdots = {\lvert{\textbf{a}_m^{\textbf{k}_m}} \rvert}, \begin{pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots\\ {\textbf{a}_m^{\textbf{k}_m}}\end{pmatrix}\in L\right\} \subseteq \mathbb{N}^{{|{\textbf{a}_1}} |}\times \cdots \times \mathbb{N}^{{|{\textbf{a}_m}} |} \end{align*} $$
is definable in
![]() $(\mathbb {N},+)$
. (Here we identify
$(\mathbb {N},+)$
. (Here we identify
![]() $(\Lambda ^m)^*$
with the subset of
$(\Lambda ^m)^*$
with the subset of
![]() $(\Lambda ^*)^m$
of tuples whose constituent strings all have the same length.)
$(\Lambda ^*)^m$
of tuples whose constituent strings all have the same length.)
The important clause of the relation is
 $\begin {pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots \\ {\textbf{a}_m^{\textbf{k}_m}}\end {pmatrix}\in L$
; the condition
$\begin {pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots \\ {\textbf{a}_m^{\textbf{k}_m}}\end {pmatrix}\in L$
; the condition
 ${| {\textbf{a}_1^{\textbf{k}_1}}|} = \cdots = {| {\textbf{a}_m^{\textbf{k}_m}}|}$
is only there so we can view
${| {\textbf{a}_1^{\textbf{k}_1}}|} = \cdots = {| {\textbf{a}_m^{\textbf{k}_m}}|}$
is only there so we can view
 $\begin {pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots \\ {\textbf{a}_m^{\textbf{k}_m}}\end {pmatrix}$
as an element of
$\begin {pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots \\ {\textbf{a}_m^{\textbf{k}_m}}\end {pmatrix}$
as an element of
![]() $(\Lambda ^m)^*$
.
$(\Lambda ^m)^*$
.
Proof Fix an automaton
![]() $(\Lambda ^m,Q,q_0,\Omega ,\delta )$
for
$(\Lambda ^m,Q,q_0,\Omega ,\delta )$
for
![]() $L $
; we show that for any
$L $
; we show that for any
![]() $q_1,q_2\in Q$
the relation
$q_1,q_2\in Q$
the relation
 $$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m) : {\lvert {\textbf{a}_1^{\textbf{k}_1}}\rvert}= \cdots = {\lvert {\textbf{a}_m^{\textbf{k}_m}}\rvert}, \delta \left( {q_1,\begin{pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots\\ {\textbf{a}_m^{\textbf{k}_m}}\end{pmatrix}}\right) = q_2\right\} \end{align*} $$
$$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m) : {\lvert {\textbf{a}_1^{\textbf{k}_1}}\rvert}= \cdots = {\lvert {\textbf{a}_m^{\textbf{k}_m}}\rvert}, \delta \left( {q_1,\begin{pmatrix}{\textbf{a}_1^{\textbf{k}_1}}\\ \vdots\\ {\textbf{a}_m^{\textbf{k}_m}}\end{pmatrix}}\right) = q_2\right\} \end{align*} $$
is definable in
![]() $(\mathbb {N},+)$
. Applying this to
$(\mathbb {N},+)$
. Applying this to
![]() $q_0$
and the elements of
$q_0$
and the elements of
![]() $\Omega $
yields the desired result.
$\Omega $
yields the desired result.
We apply induction on
![]() ${|{\textbf{a}_1} |}\cdots {| {\textbf{a}_m}|}$
. For the base case, if some
${|{\textbf{a}_1} |}\cdots {| {\textbf{a}_m}|}$
. For the base case, if some
![]() ${|{\textbf{a}_i} |} = 0$
then our relation is either empty or equivalent to all
${|{\textbf{a}_i} |} = 0$
then our relation is either empty or equivalent to all
![]() $\textbf{k}_i$
being zero, depending on whether
$\textbf{k}_i$
being zero, depending on whether
![]() $q_1 = q_2$
, and both of these are definable in
$q_1 = q_2$
, and both of these are definable in
![]() $(\mathbb {N},+)$
.
$(\mathbb {N},+)$
.
For the induction step, suppose no
![]() ${| {\textbf{a}_i}|} = 0$
. Write
${| {\textbf{a}_i}|} = 0$
. Write
![]() $\textbf{a}_i = (a_{i1},\ldots ,a_{in_i})$
and
$\textbf{a}_i = (a_{i1},\ldots ,a_{in_i})$
and
![]() $\textbf{k}_i = (k_{i1},\ldots ,k_{in_i})$
. Suppose
$\textbf{k}_i = (k_{i1},\ldots ,k_{in_i})$
. Suppose
![]() $k_{11}$
is minimum among the
$k_{11}$
is minimum among the
![]() $k_{i1}$
. For
$k_{i1}$
. For
![]() $\ell \in \mathbb {N}$
we let
$\ell \in \mathbb {N}$
we let
 $$ \begin{align*}q(\ell ) = \delta \left( {q_1, \begin{pmatrix}{a _{11}^{\ell} }\\{\vdots }\\ {a _{m1}^{\ell} }\end{pmatrix}}\right). \end{align*} $$
$$ \begin{align*}q(\ell ) = \delta \left( {q_1, \begin{pmatrix}{a _{11}^{\ell} }\\{\vdots }\\ {a _{m1}^{\ell} }\end{pmatrix}}\right). \end{align*} $$
We will use the fact that if the machine is in state
![]() $q_1$
and receives input
$q_1$
and receives input
 $\begin {pmatrix}\textbf{a}_1^{\textbf{k}_1}\\\vdots \\ {\textbf{a}_m^{\textbf{k}_m}}\end {pmatrix} $
, it will first read
$\begin {pmatrix}\textbf{a}_1^{\textbf{k}_1}\\\vdots \\ {\textbf{a}_m^{\textbf{k}_m}}\end {pmatrix} $
, it will first read
 $\begin {pmatrix}{a_{11}^{k_{11}}}\\ \vdots \\ {a_{m1}^{k_{11}}}\end {pmatrix}$
and move to state
$\begin {pmatrix}{a_{11}^{k_{11}}}\\ \vdots \\ {a_{m1}^{k_{11}}}\end {pmatrix}$
and move to state
![]() $q(k_{11})$
, after which it will process the rest of the input.
$q(k_{11})$
, after which it will process the rest of the input.
For
![]() $q'\in Q$
, let
$q'\in Q$
, let
![]() $\phi _{q'}(\textbf{k}_1,\ldots ,\textbf{k}_m)$
be the statement
$\phi _{q'}(\textbf{k}_1,\ldots ,\textbf{k}_m)$
be the statement
 $$ \begin{align*} {\lvert{ a _{12}^{k_{12}}\cdots a _{1n_1}^{k_{1n_1}}} \rvert} &= {\lvert{ a _{21}^{k_{21}-k_{11}}a _{22}^{k_{22}}\cdots a _{2n_2}^{k_{2n_2}} } \rvert}\\ &{{\kern-1.5pt}={\kern-1.5pt}}{{\kern-1pt}\cdots{\kern-1pt}} {{\kern-1.5pt}={\kern-1.5pt}}{\lvert{ a _{m1}^{k_{m1}-k_{11}}a _{m2}^{k_{m2}}\cdots a _{mn_m}^{k_{mn_m}} } \rvert} {{\kern-1pt}\wedge{\kern-1pt}} \delta \left( {q', \begin{pmatrix} \hphantom{a _{11}^{k_{11}-k_{11}}}a _{12}^{k_{12}}\cdots a _{1n_1}^{k_{1n_1}} \\ a _{21}^{k_{21}-k_{11}}a _{22}^{k_{22}}\cdots a _{2n_2}^{k_{2n_2}} \\\vdots\\ { a _{m1}^{k_{m1}-k_{11}}a _{m2}^{k_{m2}}\cdots a _{mn_m}^{k_{mn_m}} }\end{pmatrix}}\right) {{\kern-3.5pt}={\kern-1.5pt}} q_2. \end{align*} $$
$$ \begin{align*} {\lvert{ a _{12}^{k_{12}}\cdots a _{1n_1}^{k_{1n_1}}} \rvert} &= {\lvert{ a _{21}^{k_{21}-k_{11}}a _{22}^{k_{22}}\cdots a _{2n_2}^{k_{2n_2}} } \rvert}\\ &{{\kern-1.5pt}={\kern-1.5pt}}{{\kern-1pt}\cdots{\kern-1pt}} {{\kern-1.5pt}={\kern-1.5pt}}{\lvert{ a _{m1}^{k_{m1}-k_{11}}a _{m2}^{k_{m2}}\cdots a _{mn_m}^{k_{mn_m}} } \rvert} {{\kern-1pt}\wedge{\kern-1pt}} \delta \left( {q', \begin{pmatrix} \hphantom{a _{11}^{k_{11}-k_{11}}}a _{12}^{k_{12}}\cdots a _{1n_1}^{k_{1n_1}} \\ a _{21}^{k_{21}-k_{11}}a _{22}^{k_{22}}\cdots a _{2n_2}^{k_{2n_2}} \\\vdots\\ { a _{m1}^{k_{m1}-k_{11}}a _{m2}^{k_{m2}}\cdots a _{mn_m}^{k_{mn_m}} }\end{pmatrix}}\right) {{\kern-3.5pt}={\kern-1.5pt}} q_2. \end{align*} $$
That is,
![]() $\phi _{q'}$
asserts that if the machine starts in state
$\phi _{q'}$
asserts that if the machine starts in state
![]() $q'$
and receives as input
$q'$
and receives as input
 $\begin {pmatrix}\textbf{a}_1^{\textbf{k}_1}\\\vdots \\ {\textbf{a}_m^{\textbf{k}_m}} \end {pmatrix} $
with the prefix
$\begin {pmatrix}\textbf{a}_1^{\textbf{k}_1}\\\vdots \\ {\textbf{a}_m^{\textbf{k}_m}} \end {pmatrix} $
with the prefix
 $\begin {pmatrix}a_{11}^{k_{11}}\\\vdots \\ {a_{m1}^{k_{11}}} \end {pmatrix}$
deleted, then the machine ends in state
$\begin {pmatrix}a_{11}^{k_{11}}\\\vdots \\ {a_{m1}^{k_{11}}} \end {pmatrix}$
deleted, then the machine ends in state
![]() $q_2$
.
$q_2$
.
Then our relation is equivalent to the statement
 $\phi _{q(k_{11})}(\textbf{k}_1,\ldots ,\textbf{k}_m)$
. But since there are finitely many states in Q, we get that
$\phi _{q(k_{11})}(\textbf{k}_1,\ldots ,\textbf{k}_m)$
. But since there are finitely many states in Q, we get that
![]() $q(\ell ) $
is eventually periodic in
$q(\ell ) $
is eventually periodic in
![]() $\ell $
. So for
$\ell $
. So for
![]() $q'\in Q$
the statement
$q'\in Q$
the statement
![]() $ q(k_{11})=q'$
is definable in
$ q(k_{11})=q'$
is definable in
![]() $(\mathbb {N},+)$
. Moreover, for any fixed
$(\mathbb {N},+)$
. Moreover, for any fixed
![]() $q'\in Q$
the induction hypothesis yields that
$q'\in Q$
the induction hypothesis yields that
![]() $\phi _{q'}(\textbf{k}_1,\ldots ,\textbf{k}_m)$
is definable in
$\phi _{q'}(\textbf{k}_1,\ldots ,\textbf{k}_m)$
is definable in
![]() $(\mathbb {N},+)$
; thus our relation is defined in
$(\mathbb {N},+)$
; thus our relation is defined in
![]() $(\mathbb {N},+)$
by
$(\mathbb {N},+)$
by
 $\displaystyle \bigvee _{q'\in Q} (q(k_{11}) = q' \wedge \phi _{q'}(\textbf{k}_1,\ldots ,\textbf{k}_m)) $
(under the assumption that
$\displaystyle \bigvee _{q'\in Q} (q(k_{11}) = q' \wedge \phi _{q'}(\textbf{k}_1,\ldots ,\textbf{k}_m)) $
(under the assumption that
![]() $k_{11}$
is minimum among the
$k_{11}$
is minimum among the
![]() $k_{i1}$
).
$k_{i1}$
).
Similarly we get definability in the case
![]() $k_{i1}$
is minimum for some
$k_{i1}$
is minimum for some
![]() $i>1$
. So taking disjunctions we get that our relation is definable in
$i>1$
. So taking disjunctions we get that our relation is definable in
![]() $(\mathbb {N},+)$
.
$(\mathbb {N},+)$
.
Corollary 7.5. Suppose
![]() $\Gamma $
admits an F-spanning set. If
$\Gamma $
admits an F-spanning set. If
![]() $X\subseteq \Gamma ^m$
is F-automatic and
$X\subseteq \Gamma ^m$
is F-automatic and
![]() $\textbf{a}_1,\ldots ,\textbf{a}_m$
are tuples from
$\textbf{a}_1,\ldots ,\textbf{a}_m$
are tuples from
![]() $\Gamma $
then
$\Gamma $
then
 $$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m) : \begin{pmatrix} [\textbf{a}_1^{\textbf{k}_1}]_F\\ \vdots\\ {[\textbf{a}_m^{\textbf{k}_m}]_F}\end{pmatrix} \in X\right\}\subseteq \mathbb{N}^{{\lvert{\textbf{a}_1} \rvert}}\times \cdots \times \mathbb{N}^{{\lvert{\textbf{a}_m} \rvert}} \end{align*} $$
$$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m) : \begin{pmatrix} [\textbf{a}_1^{\textbf{k}_1}]_F\\ \vdots\\ {[\textbf{a}_m^{\textbf{k}_m}]_F}\end{pmatrix} \in X\right\}\subseteq \mathbb{N}^{{\lvert{\textbf{a}_1} \rvert}}\times \cdots \times \mathbb{N}^{{\lvert{\textbf{a}_m} \rvert}} \end{align*} $$
is definable in
![]() $(\mathbb {N},+)$
.
$(\mathbb {N},+)$
.
Proof By [Reference Bell and Moosa2, Lemma 5.6] there is an F-spanning set
![]() $\Sigma $
containing all the
$\Sigma $
containing all the
![]() $a_{ij}$
; one can then check that
$a_{ij}$
; one can then check that
![]() $\Sigma ^m$
is an F-spanning set for
$\Sigma ^m$
is an F-spanning set for
![]() $\Gamma ^m$
. Let
$\Gamma ^m$
. Let
![]() $L\subseteq (\Sigma ^m)^*$
be the set of representations of elements of X; so L is regular. Then by the previous lemma
$L\subseteq (\Sigma ^m)^*$
be the set of representations of elements of X; so L is regular. Then by the previous lemma
 $$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m,\ell _1,\ldots ,\ell _m) : {\lvert{\textbf{a}_1^{\textbf{k}_1}0^{\ell _1}} \rvert} = \cdots = {\lvert{\textbf{a}_m^{\textbf{k}_m}0^{\ell _m}} \rvert}, \begin{pmatrix}\textbf{a}_1^{\textbf{k}_1}0^{\ell _1}\\\vdots\\ { \textbf{a}_m^{\textbf{k}_m}0^{\ell _m}}\end{pmatrix} \in L\right\} \end{align*} $$
$$ \begin{align*}\left\{(\textbf{k}_1,\ldots ,\textbf{k}_m,\ell _1,\ldots ,\ell _m) : {\lvert{\textbf{a}_1^{\textbf{k}_1}0^{\ell _1}} \rvert} = \cdots = {\lvert{\textbf{a}_m^{\textbf{k}_m}0^{\ell _m}} \rvert}, \begin{pmatrix}\textbf{a}_1^{\textbf{k}_1}0^{\ell _1}\\\vdots\\ { \textbf{a}_m^{\textbf{k}_m}0^{\ell _m}}\end{pmatrix} \in L\right\} \end{align*} $$
is definable in
![]() $(\mathbb {N},+)$
, say by
$(\mathbb {N},+)$
, say by
![]() $\phi (\textbf{k}_1,\ldots ,\textbf{k}_m,\ell _1,\ldots ,\ell _m)$
. Then
$\phi (\textbf{k}_1,\ldots ,\textbf{k}_m,\ell _1,\ldots ,\ell _m)$
. Then
![]() $\exists \ell _1\cdots \exists \ell _m\phi (\textbf{k}_1,\ldots,\textbf{k}_m,\ell _1,\ldots ,\ell _m)$
defines the desired relation in
$\exists \ell _1\cdots \exists \ell _m\phi (\textbf{k}_1,\ldots,\textbf{k}_m,\ell _1,\ldots ,\ell _m)$
defines the desired relation in
![]() $(\mathbb {N},+)$
.
$(\mathbb {N},+)$
.
In order to apply the previous two results, we will need to relate the relations we wish to show are NIP to automatic sets. The following lemma does so. It is a straightforward generalization of a known result in classical automata theory; see for example [Reference Bruyere, Hansel, Michaux and Villemaire3, Theorem 6.1].
Lemma 7.6. Suppose
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
. If
$r>0$
. If
![]() $X\subseteq \Gamma ^m$
is definable in
$X\subseteq \Gamma ^m$
is definable in
![]() $(\Gamma ,+)$
with parameters from
$(\Gamma ,+)$
with parameters from
![]() $\Gamma $
then X is F-automatic.
$\Gamma $
then X is F-automatic.
This result is similar in flavour to the proof of Lemma 5.9, in which it came out that regular languages are closed under Boolean combinations and projection. This proof is similar, but with a complication relating to mismatched lengths when dealing with projection; we get around this by changing the set of finish states.
Proof We first check the case where X is
![]() $0$
-definable in
$0$
-definable in
![]() $(\Gamma ,+)$
; we apply structural induction on formulas. That the claim holds for
$(\Gamma ,+)$
; we apply structural induction on formulas. That the claim holds for
![]() $x = y$
and
$x = y$
and
![]() $x+y = z$
is [Reference Bell and Moosa2, Lemma 6.7]; that the claim holds for a union or complement is because regular languages are closed under union and complementation. It remains to check existential quantification.
$x+y = z$
is [Reference Bell and Moosa2, Lemma 6.7]; that the claim holds for a union or complement is because regular languages are closed under union and complementation. It remains to check existential quantification.
Suppose then that
![]() $X\subseteq \Gamma ^{m+1}$
is F-automatic. Fix an
$X\subseteq \Gamma ^{m+1}$
is F-automatic. Fix an
![]() $F^r$
-spanning set
$F^r$
-spanning set
![]() $\Sigma $
for some
$\Sigma $
for some
![]() $r>0$
; then as before one can check that
$r>0$
; then as before one can check that
![]() $\Sigma ^{m+1}$
is an
$\Sigma ^{m+1}$
is an
![]() $F^r$
-spanning set for
$F^r$
-spanning set for
![]() $\Gamma ^{m+1}$
. So by Proposition 2.6 there is an automaton
$\Gamma ^{m+1}$
. So by Proposition 2.6 there is an automaton
![]() $M = (\Sigma ^{m+1},Q,q_0,\Omega ,\delta )$
recognizing the representations over
$M = (\Sigma ^{m+1},Q,q_0,\Omega ,\delta )$
recognizing the representations over
![]() $\Sigma ^{m+1}$
of elements of X. Consider the non-deterministic automaton
$\Sigma ^{m+1}$
of elements of X. Consider the non-deterministic automaton
![]() $M' = (\Sigma ^m, Q,q_0,\Omega ',\delta ')$
where
$M' = (\Sigma ^m, Q,q_0,\Omega ',\delta ')$
where
-
•
 $\delta '(q,\textbf{a}) = \left \{\delta \left ( {q,\begin {pmatrix}\textbf{a}\\b\end {pmatrix}}\right ) : b\in \Sigma \right \}$
for
$\delta '(q,\textbf{a}) = \left \{\delta \left ( {q,\begin {pmatrix}\textbf{a}\\b\end {pmatrix}}\right ) : b\in \Sigma \right \}$
for
 $\textbf{a}\in \Sigma ^m$
, and
$\textbf{a}\in \Sigma ^m$
, and -
•
 $\Omega ' = \left \{q\in Q : \text {there is }\tau \in \Sigma ^*\text { such that }\delta \left ( {q,\begin {pmatrix}\textbf{0}^{{\lvert \tau \rvert } }\\\tau \end {pmatrix} }\right )\in \Omega \right \}$
.
$\Omega ' = \left \{q\in Q : \text {there is }\tau \in \Sigma ^*\text { such that }\delta \left ( {q,\begin {pmatrix}\textbf{0}^{{\lvert \tau \rvert } }\\\tau \end {pmatrix} }\right )\in \Omega \right \}$
.
Then if
![]() $\boldsymbol {\sigma }\in (\Sigma ^m)^*$
is accepted by
$\boldsymbol {\sigma }\in (\Sigma ^m)^*$
is accepted by
![]() $M'$
then there is
$M'$
then there is
![]() $\tau _1 \in \Sigma ^{({\lvert {\boldsymbol {\sigma }}\rvert }) }$
such that
$\tau _1 \in \Sigma ^{({\lvert {\boldsymbol {\sigma }}\rvert }) }$
such that
 $\delta \left ( {q_0,\begin {pmatrix}\boldsymbol {\sigma }\\\tau _1\end {pmatrix}}\right )\in \Omega '$
; i.e., such that there is
$\delta \left ( {q_0,\begin {pmatrix}\boldsymbol {\sigma }\\\tau _1\end {pmatrix}}\right )\in \Omega '$
; i.e., such that there is
![]() $\tau _2\in \Sigma ^*$
such that
$\tau _2\in \Sigma ^*$
such that
 $\delta \left ( {q_0,\begin {pmatrix}\boldsymbol {\sigma }\textbf{0}^{{\lvert {\tau _2} \rvert }}\\\tau _1\tau _2\end {pmatrix}}\right )\in \Omega $
. So
$\delta \left ( {q_0,\begin {pmatrix}\boldsymbol {\sigma }\textbf{0}^{{\lvert {\tau _2} \rvert }}\\\tau _1\tau _2\end {pmatrix}}\right )\in \Omega $
. So
 $\begin {pmatrix} [\boldsymbol {\sigma } ]_{F^r}\\ [\tau _1\tau _2]_{F^r}\end {pmatrix}\in X$
. Conversely suppose there is
$\begin {pmatrix} [\boldsymbol {\sigma } ]_{F^r}\\ [\tau _1\tau _2]_{F^r}\end {pmatrix}\in X$
. Conversely suppose there is
![]() $b\in \Gamma $
such that
$b\in \Gamma $
such that
 $\begin {pmatrix} [\boldsymbol {\sigma }]_{F^r}\\b\end {pmatrix}\in X$
; say
$\begin {pmatrix} [\boldsymbol {\sigma }]_{F^r}\\b\end {pmatrix}\in X$
; say
![]() $b = [\tau ] _{F^r}$
for
$b = [\tau ] _{F^r}$
for
![]() $\tau \in \Sigma ^*$
. Write
$\tau \in \Sigma ^*$
. Write
![]() $\tau =\tau _1\tau _2$
where
$\tau =\tau _1\tau _2$
where
![]() ${\lvert {\tau _1}\rvert } = {\lvert {\boldsymbol {\sigma }}\rvert }$
(replacing
${\lvert {\tau _1}\rvert } = {\lvert {\boldsymbol {\sigma }}\rvert }$
(replacing
![]() $\tau $
with some
$\tau $
with some
![]() $\tau 0^k$
if necessary). Then
$\tau 0^k$
if necessary). Then
 $\begin {pmatrix} [\boldsymbol {\sigma }\textbf{0}^{{\lvert {\tau _2}\rvert }}]_{F^r}\\ [\tau _1\tau _2]_{F^r}\end {pmatrix} = \begin {pmatrix} [\boldsymbol {\sigma } ]_{F^r}\\b\end {pmatrix}\in X$
; so
$\begin {pmatrix} [\boldsymbol {\sigma }\textbf{0}^{{\lvert {\tau _2}\rvert }}]_{F^r}\\ [\tau _1\tau _2]_{F^r}\end {pmatrix} = \begin {pmatrix} [\boldsymbol {\sigma } ]_{F^r}\\b\end {pmatrix}\in X$
; so
 $\begin {pmatrix}\boldsymbol {\sigma }\textbf{0}^{{\lvert {\tau _2}\rvert }}\\\tau _1\tau _2\end {pmatrix}$
is accepted by M. So
$\begin {pmatrix}\boldsymbol {\sigma }\textbf{0}^{{\lvert {\tau _2}\rvert }}\\\tau _1\tau _2\end {pmatrix}$
is accepted by M. So
 $\delta \left ( {q_0,\begin {pmatrix}\boldsymbol {\sigma }\\\tau _1\end {pmatrix}}\right ) \in \delta '(q_0,\boldsymbol {\sigma })\cap \Omega '$
, and
$\delta \left ( {q_0,\begin {pmatrix}\boldsymbol {\sigma }\\\tau _1\end {pmatrix}}\right ) \in \delta '(q_0,\boldsymbol {\sigma })\cap \Omega '$
, and
![]() $M'$
accepts
$M'$
accepts
![]() $\boldsymbol {\sigma }$
.
$\boldsymbol {\sigma }$
.
So
![]() $M'$
recognizes the representations over
$M'$
recognizes the representations over
![]() $\Sigma ^r$
of the projection of X away from the last coordinate. So existentially quantifying an F-automatic set results in an F-automatic set.
$\Sigma ^r$
of the projection of X away from the last coordinate. So existentially quantifying an F-automatic set results in an F-automatic set.
So if X is
![]() $0$
-definable in
$0$
-definable in
![]() $(\Gamma ,+)$
then X is F-automatic. For the general case, suppose we are given an F-automatic set
$(\Gamma ,+)$
then X is F-automatic. For the general case, suppose we are given an F-automatic set
![]() $X\subseteq \Gamma ^{m+1}$
and
$X\subseteq \Gamma ^{m+1}$
and
![]() $b\in \Gamma $
; it suffices to show that
$b\in \Gamma $
; it suffices to show that
 $\left \{\textbf{a}\in \Gamma ^m : \begin {pmatrix}\textbf{a}\\b\end {pmatrix} \in X\right \}$
is F-automatic. Fix an
$\left \{\textbf{a}\in \Gamma ^m : \begin {pmatrix}\textbf{a}\\b\end {pmatrix} \in X\right \}$
is F-automatic. Fix an
![]() $F^r$
-spanning set
$F^r$
-spanning set
![]() $\Sigma $
; fix
$\Sigma $
; fix
![]() $s_0\cdots s_{n-1} \in \Sigma ^*$
such that
$s_0\cdots s_{n-1} \in \Sigma ^*$
such that
![]() $[s_0\cdots s_{n-1}]_{F^r} = b$
. As before by Proposition 2.6 there is a DFA
$[s_0\cdots s_{n-1}]_{F^r} = b$
. As before by Proposition 2.6 there is a DFA
![]() $M= (\Sigma ^{m+1},Q,q_0,\Omega ,\delta )$
recognizing the representations over
$M= (\Sigma ^{m+1},Q,q_0,\Omega ,\delta )$
recognizing the representations over
![]() $\Sigma ^{m+1}$
of elements of X. Consider the DFA
$\Sigma ^{m+1}$
of elements of X. Consider the DFA
![]() $M' = (\Sigma ^m, Q\times \{0,\ldots ,n\},(q_0,0),\Omega ',\delta ')$
where
$M' = (\Sigma ^m, Q\times \{0,\ldots ,n\},(q_0,0),\Omega ',\delta ')$
where
 $$ \begin{align*}\delta '((q,i),\textbf{a}) = \begin{cases} \left( {\delta \left( {q,\begin{pmatrix}\textbf{a}\\s_i\end{pmatrix}}\right),i+1}\right) & {\text{if }} i < n, \\ \left( {\delta \left({q, \begin{pmatrix}\textbf{a}\\0\end{pmatrix}}\right),n}\right) &{\text{else}}, \end{cases} \end{align*} $$
$$ \begin{align*}\delta '((q,i),\textbf{a}) = \begin{cases} \left( {\delta \left( {q,\begin{pmatrix}\textbf{a}\\s_i\end{pmatrix}}\right),i+1}\right) & {\text{if }} i < n, \\ \left( {\delta \left({q, \begin{pmatrix}\textbf{a}\\0\end{pmatrix}}\right),n}\right) &{\text{else}}, \end{cases} \end{align*} $$
for
![]() $\textbf{a}\in \Sigma ^m$
, and
$\textbf{a}\in \Sigma ^m$
, and
 $$ \begin{align*}\Omega '= (\Omega \times \{n\})\cup\left\{(q,i) \in Q\times \{0,\ldots ,n-1\}: \delta \left( {q,\begin{pmatrix}\textbf{0}^{n-i}\\s_i\cdots s_{n-1}\end{pmatrix}}\right)\in\Omega\right\}. \end{align*} $$
$$ \begin{align*}\Omega '= (\Omega \times \{n\})\cup\left\{(q,i) \in Q\times \{0,\ldots ,n-1\}: \delta \left( {q,\begin{pmatrix}\textbf{0}^{n-i}\\s_i\cdots s_{n-1}\end{pmatrix}}\right)\in\Omega\right\}. \end{align*} $$
One can show by induction on
![]() ${\lvert {\boldsymbol \sigma }\rvert }$
that
${\lvert {\boldsymbol \sigma }\rvert }$
that
 $$ \begin{align*}\delta ((q_0,0),\boldsymbol\sigma ) = \begin{cases} \left( {\delta \left( {q_0,\begin{pmatrix}\boldsymbol{\sigma }\\s_0\cdots s_{{\lvert {\boldsymbol\sigma -1}\rvert}}\end{pmatrix}}\right), {\lvert {\boldsymbol\sigma }\rvert}}\right) &{\text{if }}{\lvert {\boldsymbol\sigma }\rvert}< n, \\ \left( {\delta \left( {q_0,\begin{pmatrix}\boldsymbol\sigma \\s_0\cdots s_{n-1}0^{{\lvert{\boldsymbol\sigma } \rvert}-n}\end{pmatrix}}\right), n}\right) &{\text{else}}, \end{cases} \end{align*} $$
$$ \begin{align*}\delta ((q_0,0),\boldsymbol\sigma ) = \begin{cases} \left( {\delta \left( {q_0,\begin{pmatrix}\boldsymbol{\sigma }\\s_0\cdots s_{{\lvert {\boldsymbol\sigma -1}\rvert}}\end{pmatrix}}\right), {\lvert {\boldsymbol\sigma }\rvert}}\right) &{\text{if }}{\lvert {\boldsymbol\sigma }\rvert}< n, \\ \left( {\delta \left( {q_0,\begin{pmatrix}\boldsymbol\sigma \\s_0\cdots s_{n-1}0^{{\lvert{\boldsymbol\sigma } \rvert}-n}\end{pmatrix}}\right), n}\right) &{\text{else}}, \end{cases} \end{align*} $$
for
![]() $\boldsymbol \sigma \in \Sigma ^m$
. Hence
$\boldsymbol \sigma \in \Sigma ^m$
. Hence
![]() $M'$
accepts the
$M'$
accepts the
![]() $\boldsymbol \sigma \in (\Sigma ^m)^*$
such that
$\boldsymbol \sigma \in (\Sigma ^m)^*$
such that
 $\begin {pmatrix} [\boldsymbol \sigma ]_{F^r}\\b\end {pmatrix}\in X$
; so
$\begin {pmatrix} [\boldsymbol \sigma ]_{F^r}\\b\end {pmatrix}\in X$
; so
 $\left \{\textbf{a}\in \Gamma ^m : \begin {pmatrix}\textbf{a}\\b\end {pmatrix} \in X\right \}$
is F-automatic, as desired.
$\left \{\textbf{a}\in \Gamma ^m : \begin {pmatrix}\textbf{a}\\b\end {pmatrix} \in X\right \}$
is F-automatic, as desired.
Theorem 7.7. Suppose
![]() $(\Gamma ,+) $
is a weakly minimal abelian group and admits an
$(\Gamma ,+) $
is a weakly minimal abelian group and admits an
![]() $F^r$
-spanning set for some
$F^r$
-spanning set for some
![]() $r>0$
; suppose
$r>0$
; suppose
![]() $A\subseteq \Gamma $
is F-EDP. Then
$A\subseteq \Gamma $
is F-EDP. Then
![]() $(\Gamma ,+,A)$
is NIP.
$(\Gamma ,+,A)$
is NIP.
Proof We apply [Reference Conant and Laskowski4, Theorem 2.9], which tells us that in a weakly minimal group
![]() $\Gamma $
if
$\Gamma $
if
![]() $A_{\Gamma } $
is NIP then so is
$A_{\Gamma } $
is NIP then so is
![]() $(\Gamma ,+,A)$
. Here
$(\Gamma ,+,A)$
. Here
![]() $A_{\Gamma } $
is the induced structure of
$A_{\Gamma } $
is the induced structure of
![]() $(\Gamma ,+) $
on A: the domain of
$(\Gamma ,+) $
on A: the domain of
![]() $A_{\Gamma } $
is A, and for every
$A_{\Gamma } $
is A, and for every
![]() $(\Gamma ,+)$
-definable subset X of
$(\Gamma ,+)$
-definable subset X of
![]() $\Gamma ^m$
with parameters from
$\Gamma ^m$
with parameters from
![]() $\Gamma $
its trace
$\Gamma $
its trace
![]() $X\cap A^m$
on A is an atomic relation of
$X\cap A^m$
on A is an atomic relation of
![]() $A_{\Gamma } $
. We show that
$A_{\Gamma } $
. We show that
![]() $A_{\Gamma } $
is interpretable in
$A_{\Gamma } $
is interpretable in
![]() $(\mathbb {N},+)$
, and thus is NIP.
$(\mathbb {N},+)$
, and thus is NIP.
By Lemma 7.3 we may assume A takes the form
![]() $[\textbf{a}^{\phi (\mathbb {N})}]_{F^s}$
for some
$[\textbf{a}^{\phi (\mathbb {N})}]_{F^s}$
for some
![]() $s\in r\mathbb {N}$
. So
$s\in r\mathbb {N}$
. So
![]() $\Gamma $
admits an
$\Gamma $
admits an
![]() $F^s$
-spanning set by [Reference Bell and Moosa2, Lemma 5.7]. Let
$F^s$
-spanning set by [Reference Bell and Moosa2, Lemma 5.7]. Let
![]() $\Phi \colon \mathbb {N}^{{\lvert {\textbf{a}}\rvert }}\to \Gamma $
be
$\Phi \colon \mathbb {N}^{{\lvert {\textbf{a}}\rvert }}\to \Gamma $
be
![]() $\textbf{k}\mapsto [\textbf{a}^{\textbf{k}}]_{F^s} $
; so
$\textbf{k}\mapsto [\textbf{a}^{\textbf{k}}]_{F^s} $
; so
![]() $\Phi $
is surjective
$\Phi $
is surjective
![]() $\phi (\mathbb {N}^{{\lvert {\textbf{a} } \rvert }})\twoheadrightarrow A$
. We show that
$\phi (\mathbb {N}^{{\lvert {\textbf{a} } \rvert }})\twoheadrightarrow A$
. We show that
![]() $\Phi $
defines an interpretation of
$\Phi $
defines an interpretation of
![]() $A_{\Gamma } $
in
$A_{\Gamma } $
in
![]() $(\mathbb {N},+)$
, and hence that
$(\mathbb {N},+)$
, and hence that
![]() $A_{\Gamma } $
is NIP.
$A_{\Gamma } $
is NIP.
By Corollary 7.5 the equivalence relation given by
![]() $\textbf{k}_1\sim \textbf{k}_2$
if and only if
$\textbf{k}_1\sim \textbf{k}_2$
if and only if
![]() $\Phi (\textbf{k}_1) = \Phi (\textbf{k}_2)$
is definable in
$\Phi (\textbf{k}_1) = \Phi (\textbf{k}_2)$
is definable in
![]() $(\mathbb {N},+)$
(since the diagonal in
$(\mathbb {N},+)$
(since the diagonal in
![]() $\Gamma ^{2m}$
is F-automatic by [Reference Bell and Moosa2, Lemma 6.7]). Suppose now that
$\Gamma ^{2m}$
is F-automatic by [Reference Bell and Moosa2, Lemma 6.7]). Suppose now that
![]() $X\subseteq \Gamma ^m$
is definable with parameters in
$X\subseteq \Gamma ^m$
is definable with parameters in
![]() $(\Gamma ,0,+)$
; it remains to show that
$(\Gamma ,0,+)$
; it remains to show that
![]() $ \phi (\mathbb {N}^{{\lvert {\textbf{a}}\rvert }})^m\cap (\Phi ^m)^{-1}(X) $
is definable in
$ \phi (\mathbb {N}^{{\lvert {\textbf{a}}\rvert }})^m\cap (\Phi ^m)^{-1}(X) $
is definable in
![]() $(\mathbb {N},+)$
. We get by Lemma 7.6 that X is F-automatic; so by Corollary 7.5
$(\mathbb {N},+)$
. We get by Lemma 7.6 that X is F-automatic; so by Corollary 7.5
![]() $(\Phi ^m)^{-1}(X)$
is definable in
$(\Phi ^m)^{-1}(X)$
is definable in
![]() $(\mathbb {N},+)$
. So
$(\mathbb {N},+)$
. So
![]() $\phi (\mathbb {N}^{{\lvert {\textbf{a}}\rvert }})^m\cap (\Phi ^m)^{-1}(X)$
is definable in
$\phi (\mathbb {N}^{{\lvert {\textbf{a}}\rvert }})^m\cap (\Phi ^m)^{-1}(X)$
is definable in
![]() $(\mathbb {N},+)$
, and
$(\mathbb {N},+)$
, and
![]() $\Phi $
defines an interpretation of
$\Phi $
defines an interpretation of
![]() $A_{\Gamma } $
in
$A_{\Gamma } $
in
![]() $(\mathbb {N},+)$
.
$(\mathbb {N},+)$
.
As an application of Theorem 7.7, we prove the following:
Theorem 7.8. Suppose
![]() $p\ge 7$
is prime. Then
$p\ge 7$
is prime. Then
![]() $(\mathbb {F}_p[t],+,{\times \mathord \restriction t^{\mathbb {N}}})$
is NIP, where
$(\mathbb {F}_p[t],+,{\times \mathord \restriction t^{\mathbb {N}}})$
is NIP, where
 ${\times \mathord \restriction t^{\mathbb {N}}} = \left \{\begin {pmatrix}t^i\\t^j\\t^{i+j}\end {pmatrix} : i,j\in \mathbb {N}\right \}$
.
${\times \mathord \restriction t^{\mathbb {N}}} = \left \{\begin {pmatrix}t^i\\t^j\\t^{i+j}\end {pmatrix} : i,j\in \mathbb {N}\right \}$
.
Proof Let
![]() $F\colon \mathbb {F}_p[t]\to \mathbb {F}_p[t]$
be
$F\colon \mathbb {F}_p[t]\to \mathbb {F}_p[t]$
be
![]() $f(t)\mapsto tf(t)$
. Note that
$f(t)\mapsto tf(t)$
. Note that
![]() $\mathbb {F}_p$
is an F-spanning set for
$\mathbb {F}_p$
is an F-spanning set for
![]() $\mathbb {F}_p[t]$
. Indeed, an arbitrary element of
$\mathbb {F}_p[t]$
. Indeed, an arbitrary element of
![]() $\mathbb {F}_p[t]$
is of the form
$\mathbb {F}_p[t]$
is of the form
![]() $a_0 + a_1t+\cdots + a_nt^n = [a_0a_1\cdots a_n]_F$
, and the other axioms are easily verified using the facts that
$a_0 + a_1t+\cdots + a_nt^n = [a_0a_1\cdots a_n]_F$
, and the other axioms are easily verified using the facts that
![]() $\mathbb {F}_p$
is a subgroup and
$\mathbb {F}_p$
is a subgroup and
![]() $\mathbb {F}_p\cap F(\mathbb {F}_p[t]) = \{0\}$
. Furthermore
$\mathbb {F}_p\cap F(\mathbb {F}_p[t]) = \{0\}$
. Furthermore
![]() $(\mathbb {F}_p[t],+)$
is weakly minimal: for each
$(\mathbb {F}_p[t],+)$
is weakly minimal: for each
![]() $n\in \mathbb {N}$
we have
$n\in \mathbb {N}$
we have
 $$ \begin{align*} n\mathbb{F}_p[t] &= \begin{cases} \mathbb{F}_p[t] &{\text{if }} p\nmid n, \\ 0 &{\text{else}}, \end{cases} \\ \{a\in \mathbb{F}_p[t] : na = 0\} &= \begin{cases} 0 &{\text{if }} p\nmid n, \\ \mathbb{F}_p[t] &{\text{else}}, \end{cases} \end{align*} $$
$$ \begin{align*} n\mathbb{F}_p[t] &= \begin{cases} \mathbb{F}_p[t] &{\text{if }} p\nmid n, \\ 0 &{\text{else}}, \end{cases} \\ \{a\in \mathbb{F}_p[t] : na = 0\} &= \begin{cases} 0 &{\text{if }} p\nmid n, \\ \mathbb{F}_p[t] &{\text{else}}, \end{cases} \end{align*} $$
so weak minimality follows from [Reference Conant and Laskowski4, Proposition 3.1]. So Theorem 7.7 applies, and
![]() $(\mathbb {F}_p[t],+,A)$
is NIP whenever
$(\mathbb {F}_p[t],+,A)$
is NIP whenever
![]() $A\subseteq \mathbb {F}_p[t]$
is F-EDP.
$A\subseteq \mathbb {F}_p[t]$
is F-EDP.
We encode
![]() ${\times \mathord \restriction t^{\mathbb {N}}}$
in an F-EDP subset of
${\times \mathord \restriction t^{\mathbb {N}}}$
in an F-EDP subset of
![]() $\mathbb {F}_p[t] $
. Write
$\mathbb {F}_p[t] $
. Write
![]() $\mathbb {F}_p = \mathbb {Z}/p\mathbb {Z} = \{\overline {n}: n\in \mathbb {Z}\}$
. Let
$\mathbb {F}_p = \mathbb {Z}/p\mathbb {Z} = \{\overline {n}: n\in \mathbb {Z}\}$
. Let
Note that
 $$ \begin{align*} \{\overline{3}t^{i+j}-\overline{3}t^i-\overline{3}t^j : i,j\in \mathbb{N}\setminus \{0\}\} =& \{[(\overline{0})^k(\overline{-3})(\overline{0})^{\ell} (\overline{-3})(\overline{0})^{k-1}\overline{3}]_F : k,\ell \in\mathbb{N},k>0\}\\ &\cup \{[(\overline{0})^k(\overline{-6})(\overline{0})^{k-1}\overline{3}]_F : k\in\mathbb{N}\setminus \{0\}\} \end{align*} $$
$$ \begin{align*} \{\overline{3}t^{i+j}-\overline{3}t^i-\overline{3}t^j : i,j\in \mathbb{N}\setminus \{0\}\} =& \{[(\overline{0})^k(\overline{-3})(\overline{0})^{\ell} (\overline{-3})(\overline{0})^{k-1}\overline{3}]_F : k,\ell \in\mathbb{N},k>0\}\\ &\cup \{[(\overline{0})^k(\overline{-6})(\overline{0})^{k-1}\overline{3}]_F : k\in\mathbb{N}\setminus \{0\}\} \end{align*} $$
is F-EDP as a union of F-EDP sets (see Lemma 7.2(1)). Since
![]() $t^{\mathbb {N}} = \{[(\overline {0})^k\overline {1}]_F : k \in \mathbb {N}\}$
and
$t^{\mathbb {N}} = \{[(\overline {0})^k\overline {1}]_F : k \in \mathbb {N}\}$
and
![]() $\overline {2}t^{\mathbb {N}} = \{[(\overline {0})^k\overline {2}]_F : k\in \mathbb {N}\}$
, we get that A itself is F-EDP as a union of F-EDP sets; so
$\overline {2}t^{\mathbb {N}} = \{[(\overline {0})^k\overline {2}]_F : k\in \mathbb {N}\}$
, we get that A itself is F-EDP as a union of F-EDP sets; so
![]() $(\mathbb {F}_p[t] ,+,A)$
is NIP. It remains to see that
$(\mathbb {F}_p[t] ,+,A)$
is NIP. It remains to see that
![]() ${\times \mathord \restriction t^{\mathbb {N}}}$
is definable in
${\times \mathord \restriction t^{\mathbb {N}}}$
is definable in
![]() $(\mathbb {F}_p[t],+,A)$
.
$(\mathbb {F}_p[t],+,A)$
.
Claim 7.9.
![]() $t^{\mathbb {N}}$
and
$t^{\mathbb {N}}$
and
![]() $B := \{t^{i+j} - t^i - t^j : i,j\in \mathbb {N}\setminus \{0\}\}$
are both definable in
$B := \{t^{i+j} - t^i - t^j : i,j\in \mathbb {N}\setminus \{0\}\}$
are both definable in
![]() $(\mathbb {F}_p[t] ,+,A)$
.
$(\mathbb {F}_p[t] ,+,A)$
.
Proof We first check
![]() $t^{\mathbb {N}}$
. I claim that if
$t^{\mathbb {N}}$
. I claim that if
![]() $\phi (x)$
is
$\phi (x)$
is
![]() $ (x\in A)\wedge (2x\in A)$
then
$ (x\in A)\wedge (2x\in A)$
then
![]() $\phi $
defines
$\phi $
defines
![]() $t^{\mathbb {N}}$
. It is clear that
$t^{\mathbb {N}}$
. It is clear that
![]() $\phi (\mathbb {F}_p[t] )\supseteq t^{\mathbb {N}}$
; suppose conversely that
$\phi (\mathbb {F}_p[t] )\supseteq t^{\mathbb {N}}$
; suppose conversely that
![]() $f\in \phi (\mathbb {F}_p[t] )$
. If we had
$f\in \phi (\mathbb {F}_p[t] )$
. If we had
![]() $f = \overline {2}t^i\in \overline {2}t^{\mathbb {N}}$
then
$f = \overline {2}t^i\in \overline {2}t^{\mathbb {N}}$
then
![]() $2f = \overline {4}t^i$
, and hence
$2f = \overline {4}t^i$
, and hence
![]() $2f\notin A$
(since
$2f\notin A$
(since
![]() $p\ge 7$
implies
$p\ge 7$
implies
![]() $\overline {4}\notin \{\overline {1},\overline {2},\overline {3}\}$
, and these are the only leading coefficients of elements of A). But this contradicts the assumption that
$\overline {4}\notin \{\overline {1},\overline {2},\overline {3}\}$
, and these are the only leading coefficients of elements of A). But this contradicts the assumption that
![]() $f\in \phi (\mathbb {F}_p[t])$
. Similarly if we had
$f\in \phi (\mathbb {F}_p[t])$
. Similarly if we had
![]() $f= \overline {3}t^{i+j}-\overline {3}t^i-\overline {3}t^j$
for some
$f= \overline {3}t^{i+j}-\overline {3}t^i-\overline {3}t^j$
for some
![]() $i,j$
then
$i,j$
then
![]() $2f = \overline {6}t^{i+j} - \overline {6}t^i - \overline {6}t^j$
has leading coefficient
$2f = \overline {6}t^{i+j} - \overline {6}t^i - \overline {6}t^j$
has leading coefficient
![]() $\overline {6}$
; so by similar reasoning we conclude that
$\overline {6}$
; so by similar reasoning we conclude that
![]() $2f\notin A$
, a contradiction. So having eliminated the other possibilities we conclude that
$2f\notin A$
, a contradiction. So having eliminated the other possibilities we conclude that
![]() $f\in t^{\mathbb {N}}$
, as desired. Note then that
$f\in t^{\mathbb {N}}$
, as desired. Note then that
![]() $\overline {2}t^{\mathbb {N}} = 2t^{\mathbb {N}}$
is also definable.
$\overline {2}t^{\mathbb {N}} = 2t^{\mathbb {N}}$
is also definable.
We now check B. I claim that if
![]() $\psi (x)$
is
$\psi (x)$
is
![]() $3x\in A\setminus (t^{\mathbb {N}}\cup 2t^{\mathbb {N}})$
then
$3x\in A\setminus (t^{\mathbb {N}}\cup 2t^{\mathbb {N}})$
then
![]() $\psi $
defines B. That
$\psi $
defines B. That
![]() $\psi (\mathbb {F}_p[t] )\subseteq B$
is just injectivity of
$\psi (\mathbb {F}_p[t] )\subseteq B$
is just injectivity of
![]() $f\mapsto 3f$
; that
$f\mapsto 3f$
; that
![]() $\psi (\mathbb {F}_p[t] )\supseteq B$
is that
$\psi (\mathbb {F}_p[t] )\supseteq B$
is that
![]() $\{\overline {3}t^{i+j}-\overline {3}t^i-\overline {3}t^j : i,j\in \mathbb {N}\}\cap (t^{\mathbb {N}}\cup \overline {2}t^{\mathbb {N}}) = \emptyset $
, which follows by considering the leading coefficients.
$\{\overline {3}t^{i+j}-\overline {3}t^i-\overline {3}t^j : i,j\in \mathbb {N}\}\cap (t^{\mathbb {N}}\cup \overline {2}t^{\mathbb {N}}) = \emptyset $
, which follows by considering the leading coefficients.
So it suffices to show that
![]() ${\times \mathord \restriction t^{\mathbb {N}}}$
is definable in
${\times \mathord \restriction t^{\mathbb {N}}}$
is definable in
![]() $(\mathbb {F}_p[t] ,+,t^{\mathbb {N}},B)$
. In fact if
$(\mathbb {F}_p[t] ,+,t^{\mathbb {N}},B)$
. In fact if
![]() $\phi (x,y,z)$
is
$\phi (x,y,z)$
is
then
![]() ${\times \mathord \restriction t^{\mathbb {N}}} = \phi (\mathbb {F}_p[t] )$
. It is clear that
${\times \mathord \restriction t^{\mathbb {N}}} = \phi (\mathbb {F}_p[t] )$
. It is clear that
![]() ${\times \mathord \restriction t^{\mathbb {N}}}\subseteq \phi (\mathbb {F}_p[t] )$
; for the converse suppose
${\times \mathord \restriction t^{\mathbb {N}}}\subseteq \phi (\mathbb {F}_p[t] )$
; for the converse suppose
 $\begin {pmatrix}t^i\\t^j\\t^k\end {pmatrix}\in \phi (\mathbb {F}_p[t] )$
. Note that if either of the first two disjuncts of
$\begin {pmatrix}t^i\\t^j\\t^k\end {pmatrix}\in \phi (\mathbb {F}_p[t] )$
. Note that if either of the first two disjuncts of
![]() $\phi $
holds then
$\phi $
holds then
 $\begin {pmatrix}t^i\\t^j\\t^k\end {pmatrix}\in {\times \mathord \restriction t^{\mathbb {N}}}$
; suppose then that the last holds. So there are
$\begin {pmatrix}t^i\\t^j\\t^k\end {pmatrix}\in {\times \mathord \restriction t^{\mathbb {N}}}$
; suppose then that the last holds. So there are
![]() $i',j'>0$
such that
$i',j'>0$
such that
![]() $t^k-t^i-t^j = t^{i'+j'}-t^{i'} -t^{j'} $
. Since
$t^k-t^i-t^j = t^{i'+j'}-t^{i'} -t^{j'} $
. Since
![]() $i',j'>0$
we get that the leading coefficient of the right-hand side is
$i',j'>0$
we get that the leading coefficient of the right-hand side is
![]() $\overline {1}$
; for the same to be true on the left-hand side we must have
$\overline {1}$
; for the same to be true on the left-hand side we must have
![]() $k>i,j$
, and thus
$k>i,j$
, and thus
![]() $k = i'+j'$
. So
$k = i'+j'$
. So
![]() $t^i + t^j = t^{i'} + t^{j'}$
, and
$t^i + t^j = t^{i'} + t^{j'}$
, and
![]() $\{i,j\} = \{i',j'\}$
. Thus
$\{i,j\} = \{i',j'\}$
. Thus
![]() $i+j = i'+j' = k$
, and
$i+j = i'+j' = k$
, and
 $\begin {pmatrix}t^i\\t^j\\t^k\end {pmatrix}\in {\times \mathord \restriction t^{\mathbb {N}}}$
.
$\begin {pmatrix}t^i\\t^j\\t^k\end {pmatrix}\in {\times \mathord \restriction t^{\mathbb {N}}}$
.
Acknowledgments
My thanks to Luke Franceschini for helping me work through the details of Example 3.1. Warm thanks to my advisor, Rahim Moosa, for his excellent guidance, thorough editing, and many helpful discussions. I am grateful to the reviewer for their comments, and in particular for pointing out that the notion of a length function could be simplified to its current form. This work was partially supported by an NSERC PGS-D and an NSERC CGS-D.