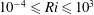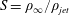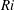1 Introduction
Vertical injection of light fluid into a denser ambient creates a flow that either bears the characteristics of a jet, if the injected momentum is dominant over the buoyant forces, or those of a plume, if the momentum that is generated by buoyancy is dominant over the momentum that is imparted at the orifice.
The instability behaviour of jets is known to be strongly affected by density variations, even if buoyancy is not taken into account. Monkewitz & Sohn (Reference Monkewitz and Sohn1988) found that jets at a jet-to-ambient density ratio below 0.72 in zero gravity display absolute instability, which leads to the self-sustained formation of ring vortices at a well-defined frequency. This phenomenon has been observed experimentally (Sreenivasan, Raghu & Kyle Reference Sreenivasan, Raghu and Kyle1989; Monkewitz et al. Reference Monkewitz, Bechert, Barsikow and Lehmann1990; Boujemaa, Amielh & Chauve Reference Boujemaa, Amielh and Chauve2004; Hallberg & Strykowski Reference Hallberg and Strykowski2006) and numerically (Lesshafft et al. Reference Lesshafft, Huerre, Sagaut and Terracol2006; Nichols, Schmid & Riley Reference Nichols, Schmid and Riley2007). Lesshafft & Huerre (Reference Lesshafft and Huerre2007) established that the absolute instability arises from non-buoyant baroclinic effects. Mollendorf & Gebhart (Reference Mollendorf and Gebhart1973) included the action of buoyancy in the form of weak forcing terms in a local instability analysis. Recently, Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017) performed a global instability analysis for light jets in the zero-Mach-number limit, achieving good agreement with the helium jet experiments of Hallberg & Strykowski (Reference Hallberg and Strykowski2006). A small Richardson number in these experiments characterises buoyant effects as being small, and the global analysis confirms that their impact on the instability behaviour is negligible in this regime.
The instability of plumes, at high Richardson numbers, has received far less attention from a theoretical perspective. Wakitani (Reference Wakitani1980) and Riley & Tveitereid (Reference Riley and Tveitereid1984) investigated the local instability characteristics, both temporal and spatial, of self-similar plumes within the limits of the Boussinesq approximation. Under the same assumption, Chakravarthy, Lesshafft & Huerre (Reference Chakravarthy, Lesshafft and Huerre2015) considered the convective/absolute nature of local instability in plumes, both in the self-similar regime far removed from the buoyancy source, and in the near-source region for one particular configuration. It was established that helical perturbations of azimuthal wavenumber
$m=1$
undergo a transition to absolute instability, due to a saddle point in the dispersion relation that is conditioned on the presence of buoyancy. However, the associated growth rates seem to be small, and their relevance for global and non-Boussinesq dynamics remains to be proved. The axisymmetric mode was found to be at most convectively unstable.
The instability of internal plumes in a confined domain appears to be a separate subject. In direct numerical simulations performed in the Boussinesq limit, Lopez & Marques (Reference Lopez and Marques2013) document a sequence of global state bifurcations in such closed flows, occurring at successive critical Rayleigh numbers. A linear global instability analysis of the same configuration (Lesshafft Reference Lesshafft2015) suggests that at least the first of these bifurcations arises due to pressure feedback between the top and bottom solid walls.
Numerous experiments have been performed on plumes with large density differences, where the Boussinesq approximation is not justified. Subbarao & Cantwell (Reference Subbarao and Cantwell1992) conducted helium-air experiments, and they reported periodic axisymmetric puffing at Reynolds and Richardson numbers,
$Re$
and
$Ri$
, above critical values. Similar observations were made by Cetegen & Kasper (Reference Cetegen and Kasper1996) for a larger range of
$Ri$
. A power law was obtained in the latter study that relates the puffing Strouhal number to
$Re$
and
$Ri$
. These experimental findings were corroborated by numerical simulations (Jiang & Luo Reference Jiang and Luo2000; Satti & Agrawal Reference Satti and Agrawal2006) and in additional recent experiments by Bharadwaj & Das (Reference Bharadwaj and Das2017). Through systematic variation of the gravity parameter, Satti & Agrawal (Reference Satti and Agrawal2006) demonstrated that the onset of self-sustained oscillations in their setting is contingent on the presence of gravity. The large majority of experiments and simulations suggest a dominant role of axisymmetric instability structures, contrary to the conclusions drawn from local instability analysis of self-similar Boussinesq plumes by Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015).
The present investigation addresses the linear instability of buoyant jets and plumes in a global and non-Boussinesq framework. The low-Mach-number approximation of McMurtry et al. (Reference McMurtry, Jou, Riley and Metcalfe1986) is used in a form where density variations arise from heating of a single-species fluid. This formulation allows one to examine the stability of buoyant jets and plumes on a continuous scale provided by the Richardson number, while the density ratio as an independent parameter characterises the departure from the Boussinesq condition. Special attention will be given to the physical origin of flow instability, by means of sensitivity analysis.
A similar approach has been pursued by Bharadwaj & Das (Reference Bharadwaj and Das2017) in their analysis of helium plumes. That study demonstrated close agreement between the occurrence of self-excited puffing in experiments and the onset of global linear instability. Furthermore, the linear analysis was shown to accurately predict the puffing frequency, even far from the instability threshold.
The paper is organised in the following manner. Section 2 introduces the governing equations and the numerical procedures employed for the computation of base flows and their instability characteristics in global and local frameworks. Global instability results are presented in § 3, followed by a discussion of the relevant physical mechanisms in § 4. The global results are complemented by a local absolute/convective analysis in § 5, which provides a link with the study by Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015) of local instability in Boussinesq settings. Conclusions are offered in § 6.
2 Problem formulation
2.1 Governing equations
A calorically perfect fluid is injected into an unstratified quiescent ambient of the same fluid at lower temperature, from a circular orifice in an adiabatic wall. In order to model a flow with strong density variations but negligible compressibility, a low-Mach-number approximation of the compressible Navier–Stokes equation is used. This approximation, which retains all the effects of variable density in the convective terms, but discards the compressible dependency of density on pressure, was introduced by McMurtry et al. (Reference McMurtry, Jou, Riley and Metcalfe1986) for a study of non-buoyant jets in the limit of zero Mach number. It was then extended to include a buoyancy term by Nichols et al. (Reference Nichols, Schmid and Riley2007) and Chandler (Reference Chandler2010), and their formulation is used in the present investigation. The dimensional governing equations in this approximation are given by
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}t}+\text{div}(\tilde{\unicode[STIX]{x1D70C}}\tilde{\boldsymbol{u}})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\unicode[STIX]{x1D70C}}\frac{\text{D}\tilde{\boldsymbol{u}}}{\text{D}t}=-\text{grad}\,\tilde{p}+\unicode[STIX]{x1D707}\left[\unicode[STIX]{x0394}\tilde{\boldsymbol{u}}+\frac{1}{3}\text{grad}(\text{div}\,\tilde{\boldsymbol{u}})\right]+g(\tilde{\unicode[STIX]{x1D70C}}_{\infty }-\tilde{\unicode[STIX]{x1D70C}})\boldsymbol{e}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\unicode[STIX]{x1D70C}}C_{p}\frac{\text{D}\tilde{T}}{\text{D}t}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}\tilde{T}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\unicode[STIX]{x1D70C}}\mathscr{R}\tilde{T}=p_{0}, & \displaystyle\end{eqnarray}$$
$\tilde{\unicode[STIX]{x1D70C}}$
,
$\tilde{\boldsymbol{u}}$
,
$\tilde{p}$
,
$\tilde{T}$
denote the dimensional density, velocity, pressure and temperature,
$\tilde{\unicode[STIX]{x1D70C}}_{\infty }$
is the ambient density,
$g$
is the acceleration due to gravity,
$\unicode[STIX]{x1D6FC}$
is the thermal conductivity,
$C_{p}$
is the specific heat,
$\unicode[STIX]{x1D707}$
is the dynamic viscosity, and
$\mathscr{R}$
is the specific gas constant. Note that the pressure in this formulation is split into a thermodynamic component
$p_{0}$
, which is constant throughout the flow, and a fluctuating hydrodynamic component
$\tilde{p}$
. While the continuity and momentum equations (2.1a
) and (2.1b
) are of the same form as in the fully compressible case, the energy equation (2.1c
) simplifies to a simple advection–diffusion equation for temperature.
In dimensionless form, scaled with the nozzle radius
$R$
, the inlet centreline velocity
$\tilde{u} _{j}$
, the temperature difference
$\tilde{T}_{j}-\tilde{T}_{\infty }$
between inflowing and ambient fluid, and the ambient density
$\tilde{\unicode[STIX]{x1D70C}}_{\infty }$
, equations (2.1) become
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}+\text{div}(\unicode[STIX]{x1D70C}\boldsymbol{u})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}\boldsymbol{u}}{\text{D}t}=-\text{grad}\,p+\frac{1}{ReS}\left[\unicode[STIX]{x0394}\boldsymbol{u}+\frac{1}{3}\text{grad}(\text{div}\,\boldsymbol{u})\right]+\frac{Ri}{S-1}(1-\unicode[STIX]{x1D70C})\boldsymbol{e}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}T}{\text{D}t}=\frac{1}{PrReS}\unicode[STIX]{x0394}T. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}(1+T(S-1))=1. & \displaystyle\end{eqnarray}$$
$T=(\tilde{T}-\tilde{T}_{\infty })/(\tilde{T}_{j}-\tilde{T}_{\infty })$
is used, and in all further calculations, this variable is expressed in terms of
$\unicode[STIX]{x1D70C}$
by use of (2.2d
). The flow is characterised by the following parameters: 
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Prandtl number}\quad Pr=\frac{\unicode[STIX]{x1D707}C_{P}}{\unicode[STIX]{x1D6FC}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{density ratio}\quad S=\frac{\tilde{\unicode[STIX]{x1D70C}}_{\infty }}{\tilde{\unicode[STIX]{x1D70C}}_{j}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Reynolds number}\quad Re=\frac{\tilde{\unicode[STIX]{x1D70C}}_{j}\tilde{u} _{j}R}{\unicode[STIX]{x1D707}}\quad \text{and} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Richardson number}\quad Ri=gR\frac{(\tilde{\unicode[STIX]{x1D70C}}_{\infty }-\tilde{\unicode[STIX]{x1D70C}}_{j})}{\tilde{\unicode[STIX]{x1D70C}}_{j}\tilde{u} _{j}^{2}}. & \displaystyle\end{eqnarray}$$
In the homogeneous limit
$S\rightarrow 1$
, the state equation (2.2d
) prescribes
$\unicode[STIX]{x1D70C}\rightarrow 1$
, and the system (2.2) is then identical to the Boussinesq equations used in Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015), provided
$\unicode[STIX]{x1D70C}-1$
is taken to be of order
$S-1$
; the present formulation is therefore consistent with our earlier study. A rigorous derivation of the Boussinesq equations and a discussion on the underlying assumptions may be found in Tritton (Reference Tritton2012).
2.2 Base flow
In a cylindrical coordinate system
$(r,\unicode[STIX]{x1D703},z)$
, the flow variables
$q=(\unicode[STIX]{x1D70C},\boldsymbol{u},p,T)^{\text{T}}$
are split into steady and unsteady components as
$$\begin{eqnarray}\displaystyle \boldsymbol{q}(r,\unicode[STIX]{x1D703},z,t)=\overline{\boldsymbol{q}}(r,\unicode[STIX]{x1D703},z)+\boldsymbol{q}^{\prime }(r,\unicode[STIX]{x1D703},z,t). & & \displaystyle\end{eqnarray}$$
The numerical tools used for the construction of the base flow, as well as for the linear perturbation analysis described in § 2.3, are very similar to those employed by Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017), except that density variations are modelled as an effect of heating, rather than species mixing. Equations (2.2) are discretised with finite elements in FreeFEM
$++$
, and a steady axisymmetric solution
$\overline{\boldsymbol{q}}$
is obtained from Newton–Raphson iterations (Garnaud et al.
Reference Garnaud, Lesshafft, Schmid and Huerre2013). The numerical domain is 80 radii long in the streamwise direction and 30 radii in the transverse direction. Iterations are performed until all flow quantities are converged to within
$10^{-9}$
times their maximum values. At the inlet,
$z=0$
, boundary conditions
$$\begin{eqnarray}\displaystyle \overline{u}_{z}=\frac{1}{2}+\frac{1}{2}\tanh \left[\frac{5}{2}\left(\frac{1}{r}-r\right)\right],\quad \overline{u}_{r}=0\quad \text{and}\quad \overline{\unicode[STIX]{x1D70C}}=1-\left(1-\frac{1}{S}\right)\overline{u}_{z} & & \displaystyle\end{eqnarray}$$
are prescribed for the axial velocity
$\overline{u}_{z}$
, the radial velocity
$\overline{u}_{r}$
and the density
$\overline{\unicode[STIX]{x1D70C}}$
. The initial shear layer momentum thickness is 10 % of the nozzle radius. All other boundary conditions are specified as
$$\begin{eqnarray}\displaystyle \displaystyle \frac{1}{Re}\frac{\unicode[STIX]{x2202}\overline{\boldsymbol{u}}}{\unicode[STIX]{x2202}r}-\overline{p}\boldsymbol{e}_{r}=0,\quad \overline{\unicode[STIX]{x1D70C}}=1\quad \text{at}~r=r_{max}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{1}{Re}\frac{\unicode[STIX]{x2202}\overline{\boldsymbol{u}}}{\unicode[STIX]{x2202}z}-\overline{p}\boldsymbol{e}_{z}=0,\quad \frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}z}=0\quad \text{at}~z=z_{max}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x2202}\overline{u}_{z}}{\unicode[STIX]{x2202}r}=\overline{u}_{r}=\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}r}=\frac{\unicode[STIX]{x2202}\overline{p}}{\unicode[STIX]{x2202}r}=0\quad \text{at}~r=0. & & \displaystyle\end{eqnarray}$$
These boundary conditions are obtained from the kinematic constraints on the axis (Khorrami, Malik & Ash Reference Khorrami, Malik and Ash1989), and by imposing zero normal stresses at
$r_{max}$
and
$z_{max}$
, together with Dirichlet and Neumann conditions for the density.
As the objective is to characterise the role of buoyancy in the instability dynamics, the main parameters to be varied are the Richardson number and the density ratio. The ranges of parameters
$10^{-4}\leqslant Ri\leqslant 10^{3}$
and
$1.05\leqslant S\leqslant 7$
will be investigated. The effect of the Reynolds number above a value of 100 is found to be weak, and a standard value of
$Re=200$
(in some cases
$Re=500$
) will be used, while
$Pr=0.7$
is maintained throughout.
Figure 1. Axisymmetric steady base flows obtained for
$Ri=10^{-4}$
(a,b) and for
$Ri=10^{3}$
(c,d). Axial velocity (a,c) and density (b,d) are shown in the (
$r,z$
) plane.
Figure 2. Variations of the centreline velocity along
$z$
. (a)
$Ri=10^{-4}$
; (b)
$Ri=10^{3}$
.
For a strong density ratio
$S=7$
, and the two extreme values
$Ri=10^{-4}$
and
$Ri=10^{3}$
, steady base flow profiles of axial velocity and density are shown in figure 1. The flow at low
$Ri$
is dominated by the momentum of the injected fluid, which diffuses radially with axial distance under the effect of viscosity. This is clearly the case of a jet, in a configuration where buoyancy has no noticeable impact on the base flow dynamics, despite the strong density variations. The flow at high
$Ri$
, in contrast, is principally driven by the buoyancy force, as the injected momentum is negligibly weak in comparison. The fluid in this case is not pushed out of the orifice, but rather pulled out by buoyancy, forming a slender rising column around the axis (note the different radial scales in figure 1). This flow is characteristic of a plume, and it is often called a ‘lazy’ plume, as the momentum at its base is much lower than that of a self-similar profile, where momentum and buoyancy are in balance.
Between the two extremes shown in figure 1, the aspect of the base flow at different Richardson numbers changes gradually. Cases with
$Ri<1$
will be denoted ‘buoyant jets’ in the following, as opposed to ‘plumes’ with
$Ri>1$
. Vertical variations of the centreline velocity are shown in figure 2 for the same two configurations as in figure 1. The jet, at
$Ri=10^{-4}$
, exhibits a short potential core region, where the centreline velocity is constant, followed by hyperbolic decay. The plume flow, at
$Ri=10^{3}$
, accelerates progressively with vertical distance from the inlet, and the centreline velocity approaches asymptotically a limit value in the self-similar regime (Yih Reference Yih1988). Buoyant jets at low but finite Richardson number behave as plumes at large distances from the nozzle, when their excess momentum is sufficiently diffused. While a jet entrains ambient fluid only through momentum diffusion, entrainment into a plume tends to be much stronger due to its continuous production of axial momentum. The plume base flow presented in figure 1(c,d) is particularly marked by radial entrainment close to
$z=0$
.
2.3 Linear stability problem
Infinitesimal perturbations of a steady base flow are sought with a global ansatz
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D70C}^{\prime },\boldsymbol{u}^{\prime },p^{\prime },T^{\prime }]^{\text{T}}=[\hat{\unicode[STIX]{x1D70C}}(r,z),\hat{\boldsymbol{u}}(r,z),\hat{p}(r,z),\hat{T}(r,z)]^{\text{T}}\text{e}^{\text{i}(m\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}t)}+\text{c.c.} & & \displaystyle\end{eqnarray}$$
The integer
$m$
denotes the azimuthal wavenumber and
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D714}_{i}$
is a complex frequency. Upon linearising the governing equations (2.2), and substitution of (2.10), the linear perturbation equations are found as
$$\begin{eqnarray}\displaystyle -\text{i}\unicode[STIX]{x1D714}\hat{\unicode[STIX]{x1D70C}}+\text{div}_{m}(\hat{\unicode[STIX]{x1D70C}}\,\overline{\boldsymbol{u}}+\overline{\unicode[STIX]{x1D70C}}\,\hat{\boldsymbol{u}})=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\text{i}\unicode[STIX]{x1D714}\overline{\unicode[STIX]{x1D70C}}\hat{\boldsymbol{u}}+\overline{\unicode[STIX]{x1D70C}}[(\text{grad}_{m}\overline{\boldsymbol{u}})\boldsymbol{\cdot }\hat{\boldsymbol{u}}+(\text{grad}_{m}\hat{\boldsymbol{u}})\boldsymbol{\cdot }\overline{\boldsymbol{u}}]+\hat{\unicode[STIX]{x1D70C}}(\text{grad}_{m}\overline{\boldsymbol{u}})\boldsymbol{\cdot }\overline{\boldsymbol{u}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{grad}_{m}\hat{p}-\frac{Ri}{S-1}\hat{\unicode[STIX]{x1D70C}}\boldsymbol{e}_{z}+\frac{1}{ReS}\left[\unicode[STIX]{x1D6E5}_{m}\hat{\boldsymbol{u}}+\frac{1}{3}\text{grad}_{m}(\text{div}_{m}\hat{\boldsymbol{u}})\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}\unicode[STIX]{x1D714}\overline{\unicode[STIX]{x1D70C}}\hat{T}+\overline{\unicode[STIX]{x1D70C}}[(\text{grad}_{m}\overline{T})\boldsymbol{\cdot }\hat{\boldsymbol{u}}+(\text{grad}_{m}\hat{T})\boldsymbol{\cdot }\overline{\boldsymbol{u}}]+\hat{\unicode[STIX]{x1D70C}}(\text{grad}_{m}\overline{T})\boldsymbol{\cdot }\overline{\boldsymbol{u}}=\frac{1}{PrReS}\unicode[STIX]{x1D6E5}_{m}\hat{T}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\unicode[STIX]{x1D70C}}+\overline{\unicode[STIX]{x1D70C}}^{2}\hat{T}(S-1)=0. & \displaystyle\end{eqnarray}$$
$m$
in order to indicate that azimuthal derivatives are replaced with a factor
$\text{i}m$
; these operators are documented in appendix A. While the base flow is taken to be swirl free,
$\overline{u}_{\unicode[STIX]{x1D703}}=0$
, the azimuthal perturbation velocity
$u_{\unicode[STIX]{x1D703}}^{\prime }$
may in general be non-zero. Homogeneous Dirichlet conditions are imposed on
$\hat{\boldsymbol{u}}$
and
$\hat{\unicode[STIX]{x1D70C}}$
at the inlet,
$z=0$
, and a homogeneous Neumann condition is prescribed for
$\hat{p}$
. On the axis, depending on the azimuthal mode considered, appropriate boundary conditions as detailed in Khorrami et al. (Reference Khorrami, Malik and Ash1989) and Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015) are enforced. On the outer boundaries at
$r_{max}$
and
$z_{max}$
, no-stress conditions consistent with (2.9) are used.
The system (2.11) is cast into the form of an eigenvalue problem
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}B\hat{\boldsymbol{q}}=L\hat{\boldsymbol{q}}. & & \displaystyle\end{eqnarray}$$
According to the ansatz (2.10), the real part of the eigenvalue,
$\unicode[STIX]{x1D714}_{r}$
, represents the oscillation frequency while the imaginary part,
$\unicode[STIX]{x1D714}_{i}$
, is the growth rate of the perturbation. As before, the variable
$\hat{T}$
is eliminated through the equation of state (2.11d
). So-called global eigenmodes are computed by resolving
$\hat{\unicode[STIX]{x1D70C}}$
,
$\hat{\boldsymbol{u}}$
and
$\hat{p}$
in both
$r$
and
$z$
, such that spatial variations of the base flow and the perturbation quantities are accounted for without further limiting assumptions (Theofilis Reference Theofilis2003). The eigenvalue problem (2.12) is then solved with an iterative shift-invert Arnoldi algorithm, in the same way as in Garnaud et al. (Reference Garnaud, Lesshafft, Schmid and Huerre2013), with an accuracy close to machine precision.
In addition, a local analysis is performed in § 5, in order to identify the absolute mode in a parallel base flow (Huerre & Monkewitz Reference Huerre and Monkewitz1990). Perturbations (2.10) are then Fourier-transformed in
$z$
, leading to the standard ansatz
$$\begin{eqnarray}\displaystyle [\hat{\unicode[STIX]{x1D70C}}(r,z),\hat{\boldsymbol{u}}(r,z),\hat{p}(r,z),\hat{T}(r,z)]^{\text{T}}=[\check{\unicode[STIX]{x1D70C}}(r),\check{\boldsymbol{u}}(r),\check{p}(r),{\check{T}}(r)]^{\text{T}}\text{e}^{\text{i}kz}. & & \displaystyle\end{eqnarray}$$
3 Global spectra and eigenfunctions
Instability results obtained from the global formulation (2.10) are presented first for axisymmetric modes,
$m=0$
, since experimental and numerical evidence suggests their leading role in the self-sustained dynamics of plumes, as discussed in § 1. A brief discussion of helical perturbations,
$m=1$
, follows in § 3.2.
3.1 Axisymmetric perturbations
Eigenvalues
$\unicode[STIX]{x1D714}$
obtained for two configurations,
$Ri=10^{-4}$
and
$10^{3}$
, with otherwise identical parameters
$S=7$
and
$Re=200$
, are presented in figure 3 as black symbols. These are the two extreme jet and plume cases discussed in § 2.2.
Figure 3. Global spectra of axisymmetric perturbations (
$m=0$
), for the two configurations shown in figure 1. (a)
$Ri=10^{-4}$
, jet case; (b)
$Ri=10^{3}$
, plume case.
$Re=200$
and
$S=7$
are set identically for both cases. True eigenvalues (○) are compared to their counterparts (+) that are obtained when the buoyancy term in (2.11b
) is removed.
The jet, at
$Ri=10^{-4}$
(figure 3
a), exhibits one unstable mode with
$\unicode[STIX]{x1D714}=0.558+0.025\text{i}$
. When buoyancy effects are eliminated, by setting
$Ri=0$
in the perturbation equations but still using the same base flow, eigenvalues shown as red crosses are obtained; visibly, the buoyancy term in the perturbation equations has no significant impact on the instability dynamics. This observation, as well as the overall appearance of the spectrum, is fully consistent with the non-buoyant and slightly buoyant results of Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017), and many more details on the unstable eigenmode of pure jets are provided in their study.
The plume, at
$Ri=10^{3}$
(figure 3
b), possesses five unstable modes, one being strongly dominant with
$\unicode[STIX]{x1D714}=29.4+11.3\text{i}$
. When the perturbation Richardson number is set to zero in this configuration, all unstable modes vanish from the spectrum. It can be concluded that buoyancy plays a determining role for the instability of this plume, not only by setting up the base flow, but also by the coupling of density and velocity perturbations. It is also noted that the high-
$Ri$
plume base flow is not subject to the non-buoyant instability that affects the low-
$Ri$
jet.
Unstable eigenvalues of the plume take on significantly higher values, both in their real and in their imaginary parts, than those of the jet. This is clearly a result of the scaling with the inflow centreline velocity, which appropriately characterises a jet, but is less pertinent for ‘lazy’ plumes. A common scaling is employed here for the sake of consistency across the full range of Richardson number values; if only high-
$Ri$
plumes were considered, a buoyancy-based velocity scaling would be more suitable.
The distinct nature of the instability modes of the jet and the plume flows is also apparent in the shape of their eigenfunctions. Figure 4 shows the spatial distribution of the axial velocity amplitude in the dominant modes for the two respective cases. At low Richardson number, the maximum perturbation amplitude is found on the centreline, 12 radii downstream of the nozzle. Perturbations are confined inside the jet column, as documented in more detail by Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017). In the high-
$Ri$
plume, the spatial eigenmode structure is very different: the maximum amplitude is located inside the mixing layer very close to the inflow, in the region where the density gradient in the base flow is maximal.
Figure 4. Spatial distributions of axial velocity eigenfunctions
$\hat{u} _{z}$
, corresponding to the most unstable modes of the two respective cases shown in figure 3. (a) Jet at
$Ri=10^{-4}$
,
$S=7$
and
$Re=200$
; (b) plume at
$Ri=10^{3}$
,
$S=7$
and
$Re=200$
.
In the reference experiments by Cetegen & Kasper (Reference Cetegen and Kasper1996) and Bharadwaj & Das (Reference Bharadwaj and Das2017), a slightly different definition is chosen for the Richardson number, which corresponds to
$2Ri/S$
in our nomenclature. Variations of the dominant eigenvalue in the present analysis are therefore presented as functions of
$Ri/S$
in figure 5 in order to facilitate a comparison. The baseline case, with
$Re=200$
,
$S=7$
and inflow conditions (2.8), is represented by solid circles. Eigenvalues of this configuration display continuous variations both in the Strouhal number
$St=\unicode[STIX]{x1D714}_{r}/(2\unicode[STIX]{x03C0})$
and in the growth rate
$\unicode[STIX]{x1D714}_{i}$
. Strouhal number values are asymptotically constant in the low-
$Ri/S$
regime, whereas they follow a power law at values
$Ri/S>0.1$
. A regression fit yields the dependence
$St=0.55(Ri/S)^{0.43}$
, which is in good agreement with experimental results in the range
$1\leqslant Ri/S\leqslant 250$
: after conversion to the present definition of the Richardson number, the power law determined by Cetegen & Kasper (Reference Cetegen and Kasper1996) in this regime is given by
$St=0.52(Ri/S)^{0.38}$
(shown as a line in figure 5
a), and the corresponding measurements of Bharadwaj & Das (Reference Bharadwaj and Das2017) for plumes from an orifice convert to
$St=0.51(Ri/S)^{0.39}$
. A different scaling, measured as
$St\propto (Ri/S)^{0.28}$
for
$Ri/S>250$
by Cetegen & Kasper (Reference Cetegen and Kasper1996), is outside the parameter range considered here. The growth rate in the baseline configuration, shown in figure 5(b), increases monotonically with
$Ri/S$
, and it is positive throughout.
Eigenvalues from three other flow configurations are included in figure 5 in order to assess the sensitivity of the instability with respect to the Reynolds number, to the density ratio and to the inlet velocity profile. With the standard profile (2.8), parameter combinations
$Re=500$
,
$S=7$
(open circles) and
$Re=200$
,
$S=4.5$
(squares) are chosen. The Strouhal number values in figure 5(a) are barely affected by these changes, and the growth rates in figure 5(b) follow a similar trend as in the baseline case. The less heated configuration (squares) is stable at
$Ri<0.1$
, consistent with the analysis by Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017).
Triangle symbols indicate results for a special case where
$Re=200$
and
$S=7$
are maintained, but the velocity inlet profile is changed to a parabolic pipe flow, while the density profile is still given by (2.8). This flow case is introduced in order to better approach the experimental conditions of Subbarao & Cantwell (Reference Subbarao and Cantwell1992) and Cetegen & Kasper (Reference Cetegen and Kasper1996), where the fluid exits from a nozzle as a developed laminar pipe flow. This change in the velocity profile has barely any effect on the Strouhal number across all
$Ri/S$
values, but it does inhibit the global instability in the low-
$Ri/S$
regime. The latter is consistent with the absence of self-excited behaviour at low
$Ri$
in the experiments of Subbarao & Cantwell (Reference Subbarao and Cantwell1992) and Cetegen & Kasper (Reference Cetegen and Kasper1996), and in the simulations of Satti & Agrawal (Reference Satti and Agrawal2006).
Figure 5. (a) Strouhal number and (b) growth rate of the global eigenvalue
$\unicode[STIX]{x1D714}$
, as a function of
$Ri/S$
. Legend: (●)
$Re=200$
,
$S=7$
; (○)
$Re=500$
,
$S=7$
; (▫)
$Re=200$
,
$S=4.5$
; (▵)
$Re=200$
,
$S=7$
, with parabolic inlet velocity profile. All other configurations take the inlet velocity profile (2.8). (——) Power law from the Cetegen & Kasper (Reference Cetegen and Kasper1996) experiments, rescaled to match the present definition of
$Ri$
.
As the effect of heating enters the problem both through the density ratio
$S$
and through the Richardson number
$Ri$
, the onset of instability is examined for independent variations of these two parameters. The main results of the local (see § 5) and global instability analyses are summarised in the state diagram in the (
$Ri,S$
) plane shown in figure 6. The thin line delineates the neutral boundary separating locally convectively unstable inlet base flows (in white below the curve) from locally absolutely unstable ones (in blue and red above the curve). The thick neutral line separates the globally stable states (in white and blue below the curve) from the globally unstable states (in red above the curve). In the white area, convective instability prevails, and in the blue and red areas, absolute instability prevails. Along a diagonal line in the state diagram, the flow changes from convectively unstable to absolutely unstable to globally unstable, once the absolutely unstable region is large enough. For buoyant jets (low
$Ri$
) and plumes (large
$Ri$
) the same sequence takes place as
$S$
increases at a given
$Ri$
. Note that the globally unstable domain is reached much ‘sooner’ for plumes than for buoyant jets. The dip in the global stability neutral curve for
$Ri$
of order unity signals a gradual shift from a shear-dominated instability to a buoyancy-dominated instability, as further discussed in § 4.
Figure 6. Instability regimes in the
$S$
–
$Ri$
plane for the axisymmetric mode at
$Re=200$
. The thick line denotes the global stability boundary, and the thin line denotes the boundary between local convective and absolute instability of the inlet profile.
3.2 Helical perturbations
The local analysis of plumes in the Boussinesq limit
$S\rightarrow 1$
by Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015) concluded that absolute instability only occurs for helical perturbations,
$m=1$
, whereas axisymmetric perturbations in that setting were found to be only convectively unstable. Although the global instability of axisymmetric eigenmodes in non-Boussinesq situations, as documented above, appears to be fully consistent with experimental and numerical observations of self-excited behaviour, the possibility of helical global instabilities remains to be explored.
Figure 7. Global spectrum of helical perturbations (
$m=1$
), for the configuration
$S=7$
,
$Ri=1$
and
$Re=200$
. Results from two calculations are shown: (○) without absorbing layer; (●) with absorbing layer at
$z>30$
.
Eigenvalues pertaining to helical instability modes are displayed in figure 7 for two different calculations, both for the same physical parameter setting
$S=7$
,
$Ri=1$
and
$Re=200$
. One case, represented by blue unfilled circles, was computed with the same boundary conditions as all previous results. A branch of regularly spaced modes is seen to be unstable over the interval
$0.8\leqslant \unicode[STIX]{x1D714}_{r}\leqslant 4$
. The features of this branch are very similar to several jet cases discussed by Coenen et al. (Reference Coenen, Lesshafft, Garnaud and Sevilla2017), as well as observations made in many different flow cases, especially in the boundary layer calculations by Åkervik et al. (Reference Åkervik, Ehrenstein, Gallaire and Henningson2008). In a recent study (Lesshafft Reference Lesshafft2017), the occurrence of such ‘arc branches’ is ascribed to the presence of spurious pressure feedback from the downstream end of a truncated flow domain, and it is predicted that artificial damping near the outflow should be effective in reducing the growth rate of such unphysical modes.
Indeed, if artificial damping is applied in an ‘absorbing layer’ (Colonius Reference Colonius2004) at
$z>30$
, the growth rates of the arc branch modes decrease, and all modes recede to the stable half-plane if the damping is sufficiently strong. Such a case is represented by red filled circles in figure 7, where a damping term
$-\unicode[STIX]{x1D706}(z)\hat{\boldsymbol{q}}$
has been added to the right-hand side of (2.12). The damping coefficient
$\unicode[STIX]{x1D706}(z)$
ramps up from zero to 16, over the interval
$30<z<50$
, according to equation (2.4) of Chomaz (Reference Chomaz2003). No unstable helical modes are found with this boundary treatment. In contrast, the same artificial damping has no discernible effect on the unstable eigenvalues for axisymmetric perturbations shown in figure 3. This behaviour is in full agreement with the arguments of Lesshafft (Reference Lesshafft2017), as
$m=0$
perturbations are locally stable in the downstream flow region, whereas
$m=1$
perturbations remain convectively unstable, as will be shown in § 5.
4 Influence of buoyant, baroclinic and shear-related mechanisms
The results discussed in § 3.1 suggest that different mechanisms drive the global instability dynamics in the low- and the high-
$Ri$
regimes. These mechanisms are investigated in the present section, on the basis of the formalism proposed by Marquet & Lesshafft (Reference Marquet and Lesshafft2015). This formalism is introduced here in a slightly different and weaker manner, which is sufficient for the present purpose.
A sensitivity analysis is to be performed, in order to quantify the influence of the various forces in the momentum equation onto the unstable growth of velocity perturbations. The latter are governed by the equation
$$\begin{eqnarray}\displaystyle -\text{i}\unicode[STIX]{x1D714}\hat{\boldsymbol{u}}={\mathcal{C}}+{\mathcal{S}}+{\mathcal{P}}+{\mathcal{B}}+{\mathcal{V}}, & & \displaystyle\end{eqnarray}$$
with the right-hand-side terms
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{C}}=-(\text{grad}\,\hat{\boldsymbol{u}})\boldsymbol{\cdot }\overline{\boldsymbol{u}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{S}}=-(\text{grad}\,\overline{\boldsymbol{u}})\boldsymbol{\cdot }\hat{\boldsymbol{u}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{P}}=-\frac{\text{grad}\,\hat{p}}{\overline{\unicode[STIX]{x1D70C}}}+\frac{\hat{\unicode[STIX]{x1D70C}}\,\text{grad}\,\overline{p}}{\overline{\unicode[STIX]{x1D70C}}^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}=-\frac{Ri}{S-1}\frac{\hat{\unicode[STIX]{x1D70C}}}{\overline{\unicode[STIX]{x1D70C}}^{2}}\boldsymbol{e}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{V}}=\frac{1}{ReS}\left[\frac{1}{\overline{\unicode[STIX]{x1D70C}}}\left(\unicode[STIX]{x0394}\hat{\boldsymbol{u}}+\frac{\text{grad}(\text{div}\,\hat{\boldsymbol{u}})}{3}\right)-\frac{\hat{\unicode[STIX]{x1D70C}}}{\overline{\unicode[STIX]{x1D70C}}^{2}}\left(\unicode[STIX]{x0394}\overline{\boldsymbol{u}}+\frac{\text{grad}(\text{div}\,\overline{\boldsymbol{u}})}{3}\right)\right]. & \displaystyle\end{eqnarray}$$
${\mathcal{C}}$
, base flow shear
${\mathcal{S}}$
, pressure force
${\mathcal{P}}$
, buoyancy
${\mathcal{B}}$
, and viscous diffusion
${\mathcal{V}}$
. As only axisymmetric
$m=0$
perturbations are considered in this chapter, it is not necessary to append a subscript
$m$
to the differential operators.
For a better physical discussion, the pressure force can be split into a divergence-free (baroclinic) and a curl-free (barotropic) component; the former is linked to the baroclinic torque in the vorticity equation, after application of the curl operator to (4.1), whereas the latter does not affect the evolution of perturbation vorticity.
A Helmholtz decomposition is performed on the pressure force
${\mathcal{P}}$
, such that
$$\begin{eqnarray}\displaystyle {\mathcal{P}}=\text{curl}\,{\mathcal{A}}-\text{grad}\,\unicode[STIX]{x1D719}, & & \displaystyle\end{eqnarray}$$
where
${\mathcal{A}}$
and
$\unicode[STIX]{x1D719}$
are found from
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{A}}=\frac{1}{4\unicode[STIX]{x03C0}}(\text{curl}\,{\mathcal{P}})\otimes (1/\boldsymbol{r}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}=\frac{1}{4\unicode[STIX]{x03C0}}(\text{div}\,{\mathcal{P}})\otimes (1/\boldsymbol{r}). & \displaystyle\end{eqnarray}$$
$\otimes$
denotes a convolution over the entire volume
$V$
of the numerical domain, and
$\boldsymbol{r}$
represents any position in
$V$
. This decomposition is performed numerically, such that
${\mathcal{P}}={\mathcal{P}}_{1}+{\mathcal{P}}_{2}$
is explicitly obtained, with a baroclinic component
${\mathcal{P}}_{1}$
and a barotropic component
${\mathcal{P}}_{2}$
.
Further analysis is restricted to the action of shear, baroclinic and buoyant forces, because all other contributions are found to be strictly stabilising at all Richardson numbers. The dependence of an eigenvalue
$\unicode[STIX]{x1D714}$
on these three components is obtained by introducing small variations into (4.1),
$$\begin{eqnarray}\displaystyle -\text{i}\unicode[STIX]{x1D714}\hat{\boldsymbol{u}}={\mathcal{C}}+(1+\unicode[STIX]{x1D700}_{S}){\mathcal{S}}+(1+\unicode[STIX]{x1D700}_{P}){\mathcal{P}}_{1}+{\mathcal{P}}_{2}+(1+\unicode[STIX]{x1D700}_{B}){\mathcal{B}}+{\mathcal{V}}, & & \displaystyle\end{eqnarray}$$
from where sensitivities can be defined as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{S}\unicode[STIX]{x1D714}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{S}}=\frac{\langle \hat{\boldsymbol{q}}^{\dagger },{\mathcal{S}}\rangle }{\langle \hat{\boldsymbol{q}}^{\dagger },B\hat{\boldsymbol{q}}\rangle },\quad \unicode[STIX]{x2202}_{P}\unicode[STIX]{x1D714}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{P}}=\frac{\langle \hat{\boldsymbol{q}}^{\dagger },{\mathcal{P}}_{1}\rangle }{\langle \hat{\boldsymbol{q}}^{\dagger },B\hat{\boldsymbol{q}}\rangle },\quad \unicode[STIX]{x2202}_{B}\unicode[STIX]{x1D714}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{B}}=\frac{\langle \hat{\boldsymbol{q}}^{\dagger },{\mathcal{B}}\rangle }{\langle \hat{\boldsymbol{q}}^{\dagger },B\hat{\boldsymbol{q}}\rangle }. & & \displaystyle\end{eqnarray}$$
Note that the terms
${\mathcal{S}}$
,
${\mathcal{P}}_{1}$
and
${\mathcal{B}}$
contain components of the eigenvector
$\hat{\boldsymbol{q}}$
, and that
$\hat{\boldsymbol{q}}^{\dagger }$
is the associated adjoint eigenvector, defined with respect to the scalar product
$\langle \cdot ,\cdot \rangle$
. A standard non-weighted discrete scalar product has been chosen in the present calculations, but the scalar quantities
$\unicode[STIX]{x2202}\unicode[STIX]{x1D714}$
in (4.6) are independent of this choice, as demonstrated by Marquet & Lesshafft (Reference Marquet and Lesshafft2015).
The sensitivities (4.6) are interpreted in the following way. An infinitesimally small positive value
$\unicode[STIX]{x1D700}_{S}$
proportionally increases the strength of the shear-related force term, resulting in an eigenvalue variation
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}=\unicode[STIX]{x1D700}_{S}\unicode[STIX]{x2202}_{S}\unicode[STIX]{x1D714}$
. If the imaginary part of
$\unicode[STIX]{x2202}_{S}\unicode[STIX]{x1D714}$
is positive, then
${\mathcal{S}}$
has a destabilising effect; if it is negative, then
${\mathcal{S}}$
acts in a stabilising way. The same reasoning applies to
$\unicode[STIX]{x2202}_{P}\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x2202}_{B}\unicode[STIX]{x1D714}$
. The three sensitivities are commensurate, so that a larger absolute value of one compared to another indicates a stronger stabilising or destabilising effect.
Figure 8. Sensitivity of the growth rate with respect to (▴) shear, (●) baroclinic and (▪) buoyancy terms, as functions of the Richardson number, with parameters
$S=7$
and
$Re=200$
.
Results from this analysis are presented in figure 8 over the full range of
$Ri$
values, for the standard setting
$S=7$
and
$Re=200$
. Imaginary values of
$\unicode[STIX]{x2202}_{S}\unicode[STIX]{x1D714}$
,
$\unicode[STIX]{x2202}_{P}\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x2202}_{B}\unicode[STIX]{x1D714}$
are shown in two separate diagrams for low and high Richardson numbers, for better readability. In the jet regime
$Ri<1$
, the strongest destabilising force is due to the base flow shear. At very low
$Ri$
, the effect of buoyancy vanishes, while the baroclinic force provides a small additional destabilisation. The local analysis of Lesshafft & Huerre (Reference Lesshafft and Huerre2007) demonstrated that the baroclinic torque is the determining ingredient that renders a non-buoyant heated jet absolutely unstable, through co-operation with the basic shear instability. The present global results are consistent with that conclusion. In the plume regime
$Ri>1$
, the buoyancy force becomes strongly destabilising, dominating all other contributions for
$Ri>5$
. Shear and baroclinic effects are negligible in comparison at very high
$Ri$
; the baroclinic force even becomes stabilising above
$Ri=100$
.
It is concluded that the observed global instability in the jet and plume regimes indeed involve distinct physical mechanisms. In buoyant jets at low Richardson number, the dynamics are driven by a shear instability, which is strengthened by a baroclinic force. In high-
$Ri$
plumes, the instability arises principally from buoyancy effects. These conclusions are fully consistent with the results of Bharadwaj & Das (Reference Bharadwaj and Das2017), who observed that the leading eigenmode could be stabilised through artificial compensation of the baroclinic torque at low
$Ri$
, and through suppression of the buoyancy force at high
$Ri$
.
5 Local analysis
The results so far have shown a dominance of axisymmetric global instabilities, which is in stark contrast to our earlier local analysis in the
$S\rightarrow 1$
Boussinesq limit (Chakravarthy et al.
Reference Chakravarthy, Lesshafft and Huerre2015), where absolute instability was found only for helical perturbations. The absolute/convective nature of local instability in non-Boussinesq settings is now investigated.
Figure 9. Variation of the absolute frequency
$\unicode[STIX]{x1D714}_{0}$
with streamwise location
$z$
for the axisymmetric mode
$m=0$
and
$Ri=10^{-4}$
(a,c) and
$Ri=10^{2}$
(b,d) at
$S=7$
,
$Re=200$
.
The same algorithm as in Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015) is used for tracking saddle points of the local dispersion relation in the complex
$k$
plane. Again, the group-velocity root-finding procedure of Lesshafft & Marquet (Reference Lesshafft and Marquet2010) has been found to be more efficient and robust than the classical Briggs or the cusp map methods (see Schmid & Henningson Reference Schmid and Henningson2001).
5.1 Axisymmetric perturbations,
$m=0$
For the standard setting
$S=7$
and
$Re=200$
, and for Richardson numbers of
$10^{-4}$
and
$10^{2}$
, variations of the absolute frequency
$\unicode[STIX]{x1D714}_{0}$
along the streamwise
$z$
direction are shown in figure 9. In the more extreme case
$Ri=10^{3}$
, numerical difficulties led to unreliable results. In both configurations, the flow is found to be absolutely unstable (
$\unicode[STIX]{x1D714}_{0,i}>0$
) over a streamwise interval of 6 or 7 radii downstream of the inlet. In the weakly non-parallel case of
$Ri=10^{-4}$
, the real part
$\unicode[STIX]{x1D714}_{0,r}$
shows moderate variations around a value of 0.5, in reasonable agreement with the global frequency
$\unicode[STIX]{x1D714}_{r}=0.56$
as given in figure 5(a). In the strongly non-parallel setting
$Ri=10^{2}$
,
$\unicode[STIX]{x1D714}_{0,r}$
displays a variation between 1.3 and 80 over the absolutely unstable interval. This is not inconsistent with the global frequency
$\unicode[STIX]{x1D714}_{r}=10.99$
, but it does not provide a means of predicting
$\unicode[STIX]{x1D714}_{r}$
at leading order.
Nonetheless, the link between local absolute and global instability of axisymmetric perturbations is very plausibly confirmed by these results, both in the low- and in the high-Richardson-number regime. The neutral curve for the onset of absolute instability in the (
$Ri,S$
) plane is reported in figure 6 for axisymmetric perturbations at
$z=0$
. It is found that the transition from convective to absolute local instability at the inlet, with increasing
$Ri$
and
$S$
, occurs before global instability sets in. This is consistent with the common observation, both in model problems (Chomaz, Huerre & Redekopp Reference Chomaz, Huerre and Redekopp1991) and in slowly varying flow (e.g. Lesshafft, Huerre & Sagaut Reference Lesshafft, Huerre and Sagaut2007), that absolute instability must prevail over a sufficiently long streamwise region with sufficient growth rate in order to prompt a global instability.
5.2 Helical perturbations,
$m=1$
The saddle point in the complex
$k$
plane that is associated with helical absolute instability in the study of Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015) is also recovered in the analysis of the present inflow profiles. The absolute growth rate
$\unicode[STIX]{x1D714}_{0,i}$
for
$m=1$
perturbations at
$z=0$
is displayed in figure 10(a) as a function of
$S$
, for parameters
$Ri=1$
and
$Re=200$
. A unity Richardson number is chosen here for comparison with the analysis in § 3 of Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015), but higher values of
$Ri$
lead to the same conclusions. The density ratio
$S$
characterises the departure from the Boussinesq limit, and it is seen to have a very weak effect on the growth rate
$\unicode[STIX]{x1D714}_{0,i}$
of the absolute helical mode.
The spatial variation of
$\unicode[STIX]{x1D714}_{0,i}$
, over a short interval of
$z$
adjacent to the inlet, is shown in figure 10(b) for the highly non-Boussinesq setting
$S=7$
; values beyond this streamwise region could not be obtained with sufficient confidence, due to numerical difficulties. The absolute helical growth rate at
$S=7$
displays the same qualitative characteristics as the one described in Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015) for the Boussinesq limit: the growth rate declines quickly downstream of the inlet, perhaps asymptotically tending towards zero. It is not surprising that under these conditions the weak absolute instability of
$m=1$
perturbations does not lead to a global flow destabilisation, as was found in § 3.2.
Figure 10. Absolute growth rate
$\unicode[STIX]{x1D714}_{0,i}$
of helical perturbations, for
$Re=200$
and
$Ri=1$
: (a) at the inlet, as a function of the density ratio
$S$
; (b) as a function of
$z$
, for
$S=7$
.
6 Conclusions
The linear instability dynamics in spatially developing buoyant jets and plumes have been investigated for a wide range of values of the Richardson number and the fluid density ratio. In the limit of zero Mach number, all variable-density effects have been taken into account in the mathematical formulation, so that configurations outside the realm of validity of the Boussinesq approximation could be considered.
Axisymmetric global instability modes have been found and documented over the entire investigated range of parameters, whereas no helical global instability could be identified. Some doubts remain only in the regime of very high Richardson number,
$Ri>100$
, where spurious helical modes could not be entirely stabilised due to numerical limitations. The preponderance of axisymmetric instability is in agreement with experimental observations by Subbarao & Cantwell (Reference Subbarao and Cantwell1992), Cetegen & Kasper (Reference Cetegen and Kasper1996) and Bharadwaj & Das (Reference Bharadwaj and Das2017), who reported axisymmetric puffing in free plumes. The present global analysis furthermore reproduces the experimentally measured frequencies with satisfactory accuracy. In particular, the experimental power law
$\unicode[STIX]{x1D714}_{r}\propto (Ri/S)^{0.38}$
has been retrieved as
$\unicode[STIX]{x1D714}_{r}\propto (Ri/S)^{0.43}$
in the present calculations. It is noted that Bharadwaj & Das (Reference Bharadwaj and Das2017) found even closer agreement from their linear analysis, which was designed to specifically model helium plumes, as opposed to thermal plumes in the present study.
The physical mechanisms behind global instability have been characterised by means of a sensitivity analysis. As proposed by Marquet & Lesshafft (Reference Marquet and Lesshafft2015), the sensitivity of the perturbation growth rate with respect to individual terms in the linear equations has been evaluated, which provides a quantitative measure for the stabilising or destabilising role of mechanisms represented by these terms. The main conclusion is that instability in the low-
$Ri$
jet regime is caused primarily by a shear mechanism, aided by a baroclinic force that arises from density variations, whereas the instability in the high-
$Ri$
plume regime is brought about principally by way of the buoyancy force, with a small contribution from shear. Nothing in the results indicates an abrupt switching between two distinct instability modes; the most unstable mode appears instead to vary smoothly as a function of
$Ri$
, with a gradual shift from the dominance of one mechanism to a dominance of the other.
These global results contrast with the conclusions of Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015), on the basis of local analysis in the Boussinesq limit, that the instability dynamics of self-similar plumes are dominated by helical perturbations. In particular, that earlier study showed axisymmetric perturbations to be only convectively unstable, whereas helical perturbations exhibit absolute instability, as well as larger temporal growth at real wavenumbers than axisymmetric modes. The global analysis in the present study was performed on base flows that develop from an orifice with prescribed inlet profiles, and that only relax asymptotically in the streamwise direction towards a self-similar flow solution. Close to the orifice, these base flows are markedly different from self-similar conditions, and this is the flow region where unstable axisymmetric perturbations reside in high-
$Ri$
plumes, according to the present results (see figure 4
b). Global instability in low-
$Ri$
buoyant jets has been shown to depend on baroclinic effects, which are absent in the Boussinesq approximation. The Boussinesq framework used by Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015) is therefore inappropriate for an instability analysis in this regime.
It has finally been demonstrated, for selected configurations, that the global instability characteristics are consistent with the absolute or convective nature of local instability. All globally unstable settings in the (
$Ri,S$
) plane, with
$Re=200$
, feature an absolutely unstable flow region in the vicinity of the inflow. In the examined cases, the absolute growth rate of axisymmetric perturbations is significantly larger than that of helical perturbations, and it remains positive over a longer streamwise region. Although absolute instability also arises for helical perturbations, it appears to be too weak to set off a global instability.
It must be cautioned that the conclusions drawn from the present results may not be easily extendable to generic plume and jet flows. In particular, the instability characteristics seem to be rather sensitive to details of the inflow profiles: with similar but not identical inflow profiles, axisymmetric perturbations are absolutely unstable in the present settings, but convectively unstable in the configuration of Chakravarthy et al. (Reference Chakravarthy, Lesshafft and Huerre2015). Test calculations, documented in Chakravarthy (Reference Chakravarthy2015), indicate that the functional shape of the density profile has a marked influence on the local stability characteristics, even when the mixing layer thickness is matched. Subbarao & Cantwell (Reference Subbarao and Cantwell1992) point out, for instance, that helium release and diffusion flames create plumes with very distinct density variations, which therefore may present quite different instability dynamics. It can also not be ruled out that nonlinear effects alter the threshold of global instability (Couairon & Chomaz Reference Couairon and Chomaz1997). The influence of the Prandtl number has not been investigated in this study, but it has been shown by Lakkaraju & Alam (Reference Lakkaraju and Alam2007) that the instability behaviour of planar plumes undergoes qualitative changes as
$Pr$
is varied far from unity.
Acknowledgements
The authors are grateful to W. Coenen for his aid with the adjoint implementation in FreeFEM
$++$
, to O. Marquet for his contribution to the sensitivity analysis, and to Professor D. Das for precious comments on the comparison with experiments. This work has been funded by the DGA under grant no. LADX2331 and by the Agence Nationale de la Recherche under the ‘Cool Jazz’ project. R.V.K.C. was supported by a PhD fellowship from École Polytechnique.
Appendix A. Differential operator definitions for azimuthally decomposed field quantities
The operators for divergence, gradient, Laplacian and advection in cylindrical coordinates in equations (2.11) are written with a subscript
$m$
. This is meant to express that azimuthal derivatives of perturbations (2.10) are included in these operators in the form of terms in
$m$
, such that formally
$$\begin{eqnarray}\displaystyle & \displaystyle \text{grad}\,(\hat{\boldsymbol{u}}\,\text{e}^{\text{i}m\unicode[STIX]{x1D703}})=(\text{grad}_{m}\hat{\boldsymbol{u}})\,\text{e}^{\text{i}m\unicode[STIX]{x1D703}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{div}\,(\hat{\boldsymbol{u}}\,\text{e}^{\text{i}m\unicode[STIX]{x1D703}})=(\text{div}_{m}\hat{\boldsymbol{u}})\,\text{e}^{\text{i}m\unicode[STIX]{x1D703}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}(\hat{\boldsymbol{u}}\,\text{e}^{\text{i}m\unicode[STIX]{x1D703}})=(\unicode[STIX]{x1D6E5}_{m}\hat{\boldsymbol{u}})\,\text{e}^{\text{i}m\unicode[STIX]{x1D703}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{div}_{m}(\hat{\unicode[STIX]{x1D70C}}\overline{\boldsymbol{u}}+\overline{\unicode[STIX]{x1D70C}}\boldsymbol{u})=\frac{1}{r}\unicode[STIX]{x2202}_{r}(r\hat{\unicode[STIX]{x1D70C}}\overline{u}_{r}+r\overline{\unicode[STIX]{x1D70C}}\hat{u} _{r})+\frac{\text{i}m}{r}\overline{\unicode[STIX]{x1D70C}}\hat{u} _{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{z}(\hat{\unicode[STIX]{x1D70C}}\overline{u}_{z}+\overline{\unicode[STIX]{x1D70C}}\hat{u} _{z}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\text{grad}_{m}\overline{\boldsymbol{u}})\boldsymbol{\cdot }\hat{\boldsymbol{u}}=[\hat{u} _{r}\unicode[STIX]{x2202}_{r}\overline{u}_{r}+\hat{u} _{z}\unicode[STIX]{x2202}_{z}\overline{u}_{r}]\boldsymbol{e}_{r}+\frac{\hat{u} _{\unicode[STIX]{x1D703}}\overline{u}_{r}}{r}\boldsymbol{e}_{\unicode[STIX]{x1D703}}+[\hat{u} _{r}\unicode[STIX]{x2202}_{r}\overline{u}_{z}+\hat{u} _{z}\unicode[STIX]{x2202}_{z}\overline{u}_{z}]\boldsymbol{e}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\text{grad}_{m}\hat{\boldsymbol{u}})\boldsymbol{\cdot }\overline{\boldsymbol{u}} & = & \displaystyle [\overline{u}_{r}\unicode[STIX]{x2202}_{r}\hat{u} _{r}+\overline{u}_{z}\unicode[STIX]{x2202}_{z}\hat{u} _{r}]\boldsymbol{e}_{r}+[\overline{u}_{r}\unicode[STIX]{x2202}_{r}\hat{u} _{\unicode[STIX]{x1D703}}+\overline{u}_{z}\unicode[STIX]{x2202}_{z}\hat{u} _{\unicode[STIX]{x1D703}}]\boldsymbol{e}_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,[\overline{u}_{r}\unicode[STIX]{x2202}_{r}\hat{u} _{z}+\overline{u}_{z}\unicode[STIX]{x2202}_{z}\hat{u} _{z}]\boldsymbol{e}_{z},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\text{grad}_{m}\overline{T})\boldsymbol{\cdot }\hat{\boldsymbol{u}}=\hat{u} _{r}\unicode[STIX]{x2202}_{r}\overline{T}+\hat{u} _{z}\unicode[STIX]{x2202}_{z}\overline{T} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\text{grad}_{m}\hat{T})\boldsymbol{\cdot }\overline{\boldsymbol{u}}=\overline{u}_{r}\unicode[STIX]{x2202}_{r}\hat{T}+\overline{u}_{z}\unicode[STIX]{x2202}_{z}\hat{T}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{grad}_{m}\hat{p}=\unicode[STIX]{x2202}_{r}\hat{p}\,\boldsymbol{e}_{r}+\frac{\text{i}m}{r}\hat{p}\,\boldsymbol{e}_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{z}\hat{p}\,\boldsymbol{e}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{grad}_{m}(\text{div}_{m}\hat{\boldsymbol{u}}) & = & \displaystyle \left[\unicode[STIX]{x2202}_{r}\frac{\unicode[STIX]{x2202}_{r}(r\hat{u} _{r})}{r}-\frac{2\text{i}m}{r^{2}}\hat{u} _{\unicode[STIX]{x1D703}}+\frac{\text{i}m}{r}\unicode[STIX]{x2202}_{r}\hat{u} _{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{rz}\hat{u} _{z}\right]\boldsymbol{e}_{r}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{r}\left[\text{i}m\unicode[STIX]{x2202}_{r}\hat{u} _{r}+\frac{\text{i}m}{r}\hat{u} _{r}-\frac{m^{2}}{r}\hat{u} _{\unicode[STIX]{x1D703}}+\text{i}m\unicode[STIX]{x2202}_{z}\hat{u} _{z}\right]\boldsymbol{e}_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\unicode[STIX]{x2202}_{rz}\hat{u} _{r}+\frac{\unicode[STIX]{x2202}_{z}\hat{u} _{r}}{r}+\frac{\text{i}m}{r}\unicode[STIX]{x2202}_{z}\hat{u} _{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{zz}\hat{u} _{z}\right]\boldsymbol{e}_{z},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{m}\hat{\boldsymbol{u}} & = & \displaystyle \left[\unicode[STIX]{x2202}_{r}\frac{\unicode[STIX]{x2202}_{r}(r\hat{u} _{r})}{r}-\frac{m^{2}}{r^{2}}\hat{u} _{r}+\unicode[STIX]{x2202}_{zz}\hat{u} _{r}-\frac{2\text{i}m}{r^{2}}\hat{u} _{\unicode[STIX]{x1D703}}\right]\boldsymbol{e}_{r}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\unicode[STIX]{x2202}_{r}\frac{\unicode[STIX]{x2202}_{r}(r\hat{u} _{\unicode[STIX]{x1D703}})}{r}-\frac{m^{2}}{r^{2}}\hat{u} _{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{zz}\hat{u} _{\unicode[STIX]{x1D703}}+\frac{2\text{i}m}{r^{2}}\hat{u} _{r}\right]\boldsymbol{e}_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{\unicode[STIX]{x2202}_{r}(r\unicode[STIX]{x2202}_{r}\hat{u} _{z})}{r}-\frac{m^{2}}{r^{2}}\hat{u} _{z}+\unicode[STIX]{x2202}_{zz}\hat{u} _{z}\right]\boldsymbol{e}_{z},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}_{m}\hat{T}=\frac{\unicode[STIX]{x2202}_{r}(r\unicode[STIX]{x2202}_{r}\hat{T})}{r}-\frac{m^{2}}{r^{2}}\hat{T}+\unicode[STIX]{x2202}_{zz}\hat{T}. & \displaystyle\end{eqnarray}$$
