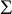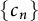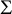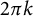1 Introduction and main results
Let
![]() $(\Sigma ,g)$
be a compact Riemannian surface with boundary. In this paper, we always assume that
$(\Sigma ,g)$
be a compact Riemannian surface with boundary. In this paper, we always assume that
![]() $\Sigma $
is connected and the boundary of
$\Sigma $
is connected and the boundary of
![]() $\Sigma $
is nonempty and smooth. Consider the Steklov problem defined in the following way
$\Sigma $
is nonempty and smooth. Consider the Steklov problem defined in the following way
 $$ \begin{align*} \begin{cases} \Delta u=0&\text{in } \Sigma,\\ \frac{\partial u}{\partial n}=\sigma u&\text{on } \partial \Sigma, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta u=0&\text{in } \Sigma,\\ \frac{\partial u}{\partial n}=\sigma u&\text{on } \partial \Sigma, \end{cases} \end{align*} $$
where
![]() $\Delta =-\operatorname {div}_g \circ \operatorname {grad}_g$
is the Laplace–Beltrami operator and
$\Delta =-\operatorname {div}_g \circ \operatorname {grad}_g$
is the Laplace–Beltrami operator and
![]() $\frac {\partial }{\partial n}$
is the outward unit normal vector field along the boundary. The collection of all numbers
$\frac {\partial }{\partial n}$
is the outward unit normal vector field along the boundary. The collection of all numbers
![]() $\sigma $
for which the Steklov problem admits a solution is called the Steklov spectrum of the surface
$\sigma $
for which the Steklov problem admits a solution is called the Steklov spectrum of the surface
![]() $\Sigma $
. The Steklov spectrum is a discrete set of real numbers called Steklov eigenvalues with finite multiplicities satisfying the following condition (see e.g., [Reference Girouard and PolterovichGP17])
$\Sigma $
. The Steklov spectrum is a discrete set of real numbers called Steklov eigenvalues with finite multiplicities satisfying the following condition (see e.g., [Reference Girouard and PolterovichGP17])
The Steklov spectrum enables us to define the following homothety-invariant functional on the set
![]() $\mathcal {R}(\Sigma )$
of Riemannian metrics on
$\mathcal {R}(\Sigma )$
of Riemannian metrics on
![]() $\Sigma $
$\Sigma $
where
![]() $L_g(\partial \Sigma )$
stands for the length of the boundary of
$L_g(\partial \Sigma )$
stands for the length of the boundary of
![]() $\Sigma $
in the metric g. The functional
$\Sigma $
in the metric g. The functional
![]() $\overline {\sigma }_k(\Sigma ,g)$
is called the k-th normalized Steklov eigenvalue. It was shown in [Reference Colbois, El Soufi and GirouardCSG11] (see also [Reference HassannezhadHas11, Reference KokarevKok14]) that if
$\overline {\sigma }_k(\Sigma ,g)$
is called the k-th normalized Steklov eigenvalue. It was shown in [Reference Colbois, El Soufi and GirouardCSG11] (see also [Reference HassannezhadHas11, Reference KokarevKok14]) that if
![]() $\Sigma $
is an orientable surface, then the functional
$\Sigma $
is an orientable surface, then the functional
![]() $\overline {\sigma }_k(\Sigma ,g)$
is bounded from above. Moreover, the following theorem holds
$\overline {\sigma }_k(\Sigma ,g)$
is bounded from above. Moreover, the following theorem holds
Theorem 1.1 [Reference Girouard and PolterovichGP]
Let
![]() $(\Sigma ,g)$
be a compact orientable surface of genus
$(\Sigma ,g)$
be a compact orientable surface of genus
![]() $\gamma $
with l boundary components. Then one has
$\gamma $
with l boundary components. Then one has
In this paper, we prove that a similar estimate holds for nonorientable surfaces.
Theorem 1.2 Let
![]() $\Sigma $
be a compact nonorientable surface of genus
$\Sigma $
be a compact nonorientable surface of genus
![]() $\gamma $
with l boundary components. Then one has
$\gamma $
with l boundary components. Then one has
Here, the genus of a nonorientable surface is defined as the genus of its orientable cover.
Remark 1.1 The estimate in Theorem 1.1 has been improved in [Reference KarpukhinKar17] by a bound which is linear in
![]() $k+\gamma +l$
instead of
$k+\gamma +l$
instead of
![]() $k(\gamma +l)$
. However, the proof of this result uses orientability in an essential way, see [Reference KarpukhinKar17, Section 6]. It would be interesting to obtain a similar improvement in Theorem 1.2.
$k(\gamma +l)$
. However, the proof of this result uses orientability in an essential way, see [Reference KarpukhinKar17, Section 6]. It would be interesting to obtain a similar improvement in Theorem 1.2.
Theorems 1.1 and 1.2 enable us to define the following functionals
and
Remark 1.2 Note that we cannot define the functionals
![]() $\sigma ^*_k(\Sigma )$
and
$\sigma ^*_k(\Sigma )$
and
![]() $\sigma ^*_k(\Sigma ,[g])$
in higher dimensions. Indeed, it was proved in the paper [Reference Colbois, El Soufi and GirouardCSG19] that if
$\sigma ^*_k(\Sigma ,[g])$
in higher dimensions. Indeed, it was proved in the paper [Reference Colbois, El Soufi and GirouardCSG19] that if
![]() $n=\dim M \geq 3$
then the functional
$n=\dim M \geq 3$
then the functional
![]() $\overline {\sigma }_k(M,g):=\sigma _k(g)Vol(\partial M, g)^{1/(n-1)}$
, where
$\overline {\sigma }_k(M,g):=\sigma _k(g)Vol(\partial M, g)^{1/(n-1)}$
, where
![]() $Vol(\partial M, g)$
denotes the volume of the boundary with respect to the metric g, is not bounded from above on the set of Riemannian metrics
$Vol(\partial M, g)$
denotes the volume of the boundary with respect to the metric g, is not bounded from above on the set of Riemannian metrics
![]() $\mathcal R(M)$
. Moreover, it is not even bounded from above in the conformal class
$\mathcal R(M)$
. Moreover, it is not even bounded from above in the conformal class
![]() $[g]$
.
$[g]$
.
The functional
![]() $\sigma ^*_k(\Sigma )$
is an object of intensive research during the last decade (see e.g., [Reference Fraser and SchoenFS11, Reference Fraser and SchoenFS16, Reference Colbois, Girouard and RaveendranCGR18, Reference PetridesPet19, Reference Girouard and LagacéGL20, Reference Matthiesen and PetridesMP20a]).
$\sigma ^*_k(\Sigma )$
is an object of intensive research during the last decade (see e.g., [Reference Fraser and SchoenFS11, Reference Fraser and SchoenFS16, Reference Colbois, Girouard and RaveendranCGR18, Reference PetridesPet19, Reference Girouard and LagacéGL20, Reference Matthiesen and PetridesMP20a]).
The functional
![]() $\sigma ^*_k(\Sigma ,[g])$
which is called the kth conformal Steklov eigenvalue is less studied. Let us mention some results concerning
$\sigma ^*_k(\Sigma ,[g])$
which is called the kth conformal Steklov eigenvalue is less studied. Let us mention some results concerning
![]() $\sigma ^*_k(\Sigma ,[g])$
. First, since the disc admits the unique conformal structure one can conclude that
$\sigma ^*_k(\Sigma ,[g])$
. First, since the disc admits the unique conformal structure one can conclude that
![]() $\sigma ^*_k(\mathbb D^2,[g_{can}])=\sigma ^*_k(\mathbb D^2),$
where
$\sigma ^*_k(\mathbb D^2,[g_{can}])=\sigma ^*_k(\mathbb D^2),$
where
![]() $g_{can}$
stands for the Euclidean metric on
$g_{can}$
stands for the Euclidean metric on
![]() $\mathbb D^2$
with unit boundary length. The value of
$\mathbb D^2$
with unit boundary length. The value of
![]() $\sigma ^*_k(\mathbb D^2)$
is known:
$\sigma ^*_k(\mathbb D^2)$
is known:
![]() $\sigma ^*_k(\mathbb D^2)=2\pi k$
(see [Reference WeinstockWei54] for
$\sigma ^*_k(\mathbb D^2)=2\pi k$
(see [Reference WeinstockWei54] for
![]() $k=1$
and [Reference Girouard and PolterovichGP10] for all
$k=1$
and [Reference Girouard and PolterovichGP10] for all
![]() $k \geq 1$
). Let us also mention the resent paper [Reference Fraser and SchoenFS20], where the authors particularly obtain new results about the functional
$k \geq 1$
). Let us also mention the resent paper [Reference Fraser and SchoenFS20], where the authors particularly obtain new results about the functional
![]() $\sigma ^*_k(\mathbb D^2)$
.
$\sigma ^*_k(\mathbb D^2)$
.
The functional
![]() $\sigma ^*_k(\Sigma ,[g])$
is the main research object of the paper [Reference PetridesPet19].
$\sigma ^*_k(\Sigma ,[g])$
is the main research object of the paper [Reference PetridesPet19].
Theorem 1.3 [Reference PetridesPet19]
For every Riemannian metric g on a compact surface
![]() $\Sigma $
with boundary one has
$\Sigma $
with boundary one has
particularly
Moreover, if the inequality (1.1) is strict then there exists a Riemannian metric
![]() $\tilde g\in [g]$
such that
$\tilde g\in [g]$
such that
![]() $\overline \sigma _k(\Sigma ,\tilde g)=\sigma ^*_k(\Sigma ,[g])$
.
$\overline \sigma _k(\Sigma ,\tilde g)=\sigma ^*_k(\Sigma ,[g])$
.
New interesting results about the functional
![]() $\sigma ^*_k(\Sigma ,[g])$
were recently obtained in the paper [Reference Karpukhin and SternKS20].
$\sigma ^*_k(\Sigma ,[g])$
were recently obtained in the paper [Reference Karpukhin and SternKS20].
Remark 1.3 The result analogous to Theorem 1.3 for the conformal spectrum of the Laplace–Beltrami operator on closed surfaces also holds (see [Reference Nadirashvili and SireNS15a, Reference Nadirashvili and SireNS15b, Reference PetridesPet14, Reference PetridesPet18, Reference Karpukhin, Nadirashvili, Penskoi and PolterovichKNPP20]). For further information concerning the spectrum of the Laplace–Beltrami operator on closed surfaces see the surveys [Reference PenskoĭPen13, Reference PenskoĭPen19] and references therein.
It is easy to see that the connection between the functionals
![]() $\sigma ^*_k(\Sigma )$
and
$\sigma ^*_k(\Sigma )$
and
![]() $\sigma ^*_k(\Sigma ,[g])$
is expressed by the formula
$\sigma ^*_k(\Sigma ,[g])$
is expressed by the formula
One can ask what do we get if we replace
![]() $\sup _{[g]}$
by
$\sup _{[g]}$
by
![]() $\inf _{[g]}$
in this formula? In this case, we get the following quantity
$\inf _{[g]}$
in this formula? In this case, we get the following quantity
It is an analog of the Friedlander–Nadirashvili invariant of closed manifolds. The first Friedlander–Nadirashvili invariant of a closed manifold was introduced in the paper [Reference Friedlander and NadirashviliFN99] in 1999. The kth Nadirashvili–Friedlander invariant of a closed surface has been recently studied in the paper [Reference Karpukhin and MedvedevKM20].
In the study of functionals like
![]() $\sigma ^*_k(\Sigma )$
and
$\sigma ^*_k(\Sigma )$
and
![]() $I^{\sigma }_k(\Sigma )$
, one considers maximizing and minimizing sequences of conformal classes
$I^{\sigma }_k(\Sigma )$
, one considers maximizing and minimizing sequences of conformal classes
![]() $\{c_n\}$
on the moduli space of conformal classes on
$\{c_n\}$
on the moduli space of conformal classes on
![]() $\Sigma $
, i.e.,
$\Sigma $
, i.e.,
![]() $\sigma ^*_k(\Sigma ,c_n) \to \sigma ^*_k(\Sigma )$
or
$\sigma ^*_k(\Sigma ,c_n) \to \sigma ^*_k(\Sigma )$
or
![]() $\sigma ^*_k(\Sigma ,c_n) \to I^{\sigma }_k(\Sigma )$
as
$\sigma ^*_k(\Sigma ,c_n) \to I^{\sigma }_k(\Sigma )$
as
![]() $n\to \infty $
. Due to the Uniformization theorem conformal classes on
$n\to \infty $
. Due to the Uniformization theorem conformal classes on
![]() $\Sigma $
are in one-to-one correspondence (up to an isometry) with metrics on
$\Sigma $
are in one-to-one correspondence (up to an isometry) with metrics on
![]() $\Sigma $
of constant Gauss curvature and geodesic boundary. Therefore, any sequence of conformal classes
$\Sigma $
of constant Gauss curvature and geodesic boundary. Therefore, any sequence of conformal classes
![]() $\{c_n\}$
on
$\{c_n\}$
on
![]() $\Sigma $
corresponds to a sequence of Riemannian surfaces of constant Gauss curvature and geodesic boundary
$\Sigma $
corresponds to a sequence of Riemannian surfaces of constant Gauss curvature and geodesic boundary
![]() $\{(\Sigma ,h_n)\},~h_n\in c_n$
and we can consider the moduli space of conformal classes on
$\{(\Sigma ,h_n)\},~h_n\in c_n$
and we can consider the moduli space of conformal classes on
![]() $\Sigma $
as the set of all
$\Sigma $
as the set of all
![]() $(\Sigma ,h)$
, where h is a metric of constant Gauss curvature and geodesic boundary, endowed with
$(\Sigma ,h)$
, where h is a metric of constant Gauss curvature and geodesic boundary, endowed with
![]() $C^{\infty }$
-topology (see Section 4). Note that the moduli space of conformal structures is a noncompact topological space. For any sequence
$C^{\infty }$
-topology (see Section 4). Note that the moduli space of conformal structures is a noncompact topological space. For any sequence
![]() $\{c_n\}$
there are two possible scenarios: either this sequence remains in a compact part of the moduli space or it escapes to infinity. Let
$\{c_n\}$
there are two possible scenarios: either this sequence remains in a compact part of the moduli space or it escapes to infinity. Let
![]() $(\Sigma _{\infty }, c_{\infty })$
denote the limiting space, i.e.,
$(\Sigma _{\infty }, c_{\infty })$
denote the limiting space, i.e.,
![]() $(\Sigma _{\infty }, c_{\infty })=\lim _{n\to \infty }(\Sigma ,c_n)$
. We compactify
$(\Sigma _{\infty }, c_{\infty })=\lim _{n\to \infty }(\Sigma ,c_n)$
. We compactify
![]() $\Sigma _{\infty }$
if necessary. Let
$\Sigma _{\infty }$
if necessary. Let
![]() $\widehat {\Sigma _{\infty }}$
denote the compactified limiting space. It turns out that if the first scenario realizes, then we get
$\widehat {\Sigma _{\infty }}$
denote the compactified limiting space. It turns out that if the first scenario realizes, then we get
![]() $\widehat {\Sigma _{\infty }}=\Sigma $
and
$\widehat {\Sigma _{\infty }}=\Sigma $
and
![]() $c_{\infty }$
is a genuine conformal class on
$c_{\infty }$
is a genuine conformal class on
![]() $\Sigma $
for which the value
$\Sigma $
for which the value
![]() $\sigma ^*_k(\Sigma )$
or
$\sigma ^*_k(\Sigma )$
or
![]() $I^{\sigma }_k(\Sigma )$
is attained. If the second scenario realizes, then we say that the sequence
$I^{\sigma }_k(\Sigma )$
is attained. If the second scenario realizes, then we say that the sequence
![]() $\{c_n\}$
degenerates. It turns out that in this case there exists a finite collection of pairwise disjoint geodesics for the metrics
$\{c_n\}$
degenerates. It turns out that in this case there exists a finite collection of pairwise disjoint geodesics for the metrics
![]() $h_n$
whose lengths in
$h_n$
whose lengths in
![]() $h_n$
tend to
$h_n$
tend to
![]() $0$
as n tends to
$0$
as n tends to
![]() $\infty $
. We refer to these geodesics as pinching or collapsing. They can be of the following three types: the collapsing boundary components, the collapsing geodesics with no self-intersection crossing the boundary
$\infty $
. We refer to these geodesics as pinching or collapsing. They can be of the following three types: the collapsing boundary components, the collapsing geodesics with no self-intersection crossing the boundary
![]() $\partial \Sigma $
at two points and the collapsing geodesics with no self-intersection which do not cross
$\partial \Sigma $
at two points and the collapsing geodesics with no self-intersection which do not cross
![]() $\partial \Sigma $
. Note that in this case, the topology of
$\partial \Sigma $
. Note that in this case, the topology of
![]() $\Sigma $
necessarily changes when we pass to the limit as
$\Sigma $
necessarily changes when we pass to the limit as
![]() $n\to \infty $
, i.e., the compact surfaces
$n\to \infty $
, i.e., the compact surfaces
![]() $\widehat \Sigma _{\infty }$
and
$\widehat \Sigma _{\infty }$
and
![]() $\Sigma $
are of different topological types. In particular, the surface
$\Sigma $
are of different topological types. In particular, the surface
![]() $\widehat \Sigma _{\infty }$
can be disconnected (see Figure 1). We refer to Section 4 for more details.
$\widehat \Sigma _{\infty }$
can be disconnected (see Figure 1). We refer to Section 4 for more details.

Figure 1: An example of a degenerating sequence of conformal classes
![]() $\{c_n\}$
on a surface
$\{c_n\}$
on a surface
![]() $\Sigma $
of genus
$\Sigma $
of genus
![]() $2$
with
$2$
with
![]() $4$
boundary components. (a) The red curves correspond to collapsing geodesics for the sequence of metrics of constant Gauss curvature and geodesic boundary
$4$
boundary components. (a) The red curves correspond to collapsing geodesics for the sequence of metrics of constant Gauss curvature and geodesic boundary
![]() $\{h_n\}, ~h_n\in c_n$
corresponding to the degenerating sequence of conformal classes
$\{h_n\}, ~h_n\in c_n$
corresponding to the degenerating sequence of conformal classes
![]() $\{c_n\}$
. (b) The compactified limiting space
$\{c_n\}$
. (b) The compactified limiting space
![]() $\widehat {\Sigma _{\infty }}$
(see Section 4). The black points correspond to the points of compactification. (c) The surface
$\widehat {\Sigma _{\infty }}$
(see Section 4). The black points correspond to the points of compactification. (c) The surface
![]() $\widehat {\Sigma _{\infty }}$
is homeomorphic to the disjoint union of a disc and a surface of genus
$\widehat {\Sigma _{\infty }}$
is homeomorphic to the disjoint union of a disc and a surface of genus
![]() $1$
with
$1$
with
![]() $1$
boundary component.
$1$
boundary component.
The following theorem establishes the correspondence between
![]() $\sigma ^*_k(\widehat \Sigma _{\infty },c_{\infty })$
and the limit of
$\sigma ^*_k(\widehat \Sigma _{\infty },c_{\infty })$
and the limit of
![]() $\sigma ^*_k(\Sigma ,c_n)$
when the sequence of conformal classes
$\sigma ^*_k(\Sigma ,c_n)$
when the sequence of conformal classes
![]() $c_n$
degenerates (see Section 4 for the definition). It is an analog of [Reference Karpukhin and MedvedevKM20, Theorem 2.8] for the Steklov setting.
$c_n$
degenerates (see Section 4 for the definition). It is an analog of [Reference Karpukhin and MedvedevKM20, Theorem 2.8] for the Steklov setting.
Theorem 1.4 Let
![]() $\Sigma $
be a compact surface of genus
$\Sigma $
be a compact surface of genus
![]() $\gamma $
with
$\gamma $
with
![]() $l>0$
boundary components and let
$l>0$
boundary components and let
![]() $c_n\to c_{\infty }$
be a degenerating sequence of conformal classes. Consider the corresponding sequence
$c_n\to c_{\infty }$
be a degenerating sequence of conformal classes. Consider the corresponding sequence
![]() $\{h_n\}$
of metrics of constant Gauss curvature and geodesic boundary. Suppose that there exist
$\{h_n\}$
of metrics of constant Gauss curvature and geodesic boundary. Suppose that there exist
![]() $s_1$
collapsing boundary components and
$s_1$
collapsing boundary components and
![]() $s_2$
collapsing geodesics with no self-intersection which cross the boundary at two points. Moreover, suppose that
$s_2$
collapsing geodesics with no self-intersection which cross the boundary at two points. Moreover, suppose that
![]() $\widehat {\Sigma _{\infty }}$
has m connected components
$\widehat {\Sigma _{\infty }}$
has m connected components
![]() $\Sigma _{\gamma _{i},l_i}$
of genus
$\Sigma _{\gamma _{i},l_i}$
of genus
![]() $\gamma _i$
with
$\gamma _i$
with
![]() $l_i>0$
boundary components,
$l_i>0$
boundary components,
![]() $\gamma _i+l_i<\gamma +l$
,
$\gamma _i+l_i<\gamma +l$
,
![]() $i=1,\ldots ,m$
. Then one has
$i=1,\ldots ,m$
. Then one has
 $$ \begin{align*} \lim_{n \to \infty} \sigma^*_k (\Sigma, c_n)= \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_i}(\Sigma_{\gamma_{i},l_i}, c_{\infty})+\sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2)\bigg), \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \sigma^*_k (\Sigma, c_n)= \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_i}(\Sigma_{\gamma_{i},l_i}, c_{\infty})+\sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2)\bigg), \end{align*} $$
where the maximum is taken over all possible combinations of indices such that
 $$ \begin{align*} \sum_{i=1}^{m} k_i + \sum_{i=1}^{s_1+s_2} r_i = k. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{m} k_i + \sum_{i=1}^{s_1+s_2} r_i = k. \end{align*} $$
Remark 1.4 Let
![]() $\Sigma $
denote either cylinder or the Möbius band. Theorem 1.4 particularly implies that if the sequence of conformal classes
$\Sigma $
denote either cylinder or the Möbius band. Theorem 1.4 particularly implies that if the sequence of conformal classes
![]() $\{c_n\}$
on
$\{c_n\}$
on
![]() $\Sigma $
degenerates then we necessarily have:
$\Sigma $
degenerates then we necessarily have:
Remark 1.5 In Theorem 1.4 the sequence
![]() $\{h_n\}$
can also have collapsing geodesics not crossing the boundary of
$\{h_n\}$
can also have collapsing geodesics not crossing the boundary of
![]() $\Sigma $
. Moreover, it can happen that the limiting space
$\Sigma $
. Moreover, it can happen that the limiting space
![]() $\widehat {\Sigma _{\infty }}$
has closed components (see Figure 2). Anyway, in Theorem 1.4 we take only components of
$\widehat {\Sigma _{\infty }}$
has closed components (see Figure 2). Anyway, in Theorem 1.4 we take only components of
![]() $\widehat {\Sigma _{\infty }}$
which have nonempty boundary.
$\widehat {\Sigma _{\infty }}$
which have nonempty boundary.

Figure 2: An example of a degenerating sequence of conformal classes
![]() $\{c_n\}$
on a surface of genus
$\{c_n\}$
on a surface of genus
![]() $2$
with
$2$
with
![]() $1$
boundary components such that the limiting space contains a closed component. In Theorem 1.4, we take only the component on the left which has nonempty boundary. Note that in this case
$1$
boundary components such that the limiting space contains a closed component. In Theorem 1.4, we take only the component on the left which has nonempty boundary. Note that in this case
![]() $s_1=s_2=0$
.
$s_1=s_2=0$
.
The main tool that we use in the proof of Theorem 1.4 is the Steklov–Neumann boundary problem also known as the sloshing problem. Let
![]() $\Omega $
be a Lipschitz domain in
$\Omega $
be a Lipschitz domain in
![]() $(\Sigma ,g)$
such that
$(\Sigma ,g)$
such that
![]() $\overline \Omega \cap \partial \Sigma = \partial ^S\Omega \neq \varnothing $
. Let
$\overline \Omega \cap \partial \Sigma = \partial ^S\Omega \neq \varnothing $
. Let
![]() $\partial ^N\Omega =\partial \Omega \setminus \partial \Sigma $
. Then the Steklov–Neumann problem is defined as:
$\partial ^N\Omega =\partial \Omega \setminus \partial \Sigma $
. Then the Steklov–Neumann problem is defined as:
 $$ \begin{align*} \begin{cases} \Delta_g u=0&\text{in } \Omega,\\ \frac{\partial u}{\partial n}=0&\text{on } \partial^N\Omega,\\ \frac{\partial u}{\partial n}=\sigma^Nu&\text{on } \partial^S\Omega. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_g u=0&\text{in } \Omega,\\ \frac{\partial u}{\partial n}=0&\text{on } \partial^N\Omega,\\ \frac{\partial u}{\partial n}=\sigma^Nu&\text{on } \partial^S\Omega. \end{cases} \end{align*} $$
The numbers
![]() $\sigma ^N$
for which the Steklov–Neumann problem admits a solution are called Steklov–Neumann eigenvalues. It is known (see [Reference Banuelos, Kulczycki, Polterovich and SiudejaBKPS10] and references therein) that the set of Steklov–Neumann eigenvalues is not empty and discrete
$\sigma ^N$
for which the Steklov–Neumann problem admits a solution are called Steklov–Neumann eigenvalues. It is known (see [Reference Banuelos, Kulczycki, Polterovich and SiudejaBKPS10] and references therein) that the set of Steklov–Neumann eigenvalues is not empty and discrete
Every Steklov–Neumann eigenvalue admits the following variational characterization:
 $$ \begin{align*} \sigma^N_k(g)=\inf_{V_k\subset \mathcal H^1(\Omega)}\sup_{0 \neq u \in V_k}\frac{\int_{\Omega}|\nabla u|^2dv_g}{\int_{\partial^S\Omega}u^2ds_g}, \end{align*} $$
$$ \begin{align*} \sigma^N_k(g)=\inf_{V_k\subset \mathcal H^1(\Omega)}\sup_{0 \neq u \in V_k}\frac{\int_{\Omega}|\nabla u|^2dv_g}{\int_{\partial^S\Omega}u^2ds_g}, \end{align*} $$
where the infimum is taken over all k-dimensional subspaces of the space
![]() $\mathcal H^1(\Omega )=\{u\in H^1(\Omega ,g)~|~\int _{\partial ^S\Omega } uds_g=0\}$
.
$\mathcal H^1(\Omega )=\{u\in H^1(\Omega ,g)~|~\int _{\partial ^S\Omega } uds_g=0\}$
.
Similarly to the case of the Steklov problem we define normalized Steklov–Neumann eigenvalues as
In this notation, we always indicate the Steklov part of the boundary at the second place. Sometimes, we also use the notation
![]() $\sigma ^N_k(\Omega , \partial ^S\Omega ,g)$
for
$\sigma ^N_k(\Omega , \partial ^S\Omega ,g)$
for
![]() $\sigma ^N_k(\Omega ,g)$
to emphasize that the Steklov boundary condition is imposed on
$\sigma ^N_k(\Omega ,g)$
to emphasize that the Steklov boundary condition is imposed on
![]() $\partial ^S\Omega $
.
$\partial ^S\Omega $
.
Remark 1.6 Consider
![]() $\Omega $
as a surface with Lipschitz boundary. It also follows from [Reference KokarevKok14, Theorem
$\Omega $
as a surface with Lipschitz boundary. It also follows from [Reference KokarevKok14, Theorem
![]() ${A}_k$
] that the quantity
${A}_k$
] that the quantity
![]() $\overline \sigma ^N_k(\Omega , \partial ^S\Omega ,g)$
is bounded from above on
$\overline \sigma ^N_k(\Omega , \partial ^S\Omega ,g)$
is bounded from above on
![]() $[g]$
and we can define the invariant
$[g]$
and we can define the invariant
![]() $\sigma ^{N*}_k(\Omega , \partial ^S\Omega ,[g])$
in the same way as the invariant
$\sigma ^{N*}_k(\Omega , \partial ^S\Omega ,[g])$
in the same way as the invariant
![]() $\sigma ^{*}_k(\Sigma ,[g])$
.
$\sigma ^{*}_k(\Sigma ,[g])$
.
Theorem 1.4 enables us to establish the value of
![]() $I^{\sigma }_k$
.
$I^{\sigma }_k$
.
Theorem 1.5 Let
![]() $\Sigma $
be a compact surface with boundary. Then one has
$\Sigma $
be a compact surface with boundary. Then one has
![]() $I^{\sigma }_k(\Sigma )=I^{\sigma }_k(\mathbb D^2)=2\pi k$
.
$I^{\sigma }_k(\Sigma )=I^{\sigma }_k(\mathbb D^2)=2\pi k$
.
1.1 Discussion
Let us discuss the estimate obtained in Theorem 1.2. The first estimate on
![]() $\overline {\sigma }_1(\Sigma ,g)$
where
$\overline {\sigma }_1(\Sigma ,g)$
where
![]() $\Sigma $
is a nonorientable surface of genus
$\Sigma $
is a nonorientable surface of genus
![]() $\gamma $
with boundary was obtained in the paper [Reference SchoenSch13]. It reads
$\gamma $
with boundary was obtained in the paper [Reference SchoenSch13]. It reads
if
![]() $\gamma \geq 1$
and
$\gamma \geq 1$
and
if
![]() $\gamma =0$
. Moreover, it follows from the papers [Reference KokarevKok14, Reference KarpukhinKar16] that
$\gamma =0$
. Moreover, it follows from the papers [Reference KokarevKok14, Reference KarpukhinKar16] that
where
![]() $[x]$
stands for the integer part of the number x.
$[x]$
stands for the integer part of the number x.
Very recently, in the paper [Reference Karpukhin and SternKS20], estimate (1.3) has been improved and extended for
![]() $k=2$
: consider
$k=2$
: consider
![]() $\Sigma $
as a domain with smooth boundary on a closed surface M, then one has
$\Sigma $
as a domain with smooth boundary on a closed surface M, then one has
In this estimate,
![]() $\Lambda _k(M):=\sup _{g\in \mathcal R(M)} \lambda _k(g)\operatorname {Vol}(M,g)$
, where
$\Lambda _k(M):=\sup _{g\in \mathcal R(M)} \lambda _k(g)\operatorname {Vol}(M,g)$
, where
![]() $\lambda _k(g)$
is the kth Laplace eigenvalue of the metric g,
$\lambda _k(g)$
is the kth Laplace eigenvalue of the metric g,
![]() $\operatorname {Vol}(M,g)$
is the volume of M in the metric g and
$\operatorname {Vol}(M,g)$
is the volume of M in the metric g and
![]() $\mathcal R(M)$
is the set of Riemannian metrics on M. Note that estimate (1.4) does not depend on the number of boundary components. Combining estimate (1.4) with our estimate we get
$\mathcal R(M)$
is the set of Riemannian metrics on M. Note that estimate (1.4) does not depend on the number of boundary components. Combining estimate (1.4) with our estimate we get
Particularly, for the Möbius band one has
since
![]() $\mathbb {MB} \subset \mathbb {RP}^2$
. The value
$\mathbb {MB} \subset \mathbb {RP}^2$
. The value
![]() $\Lambda _k(\mathbb {RP}^2)$
is known for all k (see [Reference KarpukhinKar20]):
$\Lambda _k(\mathbb {RP}^2)$
is known for all k (see [Reference KarpukhinKar20]):
![]() $\Lambda _k(\mathbb {RP}^2)=4\pi (2k+1)$
. Hence,
$\Lambda _k(\mathbb {RP}^2)=4\pi (2k+1)$
. Hence,
In the paper [Reference Fraser and SchoenFS16] it was shown that
![]() $\overline {\sigma }_1(\mathbb {MB},g) \leq 2\pi \sqrt {3}$
which is obviously
$\overline {\sigma }_1(\mathbb {MB},g) \leq 2\pi \sqrt {3}$
which is obviously
![]() $\leq 8\pi $
.
$\leq 8\pi $
.
We proceed with the discussion of the functional
![]() $I^{\sigma }_k$
. Unlike Theorem 1.4 in [Reference Karpukhin and MedvedevKM20], Theorem 1.5 says nothing about conformal classes on which the value
$I^{\sigma }_k$
. Unlike Theorem 1.4 in [Reference Karpukhin and MedvedevKM20], Theorem 1.5 says nothing about conformal classes on which the value
![]() $I^{\sigma }_k(\Sigma )$
is attained. We conjecture that
$I^{\sigma }_k(\Sigma )$
is attained. We conjecture that
Conjecture 1.6 The infimum
![]() $I^{\sigma }_k(\Sigma )$
is attained if and only if
$I^{\sigma }_k(\Sigma )$
is attained if and only if
![]() $\Sigma $
is diffeomorphic to the disc
$\Sigma $
is diffeomorphic to the disc
![]() $\mathbb D^2$
.
$\mathbb D^2$
.
Note that this conjecture would be a corollary of the following one
Conjecture 1.7 Let
![]() $\Sigma $
be a compact surface nondiffeomorphic to the disc. Then for every conformal class c on
$\Sigma $
be a compact surface nondiffeomorphic to the disc. Then for every conformal class c on
![]() $\Sigma $
one has
$\Sigma $
one has
This conjecture is an analog of the Petrides rigidity theorem for the first conformal Laplace eigenvalue [Reference PetridesPet14, Theorem 1]. Recently this conjecture has been confirmed in the case of the cylinder and the Möbius band (see [Reference Matthiesen and PetridesMP20b]). We plan to tackle Conjectures 1.6 and 1.7 in the subsequent papers.
Let us discuss the analogy between the quantity
![]() $I^{\sigma }_k$
and the Friedlander–Nadirashvili invariant of closed surfaces
$I^{\sigma }_k$
and the Friedlander–Nadirashvili invariant of closed surfaces
![]() $I_k$
. In the paper [Reference Karpukhin and MedvedevKM20], it was conjectured that
$I_k$
. In the paper [Reference Karpukhin and MedvedevKM20], it was conjectured that
![]() $I_k$
are invariants of cobordisms of closed surfaces (see Conjecture 1.8). Similarly, one can see that
$I_k$
are invariants of cobordisms of closed surfaces (see Conjecture 1.8). Similarly, one can see that
![]() $I^{\sigma }_k$
are invariants of cobordisms of compact surfaces with boundary. Let us recall that two compact surfaces with boundary
$I^{\sigma }_k$
are invariants of cobordisms of compact surfaces with boundary. Let us recall that two compact surfaces with boundary
![]() $(\Sigma _1,\partial \Sigma _1)$
and
$(\Sigma _1,\partial \Sigma _1)$
and
![]() $(\Sigma _2,\partial \Sigma _2)$
are called cobordant if there exists a three-dimensional manifold with corners
$(\Sigma _2,\partial \Sigma _2)$
are called cobordant if there exists a three-dimensional manifold with corners
![]() $\Omega $
whose boundary is
$\Omega $
whose boundary is
![]() $\Sigma _1\cup _{\partial \Sigma _1} W \cup _{\partial \Sigma _2}\Sigma _2$
, where W is a cobordism of
$\Sigma _1\cup _{\partial \Sigma _1} W \cup _{\partial \Sigma _2}\Sigma _2$
, where W is a cobordism of
![]() $\partial \Sigma _1$
and
$\partial \Sigma _1$
and
![]() $\partial \Sigma _2$
(i.e., W is a surface with boundary
$\partial \Sigma _2$
(i.e., W is a surface with boundary
![]() $\partial \Sigma _1\sqcup \partial \Sigma _2$
). Following [Reference Borodzik, Némethi and RanickiBNR16] we denote a cobordism of two surfaces
$\partial \Sigma _1\sqcup \partial \Sigma _2$
). Following [Reference Borodzik, Némethi and RanickiBNR16] we denote a cobordism of two surfaces
![]() $(\Sigma _1,\partial \Sigma _1)$
and
$(\Sigma _1,\partial \Sigma _1)$
and
![]() $(\Sigma _2,\partial \Sigma _2)$
by
$(\Sigma _2,\partial \Sigma _2)$
by
![]() $(\Omega ;\Sigma _1,\Sigma _2,W;\partial \Sigma _1,\partial \Sigma _2)$
. One can easily see that the cobordisms of surfaces with boundary are trivial. Indeed, we can construct the following cobordism of a surface
$(\Omega ;\Sigma _1,\Sigma _2,W;\partial \Sigma _1,\partial \Sigma _2)$
. One can easily see that the cobordisms of surfaces with boundary are trivial. Indeed, we can construct the following cobordism of a surface
![]() $(\Sigma ,\partial \Sigma )$
and
$(\Sigma ,\partial \Sigma )$
and
![]() $(\varnothing , \varnothing )$
:
$(\varnothing , \varnothing )$
:
![]() $(\Sigma \times [0,1];\Sigma \times \{0\}, \varnothing ,\partial \Sigma \times [0,1]\cup \Sigma \times \{1\};\partial \Sigma , \varnothing )$
. A fundamental fact about cobordisms of surfaces with boundary is Theorem about splitting cobordisms (see [Reference Borodzik, Némethi and RanickiBNR16, Theorem 4.18]) which says that every cobordism of compact surfaces with boundary can be split into a sequence of cobordisms given by a handle attachment and cobordisms given by a half-handle attachment. We refer to [Reference Borodzik, Némethi and RanickiBNR16] for definitions and further information about cobordisms of compact manifolds with boundary. Analysing the proof of Theorem 1.5 one can remark that the value of
$(\Sigma \times [0,1];\Sigma \times \{0\}, \varnothing ,\partial \Sigma \times [0,1]\cup \Sigma \times \{1\};\partial \Sigma , \varnothing )$
. A fundamental fact about cobordisms of surfaces with boundary is Theorem about splitting cobordisms (see [Reference Borodzik, Némethi and RanickiBNR16, Theorem 4.18]) which says that every cobordism of compact surfaces with boundary can be split into a sequence of cobordisms given by a handle attachment and cobordisms given by a half-handle attachment. We refer to [Reference Borodzik, Némethi and RanickiBNR16] for definitions and further information about cobordisms of compact manifolds with boundary. Analysing the proof of Theorem 1.5 one can remark that the value of
![]() $I^{\sigma }_k$
does not change under handle and half-handle attachments. Since by this procedure any surface
$I^{\sigma }_k$
does not change under handle and half-handle attachments. Since by this procedure any surface
![]() $\Sigma $
can be reduced to the disc, we get
$\Sigma $
can be reduced to the disc, we get
![]() $I^{\sigma }_k(\Sigma )=I^{\sigma }_k(\mathbb D^2)=2\pi k$
.
$I^{\sigma }_k(\Sigma )=I^{\sigma }_k(\mathbb D^2)=2\pi k$
.
1.2 Plan of the paper
The paper is organized in the following way. In Section 2, we collect all the analytic facts which are necessary for the proof of Theorem 1.4. The main result here is Proposition 2.6. In Section 3, we prove Theorem 1.2 using the techniques developed in the previous section. Section 4 represents the geometric part of the paper. Here, we describe convergence on the moduli space of conformal structures on a surface with boundary. Section 5 is devoted to the proof of Theorem 1.4. In Section 6, we deduce Theorem 1.5 from Theorem 1.4. Finally, Section 7 contains some auxiliary technical results.
2 Analytic background
Here, we provide a necessary analytic background that we will use in the proof of Theorem 1.4 in Section 5. The propositions in this section are analogs of the propositions in [Reference Karpukhin and MedvedevKM20, Section 4]. We postpone the proof of a proposition to Section 7.2 every time when it follows the exactly same way as the proof of an analogous proposition in [Reference Karpukhin and MedvedevKM20, Section 4].
2.1 Convergence of Steklov–Neumann spectrum
We start with the following convergence result.
Lemma 2.1 Let
![]() $(M, g)$
be a compact Riemannian manifold with boundary. Consider a finite collection
$(M, g)$
be a compact Riemannian manifold with boundary. Consider a finite collection
![]() $\{ B_{\epsilon }(p_i) \}_{i=1}^l$
of geodesic balls of radius
$\{ B_{\epsilon }(p_i) \}_{i=1}^l$
of geodesic balls of radius
![]() $\epsilon $
centred at some points
$\epsilon $
centred at some points
![]() $p_1,\ldots ,p_l \in M$
. Then the spectrum of the Steklov–Neumann problem
$p_1,\ldots ,p_l \in M$
. Then the spectrum of the Steklov–Neumann problem
 $$ \begin{align*} \begin{cases} \Delta_gu=0&\text{in } M\setminus \cup^l_{i=1}B_{\epsilon}(p_i),\\ \frac{\partial u}{\partial n}=0&\text{on } \cup^l_{i=1} \partial B_{\epsilon}(p_i) \setminus \partial M,\\ \frac{\partial u}{\partial n}=\lambda^N_k(M \setminus \cup^l_{i=1}B_{\epsilon}(p_i), g) u&\text{on } \partial M \setminus \cup^l_{i=1} \partial B_{\epsilon}(p_i) \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_gu=0&\text{in } M\setminus \cup^l_{i=1}B_{\epsilon}(p_i),\\ \frac{\partial u}{\partial n}=0&\text{on } \cup^l_{i=1} \partial B_{\epsilon}(p_i) \setminus \partial M,\\ \frac{\partial u}{\partial n}=\lambda^N_k(M \setminus \cup^l_{i=1}B_{\epsilon}(p_i), g) u&\text{on } \partial M \setminus \cup^l_{i=1} \partial B_{\epsilon}(p_i) \end{cases} \end{align*} $$
converges to the Steklov spectrum of
![]() $(M,g)$
as
$(M,g)$
as
![]() $\epsilon \to 0$
.
$\epsilon \to 0$
.
Proof For the sake of simplicity, we only consider the case of one ball that we denote by
![]() $B_{\epsilon }$
centred at
$B_{\epsilon }$
centred at
![]() $p \in M$
. First, we consider the case when
$p \in M$
. First, we consider the case when
![]() $B_{\epsilon } \cap \partial M \neq \varnothing $
, i.e.,
$B_{\epsilon } \cap \partial M \neq \varnothing $
, i.e.,
![]() $p\in \partial M$
.
$p\in \partial M$
.
Let
![]() $\mathcal E(u)$
denote the extension of the function u by the unique solution of the problem
$\mathcal E(u)$
denote the extension of the function u by the unique solution of the problem
 $$ \begin{align*} \begin{cases} \Delta_g\mathcal E(u)=0&\text{in } B_{\epsilon},\\ \frac{\partial \mathcal E(u)}{\partial n}=0&\text{on } \partial M \cap \partial B_{\epsilon},\\ \mathcal E(u)= u&\text{on } \partial B_{\epsilon} \setminus \partial M. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_g\mathcal E(u)=0&\text{in } B_{\epsilon},\\ \frac{\partial \mathcal E(u)}{\partial n}=0&\text{on } \partial M \cap \partial B_{\epsilon},\\ \mathcal E(u)= u&\text{on } \partial B_{\epsilon} \setminus \partial M. \end{cases} \end{align*} $$
Claim 1. The operator
![]() $\mathcal E(u)$
is uniformly bounded.
$\mathcal E(u)$
is uniformly bounded.
Proof The proof is similar to the proof of uniform boundedness of the harmonic continuation operator into small geodesic balls [Reference Rauch and TaylorRT75, Example 1]. Fix
![]() $0<r<\epsilon $
and let
$0<r<\epsilon $
and let
![]() $B_r$
denote a geodesic ball of radius r with the same center as
$B_r$
denote a geodesic ball of radius r with the same center as
![]() $B_{\epsilon }$
. One has
$B_{\epsilon }$
. One has
and
Inequality (2.1) follows from estimate (7.1) and the trace inequality
Suppose that inequality (2.2) was false. Then, there exists a sequence of functions
![]() $\{u_n\}$
in
$\{u_n\}$
in
![]() $H^1(M\setminus B_r,g)$
such that
$H^1(M\setminus B_r,g)$
such that
and
Consider
![]() $\alpha _n=\frac {1}{Vol(M\setminus B_r,g)}\int _{M\setminus B_r}u_ndv_g$
. We show that
$\alpha _n=\frac {1}{Vol(M\setminus B_r,g)}\int _{M\setminus B_r}u_ndv_g$
. We show that
Indeed, by the generalized Poincaré inequality one has
moreover
Note that
![]() $\mathcal E(u_n-\alpha _n)=\mathcal E(u_n)-\alpha _n$
. Then, we can prove inequality (2.2)
$\mathcal E(u_n-\alpha _n)=\mathcal E(u_n)-\alpha _n$
. Then, we can prove inequality (2.2)
 $$ \begin{align*} ||\nabla \mathcal E(u_n)||_{L^2(B_r,g)} &=||\nabla \mathcal E(u_n-\alpha_n)||_{L^2(B_r,g)} \leq || \mathcal E(u_n-\alpha_n)||_{H^1(B_r,g)} \\ &\leq ||u_n-\alpha_n||_{H^{1/2}(\partial B_r \setminus \partial M,g)} \leq C||u_n-\alpha_n||_{H^{1}(M\setminus B_r,g)} \leq C/n, \end{align*} $$
$$ \begin{align*} ||\nabla \mathcal E(u_n)||_{L^2(B_r,g)} &=||\nabla \mathcal E(u_n-\alpha_n)||_{L^2(B_r,g)} \leq || \mathcal E(u_n-\alpha_n)||_{H^1(B_r,g)} \\ &\leq ||u_n-\alpha_n||_{H^{1/2}(\partial B_r \setminus \partial M,g)} \leq C||u_n-\alpha_n||_{H^{1}(M\setminus B_r,g)} \leq C/n, \end{align*} $$
where in the second and third inequalities, we have used in order estimate (7.1) and the trace inequality. We got a contradiction. Hence, inequality (2.2) is true.
Note that for any
![]() $\rho r<\epsilon $
the first inequality scales as
$\rho r<\epsilon $
the first inequality scales as
while the second inequality scales as
Therefore,
![]() $||\mathcal E(u)||^2_{H^1(B_{\rho r},g)} \leq C||u||^2_{L^2(M\setminus B_{\rho r},g)}+C||\nabla u||^2_{L^2(M\setminus B_{\rho r},g)}$
for
$||\mathcal E(u)||^2_{H^1(B_{\rho r},g)} \leq C||u||^2_{L^2(M\setminus B_{\rho r},g)}+C||\nabla u||^2_{L^2(M\setminus B_{\rho r},g)}$
for
![]() $\epsilon $
small enough.▪
$\epsilon $
small enough.▪
Claim 2. One has
Proof We only consider the case of
![]() $B_{\epsilon } \cap \partial M\neq \varnothing $
. The case of
$B_{\epsilon } \cap \partial M\neq \varnothing $
. The case of
![]() $B_{\epsilon } \cap \partial M=\varnothing $
is easier and follows the exactly same arguments. The proof is similar to the proof of [Reference BogoselBog17, Theorem 3.5].
$B_{\epsilon } \cap \partial M=\varnothing $
is easier and follows the exactly same arguments. The proof is similar to the proof of [Reference BogoselBog17, Theorem 3.5].
Let
![]() $V_k$
be a k-dimensional subspace of
$V_k$
be a k-dimensional subspace of
![]() $H^1(M,g)$
and
$H^1(M,g)$
and
![]() $v\in V_k$
such that
$v\in V_k$
such that
 $$ \begin{align*} \sigma_k(M,g)=\max_{u\in V_k\setminus \{0\}}\frac{\int_M|\nabla u|^2dv_g}{\int_{\partial M}u^2ds_g}. \end{align*} $$
$$ \begin{align*} \sigma_k(M,g)=\max_{u\in V_k\setminus \{0\}}\frac{\int_M|\nabla u|^2dv_g}{\int_{\partial M}u^2ds_g}. \end{align*} $$
Let
![]() $u_1,\ldots ,u_k$
be an orthonormal basis in
$u_1,\ldots ,u_k$
be an orthonormal basis in
![]() $V_k$
. We modify the functions
$V_k$
. We modify the functions
![]() $u_i, i= 1,\ldots ,k$
as
$u_i, i= 1,\ldots ,k$
as
Then,
![]() $\int _{\partial M\setminus \partial B_{\epsilon }}u_{i,\epsilon }ds_g=0$
. Consider the space
$\int _{\partial M\setminus \partial B_{\epsilon }}u_{i,\epsilon }ds_g=0$
. Consider the space
![]() $V_{k,\epsilon }:=span(u_{1,\epsilon },\ldots ,u_{k,\epsilon })$
. Since
$V_{k,\epsilon }:=span(u_{1,\epsilon },\ldots ,u_{k,\epsilon })$
. Since
![]() $\dim V_{k,\epsilon }=k$
one has
$\dim V_{k,\epsilon }=k$
one has
 $$ \begin{align*} \sigma^N_k(M\setminus B_{\epsilon},g) \leq \max_{u_{\epsilon} \in V_{k,\epsilon}\setminus\{0\}}\frac{\int_{M\setminus B_{\epsilon}}|\nabla u_{\epsilon}|^2dv_g}{\int_{\partial M\setminus \partial B_{\epsilon}}u_{\epsilon}^2ds_g}. \end{align*} $$
$$ \begin{align*} \sigma^N_k(M\setminus B_{\epsilon},g) \leq \max_{u_{\epsilon} \in V_{k,\epsilon}\setminus\{0\}}\frac{\int_{M\setminus B_{\epsilon}}|\nabla u_{\epsilon}|^2dv_g}{\int_{\partial M\setminus \partial B_{\epsilon}}u_{\epsilon}^2ds_g}. \end{align*} $$
Moreover, since the dimension of
![]() $V_{k,\epsilon }$
is finite then there exists a function
$V_{k,\epsilon }$
is finite then there exists a function
![]() $v_{\epsilon }\in V_{k,\epsilon }$
such that
$v_{\epsilon }\in V_{k,\epsilon }$
such that
 $$ \begin{align} \sigma^N_k(M\setminus B_{\epsilon},g) \leq \frac{\int_{M\setminus B_{\epsilon}}|\nabla v_{\epsilon}|^2dv_g}{\int_{\partial M\setminus \partial B_{\epsilon}}v_{\epsilon}^2ds_g}. \end{align} $$
$$ \begin{align} \sigma^N_k(M\setminus B_{\epsilon},g) \leq \frac{\int_{M\setminus B_{\epsilon}}|\nabla v_{\epsilon}|^2dv_g}{\int_{\partial M\setminus \partial B_{\epsilon}}v_{\epsilon}^2ds_g}. \end{align} $$
Let
![]() $v_{\epsilon }=\sum ^k_{i=1}c_iu_{i,\epsilon }$
. We build the following function
$v_{\epsilon }=\sum ^k_{i=1}c_iu_{i,\epsilon }$
. We build the following function
![]() $v=\sum ^k_{i=1}c_iu_{i} \in V_k\subset H^1(M,g)$
. Note that
$v=\sum ^k_{i=1}c_iu_{i} \in V_k\subset H^1(M,g)$
. Note that
![]() $\nabla v_{\epsilon }=\sum ^k_{i=1}c_i\nabla u_{i,\epsilon }=\sum ^k_{i=1}c_i\nabla u_{i}=\nabla v$
on
$\nabla v_{\epsilon }=\sum ^k_{i=1}c_i\nabla u_{i,\epsilon }=\sum ^k_{i=1}c_i\nabla u_{i}=\nabla v$
on
![]() $M\setminus B_{\epsilon }$
. Thus,
$M\setminus B_{\epsilon }$
. Thus,
![]() $\int _{M\setminus B_{\epsilon }}|\nabla v_{\epsilon }|^2dv_g=\int _{M\setminus B_{\epsilon }}|\nabla v|^2dv_g\to \int _{M}|\nabla v|^2dv_g$
as
$\int _{M\setminus B_{\epsilon }}|\nabla v_{\epsilon }|^2dv_g=\int _{M\setminus B_{\epsilon }}|\nabla v|^2dv_g\to \int _{M}|\nabla v|^2dv_g$
as
![]() $\epsilon \to 0$
. Moreover, it is easy to see that
$\epsilon \to 0$
. Moreover, it is easy to see that
 $$ \begin{align*} &\int_{\partial M\setminus \partial B_{\epsilon}}v_{\epsilon}^2ds_g=\sum_ic^2_i\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}u^2_idv_g-\frac{1}{L(\partial M\setminus \partial B_{\epsilon},g)}\bigg(\int_{\partial M\setminus \partial B_{\epsilon}}u_ids_g\bigg)^2\bigg)\\ & \quad +\sum_{i\neq j}2c_ic_j\bigg(\int_{\partial M\setminus \partial B_{\epsilon}}u_iu_jds_g-\frac{1}{L(\partial M\setminus \partial B_{\epsilon},g)}\int_{\partial M\setminus \partial B_{\epsilon}}u_ids_g\int_{\partial M\setminus \partial B_{\epsilon}}u_jds_g\bigg), \end{align*} $$
$$ \begin{align*} &\int_{\partial M\setminus \partial B_{\epsilon}}v_{\epsilon}^2ds_g=\sum_ic^2_i\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}u^2_idv_g-\frac{1}{L(\partial M\setminus \partial B_{\epsilon},g)}\bigg(\int_{\partial M\setminus \partial B_{\epsilon}}u_ids_g\bigg)^2\bigg)\\ & \quad +\sum_{i\neq j}2c_ic_j\bigg(\int_{\partial M\setminus \partial B_{\epsilon}}u_iu_jds_g-\frac{1}{L(\partial M\setminus \partial B_{\epsilon},g)}\int_{\partial M\setminus \partial B_{\epsilon}}u_ids_g\int_{\partial M\setminus \partial B_{\epsilon}}u_jds_g\bigg), \end{align*} $$
which converges to
![]() $\int _{\partial M}v^2ds_g$
as
$\int _{\partial M}v^2ds_g$
as
![]() $\epsilon \to 0$
. Then (2.3) implies
$\epsilon \to 0$
. Then (2.3) implies
 $$ \begin{align*} \limsup_{\epsilon \to 0}\sigma^N_k(M\setminus B_{\epsilon},g) \leq \limsup_{\epsilon \to 0} \frac{\int_{M\setminus B_{\epsilon}}|\nabla v_{\epsilon}|^2dv_g}{\int_{\partial M\setminus \partial B_{\epsilon}}v_{\epsilon}^2ds_g}= \frac{\int_{M}|\nabla v|^2dv_g}{\int_{\partial M}v^2ds_g} \leq \sigma_k(M,g). \end{align*} $$
$$ \begin{align*} \limsup_{\epsilon \to 0}\sigma^N_k(M\setminus B_{\epsilon},g) \leq \limsup_{\epsilon \to 0} \frac{\int_{M\setminus B_{\epsilon}}|\nabla v_{\epsilon}|^2dv_g}{\int_{\partial M\setminus \partial B_{\epsilon}}v_{\epsilon}^2ds_g}= \frac{\int_{M}|\nabla v|^2dv_g}{\int_{\partial M}v^2ds_g} \leq \sigma_k(M,g). \end{align*} $$
▪
Now, we are ready to prove the Lemma. The proof is similar to the proof of [Reference Matthiesen and SiffertMS20, Lemma 3.2]. Let
![]() $u_{\epsilon }$
be a normalized
$u_{\epsilon }$
be a normalized
![]() $\sigma ^N_k$
-eigenfunction. By Claim 2
$\sigma ^N_k$
-eigenfunction. By Claim 2
![]() $u_{\epsilon }$
are uniformly bounded. If
$u_{\epsilon }$
are uniformly bounded. If
![]() $B_{\epsilon } \cap \partial M=\varnothing $
, then we take the harmonic continuation into
$B_{\epsilon } \cap \partial M=\varnothing $
, then we take the harmonic continuation into
![]() $B_{\epsilon }$
. It is known that the operators of harmonic continuation into
$B_{\epsilon }$
. It is known that the operators of harmonic continuation into
![]() $B_{\epsilon }$
are uniformly bounded (see [Reference Rauch and TaylorRT75, Example 1]). Otherwise we extend
$B_{\epsilon }$
are uniformly bounded (see [Reference Rauch and TaylorRT75, Example 1]). Otherwise we extend
![]() $u_{\epsilon }$
into
$u_{\epsilon }$
into
![]() $B_{\epsilon }$
by
$B_{\epsilon }$
by
![]() $\mathcal E(u_{\epsilon })$
. By Claim 1 these operators are also uniformly bounded. Therefore, we get a uniformly bounded in
$\mathcal E(u_{\epsilon })$
. By Claim 1 these operators are also uniformly bounded. Therefore, we get a uniformly bounded in
![]() $H^1(M,g)$
sequence
$H^1(M,g)$
sequence
![]() $\{\tilde u_{\epsilon }\}$
. Then there exists
$\{\tilde u_{\epsilon }\}$
. Then there exists
![]() $\epsilon _l\to 0$
such that
$\epsilon _l\to 0$
such that
![]() $\tilde u_{\epsilon _l} \rightharpoonup u$
in
$\tilde u_{\epsilon _l} \rightharpoonup u$
in
![]() $H^1(M,g)$
. Thus,
$H^1(M,g)$
. Thus,
![]() $\tilde u_{\epsilon _l} \to u$
in
$\tilde u_{\epsilon _l} \to u$
in
![]() $L^2(M,g)$
by the Rellich–Kondrachov embedding theorem. The standard elliptic estimates imply
$L^2(M,g)$
by the Rellich–Kondrachov embedding theorem. The standard elliptic estimates imply
![]() $u_{\epsilon _l} \to u$
in
$u_{\epsilon _l} \to u$
in
![]() $C^{\infty }_{loc}(M\setminus \{p\})$
. Consider a function
$C^{\infty }_{loc}(M\setminus \{p\})$
. Consider a function
![]() $\varphi \in C^{\infty }_c(M\setminus \{p\})$
such that
$\varphi \in C^{\infty }_c(M\setminus \{p\})$
such that
![]() $supp(\varphi ) \subset M\setminus B_R$
for a ball
$supp(\varphi ) \subset M\setminus B_R$
for a ball
![]() $B_R$
centered at p with R fixed. Extracting a subsequence by Claim 2 one can assume that
$B_R$
centered at p with R fixed. Extracting a subsequence by Claim 2 one can assume that
![]() $\sigma ^N_k(M\setminus B_{\epsilon _l},g)\to \sigma $
. Then we have
$\sigma ^N_k(M\setminus B_{\epsilon _l},g)\to \sigma $
. Then we have
 $$ \begin{align*} \int_M\langle \nabla u, \nabla \varphi \rangle dv_g &= \lim_{l\to 0}\int_{M\setminus B_R}\langle \nabla u_{\epsilon_l}, \nabla \varphi \rangle dv_g \\ &=\lim_{l\to 0}\sigma^N_k(M\setminus B_{\epsilon_l},g)\int_{M\setminus B_R} u_{\epsilon_l} \varphi dv_g=\sigma\int_Mu\varphi dv_g. \end{align*} $$
$$ \begin{align*} \int_M\langle \nabla u, \nabla \varphi \rangle dv_g &= \lim_{l\to 0}\int_{M\setminus B_R}\langle \nabla u_{\epsilon_l}, \nabla \varphi \rangle dv_g \\ &=\lim_{l\to 0}\sigma^N_k(M\setminus B_{\epsilon_l},g)\int_{M\setminus B_R} u_{\epsilon_l} \varphi dv_g=\sigma\int_Mu\varphi dv_g. \end{align*} $$
Hence, u is an eigenfunction with eigenvalue
![]() $\sigma $
. Thus all accumulation points of
$\sigma $
. Thus all accumulation points of
![]() $\{\sigma ^N_k(M\setminus B_{\epsilon _l},g)\}$
are in the Steklov spectrum of M. Our aim now is to show that
$\{\sigma ^N_k(M\setminus B_{\epsilon _l},g)\}$
are in the Steklov spectrum of M. Our aim now is to show that
![]() $\sigma =\sigma _k(M,g)$
. We will do this by showing that the u is orthogonal in
$\sigma =\sigma _k(M,g)$
. We will do this by showing that the u is orthogonal in
![]() $L^2(\partial M,g)$
to the first
$L^2(\partial M,g)$
to the first
![]() $k-1$
Steklov eigenfunctions of
$k-1$
Steklov eigenfunctions of
![]() $(M,g)$
. We use the proof by induction.
$(M,g)$
. We use the proof by induction.
Let
![]() $u_{\epsilon }$
be a first Steklov–Neumann eigenfunction of
$u_{\epsilon }$
be a first Steklov–Neumann eigenfunction of
![]() $(M\setminus B_{\epsilon },g)$
. We have already shown that
$(M\setminus B_{\epsilon },g)$
. We have already shown that
![]() $\tilde u_{\epsilon } \rightharpoonup u$
in
$\tilde u_{\epsilon } \rightharpoonup u$
in
![]() $H^1(M,g)$
then by the trace embedding theorem one has
$H^1(M,g)$
then by the trace embedding theorem one has
![]() $\tilde u_{\epsilon } \to u$
in
$\tilde u_{\epsilon } \to u$
in
![]() $H^{1/2}(\partial M,g)$
and hence in
$H^{1/2}(\partial M,g)$
and hence in
![]() $L^2(\partial M,g)$
. In particular, one has
$L^2(\partial M,g)$
. In particular, one has
![]() $||u_{\epsilon }-{u||_{L^2(\partial M\setminus \partial B_{\epsilon },g)}\to 0}$
as
$||u_{\epsilon }-{u||_{L^2(\partial M\setminus \partial B_{\epsilon },g)}\to 0}$
as
![]() $\epsilon \to 0$
. Then
$\epsilon \to 0$
. Then
 $$ \begin{align*} &\left|\int_{\partial M\setminus\partial B_{\epsilon}}(u_{\epsilon} -u)ds_g\right| \leq \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} -u|ds_g \\ &\quad \leq L(\partial M\setminus \partial B_{\epsilon},g)^{1/2}||u_{\epsilon}-u||_{L^2(\partial M\setminus\partial B_{\epsilon},g)}^{1/2}, \end{align*} $$
$$ \begin{align*} &\left|\int_{\partial M\setminus\partial B_{\epsilon}}(u_{\epsilon} -u)ds_g\right| \leq \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} -u|ds_g \\ &\quad \leq L(\partial M\setminus \partial B_{\epsilon},g)^{1/2}||u_{\epsilon}-u||_{L^2(\partial M\setminus\partial B_{\epsilon},g)}^{1/2}, \end{align*} $$
which converges tp
![]() $0$
as
$0$
as
![]() $\epsilon \to 0$
. Since
$\epsilon \to 0$
. Since
![]() $\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } ds_g=0$
one then has that
$\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } ds_g=0$
one then has that
![]() $\lim _{\epsilon \to 0}\int _{\partial M\setminus \partial B_{\epsilon }}uds_g=\int _{\partial M}uds_g=0$
. Therefore, u cannot be a constant and since by Claim 2
$\lim _{\epsilon \to 0}\int _{\partial M\setminus \partial B_{\epsilon }}uds_g=\int _{\partial M}uds_g=0$
. Therefore, u cannot be a constant and since by Claim 2
![]() $\limsup _{\epsilon \to 0}\sigma ^N_1(M\setminus B_{\epsilon },g)=\sigma \leq \sigma _1(M,g)$
and
$\limsup _{\epsilon \to 0}\sigma ^N_1(M\setminus B_{\epsilon },g)=\sigma \leq \sigma _1(M,g)$
and
![]() $\sigma $
belongs to the Steklov spectrum of
$\sigma $
belongs to the Steklov spectrum of
![]() $(M,g)$
we conclude that u is a first Steklov eigenfunction of
$(M,g)$
we conclude that u is a first Steklov eigenfunction of
![]() $(M,g)$
and
$(M,g)$
and
![]() $\sigma =\sigma _1(M,g)$
.
$\sigma =\sigma _1(M,g)$
.
Now suppose that
![]() $\limsup _{\epsilon \to 0}\sigma ^N_i(M\setminus B_{\epsilon },g)= \sigma _i(M,g)$
for any
$\limsup _{\epsilon \to 0}\sigma ^N_i(M\setminus B_{\epsilon },g)= \sigma _i(M,g)$
for any
![]() $i<k$
. Let
$i<k$
. Let
![]() $u_{\epsilon }$
be a kth Steklov–Neumann eigenfucntion of
$u_{\epsilon }$
be a kth Steklov–Neumann eigenfucntion of
![]() $(M\setminus B_{\epsilon },g)$
. Since
$(M\setminus B_{\epsilon },g)$
. Since
![]() $\tilde u_{\epsilon } \rightharpoonup u$
in
$\tilde u_{\epsilon } \rightharpoonup u$
in
![]() $H^1(M,g),$
then the trace embedding theorem implies that
$H^1(M,g),$
then the trace embedding theorem implies that
![]() $\tilde u_{\epsilon } \to u$
in
$\tilde u_{\epsilon } \to u$
in
![]() $H^{1/2}(\partial M,g)$
in particular
$H^{1/2}(\partial M,g)$
in particular
![]() $\tilde u_{\epsilon } \to u$
in
$\tilde u_{\epsilon } \to u$
in
![]() $L^{2}(\partial M,g)$
whence
$L^{2}(\partial M,g)$
whence
![]() $||u_{\epsilon }-u||_{L^2(\partial M\setminus \partial B_{\epsilon },g)}\to 0$
. Let
$||u_{\epsilon }-u||_{L^2(\partial M\setminus \partial B_{\epsilon },g)}\to 0$
. Let
![]() $v_{\epsilon }$
be an ith Steklov–Neumann eigenfunction of
$v_{\epsilon }$
be an ith Steklov–Neumann eigenfunction of
![]() $(M\setminus B_{\epsilon },g)$
with
$(M\setminus B_{\epsilon },g)$
with
![]() $i<k$
. Then
$i<k$
. Then
![]() $\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } v_{\epsilon } ds_g=0;$
moreover, we have supposed that v is an ith Steklov eigenfunction of
$\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } v_{\epsilon } ds_g=0;$
moreover, we have supposed that v is an ith Steklov eigenfunction of
![]() $(M,g)$
. One has
$(M,g)$
. One has
 $$ \begin{align*} & \left|\int_{\partial M\setminus\partial B_{\epsilon}}(u_{\epsilon} v_{\epsilon} -uv)ds_g\right| \\ &\quad\leq \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} v_{\epsilon} -uv|ds_g= \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} v_{\epsilon} -u_{\epsilon} v+u_{\epsilon} v-uv|ds_g \\ &\quad\leq \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} (v_{\epsilon} -v)|ds_g+\int_{\partial M\setminus\partial B_{\epsilon}}|v (u_{\epsilon} -u)|ds_g \\ &\quad\leq \bigg(\int_{\partial M\setminus\partial B_{\epsilon}}u^2_{\epsilon} ds_g \bigg)^{1/2}\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}(v_{\epsilon}-v)^2 ds_g \bigg)^{1/2} \\ &\qquad+\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}v^2_{\epsilon} ds_g \bigg)^{1/2}\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}(u_{\epsilon}-u)^2 ds_g \bigg)^{1/2}\to 0~\text{as } \epsilon \to 0. \end{align*} $$
$$ \begin{align*} & \left|\int_{\partial M\setminus\partial B_{\epsilon}}(u_{\epsilon} v_{\epsilon} -uv)ds_g\right| \\ &\quad\leq \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} v_{\epsilon} -uv|ds_g= \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} v_{\epsilon} -u_{\epsilon} v+u_{\epsilon} v-uv|ds_g \\ &\quad\leq \int_{\partial M\setminus\partial B_{\epsilon}}|u_{\epsilon} (v_{\epsilon} -v)|ds_g+\int_{\partial M\setminus\partial B_{\epsilon}}|v (u_{\epsilon} -u)|ds_g \\ &\quad\leq \bigg(\int_{\partial M\setminus\partial B_{\epsilon}}u^2_{\epsilon} ds_g \bigg)^{1/2}\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}(v_{\epsilon}-v)^2 ds_g \bigg)^{1/2} \\ &\qquad+\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}v^2_{\epsilon} ds_g \bigg)^{1/2}\bigg(\int_{\partial M\setminus\partial B_{\epsilon}}(u_{\epsilon}-u)^2 ds_g \bigg)^{1/2}\to 0~\text{as } \epsilon \to 0. \end{align*} $$
Hence,
![]() $\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } v_{\epsilon } ds_g\to \int _{\partial M}u v ds_g$
as
$\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } v_{\epsilon } ds_g\to \int _{\partial M}u v ds_g$
as
![]() $\epsilon \to 0$
. But
$\epsilon \to 0$
. But
![]() $\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } v_{\epsilon } ds_g=0$
for all
$\int _{\partial M\setminus \partial B_{\epsilon }}u_{\epsilon } v_{\epsilon } ds_g=0$
for all
![]() $\epsilon $
. Thus,
$\epsilon $
. Thus,
![]() $\int _{\partial M}u v ds_g=0$
. We conclude that u is orthogonal in
$\int _{\partial M}u v ds_g=0$
. We conclude that u is orthogonal in
![]() $L^2(\partial M,g)$
to the first
$L^2(\partial M,g)$
to the first
![]() $k-1$
Steklov eigenfunctions. Thus,
$k-1$
Steklov eigenfunctions. Thus,
![]() $\sigma =\sigma ^N_k(M,g)$
.▪
$\sigma =\sigma ^N_k(M,g)$
.▪
We endow the set of Riemannian metrics on
![]() $\Sigma $
with the
$\Sigma $
with the
![]() $C^{\infty }-$
topology. Then the following “continuity” result holds.
$C^{\infty }-$
topology. Then the following “continuity” result holds.
Proposition 2.2 Let
![]() $\Sigma $
be a surface with boundary and
$\Sigma $
be a surface with boundary and
![]() $\Omega \subset \Sigma $
be a Lipschitz domain. Let the sequence of Riemannian metrics
$\Omega \subset \Sigma $
be a Lipschitz domain. Let the sequence of Riemannian metrics
![]() $g_m$
on
$g_m$
on
![]() $\Sigma $
converge in
$\Sigma $
converge in
![]() $C^{\infty }-$
topology to the metric g. Then
$C^{\infty }-$
topology to the metric g. Then
![]() $\sigma ^*_k(\Sigma ,[g_m])\to \sigma ^*_k(\Sigma ,[g])$
. Similarly, if
$\sigma ^*_k(\Sigma ,[g_m])\to \sigma ^*_k(\Sigma ,[g])$
. Similarly, if
![]() $h_m|_{\overline \Omega }$
converge to
$h_m|_{\overline \Omega }$
converge to
![]() $g|_{\overline \Omega }$
in
$g|_{\overline \Omega }$
in
![]() $C^{\infty }$
-topology, then
$C^{\infty }$
-topology, then
![]() $\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [h_m|_{\overline \Omega }])\to \sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g|_{\overline \Omega }])$
.
$\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [h_m|_{\overline \Omega }])\to \sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g|_{\overline \Omega }])$
.
Proof We provide a proof for the functional
![]() $\sigma ^*_k(\Sigma ,[g])$
. The proof for the functional
$\sigma ^*_k(\Sigma ,[g])$
. The proof for the functional
![]() $\sigma ^{N*}_k(\Omega ,[g|_{\overline \Omega }])$
follows the exactly same arguments.
$\sigma ^{N*}_k(\Omega ,[g|_{\overline \Omega }])$
follows the exactly same arguments.
Choose any
![]() $\varepsilon>0$
and consider m large enough. One has
$\varepsilon>0$
and consider m large enough. One has
where f is any positive smooth function on
![]() $\Sigma $
. Then by [Reference Colbois, Girouard and RaveendranCGR18, Proposition 32] one has
$\Sigma $
. Then by [Reference Colbois, Girouard and RaveendranCGR18, Proposition 32] one has
Taking the supremum over all f yields
which completes the proof since this inequality holds for any
![]() $\varepsilon>0$
.▪
$\varepsilon>0$
.▪
2.2 Discontinuous metrics
Let
![]() $\Sigma $
be a compact surface with boundary. Consider a set of pairwise disjoint Lipschitz domains
$\Sigma $
be a compact surface with boundary. Consider a set of pairwise disjoint Lipschitz domains
![]() $\{\Omega _i\}^s_{i=1}$
in
$\{\Omega _i\}^s_{i=1}$
in
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
. Let
$\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
. Let
![]() $C^{\infty }_+(\Sigma ,\{\Omega _i\})$
denote a set of functions on
$C^{\infty }_+(\Sigma ,\{\Omega _i\})$
denote a set of functions on
![]() $\bigcup ^s_{i=1} \overline \Omega _i$
such that
$\bigcup ^s_{i=1} \overline \Omega _i$
such that
![]() $\rho \in C^{\infty }_+(\Sigma ,\{\Omega _i\})$
means that
$\rho \in C^{\infty }_+(\Sigma ,\{\Omega _i\})$
means that
![]() $\rho |_{\Omega _i} = \rho _i\in C^{\infty }(\overline \Omega _i)$
are positive for every i. Similarly,
$\rho |_{\Omega _i} = \rho _i\in C^{\infty }(\overline \Omega _i)$
are positive for every i. Similarly,
![]() $C^{\infty }(\Sigma ,\{\Omega _i\})$
denotes a set of “smooth” functions on
$C^{\infty }(\Sigma ,\{\Omega _i\})$
denotes a set of “smooth” functions on
![]() $\bigcup ^s_{i=1} \overline \Omega _i$
. We introduce discontinuous metrics on
$\bigcup ^s_{i=1} \overline \Omega _i$
. We introduce discontinuous metrics on
![]() $\Sigma $
defined as
$\Sigma $
defined as
![]() $\rho g\in [g]$
, where
$\rho g\in [g]$
, where
![]() $\rho \in C^{\infty }_+(\Sigma ,\{\Omega _i\})$
and g is a genuine Riemannian metric. The set
$\rho \in C^{\infty }_+(\Sigma ,\{\Omega _i\})$
and g is a genuine Riemannian metric. The set
![]() $C^{k}(\Sigma ,\{\Omega _i\})$
of functions which are of class
$C^{k}(\Sigma ,\{\Omega _i\})$
of functions which are of class
![]() $C^k$
in every
$C^k$
in every
![]() $\overline \Omega _i$
is defined in a similar way. The Steklov spectrum of the metric
$\overline \Omega _i$
is defined in a similar way. The Steklov spectrum of the metric
![]() $\rho g$
is defined as the set of critical values of the Rayleigh quotient
$\rho g$
is defined as the set of critical values of the Rayleigh quotient
 $$ \begin{align*} R_{\rho g}[\varphi]=\frac{\int_{\Sigma} | \nabla_g \varphi|^2_g dv_g}{\int_{\partial \Sigma} \rho^{\frac{1}{2}} \varphi^2 ds_g}. \end{align*} $$
$$ \begin{align*} R_{\rho g}[\varphi]=\frac{\int_{\Sigma} | \nabla_g \varphi|^2_g dv_g}{\int_{\partial \Sigma} \rho^{\frac{1}{2}} \varphi^2 ds_g}. \end{align*} $$
This is the Rayleigh quotient of the Steklov problem with density
![]() $\rho $
. The Steklov spectrum with density
$\rho $
. The Steklov spectrum with density
![]() $\rho $
is well-defined for any non-negative
$\rho $
is well-defined for any non-negative
![]() $\rho \in L^{\infty }(\Sigma ,g)$
(see [Reference KokarevKok14, Proposition 1.3]). Elliptic regularity implies that the eigenfunctions are at least
$\rho \in L^{\infty }(\Sigma ,g)$
(see [Reference KokarevKok14, Proposition 1.3]). Elliptic regularity implies that the eigenfunctions are at least
![]() $1/2$
-Hölder continuous on
$1/2$
-Hölder continuous on
![]() $\partial \Sigma $
. Therefore, Steklov eigenvalues of the metric
$\partial \Sigma $
. Therefore, Steklov eigenvalues of the metric
![]() $\rho g$
admit the following variational characterization
$\rho g$
admit the following variational characterization
where
![]() $E_{k+1}$
ranges over all
$E_{k+1}$
ranges over all
![]() $(k+1)$
-dimensional subspaces of
$(k+1)$
-dimensional subspaces of
![]() $C^0(\Sigma )$
.
$C^0(\Sigma )$
.
We introduce the following notation
where
![]() $\bar \sigma _k(\rho g)$
is the normalized kth eigenvalue given by
$\bar \sigma _k(\rho g)$
is the normalized kth eigenvalue given by
The following lemma particularly asserts that the quantity
![]() $\sigma ^*_k(\Sigma ,\{\Omega _i\},[g])$
is well-defined.
$\sigma ^*_k(\Sigma ,\{\Omega _i\},[g])$
is well-defined.
Lemma 2.3 Let
![]() $(\Sigma ,g)$
be a Riemannian surface with boundary. Consider a set of pairwise disjoint Lipschitz domains
$(\Sigma ,g)$
be a Riemannian surface with boundary. Consider a set of pairwise disjoint Lipschitz domains
![]() $\Omega _i$
such that
$\Omega _i$
such that
![]() $\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
. Then one has
$\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
. Then one has
Proof The proof follows the same steps as the proof of Lemma 2 in the paper [Reference Friedlander and NadirashviliFN99]. We provide it here.
Since the set of discontinuous metrics is larger than the set of continuous ones, we have
![]() $\sigma ^*_k(\Sigma ,\{\Omega _i\},[g])) \geq \sigma ^*_k(\Sigma ,[g])$
. Therefore, we have to prove that
$\sigma ^*_k(\Sigma ,\{\Omega _i\},[g])) \geq \sigma ^*_k(\Sigma ,[g])$
. Therefore, we have to prove that
which is equivalent to
where
![]() $\rho \in C^{\infty }_{+}(\Sigma ,\{\Omega _i\})$
and
$\rho \in C^{\infty }_{+}(\Sigma ,\{\Omega _i\})$
and
![]() $ \int _{\partial \Sigma } \rho ^{1/2}ds_g =1$
.
$ \int _{\partial \Sigma } \rho ^{1/2}ds_g =1$
.
Let
![]() $E_k$
be the eigenspace corresponding to the kth Steklov eigenvalue of the metric
$E_k$
be the eigenspace corresponding to the kth Steklov eigenvalue of the metric
![]() $\rho g$
. We put
$\rho g$
. We put
For any
![]() $\varepsilon>0$
we consider the functional
$\varepsilon>0$
we consider the functional
It immediately follows that
![]() $\mathcal {F}_{\rho }[u] \geq \varepsilon , \forall u\in S$
.
$\mathcal {F}_{\rho }[u] \geq \varepsilon , \forall u\in S$
.
Let
![]() $0<a:=\min _{\cup \{\Omega _i\}}\rho $
and
$0<a:=\min _{\cup \{\Omega _i\}}\rho $
and
![]() $\max _{\cup \{\Omega _i\}}=:b<\infty $
. We define a smooth nondecreasing function
$\max _{\cup \{\Omega _i\}}=:b<\infty $
. We define a smooth nondecreasing function
![]() $\chi (t)$
on
$\chi (t)$
on
![]() $\mathbb {R}_+$
that equals zero if
$\mathbb {R}_+$
that equals zero if
![]() $t<1/2$
and equals 1 when
$t<1/2$
and equals 1 when
![]() $t>1$
and define the following parametrized family of functions:
$t>1$
and define the following parametrized family of functions:
 $$ \begin{align*} \rho_{\delta}(x) = \begin{cases} \rho(x) &\text{if } x \notin U,\\ \rho(x)\chi \big(\frac{d^2(x)}{\delta}\big)+b\big(1-\chi \big(\frac{d^2(x)}{\delta}\big)\big) &\text{if } x \in U, \end{cases} \end{align*} $$
$$ \begin{align*} \rho_{\delta}(x) = \begin{cases} \rho(x) &\text{if } x \notin U,\\ \rho(x)\chi \big(\frac{d^2(x)}{\delta}\big)+b\big(1-\chi \big(\frac{d^2(x)}{\delta}\big)\big) &\text{if } x \in U, \end{cases} \end{align*} $$
where d is the distance function from a point
![]() $x\in \Sigma $
to
$x\in \Sigma $
to
![]() $\cup \{\partial \Omega _i\cap \partial \Omega _j\},~i\neq j$
and U is a sufficiently small tubular neighborhood of
$\cup \{\partial \Omega _i\cap \partial \Omega _j\},~i\neq j$
and U is a sufficiently small tubular neighborhood of
![]() $\cup \{\partial \Omega _i\cap \partial \Omega _j\},~i\neq j$
where
$\cup \{\partial \Omega _i\cap \partial \Omega _j\},~i\neq j$
where
![]() $d^2$
is smooth. We have:
$d^2$
is smooth. We have:
-
(i)
 $\big (\frac {a}{b}\big )\rho \leq \rho _{\delta } \leq \big (\frac {b}{a}\big ) \rho $
;
$\big (\frac {a}{b}\big )\rho \leq \rho _{\delta } \leq \big (\frac {b}{a}\big ) \rho $
; -
(ii)
 $\lim _{\delta \to 0} \int _{\partial \Sigma } \rho ^{1/2}_{\delta } ds_g=1$
; and
$\lim _{\delta \to 0} \int _{\partial \Sigma } \rho ^{1/2}_{\delta } ds_g=1$
; and -
(iii)
 $\lim _{\delta \to 0} \int _{\partial \Sigma } |\rho ^{1/2}_{\delta } - \rho ^{1/2}|^q ds_g=0, \forall q<\infty $
.
$\lim _{\delta \to 0} \int _{\partial \Sigma } |\rho ^{1/2}_{\delta } - \rho ^{1/2}|^q ds_g=0, \forall q<\infty $
.
We want to prove that
![]() $\mathcal {F}_{\rho _{\delta }}[u] \geq 0, \forall u \in S$
.
$\mathcal {F}_{\rho _{\delta }}[u] \geq 0, \forall u \in S$
.
Consider
![]() $T=(\sigma _k(\Sigma ,\rho g) -\varepsilon )\sqrt {\frac {b}{a}}$
and divide the set S into two parts
$T=(\sigma _k(\Sigma ,\rho g) -\varepsilon )\sqrt {\frac {b}{a}}$
and divide the set S into two parts
![]() $S_1$
and
$S_1$
and
![]() $S_2$
:
$S_2$
:
 $$ \begin{align*} S_1 &:=\left\{u \in S | \int_{\Sigma} |\nabla_g u|^2 dv_g \geq T\right\}, \\ S_2&:=S \setminus S_1= \left\{u \in S | \int_{\Sigma} |\nabla_g u|^2 dv_g < T\right\}. \end{align*} $$
$$ \begin{align*} S_1 &:=\left\{u \in S | \int_{\Sigma} |\nabla_g u|^2 dv_g \geq T\right\}, \\ S_2&:=S \setminus S_1= \left\{u \in S | \int_{\Sigma} |\nabla_g u|^2 dv_g < T\right\}. \end{align*} $$
If
![]() $u \in S_1$
then
$u \in S_1$
then
 $$ \begin{align*} \mathcal{F}_{\rho_{\delta}}[u] &= \int_{\Sigma}|\nabla_gu|^2dv_g-(\sigma_k(\Sigma,\rho g)-\varepsilon)\int_{\partial\Sigma}\rho_{\delta}^{1/2}u^2ds_g \\ &\geq (\sigma_k(\Sigma,\rho g)-\varepsilon)\left(\sqrt{\frac{b}{a}}-\int_{\partial\Sigma}\rho_{\delta}^{1/2}u^2ds_g\right) \\ &\geq(\sigma_k(\Sigma,\rho g)-\varepsilon)\sqrt{\frac{b}{a}}\left(1-\int_{\partial\Sigma}\rho^{1/2}u^2ds_g\right)=0. \end{align*} $$
$$ \begin{align*} \mathcal{F}_{\rho_{\delta}}[u] &= \int_{\Sigma}|\nabla_gu|^2dv_g-(\sigma_k(\Sigma,\rho g)-\varepsilon)\int_{\partial\Sigma}\rho_{\delta}^{1/2}u^2ds_g \\ &\geq (\sigma_k(\Sigma,\rho g)-\varepsilon)\left(\sqrt{\frac{b}{a}}-\int_{\partial\Sigma}\rho_{\delta}^{1/2}u^2ds_g\right) \\ &\geq(\sigma_k(\Sigma,\rho g)-\varepsilon)\sqrt{\frac{b}{a}}\left(1-\int_{\partial\Sigma}\rho^{1/2}u^2ds_g\right)=0. \end{align*} $$
Let us show that
![]() $||u||_{L^p(\partial \Sigma ,g)}$
with
$||u||_{L^p(\partial \Sigma ,g)}$
with
![]() $p\geq 2$
is bounded for any
$p\geq 2$
is bounded for any
![]() $u \in S_2$
. We consider the following operator
$u \in S_2$
. We consider the following operator
![]() $L[u]:=\int _{\partial \Sigma }u\rho ^{1/2}ds_g$
. For this operator, one has
$L[u]:=\int _{\partial \Sigma }u\rho ^{1/2}ds_g$
. For this operator, one has
which implies that
![]() $L\in H^{-1}(\Sigma ,g)$
. Here, we used in order the boundedness of
$L\in H^{-1}(\Sigma ,g)$
. Here, we used in order the boundedness of
![]() $\rho $
, the Cauchy–Schwarz and the trace inequalities. We also used the convention that C denotes any positive constant depending only on
$\rho $
, the Cauchy–Schwarz and the trace inequalities. We also used the convention that C denotes any positive constant depending only on
![]() $\Sigma $
. [Reference Adams and HedbergAH96, Lemma 8.3.1] applied to the operator L implies that there exists a constant
$\Sigma $
. [Reference Adams and HedbergAH96, Lemma 8.3.1] applied to the operator L implies that there exists a constant
![]() $C>0$
depending only on
$C>0$
depending only on
![]() $\Sigma $
such that
$\Sigma $
such that
where we used the fact that
![]() $L[u]=0~\forall u\in S$
. By the trace theorem one then has
$L[u]=0~\forall u\in S$
. By the trace theorem one then has
where
![]() $C"=C'(CT+T)$
. Finally by the Sobolev embedding theorem (see for instance [Reference Di Nezza, Palatucci and ValdinociDNPV12, Theorem 6.9]) we get
$C"=C'(CT+T)$
. Finally by the Sobolev embedding theorem (see for instance [Reference Di Nezza, Palatucci and ValdinociDNPV12, Theorem 6.9]) we get
where
![]() $\tilde C=C"'\sqrt {C"}$
. Therefore, if
$\tilde C=C"'\sqrt {C"}$
. Therefore, if
![]() $u \in S_2$
then
$u \in S_2$
then
 $$ \begin{align*} \mathcal{F}_{\rho_{\delta}}[u] &= \int_{\Sigma}|\nabla_gu|^2dv_g-(\sigma_k(\Sigma,\rho g)-\varepsilon)\int_{\partial\Sigma}\rho_{\delta}^{1/2}u^2ds_g \\ &=\int_{\Sigma}|\nabla_gu|^2dv_g- (\sigma_k(\Sigma,\rho g)-\varepsilon)-(\sigma_k(\Sigma,\rho g)-\varepsilon) \int_{\partial\Sigma} (\rho_{\delta}^{1/2}-\rho^{1/2}) u^2ds_g \\ &\geq \varepsilon-(\sigma_k(\Sigma,\rho g)-\varepsilon) \bigg(\int_{\partial\Sigma} (\rho_{\delta}^{1/2}-\rho^{1/2})^qds_g\bigg)^{1/q} \bigg(\int_{\partial\Sigma}|u|^pds_g\bigg)^{2/p} \\ &\geq \varepsilon-(\sigma_k(\Sigma,\rho g)-\varepsilon)\frac{\varepsilon}{\sigma_k(\Sigma,\rho g)-\varepsilon}=0. \end{align*} $$
$$ \begin{align*} \mathcal{F}_{\rho_{\delta}}[u] &= \int_{\Sigma}|\nabla_gu|^2dv_g-(\sigma_k(\Sigma,\rho g)-\varepsilon)\int_{\partial\Sigma}\rho_{\delta}^{1/2}u^2ds_g \\ &=\int_{\Sigma}|\nabla_gu|^2dv_g- (\sigma_k(\Sigma,\rho g)-\varepsilon)-(\sigma_k(\Sigma,\rho g)-\varepsilon) \int_{\partial\Sigma} (\rho_{\delta}^{1/2}-\rho^{1/2}) u^2ds_g \\ &\geq \varepsilon-(\sigma_k(\Sigma,\rho g)-\varepsilon) \bigg(\int_{\partial\Sigma} (\rho_{\delta}^{1/2}-\rho^{1/2})^qds_g\bigg)^{1/q} \bigg(\int_{\partial\Sigma}|u|^pds_g\bigg)^{2/p} \\ &\geq \varepsilon-(\sigma_k(\Sigma,\rho g)-\varepsilon)\frac{\varepsilon}{\sigma_k(\Sigma,\rho g)-\varepsilon}=0. \end{align*} $$
In the last inequality, we put
 $$ \begin{align*} \bigg(\int_{\partial\Sigma}(\rho_{\delta}^{1/2}-\rho^{1/2})^qds_g\bigg)^{1/q}\bigg(\int_{\partial\Sigma}|u|^pds_g\bigg)^{2/p}= \frac{\varepsilon}{\sigma_k(\Sigma,\rho g)-\varepsilon} \end{align*} $$
$$ \begin{align*} \bigg(\int_{\partial\Sigma}(\rho_{\delta}^{1/2}-\rho^{1/2})^qds_g\bigg)^{1/q}\bigg(\int_{\partial\Sigma}|u|^pds_g\bigg)^{2/p}= \frac{\varepsilon}{\sigma_k(\Sigma,\rho g)-\varepsilon} \end{align*} $$
since
![]() $\int _{\partial \Sigma }(\rho _{\delta }^{1/2}-\rho ^{1/2})^qds_g \to 0$
as
$\int _{\partial \Sigma }(\rho _{\delta }^{1/2}-\rho ^{1/2})^qds_g \to 0$
as
![]() $\delta \to 0$
and
$\delta \to 0$
and
![]() $\int _{\partial \Sigma }|u|^pds_g<+\infty $
.
$\int _{\partial \Sigma }|u|^pds_g<+\infty $
.
Hence,
![]() $\mathcal {F}_{\rho _{\delta }}[u] \geq 0, \forall u \in S$
which implies
$\mathcal {F}_{\rho _{\delta }}[u] \geq 0, \forall u \in S$
which implies
![]() $\sigma _k(\Sigma ,\rho _{\delta } g) \geq \sigma _k (\Sigma , \rho g) -\varepsilon $
. We then have
$\sigma _k(\Sigma ,\rho _{\delta } g) \geq \sigma _k (\Sigma , \rho g) -\varepsilon $
. We then have
Therefore,
![]() $\sigma ^*_k (\Sigma , [g]) \geq \sigma _k (\Sigma , \rho g) L_{\rho _{\delta } g}(\partial \Sigma ) -\varepsilon L_{\rho _{\delta } g}(\partial \Sigma )$
. Letting
$\sigma ^*_k (\Sigma , [g]) \geq \sigma _k (\Sigma , \rho g) L_{\rho _{\delta } g}(\partial \Sigma ) -\varepsilon L_{\rho _{\delta } g}(\partial \Sigma )$
. Letting
![]() $\delta \to 0$
one then gets
$\delta \to 0$
one then gets
![]() $\sigma ^*_k (\Sigma , [g]) \geq \sigma _k (\Sigma , \rho g)-\varepsilon $
that implies (2.4) since
$\sigma ^*_k (\Sigma , [g]) \geq \sigma _k (\Sigma , \rho g)-\varepsilon $
that implies (2.4) since
![]() $\varepsilon $
is arbitrary small.▪
$\varepsilon $
is arbitrary small.▪
Lemma 2.3 implies the following lemma whose proof is postponed to Section 7.2.
Lemma 2.4 Let
![]() $(\Sigma ,g)$
be a Riemannian surface with boundary. Consider a set of pairwise disjoint domains
$(\Sigma ,g)$
be a Riemannian surface with boundary. Consider a set of pairwise disjoint domains
![]() $\Omega _i$
such that
$\Omega _i$
such that
![]() $\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
and
$\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
and
![]() $\Omega _i\cap \partial \Sigma =\partial ^S\Omega _i$
. Let
$\Omega _i\cap \partial \Sigma =\partial ^S\Omega _i$
. Let
![]() $(\Omega ,h) = \sqcup (\overline \Omega _i,g|_{\overline \Omega _i})$
and
$(\Omega ,h) = \sqcup (\overline \Omega _i,g|_{\overline \Omega _i})$
and
![]() $\partial ^S\Omega =\sqcup \partial ^S\Omega _i$
. Then for all
$\partial ^S\Omega =\sqcup \partial ^S\Omega _i$
. Then for all
![]() $k \geq 0$
one has
$k \geq 0$
one has
2.3 Steklov–Neumann spectrum of a subdomain
This section is devoted to the following technical lemma
Lemma 2.5 Let
![]() $\rho _{\delta } \in C^{\infty }_+(\Sigma ,\{\Omega ,\Sigma \setminus \Omega \})$
such that
$\rho _{\delta } \in C^{\infty }_+(\Sigma ,\{\Omega ,\Sigma \setminus \Omega \})$
such that
![]() $\rho _{\delta }|_{\Omega }\equiv 1$
and
$\rho _{\delta }|_{\Omega }\equiv 1$
and
![]() $\rho _{\delta }|_{\Sigma \setminus \Omega }\equiv \delta $
. Then one has
$\rho _{\delta }|_{\Sigma \setminus \Omega }\equiv \delta $
. Then one has
where
![]() $\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , g)$
is the kth Steklov–Neumann eigenvalue of the domain
$\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , g)$
is the kth Steklov–Neumann eigenvalue of the domain
![]() $(\Omega ,g)$
and
$(\Omega ,g)$
and
![]() $\partial ^S\Omega =\partial \Sigma \cap \Omega \neq \varnothing $
.
$\partial ^S\Omega =\partial \Sigma \cap \Omega \neq \varnothing $
.
Proof The idea of the proof comes from the proof of [Reference Enciso and Peralta-SalasEPS15, Section 2, Step 2].
Case I. First, we consider the case when
![]() $\Omega ^c \cap \partial \Sigma \neq \varnothing $
. Let
$\Omega ^c \cap \partial \Sigma \neq \varnothing $
. Let
![]() $\Omega ^c$
denotes
$\Omega ^c$
denotes
![]() $int(\Sigma \setminus \Omega )$
and
$int(\Sigma \setminus \Omega )$
and
![]() $\partial ^S\Omega ^c=\partial \Omega ^c \cap \partial \Sigma $
. Since by elliptic regularity eigenfunctions of the Steklov problem with bounded density are in
$\partial ^S\Omega ^c=\partial \Omega ^c \cap \partial \Sigma $
. Since by elliptic regularity eigenfunctions of the Steklov problem with bounded density are in
![]() $H^1$
on the boundary we can restrict ourselves to the space
$H^1$
on the boundary we can restrict ourselves to the space
![]() $H^1(\partial \Sigma ,g)$
. More precisely, let
$H^1(\partial \Sigma ,g)$
. More precisely, let
![]() $\psi $
be an eigenfunction with eigenvalue
$\psi $
be an eigenfunction with eigenvalue
![]() $\sigma $
then by elliptic regularity:
$\sigma $
then by elliptic regularity:
for some positive constant C. This implies
 $$ \begin{align*} \frac{||\nabla \psi||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}}{||\psi||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}} \leq C(\sigma^2+1)-1. \end{align*} $$
$$ \begin{align*} \frac{||\nabla \psi||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}}{||\psi||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}} \leq C(\sigma^2+1)-1. \end{align*} $$
More generally we see that if
![]() $\varphi \in \operatorname {span}\langle \psi _0,\ldots ,\psi _k \rangle $
, where
$\varphi \in \operatorname {span}\langle \psi _0,\ldots ,\psi _k \rangle $
, where
![]() $\psi _i$
is in the ith eigenspace of
$\psi _i$
is in the ith eigenspace of
![]() $(\Sigma ,g_{\delta })$
then there exists a constant
$(\Sigma ,g_{\delta })$
then there exists a constant
![]() $C_k>0$
such that
$C_k>0$
such that
 $$ \begin{align*} \frac{||\nabla \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}}{|| \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}} \leq C_k. \end{align*} $$
$$ \begin{align*} \frac{||\nabla \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}}{|| \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}} \leq C_k. \end{align*} $$
Therefore, we set
 $$ \begin{align*} \mathcal H &:=\{\varphi \in H^1(\partial\Sigma,g)~|~\frac{||\nabla \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}}{|| \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}} \leq C_k\}, \\ \mathcal{H}_1 &:=\left\{\varphi \in \mathcal H ~|~\frac{\partial\hat\varphi}{\partial n}=0~\text{on } \partial^S\Omega^c\right\}, \end{align*} $$
$$ \begin{align*} \mathcal H &:=\{\varphi \in H^1(\partial\Sigma,g)~|~\frac{||\nabla \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}}{|| \varphi ||^2_{L^2(\partial\Sigma,\rho_{\delta} g)}} \leq C_k\}, \\ \mathcal{H}_1 &:=\left\{\varphi \in \mathcal H ~|~\frac{\partial\hat\varphi}{\partial n}=0~\text{on } \partial^S\Omega^c\right\}, \end{align*} $$
where
![]() $\hat \varphi $
stands for the harmonic continuation of
$\hat \varphi $
stands for the harmonic continuation of
![]() $\varphi $
into
$\varphi $
into
![]() $\Sigma $
and
$\Sigma $
and
Claim 1. One has
for any metric
![]() $\widetilde g\in [g]$
.
$\widetilde g\in [g]$
.
Proof
 $$ \begin{align*} \int_{\Sigma}\langle\nabla \hat\varphi, \nabla \hat\psi \rangle_{\tilde g} dv_{\tilde g}&=\int_{\Sigma} \Delta_{\tilde g} \hat\varphi \hat\psi dv_{\tilde g}+\int_{\partial \Sigma}\frac{\partial\hat\varphi}{\partial \tilde n}\psi ds_{\tilde g}\\ &=\int_{\partial^S\Omega^c}\frac{\partial\hat\varphi}{\partial \tilde n}\psi ds_{\tilde g}+\int_{\partial^S\Omega}\frac{\partial\hat\varphi}{\partial \tilde n}\psi ds_{\tilde g}=0. \end{align*} $$
$$ \begin{align*} \int_{\Sigma}\langle\nabla \hat\varphi, \nabla \hat\psi \rangle_{\tilde g} dv_{\tilde g}&=\int_{\Sigma} \Delta_{\tilde g} \hat\varphi \hat\psi dv_{\tilde g}+\int_{\partial \Sigma}\frac{\partial\hat\varphi}{\partial \tilde n}\psi ds_{\tilde g}\\ &=\int_{\partial^S\Omega^c}\frac{\partial\hat\varphi}{\partial \tilde n}\psi ds_{\tilde g}+\int_{\partial^S\Omega}\frac{\partial\hat\varphi}{\partial \tilde n}\psi ds_{\tilde g}=0. \end{align*} $$
▪
For the sake of simplicity, we use the symbols
![]() $\sigma ^{\delta }_k$
for
$\sigma ^{\delta }_k$
for
![]() $\sigma _k(\rho _{\delta } g)$
,
$\sigma _k(\rho _{\delta } g)$
,
![]() $g_{\delta }$
for
$g_{\delta }$
for
![]() $\rho _{\delta } g$
and
$\rho _{\delta } g$
and
![]() $R_{\delta }$
for the Rayleigh quotient
$R_{\delta }$
for the Rayleigh quotient
 $$ \begin{align*} R_{\delta}[\varphi]=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g_{\delta}}dv_{g_{\delta}}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}. \end{align*} $$
$$ \begin{align*} R_{\delta}[\varphi]=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g_{\delta}}dv_{g_{\delta}}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}. \end{align*} $$
Claim 2. There exists a constant that we also denote by
![]() $C_k>0$
such that
$C_k>0$
such that
![]() $\sigma ^{\delta }_k \leq C_k$
.
$\sigma ^{\delta }_k \leq C_k$
.
Proof Theorem 1.1 implies that there exists a constant
![]() $C(k)>0$
such that
$C(k)>0$
such that
By Lemma 2.3 for every
![]() $\delta $
one has
$\delta $
one has
Therefore,
 $$ \begin{align*} \sigma^{\delta}_k \leq \frac{C(k)}{L_{g_{\delta}}(\partial \Sigma)}=\frac{C(k)}{L_{g}(\partial^S\Omega)+ \delta ^{1/2}L_{g}(\partial^S \Omega^c)} \leq \frac{C(k)}{L_{g}(\partial^S \Omega)}=C_k. \end{align*} $$
$$ \begin{align*} \sigma^{\delta}_k \leq \frac{C(k)}{L_{g_{\delta}}(\partial \Sigma)}=\frac{C(k)}{L_{g}(\partial^S\Omega)+ \delta ^{1/2}L_{g}(\partial^S \Omega^c)} \leq \frac{C(k)}{L_{g}(\partial^S \Omega)}=C_k. \end{align*} $$
▪
Let
![]() $W_k$
be the set of
$W_k$
be the set of
![]() $k+1$
-dimensional subspaces of
$k+1$
-dimensional subspaces of
![]() $\mathcal H$
satisfying the condition that
$\mathcal H$
satisfying the condition that
![]() ${R_{\delta }}|_{W_k} \leq C_k$
. Claim 2 particularly implies that the space spanned by the first
${R_{\delta }}|_{W_k} \leq C_k$
. Claim 2 particularly implies that the space spanned by the first
![]() $k+1$
eigenfunctions is in
$k+1$
eigenfunctions is in
![]() $W_k$
, i.e.,
$W_k$
, i.e.,
![]() $W_k\ne \varnothing $
.
$W_k\ne \varnothing $
.
Consider the operator
![]() $\mathcal E$
defined in section 2.1 by
$\mathcal E$
defined in section 2.1 by
 $$ \begin{align*} \begin{cases} \Delta_{g} \mathcal E(u)=0&\text{in } \Sigma,\\ \frac{\partial \mathcal E(u)}{\partial n}=0&\text{on } \partial^S\Omega^c,\\ \mathcal E(u)=u&\text{on } \partial^S\Omega. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta_{g} \mathcal E(u)=0&\text{in } \Sigma,\\ \frac{\partial \mathcal E(u)}{\partial n}=0&\text{on } \partial^S\Omega^c,\\ \mathcal E(u)=u&\text{on } \partial^S\Omega. \end{cases} \end{align*} $$
For a function
![]() $\varphi \in H^1(\partial \Sigma ,g),$
we fix its decomposition
$\varphi \in H^1(\partial \Sigma ,g),$
we fix its decomposition
![]() $\varphi _1+\varphi _2$
with
$\varphi _1+\varphi _2$
with
 $$ \begin{align*} \varphi_1= \begin{cases} \varphi&\text{on } \partial^S\Omega,\\ \mathcal E(\varphi)&\text{on } \partial^S\Omega^c \end{cases} \end{align*} $$
$$ \begin{align*} \varphi_1= \begin{cases} \varphi&\text{on } \partial^S\Omega,\\ \mathcal E(\varphi)&\text{on } \partial^S\Omega^c \end{cases} \end{align*} $$
and
![]() $\varphi _2=\varphi _1-\varphi $
. Note that
$\varphi _2=\varphi _1-\varphi $
. Note that
![]() $\hat \varphi _1=\mathcal E(\varphi _1).$
$\hat \varphi _1=\mathcal E(\varphi _1).$
Claim 3. For every
![]() $\varphi \in V \in W_k$
there exists a constant
$\varphi \in V \in W_k$
there exists a constant
![]() $C>0$
such that
$C>0$
such that
Proof By Claim 1, one has
Further, since
![]() $\varphi \in V \in W_k$
, we have
$\varphi \in V \in W_k$
, we have
 $$ \begin{align*} C_k \geq R_{\delta}[\varphi]&=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2dv_{g}+\int_{\Sigma}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \\ &\geq \frac{\int_{\Omega^c}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{1}{\delta^{1/2}}\frac{\int_{\Omega^c}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial^S\Omega^c} \varphi^2_2 ds_{g}}\frac{||\varphi_2||^2_{L^2(\partial^S\Omega^c, g_{\delta})}}{||\varphi||^2_{L^2(\partial \Sigma, g_{\delta})}} \\ &\geq \frac{\sigma^D_1(\Omega^c,\partial^S\Omega^c, g)}{\sqrt{\delta}} \frac{||\varphi_2||^2_{L^2(\partial^S\Omega^c, g_{\delta})}}{||\varphi||^2_{L^2 (\partial \Sigma, g_{\delta})}}, \end{align*} $$
$$ \begin{align*} C_k \geq R_{\delta}[\varphi]&=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2dv_{g}+\int_{\Sigma}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \\ &\geq \frac{\int_{\Omega^c}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{1}{\delta^{1/2}}\frac{\int_{\Omega^c}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial^S\Omega^c} \varphi^2_2 ds_{g}}\frac{||\varphi_2||^2_{L^2(\partial^S\Omega^c, g_{\delta})}}{||\varphi||^2_{L^2(\partial \Sigma, g_{\delta})}} \\ &\geq \frac{\sigma^D_1(\Omega^c,\partial^S\Omega^c, g)}{\sqrt{\delta}} \frac{||\varphi_2||^2_{L^2(\partial^S\Omega^c, g_{\delta})}}{||\varphi||^2_{L^2 (\partial \Sigma, g_{\delta})}}, \end{align*} $$
where
![]() $\sigma ^D_1(\Omega ^c,\partial ^S\Omega ^c, g)$
is the first nonzero Steklov–Dirichlet eigenvalue of
$\sigma ^D_1(\Omega ^c,\partial ^S\Omega ^c, g)$
is the first nonzero Steklov–Dirichlet eigenvalue of
![]() $(\Omega ^c,g)$
(see [Reference Banuelos, Kulczycki, Polterovich and SiudejaBKPS10]).▪
$(\Omega ^c,g)$
(see [Reference Banuelos, Kulczycki, Polterovich and SiudejaBKPS10]).▪
Claim 4. For every
![]() $\varphi \in V \in W_k$
and for every sufficiently small
$\varphi \in V \in W_k$
and for every sufficiently small
![]() $\delta $
there exists a constant
$\delta $
there exists a constant
![]() $C>0$
such that
$C>0$
such that
Proof One has
 $$ \begin{align*} ||\varphi||^2_{L^2(\partial \Sigma, g_{\delta})}&=\int_{\partial^S\Omega^c}(\varphi_1+\varphi_2)^2dv_{s_{\delta}}+\int_{\partial^S\Omega}\varphi^2_1ds_{g_{\delta}} \\ &\leq \bigg(1+\frac{1}{\varepsilon}\bigg) \int_{\partial \Sigma}\varphi_2^2ds_{g_{\delta}}+(1+\varepsilon) \int_{\partial \Sigma}\varphi^2_1ds_{g_{\delta}}, \end{align*} $$
$$ \begin{align*} ||\varphi||^2_{L^2(\partial \Sigma, g_{\delta})}&=\int_{\partial^S\Omega^c}(\varphi_1+\varphi_2)^2dv_{s_{\delta}}+\int_{\partial^S\Omega}\varphi^2_1ds_{g_{\delta}} \\ &\leq \bigg(1+\frac{1}{\varepsilon}\bigg) \int_{\partial \Sigma}\varphi_2^2ds_{g_{\delta}}+(1+\varepsilon) \int_{\partial \Sigma}\varphi^2_1ds_{g_{\delta}}, \end{align*} $$
for every
![]() $\varepsilon>0$
. Applying Claim 3, we obtain
$\varepsilon>0$
. Applying Claim 3, we obtain
and hence,
Choosing
![]() $\varepsilon =\delta ^{1/4}$
completes the proof.▪
$\varepsilon =\delta ^{1/4}$
completes the proof.▪
Claim 5. For every
![]() $\varphi \in V \in W_k$
and for every sufficiently small
$\varphi \in V \in W_k$
and for every sufficiently small
![]() $\delta ,$
there exists a constant
$\delta ,$
there exists a constant
![]() $C>0$
such that
$C>0$
such that
Proof
 $$ \begin{align*} C_k \geq \frac{\int_{\partial\Sigma}|\nabla \varphi|^2_{g_{\delta}}dv_{g_{\delta}}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \geq \frac{\int_{\partial^S\Omega}|\nabla \varphi|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{\int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}, \end{align*} $$
$$ \begin{align*} C_k \geq \frac{\int_{\partial\Sigma}|\nabla \varphi|^2_{g_{\delta}}dv_{g_{\delta}}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \geq \frac{\int_{\partial^S\Omega}|\nabla \varphi|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{\int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}, \end{align*} $$
since
![]() $\varphi =\varphi _1$
on
$\varphi =\varphi _1$
on
![]() $\partial ^S\Omega $
. Then by Claim 4, one has
$\partial ^S\Omega $
. Then by Claim 4, one has
 $$ \begin{align*} C_k \geq\frac{\int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \geq \frac{1}{1+C\delta^{1/4}}\frac{\int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}}}, \end{align*} $$
$$ \begin{align*} C_k \geq\frac{\int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \geq \frac{1}{1+C\delta^{1/4}}\frac{\int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g}}{\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}}}, \end{align*} $$
which implies
 $$ \begin{align} \begin{aligned} \int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g} &\leq C_k(1+C\delta^{1/4})\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}} \\ &= C_k(1+C\delta^{1/4})\bigg(\!\int_{\partial^S\Omega} \varphi_1^2 ds_{g}+\delta^{1/2}\int_{\partial^S\Omega^c} \varphi_1^2 ds_{g}\bigg). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{\partial^S\Omega}|\nabla \varphi_1|^2_{g}ds_{g} &\leq C_k(1+C\delta^{1/4})\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}} \\ &= C_k(1+C\delta^{1/4})\bigg(\!\int_{\partial^S\Omega} \varphi_1^2 ds_{g}+\delta^{1/2}\int_{\partial^S\Omega^c} \varphi_1^2 ds_{g}\bigg). \end{aligned} \end{align} $$
For the rest of the proof C stands for any positive constant depending possibly on
![]() $\Sigma $
and g but not on
$\Sigma $
and g but not on
![]() $\delta $
or
$\delta $
or
![]() $\varphi $
.
$\varphi $
.
Note that
![]() $\partial ^s\Omega $
has positive capacity (see [Reference Henrot and PierreHP18, pp.102-105]). Applying in order the trace inequality, estimate (7.1), the Sobolev embedding and inequality (2.5) yield
$\partial ^s\Omega $
has positive capacity (see [Reference Henrot and PierreHP18, pp.102-105]). Applying in order the trace inequality, estimate (7.1), the Sobolev embedding and inequality (2.5) yield
 $$ \begin{align*} ||\varphi_1||^2_{L^2(\partial^S\Omega^c,g)} \leq C||\hat \varphi_1||^2_{H^1(\Sigma,g)} &\leq C||\varphi_1||^2_{H^{1/2}(\partial^S\Omega,g)} \\ &\leq C||\varphi_1||^2_{H^{1}(\partial^S\Omega,g)}=C(||\varphi_1||^2_{L^{2}(\partial^S\Omega,g)}+||\nabla \varphi_1||^2_{L^{2}(\partial^S\Omega,g)}) \\ &\leq C(1+C\delta^{1/4})\big(||\varphi_1||^2_{L^{2}(\partial^S\Omega,g)}+\delta^{1/2}||\varphi_1||^2_{L^{2}(\partial^S\Omega^c,g)}\big), \end{align*} $$
$$ \begin{align*} ||\varphi_1||^2_{L^2(\partial^S\Omega^c,g)} \leq C||\hat \varphi_1||^2_{H^1(\Sigma,g)} &\leq C||\varphi_1||^2_{H^{1/2}(\partial^S\Omega,g)} \\ &\leq C||\varphi_1||^2_{H^{1}(\partial^S\Omega,g)}=C(||\varphi_1||^2_{L^{2}(\partial^S\Omega,g)}+||\nabla \varphi_1||^2_{L^{2}(\partial^S\Omega,g)}) \\ &\leq C(1+C\delta^{1/4})\big(||\varphi_1||^2_{L^{2}(\partial^S\Omega,g)}+\delta^{1/2}||\varphi_1||^2_{L^{2}(\partial^S\Omega^c,g)}\big), \end{align*} $$
which implies the required inequality for
![]() $\delta $
small enough.▪
$\delta $
small enough.▪
Further, by the fact that
![]() $\int _{\Sigma }\langle \nabla \hat \varphi _1, \nabla \hat \varphi _2 \rangle _{g} dv_{g}=0$
and by Claim 4 for every
$\int _{\Sigma }\langle \nabla \hat \varphi _1, \nabla \hat \varphi _2 \rangle _{g} dv_{g}=0$
and by Claim 4 for every
![]() $\varphi \in V \in W_k$
and one has
$\varphi \in V \in W_k$
and one has
 $$ \begin{align*} R_{\delta}[\varphi] &=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}+\int_{\Sigma}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \\ &\geq \frac{1}{1+C\delta^{1/4}} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}+\int_{\Sigma}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}}} \\ &\geq \frac{1}{1+C\delta^{1/4}} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}}}=\frac{1}{1+C\delta^{1/4}} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi_1^2 dv_{g}+\delta^{1/2}\int_{\partial^S\Omega^c}\varphi_1^2 dv_{g}} \end{align*} $$
$$ \begin{align*} R_{\delta}[\varphi] &=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}}=\frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}+\int_{\Sigma}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \\ &\geq \frac{1}{1+C\delta^{1/4}} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}+\int_{\Sigma}|\nabla \hat\varphi_2|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}}} \\ &\geq \frac{1}{1+C\delta^{1/4}} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi_1^2 ds_{g_{\delta}}}=\frac{1}{1+C\delta^{1/4}} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi_1^2 dv_{g}+\delta^{1/2}\int_{\partial^S\Omega^c}\varphi_1^2 dv_{g}} \end{align*} $$
and by Claim 5, we get
 $$ \begin{align*} R_{\delta}[\varphi] &\geq\frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi_1^2 ds_{g}} \\ &\geq \frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} \frac{\int_{\Omega}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi_1^2 ds_{g}} \\ &\geq\frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} R^N_{(\Omega,\partial^S\Omega, g)}[\varphi_{|_{\Omega}}], \end{align*} $$
$$ \begin{align*} R_{\delta}[\varphi] &\geq\frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} \frac{\int_{\Sigma}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi_1^2 ds_{g}} \\ &\geq \frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} \frac{\int_{\Omega}|\nabla \hat\varphi_1|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi_1^2 ds_{g}} \\ &\geq\frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} R^N_{(\Omega,\partial^S\Omega, g)}[\varphi_{|_{\Omega}}], \end{align*} $$
where
![]() $R^N_{(\Omega ,\partial ^S\Omega , g)}$
denotes the Rayleigh quotient for the Steklov–Neumann problem in the domain
$R^N_{(\Omega ,\partial ^S\Omega , g)}$
denotes the Rayleigh quotient for the Steklov–Neumann problem in the domain
![]() $(\Omega ,g)$
.
$(\Omega ,g)$
.
Let
![]() $V=\operatorname {span}\langle \psi _0,\ldots ,\psi _k \rangle $
, where
$V=\operatorname {span}\langle \psi _0,\ldots ,\psi _k \rangle $
, where
![]() $\psi _i$
is in the ith eigenspace of
$\psi _i$
is in the ith eigenspace of
![]() $(\Sigma ,g_{\delta })$
. Then
$(\Sigma ,g_{\delta })$
. Then
 $$ \begin{align} \begin{aligned} \sigma^{\delta}_k &=\max_{\varphi \in V}R_{\delta}[\varphi] \geq \frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} \max_{\varphi \in V}R^N_{(\Omega,\partial^S\Omega, g)}[\varphi_{|_{\Omega}}] \\ &\geq \frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)}\sigma^N_k(\Omega,\partial^S\Omega, g), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sigma^{\delta}_k &=\max_{\varphi \in V}R_{\delta}[\varphi] \geq \frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)} \max_{\varphi \in V}R^N_{(\Omega,\partial^S\Omega, g)}[\varphi_{|_{\Omega}}] \\ &\geq \frac{1}{(1+C\delta^{1/4})(1+\delta^{1/2}C)}\sigma^N_k(\Omega,\partial^S\Omega, g), \end{aligned} \end{align} $$
since the restriction to
![]() $\Omega $
of the functions
$\Omega $
of the functions
![]() $\psi _i$
form the space of the same dimension by unique continuation. Finally, passing to the
$\psi _i$
form the space of the same dimension by unique continuation. Finally, passing to the
![]() $\liminf $
as
$\liminf $
as
![]() $\delta \to 0$
in (2.6) yields the lemma.
$\delta \to 0$
in (2.6) yields the lemma.
Case II. The case when
![]() $\Omega ^c \cap \partial \Sigma =\varnothing $
is trivial. Indeed, in this case, we have
$\Omega ^c \cap \partial \Sigma =\varnothing $
is trivial. Indeed, in this case, we have
![]() $\partial ^S\Omega =\partial \Sigma $
. Then for any function
$\partial ^S\Omega =\partial \Sigma $
. Then for any function
![]() $\varphi ,$
one has
$\varphi ,$
one has
 $$ \begin{align*} R_{\delta}[\varphi]=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \geq \frac{\int_{\Omega}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi^2 ds_{g}}=R^N_{(\Omega,\partial^S\Omega, g)}[\varphi_{|_{\Omega}}]. \end{align*} $$
$$ \begin{align*} R_{\delta}[\varphi]=\frac{\int_{\Sigma}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial \Sigma} \varphi^2 ds_{g_{\delta}}} \geq \frac{\int_{\Omega}|\nabla \hat\varphi|^2_{g}dv_{g}}{\int_{\partial^S\Omega} \varphi^2 ds_{g}}=R^N_{(\Omega,\partial^S\Omega, g)}[\varphi_{|_{\Omega}}]. \end{align*} $$
Therefore, considering
![]() $V=\operatorname {span}\langle \psi _0,\ldots ,\psi _k \rangle $
, where
$V=\operatorname {span}\langle \psi _0,\ldots ,\psi _k \rangle $
, where
![]() $\psi _i$
is in the ith eigenspace of
$\psi _i$
is in the ith eigenspace of
![]() $(\Sigma ,g_{\delta })$
yields
$(\Sigma ,g_{\delta })$
yields
Taking
![]() $\liminf $
as
$\liminf $
as
![]() $\delta \to 0$
completes the proof.
$\delta \to 0$
completes the proof.
Lemma 2.5 is the key ingredient in the proof of the following proposition. We postpone the proof to Section 7.2.
Proposition 2.6 Let
![]() $(\Sigma ,g)$
be a Riemannian surface with boundary,
$(\Sigma ,g)$
be a Riemannian surface with boundary,
![]() $\Omega \subset \Sigma $
a Lipschitz domain and
$\Omega \subset \Sigma $
a Lipschitz domain and
![]() $\partial ^S\Omega =\partial \Sigma \cap \Omega \neq \varnothing $
. Then for all k one has
$\partial ^S\Omega =\partial \Sigma \cap \Omega \neq \varnothing $
. Then for all k one has
Similarly, let
![]() $(\Sigma ,g)$
be a Riemannian surface whose boundary. Let
$(\Sigma ,g)$
be a Riemannian surface whose boundary. Let
![]() $\partial ^S\Sigma $
denote all boundary components with the Steklov boundary condition and
$\partial ^S\Sigma $
denote all boundary components with the Steklov boundary condition and
![]() $\Omega \subset \Sigma $
be a Lipschitz domain such that
$\Omega \subset \Sigma $
be a Lipschitz domain such that
![]() $\partial ^S\Omega \subset \partial ^S\Sigma $
. Then for all k one has
$\partial ^S\Omega \subset \partial ^S\Sigma $
. Then for all k one has
As a corollary of Proposition 2.6, we get
Corollary 2.7 Let
![]() $(M, g)$
be a compact Riemannian surface with boundary. Consider a sequence
$(M, g)$
be a compact Riemannian surface with boundary. Consider a sequence
![]() $\{ K_n \}$
of smooth domains
$\{ K_n \}$
of smooth domains
![]() $K_n \subset M$
such that
$K_n \subset M$
such that
-
•
 $K_r \subset K_s \ \forall r>s$
and
$K_r \subset K_s \ \forall r>s$
and -
•
 $\cap _n K_n=\{p_1,\ldots ,p_l\}$
for some points
$\cap _n K_n=\{p_1,\ldots ,p_l\}$
for some points
 $p_1,\ldots ,p_l \in M$
.
$p_1,\ldots ,p_l \in M$
.
Then one has
The proof is postponed to Section 7.2.
2.4 Disconnected surfaces
The proofs of two lemmas below follow the exactly same arguments as the proofs of Lemmas 4.9 and 4.10 in [Reference Karpukhin and MedvedevKM20]. Their proofs are postponed to Section 7.2.
Lemma 2.8 Let
![]() $(\Omega ,g) = \sqcup _{i=1}^s(\Omega _i,g_i)$
be a disjoint union of Riemannian surfaces with Lipschitz boundary. Set
$(\Omega ,g) = \sqcup _{i=1}^s(\Omega _i,g_i)$
be a disjoint union of Riemannian surfaces with Lipschitz boundary. Set
![]() $\partial ^S\Omega =\sqcup _{i=1}^s\partial ^S\Omega _i$
. Then for all
$\partial ^S\Omega =\sqcup _{i=1}^s\partial ^S\Omega _i$
. Then for all
![]() $k>0$
one has
$k>0$
one has
 $$ \begin{align*} \sigma^{N*}_k(\Omega,\partial^S\Omega, [g]) = \max_{\sum\limits_{i=1}^s k_i=k,\,\,\,k_i>0}\,\,\sum_{i=1}^s\sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g_i]). \end{align*} $$
$$ \begin{align*} \sigma^{N*}_k(\Omega,\partial^S\Omega, [g]) = \max_{\sum\limits_{i=1}^s k_i=k,\,\,\,k_i>0}\,\,\sum_{i=1}^s\sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g_i]). \end{align*} $$
Lemma 2.9 Let
![]() $(\Sigma ,g)$
be a Riemannian surface with boundary. Consider a set of pairwise disjoint Lipschitz domains
$(\Sigma ,g)$
be a Riemannian surface with boundary. Consider a set of pairwise disjoint Lipschitz domains
![]() $\{\Omega _i\}^s_{i=1}$
in
$\{\Omega _i\}^s_{i=1}$
in
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
and
$\Sigma =\bigcup ^s_{i=1} \overline \Omega _i$
and
![]() $\Omega _i\cap \partial \Sigma =\partial ^S\Omega _i \neq \varnothing $
for
$\Omega _i\cap \partial \Sigma =\partial ^S\Omega _i \neq \varnothing $
for
![]() $1 \leq i \leq s'$
. Then one has
$1 \leq i \leq s'$
. Then one has
 $$ \begin{align*} \sigma^{*}_k(\Sigma, [g]) \geq \max_{\sum_{i=1}^{s'} k_i=k,\,\,\,k_i \geq 0} \sum^{s'}_{i=1} \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g]). \end{align*} $$
$$ \begin{align*} \sigma^{*}_k(\Sigma, [g]) \geq \max_{\sum_{i=1}^{s'} k_i=k,\,\,\,k_i \geq 0} \sum^{s'}_{i=1} \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g]). \end{align*} $$
3 Proof of Theorem 1.2
The proof is inspired by the methods of the papers [Reference Yang and YauYY80, Reference Girouard and PolterovichGP, Reference KarpukhinKar16]. Let
![]() $\Sigma $
be a nonorientable compact surface of genus
$\Sigma $
be a nonorientable compact surface of genus
![]() $\gamma $
and l boundary components. We pass to its orientable cover
$\gamma $
and l boundary components. We pass to its orientable cover
![]() $\pi \colon \widetilde \Sigma \to \Sigma $
. Note that
$\pi \colon \widetilde \Sigma \to \Sigma $
. Note that
![]() $\Sigma $
is of genus
$\Sigma $
is of genus
![]() $\gamma $
and has
$\gamma $
and has
![]() $2l$
boundary components. Let
$2l$
boundary components. Let
![]() $\tau $
denote the involution exchanging the sheets of
$\tau $
denote the involution exchanging the sheets of
![]() $\pi $
. If h is a metric on
$\pi $
. If h is a metric on
![]() $\Sigma $
then
$\Sigma $
then
![]() $g:=\pi ^*h$
is a metric on
$g:=\pi ^*h$
is a metric on
![]() $\widetilde \Sigma $
invariant with respect to
$\widetilde \Sigma $
invariant with respect to
![]() $\tau $
, i.e.,
$\tau $
, i.e.,
![]() $\tau $
is an isometry of g. Let
$\tau $
is an isometry of g. Let
![]() $\mathcal D_{\widetilde \Sigma }$
be the Dirichlet-to-Neumann map acting on functions on
$\mathcal D_{\widetilde \Sigma }$
be the Dirichlet-to-Neumann map acting on functions on
![]() $\widetilde \Sigma $
. Then
$\widetilde \Sigma $
. Then
![]() $\tau \circ \mathcal D_{\widetilde \Sigma }=\mathcal D_{\widetilde \Sigma }\circ \tau $
and hence Steklov eigenfunctions are divided into
$\tau \circ \mathcal D_{\widetilde \Sigma }=\mathcal D_{\widetilde \Sigma }\circ \tau $
and hence Steklov eigenfunctions are divided into
![]() $\tau $
-odd and
$\tau $
-odd and
![]() $\tau $
-even ones. The corresponding Steklov eigenvalues are also divided into odd and even ones. Let
$\tau $
-even ones. The corresponding Steklov eigenvalues are also divided into odd and even ones. Let
![]() $\sigma ^{\tau }_k(\widetilde \Sigma ,g)$
the kth
$\sigma ^{\tau }_k(\widetilde \Sigma ,g)$
the kth
![]() $\tau $
-even Steklov eigenvalue. Then
$\tau $
-even Steklov eigenvalue. Then
![]() $\sigma ^{\tau }_k(\widetilde \Sigma ,g)=\sigma _k(\Sigma ,h)$
.
$\sigma ^{\tau }_k(\widetilde \Sigma ,g)=\sigma _k(\Sigma ,h)$
.
By a well-known theorem of Ahlfors [Reference AhlforsAhl50], there exists a proper conformal branched cover
![]() $\psi \colon (\widetilde \Sigma ,g) \to (\mathbb D^2,g_{can})$
. The word “proper” means
$\psi \colon (\widetilde \Sigma ,g) \to (\mathbb D^2,g_{can})$
. The word “proper” means
![]() $\psi (\partial \widetilde \Sigma )=\mathbb S^1$
. Let d be its degree. Define the following pushed-forward metric
$\psi (\partial \widetilde \Sigma )=\mathbb S^1$
. Let d be its degree. Define the following pushed-forward metric
![]() $g^*$
on
$g^*$
on
![]() $\mathbb D^2$
: consider a neighborhood U of a nonbranching point
$\mathbb D^2$
: consider a neighborhood U of a nonbranching point
![]() $p\in \mathbb D^2$
. Its pre-image is a collection of d neighborhoods
$p\in \mathbb D^2$
. Its pre-image is a collection of d neighborhoods
![]() $U_i, i=1,\ldots ,d$
on
$U_i, i=1,\ldots ,d$
on
![]() $\widetilde \Sigma $
. Moreover,
$\widetilde \Sigma $
. Moreover,
![]() $\psi _i:=\psi _{|_{U_i}}\colon U_i\to U$
is a diffeomorphism. Then the metric
$\psi _i:=\psi _{|_{U_i}}\colon U_i\to U$
is a diffeomorphism. Then the metric
![]() $g^*$
is defined on U as
$g^*$
is defined on U as
![]() $\sum (\psi ^{-1}_i)^*g$
. The metric
$\sum (\psi ^{-1}_i)^*g$
. The metric
![]() $g^*$
is a metric on
$g^*$
is a metric on
![]() $\mathbb D^2$
with isolated conical singularities at branching points of
$\mathbb D^2$
with isolated conical singularities at branching points of
![]() $\psi $
. The following lemma is trivial
$\psi $
. The following lemma is trivial
Lemma 3.1 For any function
![]() $u\in C^{\infty }(\mathbb D^2)$
one has
$u\in C^{\infty }(\mathbb D^2)$
one has
and
Further, suppose that there exists an involution
![]() $\iota $
of
$\iota $
of
![]() $\mathbb D^2$
such that
$\mathbb D^2$
such that
Lemma 3.2 The involution
![]() $\iota $
is an isometry of
$\iota $
is an isometry of
![]() $(\mathbb D^2,g^*)$
.
$(\mathbb D^2,g^*)$
.
Proof Indeed, let the neighborhood
![]() $U\subset \mathbb D^2$
be small enough and do not contain branching points. Then
$U\subset \mathbb D^2$
be small enough and do not contain branching points. Then
![]() $\psi ^{-1}(U)=\sqcup ^d_{i=1} U_i$
and applying
$\psi ^{-1}(U)=\sqcup ^d_{i=1} U_i$
and applying
![]() $\tau $
one gets:
$\tau $
one gets:
![]() $\tau (\psi ^{-1}(U))=\sqcup ^d_{i=1} \tau (U_i)$
. Note that condition (3.1) implies
$\tau (\psi ^{-1}(U))=\sqcup ^d_{i=1} \tau (U_i)$
. Note that condition (3.1) implies
![]() $\tau (\psi ^{-1}(U))=\psi ^{-1}(\iota (U))$
. Whence
$\tau (\psi ^{-1}(U))=\psi ^{-1}(\iota (U))$
. Whence
![]() $\psi ^{-1}(\iota (U))=\sqcup ^d_{i=1} \tau (U_i)$
. Let
$\psi ^{-1}(\iota (U))=\sqcup ^d_{i=1} \tau (U_i)$
. Let
![]() $\widetilde {\psi _i}:=\psi _{\tau (U_i)}$
. Then on U, one has
$\widetilde {\psi _i}:=\psi _{\tau (U_i)}$
. Then on U, one has
 $$ \begin{align*} g^* &=\sum^d_{i=1} (\widetilde{\psi_i}^{-1})^*g=\sum^d_{i=1} (\widetilde{\psi_i}^{-1})^*\tau^*g = \sum^d_{i=1} (\widetilde{\psi_i}^{-1}\circ\tau)^*g \\ &= \sum^d_{i=1} (\iota\circ\widetilde{\psi_i}^{-1})^*g = \sum^d_{i=1}\iota^*(\widetilde{\psi_i}^{-1})^*g=\iota^*g^*. \end{align*} $$
$$ \begin{align*} g^* &=\sum^d_{i=1} (\widetilde{\psi_i}^{-1})^*g=\sum^d_{i=1} (\widetilde{\psi_i}^{-1})^*\tau^*g = \sum^d_{i=1} (\widetilde{\psi_i}^{-1}\circ\tau)^*g \\ &= \sum^d_{i=1} (\iota\circ\widetilde{\psi_i}^{-1})^*g = \sum^d_{i=1}\iota^*(\widetilde{\psi_i}^{-1})^*g=\iota^*g^*. \end{align*} $$
▪
Consider a jth
![]() $\iota $
-even eigenfunction
$\iota $
-even eigenfunction
![]() $u_j$
on
$u_j$
on
![]() $(\mathbb D^2,g^*)$
with corresponding eigenvalue
$(\mathbb D^2,g^*)$
with corresponding eigenvalue
![]() $\sigma ^{\iota }_j(\mathbb D^2,g^*)$
. Then the function
$\sigma ^{\iota }_j(\mathbb D^2,g^*)$
. Then the function
![]() $\psi ^*u_j$
on
$\psi ^*u_j$
on
![]() $\widetilde \Sigma $
is
$\widetilde \Sigma $
is
![]() $\tau $
-even and hence it projects to a well-defined function
$\tau $
-even and hence it projects to a well-defined function
![]() $v_j$
on
$v_j$
on
![]() $\Sigma $
. We can construct the following function
$\Sigma $
. We can construct the following function
![]() $v=\sum _{j=0}^{k-1}c_jv_j$
. Note that
$v=\sum _{j=0}^{k-1}c_jv_j$
. Note that
![]() $\pi ^*v=\sum _{j=0}^{k-1}c_j\psi ^*u_j=\psi ^*u$
, where
$\pi ^*v=\sum _{j=0}^{k-1}c_j\psi ^*u_j=\psi ^*u$
, where
![]() $u:=\sum _{j=0}^{k-1}c_ju_j$
. Further, let
$u:=\sum _{j=0}^{k-1}c_ju_j$
. Further, let
![]() $w_i$
denote an ith eigenfunction on
$w_i$
denote an ith eigenfunction on
![]() $\Sigma $
with eigenvalue
$\Sigma $
with eigenvalue
![]() $\sigma _i(\Sigma ,h)$
. It is easy to see that one can always find some coefficients
$\sigma _i(\Sigma ,h)$
. It is easy to see that one can always find some coefficients
![]() $c_0,\ldots ,c_{k-1}$
such that
$c_0,\ldots ,c_{k-1}$
such that
![]() $\int _{\partial \Sigma }v w_idv_h=0, i=0,\ldots ,k-1$
. Then, we can use v as a test function for
$\int _{\partial \Sigma }v w_idv_h=0, i=0,\ldots ,k-1$
. Then, we can use v as a test function for
![]() $\sigma _k(\Sigma ,h)$
:
$\sigma _k(\Sigma ,h)$
:
 $$ \begin{align*} \sigma_k(\Sigma,h) \leq \frac{\int_{\Sigma}|\nabla_{h} v|^2dv_{h}}{\int_{\partial\Sigma}v^2dv_{h}}=\frac{\int_{\widetilde\Sigma}|\nabla_{g} \psi^*u|^2dv_{g}}{\int_{\partial\widetilde\Sigma}(\psi^*u)^2dv_{g}}=d\frac{\int_{\mathbb D^2}|\nabla_{g^*} u|^2dv_{g^*}}{\int_{\mathbb S^1}u^2dv_{g^*}}=d\sigma^{\iota}_k(\mathbb D^2,g^*), \end{align*} $$
$$ \begin{align*} \sigma_k(\Sigma,h) \leq \frac{\int_{\Sigma}|\nabla_{h} v|^2dv_{h}}{\int_{\partial\Sigma}v^2dv_{h}}=\frac{\int_{\widetilde\Sigma}|\nabla_{g} \psi^*u|^2dv_{g}}{\int_{\partial\widetilde\Sigma}(\psi^*u)^2dv_{g}}=d\frac{\int_{\mathbb D^2}|\nabla_{g^*} u|^2dv_{g^*}}{\int_{\mathbb S^1}u^2dv_{g^*}}=d\sigma^{\iota}_k(\mathbb D^2,g^*), \end{align*} $$
where we used Lemma 3.1. Moreover, the second identity in Lemma 3.1 implies
![]() $L_{g^*}(\mathbb S^1)=L_g(\partial \widetilde \Sigma )=2L_h(\partial \Sigma )$
. Whence
$L_{g^*}(\mathbb S^1)=L_g(\partial \widetilde \Sigma )=2L_h(\partial \Sigma )$
. Whence
Consider a conformal map
![]() $\psi $
between surfaces with involution
$\psi $
between surfaces with involution
![]() $\psi \colon (\widetilde \Sigma , \tau ) \to (\mathbb D^2, \iota )$
of minimal degree d. The map
$\psi \colon (\widetilde \Sigma , \tau ) \to (\mathbb D^2, \iota )$
of minimal degree d. The map
![]() $\psi $
is conformal, moreover, every involution exchanging the orientation on
$\psi $
is conformal, moreover, every involution exchanging the orientation on
![]() $\mathbb D^2$
is conjugate to the involution
$\mathbb D^2$
is conjugate to the involution
![]() $\iota _0(z):=\bar z$
, where we identify
$\iota _0(z):=\bar z$
, where we identify
![]() $\mathbb D^2$
with the unit disc on the complex plane. Therefore, without loss of generality, we can assume that
$\mathbb D^2$
with the unit disc on the complex plane. Therefore, without loss of generality, we can assume that
![]() $\iota =\iota _0$
. The fixed point set of
$\iota =\iota _0$
. The fixed point set of
![]() $\iota _0$
is the diameter
$\iota _0$
is the diameter
![]() $\{z\in \mathbb D^2~|~Re(z)=0\}$
. Let
$\{z\in \mathbb D^2~|~Re(z)=0\}$
. Let
![]() $H\mathbb D^2$
denote a half-disc for example the right one and
$H\mathbb D^2$
denote a half-disc for example the right one and
![]() $\partial ^SH\mathbb D^2$
is the right half-circle. Thus,
$\partial ^SH\mathbb D^2$
is the right half-circle. Thus,
![]() $\sigma ^{\iota _0}_k(\mathbb D^2,g^*)=\sigma ^N_k(H\mathbb {D}^2,\partial ^SH\mathbb {D}^2, g^*)$
and inequality (3.2) implies:
$\sigma ^{\iota _0}_k(\mathbb D^2,g^*)=\sigma ^N_k(H\mathbb {D}^2,\partial ^SH\mathbb {D}^2, g^*)$
and inequality (3.2) implies:
 $$ \begin{align} \begin{aligned} &\overline\sigma_k(\Sigma,h) \leq \frac{d}{2}\sigma^{\iota}_k(\mathbb D^2,g^*)L_{g^*}(\mathbb S^1)=d\overline\sigma^N_k(H\mathbb {D}^2,\partial^SH\mathbb{D}^2, g^*) \\ &\quad \leq d\sigma^{N*}_k(H\mathbb {D}^2,\partial^SH\mathbb{D}^2, [g^*]) \leq d\sigma^{*}_k(\mathbb {D}^2, [g_{can}])=2\pi k d, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\overline\sigma_k(\Sigma,h) \leq \frac{d}{2}\sigma^{\iota}_k(\mathbb D^2,g^*)L_{g^*}(\mathbb S^1)=d\overline\sigma^N_k(H\mathbb {D}^2,\partial^SH\mathbb{D}^2, g^*) \\ &\quad \leq d\sigma^{N*}_k(H\mathbb {D}^2,\partial^SH\mathbb{D}^2, [g^*]) \leq d\sigma^{*}_k(\mathbb {D}^2, [g_{can}])=2\pi k d, \end{aligned} \end{align} $$
where in the last inequality, we used Lemma 2.6 and the fact that there exists a unique up to an isometry conformal class
![]() $[g_{can}]$
on
$[g_{can}]$
on
![]() $\mathbb D^2$
. We want to estimate d in formula (3.3). It is known that there exists a proper conformal branched cover
$\mathbb D^2$
. We want to estimate d in formula (3.3). It is known that there exists a proper conformal branched cover
![]() $f\colon (\widetilde \Sigma , g) \to (\mathbb D^2,g_{can})$
of degree
$f\colon (\widetilde \Sigma , g) \to (\mathbb D^2,g_{can})$
of degree
![]() $d'\leq \gamma +2l$
(see [Reference GabardGab06]). One can construct the following map
$d'\leq \gamma +2l$
(see [Reference GabardGab06]). One can construct the following map
![]() $F(x):=f(x)\bar f(\tau (x))$
. Note that
$F(x):=f(x)\bar f(\tau (x))$
. Note that
![]() $\bar F(x)=F(\tau (x))=\iota (F(x))$
and hence
$\bar F(x)=F(\tau (x))=\iota (F(x))$
and hence
![]() $\iota =\iota _0$
. Moreover, F is proper and the degree of F is not greater than
$\iota =\iota _0$
. Moreover, F is proper and the degree of F is not greater than
![]() $2d'=2(\gamma +2l)$
. Hence, there exists a proper map between
$2d'=2(\gamma +2l)$
. Hence, there exists a proper map between
![]() $(\widetilde \Sigma , \tau )$
and
$(\widetilde \Sigma , \tau )$
and
![]() $(\mathbb D^2,\iota _0)$
of degree not exceeding
$(\mathbb D^2,\iota _0)$
of degree not exceeding
![]() $2d'=2(\gamma +2l)$
satisfying (3.1). Inequality (3.3) then implies
$2d'=2(\gamma +2l)$
satisfying (3.1). Inequality (3.3) then implies
4 Geometric background
The aim of this section is the proof of Theorem 1.4. For this purpose, we provide a necessary background concerning the geometry of moduli space of conformal classes on a surface with boundary. We start with closed orientable surfaces.
4.1 Closed orientable surfaces
Let us recall the Uniformization theorem.
Theorem 4.1 Let
![]() $\Sigma $
be a closed surface and g be a Riemannian metric on it. Then in the conformal class
$\Sigma $
be a closed surface and g be a Riemannian metric on it. Then in the conformal class
![]() $[g]$
, there exists a unique (up to an isometry) metric h of constant Gauss curvature and fixed area. The area assumption is unnecessary except in the case of the torus for which we fix the volume of h to be equal to
$[g]$
, there exists a unique (up to an isometry) metric h of constant Gauss curvature and fixed area. The area assumption is unnecessary except in the case of the torus for which we fix the volume of h to be equal to
![]() $1$
.
$1$
.
Remark 4.1 It follows from the Gauss–Bonnet theorem that the metric h in the Uniformization theorem is of Gauss curvature
![]() $1$
in the case of the sphere,
$1$
in the case of the sphere,
![]() $0$
in the case of the torus and
$0$
in the case of the torus and
![]() $-1$
in the rest cases.
$-1$
in the rest cases.
Recall that a Riemannian metric h of constant Gaussian curvature
![]() $-1$
is called hyperbolic and a Riemannian surface
$-1$
is called hyperbolic and a Riemannian surface
![]() $(\Sigma ,h)$
endowed with a hyperbolic metric h is called a hyperbolic surface. Note also that a hyperbolic surface is necessarily of negative Euler characteristic. We also say that the torus endowed with a metric of curvature
$(\Sigma ,h)$
endowed with a hyperbolic metric h is called a hyperbolic surface. Note also that a hyperbolic surface is necessarily of negative Euler characteristic. We also say that the torus endowed with a metric of curvature
![]() $h=0$
is a flat torus and the sphere endowed with the metric
$h=0$
is a flat torus and the sphere endowed with the metric
![]() $h=1$
is the standard (round) sphere.
$h=1$
is the standard (round) sphere.
4.2 Hyperbolic surfaces
We recall that a pair of pants is a compact surface of genus
![]() $0$
with
$0$
with
![]() $3$
boundary components. The following theorem plays an underlying role in the theory of hyperbolic surfaces.
$3$
boundary components. The following theorem plays an underlying role in the theory of hyperbolic surfaces.
Theorem 4.2 (Collar theorem (see e.g., [Reference BuserBus92]))
Let
![]() $(\Sigma ,h)$
be an orientable compact hyperbolic surface of genus
$(\Sigma ,h)$
be an orientable compact hyperbolic surface of genus
![]() $\gamma \geq 2$
and let
$\gamma \geq 2$
and let
![]() $c_1,c_2,\ldots ,c_m$
be pairwise disjoint simple closed geodesics on
$c_1,c_2,\ldots ,c_m$
be pairwise disjoint simple closed geodesics on
![]() $(\Sigma ,h)$
. Then the following holds
$(\Sigma ,h)$
. Then the following holds
-
(i)
 $m \leq 3 \gamma -3$
.
$m \leq 3 \gamma -3$
. -
(ii) There exist simple closed geodesics
 $c_{m+1},\ldots ,c_{3 \gamma -3}$
which, together with
$c_{m+1},\ldots ,c_{3 \gamma -3}$
which, together with
 $c_1,\ldots ,c_m$
, decompose
$c_1,\ldots ,c_m$
, decompose
 $\Sigma $
into pairs of pants.
$\Sigma $
into pairs of pants. -
(iii) The collars
of widths $$ \begin{align*} \mathcal{C}(c_i)=\big\{p\in\Sigma~|~ dist(p,c_i) \leq w(c_i)\big\} \end{align*} $$
are pairwise disjoint for
$$ \begin{align*} \mathcal{C}(c_i)=\big\{p\in\Sigma~|~ dist(p,c_i) \leq w(c_i)\big\} \end{align*} $$
are pairwise disjoint for $$ \begin{align*} w(c_i)=\frac{\pi}{l(c_i)}\bigg(\pi-2\arctan\bigg(\sinh\frac{l(c_i)}{2}\bigg)\bigg) \end{align*} $$
$$ \begin{align*} w(c_i)=\frac{\pi}{l(c_i)}\bigg(\pi-2\arctan\bigg(\sinh\frac{l(c_i)}{2}\bigg)\bigg) \end{align*} $$
 $i=1,\ldots ,3 \gamma -3$
.
$i=1,\ldots ,3 \gamma -3$
.
-
(iv) Each
 $\mathcal {C}(c_i)$
is isometric to the cylinder with the Riemannian metric
$\mathcal {C}(c_i)$
is isometric to the cylinder with the Riemannian metric $$ \begin{align*} \big\{(t,\theta)| -w(c_i)<t<w(c_i),\,\theta\in\mathbb{R}/2\pi\mathbb{Z}\big\} \end{align*} $$
$$ \begin{align*} \big\{(t,\theta)| -w(c_i)<t<w(c_i),\,\theta\in\mathbb{R}/2\pi\mathbb{Z}\big\} \end{align*} $$
 $$ \begin{align*} \bigg(\frac{l(c_i)}{2\pi \cos\big(\frac{l(c_i)}{2\pi}t\big)}\bigg)^2\big(dt^2+d\theta^2\big). \end{align*} $$
$$ \begin{align*} \bigg(\frac{l(c_i)}{2\pi \cos\big(\frac{l(c_i)}{2\pi}t\big)}\bigg)^2\big(dt^2+d\theta^2\big). \end{align*} $$
The decomposition of
![]() $(\Sigma ,h)$
into pair of pants which we denote by
$(\Sigma ,h)$
into pair of pants which we denote by
![]() $\mathcal {P}$
is called the pants decomposition. We also say that the geodesics
$\mathcal {P}$
is called the pants decomposition. We also say that the geodesics
![]() $c_1,\ldots ,c_{3 \gamma -3}$
form
$c_1,\ldots ,c_{3 \gamma -3}$
form
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
4.3 Convergence of hyperbolic metrics
We endow the set of hyperbolic metrics on a given surface
![]() $\Sigma $
with
$\Sigma $
with
![]() $C^{\infty }-$
topology. In this section, we describe the convergence on this topological set which is called the moduli space of conformal classes on
$C^{\infty }-$
topology. In this section, we describe the convergence on this topological set which is called the moduli space of conformal classes on
![]() $\Sigma $
. Essentially, two cases can happen: the injectivity radii of a sequence of hyperbolic metrics do not go to
$\Sigma $
. Essentially, two cases can happen: the injectivity radii of a sequence of hyperbolic metrics do not go to
![]() $0$
or they do. The first case is described by Mumford’s compactness theorem and the second one is treated by the Deligne–Mumford compactification.
$0$
or they do. The first case is described by Mumford’s compactness theorem and the second one is treated by the Deligne–Mumford compactification.
Proposition 4.3 (Mumford’s compactness theorem (see e.g., [Reference HummelHum97]))
Let
![]() $\{h_n\}$
be a sequence of hyperbolic metrics on a surface
$\{h_n\}$
be a sequence of hyperbolic metrics on a surface
![]() $\Sigma $
of genus
$\Sigma $
of genus
![]() $\geq 2$
. Assume that the injectivity radii
$\geq 2$
. Assume that the injectivity radii
![]() $\operatorname {inj}(\Sigma ,h_n)$
satisfy
$\operatorname {inj}(\Sigma ,h_n)$
satisfy
![]() $\limsup \limits _{n\to \infty }\operatorname {inj}(\Sigma ,h_n)>0$
. Then there exists a subsequence
$\limsup \limits _{n\to \infty }\operatorname {inj}(\Sigma ,h_n)>0$
. Then there exists a subsequence
![]() $\{h_{n_k}\}$
, sequence
$\{h_{n_k}\}$
, sequence
![]() $\{\Phi _k\}$
of smooth automorphisms of
$\{\Phi _k\}$
of smooth automorphisms of
![]() $\Sigma $
and a hyperbolic metric
$\Sigma $
and a hyperbolic metric
![]() $h_{\infty }$
on
$h_{\infty }$
on
![]() $\Sigma $
such that the sequence of hyperbolic metrics
$\Sigma $
such that the sequence of hyperbolic metrics
![]() $\{\Phi _k^*h_{n_k}\}$
converges in
$\{\Phi _k^*h_{n_k}\}$
converges in
![]() $C^{\infty }$
-topology to
$C^{\infty }$
-topology to
![]() $h_{\infty }$
.
$h_{\infty }$
.
If
![]() $\lim \limits _{n\to \infty }\operatorname {inj}(\Sigma ,h_n)=0$
then we say that the sequence
$\lim \limits _{n\to \infty }\operatorname {inj}(\Sigma ,h_n)=0$
then we say that the sequence
![]() $\{h_n\}$
degenerates. The thick-thin decomposition implies that if the sequence
$\{h_n\}$
degenerates. The thick-thin decomposition implies that if the sequence
![]() $\{h_n\}$
degenerates then for each n there exists a collection
$\{h_n\}$
degenerates then for each n there exists a collection
![]() $\{c_1^n,\ldots ,c_s^n\}$
of disjoint simple closed geodesics in
$\{c_1^n,\ldots ,c_s^n\}$
of disjoint simple closed geodesics in
![]() $(\Sigma ,h_n)$
whose lengths tend to
$(\Sigma ,h_n)$
whose lengths tend to
![]() $0$
and the length of any geodesic in the complement
$0$
and the length of any geodesic in the complement
![]() $\Sigma _n =\Sigma \backslash (c_1^n\cup \cdots \cup c_s^n)$
is bounded from below by a constant independent of n. We call the geodesics
$\Sigma _n =\Sigma \backslash (c_1^n\cup \cdots \cup c_s^n)$
is bounded from below by a constant independent of n. We call the geodesics
![]() $\{c_1^n,\ldots ,c_s^n\}$
“pinching” or “collapsing.” The surface
$\{c_1^n,\ldots ,c_s^n\}$
“pinching” or “collapsing.” The surface
![]() $(\Sigma _n, h_n)$
is possibly a disconnected hyperbolic surface with geodesic boundary. Let
$(\Sigma _n, h_n)$
is possibly a disconnected hyperbolic surface with geodesic boundary. Let
![]() $\widehat {\Sigma _{\infty }}$
denote the surface having the same connected components as
$\widehat {\Sigma _{\infty }}$
denote the surface having the same connected components as
![]() $\Sigma _n$
, but with boundary component replaced by marked points. Note that each sequence
$\Sigma _n$
, but with boundary component replaced by marked points. Note that each sequence
![]() $\{c_i^n\}$
corresponds to a pair of marked points
$\{c_i^n\}$
corresponds to a pair of marked points
![]() $\{p_i,q_i\}$
on
$\{p_i,q_i\}$
on
![]() $\widehat {\Sigma _{\infty }}$
,
$\widehat {\Sigma _{\infty }}$
,
![]() $i=1,\ldots ,s$
. Then the punctured surface
$i=1,\ldots ,s$
. Then the punctured surface
![]() $\widehat {\Sigma _{\infty }}\backslash \{p_1,q_1,\ldots ,p_s,q_s\}$
that we denote by
$\widehat {\Sigma _{\infty }}\backslash \{p_1,q_1,\ldots ,p_s,q_s\}$
that we denote by
![]() $\Sigma _{\infty }$
admits the unique hyperbolic metric
$\Sigma _{\infty }$
admits the unique hyperbolic metric
![]() $h_{\infty }$
with cusps at punctures. Now we are ready to formulate one of the underlying results in the theory of moduli spaces of Riemann surfaces.
$h_{\infty }$
with cusps at punctures. Now we are ready to formulate one of the underlying results in the theory of moduli spaces of Riemann surfaces.
Proposition 4.4 (Deligne–Mumford compactification (see e.g., [Reference HummelHum97]))
Let
![]() $(\Sigma , h_n)$
be a sequence of hyperbolic surfaces such that
$(\Sigma , h_n)$
be a sequence of hyperbolic surfaces such that
![]() $\operatorname {inj}(\Sigma ,h_n)\to 0$
. Then up to a choice of subsequence, there exists a sequence of diffeomorphisms
$\operatorname {inj}(\Sigma ,h_n)\to 0$
. Then up to a choice of subsequence, there exists a sequence of diffeomorphisms
![]() $\Psi _n: \Sigma _{\infty } \to \Sigma _n$
such that the sequence
$\Psi _n: \Sigma _{\infty } \to \Sigma _n$
such that the sequence
![]() $\{\Psi ^*_n h_n\}$
of hyperbolic metrics converges in
$\{\Psi ^*_n h_n\}$
of hyperbolic metrics converges in
![]() $C_{\mathrm {loc}}^{\infty }$
-topology to the complete hyperbolic metric
$C_{\mathrm {loc}}^{\infty }$
-topology to the complete hyperbolic metric
![]() $h_{\infty }$
on
$h_{\infty }$
on
![]() $\Sigma _{\infty }$
. Furthermore, there exists a metric of locally constant curvature
$\Sigma _{\infty }$
. Furthermore, there exists a metric of locally constant curvature
![]() $\widehat {h_{\infty }}$
on
$\widehat {h_{\infty }}$
on
![]() $\widehat {\Sigma _{\infty }}$
such that its restriction to
$\widehat {\Sigma _{\infty }}$
such that its restriction to
![]() $\Sigma _{\infty }$
is conformal to
$\Sigma _{\infty }$
is conformal to
![]() $h_{\infty }$
.
$h_{\infty }$
.
We call
![]() $(\widehat {\Sigma _{\infty }},\widehat {h_{\infty }})$
a limiting space of the sequence
$(\widehat {\Sigma _{\infty }},\widehat {h_{\infty }})$
a limiting space of the sequence
![]() $(\Sigma ,h_n)$
. We also say that the limit of conformal classes
$(\Sigma ,h_n)$
. We also say that the limit of conformal classes
![]() $[h_n]$
is the conformal class
$[h_n]$
is the conformal class
![]() $[\widehat {h_{\infty }}]$
on
$[\widehat {h_{\infty }}]$
on
![]() $\widehat {\Sigma _{\infty }}$
.
$\widehat {\Sigma _{\infty }}$
.
Remark 4.2 We emphazise that
![]() $\widehat {h_{\infty }}$
has locally constant curvature, since
$\widehat {h_{\infty }}$
has locally constant curvature, since
![]() $\widehat {\Sigma _{\infty }}$
is possibly disconnected and different connected components could have different signs of Euler characteristic.
$\widehat {\Sigma _{\infty }}$
is possibly disconnected and different connected components could have different signs of Euler characteristic.
4.4 Orientable surfaces with boundary of negative Euler characteristic
Our exposition of this topic essentially follows the book [Reference JostJos07].
Let
![]() $\Sigma $
be an orientable surface of genus
$\Sigma $
be an orientable surface of genus
![]() $\gamma $
with l boundary components. Consider its Schottky double
$\gamma $
with l boundary components. Consider its Schottky double
![]() $\Sigma ^d$
defined in following way. We identify
$\Sigma ^d$
defined in following way. We identify
![]() $\Sigma $
with another copy
$\Sigma $
with another copy
![]() $\Sigma '$
of
$\Sigma '$
of
![]() $\Sigma $
with opposite orientation along the common boundary. We get a closed oriented surface of genus
$\Sigma $
with opposite orientation along the common boundary. We get a closed oriented surface of genus
![]() $2\gamma +l-1$
. For example, the Schottky double of the disk is the sphere and the Schottky double of the cylinder is the torus. In the rest cases we always get a hyperbolic surface as the Schottky double. We endow the surface
$2\gamma +l-1$
. For example, the Schottky double of the disk is the sphere and the Schottky double of the cylinder is the torus. In the rest cases we always get a hyperbolic surface as the Schottky double. We endow the surface
![]() $\Sigma $
with a metric g. The next theorem plays a role of the Uniformization theorem for surfaces with boundary.
$\Sigma $
with a metric g. The next theorem plays a role of the Uniformization theorem for surfaces with boundary.
Proposition 4.5 [Reference Osgood, Phillips and SarnakOPS88]
In the conformal class
![]() $[g]$
of a metric g on the surface
$[g]$
of a metric g on the surface
![]() $\Sigma $
, there exists a unique (up to an isometry) metric of constant Gauss curvature and geodesic boundary. More precisely, this metric is of curvature
$\Sigma $
, there exists a unique (up to an isometry) metric of constant Gauss curvature and geodesic boundary. More precisely, this metric is of curvature
![]() $1$
in the case of
$1$
in the case of
![]() $\mathbb D^2$
, of the curvature
$\mathbb D^2$
, of the curvature
![]() $0$
in the case of the cylinder and of curvature
$0$
in the case of the cylinder and of curvature
![]() $-1$
in the rest cases.
$-1$
in the rest cases.
Denote the metric of constant Gauss curvature and geodesic boundary from Theorem 4.5 by h. Consider a Riemannian surface with boundary
![]() $(\Sigma , h)$
. Its Schottky double admits the metric
$(\Sigma , h)$
. Its Schottky double admits the metric
![]() $h^d$
defined as
$h^d$
defined as
![]() $h^d_{|_{\Sigma }}=h$
and
$h^d_{|_{\Sigma }}=h$
and
![]() $h^d_{|_{\Sigma }'}=h$
. It is a metric of constant curvature and the involution
$h^d_{|_{\Sigma }'}=h$
. It is a metric of constant curvature and the involution
![]() $\iota : \Sigma ^d \to \Sigma ^d$
that interchanges
$\iota : \Sigma ^d \to \Sigma ^d$
that interchanges
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
becomes an isometry with
$\Sigma '$
becomes an isometry with
![]() $\partial \Sigma $
as the fixed set. Moreover,
$\partial \Sigma $
as the fixed set. Moreover,
![]() $(\Sigma ,h_n)=(\Sigma ^d,h^d_n)/\iota $
.
$(\Sigma ,h_n)=(\Sigma ^d,h^d_n)/\iota $
.
Theorem 4.5 also says that the set of conformal classes on the surface
![]() $\Sigma $
with boundary is in one-to-one correspondence with the set of metrics of constant Gauss curvature and geodesic boundary which is in the one-to-one correspondence with the set of “symmetric” metrics (metrics that go to themselves under the involution
$\Sigma $
with boundary is in one-to-one correspondence with the set of metrics of constant Gauss curvature and geodesic boundary which is in the one-to-one correspondence with the set of “symmetric” metrics (metrics that go to themselves under the involution
![]() $\iota $
) of constant curvature on the Schottky double. We endow the set of metrics of constant Gauss curvature and geodesic boundary with
$\iota $
) of constant curvature on the Schottky double. We endow the set of metrics of constant Gauss curvature and geodesic boundary with
![]() $C^{\infty }-$
topology. Consider a sequence of conformal classes
$C^{\infty }-$
topology. Consider a sequence of conformal classes
![]() $\{c_n\}$
on
$\{c_n\}$
on
![]() $\Sigma $
. It uniquely defines a sequence of “symmetric” metrics of constant curvature
$\Sigma $
. It uniquely defines a sequence of “symmetric” metrics of constant curvature
![]() $\{h^d_n\}$
on
$\{h^d_n\}$
on
![]() $\Sigma ^d$
. For this sequence, we have the same dichotomy as we have seen in the previous sections. Precisely, either
$\Sigma ^d$
. For this sequence, we have the same dichotomy as we have seen in the previous sections. Precisely, either
![]() $\operatorname {inj} (\Sigma ^d,h^d_n) \nrightarrow 0$
or
$\operatorname {inj} (\Sigma ^d,h^d_n) \nrightarrow 0$
or
![]() $\operatorname {inj} (\Sigma ^d,h^d_n)\to 0$
. In the first case we get a genuine Riemannian metric on
$\operatorname {inj} (\Sigma ^d,h^d_n)\to 0$
. In the first case we get a genuine Riemannian metric on
![]() $\Sigma ^d$
which is obviously “symmetric” and of constant curvature while in the second case one can find a set of simple closed geodesics
$\Sigma ^d$
which is obviously “symmetric” and of constant curvature while in the second case one can find a set of simple closed geodesics
![]() $\{c_1^n,\dots ,c_s^n\},$
where
$\{c_1^n,\dots ,c_s^n\},$
where
![]() $s \leq 6\gamma +3l-6$
whose lengths
$s \leq 6\gamma +3l-6$
whose lengths
![]() $l_{h^d_n}(c_i^n)\to 0$
. For the geodesics
$l_{h^d_n}(c_i^n)\to 0$
. For the geodesics
![]() $c_i^n$
there exist two possibilities: either
$c_i^n$
there exist two possibilities: either
![]() $\iota (c_i^n)=c_i^n$
or
$\iota (c_i^n)=c_i^n$
or
![]() $\iota (c_i^n)=c_j^n$
with
$\iota (c_i^n)=c_j^n$
with
![]() $j \neq i$
. The first possibility implies that the geodesic
$j \neq i$
. The first possibility implies that the geodesic
![]() $c_i^n$
crosses
$c_i^n$
crosses
![]() $\partial \Sigma $
which corresponds to two situations as well: either
$\partial \Sigma $
which corresponds to two situations as well: either
![]() $c_i^n$
has exactly two points of intersection with
$c_i^n$
has exactly two points of intersection with
![]() $\partial \Sigma $
or it belongs to
$\partial \Sigma $
or it belongs to
![]() $\partial \Sigma $
, i.e., it is one of the boundary components. The second possibility implies that
$\partial \Sigma $
, i.e., it is one of the boundary components. The second possibility implies that
![]() $c_i^n$
does not crosse
$c_i^n$
does not crosse
![]() $\partial \Sigma $
. Taking quotient by
$\partial \Sigma $
. Taking quotient by
![]() $\iota $
, we then get three types of pinching geodesics on
$\iota $
, we then get three types of pinching geodesics on
![]() $(\Sigma ,h_n)$
with
$(\Sigma ,h_n)$
with
![]() $\operatorname {inj} (\Sigma ,h_n) \to 0$
: pinching boundary components, pinching simple geodesics which have exactly two points of intersection with the boundary and pinching simple closed geodesics which do not cross the boundary.
$\operatorname {inj} (\Sigma ,h_n) \to 0$
: pinching boundary components, pinching simple geodesics which have exactly two points of intersection with the boundary and pinching simple closed geodesics which do not cross the boundary.
4.5 Nonorientable surface with boundary of negative Euler characteristic
Let
![]() $\Sigma $
be a compact nonorientable surface with l boundary components. Note that the Uniformization Theorem 4.5 also holds for nonorientable surfaces. Pick a metric h of constant Gauss curvature and geodesic boundary. We pass to the orientable cover that we denote by
$\Sigma $
be a compact nonorientable surface with l boundary components. Note that the Uniformization Theorem 4.5 also holds for nonorientable surfaces. Pick a metric h of constant Gauss curvature and geodesic boundary. We pass to the orientable cover that we denote by
![]() $\widetilde \Sigma $
. The surface
$\widetilde \Sigma $
. The surface
![]() $\widetilde \Sigma $
is a compact orientable surface with
$\widetilde \Sigma $
is a compact orientable surface with
![]() $2l$
boundary components. The pull-back of the metric h that we denote by
$2l$
boundary components. The pull-back of the metric h that we denote by
![]() $\tilde h$
is a metric of constant Gauss curvature and with geodesic boundary. Moreover, this metric is invariant under the involution changing the orientation on
$\tilde h$
is a metric of constant Gauss curvature and with geodesic boundary. Moreover, this metric is invariant under the involution changing the orientation on
![]() $\widetilde \Sigma $
. Consider a sequence
$\widetilde \Sigma $
. Consider a sequence
![]() $\{h_n\}$
on
$\{h_n\}$
on
![]() $\Sigma $
of metrics of constant Gauss curvature and geodesic boundary such that
$\Sigma $
of metrics of constant Gauss curvature and geodesic boundary such that
![]() $\operatorname {inj}(\Sigma ,h_n)\to 0$
as
$\operatorname {inj}(\Sigma ,h_n)\to 0$
as
![]() $n\to \infty $
. This sequence corresponds to the sequence
$n\to \infty $
. This sequence corresponds to the sequence
![]() $\{\tilde h_n\}$
on
$\{\tilde h_n\}$
on
![]() $\widetilde \Sigma $
such that
$\widetilde \Sigma $
such that
![]() $\operatorname {inj}(\widetilde \Sigma ,\tilde h_n)\to 0$
as
$\operatorname {inj}(\widetilde \Sigma ,\tilde h_n)\to 0$
as
![]() $n\to \infty $
. As we discussed in the previous section for the sequence
$n\to \infty $
. As we discussed in the previous section for the sequence
![]() $\{\tilde h_n\}$
, one can find pinching geodesics of the following three types: pinching boundary components, pinching simple geodesics crossing the boundary at two points and pinching simple closed geodesics which do not cross the boundary. Note that for the geodesics of the second type the points of intersection with the boundary are not identified under the involution. Indeed, if the were identified then the corresponding pinching geodesic had fixed ends under the involution. Applying the involution to this geodesic we would get a pinching closed geodesic crossing the boundary at two points which is not one of the possible types of pinching geodesics. Consider now the geodesics of the third type. For every such geodesic there are two possible cases: either this geodesic maps to itself under the involution changing the orientation or it maps to another simple closed geodesic which does not cross the boundary. Then taking the quotient by the involution changing the orientation we get two types of simple closed geodesics on
$\{\tilde h_n\}$
, one can find pinching geodesics of the following three types: pinching boundary components, pinching simple geodesics crossing the boundary at two points and pinching simple closed geodesics which do not cross the boundary. Note that for the geodesics of the second type the points of intersection with the boundary are not identified under the involution. Indeed, if the were identified then the corresponding pinching geodesic had fixed ends under the involution. Applying the involution to this geodesic we would get a pinching closed geodesic crossing the boundary at two points which is not one of the possible types of pinching geodesics. Consider now the geodesics of the third type. For every such geodesic there are two possible cases: either this geodesic maps to itself under the involution changing the orientation or it maps to another simple closed geodesic which does not cross the boundary. Then taking the quotient by the involution changing the orientation we get two types of simple closed geodesics on
![]() $\Sigma $
which do not crosse the boundary: one-sided geodesics which are the images of the geodesics described in the first case and two-sided geodesics which are the images of the geodesics described in the second case. The collars of one-sided geodesics are nothing but Möbius bands while the collars of two-sided geodesics are cylinders. Therefore, if
$\Sigma $
which do not crosse the boundary: one-sided geodesics which are the images of the geodesics described in the first case and two-sided geodesics which are the images of the geodesics described in the second case. The collars of one-sided geodesics are nothing but Möbius bands while the collars of two-sided geodesics are cylinders. Therefore, if
![]() $\operatorname {inj}(\Sigma ,h_n)\to 0$
as
$\operatorname {inj}(\Sigma ,h_n)\to 0$
as
![]() $n\to \infty $
, then one can find pinching geodesics of the following types: pinching boundary components, pinching simple geodesics which have exactly two points of intersection with the boundary, one-sided pinching simple closed geodesics not crossing the boundary and two-sided pinching simple closed geodesics not crossing the boundary.
$n\to \infty $
, then one can find pinching geodesics of the following types: pinching boundary components, pinching simple geodesics which have exactly two points of intersection with the boundary, one-sided pinching simple closed geodesics not crossing the boundary and two-sided pinching simple closed geodesics not crossing the boundary.
4.6 Surfaces with boundary of non-negative Euler characteristic
Here we consider the cases of the disc, the cylinder
![]() $\mathcal C$
and the Möbius band
$\mathcal C$
and the Möbius band
![]() $\mathbb {MB}$
.
$\mathbb {MB}$
.
It is known that the disc has a unique conformal class (up to an isometry). We denote this conformal class as
![]() $[g_{can}]$
or
$[g_{can}]$
or
![]() $c_{can}$
, where
$c_{can}$
, where
![]() $g_{can}$
is the flat metric on the disc
$g_{can}$
is the flat metric on the disc
![]() $\mathbb D^2$
with unit boundary length.
$\mathbb D^2$
with unit boundary length.
Accordingly to Theorem 4.5 in a conformal class on
![]() $\mathcal C$
there exists a flat metric with geodesic boundary, i.e., a metric on the right circular cylinder. This metric is unique if we fix the length of the boundary. The right circular cylinder is uniquely determined by its height. Therefore, conformal classes on
$\mathcal C$
there exists a flat metric with geodesic boundary, i.e., a metric on the right circular cylinder. This metric is unique if we fix the length of the boundary. The right circular cylinder is uniquely determined by its height. Therefore, conformal classes on
![]() $\mathcal C$
are in one-to-one correspondence with heights of right circular cylinders, i.e., the set of conformal classes is
$\mathcal C$
are in one-to-one correspondence with heights of right circular cylinders, i.e., the set of conformal classes is
![]() $\mathbb R_{>0}$
. We will identify conformal classes on
$\mathbb R_{>0}$
. We will identify conformal classes on
![]() $\mathcal C$
with points of
$\mathcal C$
with points of
![]() $\mathbb R_{>0}$
. We say that the sequence
$\mathbb R_{>0}$
. We say that the sequence
![]() $\{c_n\}$
of conformal classes degenerates if either
$\{c_n\}$
of conformal classes degenerates if either
![]() $c_n \to 0$
or
$c_n \to 0$
or
![]() $c_n\to \infty $
. The case
$c_n\to \infty $
. The case
![]() $c_n \to 0$
corresponds to a pinching geodesic having intersection with two boundary components (i.e., the generatrix of the right circular cylinder). The case
$c_n \to 0$
corresponds to a pinching geodesic having intersection with two boundary components (i.e., the generatrix of the right circular cylinder). The case
![]() $c_n\to \infty $
corresponds to pinching boundary components.
$c_n\to \infty $
corresponds to pinching boundary components.
In the case of the Möbius band we also use Theorem 4.5 which implies that in every conformal class on
![]() $\mathbb {MB}$
there exists a flat metric with geodesic boundary which is unique if we fix the length of the boundary. Passing to the orientable cover and pulling back the flat metric from
$\mathbb {MB}$
there exists a flat metric with geodesic boundary which is unique if we fix the length of the boundary. Passing to the orientable cover and pulling back the flat metric from
![]() $\mathbb {MB}$
we get a flat cylinder with geodesic boundary. Then the discussion in the previous paragraph implies that the conformal classes on
$\mathbb {MB}$
we get a flat cylinder with geodesic boundary. Then the discussion in the previous paragraph implies that the conformal classes on
![]() $\mathbb {MB}$
are also encoded by
$\mathbb {MB}$
are also encoded by
![]() $\mathbb R_{>0}$
. Identifying again conformal classes on
$\mathbb R_{>0}$
. Identifying again conformal classes on
![]() $\mathbb {MB}$
with points of
$\mathbb {MB}$
with points of
![]() $\mathbb R_{>0}$
, we get two possible cases for a sequence of conformal classes
$\mathbb R_{>0}$
, we get two possible cases for a sequence of conformal classes
![]() $\{c_n\}$
: either
$\{c_n\}$
: either
![]() $c_n \to 0$
or
$c_n \to 0$
or
![]() $c_n\to \infty $
. In both cases, we say that the sequence
$c_n\to \infty $
. In both cases, we say that the sequence
![]() $\{c_n\}$
degenerates. The first case corresponds to a pinching geodesic having two points of intersection with boundary. The second case corresponds to the collapsing boundary.
$\{c_n\}$
degenerates. The first case corresponds to a pinching geodesic having two points of intersection with boundary. The second case corresponds to the collapsing boundary.
5 Proof of Theorem 1.4
Negative Euler characteristic. Let
![]() $\Sigma $
be a surface with boundary and
$\Sigma $
be a surface with boundary and
![]() $c_n\to c_{\infty }$
a degenerating sequence of conformal classes. Consider the corresponding sequence of metrics
$c_n\to c_{\infty }$
a degenerating sequence of conformal classes. Consider the corresponding sequence of metrics
![]() $h_n$
of constant Gauss curvature and geodesic boundary. Then as we have noticed in Section 4.4, one can find
$h_n$
of constant Gauss curvature and geodesic boundary. Then as we have noticed in Section 4.4, one can find
![]() $s=s_1+s_2+s_3$
pinching geodesics of the following three types:
$s=s_1+s_2+s_3$
pinching geodesics of the following three types:
![]() $s_1$
pinching boundary components,
$s_1$
pinching boundary components,
![]() $s_2$
pinching geodesics that have two points of intersection with boundary and
$s_2$
pinching geodesics that have two points of intersection with boundary and
![]() $s_3$
pinching simple closed geodesics that do not intersect the boundary.
$s_3$
pinching simple closed geodesics that do not intersect the boundary.
We introduce the following notations
-
•
 $\gamma ^n_i$
for collapsing geodesics,
$\gamma ^n_i$
for collapsing geodesics,
 $i=1,\ldots ,s$
. If we do not indicate the superscript then the symbol
$i=1,\ldots ,s$
. If we do not indicate the superscript then the symbol
 $\gamma _i$
stands for the genus;
$\gamma _i$
stands for the genus; -
•
 $\mathcal {C}^n_i$
for collars of collapsing geodesics,
$\mathcal {C}^n_i$
for collars of collapsing geodesics,
 $i=1,\ldots ,s$
. Their widths are denoted by
$i=1,\ldots ,s$
. Their widths are denoted by
 $w^n_i$
. Moreover,
$w^n_i$
. Moreover,
 $\mathcal {C}^n_i:=\{(t,\theta )~|~0 \leq t<w^n_i,~0 \leq \theta \leq 2\pi \}$
for
$\mathcal {C}^n_i:=\{(t,\theta )~|~0 \leq t<w^n_i,~0 \leq \theta \leq 2\pi \}$
for
 $1 \leq i \leq s_1$
and
$1 \leq i \leq s_1$
and
 $\mathcal {C}^n_i:=\{(t,\theta )~|~-w^n_i<t<w^n_i,~0 \leq \theta \leq 2\pi \}$
for
$\mathcal {C}^n_i:=\{(t,\theta )~|~-w^n_i<t<w^n_i,~0 \leq \theta \leq 2\pi \}$
for
 $s_1+1 \leq i \leq s$
(if the geodesic is one-sided then we consider
$s_1+1 \leq i \leq s$
(if the geodesic is one-sided then we consider
 $\mathcal {C}^n_i:=\{(t,\theta )~|~-w^n_i< t<w^n_i,~0 \leq \theta \leq 2\pi \}/\sim $
, where
$\mathcal {C}^n_i:=\{(t,\theta )~|~-w^n_i< t<w^n_i,~0 \leq \theta \leq 2\pi \}/\sim $
, where
 $\sim $
stands for
$\sim $
stands for
 $(t,\theta )\sim (-t,\pi +\theta )$
). Note that geodesics correspond to the line
$(t,\theta )\sim (-t,\pi +\theta )$
). Note that geodesics correspond to the line
 $\{t=0\}$
, the segments
$\{t=0\}$
, the segments
 $\{\theta =0\}$
and
$\{\theta =0\}$
and
 $\{\theta =2\pi \}$
are identified for
$\{\theta =2\pi \}$
are identified for
 $1 \leq i \leq s_1$
and for
$1 \leq i \leq s_1$
and for
 $s_1+s_2+1 \leq i \leq s$
and they are not identified for
$s_1+s_2+1 \leq i \leq s$
and they are not identified for
 $s_1+1 \leq i \leq s_1+s_2$
and correspond to the segments of intersection with the boundary;
$s_1+1 \leq i \leq s_1+s_2$
and correspond to the segments of intersection with the boundary; -
• for
 $0<a<w^n_i$
, we denote
$0<a<w^n_i$
, we denote
 $\mathcal C^n_i(0,a)$
the subset
$\mathcal C^n_i(0,a)$
the subset
 $\{(t, \theta )\,|~0 \leq t \leq a, 0 \leq \theta \leq 2\pi \}\subset {\mathcal {C}}^n_i$
for
$\{(t, \theta )\,|~0 \leq t \leq a, 0 \leq \theta \leq 2\pi \}\subset {\mathcal {C}}^n_i$
for
 $1 \leq i \leq s_1$
and for
$1 \leq i \leq s_1$
and for
 $-w^n_i< a< b< w^n_i$
, we denote
$-w^n_i< a< b< w^n_i$
, we denote
 $\mathcal C^n_i(a,b)$
the subset
$\mathcal C^n_i(a,b)$
the subset
 $\{(t, \theta )\,|~a \leq t \leq b, 0 \leq \theta \leq 2\pi \}\subset {\mathcal {C}}^n_i$
for
$\{(t, \theta )\,|~a \leq t \leq b, 0 \leq \theta \leq 2\pi \}\subset {\mathcal {C}}^n_i$
for
 $s_1+1 \leq i \leq s$
;
$s_1+1 \leq i \leq s$
; -
•
 $\Gamma ^n_i:=\{(t,\theta )\in \mathcal {C}^n_i~|~\theta =0$
or
$\Gamma ^n_i:=\{(t,\theta )\in \mathcal {C}^n_i~|~\theta =0$
or
 $\theta =2\pi \}$
for
$\theta =2\pi \}$
for
 $s_1+1 \leq i \leq s_1+s_2$
;
$s_1+1 \leq i \leq s_1+s_2$
; -
• for
 $-w^n_i< a< b< w^n_i$
, we set
$-w^n_i< a< b< w^n_i$
, we set
 $\Gamma ^n_i(a,b):=\{(t,\theta )\in \Gamma ^n_i~|~a \leq t \leq b\}$
for
$\Gamma ^n_i(a,b):=\{(t,\theta )\in \Gamma ^n_i~|~a \leq t \leq b\}$
for
 $s_1+1 \leq i \leq s_1+s_2$
;
$s_1+1 \leq i \leq s_1+s_2$
; -
•
 $\Sigma ^n_j$
for the jth connected component of
$\Sigma ^n_j$
for the jth connected component of
 $\Sigma \setminus \cup ^s_{i=1} \mathcal {C}^n_i$
. We enumerate
$\Sigma \setminus \cup ^s_{i=1} \mathcal {C}^n_i$
. We enumerate
 $\Sigma ^n_j$
by
$\Sigma ^n_j$
by
 $1 \leq j \leq M$
such that M denotes the number of
$1 \leq j \leq M$
such that M denotes the number of
 $\Sigma ^n_j$
and for all
$\Sigma ^n_j$
and for all
 $1 \leq j \leq m$
one has
$1 \leq j \leq m$
one has
 $\Sigma ^n_j \cap \partial \Sigma \neq \varnothing $
;
$\Sigma ^n_j \cap \partial \Sigma \neq \varnothing $
; -
• let
 $\alpha ^n = \cup _{i=1}^{s_1+s_2}\{\alpha ^n_{i,-},\alpha ^n_{i,+}\}$
, where
$\alpha ^n = \cup _{i=1}^{s_1+s_2}\{\alpha ^n_{i,-},\alpha ^n_{i,+}\}$
, where
 $0 \leq \alpha ^n_{i,\pm }< w^n_i$
. We denote by
$0 \leq \alpha ^n_{i,\pm }< w^n_i$
. We denote by
 $\Sigma ^n_j(\alpha ^n)$
the connected component of which contains
$\Sigma ^n_j(\alpha ^n)$
the connected component of which contains $$ \begin{align*} \Sigma \setminus \bigg(\bigcup^{s_1+s_2}_{i=1}{\mathcal{C}}_i^n(\alpha^n_{i,-},\alpha^n_{i,+}) \cup \bigcup^{s}_{i=s_1+s_2+1} \gamma^n_i\bigg) \end{align*} $$
$$ \begin{align*} \Sigma \setminus \bigg(\bigcup^{s_1+s_2}_{i=1}{\mathcal{C}}_i^n(\alpha^n_{i,-},\alpha^n_{i,+}) \cup \bigcup^{s}_{i=s_1+s_2+1} \gamma^n_i\bigg) \end{align*} $$
 $\Sigma _j^n$
;
$\Sigma _j^n$
;
-
• for
 $\alpha ^n = \cup _{i=1}^{s_1+s_2}\{\alpha ^n_{i,-},\alpha ^n_{i,+}\}$
, where
$\alpha ^n = \cup _{i=1}^{s_1+s_2}\{\alpha ^n_{i,-},\alpha ^n_{i,+}\}$
, where
 $0 \leq \alpha ^n_{i,\pm }< w^n_i$
we set
$0 \leq \alpha ^n_{i,\pm }< w^n_i$
we set
 $I^n_j(\alpha ^n)=\Sigma ^n_j(\alpha ^n)\cap \partial \Sigma $
and
$I^n_j(\alpha ^n)=\Sigma ^n_j(\alpha ^n)\cap \partial \Sigma $
and
 $I^n_j=\Sigma ^n_j \cap \partial \Sigma $
where
$I^n_j=\Sigma ^n_j \cap \partial \Sigma $
where
 $1 \leq j \leq m$
;
$1 \leq j \leq m$
; -
• we use the notation
 $a_n \ll b_n$
for two sequences
$a_n \ll b_n$
for two sequences
 $\{a_n\}$
and
$\{a_n\}$
and
 $\{b_n\}$
satisfying
$\{b_n\}$
satisfying
 $a_n, b_n \to +\infty $
and
$a_n, b_n \to +\infty $
and
 $\frac {a_n}{b_n} \to 0$
as
$\frac {a_n}{b_n} \to 0$
as
 $n \to \infty $
.
$n \to \infty $
.
5.1 Inequality
 $\geq $
$\geq $
We prove that
 $$ \begin{align} \liminf_{n \to \infty} \sigma^*_k (\Sigma, c_n) \geq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg), \end{align} $$
$$ \begin{align} \liminf_{n \to \infty} \sigma^*_k (\Sigma, c_n) \geq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg), \end{align} $$
For this aim we consider the domains
![]() ${\mathcal {C}}^n_i(0,\alpha _{i,+}^n)$
for
${\mathcal {C}}^n_i(0,\alpha _{i,+}^n)$
for
![]() $1 \leq i \leq s_1$
,
$1 \leq i \leq s_1$
,
![]() ${\mathcal {C}}^n_i(\alpha _{i,-}^n,\alpha _{i,+}^n)$
for
${\mathcal {C}}^n_i(\alpha _{i,-}^n,\alpha _{i,+}^n)$
for
![]() $1+s_1 \leq i \leq s_1+s_2$
, where
$1+s_1 \leq i \leq s_1+s_2$
, where
![]() $ w^n_i - \alpha _{i,\pm }^n \ll w^n_i$
,
$ w^n_i - \alpha _{i,\pm }^n \ll w^n_i$
,
![]() $\alpha _{i,\pm }^n\to \infty $
and the domains
$\alpha _{i,\pm }^n\to \infty $
and the domains
![]() $\Sigma _j^n(\alpha ^n)$
for
$\Sigma _j^n(\alpha ^n)$
for
![]() $1 \leq j \leq m$
. By Lemma 2.9, we have
$1 \leq j \leq m$
. By Lemma 2.9, we have
 $$ \begin{align} \begin{aligned} &\sigma^*_k(\Sigma, c_n) \geq \max \bigg(\sum^{s_1}_{i=1}\sigma^{N*}_{r_{i}}({\mathcal{C}}^n_i(0,\alpha_{i,+}^n), \gamma^n_i, c_n) \\ &\quad +\sum^{s_1+s_2}_{i=1+s_1}\!\sigma^{N*}_{r_{i}}({\mathcal{C}}^n_i(\alpha_{i,-}^n,\alpha_{i,+}^n),\Gamma^n_i(\alpha_{i,-}^n,\alpha_{i,+}^n), c_n)+\sum^{m}_{j=1}\sigma^{N*}_{k_{j}}\!(\!\Sigma_j^n(\alpha^n), I^n_j(\alpha^n), c_n)\bigg). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\sigma^*_k(\Sigma, c_n) \geq \max \bigg(\sum^{s_1}_{i=1}\sigma^{N*}_{r_{i}}({\mathcal{C}}^n_i(0,\alpha_{i,+}^n), \gamma^n_i, c_n) \\ &\quad +\sum^{s_1+s_2}_{i=1+s_1}\!\sigma^{N*}_{r_{i}}({\mathcal{C}}^n_i(\alpha_{i,-}^n,\alpha_{i,+}^n),\Gamma^n_i(\alpha_{i,-}^n,\alpha_{i,+}^n), c_n)+\sum^{m}_{j=1}\sigma^{N*}_{k_{j}}\!(\!\Sigma_j^n(\alpha^n), I^n_j(\alpha^n), c_n)\bigg). \end{aligned} \end{align} $$
For
![]() $1 \leq i \leq s_1$
, we define the conformal maps
$1 \leq i \leq s_1$
, we define the conformal maps
![]() $\Psi _i^n\colon ({\mathcal {C}}^n_i(0,\alpha _{i,+}^n), c_n) \to (\mathbb {D}^2, [g_{can}])$
as
$\Psi _i^n\colon ({\mathcal {C}}^n_i(0,\alpha _{i,+}^n), c_n) \to (\mathbb {D}^2, [g_{can}])$
as
The images of
![]() $\Psi _i^n$
are the annuli
$\Psi _i^n$
are the annuli
![]() $\mathbb D^2 \setminus \mathbb D^2_{e^{-\alpha _{i,+}^n}}$
exhausting
$\mathbb D^2 \setminus \mathbb D^2_{e^{-\alpha _{i,+}^n}}$
exhausting
![]() $\mathbb D^2$
as
$\mathbb D^2$
as
![]() $n \to \infty .$
We also note that
$n \to \infty .$
We also note that
![]() $\Psi _i^n(\gamma ^n_i)=\mathbb S^1$
.
$\Psi _i^n(\gamma ^n_i)=\mathbb S^1$
.
For
![]() $s_1+1 \leq i \leq s_1+s_2$
, we define the conformal maps
$s_1+1 \leq i \leq s_1+s_2$
, we define the conformal maps
![]() $\Psi _i^n\colon ({\mathcal {C}}^n_i(\alpha _{i,-}^n,\alpha _{i,+}^n), c_n) \to (\mathbb {D}^2, [g_{can}])$
as
$\Psi _i^n\colon ({\mathcal {C}}^n_i(\alpha _{i,-}^n,\alpha _{i,+}^n), c_n) \to (\mathbb {D}^2, [g_{can}])$
as
 $$ \begin{align*} \Psi_i^n(t,\theta)=\tan\left(\frac{\theta-\pi+\sqrt{-1}t}{4}\right). \end{align*} $$
$$ \begin{align*} \Psi_i^n(t,\theta)=\tan\left(\frac{\theta-\pi+\sqrt{-1}t}{4}\right). \end{align*} $$
The images of
![]() $\Psi _i^n$
that we denote by
$\Psi _i^n$
that we denote by
![]() $\Omega _{i}^n$
exhaust
$\Omega _{i}^n$
exhaust
![]() $\mathbb D^2$
as
$\mathbb D^2$
as
![]() $n \to \infty .$
We also denote the image of
$n \to \infty .$
We also denote the image of
![]() $\Gamma ^n_i(\alpha _{i,-}^n,\alpha _{i,+}^n)$
by
$\Gamma ^n_i(\alpha _{i,-}^n,\alpha _{i,+}^n)$
by
![]() $\partial ^S\Omega _{i}^n$
. Note that
$\partial ^S\Omega _{i}^n$
. Note that
![]() $\partial ^S\Omega _{i}^n$
exhaust
$\partial ^S\Omega _{i}^n$
exhaust
![]() $\mathbb S^1$
as
$\mathbb S^1$
as
![]() $n\to \infty $
.
$n\to \infty $
.
Finally, we take restrictions of the diffeomorphisms
![]() $\Psi _n^{-1}$
given by Proposition 4.4 to obtain the conformal maps
$\Psi _n^{-1}$
given by Proposition 4.4 to obtain the conformal maps
![]() $\check \Psi _j^n\colon ({\Sigma }_j^n(\alpha ^n),c_n)\to (\Sigma _{\infty },\Psi _n^*c_n)$
where
$\check \Psi _j^n\colon ({\Sigma }_j^n(\alpha ^n),c_n)\to (\Sigma _{\infty },\Psi _n^*c_n)$
where
![]() $1 \leq j \leq m$
. Let
$1 \leq j \leq m$
. Let
![]() $\check \Omega _{j}^n \subset \Sigma _{\infty }$
be the the image of
$\check \Omega _{j}^n \subset \Sigma _{\infty }$
be the the image of
![]() $\check \Psi _j^n$
and
$\check \Psi _j^n$
and
![]() $\partial ^S\check \Omega _{j}^n:=\check \Psi _j^n(I^n_j(\alpha ^n))$
. The following lemma holds
$\partial ^S\check \Omega _{j}^n:=\check \Psi _j^n(I^n_j(\alpha ^n))$
. The following lemma holds
Lemma 5.1 Let
![]() $\Sigma ^{\infty }_j$
be the connected component
$\Sigma ^{\infty }_j$
be the connected component
![]() $\check \Psi ^n_j(\Sigma ^n_j)\subset \Sigma _{\infty }$
where
$\check \Psi ^n_j(\Sigma ^n_j)\subset \Sigma _{\infty }$
where
![]() $1 \leq j \leq m$
. Then the domains
$1 \leq j \leq m$
. Then the domains
![]() $\check \Omega _j^n$
exhaust
$\check \Omega _j^n$
exhaust
![]() $\Sigma ^{\infty }_j$
and
$\Sigma ^{\infty }_j$
and
![]() $\partial ^S\check \Omega _{j}^n$
exhaust
$\partial ^S\check \Omega _{j}^n$
exhaust
![]() $\partial \Sigma ^{\infty }_j$
.
$\partial \Sigma ^{\infty }_j$
.
Proof Passing to the Schottky double of the surface
![]() $\Sigma $
, we immediately deduce this lemma from [Reference Karpukhin and MedvedevKM20, Lemma 5.1].▪
$\Sigma $
, we immediately deduce this lemma from [Reference Karpukhin and MedvedevKM20, Lemma 5.1].▪
Further, we apply the conformal transformations to (5.2) to get
 $$ \begin{align} \begin{aligned} &\sigma^*_k(\Sigma, c_n) \geq \max\bigg(\sum^{s_1}_{i=1}\sigma^{N*}_{r_{i}}(\mathbb D^2 \setminus\mathbb D^2_{e^{-\alpha_{i,+}^n}}, \mathbb S^1, [g_{can}]) \\ &\quad +\sum^{s_1+s_2}_{i=1+s_1}\sigma^{N*}_{r_{i}}(\Omega_{i}^n, \partial^S\Omega_{i}^n, [g_{can}])+\sum^{m}_{j=1}\sigma^{N*}_{k_{j}}(\check\Omega_j^n, \partial^S\check\Omega_{j}^n, [(\Psi^n)^*h_n])\bigg). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\sigma^*_k(\Sigma, c_n) \geq \max\bigg(\sum^{s_1}_{i=1}\sigma^{N*}_{r_{i}}(\mathbb D^2 \setminus\mathbb D^2_{e^{-\alpha_{i,+}^n}}, \mathbb S^1, [g_{can}]) \\ &\quad +\sum^{s_1+s_2}_{i=1+s_1}\sigma^{N*}_{r_{i}}(\Omega_{i}^n, \partial^S\Omega_{i}^n, [g_{can}])+\sum^{m}_{j=1}\sigma^{N*}_{k_{j}}(\check\Omega_j^n, \partial^S\check\Omega_{j}^n, [(\Psi^n)^*h_n])\bigg). \end{aligned} \end{align} $$
It follows from Corollary 2.7 that the first two terms on the right hand side converge to
![]() $\sigma _{r_{i}}(\mathbb D^2, [g_{can}])$
. To complete the proof we will need the following lemma
$\sigma _{r_{i}}(\mathbb D^2, [g_{can}])$
. To complete the proof we will need the following lemma
Lemma 5.2 Let
![]() $\widehat {\Sigma _j^{\infty }}\subset \widehat {\Sigma _{\infty }}$
be a closure of
$\widehat {\Sigma _j^{\infty }}\subset \widehat {\Sigma _{\infty }}$
be a closure of
![]() $\Sigma _j^{\infty }$
,
$\Sigma _j^{\infty }$
,
![]() $1 \leq j \leq m$
. Then for all r one has
$1 \leq j \leq m$
. Then for all r one has
We postpone the proof to Section 7.3.
Finally, taking
![]() $\liminf _{n\to \infty }$
in (5.3) completes the proof of (5.1).
$\liminf _{n\to \infty }$
in (5.3) completes the proof of (5.1).
5.2 Inequality
 $\leq $
$\leq $
We prove the inverse inequality,
 $$ \begin{align} \limsup_{n \to \infty} \sigma^*_k (\Sigma, c_n) \leq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg). \end{align} $$
$$ \begin{align} \limsup_{n \to \infty} \sigma^*_k (\Sigma, c_n) \leq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg). \end{align} $$
For this aim we choose a subsequence
![]() $c_{n_m}$
such that
$c_{n_m}$
such that
Then we relabel the subsequence and denote it by
![]() $\{c_n\}$
. Therefore, one can choose subsequences without changing the value of
$\{c_n\}$
. Therefore, one can choose subsequences without changing the value of
![]() $\limsup $
.
$\limsup $
.
Case 1. Suppose that up to a choice of a subsequence the following inequality holds
Then by [Reference PetridesPet19, Theorem 2] in the conformal class
![]() $c_n$
there exists a metric
$c_n$
there exists a metric
![]() $g_n$
of unit boundary length induced from a harmonic immersion with free boundary
$g_n$
of unit boundary length induced from a harmonic immersion with free boundary
![]() $\Phi _n$
to some
$\Phi _n$
to some
![]() $N(n)$
-dimensional ball
$N(n)$
-dimensional ball
![]() $\mathbb {B}^{N(n)}$
, i.e.,
$\mathbb {B}^{N(n)}$
, i.e.,
 $$ \begin{align*} g_n=\frac{\langle \Phi_n, \partial_{\nu_n}\Phi_n\rangle_{h_n}}{\sigma^*_k(\Sigma, c_n)}h_n \end{align*} $$
$$ \begin{align*} g_n=\frac{\langle \Phi_n, \partial_{\nu_n}\Phi_n\rangle_{h_n}}{\sigma^*_k(\Sigma, c_n)}h_n \end{align*} $$
and such that
![]() $\sigma _k(g_n)=\sigma ^*_k(\Sigma , c_n)$
. Here, the metric
$\sigma _k(g_n)=\sigma ^*_k(\Sigma , c_n)$
. Here, the metric
![]() $h_n$
is the canonical representative in the conformal class
$h_n$
is the canonical representative in the conformal class
![]() $c_n$
. It is known that for any compact surface the multiplicity of
$c_n$
. It is known that for any compact surface the multiplicity of
![]() $\sigma _k(g_n)$
is bounded from above by a constant depending only on k and the topology of
$\sigma _k(g_n)$
is bounded from above by a constant depending only on k and the topology of
![]() $\Sigma $
(see for instance [Reference Fraser and SchoenFS12, Reference Karpukhin, Kokarev and PolterovichKKP14]). Therefore, one can choose the number
$\Sigma $
(see for instance [Reference Fraser and SchoenFS12, Reference Karpukhin, Kokarev and PolterovichKKP14]). Therefore, one can choose the number
![]() $N(n)$
large enough such that
$N(n)$
large enough such that
![]() $N(n)$
does not depend on n.
$N(n)$
does not depend on n.
Assume that for the sequence
![]() $\{c_n\}$
the following inequality holds
$\{c_n\}$
the following inequality holds
 $$ \begin{align} \limsup_{n \to \infty} \sigma^*_k (\Sigma, c_n)> \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg). \end{align} $$
$$ \begin{align} \limsup_{n \to \infty} \sigma^*_k (\Sigma, c_n)> \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg). \end{align} $$
For
![]() $1 \leq i \leq s_1$
we consider the conformal map
$1 \leq i \leq s_1$
we consider the conformal map
![]() $\Psi ^n_i: (\mathcal C^n_i, c_n) \to (\mathbb D^2,[g_{can}])$
defined as
$\Psi ^n_i: (\mathcal C^n_i, c_n) \to (\mathbb D^2,[g_{can}])$
defined as
![]() $\Psi ^n_i(\theta ,t)=e^{\sqrt {-1}(\theta +\sqrt {-1}t)}$
. The image of this map is nothing but
$\Psi ^n_i(\theta ,t)=e^{\sqrt {-1}(\theta +\sqrt {-1}t)}$
. The image of this map is nothing but
![]() $\mathbb D^2\setminus \mathbb D^2_{e^{-w^n_i}}$
which exhausts
$\mathbb D^2\setminus \mathbb D^2_{e^{-w^n_i}}$
which exhausts
![]() $\mathbb D^2$
as
$\mathbb D^2$
as
![]() $n\to \infty $
. The image of a pinching geodesic is
$n\to \infty $
. The image of a pinching geodesic is
![]() $\mathbb S^1$
. Then the map
$\mathbb S^1$
. Then the map
![]() $\Phi ^n_i:=\Phi _n\circ (\Psi ^n_i)^{-1}: \mathbb D^2\setminus \mathbb D^2_{e^{-w^n_i}}\to \mathbb B^N$
satisfies the bubble convergence theorem for harmonic maps with free boundary [Reference Laurain and PetridesLP17, Theorem 1]. Hence, there exist a regular harmonic map with free boundary
$\Phi ^n_i:=\Phi _n\circ (\Psi ^n_i)^{-1}: \mathbb D^2\setminus \mathbb D^2_{e^{-w^n_i}}\to \mathbb B^N$
satisfies the bubble convergence theorem for harmonic maps with free boundary [Reference Laurain and PetridesLP17, Theorem 1]. Hence, there exist a regular harmonic map with free boundary
![]() $\Phi _i: \mathbb D^2 \to \mathbb B^N$
and some harmonic extensions of nonconstant
$\Phi _i: \mathbb D^2 \to \mathbb B^N$
and some harmonic extensions of nonconstant
![]() $1/2$
-harmonic maps
$1/2$
-harmonic maps
![]() $\omega ^i_1,\dots ,\omega ^i_{t_i}: \mathbb D^2 \to \mathbb B^N$
such that
$\omega ^i_1,\dots ,\omega ^i_{t_i}: \mathbb D^2 \to \mathbb B^N$
such that
 $$ \begin{align*} \int_{\mathbb D^2}|\nabla \Phi_i|^2dv_{g_{can}}+\sum^{t_j}_{j=1}\int_{\mathbb D^2}|\nabla \omega^j_{t_i}|^2dv_{g_{can}} = \lim_{n\to\infty} \int_{\gamma^n_i}ds_{g_n}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb D^2}|\nabla \Phi_i|^2dv_{g_{can}}+\sum^{t_j}_{j=1}\int_{\mathbb D^2}|\nabla \omega^j_{t_i}|^2dv_{g_{can}} = \lim_{n\to\infty} \int_{\gamma^n_i}ds_{g_n}. \end{align*} $$
We denote
![]() $\lim _{n\to \infty }\int _{\gamma ^n_i}ds_{g_n}$
by
$\lim _{n\to \infty }\int _{\gamma ^n_i}ds_{g_n}$
by
![]() $m_i$
.
$m_i$
.
Proposition 5.3 For
![]() $s_1+1 \leq i \leq s_1+s_2$
there exist integers
$s_1+1 \leq i \leq s_1+s_2$
there exist integers
![]() $t_{i} \geq 0$
, non-negative sequences
$t_{i} \geq 0$
, non-negative sequences
![]() $\{a_{i,l}^n\}, \{b_{i,l}^n\}$
with
$\{a_{i,l}^n\}, \{b_{i,l}^n\}$
with
![]() $1 \leq l \leq t_{i}$
and a sequence
$1 \leq l \leq t_{i}$
and a sequence
![]() $\{\alpha ^n_i\}$
such that
$\{\alpha ^n_i\}$
such that
and
Moreover, there exists a set
![]() $J \subset \{1,\ldots ,m\}$
such that for every
$J \subset \{1,\ldots ,m\}$
such that for every
![]() $j \in J$
one has
$j \in J$
one has
satisfying
 $$ \begin{align*} \sum^{s_1}_{i=1} m_{i}+\sum^{s_1+s_2}_{i=1} \sum^{t_i}_{l=s_1+1}m_{i,l}+\sum_{j\in J}m_j=1, \end{align*} $$
$$ \begin{align*} \sum^{s_1}_{i=1} m_{i}+\sum^{s_1+s_2}_{i=1} \sum^{t_i}_{l=s_1+1}m_{i,l}+\sum_{j\in J}m_j=1, \end{align*} $$
with
![]() $s_1+\sum ^{s_1+s_2}_{i=s_1+1}t_i$
is maximal.
$s_1+\sum ^{s_1+s_2}_{i=s_1+1}t_i$
is maximal.
Proof The proof follows the proofs of Claim 16, Claim 17 by [Reference PetridesPet19]. Precisely, denying the proposition one can construct
![]() $k+1$
test-functions such that
$k+1$
test-functions such that
![]() $\sigma _k(g_n) \leq o(1)$
which contradicts inequality (1.2). The construction of these functions is given in the proofs of Claim 16, Claim 17 by [Reference PetridesPet19]. Note that these functions equal
$\sigma _k(g_n) \leq o(1)$
which contradicts inequality (1.2). The construction of these functions is given in the proofs of Claim 16, Claim 17 by [Reference PetridesPet19]. Note that these functions equal
![]() $1$
on
$1$
on
![]() $\Sigma ^n_j$
for every
$\Sigma ^n_j$
for every
![]() $m+1 \leq j \leq M$
.▪
$m+1 \leq j \leq M$
.▪
We proceed with considering a sequence
![]() $\{d_{i,l}^n\}$
where
$\{d_{i,l}^n\}$
where
![]() $s_1+1 \leq i \leq s_1+s_2$
and
$s_1+1 \leq i \leq s_1+s_2$
and
![]() $1 \leq l \leq t_i$
such that
$1 \leq l \leq t_i$
such that
Let
![]() $q^n_{i,l}\ll a^n_{i,l}$
,
$q^n_{i,l}\ll a^n_{i,l}$
,
![]() $q^n_{i,l}\to +\infty $
. Consider the conformal maps
$q^n_{i,l}\to +\infty $
. Consider the conformal maps
defined as
 $$ \begin{align*} \Psi_{i,l}^n(t,\theta)=\tan\bigg(\frac{\theta-\pi+\sqrt{-1}(t-t_{i,l}^n)}{4}\bigg) \end{align*} $$
$$ \begin{align*} \Psi_{i,l}^n(t,\theta)=\tan\bigg(\frac{\theta-\pi+\sqrt{-1}(t-t_{i,l}^n)}{4}\bigg) \end{align*} $$
Let
and
Then
![]() $D_{i,j}^n$
exhausts
$D_{i,j}^n$
exhausts
![]() $\mathbb D^2$
and
$\mathbb D^2$
and
![]() $S_{i,j}^n$
exhausts
$S_{i,j}^n$
exhausts
![]() $\mathbb S^1$
as
$\mathbb S^1$
as
![]() $n\to \infty $
. We also set
$n\to \infty $
. We also set
Consider the map
![]() $\Phi _{i,l}^n=\Phi _n \circ (\Psi _{i,l}^n)^{-1}\colon (D_{i,j}^n,S_{i,j}^n) \to (\mathbb B^{N},\mathbb S^{N-1})$
. We endow
$\Phi _{i,l}^n=\Phi _n \circ (\Psi _{i,l}^n)^{-1}\colon (D_{i,j}^n,S_{i,j}^n) \to (\mathbb B^{N},\mathbb S^{N-1})$
. We endow
![]() $D_{i,j}^n$
with the metric
$D_{i,j}^n$
with the metric
![]() $(\Psi _{i,l}^n)_*g_n$
and
$(\Psi _{i,l}^n)_*g_n$
and
![]() $\mathbb B^{N}$
with the Euclidean metric. Then the map
$\mathbb B^{N}$
with the Euclidean metric. Then the map
![]() $\Phi _{i,l}^n$
is harmonic with free boundary since
$\Phi _{i,l}^n$
is harmonic with free boundary since
![]() $\Phi _n$
is harmonic with free boundary and
$\Phi _n$
is harmonic with free boundary and
![]() $\Psi _{i,l}^n$
is conformal. Moreover, it is shown in [Reference PetridesPet19] that the measure
$\Psi _{i,l}^n$
is conformal. Moreover, it is shown in [Reference PetridesPet19] that the measure
![]() $\boldsymbol {1}_{S_{i,j}^n}\langle \Phi _{i,l}^n,\partial _{\nu }\Phi _{i,l}^n\rangle _{g_{can}}ds_{g_{can}}$
does not concentrate at the poles
$\boldsymbol {1}_{S_{i,j}^n}\langle \Phi _{i,l}^n,\partial _{\nu }\Phi _{i,l}^n\rangle _{g_{can}}ds_{g_{can}}$
does not concentrate at the poles
![]() $(0,1)$
and
$(0,1)$
and
![]() $(0,-1)$
of
$(0,-1)$
of
![]() $\mathbb {D}^2$
. Indeed, if the measure concentrated at the poles then one would obtain a contradiction with the maximality of
$\mathbb {D}^2$
. Indeed, if the measure concentrated at the poles then one would obtain a contradiction with the maximality of
![]() $s_1+\sum ^{s_1+s_2}_{i=s_1+1}t_i$
.
$s_1+\sum ^{s_1+s_2}_{i=s_1+1}t_i$
.
The exactly same procedure can be carried out for components
![]() $\Sigma _j^n(\alpha ^n)$
,
$\Sigma _j^n(\alpha ^n)$
,
![]() $j\in J$
. The only difference is that now we use restrictions of diffeomorphisms
$j\in J$
. The only difference is that now we use restrictions of diffeomorphisms
![]() $\Psi ^n$
given by Proposition 4.4 instead of the explicit harmonic map as above. As a result, one obtains domains
$\Psi ^n$
given by Proposition 4.4 instead of the explicit harmonic map as above. As a result, one obtains domains
![]() $\check \Omega ^n_j\subset \Sigma _{\infty }$
and harmonic maps with free boundary
$\check \Omega ^n_j\subset \Sigma _{\infty }$
and harmonic maps with free boundary
![]() $\check \Phi ^n_j\colon \check \Omega ^n_j\to \mathbb {B}^N$
such that the measure
$\check \Phi ^n_j\colon \check \Omega ^n_j\to \mathbb {B}^N$
such that the measure
![]() $\boldsymbol {1}_{\partial \check \Omega _j^n}\langle \Phi _{i,l}^n,\partial _{\nu }\Phi _{i,l}^n\rangle _{g_{can}}ds_{g_{can}}$
does not concentrate at the marked points of
$\boldsymbol {1}_{\partial \check \Omega _j^n}\langle \Phi _{i,l}^n,\partial _{\nu }\Phi _{i,l}^n\rangle _{g_{can}}ds_{g_{can}}$
does not concentrate at the marked points of
![]() $\widehat {\Sigma _{\infty }}$
.
$\widehat {\Sigma _{\infty }}$
.
Now thanks to inequality (5.5), we can construct
![]() $k+1$
well-defined test-functions for the Rayleigh quotient of
$k+1$
well-defined test-functions for the Rayleigh quotient of
![]() $\sigma _k$
using the limit functions of the sequences of maps
$\sigma _k$
using the limit functions of the sequences of maps
![]() $\hat \Phi _{i,l}^n$
and
$\hat \Phi _{i,l}^n$
and
![]() $\hat \Phi _i^n$
as it was shown in [Reference PetridesPet19]. Precisely, let
$\hat \Phi _i^n$
as it was shown in [Reference PetridesPet19]. Precisely, let
![]() $p_{i}$
be the maximal integers such that
$p_{i}$
be the maximal integers such that
 $$ \begin{align} \frac{\sigma^*_{p_{i}}(\mathbb{D}^2)}{m_{i}}<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n), \end{align} $$
$$ \begin{align} \frac{\sigma^*_{p_{i}}(\mathbb{D}^2)}{m_{i}}<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n), \end{align} $$
where
![]() $1 \leq i \leq s_1$
,
$1 \leq i \leq s_1$
,
![]() $p_{i,l}$
the maximal integers such that
$p_{i,l}$
the maximal integers such that
 $$ \begin{align} \frac{\sigma^*_{p_{i,l}}(\mathbb{D}^2)}{m_{i,l}}<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n), \end{align} $$
$$ \begin{align} \frac{\sigma^*_{p_{i,l}}(\mathbb{D}^2)}{m_{i,l}}<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n), \end{align} $$
where
![]() $s_1+1 \leq i \leq s_1+s_2$
and
$s_1+1 \leq i \leq s_1+s_2$
and
![]() $p_j$
the maximal integers such that
$p_j$
the maximal integers such that
 $$ \begin{align} \frac{\sigma^*_{p_{j}}(\widehat{\Sigma_j^{\infty}}, \widehat{c_{\infty}})}{m_{j}}<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n),~j\in J. \end{align} $$
$$ \begin{align} \frac{\sigma^*_{p_{j}}(\widehat{\Sigma_j^{\infty}}, \widehat{c_{\infty}})}{m_{j}}<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n),~j\in J. \end{align} $$
Then one has
 $$ \begin{align*} \begin{array}{c} \sigma^*_{p_{i}+1}(\mathbb{D}^2) \geq m_{i}\displaystyle\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n),~1 \leq i \leq s_1, \\ \sigma^*_{p_{i,l}+1}(\mathbb{D}^2) \geq m_{i,l}\displaystyle\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n),~s_1+1 \leq i \leq s_1+s_2 \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c} \sigma^*_{p_{i}+1}(\mathbb{D}^2) \geq m_{i}\displaystyle\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n),~1 \leq i \leq s_1, \\ \sigma^*_{p_{i,l}+1}(\mathbb{D}^2) \geq m_{i,l}\displaystyle\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n),~s_1+1 \leq i \leq s_1+s_2 \end{array} \end{align*} $$
and
If
![]() $\sum ^{s_1}_{i=1} (p_{i}+1)+\sum ^{s_1+s_2}_{i=s_1+1} \sum ^{t_i}_{l=1} (p_{i,l}+1)+\sum _{j \in J}(p_j+1) \leq k$
then by inequality (5.5) we have
$\sum ^{s_1}_{i=1} (p_{i}+1)+\sum ^{s_1+s_2}_{i=s_1+1} \sum ^{t_i}_{l=1} (p_{i,l}+1)+\sum _{j \in J}(p_j+1) \leq k$
then by inequality (5.5) we have
 $$ \begin{align*} \sum^{s_1}_{i=1} \sigma^*_{p_{i}+1}(\mathbb{D}^2)+\sum^{s_1+s_2}_{i=s_1+1} \sum^{t_i}_{l=1}\sigma^*_{p_{i,l}+1}(\mathbb{D}^2)+ \sum_{j \in J}\sigma^*_{p_{j}+1}(\widehat{\Sigma_j^{\infty}}, \widehat{c_{\infty}})<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n), \end{align*} $$
$$ \begin{align*} \sum^{s_1}_{i=1} \sigma^*_{p_{i}+1}(\mathbb{D}^2)+\sum^{s_1+s_2}_{i=s_1+1} \sum^{t_i}_{l=1}\sigma^*_{p_{i,l}+1}(\mathbb{D}^2)+ \sum_{j \in J}\sigma^*_{p_{j}+1}(\widehat{\Sigma_j^{\infty}}, \widehat{c_{\infty}})<\limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n), \end{align*} $$
which implies
![]() $\sum ^{s_1}_{i=1} m_{i}+\sum ^{s_1+s_2}_{i=s_1+1} \sum ^{t_i}_{l=1}m_{i,l}+\sum _{j\in J}m_j < 1$
and we arrive at a contradiction with Proposition 5.3. Hence,
$\sum ^{s_1}_{i=1} m_{i}+\sum ^{s_1+s_2}_{i=s_1+1} \sum ^{t_i}_{l=1}m_{i,l}+\sum _{j\in J}m_j < 1$
and we arrive at a contradiction with Proposition 5.3. Hence,
![]() $\sum ^{s_1}_{i=1} (p_{i}+1)+\sum ^{s_1+s_2}_{i=s_1+1} \sum ^{t_i}_{l=1} (p_{i,l}+1)+\sum _{j \in J}({p_j+1}) \geq k+1$
.
$\sum ^{s_1}_{i=1} (p_{i}+1)+\sum ^{s_1+s_2}_{i=s_1+1} \sum ^{t_i}_{l=1} (p_{i,l}+1)+\sum _{j \in J}({p_j+1}) \geq k+1$
.
Further, let
![]() $dv_{g^{i}_{\infty }}=\lim _{n \to \infty } (\Psi _{i}^n)_*dv_{g_n}$
,
$dv_{g^{i}_{\infty }}=\lim _{n \to \infty } (\Psi _{i}^n)_*dv_{g_n}$
,
![]() $dv_{g^{i,l}_{\infty }}=\lim _{n \to \infty } (\Psi _{i,l}^n)_*dv_{g_n}$
and
$dv_{g^{i,l}_{\infty }}=\lim _{n \to \infty } (\Psi _{i,l}^n)_*dv_{g_n}$
and
![]() $dv_{g^j_{\infty }}=\lim _{n \to \infty } (\Psi _j^n)^*dv_{g_n}$
. Denote by
$dv_{g^j_{\infty }}=\lim _{n \to \infty } (\Psi _j^n)^*dv_{g_n}$
. Denote by
![]() $\widehat {dv_{g^{i}_{\infty }}}$
,
$\widehat {dv_{g^{i}_{\infty }}}$
,
![]() $\widehat {dv_{g^{i,l}_{\infty }}}$
and
$\widehat {dv_{g^{i,l}_{\infty }}}$
and
![]() $\widehat {dv_{g^j_{\infty }}}$
the measures induced by the compactification on
$\widehat {dv_{g^j_{\infty }}}$
the measures induced by the compactification on
![]() $\mathbb {D}^2$
for
$\mathbb {D}^2$
for
![]() $1 \leq i \leq s_1$
and
$1 \leq i \leq s_1$
and
![]() $s_1+1 \leq i \leq s_1+s_2$
and on
$s_1+1 \leq i \leq s_1+s_2$
and on
![]() $\widehat {\Sigma _j^{\infty }}$
, respectively. These measures are well-defined due to the nonconcentration argument explained above. Take orthonormal families of eigenfucntions
$\widehat {\Sigma _j^{\infty }}$
, respectively. These measures are well-defined due to the nonconcentration argument explained above. Take orthonormal families of eigenfucntions
![]() $(\phi ^0_i,\ldots ,\phi ^{p_{i}}_i)$
in
$(\phi ^0_i,\ldots ,\phi ^{p_{i}}_i)$
in
![]() $L^2(\mathbb {D}^2, \widehat {dv_{g^{i}_{\infty }}}) \ 1 \leq i \leq s_1$
,
$L^2(\mathbb {D}^2, \widehat {dv_{g^{i}_{\infty }}}) \ 1 \leq i \leq s_1$
,
![]() $(\phi ^0_i,\ldots ,\phi ^{p_{i,l}}_i)$
in
$(\phi ^0_i,\ldots ,\phi ^{p_{i,l}}_i)$
in
![]() $L^2(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}}) \ s_1+1 \leq i \leq s_1+s_2$
and
$L^2(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}}) \ s_1+1 \leq i \leq s_1+s_2$
and
![]() $(\psi ^0_j,\ldots ,\psi ^{p_{j}}_j)$
in
$(\psi ^0_j,\ldots ,\psi ^{p_{j}}_j)$
in
![]() $L^2(\widehat {\Sigma _j^{\infty }}, \widehat {dv_{g^j_{\infty }}})$
such that for
$L^2(\widehat {\Sigma _j^{\infty }}, \widehat {dv_{g^j_{\infty }}})$
such that for
![]() $0 \leq e \leq p_{i}$
the function
$0 \leq e \leq p_{i}$
the function
![]() $\phi ^e_i$
is an eigenfunction with eigenvalue
$\phi ^e_i$
is an eigenfunction with eigenvalue
![]() $\sigma _e(\widehat {dv_{g^{i}_{\infty }}})$
on
$\sigma _e(\widehat {dv_{g^{i}_{\infty }}})$
on
![]() $\mathbb {D}^2$
, for
$\mathbb {D}^2$
, for
![]() $0 \leq e \leq p_{i,l}$
the function
$0 \leq e \leq p_{i,l}$
the function
![]() $\phi ^e_i$
is an eigenfunction with eigenvalue
$\phi ^e_i$
is an eigenfunction with eigenvalue
![]() $\sigma _e(\widehat {dv_{g^{i,l}_{\infty }}})$
on
$\sigma _e(\widehat {dv_{g^{i,l}_{\infty }}})$
on
![]() $\mathbb {D}^2$
and for
$\mathbb {D}^2$
and for
![]() $0 \leq r \leq p_{j}$
the function
$0 \leq r \leq p_{j}$
the function
![]() $\psi ^r_j$
is an eigenfunction with eigenvalue
$\psi ^r_j$
is an eigenfunction with eigenvalue
![]() $\sigma _r(\widehat {dv_{g^j_{\infty }}})$
on
$\sigma _r(\widehat {dv_{g^j_{\infty }}})$
on
![]() $\widehat {\Sigma _j^{\infty }}$
. The standard capacity computations (see for instance [Reference PetridesPet19, Claim 1]) imply the existence of smooth functions supported in a geodesic ball of a Riemannian manifold and having bounded Dirichlet energy. More precisely, there exist positive smooth functions
$\widehat {\Sigma _j^{\infty }}$
. The standard capacity computations (see for instance [Reference PetridesPet19, Claim 1]) imply the existence of smooth functions supported in a geodesic ball of a Riemannian manifold and having bounded Dirichlet energy. More precisely, there exist positive smooth functions
![]() $\eta _i$
,
$\eta _i$
,
![]() $\eta _{i,l}$
, and
$\eta _{i,l}$
, and
![]() $\eta _j$
for
$\eta _j$
for
![]() $(\mathbb {D}^2, \widehat {dv_{g^{i}_{\infty }}})$
,
$(\mathbb {D}^2, \widehat {dv_{g^{i}_{\infty }}})$
,
![]() $(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}})$
, and
$(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}})$
, and
![]() $(\widehat {\Sigma _j^{\infty }}, \widehat {dv_{g^j_{\infty }}}),$
respectively supported in geodesic balls
$(\widehat {\Sigma _j^{\infty }}, \widehat {dv_{g^j_{\infty }}}),$
respectively supported in geodesic balls
![]() $B(x,r)$
centered at the compactification points x of radius r such that
$B(x,r)$
centered at the compactification points x of radius r such that
![]() $\eta \in C^{\infty }_0(B(x,r))$
and
$\eta \in C^{\infty }_0(B(x,r))$
and
![]() $\eta =1$
on
$\eta =1$
on
![]() $B(x,\rho _n r)\subset B(x,r)$
, where
$B(x,\rho _n r)\subset B(x,r)$
, where
![]() $\rho _n\to 0$
as
$\rho _n\to 0$
as
![]() $n\to \infty $
and
$n\to \infty $
and
![]() $\int _{\Omega }|\nabla \eta |^2_gdv_g \leq \frac {C}{\log \frac {1}{\rho _n}},$
where
$\int _{\Omega }|\nabla \eta |^2_gdv_g \leq \frac {C}{\log \frac {1}{\rho _n}},$
where
![]() $\eta $
is one of the functions
$\eta $
is one of the functions
![]() $\eta _i$
,
$\eta _i$
,
![]() $\eta _{i,l}$
and
$\eta _{i,l}$
and
![]() $\eta _j$
,
$\eta _j$
,
![]() $(\Omega ,dv_g)$
is one of the corresponding manifolds
$(\Omega ,dv_g)$
is one of the corresponding manifolds
![]() $(\mathbb {D}^2, \widehat {dv_{g^{i}_{\infty }}})$
,
$(\mathbb {D}^2, \widehat {dv_{g^{i}_{\infty }}})$
,
![]() $(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}})$
and
$(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}})$
and
![]() $(\widehat {\Sigma _j^{\infty }}, \widehat {dv_{g^j_{\infty }}})$
. Moreover, if
$(\widehat {\Sigma _j^{\infty }}, \widehat {dv_{g^j_{\infty }}})$
. Moreover, if
![]() $(\Omega ,dv_g)=(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}})$
then we additionally require
$(\Omega ,dv_g)=(\mathbb {D}^2, \widehat {dv_{g^{i,l}_{\infty }}})$
then we additionally require
![]() $\rho _n$
to satisfy
$\rho _n$
to satisfy
![]() $\partial D^n_{i,l}\setminus S^n_{i,l} \subset B(x,\rho _n r)$
. Then, we define the desired test-functions as
$\partial D^n_{i,l}\setminus S^n_{i,l} \subset B(x,\rho _n r)$
. Then, we define the desired test-functions as
extended by 0 on
![]() $\Sigma $
,
$\Sigma $
,
extended by 0 on
![]() $\Sigma $
and
$\Sigma $
and
extended by 0 on
![]() $\Sigma $
. Note that all these functions have pairwise disjoint supports. Then from the variational characterization of
$\Sigma $
. Note that all these functions have pairwise disjoint supports. Then from the variational characterization of
![]() $\sigma _k(g_n)$
one gets
$\sigma _k(g_n)$
one gets
 $$ \begin{align*} \sigma_k(g_n) &\leq \max \bigg\{\max_{1 \leq i \leq s_1} \frac{\int_{\Sigma}|\nabla \xi^e_i|^2_{g_n}dv_{g_n}}{\int_{\partial \Sigma} (\xi^e_i)^2 ds_{g_n}}, \max_{s_1+1 \leq i \leq s_1+s_2} \frac{\int_{\Sigma}|\nabla \xi^e_{i,l}|^2_{g_n}dv_{g_n}}{\int_{\partial \Sigma} (\xi^e_{i,l})^2 ds_{g_n}}, \\ & \quad \max_{j \in J} \frac{\int_{\Sigma}|\nabla \xi^r_j|^2_{g_n}dv_{g_n}}{\int_{\partial\Sigma} (\xi^r_j)^2 ds_{g_n}} \bigg\}, \end{align*} $$
$$ \begin{align*} \sigma_k(g_n) &\leq \max \bigg\{\max_{1 \leq i \leq s_1} \frac{\int_{\Sigma}|\nabla \xi^e_i|^2_{g_n}dv_{g_n}}{\int_{\partial \Sigma} (\xi^e_i)^2 ds_{g_n}}, \max_{s_1+1 \leq i \leq s_1+s_2} \frac{\int_{\Sigma}|\nabla \xi^e_{i,l}|^2_{g_n}dv_{g_n}}{\int_{\partial \Sigma} (\xi^e_{i,l})^2 ds_{g_n}}, \\ & \quad \max_{j \in J} \frac{\int_{\Sigma}|\nabla \xi^r_j|^2_{g_n}dv_{g_n}}{\int_{\partial\Sigma} (\xi^r_j)^2 ds_{g_n}} \bigg\}, \end{align*} $$
and passing to
![]() $\limsup $
as
$\limsup $
as
![]() $n\to \infty $
, we get
$n\to \infty $
, we get
 $$ \begin{align*} \limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n) &\leq \max\bigg\{\max_{1 \leq i \leq s_1} \frac{\sigma^*_{p_{i}}(\mathbb{D}^2)}{m_{i}}, \max_{s_1+1 \leq i \leq s_1+s_2} \frac{\sigma^*_{p_{i,l}}(\mathbb{D}^2)}{m_{i,l}},\\ &\quad \max_{j \in J}\frac{\sigma^*_{p_{j}}(\widehat{\Sigma_j^{\infty}}, \widehat{c_{\infty}})}{m_{j}}\bigg\} \end{align*} $$
$$ \begin{align*} \limsup_{n\to\infty}\sigma^*_k(\Sigma,c_n) &\leq \max\bigg\{\max_{1 \leq i \leq s_1} \frac{\sigma^*_{p_{i}}(\mathbb{D}^2)}{m_{i}}, \max_{s_1+1 \leq i \leq s_1+s_2} \frac{\sigma^*_{p_{i,l}}(\mathbb{D}^2)}{m_{i,l}},\\ &\quad \max_{j \in J}\frac{\sigma^*_{p_{j}}(\widehat{\Sigma_j^{\infty}}, \widehat{c_{\infty}})}{m_{j}}\bigg\} \end{align*} $$
which contradicts (5.6), (5.7), and (5.8). This means that if inequality (5.5) holds then the sequence
![]() $\{c_n\}$
cannot degenerate. We arrived at a contradiction and inequality (5.4) is proved.
$\{c_n\}$
cannot degenerate. We arrived at a contradiction and inequality (5.4) is proved.
Remark 5.1 Note that if
![]() $s_2=0$
, i.e., there are no pinching geodesics having intersection with boundary components, then we take the set J as
$s_2=0$
, i.e., there are no pinching geodesics having intersection with boundary components, then we take the set J as
![]() $J=\{1,\ldots ,m\}$
, i.e., we consider
$J=\{1,\ldots ,m\}$
, i.e., we consider
![]() $\Sigma ^n_j(\alpha ^n)$
, where
$\Sigma ^n_j(\alpha ^n)$
, where
![]() $1 \leq j \leq m$
. If all the boundary components are getting pinched then we set
$1 \leq j \leq m$
. If all the boundary components are getting pinched then we set
![]() $J=\varnothing $
and we only have deal with the functions
$J=\varnothing $
and we only have deal with the functions
![]() $ \xi ^e_i=(\Psi _{i}^n)^{-1}\eta _i\phi ^e_i$
extended by 0 on
$ \xi ^e_i=(\Psi _{i}^n)^{-1}\eta _i\phi ^e_i$
extended by 0 on
![]() $\Sigma $
and
$\Sigma $
and
![]() $\sigma ^*_{p_{i}}(\mathbb {D}^2)$
where
$\sigma ^*_{p_{i}}(\mathbb {D}^2)$
where
![]() $1 \leq i \leq s_1$
. If
$1 \leq i \leq s_1$
. If
![]() $s_1=s_2=0$
, i.e., only geodesics of the third type are getting pinched then we only have deal with functions
$s_1=s_2=0$
, i.e., only geodesics of the third type are getting pinched then we only have deal with functions
![]() $\xi ^r_j=\Psi _j^n\eta _j\psi ^r_j,~j\in J$
extended by 0 on
$\xi ^r_j=\Psi _j^n\eta _j\psi ^r_j,~j\in J$
extended by 0 on
![]() $\Sigma $
and
$\Sigma $
and
![]() $\sigma ^*_{p_{j}}(\widehat {\Sigma _j^{\infty }}, \widehat {c_{\infty }})$
where
$\sigma ^*_{p_{j}}(\widehat {\Sigma _j^{\infty }}, \widehat {c_{\infty }})$
where
![]() $J=\{1,\ldots ,m\}$
.
$J=\{1,\ldots ,m\}$
.
Case 2. Assume that up to a choice of a subsequence the following inequality holds
then we prove inequality (5.4) by induction.
Consider the case
![]() $k=1$
then by inequality (1.2)
$k=1$
then by inequality (1.2)
![]() $\sigma ^*_1(\Sigma , c_n) \geq 2\pi $
. Suppose that up to a choice of a subsequence one has
$\sigma ^*_1(\Sigma , c_n) \geq 2\pi $
. Suppose that up to a choice of a subsequence one has
![]() $\sigma ^*_1(\Sigma , c_n)> 2\pi $
. Then the case
$\sigma ^*_1(\Sigma , c_n)> 2\pi $
. Then the case
![]() $k=1$
falls under Case 1. Otherwise one has
$k=1$
falls under Case 1. Otherwise one has
![]() $\limsup _{n \to \infty } \sigma ^*_1(\Sigma , c_n)=2\pi $
and the inequality (5.4) reads as
$\limsup _{n \to \infty } \sigma ^*_1(\Sigma , c_n)=2\pi $
and the inequality (5.4) reads as
which is true. The base of induction is proved.
Suppose that the inequality holds for all numbers
![]() $k'\leq k$
. We show that it also holds for
$k'\leq k$
. We show that it also holds for
![]() $k+1$
. Indeed, one has
$k+1$
. Indeed, one has
and we get
 $$ \begin{align*} \limsup_{n \to \infty}\sigma^*_{k+1} (\Sigma, c_n) &\leq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg)+\sigma^*_1(\mathbb{D}^2) \\ &\leq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg), \end{align*} $$
$$ \begin{align*} \limsup_{n \to \infty}\sigma^*_{k+1} (\Sigma, c_n) &\leq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg)+\sigma^*_1(\mathbb{D}^2) \\ &\leq \max \bigg(\sum^{m}_{i=1} \sigma^*_{k_{i}}(\Sigma_{\gamma_{i},l_i},c_{\infty})+ \sum_{i=1}^{s_1+s_2}\sigma^*_{r_i}(\mathbb{D}^2) \bigg), \end{align*} $$
where the maximum is taken over all possible combinations of indices such that
 $$ \begin{align*} \sum_{i=1}^{m} k_i + \sum_{i=1}^{s_1+s_2} r_i = k+1, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{m} k_i + \sum_{i=1}^{s_1+s_2} r_i = k+1, \end{align*} $$
since the term
![]() $\sigma ^*_1(\mathbb {D}^2)$
can be absorbed by one of the terms inside
$\sigma ^*_1(\mathbb {D}^2)$
can be absorbed by one of the terms inside
![]() $\max $
using inequality (1.1). The proof is complete.
$\max $
using inequality (1.1). The proof is complete.
Zero Euler characteristic. The case of the cylinder was essentially considered in [Reference PetridesPet19, Section 7.1]. Indeed, it was proved that if the sequence of conformal classes
![]() $\{c_n\}$
degenerates then
$\{c_n\}$
degenerates then
 $$ \begin{align*} \lim_{n\to\infty}\sigma^*_k(\mathcal C,c_n) \leq \max_{i_1+\cdots+i_s=k}\sum^s_{q=1}\sigma^*_{i_q}(\mathbb D^2)=2\pi k. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\sigma^*_k(\mathcal C,c_n) \leq \max_{i_1+\cdots+i_s=k}\sum^s_{q=1}\sigma^*_{i_q}(\mathbb D^2)=2\pi k. \end{align*} $$
Applying then inequality (1.2), one immediately gets that
![]() $\lim _{n\to \infty }\sigma ^*_k(\mathcal C,c_n)=2\pi k$
.
$\lim _{n\to \infty }\sigma ^*_k(\mathcal C,c_n)=2\pi k$
.
Consider the case of the Möbius band. If the sequence
![]() $\{c_n\}$
goes to
$\{c_n\}$
goes to
![]() $0$
then it follows from [Reference PetridesPet19, Section 7.1] that
$0$
then it follows from [Reference PetridesPet19, Section 7.1] that
 $$ \begin{align} \lim_{n\to\infty}\sigma^*_k(\mathbb{MB},c_n) \leq \max_{i_1+\cdots+i_s=k}\sum^s_{q=1}\sigma^*_{i_q}(\mathbb D^2)=2\pi k. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\sigma^*_k(\mathbb{MB},c_n) \leq \max_{i_1+\cdots+i_s=k}\sum^s_{q=1}\sigma^*_{i_q}(\mathbb D^2)=2\pi k. \end{align} $$
Indeed, we pass to the orientable cover which is a cylinder. Then inequality (5.9) follows from [Reference PetridesPet19, Section 7.1, the case
![]() ${R}_{\alpha}\to 1$
as
${R}_{\alpha}\to 1$
as
![]() $\alpha \to +\infty$
in Petrides’ notations].
$\alpha \to +\infty$
in Petrides’ notations].
If the sequence
![]() $\{c_n\}$
goes to
$\{c_n\}$
goes to
![]() $\infty $
then we prove that inequality (5.9) also holds. The proof follows the exactly same arguments as in the proof of inequality (5.4). The analog of the Case 1 for
$\infty $
then we prove that inequality (5.9) also holds. The proof follows the exactly same arguments as in the proof of inequality (5.4). The analog of the Case 1 for
![]() $\mathbb {MB}$
corresponds to the case of pinching boundary (see Remark (5.1)).
$\mathbb {MB}$
corresponds to the case of pinching boundary (see Remark (5.1)).
Therefore, in both cases inequality (5.9) holds. Applying inequality (1.2) once again we then get that
![]() $\lim _{n\to \infty }\sigma ^*_k(\mathbb {MB},c_n)=2\pi k$
.
$\lim _{n\to \infty }\sigma ^*_k(\mathbb {MB},c_n)=2\pi k$
.
6 Proof of Theorem 1.5
For the proof of Theorem 1.5, we will need to choose a “nice” degenerating sequence of conformal classes, i.e., a degenerating sequence of conformal classes such that the limiting space looks as simple as possible.
Lemma 6.1 Let
![]() $\Sigma $
be a compact surface with boundary of negative Euler characteristic. Then there exists a degenerating sequence of conformal classes such that the limiting space is the disc.
$\Sigma $
be a compact surface with boundary of negative Euler characteristic. Then there exists a degenerating sequence of conformal classes such that the limiting space is the disc.
Proof The proof is purely topological.
Assume that
![]() $\Sigma $
is orientable. Then we consider collapsing geodesics shown in Figure 3. Passing to the limit when the lengths of all pinching geodesics tend to zero and using the one-point cusps compactification we get an orientable surface of genus 0 with one boundary component, i.e., the disc.
$\Sigma $
is orientable. Then we consider collapsing geodesics shown in Figure 3. Passing to the limit when the lengths of all pinching geodesics tend to zero and using the one-point cusps compactification we get an orientable surface of genus 0 with one boundary component, i.e., the disc.

Figure 3: Orientable surface with boundary. The lengths of all red geodesics tend to zero.
If
![]() $\Sigma $
is nonorientable then we pass to its orientable cover and we consider collapsing geodesics shown in Figure 4 for genus
$\Sigma $
is nonorientable then we pass to its orientable cover and we consider collapsing geodesics shown in Figure 4 for genus
![]() $0$
and Figure 5 for genus
$0$
and Figure 5 for genus
![]() $\neq 0$
(the pictures are symmetric with respect to the involution changing the orientation, “the antipodal map”). Passing to the limit when the lengths of all pinching geodesics tend to zero and using the one-point cusps compactification, we get a disconnected surface with two connected components which are topologically discs. The involution changing the orientation maps one component to another one and hence passing to the quotient by this involution we get just one disc.▪
$\neq 0$
(the pictures are symmetric with respect to the involution changing the orientation, “the antipodal map”). Passing to the limit when the lengths of all pinching geodesics tend to zero and using the one-point cusps compactification, we get a disconnected surface with two connected components which are topologically discs. The involution changing the orientation maps one component to another one and hence passing to the quotient by this involution we get just one disc.▪

Figure 4: Orientable cover of a non-orientable surface of genus
![]() $0$
with boundary. The lengths of all red geodesics tend to zero.
$0$
with boundary. The lengths of all red geodesics tend to zero.

Figure 5: Orientable cover of a non-orientable surface of genus
![]() $\neq 0$
with boundary. The lengths of all red geodesics tend to zero.
$\neq 0$
with boundary. The lengths of all red geodesics tend to zero.
Now we are ready to prove Theorem 1.5.
Zero Euler characteristic. Let
![]() $\Sigma $
be either the cylinder
$\Sigma $
be either the cylinder
![]() $\mathcal C$
or the Möbius band
$\mathcal C$
or the Möbius band
![]() $\mathbb {MB}$
. Then this case immediately follows from Theorem 1.4 by Remark 1.4. Indeed, if
$\mathbb {MB}$
. Then this case immediately follows from Theorem 1.4 by Remark 1.4. Indeed, if
![]() $\{c_n\}$
denotes a degenerating sequence of conformal classes on
$\{c_n\}$
denotes a degenerating sequence of conformal classes on
![]() $\Sigma $
then by Theorem 1.4:
$\Sigma $
then by Theorem 1.4:
But
![]() $I^{\sigma }_k(\Sigma ) \geq 2\pi k$
by (1.2). Thus,
$I^{\sigma }_k(\Sigma ) \geq 2\pi k$
by (1.2). Thus,
![]() $I^{\sigma }_k(\Sigma )=\lim _{n\to \infty }\sigma ^*_k(\Sigma ,c_n)=2\pi k$
and the degenerating sequence
$I^{\sigma }_k(\Sigma )=\lim _{n\to \infty }\sigma ^*_k(\Sigma ,c_n)=2\pi k$
and the degenerating sequence
![]() $\{c_n\}$
is minimizing.
$\{c_n\}$
is minimizing.
Negative Euler characteristic. By Lemma 6.1, there exists a sequence of conformal classes
![]() $\{c_n\}$
such that the limiting space
$\{c_n\}$
such that the limiting space
![]() $\widehat {\Sigma _{\infty }}$
is the disc. Then by Theorem 1.4, we have
$\widehat {\Sigma _{\infty }}$
is the disc. Then by Theorem 1.4, we have
Moreover, we know that
![]() $\sigma ^*_k(\mathbb {D}^2) = 2\pi k$
. Hence,
$\sigma ^*_k(\mathbb {D}^2) = 2\pi k$
. Hence,
Finally, by (1.2) one has
![]() $I^{\sigma }_k(\Sigma ) \geq 2\pi k$
whence
$I^{\sigma }_k(\Sigma ) \geq 2\pi k$
whence
![]() $I^{\sigma }_k(\Sigma )=2\pi k$
which completes the proof.
$I^{\sigma }_k(\Sigma )=2\pi k$
which completes the proof.
7 Appendix
7.1 A well-posed problem
In this section, we consider the problem
 $$ \begin{align} \begin{cases} \Delta u=0&\text{in } M,\\ u=g&\text{on } D,\\ \frac{\partial u}{\partial n}=0&\text{on } N, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta u=0&\text{in } M,\\ u=g&\text{on } D,\\ \frac{\partial u}{\partial n}=0&\text{on } N, \end{cases} \end{align} $$
where
![]() $(M,h)$
is a Riemannian manifold with boundary such that
$(M,h)$
is a Riemannian manifold with boundary such that
![]() $\overline D\cup \overline N=\partial M$
and D has positive capacity.
$\overline D\cup \overline N=\partial M$
and D has positive capacity.
Let G be a smooth function such that
![]() $G_{|_D}=g$
and consider the function
$G_{|_D}=g$
and consider the function
![]() $v=G-u$
. Then substituting
$v=G-u$
. Then substituting
![]() $u=G-v$
into (7.1) implies:
$u=G-v$
into (7.1) implies:
 $$ \begin{align} \begin{cases} \Delta v=\Delta G&\text{in } M,\\ v=0&\text{on } D,\\ \frac{\partial u}{\partial n}=\frac{\partial G}{\partial n}&\text{on } N. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \Delta v=\Delta G&\text{in } M,\\ v=0&\text{on } D,\\ \frac{\partial u}{\partial n}=\frac{\partial G}{\partial n}&\text{on } N. \end{cases} \end{align} $$
We introduce the space
![]() $H^1_D(M,h)$
as the closure in
$H^1_D(M,h)$
as the closure in
![]() $H^1$
-norm of
$H^1$
-norm of
![]() $C^{\infty }$
-functions vanishing on D. For a function
$C^{\infty }$
-functions vanishing on D. For a function
![]() $u \in H^1_D(M,h),$
we have the following coercivity inequality:
$u \in H^1_D(M,h),$
we have the following coercivity inequality:
with the best constant
![]() $C=\frac {1}{\sqrt {\lambda ^{DN}_1(M,h)}}$
, where
$C=\frac {1}{\sqrt {\lambda ^{DN}_1(M,h)}}$
, where
![]() $\lambda ^{DN}_1(M,h)$
is the first non zero eigenvalue of the mixed problem
$\lambda ^{DN}_1(M,h)$
is the first non zero eigenvalue of the mixed problem
 $$ \begin{align*} \begin{cases} \Delta u=\lambda u&\text{in } M,\\ u=0&\text{on } D,\\ \frac{\partial u}{\partial n}=0&\text{on } N. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Delta u=\lambda u&\text{in } M,\\ u=0&\text{on } D,\\ \frac{\partial u}{\partial n}=0&\text{on } N. \end{cases} \end{align*} $$
By the Lax–Milgram theorem and by virtue of the inequality (7.3) the problem (7.2) admits a unique solution on the space
![]() $H^1_D(M,h)$
. Thus, problem (7.1) also has a solution. Moreover, it is easy to see that this solution is unique.
$H^1_D(M,h)$
. Thus, problem (7.1) also has a solution. Moreover, it is easy to see that this solution is unique.
Our aim now is the following lemma.
Lemma 7.1 Let u satisfy the problem (7.1). Then one has
Proof The weak formulation of (7.1) reads
Let G be any continuation of the function g into M, i.e.,
![]() $G\in H^1(M,h)$
is any function such that
$G\in H^1(M,h)$
is any function such that
![]() $G_{|_D}=g$
. Then substituting
$G_{|_D}=g$
. Then substituting
![]() $v=u-G$
in the previous identity yields
$v=u-G$
in the previous identity yields
whence
Further, it is easy to see that
Moreover, since
![]() $u-G\in H^1_D(M,h)$
one has
$u-G\in H^1_D(M,h)$
one has
Substituting it in the previous inequality, we get
Plugging (7.4) in (7.5) yields
for any function
![]() $G\in H^1(M,h)$
such that
$G\in H^1(M,h)$
such that
![]() $G_{|_D}=g$
.
$G_{|_D}=g$
.
Lemma 7.2 The norms
are equivalent.
Proof By the trace inequality there exists a positive constant
![]() $C_1$
such that for every
$C_1$
such that for every
![]() $G\in H^1(M,h)$
one has
$G\in H^1(M,h)$
one has
which implies:
Further, we construct a continuation
![]() $G'\in H^1(M,h)$
of g with the property that there exists a positive constant
$G'\in H^1(M,h)$
of g with the property that there exists a positive constant
![]() $C_2$
such that for every
$C_2$
such that for every
![]() $g\in H^{1/2}(D,h)$
one has:
$g\in H^{1/2}(D,h)$
one has:
Let
![]() $\tilde g$
be any continuation of g on
$\tilde g$
be any continuation of g on
![]() $\partial M$
such that
$\partial M$
such that
![]() $||\tilde g||_{H^{1/2}(N,h)} \leq ||g||_{H^{1/2}(D,h)}$
. Therefore,
$||\tilde g||_{H^{1/2}(N,h)} \leq ||g||_{H^{1/2}(D,h)}$
. Therefore,
![]() $||\tilde g||_{H^{1/2}(\partial M,h)} \leq \sqrt {2}||g||_{H^{1/2}(D,h)}<\infty $
and
$||\tilde g||_{H^{1/2}(\partial M,h)} \leq \sqrt {2}||g||_{H^{1/2}(D,h)}<\infty $
and
![]() $\tilde g\in H^{1/2}(\partial M,h)$
. Then we take the harmonic continuation of
$\tilde g\in H^{1/2}(\partial M,h)$
. Then we take the harmonic continuation of
![]() $\tilde g$
into M as
$\tilde g$
into M as
![]() $G'$
. By [Reference TaylorTay11, Proposition 1.7] there exists a positive constant that
$G'$
. By [Reference TaylorTay11, Proposition 1.7] there exists a positive constant that
![]() $C_3$
such that:
$C_3$
such that:
Since
![]() $||\tilde g||_{H^{1/2}(\partial M,h)} \leq \sqrt {2}||g||_{H^{1/2}(D,h)}$
we get (7.9) with
$||\tilde g||_{H^{1/2}(\partial M,h)} \leq \sqrt {2}||g||_{H^{1/2}(D,h)}$
we get (7.9) with
![]() $C_2=\sqrt {2}C_3$
.
$C_2=\sqrt {2}C_3$
.
Therefore, (7.8) and (7.9) imply:
whence
 $$ \begin{align*} \begin{array}{c} C_2^{-1}\displaystyle\inf_{G\in H^1(M,h),~G_{|_D}=g}||G||_{H^1(M,h)} \leq ||g||_{H^{1/2}(D,h)} \leq \\ \leq C_1\displaystyle\inf_{G\in H^1(M,h),~G_{|_D}=g}||G||_{H^1(M,h)}, \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c} C_2^{-1}\displaystyle\inf_{G\in H^1(M,h),~G_{|_D}=g}||G||_{H^1(M,h)} \leq ||g||_{H^{1/2}(D,h)} \leq \\ \leq C_1\displaystyle\inf_{G\in H^1(M,h),~G_{|_D}=g}||G||_{H^1(M,h)}, \end{array} \end{align*} $$
since
And lemma follows.▪
Finally, taking the infimum over all
![]() $G\in H^1(M,h)$
such that
$G\in H^1(M,h)$
such that
![]() $G_{|_D}=g$
in (7.7) and using Lemma 7.2 complete the proof.▪
$G_{|_D}=g$
in (7.7) and using Lemma 7.2 complete the proof.▪
7.2 Proofs of propositions of Section 2
This section contains the proofs of propositions in Section 2 analogous to propositions in [Reference Karpukhin and MedvedevKM20, Section 4] whose adaptation to the Steklov setting is rather technical.
Proof of Lemma 2.4 Let
![]() $h^m\in [h]$
be a maximizing sequence of metrics for
$h^m\in [h]$
be a maximizing sequence of metrics for
![]() $\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [h])$
and
$\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [h])$
and
![]() $g^m\in [g]$
be a discontinuous metric on
$g^m\in [g]$
be a discontinuous metric on
![]() $\Sigma $
defined as
$\Sigma $
defined as
![]() $g|_{\Omega _i} = h_i$
. By the variational characterization of eigenvalues for all k one has
$g|_{\Omega _i} = h_i$
. By the variational characterization of eigenvalues for all k one has
![]() $\sigma _k(\Sigma ,g^m) \geq \sigma ^N(\Omega ,h^m)$
since the set of test functions for the Steklov–Neumann eigenvalues
$\sigma _k(\Sigma ,g^m) \geq \sigma ^N(\Omega ,h^m)$
since the set of test functions for the Steklov–Neumann eigenvalues
![]() $C^0(\Sigma ,\{\Omega _i\})$
is larger than the set
$C^0(\Sigma ,\{\Omega _i\})$
is larger than the set
![]() $C^0(\Sigma )$
of test functions for
$C^0(\Sigma )$
of test functions for
![]() $\sigma _k(\Sigma ,g^m)$
. Using the fact that
$\sigma _k(\Sigma ,g^m)$
. Using the fact that
![]() $L_{g^m}(\partial \Sigma )=\sum _iL_{h^m}(\partial ^S \Omega _i) \geq L_{g^m}(\partial ^S \Omega _i)$
for any i and taking the limit as
$L_{g^m}(\partial \Sigma )=\sum _iL_{h^m}(\partial ^S \Omega _i) \geq L_{g^m}(\partial ^S \Omega _i)$
for any i and taking the limit as
![]() $m\to \infty $
we get
$m\to \infty $
we get
Finally by Lemma 2.3 one gets
▪
Proof of Proposition 2.6 The proof is similar for both cases. The obvious analog of Lemma 2.5 for the second case holds since its proof follows the exactly same arguments as the proof of Lemma 2.5. For that reason we only provide the proof of Proposition 2.6 for the first case.
Take a maximizing sequence of metrics
![]() $\{h_i~ |~ h_i \in [g|_{\Omega }]\}$
for the functional
$\{h_i~ |~ h_i \in [g|_{\Omega }]\}$
for the functional
![]() $\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [g])$
, i.e.,
$\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [g])$
, i.e.,
Let
![]() $h_i=f_i g|_{\Omega }$
, where
$h_i=f_i g|_{\Omega }$
, where
![]() $f_i \in C^{\infty }_+(\bar \Omega )$
. We then define the metric
$f_i \in C^{\infty }_+(\bar \Omega )$
. We then define the metric
![]() $\widetilde {h_i}=\widetilde {f_i} g$
on
$\widetilde {h_i}=\widetilde {f_i} g$
on
![]() $\Sigma $
, where
$\Sigma $
, where
![]() $\widetilde {f_i}$
is any positive continuation of the function
$\widetilde {f_i}$
is any positive continuation of the function
![]() $f_i$
into
$f_i$
into
![]() $\Omega ^c$
. It enables us to consider the metric
$\Omega ^c$
. It enables us to consider the metric
![]() $\rho _{\delta } \widetilde {h_i}$
, where as before
$\rho _{\delta } \widetilde {h_i}$
, where as before
 $$ \begin{align*} \rho_{\delta}= \begin{cases} 1&\text{in } \Omega,\\ \delta&\text{in } \Sigma\setminus\Omega. \end{cases} \end{align*} $$
$$ \begin{align*} \rho_{\delta}= \begin{cases} 1&\text{in } \Omega,\\ \delta&\text{in } \Sigma\setminus\Omega. \end{cases} \end{align*} $$
Lemma 2.5 implies
Moreover,
![]() $L_{\rho _{\delta }\widetilde {h_i}}(\partial \Sigma )\to L_{h_i}(\partial ^S\Omega )$
. By Lemma 2.3, we have
$L_{\rho _{\delta }\widetilde {h_i}}(\partial \Sigma )\to L_{h_i}(\partial ^S\Omega )$
. By Lemma 2.3, we have
Therefore, passing to the limit as
![]() $i \to \infty $
one gets,
$i \to \infty $
one gets,
▪
Proof of Corollary 2.7 We show that
Let
![]() $g^m$
be a maximizing sequence for the functional
$g^m$
be a maximizing sequence for the functional
![]() $\sigma ^*_k(M, [g])$
. For a fixed
$\sigma ^*_k(M, [g])$
. For a fixed
![]() $m,$
we consider geodesic balls
$m,$
we consider geodesic balls
![]() $B_{\epsilon _n}(p_i)$
of radius
$B_{\epsilon _n}(p_i)$
of radius
![]() $\epsilon _n\to 0$
in metric
$\epsilon _n\to 0$
in metric
![]() $g^m$
centered at the points
$g^m$
centered at the points
![]() $p_1,\ldots ,p_l \in M$
such that
$p_1,\ldots ,p_l \in M$
such that
![]() $K_n \subset \cup ^l_{i=1}B_{\epsilon _n}(p_i)$
. We see that
$K_n \subset \cup ^l_{i=1}B_{\epsilon _n}(p_i)$
. We see that
![]() $M\setminus \cup ^l_{i=1}B_{\epsilon _n}(p_i) \subset M\setminus K_n$
. Then by Proposition 2.6 one has
$M\setminus \cup ^l_{i=1}B_{\epsilon _n}(p_i) \subset M\setminus K_n$
. Then by Proposition 2.6 one has
 $$ \begin{align} \begin{aligned} & \sigma^{N*}_k(M \setminus K_n, \partial M \setminus \partial K_n, [g]) \\ &\quad \geq\sigma^{N*}_k(M\setminus \cup^l_{i=1}B_{\epsilon_n}(p_i), \partial M\setminus \cup^l_{i=1}\partial B_{\epsilon_n}(p_i), [g]) \\ &\quad \geq \bar\sigma^{N}_k(M\setminus \cup^l_{i=1}B_{\epsilon_n}(p_i), \partial M\setminus \cup^l_{i=1}\partial B_{\epsilon_n}(p_i), g^m). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \sigma^{N*}_k(M \setminus K_n, \partial M \setminus \partial K_n, [g]) \\ &\quad \geq\sigma^{N*}_k(M\setminus \cup^l_{i=1}B_{\epsilon_n}(p_i), \partial M\setminus \cup^l_{i=1}\partial B_{\epsilon_n}(p_i), [g]) \\ &\quad \geq \bar\sigma^{N}_k(M\setminus \cup^l_{i=1}B_{\epsilon_n}(p_i), \partial M\setminus \cup^l_{i=1}\partial B_{\epsilon_n}(p_i), g^m). \end{aligned} \end{align} $$
Note that
![]() $L(\partial M \setminus \cup ^l_{i=1}\partial B_{\epsilon _n}(p_i), g^m)\to L(\partial M, g^m)$
as
$L(\partial M \setminus \cup ^l_{i=1}\partial B_{\epsilon _n}(p_i), g^m)\to L(\partial M, g^m)$
as
![]() $n\to \infty $
and by Lemma 2.1 one has
$n\to \infty $
and by Lemma 2.1 one has
![]() $\sigma ^{N}_k(M\setminus \cup ^l_{i=1}B_{\epsilon _n}(p_i), \partial M\setminus \cup ^l_{i=1}\partial B_{\epsilon _n}(p_i), g^m)\to \sigma _k(M,g^m)$
. Hence,
$\sigma ^{N}_k(M\setminus \cup ^l_{i=1}B_{\epsilon _n}(p_i), \partial M\setminus \cup ^l_{i=1}\partial B_{\epsilon _n}(p_i), g^m)\to \sigma _k(M,g^m)$
. Hence,
![]() $\bar \sigma ^{N}_k(M\setminus \cup ^l_{i=1}B_{\epsilon _n}(p_i), \partial M\setminus \cup ^l_{i=1}\partial B_{\epsilon _n}(p_i), g^m) \to \bar \sigma _k(M,g^m)$
as
$\bar \sigma ^{N}_k(M\setminus \cup ^l_{i=1}B_{\epsilon _n}(p_i), \partial M\setminus \cup ^l_{i=1}\partial B_{\epsilon _n}(p_i), g^m) \to \bar \sigma _k(M,g^m)$
as
![]() $n\to \infty $
. Taking
$n\to \infty $
. Taking
![]() $\liminf _{n\to \infty }$
in (7.10) one then gets
$\liminf _{n\to \infty }$
in (7.10) one then gets
Passing to the limit as
![]() $m\to \infty $
, we get the desired inequality.
$m\to \infty $
, we get the desired inequality.
The inequality
follows from Proposition 2.6. This completes the proof.▪
Proof of Lemma 2.8 Essentially the idea of the proof comes from the paper [Reference Wolf and KellerWK94]. We denote by
![]() $\partial ^S\Omega $
the part of the boundary with the Steklov boundary condition. We also call
$\partial ^S\Omega $
the part of the boundary with the Steklov boundary condition. We also call
![]() $\partial ^S\Omega $
“Steklov boundary” and
$\partial ^S\Omega $
“Steklov boundary” and
![]() $L_g(\partial ^S\Omega )$
“the length of Steklov boundary” in metric g.
$L_g(\partial ^S\Omega )$
“the length of Steklov boundary” in metric g.
Inequality
![]() $\boldsymbol \geq $
.
$\boldsymbol \geq $
.
Fix the indices
![]() $k_i>0$
satisfying
$k_i>0$
satisfying
![]() $\sum k_i=k$
and consider a maximizing sequence of metrics
$\sum k_i=k$
and consider a maximizing sequence of metrics
![]() $\{g_i^m\}$
such that
$\{g_i^m\}$
such that
![]() $\bar \sigma ^N_{k_i}(\Omega _i,\partial ^S\Omega _i, g^m_i)\to \sigma ^{N*}_{k_i}(\Omega _i,\partial ^S\Omega _i, [g_i])$
. One can assume that
$\bar \sigma ^N_{k_i}(\Omega _i,\partial ^S\Omega _i, g^m_i)\to \sigma ^{N*}_{k_i}(\Omega _i,\partial ^S\Omega _i, [g_i])$
. One can assume that
![]() $\sigma ^N_{k_i}(\Omega _i,\partial ^S\Omega _i, g^m_i)=\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g])$
. Then, one has
$\sigma ^N_{k_i}(\Omega _i,\partial ^S\Omega _i, g^m_i)=\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g])$
. Then, one has
 $$ \begin{align*} L_{g^m_i}(\partial^S\Omega_i)\to \frac{\sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g_i])}{\sigma^{N*}_{k}(\Omega,\partial^S\Omega, [g])}. \end{align*} $$
$$ \begin{align*} L_{g^m_i}(\partial^S\Omega_i)\to \frac{\sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g_i])}{\sigma^{N*}_{k}(\Omega,\partial^S\Omega, [g])}. \end{align*} $$
Let
![]() $\{g^m\}$
be a sequence of metrics on
$\{g^m\}$
be a sequence of metrics on
![]() $\Omega $
defined as
$\Omega $
defined as
![]() $g^m|_{\Omega _i}=g^m_i$
. Then for large enough m one has that
$g^m|_{\Omega _i}=g^m_i$
. Then for large enough m one has that
![]() $\sigma ^N_k(\Omega ,\partial ^S\Omega , g^m) = \sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g])$
, since the spectrum of disjoint union is the union of spectra of each component. By definition of
$\sigma ^N_k(\Omega ,\partial ^S\Omega , g^m) = \sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g])$
, since the spectrum of disjoint union is the union of spectra of each component. By definition of
![]() $\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [g])$
we also have
$\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [g])$
we also have
i.e.,
![]() $L_{g^m}(\partial ^S\Omega ) \leq 1$
. Thus, one has
$L_{g^m}(\partial ^S\Omega ) \leq 1$
. Thus, one has
 $$ \begin{align*} 1 \geq L_{g^m}(\partial^S\Omega) = \sum_iL_{g^m_i}(\partial^S\Omega_i)\to \frac{\sum_i \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g_i])}{\sigma^{N*}_{k}(\Omega,\partial^S\Omega, [g])}. \end{align*} $$
$$ \begin{align*} 1 \geq L_{g^m}(\partial^S\Omega) = \sum_iL_{g^m_i}(\partial^S\Omega_i)\to \frac{\sum_i \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g_i])}{\sigma^{N*}_{k}(\Omega,\partial^S\Omega, [g])}. \end{align*} $$
Passing to the limit
![]() $m\to \infty $
yields the inequality.
$m\to \infty $
yields the inequality.
Inequality
![]() $\boldsymbol \leq $
$\boldsymbol \leq $
Assume the contrary, i.e.,
 $$ \begin{align} \sigma^{N*}_k(\Omega, \partial^S\Omega, [g])> \max_{\sum\limits_{i=1}^s k_i=k,\,\,\,k_i>0}\,\,\sum_{i=1}^s\sigma^{N*}_{k_i}(\Omega_i, \partial^S\Omega_i, [g_i]). \end{align} $$
$$ \begin{align} \sigma^{N*}_k(\Omega, \partial^S\Omega, [g])> \max_{\sum\limits_{i=1}^s k_i=k,\,\,\,k_i>0}\,\,\sum_{i=1}^s\sigma^{N*}_{k_i}(\Omega_i, \partial^S\Omega_i, [g_i]). \end{align} $$
Consider a maximizing sequence of metrics
![]() $\{g^m\}$
of unit total length of Steklov boundary such that
$\{g^m\}$
of unit total length of Steklov boundary such that
![]() $\sigma ^N_{k}(\Omega ,\partial ^S\Omega , g^m)\to \sigma ^{N*}_{k}(\Omega ,\partial ^S\Omega , [g])$
. Let
$\sigma ^N_{k}(\Omega ,\partial ^S\Omega , g^m)\to \sigma ^{N*}_{k}(\Omega ,\partial ^S\Omega , [g])$
. Let
![]() $g_i^m$
be a restriction of
$g_i^m$
be a restriction of
![]() $g^m$
to
$g^m$
to
![]() $\Omega _i$
and
$\Omega _i$
and
![]() $d^m_i$
be the largest number satisfying
$d^m_i$
be the largest number satisfying
![]() $\sigma ^N_{d^m_i}(\Omega _i,\partial ^S\Omega _i, g_i^m)<\sigma ^{N*}_k(\Omega ,\partial ^S\Omega ,[g])$
and
$\sigma ^N_{d^m_i}(\Omega _i,\partial ^S\Omega _i, g_i^m)<\sigma ^{N*}_k(\Omega ,\partial ^S\Omega ,[g])$
and
![]() $\limsup _{m\to \infty }\sigma ^N_{d^m_i}(\Omega _i, \partial ^S\Omega _i, g_i^m)<\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g])$
. Let
$\limsup _{m\to \infty }\sigma ^N_{d^m_i}(\Omega _i, \partial ^S\Omega _i, g_i^m)<\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g])$
. Let
![]() $L^m_i$
denote
$L^m_i$
denote
![]() $L_{g^m_i}(\partial ^S\Omega _i)$
. Then, we have
$L_{g^m_i}(\partial ^S\Omega _i)$
. Then, we have
![]() $d^m_i \leq k$
and
$d^m_i \leq k$
and
![]() $L^m_i \leq 1$
. Therefore, up to a choice of a subsequence one can assume that
$L^m_i \leq 1$
. Therefore, up to a choice of a subsequence one can assume that
![]() $d^m_i = d_i$
does not depend on m and
$d^m_i = d_i$
does not depend on m and
![]() $L^m_i\to L_i$
as
$L^m_i\to L_i$
as
![]() $m\to \infty $
.
$m\to \infty $
.
We claim that
![]() $\sum _i(d_i+1) \geq k+1$
. Otherwise, by (7.11) and definition of
$\sum _i(d_i+1) \geq k+1$
. Otherwise, by (7.11) and definition of
![]() $d_i$
we have
$d_i$
we have
 $$ \begin{align*} \sigma^{N*}_k(\Omega,\partial^S\Omega, [g]) \sum_i L_i &\leq \sum_i \displaystyle\limsup_{m\to\infty}\bar\sigma^N_{d_i+1}(\Omega_i,\partial^S\Omega_i, g^m_i) \\ &\leq \sum_i\sigma^{N*}_{d_i+1}(\Omega_i,\partial^S\Omega_i, [g])<\sigma^{N*}_k(\Omega,\partial^S\Omega, [g]). \end{align*} $$
$$ \begin{align*} \sigma^{N*}_k(\Omega,\partial^S\Omega, [g]) \sum_i L_i &\leq \sum_i \displaystyle\limsup_{m\to\infty}\bar\sigma^N_{d_i+1}(\Omega_i,\partial^S\Omega_i, g^m_i) \\ &\leq \sum_i\sigma^{N*}_{d_i+1}(\Omega_i,\partial^S\Omega_i, [g])<\sigma^{N*}_k(\Omega,\partial^S\Omega, [g]). \end{align*} $$
Moreover,
![]() $\sum _i L_i=1$
since
$\sum _i L_i=1$
since
![]() $g^m$
are of unit Steklov boundary length. Thus, we arrive at
$g^m$
are of unit Steklov boundary length. Thus, we arrive at
![]() $\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [g])<\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g]),$
which is a contradiction.
$\sigma ^{N*}_k(\Omega , \partial ^S\Omega , [g])<\sigma ^{N*}_k(\Omega ,\partial ^S\Omega , [g]),$
which is a contradiction.
Therefore, the inequality
![]() $\sum (d_i+1) \geq k+1$
holds. Since the spectrum of a union is a union of spectra, we have
$\sum (d_i+1) \geq k+1$
holds. Since the spectrum of a union is a union of spectra, we have
hence
 $$ \begin{align*} \sigma^{N*}_k(\Omega,\partial^S\Omega, g) &= \limsup_{m\to\infty}\sigma^N_k(\Omega, \partial^S\Omega, g^m) \leq \max_i \limsup_{m\to\infty}\sigma_{d_i}(\Omega_i,g^m_i) \\ &< \sigma^{N*}_k(\Omega,\partial^S\Omega, [g]). \end{align*} $$
$$ \begin{align*} \sigma^{N*}_k(\Omega,\partial^S\Omega, g) &= \limsup_{m\to\infty}\sigma^N_k(\Omega, \partial^S\Omega, g^m) \leq \max_i \limsup_{m\to\infty}\sigma_{d_i}(\Omega_i,g^m_i) \\ &< \sigma^{N*}_k(\Omega,\partial^S\Omega, [g]). \end{align*} $$
Since
![]() $g^m$
are of unit Steklov boundary length we arrive at a contradiction.▪
$g^m$
are of unit Steklov boundary length we arrive at a contradiction.▪
Proof of Lemma 2.9 Fix indices
![]() $k_i \geq 0$
such that
$k_i \geq 0$
such that
![]() $\sum _{i=1}^{s'} k_i=k$
and set
$\sum _{i=1}^{s'} k_i=k$
and set
![]() $I = \{i\,|\,k_i>0\}$
. Let
$I = \{i\,|\,k_i>0\}$
. Let
![]() $\Omega _1 = \cup _{i\in I}\overline \Omega _i\subset \Sigma ,~\partial ^S\Omega _1 = \cup _{i\in I}\partial ^S\Omega _i,~(\Omega _2,h) = \sqcup _{i\in I}(\overline \Omega _i,g_{\overline \Omega _i})$
and
$\Omega _1 = \cup _{i\in I}\overline \Omega _i\subset \Sigma ,~\partial ^S\Omega _1 = \cup _{i\in I}\partial ^S\Omega _i,~(\Omega _2,h) = \sqcup _{i\in I}(\overline \Omega _i,g_{\overline \Omega _i})$
and
![]() $\partial ^S\Omega _2 = \sqcup _{i\in I}\partial ^S\Omega _i$
. One gets
$\partial ^S\Omega _2 = \sqcup _{i\in I}\partial ^S\Omega _i$
. One gets
 $$ \begin{align*} \sigma^*_k(\Sigma,[g]) &\geq \sigma^{N*}_k(\Omega_1,\partial^S\Omega_1, [g]) \geq \sigma^{N*}_k(\Omega_2, \partial^S\Omega_2, [h]) \\ & \geq \sum_{i\in I} \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g])=\sum^{s'}_{i=1} \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g]), \end{align*} $$
$$ \begin{align*} \sigma^*_k(\Sigma,[g]) &\geq \sigma^{N*}_k(\Omega_1,\partial^S\Omega_1, [g]) \geq \sigma^{N*}_k(\Omega_2, \partial^S\Omega_2, [h]) \\ & \geq \sum_{i\in I} \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g])=\sum^{s'}_{i=1} \sigma^{N*}_{k_i}(\Omega_i,\partial^S\Omega_i, [g]), \end{align*} $$
where we used in order: Proposition 2.6, Lemmas 2.4 and 2.8 and the fact that
![]() $\sigma ^{N*}_0(\Omega _j,\partial ^S\Omega _j, [g])=0$
for any j in the last equality.▪
$\sigma ^{N*}_0(\Omega _j,\partial ^S\Omega _j, [g])=0$
for any j in the last equality.▪
7.3 Proof of Lemma 5.2
Fix
![]() $\varepsilon>0$
. An application of Corollary 2.7 to a compact exhaustion of
$\varepsilon>0$
. An application of Corollary 2.7 to a compact exhaustion of
![]() $\Sigma ^{\infty }_j$
yields the existence of a compact set
$\Sigma ^{\infty }_j$
yields the existence of a compact set
![]() $K\subset \Sigma ^{\infty }_j\subset \widehat {\Sigma _j^{\infty }}$
such that
$K\subset \Sigma ^{\infty }_j\subset \widehat {\Sigma _j^{\infty }}$
such that
where
![]() $\partial ^SK=K\cap \partial \Sigma ^{\infty }_j \neq \varnothing $
. Since
$\partial ^SK=K\cap \partial \Sigma ^{\infty }_j \neq \varnothing $
. Since
![]() $\check \Omega _j^n$
exhaust
$\check \Omega _j^n$
exhaust
![]() $\Sigma ^{\infty }_j$
, then for all large enough n one has
$\Sigma ^{\infty }_j$
, then for all large enough n one has
![]() $K\subset \check \Omega _j^n$
. Then, by Proposition 2.6
$K\subset \check \Omega _j^n$
. Then, by Proposition 2.6
Taking
![]() $\liminf $
of both sides in the above inequality and using Proposition 2.2 yields
$\liminf $
of both sides in the above inequality and using Proposition 2.2 yields
Since
![]() $\varepsilon $
is arbitrary, this completes the proof.
$\varepsilon $
is arbitrary, this completes the proof.
Acknowledgment
The author would like to express his gratitude to Iosif Polterovich, Mikhail Karpukhin, Alexandre Girouard, and Bruno Colbois for stimulating discussions and useful remarks during the preparation of the paper. The author is also thankful to the reviewers for valuable remarks and helpful suggestions. This research is a part of author’s PhD thesis at the Université de Montréal under the supervision of Iosif Polterovich.