NOMENCLATURE
- j
-
empty gate (i = 1, . . ., m)
- k
-
position index of restricted gate
- l
-
ordinary gate between (l=1, . . ., n)
- AGAP
-
Airport Gate Assignment Problem
- AGRP
-
Aircraft Ground Routing Problem
- AIP
-
Aeronautical Information Publication
- ASDE
-
Airport Surface Detection Radar
- ATC
-
Air Traffic Control
- ATM
-
Air Traffic Management
- BADA
-
Base Of Aircraft Database
- FAP
-
Final Approach Point
- FIC
-
Flight Information Centre
- GA
-
Genetic Algorithm
- HDG&TA
-
Hybrid Dynamic Gate And Taxiway Algorithm
- ICAO
-
International Civil Aviation Organisation
- MoTa
-
Modern Taxiing
- Ne
-
number of empty gates
- PI
-
priority index of gate
- SESAR
-
Single European Sky ATM Research
- SIBT
-
Scheduled In-Block Time
- SOBT
-
Scheduled Out-Block Time
- SMAN
-
Surface Manager
- SMR
-
Surface Movement Radar
- TRACC
-
Taxi Routing For Aircraft: Creation And Controlling
- TS
-
Tabu Search
- X0
-
initial position of the intended aircraft
- X i
-
taxiway points
- P i
-
possible parking positions in the solution set
1.0 INTRODUCTION
The rapid increase in the demand for air transportation over the last four decades has led to serious capacity problems that have introduced delays, congestion, extra operational costs, adverse environmental impacts and passenger dissatisfaction at major airports. Airport capacity refers to the capability to accommodate flight operations (arriving and departing traffic) in a specified period of time(Reference Ashford and Wright1). Although airport capacity analysis requires a thorough investigation of the capacities of its airside and landside components, numerous studies have shown that physical and operational constraints on airside components (runway systems, taxiway networks and parking positions) primarily limit the overall capacity of the airport(Reference Janic2). The efficient management of existing airside resources seems to be the most effective and practical approach to overcome these capacity and traffic flow problems(Reference Cetek, Cavcar, Cinar and Aybek3).
Aircraft parking position assignment and ground-movement planning processes are among the most critical and interrelated issues for the efficient management of airside resources, especially at major hubs. The first issue is referred to as the Aircraft Gate Assignment Problem (AGAP) and involves finding an appropriate assignment schedule for arriving aircraft to available gates at terminal buildings or remote parking stands in apron areas in order to improve certain performance criteria regarding aircraft or passenger operations(Reference Atkin, Burke and Ravizza4). The second issue is referred to as The Aircraft Ground Routing Problem (AGRP) and comprises routing and scheduling surface movements of arriving and departing aircraft along the taxiway network between runway exit or entry points and parking positions in the most effective manner without violating operational and safety constraints(Reference Guépet, Briant, Gayon and Acuna-Agost5). These two problems are closely interrelated, such that a gate assignment solely based on airline or passenger requirements may lead to inefficient use of the taxiway network while ground routing that is focussed on efficient traffic flow may result in the ineffective utilisation of existing gates. Both cases cause delays and congestion in movement areas (runways, taxiways and aprons), affect other operations (runway arrival and departure management) adversely, and reduce the overall capacity of the airport.
Although the ICAO Global Air Navigation Plan(6) and SESAR European ATM Master Plan(7) aim at the full integration of airport operations through the use of automation and collaborative decision making, the current practice is that parking position assignment and ground routing processes are handled separately by different agents. Managers of ramp units execute the parking position assignment process using specific information management systems that process estimated flight schedules. Ground controllers in the ATC tower ensure the safe separation of aircraft on taxiways and apron areas manually or with the assistance of various systems such as Surface Movement Radar (SMR) and Airport Surface Detection Equipment (ASDE)(Reference Marks and Rietsema8) and decision support systems such as Surface Manager (SMAN)(Reference Kjenstad, Mannino, Nordlander, Schittekat and Smedsrud9). Both the level of coordination between ramp and tower units and the level of integration between their decision support tools and systems are not sufficient for efficient airport operations.
Numerous researchers have proposed various optimisation models to solve AGAP using mathematical programming (Babic et al(Reference Babic, Teodorovic and Tošic10), Bihr(Reference Bihr11), and Yan and Huo(Reference Yan and Huo12)), heuristic methods (Mangoubi and Mathaisel(Reference Mangoubi and Mathaisel13), Haghani and Chen(Reference Haghani and Chen14), Wipro Technologies Teams(15)) and meta-heuristic approaches (Ding et al(Reference Ding, Lim, Rodrigues and Zhu16), Xu and Bailey(Reference Xu and Bailey17), Drexl and Nikulin(Reference Drexl and Nikulin18), and Cheng et al(Reference Cheng, Ho and Kwan19)). These studies primarily focused on improving one or more landside performance criteria based on the requirements of airlines or passengers (such as minimum walking distances, minimum connection and waiting times, maximum number of gated flights, maximum total gate assignment preference, etc.) and often ignored the effect of aircraft ground movements in taxiways and aprons.
Other researchers have recently addressed the issues of gate assignment affecting aircraft ground movements. For example, Kim et al(Reference KIM, Feron and Clarke20,Reference Kim, Feron, Clarke, Marzuoli and Delahaye21) developed alternative gate assignment models which account for the effect of aircraft ground movements in a limited scope. The proposed models minimise aircraft taxi times and taxi delays in addition to passenger transit times using Tabu Search (TS) and Genetic Algorithm (GA) meta-heuristics. Neuman and Atkin(Reference Neuman and Atkin22) considered the effects of potential conflicts at taxiways near gates in their gate assignment algorithm based on mixed-integer programming. These studies made important contribution to the integration of gate assignment and ground movement operations, but they confined their scope to taxiways around parking positions rather than the entire movement area of the airport. This limitation is adapted due to the impracticability of optimising ground movement and gate assignment operations simultaneously(Reference Atkin, Burke and Ravizza4).
Similar to AGAP, various optimisation models were employed to solve AGRP. Atkin et al(Reference Atkin, Burke and Ravizza4) provided a concise overview and comparison of these models and emphasised the necessity of their integration to the gate assignment process. In addition to these studies, there are several ongoing projects regarding taxi routing management within the SESAR WPE Long Term and Innovative Research such as TRACC(Reference Gerdes and Temme23) and MoTa(Reference Chua, Cousy, Andre and Causse24). Both projects aim to develop decision support systems providing pre-tactical and tactical conflict-free taxi route advice for air traffic controllers. Although some of these studies, such as Ravizza et al(Reference Ravizza, Atkin and Burke25) and Stergianos et al(Reference Stergianos, Atkin, Schittekat, Nordlander, Gerada and Morvan26) included gate assignment-related issues (for example, the effects of stand holding and pushback strategies on taxi routing), none of them intended to attempt the creation of a gate assignment or reassignment process.
Although optimisation based approaches for AGAP and AGRP problems ensure optimal or near-optimal solutions which work well for offline planning because of their static nature, they usually perform poorly in online real-time operations in which stochastic delays are introduced due to latencies and disruptions in flight schedules, variations in aircraft performances, uncertainties in weather conditions, emergency situations and other unexpected factors. Especially for AGAP, several methods were proposed to make the assignment models more robust against the dynamic changes. Bolat(Reference Bolat27) studied the utilisation of buffer times to absorb unforeseen delays. Gu and Chung(Reference Gu and Chung28) developed a gate reassignment model based on a global search technique of Genetic Algorithm (GA). Yan et al(Reference Yan, Shieh and Chen29) introduced a simulation framework to examine the impact of stochastic flight delays on static gate assignments and to assess buffer times between aircraft. Though these approaches improve the robustness of gate assignments, more flexible techniques are required to fully cope with the dynamic nature of the more complex problems that arise from integrated airport operations.
Optimisation-based methods feature a number of shortcomings, such as the inability to create realistic models of complex airport operations or to build in a robustness against the dynamic and stochastic behaviour of air traffic, as well as the long computation times required. A knowledge-based system, however, is a practical and effective candidate to solve integrated parking position and ground movement problems. Previously, several knowledge-based models were developed for the solution of AGAP by Brazile and Swigger(Reference Brazile and Swigger30), Gossling(Reference Gossling31) and Cheng(Reference Cheng32,Reference Cheng33) , while Chua et al(Reference Chua, Cousy, Andre and Causse24) proposed such an approach to solve AGRP, but no integrated knowledge-based approach has been introduced for gate assignment and ground movement operations.
This study proposes a hybrid dynamic system: an integrated methodology of taxi path and gate assignment using a knowledge-based decision making approach to model effectively time variant and realistic operational features of aircraft gate management and route planning effectively. The proposed model aims to allocate the most suitable parking positions with minimum taxi time and taxi delay among their reduced solution set, satisfying pre-defined decision criteria within a short-term planning window as well as monitoring ground movements and reassigning taxi paths and parking positions in real time if necessary. In order to analyse the benefits, the proposed hybrid dynamic system was adapted to SIMMOD Pro, a fast-time simulation tool, as an embedded decision model which was tested for Istanbul Ataturk Airport as the alternative scenario. The current gate assignment and ground traffic control rules and procedures used at the airport were also modelled in the simulation environment as the baseline scenario. The alternative and baseline scenarios were compared in terms of their simulation results, including total and average taxi times and taxi delays, departure queue delays, hourly throughput and the utilisation of parking positions.
The remainder of this study is organised in the following order. Section 2 presents the description of the proposed hybrid dynamic gate and taxiway assignment methodology. Section 3 provides the description of the fast-time simulation model and scenarios for Istanbul Ataturk Airport. The simulation results of the alternative and baseline scenarios are presented in Section 4. The conclusions drawn from these results are discussed in Section 5.
2.0 MODEL DESCRIPTION
2.1 Hybrid dynamic gate and taxiway assignment methodology
As an alternative to current systems, the Hybrid Dynamic Gate and Taxiway Assignment (HDG&TA) system is proposed as a conceptual model capable of providing a robust and automated parking position and taxi path assignment process at airports. ‘Hybrid’ refers to the use of combined data analysis and knowledge-based techniques in parking position and taxiway assignment, and ‘dynamic’ indicates the ability of the system to check changes in the traffic and update assignments during the entire process. The model consists of a general assignment algorithm, which can receive real-time flight data from the available surveillance systems as decision inputs, and send gate and taxiway assignment instructions as outputs to Air Traffic Control (ATC) and ramp towers at airports (Fig. 1). The general algorithm performs parking position and taxiway assignments for arriving aircraft prior to their entrance to the final approach course based on gate exit times and the ground movements of departing aircraft. Taxiway planning for departing aircraft is also performed depending on gate and taxiway assignments of arriving aircraft. The system can acquire the airborne position and related flight information of arriving aircraft from primary and secondary surveillance radars, while it can track movements of aircraft at gates and on taxiways from airport surface movement radars or detection equipment.

Figure 1. System architecture of the Hybrid Dynamic Gate and Taxiway Assignment (HDG&TA) model.
The model attempts to take account of all major capacity and traffic flow constraints of airside elements in order to represent the operational air traffic environment realistically. These constraints include physical limitations such as positions, geometric configurations and dimensions of runways, taxiways, aprons, gates and open parking positions; differences in aircraft performance and flight operation types; ATC rules, procedures and separation minima; runway changes due to wind; traffic density; airline gate demands; parking durations; and travel times of ground services. On the other hand, the following assumptions and limitations have been imposed on the model in order to formulate an efficient algorithm search for a feasible solution for gate and taxiway assignments under these constraints:
-
(1) Operational constraints involving airport landside elements such as the capacity of passenger and cargo terminal buildings, passenger walking distances or customer service satisfaction are excluded in the model.
-
(2) Air traffic controllers working in the ground position of the ATC tower and ramp tower controllers have access to gate and taxiway assignment recommendations of arriving and departing aircraft through a special data link.
-
(3) Arriving aircraft start their descent for landing at the Final Approach Point (FAP) located at 10 NM from the runway threshold. A circular zone with a 2 NM radius centred at FAP is accepted as a buffer area. The gate and taxiway assignment process for an aircraft commences as it enters this buffer area.
-
(4) The minimum radar separation distance is accepted as 4 NM for arriving aircraft on the same final approach path.
-
(5) Wake turbulence separation minima between aircraft are determined according to time-based and distance-based separation standards set by ICAO for the approach and departure phases of flight(34). ICAO sets these minima based on a classification of aircraft types into three categories according to the maximum take-off mass such that heavy (136,000 kg or more), medium (7,000–136,000 kg) and light (7,000 kg or less).
-
(6) Approach and departure airspeeds of aircraft are estimated in three representative performance groups (heavy, medium and light) based on wake turbulence categories specified by ICAO. Using aircraft type designators(35) and the Base of Aircraft Database (BADA)(Reference NUIC36), corresponding airspeed values of each performance group are determined as the weighted average of aircraft types available in the air traffic data.
-
(7) Light category aircraft are assigned to pre-defined parking locations such as general aviation aprons only. Gates and remote parking stands are allocated to heavy- and medium-category aircraft.
-
(8) Each parking position has a fixed ground service travel time measured with respect to a common ground service area. These fixed values correspond to average travel times provided by ground service operators. Therefore, any variation in these travelling times due to aircraft and vehicle traffic interactions are ignored in the model.
-
(9) Although the model is capable of reducing adverse impacts of emergency situations such as runway, apron or taxiway closures due to accidents or aircraft failures, and these effects on gate and taxiway assignment are not considered in the study.
The model uses five decision criteria hierarchically for planning the assignment process of suitable parking positions and taxiways for each aircraft (Fig. 2). The first two criteria are connected with the parking position planning process whereas the last three criteria concern the taxi path-planning process. The first decision criterion of planning considers the parking duration required by the aircraft. This duration is the period between Scheduled In-Block Time (SIBT) when the aircraft reaches its gate and the Scheduled Out-Block Time (SOBT) when the aircraft departs the gate. Aircraft with shorter parking durations have priority for the assignment of gates at the terminal buildings while aircraft with longer parking durations, (e.g., overnight parking), are assigned to remote parking stands. Besides the parking duration, the gate or remote parking preference of the airline is also taken into account during the planning phase.

Figure 2. Dependency and hierarchy of decision criteria for parking position and taxi path assignment.
The second decision criterion is based on the physical constraints of parking positions and the operational requirements of airlines. Physical constraints include aircraft type and gate size compatibility, which depend on the wingspan, fuselage length and the turn radius of aircraft, and also the safety clearances and spacing between parking positions(Reference Kazda and Caves37). Operational requirements of airlines comprise airline-specific gate reservations at the airport, type of flight mission (international or domestic), and operation (passenger or cargo), the security restrictions depending on the origin of the flight, and the parking demands at hangars for receiving technical services. Based on these constraints, the model determines parking position options for assignment.
The third criterion is set to search for a suitable parking position located at the shortest distance from the estimated position of the aircraft after landing. This criterion utilises a comparative analysis for gate properties along with shortest path calculations. While the model calculates taxi path distances and arrival times of the aircraft to potential gates based on their ground position and taxi speed information, it performs comparative checks for the availability of these gates at calculated arrival times under their physical and operational constraints described by the second criterion.
The fourth criterion considers the selection of a conflict-free taxi path to the assigned gate. The taxi path assignment algorithm checks for possible conflicts dynamically at taxiway intersections and for congestion on taxiways along the shortest taxi path to the assigned gate. In case of any conflict or congestion along the shortest taxi path, alternative taxi paths are also checked for conflicts in order to determine the minimum delay taxi path from the estimated position of the aircraft after landing to the assigned gate.
The final criterion of the process is the travel time of ground services to the assigned gate. This criterion is activated only when the model finds more than one feasible parking positions under the constraints of the first four decision criteria. As ground services (fuel tanks, catering cars, passenger transfer vehicles, etc.) are based in specific areas of the airport, the average travel time to each gate or parking position has been defined by the ground service operators. Longer travel times may adversely affect the aircraft turnaround process such that they introduce delays in actual parking duration at assigned gates or parking positions. In order to minimise these delays, the model compares the pre-defined travel times to each alternative gate and chooses the one closest to the ground services area.
2.2 General algorithm
The aim of the HDG&TA model is to allocate the most suitable parking position providing the minimum taxi time and taxi delay while fulfilling the required criteria set for decision making. The algorithm continuously checks the availability of arriving aircraft within a buffer zone around the FAP (Fig. 3) to initiate the entire process. If no aircraft are detected within the buffer zone, the algorithm will wait in standby position.
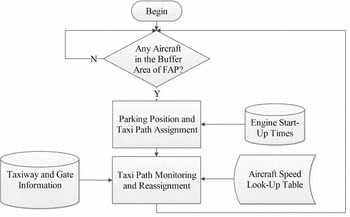
Figure 3. General algorithm of the Hybrid Dynamic Gate and Taxiway Assignment (HDG&TA) system.
The general algorithm consists of two steps: a parking position and taxi path assignment sub-algorithm, and a taxi path monitoring and reassignment sub-algorithm (Fig. 3). Each sub-algorithm contains a decision tree based on the relevant criteria set. As the first step is initiated, the algorithm searches for parking positions to define a smaller feasible set of alternatives based on the first two decision criteria. Then the algorithm calculates estimated taxi times and taxi delays for every possible alternative taxi path of this solution set. Among these alternatives, the parking position and corresponding taxi path with the minimum taxi time and taxi delay are assigned to the arriving aircraft. This assignment process is handled separately for gates and remote parking stands.
The second step checks for any possible difference in taxi time and delay between the assigned and actual taxi paths using ground radar data while the aircraft taxies. If any difference is detected due to unforeseen changes in the ground traffic flow, the sub-algorithm will recalculate the taxi times and delays for each alternative taxi path. Where necessary, a new taxi path will be reassigned to the aircraft to ensure minimum taxi time and delay. In other words, these two steps are integrated such that if one step has to change its solution due to any updates or disruptions in traffic flow or operational conditions, the other step alters its solution accordingly.
For system input, the algorithm uses three distinct databases storing engine start-up times, gate and taxiway information, and aircraft speed data. The engine start-up time database stores the actual engine start-up times kept by the Flight Information Centre (FIC) based on departure readiness of aircraft parking at gates and remote stands. The gate and taxiway information database stores data acquired from ground radar regarding parking position availability and taxiway convenience for aircraft during their entire operation span at the airport. The same database also contains the physical constraints of parking positions specified in the Aeronautical Information Publications (AIPs) and ramp tower procedures. The aircraft speed database holds approach/departure airspeed look-up tables based on aircraft performance groups and taxiing speed depending on operational restrictions. Using these speed restrictions, taxi-in and taxi-out durations are calculated for each aircraft operating on the ground.
2.2.1 Parking position and taxi path assignment
When the sub-algorithm (Fig. 4) starts, it checks the weight category of the arriving aircraft in order to search for appropriate gates at the airport. In the event that empty gates are available for medium- or heavy-category aircraft, the algorithm will define a priority index i (i = 1, . . ., m) for each gate based on the information acquired from the parking position planning decision database. The algorithm runs all of its queries from the gate with the highest-priority index (i = 1) to the one with the lowest-priority index (i = m). The gate assignment process is initiated based on the parking position preference of the aircraft. If the aircraft has a remote parking-stand preference, the gate assignment step will be skipped and the remote parking-stand algorithm will be initiated. Since the remote parking assignment algorithm runs a similar process under the similar constraints imposed by the second decision criterion, it is not presented here for brevity.

Figure 4. Parking position and taxi path assignment algorithm.
When the airline prefers to park at a specific gate, the algorithm will start the medium or heavy gate assignment sub-process represented by yellow blocks. These sub-processes check whether or not the empty gates are in areas of restricted use. If there are any physical constraints at the gates, the algorithm will implement the restricted-gate assignment rules for the corresponding aircraft category. When the gate assignment sub-processes find a suitable gate for the aircraft among the indexed gates, the taxi path assignment sub-process is started.
When there is no empty gate at the airport or the gate assignment sub-process finds no suitable gate for the aircraft, the algorithm will check the availability of gates occupied by other aircraft in the same weight category. If the algorithm finds such gates, it will proceed to the next query, or else will start the remote parking-stand assignment process. In the next query, the algorithm estimates the difference between SOBT of departing aircraft at these gates and the FAP entry time of the arriving aircraft. This difference equals the approximate taxi time of the arriving aircraft to these gates. The algorithm then checks the approximate taxi time to each gate sequentially. If the taxi time to a gate is less than a reference decision value, it can be added to the gate assignment solution set of the arriving aircraft. This reference decision value is accepted as the mean taxi-in value measured at the airport of concern (i.e., 10 minutes for LTBA) by Eurocontrol(38). After the creation of the solution set, the algorithm evaluates the alternative taxi paths for the gates in the solution set. In Fig. 5, the parking solution with associated alternative taxi paths are presented for an aircraft as an example. R0 is the initial position of the aircraft, P i are the possible parking positions and Xi,j refers to the taxiway sections in the solution set. Unobstructed taxi times and taxi delays between the estimated runway exit point and the parking positions in the solution set are calculated for each taxi path. Therefore, the gate and corresponding taxi path having the minimum taxi time and taxi delay is assigned to the intended aircraft. The algorithm then updates the status of gates and returns to the beginning of the process. The assigned taxi path status is also written to the memory mapping database, which will be explained in Section 2.2.2. If no gates are found after this query, the same steps will be repeated for remote parking stands.

Figure 5. Alternative taxi paths for possible parking positions in solution set.
At airports, some of the gates may be subject to conditional use for aircraft of certain types or weight category due to restrictions imposed by other aircraft parking at neighbouring gates. These restrictions are specific to the physical or operational constraints of the airport concerned. In this paper, two restricted gate assignment rules are adopted from the sample airport to provide a realistic representation for the case study in Section 3. These rules are as follows:
-
(1) If a heavy-category aircraft is parked to the right of a restricted empty gate, a medium-category aircraft will be permitted to use this restricted gate only when the left adjacent gate is empty.
-
(2) A heavy-category aircraft can use a restricted gate if there is no heavy category aircraft parked at the right adjacent gate.
Rule 1 and 2 are handled by the medium-category assignment sub-process (Fig. 6) and the heavy-category assignment process (Fig. 7). Each sub-process checks if empty gates lie in an area of restricted use according to their priority index, i. The area of restricted use can be described as a linear row of gates with a unique position index k ranging from 1–n (Fig. 6). The range of k is a user-defined parameter (e.g., gate number), therefore, it remains unchanged during the entire assignment process. If the empty gate i has no restrictions, it will be assigned to the arriving aircraft directly. Where gate i (e.g., i = m – j where 1 ≤ j ≤ m) is in the area of restricted use, the sub-process of the relevant category checks the occupancy status of adjacent gates to its left and right (e.g., k = n – (l+1) and k = n – (l–1), respectively, where 1 ≤ l ≤ n). The occupancy status of adjacent gates indicates whether heavy, medium or no aircraft are parked at them. Each sub-process implements its assignment rule using a set of queries shown in Figs. 7 and 8. If the gate i satisfies the conditions of the relevant rule, the sub-process assigns it to the arriving aircraft. If not, the algorithm will move to the next empty gate, i + 1. These queries are repeated until the sub-process finds a gate (i.e., i ≤ m) that satisfys the assignment rule. If no such gate is found, the algorithm leaves the sub-process.

Figure 6. Representation of empty and occupied gates within the area of restricted use.

Figure 7. Medium-category gate assignment sub-process.
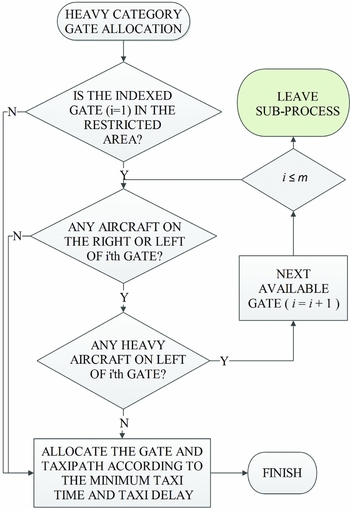
Figure 8. Heavy-category gate assignment sub-process.
2.2.2 Taxi path monitoring and reassignment
The primary aim of this step (Fig. 9) is to ensure that all aircraft travel along the assigned taxi paths having the minimum taxi time and taxi delay during real-time ground movements. These taxi paths are already recorded in the mapping database in the previous step. This database stores the occupancy status of all taxiway sections constituting these taxi paths using a 3D matrix in time-space format (Fig. 10).

Figure 9. Taxi path monitoring and reassignment algorithm.

Figure 10. Taxiway occupation status 3D matrix.
The matrix consists of three axes: taxiway, time and time penalty. Taxiway axis includes all taxiway sections constituting the taxiway network of the airport. Therefore, every possible taxi path for each aircraft can be represented on the taxiway-time plane in order to detect any conflict in the assignment and monitoring phases. If a taxiway section is occupied by two aircraft at the same instant, the aircraft that arrives later to the taxiway section will receive a taxi delay shown in the time penalty axis. The amount of this delay is equal to the occupancy time of the taxiway by the first aircraft. For example, Fig. 11 shows two aircraft taxiing along T1-T7 and T7-T1 having a conflict on taxiway segment T4 at 10:02:00. Aircraft 1 has no delay because it is the first aircraft entering T4, but Aircraft 2 receives a 1-minute delay as a penalty while it waits for Aircraft 1 to exit T4.

Figure 11. An illustrative example of conflict detection in the mapping database.
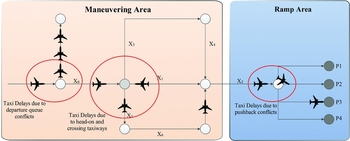
After the assignment of the taxi path and parking position in the first step, the ground movement of each aircraft is monitored continuously by radar for possible unforeseen delays along its taxi path by reviewing the ground radar data and mapping database. There are three possible causes of delay while aircraft taxies on the ground (Fig. 12). These delays can be due to departure queue conflicts, head-on and crossing taxiway conflicts, and pushback conflicts with other aircraft. During the monitoring of the aircraft by ground radar, delays are written to the mapping database continuously.

Figure 12. Taxi delays possible on the manoeuvring and ramp area.
The algorithm checks the assigned taxi path for these possible conflicts and congestion. In case of no conflict or congestion, the algorithm will let the aircraft maintain its assigned taxi path. If not, the algorithm examines the traffic situation in alternative taxi paths between the aircraft's current position and the assigned parking position.
This inquiry is repeated until the sub-process finds the conflict-free taxi path with minimum taxi time and taxi delay among the alternatives stored in the mapping database, and then it reassigns this new taxi path to the aircraft. If the system finds no conflict-free taxi path for the assigned gate, the algorithm returns to its first step to search for other possible parking positions that have conflict-free taxi paths. Dashed lines in Fig. 9 represent these dynamic updates. The algorithm performs these checks until each aircraft reaches its assigned parking position. Taxi path of departing aircraft is assigned in the same manner. Their taxi paths are also written to the memory-mapping database to control their movements.
3.0 CASE STUDY: ISTANBUL ATATURK AIRPORT
3.1 Fast-time simulation methodology
Istanbul Ataturk Airport (LTBA) is chosen as the sample airport to analyse the impact of the HDG&TA system on traffic flow in airport movement areas. LTBA is one of the fastest-growing major airports in Europe with an annual average traffic increase of 8.0% during the last 8 years(39,40) . As the largest airport in Turkey, it serves 49.4% of all international flights and 20.4% of all domestic flights in the country(40). Despite this large traffic demand, the airport has a limited area for expansion and construction of new airside infrastructure. Therefore, airside capacity improvements mainly rely on the efficient use of the existing runways, taxiways, aprons and parking positions.
A fast-time simulation study has been conducted to compare the current gate assignment and ground control procedures, and the proposed HDG&TA model in terms of throughput, ground travelling times, delays and departure queues, and bottlenecks at movement areas. The simulation model of LTBA was constructed using SIMMOD Pro, an advanced discrete-event simulation tool for airport and airspace operations. Using node-link definitions of SIMMOD Pro, runway systems, taxiway network, gates and remote parking stands, and the final approach and initial climb paths within the control zone (CTR) of LTBA can be modelled in great detail. Besides these modelling capabilities, its Profile Builder feature allows the definition of decision trees and its airfield logic permits the modelling of pre-defined, alternate or free taxi paths with minimum travelling time. Using these capabilities, both current and proposed decision models for gate and taxiway assignment were implemented in the airport model under baseline and alternative scenarios, respectively.
The airside airport layout was based on the aerodrome charts and data in the Aeronautical Information Publication (AIP) released by the national air navigation service provider, DHMI. The date of 26 June 2012 was selected as a typical busy day with 1,040 operations based on the analysis of annual traffic data from LTBA(Reference Guclu41). The traffic schedule of the typical busy day was gathered from DHMI and the airport operator, TAV. The peak period between 17:00 and 21:00 was simulated for baseline and alternative scenarios. Details regarding the airport layout, traffic characteristics and scenarios will be described in the following sections.
3.2 Airport layout and parking positions
Istanbul Ataturk Airport accommodates 36 gates and 75 remote parking stands according to the parking and docking configuration of 2012. Ground operations are divided into north and south ground sectors (Fig. 13)(Reference Genc, Erol, Eksin, Berber and Guleryuz42).

Figure 13. Parking positions, numbers and locations(38).
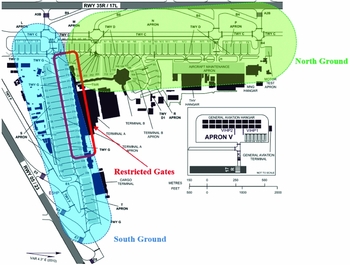
The south sector includes 17 gates (208–225) and 29 remote parking stands whereas the north sector includes 19 gates (101 –112 and 201–207) and 46 remote parking stands. Gates 205–223 are subject to the rules of restricted use as described in Section 2.2.1.
3.3 Traffic analysis
The traffic summary of the peak period on 26 June 2012 is analysed for the scenarios. During this 4-hour period, 108 arrivals and 94 departures totalling 202 operations took place. The highest throughput was seen from 18:00 to 19:00 with 58 operations, of which 32 were arrivals and 26 were departures. According to the traffic data, all departures took off either from 35R or 35L except for five from 05, whereas all arrivals landed on 05 except one on 35R during the specified period. Of the traffic during this period, 89% were medium-category aircraft and 11% were heavy-category aircraft. International and domestic flights were 62% and 38% of the total traffic, respectively.
3.4 Simulation scenarios
The currently used and HDG&TA models were represented under the baseline and alternative scenarios, respectively. Both scenarios were tested in the same simulation model for the specified peak-time traffic input. Arrival/departure times and parking (turnaround) durations were acquired from the actual traffic data as simulation inputs for both scenarios. During simulations, all arriving flights were injected to the simulation at the FAPs. Departing flights, which arrived before the simulation start time, were injected to the simulation at their assigned parking positions in the traffic data.
The baseline scenario represents the current parking position and taxiway assignment process based on the actual traffic in the specified peak-traffic period. At Istanbul Ataturk Airport, ramp unit operators perform parking position assignments using ROTA software. ROTA software consists of a resource management system based on a rule and optimisation engine(Reference Genc, Erol, Eksin, Berber and Guleryuz42). The rule engine is a task-oriented module which manages the relationship between resources and tasks. The optimisation engine provides advisories for the predefined airport operational rules by giving scores to solve the unforeseen changes in the terminal schedule. In the baseline scenario, the gate assignment output of ROTA for the given flight data was imported to SIMMOD Pro to model the current real-world gate assignment practice. Ground movements handled by ATC Tower were also modelled based on ground control procedures described by the AIP(43). According to this procedure, each aircraft should use a pre-defined taxi path depending on the location of its assigned parking position. For instance, aircraft taxiing to parking positions in the south ground area use taxiway G, whereas aircraft taxiing to parking position in the north ground area use taxiway F without crossing the apron area of restricted gates (Fig. 12). In case there is any conflict in a taxiway or parking position assignment aircraft are held at the closest staggering point during the scenario. These pre-defined taxi paths were described in the rule base of the baseline scenario.
The HDG&TA model was implemented as the alternative scenario by using the profile builder feature of SIMMOD Pro. In the first hour of this scenario (17:00–18:00), the taxiway assignment algorithm was executed only to provide a ‘warm-up period’ for the parking position assignment algorithm. Therefore, the assignment of gates and remote parking stands were performed based on the current technique using actual parking position data. After the warm-up period, the parking position assignment algorithm started running for the given flight schedules between 18:00 and 21:00.
The data obtained as a result of testing these scenarios were compiled from standard SIMMOD report files (SIMU26 and SIMU48). These data included quantitative evaluations related to system performance parameters (hourly throughput, travelling times, delays and queue lengths). Computer animations were also obtained to compare the differences in traffic flow for both simulation scenarios (Fig. 14). These outputs enable the comparison of the conventional and alternative (HDG&TA) techniques in terms of their impact on traffic flow in the movement areas of the selected airport.

Figure 14. Screenshots of baseline (left) and alternative (right) simulation scenarios taken at 20:42:39. In the baseline scenario, significant congestion can be observed at intersection points of G and D as well as in rapid-exit taxiways since the scenario is not as robust as the alternative scenario against disruptions in flight schedules.
4.0 RESULTS
After running both scenarios, five different analyses were performed to compare their impact on the traffic flow and capacity of the airport. First, the general results of the 4-hour simulations were compared in terms of total taxi times and taxi delays. In the second part, the hourly distribution results were presented for throughput for both scenarios. Third, the simulated peak-hour traffic between 18:00 and 19:00 was analysed for utilisation of runways, taxi times and departure queue delays. Fourth, the congestion points during the simulation were analysed. Finally, gate utilisation was assessed for both scenarios.
4.1 General analysis of traffic flow
An overview of the 4-hour simulation results presented in Tables 1 and 2 for arriving and departing traffic sequences, respectively. Table 1 indicates total throughput, approach time and delay, arrival taxi time and delay that occurred during the baseline and alternative scenarios. As arrival times to FAP and runway threshold are identical in both scenarios, there is no difference in flight time and delays during the approach phase for the 108 arriving flights as shown. Arrival taxi time and delay, however, are reduced in the alternative scenario by 17.9% and 93.8%, respectively, due to the positive impact of the HDG&TA model.
Table 1 Comparison of arrival times and delays for approach and arrival taxi phases

Table 2 Comparison of departure taxi times and ground delays

Table 2 presents the total taxi time and ground delay including holdings at departure queue points. The alternative scenario decreased the total departure taxi time by 14.1%, compared to the baseline scenario for the 94 departing flights during the simulation. Departure taxi and queue delays were also reduced by 12.3% and 6.6%, respectively.
According to these results, the HDG&TA algorithm significantly improves the total ground travelling time and delay without adversely affecting the arrival approach time and delay during the simulation time.
4.2 Analysis of hourly distribution results
After reviewing the overall results of the simulation, the hourly distribution of throughput was analysed separately for arrival and departure movements for both scenarios. The hourly traffic throughput of the simulated baseline and alternative scenarios are presented in Table 3. Although the actual peak hour took place at 19:00–20:00, the simulated peak hour for both scenarios occurred 1 hour earlier, as flights that entered the system before 17:00 were not included in the simulations. Therefore, the first hour of the simulation can be considered as the warm-up period. During the simulated peak hour, the alternative scenario increased throughput by two departures and therefore relieved the traffic flow better than the baseline scenario for the next hour from 19:00 to 20:00.
Table 3 Baseline operation throughput during simulation

4.3. Peak-hour analysis
Table 4 provides a detailed breakdown for the performance of the two scenarios at the simulated peak-hour period. The alternative scenario slightly improves runway usage for both departing and arriving aircraft. Additionally, the average taxi time of arriving and departing aircraft is reduced significantly, especially the average arrival and departure taxi time, which are reduced by 0.8 and 0.6 minutes per aircraft, respectively.
Table 4 Baseline and alternative scenario comparisons at peak hour

The average delay time per aircraft at the departure queue point is also decreased slightly in the alternative scenario. Although some of the peak-hour improvements made by the alternative scenario may seem limited, their contribution to arrival-departure flow management are significant during the subsequent hours of simulation.
4.4 Taxi delay points at the movement area
In addition to traffic flow results, the degree and location of taxi delays in the movement areas were compared for both scenarios. Figure 15 presents the frequency distribution of ground delay points in the baseline and alternative scenarios according to delay time intervals. During the simulations, ground delays occurred due to conflicts at the taxiway intersections and by being held in departure queues. Analysis of the results shows that ground delays under 150 seconds were observed at taxiway intersections whereas those over 150 seconds were observed in departure queues. In terms of taxi delays, the baseline scenario has higher frequencies for both delays under 20 seconds and over 60 seconds than the alternative scenario. Though the alternative scenario has relatively higher ground delay points for the interval of 20–40 seconds, it has fewer delay points and times in overall distribution, since the HDG&TA model prevented ground holding of more than 40 seconds by managing the ground movements of aircraft. In the alterative scenario, all departure queue delays (totalling 954 seconds) were confined to the departure queue point. In the baseline scenario, on the other hand, two points received departure queue-related delays (i.e., 954 and 1,199 seconds).

Figure 15. Frequency distribution of ground delay points in baseline and alternative scenarios.
The locations of the points with the highest taxi delays are presented in Fig. 16 for the baseline and alternative scenarios, respectively. In the baseline scenario (Fig. 16), the highest taxi delays occurred at the intersections of D and G taxiways (point 1), and taxiway F and the rapid exit of runway 05 (point 2). Major congestion also occurs along D taxiway (point 3 and points 5–8) and D1 (point 4).

Figure 16. Taxi delay points in baseline and alternative scenario, respectively.
The alternative scenario, on the other hand, decreases the delays at these points significantly as shown in Fig. 16. Although points with moderate delays (i.e. 20–40 seconds) are increased especially along D1 taxiway, they have a limited impact on the overall traffic flow in frequently used taxiways such as G and D. This is mainly because the HDG&TA model prevents most of the ground holding at these intersections by using alternative conflict-free taxiways and distributes the traffic flow to a wider area. Taxi delays at points 1–8 in Fig. 16 are compared quantitatively for both scenarios in Table 5.
Table 5 Taxi congestion points delay comparison in minutes

4.5 Gate utilisation
In order to evaluate the impact of the HDG&TA model on parking positions, the average occupancy time and utilisation of parking positions are compared in Table 6. While gate utilisation is decreased by 8.1% in the alternative scenario, remote parking stand utilisation is increased by 5.1%. This result indicates that the HDG&TA algorithm performs a more balanced distribution between gates and remote parking stands than the baseline model during parking position assignment. The alternative scenario results in a significant improvement in gate capacities, since it decreases the average occupancy time by 25.7 minutes for gates. However, the average occupancy time for remote parking stands is increased by only 15 minutes. In total, 108 aircraft were assigned to parking positions during the simulation of both scenarios. In the baseline scenario, all assignments were done according to actual assignment data. In the alternative scenario, however, the first 22 assignments were made according to the traffic data during the warm-up period from 17:00 to 18:00, and the remaining 86 assignments were performed by HDG&TA. The number of aircraft assigned to gates and remote parking stands in the alternative scenario are equal to those in the baseline scenario (41 and 67, respectively). This equality shows that HDG&TA complies successfully with the airline parking position preferences imposed by the first decision criterion. Although the distribution between gates and remote stands is the same, HDG&TA managed to assign more aircraft to the remote stands closer to the terminal buildings in order to decrease the taxi time and taxi delays.
Table 6 Average occupancy time and utilisation of parking positions in baseline and alternative scenarios

The total gate and remote usage times are slightly less in the alternative scenario. The reason for this reduction is the efficient management of aircraft ground movements, especially around the ramp area (i.e., pushback movements). In the baseline scenario, due to the taxiing traffic, some of the aircraft had to hold at their stands during the simulation. For that reason, the total utilisation of the parking positions in baseline scenario became slightly higher than the alternative scenario.
5.0 CONCLUSION
This study provides a comparative analysis between the conventional and the proposed HDG&TA approaches in terms of air traffic flow and gate utilisation. The proposed algorithm seeks conflict-free taxi paths with minimum taxi time and taxi delay for departing and arriving aircraft sequences while it assigns parking positions according to a pre-defined set of decision criteria such as airline demands, parking durations, and the physical compatibility of gates and remote stands. The potential benefits of the algorithm were tested for Istanbul Ataturk Airport simulation model created using SIMMOD Pro.
The HDG&TA provided a quantitative and qualitative improvement in the overall efficiency of airside operations using an integrated planning and monitoring process for parking position assignment and ground movement operations. This method implemented in the alternative scenario increased peak-hour throughput since it expedited the flow of arriving and departing aircraft and also reduced conflicts and delays at taxiway intersections in the airport movement area. Taxi-in and taxi-out times were decreased considerably in the alternative scenario. It resulted in reducing congestion points, ground holdings and queue delays leading to more effective management of taxiway systems, runways and aprons than the current separated airport operations. Besides these improvements in airside components, it contributed to the efficiency of landside operations indirectly. For example, passenger transfer times between remote stands and terminal buildings could potentially be reduced because more aircraft were assigned to remote stands closer to terminal building as presented in results.
The proposed HDG&TA offers an integrated operational approach for gate and taxiway management at major airports and a helpful insight for the development of computer-based decision making tools for the improvement of air traffic flow and capacity in movement areas. The model can be extended to a complete airside and landside gate management decision support system through the inclusion of airport terminal and passenger flow constraints. Future work will focus on a comparison of the efficiency of HDG&TA with other optimisation based approaches to seek their possible inclusion and to improve its efficiency further.
ACKNOWLEDGEMENTS
This study was supported by Anadolu University Scientific Research Projects Commission under the grant no:1307F297.