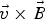Introduction
The charged particle trapping and accelerating with a laser field is a fascinating concept since last few decades (Tajima & Dawson, Reference Tajima and Dawson1979; Sprangle et al., Reference Sprangle, Esarey and Krall1996; Umstadter, Reference Umstadter2003). The rising interests to accelerate electron with a high energy remain a motivation for the investigation and development of advanced electron acceleration techniques (Leemans et al., Reference Leemans, Nagler, Gonsalves, Toth, Nakamura, Geddes, Esarey, Schroeder and Hooker2006; Ghotra & Kant, Reference Ghotra and Kant2015a). Several theoretical and experimental models are proposed by various researchers that report an effective energy gained by the electron during interaction with ultra-short and intense laser pulse (Geddes et al., Reference Geddes, Toth, Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Joshi, Reference Joshi2007; Malka et al., Reference Malka, Faur, Gauduel, Lefebvre, Rousse and Phuoc2008; Ghotra & Kant, Reference Ghotra and Kant2015b; Albert et al., Reference Albert, Lemos, Shaw, Pollock, Goyon, Schumaker, Saunders, Marsh, Pak, Ralph, Martins, Amorim, Falcone, Glenzer, Moody and Joshi2017; Mohammed et al., Reference Mohammed, Ghotra, Kaur, Hafeez and Kant2017; Wallin et al., Reference Wallin, Gonoskov, Harvey, Lundh and Marklund2017). The energy gained by the electron is sensitive to laser's power, beam waist, and pulse duration (Ghotra & Kant, Reference Ghotra and Kant2017; Fortin et al., Reference Fortin, Piche and Varin2010). Laser–plasma interactions indicate that there is a generation of superponderomotive electrons due to a non-wake-field interaction between a laser pulse and a longitudinal electric field (Robinson et al., Reference Robinson, Arefiev and Neely2013). There appears a dephasing that reduces the electron acceleration. The longitudinal electric field acts as an extra field that could reduce the dephasing rate for an efficient acceleration. Vacuum-based acceleration of electron has some advantages over plasma as it presents a greater group velocity of a laser pulse, and also the plasma-related instabilities are absent in vacuum, which appears as a better option for laser–electron interaction. Further, it is much easier to inject a pre-accelerated electron in vacuum than in plasma. Gaussian laser fields with appropriate profiles prove their suitability for effective acceleration of electron because of their ability of achieving a high energy with restricted spread and small divergence of electron beams (Fortin et al., Reference Fortin, Piche and Varin2010). The Gaussian laser beam fields and their propagation properties are dependent on laser beam frequency ω, intensity parameter a 0, beam waist radius r 0 at the focus, pulse duration τ and Rayleigh length ![]() $Z_{\rm R} = kr_0^2 /2$. A few MeV of electron energy gain was observed with intensity above
$Z_{\rm R} = kr_0^2 /2$. A few MeV of electron energy gain was observed with intensity above ![]() $10^{19}{\rm W/cm}^{\rm 2} $ with a Gaussian laser beam (Ghotra & Kant, Reference Ghotra and Kant2016a). The parameters such as external magnetic field, frequency variations and polarization characteristics of laser pulse influence the electron dynamics, and hence the electron energy gain (Ghotra & Kant, Reference Ghotra and Kant2016a; Salamin, Reference Salamin2017). The transverse electromagnetic (TEM) mode index-driven intensity variations of electromagnetic fields were investigated with intense laser beams (Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Gu et al., Reference Gu, Yu, Klimo, Esirkepov, Bulanov, Weber and Korn2016; Ghotra & Kant, Reference Ghotra and Kant2016b). Beam that involves a product of Hermite with Gaussian functions configures Hermite–Gaussian (HG) beam. The propagation characteristics of HG beam can be expressed in terms of different modes and represented as TEMmn, where m and n correspond to the mode indices. The lowest order mode (TEM00) of such beam represents a Gaussian beam. An experiment was conducted using HG laser beam with distinct modes (0, 0), (0, 1), (0, 2), (0, 3), and (0, 4) to investigate the emergence of mega gauss ordered persisting magnetic field due to relativistic electrons in plasma (Flacco et al., Reference Flacco, Vieira, Lifschitz, Sylla, Kahaly, Veltcheva, Silva and Malka2015). The polarization characteristics of a Gaussian laser beam indicate higher energy gain by the electron with a circularly polarized (CP) laser beam in comparison with a linearly polarized (LP) laser beam. The accelerated electron disperses with a low energy for a Gaussian TEM00 mode due to a strong transverse ponderomotive force. However, for an effective acceleration, the externally applied inhomogeneous magnetic field ensures a better trapping of electron near the focus of Gaussian laser pulse with TEM00 mode (Saberi & Maraghechi, Reference Saberi and Maraghechi2015). The HG beam with its higher modes enforces a better confining of electron close to its focus axis with TEM00 mode due to their characteristics intensity distributions. The electron acceleration under the influence of TEM modes of HG laser beam was investigated, which depicts that a lower mode indexed HG laser beam enforces a small acceleration of electron for longer distance, whereas, a higher mode indexed HG laser beam enforces a larger acceleration of electron for smaller distance without application of any external magnetic field (Ghotra & Kant, Reference Ghotra and Kant2016b). The detrimental effect of the B-fields on electron and ion acceleration has been evoked in an experimental and simulation study (Nakatsutsumi et al., Reference Nakatsutsumi, Sentoku, Korzhimanov, Chen, Buffechoux, Kon, Atherton, Audebert, Geissel, Hurd, Kimmel, Rambo, Schollmeier, Schwarz, Starodubtsev, Gremillet, Kodama and Fuchs2018). The inductive generation of the B-field is mainly determined by the spatio-temporal variations of the longitudinal sheath field: ∂B z/∂t = ∂E x/∂t. Those fields can be strong enough (~105 T at laser intensities ~1021 W cm–2) to magnetize the sheath electrons and deflect protons off the accelerating region, hence degrading the maximum energy. Such spatiotemporal-restricted magnetic field has larger impact on electron acceleration in plasma. The effect can be neglected for the case of direct laser acceleration (DLA) of electron in vacuum.
$10^{19}{\rm W/cm}^{\rm 2} $ with a Gaussian laser beam (Ghotra & Kant, Reference Ghotra and Kant2016a). The parameters such as external magnetic field, frequency variations and polarization characteristics of laser pulse influence the electron dynamics, and hence the electron energy gain (Ghotra & Kant, Reference Ghotra and Kant2016a; Salamin, Reference Salamin2017). The transverse electromagnetic (TEM) mode index-driven intensity variations of electromagnetic fields were investigated with intense laser beams (Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Gu et al., Reference Gu, Yu, Klimo, Esirkepov, Bulanov, Weber and Korn2016; Ghotra & Kant, Reference Ghotra and Kant2016b). Beam that involves a product of Hermite with Gaussian functions configures Hermite–Gaussian (HG) beam. The propagation characteristics of HG beam can be expressed in terms of different modes and represented as TEMmn, where m and n correspond to the mode indices. The lowest order mode (TEM00) of such beam represents a Gaussian beam. An experiment was conducted using HG laser beam with distinct modes (0, 0), (0, 1), (0, 2), (0, 3), and (0, 4) to investigate the emergence of mega gauss ordered persisting magnetic field due to relativistic electrons in plasma (Flacco et al., Reference Flacco, Vieira, Lifschitz, Sylla, Kahaly, Veltcheva, Silva and Malka2015). The polarization characteristics of a Gaussian laser beam indicate higher energy gain by the electron with a circularly polarized (CP) laser beam in comparison with a linearly polarized (LP) laser beam. The accelerated electron disperses with a low energy for a Gaussian TEM00 mode due to a strong transverse ponderomotive force. However, for an effective acceleration, the externally applied inhomogeneous magnetic field ensures a better trapping of electron near the focus of Gaussian laser pulse with TEM00 mode (Saberi & Maraghechi, Reference Saberi and Maraghechi2015). The HG beam with its higher modes enforces a better confining of electron close to its focus axis with TEM00 mode due to their characteristics intensity distributions. The electron acceleration under the influence of TEM modes of HG laser beam was investigated, which depicts that a lower mode indexed HG laser beam enforces a small acceleration of electron for longer distance, whereas, a higher mode indexed HG laser beam enforces a larger acceleration of electron for smaller distance without application of any external magnetic field (Ghotra & Kant, Reference Ghotra and Kant2016b). The detrimental effect of the B-fields on electron and ion acceleration has been evoked in an experimental and simulation study (Nakatsutsumi et al., Reference Nakatsutsumi, Sentoku, Korzhimanov, Chen, Buffechoux, Kon, Atherton, Audebert, Geissel, Hurd, Kimmel, Rambo, Schollmeier, Schwarz, Starodubtsev, Gremillet, Kodama and Fuchs2018). The inductive generation of the B-field is mainly determined by the spatio-temporal variations of the longitudinal sheath field: ∂B z/∂t = ∂E x/∂t. Those fields can be strong enough (~105 T at laser intensities ~1021 W cm–2) to magnetize the sheath electrons and deflect protons off the accelerating region, hence degrading the maximum energy. Such spatiotemporal-restricted magnetic field has larger impact on electron acceleration in plasma. The effect can be neglected for the case of direct laser acceleration (DLA) of electron in vacuum.
In this manuscript, an external axial magnetic field is employed to analyze the effect of distinct TEM modes of Hermite function on DLA of electron with a relativistic three-dimensional single-particle code using a CP Gaussian laser beam. Electron acceleration is shown to be influenced by the beam width parameter, propagation distance in terms of Rayleigh length, laser spot size, mode indices, and applied magnetic field. The influence of laser beam width parameter has been investigated on electron acceleration with distinct values of laser intensity and externally applied axial magnetic field in vacuum. The energy gained by the electron for distinct TEM modes (0, 1), (0, 2), and (0, 3) with respect to propagation distance has been analyzed without and with axial magnetic field. The acceleration distance is expressed in terms of Rayleigh length for distinct mode indices. The external magnetic field plays a vital role in controlling the electron dynamics. It strengthens the ![]() $\vec v \times \vec B$ force component of the fields for the occurrence of strong betatron resonance, which enhances electron oscillations. Hence, it ensures the confining of electron in close orbit around the axis of propagation of laser pulse. With lower mode index, the electron's acceleration remains small and focused toward the axis, the external magnetic field enhances the acceleration, and hence electron energy gain by confining the oscillations. However, with higher mode index where electron appears with larger acceleration for smaller distance, the magnetic field ensures the confining of electron around the axis for larger accelerating distance with enhanced energy gain. Presented results of electron energy gain with propagation distance under the influence of suitable magnetic field may be helpful in the development of better table-top electron accelerators of diverse dimensions and capabilities. The role of distinct mode indices and external magnetic field can be utilized for the formulation of desired-sized accelerators based on the accelerating distance of electron. The content in other sections of this paper is organized as follows. Section “Evolution of CP–HG beam” describes about the field distributions of a CP–HG laser beam, section “Relativistic analysis based on electron dynamics” describes the electron dynamics to relate the electron acceleration during interaction with laser and external fields. Outcomes are explained in section “Results and discussion”. Lastly, a conclusion is drawn and presented in section “Conclusion”.
$\vec v \times \vec B$ force component of the fields for the occurrence of strong betatron resonance, which enhances electron oscillations. Hence, it ensures the confining of electron in close orbit around the axis of propagation of laser pulse. With lower mode index, the electron's acceleration remains small and focused toward the axis, the external magnetic field enhances the acceleration, and hence electron energy gain by confining the oscillations. However, with higher mode index where electron appears with larger acceleration for smaller distance, the magnetic field ensures the confining of electron around the axis for larger accelerating distance with enhanced energy gain. Presented results of electron energy gain with propagation distance under the influence of suitable magnetic field may be helpful in the development of better table-top electron accelerators of diverse dimensions and capabilities. The role of distinct mode indices and external magnetic field can be utilized for the formulation of desired-sized accelerators based on the accelerating distance of electron. The content in other sections of this paper is organized as follows. Section “Evolution of CP–HG beam” describes about the field distributions of a CP–HG laser beam, section “Relativistic analysis based on electron dynamics” describes the electron dynamics to relate the electron acceleration during interaction with laser and external fields. Outcomes are explained in section “Results and discussion”. Lastly, a conclusion is drawn and presented in section “Conclusion”.
Evolution of CP–HG beam
A CP–HG laser beam is considered to be propagating in the z-direction. Under paraxial approximation, the transverse electric field components can be expressed as (Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Gu et al., Reference Gu, Yu, Klimo, Esirkepov, Bulanov, Weber and Korn2016):
 $$\eqalign{E_x (r,z,t) =& \displaystyle{{E_0} \over {\,f\,({\rm \xi} )}}\exp \,(i{\rm \phi} )H_{\rm m} \left( {\displaystyle{{\sqrt 2} \over {r_0 f\,({\rm \xi} )}}x} \right)\cr & \times \exp \left( { - \displaystyle{{(t - ((z - z_{\rm L} )/c))^2} \over {{\rm \tau} ^2}} - \displaystyle{{r^2} \over {r_0^2 f^2}}} \right),}$$
$$\eqalign{E_x (r,z,t) =& \displaystyle{{E_0} \over {\,f\,({\rm \xi} )}}\exp \,(i{\rm \phi} )H_{\rm m} \left( {\displaystyle{{\sqrt 2} \over {r_0 f\,({\rm \xi} )}}x} \right)\cr & \times \exp \left( { - \displaystyle{{(t - ((z - z_{\rm L} )/c))^2} \over {{\rm \tau} ^2}} - \displaystyle{{r^2} \over {r_0^2 f^2}}} \right),}$$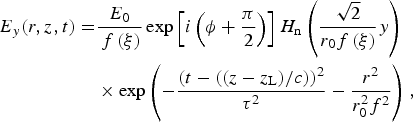 $$\eqalign{E_y (r,z,t) =& \displaystyle{{E_0} \over {\,f\,({\rm \xi} )}}\exp \left[ {i\left( {{\rm \phi} + \displaystyle{{\rm \pi} \over 2}} \right)} \right]H_{\rm n} \left( {\displaystyle{{\sqrt 2} \over {r_0 f\,({\rm \xi} )}}y} \right)\cr & \times \exp \left( { - \displaystyle{{(t - ((z - z_{\rm L} )/c))^2} \over {{\rm \tau} ^2}} - \displaystyle{{r^2} \over {r_0^2 f^2}}} \right),}$$
$$\eqalign{E_y (r,z,t) =& \displaystyle{{E_0} \over {\,f\,({\rm \xi} )}}\exp \left[ {i\left( {{\rm \phi} + \displaystyle{{\rm \pi} \over 2}} \right)} \right]H_{\rm n} \left( {\displaystyle{{\sqrt 2} \over {r_0 f\,({\rm \xi} )}}y} \right)\cr & \times \exp \left( { - \displaystyle{{(t - ((z - z_{\rm L} )/c))^2} \over {{\rm \tau} ^2}} - \displaystyle{{r^2} \over {r_0^2 f^2}}} \right),}$$where E 0 and ϕ are the field amplitude and phase of HG laser beam, respectively; m, n represent the indices of a Hermite-polynomial H m,n function; τ and r 0 are the laser's pulse duration and spot size, respectively; r 2 = x 2 + y 2, z L is the initial pulse peak position; and c is the speed of light in vacuum. The beam width parameter of laser is expressed in terms of function f(ξ) as:
where ξ = z/Z R is the propagation distance normalized in terms of Rayleigh length ![]() $Z_{\rm R} = kr_0^2 /2$, k and ω0 are the laser's wave number and frequency, respectively,
$Z_{\rm R} = kr_0^2 /2$, k and ω0 are the laser's wave number and frequency, respectively, ![]() ${\rm \phi} = {\rm \omega} _0 t - kz + {\rm (}n + m + {\rm 1)} \tan ^{ - 1} ({\rm \xi} ) - r^2 z/(Z_{\rm R} r_0^2 f^2 ) + {\rm \phi} _0 $, hence (n + m + 1)tan−1 (ξ) expresses the Guoy phase, and ϕ0 is the initial phase.
${\rm \phi} = {\rm \omega} _0 t - kz + {\rm (}n + m + {\rm 1)} \tan ^{ - 1} ({\rm \xi} ) - r^2 z/(Z_{\rm R} r_0^2 f^2 ) + {\rm \phi} _0 $, hence (n + m + 1)tan−1 (ξ) expresses the Guoy phase, and ϕ0 is the initial phase.
The longitudinal components of the electric and magnetic fields are expressed by paraxial ray approximation as:
The amplitude of the longitudinal laser field in vacuum is only about 0.03E0 for a Gaussian laser beam (Xiao et al., Reference Xiao, Huang, Ju, Li, Yang, Yang, Wu, Zhang, Qiao, Ruan, Zhou and He2016) indicating a very small longitudinal laser field in comparison with transverse components. In our presented equation (4), the longitudinal electric field component is smaller by a factor of (1/k) as compared with transverse field components. Thus, the contribution of longitudinal electric field component in our model is very small for DLA of electron in comparison with transverse component in vacuum.
The externally applied axial magnetic field is in longitudinal direction of laser pulse. Such axial magnetic field is expressed as (Ghotra & Kant, Reference Ghotra and Kant2017):
where B 0 is the magnetic field amplitude.
Relativistic analysis based on electron dynamics
The relativistic equations governing the momentum and energy of the accelerated electron in consideration of externally applied axial magnetic field are expressed as:
where p x,y,z represents the momentum coordinates and ![]() $\vec p = {\rm \gamma} \,m_0 \vec v$; βx,y,z represents the normalized velocity coordinates and
$\vec p = {\rm \gamma} \,m_0 \vec v$; βx,y,z represents the normalized velocity coordinates and ![]() ${\rm \vec \beta} = \vec v/c$;
${\rm \vec \beta} = \vec v/c$; ![]() ${\rm \gamma} ^2 = 1 + (p_x^2 + p_y^2 + p_z^2 )/(m_0 c)^2 $ is the Lorentz factor; − e and m 0 are the charge and rest mass of the electron. The other used parameters are normalized as follow:
${\rm \gamma} ^2 = 1 + (p_x^2 + p_y^2 + p_z^2 )/(m_0 c)^2 $ is the Lorentz factor; − e and m 0 are the charge and rest mass of the electron. The other used parameters are normalized as follow:
 $$\eqalign{& a_0 \to \displaystyle{{eE_0} \over {m_0 {\rm \omega} _0 c}},\,{\rm \tau ^{\prime}} \to {\rm \omega} _0 {\rm \tau}, \,r^{\prime}_0 \to \displaystyle{{{\rm \omega} _0 r_0} \over c},\,z^{\prime}_{\rm L} \to \displaystyle{{{\rm \omega} _0 z_{\rm L}} \over c},\,x^{\prime} \cr & \to \displaystyle{{{\rm \omega} _0 x} \over c},\, y^{\prime} \to \displaystyle{{{\rm \omega} _0 y} \over c},\,z^{\prime} \to \displaystyle{{{\rm \omega} _0 z} \over c}, \cr & {\rm \beta} _x \to \displaystyle{{v_x} \over c},\,{\rm \beta} _y \to \displaystyle{{v_y} \over c},\,{\rm \beta} _z \to \displaystyle{{v_z} \over c},\,t^{\prime} \to {\rm \omega} _0 t,\,p^{\prime}_0 \to \displaystyle{{\,p_0} \over {m_0 c}},\,p^{\prime}_x \cr & \to \displaystyle{{\,p_x} \over {m_0 c}},\, p^{\prime}_y \to \displaystyle{{\,p_y} \over {m_0 c}}, \cr & p^{\prime}_z \to \displaystyle{{\,p_z} \over {m_0 c}},\,k^{\prime} \to \displaystyle{{ck} \over {{\rm \omega} _0}} \,\,{\rm and}\,\,b_0 \to \displaystyle{{eB_0} \over {m_0 {\rm \omega} _0 c}}.} $$
$$\eqalign{& a_0 \to \displaystyle{{eE_0} \over {m_0 {\rm \omega} _0 c}},\,{\rm \tau ^{\prime}} \to {\rm \omega} _0 {\rm \tau}, \,r^{\prime}_0 \to \displaystyle{{{\rm \omega} _0 r_0} \over c},\,z^{\prime}_{\rm L} \to \displaystyle{{{\rm \omega} _0 z_{\rm L}} \over c},\,x^{\prime} \cr & \to \displaystyle{{{\rm \omega} _0 x} \over c},\, y^{\prime} \to \displaystyle{{{\rm \omega} _0 y} \over c},\,z^{\prime} \to \displaystyle{{{\rm \omega} _0 z} \over c}, \cr & {\rm \beta} _x \to \displaystyle{{v_x} \over c},\,{\rm \beta} _y \to \displaystyle{{v_y} \over c},\,{\rm \beta} _z \to \displaystyle{{v_z} \over c},\,t^{\prime} \to {\rm \omega} _0 t,\,p^{\prime}_0 \to \displaystyle{{\,p_0} \over {m_0 c}},\,p^{\prime}_x \cr & \to \displaystyle{{\,p_x} \over {m_0 c}},\, p^{\prime}_y \to \displaystyle{{\,p_y} \over {m_0 c}}, \cr & p^{\prime}_z \to \displaystyle{{\,p_z} \over {m_0 c}},\,k^{\prime} \to \displaystyle{{ck} \over {{\rm \omega} _0}} \,\,{\rm and}\,\,b_0 \to \displaystyle{{eB_0} \over {m_0 {\rm \omega} _0 c}}.} $$The coupled differential equations (7)–(10) with all normalized parameters have been solved numerically with a computer programing for the electron dynamics and electron energy gain.
The electron is assumed to be pre-accelerated and injected initially at a small angle δ with respect to the laser propagation axis with momentum (Ghotra & Kant, Reference Ghotra and Kant2015a, Reference Ghotra and Kantb):
where p 0 is the initial momentum of the injected electron.
Results and discussion
The numerical analysis is based on the following dimensionless parameters: a 0 = 5 (represents laser intensity ![]() $I \sim 6.92 \times 10^{19}{\rm W/cm}^{\rm 2}$), a 0 = 25 (
$I \sim 6.92 \times 10^{19}{\rm W/cm}^{\rm 2}$), a 0 = 25 (![]() $I \sim 8.5 \times 10^{20}{\rm W/cm}^2 $), a 0 = 50 (
$I \sim 8.5 \times 10^{20}{\rm W/cm}^2 $), a 0 = 50 (![]() $I \sim 6.8 \times 10^{21}{\rm W/cm}^{\rm 2} $); r′0 = 150 (represents laser spot size
$I \sim 6.8 \times 10^{21}{\rm W/cm}^{\rm 2} $); r′0 = 150 (represents laser spot size ![]() $r_0 \sim 25 {\rm \mu m}$), r′0 = 300 (
$r_0 \sim 25 {\rm \mu m}$), r′0 = 300 (![]() $r_0 \sim 50 {\rm \mu m}$), r′0 = 450 (
$r_0 \sim 50 {\rm \mu m}$), r′0 = 450 (![]() $r_0 \sim 75 {\rm \mu m}$), τ′L = 70 (represents laser pulse duration τL = 200fs); z′L = 0; initially the electron is at x′i = 0, y′i = 0, and z′i = 0; initial phase ϕ0 = 0, and b 0 = 0.006 (represents magnetic field of 0.64MG), b = 0.06 (~6.4MG); δ = 10° and p′0 = 1. The laser pulse peak power is about
$r_0 \sim 75 {\rm \mu m}$), τ′L = 70 (represents laser pulse duration τL = 200fs); z′L = 0; initially the electron is at x′i = 0, y′i = 0, and z′i = 0; initial phase ϕ0 = 0, and b 0 = 0.006 (represents magnetic field of 0.64MG), b = 0.06 (~6.4MG); δ = 10° and p′0 = 1. The laser pulse peak power is about ![]() $0.67 {\rm PW}$, which corresponds to intensity parameter a 0 = 5 with r′0 = 150. In the present scenario, the laser pulse peak power in the range of PW is feasible and observed experimentally (Spinka & Haefner, Reference Spinka and Haefner2017; Dabu, Reference Dabu2017).
$0.67 {\rm PW}$, which corresponds to intensity parameter a 0 = 5 with r′0 = 150. In the present scenario, the laser pulse peak power in the range of PW is feasible and observed experimentally (Spinka & Haefner, Reference Spinka and Haefner2017; Dabu, Reference Dabu2017).
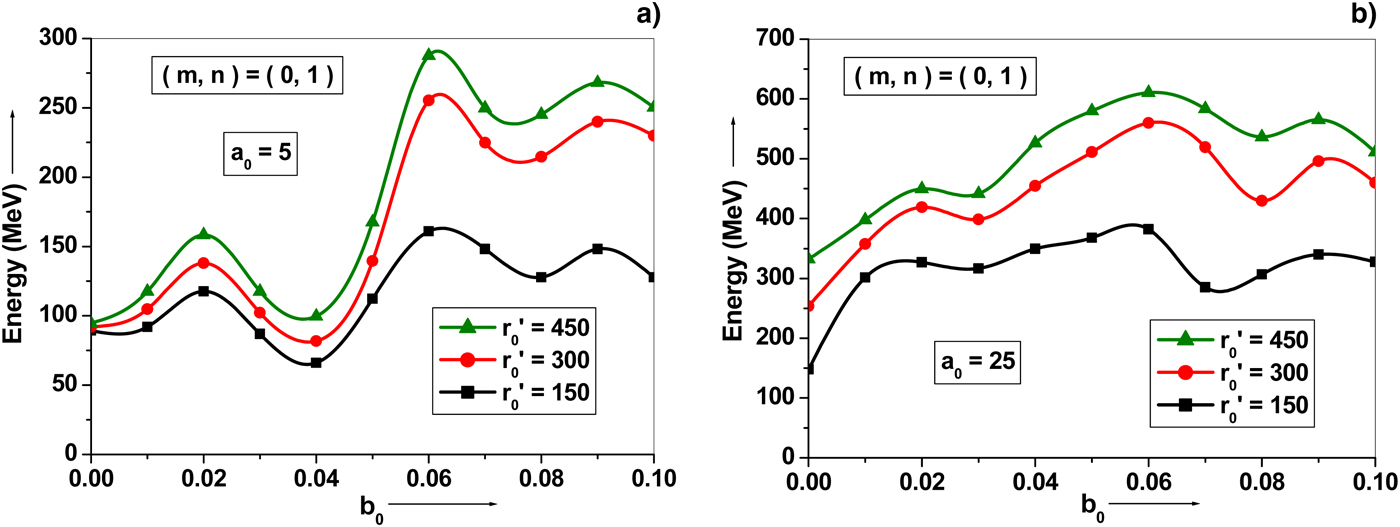
In Figure 1, the electron energy gain is analyzed as a function of normalized axial magnetic field b 0 for the mode index (m, n) = (0, 1) with normalized intensity parameter a 0 = 5 and 25 for different values of normalized laser spot size r′0 = 150, 300 and 450. The higher energy gain is depicted at the optimized value of magnetic field, which determines the resonance to maximize the electron energy gain. The magnetic field determines the cyclotron resonance for electron acceleration by laser in vacuum. The magnetic field determines the cyclotron resonance for electron acceleration by a laser beam in vacuum. For a TEM HG mode laser beam, the phase velocity v ph is different for different TEM mode indices making resonant frequency different with different modes. Resonance occurs when the laser frequency ωL coincides with betatron frequency ωβ (Ghotra & Kant, Reference Ghotra and Kant2016a). The betatron oscillation frequency can be related from the transverse motion of electron, where ![]() ${\rm \omega} _{\rm \beta} = \sqrt {ev_z B_0 /{\rm \gamma} m_0 r_0 c} $. With ωL = ω0 (1 − v z/v ph) the resonance condition is
${\rm \omega} _{\rm \beta} = \sqrt {ev_z B_0 /{\rm \gamma} m_0 r_0 c} $. With ωL = ω0 (1 − v z/v ph) the resonance condition is ![]() $eB_0 /m_0 r_0 \omega _0^2 = ({\rm \gamma} c/v_z )(1 - v_z /v_{{\rm ph}} )^2 $. Thus, the different TEM mode indices affect the resonance. In Figure 1a, the resonance appears at normalized axial magnetic field b 0 = 0.06 where the electron energy gain is maximum. The axial magnetic field strengthens the
$eB_0 /m_0 r_0 \omega _0^2 = ({\rm \gamma} c/v_z )(1 - v_z /v_{{\rm ph}} )^2 $. Thus, the different TEM mode indices affect the resonance. In Figure 1a, the resonance appears at normalized axial magnetic field b 0 = 0.06 where the electron energy gain is maximum. The axial magnetic field strengthens the ![]() $\vec v \times \vec B$ force experienced by the electron, and hence contributes significantly for enhancing electron energy gain for a trapped electron. The observed energy gain of about
$\vec v \times \vec B$ force experienced by the electron, and hence contributes significantly for enhancing electron energy gain for a trapped electron. The observed energy gain of about ![]() $100 {\rm MeV}$, with a 0 = 5 at r′0 = 300 without magnetic field is increased to
$100 {\rm MeV}$, with a 0 = 5 at r′0 = 300 without magnetic field is increased to ![]() $250 {\rm MeV}$ with axial magnetic field of
$250 {\rm MeV}$ with axial magnetic field of ![]() $6 {\rm MG}$ (corresponds to normalized value b 0 = 0.06). Thus, the higher energy gain appears at a particular value of axial magnetic field. Liu et al. (Reference Liu, He and Chen2004) investigated that a strong magnetic field of the order of
$6 {\rm MG}$ (corresponds to normalized value b 0 = 0.06). Thus, the higher energy gain appears at a particular value of axial magnetic field. Liu et al. (Reference Liu, He and Chen2004) investigated that a strong magnetic field of the order of ![]() $100 {\rm MG}$ is required to accelerate a rest electron to a few MeV of energy with an intense laser pulse of peak intensity
$100 {\rm MG}$ is required to accelerate a rest electron to a few MeV of energy with an intense laser pulse of peak intensity ![]() $2 \times 10^{19}{\rm W/cm}^{\rm 2} $. In our model, the axial magnetic field under
$2 \times 10^{19}{\rm W/cm}^{\rm 2} $. In our model, the axial magnetic field under ![]() $6 {\rm MG}$ is sufficient to accelerate electron to a few
$6 {\rm MG}$ is sufficient to accelerate electron to a few ![]() $100 {\rm MeV}$ of energy using a (0, 1) mode of a CP–HG laser pulse of peak intensity
$100 {\rm MeV}$ of energy using a (0, 1) mode of a CP–HG laser pulse of peak intensity ![]() $6.92 \times 10^{19}{\rm W/cm}^2 $. The energy gain is comparatively higher under the influence of axial magnetic field than without axial magnetic field for intensity parameter a 0 = 25 as depicted in Figure 1b. With b 0 = 0.06 and r′0 = 450, the observed value is almost double with magnetic field than that without magnetic field. The axial magnetic field has been optimized for a set of laser parameters. This optimization is solely a base for maximum energy gained by the electron during interaction with a CP–HG laser pulse.
$6.92 \times 10^{19}{\rm W/cm}^2 $. The energy gain is comparatively higher under the influence of axial magnetic field than without axial magnetic field for intensity parameter a 0 = 25 as depicted in Figure 1b. With b 0 = 0.06 and r′0 = 450, the observed value is almost double with magnetic field than that without magnetic field. The axial magnetic field has been optimized for a set of laser parameters. This optimization is solely a base for maximum energy gained by the electron during interaction with a CP–HG laser pulse.
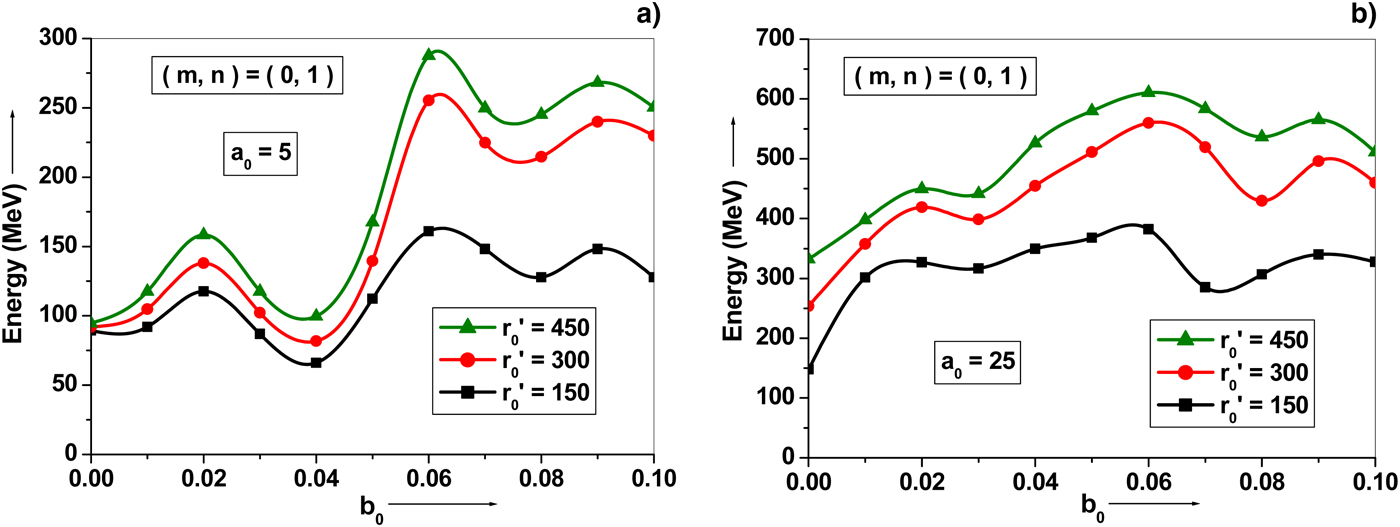
Fig. 1. Evolution of electron energy gain with a normalized function of axial magnetic field b 0 for a TEM CP–HG laser pulse with mode index (m, n) = (0, 1), for different values of laser spot sizes r′0 = 150, 300, and 450 at (a) a 0 = 5 and (b) a 0 = 25. The other used parameters are ϕ0 = 0 and τ′L = 70.
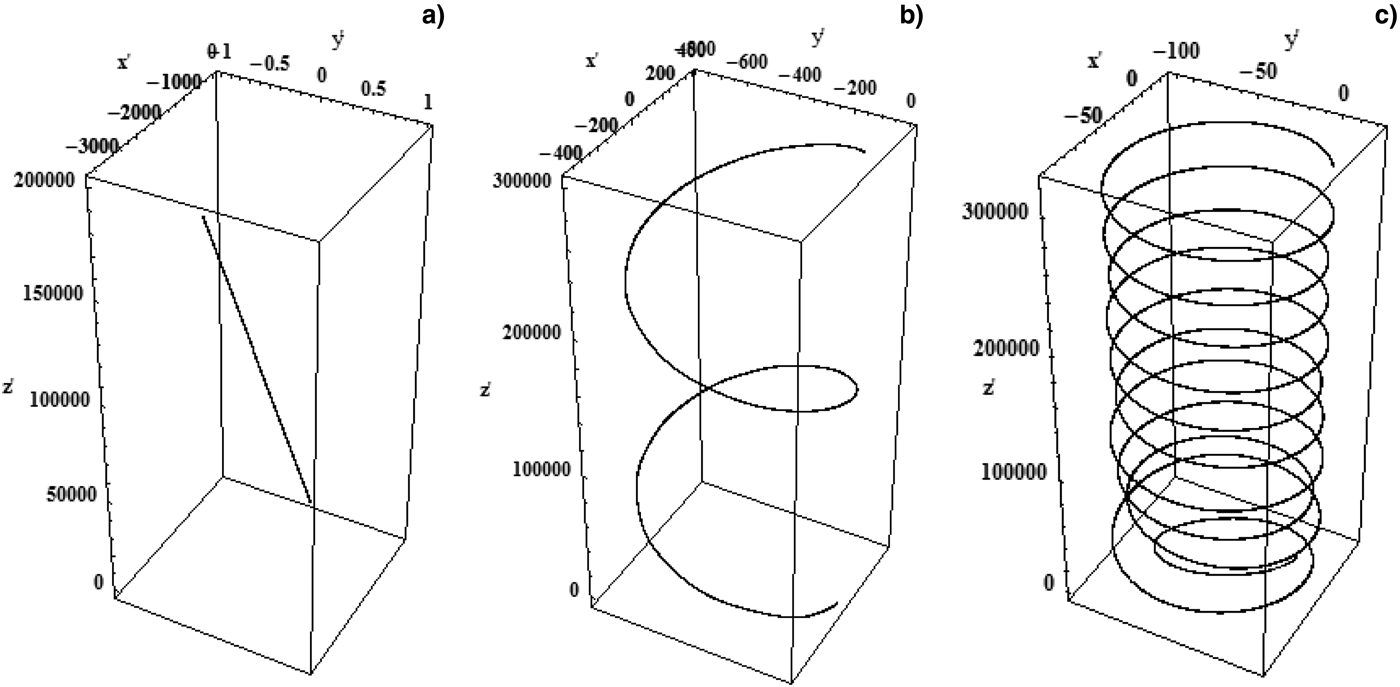
Figure 2 shows the electron trajectories with laser intensity parameter a 0 = 5 at r′0 = 150 with and without optimized magnetic field. In Figure 2a, a de-phased electron trajectory appears in the absence of axial magnetic field. A phased electron trajectory with an inefficient acceleration appears in Figure 2b with a smaller magnetic field b 0 = 0.006 (![]() $0.64 {\rm MG}$). An effective acceleration of electron appears with an optimized magnetic field, b 0 = 0.06 (6.4MG) as depicted in Figure 2c. As appearing in Figure 2a without magnetic field, the scattering of electron goes on increasing with the propagation distance, whereas it is much reduced due to an axially applied magnetic field as depicted in Figure 2b. As per Figure 2c, more reduction in the scattering of electron is observed with optimized magnetic field b 0 = 0.06. Saberi & Maraghechi (Reference Saberi and Maraghechi2015) proposed that the optimized magnetic field parameter enforces the trapping of electron at the focus of laser pulse for stronger cyclotron resonance. Due to which the electron accelerated effectively with high energy gain. Dai et al. (Reference Dai, Li, Zang and Tian2011) reported that the transverse component of electric field deflects the electron away from the beam axis when injected in the path of laser pulse. In our model, such deflection of electron away from the beam axis is controlled by using a smaller and optimized magnetic field along the longitudinal axis of a HG laser beam. The employed magnetic field is almost ten times smaller in comparison with the magnetic field stated by Liu et al. (Reference Liu, He and Chen2004) for laser magnetic resonance acceleration mechanism. The axial magnetic field can hold the accelerated electron around the axis of propagation of laser pulse due to cyclotron rotation (Akou & Hamedi, Reference Akou and Hamedi2015). Thus, the optimized axial magnetic field supports effective acceleration of electron. The axial magnetic field is highly supportive in controlling the electron that is going out of phase with the saturation of betatron resonance. Figure 2c presents a confined trajectory of electron orbit for a set of optimized parameters during laser–electron interaction.
$0.64 {\rm MG}$). An effective acceleration of electron appears with an optimized magnetic field, b 0 = 0.06 (6.4MG) as depicted in Figure 2c. As appearing in Figure 2a without magnetic field, the scattering of electron goes on increasing with the propagation distance, whereas it is much reduced due to an axially applied magnetic field as depicted in Figure 2b. As per Figure 2c, more reduction in the scattering of electron is observed with optimized magnetic field b 0 = 0.06. Saberi & Maraghechi (Reference Saberi and Maraghechi2015) proposed that the optimized magnetic field parameter enforces the trapping of electron at the focus of laser pulse for stronger cyclotron resonance. Due to which the electron accelerated effectively with high energy gain. Dai et al. (Reference Dai, Li, Zang and Tian2011) reported that the transverse component of electric field deflects the electron away from the beam axis when injected in the path of laser pulse. In our model, such deflection of electron away from the beam axis is controlled by using a smaller and optimized magnetic field along the longitudinal axis of a HG laser beam. The employed magnetic field is almost ten times smaller in comparison with the magnetic field stated by Liu et al. (Reference Liu, He and Chen2004) for laser magnetic resonance acceleration mechanism. The axial magnetic field can hold the accelerated electron around the axis of propagation of laser pulse due to cyclotron rotation (Akou & Hamedi, Reference Akou and Hamedi2015). Thus, the optimized axial magnetic field supports effective acceleration of electron. The axial magnetic field is highly supportive in controlling the electron that is going out of phase with the saturation of betatron resonance. Figure 2c presents a confined trajectory of electron orbit for a set of optimized parameters during laser–electron interaction.
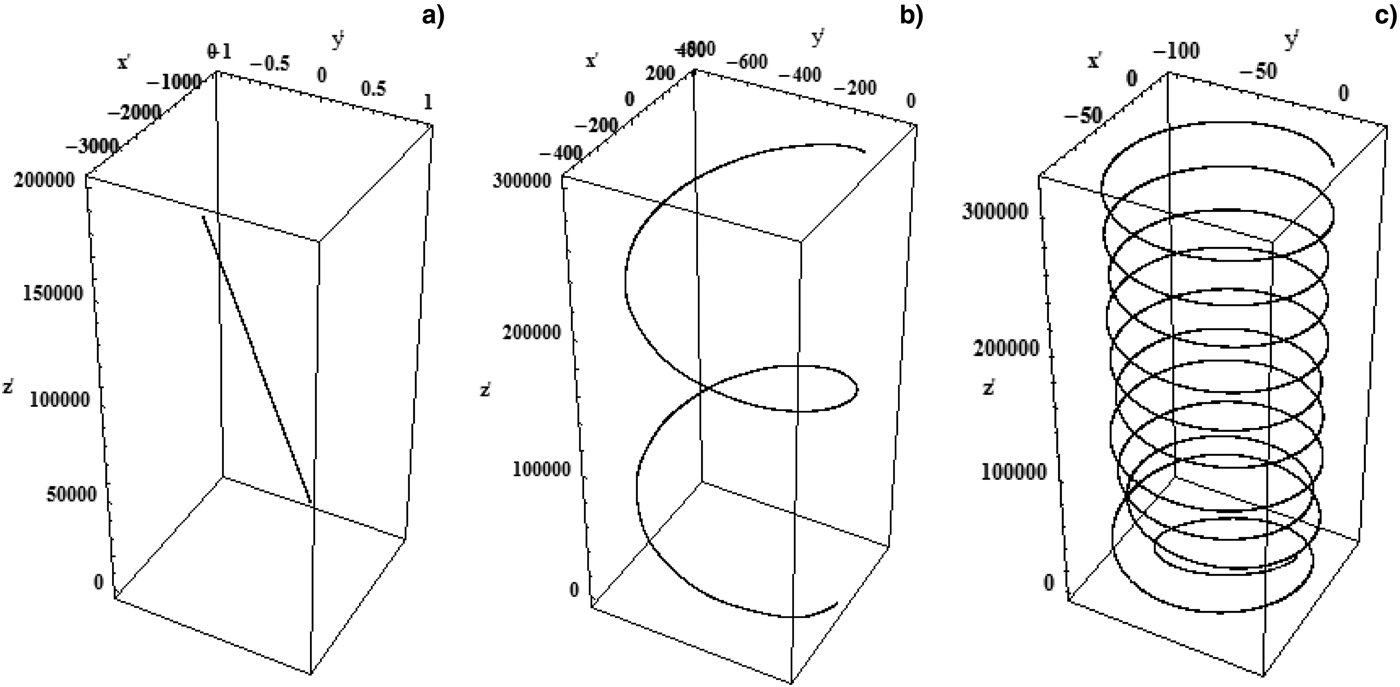
Fig. 2. Three-dimensional plots for electron trajectory without and with applied axial magnetic field for a TEM CP–HG laser pulse with mode index (m, n) = (0, 1) for a 0 = 5 with (a) b 0 = 0, (b) b 0 = 0.006, and (c) b 0 = 0.06. The other parameters are r′0 = 150, ϕ0 = 0, and τ′L = 70.
Figure 3 represents the electron energy gain variations for the mode (m, n) = (0, 1) with a normalized function of propagation distance ξ. The graphs have been plotted with distinct intensity parameters a 0 and laser spot sizes r′0 in the absence and presence of magnetic field. Electron energy gain remains high for the higher intensity parameter with the same spot size. Figure 3a depicts electron energy gain of about ![]() $600 {\rm MeV}$ with r′0 = 150 and a 0 = 50. Hartemann et al. (Reference Hartemann, Fochs, Sage, Luhmann, Woodworth, Perry, Chen and Kerman1995) analyzed the role played by a beam focus for attaining a high energy gained by an accelerating particle. The beam width parameter influences the accelerating distance expressed in terms of Rayleigh length with a Gaussian beam. The plots also show the variation of beam width function f(ξ) with an increasing normalized propagation distance. The laser's beam width increases as the laser pulse propagates through the vacuum. For the smaller value of beam width parameter, stronger electron acceleration is depicted and vice versa. Thus, an effective electron energy gain is seen with a smaller value of beam width parameter at a small distance. The acceleration of electron appear due to the asymmetry in the intensity distribution of a CP–HG laser beam. It ensures the electron trapping, acceleration, and energy gain during the interaction with the leading part of the laser pulse where the electron first gains high energy. This energy gain almost saturates while reaching to the trailing end of the pulse. The calculated acceleration distance with a LP-chirped laser pulse for electron energy gain is almost three times the Rayleigh length with a large spot size r′0 = 900 in vacuum (Ghotra & Kant, Reference Ghotra and Kant2015b). The observed acceleration distance is about six times higher the Rayleigh length for a CP–HG laser pulse with a smaller initial laser spot size, r′0 = 300 as depicted from Figure 3b. Figure 3c shows the electron energy gain with a larger spot size. Initially, the electron gains high energy from laser fields and soon after decelerated at larger propagation distance where the weakening of laser field appears. The electron is accelerated where laser field strength is high and decelerated with energy loss where field strength is low. This makes an efficient acceleration of electron. However, the deceleration appears smaller as it is controlled with the externally applied axial magnetic field. Hence, a comparative higher electron energy gain is observed in the presence of axial magnetic field than that without any additional magnetic field.
$600 {\rm MeV}$ with r′0 = 150 and a 0 = 50. Hartemann et al. (Reference Hartemann, Fochs, Sage, Luhmann, Woodworth, Perry, Chen and Kerman1995) analyzed the role played by a beam focus for attaining a high energy gained by an accelerating particle. The beam width parameter influences the accelerating distance expressed in terms of Rayleigh length with a Gaussian beam. The plots also show the variation of beam width function f(ξ) with an increasing normalized propagation distance. The laser's beam width increases as the laser pulse propagates through the vacuum. For the smaller value of beam width parameter, stronger electron acceleration is depicted and vice versa. Thus, an effective electron energy gain is seen with a smaller value of beam width parameter at a small distance. The acceleration of electron appear due to the asymmetry in the intensity distribution of a CP–HG laser beam. It ensures the electron trapping, acceleration, and energy gain during the interaction with the leading part of the laser pulse where the electron first gains high energy. This energy gain almost saturates while reaching to the trailing end of the pulse. The calculated acceleration distance with a LP-chirped laser pulse for electron energy gain is almost three times the Rayleigh length with a large spot size r′0 = 900 in vacuum (Ghotra & Kant, Reference Ghotra and Kant2015b). The observed acceleration distance is about six times higher the Rayleigh length for a CP–HG laser pulse with a smaller initial laser spot size, r′0 = 300 as depicted from Figure 3b. Figure 3c shows the electron energy gain with a larger spot size. Initially, the electron gains high energy from laser fields and soon after decelerated at larger propagation distance where the weakening of laser field appears. The electron is accelerated where laser field strength is high and decelerated with energy loss where field strength is low. This makes an efficient acceleration of electron. However, the deceleration appears smaller as it is controlled with the externally applied axial magnetic field. Hence, a comparative higher electron energy gain is observed in the presence of axial magnetic field than that without any additional magnetic field.

Fig. 3. Electron energy gain variations for (m, n) = (0, 1) with a normalized function of propagation distance ξ and laser beam width parameter f(ξ) with b 0 = 0 and b 0 = 0.06 for the different values of intensity parameter a 0 = 5, 25, and 50 for (a) r′0 = 150, (b) r′0 = 300, and (c) r′0 = 450. The other parameters are τ′L = 70, ϕ0 = 0, p′0 = 1, z′L = 0, x′i = 0, y′i = 0, and z′i = 0.
Figure 4 represents the electron energy gain variations without and with magnetic field as a function of ξ for the mode index (m, n) = (0, 2) with different intensity parameters a = 5, 25, 50 and at different values of laser spot size: (a) r′0 = 150, (b) r′0 = 300, and (c) r′0 = 450. Electron attains the maximum energy gain at shorter distance for higher values of intensity and decelerated with lower values of intensity and then saturates for longer distance. The deceleration remains smaller in the presence of axial magnetic field. The electron retains significant amount of energy at longer distance with magnetic field even in the presence of a weak laser field as depicted in Figures 4a–4c.

Fig. 4. Electron energy gain variations for (m, n) = (0, 2) with a normalized function of propagation distance ξ for b 0 = 0 and b 0 = 0.06 and the intensity parameters a 0 = 5, 25, and 50 for (a) r′0 = 150, (b) r′0 = 300, and (c) r′0 = 450. The other parameters are τ′L = 70, ϕ0 = 0, p′0 = 1, z′L = 0, x′i = 0, y′i = 0, and z′i = 0.
Figure 5 represents the electron energy gain variations without and with magnetic field as a function of ξ for the mode index (m, n) = (0, 3) with different spot size and intensity parameters. In Figures 5b and 5c, the variation has been plotted for r′0 = 300 and 450. The electron energy gain in the range of GeV is observed with laser intensity ![]() $I \sim 6.8 \times 10^{21}{\rm W/cm}^{\rm 2} $ (for a 0 = 50) and spot size r′0 = 300. Higher electron energy gain of about
$I \sim 6.8 \times 10^{21}{\rm W/cm}^{\rm 2} $ (for a 0 = 50) and spot size r′0 = 300. Higher electron energy gain of about ![]() $ \sim 1.65 {\rm GeV}$ is observed for r′0 = 150 with the same intensity (a 0 = 50) as depicted in Figure 5c). The calculated accelerating distance is about three times the Rayleigh length in this case. It is also shown that the electron gains higher energy quickly with the higher mode indices in vacuum but retains only a smaller portion of gained energy for larger propagation distance in the absence of magnetic field. However, in the presence of magnetic field, it retains higher energy for longer distances. The intensity variations with higher mode indices report a weak field at larger propagation distance. Thus, with higher modes, the electron is unable to retain its gained energy for the larger propagation distances. Such loss is controlled when external magnetic field is applied. Thus, the energy loss under the influence of external applied axial magnetic field is comparatively smaller than that without magnetic field.
$ \sim 1.65 {\rm GeV}$ is observed for r′0 = 150 with the same intensity (a 0 = 50) as depicted in Figure 5c). The calculated accelerating distance is about three times the Rayleigh length in this case. It is also shown that the electron gains higher energy quickly with the higher mode indices in vacuum but retains only a smaller portion of gained energy for larger propagation distance in the absence of magnetic field. However, in the presence of magnetic field, it retains higher energy for longer distances. The intensity variations with higher mode indices report a weak field at larger propagation distance. Thus, with higher modes, the electron is unable to retain its gained energy for the larger propagation distances. Such loss is controlled when external magnetic field is applied. Thus, the energy loss under the influence of external applied axial magnetic field is comparatively smaller than that without magnetic field.

Fig. 5. Electron energy gain variations for (m, n) = (0, 3) with a normalized function of propagation distance ξ for b 0 = 0 and b 0 = 0.06 and the intensity parameters as: a 0 = 5, 25, and 50 at (a) r′0 = 150, (b) r′0 = 300, and (c) r′0 = 450. The other parameters are τ′L = 70, ϕ0 = 0, p′0 = 1, z′L = 0, x′i = 0, y′i = 0, and z′i = 0.
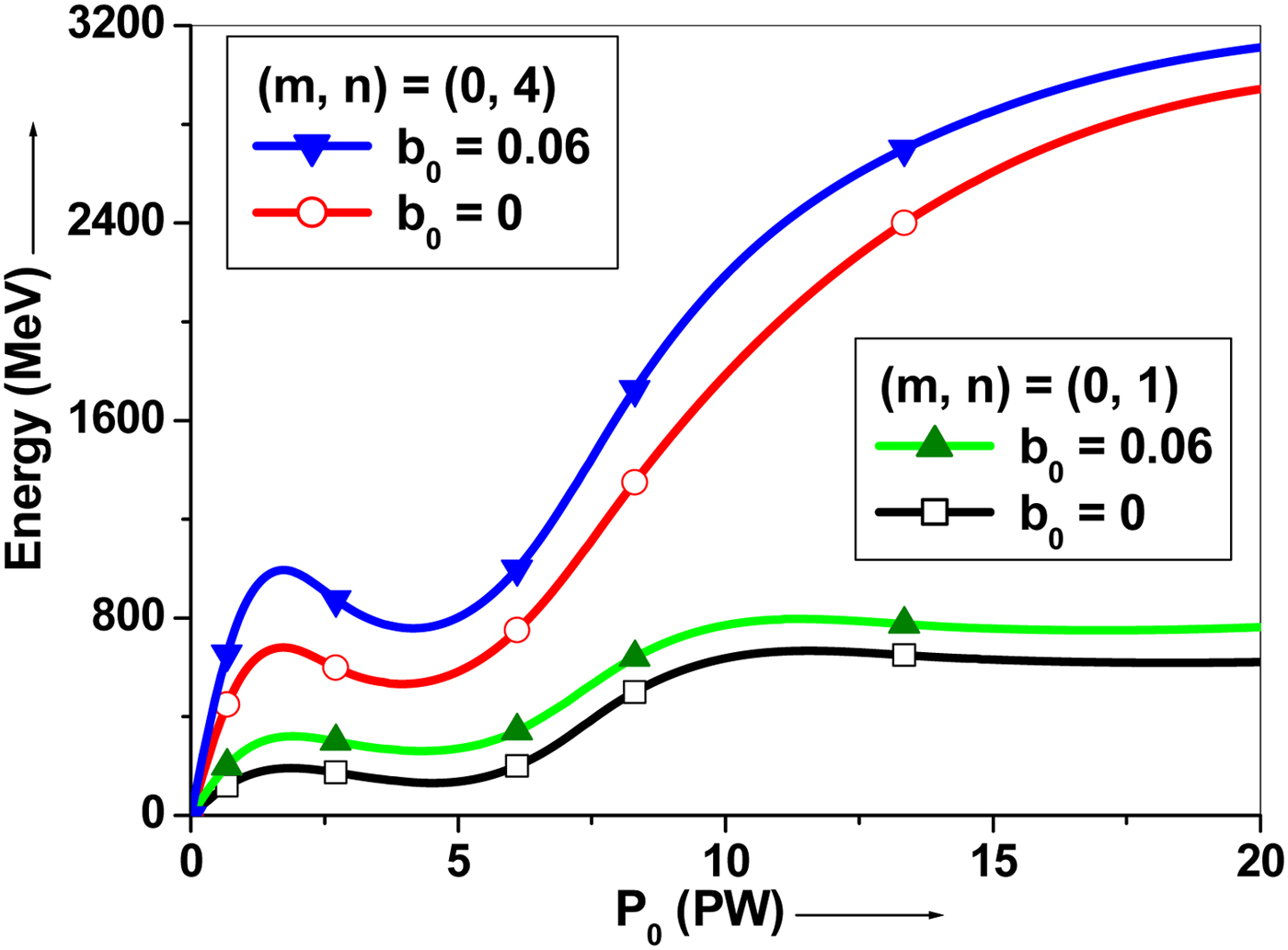
Figure 6 shows the electron energy gain without and with magnetic field as a function of laser peak power for mode indices (m, n) = (0, 1) and (0, 4). The observed electron energy gain increases with increase in laser peak power. The energy gained by the electron is above ![]() $1.5 {\rm GeV}$ at a peak power of about
$1.5 {\rm GeV}$ at a peak power of about ![]() $10 {\rm PW}$ with mode index (0, 4), whereas it is about
$10 {\rm PW}$ with mode index (0, 4), whereas it is about ![]() $0.5 {\rm GeV}$ with mode index (0, 1) in the absence of magnetic field in vacuum. The electron energy gain is above
$0.5 {\rm GeV}$ with mode index (0, 1) in the absence of magnetic field in vacuum. The electron energy gain is above ![]() $2{\rm GeV}$ at a peak power of
$2{\rm GeV}$ at a peak power of ![]() $10 {\rm PW}$ with mode index (0, 4) in the presence of magnetic field in vacuum. Such high-energy PW class of lasers is feasible experimentally. The configuration of the hybrid amplification of
$10 {\rm PW}$ with mode index (0, 4) in the presence of magnetic field in vacuum. Such high-energy PW class of lasers is feasible experimentally. The configuration of the hybrid amplification of ![]() $2 \times 10 {\rm PW}$ femtosecond laser system of the Extreme Light Infrastructure – Nuclear Physics (ELI-NP) facility is described (Dabu, Reference Dabu2017). The depicted gain with magnetic field is about
$2 \times 10 {\rm PW}$ femtosecond laser system of the Extreme Light Infrastructure – Nuclear Physics (ELI-NP) facility is described (Dabu, Reference Dabu2017). The depicted gain with magnetic field is about ![]() $30\% $ higher than that without magnetic field. Thus, the electron energy gain is appeared sensitive to laser power and mode indices, it increases with increasing the mode index for the same magnitude of laser power for HG laser beam. An electron energy gain of about
$30\% $ higher than that without magnetic field. Thus, the electron energy gain is appeared sensitive to laser power and mode indices, it increases with increasing the mode index for the same magnitude of laser power for HG laser beam. An electron energy gain of about ![]() $262 {\rm MeV}$ was observed with a CP Gaussian laser pulse of peak intensity
$262 {\rm MeV}$ was observed with a CP Gaussian laser pulse of peak intensity ![]() $ \sim 10^{20}{\rm W/cm}^{\rm 2} $ (Niu et al., Reference Niu, He, Qiao and Zhou2008). However, in our case, the observed energy gain is much higher when the higher mode index has been investigated with the same intensity than that with lower mode index for CP–HG laser pulse. Magnetic field above
$ \sim 10^{20}{\rm W/cm}^{\rm 2} $ (Niu et al., Reference Niu, He, Qiao and Zhou2008). However, in our case, the observed energy gain is much higher when the higher mode index has been investigated with the same intensity than that with lower mode index for CP–HG laser pulse. Magnetic field above ![]() $10 {\rm MG}$ was considered with a CP Gaussian laser beam to attain energy gain above
$10 {\rm MG}$ was considered with a CP Gaussian laser beam to attain energy gain above ![]() $100 {\rm MeV}$ (Sharma & Tripathi, Reference Sharma and Tripathi2009; Gupta & Ryu, Reference Gupta and Ryu2005). In our study of electron acceleration with a mode index influenced CP–HG laser beams shows the higher energy gain in GeV range with a much smaller magnetic field of about
$100 {\rm MeV}$ (Sharma & Tripathi, Reference Sharma and Tripathi2009; Gupta & Ryu, Reference Gupta and Ryu2005). In our study of electron acceleration with a mode index influenced CP–HG laser beams shows the higher energy gain in GeV range with a much smaller magnetic field of about ![]() $6.4 {\rm MG}$ even for mode index (0, 2).
$6.4 {\rm MG}$ even for mode index (0, 2).
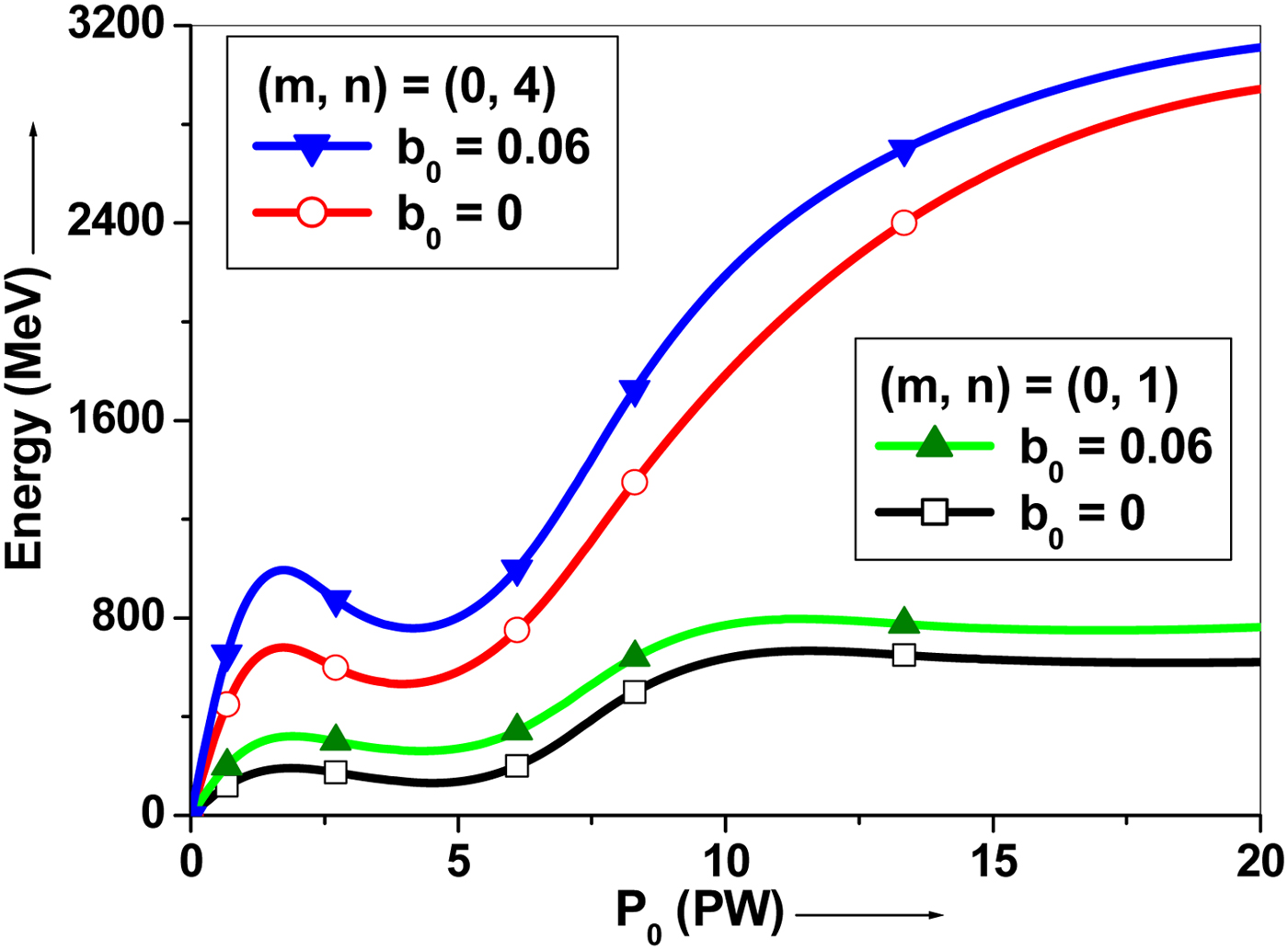
Fig. 6. Evolution of electron energy gain with laser peak power for b 0 = 0 and b 0 = 0.06 and the mode indices (m, n) = (0, 1) and (0, 4). The other parameters are same as referred in Figure 3.
Conclusion
The influence of intensity and power distribution in distinct TEM modes of HG laser on DLA of electron under the influence of axial magnetic field has been highlighted in this study. The role of laser beam width parameter has been reported for electron acceleration using a CP–HG laser beam. Using laser intensity a 0 = 25 (![]() $I \sim 8.5 \times 10^{20}{\rm W/cm}^{\rm 2} $) and laser spot size r′0 = 150 (
$I \sim 8.5 \times 10^{20}{\rm W/cm}^{\rm 2} $) and laser spot size r′0 = 150 (![]() $ \sim 25 {\rm \mu m}$) for mode (0, 4), electron energy gain of above
$ \sim 25 {\rm \mu m}$) for mode (0, 4), electron energy gain of above ![]() $1 {\rm GeV}$ is observed due to externally applied axial magnetic field. The laser peak power for such case is calculated as
$1 {\rm GeV}$ is observed due to externally applied axial magnetic field. The laser peak power for such case is calculated as ![]() $8.3 {\rm PW}$. Though, the electron energy gain for higher modes is high, but it suffers with de-phasing of electron at shorter distance in the absence of any additional magnetic field. The applied magnetic field of about
$8.3 {\rm PW}$. Though, the electron energy gain for higher modes is high, but it suffers with de-phasing of electron at shorter distance in the absence of any additional magnetic field. The applied magnetic field of about ![]() $6.4 {\rm MG}$ restricts such dephasing even with a laser intensity of about
$6.4 {\rm MG}$ restricts such dephasing even with a laser intensity of about ![]() $10^{20}{\rm W/cm}^{\rm 2} $. About 30% higher electron energy gain is observed with magnetic field than that without magnetic field. With a suitable selection of laser parameters such as intensity, beam spot size, mode index, and optimized magnetic field, the electron is accelerated up to the order of GeV energy. The role of distinct mode indices under the influence of axial magnetic field can be utilized for the formulation of desired-sized accelerators based on the accelerating distance of electron. Thus, the obtained results with distinct TEM modes with the role of magnetic field will be helpful in the development of better table-top accelerators of diverse needs.
$10^{20}{\rm W/cm}^{\rm 2} $. About 30% higher electron energy gain is observed with magnetic field than that without magnetic field. With a suitable selection of laser parameters such as intensity, beam spot size, mode index, and optimized magnetic field, the electron is accelerated up to the order of GeV energy. The role of distinct mode indices under the influence of axial magnetic field can be utilized for the formulation of desired-sized accelerators based on the accelerating distance of electron. Thus, the obtained results with distinct TEM modes with the role of magnetic field will be helpful in the development of better table-top accelerators of diverse needs.
Acknowledgments
This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) grants EP/J018171/1, EP/J500094/1 and EP/N028694/1, and the EC H2020 LASERLAB-EUROPE (grant no. 654148) and EuPRAXIA (grant no. 653782). This research was also supported in part by the International Centre for Theoretical Sciences (ICTS) during a visit for participating in the program – Laser Plasma Accelerator (Code: ICTS/Prog-LPA/2017/3).