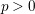1 Introduction
Let 
$p$ be a prime, 
$k$ be a field, 
$W=W(k)$ be the ring of Witt vectors of 
$k$, and 
$W_{2}(k)=W/(p^{2}W)$ be the ring of Witt vectors of length two of 
$k$, and let 
$X$ be a smooth projective variety over 
$k$. For 
$k=\mathbb{C}$, it is well known, and elementary to prove, that if 
$X$ has trivial tangent bundle, then 
$X$ is an abelian variety. In [Reference Igusa10], it was shown that this is false in characteristic 
$p>0$. In [Reference Mehta and Srinivas18], the authors studied ordinary varieties with trivial tangent bundle and proved that they have many properties similar to abelian varieties, including the Serre–Tate theory of canonical liftings. In Theorem 2.4, I present two equivalent crystalline characterizations of abelian varieties amongst the class of varieties with trivial tangent bundle. My characterization is the following: a smooth, projective variety 
$X$ with trivial tangent bundle is an abelian variety if and only if it has a smooth Picard scheme and satisfies Hodge symmetry in cohomology degree one (I call such a variety Picard–Hodge Symmetric, see Def. 2.3). Another equivalent characterization is given in terms of what I call minimally Mazur–Ogus varieties (see Def. 2.1). A smooth, projective variety is a minimally Mazur–Ogus variety if 
$H_{\text{cris}}^{2}(X/W)$ is torsion-free and Hodge–de Rham spectral sequence degenerates at 
$E_{1}$ in degree one. In Corollary 2.11, I show that if a smooth projective variety X with trivial tangent bundle lifts to 
$W_{2}$ and if the second crystalline cohomology 
$H_{\text{cris}}^{2}(X/W)$ of 
$X/W$ is torsion-free, then 
$X/k$ is an abelian variety. In Remark 2.13, I discuss a natural question raised by Li in his emails to me about weakening the hypothesis of Theorem 2.4.
In [Reference Li16, Conjecture 4.1], it is conjectured that if 
$p>3$, then every smooth, projective variety with trivial tangent bundle is an abelian variety. I show in Theorem 3.1 that this conjecture is true in dimension two.
In dimension two, the most famous example of a surface in characteristic 
$p=2$ with trivial tangent bundle and which is not an abelian variety is due to [Reference Igusa10] (Igusa surface for 
$p=2$ has been studied by many authors including Torsten Ekedahl; for a recent treatment of the Igusa surface for 
$p=2$, see [Reference Chai4]). Let me note that the Igusa surface of characteristic 
$p=2$ also has a less well-known cousin in characteristic 
$p=3$ (see Proposition 5.3 for a construction).
I observe in Theorem 3.6 that if 
$p=2$, then for every 
$g\geqslant 2$ and for every 
$1\leqslant r<g$, there is a family of varieties of dimension 
$g$ with trivial tangent bundle and which are not abelian varieties. This family is parameterized by 
${\mathcal{A}}_{r}^{\text{ord}}[p]\times {\mathcal{A}}_{g-r}$ where 
${\mathcal{A}}_{g}$ is the moduli stack of abelian varieties of dimension 
$g$ and the superscript “ord” stands for the “ordinary locus” and 
${\mathcal{A}}_{r}^{\text{ord}}[p]$ is the moduli stack of ordinary abelian varieties with a point of order 
$p$ (and more generally by 
${\mathcal{U}}_{r}^{{\geqslant}1}[p]\times {\mathcal{A}}_{g-r}$ where 
${\mathcal{U}}_{r}^{{\geqslant}1}[p]$ is the stack abelian varieties of 
$p$-rank at least one equipped with a point of order 
$p$). For 
$p=3$ one has a slightly weaker result—see Theorem 3.8.
In Remark 3.9, I note that the two conditions, minimally Mazur–Ogus and Picard–Hodge symmetry in Theorem 2.4, cannot be weakened or relaxed. In general, the presence of torsion in crystalline cohomology and nondegeneration of Hodge–de Rham are not correlated conditions.
In Theorem 4.1, I show that a smooth, projective, ordinary variety with trivial tangent bundle is an abelian variety if and only if its second crystalline cohomology is torsion-free.
In [Reference Li16, Theorem 4.2] (also see [Reference Li15]), it is shown that if 
$p>2$ and 
$X$ is ordinary with trivial tangent bundle, then 
$X$ is an abelian variety. In Theorem 5.2, I give a new proof of Li’s remarkable theorem [Reference Li16, Theorem 4.2] and, in fact, I prove a sharpening of [Reference Li16, Theorem 4.2] and [Reference Mehta and Srinivas18]. I show that for 
$p=2$, any smooth, projective, ordinary variety with trivial tangent bundle has a minimal Galois étale cover (see Def. 5.1) by an abelian variety with a Galois group of exponent 
$p=2$. Li’s approach is based on infinitesimal group actions, while I use Serre–Tate canonical liftings (of abelian varieties) and the theory of complex multiplication and its influence on the slopes of Frobenius (see [Reference Yu20]).
In the light of my characterization (Theorem 2.4), especially because torsion in the second crystalline cohomology can occur for any prime 
$p$, it seems to me that perhaps the original conjecture of Li (see [Reference Li16, Conjecture 4.1]) needs to be modified. In fact, there are two distinct versions of Li’s conjecture which I conjecture. The first version is the fixed characteristic version which says that there exists an integer 
$n_{1}(p)$ such that if 
$X$ is any variety of dimension less than 
$n_{1}(p)$ with trivial tangent bundle over an algebraically closed field of characteristic 
$p>0$, it is an abelian variety (see Conjecture 6.3).
The fixed dimension version (see Conjecture 6.1), inspired by [Reference Liedtke17], says that for any fixed integer, 
$d\geqslant 2$. There exists an integer 
$n_{0}(d)$ such that any smooth, projective variety 
$X/k$ with dimension 
$d$ and with trivial tangent bundle is an abelian variety if 
$p>n_{0}(d)$. (Clearly, for 
$d=1$, one has 
$n_{0}(1)=1$; for 
$d=2$, 
$n_{0}(2)=3$ by Theorem 3.1.)
2 Characterization of abelian varieties
In this section, I give a crystalline characterization of abelian varieties in the class of smooth, projective varieties with trivial tangent bundle. My characterization requires the following two definitions.
Definition 2.1. Let 
$X$ be a smooth, projective variety over an algebraically closed field 
$k$ with 
$\text{char}(k)=p>0$. I say that 
$X$ is a minimally Mazur–Ogus variety if 
$X$ satisfies the following two conditions:
(1)
$H_{\text{cris}}^{2}(X/W)$ is torsion-free;(2) the Hodge to de Rham spectral sequence degenerates at
$E_{1}$ in degree one.
Remark 2.2. Conditions underlying Mazur–Ogus varieties were introduced in [Reference Ogus19], where a number of their properties are studied; the nomenclature, I believe, is due to Torsten Ekedahl. A smooth, projective variety 
$X$ is a Mazur–Ogus variety if 
$H_{\text{cris}}^{\ast }(X/W)$ is torsion-free and the Hodge–de Rham spectral sequence degenerates 
$E_{1}$. Also note that for any smooth, projective variety, 
$H_{\text{cris}}^{1}(X/W)$ is canonically identified with the crystalline cohomology 
$H_{\text{cris}}^{1}(\text{Alb}(X)/W)$ of the Albanese variety 
$\text{Alb}(X)$ of 
$X$, and as the crystalline cohomology of an abelian variety is always torsion-free, one sees that 
$H_{\text{cris}}^{1}(X/W)$ is always torsion-free or zero (if 
$\text{Alb}(X)=0$). Hence, one considers the torsion-freeness of 
$H_{\text{cris}}^{2}(X/W)$ as a minimal hypothesis.
Definition 2.3. Let 
$X$ be a smooth, projective variety over an algebraically closed field 
$k$ with 
$\text{char}(k)=p>0$. I say that 
$X$ is a Picard–Hodge symmetric variety if it satisfies the following two conditions:
(1) the Picard scheme of
$X$ is smooth;(2) Hodge symmetry holds for
$H_{\text{dR}}^{1}(X/k)$.
The main theorem of this section is the following characterization theorem alluded to in Section 1.
Theorem 2.4. Let 
$X/k$ be any smooth, projective variety with trivial tangent bundle over an algebraically closed field 
$k$ of 
$\text{char}(k)=p>0$. Then the following are equivalent:
(i)
$X$ is a minimally Mazur–Ogus variety,(ii)
$X$ is a Picard–Hodge symmetric variety,(iii)
$X$ is an abelian variety.
Proof. Let us prove 
$(1)\Rightarrow (2)\Rightarrow (3)\Rightarrow (1)$. Let us begin with 
$(1)\Rightarrow (2)$. Assume that 
$X$ is minimally Mazur–Ogus. The fact that 
$H_{\text{cris}}^{2}(X/W)$ is torsion-free implies that 
$\operatorname{Pic}(X)$ is reduced (see [Reference Illusie11, Proposition 5.16, page 632]), and by the universal coefficient theorem for crystalline cohomology ([Reference Berthelot and Ogus1, Section 7.6, page 7–34] with 
$A_{0}=k$, 
$A=W$), one sees that
$$\begin{eqnarray}H_{\text{cris}}^{1}(X/W)\otimes _{W}k\overset{{\sim}}{\longrightarrow }H_{\text{dR}}^{1}(X/k).\end{eqnarray}$$ As Hodge to de Rham spectral sequence degenerates at 
$E_{1}$ in degree one, one sees that
$$\begin{eqnarray}\dim (H_{\text{dR}}^{1}(X/k))=h^{0,1}+h^{1,0}.\end{eqnarray}$$As the Picard variety is reduced, one has
$$\begin{eqnarray}\dim (H_{\text{cris}}^{1}(X/W)\otimes _{W}k)=2h^{0,1}\end{eqnarray}$$and the degeneration of the Hodge–de Rham spectral sequence in degree one means that
$$\begin{eqnarray}2h^{0,1}=h^{1,0}+h^{0,1}.\end{eqnarray}$$Thus, one sees that
$$\begin{eqnarray}h^{1,0}=h^{0,1}.\end{eqnarray}$$ Putting all this together, one sees that 
$X$ is a Picard–Hodge symmetric variety. Thus, one sees that (1)
$\Rightarrow$(2).
Now I prove (2)
$\Rightarrow$(3). Suppose that 
$X$ is a Picard–Hodge symmetric variety and 
$X$ has trivial tangent bundle, so 
$H^{0}(X,\unicode[STIX]{x1D6FA}_{X}^{1})$ has dimension 
$n=\dim (X)$. As 
$X$ is a Picard–Hodge symmetric, one sees that
$$\begin{eqnarray}h^{0,1}=h^{1,0}=\dim (X).\end{eqnarray}$$ Thus, 
$\dim (\operatorname{Pic}(X))=\dim (X)$, and by the hypothesis of (2), 
$\operatorname{Pic}(X)$ is reduced. Hence, the dual of Picard variety is also the Albanese variety: dual of 
$\operatorname{Pic}^{0}(X)=\text{Alb}(X)$ and, in particular,
$$\begin{eqnarray}\dim (X)=\dim (\operatorname{Pic}(X))=\dim (\text{Alb}(X)).\end{eqnarray}$$ Let 
$X\rightarrow \text{Alb}(X)$ be the Albanese morphism. By [Reference Mehta and Srinivas18, Lemma 1.4], one sees that the Albanese morphism 
$X\rightarrow \text{Alb}(X)$ is a smooth surjective morphism with connected fibers and 
$\unicode[STIX]{x1D6FA}_{X/\text{Alb}(X)}^{1}=0$. So 
$X\rightarrow \text{Alb}(X)$ is a finite, surjective étale morphism with connected fibers and, hence, it is an isomorphism.
Now it remains to prove that (3)
$\Rightarrow$(1). This is standard (see [Reference Illusie11]).◻
The following corollary of [Reference Deligne and Illusie6] and Theorem 2.4 is immediate as one has the degeneration of Hodge–de Rham spectral sequence in dimensions 
${\leqslant}p-1$ for any 
$p$ (and hence in dimension one for any 
$p\geqslant 2$).
Corollary 2.11. Let 
$X/k$ be a smooth, projective variety with trivial tangent bundle. Suppose 
$X$ satisfies the following:
(1)
$H_{\text{cris}}^{2}(X/W)$ is torsion-free;(2)
$X$ lifts to $W_{2}$.
Then 
$X$ is an abelian variety.
Remark 2.12. Let me point out that for the Igusa surface (
$p=2,3$), 
$H_{\text{cris}}^{2}(X/W)$ is not torsion-free (but Hodge–de Rham degenerates at 
$E_{1}$ in degree one) and Hodge symmetry is true in dimension one, but 
$\operatorname{Pic}(X)$ is not reduced. See Proposition 5.3 for the construction of the Igusa surfaces and higher dimensional examples of such varieties.
Remark 2.13. In his recent email to me, KeZheng Li has suggested that, perhaps, any smooth, projective variety with trivial tangent bundle and reduced Picard scheme is an abelian variety. This is certainly a natural expectation. I include some comments on this question.
First, let me point out that there are two important numbers 
$\dim (X)=\dim H^{0}(X,\unicode[STIX]{x1D6FA}_{X}^{1})$ and 
$\dim (\operatorname{Pic}(X))=\dim H^{1}(X,{\mathcal{O}}_{X})$ which must be equal if this assertion holds. On the other hand, even if 
$\operatorname{Pic}(X)$ is reduced, it seems difficult to prove that these two numbers are equal without some additional crystalline torsion-freeness hypothesis. Note that the pull-back of one-forms on 
$\operatorname{Pic}(X)=\text{Alb}(X)$, by 
$X\rightarrow \text{Alb}(X)$, lands inside the subspace of closed one-forms 
$H^{0}(X,Z_{1}\unicode[STIX]{x1D6FA}_{X}^{1})$ and all of the following inclusions
$$\begin{eqnarray}H^{0}(\text{Alb}(X),\unicode[STIX]{x1D6FA}_{\text{Alb}(X)}^{1})\subset H^{0}(X,Z_{1}\unicode[STIX]{x1D6FA}_{X}^{1})\subset H^{0}(X,\unicode[STIX]{x1D6FA}_{X}^{1})\end{eqnarray}$$ are strict in general. By [Reference Illusie11, Proposition 5.16, page 632], the hypothesis that 
$H_{\text{cris}}^{2}(X/W)$ is torsion-free is equivalent to the reducedness of 
$\operatorname{Pic}(X)$ and the equality 
$H^{0}(\text{Alb}(X),\unicode[STIX]{x1D6FA}_{\text{Alb}(X)}^{1})=H^{0}(X,Z_{1}\unicode[STIX]{x1D6FA}_{X}^{1})$. In particular, the second inclusion does not become an equality even if we assume 
$H_{\text{cris}}^{2}(X/W)$ is torsion-free, and so it is not possible to work with a simpler hypothesis: 
$\operatorname{Pic}(X)$ is reduced at the moment.
Second, let me point out that the reducedness of the Picard scheme controls only a part of the crystalline torsion which may arise in this situation. Torsion arising from the nonreducedness of 
$\operatorname{Pic}(X)$ is of a fairly mild sort (“divisorial torsion” in the terminology of [Reference Illusie11]). But Ekedahl has shown that the self-product of the Igusa-type surface with itself carries exotic torsion in 
$H^{3}$. It is possible that a similar example (of dimension bigger than two) exists in which 
$H_{\text{cris}}^{2}(X/W)$ has exotic torsion since there is a plethora of examples (see Theorem 3.6) in any dimension for 
$p=2$ and one can probably use deformation theory to provide examples with subtler torsion behavior.
So relaxing the conditions in Theorem 2.4 seems a bit too optimistic (to me) and, at any rate, requires a fuller understanding of the crystalline cohomology of varieties with trivial tangent bundles (which I do not possess).
It is possible to provide alternate formulations of Theorem 2.4, but I have chosen ones which are easiest to deal with in practice.
3 Surfaces with trivial tangent bundle
Let 
$X/k$ be a smooth projective variety over an algebraically closed field of characteristic 
$p>0$. The main theorem of this section is the following. This was conjectured by KeZheng Li in [Reference Li16, Conjecture 4.1].
Theorem 3.1. Let 
$X/k$ be a smooth projective surface over an algebraically closed field of characteristic 
$p>3$ and assume that the tangent bundle 
$T_{X}$ of 
$X$ is trivial. Then 
$X$ is an abelian surface.
Proof. As 
$T_{X}={\mathcal{O}}_{X}\oplus {\mathcal{O}}_{X}$, one sees that 
$\unicode[STIX]{x1D6FA}_{X}^{1}=O_{X}\oplus {\mathcal{O}}_{X}$ and so 
$\unicode[STIX]{x1D6FA}_{X}^{2}={\mathcal{O}}_{X}$. Thus, 
$c_{1}(X)=0$, and also as 
$T_{X}$ is trivial, one sees that 
$c_{2}(X)=0$. Now it is immediate by the adjunction formula (see [Reference Hartshorne9, Chap V, Proposition 1.5]) that 
$X$ is a minimal surface of Kodaira dimension 
$\unicode[STIX]{x1D705}(X)=0$.
By Noether’s formula 
$12\unicode[STIX]{x1D712}({\mathcal{O}}_{X})=c_{1}^{2}+c_{2}$ (see [Reference Hartshorne9]), one sees that
$$\begin{eqnarray}\unicode[STIX]{x1D712}({\mathcal{O}}_{X})=0.\end{eqnarray}$$This means
$$\begin{eqnarray}\unicode[STIX]{x1D712}({\mathcal{O}}_{X})=0=h^{0}-h^{0,1}+h^{0,2};\end{eqnarray}$$ as 
$K_{X}={\mathcal{O}}_{X}$ by Serre duality, one sees that 
$H^{2}({\mathcal{O}}_{X})=H^{0}({\mathcal{O}}_{X})$ and, hence, that
$$\begin{eqnarray}h^{0,1}=2.\end{eqnarray}$$ Next, 
$c_{2}=0$ gives
$$\begin{eqnarray}c_{2}=b_{0}-b_{1}+b_{2}-b_{3}+b_{4}=2-2b_{1}+b_{2}=0.\end{eqnarray}$$ Thus, one sees that 
$b_{1}\neq 0$ and one has 
$b_{2}\neq 0$ because 
$X$ is projective (the Chern class of any ample class is nonzero in 
$H_{\acute{\text{e}}\text{t}}^{2}(X,\mathbb{Q}_{\ell })$). Now 
$b_{1}$ is even as 
$b_{1}$ is the Tate module of the Albanese variety of 
$X$ (which is reduced by definition). Thus, one has 
$b_{1}\geqslant 2$.
Then by [Reference Bombieri and Mumford3, page 25], one sees that there are exactly two possibilities for the pair 
$(b_{1},b_{2})$: either 
$(b_{1},b_{2})=(4,6)$ or 
$(b_{1},b_{2})=(2,2)$. If one is in the first case, by classification of [Reference Bombieri and Mumford3, page 25], 
$X$ is an abelian surface.
If not, one is in the second case. In this case, one has 
$b_{1}=2$, so 
$q=1$ and 
$h^{1}({\mathcal{O}}_{X})=2$. Thus, one sees that 
$\operatorname{Pic}(X)$ is nonreduced, and at any rate the surface 
$X$ is hyperelliptic and as 
$p>3$, classification (see [Reference Bombieri and Mumford3, page 37]) shows that the order of 
$K_{X}$ must be one of 
$2,3,4,6$ which is at any rate 
${>}1$. On the other hand, one has 
$K_{X}={\mathcal{O}}_{X}$. Thus, 
$X$ cannot be hyperelliptic.
So one sees that the second case cannot occur and 
$X$ is an abelian surface as asserted.◻
By a family of varieties with trivial tangent bundle, I mean a proper, flat 
$1$-morphism of stacks 
$f:X\rightarrow M$, with 
$M$ being a Deligne–Mumford stack (over schemes over 
$k$) such that 
$f$ is schematic and for every morphism of stacks 
$\operatorname{Spec}(k^{\prime })\rightarrow M$ with 
$k^{\prime }\supset k$ a field, the fiber product 
$X\times _{M}\operatorname{Spec}(k^{\prime })$ is a geometrically connected, smooth, projective scheme over 
$k^{\prime }$ with trivial tangent bundle.
The construction of Igusa surface ([Reference Igusa10]) leads to the following (for another variant of this construction, see Proposition 5.3). For 
$g\geqslant 1$, let 
${\mathcal{A}}_{g}$ be moduli stack of abelian varieties of dimension 
$g$ over 
$k$ (see [Reference Faltings and Chai7, Reference Fogarty and Mumford8]). Let 
${\mathcal{A}}_{g}^{\text{ord}}[p]$ be the stack of ordinary abelian varieties with a point of order 
$p$ and let 
${\mathcal{A}}_{g}$ be the moduli stack of abelian varieties of dimension 
$g$ over 
$k$; more generally, let 
${\mathcal{U}}_{g}^{{\geqslant}1}[p]$ be the stack of moduli of abelian varieties of dimension 
$g$ parameterizing abelian varieties with a point of order 
$p$. These stacks come equipped with morphisms 
${\mathcal{U}}_{g}^{{\geqslant}1}[p]\rightarrow {\mathcal{A}}_{g}$ and 
${\mathcal{A}}_{g}^{\text{ord}}[p]\rightarrow {\mathcal{A}}_{g}$ which forget the point of order 
$p$ (in each of the two cases). The images of these morphisms are open and dense substacks of 
${\mathcal{A}}_{g}$ parameterizing abelian varieties of 
$p$-rank at least one and ordinary abelian varieties, respectively.
Theorem 3.6. Let 
$k$ be an algebraically closed field of characteristic 
$p=2$. Then for every 
$g\geqslant 2$ and for any 
$1\leqslant r<g$, there exists a family, parameterized by 
${\mathcal{U}}_{r}^{{\geqslant}1}[p]\times {\mathcal{A}}_{g-r}$ of smooth, projective varieties of dimension 
$g$ over 
$k$ which are not abelian varieties and with trivial tangent bundles. In particular, there is a family parameterized by 
${\mathcal{A}}_{r}^{\text{ord}}[p]\times {\mathcal{A}}_{g-r}$ of smooth, projective varieties of dimension 
$g$ over 
$k$ which are not abelian varieties and with trivial tangent bundles.
Proof. First, let me recall the following version of Igusa’s construction (see [Reference Igusa10]). For additional variants of Igusa’s construction, see Proposition 5.3. Let 
$B_{1}$ be an abelian variety of dimension 
$r$ over 
$k$ with 
$p$-rank at least one (note 
$p=2$) and let 
$t\in B_{1}[2](k)$ be a nontrivial two-torsion point. Let 
$B_{2}$ be any abelian variety over 
$k$ of dimension 
$g-r$. Then consider the Igusa action on 
$A=B_{1}\times B_{2}\rightarrow B_{1}\times B_{2}$ given by 
$(x,y)\mapsto (x+t,-y)$. Then this gives an action of 
$\mathbb{Z}/2$ on 
$A$ which is fixed-point-free and
$$\begin{eqnarray}H^{0}(A,\unicode[STIX]{x1D6FA}_{A}^{1})^{\mathbb{Z}/2}=H^{0}(A,\unicode[STIX]{x1D6FA}_{A}^{1}),\end{eqnarray}$$ as 
$\mathbb{Z}/2$ acts by translation on the first factor and so acts trivially on one-forms of 
$B_{1}$, and on the second factor, the action on the space of one-forms of 
$B_{2}$ is by 
$-1=1$ and hence is trivial on the space of one-forms on the second factor as well. Let 
$X$ be the quotient of 
$A$ by this 
$\mathbb{Z}/2$ action. Then 
$T_{X}$ is trivial (as 
$H^{0}(X,T_{X})=H^{0}(A,T_{A})$). On the other hand, by Igusa, 
$\operatorname{Alb}(X)=B_{1}/\langle t\rangle$ and so 
$X$ is not an abelian variety and 
$\operatorname{Pic}(X)$ is not reduced.
Now one simply has to note that one can carry out Igusa’s construction on the universal abelian scheme over the moduli stack of abelian schemes (of the above sort). ◻
For 
$p=3$, the result is a little weaker; by simply taking products with an abelian variety, one gets the following.
Theorem 3.8. Let 
$p=3$ and 
$k$ be an algebraically closed field of characteristic 
$p$. Then for every 
$g\geqslant 2$ and every integer 
$1\leqslant r\leqslant g-1$, there exists a family parameterized by 
${\mathcal{U}}_{r}^{{\geqslant}1}[p]$ of smooth, projective varieties of dimension 
$g$ over 
$k$ which are not abelian varieties and with trivial tangent bundle.
Proof. This is immediate from Proposition 5.3 which will be proved later. In the notation of that proposition, take 
$N=g$, 
$n=g-r$, and 
$A$ to be an abelian variety of dimension 
$r$ equipped with a point of order 
$p$ and for 
$1\leqslant i\leqslant n=g-r$, let 
$A_{i}=E$, where 
$E$ is the elliptic curve with automorphism of order three described in the proof of Proposition 5.3.◻
Remark 3.9. Note that for the Igusa surface, one has 
$\dim H^{0}(X,\unicode[STIX]{x1D6FA}_{X}^{1})=\dim H^{1}(X,{\mathcal{O}}_{X})$, so Hodge symmetry holds and Hodge–de Rham does degenerate at 
$E_{1}$, but 
$\operatorname{Pic}(X)$ is not reduced and 
$H_{\text{cris}}^{2}(X/W)$ has torsion. Varieties 
$X$, constructed as in Theorem 3.6 from ordinary abelian varieties, have the property that they are ordinary with trivial tangent bundle; one has lifting to 
$W_{2}$ (by [Reference Joshi12, Theorem 9.1] of V. B. Mehta) and hence Hodge–de Rham degenerates in dimension 
${<}p$ (by [Reference Deligne and Illusie6]), but 
$H_{\text{cris}}^{2}(X/W)$ is not torsion-free. Thus, these varieties are neither Picard–Hodge symmetric nor are they minimally Mazur–Ogus.
4 Ordinary varieties with trivial tangent bundle
I give a proof of the following theorem.
Theorem 4.1. Let 
$X$ be a smooth, projective variety with trivial tangent bundle. Then the following are equivalent:
- $(1)$
- $X$ is ordinary and minimally Mazur–Ogus,
- $(1^{\prime })$
- $X$ is ordinary and Picard–Hodge symmetric,
- $(2)$
- $X$ is Frobenius split and minimally Mazur–Ogus,
- $(2^{\prime })$
- $X$ is Frobenius split and Picard–Hodge symmetric,
- $(3)$
- $X$ is ordinary and $H_{\text{cris}}^{2}(X/W)$ is torsion-free,
- $(3^{\prime })$
- $X$ is Frobenius split and $H_{\text{cris}}^{2}(X/W)$ is torsion-free,
- $(4)$
- $X$ is an ordinary abelian variety.
Proof. The equivalences 
$(1)\;\Longleftrightarrow \;(1^{\prime })$ and 
$(2)\;\Longleftrightarrow \;(2^{\prime })$ are clear from the proof of Theorem 2.4. The equivalence 
$(3)\;\Longleftrightarrow \;(3^{\prime })$ is [Reference Mehta and Srinivas18, Lemma 1.1]. The equivalence (1) 
$\;\Longleftrightarrow \;$ (2) is immediate from [Reference Mehta and Srinivas18, Lemma 1.1] as 
$X$ is ordinary if and only if 
$X$ is Frobenius split. Now (2) 
$\;\Longrightarrow \;$ (3) is clear from Definition 2.1 and by [Reference Mehta and Srinivas18]. Now to prove (3) 
$\;\Longrightarrow \;$ (4). This is immediate from Theorem 2.4, provided one proves that Hodge–de Rham spectral sequence degenerates at 
$E_{1}$ in degree 
${\leqslant}1$. In other words, one has to show that the hypothesis of 
$(3)$ implies that 
$X$ is minimally Mazur–Ogus. This is proved as follows. Any smooth, projective variety with trivial tangent bundle is ordinary if and only if it is Frobenius split (see [Reference Mehta and Srinivas18, Lemma 1.1]). A result of Mehta (see [Reference Joshi12, Theorem 9.1]) says that a Frobenius split variety 
$X$ lifts to 
$W_{2}$ and hence Hodge–de Rham degenerates in dimension 
${\leqslant}p-1$ by [Reference Deligne and Illusie6, Corollaire 2.4]. Hence, one has degeneration in dimension one for any 
$p\geqslant 2$. Hence, the hypothesis of (3) implies that 
$X$ is Mazur–Ogus. So the assertion (3) 
$\;\Longrightarrow \;$ (4) follows from Theorem 2.4. Now (4) 
$\;\Longrightarrow \;$ (1) is standard (see [Reference Illusie11]).◻
Corollary 4.2. Let 
$X$ be a smooth, projective, ordinary variety with trivial tangent bundle. Then 
$X$ is an (ordinary) abelian variety if and only if 
$H_{\text{cris}}^{2}(X/W)$ is torsion-free.
5 New proof of Li’s theorem
In this section, I give a new proof of Li’s theorem (see [Reference Li15, Reference Li16]) and prove the following refinement.
Definition 5.1. Let 
$X$ be a smooth, projective variety with trivial tangent bundle and suppose 
$A\rightarrow X$ is Galois an étale cover by an abelian variety. I say that 
$A\rightarrow X$ is a minimal Galois étale cover of 
$X$ if whenever there exists a factorization of 
$A\rightarrow X$ into étale morphisms 
$A\rightarrow A^{\prime }\rightarrow X$ with 
$A^{\prime }$ an abelian variety and 
$A^{\prime }\rightarrow X$ Galois, then the morphism 
$A\rightarrow A^{\prime }$ is an isomorphism.
Theorem 5.2. Let 
$k$ be an algebraically closed field of characteristic 
$p>0$. Let 
$X/k$ be a smooth, projective, ordinary variety with trivial tangent bundle.
(1) Either
$X$ is an abelian variety or(2)
$p=2$ and $X$ has a minimal Galois étale cover by an abelian variety with Galois group of exponent $p$ (i.e., every element is of order $p$).
Proof. Let 
$X$ be as in the statement of the theorem and suppose 
$X$ is not an abelian variety. By [Reference Mehta and Srinivas18], there exists an ordinary abelian variety 
$A/k$ and a finite, Galois étale morphism 
$A\rightarrow X$ with Galois group 
$G$ of order a power of 
$p$ which acts freely on 
$X$. By passing to a quotient of 
$G$ if needed, one may assume that 
$A\rightarrow X$ is a minimal Galois étale cover of 
$X$. In particular, 
$A$ carries fixed-point-free automorphisms 
$\unicode[STIX]{x1D70E}:A\rightarrow A$ of order 
$d=p^{m}$, a power of 
$p$. If 
$d=1$ for every element of 
$G$, then this is already the case (1), so there is nothing to do; if 
$d=2$ for every element of 
$G$, then one is in the case (2), so again there is nothing to prove. So assume 
$d=p^{m}\geqslant 3$ for some element 
$\unicode[STIX]{x1D70E}\in G$.
Then, by [Reference Lange14, Lemma 3.3] (the proof given there is characteristic-free, and the argument is sketched below for convenience), there are abelian varieties 
$A_{1},A_{2}$ such that 
$A$ is isogenous to 
$A_{1}\times A_{2}$ and that 
$\unicode[STIX]{x1D70E}|_{A_{1}}$ is a translation, and 
$\unicode[STIX]{x1D70E}|_{A_{2}}$ is an automorphism (possibly with fixed points) of order a power of 
$d$. Indeed, write 
$\unicode[STIX]{x1D70E}=t_{x}\circ \unicode[STIX]{x1D70E}^{\prime }$ where 
$t_{x}$ is a translation, 
$\unicode[STIX]{x1D70E}^{\prime }$ an automorphism of order a power of 
$d$ and one may take 
$A_{1}$ to be the connected component of 
$\ker (1-\unicode[STIX]{x1D70E}^{\prime })$ and 
$A_{2}=\text{image}(1-\unicode[STIX]{x1D70E}^{\prime })$. As 
$A$ is ordinary, so are 
$A_{1}$ and 
$A_{2}$. One assumes, without loss of generality, that 
$\unicode[STIX]{x1D70E}^{\prime }$ is a homomorphism of 
$A_{2}$. Now 
$(A_{2},\unicode[STIX]{x1D70E}^{\prime })$ admits a canonical Serre–Tate lifting to 
$W(k)$ (see [Reference Mehta and Srinivas18, Theorem 1(2) of Appendix]), and, in particular, a lifting 
$(B_{2},\unicode[STIX]{x1D70E}^{\prime })$ of 
$(A_{2},\unicode[STIX]{x1D70E}^{\prime })$ to complex numbers exists. So starting with 
$X$, one has arrived at an abelian variety 
$B_{2}$ over 
$W(k)$ and an automorphism 
$\unicode[STIX]{x1D70E}^{\prime }:B_{2}\rightarrow B_{2}$ of finite order, with possibly finitely many fixed points. Replacing 
$B_{2}$ by a subabelian variety if needed, one may assume that 
$\unicode[STIX]{x1D70E}^{\prime }$ is not a translation on any subvariety of 
$B_{2}$.
Now I proceed by an algebraic variant of [Reference Birkenhake and Lange2, Proposition 13.2.5 and Theorem 13.3.2]. This is done as follows. Let 
$\unicode[STIX]{x1D6F7}_{d}(X)$ be the 
$d$-cyclotomic polynomial. So 
$\unicode[STIX]{x1D6F7}_{d}(X)|(X^{d}-1)$ and 
$\unicode[STIX]{x1D6F7}_{d}(X)$ is irreducible and the primitive 
$d$th roots of unity are its only roots. Let 
$f$ be the endomorphism 
$\frac{{\unicode[STIX]{x1D70E}^{\prime }}^{d}-1}{\unicode[STIX]{x1D6F7}_{d}(\unicode[STIX]{x1D70E}^{\prime })}$ of 
$B_{2}$, i.e., consider the polynomial
$$\begin{eqnarray}f(X)=\frac{X^{d}-1}{\unicode[STIX]{x1D6F7}_{d}(X)}\in \mathbb{Z}[X]\end{eqnarray}$$ and consider the endomorphism 
$f:=f(\unicode[STIX]{x1D70E}^{\prime }):B_{2}\rightarrow B_{2}$. Consider the subvariety
$$\begin{eqnarray}B_{3}=f(B_{2})\subset B_{2}.\end{eqnarray}$$ Then 
$B_{3}$ is an abelian variety annihilated by 
$\unicode[STIX]{x1D6F7}_{d}(\unicode[STIX]{x1D70E}^{\prime })$ and hence is naturally a 
$\mathbb{Z}[\unicode[STIX]{x1D701}_{d}]$-module. Moreover, 
$B_{3}$ has good ordinary reduction at 
$p$, denoted as 
$A_{3}$, and, in particular, 
$H_{\text{dR}}^{1}(B_{3}/W)=H_{\text{cris}}^{1}(A_{3}/W)$ is a 
$\mathbb{Z}[\unicode[STIX]{x1D701}_{d}]\otimes _{\mathbb{Z}_{p}}W(k)$-module which is finitely generated and 
$\mathbb{Z}[\unicode[STIX]{x1D701}_{d}]$-torsion-free and, hence, projective of rank 
$k=2\dim (B_{3})/\unicode[STIX]{x1D719}(d)$. Now every finitely generated projective module over 
$\mathbb{Z}[\unicode[STIX]{x1D701}_{d}]$ of rank 
$k$ is a direct sum of ideals 
$I_{1}\oplus I_{2}\oplus \cdots \oplus I_{k}$ of 
$\mathbb{Z}[\unicode[STIX]{x1D701}_{d}]$. Using this, one sees that, up to isogeny, one may factor 
$B_{3}$ into product of 
$k$ abelian varieties 
$B_{3,1},\ldots ,B_{3,k}$ each of dimension 
$\unicode[STIX]{x1D719}(d)/2$ (over 
$\mathbb{C}$, this is proved by an analytic argument, attributed to an unpublished result of S. Roan in [Reference Birkenhake and Lange2, Theorem 13.2.5]). Each of these varieties has (possibly up to isogeny) 
$\mathbb{Z}[\unicode[STIX]{x1D701}_{d}]{\hookrightarrow}\operatorname{End}(B_{3,i})$ and as 
$2\dim (B_{3,i})=\unicode[STIX]{x1D719}(d)$, so each has complex multiplication by 
$\mathbb{Z}[\unicode[STIX]{x1D701}_{d}]$. Fix one of these abelian varieties, say, 
$B_{3,1}$. Then by a basic result [Reference Lang13, Theorem 3.1, page 8], 
$B_{3,1}$ is isotypic with a simple abelian variety factor 
$B$ with complex multiplication by a CM subfield of 
$\mathbb{Q}(\unicode[STIX]{x1D701}_{d})$. Further, 
$B$ has good ordinary reduction at 
$p$ (by virtue of its construction from 
$B_{3,1}$ which has ordinary reduction at 
$p$).
On the other hand, note that 
$p$ is totally ramified in the cyclotomic field 
$\mathbb{Q}(\unicode[STIX]{x1D701}_{d})$ as 
$d=p^{m}\geqslant 3$, so 
$p$ is also totally ramified in the CM subfield for 
$B$. Hence, one sees, by [Reference Yu20] or [Reference Chai, Conrad and Oort5, Propositions 3.7.1.6 and 4.2.6], that the special fiber of 
$B$ at 
$p$ is isoclinic of positive slope (equal to half). So it cannot be ordinary. This is a contradiction.
Thus, 
$d=p^{m}\leqslant 2$ and if 
$X$ is not an abelian variety, then one is in case (2). This completes the proof.◻
If 
$A$ is an abelian variety, then 
$A$ acts on itself by translations. In particular, translation by a nontrivial point of order 
$p$ is an automorphism of 
$A$ of order 
$p$. In what follows, I say that an automorphism 
$\unicode[STIX]{x1D70C}:A\rightarrow A$ is a nontrivial automorphism if 
$\unicode[STIX]{x1D70C}$ is not a pure translation. Before proceeding, let me point out the following variant of [Reference Igusa10].
Proposition 5.3. For every algebraically closed field 
$k$ of characteristic 
$p=2$ or 
$p=3$, and for every 
$n\geqslant 1$ and every integer 
$N>n$, there exists a smooth, projective variety 
$X/k$, of 
$\dim (X)=N$, with trivial tangent bundle and a minimal Galois étale cover with 
$G=(\mathbb{Z}/p)^{n}$.
Proof. Let 
$A,A_{1},A_{2},\ldots ,A_{n}$ be abelian varieties over 
$k$ satisfying the following conditions:
(1) let
$\unicode[STIX]{x1D70C}_{i}:A_{i}\rightarrow A_{i}$, for $1\leqslant i\leqslant n$, be a nontrivial automorphism of order $p$, such that for every $i$ the subspace of $\unicode[STIX]{x1D70C}_{i}$-invariant one-forms $H^{0}(A_{i},\unicode[STIX]{x1D6FA}_{A_{i}}^{1})^{\langle \unicode[STIX]{x1D70C}_{i}\rangle }=H^{0}(A_{i},\unicode[STIX]{x1D6FA}_{A_{i}}^{1})$;(2) one has
$\dim (A)+\dim (A_{1})+\cdots +\dim (A_{n})=N$;(3) suppose
$A$ has $p$-rank at least one.
For 
$p=2$, any abelian varieties 
$A,A_{1},\ldots ,A_{n}$ satisfying the last two conditions satisfy the first with the automorphism 
$\unicode[STIX]{x1D70C}_{i}:A_{i}\rightarrow A_{i}$ being 
$\unicode[STIX]{x1D70C}_{i}(x)=-x$ for all 
$x\in A_{i}$ for 
$1\leqslant i\leqslant n$. The condition on invariant forms is trivially satisfied as 
$-1=+1$ because 
$p=2$.
For 
$p=3$, consider an elliptic curve 
$E/k$ with a nontrivial automorphism of order 
$p=3$. Let 
$A_{i}=E$ for 
$1\leqslant i\leqslant n$. The condition on invariants is trivially satisfied as 
$\mathbb{Z}/p=\mathbb{Z}/3$ operates unipotently on 
$H^{0}(E,\unicode[STIX]{x1D6FA}_{E}^{1})$. As any unipotent action has a nonzero subspace of invariants and as 
$H^{0}(E,\unicode[STIX]{x1D6FA}_{E}^{1})$ is one-dimensional, all one-forms are invariant under this nontrivial automorphism of order three.
Taking 
$p=3$, 
$N=2$, and 
$n=1$ and let 
$A=E^{\prime }$ be any ordinary elliptic curve and 
$A_{1}=E$ be an elliptic curve with an automorphism of order 
$p=3$ (any such elliptic curve is supersingular and one can take 
$E$ to be the curve 
$y^{2}=x^{3}-x$ with the automorphism 
$\unicode[STIX]{x1D70C}(x,y)=(x+1,y)$). This, as above, gives a smooth projective surface 
$X$ which is the 
$p=3$ variant of Igusa surface for 
$p=2$ which is described in [Reference Igusa10], [Reference Chai4]. By construction, 
$X$ is the quotient of 
$E^{\prime }\times E$ by the fixed-point-free automorphism group generated by 
$(z,w)\mapsto (z+t,\unicode[STIX]{x1D70C}(w))$ for 
$z,t\in E^{\prime }$ with 
$t$ being a generator of 
$E^{\prime }[3](k)\simeq \mathbb{Z}/3$ and 
$w\in E$.
Thus, for any 
$p=2,3$, one has abelian varieties satisfying all the three conditions. Let 
$t\in A[p]$ with 
$t\neq 0$ be a point on 
$A$ of order 
$p$. Let 
$G=(\mathbb{Z}/p)^{n}$ and consider its elements as vectors 
$(g,g_{2},\ldots ,g_{n-1})$ with entries in 
$\mathbb{Z}/p$, and let 
$G$ operate on
$$\begin{eqnarray}B=A\times A_{1}\times A_{2}\times \cdots \times A_{n}\end{eqnarray}$$as follows:
$$\begin{eqnarray}(1,g_{2},\ldots ,g_{n})\cdot (x,x_{1},\ldots ,x_{n})=(x+t,\unicode[STIX]{x1D70C}_{1}(x_{1}),\unicode[STIX]{x1D70C}_{2}^{g_{2}}(x_{2}),\ldots ,\unicode[STIX]{x1D70C}_{n}^{g_{n}}(x_{n})),\end{eqnarray}$$ and with the usual convention 
$\unicode[STIX]{x1D70C}_{i}^{0}=1$ (note the asymmetry in my notation and construction—this is intended to include Igusa surfaces for 
$n=1$, 
$N=2$). Then 
$G$ acts free of fixed points and the quotient 
$X=B/G$ is a smooth, projective variety with trivial tangent bundle with minimal étale cover with Galois group 
$G$ and 
$\dim (X)=N$.◻
Remark 5.4. Let me give an example of an abelian variety 
$A$ in characteristic 
$p>3$ with 
$\dim (A)>1$ and a nontrivial automorphism 
$\unicode[STIX]{x1D70C}:A\rightarrow A$ of order 
$p$, which shows that the condition on space of invariants is not satisfied in general. Let 
$A$ be the Jacobian of the hyperelliptic curve 
$y^{2}=x^{p}-x$. Then the automorphism 
$(x,y)\mapsto (x+1,y)$ of 
$y^{2}=x^{p}-x$ is an automorphism of order 
$p$ of this curve (and hence of 
$A$). Using a standard basis for computing forms, one checks that the subspace of invariant forms is not of dimension equal to 
$\dim (A)$. For example, for 
$p=5$, this curve has genus 
$g=2$ and the standard basis for 
$H^{0}(A,\unicode[STIX]{x1D6FA}_{A}^{1})$ is 
$\frac{dx}{y},\frac{xdx}{y}$. The action of the automorphism 
$(x,y)\mapsto (x+1,y)$ is then given by 
$\{\frac{dx}{y},\frac{xdx}{y}\}\mapsto \{\frac{dx}{y},\frac{(x+1)dx}{y}\}$ which is unipotent and its space of invariants is one-dimensional (and not equal to 
$g=2$). More generally, if 
$\langle u\rangle$ is the group of automorphisms generated by a unipotent linear map 
$u:V\rightarrow V$, where 
$V$ is a finite-dimensional vector space 
$V$ over an algebraically closed field 
$k$ (of characteristic 
$p>0$), then space of 
$u$ invariants 
$V^{\langle u\rangle }=V$ if and only 
$u=1$.
6 Variants of Li’s conjecture
In [Reference Li16, Conjecture 4.1], it was conjectured that for 
$p>3$, every smooth, projective variety with trivial tangent bundle is an abelian variety. Let me remark that the construction in Proposition 5.3 also works for 
$p>3$, except for the fact that I do not know how to construct abelian varieties satisfying the hypothesis on invariant forms in condition (1) above. But it is possible that abelian varieties satisfying conditions (1)–(3) in the proof of Proposition 5.3 might exist for sufficiently large 
$p$. Hence, in the light of this remark and Theorem 2.4, it seems to me that perhaps the conjecture of [Reference Li16, Conjecture 4.1] needs to be modified. In fact, I propose two separate conjectures, depending on whether one fixes the characteristic or one fixes the dimension. Both the conjectures should be true. The fixed dimension version is inspired by [Reference Liedtke17]. I note that Conjecture 6.1 replaces [Reference Li16, Conjecture 4.1].
Conjecture 6.1. (Fixed dimension version)
Let 
$d$ be a fixed positive integer. Let 
$k$ be an algebraically closed field of characteristic 
$p>0$. Then there exists a positive integer 
$n_{0}(d)$ satisfying the following property: if 
$p>n_{0}(d)$ and if X is a smooth projective variety over 
$k$ with trivial tangent bundle of dimension 
$d$, then X is an abelian variety.
Note that for 
$d=1$, 
$n_{0}(d)=1$; for 
$d=2$, one has 
$n_{0}(d)=3$ (by Theorem 3.1).
Before I state the fixed characteristic version, let us make the following elementary observation.
Lemma 6.2. Let 
$p$ be a fixed prime number. Let 
$k$ be an algebraically closed field of characteristic 
$p>0$. Then there exists a positive integer 
$n_{1}(p)$ satisfying the following property: if 
$X$ is a smooth projective variety over 
$k$ with trivial tangent bundle of dimension less than 
$n_{1}(p)$, then 
$X$ is an abelian variety.
Proof. Suppose, for a given 
$p$, there exists a smooth, projective variety 
$Z$ with trivial tangent bundle which is not an abelian variety. Then for every integer 
$n\geqslant \dim (Z)$, there exists a variety 
$Y$ of this sort with 
$\dim (Y)=n$. Indeed, one may simply take 
$Y=Z\times E^{n-\dim (Z)}$ for any elliptic curve 
$E$. So take a variety 
$Z$ with the above properties of the smallest dimension and let 
$n_{1}(p)=\dim (Z)$. If no such variety 
$Z$ exists, one can simply take 
$n_{1}(p)=0$. Then every smooth projective variety 
$X$ of dimension 
$\dim (X)<n_{1}(p)$ is an abelian variety by construction.◻
For 
$p=2,3$, 
$n_{1}(p)=2$ by Theorem 3.1. The following is the fixed characteristic version of the conjecture.
Conjecture 6.3. (Fixed characteristic version)
Let 
$p$ be any fixed prime number. The number 
$n_{1}(p)$ constructed in Lemma 6.2 has the property that 
$n_{1}(p)\geqslant 4$ for 
$p\geqslant 5$.
Acknowledgment
I would like to thank Vikram Mehta for directing me to [Reference Li16] and for many conversations around Li’s conjecture. Many years ago (around 1991–1992), Vikram had explained to me his paper with Srinivas (see [Reference Mehta and Srinivas18]), and more recently, during my visit to India in 2012, we had many lucid conversations on topics of common interest (we were studying some questions on fundamental group schemes). I was amazed by his incredible energy and zest for mathematics while facing an illness which ultimately took him from us.
I proved Theorem 2.4 while I was on a visit to RIMS, Kyoto in 2011. I thank RIMS, Kyoto for providing excellent hospitality and I am grateful to Shinichi Mochizuki for giving me an opportunity to visit RIMS. I thank KeZheng Li for answering many of my elementary and naive questions about his papers [Reference Li15, Reference Li16], and for his comments and corrections. I thank Brian Conrad for pointing out [Reference Yu20]. Finally, it is a pleasure to thank the referee for many comments and corrections which have improved the readability of this paper.
