2. NONLINEAR PARAXIAL EQUATION

One of the simplest nonlinear equations is the nonlinear paraxial equation for a complex valued field Ψ(x,t) over a spatial domain Ω ⊂ R^D (Osman, 1998):

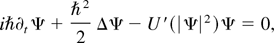
where U′ is the first derivative of a twice-differentiable nonlinear real-valued function and ħ is a positive parameter. The parameter ħ is analogous to Planck's constant, which in the quantum setting is usually very small when evaluated in the natural dimensional scales of the equation as determined by its initial and boundary conditions. For the moment, the precise specification of the domain Ω and the nature of the boundary conditions are left vague in order to make some general statements regarding the structure of Eq. (1). The nonlinear function U : R₊ → R is the potential energy density of the field and is clearly seen when the nonlinear paraxial equation, Eq. (1), is recast as a Hamiltonian system in the form

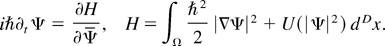
The associated Poisson bracket of any two functionals F and G is given by

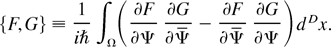
The evolution of any functional F under the nonlinear paraxial equation flow (1) is then

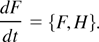
This Hamiltonian structure plays a major role in our analysis. Associated with the nonlinear paraxial equation, (1), are the local conservation laws corresponding to mass, momentum, and energy conservation. Their densities ρ, μ, and ε, respectively, are given by

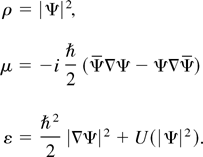
The mass and momentum densities determine the field φ up to a constant phase; the energy density can be written in terms of them as

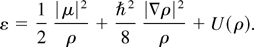
The local conservative laws are then

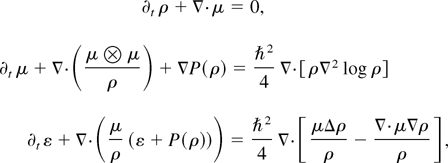
where P(ρ) ≡ ρU′(ρ) − U(ρ).

The first two of these are a closed system govering ρ and μ that has the form of a perturbation of the compressible Euler equations of fluid dynamics with the “pressure” given by P(ρ). If the “Euler part” of these equations is to be hyperbolic, then the “pressure” P(ρ) must be a strictly increasing function of ρ; in that case P′(ρ) = ρU′′(ρ) > 0. This means that U must be a strictly convex function of ρ and corresponds to a “defocusing” nonlinear paraxial equation. In this context a “focusing” nonlinear paraxial equation can be understood as a fluid whose pressure decreases when the mass density increases, a phenomenon leading to the development of mass concentrations.

3. THE SEMICLASSICAL LIMIT

The “semiclassical limit” of the nonlinear paraxial equation can be described as follows. Consider the family, parameterized by ħ > 0, of solutions Ψ^(ħ)(x,t) to the Cauchy problems (Osman, 1998):

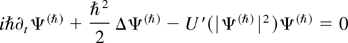
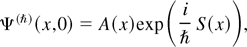
where the (nonnegative) amplitude A(x) and (real) phase S(x) are assumed to be smooth and independent of ħ. The initial conserved densities are then

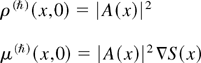
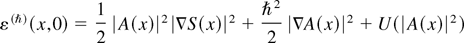
The general problem of the semiclassical limit is to determine the limiting behavior of any function of the field Ψ^(ħ) as ħ → 0, in particular, to ascertain the existence (in some sense) of the limits of the conserved densities:

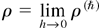
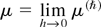
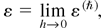
and if the limits exist, to determine their dynamics.

Arguing formally, it is natural to conjecture for the defocusing case that the 0(ħ²) dispersive terms appearing in Eq. (7) are negligible, as ħ → 0 and that the limiting densities ρ and μ satisfy the hyperbolic system (the Euler system)

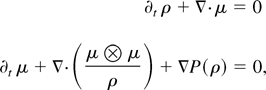
with initial conditions inferred from Eq. (9a) given by

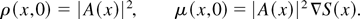
This argument is self-consistent only so long as the solution of the Euler system (11) remains classical. In that case, the limiting energy density will be given by

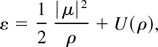
and will satisfy

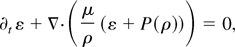
hence, playing the role of a Lax entropy for the Euler system (11). The genuinely nonlinear nature of the Euler system (11) will ensure that its classical solution will develop singular behavior (an infinite derivative) for all but rarefaction initial data. At the instant such a breaking occurs, the formally small dispersive terms on the right side of (11) will no longer be negligible, and the above characterization of the semiclassical limit will break down. Because this small regularizing term is dispersive, one expects that the impending singularity in ρ and μ will be regularized by the development of small wavelength oscillations.

4. THE NUMERICAL EXPERIMENTS ON THE ONSET OF BREAKING

Numerics are to be used to illustrate the breakdown of the “Euler” description of the semiclassical limit for the defocusing nonlinear paraxial equation (Fornberg & Whitman, 1978, p. 289). The problem is cast in one spatial dimension with a cubic nonlinearity (Osman, 1998):

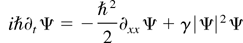
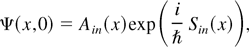
where γ here is a positive constant. For this one-dimensional case, the Euler system in Eq. (11a), describing the formal semiclassical limit, reduces to the initial value problem:

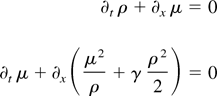
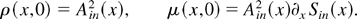
Riemann invariants for the Euler system (15a) are given by

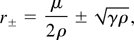
and the system can be placed in the Riemann invariant form

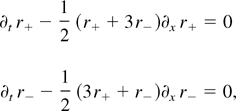
with the initial conditions

5. THE NUMERICAL EXPERIMENTS ON THE POSTBREAKING PHENOMENA

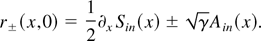
Another method for deriving the reduced system in Equation (15a) is the classical WKB method. It considers

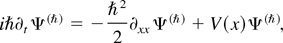
and begins with the Ansatz that Ψ^(ħ) is in the form

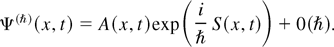
Inserting this Ansatz into the nonlinear paraxial equation (18), and balancing the leading two powers of ħ yields

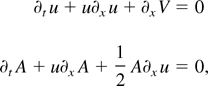
where u = ∂_xS, which is equivalent to the reduced system in Eq. (15a) upon making the identifications

The development of a singularity in this reduced system must then be interpreted as a breakdown in the Ansatz equation (19). After the breakdown, the time of the wave forms no longer continue to resemble that of the Ansatz.

In linear theories such as quantum mechanics and classical electromagnetism, the presence of singularities in reduced systems and their consequences for the full system are well understood. For example, in quantum mechanics the characteristics of the reduced hyperbolic system (20) are the paths of classical particles in the conservative force field F(x) = −∂_xV(x), which is defined in terms of the prescribed potential energy function V(x). In this manner, classical mechanics arises as the semiclassical limit of quantum mechanics. (In the electromagnetic setting, the characteristics are the “rays” of “geometrical optics”.)

Singularities in the reduced semiclassical equations result from foci and envelopes of families of these classical paths. These envelopes separate regions in the (x,t) plane that consist of points lying on only one classical path from regions consisting of points that lie on multiple paths. Along these envelopes (called caustics), neighboring rays coalesce and geometric conservation law properties of the transport equation for the amplitude A(x,t) force |A| to diverge along these caustics.

More mathematically, in the linear case of quantum mechanics, the reduced hyperbolic system is degenerate in the sense that the eikonal equation for k and the eikonal equation for A have identical characteristics. Because the eikonal equation does not depend upon the amplitude A, it can be solved first, and its characteristics are the classical paths. The transport equation for the amplitude A is then integrated along these classical paths, and geometrical consideration forces |A| to diverge along caustic envelopes. This divergence of the amplitude A is a direct consequence of the degeneracy of system in Equation (20).

The caustic behavior can be present even in the trivial case of the free paraxial equation (with V(x) = 0) provided one begins with compressional initial data such as

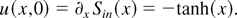
In this V(x) = 0 case, the solution Ψ^(ħ)(x,t) of initial value problem equation (14a) can be represented exactly as a Fourier integral:

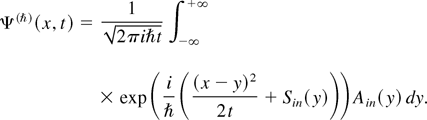
The behavior Ψ^(ħ)(x,t) as ħ → 0, uniformly in (x,t), can be obtained from an asymptotic (stationary phase) evaluation of this integral. The result shows that, away from the characteristic envelopes, Ψ^(ħ)(x,t) behaves asymptotically as the linear superposition

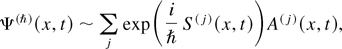
where the index j in the sum runs over different classical paths through the point (x,t), and S^(j) is the classical path. A^(j) is computed by integrating the transport equation along the jth classical path, with adjustments by phase shifts of the form exp(in^(j)π/4). The integers n^(j) are computed from the number of times the jth path touches the caustic envelope.

In the linear case for general V(x), the classical paths are not straight lines and the asymptotic behavior cannot be calculated with Fourier theory. Nevertheless, the asymptotic behavior is still given by the superposition of Eq. (24). Using the method of characteristics for the eikonal equation, one constructs a surface u = u(x,t) over the (x,t) plane. With this surface, one integrates the transport equation for A(x,t) and assembles the formula in Eq. (24). Arguments from the theory of uniform asymptotic expansions then show that the formula in Eq. (24) is asymptotically valid except at the focus and along the characteristic envelopes, the only effect of which is phase shifts of integer multiples of π/4.

In the linear case, the qualitative consequence of the formula in Eq. (24) is striking. Before the caustic, only one classical path passes through each space time point (x,t); only one term appears in the sum in Eq. (24); the intensity |A(x,t)|² is slowly varying on the ħ scale. After the caustic, three classical paths pass through each point (x,t), three terms appear in the sum, and the intensity |A(x,t)|² is

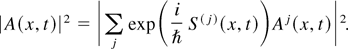
This has rapid oscillations on the ħ scale due to phase interference between the three terms in the sum. Mathematically, these rapid oscillations prevent strong convergence after the caustic. In summary, in this linear case the weak limit can be constructed simply by summing over the contributions from each classical path, with interference between terms in this sum causing rapid oscillations (Osman, 1998).

6. NONLINEAR SIMULATIONS OF DEFOCUSING AND FOCUSING CASES

Numerical results that illustrate the contrast formations of oscillations in solutions of Eq. (14a) (Osman, 1998) for the linear (γ = 0), the nonlinear defocusing (γ > 0), and the nonlinear focusing (γ < 0) cases are shown in this section. The linear case (γ = 0) is considered to illustrate the semiclassical linear theory just described. Figure 1 shows |Ψ(x,t)| as a surface over the (x,t) plane, and clearly contains one focus of that theory, from which two caustics emanate.

The amplitude |Ψ(ħ)| for the linear (γ = 0) paraxial equation as a surface over the (x,t) plane, for ħ = 0.1.

Figure 2a shows that the defocusing case is treated here with a repulsive nonlinearity (γ > 0). As in the linear case, oscillation intensity forms at specific points in space and time, and then persists.

a: The amplitude |Ψ(ħ)| for the defocusing (γ > 0) nonlinear paraxial equation as a surface over the (x,t) plane, for ħ = 0.1. b: The comparison result for the linear (γ = 0) paraxial equation.

In the defocusing case, these oscillations form two packets, one travelling to the right and the other to the left. The central region of the spatial profile that separates the two oscillatory regions is a quiescent plateau at times beyond the focus. However, when compared with the linear case, several distinguishing features arise from the nonlinearity. First, the amplitude |Ψ(x,t)| is much less intense at the focus than in the linear case, which is depicted from the same perspective in Figure 2b.

The response in the focusing case is treated here with an attractive nonlinearity (γ < 0; Fig. 3a). Indeed, the defocusing case had the mildest response, followed by the linear case, with the most extreme behavior found with focusing nonlinearity. It is the focusing nonlinearity that supports solitons in one spatial dimension and that blows up in finite time in two or more dimensions.

a: The amplitude |Ψ(ħ)| for the focusing (γ < 0) nonlinear paraxial equation as a surface over the (x,t) plane, for ħ = 0.1. b: An enlargement of the oscillatory region from (a).

The blowup of a portion of the oscillatory region shown in Figure 3b admits the intriguing interpretation of these oscillations as a dense “sea of solitons,” located near the center of the spatial profile, with a sharp boundary separating the oscillatory from the quiescent regions of space.