Published online by Cambridge University Press: 28 April 2005
We study the sustainability of long-run growth in a two-sector economy where a renewable natural resource is exploited under private property rights. We obtain short- and long-run growth trajectories in closed form, examine transitional dynamics, and characterize convergence properties. We find conditions for sustainable long-run growth, which depend on the harvesting rate, and show that the speed of convergence decreases during transition. We identify a stronger version of Hartwick's rule and analyze parameter dependences for endogenous variables. Economic growth relies less on abundance or scarcity of natural resources than on the way they are managed.
It is commonly accepted in natural resources economics that there is a strong connection between resource endowments and economic growth results. Evidence on historical episodes as well as post-World War II examples are used to analyze this relationship. Sachs and Warner (1995) point out that countries with abundant natural resources tend to grow more slowly than countries poorly endowed. A negative relationship between high natural resource intensity, namely, a high value of resource-based exports to GDP, and the rate of growth appears as a robust empirical fact, with many examples showing resource-poor economies that outperform resource-rich economies in terms of economic growth. Sachs and Warner (2001) even refer to the curse of natural resources, after exploring and statistically rejecting the possibility of a spurious negative correlation between natural resources and growth.
There is, however, the traditional viewpoint according to which most of the current rich economies once developed with the aid of their natural resources. However, this argument seems to work as a counterexample only for periods, regions, and natural resources for which high transportation costs made proximity decisive for physical availability. On the other hand, Sachs and Warner (2001) and Gylfason and Zoega (2001) show that such historical examples correspond to countries such as the UK and the USA, where the natural resource intensity measured as a percentage of GDP, was much smaller than the ratios observed in the well-endowed countries during the second half of the twentieth century.
The literature refers to multiple social, political, and economic factors explaining the adverse effects of resource abundance on growth. Nevertheless, the most accepted explanation focuses on two elements: the direct effect known as Dutch disease (unfavorable exchange rate with high price levels and wages, as well as dependence on primary exports), and the indirect crowding-out effect that flows through human and social capital deterrence. Gylfason (2001a,b) empirically analyzes these effects and finds that in most countries that are rich in natural resources, the rates of growth of per capita production over the long term have been lower than in other countries that are less well endowed. Hence, economic growth varies inversely with natural resource abundance. However, it has to be emphasized that the problem may not be the existence of natural wealth as such, but rather the lack of reaction face to the dangers that accompany the gifts of nature. In any case, it seems less than obvious that abundant natural resources will always prevent the emergence of a dynamic economy or that the discovery of such resources acts to dampen an already developed economy. Natural resources can be a blessing or a curse as long as they bring risks: abundant natural resources may imbue people with a false sense of security and lead governments to lose sight of the need for good economic management. In contrast, countries without natural resources have a smaller margin for error and they have to manage efficiently in search of growth improvements. Auty (2001) considers two kinds of development models on the basis of the attributes and qualities of political institutions: the competitive industrialization model that shows virtuous social and economic circles, and applies to extreme resource-poor countries; and the staple trap model, which especially applies to resource-abundant countries. Rodríguez and Sachs (1999) suggests that resource-rich countries grow more slowly because they are living beyond their means. Hence, the adjustment of income per capita to its steady state comes from above, displaying negative rates of growth during the transition. These authors show that it can be optimal for resource-rich countries to overshoot their long-run equilibrium growth path.
The scarce theoretical literature concerning the relationship between natural resources availability and economic growth usually refers to nonrenewable resources in the context of neoclassical exogenous growth models. As Brown (2000) remarks, technical complexities have led to a limited role for renewable resources in growth models. Although, in recent years, some articles have been filling the hole [i.e., Tahvonen and Kuuluvainen (1991, 1993), Ayong Le Kama (2001), and Wirl (2004)], they still develop into the neoclassical tradition, enlarged just to include an environmental resource sector. Two significant exceptions are Mourmouras (1991) and Gylfason et al. (1999). The first author studies interactions between capital accumulation and renewable resource exploitation in an overlapping generations model. Gylfason et al. build a stochastic two-sector endogenous growth model with tradable and nontradable goods, respectively. They study the consequences from specialization as well as conditions for the emergence of a secondary human-capital-intensive sector, which is the only one that may engender sustained growth. In this paper, however, we come up with a two-sector endogenous growth model à la Lucas (1988), where a single consumption good is obtained using a renewable resource (natural capital) in combination with physical capital. Both inputs are essential for production and, up to some degree, technical substitutes. In this resource-based-economy model, we study the feasibility for sustainable long-run growth. A renewable resource has the capacity to grow in size over time, being able to supply increasing productive inputs to the final-good sector forever without bound. This capability, however, does not materialize automatically because it depends on the endogenous rate of extraction as well as on the exogenous intrinsic rate of growth. The latter mainly arises from natural demographic behavior of the resource stock, but also may be influenced by human ecologically based interventions.
According to Hardin (1968), Clark (1973), Brander and Taylor (1998), and Brown (2000), in the absence of property rights the inefficient overexploitation of natural resources leads the economy to collapse. To avoid this tragedy of the open-access regime, a matter that is beyond the goal of this paper, we assume a private property rights system properly defined over the natural resource. In particular, the stock of natural capital is equally and uniformly owned by consumers. Accordingly, firms do not have open access to the stock because they have to pay the consumers a unit price for the harvested resource. Nevertheless, though the usual market failure caused by nonexcludability had been removed, we introduce a production externality in the final-good sector associated with the natural resource. This assumption is not fundamental for the results in our model, but it enlarges the framework for discussion and opens the possibility for multiple equilibrium paths in connection with the existence, at the aggregate level, of increasing returns to scale over accumulable factors. The presence of an externality in this model, however, makes it necessary to distinguish between the competitive equilibrium solution and the socially optimal solution. In this paper, we focus on the competitive suboptimal equilibrium results.
In this context, we study whether long-run growth may be sustainable in a natural-resource-based competitive economy. Further, we analyze the long-run growth trajectories, examine transitional dynamics, and characterize convergence properties. We find conditions for sustainable long-run growth, which crucially depend on the chosen harvesting rate. We obtain long- as well as short-run trajectories in closed form for all the variables in levels, and show how they can be used to characterize cases of overtaking among different countries. Moreover, we find that every short-run trajectory converges to another long-run one, with the speed of convergence decreasing during transition. We also identify a savings rule that plays the role of the well-known Hartwick's rule in our model. Finally, we supply an exhaustive study of dependences on parameters for all the endogenous variables. Our results show, like those of Gylfason et al. (1999), that natural resource endowments may be a mixed blessing. Usually, abundance is considered as a misfortune, but this is not necessarily true because a higher or lower positive growth is in large measure a matter of choice, and then an endogenously determined outcome. Economic growth relies less on abundance or scarcity of natural resources than on the way they are managed.
The article is organized as follows. In Section 2, we describe the model economy. In Section 3, we solve the intertemporal optimization problem for a competitive economy, and provide the dynamic system that governs its state over time. In Section 4, we show the main analytical competitive equilibrium results. In Section 5, we study economic features associated with equilibrium trajectories, particularly the properties of sustainability, growth, and convergence. In Section 6, we conclude. The complete closed-form solution to the dynamic system is supplied in the Appendix.
We consider a closed and competitive economy that is populated by many identical and infinitely lived agents. Population, which we assume constant, is denoted by N. Individual preferences are represented by a CIES function, 0<σ−1[lg ]1, for consumption
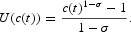
There are two sectors in the economy, the natural resource and the final-good sector.
There is a renewable natural resource,1
According to Stiglitz (1980), a renewable natural resource is a commodity or factor that is provided by nature and not produced, or producible, by man. It is renewable in the sense of a stock that can be maintained, provided it is not consumed too rapidly, or because its supply can be increased after utilization.
The stock of natural capital at date t is denoted by Q(t). We assume that such a stock is composed of homogeneous units and it changes over time because of two different flows that have opposite and offsetting effects on the stock. First, in the absence of any human economically based intervention, the natural resource evolves according to a biotic law of motion that implies exponential growth at a constant rate δ>0.2
This means that the natural resource is not subject to the traditional biological laws that apply to animal species, commonly represented by the logistic equation, or that we abstract from the negative feedbacks associated with overcrowding and environmental resistance. See Peterson and Fisher (1977), as well as Shone (1997) and Perman et al. (1999), for an integrated study of all these biological and economic concepts from an analytical point of view.
As Stiglitz (1980) points out, natural resources require human activity to convert them into a useful form and indeed to extract them, but for simplicity we assume here that extraction costs are negligible.
The extraction rate is an endogenous variable, and the way the economy decides its value has direct effects on the opportunity set for present and future consumption. If the resource is harvested for too long at a rate exceeding its regeneration capabilities, the stock of natural capital will decrease over time.4
Even though natural capital is renewable, this does not mean that it should be inexhaustible. In fact, there is a crucial difference between physical and natural capital: The first one may be used repeatedly without any consequence to its available quantity because only depreciation can reduce it, but the second one disappears automatically from the stock as it is used for production.
This expression may be encompassed in a more general law of motion for animal species that are subject to human harvesting:
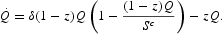
Our equation, then, comes immediately under the particular assumption of no saturation level or an infinite carrying capacity Sc, the maximum stock that the habitat can support.
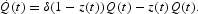
Production of the final single good is carried out by many identical competitive firms with technology represented by a Cobb-Douglas function Yi=AKβi(ziQ)1−βQγa. Production, Yi, depends positively on the stock of physical capital, Ki, on the amount of natural resource that is harvested, destroyed, or transformed each period, ziQ, as well as on the aggregate stock of natural capital, Qa. The latter plays the role of an external effect in the production process, given that all firms benefit from it, but none of the individual harvesting decisions have a significant effect on the aggregate. This externality affects productivity of all private factors of production. It represents the positive effect that the size of the natural stock exerts on the flow of produced goods, simply by augmenting total factor productivity or under the form of a lower implicit cost and a greater implicit quality associated with the harvested natural resource.6
For example, in the case of the forest resource and wooded land, a lower stock might imply either more time and a greater distance to find wood of a certain quality, which must be considered as a higher implicit price, or a lower quality of the harvested wood for a given implicit price. Given that our model does not consider explicitly these elements, which are important for harvesters in their decisionmaking processes, they are indirectly taken into account under the form of a positive external effect.
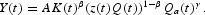
Technology shows constant returns to scale over private internal factors. For fixed Qa, there are diminishing returns to K and Q. If, however, Qa rises along with K, diminishing returns will not arise because of the increasing returns to scale with respect to all the accumulable factors taken together; that is, there are increasing returns to scale at the social level. In this function the efficiency parameter A roughly represents the constant technological level in final-goods sector, parameter β is the elasticity of output with respect to physical capital, and parameter γ is a positive constant capturing the weight of the external effects.
Output may be allocated to either aggregate consumption or physical capital accumulation.7
As previously set, we do not consider explicit extraction costs, which are usually modeled as reducing the amount of output available for consumption and investment.
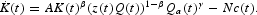
The optimization problem facing this economy, for a given constant intertemporal discount rate ρ>0, consists in choosing the controls c(t) and z(t) ∀t[ges ]0 such that
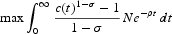
subject to (2) and (4), for K(0)=K0>0 and Q(0)=Q0>0 given.
Because of the technological externality, the economy does not fulfil the required assumptions for the basic welfare theorems to be satisfied. Consequently, the competitive solution of this problem does not correspond to a social optimum. The external effect introduces a distortion between private and social marginal productivity of natural capital, and the intertemporal growth paths are not optimal growth paths in the sense of Pareto. In this paper, we focus on the study of the competitive suboptimal equilibrium and its outcomes, which is still compatible with the presence of increasing returns to scale because of the nonincreasing private returns to both capitals. Therefore, individual agents face a concave optimization problem, as long as the representative agent takes Qa(t) as given when he decides the variables under his control. From now on, we consider the constant population N normalized to 1 and remove the time subscripts from the variables. The current-value Hamiltonian associated with the previous intertemporal optimization problem is8
In the underlying decentralized optimization problem, each competitive firm faces the stationary problem
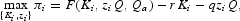
and the consumers side solves the intertemporal optimization problem (P), but taking into account the dynamic constraint
instead of (4). Price q represents the market price of natural resource paid by firms to consumers, r is the interest rate, and in equilibrium:
Given the assumption of constant returns to scale at the private level, output exactly exhausts by paying the inputs according to their marginal productivities. Hence, aggregate economic rents Π become zero.
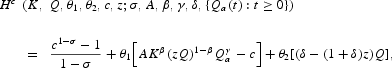
where θ1 and θ2 are the costate variables (shadow prices) associated with K and Q, respectively. The first-order necessary conditions arising from Pontryagin's maximum principle, under the equilibrium condition Qa=Q that makes individual decisions compatible at the aggregate level, are
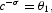
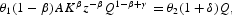
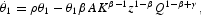
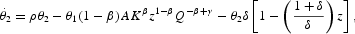
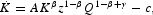
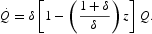
The boundary conditions are K0 and Q0 and
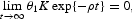
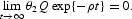
Equation (6) shows that on the margin, the final good must be equally valuable in its two uses: consumption and physical capital accumulation. Namely, the marginal utility of consumption must be equal to the marginal value (implicit price) of physical capital. Equation (7) shows that, at equilibrium, the value of the marginal productivity of natural resource (in case of being harvested) must be equal to the value of its marginal contribution to natural capital accumulation (in case of being saved). The Euler equation (8) states that the marginal productivity of physical capital (the benefit of delaying consumption) equals its rental price, which in the absence of depreciation is given by the difference between the discount rate and the rate of physical capital gains or losses,
. The Euler equation (9) supplies an intertemporal efficiency condition to be satisfied in the process of natural capital allocation. The value, in terms of natural capital, of the marginal productivity of Q in the final-good sector must be equal to its opportunity cost: the difference between the discount rate and the rate of change of the aggregate shadow value of the natural capital stock. This is a modified version of the Hotelling rule, which imposes intertemporal efficiency to the resource extraction activities. After substituting the static efficiency condition (7) into (9), we find that dynamic efficiency requires the intrinsic exogenous rate of growth of natural resource (the benefit of waiting) to be equal to the difference between the discount rate and the rate of capital gains or losses associated with natural capital (the opportunity cost),
.
From (6) and (7), we get the control functions
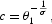
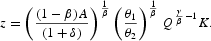
Substituting these expressions in (8)–(11), we obtain the dynamic system
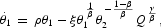
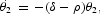
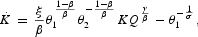
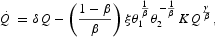
where K and Q represent either the aggregate as well as per capita levels of physical and natural capital, respectively, and
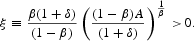
These equations, together with the initial conditions K0 and Q0, and the transversality conditions (12) and (13), make the competitive equilibrium dynamics completely determined over time.
The complete closed-form solution for the variables of the dynamic system (16)–(19), as well as for the controls of the model, can be found in the Appendix. There, we have solved it under the assumption σ=β. Our solution shows that trajectories are different depending on the parameter configuration. There are two disjoint sets of parameter values for which at least one solution trajectory under competitive equilibrium conditions exists. One of them implies a multiplicity of solutions and, hence, indeterminacy. It is the case of multiple solution trajectories starting from the same initial conditions, all of them converging to a unique steady state or balanced growth path. Nevertheless, this case is very implausible because of its counterintuitive predictions. For example, the long-run rate of growth emerges as positively related to the discount rate, whereas the rate of extraction from the natural resource stock shows a negative dependence on this parameter. Consequently, we focus on the parameter subspace which ensures the existence of a unique solution trajectory for every variable. This is the case where the externality is not too strong. In what follows, we summarize the competitive equilibrium results for natural capital, extraction rate, physical capital, output, and the ratio between the two capital stocks.
Result 1. Under the competitive equilibrium conditions, if γ<β and δ(1+γ−β)−ρ<0, then
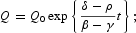
Result 2. Under the competitive equilibrium conditions, if γ<β and δ(1+γ−β)−ρ<0, then
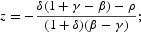
Result 3. Under the competitive equilibrium conditions, if γ<β and −[(β−γ)/β]ρ<δ(1+γ−β)−ρ<0, then
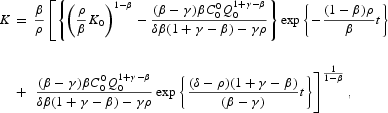
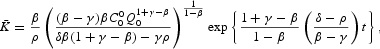
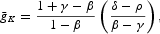
Combining the previous results into the production function we get Result 4.
Result 4. Under the competitive equilibrium conditions, if γ<β and −[(β−γ)/β]ρ<δ(1+γ−β)−ρ<0, then
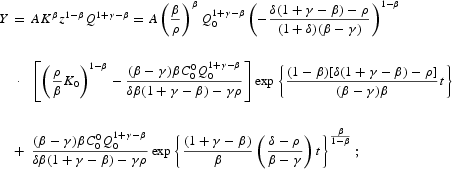

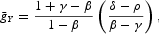
And using the previous results on Q and K, we obtain Result 5.
Result 5. Under the competitive equilibrium conditions, if γ<β, δβ>γρ, and −[(β−γ)/β]ρ<δ(1+γ−β)−ρ<0, then

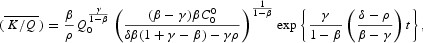
In this section we interpret the previous results stressing the properties of the model in terms of long-run sustainability and growth as well as short-run growth and convergence.
We find that
is positive when δ>ρ. In such a case, using the value of z, we get positive long-run growth for Q associated with a harvesting rate lower than zS=δ/(1+δ).9
The value zS represents the harvesting rate for which the stock of natural capital remains constant over time.
,
, and
. In the alternative case where δ<ρ, results are reversed, associated with a harvesting rate greater than zS. In short, positive long-run growth is sustainable as long as z<zS. Given that zS is increasing with the intrinsic growth rate of natural capital, δ, several exogenous factors affecting birth and death rates, as well as off-the-model human ecologically based interventions, may have an important positive impact on the margins for sustainable growth. Usually, sustainability means a state with a sustained long-run level of per capita consumption in which the natural capital stock, or its flow of resource services, is nondeclining through time. In this paper, we go further, supplying conditions for a positive and sustained long-run rate of growth of consumption per capita. Our results show that, under a well-defined system of property rights, an efficient private management of the natural resource, in both senses intra- and intertemporally, can produce sustainable economic growth even if the presence of a productive externality makes this competitive outcome suboptimal from a social point of view.
The common long-run value of the rate of growth associated with physical capital, consumption, and production,
, depends positively on parameter δ, which represents the biotic rate of growth of natural capital, but negatively on the rate of discount, ρ. These two relationships hold irrespective of the sign of growth. Moreover, this rate of growth depends positively on the parameter associated with externality, γ, when the economy experiences positive growth, δ>ρ, but it changes to the opposite when there is negative growth, δ<ρ. Because of the presence of the externality, the effect of the physical capital share in goods sector, β, on the long-run rate of growth is ambiguous. However, as long as the value of γ is small enough, we can expect a negative effect when δ>ρ and a positive one when δ<ρ. On the other hand, the rate of growth of natural capital,
, depends positively on the parameter δ and negatively on ρ, regardless of the sign of growth. This rate, instead, depends negatively on β and positively on γ when the economy experiences positive growth, changing to the opposite when there is negative growth.
Looking now at the harvesting rate z, we can see that it depends negatively on the intrinsic growth rate δ, and positively on the rate of discount, ρ, irrespective of what happens in terms of growth. However, the harvesting rate increases with β and decreases with γ only when the rate of growth in the economy is positive; otherwise these effects are reversed.
Consequently, an increase in δ that expands the margins for sustainability, because it increases zS and reduces z, has an additional positive effect because it increases the values of the long-run rates of growth
and
. On the other hand, a more patient society chooses a lower harvesting rate and reaches a greater long-run rate of growth. The same is true for an economy with a slightly stronger externality and a lower physical capital share, as long as such economy experiences positive growth. Moreover, in a more patient society, positive long-run growth is still compatible with a natural capital subject to lower biotic rates of growth.
In the short run, however, from (20) the rate of growth of per capita production can be written as
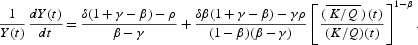
From Result 3, the rate of growth of physical capital stock, which is equal to the rate of growth of per capita consumption according to (A.26), is
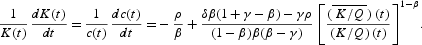
The rates of growth for Y, c, and K are above or below their common long-run rate of growth,
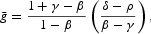
depending on whether the ratio (K/Q) is below or above its long-run level
. The latter, in turn, depends on whether
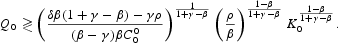
Hence, short-run transitional rates of growth converge, from above or below,10
When δ>ρ, convergence from above occurs for short-run rates of growth always positive, but convergence from below may be found even for initially negative short-run rates of growth crossing the zero axis in finite time. When δ<ρ, convergence from below occurs for short-run rates of growth always negative, but convergence from above may be found even for initially positive short-run rates of growth crossing the zero axis in finite time.
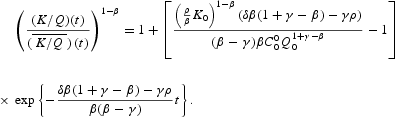
Coming back to the levels of the variables, in the short run, trajectories for K and Y show transitional dynamics as well as convergence to their long-run levels and rates of growth. There are no transitional dynamics for Q and z. The ratio between capital stocks shows transitional dynamics and convergence in both their levels and rates of growth. It has to be remarked that, although the long-run trajectory for Q depends on the initial condition Q0, those of K and Y do not depend on K0, but only on Q0. Actually, this means that what matters for the long-run levels of per capita production is not the initial endowment of physical capital but the endowment of natural resources.11
This particular result strongly depends on the assumption σ=β. In general, things are not so simple but it is a worthwhile example, which helps us to learn about some complex relationships.
If we take two similar countries A and B, with the only difference in their initial endowments of physical and natural capital, they will converge to the same rate of growth. However, during the transition, their growth rates may differ due to differences in the levels of both natural and physical capital stocks. According to (24), the short-run rate of growth of production per capita depends positively on the distance between the short-run and long-run levels of the ratio K/Q. Instead, in terms of the levels of production per capita there could be overtaking, divergence without overtaking, or convergence, depending on the initial conditions.12
This is true only for the case where variables experience positive growth because in the opposite case, when δ<ρ, the only feasible result is convergence, but convergence to zero.
. Here, overtaking appears as absolutely dependent on the initial endowments of natural capital across countries and does not depend on the rate of extraction that they choose during the transition. The resource-rich country will always emerge in finite time as the richest country. Second, pure divergence without overtaking also appears in this model when we observe a relatively resource-rich country A, QA0>QB0, endowed with a higher initial physical capital stock, KA0 [gE ] KB0. In such a case, we have YA(0)>YB(0) and also
in the long run. Third, we can still observe convergence in levels for any initial distribution of physical capital stocks, KA0>rlessKB0, if we have two equal resource-rich countries, QA0=QB0. In such a case, although YA(0)>rlessYB(0), we will observe that, in the long run,
. In summary, all these cases show how much more relevant is natural capital over physical capital, in determining the pattern of growth for different countries over time.
From the definition of speed of convergence and using (20)–(23), we get
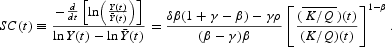
This expression gives the speed of convergence of the current production level to the long-run level. It approaches, from above or below, to the long-run value
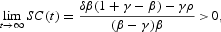
depending on whether
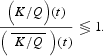
The long-run value of the speed of convergence depends positively on the natural resource intrinsic growth rate, δ, and negatively on the intertemporal rate of discount, ρ. It also depends positively on the externality, γ, when δ>ρ but negatively when δ<ρ. The effect of β is ambiguous.
In general, to the extent that as countries develop their current K/Q values and per capita production levels approach the long-run ones from below, then (27) shows that the speed of convergence decreases during the transition. Furthermore, as long as sustainability is ensured, the rates of growth during the transition are always positive. The picture that Rodríguez and Sachs (1999) describe in terms of short-run evolution for per capita production has nothing to do with ours. They find that, for a developing country, convergence to the steady-state levels occurs from above and predict negative rates of growth during the transition. According to those authors, natural capital abundance allows an economy to afford extraordinary consumption possibilities and, hence, on the transition to the steady state, it grows more slowly because they have an unsustainably high level of income. Nevertheless, the process of convergence in our model does not produce anything comparable to their mechanism of overshooting.
From the definition of saving rate and using our solutions for K, c, and Y as well as (22) and (23), we obtain
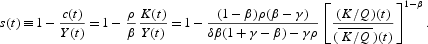
Under the condition δ>ρ, the saving rate converges, from above or below, to its unique long-run value
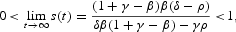
depending on whether
. The long-run saving rate depends positively on δ, as well as on the size of the externality, γ. Moreover, it depends negatively on the discount rate, ρ, but the sign of the effect associated with β is ambiguous. This sign will be positive or negative depending on whether β[gl ](1+γ)/2, if and only if γ ≠ 0. Otherwise, this parameter would not have any influence on the asymptotic saving rate.
The result in (28) connects with the well-known Hartwick's rule, which was developed in the context of a neoclassical growth model with a depletable nonrenewable natural resource. It is a savings rule that concerns the rate at which physical capital must be accumulated to compensate for the diminishing natural resource.13
Rodríguez and Sachs (1999) suggest that an economy has to invest its temporary resource windfalls in international assets that pay permanent annuities, and then consume the interest it earns on such assets.
In a recent paper, Gylfason and Zoega (2001) analyze from a theoretical point of view the influence of natural resource abundance on the saving rate, the rate of growth, and the speed of convergence. They carry out the above study using both a neoclassical growth model as well as an endogenous growth model à la Romer, expanded to include natural resources. In the context of the former, those authors show that the share of natural capital in national income has a negative impact on the saving rate as well as on the long-run level of output per capita, but a positive one on the speed of convergence. In the context of the second model, they show that the saving rate as well as the long-run rate of growth depend negatively on the natural capital share. For now, in this two-sector endogenous growth model, our results show that the long-run value of the saving rate does not depend on the share of natural capital in national income, 1−β, if we make comparable the models assuming γ=0. We confirm their result concerning the speed of convergence but, we find instead, that the long-run rate of growth depends positively on the natural capital share.
Experience seems to show that abundant natural wealth, if not well managed, reduces economic growth in the long run. It does provide nations with short-term increased wealth, but in the long term, this may slow economic growth. In particular, inasmuch as natural resource abundance involves open access to scarce natural resources by private agents, inefficient harvesting and overexploitation will necessarily appear. Here, we showed that under a well-defined system of property rights, the efficient management of the natural resource use can produce sustainable growth, even if the presence of a productive externality makes this competitive outcome suboptimal from a social point of view. If agents are impatient, positive long-run growth is only possible when the natural resource experiences a high biotic rate of growth. An increase in the intrinsic rate of growth of natural resource expands the margins for sustainability and has an additional positive effect on the long-run rate of growth. Moreover, a patient society chooses a lower harvesting rate and reaches a greater long-run rate of growth. We also showed that in the short run, production and consumption show transitional dynamics as well as convergence to their long-run levels and rates of growth. During transition, the speed of convergence decreases. In the particular case of no externality affecting production, our model predicts that the saving rate does not depend on the natural capital share; the long-run rate of growth and the speed of convergence depend positively, and the extraction rate negatively. In general, we can explain most of the empirical facts described by Gylfason and Zoega (2001) and Gylfason (2001a,b). If we consider two differently endowed economies, they will converge in rates of growth whenever they share the same technological and preference parameters. However, things are very different in terms of the levels of variables since there could be overtaking, divergence without overtaking, or convergence, depending on the initial conditions. In any case, the prominent importance of natural capital for growth has to be noted.
Our analytical results have been obtained under the simplifying assumption that the inverse of the intertemporal elasticity of substitution equals the physical capital share. This imposes three shortcomings: consumption is proportional to physical capital stock, the initial physical capital stock does not appear to be determining any of the long-run balanced growth paths, and transitional dynamics are partially simplified. Consequently, our model has to be considered only as an indicative theory of the growth process in economies where production is obtained using a renewable natural resource in combination with other factors.
Given the nature of the model and its assumptions, we find different opportunities for public intervention. First, governmental organizations, mainly national and international, have an important role to play by establishing a well-functioning legal system that enhances private property rights or well-managed common ownership. Second, governmental organizations coordinated at different levels, mainly regional and local, can play a major role undertaking active ecological and environmental policies that, by affecting the intrinsic rate of growth of natural resources, expand the margins for sustainable economic growth. Finally, by means of a direct regulation, optimal taxes and subsidies can be designed to create appropriate incentives for private behavior to eliminate the wedge between decentralized and social planner solutions. In future research, we will take the natural-resource-based economy described in this paper and study the solution to the social optimum problem as well as the issue of tax regulation and the problem of resource exploitation under an open access regime.
Here we solve in closed form the nonlinear dynamic system (16)–(19), together with the initial conditions K0 and Q0 and the transversality conditions (12) and (13), and supply the analytical solution trajectories for its variables. The assumption required to do this, as in Xie (1994), is that the inverse of the intertemporal elasticity of substitution equals the elasticity of final-good production with respect to physical capital stock, that is, the physical capital share. We characterize the parameter space with some constraints that define different subspaces where states, costates, and controls may follow a unique equilibrium trajectory, a multiplicity of equilibrium trajectories, or even no equilibrium trajectory at all.
PROPOSITION 1. Along any equilibrium path, θ2 grows permanently at a constant rate, −(δ−ρ)[lg ]0. Each of these paths, in turn, represents a balanced growth path for θ2.
Proof. From (17), we obtain
constant. Hence,

where θ2(0) has still to be determined.
Consider now the instrumental variable X defined as
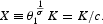
By totally differentiating and substituting from (16) and (18), we get
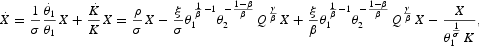
which, under the assumption σ=β, transforms into the following linear differential equation with constant coefficients
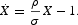
Given K0 and a certain initial value θ1(0), for the moment unknown, we can generate an initial condition for X, namely
. Then, a particular solution to (A.3) is

The transversality condition (12) allows us to establish and prove Proposition 2.
PROPOSITION 2. Along any equilibrium path, X remains constant at the stationary value
.
Proof. From (A.2) and (A.4), under the assumption σ=β, we get
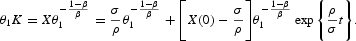
Then, (12) may be written as
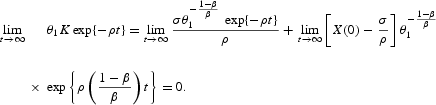
Given that X is always nonnegative, the transversality condition imposes as a necessary but not sufficient condition
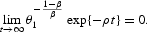
Consequently, looking at the second right-hand term of (A.5), we realize that the transversality condition also imposes the constraint X(0)=σ/ρ, from which we deduce the stationarity of X simply by substituting in (A.4). This is the unique nonexplosive solution trajectory for X, a constant value given by its initial condition. This result implies a particular and well-defined initial value for θ1:
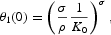
where σ=β.
PROPOSITION 3. Under the competitive equilibrium conditions:
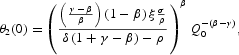
Proof. Using the previous result on X, we come back to the system (16)–(19), which now may be sequentially solved in closed form. Substitute the results from Propositions 1 and 2 in (19), getting
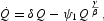
where
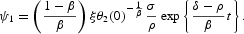
Equation (A.8) may be solved in two steps using Bernoulli's method, which leads to the general solution
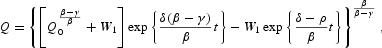
where
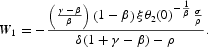
The transversality condition (13), in turn, may be written as
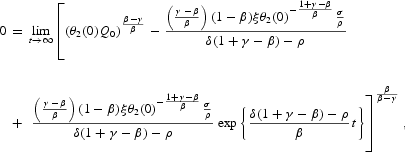
and the different cases in Proposition 3 arise automatically.
From Proposition 3, we find that θ2(0) admits the general specification
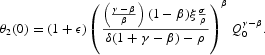
This expression corresponds to case (i) under the additional constraints γ>β and δ(1+γ−β)−ρ>0 for any ε[gl ]0. Moreover, it corresponds to case (iv) under the alternative set of constraints: ε=0, γ<β, and δ(1+γ−β)−ρ<0. On the other hand, the coefficient W1 appearing in (A.9) may be simplified by defining
, where
and Δ[gl ]0, depending on whether ε[lg ]0. Now, we can use this definition to derive a general expression for Q, which encompasses the two cases (i) and (iv) from Proposition 3:
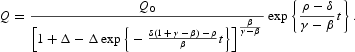
This expression corresponds to case (i) under γ>β and δ(1+γ−β)−ρ>0, for any Δ[gl ]0. It shows a multiplicity of solution trajectories for Q because of the indeterminate value of parameter Δ. Moreover, it corresponds to case (iv) under ε=Δ=0, γ<β, and δ(1+γ−β)−ρ<0, showing a unique solution trajectory for Q because in this case Δ takes a definite value.
PROPOSITION 4. Under the competitive equilibrium conditions:
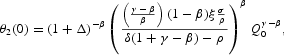
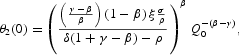
Otherwise, no equilibrium path for θ2 exists.
Proof. Take (A.1) and substitute θ2(0) from (A.11). Then,
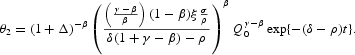
Multiplicity arises from the indeterminate value of Δ, whereas in case (b), where Δ=0, the indeterminacy disappears and we get a unique trajectory.
COROLLARY 1. The equilibrium paths for θ2 and Q take only positive values if and only if Δ>−1.
Proof. From (A.13), given the correlation among the signs of the parameter constraints as shown in Proposition 4, the positiveness of θ2 depends on the constraint Δ>−1, alone. From (A.12), the positiveness of Q also depends on Δ>−1, given the sign of the constraints in Proposition 3.
PROPOSITION 5. If γ>β, δ(1+γ−β)−ρ>0, and Δ>−1, then any of the multiple equilibrium trajectories for Q starting from Q0, while describing transitional dynamics, approaches asymptotically to an undetermined positive balanced growth path where the natural capital stock grows permanently at a constant rate
, depending on whether ρ[gl ]δ.
Proof. Under the above parameter constraints, taking the limit of (A.12), we find that, in the long run, any of the multiple equilibrium trajectories for Q evolve transitionally, approaching their associated balanced growth path:
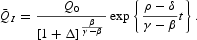
Along these asymptotic paths, Q is positive and grows at a constant rate, which is positive or negative according to ρ[gl ]δ.
PROPOSITION 6. If γ<β and δ(1+γ−β)−ρ<0, then associated with the unique equilibrium trajectory for Q starting from Q0, transitional dynamics do not exist at all, and the natural capital stock grows forever along such a positive balanced growth path at a constant rate
depending on whether δ[gl ]ρ.
Proof. Under the constraint of a weak externality γ<β and δ(1+γ−β)−ρ<0, and by Proposition 3, Δ=0. Then, substituting in (A.12), we directly get the balanced growth path
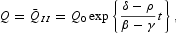
along which Q is positive and grows without transition at a constant rate, which is positive or negative according to δ[gl ]ρ.
PROPOSITION 7. Under the competitive equilibrium conditions:
Otherwise, no equilibrium path exists for θ1 starting from θ1(0).
Proof. Substituting (A.12) and (A.13) into (16), we get
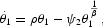
where
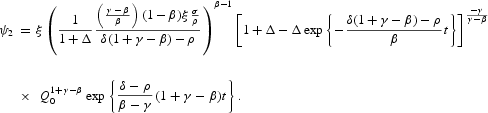
Equation (A.16) may be solved as before, applying Bernoulli's method, which leads to the solution
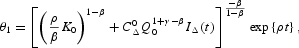
where
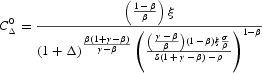
is an indeterminate constant, which depends on the value of parameter Δ, and IΔ(t) represents the following definite integral, which also depends on Δ:

Equation (A.17) gives a continuum of solution trajectories for θ1 depending on the indeterminate value of Δ as well as on the value of the remaining structural parameters. Hence, we study this expression under the two sets of parameter constraints.
First, consider γ>β and δ(1+γ−β)−ρ>0. Then, the transversality condition (A.5), which imposes limt→∞θ−(1−β)/β1exp{−ρt}=0, given (A.17) may be simplified to limt→∞IΔ(t)exp{−(ρ/β)t}=0. Under the above parameter constraints, the integrand function in (A.18) converges in the long run to the pure exponential function
. This suggest a bound to the function IΔ(t) as
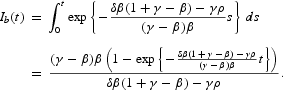
Then, if we take the transversality condition in the limit as t tends to infinity, we can rewrite the previous necessary condition in terms of the bounding function just introduced: limt→∞Ib(t)exp{−(ρ/β)t}=0. It is easy to see that, under the prevailing set of parameter constraints, this condition always holds and no other parameter constraint is needed.
Second, consider γ<β, δ(1+γ−β)−ρ<0 and Δ=0. In this case (A.17) simplifies to
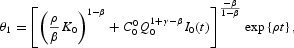
where
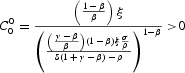
is the value for the constant C0Δ when Δ=0, and
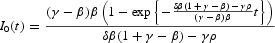
represents the solution to the integral function IΔ(t) under Δ=0. After some substitutions and rearranging terms, we get
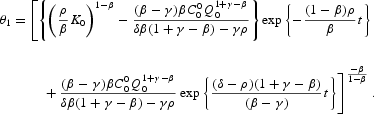
Therefore, given (A.19) and the prevailing set of parameter constraints, the transversality condition (A.5) will always be met with no additional constraint on the parameters. In this case, there exists a unique equilibrium path for θ1 starting from θ1(0).
PROPOSITION 8. Under the competitive equilibrium conditions:
Otherwise, no equilibrium path exists for K starting from K0.
Proof. Given (A.2), Proposition 2, and (A.17), we get
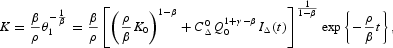
which, associated with the parameter constraints γ>β and δ(1+γ−β)−ρ>0, shows a continuum of solution trajectories for K depending on the indeterminate value of Δ. Instead, when the prevailing set of parameter constraints is γ<β, δ(1+γ−β)−ρ<0, and Δ=0, the expression simplifies to
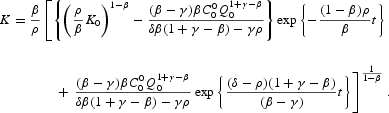
In this case, there exists a unique equilibrium path for K starting from K0. Given the direct relationship between K and θ1, the different cases in Proposition 8 are the counterpart of such displayed in Proposition 7.
COROLLARY 2. In the case where γ>β and δ(1+γ−β)−ρ>0, if Δ>−1, and δβ(1+γ−β)−γρ<0, then the multiple equilibrium paths for θ1 and K take only positive values.
Proof. Looking at (A.17) and (A.20), if C0Δ and IΔ(t) are always positive, then we get always positive, values for θ1 and K. Given the signs of the parameter constraints, both C0Δ and I(t) are always positive if Δ>−1 and δβ(1+γ−β)−γρ<0.
COROLLARY 3. In the case where γ<β and δ(1+γ−β)−ρ<0, and hence Δ=0, if δβ(1+γ−β)−γρ>0, then the unique equilibrium paths for θ1 and K take only positive values.
Proof. This result is immediate from (A.19) and (A.21).
PROPOSITION 9. If γ>β, δ(1+γ−β)−ρ>0, δβ(1+γ−β)−γρ<0, and Δ>−1, then any of the multiple equilibrium trajectories for K starting from K0, while describing transitional dynamics, approaches asymptotically to an undetermined positive balanced growth path where the physical capital stock grows permanently at a constant rate
depending on whether ρ[gl ]δ.
Proof. Under the above parameter constraints, taking the limit of (A.17), we find that, in the long run, any of the multiple-equilibrium trajectories for θ1 evolve transitionally, approaching its associated balanced growth path
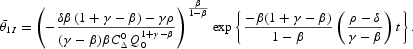
Then, given definition (A.2) and Proposition 2, in the long run, any of the multiple-equilibrium trajectories for K evolve transitionally, approaching its associated balanced growth path
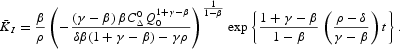
Along these asymptotic paths, K and θ1 are both positive and grow at a constant rate. It is easy to see that these variables evolve in opposite directions: K increases (decreases) while θ1 decreases (increases), depending on whether ρ[gl ]δ.
PROPOSITION 10. If γ<β, δ(1+γ−β)−ρ<0 and δβ(1+γ−β)−γρ>0, then the unique equilibrium trajectory for K starting from K0, while describing transitional dynamics, approaches asymptotically to the unique positive balanced growth path where the physical capital stock grows permanently at a constant rate
depending on whether δ[gl ]ρ.
Proof. Under the constraint of a weak externality γ<β and δ(1+γ−β)−ρ<0, but also Δ=0. Therefore, taking the limit of (A.21), we find that in the long run, the unique equilibrium trajectory for K evolves transitionally, approaching the unique balanced growth path

Along this path, K is positive and grows at a constant rate, which is positive or negative depending on whether δ[gl ]ρ.
Moreover, to have a complete description of prices, we use definition (A.2) and Proposition 2 to see that in the long run, the unique equilibrium trajectory for θ1 evolves transitionally, approaching the unique balanced growth path
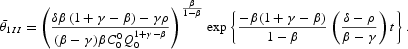
Along this path, θ1 is positive and its constant rate of growth shows, with respect to K, the opposite sign.
PROPOSITION 11. Under the competitive equilibrium conditions:
Proof. Given (14), (A.2), and Proposition 2, we get
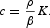
Consequently, all the statements in this proposition have been indirectly proved in the proofs of previous propositions concerning variable K.
PROPOSITION 12. Under the competitive equilibrium conditions:
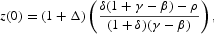
Otherwise, no equilibrium path exists for z.
Proof. Given Proposition 2, (A.12), and (A.13), the control function (15) may be reduced to
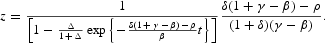
When γ>β and δ(1+γ−β)−ρ>0, (A.27) gives a continuum of solution trajectories for z because of the indeterminate value of Δ. Moreover, in the long run, any of the multiple-equilibrium trajectories for z evolve transitionally, approaching the same constant path
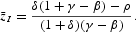
When γ<β and δ(1+γ−β)−ρ<0, given Δ=0, the indeterminacy disappears and we find a unique and constant equilibrium trajectory

In this case, there are no transitional dynamics for z.
PROPOSITION 13. Under the competitive equilibrium conditions:
Proof. From the proof of the preceding proposition, in case (a), any of the multiple-equilibrium trajectories for z starting from the indeterminate value
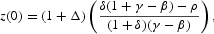
approaches monotonically to
, as given in (A.28). It is easy to prove that 1>z(0)>0 if and only if (γ−β+ρ−δ)/[δ(1+γ−β)−ρ]>Δ>−1, but also that
if and only if γ−β+ρ−δ>0. In case (b), variable z follows a constant trajectory associated with the initial value
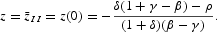
In this case, constraint 1>z>0 holds if and only if γ−β+ρ−δ<0.
We thank two anonymous referees for their helpful comments. Authors acknowledge the support of the Belgian research programmes PAI P5/10 and ARC 03/08-302, and the financial support from the Spanish CICYT, Projects SEC99-0820 and SEC2000-0260. Ruiz-Tamarit also acknowledges the grant PR2003-0107 from the Secretaría de Estado de Educación y Universidades, Spanish MECD.