1. INTRODUCTION
Global Navigation Satellite System (GNSS) is a general term used for a satellite navigation system that provides global coverage. GNSS receivers greatly benefit from the modernisation of the existing GNSS constellations such as the Global Positioning System (GPS) and Globalnaya Navigatsionnaya Sputnikovaya Sistema (GLONASS) as well as from the launch of new ones such as Galileo and BeiDou (BDS or Compass). Combining these GNSS constellations (effectively as multi-GNSS constellations) can significantly improve positioning performance in urban canyons and heavily shadowed areas. For instance, to improve the positioning performance, BeiDou, GLONASS and Galileo constellations can be utilised to augment GPS receivers by offering more useful satellites (Liu et al., Reference Liu, Shi, Li and Wan2006; Ong et al., Reference Ong, Petovello and Lachapelle2009; Wang et al., Reference Wang, Knight and Lu2011). They can also be introduced into GPS receivers to improve the performance of Receiver Autonomous Integrity Monitoring (RAIM) (Hewitson and Wang, Reference Hewitson and Wang2006; Liu et al., Reference Liu, Lu, Cui and Feng2007; Wang and Ober, Reference Wang and Ober2009; Teng and Shi, Reference Teng and Shi2012).
In multi-GNSS constellations, the positioning accuracy is mainly affected by the ranging errors and the satellite geometry. The geometry is referred to as the Geometric Dilution of Precision (GDOP), which is frequently thought of as a number signifying the effect of satellite geometry on the positioning accuracy (Zhao et al., Reference Zhao, Ou and Yuan2005; Wu et al., Reference Wu, Su and Ho2011; Yang et al., Reference Yang, Peng, Dong, Fan, Liu and Wang2011b). In addition, GDOP can also be widely utilized for selecting the satellites for positioning calculation (Zhang et al., Reference Zhang, Zhang and Qin2008; Blanco-Delgado and Nunes, Reference Blanco-Delgado and Nunes2010a). Among the metrics of GDOP, the change of GDOP is of great importance.
In a single constellation, Yarlagadda et al. (Reference Yarlagadda, Ali, Al-Dhahir and Hershey2000) discussed the change of GDOP. The results show that adding one satellite into the existing constellation decreases GDOP. Actually, in multi-GNSS constellations, when one or more satellites are added into the existing constellations, the added satellites may or may not belong to the tracked existing constellations. This will make the changes of GDOPs more complicated. It is important to look into some new characteristics of the GDOPs for multi-GNSS scenarios. Our studies have identified such new characteristics.
The remaining parts of this paper are organized as follows. Section 2 briefly reviews the calculation method of GDOP in multi-GNSS constellations. Section 3 discusses the changes of GDOP with the constellations of the added satellites in multi-GNSS constellations. Numerical experiments are given in Section 4, and the paper is concluded in Section 5.
2. GDOP CALCULATION IN MULTI-GNSS CONSTELLATIONS
In multi-GNSS constellations, the incompatibility of different constellations, mainly referring to the coordinate and time system errors between them, should be taken into account. The difference between the International Terrestrial Reference Framework (ITRF) and the coordinate reference framework of GPS, Galileo and BeiDou (respectively, WGS-84, CTRF, and CGCS 2000) is only a few centimetres. Their difference can be ignored for navigation (Hofmann-Wellenhof et al., Reference Hofmann-Wellenhof, Lichtenegger and Walse2008; Yang, Reference Yang2009). The PZ-90 coordinate system of GLONASS is a little different from ITRF. Yang et al. (Reference Yang, Li, Xu, Tang, Guo and He2011a) analysed the difference of the coordinate system errors between these different constellations, and concluded that the difference of coordinate system has no influence on the calculation of GDOP.
On the other hand, there are generally two ways to deal with the differences in the time systems (Kaplan and Hegarty, Reference Kaplan and Hegarty2006; Hofmann-Wellenhof et al., Reference Hofmann-Wellenhof, Lichtenegger and Walse2008). One is broadcasting the time difference between different constellations in the broadcast ephemeris and the other is adding one unknown time system error parameter in the process of positioning calculation. In our studies, the latter is considered. Thus, the GDOP in the single point positioning with multi-GNSS constellations is defined as:
$$GDOP = \sqrt {tr\left[ {\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n} \right)^{ - 1}} \right]} $$where Hn is called the geometric matrix, and Qn is the weight matrix related to the measurement noise with the multi-GNSS constellations. They are given by:
$${\bi H}_n = \left[ {\matrix{ {{\bi H}_A} & {{\bi 1}_A} & {{\bi 0}_A} & {{\bi 0}_A} & \ldots \cr {{\bi H}_B} & {{\bi 0}_B} & {{\bi 1}_B} & {{\bi 0}_B} & \ldots \cr {{\bi H}_C} & {{\bi 0}_C} & {{\bi 0}_C} & {{\bi 1}_C} & \ldots \cr \ldots & \ldots & \ldots & \ldots & \ldots \cr}} \right],\quad {\bi Q}_n = \left[ {\matrix{ {{\bi Q}_A} & {} & {} & {} \cr {} & {{\bi Q}_B} & {} & {} \cr {} & {} & {{\bi Q}_C} & {} \cr {} & {} & {} & \ldots \cr}} \right]$$In Equation (2), the subscripts γ=A, B, C, … denote the different constellations (such as GPS, GLONASS, Galileo and BeiDou). Correspondingly, Hγ and Qγ are the geometric matrix and the weight matrix in γ. Defining n γ as the number of tracked satellites in γ, and then n=n A+ n B+n C+… denotes the total number of satellites. The ones vectors (1γ) and the zeros vectors (0γ) are located in different columns in order to get each receiver clock bias, because the biases for different constellations are different (Choi et al., Reference Choi, Blanch, Akos, Heng, Gao, Walter and Enge2011; Wang et al., Reference Wang, Knight and Lu2011).
Moreover, Qn is a block diagonal matrix and Qγ are diagonal matrices. The weight matrix Qn is introduced in Equation (1) as the GDOP calculation with the multi-GNSS constellations requires proper weighting of individual satellites' range measurement. In addition, Qn also permits the quantification of the non-geometric effect of some factors. More details about it and the impact of different measurement errors are discussed in Blanco-Delgado and Nunes (Reference Blanco-Delgado and Nunes2010b).
Supposing hi denotes the direction cosine vector between the receiver and the corresponding satellite, and then the matrix Hγ in Equation (2) is expressed as:
$${\bi H}_A = \left[ {\matrix{ {{\bi h}_1} \cr \ldots \cr {{\bi h}_{n_A}} \cr}} \right],\quad {\bi H}_B = \left[ {\matrix{ {{\bi h}_{n_A + 1}} \cr \ldots \cr {{\bi h}_{n_A + n_B}} \cr}} \right],\quad H_C = \left[ {\matrix{ {{\bi h}_{n_A + {n_B + 1}}} \cr \ldots \cr {{\bi h}_{n_A + _{n_B} + _{n_C}}} \cr}} \right], \ldots $$In Equation (3), the direction cosine vector hi can be calculated by the approximate position of the receiver and the position of the corresponding satellite.
3. CHANGE OF GDOP IN MULTI-GNSS CONSTELLATIONS
In multi-GNSS constellations, adding satellites has influences on the geometric matrix, and changes the GDOP consequently. In this section, we take multi-GNSS constellations including two single constellations (A and B) as an example, and then add satellites to show the change of GDOP. For the convenience of discussion, the multi-GNSS constellations including A and B can be written as A/B for short.
From the point of the constellation of the added satellites, three different cases will be taken into consideration. They are listed in Table 1.
Table 1. Three different cases of adding satellites.
3.1. Adding satellites from the existing constellations (Case 1)
When one satellite from the initial set of satellites is added (in this section, one satellite from B is added into A/B), the geometric matrix and the weight matrix in Equation (2) can be described as:
$${\bi H}_{(n + 1)} = \left[ {\matrix{ {{\bi H}_A} & {{\bi 1}_A} & {{\bi 0}_A} \cr {{\bi H}_B} & {{\bi 0}_B} & {{\bi 1}_B} \cr {{\bi h}_B} & 0 & 1 \cr}} \right],\quad {\bi Q}_{(n + 1)} = \left[ {\matrix{ {{\bi Q}_A} & {} & {} \cr {} & {{\bi Q}_B} & {} \cr {} & {} & {q_{(n + 1)}} \cr}} \right]$$where hB denotes the direction cosine vector, and q (n+1) is the weight value relative to the added satellite. Assuming h=[hB 1 0], then Equation (4) can be written as:
$${\bi H}_{(n + 1)} = \left[ {\matrix{ {{\bi H}_n} \cr {\bi h} \cr}} \right],\quad {\bi Q}_{(n + 1)} = \left[ {\matrix{ {{\bi Q}_n} & {} \cr {} & {q_{(n + 1)}} \cr}} \right]$$From Equation (5), we can obtain:
$${\bi H}_{(n + 1)}^T {\bi Q}_{(n + 1)} {\bi H}_{(n + 1)} = {\bi H}_n^T {\bi Q}_n {\bi H}_n + q_{(n + 1)} {\bi h}^T {\bi h}$$According to the expression of GDOP in Equation (1), we have:
$$GDOP_{(n + 1)}^2 = tr\left[ {\left( {{\bi H}_{(n + 1)}^T {\bi Q}_{(n + 1)} {\bi H}_{(n + 1)}} \right)^{ - 1}} \right] = tr\left[ {\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n + q_{(n + 1)} {\bi h}^T {\bi h}} \right)^{ - 1}} \right]$$Let
$${\bi H}_n^T {\bi Q}_n {\bi H}_n = {\bi U\Lambda U}^T $$where U is an orthogonal matrix, and 
${\bi \Lambda} = diag\left[ {\lambda _1, \cdots, \lambda _5} \right]$ is a diagonal matrix. As 
${\bi H}_n^T {\bi Q}_n {\bi H}_n $ is a symmetric and positive definite matrix, then its diagonal elements are positive (Horn and Johnson, Reference Horn and Johnson2010). Taking the inverse of both sides of Equation (8) results in:
$$\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n} \right)^{ - 1} = \left( {{\bi U\Lambda U}^T} \right)^{ - 1} = {\bi U\Lambda} ^{ - 1} {\bi U}^T $$Substituting Equations (8) into (7), then the latter can be transformed as
$$\eqalign{tr\left[ {\left( {{\bi H}_{_{\left( {n + 1} \right)}} ^T {\bi Q}_{_{\left( {n + 1} \right)}} {\bi H}_{_{\left( {n + 1} \right)}}} \right)^{ - 1}} \right] & = tr\left[ {\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n + q_{\left( {n + 1} \right)} {\bi h}^T {\bi h}} \right)^{ - 1}} \right] \cr & = tr\left\{ {\left[ {{\bi U}\left( {{\bi \Lambda} + q_{\left( {n + 1} \right)} {\bi U}^T {\bi h}^T {\bi hU}} \right){\bi U}^T} \right]^{ - 1}} \right\} \cr & = tr\left[ {{\bi U}\left( {{\bi \Lambda} + {\bi \alpha} ^T {\bi \alpha}} \right)^{ - 1} {\bi U}^T} \right]} $$In Equation (10), α can be given by
$${\bi \alpha} = \sqrt {q_{\left( {n + 1} \right)}} {\bi hU} = \left[ {\alpha _1 \;\;\alpha _2 \;\;\alpha _3 \;\;\alpha _4 \;\;\alpha _5} \right]$$Applying the Sherman-Morrison formula (Sherman and Morrison, Reference Sherman and Morrison1949; Reference Sherman and Morrison1950), we can obtain:
$$\left( {{\bi \Lambda} + {\bi \alpha} ^T {\bi \alpha}} \right)^{ - 1} = {\bi \Lambda} ^{ - 1} - \displaystyle{{{\bi \Lambda} ^{ - 1} {\bi \alpha} ^T {\bi \alpha \Lambda} ^{ - 1}} \over {1 + {\bi \alpha \Lambda} ^{ - 1} {\bi \alpha} ^T}} = {\bi \Lambda} ^{ - 1} -\beta \left( {{\bi \alpha} ^*} \right)^T \left( {{\bi \alpha} ^*} \right)$$where
$${\bi \alpha} ^* = {\bi \alpha \Lambda} ^{ - 1},\quad \beta = \displaystyle{1 \over {1 + \gamma}} $$In Equation (13), γ can be calculated by
$$\gamma = \sum\limits_{i = 1}^5 {\displaystyle{{\alpha _i^2} \over {\lambda _i}}} $$The substitution of Equations (12) into (10) leads to
$$\eqalign{tr\left[ {\left( {{\bi H}_{(n + 1)}^T {\bi Q}_{(n + 1)} {\bi H}_{(n + 1)}} \right)^{ - 1}} \right] & = tr\left( {{\bi U\Lambda}} ^{ - 1} {\bi U}^T} \right) - \beta \cdot tr\left[ {{\bi U}\left( {{\bi \alpha} ^*} \right)^T \left( {{\bi \alpha} ^*} \right){\bi U}^T} \right] \cr & = tr\left[ {\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n} \right)^{ - 1}} \right] - \beta \cdot tr\left[ {\left( {{\bi \alpha} ^*} \right)^T \left( {{\bi \alpha} ^*} \right)} \right]} $$Combining Equations (15) with (7) gives
$$GDOP_{(n + 1)}^2 = GDOP_n^2 - \beta \cdot tr\left[ {\left( {{\bi \alpha} ^*} \right)^T \left( {{\bi \alpha} ^*} \right)} \right] = GDOP_n^2 - p$$where
$$p = \beta \cdot tr\left[ {\left( {{\bi \alpha} ^*} \right)^T \left( {{\bi \alpha} ^*} \right)} \right] = \displaystyle{1 \over {1 + \gamma}} \left[ {\sum\limits_{i = 1}^5 {\left( {\displaystyle{{\alpha _i} \over {\lambda _i}}} \right)^2}} \right] \gt 0$$Accordingly,
$$GDOP_{(n + 1)} \lt GDOP_n $$The inequality in Equation (18) shows that adding one satellite from B into A/B, the GDOP value always decreases. Similarly, the same conclusion is also obtained when one satellite from A is added into A/B. Accordingly, in the multi-GNSS constellations, if the added satellite is from the existing constellations within the current solution, increasing the number of satellites always reduces the GDOP.
3.2. Adding satellites from one different constellation (Case 2)
Adding a satellite from a different constellation, i.e., adding one satellite from C into A/B, the change of GDOP will be discussed in this section. Similar to Equation (2), the geometric matrix and the weight matrix in those circumstances are given by:
$${\bi \vec H}_{(n + 1)} = \left[ {\matrix{ {{\bi H}_A} & {{\bi 1}_A} & {{\bi 0}_A} & {{\bi 0}_A} \cr {{\bi H}_B} & {{\bi 0}_B} & {{\bi 1}_B} & {{\bi 0}_B} \cr {{\bi h}_C} & 0 & 0 & 1 \cr}} \right],\quad {\bi \vec Q}_{(n + 1)} = \left[ {\matrix{ {{\bi Q}_A} & {} & {} \cr {} & {{\bi Q}_B} & {} \cr {} & {} & {\vec q_{(n + 1)}} \cr}} \right]$$where hC denotes the direction cosine vector, and 
$\vec q_{(n + 1)} $ is the weight value relative to the added satellite. Defining 
${\bi \vec h =} \left[ {\matrix{ {{\bi h}_C} & 0 & 0 \cr}} \right]$, and then we can partition the unitary matrix and the weight matrix described in Equation (19) as
$${\bi \vec H}_{(n + 1)} = \left[ {\matrix{ {{\bi H}_n} & {{\bi 0}_{A + B}} \cr {{\bi \vec h}} & 1 \cr}} \right],\quad {\bi \vec Q}_{(n + 1)} = \left[ {\matrix{ {{\bi Q}_n} & {} \cr {} & {\vec q_{(n + 1)}} \cr}} \right]$$Therefore,
$${\bi \vec H}_{(n + 1)}^T {\bi \vec Q}_{(n + 1)} {\bi \vec H}_{(n + 1)} = \left[ {\matrix{ {{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}} & {\vec q_{(n + 1)} {\bi \vec h}^T} \cr {\vec q_{(n + 1)} {\bi \vec h}} & {\vec q_{(n + 1)}} \cr}} \right]$$According to Hotelling (Reference Hotelling1943a) and (Reference Hotelling1943b), taking the inverse of both sides of Equation (21) results in
$$\hskip-14pt\eqalign{& \left( {{\bi \vec H}^T _{(n + 1)} {\bi \vec Q}_{(n + 1)} {\bi \vec H}_{(n + 1)}} \right)^{ - 1} \cr & = \left[ {\matrix{ {\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n} \right)^{ - 1}} & \ldots \cr \ldots & {\left( {\vec q_{(n + 1)} - \vec q_{(n + 1)} {\bi \vec h}\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}} \right)^{ - 1} \vec q_{(n + 1)} {\bi \vec h}^T} \right)^{ - 1}} \cr}} \right]} $$Therefore,
$$\eqalign{& tr\left[ {\left( {{\bi \vec H}_{(n + 1)}^T {\bi \vec Q}_{(n + 1)} {\bi \vec H}_{(n + 1)}} \right)^{ - 1}} \right] \cr & = tr\left[ {\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n} \right)^{ - 1}} \right] + tr\left[ {\left( {\vec q_{(n + 1)} - \vec q_{(n + 1)} {\bi \vec h}\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}} \right)^{ - 1} \vec q_{(n + 1)} {\bi \vec h}^T} \right)^{ - 1}} \right]} $$Based on the expression of GDOP, Equation (23) can be simplified as
$$\overrightarrow {GDOP} _{(n + 1)}^2 = GDOP_n^2 + q$$where
$$q = tr\left[ {\left( {\vec q_{(n + 1)} - \vec q_{(n + 1)} {\bi \vec h}\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}} \right)^{ - 1} \vec q_{(n + 1)} {\bi \vec h}^T} \right)^{ - 1}} \right] \gt 0$$From Equation (25), as detailed in the Appendix, we can obtain
$$\overrightarrow {GDOP} _{(n + 1)} \gt GDOP_n $$This is different from the change of GDOP in Section 3.1, and Equation (26) demonstrates that adding one satellite from a third constellation causes the increase of the GDOP.
However, if we continually add a second satellite (from C) into A/B, the geometric matrix and the weight matrix in Equation (19) can be written as
$${\bi \vec H}_{(n + 2)} = \left[ {\matrix{ {} & {{\bi \vec H}_{(n + 1)}} \hskip-12pt & {} & {} \cr {h'_C} & 0 & 0 & 1 \cr}} \right] = \left[ {\matrix{ {{\bi \vec H}_{(n + 1)}} \cr {{\bi h'}} \cr}} \right],\quad {\bi \vec Q}_{(n + 2)} = \left[ {\matrix{ {{\bi \vec Q}_{(n + 1)}} & {} \cr {} & {\vec q_{(n + 2)}} \cr}} \right]$$where 
${\bi h'}_C $ denotes the direction cosine vector, and 
$\vec q_{(n + 2)} $ is the weight value relative to the added satellite. Then the GDOP is calculated by
$$\overrightarrow {GDOP} _{(n + 2)} = \sqrt {tr\left[ {\left( {{\bi \vec H}_{(n + 2)}^T {\bi \vec Q}_{(n + 2)} {\bi \vec H}_{(n + 2)}} \right)^{ - 1}} \right]} $$ It is clear to see that the structures of 
${\bi \vec H}_{(n + 2)} $ and 
${\bi \vec Q}_{(n + 2)} $ in Equation (27) and 
${\bi H}_{(n + 1)} $ and 
${\bi Q}_{(n + 1)} $ in Equation (5) are similar. Thus, the steps of comparing 
$\overrightarrow {GDOP} _{(n + 2)} $ with
$\overrightarrow {GDOP} _{(n + 1)} $ are the same as those of comparing 
$GDOP_{(n + 1)} $ to GDOP n. That is,
$$\overrightarrow {GDOP} _{(n + 2)} \lt \overrightarrow {GDOP} _{(n + 1)} $$Combining Equations (26) and (29) leads to
$$\left\{ \matrix{\overrightarrow {GDOP} _{(n + 1)} \gt GDOP_n \cr \overrightarrow {GDOP} _{(n + 2)} \lt \overrightarrow {GDOP} _{(n + 1)} } \right.$$The inequalities in Equation (30) show that adding one satellite from a third constellation into the existing constellations causes the increase of the GDOP. Continually adding additional satellites, however, causes the decrease of the GDOP.
However, whether 
$\overrightarrow {GDOP} _{(n + 2)} $ is larger than GDOP n or not is unknown. Thus, it is worth mentioning that in this case the simultaneous addition of two satellites from a third constellation may result in a decrease or increase of GDOP depending on the relative positions of the added satellites.
3.3. Adding satellites from two different constellations (Case 3)
If the two satellites which are from another two different constellations (C and D) are simultaneously added into A/B, the geometric matrix and the weight matrix in this case are given by
$$\eqalign{{\bi {\mathop{H}\limits^{\leftarrow}} } _{(n + 2)} = \left[ {\matrix{ {{\bi H}_A} & {{\bi 1}_A} & {{\bi 0}_A} & {{\bi 0}_A} & {{\bi 0}_A} \cr {{\bi H}_B} & {{\bi 0}_B} & {{\bi 1}_B} & {{\bi 0}_B} & {{\bi 0}_B} \cr {{\bi h}_C} & 0 & 0 & 1 & 0 \cr {{\bi h}_D} & 0 & 0 & 0 & 1 \cr}} \right],\quad {\bi {\mathop{Q}\limits^{\leftarrow}} } _{(n + 2)} = \left[ {\matrix{ {{\bi Q}_A} & {} & {} & {} \cr {} & {{\bi Q}_B} & {} & {} \cr {} & {} & {\vec {q}}_{(n + 1)} & {} \cr {} & {} & {} & {{\mathop{q}\limits^{\leftarrow}} } _{(n + 2)}} \cr}} \right]$$where hC and hD denote the direction cosine vectors relative to the added satellites belonging to the C and D constellations, and 
$\vec q_{(n + 1)} $ and 
${{\mathop{q}\limits^{\leftarrow}} } _{(n + 2)} $ are the weight values relative to the two satellites, respectively. Let 
${\bi{\mathop{h}\limits^{\leftarrow}} } {\rm = [}{\bi h}_D\; {\rm 0}\;{\rm 0}\;{\rm 0]}$, then we partition 
${\mathop {\bi H}\limits^{\leftarrow}} _{(n + 2)} $ and 
$ {\mathop{\bi Q}\limits^{\leftarrow}}}_{(n + 2)} $ in Equation (31) as
$${\bi {\mathop{H}\limits^{\leftarrow}} } _{(n + 2)} = \left[ {\matrix{ {{\bi \vec H}_{(n + 1)}} & {{\bi 0}_{A + B + 1}} \cr {\bi {\mathop{h}\limits^{\leftarrow}} } & 1 \cr}} \right],\quad{\bi {\mathop{Q}\limits^{\leftarrow}} } _{(n + 2)} = \left[ {\matrix{ {{\bi \vec Q}_{(n + 1)}} & {} \cr {} & {{\mathop{q}\limits^{\leftarrow}} }_{(n + 2)}} \cr}} \right]$$where 
${\mathop {\bi H}\limits^{\rightarrow}} _{(n + 1)} $ and 
${\mathop {\bi Q}\limits^{\rightarrow} _{(n + 1)} $ are defined in Equation (19).
Therefore,
$${\bi {\mathop{H}\limits^{\leftarrow}} } _{(n + 2)}^T {\bi {\mathop{Q}\limits^{\leftarrow}} } _{(n + 2)} {\bi {\mathop{H}\limits^{\leftarrow}} } _{(n + 2)} = \left[ {\matrix{ {{\bi \vec H}_{(n + 1)}^T {\bi \vec Q}_{(n + 1)} {\bi \vec H}_{(n + 1)} + {{\mathop{q}\limits^{\leftarrow}} } _{(n + 2)} {\bi {\mathop{h}\limits^{\leftarrow}} } ^T {\bi {\mathop{h}\limits^{\leftarrow}} }} & {{{\mathop{q}\limits^{\leftarrow}} } _{(n + 2)} {\bi {\mathop{h}\limits^{\leftarrow}} }^T} \cr {{\mathop{q}\limits^{\leftarrow}} } _{(n + 2)} {\bi {\mathop{h}\limits^{\leftarrow}} } & {{{\mathop{q}\limits^{\leftarrow}} } _{(n + 2)}} \cr}} \right]$$From Section 3.2, it is clear to see that the form of Equation (33) is similar to that of Equation (21). Thus, the inequality in Equation (34) can be obtained by means of the same steps as listed in Section 3.2.
$$tr\left[ {\left( {\bi {\mathop{H}\limits^{\leftarrow}} } _{(n + 2)}^T {\bi {\mathop{Q}\limits^{\leftarrow}} } _{(n + 2)} {\bi {\mathop{H}\limits^{\leftarrow}} } _{(n + 2)}} \right)^{ - 1}} \right] \gt tr\left[ {\left( {{\bi \vec H}_{(n + 1)}^T {\bi \vec Q}_{(n + 1)} {\bi \vec H}_{(n + 1)}} \right)^{ - 1}} \right]$$According to the expression of GDOP, then we have
$$\overleftarrow {GDOP} _{(n + 2)} \gt \overrightarrow {GDOP} _{(n + 1)} $$Combining Equations (35) and (26), Equation (36) can be obtained.
$$\overleftarrow {GDOP} _{(n + 2)} \gt GDOP_n $$Equation (36) indicates that GDOP increases when two satellites from two different constellations are simultaneously added to the existing constellations.
3.4. Further Discussion on the Change of GDOP
From Section 3.1 to 3.3, we take the multi-GNSS constellations (A/B) as an example, and discuss the change of GDOP. Actually, if the multi-GNSS constellations are composed of three different single constellations (i.e., A/B/C for short), the change of GDOP is similar.
Compared to A/B, the structures of the geometric matrix and the weight matrix in A/B/C are similar. Only the dimensions are different. Consequently, the change of GDOP can also be derived by means of similar procedures. That is, if the added satellite is from A, B, or C, the GDOP always decreases. However, if it is from other constellations, different numbers of added satellites have different impacts on the change of GDOP. When one satellite is added, the GDOP increases, while adding a second one decreases the GDOP.
4. NUMERICAL EXPERIMENTS
In this section, we also take A/B as an example to verify the change of GDOP through numerical experiments. For convenience of discussion, we assume that the weight matrix is an identity one.
4.1. Data collection and description
The experimental data are obtained from Lundberg (Reference Lundberg2001), and they are presented in metres. Table 2 illustrates the three-dimensional coordinates and pseudo-ranges of the eight satellites. The multi-GNSS constellations (A/B) consist of the first six satellites (S1–S6), and the other two satellites (S7, S8) are added into A/B for analysing the change of GDOP. Additionally, the first three (S1–S3) and the other three satellites (S4–S6) in A/B belong to A and B, respectively.
Table 2. Coordinates and pseudo-ranges of eight satellites.
4.2. Change of GDOP
Using the coordinates and pseudo-ranges of the eight satellites in Table 2, the GDOP values are shown in Table 3. In this table, GDOP A, GDOPB and 
$\overrightarrow {GDOP} _C $ denote the GDOP for the case of adding satellites from A, B and C, respectively. Additionally, when two satellites (from C and D) are added, the GDOP is denoted as 
$\overleftarrow {GDOP} _{CD} $.
Table 3. GDOP values of three cases.
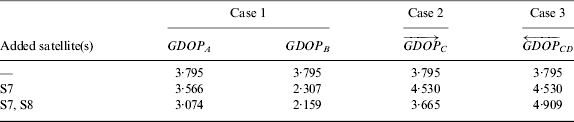
Based on the GDOP values shown in Table 3, it is clear to see that:
(1) Adding satellites which belong to the existing constellations always reduces the GDOP. Taking GDOP A as an example, when S7 is added, the GDOP decreases from 3·795 to 3·566. The change of GDOP in conditions of adding one satellite from B into A/B is the same.
(2) When the added satellite is from the existing constellations, the first difference of the GDOP values in Table 3, namely, the extent of decrease in the GDOP, does not always increase or reduce. This is different from the change of GDOP itself. For instance, ΔGDOP A (the abbreviation of the first difference of GDOP A) are 0·229 and 0·492, respectively. That is, the differences are on the increase. However, ΔGDOP B (the abbreviation of the first difference of GDOP B) are 1·488 and 0·148, respectively. Compared to the former, the latter becomes smaller.
(3) In contrast to the change of GDOP in Case 1, the GDOP in Case 2 does not always decrease. Namely, the different number of the added satellites has different influences on the change of GDOP. For instance, when S7 is added, the GDOP value (
$\overrightarrow {GDOP} _C $) increases from 3·795 to 4·530. While continually adding a second one (S8) causes the decrease of the GDOP, and it decreases from 4·530 to 3·665.(4) Moreover, when the two added satellites are from two different constellations, the GDOP is on the increase. In Table 3, if S7 (from C) and S8 (from D) are added into A/B, the GDOP increases from 3·795 to 4·909.
5. CONCLUSIONS
The influences of the constellation of the added satellites on the change of GDOP in the existing single point positioning for multi-GNSS constellations have been derived theoretically in this paper. The results demonstrate that when the added satellites belong to the existing constellations, the GDOP always decreases with the number of satellites. However, if the added satellites are from different constellations, the different numbers of the added satellites lead to different changes of GDOP. Such new characteristics have provided more knowledge and deeper insights into the GDOPs, which is very important in the selection of satellites for various positioning, navigation, and timing applications.
Besides the GDOP, the Position Dilution of Precision (PDOP), the Horizontal Dilution of Precision (HDOP) and the Vertical Dilution of Precision (VDOP) are several other important parameters with multi-GNSS constellations. Further research is underway to theoretically analyse their performance.
APPENDIX: TO DETERMINE THE PARAMETER SIGN
The proof of Equation (25) is given in this section. Using Equation (8), then
$${\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h} = {\bi U\Lambda U}^T + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}$$Taking the inverse of both sides of Equation (A1) leads to
$$\eqalign{\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}} \right)^{ - 1} & = \left( {{\bi U\Lambda U}^T + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}} \right)^{ - 1} \cr & = \left[ {{\bi U}\left( {{\bi \Lambda} + \vec q_{(n + 1)} {\bi U}^T {\bi \vec h}^T {\bi \vec hU}} \right){\bi U}^T} \right]^{ - 1} \cr & = {\bi U}\left( {{\bi \Lambda} + {\bf \upsilon} ^T {\bf \upsilon}} \right)^{ - 1} {\bi U}^T} $$where the vector 
${\bi \upsilon} = \sqrt {\vec q_{(n + 1)}} {\bi \vec hU}$ with the elements 
$ \upsilon _i (i = 1, \cdots, 5)\!\!$. Based on Equation (A2), then we have
$$\vec q_{(n + 1)} {\bi \vec h}\,{\rm (}{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}{\rm )}^{ - 1} \,\vec q_{(n + 1)} {\bi \vec h}^T {\rm =} \;\vec q_{(n + 1)} {\bi \upsilon} {\rm (}{\bi \Lambda} {\rm +} {\bi \upsilon} ^T {\bi \upsilon} )^{ - 1} {\bi \upsilon} ^T $$By means of the Sherman-Morrison formula, we can write
$$\left( {{\bi \Lambda} {\rm +} {\bi \upsilon} ^T {\bi \upsilon}} \right)^{ - 1} = {\bi \Lambda} ^{ - 1} - \displaystyle{{\bi \Lambda} ^{ - 1} {\bi \upsilon} ^T {\bi \upsilon \Lambda} ^{ - 1} \over {1 + {\bi \upsilon \Lambda} ^{ - 1} {\bi \upsilon} ^T}} = {\bi \Lambda} ^{ - 1} - {\displaystyle{1 \over {1 + \vec \gamma}}} \left( {{\bi \Lambda} ^{ - 1} {\bi \upsilon} ^T {\bi \upsilon \Lambda} ^{ - 1}} \right)$$where
$$\vec \gamma = {\bi \upsilon \Lambda} ^{ - 1} {\bi \upsilon} ^T = \sum\limits_{i = 1}^5 {\left( {\displaystyle{{{\bi \upsilon} _i^2} \over {\lambda _i}}} \right)} $$The substitution of Equations (A4) and (A5) into (A3) leads to
$$\vec q_{(n + 1)} {\bi \vec h}\,{\rm (}{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}{\rm )}^{ - 1} \,\vec q_{(n + 1)} {\bi \vec h}^T {\rm =} \vec q_{(n + 1)} {\displaystyle{{{\rm \vec \gamma}} \over {1 + {\rm \vec \gamma}}}} $$Therefore,
$$\vec q_{(n + 1)} {\rm -} \vec q_{(n + 1)} {\bi \vec h}\,{\rm (}{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}{\rm )}^{ - 1} \,\vec q_{(n + 1)} {\bi \vec h}^T {\rm =} {\displaystyle{{\vec q_{(n + 1)}} \over {1 + {\rm \vec \gamma}}}} $$Furthermore,
$$q = tr\left[ {\left( {\vec q_{(n + 1)} {\rm -} \vec q_{(n + 1)} {\bi \vec h}\,\left( {{\bi H}_n^T {\bi Q}_n {\bi H}_n + \vec q_{(n + 1)} {\bi \vec h}^T {\bi \vec h}} \right)^{ - 1} \,\vec q_{(n + 1)} {\bi \vec h}^T} \right)^{ - 1}} \right]{\rm =} {\displaystyle{{1 + {\rm \vec \gamma}} \over {\vec q_{(n + 1)}}}} \gt 0$$
