1. INTRODUCTION
Teaching graduate econometrics means covering three different kinds of
subject matter: a grounding in the theory of econometrics, a long laundry
list of available econometric techniques, and an introduction to the fact
that the practice of linking models and data is every bit as untidy as
mathematical statistics is neat. I assign Econometric Theory and
Methods (ETM) as a primary text in our first Ph.D.
econometrics course. ETM is in charge of getting the students
their theoretical grounding. I also assign Greene's excellent
Econometric Analysis (2003) for its
coverage of a long list of techniques. My laptop, EViews, and I, together
with a whole lot of real data, are responsible for being untidy.
ETM's forte is that it presents econometric theory in a
consistent, methodical sequence that gives students mathematical tools
immediately applicable to econometric theory. Written by renowned
econometricians, ETM reflects the authors' personal tastes
in choice of which mathematical techniques to emphasize. The book contains
what the authors find most important and leaves out other material. There
is considerable use of projection matrices, artificial regressions, and
Gauss–Newton regressions, and more space than is usual is spent on
the geometry of least squares. The method of moments is the underlying
statistical principle through most of the text. Bootstrapping is
introduced early on. Although occasionally idiosyncratic in their choice
of material, the authors keep the book to the point and, admirably, on the
short side. ETM is 750 pages. As comparisons, Greene (2003) is 1,026 pages; Hayashi's
Econometrics (2000) is 683 pages;
Ruud's An Introduction to Classical Econometric Theory
(2000) is 951 pages; the authors' 1993
Estimation and Inference in Econometrics (1993) is 874 pages.1
Note
that ETM isn't a new edition of Estimation and
Inference. There are significant similarities, but ETM is a
new—and even better—book.
As an indication of how
much more econometrics there is now, the
1984
vintage third edition of Johnston's
Econometric
Methods—a favorite of many connoisseurs—is only 508
pages.
In their preface the authors discuss two themes that help organize the
book: advances in computation and the use of unbiased estimating
equations. Keeping to these themes is clearly an important element in the
book's straightforward presentation. (Note that “advances in
computation” means mostly bootstrapping and the use of artificial
regressions. There is a discussion of the method of simulated moments, but
not for example Markov Chain Monte Carlo [MCMC] methods.)
So what's missing? ETM is much less an encyclopedia or
reference book than is Greene. As an example, ETM spends 50 pages
on discrete and limited dependent variables. Greene spends 140 pages.
Similarly ETM gives an excellent 5-page introduction to the
vector autoregression (VAR). Greene uses 19 pages and discusses more
aspects. Both approaches are valuable, and there is limited time in a
first-year econometrics course. A student using ETM will know the
basics of limited dependent variable models and what a VAR is but will
have to look elsewhere to bring his or her knowledge to the level where
the techniques can be applied.
The more striking omission is that ETM contains neither
illustrative applications nor any examples using data. (There are a small
number of applied examples in the chapter end exercises. Data for these
are on the text Web site.) This would be fatal in a self-teaching book.
Fortunately, the market for self-taught graduate econometrics is
vanishingly small, and ETM use will invariably be accompanied by
a skilled and lively graduate econometrics instructor. In other words,
ETM needs to be supplemented with another source for all the
practical stuff.
2. CHAPTER-BY-CHAPTER REVIEW
The opening chapter of ETM is called “Regression
Models.” The book opens with the definition of a simple linear
regression,
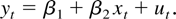
This first chapter gives a good sense of the flavor of the book, both
in terms of strengths and in noting practical areas that require some
supplementation.
The opening pages talk through equation (2.1) sufficiently clearly
that after only three pages a reader has a basic understanding of what you
get out of a regression. On the other hand, the simple regression is
illustrated with equation (2.1) but without the traditional scatter
diagram showing points in (y,x). It is hard to imagine
that a student who has never seen a regression can learn from the equation
without a picture.
Major negative? Not necessarily. First, students starting a graduate
econometrics course almost certainly bring with them a rough idea of what
a regression is. Second, it's not difficult to show the traditional
scatter diagram in class. On the other hand, the absence of a scatter
diagram surely makes the concept of a residual less intuitive. (For
comparison, Greene does provide a scatter diagram; Hayashi does not.)
ETM announces that equation (2.1) might be a consumption
function relating household consumption in year t to measured
disposable income; β2 is the marginal propensity to
consume; and β1 is autonomous consumption. It is not that
difficult to teach graduate students to regress y on x
and to then give an interpretation of the resulting computer output. It is
extraordinarily difficult to dissuade students from running regressions
with endogenous variables on the right-hand side. (I find it somewhat
effective to have my labor economist wife make a guest appearance during
lecture to threaten mayhem upon any student who runs such a regression.
But this option may not be available to most econometricians.) Page 1 of a
text is not the place to bring up endogeneity, but couldn't we have
an example that doesn't leave something to unlearn? Mind you, both
Greene and Hayashi open with the Keynesian consumption function as the
first example.
Writing style is probably less important than content. On the other
hand, students are going to—it is hoped—spend many, many hours
with the text. Davidson and MacKinnon write delightfully and are unafraid
to say what they mean in a straightforward way. I find their use of
language engaging. Here is one example taken from a footnote:
In this book, all logarithms are natural logarithms….
Some authors use “ln” to denote natural logarithms and
“log” to denote base 10 logarithms. Since econometricians
should never have any use for base 10 logarithms, we avoid this
aesthetically displeasing notation.
Chapter 2 presents the geometry of linear regression. A thorough
review of the geometry of vector spaces is followed by everything you ever
wanted students to know about the geometry of least squares. Emphasis is
given to the use of projection matrices because these play an important
role in the algebra of regressions. The Frisch–Waugh–Lovell
(FWL) theorem is proved and discussed at length. FWL states that
β1 in the regression y = X1
β1 + X2 β2 + u
can be estimated by forming the residuals from a regression of y
on X2 and the residuals from a regression of
X1 on X2 and regressing the former
on the latter. Three applications of FWL are given: sweeping out the
dummies, removing a deterministic time trend from a regression, and the
relation between several measures of goodness of fit. The final section
discusses influential observations and leverage.
The third chapter turns to the statistical properties of ordinary
least squares (OLS). Least squares is shown to be unbiased if the
right-hand-side variables are exogenous, implying
E(u|X) = 0, but not necessarily if the
right-hand-side variables are merely predetermined,
E(ut|Xt)
= 0. As an algebraic illustration of the latter point the authors consider
the regression of yt on
yt−1 given independent and identically
distributed (i.i.d.) errors, pointing out that least squares is not
unbiased. This is true but not helpful. Endogeneity is an important source
of bias in least squares. Measurement error is an important source of
bias. Selection is an important source of bias. Lagged dependent variables
with serially correlated errors are an important source of bias. The
presence of a lagged dependent variable with i.i.d. errors is not an
important source of bias. Although mathematically an estimator either is
unbiased or it isn't, the untidy part of econometrics involves
learning when biases are likely to be large or small. Some other example
would have been better here.
Continuing, the third chapter explains probability limits and
consistency, gives the covariance of OLS, proves the Gauss–Markov
theorem, discusses the relation between error terms and residuals, gives a
good discussion of misspecification, and concludes with defining
R2 and discussing goodness of fit.
The fourth chapter covers hypothesis testing. The chapter opens with a
discussion of the principles of hypothesis testing and proceeds to work
through t- and F-tests. The discussion is both thorough
and succinct. As might be expected from the authors the bootstrap is
introduced as a standard tool, rather than exotica relegated to the back
of the book.
Chapter 5 covers confidence intervals. In addition to the obvious
material, this chapter discusses bootstrap confidence regions and
confidence regions in multiple dimensions. Heteroskedasticity-consistent
covariance matrices are explained. So is the delta method for nonlinear
hypothesis tests.
The sixth chapter takes up nonlinear regression. This is earlier than
is traditional. But the early placement has two advantages. First, with
modern software nonlinear regression is not much harder to execute than is
linear regression. Second, this permits introduction of the
Gauss–Newton regression, a tool that the authors use later in the
book for computing both linear and nonlinear tests. The chapter
concentrates on estimation and testing but gives little in the way of
examples of useful nonlinear functional forms or in the way of guidance in
the interpretation of nonlinear models. The chapter explores several basic
optimization algorithms. Such algorithms are useful not only in
econometrics but in the growing areas of economics that employ significant
computation. The discussion of optimization is terrific, as one would
expect from the authors. They make it look almost too easy, so an
additional word of warning that numerical computation is a difficult field
might have been in order.
Generalized least squares is introduced in chapter 7. Along with the
discussion, autoregressive (AR) and moving average (MA) processes are
introduced. Several tests for serial correlation are given. It is
noteworthy that the Durbin–Watson (DW) statistic is explained
clearly, identified as the most popular test for serial correlation, and
then it is explained why the DW is now obsolete and should not be used.
Panel data are briefly introduced in this chapter, and the fixed effect
and random effect models are explained.
The eighth chapter covers instrumental variable estimation, beginning
with brief discussions of errors-in-variables and simultaneous equation
systems. (The latter is discussed in depth in chapter 12.) The discussion
covers finite-sample properties, test of overidentifying restrictions,
Durbin–Wu–Hausman tests, and instrumental variable estimation
of nonlinear models. Chapter 9 moves to generalized method of moments
(GMM). The discussion begins with using GMM for the linear regression
model, which is a good way to build intuition. Careful discussion is given
to alternative formulations of the GMM estimator and to heteroskedasticity
and autocorrelation consistent estimation. A variety of tests are
discussed. The chapter concludes with an introduction to the method of
simulated moments.
Up to this point in the text the underlying estimation theory is based
on method of moments. Chapter 10 turns to maximum likelihood estimation
(MLE). In addition to explaining MLE, the authors use this opportunity to
introduce the likelihood ratio, Wald, and Lagrange multiplier trio.
Chapter 11 begins with logit and probit models. (It would be nice if a
little more time were spent on interpreting results, something students
frequently—and even experts sometimes—have trouble with.)
Multinomial, ordered, and nested models are then presented. Models for
count data, censored and truncated models, selection models, and duration
models are all introduced briefly and clearly.
Multivariate regression models are covered in chapter 12. The chapter
begins with seemingly unrelated regression, including nonlinear systems.
Simultaneous equation models are then covered. GMM, three-stage least
squares (3SLS), full information maximum likelihood (FIML), and limited
information maximum likelihood (LIML) are discussed. Structural and
reduced forms are given, although there is no discussion of the
interpretation of the reduced form.
Chapter 13 goes over methods for stationary time series. The chapter
opens with autoregressive moving average (ARMA) models. Estimation is
discussed, including some of the practical difficulties of MA estimation.
Distributed lag models come next, including partial adjustment,
autoregressive distributed lag, and error-correction models. Neither
polynomial distributed lag nor adaptive expectations models are discussed.
An unusually thorough discussion of seasonal adjustment is given. Basic
autoregressive conditional heteroskedasticity (ARCH) and generalized
autoregressive conditional heteroskedasticity (GARCH) models are given.
VARs are discussed extremely briefly, without mention of identification
issues, impulse response functions, or variance decompositions.
Chapter 14 turns to unit roots and cointegration. The chapter opens by
building the idea of a random walk. The subject is then motivated with a
discussion of spurious regressions. Unit root tests are discussed,
followed by a discussion of cointegration and tests for cointegration.
Chapter 15 concludes the text with an examination of specification
testing. A number of tests based on artificial regressions are presented.
There are then a section on nonnested hypothesis tests, a very brief
discussion of model selection based on the Akaike information criterion
(AIC) and Bayesian information criterion (BIC), and an introduction to
nonparametric estimation.
