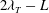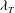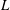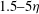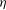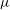1. Introduction
The interaction between the different scales of turbulence has been the subject of a great many investigations in the past few years. According to the classical theory of turbulence, turbulent kinetic energy is produced at large scales, and it is then transferred on average to ever smaller scales in an inviscid process, before being dissipated into heat (Richardson Reference Richardson1926; Pope Reference Pope2000). The classical theory of turbulence considers the mechanism of energy transfer to be universal (Pope Reference Pope2000). Furthermore, some properties of the small scales of turbulence have been observed to be independent of the flow under investigation; see Sreenivasan & Antonia (Reference Sreenivasan and Antonia1997), Elsinga & Marusic (Reference Elsinga and Marusic2010), Wei et al. (Reference Wei, Elsinga, Brethouwer, Schlatter and Johansson2014), among others. Despite the universality of various important features of turbulence, several works have reported that in turbulent boundary layers (TBLs) the large-scale motions appear to interact with the viscous scales in a different way depending on the distance from the wall (Hutchins & Marusic Reference Hutchins and Marusic2007a ; Chung & McKeon Reference Chung and McKeon2010; Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009; Ganapathisubramani et al. Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012). Although such interaction between the large-scale and small-scale motions has lately aroused deep interest, shear flows other than boundary layers have scarcely been tackled in the literature. Only a mixing layer has been studied so far (Buxton Reference Buxton2011; Buxton & Ganapathisubramani Reference Buxton and Ganapathisubramani2014).
In turbulence, the clear separation of the scales is achieved in flows at high Reynolds number. However, the ratio between the large scales and the small scales of turbulence (dynamic range) is almost proportional to the Reynolds number of the flow, thus making the simultaneous tracking of the entire range of scales difficult. For these reasons, the recent works on scale interaction in TBLs at high Reynolds numbers rely on HWA data, as it offers a large temporal dynamic range. Some early indications of top-down interaction in the boundary layer were found in the work by Hutchins & Marusic (Reference Hutchins and Marusic2007b ), who noticed that the very large-scale motions influence the near-wall turbulence, which was originally regarded as an independent region of the TBL (Jiménez & Pinelli Reference Jiménez and Pinelli1999; Schoppa & Hussain Reference Schoppa and Hussain2002). Two years later, these qualitative observations led Mathis et al. (Reference Mathis, Hutchins and Marusic2009) to quantify the large-scale modulation of the small scales in a TBL at high Reynolds number. The authors applied a procedure similar to Bandyopadhyay & Hussain (Reference Bandyopadhyay and Hussain1984). They reconstructed two signals representative of the large- and small-scale motions (named large-scale and small-scale signal, respectively) by applying a spectral filter on time series from HWA. The Taylor hypothesis of frozen turbulence (Taylor Reference Taylor1938) made it possible to create an analogy between the length scales of turbulence and the frequency content of the signal. The small-scale signal was then Hilbert-transformed and low-pass filtered, in order to create a signal representative of the local small-scale activity. It can be thought of as the filtered envelope of the small-scale signal. The correlation coefficients between this signal and the large-scale signal were computed at different distances from the wall. This procedure made it possible to retrieve an estimate of the local degree of amplitude modulation. It was found that the near-wall region is characterized by a positive top-down interaction, i.e. positive fluctuations of the large-scale signal induce a local increment to the amplitude of the small-scale signal. On the other hand, further from the wall, a phase reversal was reported (see also Chung & McKeon Reference Chung and McKeon2010; Jacobi & McKeon Reference Jacobi and McKeon2013), with the small-scale signal being statistically less intense for positive large-scale fluctuations.
However, Schlatter & Örlü (Reference Schlatter and Örlü2010) found that the correlation coefficient between the large-scale signal and the envelope of the small-scale signal is not an independent tool to quantify the degree of amplitude modulation. It was shown that a synthetic signal characterized by the same skewness as the original signal also has the same value for the correlation coefficient. The authors therefore invoked a note of caution. Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011) suggested the use of two-point correlation to overcome this limitation, and proved that the physical phenomenon observed by Mathis et al. (Reference Mathis, Hutchins and Marusic2009) is not an artifact of the mathematical tool used in that quantification. Later, Mathis et al. (Reference Mathis, Marusic, Hutchins and Sreenivasan2011) decomposed the skewness factor into contributions from large- and small-scale signals. They found that one of the terms constituting the skewness factor closely resembles the correlation coefficient used to quantify amplitude modulation. In particular, that term becomes more and more similar to the skewness factor of the signal for increasing the Reynolds number of the flow, which explains the analogy between skewness factor and correlation coefficient. Recently, Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) showed that the small-scale amplitude grows with increasing values of the large-scale fluctuation in the near-wall region, whereas in the outer region the small-scale amplitude decreases with increasing large-scale fluctuation. In particular, the small-scale signal is more amplitude-modulated when the strength of the large-scale fluctuation increases. Furthermore, a method based on the number of occurrences of local maxima and minima of the signal made it possible to explore effects of frequency modulation. The frequency of the small-scale signal was reported to be higher for positive large-scale fluctuations and lower for negative large-scale fluctuations. This evidence is stronger in the near-wall region, and it becomes weaker at a distance from the wall larger than 100 wall units. In that work, the authors hypothesized that both the frequency and amplitude modulation are the result of a change in the local Reynolds number of the flow.
The top-down interaction between the scales of turbulence has so far been studied very intensively in boundary layers, with the further aim of controlling the activity of the viscous scales in the near-wall region (Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010; Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2011). The large-scale modulation of the small scale has barely been explored in free shear flows. An extensive analysis of the phenomenon in different flows was performed by Bandyopadhyay & Hussain (Reference Bandyopadhyay and Hussain1984), who examined a wake, a mixing layer, and a jet. They found that a wake and a jet behave in a similar way to the near-wall region of a TBL, i.e. the small-scale signal exhibits a stronger amplitude for positive fluctuations of the large-scale signal, independently of the radial location. The mixing layer, on the other hand, presents a phase reversal between large- and small-scale signals analogous to the outer region of a TBL. In the present study, the nature of the interaction between large- and small-scale velocity fluctuations is examined in a turbulent jet at high Reynolds number. The mean shear vanishes at the centreline of a far-field jet, which represents an important difference with respect to boundary layers and mixing layers.
The far field of a jet is characterized by isotropy of the small scales on average (Pope Reference Pope2000; Ganapathisubramani, Lakshminarasimhan & Clemens Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008; Cardesa et al.
Reference Cardesa, Mistry, Gan and Dawson2013). Nevertheless, the small-scale motions were observed to be highly intermittent locally and inhomogeneous in a large number of works (She, Jackson & Orszag Reference She, Jackson and Orszag1990; Shen & Warhaft Reference Shen and Warhaft2000; Ishihara, Toshiyuki & Kaneda Reference Ishihara, Toshiyuki and Kaneda2009; Fiscaletti, Westerweel & Elsinga Reference Fiscaletti, Westerweel and Elsinga2014, among others). This inhomogeneity reinforces with increase in the Reynolds number of the flow. Moreover, the small-scale motions were observed to organize themselves into coherent structures. For example, intense vorticity appears in the shape of vortex tubes (Siggia Reference Siggia1981; Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Vincent & Meneguzzi Reference Vincent and Meneguzzi1991), called ‘worms’ after the work by Jiménez et al. (Reference Jiménez, Wray, Saffman and Rogallo1993). These worms have a characteristic diameter of approximately
$10{\it\eta}$
over a very large range of Reynolds numbers based on the Taylor scale (Kaneda & Ishihara Reference Kaneda and Ishihara2006; Ishihara, Kaneda & Hunt Reference Ishihara, Kaneda and Hunt2013; Fiscaletti et al.
Reference Fiscaletti, Westerweel and Elsinga2014), whereas their length was proposed to scale with the integral length scale of the flow (Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993; Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008). Consistent with the high intermittency of turbulence at the small-scale level, the worm-like structures were observed to cluster in regions of flow of intense shear (Worth & Nickels Reference Worth and Nickels2011; Ishihara et al.
Reference Ishihara, Kaneda and Hunt2013), and high rate of dissipation (Vincent & Meneguzzi Reference Vincent and Meneguzzi1994; Chacin & Cantwell Reference Chacin and Cantwell2000; Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008). On the other hand, with the intense vortices gathering in clusters, large portions of the flow are characterized by very low vorticity.
The present study aims at a detailed assessment of amplitude and frequency modulation of the small scales in a jet at high Reynolds number. In the first part of the investigation, the scale interaction is examined with HWA. The use of HWA, however, requires application of the Taylor hypothesis of frozen turbulence if length scales are to be considered, which has already been reported in the past to be a considerable source of bias (Zaman & Hussain Reference Zaman and Hussain1981; del Álamo & Jiménez Reference del Álamo and Jiménez2009). For this reason, the phenomenon is studied in the second part with long-range
${\it\mu}$
PIV. In this way, amplitude and spatial frequency modulation can be quantified without any need for conversion of the signal from the time domain to the spatial domain typical of HWA. This will be shown to greatly affect the level of amplitude modulation. Moreover, long-range
${\it\mu}$
PIV allows exploration of the relation between amplitude modulation and the coherent structures. Finally, we speculate on the implications of these findings for TBL flows.
2. Experiments
The air jet under investigation issued from a round nozzle with an exit diameter of
$D=8~\text{mm}$
. The flow velocity at the nozzle exit is
$125~\text{m}~\text{s}^{-1}$
, as established in a separate measurement with a Pitot tube of 1.5 mm in diameter. The non-dimensional numbers at the nozzle can be estimated: Reynolds number
$\mathit{Re}=6.6\times 10^{4}$
and Mach number
$\mathit{Ma}=0.37$
. The inlet chamber upstream of the nozzle consists of a diffuser with an angle of about 22°, followed by a series of five fine irregular mesh screens with an average mesh size of about
$1~\text{mm}^{2}$
, intended to reduce the size of the largest scales present in the flow. A 25:1 contraction is followed by a round nozzle, whose edges are slightly chamfered. Further details of the settling chamber and the shape of the nozzle can be found in Slot et al. (Reference Slot, Moore, Delfos and Boersma2009). Two different techniques were used to measure the jet flow: HWA and long-range microscopic particle image velocimetry (long-range
${\it\mu}$
PIV).
2.1. Hot-wire anemometry
The measurements were performed at a downstream distance of 70 nozzle diameters from the nozzle exit, at two different radial locations, namely at the centreline and at
$0.2~r_{1/2}$
, where
$r_{1/2}$
is the jet’s half-width. At this stage, the turbulence of the flow is fully developed, and the jet is characterized by its typical self-similar behaviour, as demonstrated in Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014). The sensor, a tungsten Dantec 55P11, was operated in constant temperature mode, with an overheat ratio of 0.7. In this way, its temperature was kept approximately constant at
$220\,^{\circ }\text{C}$
throughout the entire measurement process. The length of the sensor was 1.25 mm and its diameter was
$5~{\rm\mu}\text{m}$
, equivalent to
$23{\it\eta}$
and
$0.09{\it\eta}$
respectively, where
${\it\eta}$
is the Kolmogorov length scale of the flow at the measurement location. The feedback control of the wire temperature was established through a Dantec Dynamics 56C17 CTA Bridge. Data were acquired at a frequency of 200 kHz, over a time of 4 s per run (
$8\times 10^{5}$
samples). An estimate of the dissipation rate in jets is provided using the approximation (Panchapakesan & Lumley Reference Panchapakesan and Lumley1993)
$$\begin{eqnarray}{\it\varepsilon}\approx 0.015\frac{U_{c}^{3}}{r_{1/2}},\end{eqnarray}$$
where
$U_{c}$
is the centreline velocity and
$r_{1/2}$
is the jet’s half-width. Based on the dissipation rate at the above-mentioned measurement location, the size of the Kolmogorov scale
${\it\eta}$
is estimated to be
$57~{\rm\mu}\text{m}$
, which corresponds to a frequency of 30 kHz at the jet centreline when employing Taylor’s hypothesis. Since, for frequencies higher than 22 kHz, the measurement noise dramatically affects the signal, a low-pass filtering at this cut-off frequency had to be applied. As a consequence, the minimum size of the eddies that the measurement can resolve is estimated to be
$90~{\rm\mu}\text{m}$
, corresponding to about 1.5 Kolmogorov length scales. Moreover, an estimate of the Taylor microscale
${\it\lambda}_{T}$
was obtained from the expression (Taylor Reference Taylor1935)
$$\begin{eqnarray}{\it\lambda}_{T}=u^{\prime }\sqrt{15\frac{{\it\nu}}{{\it\varepsilon}}},\end{eqnarray}$$
where
$u^{\prime }$
is the root mean square (r.m.s.) of the axial velocity. Moreover, the integral length scale of the flow (
$L$
) can be estimated by
$$\begin{eqnarray}L\sim {\it\eta}\,\mathit{Re}^{3/4}.\end{eqnarray}$$
From the calculation, the Taylor microscale
${\it\lambda}_{T}$
is
$2.19~\text{mm}$
, and the integral length scale of the flow
$L$
is
$43~\text{mm}$
. The Reynolds number based on the Taylor microscale
$(\mathit{Re}_{{\it\lambda}})$
was estimated to be 367. Table 1 provides a summary of the macroscopic characteristics of the jet flow.
Table 1. Macroscopic characteristics of the jet flow as estimated from HWA and Pitot tube measurements.
2.2. Long-range
${\it\mu}$
PIV
The PIV measurement was performed at the same downstream distance of 70 nozzle diameters from the nozzle exit, in proximity to the centreline. The measurement plane was parallel to the axis of the jet. A detailed description of the experiment and its validation based on the main statistical properties of the turbulence are given in Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014). Here we only give a brief overview of the main characteristics of the PIV system. The long-range microscope used in the
${\it\mu}$
PIV system is the Questar QM-1, with a magnification factor of 2.5, and with a working distance of 560 mm. The working distance is more than an order of magnitude higher than the jet’s half-width at the measurement location (52.2 mm), which is deemed sufficient to avoid any perturbative effect on the flow.
As seeding tracers,
$1~{\rm\mu}\text{m}$
DEHS particles (Di(2-ethylhexyl) sebacate, sebacic acid) generated from a Laskin nozzle were used. The response time of this seeding is about two orders of magnitude lower than the Kolmogorov time scale, so that the velocity fluctuations in the flow can be tracked accurately.
A total of
$11\,000$
image pairs were collected at an acquisition frequency of 5 Hz. The dataset of image pairs was processed through a cross-correlation algorithm, implemented in the software DaVis by LaVision. A two-pass refinement of the grid was adopted, with a final interrogation window of
$64\times 64~\text{pixels}$
, and a 50 % window overlap. The size of the interrogation window was
$160~{\rm\mu}\text{m}$
, which corresponds to 2.9 Kolmogorov length scales at the measurement location. The thickness of the light sheet was almost equal in size (
$180~{\rm\mu}\text{m}$
). The field of view was
$3.43\times 2.60~\text{mm}$
, equivalent to
$1.68{\it\lambda}_{T}\times 1.26{\it\lambda}_{T}$
, where
${\it\lambda}_{T}$
is the Taylor length scale as derived from the
${\it\mu}$
PIV data. A time delay of
$3~{\rm\mu}\text{s}$
was chosen between the first and second laser pulses, yielding an average particle displacement of 11.8 pixels, which corresponds to
$9.78~\text{m}~\text{s}^{-1}$
. The flow characteristics as estimated from
${\it\mu}$
PIV are comparable to those from HWA, and they can be found in table 4 of Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014). The Taylor and Kolmogorov length scales appearing in the non-dimensionalization of physical quantities computed from
${\it\mu}$
PIV data were estimated from
${\it\mu}$
PIV data. The coordinate system
$x_{i}$
and corresponding velocity components
$u_{i}$
for the
${\it\mu}$
PIV dataset are defined as follows: subscripts 1 and 2 represent the axial and radial directions respectively; subscript 3 indicates the direction perpendicular to the measurement plane.
3. Methods for scale separation and coherent structures identification
In this work we address the amplitude and frequency modulation of the small scales of turbulence by the large scales. We rely on the present datasets from both HWA and long-range
${\it\mu}$
PIV. In order to extract large- and small-scale information from both measurement techniques a further treatment of the data is required, which is described next.
3.1. The filtering of the HWA data
Figure 1 shows the velocity power spectrum. The
$-5/3$
slope in the inertial range of the energy cascade develops over two decades. This demonstrates the highly turbulent nature of the flow, and the clear separation of the large scales and the small scales. In figure 1 we present a low-frequency and high-frequency band, which are taken to be representative of the large-scale signal and the small-scale signal, respectively. In particular, the low-frequency signal is associated with length scales between
$2{\it\lambda}_{T}$
and
$L$
, whereas the high-frequency signal is associated with length scales between
$1.5{\it\eta}$
and
$5{\it\eta}$
. The velocity is band-pass filtered in the frequency domain, and the frequency components not belonging to the frequency band of interest are set to zero. The new small-scale and large-scale velocity signals are then obtained by applying the inverse fast Fourier transform.
Figure 1. Velocity power spectrum of a hot-wire signal taken at the jet centreline, at a downstream distance of 70 nozzle diameters.
3.2. The processing of the long-range
${\it\mu}$
PIV data
In the
${\it\mu}$
PIV measurement, the field of view (
$1.68{\it\lambda}_{T}\times 1.26{\it\lambda}_{T}$
) is not large enough to fully capture the large scales of turbulence, as defined above for HWA. Therefore the fluctuating axial velocity component averaged over the field of view was considered as the instantaneous local large-scale velocity fluctuation instead. The vector spacing in the
${\it\mu}$
PIV measurement is
$1.5{\it\eta}$
, which is also the size of the smallest eddies that can be resolved with HWA, under the hypothesis of frozen turbulence.
Furthermore, taking advantage of the planar velocity data we analysed the link between the intense vortices or intense dissipation, and the strength of the local large-scale fluctuation. In this analysis the intense dissipation, vorticity and vortical motion are considered to be associated with (or representative of) the small scales of motion. In this section we illustrate the criterion adopted for the detection of the vortices, and for locating their centres. The criterion uses the imaginary part of the eigenvalues of the reduced velocity gradient tensor (VGT),
${\it\lambda}_{ci}$
, where non-zero values indicate a local swirling motion. It is therefore known as the
${\it\lambda}_{ci}$
-criterion, or swirling strength, and it was first proposed by Zhou et al. (Reference Zhou, Adrian, Balachandar and Kendall1999). If
${\it\lambda}_{ci}$
is higher than a certain threshold, a vortex is said to be detected. A threshold value for
${\it\lambda}_{ci}~({\it\lambda}_{ci,thr})$
was determined as a multiple of the r.m.s. of
${\it\lambda}_{ci}$
, computed on the dataset where
${\it\lambda}_{ci}$
was non-zero. A vortex is detected if either one point or cluster of multiple points was characterized by
$$\begin{eqnarray}{\it\lambda}_{ci}>K\,{\it\lambda}_{ci,rms},\end{eqnarray}$$
where
$K$
is a constant. In order to determine the subgrid position of the centre of each vortex, we computed the centroid of the
${\it\lambda}_{ci}$
distribution within the vortex core.
The convection velocity of a vortex could also be estimated. As an initial approximation, the fluid velocity at the centroid of a vortex can be considered as the convection velocity of that vortex,
$V$
.
Furthermore, we will analyse the behaviour of the regions of intense dissipation, with a particular focus on their convection velocities, and their rate of occurrence. The estimate of the local turbulent dissipation rate stemmed from
$$\begin{eqnarray}{\it\varepsilon}=2{\it\nu}\left(\unicode[STIX]{x1D63C}(1,1)^{2}+2\left(\frac{\unicode[STIX]{x1D63C}(2,1)+\unicode[STIX]{x1D63C}(1,2)}{2}\right)^{2}+\unicode[STIX]{x1D63C}(2,2)^{2}\right),\end{eqnarray}$$
where
$\unicode[STIX]{x1D63C}$
is the reduced (two-dimensional) VGT in a point. A region of intense dissipation is detected if either one point or a cluster of multiple points was characterized by:
$$\begin{eqnarray}{\it\varepsilon}>K_{{\it\varepsilon}}\,{\it\varepsilon}_{rms}\end{eqnarray}$$
where
$K_{{\it\varepsilon}}$
is a constant. Analogous to the intense vortices, the subgrid position of the centre of each region of intense dissipation was identified by calculating the centroid of the
${\it\varepsilon}$
distribution within the points belonging to the region of intense dissipation. In the following, we refer to convection velocity of a region of intense dissipation
$V_{{\it\varepsilon}}$
as the axial flow velocity at the centre of the dissipation structure.
Figure 2. Sample from the velocity signal (top) with the corresponding small-scale and large-scale components (bottom).
4. Amplitude modulation
In figure 2, part of the raw velocity signal (top) is shown, with the corresponding large-scale signal and small-scale signal content (bottom). It appears that the small scales are affected by the large-scale motions. When the large-scale fluctuation is positive the small-scale fluctuations are typically more intense. The large scales thus have a role in modulating the amplitude of the dissipative scales, similar to the observations of Hutchins & Marusic (Reference Hutchins and Marusic2007b ) in the near-wall region. This trend is more evident in figure 3, where the probability density functions (p.d.f.s) of the small-scale velocity fluctuations are presented, conditioned on the large positive and large negative fluctuations in the corresponding large-scale signal. The threshold of the large-scale fluctuation was taken to be its r.m.s. value. The variance of the p.d.f. conditioned on the positive fluctuations of the large-scale signal is clearly higher than the variance for the negative large-scale fluctuations: this demonstrates that the sign of the large-scale fluctuations has a modulating effect on the small-scale turbulent activity.
Figure 3. Probability density function of the small-scale fluctuations, conditioned on the large positive (continuous line) and large negative (dashed line) fluctuations of the large-scale signal.
Nevertheless, the variance of the conditional p.d.f. does not provide a detailed description of the relation between the strength of the large-scale signal and the amplitude modulation of the small-scale motions. Hence, a procedure similar to that detailed in Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) was applied to the present experimental dataset. In the following, we let
$u_{L}^{\ast }$
denote the fluctuations of the large-scale signal non-dimensionalized by the average centreline velocity
$U_{c}~(u_{L}^{\ast }=u_{L}^{}/U_{c})$
. The aforementioned procedure consists of the following steps.
-
(i) Equally spaced
$u_{L}^{\ast }$
bins were created, with a spacing of 0.05 ranging from
$u_{L}^{\ast }=-0.4$
to
$u_{L}^{\ast }=0.4$
. A bin spacing of 0.05 was chosen as a balance between the bin size and the number of samples within each bin. With such a size, the minimum amount of samples falling within each bin was larger than 1000. -
(ii) Each large-scale sample is associated with a small-scale sample at the same instant in time.
-
(iii) The associated sample of the small-scale signal was included in a group, corresponding to one of the
$u_{L}^{\ast }$
bins, effectively creating an independent new small-scale velocity series for each
$u_{L}^{\ast }$
bin. -
(iv) The r.m.s. of the samples contained in each group was then computed, and this small-scale r.m.s. represents the amplitude of the small scales conditioned on the strength of the respective large-scale signal,
${\it\sigma}_{u_{L}}$
. The r.m.s. was non-dimensionalized by the r.m.s. of the entire small-scale fluctuations at the centreline
${\it\sigma}_{c}$
, and therefore
${\it\sigma}_{u_{L}}^{\ast }={\it\sigma}_{u_{L}}/{\it\sigma}_{c}$
.
The analysis was conducted for datasets from two different radial positions, namely at the centreline and at 0.2 non-dimensional radii. Figure 4 shows the result of this procedure for the two different radial locations. The amplitude modulation effects are linear for fluctuations of the large-scale signal close to zero. Nevertheless, the interaction between the large- and small-scale motions is generally nonlinear, especially for
$u_{L}^{\ast }<0$
. We can also observe that the trend does not change with the radial location of the jet. This is consistent with Bandyopadhyay & Hussain (Reference Bandyopadhyay and Hussain1984), where the correlation coefficients between the large-scale signal and the envelope of the small-scale signal are observed to remain constant across different radial positions.
Figure 4. Root mean square of the p.d.f. of the small-scale signal
${\it\sigma}_{u_{L}}^{\ast }={\it\sigma}_{u_{L}}/{\it\sigma}_{c}$
, conditioned on the fluctuations of the large-scale signal
$u_{L}$
, at the centreline position (continuous line, ○), and at 0.2 non-dimensional radii (dashed line, ◃). A dotted line (*) has been added, which represents the amount of variance of the p.d.f. of the small-scale signal generated in the conversion from time series into space series, as obtained from (9.6) (see § 9).
Moreover, the correlation coefficient (
$R$
) between the large-scale signal and the envelope of the small-scale signal allowed further evaluation of the interaction between the scales. The envelope of the small-scale signal is calculated following the approach by Mathis et al. (Reference Mathis, Hutchins and Marusic2009). The Hilbert transform was first applied to the small-scale signal. For the envelope, we filtered the Hilbert-transformed signal using the same spectral filter as for the large-scale fluctuations. To estimate a possible time delay in the interaction between the scales, we calculated the correlation coefficient
$R$
for different time shifts
${\rm\Delta}t$
of the two signals. As a convention, a negative time shift is equivalent to delaying the small-scale signal. Figure 5 shows the result of this procedure. The maximum correlation coefficient (
$R=0.65$
) is found for a negative shift of
$1.8\times 10^{-4}~\text{s}$
, implying a delay in the scale interaction. This shift is almost equal to the Kolmogorov time scale
${\it\tau}_{{\it\eta}}=2\times 10^{-4}~\text{s}$
. The interaction between large and small scales can therefore be considered concurrent.
Figure 5. Correlation coefficients
$R$
for different relative time shifts between the large-scale signal and the envelope of the small-scale signal (following Mathis et al.
Reference Mathis, Hutchins and Marusic2009).
A test was performed to check the sensitivity of small-scale amplitude modulation to the choice of the large-scale frequency content. In this test, the large-scale signal was associated with the ranges
${\it\lambda}_{T}-L$
, and
$3{\it\lambda}_{T}-L$
, in which the lower limit of the range was varied with respect to the definition of large-scale motions introduced in § 3,
$2{\it\lambda}_{T}-L$
. The small-scale signal was kept the same as before. With these new large-scale bounds, the analysis presented in this section was repeated, and the results showed that changes in the strength of the physical phenomenon are negligible.
5. Frequency modulation
In this section the frequency modulation of the small-scale motions is examined. We apply the peak and valley counting (PVC) method (Ganapathisubramani et al.
Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) to the present dataset of HWA, with the aim of quantifying the extent of frequency modulation with the strength of large-scale fluctuation. This approach is based on the counting of the local number of peaks and valleys (hence its name) in the small-scale signal over a certain time segment. The metric was developed with the aim of overcoming the limitations linked with the zero-crossing method. A
$u_{L}^{\ast }$
binning with a spacing of 0.05 ranging from
$u_{L}^{\ast }=-0.4$
to
$u_{L}^{\ast }=0.4$
was created for the large-scale fluctuations, similar to what was done in § 4. Moreover, the time series of both the large- and small-scale fluctuations were divided into segments of 100 samples each (corresponding to
$5\times 10^{-4}~\text{s}$
). This segment size was chosen as the ratio between the acquisition frequency and 2001 Hz, a frequency intermediate between the large- and small-scale motions. With such a bin size and time segment, the minimum amount of samples falling within each bin was 400. The number of local maxima and minima of the small-scale signal within each time segment was then determined. A representative frequency of occurrence of local maxima and minima per unit length
$\langle f_{m}\rangle$
was obtained by dividing the number of local maxima and minima by
$10^{-3}~\text{s}$
, i.e. twice the length of the time segment. Eventually, the number of local maxima and minima was conditionally averaged depending on the local strength of the large-scale fluctuation
$u_{L}^{\ast }$
. In figure 6, the result of the application of the PVC scheme to the hot-wire dataset is presented, for the signals acquired at the centreline and at 0.2 non-dimensional radii. The two graphs show a similar trend for both the radial positions within the jet. It can be seen that the frequency of the small-scale signal increases statistically with the strength of the large-scale fluctuations. As for the amplitude modulation, the relation is generally nonlinear.
Figure 6. Local frequency of the small-scale signal
$\langle f_{m}\rangle$
, conditioned on the fluctuations of the large-scale signal, for a signal acquired at the centreline position (continuous line, ○), and at 0.2 non-dimensional radii (dashed line, ◃), both at
$x/D=70$
.
However, the frequency modulation can also be regarded as a frequency dependence in the amplitude modulation, that is, different frequencies experience a different level of amplitude modulation (for a given
$u_{L}^{\ast }$
). It thus appears that the higher frequencies of the small-scale signal are more amplitude-modulated. If we look at this in the frequency domain, we can expect that the higher wavenumbers within the viscous region are subject to stronger amplitude modulation. This would have an important implication. The behaviour of the large scales alters the shape of the velocity power spectrum locally. In particular, the small-scale frequency band is expected to become flatter for positive fluctuations of the large-scale signal, and steeper for negative fluctuations. In order to verify this, the following procedure was implemented.
-
(i) First, the small-scale signal was divided into segments of length corresponding to 200 time samples (
$10^{-3}~\text{s}$
). -
(ii) A hamming filter was applied to the segments of the small-scale signal.
-
(iii) From all the filtered segments, we selected only those with a particular value of
$u_{L}^{\ast }$
in the corresponding large-scale signal. -
(iv) The selected pieces of the small-scale signal were juxtaposed, thus generating new signals.
-
(v) The power spectra for each of these conditional signals were calculated. Finally, the obtained conditional power spectrum was normalized by its value at
$k{\it\eta}=10^{-0.6}$
, to compensate for the differences in the energy content and emphasize the slope of the spectrum.
This scheme was applied for three different
$u_{L}^{\ast }$
. The results are shown in figure 7. The power spectrum was first conditioned on strong large-scale fluctuations
$u_{L}^{\ast }$
ranging between 0.3 and 0.35 (positive fluctuations), then between
$-0.35$
and
$-0.3$
(negative fluctuations), and eventually for randomly selected segments of the small-scale signal (unconditional
$u_{L}^{\ast }$
). As predicted, the slope of the line indicating strong negative fluctuation is the steepest, whereas the slope for strong positive fluctuation is flatter. This supports the earlier statement that the amplitude modulation of the small-scale signal is frequency-dependent, and that the degree of amplitude modulation increases at higher frequencies. Consistent with this finding, Fiscaletti et al. (Reference Fiscaletti, Elsinga, Ganapathisubramani and Westerweel2013) obtained that small-scale signals associated with higher frequencies present a higher amplitude modulation when quantified as in § 4.
Figure 7. Power spectra of conditionally selected segments of the small-scale signal. The positive fluctuation line is obtained for
$u_{L}^{\ast }$
ranging between 0.3 and 0.35, the negative fluctuation line is between
$-0.35$
and
$-0.3$
, and the line labelled ‘Unconditional’ is obtained for unconditional
$u_{L}^{\ast }$
(randomly selected segments of the small-scale signal).
Figure 8. Joint probability density function between the r.m.s. vorticity over each field of view
${\it\omega}_{rms}$
and the average axial velocity over each field of view. The vorticity was normalized over the total r.m.s. vorticity, and the average axial velocity over the average axial velocity of the flow.
6. The coupling between small-scale flow structures and large-scale fluctuations
The observed small-scale amplitude modulation leads us to hypothesize that vorticity and dissipation, which are closely associated with small scales, are on average more intense in regions of positive large-scale fluctuations. In order to check this assumption, the joint probability density functions (j.p.d.f.s) between the r.m.s. vorticity and dissipation and the large-scale velocity fluctuations
$u_{L}^{\ast }$
were calculated from the PIV velocity fields. Note that the large-scale velocity fluctuation was taken as the average axial velocity fluctuation over the field of view, as explained in § 3. The number of samples considered was 11 000, namely the total number of velocity fields acquired from
${\it\mu}$
PIV. The results are shown in figures 8 and 9. At negative large-scale fluctuations, the vorticity r.m.s. is mostly lower than the average r.m.s. of the vorticity magnitude, computed over all the samples. A similar trend can be observed for the dissipation r.m.s. Moreover, as the large-scale fluctuations increase, vorticity and dissipation r.m.s. tend to increase too. Therefore, regions of the flow that have a large-scale axial velocity higher than the average axial velocity of the flow are characterized by higher levels of vorticity and dissipation, and vice versa.
Figure 9. Joint probability density function between the r.m.s. rate of dissipation over each field of view
${\it\varepsilon}_{rms}$
and the average axial velocity over each field of view. The rate of dissipation was normalized over the total r.m.s. rate of dissipation, and the average axial velocity over the average axial velocity of the flow.
This finding is consistent with amplitude modulation observed in § 4 based on the HWA data. Furthermore, we estimated the amplitude modulation from the long-range
${\it\mu}$
PIV dataset for comparison with HWA. We applied a procedure similar to that used in § 4, for the HWA dataset. The procedure consists of the following steps.
-
(i) The axial small-scale velocity r.m.s. and the vorticity r.m.s. of each of the 11 000 vector fields was calculated, relative to the average axial velocity and vorticity computed over the vector field, respectively.
-
(ii) Equally spaced bins with a spacing of 0.125 ranging from
$u_{L}^{\ast }=-0.375$
to
$u_{L}^{\ast }=0.375$
were created. -
(iii) Depending on the value of the
$u_{L}^{\ast }$
, the associated axial velocity r.m.s. and vorticity r.m.s. was included in a group, corresponding to one of the
$u_{L}^{\ast }$
bins. -
(iv) The average axial velocity r.m.s. and vorticity r.m.s. included in each
$u_{L}^{\ast }$
bin were computed.
The results of these calculations are given in figure 10. A first consideration that can be retrieved from these graphs is that the axial velocity r.m.s. and the vorticity r.m.s. provide almost the same results when it comes to the quantification of the amplitude modulation. Amplitude modulation from PIV shows a trend similar to the HWA analysis. However, the nonlinearity observed for strongly negative large-scale fluctuations in the analysis of HWA time series (figure 4) cannot be found in PIV (figure 10). Moreover, we can see that the level of amplitude modulation for long-range
${\it\mu}$
PIV is much lower than for HWA (i.e. the slope of the graph is smaller). In particular, we can notice that the amplitude modulation for strongly positive fluctuations (
$u_{L}^{\ast }>0.3$
) and strongly negative fluctuations (
$u_{L}^{\ast }<-0.3$
) is around
$10\,\%$
of the unconditional r.m.s. (figure 10), whereas it reaches values up to
$35\,\%{-}40\,\%$
if we look at the dataset from HWA (figure 4). This overestimation of the amplitude modulation from HWA can be attributed to the Taylor hypothesis of frozen turbulence in the conversion from time to space series of HWA, which is discussed in § 9.
Figure 10. Average axial velocity r.m.s. (continuous line, ○) and average vorticity r.m.s. (dashed line, ◃) computed over each vector field, conditioned on the fluctuations of the large-scale signal
$u_{L}$
, from the long-range
${\it\mu}$
PIV dataset.
7. The conditional size of the vorticity structures
Next, we examine the size of the coherent structures of vorticity depending on the large-scale flow velocity. This is of interest since changes in structure size could potentially be linked to frequency modulation observed in the previous sections. An indication of the diameter of the vortices (called ‘worms’) can be found in the literature for flows at different
$\mathit{Re}_{{\it\lambda}}$
. In this respect, Jiménez et al. (Reference Jiménez, Wray, Saffman and Rogallo1993) showed that the core diameter of these intense vortices scales with the Kolmogorov length scale. This inference was obtained from DNS simulations of isotropic turbulence run at different Reynolds numbers. Nevertheless, the Taylor microscale Reynolds number (
$\mathit{Re}_{{\it\lambda}}$
) of these simulations was never higher than 150 (
$\mathit{Re}_{{\it\lambda}}<150$
). Kaneda & Ishihara (Reference Kaneda and Ishihara2006) have recently examined the size of the intense vortices in a DNS of homogeneous isotropic turbulence at a Taylor microscale Reynolds number higher than 1000 (
$\mathit{Re}_{{\it\lambda}}>1000$
). Ganapathisubramani et al. (Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008) confirmed from experiments the characteristic size and spatial organization of the structures of intense vorticity previously observed; subsequently, Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014) were able to investigate experimentally the scaling of the worms at a Taylor microscale Reynolds number (
$\mathit{Re}_{{\it\lambda}}$
) of around 350. In all the aforementioned works, the characteristic core diameter of the structures of intense vorticity was found to range between
$8{\it\eta}$
and
$12{\it\eta}$
. In the present work, the size of the coherent structures of vorticity is analysed conditioned on positive and negative large-scale fluctuations. Recall that the average of the axial velocity over the field of view was regarded as the large-scale fluctuation in the
${\it\mu}$
PIV measurement. An estimate of the average size of the intense vortices can be obtained from the autocorrelation coefficient map of the out-of-plane vorticity
${\it\omega}_{3}$
. In figure 11, the cross-sections of the autocorrelation peak are given conditioned on
$u_{L}^{\ast }<-0.3$
and
$u_{L}^{\ast }>0.3$
. The number of samples that contributed to the autocorrelation map were 1415 for
$u_{L}^{\ast }>0.3$
, and 1408 for
$u_{L}^{\ast }<-0.3$
. As a threshold for the identification of the characteristic core radius, we considered an autocorrelation coefficient of 0.5 (figure 11). It can be inferred that the characteristic diameter of the structures of intense vorticity is larger (
${\approx}12.2{\it\eta}$
) if conditioned on
$u_{L}^{\ast }<-0.3$
, and smaller (
${\approx}11.8{\it\eta}$
) if conditioned on
$u_{L}^{\ast }>0.3$
of around
$3.3\,\%$
depending on
$u_{L}^{\ast }$
. Furthermore, we analysed the spatial extent of the 500 most intense vortices, detected for large-scale fluctuations
$u_{L}^{\ast }>0.3$
as well as the 500 most intense vortices within
$u_{L}^{\ast }<-0.3$
regions. The intensity of each vortex was evaluated as the maximum value of
${\it\lambda}_{ci}$
among the points making up each vortex. With the aim of quantifying the extension of the 500 vortices, the point characterized by the highest
${\it\lambda}_{ci}$
was surrounded by a square box of
$15{\it\eta}\times 15{\it\eta}$
in size (so as to include the entire core diameter of the vortex, expected to be around
$10{-}12{\it\eta}$
, as mentioned above). The number of points of the box complying with
$$\begin{eqnarray}{\it\lambda}_{ci}>C_{e}\,{\it\lambda}_{ci,max}\end{eqnarray}$$
were considered as part of the vortex, and represented an estimate of the characteristic area of each vortex. The result depends on the chosen value of the
$C_{e}$
parameter. The procedure was developed for its intrinsic robustness, and yielded the graph in figure 12, showing the square root of the average intense vortex area conditioned on
$u_{L}^{\ast }<-0.3$
and
$u_{L}^{\ast }>-0.3$
for different
$C_{e}$
. The square root of the area in this case is again a measure for the characteristic vortex diameter. It can be seen that the intense vortices located in regions of strongly positive fluctuations are smaller than the intense vortices located in regions of strongly negative fluctuations. These observations are consistent with the analysis of the
${\it\omega}_{3}$
autocorrelation peaks discussed above.
Figure 11. Autocorrelation coefficient maps of the out-of-plane vorticity for in-plane shifts
$r$
, conditioned on the large-scale signal
$u_{L}^{\ast }>0.3$
(dashed line, ◃) and
$u_{L}^{\ast }<-0.3$
(continuous line, ○). The local fluctuation of the large-scale signal is defined in § 3;
${\it\mu}$
PIV data have been analysed here.
Figure 12. Characteristic size of the 500 most intense vortices for different values of the threshold
$C_{e}$
(7.1), conditioned on
$u_{L}^{\ast }>0.3$
(dashed line) and
$u_{L}^{\ast }<-0.3$
(continuous line).
Moreover, we estimated the size of a ‘local’ Kolmogorov length scale for positive and negative fluctuations of the large-scale signal from the dataset of HWA. The rate of dissipation conditioned on the strength of the large-scale fluctuations was therefore computed. In particular, the Kolmogorov length scale was estimated for
$u_{L}^{\ast }>0.3$
(strongly positive fluctuations) and for
$u_{L}^{\ast }<-0.3$
(strongly negative fluctuations). On the unfiltered velocity fluctuations, we applied the following central difference scheme, which relies on the hypothesis of isotropy, already generally ascertained in Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014) for the experimental object of the present analysis:
$$\begin{eqnarray}{\it\varepsilon}=\left\langle 15{\it\nu}\left[(u(i+1)-u(i-1))\!\left/2\left(\frac{\bar{U}+u(i)}{f}\right)\right.\right]^{2}\right\rangle ,\end{eqnarray}$$
where
$f$
is the acquisition frequency. From this, we retrieved the rate of dissipation conditioned on the positive (
${\it\varepsilon}^{+}$
) and negative (
${\it\varepsilon}^{-}$
) fluctuations of the large-scale signal. The conditional Kolmogorov length scale could then be computed, yielding
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}^{+}=\left(\frac{{\it\nu}^{3}}{{\it\varepsilon}^{+}}\right)^{(1/4)}=56.0~{\rm\mu}\text{m}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}^{-}=\left(\frac{{\it\nu}^{3}}{{\it\varepsilon}^{-}}\right)^{(1/4)}=57.3~{\rm\mu}\text{m}, & \displaystyle\end{eqnarray}$$
${\it\varepsilon}^{+}=366.4~\text{m}^{2}~\text{s}^{-3}$
and
${\it\varepsilon}^{-}=333.8~\text{m}^{2}~\text{s}^{-3}$
. Therefore the positive large-scale fluctuations are associated with a stronger rate of dissipation locally and a smaller size of the local Kolmogorov length scale. The percentage difference in the two estimated Kolmogorov length scales is
$2.3\,\%$
. This is in good agreement with the percentage difference found earlier for the characteristic diameter of the vortices, which are known to scale on
${\it\eta}$
.
To summarize, an increase in the strength of the large-scale fluctuations (
$u_{L}^{\ast }\uparrow$
) is associated with a decrease in the size of the local Kolmogorov length scale (
${\it\eta}\downarrow$
). This change was estimated to be in the order of 2 %–3 % if we move from strongly positive fluctuations (
$u_{L}^{\ast }>0.3$
) to strongly negative fluctuations (
$u_{L}^{\ast }<-0.3$
). In relation to the observed magnitude of the amplitude and frequency modulation, these size effects can thus be considered negligible.
8. The conditional intensity of the coherent structures
In the previous section we showed that the size of the coherent structures of vorticity does not change significantly with
$u_{L}^{\ast }$
. If the structure size is unaffected, the observed amplitude modulation must then be explained by the spatial distribution of the intense coherent structures relative to the large-scale motions, which will be examined next. The criterion for the detection of the intense vortices and the identification of their centres is detailed in § 3. We assigned different values to the threshold parameter
$K$
in (3.1), thus detecting a decreasing number of vortices with increasing values of
$K$
. The vortex convection velocity (
$V$
) was then taken as the measured flow velocity at the centre. A summary of the total number of vortices and their average convection velocity for a given threshold
$K$
is provided in table 2. The average velocity at which the intense vortices are convected downstream is always higher than the mean axial component of the velocity (
$\bar{U}=9.78~\text{m}~\text{s}^{-1}$
). In particular, the vortices characterized by higher
${\it\lambda}_{ci}$
tend to be convected at higher velocities. Further evidence of this trend can be found in the j.p.d.f. between the convection velocity of the vortices and their intensity, taken as the peak
${\it\lambda}_{ci}$
of the vortex. The j.p.d.f. was computed for
$K=3$
, thus examining a total number of 16 662 vortices (second row of table 2). The resulting j.p.d.f. is shown in figure 13. It can be observed that the most intense vortices are characterized by higher convection velocities, which means that they are found more often in high-velocity regions of the flow, as compared to regions characterized by low velocity.
Table 2. Average convection velocities of the vortices
$\bar{V}$
(second column) after applying different thresholds
$K$
for
${\it\lambda}_{ci}$
(3.1).
$N$
represents the total number of vortices found for the given value of
$K$
. Note that the average convection velocities of the vortices are higher than the average axial velocity of the flow, at
$\bar{U}=9.78~\text{m}~\text{s}^{-1}$
.
Figure 13. Joint probability density function between the strength of the intense vortices
${\it\lambda}_{ci}$
and their axial convection velocity
$V$
. The intense vortices were detected with the
${\it\lambda}_{ci}$
-criterion (after Zhou et al.
Reference Zhou, Adrian, Balachandar and Kendall1999, (3.1)), with
$K=3$
. The j.p.d.f. is based on 16 662 samples (second row of table 2).
As already ascertained in other works (i.e. Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008; Fiscaletti et al.
Reference Fiscaletti, Westerweel and Elsinga2014), the regions of intense dissipation appear in the vicinity of intense vortices. A similar trend to that observed for the average absolute vorticity could therefore also be expected for the structures of intense dissipation rate. In order to identify the regions of intense dissipation we used (3.3) for different values of the parameter
$K_{{\it\varepsilon}}$
. The flow velocity at the centroids of each region of intense dissipation was evaluated and taken as the convection velocity. In table 3 we give a summary of the whole number of regions of intense dissipation, and the average convection velocity (
$V_{{\it\varepsilon}}$
) for a given threshold
$K_{{\it\varepsilon}}$
. Similar to the vortices, the structures of intense dissipation are convected downstream at a velocity higher than the average flow velocity, and increasing with the strength
$K_{{\it\varepsilon}}$
. We compute the j.p.d.f. between the convection velocities of the regions of intense dissipation and their dissipation rate. Equation (3.3) was used to identify the regions of intense dissipation, with
$K_{{\it\varepsilon}}=3$
as value of the
$K_{{\it\varepsilon}}$
parameter. The j.p.d.f. is given in figure 14. As for the structures of vorticity, the structures of intense dissipation characterized by higher intensity are typically convected downstream at higher velocities.
Table 3. Average convection velocities of the regions of intense dissipation
$\bar{V_{{\it\varepsilon}}}$
(second column) after applying different thresholds
$K_{{\it\varepsilon}}$
for
${\it\varepsilon}$
(3.3).
$N$
represents the total number of regions of intense dissipation found for the given value of
$K_{{\it\varepsilon}}$
. Note that the average convection velocities of the regions of intense dissipation are higher than the average axial velocity of the flow, at
$\bar{U}=9.78~\text{m}~\text{s}^{-1}$
.
Figure 14. Joint probability density function between the rate of dissipation of the regions of intense dissipation
${\it\varepsilon}$
and their axial convection velocity
$V_{{\it\varepsilon}}$
. The regions of intense dissipation were detected with the criterion detailed in § 3 (3.3), with
$K_{{\it\varepsilon}}=3$
. The j.p.d.f. is based on 17 057 samples (second row of table 3).
To summarize, more intense small-scale structures (i.e. vortices and dissipation structures) are typically located within regions of high flow velocity, so they are expected to be convected at higher velocity. This finding can be related to the evidence of amplitude and frequency modulation described in previous sections. In particular, the positive correlation between the intensity of a vortex and its convection velocity can be directly related to the trend between the strength of the large-scale fluctuation and the local standard deviation of the small-scale signal (figure 4).
9. The effects of the Taylor hypothesis of frozen turbulence
We now move to the evidence of frequency modulation that was ascertained in § 5. In that section the local strength of the large-scale fluctuations was found to modulate the number of peaks and valleys of the small-scale signal locally (figure 6). This was regarded as evidence of frequency modulation, with the amplitude modulation being frequency-dependent. Moreover, a frequency dependence in the already ascertained amplitude modulation implies a local change of the slope of the power spectrum conditioned on the local strength of the large-scale fluctuation. In this respect, the two conditional spectra in figure 7 were interpreted as evidence of frequency modulation. However, if we admit that the small-scale structures do not change in size, as ascertained in § 7, the frequency modulation is then a direct consequence of the different convection velocities at which the intense vortices are convected downstream. In particular, the small-scale fluctuations residing in a positive large-scale fluctuation (
$u_{L}^{\ast }>0$
) will probably be convected past the hot-wire probe faster (than the average flow velocity), resulting in an increased number of peaks and valleys per unit time (
$V\uparrow$
implies
$P\& V\uparrow$
) relative to the same-sized small-scale features in a negative
$u_{L}^{\ast }$
associated with lower convection velocity. If we analyse more carefully the two conditional power spectra (figure 7), we can see that they collapse onto each other for the first part of the viscous region (for
$k{\it\eta}$
ranging between
$10^{-0.6}$
and
$10^{-0.42}$
). Furthermore, the spectra without rescaling the vertical axis (figure 15
a) seem to have the same shape in the region
$10^{-0.6}{-}10^{-0.42}$
, and thus mainly reveal an offset. Nevertheless, it is possible to compensate to first order for the non-constant convection velocity in the conditional spectra, using
$$\begin{eqnarray}\frac{{\rm\Delta}k}{k_{T}}=\frac{u_{L}}{U_{c}}-1,\end{eqnarray}$$
where
${\rm\Delta}k$
is the wavenumber shift of the conditional spectrum relative to the Taylor hypothesis (which is to be compensated),
$k_{T}$
is the wavenumber after application of the Taylor hypothesis at constant convection velocity by the mean flow
$U_{c}$
, i.e. the average axial velocity of the flow (
$U_{c}=10.56~\text{m}~\text{s}^{-1}$
); the large-scale velocity fluctuation
$u_{L}$
is then taken as the difference between the real convection velocity of the conditional small scales and
$U_{c}$
. For the present conditional spectra,
$u_{L}=0.3U_{c}$
for the positive large-scale fluctuations, and
$u_{L}=-0.3U_{c}$
for the negative. The result of this compensating shift is given in figure 15(b). The two conditional spectra (figure 15
b) now overlap on the unconditional one, thus strongly suggesting that the three power spectra are actually different portions of the same spatial power spectrum. Moreover, the collapse of the conditional spectra (figure 15
b) supports that the modulation in frequency of the small scales can largely be explained as an effect induced by variations in the convection velocity of the same small (spatial) scales.
Figure 15. Power spectra of conditionally selected segments of the small-scale signal, (a) before and (b) after the compensation for the horizontal offset induced by the Taylor hypothesis of frozen turbulence in the conversion of time series into space series. The positive fluctuation line is obtained for
$u_{L}^{\ast }$
ranging between 0.3 and 0.35, the negative fluctuation line is between
$-0.35$
and
$-0.3$
, and the line labelled ‘Unconditional’ is obtained for unconditional
$u_{L}^{\ast }$
(randomly selected segments of the small-scale signal).
The application of the Taylor hypothesis in the conversion of time series into space series also affects the estimate of the amplitude modulation from HWA data (figure 4). The adoption of the same band-pass frequencies independently of the local convection velocity leads to a different spatial frequency content in the various segments of the small-scale signal, depending on the strength and the sign of the associated large-scale fluctuations. As a consequence, the power spectrum conditioned on strongly positive fluctuations includes energy contributions from lower spatial frequencies than those corresponding to the prescribed range of
$1.5{-}5{\it\eta}$
(§ 3), whereas the power spectrum conditioned on strongly negative fluctuations includes contributions from higher spatial frequencies than those corresponding to the prescribed range
$1.5{-}5{\it\eta}$
(figure 15
b). Because of the slope in the power spectrum, this produces a larger energy content in the power spectrum conditioned on strongly positive fluctuations, and vice versa. Therefore, all the segments of the small-scale signal associated with positive large-scale fluctuations contain an increment of energy produced by the Taylor hypothesis. This energy increment can be estimated by comparing the amplitude modulation from HWA (figure 4) and from long-range
${\it\mu}$
PIV (figure 10). In fact, data from long-range
${\it\mu}$
PIV are not affected by such a frequency shift (because the spatial frequencies are measured directly), so they can thus be considered representative of the real amplitude modulation in space. For turbulent jet flow, we can assess that around 75 % of the amplitude modulation estimated from HWA comes from the conversion from time series into space series, namely by application of the Taylor hypothesis of frozen turbulence.
An estimate of the amount of amplitude modulation in consequence of the conversion from time series into space series can also be obtained analytically. Consider the turbulent kinetic energy of the signal at a certain wave number
$\widehat{E}(k)$
, which can be modelled by a power law in the small-scale range:
$$\begin{eqnarray}\widehat{E}(k)=C\,k^{-p}={\textstyle \frac{1}{2}}u_{k}^{2},\end{eqnarray}$$
where, from experimental data,
$p$
is approximately 2 in the range of
$k{\it\eta}$
between 1.5 and 5,
$C$
is a constant independent of
$k$
, and
$u_{k}$
is the velocity fluctuation associated with
$k$
. Equation (9.2) can be rewritten as
$$\begin{eqnarray}|u_{k}|=\widehat{C}\,k^{-(p/2)},\end{eqnarray}$$
where
$\widehat{C}=\sqrt{2C}$
. The wavenumber
$\bar{k}$
(in space) can be replaced by the ratio between the frequency (
$f_{k}$
) and the local convection velocity. The local convection velocity can be approximated as the sum between the mean velocity of the flow, and local large-scale velocity fluctuation (
$U_{CV}=U_{c}+u_{L}$
). The smaller scales contain much less and can therefore be neglected. We obtain
$$\begin{eqnarray}\bar{k}=\frac{f_{k}}{U_{c}+u_{L}}\end{eqnarray}$$
which, if plugged into (9.3), yields
$$\begin{eqnarray}|u_{k}|=\widehat{C}\left(\frac{f_{k}}{U_{c}+u_{L}}\right)^{-(p/2)}.\end{eqnarray}$$
If this expression for
$u_{k}$
is expanded in Taylor series, we can estimate the local amplitude of the small-scale signal in relation to the strength and the sign of the large-scale fluctuation (
$u_{L}$
):
$$\begin{eqnarray}\displaystyle |u_{k}| & = & \displaystyle |u_{k}|\left.\vphantom{\frac{\partial |u_{k}|}{\partial u_{L}}}\right|_{(u_{L}=0)}+\left.\frac{\partial |u_{k}|}{\partial u_{L}}\right|_{(u_{L}=0)}u_{L}+\text{h.o.t.}\nonumber\\ \displaystyle & {\approx} & \displaystyle \left(\frac{f_{k}}{U_{c}}\right)^{-(p/2)}\left(1+\frac{p}{2}\frac{u_{L}}{U_{c}}\right).\end{eqnarray}$$
If now in a HWA measurement the small scales are defined by a constant temporal frequency
$f_{k}$
, then it can be seen from this equation that the observed amplitude of the small-scale signal increases/decreases linearly with the strength of the positive/negative large-scale fluctuations. This linear trend is added to figure 4 (dotted line, *). If we consider a large-scale fluctuation of
$u_{L}/U_{c}=0.3$
and
$p=2$
, we obtain that the amount of amplitude modulation generated in the conversion of the time series into space series is 0.3. The amplitude modulation obtained from the analysis described in § 4 is 0.42 for the signal at the centreline. This means that the amount of amplitude modulation introduced in the conversion of the hot-wire signal from time series into space series accounts for around
$70\,\%$
of the total amplitude modulation. This analytical result compares well with the observed difference in modulation from HWA and PIV (§ 4).
Overall, this overestimation can also be interpreted as the difference between the scale interactions in space and time. Based on the comparison, it can be seen that the interactions in time (i.e. in hot-wire data) appears to be more ‘active’ than interactions in space. This suggests that flow evolution in time is perhaps more important to scale interactions compared to the concurrent spatial structure.
10. Analysis of a turbulent boundary layer
We now explore how the present findings for jet flow may apply to TBL flow. From the analysis of jet flow we learned that the observed amplitude modulation in a jet can be viewed as a spatial (inhomogeneous) organization of the small scales. In particular, the small-scale vortices are more often located in high-velocity regions as opposed to the low-speed regions within the jet. If we assume that in a TBL the size of the small-scale features does not change significantly, as in the jet, or if we simply consider a specific physical length scale within the small-scale range, we can relate this spatial organization to amplitude and frequency modulation in frequency space (HWA), as mentioned. Regarding the spatial organization of the small scales or alternatively the vortex structures, the experimental studies by Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000) and Elsinga et al. (Reference Elsinga, Adrian, van Oudheusden and Scarano2010), and the DNS simulations by del Álamo & Jiménez (Reference del Álamo and Jiménez2009) are examined here.
In figure 21 of the work by Adrian et al. (Reference Adrian, Meinhart and Tomkins2000), the conditionally averaged streamwise convection velocities of the coherent structures of vorticity are presented at different wall distances. It can be observed that for small distances from the wall, the streamwise convection velocities are almost equal to the average streamwise velocity of the flow. However, if we move to the outer region, the streamwise convection velocities are lower than the average streamwise velocity of the flow. In their investigation, the Reynolds number of the flow is
$\mathit{Re}_{{\it\theta}}=7705$
, corresponding to a Reynolds number based on the Taylor microscale higher than 350. Subsequently, the DNS simulations by del Álamo & Jiménez (Reference del Álamo and Jiménez2009) and the experiments by Elsinga et al. (Reference Elsinga, Adrian, van Oudheusden and Scarano2010) confirmed this trend. In the outer region of a TBL, the convection velocities of the coherent structures of vorticity are lower than the local average velocity of the flow, which explains the stronger activity of the small scales for negative fluctuations of the large-scale signal, as found from HWA data. Furthermore, figure 2(a) of del Álamo & Jiménez (Reference del Álamo and Jiménez2009) shows the streamwise convection velocities of the small scales (i.e. small wave length), in a channel flow. The bottom graph reveals that at 10 wall units distance from the wall the convection velocities are higher than the local average streamwise velocities of the flow. This implies that, in the near-wall region of the boundary layer, the small-scale structures are typically located in large-scale high-speed regions, thus producing the positive amplitude modulation effects already ascertained in the aforementioned studies.
Moreover, the observations of §§ 6 and 9 have shown that the effects produced by variations in convection velocity are embedded in the amplitude modulation measured with HWA. These effects led us to estimate the amplitude modulation to be four times higher when based on time series (HWA) as opposed to that returned in space by PIV. We showed that, in the viscous region of the spectrum, all the spectra conditioned on the strength of the large-scale fluctuation collapse approximately on the same spectrum when a compensating horizontal shift is introduced (figure 15). From the experimental dataset described in the work by Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012), we intend to verify if an analogous collapse in the conditional spectra can be found in the near-wall region of a TBL. Figure 16(a) provides the result of this analysis. As can be observed, the three spectra conditioned on strongly positive, zero, and strongly negative fluctuations of the large-scale signal show a collapse for an interval of non-dimensional frequencies
$((2{\rm\pi}f/U){\it\delta})$
between
$4\times 10^{2}$
and
$3\times 10^{3}$
. This frequency range represents only a small and low energetic portion of the whole interval of frequencies representative of the small-scale motions, as defined in the work by Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012). This implies that only the frequency modulation can be explained as the result of the Taylor hypothesis. Frequency modulation has been determined by means of the peak and valley counting method (PVC), and the number of local maxima and minima is mainly determined by the high-frequency components of the signal. Therefore the collapse of the three spectra at the high frequencies shows that the frequency modulation is actually the result of different convection velocities of the structures of vorticity, analogous to the jet. It is instead more difficult to draw conclusions for amplitude modulation. Many factors cause the analysis in the near-wall region of a TBL to be different from that in jet flow: (i) the important phase delay in the top-down interaction between scales, as shown by Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) (their figure 11a), (ii) the different definition of the small-scale motions between the present investigation (
${<}5{\it\eta}$
) and the works from the literature on TBLs (typically
${<}{\it\delta}$
), (iii) the modest slope of the power spectrum in the near-wall region, for the most energetic frequencies.
Figure 16. Conditional power spectra of the small scales as a function of wavenumber at (a,b)
$y^{+}=15$
and (c,d)
$y/{\it\delta}=0.1$
. The horizontal axis shows the wavenumber computed with free-stream velocity (a,c) and with an appropriate local convection velocity (b,d). The different lines show the conditional spectra of the small scales for
$u_{L}^{\ast }=-3$
, 0 and 3. Note the collapse of the spectra at higher frequencies at
$y^{+}=15$
and increased deviation at
$y/{\it\delta}=0.1$
when the correction for local convection velocity is employed. Figure adapted from Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012).
It is also of interest to move to the outer region of a TBL and perform the same analysis. The outer region is characterized by a negative correlation coefficient between the large-scale and small-scale signals. In this region of the flow we expect that the spectrum conditioned on positive large-scale fluctuations has a lower energy content than the spectrum conditioned on negative large-scale fluctuations, as a consequence of amplitude modulation. Analogously to the near-wall region, the three conditional spectra from Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) are given in figure 16(c,d). It can be observed that the difference in the energy content of the three spectra is small, even without any horizontal compensating shift. This is probably due to the simultaneous effects of both the local convection velocities and the amplitude modulation, which seem to be of the same importance, with the effect of the amplitude modulation being prevalent. Furthermore, the overlap of the three conditional spectra suggests that the amount of frequency modulation is small in this region of the flow. This is consistent with the finding by Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012), their figure 8. If we then account for the effect of the local convection velocities, and introduce a horizontal shift, the three spectra diverge from each other. In figure 16(b,d), we observe the effect of this horizontal shift. Similarly to the near-wall region of the TBL, for the outer region it is also difficult to draw firm conclusions on the amplitude modulation, only on the basis of the conditional spectra. However, the divergence of the conditional spectra after the compensation suggests that the Taylor hypothesis leads to underestimation of the amplitude modulation in the outer region of a TBL, at the high frequencies of the interval. This warrants further investigation in the future.
To summarize, the effects of the local convection velocities in the conditional spectra as described in detail in §§ 6 and 9 have been compensated by applying a horizontal shift in frequency (figure 16). In the inner region of the TBL, the conditional spectra tend to collapse at the high frequencies mostly at scales smaller than the local Taylor length scale
${\it\lambda}_{T}$
. This is evidence that the frequency modulation found in the near-wall region of a TBL (Ganapathisubramani et al.
Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012, figure 8) occurs in time series and not in physical space. However, it is more difficult to interpret the implications that this effect can have on the amplitude modulation quantified in the literature as those including length scales up to
${\it\delta}$
in the small-scale signals. In the outer region of the TBL, the conditional spectra diverge after compensating for the local convection velocities, which could indicate that the amplitude modulation is underpredicted when converting from a time-frame into a space-frame. Nevertheless, further investigations based on PIV data at high resolution are required to quantify the amplitude modulation in a TBL, in physical space.
11. Conclusions
In the present work, amplitude and frequency modulation of the small scales of turbulence in a jet at high Reynolds number has been investigated experimentally using both HWA and PIV. Data were acquired at 70 nozzle diameters downstream from the nozzle, thus in the fully developed region. HWA time series were converted into space series after applying the Taylor hypothesis of frozen turbulence. By making use of a spectral filter, two signals were reconstructed from the original signal, one representative of the large scales (large-scale signal), and another representative of the small scales (small-scale signal). It was found that when the large-scale signal fluctuates positively, the small-scale signal is stronger in amplitude (amplitude modulation), and presents an increase in its number of local maxima and minima locally (frequency modulation). The opposite behaviour was found for negative fluctuations of the large-scale signal. The response of the small-scale motions to amplitude modulation can be considered instantaneous, being one Kolmogorov time scale. Moreover, the local standard deviation of the small-scale signal (representative of the amplitude of the small-scale signal) increases with the local strength of the large-scale fluctuations, similar to the near-wall region of a TBL (Ganapathisubramani et al. Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012). The trend is linear for fluctuations of the large-scale signal of modest size, but is generally nonlinear.
Amplitude and frequency modulation was further investigated with long-range
${\it\mu}$
PIV. The use of PIV permits spatial resolution of the small scale of turbulence without the need for the Taylor hypothesis of frozen turbulence. The size of the structures of intense vorticity conditioned on strongly positive and strongly negative large-scale fluctuations was examined. It was observed that the size of the structures of vorticity does not change significantly in relation to the large-scale velocity fluctuation, meaning that there is no significant spatial frequency modulation in PIV. The coherent structures of intense vorticity were found to be characterized statistically by velocities higher than the mean velocity of the flow. The structures of intense dissipation, which are located in close vicinity to the structures of vorticity (consistent with Ganapathisubramani et al.
Reference Ganapathisubramani, Lakshminarasimhan and Clemens2008), presented a similar trend. These findings led us to link amplitude modulation from PIV to the spatially inhomogeneous distribution of the coherent structures of vorticity and of intense dissipation. In particular, these coherent structures tend to be located in high-velocity regions of the flow.
The analysis from the PIV data shows that the amount of amplitude modulation is
$25\,\%$
of the value measured with HWA. This overestimation of the amplitude modulation from hot-wire signals was attributed to application of the Taylor hypothesis of frozen turbulence in the analysis of hot-wire signals. In fact, the fixed spectral band filter used to obtain the large- and small-scale signals does not consider the local convection velocity, but rather the mean velocity of the flow. This leads to a different spatial frequency content within the same small-scale signal depending on the local strength of large-scale fluctuation. The conditional spectra overlap when a compensating shift is introduced based on the local convection velocity (approximated by the local strength of the large-scale fluctuation), which clarifies the effect of the Taylor hypothesis in estimating amplitude and frequency modulation from HWA. This effect has also been shown analytically in the paper. It must be noted that this overestimation of amplitude modulation in hot-wire time-series compared to the PIV data can also be interpreted physically as the difference between scale interactions in space and time. It seems that temporal interactions across scales are stronger and more active compared to the concurrent spatial interactions. This suggests that the comparison between amplitude modulation in space and in time must be carried out in different flows in order to highlight the differences in the interaction between spatial and temporal scales. To the best of our knowledge, this is the first and only study thus far to make this direct comparison. All previous studies utilize either time-series data (Bandyopadhyay & Hussain Reference Bandyopadhyay and Hussain1984; Mathis et al.
Reference Mathis, Hutchins and Marusic2009; Ganapathisubramani et al.
Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) or simply have PIV data (Buxton & Ganapathisubramani Reference Buxton and Ganapathisubramani2014).
Finally, the implications of the present findings to a TBL were explored. The evidence from the literature suggests that in the near wall the structures of vorticity present, on average, convection velocities higher than the local average velocity of the flow, whereas the opposite behaviour occurs in the outer region. Following our argument developed for jet flow, the frequency modulation found in Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012) is largely associated with varying convection velocities of the small scales (below a Taylor length). In the outer layer, the modulation of the high-frequency part of the small scales is underestimated when evaluated from velocity time-series.
Acknowledgements
B.G. acknowledges the support from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013), ERC grant agreement 277472.
