1. INTRODUCTION
In general, the lasers are characterized by non-uniform radial intensity profile and the non-linear effects invoked by the propagation of such electromagnetic (em) beams in the plasmas are highly sensitive to the irradiance distribution along the wave front of the beam (Sodha et al., Reference Sodha, Ghatak and Tripathi1976). As the beam propagates in the plasma, the electrons/ions redistribute itself under the influence of non-uniform irradiance profile and this self-consistent redistribution cause non-linearities in the plasma, characterized by dielectric function. Among many of the non-linear phenomena associated with interplay between em beam and plasma, self-focusing/defocusing is of considerable interest (Sodha et al., Reference Sodha, Ghatak and Tripathi1976; Hora, Reference Hora1991; Sprangle & Esarey, Reference Sprangle and Esarey1991; Berge, Reference Berge1998; Saini & Gill, Reference Saini and Gill2006; Yu et al., Reference Yu, Yu, Xu, Tian, Chen and Wong2007) on account of its relevance to promising applications in inertial confinement fusion (ICF) (Tabak et al., Reference Tabak, Hammer, Glinisky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Deutsh et al., Reference Deutsh, Furukaw, Mima, Murakami and Nishihara1996), charged particle acceleration (Sprangle et al., Reference Sprangle, Esarey, Ting and Joyce1988; Umstadter et al., Reference Umstadter, Chen, Maksimchuk, Mourou and Wagner1996), X-ray generation (Eder et al., Reference Eder, Amendt, Da Silva, London, Mac Gowan, Mathews, Penetrante, Rosen, Silks, Donnelly, Falcone and Strobel1994), and ionospheric modification (Gurevich, Reference Gurevich1978). The investigations exploring the laser propagation dynamics in plasmas frequently take account of Gaussian nature of the irradiance profile of the laser where the intensity peaks at the central axis and falls off radially. However, in the last few years significant interest has been gained by optical beams with zero central intensity (Sodha et al., Reference Sodha, Ghatak and Tripathi1974; Reference Sodha, Mishra and & Misra2009a; Reference Sodha, Mishra and Misra2009b; Gupta et al., Reference Gupta, Rafat and Sharma2011a; Reference Gupta, Sharma, Rafat and Sharma2009b; Khamedi & Bahrampour, Reference Khamedi and Bahrampour2013; Sharma et al., Reference Sharma, Sodha, Misra and Mishra2013; Misra et al., Reference Misra, Mishra, Sodha and Tripathi2014) because of its numerous applications in modern atomic optics and plasma physics. In particular, the off-axis dipole-like potential associated with the central shadow beams can be utilized to guide and trap the atoms; this effect has drawn significant attention to the central shadow beam dynamics (O'Neil et al., Reference O'neil, Macvicar, Allen and Padgett2002). The theoretical and analytical investigations describing the propagation dynamics of central shadow (in particular hollow Gaussian) beams in plasma, predicts weak divergence of hollow beams than that for Gaussian profile; such beams thus can be utilized to achieve large-energy transport in the plasma (Misra et al., Reference Misra, Mishra, Sodha and Tripathi2014). Apart from the hollow Gaussian beams (HGBs), another class of central shadow beams is described by the Laguerre–Gaussian (LG) (Sueda et al., Reference Sueda, Miyaji, Miyanaga and Nakatsuka2004) profile; in particular such beams besides a non-Gaussian intensity modulation comprises an inherent orbital angular momentum (l). The general algebraic form of LG profile can be expressed as
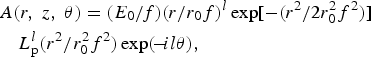 $$\eqalign{& A\lpar r\comma \; z\comma \; {\rm \theta} \rpar = \lpar E_0 /f\rpar \lpar r/r_0 f\rpar ^l \, \hbox{exp}[ - \lpar r^2 /2r_0^2 f^2 \rpar ] \cr & \quad L_{\rm p}^l \lpar r^2 /r_0^2 f^2 \rpar \, \hbox{exp}\lpar \!-\! il{\rm \theta} \rpar \comma \; } $$
$$\eqalign{& A\lpar r\comma \; z\comma \; {\rm \theta} \rpar = \lpar E_0 /f\rpar \lpar r/r_0 f\rpar ^l \, \hbox{exp}[ - \lpar r^2 /2r_0^2 f^2 \rpar ] \cr & \quad L_{\rm p}^l \lpar r^2 /r_0^2 f^2 \rpar \, \hbox{exp}\lpar \!-\! il{\rm \theta} \rpar \comma \; } $$where p refers the radial index, r 0f refers to the half-waist width, f is the beam width parameter, θ is the azimuthal angle, and E 0 is the amplitude of the electric field.
This can readily be seen that the LG beam displays an off-axis (r ≠ 0) intensity maxima. As an em beam propagates in the plasma, it may trigger the non-linear effects depending on the laser intensity and the beam can undergo continuous focusing/defocusing. The situation when the LG beam in the self-focusing regime, the axial trapping efficiency of the optical tweezers gets significantly enhanced. The propagation dynamics of such LG beams in the non-linear (in particular the Kerr dielectric) medium has recently been investigated by Thakur and Berakdar (Reference Thakur and Berakdar2010) and Khamedi and Bahrampour (Reference Khamedi and Bahrampour2013); however, these analyses are based on paraxial approximation whose validity is limited to the finite region near the central axis (i.e., r = 0). It is necessary to point out here that paraxial approximation in general is applicable to Gaussian beams where the non-linear effects are pronounced in the vicinity of its intensity maximum, that is, at the central axis. Hence, the use of paraxial approximation in analyzing the propagation dynamics of central shadow LG (off-axis) beams is inconsistent and the formulation should be modified. The applicability of paraxial approach in the vicinity of off-axis (r ≠ 0) intensity maxima in particular for the HGBs has been examined in recent studies (Misra & Mishra, Reference Misra and Mishra2008; Reference Misra and Mishra2009a; Reference Misra and Mishra2009b; Sodha et al., Reference Sodha, Mishra and & Misra2009a; Reference Sodha, Mishra and Misra2009b).
Apart from individual beam dynamics, the phenomenon of mutual interaction of multiple beams has numerous applications in filamentation, optics, electron acceleration, and trapping of atoms (Sprangle et al., Reference Sprangle, Esarey, Ting and Joyce1988; Sprangle & Esarey, Reference Sprangle and Esarey1991; Umstadter et al., Reference Umstadter, Chen, Maksimchuk, Mourou and Wagner1996; Scheller et al., Reference Scheller, Mills, Miri, Cheng, Moloney, Kolesik, Polynkin and Christodoulides2014). The focusing/de-focusing of two or more Gaussian em-coaxial beams in the plasma have been extensively studied (Sodha et al., Reference Sodha, Ghatak and Tripathi1976; Reference Sodha and Sharma1979; Reference Sodha, Sharma and Agarwal2008; Konar & Jana, Reference Konar and Jana2005; Gupta et al., Reference Gupta, Rafat and Sharma2011a; Reference Gupta, Sharma, Rafat and Sharma2011b) and the influence of basic saturating non-linearities, for example, ponderomotive, collisional, and relativistic on the beam dynamics has been explored. In such cases, the plasma density redistribution and hence the dielectric function gets modified by the combined effect of intensities of both the em beams. In coaxial propagation, the propagation dynamics (i.e., focusing/de-focusing) of one beam is influenced by the other beam and hence one beam can be utilized as the controlling tool for the other beam (Sodha et al., Reference Sodha, Sharma and Agarwal2008). The cross-focusing of two HGBs in the relativistic regime has been analyzed by Gupta et al. (Reference Gupta, Rafat and Sharma2011a; Reference Gupta, Sharma, Rafat and Sharma2011b); however, the mutual influence of the beams on one another and dielectric function is not very clear from their analysis. In this study, we aim to demonstrate that how the coaxial propagation of LG (in particular the L 01 mode) and Gaussian beams mutually influences each other dynamics in different non-linear plasma regimes. The existence of such beams has been experimentally verified by Brijesh et al. (Reference Brijesh, Kessler, Zuegel and Meyerhofer2007) who were able to generate the horseshoe-shaped longitudinal beam; it is primarily a coaxial combination of LG and Gaussian modes. Another motivation comes from a recent work (Scheller et al., Reference Scheller, Mills, Miri, Cheng, Moloney, Kolesik, Polynkin and Christodoulides2014) where the length of the laser-induced filaments in air is enhanced significantly when an annular beam is coupled with the Gaussian mode; such enhanced filamentation has promising applications in remote sensing (Luo et al., Reference Luo, Xu, Hosseini, Daigle, Theberge, Sharifi and Chin2006), atto-second physics (Stibenz et al., Reference Stibenz, Zhavoronkov and Steinmeyer2006), channeling microwaves (Ren et al., Reference Ren, Alshershby, Qin, Hao and Lin2013), and lightning protection (Kasparian et al., Reference Kasparian, Ackermann, Andre, Mechain, Mejean, Prade, Rohwetter, Salmon, Stelmaszczkyk, YU, Mysyrowicz, Sauerbrey, Woste and Wolf2008).
In this analysis, a formalism describing the non-linear coaxial propagation dynamics of finite size intense coherent LG (L 01 mode) and Gaussian beams, in a plasma characterized by ponderomotive and relativistic non-linearities has been developed. The formulation is based on paraxial and a modified paraxial-like approach, applicable to the Gaussian and central shadow LG beams have been utilized to investigate the space evolution and consequent transverse focusing/defocusing of the coupled mode; as discussed before the plasma modification in such case is influenced by the intensity profiles of both the beams. The details of the paraxial-like approach can be seen from the recent literature (Misra & Mishra, Reference Misra and Mishra2008; Sodha et al., Reference Sodha, Mishra and & Misra2009a; Sharma et al., Reference Sharma, Sodha, Misra and Mishra2013) where it is applied to study the non-linear propagation of dark hollow Gaussian beams (DHGBs) in a plasma. The propagation of an em beam is characterized by non-linear Schrödinger wave equation (NLSE). Using the paraxial and paraxial-like approaches for the two beams viz. Gaussian and LG (L 01 mode) beams, the NLSE is solved and a set of non-linear coupled differential equation describing the space evolution of beam width parameters (f, i.e., electric field) and phase have been derived; this space evolution describes the coaxial propagation of the Gaussian and LG beams as in advances in plasmas. The deviation of the propagation characteristic of the coupled mode (Gaussian plus L01 mode) from that in case of individual beam has been demonstrated graphically. The critical curves characterizing the region of focusing/defocusing in radius-intensity space and consequent transverse self-compression of the coaxial mode of propagation in plasma characterized by different non-linearities viz. ponderomotive and relativistic regimes have been examined in this paper. In the next section, the focusing equation for Gaussian and LG profiles has been established and the critical condition for the propagation of beams in the self-trapped mode is discussed. In Section 3, the effective dielectric function of the plasma under the influence of the coaxial beams corresponding to ponderomotive and relativistic non-linearities has been evaluated. Section 4 includes the discussion on the numerical results based on analysis, whereas a summary of the outcome in Section 5 concludes the paper.
2. ANALYSIS
2.1. Propagation
Consider the coaxial propagation of coherent circularly polarized LG and Gaussian beams in a homogeneous plasma with its electric vector polarized along the z-axis; the laser beams are considered to be of same frequency (ω). It is convenient to express the electric field vectors El and Eg associated with these beams in cylindrical coordinate system with azimuthal symmetry and can be expressed as
and
where A l(r, z) = (E 0l/f l)(r/r 0lf l)lexp[−(r 2/2r 0l2f l2)]L pl(r 2/r 0l2f l2)exp(−iφl), A g(r, z) = (E 0g/f g)exp[−(r 2/2r 0g2f g2)], E 0l and E 0g refers to the maximum amplitude of the LG and Gaussian beams of initial width r 0l & r 0g (in space), L pl is the associated Laguerre polynomial, l & p refer the binomial coefficients characterizing intensity modulation on the wavefront and φl refers the initial phase difference between the electric field vectors between Gaussian (Eg) and LG (El) beams in coaxial propagation. The dispersion relation characterize the em field in a plasma and can be expressed as ω2 = (c 2k 2 + ωp2), where ωp is the plasma frequency, k[=(ω/c)ε0j1/2] refers to the wave number associated with the em beam, ε0j is the dielectric function corresponding to the axis of maximum electric field on the wavefront of the beam and c refers to the speed of light in vacuum; here j stands for LG (L 01 mode) and Gaussian profiles of the beam.
The NLSE) describing the propagation of an em beam in a plasma (Sodha et al., Reference Sodha, Ghatak and Tripathi1976); following the Jeffreys–Wentzel–Kramers–Brillouin (JWKB) approximation (Ghatak & Loknathan, Reference Ghatak and Loknathan2004) for a slowly varying amplitude of the wave with propagation distance z (i.e., the term ∂ 2A j/∂ z 2 is neglected), the wave equation characterizing the electric field vector takes the form
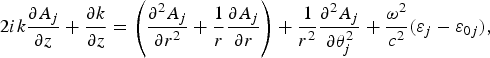 $$2ik\displaystyle{{\partial A_j } \over {\partial z}} + \displaystyle{{{\rm \partial} k} \over {\partial z}} = \left({\displaystyle{{\partial^2 A_j } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A_j } \over {\partial r}}} \right)+ \displaystyle{1 \over {r^2 }}\displaystyle{{\partial ^2 A_j } \over {\partial {\rm \theta} _j^2 }} + \displaystyle{{{\rm \omega} ^2 } \over {c^2 }}\lpar {\rm \varepsilon} _j - {\rm \varepsilon} _{0j} \rpar \comma \; $$
$$2ik\displaystyle{{\partial A_j } \over {\partial z}} + \displaystyle{{{\rm \partial} k} \over {\partial z}} = \left({\displaystyle{{\partial^2 A_j } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A_j } \over {\partial r}}} \right)+ \displaystyle{1 \over {r^2 }}\displaystyle{{\partial ^2 A_j } \over {\partial {\rm \theta} _j^2 }} + \displaystyle{{{\rm \omega} ^2 } \over {c^2 }}\lpar {\rm \varepsilon} _j - {\rm \varepsilon} _{0j} \rpar \comma \; $$where εj refers the dielectric function of the plasma and j stands for Gaussian and LG beams.
The first two terms in the right-hand side of the above equation refer to the contribution in field evolution due to diffraction and phase variation; the manifestation of these terms with plasma non-linear effects (last term) causes the transverse focusing/defocusing of the em beam as it propagates in the plasma. The non-linearity in plasma primarily arises on account of electron density modification due to non-uniformity in the irradiance profile of the beam. The solution for Eq. (4) can be written as (Sodha et al., Reference Sodha, Ghatak and Tripathi1976)
where S j(r, z) refers to the eikonal associated with the LG and Gaussian beam propagations.
Substituting for A j(r, z, θ j) in Eq. (4) and comparing the real and imaginary terms one gets (Thakur & Berakdar, Reference Thakur and Berakdar2010; Misra et al., Reference Misra, Mishra, Sodha and Tripathi2014)
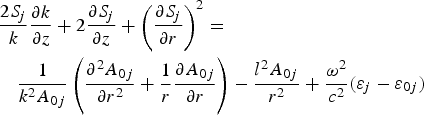 $$\eqalign{&\displaystyle{{2S_j } \over k}\displaystyle{{\partial k} \over {\partial z}} + 2\displaystyle{{\partial S_j } \over {\partial z}} + \left({\displaystyle{{\partial S_j } \over {\partial r}}} \right)^2 = \cr & \quad \displaystyle{1 \over {k^2 A_{0j} }}\left({\displaystyle{{\partial^2 A_{0j} } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A_{0j} } \over {\partial r}}} \right)- \displaystyle{{l^2 A_{0j} } \over {r^2 }} + \displaystyle{{{\rm \omega} _{}^2 } \over {c^2 }}\lpar {\rm \varepsilon} _j - {\rm \varepsilon} _{0j} \rpar } $$
$$\eqalign{&\displaystyle{{2S_j } \over k}\displaystyle{{\partial k} \over {\partial z}} + 2\displaystyle{{\partial S_j } \over {\partial z}} + \left({\displaystyle{{\partial S_j } \over {\partial r}}} \right)^2 = \cr & \quad \displaystyle{1 \over {k^2 A_{0j} }}\left({\displaystyle{{\partial^2 A_{0j} } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A_{0j} } \over {\partial r}}} \right)- \displaystyle{{l^2 A_{0j} } \over {r^2 }} + \displaystyle{{{\rm \omega} _{}^2 } \over {c^2 }}\lpar {\rm \varepsilon} _j - {\rm \varepsilon} _{0j} \rpar } $$and
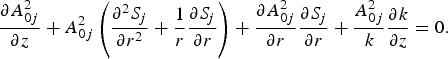 $$\displaystyle{{\partial A_{0j}^2 } \over {\partial z}} + A_{0j}^2 \left({\displaystyle{{\partial^2 S_j } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial S_j } \over {\partial r}}} \right)+ \displaystyle{{\partial A_{0j}^2 } \over {\partial r}}\displaystyle{{\partial S_j } \over {\partial r}} + \displaystyle{{A_{0j}^2 } \over k}\displaystyle{{\partial k} \over {\partial z}} = 0. $$
$$\displaystyle{{\partial A_{0j}^2 } \over {\partial z}} + A_{0j}^2 \left({\displaystyle{{\partial^2 S_j } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial S_j } \over {\partial r}}} \right)+ \displaystyle{{\partial A_{0j}^2 } \over {\partial r}}\displaystyle{{\partial S_j } \over {\partial r}} + \displaystyle{{A_{0j}^2 } \over k}\displaystyle{{\partial k} \over {\partial z}} = 0. $$It is noticed that Gaussian and LG beams have different intensity profiles and characterized by on-axis and off-axis maxima, respectively; thus it is instructive that the dynamics of each beam should be analyzed in the vicinity of its intensity maxima.
2.1.1. LG Beam: L01 Mode
As discussed earlier, LG beam displays an off-axis intensity profile and the above set of equations [Eq. (5)] should be transferred to the axis (r ≠ 0) in the vicinity of intensity maximum. For the sake of simplicity in the analysis, the propagation dynamics of a specific LG profile corresponding to L 01 mode has been considered herein. For this particular case (i.e., L 01 mode) the intensity maximum occurs at r = r 0lf l. To proceed further a paraxial-like approach (Misra & Mishra, Reference Misra and Mishra2008; Sodha et al., Reference Sodha, Mishra and & Misra2009a) analogous to that of paraxial approximation is adopted where the coordinate system is transformed from (r, z) to (η l, z) space such that
where r 0lf l(z) is the width of the beam and r = r 0lf l represents the position of the maximum irradiance on the wavefront as it advances in the plasma. In the vicinity of off-axis maxima, it is justified to expand other relevant parameters around intensity maximum, that is, η l = 0. Using this relation the set of Eqs (6) thus transformed as (Misra & Mishra, Reference Misra and Mishra2008)
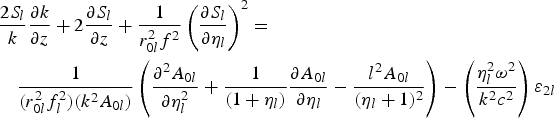 $$\eqalign{& \displaystyle{{2S_l } \over k}\displaystyle{{\partial k} \over {\partial z}} + 2\displaystyle{{\partial S_l } \over {\partial z}} + \displaystyle{1 \over {r_{0l}^2 f^2 }}\left({\displaystyle{{\partial S_l } \over {\partial \eta_l }}} \right)^2 = \cr & \quad \displaystyle{1 \over {\lpar r_{0l}^2 f_l^2 \rpar \lpar k^2 A_{0l} \rpar }}\left({\displaystyle{{\partial^2 A_{0l} } \over {\partial \eta_l^2 }} + \displaystyle{1 \over {\lpar 1 + \eta_l \rpar }}\displaystyle{{\partial A_{0l} } \over {\partial \eta_l }} - \displaystyle{{l^2 A_{0l} } \over {\lpar \eta_l + 1\rpar^2 }}} \right)- \left({\displaystyle{{\eta_l^2 \omega^2 } \over {k^2 c^2 }}} \right)\varepsilon _{2l}} $$
$$\eqalign{& \displaystyle{{2S_l } \over k}\displaystyle{{\partial k} \over {\partial z}} + 2\displaystyle{{\partial S_l } \over {\partial z}} + \displaystyle{1 \over {r_{0l}^2 f^2 }}\left({\displaystyle{{\partial S_l } \over {\partial \eta_l }}} \right)^2 = \cr & \quad \displaystyle{1 \over {\lpar r_{0l}^2 f_l^2 \rpar \lpar k^2 A_{0l} \rpar }}\left({\displaystyle{{\partial^2 A_{0l} } \over {\partial \eta_l^2 }} + \displaystyle{1 \over {\lpar 1 + \eta_l \rpar }}\displaystyle{{\partial A_{0l} } \over {\partial \eta_l }} - \displaystyle{{l^2 A_{0l} } \over {\lpar \eta_l + 1\rpar^2 }}} \right)- \left({\displaystyle{{\eta_l^2 \omega^2 } \over {k^2 c^2 }}} \right)\varepsilon _{2l}} $$and
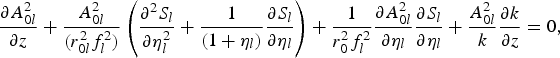 $$\eqalign{\displaystyle{{\partial A_{0l}^2 } \over {\partial z}} + \displaystyle{{A_{0l}^2 } \over {\lpar r_{0l}^2 f_l^2 \rpar }}\left({\displaystyle{{\partial^2 S_l } \over {\partial \eta_l^2 }} + \displaystyle{1 \over {\lpar 1 + \eta_l \rpar }}\displaystyle{{\partial S_l } \over {\partial \eta_l }}} \right)+ \displaystyle{1 \over {r_0^2 f_l^2 }}\displaystyle{{\partial A_{0l}^2 } \over {\partial \eta _l }}\displaystyle{{\partial S_l } \over {\partial \eta _l }} + \displaystyle{{A_{0l}^2 } \over k}\displaystyle{{\partial k} \over {\partial z}} = 0\comma} \; $$
$$\eqalign{\displaystyle{{\partial A_{0l}^2 } \over {\partial z}} + \displaystyle{{A_{0l}^2 } \over {\lpar r_{0l}^2 f_l^2 \rpar }}\left({\displaystyle{{\partial^2 S_l } \over {\partial \eta_l^2 }} + \displaystyle{1 \over {\lpar 1 + \eta_l \rpar }}\displaystyle{{\partial S_l } \over {\partial \eta_l }}} \right)+ \displaystyle{1 \over {r_0^2 f_l^2 }}\displaystyle{{\partial A_{0l}^2 } \over {\partial \eta _l }}\displaystyle{{\partial S_l } \over {\partial \eta _l }} + \displaystyle{{A_{0l}^2 } \over k}\displaystyle{{\partial k} \over {\partial z}} = 0\comma} \; $$where εl (η l, z) = ε0l (z) − η l2 ε2l (z) and like the paraxial theory the present analysis is strictly applicable when η l≪1. In paraxial regime, the solution of Eqs. (8) can be written as
and
where βl = r 0l2f l (∂f l /∂z), Θl(z) is the arbitrary phase function describing the departure of the curvature from spherical nature and f l refers to the beam width parameter that characterizes the irradiance profile as it propagates in the plasma.
The solutions for A 0l2 and S l is consistent with Eq. (8b) and essentially characterize the maintenance of the shape of the beam as it advances through the plasma. Substituting for A 0l2, S l, and εl in Eq. (8a) and equating the coefficients of η l0 and η l2 on both sides of the resulting equation one obtains
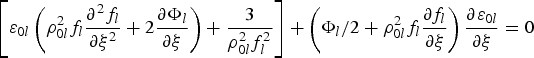 $$\eqalign{\left[{\varepsilon_{0l} \left({\rho_{0l}^2 f_l \displaystyle{{\partial^2 f_l } \over {\partial \xi^2 }} + 2\displaystyle{{\partial \Phi_l } \over {\partial \xi }}} \right)+ \displaystyle{3 \over {\rho_{0l}^2 f_l^2 }}} \right]+ \left({\Phi_l /2 + \rho_{0l}^2 f_l \displaystyle{{\partial f_l } \over {\partial \xi }}} \right)\displaystyle{{\partial \varepsilon _{0l} } \over {\partial \xi }} = 0} $$
$$\eqalign{\left[{\varepsilon_{0l} \left({\rho_{0l}^2 f_l \displaystyle{{\partial^2 f_l } \over {\partial \xi^2 }} + 2\displaystyle{{\partial \Phi_l } \over {\partial \xi }}} \right)+ \displaystyle{3 \over {\rho_{0l}^2 f_l^2 }}} \right]+ \left({\Phi_l /2 + \rho_{0l}^2 f_l \displaystyle{{\partial f_l } \over {\partial \xi }}} \right)\displaystyle{{\partial \varepsilon _{0l} } \over {\partial \xi }} = 0} $$and
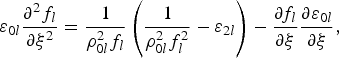 $${\rm \varepsilon} _{0l} \displaystyle{{\partial ^2 f_l } \over {\partial \xi ^2 }} = \displaystyle{1 \over {\rho _{0l}^2 f_l }}\left({\displaystyle{1 \over {\rho_{0l}^2 f_l^2 }} - {\rm \varepsilon}_{2l} } \right)- \displaystyle{{\partial f_l } \over {\partial {\rm \xi} }}\displaystyle{{\partial {\rm \varepsilon} _{0l} } \over {\partial {\rm \xi} }}\comma \; $$
$${\rm \varepsilon} _{0l} \displaystyle{{\partial ^2 f_l } \over {\partial \xi ^2 }} = \displaystyle{1 \over {\rho _{0l}^2 f_l }}\left({\displaystyle{1 \over {\rho_{0l}^2 f_l^2 }} - {\rm \varepsilon}_{2l} } \right)- \displaystyle{{\partial f_l } \over {\partial {\rm \xi} }}\displaystyle{{\partial {\rm \varepsilon} _{0l} } \over {\partial {\rm \xi} }}\comma \; $$where ρ 0l = (r 0lω/c), Φl = (Θlω/c), and ξ = (zω/c).
The set of equations [Eq. (10)] characterizes the spatial evolution of the electric field envelop of LG (L 01 mode) beam as it propagates in the plasma; in this course the transverse focusing/defocusing of the beam occurs. It should be noted here that the wave equations [Eqs. (7)–(10)] strictly correspond to the L 01 mode of LG beam; however, the similar analysis based on the paraxial-like approach can be performed for various orders (i.e., arbitrary l & p) of off-axis LG intensity profiles.
2.1.2. Gaussian Beam
In case of Gaussian beam, the intensity maximum occurs at r = 0. Following earlier analyses (Sharma et al., Reference Sharma, Borhanian and Kourakis2009) based on paraxial approximation, the coupled differential equations describing the beam width parameter and phase in corresponding to Gaussian wavefront in the plasma can be written as
and
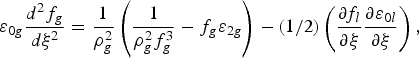 $${\rm \varepsilon} _{0g} \displaystyle{{d^2 f_g } \over {d{\rm\xi} ^2 }} = \displaystyle{1 \over {\rho _g^2 }}\left({\displaystyle{1 \over {\rho_g^2 f_g^3 }} - f_g {\rm \varepsilon}_{2g} } \right)- \lpar 1/2\rpar \left({\displaystyle{{\partial f_l } \over {\partial {\rm\xi} }}\displaystyle{{\partial {\rm \varepsilon}_{0l} } \over {\partial {\rm\xi} }}} \right)\comma \; $$
$${\rm \varepsilon} _{0g} \displaystyle{{d^2 f_g } \over {d{\rm\xi} ^2 }} = \displaystyle{1 \over {\rho _g^2 }}\left({\displaystyle{1 \over {\rho_g^2 f_g^3 }} - f_g {\rm \varepsilon}_{2g} } \right)- \lpar 1/2\rpar \left({\displaystyle{{\partial f_l } \over {\partial {\rm\xi} }}\displaystyle{{\partial {\rm \varepsilon}_{0l} } \over {\partial {\rm\xi} }}} \right)\comma \; $$where ρ 0g = (r 0gω/c) and Φg = (Θgω/c). The above equations [Eqs (11)] characterizing f g and Φg are consistent with the irradiance profile
with εg (r,z) = ε0g (z) − η g2 ε2g (z), η g = (r/r 0g).
It is interesting to note here that the algebraic form of the focusing equation [i.e., Eqs. (10b)–(11b)] is similar to that obtained in references (Nasalski, Reference Nasalski1995; Reference Nasalski1996; Thakur & Berkdar, Reference Thakur and Berakdar2010), where laser propagation dynamics in Kerr dielectric medium corresponding to Gaussian and LG profiles has been explored. In contrast to quadratic dependence of the dielectric function on the laser field in Kerr medium, the plasma exhibits saturating nature of non-linearity; this causes the oscillatory focusing/defocusing as the laser beam propagates in the plasma.
The set of Eqs. (10) and (11) is coupled through the dielectric function and characterize the coaxial propagation of the LG (L 01 mode) and Gaussian beams. Using appropriate expressions for ε corresponding to plasma with dominant ponderomotive and relativistic non-linearities in addition to initial boundary conditions (corresponding to plane wavefront of the pulse at z = 0) viz.Φl(0) = Φg(0) = 0, f l(0) = f g(0) = 1 and f l′ (0) = f g′ (0) = 0, the equations can numerically be solved to evaluate the beam width parameter and phase dependence on the propagation distance ξ; for our computations Mathematica software is used. The knowledge of f j and Φj leads to the information about spatial evolution of intensity profile as it propagates in the plasma.
2.2. Critical Condition for Focusing: Critical Curve
For an initial plane wavefront (i.e., df j/dξ = 0) of the beam, (d 2f j/dξ2)ξ=0 = 0 refers to f j(ξ) = 1 and the beam can propagate without convergence or divergence in plasma; this refers the critical condition for focusing of the em beam. Thus by substituting (d 2f j/dξ2)ξ=0 = 0 in Eqs. (10b) and (11b), one obtains a relation between dimensionless initial width of the beam ρ j(=r jω/c) and initial irradiance EE*, as the critical curve that ensures the propagation of the beam in the self-trapped mode. The critical condition is thus given by Sharma et al. (Reference Sharma, Prakash, Verma and Sodha2003)
The beam displays self-focusing for the condition (d 2f j/dξ2) < 0, whereas in case of (d 2f j/dξ2)>0 the beam undergoes either oscillatory or steady divergence.
3. DIELECTRIC FUNCTION OF THE PLASMA
The non-linear propagation of any beam in the plasma is characterized by the non-linear dielectric function that is in the present analysis, modified by the coupling of fields (intensities) of both the beams. The spatial profile of the dielectric function as a consequence of the combined intensity profile (derived later) drives the non-linear effects in the plasma and hence propagation dynamics of the beams. Following Sodha et al. (Reference Sodha, Ghatak and Tripathi1974), the effective dielectric function of the plasma can be expressed as
where Ω = (ωpe/ω), ωpe = (4π n e0e 2/m e)1/2 is the electron plasma frequency, n e is the plasma density in the presence of em field, n e0 refers the undisturbed plasma density, m e is the mass of the electron, and e is the electronic charge.
As mentioned before, the plasma density redistribution and hence the effective dielectric function is determined by combined intensities of LG and Gaussian beams. The effective irradiance generated by LG (L 01 mode) and Gaussian beams can be written as
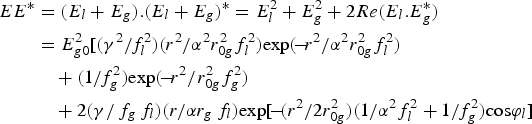 $$\eqalign{E{E^{\ast} } &= \lpar {E_l} + {E_g}\rpar .{\lpar {E_l} + {E_g}\rpar ^{\ast}} = E_l^2 + E_g^2 + 2Re\lpar {E_l}.E_g^{\ast} \rpar \cr & = E_{g0}^2 [ {\lpar {\gamma^2}/f_l^2 \rpar \lpar {r^2}/{\alpha^2}r_{0g}^2 f_l^2 \rpar \hbox{exp}\lpar \!-\! {r^2}/{\alpha^2}r_{0g}^2 f_l^2 \rpar } \cr & \quad + \lpar 1/f_g^2 \rpar \hbox{exp}\lpar \!-\! {r^2}/r_{0g}^2 f_g^2 \rpar \cr & \quad + { 2\lpar \gamma /{\,f_g}{\,f_l}\rpar \lpar r/\alpha {r_g}{\,f_l}\rpar \hbox{exp}[ \!-\! \lpar {r^2}/2r_{0g}^2 \rpar \lpar 1/{\alpha^2}f_l^2 + 1/f_g^2 \rpar \hbox{cos}{{\rm \varphi}_l}} ] } $$
$$\eqalign{E{E^{\ast} } &= \lpar {E_l} + {E_g}\rpar .{\lpar {E_l} + {E_g}\rpar ^{\ast}} = E_l^2 + E_g^2 + 2Re\lpar {E_l}.E_g^{\ast} \rpar \cr & = E_{g0}^2 [ {\lpar {\gamma^2}/f_l^2 \rpar \lpar {r^2}/{\alpha^2}r_{0g}^2 f_l^2 \rpar \hbox{exp}\lpar \!-\! {r^2}/{\alpha^2}r_{0g}^2 f_l^2 \rpar } \cr & \quad + \lpar 1/f_g^2 \rpar \hbox{exp}\lpar \!-\! {r^2}/r_{0g}^2 f_g^2 \rpar \cr & \quad + { 2\lpar \gamma /{\,f_g}{\,f_l}\rpar \lpar r/\alpha {r_g}{\,f_l}\rpar \hbox{exp}[ \!-\! \lpar {r^2}/2r_{0g}^2 \rpar \lpar 1/{\alpha^2}f_l^2 + 1/f_g^2 \rpar \hbox{cos}{{\rm \varphi}_l}} ] } $$with α(=r 0l/r 0g) and γ = E l0/E g0.
In the paraxial regime, the effective irradiance [EE*, Eq. (15)] can be expanded around its intensity maximum. Thus for Gaussian beam (r = 0), one gets
where a g = (E g02/f g2), b g = E g02(2γ/αf gf l2) cosφl, and c g = E g02[(γ2/α2f l4) − (1/f g4)].
Similarly in the case of L 01 mode of the LG beam, EE* in the vicinity of irradiance maximum (i.e., η l = 0) can be written as
where a l = E g02[(γ 2/f l2)exp(−1) + (1/f g2)exp(−α 2f lg2) + (2γ/f gf l) exp[−(1+α 2f lg2)/2]cosφl], b l = −E g02(α 2f lg2)[(2/f g2)exp(−α 2f lg2) + (2γ/f gf l)exp[−(1+α 2f lg2)/2]cosφl], c l = −E g02[(2γ 2/f l2) exp(−1) − (1/f g2)(α 2f lg2)exp(−α 2f lg2) + (2γ/f gf l)exp[−(1+ α 2f lg2)/2]cosφl], and f lg = (f l/f g).
3.1. Evaluation of Dielectric Function
3.1.1. Ponderomotive Non-Linearity
In collisionless plasmas under influence of an em radiation, the redistribution of the electron density is determined by the balance of ponderomotive force with electron gas pressure gradient and the space charge electric field; the magnitude of the ponderomotive force is proportional to the gradient of beam irradiance. Such non-linearity sets in a period of the order of ωpi−1. For a collisionless plasma at moderate power of the beam (when the quiver speed of the electron is much smaller than the speed of light in vacuum), the modified electron density function n e is given by (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1976),
where β = (e 2/8k bT 0m eω2), k b is the Boltzmann constant, and T 0 is the temperature of the atoms/ions. By substituting Eq. (17) into (14), one obtains
 $$\eqalign{{\rm \varepsilon} _j \lpar r\comma \; z\rpar &= {\rm \varepsilon} _{0j} \lpar z\rpar - \eta _j^2 {\rm \varepsilon} _{2j} \lpar z\rpar = 1 - \Omega ^2 \, \hbox{exp}\lpar - {\rm \beta} EE^ {\ast} \rpar \cr & \approx [ 1 - \Omega ^2 \, \hbox{exp}\lpar - {\rm \beta} a_j \rpar ] - \eta _j^2 [ \Omega ^2 \lpar {\rm \beta} c_j - {\rm \beta} ^2 b_j^2 /2\rpar \, \hbox{exp}\lpar \!-\! {\rm \beta} a_j \rpar ] .} $$
$$\eqalign{{\rm \varepsilon} _j \lpar r\comma \; z\rpar &= {\rm \varepsilon} _{0j} \lpar z\rpar - \eta _j^2 {\rm \varepsilon} _{2j} \lpar z\rpar = 1 - \Omega ^2 \, \hbox{exp}\lpar - {\rm \beta} EE^ {\ast} \rpar \cr & \approx [ 1 - \Omega ^2 \, \hbox{exp}\lpar - {\rm \beta} a_j \rpar ] - \eta _j^2 [ \Omega ^2 \lpar {\rm \beta} c_j - {\rm \beta} ^2 b_j^2 /2\rpar \, \hbox{exp}\lpar \!-\! {\rm \beta} a_j \rpar ] .} $$Here εj(r, z) refer to the dielectric function for LG (L 01 mode) and Gaussian beams in the vicinity of their intensity maximum.
3.1.2. Relativistic Non-Linearity
In the presence of high-intensity em radiation, the electrons may gain the quiver speed equivalent to the light speed in vacuum. This causes relativistic variation in the electron mass and consequent change in plasma frequency leads to the redistribution of electrons and triggers relativistic non-linearity (Hora, Reference Hora1975). This non-linearity sets in a period of the order of ωpe−1. The dielectric function in the case of circularly polarized beam can be expressed as (Hora, Reference Hora1991)
where ς = (e 2/m e2ω2c 2). The dielectric function in the vicinity of intensity maxima can be written as
 $$\eqalign{{\rm \varepsilon} _j \lpar r\comma \; z\rpar &= {\rm \varepsilon} _{0j} \lpar z\rpar - \eta _j^2 {\rm \varepsilon} _{2j} \lpar z\rpar = 1 - \Omega ^2 \lpar 1 + \varsigma EE^{\ast} \rpar ^{ - 1/2} \cr & \approx [ 1 - \Omega ^2 \lpar 1 + \varsigma a_j \rpar ^{ - 1/2} ] - \eta _j^2 \lpar \Omega ^2 /2\rpar \lpar 1 + \varsigma a_j \rpar ^{ - 3/2} \cr & \quad [ \varsigma c_j - \lpar 3/4\rpar \varsigma ^2 b_j^2 \lpar 1 + \varsigma a_j \rpar ^{ - 1} ] .} $$
$$\eqalign{{\rm \varepsilon} _j \lpar r\comma \; z\rpar &= {\rm \varepsilon} _{0j} \lpar z\rpar - \eta _j^2 {\rm \varepsilon} _{2j} \lpar z\rpar = 1 - \Omega ^2 \lpar 1 + \varsigma EE^{\ast} \rpar ^{ - 1/2} \cr & \approx [ 1 - \Omega ^2 \lpar 1 + \varsigma a_j \rpar ^{ - 1/2} ] - \eta _j^2 \lpar \Omega ^2 /2\rpar \lpar 1 + \varsigma a_j \rpar ^{ - 3/2} \cr & \quad [ \varsigma c_j - \lpar 3/4\rpar \varsigma ^2 b_j^2 \lpar 1 + \varsigma a_j \rpar ^{ - 1} ] .} $$As can be seen from the final expressions for dielectric function, it is influenced by the irradiance profile of both the beams that are coupled through the phase difference between them; manifesting the appropriate expressions for the dielectric function [Eqs. (18) and (20)] with the beam dynamics equations [Eqs. (10) and (11)], coaxial (or coupled mode) propagation of LG (L 01 mode) and Gaussian beams has been analyzed and discussed in the next section.
4. NUMERICAL RESULTS AND DISCUSSION
For a numerical appreciation of the analytical formulation and physics understanding of the coaxial propagation dynamics of central shadow LG (L 01 mode in particular) and Gaussian em beams, critical curve, and non-linear space evolution are computed for an arbitrarily set of laser–plasma parameters and different kind of basic non-linearities; the estimates have been illustrated graphically. The propagation of the beams in the plasma is primarily characterized by dielectric function that becomes a complex function of electric fields of both the beams in coupled mode. The critical curves viz. the relation between initial irradiance g j(=β E 0j2orς E 0j2) and initial beam width parameter (ρ j) has been obtained using Eq. (13) and the appropriate expression for the transverse component of dielectric function and non-linearities. The non-linear space evolution of the beam width parameters (f j) and eikonal phase (Θj) has been obtained by simultaneous numerical integration of Eqs. (10) and (11) along with the suitable laser plasma parameters and appropriate boundary conditions (as stated in the last paragraph of Section 2.1.2). The effect of varying initial laser parameters of both beams viz. initial width (ρ j), initial irradiance (g j), and initial phase difference (φl) on non-linear coaxial propagation dynamics and transverse compression have been evaluated and presented in the form of curves. The computations have been performed for the following standard set of parameters viz. β E 0g2(=ς E 0g2) = 5, β E 0l2(=ς E 0l2) = 2, γ 2 = 2/5, α = 1, Ω2 = 0.8, and φl = π/4; the choice of these normalized parameters refers to laser propagation in the weakly relativistic plasma regime having uniform background plasma density n e0~1018 cm−3, laser wavelength λ~10 µm, and intensity I 0 ≈ 1017 W/cm2, respectively. The effect of various laser–plasma parameters on the critical curves and beam parameters has been studied by varying one and keeping others the same.
The critical curves (cc's) corresponding to dominant ponderomotive non-linearities have been illustrated in the set of Figure 1. The critical curves describe the self-trapping mode of the propagation of the em beams and characterize the em beam propagation in (ρ j,g j) space. It can readily be seen from Eq. (13) that the initial beam width (i.e., ρ j−2) follows the behavior similar to that of transverse (azimuthal) component of the dielectric function ε2j. The critical curve divides the (ρ j,g j) space primarily in two regions where the propagation of em beam is characterized by self (oscillatory)-focusing (region below cc) and oscillatory defocusing (region above in proximity of cc), or steady defocusing (region far away from cc). The figures also indicate the fact that the beam having large ρ j and large irradiance in the self-focusing region, gives rise to larger non-linear effects. The parameters corresponding to an initial point (ρ j,g j) lying on critical curves correspond to (d 2f/d ξ 2)ξ=0 = 0 and for an initially plane wavefront (df/d ξ) = 0, f remains constant and the beam propagates without convergence or divergence in plasma; such self-trapped motion of the beam is termed as stationary spatial soliton propagation. As stated before, the phase difference φl describes the coupling of electric field vectors associated with Gaussian and LG (L 01 mode) beams and effectively characterize the intensity pattern and propagation of the coupled mode. The effect of varying φl on critical curves (ρ g−2 − g g) corresponding to ponderomotive non-linearity for the given values of parameters α & g l (=β E 0l2), has been illustrated in Figure 1a. The figure indicates that the self-focusing region decreases with increasing φl; this nature can be attributed to large coupling between the coaxial beams with decreasing φl which enhances the effective irradiance of the beam and therefore more pronounced non-linear effects. It is seen that the self-focusing region decreases with the increasing value of the parameter α; this behavior has been displayed in Figure 1b and can be understood in terms of decrease in effective intensity [via Eqs. (16) and (18)] with increasing α. The self-focusing region is seen to increase with increasing parameter g l; this nature has been displayed in Figure 1c. Similarly the critical curves can also be obtained in terms of parameters associated with LG beams, that is (ρ l−2 − g l) for given values of α and g g; however, these curves are another way of presentation of cc's and carry the same information as described in the case of Figure 1. The dependence of critical curves corresponding to dominant relativistic non-linearity has been displayed in the set of Figure 2; the nature of the curves is similar to that obtained in the case of ponderomotive non-linearity (Fig. 1) and physically interpretable in the similar fashion. These critical curves characterize the regions for self-focusing and oscillatory/steady divergence and valid throughout the propagation dynamics.

Fig. 1. Dependence of cc's (ρ g−2 − g g) on (a) phase φl associated with LG beams, (b) parameter α and (c) irradiance of LG beams g l corresponding to ponderomotive non-linearity for the standard set of parameters stated in the text.

Fig. 2. Dependence of cc's (ρ g−2 − g g) on (a) phase φl associated with LG beams, (b) parameter α and (c) irradiance of LG beams g l corresponding to relativistic non-linearity for the standard set of parameters stated in the text.
The dependence of beam width parameters associated with coaxial propagation of LG (f l) and Gaussian (f g) beams in the plasma having dominant ponderomotive non-linearity has been illustrated in Figure 3a (solid lines). It is seen that during coaxial propagation each beam mutually influence the dynamics of the other beam; in order to illustrate this fact the independent propagation of individual beams has been shown by broken lines in the figure. It can be seen from the figure that the additional influence of LG beam in coupled mode propagation causes the focusing of the Gaussian beam as it advances through the plasma. The effect of coaxial propagation on space evolution of the eikonal phase associated with LG (Φl) and Gaussian (Φg) beams (as in Fig. 3a) has been displayed in Figure 3b. The behavior of the curves corresponding to coaxial propagation is in well conformance with the critical curves as shown in Figure 1. The effect of phase difference (i.e., φl) on coaxial propagation of the beams corresponding to φl = π/4 & π/8 has been displayed in Figure 4a. The figure reflects the strong coupling in case of φl = π/4 as the focusing curves approach each other; this nature is well appreciated with critical curves in Figure 1a. The co-axial beam is seen to exhibit larger focusing with increasing parameter α and is shown in Figure 4b. The increase in α effectively refers to large initial beam width (ρ l) associated with the LG mode (for constant ρ g) that enhances non-linearity and hence the focusing. Further the influence of the initial irradiance of the LG mode on the non-linear propagation dynamics of Gaussian beam coaxially has been displayed in Figure 4c; the strong non-linear effects in the case of g l = 5 can be understood as a consequence of critical curves displayed in Figure 1c. The figures corresponding to the coupled mode propagation suggest that the dynamics of one beam can be controlled up to significant extent by varying the parameters of the other beam.

Fig. 3. Space evolution of the (a) beam width parameters (f j) and (b) phase (Φj) corresponding to ponderomotive non-linearity for the standard set of parameters stated in the text with φl = π/6; solid lines refer to coaxial propagation, while the broken curves correspond to separate propagation of Gaussian (f g, black lines) and LG (f l, red lines) beams.

Fig. 4. Space evolution of the beam width parameters (f j) corresponding to ponderomotive non-linearity for the standard set of parameters stated in the text. Panel (a) corresponds to varying phase φl(=π/4, solid) and φl(=π/8, broken), panel (b) refers to varying parameter α(=1, solid) and α(=1.5, broken), panel (c) refers to varying irradiance of LG beam g l(=2, solid) and g l(=5, broken); red and black color lines refer to f l and f g, respectively.
The beam width parameters f's certainly describe the evolution of electric field or intensity envelop (i.e., EE*) of the em beam and hence the power (energy) transfer as it advances through the plasma. In order to have an idea of the radial distribution of the intensity during coaxial propagation of LG–Gaussian modes, the space evolution of the effective irradiance profile in non-linear regime of the plasma characterized by dominant ponderomotive non-linearity has been displayed in Figure 5; the distribution is shown at different ξ values for the parameters g g = 10, g l = 5, α = 3, and φl = π/6. It is shown that during coaxial propagation, the beam dynamics mutually influence each other and gives rise to large non-linear effects; as a consequence the transverse laser field itself gets modified as it advances through the plasma. It can be seen from the figure that on account of mutual focusing/defocusing the radial distribution of intensity displays compression/rarefaction of the beams; the intensity distribution of LG and Gaussian modes independently has been shown by the broken curves. It is also noticed that the coupling of Gaussian mode with annular (L 01 mode) field profile leads to significant enhancement (e.g., ξ = 36) in its irradiance as beam propagates through the plasma; this nature is qualitatively similar as obtained in one of the recent experimental investigation (Scheller et al., Reference Scheller, Mills, Miri, Cheng, Moloney, Kolesik, Polynkin and Christodoulides2014). The spatial evolution of such profiles (characterized by potential dipoles) can also efficiently be utilized for trapping of plasma particles. Furthermore, it is also necessary to point out that a specific case, that is, propagation dynamics of LG em beam corresponding to L 01 mode has been considered herein the analysis however the methodology of paraxial-like approach can be extended to investigate the propagation dynamics of higher order LG modes.

Fig. 5. Space evolution of the radial distribution of the beam irradiance (EE*/E 0g2) as a function of parameters (ξ); the figure corresponds to dominant ponderomotive non-linearity for the parameters g g = 10, g l = 5, α = 3, and& ϕl = π/6.
5. SUMMARY
A formalism describing the non-linear coaxial propagation dynamics of finite size intense LG (L 01 mode) and Gaussian beams in a plasma characterized by ponderomotive and relativistic non-linearities has been established. In order to analyze the off-axis contribution of annular LG beams the formulation takes account of paraxial-like approach, while usual paraxial approximation is utilized to analyze the dynamics of Gaussian mode propagation. The dynamics of coaxial propagation is coupled through the dielectric function which is considered to be a function of combined electric field of both the propagating modes. The coaxial propagation dynamics is described by NLSE which governs the spatial evolution of the coupled mode as it advances through the plasma. Based on this analysis, the critical curves and space evolution of beam width parameter (f j) and phase (Φj) of coupled mode have been computed and presented graphically. The critical curves predict the regimes of oscillatory (self) focusing/defocusing and steady divergence of the coupled mode propagation; this characteristic feature is a consequence of competing phenomenon of diffraction with non-linear effects. It is shown that the coupling of Gaussian profile with L 01 mode significantly enhances its intensity as the coupled mode advances through the plasma. The focusing dynamics of such profiles (i.e., existence of sharp potential dipoles) is of relevance to the particle/atomic trapping and efficient energy transport which has significantly enhanced due to self-focusing of the coaxial beams.
ACKNOWLEDGEMENTS
One of the authors (SM) is grateful to the Department of Science and Technology (DST) for the financial support for the work.



