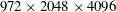1 Introduction
The mechanism of vorticity growth in the incompressible three-dimensional (3D) Euler equations, in the absence of a physical boundary, has been addressed in numerous studies because of its relation to a possible finite-time blowup and subsequent transition to turbulence. Several analytical blowup and no-blowup criteria have been established; see the reviews in Chae (Reference Chae, Dafermos and Pokorny2008) and Gibbon (Reference Gibbon2008). In parallel, a large amount of effort has been made with numerical analysis. In one of the early numerical studies, Brachet et al. (Reference Brachet, Meneguzzi, Vincent, Politano and Sulem1992) examined the evolution of periodic flows in
![]() $256^{3}$
grids for random initial conditions and in
$256^{3}$
grids for random initial conditions and in
![]() $864^{3}$
grids for the symmetric Taylor–Green vortex. In all cases, the maximum of vorticity grew nearly exponentially with time, and the regions of high vorticity were confined within pancake-like structures (thin vortex sheets). An exact solution of the Euler equations was suggested as a model for asymptotic pancake development, with the relation
$864^{3}$
grids for the symmetric Taylor–Green vortex. In all cases, the maximum of vorticity grew nearly exponentially with time, and the regions of high vorticity were confined within pancake-like structures (thin vortex sheets). An exact solution of the Euler equations was suggested as a model for asymptotic pancake development, with the relation
![]() $\unicode[STIX]{x1D714}_{max}(t)\propto 1/\ell (t)$
between the vorticity maximum and the pancake thickness. Since the tendency towards a vortex sheet should suppress three-dimensionality of the flow, formation of a finite-time singularity is not expected. It should be recalled that the dynamics of the two-dimensional (2D) Euler equations is known to be regular; see Majda & Bertozzi (Reference Majda and Bertozzi2002) and the related discussion in Pumir & Siggia (Reference Pumir and Siggia1990) and Ohkitani (Reference Ohkitani2008). Thus, further numerical studies were mainly concentrated on carefully designed initial conditions providing enhanced vorticity growth. We refer to Gibbon (Reference Gibbon2008) and Agafontsev, Kuznetsov & Mailybaev (Reference Agafontsev, Kuznetsov and Mailybaev2015) for a brief review, as well as to Hou (Reference Hou2009), Bustamante & Brachet (Reference Bustamante and Brachet2012) and Kerr (Reference Kerr2013) for examples of recent numerical works. It is fair to say that we do not possess sufficiently reliable evidence supporting the blowup hypothesis yet.
$\unicode[STIX]{x1D714}_{max}(t)\propto 1/\ell (t)$
between the vorticity maximum and the pancake thickness. Since the tendency towards a vortex sheet should suppress three-dimensionality of the flow, formation of a finite-time singularity is not expected. It should be recalled that the dynamics of the two-dimensional (2D) Euler equations is known to be regular; see Majda & Bertozzi (Reference Majda and Bertozzi2002) and the related discussion in Pumir & Siggia (Reference Pumir and Siggia1990) and Ohkitani (Reference Ohkitani2008). Thus, further numerical studies were mainly concentrated on carefully designed initial conditions providing enhanced vorticity growth. We refer to Gibbon (Reference Gibbon2008) and Agafontsev, Kuznetsov & Mailybaev (Reference Agafontsev, Kuznetsov and Mailybaev2015) for a brief review, as well as to Hou (Reference Hou2009), Bustamante & Brachet (Reference Bustamante and Brachet2012) and Kerr (Reference Kerr2013) for examples of recent numerical works. It is fair to say that we do not possess sufficiently reliable evidence supporting the blowup hypothesis yet.
In our previous study, see Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), we returned to the problem of vorticity growth from generic large-scale initial conditions and focused on numerical description of flow details with high resolution. Two simulations were carried out with grids of up to
![]() $486\times 1024\times 2048$
and
$486\times 1024\times 2048$
and
![]() $1152\times 384\times 2304$
for initial conditions designated as
$1152\times 384\times 2304$
for initial conditions designated as
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
. Self-similar development of the pancake-like regions of high vorticity was observed. However, significantly different exponents (
$I_{2}$
. Self-similar development of the pancake-like regions of high vorticity was observed. However, significantly different exponents (
![]() $\unicode[STIX]{x1D6FD}_{2}/\unicode[STIX]{x1D6FD}_{1}\approx 2/3$
) were measured for the maximum vorticity growth
$\unicode[STIX]{x1D6FD}_{2}/\unicode[STIX]{x1D6FD}_{1}\approx 2/3$
) were measured for the maximum vorticity growth
![]() $\unicode[STIX]{x1D714}_{max}(t)\propto \text{e}^{\unicode[STIX]{x1D6FD}_{2}t}$
and the pancake compression in the transversal direction
$\unicode[STIX]{x1D714}_{max}(t)\propto \text{e}^{\unicode[STIX]{x1D6FD}_{2}t}$
and the pancake compression in the transversal direction
![]() $\ell (t)\propto \text{e}^{-\unicode[STIX]{x1D6FD}_{1}t}$
, demonstrating that the pancake model with
$\ell (t)\propto \text{e}^{-\unicode[STIX]{x1D6FD}_{1}t}$
, demonstrating that the pancake model with
![]() $\unicode[STIX]{x1D714}_{max}(t)\propto 1/\ell (t)$
suggested in Brachet et al. (Reference Brachet, Meneguzzi, Vincent, Politano and Sulem1992) is insufficient. Pancake structures emerged in increasing number with time. These structures provided the leading contribution to the energy spectrum, where we observed the gradual formation of the Kolmogorov spectrum,
$\unicode[STIX]{x1D714}_{max}(t)\propto 1/\ell (t)$
suggested in Brachet et al. (Reference Brachet, Meneguzzi, Vincent, Politano and Sulem1992) is insufficient. Pancake structures emerged in increasing number with time. These structures provided the leading contribution to the energy spectrum, where we observed the gradual formation of the Kolmogorov spectrum,
![]() $E(k)\propto k^{-5/3}$
, in a fully inviscid flow.
$E(k)\propto k^{-5/3}$
, in a fully inviscid flow.
In the present paper, we demonstrate that the asymptotic pancake evolution can be described by a new exact solution of the Euler equations, which combines a shear flow aligned with an asymmetric straining flow. This solution represents an essential generalization of the pancake model of Brachet et al. (Reference Brachet, Meneguzzi, Vincent, Politano and Sulem1992) and agrees with the numerical data. We illustrate our results with the simulation with the
![]() $I_{1}$
initial condition from Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), performed here in an eight times larger grid of up to
$I_{1}$
initial condition from Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), performed here in an eight times larger grid of up to
![]() $972\times 2048\times 4096$
, and concentrate our analysis on the main pancake structure containing the global vorticity maximum. We checked that other pancake structures, as well as pancakes developing in simulations with different initial conditions, also agree with the exact solution.
$972\times 2048\times 4096$
, and concentrate our analysis on the main pancake structure containing the global vorticity maximum. We checked that other pancake structures, as well as pancakes developing in simulations with different initial conditions, also agree with the exact solution.
The paper is organized as follows. Section 2 describes the numerical method and demonstrates general properties of a pancake structure. The exact solution of the 3D Euler equations is proposed in § 3 as a model for asymptotic pancake evolution. In § 4, we provide several numerical tests comparing the analytical model with the simulations. The final section contains conclusions.
2 Pancake vorticity structures
We analyse the evolution of high-vorticity regions with numerical simulations of the Euler equations (in the vorticity formulation),
in the periodic box
![]() $\boldsymbol{r}=(x,y,z)\in [-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]^{3}$
. The pseudospectral Runge–Kutta fourth-order method is used, together with the Fourier cutoff function suggested in Hou & Li (Reference Hou and Li2007) to avoid the bottle-neck instability. The inverse of the curl operator and all spatial derivatives are calculated in the Fourier space. We start from initial condition
$\boldsymbol{r}=(x,y,z)\in [-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]^{3}$
. The pseudospectral Runge–Kutta fourth-order method is used, together with the Fourier cutoff function suggested in Hou & Li (Reference Hou and Li2007) to avoid the bottle-neck instability. The inverse of the curl operator and all spatial derivatives are calculated in the Fourier space. We start from initial condition
![]() $I_{1}$
of Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), which represents a perturbation of the shear flow
$I_{1}$
of Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), which represents a perturbation of the shear flow
![]() $\unicode[STIX]{x1D714}_{x}=\sin z$
,
$\unicode[STIX]{x1D714}_{x}=\sin z$
,
![]() $\unicode[STIX]{x1D714}_{y}=\cos z$
,
$\unicode[STIX]{x1D714}_{y}=\cos z$
,
![]() $\unicode[STIX]{x1D714}_{z}=0$
. Taking advantage of the anisotropy of the vorticity field, we use an adaptive anisotropic rectangular grid, which is uniform along each direction and adapted independently along each coordinate. For more details of the numerical scheme, see Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), where it was verified that the accuracy within the simulation time interval is very high and is not affected by the Fourier cutoff filter. The simulation previously stopped at time
$\unicode[STIX]{x1D714}_{z}=0$
. Taking advantage of the anisotropy of the vorticity field, we use an adaptive anisotropic rectangular grid, which is uniform along each direction and adapted independently along each coordinate. For more details of the numerical scheme, see Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), where it was verified that the accuracy within the simulation time interval is very high and is not affected by the Fourier cutoff filter. The simulation previously stopped at time
![]() $t=6.89$
with the grid
$t=6.89$
with the grid
![]() $486\times 1024\times 2048$
is continued here until
$486\times 1024\times 2048$
is continued here until
![]() $t=7.75$
with the eight times larger final grid
$t=7.75$
with the eight times larger final grid
![]() $972\times 2048\times 4096$
, when the thinnest pancake structure is resolved with
$972\times 2048\times 4096$
, when the thinnest pancake structure is resolved with
![]() $10$
grid points at the level of vorticity half-maximum. The results of the two simulations converge perfectly at the same times. Both the energy
$10$
grid points at the level of vorticity half-maximum. The results of the two simulations converge perfectly at the same times. Both the energy
![]() $E=(1/2)\int \boldsymbol{v}^{2}\,\text{d}^{3}\boldsymbol{r}$
and the helicity
$E=(1/2)\int \boldsymbol{v}^{2}\,\text{d}^{3}\boldsymbol{r}$
and the helicity
![]() $\unicode[STIX]{x1D6FA}=\int (\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D74E})\,\text{d}^{3}\boldsymbol{r}$
are conserved, with a relative error smaller than
$\unicode[STIX]{x1D6FA}=\int (\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D74E})\,\text{d}^{3}\boldsymbol{r}$
are conserved, with a relative error smaller than
![]() $10^{-11}$
.
$10^{-11}$
.

Figure 1. (a) Global vorticity maximum as a function of time (logarithmic vertical scale). The red dashed line indicates the slope
![]() $\propto \text{e}^{\unicode[STIX]{x1D6FD}_{2}t}$
, with
$\propto \text{e}^{\unicode[STIX]{x1D6FD}_{2}t}$
, with
![]() $\unicode[STIX]{x1D6FD}_{2}=0.5$
. The thin vertical line marks the final simulation time
$\unicode[STIX]{x1D6FD}_{2}=0.5$
. The thin vertical line marks the final simulation time
![]() $t=6.89$
in Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015). (b) Regions of the largest vorticity,
$t=6.89$
in Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015). (b) Regions of the largest vorticity,
![]() $\unicode[STIX]{x1D714}\geqslant 0.85\unicode[STIX]{x1D714}_{max}(t)$
, at different times. The colour represents the vorticity in the midplane of the pancake, from blue for
$\unicode[STIX]{x1D714}\geqslant 0.85\unicode[STIX]{x1D714}_{max}(t)$
, at different times. The colour represents the vorticity in the midplane of the pancake, from blue for
![]() $0.85\unicode[STIX]{x1D714}_{max}(t)$
to yellow for
$0.85\unicode[STIX]{x1D714}_{max}(t)$
to yellow for
![]() $\unicode[STIX]{x1D714}_{max}(t)$
. The structures are shifted vertically for better visualization. (c) Characteristic spatial scales
$\unicode[STIX]{x1D714}_{max}(t)$
. The structures are shifted vertically for better visualization. (c) Characteristic spatial scales
![]() $\ell _{1}$
(black),
$\ell _{1}$
(black),
![]() $\ell _{2}$
(blue) and
$\ell _{2}$
(blue) and
![]() $\ell _{3}$
(red) of the pancake structure. The red dashed line indicates the slope
$\ell _{3}$
(red) of the pancake structure. The red dashed line indicates the slope
![]() $\propto \text{e}^{-\unicode[STIX]{x1D6FD}_{1}t}$
, with
$\propto \text{e}^{-\unicode[STIX]{x1D6FD}_{1}t}$
, with
![]() $\unicode[STIX]{x1D6FD}_{1}=0.74$
.
$\unicode[STIX]{x1D6FD}_{1}=0.74$
.
Figure 1(a) shows the evolution of the global vorticity maximum
![]() $\unicode[STIX]{x1D714}_{max}(t)=\max _{\boldsymbol{r}}|\unicode[STIX]{x1D74E}(\boldsymbol{r},t)|$
, demonstrating the vorticity increase from
$\unicode[STIX]{x1D714}_{max}(t)=\max _{\boldsymbol{r}}|\unicode[STIX]{x1D74E}(\boldsymbol{r},t)|$
, demonstrating the vorticity increase from
![]() $\unicode[STIX]{x1D714}_{max}(0)=1.5$
up to
$\unicode[STIX]{x1D714}_{max}(0)=1.5$
up to
![]() $18.4$
at
$18.4$
at
![]() $t=7.75$
and the asymptotically exponential vorticity growth at late times. Figure 1(b) shows the three-dimensional regions containing the vorticity
$t=7.75$
and the asymptotically exponential vorticity growth at late times. Figure 1(b) shows the three-dimensional regions containing the vorticity
![]() $\unicode[STIX]{x1D714}=|\unicode[STIX]{x1D74E}|\geqslant 0.85\unicode[STIX]{x1D714}_{max}(t)$
at different times, and one can clearly see the formation of a thin pancake structure. It is convenient to introduce the pancake midplane as a surface, where the vorticity attains a maximum within the pancake thickness. The colour in figure 1(b) describes the midplane vorticity, from blue for
$\unicode[STIX]{x1D714}=|\unicode[STIX]{x1D74E}|\geqslant 0.85\unicode[STIX]{x1D714}_{max}(t)$
at different times, and one can clearly see the formation of a thin pancake structure. It is convenient to introduce the pancake midplane as a surface, where the vorticity attains a maximum within the pancake thickness. The colour in figure 1(b) describes the midplane vorticity, from blue for
![]() $0.85\unicode[STIX]{x1D714}_{max}(t)$
to yellow for
$0.85\unicode[STIX]{x1D714}_{max}(t)$
to yellow for
![]() $\unicode[STIX]{x1D714}_{max}(t)$
. At
$\unicode[STIX]{x1D714}_{max}(t)$
. At
![]() $t=3$
and
$t=3$
and
![]() $4$
, the pancake spans the whole periodic domain in the
$4$
, the pancake spans the whole periodic domain in the
![]() $x$
-direction; for larger times, its lateral sizes decrease, but eventually stabilize and remain almost constant at
$x$
-direction; for larger times, its lateral sizes decrease, but eventually stabilize and remain almost constant at
![]() $t\geqslant 6$
. On the contrary, the thickness keeps decreasing rapidly. Thus, at late times, vorticity variations become large (small) in transversal (tangential) directions to the pancake.
$t\geqslant 6$
. On the contrary, the thickness keeps decreasing rapidly. Thus, at late times, vorticity variations become large (small) in transversal (tangential) directions to the pancake.
The local geometry of the thin structure can be studied using the Hessian matrix
![]() $\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D714}^{2}$
of second derivatives of
$\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D714}^{2}$
of second derivatives of
![]() $\unicode[STIX]{x1D714}^{2}$
with respect to
$\unicode[STIX]{x1D714}^{2}$
with respect to
![]() $(x,y,z)$
, computed at the point of maximum vorticity; the location of the latter in between the grid nodes is approximated with the second-order finite-difference scheme. The (unit) normal vector
$(x,y,z)$
, computed at the point of maximum vorticity; the location of the latter in between the grid nodes is approximated with the second-order finite-difference scheme. The (unit) normal vector
![]() $\boldsymbol{n}_{1}$
to the pancake is defined as the eigenvector corresponding to the largest of the three eigenvalues
$\boldsymbol{n}_{1}$
to the pancake is defined as the eigenvector corresponding to the largest of the three eigenvalues
![]() $|\unicode[STIX]{x1D706}_{1}|\geqslant |\unicode[STIX]{x1D706}_{2}|\geqslant |\unicode[STIX]{x1D706}_{3}|$
of the Hessian. The pancake thickness
$|\unicode[STIX]{x1D706}_{1}|\geqslant |\unicode[STIX]{x1D706}_{2}|\geqslant |\unicode[STIX]{x1D706}_{3}|$
of the Hessian. The pancake thickness
![]() $\ell _{1}$
, as well as its lateral scales
$\ell _{1}$
, as well as its lateral scales
![]() $\ell _{2}$
and
$\ell _{2}$
and
![]() $\ell _{3}$
, can be estimated with the local second-order approximation as
$\ell _{3}$
, can be estimated with the local second-order approximation as
![]() $\ell _{i}=\sqrt{2\unicode[STIX]{x1D714}_{max}^{2}/|\unicode[STIX]{x1D706}_{i}|}$
; see Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015). Figure 1(c) shows these characteristic scales as functions of time. At late times, the pancake thickness
$\ell _{i}=\sqrt{2\unicode[STIX]{x1D714}_{max}^{2}/|\unicode[STIX]{x1D706}_{i}|}$
; see Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015). Figure 1(c) shows these characteristic scales as functions of time. At late times, the pancake thickness
![]() $\ell _{1}$
is exponentially decreasing, while the dimensions
$\ell _{1}$
is exponentially decreasing, while the dimensions
![]() $\ell _{2}$
and
$\ell _{2}$
and
![]() $\ell _{3}$
do not change substantially, in agreement with the three-dimensional picture in figure 1(b). Thus, the pancake develops only one small scale corresponding to its transversal direction, and the vorticity growth is locally one-dimensional. The span-to-thickness ratio grows exponentially, reaching
$\ell _{3}$
do not change substantially, in agreement with the three-dimensional picture in figure 1(b). Thus, the pancake develops only one small scale corresponding to its transversal direction, and the vorticity growth is locally one-dimensional. The span-to-thickness ratio grows exponentially, reaching
![]() $\ell _{2}/\ell _{1}\sim \ell _{3}/\ell _{1}\gtrsim 100$
at the final time
$\ell _{2}/\ell _{1}\sim \ell _{3}/\ell _{1}\gtrsim 100$
at the final time
![]() $t=7.75$
. The vorticity vector within the pancake structure is tangent to the pancake midplane and oriented roughly anti-parallel to the
$t=7.75$
. The vorticity vector within the pancake structure is tangent to the pancake midplane and oriented roughly anti-parallel to the
![]() $y$
-axis.
$y$
-axis.
3 Exact solution of the Euler equations as a model for pancake evolution
Following the numerical results, we suggest an analytical model for the vorticity growth. Assuming that in Cartesian coordinates
![]() $\boldsymbol{a}=a_{1}\boldsymbol{n}_{1}+a_{2}\boldsymbol{n}_{2}+a_{3}\boldsymbol{n}_{3}$
the vorticity changes only along the
$\boldsymbol{a}=a_{1}\boldsymbol{n}_{1}+a_{2}\boldsymbol{n}_{2}+a_{3}\boldsymbol{n}_{3}$
the vorticity changes only along the
![]() $a_{1}$
-axis and is oriented along the
$a_{1}$
-axis and is oriented along the
![]() $a_{2}$
-axis, we write
$a_{2}$
-axis, we write
where
![]() $\unicode[STIX]{x1D6FA}(t)$
is the characteristic vorticity amplitude and
$\unicode[STIX]{x1D6FA}(t)$
is the characteristic vorticity amplitude and
![]() $\ell _{1}(t)$
is the pancake thickness. The ansatz (3.1) contains a derivative (denoted by a prime) of an arbitrary function
$\ell _{1}(t)$
is the pancake thickness. The ansatz (3.1) contains a derivative (denoted by a prime) of an arbitrary function
![]() $f(\unicode[STIX]{x1D709})$
taken at
$f(\unicode[STIX]{x1D709})$
taken at
![]() $\unicode[STIX]{x1D709}=a_{1}/\ell _{1}(t)$
. One can check that (3.1) together with the velocity field
$\unicode[STIX]{x1D709}=a_{1}/\ell _{1}(t)$
. One can check that (3.1) together with the velocity field
 $$\begin{eqnarray}\displaystyle \boldsymbol{v}(\boldsymbol{a},t)=-\unicode[STIX]{x1D6FA}(t)\ell _{1}(t)f\left(\frac{a_{1}}{\ell _{1}(t)}\right)\boldsymbol{n}_{3}+\left(\begin{array}{@{}c@{}}-\unicode[STIX]{x1D6FD}_{1}(t)a_{1}\\ \unicode[STIX]{x1D6FD}_{2}(t)a_{2}\\ \unicode[STIX]{x1D6FD}_{3}(t)a_{3}\end{array}\right) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{v}(\boldsymbol{a},t)=-\unicode[STIX]{x1D6FA}(t)\ell _{1}(t)f\left(\frac{a_{1}}{\ell _{1}(t)}\right)\boldsymbol{n}_{3}+\left(\begin{array}{@{}c@{}}-\unicode[STIX]{x1D6FD}_{1}(t)a_{1}\\ \unicode[STIX]{x1D6FD}_{2}(t)a_{2}\\ \unicode[STIX]{x1D6FD}_{3}(t)a_{3}\end{array}\right) & & \displaystyle\end{eqnarray}$$
represents an exact solution of the Euler equations (2.1), where
![]() $\unicode[STIX]{x1D6FD}_{1}(t)$
,
$\unicode[STIX]{x1D6FD}_{1}(t)$
,
![]() $\unicode[STIX]{x1D6FD}_{2}(t)$
and
$\unicode[STIX]{x1D6FD}_{2}(t)$
and
![]() $\unicode[STIX]{x1D6FD}_{3}(t)$
are given by
$\unicode[STIX]{x1D6FD}_{3}(t)$
are given by
with the dots denoting time derivatives. The velocity (3.2) is a superposition of the shear flow
![]() $-\unicode[STIX]{x1D6FA}\ell _{1}f(a_{1}/\ell _{1})\boldsymbol{n}_{3}$
and the asymmetric irrotational straining flow
$-\unicode[STIX]{x1D6FA}\ell _{1}f(a_{1}/\ell _{1})\boldsymbol{n}_{3}$
and the asymmetric irrotational straining flow
![]() $(-\unicode[STIX]{x1D6FD}_{1}a_{1},\unicode[STIX]{x1D6FD}_{2}a_{2},\unicode[STIX]{x1D6FD}_{3}a_{3})$
, and satisfies the Euler equations
$(-\unicode[STIX]{x1D6FD}_{1}a_{1},\unicode[STIX]{x1D6FD}_{2}a_{2},\unicode[STIX]{x1D6FD}_{3}a_{3})$
, and satisfies the Euler equations
![]() $\dot{\boldsymbol{v}}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}=-\unicode[STIX]{x1D735}p$
with the pressure
$\dot{\boldsymbol{v}}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}=-\unicode[STIX]{x1D735}p$
with the pressure
It should be noted that the pressure is determined entirely by the coefficients
![]() $\unicode[STIX]{x1D6FD}_{1}$
,
$\unicode[STIX]{x1D6FD}_{1}$
,
![]() $\unicode[STIX]{x1D6FD}_{2}$
and
$\unicode[STIX]{x1D6FD}_{2}$
and
![]() $\unicode[STIX]{x1D6FD}_{3}$
of the straining flow. A uniform velocity field with an arbitrary time dependence
$\unicode[STIX]{x1D6FD}_{3}$
of the straining flow. A uniform velocity field with an arbitrary time dependence
![]() $(0,v_{b2}(t),v_{b3}(t))$
can be added to (3.2). This field, describing a drift of the pancake structure, leads to the change of pressure as
$(0,v_{b2}(t),v_{b3}(t))$
can be added to (3.2). This field, describing a drift of the pancake structure, leads to the change of pressure as
![]() $p\rightarrow p-a_{2}(\unicode[STIX]{x1D6FD}_{2}v_{b2}+\dot{v}_{b2})-a_{3}(\unicode[STIX]{x1D6FD}_{3}v_{b3}+\dot{v}_{b3})$
.
$p\rightarrow p-a_{2}(\unicode[STIX]{x1D6FD}_{2}v_{b2}+\dot{v}_{b2})-a_{3}(\unicode[STIX]{x1D6FD}_{3}v_{b3}+\dot{v}_{b3})$
.
The suggested solution is an essential generalization of the pancake model of Brachet et al. (Reference Brachet, Meneguzzi, Vincent, Politano and Sulem1992); the latter is obtained as a special case with
![]() $\unicode[STIX]{x1D6FA}=\ell _{1}^{-1}=\text{e}^{t/T}$
,
$\unicode[STIX]{x1D6FA}=\ell _{1}^{-1}=\text{e}^{t/T}$
,
![]() $\unicode[STIX]{x1D6FD}_{1,2}=1/T$
,
$\unicode[STIX]{x1D6FD}_{1,2}=1/T$
,
![]() $\unicode[STIX]{x1D6FD}_{3}=0$
. The solution (3.1)–(3.4) has infinite energy in
$\unicode[STIX]{x1D6FD}_{3}=0$
. The solution (3.1)–(3.4) has infinite energy in
![]() $\mathbb{R}^{3}$
and allows for an arbitrary time dependence of
$\mathbb{R}^{3}$
and allows for an arbitrary time dependence of
![]() $\unicode[STIX]{x1D6FA}(t)$
and
$\unicode[STIX]{x1D6FA}(t)$
and
![]() $\ell _{1}(t)$
, in particular, the one leading to a finite-time blowup. In addition to an arbitrary function
$\ell _{1}(t)$
, in particular, the one leading to a finite-time blowup. In addition to an arbitrary function
![]() $f(\unicode[STIX]{x1D709})$
, the new solution is characterized by a single dimensionless parameter
$f(\unicode[STIX]{x1D709})$
, the new solution is characterized by a single dimensionless parameter
describing the asymmetry of the straining flow in (3.2). In our numerical simulations, nearly exponential behaviour for
![]() $\unicode[STIX]{x1D6FA}(t)$
(vorticity maximum) and
$\unicode[STIX]{x1D6FA}(t)$
(vorticity maximum) and
![]() $\ell _{1}(t)$
is observed, see figure 1(a,c), which corresponds to constant numbers for
$\ell _{1}(t)$
is observed, see figure 1(a,c), which corresponds to constant numbers for
![]() $\unicode[STIX]{x1D6FD}_{1}$
,
$\unicode[STIX]{x1D6FD}_{1}$
,
![]() $\unicode[STIX]{x1D6FD}_{2}$
and
$\unicode[STIX]{x1D6FD}_{2}$
and
![]() $\unicode[STIX]{x1D6FD}_{3}$
in (3.3). Then, the asymmetry parameter defines the exponent in the power-law relation
$\unicode[STIX]{x1D6FD}_{3}$
in (3.3). Then, the asymmetry parameter defines the exponent in the power-law relation
between the vorticity amplitude and the pancake thickness. Consequently, in the transversal direction, the velocity has variation
![]() $\unicode[STIX]{x1D6FF}v_{3}\propto \unicode[STIX]{x1D6FA}\ell _{1}\propto \ell _{1}^{1-\unicode[STIX]{x1D701}}$
at the scale of the pancake thickness
$\unicode[STIX]{x1D6FF}v_{3}\propto \unicode[STIX]{x1D6FA}\ell _{1}\propto \ell _{1}^{1-\unicode[STIX]{x1D701}}$
at the scale of the pancake thickness
![]() $\unicode[STIX]{x1D6FF}a_{1}\sim \ell _{1}$
, and this variation vanishes for
$\unicode[STIX]{x1D6FF}a_{1}\sim \ell _{1}$
, and this variation vanishes for
![]() $\unicode[STIX]{x1D701}<1$
(i.e.
$\unicode[STIX]{x1D701}<1$
(i.e.
![]() $\unicode[STIX]{x1D70E}<1$
) as
$\unicode[STIX]{x1D70E}<1$
) as
![]() $\ell _{1}\rightarrow 0$
.
$\ell _{1}\rightarrow 0$
.
The solution (3.1)–(3.4) can be extended for the Navier–Stokes equations with kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
, if the function
$\unicode[STIX]{x1D708}$
, if the function
![]() $f(\unicode[STIX]{x1D709},t)$
changes with time as
$f(\unicode[STIX]{x1D709},t)$
changes with time as
![]() $f_{t}-(\unicode[STIX]{x1D708}/\ell _{1}^{2})f_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}=0$
. The latter becomes the heat equation after a simple transformation of time,
$f_{t}-(\unicode[STIX]{x1D708}/\ell _{1}^{2})f_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}=0$
. The latter becomes the heat equation after a simple transformation of time,
![]() $\unicode[STIX]{x1D70F}=\int \,\text{d}t/\ell _{1}^{2}(t)$
. For the axisymmetric straining flow with
$\unicode[STIX]{x1D70F}=\int \,\text{d}t/\ell _{1}^{2}(t)$
. For the axisymmetric straining flow with
![]() $\unicode[STIX]{x1D6FD}_{2}=\unicode[STIX]{x1D6FD}_{3}=\unicode[STIX]{x1D6FD}_{1}/2$
, the suggested solution becomes the special case of the Lundgren stretched-spiral vortex; see Lundgren (Reference Lundgren1982). It should be noted that solutions of the Navier–Stokes equations in the form of stretched vortices embedded in a uniform straining flow were first studied by Burgers (Reference Burgers1948); see also Prochazka & Pullin (Reference Prochazka and Pullin1998), Pullin & Saffman (Reference Pullin and Saffman1998), Gibbon, Fokas & Doering (Reference Gibbon, Fokas and Doering1999) and Maekawa (Reference Maekawa2009).
$\unicode[STIX]{x1D6FD}_{2}=\unicode[STIX]{x1D6FD}_{3}=\unicode[STIX]{x1D6FD}_{1}/2$
, the suggested solution becomes the special case of the Lundgren stretched-spiral vortex; see Lundgren (Reference Lundgren1982). It should be noted that solutions of the Navier–Stokes equations in the form of stretched vortices embedded in a uniform straining flow were first studied by Burgers (Reference Burgers1948); see also Prochazka & Pullin (Reference Prochazka and Pullin1998), Pullin & Saffman (Reference Pullin and Saffman1998), Gibbon, Fokas & Doering (Reference Gibbon, Fokas and Doering1999) and Maekawa (Reference Maekawa2009).
4 Comparison with the numerical simulations
In simulations, we define the local coordinate system
![]() $(a_{1},a_{2},a_{3})$
for the pancake structure in the following way. The origin is chosen at the point of the global vorticity maximum, where we also compute the pancake normal vector
$(a_{1},a_{2},a_{3})$
for the pancake structure in the following way. The origin is chosen at the point of the global vorticity maximum, where we also compute the pancake normal vector
![]() $\boldsymbol{n}_{1}$
of the
$\boldsymbol{n}_{1}$
of the
![]() $a_{1}$
-axis, as described in § 2. According to the exact solution (3.1), the
$a_{1}$
-axis, as described in § 2. According to the exact solution (3.1), the
![]() $a_{2}$
-axis should be parallel to the vorticity vector
$a_{2}$
-axis should be parallel to the vorticity vector
![]() $\unicode[STIX]{x1D74E}$
. However, in simulations, the angle between
$\unicode[STIX]{x1D74E}$
. However, in simulations, the angle between
![]() $\boldsymbol{n}_{1}$
and
$\boldsymbol{n}_{1}$
and
![]() $\unicode[STIX]{x1D74E}$
may differ from
$\unicode[STIX]{x1D74E}$
may differ from
![]() $90^{\circ }$
. We checked that this difference, in fact, is tiny, reaching
$90^{\circ }$
. We checked that this difference, in fact, is tiny, reaching
![]() $0.02^{\circ }$
at the final time. Thereby, we define the
$0.02^{\circ }$
at the final time. Thereby, we define the
![]() $a_{2}$
-axis with the direction
$a_{2}$
-axis with the direction
![]() $\boldsymbol{n}_{2}=c[\unicode[STIX]{x1D74E}-(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{n}_{1})\boldsymbol{n}_{1}]$
, where
$\boldsymbol{n}_{2}=c[\unicode[STIX]{x1D74E}-(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{n}_{1})\boldsymbol{n}_{1}]$
, where
![]() $(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{n}_{1})\boldsymbol{n}_{1}$
is a small correction and the prefactor
$(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{n}_{1})\boldsymbol{n}_{1}$
is a small correction and the prefactor
![]() $c$
is chosen such that
$c$
is chosen such that
![]() $\Vert \boldsymbol{n}_{2}\Vert =1$
. Finally, the
$\Vert \boldsymbol{n}_{2}\Vert =1$
. Finally, the
![]() $a_{3}$
-axis has the direction
$a_{3}$
-axis has the direction
![]() $\boldsymbol{n}_{3}=\boldsymbol{n}_{1}\times \boldsymbol{n}_{2}$
. It should be noted that this coordinate system is computed at each moment of time, which is necessary to account for a possible drift of the whole structure. We choose the vorticity amplitude as the maximum vorticity,
$\boldsymbol{n}_{3}=\boldsymbol{n}_{1}\times \boldsymbol{n}_{2}$
. It should be noted that this coordinate system is computed at each moment of time, which is necessary to account for a possible drift of the whole structure. We choose the vorticity amplitude as the maximum vorticity,
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}_{max}$
, and compute coefficients
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}_{max}$
, and compute coefficients
![]() $\unicode[STIX]{x1D6FD}_{1}$
,
$\unicode[STIX]{x1D6FD}_{1}$
,
![]() $\unicode[STIX]{x1D6FD}_{2}$
and
$\unicode[STIX]{x1D6FD}_{2}$
and
![]() $\unicode[STIX]{x1D6FD}_{3}$
according to (3.3).
$\unicode[STIX]{x1D6FD}_{3}$
according to (3.3).

Figure 2. (a) Normalized vorticity component
![]() $\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{max}$
as a function of
$\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{max}$
as a function of
![]() $\unicode[STIX]{x1D709}=a_{1}/\ell _{1}$
at different times. (b) Comparison of the logarithmic derivatives
$\unicode[STIX]{x1D709}=a_{1}/\ell _{1}$
at different times. (b) Comparison of the logarithmic derivatives
![]() $\unicode[STIX]{x1D6FD}_{1}=-\dot{\ell }_{1}/\ell _{1}$
and
$\unicode[STIX]{x1D6FD}_{1}=-\dot{\ell }_{1}/\ell _{1}$
and
![]() $\unicode[STIX]{x1D6FD}_{2}=\dot{\unicode[STIX]{x1D714}}_{max}/\unicode[STIX]{x1D714}_{max}$
with the velocity gradients
$\unicode[STIX]{x1D6FD}_{2}=\dot{\unicode[STIX]{x1D714}}_{max}/\unicode[STIX]{x1D714}_{max}$
with the velocity gradients
![]() $-\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
and
$-\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
and
![]() $\unicode[STIX]{x2202}v_{2}/\unicode[STIX]{x2202}a_{2}$
computed at the global vorticity maximum; see (4.2). After prior computation of the time derivatives,
$\unicode[STIX]{x2202}v_{2}/\unicode[STIX]{x2202}a_{2}$
computed at the global vorticity maximum; see (4.2). After prior computation of the time derivatives,
![]() $\ell _{1}$
and
$\ell _{1}$
and
![]() $\unicode[STIX]{x1D714}_{max}$
are smoothed with the weighted local regression (lowess filter); see Cleveland, Devlin & Grosse (Reference Cleveland, Devlin and Grosse1988).
$\unicode[STIX]{x1D714}_{max}$
are smoothed with the weighted local regression (lowess filter); see Cleveland, Devlin & Grosse (Reference Cleveland, Devlin and Grosse1988).
In this section, we provide several numerical tests supporting the pancake model proposed in § 3. The first test is related to self-similarity of the transversal vorticity profile, which should be kept, according to (3.1), as
This is confirmed in figure 2(a), where the vorticity profile
![]() $\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{max}$
along the
$\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D714}_{max}$
along the
![]() $a_{1}$
-axis is shown at different times. The self-similarity region grows with time in the
$a_{1}$
-axis is shown at different times. The self-similarity region grows with time in the
![]() $\unicode[STIX]{x1D709}$
-coordinate, remaining finite in physical space, where it matches with the background flow. It should be noted that the function
$\unicode[STIX]{x1D709}$
-coordinate, remaining finite in physical space, where it matches with the background flow. It should be noted that the function
![]() $f(\unicode[STIX]{x1D709})$
may be arbitrary; in our simulations, different vorticity profiles are obtained for different pancakes and initial conditions.
$f(\unicode[STIX]{x1D709})$
may be arbitrary; in our simulations, different vorticity profiles are obtained for different pancakes and initial conditions.
For the analysis of the velocity field, one should take into account a drift of the pancake structure by a background flow with non-trivial time dependence. However, this difficulty can be avoided if we examine the velocity gradient, which for the pancake model solution (3.1)–(3.4) has the form
 $$\begin{eqnarray}\displaystyle [\unicode[STIX]{x2202}v_{i}/\unicode[STIX]{x2202}a_{j}]=\left(\begin{array}{@{}ccc@{}}-\unicode[STIX]{x1D6FD}_{1} & 0 & 0\\ 0 & \unicode[STIX]{x1D6FD}_{2} & 0\\ -\unicode[STIX]{x1D714}_{2} & 0 & \unicode[STIX]{x1D6FD}_{3}\end{array}\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x2202}v_{i}/\unicode[STIX]{x2202}a_{j}]=\left(\begin{array}{@{}ccc@{}}-\unicode[STIX]{x1D6FD}_{1} & 0 & 0\\ 0 & \unicode[STIX]{x1D6FD}_{2} & 0\\ -\unicode[STIX]{x1D714}_{2} & 0 & \unicode[STIX]{x1D6FD}_{3}\end{array}\right). & & \displaystyle\end{eqnarray}$$
In figure 2(b), we compare at different times the logarithmic derivatives
![]() $\unicode[STIX]{x1D6FD}_{1}=-\dot{\ell }_{1}/\ell _{1}$
and
$\unicode[STIX]{x1D6FD}_{1}=-\dot{\ell }_{1}/\ell _{1}$
and
![]() $\unicode[STIX]{x1D6FD}_{2}=\dot{\unicode[STIX]{x1D714}}_{max}/\unicode[STIX]{x1D714}_{max}$
with the velocity gradients
$\unicode[STIX]{x1D6FD}_{2}=\dot{\unicode[STIX]{x1D714}}_{max}/\unicode[STIX]{x1D714}_{max}$
with the velocity gradients
![]() $-\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
and
$-\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
and
![]() $\unicode[STIX]{x2202}v_{2}/\unicode[STIX]{x2202}a_{2}$
evaluated at the global vorticity maximum. One can see very good overall agreement, with a larger deviation for
$\unicode[STIX]{x2202}v_{2}/\unicode[STIX]{x2202}a_{2}$
evaluated at the global vorticity maximum. One can see very good overall agreement, with a larger deviation for
![]() $-\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
at
$-\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
at
![]() $t=7$
. This deviation can be attributed to the variation (up to 20 %) of the velocity derivative within the pancake thickness. At the final simulation time
$t=7$
. This deviation can be attributed to the variation (up to 20 %) of the velocity derivative within the pancake thickness. At the final simulation time
![]() $t=7.75$
and at the global vorticity maximum, the numerical velocity gradient is given by
$t=7.75$
and at the global vorticity maximum, the numerical velocity gradient is given by
 $$\begin{eqnarray}\displaystyle [\unicode[STIX]{x2202}v_{i}/\unicode[STIX]{x2202}a_{j}]_{\boldsymbol{a}=0}=\left(\begin{array}{@{}ccc@{}}-0.72 & -0.04 & -0.03\\ -0.11 & 0.53 & -0.09\\ -18.42 & -0.04 & 0.19\end{array}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x2202}v_{i}/\unicode[STIX]{x2202}a_{j}]_{\boldsymbol{a}=0}=\left(\begin{array}{@{}ccc@{}}-0.72 & -0.04 & -0.03\\ -0.11 & 0.53 & -0.09\\ -18.42 & -0.04 & 0.19\end{array}\right), & & \displaystyle\end{eqnarray}$$
confirming that there is a single large
![]() $(3,1)$
-component,
$(3,1)$
-component,
![]() $\unicode[STIX]{x2202}v_{3}/\unicode[STIX]{x2202}a_{1}\approx -\unicode[STIX]{x1D714}_{max}$
. The diagonal components corresponding to the straining flow are in very good agreement with the coefficients
$\unicode[STIX]{x2202}v_{3}/\unicode[STIX]{x2202}a_{1}\approx -\unicode[STIX]{x1D714}_{max}$
. The diagonal components corresponding to the straining flow are in very good agreement with the coefficients
![]() $-\unicode[STIX]{x1D6FD}_{1}=-0.74$
,
$-\unicode[STIX]{x1D6FD}_{1}=-0.74$
,
![]() $\unicode[STIX]{x1D6FD}_{2}=0.53$
and
$\unicode[STIX]{x1D6FD}_{2}=0.53$
and
![]() $\unicode[STIX]{x1D6FD}_{3}=0.21$
, while the remaining components,
$\unicode[STIX]{x1D6FD}_{3}=0.21$
, while the remaining components,
![]() $(1,2)$
,
$(1,2)$
,
![]() $(1,3)$
,
$(1,3)$
,
![]() $(2,1)$
,
$(2,1)$
,
![]() $(2,3)$
and
$(2,3)$
and
![]() $(3,2)$
corresponding to vanishing elements in (4.2) are small.
$(3,2)$
corresponding to vanishing elements in (4.2) are small.

Figure 3. (a) Pancake midplane (vorticity above 70 % of the maximum value) in the projection to the
![]() $(x,y)$
-plane. The arrows show projections of the vorticity vector, scaled by a factor of
$(x,y)$
-plane. The arrows show projections of the vorticity vector, scaled by a factor of
![]() $0.025$
. The coordinates are shifted to place the vorticity maximum at the origin. (b) Velocity derivatives
$0.025$
. The coordinates are shifted to place the vorticity maximum at the origin. (b) Velocity derivatives
![]() $\unicode[STIX]{x2202}v_{i}/\unicode[STIX]{x2202}a_{j}$
evaluated at different points of the pancake midplane; marked with
$\unicode[STIX]{x2202}v_{i}/\unicode[STIX]{x2202}a_{j}$
evaluated at different points of the pancake midplane; marked with
![]() $(i,j)$
. (c) Normalized vorticity profile
$(i,j)$
. (c) Normalized vorticity profile
![]() $\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D6FA}$
in the direction perpendicular to the midplane, at five different points corresponding to the red dots in (a). The red line corresponding to the centre of the pancake is the same as in figure 2(a).
$\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D6FA}$
in the direction perpendicular to the midplane, at five different points corresponding to the red dots in (a). The red line corresponding to the centre of the pancake is the same as in figure 2(a).
The previous tests confirmed that the pancake model solution agrees with the flow in the vicinity of the global vorticity maximum. However, this model cannot describe the whole region of high vorticity, since the pancake is not completely flat, with deviations from the plane
![]() $a_{1}=0$
much larger than the pancake thickness; see figure 1(b). Nevertheless, we can check whether the model approximates the pancake locally, at every nearly flat pancake segment. For this purpose, we consider the final time and isolate the principal part of the pancake with vorticity
$a_{1}=0$
much larger than the pancake thickness; see figure 1(b). Nevertheless, we can check whether the model approximates the pancake locally, at every nearly flat pancake segment. For this purpose, we consider the final time and isolate the principal part of the pancake with vorticity
![]() $\unicode[STIX]{x1D714}\geqslant 0.7\unicode[STIX]{x1D714}_{max}$
; the isolated region is roughly parallel to the
$\unicode[STIX]{x1D714}\geqslant 0.7\unicode[STIX]{x1D714}_{max}$
; the isolated region is roughly parallel to the
![]() $(x,y)$
-plane. Despite the fact that this region is very thin,
$(x,y)$
-plane. Despite the fact that this region is very thin,
![]() $\ell _{1}\sim 0.01$
, its lateral dimensions are comparable to the size of the numerical box, as shown by the projection to the
$\ell _{1}\sim 0.01$
, its lateral dimensions are comparable to the size of the numerical box, as shown by the projection to the
![]() $(x,y)$
-plane in figure 3(a). Within this region, we define the pancake midplane
$(x,y)$
-plane in figure 3(a). Within this region, we define the pancake midplane
![]() $z=z_{m}(x,y)$
, chosen as points of maximum vorticity,
$z=z_{m}(x,y)$
, chosen as points of maximum vorticity,
![]() $\max _{z}\unicode[STIX]{x1D714}$
, for the given values of
$\max _{z}\unicode[STIX]{x1D714}$
, for the given values of
![]() $x$
and
$x$
and
![]() $y$
. Then, at each point
$y$
. Then, at each point
![]() $\boldsymbol{r}_{m}=(x,y,z_{m}(x,y))$
of the midplane, we define the new local coordinates
$\boldsymbol{r}_{m}=(x,y,z_{m}(x,y))$
of the midplane, we define the new local coordinates
![]() $(a_{1},a_{2},a_{3})$
, using the first eigenvector of the Hessian matrix and the vorticity vector, as described above in this section. It should be noted that
$(a_{1},a_{2},a_{3})$
, using the first eigenvector of the Hessian matrix and the vorticity vector, as described above in this section. It should be noted that
![]() $(x,y)$
serve as parameters in this representation, while the coordinates
$(x,y)$
serve as parameters in this representation, while the coordinates
![]() $(a_{1},a_{2},a_{3})$
explore the neighbourhood of
$(a_{1},a_{2},a_{3})$
explore the neighbourhood of
![]() $\boldsymbol{r}_{m}$
.
$\boldsymbol{r}_{m}$
.
First, we verified numerically that, within the pancake, the vorticity vector is tangent to the midplane and almost unidirectional. This is illustrated in figure 3(a), where projections to the
![]() $(x,y)$
-plane of the vorticity vector are shown by arrows, which are scaled (multiplied by
$(x,y)$
-plane of the vorticity vector are shown by arrows, which are scaled (multiplied by
![]() $0.025$
) to fit the plot. At several distant points on the midplane, we considered the vorticity profile
$0.025$
) to fit the plot. At several distant points on the midplane, we considered the vorticity profile
![]() $\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D6FA}$
as a function of
$\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D6FA}$
as a function of
![]() $a_{1}/\ell _{1}$
, where
$a_{1}/\ell _{1}$
, where
![]() $\unicode[STIX]{x1D6FA}=\max _{z}\unicode[STIX]{x1D714}$
is the vorticity at the corresponding point on the midplane. At every point, a convergence similar to figure 2(a) is observed, showing that the vorticity profile changes with time self-similarly according to (4.1); the convergence gets worse near the pancake border. The vorticity profile varies from point to point; this means that the function
$\unicode[STIX]{x1D6FA}=\max _{z}\unicode[STIX]{x1D714}$
is the vorticity at the corresponding point on the midplane. At every point, a convergence similar to figure 2(a) is observed, showing that the vorticity profile changes with time self-similarly according to (4.1); the convergence gets worse near the pancake border. The vorticity profile varies from point to point; this means that the function
![]() $f(\unicode[STIX]{x1D709})$
of the model (3.1) changes along the pancake. The magnitude of this variation can be seen in figure 3(c), which presents the final-time vorticity profiles
$f(\unicode[STIX]{x1D709})$
of the model (3.1) changes along the pancake. The magnitude of this variation can be seen in figure 3(c), which presents the final-time vorticity profiles
![]() $\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D6FA}$
at five different points marked with red dots in panel (a) of the same figure. It should be noted that a specific form of
$\unicode[STIX]{x1D714}_{2}/\unicode[STIX]{x1D6FA}$
at five different points marked with red dots in panel (a) of the same figure. It should be noted that a specific form of
![]() $f(\unicode[STIX]{x1D709})$
is not important in the exact solution (3.1)–(3.2). Thus, this function accounts for the local self-similarity only, while its variations along the pancake may be captured by a next-order correction to our model.
$f(\unicode[STIX]{x1D709})$
is not important in the exact solution (3.1)–(3.2). Thus, this function accounts for the local self-similarity only, while its variations along the pancake may be captured by a next-order correction to our model.

Figure 4. (a) Relation between the vorticity local maxima
![]() $\unicode[STIX]{x1D714}_{max}(t)$
and the respective characteristic lengths
$\unicode[STIX]{x1D714}_{max}(t)$
and the respective characteristic lengths
![]() $\ell _{1}(t)$
during the evolution of the pancake structures. The lines represent the evolution of the maxima with increasing time, with the red dots corresponding to the final simulation time. The dashed red line indicates the power-law scaling
$\ell _{1}(t)$
during the evolution of the pancake structures. The lines represent the evolution of the maxima with increasing time, with the red dots corresponding to the final simulation time. The dashed red line indicates the power-law scaling
![]() $\unicode[STIX]{x1D714}_{max}\propto \ell _{1}^{-2/3}$
. (b) The same graph for a different simulation with a generic initial condition and the final grid
$\unicode[STIX]{x1D714}_{max}\propto \ell _{1}^{-2/3}$
. (b) The same graph for a different simulation with a generic initial condition and the final grid
![]() $1152\times 972\times 864$
.
$1152\times 972\times 864$
.
The structure of the gradient (4.2) is confirmed in figure 3(b) along the whole pancake midplane. The components
![]() $(1,2)$
,
$(1,2)$
,
![]() $(1,3)$
,
$(1,3)$
,
![]() $(2,1)$
,
$(2,1)$
,
![]() $(2,3)$
and
$(2,3)$
and
![]() $(3,2)$
are concentrated in the middle of the figure: they are approximately one order of magnitude smaller than the diagonal components and more than two orders of magnitude smaller than the
$(3,2)$
are concentrated in the middle of the figure: they are approximately one order of magnitude smaller than the diagonal components and more than two orders of magnitude smaller than the
![]() $(3,1)$
-component related to the vorticity. The large
$(3,1)$
-component related to the vorticity. The large
![]() $(3,1)$
-component does not fit to the vertical range of the figure, but it is in excellent agreement with the vorticity,
$(3,1)$
-component does not fit to the vertical range of the figure, but it is in excellent agreement with the vorticity,
![]() $\unicode[STIX]{x2202}v_{3}/\unicode[STIX]{x2202}a_{1}\approx -\unicode[STIX]{x1D714}$
, with the difference below 0.6 %. The diagonal components
$\unicode[STIX]{x2202}v_{3}/\unicode[STIX]{x2202}a_{1}\approx -\unicode[STIX]{x1D714}$
, with the difference below 0.6 %. The diagonal components
![]() $\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
(blue) and
$\unicode[STIX]{x2202}v_{1}/\unicode[STIX]{x2202}a_{1}$
(blue) and
![]() $\unicode[STIX]{x2202}v_{2}/\unicode[STIX]{x2202}a_{2}$
(red) vary significantly along the midplane. We do not show
$\unicode[STIX]{x2202}v_{2}/\unicode[STIX]{x2202}a_{2}$
(red) vary significantly along the midplane. We do not show
![]() $\unicode[STIX]{x2202}v_{3}/\unicode[STIX]{x2202}a_{3}$
due to its exact relation to
$\unicode[STIX]{x2202}v_{3}/\unicode[STIX]{x2202}a_{3}$
due to its exact relation to
![]() $(1,1)$
- and
$(1,1)$
- and
![]() $(2,2)$
-components, originating from incompressibility of the flow,
$(2,2)$
-components, originating from incompressibility of the flow,
![]() $\text{div}\,\boldsymbol{v}=0$
. With these observations, we confirm that, for every nearly flat pancake segment, the flow can be approximated by the pancake model solution suggested in § 3.
$\text{div}\,\boldsymbol{v}=0$
. With these observations, we confirm that, for every nearly flat pancake segment, the flow can be approximated by the pancake model solution suggested in § 3.
As was noticed in Agafontsev et al. (Reference Agafontsev, Kuznetsov and Mailybaev2015), at late times the pancakes develop according to the Kolmogorov-like power law
This tendency is clearly seen in figure 4(a), where all other local vorticity maxima are shown and the
![]() $2/3$
-slope is represented by the dashed line. We stress that the pancake model solution (3.1)–(3.4) allows for an arbitrary power-law exponent
$2/3$
-slope is represented by the dashed line. We stress that the pancake model solution (3.1)–(3.4) allows for an arbitrary power-law exponent
![]() $\unicode[STIX]{x1D701}$
. Thus, the universality of the asymptotic value
$\unicode[STIX]{x1D701}$
. Thus, the universality of the asymptotic value
![]() $\unicode[STIX]{x1D701}=2/3$
, which corresponds to the asymmetry parameter
$\unicode[STIX]{x1D701}=2/3$
, which corresponds to the asymmetry parameter
![]() $\unicode[STIX]{x1D70E}=1/3$
of the straining flow, goes beyond this solution. We think that restrictions on the power law may come from the non-local interactions of the pancakes and the background flow.
$\unicode[STIX]{x1D70E}=1/3$
of the straining flow, goes beyond this solution. We think that restrictions on the power law may come from the non-local interactions of the pancakes and the background flow.
All of the results presented so far relate to the main pancake structure from the simulation with the
![]() $I_{1}$
initial condition. We confirmed that several other pancake structures, associated with some of the local vorticity maxima shown in figure 4(a), also agree with the pancake model solution. We performed a series of simulations in grids with a total number of nodes of
$I_{1}$
initial condition. We confirmed that several other pancake structures, associated with some of the local vorticity maxima shown in figure 4(a), also agree with the pancake model solution. We performed a series of simulations in grids with a total number of nodes of
![]() $1024^{3}$
, starting from fully generic (large-scale) initial conditions. The regions of high vorticity, emerging from such initial flows, have arbitrary orientation, which does not allow us to use anisotropic grids effectively. Thereby, such simulations yield considerably smaller overall vorticity enhancement. However, these regions represent pancake-like structures developing close to the model solution (3.1)–(3.4), and the same relation (4.4) between the vorticity maximum and the pancake thickness is observed; see the example of one such simulation in figure 4(b).
$1024^{3}$
, starting from fully generic (large-scale) initial conditions. The regions of high vorticity, emerging from such initial flows, have arbitrary orientation, which does not allow us to use anisotropic grids effectively. Thereby, such simulations yield considerably smaller overall vorticity enhancement. However, these regions represent pancake-like structures developing close to the model solution (3.1)–(3.4), and the same relation (4.4) between the vorticity maximum and the pancake thickness is observed; see the example of one such simulation in figure 4(b).
5 Conclusions
We have studied high-vorticity regions developing in the 3D incompressible Euler equations from generic large-scale initial conditions. These regions represent pancake-like structures of increasing vorticity, which compress in a self-similar way in the transversal direction. Led by this observation, we proposed a novel exact solution of the 3D Euler equations, which describes this behaviour asymptotically. The proposed solution combines a shear flow aligned with an asymmetric irrotational straining flow, and is characterized by a single asymmetry parameter and an arbitrary transversal vorticity profile. It should be noted that a pancake structure is not completely flat, with deviations much larger than the pancake thickness. It is remarkable that the proposed analytical model describes locally every nearly flat pancake segment, while the model parameters may change from one segment to another. The latter may be captured in next-order corrections to our pancake model, which is an interesting topic for future studies. In simulations, we observe exponential evolution of the vorticity maximum and pancake thickness, with a Kolmogorov-like relation between the two,
![]() $\unicode[STIX]{x1D714}_{max}(t)\propto \ell _{1}(t)^{-2/3}$
. This behaviour is not required by the suggested model, and presumably relates to non-local effects.
$\unicode[STIX]{x1D714}_{max}(t)\propto \ell _{1}(t)^{-2/3}$
. This behaviour is not required by the suggested model, and presumably relates to non-local effects.
Acknowledgements
Simulations were performed at the Novosibirsk Supercomputer Center (NSU) and the Data Center of IMPA (Rio de Janeiro). The work of D.S.A. and E.A.K. was supported by the Russian Science Foundation (grant 14-22-00174). D.S.A. acknowledges the support from IMPA during visits to Brazil. A.A.M. was supported by the CNPq (grant 302351/2015-9) and the Program FAPERJ Pensa Rio (grant E-26/210.874/2014).