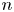1. Introduction
Navigators used to plot on a map lines of position or lines of bearing, which are rays emanating from a landmark (e.g., a lighthouse or radio beacon) at a particular bearing (angle relative to north) that was estimated to be the direction from the landmark (which we also refer to as observation point) to the ship or plane. Two such rays usually intersect at a point, which the navigator would take as an estimate of the true position of the craft. Navigators were encouraged to plot three rays, to make position estimation more robust. The three rays normally created a triangle, called a cocked hat (Dear and Kemp, Reference Dear and Kemp2006), as shown in Figure 1. The properties of the cocked hat have been investigated thoroughly (His Majesty's Navigation School, 1938; Stansfield, Reference Stansfield1947; Daniels, Reference Daniels1951; Anderson, Reference Anderson1952; Cotter, Reference Cotter1961; Williams, Reference Williams1991; Cook, Reference Cook1993; Stuart, Reference Stuart2019), to help navigators interpret it and make good navigation decisions. The aim of this paper is to analyse the conditions under which an elegant property of the cocked hat holds. That property was stated without a proof more than 80 years ago (His Majesty's Navigation School, 1938), proved informally (and essentially incorrectly) 70 years ago (Stansfield, Reference Stansfield1947), and has been widely disseminated ever since (Daniels, Reference Daniels1951; The Open University, 1984; Williams, Reference Williams1991; Cook, Reference Cook1993; Denny, Reference Denny2012), including in course material (The Open University, 1984) and in a popular science book (Denny, Reference Denny2012). The mathematically incorrect explanation in the Open University video (The Open University; 1984), which is presented there as a proof, demonstrates that it was widely believed that this explanation is indeed a proof when in fact it is not.

Figure 1. Three observation points ![]() $P_1,P_2,P_3$, the target
$P_1,P_2,P_3$, the target ![]() $F$, the three rays and the cocked hat (shaded)
$F$, the three rays and the cocked hat (shaded)
The property that we are interested in is the probability of the cocked hat containing the true position being ![]() $1/4$. Under what conditions is this statement true?
$1/4$. Under what conditions is this statement true?
This claim first appeared in a 1938 navigation manual (His Majesty's Navigation School, 1938, p. 166), without a proof and with only informal conditions on the error angles at the three landmarks, which we denote ![]() $P_{1}$,
$P_{1}$, ![]() $P_{2}$ and
$P_{2}$ and ![]() $P_{3}$ (see Figure 1). The error angles
$P_{3}$ (see Figure 1). The error angles ![]() $\epsilon _{1}$,
$\epsilon _{1}$, ![]() $\epsilon _{2}$ and
$\epsilon _{2}$ and ![]() $\epsilon _{3}$ are between the plotted rays, which we denote
$\epsilon _{3}$ are between the plotted rays, which we denote ![]() $R_{1}$,
$R_{1}$, ![]() $R_{2}$ and
$R_{2}$ and ![]() $R_{3}$ and the rays
$R_{3}$ and the rays ![]() $r_i$ from
$r_i$ from ![]() $P_{i}$ to the true position of the craft, which we denote by
$P_{i}$ to the true position of the craft, which we denote by ![]() $F$ (see Figure 1). The informal conditions are that the errors are independent (the manual does not use this term, but this is what it means) and fairly small, around 1 degree. A 1947 paper by Stansfield (Stansfield, Reference Stansfield1947)Footnote 1 cites the claim, gives more formal conditions for it and sketches a proof. The conditions that Stansfield specified are remarkably weak: he claims that the result would hold if only two of the three errors have zero median. Stansfield writes that this assumption is equivalent to the following: ‘for two of the stations the observed bearings are equally likely to pass to the right or the left of the true position’.
$F$ (see Figure 1). The informal conditions are that the errors are independent (the manual does not use this term, but this is what it means) and fairly small, around 1 degree. A 1947 paper by Stansfield (Stansfield, Reference Stansfield1947)Footnote 1 cites the claim, gives more formal conditions for it and sketches a proof. The conditions that Stansfield specified are remarkably weak: he claims that the result would hold if only two of the three errors have zero median. Stansfield writes that this assumption is equivalent to the following: ‘for two of the stations the observed bearings are equally likely to pass to the right or the left of the true position’.
A 1951 paper by Daniels (Reference Daniels1951) states Stansfield's result in a more modern statistical language, saying that the cocked hat is a ![]() $25\%$ distribution-free confidence region; the term distribution-free means that the result is not dependent on a particular error distribution, say Gaussian, but only on a parameter of the distribution, here the zero median.Footnote 2 Daniels then considers the case of
$25\%$ distribution-free confidence region; the term distribution-free means that the result is not dependent on a particular error distribution, say Gaussian, but only on a parameter of the distribution, here the zero median.Footnote 2 Daniels then considers the case of ![]() $n$ landmarks and
$n$ landmarks and ![]() $n$ rays starting from there. The lines of these rays split the plane into finitely connected components, some of them bounded, some of them not. Daniels claims without proof a particular formula,
$n$ rays starting from there. The lines of these rays split the plane into finitely connected components, some of them bounded, some of them not. Daniels claims without proof a particular formula, ![]() ${2n}/{2^{n}}$, for the probability that
${2n}/{2^{n}}$, for the probability that ![]() $F$ belongs to the union of the unbounded components. The
$F$ belongs to the union of the unbounded components. The ![]() $25\%$-probability result was incorrectly extended again by WilliamsFootnote 3 in 1991. He claimed specific probabilities that the open regions around the cocked hat contain
$25\%$-probability result was incorrectly extended again by WilliamsFootnote 3 in 1991. He claimed specific probabilities that the open regions around the cocked hat contain ![]() $F$, again with only an informal specification of the assumptions and with only a sketch of the proof. Williams's claims were shown to be false by Cook (Reference Cook1993), using specific error distributions, to which Williams answered with a witty (but scientifically wrong) rebuttal. Cook also repeated the claim that the probability of the cocked hat contains
$F$, again with only an informal specification of the assumptions and with only a sketch of the proof. Williams's claims were shown to be false by Cook (Reference Cook1993), using specific error distributions, to which Williams answered with a witty (but scientifically wrong) rebuttal. Cook also repeated the claim that the probability of the cocked hat contains ![]() $F$ is
$F$ is ![]() $1/4$.
$1/4$.
Our aim in this paper is to show that the ![]() $25\%$-probability result is valid only for error distributions that guarantee that the three rays intersect at three distinct points and form a triangle.
$25\%$-probability result is valid only for error distributions that guarantee that the three rays intersect at three distinct points and form a triangle.
We note that the use of the cocked hat in navigation is today obsolete, having been replaced by estimation of confidence regions, usually circles or ellipses, by computer algorithms.
2. Generalisations to rays that do not intersect
Two rays in the plane can intersect, but they can also fail to intersect. Lines of position plotted by navigators almost always intersected, because the error angles were small. Also, navigators were taught to choose landmarks so that no angle at the intersection is smaller than about 50 degrees – a small angle at the intersection implies ill-conditioning (high sensitivity of the intersection point to bearing errors).
Stansfield's formulation of the problem uses much more general assumptions on the errors, and no assumption about angles at the intersections. Stansfield, Daniels and the authors that followed only require that the three errors ![]() $\varepsilon _1,\varepsilon _2,\varepsilon _3 \in (-\pi ,\pi ]$ are random and independent, and that the median of their distributions is zero. We replace the zero-median assumption by a consistent but slightly more general condition, namely
$\varepsilon _1,\varepsilon _2,\varepsilon _3 \in (-\pi ,\pi ]$ are random and independent, and that the median of their distributions is zero. We replace the zero-median assumption by a consistent but slightly more general condition, namely
for every ![]() $i \in [n]$, where
$i \in [n]$, where ![]() $[n]$ is a shorthand for the set
$[n]$ is a shorthand for the set ![]() $\{1,2,\ldots ,n\}$. This means in particular that the target is never on
$\{1,2,\ldots ,n\}$. This means in particular that the target is never on ![]() $R_i$, which is a necessity because if
$R_i$, which is a necessity because if ![]() $\mathrm {Prob}(\epsilon _{i}=0)>0$ were allowed, then
$\mathrm {Prob}(\epsilon _{i}=0)>0$ were allowed, then ![]() $\mathrm {Prob}(F \in \Delta )$ could be close to one (e.g., if
$\mathrm {Prob}(F \in \Delta )$ could be close to one (e.g., if ![]() $\mathrm {Prob}(\epsilon _{i}=0)$ is close to one), implying that the
$\mathrm {Prob}(\epsilon _{i}=0)$ is close to one), implying that the ![]() $1/4$ result does not hold in this case. We also consider the restriction of the errors to
$1/4$ result does not hold in this case. We also consider the restriction of the errors to ![]() $[-\pi /2,\pi /2]$.
$[-\pi /2,\pi /2]$.
Under these weak assumptions on the error distribution, the three rays might fail to form a triangle (the cocked hat). How can we formally express the ![]() $25\%$-probability result when rays may fail to intersect? We propose four ways to express the result; the first three are fairly natural but are not sufficient for the
$25\%$-probability result when rays may fail to intersect? We propose four ways to express the result; the first three are fairly natural but are not sufficient for the ![]() $1/4$ result, even under the restriction
$1/4$ result, even under the restriction ![]() $\epsilon _{i}\in [-\pi /2,\pi /2]$; the fourth is not particularly natural but is the only correct statement of the result.
$\epsilon _{i}\in [-\pi /2,\pi /2]$; the fourth is not particularly natural but is the only correct statement of the result.
Conjunction formulation. The probability that the three rays intersect at three points and that the triangle that they form contains ![]() $F$ is
$F$ is ![]() $1/4$. In this formulation, we allow error distributions that could generate non-intersecting rays and we hope to prove that the probability that the rays intersect at fewer than three points or that the triangle does not contain
$1/4$. In this formulation, we allow error distributions that could generate non-intersecting rays and we hope to prove that the probability that the rays intersect at fewer than three points or that the triangle does not contain ![]() $F$ is exactly
$F$ is exactly ![]() $3/4$. This is false.
$3/4$. This is false.
Conditional probability formulation. The conditional probability that the triangle that the rays form contains ![]() $F$, conditioned on the rays forming a triangle, is
$F$, conditioned on the rays forming a triangle, is ![]() $1/4$. In this formulation we again allow error distributions that generate non-intersecting rays, and we hope to prove that if the rays intersect at three points, then the probability that the triangle contains
$1/4$. In this formulation we again allow error distributions that generate non-intersecting rays, and we hope to prove that if the rays intersect at three points, then the probability that the triangle contains ![]() $F$ is
$F$ is ![]() $1/4$. We do not care with what probability the rays fail to form a triangle. This again is false.
$1/4$. We do not care with what probability the rays fail to form a triangle. This again is false.
Lines formulation. We extend the rays ![]() $r_{i}$ to infinite lines
$r_{i}$ to infinite lines ![]() $\ell _{i}$, which always form a triangle, and we hope to show that the triangle that they form contains
$\ell _{i}$, which always form a triangle, and we hope to show that the triangle that they form contains ![]() $F$ with probability
$F$ with probability ![]() $1/4$. Here we must restrict
$1/4$. Here we must restrict ![]() $\epsilon _{i}\in [-\pi /2,\pi /2]$, otherwise the same line could appear both on the left and on the right of
$\epsilon _{i}\in [-\pi /2,\pi /2]$, otherwise the same line could appear both on the left and on the right of ![]() $F$. Again, this claim is false.
$F$. Again, this claim is false.
Constrained distribution formulation. We assume that the distribution of errors is such that every pair of rays always intersects and we hope to show that the probability that the triangle contains ![]() $F$ is
$F$ is ![]() $1/4$. We do not permit distributions under which two of the rays might fail to intersect. We show below that in this case
$1/4$. We do not permit distributions under which two of the rays might fail to intersect. We show below that in this case ![]() $\mathrm {Prob}(F \in \Delta )= 1/4$.
$\mathrm {Prob}(F \in \Delta )= 1/4$.
We note that, from the navigator's perspective, the conditional probability is the most natural. You plot three rays. If they do not intersect at three points, you discard the measurements and try again, because you either picked bad observation points (e.g., two of them and your ship are almost collinear) or at least one of the bearings is way off. If they do intersect at three points, you want to know the (conditional) probability that the cocked hat contains ![]() $F$. From the statistician's perspective, any of the first three formulations makes sense. The fourth makes less statistical sense, because it is unusual to assume that independent error distributions satisfy some global structural constraint. In particular, it appears that Daniels may have believed that the lines formulation is correct, because he writes about geometrical lines in the plane, not about rays. He writes ‘a particular set of
$F$. From the statistician's perspective, any of the first three formulations makes sense. The fourth makes less statistical sense, because it is unusual to assume that independent error distributions satisfy some global structural constraint. In particular, it appears that Daniels may have believed that the lines formulation is correct, because he writes about geometrical lines in the plane, not about rays. He writes ‘a particular set of ![]() $n$ lines, no two of which are parallel, divides the plane in to
$n$ lines, no two of which are parallel, divides the plane in to ![]() $\frac {1}{2}(n^{2}+n+2)$ polygons’.
$\frac {1}{2}(n^{2}+n+2)$ polygons’.
3. Counterexamples
We now show that the Conjunction, Conditional probability and Lines formulations are all false by giving counterexamples. Every example is a two-ray distribution that is concentrated on two rays ![]() $R_i^{+}$ and
$R_i^{+}$ and ![]() $R_i^{-}$:
$R_i^{-}$: ![]() $\mathrm {Prob}(R_i=R_i^{+})=\mathrm {Prob}(R_i=R_i^{-})=\frac 12$. This is no coincidence, as we will see at the end of this section.
$\mathrm {Prob}(R_i=R_i^{+})=\mathrm {Prob}(R_i=R_i^{-})=\frac 12$. This is no coincidence, as we will see at the end of this section.
In the first example ![]() $F$ is in the centroid of an equilateral triangle whose vertices are
$F$ is in the centroid of an equilateral triangle whose vertices are ![]() $P_{1}$,
$P_{1}$, ![]() $P_{2}$ and
$P_{2}$ and ![]() $P_{3}$. Figure 2 (left) shows the two-ray error distributions. It is easy to see that
$P_{3}$. Figure 2 (left) shows the two-ray error distributions. It is easy to see that ![]() $R_{i}^{+}$ intersects neither
$R_{i}^{+}$ intersects neither ![]() $R_{i+1}^{+}$ nor
$R_{i+1}^{+}$ nor ![]() $R_{i+1}^{-}$ (subscripts are meant modulo
$R_{i+1}^{-}$ (subscripts are meant modulo ![]() $3$). Therefore, if
$3$). Therefore, if ![]() $R_{i}^{+}$ is selected, then a cocked hat does not form. On the other hand, if
$R_{i}^{+}$ is selected, then a cocked hat does not form. On the other hand, if ![]() $R_{1}^{-}$,
$R_{1}^{-}$, ![]() $R_{2}^{-}$ and
$R_{2}^{-}$ and ![]() $R_{3}^{-}$ are selected, then they form a cocked hat that contains
$R_{3}^{-}$ are selected, then they form a cocked hat that contains ![]() $F$. Therefore,
$F$. Therefore,
 \begin{align*} \mathrm{Prob}(F\in\triangle \,|\, \text{ the rays form a cocked hat }\triangle) & = 1,\\ \mathrm{Prob}(\text{the rays form a cocked hat }\triangle\text{ and }F\in\triangle) & = \frac{1}{8}. \end{align*}
\begin{align*} \mathrm{Prob}(F\in\triangle \,|\, \text{ the rays form a cocked hat }\triangle) & = 1,\\ \mathrm{Prob}(\text{the rays form a cocked hat }\triangle\text{ and }F\in\triangle) & = \frac{1}{8}. \end{align*}
This shows both that the Conjunction formulation is false and that the Conditional probability formulation is false. Note that all the error angles have magnitude less than ![]() $\pi /2$, so these formulations are false even with this restriction.
$\pi /2$, so these formulations are false even with this restriction.

Figure 2. Two counterexamples
Figure 2 (right) shows another two-ray distribution. The error magnitudes are less than ![]() $\pi /2$, actually as small as you wish. The true position
$\pi /2$, actually as small as you wish. The true position ![]() $F$ lies outside all the triangles that the lines form, so the probability that the cocked hat (in the Lines formulation) contains
$F$ lies outside all the triangles that the lines form, so the probability that the cocked hat (in the Lines formulation) contains ![]() $F$ is zero. We can move
$F$ is zero. We can move ![]() $F$ to the right by any amount and
$F$ to the right by any amount and ![]() $F \notin \Delta$ will still hold. This example also shows that the conditional probability that a cocked hat formed by three rays contains
$F \notin \Delta$ will still hold. This example also shows that the conditional probability that a cocked hat formed by three rays contains ![]() $F$ can also be zero.
$F$ can also be zero.
The last example, given in Figure 3, shows that the probability that the triangle formed by the extension of the rays to lines contains ![]() $F$ can be
$F$ can be ![]() $1$. We again note that the error angles are bounded in magnitude by
$1$. We again note that the error angles are bounded in magnitude by ![]() $\pi /2$. In this example the three rays do not have three intersection points, so the cocked hat appears with probability zero. So this is another counterexample to the Conjunction formulation.
$\pi /2$. In this example the three rays do not have three intersection points, so the cocked hat appears with probability zero. So this is another counterexample to the Conjunction formulation.

Figure 3. The third counterexample
We close this section with a remark on two-ray distributions. The set of (Borel) probability distributions satisfying condition (2.1) is convex, and its extreme points are exactly the two-ray distributions, as one can easily check. Moreover, ![]() $\mathrm {Prob}(F \in \Delta )$ is a linear function on the product of the distributions
$\mathrm {Prob}(F \in \Delta )$ is a linear function on the product of the distributions ![]() $\mu _1,\mu _2,\mu _3$, where
$\mu _1,\mu _2,\mu _3$, where ![]() $\mu _i$ is the probability distribution of the ray
$\mu _i$ is the probability distribution of the ray ![]() $R_i$. Indeed, denoting by
$R_i$. Indeed, denoting by ![]() $I(E)$ the indicator function of an event
$I(E)$ the indicator function of an event ![]() $E$, we have
$E$, we have
a linear function of each ![]() $\mu _i$, so if it takes the value
$\mu _i$, so if it takes the value ![]() $1/4$ on the two-ray distributions, then it takes the same value on all distributions satisfying (2.1). We will come back to such distributions again in Section 5.
$1/4$ on the two-ray distributions, then it takes the same value on all distributions satisfying (2.1). We will come back to such distributions again in Section 5.
4. Intersecting rays
We now start the analysis when rays must intersect in pairs. We assume throughout that the ![]() $n+1$ points
$n+1$ points ![]() $P_{1},\ldots ,P_{n},F$ are in general position, so that no three are collinear and so that no other degeneracies arise.
$P_{1},\ldots ,P_{n},F$ are in general position, so that no three are collinear and so that no other degeneracies arise.
We introduce some notation. We let ![]() $\overrightarrow {XY}$ denote the ray emanating from
$\overrightarrow {XY}$ denote the ray emanating from ![]() $X$ in the direction of
$X$ in the direction of ![]() $Y$ when
$Y$ when ![]() $X$ and
$X$ and ![]() $Y$ are distinct points in the plane; here we assume that
$Y$ are distinct points in the plane; here we assume that ![]() $X \notin \overrightarrow {XY}$. Thus
$X \notin \overrightarrow {XY}$. Thus ![]() $r_i=\overrightarrow {P_{i}F}$ is the ray starting at
$r_i=\overrightarrow {P_{i}F}$ is the ray starting at ![]() $P_{i}$ in the direction of the target
$P_{i}$ in the direction of the target ![]() $F$, and
$F$, and ![]() $\ell _i$ is the line containing
$\ell _i$ is the line containing ![]() $r_i$. From each
$r_i$. From each ![]() $P_i$ out goes a random ray
$P_i$ out goes a random ray ![]() $R_i$ making a (signed) angle
$R_i$ making a (signed) angle ![]() $\varepsilon _i\in (-\pi ,\pi )$ with
$\varepsilon _i\in (-\pi ,\pi )$ with ![]() $r_i$. Our basic assumption, besides (2.1), is that two random rays always intersect, that is, for distinct
$r_i$. Our basic assumption, besides (2.1), is that two random rays always intersect, that is, for distinct ![]() $i,j \in [n]$ we have
$i,j \in [n]$ we have
So rays ![]() $R_i$ and
$R_i$ and ![]() $R_j$ intersect almost surely but their intersection point is not
$R_j$ intersect almost surely but their intersection point is not ![]() $P_i$ or
$P_i$ or ![]() $P_j$ because of our convention that
$P_j$ because of our convention that ![]() $X \notin \overrightarrow {XY}$ .
$X \notin \overrightarrow {XY}$ .
Further notation: ![]() $h_i^{-}$ (respectively
$h_i^{-}$ (respectively ![]() $h_i^{+}$) are the half-planes bounded by
$h_i^{+}$) are the half-planes bounded by ![]() $\ell _i$, with
$\ell _i$, with ![]() $h_i^{-}$ consisting of points
$h_i^{-}$ consisting of points ![]() $X$ such that the ray
$X$ such that the ray ![]() $\overrightarrow {P_iX}$ comes from a clockwise rotation from
$\overrightarrow {P_iX}$ comes from a clockwise rotation from ![]() $r_i$ with angle less than
$r_i$ with angle less than ![]() $\pi$, and
$\pi$, and ![]() $h_i^{+}$ is its complementary half-plane. When
$h_i^{+}$ is its complementary half-plane. When ![]() $r$ and
$r$ and ![]() $r'$ are two rays we denote by
$r'$ are two rays we denote by ![]() $\mathrm {cone}(P_i,r,r')$ the cone whose apex is
$\mathrm {cone}(P_i,r,r')$ the cone whose apex is ![]() $P_i$ and whose bounding rays are translated copies of
$P_i$ and whose bounding rays are translated copies of ![]() $r$ and
$r$ and ![]() $r'$. Such a cone always has angle less than
$r'$. Such a cone always has angle less than ![]() $\pi$, because
$\pi$, because ![]() $r$ and
$r$ and ![]() $r'$ will never have opposite directions.
$r'$ will never have opposite directions.
Define ![]() $C_{ij}=\mathrm {cone}(P_i,r_j,\overrightarrow {P_iP_j})$ for distinct
$C_{ij}=\mathrm {cone}(P_i,r_j,\overrightarrow {P_iP_j})$ for distinct ![]() $i,j \in [n]$.
$i,j \in [n]$.
Lemma 4.1 The cone ![]() $C_{ij}$ contains
$C_{ij}$ contains ![]() $r_i$ and
$r_i$ and ![]() $\mathrm {Prob}( R_i \subset C_{ij})=1$.
$\mathrm {Prob}( R_i \subset C_{ij})=1$.
Proof. Assume first that ![]() $P_j \in h_i^{-}$. We define first the cones
$P_j \in h_i^{-}$. We define first the cones ![]() $C_{ij}^{-}=\mathrm {cone}(P_i,r_i, \overrightarrow {P_iP_j})$ and
$C_{ij}^{-}=\mathrm {cone}(P_i,r_i, \overrightarrow {P_iP_j})$ and ![]() $C_{ij}^{+}=\mathrm {cone}(P_i,r_i,r_j)$; see Figure 4. Note that the angle of
$C_{ij}^{+}=\mathrm {cone}(P_i,r_i,r_j)$; see Figure 4. Note that the angle of ![]() $C_{ij}^{-}$ (respectively
$C_{ij}^{-}$ (respectively ![]() $C_{ij}^{+}$) is equal to the angle at
$C_{ij}^{+}$) is equal to the angle at ![]() $P_i$ (and at
$P_i$ (and at ![]() $F$) of the triangle with vertices
$F$) of the triangle with vertices ![]() $P_i,P_j,F$. Then
$P_i,P_j,F$. Then ![]() $C_{ij}=C_{ij}^{-} \cup C_{ij}^{+}$ because the angle of this cone is the sum of the angles of
$C_{ij}=C_{ij}^{-} \cup C_{ij}^{+}$ because the angle of this cone is the sum of the angles of ![]() $C_{ij}^{-}$ and
$C_{ij}^{-}$ and ![]() $C_{ij}^{+}$, so smaller than
$C_{ij}^{+}$, so smaller than ![]() $\pi$. Then
$\pi$. Then ![]() $r_i \subset C_{ij}$ indeed, as shown in Figure 4 (left).
$r_i \subset C_{ij}$ indeed, as shown in Figure 4 (left).

Figure 4. Illustration for Lemma 4.1: the case ![]() $P_j \in h_i^{-}$ on the left, and the case
$P_j \in h_i^{-}$ on the left, and the case ![]() $P_j \in h_i^{+}$ on the right
$P_j \in h_i^{+}$ on the right
Suppose now that ![]() $\varepsilon _i>0$, which is the same as
$\varepsilon _i>0$, which is the same as ![]() $R_i \subset h_i^{+}$. If
$R_i \subset h_i^{+}$. If ![]() $R_i$ does not lie in
$R_i$ does not lie in ![]() $C_{ij}^{+}$, then
$C_{ij}^{+}$, then ![]() $R_i \subset h_i^{+}\setminus C_{ij}^{+}$. The last set is a convex cone, disjoint from
$R_i \subset h_i^{+}\setminus C_{ij}^{+}$. The last set is a convex cone, disjoint from ![]() $h_j^{-}$, as they are separated by the line
$h_j^{-}$, as they are separated by the line ![]() $\ell _j$. So no
$\ell _j$. So no ![]() $R_j$ with
$R_j$ with ![]() $\varepsilon _j<0$ can intersect
$\varepsilon _j<0$ can intersect ![]() $R_i$, contradicting (4.1). So
$R_i$, contradicting (4.1). So ![]() $R_i \subset C_{ij}^{+}$.
$R_i \subset C_{ij}^{+}$.
Let ![]() $h$ denote the half-plane containing
$h$ denote the half-plane containing ![]() $F$ and bounded by the line through
$F$ and bounded by the line through ![]() $P_i$ and
$P_i$ and ![]() $P_j$. Observe that by the previous argument
$P_j$. Observe that by the previous argument ![]() $R_j \subset h$ because the complementary half-plane to
$R_j \subset h$ because the complementary half-plane to ![]() $h$ is disjoint from
$h$ is disjoint from ![]() $C_{ij}^{+}$, so
$C_{ij}^{+}$, so ![]() $R_j$ can intersect
$R_j$ can intersect ![]() $R_i \subset C_{ij}^{+}$ only if it lies in
$R_i \subset C_{ij}^{+}$ only if it lies in ![]() $h$.
$h$.
Suppose next that ![]() $\varepsilon _i<0$. We show that
$\varepsilon _i<0$. We show that ![]() $R_i \subset C_{ij}^{-}$. If not, then
$R_i \subset C_{ij}^{-}$. If not, then ![]() $R_i \subset h_i^{-}\setminus C_{ij}^{-}$. The last set is a convex cone again, disjoint from
$R_i \subset h_i^{-}\setminus C_{ij}^{-}$. The last set is a convex cone again, disjoint from ![]() $h$, so
$h$, so ![]() $R_i\cap R_j=\emptyset$ for all
$R_i\cap R_j=\emptyset$ for all ![]() $R_j$ with
$R_j$ with ![]() $\varepsilon _j<0$, contradicting (4.1).
$\varepsilon _j<0$, contradicting (4.1).
The argument for the case ![]() $P_j \in h_i^{+}$ is symmetric (see Figure 4 (right)), but otherwise identical and is therefore omitted.
$P_j \in h_i^{+}$ is symmetric (see Figure 4 (right)), but otherwise identical and is therefore omitted.
We remark here that Lemma 4.1 implies that the cone ![]() ${\bigcap} _{j\ne i} C_{ij}$ is convex (that is, its angle is smaller than
${\bigcap} _{j\ne i} C_{ij}$ is convex (that is, its angle is smaller than ![]() $\pi$), it contains
$\pi$), it contains ![]() $r_i$, and
$r_i$, and ![]() $\mathrm {Prob}(R_i \subset {\bigcap} _{j\ne i} C_{ij})=1$, of course only if
$\mathrm {Prob}(R_i \subset {\bigcap} _{j\ne i} C_{ij})=1$, of course only if ![]() $n\ge 2$. (For
$n\ge 2$. (For ![]() $n=1$, condition (4.1) is void.) Define
$n=1$, condition (4.1) is void.) Define ![]() $K_i$ as the smallest (with respect to inclusion) convex cone satisfying
$K_i$ as the smallest (with respect to inclusion) convex cone satisfying ![]() $\mathrm {Prob}(R_i \subset K_i)=1$. Note that
$\mathrm {Prob}(R_i \subset K_i)=1$. Note that ![]() $K_i \subset {\bigcap} _{j\ne i} C_{ij}$. For later reference we state the following corollary.
$K_i \subset {\bigcap} _{j\ne i} C_{ij}$. For later reference we state the following corollary.
Corollary 4.1 Under conditions (2.1) and (4.1) ![]() $K_i$ is a convex cone,
$K_i$ is a convex cone, ![]() $r_i\subset K_i$ and
$r_i\subset K_i$ and ![]() $\mathrm {Prob}(R_i\subset K_i)=1$ for every
$\mathrm {Prob}(R_i\subset K_i)=1$ for every ![]() $i\in [n]$.
$i\in [n]$.
Proof. Set ![]() $T=\mathrm {conv} \{P_1,P_2,P_3,F\}$, the convex hull of
$T=\mathrm {conv} \{P_1,P_2,P_3,F\}$, the convex hull of ![]() $P_1,P_2,P_3$ and
$P_1,P_2,P_3$ and ![]() $F$. We will have to consider three cases separately: when
$F$. We will have to consider three cases separately: when ![]() $T$ is a triangle with
$T$ is a triangle with ![]() $F$ inside
$F$ inside ![]() $T$ (Case 1); when
$T$ (Case 1); when ![]() $T$ is a triangle with
$T$ is a triangle with ![]() $F$ a vertex of
$F$ a vertex of ![]() $T$ (Case 2); and when
$T$ (Case 2); and when ![]() $T$ is a quadrilateral (Case 3).
$T$ is a quadrilateral (Case 3).
Case 1. Define ![]() $C_i=\mathrm {cone}(P_i,\overrightarrow {P_iP_{i-1}},\overrightarrow {P_iP_{i+1}})$ for
$C_i=\mathrm {cone}(P_i,\overrightarrow {P_iP_{i-1}},\overrightarrow {P_iP_{i+1}})$ for ![]() $i=1,2,3$, where the subscripts are taken mod
$i=1,2,3$, where the subscripts are taken mod ![]() $3$; see Figure 5 (left).
$3$; see Figure 5 (left).

Figure 5. The cone ![]() $C_2$ in Case 1 (left) and Case 2 (right)
$C_2$ in Case 1 (left) and Case 2 (right)
We claim that ![]() $R_i \subset C_i$ for all
$R_i \subset C_i$ for all ![]() $i$. By symmetry it suffices to show this for
$i$. By symmetry it suffices to show this for ![]() $i=2$. By Lemma 4.1
$i=2$. By Lemma 4.1 ![]() $R_2 \subset C_{21}\cap C_{23}$. So it is enough to check that
$R_2 \subset C_{21}\cap C_{23}$. So it is enough to check that ![]() $C_2 = C_{21}\cap C_{23}$, and this is evident: the rays bounding
$C_2 = C_{21}\cap C_{23}$, and this is evident: the rays bounding ![]() $C_2$ are
$C_2$ are ![]() $\overrightarrow {P_2P_{1}}$ (which bounds
$\overrightarrow {P_2P_{1}}$ (which bounds ![]() $C_{21}$) and
$C_{21}$) and ![]() $\overrightarrow {P_2P_3}$ (which bounds
$\overrightarrow {P_2P_3}$ (which bounds ![]() $C_{23}$).
$C_{23}$).
We can now finish the proof of the theorem in Case 1. There are eight sub-cases with equal probabilities that correspond to the signs of ![]() $\epsilon _{1}$,
$\epsilon _{1}$, ![]() $\epsilon _{2}$ and
$\epsilon _{2}$ and ![]() $\epsilon _{3}$, as shown in Figure 6. Only in two of them, namely when all
$\epsilon _{3}$, as shown in Figure 6. Only in two of them, namely when all ![]() $\epsilon _{i}$ have the same sign, do we have
$\epsilon _{i}$ have the same sign, do we have ![]() $F\in \triangle$, so the probability of this event is
$F\in \triangle$, so the probability of this event is ![]() $1/4$.
$1/4$.

Figure 6. Illustration for the proof of Theorem 4.1
Case 2. We assume (by symmetry) that ![]() $P_2$ is inside the triangle
$P_2$ is inside the triangle ![]() $T$. We define the cones
$T$. We define the cones ![]() $C_1=\mathrm {cone}(P_1,r_2,\overrightarrow {P_1P_2})$,
$C_1=\mathrm {cone}(P_1,r_2,\overrightarrow {P_1P_2})$, ![]() $C_2=\mathrm {cone}(P_2,r_1,r_3)$ and
$C_2=\mathrm {cone}(P_2,r_1,r_3)$ and ![]() $C_3=\mathrm {cone}(P_3,r_2,\overrightarrow {P_3P_2})$ and we claim that
$C_3=\mathrm {cone}(P_3,r_2,\overrightarrow {P_3P_2})$ and we claim that ![]() $R_i \subset C_i$ for all
$R_i \subset C_i$ for all ![]() $i$. From Lemma 4.1 we have that
$i$. From Lemma 4.1 we have that ![]() $R_2 \subset C_{21}\cap C_{23}$. The bounding rays of
$R_2 \subset C_{21}\cap C_{23}$. The bounding rays of ![]() $C_2$ are a translate of
$C_2$ are a translate of ![]() $r_2$ (bounding
$r_2$ (bounding ![]() $C_{21}$) and a translate of
$C_{21}$) and a translate of ![]() $r_3$ (bounding
$r_3$ (bounding ![]() $C_{23}$), so
$C_{23}$), so ![]() $C_2 = C_{21}\cap C_{23}$ (see Figure 5 (right)).
$C_2 = C_{21}\cap C_{23}$ (see Figure 5 (right)).
The cases ![]() $i=1$ and
$i=1$ and ![]() $3$ are symmetric and very simple. We only consider
$3$ are symmetric and very simple. We only consider ![]() $i=1$. Again, by Lemma 4.1
$i=1$. Again, by Lemma 4.1 ![]() $R_1 \subset C_{12}$ and then
$R_1 \subset C_{12}$ and then ![]() $C_1= C_{12}$ implying
$C_1= C_{12}$ implying ![]() $R_1 \subset C_1$.
$R_1 \subset C_1$.
Again, there are eight subcases, corresponding to the eight possible sign patterns of ![]() $\varepsilon _1,\varepsilon _2,\varepsilon _3$. It is easy to see that
$\varepsilon _1,\varepsilon _2,\varepsilon _3$. It is easy to see that ![]() $F \in \Delta$ in exactly two of them.
$F \in \Delta$ in exactly two of them.
Case 3. We assume again by symmetry that the segment ![]() $P_2F$ is a diagonal of the quadrilateral
$P_2F$ is a diagonal of the quadrilateral ![]() $T$. Define cones
$T$. Define cones ![]() $C_1=\mathrm {cone}(P_1,r_2,\overrightarrow {P_1P_3})$,
$C_1=\mathrm {cone}(P_1,r_2,\overrightarrow {P_1P_3})$, ![]() $C_2=\mathrm {cone}(P_2,r_1,r_3)$ and
$C_2=\mathrm {cone}(P_2,r_1,r_3)$ and ![]() $C_3=\mathrm {cone}(P_3,r_2,\overrightarrow {P_3P_2})$. We claim again that
$C_3=\mathrm {cone}(P_3,r_2,\overrightarrow {P_3P_2})$. We claim again that ![]() $R_i \subset C_i$ for all
$R_i \subset C_i$ for all ![]() $i$. The proof is similar to the previous ones using Lemma 4.1 and is omitted here. Again,
$i$. The proof is similar to the previous ones using Lemma 4.1 and is omitted here. Again, ![]() $F \in \Delta$ in exactly two out of the eight cases.
$F \in \Delta$ in exactly two out of the eight cases.
5. Daniels’ statement
We assume now that there are ![]() $n\ge 3$ observation points
$n\ge 3$ observation points ![]() $P_1,\ldots ,P_n$ plus the target point
$P_1,\ldots ,P_n$ plus the target point ![]() $F$ and that these
$F$ and that these ![]() $n+1$ points are in general position. A random ray
$n+1$ points are in general position. A random ray ![]() $R_i$ starts at each
$R_i$ starts at each ![]() $P_i$ satisfying conditions (2.1) and (4.1). The lines of the rays
$P_i$ satisfying conditions (2.1) and (4.1). The lines of the rays ![]() $R_i$ split the plane into connected components. Let
$R_i$ split the plane into connected components. Let ![]() $U$ denote the union of the
$U$ denote the union of the ![]() $2n$ unbounded components. Here comes Daniels’ statement.
$2n$ unbounded components. Here comes Daniels’ statement.
Theorem 5.1 Under conditions (2.1) and (4.1) we have
The case ![]() $n=2$ is trivial and not interesting. The case
$n=2$ is trivial and not interesting. The case ![]() $n=3$ is just Theorem 4.1. We note that condition (4.1) is a necessity, even for
$n=3$ is just Theorem 4.1. We note that condition (4.1) is a necessity, even for ![]() $n=3$, as the counterexamples in Section 3 show.
$n=3$, as the counterexamples in Section 3 show.
We are going to prove this theorem under the assumption that each ![]() $R_i$ is a two-ray distribution, that is,
$R_i$ is a two-ray distribution, that is, ![]() $\mathrm {Prob}(R_i=R_i^{+})=\mathrm {Prob}(R_i=R_i^{-})=1/2$ and explain, after the proof, how this special case implies the theorem. We also assume that the
$\mathrm {Prob}(R_i=R_i^{+})=\mathrm {Prob}(R_i=R_i^{-})=1/2$ and explain, after the proof, how this special case implies the theorem. We also assume that the ![]() $2n$ rays
$2n$ rays ![]() $R_i^{+},R_i^{-}$, together with the points
$R_i^{+},R_i^{-}$, together with the points ![]() $P_1,\ldots ,P_n,F$ are in general position. This is not a serious restriction because the general case of two-ray distributions follows from this by a routine limiting argument.
$P_1,\ldots ,P_n,F$ are in general position. This is not a serious restriction because the general case of two-ray distributions follows from this by a routine limiting argument.
Proof. To simplify the exposition, we set ![]() $D_i=\mathrm {cone}(P_i,R_i^{+},R_i^{-})$, which is equivalent to
$D_i=\mathrm {cone}(P_i,R_i^{+},R_i^{-})$, which is equivalent to ![]() $D_i=\mathrm {conv}(R_i^{+} \cup R_i^{-})$. Lemma 4.1 implies that
$D_i=\mathrm {conv}(R_i^{+} \cup R_i^{-})$. Lemma 4.1 implies that ![]() $r_i \subset D_i$ for every
$r_i \subset D_i$ for every ![]() $i\in [n]$. Let
$i\in [n]$. Let ![]() $S$ be a circle centred at
$S$ be a circle centred at ![]() $F$ such that
$F$ such that ![]() $S\subset D_i$ for every
$S\subset D_i$ for every ![]() $i\in [n]$. Observe that for distinct
$i\in [n]$. Observe that for distinct ![]() $i,j\in [n]$, the intersection
$i,j\in [n]$, the intersection ![]() $D_i\cap D_j$ is a convex quadrilateral containing
$D_i\cap D_j$ is a convex quadrilateral containing ![]() $S$ and of course
$S$ and of course ![]() $F$; see Figure 7 (left). This follows from condition (4.1): both
$F$; see Figure 7 (left). This follows from condition (4.1): both ![]() $R_i^{+}$ and
$R_i^{+}$ and ![]() $R_i^{-}$ intersect both
$R_i^{-}$ intersect both ![]() $R_j^{+}$ and
$R_j^{+}$ and ![]() $R_j^{-}$ and the four intersection points are the vertices of
$R_j^{-}$ and the four intersection points are the vertices of ![]() $D_i\cap D_j$, which is then a convex quadrilateral.
$D_i\cap D_j$, which is then a convex quadrilateral.

Figure 7. The intersection ![]() $D_i\cap D_j$ and the translated cone
$D_i\cap D_j$ and the translated cone ![]() $D_i^{*}$
$D_i^{*}$
Let ![]() $L_i^{+}$ (respectively
$L_i^{+}$ (respectively ![]() $L_i^{-}$) denote the line of the ray
$L_i^{-}$) denote the line of the ray ![]() $R_i^{+}$ (and
$R_i^{+}$ (and ![]() $R_i^{-}$). For a selection
$R_i^{-}$). For a selection ![]() $\delta _1,\ldots ,\delta _n \in \{1,-1\}$ of signs, the lines
$\delta _1,\ldots ,\delta _n \in \{1,-1\}$ of signs, the lines ![]() $L_1^{\delta _1},\ldots ,L_n^{\delta _n}$ split the plane into finitely many connected components. We are going to show that, out of the
$L_1^{\delta _1},\ldots ,L_n^{\delta _n}$ split the plane into finitely many connected components. We are going to show that, out of the ![]() $2^{n}$ possible selections, there are exactly
$2^{n}$ possible selections, there are exactly ![]() $2n$ for which
$2n$ for which ![]() $F$ lies in an unbounded component.
$F$ lies in an unbounded component.
We reduce this statement to another one about arcs on the unit circle. First comes a simpler reduction. Translate each cone ![]() $D_i$ into a new (and actually unique) position
$D_i$ into a new (and actually unique) position ![]() $D_i^{*}$ so that its rays touch the circle
$D_i^{*}$ so that its rays touch the circle ![]() $S$ (see Figure 7 (right)). Let
$S$ (see Figure 7 (right)). Let ![]() $Q_i^{+},M_i^{+}$ (respectively
$Q_i^{+},M_i^{+}$ (respectively ![]() $Q_i^{-},M_i^{-}$) be the translated copies of
$Q_i^{-},M_i^{-}$) be the translated copies of ![]() $R_i^{+},L_i^{+}$ (and
$R_i^{+},L_i^{+}$ (and ![]() $R_i^{-},L_i^{-}$). Note that
$R_i^{-},L_i^{-}$). Note that ![]() $D_i^{*}\cap D_j^{*}$ is again a convex quadrilateral.
$D_i^{*}\cap D_j^{*}$ is again a convex quadrilateral.
We claim next that, for a fixed selection ![]() $\delta _1,\ldots ,\delta _n$ of signs,
$\delta _1,\ldots ,\delta _n$ of signs, ![]() $F$ lies in an unbounded component for the lines
$F$ lies in an unbounded component for the lines ![]() $L_1^{\delta _1},\ldots ,L_n^{\delta _n}$ if and only if it lies in the corresponding unbounded component for the lines
$L_1^{\delta _1},\ldots ,L_n^{\delta _n}$ if and only if it lies in the corresponding unbounded component for the lines ![]() $M_1^{\delta _1},\ldots ,M_n^{\delta _n}$. This is simple. The point
$M_1^{\delta _1},\ldots ,M_n^{\delta _n}$. This is simple. The point ![]() $F$ lies in an unbounded component for the lines
$F$ lies in an unbounded component for the lines ![]() $L_i^{\delta _i}$ if and only if there is a half-line
$L_i^{\delta _i}$ if and only if there is a half-line ![]() $R$ starting at
$R$ starting at ![]() $F$ and disjoint from each
$F$ and disjoint from each ![]() $L_i ^{\delta _i}$, which happens if and only if
$L_i ^{\delta _i}$, which happens if and only if ![]() $R$ is disjoint from the lines
$R$ is disjoint from the lines ![]() $M_i ^{\delta _i}$ as well.
$M_i ^{\delta _i}$ as well.
Assume now that ![]() $S$ is the unit circle. Let
$S$ is the unit circle. Let ![]() $a_i^{+}$ (respectively
$a_i^{+}$ (respectively ![]() $a_i^{-}$) be the points where
$a_i^{-}$) be the points where ![]() $M_i^{+}$ (and
$M_i^{+}$ (and ![]() $M_i^{-}$) touch
$M_i^{-}$) touch ![]() $S$, and let
$S$, and let ![]() $A_i$ be the shorter arc on
$A_i$ be the shorter arc on ![]() $S$ between
$S$ between ![]() $a_i^{+}$ and
$a_i^{+}$ and ![]() $a_i^{-}$; see Figure 7 (right). It is clear that
$a_i^{-}$; see Figure 7 (right). It is clear that ![]() $a_i^{+}$ and
$a_i^{+}$ and ![]() $a_i^{-}$ are not opposite points on
$a_i^{-}$ are not opposite points on ![]() $S$, so
$S$, so ![]() $A_i$ is well defined. These arcs completely determine
$A_i$ is well defined. These arcs completely determine ![]() $D_i^{*}$. They satisfy the following conditions:
$D_i^{*}$. They satisfy the following conditions:
(i) each
 $A_i$ is shorter than
$A_i$ is shorter than  $\pi$, and
$\pi$, and(ii)
 $A_i\cup A_j$ is an arc in
$A_i\cup A_j$ is an arc in  $S$ longer than
$S$ longer than  $\pi$ for all
$\pi$ for all  $i,j\in [n],\ i\ne j$.
$i,j\in [n],\ i\ne j$.
The latter condition follows from the fact that ![]() $D_i^{*}\cap D_j^{*}$ is a convex quadrilateral.
$D_i^{*}\cap D_j^{*}$ is a convex quadrilateral.
We call a selection ![]() $\delta _1,\ldots ,\delta _n$ special if it gives an unbounded component containing
$\delta _1,\ldots ,\delta _n$ special if it gives an unbounded component containing ![]() $F$. We claim that a selection is special if and only if the points
$F$. We claim that a selection is special if and only if the points ![]() $a_1^{\delta _1},\ldots ,a_n^{\delta _n}$ lie on an arc of
$a_1^{\delta _1},\ldots ,a_n^{\delta _n}$ lie on an arc of ![]() $S$ shorter than
$S$ shorter than ![]() $\pi$. This is also simple. If there is such an arc, call it
$\pi$. This is also simple. If there is such an arc, call it ![]() $I$ and let
$I$ and let ![]() $Q$ be the centre point of the complementary arc
$Q$ be the centre point of the complementary arc ![]() $S \setminus I$. The ray
$S \setminus I$. The ray ![]() $\overrightarrow {FQ}$ avoids every line
$\overrightarrow {FQ}$ avoids every line ![]() $M_i^{\delta _i}$. If there is no such arc, then the connected component containing
$M_i^{\delta _i}$. If there is no such arc, then the connected component containing ![]() $F$ (and
$F$ (and ![]() $S$) is bounded, as one can check easily. Therefore it suffices to prove the following lemma.
$S$) is bounded, as one can check easily. Therefore it suffices to prove the following lemma.
Lemma 5.1 Under the above conditions, there are exactly ![]() $2n$ special selections.
$2n$ special selections.
Proof. For a special selection ![]() $\delta =(\delta _1,\ldots ,\delta _n)$, let
$\delta =(\delta _1,\ldots ,\delta _n)$, let ![]() $I(\delta )$ denote the shortest arc on
$I(\delta )$ denote the shortest arc on ![]() $S$ containing every
$S$ containing every ![]() $a_i^{\delta _i}$,
$a_i^{\delta _i}$, ![]() $i\in [n]$. Thus
$i\in [n]$. Thus ![]() $I(\delta )$ is the shorter arc between points
$I(\delta )$ is the shorter arc between points ![]() $a_i^{\delta _i}$ and
$a_i^{\delta _i}$ and ![]() $a_j^{\delta _j}$ for some distinct
$a_j^{\delta _j}$ for some distinct ![]() $i,j\in [n]$, and they are the endpoints of
$i,j\in [n]$, and they are the endpoints of ![]() $I(\delta )$.
$I(\delta )$.
Claim 5.1 Each ![]() $a_i^{+}$ (and
$a_i^{+}$ (and ![]() $a_i^{-}$) is the endpoint of
$a_i^{-}$) is the endpoint of ![]() $I(\delta )$ for exactly two special selections
$I(\delta )$ for exactly two special selections ![]() $\delta$.
$\delta$.
It suffices to prove this claim, since it implies Lemma 5.1 and then Theorem 5.1 as well.
Proof of the claim. It is enough to work with ![]() $a_1^{+}$. Using the notation on Figure 8, we assume that
$a_1^{+}$. Using the notation on Figure 8, we assume that ![]() $a_1^{-}$ is from the half-circle
$a_1^{-}$ is from the half-circle ![]() $S^{+}$ so
$S^{+}$ so ![]() $A_1\subset S^{+}$.
$A_1\subset S^{+}$.

Figure 8. The definition of ![]() $S^{+}$ and
$S^{+}$ and ![]() $S^{-}$
$S^{-}$
Define ![]() $X=\{a_1^{+},a_1^{-},\ldots ,a_n^{+},a_n^{-}\}$ and
$X=\{a_1^{+},a_1^{-},\ldots ,a_n^{+},a_n^{-}\}$ and ![]() $Y=X \setminus \{a_1^{+},a_1^{-}\}$. Observe first that
$Y=X \setminus \{a_1^{+},a_1^{-}\}$. Observe first that ![]() $S^{+}$ cannot contain any
$S^{+}$ cannot contain any ![]() $A_i$,
$A_i$, ![]() $i>1$, as otherwise
$i>1$, as otherwise ![]() $A_1,A_i\subset S^{+}$, contradicting condition (ii). Moreover,
$A_1,A_i\subset S^{+}$, contradicting condition (ii). Moreover, ![]() $S^{-}$ cannot contain two arcs
$S^{-}$ cannot contain two arcs ![]() $A_i,A_j$ with distinct
$A_i,A_j$ with distinct ![]() $i,j>1$ because of condition (ii) again. It follows then that
$i,j>1$ because of condition (ii) again. It follows then that ![]() $|S^{+}\cap Y|=n-1$ or
$|S^{+}\cap Y|=n-1$ or ![]() $n-2$.
$n-2$.
Case 1: when ![]() $|S^{+}\cap Y|=n-1$. Then
$|S^{+}\cap Y|=n-1$. Then ![]() $|S^{-}\cap Y|=n-1$ as well and
$|S^{-}\cap Y|=n-1$ as well and ![]() $S^{+}$ contains exactly one element from each pair
$S^{+}$ contains exactly one element from each pair ![]() $\{a_i^{+},a_i^{-}\}$,
$\{a_i^{+},a_i^{-}\}$, ![]() $i>1$, and then so does
$i>1$, and then so does ![]() $S^{-}$. This gives exactly two special selections
$S^{-}$. This gives exactly two special selections ![]() $\delta$ and
$\delta$ and ![]() $\varepsilon$ with
$\varepsilon$ with ![]() $I(\delta )\subset S^{+}$ and
$I(\delta )\subset S^{+}$ and ![]() $I(\varepsilon )\subset S^{-}$, with
$I(\varepsilon )\subset S^{-}$, with ![]() $a_1^{+}$ an endpoint of both.
$a_1^{+}$ an endpoint of both.
Case 2: when ![]() $|S^{+}\cap Y|=n-2$. Then
$|S^{+}\cap Y|=n-2$. Then ![]() $S^{+}$ contains no
$S^{+}$ contains no ![]() $I(\delta )$ with
$I(\delta )$ with ![]() $\delta$ special,
$\delta$ special, ![]() $|S^{-}\cap Y|=n$ and so
$|S^{-}\cap Y|=n$ and so ![]() $A_i\subset S^{-}$ for a unique
$A_i\subset S^{-}$ for a unique ![]() $i>1$. This again gives two special selections
$i>1$. This again gives two special selections ![]() $\delta$ and
$\delta$ and ![]() $\varepsilon$ where
$\varepsilon$ where ![]() $a_1^{+}$ is the endpoint of
$a_1^{+}$ is the endpoint of ![]() $I(\delta )$ and
$I(\delta )$ and ![]() $I(\varepsilon )$. In fact
$I(\varepsilon )$. In fact ![]() $\delta$ and
$\delta$ and ![]() $\varepsilon$ coincide except at position
$\varepsilon$ coincide except at position ![]() $i$:
$i$: ![]() $\delta _j=\varepsilon _j$ for all
$\delta _j=\varepsilon _j$ for all ![]() $j\in [n]$ but
$j\in [n]$ but ![]() $j=i$ and
$j=i$ and ![]() $\delta _1=\varepsilon _1=1$.
$\delta _1=\varepsilon _1=1$.
We explain now how the case of two-ray distributions implies Theorem 5.1, or rather give a sketch of this and leave the technical details to the interested reader. Assume each ray ![]() $R_i$ follows a generic distribution
$R_i$ follows a generic distribution ![]() $\mu _i$ for all
$\mu _i$ for all ![]() $i \in [n]$ still satisfying conditions (2.1) and (4.1). Note that, by Corollary 4.1,
$i \in [n]$ still satisfying conditions (2.1) and (4.1). Note that, by Corollary 4.1, ![]() $\mathrm {Prob}(R_i \subset K_i)=1$. Using this, one can check that every
$\mathrm {Prob}(R_i \subset K_i)=1$. Using this, one can check that every ![]() $\mu _i$ can be approximated with high precision by a convex combination of two-ray distributions, each having
$\mu _i$ can be approximated with high precision by a convex combination of two-ray distributions, each having ![]() $R_i^{+},R_i^{-}\subset K_i$. One has to show as well that this approximation can be chosen so that
$R_i^{+},R_i^{-}\subset K_i$. One has to show as well that this approximation can be chosen so that ![]() $R_i^{\delta _i}\cap R_j^{\delta _j}\ne \emptyset$ for distinct
$R_i^{\delta _i}\cap R_j^{\delta _j}\ne \emptyset$ for distinct ![]() $i,j \in [n]$ and for every choice of signs
$i,j \in [n]$ and for every choice of signs ![]() $\delta _i,\delta _j$. As in (3.1),
$\delta _i,\delta _j$. As in (3.1), ![]() $\mathrm {Prob}(F \in U)$ is a linear function of the underlying distributions
$\mathrm {Prob}(F \in U)$ is a linear function of the underlying distributions ![]() $\mu _i$, and this linear function equals
$\mu _i$, and this linear function equals ![]() $2n/2^{n}$ on the product of two-ray distributions. Therefore, this linear function equals
$2n/2^{n}$ on the product of two-ray distributions. Therefore, this linear function equals ![]() $2n/2^{n}$ on any convex combination of products of two-ray distributions and consequently
$2n/2^{n}$ on any convex combination of products of two-ray distributions and consequently ![]() $\mathrm {Prob}(F \in U)$ must be equal to
$\mathrm {Prob}(F \in U)$ must be equal to ![]() $2n/2^{n}$ on the product of the
$2n/2^{n}$ on the product of the ![]() $\mu _i$.
$\mu _i$.
Financial statement
The first author was partially supported by Hungarian National Research grants 131529, 131696 and KKP-133819. The last author was partially supported by grants 965/15, 863/15 and 1919/19 from the Israel Science Foundation and by a grant from the Israeli Ministry of Science and Technology. We thank Gil Kalai for connecting the three of us in this piece of research.