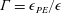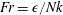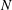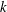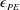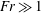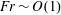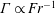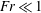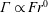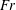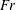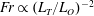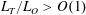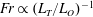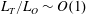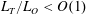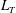1 Introduction
Diapycnal (irreversible) mixing is critical for maintaining the oceanic meridional overturning circulation and other important related issues such as global mass and heat budgets, ocean productivity etc. (Munk & Wunsch Reference Munk and Wunsch1998). Hence, an accurate estimate of mixing in oceanic flows is essential but remains challenging due to complexities associated primarily with density stratification and limitations associated with direct measurements of pertinent turbulence quantities (Venayagamoorthy & Koseff Reference Venayagamoorthy and Koseff2016; Gregg et al. Reference Gregg, D’Asaro, Riley and Kunze2018). For instance, it is well known that internal wave motions are prevalent in density stratified flows and hence contaminate flux measurements. Thus, a number of indirect techniques are commonly used in practice in oceanography to infer turbulent heat and momentum fluxes. For example, the popular Osborn (Reference Osborn1980) model recasts the diapycnal diffusivity for a homogeneous and stationary flow as
$$\begin{eqnarray}K_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D6E4}\frac{\unicode[STIX]{x1D716}}{N^{2}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E4}=R_{f}/(1-R_{f})$
is a mixing coefficient and
$R_{f}$
is the mixing efficiency,
$\unicode[STIX]{x1D716}$
is the rate of dissipation of turbulent kinetic energy and
$N=\sqrt{(-g/\unicode[STIX]{x1D70C})(\text{d}\langle \unicode[STIX]{x1D70C}\rangle /\text{d}z)}$
is the buoyancy frequency. Assuming that both
$\unicode[STIX]{x1D716}$
and
$N$
are readily measurable in the ocean (albeit based on some underlying assumptions such as local isotropy of small scales and choices on how
$N$
is computed; see, for example, Arthur et al. (Reference Arthur, Venayagamoorthy, Koseff and Fringer2017) for a discussion on
$N$
), then clearly the only remaining quantity that needs to be quantified for computing
$K_{\unicode[STIX]{x1D70C}}$
is the mixing coefficient
$\unicode[STIX]{x1D6E4}$
. In practice,
$\unicode[STIX]{x1D6E4}$
is typically considered to have a canonical constant value of 0.2 (
$R_{f}\approx 0.17$
) (Osborn Reference Osborn1980). The constancy of
$\unicode[STIX]{x1D6E4}$
has been the subject of extensive debate over the last few decades (Gregg et al.
Reference Gregg, D’Asaro, Riley and Kunze2018). In fact, a number of different parameterizations for the mixing efficiency have been proposed that are primarily based on one of three fundamental dimensionless parameters. These are the gradient Richardson number
$Ri$
, the buoyancy Reynolds number
$Re_{b}$
and the turbulent Froude number
$Fr$
. We note that it has been argued that a multi-parameter framework might be necessary to adequately parameterize mixing (Mater & Venayagamoorthy Reference Mater and Venayagamoorthy2014; Monismith, Koseff & White Reference Monismith, Koseff and White2018). However, from a practical standpoint, it is useful to identify an optimal single parameter that can be used to infer the state of turbulence and mixing efficiency. This is the primary impetus behind this current study.
It might be argued that a popular dimensionless number for parameterization of mixing is the buoyancy Reynolds (or Gibson) number
$Re_{b}=\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}N^{2}$
, where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. This is mainly because it is readily computable from quantities that are measurable in the ocean. It has been argued that in strongly stratified flows,
$\unicode[STIX]{x1D6E4}$
is generally constant (typically assumed to be
${\sim}0.2$
in practice) up to some critical value of
$Re_{b}$
and then gradually decreases like
$\unicode[STIX]{x1D6E4}\propto Re_{b}^{-1/2}$
, as stratification weakens (Shih et al.
Reference Shih, Koseff, Ivey and Ferziger2005; Lozovatsky & Fernando Reference Lozovatsky and Fernando2013; Salehipour & Peltier Reference Salehipour and Peltier2015; Monismith et al.
Reference Monismith, Koseff and White2018). However, there is no consensus on a definitive critical value of
$Re_{b}$
at which the transition from a constant value to a functional dependence on
$Re_{b}$
occurs as evident from analysis of data obtained from different numerical simulations and field measurements. For example, Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) and Salehipour & Peltier (Reference Salehipour and Peltier2015) found a critical
$Re_{b}$
of order
$10^{2}$
while Lozovatsky & Fernando (Reference Lozovatsky and Fernando2013) found this transition to occur around
$10^{4}$
. Using different data sets, Monismith et al. (Reference Monismith, Koseff and White2018) noticed that for high value of
$Re_{b}$
, mixing efficiency is not constant and varies with
$Re_{b}$
. However, there is no unique relation of
$R_{f}$
with
$Re_{b}$
. On the other hand, parameterizations based on the gradient Richardson number
$Ri=N^{2}/S^{2}$
(where
$S$
is the mean shear rate) suggest that
$R_{f}$
increases with
$Ri$
in the shear-dominated or weakly stratified flow up to a critical value of gradient Richardson number (
$Ri\sim 0.25$
) (Linden Reference Linden1979) and approaches a constant value for high-
$Ri$
regime (Venayagamoorthy & Koseff Reference Venayagamoorthy and Koseff2016). However, it should be noted that
$Ri$
is restricted to shear-driven turbulence and hence is not practically useful for quantifying mixing in the absence of mean shear. Therefore, while
$Ri$
and
$Re_{b}$
may appear to be convenient parameters for quantifying mixing, they may not be useful for robust characterizations of the local state of turbulence and associated mixing in stratified flows for the aforementioned reasons.
The turbulent Froude number
$Fr=\unicode[STIX]{x1D716}/Nk$
(where
$k$
is the turbulent kinetic energy) is perhaps a better-suited parameter (Ivey & Imberger Reference Ivey and Imberger1991; Shih et al.
Reference Shih, Koseff, Ferziger and Rehmann2000), but least investigated in the context of oceanography because it is difficult to compute directly from measurable quantities in the field. It is worth noting that
$Fr$
can be viewed as a competition of time scales (i.e. between the turbulence time scale
$T_{L}=k/\unicode[STIX]{x1D716}$
and the buoyancy time scale
$N^{-1}$
). Hence,
$Fr$
is indicator of the local state of turbulence in a stably stratified flow. For high
$Fr$
(weak stratification), it has been shown using simple scaling analysis that
$\unicode[STIX]{x1D6E4}\sim Fr^{-2}$
, and this has been verified using direct numerical simulation (DNS) results (Maffioli, Brethouwer & Lindborg Reference Maffioli, Brethouwer and Lindborg2016). For strongly stratified flows (i.e. for
$Fr<1$
), DNS data show that
$\unicode[STIX]{x1D6E4}$
approaches a constant value provided the irreversible definition is used (i.e.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D716}_{PE}/\unicode[STIX]{x1D716}$
) (Peltier & Caulfield Reference Peltier and Caulfield2003; Venayagamoorthy & Stretch Reference Venayagamoorthy and Stretch2010). However, to our knowledge, no physically based quantitative arguments have been presented to support the constancy of
$\unicode[STIX]{x1D6E4}$
in the low-
$Fr$
limit as well as how
$\unicode[STIX]{x1D6E4}$
should vary in the transition region between the low-
$Fr$
and the high-
$Fr$
limits. In the present work, our key goal is to show that the turbulent Froude number is indeed likely to be an optimal single parameter of choice that can provide a basis for inferring the state of turbulence and for parameterizing the irreversible mixing efficiency in stratified flows.
In the light of the discussions presented above, it is clear that despite the numerous studies on this topic, there is still no universal consensus on what the optimal parameter of choice is for quantifying
$\unicode[STIX]{x1D6E4}$
(Mater & Venayagamoorthy Reference Mater and Venayagamoorthy2014; Gregg et al.
Reference Gregg, D’Asaro, Riley and Kunze2018), and, more importantly, a robust and practically useful parameterization of
$\unicode[STIX]{x1D6E4}$
(or equivalently the mixing efficiency
$R_{f}$
) remains elusive. In what follows, we present a new formulation for the mixing efficiency in stably stratified turbulence using scaling arguments in § 2. This is followed by a brief description of the DNS data that are used for testing the proposed formulations in § 3. Results to highlight the fidelity of the proposed scaling relationships are presented in § 4 and concluding remarks are made in § 5.
2 Theoretical analysis
2.1 Parameterization of
$\unicode[STIX]{x1D6E4}$
as a function of
$Fr$
In the limit of high
$Fr$
, considering a balance between advection and background stratification terms in the buoyancy equation, Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) have shown that
$\unicode[STIX]{x1D6E4}\propto Fr^{-2}$
. Their DNS data also suggest that
$\unicode[STIX]{x1D6E4}$
approaches a constant for low
$Fr$
. Here, we use different scaling arguments that consider dominant time scales governing the flow for different stratified conditions (i.e. from weak to strong stratification) to derive the functional dependence of
$\unicode[STIX]{x1D6E4}$
on
$Fr$
. It is important to clarify that a strongly stratified flow
$(Fr\ll 1)$
can be classified into two different regimes depending on the value of
$Re_{b}$
, viz., viscosity-affected regime (
$Re_{b}\ll 1$
) and strongly stratified regime
$(Re_{b}\gg 1)$
. Note the viscosity-affected regime is virtually non-turbulent (Brethouwer et al.
Reference Brethouwer, Billant, Lindberg and Chomaz2007). Given that the focus is on turbulent flows that are affected by buoyancy, the viscosity-affected region can be neglected without loss of generality in the discussion that follows (i.e. flow with
$Re_{b}<1$
). Hence, it might be instructive to classify stably stratified flows into roughly three flow regimes based on the turbulent Froude number. As such, it can be expected that the functional relationship of
$\unicode[STIX]{x1D6E4}$
and
$Fr$
should be different for each of these different regimes. This is because, the transition between weakly stratified regime and strongly stratified regime does not happen at one single value of
$Fr$
. There should be an intermediate regime in between which is influenced by buoyancy (i.e. moderately stratified), where both stratification and turbulence are important. We note that Rehmann (Reference Rehmann2004) has also suggested three different regimes for quantifying
$R_{f}$
as a function of grid Richardson number for weak, moderate and strong stratification, respectively.
2.1.1 Weakly stratified regime
$(Fr\gg \mathit{O}(1))$
For a weakly stratified fluid or in the limit of high
$Fr$
, it is clear that density acts as a passive scalar since the flow is nearly isotropic and hence there is very little to negligible diapycnal mixing (Holford & Linden Reference Holford and Linden1999). The dominant time scale is therefore the turbulent time scale,
$T_{L}=k/\unicode[STIX]{x1D716}$
. Thus, the vertical displacement of fluid particles
$L_{disp}\sim w^{\prime }T_{L}$
, where
$w^{\prime }$
is the vertical velocity. From this, the density fluctuation
$\unicode[STIX]{x1D70C}^{\prime }\sim w^{\prime }T_{L}(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z)$
, where
$\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z$
is the background density gradient. Hence, the buoyancy flux
$B=-(g/\unicode[STIX]{x1D70C})\langle \unicode[STIX]{x1D70C}^{\prime }w^{\prime }\rangle \sim -(g/\unicode[STIX]{x1D70C})w^{\prime 2}T_{L}(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z)=w^{\prime 2}N^{2}T_{L}$
. Also for this case, the turbulent kinetic energy
$k\sim w^{\prime 2}$
and its rate of dissipation
$\unicode[STIX]{x1D716}\sim w^{\prime 2}/T_{L}$
, by assuming that dissipation rate of
$k$
is independent of buoyancy effects. Based on these arguments, it follows that the mixing coefficient for the weakly stratified regime should scale as
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}=\frac{B}{\unicode[STIX]{x1D716}}=\frac{\unicode[STIX]{x1D716}_{PE}}{\unicode[STIX]{x1D716}}\sim \frac{w^{\prime 2}N^{2}T_{L}}{w^{\prime 2}/T_{L}}=Fr^{-2}.\end{eqnarray}$$
We note that the end result shown in (2.1) is identical to that found in the DNS study by Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) for weakly stratified turbulent flows.
2.1.2 Moderately stratified regime
$(Fr\sim \mathit{O}(1))$
For a moderately stratified turbulent flow, it is reasonable to assume that buoyancy effects would begin to influence the dynamics during the active mixing period. Hence, both the buoyancy time scale
$N^{-1}$
and turbulent time scale
$T_{L}$
are important but are not necessarily equal. We assume that buoyancy time scale sets the vertical displacement of fluid particles, i.e.
$L_{disp}\sim w^{\prime }/N$
and the density fluctuation
$\unicode[STIX]{x1D70C}^{\prime }\sim (w^{\prime }/N)(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z)$
. Hence, the buoyancy flux
$B\sim -(g/\unicode[STIX]{x1D70C})(w^{\prime 2}/N)(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z)=w^{\prime 2}N$
. By assuming independence of the dissipation rate of
$k$
from buoyancy effects (i.e. the relevant time scale is
$T_{L}$
), it follows that
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}\sim \frac{w^{\prime 2}N}{w^{\prime 2}/T_{L}}=Fr^{-1}.\end{eqnarray}$$
This is a new scaling result for the transition region that is sandwiched between the weakly stratified and strongly stratified flow regimes.
2.1.3 Strongly stratified regime
$(Fr\ll \mathit{O}(1))$
In the limit of strong stratification, the buoyancy effects will be dominant and hence it is reasonable to assume that the dominant time scale will be only the buoyancy time scale
$N^{-1}$
. This implies that a bulk of the turbulent kinetic energy dissipates within one buoyancy period. From this, it follows that
$\unicode[STIX]{x1D716}\sim w^{\prime 2}N$
. Also here,
$L_{disp}\sim w^{\prime }/N$
,
$\unicode[STIX]{x1D70C}^{\prime }\sim (w^{\prime }/N)(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z)$
and
$B\sim w^{\prime 2}N$
. Hence, the mixing efficiency scales as
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}\sim \frac{w^{\prime 2}NN^{-1}}{w^{\prime 2}}=\text{const.}\sim Fr^{0}.\end{eqnarray}$$
We note that this new scaling result provides a physically based underpinning for what has been observed from different data obtained from DNS, field and laboratory experiments concerning the constancy of the irreversible mixing efficiency in the strongly stratified regime.
2.2 Inferring
$Fr$
from Ozmidov and Thorpe length scales
As we have argued, the turbulent Froude number can be used to diagnose the state of turbulence and parameterize the mixing efficiency in stably stratified turbulent flows. However, its use is limited in practice due to reasons already mentioned. Here, we propose a novel approach to estimate
$Fr$
using measurable turbulent length scales in oceanic flows.
A fundamental length scale that provides a measure of overturning length scale in a stratified flow is the well-known Ellison length scale (Ellison Reference Ellison1957) defined as
$$\begin{eqnarray}L_{E}=\frac{\langle \unicode[STIX]{x1D70C}^{\prime 2}\rangle ^{1/2}}{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z},\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}^{\prime }$
is the turbulent density fluctuation,
$\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /\unicode[STIX]{x2202}z$
is the mean background density gradient and
$\langle \,\rangle$
represents ensemble average. Conceptually,
$L_{E}$
is obtained from three-dimensional resorting of instantaneous density fields to a reference state of minimum potential energy (Winters et al.
Reference Winters, Lombard, Riley and D’Asaro1995). However, in the context of oceanography, instantaneous density is measured using vertical profilers on moorings or dropped from research vessels. In the limit of available one-dimensional vertical profiles, statistically
$L_{E}$
represents the largest overturns in the flow and gives an indication of the available potential energy per unit mass. A similar and relatively simpler kinematic length scale obtained from instantaneous vertical density profiles is the Thorpe length scale,
$L_{T}$
(Thorpe Reference Thorpe1977). In a statistical sense, both
$L_{T}$
and
$L_{E}$
represent a measure of the vertical distance travelled by fluid parcels in order to achieve an equilibrium position through adiabatic resorting. Thus, for one-dimensional vertical profiles, both
$L_{T}$
and
$L_{E}$
should be equivalent, a result that has been verified in previous studies (Itsweire et al.
Reference Itsweire, Koseff, Briggs and Ferziger1993; Mater, Schaad & Venayagamoorthy Reference Mater, Schaad and Venayagamoorthy2013). Another length scale that is often used to represent the size of a turbulent eddy in stratified turbulence was suggested by Ozmidov (Reference Ozmidov1965) through a dimensionally constructed length scale commonly known as the Ozmidov length scale (
$L_{O}$
) that is defined as
$$\begin{eqnarray}L_{O}=(\unicode[STIX]{x1D716}/N^{3})^{1/2}.\end{eqnarray}$$
Here
$L_{O}$
is the length scale at which inertial forces balance the buoyancy forces, in such a way that
$L_{O}$
represents the largest (isotropic) eddy unaffected by buoyancy.
The ratio of these two length scales has been used to denote the age of a turbulent event (Smyth, Moum & Caldwell Reference Smyth, Moum and Caldwell2001). Mater et al. (Reference Mater, Schaad and Venayagamoorthy2013) suggested that
$L_{T}$
and
$L_{O}$
are equivalent only for turbulent Froude number of order one. Here, we delve further to show that the ratio of
$L_{T}/L_{O}$
or, more explicitly,
$L_{E}/L_{O}$
is not only a signature of the age of turbulence but, more importantly, is a quantitative representation of the strength of stratification in a turbulent flow similar to the concept of a turbulent Froude number. A quantitative relationship between
$L_{E}/L_{O}$
and
$Fr$
can be derived as follows. The ratio of the Ellison length scale to the Ozmidov length scale can be written as
$$\begin{eqnarray}\frac{L_{E}}{L_{O}}=\frac{\langle \unicode[STIX]{x1D70C}^{\prime 2}\rangle ^{1/2}N^{3/2}}{(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}\rangle /dz)\unicode[STIX]{x1D716}^{1/2}}=\frac{\langle \unicode[STIX]{x1D70C}^{\prime 2}\rangle ^{1/2}}{\unicode[STIX]{x1D716}^{1/2}}\frac{g}{\unicode[STIX]{x1D70C}}N^{-1/2}.\end{eqnarray}$$
In the limit of strong stratification,
$(g/\unicode[STIX]{x1D70C})\langle \unicode[STIX]{x1D70C}^{\prime 2}\rangle ^{1/2}$
represents a gravitational acceleration term which can be expected to scale with the velocity scale
$k^{1/2}$
and time scale
$N^{-1}$
, such that
$\langle \unicode[STIX]{x1D70C}^{\prime 2}\rangle ^{1/2}(g/\unicode[STIX]{x1D70C})\sim wN\sim k^{1/2}N$
. Thus, in the strongly stratified regime
$(Fr<\mathit{O}(1))$
, the length-scale ratio can be written as
$$\begin{eqnarray}\frac{L_{E}}{L_{O}}\sim \frac{k^{1/2}N}{\unicode[STIX]{x1D716}^{1/2}N^{1/2}}=(kN/\unicode[STIX]{x1D716})^{1/2}=Fr^{-1/2}.\end{eqnarray}$$
This can be rewritten to express
$Fr$
in terms of
$L_{T}/L_{O}$
as
$$\begin{eqnarray}Fr\sim (L_{E}/L_{O})^{-2}\sim (L_{T}/L_{O})^{-2}.\end{eqnarray}$$
We note that this scaling also verifies the results by Mater et al. (Reference Mater, Schaad and Venayagamoorthy2013) which show that for strongly stratified regime,
$L_{T}\sim L_{kN}=(k/N^{2})^{1/2}$
, where
$L_{kN}$
is an overturning length scale in the buoyancy dominated regime such that
$L_{T}/L_{O}\sim Fr^{-1/2}$
.
For the moderately stratified regime where
$Fr\sim \mathit{O}(1)$
, it directly follows that the length-scale ratio,
$L_{E}/L_{O}\sim Fr^{-1}$
. Hence,
$Fr$
scales with
$L_{E}/L_{O}$
as
$$\begin{eqnarray}Fr\sim (L_{E}/L_{O})^{-1}\sim (L_{T}/L_{O})^{-1}.\end{eqnarray}$$
Now, for a weakly stratified turbulent flow or in the limit of high Froude number
$Fr>O(1)$
, the Thorpe length scale as well as the Ellison length scale should scale with the isotropic turbulent length scale
$L_{k\unicode[STIX]{x1D716}}=k^{3/2}/\unicode[STIX]{x1D716}$
(Luketina & Imberger Reference Luketina and Imberger1989; Ivey & Imberger Reference Ivey and Imberger1991). Thus,
$L_{E}\sim L_{T}\sim L_{k\unicode[STIX]{x1D716}}=k^{3/2}/\unicode[STIX]{x1D716}$
. With this information, the length-scale ratio,
$L_{E}/L_{O}$
, for a weakly stratified flow can be written as
$$\begin{eqnarray}\frac{L_{E}}{L_{O}}\sim \frac{k^{3/2}/\unicode[STIX]{x1D716}}{\unicode[STIX]{x1D716}^{1/2}/N^{3/2}}=(kN/\unicode[STIX]{x1D716})^{3/2}=Fr^{-3/2},\end{eqnarray}$$
which translates to
$$\begin{eqnarray}Fr\sim (L_{E}/L_{O})^{-2/3}\sim (L_{T}/L_{O})^{-2/3},\end{eqnarray}$$
similar to the scaling provided by Ivey & Imberger (Reference Ivey and Imberger1991). Given that both
$L_{T}$
and
$L_{O}$
are directly measurable in the ocean using conductivity-temperature-depth (CTD) and microstructure profilers, equations (2.8), (2.9) and (2.11) are key scaling results that can be used to obtain direct estimates of
$Fr$
in the field. The scaling arguments presented for both
$\unicode[STIX]{x1D6E4}$
and
$Fr$
are tested using three independent DNS data sets in what follows.
Figure 1. Mixing coefficient
$\unicode[STIX]{x1D6E4}$
as a function of turbulent Froude number
$Fr$
. The colour bar shows values of
$Re_{b}$
. Star: decaying DNS; circle: forced DNS of Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016); square: sheared DNS of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005). Solid lines display the scaling relations derived in § 2.1.
3 Data sources
Three independent DNS data sets are considered to test the veracity of our proposed scaling arguments. The first data set is from our own set of DNS of decaying homogeneous stably stratified turbulence. These simulations were carried out using a pseudo-spectral DNS code developed by Riley, Metcalfe & Weissman (Reference Riley, Metcalfe, Weissman and West1981) for stably stratified homogeneous turbulent flows. A cubical periodic domain of dimension
$2\unicode[STIX]{x03C0}$
with
$512^{3}$
grid points was considered for all the simulations. The turbulent flow was initialized with a Gaussian isotropic three-dimensional solenoidal velocity field and allowed to evolve and decay under the influence of a constant background stratification. Flow was characterized with an initial Reynolds number of 1000 defined as
$Re_{0}=u_{0}L_{0}/\unicode[STIX]{x1D708}$
, where
$u_{0}=1$
is the initial velocity scale and
$L_{0}=1$
is the initial length scale. Background stratification was characterized with an initial Richardson number
$Ri_{0}=(NL_{0}/u_{0})^{2}$
. Four DNS simulations were performed for the present study with
$Ri_{0}=0.01$
, 0.1, 1.0 and 10, respectively, for a duration of
$5L_{0}/u_{0}$
. Further details of the simulations are given in Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2018). The second data set was obtained from a high-resolution DNS study of stratified turbulence by Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016). A body force was included in their numerical simulations in order to achieve stationary turbulence. They used isotropic forcing for most of the simulations and two-dimensional vortical forcing was used for a few simulations to achieve a strongly stratified regime with buoyancy Reynolds number greater than
$10$
. The third data set was obtained from DNS study of homogeneous sheared stably stratified turbulence by Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005). These simulations are for temporally developing homogeneous turbulence with constant mean shear and constant background stratification. These simulations were performed at a relatively lower resolution (
$128^{3}$
) compared to the other two data sets but include the effects of background shear.
4 Results
4.1 Mixing coefficient as a function of turbulent Froude number
Figure 2. Mixing coefficient
$\unicode[STIX]{x1D6E4}$
as a function of buoyancy Reynold number
$Re_{b}$
for decaying DNS (star), forced DNS of Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) (circle) and sheared DNS of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) (square). Solid line indicates the functional relation of
$\unicode[STIX]{x1D6E4}$
and
$Re_{b}$
proposed by Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005).
Figure 1 shows the mixing coefficient
$\unicode[STIX]{x1D6E4}$
as a function of turbulent Froude number for decaying, forced and sheared DNS data. The buoyancy Reynolds number
$Re_{b}$
is also shown in the colour bar for reference. There are two observations that are noteworthy. The first key observation that can be made from figure 1 is that all the data collapse reasonably well on to the lines given by the new scaling results for
$\unicode[STIX]{x1D6E4}$
proposed in § 2.1. These data show that in the strongly stratified flow regime (
$Fr\ll 1$
),
$\unicode[STIX]{x1D6E4}$
is approximately a constant. In the moderately stratified flow regime (
$Fr\sim \mathit{O}(1)$
),
$\unicode[STIX]{x1D6E4}\propto Fr^{-1}$
, and for the weakly stratified flow regime (
$Fr\gg 1$
),
$\unicode[STIX]{x1D6E4}\propto Fr^{-2}$
, which is also in agreement with what has been previously shown by Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) in the limit of high
$Fr$
.
Second, it appears that there is no unique relationship between
$\unicode[STIX]{x1D6E4}$
and buoyancy Reynolds number
$Re_{b}$
. In order to see this point clearly, the mixing coefficient
$\unicode[STIX]{x1D6E4}$
as a function of
$Re_{b}$
is shown in figure 2 for all three data sets. The
$Fr$
is also shown in the colour bar to facilitate cross-referencing with figure 1. It can be seen that
$\unicode[STIX]{x1D6E4}$
is approximately constant for strongly stratified flows (i.e. low values of
$Fr$
). However, it is evident that the transition of
$\unicode[STIX]{x1D6E4}$
from a constant value to a functional dependence on
$Re_{b}$
is not unique. For example, for various flows which have
$Re_{b}=10^{3}$
, the measured values of
$\unicode[STIX]{x1D6E4}$
can differ by over an order of magnitude as shown in figure 2. These results highlight how
$Re_{b}$
is an ambiguous parameter for quantifying mixing in stratified flows. We note that the ambiguity associated with
$Re_{b}$
has been discussed in previous studies (Mater & Venayagamoorthy Reference Mater and Venayagamoorthy2014; Holleman, Geyer & Ralston Reference Holleman, Geyer and Ralston2016; Scotti & White Reference Scotti and White2016; Monismith et al.
Reference Monismith, Koseff and White2018). Based on the results shown in figures 1 and 2, it is plausible to suggest that
$Fr$
might be an optimal (single) parameter that can be used to parameterize the mixing efficiency.
Figure 3. Froude number as a function of
$L_{E}/L_{O}$
for decaying DNS (star), forced DNS (circle) and sheared DNS (square) data with
$Re_{b}$
in colour bar. Solid lines display the scaling relations derived in § 2.2.
4.2 Inferring the state of turbulence
We have seen in figure 1 that the mixing coefficient is well described by the scaling results in § 2.1. However, as discussed in § 2.2, there is the impending issue of how to estimate
$Fr$
from measurable quantities in the field. To this end, scaling arguments to find relationships between
$L_{E}/L_{O}$
and turbulent Froude number were presented in § 2.2. The results presented in figure 3 for decaying, sheared and forced DNS data validate the scaling results shown in (2.8), (2.9), and (2.11), respectively. The data indicate that
$Fr\sim (L_{E}/L_{O})^{-2/3}$
for
$(L_{E}/L_{O})<\mathit{O}(1)$
,
$Fr\sim (L_{E}/L_{O})^{-1}$
for
$(L_{E}/L_{O})\sim \mathit{O}(1)$
and
$Fr\sim (L_{E}/L_{O})^{-2}$
for
$(L_{E}/L_{O})>\mathit{O}(1)$
. By combining the scaling results provided for
$\unicode[STIX]{x1D6E4}$
and
$Fr$
(as shown in figures 1 and 3), the scaling relationship between
$\unicode[STIX]{x1D6E4}$
and the (field) measurable length-scale ratio
$L_{E}/L_{O}$
can be also established for practical purposes as follows: for weakly stratified regime,
$\unicode[STIX]{x1D6E4}\sim (L_{E}/L_{O})^{4/3}$
; for moderately stratified regime,
$\unicode[STIX]{x1D6E4}\sim (L_{E}/L_{O})^{1}$
; and for the strongly stratified regime where
$\unicode[STIX]{x1D6E4}$
is approximately constant,
$\unicode[STIX]{x1D6E4}\sim (L_{E}/L_{O})^{0}$
. The DNS data are in good agreement with these results, as shown in figure 4. We note that, using a least squares fitted power law relationship, Smyth et al. (Reference Smyth, Moum and Caldwell2001) found that
$\unicode[STIX]{x1D6E4}\sim (L_{T}/L_{O})^{0.6}$
, which may be acceptable for the moderately stratified regime. In a recent study, using measurements made in the ocean, Ijichi & Hibiya (Reference Ijichi and Hibiya2018) have also shown that
$\unicode[STIX]{x1D6E4}\sim (L_{T}/L_{O})^{4/3}$
, similar to the scaling provided here for
$Fr>\mathit{O}(1)$
. The results presented here are indeed powerful because they show that with
$L_{T}$
and
$L_{O}$
known (i.e. measurable), it is possible to estimate
$Fr$
from field measurements and hence identify the state of turbulence in stratified flows in the field. This in turn permits the use of a more accurate parameterization to predict
$\unicode[STIX]{x1D6E4}$
which is crucial for obtaining robust estimates of diapycnal mixing.
Figure 4. Mixing coefficient
$\unicode[STIX]{x1D6E4}$
as a function of
$L_{E}/L_{O}$
for decaying DNS (star), forced DNS (circle) and sheared DNS (square) data with
$Fr$
in colour bar. Solid lines display the scaling relations.
5 Concluding remarks
In this paper we first derived new scaling results for
$\unicode[STIX]{x1D6E4}$
as a function of
$Fr$
as well as for
$Fr$
as a function of
$L_{T}/L_{O}$
. We then used direct numerical simulation data from three independent studies to validate the scaling results. Three significant findings can be noted from the above discussions. First, scaling results that are validated using high-resolution DNS data show that the mixing coefficient scales with the turbulent Froude number in a universal manner, noting, however, that the functional dependence on
$Fr$
is different for the three different flow regimes. Second, the results show that
$Re_{b}$
is an ambiguous parameter and hence parameterizations of
$\unicode[STIX]{x1D6E4}$
based on
$Re_{b}$
are not unique. The third key finding is that the ratio
$L_{T}/L_{O}$
not only is a representation of the age of turbulence, as has been previously suggested (i.e. young turbulence or old turbulence), but also represents the state of the flow (i.e. whether the flow is in a strongly stratified regime or in a weakly stratified regime). This finding will be useful in oceanography for inferring the state of turbulence and thereby facilitate the use of the more appropriate parameterizations for
$\unicode[STIX]{x1D6E4}$
that have been formulated in this study. To the knowledge of authors, this is the first time such an analysis has been carried out to both identify the state of turbulence and quantify the mixing efficiency using a single parameter in an unambiguous manner. The natural next steps are to perform further tests with more complex forcing conditions and evaluate the utility of the proposed parameterizations in the field.
Acknowledgements
The authors are grateful to the anonymous referees for their constructive comments and recommendations. We wish to thank Dr A. Maffioli and Dr L. Shih for providing their DNS data and Professor J. Riley for providing his DNS code. S.K.V. also wishes especially to thank Professor D. Stretch for inspiring him to study stratified turbulence and for many insightful discussions. We gratefully acknowledge the support of both the Office of Naval Research under grant no. N00014-16-1-3015 (Scientific Officers: Dr T. Paluszkiewicz and Dr S. Harper) and the National Science Foundation under CAREER grant OCE-1151838.
