Hostname: page-component-6dbcb7884d-cm8hq Total loading time: 0 Render date: 2025-02-13T19:33:51.597Z Has data issue: false hasContentIssue false
  • English
  • Français

On the inference of the state of turbulence and mixing efficiency in stably stratified flows

Published online by Cambridge University Press:  21 March 2019

Amrapalli Garanaik  and
Subhas K. Venayagamoorthy Open the ORCID record for Subhas K. Venayagamoorthy [Opens in a new window]
Amrapalli Garanaik
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
Subhas K. Venayagamoorthy*
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
*
†Email address for correspondence: vskaran@colostate.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Scaling arguments are presented to quantify the widely used diapycnal (irreversible) mixing coefficient 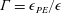$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D716}_{PE}/\unicode[STIX]{x1D716}$ in stratified flows as a function of the turbulent Froude number 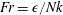$Fr=\unicode[STIX]{x1D716}/Nk$. Here, 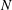$N$ is the buoyancy frequency, 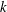$k$ is the turbulent kinetic energy, $\unicode[STIX]{x1D716}$ is the rate of dissipation of turbulent kinetic energy and 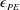$\unicode[STIX]{x1D716}_{PE}$ is the rate of dissipation of turbulent potential energy. We show that for 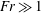$Fr\gg 1$, $\unicode[STIX]{x1D6E4}\propto Fr^{-2}$, for 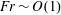$Fr\sim \mathit{O}(1)$, 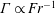$\unicode[STIX]{x1D6E4}\propto Fr^{-1}$ and for 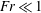$Fr\ll 1$, 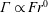$\unicode[STIX]{x1D6E4}\propto Fr^{0}$. These scaling results are tested using high-resolution direct numerical simulation (DNS) data from three different studies and are found to hold reasonably well across a wide range of 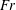$Fr$ that encompasses weakly stratified to strongly stratified flow conditions. Given that the $Fr$ cannot be readily computed from direct field measurements, we propose a practical approach that can be used to infer the 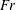$Fr$ from readily measurable quantities in the field. 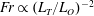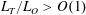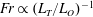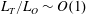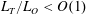Scaling analyses show that $Fr\propto (L_{T}/L_{O})^{-2}$ for $L_{T}/L_{O}>O(1)$, $Fr\propto (L_{T}/L_{O})^{-1}$ for $L_{T}/L_{O}\sim O(1)$, and $Fr\propto (L_{T}/L_{O})^{-2/3}$ for $L_{T}/L_{O}<O(1)$, where 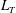$L_{T}$ is the Thorpe length scale and $L_{O}$ is the Ozmidov length scale. These formulations are also tested with DNS data to highlight their validity. These novel findings could prove to be a significant breakthrough not only in providing a unifying (and practically useful) parameterization for the mixing efficiency in stably stratified turbulence but also for inferring the dynamic state of turbulence in geophysical flows.

JFM classification

Geophysical and Geological Flows: Stratified flows Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 323 - 333
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, R. S., Venayagamoorthy, S. K., Koseff, J. R. & Fringer, O. B. 2017 How we compute N matters to estimates of mixing in stratified flows. J. Fluid Mech. 831, R2.Google Scholar
Brethouwer, G., Billant, P., Lindberg, E. & Chomaz, J. M. 2007 Scaling analysis and simulation of strongly statified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Ellison, T. H. 1957 Turbulent transport of heat and momentum from an infinite rough plane. J. Fluid Mech. 2, 456–466.Google Scholar
Garanaik, A. & Venayagamoorthy, S. K. 2018 Assessment of small-scale anisotropy in stably stratified turbulent flows using direct numerical simulations. Phys. Fluids 30, 126602.Google Scholar
Gregg, M. C., D’Asaro, E. A., Riley, J. J. & Kunze, E. 2018 Mixing efficiency in the ocean. Annu. Rev. Marine Sci. 10 (1), 443–473.Google Scholar
Holford, J. M. & Linden, P. F. 1999 Turbulent mixing in a stratified fluid. Dyn. Atmos. Oceans 30, 173–198.Google Scholar
Holleman, R. C., Geyer, W. R. & Ralston, D. K. 2016 Stratified turbulence and mixing efficiency in a salt wedge estuary. J. Phys. Oceanogr. 46, 1769–1783.Google Scholar
Ijichi, T. & Hibiya, T. 2018 Observed variations in turbulent mixing efficiency in the deep ocean. J. Phys. Oceanogr. 48, 1815–1830.Google Scholar
Itsweire, E. C., Koseff, J. R., Briggs, D. A. & Ferziger, J. H. 1993 Turbulence in stratified shear flows: implications for interpreting shear-induced mixing in the ocean. J. Phys. Oceanogr. 23, 1508–1522.Google Scholar
Ivey, G. N. & Imberger, J. 1991 On the nature of turbulence in a stratified fluid. Part I. The energetics of mixing. J. Phys. Oceanogr. 21, 650–659.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13, 3–23.Google Scholar
Lozovatsky, I. D. & Fernando, H. J. S. 2013 Mixing efficiency in natural flows. Phil. Trans. R. Soc. Lond. A 371, 4662–4672.Google Scholar
Luketina, D. & Imberger, J. 1989 Turbulence and entrainment in a buoyant surface plume. J. Geophys. Res. 94 (C9), 12619–12636.Google Scholar
Maffioli, A., Brethouwer, G. & Lindborg, E. 2016 Mixing efficiency in stratified turbulence. J. Fluid Mech. 794, R3.Google Scholar
Mater, B. D., Schaad, S. M. & Venayagamoorthy, S. K. 2013 Relevance of the Thorpe scale in stably stratified turbulence. Phys. Fluids 25, 076604.Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014 The quest for an unambiguous parameterization of mixing efficiency in stably stratified geophysical flows. Geophys. Res. Lett. 41, 4646–4653.Google Scholar
Monismith, S. G., Koseff, J. R. & White, B. L. 2018 Mixing efficiency in the presence of stratification: when is it constant? Geophys. Res. Lett. 45, 5627–5634.Google Scholar
Munk, W. & Wunsch, C. 1998 Abyssal receipes II: energetics of tidal and wind mixing. Deep Sea Res. 45, 1977–2010.Google Scholar
Osborn, T. R. 1980 Estimates of the rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.Google Scholar
Ozmidov, R. V. 1965 On the turbulent exchange in a stably stratified ocean. Izv. Acad. Sci., USSR, Atmos. Ocean. Phys. 1, 853–860.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Rehmann, C. R. 2004 Scaling for the mixing efficiency of stratified grid turbulence. J. Hydraul. Res. 42, 35–42.Google Scholar
Riley, J. J., Metcalfe, R. W. & Weissman, M. A. 1981 Direct numerical simulations of homogeneous turbulence in density stratified fluids. In Nonlinear Properties of Internal Waves AIP Conf. Proc. 76 (ed. West, B. J.), pp. 79–112. AIP.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Scotti, A. & White, B. 2016 The mixing efficiency of stratified turbulent boundary layer. J. Phys. Oceanogr. 46, 3181–3191.Google Scholar
Shih, L. H., Koseff, J. R., Ferziger, J. H. & Rehmann, C. R. 2000 Scalling and parameterization of stratified homogeneous turbulent shear flow. J. Fluid Mech. 412, 1–20.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Smyth, W. D, Moum, J. N. & Caldwell, D. R. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31 (8), 1969–1992.Google Scholar
Thorpe, S. A. 1977 Turbulence and mixing in a Scotish loch. Phil. Trans. R. Soc. Lond. A 286, 125–181.Google Scholar
Venayagamoorthy, S. K. & Koseff, J. 2016 On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 798, R1.Google Scholar
Venayagamoorthy, S. K. & Stretch, D. D. 2010 On the turbulent Prandtl number in homogeneous stably stratified turbulence. J. Fluid Mech. 644, 359–369.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar