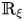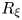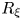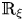1. Introduction
In the class of complex Grassmannians of rank 2, we can give the examples of Hermitian symmetric spaces ![]() $G_{2}(\mathbb {C}^{m+2})=SU_{m+2}/S(U_2U_m)$ and
$G_{2}(\mathbb {C}^{m+2})=SU_{m+2}/S(U_2U_m)$ and ![]() $G_{2}^{*}(\mathbb {C}^{m+2})=SU_{2,m}/S(U_2U_m)$, which are said to be complex two-plane Grassmannians of compact type and complex hyperbolic two-plane Grassmannians of non-compact type, respectively. They are viewed as Hermitian symmetric spaces and quaternionic Kähler symmetric spaces equipped with the Kähler structure
$G_{2}^{*}(\mathbb {C}^{m+2})=SU_{2,m}/S(U_2U_m)$, which are said to be complex two-plane Grassmannians of compact type and complex hyperbolic two-plane Grassmannians of non-compact type, respectively. They are viewed as Hermitian symmetric spaces and quaternionic Kähler symmetric spaces equipped with the Kähler structure ![]() $J$ and the quaternionic Kähler structure
$J$ and the quaternionic Kähler structure ![]() $\mathcal {J}=\mathrm {span}\{J_{1}, J_{2}, J_{3}\}$ (see [Reference Berndt and Suh6, Reference Eberlein11, Reference Kobayashi and Nomizu15, Reference Suh31, Reference Suh33, Reference Suh38]). Among them, in this paper we will consider our subject on complex two-plane Grassmannians and its real hypersurfaces with cyclic parallel structure Jacobi operator.
$\mathcal {J}=\mathrm {span}\{J_{1}, J_{2}, J_{3}\}$ (see [Reference Berndt and Suh6, Reference Eberlein11, Reference Kobayashi and Nomizu15, Reference Suh31, Reference Suh33, Reference Suh38]). Among them, in this paper we will consider our subject on complex two-plane Grassmannians and its real hypersurfaces with cyclic parallel structure Jacobi operator.
Now let us denote by ![]() ${G_2({\mathbb {C}}^{m+2})}=SU_{m+2}/S(U_2U_m)$ the set of all complex 2-dimensional linear subspaces in the complex Euclidean space
${G_2({\mathbb {C}}^{m+2})}=SU_{m+2}/S(U_2U_m)$ the set of all complex 2-dimensional linear subspaces in the complex Euclidean space ![]() $\mathbb {C}^{m+2}$. If
$\mathbb {C}^{m+2}$. If ![]() $m = 1$, then we see that
$m = 1$, then we see that ![]() $G_{2}(\mathbb {C}^{3})$ is isometric to the 2-dimensional complex projective space
$G_{2}(\mathbb {C}^{3})$ is isometric to the 2-dimensional complex projective space ![]() $\mathbb {C} P^{2}$ with constant holomorphic sectional curvature 8. And the isomorphism
$\mathbb {C} P^{2}$ with constant holomorphic sectional curvature 8. And the isomorphism ![]() $\mathrm {Spin} (6) \simeq SU(4)$ yields an isometry between
$\mathrm {Spin} (6) \simeq SU(4)$ yields an isometry between ![]() $G_{2}(\mathbb {C}^{4})$ and the real Grassmann manifold
$G_{2}(\mathbb {C}^{4})$ and the real Grassmann manifold ![]() $G_{2}^{+}(\mathbb {R}^{6})$ of oriented 2-dimensional linear subspaces in
$G_{2}^{+}(\mathbb {R}^{6})$ of oriented 2-dimensional linear subspaces in ![]() $\mathbb {R}^{6}$. So, we will consider
$\mathbb {R}^{6}$. So, we will consider ![]() $m \geq 3$ hereafter, unless otherwise stated.
$m \geq 3$ hereafter, unless otherwise stated.
Recall that a non-zero vector field ![]() $X$ of Hermitian symmetric spaces
$X$ of Hermitian symmetric spaces ![]() $(\bar M, g)$ of rank 2 is called singular if it is tangent to more than one maximal flat in
$(\bar M, g)$ of rank 2 is called singular if it is tangent to more than one maximal flat in ![]() $\bar M$. In particular, there are exactly two types of singular tangent vectors
$\bar M$. In particular, there are exactly two types of singular tangent vectors ![]() $X$ of
$X$ of ![]() $G_{2}(\mathbb {C}^{m+2})$ which are characterized by the geometric properties
$G_{2}(\mathbb {C}^{m+2})$ which are characterized by the geometric properties ![]() $JX \in {\mathcal {J}}X$ and
$JX \in {\mathcal {J}}X$ and ![]() $JX \perp {\mathcal {J}}X$ (see [Reference Berndt3, Reference Berndt and Suh4]).
$JX \perp {\mathcal {J}}X$ (see [Reference Berndt3, Reference Berndt and Suh4]).
The Riemannian curvature tensor ![]() $\bar R$ of
$\bar R$ of ![]() ${G_2({\mathbb {C}}^{m+2})}$ is locally given by
${G_2({\mathbb {C}}^{m+2})}$ is locally given by
 \begin{equation*} \begin{split} & + \sum_{\nu=1}^{3}\big \{ g(J_{\nu}Y, Z) J_{\nu} X - g(J_{\nu}X, Z) J_{\nu}Y - 2g(J_{\nu}X, Y) J_{\nu}Z \big \} \\ & + \sum_{\nu=1}^{3}\big \{ g(J_{\nu}J Y, Z) J_{\nu} JX - g(J_{\nu}JX, Z) J_{\nu}JY \big \}, \end{split} \end{equation*}
\begin{equation*} \begin{split} & + \sum_{\nu=1}^{3}\big \{ g(J_{\nu}Y, Z) J_{\nu} X - g(J_{\nu}X, Z) J_{\nu}Y - 2g(J_{\nu}X, Y) J_{\nu}Z \big \} \\ & + \sum_{\nu=1}^{3}\big \{ g(J_{\nu}J Y, Z) J_{\nu} JX - g(J_{\nu}JX, Z) J_{\nu}JY \big \}, \end{split} \end{equation*}
where ![]() $\{J_{1}$,
$\{J_{1}$, ![]() $J_{2}$,
$J_{2}$, ![]() $J_{3}\}$ is any canonical local basis of
$J_{3}\}$ is any canonical local basis of ![]() $\mathcal {J}$ and the tensor
$\mathcal {J}$ and the tensor ![]() $g$ of type (0,2) stands for the Riemannian metric on complex two-plane Grassmannians
$g$ of type (0,2) stands for the Riemannian metric on complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$ (see [Reference Berndt3, Reference Berndt and Suh4, Reference Berndt and Suh9]).
${G_2({\mathbb {C}}^{m+2})}$ (see [Reference Berndt3, Reference Berndt and Suh4, Reference Berndt and Suh9]).
For a real hypersurface ![]() $M$ in complex two-plane Grassmannians
$M$ in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$, we have the following two natural geometric conditions: the
${G_2({\mathbb {C}}^{m+2})}$, we have the following two natural geometric conditions: the ![]() $1$-dimensional distribution
$1$-dimensional distribution ![]() $\mathcal {C}^{\bot }= \mathrm {span} \{\xi \}$ and the
$\mathcal {C}^{\bot }= \mathrm {span} \{\xi \}$ and the ![]() $3$-dimensional distribution
$3$-dimensional distribution ![]() $\mathcal {Q}^{\bot } = \mathrm {span}\{\xi _{1},\xi _{2}, \xi _{3}\}$ are invariant under the shape operator
$\mathcal {Q}^{\bot } = \mathrm {span}\{\xi _{1},\xi _{2}, \xi _{3}\}$ are invariant under the shape operator ![]() $A$ of
$A$ of ![]() $M$. Here the almost contact structure vector field
$M$. Here the almost contact structure vector field ![]() $\xi$ defined by
$\xi$ defined by ![]() $\xi = -JN$ is said to be a Reeb vector field, where
$\xi = -JN$ is said to be a Reeb vector field, where ![]() $N$ denotes a local unit normal vector field of
$N$ denotes a local unit normal vector field of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$. The almost contact 3-structure vector fields
${G_2({\mathbb {C}}^{m+2})}$. The almost contact 3-structure vector fields ![]() $\xi _{1},\xi _{2},\xi _{3}$ spanning the 3-dimensional distribution
$\xi _{1},\xi _{2},\xi _{3}$ spanning the 3-dimensional distribution ![]() $\mathcal {Q}^{\bot }$ of
$\mathcal {Q}^{\bot }$ of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ are defined by
${G_2({\mathbb {C}}^{m+2})}$ are defined by ![]() $\xi _{\nu } = - J_{\nu } N$
$\xi _{\nu } = - J_{\nu } N$ ![]() $(\nu =1, 2, 3$), such that
$(\nu =1, 2, 3$), such that ![]() $TM = \mathcal {Q} \oplus \mathcal {Q}^{\bot } = \mathcal {C} \oplus \mathcal {C}^{\bot }$. By using these invariant conditions for two kinds of distributions
$TM = \mathcal {Q} \oplus \mathcal {Q}^{\bot } = \mathcal {C} \oplus \mathcal {C}^{\bot }$. By using these invariant conditions for two kinds of distributions ![]() $\mathcal {C}^{\bot }$ and
$\mathcal {C}^{\bot }$ and ![]() $\mathcal {Q}^{\bot }$ in
$\mathcal {Q}^{\bot }$ in ![]() $T{G_2({\mathbb {C}}^{m+2})}$, Berndt and Suh gave a classification of real hypersurfaces in complex two-plane Grassmannians as follows:
$T{G_2({\mathbb {C}}^{m+2})}$, Berndt and Suh gave a classification of real hypersurfaces in complex two-plane Grassmannians as follows:
Theorem A [Reference Berndt and Suh4]
Let ![]() $M$ be a connected real hypersurface in complex two-plane Grassmannians
$M$ be a connected real hypersurface in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. Then both
$m \geq 3$. Then both ![]() $\mathcal {C}^{\bot }$ and
$\mathcal {C}^{\bot }$ and ![]() ${{\mathcal {Q}}^{\bot }}$ are invariant under the shape operator
${{\mathcal {Q}}^{\bot }}$ are invariant under the shape operator ![]() $A$ of
$A$ of ![]() $M$ if and only if
$M$ if and only if
(
 $\mathcal{T}_{A}$)
$\mathcal{T}_{A}$)  $M$ is an open part of a tube around a totally geodesic
$M$ is an open part of a tube around a totally geodesic  ${G_2({\mathbb {C}}^{m+1})}$ in
${G_2({\mathbb {C}}^{m+1})}$ in  ${G_2({\mathbb {C}}^{m+2})}$, or
${G_2({\mathbb {C}}^{m+2})}$, or(
 $\mathcal{T}_{B}$)
$\mathcal{T}_{B}$)  $m$ is even, say
$m$ is even, say  $m=2n$, and
$m=2n$, and  $M$ is an open part of a tube around a totally geodesic
$M$ is an open part of a tube around a totally geodesic  ${\mathbb {H}}P^{n}$ in
${\mathbb {H}}P^{n}$ in  ${G_2({\mathbb {C}}^{m+2})}$.
${G_2({\mathbb {C}}^{m+2})}$.
On the other hand, we say that a real hypersurface ![]() $M$ in complex two-plane Grassmannians
$M$ in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$ is Hopf if and only if the Reeb vector field
${G_2({\mathbb {C}}^{m+2})}$ is Hopf if and only if the Reeb vector field ![]() $\xi$ is Hopf, that is,
$\xi$ is Hopf, that is, ![]() $A\xi \in \mathcal {C}^{\bot }$. In addition, when the distribution
$A\xi \in \mathcal {C}^{\bot }$. In addition, when the distribution ![]() $\mathcal {Q}^{\bot }$ of
$\mathcal {Q}^{\bot }$ of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ is invariant under the shape operator,
${G_2({\mathbb {C}}^{m+2})}$ is invariant under the shape operator, ![]() $M$ is said to be a
$M$ is said to be a ![]() $\mathcal {Q}^{\bot }$-invariant real hypersurface.
$\mathcal {Q}^{\bot }$-invariant real hypersurface.
Moreover, we say that the Reeb flow of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ is isometric, when the Reeb vector field
${G_2({\mathbb {C}}^{m+2})}$ is isometric, when the Reeb vector field ![]() $\xi$ of
$\xi$ of ![]() $M$ is Killing. It implies that the metric tensor
$M$ is Killing. It implies that the metric tensor ![]() $g$ of
$g$ of ![]() $M$ is invariant under the Reeb flow of
$M$ is invariant under the Reeb flow of ![]() $\xi$, that is,
$\xi$, that is, ![]() $\mathcal {L}_{\xi }g =0$ where
$\mathcal {L}_{\xi }g =0$ where ![]() $\mathcal {L}_{\xi }$ denotes the Lie derivative along the direction of
$\mathcal {L}_{\xi }$ denotes the Lie derivative along the direction of ![]() $\xi$. Related to this notion, for complex two-plane Grassmannians
$\xi$. Related to this notion, for complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$, Berndt and Suh gave a remarkable characterization for real hypersurface of type
${G_2({\mathbb {C}}^{m+2})}$, Berndt and Suh gave a remarkable characterization for real hypersurface of type ![]() $(\mathcal {T}_{A})$ mentioned in theorem
$(\mathcal {T}_{A})$ mentioned in theorem ![]() ${\rm A}$ (see [Reference Berndt and Suh5]).
${\rm A}$ (see [Reference Berndt and Suh5]).
Indeed, the notion of isometric Reeb flow is regarded as a typical example of Killing vector fields which are classical objects of differential geometry. As mentioned above, Killing vector fields are defined by vanishing of the Lie derivative of metric tensor ![]() $g$ with respect to a vector
$g$ with respect to a vector ![]() $X$, that is,
$X$, that is, ![]() $\mathcal {L}_{X}g=0$. Recently, the notion of isometric Reeb flow is considered for real hypersurfaces in Hermitian symmetric spaces including complex Grassmannians and complex quadrics, etc. (see [Reference Berndt and Suh5, Reference Berndt and Suh7, Reference Suh32, Reference Suh35]). By using Lie algebraic method given in [Reference Adams1, Reference Ballmann2, Reference Borel and De Siebenthal10], Berndt–Suh [Reference Berndt and Suh8] gave a complete classification of real hypersurfaces with isometric Reeb flow in Hermitian symmetric spaces.
$\mathcal {L}_{X}g=0$. Recently, the notion of isometric Reeb flow is considered for real hypersurfaces in Hermitian symmetric spaces including complex Grassmannians and complex quadrics, etc. (see [Reference Berndt and Suh5, Reference Berndt and Suh7, Reference Suh32, Reference Suh35]). By using Lie algebraic method given in [Reference Adams1, Reference Ballmann2, Reference Borel and De Siebenthal10], Berndt–Suh [Reference Berndt and Suh8] gave a complete classification of real hypersurfaces with isometric Reeb flow in Hermitian symmetric spaces.
Let us consider a Killing tensor field which is a generalization of a Killing vector field on ![]() $(\bar M, g)$. Let
$(\bar M, g)$. Let ![]() $\mathbb {K}$ be a tensor field of type
$\mathbb {K}$ be a tensor field of type ![]() $(0,k)$ on
$(0,k)$ on ![]() $(\bar M, g)$. Then,
$(\bar M, g)$. Then, ![]() $\mathbb {K}$ is said to be Killing if the complete symmetrization of
$\mathbb {K}$ is said to be Killing if the complete symmetrization of ![]() $\nabla \mathbb {K}$ vanishes. That is, it means that
$\nabla \mathbb {K}$ vanishes. That is, it means that ![]() $\mathbb {K}$ satisfies
$\mathbb {K}$ satisfies
for any vector field ![]() $X$. It follows that for such a Killing tensor, the expression
$X$. It follows that for such a Killing tensor, the expression ![]() $\mathbb {K} (\dot {\gamma }, \dot {\gamma }, \cdots , \dot {\gamma })$ is constant along any geodesic
$\mathbb {K} (\dot {\gamma }, \dot {\gamma }, \cdots , \dot {\gamma })$ is constant along any geodesic ![]() $\gamma$ (see [Reference Semmelmann29]). In particular, the existing literature on symmetric Killing tensors is huge, especially coming from theoretical physics (see [Reference Heil, Moroianu and Semmelmann12, Reference Semmelmann29]). As examples of such a symmetric Killing tensor, real hypersurfaces in complex two-plane Grassmannians
$\gamma$ (see [Reference Semmelmann29]). In particular, the existing literature on symmetric Killing tensors is huge, especially coming from theoretical physics (see [Reference Heil, Moroianu and Semmelmann12, Reference Semmelmann29]). As examples of such a symmetric Killing tensor, real hypersurfaces in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$ with Killing shape operator were considered by Lee and Suh (see [Reference Lee and Suh20]). Recently, Lee, Woo and Suh [Reference Lee, Woo and Suh21] considered the notion of Killing normal Jacobi operator of Hopf real hypersurfaces in complex Grassmannians of rank 2. In addition, Suh gave a classification for Hopf real hypersurfaces with Killing Ricci tensor in complex Grassmannians of rank 2 (see [Reference Suh36, Reference Suh37]).
${G_2({\mathbb {C}}^{m+2})}$ with Killing shape operator were considered by Lee and Suh (see [Reference Lee and Suh20]). Recently, Lee, Woo and Suh [Reference Lee, Woo and Suh21] considered the notion of Killing normal Jacobi operator of Hopf real hypersurfaces in complex Grassmannians of rank 2. In addition, Suh gave a classification for Hopf real hypersurfaces with Killing Ricci tensor in complex Grassmannians of rank 2 (see [Reference Suh36, Reference Suh37]).
Now, we define a structure Jacobi tensor ![]() $\mathbb {R}_{\xi }$ which is a symmetric tensor field of type (0,2) on
$\mathbb {R}_{\xi }$ which is a symmetric tensor field of type (0,2) on ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ given by
${G_2({\mathbb {C}}^{m+2})}$ given by
for any tangent vector fields ![]() $Y$ and
$Y$ and ![]() $Z$ on
$Z$ on ![]() $M$. Here,
$M$. Here, ![]() ${R_{\xi }}$ is a symmetric tensor field of type (1,1) on
${R_{\xi }}$ is a symmetric tensor field of type (1,1) on ![]() $M$ (so-called, the structure Jacobi operator of
$M$ (so-called, the structure Jacobi operator of ![]() $M$). If the structure Jacobi tensor
$M$). If the structure Jacobi tensor ![]() $\mathbb {R}_{\xi }$ satisfies
$\mathbb {R}_{\xi }$ satisfies
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$, then
$M$, then ![]() $\mathbb {R}_{\xi }$ is said to be Killing. Taking the covariant derivative of (1.2), the property of Killing with respect to
$\mathbb {R}_{\xi }$ is said to be Killing. Taking the covariant derivative of (1.2), the property of Killing with respect to ![]() $\mathbb {R}_{\xi }$ becomes
$\mathbb {R}_{\xi }$ becomes
By virtue of the linearization, (1.3) can be rearranged as
for any tangent vector fields ![]() $X$,
$X$, ![]() $Y$ and
$Y$ and ![]() $Z \in TM$. If the structure Jacobi operator
$Z \in TM$. If the structure Jacobi operator ![]() ${R_{\xi }}$ of
${R_{\xi }}$ of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ satisfies (1.4), we say that
${G_2({\mathbb {C}}^{m+2})}$ satisfies (1.4), we say that ![]() ${R_{\xi }}$ is cyclic parallel. Moreover, by local existence and uniqueness theorem for geodesics, (1.4) can be interpreted that the structure Jacobi curvature
${R_{\xi }}$ is cyclic parallel. Moreover, by local existence and uniqueness theorem for geodesics, (1.4) can be interpreted that the structure Jacobi curvature ![]() ${\mathbb {R}}_{\xi }(\dot \gamma , \dot \gamma ):=g({R_{\xi }} \dot \gamma , \dot \gamma )$ is constant along the geodesic
${\mathbb {R}}_{\xi }(\dot \gamma , \dot \gamma ):=g({R_{\xi }} \dot \gamma , \dot \gamma )$ is constant along the geodesic ![]() $\gamma$ with
$\gamma$ with ![]() $\gamma (0)=p$ and
$\gamma (0)=p$ and ![]() ${\dot \gamma }(0)=X_{p}$ for any point
${\dot \gamma }(0)=X_{p}$ for any point ![]() $p \in M$ and any tangent vector
$p \in M$ and any tangent vector ![]() $X(p)=X_{p} \in T_{p}M$.
$X(p)=X_{p} \in T_{p}M$.
From the assumption of structure Jacobi operator being cyclic parallel, first we assert that the unit normal vector field ![]() $N$ becomes singular as follows:
$N$ becomes singular as follows:
Theorem 1 Let ![]() $M$ be a Hopf real hypersurface in complex two-plane Grassmannians
$M$ be a Hopf real hypersurface in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$ for
${G_2({\mathbb {C}}^{m+2})}$ for ![]() $m \geq 3$. If
$m \geq 3$. If ![]() $M$ has a cyclic parallel structure Jacobi operator, then the normal vector field
$M$ has a cyclic parallel structure Jacobi operator, then the normal vector field ![]() $N$ of
$N$ of ![]() $M$ is singular.
$M$ is singular.
Next, by using theorem 1 we give a classification of Hopf real hypersurfaces in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$, with cyclic parallel structure Jacobi operator as follows:
$m \geq 3$, with cyclic parallel structure Jacobi operator as follows:
Theorem 2 Let ![]() $M$ be a Hopf real hypersurface in complex two-plane Grassmannians
$M$ be a Hopf real hypersurface in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. Then the structure Jacobi operator
$m \geq 3$. Then the structure Jacobi operator ![]() ${R_{\xi }}$ of
${R_{\xi }}$ of ![]() $M$ is cyclic parallel if and only if
$M$ is cyclic parallel if and only if ![]() $M$ is locally congruent to an open part of a tube of
$M$ is locally congruent to an open part of a tube of ![]() $r = ({\pi }/{4 \sqrt {2})}$ around a totally geodesic
$r = ({\pi }/{4 \sqrt {2})}$ around a totally geodesic ![]() ${G_2({\mathbb {C}}^{m+1})}$ in
${G_2({\mathbb {C}}^{m+1})}$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$.
${G_2({\mathbb {C}}^{m+2})}$.
2. Preliminaries
As mentioned in the introduction, the complete classifications of real hypersurfaces in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$, satisfying two invariant conditions for the distributions
$m \geq 3$, satisfying two invariant conditions for the distributions ![]() $\mathcal {C}^{\bot }=\mathrm {span}\{\xi \}$ and
$\mathcal {C}^{\bot }=\mathrm {span}\{\xi \}$ and ![]() ${{\mathcal {Q}}^{\bot }}=\mathrm {span}\{\xi _{1}, \xi _{2}, \xi _{3}\}$ was given in [Reference Berndt and Suh4].
${{\mathcal {Q}}^{\bot }}=\mathrm {span}\{\xi _{1}, \xi _{2}, \xi _{3}\}$ was given in [Reference Berndt and Suh4].
In fact, in [Reference Berndt3, Reference Berndt and Suh4] Berndt and Suh gave the characterizations of the singular unit normal vector ![]() $N$ of
$N$ of ![]() $M$ in complex two-plane Grassmannians
$M$ in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$: There are two types of singular normal vector, those
${G_2({\mathbb {C}}^{m+2})}$: There are two types of singular normal vector, those ![]() $N$ for which
$N$ for which ![]() $JN \bot \mathcal {J} N$, and those for which
$JN \bot \mathcal {J} N$, and those for which ![]() $JN \in \mathcal {J} N$. In other words, it means that
$JN \in \mathcal {J} N$. In other words, it means that ![]() $\xi \in \mathcal {Q}$ or
$\xi \in \mathcal {Q}$ or ![]() $\xi \in {{\mathcal {Q}}^{\bot }}$ because
$\xi \in {{\mathcal {Q}}^{\bot }}$ because ![]() $JN=-\xi$,
$JN=-\xi$, ![]() $\mathcal {J}N=\mathrm {span}\{\xi _{1}, \xi _{2}, \xi _{3}\}={{\mathcal {Q}}^{\bot }}$, and
$\mathcal {J}N=\mathrm {span}\{\xi _{1}, \xi _{2}, \xi _{3}\}={{\mathcal {Q}}^{\bot }}$, and ![]() $TM=\mathcal {Q} \oplus {{\mathcal {Q}}^{\bot }}$. The following proposition tells us that the normal vector field
$TM=\mathcal {Q} \oplus {{\mathcal {Q}}^{\bot }}$. The following proposition tells us that the normal vector field ![]() $N$ on the model spaces of
$N$ on the model spaces of ![]() $(\mathcal {T}_{A})$ is singular of type of
$(\mathcal {T}_{A})$ is singular of type of ![]() $JN \in \mathcal {J} N$, that is,
$JN \in \mathcal {J} N$, that is, ![]() $\xi \in {{\mathcal {Q}}^{\bot }}$.
$\xi \in {{\mathcal {Q}}^{\bot }}$.
Proposition A [Reference Berndt and Suh4, Reference Berndt and Suh9]
Let ![]() $(\mathcal {T}_{A})$ be the tube of radius
$(\mathcal {T}_{A})$ be the tube of radius ![]() $0 < r < \frac {\pi }{\sqrt {8}}$ around the totally geodesic
$0 < r < \frac {\pi }{\sqrt {8}}$ around the totally geodesic ![]() ${G_2({\mathbb {C}}^{m+1})}$ in
${G_2({\mathbb {C}}^{m+1})}$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$. Then the following statements hold:
${G_2({\mathbb {C}}^{m+2})}$. Then the following statements hold:
1.
 $(\mathcal {T}_{A})$ is a Hopf hypersurface.
$(\mathcal {T}_{A})$ is a Hopf hypersurface.2. Every unit normal vector field
 $N$ of
$N$ of  $(\mathcal {T}_{A})$ is singular and of type
$(\mathcal {T}_{A})$ is singular and of type  $JN \in \mathcal {J} N$.
$JN \in \mathcal {J} N$.3. The eigenvalues and their corresponding eigenspaces and multiplicities are given in Table 1.
4. The Reeb flow on
 $(\mathcal {T}_{A})$ is isometric.
$(\mathcal {T}_{A})$ is isometric.
Table 1. Principal curvatures of a model space of type ![]() $(\mathcal {T}_{A})$
$(\mathcal {T}_{A})$

In proposition ![]() ${\rm A}$, the notion of isometric Reeb flow gave a kind of characterizations of real hypersurface of type
${\rm A}$, the notion of isometric Reeb flow gave a kind of characterizations of real hypersurface of type ![]() $(\mathcal {T}_{A})$. Like for such an investigation, many geometric conditions were considered as characterizations of the model space of
$(\mathcal {T}_{A})$. Like for such an investigation, many geometric conditions were considered as characterizations of the model space of ![]() $(\mathcal {T}_{A})$ in complex two-plane Grassmannians (see [Reference Jeong, Pérez, Suh and Woo14, Reference Machado and Pérez22, Reference Machado and Pérez23, Reference Pérez25, Reference Pérez, Lee, Suh and Woo26, Reference Pérez, Suh and Woo28, Reference Suh, Lee and Kim39, Reference Suh, Lee and Kim40]).
$(\mathcal {T}_{A})$ in complex two-plane Grassmannians (see [Reference Jeong, Pérez, Suh and Woo14, Reference Machado and Pérez22, Reference Machado and Pérez23, Reference Pérez25, Reference Pérez, Lee, Suh and Woo26, Reference Pérez, Suh and Woo28, Reference Suh, Lee and Kim39, Reference Suh, Lee and Kim40]).
On the other hand, by using the notion of isometric Reeb flow, that is, the shape operator ![]() $A$ of a Hopf real hypersurface
$A$ of a Hopf real hypersurface ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ commutes with structure tensor
${G_2({\mathbb {C}}^{m+2})}$ commutes with structure tensor ![]() $\phi$, that is,
$\phi$, that is, ![]() $A \phi = \phi A$, Berndt and Suh gave:
$A \phi = \phi A$, Berndt and Suh gave:
 \begin{equation} \begin{split} (\nabla_{X}A)Y & ={-} \eta(Y) \phi X +(X\alpha)\eta(Y) \xi + \alpha g(A \phi X, Y) \xi - g(A^{2} \phi X, Y) \xi \\ & \quad - \sum_{i=1}^{3}\big\{ \eta_{\nu}(Y)\phi_{\nu} X + g(\phi_{\nu} \xi, Y) \phi \phi_{\nu} X + 2g(\phi_{\nu} \xi, X) \phi \phi_{\nu} Y \\ & \quad + g(\phi_{\nu} \xi, X) \eta_{\nu} (Y) \xi - \eta_{\nu}(\xi) g(\phi_{\nu} X, Y) \xi + g(\phi_{\nu} X, Y){{\xi}_{\nu}} \\ & \quad - \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi + g(\phi_{\nu} \phi X, Y) \phi_{\nu} \xi \big \} \end{split} \end{equation}
\begin{equation} \begin{split} (\nabla_{X}A)Y & ={-} \eta(Y) \phi X +(X\alpha)\eta(Y) \xi + \alpha g(A \phi X, Y) \xi - g(A^{2} \phi X, Y) \xi \\ & \quad - \sum_{i=1}^{3}\big\{ \eta_{\nu}(Y)\phi_{\nu} X + g(\phi_{\nu} \xi, Y) \phi \phi_{\nu} X + 2g(\phi_{\nu} \xi, X) \phi \phi_{\nu} Y \\ & \quad + g(\phi_{\nu} \xi, X) \eta_{\nu} (Y) \xi - \eta_{\nu}(\xi) g(\phi_{\nu} X, Y) \xi + g(\phi_{\nu} X, Y){{\xi}_{\nu}} \\ & \quad - \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi + g(\phi_{\nu} \phi X, Y) \phi_{\nu} \xi \big \} \end{split} \end{equation}
for any tangent vector fields ![]() $X$ and
$X$ and ![]() $Y$ on
$Y$ on ![]() $M$ (see proposition 4 in [Reference Berndt and Suh5]). In fact, from (iv) in proposition
$M$ (see proposition 4 in [Reference Berndt and Suh5]). In fact, from (iv) in proposition ![]() ${\rm A}$, we see that the shape operator
${\rm A}$, we see that the shape operator ![]() $A$ of
$A$ of ![]() $(\mathcal {T}_{A})$ satisfies
$(\mathcal {T}_{A})$ satisfies ![]() $A \phi = \phi A$. Thus, the above equation (2.1) holds on
$A \phi = \phi A$. Thus, the above equation (2.1) holds on ![]() $(\mathcal {T}_{A})$ and it can be rearranged as
$(\mathcal {T}_{A})$ and it can be rearranged as
 \begin{equation} \begin{split} (\nabla_{X}A)Y & ={-} \eta(Y) \phi X + \alpha g(A \phi X, Y) \xi - g(A^{2} \phi X, Y) \xi \\ & \quad - \sum_{i=1}^{3}\big\{ \eta_{\nu}(Y)\phi_{\nu} X + g(\phi_{\nu} \xi, Y) \phi \phi_{\nu} X + 2g(\phi_{\nu} \xi, X) \phi \phi_{\nu} Y \\ & \quad + g(\phi_{\nu} \xi, X) \eta_{\nu} (Y) \xi - \eta_{\nu}(\xi) g(\phi_{\nu} X, Y) \xi + g(\phi_{\nu} X, Y){{\xi}_{\nu}} \\ & \quad - \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi + g(\phi_{\nu} \phi X, Y) \phi_{\nu} \xi \big \} \end{split} \end{equation}
\begin{equation} \begin{split} (\nabla_{X}A)Y & ={-} \eta(Y) \phi X + \alpha g(A \phi X, Y) \xi - g(A^{2} \phi X, Y) \xi \\ & \quad - \sum_{i=1}^{3}\big\{ \eta_{\nu}(Y)\phi_{\nu} X + g(\phi_{\nu} \xi, Y) \phi \phi_{\nu} X + 2g(\phi_{\nu} \xi, X) \phi \phi_{\nu} Y \\ & \quad + g(\phi_{\nu} \xi, X) \eta_{\nu} (Y) \xi - \eta_{\nu}(\xi) g(\phi_{\nu} X, Y) \xi + g(\phi_{\nu} X, Y){{\xi}_{\nu}} \\ & \quad - \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi + g(\phi_{\nu} \phi X, Y) \phi_{\nu} \xi \big \} \end{split} \end{equation}
for any tangent vector fields ![]() $X$ and
$X$ and ![]() $Y$ on
$Y$ on ![]() $T(\mathcal {T}_{A})=T_{\alpha }\oplus T_{\beta }\oplus T_{\lambda }\oplus T_{\mu }$.
$T(\mathcal {T}_{A})=T_{\alpha }\oplus T_{\beta }\oplus T_{\lambda }\oplus T_{\mu }$.
3. Fundamental equations of real hypersurfaces in  ${G_2({\mathbb {C}}^{m+2})}$
${G_2({\mathbb {C}}^{m+2})}$
We use some references [Reference Lee and Suh17, Reference Pérez and Suh27, Reference Suh34] to recall the Riemannian geometry of complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$, and some fundamental formulas including the Codazzi and Gauss equations for a real hypersurface in
$m \geq 3$, and some fundamental formulas including the Codazzi and Gauss equations for a real hypersurface in ![]() ${G_2({\mathbb {C}}^{m+2})}$.
${G_2({\mathbb {C}}^{m+2})}$.
Let ![]() $M$ be a real hypersurface of complex two-plane Grassmannians
$M$ be a real hypersurface of complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$, that is, a submanifold of
$m \geq 3$, that is, a submanifold of ![]() ${G_2({\mathbb {C}}^{m+2})}$ with real codimension one. The induced Riemannian metric on
${G_2({\mathbb {C}}^{m+2})}$ with real codimension one. The induced Riemannian metric on ![]() $M$ will also be denoted by
$M$ will also be denoted by ![]() $g$, and
$g$, and ![]() $\nabla$ denotes the Riemannian connection of
$\nabla$ denotes the Riemannian connection of ![]() $(M,g)$. Let
$(M,g)$. Let ![]() $N$ be a local unit normal field of
$N$ be a local unit normal field of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ and
${G_2({\mathbb {C}}^{m+2})}$ and ![]() $S$ the shape operator of
$S$ the shape operator of ![]() $M$ with respect to
$M$ with respect to ![]() $N$, that is,
$N$, that is, ![]() ${\bar \nabla }_{X}N = -SX$. The Kähler structure
${\bar \nabla }_{X}N = -SX$. The Kähler structure ![]() $J$ of complex two-plane Grassmannians
$J$ of complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$ induces on
${G_2({\mathbb {C}}^{m+2})}$ induces on ![]() $M$ an almost contact metric structure
$M$ an almost contact metric structure ![]() $(\phi ,\xi ,\eta ,g)$. Furthermore, let
$(\phi ,\xi ,\eta ,g)$. Furthermore, let ![]() $\{J_1, J_2, J_3 \}$ be a canonical local basis of the quaternionic Kähler structure
$\{J_1, J_2, J_3 \}$ be a canonical local basis of the quaternionic Kähler structure ![]() ${\mathcal {J}}$. Then each
${\mathcal {J}}$. Then each ![]() $J_\nu$ induces an almost contact metric structure
$J_\nu$ induces an almost contact metric structure ![]() $(\phi _\nu ,\xi _\nu ,\eta _\nu ,g)$ on
$(\phi _\nu ,\xi _\nu ,\eta _\nu ,g)$ on ![]() $M$. Now let us put
$M$. Now let us put
for any tangent vector ![]() $X$ on a real hypersurface
$X$ on a real hypersurface ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$, where
${G_2({\mathbb {C}}^{m+2})}$, where ![]() $N$ denotes a normal vector of
$N$ denotes a normal vector of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$. Then the following identities can be proved in a straightforward method and will be used frequently in subsequent calculations:
${G_2({\mathbb {C}}^{m+2})}$. Then the following identities can be proved in a straightforward method and will be used frequently in subsequent calculations:
where we have used that ![]() $J_{\nu }J_{\nu +1}=J_{\nu +2}= - J_{\nu +1}J_{\nu }$.
$J_{\nu }J_{\nu +1}=J_{\nu +2}= - J_{\nu +1}J_{\nu }$.
On the other hand, from the parallelism of ![]() $J$ and
$J$ and ![]() $\mathcal {J}$ which are defined by
$\mathcal {J}$ which are defined by
together with Gauss and Weingarten formulas, it follows that
Combining these formulas, we find the following
 \begin{equation} \begin{split} {\nabla}_X({{{\phi}}}_{\nu}{\xi}) & ={\nabla}_X({{{\phi}}}{\xi}_{\nu}) \\ & =({\nabla}_X{{{\phi}}}){\xi}_{\nu}+{{{\phi}}}({\nabla}_X{\xi}_{\nu})\\ & =q_{{\nu}+2}(X){{{\phi}}}_{{\nu}+1}{\xi}-q_{{\nu}+1}(X){{{\phi}}}_{{\nu}+2}{\xi}+{{{\phi}}}_{\nu}{{{\phi}}}AX \\ & \quad \ - g(AX,{\xi}){\xi}_{\nu}+{\eta}({\xi}_{\nu})AX. \end{split} \end{equation}
\begin{equation} \begin{split} {\nabla}_X({{{\phi}}}_{\nu}{\xi}) & ={\nabla}_X({{{\phi}}}{\xi}_{\nu}) \\ & =({\nabla}_X{{{\phi}}}){\xi}_{\nu}+{{{\phi}}}({\nabla}_X{\xi}_{\nu})\\ & =q_{{\nu}+2}(X){{{\phi}}}_{{\nu}+1}{\xi}-q_{{\nu}+1}(X){{{\phi}}}_{{\nu}+2}{\xi}+{{{\phi}}}_{\nu}{{{\phi}}}AX \\ & \quad \ - g(AX,{\xi}){\xi}_{\nu}+{\eta}({\xi}_{\nu})AX. \end{split} \end{equation}
Moreover, from ![]() $JJ_{\nu }=J_{\nu }J$,
$JJ_{\nu }=J_{\nu }J$, ![]() ${\nu }=1,2,3$, it follows that
${\nu }=1,2,3$, it follows that
Finally, using the explicit expression for the Riemannian curvature tensor ![]() $\bar {R}$ of complex two-plane Grassmannians
$\bar {R}$ of complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$ in the introduction, the Codazzi and Gauss equations of
${G_2({\mathbb {C}}^{m+2})}$ in the introduction, the Codazzi and Gauss equations of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ are given respectively by
${G_2({\mathbb {C}}^{m+2})}$ are given respectively by
 \begin{equation} \begin{split} (\nabla_XA)Y - (\nabla_YA)X & = \eta(X)\phi Y - \eta(Y)\phi X - 2g(\phi X,Y)\xi \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(X)\phi_\nu Y - \eta_\nu(Y)\phi_\nu X - 2g(\phi_\nu X,Y)\xi_\nu\big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(\phi X)\phi_\nu\phi Y - \eta_\nu(\phi Y)\phi_\nu\phi X\big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta(X)\eta_\nu(\phi Y) - \eta(Y)\eta_\nu(\phi X)\big\}\xi_{\nu} \end{split} \end{equation}
\begin{equation} \begin{split} (\nabla_XA)Y - (\nabla_YA)X & = \eta(X)\phi Y - \eta(Y)\phi X - 2g(\phi X,Y)\xi \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(X)\phi_\nu Y - \eta_\nu(Y)\phi_\nu X - 2g(\phi_\nu X,Y)\xi_\nu\big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(\phi X)\phi_\nu\phi Y - \eta_\nu(\phi Y)\phi_\nu\phi X\big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta(X)\eta_\nu(\phi Y) - \eta(Y)\eta_\nu(\phi X)\big\}\xi_{\nu} \end{split} \end{equation}and
 \begin{equation} \begin{split} R(X,Y)Z & = g(Y,Z)X - g(X,Z)Y + g({\phi}Y,Z){\phi}X - g({\phi}X,Z){\phi}Y \\ & \quad - 2g({\phi}X,Y){\phi}Z+ g(AY,Z)AX - g(AX,Z)AY \\ & \quad + \sum_{\nu=1}^{3} \Big \{g({{\phi}_{\nu}}Y,Z){{\phi}_{\nu}}X - g({{\phi}_{\nu}}X,Z){{\phi}_{\nu}}Y - 2g({{\phi}_{\nu}}X,Y){{\phi}_{\nu}}Z \\ & \quad + g({{\phi}_{\nu}}{\phi}Y,Z){{\phi}_{\nu}} {\phi}X - g({{\phi}_{\nu}}{\phi}X,Z){{{\phi}_{\nu}}}{\phi}Y \\ & \quad + \eta(X){{{\eta}_{\nu}}}(Z){{{\phi}_{\nu}}}{\phi}Y - {\eta}(Y){{{\eta}_{\nu}}}(Z){{{\phi}_{\nu}}}{\phi}X \\ & \quad + {\eta}(Y)g({{{\phi}_{\nu}}}{\phi}X,Z){{\xi}_{\nu}} - {\eta}(X)g({{{\phi}_{\nu}}}{\phi}Y,Z){{{\xi}_{\nu}}} \Big \} \end{split} \end{equation}
\begin{equation} \begin{split} R(X,Y)Z & = g(Y,Z)X - g(X,Z)Y + g({\phi}Y,Z){\phi}X - g({\phi}X,Z){\phi}Y \\ & \quad - 2g({\phi}X,Y){\phi}Z+ g(AY,Z)AX - g(AX,Z)AY \\ & \quad + \sum_{\nu=1}^{3} \Big \{g({{\phi}_{\nu}}Y,Z){{\phi}_{\nu}}X - g({{\phi}_{\nu}}X,Z){{\phi}_{\nu}}Y - 2g({{\phi}_{\nu}}X,Y){{\phi}_{\nu}}Z \\ & \quad + g({{\phi}_{\nu}}{\phi}Y,Z){{\phi}_{\nu}} {\phi}X - g({{\phi}_{\nu}}{\phi}X,Z){{{\phi}_{\nu}}}{\phi}Y \\ & \quad + \eta(X){{{\eta}_{\nu}}}(Z){{{\phi}_{\nu}}}{\phi}Y - {\eta}(Y){{{\eta}_{\nu}}}(Z){{{\phi}_{\nu}}}{\phi}X \\ & \quad + {\eta}(Y)g({{{\phi}_{\nu}}}{\phi}X,Z){{\xi}_{\nu}} - {\eta}(X)g({{{\phi}_{\nu}}}{\phi}Y,Z){{{\xi}_{\nu}}} \Big \} \end{split} \end{equation}
for any tangent vector fields ![]() $X$,
$X$, ![]() $Y$ and
$Y$ and ![]() $Z$ on
$Z$ on ![]() $M$.
$M$.
On the other hand, we can derive some important facts from the geometric condition of ![]() $M$ being Hopf, that is,
$M$ being Hopf, that is, ![]() $A\xi = \alpha \xi$ where
$A\xi = \alpha \xi$ where ![]() $\alpha = g(A\xi , \xi )$. Among them, we introduce the following formulas which are induced from the Codazzi equation:
$\alpha = g(A\xi , \xi )$. Among them, we introduce the following formulas which are induced from the Codazzi equation:
Lemma A [Reference Berndt and Suh5]
If ![]() $M$ is a connected orientable Hopf real hypersurface in complex two-plane Grassmannians
$M$ is a connected orientable Hopf real hypersurface in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$, then
$m \geq 3$, then
 \begin{equation} \mathrm{grad} \, \alpha = (\xi \alpha)\xi + 4\sum_{\nu=1}^{3} \eta_{\nu}(\xi)\phi_{\nu} \xi \end{equation}
\begin{equation} \mathrm{grad} \, \alpha = (\xi \alpha)\xi + 4\sum_{\nu=1}^{3} \eta_{\nu}(\xi)\phi_{\nu} \xi \end{equation}and
 \begin{equation} \begin{split} & 2 A \phi A X - \alpha A\phi X - \alpha \phi A X \\ & \quad = 2 \phi X + 2 \sum_{\nu=1}^{3} \big\{ \eta_{\nu} (X) \phi_{\nu} \xi - g(\phi_{\nu}\xi, X) \xi_{\nu} + \eta_{\nu} (\xi) \phi_{\nu} X \big\} \\ & \quad \quad -4 \sum_{\nu=1}^{3} \big \{ \eta(X) \eta_{\nu} (\xi) \phi_{\nu} \xi - \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \xi \big\} \end{split} \end{equation}
\begin{equation} \begin{split} & 2 A \phi A X - \alpha A\phi X - \alpha \phi A X \\ & \quad = 2 \phi X + 2 \sum_{\nu=1}^{3} \big\{ \eta_{\nu} (X) \phi_{\nu} \xi - g(\phi_{\nu}\xi, X) \xi_{\nu} + \eta_{\nu} (\xi) \phi_{\nu} X \big\} \\ & \quad \quad -4 \sum_{\nu=1}^{3} \big \{ \eta(X) \eta_{\nu} (\xi) \phi_{\nu} \xi - \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \xi \big\} \end{split} \end{equation}
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$.
${G_2({\mathbb {C}}^{m+2})}$.
4. Proof of theorem 1
Let ![]() $M$ be a Hopf real hypersurface with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians
$M$ be a Hopf real hypersurface with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$.
$m \geq 3$.
From (3.9) the structure Jacobi operator ![]() ${R_{\xi }} \in \mathrm {End}(TM)$ is given as follows
${R_{\xi }} \in \mathrm {End}(TM)$ is given as follows
 \begin{equation} \begin{split} R_{\xi}(Y) & = R(Y,\xi)\xi \\ & = Y - \eta(Y) \xi + \alpha AY - \alpha^{2} \eta(Y) \xi \\ & \quad - \sum_{\nu=1}^{3} \big\{ \eta_{\nu}(Y) {{\xi}_{\nu}} - \eta(Y) \eta_{\nu}(\xi) {{\xi}_{\nu}} - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \xi + \eta_{\nu}(\xi) \phi_{\nu} \phi Y \big \} \end{split} \end{equation}
\begin{equation} \begin{split} R_{\xi}(Y) & = R(Y,\xi)\xi \\ & = Y - \eta(Y) \xi + \alpha AY - \alpha^{2} \eta(Y) \xi \\ & \quad - \sum_{\nu=1}^{3} \big\{ \eta_{\nu}(Y) {{\xi}_{\nu}} - \eta(Y) \eta_{\nu}(\xi) {{\xi}_{\nu}} - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \xi + \eta_{\nu}(\xi) \phi_{\nu} \phi Y \big \} \end{split} \end{equation}
for any tangent vector field ![]() $Y \in TM$ (see [Reference Lee and Suh19, Reference Machado, Pérez and Suh24]).
$Y \in TM$ (see [Reference Lee and Suh19, Reference Machado, Pérez and Suh24]).
Taking the covariant derivative of (4.1) along the direction of ![]() $X$ implies
$X$ implies
 \begin{equation} \begin{split} (\nabla_{X}R_{\xi})Y & = \nabla_{X}({R_{\xi}}Y) - {R_{\xi}} (\nabla_{X}Y) \\ & ={-}g(\phi AX, Y) \xi - \eta(Y) \phi AX \\ & \quad - \sum_{\nu=1}^{3} \Big [ g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} + 2\eta(Y) g(\phi_{\nu} \xi, AX) {{\xi}_{\nu}} + \eta_{\nu}(Y) \phi_{\nu} AX \\ & \quad + 3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi + 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi \\ & \quad - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX + 3 \alpha \eta (X) g(\phi_{\nu} \xi, Y) {{\xi}_{\nu}} \\ & \quad - 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX - 4 \eta_{\nu}(\xi)g(AX, Y) \phi_{\nu} \xi \\ & \quad - 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y \Big ] \\ & \quad + g((\nabla_{X}A)\xi, \xi)AY + \alpha (\nabla_{X}A)Y - \alpha g((\nabla_{X}A)Y, \xi)\xi \\ & \quad - \alpha g(AY, \phi AX) \xi - \alpha \eta(Y) (\nabla_{X}A) \xi - \alpha \eta(Y) A \phi AX \end{split} \end{equation}
\begin{equation} \begin{split} (\nabla_{X}R_{\xi})Y & = \nabla_{X}({R_{\xi}}Y) - {R_{\xi}} (\nabla_{X}Y) \\ & ={-}g(\phi AX, Y) \xi - \eta(Y) \phi AX \\ & \quad - \sum_{\nu=1}^{3} \Big [ g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} + 2\eta(Y) g(\phi_{\nu} \xi, AX) {{\xi}_{\nu}} + \eta_{\nu}(Y) \phi_{\nu} AX \\ & \quad + 3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi + 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi \\ & \quad - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX + 3 \alpha \eta (X) g(\phi_{\nu} \xi, Y) {{\xi}_{\nu}} \\ & \quad - 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX - 4 \eta_{\nu}(\xi)g(AX, Y) \phi_{\nu} \xi \\ & \quad - 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y \Big ] \\ & \quad + g((\nabla_{X}A)\xi, \xi)AY + \alpha (\nabla_{X}A)Y - \alpha g((\nabla_{X}A)Y, \xi)\xi \\ & \quad - \alpha g(AY, \phi AX) \xi - \alpha \eta(Y) (\nabla_{X}A) \xi - \alpha \eta(Y) A \phi AX \end{split} \end{equation}
for any tangent vector fields ![]() $X$ and
$X$ and ![]() $Y$ on
$Y$ on ![]() $M$ (see [Reference Lee and Suh19]). From this and using symmetric property of the structure Jacobi operator
$M$ (see [Reference Lee and Suh19]). From this and using symmetric property of the structure Jacobi operator ![]() ${R_{\xi }}$ in
${R_{\xi }}$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$, the cyclic parallelism of the structure Jacobi operator (1.4) can be rearranged as follows:
${G_2({\mathbb {C}}^{m+2})}$, the cyclic parallelism of the structure Jacobi operator (1.4) can be rearranged as follows:
 \begin{align} 0 & = g\big((\nabla_{X}{R_{\xi}})Y, Z \big) + g\big((\nabla_{Y}{R_{\xi}})Z, X \big)+g\big((\nabla_{Z}{R_{\xi}})X, Y \big)\nonumber\\ & = g\big((\nabla_{X}{R_{\xi}})Y, Z \big) + g\big((\nabla_{Y}{R_{\xi}})X, Z \big)\nonumber \\ & \quad + g(A\phi X, Z) \eta(Y) + \eta(X) g(A \phi Y, Z) + (\xi \alpha) g(AX, Y)\eta(Z)\nonumber \\ & \quad - \alpha (\xi \alpha) \eta(X) \eta(Y) \eta(Z) + \alpha^{2} \eta(Y) g(A \phi X, Z) - \alpha \eta(Y) g(A \phi A X, Z)\nonumber \\ & \quad + \alpha \eta(Y) g(A \phi AX, Z) + \alpha \eta(X) g(A \phi AY, Z) - \alpha (\xi \alpha) \eta(X) \eta(Y) \eta(Z)\nonumber \\ & \quad + \alpha^{2} \eta(X) g(A \phi Y, Z) - \alpha \eta(X) g(A \phi A Y, Z) + \alpha g((\nabla_X A)Y, Z)\nonumber \\ & \quad + \alpha g( \phi X, Y)\eta(Z) + \alpha \eta(X)g(\phi Y, Z) + 2\alpha \eta(Y) g(\phi X, Z) \nonumber \\ & \quad + \sum_{\nu=1}^{3} \Big [ \eta_{\nu}(Y) g(A \phi_{\nu} X, Z) - 2\eta(X)\eta_{\nu}(Y) g(A \phi_{\nu} \xi, Z) + \eta_{\nu}(X) g(A \phi_{\nu} Y, Z) \nonumber\\ & \quad + 3g(\phi_{\nu} \xi, Y) g(A \phi_{\nu} \phi X, Z) - 3 \eta(X) g(\phi_{\nu} \xi, Y) g(A{{\xi}_{\nu}}, Z)\nonumber \\ & \quad + 3g(\phi_{\nu} \xi, X) g(A \phi \phi_{\nu} Y, Z) - 3 \alpha g(\phi_{\nu} \xi, X) \eta_{\nu}(Y)\eta(Z)\nonumber \\ & \quad + 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) g(AY, Z) + 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y)g(AX, Z)\nonumber\\ & \quad + 2 g(\phi_{\nu}\phi X, Y)g(A \phi_{\nu} \xi, Z) + 4 g(AX, Y) \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z)\nonumber\\ & \quad - 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z) - 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z) \Big ]\nonumber \\ & \quad + \alpha \sum_{\nu=1}^{3} \Big [ g(\phi_\nu X, Y)\eta_\nu(Z) + \eta_\nu(X)g(\phi_\nu Y, Z) + 2\eta_{\nu}(Y) g(\phi_\nu X,Z)\nonumber \\ & \quad - g(\phi_\nu\phi X, Y)g(\phi_{\nu} \xi, Z) + g(\phi_{\nu} \xi, X)g(\phi \phi_\nu Y, Z)\nonumber \\ & \quad + \eta_\nu(\phi X)\eta_{\nu}(Y) \eta(Z) + \eta(X)\eta_{\nu}(Y) g(\phi_{\nu} \xi, Z)\Big ], \end{align}
\begin{align} 0 & = g\big((\nabla_{X}{R_{\xi}})Y, Z \big) + g\big((\nabla_{Y}{R_{\xi}})Z, X \big)+g\big((\nabla_{Z}{R_{\xi}})X, Y \big)\nonumber\\ & = g\big((\nabla_{X}{R_{\xi}})Y, Z \big) + g\big((\nabla_{Y}{R_{\xi}})X, Z \big)\nonumber \\ & \quad + g(A\phi X, Z) \eta(Y) + \eta(X) g(A \phi Y, Z) + (\xi \alpha) g(AX, Y)\eta(Z)\nonumber \\ & \quad - \alpha (\xi \alpha) \eta(X) \eta(Y) \eta(Z) + \alpha^{2} \eta(Y) g(A \phi X, Z) - \alpha \eta(Y) g(A \phi A X, Z)\nonumber \\ & \quad + \alpha \eta(Y) g(A \phi AX, Z) + \alpha \eta(X) g(A \phi AY, Z) - \alpha (\xi \alpha) \eta(X) \eta(Y) \eta(Z)\nonumber \\ & \quad + \alpha^{2} \eta(X) g(A \phi Y, Z) - \alpha \eta(X) g(A \phi A Y, Z) + \alpha g((\nabla_X A)Y, Z)\nonumber \\ & \quad + \alpha g( \phi X, Y)\eta(Z) + \alpha \eta(X)g(\phi Y, Z) + 2\alpha \eta(Y) g(\phi X, Z) \nonumber \\ & \quad + \sum_{\nu=1}^{3} \Big [ \eta_{\nu}(Y) g(A \phi_{\nu} X, Z) - 2\eta(X)\eta_{\nu}(Y) g(A \phi_{\nu} \xi, Z) + \eta_{\nu}(X) g(A \phi_{\nu} Y, Z) \nonumber\\ & \quad + 3g(\phi_{\nu} \xi, Y) g(A \phi_{\nu} \phi X, Z) - 3 \eta(X) g(\phi_{\nu} \xi, Y) g(A{{\xi}_{\nu}}, Z)\nonumber \\ & \quad + 3g(\phi_{\nu} \xi, X) g(A \phi \phi_{\nu} Y, Z) - 3 \alpha g(\phi_{\nu} \xi, X) \eta_{\nu}(Y)\eta(Z)\nonumber \\ & \quad + 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) g(AY, Z) + 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y)g(AX, Z)\nonumber\\ & \quad + 2 g(\phi_{\nu}\phi X, Y)g(A \phi_{\nu} \xi, Z) + 4 g(AX, Y) \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z)\nonumber\\ & \quad - 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z) - 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z) \Big ]\nonumber \\ & \quad + \alpha \sum_{\nu=1}^{3} \Big [ g(\phi_\nu X, Y)\eta_\nu(Z) + \eta_\nu(X)g(\phi_\nu Y, Z) + 2\eta_{\nu}(Y) g(\phi_\nu X,Z)\nonumber \\ & \quad - g(\phi_\nu\phi X, Y)g(\phi_{\nu} \xi, Z) + g(\phi_{\nu} \xi, X)g(\phi \phi_\nu Y, Z)\nonumber \\ & \quad + \eta_\nu(\phi X)\eta_{\nu}(Y) \eta(Z) + \eta(X)\eta_{\nu}(Y) g(\phi_{\nu} \xi, Z)\Big ], \end{align}where we have used
 \begin{equation*} \begin{split} g((\nabla_{Z}A)\xi, X) & = (Z \alpha) \eta(X) - \alpha g(A \phi X, Z) + g(A \phi A X, Z) \\ & = (\xi \alpha) \eta(Z) \eta(X) + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z) \eta(X) \\ & \quad \ - \alpha g(A \phi X, Z) + g(A \phi A X, Z) \end{split} \end{equation*}
\begin{equation*} \begin{split} g((\nabla_{Z}A)\xi, X) & = (Z \alpha) \eta(X) - \alpha g(A \phi X, Z) + g(A \phi A X, Z) \\ & = (\xi \alpha) \eta(Z) \eta(X) + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Z) \eta(X) \\ & \quad \ - \alpha g(A \phi X, Z) + g(A \phi A X, Z) \end{split} \end{equation*}and
 \begin{equation*} \begin{split} & g((\nabla_ZA)X, Y) \\ & = g((\nabla_X A)Z, Y) + \eta(Z)g( \phi X, Y) - \eta(X)g(\phi Z, Y) - 2g(\phi Z,X)\eta(Y) \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(Z)g(\phi_\nu X, Y) - \eta_\nu(X)g(\phi_\nu Z, Y) - 2g(\phi_\nu Z,X)\eta_{\nu}(Y) \big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(\phi Z)g(\phi_\nu\phi X, Y) - \eta_\nu(\phi X)g(\phi_\nu\phi Z, Y) \big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta(Z)\eta_\nu(\phi X) - \eta(X)\eta_\nu(\phi Z)\big\}\eta_{\nu}(Y) \end{split} \end{equation*}
\begin{equation*} \begin{split} & g((\nabla_ZA)X, Y) \\ & = g((\nabla_X A)Z, Y) + \eta(Z)g( \phi X, Y) - \eta(X)g(\phi Z, Y) - 2g(\phi Z,X)\eta(Y) \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(Z)g(\phi_\nu X, Y) - \eta_\nu(X)g(\phi_\nu Z, Y) - 2g(\phi_\nu Z,X)\eta_{\nu}(Y) \big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta_\nu(\phi Z)g(\phi_\nu\phi X, Y) - \eta_\nu(\phi X)g(\phi_\nu\phi Z, Y) \big\} \\ & \quad + \sum_{\nu=1}^{3} \big\{\eta(Z)\eta_\nu(\phi X) - \eta(X)\eta_\nu(\phi Z)\big\}\eta_{\nu}(Y) \end{split} \end{equation*}
for any tangent vector fields ![]() $X$,
$X$, ![]() $Y$ and
$Y$ and ![]() $Z$ on
$Z$ on ![]() $M$. Deleting
$M$. Deleting ![]() $Z$ from (4.3) and using (4.2) gives
$Z$ from (4.3) and using (4.2) gives
 \begin{align} & -g(\phi AX, Y) \xi - \eta(Y) \phi AX -g(\phi AY, X) \xi - \eta(X) \phi AY + \eta(Y)A\phi X \nonumber\\ & + \eta(X) A \phi Y + (\xi \alpha) g(AX, Y) \xi - 2 \alpha (\xi \alpha) \eta(X) \eta(Y) \xi + \alpha^{2} \eta(Y) A \phi X \nonumber\\ & + \alpha^{2} \eta(X) A \phi Y + \alpha (\nabla_X A)Y + \alpha g(\phi X, Y)\xi + \alpha \eta(X) \phi Y + 2\alpha \eta(Y) \phi X \nonumber\\ & - \sum_{\nu=1}^{3} \Big [ g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} + 2\eta(Y) g(\phi_{\nu} \xi, AX) {{\xi}_{\nu}} + \eta_{\nu}(Y) \phi_{\nu} AX \nonumber\\ & +3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi + 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX \nonumber\\ &+ 3 \alpha \eta (X) g(\phi_{\nu} \xi, Y) {{\xi}_{\nu}} - 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX \nonumber\\ & \quad \quad \quad - 4 \eta_{\nu}(\xi)g(AX, Y) \phi_{\nu} \xi - 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y \nonumber\\ &+ g(\phi_{\nu} AY, X) {{\xi}_{\nu}} + 2\eta(X) g(\phi_{\nu} \xi, AY) {{\xi}_{\nu}} + \eta_{\nu}(X) \phi_{\nu} AY \nonumber\\ &+3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi + 3 \eta(X) \eta_{\nu}(AY) \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \nonumber\\ & + 3 \alpha \eta (Y) g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} - 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) AY \nonumber\\ & - 4 \eta_{\nu}(\xi)g(AY, X) \phi_{\nu} \xi - 2g(\phi_{\nu} \xi, AY) \phi_{\nu}\phi X \Big ] \nonumber\\ & + \sum_{\nu=1}^{3} \Big [ \eta_{\nu}(Y) A \phi_{\nu} X - 2\eta(X)\eta_{\nu}(Y) A \phi_{\nu} \xi + \eta_{\nu}(X) A \phi_{\nu} Y \nonumber\\ &+ 3g(\phi_{\nu} \xi, Y) A \phi_{\nu} \phi X - 3 \eta(X) g(\phi_{\nu} \xi, Y) A{{\xi}_{\nu}} \nonumber\\ &+ 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 3 \alpha g(\phi_{\nu} \xi, X) \eta_{\nu}(Y)\xi \nonumber\\ &+ 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) AY + 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX \nonumber\\ &+ 2 g(\phi_{\nu}\phi X, Y) A \phi_{\nu} \xi + 4 g(AX, Y)\eta_{\nu}(\xi) \phi_{\nu} \xi \nonumber\\ &- 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) \phi_{\nu} \xi - 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) \phi_{\nu} \xi \Big ] \nonumber\\ & + \alpha \sum_{\nu=1}^{3} \Big [ g(\phi_\nu X, Y) {{\xi}_{\nu}} + \eta_\nu(X) \phi_\nu Y + 2\eta_{\nu}(Y) \phi_\nu X - g(\phi_\nu\phi X, Y) \phi_{\nu} \xi\nonumber\\ & + g(\phi_{\nu} \xi, X) \phi \phi_\nu Y + \eta_\nu(\phi X)\eta_{\nu}(Y) \xi + \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi \Big ]\nonumber\\ & + g((\nabla_{X}A)\xi, \xi)AY - \alpha g((\nabla_{X}A)Y, \xi)\xi - \alpha g(AY, \phi AX) \xi \nonumber\\ & - \alpha \eta(Y) A \phi AX + g((\nabla_{Y}A)\xi, \xi)AX - \alpha g((\nabla_{Y}A)X, \xi)\xi \nonumber\\ & - \alpha g(AX, \phi AY) \xi - \alpha \eta(X) A \phi AY + \alpha (\nabla_{X}A)Y - \alpha \eta(Y) (\nabla_{X}A) \xi \nonumber\\ & + \alpha (\nabla_{Y}A)X - \alpha \eta(X) (\nabla_{Y}A) \xi =0. \end{align}
\begin{align} & -g(\phi AX, Y) \xi - \eta(Y) \phi AX -g(\phi AY, X) \xi - \eta(X) \phi AY + \eta(Y)A\phi X \nonumber\\ & + \eta(X) A \phi Y + (\xi \alpha) g(AX, Y) \xi - 2 \alpha (\xi \alpha) \eta(X) \eta(Y) \xi + \alpha^{2} \eta(Y) A \phi X \nonumber\\ & + \alpha^{2} \eta(X) A \phi Y + \alpha (\nabla_X A)Y + \alpha g(\phi X, Y)\xi + \alpha \eta(X) \phi Y + 2\alpha \eta(Y) \phi X \nonumber\\ & - \sum_{\nu=1}^{3} \Big [ g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} + 2\eta(Y) g(\phi_{\nu} \xi, AX) {{\xi}_{\nu}} + \eta_{\nu}(Y) \phi_{\nu} AX \nonumber\\ & +3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi + 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX \nonumber\\ &+ 3 \alpha \eta (X) g(\phi_{\nu} \xi, Y) {{\xi}_{\nu}} - 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX \nonumber\\ & \quad \quad \quad - 4 \eta_{\nu}(\xi)g(AX, Y) \phi_{\nu} \xi - 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y \nonumber\\ &+ g(\phi_{\nu} AY, X) {{\xi}_{\nu}} + 2\eta(X) g(\phi_{\nu} \xi, AY) {{\xi}_{\nu}} + \eta_{\nu}(X) \phi_{\nu} AY \nonumber\\ &+3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi + 3 \eta(X) \eta_{\nu}(AY) \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \nonumber\\ & + 3 \alpha \eta (Y) g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} - 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) AY \nonumber\\ & - 4 \eta_{\nu}(\xi)g(AY, X) \phi_{\nu} \xi - 2g(\phi_{\nu} \xi, AY) \phi_{\nu}\phi X \Big ] \nonumber\\ & + \sum_{\nu=1}^{3} \Big [ \eta_{\nu}(Y) A \phi_{\nu} X - 2\eta(X)\eta_{\nu}(Y) A \phi_{\nu} \xi + \eta_{\nu}(X) A \phi_{\nu} Y \nonumber\\ &+ 3g(\phi_{\nu} \xi, Y) A \phi_{\nu} \phi X - 3 \eta(X) g(\phi_{\nu} \xi, Y) A{{\xi}_{\nu}} \nonumber\\ &+ 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 3 \alpha g(\phi_{\nu} \xi, X) \eta_{\nu}(Y)\xi \nonumber\\ &+ 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) AY + 4 \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX \nonumber\\ &+ 2 g(\phi_{\nu}\phi X, Y) A \phi_{\nu} \xi + 4 g(AX, Y)\eta_{\nu}(\xi) \phi_{\nu} \xi \nonumber\\ &- 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) \phi_{\nu} \xi - 4 \alpha \eta(X) \eta(Y) \eta_{\nu}(\xi) \phi_{\nu} \xi \Big ] \nonumber\\ & + \alpha \sum_{\nu=1}^{3} \Big [ g(\phi_\nu X, Y) {{\xi}_{\nu}} + \eta_\nu(X) \phi_\nu Y + 2\eta_{\nu}(Y) \phi_\nu X - g(\phi_\nu\phi X, Y) \phi_{\nu} \xi\nonumber\\ & + g(\phi_{\nu} \xi, X) \phi \phi_\nu Y + \eta_\nu(\phi X)\eta_{\nu}(Y) \xi + \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi \Big ]\nonumber\\ & + g((\nabla_{X}A)\xi, \xi)AY - \alpha g((\nabla_{X}A)Y, \xi)\xi - \alpha g(AY, \phi AX) \xi \nonumber\\ & - \alpha \eta(Y) A \phi AX + g((\nabla_{Y}A)\xi, \xi)AX - \alpha g((\nabla_{Y}A)X, \xi)\xi \nonumber\\ & - \alpha g(AX, \phi AY) \xi - \alpha \eta(X) A \phi AY + \alpha (\nabla_{X}A)Y - \alpha \eta(Y) (\nabla_{X}A) \xi \nonumber\\ & + \alpha (\nabla_{Y}A)X - \alpha \eta(X) (\nabla_{Y}A) \xi =0. \end{align}On the other hand, by using the Codazzi equation (3.8) and (3.10) in the latter part of (4.4), we obtain
 \begin{align} & g((\nabla_{X}A)\xi, \xi)AY - \alpha g((\nabla_{X}A)Y, \xi)\xi - \alpha g(AY, \phi AX) \xi - \alpha \eta(Y) A \phi AX\nonumber\\ & + g((\nabla_{Y}A)\xi, \xi)AX - \alpha g((\nabla_{Y}A)X, \xi)\xi - \alpha g(AX, \phi AY) \xi - \alpha \eta(X) A \phi AY\nonumber\\ & + \alpha (\nabla_{X}A)Y + \alpha (\nabla_{Y}A)X - \alpha \eta(Y) (\nabla_{X}A) \xi - \alpha \eta(X) (\nabla_{Y}A) \xi\nonumber\\ & = (\xi \alpha) \eta(X) AY + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) AY - \alpha g(A\phi AX, Y) \xi \nonumber\\ & \quad - \alpha \eta(Y) A \phi AX -\alpha (\xi \alpha) \eta(X) \eta(Y)\xi - 4\alpha \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \eta(Y)\xi \nonumber\\ & \quad - \alpha^{2} g(\phi AX,Y) \xi + \alpha g(A \phi AX, Y) \xi + (\xi \alpha) \eta(Y) AX \nonumber\\ & \quad + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX + \alpha g(A\phi AX, Y) \xi \nonumber\\ & \quad - \alpha \eta(X) A \phi AY -\alpha (\xi \alpha) \eta(X) \eta(Y) \xi \nonumber\\ & \quad -4 \alpha \sum_{\nu=1}^{3} \eta_{\nu}(\xi) \eta(X) g(\phi_{\nu} \xi, Y) \xi - \alpha^{2} g(\phi AY,X)\xi + \alpha g(A \phi AY, X) \xi \nonumber\\ & \quad + 2 \alpha (\nabla_X A)Y + \alpha \eta(Y)\phi X - \alpha \eta(X)\phi Y - 2\alpha g(\phi Y,X)\xi \nonumber\\ & \quad+ \alpha \sum_{\nu=1}^{3} \big \{ \eta_\nu(Y)\phi_\nu X - \eta_\nu(X)\phi_\nu Y - 2g(\phi_\nu Y,X)\xi_\nu \eta_\nu(\phi Y)\phi_\nu\phi X \big \}\nonumber\\ & \quad + \alpha \sum_{\nu=1}^{3} \big \{ - \eta_\nu(\phi X)\phi_\nu\phi Y + \eta(Y)\eta_\nu(\phi X){{\xi}_{\nu}} - \eta(X)\eta_\nu(\phi Y)\xi_{\nu} \big \}\nonumber\\ & \quad-\alpha \eta(Y) \{(\xi \alpha) \eta(X) \xi + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \xi + \alpha \phi AX - A\phi AX \big \}\nonumber\\ & \quad-\alpha \eta(X) \{(\xi \alpha) \eta(Y) \xi + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) \xi + \alpha \phi AY - A\phi AY \big \}. \end{align}
\begin{align} & g((\nabla_{X}A)\xi, \xi)AY - \alpha g((\nabla_{X}A)Y, \xi)\xi - \alpha g(AY, \phi AX) \xi - \alpha \eta(Y) A \phi AX\nonumber\\ & + g((\nabla_{Y}A)\xi, \xi)AX - \alpha g((\nabla_{Y}A)X, \xi)\xi - \alpha g(AX, \phi AY) \xi - \alpha \eta(X) A \phi AY\nonumber\\ & + \alpha (\nabla_{X}A)Y + \alpha (\nabla_{Y}A)X - \alpha \eta(Y) (\nabla_{X}A) \xi - \alpha \eta(X) (\nabla_{Y}A) \xi\nonumber\\ & = (\xi \alpha) \eta(X) AY + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) AY - \alpha g(A\phi AX, Y) \xi \nonumber\\ & \quad - \alpha \eta(Y) A \phi AX -\alpha (\xi \alpha) \eta(X) \eta(Y)\xi - 4\alpha \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \eta(Y)\xi \nonumber\\ & \quad - \alpha^{2} g(\phi AX,Y) \xi + \alpha g(A \phi AX, Y) \xi + (\xi \alpha) \eta(Y) AX \nonumber\\ & \quad + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) AX + \alpha g(A\phi AX, Y) \xi \nonumber\\ & \quad - \alpha \eta(X) A \phi AY -\alpha (\xi \alpha) \eta(X) \eta(Y) \xi \nonumber\\ & \quad -4 \alpha \sum_{\nu=1}^{3} \eta_{\nu}(\xi) \eta(X) g(\phi_{\nu} \xi, Y) \xi - \alpha^{2} g(\phi AY,X)\xi + \alpha g(A \phi AY, X) \xi \nonumber\\ & \quad + 2 \alpha (\nabla_X A)Y + \alpha \eta(Y)\phi X - \alpha \eta(X)\phi Y - 2\alpha g(\phi Y,X)\xi \nonumber\\ & \quad+ \alpha \sum_{\nu=1}^{3} \big \{ \eta_\nu(Y)\phi_\nu X - \eta_\nu(X)\phi_\nu Y - 2g(\phi_\nu Y,X)\xi_\nu \eta_\nu(\phi Y)\phi_\nu\phi X \big \}\nonumber\\ & \quad + \alpha \sum_{\nu=1}^{3} \big \{ - \eta_\nu(\phi X)\phi_\nu\phi Y + \eta(Y)\eta_\nu(\phi X){{\xi}_{\nu}} - \eta(X)\eta_\nu(\phi Y)\xi_{\nu} \big \}\nonumber\\ & \quad-\alpha \eta(Y) \{(\xi \alpha) \eta(X) \xi + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \xi + \alpha \phi AX - A\phi AX \big \}\nonumber\\ & \quad-\alpha \eta(X) \{(\xi \alpha) \eta(Y) \xi + 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) g(\phi_{\nu} \xi, Y) \xi + \alpha \phi AY - A\phi AY \big \}. \end{align} From now on, we want to prove that the normal vector field ![]() $N$ of a Hopf real hypersurface
$N$ of a Hopf real hypersurface ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ is singular. Then by the meaning of singularity mentioned in the introduction, we see that either
${G_2({\mathbb {C}}^{m+2})}$ is singular. Then by the meaning of singularity mentioned in the introduction, we see that either ![]() $\xi \in \mathcal {Q}$ or
$\xi \in \mathcal {Q}$ or ![]() $\xi \in {{\mathcal {Q}}^{\bot }}$ where
$\xi \in {{\mathcal {Q}}^{\bot }}$ where ![]() $\mathcal {Q}$ is the maximal quaternionic subbundle of
$\mathcal {Q}$ is the maximal quaternionic subbundle of ![]() $TM = \mathcal {Q} \oplus {{\mathcal {Q}}^{\bot }}$. In order to do this, we may put the Reeb vector field
$TM = \mathcal {Q} \oplus {{\mathcal {Q}}^{\bot }}$. In order to do this, we may put the Reeb vector field ![]() $\xi$ as follows:
$\xi$ as follows:
for unit vector fields ![]() ${X_{0}} \in \mathcal {Q}$ and
${X_{0}} \in \mathcal {Q}$ and ![]() ${{\xi }_1} \in {{\mathcal {Q}}^{\bot }}$ with
${{\xi }_1} \in {{\mathcal {Q}}^{\bot }}$ with ![]() $\eta ({X_{0}}) \eta ({{\xi }_1}) \neq 0$. By using the notation (*) we obtain that the Reeb function
$\eta ({X_{0}}) \eta ({{\xi }_1}) \neq 0$. By using the notation (*) we obtain that the Reeb function ![]() $\alpha$ is constant along the direction of
$\alpha$ is constant along the direction of ![]() $\xi$ if and only if the distribution
$\xi$ if and only if the distribution ![]() $\mathcal {Q}$- or the
$\mathcal {Q}$- or the ![]() $\mathcal {Q}^{\bot }$-component of the structure vector field
$\mathcal {Q}^{\bot }$-component of the structure vector field ![]() $\xi$ is invariant by the shape operator, that is
$\xi$ is invariant by the shape operator, that is ![]() $A {X_{0}} = \alpha {X_{0}}$ and
$A {X_{0}} = \alpha {X_{0}}$ and ![]() $A {{\xi }_1} = \alpha {{\xi }_1}$ (see [Reference Jeong, Machado, Pérez and Suh13, Reference Lee and Suh18]). From this fact, we obtain the following useful formulas for Hopf real hypersurfaces in
$A {{\xi }_1} = \alpha {{\xi }_1}$ (see [Reference Jeong, Machado, Pérez and Suh13, Reference Lee and Suh18]). From this fact, we obtain the following useful formulas for Hopf real hypersurfaces in ![]() ${G_2({\mathbb {C}}^{m+2})}$.
${G_2({\mathbb {C}}^{m+2})}$.
Lemma 4.1 Let ![]() $M$ be a Hopf real hypersurface with non-vanishing geodesic Reeb flow in
$M$ be a Hopf real hypersurface with non-vanishing geodesic Reeb flow in ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. If the distribution
$m \geq 3$. If the distribution ![]() $\mathcal {Q}$ or
$\mathcal {Q}$ or ![]() $\mathcal {Q}^{\bot }$ component of the structure vector field
$\mathcal {Q}^{\bot }$ component of the structure vector field ![]() $\xi$ is invariant by the shape operator, then the following formulas hold:
$\xi$ is invariant by the shape operator, then the following formulas hold:
1.
 $A \phi {X_{0}} = \mu \phi {X_{0}}$,
$A \phi {X_{0}} = \mu \phi {X_{0}}$,2.
 $A \phi {{\xi }_1} = \mu \phi {{\xi }_1}$,
$A \phi {{\xi }_1} = \mu \phi {{\xi }_1}$,3.
 $A \phi _{1} {X_{0}} = \mu \phi _{1} {X_{0}}$
$A \phi _{1} {X_{0}} = \mu \phi _{1} {X_{0}}$
where the function ![]() $\mu$ is given by
$\mu$ is given by ![]() $\mu = ({\alpha ^{2}+ 4 \eta ^{2}({X_{0}})}/{\alpha })$.
$\mu = ({\alpha ^{2}+ 4 \eta ^{2}({X_{0}})}/{\alpha })$.
Proof. Putting ![]() $X = {X_{0}}$ in (3.11) and using
$X = {X_{0}}$ in (3.11) and using ![]() $A{X_{0}} = \alpha {X_{0}}$, it yields
$A{X_{0}} = \alpha {X_{0}}$, it yields
where we have used ![]() $g(\phi _{\nu } \xi , {X_{0}}) =0$ for
$g(\phi _{\nu } \xi , {X_{0}}) =0$ for ![]() $\nu =1,2,3$ and
$\nu =1,2,3$ and ![]() $\eta _{2}(\xi ) = \eta _{3}(\xi )=0$.
$\eta _{2}(\xi ) = \eta _{3}(\xi )=0$.
On the other hand, by (*) we obtain
In addition, from (*) and ![]() $\phi _{1} \xi = \phi _{1} \xi$ we have
$\phi _{1} \xi = \phi _{1} \xi$ we have
 \begin{equation*} \begin{split} 0 = \phi \xi & = \eta({X_{0}}) \phi {X_{0}} + \eta({{\xi}_1}) \phi {{\xi}_1} \\ & = \eta({X_{0}}) \phi {X_{0}} + \eta({{\xi}_1}) \phi_{1} \xi \\ & = \eta({X_{0}}) \phi {X_{0}} + \eta({{\xi}_1}) \eta({X_{0}}) \phi_{1} {X_{0}}, \end{split} \end{equation*}
\begin{equation*} \begin{split} 0 = \phi \xi & = \eta({X_{0}}) \phi {X_{0}} + \eta({{\xi}_1}) \phi {{\xi}_1} \\ & = \eta({X_{0}}) \phi {X_{0}} + \eta({{\xi}_1}) \phi_{1} \xi \\ & = \eta({X_{0}}) \phi {X_{0}} + \eta({{\xi}_1}) \eta({X_{0}}) \phi_{1} {X_{0}}, \end{split} \end{equation*}which means
because of ![]() $\eta ({X_{0}}) \eta ({{\xi }_1})\neq 0$. Substituting (4.7) and (4.8) to (4.6), we get
$\eta ({X_{0}}) \eta ({{\xi }_1})\neq 0$. Substituting (4.7) and (4.8) to (4.6), we get
Since ![]() $M$ has non-vanishing geodesic Reeb flow, we see that the vector field
$M$ has non-vanishing geodesic Reeb flow, we see that the vector field ![]() $\phi {X_{0}}$ is principal with corresponding principal curvature
$\phi {X_{0}}$ is principal with corresponding principal curvature ![]() $\mu = ({\alpha ^{2}+ 4 \eta ^{2}({X_{0}})}/{\alpha })$.
$\mu = ({\alpha ^{2}+ 4 \eta ^{2}({X_{0}})}/{\alpha })$.
Similarly, using (4.7) and (4.8), together with ![]() $\eta ({X_{0}}) \eta ({{\xi }_1}) \neq 0$, the formula (4.6) gives (b) and (c).
$\eta ({X_{0}}) \eta ({{\xi }_1}) \neq 0$, the formula (4.6) gives (b) and (c).
When the Reeb function ![]() $\alpha$ is vanishing, Pérez and Suh gave the following
$\alpha$ is vanishing, Pérez and Suh gave the following
Lemma B [Reference Pérez and Suh27]
Let ![]() $M$ be a Hopf real hypersurface in
$M$ be a Hopf real hypersurface in ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. If
$m \geq 3$. If ![]() $M$ has vanishing geodesic Reeb flow, then the unit normal vector field
$M$ has vanishing geodesic Reeb flow, then the unit normal vector field ![]() $N$ of
$N$ of ![]() $M$ is singular, that is, either
$M$ is singular, that is, either ![]() $\xi \in \mathcal {Q}$ or
$\xi \in \mathcal {Q}$ or ![]() $\xi \in \mathcal {Q}^{\bot }$.
$\xi \in \mathcal {Q}^{\bot }$.
Remark 4.2 By using the method in the proof of lemma ![]() ${\rm B}$, we can assert that if
${\rm B}$, we can assert that if ![]() $M$ is a Hopf real hypersurface with constant Reeb curvature, then the unit normal vector field
$M$ is a Hopf real hypersurface with constant Reeb curvature, then the unit normal vector field ![]() $N$ of
$N$ of ![]() $M$ is singular. In fact, since
$M$ is singular. In fact, since ![]() $M$ has constant Reeb function, (3.10) becomes
$M$ has constant Reeb function, (3.10) becomes
 \[ 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) \phi_{\nu} \xi=0 \]
\[ 4 \sum_{\nu=1}^{3} \eta_{\nu}(\xi) \phi_{\nu} \xi=0 \]
By using (*), this equation yields ![]() $\eta ({{\xi }_1}) \phi _{1} \xi =0$. From our assumption of
$\eta ({{\xi }_1}) \phi _{1} \xi =0$. From our assumption of ![]() $\eta (X)\eta ({{\xi }_1}) \neq 0$ and (4.7), it leads to
$\eta (X)\eta ({{\xi }_1}) \neq 0$ and (4.7), it leads to ![]() $\phi _{1} {X_{0}} =0$. Taking the inner product with
$\phi _{1} {X_{0}} =0$. Taking the inner product with ![]() $\phi _{1} {X_{0}}$, it implies
$\phi _{1} {X_{0}}$, it implies
which gives us a contradiction.
By using lemma ![]() ${\rm B}$, in the latter part of this section, we prove that the normal vector field
${\rm B}$, in the latter part of this section, we prove that the normal vector field ![]() $N$ of
$N$ of ![]() $M$ is singular, when a Hopf real hypersurface
$M$ is singular, when a Hopf real hypersurface ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$ has non-vanishing geodesic Reeb flow
${G_2({\mathbb {C}}^{m+2})}$ has non-vanishing geodesic Reeb flow ![]() $\alpha =g(A\xi , \xi )$.
$\alpha =g(A\xi , \xi )$.
Lemma 4.3 Let ![]() $M$ be a Hopf real hypersurface with non-vanishing geodesic Reeb flow in complex two-plane Grassmannians
$M$ be a Hopf real hypersurface with non-vanishing geodesic Reeb flow in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. If the structure Jacobi operator
$m \geq 3$. If the structure Jacobi operator ![]() ${R_{\xi }}$ of
${R_{\xi }}$ of ![]() $M$ is cyclic parallel, then the unit normal vector field
$M$ is cyclic parallel, then the unit normal vector field ![]() $N$ of
$N$ of ![]() $M$ is singular.
$M$ is singular.
Proof. In [Reference Lee and Loo16], Lee and Loo show that if ![]() $M$ is Hopf, then the Reeb function
$M$ is Hopf, then the Reeb function ![]() $\alpha$ is constant along the direction of structure vector field
$\alpha$ is constant along the direction of structure vector field ![]() $\xi$, that is,
$\xi$, that is, ![]() $\xi \alpha =0$. Then we see that the distribution
$\xi \alpha =0$. Then we see that the distribution ![]() $\mathcal {Q}$- and the
$\mathcal {Q}$- and the ![]() $\mathcal {Q}^{\bot }$-component of
$\mathcal {Q}^{\bot }$-component of ![]() $\xi$ are invariant by the shape operator
$\xi$ are invariant by the shape operator ![]() $A$, that is
$A$, that is ![]() $A{X_{0}} = \alpha {X_{0}}$ and
$A{X_{0}} = \alpha {X_{0}}$ and ![]() $A{{\xi }_1} = \alpha {{\xi }_1}$.
$A{{\xi }_1} = \alpha {{\xi }_1}$.
Bearing in mind of these facts, putting ![]() $X={X_{0}}$ and
$X={X_{0}}$ and ![]() $Y= {{\xi }_1}$ in (4.4) and using (4.5), we obtain
$Y= {{\xi }_1}$ in (4.4) and using (4.5), we obtain
 \begin{equation*} \begin{split} & \quad - \alpha \eta({X_{0}}) \phi {{\xi}_1} + \mu \eta({{\xi}_1}) \phi {X_{0}} + \mu \eta({X_{0}}) \phi {{\xi}_1} + 3\alpha (\nabla_{{X_{0}}} A){{\xi}_1} + 2\alpha \eta({{\xi}_1}) \phi {X_{0}} \\ & \quad -\alpha^{3} \eta({{\xi}_1}) \phi {X_{0}} + \mu \alpha^{2} \eta({{\xi}_1}) \phi {X_{0}} - \alpha^{3} \eta({X_{0}}) \phi {{\xi}_1} + \mu \alpha^{2} \eta({X_{0}}) \phi {{\xi}_1} \\ & \quad + \sum_{\nu=1}^{3} \Big [ \alpha \eta_{\nu}({{\xi}_1}) \phi_{\nu} {X_{0}} - 3 \alpha g(\phi_{\nu} {X_{0}}, \phi {{\xi}_1}) \phi_{\nu} \xi - 2 \alpha \eta({X_{0}}) \eta_{\nu}({{\xi}_1}) \phi_{\nu} \xi + \eta_{\nu}({{\xi}_1}) A \phi_{\nu} {X_{0}} \\ & \quad \quad \quad \quad - 2\eta({X_{0}})\eta_{\nu}({{\xi}_1}) A \phi_{\nu} \xi - 8 \alpha \eta({X_{0}}) \eta({{\xi}_1}) \eta_{\nu}(\xi) \phi_{\nu} \xi + \alpha \eta_\nu({{\xi}_1})\phi_\nu {X_{0}} \Big ] =0, \end{split} \end{equation*}
\begin{equation*} \begin{split} & \quad - \alpha \eta({X_{0}}) \phi {{\xi}_1} + \mu \eta({{\xi}_1}) \phi {X_{0}} + \mu \eta({X_{0}}) \phi {{\xi}_1} + 3\alpha (\nabla_{{X_{0}}} A){{\xi}_1} + 2\alpha \eta({{\xi}_1}) \phi {X_{0}} \\ & \quad -\alpha^{3} \eta({{\xi}_1}) \phi {X_{0}} + \mu \alpha^{2} \eta({{\xi}_1}) \phi {X_{0}} - \alpha^{3} \eta({X_{0}}) \phi {{\xi}_1} + \mu \alpha^{2} \eta({X_{0}}) \phi {{\xi}_1} \\ & \quad + \sum_{\nu=1}^{3} \Big [ \alpha \eta_{\nu}({{\xi}_1}) \phi_{\nu} {X_{0}} - 3 \alpha g(\phi_{\nu} {X_{0}}, \phi {{\xi}_1}) \phi_{\nu} \xi - 2 \alpha \eta({X_{0}}) \eta_{\nu}({{\xi}_1}) \phi_{\nu} \xi + \eta_{\nu}({{\xi}_1}) A \phi_{\nu} {X_{0}} \\ & \quad \quad \quad \quad - 2\eta({X_{0}})\eta_{\nu}({{\xi}_1}) A \phi_{\nu} \xi - 8 \alpha \eta({X_{0}}) \eta({{\xi}_1}) \eta_{\nu}(\xi) \phi_{\nu} \xi + \alpha \eta_\nu({{\xi}_1})\phi_\nu {X_{0}} \Big ] =0, \end{split} \end{equation*}
where we have used ![]() $g(\phi {{\xi }_1}, {X_{0}}) = - g(\phi {X_{0}}, {{\xi }_1})=0$ and
$g(\phi {{\xi }_1}, {X_{0}}) = - g(\phi {X_{0}}, {{\xi }_1})=0$ and
for all ![]() $\nu =1,2,3$. Since
$\nu =1,2,3$. Since ![]() $\eta _{2}(\xi )=\eta _{3}(\xi )=0$, together with
$\eta _{2}(\xi )=\eta _{3}(\xi )=0$, together with ![]() $g(\phi _{1} {X_{0}}, \phi _{1} {X_{0}}) = 1$, this equation can be rearranged as
$g(\phi _{1} {X_{0}}, \phi _{1} {X_{0}}) = 1$, this equation can be rearranged as
 \begin{equation} \begin{split} & - \alpha \eta({X_{0}}) \phi {{\xi}_1} + \mu \eta({{\xi}_1}) \phi {X_{0}} + \mu \eta({X_{0}}) \phi {{\xi}_1} + 3\alpha (\nabla_{{X_{0}}} A){{\xi}_1} \\ & + 2\alpha \eta({{\xi}_1}) \phi {X_{0}} -\alpha^{3} \eta({{\xi}_1}) \phi {X_{0}} + \mu \alpha^{2} \eta({{\xi}_1}) \phi {X_{0}} \\ & - \alpha^{3} \eta({X_{0}}) \phi {{\xi}_1} + \mu \alpha^{2} \eta({X_{0}}) \phi {{\xi}_1} + 2 \alpha \phi_{1} {X_{0}} - 5 \alpha \eta({X_{0}}) \phi \xi_{1}\\ & + \mu \phi_{1} {X_{0}} - 2\mu \eta({X_{0}}) \phi_{1} \xi - 8 \alpha \eta({X_{0}}) \big(\eta({{\xi}_1})\big)^{2} \phi_{1} \xi =0. \end{split} \end{equation}
\begin{equation} \begin{split} & - \alpha \eta({X_{0}}) \phi {{\xi}_1} + \mu \eta({{\xi}_1}) \phi {X_{0}} + \mu \eta({X_{0}}) \phi {{\xi}_1} + 3\alpha (\nabla_{{X_{0}}} A){{\xi}_1} \\ & + 2\alpha \eta({{\xi}_1}) \phi {X_{0}} -\alpha^{3} \eta({{\xi}_1}) \phi {X_{0}} + \mu \alpha^{2} \eta({{\xi}_1}) \phi {X_{0}} \\ & - \alpha^{3} \eta({X_{0}}) \phi {{\xi}_1} + \mu \alpha^{2} \eta({X_{0}}) \phi {{\xi}_1} + 2 \alpha \phi_{1} {X_{0}} - 5 \alpha \eta({X_{0}}) \phi \xi_{1}\\ & + \mu \phi_{1} {X_{0}} - 2\mu \eta({X_{0}}) \phi_{1} \xi - 8 \alpha \eta({X_{0}}) \big(\eta({{\xi}_1})\big)^{2} \phi_{1} \xi =0. \end{split} \end{equation}From (4.7) and (4.8), (4.9) becomes
 \begin{equation} \begin{split} & \eta^{2}({X_{0}}) \big \{ - 6\alpha - \mu - \alpha^{3} + \mu \alpha^{2} - 8 \alpha \eta^{2}({{\xi}_1}) \big\}\phi_{1} {X_{0}} \\ & \quad - \eta^{2}({{\xi}_1})\big \{ \mu + 2\alpha -\alpha^{3} + \mu \alpha^{2} \big \} \phi_{1} {X_{0}} \\ & \quad + ( 2 \alpha + \mu ) \phi_{1} {X_{0}} + 3\alpha (\nabla_{{X_{0}}} A){{\xi}_1} =0. \end{split} \end{equation}
\begin{equation} \begin{split} & \eta^{2}({X_{0}}) \big \{ - 6\alpha - \mu - \alpha^{3} + \mu \alpha^{2} - 8 \alpha \eta^{2}({{\xi}_1}) \big\}\phi_{1} {X_{0}} \\ & \quad - \eta^{2}({{\xi}_1})\big \{ \mu + 2\alpha -\alpha^{3} + \mu \alpha^{2} \big \} \phi_{1} {X_{0}} \\ & \quad + ( 2 \alpha + \mu ) \phi_{1} {X_{0}} + 3\alpha (\nabla_{{X_{0}}} A){{\xi}_1} =0. \end{split} \end{equation} On the other hand, from (3.4) and (3.10), the assumption ![]() $A{{\xi }_1} = \alpha {{\xi }_1}$ yields
$A{{\xi }_1} = \alpha {{\xi }_1}$ yields
 \begin{equation*} \begin{split} (\nabla_{X}A)\xi_{1} & = (X \alpha) {{\xi}_1} + \alpha \nabla_{X}{{\xi}_1} - A(\nabla_{X}{{\xi}_1}) \\ & = 4\eta({{\xi}_1}) g(\phi_{1} \xi, X) {{\xi}_1} + \alpha \{ q_{3}(X) {{\xi}_2} - q_{2}(X) {{\xi}_3} + \phi_{1} AX\} \\ & \quad \ - q_{3}(X) A{{\xi}_2} + q_{2}(X) A{{\xi}_3} - A\phi_{1} AX \end{split} \end{equation*}
\begin{equation*} \begin{split} (\nabla_{X}A)\xi_{1} & = (X \alpha) {{\xi}_1} + \alpha \nabla_{X}{{\xi}_1} - A(\nabla_{X}{{\xi}_1}) \\ & = 4\eta({{\xi}_1}) g(\phi_{1} \xi, X) {{\xi}_1} + \alpha \{ q_{3}(X) {{\xi}_2} - q_{2}(X) {{\xi}_3} + \phi_{1} AX\} \\ & \quad \ - q_{3}(X) A{{\xi}_2} + q_{2}(X) A{{\xi}_3} - A\phi_{1} AX \end{split} \end{equation*}
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$. From this, taking the inner product with
$M$. From this, taking the inner product with ![]() $\phi _{1} {X_{0}}$ to (4.10) and (3.4), together with
$\phi _{1} {X_{0}}$ to (4.10) and (3.4), together with ![]() $\alpha \mu = \alpha ^{2}+ 4 \eta ^{2}({X_{0}})$, we get
$\alpha \mu = \alpha ^{2}+ 4 \eta ^{2}({X_{0}})$, we get
 \begin{equation} \begin{split} & \eta^{2}({X_{0}}) \big \{ - 14 \alpha - \mu + 12 \alpha \eta^{2}({X_{0}})\big\} - \eta^{2}({{\xi}_1})\big \{ \mu + 2\alpha + 4 \alpha \eta^{2}({X_{0}}) \big \} \\ & \quad + 2 \alpha + \mu -12 \alpha \eta^{2}({X_{0}})=0, \end{split} \end{equation}
\begin{equation} \begin{split} & \eta^{2}({X_{0}}) \big \{ - 14 \alpha - \mu + 12 \alpha \eta^{2}({X_{0}})\big\} - \eta^{2}({{\xi}_1})\big \{ \mu + 2\alpha + 4 \alpha \eta^{2}({X_{0}}) \big \} \\ & \quad + 2 \alpha + \mu -12 \alpha \eta^{2}({X_{0}})=0, \end{split} \end{equation}
where we have used ![]() $g(\phi _{1} {X_{0}}, \phi _{1} {X_{0}}) = 1$,
$g(\phi _{1} {X_{0}}, \phi _{1} {X_{0}}) = 1$, ![]() $\eta ^{2}({X_{0}}) + \eta ^{2}({{\xi }_1})=1$, and
$\eta ^{2}({X_{0}}) + \eta ^{2}({{\xi }_1})=1$, and
By using non-vanishing Reeb function ![]() $\alpha \neq 0$ and
$\alpha \neq 0$ and ![]() $\alpha \mu = \alpha ^{2}+ 4 \eta ^{2}({X_{0}})$, together with
$\alpha \mu = \alpha ^{2}+ 4 \eta ^{2}({X_{0}})$, together with ![]() $\eta ^{2}({{\xi }_1}) = 1 - \eta ^{2}({X_{0}})$, (4.11) becomes
$\eta ^{2}({{\xi }_1}) = 1 - \eta ^{2}({X_{0}})$, (4.11) becomes
By virtue of ![]() $\xi = \eta ({X_{0}}) {X_{0}} + \eta ({{\xi }_1}){{\xi }_1}$ in (*) for
$\xi = \eta ({X_{0}}) {X_{0}} + \eta ({{\xi }_1}){{\xi }_1}$ in (*) for ![]() $\eta ({X_{0}})\eta ({{\xi }_1}) \neq 0$, and our assumption of non-vanishing geodesic Reeb flow, that is,
$\eta ({X_{0}})\eta ({{\xi }_1}) \neq 0$, and our assumption of non-vanishing geodesic Reeb flow, that is, ![]() $\alpha \neq 0$, (4.12) implies that
$\alpha \neq 0$, (4.12) implies that ![]() $\eta ^{2} ({X_{0}}) = \frac {7}{4}$. Since the structure vector field
$\eta ^{2} ({X_{0}}) = \frac {7}{4}$. Since the structure vector field ![]() $\xi$ is unit, we should have
$\xi$ is unit, we should have ![]() $\eta ^{2}({X_{0}})+ \eta ^{2}({{\xi }_1}) =1$. From these facts, we obtain
$\eta ^{2}({X_{0}})+ \eta ^{2}({{\xi }_1}) =1$. From these facts, we obtain ![]() $\eta ^{2}({{\xi }_1}) =~- \frac {3}{4}$. It makes a contradiction. This means that either
$\eta ^{2}({{\xi }_1}) =~- \frac {3}{4}$. It makes a contradiction. This means that either ![]() $\xi =\eta ({X_{0}}){X_{0}} = \pm {X_{0}} \in \mathcal {Q}$ or
$\xi =\eta ({X_{0}}){X_{0}} = \pm {X_{0}} \in \mathcal {Q}$ or ![]() $\xi =\eta ({{\xi }_1}){{\xi }_1} = \pm {{\xi }_1} \in {{\mathcal {Q}}^{\bot }}$, which gives the unit normal vector field
$\xi =\eta ({{\xi }_1}){{\xi }_1} = \pm {{\xi }_1} \in {{\mathcal {Q}}^{\bot }}$, which gives the unit normal vector field ![]() $N$ is singular.
$N$ is singular.
Summing up lemmas ![]() ${\rm B}$ and 4.3, we assert that our theorem 1 in the introduction.
${\rm B}$ and 4.3, we assert that our theorem 1 in the introduction.
5. Cyclic parallel structure Jacobi operator for  $JN \in \mathcal {J} N$
$JN \in \mathcal {J} N$
Hereafter, let ![]() $M$ be a Hopf real hypersurface with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians
$M$ be a Hopf real hypersurface with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$ for
${G_2({\mathbb {C}}^{m+2})}$ for ![]() $m \geq 3$. Then by theorem 1, our discussions can be divided into two cases accordingly as the Reeb vector field
$m \geq 3$. Then by theorem 1, our discussions can be divided into two cases accordingly as the Reeb vector field ![]() $\xi \in {{\mathcal {Q}}^{\bot }}$ or
$\xi \in {{\mathcal {Q}}^{\bot }}$ or ![]() $\xi \in \mathcal {Q}$.
$\xi \in \mathcal {Q}$.
In this section, we consider the case of ![]() $\xi \in {{\mathcal {Q}}^{\bot }}$ (i.e.
$\xi \in {{\mathcal {Q}}^{\bot }}$ (i.e. ![]() $JN \in \mathcal {J} N$ where
$JN \in \mathcal {J} N$ where ![]() $N$ is a unit normal vector field on
$N$ is a unit normal vector field on ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$). Since
$m \geq 3$). Since ![]() ${{\mathcal {Q}}^{\bot }}$ is 3-dimensional distribution defined by
${{\mathcal {Q}}^{\bot }}$ is 3-dimensional distribution defined by ![]() ${{\mathcal {Q}}^{\bot }} = \mathrm {span}\{{{\xi }_1}, {{\xi }_2}, {{\xi }_3} \}$, we may put
${{\mathcal {Q}}^{\bot }} = \mathrm {span}\{{{\xi }_1}, {{\xi }_2}, {{\xi }_3} \}$, we may put ![]() $\xi = {{\xi }_1}$. From this, we give an important lemma as follows.
$\xi = {{\xi }_1}$. From this, we give an important lemma as follows.
Lemma 5.1 Let ![]() $M$ be a real hypersurface in complex two-plane Grassmannians
$M$ be a real hypersurface in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. Let
$m \geq 3$. Let ![]() $J_{1} \in \mathcal {J}$ be the almost Hermitian structure such that
$J_{1} \in \mathcal {J}$ be the almost Hermitian structure such that ![]() $JN = J_{1}N$ (or
$JN = J_{1}N$ (or ![]() $\xi = {{\xi }_1})$. Then we obtain
$\xi = {{\xi }_1})$. Then we obtain
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$.
$M$.
Proof. Differentiating ![]() $\xi = {{\xi }_1}$ along any vector field
$\xi = {{\xi }_1}$ along any vector field ![]() $X \in TM$ and using (3.4), we obtain
$X \in TM$ and using (3.4), we obtain
Taking the inner product of (5.1) with ![]() ${{\xi }_2}$ and
${{\xi }_2}$ and ![]() ${{\xi }_3}$, we obtain
${{\xi }_3}$, we obtain
and
respectively. It follows that
From this, (5.1) becomes
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$. Moreover, taking the symmetric part of (5.2) we obtain
$M$. Moreover, taking the symmetric part of (5.2) we obtain
Then, by virtue of lemma 5.1, we prove the following
Lemma 5.2 Let ![]() $M$ be a Hopf hypersurface with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians
$M$ be a Hopf hypersurface with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m\geq 3$. If the Reeb vector field
$m\geq 3$. If the Reeb vector field ![]() $\xi$ belongs to
$\xi$ belongs to ![]() ${{\mathcal {Q}}^{\bot }}$ (i.e.
${{\mathcal {Q}}^{\bot }}$ (i.e. ![]() $\xi ={{\xi }_1}$), then the distribution
$\xi ={{\xi }_1}$), then the distribution ![]() ${{\mathcal {Q}}^{\bot }}$ is invariant by the shape operator
${{\mathcal {Q}}^{\bot }}$ is invariant by the shape operator ![]() $A$ of
$A$ of ![]() $M$, that is,
$M$, that is, ![]() $g(A\mathcal {Q}, {{\mathcal {Q}}^{\bot }})=0$.
$g(A\mathcal {Q}, {{\mathcal {Q}}^{\bot }})=0$.
Proof. By (3.10) we obtain ![]() $X \alpha = (\xi \alpha )\eta (X)$ for any
$X \alpha = (\xi \alpha )\eta (X)$ for any ![]() $X \in TM$, when the Reeb vector field
$X \in TM$, when the Reeb vector field ![]() $\xi$ belongs to the distribution
$\xi$ belongs to the distribution ![]() $\mathcal {Q}$. From this and taking the inner product of (4.4) with
$\mathcal {Q}$. From this and taking the inner product of (4.4) with ![]() $\xi$, we have
$\xi$, we have
 \begin{equation*} \begin{split} & -g(\phi AX, Y) + g(A \phi X, Y) + (\xi \alpha) g(AX, Y) - \alpha (\xi \alpha) \eta(X) \eta(Y)+ 3 \alpha^{2} g(\phi AX, Y) \\ & - \alpha g(A\phi AX, Y) + 3\alpha g(\phi X, Y) +\alpha^{2} g(A \phi X, Y)-\alpha^{2} g(\phi AX,Y) \\ & + \sum_{\nu=1}^{3} \Big [ -\eta_{\nu}(\xi) g(\phi_{\nu} AX, Y) - g(\phi_{\nu} \xi, AX)\eta_{\nu}(Y) - 3 g(AX,{{\xi}_{\nu}})g(\phi_{\nu} \xi, Y)\\ & \quad \quad \quad + 4 \alpha \eta_{\nu}(\xi) \eta(X) g(\phi_{\nu} \xi, Y)+ \eta_{\nu}(\xi) g(A \phi_{\nu} X, Y) - \eta_{\nu}(X) g(\phi_{\nu} \xi, AY) \\ & \quad \quad \quad - 3g(\phi_{\nu} \xi, X)g({{\xi}_{\nu}}, AY)+ 4 \alpha \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \eta(Y) \\ & \quad \quad \quad - 9 \alpha g(\phi_{\nu} \xi, X)\eta_{\nu}(Y) - 3 \alpha \eta_{\nu}(X) g(\phi_{\nu} \xi, Y )+ 3 \alpha \eta_{\nu}(\xi) g(\phi_\nu X, Y) \Big ] =0, \end{split} \end{equation*}
\begin{equation*} \begin{split} & -g(\phi AX, Y) + g(A \phi X, Y) + (\xi \alpha) g(AX, Y) - \alpha (\xi \alpha) \eta(X) \eta(Y)+ 3 \alpha^{2} g(\phi AX, Y) \\ & - \alpha g(A\phi AX, Y) + 3\alpha g(\phi X, Y) +\alpha^{2} g(A \phi X, Y)-\alpha^{2} g(\phi AX,Y) \\ & + \sum_{\nu=1}^{3} \Big [ -\eta_{\nu}(\xi) g(\phi_{\nu} AX, Y) - g(\phi_{\nu} \xi, AX)\eta_{\nu}(Y) - 3 g(AX,{{\xi}_{\nu}})g(\phi_{\nu} \xi, Y)\\ & \quad \quad \quad + 4 \alpha \eta_{\nu}(\xi) \eta(X) g(\phi_{\nu} \xi, Y)+ \eta_{\nu}(\xi) g(A \phi_{\nu} X, Y) - \eta_{\nu}(X) g(\phi_{\nu} \xi, AY) \\ & \quad \quad \quad - 3g(\phi_{\nu} \xi, X)g({{\xi}_{\nu}}, AY)+ 4 \alpha \eta_{\nu}(\xi) g(\phi_{\nu} \xi, X) \eta(Y) \\ & \quad \quad \quad - 9 \alpha g(\phi_{\nu} \xi, X)\eta_{\nu}(Y) - 3 \alpha \eta_{\nu}(X) g(\phi_{\nu} \xi, Y )+ 3 \alpha \eta_{\nu}(\xi) g(\phi_\nu X, Y) \Big ] =0, \end{split} \end{equation*}where we have used
and
for any tangent vector fields ![]() $X$ and
$X$ and ![]() $Y$ on
$Y$ on ![]() $M$.
$M$.
On the other hand, from the assumption ![]() $\xi = {{\xi }_1} \in {{\mathcal {Q}}^{\bot }}$ we get
$\xi = {{\xi }_1} \in {{\mathcal {Q}}^{\bot }}$ we get ![]() $\phi _{2} \xi = \phi _{2} {{\xi }_1} = -{{\xi }_3}$ and
$\phi _{2} \xi = \phi _{2} {{\xi }_1} = -{{\xi }_3}$ and ![]() $\phi _{3} \xi = \phi _{3} {{\xi }_1} = {{\xi }_2}$. By using these formulas into the preceding equation, we get
$\phi _{3} \xi = \phi _{3} {{\xi }_1} = {{\xi }_2}$. By using these formulas into the preceding equation, we get
 \begin{equation} \begin{split} & -g(\phi AX, Y) + g(A \phi X, Y) + (\xi \alpha) g(AX, Y) - \alpha (\xi \alpha) \eta(X) \eta(Y)\\ & + 2 \alpha^{2} g(\phi AX, Y) - \alpha g(A\phi AX, Y) + 3\alpha g(\phi X, Y) +\alpha^{2} g(A \phi X, Y) \\ & -g(\phi_{1} AX, Y) - 2 \eta_{3}(AX) \eta_{2}(Y) + 2 \eta_{2}(AX) \eta_{3}(Y) \\ & + g(A\phi_{1} X, Y) - 2 \eta_{2}(X) g(A{{\xi}_3}, Y) + 2 \eta_{3}(X) g(A{{\xi}_2}, Y) \\ & + 6\alpha \eta_{3}(X)\eta_{2}(Y) - 6\alpha \eta_{2}(X) \eta_{3}(Y) + 3 \alpha g(\phi_{1}X, Y) =0. \end{split} \end{equation}
\begin{equation} \begin{split} & -g(\phi AX, Y) + g(A \phi X, Y) + (\xi \alpha) g(AX, Y) - \alpha (\xi \alpha) \eta(X) \eta(Y)\\ & + 2 \alpha^{2} g(\phi AX, Y) - \alpha g(A\phi AX, Y) + 3\alpha g(\phi X, Y) +\alpha^{2} g(A \phi X, Y) \\ & -g(\phi_{1} AX, Y) - 2 \eta_{3}(AX) \eta_{2}(Y) + 2 \eta_{2}(AX) \eta_{3}(Y) \\ & + g(A\phi_{1} X, Y) - 2 \eta_{2}(X) g(A{{\xi}_3}, Y) + 2 \eta_{3}(X) g(A{{\xi}_2}, Y) \\ & + 6\alpha \eta_{3}(X)\eta_{2}(Y) - 6\alpha \eta_{2}(X) \eta_{3}(Y) + 3 \alpha g(\phi_{1}X, Y) =0. \end{split} \end{equation}
Deleting ![]() $Y$ from (5.4), we get
$Y$ from (5.4), we get
 \begin{equation} \begin{split} & - \phi AX + A \phi X + (\xi \alpha) AX - \alpha (\xi \alpha) \eta(X) \xi + 2 \alpha^{2} \phi AX - \alpha A\phi AX +\alpha^{2} A \phi X \\ & -\phi_{1} AX - 2 \eta_{3}(AX) {{\xi}_2} + 2 \eta_{2}(AX) \xi_{3} + A\phi_{1} X - 2 \eta_{2}(X) A{{\xi}_3} + 2 \eta_{3}(X) A{{\xi}_2} \\ & + 3\alpha \big \{ 2\eta_{3}(X)\xi_{2} - 2\eta_{2}(X) \xi_{3} + \phi X + \phi_{1}X \big \}=0 \end{split} \end{equation}
\begin{equation} \begin{split} & - \phi AX + A \phi X + (\xi \alpha) AX - \alpha (\xi \alpha) \eta(X) \xi + 2 \alpha^{2} \phi AX - \alpha A\phi AX +\alpha^{2} A \phi X \\ & -\phi_{1} AX - 2 \eta_{3}(AX) {{\xi}_2} + 2 \eta_{2}(AX) \xi_{3} + A\phi_{1} X - 2 \eta_{2}(X) A{{\xi}_3} + 2 \eta_{3}(X) A{{\xi}_2} \\ & + 3\alpha \big \{ 2\eta_{3}(X)\xi_{2} - 2\eta_{2}(X) \xi_{3} + \phi X + \phi_{1}X \big \}=0 \end{split} \end{equation}
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$.
$M$.
On the other hand, when ![]() $\xi ={{\xi }_1} \in \mathcal {Q}$, (3.11) gives us
$\xi ={{\xi }_1} \in \mathcal {Q}$, (3.11) gives us
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$. Substituting (5.6) into (5.5), it follows that
$M$. Substituting (5.6) into (5.5), it follows that
 \begin{equation*} \begin{split} & -\phi AX + A \phi X + (\xi \alpha) AX - \alpha (\xi \alpha) \eta(X) \xi + 2 \alpha^{2} \phi AX - \alpha A\phi AX +\alpha^{2} A \phi X \\ & -\phi_{1} AX - 2 \eta_{3}(AX) {{\xi}_2} + 2 \eta_{2}(AX) \xi_{3} + A\phi_{1} X - 2 \eta_{2}(X) A{{\xi}_3} + 2 \eta_{3}(X) A{{\xi}_2} \\ & + 3\alpha \big \{ A\phi AX - \frac{\alpha}{2} A \phi X - \frac{\alpha}{2} \phi AX \big \}=0, \end{split} \end{equation*}
\begin{equation*} \begin{split} & -\phi AX + A \phi X + (\xi \alpha) AX - \alpha (\xi \alpha) \eta(X) \xi + 2 \alpha^{2} \phi AX - \alpha A\phi AX +\alpha^{2} A \phi X \\ & -\phi_{1} AX - 2 \eta_{3}(AX) {{\xi}_2} + 2 \eta_{2}(AX) \xi_{3} + A\phi_{1} X - 2 \eta_{2}(X) A{{\xi}_3} + 2 \eta_{3}(X) A{{\xi}_2} \\ & + 3\alpha \big \{ A\phi AX - \frac{\alpha}{2} A \phi X - \frac{\alpha}{2} \phi AX \big \}=0, \end{split} \end{equation*}which implies
 \begin{equation} \begin{split} & ({-}2 + 7\alpha^{2}) \phi AX + (2- \alpha^{2}) A \phi X + 2(\xi \alpha) AX - 2\alpha (\xi \alpha) \eta(X) \xi \\ & \quad + 4 \alpha A\phi AX - 2 \big \{ \phi_{1} AX + 2 \eta_{3}(AX) {{\xi}_2} -2 \eta_{2}(AX) \xi_{3} \big \} \\ & \quad + 2 \big \{ A\phi_{1} X - 2 \eta_{2}(X) A{{\xi}_3} +2 \eta_{3}(X) A{{\xi}_2} \big \} =0 \end{split} \end{equation}
\begin{equation} \begin{split} & ({-}2 + 7\alpha^{2}) \phi AX + (2- \alpha^{2}) A \phi X + 2(\xi \alpha) AX - 2\alpha (\xi \alpha) \eta(X) \xi \\ & \quad + 4 \alpha A\phi AX - 2 \big \{ \phi_{1} AX + 2 \eta_{3}(AX) {{\xi}_2} -2 \eta_{2}(AX) \xi_{3} \big \} \\ & \quad + 2 \big \{ A\phi_{1} X - 2 \eta_{2}(X) A{{\xi}_3} +2 \eta_{3}(X) A{{\xi}_2} \big \} =0 \end{split} \end{equation}
for any ![]() $X \in TM$. Bearing in mind of (5.2) and (5.3), the above equation reduces to
$X \in TM$. Bearing in mind of (5.2) and (5.3), the above equation reduces to
and
respectively. Substituting (5.9) and (5.10) into (5.7), it becomes
 \begin{equation*} \begin{split} & ({-}2 + 7\alpha^{2}) \phi AX + (2- \alpha^{2}) A \phi X + 2(\xi \alpha) AX - 2\alpha (\xi \alpha) \eta(X) \xi + 4 \alpha A\phi AX \\ & - 2 \big \{ \phi_{1} AX + \phi AX - \phi_{1}AX \big \} + 2 \big \{ A\phi_{1} X - A \phi X + A \phi_{1}X \big \} =0, \end{split} \end{equation*}
\begin{equation*} \begin{split} & ({-}2 + 7\alpha^{2}) \phi AX + (2- \alpha^{2}) A \phi X + 2(\xi \alpha) AX - 2\alpha (\xi \alpha) \eta(X) \xi + 4 \alpha A\phi AX \\ & - 2 \big \{ \phi_{1} AX + \phi AX - \phi_{1}AX \big \} + 2 \big \{ A\phi_{1} X - A \phi X + A \phi_{1}X \big \} =0, \end{split} \end{equation*}which yields
Subtracting (5.11) from (5.8), we have ![]() $A \phi X = A \phi _{1} X$, which means that
$A \phi X = A \phi _{1} X$, which means that ![]() $\phi A X = \phi _{1} AX$ for any tangent vector field
$\phi A X = \phi _{1} AX$ for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$. From this, (5.2) becomes
$M$. From this, (5.2) becomes
for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$. Taking the inner product of (5.12) with
$M$. Taking the inner product of (5.12) with ![]() ${{\xi }_2}$ (resp.
${{\xi }_2}$ (resp. ![]() ${{\xi }_3}$), we get the following for any tangent vector field
${{\xi }_3}$), we get the following for any tangent vector field ![]() $X$ on
$X$ on ![]() $M$
$M$
which means that ![]() $g(A\mathcal {Q}, {{\mathcal {Q}}^{\bot }})=0$. It gives a complete proof of lemma 5.2.
$g(A\mathcal {Q}, {{\mathcal {Q}}^{\bot }})=0$. It gives a complete proof of lemma 5.2.
By theorem ![]() ${\rm A}$ and proposition
${\rm A}$ and proposition ![]() ${\rm A}$, lemma 5.2 assures that if a Hopf real hypersurface satisfies all of geometric conditions mentioned in lemma 5.2, then
${\rm A}$, lemma 5.2 assures that if a Hopf real hypersurface satisfies all of geometric conditions mentioned in lemma 5.2, then ![]() $M$ is locally congruent to an open part of the model spaces of type
$M$ is locally congruent to an open part of the model spaces of type ![]() $(\mathcal {T}_{A})$.
$(\mathcal {T}_{A})$.
From now on, we will check whether a real hypersurface of type ![]() $(\mathcal {T}_{A})$ satisfies our hypothesis given in lemma 5.2. By proposition A mentioned in §2, we see that such real hypersurface is Hopf and its normal vector field satisfies
$(\mathcal {T}_{A})$ satisfies our hypothesis given in lemma 5.2. By proposition A mentioned in §2, we see that such real hypersurface is Hopf and its normal vector field satisfies ![]() $JN \in \mathcal {J}N$.
$JN \in \mathcal {J}N$.
In the remaining part of this section, we want to check if the structure Jacobi operator ![]() ${R_{\xi }}$ for a model space of type
${R_{\xi }}$ for a model space of type ![]() $(\mathcal {T}_{A})$ satisfies the cyclic parallelism. In order to do this, we want to find some necessary and sufficient conditions for structure Jacobi operator
$(\mathcal {T}_{A})$ satisfies the cyclic parallelism. In order to do this, we want to find some necessary and sufficient conditions for structure Jacobi operator ![]() ${R_{\xi }}$ of a real hypersurface
${R_{\xi }}$ of a real hypersurface ![]() $(\mathcal {T}_{A})$ to be cyclic parallel according to each eigenspace including the vector
$(\mathcal {T}_{A})$ to be cyclic parallel according to each eigenspace including the vector ![]() $Y$.
$Y$.
From such a view point, first, we consider the following case.
Case A. ![]() $Y \in T_{\lambda }$
$Y \in T_{\lambda }$
In other words, from (4.4) and (4.5), together with (2.2), the structure Jacobi operator ![]() ${R_{\xi }}$ of a real hypersurface of type
${R_{\xi }}$ of a real hypersurface of type ![]() $(\mathcal {T}_{A})$ satisfies the following for any tangent vector field
$(\mathcal {T}_{A})$ satisfies the following for any tangent vector field ![]() $X \in T(\mathcal {T}_{A})$
$X \in T(\mathcal {T}_{A})$
 \begin{equation} \begin{split} & 3\alpha ( \lambda^{2}- \alpha \lambda -2 )g(\phi Y, X) \xi -2 (2 \alpha - \beta - \lambda) g(\phi_{2}Y, X) {{\xi}_2} \\ & \quad -2 (2 \alpha - \beta - \lambda) g(\phi_{3}Y, X) {{\xi}_3} -2 (2 \alpha - \beta - \lambda) \eta_{2}(X) \phi_{2}Y \\ & \quad -2 (2 \alpha - \beta - \lambda) \eta_{3}(X) \phi_{3}Y =0, \end{split} \end{equation}
\begin{equation} \begin{split} & 3\alpha ( \lambda^{2}- \alpha \lambda -2 )g(\phi Y, X) \xi -2 (2 \alpha - \beta - \lambda) g(\phi_{2}Y, X) {{\xi}_2} \\ & \quad -2 (2 \alpha - \beta - \lambda) g(\phi_{3}Y, X) {{\xi}_3} -2 (2 \alpha - \beta - \lambda) \eta_{2}(X) \phi_{2}Y \\ & \quad -2 (2 \alpha - \beta - \lambda) \eta_{3}(X) \phi_{3}Y =0, \end{split} \end{equation}
where ![]() $T(\mathcal {T}_{A})$ denotes a tangent space of type
$T(\mathcal {T}_{A})$ denotes a tangent space of type ![]() $(\mathcal {T}_{A})$ and we have used
$(\mathcal {T}_{A})$ and we have used ![]() $\phi \phi _{2} Y = \phi _{2} \phi Y = - \phi _{3}Y \in T_{\mu }$ and
$\phi \phi _{2} Y = \phi _{2} \phi Y = - \phi _{3}Y \in T_{\mu }$ and ![]() $\phi \phi _{3} Y = \phi _{3} \phi Y = \phi _{2}Y \in T_{\mu }$ for any
$\phi \phi _{3} Y = \phi _{3} \phi Y = \phi _{2}Y \in T_{\mu }$ for any ![]() $Y \in T_{\lambda }$.
$Y \in T_{\lambda }$.
From now on, we want to check a solution of the equation (5.14) to be satisfied for type ![]() $(\mathcal {T}_{A})$. In fact, the left side of (5.14) depends on the eigenspaces of
$(\mathcal {T}_{A})$. In fact, the left side of (5.14) depends on the eigenspaces of ![]() $(\mathcal {T}_{A})$ and is given as
$(\mathcal {T}_{A})$ and is given as
 \begin{equation*} \mathrm{Left\ side\ of\ } (5.14) = \left\{ \begin{array}{@{}ll} 0 & \mbox{for} \ X \in T_{\alpha}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{2}Y & \mbox{for} \ X ={{\xi}_2} \in T_{\beta}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{3}Y & \mbox{for} \ X={{\xi}_3} \in T_{\beta}, \\ 3\alpha ( \lambda^{2}- \alpha \lambda -2 )g(\phi Y, X) \xi & \mbox{for} \ X \in T_{\lambda}, \\ - 2 (2 \alpha - \beta - \lambda) g(\phi_{2}Y, X) ({{\xi}_2} + {{\xi}_3}) & \mbox{for} \ X \in T_{\mu} \\ \end{array}\right. \end{equation*}
\begin{equation*} \mathrm{Left\ side\ of\ } (5.14) = \left\{ \begin{array}{@{}ll} 0 & \mbox{for} \ X \in T_{\alpha}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{2}Y & \mbox{for} \ X ={{\xi}_2} \in T_{\beta}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{3}Y & \mbox{for} \ X={{\xi}_3} \in T_{\beta}, \\ 3\alpha ( \lambda^{2}- \alpha \lambda -2 )g(\phi Y, X) \xi & \mbox{for} \ X \in T_{\lambda}, \\ - 2 (2 \alpha - \beta - \lambda) g(\phi_{2}Y, X) ({{\xi}_2} + {{\xi}_3}) & \mbox{for} \ X \in T_{\mu} \\ \end{array}\right. \end{equation*} for ![]() $Y \in T_{\lambda }$. By using
$Y \in T_{\lambda }$. By using ![]() $\alpha = 2 \sqrt {2} \cot (2 \sqrt {2}r)=\sqrt {2}(\cot (\sqrt {2}r) - \tan (\sqrt {2}r))$ and
$\alpha = 2 \sqrt {2} \cot (2 \sqrt {2}r)=\sqrt {2}(\cot (\sqrt {2}r) - \tan (\sqrt {2}r))$ and ![]() $\lambda = - \sqrt {2} \tan (\sqrt {2}r)$ with
$\lambda = - \sqrt {2} \tan (\sqrt {2}r)$ with ![]() $r \in (0, ({\pi }/{2 \sqrt {2})})$, we get
$r \in (0, ({\pi }/{2 \sqrt {2})})$, we get ![]() $\lambda ^{2}- \alpha \lambda -2 =0$. From this, the previous formula follows
$\lambda ^{2}- \alpha \lambda -2 =0$. From this, the previous formula follows
 \begin{equation} \begin{split} & \mathrm{Left\ side\ of\ } (5.14) \\ & \quad \quad = \left\{ \begin{array}{@{}ll} 0 & \mbox{for} \ X \in T_{\alpha}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{2}Y & \mbox{for} \ X ={{\xi}_2} \in T_{\beta}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{3}Y & \mbox{for} \ X={{\xi}_3} \in T_{\beta}, \\ 0 & \mbox{for} \ X \in T_{\lambda}, \\ - 2 (2 \alpha - \beta - \lambda) g(\phi_{2}Y, X) ({{\xi}_2} + {{\xi}_3}) & \mbox{for} \ X \in T_{\mu} \end{array}\right. \end{split} \end{equation}
\begin{equation} \begin{split} & \mathrm{Left\ side\ of\ } (5.14) \\ & \quad \quad = \left\{ \begin{array}{@{}ll} 0 & \mbox{for} \ X \in T_{\alpha}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{2}Y & \mbox{for} \ X ={{\xi}_2} \in T_{\beta}, \\ - 2 (2 \alpha - \beta - \lambda) \phi_{3}Y & \mbox{for} \ X={{\xi}_3} \in T_{\beta}, \\ 0 & \mbox{for} \ X \in T_{\lambda}, \\ - 2 (2 \alpha - \beta - \lambda) g(\phi_{2}Y, X) ({{\xi}_2} + {{\xi}_3}) & \mbox{for} \ X \in T_{\mu} \end{array}\right. \end{split} \end{equation}
for ![]() $Y \in T_{\lambda }$.
$Y \in T_{\lambda }$.
Bearing in mind of proposition ![]() ${\rm A}$, if
${\rm A}$, if ![]() $r=({\pi }/{4\sqrt {2})}$, then
$r=({\pi }/{4\sqrt {2})}$, then ![]() $2 \alpha - \beta - \lambda =0$. Hence, when
$2 \alpha - \beta - \lambda =0$. Hence, when ![]() $Y \in T_{\lambda }$, the structure Jacobi operator
$Y \in T_{\lambda }$, the structure Jacobi operator ![]() ${R_{\xi }}$ is cyclic parallel if and only if the radius
${R_{\xi }}$ is cyclic parallel if and only if the radius ![]() $r$ of the tube
$r$ of the tube ![]() $(\mathcal {T}_{A})$ is
$(\mathcal {T}_{A})$ is ![]() $({\pi }/{4\sqrt {2})}$.
$({\pi }/{4\sqrt {2})}$.
Under these situations, we consider our problem for the other cases ![]() $Y \in T_{\alpha } \oplus T_{\beta } \oplus T_{\mu }$ as follows.
$Y \in T_{\alpha } \oplus T_{\beta } \oplus T_{\mu }$ as follows.
Case B. ![]() $Y \in T_{\alpha } \oplus T_{\beta } \oplus T_{\mu }$ where
$Y \in T_{\alpha } \oplus T_{\beta } \oplus T_{\mu }$ where ![]() $\alpha = \mu = 0$,
$\alpha = \mu = 0$, ![]() $\beta = \sqrt {2}$, and
$\beta = \sqrt {2}$, and ![]() $\lambda = - \sqrt {2}$
$\lambda = - \sqrt {2}$
By the affect of case ![]() ${\rm A}$ in
${\rm A}$ in ![]() $(\mathcal {T}_{A})$, we have seen that in order to be cyclic parallel for the structure Jacobi operator
$(\mathcal {T}_{A})$, we have seen that in order to be cyclic parallel for the structure Jacobi operator ![]() ${R_{\xi }}$ of
${R_{\xi }}$ of ![]() $(\mathcal {T}_{A})$, the radius
$(\mathcal {T}_{A})$, the radius ![]() $r$ of
$r$ of ![]() $(\mathcal {T}_{A})$ should satisfy
$(\mathcal {T}_{A})$ should satisfy ![]() $r=({\pi }/{4\sqrt {2})}$. From this fact, we obtain
$r=({\pi }/{4\sqrt {2})}$. From this fact, we obtain ![]() $\alpha = \mu = 0$,
$\alpha = \mu = 0$, ![]() $\beta = \sqrt {2}$, and
$\beta = \sqrt {2}$, and ![]() $\lambda = - \sqrt {2}$. Then, the left side of (4.4) becomes
$\lambda = - \sqrt {2}$. Then, the left side of (4.4) becomes
 \begin{equation} \begin{split} & \mathrm{Left\ side\ of\ } (4.4) \\ & ={-}g(\phi AX, Y) \xi - \eta(Y) \phi AX -g(\phi AY, X) \xi \\ & \quad - \eta(X) \phi AY + \eta(Y)A\phi X + \eta(X) A \phi Y \\ & \quad - \sum_{\nu=1}^{3} \Big [ g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} + 2\eta(Y) g(\phi_{\nu} \xi, AX) {{\xi}_{\nu}} + \eta_{\nu}(Y) \phi_{\nu} AX \\ & \quad + 3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi + 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi \\ & \quad - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX - 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y + \eta_{\nu}(X) \phi_{\nu} AY \\ & \quad - 2g(\phi_{\nu} \xi, AY) \phi_{\nu}\phi X + g(\phi_{\nu} AY, X) {{\xi}_{\nu}} + 2\eta(X) g(\phi_{\nu} \xi, AY) {{\xi}_{\nu}} \\ & \quad + 3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi + 3 \eta(X) \eta_{\nu}(AY) \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \\ & \quad - \eta_{\nu}(Y) A \phi_{\nu} X + 2\eta(X)\eta_{\nu}(Y) A \phi_{\nu} \xi - \eta_{\nu}(X) A \phi_{\nu} Y \\ & \quad - 3g(\phi_{\nu} \xi, Y) A \phi_{\nu} \phi X + 3 \eta(X) g(\phi_{\nu} \xi, Y) A{{\xi}_{\nu}} \\ & \quad - 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 2 g(\phi_{\nu}\phi X, Y) A \phi_{\nu} \xi \Big ] \end{split} \end{equation}
\begin{equation} \begin{split} & \mathrm{Left\ side\ of\ } (4.4) \\ & ={-}g(\phi AX, Y) \xi - \eta(Y) \phi AX -g(\phi AY, X) \xi \\ & \quad - \eta(X) \phi AY + \eta(Y)A\phi X + \eta(X) A \phi Y \\ & \quad - \sum_{\nu=1}^{3} \Big [ g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} + 2\eta(Y) g(\phi_{\nu} \xi, AX) {{\xi}_{\nu}} + \eta_{\nu}(Y) \phi_{\nu} AX \\ & \quad + 3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi + 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi \\ & \quad - 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX - 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y + \eta_{\nu}(X) \phi_{\nu} AY \\ & \quad - 2g(\phi_{\nu} \xi, AY) \phi_{\nu}\phi X + g(\phi_{\nu} AY, X) {{\xi}_{\nu}} + 2\eta(X) g(\phi_{\nu} \xi, AY) {{\xi}_{\nu}} \\ & \quad + 3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi + 3 \eta(X) \eta_{\nu}(AY) \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \\ & \quad - \eta_{\nu}(Y) A \phi_{\nu} X + 2\eta(X)\eta_{\nu}(Y) A \phi_{\nu} \xi - \eta_{\nu}(X) A \phi_{\nu} Y \\ & \quad - 3g(\phi_{\nu} \xi, Y) A \phi_{\nu} \phi X + 3 \eta(X) g(\phi_{\nu} \xi, Y) A{{\xi}_{\nu}} \\ & \quad - 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 2 g(\phi_{\nu}\phi X, Y) A \phi_{\nu} \xi \Big ] \end{split} \end{equation}
for any ![]() $X \in T(\mathcal {T}_{A})$ and
$X \in T(\mathcal {T}_{A})$ and ![]() $Y \in T_{\alpha } \oplus T_{\beta } \oplus T_{\mu }$.
$Y \in T_{\alpha } \oplus T_{\beta } \oplus T_{\mu }$.
Subcase B-1. ![]() $Y = \xi \in T_{\alpha }$ where
$Y = \xi \in T_{\alpha }$ where ![]() $\alpha =0$
$\alpha =0$
From this assumption, we get ![]() $A Y= A\xi =\alpha \xi =0$. Then, (5.16) becomes
$A Y= A\xi =\alpha \xi =0$. Then, (5.16) becomes
 \begin{equation} \begin{split} & - \phi AX + A\phi X - \sum_{\nu=1}^{3} \big \{ g(A\phi_{\nu} \xi, X) {{\xi}_{\nu}} + \eta_{\nu}(\xi) \phi_{\nu} AX + 3 g(A{{\xi}_{\nu}}, X) \phi_{\nu} \xi \big \} \\ & \quad + \sum_{\nu=1}^{3} \big \{ \eta_{\nu}(X) A \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, X) A {{\xi}_{\nu}} + \eta_{\nu}(\xi) A \phi_{\nu} X \big \}\\ & ={-} \phi AX + A\phi X - \phi_{1} AX + A \phi_{1} X,\end{split} \end{equation}
\begin{equation} \begin{split} & - \phi AX + A\phi X - \sum_{\nu=1}^{3} \big \{ g(A\phi_{\nu} \xi, X) {{\xi}_{\nu}} + \eta_{\nu}(\xi) \phi_{\nu} AX + 3 g(A{{\xi}_{\nu}}, X) \phi_{\nu} \xi \big \} \\ & \quad + \sum_{\nu=1}^{3} \big \{ \eta_{\nu}(X) A \phi_{\nu} \xi - 3g(\phi_{\nu} \xi, X) A {{\xi}_{\nu}} + \eta_{\nu}(\xi) A \phi_{\nu} X \big \}\\ & ={-} \phi AX + A\phi X - \phi_{1} AX + A \phi_{1} X,\end{split} \end{equation}
where we have used ![]() $\phi _{2}\xi = - {{\xi }_3}$,
$\phi _{2}\xi = - {{\xi }_3}$, ![]() $\phi _{3}\xi = {{\xi }_2}$, and
$\phi _{3}\xi = {{\xi }_2}$, and ![]() $\phi \phi _{\nu } \xi = \phi ^{2}{{\xi }_{\nu }} = - {{\xi }_{\nu }} + \eta ({{\xi }_{\nu }})\xi$. According to the composition of the eigenspaces for
$\phi \phi _{\nu } \xi = \phi ^{2}{{\xi }_{\nu }} = - {{\xi }_{\nu }} + \eta ({{\xi }_{\nu }})\xi$. According to the composition of the eigenspaces for ![]() $(\mathcal {T}_{A})$, we see that each eigenspace
$(\mathcal {T}_{A})$, we see that each eigenspace ![]() $T_{\sigma }$ of
$T_{\sigma }$ of ![]() $(\mathcal {T}_{A})$ is
$(\mathcal {T}_{A})$ is ![]() $\phi$-(or
$\phi$-(or ![]() $\phi _{1}$-)invariant, that is,
$\phi _{1}$-)invariant, that is, ![]() $\phi T_{\sigma } = \phi _{1} T_{\sigma } = T_{\sigma }$. From this, (5.17) vanishes on all eigenspaces of
$\phi T_{\sigma } = \phi _{1} T_{\sigma } = T_{\sigma }$. From this, (5.17) vanishes on all eigenspaces of ![]() $(\mathcal {T}_{A})$. So, this means that the structure Jacobi operator
$(\mathcal {T}_{A})$. So, this means that the structure Jacobi operator ![]() ${R_{\xi }}$ is cyclic parallel when
${R_{\xi }}$ is cyclic parallel when ![]() $Y \in T_{\alpha }$.
$Y \in T_{\alpha }$.
Subcase B-2. ![]() $Y \in T_{\beta }$ where
$Y \in T_{\beta }$ where ![]() $\beta = \sqrt {2}$
$\beta = \sqrt {2}$
Since ![]() $T_{\beta }=\mathrm {span}\{{{\xi }_2}, {{\xi }_3}\}$, we have the following two subcases.
$T_{\beta }=\mathrm {span}\{{{\xi }_2}, {{\xi }_3}\}$, we have the following two subcases.
•
 $Y ={{\xi }_2} \in T_{\beta }$
$Y ={{\xi }_2} \in T_{\beta }$Using
 $\alpha = 0$, (5.16) can be rearranged as
(5.18)for any eigenvector
$\alpha = 0$, (5.16) can be rearranged as
(5.18)for any eigenvector \begin{equation} \begin{split} & 6 \beta \eta_{3}(X) \xi + \beta\eta(X) {{\xi}_3} - \phi_{2} AX + 3 \phi_{3} \phi AX \\ & \quad + 2 \beta \phi_{3}\phi X + A\phi_{2} X + 3 A \phi_{3} \phi X \end{split} \end{equation}
\begin{equation} \begin{split} & 6 \beta \eta_{3}(X) \xi + \beta\eta(X) {{\xi}_3} - \phi_{2} AX + 3 \phi_{3} \phi AX \\ & \quad + 2 \beta \phi_{3}\phi X + A\phi_{2} X + 3 A \phi_{3} \phi X \end{split} \end{equation} $X$ on
$X$ on  $(\mathcal {T}_{A})$. It is well-known that for
$(\mathcal {T}_{A})$. It is well-known that for  $X \in T_{\lambda }$ (resp.
$X \in T_{\lambda }$ (resp.  $X \in T_{\mu }$), by the straightforward calculation with (3.2), we obtain
and
$X \in T_{\mu }$), by the straightforward calculation with (3.2), we obtain
and \begin{gather*} \phi_{2}\phi X \underset{X \in T_{\lambda}}= \phi_{2}\phi_{1}X \underset{3.2}{=} -\phi_{3}X \in T_{\mu} \\ \ \ (\mathrm{resp.}\ \phi_{2}\phi X \underset{X \in T_{\mu}}={-}\phi_{2}\phi_{1}X = \phi_{3}X \in T_{\lambda}), \\ \phi_{3}\phi X \underset{X \in T_{\lambda}}= \phi_{3}\phi_{1}X \underset{3.2}{=} \phi_{2}X \in T_{\mu} \\ \ \ (\mathrm{resp.} \ \phi_{3}\phi X \underset{X \in T_{\mu}}={-}\phi_{3}\phi_{1}X ={-}\phi_{2}X \in T_{\lambda} ), \end{gather*}Bearing in mind such properties, together with
\begin{gather*} \phi_{2}\phi X \underset{X \in T_{\lambda}}= \phi_{2}\phi_{1}X \underset{3.2}{=} -\phi_{3}X \in T_{\mu} \\ \ \ (\mathrm{resp.}\ \phi_{2}\phi X \underset{X \in T_{\mu}}={-}\phi_{2}\phi_{1}X = \phi_{3}X \in T_{\lambda}), \\ \phi_{3}\phi X \underset{X \in T_{\lambda}}= \phi_{3}\phi_{1}X \underset{3.2}{=} \phi_{2}X \in T_{\mu} \\ \ \ (\mathrm{resp.} \ \phi_{3}\phi X \underset{X \in T_{\mu}}={-}\phi_{3}\phi_{1}X ={-}\phi_{2}X \in T_{\lambda} ), \end{gather*}Bearing in mind such properties, together with \begin{equation*} \phi X = \phi_{1} X \in T_{\lambda} \ \ (\mathrm{resp.}\ \phi X = \phi_{1} X \in T_{\mu}). \end{equation*}
\begin{equation*} \phi X = \phi_{1} X \in T_{\lambda} \ \ (\mathrm{resp.}\ \phi X = \phi_{1} X \in T_{\mu}). \end{equation*} $\beta =\sqrt {2}$ and
$\beta =\sqrt {2}$ and  $\lambda = - \sqrt {2}$, (5.18) is identically vanishing for any tangent vector field
$\lambda = - \sqrt {2}$, (5.18) is identically vanishing for any tangent vector field  $X$ on
$X$ on  $(\mathcal {T}_{A})$.
$(\mathcal {T}_{A})$.•
 $Y ={{\xi }_3} \in T_{\beta }$
$Y ={{\xi }_3} \in T_{\beta }$Similarly, from (5.16) we obtain
(5.19)for any eigenvector \begin{equation} \begin{split} & -6 \beta \eta_{2}(X) \xi - \beta \eta(X) {{\xi}_2} - \phi_{3} AX - 3 \phi_{2} \phi AX \\ & \quad - 2 \beta \phi_{2}\phi X + A\phi_{3} X - 3 A \phi_{2} \phi X \end{split} \end{equation}
\begin{equation} \begin{split} & -6 \beta \eta_{2}(X) \xi - \beta \eta(X) {{\xi}_2} - \phi_{3} AX - 3 \phi_{2} \phi AX \\ & \quad - 2 \beta \phi_{2}\phi X + A\phi_{3} X - 3 A \phi_{2} \phi X \end{split} \end{equation} $X$ on
$X$ on  $(\mathcal {T}_{A})$. More specifically, according to each eigenspace
$(\mathcal {T}_{A})$. More specifically, according to each eigenspace  $T_{\alpha }$,
$T_{\alpha }$,  $T_{\beta }$,
$T_{\beta }$,  $T_{\lambda }$ and
$T_{\lambda }$ and  $T_{\mu }$, it follows that
where we have used
$T_{\mu }$, it follows that
where we have used \begin{equation*} (5.19) = \left\{ \begin{array}{@{}ll} - \beta {{\xi}_2} + A \phi_{3}\xi ={-} \beta {{\xi}_2} + A {{\xi}_2} = 0 & \mbox{for} \ X \in T_{\alpha}, \\ - 6 \beta \xi - \phi_{3} A {{\xi}_2} - 3 \phi_{2} \phi A {{\xi}_2} - 2 \beta \phi_{2} \phi {{\xi}_2} =0 & \mbox{for} \ X ={{\xi}_2} \in T_{\beta}, \\ - 3 \phi_{2}\phi A {{\xi}_3} - 2 \beta \phi_{2} \phi \xi_{3} - 3 A \phi_{2} \phi {{\xi}_3} = 0 & \mbox{for} \ X={{\xi}_3} \in T_{\beta}, \\ - \lambda \phi_{3}X - 3\lambda \phi_{2}\phi X - 2 \beta \phi_{2} \phi X = 2 (\lambda + \beta)\phi_{3}X=0 & \mbox{for} \ X \in T_{\lambda}, \\ - 2 \beta \phi_{2} \phi X + \lambda \phi_{3}X - 3 A \phi_{3}X ={-}2\beta (\beta + \lambda) \phi_{3}X =0 & \mbox{for} \ X \in T_{\mu}, \\ \end{array}\right. \end{equation*}
\begin{equation*} (5.19) = \left\{ \begin{array}{@{}ll} - \beta {{\xi}_2} + A \phi_{3}\xi ={-} \beta {{\xi}_2} + A {{\xi}_2} = 0 & \mbox{for} \ X \in T_{\alpha}, \\ - 6 \beta \xi - \phi_{3} A {{\xi}_2} - 3 \phi_{2} \phi A {{\xi}_2} - 2 \beta \phi_{2} \phi {{\xi}_2} =0 & \mbox{for} \ X ={{\xi}_2} \in T_{\beta}, \\ - 3 \phi_{2}\phi A {{\xi}_3} - 2 \beta \phi_{2} \phi \xi_{3} - 3 A \phi_{2} \phi {{\xi}_3} = 0 & \mbox{for} \ X={{\xi}_3} \in T_{\beta}, \\ - \lambda \phi_{3}X - 3\lambda \phi_{2}\phi X - 2 \beta \phi_{2} \phi X = 2 (\lambda + \beta)\phi_{3}X=0 & \mbox{for} \ X \in T_{\lambda}, \\ - 2 \beta \phi_{2} \phi X + \lambda \phi_{3}X - 3 A \phi_{3}X ={-}2\beta (\beta + \lambda) \phi_{3}X =0 & \mbox{for} \ X \in T_{\mu}, \\ \end{array}\right. \end{equation*} $\phi _{2}\phi {{\xi }_2} = - \phi _{2}{{\xi }_3} = -\xi$,
$\phi _{2}\phi {{\xi }_2} = - \phi _{2}{{\xi }_3} = -\xi$,  $\phi _{2}\phi {{\xi }_2} = \phi _{2}{{\xi }_2} =0$,
$\phi _{2}\phi {{\xi }_2} = \phi _{2}{{\xi }_2} =0$,  $\beta = \sqrt {2}$ and
$\beta = \sqrt {2}$ and  $\lambda =-\sqrt {2}$.
$\lambda =-\sqrt {2}$.
Subcase B-3. ![]() $Y \in T_{\mu }$ where
$Y \in T_{\mu }$ where ![]() $\mu = 0$
$\mu = 0$
Since a real hypersurface of type ![]() $(\mathcal {T}_{A})$ has isometric Reeb flow, we obtain
$(\mathcal {T}_{A})$ has isometric Reeb flow, we obtain ![]() $\phi Y \in T_{\mu =0}$, that is,
$\phi Y \in T_{\mu =0}$, that is, ![]() $A \phi Y = \phi A Y = \mu \phi Y = 0$ for any
$A \phi Y = \phi A Y = \mu \phi Y = 0$ for any ![]() $Y \in T_{\mu =0}$. From this and the construction of
$Y \in T_{\mu =0}$. From this and the construction of ![]() $T_{\mu }=\{Y \in \mathcal {Q} \, | \, \phi Y = -\phi _{1}Y \}$, we also obtain
$T_{\mu }=\{Y \in \mathcal {Q} \, | \, \phi Y = -\phi _{1}Y \}$, we also obtain ![]() $A \phi _{1} Y = - A \phi Y = 0$ for
$A \phi _{1} Y = - A \phi Y = 0$ for ![]() $Y \in T_{\mu =0}$. From these properties, (5.16) becomes
$Y \in T_{\mu =0}$. From these properties, (5.16) becomes
 \begin{equation} \begin{split} & - \sum_{\nu=1}^{3} \big \{ g(\phi_{\nu}AX, Y) {{\xi}_{\nu}} + 3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi - 2g(\phi_{\nu} \xi, AX) \phi_{\nu} \phi Y \\ & \quad \quad \quad - \eta_{\nu}(X) A \phi_{\nu} Y - 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 2 g(\phi_{\nu} \phi X, Y) A \phi_{\nu} \xi \big \} \\ & ={-}2 (\beta + \lambda) \big \{ g(\phi_{2}X, Y) {{\xi}_2} + g(\phi_{3}X, Y) {{\xi}_3} + \eta_{2}(X) \phi_{2}Y + \eta_{3}(X) \phi_{3}Y \big\}, \end{split} \end{equation}
\begin{equation} \begin{split} & - \sum_{\nu=1}^{3} \big \{ g(\phi_{\nu}AX, Y) {{\xi}_{\nu}} + 3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi - 2g(\phi_{\nu} \xi, AX) \phi_{\nu} \phi Y \\ & \quad \quad \quad - \eta_{\nu}(X) A \phi_{\nu} Y - 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 2 g(\phi_{\nu} \phi X, Y) A \phi_{\nu} \xi \big \} \\ & ={-}2 (\beta + \lambda) \big \{ g(\phi_{2}X, Y) {{\xi}_2} + g(\phi_{3}X, Y) {{\xi}_3} + \eta_{2}(X) \phi_{2}Y + \eta_{3}(X) \phi_{3}Y \big\}, \end{split} \end{equation}
where we have used ![]() $\phi _{2} \phi Y = \phi _{3}Y \in T_{\lambda }$ and
$\phi _{2} \phi Y = \phi _{3}Y \in T_{\lambda }$ and ![]() $\phi _{3} \phi Y = -\phi _{2}Y \in T_{\lambda }$ for any
$\phi _{3} \phi Y = -\phi _{2}Y \in T_{\lambda }$ for any ![]() $Y \in T_{\mu =0}$. Since
$Y \in T_{\mu =0}$. Since ![]() $\beta = \sqrt {2}$ and
$\beta = \sqrt {2}$ and ![]() $\lambda =-\sqrt {2}$, (5.20) is identically vanishing for any tangent vector field
$\lambda =-\sqrt {2}$, (5.20) is identically vanishing for any tangent vector field ![]() $X$ on
$X$ on ![]() $(\mathcal {T}_{A})$.
$(\mathcal {T}_{A})$.
Summing up these discussions, we assert that the structure Jacobi operator ![]() ${R_{\xi }}$ of a real hypersurface of type
${R_{\xi }}$ of a real hypersurface of type ![]() $(\mathcal {T}_{A})$ is cyclic parallel if and only if the radius
$(\mathcal {T}_{A})$ is cyclic parallel if and only if the radius ![]() $r$ of the tube around of type
$r$ of the tube around of type ![]() $(\mathcal {T}_{A})$ is
$(\mathcal {T}_{A})$ is ![]() $({\pi }/{4\sqrt {2})}$.
$({\pi }/{4\sqrt {2})}$.
6. Cyclic parallel structure Jacobi operator for  $JN \bot \mathcal {J} N$
$JN \bot \mathcal {J} N$
Let ![]() $M$ be a Hopf real hypersurface with cyclic parallel structure Jacobi operator
$M$ be a Hopf real hypersurface with cyclic parallel structure Jacobi operator ![]() ${R_{\xi }}$ in complex two-plane Grassmannians
${R_{\xi }}$ in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. Assume that the unit normal vector field
$m \geq 3$. Assume that the unit normal vector field ![]() $N$ of
$N$ of ![]() $M$ satisfies
$M$ satisfies ![]() $JN \bot {\mathcal {J}}N$ (i.e.
$JN \bot {\mathcal {J}}N$ (i.e. ![]() $\xi \in \mathcal {Q}$). Related to the Reeb vector field
$\xi \in \mathcal {Q}$). Related to the Reeb vector field ![]() $\xi$ of
$\xi$ of ![]() $M$ in
$M$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$, Lee and Suh gave:
${G_2({\mathbb {C}}^{m+2})}$, Lee and Suh gave:
Theorem B [Reference Lee and Suh17]
Let ![]() $M$ be a connected orientable Hopf real hypersurface in complex two-plane Grassmannians of compact type
$M$ be a connected orientable Hopf real hypersurface in complex two-plane Grassmannians of compact type ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$. Then the Reeb vector
$m \geq 3$. Then the Reeb vector ![]() $\xi$ belongs to the distribution
$\xi$ belongs to the distribution ![]() $\mathcal {Q}$ if and only if
$\mathcal {Q}$ if and only if ![]() $M$ is locally congruent to an open part of
$M$ is locally congruent to an open part of ![]() $(\mathcal {T}_{B})$: a tube around a totally geodesic
$(\mathcal {T}_{B})$: a tube around a totally geodesic ![]() $\mathbb {H} P^{n}$ in
$\mathbb {H} P^{n}$ in ![]() ${G_2({\mathbb {C}}^{m+2})}$, where
${G_2({\mathbb {C}}^{m+2})}$, where ![]() $m = 2n$.
$m = 2n$.
By virtue of theorem ![]() $1$ and theorem
$1$ and theorem ![]() ${\rm B}$, we assert that a Hopf real hypersurface
${\rm B}$, we assert that a Hopf real hypersurface ![]() $M$ in complex two-plane Grassmannians
$M$ in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$, satisfying the hypothesis in our theorem
$m \geq 3$, satisfying the hypothesis in our theorem ![]() $2$ is locally congruent to an open part of the model space mentioned in theorem
$2$ is locally congruent to an open part of the model space mentioned in theorem ![]() ${\rm B}$. Hereafter, conversely, let us check whether the structure Jacobi operator
${\rm B}$. Hereafter, conversely, let us check whether the structure Jacobi operator ![]() ${R_{\xi }}$ of the model space of type
${R_{\xi }}$ of the model space of type ![]() $(\mathcal {T}_{B})$ satisfies our assumption of cyclic parallel structure Jacobi operator.
$(\mathcal {T}_{B})$ satisfies our assumption of cyclic parallel structure Jacobi operator.
In order to do this, we introduce a proposition given in [Reference Suh30] as follows:
Proposition B Let ![]() $M$ be a connected real hypersurface in complex two-plane Grassmannians
$M$ be a connected real hypersurface in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$. Suppose that
${G_2({\mathbb {C}}^{m+2})}$. Suppose that ![]() $A\mathcal {Q} \subset \mathcal {Q}$,
$A\mathcal {Q} \subset \mathcal {Q}$, ![]() $A\xi = \alpha \xi$, and
$A\xi = \alpha \xi$, and ![]() $\xi$ is tangent to
$\xi$ is tangent to ![]() $\mathcal {Q}$. Then the quaternionic dimension
$\mathcal {Q}$. Then the quaternionic dimension ![]() $m$ of
$m$ of ![]() ${G_2({\mathbb {C}}^{m+2})}$ is even, say
${G_2({\mathbb {C}}^{m+2})}$ is even, say ![]() $m =2n$, and
$m =2n$, and ![]() $M$ has five distinct constant principal curvatures
$M$ has five distinct constant principal curvatures
with some ![]() $r \in (0, \frac {\pi }{4})$. The corresponding multiplicities are
$r \in (0, \frac {\pi }{4})$. The corresponding multiplicities are
and the corresponding eigenspaces are
 \begin{equation*} \begin{split} & T_{\alpha} = \mathbb{R} \xi = \mathcal{C}^{\bot} = \mathrm{span}\{\xi\}, \\ & T_{\beta} = \mathcal{J} J\xi = \mathrm{span}\{{{\xi}_1}, {{\xi}_2}, {{\xi}_3}\}, \\ & T_{\gamma} = \mathcal{J} \xi = \mathrm{span}\{\phi {{\xi}_1}, \phi {{\xi}_2}, \phi {{\xi}_3}\},\\ & T_{\lambda}, \ \ T_{\mu}, \end{split} \end{equation*}
\begin{equation*} \begin{split} & T_{\alpha} = \mathbb{R} \xi = \mathcal{C}^{\bot} = \mathrm{span}\{\xi\}, \\ & T_{\beta} = \mathcal{J} J\xi = \mathrm{span}\{{{\xi}_1}, {{\xi}_2}, {{\xi}_3}\}, \\ & T_{\gamma} = \mathcal{J} \xi = \mathrm{span}\{\phi {{\xi}_1}, \phi {{\xi}_2}, \phi {{\xi}_3}\},\\ & T_{\lambda}, \ \ T_{\mu}, \end{split} \end{equation*}where
In order to check the converse part, we assume that the structure Jacobi operator ![]() ${R_{\xi }}$ of our model space of type
${R_{\xi }}$ of our model space of type ![]() $(\mathcal {T}_{B})$ satisfies the property of cyclic parallelism. Accordingly, by
$(\mathcal {T}_{B})$ satisfies the property of cyclic parallelism. Accordingly, by ![]() $A \phi \xi _{\nu } =0$ for
$A \phi \xi _{\nu } =0$ for ![]() $\nu = 1,2,3$, the property (1.4) can be rearranged as
$\nu = 1,2,3$, the property (1.4) can be rearranged as
 \begin{equation} \begin{split} & g(X, A\phi Y) \xi - \eta(Y) \phi AX -g(X, \phi AY) \xi - \eta(X) \phi AY + \eta(Y)A\phi X \\ & + \eta(X) A \phi Y + \alpha^{2} \eta(Y) A \phi X + \alpha^{2} \eta(X) A \phi Y + 3\alpha (\nabla_X A)Y \\ & + \alpha g(\phi X, Y)\xi + 3\alpha \eta(Y) \phi X +\alpha^{2}g(X,A \phi Y)\xi -\alpha^{2} g(\phi AY,X)\xi \\ & - 2 \alpha g(\phi Y,X)\xi -\alpha ^{2}\eta(Y) \phi AX - \alpha^{2} \eta(X) \phi AY \\ & + \sum_{\nu=1}^{3} \Big [{-}g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} - \eta_{\nu}(Y) \phi_{\nu} AX -3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi \\ & - 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi + 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX \\ & - 3 \alpha \eta (X) g(\phi_{\nu} \xi, Y) {{\xi}_{\nu}} + 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y \\ & - g(\phi_{\nu} AY, X) {{\xi}_{\nu}} - 2\eta(X) g(\phi_{\nu} \xi, AY) {{\xi}_{\nu}} - \eta_{\nu}(X) \phi_{\nu} AY \\ & - 3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi - 3 \eta(X) \eta_{\nu}(AY) \phi_{\nu} \xi + 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \\ & - 3 \alpha \eta (Y) g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} + 2g(\phi_{\nu} \xi, AY) \phi_{\nu}\phi X +\eta_{\nu}(Y) A \phi_{\nu} X \\ & + \eta_{\nu}(X) A \phi_{\nu} Y + 3g(\phi_{\nu} \xi, Y) A \phi_{\nu} \phi X - 3 \eta(X) g(\phi_{\nu} \xi, Y) A{{\xi}_{\nu}}\\ & + 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 3 \alpha g(\phi_{\nu} \xi, X) \eta_{\nu}(Y)\xi + \alpha g(\phi_\nu X, Y) {{\xi}_{\nu}} \\ & + 2\alpha \eta_{\nu}(Y) \phi_\nu X - \alpha g(\phi_\nu\phi X, Y) \phi_{\nu} \xi + \alpha g(\phi_{\nu} \xi, X) \phi \phi_\nu Y \\ & + \alpha \eta_\nu(\phi X)\eta_{\nu}(Y) \xi +\alpha \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi + \alpha \eta_\nu(Y)\phi_\nu X \\ & - 2 \alpha g(\phi_\nu Y,X)\xi_\nu + \alpha \eta_\nu(\phi Y)\phi_\nu\phi X - \alpha \eta_\nu(\phi X)\phi_\nu\phi Y \\ & + \alpha \eta(Y)\eta_\nu(\phi X){{\xi}_{\nu}} - \alpha \eta(X)\eta_\nu(\phi Y)\xi_{\nu} \Big ]=0 \end{split} \end{equation}
\begin{equation} \begin{split} & g(X, A\phi Y) \xi - \eta(Y) \phi AX -g(X, \phi AY) \xi - \eta(X) \phi AY + \eta(Y)A\phi X \\ & + \eta(X) A \phi Y + \alpha^{2} \eta(Y) A \phi X + \alpha^{2} \eta(X) A \phi Y + 3\alpha (\nabla_X A)Y \\ & + \alpha g(\phi X, Y)\xi + 3\alpha \eta(Y) \phi X +\alpha^{2}g(X,A \phi Y)\xi -\alpha^{2} g(\phi AY,X)\xi \\ & - 2 \alpha g(\phi Y,X)\xi -\alpha ^{2}\eta(Y) \phi AX - \alpha^{2} \eta(X) \phi AY \\ & + \sum_{\nu=1}^{3} \Big [{-}g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} - \eta_{\nu}(Y) \phi_{\nu} AX -3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi \\ & - 3 \eta(Y) \eta_{\nu}(AX) \phi_{\nu} \xi + 3g(\phi_{\nu} \xi, Y) \phi_{\nu} \phi AX \\ & - 3 \alpha \eta (X) g(\phi_{\nu} \xi, Y) {{\xi}_{\nu}} + 2g(\phi_{\nu} \xi, AX) \phi_{\nu}\phi Y \\ & - g(\phi_{\nu} AY, X) {{\xi}_{\nu}} - 2\eta(X) g(\phi_{\nu} \xi, AY) {{\xi}_{\nu}} - \eta_{\nu}(X) \phi_{\nu} AY \\ & - 3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi - 3 \eta(X) \eta_{\nu}(AY) \phi_{\nu} \xi + 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \\ & - 3 \alpha \eta (Y) g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} + 2g(\phi_{\nu} \xi, AY) \phi_{\nu}\phi X +\eta_{\nu}(Y) A \phi_{\nu} X \\ & + \eta_{\nu}(X) A \phi_{\nu} Y + 3g(\phi_{\nu} \xi, Y) A \phi_{\nu} \phi X - 3 \eta(X) g(\phi_{\nu} \xi, Y) A{{\xi}_{\nu}}\\ & + 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y - 3 \alpha g(\phi_{\nu} \xi, X) \eta_{\nu}(Y)\xi + \alpha g(\phi_\nu X, Y) {{\xi}_{\nu}} \\ & + 2\alpha \eta_{\nu}(Y) \phi_\nu X - \alpha g(\phi_\nu\phi X, Y) \phi_{\nu} \xi + \alpha g(\phi_{\nu} \xi, X) \phi \phi_\nu Y \\ & + \alpha \eta_\nu(\phi X)\eta_{\nu}(Y) \xi +\alpha \eta(X)\eta_{\nu}(Y) \phi_{\nu} \xi + \alpha \eta_\nu(Y)\phi_\nu X \\ & - 2 \alpha g(\phi_\nu Y,X)\xi_\nu + \alpha \eta_\nu(\phi Y)\phi_\nu\phi X - \alpha \eta_\nu(\phi X)\phi_\nu\phi Y \\ & + \alpha \eta(Y)\eta_\nu(\phi X){{\xi}_{\nu}} - \alpha \eta(X)\eta_\nu(\phi Y)\xi_{\nu} \Big ]=0 \end{split} \end{equation}
for any tangent vector field ![]() $X$ on type
$X$ on type ![]() $(\mathcal {T}_{B})$.
$(\mathcal {T}_{B})$.
Bearing in mind of our assumption, the structure Jacobi operator ![]() ${R_{\xi }}$ for the tube of type
${R_{\xi }}$ for the tube of type ![]() $(\mathcal {T}_{B})$ is cyclic parallel, taking
$(\mathcal {T}_{B})$ is cyclic parallel, taking ![]() $Y \in T_{\alpha }$ in (6.1) yields
$Y \in T_{\alpha }$ in (6.1) yields
 \begin{equation} \begin{split} & - \phi AX + A\phi X + \alpha^{2} A \phi X + 2\alpha^{2} \phi AX - 3 \alpha A \phi AX + 3\alpha \phi X \\ & -3 \sum_{\nu=1}^{3} \Big [ \beta \eta_{\nu}(X) \phi_{\nu} \xi +3 \alpha g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} + \alpha \eta_{\nu}(X) \phi_{\nu} \xi + \beta g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} \Big ]=0, \end{split} \end{equation}
\begin{equation} \begin{split} & - \phi AX + A\phi X + \alpha^{2} A \phi X + 2\alpha^{2} \phi AX - 3 \alpha A \phi AX + 3\alpha \phi X \\ & -3 \sum_{\nu=1}^{3} \Big [ \beta \eta_{\nu}(X) \phi_{\nu} \xi +3 \alpha g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} + \alpha \eta_{\nu}(X) \phi_{\nu} \xi + \beta g(\phi_{\nu} \xi, X) {{\xi}_{\nu}} \Big ]=0, \end{split} \end{equation}
where we have used ![]() $(\nabla _{X}A)\xi = \alpha \phi AX - A \phi AX$ and
$(\nabla _{X}A)\xi = \alpha \phi AX - A \phi AX$ and ![]() $\phi \phi _{\nu } \xi = \phi ^{2}{{\xi }_{\nu }} = - {{\xi }_{\nu }}$. Furthermore, taking
$\phi \phi _{\nu } \xi = \phi ^{2}{{\xi }_{\nu }} = - {{\xi }_{\nu }}$. Furthermore, taking ![]() $X=\xi _{\mu } \in T_{\beta }$ in (6.2) follows
$X=\xi _{\mu } \in T_{\beta }$ in (6.2) follows
 \begin{equation*} \begin{split} 0 & ={-} \phi A \xi_{\mu} + A\phi \xi_{\mu} + \alpha^{2} A \phi \xi_{\mu} + 2\alpha^{2} \phi A \xi_{\mu} - 3 \alpha A \phi A \xi_{\mu} + 3\alpha \phi \xi_{\mu} \\ & \quad -3 \sum_{\nu=1}^{3} \Big [ \beta \eta_{\nu}(\xi_{\mu}) \phi_{\nu} \xi +3 \alpha g(\phi_{\nu} \xi, \xi_{\mu}) {{\xi}_{\nu}} + \alpha \eta_{\nu}(\xi_{\mu}) \phi_{\nu} \xi + \beta g(\phi_{\nu} \xi, \xi_{\mu}) {{\xi}_{\nu}} \Big ] \\ & = 2 \beta ( \alpha^{2} -2) \phi_{\mu} \xi, \end{split} \end{equation*}
\begin{equation*} \begin{split} 0 & ={-} \phi A \xi_{\mu} + A\phi \xi_{\mu} + \alpha^{2} A \phi \xi_{\mu} + 2\alpha^{2} \phi A \xi_{\mu} - 3 \alpha A \phi A \xi_{\mu} + 3\alpha \phi \xi_{\mu} \\ & \quad -3 \sum_{\nu=1}^{3} \Big [ \beta \eta_{\nu}(\xi_{\mu}) \phi_{\nu} \xi +3 \alpha g(\phi_{\nu} \xi, \xi_{\mu}) {{\xi}_{\nu}} + \alpha \eta_{\nu}(\xi_{\mu}) \phi_{\nu} \xi + \beta g(\phi_{\nu} \xi, \xi_{\mu}) {{\xi}_{\nu}} \Big ] \\ & = 2 \beta ( \alpha^{2} -2) \phi_{\mu} \xi, \end{split} \end{equation*}
which implies ![]() $\beta ( \alpha ^{2} -2) =0$. Since
$\beta ( \alpha ^{2} -2) =0$. Since ![]() $\beta = 2 \cot (2r)$ for
$\beta = 2 \cot (2r)$ for ![]() $r \in (0,({\pi }/{4}))$, we obtain
$r \in (0,({\pi }/{4}))$, we obtain ![]() $\alpha ^{2}=2$.
$\alpha ^{2}=2$.
On the other hand, taking ![]() $X \in T_{\lambda }$ in (6.2), together with
$X \in T_{\lambda }$ in (6.2), together with ![]() $\phi T_{\lambda }=T_{\mu }$, provides
$\phi T_{\lambda }=T_{\mu }$, provides
where we have used ![]() $\alpha ^{2}=2$,
$\alpha ^{2}=2$, ![]() $\lambda \mu = (\cot r) \cdot (-\tan r) =-1$, and
$\lambda \mu = (\cot r) \cdot (-\tan r) =-1$, and ![]() $\lambda + \mu = 2 \cot (2t) = \beta$.
$\lambda + \mu = 2 \cot (2t) = \beta$.
Applying a method to (6.2) that is done above, the left side of (6.2) according to each eigenspace of type ![]() $(\mathcal {T}_{\beta })$ is given as
$(\mathcal {T}_{\beta })$ is given as
 \begin{equation*} \mathrm{Left\ side \ of \ } (6.2) = \left\{ \begin{array}{@{}ll} 0 & \mbox{for} \ X \in T_{\alpha}, \\ 2 \beta (\alpha^{2} -2) \phi_{\mu} \xi & \mbox{for} \ X =\xi_{\mu} \in T_{\beta}, \\ - 6 (\beta + 2 \alpha) \xi_{\mu} & \mbox{for} \ X=\phi_{\mu} \xi \in T_{\gamma}, \\ 3 (\beta + 2 \alpha) \phi X & \mbox{for} \ X \in T_{\lambda}, \\ 3 (\beta + 2 \alpha) \phi X & \mbox{for} \ X \in T_{\mu}. \\ \end{array}\right. \end{equation*}
\begin{equation*} \mathrm{Left\ side \ of \ } (6.2) = \left\{ \begin{array}{@{}ll} 0 & \mbox{for} \ X \in T_{\alpha}, \\ 2 \beta (\alpha^{2} -2) \phi_{\mu} \xi & \mbox{for} \ X =\xi_{\mu} \in T_{\beta}, \\ - 6 (\beta + 2 \alpha) \xi_{\mu} & \mbox{for} \ X=\phi_{\mu} \xi \in T_{\gamma}, \\ 3 (\beta + 2 \alpha) \phi X & \mbox{for} \ X \in T_{\lambda}, \\ 3 (\beta + 2 \alpha) \phi X & \mbox{for} \ X \in T_{\mu}. \\ \end{array}\right. \end{equation*} Now, as the other case we consider the case ![]() $Y \in T_{\lambda }$. Then, by using
$Y \in T_{\lambda }$. Then, by using ![]() $JT_{\lambda }=T_{\mu }$ and
$JT_{\lambda }=T_{\mu }$ and ![]() $\mathcal {J} T_{\lambda }=T_{\lambda }$, equation (6.1) is rearranged as
$\mathcal {J} T_{\lambda }=T_{\lambda }$, equation (6.1) is rearranged as
 \begin{equation} \begin{split} & g(X, A\phi Y) \xi -g(X, \phi AY) \xi - \eta(X) \phi AY + \eta(X) A \phi Y + \alpha^{2} \eta(X) A \phi Y \\ & + 3\alpha (\nabla_X A)Y + \alpha g(\phi X, Y)\xi +\alpha^{2}g(X,A \phi Y)\xi \\ & -\alpha^{2} g(\phi AY,X)\xi - 2 \alpha g(\phi Y,X)\xi - \alpha^{2} \eta(X) \phi AY \\ & + \sum_{\nu=1}^{3} \Big [{-}g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} -3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi - g(\phi_{\nu} AY, X) {{\xi}_{\nu}} \\ & - \eta_{\nu}(X) \phi_{\nu} AY -3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi + 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \\ & + \eta_{\nu}(X) A \phi_{\nu} Y + \alpha g(\phi_\nu X, Y) {{\xi}_{\nu}} + 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y \\ & - \alpha g(\phi_\nu\phi X, Y) \phi_{\nu} \xi + \alpha g(\phi_{\nu} \xi, X) \phi \phi_\nu Y \\ & - 2 \alpha g(\phi_\nu Y,X)\xi_\nu + \alpha g( \phi_\nu \xi, X) \phi_\nu\phi Y \Big ] \\ & = (\mu - \lambda - 3 \alpha + \alpha^{2}\mu - \alpha^{2} \lambda) g(X, \phi Y) \xi + (\lambda + \mu + \alpha^{2} \mu - \alpha^{2} \lambda ) \eta(X) \phi Y \\ & + 3 \alpha (\nabla_{X}A) Y + \sum_{\nu=1}^{3} \Big [- 3\alpha g(\phi_{\nu}Y, X)\xi_{\nu} + (3\mu + 3\lambda - \alpha) g(\phi \phi_{\nu}Y, X) \phi_{\nu}\xi \Big ] \\ & + \sum_{\nu=1}^{3} (3\lambda + 3 \mu + 2 \alpha) g(\phi_{\nu}\xi, X) \phi \phi_{\nu} Y =0 \end{split} \end{equation}
\begin{equation} \begin{split} & g(X, A\phi Y) \xi -g(X, \phi AY) \xi - \eta(X) \phi AY + \eta(X) A \phi Y + \alpha^{2} \eta(X) A \phi Y \\ & + 3\alpha (\nabla_X A)Y + \alpha g(\phi X, Y)\xi +\alpha^{2}g(X,A \phi Y)\xi \\ & -\alpha^{2} g(\phi AY,X)\xi - 2 \alpha g(\phi Y,X)\xi - \alpha^{2} \eta(X) \phi AY \\ & + \sum_{\nu=1}^{3} \Big [{-}g(\phi_{\nu} AX, Y) {{\xi}_{\nu}} -3 g(\phi_{\nu} AX, \phi Y) \phi_{\nu} \xi - g(\phi_{\nu} AY, X) {{\xi}_{\nu}} \\ & - \eta_{\nu}(X) \phi_{\nu} AY -3 g(\phi_{\nu} AY, \phi X) \phi_{\nu} \xi + 3g(\phi_{\nu} \xi, X) \phi_{\nu} \phi AY \\ & + \eta_{\nu}(X) A \phi_{\nu} Y + \alpha g(\phi_\nu X, Y) {{\xi}_{\nu}} + 3g(\phi_{\nu} \xi, X) A \phi \phi_{\nu} Y \\ & - \alpha g(\phi_\nu\phi X, Y) \phi_{\nu} \xi + \alpha g(\phi_{\nu} \xi, X) \phi \phi_\nu Y \\ & - 2 \alpha g(\phi_\nu Y,X)\xi_\nu + \alpha g( \phi_\nu \xi, X) \phi_\nu\phi Y \Big ] \\ & = (\mu - \lambda - 3 \alpha + \alpha^{2}\mu - \alpha^{2} \lambda) g(X, \phi Y) \xi + (\lambda + \mu + \alpha^{2} \mu - \alpha^{2} \lambda ) \eta(X) \phi Y \\ & + 3 \alpha (\nabla_{X}A) Y + \sum_{\nu=1}^{3} \Big [- 3\alpha g(\phi_{\nu}Y, X)\xi_{\nu} + (3\mu + 3\lambda - \alpha) g(\phi \phi_{\nu}Y, X) \phi_{\nu}\xi \Big ] \\ & + \sum_{\nu=1}^{3} (3\lambda + 3 \mu + 2 \alpha) g(\phi_{\nu}\xi, X) \phi \phi_{\nu} Y =0 \end{split} \end{equation}
for any tangent vector field ![]() $X$ on type
$X$ on type ![]() $(\mathcal {T}_{B})$. Restricting
$(\mathcal {T}_{B})$. Restricting ![]() $X \in T_{\alpha }$ in (6.3) provides
$X \in T_{\alpha }$ in (6.3) provides
for any ![]() $Y \in T_{\lambda }$. By the equation of Codazzi (3.8), we get
$Y \in T_{\lambda }$. By the equation of Codazzi (3.8), we get
 \begin{equation*} \begin{split} (\nabla_{\xi} A)Y & = (\nabla_Y A)\xi + \phi Y + \sum_{\nu=1}^{3} \big\{- \eta_\nu(Y)\phi_\nu \xi - 3g(\phi_\nu \xi,Y)\xi_\nu \big\} \\ & = \alpha \phi AY - A \phi AY + \phi Y = (\alpha \lambda - \lambda \mu + 1) \phi Y \end{split} \end{equation*}
\begin{equation*} \begin{split} (\nabla_{\xi} A)Y & = (\nabla_Y A)\xi + \phi Y + \sum_{\nu=1}^{3} \big\{- \eta_\nu(Y)\phi_\nu \xi - 3g(\phi_\nu \xi,Y)\xi_\nu \big\} \\ & = \alpha \phi AY - A \phi AY + \phi Y = (\alpha \lambda - \lambda \mu + 1) \phi Y \end{split} \end{equation*}
for any ![]() $Y \in T_{\lambda }$. From this, (6.4) becomes
$Y \in T_{\lambda }$. From this, (6.4) becomes
Since ![]() $\alpha ^{2}=2$,
$\alpha ^{2}=2$, ![]() $\beta +2\alpha =0$,
$\beta +2\alpha =0$, ![]() $\lambda + \mu =\beta$ and
$\lambda + \mu =\beta$ and ![]() $\lambda \mu = -1$, the previous equation gives
$\lambda \mu = -1$, the previous equation gives
which gives us a contradiction. In fact, by proposition ![]() ${\rm B}$ we see that
${\rm B}$ we see that ![]() $\beta =2 \cot (2r)$,
$\beta =2 \cot (2r)$, ![]() $\lambda =\cot (r)$ and
$\lambda =\cot (r)$ and ![]() $\mu =-\tan (r)$ where
$\mu =-\tan (r)$ where ![]() $r \in (0, \frac {\pi }{4})$. From this, we get
$r \in (0, \frac {\pi }{4})$. From this, we get
which means that the function ![]() $\beta - \mu -2 \lambda$ is non-vanishing for any
$\beta - \mu -2 \lambda$ is non-vanishing for any ![]() $r \in (0, ({\pi }/{4}))$.
$r \in (0, ({\pi }/{4}))$.
Summing up those documents in this section, we can assert that there does not exist a Hopf real hypersurface in complex two-plane Grassmannians ![]() ${G_2({\mathbb {C}}^{m+2})}$,
${G_2({\mathbb {C}}^{m+2})}$, ![]() $m \geq 3$, with cyclic parallel structure Jacobi operator when the normal vector field of
$m \geq 3$, with cyclic parallel structure Jacobi operator when the normal vector field of ![]() $M$ is of type
$M$ is of type ![]() $JN \bot \mathcal {J} N$.
$JN \bot \mathcal {J} N$.
Acknowledgements
The authors would like to give their sincere gratitude to the reviewer for his/her efforts and careful reading for the manuscript. The first author was supported by grant Proj. No. NRF-2019-R1I1A1A-01050300, the second by Proj. No. NRF-2018-R1D1A1B-05040381, and the third by NRF-2020-R1A2C1A-01101518 from National Research Foundation of Korea.