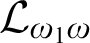1 Introduction
A central feature of elementary first-order logic is the compactness theorem, which has as a consequence the Ryll–Nardzewski theorem that any countably-categorical structure is relatively simple: for each n, there are only finitely many automorphism orbits of n-tuples. So most structures are not countably categorical, which means that no matter which elementary first-order sentences we write down, we cannot completely characterize the structure up to isomorphism.
If we strengthen our language, Scott [Reference Scott62] showed that we can characterize every countable structure up to isomorphism. The required strengthening of the language allows countably infinite conjunctions and disjunctions, so that for example we can express that an abelian group is torsion by saying that for each element x, either
![]() $x = 0$
, or
$x = 0$
, or
![]() $x + x = 0$
, or
$x + x = 0$
, or
![]() $x + x + x = 0$
, and so on. More formally, we use the logic
$x + x + x = 0$
, and so on. More formally, we use the logic
![]() $\mathcal {L}_{\omega _1 \omega }$
which is defined as follows:
$\mathcal {L}_{\omega _1 \omega }$
which is defined as follows:
Definition 1.1. Let
![]() $\tau $
be a vocabulary. The formulas of the logic
$\tau $
be a vocabulary. The formulas of the logic
![]() $\mathcal {L}_{\omega _1 \omega }(\tau )$
are built inductively as follows:
$\mathcal {L}_{\omega _1 \omega }(\tau )$
are built inductively as follows:
-
• terms and atomic formulas are defined as in elementary first-order logic;
-
• if
 $\varphi $
is a formula, so is
$\varphi $
is a formula, so is
 $\neg \varphi $
;
$\neg \varphi $
; -
• if
 $\bar {x}$
is a finite tuple of variables and X is a countable set of formulas such that for each
$\bar {x}$
is a finite tuple of variables and X is a countable set of formulas such that for each
 $\varphi \in X$
, the free variables of
$\varphi \in X$
, the free variables of
 $\varphi $
are contained within
$\varphi $
are contained within
 $\bar {x}$
, then
$\bar {x}$
, then
 and
and
 are formulas; and
are formulas; and -
• if
 $\varphi $
is a formula, then so are
$\varphi $
is a formula, then so are
 $\forall x \varphi $
and
$\forall x \varphi $
and
 $\exists x \varphi $
.
$\exists x \varphi $
.
![]() $\mathcal {L}_{\omega _1 \omega }$
does not satisfy compactness, but it does satisfy downward (though not upward) Löwenheim–Skolem for countable fragments. The book by Marker [Reference Marker45] is an excellent reference on infinitary model theory.
$\mathcal {L}_{\omega _1 \omega }$
does not satisfy compactness, but it does satisfy downward (though not upward) Löwenheim–Skolem for countable fragments. The book by Marker [Reference Marker45] is an excellent reference on infinitary model theory.
Now that we have strengthened our language, it is possible to show that each structure is characterized up to isomorphism among countable structures by a sentence of this logic [Reference Scott62]. We call this sentence a Scott sentence.
Definition 1.2. Let
![]() $\mathcal {A}$
be a countable structure. A Scott sentence for
$\mathcal {A}$
be a countable structure. A Scott sentence for
![]() $\mathcal {A}$
is a sentence
$\mathcal {A}$
is a sentence
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal {L}_{\omega _1 \omega }$
such that, up to isomorphism,
$\mathcal {L}_{\omega _1 \omega }$
such that, up to isomorphism,
![]() $\mathcal {A}$
is the only countably model of
$\mathcal {A}$
is the only countably model of
![]() $\varphi $
.
$\varphi $
.
The standard proof that every countable structure has a Scott sentence passes through the back-and-forth relations, showing that they must stabilize at some countable ordinal, and then extracting from this a Scott sentence. This Scott analysis of a structure has played an important role in the study of Vaught’s conjecture, e.g., in Morley’s theorem [Reference Morley55] that the number of non-isomorphic countable models of a theory is either at most
![]() $\aleph _1$
or is exactly
$\aleph _1$
or is exactly
![]() $2^{\aleph _0}$
. There are excellent references for these results on Vaught’s conjecture, e.g., in Marker’s book [Reference Marker45], and so we will only touch on them briefly.
$2^{\aleph _0}$
. There are excellent references for these results on Vaught’s conjecture, e.g., in Marker’s book [Reference Marker45], and so we will only touch on them briefly.
Fixing a countable structure
![]() $\mathcal {A}$
, there is some countable ordinal at which the back-and-forth relations stabilize. This introduces a way of assigning an ordinal to
$\mathcal {A}$
, there is some countable ordinal at which the back-and-forth relations stabilize. This introduces a way of assigning an ordinal to
![]() $\mathcal {A}$
, called its Scott rank. There are several slightly different variations of what it means to stabilize, leading to several different definitions of Scott rank. Equivalently the Scott rank can be thought of as measuring both the complexity of the automorphism orbits of the structure and the complexity of describing the structure.
$\mathcal {A}$
, called its Scott rank. There are several slightly different variations of what it means to stabilize, leading to several different definitions of Scott rank. Equivalently the Scott rank can be thought of as measuring both the complexity of the automorphism orbits of the structure and the complexity of describing the structure.
Another way of measuring the complexity of
![]() $\mathcal {A}$
is the least complexity of a Scott sentence for
$\mathcal {A}$
is the least complexity of a Scott sentence for
![]() $\mathcal {A}$
. To measure the complexity of
$\mathcal {A}$
. To measure the complexity of
![]() $\mathcal {L}_{\omega _1 \omega }$
formulas, we use the natural hierarchy of
$\mathcal {L}_{\omega _1 \omega }$
formulas, we use the natural hierarchy of
![]() $\Sigma _\alpha $
and
$\Sigma _\alpha $
and
![]() $\Pi _\alpha $
sentences in normal form.
$\Pi _\alpha $
sentences in normal form.
-
• An
 $\mathcal {L}_{\omega _1 \omega }$
formula is both
$\mathcal {L}_{\omega _1 \omega }$
formula is both
 $\Sigma _0$
and
$\Sigma _0$
and
 $\Pi _0$
if it is quantifier free and does not contain any infinite disjunctions or conjunctions.
$\Pi _0$
if it is quantifier free and does not contain any infinite disjunctions or conjunctions. -
• An
 $\mathcal {L}_{\omega _1 \omega }$
formula is
$\mathcal {L}_{\omega _1 \omega }$
formula is
 $\Sigma _\alpha $
if it is a countable disjunction of formulas of the form
$\Sigma _\alpha $
if it is a countable disjunction of formulas of the form
 $\exists x \phi $
where each
$\exists x \phi $
where each
 $\phi $
is
$\phi $
is
 $\Pi _\beta $
for some
$\Pi _\beta $
for some
 $\beta < \alpha $
.
$\beta < \alpha $
. -
• An
 $\mathcal {L}_{\omega _1 \omega }$
formula is
$\mathcal {L}_{\omega _1 \omega }$
formula is
 $\Pi _\alpha $
if it is a countable conjunction of formulas of the form
$\Pi _\alpha $
if it is a countable conjunction of formulas of the form
 $\forall x \phi $
where each
$\forall x \phi $
where each
 $\phi $
is
$\phi $
is
 $\Sigma _\beta $
for some
$\Sigma _\beta $
for some
 $\beta < \alpha $
.
$\beta < \alpha $
.
This approach led Montalbán [Reference Montalbán52] to define a new notion of Scott rank as the least ordinal
![]() $\alpha $
for which
$\alpha $
for which
![]() $\mathcal {A}$
has a
$\mathcal {A}$
has a
![]() $\Pi _{\alpha +1}$
Scott sentence. He proved that this is robust in the sense that there are a number of different equivalent characterizations, including the complexity of defining automorphism orbits, and the complexity of computing isomorphisms between different copies of
$\Pi _{\alpha +1}$
Scott sentence. He proved that this is robust in the sense that there are a number of different equivalent characterizations, including the complexity of defining automorphism orbits, and the complexity of computing isomorphisms between different copies of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
An even finer measurement, the Scott complexity of
![]() $\mathcal {A}$
, is the least complexity of a Scott sentence for
$\mathcal {A}$
, is the least complexity of a Scott sentence for
![]() $\mathcal {A}$
. Alvir et al. [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1] argued by means of the Wadge degrees that the only (reasonable) possible complexities are
$\mathcal {A}$
. Alvir et al. [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1] argued by means of the Wadge degrees that the only (reasonable) possible complexities are
![]() $\Sigma _\alpha $
,
$\Sigma _\alpha $
,
![]() $\Pi _\alpha $
, and
$\Pi _\alpha $
, and
![]() $\mathrm {d}\!-\Sigma _\alpha $
.
$\mathrm {d}\!-\Sigma _\alpha $
.
This article will begin with a more detailed look at the above background material. Following this, we will touch on more specialized areas. We begin with effective considerations and structures of high Scott rank. Here we give new elementary proofs, avoiding Barwise compactness and
![]() $\Sigma ^1_1$
bounding, which we think are simpler than many of those in the literature. Next, we look at results on the Scott complexity of particular structures of interest in mathematics, e.g., free groups. Finally, we discuss theories, including a brief summary of connections with Vaught’s conjecture.
$\Sigma ^1_1$
bounding, which we think are simpler than many of those in the literature. Next, we look at results on the Scott complexity of particular structures of interest in mathematics, e.g., free groups. Finally, we discuss theories, including a brief summary of connections with Vaught’s conjecture.
We also note that there is work applying the Scott analysis to separable metric spaces, which we will not cover in this survey. See [Reference Chan15, Reference Chan and Chen16, Reference Doucha19, Reference Melnikov and Nies47, Reference Yaacov, Doucha, Nies and Tsankov67]; note that [Reference Doucha19] has an erratum [Reference Doucha20].
2 Scott sentences and Scott rank
Our first step is to see why every structure has a Scott sentence. The standard way to see this is to analyse the back-and-forth relations. There are a number of different ways to define the back-and-forth relations, but from a computability-theoretic perspective the most natural is the following due to its connections with
![]() $\Sigma _\alpha $
and
$\Sigma _\alpha $
and
![]() $\Pi _\alpha $
sentences.
$\Pi _\alpha $
sentences.
Definition 2.1. The standard asymmetric back-and-forth relations
![]() $\leq _\alpha $
on
$\leq _\alpha $
on
![]() $\mathcal {A}$
, for
$\mathcal {A}$
, for
![]() $\alpha < \omega _1$
, are defined by:
$\alpha < \omega _1$
, are defined by:
-
1.
 $\bar {a} \leq _0 \bar {b}$
if
$\bar {a} \leq _0 \bar {b}$
if
 $\bar {a}$
and
$\bar {a}$
and
 $\bar {b}$
satisfy the same quantifier-free formulas from among the first
$\bar {b}$
satisfy the same quantifier-free formulas from among the first
 $|\bar {a}|$
-many formulas.
$|\bar {a}|$
-many formulas. -
2. For
 $\alpha> 0$
,
$\alpha> 0$
,
 $\bar {a} \leq _\alpha \bar {b}$
if for each
$\bar {a} \leq _\alpha \bar {b}$
if for each
 $\beta < \alpha $
and
$\beta < \alpha $
and
 $\bar {d}$
there is
$\bar {d}$
there is
 $\bar {c}$
such that
$\bar {c}$
such that
 $\bar {b} \bar {d} \leq _\beta \bar {a} \bar {c}$
.
$\bar {b} \bar {d} \leq _\beta \bar {a} \bar {c}$
.
We define
 $\bar {a} \equiv _\alpha \bar {b}$
if
$\bar {a} \equiv _\alpha \bar {b}$
if
 $\bar {a} \leq _\alpha \bar {b}$
and
$\bar {a} \leq _\alpha \bar {b}$
and
 $\bar {b} \leq _\alpha \bar {a}$
. We also define
$\bar {b} \leq _\alpha \bar {a}$
. We also define
 $\bar {a} \equiv _\infty \bar {b}$
if
$\bar {a} \equiv _\infty \bar {b}$
if
 $\bar {a} \equiv _\alpha \bar {b}$
for all
$\bar {a} \equiv _\alpha \bar {b}$
for all
![]() $\alpha < \omega _1$
.
$\alpha < \omega _1$
.
It is not hard to prove by induction that for
![]() $\alpha \geq 1$
,
$\alpha \geq 1$
,
 $\bar {a} \leq _\alpha \bar {b}$
if and only if every
$\bar {a} \leq _\alpha \bar {b}$
if and only if every
![]() $\Sigma _\alpha $
sentence true of
$\Sigma _\alpha $
sentence true of
![]() $\bar {b}$
is true of
$\bar {b}$
is true of
![]() $\bar {a}$
. Similarly,
$\bar {a}$
. Similarly,
 $\bar {a} \equiv _\infty \bar {b}$
if and only if
$\bar {a} \equiv _\infty \bar {b}$
if and only if
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
satisfy the same
$\bar {b}$
satisfy the same
![]() $\mathcal {L}_{\omega _1 \omega }$
formulas.
$\mathcal {L}_{\omega _1 \omega }$
formulas.
For each pair of tuples
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
such that
$\bar {b}$
such that
 $\bar {a} \not \equiv _\infty \bar {b}$
, choose a formula
$\bar {a} \not \equiv _\infty \bar {b}$
, choose a formula
 $\varphi _{\bar {a};\bar {b}}(\bar {x})$
such that
$\varphi _{\bar {a};\bar {b}}(\bar {x})$
such that
 $\mathcal {A} \models \varphi _{\bar {a};\bar {b}}(\bar {a})$
but
$\mathcal {A} \models \varphi _{\bar {a};\bar {b}}(\bar {a})$
but
 $\mathcal {A} \models \neg \varphi _{\bar {a};\bar {b}}(\bar {b})$
. Then define
$\mathcal {A} \models \neg \varphi _{\bar {a};\bar {b}}(\bar {b})$
. Then define
 . So we have that
. So we have that
 $\mathcal {A} \models \psi _{\bar {a}}(\bar {b})$
if and only if
$\mathcal {A} \models \psi _{\bar {a}}(\bar {b})$
if and only if
 $\bar {a} \equiv _\infty \bar {b}$
. We may also add as a conjunct to
$\bar {a} \equiv _\infty \bar {b}$
. We may also add as a conjunct to
![]() $\psi _{\bar {a}}(\bar {x})$
all of the atomic formulas true of
$\psi _{\bar {a}}(\bar {x})$
all of the atomic formulas true of
![]() $\bar {a}$
.
$\bar {a}$
.
Now define:

and

It is easy to argue by a standard back-and-forth argument that
![]() $\theta $
is a Scott sentence for
$\theta $
is a Scott sentence for
![]() $\mathcal {A}$
. We call
$\mathcal {A}$
. We call
![]() $\theta $
the canonical Scott sentence for
$\theta $
the canonical Scott sentence for
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Theorem 2.2 Scott [Reference Scott62]
Every countable structure has a Scott sentence.
Proof It is clear that
![]() $\mathcal {A} \models \theta $
. Suppose that
$\mathcal {A} \models \theta $
. Suppose that
![]() $\mathcal {B}$
is countable and
$\mathcal {B}$
is countable and
![]() $\mathcal {B} \models \theta $
. Suppose that we have a finite partial map
$\mathcal {B} \models \theta $
. Suppose that we have a finite partial map
![]() $\mathcal {A} \to \mathcal {B}$
mapping
$\mathcal {A} \to \mathcal {B}$
mapping
![]() $\bar {a}$
to
$\bar {a}$
to
![]() $\bar {b}$
with
$\bar {b}$
with
 $\psi _{\bar {a}}(\bar {b})$
. Then for such
$\psi _{\bar {a}}(\bar {b})$
. Then for such
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
:
$\bar {b}$
:
-
•
 $\bar {a}$
and
$\bar {a}$
and
 $\bar {b}$
have the same atomic type;
$\bar {b}$
have the same atomic type; -
• given
 $a' \in \mathcal {A}$
, since
$a' \in \mathcal {A}$
, since
 $\mathcal {B} \models \sigma _{\bar {a}} \wedge \psi _{\bar {a}}(\bar {b})$
, there is
$\mathcal {B} \models \sigma _{\bar {a}} \wedge \psi _{\bar {a}}(\bar {b})$
, there is
 $b' \in \mathcal {B}$
with
$b' \in \mathcal {B}$
with
 $\mathcal {B} \models \psi _{\bar {a}a'}(\bar {b}b')$
; and
$\mathcal {B} \models \psi _{\bar {a}a'}(\bar {b}b')$
; and -
• given
 $b' \in \mathcal {B}$
, since
$b' \in \mathcal {B}$
, since
 $\mathcal {B} \models \rho _{\bar {a}} \wedge \psi _{\bar {a}}(\bar {b})$
, there is
$\mathcal {B} \models \rho _{\bar {a}} \wedge \psi _{\bar {a}}(\bar {b})$
, there is
 $a' \in \mathcal {A}$
with
$a' \in \mathcal {A}$
with
 $\mathcal {B} \models \psi _{\bar {a}a'}(\bar {b}b')$
;
$\mathcal {B} \models \psi _{\bar {a}a'}(\bar {b}b')$
;
So by a back-and-forth argument we can extend our finite partial isomorphism to an isomorphism
![]() $\mathcal {A} \to \mathcal {B}$
. Thus
$\mathcal {A} \to \mathcal {B}$
. Thus
![]() $\theta $
is a Scott sentence for
$\theta $
is a Scott sentence for
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
As a corollary, by adding constants to the language, we get:
Corollary 2.3. Let
![]() $\mathcal {A}$
be a countable structure and
$\mathcal {A}$
be a countable structure and
 $\bar {a},\bar {b} \in \mathcal {A}$
. Then there is an automorphism of
$\bar {a},\bar {b} \in \mathcal {A}$
. Then there is an automorphism of
![]() $\mathcal {A}$
taking
$\mathcal {A}$
taking
![]() $\bar {a}$
to
$\bar {a}$
to
![]() $\bar {b}$
if and only if
$\bar {b}$
if and only if
 $\bar {a} \equiv _\infty \bar {b}$
.
$\bar {a} \equiv _\infty \bar {b}$
.
There are only countably many tuples
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\mathcal {A}$
, so there is a countable ordinal
$\mathcal {A}$
, so there is a countable ordinal
![]() $\alpha $
such, that for
$\alpha $
such, that for
 $\bar {a},\bar {b} \in \mathcal {A}$
, if
$\bar {a},\bar {b} \in \mathcal {A}$
, if
 $\bar {a} \not \equiv _\infty \bar {b}$
then
$\bar {a} \not \equiv _\infty \bar {b}$
then
 $\bar {a} \nleq _\alpha \bar {b}$
. We may choose the formulas
$\bar {a} \nleq _\alpha \bar {b}$
. We may choose the formulas
![]() $\varphi _{\bar {a},\bar {b}}$
to be
$\varphi _{\bar {a},\bar {b}}$
to be
![]() $\Pi _\alpha $
, so that
$\Pi _\alpha $
, so that
![]() $\psi _{\bar {a}}$
are also
$\psi _{\bar {a}}$
are also
![]() $\Pi _\alpha $
. Then the formula
$\Pi _\alpha $
. Then the formula
![]() $\theta $
is
$\theta $
is
![]() $\Pi _{\alpha + 2}$
. So there is a natural notion of rank that we can assign to
$\Pi _{\alpha + 2}$
. So there is a natural notion of rank that we can assign to
![]() $\mathcal {A}$
based on the least such ordinal
$\mathcal {A}$
based on the least such ordinal
![]() $\alpha $
. Ash and Knight [Reference Ash and Knight4] prefer the following ranks:
$\alpha $
. Ash and Knight [Reference Ash and Knight4] prefer the following ranks:
Definition 2.4. For
![]() $\bar {a} \in \mathcal {A}$
, define
$\bar {a} \in \mathcal {A}$
, define
![]() $r(\bar {a})$
as the least ordinal
$r(\bar {a})$
as the least ordinal
![]() $\alpha $
such that for all
$\alpha $
such that for all
![]() $\bar {b}$
, if
$\bar {b}$
, if
 $\bar {a} \leq _\alpha \bar {b}$
then
$\bar {a} \leq _\alpha \bar {b}$
then
 $\bar {a} \equiv _\infty \bar {b}$
. Then define:
$\bar {a} \equiv _\infty \bar {b}$
. Then define:
-
•
 $r(\mathcal {A}) = \mathrm{sup} \{r(\bar {a}) : \bar {a} \in \mathcal {A}\}$
and
$r(\mathcal {A}) = \mathrm{sup} \{r(\bar {a}) : \bar {a} \in \mathcal {A}\}$
and -
•
 $R(\mathcal {A}) = \mathrm{sup} \{r(\bar {a})+1 : \bar {a} \in \mathcal {A}\}$
.
$R(\mathcal {A}) = \mathrm{sup} \{r(\bar {a})+1 : \bar {a} \in \mathcal {A}\}$
.
If
![]() $\lambda $
is a limit ordinal, it is possible for two structures
$\lambda $
is a limit ordinal, it is possible for two structures
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
to have
$\mathcal {B}$
to have
![]() $r(\mathcal {A}) = r(\mathcal {B}) = \lambda $
, but
$r(\mathcal {A}) = r(\mathcal {B}) = \lambda $
, but
![]() $R(\mathcal {A}) = \lambda $
and
$R(\mathcal {A}) = \lambda $
and
![]() $R(\mathcal {B}) = \lambda + 1$
.
$R(\mathcal {B}) = \lambda + 1$
.
Scott’s original proof of Theorem 2.2 used symmetric back-and-forth relations
![]() $\sim _\alpha $
instead of the asymmetric ones defined above. In the definition below we extend only by single elements c and d rather than by tuples to show another possible variation.
$\sim _\alpha $
instead of the asymmetric ones defined above. In the definition below we extend only by single elements c and d rather than by tuples to show another possible variation.
Definition 2.5. The standard symmetric back-and-forth relations
![]() $\sim _\alpha $
on
$\sim _\alpha $
on
![]() $\mathcal {A}$
, for
$\mathcal {A}$
, for
![]() $\alpha < \omega _1$
, are defined by:
$\alpha < \omega _1$
, are defined by:
-
1.
 $\bar {a} \sim _0 \bar {b}$
if
$\bar {a} \sim _0 \bar {b}$
if
 $\bar {a}$
and
$\bar {a}$
and
 $\bar {b}$
satisfy the same quantifier-free formulas.
$\bar {b}$
satisfy the same quantifier-free formulas. -
2. For
 $\alpha> 0$
,
$\alpha> 0$
,
 $\bar {a} \sim _\alpha \bar {b}$
if for each
$\bar {a} \sim _\alpha \bar {b}$
if for each
 $\beta < \alpha $
and d there is c such that
$\beta < \alpha $
and d there is c such that
 $\bar {a} c \sim _\beta \bar {b} d$
, and for all c there is d such that
$\bar {a} c \sim _\beta \bar {b} d$
, and for all c there is d such that
 $\bar {a} c \sim _\beta \bar {b} d$
.
$\bar {a} c \sim _\beta \bar {b} d$
.
Again, one can argue that there is a countable ordinal
![]() $\alpha $
such that if
$\alpha $
such that if
 $\bar {a} \sim _\alpha \bar {b}$
, then
$\bar {a} \sim _\alpha \bar {b}$
, then
 $\bar {a} \sim _\beta \bar {b}$
for all
$\bar {a} \sim _\beta \bar {b}$
for all
![]() $\beta $
. We can define a rank based on these back-and-forth relations.
$\beta $
. We can define a rank based on these back-and-forth relations.
Definition 2.6. For
![]() $\bar {a} \in \mathcal {A}$
, define
$\bar {a} \in \mathcal {A}$
, define
![]() $\operatorname {\mathrm {sr}}(\bar {a})$
as the least ordinal
$\operatorname {\mathrm {sr}}(\bar {a})$
as the least ordinal
![]() $\alpha $
such that for all
$\alpha $
such that for all
![]() $\bar {b}$
, if
$\bar {b}$
, if
 $\bar {a} \sim _\alpha \bar {b}$
then
$\bar {a} \sim _\alpha \bar {b}$
then
 $\bar {a} \equiv _\infty \bar {b}$
. Then define:
$\bar {a} \equiv _\infty \bar {b}$
. Then define:
-
•
 $\operatorname {\mathrm {sr}}(\mathcal {A}) = \mathrm{sup} \{\operatorname {\mathrm {sr}}(\bar {a}) : \bar {a} \in \mathcal {A}\}$
and
$\operatorname {\mathrm {sr}}(\mathcal {A}) = \mathrm{sup} \{\operatorname {\mathrm {sr}}(\bar {a}) : \bar {a} \in \mathcal {A}\}$
and -
•
 $\operatorname {\mathrm {SR}}(\mathcal {A}) = \mathrm{sup} \{\operatorname {\mathrm {sr}}(\bar {a})+1 : \bar {a} \in \mathcal {A}\}$
.
$\operatorname {\mathrm {SR}}(\mathcal {A}) = \mathrm{sup} \{\operatorname {\mathrm {sr}}(\bar {a})+1 : \bar {a} \in \mathcal {A}\}$
.
This is what Marker [Reference Marker45] uses as the definition of Scott rank. It is from this connection with Scott’s original proof of Theorem 2.2 that the name Scott rank is given to these notions of rank, though it is unclear which rank should hold the title. In general, we prefer the ranks R and
![]() $\operatorname {\mathrm {SR}}$
over the ranks r and
$\operatorname {\mathrm {SR}}$
over the ranks r and
![]() $\operatorname {\mathrm {sr}}$
, as they contain more information. These ranks R and
$\operatorname {\mathrm {sr}}$
, as they contain more information. These ranks R and
![]() $\operatorname {\mathrm {SR}}$
agree at multiples of
$\operatorname {\mathrm {SR}}$
agree at multiples of
![]() $\omega ^2$
.
$\omega ^2$
.
There are two other possible variations on the back-and-forth relations: defining the symmetric relations
![]() $\sim _\alpha $
to extend by tuples (which is a common definition) and defining the asymmetric relations
$\sim _\alpha $
to extend by tuples (which is a common definition) and defining the asymmetric relations
![]() $\leq _\alpha $
to extend by single elements (which is rarely seen). Each of these definitions also gives rise to a notion of rank.
$\leq _\alpha $
to extend by single elements (which is rarely seen). Each of these definitions also gives rise to a notion of rank.
Another common notion of rank, used, e.g., by Sacks [Reference Sacks61] and in Marker’s book on model theory [Reference Marker44], is as follows.
Definition 2.7. Let
![]() $\mathcal {A}$
be a countable structure. We define fragments
$\mathcal {A}$
be a countable structure. We define fragments
 $\mathcal {L}_{\alpha }^{\mathcal {A}}$
of
$\mathcal {L}_{\alpha }^{\mathcal {A}}$
of
![]() $\mathcal {L}_{\omega _1 \omega }$
and
$\mathcal {L}_{\omega _1 \omega }$
and
 $\mathcal {L}_{\alpha }^{\mathcal {A}}$
-theories
$\mathcal {L}_{\alpha }^{\mathcal {A}}$
-theories
 $T_{\alpha }^{\mathcal {A}}$
as follows:
$T_{\alpha }^{\mathcal {A}}$
as follows:
-
1.
 $\mathcal {L}_0^{\mathcal {A}}$
is finitary first-order logic;
$\mathcal {L}_0^{\mathcal {A}}$
is finitary first-order logic; -
2.
 $T_\alpha ^{\mathcal {A}}$
is the complete theory of
$T_\alpha ^{\mathcal {A}}$
is the complete theory of
 $\mathcal {A}$
in
$\mathcal {A}$
in
 $\mathcal {L}_{\alpha }^{\mathcal {A}}$
;
$\mathcal {L}_{\alpha }^{\mathcal {A}}$
; -
3.
 $\mathcal {L}_{\lambda }^{\mathcal {A}}$
is the union of
$\mathcal {L}_{\lambda }^{\mathcal {A}}$
is the union of
 $\mathcal {L}_{\alpha }^{\mathcal {A}}$
for
$\mathcal {L}_{\alpha }^{\mathcal {A}}$
for
 $\alpha < \lambda $
a limit ordinal; and
$\alpha < \lambda $
a limit ordinal; and -
4.
 $\mathcal {L}_{\alpha +1}^{\mathcal {A}}$
is the least fragment of
$\mathcal {L}_{\alpha +1}^{\mathcal {A}}$
is the least fragment of
 $\mathcal {L}_{\omega _1 \omega }$
containing
$\mathcal {L}_{\omega _1 \omega }$
containing
 $\mathcal {L}_{\alpha }^{\mathcal {A}}$
and also containing, for each non-principal n-type p of
$\mathcal {L}_{\alpha }^{\mathcal {A}}$
and also containing, for each non-principal n-type p of
 $T_\alpha ^{\mathcal {A}}$
, the conjunction
$T_\alpha ^{\mathcal {A}}$
, the conjunction
 $\bigwedge p$
of all the formulas in p.
$\bigwedge p$
of all the formulas in p.
Essentially,
 $T_{\alpha +1}^{\mathcal {A}}$
gives a name to all of the non-principal types of
$T_{\alpha +1}^{\mathcal {A}}$
gives a name to all of the non-principal types of
 $T_\alpha ^{\mathcal {A}}$
, though this may then introduce new non-principal types. However, one can show that this process stabilizes and for some
$T_\alpha ^{\mathcal {A}}$
, though this may then introduce new non-principal types. However, one can show that this process stabilizes and for some
![]() $\alpha $
, all of the types of
$\alpha $
, all of the types of
 $T_{\alpha }^{\mathcal {A}}$
realized in
$T_{\alpha }^{\mathcal {A}}$
realized in
![]() $\mathcal {A}$
are principal. One can then define the Scott rank of
$\mathcal {A}$
are principal. One can then define the Scott rank of
![]() $\mathcal {A}$
to be the least
$\mathcal {A}$
to be the least
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathcal {A}$
is the atomic model of
$\mathcal {A}$
is the atomic model of
 $T_\alpha ^{\mathcal {A}}$
. This rank agrees with the previous ranks at multiples of
$T_\alpha ^{\mathcal {A}}$
. This rank agrees with the previous ranks at multiples of
![]() $\omega ^2$
. It can be useful when one wants to apply ideas from finitary model theory.
$\omega ^2$
. It can be useful when one wants to apply ideas from finitary model theory.
Gao [Reference Gao23] also introduces a notion of Scott rank based on back-and-forth games, which is similar in spirit to the ranks defined using back-and-forth relations.
A final notion of Scott rank was introduced by Montalbán [Reference Montalbán52] based on the following list of equivalent properties:
Theorem 2.8 Montalbán [Reference Montalbán52]
Let
![]() $\mathcal {A}$
be a countable structure, and
$\mathcal {A}$
be a countable structure, and
![]() $\alpha $
a countable ordinal. The following are equivalent:
$\alpha $
a countable ordinal. The following are equivalent:
-
1.
 $\mathcal {A}$
has a
$\mathcal {A}$
has a
 $\Pi _{\alpha +1}$
Scott sentence.
$\Pi _{\alpha +1}$
Scott sentence. -
2. Every automorphism orbit in
 $\mathcal {A}$
is
$\mathcal {A}$
is
 $\Sigma _\alpha $
-definable without parameters.
$\Sigma _\alpha $
-definable without parameters. -
3.
 $\mathcal {A}$
is uniformly (boldface)
$\mathcal {A}$
is uniformly (boldface)
 $\mathbf {\Delta }^0_\alpha $
-categorical.
$\mathbf {\Delta }^0_\alpha $
-categorical.
Montalbán proposed the following definition of Scott rank:
Definition 2.9. The Scott rank of a countable structure
![]() $\mathcal {A}$
is the least ordinal
$\mathcal {A}$
is the least ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathcal {A}$
has a
$\mathcal {A}$
has a
![]() $\Pi _{\alpha + 1}$
Scott sentence.
$\Pi _{\alpha + 1}$
Scott sentence.
Montalbán argued that this is the correct notion of Scott rank because it is robust in the sense that it has many equivalent characterizations via Theorem 2.8. It is this definition that we use for most of the rest of this article, except when otherwise noted.
There is a clear connection between this notion of Scott rank proposed by Montalbán and the rank R of Definition 2.4 defined using the asymmetric back-and-forth relations
![]() $\leq _\alpha $
. Given
$\leq _\alpha $
. Given
![]() $\bar {a} \in \mathcal {A}$
, the formula
$\bar {a} \in \mathcal {A}$
, the formula
![]() $\psi _{\bar {a}}$
defines the automorphism orbit of
$\psi _{\bar {a}}$
defines the automorphism orbit of
![]() $\bar {a}$
; this is because if
$\bar {a}$
; this is because if
 $\bar {a} \equiv _\infty \bar {b}$
, then the structures
$\bar {a} \equiv _\infty \bar {b}$
, then the structures
![]() $(\mathcal {A},\bar {a})$
and
$(\mathcal {A},\bar {a})$
and
 $(\mathcal {A},\bar {b})$
, with
$(\mathcal {A},\bar {b})$
, with
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
named as constants, are isomorphic. With
$\bar {b}$
named as constants, are isomorphic. With
![]() $\alpha = r(\bar {a})$
, the automorphism orbit of
$\alpha = r(\bar {a})$
, the automorphism orbit of
![]() $\bar {a}$
is defined by a
$\bar {a}$
is defined by a
![]() $\Pi _{\alpha }$
formula. Thus the Scott rank as defined by Montalbán and the rank R differ by at most one.
$\Pi _{\alpha }$
formula. Thus the Scott rank as defined by Montalbán and the rank R differ by at most one.
3 Scott complexity
There is some arbitrariness in choosing to define Scott rank using
![]() $\Pi $
formulas rather than
$\Pi $
formulas rather than
![]() $\Sigma $
formulas. Indeed, if we defined the Scott rank of a structure to be the least ordinal
$\Sigma $
formulas. Indeed, if we defined the Scott rank of a structure to be the least ordinal
![]() $\alpha $
such that the structure has a
$\alpha $
such that the structure has a
![]() $\Sigma _{\alpha +2}$
Scott sentence, then we would have the desirable property that naming constants does not change Scott rank:
$\Sigma _{\alpha +2}$
Scott sentence, then we would have the desirable property that naming constants does not change Scott rank:
![]() $\mathcal {A}$
has the same Scott rank as
$\mathcal {A}$
has the same Scott rank as
![]() $(\mathcal {A},\bar {c})$
for any tuple
$(\mathcal {A},\bar {c})$
for any tuple
![]() $\bar {c} \in \mathcal {A}$
. This follows from the following fact:
$\bar {c} \in \mathcal {A}$
. This follows from the following fact:
Theorem 3.1 Montalbán
Let
![]() $\mathcal {A}$
be a countable structure. Then
$\mathcal {A}$
be a countable structure. Then
![]() $\mathcal {A}$
has a
$\mathcal {A}$
has a
![]() $\Sigma _{\alpha +1}$
Scott sentence if and only if for some
$\Sigma _{\alpha +1}$
Scott sentence if and only if for some
![]() $\bar {c} \in \mathcal {A}$
,
$\bar {c} \in \mathcal {A}$
,
![]() $(\mathcal {A},\bar {c})$
has a
$(\mathcal {A},\bar {c})$
has a
![]() $\Pi _{\alpha }$
Scott sentence.
$\Pi _{\alpha }$
Scott sentence.
The proof of this fact is less obvious than it seems; indeed it was stated as an obvious fact without proof in [Reference Montalbán52] but a proof was first provided (for
![]() $\Sigma _3$
sentences) in [Reference Montalbán53]. A full proof appears in [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1].
$\Sigma _3$
sentences) in [Reference Montalbán53]. A full proof appears in [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1].
Moreover, defining Scott rank in this way is still robust; combining Theorems 2.8 and 3.1, we get:
Theorem 3.2. Let
![]() $\mathcal {A}$
be a countable structure, and
$\mathcal {A}$
be a countable structure, and
![]() $\alpha $
a countable ordinal. The following are equivalent:
$\alpha $
a countable ordinal. The following are equivalent:
-
1.
 $\mathcal {A}$
has a
$\mathcal {A}$
has a
 $\Sigma _{\alpha +2}$
Scott sentence.
$\Sigma _{\alpha +2}$
Scott sentence. -
2. There are parameters
 $\bar {c}$
such that every automorphism orbit in
$\bar {c}$
such that every automorphism orbit in
 $\mathcal {A}$
is
$\mathcal {A}$
is
 $\Sigma _\alpha $
-definable over
$\Sigma _\alpha $
-definable over
 $\bar {c}$
.
$\bar {c}$
. -
3.
 $\mathcal {A}$
is (boldface)
$\mathcal {A}$
is (boldface)
 $\mathbf {\Delta }^0_\alpha $
-categorical.
$\mathbf {\Delta }^0_\alpha $
-categorical.
In [Reference Montalbán54], Montalbán refers to the Scott rank of Definition 2.9 as parameterless Scott rank and the Scott rank defined using
![]() $\Sigma $
formulas as parametrized Scott rank, and uses the latter as the definition.
$\Sigma $
formulas as parametrized Scott rank, and uses the latter as the definition.
Rather than choosing between these two possibilities, one can give up on assigning a single ordinal rank, and rather say that the Scott complexity (or Scott sentence complexity) of a structure is the least complexity of a Scott sentence for that structure, e.g., if a structure has a
![]() $\Pi _3$
Scott sentence but no
$\Pi _3$
Scott sentence but no
![]() $\Sigma _3$
Scott sentence, then its Scott complexity is
$\Sigma _3$
Scott sentence, then its Scott complexity is
![]() $\Pi _3$
. (This is not yet a formal definition, as we have not specified the possible complexities of sentences.)
$\Pi _3$
. (This is not yet a formal definition, as we have not specified the possible complexities of sentences.)
Now these complexities are not totally ordered;
![]() $\Pi _\alpha $
and
$\Pi _\alpha $
and
![]() $\Sigma _\alpha $
are incomparable. So a natural question is: Can a structure have both a
$\Sigma _\alpha $
are incomparable. So a natural question is: Can a structure have both a
![]() $\Sigma _{\alpha +1}$
Scott sentence and a
$\Sigma _{\alpha +1}$
Scott sentence and a
![]() $\Pi _{\alpha +1}$
Scott sentence, but no
$\Pi _{\alpha +1}$
Scott sentence, but no
![]() $\Sigma _\alpha $
or
$\Sigma _\alpha $
or
![]() $\Pi _\alpha $
Scott sentence? The answer turns out to be yes—for example, the group
$\Pi _\alpha $
Scott sentence? The answer turns out to be yes—for example, the group
![]() $\mathbb {Z}$
has a
$\mathbb {Z}$
has a
![]() $\Sigma _3$
and a
$\Sigma _3$
and a
![]() $\Pi _3$
Scott sentence, but no
$\Pi _3$
Scott sentence, but no
![]() $\Sigma _2$
or
$\Sigma _2$
or
![]() $\Pi _2$
Scott sentence—but the following theorem of A. Miller says that the structure must then have a Scott sentence which is a conjunction of a
$\Pi _2$
Scott sentence—but the following theorem of A. Miller says that the structure must then have a Scott sentence which is a conjunction of a
![]() $\Sigma _\alpha $
sentence and a
$\Sigma _\alpha $
sentence and a
![]() $\Pi _\alpha $
sentence. We call such a sentence a
$\Pi _\alpha $
sentence. We call such a sentence a
![]() $\mathrm {d}\!-\Sigma _\alpha $
sentence, where d stands for difference, because it is the difference of two
$\mathrm {d}\!-\Sigma _\alpha $
sentence, where d stands for difference, because it is the difference of two
![]() $\Sigma _\alpha $
sentences.
$\Sigma _\alpha $
sentences.
Theorem 3.3 Miller [Reference Miller49]
Let
![]() $\mathcal {A}$
be a countable structure. Then if
$\mathcal {A}$
be a countable structure. Then if
![]() $\mathcal {A}$
has both a
$\mathcal {A}$
has both a
![]() $\Sigma _\alpha $
and a
$\Sigma _\alpha $
and a
![]() $\Pi _\alpha $
Scott sentence, it has a
$\Pi _\alpha $
Scott sentence, it has a
![]() $\mathrm {d}\!-\Sigma _\beta $
Scott sentence for some
$\mathrm {d}\!-\Sigma _\beta $
Scott sentence for some
![]() $\beta < \alpha $
.
$\beta < \alpha $
.
So for example the group
![]() $\mathbb {Z}$
has a
$\mathbb {Z}$
has a
![]() $\mathrm {d}\!-\Sigma _2$
sentence but no
$\mathrm {d}\!-\Sigma _2$
sentence but no
![]() $\Sigma _2$
or
$\Sigma _2$
or
![]() $\Pi _2$
sentence. Thus when we say that the Scott complexity of a structure is the least complexity of a Scott sentence for that structure, we have to include not just
$\Pi _2$
sentence. Thus when we say that the Scott complexity of a structure is the least complexity of a Scott sentence for that structure, we have to include not just
![]() $\Sigma _\alpha $
and
$\Sigma _\alpha $
and
![]() $\Pi _\alpha $
as complexities, but
$\Pi _\alpha $
as complexities, but
![]() $\mathrm {d}\!-\Sigma _2$
. But among these complexities, there is always a single least complexity of a Scott sentence.
$\mathrm {d}\!-\Sigma _2$
. But among these complexities, there is always a single least complexity of a Scott sentence.

Are there further possible least complexities of Scott sentences? For all of the other complexity classes of sentences we can think of, any structure with a Scott sentence of that complexity also has a simpler Scott sentence. Let us give two examples. First, if a structure has a Scott sentence which is a negation of a
![]() $\mathrm {d}\!-\Sigma _\alpha $
sentence, that is, of the form
$\mathrm {d}\!-\Sigma _\alpha $
sentence, that is, of the form
![]() $\varphi \vee \psi $
where
$\varphi \vee \psi $
where
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma _\alpha $
and
$\Sigma _\alpha $
and
![]() $\psi $
is
$\psi $
is
![]() $\Pi _\alpha $
, then one of either
$\Pi _\alpha $
, then one of either
![]() $\varphi $
or
$\varphi $
or
![]() $\psi $
is a Scott sentence on its own, and so the structure has either a
$\psi $
is a Scott sentence on its own, and so the structure has either a
![]() $\Sigma _\alpha $
or
$\Sigma _\alpha $
or
![]() $\Pi _\alpha $
Scott sentence. Second, there are complexities
$\Pi _\alpha $
Scott sentence. Second, there are complexities
![]() $n\mathrm {-}\Sigma _\alpha $
corresponding to the difference hierarchy. Suppose that a structure has a Scott sentence which is
$n\mathrm {-}\Sigma _\alpha $
corresponding to the difference hierarchy. Suppose that a structure has a Scott sentence which is
![]() $3\mathrm {-}\Sigma _\alpha $
, that is, of the form
$3\mathrm {-}\Sigma _\alpha $
, that is, of the form
![]() $(\varphi \wedge \neg \psi ) \vee \theta $
where these sentences are all
$(\varphi \wedge \neg \psi ) \vee \theta $
where these sentences are all
![]() $\Sigma _\alpha $
. Then either the
$\Sigma _\alpha $
. Then either the
![]() $\mathrm {d}\!-\Sigma _\alpha $
sentence
$\mathrm {d}\!-\Sigma _\alpha $
sentence
![]() $\varphi \wedge \neg \psi $
is a Scott sentence, or the
$\varphi \wedge \neg \psi $
is a Scott sentence, or the
![]() $\Sigma _\alpha $
sentence
$\Sigma _\alpha $
sentence
![]() $\psi $
is a Scott sentence. A similar argument works for the rest of the difference hierarchy. Empirically through arguments such as these, and by checking examples, it appears that
$\psi $
is a Scott sentence. A similar argument works for the rest of the difference hierarchy. Empirically through arguments such as these, and by checking examples, it appears that
![]() $\Sigma _\alpha $
,
$\Sigma _\alpha $
,
![]() $\Pi _\alpha $
, and
$\Pi _\alpha $
, and
![]() $\mathrm {d}\!-\Sigma _\alpha $
are the only possible Scott complexities. Thus we define:
$\mathrm {d}\!-\Sigma _\alpha $
are the only possible Scott complexities. Thus we define:
Definition 3.4. The Scott sentence complexity of a structure
![]() $\mathcal {A}$
is the least complexity, from among
$\mathcal {A}$
is the least complexity, from among
![]() $\Sigma _\alpha $
,
$\Sigma _\alpha $
,
![]() $\Pi _\alpha $
, and
$\Pi _\alpha $
, and
![]() $\mathrm {d}\!-\Sigma _\alpha $
, of a Scott sentence for
$\mathrm {d}\!-\Sigma _\alpha $
, of a Scott sentence for
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
It is desirable to have some kind of more rigorous argument that these should be the possible complexities, and that it is not just that we cannot think of any other possibilities. For this, we use a perspective that began in [Reference Miller49] of looking at the Borel complexity of the set of copies of a structure. Given a language
![]() $\mathcal {L}$
, there is a Polish space
$\mathcal {L}$
, there is a Polish space
![]() $\operatorname {\mathrm {Mod}}(\mathcal {L})$
of all
$\operatorname {\mathrm {Mod}}(\mathcal {L})$
of all
![]() $\mathcal {L}$
-structures with domain
$\mathcal {L}$
-structures with domain
![]() $\omega $
. Given a structure
$\omega $
. Given a structure
![]() $\mathcal {A} \in \operatorname {\mathrm {Mod}}(\mathcal {L})$
, let
$\mathcal {A} \in \operatorname {\mathrm {Mod}}(\mathcal {L})$
, let
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
be the set of all isomorphic copies of
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
be the set of all isomorphic copies of
![]() $\mathcal {A}$
in
$\mathcal {A}$
in
![]() $\operatorname {\mathrm {Mod}}(\mathcal {L})$
. There is a correspondence between Scott sentences of
$\operatorname {\mathrm {Mod}}(\mathcal {L})$
. There is a correspondence between Scott sentences of
![]() $\mathcal {A}$
and the complexity of
$\mathcal {A}$
and the complexity of
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
via the Lopez-Escobar theorem, and its strengthenings by Vaught and Miller.
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
via the Lopez-Escobar theorem, and its strengthenings by Vaught and Miller.
Theorem 3.5 Lopez-Escobar [Reference Lopez-Escobar40], Vaught [Reference Vaught65], and Miller [Reference Miller50]
Let
![]() $\mathbb {K}$
be a subclass of
$\mathbb {K}$
be a subclass of
![]() $\operatorname {\mathrm {Mod}}(\mathcal {L})$
which is closed under isomorphism. Then
$\operatorname {\mathrm {Mod}}(\mathcal {L})$
which is closed under isomorphism. Then
![]() $\mathbb {K}$
is
$\mathbb {K}$
is
![]() $\boldsymbol {\Sigma }^0_\alpha $
if and only if
$\boldsymbol {\Sigma }^0_\alpha $
if and only if
![]() $\mathbb {K}$
is axiomatized by an infinitary
$\mathbb {K}$
is axiomatized by an infinitary
![]() $\Sigma _\alpha $
sentence. The same is true for
$\Sigma _\alpha $
sentence. The same is true for
 $\mathbf {\Pi }^0_\alpha $
and
$\mathbf {\Pi }^0_\alpha $
and
![]() $\Pi _\alpha $
sentences, and for the difference hierarchy.
$\Pi _\alpha $
sentences, and for the difference hierarchy.
Since each structure has a Scott sentence,
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
is always Borel.
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
is always Borel.
Intuitively, the Lopez-Escobar result should extend to any natural and robust notion of complexity for sentences. So in place of looking at the least complexity of a Scott sentence for
![]() $\mathcal {A}$
, we look at the complexity of
$\mathcal {A}$
, we look at the complexity of
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
. This gives us access to additional structure via Wadge reducibility.
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
. This gives us access to additional structure via Wadge reducibility.
Definition 3.6 Wadge
Let A and B be subsets of
![]() $\operatorname {\mathrm {Mod}}(\mathcal {L})$
. We say that A is Wadge reducible to B, and write
$\operatorname {\mathrm {Mod}}(\mathcal {L})$
. We say that A is Wadge reducible to B, and write
![]() $A \leq _W B$
, if there is a continuous function f with
$A \leq _W B$
, if there is a continuous function f with
 $A = f^{-1}[B]$
, i.e.,
$A = f^{-1}[B]$
, i.e.,
The equivalence classes under this pre-order are called the Wadge degrees; we write
![]() $[A]_W$
for the Wadge degree of A. The Wadge hierarchy is the set of Wadge degrees under continuous reductions.
$[A]_W$
for the Wadge degree of A. The Wadge hierarchy is the set of Wadge degrees under continuous reductions.
With enough determinacy, the Wadge hierarchy is very well-behaved; it is well-founded and almost totally ordered (in the sense that any anti-chain has size at most two).
Theorem 3.7 Martin and Monk, AD
The Wadge order is well-founded.
Theorem 3.8 Wadge’s Lemma, AD, [Reference Wadge66]
Given
![]() $A,B \subseteq \omega ^\omega $
, either
$A,B \subseteq \omega ^\omega $
, either
![]() $A \leq _W B$
or
$A \leq _W B$
or
![]() $B \leq _W \omega ^\omega - A$
.
$B \leq _W \omega ^\omega - A$
.
Since determinacy for Borel sets is provable in ZFC, this theorem holds in ZFC for such sets. Since
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
is Borel, we will not need to use any determinacy assumptions.
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
is Borel, we will not need to use any determinacy assumptions.
In general, for each of the pointclasses
![]() $\Gamma $
from among
$\Gamma $
from among
![]() $\boldsymbol {\Sigma }^0_\alpha $
,
$\boldsymbol {\Sigma }^0_\alpha $
,
 $\mathbf {\Pi }^0_\alpha $
,
$\mathbf {\Pi }^0_\alpha $
,
![]() $\mathbf {\Delta }^0_\alpha $
,
$\mathbf {\Delta }^0_\alpha $
,
 $\mathrm {d}\!-\boldsymbol {\Sigma }^0_\alpha $
, and other pointclasses arising from the Borel or difference hierarchies, if A is Wadge-reducible to a set in
$\mathrm {d}\!-\boldsymbol {\Sigma }^0_\alpha $
, and other pointclasses arising from the Borel or difference hierarchies, if A is Wadge-reducible to a set in
![]() $\Gamma $
, then A itself is in
$\Gamma $
, then A itself is in
![]() $\Gamma $
; and moreover, there is a
$\Gamma $
; and moreover, there is a
![]() $\Gamma $
-complete set. We denote by
$\Gamma $
-complete set. We denote by
![]() $\Gamma $
the Wadge degree of a
$\Gamma $
the Wadge degree of a
![]() $\Gamma $
-complete set. So, for example,
$\Gamma $
-complete set. So, for example,
![]() $\boldsymbol {\Sigma }^0_1$
is the Wadge degree of open, but not clopen, sets.
$\boldsymbol {\Sigma }^0_1$
is the Wadge degree of open, but not clopen, sets.
Now we define:
Definition 3.9. The Scott complexity of a structure
![]() $\mathcal {A}$
is the Wadge degree of
$\mathcal {A}$
is the Wadge degree of
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
.
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
.
Of course we want to show that this is the same as Definition 3.4. (We have made a slight differentiation between the two by calling one Scott sentence complexity and the other Scott complexity; they are technically different types of objects, the former being a complexity class of sentences and the latter being a Wadge degree, though by the Lopez-Escobar theorem the two are in correspondence.) The possible Scott complexities are exactly what we expect given the discussion above:
 $\mathbf {\Pi }^0_\alpha $
,
$\mathbf {\Pi }^0_\alpha $
,
 $\boldsymbol {\Sigma }^0_\alpha $
, and
$\boldsymbol {\Sigma }^0_\alpha $
, and
 $\mathrm {d}\!-\boldsymbol {\Sigma }^0_\alpha $
. There are certain values of
$\mathrm {d}\!-\boldsymbol {\Sigma }^0_\alpha $
. There are certain values of
![]() $\alpha $
for which some of these are not possible, e.g.,
$\alpha $
for which some of these are not possible, e.g.,
![]() $\Sigma _2$
is not the Scott complexity of any structure. A complete list is as follows:
$\Sigma _2$
is not the Scott complexity of any structure. A complete list is as follows:
Theorem 3.10 Miller [Reference Miller49] and Alvir et al. [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1]
The possible Scott complexities of countable structures
![]() $\mathcal {A}$
are:
$\mathcal {A}$
are:
-
1.
 $\mathbf {\Pi }^0_\alpha $
for
$\mathbf {\Pi }^0_\alpha $
for
 $\alpha \geq 1$
,
$\alpha \geq 1$
, -
2.
 $\boldsymbol {\Sigma }^0_\alpha $
for
$\boldsymbol {\Sigma }^0_\alpha $
for
 $\alpha \geq 3$
a successor ordinal, and
$\alpha \geq 3$
a successor ordinal, and -
3.
 $\mathrm {d}\!-\boldsymbol {\Sigma }^0_\alpha $
for
$\mathrm {d}\!-\boldsymbol {\Sigma }^0_\alpha $
for
 $\alpha \geq 1$
a successor ordinal.
$\alpha \geq 1$
a successor ordinal.
There is a countable structure with each of these Wadge degrees.
Miller constructed a number of examples of structures with various Scott complexities, and also ruled out some possibilities, such as
![]() $\boldsymbol {\Sigma }^0_2$
(for relational languages). He left open the case of constructing a structure of Scott complexity
$\boldsymbol {\Sigma }^0_2$
(for relational languages). He left open the case of constructing a structure of Scott complexity
 $\boldsymbol {\Sigma }^0_{\alpha +1}$
for
$\boldsymbol {\Sigma }^0_{\alpha +1}$
for
![]() $\alpha $
a limit ordinal. Alvir et al. found such examples, and showed that these are the only possibilities.
$\alpha $
a limit ordinal. Alvir et al. found such examples, and showed that these are the only possibilities.
As a consequence of this theorem, Scott sentence complexity as in Definition 3.4 and Scott complexity as in Definition 3.9 are really the same thing, under the natural correspondence between Wadge degrees of
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
and Scott sentences for
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
and Scott sentences for
![]() $\mathcal {A}$
, that is, identifying
$\mathcal {A}$
, that is, identifying
![]() $\Sigma _\alpha $
and
$\Sigma _\alpha $
and
![]() $\boldsymbol {\Sigma }^0_\alpha $
, etc.
$\boldsymbol {\Sigma }^0_\alpha $
, etc.
4 Structures of high Scott rank
We now turn to an effective analysis of Scott complexity. We say that an ordinal
![]() $\alpha $
is X-computable if there is an X-computable linear order isomorphic to
$\alpha $
is X-computable if there is an X-computable linear order isomorphic to
![]() $\alpha $
. As there are only countably many X-computable ordinals, there must be a least non-X-computable ordinal, which we call
$\alpha $
. As there are only countably many X-computable ordinals, there must be a least non-X-computable ordinal, which we call
 $\omega _1^{X}$
(or
$\omega _1^{X}$
(or
 $\omega _1^{CK}$
when X is computable). Since any initial segment of an X-computable well-founded linear order has a X-computable presentation, the X-computable ordinals are closed downwards; the X-computable ordinals are exactly the ordinals below
$\omega _1^{CK}$
when X is computable). Since any initial segment of an X-computable well-founded linear order has a X-computable presentation, the X-computable ordinals are closed downwards; the X-computable ordinals are exactly the ordinals below
 $\omega _1^X$
.
$\omega _1^X$
.
We will give simpler and more elementary proofs than are usual in the literature, avoiding the use of
![]() $\Sigma ^1_1$
bounding, ordinal notations, or the Barwise compactness theorem. (See, e.g., [Reference Ash and Knight4] for proofs of some of these results using the Barwise compactness theorem.) Instead, our main tool will be the fact that if an X-computable tree is well-founded, then its tree rank is an X-computable ordinal. Recall that the tree rank is defined as follows:
$\Sigma ^1_1$
bounding, ordinal notations, or the Barwise compactness theorem. (See, e.g., [Reference Ash and Knight4] for proofs of some of these results using the Barwise compactness theorem.) Instead, our main tool will be the fact that if an X-computable tree is well-founded, then its tree rank is an X-computable ordinal. Recall that the tree rank is defined as follows:
-
•
 $rk(x) = 0$
if x is a leaf.
$rk(x) = 0$
if x is a leaf. -
•
 $rk(x)$
is otherwise the least ordinal (or possibly
$rk(x)$
is otherwise the least ordinal (or possibly
 $\infty $
) greater than the ranks of the children of x.
$\infty $
) greater than the ranks of the children of x.
The rank of a tree is the rank of its root node.
Theorem 4.1. Let T be an X-computable well-founded tree. Then the tree rank of T is an X-computable ordinal.
Proof sketch Given a tree
![]() $T \subseteq \omega ^{< \omega }$
we will define computably in T a linear order, called the Kleene–Brouwer order. If T is well-founded then the Kleene–Brouwer order will be as well; and in this case, the order type of the Kleene–Brouwer order will be an ordinal greater than the tree rank of T. The Kleene–Brouwer order is defined on the nodes of T by
$T \subseteq \omega ^{< \omega }$
we will define computably in T a linear order, called the Kleene–Brouwer order. If T is well-founded then the Kleene–Brouwer order will be as well; and in this case, the order type of the Kleene–Brouwer order will be an ordinal greater than the tree rank of T. The Kleene–Brouwer order is defined on the nodes of T by
![]() $s \leq _{KB} t$
if and only if
$s \leq _{KB} t$
if and only if
-
•
 $t \preceq s$
(s extends t) or
$t \preceq s$
(s extends t) or -
• there is n such that
 $s(n) < t(n)$
and
$s(n) < t(n)$
and
 $t \upharpoonright n = s \upharpoonright n$
(s is to the left of t).
$t \upharpoonright n = s \upharpoonright n$
(s is to the left of t).
If an X-computable tree T is well-founded with tree rank
![]() $\alpha $
, the Kleene–Brouwer order of T can be computed from T and hence is an X-computable presentation of an ordinal
$\alpha $
, the Kleene–Brouwer order of T can be computed from T and hence is an X-computable presentation of an ordinal
![]() $\beta \geq \alpha $
. Thus
$\beta \geq \alpha $
. Thus
![]() $\alpha $
itself is X-computable. We leave the details to the reader; they are not difficult.
$\alpha $
itself is X-computable. We leave the details to the reader; they are not difficult.
4.1 Bounds on Scott complexity
There are countably many computable structures, and hence by a simple counting argument there must be some ordinal
![]() $\alpha < \omega _1$
which is an upper bound on the Scott rank of a computable structure. Our goal in this section is to compute this bound, as well as to prove some other results along the way.
$\alpha < \omega _1$
which is an upper bound on the Scott rank of a computable structure. Our goal in this section is to compute this bound, as well as to prove some other results along the way.
For this section, it is helpful to extend the back-and-forth relations to tuples from different structures.
Definition 4.2. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be structures. The standard asymmetric back-and-forth relations
$\mathcal {B}$
be structures. The standard asymmetric back-and-forth relations
![]() $\leq _\alpha $
, for
$\leq _\alpha $
, for
![]() $\alpha < \omega _1$
, are defined for
$\alpha < \omega _1$
, are defined for
![]() $\bar {a} \in \mathcal {A}$
and
$\bar {a} \in \mathcal {A}$
and
![]() $\bar {b} \in \mathcal {B}$
of the same length by:
$\bar {b} \in \mathcal {B}$
of the same length by:
-
1.
 $(\mathcal {A},\bar {a}) \leq _0 (\mathcal {B},\bar {b})$
if
$(\mathcal {A},\bar {a}) \leq _0 (\mathcal {B},\bar {b})$
if
 $\bar {a}$
and
$\bar {a}$
and
 $\bar {b}$
satisfy the same quantifier-free formulas from among the first
$\bar {b}$
satisfy the same quantifier-free formulas from among the first
 $|\bar {a}|$
-many formulas.
$|\bar {a}|$
-many formulas. -
2. For
 $\alpha> 0$
,
$\alpha> 0$
,
 $(\mathcal {A},\bar {a}) \leq _\alpha (\mathcal {B},\bar {b})$
if for each
$(\mathcal {A},\bar {a}) \leq _\alpha (\mathcal {B},\bar {b})$
if for each
 $\beta < \alpha $
and
$\beta < \alpha $
and
 $\bar {d} \in \mathcal {B}$
there is
$\bar {d} \in \mathcal {B}$
there is
 $\bar {c} \in \mathcal {A}$
such that
$\bar {c} \in \mathcal {A}$
such that
 $(\mathcal {B},\bar {b} \bar {d}) \leq _\beta (\mathcal {A},\bar {a} \bar {c})$
.
$(\mathcal {B},\bar {b} \bar {d}) \leq _\beta (\mathcal {A},\bar {a} \bar {c})$
.
We define
![]() $\equiv _\infty $
etc. as before.
$\equiv _\infty $
etc. as before.
To begin, suppose that we have a computable structure
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Theorem 4.3 Nadel [Reference Nadel56]
Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be X-computable structures. If
$\mathcal {B}$
be X-computable structures. If
![]() $\mathcal {A} \equiv _\alpha \mathcal {B}$
for every
$\mathcal {A} \equiv _\alpha \mathcal {B}$
for every
 $\alpha < \omega _1^X$
, then
$\alpha < \omega _1^X$
, then
![]() $\mathcal {A} \cong \mathcal {B}$
.
$\mathcal {A} \cong \mathcal {B}$
.
Proof A finite partial isomorphism maps an element
![]() $\bar {a}$
of
$\bar {a}$
of
![]() $\mathcal {A}$
to a tuple
$\mathcal {A}$
to a tuple
![]() $\bar {b}$
of
$\bar {b}$
of
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
 $(\mathcal {A},\bar {a}) \equiv _0 (\mathcal {B},\bar {b})$
:
$(\mathcal {A},\bar {a}) \equiv _0 (\mathcal {B},\bar {b})$
:
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
satisfy the same atomic formulas from among the first
$\bar {b}$
satisfy the same atomic formulas from among the first
![]() $|\bar {a}|$
-many. We can form a tree of finite partial isomorphisms; the root node is the empty partial isomorphism, and the children of a node are the finite partial isomorphisms extending that node.
$|\bar {a}|$
-many. We can form a tree of finite partial isomorphisms; the root node is the empty partial isomorphism, and the children of a node are the finite partial isomorphisms extending that node.
Let T be the subtree of the tree of finite partial isomorphisms such that at the nth level, all of the finite partial isomorphism contain the first n elements of
![]() $\mathcal {A}$
in their domain, and the first n elements of
$\mathcal {A}$
in their domain, and the first n elements of
![]() $\mathcal {B}$
in their range. So T is X-computable. A path through T corresponds to a (total) isomorphism
$\mathcal {B}$
in their range. So T is X-computable. A path through T corresponds to a (total) isomorphism
![]() $\mathcal {A} \to \mathcal {B}$
.
$\mathcal {A} \to \mathcal {B}$
.
Claim 1. Consider a node
![]() $\sigma $
of T corresponding to a finite partial isomorphism
$\sigma $
of T corresponding to a finite partial isomorphism
![]() $\bar {a} \mapsto \bar {b}$
. If
$\bar {a} \mapsto \bar {b}$
. If
 $(\mathcal {A},\bar {a}) \equiv _{\alpha \cdot 4} (\mathcal {B},\bar {b})$
, then the tree rank of
$(\mathcal {A},\bar {a}) \equiv _{\alpha \cdot 4} (\mathcal {B},\bar {b})$
, then the tree rank of
![]() $\sigma $
is at least
$\sigma $
is at least
![]() $\alpha $
.
$\alpha $
.
Proof We argue by induction on
![]() $\alpha $
. We must show that for each
$\alpha $
. We must show that for each
![]() $\beta < \alpha $
, there is a child of
$\beta < \alpha $
, there is a child of
![]() $\sigma $
of tree rank at least
$\sigma $
of tree rank at least
![]() $\beta $
. Suppose without loss of generality that
$\beta $
. Suppose without loss of generality that
![]() $\sigma $
is at the nth level of the tree.
$\sigma $
is at the nth level of the tree.
First, let d be the
![]() $(n+1)$
st element of
$(n+1)$
st element of
![]() $\mathcal {B}$
. (If d is already contained in
$\mathcal {B}$
. (If d is already contained in
![]() $\bar {b}$
, then do nothing here; we assume that d is not in
$\bar {b}$
, then do nothing here; we assume that d is not in
![]() $\bar {b}$
.) Since
$\bar {b}$
.) Since
 $(\mathcal {A},\bar {a}) \equiv _{\alpha \cdot 4} (\mathcal {B},\bar {b})$
, there is
$(\mathcal {A},\bar {a}) \equiv _{\alpha \cdot 4} (\mathcal {B},\bar {b})$
, there is
![]() $c \in \mathcal {A}$
such that
$c \in \mathcal {A}$
such that
 $(\mathcal {A},\bar {a}c) \equiv _{\beta \cdot 4 + 2} (\mathcal {B},\bar {b}d)$
. Now let
$(\mathcal {A},\bar {a}c) \equiv _{\beta \cdot 4 + 2} (\mathcal {B},\bar {b}d)$
. Now let
![]() $c' \in \mathcal {A}$
be the
$c' \in \mathcal {A}$
be the
![]() $n+1$
st element of
$n+1$
st element of
![]() $\mathcal {A}$
. (Again, if
$\mathcal {A}$
. (Again, if
![]() $c'$
is already contained in
$c'$
is already contained in
![]() $\bar {a}c$
, then do nothing here; we assume that
$\bar {a}c$
, then do nothing here; we assume that
![]() $c'$
is not in
$c'$
is not in
![]() $\bar {a}c$
.) Let
$\bar {a}c$
.) Let
![]() $d' \in \mathcal {B}$
be such that
$d' \in \mathcal {B}$
be such that
 $(\mathcal {A},\bar {a}cc') \equiv _{\beta \cdot 4} (\mathcal {B},\bar {b}dd')$
. Then
$(\mathcal {A},\bar {a}cc') \equiv _{\beta \cdot 4} (\mathcal {B},\bar {b}dd')$
. Then
![]() $\bar {a}cc' \mapsto \bar {b}dd'$
is a finite partial isomorphism which is a child of
$\bar {a}cc' \mapsto \bar {b}dd'$
is a finite partial isomorphism which is a child of
![]() $\sigma $
, and by the induction hypothesis, it has tree rank at least
$\sigma $
, and by the induction hypothesis, it has tree rank at least
![]() $\beta $
.
$\beta $
.
Now
 $(\mathcal {A},\varnothing ) \equiv _{\omega _1^X} (\mathcal {B},\varnothing )$
and so the tree rank of T is at least
$(\mathcal {A},\varnothing ) \equiv _{\omega _1^X} (\mathcal {B},\varnothing )$
and so the tree rank of T is at least
 $\omega _1^X$
. Since T is X-computable, T must have a path, which is an isomorphism
$\omega _1^X$
. Since T is X-computable, T must have a path, which is an isomorphism
![]() $\mathcal {A} \to \mathcal {B}$
.⊣
$\mathcal {A} \to \mathcal {B}$
.⊣
We can easily apply this to tuples in a single structure.
Corollary 4.4 Nadel [Reference Nadel56]
Let
![]() $\mathcal {A}$
be an X-computable structures and
$\mathcal {A}$
be an X-computable structures and
 $\bar {a},\bar {b} \in \mathcal {A}$
. If
$\bar {a},\bar {b} \in \mathcal {A}$
. If
 $\bar {a} \equiv _\alpha \bar {b}$
for every
$\bar {a} \equiv _\alpha \bar {b}$
for every
 $\alpha < \omega _1^X$
, then there is an automorphism of
$\alpha < \omega _1^X$
, then there is an automorphism of
![]() $\mathcal {A}$
taking
$\mathcal {A}$
taking
![]() $\bar {a}$
to
$\bar {a}$
to
![]() $\bar {b}$
.
$\bar {b}$
.
We also get an upper bound on the Scott complexity of a computable structure.
Corollary 4.5 Nadel [Reference Nadel56]
An X-computable structure has a
 $\Pi _{\omega _1^{CK}+2}$
Scott sentence, and hence has Scott rank at most
$\Pi _{\omega _1^{CK}+2}$
Scott sentence, and hence has Scott rank at most
 $\omega _1^{CK}+1$
.
$\omega _1^{CK}+1$
.
This is true for all of the different definitions of Scott rank.
Proof By the previous corollary, if
 $\bar {a} \leq _{\omega _1^X} \bar {b}$
, then
$\bar {a} \leq _{\omega _1^X} \bar {b}$
, then
 $\bar {a}\equiv _\infty \bar {b}$
. Then as in the discussion preceding Definition 2.4, we can choose the formulas
$\bar {a}\equiv _\infty \bar {b}$
. Then as in the discussion preceding Definition 2.4, we can choose the formulas
![]() $\varphi _{\bar {a},\bar {b}}$
in the definition of the canonical Scott sentence to be
$\varphi _{\bar {a},\bar {b}}$
in the definition of the canonical Scott sentence to be
 $\Pi _{\omega _1^X}$
, so that the resulting Scott sentence is
$\Pi _{\omega _1^X}$
, so that the resulting Scott sentence is
 $\Pi _{\omega _1^X + 2}$
.
$\Pi _{\omega _1^X + 2}$
.
Next we will consider the computability of the Scott sentences of a computable structure. We give a slightly informal definition of the computable formulas of
![]() $\mathcal {L}_{\omega _1 \omega }$
. For the fully formal definition, see [Reference Ash and Knight4].
$\mathcal {L}_{\omega _1 \omega }$
. For the fully formal definition, see [Reference Ash and Knight4].
Definition 4.6.
-
• A computable
 $\Sigma _0$
or
$\Sigma _0$
or
 $\Pi _0$
formula is just a finitary quantifier-free formula.
$\Pi _0$
formula is just a finitary quantifier-free formula. -
• A computable
 $\Sigma _\alpha $
formula is a disjunction of formulas
$\Sigma _\alpha $
formula is a disjunction of formulas
 $\exists \bar {x} \psi (\bar {x})$
where the formulas
$\exists \bar {x} \psi (\bar {x})$
where the formulas
 $\psi (\bar {x})$
are computable
$\psi (\bar {x})$
are computable
 $\Pi _\beta $
for some
$\Pi _\beta $
for some
 $\beta < \alpha $
, and there is a c.e. set of codes for the formulas over which the disjunction is being taken.
$\beta < \alpha $
, and there is a c.e. set of codes for the formulas over which the disjunction is being taken. -
• A computable
 $\Pi _\alpha $
formula is a conjunction of formulas
$\Pi _\alpha $
formula is a conjunction of formulas
 $\exists \bar {x} \psi (\bar {x})$
where the formulas
$\exists \bar {x} \psi (\bar {x})$
where the formulas
 $\psi (\bar {x})$
are computable
$\psi (\bar {x})$
are computable
 $\Sigma _\beta $
for some
$\Sigma _\beta $
for some
 $\beta < \alpha $
, and the there is a c.e. set of codes for the formulas over which the conjunction is being taken.
$\beta < \alpha $
, and the there is a c.e. set of codes for the formulas over which the conjunction is being taken.
Let
![]() $\mathcal {A}$
be an X-computable structure. We will define, recursively for
$\mathcal {A}$
be an X-computable structure. We will define, recursively for
 $\alpha < \omega _1^X$
and tuples
$\alpha < \omega _1^X$
and tuples
![]() $\bar {a} \in \mathcal {A}$
, formulas
$\bar {a} \in \mathcal {A}$
, formulas
-
•
 $\varphi _{\bar {a},\alpha }$
such that
$\varphi _{\bar {a},\alpha }$
such that
 $\mathcal {B} \models \varphi _{\bar {a},\alpha }(\bar {b})$
if and only if
$\mathcal {B} \models \varphi _{\bar {a},\alpha }(\bar {b})$
if and only if
 $(\mathcal {A},\bar {a}) \leq _\alpha (\mathcal {B},\bar {b})$
and
$(\mathcal {A},\bar {a}) \leq _\alpha (\mathcal {B},\bar {b})$
and -
•
 $\psi _{\bar {a},\alpha }$
such that
$\psi _{\bar {a},\alpha }$
such that
 $\mathcal {B} \models \psi _{\bar {a},\alpha }(\bar {b})$
if and only if
$\mathcal {B} \models \psi _{\bar {a},\alpha }(\bar {b})$
if and only if
 $(\mathcal {B},\bar {b}) \leq _\alpha (\mathcal {A},\bar {a})$
.
$(\mathcal {B},\bar {b}) \leq _\alpha (\mathcal {A},\bar {a})$
.
We put
![]() $\varphi _{\bar {a},0}(\bar {x}) = \psi _{\bar {a},0}(\bar {x})$
to be the conjunction of the first
$\varphi _{\bar {a},0}(\bar {x}) = \psi _{\bar {a},0}(\bar {x})$
to be the conjunction of the first
![]() $|\bar {x}|$
-many atomic and negated atomic formulas about
$|\bar {x}|$
-many atomic and negated atomic formulas about
![]() $\bar {x}$
. For
$\bar {x}$
. For
![]() $\alpha> 0$
, we put
$\alpha> 0$
, we put
 $$ \begin{align*} \varphi_{\bar{a},\alpha}(\bar{x}) = \bigwedge_{\beta < \alpha} \; \forall \bar{y} \; \bigvee_{\bar{c} \in \mathcal{A}} \psi_{\bar{a}\bar{c},\beta}(\bar{x},\bar{y}), \end{align*} $$
$$ \begin{align*} \varphi_{\bar{a},\alpha}(\bar{x}) = \bigwedge_{\beta < \alpha} \; \forall \bar{y} \; \bigvee_{\bar{c} \in \mathcal{A}} \psi_{\bar{a}\bar{c},\beta}(\bar{x},\bar{y}), \end{align*} $$
and
 $$ \begin{align*} \psi_{\bar{a},\alpha}(\bar{x}) = \bigwedge_{\beta < \alpha} \; \bigwedge_{\bar{c} \in \mathcal{A}} \exists \bar{y} \; \varphi_{\bar{a}\bar{c},\beta}(\bar{x},\bar{y}).\end{align*} $$
$$ \begin{align*} \psi_{\bar{a},\alpha}(\bar{x}) = \bigwedge_{\beta < \alpha} \; \bigwedge_{\bar{c} \in \mathcal{A}} \exists \bar{y} \; \varphi_{\bar{a}\bar{c},\beta}(\bar{x},\bar{y}).\end{align*} $$
Both
![]() $\varphi _{\bar {a},\alpha }$
and
$\varphi _{\bar {a},\alpha }$
and
![]() $\psi _{\bar {a},\alpha }$
are computable
$\psi _{\bar {a},\alpha }$
are computable
![]() $\Pi _{\alpha \cdot 2}$
formulas.
$\Pi _{\alpha \cdot 2}$
formulas.
Suppose that
![]() $\alpha $
is an X-computable ordinal such that for all
$\alpha $
is an X-computable ordinal such that for all
 $\bar {a},\bar {b} \in \mathcal {A}$
, if
$\bar {a},\bar {b} \in \mathcal {A}$
, if
 $\bar {a} \leq _\alpha \bar {b}$
then
$\bar {a} \leq _\alpha \bar {b}$
then
 $\bar {a} \equiv _\infty \bar {b}$
. Then
$\bar {a} \equiv _\infty \bar {b}$
. Then
 $\mathcal {A} \models \psi _{\bar {a},\alpha }(\bar {b})$
if and only if
$\mathcal {A} \models \psi _{\bar {a},\alpha }(\bar {b})$
if and only if
 $\bar {a} \equiv _\infty \bar {b}$
. In the definition of the canonical Scott sentence, we may use
$\bar {a} \equiv _\infty \bar {b}$
. In the definition of the canonical Scott sentence, we may use
![]() $\psi _{\bar {a},\alpha }$
as the formula
$\psi _{\bar {a},\alpha }$
as the formula
![]() $\psi _{\bar {a}}$
. We get that the resulting Scott sentence is a computable
$\psi _{\bar {a}}$
. We get that the resulting Scott sentence is a computable
![]() $\Pi _{\alpha \cdot 2 + 2}$
sentence. (Note that this argument only works if the ordinal
$\Pi _{\alpha \cdot 2 + 2}$
sentence. (Note that this argument only works if the ordinal
![]() $\alpha $
is X-computable.) Thus we get:
$\alpha $
is X-computable.) Thus we get:
Theorem 4.7 Nadel [Reference Nadel56]
Let
![]() $\mathcal {A}$
be an X-computable structure. Then
$\mathcal {A}$
be an X-computable structure. Then
![]() $\mathcal {A}$
has Scott rank
$\mathcal {A}$
has Scott rank
 $< \omega _1^X$
if and only if
$< \omega _1^X$
if and only if
![]() $\mathcal {A}$
has an X-computable Scott sentence.
$\mathcal {A}$
has an X-computable Scott sentence.
An interesting line of investigation is to study the difference between the least-complexity Scott sentence and the least-complexity computable Scott sentence for a structure. Not much is known, though for example Ho constructed a subgroup of
![]() $\mathbb {Q}$
with a
$\mathbb {Q}$
with a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence but no computable
$\mathrm {d}\!-\Sigma _2$
Scott sentence but no computable
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence [Reference Ho33]. (The structure has computable
$\mathrm {d}\!-\Sigma _2$
Scott sentence [Reference Ho33]. (The structure has computable
![]() $\Sigma _3$
and
$\Sigma _3$
and
![]() $\Pi _3$
structures, so that Theorem 3.3 is not true for computable Scott sentences.)
$\Pi _3$
structures, so that Theorem 3.3 is not true for computable Scott sentences.)
Finally, we will prove effective versions of Theorem 4.3 and Corollary 4.4.
Theorem 4.8 Nadel [Reference Nadel56]
Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be X-computable structures. If
$\mathcal {B}$
be X-computable structures. If
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
satisfy the same X-computable infinitary formulas, then they are isomorphic.
$\mathcal {B}$
satisfy the same X-computable infinitary formulas, then they are isomorphic.
Proof For each
 $\alpha < \omega _1^X$
, we have that
$\alpha < \omega _1^X$
, we have that
![]() $\mathcal {B} \models \varphi _{\varnothing ,\alpha }$
where this is the X-computable formula defined above. This implies that
$\mathcal {B} \models \varphi _{\varnothing ,\alpha }$
where this is the X-computable formula defined above. This implies that
![]() $\mathcal {A} \leq _\alpha \mathcal {B}$
for each
$\mathcal {A} \leq _\alpha \mathcal {B}$
for each
![]() $\alpha $
. Thus
$\alpha $
. Thus
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are isomorphic by Theorem 4.3.
$\mathcal {B}$
are isomorphic by Theorem 4.3.
Corollary 4.9 Nadel [Reference Nadel56]
Let
![]() $\mathcal {A}$
be an X-computable structure. If
$\mathcal {A}$
be an X-computable structure. If
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b} \in \mathcal {A}$
satisfy the same X-computable formulas, then there is an automorphism of
$\bar {b} \in \mathcal {A}$
satisfy the same X-computable formulas, then there is an automorphism of
![]() $\mathcal {A}$
taking
$\mathcal {A}$
taking
![]() $\bar {a}$
to
$\bar {a}$
to
![]() $\bar {b}$
.
$\bar {b}$
.
4.2 Construction of structures of high Scott complexity
Corollary 4.5 is the best possible bound on the Scott complexity of an X-computable structure. Harrison [Reference Harrison26] constructed a computable linear order of order type
 $\omega _1^{CK} \cdot (1 + \mathbb {Q})$
, which has Scott complexity
$\omega _1^{CK} \cdot (1 + \mathbb {Q})$
, which has Scott complexity
 $\Pi _{\omega _1^{CK}+2}$
. It is a pseudo-well-ordering in the sense that it has no hyperarithmetic descending sequence. More generally, we can construct the Harrison linear order
$\Pi _{\omega _1^{CK}+2}$
. It is a pseudo-well-ordering in the sense that it has no hyperarithmetic descending sequence. More generally, we can construct the Harrison linear order
 $\omega _1^{X} \cdot (1 + \mathbb {Q})$
relative to any set X, which has Scott complexity
$\omega _1^{X} \cdot (1 + \mathbb {Q})$
relative to any set X, which has Scott complexity
 $\Pi _{\omega _1^{X}+2}$
. Often, the Barwise compactness theorem is used to construct the Harrison linear order, but we will give a more natural construction found in [Reference Kleene34] and which is explained in Lemma III.2.1 of [Reference Sacks60]. Our account comes from [Reference Chan14]. We will give the general overview of the argument giving most but not all of the details.
$\Pi _{\omega _1^{X}+2}$
. Often, the Barwise compactness theorem is used to construct the Harrison linear order, but we will give a more natural construction found in [Reference Kleene34] and which is explained in Lemma III.2.1 of [Reference Sacks60]. Our account comes from [Reference Chan14]. We will give the general overview of the argument giving most but not all of the details.
The relation “Y is not hyperarithmetic in X” is
 $\Sigma ^1_1(X)$
and so there is an X-computable tree T whose paths are pairs
$\Sigma ^1_1(X)$
and so there is an X-computable tree T whose paths are pairs
![]() $\langle Y,f \rangle $
where f witnesses that Y is not hyperarithmetic in X. T is X-computable uniformly in X and has no X-hyperarithmetic path. Take the Kleene-Brouwer order of T. We get an X-computable linear order L with no X-hyperarithmetic descending sequence, as given a descending sequence in L, with one more jump we can compute a path through T. Then we argue that L has order type
$\langle Y,f \rangle $
where f witnesses that Y is not hyperarithmetic in X. T is X-computable uniformly in X and has no X-hyperarithmetic path. Take the Kleene-Brouwer order of T. We get an X-computable linear order L with no X-hyperarithmetic descending sequence, as given a descending sequence in L, with one more jump we can compute a path through T. Then we argue that L has order type
 $\omega _1^X \cdot (1 + \mathbb {Q}) + \alpha $
for some
$\omega _1^X \cdot (1 + \mathbb {Q}) + \alpha $
for some
 $\alpha < \omega _1^X$
. This takes several steps:
$\alpha < \omega _1^X$
. This takes several steps:
-
• Let
 $\gamma $
be the order type of the well-founded initial segment of L. Write
$\gamma $
be the order type of the well-founded initial segment of L. Write
 $L = L_1 + L_2$
with
$L = L_1 + L_2$
with
 $L_1$
the well-founded initial segment of L. If
$L_1$
the well-founded initial segment of L. If
 $\gamma $
were a computable ordinal, then we could hyperarithmetically split L as
$\gamma $
were a computable ordinal, then we could hyperarithmetically split L as
 $L_1 + L_2$
, and
$L_1 + L_2$
, and
 $L_2$
has no least element, giving a hyperarithmetic descending sequence in L. Also, we cannot have
$L_2$
has no least element, giving a hyperarithmetic descending sequence in L. Also, we cannot have
 $\gamma> \omega _1^X$
as then we could fix some element u such that
$\gamma> \omega _1^X$
as then we could fix some element u such that
 $\{ v \in L : v < u\}$
is a computable linear ordering of order type
$\{ v \in L : v < u\}$
is a computable linear ordering of order type
 $\omega _1^X$
. Thus
$\omega _1^X$
. Thus
 $\gamma = \omega _1^X$
.
$\gamma = \omega _1^X$
. -
• Similarly, given any
 $u \in L$
, either
$u \in L$
, either
 $\{ v \in L : v \geq u\}$
is well-founded or the well-founded initial segment of
$\{ v \in L : v \geq u\}$
is well-founded or the well-founded initial segment of
 $\{ v \in L : v \geq u\}$
has order type
$\{ v \in L : v \geq u\}$
has order type
 $\omega _1^X$
. Thus
$\omega _1^X$
. Thus
 $L \cong \omega _1^X \cdot (1+L^*) + \alpha $
for some linear order
$L \cong \omega _1^X \cdot (1+L^*) + \alpha $
for some linear order
 $L^*$
and ordinal
$L^*$
and ordinal
 $\alpha $
.
$\alpha $
. -
•
 $\alpha $
must be computable, as if u is the initial element of
$\alpha $
must be computable, as if u is the initial element of
 $\alpha $
,
$\alpha $
,
 $\{v \in L : v \geq u\}$
is a computable linear order.
$\{v \in L : v \geq u\}$
is a computable linear order. -
• We claim that
 $L^*$
is dense and without endpoints. If
$L^*$
is dense and without endpoints. If
 $L^*$
had a left endpoint, then
$L^*$
had a left endpoint, then
 $\omega _1^X + \omega _1^X$
would be an initial segment of L, which we have already argued is not the case. If it had a right endpoint, then
$\omega _1^X + \omega _1^X$
would be an initial segment of L, which we have already argued is not the case. If it had a right endpoint, then
 $\omega _1^X + \alpha $
would be a final segment of L, which cannot happen because
$\omega _1^X + \alpha $
would be a final segment of L, which cannot happen because
 $\omega _1^X + \alpha $
is not X-computable. And if
$\omega _1^X + \alpha $
is not X-computable. And if
 $L^*$
was not dense then we could find elements
$L^*$
was not dense then we could find elements
 $a,b \in L$
such that
$a,b \in L$
such that
 $[a,b) \cong \omega _1^X$
, and this cannot happen as
$[a,b) \cong \omega _1^X$
, and this cannot happen as
 $\omega _1^X$
is not X-computable.
$\omega _1^X$
is not X-computable.
Now if we fix the first element a of
![]() $\alpha $
, and restrict L to the elements below a, we obtain an X-computable linear order of order type
$\alpha $
, and restrict L to the elements below a, we obtain an X-computable linear order of order type
 $\omega _1^X \cdot (1 + \mathbb {Q})$
as desired. (Up until this point, the construction has been uniform in X, and indeed we can use a trick to make this step uniform as well: we instead replace L by
$\omega _1^X \cdot (1 + \mathbb {Q})$
as desired. (Up until this point, the construction has been uniform in X, and indeed we can use a trick to make this step uniform as well: we instead replace L by
![]() $L \cdot \omega $
which has order type
$L \cdot \omega $
which has order type
 $\omega _1^X \cdot (1 + \mathbb {Q})$
.)
$\omega _1^X \cdot (1 + \mathbb {Q})$
.)
Now we have to argue that the Scott complexity of
 $\omega _1^X \cdot (1 + \mathbb {Q})$
is
$\omega _1^X \cdot (1 + \mathbb {Q})$
is
 $\Pi _{\omega _1^{X}+2}$
. We must show that it has no
$\Pi _{\omega _1^{X}+2}$
. We must show that it has no
 $\Sigma _{\omega _1^X+2}$
Scott sentence. Using Theorem 3.2, it suffices to show that there is no tuple
$\Sigma _{\omega _1^X+2}$
Scott sentence. Using Theorem 3.2, it suffices to show that there is no tuple
![]() $\bar {c}$
such that the automorphism orbits are definable by
$\bar {c}$
such that the automorphism orbits are definable by
![]() $\Sigma _{\alpha }$
formulas,
$\Sigma _{\alpha }$
formulas,
 $\alpha < \omega _1^X$
. (Note that if an orbit is definable by a
$\alpha < \omega _1^X$
. (Note that if an orbit is definable by a
 $\Sigma _{\omega _1^X}$
formula, then it is definable by a
$\Sigma _{\omega _1^X}$
formula, then it is definable by a
![]() $\Sigma _{\alpha }$
formula for some
$\Sigma _{\alpha }$
formula for some
 $\alpha < \omega _1^X$
.) The parameters
$\alpha < \omega _1^X$
.) The parameters
![]() $\bar {c}$
do not help us define the automorphism orbits because, given
$\bar {c}$
do not help us define the automorphism orbits because, given
![]() $\bar {c} = (c_1,\ldots ,c_n)$
with
$\bar {c} = (c_1,\ldots ,c_n)$
with
![]() $c_1 < c_2 < \cdots < c_n$
, between two of the parameters is a linear order of order type
$c_1 < c_2 < \cdots < c_n$
, between two of the parameters is a linear order of order type
 $\omega _1^X \cdot (1 + \mathbb {Q}) + \beta $
for some
$\omega _1^X \cdot (1 + \mathbb {Q}) + \beta $
for some
 $\beta < \omega _1^X$
. So let us ignore the parameters. (See, for example, Section 15.3.3 of [Reference Ash and Knight4] for similar arguments.) Let u be an element of the non-well-founded part of the Harrison linear order, and suppose to the contrary that
$\beta < \omega _1^X$
. So let us ignore the parameters. (See, for example, Section 15.3.3 of [Reference Ash and Knight4] for similar arguments.) Let u be an element of the non-well-founded part of the Harrison linear order, and suppose to the contrary that
![]() $\varphi (\bar {x})$
is a
$\varphi (\bar {x})$
is a
![]() $\Sigma _\alpha $
formula defining the automorphism type of u, with
$\Sigma _\alpha $
formula defining the automorphism type of u, with
 $\alpha < \omega _1^X$
. Then (using the formula
$\alpha < \omega _1^X$
. Then (using the formula
![]() $\varphi _{u,\alpha }$
from the previous section) there is an X-computable
$\varphi _{u,\alpha }$
from the previous section) there is an X-computable
![]() $\Pi _{\alpha \cdot 2}$
formula defining the automorphism orbit of u. So we may assume, after increasing
$\Pi _{\alpha \cdot 2}$
formula defining the automorphism orbit of u. So we may assume, after increasing
![]() $\alpha $
, that
$\alpha $
, that
![]() $\varphi $
is X-computable. So the automorphism orbit
$\varphi $
is X-computable. So the automorphism orbit
![]() $\{v \in L : L \models \varphi (v)\}$
of u is X-hyperarithmetic, and has no least element. Then we can find a hyperarithmetic descending sequence in L.
$\{v \in L : L \models \varphi (v)\}$
of u is X-hyperarithmetic, and has no least element. Then we can find a hyperarithmetic descending sequence in L.
Thus we obtain:
Theorem 4.10. Given
![]() $X \in 2^\omega $
, there is an X-computable linear order of Scott rank
$X \in 2^\omega $
, there is an X-computable linear order of Scott rank
 $\omega _1^{X}+1$
and Scott complexity
$\omega _1^{X}+1$
and Scott complexity
 $\Pi _{\omega _1^{X}+2}$
. Moreover, there is a uniform operator
$\Pi _{\omega _1^{X}+2}$
. Moreover, there is a uniform operator
![]() $\Phi $
such that
$\Phi $
such that
![]() $\Phi (X)$
has order type
$\Phi (X)$
has order type
 $\omega _1^X \cdot (1 + \mathbb {Q})$
, so that
$\omega _1^X \cdot (1 + \mathbb {Q})$
, so that
 $\omega _1^X = \omega _1^Y$
if and only if
$\omega _1^X = \omega _1^Y$
if and only if
![]() $\Phi ^X \cong \Phi ^Y$
.
$\Phi ^X \cong \Phi ^Y$
.
In general, we say that a structure
![]() $\mathcal {A}$
has high Scott rank/high Scott complexity if it satisfies one of the following equivalent conditions:
$\mathcal {A}$
has high Scott rank/high Scott complexity if it satisfies one of the following equivalent conditions:
-
• it does not have an X-computable Scott sentence;
-
• its Scott rank is not X-computable, i.e., at least
 $\omega _1^{\mathcal {A}}$
; and
$\omega _1^{\mathcal {A}}$
; and -
• it has Scott complexity at least
 $\Pi _{\omega _1^{\mathcal {A}}}$
.
$\Pi _{\omega _1^{\mathcal {A}}}$
.
All of the different possible definitions of Scott rank agree on whether a structure has high Scott rank, and if it does have high Scott rank, they agree on whether the Scott rank is
 $\omega _1^X$
or
$\omega _1^X$
or
 $\omega _1^X + 1$
.
$\omega _1^X + 1$
.
In terms of Scott complexity, there are five possible Scott complexities for a structure of high Scott complexity:

Structures of Scott complexity
 $\Pi _{\omega _1^{CK}}$
and
$\Pi _{\omega _1^{CK}}$
and
 $\Pi _{\omega _1^{CK}}+1$
have Scott rank
$\Pi _{\omega _1^{CK}}+1$
have Scott rank
 $\omega _1^{CK}$
, and structures of the other three Scott complexities have Scott rank
$\omega _1^{CK}$
, and structures of the other three Scott complexities have Scott rank
 $\omega _1^{CK}+1$
.
$\omega _1^{CK}+1$
.
While a computable structure with Scott rank
 $\omega _1^{CK}+1$
was known in the 1960s, it was not until the 2000s that a computable structure of Scott rank
$\omega _1^{CK}+1$
was known in the 1960s, it was not until the 2000s that a computable structure of Scott rank
 $\omega _1^{CK}$
was constructed. [Reference Makkai41] gave a complicated construction of a
$\omega _1^{CK}$
was constructed. [Reference Makkai41] gave a complicated construction of a
![]() $\Delta ^0_2$
structure with Scott rank
$\Delta ^0_2$
structure with Scott rank
 $\omega _1^{CK}$
, and later Knight and Millar gave a simpler construction while also obtaining a computable structure [Reference Knight and Millar37]. The structures they build have Scott complexity
$\omega _1^{CK}$
, and later Knight and Millar gave a simpler construction while also obtaining a computable structure [Reference Knight and Millar37]. The structures they build have Scott complexity
 $\Pi _{\omega _1^{CK}}$
.
$\Pi _{\omega _1^{CK}}$
.
Theorem 4.11 Knight and Millar [Reference Knight and Millar37]
There is a computable structure of Scott rank
 $\omega _1^{CK}$
and Scott complexity
$\omega _1^{CK}$
and Scott complexity
 $\Pi _{\omega _1^{CK}}$
. Moreover, given X, there is an X-computable structure of Scott rank
$\Pi _{\omega _1^{CK}}$
. Moreover, given X, there is an X-computable structure of Scott rank
 $\omega _1^{X}$
and Scott complexity
$\omega _1^{X}$
and Scott complexity
 $\Pi _{\omega _1^{X}}$
.
$\Pi _{\omega _1^{X}}$
.
Proof sketch The construction of Knight and Millar uses the Barwise compactness theorem to build a computable thin homogeneous tree, where these terms are defined below. We will give a proof along the same lines, building a computable thin homogeneous tree, but we will build this tree in a more constructive way and avoid using the Barwise compactness theorem. We will give a computable construction but the construction relativizes to any X.
Definition 4.12. A tree T is thin if there is a computable ordinal bound on the ordinal tree ranks at each level of the tree.
Note that there can be nodes on the tree of rank
![]() $\infty $
; the bound is just on the nodes with ordinal rank.
$\infty $
; the bound is just on the nodes with ordinal rank.
Definition 4.13. A tree T is homogeneous if:
-
• Whenever x has a successor of rank
 $\alpha $
, it has infinitely many successors of rank
$\alpha $
, it has infinitely many successors of rank
 $\alpha $
.
$\alpha $
. -
• If some element at level n has a successor of rank
 $\alpha $
, every element at level n with rank
$\alpha $
, every element at level n with rank
 $> \alpha $
has a successor of rank
$> \alpha $
has a successor of rank
 $\alpha $
.
$\alpha $
.
Such a tree is called homogeneous because any two nodes at the same level of the tree and with the same rank are automorphic, and indeed the isomorphism type of the tree is determined by which tree ranks appear at each level. One can show that a computable thin homogeneous tree has a
 $\Pi _{\omega _1^{CK}}$
Scott sentence; one writes down the conjunctions of the sentences, one for each level, which say which tree ranks show up at that level. Each of these sentences is
$\Pi _{\omega _1^{CK}}$
Scott sentence; one writes down the conjunctions of the sentences, one for each level, which say which tree ranks show up at that level. Each of these sentences is
 $\Pi _{\omega _1^{CK}}$
because there is a bound on the tree ranks at that level. Though the tree ranks at each level are bounded, if they are unbounded below
$\Pi _{\omega _1^{CK}}$
because there is a bound on the tree ranks at that level. Though the tree ranks at each level are bounded, if they are unbounded below
 $\omega _1^{CK}$
overall, the tree has Scott complexity
$\omega _1^{CK}$
overall, the tree has Scott complexity
 $\Pi _{\omega _1^{CK}}$
. See [Reference Knight and Millar37] for details.
$\Pi _{\omega _1^{CK}}$
. See [Reference Knight and Millar37] for details.
So we want to construct a thin homogeneous tree with unbounded ranks. To construct such a tree, first fix a computable presentation
![]() $\mathcal {H}$
of the Harrison linear order. By the trick of replacing each element of
$\mathcal {H}$
of the Harrison linear order. By the trick of replacing each element of
![]() $\mathcal {H}$
by a copy of
$\mathcal {H}$
by a copy of
![]() $\omega $
, we may assume that we can compute successors, predecessors, and limits in
$\omega $
, we may assume that we can compute successors, predecessors, and limits in
![]() $\mathcal {H}$
. We construct for each
$\mathcal {H}$
. We construct for each
![]() $n = 1,2,\ldots $
a set
$n = 1,2,\ldots $
a set
![]() $S_n \subseteq \mathcal {H}$
such that:
$S_n \subseteq \mathcal {H}$
such that:
-
1.
 $S_1 \subseteq S_2 \subseteq S_3 \subseteq \cdots $
,
$S_1 \subseteq S_2 \subseteq S_3 \subseteq \cdots $
, -
2.
 $\bigcup _i S_i = \mathcal {H}$
,
$\bigcup _i S_i = \mathcal {H}$
, -
3.
 $S_1$
is cofinal in
$S_1$
is cofinal in
 $\mathcal {H}$
,
$\mathcal {H}$
, -
4. each
 $S_n$
is bounded above inside the well-founded part of
$S_n$
is bounded above inside the well-founded part of
 $\mathcal {H}$
,
$\mathcal {H}$
, -
5. for each
 $a \in S_n$
which is a limit element of
$a \in S_n$
which is a limit element of
 $\mathcal {H}$
,
$\mathcal {H}$
,
 $\{b \in S_{n+1} : b < a\}$
is unbounded below a,
$\{b \in S_{n+1} : b < a\}$
is unbounded below a, -
6. for each
 $a \in S_n$
which is a successor element of
$a \in S_n$
which is a successor element of
 $\mathcal {H}$
, the predecessor of a is in
$\mathcal {H}$
, the predecessor of a is in
 $S_{n+1}$
.
$S_{n+1}$
.
Construct
![]() $S_1$
as follows. Computably list out the elements of
$S_1$
as follows. Computably list out the elements of
![]() $\mathcal {H}$
, e.g., as
$\mathcal {H}$
, e.g., as
![]() $h_1,h_2,h_3,\ldots $
Consider the elements of
$h_1,h_2,h_3,\ldots $
Consider the elements of
![]() $\mathcal {H}$
one-by-one in order, and put each element which is larger than all of the previous elements into
$\mathcal {H}$
one-by-one in order, and put each element which is larger than all of the previous elements into
![]() $S_1$
. For example, if the first nine elements are ordered as
$S_1$
. For example, if the first nine elements are ordered as
then we put
![]() $h_1$
in
$h_1$
in
![]() $S_1$
, omit
$S_1$
, omit
![]() $h_2$
because it is smaller than
$h_2$
because it is smaller than
![]() $h_2$
, put
$h_2$
, put
![]() $h_3$
and
$h_3$
and
![]() $h_4$
in
$h_4$
in
![]() $S_1$
, then omit
$S_1$
, then omit
![]() $h_5$
,
$h_5$
,
![]() $h_6$
, and
$h_6$
, and
![]() $h_7$
because they are lower than
$h_7$
because they are lower than
![]() $h_4$
, put
$h_4$
, put
![]() $h_8$
in
$h_8$
in
![]() $S_1$
, and omit
$S_1$
, and omit
![]() $h_9$
. So we get
$h_9$
. So we get
![]() $S_1 = \{h_1,h_3,h_4,h_8,\ldots \}$
. Note that the order type of
$S_1 = \{h_1,h_3,h_4,h_8,\ldots \}$
. Note that the order type of
![]() $S_1$
is
$S_1$
is
![]() $\omega $
. Only finitely many of the elements of
$\omega $
. Only finitely many of the elements of
![]() $S_1$
are in the well-founded part of
$S_1$
are in the well-founded part of
![]() $\mathcal {H}$
; this is for (4).
$\mathcal {H}$
; this is for (4).
Given
![]() $S_1,\ldots ,S_n$
, we construct
$S_1,\ldots ,S_n$
, we construct
![]() $S_{n+1}$
as follows. Each element of
$S_{n+1}$
as follows. Each element of
![]() $S_n$
will be an element of
$S_n$
will be an element of
![]() $S_{n+1}$
, satisfying (1). For each element y of
$S_{n+1}$
, satisfying (1). For each element y of
![]() $S_{n} - S_{n-1}$
which is a limit element of
$S_{n} - S_{n-1}$
which is a limit element of
![]() $\mathcal {H}$
, we can find
$\mathcal {H}$
, we can find
![]() $x \in S_{n}$
such that there are no element z of
$x \in S_{n}$
such that there are no element z of
![]() $S_{n+1}$
with
$S_{n+1}$
with
![]() $x < z < y$
. Then, in the open interval
$x < z < y$
. Then, in the open interval
![]() $\{ z \in \mathcal {H} : x < z < y\}$
we can do the same construction as we did for
$\{ z \in \mathcal {H} : x < z < y\}$
we can do the same construction as we did for
![]() $S_1$
, listing out the elements in this interval and putting each element which is greater than the previous elements into
$S_1$
, listing out the elements in this interval and putting each element which is greater than the previous elements into
![]() $S_{n+1}$
. Thus we satisfy (5). For each successor element of
$S_{n+1}$
. Thus we satisfy (5). For each successor element of
![]() $S_n$
, we put its predecessor into
$S_n$
, we put its predecessor into
![]() $S_{n+1}$
, satisfying (6). To satisfy (2), we also have to add to
$S_{n+1}$
, satisfying (6). To satisfy (2), we also have to add to
![]() $S_{n+1}$
the first element of
$S_{n+1}$
the first element of
![]() $\mathcal {H}$
which does not yet appear in
$\mathcal {H}$
which does not yet appear in
![]() $S_n$
. (4) is easy to verify, and (3) is just about
$S_n$
. (4) is easy to verify, and (3) is just about
![]() $S_1$
.
$S_1$
.
Let T a subtree of the tree of all descending sequences in
![]() $\mathcal {H}$
, with the nodes at level n being from
$\mathcal {H}$
, with the nodes at level n being from
![]() $S_n$
; i.e., the path
$S_n$
; i.e., the path
 $\bar {h} = \langle h_1,\ldots ,h_n \rangle $
has
$\bar {h} = \langle h_1,\ldots ,h_n \rangle $
has
![]() $h_1 \in S_1, h_2 \in S_2,\ldots ,h_n \in S_n$
. Given a node corresponding to the sequence
$h_1 \in S_1, h_2 \in S_2,\ldots ,h_n \in S_n$
. Given a node corresponding to the sequence
 $\bar {h} = \langle h_1,\ldots ,h_n \rangle $
, it is easy to argue using (5) and (6) that the tree rank of
$\bar {h} = \langle h_1,\ldots ,h_n \rangle $
, it is easy to argue using (5) and (6) that the tree rank of
![]() $\bar {h}$
is the order type of
$\bar {h}$
is the order type of
![]() $\{x \in \mathcal {H} : x < h_n\}$
if
$\{x \in \mathcal {H} : x < h_n\}$
if
![]() $h_n$
is in the well-founded part of
$h_n$
is in the well-founded part of
![]() $\mathcal {H}$
, and
$\mathcal {H}$
, and
![]() $\infty $
otherwise. By choice of the
$\infty $
otherwise. By choice of the
![]() $S_n$
—namely (4)—T is a thin tree. To make it homogeneous, we just need to duplicate each node infinitely many times. By (3), the root node—which is the empty sequence—has tree rank
$S_n$
—namely (4)—T is a thin tree. To make it homogeneous, we just need to duplicate each node infinitely many times. By (3), the root node—which is the empty sequence—has tree rank
![]() $\infty $
, but by (2), there is no bound on the tree ranks at all levels.⊣
$\infty $
, but by (2), there is no bound on the tree ranks at all levels.⊣
The construction of the Harrison linear order was uniform in the sense that given X, one could effectively construct the Harrison linear order relative to X. Moreover, if
 $\omega _1^X = \omega _1^Y$
, then the Harrison linear order relative to X is the same as the Harrison linear order relative to Y. One can view this as saying that the construction produces a natural/canonical structure, the Harrison linear order. On the other hand, the construction just given of an X-computable structure of Scott rank
$\omega _1^X = \omega _1^Y$
, then the Harrison linear order relative to X is the same as the Harrison linear order relative to Y. One can view this as saying that the construction produces a natural/canonical structure, the Harrison linear order. On the other hand, the construction just given of an X-computable structure of Scott rank
 $\omega _1^X$
is not uniform in this way. The structure one gets depends on the sets
$\omega _1^X$
is not uniform in this way. The structure one gets depends on the sets
![]() $S_1,S_2,\ldots $
, and these in turn depend on the particular presentation of the Harrison linear order
$S_1,S_2,\ldots $
, and these in turn depend on the particular presentation of the Harrison linear order
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Chan [Reference Chan14] asked whether there is some other uniform construction of a computable structure of Scott rank
 $\omega _1^{CK}$
. Becker [Reference Becker6] and Chan et al. (unpublished) independently showed that there is no uniform construction.
$\omega _1^{CK}$
. Becker [Reference Becker6] and Chan et al. (unpublished) independently showed that there is no uniform construction.
Theorem 4.14 Becker [Reference Becker6] and Chan et al.,
There is no Borel operator
![]() $\Phi $
such that:
$\Phi $
such that:
-
• for all
 $X,Y \in 2^\omega $
,
$X,Y \in 2^\omega $
,
 $\Phi (X) \cong \Phi (Y) \Longleftrightarrow \omega _1^X = \omega _1^Y.$
$\Phi (X) \cong \Phi (Y) \Longleftrightarrow \omega _1^X = \omega _1^Y.$
-
• for all
 $X \in 2^\omega $
,
$X \in 2^\omega $
,
 $\Phi (X)$
is a computable structure of Scott complexity strictly less than
$\Phi (X)$
is a computable structure of Scott complexity strictly less than
 $\Pi _{\omega _1^X+2}$
.
$\Pi _{\omega _1^X+2}$
.
Proof The proof we give is due to an anonymous referee. Suppose to the contrary that there was such a
![]() $\Phi $
. Since
$\Phi $
. Since
![]() $\Phi $
is Borel, for sufficiently large
$\Phi $
is Borel, for sufficiently large
![]() $\beta $
, the inverse image of a
$\beta $
, the inverse image of a
![]() $\boldsymbol {\Sigma }^0_\beta $
set under
$\boldsymbol {\Sigma }^0_\beta $
set under
![]() $\Phi $
is
$\Phi $
is
![]() $\boldsymbol {\Sigma }^0_\beta $
. Choose X such that
$\boldsymbol {\Sigma }^0_\beta $
. Choose X such that
 $\omega _1^X> \beta $
. Let
$\omega _1^X> \beta $
. Let
![]() $\mathcal {A} = \Phi (X)$
. If
$\mathcal {A} = \Phi (X)$
. If
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
is
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
is
 $\boldsymbol {\Sigma }^0_{\omega _1^X + 2}$
, then so is
$\boldsymbol {\Sigma }^0_{\omega _1^X + 2}$
, then so is
 $\Phi ^{-1}[\operatorname {\mathrm {Iso}}(\mathcal {A})]$
. But by Theorem 2.3 of [Reference Marker42], the set
$\Phi ^{-1}[\operatorname {\mathrm {Iso}}(\mathcal {A})]$
. But by Theorem 2.3 of [Reference Marker42], the set
 $\Phi ^{-1}[\operatorname {\mathrm {Iso}}(\mathcal {A})] = \{Y : \omega _1^Y = \omega _1^X\}$
is not
$\Phi ^{-1}[\operatorname {\mathrm {Iso}}(\mathcal {A})] = \{Y : \omega _1^Y = \omega _1^X\}$
is not
 $\boldsymbol {\Sigma }^0_{\omega _1^X + 2}$
.
$\boldsymbol {\Sigma }^0_{\omega _1^X + 2}$
.
Becker [Reference Becker7] later proved a number of strengthenings of this result.
Theorem 4.8 says that two computable structures that satisfy the same computable infinitary formulas are isomorphic. Given a computable structure
![]() $\mathcal {A}$
, the computable infinitary theory of
$\mathcal {A}$
, the computable infinitary theory of
![]() $\mathcal {A}$
is the collection of all the computable
$\mathcal {A}$
is the collection of all the computable
![]() $\mathcal {L}_{\omega _1 \omega }$
sentences true of
$\mathcal {L}_{\omega _1 \omega }$
sentences true of
![]() $\mathcal {A}$
. The structure of Scott rank
$\mathcal {A}$
. The structure of Scott rank
 $\omega _1^{CK}$
constructed by Knight and Millar (Theorem 4.11) is the only model, computable or not, of its computable infinitary theory; we say that its computable infinitary theory is countably categorical. On the other hand the Harrison linear order, which has Scott rank
$\omega _1^{CK}$
constructed by Knight and Millar (Theorem 4.11) is the only model, computable or not, of its computable infinitary theory; we say that its computable infinitary theory is countably categorical. On the other hand the Harrison linear order, which has Scott rank
 $\omega _1^{CK}+1$
, is not the only model of its computable infinitary theory. Millar and Sacks [Reference Millar and Sacks48] asked whether there is a computable structure of Scott rank
$\omega _1^{CK}+1$
, is not the only model of its computable infinitary theory. Millar and Sacks [Reference Millar and Sacks48] asked whether there is a computable structure of Scott rank
 $\omega _1^{CK}$
such that the computable infinitary theory is not countably categorical. This is equivalent to finding a structure of Scott complexity
$\omega _1^{CK}$
such that the computable infinitary theory is not countably categorical. This is equivalent to finding a structure of Scott complexity
 $\Pi _{\omega _1^{CK}+1}$
. (In one direction, if the computable infinitary theory of a computable structure is countably categorical, then the structure has a
$\Pi _{\omega _1^{CK}+1}$
. (In one direction, if the computable infinitary theory of a computable structure is countably categorical, then the structure has a
 $\Pi _{\omega _1^{CK}}$
Scott sentence, namely the conjunction of all the computable sentences true of it. The converse is slightly more difficult; see [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1].)
$\Pi _{\omega _1^{CK}}$
Scott sentence, namely the conjunction of all the computable sentences true of it. The converse is slightly more difficult; see [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1].)
Millar and Sacks [Reference Millar and Sacks48] produced such a structure
![]() $\mathcal {A}$
which is not hyperarithmetic, but which does have
$\mathcal {A}$
which is not hyperarithmetic, but which does have
 $\omega _1^{\mathcal {A}} = \omega _1^{CK}$
. Freer [Reference Freer22] proved the analogous result higher up: for any admissible
$\omega _1^{\mathcal {A}} = \omega _1^{CK}$
. Freer [Reference Freer22] proved the analogous result higher up: for any admissible
![]() $\alpha $
, there is a structure
$\alpha $
, there is a structure
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
 $\omega _1^{\mathcal {A}} = \alpha $
and
$\omega _1^{\mathcal {A}} = \alpha $
and
![]() $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\Pi _{\omega _1^{\mathcal {A}}+1}$
. Finally, Harrison-Trainor et al. [Reference Harrison-Trainor, Igusa and Knight31] constructed a computable example.
$\Pi _{\omega _1^{\mathcal {A}}+1}$
. Finally, Harrison-Trainor et al. [Reference Harrison-Trainor, Igusa and Knight31] constructed a computable example.
Theorem 4.15 Harrison-Trainor et al. [Reference Harrison-Trainor, Igusa and Knight31]
There is a computable structure with Scott complexity
 $\Pi _{\omega _1^{CK}+1}$
.
$\Pi _{\omega _1^{CK}+1}$
.
There are two remaining complexities,
 $\Sigma _{\omega _1^{CK}+1}$
and
$\Sigma _{\omega _1^{CK}+1}$
and
 $\mathrm {d}\!-\Sigma _{\omega _1^{CK}+1}$
. These are exactly the structures with the property that they have Scott rank
$\mathrm {d}\!-\Sigma _{\omega _1^{CK}+1}$
. These are exactly the structures with the property that they have Scott rank
 $\omega _1^{CK}+1$
, but after naming a constant, they have Scott rank
$\omega _1^{CK}+1$
, but after naming a constant, they have Scott rank
 $\omega _1^{CK}$
. This follows from Theorem 3.2 and the following corresponding result for
$\omega _1^{CK}$
. This follows from Theorem 3.2 and the following corresponding result for
![]() $\mathrm {d}\!-\Sigma _\alpha $
sentences:
$\mathrm {d}\!-\Sigma _\alpha $
sentences:
Theorem 4.16 Alvir et al. [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1]
Let
![]() $\mathcal {A}$
be a countable structure. Then
$\mathcal {A}$
be a countable structure. Then
![]() $\mathcal {A}$
has a
$\mathcal {A}$
has a
![]() $\mathrm {d}\!-\Sigma _{\alpha }$
Scott sentence if and only if for some
$\mathrm {d}\!-\Sigma _{\alpha }$
Scott sentence if and only if for some
![]() $\bar {c} \in \mathcal {A}$
,
$\bar {c} \in \mathcal {A}$
,
![]() $(\mathcal {A},\bar {c})$
has a
$(\mathcal {A},\bar {c})$
has a
![]() $\Pi _{\alpha }$
Scott sentence and the automorphism orbit of
$\Pi _{\alpha }$
Scott sentence and the automorphism orbit of
![]() $\bar {c}$
in
$\bar {c}$
in
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\Sigma _{\alpha }$
-definable.
$\Sigma _{\alpha }$
-definable.
Turetsky asked whether such structures exist. Alvir et al. [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1] showed that they do. Thus there are computable structures of all five possible high Scott complexities.
Theorem 4.17 Alvir et al., [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1]
There are computable structures of all possible high Scott complexities:
 $\Pi _{\omega _1^{CK}}$
,
$\Pi _{\omega _1^{CK}}$
,
 $\Pi _{\omega _1^{CK}+1}$
,
$\Pi _{\omega _1^{CK}+1}$
,
 $\Sigma _{\omega _1^{CK}+1}$
,
$\Sigma _{\omega _1^{CK}+1}$
,
 $\mathrm {d}\!-\Sigma _{\omega _1^{CK}+1}$
, and
$\mathrm {d}\!-\Sigma _{\omega _1^{CK}+1}$
, and
 $\Pi _{\omega _1^{CK}+2}$
.
$\Pi _{\omega _1^{CK}+2}$
.
4.3 Computably approximable structures
Theorem 4.8 says that two computable structures that satisfy the same computable infinitary formulas are isomorphic. Thus the computable infinitary theory of a computable structure characterizes the structure among computable structures. (If a computable structure does not have a countably categorical computably infinitary theory, for example the Harrison linear order or the structure of Theorem 4.15, then the other models of its computable infinitary theory are necessarily non-computable.) If we restrict our attention to computable structures only, is there a single sentence characterizing every computable structure? We call such a sentence a pseudo-Scott sentence.
Definition 4.18. Let
![]() $\mathcal {A}$
be a computable structure. A pseudo-Scott sentence for
$\mathcal {A}$
be a computable structure. A pseudo-Scott sentence for
![]() $\mathcal {A}$
is a sentence whose computable models are just the computable copies of
$\mathcal {A}$
is a sentence whose computable models are just the computable copies of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Calvert and Knight [Reference Calvert and Knight11] asked whether every computable structure has a computable infinitary pseudo-Scott sentence. A counterexample would have to be of high Scott rank, as structures of computable Scott rank have computable Scott sentences, and any Scott sentence is a pseudo-Scott sentence.
Question 4.19 Calvert and Knight [Reference Calvert and Knight11]
Is there a computable structure of noncomputable Scott rank with a computable infinitary pseudo-Scott sentence?
This question is still open. A structure without a computable Scott sentence is said to be weakly computably approximable.
Definition 4.20. A computable structure
![]() $\mathcal {A}$
of non-computable Scott rank is weakly computably approximable if every computable infinitary sentence
$\mathcal {A}$
of non-computable Scott rank is weakly computably approximable if every computable infinitary sentence
![]() $\varphi $
true in
$\varphi $
true in
![]() $\mathcal {A}$
is also true in some computable
$\mathcal {A}$
is also true in some computable
![]() $\mathcal {B} \ncong \mathcal {A}$
.
$\mathcal {B} \ncong \mathcal {A}$
.
The Harrison linear order has the property that any computable sentence true of it is also true of some other structure which is not just computable, but which has computable Scott rank. Moreover, the Harrison order has the following stronger property:
Definition 4.21. A computable structure
![]() $\mathcal {A}$
of high Scott rank is strongly computably approximable if for all
$\mathcal {A}$
of high Scott rank is strongly computably approximable if for all
![]() $\Sigma ^1_1$
sets S, there is a uniformly computable sequence
$\Sigma ^1_1$
sets S, there is a uniformly computable sequence
![]() $(\mathcal {C}_n)$
such that if
$(\mathcal {C}_n)$
such that if
![]() $n \in S$
, then
$n \in S$
, then
![]() $\mathcal {C}_n \cong \mathcal {A}$
, and if
$\mathcal {C}_n \cong \mathcal {A}$
, and if
![]() $n \notin S$
, then
$n \notin S$
, then
![]() $\mathcal {C}_n$
has computable Scott rank.
$\mathcal {C}_n$
has computable Scott rank.
One can see that the Harrison order is strongly computably approximable by a simple modification of the construction given earlier.
Calvert et al. also showed that there is also such a structure of Scott rank
 $\omega _1^{CK}$
. This can also be seen using our construction for Theorem 4.11 combined with the fact that the Harrison order is strongly computably approximable.
$\omega _1^{CK}$
. This can also be seen using our construction for Theorem 4.11 combined with the fact that the Harrison order is strongly computably approximable.
Theorem 4.22 Calvert et al. [Reference Calvert, Knight and Millar12]
There is a computable tree T of Scott rank
 $\omega _1^{CK}$
that is strongly computably approximable.
$\omega _1^{CK}$
that is strongly computably approximable.
This theorem is very useful for other constructions; for example it was used in the proofs of Theorems 4.15 and 4.17.
Not every computable structure of high Scott rank is strongly computably approximable; indeed, there is a single computable sentence all of whose models have high Scott rank.
Theorem 4.23 Harrison-Trainor [Reference Harrison-Trainor27]
For
 $\alpha = \omega _1^{CK}$
or
$\alpha = \omega _1^{CK}$
or
 $\alpha = \omega _1^{CK} + 1$
: There is a computable model
$\alpha = \omega _1^{CK} + 1$
: There is a computable model
![]() $\mathcal {A}$
of Scott rank
$\mathcal {A}$
of Scott rank
![]() $\alpha $
and a
$\alpha $
and a
![]() $\Pi ^{\mathtt {c}}_2$
sentence
$\Pi ^{\mathtt {c}}_2$
sentence
![]() $\psi $
such that
$\psi $
such that
![]() $\mathcal {A} \models \psi $
, and whenever
$\mathcal {A} \models \psi $
, and whenever
![]() $\mathcal {B}$
is any structure and
$\mathcal {B}$
is any structure and
![]() $\mathcal {B} \models \psi $
,
$\mathcal {B} \models \psi $
,
![]() $\mathcal {B}$
has Scott rank
$\mathcal {B}$
has Scott rank
![]() $\alpha $
.
$\alpha $
.
Another application of the existence of strongly computably approximable structures is a computation of the index set complexity of being of high Scott rank.
Theorem 4.24 Calvert et al. [Reference Calvert, Fokina, Goncharov, Knight, Kudinov, Morozov and Puzarenko9]
The index set
of computable structures with high Scott rank is
 $\Pi ^1_1\ m$
-complete.
$\Pi ^1_1\ m$
-complete.
They also computed the complexity of the index sets of computable structures of Scott rank
 $\omega _1^{CK}$
and
$\omega _1^{CK}$
and
 $\omega _1^{CK}+1$
; these are complete for differences of
$\omega _1^{CK}+1$
; these are complete for differences of
 $\Pi ^1_1$
sets and differences of
$\Pi ^1_1$
sets and differences of
![]() $\Sigma ^1_1$
sets respectively.
$\Sigma ^1_1$
sets respectively.
4.4 Computable categoricity and high Scott complexity
A computable structure
![]() $\mathcal {A}$
is said to be computably categorical if whenever
$\mathcal {A}$
is said to be computably categorical if whenever
![]() $\mathcal {B} \cong \mathcal {A}$
is a computable copy of
$\mathcal {B} \cong \mathcal {A}$
is a computable copy of
![]() $\mathcal {A}$
, there is a computable isomorphism from
$\mathcal {A}$
, there is a computable isomorphism from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathcal {B}$
. For a long time, an important problem was to characterize the structures which are computably categorical. It turned out that the more well-behaved notion was that of relative computable categoricity: a computable structure
$\mathcal {B}$
. For a long time, an important problem was to characterize the structures which are computably categorical. It turned out that the more well-behaved notion was that of relative computable categoricity: a computable structure
![]() $\mathcal {A}$
is relatively computably categorical if for every copy
$\mathcal {A}$
is relatively computably categorical if for every copy
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $\mathcal {A}$
, not necessarily computable, there is an isomorphism from
$\mathcal {A}$
, not necessarily computable, there is an isomorphism from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathcal {B}$
computable from
$\mathcal {B}$
computable from
![]() $\mathcal {B}$
. Relative computable categoricity is characterised by the following theorem:
$\mathcal {B}$
. Relative computable categoricity is characterised by the following theorem:
Theorem 4.25 Ash et al. [Reference Ash, Knight, Manasse and Slaman3] and Chisholm [Reference Chisholm17]
A computable structure
![]() $\mathcal {A}$
is relatively computably categorical if and only if it has a computable
$\mathcal {A}$
is relatively computably categorical if and only if it has a computable
![]() $\Sigma _1$
Scott family: there is a tuple
$\Sigma _1$
Scott family: there is a tuple
![]() $\bar {c}$
of constants and a c.e. collection
$\bar {c}$
of constants and a c.e. collection
![]() $\Phi $
of computable
$\Phi $
of computable
![]() $\Sigma _1$
formulas such that
$\Sigma _1$
formulas such that
-
1. each tuple
 $\bar {a}$
in
$\bar {a}$
in
 $\mathcal {A}$
satisfies
$\mathcal {A}$
satisfies
 $\varphi (\bar {a},\bar {c})$
for some formula
$\varphi (\bar {a},\bar {c})$
for some formula
 $\varphi \in \Phi $
and
$\varphi \in \Phi $
and -
2. whenever two tuples
 $\bar {a}$
and
$\bar {a}$
and
 $\bar {b}$
in
$\bar {b}$
in
 $\mathcal {A}$
satisfy the same formula
$\mathcal {A}$
satisfy the same formula
 $\varphi (\cdot ,\bar {c})$
from
$\varphi (\cdot ,\bar {c})$
from
 $\Phi $
, there is an automorphism of
$\Phi $
, there is an automorphism of
 $\mathcal {A}$
taking
$\mathcal {A}$
taking
 $\bar {a}$
to
$\bar {a}$
to
 $\bar {b}$
.
$\bar {b}$
.
It is not hard to see that if
![]() $\mathcal {A}$
has a computable
$\mathcal {A}$
has a computable
![]() $\Sigma _1$
Scott family, then it is relatively computably categorical; the other direction is a forcing argument. So in some sense if a structure is relatively computably categorical, then there is a good structural reason for this.
$\Sigma _1$
Scott family, then it is relatively computably categorical; the other direction is a forcing argument. So in some sense if a structure is relatively computably categorical, then there is a good structural reason for this.
As for (plain) computable categoricity, in certain classes there are good structural ways to determine whether a structure is computably categorical—e.g., a linear order is computably categorical if and only if it has finitely many adjacencies [Reference Gončarov and Dzgoev25]—but there is no good characterization in general. Goncharov [Reference Gončarov24] showed that there are structures that are computably categorical but not relatively computably categorical. Later, Downey et al. [Reference Downey, Kach, Lempp, Lewis-Pye, Montalbán and Turetsky21] showed that the set of (indices for) computably categorical structures is
 $\Pi ^1_1\ m$
-complete; this can be interpreted as meaning that there is no good characterization of computable categoricity that is simpler than the naive definition. As part of this proof, they constructed for each computable ordinal
$\Pi ^1_1\ m$
-complete; this can be interpreted as meaning that there is no good characterization of computable categoricity that is simpler than the naive definition. As part of this proof, they constructed for each computable ordinal
 $\alpha < \omega _1^{CK}$
a computably categorical structure
$\alpha < \omega _1^{CK}$
a computably categorical structure
![]() $\mathcal {A}$
which is not relatively
$\mathcal {A}$
which is not relatively
![]() $\Delta ^0_\alpha $
-categorical, i.e., it is not the case that for every
$\Delta ^0_\alpha $
-categorical, i.e., it is not the case that for every
![]() $\mathcal {B} \cong \mathcal {A}$
there is an isomorphism from
$\mathcal {B} \cong \mathcal {A}$
there is an isomorphism from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathcal {B}$
which is
$\mathcal {B}$
which is
![]() $\Delta ^0_\alpha $
in
$\Delta ^0_\alpha $
in
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
This left a gap: Is every computably categorical structure
![]() $\Delta ^0_\alpha $
-categorical for some computable ordinal
$\Delta ^0_\alpha $
-categorical for some computable ordinal
 $\alpha < \omega _1^{CK}$
? Or even, is every computably categorical structure
$\alpha < \omega _1^{CK}$
? Or even, is every computably categorical structure
![]() $\Delta ^1_1$
-categorical? (A structure is relatively
$\Delta ^1_1$
-categorical? (A structure is relatively
![]() $\Delta ^1_1$
-categorical if for every
$\Delta ^1_1$
-categorical if for every
![]() $\mathcal {B} \cong \mathcal {A}$
there is an isomorphism from
$\mathcal {B} \cong \mathcal {A}$
there is an isomorphism from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathcal {B}$
which is
$\mathcal {B}$
which is
![]() $\Delta ^1_1$
in
$\Delta ^1_1$
in
![]() $\mathcal {B}$
.) If
$\mathcal {B}$
.) If
![]() $\mathcal {A}$
is a computable structure of computable Scott rank
$\mathcal {A}$
is a computable structure of computable Scott rank
 $\alpha < \omega _1^{CK}$
, then it is relatively
$\alpha < \omega _1^{CK}$
, then it is relatively
 $\Delta ^0_{\alpha \cdot 2}$
-categorical; this follows from a similar argument as Theorem 4.8. In the other direction, one can argue that a computable structure which is relatively
$\Delta ^0_{\alpha \cdot 2}$
-categorical; this follows from a similar argument as Theorem 4.8. In the other direction, one can argue that a computable structure which is relatively
![]() $\Delta ^1_1$
-categorical must have computable Scott rank. (See Proposition 1 of [Reference Turetsky64].) So a computable structure is relatively
$\Delta ^1_1$
-categorical must have computable Scott rank. (See Proposition 1 of [Reference Turetsky64].) So a computable structure is relatively
![]() $\Delta ^1_1$
-categorical if and only if it has computable Scott rank. Turetsky [Reference Turetsky64] showed:
$\Delta ^1_1$
-categorical if and only if it has computable Scott rank. Turetsky [Reference Turetsky64] showed:
Theorem 4.26 Turetsky [Reference Turetsky64]
There is a computably categorical structure which has high Scott complexity and thus is not relatively
![]() $\Delta ^1_1$
-categorical.
$\Delta ^1_1$
-categorical.
Turetsky was also able to adapt this construction to build a structure of computable dimension 2:
Theorem 4.27 Turetsky [Reference Turetsky64]
There is a structure of computable dimension 2 with two computable copies which are not hyperarithmetically isomorphic. This structure has high Scott complexity.
This is of particular interest because up until Turetsky’s construction the only existing constructions [Reference Cholak, Goncharov, Khoussainov and Shore18, Reference Gao24, Reference Hirschfeldt, Khoussainov and Shore32] of a structure of computable dimension 2, using a method called the special component technique, build two computable copies which are not computably isomorphic, but which are
![]() $\Delta ^0_3$
isomorphic.
$\Delta ^0_3$
isomorphic.
5 Scott complexity for certain structures
Scott complexity gives a good measuring stick for studying particular structures that we are interested in. Scott complexity measures the difficulty of characterizing a structure up to isomorphism, as well as (using Theorem 2.8) the difficulty of understanding the automorphisms of the structure, and computing isomorphisms between different copies of the structure. By finding the Scott complexity of a particular structure, we come to understand the simplest way of characterizing it. Moreover, the problem of computing the Scott complexity of a structure gives us a way of testing our understanding of that structure; indeed, one longstanding open questions is:
Question 5.1. What is the Scott complexity of the pure transcendental field
![]() $\mathbb {Q}(x_1,x_2,\ldots )$
?
$\mathbb {Q}(x_1,x_2,\ldots )$
?
This highlights the fact that we do not have a good understanding of pure transcendence bases, i.e., transcendence bases which also generate the field extension. In contrast, Nielson transformations give us an excellent understanding of bases for free groups, allowing us to compute their Scott complexity; see Theorem 5.7.
To compute the Scott complexity of a structure, one usually writes down a Scott sentence of a particular complexity, and then one proves a lower bound showing that this complexity is optimal. So, for example, one might write down a
![]() $\Sigma _4$
Scott sentence for a structure
$\Sigma _4$
Scott sentence for a structure
![]() $\mathcal {A}$
, and then give a Wadge reduction f from a
$\mathcal {A}$
, and then give a Wadge reduction f from a
![]() $\boldsymbol {\Sigma }^0_4$
-complete set S to
$\boldsymbol {\Sigma }^0_4$
-complete set S to
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
, i.e., a continuous operator f such that if
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
, i.e., a continuous operator f such that if
![]() $x \in S$
then
$x \in S$
then
![]() $f(x) \cong \mathcal {A}$
, and if
$f(x) \cong \mathcal {A}$
, and if
![]() $x \notin S$
then
$x \notin S$
then
![]() $f(x) \ncong \mathcal {A}$
.
$f(x) \ncong \mathcal {A}$
.
Much of the literature takes the approach of using index sets rather than Wadge reductions.
Definition 5.2. Fix a listing
![]() $\mathcal {M}_i$
of the partial computable structures in the language of
$\mathcal {M}_i$
of the partial computable structures in the language of
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
is the index set of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
If
![]() $\mathcal {A}$
has a Scott sentence which is a computable
$\mathcal {A}$
has a Scott sentence which is a computable
![]() $\Sigma _\alpha $
sentence then
$\Sigma _\alpha $
sentence then
![]() $\mathcal {I}_{\mathcal {A}}$
will be of complexity
$\mathcal {I}_{\mathcal {A}}$
will be of complexity
![]() $\Sigma ^0_\alpha $
as a subset of
$\Sigma ^0_\alpha $
as a subset of
![]() $\omega $
. The same is true for
$\omega $
. The same is true for
![]() $\Pi _\alpha $
and
$\Pi _\alpha $
and
 $\Pi ^0_\alpha $
, and
$\Pi ^0_\alpha $
, and
![]() $\mathrm {d}\!-\Sigma _\alpha $
and
$\mathrm {d}\!-\Sigma _\alpha $
and
 $\mathrm {d}\!-\Sigma ^0_\alpha $
as well. So if we can prove, for example, that
$\mathrm {d}\!-\Sigma ^0_\alpha $
as well. So if we can prove, for example, that
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
is
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
is
 $\Sigma ^0_\alpha\ m$
-complete, then
$\Sigma ^0_\alpha\ m$
-complete, then
![]() $\mathcal {A}$
cannot have a computable
$\mathcal {A}$
cannot have a computable
![]() $\Pi _\alpha $
Scott sentence.
$\Pi _\alpha $
Scott sentence.
This strategy does not always work. Knight and McCoy [Reference Knight and McCoy36] showed that there is a structure (a particular subgroup of
![]() $\mathbb {Q}$
) for which the index set is m-complete
$\mathbb {Q}$
) for which the index set is m-complete
 $\mathrm {d}\!-\Sigma ^0_\alpha $
, but there is no computable
$\mathrm {d}\!-\Sigma ^0_\alpha $
, but there is no computable
![]() $\mathrm {d}\!-\Sigma _\alpha $
Scott sentence. The structure does however have an X-computable
$\mathrm {d}\!-\Sigma _\alpha $
Scott sentence. The structure does however have an X-computable
![]() $\mathrm {d}\!-\Sigma _\alpha $
Scott sentence, for a particular low c.e. set X used to build the subgroup. So at the computable level, the index set complexity and the Scott complexity do not always match up. To fix this, we must relativize.
$\mathrm {d}\!-\Sigma _\alpha $
Scott sentence, for a particular low c.e. set X used to build the subgroup. So at the computable level, the index set complexity and the Scott complexity do not always match up. To fix this, we must relativize.
Definition 5.3. Fix a listing
 $\mathcal {M}^X_i$
of the partial X-computable structures in the language of
$\mathcal {M}^X_i$
of the partial X-computable structures in the language of
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
 $$ \begin{align*} \mathcal{I}^X_{\mathcal{A}} = \{ i \in \omega : \mathcal{M}^X_i \cong \mathcal{A} \} \end{align*} $$
$$ \begin{align*} \mathcal{I}^X_{\mathcal{A}} = \{ i \in \omega : \mathcal{M}^X_i \cong \mathcal{A} \} \end{align*} $$
is the index set of
![]() $\mathcal {A}$
relative to X.
$\mathcal {A}$
relative to X.
So for example to show that
![]() $\mathcal {A}$
does not have any Scott sentence which is
$\mathcal {A}$
does not have any Scott sentence which is
![]() $\Pi _\alpha $
or simpler, we must show that there is a set X such that for every
$\Pi _\alpha $
or simpler, we must show that there is a set X such that for every
![]() $Y \geq _T X$
, the index set
$Y \geq _T X$
, the index set
 $\mathcal {I}^Y_{\mathcal {A}}$
relative to Y is
$\mathcal {I}^Y_{\mathcal {A}}$
relative to Y is
 $\Sigma ^Y_\alpha\ m$
-complete. This essentially works out to the same things as giving a Wadge reduction.
$\Sigma ^Y_\alpha\ m$
-complete. This essentially works out to the same things as giving a Wadge reduction.
We now turn to some examples.
Theorem 5.4 Calvert et al. [Reference Calvert, Harizanov, Knight and Miller10] and Calvert [Reference Calvert8]
Let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $\mathbb {Q}$
-vector space. Then:
$\mathbb {Q}$
-vector space. Then:
-
1. If
 $\dim (\mathcal {A}) = 1$
, then
$\dim (\mathcal {A}) = 1$
, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\Pi _2$
.
$\Pi _2$
. -
2. If
 $\infty> \dim (\mathcal {A}) > 1$
, then
$\infty> \dim (\mathcal {A}) > 1$
, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\mathrm {d}\!-\Sigma _2$
.
$\mathrm {d}\!-\Sigma _2$
. -
3. If
 $\dim (\mathcal {A}) = \infty $
, then
$\dim (\mathcal {A}) = \infty $
, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\Pi _3$
.
$\Pi _3$
.
Theorem 5.5 Calvert [Reference Calvert8]
Let
![]() $\mathcal {A}$
be an algebraically closed field. Then:
$\mathcal {A}$
be an algebraically closed field. Then:
-
1. If
 $\mathcal {A}$
has finite transcendence degree, then
$\mathcal {A}$
has finite transcendence degree, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\mathrm {d}\!-\Sigma _2$
.
$\mathrm {d}\!-\Sigma _2$
. -
2. If
 $\mathcal {A}$
has infinite transcendence degree, then
$\mathcal {A}$
has infinite transcendence degree, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\Pi _3$
.
$\Pi _3$
.
Both of these classes are examples of strongly minimal theories and hence admit a pregeometry of algebraic closure. Csima et al. (unpublished) have shown that the hardness portion of the results above are consequences of the existence of this pregeometry. Other classes of structures also admit a pregeometry with the right properties; another example is the class of real closed ordered fields. Calvert et al. [Reference Calvert, Harizanov, Knight and Miller10] first computed the complexity of Archimedean real closed ordered fields.
Theorem 5.6 Calvert et al. [Reference Calvert, Harizanov, Knight and Miller10]
Let
![]() $\mathcal {A}$
be an Archimedean real closed ordered field.
$\mathcal {A}$
be an Archimedean real closed ordered field.
-
1. If the transcendence degree is
 $0$
, then
$0$
, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\Pi _2$
.
$\Pi _2$
. -
2. If the transcendence degree of
 $\mathcal {A}$
is finite but not
$\mathcal {A}$
is finite but not
 $0$
, then
$0$
, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\mathrm {d}\!-\Sigma _2$
.
$\mathrm {d}\!-\Sigma _2$
. -
3. If the transcendence degree of
 $\mathcal {A}$
is infinite, then
$\mathcal {A}$
is infinite, then
 $\mathcal {A}$
has Scott complexity
$\mathcal {A}$
has Scott complexity
 $\Pi _3$
.
$\Pi _3$
.
They also prove a number of results on reduced abelian p-groups.
Groups have been a very fruitful area for proving interesting results about Scott complexity. This began with free groups, where Carson et al. [Reference Carson, Harizanov, Knight, Lange, McCoy, Morozov, Quinn, Safranski and Wallbaum13] and McCoy and Wallbaum [Reference McCoy and Wallbaum46] used Nielson transformations to compute the Scott complexities of free groups on various generators.
Theorem 5.7 [Reference Chan13, Reference Marker46]
-
1. For
 $n \geq 1$
, the free group
$n \geq 1$
, the free group
 $F_n$
on n generators has Scott complexity
$F_n$
on n generators has Scott complexity
 $\mathrm {d}\!-\Sigma _2$
.
$\mathrm {d}\!-\Sigma _2$
. -
2. The free group
 $F_\infty $
on infinitely many generators has Scott complexity
$F_\infty $
on infinitely many generators has Scott complexity
 $\Pi _4$
.
$\Pi _4$
.
Knight and Saraph [Reference Knight and Saraph38] continued the study of the Scott complexity of groups by looking at torsion-free abelian groups of finite rank and finitely generated groups. For groups of finite rank, Knight and Saraph show that there is always a
![]() $\Sigma _3$
Scott sentence.
$\Sigma _3$
Scott sentence.
Theorem 5.8 Knight and Saraph [Reference Knight and Saraph38]
Let G be a torsion-free abelian group of finite rank. Then G has a
![]() $\Sigma _3$
Scott sentence.
$\Sigma _3$
Scott sentence.
Moreover, they show that there are computable torsion-free abelian groups of rank one which have Scott complexity
![]() $\Sigma _3$
.
$\Sigma _3$
.
Theorem 5.9 Knight and Saraph [Reference Knight and Saraph38]
If G is a subgroup of
![]() $\mathbb {Q}$
in which
$\mathbb {Q}$
in which
![]() $1$
is not infinitely divisible by any prime, but in which
$1$
is not infinitely divisible by any prime, but in which
![]() $1$
is finitely divisible by infinitely many primes, then G has Scott complexity
$1$
is finitely divisible by infinitely many primes, then G has Scott complexity
![]() $\Sigma _3$
.
$\Sigma _3$
.
One can also analyse the computability of these Scott sentences; see [Reference Knight and Saraph38] as well as [Reference Ho33].
Knight and Saraph also show that every finitely generated group has a
![]() $\Sigma _3$
Scott sentence, and indeed the same proof works for structures of any language.
$\Sigma _3$
Scott sentence, and indeed the same proof works for structures of any language.
Theorem 5.10 Knight and Saraph [Reference Knight and Saraph38]
Every finitely generated structure has a
![]() $\Sigma _3$
Scott sentence.
$\Sigma _3$
Scott sentence.
By Theorem 5.7, every finitely generated free group has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence. Moreover, the same is true of any finitely generated abelian group and of the dihedral group.
$\mathrm {d}\!-\Sigma _2$
Scott sentence. Moreover, the same is true of any finitely generated abelian group and of the dihedral group.
Theorem 5.11 Knight and Saraph [Reference Knight and Saraph38]
Every finitely generated abelian group has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence.
$\mathrm {d}\!-\Sigma _2$
Scott sentence.
Theorem 5.12 Knight and Saraph [Reference Knight and Saraph38]
The infinite dihedral group has Scott complexity
![]() $\mathrm {d}\!-\Sigma _2$
.
$\mathrm {d}\!-\Sigma _2$
.
Next, Ho [Reference Ho33] showed that polycyclic groups (which include nilpotent groups and abelian groups) and certain solvable groups also all have computable
 $\mathrm {d}\!-\Sigma ^0_2$
Scott sentence.
$\mathrm {d}\!-\Sigma ^0_2$
Scott sentence.
Theorem 5.13 Ho [Reference Ho33]
Every finitely generated polycyclic group has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence.
$\mathrm {d}\!-\Sigma _2$
Scott sentence.
At the time, every finitely generated group that had been checked had a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence, and so Knight and Saraph asked whether every finitely generated group has a
$\mathrm {d}\!-\Sigma _2$
Scott sentence, and so Knight and Saraph asked whether every finitely generated group has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence. Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho29] answered this question by showing that there is a finitely generated group with no
$\mathrm {d}\!-\Sigma _2$
Scott sentence. Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho29] answered this question by showing that there is a finitely generated group with no
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence and hence with Scott complexity
$\mathrm {d}\!-\Sigma _2$
Scott sentence and hence with Scott complexity
![]() $\Sigma _3$
.
$\Sigma _3$
.
Theorem 5.14 Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho29]
There is a finitely-generated computable group with Scott complexity
![]() $\Sigma _3$
.
$\Sigma _3$
.
Thus the upper bound given by Theorem 5.10 is best possible.
The proof of this last theorem relied on a characterizations using a number of different equivalent conditions on when a finitely generated structure has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence.
$\mathrm {d}\!-\Sigma _2$
Scott sentence.
Theorem 5.15 Miller [Reference Miller49], Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho29], and Alvir et al. [Reference Alvir, Knight and McCoy2]
Let
![]() $\mathcal {A}$
be a finitely generated structure. The following are equivalent:
$\mathcal {A}$
be a finitely generated structure. The following are equivalent:
-
1.
 $\mathcal {A}$
has a
$\mathcal {A}$
has a
 $\mathrm {d}\!-\Sigma _2$
Scott sentence;
$\mathrm {d}\!-\Sigma _2$
Scott sentence; -
2.
 $\mathcal {A}$
has a
$\mathcal {A}$
has a
 $\Pi _3$
Scott sentence;
$\Pi _3$
Scott sentence; -
3.
 $\mathcal {A}$
is the only model of its
$\mathcal {A}$
is the only model of its
 $\Sigma _2$
theory;
$\Sigma _2$
theory; -
4. some generating tuple of
 $\mathcal {A}$
is defined by a
$\mathcal {A}$
is defined by a
 $\Pi _1$
formula;
$\Pi _1$
formula; -
5. every generating tuple of
 $\mathcal {A}$
is defined by a
$\mathcal {A}$
is defined by a
 $\Pi _1$
formula; and
$\Pi _1$
formula; and -
6.
 $\mathcal {A}$
does not contain a copy of itself as a proper
$\mathcal {A}$
does not contain a copy of itself as a proper
 $\Sigma _1$
-elementary substructure.
$\Sigma _1$
-elementary substructure.
(2) is due to Miller [Reference Miller49], (3) is due to Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho30], (4) and (5) are due to Alvir et al. [Reference Alvir, Knight and McCoy2], and (6) is due to Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho29]. It is condition (6) which seems to be the most useful for constructing examples, as it has a more semantic flavour. Alvir et al. also have a nice characterization of when a structure has a computable
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence.
$\mathrm {d}\!-\Sigma _2$
Scott sentence.
Theorem 5.16 Alvir et al. [Reference Alvir, Knight and McCoy2]
Let
![]() $\mathcal {A}$
be a finitely generated structure. The following are equivalent:
$\mathcal {A}$
be a finitely generated structure. The following are equivalent:
-
1.
 $\mathcal {A}$
has a computable
$\mathcal {A}$
has a computable
 $\mathrm {d}\!-\Sigma _2$
Scott sentence;
$\mathrm {d}\!-\Sigma _2$
Scott sentence; -
2. some generating tuple of
 $\mathcal {A}$
is defined by a computable
$\mathcal {A}$
is defined by a computable
 $\Pi _1$
formula;
$\Pi _1$
formula; -
3. every generating tuple of
 $\mathcal {A}$
is defined by a computable
$\mathcal {A}$
is defined by a computable
 $\Pi _1$
formula.
$\Pi _1$
formula.
There are indeed computable structures with a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence, but no computable
$\mathrm {d}\!-\Sigma _2$
Scott sentence, but no computable
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence; for example Theorem 2.8 of [Reference Harrison-Trainor28] gives an example of a computable finitely generated principal ideal domain which, as a module over itself, has a
$\mathrm {d}\!-\Sigma _2$
Scott sentence; for example Theorem 2.8 of [Reference Harrison-Trainor28] gives an example of a computable finitely generated principal ideal domain which, as a module over itself, has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence but no computable
$\mathrm {d}\!-\Sigma _2$
Scott sentence but no computable
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence.
$\mathrm {d}\!-\Sigma _2$
Scott sentence.
These general tools give us a way to study Scott complexity in other classes of finitely generated structures. The known result are shown in the table below. Those results which have not yet been cited are due to Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho29] and Harrison-Trainor [Reference Harrison-Trainor28].

One important class of structures for which we do not know the answer is finitely presented groups.
Question 5.17 Question 1.7 of [Reference Harrison-Trainor and Ho29] and Question 1 of [Reference Alvir, Knight and McCoy2]
Does every finitely presented group have a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence?
$\mathrm {d}\!-\Sigma _2$
Scott sentence?
The best progress towards answering this question is in [Reference Harrison-Trainor28]. There, Harrison-Trainor proves the following purely group-theoretic characterization of the finitely presented groups with a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence:
$\mathrm {d}\!-\Sigma _2$
Scott sentence:
Theorem 5.18 Harrison-Trainor [Reference Harrison-Trainor28]
Let G be a finitely presented group. Then the following are equivalent:
-
1. G does not have a
 $\mathrm {d}\!-\Sigma _2$
Scott sentence and
$\mathrm {d}\!-\Sigma _2$
Scott sentence and -
2. G contains a proper subgroup
 $H \cong G$
with the property that for every finite set of non-identity elements
$H \cong G$
with the property that for every finite set of non-identity elements
 $a_1,\ldots ,a_n \in G$
, there is a normal subgroup
$a_1,\ldots ,a_n \in G$
, there is a normal subgroup
 $H' \subseteq G$
such that
$H' \subseteq G$
such that
 $G = H' \rtimes H$
and
$G = H' \rtimes H$
and
 $a_1,\ldots ,a_k \notin H'$
.
$a_1,\ldots ,a_k \notin H'$
.
One can immediately see from this that any finitely presented Hopfian group has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence. (A Hopfian group is one which is not isomorphic to any of its proper quotients.) This includes cases such as finitely generated abelian groups and free groups for which we already knew this, as well as a few new examples such as finitely presented residually finite groups and torsion-free hyperbolic groups. We can also show that the Baumslag-Solitar groups
$\mathrm {d}\!-\Sigma _2$
Scott sentence. (A Hopfian group is one which is not isomorphic to any of its proper quotients.) This includes cases such as finitely generated abelian groups and free groups for which we already knew this, as well as a few new examples such as finitely presented residually finite groups and torsion-free hyperbolic groups. We can also show that the Baumslag-Solitar groups
![]() $B(1,n)$
, which were originally constructed specifically as examples of non-Hopfian finitely generated groups, have
$B(1,n)$
, which were originally constructed specifically as examples of non-Hopfian finitely generated groups, have
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentences.
$\mathrm {d}\!-\Sigma _2$
Scott sentences.
Paolini [Reference Paolini58] gave a sufficient condition, a weakening of Hopfianity, for an arbitrary finitely presented structure to have a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence. We say that
$\mathrm {d}\!-\Sigma _2$
Scott sentence. We say that
![]() $\mathcal {A}$
is quasi-Hopfian if there is a finite generating set
$\mathcal {A}$
is quasi-Hopfian if there is a finite generating set
![]() $\bar {a}$
of
$\bar {a}$
of
![]() $\mathcal {A}$
such that whenever
$\mathcal {A}$
such that whenever
![]() $f\colon \mathcal {A} \to \mathcal {A}$
is a surjective homomorphism of
$f\colon \mathcal {A} \to \mathcal {A}$
is a surjective homomorphism of
![]() $\mathcal {A}$
which is injective on
$\mathcal {A}$
which is injective on
![]() $\bar {a}$
, f is injective.
$\bar {a}$
, f is injective.
Theorem 5.19 Paolini [Reference Paolini58]
Let
![]() $\mathcal {A}$
be a finitely presented structure. If
$\mathcal {A}$
be a finitely presented structure. If
![]() $\mathcal {A}$
is quasi-Hopfian, then
$\mathcal {A}$
is quasi-Hopfian, then
![]() $\mathcal {A}$
has a
$\mathcal {A}$
has a
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence.
$\mathrm {d}\!-\Sigma _2$
Scott sentence.
Paolini also gives a condition on the automorphism group of a quasi-Hopfian computable structure which is sufficient to have a computable
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence. Paolini applies this to show that the free projective plane of rank 4, which is quasi-Hopfian but not Hopfian, has a computable
$\mathrm {d}\!-\Sigma _2$
Scott sentence. Paolini applies this to show that the free projective plane of rank 4, which is quasi-Hopfian but not Hopfian, has a computable
![]() $\textrm {d}-\Sigma _2$
Scott sentence. He also considers Coxeter groups of finite rank; these are Hopfian, and hence have
$\textrm {d}-\Sigma _2$
Scott sentence. He also considers Coxeter groups of finite rank; these are Hopfian, and hence have
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentences, but it takes more work to show that these Scott sentences are computable.
$\mathrm {d}\!-\Sigma _2$
Scott sentences, but it takes more work to show that these Scott sentences are computable.
The complexity of saying that a structure is finitely generated is
![]() $\Sigma _3$
. When a finitely generated structure has Scott complexity
$\Sigma _3$
. When a finitely generated structure has Scott complexity
![]() $\Sigma _3$
, is this just because it is
$\Sigma _3$
, is this just because it is
![]() $\Sigma _3$
to say that it is finitely generated? Or is the complexity of picking out the structure from among other finitely generated structures actually
$\Sigma _3$
to say that it is finitely generated? Or is the complexity of picking out the structure from among other finitely generated structures actually
![]() $\Sigma _3$
? We can ask the analogous question whenever the complexity of a structure in a class
$\Sigma _3$
? We can ask the analogous question whenever the complexity of a structure in a class
![]() $\mathcal {K}$
is the same or less than the complexity of
$\mathcal {K}$
is the same or less than the complexity of
![]() $\mathcal {K}$
. For such cases, we would like to separate the complexity of describing the class of structure from the complexity of describing the structure inside of the class.
$\mathcal {K}$
. For such cases, we would like to separate the complexity of describing the class of structure from the complexity of describing the structure inside of the class.
Definition 5.20. Let
![]() $\mathcal {A}$
be a structure in a class
$\mathcal {A}$
be a structure in a class
![]() $\mathcal {K}$
. We say that
$\mathcal {K}$
. We say that
![]() $\varphi $
is a quasi Scott sentence for
$\varphi $
is a quasi Scott sentence for
![]() $\mathcal {A}$
within
$\mathcal {A}$
within
![]() $\mathcal {K}$
if, for countable
$\mathcal {K}$
if, for countable
![]() $\mathcal {B} \in \mathcal {K}$
,
$\mathcal {B} \in \mathcal {K}$
,
The Scott complexity of
![]() $\mathcal {A}$
within
$\mathcal {A}$
within
![]() $\mathcal {K}$
is
$\mathcal {K}$
is
![]() $\Gamma \in \{\Sigma _\alpha ,\Pi _\alpha ,\mathrm {d}\!-\Sigma _\alpha \}$
if
$\Gamma \in \{\Sigma _\alpha ,\Pi _\alpha ,\mathrm {d}\!-\Sigma _\alpha \}$
if
![]() $\Gamma $
is the least complexity of a quasi Scott sentence for
$\Gamma $
is the least complexity of a quasi Scott sentence for
![]() $\mathcal {A}$
within
$\mathcal {A}$
within
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
To prove an upper bound, we just need to exhibit a quasi Scott sentence. We again prove lower bounds using a reduction. For example, to show that
![]() $\mathcal {A}$
has Scott complexity at least
$\mathcal {A}$
has Scott complexity at least
![]() $\Sigma _\alpha $
within
$\Sigma _\alpha $
within
![]() $\mathcal {K}$
, we give a Wadge reduction f from a
$\mathcal {K}$
, we give a Wadge reduction f from a
 $\boldsymbol {\Sigma }^0_\alpha $
-complete set S to
$\boldsymbol {\Sigma }^0_\alpha $
-complete set S to
![]() $\operatorname {\mathrm {Iso}}(\mathcal {A})$
with the additional property that
$\operatorname {\mathrm {Iso}}(\mathcal {A})$
with the additional property that
![]() $f(x) \in \mathcal {K}$
for all x.
$f(x) \in \mathcal {K}$
for all x.
For finitely generated structures, we have the following interesting result:
Theorem 5.21 Harrison-Trainor and Ho [Reference Harrison-Trainor and Ho30]
Every finitely generated structure has a
![]() $\Pi _3$
quasi-Scott sentence within the class of finitely generated structures.
$\Pi _3$
quasi-Scott sentence within the class of finitely generated structures.
Recall that this means that for each finitely generated structure
![]() $\mathcal {A}$
, there is a
$\mathcal {A}$
, there is a
![]() $\Pi _3$
sentence
$\Pi _3$
sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $\mathcal {A}$
is the only finitely generated model of
$\mathcal {A}$
is the only finitely generated model of
![]() $\varphi $
. In [Reference Harrison-Trainor and Ho30], Harrison-Trainor and Ho prove that there are finitely generated groups with no
$\varphi $
. In [Reference Harrison-Trainor and Ho30], Harrison-Trainor and Ho prove that there are finitely generated groups with no
![]() $\mathrm {d}\!-\Sigma _2$
quasi Scott sentence within the class of finitely generated structures. Thus the analogue for quasi Scott sentences of Theorem 3.3 is not true: if a structure has a
$\mathrm {d}\!-\Sigma _2$
quasi Scott sentence within the class of finitely generated structures. Thus the analogue for quasi Scott sentences of Theorem 3.3 is not true: if a structure has a
![]() $\Sigma _3$
and a
$\Sigma _3$
and a
![]() $\Pi _3$
quasi Scott sentence within the class of finitely generated structures, it is not necessarily true that it has a
$\Pi _3$
quasi Scott sentence within the class of finitely generated structures, it is not necessarily true that it has a
![]() $\mathrm {d}\!-\Sigma _2$
quasi Scott sentence. There are two questions that are still open about quasi Scott sentences:
$\mathrm {d}\!-\Sigma _2$
quasi Scott sentence. There are two questions that are still open about quasi Scott sentences:
Question 5.22 Question 5.7 of [Reference Harrison-Trainor and Ho29]
Give a characterization of the finitely generated structures which have a
![]() $\mathrm {d}\!-\Sigma _2$
quasi Scott sentence within the class of finitely generated structures.
$\mathrm {d}\!-\Sigma _2$
quasi Scott sentence within the class of finitely generated structures.
Question 5.23 See Section 5.3 of [Reference Harrison-Trainor and Ho30]
Is there a finitely generated structure with a
![]() $\mathrm {d}\!-\Sigma _2$
quasi Scott sentence within the class of finitely generated structures, but no
$\mathrm {d}\!-\Sigma _2$
quasi Scott sentence within the class of finitely generated structures, but no
![]() $\mathrm {d}\!-\Sigma _2$
Scott sentence?
$\mathrm {d}\!-\Sigma _2$
Scott sentence?
Recall from Theorem 5.7 that the free group
![]() $F_\infty $
on infinitely many generators has Scott complexity
$F_\infty $
on infinitely many generators has Scott complexity
![]() $\Pi _4$
. McCoy and Walbaum [Reference McCoy and Wallbaum46] show that the class of free groups is axiomatizable by a
$\Pi _4$
. McCoy and Walbaum [Reference McCoy and Wallbaum46] show that the class of free groups is axiomatizable by a
![]() $\Pi _4$
sentence. Within this class,
$\Pi _4$
sentence. Within this class,
![]() $F_\infty $
is simpler to describe. (
$F_\infty $
is simpler to describe. (
![]() $F_1$
and
$F_1$
and
![]() $F_2$
also become simpler to describe within this class.)
$F_2$
also become simpler to describe within this class.)
Theorem 5.24 [Reference Chan13, Reference Marker46]
Let
![]() $\mathcal {FG}$
be the class of free groups.
$\mathcal {FG}$
be the class of free groups.
-
1. The free group
 $F_1 \cong \mathbb {Z}$
on one generator has Scott complexity
$F_1 \cong \mathbb {Z}$
on one generator has Scott complexity
 $\Pi _1$
within
$\Pi _1$
within
 $\mathcal {FG}$
.
$\mathcal {FG}$
. -
2. The free group
 $F_2$
on two generators has Scott complexity
$F_2$
on two generators has Scott complexity
 $\Pi _2$
within
$\Pi _2$
within
 $\mathcal {FG}$
.
$\mathcal {FG}$
. -
3. For
 $n> 2$
, the free group
$n> 2$
, the free group
 $F_n$
on n generators has Scott complexity
$F_n$
on n generators has Scott complexity
 $\mathrm {d}\!-\Sigma ^0_2$
within
$\mathrm {d}\!-\Sigma ^0_2$
within
 $\mathcal {FG}$
.
$\mathcal {FG}$
. -
4. The free group
 $F_\infty $
on infinitely many generators has Scott complexity
$F_\infty $
on infinitely many generators has Scott complexity
 $\Pi _3$
within
$\Pi _3$
within
 $\mathcal {FG}$
.
$\mathcal {FG}$
.
Quasi Scott sentences are also useful for talking about very simple structures, such as the one-dimensional
![]() $\mathbb {Q}$
-vector space; then Theorem 5.4 says that the Scott complexity of
$\mathbb {Q}$
-vector space; then Theorem 5.4 says that the Scott complexity of
![]() $\mathcal {V}$
is
$\mathcal {V}$
is
![]() $\Pi _2$
. However even just saying that
$\Pi _2$
. However even just saying that
![]() $\mathcal {V}$
is a vector space is already
$\mathcal {V}$
is a vector space is already
![]() $\Pi _2$
; perhaps all the complexity is in saying that
$\Pi _2$
; perhaps all the complexity is in saying that
![]() $\mathcal {V}$
is a vector space, and it is simpler than that to say that a vector space is one-dimensional? However Calvert et al. [Reference Calvert, Harizanov, Knight and Miller10] show that the one-dimensional
$\mathcal {V}$
is a vector space, and it is simpler than that to say that a vector space is one-dimensional? However Calvert et al. [Reference Calvert, Harizanov, Knight and Miller10] show that the one-dimensional
![]() $\mathbb {Q}$
-vector space has Scott complexity
$\mathbb {Q}$
-vector space has Scott complexity
![]() $\Pi _2$
within the class of
$\Pi _2$
within the class of
![]() $\mathbb {Q}$
-vector spaces.
$\mathbb {Q}$
-vector spaces.
Quasi Scott sentences within the class of finitely generated structures are similar to quasi-finite axiomatizability. A structure is quasi-finitely axiomatizable if there is a sentence
![]() $\varphi $
of finitary first-order logic such that the structure is the only finitely generated structure satisfying
$\varphi $
of finitary first-order logic such that the structure is the only finitely generated structure satisfying
![]() $\varphi $
, that is, if it has a finitary quasi Scott sentence within the class of finitely generated structures. See the survey [Reference Nies57].
$\varphi $
, that is, if it has a finitary quasi Scott sentence within the class of finitely generated structures. See the survey [Reference Nies57].
6 Theories
Given an
![]() $\mathcal {L}_{\omega _1 \omega }$
sentence
$\mathcal {L}_{\omega _1 \omega }$
sentence
![]() $\varphi $
we can think of
$\varphi $
we can think of
![]() $\varphi $
as a theory defining the class
$\varphi $
as a theory defining the class
![]() $\{\mathcal {A} : \mathcal {A} \models \varphi \}$
. This generalizes the notion of an elementary first-order theory, as given such a theory T, the conjunction
$\{\mathcal {A} : \mathcal {A} \models \varphi \}$
. This generalizes the notion of an elementary first-order theory, as given such a theory T, the conjunction
![]() $\bigwedge T$
of all the sentences in T is an
$\bigwedge T$
of all the sentences in T is an
![]() $\mathcal {L}_{\omega _1 \omega }$
sentence.
$\mathcal {L}_{\omega _1 \omega }$
sentence.
6.1 Vaught’s conjecture
As previously mentioned, we give only the briefest overview of Vaught’s conjecture and its connections with Scott sentences.
A central question in model theory is given a theory T, how many countable models can T have? The continuum hypothesis would imply that if T has infinitely many countable models, then it can only have countably many or continuum many countable models. In descriptive set theory, one often finds (e.g., for analytic sets) that even without the continuum hypothesis, one can prove that naturally occurring sets must have cardinality countable or continuum. Vaught’s conjecture [Reference Vaught65] asks whether this is true for the number of countable models of a theory.
Conjecture 6.1 Vaught
The number of countable models of an elementary first-order theory is either countable or continuum.
It is natural to extend this conjecture to theories given by sentences of
![]() $\mathcal {L}_{\omega _1 \omega }$
.
$\mathcal {L}_{\omega _1 \omega }$
.
Morley was able to eliminate almost all of the other possibilities.
Theorem 6.2 Morley [Reference Morley55]
The number of countable models of an elementary first-order theory is either
![]() $\aleph _0$
,
$\aleph _0$
,
![]() $\aleph _1$
, or continuum.
$\aleph _1$
, or continuum.
The standard proof of this theorem rests on what is called the Scott analysis together with Silver’s theorem. The Scott analysis looks at the back-and-forth relations on all of the models of the theory, or, as in [Reference Marker44], the analysis as in Definition 2.7. This gives a level-by-level splitting of the models of the theory, e.g., at level
![]() $\alpha $
one splits the models into
$\alpha $
one splits the models into
![]() $\equiv _\alpha $
-classes. Silver’s theorem says that co-analytic equivalence relations have either countably many or continuum many equivalence classes [Reference Silver63]. So at each level
$\equiv _\alpha $
-classes. Silver’s theorem says that co-analytic equivalence relations have either countably many or continuum many equivalence classes [Reference Silver63]. So at each level
![]() $\alpha $
there are either countably many or continuum many equivalence classes. If the theory has fewer than continuum-many models, at each level
$\alpha $
there are either countably many or continuum many equivalence classes. If the theory has fewer than continuum-many models, at each level
![]() $\alpha $
there must only be countably many equivalence classes of models. Then there are
$\alpha $
there must only be countably many equivalence classes of models. Then there are
![]() $\omega _1$
levels, hence at most
$\omega _1$
levels, hence at most
![]() $\aleph _1$
countable models.
$\aleph _1$
countable models.
Of course Vaught’s conjecture is automatically true if the continuum hypothesis is. Thus Vaught’s conjecture is often stated in a way that is independent of the continuum hypothesis. We say a sentence
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal {L}_{\omega _1 \omega }$
is scattered if it does not have a perfect set of countable models (in the space
$\mathcal {L}_{\omega _1 \omega }$
is scattered if it does not have a perfect set of countable models (in the space
![]() $\operatorname {\mathrm {Mod}}(\mathcal {L})$
). Then one can state Vaught’s conjecture as saying that any scattered theory has countably many countable models. Using the Scott analysis, one can show:
$\operatorname {\mathrm {Mod}}(\mathcal {L})$
). Then one can state Vaught’s conjecture as saying that any scattered theory has countably many countable models. Using the Scott analysis, one can show:
Theorem 6.3. The following are equivalent:
-
1.
 $\varphi $
is scattered,
$\varphi $
is scattered, -
2. for each countable
 $\alpha $
, there are only countably many
$\alpha $
, there are only countably many
 $\equiv _\alpha $
-equivalence classes of models of
$\equiv _\alpha $
-equivalence classes of models of
 $\varphi $
, and
$\varphi $
, and -
3. for each countable
 $\alpha $
, there are only countably many models of
$\alpha $
, there are only countably many models of
 $\varphi $
of Scott rank less than
$\varphi $
of Scott rank less than
 $\alpha $
.
$\alpha $
.
The Scott analysis, though not necessarily Scott rank or complexity, plays a central role in a large body of results about what a counterexample to Vaught’s conjecture would have to look like. Often, these results are about the uncountable models of the theory. One example mentioning Scott rank explicitly is:
Theorem 6.4 Harrington
A counterexample to Vaught’s Conjecture has models of arbitrarily large Scott rank below
![]() $\omega _2$
.
$\omega _2$
.
In this theorem, we need the Scott rank for uncountable structures, e.g., by extending the Scott ranks based on back-and-forth relations. Harrington’s proof was never published, but recently new proofs have independently been given by Baldwin et al. [Reference Baldwin, Friedman, Koerwien and Laskowski5], Knight et al. [Reference Knight, Montalbán and Schweber35], and Larson [Reference Larson39].
Montalbán showed that there are computability-theoretic ways of stating Vaught’s conjecture; the proof also uses an analysis of the back-and-forth relations.
Theorem 6.5. ZFC+PD; Montalbán [Reference Montalbán51]
Let
![]() $\varphi $
be an
$\varphi $
be an
![]() $\mathcal {L}_{\omega _1 \omega }$
sentence with uncountably many countable models. The following are equivalent:
$\mathcal {L}_{\omega _1 \omega }$
sentence with uncountably many countable models. The following are equivalent:
-
(V1)
 $\varphi $
is a counterexample to Vaught’s conjecture.
$\varphi $
is a counterexample to Vaught’s conjecture. -
(V2)
 $\varphi $
satisfies hyperarithmetic-is-recursive on a cone, i.e., for all sufficiently powerful oracles X, any hyperarithmetic-in-X model of
$\varphi $
satisfies hyperarithmetic-is-recursive on a cone, i.e., for all sufficiently powerful oracles X, any hyperarithmetic-in-X model of
 $\varphi $
has an X-computable copy.
$\varphi $
has an X-computable copy. -
(V3) There is an oracle relative to which,
where $$ \begin{align*} \{ \text{DgSp}(\mathcal{A}) \; : \; \mathcal{A} \models \varphi \} = \{\{X \in 2^\omega \; : \; \omega_1^X \geq \alpha\} : \alpha \in \omega_1\},\end{align*} $$
$$ \begin{align*} \{ \text{DgSp}(\mathcal{A}) \; : \; \mathcal{A} \models \varphi \} = \{\{X \in 2^\omega \; : \; \omega_1^X \geq \alpha\} : \alpha \in \omega_1\},\end{align*} $$
 $\text {DgSp}(\mathcal {A})$
is the degree spectrum of
$\text {DgSp}(\mathcal {A})$
is the degree spectrum of
 $\mathcal {A}$
, that is, the collection of sets which can compute a copy of
$\mathcal {A}$
, that is, the collection of sets which can compute a copy of
 $\mathcal {A}$
.
$\mathcal {A}$
.
As an example of an open question relating Scott rank and Vaught’s conjecture, we have:
Question 6.6 Montalbán, Berkeley Vaught’s Conjecture Workshop
A minimal theory T has the property that for any
![]() $\mathcal {L}_{\omega _1 \omega }$
-sentence
$\mathcal {L}_{\omega _1 \omega }$
-sentence
![]() $\varphi $
, exactly one of
$\varphi $
, exactly one of
![]() $T \wedge \varphi $
or
$T \wedge \varphi $
or
![]() $T \wedge \neg \varphi $
has models of arbitrarily high Scott rank. Does the existence of a minimal theory imply the existence of a counterexample to Vaught’s conjecture?
$T \wedge \neg \varphi $
has models of arbitrarily high Scott rank. Does the existence of a minimal theory imply the existence of a counterexample to Vaught’s conjecture?
6.2 Scott spectra
The results of this section were proved using the notion of Scott rank defined using symmetric back-and-forth relations (as in Definition 2.5) except with arbitrary tuples, replacing (2) of that definition with:
-
(2) For
 $\alpha> 0$
,
$\alpha> 0$
,
 $\bar {a} \sim _\alpha \bar {b}$
if for each
$\bar {a} \sim _\alpha \bar {b}$
if for each
 $\beta < \alpha $
and
$\beta < \alpha $
and
 $\bar {d}$
there is
$\bar {d}$
there is
 $\bar {c}$
such that
$\bar {c}$
such that
 $\bar {a} \bar {c} \sim _\beta \bar {b} \bar {d}$
, and for all
$\bar {a} \bar {c} \sim _\beta \bar {b} \bar {d}$
, and for all
 $\bar {c}$
there is
$\bar {c}$
there is
 $\bar {d}$
such that
$\bar {d}$
such that
 $\bar {a} \bar {c} \sim _\beta \bar {b} \bar {d}$
.
$\bar {a} \bar {c} \sim _\beta \bar {b} \bar {d}$
.
It is likely that the same or similar results can be proved for any of the definitions of Scott rank.
Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Pi _2$
sentence which we think of as similar to a theory in the sense that it defines a class of models. Many natural theories are of this form, e.g., most algebraic classes of interest such as algebraically closed fields or torsion groups. Montalbán asked whether there must be a model of
$\Pi _2$
sentence which we think of as similar to a theory in the sense that it defines a class of models. Many natural theories are of this form, e.g., most algebraic classes of interest such as algebraically closed fields or torsion groups. Montalbán asked whether there must be a model of
![]() $\varphi $
of somewhat low Scott complexity, say Scott rank 2 or less. One might expect that it would be possible to construct a model of any
$\varphi $
of somewhat low Scott complexity, say Scott rank 2 or less. One might expect that it would be possible to construct a model of any
![]() $\Pi _2$
theory without introducing any complicated types, resulting in a structure of low Scott rank. This turns out not to be the case; surprisingly, there are
$\Pi _2$
theory without introducing any complicated types, resulting in a structure of low Scott rank. This turns out not to be the case; surprisingly, there are
![]() $\Pi _2$
sentences all of whose models are very complicated.
$\Pi _2$
sentences all of whose models are very complicated.
Theorem 6.7 Harrison-Trainor [Reference Harrison-Trainor27]
Fix
![]() $\alpha < \omega _1$
. There is a
$\alpha < \omega _1$
. There is a
![]() $\Pi _2$
sentence T whose models all have Scott rank
$\Pi _2$
sentence T whose models all have Scott rank
![]() $\alpha $
.
$\alpha $
.
More generally, we can consider the collection of Scott ranks of all of the models of
![]() $\varphi $
.
$\varphi $
.
Definition 6.8. Let
![]() $\varphi $
be an
$\varphi $
be an
![]() $\mathcal {L}_{\omega _1 \omega }$
sentence. The Scott spectrum of
$\mathcal {L}_{\omega _1 \omega }$
sentence. The Scott spectrum of
![]() $\varphi $
is the collection
$\varphi $
is the collection
of Scott ranks of countable models of
![]() $\varphi $
.
$\varphi $
.
There are many natural questions about Scott spectra. For example, what kind of gaps can one have—for which
![]() $\alpha < \beta $
can a theory have models of Scott rank
$\alpha < \beta $
can a theory have models of Scott rank
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, but no models of Scott rank in between? Is there any relation between the complexity of the theory and the possible Scott spectrum? The following result of Sacks says that the Scott spectrum of a class is either bounded, or the class contains models of high Scott rank.
$\beta $
, but no models of Scott rank in between? Is there any relation between the complexity of the theory and the possible Scott spectrum? The following result of Sacks says that the Scott spectrum of a class is either bounded, or the class contains models of high Scott rank.
Theorem 6.9 Sacks [Reference Sacks59]
Let
![]() $\varphi $
be an
$\varphi $
be an
![]() $\mathcal {L}_{\omega _1 \omega }$
sentence. Suppose that the Scott rank of
$\mathcal {L}_{\omega _1 \omega }$
sentence. Suppose that the Scott rank of
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
 $\leq \omega _1^{\mathcal {M} \oplus \varphi }$
for all countable models
$\leq \omega _1^{\mathcal {M} \oplus \varphi }$
for all countable models
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\varphi $
. Then there is
$\varphi $
. Then there is
 $\alpha < \omega _1^\varphi $
such that the Scott rank of every model of
$\alpha < \omega _1^\varphi $
such that the Scott rank of every model of
![]() $\varphi $
is at most
$\varphi $
is at most
![]() $\alpha $
.
$\alpha $
.
Harrison-Trainor [Reference Harrison-Trainor27] gave a complete descriptive set-theoretic classification of the possible Scott spectra. To give this characterization, we need a few definitions.
Definition 6.10. Let
![]() $(L,\leq )$
be a linear order. The well-founded part
$(L,\leq )$
be a linear order. The well-founded part
![]() $\operatorname {\mathrm {wf}}(L)$
of L is the largest initial segment of L which is well-founded. The well-founded collapse of L,
$\operatorname {\mathrm {wf}}(L)$
of L is the largest initial segment of L which is well-founded. The well-founded collapse of L,
![]() $\operatorname {\mathrm {wfc}}(L)$
, is the order type of L after we collapse the non-well-founded part
$\operatorname {\mathrm {wfc}}(L)$
, is the order type of L after we collapse the non-well-founded part
![]() $L \setminus \operatorname {\mathrm {wf}}(L)$
to a single element.
$L \setminus \operatorname {\mathrm {wf}}(L)$
to a single element.
We can identify
![]() $\alpha \in \operatorname {\mathrm {wf}}(L)$
with the ordinal which is the order type of
$\alpha \in \operatorname {\mathrm {wf}}(L)$
with the ordinal which is the order type of
![]() $\{\beta \in L : \beta < \alpha \}$
. We can also identify
$\{\beta \in L : \beta < \alpha \}$
. We can also identify
![]() $\operatorname {\mathrm {wf}}(L)$
with its order type. If L is well-founded, with order type
$\operatorname {\mathrm {wf}}(L)$
with its order type. If L is well-founded, with order type
![]() $\alpha $
, then
$\alpha $
, then
![]() $\operatorname {\mathrm {wfc}}(L) = \operatorname {\mathrm {wf}}(L) = \alpha $
. If L is not well-founded,
$\operatorname {\mathrm {wfc}}(L) = \operatorname {\mathrm {wf}}(L) = \alpha $
. If L is not well-founded,
![]() $\operatorname {\mathrm {wfc}}(L) = \operatorname {\mathrm {wf}}(L)+1$
. We extend these operations to collections of linear orders by applying the operation to each order in the collection.
$\operatorname {\mathrm {wfc}}(L) = \operatorname {\mathrm {wf}}(L)+1$
. We extend these operations to collections of linear orders by applying the operation to each order in the collection.
Then we get the following characterization of the Scott spectra:
Theorem 6.11 Harrison-Trainor [Reference Harrison-Trainor27]; ZFC + PD
The Scott spectra of
![]() $\mathcal {L}_{\omega _1 \omega }$
-sentences are exactly the sets of the form:
$\mathcal {L}_{\omega _1 \omega }$
-sentences are exactly the sets of the form:
-
1.
 $\operatorname {\mathrm {wf}}(\mathcal {C})$
,
$\operatorname {\mathrm {wf}}(\mathcal {C})$
, -
2.
 $\operatorname {\mathrm {wfc}}(\mathcal {C})$
, or
$\operatorname {\mathrm {wfc}}(\mathcal {C})$
, or -
3.
 $\operatorname {\mathrm {wf}}(\mathcal {C}) \cup \operatorname {\mathrm {wfc}}(\mathcal {C}),$
$\operatorname {\mathrm {wf}}(\mathcal {C}) \cup \operatorname {\mathrm {wfc}}(\mathcal {C}),$
where
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $\boldsymbol {\Sigma }^1_1$
class of linear orders of
$\boldsymbol {\Sigma }^1_1$
class of linear orders of
![]() $\omega $
.
$\omega $
.
The more difficult and most useful part of this characterization is to show that each such collection of ordinals is the Scott spectrum of a theory. This direction is provable within ZFC and does not use the set-theoretic assumption of projective determinacy. One can use this direction to construct interesting examples of Scott spectra, such as the collection of successor ordinals, or the collection of admissible ordinals.
Harrison-Trainor also proved that
![]() $\Pi _2$
theories are enough to get all of the Scott spectra.
$\Pi _2$
theories are enough to get all of the Scott spectra.
Theorem 6.12 Harrison-Trainor [Reference Harrison-Trainor27]
Each Scott spectrum is the Scott spectrum of a
 $\Pi ^{\mathtt {in}}_2$
sentence.
$\Pi ^{\mathtt {in}}_2$
sentence.
For example, for every pair of ordinals
![]() $\alpha < \beta $
,
$\alpha < \beta $
,
![]() $\{\alpha ,\beta \}$
is a Scott spectrum.
$\{\alpha ,\beta \}$
is a Scott spectrum.
6.3 Scott height
Of the countably many computable
![]() $\mathcal {L}_{\omega _1 \omega }$
sentences, some of them have a Scott spectrum which is unbounded below
$\mathcal {L}_{\omega _1 \omega }$
sentences, some of them have a Scott spectrum which is unbounded below
![]() $\omega _1$
, and others are bounded below
$\omega _1$
, and others are bounded below
![]() $\omega _1$
. Since there are only countably many computable sentences, of all those that are bounded below
$\omega _1$
. Since there are only countably many computable sentences, of all those that are bounded below
![]() $\omega _1$
, there must be some countable ordinal which is the least common upper bound for all of them. Using
$\omega _1$
, there must be some countable ordinal which is the least common upper bound for all of them. Using
![]() $\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
for the computable
$\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
for the computable
![]() $\mathcal {L}_{\omega _1 \omega }$
sentences, we define:
$\mathcal {L}_{\omega _1 \omega }$
sentences, we define:
Definition 6.13. The Scott height
 $\operatorname {\mathrm {sh}}(\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega })$
of
$\operatorname {\mathrm {sh}}(\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega })$
of
![]() $\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
is the least ordinal
$\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
is the least ordinal
![]() $\alpha < \omega _1$
such that if
$\alpha < \omega _1$
such that if
![]() $\varphi $
is a computable
$\varphi $
is a computable
![]() $\mathcal {L}_{\omega _1 \omega }$
sentence whose Scott spectrum is bounded below
$\mathcal {L}_{\omega _1 \omega }$
sentence whose Scott spectrum is bounded below
![]() $\omega _1$
, then the Scott spectrum of
$\omega _1$
, then the Scott spectrum of
![]() $\varphi $
is bounded below
$\varphi $
is bounded below
![]() $\alpha $
.
$\alpha $
.
The Scott height is a way of measuring how far the computable sentences can “reach” up the class of countable ordinals.
Sacks and Marker made significant progress towards computing the Scott height of
![]() $\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
. Sacks [Reference Sacks59] showed that
$\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
. Sacks [Reference Sacks59] showed that
 $\operatorname {\mathrm {sh}}(\mathcal {L}^{\mathtt {c}}_{\omega _1,\omega }) \leq \delta ^1_2$
, where
$\operatorname {\mathrm {sh}}(\mathcal {L}^{\mathtt {c}}_{\omega _1,\omega }) \leq \delta ^1_2$
, where
![]() $\delta ^1_2$
is the least ordinal which has no
$\delta ^1_2$
is the least ordinal which has no
![]() $\Delta ^1_2$
presentation. Marker [Reference Marker43] was able to resolve this question for pseudo-elementary classes.
$\Delta ^1_2$
presentation. Marker [Reference Marker43] was able to resolve this question for pseudo-elementary classes.
Definition 6.14. A class
![]() $\mathcal {C}$
of structures in a language
$\mathcal {C}$
of structures in a language
![]() $\mathcal {L}$
is an
$\mathcal {L}$
is an
![]() $\mathcal {L}_{\omega _1 \omega }$
-pseudo-elementary class (
$\mathcal {L}_{\omega _1 \omega }$
-pseudo-elementary class (
 $PC_{\mathcal {L}_{\omega _1 \omega }}$
-class) if there is an
$PC_{\mathcal {L}_{\omega _1 \omega }}$
-class) if there is an
![]() $\mathcal {L}_{\omega _1 \omega }$
-sentence
$\mathcal {L}_{\omega _1 \omega }$
-sentence
![]() $\varphi $
in an expanded language
$\varphi $
in an expanded language
![]() $\mathcal {L}' \supseteq \mathcal {L}$
such that the structures in
$\mathcal {L}' \supseteq \mathcal {L}$
such that the structures in
![]() $\mathcal {C}$
are the reducts to
$\mathcal {C}$
are the reducts to
![]() $\mathcal {L}$
of the models of
$\mathcal {L}$
of the models of
![]() $\varphi $
.
$\varphi $
.
![]() $\mathcal {C}$
is a computable
$\mathcal {C}$
is a computable
 $PC_{\mathcal {L}_{\omega _1 \omega }}$
-class if
$PC_{\mathcal {L}_{\omega _1 \omega }}$
-class if
![]() $\varphi $
is a computable sentence.
$\varphi $
is a computable sentence.
We can define the Scott height of
 $PC_{\mathcal {L}_{\omega _1 \omega }}$
in a similar way to the Scott height of
$PC_{\mathcal {L}_{\omega _1 \omega }}$
in a similar way to the Scott height of
![]() $\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
, except that now we consider all
$\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }$
, except that now we consider all
![]() $\mathcal {L}_{\omega _1 \omega }$
-pseudo-elementary classes which are the reducts of the models of a computable sentence. Marker [Reference Marker43] showed that
$\mathcal {L}_{\omega _1 \omega }$
-pseudo-elementary classes which are the reducts of the models of a computable sentence. Marker [Reference Marker43] showed that
 $\operatorname {\mathrm {sh}}(PC_{\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }}) = \delta ^1_2$
. Finally, Harrison-Trainor [Reference Harrison-Trainor27] showed that every Scott spectrum of a pseudo-elementary
$\operatorname {\mathrm {sh}}(PC_{\mathcal {L}^{\mathtt {c}}_{\omega _1 \omega }}) = \delta ^1_2$
. Finally, Harrison-Trainor [Reference Harrison-Trainor27] showed that every Scott spectrum of a pseudo-elementary
![]() $\mathcal {L}_{\omega _1 \omega }$
-class is the Scott spectrum of an
$\mathcal {L}_{\omega _1 \omega }$
-class is the Scott spectrum of an
![]() $\mathcal {L}_{\omega _1 \omega }$
-sentence.
$\mathcal {L}_{\omega _1 \omega }$
-sentence.
Theorem 6.15 Harrison-Trainor [Reference Harrison-Trainor27]
Every Scott spectrum of a pseudo-elementary
![]() $\mathcal {L}_{\omega _1 \omega }$
-class is the Scott spectrum of an
$\mathcal {L}_{\omega _1 \omega }$
-class is the Scott spectrum of an
![]() $\mathcal {L}_{\omega _1 \omega }$
-sentence. Moreover, every Scott spectrum of a computable pseudo-elementary
$\mathcal {L}_{\omega _1 \omega }$
-sentence. Moreover, every Scott spectrum of a computable pseudo-elementary
![]() $\mathcal {L}_{\omega _1 \omega }$
-class is the Scott spectrum of a computable
$\mathcal {L}_{\omega _1 \omega }$
-class is the Scott spectrum of a computable
![]() $\mathcal {L}_{\omega _1 \omega }$
-sentence.
$\mathcal {L}_{\omega _1 \omega }$
-sentence.
Combined, all of these results allow us to compute the Scott height.
Corollary 6.16 Sacks [Reference Sacks59], Marker [Reference Marker43], and Harrison-Trainor [Reference Harrison-Trainor27]
 $\operatorname {\mathrm {sh}}(\mathcal {L}^{\mathtt {c}}_{\omega _1,\omega }) = \delta ^1_2$
.
$\operatorname {\mathrm {sh}}(\mathcal {L}^{\mathtt {c}}_{\omega _1,\omega }) = \delta ^1_2$
.
Marker also studies Scott heights for other types of classes. We say that a class is co-pseudo-elementary
![]() $\mathcal {L}_{\omega _1 \omega }$
, or
$\mathcal {L}_{\omega _1 \omega }$
, or
 $c\mathcal {PC}_{\mathcal {L}_{\omega _1 \omega }}$
, if it is the complement of a pseudo-elementary class. Then Marker [Reference Marker43] shows that:
$c\mathcal {PC}_{\mathcal {L}_{\omega _1 \omega }}$
, if it is the complement of a pseudo-elementary class. Then Marker [Reference Marker43] shows that:
Theorem 6.17 Marker [Reference Marker43]
 $\operatorname {\mathrm {sh}}(c\mathcal {PC}_{\mathcal {L}_{\omega _1 \omega }}) = \gamma ^1_2$
.
$\operatorname {\mathrm {sh}}(c\mathcal {PC}_{\mathcal {L}_{\omega _1 \omega }}) = \gamma ^1_2$
.
Here,
![]() $\gamma ^1_2$
is the least ordinal such that any non-empty
$\gamma ^1_2$
is the least ordinal such that any non-empty
 $\Pi ^1_2$
class of ordinals contains an ordinal below
$\Pi ^1_2$
class of ordinals contains an ordinal below
![]() $\gamma ^1_2$
. (By a
$\gamma ^1_2$
. (By a
 $\Pi ^1_2$
class of ordinals, we mean a
$\Pi ^1_2$
class of ordinals, we mean a
 $\Pi ^1_2$
class of presentations of linear orders on domain
$\Pi ^1_2$
class of presentations of linear orders on domain
![]() $\omega $
.) We have
$\omega $
.) We have
 $\gamma ^1_2> \delta ^1_2$
.
$\gamma ^1_2> \delta ^1_2$
.