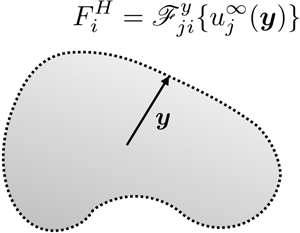
1. Introduction
Intricate coupling between particles, multi-length scale flow structures and different types of transport processes make it challenging to obtain solutions of field equations governing transport processes in colloidal suspensions. For example, computation of the charge distribution in a flowing suspension requires solution of coupled Stokes, Poisson and advection–diffusion equations which typically involve many-body interactions. This issue may be resolved by reciprocal relations that relate particle motion to ambient physical and chemical fields, allowing one to compute particle motion without solving the full field equations. The notion of relating particle motion to macroscopic fields has its origin in the celebrated result of Faxén (Reference Faxén1922), who showed that the force and torque on a sphere of radius 
$a$ with no-slip boundaries held fixed at point 
$\boldsymbol {y}$ in an ambient fluid of viscosity 
$\eta$ can be computed from the action of integro-differential operators on the far-field velocity
$u_i^{\infty }$
\begin{gather} F_i^{H} = 6{\rm \pi}\eta a\int u_i^{\infty}(\boldsymbol{\xi})\left(1 + \frac{a^{2}}{6}\nabla^{2}_y\right) \delta(\boldsymbol{\xi}-\boldsymbol{y})\, \textrm{d}\boldsymbol{\xi}, \end{gather}
\begin{gather}L_i^{H} = 4{\rm \pi}\eta a^{3} \varepsilon_{ijk}\int u_k^{\infty}(\boldsymbol{\xi}) \frac{\partial}{\partial y_j}\delta(\boldsymbol{\xi} - \boldsymbol{y}) \, \textrm{d} \boldsymbol{\xi}, \end{gather}
where 
$F_i^{H}$ and 
$L_i^{H}$ are the hydrodynamic force and torque, respectively. Here, 
$\boldsymbol{\xi}$ is an integration variable and 
$\varepsilon_{ijk}$ is the Levi-Civita symbol. Generalization of Faxén's original result includes extensions to higher-order traction moments (Batchelor & Green Reference Batchelor and Green1972; Jeffrey, Morris & Brady Reference Jeffrey, Morris and Brady1993), to rigid non-spherical particles (Kim Reference Kim1985) and to particles of other material compositions such as rigid droplets (Rallison Reference Rallison1978). Extensions to coupled physical and chemical transport processes have been limited, and include thermophoresis of rigid spheres (Mohan & Brenner Reference Mohan and Brenner2005) and droplets (Bafaluy et al. Reference Bafaluy, Pagonabarraga, Rubi and Bedeaux1995). Derivation of each of these ‘generalized Faxén formulas’ requires a separate (sometimes lengthy) proof, suggesting the need for a generalized framework.
Here, we present a framework for computing generalized Faxén formulas that can be broadly applied to any coupled transport processes. Our results allow one to obtain equations of motion for particles that can be used as the theoretical underpinning for computational frameworks studying the particle-scale dynamics and properties of suspensions in which physical and chemical rate processes are coupled.
2. Results
It has been noted that the functional forms of the Faxén formulas are remarkably similar to the corresponding singularity solutions of the velocity fields around a particle held fixed in a uniform flow of velocity 
$U_i^{\infty }$ and angular velocity 
$\varOmega _i^{\infty }$, where the latter are given by
\begin{gather} u_i(\boldsymbol{x}) = U_i^{\infty} - 6{\rm \pi}\eta aU_j^{\infty}\int {\mathsf{J}}_{ji}(\boldsymbol{\xi},\boldsymbol{x})\left(1 + \frac{a^{2}}{6}\nabla_y^{2}\right)\delta(\boldsymbol{\xi}-\boldsymbol{y})\, \textrm{d} \boldsymbol{\xi}, \end{gather}
\begin{gather} u_i(\boldsymbol{x}) = \varepsilon_{ijk}\varOmega_j^{\infty} r_k - 4{\rm \pi}\eta a^{3} \varepsilon_{jk\ell}\varOmega_\ell^{\infty}\int {\mathsf{J}}_{ki}(\boldsymbol{\xi},\boldsymbol{x}) \frac{\partial}{\partial y_j}\delta(\boldsymbol{\xi} - \boldsymbol{y}) \, \textrm{d} \boldsymbol{\xi}. \end{gather}Here,
\begin{equation} {\mathsf{J}}_{ji}(\boldsymbol{x},\boldsymbol{y}) = \frac{1}{8{\rm \pi}\eta a}\left(\frac{\delta_{ij}}{|\boldsymbol{x}-\boldsymbol{y}|} + \frac{(x_i-y_i)(x_j-y_j)}{|\boldsymbol{x}-\boldsymbol{y}|^{3}}\right) \end{equation}
is the Stokeslet, the Green's function of the Stokes equations for an unbound domain, which generates the velocity field induced by a point force 
$f_i$ located at 
$\boldsymbol {y}$: 
$u_i(\boldsymbol {x})={\mathsf{J}}_{ij}(\boldsymbol {x},\boldsymbol {y})\,f_j$, and 
$\delta_{ij}$ is the Kronecker delta. This correspondence is not a coincidence. Indeed, Hinch (Reference Hinch1977) noted that the ‘similarity is rooted in the [Lorentz] reciprocal theorem for Stokes flow’. Later, Kim (Reference Kim1985) provided a proof of this duality for arbitrarily shaped, rigid particles using the Lorentz reciprocal theorem; another elegant proof, attributed to Hinch, is given in Kim & Karrila (Reference Kim and Karrila1991). An extension of this proof to rigid droplets and to heat conduction in particles of arbitrary thermal conductivity emphasized the role of internal singularities in two phase flow problems (Kim & Lu Reference Kim and Lu1987). The authors deduced via these cases that the singularity solution/Faxén operator duality reflects a symmetry of the Stokes equations arising from the Lorentz reciprocal theorem (Hinch Reference Hinch1977; Kim Reference Kim1985; Kim & Lu Reference Kim and Lu1987), and they inferred but did not prove a more general duality. Prior mathematical proofs thus excluded important cases such as porous, core/shell, deformable and slip-stick particles, and flows with coupled transport processes such as diffusiophoresis or electrophoresis. A more comprehensive and widely useful formulation of the Faxén/singularity solution duality requires a general proof amenable to treatment of both arbitrary particle compositions and coupled transport processes.
Constructing such a proof is the primary purpose of this manuscript. The Faxén/singularity solution duality can be expressed in the operator notation of Kim (Reference Kim1985) as a relationship between the Faxén operators for the hydrodynamic force and torque on a single particle of a given shape and material composition,
\begin{gather} F_i^{H} = \mathscr{F}_{ji}^{y}\{u_j^{\infty}(\boldsymbol{y})\}, \end{gather}
\begin{gather}L_i^{H} = \mathscr{L}_{ji}^{y} \{u_j^{\infty}(\boldsymbol{y})\} , \end{gather}
and the singularity solutions for the velocity field exterior to that same particle held fixed in a fluid with constant far-field velocity 
$U_i^{\infty }$ and constant rotation rate 
$\varOmega _i^{\infty }$:
\begin{gather} u_i(\boldsymbol{x}) = U_i^{\infty} - \mathscr{F}_{jk}^{y}\{{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\} U_k^{\infty}, \end{gather}
\begin{gather}u_i(\boldsymbol{x}) = \varepsilon_{ijk}\varOmega_j^{\infty} r_k - \mathscr{L}_{jk}^{y}\{{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\}\varOmega_k^{\infty}, \end{gather}
where 
$\mathscr {F}_{ij}^{y}$ and 
$\mathscr {L}_{ij}^{y}$ are linear operators and 
$\boldsymbol {r}=\boldsymbol {x}-\boldsymbol {y}$ is the position of a material point in the fluid relative to the particle. The superscript 
$y$ indicates that the operator acts on the particle coordinate 
$\boldsymbol {y}$. Note that, while Kim assumed that the operators act on the unbound Green's function, we can readily extend this duality to singularity solutions acting on arbitrary Green's functions, including a point-force interior to a sphere (Oseen Reference Oseen1927), near a planar wall (Blake Reference Blake1971) or between two walls (Liron & Mochon Reference Liron and Mochon1976). This extension requires some care. The symmetry of the unbound Green's function 
${\mathsf{J}}_{ij}(\boldsymbol {x},\boldsymbol {y})={\mathsf{J}}_{ij}(\boldsymbol {y},\boldsymbol {x})={\mathsf{J}}_{ji}(\boldsymbol {y},\boldsymbol {x})$ allows one to freely exchange the index on which the operators 
$\mathscr {F}_{ij}^{y}$ and 
$\mathscr {L}_{ij}^{y}$ act. The more limited symmetries of the general Green's function 
${\mathsf{J}}_{ij}(\boldsymbol {x},\boldsymbol {y})={\mathsf{J}}_{ji}(\boldsymbol {y},\boldsymbol {x})$ lead to the requirement that the operators act on the first index of the Green's function. In support of this extension, we note that Faxén/singularity solution duality has been verified by direct computation for no-slip spheres between parallel walls (Swan & Brady Reference Swan and Brady2010) and interior to spherical cavities (Aponte-Rivera & Zia Reference Aponte-Rivera and Zia2016).
The duality can be understood as a reciprocal relation; in (2.4) the operators 
$\mathscr {F}_{ij}^{y}$ and 
$\mathscr {L}_{ij}^{y}$ act on the Stokeslet to satisfy the boundary conditions on the particle surface for specified flows. These same operators act on the 
$u_i^{\infty }(\boldsymbol {y})$ in (2.3) to extract moments of the traction and give the hydrodynamic force and torque that arise from the arbitrary far-field flow. In this sense, the operators may be understood as generalized resistance tensors that act on a velocity field to produce the hydrodynamic force and torque. All familiar hydrodynamic resistance tensors are encoded inside these operators, for instance, 
$\mathscr {F}_{ji}^{y}\{U_j^{\infty }\}={\mathsf{R}}_{ij}^{FU}U_j^{\infty }$.
The benefits this duality holds are twofold: First, the Faxén operators can be obtained analytically or numerically from the solution of simple boundary value problems, allowing one to calculate particle motion in arbitrary flow fields by solving for motion of that same particle in a much simpler flow. Second, the operators 
$\mathscr {F}_{ij}^{y}$ and 
$\mathscr {L}_{ij}^{y}$ can be expressed as positive semi-definite operators, making them ideal for implementation into simulations. However, a proof of this duality for general particle types or for suspensions with coupled transport processes, which is the aim of this work, is currently lacking.
The prior proofs of duality of (2.3) and (2.4) for rigid particles (Kim Reference Kim1985) and spherical droplets and heat conduction (Kim & Lu Reference Kim and Lu1987) relied on the Lorentz reciprocal theorem and thus require detailed knowledge of the boundary conditions on all particlesurfaces. One could hypothetically construct similar proofs for particles of other material compositions, e.g. porous, linear–viscoelastic, charged, or drop with mobile surfactant, but one would need to construct a separate proof in each case, requiring the development of reciprocal relations for each boundary condition, no small task. Furthermore, one must construct a different proof for each traction moment, e.g. force, torque, stresslet. A more general approach, i.e. one that is independent of the particle boundary conditions, would allow us to bypass this complexity and to prove the operator duality for particles of arbitrary shape and composition and, as we will show, we could thence readily extend the methods to coupled transport processes such as diffusiophoresis (coupled momentum and mass transport) and electrophoresis.
We recognized that this general approach can be found by invoking energy methods that give reciprocity between operators rather than between fields. We note that the Faxén operators themselves must encode the boundary conditions because they arise as solutions to partial differential equations. This suggests that we could construct a proof of the relationship between Faxén formulas and singularity solutions for particles of arbitrary composition provided that expressions for the operators appearing in the singularity solutions are known. We thus seek to obtain an explicit representation of these operators.
We seek a general operator 
$\mathscr {A}_i^{y}$ that is the sole and sufficient carrier of boundary conditions on a particle of arbitrary shape and composition that produces velocity field exterior to a particle held fixed in an arbitrary far-field velocity field 
$u_i^{\infty }(\boldsymbol {x})$ as
\begin{equation} u_i(\boldsymbol{x}) = u_i^{\infty}(\boldsymbol{x}) - \mathscr{A}_j^{y}\{{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\}. \end{equation}
The operators 
$\mathscr {F}_{ij}^{y}U_j^{\infty }$ and 
$\mathscr {L}_{ij}^{y}\varOmega _j^{\infty }$ are particular examples of 
$\mathscr {A}_i^{y}$ for specialized far-field flows. We seek a particular representation of 
$\mathscr {A}_j^{y}$ that is made valid for all particles regardless of shape or composition by encoding the boundary conditions on the particle surface 
$S_p$. The boundary integral representation due to Ladyzhenskaya (Reference Ladyzhenskaya1969) yields an expression for the fluid velocity external to the particle
\begin{equation} u_i(\boldsymbol{x}) = u_i^{\infty}(\boldsymbol{x}) - \int_{S_{p}(\boldsymbol{y})} \left[{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x}) \sigma_{jk}n_k - \varSigma_{jki}(\boldsymbol{y},\boldsymbol{x}) u_kn_j \right] \textrm{d} S_y, \end{equation}
where 
$n_i$ is the outward-facing unit normal of the particle. Notably, the fluid velocity field is specified entirely by the far-field velocity and an integral operator encoding how the boundary values of the hydrodynamic stress 
$\sigma _{jk}$ and the fluid velocity 
$u_k$ on 
$S_p$ are propagated via the corresponding Stokes-flow singularities, the Stokeslet 
${\mathsf{J}}_{ji}$ and its conjugate stress field
\begin{equation} \varSigma_{jki}(\boldsymbol{x},\boldsymbol{y}) =-\frac{1}{4{\rm \pi}}\delta_{jk}\frac{x_i-y_i}{|\boldsymbol{x}-\boldsymbol{y}|^{3}} + \eta\left(\frac{\partial {\mathsf{J}}_{ji}}{\partial x_k} + \frac{\partial {\mathsf{J}}_{ki}}{\partial x_j}\right). \end{equation}
In incompressible flows, the double-layer operator, the second term in (2.6), acts only on the parts of 
$\varSigma _{jki}$ that can be described with a Stokeslet, thus justifying the functional forms of (2.3) and (2.4). This can be readily shown from a Taylor series expansion of the double layer; the pressure singularity in the zeroth-order term of the expansion vanishes from compressibility, while higher-order derivatives of the pressure singularity can be expressed in terms of the Stokeslet using the relation 
$\eta \nabla ^{2}_xu_i=\partial p/\partial x_i$. This property of the double layer arises because pressure serves as a Lagrange multiplier enforcing incompressibility, and is fully determined by the velocity field to within an additive constant in all incompressible, Newtonian flows (Beris & Edwards Reference Beris and Edwards1994). An alternative representation would be required if one wished to compute Faxén operators for moments of the pressure (Jeffrey et al. Reference Jeffrey, Morris and Brady1993).
Hence, comparing (2.5) and (2.6) reveals a representation of the operator 
$\mathscr {A}_i^{y}$ that is valid for particles of arbitrary shape and composition
\begin{equation} \mathscr{A}_j^{y}\{ {\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\} = \int_{S_p(\boldsymbol{y})} \left[{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x}) \sigma_{jk}n_k - \varSigma_{jki}(\boldsymbol{y},\boldsymbol{x})u_kn_j \right] \textrm{d} S_y. \end{equation}
We will use this representation to prove the duality between generalized Faxén formulas and singularity solutions. The proof that follows applies as written to particles in an unbound fluid, and to particles confined by external walls or boundaries by replacing 
${\mathsf{J}}_{ji}$ and 
$\varSigma _{jki}$ with the appropriate Green's functions.
We will now apply energy methods to this integral representation of Stokes flow in order to prove the Faxén formula/singularity solution duality. The functional 
$\mathscr {A}_i^{y}\{ u_i^{\infty }(\boldsymbol {y}) \}$ gives the increase in the rate of work arising from the presence of the particle in response to the far-field flow. This can be shown through explicit representation of the action of 
$\mathscr {A}_i^{y}$ on 
$u_i^{\infty }$
\begin{equation} \mathscr{A}_i^{y}\{ u_i^{\infty}(\boldsymbol{y}) \} =\int_{S_p(\boldsymbol{y})} \left(u_i^{\infty}(\boldsymbol{\xi})\sigma_{ij}n_j - u_i\sigma_{ij}^{\infty}(\boldsymbol{\xi})n_j\right) \textrm{d} S_\xi, \end{equation}
where 
$S_p(\boldsymbol {y})$ is the particle surface and 
$\sigma _{ij}^{\infty }$ is the stress generated by the far-field flow. Taylor expanding the far-field velocity about the particle centre yields
\begin{equation} u_i^{\infty}(\boldsymbol{x}) = U_i^{\infty} + \varepsilon_{ijk}\varOmega_j^{\infty} r_k + {\mathsf{E}}_{ij}^{\kern0.8pt\infty} r_j + \cdots, \quad \sigma_{ij}^{\infty} = 2\eta {\mathsf{E}}_{ij}^{\kern0.8pt\infty} + \cdots, \end{equation}
where 
${\mathsf{E}}_{ij}^{\kern0.8pt\infty }$ is the shear rate far from the particle, which upon substitution into (2.9) yields
\begin{equation} \mathscr{A}_i^{y}\{ u_i^{\infty}(\boldsymbol{y}) \} = F_i^{H}U_i^{\infty} + L_i^{H}\varOmega_j^{\infty} + {\mathsf{S}}_{ij}^{H}{\mathsf{E}}_{ij}^{\kern0.8pt\infty} + \cdots, \end{equation}which is identically the rate of work required to generate the flow in the presence of the particles (Batchelor Reference Batchelor1970). Here,
\begin{equation} {\mathsf{S}}_{ij}^{H}=\int_{S_p(\boldsymbol{y})}\tfrac{1}{2}\left(\sigma_{ik}n_kr_j+\sigma_{jk}n_kr_i - \tfrac{2}{3}\delta_{ij}\sigma_{k\ell}n_kr_\ell\right) \textrm{d} S - \eta\int_{S_p(\boldsymbol{y})}(u_in_j+u_jn_i)\, \textrm{d} S \end{equation}
is the (irreducible) hydrodynamic stresslet. Note, the rate of work expression does not truncate at the stresslet, and continues ad infinitum to higher-order force moments (cf. appendix A of Dolata & Zia Reference Dolata and Zia2020). The above working is at the heart of the singularity/Faxén duality: the operator 
$\mathscr {A}_i^{y}$ acts on the Stokeslet in (2.9) to produce flow, and on the far-field velocity in (2.11) to yield the rate of work.
This can readily be used to prove a theorem of (the rate of) virtual work for the operator 
$\mathscr {A}_i^{y}$. The right-hand side of (2.11) can be represented as 
$\mathcal {F}^{\intercal }\mathcal {U}$, where 
$\mathcal {F}$ is a generalized force vector containing every traction moment that acts on the particle surface, and 
$\mathcal {U}$ is a generalized velocity vector containing all fluid velocity derivatives. The linearity of Stokes flow dictates that the generalized force can be related to the generalized velocity through the grand resistance matrix 
$\mathcal {R}^{FU}$ as 
$\mathcal {F}=\mathcal {R}^{FU}\mathcal {U}$, giving the right-hand side of (2.11) as 
$\mathcal {U}^{\intercal }\mathcal {R}^{FU}\mathcal {U}$. The virtual rate of work done by some arbitrary auxiliary velocity field 
$\tilde {u}_i^{\infty }$ is found by expanding 
$\mathscr {A}_i^{y}\{\tilde {u}_i^{\infty }(\boldsymbol {y}) \}$ in the same way; we find that the virtual work done by the actual traction generated by particle motion via the virtual auxiliary velocity field is 
$\mathscr {A}_i^{y}\{\tilde {u}_i^{\infty }(\boldsymbol {y}) \} = \tilde {\mathcal {U}}^{\intercal }\mathcal {R}^{FU}\mathcal {U}$. From the symmetry of the grand resistance matrix, we have 
$\tilde {\mathcal {U}}^{\intercal }\mathcal {R}^{FU}\mathcal {U}=\mathcal {U}^{\intercal }\mathcal {R}^{FU}\tilde {\mathcal {U}}$, which immediately implies
\begin{equation} \mathscr{A}_i^{y}\{ \tilde{u}_i^{\infty}(\boldsymbol{y}) \} = \tilde{\mathscr{A}}_i^{y}\{u_i^{\infty}(\boldsymbol{y}) \}, \end{equation}
where 
$\tilde {\mathscr {A}}_i^{y}$ is an auxiliary operator that enforces the boundary conditions on 
$S_p$ for the far-field flow 
$\tilde {u}_i^{\infty }$.
Our operator reciprocity broadens prior understanding that the Faxén formula/singularity solution duality is a consequence of the Lorentz reciprocal theorem. Earlier works proved that this duality and its connection to the Lorentz reciprocal theorem holds under specific boundary conditions (Kim Reference Kim1985; Kim & Lu Reference Kim and Lu1987), but did not generalize beyond those specific boundary conditions, possibly because each new particle type would require a completely new proof. Our method bypasses the need to repeat the proof for each particle type, by working with the singularity operators that encode the boundary conditions, rather than the specific velocity and stress fields generated by these operators. We thus provide general proof that the Faxén formula/singularity solution duality is a consequence of the Lorentz reciprocal theorem, which holds for arbitrary particle composition (rigid, porous, deformable, micropolar, etc.). Together, the broader understanding and general proof provides a framework which we will subsequently use to model coupled transport processes.
We can now prove the relation between Faxén's formulas and the associated singularity solutions through appropriate choice of the auxiliary velocity field. For instance, if we set 
$\tilde {u}_i^{\infty }~=~\tilde {U}_i^{\infty }$ in (2.13), then 
$\tilde {\mathscr {A}}_i^{y}=\mathscr {F}_{ij}^{y}\tilde {U}_j^{\infty }$ as defined by (2.4a), and
\begin{equation} F_i^{H} \tilde{U}_i^{\infty} = \mathscr{F}_{ji}^{y}\{u_j^{\infty}(\boldsymbol{y})\}\tilde{U}_i^{\infty}, \end{equation}where the left-hand side follows from (2.11). The far-field velocity is arbitrary and may be removed using orthogonality arguments, thus proving the duality between the singularity solution operator and the Faxén operator. This procedure can be repeated for all higher-order velocity derivatives, proving that the operator duality holds for all traction moments and for particles of arbitrary shape, surface conditions and composition. We observe that the proven duality between generalized Faxén relations and singularity solutions should be understood as restatements of the symmetry of the grand resistance matrix, which was used to prove (2.13). An extension of this results to a system without an obvious definition for a grand resistance matrix, namely a deforming droplet, is given in § 3.2.
In order to extend our proof to coupled transport processes, we are guided by the Onsager–Casimir reciprocal relations (Onsager Reference Onsager1931a,Reference Onsagerb; Casimir Reference Casimir1945), which lead to symmetry relations between thermodynamic fluxes and forces in the entropy production equation. The linearity of the Newtonian stress tensor in the symmetric part of the velocity gradient is implied by the Onsager–Casimir relations. The symmetry of the stress tensor and its linearity in the velocity gradient also lead directly to the Lorentz reciprocal theorem, and ultimately to the existence and symmetry of the grand resistance matrix. We may then view the symmetry of the grand resistance matrix, and hence the operator reciprocal relation given in (2.13), as a corollary of the Onsager–Casimir reciprocal relations. Following this line of reasoning implies the existence of an extended Grand Resistance matrix that encodes the virtual work done by imposed macroscopic fields (velocity, temperature, potential, etc.) on the associated flux (traction, heat flux, current, etc.) on the particle surface. The important outcome of this approach is that we can derive reciprocal relations between operators for coupled transport processes, simply by leveraging the expanded grand resistance matrix.
We can represent general transport processes with a field variable and its gradients and the associated moments of the flux of a conserved quantity evaluated at the particle surface. In the case of momentum transport, these quantities are the fluid velocity field and the corresponding momentum flux, where the latter is characterized by the fluid stress tensor that in turn produces traction moments on immersed surfaces. More generally, we can represent momentum flux and other arbitrary transport processes of a continuous phase such as molecular diffusiophoresis, electrophoresis or thermophoresis via a generalized state vector 
$\varPhi$ that contains the far-field values 
$\boldsymbol {\phi }^{\infty }$ of a field variable 
$\boldsymbol {\phi }$ (e.g. velocity, chemical potential, electric potential, temperature) and its spatial gradients. The generalized current or transport flux of the affinity 
$\boldsymbol {\phi }$ and its moments, evaluated at the particle surface, can be represented by a generalized vector 
$\mathcal {J}$.
The affinity drives current, a rate of transport, producing work at a rate 
${\dot {W}= \pm \mathcal {J}\varPhi }$. The sign of the rate of work is physically important and depends on the parity of the transport process under time reversal. For instance, momentum transport is time reversible, and 
$\dot {W}=\mathcal {J}\varPhi$ with 
$\mathcal {J}=\mathcal {F}$ and 
$\varPhi = \mathcal {U}$ as above. In contradistinction are time irreversible transport processes where 
$\dot {W}= -\varPhi \mathcal {J}$, such as diffusion of solute, where 
$\varPhi$ contains the gradient of the chemical potential and 
$\mathcal {J}$ contains the moments of molar flux. In the linear regime, the current 
$\mathcal {J}$ is linear in the inducing driving force 
$\varPhi$, where the strength of the current is set by a generalized resistance matrix 
$\mathcal {R}^{J\phi }$, which is assumed symmetric. It is shown in appendix A that this assumption holds true provided a generalized Lorentz reciprocal theorem is satisfied in the particle interior. In the case of coupled physical and chemical transport processes, fluid motion can induce a generalized current 
$\mathcal {J}$ linear in the driving flow 
$\mathcal {U}$ as 
$\mathcal {J}=\mathcal {R}^{JU}\mathcal {U}$. Likewise, the companion coupled field variable can induce hydrodynamic forces on particle surfaces expressed as 
$\mathcal {F}=\mathcal {R}^{F\phi }\varPhi$. As shown in appendix A, there is a reciprocity between these coupled fluxes: 
$\mathcal {R}^{JU} = \pm (\mathcal {R}^{F\phi })^{\intercal }$, where the sign again depends on the parity of the transport processes under time reversal.
In many cases of interest, 
$\phi$ is a harmonic function (i.e. a solution of the Laplace equation) and the flux is given by 
$-\alpha \partial \phi /\partial x_i$, where 
$\alpha$ is a transport coefficient; examples include diffusiophoresis, where 
$\alpha$ is a diffusivity, and the thin double-layer limit of electrokinetic transport phenomena, where 
$\alpha$ is the ionic conductivity. Treatment of the case of finite double layers requires a small modification to the proof, and is discussed in § 3.4. The value of 
$\phi$ at a material point may be given as
\begin{equation} \phi(\boldsymbol{x}) = \phi^{\infty}(\boldsymbol{x}) - \mathscr{C}^{y}\{G(\boldsymbol{y},\boldsymbol{x})\}, \end{equation}
in analogy with (2.5), where 
$\mathscr {C}^{y}$ is an operator that acts on the Laplace Green's function
\begin{equation} G(\boldsymbol{x},\boldsymbol{y}) = \mp\frac{1}{4{\rm \pi}\alpha|\boldsymbol{x}-\boldsymbol{y}|} \end{equation}
to satisfy the boundary conditions of 
$\phi$ on 
$S_p$, i.e. to produce the potential. We note that the sign in (2.16) is consistent with the rate of work done. We use the integral representation of the Laplace equation, often termed Green's third identity, in a manner completely analogous to the proof above where we obtained the energy dissipation from the Ladyzhenskaya (Reference Ladyzhenskaya1969) integral representation, to prove that
\begin{equation} \mathscr{C}^{y}\{\phi^{\infty}(\boldsymbol{y})\} = \pm \mathcal{J}\varPhi, \end{equation}
in analogy to (2.11). That is, 
$\mathscr {C}$ acts on the imposed potential to do work. A straightforward generalization of our theorem of virtual work (cf. (2.13)) to coupled physical and chemical transport processes is then implied by the symmetry of the generalized grand resistance matrix
\begin{equation} \mathscr{A}_i^{y}\{ \tilde{u}_i^{\infty}(\boldsymbol{y}) \} + \mathscr{C}^{y}\{\tilde{\phi}^{\infty}(\boldsymbol{y}) \} = \tilde{\mathscr{A}}_i^{y}\{ u_i^{\infty}(\boldsymbol{y}) \} + \tilde{\mathscr{C}}^{y}\{\phi^{\infty}(\boldsymbol{y}) \}. \end{equation}
Equation (2.18) is an extension of our generalized theorem of virtual work, and gives a reciprocal relation between the operator 
$\mathscr {A}_i^{y}$ that generates flow exterior to a particle and the operator 
$\mathscr{C}^y$ which generates harmonic functions; as will be shown, (2.18) will form the basis for calculating Faxén relations for systems with coupled physical and chemical transport processes.
As shown in appendix A, the symmetry relations underpinning (2.18) will hold provided that the governing equations of the velocity and potential interior to the particle obey a generalized Lorentz reciprocal theorem
\begin{equation} \int_{V_p} \frac{\partial}{\partial x_j}\left(u_i\tilde{\sigma}_{ij} \pm \phi \tilde{j}_j \right) \textrm{d} V = \int_{V_p} \frac{\partial}{\partial x_j}\left(\tilde{u}_i\sigma_{ij} \pm \tilde{\phi} j_j \right) \textrm{d} V, \end{equation}where the volume integral is taken both the particle interior and the infinitesimally thin boundary layer between the particle and fluid. The importance of the fields interior to the particle should not be a surprise; indeed, Kim & Lu (Reference Kim and Lu1987) emphasized the importance of internal singularities in their proof of the Faxén/singularity solution duality for spherical droplets. The requirements for (2.19) to hold are not severe. For rigid, solid particles and perfect conductors, this reduces to the standard forms of the Lorentz reciprocal theorem and Green's second identity because stresses and currents are localized to the particle surface. This generalized Lorentz reciprocal theorem holds for many other physical cases of interest, such as droplets with zero surface tension or with viscous interfacial stresses, porous particles governing by Brinkman's or Darcy's equations, as well as composite particles constructed from multiple different material. Additionally, it has been proven to hold for electrokinetic phenomena in Newtonian fluids (Brunet & Ajdari Reference Brunet and Ajdari2004). However, there exists some problems of great interest for which this generalized Lorentz reciprocal theorem does not hold, such as, for instance, the case of a droplet with finite surface tension. This is a minor limitation of the model. One can still derive Faxén laws for such system by invoking linearity of the governing equation external to the particle to express the fluid velocity and other coupled processes as the superposition of solutions of two model problems: one where (2.18) holds and hence a Faxén law exists, and a second problem encoding degrees of freedom internal to the particle. This idea is explored further in § 3.2, where Faxén laws for deformable droplets are derived.
3. Example problems
In this section, we employ the general framework derived in the prior sections to study four example problems. In § 3.1, we derive expressions for Faxén formulas for the hydrodynamic force on a spherical particle of arbitrary composition. The Faxén law for the stresslet exerted on a deformable droplet is derived in § 3.2, demonstrating that our method can be applied to deformable particles. The influence of coupled physical and chemical transport problems is studied in § 3.3, where we compute a Faxén formula for the electrophoretic force on a particle of arbitrary shape. Finally, we investigate the influence of body forces and charges, which have heretofore been neglected, through the canonical problem of the electroviscous effect in § 3.4.
3.1. Hydrodynamic drag on spherical particles of arbitrary composition
From symmetry considerations, the Faxén formula for the hydrodynamic drag on spherical particles of arbitrary shape and composition can be written as
\begin{equation} F_i^{H} = \frac{4{\rm \pi}\eta a}{3}\int u_i^{\infty}(\boldsymbol{\xi})\left(\,f_1 + a^{2}f_2\nabla^{2}_y\right) \delta(\boldsymbol{\xi}-\boldsymbol{y})\, \textrm{d}\boldsymbol{\xi}, \end{equation}
where 
$f_1$ and 
$f_2$ are constants that depend on the boundary conditions at the particle surface and on the equations of motion internal to the particle, and are directly related to the coefficients in the singularity solution through the singularity/Faxén duality. This general formula extends the results of Kim (Reference Kim1985) and Kim & Lu (Reference Kim and Lu1987) for rigid particles and spherical droplets to arbitrary particle compositions, and explains the functional similarity between singularity solutions and Faxén formulas for solid spheres (Faxén Reference Faxén1922), spherical droplets with infinite surface tension (Rallison Reference Rallison1978), porous spheres using Darcy's (Palaniappan Reference Palaniappan1993) and Brinkman's (Padmavathi, Amaranath & Nigam Reference Padmavathi, Amaranath and Nigam1993) models, double emulsions (Haj-Hariri, Nadim & Borhan Reference Haj-Hariri, Nadim and Borhan1993), composite particles consisting of a solid core with a porous covering (Chen & Ye Reference Chen and Ye2000) and, after typological errors are corrected in their work, spheres with a Navier-slip boundary condition (Sri Padmavati & Amaranath Reference Sri Padmavati and Amaranath2004). A Faxén law of the general form of (3.1) will exist for all spherical particles that have translation described by a quasi-linear boundary value problem. This restriction is not severe. One can construct quasi-linear Faxén operators for particles with elastic stresses or other internal degrees of freedom, which typically involve nonlinear boundary conditions, by introducing evolution equations for these additional degrees of freedom. This idea is discussed further in the next section.
3.2. Faxén formulas for deformable droplets
A spherical droplet will deform under an imposed flow due to unequal normal stresses across its surface. In general, the shape of the deformed particle is a nonlinear function of the imposed flow, suggesting that, at first glance, there is no grand resistance matrix. This, however, is not the case. The linearity of the Stokes equations allows us to express the velocity field exterior to a deforming sphere as the superposition of two flows. The first is the flow exterior to a droplet with zero surface tension; a droplet with zero surface tension will have a grand resistance matrix dependent on the instantaneous shape of the particle at a given moment because the droplet dynamics is reversible and arises only from the imposed flow. The second flow is the retraction of the droplet towards its equilibrium shape due to surface tension. This second flow is independent of the far-field flow and depends only on the shape and material properties of the droplet. We use this partition of the flow to derive Faxén formulas for the stresslet and degenerate octupole moment induced on an inviscid droplet, and demonstrate how they may be used to compute the time evolution of the stresslet under arbitrary imposed flows when supplemented with kinetic equations for the surface deformations.
The boundary conditions for a droplet of viscosity 
$\lambda \eta$ and surface tension 
$\gamma$ are givenas
\begin{equation} u_i \to u_i^{\infty}(\boldsymbol{x})\quad \textrm{as}\ r\to\infty, \quad u_i = \hat{u}_i\quad \textrm{on}\ S_p, \quad \sigma_{ij}n_j = \hat{\sigma}_{ij}n_j + \gamma n_i\frac{\partial n_i}{\partial x_i}\quad \textrm{on}\ S_p, \end{equation}where the hat represents the field values interior to the droplet. The linearity of the Stokes equations allows us to re-express the flow as the superposition of two flows: the flow around a zero surface tension droplet under an imposed far-field flow
\begin{equation} u_i \to u_i^{\infty}(\boldsymbol{x})\quad \textrm{as}\ r\to\infty, \quad u_i = \hat{u}_i\quad \textrm{on}\ S_p, \quad \sigma_{ij}n_j = \hat{\sigma}_{ij}n_j, \end{equation}and droplet retraction due to surface tension
\begin{equation} u_i \to 0\quad \textrm{as}\ r\to\infty, \quad u_i = \hat{u}_i\quad \textrm{on} \ S_p, \quad \sigma_{ij}n_j = \hat{\sigma}_{ij}n_j + \gamma n_i\frac{\partial n_i}{\partial x_i}\quad \textrm{on}\ S_p. \end{equation}This decomposition has previously been employed to study the deformation of droplets under shear flow (Yu & Bousmina Reference Yu and Bousmina2003). We may therefore express the total solution to flow around a droplet as
\begin{equation} u_i(\boldsymbol{x}) = u_i^{\infty}(\boldsymbol{x}) - \mathscr{A}_j^{y,{flow}}\{{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\} - \mathscr{A}_j^{y,{ST}}\{{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\}. \end{equation}
The operator 
$\mathscr {A}_j^{y,{flow}}$ encodes the flow induced by the presence of a zero surface tension droplet in the far-field flow and satisfies (3.3); it is dependent on both the instantaneous shape of the deformed droplet and the imposed flow, and encodes the grand resistance matrix for a droplet of a given shape with no surface tension. The operator 
$\mathscr {A}_j^{y,{ST}}$ encodes the droplet retraction due to surface tension and satisfies (3.4). This operator depends only on the instantaneous shape and material properties of the droplet, and is independent of the flow.
We can now obtain expressions for the Faxén formula for the stresslet on a deforming droplet using these operators. Recall from (2.11) that 
$\mathscr {A}_j^{y}\{{\mathsf{E}}_{ji}^{\kern0.8pt\infty } r_i\}={\mathsf{S}}_{ij}^{H}{\mathsf{E}}_{ji}^{\kern0.8pt\infty }.$ Let 
$\mathscr {A}_k^{y,{flow}}={\mathsf{E}}_{ij}^{\kern0.8pt\infty }\mathscr {E}_{kij}^{y}$ be the operator that encodes the flow around a zero surface tension droplet with the far-field velocity 
$u_i^{\infty } ={\mathsf{E}}_{ij}^{\kern0.8pt\infty } r_j$. It follows from the Faxén/singularity solution duality that
\begin{equation} {\mathsf{S}}_{ij}^{H} = \mathscr{E}_{kij}^{y}\{u_k^{\infty}(\boldsymbol{y})\} + \varDelta_{ijk\ell}^{(2,2)}\mathscr{A}_k^{y,{ST}}\{r_\ell\}, \end{equation}
where 
$\varDelta _{ijk\ell }^{(2,2)}=\tfrac {1}{2}\delta _{ik}\delta _{j\ell } + \tfrac {1}{2}\delta _{i\ell }\delta _{jk} - \tfrac {1}{3}\delta _{ij}\delta _{k\ell }$ projects a second-rank tensor into fully symmetric and traceless form. The first term in (3.6) is the Faxén formula for the stresslet on a droplet with zero surface tension and the second term is the additional stresslet arising from surface-tension-induced deformation of the droplet.
These expressions are exact for droplets of arbitrary shape, viscosity and surface tension. Their key utility is revealed in flows for which the droplet shape has an analytical description. In the large deformation limit, this is typically done by employing area (Wetzel & Tucker Reference Wetzel and Tucker1999) or volume (Wetzel & Tucker Reference Wetzel and Tucker2001; Jackson & Tucker Reference Jackson and Tucker2003; Yu & Bousmina Reference Yu and Bousmina2003) tensors. Here, we will instead examine the small deformation regime. For small deformations, the droplet shape can be expanded in spherical harmonics (Frankel & Acrivos Reference Frankel and Acrivos1970). To linear order, only the second-degree spherical harmonic, which we describe with a symmetric, traceless tensor 
${\mathsf{F}}_{ij}$, contributes to the stresslet, meaning the droplet shape is described by the shape function
\begin{equation} f(\boldsymbol{r}) = a\left(1 + \frac{r_ir_j}{r^{2}} {\mathsf{F}}_{ij}\right) - r, \end{equation}
which vanishes on the droplet surface. Consistency requires that 
${\mathsf{F}}_{ij}$ is asymptotically small, so that droplet shape can be evaluated as a sphere to linear order.
From Frankel & Acrivos (Reference Frankel and Acrivos1970), the operator encoding surface retraction is given as
\begin{align} &\mathscr{A}_j^{y,{ST}}\{{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\} \nonumber\\ &\quad = \frac{8{\rm \pi}\eta a^{3}}{3} \frac{4\gamma}{\eta a(2\lambda + 3)} {\mathsf{F}}_{jk} \int {\mathsf{J}}_{ji}(\boldsymbol{\xi},\boldsymbol{x}) \left(1 + \frac{a^{2}(3\lambda + 2)}{2(19\lambda+16)} \nabla_y^{2} \right)\frac{\partial}{\partial y_k} \delta(\boldsymbol{\xi} - \boldsymbol{y})\, \textrm{d}\boldsymbol{\xi}. \end{align}Substituting (3.8) into (3.6) yields the Faxén law for a slightly deformed viscous droplet
\begin{equation} {\mathsf{S}}_{ij}^{H} = \mathscr{E}_{kij}^{y}\{u_k^{\infty}(\boldsymbol{y})\} + \frac{8{\rm \pi}\eta a^{3}}{3} \frac{4\gamma}{\eta a(2\lambda + 3)} {\mathsf{F}}_{ij}, \end{equation}
where 
$\mathscr {E}_{kij}^{y}$ is yet to be determined. The Faxén law for the stresslet can be combined with the kinematic condition
\begin{equation} n_iu_i = \frac{1}{|\boldsymbol{\nabla} f|}\frac{ \textrm{d} f(\boldsymbol{r})}{ \textrm{d} t}, \end{equation}to obtain an expression for the temporal evolution for the stresslet.
The kinematic condition (3.10) reveals that the deformation of the droplet is given by the flow normal to its surface. The flow arising from surface tension is given by (3.8), while the flow arising from the deformation induced by the (arbitrary) far-field flow is given by the multipole expansion
\begin{equation} u_i = u_i^{\infty}(\boldsymbol{x}) -\int {\mathsf{J}}_{ji}(\boldsymbol{\xi},\boldsymbol{x}) \left({\mathsf{S}}_{jk}^{\kern0.8pt H,{flow}} + {\mathsf{O}}_{jk}^{\kern0.8pt H,{flow}}\nabla_y^{2} \right)\frac{\partial}{\partial y_k}\delta(\boldsymbol{\xi} - \boldsymbol{y}) \, \textrm{d}\boldsymbol{\xi} + \cdots. \end{equation}
Here, 
${\mathsf{O}}_{ij}^{\kern0.8pt H,{flow}}$ is the degenerate octupole moment arising from the imposed flow; symmetry considerations indicate that other force moments (force, torque, quadrupole moments) will not contribute to the evolution of 
${\mathsf{F}}_{ij}$. Substituting (3.8) and (3.11) into (3.10) yields an equation for the droplet deformation rate
\begin{equation} r_in_j\frac{ \textrm{d} {\mathsf{F}}_{ij}}{ \textrm{d} t} = \left(-\frac{40 \gamma (\lambda +1)}{\eta (2 \lambda +3) (19 \lambda +16)}{\mathsf{F}}_{ij} - \frac{3}{8{\rm \pi}\eta a^{2}}{\mathsf{S}}_{ij}^{\kern0.8pt H,flow} + \frac{9}{4{\rm \pi}\eta a^{4}}{\mathsf{S}}_{ij}^{\kern0.8pt H,flow}\right)n_in_j + n_iv_i^{\infty} . \end{equation}
Multiplying by 
$n_kn_\ell$ and integrating over the surface of the sphere gives a differential equation for the droplet shape
\begin{equation} \frac{ \textrm{d} {\mathsf{F}}_{ij}}{ \textrm{d} t} = -\frac{40 \gamma (\lambda +1)}{a\eta (2 \lambda +3) (19 \lambda +16)}{\mathsf{F}}_{ij} - \frac{3}{8{\rm \pi}\eta a^{3}}{\mathsf{S}}_{ij}^{\kern0.8pt H,flow} + \frac{9}{4{\rm \pi}\eta a^{5}}{\mathsf{O}}_{ij}^{\kern0.8pt H,flow} + \left(1 + \frac{a^{2}}{14}\nabla^{2}\right){\mathsf{E}}_{ij}^{\kern0.8pt\infty}, \end{equation}
where 
${\mathsf{E}}_{ij}^{\kern0.8pt\infty }$ and 
$\nabla ^{2}{\mathsf{E}}_{ij}^{\kern0.8pt\infty }$ are evaluated at the centre of the sphere. All that remains is to derive expressions for the flow-induced stresslet and octupole moment. The Faxén operator for the stresslet can be obtained from the known solution of the velocity field around a spherical droplet with no surface tension embedded in a constant shear rate field (Taylor Reference Taylor1934)
\begin{equation} \mathscr{E}_{kij}^{y}\{u_k^{\infty}(\boldsymbol{y})\} = \frac{8{\rm \pi}\eta a^{3}}{3}\frac{5\lambda - 5}{2\lambda + 3}\varDelta_{ijk\ell}^{(2,2)} \int u_k^{\infty}(\boldsymbol{\xi})\left(1 + \frac{a^{2}}{10}\nabla_y^{2} \right)\frac{\partial}{\partial y_\ell} \delta(\boldsymbol{\xi} - \boldsymbol{y}) \, \textrm{d}\boldsymbol{\xi}. \end{equation}The Faxén operator for the octupole moment is found from the solution solution of a zero surface tension droplet in a flow where the Laplacian of the far-field shear rate is constant
\begin{equation} \mathscr{O}_{kij}^{y}\{u_k^{\infty}(\boldsymbol{y})\} = \frac{4{\rm \pi}\eta a^{3}}{3}\frac{\lambda - 1}{2\lambda + 3} \varDelta_{ijk\ell}^{(2,2)}\int u_k^{\infty}(\boldsymbol{\xi})\left(1 + \frac{5a^{2}}{42}\frac{19\lambda + 18}{19\lambda + 16}\nabla_y^{2} \right)\frac{\partial}{\partial y_\ell} \delta(\boldsymbol{\xi} - \boldsymbol{y}) \, \textrm{d}\boldsymbol{\xi}. \end{equation}
These Faxén operators, together with the evolution equation (3.9) and (3.13), yield equations allowing for the computation of the stresslet on a deformable droplet in the linear response regime. Our result is valid for all transient flows, provided the deformation is small. In the steady state limit, 
${\mathsf{F}}_{ij}$ can be computed from (3.13), which upon insertion into (3.9), yields
\begin{equation} {\mathsf{S}}_{ij}^{H} = \frac{8{\rm \pi}\eta a^{3}}{3}\frac{5\lambda + 2}{2\lambda + 2} \varDelta_{ijk\ell}^{(2,2)}\int u_k^{\infty}(\boldsymbol{\xi})\left(1 + \frac{a^{2}\lambda}{10\lambda + 4}\nabla_y^{2} \right)\frac{\partial}{\partial y_\ell} \delta(\boldsymbol{\xi} - \boldsymbol{y}) \, \textrm{d}\boldsymbol{\xi}, \end{equation}which recovers the known result for a spherical droplet (Rallison Reference Rallison1978).
We have derived a Faxén formula for the stresslet exerted on a deformable droplet in the linear response regime. This result can readily be extended to higher-order terms in the deformation using well-known mathematical methods for computing flows around slightly deformed droplets (Frankel & Acrivos Reference Frankel and Acrivos1970). It would also be straightforward to extend these results to other constitutive equations for droplet interfaces, such as the elastic interfaces that arise in elastic capsules (Barthès-Biesel & Rallison Reference Barthès-Biesel and Rallison1981), or interfaces with Marangoni stresses arising from mobile surfactants (Danov Reference Danov2001). Finally, these results can be extended to large deformations, provided one can identify an appropriate shape parameterization.
3.3. Electrophoretic force on a rigid particle of arbitrary shape
We will use the reciprocal relation (2.18) to obtain expressions for hydrodynamic traction moments induced on a particle held fixed in the presence of an imposed potential field 
$\phi ^{\infty }$. For ease of discussion, we choose the generic potential 
$\phi$ to represent the electric potential arising from the presence of dissolved ions. However, the results are general for any analogous transport process. Computation of the Faxén formulas for the phoretic force and torque, that is, the hydrodynamic forces and torques induced on a particle by an arbitrary far-field potential 
$\phi ^{\infty }$, requires the selection of the appropriate auxiliary problem. Force and translational velocity are conjugate variables, which suggests that the phoretic force can be computed from the streaming potential problem for a charged particle. In this problem, a particle is held fixed in a uniform velocity field 
$U_i^{\infty }$ in the absence of any far-field potential (
$\phi ^{\infty }=0$), distorting the velocity field. At the same time, shearing flows normal to the double layer (i.e. normal stresses) induce a current within the double layer, and hence generate an electric field. Conservation of charge within the double layer leads to a relationship between the stresses and ionic current normal to the double layer (Bike & Prieve Reference Bike and Prieve1992), requiring the addition of the electric potential 
$\phi$ to our set of singularity solutions
\begin{gather} u_i(\boldsymbol{x}) = U_i^{\infty} - \mathscr{F}_{jk}^{y}\{{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\} U_k^{\infty}, \end{gather}
\begin{gather}p(\boldsymbol{x}) = - \mathscr{F}_{ij}^{y}\{\mathcal{P}_i(\boldsymbol{y},\boldsymbol{x})\}U_j^{\infty}, \end{gather}
\begin{gather}\phi(\boldsymbol{x}) = -\mathscr{S}^{y}_i \{G(\boldsymbol{y},\boldsymbol{x})\}U_i^{\infty}. \end{gather}
Here, the operator acting on the pressure is the same as that on the fluid velocity, since both arise as solution to the same linear equation, and the operator 
$\mathscr {S}^{y}_i$ yields the streaming potential induced by fluid motion. Note that we have also included the fluid pressure 
$p$ in our set of singularity solutions. In incompressible flows, the pressure contains no additional information that is not already expressed by the velocity field; the pressure is simply a Lagrange multiplier that enforces compressibility. All information about the flow is encoded in the operator 
$\mathscr {F}_{ij}^{y}$, which generates both the velocity and pressure field. Thus, the inclusion of the pressure is not a matter of physical necessity. Indeed, one could use the relationship 
$\eta \nabla ^{2}_xu_i=\partial p/\partial x_i$ to re-express everything that follows in terms of the Stokeslet. Rather, we include the pressure in order to simplify our derivations by leveraging the relationship between the unbound pressure Green's function 
$\mathcal {P}_i$ and (2.16), the Green's function for the potential
\begin{equation} \mathcal{P}_i(\boldsymbol{y},\boldsymbol{x}) = -\alpha \frac{\partial G(\boldsymbol{y},\boldsymbol{x})}{\partial y_i}. \end{equation}
The apparent sign inconsistency of (3.18) with (2.16) arises because it is the electric field 
$E_i=-\partial \phi /\partial x_i$ that should appear in the virtual work production expression, rather than the potential itself.
We substitute the auxiliary problem (3.17) into the right-hand side of (2.18) by setting 
${\tilde {\mathscr {A}}_i^{y}=\mathscr {F} _{ij}^{y}\tilde {U}_j^{\infty }}$ and 
$\tilde {\mathscr {C}}^{y} = \mathscr {S}_i^{y}\tilde {U}_i^{\infty }$, which yields
\begin{equation} F_i^{H} \tilde{U}_i^{\infty} = \mathscr{F}_{ji}^{y}\{u_j^{\infty}(\boldsymbol{y})\}\tilde{U}_i^{\infty} + \mathscr{S}_{i}^{y}\{\phi^{\infty}(\boldsymbol{y})\}\tilde{U}_i^{\infty}, \end{equation}
where the left-hand side again follows from the virtual work done by the imposed fields and the electrostatic work is zero by prescription of no imposed far-field potential. Equation (3.19) is a general Faxén formula for the hydrodynamic force on the surface of a particle held fixed in an imposed arbitrary flow field and arbitrary far-field potential. The first term on right-hand side of (3.19) is the generalized Faxén formula for the hydrodynamic force induced by a far-field velocity, and the second term reveals that the operator 
$\mathscr {S}_i^{y}$ that acts on the far-field potential to give the phoretic force is identical to that which acts on the Laplace Green's function to give the potential field. Equivalent Faxén operators for higher-order phoretic traction moments are found by choosing the appropriate far-field velocity. We have thus extended the Faxén formula/singularity solution duality to coupled chemical and physical transport processes.
In general, obtaining specific expressions for the phoretic Faxén 
$\mathscr {S}^{y}_i$ in (3.19) for a specific particle type (e.g. of a certain shape, composition and surface charge) requires solution of the relevant boundary value problem. Here, we will give explicit expressions for one such problem, namely, the phoretic (electro-hydrodynamic) force arising on the surface of a particle with a thin ionic double layer. For rigid particles with thin double layers, fluid velocity is unchanged by the presence of the ions, but the pressure gradient induces a current, coupling the pressure and the potential at the boundary. The resultant surface boundary condition is (Bike & Prieve Reference Bike and Prieve1992)
\begin{equation} \alpha n_i\frac{\partial\phi}{\partial x_i} = \mu n_i\frac{\partial p}{\partial x_i} \quad \textrm{on}\ S_p, \end{equation}
where 
$\mu$ is the electrophoretic mobility. Substituting (3.17b) and (3.17c) into (3.20) and relating the pressure and potential Green's functions through (3.18) yields the operator sought
\begin{equation} \mathscr{S}_i^{y} = -\mathscr{F}_{ji}^{y}\frac{\partial}{\partial y_j} . \end{equation}Extending this result to the torque by imposing a far-field rotation as in (2.4b), we immediately obtain the phoretic force and torque from our proven duality
\begin{equation} F_i^{phor} = -\mu\mathscr{F}_{ji}^{y} \left\{\frac{\partial\phi^{\infty}(\boldsymbol{y})}{\partial y_j} \right\}, \quad L_i^{phor} = -\mu\mathscr{L}_{ji}^{y}\left\{\frac{\partial\phi^{\infty}(\boldsymbol{y})}{\partial y_j} \right\}. \end{equation}
We thus find that the Faxén operators for the force induced by the far-field velocity and the far-field potential are identical in the thin double-layer limit; the solution of Morrison Jr. (Reference Morrison1970) for electrophoretic motion of an arbitrarily shaped particle indicates that a similar duality exists between the first moment of the ionic current induced by a far-field flow and a far-field potential. Our specific result (2.24) recovers the known result that in the thin double-layer limit, all particles acted on by a linear potential 
$\phi ^{\infty } = -g_i^{\infty } y_j$ obtain the same phoretic velocity 
$U_i=\mu g_i^{\infty }$ and zero rotational velocity 
$(\varOmega _i=0)$ regardless of shape or size (Smoluchowski Reference Smoluchowski1903; Morrison Jr. Reference Morrison1970). Particle velocities can be obtained using our expressions for phoretic traction moments from the following overdamped equations of motion:
\begin{equation} \left(\begin{matrix} F_i^{H} \\ L_i^{H} \end{matrix}\right) = -\left(\begin{matrix} {\mathsf{R}}^{\kern0.8pt FU}_{ij} & {\mathsf{R}}_{ji}^{\kern0.8pt LU}\\ {\mathsf{R}}_{ij}^{\kern0.8pt LU} & {\mathsf{R}}_{ij}^{\varOmega L} \end{matrix}\right) \left(\begin{matrix} U_j \\ \varOmega_j \end{matrix}\right) + \left(\begin{matrix} \mathscr{F}_{ji}^{y} & -\mu\mathscr{F}_{ji}^{y}\frac{\partial}{\partial y_j}\\ \mathscr{L}_{ji}^{y} & -\mu\mathscr{L}_{ji}^{y}\frac{\partial}{\partial y_j} \end{matrix}\right) \left(\begin{matrix} u_j^{\infty}(\boldsymbol{y}) \\ \phi^{\infty}(\boldsymbol{y}) \end{matrix}\right) = \left(\begin{matrix} 0 \\ 0 \end{matrix}\right), \end{equation}
where 
$U_i$ and 
$\varOmega _i$ are the translational and rotational velocities of the particle, respectively, and 
${\mathsf{R}}_{ij}^{\kern0.8pt FU}$, 
${\mathsf{R}}_{ij}^{\kern0.8pt LU}$ and 
${\mathsf{R}}_{ij}^{\kern0.8pt L\varOmega }$ are resistance tensors. Setting 
$\phi ^{\infty } = -g_i^{\infty } y_j$, and solving yields 
$U_i=\mu g_i^{\infty }$ and 
$\varOmega _i=0$ in agreement with Smoluchowski and Morrison Jr.
3.4. Fluids acted on by body forces
In the prior sections, we have restricted ourselves to flows with no body forces or charges. This is in general a good approximation in Stokes flow, but can fail in systems with coupled physical and chemical transport processes. For instance, charged ions can exert an electrostatic force on the fluid and dissolved molecules can induce an osmotic force on the fluid during diffusiophoresis. Our proof can readily be extended to a fluid acted on by a body force 
$f_i$ with two small changes. First, the integral representation in (2.8) must be modified by the addition of a body force term
\begin{equation} \mathscr{A}_j^{y}\{ {\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x})\} = \int_{S_p(\boldsymbol{y})} \left[{\mathsf{J}}_{ji}(\boldsymbol{y},\boldsymbol{x}) \sigma_{jk}n_k - \varSigma_{jki}(\boldsymbol{y},\boldsymbol{x})u_kn_j\right] \textrm{d} S_y - \int_{V\notin V_p(\boldsymbol{y})} f_j{\mathsf{J}}_{ji}\{(\boldsymbol{y},\boldsymbol{x})\}\, \textrm{d} V, \end{equation}where the volume integral is taken external to the sphere. Second, the generalized Lorentz reciprocal theorem given in (2.19) must be extended to the region of fluid that contains body forces. With these modifications, one then finds that
\begin{equation} \mathscr{A}_i^{y}\{ u_i^{\infty}(\boldsymbol{y}) \} = F_iU_i^{\infty} + L_i\varOmega_j^{\infty} + {\mathsf{S}}_{ij}{\mathsf{E}}_{ij}^{\kern0.8pt\infty} + \cdots, \end{equation}where the force moments now are the total force exerted on the particle, i.e. the sum of viscous and body forces. The singularity solution/Faxén formula duality then holds provided the existence of a grand resistance matrix. In electrophoresis, this requires that the Péclet number is small, so that the distribution of ions is only slightly perturbed by the flow (Brunet & Ajdari Reference Brunet and Ajdari2004). All of the dualities discussed prior (force/translation, torque/rotation, stresslet/strain, etc.) will then hold for fluids acted on by a body force.
In general, obtaining singularity solutions for a fluid acted on by a body force is a challenging task due to the presence of the body force integral. However, if the body force is localized near the particle so that 
$\lim _{r\to \infty } r^{n}f_i(\boldsymbol {r})=0$ for all 
$n>0$, the body force integral can be Taylor expanded and it is sufficient to consider the asymptotic form of the singularity solution far from the particle. This follows from the fact that the hydrodynamic stresslet evaluated on a far-field surface is identical to the total stresslet evaluated in the vicinity of the particle (Ohshima Reference Ohshima2006).
We will use this extension of our method to compute the Faxén law for the stresslet induced on a charged droplet of viscosity 
$\lambda \eta$ immersed in an electrolyte containing 
$N$ ionic species. Recall that the singularity operator for the flow around a particle generates the Faxén law for the stresslet. Ohshima (Reference Ohshima2006) gave an analytical solution for the velocity field around a charged sphere in a straining flow, from which we immediately obtain the Faxén law for the stresslet on a charged droplet
\begin{equation} {\mathsf{S}}_{ij} = \frac{8{\rm \pi}\eta a^{3}}{3}\varDelta_{ijk\ell}^{(2,2)} \int u_k^{\infty}(\boldsymbol{\xi})\left(s_2 + \frac{a^{2}s_2}{2}\nabla_y^{2} \right)\frac{\partial}{\partial y_\ell} \delta(\boldsymbol{\xi} - \boldsymbol{y})\, \textrm{d}\boldsymbol{\xi} \end{equation}where
\begin{gather} s_1 = \frac{5\lambda + 2}{2\lambda +2} + \int_a^{\infty}\left(\frac{3\lambda a^{2}}{20\lambda + 20} - \frac{(5\lambda + 2)x^{2}}{20\lambda + 20} + \frac{x^{5}}{10 a^{3}} \right)G(x)\, \textrm{d} x, \end{gather}
\begin{gather}s_2 = \frac{\lambda}{2\lambda + 2} + \int_a^{\infty}\left(\frac{(5\lambda -2)a^{2}}{140\lambda + 140} - \frac{\lambda x^{2}}{20\lambda + 20} + \frac{x^{7}}{70 a^{5}} \right)G(x)\, \textrm{d} x, \end{gather}and
\begin{equation} G(r) = -\frac{2e}{\eta r^{2}}\frac{ \textrm{d} y}{ \textrm{d} r}\sum_{i=1}^{N}Z_i^{2}n_i^{\infty}\exp(-Z_iy)g_i(r), \quad y = \frac{e\phi^{(0)}}{kT}. \end{equation}
Here, 
$e$ is the charge of an electron, 
$Z_i$ and 
$n_i^{\infty }$ are the valency and unperturbed number density of species 
$i$, 
$\phi ^{(0)}$ is the electrostatic potential at thermodynamic equilibrium and 
$k$ is Boltzmann's constant. The function 
$g_i(r)$ encodes how the electrochemical potential of species 
$i$ distorted by the flow
\begin{equation} \mu_i = -Z_ie\frac{g_i(r)}{r^{2}}\boldsymbol{r}\boldsymbol{\cdot}\boldsymbol{\mathsf{E}}^{\infty}\boldsymbol{\cdot}\boldsymbol{r} \quad \textrm{(no summation on $i$)}, \end{equation}and is obtained from numerical solution of the ion transport equations. This Faxén law recovers the calculation of the electroviscous effect for droplets given by Ohshima (Reference Ohshima2006) in the limit of constant shear rate, and reduces to the Faxén formula for the viscous droplet (Rallison Reference Rallison1978) in the limit where the electroviscous terms vanish.
4. Conclusions
In this work, we have proven a duality relating Faxén formulas to singularity solutions and extended the results to the case of coupled physical and chemical transport processes. The utility of our proof is twofold. First, it shows that the Faxén formula for a given problem can be inferred directly from the singularity solution for the associated boundary value problem; and second, it explains that the Faxén/singularity solution duality is a consequence of a generalized Lorentz reciprocal relation interior to the particle. We demonstrated the utility of the expanded method by deriving Faxén formulas for the phoretic force and torque exerted on a particle in the thin double-layer limit, which recovered prior derivations in the limit of a constant far-field gradient. Our proof, constructed from the integral representation of the Stokes and Laplace equations to generate reciprocal relations between operators, can readily be extended to any other governing equation for which an appropriate integral representation can be identified.
Moving forward, the proofs developed in this work provide a natural framework for the extension of existing simulation methods. The integral representation of the Faxén formulas could be used to derive generalized Rotne–Prager tensors for coupled transport processes following the method of Wajnryb et al. (Reference Wajnryb, Mizerski, Zuk and Szymczak2013). Furthermore, our results could be used to incorporating hydrodynamic interactions into the Laplacian dynamics (Bonnecaze & Brady Reference Bonnecaze and Brady1990; Yan & Brady Reference Yan and Brady2016) framework. One could imagine using (3.23) and similar equations derived for other boundary conditions to serve as a theoretical basis for extending dynamic simulations to systems involving couplings between momentum and mass, charge or heat transport.
The generality of our method also allows immediate application to heterogeneous media. The expressions obtained from our framework are valid for arbitrary external fields, allowing one to derive expressions for forces arising from statistically non-uniform fields. For instance, one can imagine computing the stresslet induced by non-uniform electric fields. Interestingly, (2.8) implies that the pressure gradient can induce forces, torques, stresslets etc. for particles on which the double-layer operator does not vanish, which suggests that the pressure gradient may play a role in the dynamics of suspensions of deformable or porous particles, the latter of which permits a particularly simple representation of the singularity operators (Masoud, Stone & Shelley Reference Masoud, Stone and Shelley2013). Such dynamics, if it exists, could be studied by using the results of this paper to compute traction moments arising from the pressure gradient, and the method of Dolata & Zia (Reference Dolata and Zia2020) to compute the suspension stress.
Acknowledgement
This work was supported in part by an Office of Naval Research Young Investigator Award (No. N00014-14-1-0744).
Declaration of interests
The authors report no conflict of interest.
Appendix A.
Here, we derive the necessary and sufficient conditions required for the symmetry of the generalized grand resistance matrix. Consider the integral
\begin{equation} \int_{S_\infty} \left(u_i\tilde{\sigma}_{ij}n_j \pm\phi \tilde{j}_in_i \right) \textrm{d} S - \int_{S_\infty} \left(\tilde{u}_i\sigma_{ij}n_j \pm \tilde{\phi} j_i n_i\right) \textrm{d} S, \end{equation}
over the surface 
$S_\infty$ located far from the particle. A straightforward working reveals that this quantity is equivalent to
\begin{equation} (\tilde{\mathcal{F}}^{\intercal}\mathcal{U} \pm \tilde{\mathcal{J}}^{\intercal}\varPhi) - (\mathcal{F}^{\intercal}\tilde{\mathcal{U}} \pm \mathcal{J}^{\intercal}\tilde{\varPhi}), \end{equation}
where we have used the facts that the fluxes 
$\mathcal {F}$ and 
$\mathcal {J}$ evaluated at 
$S_\infty$ are identical to those evaluated at 
$S_p$ due to the conservation laws, and that the singularity operators produce fields that decay as 
$1/r$ or faster. Application of the divergence theorem to (A 1) gives
\begin{equation} -\int_{V_p} \frac{\partial}{\partial x_j}\left(u_i\tilde{\sigma}_{ij} \pm \phi\tilde{j}_j \right) \textrm{d} V + \int_{V_p} \frac{\partial}{\partial x_j}\left(\tilde{u}_i\sigma_{ij} \pm \tilde{\phi} j_j\right) \textrm{d} V, \end{equation}where the volume integrals are taken over the particle interior. In deriving (A 3) we assume that the field variables are continuous across the particle surface. As discussed by Nadim (Reference Nadim1996), this assumption does not cause a loss of generality because jump conditions can be interpreted as volumetric forces present in a infinitesimally thin surface layer between the particle and fluid. If this volume integral vanishes, equating (A 3) with (A 2) yields the relation
\begin{equation} \tilde{\mathcal{F}}^{\intercal}\mathcal{U} + \pm \tilde{\mathcal{J}}^{\intercal}\varPhi = \mathcal{F}^{\intercal}\tilde{\mathcal{U}} + \pm \mathcal{J}^{\intercal}\tilde{\varPhi}, \end{equation}from which the symmetry of the generalized grand resistance matrix readily follows.
