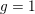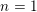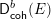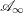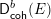1 Introduction
1.1
The initial form of mirror symmetry, as described in 1991 by Candelas, de la Ossa, Green and Parkes [Reference Candelas, de la Ossa, Green and ParkesCdGP91], centered on the surprising prediction that the genus-zero Gromov–Witten invariants of a quintic ![]() $3$-fold
$3$-fold ![]() $\check{X\,}\!$ could be computed by solving a differential equation governing the variation of Hodge structure associated to another space, the so-called mirror quintic
$\check{X\,}\!$ could be computed by solving a differential equation governing the variation of Hodge structure associated to another space, the so-called mirror quintic ![]() $X$. Many other such mirror pairs
$X$. Many other such mirror pairs ![]() $(X,\check{X\,}\!)$ were later found in physics, satisfying similar relationships between the genus-zero Gromov–Witten invariants of
$(X,\check{X\,}\!)$ were later found in physics, satisfying similar relationships between the genus-zero Gromov–Witten invariants of ![]() $\check{X\,}\!$ and the variation of Hodge structure of
$\check{X\,}\!$ and the variation of Hodge structure of ![]() $X$.
$X$.
1.2
A far-reaching generalization of mirror symmetry was proposed several years later by Kontsevich [Reference KontsevichKon95] in his address to the 1994 International Congress of Mathematicians. He conjectured that the more fundamental relationship between the spaces ![]() $X$ and
$X$ and ![]() $\check{X\,}\!$ in a mirror pair should be the existence of a derived equivalence between the derived category
$\check{X\,}\!$ in a mirror pair should be the existence of a derived equivalence between the derived category ![]() $\mathsf{D}_{\mathsf{coh}}^{b}(X)$ of coherent sheaves on
$\mathsf{D}_{\mathsf{coh}}^{b}(X)$ of coherent sheaves on ![]() $X$ and the Fukaya category
$X$ and the Fukaya category ![]() $\mathsf{Fuk}(\check{X\,}\!)$ of
$\mathsf{Fuk}(\check{X\,}\!)$ of ![]() $\check{X\,}\!$. This statement became known as the homological mirror symmetry conjecture.
$\check{X\,}\!$. This statement became known as the homological mirror symmetry conjecture.
1.3
Implicit in Kontsevich’s proposal was the idea that the equality of numerical invariants predicted by the original version of mirror symmetry should follow tautologically from the homological mirror symmetry conjecture. To achieve this one needs to construct categorical Gromov–Witten invariants: invariants associated to an ![]() $\mathscr{A}_{\infty }$ triangulated category
$\mathscr{A}_{\infty }$ triangulated category ![]() $\mathscr{C}$, with the property that they recover the classical Gromov–Witten invariants of the space
$\mathscr{C}$, with the property that they recover the classical Gromov–Witten invariants of the space ![]() $\check{X\,}\!$ when the target category
$\check{X\,}\!$ when the target category ![]() $\mathscr{C}$ is taken to be
$\mathscr{C}$ is taken to be ![]() $\mathsf{Fuk}(\check{X\,}\!)$. Once one has such invariants, evaluating them on
$\mathsf{Fuk}(\check{X\,}\!)$. Once one has such invariants, evaluating them on ![]() $\mathsf{D}_{\mathsf{coh}}^{b}(X)$ yields new invariants of
$\mathsf{D}_{\mathsf{coh}}^{b}(X)$ yields new invariants of ![]() $X$, the so-called B-model Gromov–Witten invariants of
$X$, the so-called B-model Gromov–Witten invariants of ![]() $X$. These invariants are defined for any genus, not just for genus zero. (The genus-zero B-model invariants are expected to match the data of the variation of Hodge structures used before.) The categorical nature of the construction automatically implies, for a pair of spaces
$X$. These invariants are defined for any genus, not just for genus zero. (The genus-zero B-model invariants are expected to match the data of the variation of Hodge structures used before.) The categorical nature of the construction automatically implies, for a pair of spaces ![]() $(X,\check{X\,}\!)$ which satisfies homological mirror symmetry, that the B-model invariants of
$(X,\check{X\,}\!)$ which satisfies homological mirror symmetry, that the B-model invariants of ![]() $X$ match the Gromov–Witten invariants of
$X$ match the Gromov–Witten invariants of ![]() $\check{X\,}\!$.
$\check{X\,}\!$.
1.4
Genus-zero categorical Gromov–Witten invariants satisfying the desired properties were defined in 2015 by Ganatra, Perutz and Sheridan [Reference Ganatra, Perutz and SheridanGPS15] following ideas of Saito [Reference SaitoSai83a, Reference SaitoSai83b] and Barannikov [Reference BarannikovBar01]. However, according to the authors, this approach does not extend to positive genus.
For arbitrary genus Costello [Reference CostelloCos09] proposed a definition of categorical invariants associated to a cyclic ![]() $\mathscr{A}_{\infty }$-algebra (or category), following ideas of Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS09]. Unfortunately many details of [Reference CostelloCos09] were left open, and computing explicit examples turned out to be a difficult task. Costello (unpublished) computed one example where the target algebra is the ground field (corresponding to the case where the target space
$\mathscr{A}_{\infty }$-algebra (or category), following ideas of Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS09]. Unfortunately many details of [Reference CostelloCos09] were left open, and computing explicit examples turned out to be a difficult task. Costello (unpublished) computed one example where the target algebra is the ground field (corresponding to the case where the target space ![]() $X$ is a point). No other explicit computations of Costello’s invariants exist. Costello and Li [Reference Costello and LiCL12] wrote:
$X$ is a point). No other explicit computations of Costello’s invariants exist. Costello and Li [Reference Costello and LiCL12] wrote:
A candidate for the B-model partition function associated to a Calabi–Yau category was proposed in [Reference CostelloCos07, Reference CostelloCos05, Reference Kontsevich and SoibelmanKS09] based on a classification of a class of 2-dimensional topological field theories. Unfortunately, it is extremely difficult to compute this B-model partition function.
1.5
In this paper we compute the ![]() $g=1$,
$g=1$, ![]() $n=1$ B-model categorical invariant of an elliptic curve
$n=1$ B-model categorical invariant of an elliptic curve ![]() $E_{\unicode[STIX]{x1D70F}}$, starting from Costello’s definition and using as input an
$E_{\unicode[STIX]{x1D70F}}$, starting from Costello’s definition and using as input an ![]() $\mathscr{A}_{\infty }$ model of the derived category
$\mathscr{A}_{\infty }$ model of the derived category ![]() $\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$ proposed by Polishchuk [Reference PolishchukPol11]. It is the first computation of a categorical Gromov–Witten invariant with non-trivial target and positive genus.
$\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$ proposed by Polishchuk [Reference PolishchukPol11]. It is the first computation of a categorical Gromov–Witten invariant with non-trivial target and positive genus.
More precisely, for a complex number ![]() $\unicode[STIX]{x1D70F}$ in the upper-half plane
$\unicode[STIX]{x1D70F}$ in the upper-half plane ![]() $\mathbb{H}$, let
$\mathbb{H}$, let ![]() $E_{\unicode[STIX]{x1D70F}}$ denote the elliptic curve of modular parameter
$E_{\unicode[STIX]{x1D70F}}$ denote the elliptic curve of modular parameter ![]() $\unicode[STIX]{x1D70F}$,
$\unicode[STIX]{x1D70F}$, ![]() $E_{\unicode[STIX]{x1D70F}}=\mathbb{C}/\mathbb{Z}\oplus \mathbb{Z}\unicode[STIX]{x1D70F}$. For each such
$E_{\unicode[STIX]{x1D70F}}=\mathbb{C}/\mathbb{Z}\oplus \mathbb{Z}\unicode[STIX]{x1D70F}$. For each such ![]() $\unicode[STIX]{x1D70F}$ we compute a complex number
$\unicode[STIX]{x1D70F}$ we compute a complex number ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$, the corresponding B-model categorical invariant. Regarding the result as a function of
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$, the corresponding B-model categorical invariant. Regarding the result as a function of ![]() $\unicode[STIX]{x1D70F}$, we obtain the so-called B-model Gromov–Witten potential, a complex-valued function on the upper half plane.
$\unicode[STIX]{x1D70F}$, we obtain the so-called B-model Gromov–Witten potential, a complex-valued function on the upper half plane.
1.6
Mirror symmetry predicts the result of the above computation. There is a standard way to collect the classical ![]() $g=1$,
$g=1$, ![]() $n=1$ Gromov–Witten invariants of an elliptic curve in a generating power series, the A-model Gromov–Witten potential
$n=1$ Gromov–Witten invariants of an elliptic curve in a generating power series, the A-model Gromov–Witten potential ![]() $F_{1,1}^{\mathsf{A}}(q)$. The result is known through work of Dijkgraaf [Reference DijkgraafDij95]:
$F_{1,1}^{\mathsf{A}}(q)$. The result is known through work of Dijkgraaf [Reference DijkgraafDij95]:
Here ![]() $E_{2}$ is the standard Eisenstein holomorphic, quasi-modular form of weight 2, expanded at
$E_{2}$ is the standard Eisenstein holomorphic, quasi-modular form of weight 2, expanded at ![]() $q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70F})$. In this computation, the inserted class at the one puncture is
$q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70F})$. In this computation, the inserted class at the one puncture is ![]() $[\mathsf{pt}]^{\mathsf{PD}}$, the Poincaré dual class of a point.
$[\mathsf{pt}]^{\mathsf{PD}}$, the Poincaré dual class of a point.
The prediction of mirror symmetry is that the A- and B-model potentials should match after the Kähler and complex moduli spaces are identified via the mirror map, which in the case of elliptic curves takes the form
Thus the prediction of mirror symmetry is that the B-model potential should equal
1.7
To get our computation off the ground we need a cyclic ![]() $\mathscr{A}_{\infty }$-algebra model of the derived category
$\mathscr{A}_{\infty }$-algebra model of the derived category ![]() $\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$. Such an algebra was described by Polishchuk [Reference PolishchukPol11], using structure constants that are modular, almost holomorphic forms. We denote this
$\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$. Such an algebra was described by Polishchuk [Reference PolishchukPol11], using structure constants that are modular, almost holomorphic forms. We denote this ![]() $\mathscr{A}_{\infty }$-algebra by
$\mathscr{A}_{\infty }$-algebra by ![]() $A_{\unicode[STIX]{x1D70F}}$. We will use both Polishchuk’s original algebra, and a gauge-equivalent modification of it whose structure constants are quasi-modular, holomorphic forms. The interplay between calculations in these two models, via the Kaneko–Zagier theory of quasi-modular forms, will form a central part of our final computation.
$A_{\unicode[STIX]{x1D70F}}$. We will use both Polishchuk’s original algebra, and a gauge-equivalent modification of it whose structure constants are quasi-modular, holomorphic forms. The interplay between calculations in these two models, via the Kaneko–Zagier theory of quasi-modular forms, will form a central part of our final computation.
1.8
Like in the classical Gromov–Witten calculation, in order to get a non-trivial answer in the B-model computation we need to insert a certain Hochschild class ![]() $[\unicode[STIX]{x1D709}]\in \mathit{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$ at the puncture, mirror dual to
$[\unicode[STIX]{x1D709}]\in \mathit{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$ at the puncture, mirror dual to ![]() $[\mathsf{pt}]^{\mathsf{PD}}$. This class will be represented by the Hochschild chain in
$[\mathsf{pt}]^{\mathsf{PD}}$. This class will be represented by the Hochschild chain in ![]() $A_{\unicode[STIX]{x1D70F}}^{\otimes 1}$,
$A_{\unicode[STIX]{x1D70F}}^{\otimes 1}$,
(The identification of ![]() $E_{\unicode[STIX]{x1D70F}}$ with
$E_{\unicode[STIX]{x1D70F}}$ with ![]() $\mathbb{C}/\mathbb{Z}\oplus \mathbb{Z}\unicode[STIX]{x1D70F}$ yields a well-defined class
$\mathbb{C}/\mathbb{Z}\oplus \mathbb{Z}\unicode[STIX]{x1D70F}$ yields a well-defined class ![]() $d\bar{z}$ in
$d\bar{z}$ in ![]() $H^{1}(E_{\unicode[STIX]{x1D70F}},\mathscr{O}_{E_{\unicode[STIX]{x1D70F}}})$. This group is a direct summand of
$H^{1}(E_{\unicode[STIX]{x1D70F}},\mathscr{O}_{E_{\unicode[STIX]{x1D70F}}})$. This group is a direct summand of ![]() $A_{\unicode[STIX]{x1D70F}}$. Therefore
$A_{\unicode[STIX]{x1D70F}}$. Therefore ![]() $\unicode[STIX]{x1D709}$ is a well-defined element of homological degree
$\unicode[STIX]{x1D709}$ is a well-defined element of homological degree ![]() $(-1)$ of the algebra
$(-1)$ of the algebra ![]() $A_{\unicode[STIX]{x1D70F}}$, and as such it gives rise to a class in
$A_{\unicode[STIX]{x1D70F}}$, and as such it gives rise to a class in ![]() $\mathit{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$.)
$\mathit{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$.)
The following theorem is the main result of this paper.
Theorem 1.9. With insertion of the class ![]() $[\unicode[STIX]{x1D709}]$, Costello’s categorical Gromov–Witten invariant of
$[\unicode[STIX]{x1D709}]$, Costello’s categorical Gromov–Witten invariant of ![]() $A_{\unicode[STIX]{x1D70F}}$ at
$A_{\unicode[STIX]{x1D70F}}$ at ![]() $g=1$,
$g=1$, ![]() $n=1$ equals
$n=1$ equals
1.10
We interpret this result in two ways. On the one hand, we think of it as confirmation of the mirror symmetry prediction at ![]() $g=1$ as in § 1.6. On the other hand, through the prism of homological mirror symmetry we can view our result as a statement about the Fukaya category of the family
$g=1$ as in § 1.6. On the other hand, through the prism of homological mirror symmetry we can view our result as a statement about the Fukaya category of the family ![]() $\check{E\,}\!_{\unicode[STIX]{x1D70C}}$ which is the mirror to the family
$\check{E\,}\!_{\unicode[STIX]{x1D70C}}$ which is the mirror to the family ![]() $E_{\unicode[STIX]{x1D70F}}$ of elliptic curves. Indeed, from work of Polishchuk and Zaslow [Reference Polishchuk and ZaslowPZ98] we know that homological mirror symmetry holds for elliptic curves. The authors construct an equivalence
$E_{\unicode[STIX]{x1D70F}}$ of elliptic curves. Indeed, from work of Polishchuk and Zaslow [Reference Polishchuk and ZaslowPZ98] we know that homological mirror symmetry holds for elliptic curves. The authors construct an equivalence
where ![]() $\check{E\,}\!$ is the 2-torus mirror to
$\check{E\,}\!$ is the 2-torus mirror to ![]() $E_{\unicode[STIX]{x1D70F}}$, endowed with a certain complexified Kähler class
$E_{\unicode[STIX]{x1D70F}}$, endowed with a certain complexified Kähler class ![]() $\unicode[STIX]{x1D70C}$. Therefore our computation, which is a priori about
$\unicode[STIX]{x1D70C}$. Therefore our computation, which is a priori about ![]() $\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$, can be reinterpreted as a calculation about
$\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$, can be reinterpreted as a calculation about ![]() $\mathsf{Fuk}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$. From this perspective we regard Theorem 1.9 as verification of the prediction that Costello’s categorical Gromov–Witten invariants of the Fukaya category agree (in this case) with the classical ones of the underlying space, as computed by Dijkgraaf.
$\mathsf{Fuk}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$. From this perspective we regard Theorem 1.9 as verification of the prediction that Costello’s categorical Gromov–Witten invariants of the Fukaya category agree (in this case) with the classical ones of the underlying space, as computed by Dijkgraaf.
1.11
There is one important aspect of Costello’s work that we have suppressed in the above discussion. In order to extract an actual Gromov–Witten potential from a cyclic ![]() $\mathscr{A}_{\infty }$-algebra
$\mathscr{A}_{\infty }$-algebra ![]() $A$ (as opposed to a line in a certain Fock space) we need to choose a splitting of the Hodge filtration on the periodic cyclic homology of
$A$ (as opposed to a line in a certain Fock space) we need to choose a splitting of the Hodge filtration on the periodic cyclic homology of ![]() $A$. The correct splitting is forced on us by mirror symmetry. The Hochschild and cyclic homology of
$A$. The correct splitting is forced on us by mirror symmetry. The Hochschild and cyclic homology of ![]() $A_{\unicode[STIX]{x1D70F}}$ agree with those of
$A_{\unicode[STIX]{x1D70F}}$ agree with those of ![]() $E_{\unicode[STIX]{x1D70F}}$, as they are derived invariants. Under this identification, a splitting of the Hodge filtration is the choice of a splitting of the natural projection
$E_{\unicode[STIX]{x1D70F}}$, as they are derived invariants. Under this identification, a splitting of the Hodge filtration is the choice of a splitting of the natural projection
Mirror symmetry imposes the requirement that the lift of ![]() $[\unicode[STIX]{x1D709}]$ must be invariant under monodromy around the cusp, which in turn uniquely determines the lifting. It is with this choice that we carry out the computations in Theorem 1.9. See § 9 for more details.
$[\unicode[STIX]{x1D709}]$ must be invariant under monodromy around the cusp, which in turn uniquely determines the lifting. It is with this choice that we carry out the computations in Theorem 1.9. See § 9 for more details.
1.12
There is another approach to higher-genus invariants in the B-model, due to Costello and Li [Reference Costello and LiCL12, Reference LiLi11, Reference LiLi12, Reference LiLi16], inspired by the Bershadsky–Cecotti–Ooguri–Vafa (BCOV) construction in physics [Reference Bershadsky, Cecotti, Ooguri and VafaBCOV94].
These other invariants also depend on a choice of splitting of the Hodge filtration. In their works Costello and Li analyzed the BCOV-type invariants of elliptic curves obtained from arbitrary splittings of the Hodge filtration and showed that these invariants satisfy the Virasoro constraints. Moreover, they studied a family of splittings depending on a parameter ![]() $\unicode[STIX]{x1D70E}\in \mathbb{H}$ and proved the modularity of the corresponding BCOV potentials. The monodromy invariant splitting that we consider corresponds to the limiting splitting
$\unicode[STIX]{x1D70E}\in \mathbb{H}$ and proved the modularity of the corresponding BCOV potentials. The monodromy invariant splitting that we consider corresponds to the limiting splitting ![]() $\unicode[STIX]{x1D70E}\rightarrow \mathtt{i}\infty$. We have learned the idea that this is the correct one for mirror symmetry from conversations with Costello and Li.
$\unicode[STIX]{x1D70E}\rightarrow \mathtt{i}\infty$. We have learned the idea that this is the correct one for mirror symmetry from conversations with Costello and Li.
1.13
The BCOV-type invariants have the advantage that they give a more geometric definition of B-model Gromov–Witten invariants for Calabi–Yau spaces, and are also more easily computed than the original categorical ones of Costello [Reference CostelloCos09]. In fact, for elliptic curves Li was able to establish mirror symmetry at arbitrary genus for BCOV B-model invariants, and to directly compute the potential functions in any genus and for arbitrary insertions.
However, the BCOV-type invariants are fundamentally different from the ones we study in this paper, in that they are not a priori categorical: knowing homological mirror symmetry does not allow one to conclude the equality of the A- and B-model invariants. Moreover, the BCOV approach does not immediately generalize to other non-geometric situations wherein one only has a category, and not an underlying space.
1.14 Outline of the paper
Section 2 outlines Dijkgraaf’s computation in the classical setting. Section 3 discusses mirror symmetry in the geometric setting. The next two sections review modular forms, Kaneko–Zagier theory, and Polishchuk’s ![]() $\mathscr{A}_{\infty }$-algebra. Costello’s general formalism is outlined in § 6, and the next section contains a roadmap for the computation for elliptic curves. Section 8 describes a computation, essentially due to Costello, of the string vertices for
$\mathscr{A}_{\infty }$-algebra. Costello’s general formalism is outlined in § 6, and the next section contains a roadmap for the computation for elliptic curves. Section 8 describes a computation, essentially due to Costello, of the string vertices for ![]() $\unicode[STIX]{x1D712}=-1$. The last two sections present two different ways to compute the Gromov–Witten invariant
$\unicode[STIX]{x1D712}=-1$. The last two sections present two different ways to compute the Gromov–Witten invariant ![]() $F_{1,1}^{\mathsf{B}}$ that we want. The first method involves reducing the problem to a very large linear algebra computation, which is then solved by computer. The second method, presented in § 10, gives a purely mathematical deduction of the result, using a comparison between computations in the holomorphic and modular gauges, respectively.
$F_{1,1}^{\mathsf{B}}$ that we want. The first method involves reducing the problem to a very large linear algebra computation, which is then solved by computer. The second method, presented in § 10, gives a purely mathematical deduction of the result, using a comparison between computations in the holomorphic and modular gauges, respectively.
1.15 Standing assumptions
We work over the field of complex numbers ![]() $\mathbb{C}$. Throughout the paper we will need to use various comparison results between algebraic homology theories (Hochschild, cyclic) and geometric ones (Hodge, de Rham). Most of these comparison results are in the literature; however, some appear to be known only to specialists but are not published. In particular, we have not been able to find in the literature a comparison between the algebraic Getzler–Gauss–Manin connection and the classical geometric one. We tacitly assume that they agree, but this should be considered a conjectural result. (A similar assumption is made in [Reference Ganatra, Perutz and SheridanGPS15].)
$\mathbb{C}$. Throughout the paper we will need to use various comparison results between algebraic homology theories (Hochschild, cyclic) and geometric ones (Hodge, de Rham). Most of these comparison results are in the literature; however, some appear to be known only to specialists but are not published. In particular, we have not been able to find in the literature a comparison between the algebraic Getzler–Gauss–Manin connection and the classical geometric one. We tacitly assume that they agree, but this should be considered a conjectural result. (A similar assumption is made in [Reference Ganatra, Perutz and SheridanGPS15].)
2 The classical invariants
In this section we outline Dijkgraaf’s computation [Reference DijkgraafDij95] of the classical ![]() $g=1$,
$g=1$, ![]() $n=1$ Gromov–Witten invariants of elliptic curves.
$n=1$ Gromov–Witten invariants of elliptic curves.
2.1
Let ![]() $\check{E\,}\!=\mathbb{R}^{2}/\mathbb{Z}^{2}$ denote the two-dimensional torus, endowed with any complex structure making it into an elliptic curve. (The specific choice of complex structure will not matter.) We upgrade
$\check{E\,}\!=\mathbb{R}^{2}/\mathbb{Z}^{2}$ denote the two-dimensional torus, endowed with any complex structure making it into an elliptic curve. (The specific choice of complex structure will not matter.) We upgrade ![]() $\check{E\,}\!$ to a symplectic manifold by choosing any symplectic form
$\check{E\,}\!$ to a symplectic manifold by choosing any symplectic form ![]() $\unicode[STIX]{x1D714}$ in
$\unicode[STIX]{x1D714}$ in ![]() $H^{2}(\check{E\,}\!,\mathbb{R})$ whose area is one.
$H^{2}(\check{E\,}\!,\mathbb{R})$ whose area is one.
We also fix a point ![]() $P_{0}\in \check{E\,}\!$, which we think of as determining the origin of the group structure of
$P_{0}\in \check{E\,}\!$, which we think of as determining the origin of the group structure of ![]() $\check{E\,}\!$.
$\check{E\,}\!$.
2.2
For any ![]() $\unicode[STIX]{x1D6FD}\in H_{2}(\check{E\,}\!,\mathbb{Z})$, let
$\unicode[STIX]{x1D6FD}\in H_{2}(\check{E\,}\!,\mathbb{Z})$, let ![]() $\overline{M}_{1,1}(\check{E\,}\!,\unicode[STIX]{x1D6FD})$ be the moduli space of stable maps from a stable genus-one curve with one marked point to
$\overline{M}_{1,1}(\check{E\,}\!,\unicode[STIX]{x1D6FD})$ be the moduli space of stable maps from a stable genus-one curve with one marked point to ![]() $\check{E\,}\!$ with homology class
$\check{E\,}\!$ with homology class ![]() $\unicode[STIX]{x1D6FD}$. It has virtual real dimension two. If
$\unicode[STIX]{x1D6FD}$. It has virtual real dimension two. If ![]() $\unicode[STIX]{x1D6FD}=d\cdot [\check{E\,}\!]$ for some integer
$\unicode[STIX]{x1D6FD}=d\cdot [\check{E\,}\!]$ for some integer ![]() $d>0$ then
$d>0$ then
and the virtual dimension agrees with the actual dimension. In fact the moduli space ![]() $M_{1,1}(\check{E\,}\!,\unicode[STIX]{x1D6FD})$ parametrizes in this case the pairs
$M_{1,1}(\check{E\,}\!,\unicode[STIX]{x1D6FD})$ parametrizes in this case the pairs ![]() $(f,P)$ where
$(f,P)$ where ![]() $f:E\rightarrow \check{E\,}\!$ is a degree-
$f:E\rightarrow \check{E\,}\!$ is a degree-![]() $d$ isogeny onto
$d$ isogeny onto ![]() $\check{E\,}\!$ from another elliptic curve
$\check{E\,}\!$ from another elliptic curve ![]() $E$, and
$E$, and ![]() $P$ is any point on
$P$ is any point on ![]() $E$. (There are only finitely many such isogenies possible, therefore
$E$. (There are only finitely many such isogenies possible, therefore ![]() $\dim _{\mathbb{R}}M_{1,1}(X,\unicode[STIX]{x1D6FD})=2$.)
$\dim _{\mathbb{R}}M_{1,1}(X,\unicode[STIX]{x1D6FD})=2$.)
2.3
To compute an actual numerical Gromov–Witten invariant we need to insert a cohomology class at the marked point, so that the integrand is a 2-form. Inserting a ![]() $\unicode[STIX]{x1D713}$-class from
$\unicode[STIX]{x1D713}$-class from ![]() $M_{1,1}$ gives zero, so the only choice left is to pull-back a 2-form
$M_{1,1}$ gives zero, so the only choice left is to pull-back a 2-form ![]() $\unicode[STIX]{x1D6FC}$ from
$\unicode[STIX]{x1D6FC}$ from ![]() $\check{E\,}\!=T^{2}$ via the evaluation map
$\check{E\,}\!=T^{2}$ via the evaluation map
The natural choice used is to take ![]() $\unicode[STIX]{x1D6FC}=[\mathsf{pt}]^{\mathsf{PD}}$, the Poincaré dual class to a point. If we think of this point as being
$\unicode[STIX]{x1D6FC}=[\mathsf{pt}]^{\mathsf{PD}}$, the Poincaré dual class to a point. If we think of this point as being ![]() $P_{0}$, then the associated Gromov–Witten invariant for
$P_{0}$, then the associated Gromov–Witten invariant for ![]() $\unicode[STIX]{x1D6FD}=d\cdot [\check{E\,}\!]$ will compute the number of isogenies
$\unicode[STIX]{x1D6FD}=d\cdot [\check{E\,}\!]$ will compute the number of isogenies ![]() $f:E\rightarrow \check{E\,}\!$, up to isomorphism. (Inserting
$f:E\rightarrow \check{E\,}\!$, up to isomorphism. (Inserting ![]() $\unicode[STIX]{x1D6FC}$ has the effect of requiring
$\unicode[STIX]{x1D6FC}$ has the effect of requiring ![]() $P$ to map to
$P$ to map to ![]() $P_{0}$.) This number is well known – it equals the sum
$P_{0}$.) This number is well known – it equals the sum ![]() $(\sum _{k\,\mid \,d}k)$ of divisors of
$(\sum _{k\,\mid \,d}k)$ of divisors of ![]() $d$. This can be seen by counting the number of matrices with integer coefficients, of determinant
$d$. This can be seen by counting the number of matrices with integer coefficients, of determinant ![]() $d$, up to
$d$, up to ![]() $\mathsf{SL}(2,\mathbb{Z})$ conjugation.
$\mathsf{SL}(2,\mathbb{Z})$ conjugation.
2.4
One encapsulates the result of this computation into the classical Gromov–Witten potential of the A-model
(The leading coefficient of ![]() $-1/24$ arises from a computation on
$-1/24$ arises from a computation on ![]() $\overline{M}_{1,1}$ which we will omit.) This formula equals
$\overline{M}_{1,1}$ which we will omit.) This formula equals ![]() $-{\textstyle \frac{1}{24}}E_{2}(q)$ under the change of variables
$-{\textstyle \frac{1}{24}}E_{2}(q)$ under the change of variables ![]() $\unicode[STIX]{x1D70F}=(1/2\unicode[STIX]{x1D70B}\mathtt{i})\log (q)$, where
$\unicode[STIX]{x1D70F}=(1/2\unicode[STIX]{x1D70B}\mathtt{i})\log (q)$, where ![]() $E_{2}$ is the Eisenstein holomorphic, quasi-modular normalized form of weight 2; see § 4 for details on modular forms.
$E_{2}$ is the Eisenstein holomorphic, quasi-modular normalized form of weight 2; see § 4 for details on modular forms.
3 Geometric mirror symmetry
In this section we discuss the identifications that mirror symmetry prescribes between structures of the A- and the B-models for elliptic curves. We place ourselves in the classical geometric context, where one deals with spaces and not with categories.
3.1
At its core mirror symmetry is an identification between two families of geometric structures, the A-model and the B-model. The A-model is usually a trivial family of complex manifolds, endowed with a varying complexified Kähler class (this notion is a generalization of the usual Kähler class; see below). The B-model family is a varying family of complex manifolds. The mirror map is an isomorphism
between the moduli space ![]() $\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ of complexified Kähler classes and the moduli space
$\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ of complexified Kähler classes and the moduli space ![]() $\mathscr{M}^{\mathsf{cx}}$ of complex structures. This isomorphism is not defined everywhere, but only in the neighborhood of certain limit points of these spaces, the so-called large volume and large complex structure limit points.
$\mathscr{M}^{\mathsf{cx}}$ of complex structures. This isomorphism is not defined everywhere, but only in the neighborhood of certain limit points of these spaces, the so-called large volume and large complex structure limit points.
3.2
In the case of elliptic curves both the A- and the B-model families have descriptions in terms of familiar structures. We begin by describing the A-model family.
Let ![]() $\check{E\,}\!$ denote the 2-torus
$\check{E\,}\!$ denote the 2-torus ![]() $\mathbb{R}^{2}/\mathbb{Z}^{2}$ endowed with some complex structure, as in § 2. The moduli space of complexified Kähler structures on
$\mathbb{R}^{2}/\mathbb{Z}^{2}$ endowed with some complex structure, as in § 2. The moduli space of complexified Kähler structures on ![]() $\check{E\,}\!$ is defined to be
$\check{E\,}\!$ is defined to be
In other words, a complexified Kähler class ![]() $\unicode[STIX]{x1D70C}$ on
$\unicode[STIX]{x1D70C}$ on ![]() $\check{E\,}\!$ can be written as
$\check{E\,}\!$ can be written as ![]() $\unicode[STIX]{x1D70C}=b+\mathtt{i}A$ where
$\unicode[STIX]{x1D70C}=b+\mathtt{i}A$ where ![]() $b$ is a form in
$b$ is a form in ![]() $H^{2}(\check{E\,}\!,\mathbb{R})/H^{2}(\check{E\,}\!,\mathbb{Z})$ and
$H^{2}(\check{E\,}\!,\mathbb{R})/H^{2}(\check{E\,}\!,\mathbb{Z})$ and ![]() $A\in H^{2}(\check{E\,}\!,\mathbb{R})$ represented by a symplectic form with positive area.
$A\in H^{2}(\check{E\,}\!,\mathbb{R})$ represented by a symplectic form with positive area.
The moduli space ![]() $\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ is naturally isomorphic to
$\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ is naturally isomorphic to ![]() $\mathbb{H}/\mathbb{Z}$. The correspondence
$\mathbb{H}/\mathbb{Z}$. The correspondence ![]() $\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ thus identifies a neighborhood of
$\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ thus identifies a neighborhood of ![]() $\mathtt{i}\cdot \infty$ in
$\mathtt{i}\cdot \infty$ in ![]() $\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}(\check{E\,}\!)$ (the large volume limit point) with a neighborhood of the cusp in the moduli space of complex structures of elliptic curves (the large complex structure limit point).
$\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}(\check{E\,}\!)$ (the large volume limit point) with a neighborhood of the cusp in the moduli space of complex structures of elliptic curves (the large complex structure limit point).
The map ![]() $\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ is the mirror map for elliptic curves described by Polishchuk and Zaslow [Reference Polishchuk and ZaslowPZ98]. We have used it in order to identify the A- and B-model potentials in § 1.6.
$\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ is the mirror map for elliptic curves described by Polishchuk and Zaslow [Reference Polishchuk and ZaslowPZ98]. We have used it in order to identify the A- and B-model potentials in § 1.6.
Due to the periodicity of ![]() $b$ and
$b$ and ![]() $\mathsf{Re}(\unicode[STIX]{x1D70F})$ and the positivity of
$\mathsf{Re}(\unicode[STIX]{x1D70F})$ and the positivity of ![]() $A$ and
$A$ and ![]() $\mathsf{Im}(\unicode[STIX]{x1D70F})$, it often makes more sense to use exponential coordinates on
$\mathsf{Im}(\unicode[STIX]{x1D70F})$, it often makes more sense to use exponential coordinates on ![]() $\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ and
$\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ and ![]() $\mathscr{M}^{\mathsf{cx}}$. We will write
$\mathscr{M}^{\mathsf{cx}}$. We will write ![]() $q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70C})$ or
$q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70C})$ or ![]() $q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70F})$ depending on the context, with the hope that this will not cause any confusion.
$q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70F})$ depending on the context, with the hope that this will not cause any confusion.
3.3
On the A-model side the trivial bundle over ![]() $\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ with fiber
$\mathscr{M}^{\mathsf{K}\ddot{\mathsf{a}}\mathsf{hler}}$ with fiber ![]() $H^{1-\bullet }(\check{E\,}\!,\mathbb{C})$ carries the structure of a graded variation of polarized semi-infinite Hodge structures (VSHS), in the sense of [Reference BarannikovBar01, Reference Ganatra, Perutz and SheridanGPS15]. We shall only need parts of this structure: a graded fiberwise pairing (the Poincaré pairing
$H^{1-\bullet }(\check{E\,}\!,\mathbb{C})$ carries the structure of a graded variation of polarized semi-infinite Hodge structures (VSHS), in the sense of [Reference BarannikovBar01, Reference Ganatra, Perutz and SheridanGPS15]. We shall only need parts of this structure: a graded fiberwise pairing (the Poincaré pairing ![]() $\langle \,-\,,\,-\,\rangle _{\mathsf{P}}$ given by wedge and integrate) and a flat connection, the Dubrovin connection
$\langle \,-\,,\,-\,\rangle _{\mathsf{P}}$ given by wedge and integrate) and a flat connection, the Dubrovin connection ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{D}}$ (see [Reference Ganatra, Perutz and SheridanGPS15]),
$\unicode[STIX]{x1D6FB}^{\mathsf{D}}$ (see [Reference Ganatra, Perutz and SheridanGPS15]),
where ![]() $\unicode[STIX]{x1D714}\in H^{2}(\check{E\,}\!,\mathbb{C})$ is the unique symplectic form such that
$\unicode[STIX]{x1D714}\in H^{2}(\check{E\,}\!,\mathbb{C})$ is the unique symplectic form such that ![]() $\int _{\check{E\,}\!}\unicode[STIX]{x1D714}=1$.
$\int _{\check{E\,}\!}\unicode[STIX]{x1D714}=1$.
3.4
We have a similar structure of polarized VSHS over ![]() $\mathscr{M}^{\mathsf{cx}}$ coming from the B-model. The fiber over
$\mathscr{M}^{\mathsf{cx}}$ coming from the B-model. The fiber over ![]() $\unicode[STIX]{x1D70F}\in \mathscr{M}^{\mathsf{cx}}$ of the underlying vector bundle is the graded vector space
$\unicode[STIX]{x1D70F}\in \mathscr{M}^{\mathsf{cx}}$ of the underlying vector bundle is the graded vector space ![]() $\mathit{HH}_{\bullet -1}(E_{\unicode[STIX]{x1D70F}})$. The fiberwise pairing is given by the Mukai pairing
$\mathit{HH}_{\bullet -1}(E_{\unicode[STIX]{x1D70F}})$. The fiberwise pairing is given by the Mukai pairing ![]() $\langle \,-\,,\,-\,\rangle _{\mathsf{M}}$; see [Reference CăldăraruCăl05]. We recall the formula for the Mukai pairing. The Hochschild–Kostant–Rosenberg isomorphism gives an identification
$\langle \,-\,,\,-\,\rangle _{\mathsf{M}}$; see [Reference CăldăraruCăl05]. We recall the formula for the Mukai pairing. The Hochschild–Kostant–Rosenberg isomorphism gives an identification
The Mukai pairing then becomes
where ![]() $|u|=q$ for
$|u|=q$ for ![]() $u\in H^{p}(E_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6FA}_{E_{\unicode[STIX]{x1D70F}}}^{q})$. See Ramadoss [Reference RamadossRam08] for an explanation of this sign. The factor of
$u\in H^{p}(E_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6FA}_{E_{\unicode[STIX]{x1D70F}}}^{q})$. See Ramadoss [Reference RamadossRam08] for an explanation of this sign. The factor of ![]() $1/2\unicode[STIX]{x1D70B}\mathtt{i}$ arises from the comparison of the Serre duality pairing (the residue pairing) with the wedge-and-integrate pairing. Note that this factor is missing in the comparison [Reference Ganatra, Perutz and SheridanGPS15, Conjecture 1.14]. Also note that the Todd class of an elliptic curve is trivial, so there is no correction from it as in [Reference CăldăraruCăl05].
$1/2\unicode[STIX]{x1D70B}\mathtt{i}$ arises from the comparison of the Serre duality pairing (the residue pairing) with the wedge-and-integrate pairing. Note that this factor is missing in the comparison [Reference Ganatra, Perutz and SheridanGPS15, Conjecture 1.14]. Also note that the Todd class of an elliptic curve is trivial, so there is no correction from it as in [Reference CăldăraruCăl05].
The connection is the Gauss–Manin connection ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{GM}}$ after identifying
$\unicode[STIX]{x1D6FB}^{\mathsf{GM}}$ after identifying ![]() $\mathit{HH}_{\bullet }(E_{\unicode[STIX]{x1D70F}})\cong \bigoplus _{q-p=\bullet }H^{p}(E_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6FA}_{E_{\unicode[STIX]{x1D70F}}}^{q})$ further with
$\mathit{HH}_{\bullet }(E_{\unicode[STIX]{x1D70F}})\cong \bigoplus _{q-p=\bullet }H^{p}(E_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6FA}_{E_{\unicode[STIX]{x1D70F}}}^{q})$ further with ![]() $H_{\mathsf{dR}}^{\bullet }(E_{\unicode[STIX]{x1D70F}})$ as
$H_{\mathsf{dR}}^{\bullet }(E_{\unicode[STIX]{x1D70F}})$ as ![]() $\mathbb{Z}/2\mathbb{Z}$-graded vector spaces; see [Reference GriffithsGri68]. (We are using the fact that the Hodge–de Rham spectral sequence degenerates on
$\mathbb{Z}/2\mathbb{Z}$-graded vector spaces; see [Reference GriffithsGri68]. (We are using the fact that the Hodge–de Rham spectral sequence degenerates on ![]() $E_{\unicode[STIX]{x1D70F}}$.)
$E_{\unicode[STIX]{x1D70F}}$.)
3.5
The mirror map gives an isomorphism between the A-model polarized VSHS and the B-model one. The following theorem identifies the classes ![]() $[\unicode[STIX]{x1D6FA}]\in \mathit{HH}_{1}(E_{\unicode[STIX]{x1D70F}})$ and
$[\unicode[STIX]{x1D6FA}]\in \mathit{HH}_{1}(E_{\unicode[STIX]{x1D70F}})$ and ![]() $[\unicode[STIX]{x1D709}]\in \mathit{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$ which correspond to the classes
$[\unicode[STIX]{x1D709}]\in \mathit{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$ which correspond to the classes ![]() $1\in H^{0}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$ and
$1\in H^{0}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$ and ![]() $[\mathsf{pt}]^{\mathsf{PD}}\in H^{2}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$, respectively, under this isomorphism.
$[\mathsf{pt}]^{\mathsf{PD}}\in H^{2}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$, respectively, under this isomorphism.
Proposition 3.6. Under the mirror map ![]() $\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ the class
$\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ the class ![]() $1\in H^{0}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$ corresponds to the class of the global holomorphic volume form
$1\in H^{0}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$ corresponds to the class of the global holomorphic volume form
Similarly, the class ![]() $[\mathsf{pt}]^{\mathsf{PD}}\in H^{2}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$ corresponds to the class
$[\mathsf{pt}]^{\mathsf{PD}}\in H^{2}(\check{E\,}\!_{\unicode[STIX]{x1D70C}})$ corresponds to the class
Proof. Because we are only interested in what happens in a neighborhood of the large complex limit point we have well-defined forms ![]() $dz$ and
$dz$ and ![]() $d\bar{z}$ which give bases of
$d\bar{z}$ which give bases of ![]() $H^{0}(E_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6FA}_{E_{\unicode[STIX]{x1D70F}}}^{1})$ and
$H^{0}(E_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6FA}_{E_{\unicode[STIX]{x1D70F}}}^{1})$ and ![]() $H^{1}(E_{\unicode[STIX]{x1D70F}}\mathscr{O}_{E_{\unicode[STIX]{x1D70F}}})$, respectively, on each elliptic curve
$H^{1}(E_{\unicode[STIX]{x1D70F}}\mathscr{O}_{E_{\unicode[STIX]{x1D70F}}})$, respectively, on each elliptic curve ![]() $E_{\unicode[STIX]{x1D70F}}$. The classes
$E_{\unicode[STIX]{x1D70F}}$. The classes ![]() $[\unicode[STIX]{x1D6FA}]$ and
$[\unicode[STIX]{x1D6FA}]$ and ![]() $[\unicode[STIX]{x1D709}]$ are therefore pointwise multiples of these forms. The goal is to identify which multiples they are.
$[\unicode[STIX]{x1D709}]$ are therefore pointwise multiples of these forms. The goal is to identify which multiples they are.
In the A-model we have
The relationships ![]() $q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70C})$ and
$q=\exp (2\unicode[STIX]{x1D70B}\mathtt{i}\unicode[STIX]{x1D70C})$ and ![]() $\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ force the identification
$\unicode[STIX]{x1D70C}\leftrightarrow \unicode[STIX]{x1D70F}$ force the identification
Therefore in the B-model we require
A straightforward calculation with periods shows that
and this forces the class ![]() $[\unicode[STIX]{x1D6FA}]$ to equal
$[\unicode[STIX]{x1D6FA}]$ to equal ![]() $[2\unicode[STIX]{x1D70B}\mathtt{i}\cdot dz]$.
$[2\unicode[STIX]{x1D70B}\mathtt{i}\cdot dz]$.
Similarly, the A-model identity
forces the equality
which in turn implies
as stated in § 1.8. ◻
3.7
We conclude this section with a discussion of the splitting of the Hodge filtration on the de Rham cohomology ![]() $H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$. For an elliptic curve
$H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$. For an elliptic curve ![]() $E_{\unicode[STIX]{x1D70F}}$ the Hodge filtration is expressed by the short exact sequence
$E_{\unicode[STIX]{x1D70F}}$ the Hodge filtration is expressed by the short exact sequence
or, equivalently, by the sequence
We have natural basis vectors ![]() $[dz]$ and
$[dz]$ and ![]() $[\unicode[STIX]{x1D709}]$ of the first and last vector spaces in this sequence. Thus choosing a splitting of the Hodge filtration means picking a lift
$[\unicode[STIX]{x1D709}]$ of the first and last vector spaces in this sequence. Thus choosing a splitting of the Hodge filtration means picking a lift ![]() $[\unicode[STIX]{x1D709}+f(\unicode[STIX]{x1D70F})\,dz]$ of
$[\unicode[STIX]{x1D709}+f(\unicode[STIX]{x1D70F})\,dz]$ of ![]() $[\unicode[STIX]{x1D709}]$ from
$[\unicode[STIX]{x1D709}]$ from
to ![]() $H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ for every
$H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ for every ![]() $\unicode[STIX]{x1D70F}$.
$\unicode[STIX]{x1D70F}$.
Mirror symmetry prescribes that the correct lift must be invariant under monodromy around the cusp. The following lemma characterizes this lift.
Lemma 3.8. The following conditions are equivalent for a family ![]() $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ of lifts of the family of Hochschild classes
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ of lifts of the family of Hochschild classes ![]() $[\unicode[STIX]{x1D709}]$:
$[\unicode[STIX]{x1D709}]$:
(i) the lift
 $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ is invariant under monodromy around the cusp for all
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ is invariant under monodromy around the cusp for all  $\unicode[STIX]{x1D70F}\in \mathbb{H}$;
$\unicode[STIX]{x1D70F}\in \mathbb{H}$;(ii) the family
 $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ is flat with respect to the Gauss–Manin connection.
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ is flat with respect to the Gauss–Manin connection.
Proof. Fix an identification of ![]() $E_{\unicode[STIX]{x1D70F}}$ with
$E_{\unicode[STIX]{x1D70F}}$ with ![]() $\mathbb{C}/\mathbb{Z}\oplus \mathbb{Z}\unicode[STIX]{x1D70F}$. This determines a basis
$\mathbb{C}/\mathbb{Z}\oplus \mathbb{Z}\unicode[STIX]{x1D70F}$. This determines a basis ![]() $A,B$ of cycles in
$A,B$ of cycles in ![]() $H_{1}(E_{\unicode[STIX]{x1D70F}})$ corresponding to the paths from 0 to 1 and from 0 to
$H_{1}(E_{\unicode[STIX]{x1D70F}})$ corresponding to the paths from 0 to 1 and from 0 to ![]() $\unicode[STIX]{x1D70F}$, respectively. Under the monodromy
$\unicode[STIX]{x1D70F}$, respectively. Under the monodromy ![]() $\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}+1$ around the cusp the basis
$\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}+1$ around the cusp the basis ![]() $(A,B)$ maps to
$(A,B)$ maps to ![]() $(A,A+B)$.
$(A,A+B)$.
Let ![]() $A^{\ast },B^{\ast }$ denote the basis in
$A^{\ast },B^{\ast }$ denote the basis in ![]() $H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ dual to the basis
$H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ dual to the basis ![]() $(A,B)$. Then under the same monodromy the pair
$(A,B)$. Then under the same monodromy the pair ![]() $(A^{\ast },B^{\ast })$ maps to
$(A^{\ast },B^{\ast })$ maps to ![]() $(A^{\ast }-B^{\ast },B^{\ast })$ (the inverse transpose matrix). We have
$(A^{\ast }-B^{\ast },B^{\ast })$ (the inverse transpose matrix). We have
It follows that the invariant cocycle ![]() $B^{\ast }$ is expressed in the
$B^{\ast }$ is expressed in the ![]() $(dz,d\bar{z})$ basis as
$(dz,d\bar{z})$ basis as
For a class ![]() $[\tilde{\unicode[STIX]{x1D709}}]\in H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ to be invariant under monodromy around the cusp it must be a multiple of
$[\tilde{\unicode[STIX]{x1D709}}]\in H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ to be invariant under monodromy around the cusp it must be a multiple of ![]() $B^{\ast }$. And indeed there exists a unique monodromy invariant lift of
$B^{\ast }$. And indeed there exists a unique monodromy invariant lift of ![]() $[\unicode[STIX]{x1D709}]$ from
$[\unicode[STIX]{x1D709}]$ from
to ![]() $H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$, namely
$H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$, namely
By definition of the Gauss–Manin connection, since ![]() $-B^{\ast }$ is a topological cohomology class, it is
$-B^{\ast }$ is a topological cohomology class, it is ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{GM}}$-flat and this condition uniquely identifies the family in (ii).◻
$\unicode[STIX]{x1D6FB}^{\mathsf{GM}}$-flat and this condition uniquely identifies the family in (ii).◻
3.9
We will also need in § 10 the explicit form of the Kodaira–Spencer class,
This follows from the relationship between the Kodaira–Spencer class and the Gauss–Manin connection, given by the formula
4 Quasi-modular forms and Kaneko–Zagier theory
Before we can describe Polishchuk’s ![]() $\mathscr{A}_{\infty }$ model for the derived category of an elliptic curve we need to review the theory of quasi-modular, holomorphic forms and its relationship to the theory of almost holomorphic, modular forms. Their interplay is described by Kaneko–Zagier theory; see [Reference Kanazawa and ZhouKZ15, 5.1] and [Reference Kaneko and ZagierKZ95].
$\mathscr{A}_{\infty }$ model for the derived category of an elliptic curve we need to review the theory of quasi-modular, holomorphic forms and its relationship to the theory of almost holomorphic, modular forms. Their interplay is described by Kaneko–Zagier theory; see [Reference Kanazawa and ZhouKZ15, 5.1] and [Reference Kaneko and ZagierKZ95].
4.1
The ring of holomorphic, modular forms for the group ![]() $\unicode[STIX]{x1D6E4}=\mathsf{SL}(2,\mathbb{Z})$ is isomorphic to
$\unicode[STIX]{x1D6E4}=\mathsf{SL}(2,\mathbb{Z})$ is isomorphic to ![]() $\mathbb{C}[E_{4},E_{6}]$, where
$\mathbb{C}[E_{4},E_{6}]$, where ![]() $E_{4}$ and
$E_{4}$ and ![]() $E_{6}$ are the Eisenstein modular forms of weights 4 and 6, respectively. (Since there are competing systems of notation in the literature we reserve the notation
$E_{6}$ are the Eisenstein modular forms of weights 4 and 6, respectively. (Since there are competing systems of notation in the literature we reserve the notation ![]() $E_{k}$ to mean the corresponding normalized form, in the sense that the function has been rescaled to satisfy
$E_{k}$ to mean the corresponding normalized form, in the sense that the function has been rescaled to satisfy ![]() $\lim _{\unicode[STIX]{x1D70F}\rightarrow \mathtt{i}\cdot \infty }E_{k}(\unicode[STIX]{x1D70F})=1$.)
$\lim _{\unicode[STIX]{x1D70F}\rightarrow \mathtt{i}\cdot \infty }E_{k}(\unicode[STIX]{x1D70F})=1$.)
4.2
For the purposes of this paper we need to consider certain functions on ![]() $\mathbb{H}$ which are not at the same time holomorphic and modular. Of particular interest to us is the Eisenstein form
$\mathbb{H}$ which are not at the same time holomorphic and modular. Of particular interest to us is the Eisenstein form ![]() $E_{2}$: it is still holomorphic, but it does not satisfy the usual transformation law with respect to
$E_{2}$: it is still holomorphic, but it does not satisfy the usual transformation law with respect to ![]() $\unicode[STIX]{x1D6E4}$; see [Reference Kanazawa and ZhouKZ15, 4.1]. We will call elements of the ring
$\unicode[STIX]{x1D6E4}$; see [Reference Kanazawa and ZhouKZ15, 4.1]. We will call elements of the ring ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})=\mathbb{C}[E_{2},E_{4},E_{6}]$quasi-modular holomorphic forms; the weight of such a form is defined by declaring the weight of
$\widetilde{M}(\unicode[STIX]{x1D6E4})=\mathbb{C}[E_{2},E_{4},E_{6}]$quasi-modular holomorphic forms; the weight of such a form is defined by declaring the weight of ![]() $E_{2k}$ to be
$E_{2k}$ to be ![]() $2k$.
$2k$.
4.3
While the form ![]() $E_{2}$ is not modular, the simple modification
$E_{2}$ is not modular, the simple modification
is; it satisfies the same transformation rule as regular modular forms of weight 2 with respect to the group ![]() $\unicode[STIX]{x1D6E4}$. However,
$\unicode[STIX]{x1D6E4}$. However, ![]() $E_{2}^{\ast }$ is no longer holomorphic. The functions in the ring
$E_{2}^{\ast }$ is no longer holomorphic. The functions in the ring ![]() $\mathscr{O}(\mathbb{H})[1/(\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}})]$ which are modular in the above sense (for arbitrary weights) and satisfy a suitable growth condition at the cusp form a ring
$\mathscr{O}(\mathbb{H})[1/(\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}})]$ which are modular in the above sense (for arbitrary weights) and satisfy a suitable growth condition at the cusp form a ring ![]() $\widehat{M}(\unicode[STIX]{x1D6E4})$. Its elements will be called almost holomorphic modular forms. One can show that
$\widehat{M}(\unicode[STIX]{x1D6E4})$. Its elements will be called almost holomorphic modular forms. One can show that
4.4
The rings ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})$ and
$\widetilde{M}(\unicode[STIX]{x1D6E4})$ and ![]() $\widehat{M}(\unicode[STIX]{x1D6E4})$ are closed under the actions of certain differential operators. The former is closed under the action of
$\widehat{M}(\unicode[STIX]{x1D6E4})$ are closed under the actions of certain differential operators. The former is closed under the action of ![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}$, while the latter is closed under
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}$, while the latter is closed under
where ![]() $\mathsf{wt}$ denotes the weight of the form on which
$\mathsf{wt}$ denotes the weight of the form on which ![]() $\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$ acts.
$\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$ acts.
The following theorem is the main result of Kaneko–Zagier theory [Reference Kaneko and ZagierKZ95].
Theorem 4.5. The operator
which maps an almost holomorphic, modular form
to its ‘constant term’ part ![]() $F_{0}(\unicode[STIX]{x1D70F})$ is a differential ring isomorphism. Its inverse will be denoted by
$F_{0}(\unicode[STIX]{x1D70F})$ is a differential ring isomorphism. Its inverse will be denoted by
5 Polishchuk’s algebra and its holomorphic modification
In this section we review Polishchuk’s cyclic ![]() $\mathscr{A}_{\infty }$-algebra
$\mathscr{A}_{\infty }$-algebra ![]() $A_{\unicode[STIX]{x1D70F}}$ associated to an elliptic curve
$A_{\unicode[STIX]{x1D70F}}$ associated to an elliptic curve ![]() $E_{\unicode[STIX]{x1D70F}}$. This presentation uses almost holomorphic, modular forms. The main result of this section asserts that the
$E_{\unicode[STIX]{x1D70F}}$. This presentation uses almost holomorphic, modular forms. The main result of this section asserts that the ![]() $\mathscr{A}_{\infty }$-algebra
$\mathscr{A}_{\infty }$-algebra ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ obtained by replacing these structure constants by their images under the homomorphism
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ obtained by replacing these structure constants by their images under the homomorphism ![]() $\unicode[STIX]{x1D711}$ of Theorem 4.5 yields an algebra which is gauge equivalent to
$\unicode[STIX]{x1D711}$ of Theorem 4.5 yields an algebra which is gauge equivalent to ![]() $A_{\unicode[STIX]{x1D70F}}$ and varies holomorphically with
$A_{\unicode[STIX]{x1D70F}}$ and varies holomorphically with ![]() $\unicode[STIX]{x1D70F}$.
$\unicode[STIX]{x1D70F}$.
5.1
For ![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$, let
$\unicode[STIX]{x1D70F}\in \mathbb{H}$, let ![]() $E_{\unicode[STIX]{x1D70F}}$ be the corresponding elliptic curve. We will denote its origin by
$E_{\unicode[STIX]{x1D70F}}$ be the corresponding elliptic curve. We will denote its origin by ![]() $P_{0}$. The derived category
$P_{0}$. The derived category ![]() $\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$ of coherent sheaves on the elliptic curves
$\mathsf{D}_{\mathsf{coh}}^{b}(E_{\unicode[STIX]{x1D70F}})$ of coherent sheaves on the elliptic curves ![]() $E_{\unicode[STIX]{x1D70F}}$ is compactly generated by the object
$E_{\unicode[STIX]{x1D70F}}$ is compactly generated by the object ![]() $\mathscr{F}=\mathscr{O}\oplus L$, where
$\mathscr{F}=\mathscr{O}\oplus L$, where ![]() $L$ is the degree-one line bundle
$L$ is the degree-one line bundle ![]() $L=\mathscr{O}(P_{0})$. Therefore the differential graded (dg) algebra
$L=\mathscr{O}(P_{0})$. Therefore the differential graded (dg) algebra
is derived equivalent to ![]() $E_{\unicode[STIX]{x1D70F}}$. By homological perturbation we can transfer the dg-algebra structure from
$E_{\unicode[STIX]{x1D70F}}$. By homological perturbation we can transfer the dg-algebra structure from ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{dg}}$ to a quasi-equivalent
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{dg}}$ to a quasi-equivalent ![]() $\mathscr{A}_{\infty }$-algebra structure on
$\mathscr{A}_{\infty }$-algebra structure on
The graded vector space ![]() $A_{\unicode[STIX]{x1D70F}}$ is concentrated in cohomological degrees zero and one, and
$A_{\unicode[STIX]{x1D70F}}$ is concentrated in cohomological degrees zero and one, and
5.2
Polishchuk [Reference PolishchukPol11] explicitly computes an ![]() $\mathscr{A}_{\infty }$ structure on
$\mathscr{A}_{\infty }$ structure on ![]() $A_{\unicode[STIX]{x1D70F}}$ using a particular choice of homotopy between
$A_{\unicode[STIX]{x1D70F}}$ using a particular choice of homotopy between ![]() $A_{\unicode[STIX]{x1D70F}}$ and
$A_{\unicode[STIX]{x1D70F}}$ and ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{dg}}$. In order to express his result Polishchuk chooses a basis for the six-dimensional algebra
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{dg}}$. In order to express his result Polishchuk chooses a basis for the six-dimensional algebra ![]() $A_{\unicode[STIX]{x1D70F}}$ consisting of:
$A_{\unicode[STIX]{x1D70F}}$ consisting of:
∙ the identity morphisms
 $\mathsf{id}_{\mathscr{O}}:\mathscr{O}\rightarrow \mathscr{O}$ and
$\mathsf{id}_{\mathscr{O}}:\mathscr{O}\rightarrow \mathscr{O}$ and  $\mathsf{id}_{L}:L\rightarrow L$ in
$\mathsf{id}_{L}:L\rightarrow L$ in  $A_{\unicode[STIX]{x1D70F}}^{0}$;
$A_{\unicode[STIX]{x1D70F}}^{0}$;∙ the morphisms
 $\unicode[STIX]{x1D709}:\mathscr{O}\rightarrow \mathscr{O}[1]$ and
$\unicode[STIX]{x1D709}:\mathscr{O}\rightarrow \mathscr{O}[1]$ and  $\unicode[STIX]{x1D709}_{L}:L\rightarrow L[1]$ in
$\unicode[STIX]{x1D709}_{L}:L\rightarrow L[1]$ in  $A_{\unicode[STIX]{x1D70F}}^{1}$ given by
$A_{\unicode[STIX]{x1D70F}}^{1}$ given by  $\unicode[STIX]{x1D709}=d\bar{z}$, and similarly for
$\unicode[STIX]{x1D709}=d\bar{z}$, and similarly for  $\unicode[STIX]{x1D709}_{L}$;
$\unicode[STIX]{x1D709}_{L}$;∙ the degree-zero morphism
 $\unicode[STIX]{x1D703}:\mathscr{O}\rightarrow L$ in
$\unicode[STIX]{x1D703}:\mathscr{O}\rightarrow L$ in  $A_{\unicode[STIX]{x1D70F}}^{0}$ given by the theta function
$A_{\unicode[STIX]{x1D70F}}^{0}$ given by the theta function  $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}(z,\unicode[STIX]{x1D70F})$;
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}(z,\unicode[STIX]{x1D70F})$;∙ an explicit dual morphism
 $\unicode[STIX]{x1D702}:L\rightarrow \mathscr{O}[1]$ in
$\unicode[STIX]{x1D702}:L\rightarrow \mathscr{O}[1]$ in  $A_{\unicode[STIX]{x1D70F}}^{1}$ given by the formula in [Reference PolishchukPol11, 2.2].
$A_{\unicode[STIX]{x1D70F}}^{1}$ given by the formula in [Reference PolishchukPol11, 2.2].
5.3
For our purposes it will be more convenient to work with a slightly modified basis for ![]() $A_{\unicode[STIX]{x1D70F}}$, obtained by dividing the elements of degree one in Polishchuk’s basis (
$A_{\unicode[STIX]{x1D70F}}$, obtained by dividing the elements of degree one in Polishchuk’s basis (![]() $\unicode[STIX]{x1D702}$,
$\unicode[STIX]{x1D702}$, ![]() $\unicode[STIX]{x1D709}$ and
$\unicode[STIX]{x1D709}$ and ![]() $\unicode[STIX]{x1D709}_{L}$) by the factor
$\unicode[STIX]{x1D709}_{L}$) by the factor ![]() $\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}$. We leave the degree-zero elements unchanged. The rescaled elements will still be denoted by
$\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}$. We leave the degree-zero elements unchanged. The rescaled elements will still be denoted by ![]() $\unicode[STIX]{x1D702}$,
$\unicode[STIX]{x1D702}$, ![]() $\unicode[STIX]{x1D709}$,
$\unicode[STIX]{x1D709}$, ![]() $\unicode[STIX]{x1D709}_{L}$; they differ by a factor of
$\unicode[STIX]{x1D709}_{L}$; they differ by a factor of ![]() $1/2\unicode[STIX]{x1D70B}\mathtt{i}$ from the ones that Polishchuk considers in [Reference PolishchukPol11, 2.5, Remark 2]).
$1/2\unicode[STIX]{x1D70B}\mathtt{i}$ from the ones that Polishchuk considers in [Reference PolishchukPol11, 2.5, Remark 2]).
With this rescaling the new element ![]() $\unicode[STIX]{x1D709}$ agrees with the expression in § 1.8.
$\unicode[STIX]{x1D709}$ agrees with the expression in § 1.8.
5.4
At this point we need to decide which sign conventions to use for the ![]() $\mathscr{A}_{\infty }$ axioms. There are (at least) two such conventions in the literature. In this paper we will use the so-called shifted signs, which are more common in the symplectic geometry literature and are easier to use. See [Reference ChoCho08] for a discussion of these two conventions and of ways to translate between them. Note, however, that Polishchuk [Reference PolishchukPol11] uses in the unshifted sign convention; we will make the change to the shifted convention as we go. Following [Reference ChoCho08], we will denote by
$\mathscr{A}_{\infty }$ axioms. There are (at least) two such conventions in the literature. In this paper we will use the so-called shifted signs, which are more common in the symplectic geometry literature and are easier to use. See [Reference ChoCho08] for a discussion of these two conventions and of ways to translate between them. Note, however, that Polishchuk [Reference PolishchukPol11] uses in the unshifted sign convention; we will make the change to the shifted convention as we go. Following [Reference ChoCho08], we will denote by ![]() $|x|^{\prime }$ the shifted degree of an element
$|x|^{\prime }$ the shifted degree of an element ![]() $x\in A_{\unicode[STIX]{x1D70F}}$,
$x\in A_{\unicode[STIX]{x1D70F}}$, ![]() $|x|^{\prime }=|x|-1$.
$|x|^{\prime }=|x|-1$.
5.5
Once we have fixed a global holomorphic volume form ![]() $\unicode[STIX]{x1D6FA}$ on
$\unicode[STIX]{x1D6FA}$ on ![]() $E_{\unicode[STIX]{x1D70F}}$ as in Proposition 3.6 we get an induced symmetric non-degenerate pairing on
$E_{\unicode[STIX]{x1D70F}}$ as in Proposition 3.6 we get an induced symmetric non-degenerate pairing on ![]() $A_{\unicode[STIX]{x1D70F}}$ arising from Serre duality. Correcting it by the shifted sign conventions, we obtain a skew-symmetric pairing on
$A_{\unicode[STIX]{x1D70F}}$ arising from Serre duality. Correcting it by the shifted sign conventions, we obtain a skew-symmetric pairing on ![]() $A_{\unicode[STIX]{x1D70F}}$ given by
$A_{\unicode[STIX]{x1D70F}}$ given by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}\langle \unicode[STIX]{x1D709},\mathsf{id}_{\mathscr{O}}\rangle \ & =\ & -1,\quad & \langle \unicode[STIX]{x1D709}_{L},\mathsf{id}_{L}\rangle \ & =\ & -1,\\ \langle \mathsf{id}_{\mathscr{O}},\unicode[STIX]{x1D709}\rangle \ & =\ & 1,\quad & \langle \mathsf{id}_{L},\unicode[STIX]{x1D709}_{L}\rangle \ & =\ & 1,\\ \langle \unicode[STIX]{x1D703},\unicode[STIX]{x1D702}\rangle \ & =\ & 1,\quad & \langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D703}\rangle \ & =\ & -1.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rclrcl@{}}\langle \unicode[STIX]{x1D709},\mathsf{id}_{\mathscr{O}}\rangle \ & =\ & -1,\quad & \langle \unicode[STIX]{x1D709}_{L},\mathsf{id}_{L}\rangle \ & =\ & -1,\\ \langle \mathsf{id}_{\mathscr{O}},\unicode[STIX]{x1D709}\rangle \ & =\ & 1,\quad & \langle \mathsf{id}_{L},\unicode[STIX]{x1D709}_{L}\rangle \ & =\ & 1,\\ \langle \unicode[STIX]{x1D703},\unicode[STIX]{x1D702}\rangle \ & =\ & 1,\quad & \langle \unicode[STIX]{x1D702},\unicode[STIX]{x1D703}\rangle \ & =\ & -1.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$ All other pairings between basis elements are zero. This pairing will give the cyclic structure on ![]() $A_{\unicode[STIX]{x1D70F}}$.
$A_{\unicode[STIX]{x1D70F}}$.
5.6
We will now describe Polishchuk’s formulas for the multiplications
These operations are non-trivial only when ![]() $k$ is even. The first product
$k$ is even. The first product ![]() $\unicode[STIX]{x1D707}_{2}$ is the usual Yoneda product on the
$\unicode[STIX]{x1D707}_{2}$ is the usual Yoneda product on the ![]() $\mathsf{Ext}$ algebra
$\mathsf{Ext}$ algebra ![]() $A_{\unicode[STIX]{x1D70F}}$, with a sign adjustment: the only non-zero products (apart from the obvious ones involving
$A_{\unicode[STIX]{x1D70F}}$, with a sign adjustment: the only non-zero products (apart from the obvious ones involving ![]() $\mathsf{id}$ and
$\mathsf{id}$ and ![]() $\mathsf{id}_{L}$) are
$\mathsf{id}_{L}$) are ![]() $\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}=-\unicode[STIX]{x1D709}$ and
$\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}=-\unicode[STIX]{x1D709}$ and ![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D709}_{L}$. (We will use reverse notation for composition of morphisms, so that
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D709}_{L}$. (We will use reverse notation for composition of morphisms, so that ![]() $\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}$ means
$\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}$ means ![]() $\unicode[STIX]{x1D702}\circ \unicode[STIX]{x1D703}$. The same convention shall be used for the higher products, in line with Polishchuk’s conventions.)
$\unicode[STIX]{x1D702}\circ \unicode[STIX]{x1D703}$. The same convention shall be used for the higher products, in line with Polishchuk’s conventions.)
5.7
An important feature of Polishchuk’s formulas is that they respect cyclic symmetry with respect to the inner product on ![]() $A_{\unicode[STIX]{x1D70F}}$. We will say that a homogeneous map (of some degree)
$A_{\unicode[STIX]{x1D70F}}$. We will say that a homogeneous map (of some degree)
is cyclic if it is invariant under cyclic rotation of its arguments, up to a Koszul sign determined by the shifted degrees of its arguments. The products ![]() $\unicode[STIX]{x1D707}_{k}$ will be cyclic in the sense that the tensors
$\unicode[STIX]{x1D707}_{k}$ will be cyclic in the sense that the tensors
are cyclic in the above sense. An ![]() $\mathscr{A}_{\infty }$-algebra endowed with a pairing of degree
$\mathscr{A}_{\infty }$-algebra endowed with a pairing of degree ![]() $d$ which makes the maps
$d$ which makes the maps ![]() $c_{k}$ cyclic will be said to be Calabi–Yau of degree
$c_{k}$ cyclic will be said to be Calabi–Yau of degree ![]() $d$, or
$d$, or ![]() $\text{CY}[d]$, or cyclic of degree
$\text{CY}[d]$, or cyclic of degree ![]() $d$.
$d$.
5.8
All the higher multiplications of ![]() $A_{\unicode[STIX]{x1D70F}}$ can be deduced from a single one using this cyclic symmetry. The complete list is presented in [Reference PolishchukPol11, Theorem 2.5.1], but for reference we list the formula for only one such multiplication. Explicitly, let
$A_{\unicode[STIX]{x1D70F}}$ can be deduced from a single one using this cyclic symmetry. The complete list is presented in [Reference PolishchukPol11, Theorem 2.5.1], but for reference we list the formula for only one such multiplication. Explicitly, let ![]() $a$,
$a$, ![]() $b$,
$b$, ![]() $c$,
$c$, ![]() $d$ be non-negative integers, and let
$d$ be non-negative integers, and let ![]() $s=a+b+c+d$. Then for
$s=a+b+c+d$. Then for ![]() $s$ odd we have
$s$ odd we have
and zero otherwise. In this formula ![]() $k=s+3$, and
$k=s+3$, and
is a certain almost holomorphic modular form of weight ![]() $s+1$ defined by Polishchuk in [Reference PolishchukPol11, 1.1].
$s+1$ defined by Polishchuk in [Reference PolishchukPol11, 1.1].
5.9
We associate a notion of weight to the basis elements of ![]() $A_{\unicode[STIX]{x1D70F}}$ as follows:
$A_{\unicode[STIX]{x1D70F}}$ as follows:
 $$\begin{eqnarray}\displaystyle \mathsf{wt}(\mathsf{id}) & = & \displaystyle \mathsf{wt}(\mathsf{id}_{L})=0,\nonumber\\ \displaystyle \mathsf{wt}(\unicode[STIX]{x1D703}) & = & \displaystyle \mathsf{wt}(\unicode[STIX]{x1D702})=1/2,\nonumber\\ \displaystyle \mathsf{wt}(\unicode[STIX]{x1D709}) & = & \displaystyle \mathsf{wt}(\unicode[STIX]{x1D709}_{L})=1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathsf{wt}(\mathsf{id}) & = & \displaystyle \mathsf{wt}(\mathsf{id}_{L})=0,\nonumber\\ \displaystyle \mathsf{wt}(\unicode[STIX]{x1D703}) & = & \displaystyle \mathsf{wt}(\unicode[STIX]{x1D702})=1/2,\nonumber\\ \displaystyle \mathsf{wt}(\unicode[STIX]{x1D709}) & = & \displaystyle \mathsf{wt}(\unicode[STIX]{x1D709}_{L})=1.\nonumber\end{eqnarray}$$ Note that with respect to these assignments of weights the multiplications ![]() $\unicode[STIX]{x1D707}_{k}$ are of total weight zero, and the inner product
$\unicode[STIX]{x1D707}_{k}$ are of total weight zero, and the inner product ![]() $\langle -,-\rangle$ is of total weight
$\langle -,-\rangle$ is of total weight ![]() $-1$.
$-1$.
5.10
Even though the dependence on ![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$ of the family of elliptic curves
$\unicode[STIX]{x1D70F}\in \mathbb{H}$ of the family of elliptic curves ![]() $E_{\unicode[STIX]{x1D70F}}$ is holomorphic, the associated family of
$E_{\unicode[STIX]{x1D70F}}$ is holomorphic, the associated family of ![]() $\mathscr{A}_{\infty }$-algebras
$\mathscr{A}_{\infty }$-algebras ![]() $A_{\unicode[STIX]{x1D70F}}$ does not depend holomorphically on
$A_{\unicode[STIX]{x1D70F}}$ does not depend holomorphically on ![]() $\unicode[STIX]{x1D70F}$: the structure constants
$\unicode[STIX]{x1D70F}$: the structure constants ![]() $g_{a+c,b+d}$ are not holomorphic. We think of the multiplications
$g_{a+c,b+d}$ are not holomorphic. We think of the multiplications ![]() $\{\unicode[STIX]{x1D707}_{k}\}$ as giving a 2-cocycle
$\{\unicode[STIX]{x1D707}_{k}\}$ as giving a 2-cocycle ![]() $\unicode[STIX]{x1D707}^{\ast }$ in the Hochschild cochain
$\unicode[STIX]{x1D707}^{\ast }$ in the Hochschild cochain ![]() $CC^{\bullet }(A_{\unicode[STIX]{x1D70F}})$. (The differential in this complex is
$CC^{\bullet }(A_{\unicode[STIX]{x1D70F}})$. (The differential in this complex is ![]() $[\unicode[STIX]{x1D707}^{\ast },\,-\,]$.) The failure of holomorphicity is measured by the 2-cochain
$[\unicode[STIX]{x1D707}^{\ast },\,-\,]$.) The failure of holomorphicity is measured by the 2-cochain ![]() $\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D707}^{\ast }$.
$\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D707}^{\ast }$.
The following result shows that the anti-holomorphic dependence of this family is nevertheless trivial to first order (i.e. it is zero in Hochschild cohomology). The proof is a straightforward computation.
Theorem 5.11. Let ![]() $CC^{\bullet }(A_{\unicode[STIX]{x1D70F}})$ denote the Hochschild cochain complex of
$CC^{\bullet }(A_{\unicode[STIX]{x1D70F}})$ denote the Hochschild cochain complex of ![]() $A_{\unicode[STIX]{x1D70F}}$, with differential
$A_{\unicode[STIX]{x1D70F}}$, with differential ![]() $[\unicode[STIX]{x1D707}^{\ast },\,-\,]$. Let
$[\unicode[STIX]{x1D707}^{\ast },\,-\,]$. Let ![]() $\unicode[STIX]{x1D713}_{3}:A_{\unicode[STIX]{x1D70F}}[1]^{\otimes 3}\rightarrow A_{\unicode[STIX]{x1D70F}}[1]$ be the cyclic Hochschild
$\unicode[STIX]{x1D713}_{3}:A_{\unicode[STIX]{x1D70F}}[1]^{\otimes 3}\rightarrow A_{\unicode[STIX]{x1D70F}}[1]$ be the cyclic Hochschild ![]() $1$-cochain defined by
$1$-cochain defined by
and its cyclic rotations with respect to the pairing. Then we have
5.12
The deformation induced by ![]() $\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D707}$ is trivial not just to first order: the bounding element
$\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D707}$ is trivial not just to first order: the bounding element ![]() $\unicode[STIX]{x1D713}_{3}$ can be integrated to an
$\unicode[STIX]{x1D713}_{3}$ can be integrated to an ![]() $\mathscr{A}_{\infty }$ quasi-isomorphism
$\mathscr{A}_{\infty }$ quasi-isomorphism
from ![]() $A_{\unicode[STIX]{x1D70F}}$ to a holomorphic family
$A_{\unicode[STIX]{x1D70F}}$ to a holomorphic family ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ of
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ of ![]() $\mathscr{A}_{\infty }$-algebras over
$\mathscr{A}_{\infty }$-algebras over ![]() $\mathbb{H}$. The process is similar to integrating pseudo-isotopies of
$\mathbb{H}$. The process is similar to integrating pseudo-isotopies of ![]() $\mathscr{A}_{\infty }$-algebras; see [Reference FukayaFuk10, Proposition 9.1]. We will now present the construction of the algebras
$\mathscr{A}_{\infty }$-algebras; see [Reference FukayaFuk10, Proposition 9.1]. We will now present the construction of the algebras ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ and of the
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ and of the ![]() $\mathscr{A}_{\infty }$ quasi-isomorphism
$\mathscr{A}_{\infty }$ quasi-isomorphism ![]() $f$.
$f$.
The holomorphic family ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ has the same underlying vector space as
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ has the same underlying vector space as ![]() $A_{\unicode[STIX]{x1D70F}}$ and the same basis. Its structure constants are obtained simply by applying the map
$A_{\unicode[STIX]{x1D70F}}$ and the same basis. Its structure constants are obtained simply by applying the map ![]() $\unicode[STIX]{x1D711}$ of Theorem 4.5 to the structure constants of
$\unicode[STIX]{x1D711}$ of Theorem 4.5 to the structure constants of ![]() $A_{\unicode[STIX]{x1D70F}}$, so that, for example, the multiplications of
$A_{\unicode[STIX]{x1D70F}}$, so that, for example, the multiplications of ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ are obtained by cyclic symmetry from
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ are obtained by cyclic symmetry from
Since ![]() $\unicode[STIX]{x1D711}$ is a ring map, the maps
$\unicode[STIX]{x1D711}$ is a ring map, the maps ![]() $\{\unicode[STIX]{x1D707}_{k}^{\mathsf{hol}}\}$ also satisfy the
$\{\unicode[STIX]{x1D707}_{k}^{\mathsf{hol}}\}$ also satisfy the ![]() $\mathscr{A}_{\infty }$ relations.
$\mathscr{A}_{\infty }$ relations.
5.13
One can explicitly compute ![]() $\unicode[STIX]{x1D711}(g_{a,b})$ using the recurrence formulas in [Reference PolishchukPol11, Proposition 2.6.1(ii)]. For example, we have
$\unicode[STIX]{x1D711}(g_{a,b})$ using the recurrence formulas in [Reference PolishchukPol11, Proposition 2.6.1(ii)]. For example, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}(g_{1,0}) & = & \displaystyle \unicode[STIX]{x1D711}(e_{2}^{\ast })=\unicode[STIX]{x1D711}\biggl(e_{2}-\frac{2\unicode[STIX]{x1D70B}\mathtt{i}}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}\biggr)=e_{2},\nonumber\\ \displaystyle \unicode[STIX]{x1D711}(g_{2,1}) & = & \displaystyle \unicode[STIX]{x1D711}\biggl(-g_{1,0}^{2}+\frac{5}{6}g_{3,0}\biggr)=-e_{2}^{2}+\frac{5}{6}\cdot 3!\cdot e_{4}=-e_{2}^{2}+5e_{4}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}(g_{1,0}) & = & \displaystyle \unicode[STIX]{x1D711}(e_{2}^{\ast })=\unicode[STIX]{x1D711}\biggl(e_{2}-\frac{2\unicode[STIX]{x1D70B}\mathtt{i}}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}\biggr)=e_{2},\nonumber\\ \displaystyle \unicode[STIX]{x1D711}(g_{2,1}) & = & \displaystyle \unicode[STIX]{x1D711}\biggl(-g_{1,0}^{2}+\frac{5}{6}g_{3,0}\biggr)=-e_{2}^{2}+\frac{5}{6}\cdot 3!\cdot e_{4}=-e_{2}^{2}+5e_{4}.\nonumber\end{eqnarray}$$ In general, ![]() $g_{a,b}$ is a polynomial expression with rational coefficients in
$g_{a,b}$ is a polynomial expression with rational coefficients in ![]() $e_{2k}^{\ast }$;
$e_{2k}^{\ast }$; ![]() $\unicode[STIX]{x1D711}(g_{a,b})$ is obtained by replacing
$\unicode[STIX]{x1D711}(g_{a,b})$ is obtained by replacing ![]() $e_{2}^{\ast }$ by
$e_{2}^{\ast }$ by ![]() $e_{2}$ in the same expression, leaving all the other terms unchanged.
$e_{2}$ in the same expression, leaving all the other terms unchanged.
The following theorem describes recursively the construction of the maps ![]() $f_{n}$ which assemble to give a quasi-equivalence
$f_{n}$ which assemble to give a quasi-equivalence ![]() $A_{\unicode[STIX]{x1D70F}}\cong A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$. The proof is a straightforward (though tedious) inductive calculation.
$A_{\unicode[STIX]{x1D70F}}\cong A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$. The proof is a straightforward (though tedious) inductive calculation.
Theorem 5.14. Inductively define multilinear maps
by setting ![]() $f_{1}=\mathsf{id}$ and
$f_{1}=\mathsf{id}$ and
Here the integration symbol ![]() $\int (\ldots )\,\,d\bar{\unicode[STIX]{x1D70F}}$ is formally applied to the coefficients of the tensors, and is defined by
$\int (\ldots )\,\,d\bar{\unicode[STIX]{x1D70F}}$ is formally applied to the coefficients of the tensors, and is defined by
Then the maps ![]() $\{{f_{n}\}}_{n\geqslant 1}$ form a cyclic
$\{{f_{n}\}}_{n\geqslant 1}$ form a cyclic ![]() $\mathscr{A}_{\infty }$ quasi-isomorphism
$\mathscr{A}_{\infty }$ quasi-isomorphism
6 Costello’s formalism
In this section we review Costello’s general definition of categorical Gromov–Witten invariants. In the next section we will specialize this construction to the case of the ![]() $g=1$,
$g=1$, ![]() $n=1$ invariant of an elliptic curve.
$n=1$ invariant of an elliptic curve.
6.1
Let ![]() $A$ be a cyclic
$A$ be a cyclic ![]() $\mathscr{A}_{\infty }$-algebra whose pairing is of degree
$\mathscr{A}_{\infty }$-algebra whose pairing is of degree ![]() $d$ as in § 5.7, and let
$d$ as in § 5.7, and let ![]() $\mathsf{HH}=\mathsf{HH}_{\bullet }(A)[d]$ denote the shifted Hochschild homology of
$\mathsf{HH}=\mathsf{HH}_{\bullet }(A)[d]$ denote the shifted Hochschild homology of ![]() $A$. The categorical Gromov–Witten potential that we ultimately want to construct is an element
$A$. The categorical Gromov–Witten potential that we ultimately want to construct is an element
Here ![]() $\unicode[STIX]{x1D706}$ is a formal variable used to keep track of the Euler characteristics of curves and
$\unicode[STIX]{x1D706}$ is a formal variable used to keep track of the Euler characteristics of curves and ![]() $u$ is the usual formal variable of degree
$u$ is the usual formal variable of degree ![]() $-2$ which appears in the definition of cyclic homology. It is a placeholder for keeping track of insertions of
$-2$ which appears in the definition of cyclic homology. It is a placeholder for keeping track of insertions of ![]() $\unicode[STIX]{x1D713}$ classes.
$\unicode[STIX]{x1D713}$ classes.
The invariant ![]() $F^{\mathsf{cat}}$ depends not only on the algebra
$F^{\mathsf{cat}}$ depends not only on the algebra ![]() $A$, but also on a further choice: a splitting of the Hodge filtration on the periodic cyclic homology
$A$, but also on a further choice: a splitting of the Hodge filtration on the periodic cyclic homology ![]() $\mathsf{HP}_{\bullet }(A)$ of
$\mathsf{HP}_{\bullet }(A)$ of ![]() $A$. The construction of
$A$. The construction of ![]() $F^{\mathsf{cat}}$ proceeds in two stages. First one constructs an abstract invariant
$F^{\mathsf{cat}}$ proceeds in two stages. First one constructs an abstract invariant ![]() $F^{\mathsf{abs}}$ which only depends on
$F^{\mathsf{abs}}$ which only depends on ![]() $A$. It is a state in the homology of a certain Fock space associated to
$A$. It is a state in the homology of a certain Fock space associated to ![]() $A$. The choice of splitting of the Hodge filtration is then used to identify the homology of the Fock space with
$A$. The choice of splitting of the Hodge filtration is then used to identify the homology of the Fock space with ![]() $\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$ and hence to extract
$\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$ and hence to extract ![]() $F^{\mathsf{cat}}$ from
$F^{\mathsf{cat}}$ from ![]() $F^{\mathsf{abs}}$.
$F^{\mathsf{abs}}$.
6.2
The potential thus constructed is invariant under cyclic quasi-equivalence. If ![]() $A^{\prime }$ is another cyclic
$A^{\prime }$ is another cyclic ![]() $\mathscr{A}_{\infty }$-algebra and
$\mathscr{A}_{\infty }$-algebra and ![]() $f$ is a cyclic quasi-equivalence
$f$ is a cyclic quasi-equivalence ![]() $A\cong A^{\prime }$, then
$A\cong A^{\prime }$, then ![]() $f$ induces an isomorphism
$f$ induces an isomorphism ![]() $\mathsf{HP}_{\bullet }(A)\cong \mathsf{HP}_{\bullet }(A^{\prime })$ of filtered vector spaces. The original splitting
$\mathsf{HP}_{\bullet }(A)\cong \mathsf{HP}_{\bullet }(A^{\prime })$ of filtered vector spaces. The original splitting ![]() $s$ of the Hodge filtration on
$s$ of the Hodge filtration on ![]() $\mathsf{HP}_{\bullet }(A)$ then determines a splitting
$\mathsf{HP}_{\bullet }(A)$ then determines a splitting ![]() $s^{\prime }$ of the Hodge filtration on
$s^{\prime }$ of the Hodge filtration on ![]() $\mathsf{HP}_{\bullet }(A^{\prime })$. The invariance of the Gromov–Witten invariants means that the potential associated to
$\mathsf{HP}_{\bullet }(A^{\prime })$. The invariance of the Gromov–Witten invariants means that the potential associated to ![]() $(A,s)$ is the same as that associated to
$(A,s)$ is the same as that associated to ![]() $(A^{\prime },s^{\prime })$ under the obvious identifications.
$(A^{\prime },s^{\prime })$ under the obvious identifications.
6.3
Individual Gromov–Witten invariants can be read off from ![]() $F^{\mathsf{cat}}$ as coefficients of its power series expansion. For example, in the next section we will want to compute the
$F^{\mathsf{cat}}$ as coefficients of its power series expansion. For example, in the next section we will want to compute the ![]() $g=1$,
$g=1$, ![]() $n=1$ invariant of Polishchuk’s algebra
$n=1$ invariant of Polishchuk’s algebra ![]() $A_{\unicode[STIX]{x1D70F}}$. The Euler characteristic of the curves in
$A_{\unicode[STIX]{x1D70F}}$. The Euler characteristic of the curves in ![]() $M_{1,1}$ is
$M_{1,1}$ is ![]() $\unicode[STIX]{x1D712}=-1$; thus we are interested in the
$\unicode[STIX]{x1D712}=-1$; thus we are interested in the ![]() $\unicode[STIX]{x1D706}^{-\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D706}^{1}$ part of
$\unicode[STIX]{x1D706}^{-\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D706}^{1}$ part of ![]() $F^{\mathsf{cat}}$. We want to insert the Hochschild class
$F^{\mathsf{cat}}$. We want to insert the Hochschild class ![]() $[\unicode[STIX]{x1D709}]$ (and no
$[\unicode[STIX]{x1D709}]$ (and no ![]() $\unicode[STIX]{x1D713}$-classes). This means that the Gromov–Witten invariant we are interested in is the coefficient of
$\unicode[STIX]{x1D713}$-classes). This means that the Gromov–Witten invariant we are interested in is the coefficient of ![]() $[\unicode[STIX]{x1D6FA}]u^{-1}\unicode[STIX]{x1D706}$ in the power series expansion of
$[\unicode[STIX]{x1D6FA}]u^{-1}\unicode[STIX]{x1D706}$ in the power series expansion of ![]() $F^{\mathsf{cat}}$: here
$F^{\mathsf{cat}}$: here ![]() $[\unicode[STIX]{x1D6FA}]$ is the class in
$[\unicode[STIX]{x1D6FA}]$ is the class in ![]() $\mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ which is Mukai dual to
$\mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ which is Mukai dual to ![]() $[\unicode[STIX]{x1D709}]$ (Proposition 3.6), and we have used
$[\unicode[STIX]{x1D709}]$ (Proposition 3.6), and we have used ![]() $u^{-1}$ to denote no
$u^{-1}$ to denote no ![]() $\unicode[STIX]{x1D713}$-class insertions (one
$\unicode[STIX]{x1D713}$-class insertions (one ![]() $\unicode[STIX]{x1D713}$ class would give
$\unicode[STIX]{x1D713}$ class would give ![]() $u^{-2}$, etc.).
$u^{-2}$, etc.).
We begin by describing the structures on the cyclic chain complex of ![]() $A$ that will be needed for the construction of
$A$ that will be needed for the construction of ![]() $F^{\mathsf{abs}}$.
$F^{\mathsf{abs}}$.
6.4 The circle action on Hochschild chains
Let ![]() $V$ denote the shifted Hochschild cochain complex of
$V$ denote the shifted Hochschild cochain complex of ![]() $A$,
$A$,
whose homology is ![]() $\mathsf{HH}$. Connes’
$\mathsf{HH}$. Connes’ ![]() $B$ operator is a degree-one operator on
$B$ operator is a degree-one operator on ![]() $V$. It gives a homological circle action on the dg vector space
$V$. It gives a homological circle action on the dg vector space ![]() $V$. We use it to form the periodic cyclic complex
$V$. We use it to form the periodic cyclic complex
and its negative cyclic subcomplex
The homology of these complexes are the (shifted by ![]() $d$) periodic and negative cyclic homology of
$d$) periodic and negative cyclic homology of ![]() $A$, respectively.
$A$, respectively.
6.5 The Mukai pairing
The Mukai pairing [Reference Căldăraru and WillertonCW10] is a non-degenerate symmetric pairing of degree ![]() $2d$ on
$2d$ on ![]() $\mathsf{HH}$. Shklyarov [Reference ShklyarovShk13] and Sheridan [Reference SheridanShe20] construct a lift of the Mukai pairing to the chain level. It is a symmetric bilinear form of degree
$\mathsf{HH}$. Shklyarov [Reference ShklyarovShk13] and Sheridan [Reference SheridanShe20] construct a lift of the Mukai pairing to the chain level. It is a symmetric bilinear form of degree ![]() $2d$ on
$2d$ on ![]() $V$,
$V$,
We will discuss this pairing further in § 7.4.
6.6 The higher residue pairing
The chain-level Mukai pairing on ![]() $V$ induces a
$V$ induces a ![]() $\mathbb{C}(\!(u)\!)$ sesquilinear pairing of degree
$\mathbb{C}(\!(u)\!)$ sesquilinear pairing of degree ![]() $2d$ on
$2d$ on ![]() $V_{\mathsf{Tate}}$,
$V_{\mathsf{Tate}}$,
the higher residue pairing Footnote 1 (see [Reference SheridanShe20, Definition 2 and §5.42] for details). For ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in CC_{\bullet }(A)$,
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in CC_{\bullet }(A)$, ![]() $i,j\in \mathbb{Z}$ the higher residue pairing is given by
$i,j\in \mathbb{Z}$ the higher residue pairing is given by
Laurent power series only have finitely many negative powers of ![]() $u$, hence the above formula extends by sesquilinearity to all of
$u$, hence the above formula extends by sesquilinearity to all of ![]() $V_{\mathsf{Tate}}$.
$V_{\mathsf{Tate}}$.
The higher residue pairing is a chain map with respect to ![]() $b+uB$, which makes it descend to a pairing on periodic cyclic homology. The space
$b+uB$, which makes it descend to a pairing on periodic cyclic homology. The space ![]() $V_{\mathsf{Tate}}$ is filtered by powers of
$V_{\mathsf{Tate}}$ is filtered by powers of ![]() $u$, and the pairing respects this filtration. In particular, for
$u$, and the pairing respects this filtration. In particular, for ![]() $x,y\in \mathsf{HC}_{\bullet }^{-}(A)$ we have
$x,y\in \mathsf{HC}_{\bullet }^{-}(A)$ we have ![]() $\langle x,y\rangle _{\mathsf{hres}}\in \mathbb{C}\unicode[STIX]{x27E6}u\unicode[STIX]{x27E7}$.
$\langle x,y\rangle _{\mathsf{hres}}\in \mathbb{C}\unicode[STIX]{x27E6}u\unicode[STIX]{x27E7}$.
The constant term of the power series ![]() $\langle x,y\rangle _{\mathsf{hres}}$ equals the Mukai pairing
$\langle x,y\rangle _{\mathsf{hres}}$ equals the Mukai pairing ![]() $\langle \overline{x},\overline{y}\rangle _{\mathsf{M}}$ of the reductions of
$\langle \overline{x},\overline{y}\rangle _{\mathsf{M}}$ of the reductions of ![]() $x$ and
$x$ and ![]() $y$ to Hochschild homology. However, the power series
$y$ to Hochschild homology. However, the power series ![]() $\langle x,y\rangle _{\mathsf{hres}}$ can have higher powers of
$\langle x,y\rangle _{\mathsf{hres}}$ can have higher powers of ![]() $u$ which are not computed by the above homology Mukai pairing.
$u$ which are not computed by the above homology Mukai pairing.
6.7 The ordinary residue pairing
We will also consider the residue pairing, the ![]() $\mathbb{C}$-valued pairing of degree
$\mathbb{C}$-valued pairing of degree ![]() $2d-2$ on
$2d-2$ on ![]() $V_{\mathsf{Tate}}$ obtained by taking the coefficient of
$V_{\mathsf{Tate}}$ obtained by taking the coefficient of ![]() $u^{-1}$ (the residue) in the higher residue pairing. It is skew-symmetric, and restricts to zero on the dg subspace
$u^{-1}$ (the residue) in the higher residue pairing. It is skew-symmetric, and restricts to zero on the dg subspace ![]() $V^{hS^{1}}$. We will think of
$V^{hS^{1}}$. We will think of ![]() $V^{hS^{1}}$ as a Lagrangian subspace of the symplectic vector space
$V^{hS^{1}}$ as a Lagrangian subspace of the symplectic vector space ![]() $V_{\mathsf{Tate}}$.
$V_{\mathsf{Tate}}$.
6.8 Weyl algebra and Fock module
We associate a Weyl algebra ![]() ${\mathcal{W}}$ to the symplectic vector space
${\mathcal{W}}$ to the symplectic vector space ![]() $V_{\mathsf{Tate}}$ and a Fock space
$V_{\mathsf{Tate}}$ and a Fock space ![]() $\mathscr{F}$ to its Lagrangian subspace
$\mathscr{F}$ to its Lagrangian subspace ![]() $V^{hS^{1}}$. Explicitly,
$V^{hS^{1}}$. Explicitly, ![]() ${\mathcal{W}}$ is defined as
${\mathcal{W}}$ is defined as
where ![]() $[x,y]$ is the graded commutator of
$[x,y]$ is the graded commutator of ![]() $x,y\in T^{\bullet }(V_{\mathsf{Tate}})$, and
$x,y\in T^{\bullet }(V_{\mathsf{Tate}})$, and ![]() $\mathscr{F}$ is the quotient of
$\mathscr{F}$ is the quotient of ![]() ${\mathcal{W}}$ by the left ideal generated by
${\mathcal{W}}$ by the left ideal generated by ![]() $V^{hS^{1}}\subset V^{\mathsf{Tate}}$. It is an irreducible left
$V^{hS^{1}}\subset V^{\mathsf{Tate}}$. It is an irreducible left ![]() ${\mathcal{W}}$-module.
${\mathcal{W}}$-module.
6.9 String vertices
Sen and Zwiebach [Reference Sen and ZwiebachSZ94] note that there are certain distinguished singular chains ![]() $S_{g,n}$, the string vertices, on the uncompactified moduli spaces of curves
$S_{g,n}$, the string vertices, on the uncompactified moduli spaces of curves ![]() $M_{g,n}$. They play the role of approximations of the fundamental classes of the compactified spaces
$M_{g,n}$. They play the role of approximations of the fundamental classes of the compactified spaces ![]() $\overline{M}_{g,n}$. The string vertices can be defined by recursive relations encapsulated in a differential equation known as the quantum master equation; see [Reference CostelloCos09, Theorem 1]. We will discuss string vertices in § 8.
$\overline{M}_{g,n}$. The string vertices can be defined by recursive relations encapsulated in a differential equation known as the quantum master equation; see [Reference CostelloCos09, Theorem 1]. We will discuss string vertices in § 8.
Moreover, Kontsevich and Soibelman argue that chains on moduli spaces of curves act on the cyclic chain complex of any Calabi–Yau ![]() $\mathscr{A}_{\infty }$-algebra. This action will be further explained in § 7.4.
$\mathscr{A}_{\infty }$-algebra. This action will be further explained in § 7.4.
6.10 Deformed Fock module
Costello’s main observation in [Reference CostelloCos09] is that the action of the string vertices ![]() $S_{g,n}$ on cyclic chains can be used to deform the module structure on
$S_{g,n}$ on cyclic chains can be used to deform the module structure on ![]() $\mathscr{F}$. The result is a
$\mathscr{F}$. The result is a ![]() ${\mathcal{W}}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$-module
${\mathcal{W}}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$-module ![]() $\mathscr{F}^{\mathsf{def}}$ which is a deformation of
$\mathscr{F}^{\mathsf{def}}$ which is a deformation of ![]() $\mathscr{F}$ over
$\mathscr{F}$ over ![]() $\mathbb{C}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$.
$\mathbb{C}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$.
The deformed module ![]() $\mathscr{F}^{\mathsf{def}}$ is constructed as follows. The standard Fock module
$\mathscr{F}^{\mathsf{def}}$ is constructed as follows. The standard Fock module ![]() $\mathscr{F}$ is the quotient of
$\mathscr{F}$ is the quotient of ![]() ${\mathcal{W}}$ by the left ideal generated by the relations
${\mathcal{W}}$ by the left ideal generated by the relations
The module ![]() $\mathscr{F}^{\mathsf{def}}$ is obtained by taking the quotient of
$\mathscr{F}^{\mathsf{def}}$ is obtained by taking the quotient of ![]() ${\mathcal{W}}$ by the left ideal
${\mathcal{W}}$ by the left ideal ![]() $I^{\mathsf{def}}$ generated by the deformed relations
$I^{\mathsf{def}}$ generated by the deformed relations
for all ![]() $\unicode[STIX]{x1D6FC}\in V$,
$\unicode[STIX]{x1D6FC}\in V$, ![]() $k\geqslant 0$. Here
$k\geqslant 0$. Here ![]() $\unicode[STIX]{x1D704}$ is a certain operator on chains that will be described in § 8, and
$\unicode[STIX]{x1D704}$ is a certain operator on chains that will be described in § 8, and ![]() $\unicode[STIX]{x1D70C}$ denotes the action of singular chains on cyclic chains.
$\unicode[STIX]{x1D70C}$ denotes the action of singular chains on cyclic chains.
Costello argues that for reasonable ![]() $\mathscr{A}_{\infty }$-algebras, for which the Hodge filtration splits in the sense of Definition 6.13 below, the homology
$\mathscr{A}_{\infty }$-algebras, for which the Hodge filtration splits in the sense of Definition 6.13 below, the homology ![]() $H_{\bullet }(\mathscr{F}^{\mathsf{def}})$ is a flat deformation of the Fock module
$H_{\bullet }(\mathscr{F}^{\mathsf{def}})$ is a flat deformation of the Fock module ![]() $H_{\bullet }(\mathscr{F})$ over the classical (non-dg) Weyl algebra
$H_{\bullet }(\mathscr{F})$ over the classical (non-dg) Weyl algebra ![]() $H_{\bullet }({\mathcal{W}})$.
$H_{\bullet }({\mathcal{W}})$.
6.11
Fock modules over classical Weyl algebras are rigid, and thus the above deformation must be trivial at the level of homology. This implies that there is an isomorphism
of ![]() $H_{\bullet }({\mathcal{W}})\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$-modules, unique up to multiplication by a power series in
$H_{\bullet }({\mathcal{W}})\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$-modules, unique up to multiplication by a power series in ![]() $\mathbb{C}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$ which begins with 1.
$\mathbb{C}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$ which begins with 1.
By its construction the module ![]() $H_{\bullet }(\mathscr{F}^{\mathsf{def}})$ has a canonical generator
$H_{\bullet }(\mathscr{F}^{\mathsf{def}})$ has a canonical generator ![]() $\unicode[STIX]{x1D7D9}$ (it is a quotient of
$\unicode[STIX]{x1D7D9}$ (it is a quotient of ![]() $H_{\bullet }({\mathcal{W}}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7})$ by a certain ideal). Costello defines the abstract Gromov–Witten potential
$H_{\bullet }({\mathcal{W}}\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7})$ by a certain ideal). Costello defines the abstract Gromov–Witten potential
to be the image of ![]() $\unicode[STIX]{x1D7D9}$ under the above isomorphism. The ambiguity from the above power series will not play a role for us because we only care about the leading term of
$\unicode[STIX]{x1D7D9}$ under the above isomorphism. The ambiguity from the above power series will not play a role for us because we only care about the leading term of ![]() $F^{\mathsf{abs}}$ (the
$F^{\mathsf{abs}}$ (the ![]() $\unicode[STIX]{x1D706}^{1}$ term).
$\unicode[STIX]{x1D706}^{1}$ term).
6.12 Splitting of the Hodge filtration
In order to extract a concrete categorical Gromov–Witten potential
from the abstract one we need to choose a splitting of the Hodge filtration, a notion we now make precise.
Endow the graded vector space ![]() $\mathsf{HH}$ with a trivial circle operator and define
$\mathsf{HH}$ with a trivial circle operator and define ![]() $\mathsf{HH}_{\mathsf{Tate}}=\mathsf{HH}(\!(u)\!)$. The homology level Mukai pairing on
$\mathsf{HH}_{\mathsf{Tate}}=\mathsf{HH}(\!(u)\!)$. The homology level Mukai pairing on ![]() $\mathsf{HH}$ induces a higher residue pairing on
$\mathsf{HH}$ induces a higher residue pairing on ![]() $\mathsf{HH}_{\mathsf{Tate}}$ defined by the same formula as the higher residue pairing. The higher residue pairing on
$\mathsf{HH}_{\mathsf{Tate}}$ defined by the same formula as the higher residue pairing. The higher residue pairing on ![]() $\mathsf{HH}_{\mathsf{Tate}}$ respects the grading with respect to powers of
$\mathsf{HH}_{\mathsf{Tate}}$ respects the grading with respect to powers of ![]() $u$. This grading induces a decreasing filtration on
$u$. This grading induces a decreasing filtration on ![]() $\mathsf{HH}_{\mathsf{Tate}}$, similar to the one on
$\mathsf{HH}_{\mathsf{Tate}}$, similar to the one on ![]() $H_{\bullet }(V_{\mathsf{Tate}})$.
$H_{\bullet }(V_{\mathsf{Tate}})$.
Definition 6.13. A splitting of the Hodge filtration on the periodic cyclic homology of ![]() $A$ is an isomorphism of filtered vector spaces
$A$ is an isomorphism of filtered vector spaces
which respects the higher residue pairings.
6.14
Choosing a splitting of the Hodge filtration is equivalent to assigning to each ![]() $x\in \mathsf{HH}_{i}(A)$ a lift
$x\in \mathsf{HH}_{i}(A)$ a lift ![]() $\tilde{x}\in \mathsf{HC}_{i}^{-}(A)$. This assignment is required to satisfy the property that for
$\tilde{x}\in \mathsf{HC}_{i}^{-}(A)$. This assignment is required to satisfy the property that for ![]() $x,y\in \mathsf{HH}_{\bullet }(A)$ we have
$x,y\in \mathsf{HH}_{\bullet }(A)$ we have
In other words, we impose the condition that the higher residue pairing evaluated on lifts of elements in ![]() $\mathsf{HH}$ must have no higher powers of
$\mathsf{HH}$ must have no higher powers of ![]() $u$.
$u$.
6.15
Endowing the graded vector space ![]() $\mathsf{HH}_{\mathsf{Tate}}$ with the residue Mukai pairing makes it into a symplectic vector space, and
$\mathsf{HH}_{\mathsf{Tate}}$ with the residue Mukai pairing makes it into a symplectic vector space, and ![]() $\mathsf{HH}^{hS^{1}}$ is a Lagrangian subspace. This yields a corresponding Weyl algebra
$\mathsf{HH}^{hS^{1}}$ is a Lagrangian subspace. This yields a corresponding Weyl algebra ![]() ${\mathcal{W}}_{H}$ and Fock space
${\mathcal{W}}_{H}$ and Fock space ![]() $\mathscr{F}_{H}$. The latter can be identified with
$\mathscr{F}_{H}$. The latter can be identified with ![]() $\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])$ as a
$\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])$ as a ![]() ${\mathcal{W}}_{H}$-module via the action on the generator
${\mathcal{W}}_{H}$-module via the action on the generator ![]() $\unicode[STIX]{x1D7D9}$: negative powers of
$\unicode[STIX]{x1D7D9}$: negative powers of ![]() $u$ act by multiplication, non-negative powers of
$u$ act by multiplication, non-negative powers of ![]() $u$ act by differentiation.
$u$ act by differentiation.
A choice of splitting of the Hodge filtration induces an isomorphism of Weyl algebras
and a corresponding isomorphism of Fock modules
The categorical Gromov–Witten potential ![]() $F^{\mathsf{cat}}$ that we ultimately want is defined to be
$F^{\mathsf{cat}}$ that we ultimately want is defined to be
the preimage under ![]() $S$ of the abstract Gromov–Witten potential.
$S$ of the abstract Gromov–Witten potential.
7 A roadmap to the computation
We specialize Costello’s formalism described in the previous section to the computation of the ![]() $g=1$,
$g=1$, ![]() $n=1$ invariant of elliptic curves. We complete the main calculation of Theorem 1.9, assuming a few intermediate computations which we put off to §§ 8–10.
$n=1$ invariant of elliptic curves. We complete the main calculation of Theorem 1.9, assuming a few intermediate computations which we put off to §§ 8–10.
7.1
Fix a complex number ![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$ and consider the cyclic
$\unicode[STIX]{x1D70F}\in \mathbb{H}$ and consider the cyclic ![]() $\mathscr{A}_{\infty }$-algebra
$\mathscr{A}_{\infty }$-algebra ![]() $A_{\unicode[STIX]{x1D70F}}$ discussed in § 5, whose pairing has degree
$A_{\unicode[STIX]{x1D70F}}$ discussed in § 5, whose pairing has degree ![]() $d=1$. We are interested in computing the coefficient of
$d=1$. We are interested in computing the coefficient of ![]() $[\unicode[STIX]{x1D6FA}]u^{-1}\unicode[STIX]{x1D706}$ in the potential
$[\unicode[STIX]{x1D6FA}]u^{-1}\unicode[STIX]{x1D706}$ in the potential ![]() $F^{\mathsf{cat}}$ obtained from
$F^{\mathsf{cat}}$ obtained from ![]() $A_{\unicode[STIX]{x1D70F}}$, using a splitting of the Hodge filtration on the periodic cyclic homology of
$A_{\unicode[STIX]{x1D70F}}$, using a splitting of the Hodge filtration on the periodic cyclic homology of ![]() $A_{\unicode[STIX]{x1D70F}}$ which matches at the geometric level the one described in Lemma 3.8.
$A_{\unicode[STIX]{x1D70F}}$ which matches at the geometric level the one described in Lemma 3.8.
As explained above, the computation proceeds in three steps.
(i) We first compute the string vertices
 $S_{0,3}$ and
$S_{0,3}$ and  $S_{1,1}$. (These are the only pairs
$S_{1,1}$. (These are the only pairs  $(g,n)$ with Euler characteristic
$(g,n)$ with Euler characteristic  $-1$.) The answer will be expressed as certain linear combinations of ribbon graphs, using a model for chains on decorated moduli spaces of curves due to Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS09].
$-1$.) The answer will be expressed as certain linear combinations of ribbon graphs, using a model for chains on decorated moduli spaces of curves due to Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS09].(ii) We then find an explicit splitting of the Hodge filtration on
 $\mathsf{HP}_{\bullet }(A)$ by choosing a particular lift
$\mathsf{HP}_{\bullet }(A)$ by choosing a particular lift  $[\tilde{\unicode[STIX]{x1D709}}]\in \mathsf{HC}_{-1}^{-}(A)$ of the class
$[\tilde{\unicode[STIX]{x1D709}}]\in \mathsf{HC}_{-1}^{-}(A)$ of the class  $[\unicode[STIX]{x1D709}]\in \mathsf{HH}_{-1}(A)$. This splitting is chosen to match the geometric one in Lemma 3.8.
$[\unicode[STIX]{x1D709}]\in \mathsf{HH}_{-1}(A)$. This splitting is chosen to match the geometric one in Lemma 3.8.(iii) We complete the computation by combining the results of (i) and (ii) into a calculation with Fock modules.
In this section we will outline these steps, leaving the details of the explicit computations to §§ 8–10.
7.2 The string vertices
We want to represent singular chains on ![]() $M_{g,n}$ by linear combinations of ribbon graphs, using classical results by Strebel [Reference StrebelStr84] and Penner [Reference PennerPen87] that compare the ribbon graph complex and the singular chain complex
$M_{g,n}$ by linear combinations of ribbon graphs, using classical results by Strebel [Reference StrebelStr84] and Penner [Reference PennerPen87] that compare the ribbon graph complex and the singular chain complex ![]() $C_{\bullet }(M_{g,n})$. For technical reasons explained below, the classical ribbon graph complex is not flexible enough and we need a generalization described by Kontsevich and Soibelman in [Reference Kontsevich and SoibelmanKS09, §11.6]. The details will be discussed in § 8.
$C_{\bullet }(M_{g,n})$. For technical reasons explained below, the classical ribbon graph complex is not flexible enough and we need a generalization described by Kontsevich and Soibelman in [Reference Kontsevich and SoibelmanKS09, §11.6]. The details will be discussed in § 8.
The main reason this generalization is needed is so that we can write a combinatorial model for the quantum master equation, which at the level of singular chains was described in [Reference CostelloCos09]. The combinatorial equation can then be solved recursively, degree by degree in ![]() $\unicode[STIX]{x1D706}$. The first few terms of the solution are as follows:
$\unicode[STIX]{x1D706}$. The first few terms of the solution are as follows:
and

We refer to § 8 for the meaning of these diagrams. The operator ![]() $\unicode[STIX]{x1D704}$ which turns an output into an input will also be discussed in § 8.
$\unicode[STIX]{x1D704}$ which turns an output into an input will also be discussed in § 8.
7.3 The correct lift
The class ![]() $[\unicode[STIX]{x1D6FA}]\in \mathsf{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ has a canonical lift to cyclic homology, therefore the only information needed to specify a splitting of the Hodge filtration for
$[\unicode[STIX]{x1D6FA}]\in \mathsf{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ has a canonical lift to cyclic homology, therefore the only information needed to specify a splitting of the Hodge filtration for ![]() $A_{\unicode[STIX]{x1D70F}}$ is to choose a lift
$A_{\unicode[STIX]{x1D70F}}$ is to choose a lift ![]() $[\tilde{\unicode[STIX]{x1D709}}]\in \mathsf{HC}_{-1}^{-}(A_{\unicode[STIX]{x1D70F}})$ of the Hochschild homology class
$[\tilde{\unicode[STIX]{x1D709}}]\in \mathsf{HC}_{-1}^{-}(A_{\unicode[STIX]{x1D70F}})$ of the Hochschild homology class ![]() $[\unicode[STIX]{x1D709}]\in \mathsf{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$ defined in Proposition 3.6. Such a lift will have the form
$[\unicode[STIX]{x1D709}]\in \mathsf{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$ defined in Proposition 3.6. Such a lift will have the form
for some chain ![]() $\unicode[STIX]{x1D6FC}\in CC_{1}(A_{\unicode[STIX]{x1D70F}})$ that satisfies
$\unicode[STIX]{x1D6FC}\in CC_{1}(A_{\unicode[STIX]{x1D70F}})$ that satisfies
For degree reasons any choice of ![]() $\unicode[STIX]{x1D6FC}$ satisfying this condition will uniquely determine a lift
$\unicode[STIX]{x1D6FC}$ satisfying this condition will uniquely determine a lift ![]() $\tilde{\unicode[STIX]{x1D709}}$: the higher-order terms can always be filled in to satisfy
$\tilde{\unicode[STIX]{x1D709}}$: the higher-order terms can always be filled in to satisfy ![]() $(b+uB)(\tilde{\unicode[STIX]{x1D709}})=0$, and these further choices do not change the class
$(b+uB)(\tilde{\unicode[STIX]{x1D709}})=0$, and these further choices do not change the class ![]() $[\tilde{\unicode[STIX]{x1D709}}]$ in
$[\tilde{\unicode[STIX]{x1D709}}]$ in ![]() $\mathsf{HP}_{-1}(A_{\unicode[STIX]{x1D70F}})$.
$\mathsf{HP}_{-1}(A_{\unicode[STIX]{x1D70F}})$.
We will argue in § 9 that the correct lift is characterized by the system of equations
Here ![]() $b^{1|1}$ is the operator defined in [Reference SheridanShe20, 3.11] and
$b^{1|1}$ is the operator defined in [Reference SheridanShe20, 3.11] and ![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$ is the derivative of the multiplications
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$ is the derivative of the multiplications ![]() $\{\unicode[STIX]{x1D707}_{k}\}$ of
$\{\unicode[STIX]{x1D707}_{k}\}$ of ![]() $A_{\unicode[STIX]{x1D70F}}$, viewed as a Hochschild 2-cocycle in
$A_{\unicode[STIX]{x1D70F}}$, viewed as a Hochschild 2-cocycle in ![]() $\mathsf{HH}^{2}(A_{\unicode[STIX]{x1D70F}})$.
$\mathsf{HH}^{2}(A_{\unicode[STIX]{x1D70F}})$.
These equations are linear in ![]() $\unicode[STIX]{x1D6FC}$; we will argue in § 9 that large-scale computer calculations allow us to solve this system explicitly. Alternatively, in the same section we will argue by theoretical means that this system admits a solution, and this solution is unique up to a
$\unicode[STIX]{x1D6FC}$; we will argue in § 9 that large-scale computer calculations allow us to solve this system explicitly. Alternatively, in the same section we will argue by theoretical means that this system admits a solution, and this solution is unique up to a ![]() $b$-exact term.
$b$-exact term.
7.4 The action of singular chains on cyclic chains
Kontsevich–Soibelman construct an action of their generalized ribbon graphs (thought of as chains on moduli spaces of curves) on the Hochschild chain complex of an ![]() $\mathscr{A}_{\infty }$-algebra
$\mathscr{A}_{\infty }$-algebra ![]() $A$. Specifically, to a ribbon graph
$A$. Specifically, to a ribbon graph ![]() $\unicode[STIX]{x1D6E4}$ with
$\unicode[STIX]{x1D6E4}$ with ![]() $m$ inputs and
$m$ inputs and ![]() $n$ outputs they associate a map
$n$ outputs they associate a map
of a certain degree depending on ![]() $\unicode[STIX]{x1D6E4}$. For example, the chain-level Mukai pairing is the degree-
$\unicode[STIX]{x1D6E4}$. For example, the chain-level Mukai pairing is the degree-![]() $2d$ map associated to the following graph of genus zero, two inputs and no outputs:
$2d$ map associated to the following graph of genus zero, two inputs and no outputs:

Similarly, the coproduct on the shifted Hochschild homology of a cyclic ![]() $\mathscr{A}_{\infty }$-algebra (induced by the product on Hochschild cohomology, under the Calabi–Yau identification of cohomology with shifted homology) is given by the following graph with one input and two outputs:
$\mathscr{A}_{\infty }$-algebra (induced by the product on Hochschild cohomology, under the Calabi–Yau identification of cohomology with shifted homology) is given by the following graph with one input and two outputs:
7.5 The Fock space computation
We are interested in the coefficient of ![]() $[\unicode[STIX]{x1D6FA}]u^{-1}\unicode[STIX]{x1D706}^{1}$ in the series
$[\unicode[STIX]{x1D6FA}]u^{-1}\unicode[STIX]{x1D706}^{1}$ in the series
Since the subspace ![]() $\mathsf{HH}[[u]]\subset {\mathcal{W}}_{H}$ of the Weyl algebra acts by derivation on the Fock module
$\mathsf{HH}[[u]]\subset {\mathcal{W}}_{H}$ of the Weyl algebra acts by derivation on the Fock module ![]() $\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$, this coefficient can be recovered as the constant coefficient of
$\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$, this coefficient can be recovered as the constant coefficient of ![]() $\unicode[STIX]{x1D706}^{1}$ in
$\unicode[STIX]{x1D706}^{1}$ in ![]() $[\unicode[STIX]{x1D709}]\cdot F^{\mathsf{cat}}$, where we have denoted by
$[\unicode[STIX]{x1D709}]\cdot F^{\mathsf{cat}}$, where we have denoted by ![]() $\cdot$ the action of
$\cdot$ the action of ![]() ${\mathcal{W}}_{H}$.
${\mathcal{W}}_{H}$.
Since ![]() $F^{\mathsf{cat}}$ is the preimage of the generator
$F^{\mathsf{cat}}$ is the preimage of the generator ![]() $\unicode[STIX]{x1D7D9}$ of
$\unicode[STIX]{x1D7D9}$ of ![]() $H_{\bullet }(\mathscr{F}^{\mathsf{def}})$ under the isomorphism of
$H_{\bullet }(\mathscr{F}^{\mathsf{def}})$ under the isomorphism of ![]() ${\mathcal{W}}_{H}$-modules
${\mathcal{W}}_{H}$-modules
the element ![]() $[\unicode[STIX]{x1D709}]\cdot F^{\mathsf{cat}}$ is the unique element in
$[\unicode[STIX]{x1D709}]\cdot F^{\mathsf{cat}}$ is the unique element in ![]() $\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$ satisfying
$\mathsf{Sym}(u^{-1}\mathsf{HH}[u^{-1}])\unicode[STIX]{x27E6}\unicode[STIX]{x1D706}\unicode[STIX]{x27E7}$ satisfying
(We have used here the fact that the isomorphism ![]() ${\mathcal{W}}_{H}\cong H_{\bullet }({\mathcal{W}})$ induced by the splitting maps
${\mathcal{W}}_{H}\cong H_{\bullet }({\mathcal{W}})$ induced by the splitting maps ![]() $[\unicode[STIX]{x1D709}]\in {\mathcal{W}}_{H}$ to
$[\unicode[STIX]{x1D709}]\in {\mathcal{W}}_{H}$ to ![]() $[\tilde{\unicode[STIX]{x1D709}}]$, and the second
$[\tilde{\unicode[STIX]{x1D709}}]$, and the second ![]() $\cdot$ above refers to the action of
$\cdot$ above refers to the action of ![]() $H_{\bullet }({\mathcal{W}})$.)
$H_{\bullet }({\mathcal{W}})$.)
7.6
Write the lift ![]() $[\tilde{\unicode[STIX]{x1D709}}]$ of
$[\tilde{\unicode[STIX]{x1D709}}]$ of ![]() $[\unicode[STIX]{x1D709}]$ as
$[\unicode[STIX]{x1D709}]$ as
by collecting in ![]() $\unicode[STIX]{x1D6FD}u^{2}$ the terms with powers of
$\unicode[STIX]{x1D6FD}u^{2}$ the terms with powers of ![]() $u$ greater than two. Consider
$u$ greater than two. Consider ![]() $\tilde{\unicode[STIX]{x1D709}}=\tilde{\unicode[STIX]{x1D709}}u^{0}$ as a chain-level element in
$\tilde{\unicode[STIX]{x1D709}}=\tilde{\unicode[STIX]{x1D709}}u^{0}$ as a chain-level element in ![]() $\mathscr{F}^{\mathsf{def}}$. In this module the deformed relations (6.10) give the equality
$\mathscr{F}^{\mathsf{def}}$. In this module the deformed relations (6.10) give the equality
where ![]() $T_{1},T_{2},T_{3}$ are the results of inserting
$T_{1},T_{2},T_{3}$ are the results of inserting ![]() $\tilde{\unicode[STIX]{x1D709}}$ into the three ribbon graphs that appear in the expressions for the string vertices
$\tilde{\unicode[STIX]{x1D709}}$ into the three ribbon graphs that appear in the expressions for the string vertices ![]() $S_{0,3}$ and
$S_{0,3}$ and ![]() $S_{1,1}$ as in § 7.2:
$S_{1,1}$ as in § 7.2:

Since ![]() $\tilde{T}_{2}(\tilde{\unicode[STIX]{x1D709}})$ only depends on the chain
$\tilde{T}_{2}(\tilde{\unicode[STIX]{x1D709}})$ only depends on the chain ![]() $\unicode[STIX]{x1D6FC}$, we will sometimes denote it by
$\unicode[STIX]{x1D6FC}$, we will sometimes denote it by ![]() $T_{2}(\unicode[STIX]{x1D6FC})$.
$T_{2}(\unicode[STIX]{x1D6FC})$.
7.7
Having explicit formulas for the operations ![]() $\unicode[STIX]{x1D707}_{k}$ of the algebra
$\unicode[STIX]{x1D707}_{k}$ of the algebra ![]() $A_{\unicode[STIX]{x1D70F}}$ and for the chain
$A_{\unicode[STIX]{x1D70F}}$ and for the chain ![]() $\unicode[STIX]{x1D6FC}$ allows us to compute the values of the three expressions above. This will be done with a computer calculation in § 9, and the result is that
$\unicode[STIX]{x1D6FC}$ allows us to compute the values of the three expressions above. This will be done with a computer calculation in § 9, and the result is that ![]() $T_{2}(\tilde{\unicode[STIX]{x1D709}})=T_{3}(\tilde{\unicode[STIX]{x1D709}})=0$ and
$T_{2}(\tilde{\unicode[STIX]{x1D709}})=T_{3}(\tilde{\unicode[STIX]{x1D709}})=0$ and
Thus in ![]() $\mathscr{F}^{\mathsf{def}}$ we have the equality
$\mathscr{F}^{\mathsf{def}}$ we have the equality
7.8
As written above, the expression on the right-hand side is not explicitly in the image of ![]() $S$, because the classes
$S$, because the classes ![]() $\unicode[STIX]{x1D709}$ are not (
$\unicode[STIX]{x1D709}$ are not (![]() $b+uB$)-closed while the classes in the image of
$b+uB$)-closed while the classes in the image of ![]() $S$ always are. However, we know abstractly that this must be the case, because the map
$S$ always are. However, we know abstractly that this must be the case, because the map ![]() $S$ is an isomorphism of dg modules. So all we need to do is to rewrite the expression
$S$ is an isomorphism of dg modules. So all we need to do is to rewrite the expression ![]() $(\unicode[STIX]{x1D709}u^{-1})(\unicode[STIX]{x1D709}u^{-1})$ using the Weyl algebra relations to make it appear as the image under
$(\unicode[STIX]{x1D709}u^{-1})(\unicode[STIX]{x1D709}u^{-1})$ using the Weyl algebra relations to make it appear as the image under ![]() $S$ of an element in
$S$ of an element in ![]() ${\mathcal{W}}_{H}$.
${\mathcal{W}}_{H}$.
Note that ![]() $(\tilde{\unicode[STIX]{x1D709}}u^{-1})(\tilde{\unicode[STIX]{x1D709}}u^{-1})$ is the image under
$(\tilde{\unicode[STIX]{x1D709}}u^{-1})(\tilde{\unicode[STIX]{x1D709}}u^{-1})$ is the image under ![]() $S$ of
$S$ of ![]() $([\unicode[STIX]{x1D709}]u^{-1})([\unicode[STIX]{x1D709}]u^{-1})$. For degree reasons the terms
$([\unicode[STIX]{x1D709}]u^{-1})([\unicode[STIX]{x1D709}]u^{-1})$. For degree reasons the terms ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}u$ are in the left ideal
$\unicode[STIX]{x1D6FD}u$ are in the left ideal ![]() $I^{\mathsf{def}}\;\mathsf{mod}\;\unicode[STIX]{x1D706}^{2}$ (inserting them into any of the ribbon graphs in
$I^{\mathsf{def}}\;\mathsf{mod}\;\unicode[STIX]{x1D706}^{2}$ (inserting them into any of the ribbon graphs in ![]() $S_{0,3}$ and
$S_{0,3}$ and ![]() $S_{1,1}$ gives zero). Thus we have the equality in
$S_{1,1}$ gives zero). Thus we have the equality in ![]() $\mathscr{F}^{\mathsf{def}}$
$\mathscr{F}^{\mathsf{def}}$
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D709}u^{-1})(\unicode[STIX]{x1D709}u^{-1}) & = & \displaystyle (\tilde{\unicode[STIX]{x1D709}}u^{-1}-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}u)(\tilde{\unicode[STIX]{x1D709}}u^{-1}-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}u)\nonumber\\ \displaystyle & = & \displaystyle (\tilde{\unicode[STIX]{x1D709}}u^{-1})(\tilde{\unicode[STIX]{x1D709}}u^{-1})-(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}u)(\tilde{\unicode[STIX]{x1D709}}u^{-1})\nonumber\\ \displaystyle & = & \displaystyle (\tilde{\unicode[STIX]{x1D709}}u^{-1})(\tilde{\unicode[STIX]{x1D709}}u^{-1})-\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}\rangle _{\mathsf{M}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D709}u^{-1})(\unicode[STIX]{x1D709}u^{-1}) & = & \displaystyle (\tilde{\unicode[STIX]{x1D709}}u^{-1}-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}u)(\tilde{\unicode[STIX]{x1D709}}u^{-1}-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}u)\nonumber\\ \displaystyle & = & \displaystyle (\tilde{\unicode[STIX]{x1D709}}u^{-1})(\tilde{\unicode[STIX]{x1D709}}u^{-1})-(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}u)(\tilde{\unicode[STIX]{x1D709}}u^{-1})\nonumber\\ \displaystyle & = & \displaystyle (\tilde{\unicode[STIX]{x1D709}}u^{-1})(\tilde{\unicode[STIX]{x1D709}}u^{-1})-\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}\rangle _{\mathsf{M}}.\nonumber\end{eqnarray}$$Here we have used the Weyl algebra relation
7.9
We put together all the previous computations to get
and therefore the categorical Gromov–Witten invariant we want (the constant coefficient of ![]() $\unicode[STIX]{x1D706}$ in
$\unicode[STIX]{x1D706}$ in ![]() $[\unicode[STIX]{x1D709}]\cdot F^{\mathsf{cat}}$) is
$[\unicode[STIX]{x1D709}]\cdot F^{\mathsf{cat}}$) is
We will argue in § 9 that
thus completing the computation of Theorem 1.9:
8 String vertices
In this section we discuss the quantum master equation on chains on moduli spaces of curves, and the construction of string vertices as linear combinations of ribbon graphs with rational coefficients.
8.1
Let ![]() $M_{g,n}^{\mathsf{fr}}$ denote the coarse moduli space of smooth, genus-
$M_{g,n}^{\mathsf{fr}}$ denote the coarse moduli space of smooth, genus-![]() $g$ curves with
$g$ curves with ![]() $n$ framed (parametrized), ordered outgoing boundaries. The wreath product group
$n$ framed (parametrized), ordered outgoing boundaries. The wreath product group ![]() $(S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{n}$ acts on the space
$(S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{n}$ acts on the space ![]() $M_{g,n}^{\mathsf{fr}}$, where the circles
$M_{g,n}^{\mathsf{fr}}$, where the circles ![]() $(S^{1})^{n}$ act by rotation of the framing, and the symmetric group
$(S^{1})^{n}$ act by rotation of the framing, and the symmetric group ![]() $\unicode[STIX]{x1D6F4}_{n}$ acts by permutation of the boundaries. Denote by
$\unicode[STIX]{x1D6F4}_{n}$ acts by permutation of the boundaries. Denote by ![]() $M_{g,n}=M_{g,n}^{\mathsf{fr}}/((S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{n})$ the quotient space, parametrizing smooth, genus-
$M_{g,n}=M_{g,n}^{\mathsf{fr}}/((S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{n})$ the quotient space, parametrizing smooth, genus-![]() $g$ curves with
$g$ curves with ![]() $n$ unframed, unordered outgoing boundaries. Let
$n$ unframed, unordered outgoing boundaries. Let ![]() $C_{\bullet }(M_{g,n})$ be the normalized singular chain complex of
$C_{\bullet }(M_{g,n})$ be the normalized singular chain complex of ![]() $M_{g,n}$ with rational coefficients.
$M_{g,n}$ with rational coefficients.
There is a degree-one operator
defined as the sum of all the possible ways of sewing pairs of boundary components, with a full ![]() $S^{1}$ twist. Twist-sewing also defines an odd bracket
$S^{1}$ twist. Twist-sewing also defines an odd bracket
where the gluing is performed by choosing one boundary from the first surface and one from the second surface.
Theorem 8.2 (Costello [Reference CostelloCos09, §4, Theorem 1]).
There exists, for each pair of integers ![]() $g\geqslant 0$,
$g\geqslant 0$, ![]() $n>0$ with
$n>0$ with ![]() $2-2g-n<0$, a chain
$2-2g-n<0$, a chain ![]() $S_{g,n}\in C_{\bullet }(M_{g,n})$ of degree
$S_{g,n}\in C_{\bullet }(M_{g,n})$ of degree ![]() $6g-6+2n$ such that:
$6g-6+2n$ such that:
(i)
 $S_{0,3}$ is a
$S_{0,3}$ is a  $0$-chain of degree
$0$-chain of degree  ${\textstyle \frac{1}{3!}}$;
${\textstyle \frac{1}{3!}}$;(ii) for all
 $g,n\geqslant 0$ and
$g,n\geqslant 0$ and  $2-2g-n>0$ we have
$2-2g-n>0$ we have  $$\begin{eqnarray}\unicode[STIX]{x2202}S_{g,n}+\mathop{\sum }_{\substack{ g_{1}+g_{2}=g \\ n_{1}+n_{2}=n+2}}\frac{1}{2}\{S_{g_{1},n_{1}},S_{g_{2},n_{2}}\}+\unicode[STIX]{x1D6E5}S_{g-1,n+2}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}S_{g,n}+\mathop{\sum }_{\substack{ g_{1}+g_{2}=g \\ n_{1}+n_{2}=n+2}}\frac{1}{2}\{S_{g_{1},n_{1}},S_{g_{2},n_{2}}\}+\unicode[STIX]{x1D6E5}S_{g-1,n+2}=0.\end{eqnarray}$$
Furthermore, such a collection ![]() $\{S_{g,n}\}$ is unique up to homotopy in the sense of [Reference CostelloCos09, §8].
$\{S_{g,n}\}$ is unique up to homotopy in the sense of [Reference CostelloCos09, §8].
8.3
The equation in part (ii) of the theorem is a form of the quantum master equation for chains on moduli spaces; see [Reference CostelloCos09]. It was first discovered by Sen and Zwiebach [Reference Sen and ZwiebachSZ94]. The singular chains ![]() $S_{g,n}$ solving the quantum master equation are called string vertices.
$S_{g,n}$ solving the quantum master equation are called string vertices.
8.4
In order to perform explicit computations we need to use a combinatorial model for chains on moduli spaces of curves for which the twist-sewing operations make sense. Such a combinatorial model is described by Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS09, §11.6]. Their construction gives a chain model ![]() $C_{\bullet }^{\mathsf{comb}}(M_{g,m,n}^{\mathsf{fr}})$ for the moduli space
$C_{\bullet }^{\mathsf{comb}}(M_{g,m,n}^{\mathsf{fr}})$ for the moduli space ![]() $M_{g,m,n}^{\mathsf{fr}}$ of genus-
$M_{g,m,n}^{\mathsf{fr}}$ of genus-![]() $g$ curves with
$g$ curves with ![]() $m$ inputs and
$m$ inputs and ![]() $n$ outputs which are ordered and framed. The moduli space
$n$ outputs which are ordered and framed. The moduli space ![]() $M_{g,m,n}=M_{g,m,n}^{\mathsf{fr}}/((S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{m,n})$ is defined as before. In the following, we shall make the identification of
$M_{g,m,n}=M_{g,m,n}^{\mathsf{fr}}/((S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{m,n})$ is defined as before. In the following, we shall make the identification of ![]() $M_{g,n}$ with
$M_{g,n}$ with ![]() $M_{g,0,n}$.
$M_{g,0,n}$.
However, the ribbon graph model only exists for ![]() $m\geqslant 1$ – ribbon graphs must have at least one incoming boundary component. To remedy this, Costello notes that there is a map
$m\geqslant 1$ – ribbon graphs must have at least one incoming boundary component. To remedy this, Costello notes that there is a map
obtained by switching the designation of one of the outgoing boundaries in ![]() $M_{g,0,n}$ to ‘incoming’ and summing over all such choices of outgoing boundary.
$M_{g,0,n}$ to ‘incoming’ and summing over all such choices of outgoing boundary.
8.5
We can describe the chains ![]() $S_{g,n}$ combinatorially, via the map
$S_{g,n}$ combinatorially, via the map ![]() $\unicode[STIX]{x1D704}$. Taking coinvariants of the
$\unicode[STIX]{x1D704}$. Taking coinvariants of the ![]() $(S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{1,n-1}$ action on
$(S^{1})^{n}\ltimes \unicode[STIX]{x1D6F4}_{1,n-1}$ action on ![]() $C_{\bullet }^{\mathsf{comb}}(M_{g,1,n-1}^{\mathsf{fr}})$ produces a combinatorial model of
$C_{\bullet }^{\mathsf{comb}}(M_{g,1,n-1}^{\mathsf{fr}})$ produces a combinatorial model of ![]() $C_{\bullet }(M_{g,1,n-1})$ of the form
$C_{\bullet }(M_{g,1,n-1})$ of the form
More details can be found in [Reference CostelloCos09, §5].
Thus, a chain in ![]() $C_{\bullet }^{\mathsf{comb}}(M_{g,1,n-1})$ is a decorated ribbon graph whose input and outputs are labeled by negative powers of
$C_{\bullet }^{\mathsf{comb}}(M_{g,1,n-1})$ is a decorated ribbon graph whose input and outputs are labeled by negative powers of ![]() $u$. For example, the chains
$u$. For example, the chains ![]() $\unicode[STIX]{x1D704}(S_{0,3})$ and
$\unicode[STIX]{x1D704}(S_{0,3})$ and ![]() $\unicode[STIX]{x1D704}(S_{1,1})$ that we have described in § 7.2 are elements in
$\unicode[STIX]{x1D704}(S_{1,1})$ that we have described in § 7.2 are elements in ![]() $C_{\bullet }(M_{0,1,2})$ and
$C_{\bullet }(M_{0,1,2})$ and ![]() $C_{\bullet }(M_{1,1,0})$, respectively. The vertices labeled with a cross are input vertices, which for Kontsevich–Soibelman are in the set
$C_{\bullet }(M_{1,1,0})$, respectively. The vertices labeled with a cross are input vertices, which for Kontsevich–Soibelman are in the set ![]() $V_{\mathsf{in}}$. The white vertices (little circles) in
$V_{\mathsf{in}}$. The white vertices (little circles) in ![]() $\unicode[STIX]{x1D704}(S_{0,3})$ denote output vertices in
$\unicode[STIX]{x1D704}(S_{0,3})$ denote output vertices in ![]() $V_{\mathsf{out}}$.
$V_{\mathsf{out}}$.
8.6
We now explain where the coefficients that appear in the chains defined in (7.2) come from. For
the coefficient is ![]() ${\textstyle \frac{1}{2}}$ instead of
${\textstyle \frac{1}{2}}$ instead of ![]() ${\textstyle \frac{1}{3!}}$ because when applying the map
${\textstyle \frac{1}{3!}}$ because when applying the map ![]() $\unicode[STIX]{x1D704}$ there are three choices of outgoing boundary to turn to an incoming one.
$\unicode[STIX]{x1D704}$ there are three choices of outgoing boundary to turn to an incoming one.
Next we compute ![]() $\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6E5}(S_{0,3}))\in C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$ in the moduli space of genus-one curves with one unparametrized input boundary component and zero outgoing boundary components. Since
$\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6E5}(S_{0,3}))\in C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$ in the moduli space of genus-one curves with one unparametrized input boundary component and zero outgoing boundary components. Since ![]() $\binom{3}{2}=3$, the chain
$\binom{3}{2}=3$, the chain ![]() $\unicode[STIX]{x1D6E5}(S_{0,3})$ is
$\unicode[STIX]{x1D6E5}(S_{0,3})$ is ![]() ${\textstyle \frac{1}{2}}=3\cdot {\textstyle \frac{1}{6}}$ times the result of self-sewing of any two boundary components. Self-sewing of two outgoing boundary components can be described combinatorially:
${\textstyle \frac{1}{2}}=3\cdot {\textstyle \frac{1}{6}}$ times the result of self-sewing of any two boundary components. Self-sewing of two outgoing boundary components can be described combinatorially:

8.7
The string vertex ![]() $\unicode[STIX]{x1D704}(S_{1,1})$, being a degree-two chain in
$\unicode[STIX]{x1D704}(S_{1,1})$, being a degree-two chain in ![]() $C_{2}^{\mathsf{comb}}(M_{1,1,0})$, must be a linear combination of the form
$C_{2}^{\mathsf{comb}}(M_{1,1,0})$, must be a linear combination of the form

for some ![]() $a,b\in \mathbb{Q}$. (These are all the possible ribbon graphs of even degree in
$a,b\in \mathbb{Q}$. (These are all the possible ribbon graphs of even degree in ![]() $C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$.)
$C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$.)
Denote by ![]() $\unicode[STIX]{x2202}$ the boundary operator on
$\unicode[STIX]{x2202}$ the boundary operator on ![]() $C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$, and by
$C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$, and by ![]() $D$ the circle operator which is of degree one. The total differential on the equivariant complex
$D$ the circle operator which is of degree one. The total differential on the equivariant complex ![]() $C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$ is given by
$C_{\bullet }^{\mathsf{comb}}(M_{1,1,0})$ is given by ![]() $(\unicode[STIX]{x2202}+uD)$. Then the quantum master equation for
$(\unicode[STIX]{x2202}+uD)$. Then the quantum master equation for ![]() $n=1$,
$n=1$, ![]() $g=1$ becomes
$g=1$ becomes
One can check that

and all other terms are zero. Putting these together with the quantum master equation, we conclude that the coefficients ![]() $a$,
$a$, ![]() $b$ satisfy
$b$ satisfy
Solving this gives the combinatorial model of the string vertex ![]() $S_{1,1}$:
$S_{1,1}$:

8.8
This computation is essentially due to Costello (unpublished). He used it to compute the categorical Gromov–Witten invariant at ![]() $g=1$,
$g=1$, ![]() $n=1$ of a point (we take the
$n=1$ of a point (we take the ![]() $\mathscr{A}_{\infty }$-algebra
$\mathscr{A}_{\infty }$-algebra ![]() $A$ to be
$A$ to be ![]() $\mathbb{C}$). At
$\mathbb{C}$). At ![]() $g=1$,
$g=1$, ![]() $n=1$ the insertion of the
$n=1$ the insertion of the ![]() $\unicode[STIX]{x1D713}$-class gives the coefficient
$\unicode[STIX]{x1D713}$-class gives the coefficient ![]() $1/24$ in the first term of
$1/24$ in the first term of ![]() $\unicode[STIX]{x1D704}(S_{1,1})$. This agrees with the geometric computation that
$\unicode[STIX]{x1D704}(S_{1,1})$. This agrees with the geometric computation that
9 The computer calculation
In § 7 we have argued that the computation of Theorem 1.9 can be reduced to finding the correct chain ![]() $\unicode[STIX]{x1D6FC}$ which gives the lift
$\unicode[STIX]{x1D6FC}$ which gives the lift ![]() $\tilde{\unicode[STIX]{x1D709}}$, and computing the values
$\tilde{\unicode[STIX]{x1D709}}$, and computing the values ![]() $T_{2}(\tilde{\unicode[STIX]{x1D709}})=T_{3}(\tilde{\unicode[STIX]{x1D709}})=0$,
$T_{2}(\tilde{\unicode[STIX]{x1D709}})=T_{3}(\tilde{\unicode[STIX]{x1D709}})=0$,
and
In this section we describe our initial approach to computing these values, by reducing the question of computing them to a large linear algebra problem which can be solved by computer. In the next section we will give a purely mathematical deduction of Theorem 1.9.
9.1
The fact that ![]() $T_{3}(\tilde{\unicode[STIX]{x1D709}})=0$ and
$T_{3}(\tilde{\unicode[STIX]{x1D709}})=0$ and
follows easily from the Kontsevich–Soibelman definition of the action of ribbon graphs on cyclic chains of ![]() $A_{\unicode[STIX]{x1D70F}}$. Roughly speaking, one inserts Hochschild chains at each face of a graph (marked by a cross), labels each half edges by a basis element of
$A_{\unicode[STIX]{x1D70F}}$. Roughly speaking, one inserts Hochschild chains at each face of a graph (marked by a cross), labels each half edges by a basis element of ![]() $A_{\unicode[STIX]{x1D70F}}$, then contracts these tensors using the inner product on
$A_{\unicode[STIX]{x1D70F}}$, then contracts these tensors using the inner product on ![]() $A_{\unicode[STIX]{x1D70F}}$ for every edge, and the cyclic
$A_{\unicode[STIX]{x1D70F}}$ for every edge, and the cyclic ![]() $A_{\infty }$ structure on every vertex.
$A_{\infty }$ structure on every vertex.
For example, the fact that

follows form the fact that for any choice of basis vectors ![]() $x,y$ of the algebra
$x,y$ of the algebra ![]() $A_{\unicode[STIX]{x1D70F}}$ we have
$A_{\unicode[STIX]{x1D70F}}$ we have
where ![]() $x^{\vee }$,
$x^{\vee }$, ![]() $y^{\vee }$ are dual basis vectors of
$y^{\vee }$ are dual basis vectors of ![]() $x,y$ with respect to the pairing of the algebra
$x,y$ with respect to the pairing of the algebra ![]() $A_{\unicode[STIX]{x1D70F}}$. (This corresponds to the fact that we need to label the leg of the graph labeled with a cross with
$A_{\unicode[STIX]{x1D70F}}$. (This corresponds to the fact that we need to label the leg of the graph labeled with a cross with ![]() $\unicode[STIX]{x1D709}$, label the other half-edges of the graph by basis elements of the algebra, and evaluate the corresponding cyclic operations at the vertices and the duals of the pairing at the edges.)
$\unicode[STIX]{x1D709}$, label the other half-edges of the graph by basis elements of the algebra, and evaluate the corresponding cyclic operations at the vertices and the duals of the pairing at the edges.)
Similarly, for the ribbon graph that appears in ![]() $S_{0,3}$ the input edge is labeled
$S_{0,3}$ the input edge is labeled ![]() $\unicode[STIX]{x1D709}$; the other two half edges adjacent to the trivalent vertex will be labeled
$\unicode[STIX]{x1D709}$; the other two half edges adjacent to the trivalent vertex will be labeled ![]() $\mathsf{id}_{\mathscr{O}}$ in order to get a non-trivial cyclic
$\mathsf{id}_{\mathscr{O}}$ in order to get a non-trivial cyclic ![]() $c_{3}$, and then the output is read at the output vertices as two copies of
$c_{3}$, and then the output is read at the output vertices as two copies of ![]() $\unicode[STIX]{x1D709}u^{-1}$.
$\unicode[STIX]{x1D709}u^{-1}$.
9.2
We next need to understand the conditions that single out the correct lift
of the class ![]() $\unicode[STIX]{x1D709}\in \mathsf{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$. As mentioned before, for degree reasons the only choice to be made is that of the chain
$\unicode[STIX]{x1D709}\in \mathsf{HH}_{-1}(A_{\unicode[STIX]{x1D70F}})$. As mentioned before, for degree reasons the only choice to be made is that of the chain ![]() $\unicode[STIX]{x1D6FC}\in CC_{1}(A_{\unicode[STIX]{x1D70F}})$. This chain must satisfy
$\unicode[STIX]{x1D6FC}\in CC_{1}(A_{\unicode[STIX]{x1D70F}})$. This chain must satisfy
and any choice of ![]() $\unicode[STIX]{x1D6FC}$ satisfying this equation can be extended to a class
$\unicode[STIX]{x1D6FC}$ satisfying this equation can be extended to a class ![]() $[\tilde{\unicode[STIX]{x1D709}}]\in \mathsf{HC}_{-1}^{-}(A_{\unicode[STIX]{x1D70F}})$ which is uniquely determined by
$[\tilde{\unicode[STIX]{x1D709}}]\in \mathsf{HC}_{-1}^{-}(A_{\unicode[STIX]{x1D70F}})$ which is uniquely determined by ![]() $\unicode[STIX]{x1D6FC}$. Therefore we will talk about the lift
$\unicode[STIX]{x1D6FC}$. Therefore we will talk about the lift ![]() $[\tilde{\unicode[STIX]{x1D709}}]$ determined by
$[\tilde{\unicode[STIX]{x1D709}}]$ determined by ![]() $\unicode[STIX]{x1D6FC}$.
$\unicode[STIX]{x1D6FC}$.
The following proposition will specify the correct choice of ![]() $\unicode[STIX]{x1D6FC}$ to match the geometric splitting in Lemma 3.8.
$\unicode[STIX]{x1D6FC}$ to match the geometric splitting in Lemma 3.8.
Proposition 9.3. Fix ![]() $\unicode[STIX]{x1D70F}_{0}\in \mathbb{H}$ and consider the set of chains
$\unicode[STIX]{x1D70F}_{0}\in \mathbb{H}$ and consider the set of chains ![]() $\unicode[STIX]{x1D6FC}\in CC_{1}(A_{\unicode[STIX]{x1D70F}_{0}})$ satisfying
$\unicode[STIX]{x1D6FC}\in CC_{1}(A_{\unicode[STIX]{x1D70F}_{0}})$ satisfying
(i) Among these chains there exists a unique one (up to
 $b$-exact chains)
$b$-exact chains)  $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ with the property that the chain is
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ with the property that the chain is $$\begin{eqnarray}b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{GM}})\in CC_{-1}(A_{\unicode[STIX]{x1D70F}_{0}})\end{eqnarray}$$
$$\begin{eqnarray}b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{GM}})\in CC_{-1}(A_{\unicode[STIX]{x1D70F}_{0}})\end{eqnarray}$$ $b$-exact, where
$b$-exact, where  $b^{1|1}$ is the operator defined in [Reference SheridanShe20, 3.11] and
$b^{1|1}$ is the operator defined in [Reference SheridanShe20, 3.11] and  $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$ is the derivative of the operations
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$ is the derivative of the operations  $\{\unicode[STIX]{x1D707}_{k}\}$, viewed as a Hochschild
$\{\unicode[STIX]{x1D707}_{k}\}$, viewed as a Hochschild  $2$-cocycle in
$2$-cocycle in  $\mathsf{HH}^{2}(A_{\unicode[STIX]{x1D70F}_{0}})$.
$\mathsf{HH}^{2}(A_{\unicode[STIX]{x1D70F}_{0}})$.(ii) Let
 $[\tilde{\unicode[STIX]{x1D709}}]$ be the lift of
$[\tilde{\unicode[STIX]{x1D709}}]$ be the lift of  $[\unicode[STIX]{x1D709}]$ to periodic cyclic homology corresponding to the unique chain in (i). Then its image under the Hochschild–Kostant–Rosenberg (HKR) isomorphism matches the class
$[\unicode[STIX]{x1D709}]$ to periodic cyclic homology corresponding to the unique chain in (i). Then its image under the Hochschild–Kostant–Rosenberg (HKR) isomorphism matches the class  $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ of Lemma 3.8.
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ of Lemma 3.8.
Proof. (i) In the proof of Lemma 3.8 we constructed a family ![]() $[\unicode[STIX]{x1D709}]$ of classes in
$[\unicode[STIX]{x1D709}]$ of classes in ![]() $\mathsf{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$ and a family of lifts
$\mathsf{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$ and a family of lifts ![]() $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}\in H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$, both parametrized by
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}\in H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$, both parametrized by ![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$. This family of lifts is uniquely characterized by the local condition that it is Gauss–Manin flat.
$\unicode[STIX]{x1D70F}\in \mathbb{H}$. This family of lifts is uniquely characterized by the local condition that it is Gauss–Manin flat.
Locally around ![]() $\unicode[STIX]{x1D70F}_{0}\in \mathbb{H}$ pick representatives
$\unicode[STIX]{x1D70F}_{0}\in \mathbb{H}$ pick representatives ![]() $\tilde{\unicode[STIX]{x1D709}}$ of the images
$\tilde{\unicode[STIX]{x1D709}}$ of the images ![]() $[\tilde{\unicode[STIX]{x1D709}}]$ in
$[\tilde{\unicode[STIX]{x1D709}}]$ in ![]() $\mathsf{HC}_{-1}^{-}(A_{\unicode[STIX]{x1D70F}_{0}})$ of the geometric classes
$\mathsf{HC}_{-1}^{-}(A_{\unicode[STIX]{x1D70F}_{0}})$ of the geometric classes ![]() $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}\in H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ under the inverse HKR isomorphism. Each such
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}\in H_{\mathsf{dR}}^{1}(E_{\unicode[STIX]{x1D70F}})$ under the inverse HKR isomorphism. Each such ![]() $\tilde{\unicode[STIX]{x1D709}}$ will be of the form
$\tilde{\unicode[STIX]{x1D709}}$ will be of the form
for some chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}\in CC_{1}(A_{\unicode[STIX]{x1D70F}})$ which depends on
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}\in CC_{1}(A_{\unicode[STIX]{x1D70F}})$ which depends on ![]() $\unicode[STIX]{x1D70F}$. Since
$\unicode[STIX]{x1D70F}$. Since ![]() $[\tilde{\unicode[STIX]{x1D709}}]$ depends smoothly on
$[\tilde{\unicode[STIX]{x1D709}}]$ depends smoothly on ![]() $\unicode[STIX]{x1D70F}$ we can choose
$\unicode[STIX]{x1D70F}$ we can choose ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ to also depend smoothly on
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ to also depend smoothly on ![]() $\unicode[STIX]{x1D70F}$.
$\unicode[STIX]{x1D70F}$.
We have assumed that the geometric Gauss–Manin connection ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{GM}}$ is identified with the algebraic Getzler–Gauss–Manin connection
$\unicode[STIX]{x1D6FB}^{\mathsf{GM}}$ is identified with the algebraic Getzler–Gauss–Manin connection ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{GGM}}$ under HKR. The chain-level Getzler–Gauss–Manin connection applied to a family of chains
$\unicode[STIX]{x1D6FB}^{\mathsf{GGM}}$ under HKR. The chain-level Getzler–Gauss–Manin connection applied to a family of chains ![]() $x\in CC_{\bullet }(A_{\unicode[STIX]{x1D70F}})$ is given by the following formula (see [Reference SheridanShe20, Definition 3.32]):
$x\in CC_{\bullet }(A_{\unicode[STIX]{x1D70F}})$ is given by the following formula (see [Reference SheridanShe20, Definition 3.32]):
Thus ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{GGM}}(\tilde{\unicode[STIX]{x1D709}})$ has the form
$\unicode[STIX]{x1D6FB}^{\mathsf{GGM}}(\tilde{\unicode[STIX]{x1D709}})$ has the form
The flatness of the family ![]() $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ implies that
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$ implies that ![]() $b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{GM}})$ is
$b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{GM}})$ is ![]() $b$-exact.
$b$-exact.
This shows that a family ![]() $\unicode[STIX]{x1D6FC}$ with the required property exists, at least locally around each
$\unicode[STIX]{x1D6FC}$ with the required property exists, at least locally around each ![]() $\unicode[STIX]{x1D70F}_{0}$. We will now show uniqueness. Let
$\unicode[STIX]{x1D70F}_{0}$. We will now show uniqueness. Let ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ be two chains satisfying the desired properties. Their difference is a Hochschild cycle,
$\unicode[STIX]{x1D6FC}^{\prime }$ be two chains satisfying the desired properties. Their difference is a Hochschild cycle,
so it gives a class ![]() $[\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }]\in \mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ for each
$[\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }]\in \mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ for each ![]() $\unicode[STIX]{x1D70F}$. The chain
$\unicode[STIX]{x1D70F}$. The chain ![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\in CC^{2}(A_{\unicode[STIX]{x1D70F}_{0}})$ is a cocycle, and its class in Hochschild cohomology is the negative of the Kodaira–Spencer class
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\in CC^{2}(A_{\unicode[STIX]{x1D70F}_{0}})$ is a cocycle, and its class in Hochschild cohomology is the negative of the Kodaira–Spencer class
(Note that the comparison between the algebraic and geometric Kodaira–Spencer classes has a factor of ![]() $-1$ built in; see [Reference SheridanShe20, 3.32].) Moreover, under the comparison assumption (§ 1.15), at homology level the class
$-1$ built in; see [Reference SheridanShe20, 3.32].) Moreover, under the comparison assumption (§ 1.15), at homology level the class
agrees with the contraction ![]() $-\mathsf{KS}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}})\,\lrcorner \,[\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }]$. By assumption the former is
$-\mathsf{KS}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}})\,\lrcorner \,[\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }]$. By assumption the former is ![]() $b$-exact.
$b$-exact.
Therefore we have
in ![]() $\mathsf{HH}_{-1}(A_{\unicode[STIX]{x1D70F}_{0}})$. But for elliptic curves, contraction with
$\mathsf{HH}_{-1}(A_{\unicode[STIX]{x1D70F}_{0}})$. But for elliptic curves, contraction with ![]() $\mathsf{KS}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}})$ is an isomorphism
$\mathsf{KS}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}})$ is an isomorphism ![]() $\mathsf{HH}_{1}(E_{\unicode[STIX]{x1D70F}})\stackrel{{\sim}}{\longrightarrow }\mathsf{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$. We conclude that
$\mathsf{HH}_{1}(E_{\unicode[STIX]{x1D70F}})\stackrel{{\sim}}{\longrightarrow }\mathsf{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$. We conclude that ![]() $[\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }]=0$ in
$[\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\prime }]=0$ in ![]() $\mathsf{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$, and thus
$\mathsf{HH}_{-1}(E_{\unicode[STIX]{x1D70F}})$, and thus ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ is unique up to
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ is unique up to ![]() $b$-exact chains. (This uniqueness argument was suggested to us by Sheridan.)
$b$-exact chains. (This uniqueness argument was suggested to us by Sheridan.)
(ii) This follows immediately from the arguments above for the proof of (i) and the uniqueness of ![]() $[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$.◻
$[\tilde{\unicode[STIX]{x1D709}}]^{\mathsf{geom}}$.◻
9.4
For a fixed value of ![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$ the conditions
$\unicode[STIX]{x1D70F}\in \mathbb{H}$ the conditions
and
are linear in ![]() $\unicode[STIX]{x1D6FC}$. The structure constants of the multiplications
$\unicode[STIX]{x1D6FC}$. The structure constants of the multiplications ![]() $\unicode[STIX]{x1D707}_{k}$ of
$\unicode[STIX]{x1D707}_{k}$ of ![]() $A_{\unicode[STIX]{x1D70F}}$ can be computed using the formulas in [Reference PolishchukPol11, 1.2], and their derivatives with respect to
$A_{\unicode[STIX]{x1D70F}}$ can be computed using the formulas in [Reference PolishchukPol11, 1.2], and their derivatives with respect to ![]() $\unicode[STIX]{x1D70F}$ can be computed explicitly as well. For example, we have
$\unicode[STIX]{x1D70F}$ can be computed explicitly as well. For example, we have
 $$\begin{eqnarray}\displaystyle g_{21} & = & \displaystyle {\textstyle \frac{5}{6}}g_{30}-g_{10}^{2},\nonumber\\ \displaystyle g_{41} & = & \displaystyle {\textstyle \frac{7}{10}}g_{50}-4g_{10}g_{30},\nonumber\\ \displaystyle \unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}g_{10} & = & \displaystyle \frac{g_{21}}{2\unicode[STIX]{x1D70B}\mathtt{i}}-\frac{2g_{10}}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{21} & = & \displaystyle {\textstyle \frac{5}{6}}g_{30}-g_{10}^{2},\nonumber\\ \displaystyle g_{41} & = & \displaystyle {\textstyle \frac{7}{10}}g_{50}-4g_{10}g_{30},\nonumber\\ \displaystyle \unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}g_{10} & = & \displaystyle \frac{g_{21}}{2\unicode[STIX]{x1D70B}\mathtt{i}}-\frac{2g_{10}}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}.\nonumber\end{eqnarray}$$ These are then used to write the linear operators ![]() $b$ and
$b$ and ![]() $b^{1|1}$ in the basis for
$b^{1|1}$ in the basis for ![]() $A_{\unicode[STIX]{x1D70F}}$ described in (5.3). The resulting matrices allow us to express the equations
$A_{\unicode[STIX]{x1D70F}}$ described in (5.3). The resulting matrices allow us to express the equations ![]() $b(\unicode[STIX]{x1D6FC})=-1\otimes \unicode[STIX]{x1D709}$ and
$b(\unicode[STIX]{x1D6FC})=-1\otimes \unicode[STIX]{x1D709}$ and ![]() $b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC})=0$, and a solution
$b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC})=0$, and a solution ![]() $\unicode[STIX]{x1D6FC}$ can be found in
$\unicode[STIX]{x1D6FC}$ can be found in ![]() $A_{\unicode[STIX]{x1D70F}}^{\otimes 9}\oplus A_{\unicode[STIX]{x1D70F}}^{\otimes 7}\oplus \cdots A_{\unicode[STIX]{x1D70F}}^{\otimes 3}$. We then use
$A_{\unicode[STIX]{x1D70F}}^{\otimes 9}\oplus A_{\unicode[STIX]{x1D70F}}^{\otimes 7}\oplus \cdots A_{\unicode[STIX]{x1D70F}}^{\otimes 3}$. We then use ![]() $L^{1}$ optimization techniques to find such a solution with a small number of non-zero terms; the best such solution we found has 92 non-zero terms.
$L^{1}$ optimization techniques to find such a solution with a small number of non-zero terms; the best such solution we found has 92 non-zero terms.
9.5
To complete the calculation of the potential we need to follow the procedure outlined in [Reference Kontsevich and SoibelmanKS09, §11.6] to compute the result of inserting the various chains into the corresponding ribbon graphs.
Evaluating the insertion of ![]() $\unicode[STIX]{x1D6FC}$ is a large-scale computation which needs to be done by computer, but follows the same outline as the ones above. The results are
$\unicode[STIX]{x1D6FC}$ is a large-scale computation which needs to be done by computer, but follows the same outline as the ones above. The results are

as required, completing the proof of Theorem 1.9.
9.6
In the next section we will need to prove that the potential function ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ admits a finite limit at the cusp (i.e. as
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ admits a finite limit at the cusp (i.e. as ![]() $\unicode[STIX]{x1D70F}\rightarrow \mathtt{i}\cdot \infty$). Since the structure constants of Polishchuk’s algebra
$\unicode[STIX]{x1D70F}\rightarrow \mathtt{i}\cdot \infty$). Since the structure constants of Polishchuk’s algebra ![]() $A_{\unicode[STIX]{x1D70F}}$ do extend to the cusp (in our basis, see [Reference PolishchukPol11, 2.5, Remark 2]), the result would follow immediately if we could argue that a choice for the chain
$A_{\unicode[STIX]{x1D70F}}$ do extend to the cusp (in our basis, see [Reference PolishchukPol11, 2.5, Remark 2]), the result would follow immediately if we could argue that a choice for the chain ![]() $\unicode[STIX]{x1D6FC}$ can be found which also has a finite limit at the cusp.
$\unicode[STIX]{x1D6FC}$ can be found which also has a finite limit at the cusp.
Unfortunately we will not be able to prove directly the existence of such a chain. Instead we will use an auxiliary lift ![]() $[\tilde{\unicode[STIX]{x1D709}}^{\prime }]$ of the family
$[\tilde{\unicode[STIX]{x1D709}}^{\prime }]$ of the family ![]() $[\unicode[STIX]{x1D709}]$ of Hochschild homology classes. This lift will not be Gauss–Manin flat, but by its very construction it will have a finite limit at the cusp. Using the lift
$[\unicode[STIX]{x1D709}]$ of Hochschild homology classes. This lift will not be Gauss–Manin flat, but by its very construction it will have a finite limit at the cusp. Using the lift ![]() $[\tilde{\unicode[STIX]{x1D709}}^{\prime }]$ instead of the correct Gauss–Manin flat lift in the computations will not compute the correct Gromov–Witten potential. However, comparing the result of this ‘wrong’ computation with the correct one will allow us to conclude that
$[\tilde{\unicode[STIX]{x1D709}}^{\prime }]$ instead of the correct Gauss–Manin flat lift in the computations will not compute the correct Gromov–Witten potential. However, comparing the result of this ‘wrong’ computation with the correct one will allow us to conclude that ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ extends to the cusp.
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ extends to the cusp.
9.7
The desired family of chains
which determines the lifts ![]() $\tilde{\unicode[STIX]{x1D709}}^{\prime }$ can be written explicitly. Taking
$\tilde{\unicode[STIX]{x1D709}}^{\prime }$ can be written explicitly. Taking
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime } & = & \displaystyle \mathsf{id}_{L}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\frac{1}{4}\cdot \mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\frac{1}{2E_{4}(\unicode[STIX]{x1D70F})} (9E_{2}(\unicode[STIX]{x1D70F})\cdot \mathsf{id}_{L}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,60\cdot (\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703})-12\cdot (\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709})\nonumber\\ \displaystyle & & \displaystyle +\,36\cdot \mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}-24\cdot \mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}-60\cdot \mathsf{id}_{L}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703} ),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime } & = & \displaystyle \mathsf{id}_{L}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\frac{1}{4}\cdot \mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\frac{1}{2E_{4}(\unicode[STIX]{x1D70F})} (9E_{2}(\unicode[STIX]{x1D70F})\cdot \mathsf{id}_{L}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,60\cdot (\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703})-12\cdot (\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}+\mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709})\nonumber\\ \displaystyle & & \displaystyle +\,36\cdot \mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}-24\cdot \mathsf{id}_{\mathscr{O}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}-60\cdot \mathsf{id}_{L}\unicode[STIX]{x1D702}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}\unicode[STIX]{x1D703} ),\nonumber\end{eqnarray}$$one can check by direct calculation that we have
It is obvious from the above formulas that the chain ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ extends to the cusp: its coefficients have finite limit at
$\unicode[STIX]{x1D6FC}^{\prime }$ extends to the cusp: its coefficients have finite limit at ![]() $\unicode[STIX]{x1D70F}=\mathtt{i}\cdot \infty$.
$\unicode[STIX]{x1D70F}=\mathtt{i}\cdot \infty$.
10 Proof of the main theorem
In this final section we give a purely mathematical proof of Theorem 1.9, without relying on computer calculations. The main idea is to carry out the same computation in two different gauges, Polishchuk’s modular gauge and the holomorphic gauge described in § 5, and with three different splittings of the Hodge filtration. Comparing the results of these computations will allow us to determine the Gromov–Witten potential ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$.
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$.
10.1
In a nutshell the computation of the categorical Gromov–Witten invariant ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ and of some of its variants can be reduced to the following three steps.
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ and of some of its variants can be reduced to the following three steps.
(i) Fix an
 $\mathscr{A}_{\infty }$ model
$\mathscr{A}_{\infty }$ model  $A_{\unicode[STIX]{x1D70F}}$ or
$A_{\unicode[STIX]{x1D70F}}$ or  $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ of the derived category of the elliptic curve
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ of the derived category of the elliptic curve  $E_{\unicode[STIX]{x1D70F}}$.
$E_{\unicode[STIX]{x1D70F}}$.(ii) Construct a splitting of the Hodge filtration by finding a solution
 $\unicode[STIX]{x1D6FC}$ of the equation (This
$\unicode[STIX]{x1D6FC}$ of the equation (This $$\begin{eqnarray}b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709}).\end{eqnarray}$$
$$\begin{eqnarray}b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709}).\end{eqnarray}$$ $\unicode[STIX]{x1D6FC}$ determines a lift
$\unicode[STIX]{x1D6FC}$ determines a lift  $[\tilde{\unicode[STIX]{x1D709}}]$ of
$[\tilde{\unicode[STIX]{x1D709}}]$ of  $[\unicode[STIX]{x1D709}]$ as in § 9.)
$[\unicode[STIX]{x1D709}]$ as in § 9.)(iii) Compute the final invariant as
where $$\begin{eqnarray}F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC})=T_{2}(\unicode[STIX]{x1D6FC})-{\textstyle \frac{1}{2}}\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}\rangle _{\mathsf{M}},\end{eqnarray}$$and
$$\begin{eqnarray}F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC})=T_{2}(\unicode[STIX]{x1D6FC})-{\textstyle \frac{1}{2}}\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}\rangle _{\mathsf{M}},\end{eqnarray}$$and

(Since we do not want to rely on computer calculations, we cannot assume that ![]() $T_{2}(\unicode[STIX]{x1D6FC})=0$ as we have done before.)
$T_{2}(\unicode[STIX]{x1D6FC})=0$ as we have done before.)
In this section we will use three different choices for the chain ![]() $\unicode[STIX]{x1D6FC}$ in the above process, which give three different splittings of the Hodge filtration and consequently three different potentials (only one of which is of interest from the point of view of mirror symmetry; see below). We remark that in our case, any lift of
$\unicode[STIX]{x1D6FC}$ in the above process, which give three different splittings of the Hodge filtration and consequently three different potentials (only one of which is of interest from the point of view of mirror symmetry; see below). We remark that in our case, any lift of ![]() $[\unicode[STIX]{x1D709}]$ to a negative cyclic class
$[\unicode[STIX]{x1D709}]$ to a negative cyclic class ![]() $[\tilde{\unicode[STIX]{x1D709}}]$ satisfies the symplectic condition of Definition 6.13 for degree reasons.
$[\tilde{\unicode[STIX]{x1D709}}]$ satisfies the symplectic condition of Definition 6.13 for degree reasons.
10.2
The first choice of ![]() $\unicode[STIX]{x1D6FC}$ is the chain
$\unicode[STIX]{x1D6FC}$ is the chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ described in Proposition 9.3. For this choice the corresponding lifting
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ described in Proposition 9.3. For this choice the corresponding lifting ![]() $[\tilde{\unicode[STIX]{x1D709}}]$ is Gauss–Manin flat. The chain
$[\tilde{\unicode[STIX]{x1D709}}]$ is Gauss–Manin flat. The chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ is characterized by the condition
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ is characterized by the condition
Using it in the above procedure yields the correct Gromov–Witten potential we are interested in:
In a sense that will be made precise below, the chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ depends in a holomorphic, but not modular fashion on
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ depends in a holomorphic, but not modular fashion on ![]() $\unicode[STIX]{x1D70F}$. Thus using it with the holomorphic
$\unicode[STIX]{x1D70F}$. Thus using it with the holomorphic ![]() $\mathscr{A}_{\infty }$ model
$\mathscr{A}_{\infty }$ model ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ will allow us to deduce that
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ will allow us to deduce that ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ is holomorphic in
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ is holomorphic in ![]() $\unicode[STIX]{x1D70F}$.
$\unicode[STIX]{x1D70F}$.
10.3
The second choice of ![]() $\unicode[STIX]{x1D6FC}$ is the 11-term chain
$\unicode[STIX]{x1D6FC}$ is the 11-term chain ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ described in § 9.7. The resulting potential
$\unicode[STIX]{x1D6FC}^{\prime }$ described in § 9.7. The resulting potential ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}^{\prime })$ has the property that it extends to the cusp. Comparing it with
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}^{\prime })$ has the property that it extends to the cusp. Comparing it with ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ will allow us to deduce that this potential also admits a finite limit at the cusp.
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ will allow us to deduce that this potential also admits a finite limit at the cusp.
10.4
Finally, the third choice of chain ![]() $\unicode[STIX]{x1D6FC}$ is a modular version
$\unicode[STIX]{x1D6FC}$ is a modular version ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ of
$\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ of ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$. It is a solution of the equation
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$. It is a solution of the equation
where ![]() $\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$ is the natural differential operator on almost holomorphic, modular forms described in § 4.4. Using it in the modular model
$\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$ is the natural differential operator on almost holomorphic, modular forms described in § 4.4. Using it in the modular model ![]() $A_{\unicode[STIX]{x1D70F}}$ yields a new potential
$A_{\unicode[STIX]{x1D70F}}$ yields a new potential
By its very construction it will be obvious that ![]() $F_{1,1}^{\mathsf{B},\mathsf{mod}}$ is modular.
$F_{1,1}^{\mathsf{B},\mathsf{mod}}$ is modular.
In Proposition 10.15 we will argue that we have
The following theorem is a refinement of the statement of our main result, Theorem 1.9.
Theorem 10.5. The Gromov–Witten potential function ![]() $F_{1,1}^{\mathsf{B}}:\mathbb{H}\rightarrow \mathbb{C}$ satisfies the following properties:
$F_{1,1}^{\mathsf{B}}:\mathbb{H}\rightarrow \mathbb{C}$ satisfies the following properties:
(a)
 $F_{1,1}^{\mathsf{B}}$ is holomorphic;
$F_{1,1}^{\mathsf{B}}$ is holomorphic;(b)
 $F_{1,1}^{\mathsf{B}}$ extends to the cusp;
$F_{1,1}^{\mathsf{B}}$ extends to the cusp;(c) the function
is modular of weight 2. $$\begin{eqnarray}F_{1,1}^{\mathsf{B},\mathsf{mod}}(\unicode[STIX]{x1D70F})=F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})-\frac{1}{4\unicode[STIX]{x1D70B}\mathtt{i}(\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}})}\end{eqnarray}$$
$$\begin{eqnarray}F_{1,1}^{\mathsf{B},\mathsf{mod}}(\unicode[STIX]{x1D70F})=F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})-\frac{1}{4\unicode[STIX]{x1D70B}\mathtt{i}(\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}})}\end{eqnarray}$$
Therefore we have
Proof. The proof of the fact that the potential ![]() $F_{1,1}^{\mathsf{B}}$ satisfies conditions (a)–(c) above is the content of Propositions 10.10, 10.11, and 10.15. The final statement of the theorem follows from the fact that
$F_{1,1}^{\mathsf{B}}$ satisfies conditions (a)–(c) above is the content of Propositions 10.10, 10.11, and 10.15. The final statement of the theorem follows from the fact that ![]() $-{\textstyle \frac{1}{24}}E_{2}(\unicode[STIX]{x1D70F})$ is the unique function on
$-{\textstyle \frac{1}{24}}E_{2}(\unicode[STIX]{x1D70F})$ is the unique function on ![]() $\mathbb{H}$ that satisfies conditions (a)–(c).◻
$\mathbb{H}$ that satisfies conditions (a)–(c).◻
10.6
In the remainder of this section we give precise arguments for the fact that the potential ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ satisfies conditions (a)–(c) of Theorem 10.5. We begin with a lemma which shows that the term
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ satisfies conditions (a)–(c) of Theorem 10.5. We begin with a lemma which shows that the term ![]() $T_{2}(\unicode[STIX]{x1D6FC})$ used in the definition of the potential is not affected by changing
$T_{2}(\unicode[STIX]{x1D6FC})$ used in the definition of the potential is not affected by changing ![]() $\unicode[STIX]{x1D6FC}$ by any multiple of the class
$\unicode[STIX]{x1D6FC}$ by any multiple of the class ![]() $[\unicode[STIX]{x1D6FA}]\in \mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ defined in Proposition 3.6.
$[\unicode[STIX]{x1D6FA}]\in \mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ defined in Proposition 3.6.
Lemma 10.7. We have

Proof. The Calabi–Yau structure of ![]() $A_{\unicode[STIX]{x1D70F}}$ gives an identification
$A_{\unicode[STIX]{x1D70F}}$ gives an identification
This turns the former into a graded commutative Frobenius algebra with pairing given by the Mukai pairing on homology. In turn this yields a two-dimensional topological field theory.
Moreover, under this identification the class ![]() $[\unicode[STIX]{x1D6FA}]\in \mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ is matched with a multiple of
$[\unicode[STIX]{x1D6FA}]\in \mathit{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ is matched with a multiple of ![]() $1\in \mathit{HH}^{0}(A_{\unicode[STIX]{x1D70F}})$. The field theory interpretation implies that
$1\in \mathit{HH}^{0}(A_{\unicode[STIX]{x1D70F}})$. The field theory interpretation implies that

The term ![]() $\mathsf{Tr}_{\mathit{HH}^{\bullet }(A_{\unicode[STIX]{x1D70F}})}(1)$ is the supertrace of multiplication by
$\mathsf{Tr}_{\mathit{HH}^{\bullet }(A_{\unicode[STIX]{x1D70F}})}(1)$ is the supertrace of multiplication by ![]() $1$ in the Hochschild cohomology ring
$1$ in the Hochschild cohomology ring ![]() $\mathit{HH}^{\bullet }(A_{\unicode[STIX]{x1D70F}})$, which is zero (the Euler characteristic of the graded vector space
$\mathit{HH}^{\bullet }(A_{\unicode[STIX]{x1D70F}})$, which is zero (the Euler characteristic of the graded vector space ![]() $\mathsf{HH}^{\bullet }(A_{\unicode[STIX]{x1D70F}})$).◻
$\mathsf{HH}^{\bullet }(A_{\unicode[STIX]{x1D70F}})$).◻
10.8
Let ![]() $\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D70F})$ be two families of solutions of the equation
$\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D70F})$ be two families of solutions of the equation ![]() $b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709})$. Then for every
$b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709})$. Then for every ![]() $\unicode[STIX]{x1D70F}$ the chain
$\unicode[STIX]{x1D70F}$ the chain ![]() $\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D70F})-\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D70F})$ is
$\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D70F})-\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D70F})$ is ![]() $b$-closed, and therefore it defines a class
$b$-closed, and therefore it defines a class ![]() $[\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D70F})-\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D70F})]\in \mathsf{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ which must be a multiple
$[\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D70F})-\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D70F})]\in \mathsf{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$ which must be a multiple ![]() $c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}]$ of
$c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}]$ of ![]() $[\unicode[STIX]{x1D6FA}]$.
$[\unicode[STIX]{x1D6FA}]$.
Corollary 10.9. The difference between the potentials obtained from ![]() $\unicode[STIX]{x1D6FC}_{1}$ and
$\unicode[STIX]{x1D6FC}_{1}$ and ![]() $\unicode[STIX]{x1D6FC}_{2}$ is
$\unicode[STIX]{x1D6FC}_{2}$ is
Proof. We have
 $$\begin{eqnarray}\displaystyle F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}_{1})-F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}_{2}) & = & \displaystyle T_{2}(\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2})-\frac{1}{2}\langle \unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D709}\rangle _{\mathsf{M}}\nonumber\\ \displaystyle & = & \displaystyle T_{2}(c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}])-\frac{1}{2}\langle c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}],[\unicode[STIX]{x1D709}]\rangle _{\mathsf{M}}\nonumber\\ \displaystyle & = & \displaystyle -\frac{c(\unicode[STIX]{x1D70F})}{2}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}_{1})-F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}_{2}) & = & \displaystyle T_{2}(\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2})-\frac{1}{2}\langle \unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D709}\rangle _{\mathsf{M}}\nonumber\\ \displaystyle & = & \displaystyle T_{2}(c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}])-\frac{1}{2}\langle c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}],[\unicode[STIX]{x1D709}]\rangle _{\mathsf{M}}\nonumber\\ \displaystyle & = & \displaystyle -\frac{c(\unicode[STIX]{x1D70F})}{2}.\Box \nonumber\end{eqnarray}$$Proposition 10.10. The categorical Gromov–Witten invariant ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ is a holomorphic function on
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ is a holomorphic function on ![]() $\mathbb{H}$. Moreover, it is an element of weight 2 in the graded ring
$\mathbb{H}$. Moreover, it is an element of weight 2 in the graded ring ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})_{(0)}$ obtained by localizing
$\widetilde{M}(\unicode[STIX]{x1D6E4})_{(0)}$ obtained by localizing ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})$ at the multiplicative set of elements of homogeneous weight.
$\widetilde{M}(\unicode[STIX]{x1D6E4})$ at the multiplicative set of elements of homogeneous weight.
Proof. By (6.2) and Theorem 5.14 it will be enough to prove the statement when using the algebra ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ that we defined in (5.12) as the chosen
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ that we defined in (5.12) as the chosen ![]() $\mathscr{A}_{\infty }$ model of the derived category of the elliptic curve
$\mathscr{A}_{\infty }$ model of the derived category of the elliptic curve ![]() $E_{\unicode[STIX]{x1D70F}}$. Therefore we fix the algebra
$E_{\unicode[STIX]{x1D70F}}$. Therefore we fix the algebra ![]() $A=A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$.
$A=A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$.
In Proposition 9.3 we have argued that the equations defining the chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ can always be solved locally around every
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ can always be solved locally around every ![]() $\unicode[STIX]{x1D70F}_{0}\in \mathbb{H}$, and the solution is unique up to
$\unicode[STIX]{x1D70F}_{0}\in \mathbb{H}$, and the solution is unique up to ![]() $b$-exact chains. Moreover, the corresponding lift of
$b$-exact chains. Moreover, the corresponding lift of ![]() $[\unicode[STIX]{x1D709}]$ will be Gauss–Manin flat. The proof of this result did not depend on the specific algebra we used, only on the fact that the section
$[\unicode[STIX]{x1D709}]$ will be Gauss–Manin flat. The proof of this result did not depend on the specific algebra we used, only on the fact that the section ![]() $\unicode[STIX]{x1D709}$ of the family
$\unicode[STIX]{x1D709}$ of the family ![]() $\{{A_{\unicode[STIX]{x1D70F}}\}}_{\unicode[STIX]{x1D70F}\in \mathbb{H}}$ was flat with respect to differentiation by
$\{{A_{\unicode[STIX]{x1D70F}}\}}_{\unicode[STIX]{x1D70F}\in \mathbb{H}}$ was flat with respect to differentiation by ![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}$. Using any local choice
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}$. Using any local choice ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ of such
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ of such ![]() $\unicode[STIX]{x1D6FC}$ allows us to define
$\unicode[STIX]{x1D6FC}$ allows us to define ![]() $F_{1,1}^{\mathsf{B}}$ locally on
$F_{1,1}^{\mathsf{B}}$ locally on ![]() $\mathbb{H}$.
$\mathbb{H}$.
The action of ribbon graphs on ![]() $CC_{\bullet }(A)$ is a chain map, in the sense that it intertwines the
$CC_{\bullet }(A)$ is a chain map, in the sense that it intertwines the ![]() $\unicode[STIX]{x2202}$ operator on ribbon graphs and the
$\unicode[STIX]{x2202}$ operator on ribbon graphs and the ![]() $b$ operator on chains. Both ribbon graphs involved in the definition of the potential are trivalent, therefore they are sent to zero by
$b$ operator on chains. Both ribbon graphs involved in the definition of the potential are trivalent, therefore they are sent to zero by ![]() $\unicode[STIX]{x2202}$. This implies that modifying
$\unicode[STIX]{x2202}$. This implies that modifying ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ by a
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ by a ![]() $b$-exact chain does not change the result of its insertion in these two graphs. We conclude that the locally defined potentials glue to a well-defined global potential on the entire upper half plane
$b$-exact chain does not change the result of its insertion in these two graphs. We conclude that the locally defined potentials glue to a well-defined global potential on the entire upper half plane ![]() $\mathbb{H}$.
$\mathbb{H}$.
The structure constants of the algebra ![]() $A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ are holomorphic, quasi-modular forms in the ring
$A_{\unicode[STIX]{x1D70F}}^{\mathsf{hol}}$ are holomorphic, quasi-modular forms in the ring ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})$. All the operations used to compute the Gromov–Witten potential (differentiating, solving linear systems, inserting chains into ribbon graphs) always keep us inside
$\widetilde{M}(\unicode[STIX]{x1D6E4})$. All the operations used to compute the Gromov–Witten potential (differentiating, solving linear systems, inserting chains into ribbon graphs) always keep us inside ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})_{(0)}$. (We need to allow for divisions by homogeneous weight elements of
$\widetilde{M}(\unicode[STIX]{x1D6E4})_{(0)}$. (We need to allow for divisions by homogeneous weight elements of ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})$ in order to solve linear systems.) We conclude that
$\widetilde{M}(\unicode[STIX]{x1D6E4})$ in order to solve linear systems.) We conclude that ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ is an element of
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ is an element of ![]() $\widetilde{M}(\unicode[STIX]{x1D6E4})_{(0)}$, and an easy computation shows that its weight is 2.◻
$\widetilde{M}(\unicode[STIX]{x1D6E4})_{(0)}$, and an easy computation shows that its weight is 2.◻
Proposition 10.11. The potential ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ extends to the cusp: the limit
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ extends to the cusp: the limit
exists and is finite.
Proof. We use the modular gauge ![]() $A_{\unicode[STIX]{x1D70F}}$. The structure constants of this family of
$A_{\unicode[STIX]{x1D70F}}$. The structure constants of this family of ![]() $\mathscr{A}_{\infty }$-algebras extend to the cusp [Reference PolishchukPol11, 2.5, Remark 2]. The chain
$\mathscr{A}_{\infty }$-algebras extend to the cusp [Reference PolishchukPol11, 2.5, Remark 2]. The chain ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ defined in (9.7) also extends to the cusp. The terms
$\unicode[STIX]{x1D6FC}^{\prime }$ defined in (9.7) also extends to the cusp. The terms ![]() $T_{2}(\unicode[STIX]{x1D6FC}^{\prime })$ and
$T_{2}(\unicode[STIX]{x1D6FC}^{\prime })$ and ![]() $\langle \unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D709}\rangle _{\mathsf{M}}$ are (very complicated) polynomial expressions in the structure constants of the algebra and the coefficients of
$\langle \unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D709}\rangle _{\mathsf{M}}$ are (very complicated) polynomial expressions in the structure constants of the algebra and the coefficients of ![]() $\unicode[STIX]{x1D6FC}^{\prime }$. Therefore the potential
$\unicode[STIX]{x1D6FC}^{\prime }$. Therefore the potential ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}^{\prime })$ obtained from the chain
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}^{\prime })$ obtained from the chain ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ extends to the cusp.
$\unicode[STIX]{x1D6FC}^{\prime }$ extends to the cusp.
The chains ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ and
$\unicode[STIX]{x1D6FC}^{\prime }$ and ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ both satisfy
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ both satisfy ![]() $b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709})$, thus we are in the setup of Corollary 10.9. If we argue that the function
$b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709})$, thus we are in the setup of Corollary 10.9. If we argue that the function ![]() $c(\unicode[STIX]{x1D70F})$ defined by the equality
$c(\unicode[STIX]{x1D70F})$ defined by the equality
extends to the cusp, we will be able to conclude that
also extends to the cusp, which is what we need to prove.
The expression ![]() $b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\prime })$ is a polynomial expression in the structure constants of
$b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\prime })$ is a polynomial expression in the structure constants of ![]() $A_{\unicode[STIX]{x1D70F}}$, their derivatives, and the coefficients of
$A_{\unicode[STIX]{x1D70F}}$, their derivatives, and the coefficients of ![]() $\unicode[STIX]{x1D6FC}^{\prime }$, all of which have limits at the cusp; therefore this expression also extends to the cusp. Using the defining property of
$\unicode[STIX]{x1D6FC}^{\prime }$, all of which have limits at the cusp; therefore this expression also extends to the cusp. Using the defining property of ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ that
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ that
we conclude that ![]() $b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\prime }-\unicode[STIX]{x1D6FC}^{\mathsf{GM}})$ also extends to the cusp.
$b^{1|1}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\prime }-\unicode[STIX]{x1D6FC}^{\mathsf{GM}})$ also extends to the cusp.
By HKR we conclude that
extends to the cusp. The class ![]() $\mathsf{KS}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}})$ was computed in § 3.9,
$\mathsf{KS}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}})$ was computed in § 3.9,
and therefore
It follows that ![]() $c(\unicode[STIX]{x1D70F})$ admits a finite limit at the cusp.◻
$c(\unicode[STIX]{x1D70F})$ admits a finite limit at the cusp.◻
10.12
From now on we will position ourselves in the modular gauge – we take Polishchuk’s algebra ![]() $A_{\unicode[STIX]{x1D70F}}$ as the
$A_{\unicode[STIX]{x1D70F}}$ as the ![]() $\mathscr{A}_{\infty }$ model for the elliptic curve.
$\mathscr{A}_{\infty }$ model for the elliptic curve.
Fix any ![]() $\unicode[STIX]{x1D70F}\in \mathbb{H}$. We have already shown that the equation
$\unicode[STIX]{x1D70F}\in \mathbb{H}$. We have already shown that the equation
along with ![]() $b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709})$ defines a unique (up to
$b(\unicode[STIX]{x1D6FC})=-B(\unicode[STIX]{x1D709})$ defines a unique (up to ![]() $b$-exact terms) chain
$b$-exact terms) chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ which we used to define the potential
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ which we used to define the potential ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$.
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$.
However, the resulting chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ is not modular. The point where modularity breaks down is in the computation of
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ is not modular. The point where modularity breaks down is in the computation of ![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$: even though the coefficients of
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$: even though the coefficients of ![]() $\unicode[STIX]{x1D707}^{\ast }$ are in the ring
$\unicode[STIX]{x1D707}^{\ast }$ are in the ring ![]() $\widehat{M}(\unicode[STIX]{x1D6E4})$ of almost holomorphic modular forms, the coefficients of
$\widehat{M}(\unicode[STIX]{x1D6E4})$ of almost holomorphic modular forms, the coefficients of ![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$ are no longer modular.
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }$ are no longer modular.
10.13
This observation suggests how to modify the above computation so that all the intermediate computations (and the result) stay in ![]() $\widehat{M}(\unicode[STIX]{x1D6E4})$. Namely, if we replace the equation above with
$\widehat{M}(\unicode[STIX]{x1D6E4})$. Namely, if we replace the equation above with
where ![]() $\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$ is the natural differential operator on
$\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$ is the natural differential operator on ![]() $\widehat{M}(\unicode[STIX]{x1D6E4})$,
$\widehat{M}(\unicode[STIX]{x1D6E4})$,
the solution ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ will depend in a modular, almost holomorphic way on
$\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ will depend in a modular, almost holomorphic way on ![]() $\unicode[STIX]{x1D70F}$.
$\unicode[STIX]{x1D70F}$.
Note that locally around every point in ![]() $\mathbb{H}$ such a solution
$\mathbb{H}$ such a solution ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ exists and is unique up to a
$\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ exists and is unique up to a ![]() $b$-exact chain because the operator
$b$-exact chain because the operator ![]() $\mathsf{KZ}$ of Theorem 4.5 induces an isomorphism between solutions
$\mathsf{KZ}$ of Theorem 4.5 induces an isomorphism between solutions ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ of the above equation and solutions
$\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ of the above equation and solutions ![]() $\unicode[STIX]{x1D6FC}$ of the original equation,
$\unicode[STIX]{x1D6FC}$ of the original equation,
10.14
We use the solution ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ to define a new potential,
$\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ to define a new potential,
As the operator ![]() $\mathsf{KZ}$ is a differential ring isomorphism, it follows that we have
$\mathsf{KZ}$ is a differential ring isomorphism, it follows that we have
and, in particular, ![]() $F_{1,1}^{\mathsf{B},\mathsf{mod}}$ is a modular form in
$F_{1,1}^{\mathsf{B},\mathsf{mod}}$ is a modular form in ![]() $\widehat{M}(\unicode[STIX]{x1D6E4})_{(0)}$ of weight 2.
$\widehat{M}(\unicode[STIX]{x1D6E4})_{(0)}$ of weight 2.
Proposition 10.15. We have
Therefore ![]() $F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ satisfies condition (c) of Theorem 10.5.
$F_{1,1}^{\mathsf{B}}(\unicode[STIX]{x1D70F})$ satisfies condition (c) of Theorem 10.5.
Proof. Consider the difference
It is a ![]() $b$-closed chain in
$b$-closed chain in ![]() $CC_{1}(A_{\unicode[STIX]{x1D70F}})$, thus it gives a class
$CC_{1}(A_{\unicode[STIX]{x1D70F}})$, thus it gives a class ![]() $[\unicode[STIX]{x1D6FF}]$ in
$[\unicode[STIX]{x1D6FF}]$ in ![]() $\mathsf{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$. We will show that
$\mathsf{HH}_{1}(A_{\unicode[STIX]{x1D70F}})$. We will show that
Corollary 10.9 then implies the result.
The chains ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ and
$\unicode[STIX]{x1D6FC}^{\mathsf{GM}}$ and ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ define lifts of
$\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ define lifts of ![]() $\unicode[STIX]{x1D709}$ which we denote by
$\unicode[STIX]{x1D709}$ which we denote by ![]() $\tilde{\unicode[STIX]{x1D709}}$ and
$\tilde{\unicode[STIX]{x1D709}}$ and ![]() $\tilde{\unicode[STIX]{x1D709}}^{\mathsf{mod}}$, respectively. The former is flat with respect to the Gauss–Manin connection. The main idea is to calculate
$\tilde{\unicode[STIX]{x1D709}}^{\mathsf{mod}}$, respectively. The former is flat with respect to the Gauss–Manin connection. The main idea is to calculate
in two different ways, and to compare the results.
The definition of the Getzler–Gauss–Manin connection
implicitly assumes that we have chosen a connection on the family ![]() $A_{\unicode[STIX]{x1D70F}}$ of
$A_{\unicode[STIX]{x1D70F}}$ of ![]() $\mathscr{A}_{\infty }$-algebras over
$\mathscr{A}_{\infty }$-algebras over ![]() $\mathbb{H}$ with the property that the basis elements of
$\mathbb{H}$ with the property that the basis elements of ![]() $A_{\unicode[STIX]{x1D70F}}$ are flat for this connection. This allows us to write expressions like
$A_{\unicode[STIX]{x1D70F}}$ are flat for this connection. This allows us to write expressions like ![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}(x)$, by which we mean that we write
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}(x)$, by which we mean that we write ![]() $x$ in this chosen basis and differentiate the coefficients.
$x$ in this chosen basis and differentiate the coefficients.
However there is no reason to insist on the use of such a connection – any connection ![]() $\unicode[STIX]{x1D6FB}$ will work to define the Getzler–Gauss–Manin connection, at least at the level of homology; see [Reference SheridanShe20, Corollary 3.36] for a proof of this fact. We just need to replace the formula above by
$\unicode[STIX]{x1D6FB}$ will work to define the Getzler–Gauss–Manin connection, at least at the level of homology; see [Reference SheridanShe20, Corollary 3.36] for a proof of this fact. We just need to replace the formula above by
where now we think of applying ![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}$ to arbitrary tensors.
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}$ to arbitrary tensors.
We will use two different connections ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{std}}$ and
$\unicode[STIX]{x1D6FB}^{\mathsf{std}}$ and ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{mod}}$ on the bundle
$\unicode[STIX]{x1D6FB}^{\mathsf{mod}}$ on the bundle ![]() $A_{\unicode[STIX]{x1D70F}}$ over
$A_{\unicode[STIX]{x1D70F}}$ over ![]() $\mathbb{H}$. The first,
$\mathbb{H}$. The first, ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{std}}$, is the standard connection for which the basis vectors
$\unicode[STIX]{x1D6FB}^{\mathsf{std}}$, is the standard connection for which the basis vectors ![]() $\mathsf{id}_{\mathscr{O}},\mathsf{id}_{L},\unicode[STIX]{x1D703},\unicode[STIX]{x1D702},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{L}$ are flat. Computing
$\mathsf{id}_{\mathscr{O}},\mathsf{id}_{L},\unicode[STIX]{x1D703},\unicode[STIX]{x1D702},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{L}$ are flat. Computing ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{GGM}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}(\tilde{\unicode[STIX]{x1D709}})$ using
$\unicode[STIX]{x1D6FB}^{\mathsf{GGM}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}(\tilde{\unicode[STIX]{x1D709}})$ using ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{std}}$ yields
$\unicode[STIX]{x1D6FB}^{\mathsf{std}}$ yields
Define a second connection, ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{mod}}$, on the bundle
$\unicode[STIX]{x1D6FB}^{\mathsf{mod}}$, on the bundle ![]() $A_{\unicode[STIX]{x1D70F}}$ of
$A_{\unicode[STIX]{x1D70F}}$ of ![]() $\mathscr{A}_{\infty }$-algebras by the formula
$\mathscr{A}_{\infty }$-algebras by the formula
for any basis vector ![]() $x$ of
$x$ of ![]() $A_{\unicode[STIX]{x1D70F}}$, where the weight of basis elements was defined in § 5.9. A straight-forward computation shows that
$A_{\unicode[STIX]{x1D70F}}$, where the weight of basis elements was defined in § 5.9. A straight-forward computation shows that
where the left-hand side refers to the differentiation of the tensor ![]() $\unicode[STIX]{x1D707}_{k}$ with respect to the connection
$\unicode[STIX]{x1D707}_{k}$ with respect to the connection ![]() $\unicode[STIX]{x1D6FB}$, while the right-hand side refers to the differentiation of the structure constants of the same tensor using the operator
$\unicode[STIX]{x1D6FB}$, while the right-hand side refers to the differentiation of the structure constants of the same tensor using the operator ![]() $\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$.
$\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}$.
Computing ![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{GGM}}(\tilde{\unicode[STIX]{x1D709}}^{\mathsf{mod}})$ using the connection
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{GGM}}(\tilde{\unicode[STIX]{x1D709}}^{\mathsf{mod}})$ using the connection ![]() $\unicode[STIX]{x1D6FB}^{\mathsf{mod}}$ yields
$\unicode[STIX]{x1D6FB}^{\mathsf{mod}}$ yields
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{GGM}}(\tilde{\unicode[STIX]{x1D709}}^{\mathsf{mod}}) & = & \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{mod}}(\unicode[STIX]{x1D709})-b^{1|1}(\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{mod}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{mod}})+O(u)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D709}-b^{1|1}(\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{mod}})+O(u)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D709}+O(u).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{GGM}}(\tilde{\unicode[STIX]{x1D709}}^{\mathsf{mod}}) & = & \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{mod}}(\unicode[STIX]{x1D709})-b^{1|1}(\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}^{\mathsf{mod}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{mod}})+O(u)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D709}-b^{1|1}(\widehat{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}^{\ast }\mid \unicode[STIX]{x1D6FC}^{\mathsf{mod}})+O(u)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D70F}-\bar{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D709}+O(u).\nonumber\end{eqnarray}$$Equating the two calculations above yields
Passing to Hochschild homology, we get
Since ![]() $[\unicode[STIX]{x1D6FF}]=c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}]$ for some
$[\unicode[STIX]{x1D6FF}]=c(\unicode[STIX]{x1D70F})\cdot [\unicode[STIX]{x1D6FA}]$ for some ![]() $c(\unicode[STIX]{x1D70F})$, under the HKR isomorphism this becomes
$c(\unicode[STIX]{x1D70F})$, under the HKR isomorphism this becomes
which forces ![]() $c(\unicode[STIX]{x1D70F})$ to equal
$c(\unicode[STIX]{x1D70F})$ to equal
Remark 10.16. It is worth noting that the modular splitting obtained from the chain ![]() $\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ corresponds to the complex conjugate splitting from complex algebraic geometry. This follows from a direct computation.
$\unicode[STIX]{x1D6FC}^{\mathsf{mod}}$ corresponds to the complex conjugate splitting from complex algebraic geometry. This follows from a direct computation.
Acknowledgements
We would like to thank Nick Sheridan, Kevin Costello, Si Li, Dima Arinkin, Alexander Polishchuk, and Jie Zhou for patiently listening to the various problems we ran into at different stages of the project, and for providing insight. Stephen Wright’s explanation of the use of ![]() $L^{1}$-optimization techniques has been extremely helpful for computing a small solution to the lifting problem. Some of the larger computations were carried out on the SBEL supercomputer at the University of Wisconsin, whose graceful support we acknowledge.
$L^{1}$-optimization techniques has been extremely helpful for computing a small solution to the lifting problem. Some of the larger computations were carried out on the SBEL supercomputer at the University of Wisconsin, whose graceful support we acknowledge.