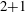1 Introduction
The Korteweg–de Vries (KdV) equation and its generalisations are successfully used to describe long weakly nonlinear internal waves that are commonly observed in the oceans (Benjamin Reference Benjamin1966; Benney Reference Benney1966; Maslowe & Redekopp Reference Maslowe and Redekopp1980; Grimshaw et al. Reference Grimshaw, Pelinovsky and Talipova1997, Reference Grimshaw, Ostrovsky, Shrira and Stepanyants1998; Grimshaw Reference Grimshaw and Grimshaw2001; Grue Reference Grue, Grue and Trulsen2006; Helfrich & Melville Reference Helfrich and Melville2006; Apel et al. Reference Apel, Ostrovsky, Stepanyants and Lynch2007), as well as to describe weakly nonlinear shallow-water surface waves (Boussinesq Reference Boussinesq1871; Korteweg & de Vries Reference Korteweg and de Vries1895; Ablowitz & Baldwin Reference Ablowitz and Baldwin2012; Chakravarty & Kodama Reference Chakravarty and Kodama2014). The waves described by these models have plane or nearly plane fronts. However, waves registered by satellite observations often look like a part of a ring, motivating the present study of annular waves (see figure 1 for the image of a nearly annular internal soliton). Observations of internal waves with curvilinear fronts have been reported in several studies, e.g. Farmer & Armi (Reference Farmer and Armi1988), Nash & Moum (Reference Nash and Moum2005) and Jackson et al. (Reference Jackson, Da Silva, Jeans, Alpers and Caruso2013). Internal waves have a strong effect on acoustic signalling, as well as impacting submersibles, offshore structures and underwater pipelines. They also significantly contribute to the ocean mixing processes. Therefore, it is important to develop a good understanding of the main properties and behaviour of these waves. In natural oceanic environments these waves often propagate over currents, for example, tides, wind-drift currents, river flows, etc. Thus, we aim to develop an asymptotic theory which could be used to model long ring waves in a stratified fluid over a shear flow. In this paper we focus on the basic balance between nonlinearity and dispersion, considering waves with cylindrical divergence on horizontal shear flows in the KdV regime.
Currently, there is considerable interest in both internal and surface waves on sheared currents. Among recent results, the effect of a shear flow on linear surface waves was studied by Ellingsen (Reference Ellingsen2014a ,Reference Ellingsen b ), while Thomas, Kharif & Manna (Reference Thomas, Kharif and Manna2012) studied how vorticity modifies the modulational instability properties of weakly nonlinear surface wave trains. Analytical considerations of the latter paper complemented a strongly nonlinear numerical analysis developed by Nwogu (Reference Nwogu2009). The complementary nature of the analytical weakly nonlinear studies and strongly nonlinear numerical modelling is also notable in the research on internal waves. Analytical studies help to identify the main trends and dependences, creating the framework for the discussion of the observed and modelled phenomena, while advanced numerical modelling allows one to describe important features of the waves in more realistic settings not amenable to theoretical analysis (see, for example, the reviews by Helfrich & Melville (Reference Helfrich and Melville2006) and Apel et al. (Reference Apel, Ostrovsky, Stepanyants and Lynch2007)).
The effects of various sheared currents on internal waves and their role in the oceanic processes have been studied by a number of authors (e.g. Lee & Beardsley Reference Lee and Beardsley1974; Voronovich, Sazonov & Shrira Reference Voronovich, Sazonov and Shrira2006; Buhler Reference Buhler2009). Modifications of large internal solitary waves by a background shear flow have been studied analytically by Choi (Reference Choi2006) and modelled numerically, for example, by Stastna & Lamb (Reference Stastna and Lamb2002) and Stastna & Walter (Reference Stastna and Walter2014), within the framework of two-dimensional simulations. Three-dimensional numerical modelling, although expensive, has also been developed. In particular, large-amplitude internal waves in the Strait of Gibraltar have been modelled by Vlasenko et al. (Reference Vlasenko, Sanchez Garrido, Stashchuk, Garcia Lafuente and Losada2009) and Sannino et al. (Reference Sannino, Sanchez Garrido, Liberti, Pratt, Gianluca, Miroslav, Piero and Paola2014). Tidal generation of internal waves in the Celtic Sea has been modelled by Vlasenko et al. (Reference Vlasenko, Stashchuk, Palmer and Inall2013, Reference Vlasenko, Stashchuk, Inall and Hopkins2014) and Grue (Reference Grue2015). We note that the waves generated in the Strait of Gibraltar are nearly annular (see figure 1), as are the waves generated near a sea mountain in the Celtic Sea (see Vlasenko et al. (Reference Vlasenko, Stashchuk, Inall and Hopkins2014, figure A1)).
Figure 1. Internal soliton generated in the Strait of Gibraltar (NASA image STS17-34-098, Lunar and Planetary Institute, http://www.lpi.usra.edu/publications/slidesets/oceans/oceanviews/oceanviews_index.shtml). A very large collection of images of various nonlinear internal waves can be found at http://www.internalwaveatlas.com/Atlas2_index.html.
The cylindrical (or concentric) Korteweg–de Vries (cKdV) equation is a universal weakly nonlinear weakly dispersive wave equation in cylindrical geometry. Originally derived in the context of ion-acoustic waves in plasma (Maxon & Viecelli Reference Maxon and Viecelli1974), it was later derived for the surface waves in a uniform fluid, first from Boussinesq equations (Miles Reference Miles1978), and then from the full Euler equations (Johnson Reference Johnson1980). Versions of the equation were also derived for internal waves in a stratified fluid without shear flow (Lipovskii Reference Lipovskii1985), and surface waves in a uniform fluid with a shear flow (Johnson Reference Johnson1990). The original equation is integrable (Dryuma Reference Druma1976; Calogero & Degasperis Reference Calogero and Degasperis1978), and there exists a useful map between cKdV and Kadomtsev–Petviashvili (KP) equations (Johnson Reference Johnson1980, Reference Johnson1997; Klein et al. Reference Klein, Matveev and Smirnov2007), while a generic shear flow leads to a non-integrable cKdV-type equation.
In this paper we study the propagation of internal and surface ring waves in a stratified fluid over a prescribed shear flow, generalising the previous studies. The paper is organised as follows. In § 2 we derive a
$2+1$
-dimensional cKdV-type model for the amplitudes of surface and internal waves, by finding an appropriate linear modal decomposition (different from the known modal decomposition in Cartesian coordinates) and using techniques from the asymptotic multiple-scale analysis. The detailed structure of the wavefronts is analysed analytically, for the case of a two-layer model with a piecewise-constant current, in § 3. We also obtain conditions guaranteeing that there are no critical levels, and calculate explicit expressions for the coefficients of the derived amplitude equation, listed in appendix B. Some conclusions are drawn in § 4.
2 Problem formulation and amplitude equation
2.1 Problem formulation
We consider a ring wave propagating in an inviscid incompressible fluid, described by the full set of Euler equations:
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}(u_{t}+uu_{x}+vu_{y}+wu_{z})+p_{x}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}(v_{t}+uv_{x}+vv_{y}+wv_{z})+p_{y}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}(w_{t}+uw_{x}+vw_{y}+ww_{z})+p_{z}+{\it\rho}g=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}_{t}+u{\it\rho}_{x}+v{\it\rho}_{y}+w{\it\rho}_{z}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{x}+v_{y}+w_{z}=0, & \displaystyle\end{eqnarray}$$
with the free surface and rigid bottom boundary conditions appropriate for oceanic conditions:
$$\begin{eqnarray}\displaystyle & \displaystyle w=h_{t}+uh_{x}+vh_{y}\quad \text{at }z=h(x,y,t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p=p_{a}\quad \text{at }z=h(x,y,t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w=0\quad \text{at }z=0. & \displaystyle\end{eqnarray}$$
Here,
$u,v,w$
are the velocity components in the
$x,y,z$
directions respectively,
$p$
is the pressure,
${\it\rho}$
is the density,
$g$
is the gravitational acceleration,
$z=h(x,y,t)$
is the free surface height (equal to the depth of the fluid under the free surface;
$z=0$
at the bottom) and
$p_{a}$
is the constant atmospheric pressure at the surface. We assume that in the basic state
$u_{0}=u_{0}(z),v_{0}=w_{0}=0,p_{0z}=-{\it\rho}_{0}g,h=h_{0}$
. Here,
$u_{0}(z)$
is a horizontal shear flow in the
$x$
direction and
${\it\rho}_{0}={\it\rho}_{0}(z)$
is a stable background density stratification (see figure 2).
Figure 2. Schematic of the problem formulation.
It is convenient to use the vertical particle displacement
${\it\zeta}$
as an additional dependent variable, which is defined by the equation
$$\begin{eqnarray}{\it\zeta}_{t}+u{\it\zeta}_{x}+v{\it\zeta}_{y}+w{\it\zeta}_{z}=w\end{eqnarray}$$
and satisfies the obvious surface boundary condition
$$\begin{eqnarray}{\it\zeta}=h-h_{0}\quad \text{at }z=h(x,y,t),\end{eqnarray}$$
where
$h_{0}$
is the unperturbed depth of the fluid.
We aim to derive an amplitude equation for the amplitudes of the long surface and internal waves. Thus, we use the following non-dimensional variables:
$$\begin{eqnarray}\displaystyle x\rightarrow {\it\lambda}x,\quad y\rightarrow {\it\lambda}y,\quad z\rightarrow h_{0}z,\quad t\rightarrow \frac{{\it\lambda}}{c^{\ast }}t,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u\rightarrow c^{\ast }u,\quad v\rightarrow c^{\ast }v,\quad w\rightarrow \frac{h_{0}c^{\ast }}{{\it\lambda}}w,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle ({\it\rho}_{0},{\it\rho})\rightarrow {\it\rho}^{\ast }({\it\rho}_{0},{\it\rho}),\quad h\rightarrow h_{0}+a{\it\eta},\quad p\rightarrow p_{a}+\int _{z}^{h_{0}}{\it\rho}^{\ast }{\it\rho}_{0}(s)g\,\text{d}s+{\it\rho}^{\ast }gh_{0}p. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Here,
${\it\lambda}$
is the wavelength,
$a$
is the wave amplitude,
$c^{\ast }$
is the typical long-wave speed of surface or internal waves (
$\sqrt{gh_{0}}$
or
$h^{\ast }N^{\ast }$
respectively, where
$N^{\ast }$
is a typical value of the buoyancy frequency, and
$h^{\ast }$
is a typical depth of the stratified layer),
${\it\rho}^{\ast }$
is the dimensional reference density of the fluid, while
${\it\rho}_{0}(z)$
is the non-dimensional function describing stratification in the basic state, and
${\it\eta}={\it\eta}(x,y,t)$
is the non-dimensional free surface perturbation. In both cases non-dimensionalisation leads to the appearance of the same small parameters in the problem, the amplitude parameter
${\it\varepsilon}=a/h_{0}$
and the wavelength parameter
${\it\delta}=h_{0}/{\it\lambda}$
. In the second case, a third small (Boussinesq) parameter will appear as well, but the Boussinesq approximation is not used in the subsequent derivation. Thus, it is natural to non-dimensionalise the general problem formulation, including both surface and internal waves, using the parameters of the faster surface waves, and to measure the speeds of the internal waves as fractions of the surface wave speed, etc. However, if one is primarily interested in the study of internal waves, it is more natural to use the typical speed of the internal waves.
Introducing the cylindrical coordinate system moving at a constant speed
$c$
(a natural choice is the flow speed at the bottom, as we will show later), considering deviations from the basic state (the same notations
$u$
and
$v$
have been used for the projections of the deviations of the speed on the new coordinate axis) and scaling the appropriate variables using the amplitude parameter
${\it\varepsilon}$
,
$$\begin{eqnarray}\displaystyle x\rightarrow ct+r\cos {\it\theta},\quad y\rightarrow r\sin {\it\theta},\quad z\rightarrow z,\quad t\rightarrow t,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u\rightarrow u_{0}(z)+{\it\varepsilon}(u\cos {\it\theta}-v\sin {\it\theta}),\quad v\rightarrow {\it\varepsilon}(u\sin {\it\theta}+v\cos {\it\theta}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w\rightarrow {\it\varepsilon}w,\quad p\rightarrow {\it\varepsilon}p,\quad {\it\rho}\rightarrow {\it\rho}_{0}+{\it\varepsilon}{\it\rho},\end{eqnarray}$$
we arrive at the following non-dimensional problem formulation in the moving cylindrical coordinate frame:
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle ({\it\rho}_{0}+{\it\varepsilon}{\it\rho})\left[u_{t}+{\it\varepsilon}\left(uu_{r}+\frac{v}{r}u_{{\it\theta}}+wu_{z}-\frac{v^{2}}{r}\right)+((u_{0}-c)u_{r}+u_{0z}w)\cos {\it\theta}\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \left.-\,(u_{0}-c)(u_{{\it\theta}}-v)\frac{\sin {\it\theta}}{r}\right]+p_{r}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle ({\it\rho}_{0}+{\it\varepsilon}{\it\rho})\left[\vphantom{\left(u_{0}\biggl(\displaystyle \frac{v_{{\it\theta}}}{r}\biggr)\right)}v_{t}+{\it\varepsilon}\left(uv_{r}+\frac{v}{r}v_{{\it\theta}}+wv_{z}+\frac{uv}{r}\right)+(u_{0}-c)v_{r}\cos {\it\theta}\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \left.-\left((u_{0}-c)\bigg(\frac{v_{{\it\theta}}}{r}+\frac{u}{r}\bigg)+u_{0z}w\right)\sin {\it\theta}\right]+\frac{p_{{\it\theta}}}{r}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\it\delta}^{2}({\it\rho}_{0}+{\it\varepsilon}{\it\rho})\left[w_{t}+{\it\varepsilon}\left(uw_{r}+\frac{v}{r}w_{{\it\theta}}+ww_{z}\right)+(u_{0}-c)\left(w_{r}\cos {\it\theta}-w_{{\it\theta}}\frac{\sin {\it\theta}}{r}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,p_{z}+{\it\rho}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}_{t}+{\it\varepsilon}\left(u{\it\rho}_{r}+\frac{v}{r}{\it\rho}_{{\it\theta}}+w{\it\rho}_{z}\right)+(u_{0}-c)\left({\it\rho}_{r}\cos {\it\theta}-{\it\rho}_{{\it\theta}}\frac{\sin {\it\theta}}{r}\right)+{\it\rho}_{0z}w=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{r}+\frac{u}{r}+\frac{v_{{\it\theta}}}{r}+w_{z}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w={\it\eta}_{t}+{\it\varepsilon}\left(u{\it\eta}_{r}+\frac{v}{r}{\it\eta}_{{\it\theta}}\right)+(u_{0}-c)\left({\it\eta}_{r}\cos {\it\theta}-{\it\eta}_{{\it\theta}}\frac{\sin {\it\theta}}{r}\right)\quad \text{at }z=1+{\it\varepsilon}{\it\eta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\varepsilon}p=\int _{1}^{1+{\it\varepsilon}{\it\eta}}{\it\rho}_{0}(s)\,\text{d}s\quad \text{at }z=1+{\it\varepsilon}{\it\eta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w=0\quad \text{at }z=0, & \displaystyle\end{eqnarray}$$
with the vertical particle displacement satisfying the following equation and boundary condition:
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\zeta}_{t}+{\it\varepsilon}\left(u{\it\zeta}_{r}+\frac{v}{r}{\it\zeta}_{{\it\theta}}+w{\it\zeta}_{z}\right)+(u_{0}-c)\left({\it\zeta}_{r}\cos {\it\theta}-{\it\zeta}_{{\it\theta}}\frac{\sin {\it\theta}}{r}\right)=w, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\zeta}={\it\eta}\quad \text{at }z=1+{\it\varepsilon}{\it\eta}. & \displaystyle\end{eqnarray}$$
For the sake of simplicity, in the subsequent derivation we impose the condition
${\it\delta}^{2}={\it\varepsilon}$
, although this is not the necessary condition. Indeed, variables can be scaled further to replace
${\it\delta}^{2}$
with
${\it\varepsilon}$
in the equations (Johnson Reference Johnson1997).
We look for a solution of this problem in the form of asymptotic multiple-scale expansions of the form
$$\begin{eqnarray}{\it\zeta}={\it\zeta}_{1}+{\it\varepsilon}{\it\zeta}_{2}+\cdots ,\end{eqnarray}$$
and similar expansions for other variables, where
$$\begin{eqnarray}{\it\zeta}_{1}=A({\it\xi},R,{\it\theta}){\it\phi}(z,{\it\theta}),\end{eqnarray}$$
with the following set of fast and slow variables:
$$\begin{eqnarray}\displaystyle {\it\xi}=rk({\it\theta})-st,\quad R={\it\varepsilon}rk({\it\theta}),\quad {\it\theta}={\it\theta}, & & \displaystyle\end{eqnarray}$$
where we define
$s$
to be the wave speed found assuming the absence of a shear flow (with
$k({\it\theta})=1$
), while for a given shear flow the function
$k({\it\theta})$
describes the distortion of the wavefront. The speed
$s$
and the function
$k({\it\theta})$
are to be determined. In this description, when a shear flow is present, the radial wave speed is not equal to
$s$
, but to
$s/k({\it\theta})$
. The choice of the fast and slow variables is similar to that in the derivation of the cKdV-type equation for the surface waves (Johnson Reference Johnson1990), with the formal range of asymptotic validity of the model being defined by the conditions
${\it\xi}\sim R\sim O(1)$
. To leading order, the wavefront at any fixed moment of time
$t$
is described by the equation
$$\begin{eqnarray}rk({\it\theta})=\text{constant},\end{eqnarray}$$
and we consider outward propagating ring waves, requiring that the function
$k({\it\theta})$
is strictly positive. By writing (2.28) we anticipate that the solution of the linearised problem allows for a modal decomposition, similar to the well-known result in the Cartesian geometry, but expect that it has a more complicated structure for the ring waves on a shear flow because of the loss of the radial symmetry in the problem formulation (the shear flow is parallel).
2.2 Amplitude equation
To leading order, assuming that perturbations of the basic state are caused only by the propagating wave, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle u_{1}=-A{\it\phi}u_{0z}\cos {\it\theta}-\frac{kF}{k^{2}+k^{^{\prime }2}}A{\it\phi}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v_{1}=A{\it\phi}u_{0z}\sin {\it\theta}-\frac{k^{\prime }F}{k^{2}+k^{^{\prime }2}}A{\it\phi}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w_{1}=A_{{\it\xi}}F{\it\phi}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{1}=\frac{{\it\rho}_{0}}{k^{2}+k^{^{\prime }2}}AF^{2}{\it\phi}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}_{1}=-{\it\rho}_{0z}A{\it\phi}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}_{1}=A{\it\phi}\quad \text{at }z=1, & \displaystyle\end{eqnarray}$$
where the function
${\it\phi}(z,{\it\theta})$
satisfies the following modal equations:
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{{\it\rho}_{0}F^{2}}{k^{2}+k^{^{\prime }2}}{\it\phi}_{z}\right)_{z}-{\it\rho}_{0z}{\it\phi}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{F^{2}}{k^{2}+k^{^{\prime }2}}{\it\phi}_{z}-{\it\phi}=0\quad \text{at }z=1, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}=0\quad \text{at }z=0, & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}F=-s+(u_{0}-c)(k\cos {\it\theta}-k^{\prime }\sin {\it\theta}),\end{eqnarray}$$
$k=k({\it\theta})$
and
$k^{\prime }=\text{d}k/\text{d}{\it\theta}$
. We now have fixed the speed of the moving coordinate frame
$c$
to be equal to the speed of the shear flow at the bottom,
$c=u_{0}(0)$
(then
$F=-s\neq 0$
at
$z=0$
, and the condition
$F{\it\phi}=0$
at
$z=0$
implies (2.39)). Of course, the physics does not depend on the choice of
$c$
(see a discussion in Johnson (Reference Johnson1990)), but our derivation shows that the mathematical formulation simplifies if we choose
$c=u_{0}(0)$
. For a given density stratification the values of the wave speed
$s$
of concentric waves, found assuming the absence of a shear flow (with
$k({\it\theta})=1$
), and the pair of functions
${\it\phi}(z,{\it\theta})$
and
$k({\it\theta})$
, found for a given shear flow, constitute solution of the modal equations (2.37)–(2.39). Assuming the absence of a shear flow, the modal equations (2.37)–(2.39) reduce to the modal equations for plane waves (e.g. Grimshaw Reference Grimshaw and Grimshaw2001, see also § 2.4). Therefore, the speed of the long concentric waves (in the absence of a shear flow) coincides with the speed of the long plane waves. Unlike the surface wave problem considered by Johnson (Reference Johnson1990), the exact form of the equations for the wave speed
$s$
and the function
$k({\it\theta})$
depends on the stratification. An example for the case of a two-layer fluid with a piecewise-constant current is discussed in § 3.
At
$O({\it\varepsilon})$
we obtain the following set of equations:
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\it\rho}_{0}\left(Fu_{2{\it\xi}}+u_{0z}w_{2}\cos {\it\theta}\right)+{\it\rho}_{1}\left(Fu_{1{\it\xi}}+u_{0z}w_{1}\cos {\it\theta}\right)+{\it\rho}_{0}\left[\vphantom{\displaystyle \frac{k}{R}}(F+s)u_{1R}\qquad \qquad \qquad \right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \left.\quad -\,(u_{0}-c)(u_{1{\it\theta}}-v_{1})\frac{k}{R}\sin {\it\theta}+(ku_{1}+k^{\prime }v_{1})u_{1{\it\xi}}+u_{1z}w_{1}\right]+k(p_{2{\it\xi}}+p_{1R})=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\it\rho}_{0}\left(Fv_{2{\it\xi}}-u_{0z}w_{2}\sin {\it\theta}\right)+{\it\rho}_{1}\left(Fv_{1{\it\xi}}-u_{0z}w_{1}\sin {\it\theta}\right)+{\it\rho}_{0}\left[\vphantom{\displaystyle \frac{k}{R}}(F+s)v_{1R}\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \left.\quad -\,(u_{0}-c)(v_{1{\it\theta}}+u_{1})\frac{k\sin {\it\theta}}{R}+(ku_{1}+k^{\prime }v_{1})v_{1{\it\xi}}+v_{1z}w_{1}\right]+\frac{kp_{1{\it\theta}}}{R}+k^{\prime }(p_{2{\it\xi}}+p_{1R})=0,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{2z}+{\it\rho}_{2}+{\it\rho}_{0}Fw_{1{\it\xi}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F{\it\rho}_{2{\it\xi}}+{\it\rho}_{0z}w_{2}+(F+s){\it\rho}_{1R}-(u_{0}-c)\frac{k}{R}{\it\rho}_{1{\it\theta}}\sin {\it\theta}+(ku_{1}+k^{\prime }v_{1}){\it\rho}_{1{\it\xi}}+w_{1}{\it\rho}_{1z}=0,\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle ku_{2{\it\xi}}+k^{\prime }v_{2{\it\xi}}+w_{2z}+ku_{1R}+\frac{k}{R}(v_{1{\it\theta}}+u_{1})+k^{\prime }v_{1R}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F{\it\zeta}_{2{\it\xi}}-w_{2}+(F+s){\it\zeta}_{1R}-(u_{0}-c)\frac{k}{R}{\it\zeta}_{1{\it\theta}}\sin {\it\theta}+(ku_{1}+k^{\prime }v_{1}){\it\zeta}_{1{\it\xi}}+w_{1}{\it\zeta}_{1z}=0; & \displaystyle\end{eqnarray}$$
and boundary conditions:
$$\begin{eqnarray}\displaystyle & \displaystyle w_{2}=0\quad \text{at }z=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{2}={\it\rho}_{0}{\it\eta}_{2}+{\textstyle \frac{1}{2}}{\it\rho}_{0z}{\it\eta}_{1}^{2}-{\it\eta}_{1}p_{1z}\quad \text{at }z=1, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle w_{2} & = & \displaystyle F{\it\eta}_{2{\it\xi}}+(F+s){\it\eta}_{1R}-(u_{0}-c)\frac{k}{R}{\it\eta}_{1{\it\theta}}\sin {\it\theta}\nonumber\\ \displaystyle & & \displaystyle +\,(ku_{1}+k^{\prime }v_{1}){\it\eta}_{1{\it\xi}}+F_{z}{\it\eta}_{1}{\it\eta}_{1{\it\xi}}-{\it\eta}_{1}w_{1z}\quad \text{at }z=1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\zeta}_{2}={\it\eta}_{2}-{\it\eta}_{1}{\it\zeta}_{1z}\quad \text{at }z=1. & \displaystyle\end{eqnarray}$$
Substituting the leading-order solution (2.28), (2.31)–(2.33) into (2.46) we obtain
$$\begin{eqnarray}w_{2}=F{\it\zeta}_{2{\it\xi}}+(F+s)A_{R}{\it\phi}-(u_{0}-c)\frac{k}{R}\sin {\it\theta}(A{\it\phi})_{{\it\theta}}-F_{z}{\it\phi}^{2}AA_{{\it\xi}}.\end{eqnarray}$$
Next, we find
$u_{2{\it\xi}}$
from (2.41) and
$v_{2{\it\xi}}$
from (2.42) and substitute them into (2.45), obtaining the following equation:
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-8.0pt}\displaystyle -(k^{2}+k^{\prime 2})p_{2{\it\xi}}+{\it\rho}_{0}(Fw_{2z}-F_{z}w_{2})={\it\rho}_{0}\left\{-\frac{k}{R}F(v_{1{\it\theta}}+u_{1})-(u_{0}-c)\frac{k}{R}\sin {\it\theta}[k(u_{1{\it\theta}}-v_{1})\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\left.k^{\prime }(v_{1{\it\theta}}+u_{1})]+s(ku_{1R}+k^{\prime }v_{1R})+\frac{1}{2}[(ku_{1}+k^{\prime }v_{1})^{2}]_{{\it\xi}}+(ku_{1}+k^{\prime }v_{1})_{z}w_{1}\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,{\it\rho}_{1}(Fw_{1z}-F_{z}w_{1})+(k^{2}+k^{^{\prime }2})p_{1R}+\frac{kk^{\prime }}{R}p_{1{\it\theta}}.\end{eqnarray}$$
On the other hand, finding
${\it\rho}_{2}$
from (2.43) and substituting it into (2.44) we get
$$\begin{eqnarray}\displaystyle Fp_{2z{\it\xi}}-{\it\rho}_{0z}w_{2}=-{\it\rho}_{0}F^{2}w_{1{\it\xi}{\it\xi}}+(F+s){\it\rho}_{1R}-(u_{0}-c)\frac{k}{R}{\it\rho}_{1{\it\theta}}\sin {\it\theta}+(ku_{1}+k^{\prime }v_{1}){\it\rho}_{1{\it\xi}}+{\it\rho}_{1z}w_{1}.\quad\end{eqnarray}$$
Equating the expressions for
$p_{2z{\it\xi}}$
from (2.52) and (2.53), using (2.51) to exclude
$w_{2}$
, substituting the leading-order solution (2.28), (2.31)–(2.36) and using the modal equation (2.37), we obtain the equation for
${\it\zeta}_{2}$
in the form
$$\begin{eqnarray}\left(\frac{{\it\rho}_{0}F^{2}}{k^{2}+k^{\prime 2}}{\it\zeta}_{2{\it\xi}z}\right)_{z}-{\it\rho}_{0z}{\it\zeta}_{2{\it\xi}}=M_{2},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \displaystyle -(k^{2}+k^{\prime 2})M_{2} & = & \displaystyle 2s({\it\rho}_{0}F{\it\phi}_{z})_{z}A_{R}+(k^{2}+k^{\prime 2}){\it\rho}_{0}F^{2}{\it\phi}A_{{\it\xi}{\it\xi}{\it\xi}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,[-(3{\it\rho}_{0}F^{2}{\it\phi}_{z}^{2})_{z}+2{\it\rho}_{0}F^{2}{\it\phi}_{z}{\it\phi}_{zz}+(2{\it\rho}_{0}F^{2}{\it\phi}{\it\phi}_{zz})_{z}]AA_{{\it\xi}}\nonumber\\ \displaystyle & & \displaystyle -\,\displaystyle \left\{{\it\rho}_{0}\left\{k(k+k^{\prime \prime })\left[\frac{F^{2}}{k^{2}+k^{\prime 2}}-\left(\frac{2k^{\prime }F}{k^{2}+k^{\prime 2}}+(u_{0}-c)\sin {\it\theta}\right)^{2}\right]{\it\phi}_{z}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,2kF\left.\left.\left(\frac{k^{\prime }F}{k^{2}+k^{\prime 2}}+(u_{0}-c)\sin {\it\theta}\right){\it\phi}_{z{\it\theta}}\right\}\right\}_{z}\frac{A}{R}\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\left\{2{\it\rho}_{0}kF\left[\frac{k^{\prime }F}{k^{2}+k^{\prime 2}}+(u_{0}-c)\sin {\it\theta}\right]{\it\phi}_{z}\right\}_{z}\frac{A_{{\it\theta}}}{R}.\end{eqnarray}$$
Next, substituting (2.51) into the boundary condition (2.47) and recalling that
${\it\phi}|_{z=0}=0$
, we obtain
$F{\it\zeta}_{2{\it\xi}}=0$
at
$z=0$
, implying that
$$\begin{eqnarray}{\it\zeta}_{2{\it\xi}}=0\quad \text{at }z=0,\end{eqnarray}$$
since
$F=-s$
at
$z=0$
by our choice of the constant
$c$
. The boundary condition (2.50) implies
$$\begin{eqnarray}{\it\eta}_{2}={\it\zeta}_{2}+A^{2}{\it\phi}{\it\phi}_{z}\quad \text{at }z=1.\end{eqnarray}$$
Substituting (2.57) into (2.48), we get
$$\begin{eqnarray}p_{2}={\it\rho}_{0}({\it\zeta}_{2}+A^{2}{\it\phi}{\it\phi}_{z})-\frac{A^{2}{\it\phi}}{k^{2}+k^{\prime 2}}({\it\rho}_{0z}F^{2}{\it\phi}_{z}+2{\it\rho}_{0}FF_{z}{\it\phi}_{z}+{\it\rho}_{0}F^{2}{\it\phi}_{zz})+\frac{1}{2}{\it\rho}_{0z}A^{2}{\it\phi}^{2}\quad \text{at }z=1.\end{eqnarray}$$
Substituting the expression (2.51) into (2.49), we obtain
$$\begin{eqnarray}F{\it\zeta}_{2{\it\xi}}=F{\it\eta}_{2{\it\xi}}-2FAA_{{\it\xi}}{\it\phi}{\it\phi}_{z},\end{eqnarray}$$
which coincides with the product of the partial derivative of
${\it\eta}_{2}$
in (2.57) with respect to
${\it\xi}$
with
$F$
. Therefore, the boundary condition (2.49) is the differential consequence of (2.57).
Differentiating (2.58) with respect to
${\it\xi}$
, using (2.52) to eliminate
$p_{2{\it\xi}}$
and using (2.49) to exclude
$w_{2}$
(all at
$z=1$
), we obtain
$$\begin{eqnarray}{\it\rho}_{0}\left[\frac{F^{2}}{k^{2}+k^{\prime 2}}{\it\zeta}_{2{\it\xi}z}-{\it\zeta}_{2{\it\xi}}\right]=N_{2}\quad \text{at }z=1,\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \displaystyle -(k^{2}+k^{\prime 2})N_{2} & = & \displaystyle 2s{\it\rho}_{0}F{\it\phi}_{z}A_{R}+[-3{\it\rho}_{0}F^{2}{\it\phi}_{z}^{2}+2{\it\rho}_{0}F^{2}{\it\phi}{\it\phi}_{zz}]AA_{{\it\xi}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,{\it\rho}_{0}\left\{k(k+k^{\prime \prime })\left[\frac{F^{2}}{k^{2}+k^{\prime 2}}-\left(\frac{2k^{\prime }F}{k^{2}+k^{\prime 2}}+(u_{0}-c)\sin {\it\theta}\right)^{2}\right]{\it\phi}_{z}\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,2kF\left.\left(\frac{k^{\prime }F}{k^{2}+k^{\prime 2}}+(u_{0}-c)\sin {\it\theta}\right){\it\phi}_{z{\it\theta}}\right\}\frac{A}{R}\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,2{\it\rho}_{0}kF\left[\frac{k^{\prime }F}{k^{2}+k^{\prime 2}}+(u_{0}-c)\sin {\it\theta}\right]{\it\phi}_{z}\frac{A_{{\it\theta}}}{R}.\end{eqnarray}$$
Thus, we obtain the non-homogeneous equation (2.54) for the function
${\it\zeta}_{2{\it\xi}}$
with the boundary conditions (2.56), (2.60). The compatibility condition
$$\begin{eqnarray}\int _{0}^{1}M_{2}{\it\phi}\,\text{d}z-[N_{2}{\it\phi}]_{z=1}=0\end{eqnarray}$$
yields the
$2+1$
-dimensional evolution equation for the slowly varying amplitude of the ring wave in the form
$$\begin{eqnarray}{\it\mu}_{1}A_{R}+{\it\mu}_{2}AA_{{\it\xi}}+{\it\mu}_{3}A_{{\it\xi}{\it\xi}{\it\xi}}+{\it\mu}_{4}\frac{A}{R}+{\it\mu}_{5}\frac{A_{{\it\theta}}}{R}=0,\end{eqnarray}$$
where the coefficients are given in terms of the solutions of the modal equations (2.37)–(2.39) by the following formulae:
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{1}=2s\int _{0}^{1}{\it\rho}_{0}F{\it\phi}_{z}^{2}\,\text{d}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{2}=-3\int _{0}^{1}{\it\rho}_{0}F^{2}{\it\phi}_{z}^{3}\,\text{d}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{3}=-(k^{2}+k^{\prime 2})\int _{0}^{1}{\it\rho}_{0}F^{2}{\it\phi}^{2}\,\text{d}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{4}=-\int _{0}^{1}\left\{\frac{{\it\rho}_{0}{\it\phi}_{z}^{2}k(k+k^{\prime \prime })}{(k^{2}+k^{\prime 2})^{2}}\left((k^{2}-3k^{\prime 2})F^{2}-4k^{\prime }(k^{2}+k^{\prime 2})(u_{0}-c)\sin {\it\theta}F\right.\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left.\left.~~-\,\sin ^{2}{\it\theta}(u_{0}-c)^{2}(k^{2}+k^{\prime 2})^{2}\right)+\frac{2{\it\rho}_{0}k}{k^{2}+k^{\prime 2}}F{\it\phi}_{z}{\it\phi}_{z{\it\theta}}(k^{\prime }F+(k^{2}+k^{\prime 2})(u_{0}-c)\sin {\it\theta})\hspace{-0.5pt}\right\}\text{d}z, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{5}=-\frac{2k}{k^{2}+k^{\prime 2}}\int _{0}^{1}{\it\rho}_{0}F{\it\phi}_{z}^{2}[k^{\prime }F+(u_{0}-c)(k^{2}+k^{\prime 2})\sin {\it\theta}]\,\text{d}z. & \displaystyle\end{eqnarray}$$
2.3 Reduction
$1$
: surface ring waves over a shear flow in a homogeneous fluid
Let us now consider a reduction of the derived equation (2.63) to the case of surface ring waves in a homogeneous fluid, studied by Johnson (Reference Johnson1980, Reference Johnson1990). Here,
${\it\rho}_{0}$
is a constant and we normalise
${\it\phi}$
by setting
${\it\phi}=1$
at
$z=1$
. The wave speed
$s$
, in the absence of a shear flow, as well as the function
$k({\it\theta})$
and the modal function
${\it\phi}$
, for a given shear flow, can be easily found from the modal equations (2.37)–(2.39). Indeed, the modal function
${\it\phi}$
is given by
$$\begin{eqnarray}{\it\phi}=(k^{2}+k^{\prime 2})\int _{0}^{z}\frac{1}{F^{2}}\,\text{d}z.\end{eqnarray}$$
Assuming first that there is no shear flow, we set
$k=1$
,
$u_{0}(z)=c=0$
, and the normalisation condition
${\it\phi}=1$
at
$z=1$
then implies
$$\begin{eqnarray}\int _{0}^{1}\frac{1}{s^{2}}\,\text{d}z=1\Longrightarrow s^{2}=1.\end{eqnarray}$$
Thus, we recover that the wave speed of the outward propagating surface ring wave in the absence of a shear flow is equal to
$1$
. Next, let us assume that there is a shear flow, then
$F=-1+(u_{0}-c)(k\cos {\it\theta}-k^{\prime }\sin {\it\theta})$
. Requiring again that
${\it\phi}=1$
at
$z=1$
we obtain the equation
$$\begin{eqnarray}(k^{2}+k^{\prime 2})\int _{0}^{1}\frac{1}{F^{2}}\,\text{d}z=1,\end{eqnarray}$$
which, of course, coincides with the generalised Burns condition (Johnson Reference Johnson1990).
The generalised Burns condition (2.71) constitutes a nonlinear first-order differential equation for the function
$k({\it\theta})$
. The function relevant to the ring wave is provided by the singular solution (the envelope of the general solution) of this equation (Johnson Reference Johnson1990, Reference Johnson1997):
$$\begin{eqnarray}\displaystyle & \displaystyle k({\it\theta})=a\cos ({\it\theta})+b(a)\sin ({\it\theta}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0=\cos {\it\theta}+b^{\prime }(a)\sin {\it\theta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle [a^{2}+b^{2}(a)]\int _{0}^{1}\frac{\text{d}z}{[1-(u_{0}(z)-c)a]^{2}}=1. & \displaystyle\end{eqnarray}$$
Indeed, the general solution
$k({\it\theta})=a\cos {\it\theta}+b(a)\sin {\it\theta}=\sqrt{a^{2}+b(a)^{2}}\sin ({\it\theta}+{\it\varphi}),$
where
$a$
is an arbitrary constant,
$b(a)$
is a constant defined by formula (2.74) and
$\tan {\it\varphi}=a/b(a)$
, cannot describe an outward propagating ring wave since
$\sin ({\it\theta}+{\it\varphi})$
is not strictly positive. However, (2.71) also has a singular solution (an additional solution, not described by the general solution but instead given by its envelope), defined by formulae (2.72)–(2.74), where
$a=a({\it\theta})$
. The singular solution does not have any free parameters and has the desired property (see Johnson Reference Johnson1990, Reference Johnson1997).
Differentiating the generalised Burns condition, we obtain
$$\begin{eqnarray}2(k+k^{\prime \prime })\int _{0}^{1}\frac{k^{\prime }F+(u_{0}-c)(k^{2}+k^{\prime 2})\sin {\it\theta}}{F^{3}}\,\text{d}z=0.\end{eqnarray}$$
Since
$k+k^{\prime \prime }\neq 0$
on the singular solution, then
$$\begin{eqnarray}{\it\mu}_{5}=-2{\it\rho}_{0}k(k^{2}+k^{\prime 2})\int _{0}^{1}\frac{k^{\prime }F+(u_{0}-c)(k^{2}+k^{\prime 2})\sin {\it\theta}}{F^{3}}\,\text{d}z=0.\end{eqnarray}$$
Thus, the derived amplitude equation (2.63) reduces to the form of the
$1+1$
-dimensional cKdV-type equation (i.e.
${\it\mu}_{5}=0$
) for any shear flow, and not just for stationary and constant shear flows, as previously thought (Johnson Reference Johnson1990, Reference Johnson1997).
Substituting the modal function (2.69) into the expressions for the remaining coefficients (2.64)–(2.67), the amplitude equation can be written as
$$\begin{eqnarray}\tilde{{\it\mu}}_{1}A_{R}+\tilde{{\it\mu}}_{2}AA_{{\it\xi}}+\tilde{{\it\mu}}_{3}A_{{\it\xi}{\it\xi}{\it\xi}}+\frac{\tilde{{\it\mu}}_{4}}{R}A=0,\end{eqnarray}$$
and the expressions for the coefficients can be brought to the previously known form (Johnson Reference Johnson1990):
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{{\it\mu}}_{1}=2(k^{2}+k^{\prime 2})I_{3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{{\it\mu}}_{2}=-3(k^{2}+k^{\prime 2})^{2}I_{4}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{{\it\mu}}_{3}=-(k^{2}+k^{\prime 2})^{2}\int _{0}^{1}\int _{z}^{1}\int _{0}^{z_{1}}\frac{F^{2}(z_{1},{\it\theta})}{F^{2}(z,{\it\theta})F^{2}(z_{2},{\it\theta})}\,\text{d}z_{2}\,\text{d}z_{1}\,\text{d}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \tilde{{\it\mu}}_{4} & = & \displaystyle \frac{-k(k+k^{\prime \prime })}{k\cos {\it\theta}-k^{\prime }\sin {\it\theta}}((k\cos {\it\theta}+3k^{\prime }\sin {\it\theta})I_{2}+4k^{\prime }\sin {\it\theta}I_{3})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3k(k+k^{\prime \prime })(k^{2}+k^{\prime 2})\sin ^{2}{\it\theta}}{(k\cos {\it\theta}-k^{\prime }\sin {\it\theta})^{2}}(I_{2}+2I_{3}+I_{4}),\end{eqnarray}$$
where
$$\begin{eqnarray}I_{n}=\int _{0}^{1}\frac{\,\text{d}z}{F^{n}},\quad \tilde{{\it\mu}}_{i}=\frac{{\it\mu}_{i}}{k^{2}+k^{\prime 2}},\quad i=\overline{1,4}.\end{eqnarray}$$
We note that unlike the formula for
$\tilde{{\it\mu}}_{3}$
above, our representation of the coefficients by the formulae (2.64)–(2.67) does not involve multiple integrals.
2.4 Reduction
$2$
: interfacial concentric waves in the absence of a shear flow
Let us now consider another reduction of the derived equation (2.63). If there is no shear flow, i.e.
$u_{0}(z)=0$
, the ring waves become concentric waves. Here,
$F=-s$
,
$k({\it\theta})=1$
and
$k^{\prime }({\it\theta})=0$
. Then
${\it\mu}_{5}=0$
, and the derived equation (2.63) again reduces to the form of the
$1+1$
-dimensional cKdV-type equation:
$$\begin{eqnarray}\tilde{{\it\mu}}_{1}A_{R}+\tilde{{\it\mu}}_{2}AA_{{\it\xi}}+\tilde{{\it\mu}}_{3}A_{{\it\xi}{\it\xi}{\it\xi}}+\frac{\tilde{{\it\mu}}_{4}}{R}A=0,\end{eqnarray}$$
and expressions for the coefficients are given by
$$\begin{eqnarray}\displaystyle \tilde{{\it\mu}}_{1}=2\int _{0}^{1}{\it\rho}_{0}{\it\phi}_{z}^{2}\,\text{d}z,\quad \tilde{{\it\mu}}_{2}=3\int _{0}^{1}{\it\rho}_{0}{\it\phi}_{z}^{3}\,\text{d}z,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{{\it\mu}}_{3}=\int _{0}^{1}{\it\rho}_{0}{\it\phi}^{2}\,\text{d}z,\quad \tilde{{\it\mu}}_{4}=\int _{0}^{1}{\it\rho}_{0}{\it\phi}_{z}^{2}\,\text{d}z,\end{eqnarray}$$
where
$$\begin{eqnarray}\tilde{{\it\mu}}_{i}=-\frac{{\it\mu}_{i}}{s^{2}},\quad i=\overline{1,4}.\end{eqnarray}$$
Here,
${\it\phi}={\it\phi}(z)$
is the modal function, satisfying the same equations as in Cartesian geometry:
$$\begin{eqnarray}\displaystyle & \displaystyle (s^{2}{\it\rho}_{0}{\it\phi}_{z})_{z}-{\it\rho}_{0z}{\it\phi}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle s^{2}{\it\phi}_{z}-{\it\phi}=0\quad \text{at }z=1, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\phi}=0\quad \text{at }z=0. & \displaystyle\end{eqnarray}$$
This reduction agrees with the equation previously derived by Lipovskii (Reference Lipovskii1985).
Thus, in both cases the derived amplitude equation (2.63) correctly reduces to the previously derived models. Importantly, in both of these previously studied cases the coefficient
${\it\mu}_{5}=0$
. However, it is not equal to zero in the general case of the waves in a stratified fluid with a shear flow. Interestingly, Johnson has caught the ‘ghost’ of the additional term in his study of the surface waves on a shear flow. However, as we noted earlier, the complicated formula for the coefficient
${\it\mu}_{5}$
given by Johnson (Reference Johnson1990) will lead to a zero coefficient for any shear flow.
3 Two-layer example: dispersion relation and wavefronts
3.1 Two-layer model
In order to clarify the general theory developed in the previous section and to illustrate the different effect of a shear flow on the wavefronts of surface and internal ring waves, here we discuss a simple piecewise-constant setting, frequently used in theoretical and laboratory studies of long internal and surface waves (figure 3; see, for example, Long Reference Long1955; Lee & Beardsley Reference Lee and Beardsley1974; Miyata Reference Miyata1985; Weidman & Zakhem Reference Weidman and Zakhem1988; Choi & Camassa Reference Choi and Camassa1999; Ramirez et al. Reference Ramirez, Renouard and Stepanyants2002; Choi Reference Choi2006; Grue Reference Grue, Grue and Trulsen2006; Voronovich et al. Reference Voronovich, Sazonov and Shrira2006; Chumakova et al. Reference Chumakova, Menzaque, Milewski, Rosales, Tabak and Turner2009; Alias, Grimshaw & Khusnutdinova Reference Alias, Grimshaw and Khusnutdinova2014; Arkhipov, Safarova & Khabakhpashev Reference Arkhipov, Safarova and Khabakhpashev2014; Boonkasame & Milewski Reference Boonkasame and Milewski2014 and references therein). In these theoretical and laboratory studies, the model is often chosen to yield explicit formulae, but is regarded as a reasonable abstraction for a background flow with smooth density and shear profiles across the interface, in the long-wave approximation. It is also necessary to note that this background flow is subject to Kelvin–Helmholtz (K–H) instability arising as short waves, which is excluded in the consideration of a long wave over a sufficiently weak shear flow both because the two-layer model is an abstraction of the actual continuous density and shear flow profiles, and due to the large separation of scales (see Turner Reference Turner1973; Craik Reference Craik1985; Drazin & Reed Reference Drazin and Reed2004 and references therein). The stability condition for the long waves in a fluid of finite depth is briefly discussed in appendix A.
Figure 3. The two-layer model.
Here, in non-dimensional form, both the density of the fluid and the shear flow are piecewise-constant functions (
$0\leqslant z\leqslant 1$
):
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}_{0}={\it\rho}_{2}H(z)+({\it\rho}_{1}-{\it\rho}_{2})H(z-d), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{0}=U_{2}H(z)+(U_{1}-U_{2})H(z-d), & \displaystyle\end{eqnarray}$$
where
$d$
is the thickness of the lower layer and
$H(z)$
is the Heaviside function.
3.2 Dispersion relation and approximations
Solution of the modal equations (2.37)–(2.39) in the two layers is given by the linear functions of
$z$
(
${\it\phi}_{1}$
is the modal function in the upper layer and
${\it\phi}_{2}$
is the modal function in the lower layer):
$$\begin{eqnarray}{\it\phi}_{1}=\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+z-1\right){\it\Lambda},\quad {\it\phi}_{2}=\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)\frac{{\it\Lambda}z}{d},\end{eqnarray}$$
where
${\it\Lambda}$
is a parameter and the continuity of
${\it\phi}$
is satisfied, while the jump condition at the interface,
$$\begin{eqnarray}\frac{\left[{\it\rho}_{0}F^{2}{\it\phi}_{z}\right]}{k^{2}+k^{\prime 2}}=[{\it\rho}_{0}]{\it\phi}\quad \text{at }z=d,\end{eqnarray}$$
provides the ‘dispersion relation’,
$$\begin{eqnarray}({\it\rho}_{2}-{\it\rho}_{1})d(1-d)(k^{2}+k^{\prime 2})^{2}-{\it\rho}_{2}[dF_{1}^{2}+(1-d)F_{2}^{2}](k^{2}+k^{\prime 2})+{\it\rho}_{2}F_{1}^{2}F_{2}^{2}=0,\end{eqnarray}$$
with
$F_{1}=-s+(U_{1}-U_{2})(k\cos {\it\theta}-k^{\prime }\sin {\it\theta}),F_{2}=-s$
. This nonlinear first-order differential equation for the function
$k({\it\theta})$
is a further generalisation of both the Burns and generalised Burns conditions (Burns Reference Burns1953; Johnson Reference Johnson1990). First, we assume that there is no shear flow and find the wave speed
$s$
by letting
$U_{1}=U_{2}=0$
, while
$k=1$
. The dispersion relation takes the standard form
$$\begin{eqnarray}{\it\rho}_{2}s^{4}-{\it\rho}_{2}s^{2}+({\it\rho}_{2}-{\it\rho}_{1})d(1-d)=0.\end{eqnarray}$$
Therefore, the wave speed in the absence of the shear flow is given by
$$\begin{eqnarray}s^{2}=\frac{{\it\rho}_{2}\pm \sqrt{{\it\rho}_{2}^{2}-4{\it\rho}_{2}({\it\rho}_{2}-{\it\rho}_{1})d(1-d)}}{2{\it\rho}_{2}}=\frac{1\pm \sqrt{(2d-1)^{2}+4{\it\rho}_{1}/{\it\rho}_{2}d(1-d)}}{2},\end{eqnarray}$$
where the upper sign should be chosen for the faster surface mode and the lower sign for the slower internal mode. For example, if
${\it\rho}_{1}=1,{\it\rho}_{2}=1.2$
and
$d=0.5$
, we obtain
$s_{sur}\approx 0.98$
and
$s_{int}\approx 0.21$
.
When the shear flow is present, equation (3.5) constitutes a nonlinear first-order differential equation for the function
$k({\it\theta})$
. We have
$$\begin{eqnarray}k^{2}+k^{\prime 2}=\frac{{\it\rho}_{2}[dF_{1}^{2}+(1-d)F_{2}^{2}]\pm \sqrt{{\it\Delta}}}{2({\it\rho}_{2}-{\it\rho}_{1})(1-d)d},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle {\it\Delta} & = & \displaystyle {\it\rho}_{2}^{2}[dF_{1}^{2}+(1-d)F_{2}^{2}]^{2}-4{\it\rho}_{2}({\it\rho}_{2}-{\it\rho}_{1})d(1-d)F_{1}^{2}F_{2}^{2}\nonumber\\ \displaystyle & = & \displaystyle {\it\rho}_{2}^{2}[dF_{1}^{2}-(1-d)F_{2}^{2}]^{2}+4{\it\rho}_{1}{\it\rho}_{2}d(1-d)F_{1}^{2}F_{2}^{2}\geqslant 0,\end{eqnarray}$$
and the upper/lower signs correspond to the internal/surface modes respectively.
The generalised Burns condition for the surface waves in a homogeneous fluid with this two-layer shear flow takes the form
$$\begin{eqnarray}(k^{2}+k^{\prime 2})\left(\frac{1-d}{F_{1}^{2}}+\frac{d}{F_{2}^{2}}\right)=1\quad \Leftrightarrow \quad [dF_{1}^{2}+(1-d)F_{2}^{2}](k^{2}+k^{\prime 2})=F_{1}^{2}F_{2}^{2},\end{eqnarray}$$
and can be recovered from our more general equation (3.5) in the limit
${\it\rho}_{2}-{\it\rho}_{1}\rightarrow 0$
.
If the density contrast is small,
${\it\rho}_{2}-{\it\rho}_{1}\ll {\it\rho}_{1},{\it\rho}_{2}$
, one can obtain a simplified equation not only for the surface mode (see (3.10)), but also for the interfacial mode, by replacing the free surface condition (2.38) with the rigid lid approximation,
$$\begin{eqnarray}{\it\phi}=0\quad \text{at }z=1.\end{eqnarray}$$
Then, the modal functions
${\it\phi}$
in the two layers are found to be
$$\begin{eqnarray}{\it\phi}_{1}={\it\Lambda}(z-1),\quad {\it\phi}_{2}=\frac{d-1}{d}{\it\Lambda}z,\end{eqnarray}$$
where
${\it\Lambda}$
is a constant, and the jump condition at
$z=d$
again provides the ‘dispersion relation’:
$$\begin{eqnarray}({\it\rho}_{2}-{\it\rho}_{1})d(1-d)(k^{2}+k^{\prime 2})={\it\rho}_{1}dF_{1}^{2}+{\it\rho}_{2}(1-d)F_{2}^{2}.\end{eqnarray}$$
Remarkably, the required singular solution
$k({\it\theta})$
of the differential equation (3.13) can be found explicitly, in the following form:
$$\begin{eqnarray}\displaystyle \displaystyle k({\it\theta}) & = & \displaystyle \text{sign}(\cos {\it\theta})\sqrt{\frac{1-{\it\alpha}(U_{1}-U_{2})+{\it\alpha}^{2}s^{2}}{1+(1-{\it\alpha}(U_{1}-U_{2}))\tan ^{2}{\it\theta}}}\left(\frac{\cos {\it\theta}}{1-{\it\alpha}(U_{1}-U_{2})}+\frac{\sin ^{2}{\it\theta}}{\cos {\it\theta}}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\frac{{\it\alpha}s\cos {\it\theta}}{1-{\it\alpha}(U_{1}-U_{2})},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle {\it\alpha}=\frac{{\it\rho}_{1}(U_{1}-U_{2})}{(1-d)({\it\rho}_{2}-{\it\rho}_{1})},\quad s^{2}=\frac{({\it\rho}_{2}-{\it\rho}_{1})d(1-d)}{{\it\rho}_{1}d+{\it\rho}_{2}(1-d)}. & & \displaystyle\end{eqnarray}$$
The solution (3.14) can be verified directly, by substituting it into (3.13). It is shown in figure 7 for the parameters
${\it\rho}_{1}=1,{\it\rho}_{2}=1.2,d=0.5$
and
$U_{1}-U_{2}=0.1$
.
Let us note that equations asymptotically equivalent to both approximate equations (3.10) and (3.13) can be formally obtained from the full dispersion relation (3.5) if we first solve it as a quadratic equation with respect to
$k^{2}+k^{\prime 2}$
, see (3.8), and then Taylor expand
$\sqrt{{\it\Delta}}$
in powers of the small parameter
$({\it\rho}_{2}-{\it\rho}_{1})/{\it\rho}_{2}$
:
$$\begin{eqnarray}k^{2}+k^{\prime 2}=\frac{{\it\rho}_{2}[dF_{1}^{2}+(1-d)F_{2}^{2}]}{2({\it\rho}_{2}-{\it\rho}_{1})(1-d)d}\left[1\pm \left(1+2\frac{({\it\rho}_{2}-{\it\rho}_{1})d(1-d)F_{1}^{2}F_{2}^{2}}{{\it\rho}_{2}[dF_{1}^{2}+(1-d)F_{2}^{2}]^{2}}+\cdots \right)\right].\end{eqnarray}$$
The approximate equations (3.10) and (3.13) correspond to the lower and upper signs in the above equation respectively.
3.3 Wavefronts
The general solution of (3.5) can be found in a form similar to the general solution of the generalised Burns condition (Johnson Reference Johnson1990), allowing us then to find the necessary singular solution relevant to the ring waves in a stratified fluid in the form
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}k({\it\theta})=a\cos {\it\theta}+b(a)\sin {\it\theta},\\ b^{\prime }(a)=-1/\tan {\it\theta},\\ a^{2}+b^{2}(a)=\displaystyle \frac{{\it\rho}_{2}[d(-s+a(U_{1}-U_{2}))^{2}+(1-d)s^{2}]\pm \sqrt{{\it\Delta}}}{2({\it\rho}_{2}-{\it\rho}_{1})d(1-d)},\end{array}\!\right\}\end{eqnarray}$$
where
$$\begin{eqnarray}{\it\Delta}={\it\rho}_{2}^{2}\left[d(-s+a(U_{1}-U_{2}))^{2}-(1-d)s^{2}\right]^{2}+4{\it\rho}_{1}{\it\rho}_{2}d(1-d)s^{2}\left[-s+a(U_{1}-U_{2})\right]^{2}.\end{eqnarray}$$
Therefore,
$$\begin{eqnarray}0\leqslant {\it\Delta}\leqslant {\it\rho}_{2}[d(-s+a(U_{1}-U_{2}))^{2}+(1-d)s^{2}].\end{eqnarray}$$
The upper sign should be chosen in (3.17) for the interfacial mode and the lower sign for the surface mode, as previously discussed. In what follows, the singular solution
$k=k({\it\theta})$
is given in parametric form:
$k=k(a),{\it\theta}={\it\theta}(a)$
, where
$a$
is a parameter.
Let us denote
$$\begin{eqnarray}a^{2}+b^{2}=\frac{{\it\rho}_{2}[d(-s+a(U_{1}-U_{2}))^{2}+(1-d)s^{2}]\pm \sqrt{{\it\Delta}}}{2({\it\rho}_{2}-{\it\rho}_{1})d(1-d)}=Q,\quad \text{where }b=b(a).\end{eqnarray}$$
Then the condition
$b^{2}=Q-a^{2}\geqslant 0$
determines the domain of
$a\in [a_{min},a_{max}]$
. We require
$k({\it\theta})$
to be positive everywhere to describe the outward propagating ring wave. Therefore, one needs to choose the interval
$[a_{min},a_{max}]$
containing
$a=0$
, since
$a$
should take both positive and negative values (in particular,
$k({\it\theta})$
should be positive at both
${\it\theta}=0$
and
${\it\theta}={\rm\pi}$
). Then,
$$\begin{eqnarray}2bb^{\prime }=Q_{a}-2a,\quad \Rightarrow b^{\prime }=\frac{Q_{a}-2a}{2b},\quad \Rightarrow \tan {\it\theta}=-\frac{2b}{Q_{a}-2a}.\end{eqnarray}$$
Therefore,
$k(a)=k({\it\theta}(a))$
can be written in the form
$$\begin{eqnarray}\displaystyle k(a)=a\cos {\it\theta}+b\sin {\it\theta}=\cos {\it\theta}(a+b\tan {\it\theta})=\text{sign}\left(-2b\frac{\cos {\it\theta}}{\tan {\it\theta}}\right)\frac{aQ_{a}-2Q}{\sqrt{(Q_{a}-2a)^{2}+4b^{2}}}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Since
$k(a)>0$
, we obtain
$$\begin{eqnarray}\text{sign}(k(a))=-\text{sign}\left[b(aQ_{a}-2Q)\frac{\cos {\it\theta}}{\tan {\it\theta}}\right]=1.\end{eqnarray}$$
When there is no shear flow,
$aQ_{a}-2Q=-2Q<0$
. Therefore, it is natural to assume that this inequality will continue to hold in the case of the relatively weak shear flow considered here, and check that it is satisfied once the solution is constructed. Moreover, in the particular case of small density contrast,
${\it\rho}_{2}-{\it\rho}_{1}\ll {\it\rho}_{1,2}$
and
$d\sim 0.5$
, this condition can be verified directly using the approximation (3.13) for the interfacial mode, which we do not discuss in detail here.
Thus, we assume that
$aQ_{a}-2Q<0$
in the interval
$[a_{min},a_{max}]$
. Then
$$\begin{eqnarray}k(a)=-\frac{aQ_{a}-2Q}{\sqrt{(Q_{a}-2a)^{2}+4b^{2}}}\end{eqnarray}$$
and
$$\begin{eqnarray}\text{sign}(b)=\text{sign}\left(\frac{\cos {\it\theta}}{\tan {\it\theta}}\right)=\text{sign}\left(\frac{\cos ^{2}{\it\theta}}{\sin {\it\theta}}\right)=\left\{\begin{array}{@{}ll@{}}1 & \text{if }{\it\theta}\in (0,{\rm\pi}),\\ -1 & \text{if }{\it\theta}\in ({\rm\pi},2{\rm\pi}).\end{array}\right.\end{eqnarray}$$
Therefore, if
${\it\theta}\in (0,{\rm\pi})$
, then
$$\begin{eqnarray}b=\sqrt{Q-a^{2}},\quad \tan {\it\theta}=-\frac{2\sqrt{Q-a^{2}}}{Q_{a}-2a},\end{eqnarray}$$
and we let
$$\begin{eqnarray}{\it\theta}=\left\{\begin{array}{@{}ll@{}}\displaystyle \arctan \left(-\frac{2\sqrt{Q-a^{2}}}{Q_{a}-2a}\right) & \text{if }Q_{a}-2a<0,\\ \displaystyle \arctan \left(-\frac{2\sqrt{Q-a^{2}}}{Q_{a}-2a}\right)+{\rm\pi} & \text{if }Q_{a}-2a>0.\end{array}\right.\end{eqnarray}$$
Similarly, if
${\it\theta}\in ({\rm\pi},2{\rm\pi})$
, then
$$\begin{eqnarray}b=-\sqrt{Q-a^{2}},\quad \tan {\it\theta}=\frac{2\sqrt{Q-a^{2}}}{Q_{a}-2a},\end{eqnarray}$$
and we let
$$\begin{eqnarray}{\it\theta}=\left\{\begin{array}{@{}ll@{}}\displaystyle \arctan \left(\frac{2\sqrt{Q-a^{2}}}{Q_{a}-2a}\right)+{\rm\pi} & \text{if }Q_{a}-2a>0,\\ \displaystyle \arctan \left(\frac{2\sqrt{Q-a^{2}}}{Q_{a}-2a}\right)+2{\rm\pi} & \text{if }Q_{a}-2a<0.\end{array}\right.\end{eqnarray}$$
Thus, we obtain the required singular solution analytically, in parametric form. The functions
$k(a),{\it\theta}(a)$
and
$k({\it\theta})$
for both surface and interfacial ring waves are shown in figures 4–6 respectively. As before, we let
${\it\rho}_{1}=1$
,
${\it\rho}_{2}=1.2$
and
$d=0.5$
, and consider several values of the strength of the shear flow.
Figure 4. The function
$k(a)$
. (a) Surface mode:
$U_{1}-U_{2}=0$
(circles),
$U_{1}-U_{2}=0.2$
(plus signs),
$U_{1}-U_{2}=0.3$
(stars) and
$U_{1}-U_{2}=0.4$
(triangles). (b) Interfacial mode:
$U_{1}-U_{2}=0$
(circles),
$U_{1}-U_{2}=0.1$
(plus signs),
$U_{1}-U_{2}=0.15$
(stars) and
$U_{1}-U_{2}=0.2$
(triangles).
Figure 5. The function
${\it\theta}(a)$
. (a) Surface mode:
$U_{1}-U_{2}=0$
(circles),
$U_{1}-U_{2}=0.2$
(plus signs),
$U_{1}-U_{2}=0.3$
(stars) and
$U_{1}-U_{2}=0.4$
(triangles). (b) Interfacial mode:
$U_{1}-U_{2}=0$
(circles),
$U_{1}-U_{2}=0.1$
(plus signs),
$U_{1}-U_{2}=0.15$
(stars) and
$U_{1}-U_{2}=0.2$
(triangles).
Figure 6. The function
$k({\it\theta})$
. (a) Surface mode:
$U_{1}-U_{2}=0$
(circles),
$U_{1}-U_{2}=0.2$
(plus signs),
$U_{1}-U_{2}=0.3$
(stars) and
$U_{1}-U_{2}=0.4$
(triangles). (b) Interfacial mode:
$U_{1}-U_{2}=0$
(circles),
$U_{1}-U_{2}=0.1$
(plus signs),
$U_{1}-U_{2}=0.15$
(stars) and
$U_{1}-U_{2}=0.2$
(triangles).
We also compare the approximate solution (3.14) for the internal waves with the exact solution (3.17) in figure 7, for the case when
$U_{1}-U_{2}=0.1$
. We can see that the simpler approximate solution is rather close to the exact solution, with the advantage that the function
$k$
can be written explicitly as a function of
${\it\theta}$
.
Next, we note that to leading order, the radial wave speed is given by
$s/k({\it\theta})$
. As discussed before, wavefronts are described by the equation
$rk({\it\theta})=$
constant. In figures 8 and 9 we show the wavefronts for the surface mode and interfacial mode of (3.5) respectively, for
${\it\rho}_{1}=1,{\it\rho}_{2}=1.2,d=0.5$
and several values of the strength of the shear flow.
Figure 8. Wavefronts of surface ring waves described by
$k({\it\theta})r=50$
(
${\it\varepsilon}=0.02$
and
$R=1$
).
Figure 9. Wavefronts of interfacial ring waves described by
$k({\it\theta})r=50$
(
${\it\varepsilon}=0.02$
and
$R=1$
).
We see that the shear flow has very different effects on the surface and internal ring waves: the surface ring waves shown in figure 8 are elongated in the direction of the shear flow, while the interfacial ring waves shown in figure 9 are squeezed in the direction of the flow. We note that, in a different setting, deformation of linear surface waves by a sheared current was recently discussed by Ellingsen (Reference Ellingsen2014a
,Reference Ellingsen
b
). We also note that when the value of
$U_{1}-U_{2}$
is increased, there is a threshold after which the equation for
$k({\it\theta})$
corresponding to interfacial waves does not have a real-valued solution. This value coincides with the critical value given by (A 1).
To understand why this happens, we consider the behaviour of
$k({\it\theta})$
around the angles
${\it\theta}=0,{\rm\pi}$
. Locally, in the area around the angles
${\it\theta}=0,{\rm\pi}$
, the ring waves can be treated as plane waves over a shear flow (propagating along or opposite to the flow). The modal equation is given by Grimshaw (Reference Grimshaw and Grimshaw2001):
$$\begin{eqnarray}\displaystyle & ({\it\rho}_{0}(C-u_{0})^{2}{\it\phi}_{z})_{z}-{\it\rho}_{0z}{\it\phi}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (C-u_{0})^{2}{\it\phi}_{z}-{\it\phi}=0\quad \text{at}~z=1, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\phi}=0\quad \text{at}~z=0. & \displaystyle\end{eqnarray}$$
In the two-layer case, the dispersion relation takes the form
$$\begin{eqnarray}d{\it\rho}_{1}(C-U_{1})^{2}-{\it\rho}_{2}(C-U_{2})^{2}(d-1+(C-U_{1})^{2})=d({\it\rho}_{1}-{\it\rho}_{2})(d-1+(C-U_{1})^{2}).\end{eqnarray}$$
This dispersion relation also follows from the results obtained by Ovsyannikov (Reference Ovsyannikov1979) for the free surface two-layer shallow-water model. Substituting the coefficients
${\it\rho}_{1}=1,{\it\rho}_{2}=1.2,~d=0.5$
into the general solution of this quartic equation, one obtains the following formula for the wave speed
$C$
:
$$\begin{eqnarray}C=\frac{U_{1}+U_{2}}{2}\pm \frac{1}{6}\sqrt{9(U_{1}-U_{2})^{2}\pm 3\sqrt{72(U_{1}-U_{2})^{2}+30}+18}.\end{eqnarray}$$
Letting the Cartesian coordinate frame move at the speed
$U_{2}$
, we now plot the four solutions for the wave speed
$C$
in figure 10. Here, the top and bottom curves show the speeds of surface waves, propagating along and opposite to the shear flow, while the curves in between show the speeds of the slower moving internal waves. Both surface and internal waves can propagate when there is no shear flow (
$U_{1}=0$
). When the strength of the shear flow is increased (
$U_{1}>0$
), the difference between the speeds of the surface waves along and opposite to the flow increases, while the similar difference for the internal waves decreases. This indicates that the wavefronts of the surface waves become elongated in the direction of the flow, while the wavefronts of the internal waves are indeed squeezed in this direction. The graph also shows the onset of the K–H instability for the long waves at
$U_{1}\approx 0.5$
, and stabilisation for values of the shear flow exceeding
$U_{1}\approx 2$
, in agreement with the results of Ovsyannikov (Reference Ovsyannikov1979). We note that the stabilisation persists within the scope of the full equations of motion (Ovsyannikov Reference Ovsyannikov1985; Lannes & Ming Reference Lannes and Ming2015).
Figure 10. Wave speeds (3.34) as functions of the strength of the shear flow.
3.4 Critical layer
The critical layer is a region in the neighbourhood of a line at which the local wave speed is equal to the shear flow speed, see Freeman & Johnson (Reference Freeman and Johnson1970) and Johnson (Reference Johnson1990, Reference Johnson2012) and references therein. In this paper we only consider a relatively weak shear flow, when the critical layer does not appear, which we justify next.
The wavefront can be described as
$$\begin{eqnarray}H(r,{\it\theta},t)=rk({\it\theta})-st=\text{constant}.\end{eqnarray}$$
Following Johnson (Reference Johnson1990, Reference Johnson1997), we find that the local wave speed in the direction
$$\begin{eqnarray}\frac{\boldsymbol{{\rm\nabla}}H}{|\boldsymbol{{\rm\nabla}}H|}=\frac{k\boldsymbol{e}_{\boldsymbol{r}}+k^{\prime }\boldsymbol{e}_{{\it\theta}}}{\sqrt{k^{2}+k^{\prime 2}}}\end{eqnarray}$$
is given by
$$\begin{eqnarray}-\frac{H_{t}}{|\boldsymbol{{\rm\nabla}}H|}=\frac{s}{\sqrt{k^{2}+k^{\prime 2}}}.\end{eqnarray}$$
Therefore, the critical layer occurs when
$$\begin{eqnarray}\frac{s}{\sqrt{k^{2}+k^{\prime 2}}}=(U_{1}-U_{2})\cos ({\it\alpha}+{\it\theta}),\quad \text{where}~\cos {\it\alpha}=\frac{k}{\sqrt{k^{2}+k^{\prime 2}}},\end{eqnarray}$$
which is equivalent to the condition
$$\begin{eqnarray}F_{1}=-s+(U_{1}-U_{2})(k\cos {\it\theta}-k^{\prime }\sin {\it\theta})=0,\end{eqnarray}$$
when the linear problem formulation fails. It should be noted that
$F_{2}=-s\neq 0$
.
We know that
$$\begin{eqnarray}F_{1{\it\theta}}=-(U_{1}-U_{2})(k+k^{\prime \prime })\sin {\it\theta},\end{eqnarray}$$
where, without loss of generality, we assume that
$U_{1}-U_{2}>0$
and
$k+k^{\prime \prime }>0$
on the selected singular solution (
$k({\it\theta})>0$
). Then,
$F_{1{\it\theta}}<0$
if
${\it\theta}\in (0,{\rm\pi})$
and
$F_{1{\it\theta}}>0$
if
${\it\theta}\in ({\rm\pi},2{\rm\pi})$
, which implies that
$F_{1}$
reaches its maximum value at
${\it\theta}=0$
. Therefore, to avoid the appearance of critical layers, we require that
$$\begin{eqnarray}F_{1}\leqslant F_{1}|_{{\it\theta}=0}=-s+(U_{1}-U_{2})k(0)<0,\end{eqnarray}$$
which yields the following constraint on the strength of the shear flow:
$$\begin{eqnarray}(U_{1}-U_{2})k(0)<s.\end{eqnarray}$$
We note that
$k(0)$
depends on
$U_{1}-U_{2}$
. However, since
$s/k({\it\theta})$
represents the radial wave speed, it is natural to impose the condition that
$s/k(0)\geqslant s$
(i.e. the downstream wave speed is greater than or equal to the speed found assuming the absence of the shear flow, see figure 10), implying that
$k(0)\leqslant 1$
. Therefore, we can replace the exact condition (3.42) with a simplified estimate:
$$\begin{eqnarray}U_{1}-U_{2}<s\leqslant \frac{s}{k(0)}.\end{eqnarray}$$
Thus, if the shear flow satisfies condition (3.43), then there are no critical layers. We note also that the long waves in the two-layer fluid are K–H stable if the shear flow satisfies the stability criterion (A 1) given in appendix A. The coefficients of the derived
$2+1$
-dimensional amplitude equation (2.63) for both surface and interfacial ring waves in this two-layer case are listed in appendix B.
4 Discussion
In this paper we have developed an asymptotic theory describing the propagation of long linear and weakly nonlinear ring waves in a stratified fluid over a shear flow in the KdV regime. The theory is based on the existence of a suitable linear modal decomposition, which has more complicated structure than the known modal decomposition in Cartesian geometry, when waves propagate along or opposite to the horizontal shear flow. In our formulation, the shear flow is parallel, while the waves in the absence of the shear flow are concentric. Thus, there is a clash of geometries, and it is not clear a priori that there is any modal decomposition.
The developed linear formulation provides, in particular, a description of the distortion of the shape of the wavefronts of the ring waves by the shear flow, which has been illustrated by considering the classical setting of a two-layer fluid with a piecewise-constant current. The wavefronts of surface and interfacial ring waves were described in terms of two branches of the singular solution of the derived nonlinear first-order differential equation, constituting further generalisation of the well-known Burns and generalised Burns conditions (Burns Reference Burns1953; Johnson Reference Johnson1990). Remarkably, the two branches of this singular solution could be described in parametric form, and an explicit analytical solution was developed for the wavefront of the interfacial mode in the case of low density contrast. The constructed solutions have revealed the qualitatively different behaviour of the wavefronts of surface and interfacial waves propagating over the same shear flow. Indeed, while the wavefront of the surface ring wave is elongated in the direction of the flow, the wavefront of the interfacial wave is squeezed in this direction.
The derived
$2+1$
-dimensional cylindrical Korteweg–de Vries-type equation constitutes generalisation of the previously derived
$1+1$
-dimensional equation for the surface waves in a homogeneous fluid over a shear flow (Johnson Reference Johnson1990) and internal waves in a stratified fluid in the absence of a shear flow (Lipovskii Reference Lipovskii1985). Strictly speaking, Johnson derived a
$2+1$
-dimensional model (Johnson Reference Johnson1990), but as a by-product of our study we have shown that the complicated formula for one of the coefficients of his equation will yield a zero coefficient for any shear flow, which then reduces the equation to a
$1+1$
-dimensional model. Finally, for the case of the two-layer model we have also derived a constraint on the strength of the shear flow, which guarantees that there are no critical layers, and obtained explicit expressions for the coefficients of the derived amplitude equation in terms of the physical and geometrical parameters of the model, which provides a fully developed asymptotic theory for this case. Further work will include numerical and analytical studies of the long weakly nonlinear ring waves using the derived equation.
It should be noted that the derived model can be generalised to include the effects of variable environment and rotation, similarly to existing studies for plane waves (see Grimshaw Reference Grimshaw and Grimshaw2001; Grimshaw et al. Reference Grimshaw, Helfrich and Johnson2013 and references therein). The modal decomposition found in this paper can be used to derive other long ring wave models, similar to the Benjamin–Ono and intermediate-depth equations for plane waves (Benjamin Reference Benjamin1967; Ono Reference Ono1975; Joseph Reference Joseph1977; Kubota et al. Reference Kubota, Ko and Dobbs1978).
Figure 11. Solitons in the Strait of Gibraltar (NASA image STS17-34-081, Lunar and Planetary Institute, http://www.lpi.usra.edu/publications/slidesets/oceans/oceanviews/oceanviews_index.shtml).
Finally, we assume that theoretical results developed in this paper are relevant to the description of the nearly annular internal waves observed in the oceans. Such waves are generated in straits (e.g. in the Strait of Gibraltar, see figure 1), in river–sea interaction zones (e.g. by a Columbia River plume, see Nash & Moum (Reference Nash and Moum2005)) and by scattering from localised topographic features (e.g. from a sea mountain in the Celtic Sea, see Vlasenko et al. (Reference Vlasenko, Stashchuk, Inall and Hopkins2014)). While the observed waves are often strongly nonlinear, previous studies of such waves within the scope of KdV-like models and their generalisations suggest that this is a useful asymptotic regime for this class of problem (see, for example, Grimshaw et al. Reference Grimshaw, Pelinovsky and Talipova1997, Reference Grimshaw, Ostrovsky, Shrira and Stepanyants1998; Apel Reference Apel2003; Grue Reference Grue, Grue and Trulsen2006; Helfrich & Melville Reference Helfrich and Melville2006; Apel et al. Reference Apel, Ostrovsky, Stepanyants and Lynch2007).
Squeezing of the wavefronts of interfacial ring waves in the direction of the shear flow should be a prominent feature, and we conjecture that this might be a factor contributing to the change of the shape of internal waves generated by an exchange flow in the Strait of Gibraltar, visible in figure 11 for the waves propagating further into the Mediterranean Sea (two groups of internal waves are indicated by white arrows), as well as to the change of the shape of the internal spiral waves generated by a tidal flow near a sea mountain in Vlasenko et al. (Reference Vlasenko, Stashchuk, Inall and Hopkins2014, figure A1). We hope that our study will help in better understanding and interpretation of numerical and observational data for internal waves in three-dimensional settings.
Acknowledgements
We thank R. Barros, W. Choi, G. A. El, R. H. J. Grimshaw, J. Grue, R. S. Johnson, L. Martina, V. B. Matveev, E. A. Kuznetsov, A. V. Mikhailov, P. A. Milewski, L. A. Ostrovsky, V. I. Shrira, Yu. A. Stepanyants, V. Vlasenko and anonymous referees for useful references, criticisms and related discussions. X.Z. thanks Xinhe Liu for useful discussions of some technical issues.
Appendix A. Stability condition for long waves
In the rigid lid approximation, the condition for the stability of the long waves in a two-layer fluid of finite depth (see figure 3) in the non-dimensional variables used in our paper is given by
$$\begin{eqnarray}(U_{1}-U_{2})^{2}<\frac{({\it\rho}_{2}-{\it\rho}_{1})\big({\it\rho}_{1}d+{\it\rho}_{2}(1-d)\big)}{{\it\rho}_{1}{\it\rho}_{2}}\end{eqnarray}$$
(Ovsyannikov Reference Ovsyannikov1979, Reference Ovsyannikov1985); see also Bontozoglou (Reference Bontozoglou1991), Boonkasame & Milewski (Reference Boonkasame and Milewski2011) and Lannes & Ming (Reference Lannes and Ming2015) and references therein. The free surface results show that long waves are stable both for small shears, as in the rigid lid case, but also for sufficiently large shears (Ovsyannikov Reference Ovsyannikov1979, Reference Ovsyannikov1985); see also Barros & Choi (Reference Barros and Choi2014) and Lannes & Ming (Reference Lannes and Ming2015).
Long interfacial waves satisfying the stability criterion (A 1) are observed both in experiments and in natural environments (for example, see the reviews by Grue (Reference Grue, Grue and Trulsen2006) and Apel et al. (Reference Apel, Ostrovsky, Stepanyants and Lynch2007)), which means that in the situations where they are observed there exist some extra mechanisms which prevent the development of the K–H instability for short-wavelength perturbations. Among such stabilising mechanisms not present in the simplified model are the continuity of the actual density and shear flow profiles, with a thin intermediate layer in between the two main layers, and surface tension (see Turner (Reference Turner1973), Boonkasame & Milewski (Reference Boonkasame and Milewski2011), Lannes & Ming (Reference Lannes and Ming2015) and references therein). The two-layer model is an abstraction of the actual continuous density and shear flow profiles, suitable for the theoretical study of long internal waves.
Appendix B. Coefficients of the cKdV-type equation
In this appendix we list the coefficients of the derived
$2+1$
-dimensional amplitude equation (2.63) for both surface and interfacial ring waves in the two-layer case.
For surface waves, we normalise
${\it\phi}$
by setting
${\it\phi}=1$
at
$z=1$
. The parameter
${\it\Lambda}$
in the modal function (3.3) is given by
$$\begin{eqnarray}{\it\Lambda}_{s}=\frac{k^{2}+k^{\prime 2}}{F_{1}^{2}}.\end{eqnarray}$$
Substituting the modal function into the formulae (2.64)–(2.68), we obtain the coefficients in the form
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{1}=\frac{2s(k^{2}+k^{\prime 2})^{2}}{F_{1}^{4}}\left((1-d){\it\rho}_{1}F_{1}+\frac{{\it\rho}_{2}F_{2}}{d}\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)^{2}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{2}=-\frac{3(k^{2}+k^{\prime 2})^{3}}{F_{1}^{6}}\left((1-d){\it\rho}_{1}F_{1}^{2}+\frac{{\it\rho}_{2}F_{2}^{2}}{d^{2}}\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)^{3}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle {\it\mu}_{3} & = & \displaystyle -\frac{(k^{2}+k^{\prime 2})^{3}}{3F_{1}^{4}}\left({\it\rho}_{1}F_{1}^{2}\left(\frac{F_{1}^{6}}{(k^{2}+k^{\prime 2})^{3}}-\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)^{3}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,{\it\rho}_{2}F_{2}^{2}d\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)^{2}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle {\it\mu}_{4} & = & \displaystyle -\frac{(1-d){\it\rho}_{1}k(k+k^{\prime \prime })(k^{2}+k^{\prime 2})}{F_{1}^{4}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(F_{1}^{2}+4k^{\prime }F_{1}(U_{1}-U_{2})\sin {\it\theta}+3(k^{2}+k^{\prime 2})(U_{1}-U_{2})^{2}\sin ^{2}{\it\theta}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\frac{{\it\rho}_{2}(k+k^{\prime \prime })kF_{2}^{2}}{dF_{1}^{4}}\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)\left((k^{2}-3k^{\prime 2})\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{4(d-1)k^{\prime }(k^{\prime }F_{1}+(U_{1}-U_{2})(k^{2}+k^{\prime 2})\sin {\it\theta})}{F_{1}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle {\it\mu}_{5} & = & \displaystyle -\frac{2k(k^{2}+k^{\prime 2})}{F_{1}^{4}}\left(\vphantom{\displaystyle \left(\frac{F_{1}^{2}}{k^{\prime 2}}\right)}(1-d){\it\rho}_{1}F_{1}(k^{\prime }F_{1}+(U_{1}-U_{2})(k^{2}+k^{\prime 2})\sin {\it\theta})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{{\it\rho}_{2}k^{\prime }F_{2}^{2}}{d}\left(\frac{F_{1}^{2}}{k^{2}+k^{\prime 2}}+d-1\right)^{2}\right),\end{eqnarray}$$
where
$$\begin{eqnarray}F_{1}=-s+(U_{1}-U_{2})(k\cos {\it\theta}-k^{\prime }\sin {\it\theta}),\quad F_{2}=-s,\end{eqnarray}$$
$$\begin{eqnarray}s^{2}=\frac{1+\sqrt{(2d-1)^{2}+4{\it\rho}_{1}/{\it\rho}_{2}d(1-d)}}{2}\end{eqnarray}$$
and the function
$k({\it\theta})$
is defined by the formula (3.17) (lower sign).
For interfacial waves, we normalise
${\it\phi}$
by setting
${\it\phi}=1$
at
$z=d$
. The parameter
${\it\Lambda}$
in the modal function (3.3) is given by
$$\begin{eqnarray}{\it\Lambda}_{i}=\frac{k^{2}+k^{\prime 2}}{F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2})}.\end{eqnarray}$$
Substituting the modal function into the formulae (2.64)–(2.68), we obtain the coefficients in the form
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{1}=2s\left(\frac{(1-d){\it\rho}_{1}F_{1}(k^{2}+k^{\prime 2})^{2}}{(F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2}))^{2}}+\frac{{\it\rho}_{2}F_{2}}{d}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\mu}_{2}=-3\left(\frac{(1-d){\it\rho}_{1}F_{1}^{2}(k^{2}+k^{\prime 2})^{3}}{(F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2}))^{3}}+\frac{{\it\rho}_{2}F_{2}^{2}}{d^{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\mu}_{3}=-\frac{{\it\rho}_{1}F_{1}^{2}}{3(F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2}))^{2}}\left(F_{1}^{6}-(F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2}))^{3}\right)-\frac{1}{3}d{\it\rho}_{2}F_{2}^{2}(k^{2}+k^{\prime 2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle {\it\mu}_{4} & = & \displaystyle -\frac{(1-d){\it\rho}_{1}k(k+k^{\prime \prime })\left((k^{2}-3k^{\prime 2})F_{1}^{2}-4k^{\prime }(k^{2}+k^{\prime 2})F_{1}(U_{1}-U_{2})\sin {\it\theta}-(U_{1}-U_{2})^{2}(k^{2}+k^{\prime 2})^{2}\sin ^{2}{\it\theta}\right)}{(F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2}))^{2}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\frac{4(1-d){\it\rho}_{1}k(k+k^{\prime \prime })F_{1}^{2}}{(F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2}))^{3}}(k^{\prime }F_{1}+(k^{2}+k^{\prime 2})(U_{1}-U_{2})\sin {\it\theta})^{2}-\frac{{\it\rho}_{2}k(k+k^{\prime \prime })(k^{2}-3k^{\prime 2})F_{2}^{2}}{d(k^{2}+k^{\prime 2})^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\mu}_{5}=-\frac{2(1-d){\it\rho}_{1}F_{1}k(k^{2}+k^{\prime 2})}{(F_{1}^{2}+(d-1)(k^{2}+k^{\prime 2}))^{2}}(k^{\prime }F_{1}+(U_{1}-U_{2})(k^{2}+k^{\prime 2})\sin {\it\theta})-\frac{2kk^{\prime }{\it\rho}_{2}F_{2}^{2}}{d(k^{2}+k^{\prime 2})},\end{eqnarray}$$
where
$$\begin{eqnarray}F_{1}=-s+(U_{1}-U_{2})(k\cos {\it\theta}-k^{\prime }\sin {\it\theta}),\quad F_{2}=-s,\end{eqnarray}$$
$$\begin{eqnarray}s^{2}=\frac{1-\sqrt{(2d-1)^{2}+4{\it\rho}_{1}/{\it\rho}_{2}d(1-d)}}{2}\end{eqnarray}$$
and the function
$k({\it\theta})$
is defined by the formula (3.17) (upper sign). For the latter, one can also use the explicit formula (3.14), obtained in the rigid lid approximation. We note that, in the general case, the coefficient
${\it\mu}_{5}$
is non-zero for both surface and interfacial waves.
