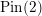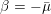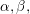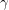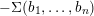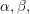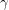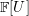1 Introduction
Let ![]() $Y$ be a closed, oriented three-manifold with
$Y$ be a closed, oriented three-manifold with ![]() $b_{1}=0$ and spin structure
$b_{1}=0$ and spin structure ![]() $\mathfrak{s}$, and let
$\mathfrak{s}$, and let  $G=\text{Pin}(2)$, the subgroup
$G=\text{Pin}(2)$, the subgroup  $S^{1}\cup jS^{1}$ of the unit quaternions. Manolescu introduced the
$S^{1}\cup jS^{1}$ of the unit quaternions. Manolescu introduced the ![]() $G$-equivariant Seiberg–Witten Floer homology
$G$-equivariant Seiberg–Witten Floer homology  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ in [Reference ManolescuMan16], and with it the suite of homology cobordism invariants
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ in [Reference ManolescuMan16], and with it the suite of homology cobordism invariants ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$. These are defined analogously to the Frøyshov invariant of the usual,
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$. These are defined analogously to the Frøyshov invariant of the usual, ![]() $S^{1}$-equivariant, Seiberg–Witten Floer homology. To construct the
$S^{1}$-equivariant, Seiberg–Witten Floer homology. To construct the ![]() $\text{Pin}(2)$-equivariant Floer theory, Manolescu does finite-dimensional approximation of the Seiberg–Witten equations for
$\text{Pin}(2)$-equivariant Floer theory, Manolescu does finite-dimensional approximation of the Seiberg–Witten equations for ![]() $(Y,\mathfrak{s})$, and obtains a
$(Y,\mathfrak{s})$, and obtains a ![]() $G$-equivariant homotopy type
$G$-equivariant homotopy type  $\mathit{SWF}(Y,\mathfrak{s})$. The invariant
$\mathit{SWF}(Y,\mathfrak{s})$. The invariant  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ is then the
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ is then the ![]() $G$-equivariant Borel homology of
$G$-equivariant Borel homology of  $\mathit{SWF}(Y,\mathfrak{s})$. As the
$\mathit{SWF}(Y,\mathfrak{s})$. As the ![]() $G$-equivariant homology of some stable homotopy type,
$G$-equivariant homology of some stable homotopy type,  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ comes with the structure of a module over
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ comes with the structure of a module over  $H^{\ast }(BG;\mathbb{F})\simeq \mathbb{F}[q,v]/(q^{3}),$ where
$H^{\ast }(BG;\mathbb{F})\simeq \mathbb{F}[q,v]/(q^{3}),$ where ![]() $\mathbb{F}$ is the field of two elements. The invariants
$\mathbb{F}$ is the field of two elements. The invariants ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$, and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$, and ![]() $\unicode[STIX]{x1D6FE}$ are defined using the module structure.
$\unicode[STIX]{x1D6FE}$ are defined using the module structure.
The invariant ![]() $\unicode[STIX]{x1D6FD}$ was then used to disprove the triangulation conjecture. Let
$\unicode[STIX]{x1D6FD}$ was then used to disprove the triangulation conjecture. Let ![]() $\unicode[STIX]{x1D703}_{3}^{H}$ denote the homology cobordism group of integral homology three-spheres. By the work of Galewski and Stern [Reference Galewski and SternGS80] and Matumoto [Reference MatumotoMat78], there exist nontriangulable manifolds in dimension at least
$\unicode[STIX]{x1D703}_{3}^{H}$ denote the homology cobordism group of integral homology three-spheres. By the work of Galewski and Stern [Reference Galewski and SternGS80] and Matumoto [Reference MatumotoMat78], there exist nontriangulable manifolds in dimension at least ![]() $5$ if and only if
$5$ if and only if ![]() $\unicode[STIX]{x1D703}_{3}^{H}$ does not contain an element
$\unicode[STIX]{x1D703}_{3}^{H}$ does not contain an element ![]() $[Y]$ of order
$[Y]$ of order ![]() $2$, with
$2$, with  $\unicode[STIX]{x1D707}(Y)=1$. However, the invariant
$\unicode[STIX]{x1D707}(Y)=1$. However, the invariant  $\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D703}_{3}^{H}\rightarrow \mathbb{Z}$ satisfies
$\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D703}_{3}^{H}\rightarrow \mathbb{Z}$ satisfies  $\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=-\unicode[STIX]{x1D6FD}(-Y,\mathfrak{s})$ and
$\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=-\unicode[STIX]{x1D6FD}(-Y,\mathfrak{s})$ and  $\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})\equiv \unicode[STIX]{x1D707}(Y,\mathfrak{s})\hspace{0.2em}{\rm mod}\hspace{0.2em}2$, from which Manolescu concludes that there exist manifolds of all dimensions at least
$\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})\equiv \unicode[STIX]{x1D707}(Y,\mathfrak{s})\hspace{0.2em}{\rm mod}\hspace{0.2em}2$, from which Manolescu concludes that there exist manifolds of all dimensions at least ![]() $5$ which cannot be triangulated.
$5$ which cannot be triangulated.
Let ![]() $Y$ be a Seifert rational homology sphere with spin structure
$Y$ be a Seifert rational homology sphere with spin structure ![]() $\mathfrak{s}$, such that the base orbifold of the Seifert fibration of
$\mathfrak{s}$, such that the base orbifold of the Seifert fibration of ![]() $Y$ has
$Y$ has ![]() $S^{2}$ as underlying space.Footnote 1 In the present paper, we use the description of the Seiberg–Witten moduli space given by Mrowka, Ozsváth and Yu [Reference Mrowka, Ozsváth and YuMOY97] to compute
$S^{2}$ as underlying space.Footnote 1 In the present paper, we use the description of the Seiberg–Witten moduli space given by Mrowka, Ozsváth and Yu [Reference Mrowka, Ozsváth and YuMOY97] to compute  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$, as a module over
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$, as a module over  $\mathbb{F}[q,v]/(q^{3})$ (here, the action of
$\mathbb{F}[q,v]/(q^{3})$ (here, the action of ![]() $v$ decreases grading by
$v$ decreases grading by ![]() $4$, and that of
$4$, and that of ![]() $q$ decreases grading by
$q$ decreases grading by ![]() $1$). The description is in terms of the Heegaard Floer homology
$1$). The description is in terms of the Heegaard Floer homology  $\mathit{HF}^{+}(Y,\mathfrak{s})$, defined in [Reference Ozsváth and SzabóOS04a, Reference Ozsváth and SzabóOS04b]. In particular, this description makes
$\mathit{HF}^{+}(Y,\mathfrak{s})$, defined in [Reference Ozsváth and SzabóOS04a, Reference Ozsváth and SzabóOS04b]. In particular, this description makes  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ quickly computable, as Ozsváth-Szabó, Némethi, and Can and Karakurt [Reference Ozsváth and SzabóOS03b, Reference NémethiNém05, Reference Can and KarakurtCK14] have developed algorithms to calculate
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ quickly computable, as Ozsváth-Szabó, Némethi, and Can and Karakurt [Reference Ozsváth and SzabóOS03b, Reference NémethiNém05, Reference Can and KarakurtCK14] have developed algorithms to calculate  $HF^{+}(Y,\mathfrak{s})$ for
$HF^{+}(Y,\mathfrak{s})$ for ![]() $Y$ a Seifert space. In order to obtain
$Y$ a Seifert space. In order to obtain  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ in terms of
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ in terms of  $HF^{+}(Y,\mathfrak{s})$, we use both the equivalence of
$HF^{+}(Y,\mathfrak{s})$, we use both the equivalence of ![]() $\mathit{HF}^{+}$ and
$\mathit{HF}^{+}$ and ![]() $\check{HM}$ due to Kutluhan, Lee and Taubes [Reference Kutluhan, Lee and TaubesKLT10], and Colin, Ghiggini and Honda [Reference Colin, Ghiggini and HondaCGH11] and Taubes [Reference TaubesTau07], and the equivalence of
$\check{HM}$ due to Kutluhan, Lee and Taubes [Reference Kutluhan, Lee and TaubesKLT10], and Colin, Ghiggini and Honda [Reference Colin, Ghiggini and HondaCGH11] and Taubes [Reference TaubesTau07], and the equivalence of ![]() $\check{HM}$ and
$\check{HM}$ and  $\mathit{SWFH}^{S^{1}}$ due to Lidman and Manolescu [Reference Lidman and ManolescuLM18]. Here
$\mathit{SWFH}^{S^{1}}$ due to Lidman and Manolescu [Reference Lidman and ManolescuLM18]. Here  $\mathit{SWFH}^{S^{1}}(Y,\mathfrak{s})$ denotes the
$\mathit{SWFH}^{S^{1}}(Y,\mathfrak{s})$ denotes the ![]() $S^{1}$-equivariant Borel homology of the stable homotopy type
$S^{1}$-equivariant Borel homology of the stable homotopy type  $\mathit{SWF}(Y,\mathfrak{s})$.
$\mathit{SWF}(Y,\mathfrak{s})$.
We will need to relate  $\mathit{SWFH}^{S^{1}}(Y,\mathfrak{s})$ and
$\mathit{SWFH}^{S^{1}}(Y,\mathfrak{s})$ and  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ when the underlying homotopy type
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ when the underlying homotopy type  $\mathit{SWF}(Y,\mathfrak{s})$ is simple enough. This should be compared with [Reference LinLin17], in which Lin calculates the
$\mathit{SWF}(Y,\mathfrak{s})$ is simple enough. This should be compared with [Reference LinLin17], in which Lin calculates the ![]() $\text{Pin}(2)$-monopole Floer homology in the setting of [Reference LinLin18] for many classes of three-manifolds
$\text{Pin}(2)$-monopole Floer homology in the setting of [Reference LinLin18] for many classes of three-manifolds ![]() $Y$ obtained by surgery on a knot. The approach there is based, similarly, on extracting information from the
$Y$ obtained by surgery on a knot. The approach there is based, similarly, on extracting information from the ![]() $S^{1}$-equivariant theory
$S^{1}$-equivariant theory  $\check{HM}(Y,\mathfrak{s})$ of [Reference Kronheimer and MrowkaKM07], when
$\check{HM}(Y,\mathfrak{s})$ of [Reference Kronheimer and MrowkaKM07], when  $\check{HM}(Y,\mathfrak{s})$ is simple enough.
$\check{HM}(Y,\mathfrak{s})$ is simple enough.
To state the calculation of  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$, let
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$, let ![]() ${\mathcal{T}}^{+}$ denote
${\mathcal{T}}^{+}$ denote  $\mathbb{F}[U,U^{-1}]/U\mathbb{F}[U]$, and
$\mathbb{F}[U,U^{-1}]/U\mathbb{F}[U]$, and  ${\mathcal{T}}^{+}(i)=\mathbb{F}[U^{-i+1},U^{-i+2},\ldots ]/U\mathbb{F}[U]$, with
${\mathcal{T}}^{+}(i)=\mathbb{F}[U^{-i+1},U^{-i+2},\ldots ]/U\mathbb{F}[U]$, with  $\deg (U)=-2$. We also introduce the notation
$\deg (U)=-2$. We also introduce the notation ![]() ${\mathcal{V}}^{+}$ to denote
${\mathcal{V}}^{+}$ to denote  $\mathbb{F}[v,v^{-1}]/v\mathbb{F}[v]$, and
$\mathbb{F}[v,v^{-1}]/v\mathbb{F}[v]$, and  ${\mathcal{V}}^{+}(i)=\mathbb{F}[v^{-i+1},v^{-i+2},\ldots ]/v\mathbb{F}[v]$, with
${\mathcal{V}}^{+}(i)=\mathbb{F}[v^{-i+1},v^{-i+2},\ldots ]/v\mathbb{F}[v]$, with  $\deg (v)=-4$. For any graded module
$\deg (v)=-4$. For any graded module ![]() $M$, let
$M$, let ![]() $M_{n}$ denote the submodule of homogeneous elements of degree
$M_{n}$ denote the submodule of homogeneous elements of degree ![]() $n$, and define
$n$, and define ![]() $M[k]$ by
$M[k]$ by  $M[k]_{n}=M_{n+k}$. Let
$M[k]_{n}=M_{n+k}$. Let  ${\mathcal{T}}_{d}^{+}(n)={\mathcal{T}}^{+}(n)[-d]$ and
${\mathcal{T}}_{d}^{+}(n)={\mathcal{T}}^{+}(n)[-d]$ and  ${\mathcal{V}}_{d}^{+}(n)={\mathcal{V}}^{+}(n)[-d]$. The module
${\mathcal{V}}_{d}^{+}(n)={\mathcal{V}}^{+}(n)[-d]$. The module ![]() ${\mathcal{T}}_{d}^{+}(n)$ is then supported in degrees from
${\mathcal{T}}_{d}^{+}(n)$ is then supported in degrees from ![]() $d$ to
$d$ to  $d+2(n-1)$, with the parity of
$d+2(n-1)$, with the parity of ![]() $d$.
$d$.
Fix ![]() $Y$ a Seifert rational homology three-sphere with negative fibration; that is, the orbifold line bundle of
$Y$ a Seifert rational homology three-sphere with negative fibration; that is, the orbifold line bundle of ![]() $Y$ is of negative degree (see § 5). For example, the Brieskorn sphere
$Y$ is of negative degree (see § 5). For example, the Brieskorn sphere  $\unicode[STIX]{x1D6F4}(a_{1},\ldots ,a_{n})$, for coprime
$\unicode[STIX]{x1D6F4}(a_{1},\ldots ,a_{n})$, for coprime ![]() $a_{i}$, is of negative fibration. Using Corollary 5.4 we may write
$a_{i}$, is of negative fibration. Using Corollary 5.4 we may write
 $$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+}\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\,\oplus \,J^{\oplus 2}[-s],\end{eqnarray}$$
$$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+}\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\,\oplus \,J^{\oplus 2}[-s],\end{eqnarray}$$ for some constants  $s,d_{i},n_{i},N$ and some
$s,d_{i},n_{i},N$ and some ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module ![]() $J$, all determined by
$J$, all determined by ![]() $(Y,\mathfrak{s})$. Moreover,
$(Y,\mathfrak{s})$. Moreover,  $d_{i+1}>d_{i},n_{i+1}<n_{i}$ for all
$d_{i+1}>d_{i},n_{i+1}<n_{i}$ for all ![]() $i$. Roughly, in terms of Seiberg–Witten theory, the term
$i$. Roughly, in terms of Seiberg–Witten theory, the term  ${\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+}$ accounts for the reducible critical point, and the modules
${\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+}$ accounts for the reducible critical point, and the modules
 $$\begin{eqnarray}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\quad \text{and}\quad {\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\quad \text{and}\quad {\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\end{eqnarray}$$ account for the irreducibles which cancel against the bottom of the infinite ![]() $U$-tower. The term
$U$-tower. The term ![]() $J^{\oplus 2}$ accounts for the other irreducibles.
$J^{\oplus 2}$ accounts for the other irreducibles.
Let us denote by ![]() $\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}$ the restriction functor from the map of modules
$\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}$ the restriction functor from the map of modules  $\mathbb{F}[v]\rightarrow \mathbb{F}[U]$ given by
$\mathbb{F}[v]\rightarrow \mathbb{F}[U]$ given by  $v\rightarrow U^{2}$. The restriction functor converts
$v\rightarrow U^{2}$. The restriction functor converts ![]() ${\mathcal{T}}_{d}^{+}(n)$ to
${\mathcal{T}}_{d}^{+}(n)$ to  ${\mathcal{V}}_{d}^{+}(\lfloor (n+1)/2\rfloor )\oplus {\mathcal{V}}_{d+2}^{+}(\lfloor n/2\rfloor )$.
${\mathcal{V}}_{d}^{+}(\lfloor (n+1)/2\rfloor )\oplus {\mathcal{V}}_{d+2}^{+}(\lfloor n/2\rfloor )$.
Theorem 1.1. Let ![]() $Y$ be a Seifert rational homology three-sphere of negative fibration, fibering over an orbifold with underlying space
$Y$ be a Seifert rational homology three-sphere of negative fibration, fibering over an orbifold with underlying space ![]() $S^{2}$, and let
$S^{2}$, and let ![]() $\mathfrak{s}$ be a spin structure on
$\mathfrak{s}$ be a spin structure on ![]() $Y$. Let
$Y$. Let  $\mathit{HF}^{+}(Y,\mathfrak{s})$ be as in (1). Then there exist constants
$\mathit{HF}^{+}(Y,\mathfrak{s})$ be as in (1). Then there exist constants ![]() $(a_{i},b_{i})$ and an
$(a_{i},b_{i})$ and an  $\mathbb{F}[q,v]/(q^{3})$-module
$\mathbb{F}[q,v]/(q^{3})$-module ![]() $J^{\prime \prime }$, specified in Corollary 5.4 and depending only on the sequence
$J^{\prime \prime }$, specified in Corollary 5.4 and depending only on the sequence ![]() $(d_{i},n_{i})$, so that, as an
$(d_{i},n_{i})$, so that, as an ![]() $\mathbb{F}[v]$-module,
$\mathbb{F}[v]$-module,
 $$\begin{eqnarray}\displaystyle \mathit{SWFH}^{G}(Y,\mathfrak{s}) & = & \displaystyle {\mathcal{V}}_{s+4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{s+1}^{+}\oplus {\mathcal{V}}_{s+2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i=1}^{N^{\prime }}{\mathcal{V}}_{s+a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus J^{\prime \prime }[-s]\oplus \text{res}_{\mathbb{ F}[v]}^{\mathbb{F}[U]}J[-s].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{SWFH}^{G}(Y,\mathfrak{s}) & = & \displaystyle {\mathcal{V}}_{s+4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{s+1}^{+}\oplus {\mathcal{V}}_{s+2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i=1}^{N^{\prime }}{\mathcal{V}}_{s+a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus J^{\prime \prime }[-s]\oplus \text{res}_{\mathbb{ F}[v]}^{\mathbb{F}[U]}J[-s].\nonumber\end{eqnarray}$$ The ![]() $q$-action is given by the isomorphism
$q$-action is given by the isomorphism  ${\mathcal{V}}_{s+2}^{+}\rightarrow {\mathcal{V}}_{s+1}^{+}$ and the map
${\mathcal{V}}_{s+2}^{+}\rightarrow {\mathcal{V}}_{s+1}^{+}$ and the map  ${\mathcal{V}}_{s+1}^{+}\rightarrow {\mathcal{V}}_{s+4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}$, which is an
${\mathcal{V}}_{s+1}^{+}\rightarrow {\mathcal{V}}_{s+4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}$, which is an ![]() $\mathbb{F}$-vector space isomorphism in all degrees at least
$\mathbb{F}$-vector space isomorphism in all degrees at least  $s+4\lfloor (d_{1}+2n_{1}+1)/4\rfloor$ and vanishes otherwise. Further,
$s+4\lfloor (d_{1}+2n_{1}+1)/4\rfloor$ and vanishes otherwise. Further, ![]() $q$ annihilates
$q$ annihilates  $\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J[-s]$ and
$\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J[-s]$ and  $\bigoplus _{i=1}^{N^{\prime }}{\mathcal{V}}_{s+a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)$. The action of
$\bigoplus _{i=1}^{N^{\prime }}{\mathcal{V}}_{s+a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)$. The action of ![]() $q$ on
$q$ on ![]() $J^{\prime \prime }$ is specified in Corollary 5.4.
$J^{\prime \prime }$ is specified in Corollary 5.4.
Theorem 1.1 specifies ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},$ and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},$ and ![]() $\unicode[STIX]{x1D6FE}$, which we state as Corollary 1.2. For
$\unicode[STIX]{x1D6FE}$, which we state as Corollary 1.2. For ![]() $Y$ an integral homology three-sphere, let
$Y$ an integral homology three-sphere, let ![]() $d(Y)$ be the Heegaard Floer correction term [Reference Ozsváth and SzabóOS03a]. Using Theorems 1.1 and 1.3 below we obtain the following.
$d(Y)$ be the Heegaard Floer correction term [Reference Ozsváth and SzabóOS03a]. Using Theorems 1.1 and 1.3 below we obtain the following.
(a) Let
 $Y$ be a Seifert integral homology sphere of negative fibration. Then
$Y$ be a Seifert integral homology sphere of negative fibration. Then  $\unicode[STIX]{x1D6FD}(Y)=\unicode[STIX]{x1D6FE}(Y)=-\bar{\unicode[STIX]{x1D707}}(Y)$, and
$\unicode[STIX]{x1D6FD}(Y)=\unicode[STIX]{x1D6FE}(Y)=-\bar{\unicode[STIX]{x1D707}}(Y)$, and  $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(Y)=\left\{\begin{array}{@{}ll@{}}d(Y)/2\quad & \text{if }d(Y)/2\equiv -\bar{\unicode[STIX]{x1D707}}(Y)\hspace{0.2em}{\rm mod}\hspace{0.2em}2,\\ d(Y)/2+1\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(Y)=\left\{\begin{array}{@{}ll@{}}d(Y)/2\quad & \text{if }d(Y)/2\equiv -\bar{\unicode[STIX]{x1D707}}(Y)\hspace{0.2em}{\rm mod}\hspace{0.2em}2,\\ d(Y)/2+1\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$(b) Let
 $Y$ be a Seifert integral homology sphere of positive fibration. Then
$Y$ be a Seifert integral homology sphere of positive fibration. Then  $\unicode[STIX]{x1D6FC}(Y)=\unicode[STIX]{x1D6FD}(Y)=-\bar{\unicode[STIX]{x1D707}}(Y),$ and
$\unicode[STIX]{x1D6FC}(Y)=\unicode[STIX]{x1D6FD}(Y)=-\bar{\unicode[STIX]{x1D707}}(Y),$ and  $$\begin{eqnarray}\unicode[STIX]{x1D6FE}(Y)=\left\{\begin{array}{@{}ll@{}}d(Y)/2\quad & \text{if }d(Y)/2\equiv -\bar{\unicode[STIX]{x1D707}}(Y)\hspace{0.2em}{\rm mod}\hspace{0.2em}2,\\ d(Y)/2-1\quad & \text{otherwise. }\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}(Y)=\left\{\begin{array}{@{}ll@{}}d(Y)/2\quad & \text{if }d(Y)/2\equiv -\bar{\unicode[STIX]{x1D707}}(Y)\hspace{0.2em}{\rm mod}\hspace{0.2em}2,\\ d(Y)/2-1\quad & \text{otherwise. }\end{array}\right.\end{eqnarray}$$
From Corollary 1.2, we see that for Seifert integral homology spheres the Manolescu invariants ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$, and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$, and ![]() $\unicode[STIX]{x1D6FE}$ are all determined by
$\unicode[STIX]{x1D6FE}$ are all determined by ![]() $d$ and
$d$ and ![]() $\bar{\unicode[STIX]{x1D707}}$. In particular,
$\bar{\unicode[STIX]{x1D707}}$. In particular, ![]() $\unicode[STIX]{x1D6FC}$,
$\unicode[STIX]{x1D6FC}$, ![]() $\unicode[STIX]{x1D6FD}$, and
$\unicode[STIX]{x1D6FD}$, and ![]() $\unicode[STIX]{x1D6FE}$ provide no new obstructions to Seifert spaces bounding acyclic four-manifolds.
$\unicode[STIX]{x1D6FE}$ provide no new obstructions to Seifert spaces bounding acyclic four-manifolds.
In [Reference ManolescuMan16], Manolescu also conjectured that for all spin Seifert rational homology spheres  $\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=-\bar{\unicode[STIX]{x1D707}}(Y,\mathfrak{s})$, where
$\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=-\bar{\unicode[STIX]{x1D707}}(Y,\mathfrak{s})$, where ![]() $\bar{\unicode[STIX]{x1D707}}$ is the Neumann–Siebenmann invariant defined in [Reference NeumannNeu80, Reference SiebenmannSie80]. We are able to prove part of this conjecture.
$\bar{\unicode[STIX]{x1D707}}$ is the Neumann–Siebenmann invariant defined in [Reference NeumannNeu80, Reference SiebenmannSie80]. We are able to prove part of this conjecture.
Theorem 1.3. Let ![]() $Y$ be a Seifert integral homology three-sphere. Then
$Y$ be a Seifert integral homology three-sphere. Then  $\unicode[STIX]{x1D6FD}(Y)=-\bar{\unicode[STIX]{x1D707}}(Y)$.
$\unicode[STIX]{x1D6FD}(Y)=-\bar{\unicode[STIX]{x1D707}}(Y)$.
We prove Theorem 1.3 by showing that ![]() $\unicode[STIX]{x1D6FD}$ is controlled by the degree of the reducible, and by using a result of Ruberman and Saveliev [Reference Ruberman and SavelievRS11] that gives
$\unicode[STIX]{x1D6FD}$ is controlled by the degree of the reducible, and by using a result of Ruberman and Saveliev [Reference Ruberman and SavelievRS11] that gives ![]() $\bar{\unicode[STIX]{x1D707}}$ as a sum of eta invariants.
$\bar{\unicode[STIX]{x1D707}}$ as a sum of eta invariants.
Fukumoto, Furuta and Ue showed in [Reference Fukumoto, Furuta and UeFFU01] that ![]() $\bar{\unicode[STIX]{x1D707}}$ is a homology cobordism invariant for many classes of Seifert spaces, and Saveliev [Reference SavelievSav02] extended this to show that Seifert integral homology spheres with
$\bar{\unicode[STIX]{x1D707}}$ is a homology cobordism invariant for many classes of Seifert spaces, and Saveliev [Reference SavelievSav02] extended this to show that Seifert integral homology spheres with ![]() $\bar{\unicode[STIX]{x1D707}}\neq 0$ have infinite order in
$\bar{\unicode[STIX]{x1D707}}\neq 0$ have infinite order in ![]() $\unicode[STIX]{x1D703}_{3}^{H}$. Theorem 1.3 generalizes the result of Fukumoto, Furuta and Ue, showing that the Neumann–Siebenmann invariant
$\unicode[STIX]{x1D703}_{3}^{H}$. Theorem 1.3 generalizes the result of Fukumoto, Furuta and Ue, showing that the Neumann–Siebenmann invariant ![]() $\bar{\unicode[STIX]{x1D707}}$, restricted to Seifert integral homology spheres, is a homology cobordism invariant.
$\bar{\unicode[STIX]{x1D707}}$, restricted to Seifert integral homology spheres, is a homology cobordism invariant.
For Seifert spaces with  $\mathit{HF}^{+}(Y,\mathfrak{s})$ of a special form,
$\mathit{HF}^{+}(Y,\mathfrak{s})$ of a special form,  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ may be expressed more compactly than is evident in the statement of Theorem 1.1. If
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ may be expressed more compactly than is evident in the statement of Theorem 1.1. If ![]() $Y$ is of negative fibration and
$Y$ is of negative fibration and
 $$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{d}^{+}\oplus {\mathcal{T}}_{-2n+1}^{+}(m)\oplus \bigoplus _{i\in I}{\mathcal{T}}_{a_{i}}^{+}(m_{i})^{\oplus 2},\end{eqnarray}$$
$$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{d}^{+}\oplus {\mathcal{T}}_{-2n+1}^{+}(m)\oplus \bigoplus _{i\in I}{\mathcal{T}}_{a_{i}}^{+}(m_{i})^{\oplus 2},\end{eqnarray}$$ for some index set ![]() $I$, we say that
$I$, we say that ![]() $(Y,\mathfrak{s})$ is of projective type. We will say that
$(Y,\mathfrak{s})$ is of projective type. We will say that ![]() $Y$ is of projective type if
$Y$ is of projective type if ![]() $Y$ is an integral homology sphere such that (2) holds. There are many examples of such Seifert spaces, among them
$Y$ is an integral homology sphere such that (2) holds. There are many examples of such Seifert spaces, among them  $\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$, by work of Némethi and Borodzik [Reference NémethiNém07, Reference Borodzik and NémethiBN13] and Tweedy [Reference TweedyTwe13]. The condition (2) also admits a natural expression in terms of graded roots; see § 5.2.
$\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$, by work of Némethi and Borodzik [Reference NémethiNém07, Reference Borodzik and NémethiBN13] and Tweedy [Reference TweedyTwe13]. The condition (2) also admits a natural expression in terms of graded roots; see § 5.2.
Theorem 1.4. If ![]() $(Y,\mathfrak{s})$ is of projective type, as in (2), with
$(Y,\mathfrak{s})$ is of projective type, as in (2), with ![]() $m\neq 0$, then we have the following.
$m\neq 0$, then we have the following.
If  $d\equiv 2n+2$ mod
$d\equiv 2n+2$ mod ![]() $4$,
$4$,
 $$\begin{eqnarray}\displaystyle \mathit{SWFH}^{G}(Y,\mathfrak{s}) & = & \displaystyle {\mathcal{V}}_{d+2}^{+}\oplus {\mathcal{V}}_{-2n+1}^{+}\oplus {\mathcal{V}}_{-2n+2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus {\mathcal{V}}_{-2n+3}^{+}\biggl(\biggl\lfloor\frac{m}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}}^{+}\biggl(\biggl\lfloor\frac{m_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}+2}^{+}\biggl(\biggl\lfloor\frac{m_{i}}{2}\biggr\rfloor\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{SWFH}^{G}(Y,\mathfrak{s}) & = & \displaystyle {\mathcal{V}}_{d+2}^{+}\oplus {\mathcal{V}}_{-2n+1}^{+}\oplus {\mathcal{V}}_{-2n+2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus {\mathcal{V}}_{-2n+3}^{+}\biggl(\biggl\lfloor\frac{m}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}}^{+}\biggl(\biggl\lfloor\frac{m_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}+2}^{+}\biggl(\biggl\lfloor\frac{m_{i}}{2}\biggr\rfloor\biggr).\end{eqnarray}$$ If ![]() $d\equiv 2n$ mod
$d\equiv 2n$ mod ![]() $4$,
$4$,
 $$\begin{eqnarray}\displaystyle \mathit{SWFH}^{G}(Y,\mathfrak{s}) & = & \displaystyle {\mathcal{V}}_{d}^{+}\oplus {\mathcal{V}}_{-2n+1}^{+}\oplus {\mathcal{V}}_{-2n+2}^{+}\oplus {\mathcal{V}}_{-2n+3}^{+}\biggl(\biggl\lfloor\frac{m}{2}\biggr\rfloor\biggr)\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i\in I}{\mathcal{V}}_{a_{i}}^{+}\biggl(\biggl\lfloor\frac{m_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}+2}^{+}\biggl(\biggl\lfloor\frac{m_{i}}{2}\biggr\rfloor\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{SWFH}^{G}(Y,\mathfrak{s}) & = & \displaystyle {\mathcal{V}}_{d}^{+}\oplus {\mathcal{V}}_{-2n+1}^{+}\oplus {\mathcal{V}}_{-2n+2}^{+}\oplus {\mathcal{V}}_{-2n+3}^{+}\biggl(\biggl\lfloor\frac{m}{2}\biggr\rfloor\biggr)\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i\in I}{\mathcal{V}}_{a_{i}}^{+}\biggl(\biggl\lfloor\frac{m_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}+2}^{+}\biggl(\biggl\lfloor\frac{m_{i}}{2}\biggr\rfloor\biggr).\end{eqnarray}$$ The ![]() $q$-action is given by the isomorphism
$q$-action is given by the isomorphism  ${\mathcal{V}}_{-2n+2}^{+}\rightarrow {\mathcal{V}}_{-2n+1}^{+}$ and the map
${\mathcal{V}}_{-2n+2}^{+}\rightarrow {\mathcal{V}}_{-2n+1}^{+}$ and the map  ${\mathcal{V}}_{-2n+1}^{+}\rightarrow {\mathcal{V}}_{d+2}^{+}$ (if
${\mathcal{V}}_{-2n+1}^{+}\rightarrow {\mathcal{V}}_{d+2}^{+}$ (if  $d\equiv 2n+2\;\text{mod}\;4$), or
$d\equiv 2n+2\;\text{mod}\;4$), or  ${\mathcal{V}}_{-2n+1}^{+}\rightarrow {\mathcal{V}}_{d}^{+}$ (if
${\mathcal{V}}_{-2n+1}^{+}\rightarrow {\mathcal{V}}_{d}^{+}$ (if  $d\equiv 2n\;\text{mod}\;4$), which is an
$d\equiv 2n\;\text{mod}\;4$), which is an ![]() $\mathbb{F}$-vector space isomorphism in all degrees at least
$\mathbb{F}$-vector space isomorphism in all degrees at least ![]() $d+2$ (respectively,
$d+2$ (respectively, ![]() $d$), and vanishes otherwise. In (3) and (4),
$d$), and vanishes otherwise. In (3) and (4), ![]() $q$ acts on
$q$ acts on  ${\mathcal{V}}_{-2n+3}^{+}(\lfloor m/2\rfloor )$ as the unique nonzero map
${\mathcal{V}}_{-2n+3}^{+}(\lfloor m/2\rfloor )$ as the unique nonzero map  ${\mathcal{V}}_{-2n+3}^{+}(\lfloor m/2\rfloor )\rightarrow {\mathcal{V}}_{-2n+2}^{+}$ if
${\mathcal{V}}_{-2n+3}^{+}(\lfloor m/2\rfloor )\rightarrow {\mathcal{V}}_{-2n+2}^{+}$ if ![]() $m\geqslant 2$. The action of
$m\geqslant 2$. The action of ![]() $q$ annihilates
$q$ annihilates  $\bigoplus _{i\in I}{\mathcal{V}}_{a_{i}}^{+}(\lfloor (m_{i}+1)/2\rfloor )\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}+2}^{+}(\lfloor m_{i}/2\rfloor )$.
$\bigoplus _{i\in I}{\mathcal{V}}_{a_{i}}^{+}(\lfloor (m_{i}+1)/2\rfloor )\oplus \bigoplus _{i\in I}{\mathcal{V}}_{a_{i}+2}^{+}(\lfloor m_{i}/2\rfloor )$.
If ![]() $m=0$, we define
$m=0$, we define ![]() $n$ by
$n$ by  $d=-2n$, in which case (4) again holds, and the
$d=-2n$, in which case (4) again holds, and the ![]() $q$ action is as before.
$q$ action is as before.
To prove Theorem 1.1, we use [Reference Mrowka, Ozsváth and YuMOY97] to show that a space representative of the stable homotopy type  $\mathit{SWF}(Y,\mathfrak{s})$, away from the reducible, naturally splits into two disjoint pieces, which are interchanged by the action of
$\mathit{SWF}(Y,\mathfrak{s})$, away from the reducible, naturally splits into two disjoint pieces, which are interchanged by the action of ![]() $j\in G$. For
$j\in G$. For ![]() $Z$ a topological space with
$Z$ a topological space with ![]() $G$-action let
$G$-action let  $Z^{S^{1}}\subset Z$ denote the subset fixed by
$Z^{S^{1}}\subset Z$ denote the subset fixed by ![]() $S^{1}\subset G$. Say
$S^{1}\subset G$. Say
 $$\begin{eqnarray}X=\mathit{SWF}(Y,\mathfrak{s})/(\mathit{SWF}(Y,\mathfrak{s})^{S^{1}}).\end{eqnarray}$$
$$\begin{eqnarray}X=\mathit{SWF}(Y,\mathfrak{s})/(\mathit{SWF}(Y,\mathfrak{s})^{S^{1}}).\end{eqnarray}$$Then
 $$\begin{eqnarray}X=X_{+}\vee jX_{+}.\end{eqnarray}$$
$$\begin{eqnarray}X=X_{+}\vee jX_{+}.\end{eqnarray}$$ That is, ![]() $X$ is a wedge sum of two components related by the action of
$X$ is a wedge sum of two components related by the action of ![]() $j$. Then the chain complex of
$j$. Then the chain complex of  $EG\wedge _{G}\mathit{SWF}(Y,\mathfrak{s})$, used to compute the
$EG\wedge _{G}\mathit{SWF}(Y,\mathfrak{s})$, used to compute the ![]() $G$-Borel homology, is closely related to the chain complex of
$G$-Borel homology, is closely related to the chain complex of  $ES^{1}\wedge _{S^{1}}\mathit{SWF}(Y,\mathfrak{s})$, whose homology is the
$ES^{1}\wedge _{S^{1}}\mathit{SWF}(Y,\mathfrak{s})$, whose homology is the ![]() $S^{1}$-Borel homology of
$S^{1}$-Borel homology of  $\mathit{SWF}(Y,\mathfrak{s})$. A careful, but entirely elementary, analysis of the differentials in these two complexes then yields Theorem 1.1.
$\mathit{SWF}(Y,\mathfrak{s})$. A careful, but entirely elementary, analysis of the differentials in these two complexes then yields Theorem 1.1.
1.1 Local equivalence
We call rational homology three-spheres ![]() $Y_{1}$ and
$Y_{1}$ and ![]() $Y_{2}$ (integral) homology cobordant if there exists a compact oriented four-manifold
$Y_{2}$ (integral) homology cobordant if there exists a compact oriented four-manifold ![]() $W$ with
$W$ with  $\unicode[STIX]{x2202}W=Y_{1}\amalg -Y_{2}$ so that the maps induced by inclusion
$\unicode[STIX]{x2202}W=Y_{1}\amalg -Y_{2}$ so that the maps induced by inclusion  $H_{\ast }(Y_{i};\mathbb{Z})\rightarrow H_{\ast }(W;\mathbb{Z})$ are isomorphisms for
$H_{\ast }(Y_{i};\mathbb{Z})\rightarrow H_{\ast }(W;\mathbb{Z})$ are isomorphisms for ![]() $i=1,2$.
$i=1,2$.
Manolescu’s construction of  $\mathit{SWF}(Y,\mathfrak{s})$ contains more information about homology cobordism than the invariants
$\mathit{SWF}(Y,\mathfrak{s})$ contains more information about homology cobordism than the invariants ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},$ and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},$ and ![]() $\unicode[STIX]{x1D6FE}$. Namely, a spin cobordism
$\unicode[STIX]{x1D6FE}$. Namely, a spin cobordism ![]() $W$ from
$W$ from ![]() $Y_{1}$ to
$Y_{1}$ to ![]() $Y_{2}$ with
$Y_{2}$ with  $b_{2}(W)=0$ induces a map
$b_{2}(W)=0$ induces a map  $\mathit{SWF}(Y_{1},\mathfrak{s}_{1})\rightarrow \mathit{SWF}(Y_{2},\mathfrak{s}_{2})$ which is a homotopy equivalence on
$\mathit{SWF}(Y_{1},\mathfrak{s}_{1})\rightarrow \mathit{SWF}(Y_{2},\mathfrak{s}_{2})$ which is a homotopy equivalence on ![]() $S^{1}$-fixed point sets. We call two
$S^{1}$-fixed point sets. We call two ![]() $G$-spaces
$G$-spaces ![]() $X_{1},X_{2}$locally equivalent if there exist
$X_{1},X_{2}$locally equivalent if there exist ![]() $G$-equivariant stable maps
$G$-equivariant stable maps  $X_{1}\rightarrow X_{2}$ and
$X_{1}\rightarrow X_{2}$ and  $X_{2}\rightarrow X_{1}$ which induce homotopy equivalences on fixed point sets. The local equivalence class
$X_{2}\rightarrow X_{1}$ which induce homotopy equivalences on fixed point sets. The local equivalence class  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{l}}$ is then a homology cobordism invariant of
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{l}}$ is then a homology cobordism invariant of ![]() $(Y,\mathfrak{s})$. The local equivalence class
$(Y,\mathfrak{s})$. The local equivalence class  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{l}}$ determines
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{l}}$ determines  $\unicode[STIX]{x1D6FC}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})$ and
$\unicode[STIX]{x1D6FC}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})$ and ![]() $\unicode[STIX]{x1D6FE}(Y,\mathfrak{s})$.
$\unicode[STIX]{x1D6FE}(Y,\mathfrak{s})$.
For a more computable version of local equivalence, we introduce chain local equivalence, using the ![]() $C_{\ast }(G)$-equivariant chain complex associated to a
$C_{\ast }(G)$-equivariant chain complex associated to a ![]() $G$-CW complex. The chain local equivalence class of a
$G$-CW complex. The chain local equivalence class of a ![]() $G$-space
$G$-space ![]() $X$, denoted
$X$, denoted ![]() $[X]_{\text{cl}}$, takes values in the set
$[X]_{\text{cl}}$, takes values in the set ![]() $\mathfrak{CE}$ of homotopy-equivalence classes of chain complexes of a certain form. In particular, using the chain local equivalence class we have the following result.
$\mathfrak{CE}$ of homotopy-equivalence classes of chain complexes of a certain form. In particular, using the chain local equivalence class we have the following result.
Corollary 1.5. Let ![]() $Y$ be a rational homology three-sphere with spin structure
$Y$ be a rational homology three-sphere with spin structure ![]() $\mathfrak{s}$. Then there is a homology-cobordism invariant,
$\mathfrak{s}$. Then there is a homology-cobordism invariant,  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$, the connected Seiberg–Witten Floer homology of
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$, the connected Seiberg–Witten Floer homology of ![]() $(Y,\mathfrak{s})$, taking values in isomorphism classes of
$(Y,\mathfrak{s})$, taking values in isomorphism classes of ![]() $\mathbb{F}[U]$-modules. More specifically,
$\mathbb{F}[U]$-modules. More specifically,  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ is the isomorphism class of a summand of
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ is the isomorphism class of a summand of  $\mathit{HF}_{\text{red}}(Y,\mathfrak{s})$.
$\mathit{HF}_{\text{red}}(Y,\mathfrak{s})$.
The connected Seiberg–Witten Floer homology is constructed using the CW chain complex of a space representative ![]() $X$ of
$X$ of  $\mathit{SWF}(Y,\mathfrak{s})$. The CW chain complex
$\mathit{SWF}(Y,\mathfrak{s})$. The CW chain complex  $C_{\ast }^{\text{CW}}(X)$ splits, as a module over
$C_{\ast }^{\text{CW}}(X)$ splits, as a module over  $C_{\ast }^{\text{CW}}(G)$, into a direct sum of two subcomplexes, with one summand attached to the
$C_{\ast }^{\text{CW}}(G)$, into a direct sum of two subcomplexes, with one summand attached to the ![]() $S^{1}$-fixed-point set, and the other a free
$S^{1}$-fixed-point set, and the other a free  $C_{\ast }^{\text{CW}}(G)$-module. Roughly, the
$C_{\ast }^{\text{CW}}(G)$-module. Roughly, the ![]() $S^{1}$-Borel homology of the former component is
$S^{1}$-Borel homology of the former component is  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$.
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$.
In the calculation of  $\mathit{SWFH}^{G}(Y,\mathfrak{s})$ for Seifert spaces, we provide enough information about the
$\mathit{SWFH}^{G}(Y,\mathfrak{s})$ for Seifert spaces, we provide enough information about the ![]() $G$-equivariant chain complex of
$G$-equivariant chain complex of  $\mathit{SWF}(Y,\mathfrak{s})$ to calculate the chain local equivalence class
$\mathit{SWF}(Y,\mathfrak{s})$ to calculate the chain local equivalence class  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$ of Seifert spaces. As a corollary, we obtain the following.
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$ of Seifert spaces. As a corollary, we obtain the following.
Corollary 1.6. The sets  $\{{d_{i}\}}_{i},\{{n_{i}\}}_{i}$ in Theorem 1.1 are integral homology cobordism invariants of negative Seifert fiber spaces. That is: say
$\{{d_{i}\}}_{i},\{{n_{i}\}}_{i}$ in Theorem 1.1 are integral homology cobordism invariants of negative Seifert fiber spaces. That is: say ![]() $Y_{1}$ and
$Y_{1}$ and ![]() $Y_{2}$ are negative Seifert integral homology spheres with
$Y_{2}$ are negative Seifert integral homology spheres with ![]() $Y_{1}$ homology cobordant to
$Y_{1}$ homology cobordant to ![]() $Y_{2}$; let
$Y_{2}$; let ![]() $S_{i}$ be the set of isomorphism classes of simple summands of
$S_{i}$ be the set of isomorphism classes of simple summands of  $\mathit{HF}^{+}(Y_{i})$ that occur an odd number of times in the decomposition (1); then
$\mathit{HF}^{+}(Y_{i})$ that occur an odd number of times in the decomposition (1); then  $S_{1}=S_{2}$.
$S_{1}=S_{2}$.
We obtain Corollary 1.6 by showing that ![]() $\{{d_{i}\}}_{i}$ and
$\{{d_{i}\}}_{i}$ and ![]() $\{{n_{i}\}}_{i}$ determine
$\{{n_{i}\}}_{i}$ determine  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$.
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$.
Corollary 1.7. Let ![]() $(Y_{1},\mathfrak{s}_{1})$ be a negative Seifert rational homology three-sphere with spin structure, with
$(Y_{1},\mathfrak{s}_{1})$ be a negative Seifert rational homology three-sphere with spin structure, with  $\mathit{HF}^{+}(Y_{1},\mathfrak{s}_{1})$ as in (1). Then
$\mathit{HF}^{+}(Y_{1},\mathfrak{s}_{1})$ as in (1). Then
 $$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(Y_{1},\mathfrak{s}_{1})=\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i}).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(Y_{1},\mathfrak{s}_{1})=\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i}).\end{eqnarray}$$ In particular, if ![]() $Y_{1}$ is an integral homology sphere and
$Y_{1}$ is an integral homology sphere and ![]() $Y_{2}$ is any integral homology sphere homology cobordant to
$Y_{2}$ is any integral homology sphere homology cobordant to ![]() $Y_{1}$, then
$Y_{1}$, then  $\check{HM}(Y_{2})\cong \mathit{HF}^{+}(Y_{2})$ contains a summand isomorphic to (6), as
$\check{HM}(Y_{2})\cong \mathit{HF}^{+}(Y_{2})$ contains a summand isomorphic to (6), as ![]() $\mathbb{F}[U]$-modules.
$\mathbb{F}[U]$-modules.
Remark 1.8. In fact,  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ is an invariant of spin rational homology cobordism, for
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ is an invariant of spin rational homology cobordism, for ![]() $Y$ a rational homology three-sphere.
$Y$ a rational homology three-sphere.
From Corollary 1.7 and (1), we see that for Seifert integral homology spheres ![]() $Y$,
$Y$,  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})=0$ if and only if
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})=0$ if and only if  $d(Y,\mathfrak{s})/2=-\bar{\unicode[STIX]{x1D707}}(Y,\mathfrak{s})$. As an application of the Corollaries 1.5 and 1.7, we have the following result.
$d(Y,\mathfrak{s})/2=-\bar{\unicode[STIX]{x1D707}}(Y,\mathfrak{s})$. As an application of the Corollaries 1.5 and 1.7, we have the following result.
Corollary 1.9. The spaces  $\unicode[STIX]{x1D6F4}(5,7,13)$ and
$\unicode[STIX]{x1D6F4}(5,7,13)$ and  $\unicode[STIX]{x1D6F4}(7,10,17)$ satisfy
$\unicode[STIX]{x1D6F4}(7,10,17)$ satisfy
 $$\begin{eqnarray}\displaystyle & \displaystyle d(\unicode[STIX]{x1D6F4}(5,7,13))=d(\unicode[STIX]{x1D6F4}(7,10,17))=2, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F4}(5,7,13))=\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F4}(7,10,17))=0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d(\unicode[STIX]{x1D6F4}(5,7,13))=d(\unicode[STIX]{x1D6F4}(7,10,17))=2, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F4}(5,7,13))=\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F4}(7,10,17))=0. & \displaystyle \nonumber\end{eqnarray}$$ However,  $\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(5,7,13))={\mathcal{T}}_{1}^{+}(1)$, while
$\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(5,7,13))={\mathcal{T}}_{1}^{+}(1)$, while
 $$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(7,10,17))={\mathcal{T}}_{-1}^{+}(2)\oplus {\mathcal{T}}_{-1}^{+}(1).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(7,10,17))={\mathcal{T}}_{-1}^{+}(2)\oplus {\mathcal{T}}_{-1}^{+}(1).\end{eqnarray}$$ Thus  $\unicode[STIX]{x1D6F4}(5,7,13)$ and
$\unicode[STIX]{x1D6F4}(5,7,13)$ and  $\unicode[STIX]{x1D6F4}(7,10,17)$ are not homology cobordant, despite having the same
$\unicode[STIX]{x1D6F4}(7,10,17)$ are not homology cobordant, despite having the same ![]() $d$,
$d$, ![]() $\bar{\unicode[STIX]{x1D707}}$,
$\bar{\unicode[STIX]{x1D707}}$, ![]() $\unicode[STIX]{x1D6FC}$,
$\unicode[STIX]{x1D6FC}$, ![]() $\unicode[STIX]{x1D6FD}$, and
$\unicode[STIX]{x1D6FD}$, and ![]() $\unicode[STIX]{x1D6FE}$ invariants.
$\unicode[STIX]{x1D6FE}$ invariants.
There are many other examples of homology cobordism classes that are distinguished by ![]() $d_{i},n_{i}$, but not by
$d_{i},n_{i}$, but not by ![]() $d$ and
$d$ and ![]() $\bar{\unicode[STIX]{x1D707}}$. As an example, we have the following corollary.
$\bar{\unicode[STIX]{x1D707}}$. As an example, we have the following corollary.
Corollary 1.10. The Seifert space  $\unicode[STIX]{x1D6F4}(7,10,17)$ is not homology cobordant to
$\unicode[STIX]{x1D6F4}(7,10,17)$ is not homology cobordant to  $\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$ for any
$\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$ for any ![]() $p,q,n$.
$p,q,n$.
This result follows from Corollary 1.6. Indeed, since  $\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$ are of projective type,
$\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$ are of projective type,  $\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1))$ is a simple
$\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1))$ is a simple ![]() $\mathbb{F}[U]$-module, using the definition (2) and equation (6). Using (7), Corollary 1.10 follows.
$\mathbb{F}[U]$-module, using the definition (2) and equation (6). Using (7), Corollary 1.10 follows.
Moreover, using a calculation from [Reference ManolescuMan13], we are able to show the existence of three-manifolds not homology cobordant to any Seifert fiber space. This result is also due to Frøyshov using instanton homology, and has been independently proved by Lin [Reference LinLin17]. For example, we have the following.
Corollary 1.11. The connected sum  $\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11)$ is not homology cobordant to any Seifert fiber space.
$\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11)$ is not homology cobordant to any Seifert fiber space.
Proof. In [Reference ManolescuMan13], Manolescu shows  $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=2$, while
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=2$, while  $\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=0$. In addition,
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=0$. In addition,  $d(\unicode[STIX]{x1D6F4}(2,3,11))=2$, so
$d(\unicode[STIX]{x1D6F4}(2,3,11))=2$, so  $d(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=4$. To obtain a contradiction, say first that
$d(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=4$. To obtain a contradiction, say first that  $\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11)$ is homology cobordant to a negative Seifert space
$\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11)$ is homology cobordant to a negative Seifert space ![]() $Y$. Corollary 1.2 implies
$Y$. Corollary 1.2 implies
 $$\begin{eqnarray}2=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=\unicode[STIX]{x1D6FD}(Y)=\unicode[STIX]{x1D6FE}(Y)=\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=0,\end{eqnarray}$$
$$\begin{eqnarray}2=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=\unicode[STIX]{x1D6FD}(Y)=\unicode[STIX]{x1D6FE}(Y)=\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))=0,\end{eqnarray}$$ a contradiction. Say instead that  $\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11)$ is homology cobordant to a positive Seifert space
$\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11)$ is homology cobordant to a positive Seifert space ![]() $Y$. Then by Corollary 1.2,
$Y$. Then by Corollary 1.2,  $\unicode[STIX]{x1D6FE}(Y)=d(Y)/2=d(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))/2=2$. However,
$\unicode[STIX]{x1D6FE}(Y)=d(Y)/2=d(\unicode[STIX]{x1D6F4}(2,3,11)\#\unicode[STIX]{x1D6F4}(2,3,11))/2=2$. However,  $\unicode[STIX]{x1D6FE}(Y)=0$. Again we have a contradiction, completing the proof.◻
$\unicode[STIX]{x1D6FE}(Y)=0$. Again we have a contradiction, completing the proof.◻
Note that Corollary 1.11 readily implies the following statement for knots.
Corollary 1.12. There exist knots, such as the connected sum of torus knots  $T(3,11)\#T(3,11)$, which are not concordant to any Montesinos knot.
$T(3,11)\#T(3,11)$, which are not concordant to any Montesinos knot.
We also have that many Seifert integral homology spheres of negative fibration are not homology cobordant to any Seifert integral homology sphere of positive fibration. For instance we have the following.
Corollary 1.13. The Seifert spaces  $\unicode[STIX]{x1D6F4}(2,3,12k+7)$, for
$\unicode[STIX]{x1D6F4}(2,3,12k+7)$, for ![]() $k\geqslant 0$, are not homology cobordant to
$k\geqslant 0$, are not homology cobordant to  $-\unicode[STIX]{x1D6F4}(a_{1},a_{2},\ldots ,a_{n})$ for any choice of relatively prime
$-\unicode[STIX]{x1D6F4}(a_{1},a_{2},\ldots ,a_{n})$ for any choice of relatively prime ![]() $a_{i}$.
$a_{i}$.
This corollary is a direct consequence of Corollary 1.2, which shows that if ![]() $Y$ is a negative Seifert space with
$Y$ is a negative Seifert space with  $d(Y)/2\neq -\bar{\unicode[STIX]{x1D707}}(Y)$, then
$d(Y)/2\neq -\bar{\unicode[STIX]{x1D707}}(Y)$, then ![]() $Y$ is not homology cobordant to any positive Seifert space. We note
$Y$ is not homology cobordant to any positive Seifert space. We note  $d(\unicode[STIX]{x1D6F4}(2,3,12k+7))=0$ and
$d(\unicode[STIX]{x1D6F4}(2,3,12k+7))=0$ and  $\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F4}(2,3,12k+7))=1$, and the corollary follows. This should be compared with a result of Fintushel and Stern [Reference Fintushel and SternFS85] that gives a similar conclusion: if
$\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D6F4}(2,3,12k+7))=1$, and the corollary follows. This should be compared with a result of Fintushel and Stern [Reference Fintushel and SternFS85] that gives a similar conclusion: if  $R(a_{1},\ldots ,a_{n})>0$, then
$R(a_{1},\ldots ,a_{n})>0$, then  $\unicode[STIX]{x1D6F4}(a_{1},\ldots ,a_{n})$ is not oriented cobordant to any connected sum of positive Seifert homology spheres by a positive definite cobordism
$\unicode[STIX]{x1D6F4}(a_{1},\ldots ,a_{n})$ is not oriented cobordant to any connected sum of positive Seifert homology spheres by a positive definite cobordism ![]() $W$, where
$W$, where  $H_{1}(W;\mathbb{Z})$ contains no
$H_{1}(W;\mathbb{Z})$ contains no![]() $2$-torsion. However, there are examples with
$2$-torsion. However, there are examples with ![]() $R<0$, but
$R<0$, but  $d/2\neq -\bar{\unicode[STIX]{x1D707}}$, so we can apply Corollary 1.2. For instance,
$d/2\neq -\bar{\unicode[STIX]{x1D707}}$, so we can apply Corollary 1.2. For instance,  $\unicode[STIX]{x1D6F4}(2,3,7)$ has
$\unicode[STIX]{x1D6F4}(2,3,7)$ has ![]() $R$-invariant
$R$-invariant ![]() $-1$, but
$-1$, but  $d/2\neq -\bar{\unicode[STIX]{x1D707}}$. Thus, Corollary 1.13 is not detected by the
$d/2\neq -\bar{\unicode[STIX]{x1D707}}$. Thus, Corollary 1.13 is not detected by the ![]() $R$-invariant, nor the
$R$-invariant, nor the ![]() $d$-invariant, since
$d$-invariant, since  $d(\unicode[STIX]{x1D6F4}(2,3,12k+7))=0$.
$d(\unicode[STIX]{x1D6F4}(2,3,12k+7))=0$.
The organization of the paper is as follows. In § 2 we provide the necessary equivariant topology constructions and define local and chain local equivalence. We also provide means for computing chain local equivalence class, particularly Lemma 2.24, as well as the definition of connected homology. In § 3 we compute the ![]() $G$-Borel homology of
$G$-Borel homology of ![]() $j$-split spaces. In § 4 we review the finite-dimensional approximation of [Reference ManolescuMan16]. In § 5 we recall the results of [Reference Mrowka, Ozsváth and YuMOY97] and prove Theorems 1.1, 1.3, and 1.4. In § 6 we provide applications and examples of the homology calculation. Throughout the paper all homology will be taken with
$j$-split spaces. In § 4 we review the finite-dimensional approximation of [Reference ManolescuMan16]. In § 5 we recall the results of [Reference Mrowka, Ozsváth and YuMOY97] and prove Theorems 1.1, 1.3, and 1.4. In § 6 we provide applications and examples of the homology calculation. Throughout the paper all homology will be taken with  $\mathbb{F}=\mathbb{Z}/2$ coefficients, unless stated otherwise.
$\mathbb{F}=\mathbb{Z}/2$ coefficients, unless stated otherwise.
2 Spaces of type SWF
2.1  $G$-CW complexes
$G$-CW complexes
In this section we recall the definition of spaces of type SWF from [Reference ManolescuMan16], and introduce local equivalence. Spaces of type SWF are the output of the construction of the Seiberg–Witten Floer stable homotopy type of [Reference ManolescuMan03] and [Reference ManolescuMan16]; see § 4.
First, we recall some basics of equivariant algebraic topology from [Reference tom DiecktDie87]. The reader is encouraged to consult both [Reference ManolescuMan16] and [Reference tom DiecktDie87] for a fuller discussion. For now, ![]() $G$ will denote a compact Lie group. We define a
$G$ will denote a compact Lie group. We define a ![]() $G$-equivariant
$G$-equivariant ![]() $k$-cell as a copy of
$k$-cell as a copy of  $G/H\times D^{k}$, where
$G/H\times D^{k}$, where ![]() $H$ is a closed subgroup of
$H$ is a closed subgroup of ![]() $G$. A (finite) equivariant
$G$. A (finite) equivariant ![]() $G$-CW decomposition of a relative
$G$-CW decomposition of a relative ![]() $G$-space
$G$-space ![]() $(X,A)$, where the action of
$(X,A)$, where the action of ![]() $G$ takes
$G$ takes ![]() $A$ to itself, is a filtration
$A$ to itself, is a filtration  $(X_{n}|n\in \mathbb{Z}_{{\geqslant}0})$ such that:
$(X_{n}|n\in \mathbb{Z}_{{\geqslant}0})$ such that:
∙
 $A\subset X_{0}$ and
$A\subset X_{0}$ and  $X=X_{n}$ for
$X=X_{n}$ for  $n$ sufficiently large;
$n$ sufficiently large;∙ the space
 $X_{n}$ is obtained from
$X_{n}$ is obtained from  $X_{n-1}$ by attaching
$X_{n-1}$ by attaching  $G$-equivariant
$G$-equivariant  $n$-cells.
$n$-cells.
When ![]() $A$ is a point, we call
$A$ is a point, we call ![]() $(X,A)$ a pointed
$(X,A)$ a pointed ![]() $G$-CW complex. We always assume that
$G$-CW complex. We always assume that ![]() $G$ acts on the left.
$G$ acts on the left.
Let ![]() $EG$ be the total space of the universal bundle of
$EG$ be the total space of the universal bundle of ![]() $G$. For two pointed
$G$. For two pointed ![]() $G$-spaces
$G$-spaces ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{2}$, write
$X_{2}$, write
 $$\begin{eqnarray}X_{1}\wedge _{G}X_{2}=(X_{1}\wedge X_{2})/(gx_{1}\times x_{2}\sim x_{1}\times g^{-1}x_{2}).\end{eqnarray}$$
$$\begin{eqnarray}X_{1}\wedge _{G}X_{2}=(X_{1}\wedge X_{2})/(gx_{1}\times x_{2}\sim x_{1}\times g^{-1}x_{2}).\end{eqnarray}$$ The Borel homology of a pointed ![]() $G$-space
$G$-space ![]() $X$ is given by
$X$ is given by
 $$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X)=\tilde{H}_{\ast }(EG_{+}\wedge _{G}X),\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X)=\tilde{H}_{\ast }(EG_{+}\wedge _{G}X),\end{eqnarray}$$ where ![]() $EG_{+}$ is
$EG_{+}$ is ![]() $EG$ with a disjoint basepoint. Similarly, we define Borel cohomology:
$EG$ with a disjoint basepoint. Similarly, we define Borel cohomology:
 $$\begin{eqnarray}\tilde{H}_{G}^{\ast }(X)=\tilde{H}^{\ast }(EG_{+}\wedge _{G}X).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{G}^{\ast }(X)=\tilde{H}^{\ast }(EG_{+}\wedge _{G}X).\end{eqnarray}$$Additionally, we have a map given by projecting to the first factor:
 $$\begin{eqnarray}f:EG_{+}\wedge _{G}X\rightarrow BG_{+}.\end{eqnarray}$$
$$\begin{eqnarray}f:EG_{+}\wedge _{G}X\rightarrow BG_{+}.\end{eqnarray}$$ From ![]() $f$ we have a map
$f$ we have a map  $p_{G}=f^{\ast }:H^{\ast }(BG)\rightarrow \tilde{H}_{G}^{\ast }(X)$. Then
$p_{G}=f^{\ast }:H^{\ast }(BG)\rightarrow \tilde{H}_{G}^{\ast }(X)$. Then  $H^{\ast }(BG)$ acts on
$H^{\ast }(BG)$ acts on ![]() $\tilde{H}_{\ast }^{G}(X)$, by composing
$\tilde{H}_{\ast }^{G}(X)$, by composing ![]() $p_{G}$ with the cap product action of
$p_{G}$ with the cap product action of ![]() $\tilde{H}_{G}^{\ast }(X)$ on
$\tilde{H}_{G}^{\ast }(X)$ on ![]() $\tilde{H}_{\ast }^{G}(X)$. We may also define the unpointed version of the above constructions in an apparent way.
$\tilde{H}_{\ast }^{G}(X)$. We may also define the unpointed version of the above constructions in an apparent way.
As an example, consider the case ![]() $G=S^{1}$. Here
$G=S^{1}$. Here  $BS^{1}=\mathbb{C}P^{\infty }$, so
$BS^{1}=\mathbb{C}P^{\infty }$, so  $H^{\ast }(BS^{1})=\mathbb{F}[U]$, with
$H^{\ast }(BS^{1})=\mathbb{F}[U]$, with  $\text{deg}\,U=2$. Then
$\text{deg}\,U=2$. Then ![]() $\mathbb{F}[U]$ acts on
$\mathbb{F}[U]$ acts on  $H_{\ast }^{S^{1}}(X)$, for
$H_{\ast }^{S^{1}}(X)$, for ![]() $X$ any
$X$ any ![]() $S^{1}$-space.
$S^{1}$-space.
From now on we let  $G=\text{Pin}(2)$. The group
$G=\text{Pin}(2)$. The group  $G=\text{Pin}(2)$ is the set
$G=\text{Pin}(2)$ is the set  $S^{1}\cup jS^{1}\subset \mathbb{H}$, where
$S^{1}\cup jS^{1}\subset \mathbb{H}$, where ![]() $S^{1}$ is the unit circle in the
$S^{1}$ is the unit circle in the ![]() $\langle 1,i\rangle$ plane. The group action of
$\langle 1,i\rangle$ plane. The group action of ![]() $G$ is induced from the group action of the unit quaternions. Manolescu shows in [Reference ManolescuMan16] that
$G$ is induced from the group action of the unit quaternions. Manolescu shows in [Reference ManolescuMan16] that  $H^{\ast }(BG)=\mathbb{F}[q,v]/(q^{3})$, where
$H^{\ast }(BG)=\mathbb{F}[q,v]/(q^{3})$, where  $\text{deg}\,q=1$ and
$\text{deg}\,q=1$ and  $\text{deg}\,v=4$, so
$\text{deg}\,v=4$, so ![]() $\tilde{H}_{\ast }^{G}(X)$ is naturally an
$\tilde{H}_{\ast }^{G}(X)$ is naturally an  $\mathbb{F}[q,v]/(q^{3})$-module for
$\mathbb{F}[q,v]/(q^{3})$-module for ![]() $X$ a pointed
$X$ a pointed ![]() $G$-space. Moreover
$G$-space. Moreover  $S^{\infty }=S(\mathbb{H}^{\infty })$ has a free action by the quaternions, making
$S^{\infty }=S(\mathbb{H}^{\infty })$ has a free action by the quaternions, making ![]() $S^{\infty }$ a free
$S^{\infty }$ a free ![]() $G$-space. Since
$G$-space. Since ![]() $S^{\infty }$ is contractible, we identify
$S^{\infty }$ is contractible, we identify  $EG=S^{\infty }$. We may view
$EG=S^{\infty }$. We may view  $EG=S^{\infty }$ also as
$EG=S^{\infty }$ also as ![]() $ES^{1}$ (as an
$ES^{1}$ (as an ![]() $S^{1}$-space) by forgetting the action of
$S^{1}$-space) by forgetting the action of ![]() $j$.
$j$.
We will also need to relate ![]() $G$-Borel homology and
$G$-Borel homology and ![]() $S^{1}$-Borel homology. Consider
$S^{1}$-Borel homology. Consider
 $$\begin{eqnarray}f:\mathbb{C}P^{\infty }=BS^{1}\rightarrow BG,\end{eqnarray}$$
$$\begin{eqnarray}f:\mathbb{C}P^{\infty }=BS^{1}\rightarrow BG,\end{eqnarray}$$ the map given by quotienting by the action of ![]() $j\in G$ on
$j\in G$ on  $BS^{1}=ES^{1}/S^{1}$. Then we have the following fact (for a proof, see [Reference ManolescuMan16, Example 2.11]).
$BS^{1}=ES^{1}/S^{1}$. Then we have the following fact (for a proof, see [Reference ManolescuMan16, Example 2.11]).
Fact 2.1. The natural map
 $$\begin{eqnarray}f^{\ast }=\text{res}_{S^{1}}^{G}:H^{\ast }(BG)\rightarrow H^{\ast }(BS^{1})\end{eqnarray}$$
$$\begin{eqnarray}f^{\ast }=\text{res}_{S^{1}}^{G}:H^{\ast }(BG)\rightarrow H^{\ast }(BS^{1})\end{eqnarray}$$ is an isomorphism in degrees divisible by ![]() $4$, and zero otherwise. In particular,
$4$, and zero otherwise. In particular,  $v\rightarrow U^{2}$.
$v\rightarrow U^{2}$.
Moreover, for ![]() $X$ a
$X$ a ![]() $G$-space, we have a natural map
$G$-space, we have a natural map
 $$\begin{eqnarray}g:EG_{+}\wedge _{S^{1}}X\rightarrow EG_{+}\wedge _{G}X.\end{eqnarray}$$
$$\begin{eqnarray}g:EG_{+}\wedge _{S^{1}}X\rightarrow EG_{+}\wedge _{G}X.\end{eqnarray}$$ The map ![]() $g$ induces a map
$g$ induces a map
 $$\begin{eqnarray}g_{\ast }=\text{cor}_{G}^{S^{1}}:\tilde{H}_{\ast }^{S^{1}}(X)\rightarrow \tilde{H}_{\ast }^{G}(X),\end{eqnarray}$$
$$\begin{eqnarray}g_{\ast }=\text{cor}_{G}^{S^{1}}:\tilde{H}_{\ast }^{S^{1}}(X)\rightarrow \tilde{H}_{\ast }^{G}(X),\end{eqnarray}$$ called the corestriction map. As a Corollary of Fact 2.1, we have a relationship between the action of ![]() $U$ and
$U$ and ![]() $v$ (see [Reference tom DiecktDie87, § III.1]).
$v$ (see [Reference tom DiecktDie87, § III.1]).
Fact 2.2. Let ![]() $X$ be a
$X$ be a ![]() $G$-space. Then, for every
$G$-space. Then, for every  $x\in H_{\ast }^{S^{1}}(X)$,
$x\in H_{\ast }^{S^{1}}(X)$,
 $$\begin{eqnarray}v(\text{cor}_{G}^{S^{1}}(x))=\text{cor}_{G}^{S^{1}}(U^{2}x).\end{eqnarray}$$
$$\begin{eqnarray}v(\text{cor}_{G}^{S^{1}}(x))=\text{cor}_{G}^{S^{1}}(U^{2}x).\end{eqnarray}$$ We shall use that Borel homology with ![]() $\mathbb{F}$ coefficients behaves well with respect to suspension. If
$\mathbb{F}$ coefficients behaves well with respect to suspension. If ![]() $V$ is a finite-dimensional (real) representation of
$V$ is a finite-dimensional (real) representation of ![]() $G$, let
$G$, let ![]() $V^{+}$ be the one-point compactification, where
$V^{+}$ be the one-point compactification, where ![]() $G$ acts trivially on
$G$ acts trivially on  $V^{+}-V$. Then
$V^{+}-V$. Then  $\unicode[STIX]{x1D6F4}^{V}X=V^{+}\wedge X$ will be called the suspension of
$\unicode[STIX]{x1D6F4}^{V}X=V^{+}\wedge X$ will be called the suspension of ![]() $X$ by the representation
$X$ by the representation ![]() $V$.
$V$.
We mention the following representations of ![]() $G$:
$G$:
∙ let
 $\tilde{\mathbb{R}}^{s}$ be the vector space
$\tilde{\mathbb{R}}^{s}$ be the vector space  $\mathbb{R}^{s}$ on which
$\mathbb{R}^{s}$ on which  $j$ acts by
$j$ acts by  $-1$, and
$-1$, and  $e^{i\unicode[STIX]{x1D703}}$ acts by the identity, for all
$e^{i\unicode[STIX]{x1D703}}$ acts by the identity, for all  $\unicode[STIX]{x1D703}$;
$\unicode[STIX]{x1D703}$;∙ we let
 $\tilde{\mathbb{C}}$ be the representation of
$\tilde{\mathbb{C}}$ be the representation of  $G$ on
$G$ on  $\mathbb{C}$ where
$\mathbb{C}$ where  $j$ acts by
$j$ acts by  $-1$, and
$-1$, and  $e^{i\unicode[STIX]{x1D703}}$ acts by the identity for all
$e^{i\unicode[STIX]{x1D703}}$ acts by the identity for all  $\unicode[STIX]{x1D703}$;
$\unicode[STIX]{x1D703}$;∙ the quaternions
 $\mathbb{H}$, on which
$\mathbb{H}$, on which  $G$ acts by multiplication on the left.
$G$ acts by multiplication on the left.
Definition 2.3. Let  $s\in \mathbb{Z}_{{\geqslant}0}$. A space of type SWF at level
$s\in \mathbb{Z}_{{\geqslant}0}$. A space of type SWF at level ![]() $s$ is a pointed finite
$s$ is a pointed finite ![]() $G$-CW complex
$G$-CW complex ![]() $X$ with:
$X$ with:
∙ the
 $S^{1}$-fixed-point set
$S^{1}$-fixed-point set  $X^{S^{1}}$ is
$X^{S^{1}}$ is  $G$-homotopy equivalent to
$G$-homotopy equivalent to  $(\tilde{\mathbb{R}}^{s})^{+}$;
$(\tilde{\mathbb{R}}^{s})^{+}$;∙ the action of
 $G$ on
$G$ on  $X-X^{S^{1}}$ is free.
$X-X^{S^{1}}$ is free.
Remark 2.4. We list some examples of spaces of type SWF. The simplest space of type SWF is ![]() $S^{0}$. More interesting examples may be produced as follows. Let
$S^{0}$. More interesting examples may be produced as follows. Let ![]() $X$ be a free, finite
$X$ be a free, finite ![]() $G$-CW complex. Define
$G$-CW complex. Define
 $$\begin{eqnarray}\tilde{\unicode[STIX]{x1D6F4}}X=X\times [0,1]/(0,x)\sim (0,x^{\prime })\quad \text{and}\quad (1,x)\sim (1,x^{\prime })\quad \text{for}\;\text{all}\;x,x^{\prime }\in X.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D6F4}}X=X\times [0,1]/(0,x)\sim (0,x^{\prime })\quad \text{and}\quad (1,x)\sim (1,x^{\prime })\quad \text{for}\;\text{all}\;x,x^{\prime }\in X.\end{eqnarray}$$ We call ![]() $\tilde{\unicode[STIX]{x1D6F4}}X$ the unreduced suspension of
$\tilde{\unicode[STIX]{x1D6F4}}X$ the unreduced suspension of ![]() $X$. Here
$X$. Here ![]() $G$ acts on
$G$ acts on ![]() $\tilde{\unicode[STIX]{x1D6F4}}X$ by multiplication on the first factor. We fix one of the cone points as the base point. Then the
$\tilde{\unicode[STIX]{x1D6F4}}X$ by multiplication on the first factor. We fix one of the cone points as the base point. Then the ![]() $S^{1}$-fixed-point set is precisely
$S^{1}$-fixed-point set is precisely  $S^{0}\subset \tilde{\unicode[STIX]{x1D6F4}}X$, and
$S^{0}\subset \tilde{\unicode[STIX]{x1D6F4}}X$, and ![]() $\tilde{\unicode[STIX]{x1D6F4}}X$ is a space of type SWF. As a particular example, let
$\tilde{\unicode[STIX]{x1D6F4}}X$ is a space of type SWF. As a particular example, let ![]() $X=G$, where
$X=G$, where ![]() $G$ acts on
$G$ acts on ![]() $X$ by multiplication on the left, as usual. Then
$X$ by multiplication on the left, as usual. Then ![]() $\tilde{\unicode[STIX]{x1D6F4}}X$ is, topologically, the suspension of two disjoint circles.
$\tilde{\unicode[STIX]{x1D6F4}}X$ is, topologically, the suspension of two disjoint circles.
We also find it convenient to recall the definition of reduced Borel homology, for spaces ![]() $X$ of type SWF:
$X$ of type SWF:
 $$\begin{eqnarray}\tilde{H}_{\ast ,\text{red}}^{S^{1}}(X)=\tilde{H}_{\ast }^{S^{1}}(X)/\text{Im}\,U^{N},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast ,\text{red}}^{S^{1}}(X)=\tilde{H}_{\ast }^{S^{1}}(X)/\text{Im}\,U^{N},\end{eqnarray}$$ for ![]() $N\gg 0$. Indeed, for all
$N\gg 0$. Indeed, for all ![]() $N$ sufficiently large
$N$ sufficiently large  $\text{Im}\,U^{N}=\text{Im}\,U^{N+1}$, so
$\text{Im}\,U^{N}=\text{Im}\,U^{N+1}$, so  $\tilde{H}_{\ast ,\text{red}}^{S^{1}}(X)$ is well defined.
$\tilde{H}_{\ast ,\text{red}}^{S^{1}}(X)$ is well defined.
Associated to a space ![]() $X$ of type SWF at level
$X$ of type SWF at level ![]() $s$, we take the Borel cohomology
$s$, we take the Borel cohomology ![]() $\tilde{H}_{G}^{\ast }(X)$, from which we define
$\tilde{H}_{G}^{\ast }(X)$, from which we define  $a(X),b(X),$ and
$a(X),b(X),$ and ![]() $c(X)$ as in [Reference ManolescuMan16]:
$c(X)$ as in [Reference ManolescuMan16]:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}a(X)=\text{min}\{r\equiv s\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{G}^{r}(X),v^{l}x\neq 0\;\text{for}\;\text{all}\;l\geqslant 0\},\\[2.0pt] b(X)=\text{min}\{r\equiv s+1\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{G}^{r}(X),v^{l}x\neq 0\;\text{for}\;\text{all}\;l\geqslant 0\}-1,\\[2.0pt] c(X)=\text{min}\{r\equiv s+2\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{G}^{r}(X),v^{l}x\neq 0\;\text{for}\;\text{all}\;l\geqslant 0\}-2.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}a(X)=\text{min}\{r\equiv s\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{G}^{r}(X),v^{l}x\neq 0\;\text{for}\;\text{all}\;l\geqslant 0\},\\[2.0pt] b(X)=\text{min}\{r\equiv s+1\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{G}^{r}(X),v^{l}x\neq 0\;\text{for}\;\text{all}\;l\geqslant 0\}-1,\\[2.0pt] c(X)=\text{min}\{r\equiv s+2\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{G}^{r}(X),v^{l}x\neq 0\;\text{for}\;\text{all}\;l\geqslant 0\}-2.\end{array} & & \displaystyle\end{eqnarray}$$ The well-definedness of ![]() $a,b$, and
$a,b$, and ![]() $c$ follows from the equivariant localization theorem (see [Reference tom DiecktDie87] § III). We also list an equivalent definition of
$c$ follows from the equivariant localization theorem (see [Reference tom DiecktDie87] § III). We also list an equivalent definition of ![]() $a,b$, and
$a,b$, and ![]() $c$ from [Reference ManolescuMan16], using homology:
$c$ from [Reference ManolescuMan16], using homology:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}a(X)=\text{min}\;\{r\equiv s\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{r}^{G}(X),x\in \text{Im}\,v^{l}\;\text{for}\;\text{all}\;l\geqslant 0\},\\[2.0pt] b(X)=\text{min}\;\{r\equiv s+1\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{r}^{G}(X),x\in \text{Im}\,v^{l}\;\text{for}\;\text{all}\;l\geqslant 0\}-1,\\[2.0pt] c(X)=\text{min}\;\{r\equiv s+2\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{r}^{G}(X),x\in \text{Im}\,v^{l}\;\text{for}\;\text{all}\;l\geqslant 0\}-2.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}a(X)=\text{min}\;\{r\equiv s\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{r}^{G}(X),x\in \text{Im}\,v^{l}\;\text{for}\;\text{all}\;l\geqslant 0\},\\[2.0pt] b(X)=\text{min}\;\{r\equiv s+1\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{r}^{G}(X),x\in \text{Im}\,v^{l}\;\text{for}\;\text{all}\;l\geqslant 0\}-1,\\[2.0pt] c(X)=\text{min}\;\{r\equiv s+2\;\text{mod}\;4\mid \exists \,x\in \tilde{H}_{r}^{G}(X),x\in \text{Im}\,v^{l}\;\text{for}\;\text{all}\;l\geqslant 0\}-2.\end{array} & & \displaystyle\end{eqnarray}$$Remark 2.5. The Manolescu invariants of [Reference ManolescuMan16] are defined in terms of ![]() $a,b$, and
$a,b$, and ![]() $c$, as we will review in § 4.
$c$, as we will review in § 4.
Definition 2.6 (see [Reference ManolescuMan14]).
Let ![]() $X$ and
$X$ and ![]() $X^{\prime }$ be spaces of type SWF,
$X^{\prime }$ be spaces of type SWF,  $m,m^{\prime }\in \mathbb{Z}$, and
$m,m^{\prime }\in \mathbb{Z}$, and  $n,n^{\prime }\in \mathbb{Q}$. We say that the triples
$n,n^{\prime }\in \mathbb{Q}$. We say that the triples  $(X,m,n)$ and
$(X,m,n)$ and  $(X^{\prime },m^{\prime },n^{\prime })$ are stably equivalent if
$(X^{\prime },m^{\prime },n^{\prime })$ are stably equivalent if  $n-n^{\prime }\in \mathbb{Z}$ and there exists a
$n-n^{\prime }\in \mathbb{Z}$ and there exists a ![]() $G$-equivariant homotopy equivalence, for some
$G$-equivariant homotopy equivalence, for some ![]() $r\gg 0$ and some nonnegative
$r\gg 0$ and some nonnegative ![]() $M\in \mathbb{Z}$ and
$M\in \mathbb{Z}$ and ![]() $N\in \mathbb{Q}$:
$N\in \mathbb{Q}$:
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{r\mathbb{R}}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}X\rightarrow \unicode[STIX]{x1D6F4}^{r\mathbb{R}}\unicode[STIX]{x1D6F4}^{(M^{\prime }-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}X^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{r\mathbb{R}}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}X\rightarrow \unicode[STIX]{x1D6F4}^{r\mathbb{R}}\unicode[STIX]{x1D6F4}^{(M^{\prime }-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}X^{\prime }.\end{eqnarray}$$ Let ![]() $\mathfrak{E}$ be the set of equivalence classes of triples
$\mathfrak{E}$ be the set of equivalence classes of triples  $(X,m,n)$ for
$(X,m,n)$ for ![]() $X$ a space of type
$X$ a space of type ![]() $\text{SWF}$,
$\text{SWF}$, ![]() $m\in \mathbb{Z}$,
$m\in \mathbb{Z}$, ![]() $n\in \mathbb{Q}$, under the equivalence relation of stable
$n\in \mathbb{Q}$, under the equivalence relation of stable ![]() $G$-equivalence.Footnote 2 The set
$G$-equivalence.Footnote 2 The set ![]() $\mathfrak{E}$ may be considered as a subcategory of the
$\mathfrak{E}$ may be considered as a subcategory of the ![]() $G$-equivariant Spanier–Whitehead category [Reference ManolescuMan16], by viewing
$G$-equivariant Spanier–Whitehead category [Reference ManolescuMan16], by viewing  $(X,m,n)$ as the formal desuspension of
$(X,m,n)$ as the formal desuspension of ![]() $X$ by
$X$ by ![]() $m$ copies of
$m$ copies of ![]() $\tilde{\mathbb{R}}^{+}$ and
$\tilde{\mathbb{R}}^{+}$ and ![]() $n$ copies of
$n$ copies of ![]() $\mathbb{H}^{+}$. For
$\mathbb{H}^{+}$. For  $(X,m,n),(X^{\prime },m^{\prime },n^{\prime })\in \mathfrak{E}$, a map
$(X,m,n),(X^{\prime },m^{\prime },n^{\prime })\in \mathfrak{E}$, a map  $(X,m,n)\rightarrow (X^{\prime },m^{\prime },n^{\prime })$ is simply a map as in (11) that need not be a homotopy equivalence. We define Borel homology for
$(X,m,n)\rightarrow (X^{\prime },m^{\prime },n^{\prime })$ is simply a map as in (11) that need not be a homotopy equivalence. We define Borel homology for  $(X,m,n)\in \mathfrak{E}$ by
$(X,m,n)\in \mathfrak{E}$ by
 $$\begin{eqnarray}\tilde{H}_{\ast }^{G}((X,m,n))=\tilde{H}_{\ast }^{G}(X)[m+4n].\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{G}((X,m,n))=\tilde{H}_{\ast }^{G}(X)[m+4n].\end{eqnarray}$$ In (12), we needed to use the suspension-invariance  $\tilde{H}_{\ast }^{G}(\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}}X)=\tilde{H}_{\ast }^{G}(X)[-1]$, which only holds with
$\tilde{H}_{\ast }^{G}(\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}}X)=\tilde{H}_{\ast }^{G}(X)[-1]$, which only holds with ![]() $\mathbb{Z}/2$-coefficients. For
$\mathbb{Z}/2$-coefficients. For ![]() $\mathbb{Z}$-coefficients and other cohomology theories there need not be suspension-invariance of the same form and
$\mathbb{Z}$-coefficients and other cohomology theories there need not be suspension-invariance of the same form and ![]() $\mathfrak{E}$ must be replaced with a category involving suspension only by certain representations (cf. [Reference ManolescuMan14, Remark 4.4]).
$\mathfrak{E}$ must be replaced with a category involving suspension only by certain representations (cf. [Reference ManolescuMan14, Remark 4.4]).
Definition 2.7. We call  $X_{1},X_{2}\in \mathfrak{E}$locally equivalent if there exist
$X_{1},X_{2}\in \mathfrak{E}$locally equivalent if there exist ![]() $G$-equivariant (stable) maps
$G$-equivariant (stable) maps
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}:X_{1}\rightarrow X_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}:X_{2}\rightarrow X_{1}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}:X_{1}\rightarrow X_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}:X_{2}\rightarrow X_{1}, & \displaystyle \nonumber\end{eqnarray}$$ which are ![]() $G$-homotopy equivalences on the
$G$-homotopy equivalences on the ![]() $S^{1}$-fixed-point set. For such
$S^{1}$-fixed-point set. For such ![]() $X_{1},X_{2}$, we write
$X_{1},X_{2}$, we write  $X_{1}\equiv _{l}X_{2}$, and let
$X_{1}\equiv _{l}X_{2}$, and let ![]() $\mathfrak{LE}$ denote the set of local equivalence classes.
$\mathfrak{LE}$ denote the set of local equivalence classes.
Local equivalence is easily seen to be an equivalence relation. The set ![]() $\mathfrak{LE}$ comes with an abelian group structure, with multiplication given by smash product. One may check that inverses are given by Spanier–Whitehead duality.
$\mathfrak{LE}$ comes with an abelian group structure, with multiplication given by smash product. One may check that inverses are given by Spanier–Whitehead duality.
2.2  $G$-CW decompositions of
$G$-CW decompositions of  $G$-spaces
$G$-spaces
Throughout this section ![]() $X$ will denote a space of type SWF. Here we will give example
$X$ will denote a space of type SWF. Here we will give example ![]() $G$-CW decompositions and construct a
$G$-CW decompositions and construct a ![]() $G$-CW structure on smash products of
$G$-CW structure on smash products of ![]() $G$-spaces.
$G$-spaces.
For ![]() $W$ a CW complex, we write
$W$ a CW complex, we write  $C_{\ast }^{\text{CW}}(W)$ for the corresponding cellular (CW) chain complex. We fix a convenient CW decomposition of
$C_{\ast }^{\text{CW}}(W)$ for the corresponding cellular (CW) chain complex. We fix a convenient CW decomposition of ![]() $G$. The
$G$. The ![]() $0$-cells are the points
$0$-cells are the points  $1,j,j^{2},j^{3}$ in
$1,j,j^{2},j^{3}$ in ![]() $G$, and the
$G$, and the ![]() $1$-cells are
$1$-cells are  $s,js,j^{2}s,j^{3}s$, where
$s,js,j^{2}s,j^{3}s$, where  $s=\{e^{i\unicode[STIX]{x1D703}}\in S^{1}\mid \unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x1D70B})\}$. We identify each of the cells of this CW decomposition with its image in
$s=\{e^{i\unicode[STIX]{x1D703}}\in S^{1}\mid \unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x1D70B})\}$. We identify each of the cells of this CW decomposition with its image in  $C_{\ast }^{\text{CW}}(G)$, the corresponding
$C_{\ast }^{\text{CW}}(G)$, the corresponding ![]() $CW$ chain complex of
$CW$ chain complex of ![]() $G$. Then
$G$. Then  $\unicode[STIX]{x2202}(s)=1+j^{2}$. To ease notation, we will refer to
$\unicode[STIX]{x2202}(s)=1+j^{2}$. To ease notation, we will refer to  $C_{\ast }^{\text{CW}}(G)$ by
$C_{\ast }^{\text{CW}}(G)$ by ![]() ${\mathcal{G}}$.
${\mathcal{G}}$.
We will use that this CW decomposition also induces a CW decomposition of ![]() $S^{1}$, for which
$S^{1}$, for which  $C_{\ast }^{\text{CW}}(S^{1})$ is the subcomplex of
$C_{\ast }^{\text{CW}}(S^{1})$ is the subcomplex of ![]() ${\mathcal{G}}$ generated by
${\mathcal{G}}$ generated by  $1,j^{2},s,j^{2}s$.
$1,j^{2},s,j^{2}s$.
A ![]() $G$-CW decomposition of
$G$-CW decomposition of ![]() $X$ also induces a CW decomposition of
$X$ also induces a CW decomposition of ![]() $X$, using the decomposition of
$X$, using the decomposition of ![]() $G$ into cells as above, which we will call a
$G$ into cells as above, which we will call a ![]() $G$-compatible CW decomposition of
$G$-compatible CW decomposition of ![]() $X$.
$X$.
Example 2.8. Note that the representation ![]() $(\tilde{\mathbb{R}}^{s})^{+}$ admits a
$(\tilde{\mathbb{R}}^{s})^{+}$ admits a ![]() $G$-CW decomposition with
$G$-CW decomposition with ![]() $0$-skeleton a copy of
$0$-skeleton a copy of ![]() $S^{0}$ on which
$S^{0}$ on which ![]() $G$ acts trivially, and an
$G$ acts trivially, and an ![]() $i$-cell
$i$-cell ![]() $c_{i}$ of the form
$c_{i}$ of the form  $D^{i}\times \mathbb{Z}/2$ for
$D^{i}\times \mathbb{Z}/2$ for ![]() $i\leqslant s$. One of the two points of the
$i\leqslant s$. One of the two points of the ![]() $0$-skeleton of
$0$-skeleton of ![]() $(\tilde{\mathbb{R}}^{s})^{+}$ is fixed as the basepoint.
$(\tilde{\mathbb{R}}^{s})^{+}$ is fixed as the basepoint.
Example 2.9. We find a CW decomposition for ![]() $\mathbb{H}^{+}$ as a
$\mathbb{H}^{+}$ as a ![]() $G$-space. We write elements of
$G$-space. We write elements of ![]() $\mathbb{H}$ as pairs of complex numbers
$\mathbb{H}$ as pairs of complex numbers  $(z,w)=(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2}e^{i\unicode[STIX]{x1D703}_{2}})$ in polar coordinates. The action of
$(z,w)=(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2}e^{i\unicode[STIX]{x1D703}_{2}})$ in polar coordinates. The action of ![]() $j$ is then given by
$j$ is then given by  $j(z,w)=(-\bar{w},\bar{z})$. Fix the point at infinity as the base point. We let
$j(z,w)=(-\bar{w},\bar{z})$. Fix the point at infinity as the base point. We let ![]() $(0,0)$ be the (
$(0,0)$ be the (![]() $G$-invariant)
$G$-invariant) ![]() $0$-cell labeled
$0$-cell labeled ![]() $r_{0}$. We let
$r_{0}$. We let ![]() $y_{1}$ be the
$y_{1}$ be the ![]() $G$-
$G$-![]() $1$-cell given by the orbit of
$1$-cell given by the orbit of  $\{(r_{1},0)\mid r_{1}>0\}$:
$\{(r_{1},0)\mid r_{1}>0\}$:
 $$\begin{eqnarray}\{(r_{1}e^{i\unicode[STIX]{x1D703}},r_{2}e^{i\unicode[STIX]{x1D703}})\mid \,r_{1}r_{2}=0\}.\end{eqnarray}$$
$$\begin{eqnarray}\{(r_{1}e^{i\unicode[STIX]{x1D703}},r_{2}e^{i\unicode[STIX]{x1D703}})\mid \,r_{1}r_{2}=0\}.\end{eqnarray}$$ We take ![]() $y_{2}$ the
$y_{2}$ the ![]() $G$-
$G$-![]() $2$-cell given by the orbit of
$2$-cell given by the orbit of  $\{(r_{1},r_{2})\mid r_{1}r_{2}\neq 0\}$:
$\{(r_{1},r_{2})\mid r_{1}r_{2}\neq 0\}$:
 $$\begin{eqnarray}\{(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2}e^{i\unicode[STIX]{x1D703}_{2}})\mid \,\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D703}_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D70B},r_{1}r_{2}\neq 0\}.\end{eqnarray}$$
$$\begin{eqnarray}\{(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2}e^{i\unicode[STIX]{x1D703}_{2}})\mid \,\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D703}_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D70B},r_{1}r_{2}\neq 0\}.\end{eqnarray}$$ Finally, ![]() $y_{3}$ consists of the orbit of
$y_{3}$ consists of the orbit of  $\{(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2})\mid \unicode[STIX]{x1D703}_{1}\in (0,\unicode[STIX]{x1D70B}),\;r_{1}r_{2}\neq 0\}$:
$\{(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2})\mid \unicode[STIX]{x1D703}_{1}\in (0,\unicode[STIX]{x1D70B}),\;r_{1}r_{2}\neq 0\}$:
 $$\begin{eqnarray}\{(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2}e^{i\unicode[STIX]{x1D703}_{2}})\mid \,\unicode[STIX]{x1D703}_{1}\neq \unicode[STIX]{x1D703}_{2}\;\text{mod}\;\unicode[STIX]{x1D70B},r_{1}r_{2}\neq 0\}.\end{eqnarray}$$
$$\begin{eqnarray}\{(r_{1}e^{i\unicode[STIX]{x1D703}_{1}},r_{2}e^{i\unicode[STIX]{x1D703}_{2}})\mid \,\unicode[STIX]{x1D703}_{1}\neq \unicode[STIX]{x1D703}_{2}\;\text{mod}\;\unicode[STIX]{x1D70B},r_{1}r_{2}\neq 0\}.\end{eqnarray}$$ We now give  $X_{1}\wedge X_{2}$ a
$X_{1}\wedge X_{2}$ a ![]() $G$-CW structure for
$G$-CW structure for ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{2}$ spaces of type SWF. To do so, we proceed cell by cell on both factors, so we need only find a
$X_{2}$ spaces of type SWF. To do so, we proceed cell by cell on both factors, so we need only find a ![]() $G$-CW structure on
$G$-CW structure on ![]() $G\times G$,
$G\times G$,  $\mathbb{Z}/2\times G$, and
$\mathbb{Z}/2\times G$, and  $\mathbb{Z}/2\times \mathbb{Z}/2$, each with the diagonal
$\mathbb{Z}/2\times \mathbb{Z}/2$, each with the diagonal ![]() $G$-action. The space
$G$-action. The space  $\mathbb{Z}/2\times G$ has a
$\mathbb{Z}/2\times G$ has a ![]() $G$-CW decomposition as
$G$-CW decomposition as ![]() $G\amalg G$, as may be seen directly, and
$G\amalg G$, as may be seen directly, and  $\mathbb{Z}/2\times \mathbb{Z}/2$ may be written as a disjoint union of
$\mathbb{Z}/2\times \mathbb{Z}/2$ may be written as a disjoint union of ![]() $G$-
$G$-![]() $0$-cells
$0$-cells  $\mathbb{Z}/2\amalg \mathbb{Z}/2$.
$\mathbb{Z}/2\amalg \mathbb{Z}/2$.
Example 2.10. The ![]() $G$-CW structure on
$G$-CW structure on ![]() $G\times G$ is more complicated. Note that the product CW decomposition on
$G\times G$ is more complicated. Note that the product CW decomposition on ![]() $G\times G$ is not equivariant. We choose a homotopy
$G\times G$ is not equivariant. We choose a homotopy  $\unicode[STIX]{x1D719}_{t}:G\times G\rightarrow G\times G$ as in Figure 1, with
$\unicode[STIX]{x1D719}_{t}:G\times G\rightarrow G\times G$ as in Figure 1, with  $t\in [0,1]$,
$t\in [0,1]$,  $\unicode[STIX]{x1D719}_{0}=\text{Id},$ and
$\unicode[STIX]{x1D719}_{0}=\text{Id},$ and  $\unicode[STIX]{x1D719}_{1}(G\times G)$ shown. The arrows depict the action of
$\unicode[STIX]{x1D719}_{1}(G\times G)$ shown. The arrows depict the action of ![]() $S^{1}$. On the left, the diagonal lines show the
$S^{1}$. On the left, the diagonal lines show the ![]() $G$-action before homotopy. For example, the homotopy
$G$-action before homotopy. For example, the homotopy ![]() $\unicode[STIX]{x1D719}$ takes the line
$\unicode[STIX]{x1D719}$ takes the line  $\ell =\{(e^{i\unicode[STIX]{x1D703}}\times e^{i\unicode[STIX]{x1D703}})\mid \unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x1D70B})\}$, the first half of the diagonal in
$\ell =\{(e^{i\unicode[STIX]{x1D703}}\times e^{i\unicode[STIX]{x1D703}})\mid \unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x1D70B})\}$, the first half of the diagonal in  $S^{1}\times S^{1}$, to the sum of CW cells:
$S^{1}\times S^{1}$, to the sum of CW cells:
 $$\begin{eqnarray}s\otimes 1+j^{2}\otimes s.\end{eqnarray}$$
$$\begin{eqnarray}s\otimes 1+j^{2}\otimes s.\end{eqnarray}$$ The arrows on the right show the ![]() $G$-action on
$G$-action on ![]() $G\times G$ given by
$G\times G$ given by
 $$\begin{eqnarray}g(g_{1}\times g_{2})=\unicode[STIX]{x1D719}_{1}(g\unicode[STIX]{x1D719}_{1}^{-1}(g_{1}\times g_{2})).\end{eqnarray}$$
$$\begin{eqnarray}g(g_{1}\times g_{2})=\unicode[STIX]{x1D719}_{1}(g\unicode[STIX]{x1D719}_{1}^{-1}(g_{1}\times g_{2})).\end{eqnarray}$$ The action (13) is clearly cellular with respect to the product CW structure of ![]() $G\times G$. Then
$G\times G$. Then ![]() $G\times G$ admits a
$G\times G$ admits a ![]() $G$-CW-decomposition so that the induced CW decomposition is the product CW decomposition of
$G$-CW-decomposition so that the induced CW decomposition is the product CW decomposition of ![]() $G\times G$.
$G\times G$.
Now, let ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{2}$ be spaces of type SWF. We then give
$X_{2}$ be spaces of type SWF. We then give  $X_{1}\wedge X_{2}$ a
$X_{1}\wedge X_{2}$ a ![]() $G$-CW decomposition proceeding cell-by-cell. That is, for
$G$-CW decomposition proceeding cell-by-cell. That is, for ![]() $G$-cells
$G$-cells  $e_{1}\subseteq X_{1},e_{2}\subseteq X_{2}$ we give
$e_{1}\subseteq X_{1},e_{2}\subseteq X_{2}$ we give ![]() $e_{1}\wedge e_{2}$ the appropriate
$e_{1}\wedge e_{2}$ the appropriate ![]() $G$-CW decomposition as constructed above. This is possible because the cells
$G$-CW decomposition as constructed above. This is possible because the cells ![]() $e_{i}$ are necessarily of the form
$e_{i}$ are necessarily of the form ![]() $D^{k}$,
$D^{k}$,  $\mathbb{Z}/2\times D^{k}$, or
$\mathbb{Z}/2\times D^{k}$, or ![]() $G\times D^{k}$. In particular, the construction of a
$G\times D^{k}$. In particular, the construction of a ![]() $G$-CW structure on
$G$-CW structure on  $X_{1}\wedge X_{2}$ gives us a
$X_{1}\wedge X_{2}$ gives us a ![]() $G$-CW structure for suspensions. For
$G$-CW structure for suspensions. For ![]() $V$ a finite-dimensional
$V$ a finite-dimensional ![]() $G$-representation which is a direct sum of copies of
$G$-representation which is a direct sum of copies of ![]() $\mathbb{R},\tilde{\mathbb{R}},$ and
$\mathbb{R},\tilde{\mathbb{R}},$ and ![]() $\mathbb{H}$, we have
$\mathbb{H}$, we have  $\unicode[STIX]{x1D6F4}^{V}X=V^{+}\wedge X$, and so we give
$\unicode[STIX]{x1D6F4}^{V}X=V^{+}\wedge X$, and so we give ![]() $\unicode[STIX]{x1D6F4}^{V}X$ the smash product
$\unicode[STIX]{x1D6F4}^{V}X$ the smash product ![]() $G$-CW decomposition.
$G$-CW decomposition.

Figure 1. Homotopy of the action of ![]() $G$ on
$G$ on ![]() $G\times G$.
$G\times G$.
Finally, we construct a CW structure for the ![]() $G$-smash product
$G$-smash product  $X_{1}\wedge _{G}X_{2}=(X_{1}\wedge X_{2})/G$ (where
$X_{1}\wedge _{G}X_{2}=(X_{1}\wedge X_{2})/G$ (where ![]() $G$ acts diagonally). More generally, we describe a CW structure for the quotient
$G$ acts diagonally). More generally, we describe a CW structure for the quotient ![]() $W/G$ for
$W/G$ for ![]() $W$ a
$W$ a ![]() $G$-CW complex. Indeed, let
$G$-CW complex. Indeed, let  $W=\bigcup e_{i}$ a
$W=\bigcup e_{i}$ a ![]() $G$-CW complex, where
$G$-CW complex, where  $e_{i}=G/H_{i}\times D^{k(i)}$ are equivariant
$e_{i}=G/H_{i}\times D^{k(i)}$ are equivariant ![]() $G$-cells for some function
$G$-cells for some function ![]() $k$, and
$k$, and ![]() $H_{i}\subseteq G$ are subgroups. Then
$H_{i}\subseteq G$ are subgroups. Then ![]() $W/G$ admits a CW decomposition given by
$W/G$ admits a CW decomposition given by  $W/G=\bigcup e_{i}/G=\bigcup D^{k(i)}$.
$W/G=\bigcup e_{i}/G=\bigcup D^{k(i)}$.
2.3 Modules from  $G$-CW decompositions
$G$-CW decompositions
Throughout this section ![]() $X$ will denote a space of type SWF. Here we will show that the CW chain complex of
$X$ will denote a space of type SWF. Here we will show that the CW chain complex of ![]() $X$ inherits a module structure from the action of
$X$ inherits a module structure from the action of ![]() $G$, and we will define chain local equivalence.
$G$, and we will define chain local equivalence.
From the group structure of ![]() $G$,
$G$,  $C_{\ast }^{\text{CW}}(G)={\mathcal{G}}$ acquires an algebra structure. Namely, the multiplication map
$C_{\ast }^{\text{CW}}(G)={\mathcal{G}}$ acquires an algebra structure. Namely, the multiplication map  $G\times G\rightarrow G$ gives a map
$G\times G\rightarrow G$ gives a map  $C_{\ast }^{\text{CW}}(G)\otimes _{\mathbb{F}}C_{\ast }^{\text{CW}}(G)\rightarrow C_{\ast }^{\text{CW}}(G)$. Here, we have used the product
$C_{\ast }^{\text{CW}}(G)\otimes _{\mathbb{F}}C_{\ast }^{\text{CW}}(G)\rightarrow C_{\ast }^{\text{CW}}(G)$. Here, we have used the product ![]() $G$-CW decomposition of
$G$-CW decomposition of ![]() $G\times G$, from Example 2.10, for which the multiplication map is cellular. A small calculation yields
$G\times G$, from Example 2.10, for which the multiplication map is cellular. A small calculation yields
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(G)\cong \mathbb{F}\langle s,j\rangle /(sj=j^{3}s,s^{2}=0,j^{4}=1).\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(G)\cong \mathbb{F}\langle s,j\rangle /(sj=j^{3}s,s^{2}=0,j^{4}=1).\end{eqnarray}$$ For any ![]() $G$-compatible decomposition of
$G$-compatible decomposition of ![]() $X$, the relative CW chain complex
$X$, the relative CW chain complex  $C_{\ast }^{\text{CW}}(X,\text{pt})$, which we will call the reduced
$C_{\ast }^{\text{CW}}(X,\text{pt})$, which we will call the reduced ![]() $G$-CW chain complex of
$G$-CW chain complex of ![]() $X$, inherits the structure of a
$X$, inherits the structure of a ![]() ${\mathcal{G}}$-chain complex, as the (cellular) map
${\mathcal{G}}$-chain complex, as the (cellular) map  $G\times X\rightarrow X$ gives a map
$G\times X\rightarrow X$ gives a map  ${\mathcal{G}}\times C_{\ast }^{\text{CW}}(X,\text{pt})\rightarrow C_{\ast }^{\text{CW}}(X,\text{pt})$. That is,
${\mathcal{G}}\times C_{\ast }^{\text{CW}}(X,\text{pt})\rightarrow C_{\ast }^{\text{CW}}(X,\text{pt})$. That is,  $C_{\ast }^{\text{CW}}(X,\text{pt})$ is a module over
$C_{\ast }^{\text{CW}}(X,\text{pt})$ is a module over ![]() ${\mathcal{G}}$, such that, for
${\mathcal{G}}$, such that, for  $z\in C_{\ast }^{\text{CW}}(X,\text{pt})$, and
$z\in C_{\ast }^{\text{CW}}(X,\text{pt})$, and ![]() $a\in {\mathcal{G}}$,
$a\in {\mathcal{G}}$,  $\unicode[STIX]{x2202}(az)=a\unicode[STIX]{x2202}(z)+\unicode[STIX]{x2202}(a)z$. The assertion that
$\unicode[STIX]{x2202}(az)=a\unicode[STIX]{x2202}(z)+\unicode[STIX]{x2202}(a)z$. The assertion that  $(gh)x=g(hx)$ for
$(gh)x=g(hx)$ for  $g,h\in {\mathcal{G}}$ and
$g,h\in {\mathcal{G}}$ and  $x\in C_{\ast }^{\text{CW}}(X,\text{pt})$ follows from the fact that the map
$x\in C_{\ast }^{\text{CW}}(X,\text{pt})$ follows from the fact that the map  $G\times X\rightarrow X$ is a group action. More concretely, having fixed a
$G\times X\rightarrow X$ is a group action. More concretely, having fixed a ![]() $G$-compatible CW decomposition of
$G$-compatible CW decomposition of ![]() $X$,
$X$,  $C_{\ast }^{\text{CW}}(X)$ is a
$C_{\ast }^{\text{CW}}(X)$ is a ![]() ${\mathcal{G}}$-module with basis (over
${\mathcal{G}}$-module with basis (over ![]() ${\mathcal{G}}$) given by the set of
${\mathcal{G}}$) given by the set of ![]() $G$-cells.
$G$-cells.
We find the module structure for the Examples 2.8–2.10 of § 2.2.
Example 2.11. Consider the ![]() ${\mathcal{G}}$-chain complex structure of
${\mathcal{G}}$-chain complex structure of  $C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$ from Example 2.8. Each equivariant cell
$C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$ from Example 2.8. Each equivariant cell ![]() $c_{i}$ is itself the
$c_{i}$ is itself the ![]() $\mathbb{Z}/2$-orbit of a nonequivariant cell
$\mathbb{Z}/2$-orbit of a nonequivariant cell  $c_{i}^{\prime }=D^{i}\times 0$. Identifying
$c_{i}^{\prime }=D^{i}\times 0$. Identifying ![]() $c_{i}^{\prime }$ with its image in
$c_{i}^{\prime }$ with its image in  $C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$, we have
$C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$, we have  $\unicode[STIX]{x2202}(c_{0}^{\prime })=0,\unicode[STIX]{x2202}(c_{1}^{\prime })=c_{0}^{\prime },$ and
$\unicode[STIX]{x2202}(c_{0}^{\prime })=0,\unicode[STIX]{x2202}(c_{1}^{\prime })=c_{0}^{\prime },$ and  $\unicode[STIX]{x2202}(c_{i}^{\prime })=(1+j)c_{i-1}^{\prime }$ for
$\unicode[STIX]{x2202}(c_{i}^{\prime })=(1+j)c_{i-1}^{\prime }$ for ![]() $i\geqslant 2$. One may check that the action of
$i\geqslant 2$. One may check that the action of ![]() ${\mathcal{G}}$ is given by the relations
${\mathcal{G}}$ is given by the relations  $jc_{0}^{\prime }=c_{0}^{\prime }$,
$jc_{0}^{\prime }=c_{0}^{\prime }$,  $j^{2}c_{i}^{\prime }=c_{i}^{\prime }$ for
$j^{2}c_{i}^{\prime }=c_{i}^{\prime }$ for ![]() $i\geqslant 1$, and
$i\geqslant 1$, and ![]() $sc_{i}^{\prime }=0$ for all
$sc_{i}^{\prime }=0$ for all ![]() $i$ (in particular, the CW cells of
$i$ (in particular, the CW cells of  $((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$ are precisely
$((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$ are precisely  $c_{0}^{\prime },c_{1}^{\prime },\ldots ,c_{s}^{\prime }$ and
$c_{0}^{\prime },c_{1}^{\prime },\ldots ,c_{s}^{\prime }$ and  $jc_{1}^{\prime },\ldots ,jc_{s}^{\prime }$, and all of these are distinct).
$jc_{1}^{\prime },\ldots ,jc_{s}^{\prime }$, and all of these are distinct).
Example 2.12. We also find the ![]() ${\mathcal{G}}$-chain complex structure of
${\mathcal{G}}$-chain complex structure of  $C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$ from Example 2.9. We choose CW cells
$C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$ from Example 2.9. We choose CW cells ![]() $r_{0}^{\prime },y_{i}^{\prime }$, as in Example 2.9, whose orbits are
$r_{0}^{\prime },y_{i}^{\prime }$, as in Example 2.9, whose orbits are ![]() $r_{0},y_{i}$. One may check that the differentials are given by
$r_{0},y_{i}$. One may check that the differentials are given by
 $$\begin{eqnarray}\unicode[STIX]{x2202}(r_{0}^{\prime })=0,\quad \unicode[STIX]{x2202}y_{1}^{\prime }=r_{0}^{\prime },\quad \unicode[STIX]{x2202}y_{2}^{\prime }=(1+j)y_{1}^{\prime },\quad \text{and}\quad \unicode[STIX]{x2202}y_{3}^{\prime }=sy_{1}^{\prime }+(1+j)y_{2}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(r_{0}^{\prime })=0,\quad \unicode[STIX]{x2202}y_{1}^{\prime }=r_{0}^{\prime },\quad \unicode[STIX]{x2202}y_{2}^{\prime }=(1+j)y_{1}^{\prime },\quad \text{and}\quad \unicode[STIX]{x2202}y_{3}^{\prime }=sy_{1}^{\prime }+(1+j)y_{2}^{\prime }.\end{eqnarray}$$ The ![]() ${\mathcal{G}}$-action on the fixed-point set,
${\mathcal{G}}$-action on the fixed-point set, ![]() $r_{0}^{\prime }$, is necessarily trivial. However, elsewhere the
$r_{0}^{\prime }$, is necessarily trivial. However, elsewhere the ![]() $G$-action on
$G$-action on  $(\mathbb{H}^{+},\text{pt})$ is free, and so the submodule (not a subcomplex, however) of
$(\mathbb{H}^{+},\text{pt})$ is free, and so the submodule (not a subcomplex, however) of  $C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$ generated by
$C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$ generated by  $y_{1}^{\prime },y_{2}^{\prime },y_{3}^{\prime }$ is
$y_{1}^{\prime },y_{2}^{\prime },y_{3}^{\prime }$ is ![]() ${\mathcal{G}}$-free, specifying the
${\mathcal{G}}$-free, specifying the ![]() ${\mathcal{G}}$-module structure of
${\mathcal{G}}$-module structure of  $C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$.
$C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$.
Example 2.13. The CW chain complex of the usual product CW structure on ![]() $G\times G$ becomes a
$G\times G$ becomes a ![]() ${\mathcal{G}}$-module via
${\mathcal{G}}$-module via
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(G\times G)=C_{\ast }^{\text{CW}}(G)\otimes _{\mathbb{ F}}C_{\ast }^{\text{CW}}(G),\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(G\times G)=C_{\ast }^{\text{CW}}(G)\otimes _{\mathbb{ F}}C_{\ast }^{\text{CW}}(G),\end{eqnarray}$$ where the action of ![]() ${\mathcal{G}}$ is given by
${\mathcal{G}}$ is given by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}s(a\otimes b)=sa\otimes b+j^{2}a\otimes sb,\\ j(a\otimes b)=ja\otimes jb.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}s(a\otimes b)=sa\otimes b+j^{2}a\otimes sb,\\ j(a\otimes b)=ja\otimes jb.\end{array} & & \displaystyle\end{eqnarray}$$ The differentials are induced by those of the usual product CW structure on ![]() $G\times G$.
$G\times G$.
For  $X_{1}\wedge X_{2}$ with the
$X_{1}\wedge X_{2}$ with the ![]() $G$-CW decomposition described in § 2.2, we have
$G$-CW decomposition described in § 2.2, we have
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(X_{1}\wedge X_{2},\text{pt})=C_{\ast }^{\text{CW}}(X_{1},\text{pt})\otimes _{\mathbb{F}}C_{\ast }^{\text{CW}}(X_{2},\text{pt}),\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(X_{1}\wedge X_{2},\text{pt})=C_{\ast }^{\text{CW}}(X_{1},\text{pt})\otimes _{\mathbb{F}}C_{\ast }^{\text{CW}}(X_{2},\text{pt}),\end{eqnarray}$$ as ![]() ${\mathcal{G}}$-chain complexes, using (15).
${\mathcal{G}}$-chain complexes, using (15).
Furthermore the CW chain complex for the ![]() $G$-smash product
$G$-smash product  $X_{1}\wedge _{G}X_{2}$ is given by
$X_{1}\wedge _{G}X_{2}$ is given by
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(X_{1}\wedge _{G}X_{2},\text{pt})\simeq C_{\ast }^{\text{CW}}(X_{1}\wedge X_{2},\text{pt})/{\mathcal{G}}.\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(X_{1}\wedge _{G}X_{2},\text{pt})\simeq C_{\ast }^{\text{CW}}(X_{1}\wedge X_{2},\text{pt})/{\mathcal{G}}.\end{eqnarray}$$ Here, the right-hand side is defined by quotienting by the action of ![]() $(1+j)$ and
$(1+j)$ and ![]() $s$. One may check directly that the result is a chain complex.
$s$. One may check directly that the result is a chain complex.
We will write elements of the latter as  $x_{1}\otimes _{{\mathcal{G}}}x_{2}$. Note that Borel homology
$x_{1}\otimes _{{\mathcal{G}}}x_{2}$. Note that Borel homology ![]() $\tilde{H}_{\ast }^{G}(X)$ is calculated using a
$\tilde{H}_{\ast }^{G}(X)$ is calculated using a ![]() $G$-smash product, and so may be computed from the following chain complex:
$G$-smash product, and so may be computed from the following chain complex:
 $$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X)=H((C_{\ast }^{\text{CW}}(EG)\otimes _{\mathbb{ F}}C_{\ast }^{\text{CW}}(X,\text{pt}))/{\mathcal{G}},\unicode[STIX]{x2202}).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X)=H((C_{\ast }^{\text{CW}}(EG)\otimes _{\mathbb{ F}}C_{\ast }^{\text{CW}}(X,\text{pt}))/{\mathcal{G}},\unicode[STIX]{x2202}).\end{eqnarray}$$ In (18), we choose some fixed ![]() $G$-CW decomposition of
$G$-CW decomposition of ![]() $EG$ to define
$EG$ to define  $C_{\ast }^{\text{CW}}(EG)$. Following (18), we make a definition.
$C_{\ast }^{\text{CW}}(EG)$. Following (18), we make a definition.
Definition 2.14. Let ![]() $Z$ a
$Z$ a ![]() ${\mathcal{G}}$-chain complex. We define the
${\mathcal{G}}$-chain complex. We define the ![]() $G$-Borel homology of
$G$-Borel homology of ![]() $Z$ by
$Z$ by
 $$\begin{eqnarray}H_{\ast }^{G}(Z)=H(C_{\ast }^{\text{CW}}(EG)\otimes _{{\mathcal{G}}}Z,\unicode[STIX]{x2202}),\end{eqnarray}$$
$$\begin{eqnarray}H_{\ast }^{G}(Z)=H(C_{\ast }^{\text{CW}}(EG)\otimes _{{\mathcal{G}}}Z,\unicode[STIX]{x2202}),\end{eqnarray}$$ and similarly for ![]() $S^{1}$-Borel homology:
$S^{1}$-Borel homology:
 $$\begin{eqnarray}H_{\ast }^{S^{1}}(Z)=H(C_{\ast }^{\text{CW}}(EG)\otimes _{C_{\ast }^{\text{CW}}(S^{1})}Z,\unicode[STIX]{x2202}),\end{eqnarray}$$
$$\begin{eqnarray}H_{\ast }^{S^{1}}(Z)=H(C_{\ast }^{\text{CW}}(EG)\otimes _{C_{\ast }^{\text{CW}}(S^{1})}Z,\unicode[STIX]{x2202}),\end{eqnarray}$$ where  $C_{\ast }^{\text{CW}}(S^{1})$ is viewed as a subcomplex of
$C_{\ast }^{\text{CW}}(S^{1})$ is viewed as a subcomplex of ![]() ${\mathcal{G}}$.
${\mathcal{G}}$.
Note then that the ![]() ${\mathcal{G}}$-module
${\mathcal{G}}$-module  $C_{\ast }^{\text{CW}}(X,\text{pt})$ determines
$C_{\ast }^{\text{CW}}(X,\text{pt})$ determines ![]() $\tilde{H}_{\ast }^{G}(X)$ for
$\tilde{H}_{\ast }^{G}(X)$ for ![]() $X$ a space of type SWF.
$X$ a space of type SWF.
Definition 2.15. A ![]() ${\mathcal{G}}$-chain complex
${\mathcal{G}}$-chain complex ![]() $Z$of type SWF at level
$Z$of type SWF at level ![]() $s$ is a
$s$ is a ![]() ${\mathcal{G}}$-chain complex
${\mathcal{G}}$-chain complex ![]() $Z$ generated by
$Z$ generated by
 $$\begin{eqnarray}\{c_{0},c_{1},c_{2},\ldots ,c_{s}\}\,\cup \,\mathop{\bigcup }_{i\in I}\{x_{i}\},\end{eqnarray}$$
$$\begin{eqnarray}\{c_{0},c_{1},c_{2},\ldots ,c_{s}\}\,\cup \,\mathop{\bigcup }_{i\in I}\{x_{i}\},\end{eqnarray}$$ subject to the following conditions (perhaps with an overall grading shift). The element ![]() $c_{i}$ is of degree
$c_{i}$ is of degree ![]() $i$, and
$i$, and ![]() $I$ is some finite index set. The only relations are
$I$ is some finite index set. The only relations are  $j^{2}c_{i}=c_{i},sc_{i}=0,jc_{0}=c_{0}$. The differentials are given by
$j^{2}c_{i}=c_{i},sc_{i}=0,jc_{0}=c_{0}$. The differentials are given by  $\unicode[STIX]{x2202}c_{0}=0$,
$\unicode[STIX]{x2202}c_{0}=0$,  $\unicode[STIX]{x2202}c_{1}=c_{0}$, and
$\unicode[STIX]{x2202}c_{1}=c_{0}$, and  $\unicode[STIX]{x2202}c_{i}=(1+j)c_{i-1}$ for
$\unicode[STIX]{x2202}c_{i}=(1+j)c_{i-1}$ for  $2\leqslant i\leqslant s$. The submodule generated by
$2\leqslant i\leqslant s$. The submodule generated by ![]() $\{{x_{i}\}}_{i\in I}$ is free under the action of
$\{{x_{i}\}}_{i\in I}$ is free under the action of ![]() ${\mathcal{G}}$. We call the submodule generated by
${\mathcal{G}}$. We call the submodule generated by ![]() $\{{c_{i}\}}_{i}$ the fixed-point set (or fixed-point subcomplex) of
$\{{c_{i}\}}_{i}$ the fixed-point set (or fixed-point subcomplex) of ![]() $Z$.
$Z$.
Note that the fixed-point subcomplex is part of the data of a complex of type SWF.
Chain complexes of type SWF are to be thought of as reduced ![]() $G$-CW chain complexes of spaces of type SWF. Indeed, all spaces
$G$-CW chain complexes of spaces of type SWF. Indeed, all spaces ![]() $X$ of type SWF have reduced
$X$ of type SWF have reduced ![]() $G$-CW chain complex homotopy equivalent to a complex of type SWF. To see this, we first choose a homotopy equivalence
$G$-CW chain complex homotopy equivalent to a complex of type SWF. To see this, we first choose a homotopy equivalence  $X^{S^{1}}\simeq (\tilde{\mathbb{R}}^{s})^{+}$ and decompose the latter according to the CW decomposition of Example 2.8. We note that
$X^{S^{1}}\simeq (\tilde{\mathbb{R}}^{s})^{+}$ and decompose the latter according to the CW decomposition of Example 2.8. We note that ![]() $X^{S^{1}}$ is a
$X^{S^{1}}$ is a ![]() $G$-CW subcomplex of
$G$-CW subcomplex of ![]() $X$, and all cells of
$X$, and all cells of  $(X,X^{S^{1}})$ are free
$(X,X^{S^{1}})$ are free ![]() $G$-cells, since
$G$-cells, since ![]() $X$ is a space of type SWF. Then
$X$ is a space of type SWF. Then ![]() $X$ is homotopy-equivalent to a space obtained by attaching
$X$ is homotopy-equivalent to a space obtained by attaching ![]() $X/X^{S^{1}}$ to
$X/X^{S^{1}}$ to ![]() $(\tilde{\mathbb{R}}^{s})^{+}$. By a cellular approximation we obtain a chain map,
$(\tilde{\mathbb{R}}^{s})^{+}$. By a cellular approximation we obtain a chain map,
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(X/X^{S^{1}},\text{pt})\rightarrow C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{\mathbb{R}}(\tilde{\mathbb{R}}^{s})^{+},\text{pt}),\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(X/X^{S^{1}},\text{pt})\rightarrow C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{\mathbb{R}}(\tilde{\mathbb{R}}^{s})^{+},\text{pt}),\end{eqnarray}$$ whose mapping cone is homotopy equivalent to  $C_{\ast }^{\text{CW}}(X,\text{pt})[-1]$. However, any two equivariant CW complexes for
$C_{\ast }^{\text{CW}}(X,\text{pt})[-1]$. However, any two equivariant CW complexes for ![]() $(\tilde{\mathbb{R}}^{s})^{+}$ are chain homotopy equivalent. To see this, first note that for any such CW decomposition, the standard CW chain complex
$(\tilde{\mathbb{R}}^{s})^{+}$ are chain homotopy equivalent. To see this, first note that for any such CW decomposition, the standard CW chain complex  $\langle c_{0},\ldots ,c_{s}\rangle$ admits a quasi-isomorphism to
$\langle c_{0},\ldots ,c_{s}\rangle$ admits a quasi-isomorphism to  $C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$. This induces a quasi-isomorphism
$C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$. This induces a quasi-isomorphism  $\langle c_{1},\ldots ,c_{s}\rangle \rightarrow C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},S^{0})$. That is, we have a quasi-isomorphism between free
$\langle c_{1},\ldots ,c_{s}\rangle \rightarrow C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},S^{0})$. That is, we have a quasi-isomorphism between free ![]() $\mathbb{Z}_{2}$-complexes. By [Reference WeibelWei94, Theorem 10.4.8], these complexes are in fact homotopy equivalent, from which it also follows that
$\mathbb{Z}_{2}$-complexes. By [Reference WeibelWei94, Theorem 10.4.8], these complexes are in fact homotopy equivalent, from which it also follows that  $C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})\simeq \langle c_{0},\ldots ,c_{s}\rangle$. Similarly, we obtain that any two equivariant CW complexes for
$C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})\simeq \langle c_{0},\ldots ,c_{s}\rangle$. Similarly, we obtain that any two equivariant CW complexes for  $\unicode[STIX]{x1D6F4}^{\mathbb{R}}(\tilde{\mathbb{R}}^{s})^{+}$ are chain homotopy equivalent. Then we may replace (22) with the same sequence, using the standard CW complex structure on
$\unicode[STIX]{x1D6F4}^{\mathbb{R}}(\tilde{\mathbb{R}}^{s})^{+}$ are chain homotopy equivalent. Then we may replace (22) with the same sequence, using the standard CW complex structure on ![]() $(\tilde{\mathbb{R}}^{s})^{+}$, and we see that
$(\tilde{\mathbb{R}}^{s})^{+}$, and we see that  $C_{\ast }^{\text{CW}}(X,\text{pt})$ is homotopy-equivalent to a chain complex of type SWF.
$C_{\ast }^{\text{CW}}(X,\text{pt})$ is homotopy-equivalent to a chain complex of type SWF.
Let ![]() $\tilde{\oplus }$ denote a direct sum of
$\tilde{\oplus }$ denote a direct sum of ![]() ${\mathcal{G}}$-modules that need not be a direct sum of chain complexes. Note that a choice of decomposition
${\mathcal{G}}$-modules that need not be a direct sum of chain complexes. Note that a choice of decomposition ![]() $R\,\tilde{\oplus }\,F$ of a chain complex of type SWF, where
$R\,\tilde{\oplus }\,F$ of a chain complex of type SWF, where  $R=\langle c_{0},\ldots ,c_{s}\rangle$ and
$R=\langle c_{0},\ldots ,c_{s}\rangle$ and  $F=\text{span}_{i}\{x_{i}\}$, is not part of the data in the definition. However, for a space
$F=\text{span}_{i}\{x_{i}\}$, is not part of the data in the definition. However, for a space ![]() $X$ of type SWF,
$X$ of type SWF,  $C_{\ast }^{\text{CW}}(X,\text{pt})$ comes with a preferred fixed-subset (from fixed cells), and much of what follows could be rephrased where the decomposition is part of the data of a complex of type SWF (this will turn out to be somewhat immaterial; cf. Lemma 2.24).
$C_{\ast }^{\text{CW}}(X,\text{pt})$ comes with a preferred fixed-subset (from fixed cells), and much of what follows could be rephrased where the decomposition is part of the data of a complex of type SWF (this will turn out to be somewhat immaterial; cf. Lemma 2.24).
To introduce chain local equivalence, we will consider the CW chain complexes coming from suspensions. For a module ![]() $M$ and a submodule
$M$ and a submodule ![]() $S\subseteq M$, we let
$S\subseteq M$, we let  $\langle S\rangle \subseteq M$ denote the subset generated by
$\langle S\rangle \subseteq M$ denote the subset generated by ![]() $S$.
$S$.
Note that, by Example 2.11 and the ![]() $G$-CW decomposition constructed in § 2.2 for suspensions, for
$G$-CW decomposition constructed in § 2.2 for suspensions, for ![]() $X$ a space of type SWF:
$X$ a space of type SWF:
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}}X,\text{pt})=\langle c_{0},c_{1}\rangle \,\otimes _{\mathbb{F}}\,C_{\ast }^{\text{CW}}(X,\text{pt}),\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}}X,\text{pt})=\langle c_{0},c_{1}\rangle \,\otimes _{\mathbb{F}}\,C_{\ast }^{\text{CW}}(X,\text{pt}),\end{eqnarray}$$ with relations  $\unicode[STIX]{x2202}c_{1}=c_{0}$,
$\unicode[STIX]{x2202}c_{1}=c_{0}$,  $j^{2}c_{1}=c_{1},jc_{0}=c_{0},sc_{0}=sc_{1}=0$. The differential on the right is given by
$j^{2}c_{1}=c_{1},jc_{0}=c_{0},sc_{0}=sc_{1}=0$. The differential on the right is given by  $\unicode[STIX]{x2202}(a\otimes b)=\unicode[STIX]{x2202}(a)\otimes b+a\otimes \unicode[STIX]{x2202}(b)$. Similarly, using Example 2.12:
$\unicode[STIX]{x2202}(a\otimes b)=\unicode[STIX]{x2202}(a)\otimes b+a\otimes \unicode[STIX]{x2202}(b)$. Similarly, using Example 2.12:
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{\mathbb{H}}X,\text{pt})=\langle r_{0},y_{1},y_{2},y_{3}\rangle \,\otimes _{\mathbb{F}}\,C_{\ast }^{\text{CW}}(X,\text{pt}),\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{\mathbb{H}}X,\text{pt})=\langle r_{0},y_{1},y_{2},y_{3}\rangle \,\otimes _{\mathbb{F}}\,C_{\ast }^{\text{CW}}(X,\text{pt}),\end{eqnarray}$$ with the product differential on the right, and differentials for the ![]() $y_{i}$ given as in Example 2.12.
$y_{i}$ given as in Example 2.12.
For ![]() $V=\mathbb{H}$,
$V=\mathbb{H}$, ![]() $\tilde{\mathbb{R}}$, or
$\tilde{\mathbb{R}}$, or ![]() $\mathbb{R}$, and
$\mathbb{R}$, and ![]() $Z$ a
$Z$ a ![]() ${\mathcal{G}}$-chain complex, we set
${\mathcal{G}}$-chain complex, we set
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}Z=C_{\ast }^{\text{CW}}(V^{+},\text{pt})\,\otimes _{\mathbb{ F}}\,Z,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}Z=C_{\ast }^{\text{CW}}(V^{+},\text{pt})\,\otimes _{\mathbb{ F}}\,Z,\end{eqnarray}$$ with ![]() ${\mathcal{G}}$-action given by
${\mathcal{G}}$-action given by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}s(a\otimes b)=(sa\otimes b)+(j^{2}a\otimes sb),\\[2.0pt] j(a\otimes b)=ja\otimes jb.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}s(a\otimes b)=(sa\otimes b)+(j^{2}a\otimes sb),\\[2.0pt] j(a\otimes b)=ja\otimes jb.\end{array} & & \displaystyle\end{eqnarray}$$ The chain complexes  $C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$ and
$C_{\ast }^{\text{CW}}(\mathbb{H}^{+},\text{pt})$ and  $C_{\ast }^{\text{CW}}(\tilde{\mathbb{R}}^{+},\text{pt})$ were given in Examples 2.11 and 2.12, respectively. Also,
$C_{\ast }^{\text{CW}}(\tilde{\mathbb{R}}^{+},\text{pt})$ were given in Examples 2.11 and 2.12, respectively. Also,  $C_{\ast }^{\text{CW}}(\mathbb{R}^{+},\text{pt})=\langle c_{1}\rangle$, where
$C_{\ast }^{\text{CW}}(\mathbb{R}^{+},\text{pt})=\langle c_{1}\rangle$, where  $jc_{1}=c_{1},sc_{1}=0$, and
$jc_{1}=c_{1},sc_{1}=0$, and  $\text{deg}\,c_{1}=1$. Hence, for example,
$\text{deg}\,c_{1}=1$. Hence, for example,
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\mathbb{R}}Z=Z[-1].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\mathbb{R}}Z=Z[-1].\end{eqnarray}$$Lemma 2.16. Let ![]() $V=\mathbb{H}$,
$V=\mathbb{H}$, ![]() $\tilde{\mathbb{R}}$, or
$\tilde{\mathbb{R}}$, or ![]() $\mathbb{R}$. If
$\mathbb{R}$. If  $Z=C_{\ast }^{\text{CW}}(X,\text{pt})$ for
$Z=C_{\ast }^{\text{CW}}(X,\text{pt})$ for ![]() $X$ a space of type SWF, then
$X$ a space of type SWF, then  $\unicode[STIX]{x1D6F4}^{V}Z=C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{V}X,\text{pt})$.
$\unicode[STIX]{x1D6F4}^{V}Z=C_{\ast }^{\text{CW}}(\unicode[STIX]{x1D6F4}^{V}X,\text{pt})$.
For  $V=\mathbb{H}^{i}\oplus \tilde{\mathbb{R}}^{j}\oplus \mathbb{R}^{k}$ for some constants
$V=\mathbb{H}^{i}\oplus \tilde{\mathbb{R}}^{j}\oplus \mathbb{R}^{k}$ for some constants ![]() $i,j,k$, we define
$i,j,k$, we define ![]() $\unicode[STIX]{x1D6F4}^{V}Z$ by
$\unicode[STIX]{x1D6F4}^{V}Z$ by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}Z=(\unicode[STIX]{x1D6F4}^{\mathbb{H}})^{i}(\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}})^{j}(\unicode[STIX]{x1D6F4}^{\mathbb{R}})^{k}Z,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}Z=(\unicode[STIX]{x1D6F4}^{\mathbb{H}})^{i}(\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}})^{j}(\unicode[STIX]{x1D6F4}^{\mathbb{R}})^{k}Z,\end{eqnarray}$$ where ![]() $(\unicode[STIX]{x1D6F4}^{\mathbb{H}})^{i}$ denotes applying
$(\unicode[STIX]{x1D6F4}^{\mathbb{H}})^{i}$ denotes applying ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}}$
$\unicode[STIX]{x1D6F4}^{\mathbb{H}}$![]() $i$ times, and so for
$i$ times, and so for ![]() $\tilde{\mathbb{R}}$ and
$\tilde{\mathbb{R}}$ and ![]() $\mathbb{R}$. Then
$\mathbb{R}$. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}\unicode[STIX]{x1D6F4}^{W}Z\simeq \unicode[STIX]{x1D6F4}^{W}\unicode[STIX]{x1D6F4}^{V}Z,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}\unicode[STIX]{x1D6F4}^{W}Z\simeq \unicode[STIX]{x1D6F4}^{W}\unicode[STIX]{x1D6F4}^{V}Z,\end{eqnarray}$$ for two ![]() $G$-representations
$G$-representations ![]() $V,W$, each a direct sum of copies of
$V,W$, each a direct sum of copies of ![]() $\mathbb{H},\mathbb{R},\tilde{\mathbb{R}}$.
$\mathbb{H},\mathbb{R},\tilde{\mathbb{R}}$.
Definition 2.17. Let ![]() $Z_{i}$ be chain complexes of type SWF,
$Z_{i}$ be chain complexes of type SWF,  $m_{i}\in \mathbb{Z},n_{i}\in \mathbb{Q}$, for
$m_{i}\in \mathbb{Z},n_{i}\in \mathbb{Q}$, for ![]() $i=1,2$. We call
$i=1,2$. We call  $(Z_{1},m_{1},n_{1})$ and
$(Z_{1},m_{1},n_{1})$ and  $(Z_{2},m_{2},n_{2})$chain stably equivalent if
$(Z_{2},m_{2},n_{2})$chain stably equivalent if  $n_{1}-n_{2}\in \mathbb{Z}$ and there exist
$n_{1}-n_{2}\in \mathbb{Z}$ and there exist  $M\in \mathbb{Z},N\in \mathbb{Q}$ and maps
$M\in \mathbb{Z},N\in \mathbb{Q}$ and maps
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\leftarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\leftarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$which are chain homotopy equivalences.
Remark 2.18. We do not consider suspensions by ![]() $\mathbb{R}$, unlike in the case of stable equivalence for spaces, since by (26), no new maps are obtained by suspending by
$\mathbb{R}$, unlike in the case of stable equivalence for spaces, since by (26), no new maps are obtained by suspending by ![]() $\mathbb{R}$.
$\mathbb{R}$.
Chain stable equivalence is an equivalence relation, and we denote the set of chain stable equivalence classes by ![]() $\mathfrak{CE}$.
$\mathfrak{CE}$.
Lemma 2.19. Associated to an element  $(X,m,n)\in \mathfrak{C}$ there is a well-defined element
$(X,m,n)\in \mathfrak{C}$ there is a well-defined element  $(C_{\ast }^{\text{CW}}(X,\text{pt}),m,n)\in \mathfrak{CE}$.
$(C_{\ast }^{\text{CW}}(X,\text{pt}),m,n)\in \mathfrak{CE}$.
Proof. Say that  $[(X_{1},m_{1},n_{1})]=[(X_{2},m_{2},n_{2})]\in \mathfrak{C}$ with
$[(X_{1},m_{1},n_{1})]=[(X_{2},m_{2},n_{2})]\in \mathfrak{C}$ with ![]() $G$-CW decompositions
$G$-CW decompositions ![]() $C_{i}$ of
$C_{i}$ of ![]() $X_{i}$. We will show that
$X_{i}$. We will show that
 $$\begin{eqnarray}[(C_{\ast }^{\text{CW}}(X_{1},\text{pt}),m_{1},n_{1})]=[(C_{\ast }^{\text{CW}}(X_{2},\text{pt}),m_{2},n_{2})]\in \mathfrak{CE},\end{eqnarray}$$
$$\begin{eqnarray}[(C_{\ast }^{\text{CW}}(X_{1},\text{pt}),m_{1},n_{1})]=[(C_{\ast }^{\text{CW}}(X_{2},\text{pt}),m_{2},n_{2})]\in \mathfrak{CE},\end{eqnarray}$$ where  $C_{\ast }^{\text{CW}}(X_{i},\text{pt})$ is the
$C_{\ast }^{\text{CW}}(X_{i},\text{pt})$ is the ![]() ${\mathcal{G}}$-chain complex associated to the
${\mathcal{G}}$-chain complex associated to the ![]() $G$-CW decomposition
$G$-CW decomposition ![]() $C_{i}$ of
$C_{i}$ of ![]() $X_{i}$. (In the case
$X_{i}$. (In the case  $X_{1}\simeq X_{2}$, and
$X_{1}\simeq X_{2}$, and  $m_{1}=m_{2},n_{1}=n_{2}$, we are showing that the corresponding element in
$m_{1}=m_{2},n_{1}=n_{2}$, we are showing that the corresponding element in ![]() $\mathfrak{CE}$ does not depend on the choice of
$\mathfrak{CE}$ does not depend on the choice of ![]() $G$-CW decomposition.) By hypothesis, there are homotopy equivalences
$G$-CW decomposition.) By hypothesis, there are homotopy equivalences ![]() $f$ and
$f$ and ![]() $g$:
$g$:
 $$\begin{eqnarray}\displaystyle & \displaystyle f:\unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}X_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}X_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle g:\unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}X_{2}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}X_{1}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f:\unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}X_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}X_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle g:\unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}X_{2}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}X_{1}. & \displaystyle \nonumber\end{eqnarray}$$ By the equivariant cellular approximation theorem (see [Reference WanerWan80]), we may homotope ![]() $f$ and
$f$ and ![]() $g$ to cellular maps (where the cell structures of suspensions are given as in (24)):
$g$ to cellular maps (where the cell structures of suspensions are given as in (24)):
 $$\begin{eqnarray}\displaystyle & \displaystyle f^{\text{CW}}:\unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle g^{\text{CW}}:\unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{2}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{1}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f^{\text{CW}}:\unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle g^{\text{CW}}:\unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{2}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{1}. & \displaystyle \nonumber\end{eqnarray}$$ Since ![]() $f$ and
$f$ and ![]() $g$ are homotopy equivalences, so are
$g$ are homotopy equivalences, so are ![]() $f^{\text{CW}}$ and
$f^{\text{CW}}$ and ![]() $g^{\text{CW}}$. The cellular maps
$g^{\text{CW}}$. The cellular maps ![]() $f^{\text{CW}}$ and
$f^{\text{CW}}$ and ![]() $g^{\text{CW}}$ induce maps
$g^{\text{CW}}$ induce maps ![]() $f_{\ast }$ and
$f_{\ast }$ and ![]() $g_{\ast }$:
$g_{\ast }$:
 $$\begin{eqnarray}\displaystyle & \displaystyle f_{\ast }:\unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{1},\text{pt})\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{2},\text{pt}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle g_{\ast }:\unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{2},\text{pt})\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{1},\text{pt}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{\ast }:\unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{1},\text{pt})\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{2},\text{pt}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle g_{\ast }:\unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{2},\text{pt})\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}C_{\ast }^{\text{CW}}(X_{1},\text{pt}). & \displaystyle \nonumber\end{eqnarray}$$These are chain homotopy equivalences, by construction, and so we obtain (31), as needed. ◻
Definition 2.20. Let ![]() $Z_{i}$ be chain complexes of type SWF,
$Z_{i}$ be chain complexes of type SWF,  $m_{i}\in \mathbb{Z},n_{i}\in \mathbb{Q}$, for
$m_{i}\in \mathbb{Z},n_{i}\in \mathbb{Q}$, for ![]() $i=1,2$. We call
$i=1,2$. We call  $(Z_{1},m_{1},n_{1})$ and
$(Z_{1},m_{1},n_{1})$ and  $(Z_{2},m_{2},n_{2})$chain locally equivalent, written
$(Z_{2},m_{2},n_{2})$chain locally equivalent, written  $(Z_{1},m_{1},n_{1})\equiv _{cl}(Z_{2},m_{2},n_{2})$, if there exist
$(Z_{1},m_{1},n_{1})\equiv _{cl}(Z_{2},m_{2},n_{2})$, if there exist  $M\in \mathbb{Z},N\in \mathbb{Q}$ and maps
$M\in \mathbb{Z},N\in \mathbb{Q}$ and maps
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\rightarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\leftarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}^{(N-n_{1})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{1})\tilde{\mathbb{R}}}Z_{1}\leftarrow \unicode[STIX]{x1D6F4}^{(N-n_{2})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M-m_{2})\tilde{\mathbb{R}}}Z_{2}, & \displaystyle\end{eqnarray}$$which are chain homotopy equivalences on fixed-point sets.
We call a map as in (32) or (33) a chain local equivalence. By the condition ‘is a homotopy equivalence on fixed-point sets’ we mean that the maps restrict to homotopy equivalences of  $\langle c_{0},\ldots ,c_{s}\rangle$ (in particular, we require that the chain maps in (32)–(33) send fixed-point sets to fixed-point sets).
$\langle c_{0},\ldots ,c_{s}\rangle$ (in particular, we require that the chain maps in (32)–(33) send fixed-point sets to fixed-point sets).
Elements  $Z_{1},Z_{2}\in \mathfrak{CE}$ are chain locally equivalent if and only if there are chain local equivalences
$Z_{1},Z_{2}\in \mathfrak{CE}$ are chain locally equivalent if and only if there are chain local equivalences  $Z_{1}\rightarrow Z_{2}$ and
$Z_{1}\rightarrow Z_{2}$ and  $Z_{2}\rightarrow Z_{1}$. There are pairs of chain complexes with a chain local equivalence in one direction but not the other; these are not chain locally equivalent complexes. Chain local equivalence is an equivalence relation. Denote the set of chain local equivalence classes by
$Z_{2}\rightarrow Z_{1}$. There are pairs of chain complexes with a chain local equivalence in one direction but not the other; these are not chain locally equivalent complexes. Chain local equivalence is an equivalence relation. Denote the set of chain local equivalence classes by ![]() $\mathfrak{CLE}$. The set
$\mathfrak{CLE}$. The set ![]() $\mathfrak{CLE}$ is naturally an abelian group, with multiplication given by the tensor product (over
$\mathfrak{CLE}$ is naturally an abelian group, with multiplication given by the tensor product (over ![]() $\mathbb{F}$, with
$\mathbb{F}$, with ![]() ${\mathcal{G}}$-action as above). To discuss inverses in
${\mathcal{G}}$-action as above). To discuss inverses in ![]() $\mathfrak{CLE}$, we take a brief discursion.
$\mathfrak{CLE}$, we take a brief discursion.
Note that it is not obvious that chain homotopy equivalent complexes of type SWF are chain locally equivalent, as there may be self-homotopy-equivalences of a complex that do not take fixed-point sets to fixed-point sets. Note, however, that any two ![]() ${\mathcal{G}}$-chain complexes coming from a space of type SWF with different
${\mathcal{G}}$-chain complexes coming from a space of type SWF with different ![]() $G$-CW decompositions are necessarily homotopy-equivalent by a chain map preserving the subcomplex of the fixed point set (coinciding with the notion of the ‘fixed-point set’ of a chain complex of type SWF), by the equivariant cellular approximation theorem. For more general
$G$-CW decompositions are necessarily homotopy-equivalent by a chain map preserving the subcomplex of the fixed point set (coinciding with the notion of the ‘fixed-point set’ of a chain complex of type SWF), by the equivariant cellular approximation theorem. For more general ![]() ${\mathcal{G}}$-chain complexes, we have Lemma 2.26 below, which states that the chain homotopy type determines the chain local equivalence class.
${\mathcal{G}}$-chain complexes, we have Lemma 2.26 below, which states that the chain homotopy type determines the chain local equivalence class.
Inverses are given by dual chain complexes. Note that  $\text{Hom}(Z;\mathbb{F})$ will not usually be a chain complex of type SWF; however, some suspension of it will be chain homotopy equivalent to a chain complex of type SWF; see Lemma 2.27. In the case of chain complexes of type SWF arising as CW-chain complexes, inverses are more readily understood. Here, we recall from [Reference ManolescuMan16] that the Spanier–Whitehead dual of a space of type SWF is again a space of type SWF, from which the existence of group inverses (for chain complexes coming from spaces) follows.
$\text{Hom}(Z;\mathbb{F})$ will not usually be a chain complex of type SWF; however, some suspension of it will be chain homotopy equivalent to a chain complex of type SWF; see Lemma 2.27. In the case of chain complexes of type SWF arising as CW-chain complexes, inverses are more readily understood. Here, we recall from [Reference ManolescuMan16] that the Spanier–Whitehead dual of a space of type SWF is again a space of type SWF, from which the existence of group inverses (for chain complexes coming from spaces) follows.
2.4 Calculating the chain local equivalence class
In this section we will obtain a description of ![]() $\mathfrak{CLE}$ more amenable to calculations than the definition. Throughout this section
$\mathfrak{CLE}$ more amenable to calculations than the definition. Throughout this section ![]() $Z$ will denote a chain complex of type SWF. The main result is Lemma 2.24, which allows us to determine if
$Z$ will denote a chain complex of type SWF. The main result is Lemma 2.24, which allows us to determine if  $(Z_{1},m_{1},n_{1})$ and
$(Z_{1},m_{1},n_{1})$ and  $(Z_{2},m_{2},n_{2})$ are chain locally equivalent without checking all possible
$(Z_{2},m_{2},n_{2})$ are chain locally equivalent without checking all possible ![]() $M,N$.
$M,N$.
For ![]() $Z$ a chain complex of type SWF, we will let
$Z$ a chain complex of type SWF, we will let ![]() $Z$ also denote the element
$Z$ also denote the element  $(Z,0,0)\in \mathfrak{CE}$.
$(Z,0,0)\in \mathfrak{CE}$.
Definition 2.21. Let ![]() $R$ be the fixed-point set of
$R$ be the fixed-point set of ![]() $Z$. If
$Z$. If  $\text{deg}\,r<\text{deg}\,x$ for all nonzero homogeneous
$\text{deg}\,r<\text{deg}\,x$ for all nonzero homogeneous  $x\in (Z/R)$ and
$x\in (Z/R)$ and ![]() $r\in R$, we say that the chain complex
$r\in R$, we say that the chain complex ![]() $Z$ is a suspensionlike complex.
$Z$ is a suspensionlike complex.
Remark 2.22. Let ![]() $X$ be a free, finite
$X$ be a free, finite ![]() $G$-CW complex. Then the reduced
$G$-CW complex. Then the reduced ![]() $G$-CW chain complex of
$G$-CW chain complex of ![]() $\tilde{\unicode[STIX]{x1D6F4}}X$, the unreduced suspension of
$\tilde{\unicode[STIX]{x1D6F4}}X$, the unreduced suspension of ![]() $X$, is a suspensionlike chain complex.
$X$, is a suspensionlike chain complex.
For  $Z_{1},Z_{2}\in \mathfrak{CLE}$, we call a local equivalence
$Z_{1},Z_{2}\in \mathfrak{CLE}$, we call a local equivalence  $Z_{1}\rightarrow Z_{2}$ (without needing to suspend either complex) an unstable local map.
$Z_{1}\rightarrow Z_{2}$ (without needing to suspend either complex) an unstable local map.
Lemma 2.23. Let  $Z_{i}=R_{i}\,\tilde{\oplus }\,F_{i}$ for
$Z_{i}=R_{i}\,\tilde{\oplus }\,F_{i}$ for ![]() $i=1,2$ be suspensionlike chain complexes at level
$i=1,2$ be suspensionlike chain complexes at level ![]() $s$ with unstable local maps
$s$ with unstable local maps  $Z_{1}\leftrightarrow Z_{2}$. Then there exist suspensionlike chain complexes
$Z_{1}\leftrightarrow Z_{2}$. Then there exist suspensionlike chain complexes ![]() $Z_{i}^{\prime }$ at level
$Z_{i}^{\prime }$ at level ![]() $0$ with
$0$ with  $\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }\simeq Z_{i}$, and unstable local maps
$\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }\simeq Z_{i}$, and unstable local maps  $Z_{1}^{\prime }\leftrightarrow Z_{2}^{\prime }$.
$Z_{1}^{\prime }\leftrightarrow Z_{2}^{\prime }$.
Proof. We may assume ![]() $s>0$, as otherwise the statement is vacuous. To construct
$s>0$, as otherwise the statement is vacuous. To construct ![]() $Z_{i}^{\prime }$, observe that the image
$Z_{i}^{\prime }$, observe that the image  $\text{Im}\,\unicode[STIX]{x2202}|_{F_{i}}\cap R_{i}$, must be either
$\text{Im}\,\unicode[STIX]{x2202}|_{F_{i}}\cap R_{i}$, must be either  $\{(1+j)c_{s}\}$ or empty, and in the latter case the lemma is trivial, so we assume that the former holds. Then, construct a new complex
$\{(1+j)c_{s}\}$ or empty, and in the latter case the lemma is trivial, so we assume that the former holds. Then, construct a new complex  $Z_{i}^{\prime }=\langle f\rangle \,\tilde{\oplus }\,F_{i}[s]$, where the boundary map
$Z_{i}^{\prime }=\langle f\rangle \,\tilde{\oplus }\,F_{i}[s]$, where the boundary map  $F_{i}[s]\rightarrow \langle f\rangle$ is obtained as the boundary map
$F_{i}[s]\rightarrow \langle f\rangle$ is obtained as the boundary map  $F_{i}\rightarrow \langle (1+j)c_{s}\rangle$. It is clear that an unstable local map
$F_{i}\rightarrow \langle (1+j)c_{s}\rangle$. It is clear that an unstable local map  $Z_{1}\rightarrow Z_{2}$ induces an unstable local map
$Z_{1}\rightarrow Z_{2}$ induces an unstable local map  $Z_{1}^{\prime }\rightarrow Z_{2}^{\prime }$, and we are left with showing
$Z_{1}^{\prime }\rightarrow Z_{2}^{\prime }$, and we are left with showing  $Z_{i}\simeq \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }$.
$Z_{i}\simeq \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }$.
To see this, we view ![]() $\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }$ as the mapping cone of
$\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }$ as the mapping cone of
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}\langle f\rangle [-1].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}\langle f\rangle [-1].\end{eqnarray}$$ We claim  $\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]\simeq F_{i}$. To see this, construct a map
$\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]\simeq F_{i}$. To see this, construct a map  $F_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]$ by
$F_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]$ by  $x\rightarrow (1+j)c_{s}\otimes x[s]$; it is straightforward to check that this map is a quasi-isomorphism. By [Reference WeibelWei94, Theorem 10.4.8], and using that
$x\rightarrow (1+j)c_{s}\otimes x[s]$; it is straightforward to check that this map is a quasi-isomorphism. By [Reference WeibelWei94, Theorem 10.4.8], and using that ![]() $\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}^{s}}}F_{i}$ is free, this map admits a homotopy inverse, establishing the claim. Then, the mapping cone (34) is homotopy equivalent to the mapping cone of some
$\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}^{s}}}F_{i}$ is free, this map admits a homotopy inverse, establishing the claim. Then, the mapping cone (34) is homotopy equivalent to the mapping cone of some  $F_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}\langle f\rangle [-1]\cong R_{i}[-1]$. In particular, the map
$F_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}\langle f\rangle [-1]\cong R_{i}[-1]$. In particular, the map  $F_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]$ constructed above commutes with the boundary maps in the construction of
$F_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F_{i}[s]$ constructed above commutes with the boundary maps in the construction of ![]() $Z_{i}^{\prime }$ and in (34). Then we have a map
$Z_{i}^{\prime }$ and in (34). Then we have a map  $\unicode[STIX]{x1D719}:Z_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }$, which is a quasi-isomorphism; that is, the mapping cone
$\unicode[STIX]{x1D719}:Z_{i}\rightarrow \unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z_{i}^{\prime }$, which is a quasi-isomorphism; that is, the mapping cone  $\text{Cone}(\unicode[STIX]{x1D719})$ is trivial in the derived category. Since
$\text{Cone}(\unicode[STIX]{x1D719})$ is trivial in the derived category. Since  $\text{Cone}(\unicode[STIX]{x1D719})$ is homotopy-equivalent to a free complex, it is also trivial in the homotopy category, and so
$\text{Cone}(\unicode[STIX]{x1D719})$ is homotopy-equivalent to a free complex, it is also trivial in the homotopy category, and so ![]() $\unicode[STIX]{x1D719}$ is a homotopy equivalence, as needed.◻
$\unicode[STIX]{x1D719}$ is a homotopy equivalence, as needed.◻
Lemma 2.24. Let ![]() $Z_{1}$ and
$Z_{1}$ and ![]() $Z_{2}$ be locally equivalent suspensionlike chain complexes of type SWF. Then there exist unstable local maps
$Z_{2}$ be locally equivalent suspensionlike chain complexes of type SWF. Then there exist unstable local maps
 $$\begin{eqnarray}Z_{1}\leftrightarrow Z_{2},\end{eqnarray}$$
$$\begin{eqnarray}Z_{1}\leftrightarrow Z_{2},\end{eqnarray}$$ without needing to suspend ![]() $Z_{i}$.
$Z_{i}$.
Proof. By Lemma 2.23, we may assume that ![]() $Z_{1}$ and
$Z_{1}$ and ![]() $Z_{2}$ are level
$Z_{2}$ are level ![]() $0$ and suspensionlike. It then suffices to show that if there are unstable local maps
$0$ and suspensionlike. It then suffices to show that if there are unstable local maps  $\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{1}\leftrightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{2}$, then there are unstable local maps
$\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{1}\leftrightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{2}$, then there are unstable local maps  $Z_{1}\leftrightarrow Z_{2}$.
$Z_{1}\leftrightarrow Z_{2}$.
Let  $Z_{i}=R_{i}\,\tilde{\oplus }\,F_{i}$. That is,
$Z_{i}=R_{i}\,\tilde{\oplus }\,F_{i}$. That is, ![]() $Z_{i}$ is the mapping cone of a map
$Z_{i}$ is the mapping cone of a map  $F_{i}\rightarrow R_{i}[-1]$. Now,
$F_{i}\rightarrow R_{i}[-1]$. Now,  $\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{i}=\unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{i}\,\tilde{\oplus }\,\unicode[STIX]{x1D6F4}^{\mathbb{H}}F_{i}$. We claim
$\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{i}=\unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{i}\,\tilde{\oplus }\,\unicode[STIX]{x1D6F4}^{\mathbb{H}}F_{i}$. We claim  $\unicode[STIX]{x1D6F4}^{\mathbb{H}}F_{i}\simeq F_{i}[-4]$. First, we have a quasi-isomorphism
$\unicode[STIX]{x1D6F4}^{\mathbb{H}}F_{i}\simeq F_{i}[-4]$. First, we have a quasi-isomorphism  $F_{i}[-4]\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}F_{i}$ by
$F_{i}[-4]\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}F_{i}$ by  $x[-4]\rightarrow s(1+j)^{3}y_{3}\otimes x$. Further, any free finite
$x[-4]\rightarrow s(1+j)^{3}y_{3}\otimes x$. Further, any free finite ![]() ${\mathcal{G}}$-chain complex
${\mathcal{G}}$-chain complex ![]() $F$ with
$F$ with  $H(F)=0$ is nullhomotopic (the verification of this is similar to the construction of projective resolutions in abelian categories). It follows that free finite quasi-isomorphic
$H(F)=0$ is nullhomotopic (the verification of this is similar to the construction of projective resolutions in abelian categories). It follows that free finite quasi-isomorphic ![]() ${\mathcal{G}}$-chain complexes are in fact homotopy equivalent, giving the claim. In particular,
${\mathcal{G}}$-chain complexes are in fact homotopy equivalent, giving the claim. In particular, ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{i}$ is homotopy equivalent to the mapping cone of a map
$\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{i}$ is homotopy equivalent to the mapping cone of a map  $F_{i}[-4]\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{i}[-1]$. However, since
$F_{i}[-4]\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{i}[-1]$. However, since ![]() $Z_{i}$ is suspensionlike, we have that
$Z_{i}$ is suspensionlike, we have that ![]() $F_{i}[-4]$ is concentrated in degree at least
$F_{i}[-4]$ is concentrated in degree at least ![]() $5$, while
$5$, while  $s(1+j)^{3}y_{3}[-1]$ is the only cycle in degree
$s(1+j)^{3}y_{3}[-1]$ is the only cycle in degree ![]() $5$. It is then readily checked that the map
$5$. It is then readily checked that the map  $F_{i}[-4]\rightarrow \langle s(1+j)^{3}y_{3}[-1]\rangle$ defining (a complex homotopy equivalent to)
$F_{i}[-4]\rightarrow \langle s(1+j)^{3}y_{3}[-1]\rangle$ defining (a complex homotopy equivalent to) ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{i}$ is identical to the map
$\unicode[STIX]{x1D6F4}^{\mathbb{H}}Z_{i}$ is identical to the map  $F_{i}\rightarrow R_{i}$ defining
$F_{i}\rightarrow R_{i}$ defining ![]() $Z_{i}$.
$Z_{i}$.
Now, say we have local equivalences  $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{1}\,\tilde{\oplus }\,F_{1}[-4]\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{2}\,\tilde{\oplus }\,F_{2}[-4]$. For grading reasons,
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{1}\,\tilde{\oplus }\,F_{1}[-4]\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{2}\,\tilde{\oplus }\,F_{2}[-4]$. For grading reasons, ![]() $\unicode[STIX]{x1D719}$ must send
$\unicode[STIX]{x1D719}$ must send  $\unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{1}\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{2}$. In particular, there is then a map of exact sequences as follows.
$\unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{1}\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{2}$. In particular, there is then a map of exact sequences as follows.

Any local map ![]() $\unicode[STIX]{x1D719}$ sends
$\unicode[STIX]{x1D719}$ sends  $s(1+j)^{3}y_{3}\otimes c_{0}\in \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{1}\rightarrow s(1+j)^{3}y_{3}\otimes c_{0}\in \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{2}$, as is a straightforward check. Then we inherit a local map
$s(1+j)^{3}y_{3}\otimes c_{0}\in \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{1}\rightarrow s(1+j)^{3}y_{3}\otimes c_{0}\in \unicode[STIX]{x1D6F4}^{\mathbb{H}}R_{2}$, as is a straightforward check. Then we inherit a local map  $\unicode[STIX]{x1D713}:Z_{1}\rightarrow Z_{2}$ by defining it separately on the fixed point set and on
$\unicode[STIX]{x1D713}:Z_{1}\rightarrow Z_{2}$ by defining it separately on the fixed point set and on ![]() $F_{1}$. That is, set
$F_{1}$. That is, set  $\unicode[STIX]{x1D713}(c_{0})=c_{0}$, and for
$\unicode[STIX]{x1D713}(c_{0})=c_{0}$, and for ![]() $x\in F_{1}$, set
$x\in F_{1}$, set  $\unicode[STIX]{x1D713}(x)=\unicode[STIX]{x1D719}(x[-4])$. The map
$\unicode[STIX]{x1D713}(x)=\unicode[STIX]{x1D719}(x[-4])$. The map ![]() $\unicode[STIX]{x1D713}$ commutes with the boundary
$\unicode[STIX]{x1D713}$ commutes with the boundary  $F_{i}\rightarrow R_{i}[-1]$ using
$F_{i}\rightarrow R_{i}[-1]$ using  $\unicode[STIX]{x1D719}(s(1+j)^{3}y_{3}\otimes c_{0})=s(1+j)^{3}y_{3}\otimes c_{0}$ and the construction of the boundary map
$\unicode[STIX]{x1D719}(s(1+j)^{3}y_{3}\otimes c_{0})=s(1+j)^{3}y_{3}\otimes c_{0}$ and the construction of the boundary map  $F_{i}[-4]\rightarrow \langle s(1+j)^{3}y_{3}\rangle [-1]$. Then,
$F_{i}[-4]\rightarrow \langle s(1+j)^{3}y_{3}\rangle [-1]$. Then, ![]() $\unicode[STIX]{x1D713}$ is a local map, and we similarly construct a local map going the other direction, completing the proof.◻
$\unicode[STIX]{x1D713}$ is a local map, and we similarly construct a local map going the other direction, completing the proof.◻
Lemma 2.24 states that if  $\unicode[STIX]{x1D6F4}^{(N_{0}-n_{i})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M_{0}-m_{i})\tilde{\mathbb{R}}}Z_{i}$ are suspensionlike, then if
$\unicode[STIX]{x1D6F4}^{(N_{0}-n_{i})\mathbb{H}}\unicode[STIX]{x1D6F4}^{(M_{0}-m_{i})\tilde{\mathbb{R}}}Z_{i}$ are suspensionlike, then if  $(Z_{1},m_{1},n_{1})$ and
$(Z_{1},m_{1},n_{1})$ and  $(Z_{2},m_{2},n_{2})$ are (stably) locally equivalent, there is a local equivalence realized by genuine (unstable) chain maps after suspending the complexes
$(Z_{2},m_{2},n_{2})$ are (stably) locally equivalent, there is a local equivalence realized by genuine (unstable) chain maps after suspending the complexes ![]() $Z_{i}$ by
$Z_{i}$ by  $(N_{0}-n_{i})\mathbb{H}\oplus (M_{0}-m_{i})\tilde{\mathbb{R}}$.
$(N_{0}-n_{i})\mathbb{H}\oplus (M_{0}-m_{i})\tilde{\mathbb{R}}$.
Finally, to take advantage of Lemma 2.24, we need to know that many complexes admit suspensionlike representatives.
Lemma 2.25. Let ![]() $Z$ a chain complex of type SWF. Then some suspension
$Z$ a chain complex of type SWF. Then some suspension ![]() $\unicode[STIX]{x1D6F4}^{V}Z$ is homotopy equivalent (in fact, locally equivalent) to a suspensionlike chain complex.
$\unicode[STIX]{x1D6F4}^{V}Z$ is homotopy equivalent (in fact, locally equivalent) to a suspensionlike chain complex.
Proof. This is much as the proof of Lemma 2.24. We express  $Z=R\,\tilde{\oplus }\,F$, with fixed point set
$Z=R\,\tilde{\oplus }\,F$, with fixed point set ![]() $R$. Then
$R$. Then ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}Z$ is a chain complex homotopy equivalent to
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}Z$ is a chain complex homotopy equivalent to  $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R\,\tilde{\oplus }\,F[-4n]$, and moreover the chain homotopy equivalence is the identity on
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R\,\tilde{\oplus }\,F[-4n]$, and moreover the chain homotopy equivalence is the identity on ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ (whence, a local equivalence). In the case
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ (whence, a local equivalence). In the case ![]() $s=0$,
$s=0$, ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ is a suspensionlike chain complex, and so then is
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ is a suspensionlike chain complex, and so then is  $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R\,\tilde{\oplus }\,F[-4n]$, finishing the proof.
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R\,\tilde{\oplus }\,F[-4n]$, finishing the proof.
For ![]() $s>0$, there is a subcomplex, inducing a quasi-isomorphism,
$s>0$, there is a subcomplex, inducing a quasi-isomorphism,  $H_{n}\subset \unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ given by
$H_{n}\subset \unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ given by ![]() $R$ along with generators
$R$ along with generators  $y_{4k+1},y_{4k+2},y_{4k+3}$ for
$y_{4k+1},y_{4k+2},y_{4k+3}$ for  $0\leqslant k\leqslant n-1$, that satisfy relations as in Example 2.9. In fact,
$0\leqslant k\leqslant n-1$, that satisfy relations as in Example 2.9. In fact, ![]() $H_{n}$ and
$H_{n}$ and ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ are two different CW chain complexes coming from different
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ are two different CW chain complexes coming from different ![]() $G$-CW decompositions of
$G$-CW decompositions of  $(\tilde{\mathbb{R}}^{s}\oplus \mathbb{H}^{n})^{+}$. The cone of
$(\tilde{\mathbb{R}}^{s}\oplus \mathbb{H}^{n})^{+}$. The cone of  $H_{n}\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ is zero in the derived category, and is homotopy equivalent to a free complex, so is nullhomotopic, as in the proof of Lemma 2.24. Using that
$H_{n}\rightarrow \unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}R$ is zero in the derived category, and is homotopy equivalent to a free complex, so is nullhomotopic, as in the proof of Lemma 2.24. Using that ![]() $H_{n}$ is suspensionlike, we obtain that
$H_{n}$ is suspensionlike, we obtain that ![]() $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}Z$ is homotopy equivalent to a suspensionlike chain complex
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{n}}Z$ is homotopy equivalent to a suspensionlike chain complex  $H_{n}\,\tilde{\oplus }\,F[-4n]$.◻
$H_{n}\,\tilde{\oplus }\,F[-4n]$.◻
Similarly, we can show the following result.
Lemma 2.26. Let  $Z_{1}=Z_{2}\in \mathfrak{CE}$. Then
$Z_{1}=Z_{2}\in \mathfrak{CE}$. Then  $Z_{1}=Z_{2}\in \mathfrak{CLE}$.
$Z_{1}=Z_{2}\in \mathfrak{CLE}$.
Proof. We may assume that ![]() $Z_{1},Z_{2}$ are chain complexes of type SWF (that is, we have already suspended suitably). By Lemma 2.25, after further suspending, we can assume that
$Z_{1},Z_{2}$ are chain complexes of type SWF (that is, we have already suspended suitably). By Lemma 2.25, after further suspending, we can assume that ![]() $Z_{1},Z_{2}$ are chain homotopy equivalent suspensionlike complexes. We have used in this step that the suspensionlike representatives of the (stable) chain homotopy equivalence class generated by Lemma 2.25 are locally equivalent to the original complexes. Now, any chain map
$Z_{1},Z_{2}$ are chain homotopy equivalent suspensionlike complexes. We have used in this step that the suspensionlike representatives of the (stable) chain homotopy equivalence class generated by Lemma 2.25 are locally equivalent to the original complexes. Now, any chain map  $\unicode[STIX]{x1D719}:Z_{1}\rightarrow Z_{2}$, for
$\unicode[STIX]{x1D719}:Z_{1}\rightarrow Z_{2}$, for ![]() $Z_{i}$ suspensionlike, sends
$Z_{i}$ suspensionlike, sends  $R_{1}\rightarrow R_{2}$ for grading reasons. In particular, a chain homotopy equivalence
$R_{1}\rightarrow R_{2}$ for grading reasons. In particular, a chain homotopy equivalence  $\unicode[STIX]{x1D719}:Z_{1}\rightarrow Z_{2}$ must induce a homotopy equivalence on fixed-point sets, as needed.◻
$\unicode[STIX]{x1D719}:Z_{1}\rightarrow Z_{2}$ must induce a homotopy equivalence on fixed-point sets, as needed.◻
We have a result similar to Lemma 2.25 relating to duality.
Lemma 2.27. Let ![]() $Z$ be a chain complex of type SWF. Then
$Z$ be a chain complex of type SWF. Then  $\unicode[STIX]{x1D6F4}^{V}\text{Hom}(Z;\mathbb{F})$ is chain-homotopy equivalent to a complex of type SWF for
$\unicode[STIX]{x1D6F4}^{V}\text{Hom}(Z;\mathbb{F})$ is chain-homotopy equivalent to a complex of type SWF for ![]() $V$ sufficiently large.
$V$ sufficiently large.
Proof. Write  $Z=R\,\tilde{\oplus }\,F$. Then
$Z=R\,\tilde{\oplus }\,F$. Then  $\text{Hom}(Z;\mathbb{F})=R^{\vee }\,\tilde{\oplus }\,F^{\vee }$, but where the differential is now from
$\text{Hom}(Z;\mathbb{F})=R^{\vee }\,\tilde{\oplus }\,F^{\vee }$, but where the differential is now from ![]() $R^{\vee }$ to
$R^{\vee }$ to ![]() $F^{\vee }$. We identify
$F^{\vee }$. We identify ![]() $R^{\vee }$ with
$R^{\vee }$ with ![]() $R$ by sending
$R$ by sending  $((1+j)c_{i})^{\vee }\rightarrow c_{i}$. Let
$((1+j)c_{i})^{\vee }\rightarrow c_{i}$. Let  $V=\mathbb{H}^{n}$ for some
$V=\mathbb{H}^{n}$ for some ![]() $n$ sufficiently large. Then
$n$ sufficiently large. Then  $\unicode[STIX]{x1D6F4}^{V}\text{Hom}(Z;\mathbb{F})$ is the mapping cone
$\unicode[STIX]{x1D6F4}^{V}\text{Hom}(Z;\mathbb{F})$ is the mapping cone  $\unicode[STIX]{x1D6F4}^{V}R^{\vee }\rightarrow \unicode[STIX]{x1D6F4}^{V}F^{\vee }[-1]$, which is homotopy equivalent to a mapping cone
$\unicode[STIX]{x1D6F4}^{V}R^{\vee }\rightarrow \unicode[STIX]{x1D6F4}^{V}F^{\vee }[-1]$, which is homotopy equivalent to a mapping cone  $\unicode[STIX]{x1D6F4}^{V}R\rightarrow F[-1-4n]$. Then, for
$\unicode[STIX]{x1D6F4}^{V}R\rightarrow F[-1-4n]$. Then, for ![]() $n$ sufficiently large, the connecting morphism restricted to
$n$ sufficiently large, the connecting morphism restricted to  $R\subset \unicode[STIX]{x1D6F4}^{V}R$ must vanish for grading reasons. The resulting complex is then of type SWF.◻
$R\subset \unicode[STIX]{x1D6F4}^{V}R$ must vanish for grading reasons. The resulting complex is then of type SWF.◻
Finally, we remark that we could simplify the discussion of duality by defining a variant of ![]() $\mathfrak{CLE}$ using only chain complexes that are homotopy-equivalent to the CW chain complex associated to actual
$\mathfrak{CLE}$ using only chain complexes that are homotopy-equivalent to the CW chain complex associated to actual ![]() $G$-spaces of type SWF.
$G$-spaces of type SWF.
2.5 Inessential subcomplexes and connected quotient complexes
In this section, we show how Lemma 2.24 allows for a convenient characterization of chain locally equivalent complexes. We then define connected ![]() $S^{1}$-homology of spaces of type SWF, which we will use later to define
$S^{1}$-homology of spaces of type SWF, which we will use later to define  $\mathit{SWFH}_{\text{conn}}$ as in Corollary 1.5.
$\mathit{SWFH}_{\text{conn}}$ as in Corollary 1.5.
Definition 2.28. Take ![]() $Z$ a chain complex of type SWF, and let
$Z$ a chain complex of type SWF, and let ![]() $R\subset Z$ be the fixed-point set. For any subcomplex
$R\subset Z$ be the fixed-point set. For any subcomplex ![]() $M\subset Z$ such that
$M\subset Z$ such that  $M\cap R=\{0\}$, the projection
$M\cap R=\{0\}$, the projection  $Z\rightarrow Z/M$ is a chain homotopy equivalence on
$Z\rightarrow Z/M$ is a chain homotopy equivalence on ![]() $R$. If there exists a map of chain complexes
$R$. If there exists a map of chain complexes  $Z/M\rightarrow Z$ that is a chain homotopy equivalence on
$Z/M\rightarrow Z$ that is a chain homotopy equivalence on ![]() $R$, we say that
$R$, we say that ![]() $M$ is an inessential subcomplex.
$M$ is an inessential subcomplex.
If ![]() $M$ is inessential, then
$M$ is inessential, then  $Z/M\equiv _{cl}Z$. We order inessential subcomplexes by inclusion,
$Z/M\equiv _{cl}Z$. We order inessential subcomplexes by inclusion,  $N\leqslant M$ if
$N\leqslant M$ if  $N\subseteq M$. We show that there is a unique ‘minimal’ model
$N\subseteq M$. We show that there is a unique ‘minimal’ model ![]() $Z/N$ locally equivalent to
$Z/N$ locally equivalent to ![]() $Z$.
$Z$.
Lemma 2.29. Let ![]() $M\subset Z$ be an inessential subcomplex, maximal with respect to inclusion. Then a map
$M\subset Z$ be an inessential subcomplex, maximal with respect to inclusion. Then a map  $f:Z/M\rightarrow Z$ which is a homotopy equivalence on fixed-point sets is injective.
$f:Z/M\rightarrow Z$ which is a homotopy equivalence on fixed-point sets is injective.
Proof. Indeed, say  $f:Z/M\rightarrow Z$ is a local equivalence with nonzero kernel. Let
$f:Z/M\rightarrow Z$ is a local equivalence with nonzero kernel. Let ![]() $R_{1}$ denote the fixed-point set of
$R_{1}$ denote the fixed-point set of ![]() $Z/M$ and
$Z/M$ and ![]() $R_{2}$ denote the fixed-point set of
$R_{2}$ denote the fixed-point set of ![]() $Z$. Since
$Z$. Since ![]() $f$ restricts to a homotopy equivalence on the fixed-point sets, then
$f$ restricts to a homotopy equivalence on the fixed-point sets, then  $(\text{ker}\,f)\cap R_{1}=\{0\}$. Let
$(\text{ker}\,f)\cap R_{1}=\{0\}$. Let  $\unicode[STIX]{x1D70B}:Z\rightarrow Z/M$ be the projection map. Then
$\unicode[STIX]{x1D70B}:Z\rightarrow Z/M$ be the projection map. Then ![]() $f$ induces a map
$f$ induces a map  $Z/(\unicode[STIX]{x1D70B}^{-1}(\text{ker}\,f))\rightarrow Z$, and by
$Z/(\unicode[STIX]{x1D70B}^{-1}(\text{ker}\,f))\rightarrow Z$, and by  $(\text{ker}\,f)\cap R_{1}=\{0\}$, this map is a homotopy-equivalence on fixed-point sets. Additionally, we have
$(\text{ker}\,f)\cap R_{1}=\{0\}$, this map is a homotopy-equivalence on fixed-point sets. Additionally, we have  $\unicode[STIX]{x1D70B}^{-1}(\text{ker}\,f)\cap R_{2}=\{0\}$. Then
$\unicode[STIX]{x1D70B}^{-1}(\text{ker}\,f)\cap R_{2}=\{0\}$. Then  $\unicode[STIX]{x1D70B}^{-1}(\text{ker}\,f)$ is an inessential submodule, and it (strictly) contains
$\unicode[STIX]{x1D70B}^{-1}(\text{ker}\,f)$ is an inessential submodule, and it (strictly) contains ![]() $M$, contradicting that
$M$, contradicting that ![]() $M$ was maximal. Then
$M$ was maximal. Then ![]() $f$ was injective, as needed.◻
$f$ was injective, as needed.◻
Lemma 2.30. Let ![]() $Z$ be a chain complex of type SWF and let
$Z$ be a chain complex of type SWF and let  $M,N\subset Z$ be inessential subcomplexes, with
$M,N\subset Z$ be inessential subcomplexes, with ![]() $M$ and
$M$ and ![]() $N$ maximal with respect to inclusion. Then
$N$ maximal with respect to inclusion. Then  $Z/M\cong Z/N$, where
$Z/M\cong Z/N$, where ![]() $\cong$ denotes isomorphism of
$\cong$ denotes isomorphism of ![]() ${\mathcal{G}}$-chain complexes.
${\mathcal{G}}$-chain complexes.
Proof. Indeed, if there exist maps  $\unicode[STIX]{x1D6FC}:Z/M\rightarrow Z,$ and
$\unicode[STIX]{x1D6FC}:Z/M\rightarrow Z,$ and  $\unicode[STIX]{x1D6FD}:Z/N\rightarrow Z$ as above, consider the composition
$\unicode[STIX]{x1D6FD}:Z/N\rightarrow Z$ as above, consider the composition
 $$\begin{eqnarray}\unicode[STIX]{x1D719}:Z/N\rightarrow Z\rightarrow Z/M.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}:Z/N\rightarrow Z\rightarrow Z/M.\end{eqnarray}$$ In particular, we have a map  $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D719}:Z/N\rightarrow Z$, which is injective by Lemma 2.29. It then follows that
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D719}:Z/N\rightarrow Z$, which is injective by Lemma 2.29. It then follows that ![]() $\unicode[STIX]{x1D719}$ is injective. We also have
$\unicode[STIX]{x1D719}$ is injective. We also have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}:Z/M\rightarrow Z\rightarrow Z/N. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}:Z/M\rightarrow Z\rightarrow Z/N. & & \displaystyle \nonumber\end{eqnarray}$$ As before, ![]() $\unicode[STIX]{x1D713}$ is injective. Then, since we have injective chain maps between
$\unicode[STIX]{x1D713}$ is injective. Then, since we have injective chain maps between ![]() $Z/N$ and
$Z/N$ and ![]() $Z/M$, finite-dimensional
$Z/M$, finite-dimensional ![]() $\mathbb{F}$-complexes, the two chain complexes must have the same dimension. An injective map between complexes of the same dimension is bijective, and, finally, a bijective
$\mathbb{F}$-complexes, the two chain complexes must have the same dimension. An injective map between complexes of the same dimension is bijective, and, finally, a bijective ![]() ${\mathcal{G}}$-chain complex map is a
${\mathcal{G}}$-chain complex map is a ![]() ${\mathcal{G}}$-chain complex isomorphism.◻
${\mathcal{G}}$-chain complex isomorphism.◻
Lemma 2.31. Let ![]() $Z$ be a chain complex of type SWF and
$Z$ be a chain complex of type SWF and ![]() $M$ a maximal inessential subcomplex of
$M$ a maximal inessential subcomplex of ![]() $Z$. We have a (noncanonical) decomposition of
$Z$. We have a (noncanonical) decomposition of ![]() $Z$:
$Z$:
 $$\begin{eqnarray}Z=(Z/M)\oplus M,\end{eqnarray}$$
$$\begin{eqnarray}Z=(Z/M)\oplus M,\end{eqnarray}$$ where the isomorphism class of ![]() $Z/M$ is an invariant of
$Z/M$ is an invariant of ![]() $Z$, independent of the choice of maximal inessential subcomplex
$Z$, independent of the choice of maximal inessential subcomplex ![]() $M\subseteq Z$.
$M\subseteq Z$.
Proof. Let  $\unicode[STIX]{x1D6FD}:Z/M\rightarrow Z$ be a homotopy equivalence on fixed-point sets. The map
$\unicode[STIX]{x1D6FD}:Z/M\rightarrow Z$ be a homotopy equivalence on fixed-point sets. The map ![]() $\unicode[STIX]{x1D6FD}$ is injective by Lemma 2.29. Let
$\unicode[STIX]{x1D6FD}$ is injective by Lemma 2.29. Let ![]() $\unicode[STIX]{x1D70B}$ be the projection
$\unicode[STIX]{x1D70B}$ be the projection  $Z\rightarrow Z/M$. We note that
$Z\rightarrow Z/M$. We note that ![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is a map
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is a map  $Z/M\rightarrow Z$ which is a homotopy equivalence on the fixed point set, and so by Lemma 2.29,
$Z/M\rightarrow Z$ which is a homotopy equivalence on the fixed point set, and so by Lemma 2.29, ![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is injective. Then
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is injective. Then ![]() $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is also injective.
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is also injective.
We have a map  $\unicode[STIX]{x1D6FD}\oplus i:(Z/M)\oplus M\rightarrow Z$, where
$\unicode[STIX]{x1D6FD}\oplus i:(Z/M)\oplus M\rightarrow Z$, where ![]() $i$ is the inclusion
$i$ is the inclusion  $i:M\rightarrow Z$. We check that
$i:M\rightarrow Z$. We check that ![]() $\unicode[STIX]{x1D6FD}\oplus i$ is injective. Indeed, if
$\unicode[STIX]{x1D6FD}\oplus i$ is injective. Indeed, if  $(\unicode[STIX]{x1D6FD}\oplus i)(z\oplus m)=0$, we have
$(\unicode[STIX]{x1D6FD}\oplus i)(z\oplus m)=0$, we have  $\unicode[STIX]{x1D6FD}(z)=m$. By definition,
$\unicode[STIX]{x1D6FD}(z)=m$. By definition,  $\unicode[STIX]{x1D70B}(m)=0$, while
$\unicode[STIX]{x1D70B}(m)=0$, while ![]() $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is injective. It follows that
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}$ is injective. It follows that  $m=z=0$, and
$m=z=0$, and ![]() $\unicode[STIX]{x1D6FD}\oplus i$ is injective. Then
$\unicode[STIX]{x1D6FD}\oplus i$ is injective. Then  $Z/M\oplus M\rightarrow Z$ is an injective map of
$Z/M\oplus M\rightarrow Z$ is an injective map of ![]() $\mathbb{F}$-vector spaces of the same dimension, and so is an isomorphism (of
$\mathbb{F}$-vector spaces of the same dimension, and so is an isomorphism (of ![]() ${\mathcal{G}}$-chain complexes). Since, by Lemma 2.30, the isomorphism class of
${\mathcal{G}}$-chain complexes). Since, by Lemma 2.30, the isomorphism class of ![]() $Z/M$ is independent of
$Z/M$ is independent of ![]() $M$, we obtain that the isomorphism class of
$M$, we obtain that the isomorphism class of ![]() $Z/M$ is a well-defined invariant of
$Z/M$ is a well-defined invariant of ![]() $Z$.◻
$Z$.◻
Definition 2.32. For ![]() $Z$ a chain complex of type SWF, let
$Z$ a chain complex of type SWF, let ![]() $Z_{\text{conn}}$ denote
$Z_{\text{conn}}$ denote  $Z/Z_{\text{iness}}$, for
$Z/Z_{\text{iness}}$, for  $Z_{\text{iness}}\subseteq Z$ a maximal inessential subcomplex. We call
$Z_{\text{iness}}\subseteq Z$ a maximal inessential subcomplex. We call ![]() $Z_{\text{conn}}$ the connected complex of
$Z_{\text{conn}}$ the connected complex of ![]() $Z$.
$Z$.
Theorem 2.33. Let ![]() $Z$ be a suspensionlike chain complex of type SWF. Then for
$Z$ be a suspensionlike chain complex of type SWF. Then for ![]() $W$ another suspensionlike complex of type SWF,
$W$ another suspensionlike complex of type SWF,  $Z\equiv _{cl}W$ if and only if
$Z\equiv _{cl}W$ if and only if  $Z_{\text{conn}}\simeq W_{\text{conn}}$.
$Z_{\text{conn}}\simeq W_{\text{conn}}$.
Proof. By Lemma 2.31, we may write  $Z=Z_{\text{conn}}\oplus Z_{\text{iness}},W=W_{\text{conn}}\oplus W_{\text{iness}}$, with
$Z=Z_{\text{conn}}\oplus Z_{\text{iness}},W=W_{\text{conn}}\oplus W_{\text{iness}}$, with  $Z_{\text{iness}},W_{\text{iness}}$ maximal inessential subcomplexes. Say we have local equivalences (we need not consider suspensions, by Lemma 2.24)
$Z_{\text{iness}},W_{\text{iness}}$ maximal inessential subcomplexes. Say we have local equivalences (we need not consider suspensions, by Lemma 2.24)
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}:Z_{\text{conn}}\oplus Z_{\text{iness}}\rightarrow W_{\text{conn}}\oplus W_{\text{iness}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}:W_{\text{conn}}\oplus W_{\text{iness}}\rightarrow Z_{\text{conn}}\oplus Z_{\text{iness}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}:Z_{\text{conn}}\oplus Z_{\text{iness}}\rightarrow W_{\text{conn}}\oplus W_{\text{iness}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D713}:W_{\text{conn}}\oplus W_{\text{iness}}\rightarrow Z_{\text{conn}}\oplus Z_{\text{iness}}. & \displaystyle \nonumber\end{eqnarray}$$ We restrict ![]() $\unicode[STIX]{x1D719}$ and
$\unicode[STIX]{x1D719}$ and ![]() $\unicode[STIX]{x1D713}$ to
$\unicode[STIX]{x1D713}$ to ![]() $Z_{\text{conn}}$ and
$Z_{\text{conn}}$ and ![]() $W_{\text{conn}}$, since it is clear that
$W_{\text{conn}}$, since it is clear that  $Z_{\text{conn}}\oplus Z_{\text{iness}}$ is chain locally equivalent to
$Z_{\text{conn}}\oplus Z_{\text{iness}}$ is chain locally equivalent to ![]() $Z_{\text{conn}}$, and likewise for
$Z_{\text{conn}}$, and likewise for ![]() $W_{\text{conn}}$. Further, we project the image of
$W_{\text{conn}}$. Further, we project the image of ![]() $\unicode[STIX]{x1D719}$ and
$\unicode[STIX]{x1D719}$ and ![]() $\unicode[STIX]{x1D713}$ to
$\unicode[STIX]{x1D713}$ to ![]() $W_{\text{conn}}$ and
$W_{\text{conn}}$ and ![]() $Z_{\text{conn}}$, respectively. Call the resulting maps
$Z_{\text{conn}}$, respectively. Call the resulting maps ![]() $\unicode[STIX]{x1D719}_{0}$ and
$\unicode[STIX]{x1D719}_{0}$ and ![]() $\unicode[STIX]{x1D713}_{0}$. If
$\unicode[STIX]{x1D713}_{0}$. If ![]() $\unicode[STIX]{x1D719}_{0}$ had a nontrivial kernel, then we would obtain by composition a local equivalence:
$\unicode[STIX]{x1D719}_{0}$ had a nontrivial kernel, then we would obtain by composition a local equivalence:
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D719}_{0}:Z_{\text{conn}}/\text{ker}\,\unicode[STIX]{x1D719}_{0}\rightarrow Z_{\text{conn}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D719}_{0}:Z_{\text{conn}}/\text{ker}\,\unicode[STIX]{x1D719}_{0}\rightarrow Z_{\text{conn}}.\end{eqnarray}$$ Composing with the inclusion  $\unicode[STIX]{x1D704}:Z_{\text{conn}}\rightarrow Z$ gives a chain local map
$\unicode[STIX]{x1D704}:Z_{\text{conn}}\rightarrow Z$ gives a chain local map  $\unicode[STIX]{x1D704}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D719}_{0}:Z_{\text{conn}}/\text{ker}\;\unicode[STIX]{x1D719}_{0}\rightarrow Z$, so by Lemma 2.29,
$\unicode[STIX]{x1D704}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D719}_{0}:Z_{\text{conn}}/\text{ker}\;\unicode[STIX]{x1D719}_{0}\rightarrow Z$, so by Lemma 2.29, ![]() $\unicode[STIX]{x1D704}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D719}_{0}$ is injective. Thus,
$\unicode[STIX]{x1D704}\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D719}_{0}$ is injective. Thus, ![]() $\unicode[STIX]{x1D719}_{0}$ is injective. Similarly
$\unicode[STIX]{x1D719}_{0}$ is injective. Similarly ![]() $\unicode[STIX]{x1D713}_{0}$ is injective, so we obtain an isomorphism of chain complexes
$\unicode[STIX]{x1D713}_{0}$ is injective, so we obtain an isomorphism of chain complexes  $Z_{\text{conn}}\cong W_{\text{conn}}$. Conversely, a homotopy equivalence
$Z_{\text{conn}}\cong W_{\text{conn}}$. Conversely, a homotopy equivalence  $Z_{\text{conn}}\rightarrow W_{\text{conn}}$ yields a local equivalence
$Z_{\text{conn}}\rightarrow W_{\text{conn}}$ yields a local equivalence  $Z\rightarrow W$ by the composition
$Z\rightarrow W$ by the composition
 $$\begin{eqnarray}Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z_{\text{conn}}\rightarrow W_{\text{conn}}\rightarrow W,\end{eqnarray}$$
$$\begin{eqnarray}Z\xrightarrow[{}]{\unicode[STIX]{x1D70B}}Z_{\text{conn}}\rightarrow W_{\text{conn}}\rightarrow W,\end{eqnarray}$$ where  $\unicode[STIX]{x1D70B}:Z\rightarrow Z_{\text{conn}}$ is projection to the first summand.◻
$\unicode[STIX]{x1D70B}:Z\rightarrow Z_{\text{conn}}$ is projection to the first summand.◻
The next corollary allows us to view the chain local equivalence type of a space of type SWF in ![]() $\mathfrak{CE}$ instead of
$\mathfrak{CE}$ instead of ![]() $\mathfrak{CLE}$.
$\mathfrak{CLE}$.
Corollary 2.34. In the language of Theorem 2.33, there is an injection  $B:\mathfrak{CLE}\rightarrow \mathfrak{CE}$ given by
$B:\mathfrak{CLE}\rightarrow \mathfrak{CE}$ given by  $[(Z,m,n)]\rightarrow [(Z_{\text{conn}},m,n)]$, for
$[(Z,m,n)]\rightarrow [(Z_{\text{conn}},m,n)]$, for  $(Z,m,n)$ a representative of the class
$(Z,m,n)$ a representative of the class  $[(Z,m,n)]$ with
$[(Z,m,n)]$ with ![]() $Z$ suspensionlike.
$Z$ suspensionlike.
Proof. Fix  $[(Z,m,n)]=[(Z^{\prime },m^{\prime },n^{\prime })]\in \mathfrak{CLE}$ with
$[(Z,m,n)]=[(Z^{\prime },m^{\prime },n^{\prime })]\in \mathfrak{CLE}$ with ![]() $Z$ and
$Z$ and ![]() $Z^{\prime }$ suspensionlike; we will show that
$Z^{\prime }$ suspensionlike; we will show that  $[(Z_{\text{conn}},m,n)]=[(Z_{\text{conn}}^{\prime },m^{\prime },n^{\prime })]$ in
$[(Z_{\text{conn}},m,n)]=[(Z_{\text{conn}}^{\prime },m^{\prime },n^{\prime })]$ in ![]() $\mathfrak{CE}$. First, we observe that, for
$\mathfrak{CE}$. First, we observe that, for  $V=\mathbb{H},\tilde{\mathbb{R}}$:
$V=\mathbb{H},\tilde{\mathbb{R}}$:
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}Z_{\text{conn}}\simeq (\unicode[STIX]{x1D6F4}^{V}Z)_{\text{conn}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{V}Z_{\text{conn}}\simeq (\unicode[STIX]{x1D6F4}^{V}Z)_{\text{conn}}.\end{eqnarray}$$ We have, for ![]() $M,N$ sufficiently large,
$M,N$ sufficiently large,
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}Z\leftrightarrows \unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}Z^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}Z\leftrightarrows \unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}Z^{\prime }.\end{eqnarray}$$ Here the maps in both directions are local equivalences. Choosing  $M\geqslant \text{max}\{m,m^{\prime }\}\,$ and
$M\geqslant \text{max}\{m,m^{\prime }\}\,$ and  $N\geqslant \text{max}\,\{n,n^{\prime }\}$ guarantees that both
$N\geqslant \text{max}\,\{n,n^{\prime }\}$ guarantees that both
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}Z\quad \text{and}\quad \unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}Z^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}Z\quad \text{and}\quad \unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}Z^{\prime }\end{eqnarray}$$are suspensionlike. Then, by Theorem 2.33, we have a homotopy equivalence:
 $$\begin{eqnarray}(\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}Z)_{\text{conn}}\rightarrow (\unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}Z^{\prime })_{\text{conn}}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}Z)_{\text{conn}}\rightarrow (\unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}Z^{\prime })_{\text{conn}}.\end{eqnarray}$$However, by (37), we obtain a homotopy equivalence:
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}(Z_{\text{conn}})\rightarrow \unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}(Z_{\text{conn}}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{(M-m)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n)\mathbb{H}}(Z_{\text{conn}})\rightarrow \unicode[STIX]{x1D6F4}^{(M-m^{\prime })\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{(N-n^{\prime })\mathbb{H}}(Z_{\text{conn}}^{\prime }).\end{eqnarray}$$ Then  $[(Z_{\text{conn}},m,n)]=[(Z_{\text{conn}}^{\prime },m^{\prime },n^{\prime })]\in \mathfrak{CE}$, as needed. Finally, we show
$[(Z_{\text{conn}},m,n)]=[(Z_{\text{conn}}^{\prime },m^{\prime },n^{\prime })]\in \mathfrak{CE}$, as needed. Finally, we show ![]() $B$ is injective. If
$B$ is injective. If  $(Z_{\text{conn}},m,n)$ is stably equivalent to
$(Z_{\text{conn}},m,n)$ is stably equivalent to  $(Z_{\text{conn}}^{\prime },m^{\prime },n^{\prime })$, then
$(Z_{\text{conn}}^{\prime },m^{\prime },n^{\prime })$, then  $(Z,m,n)$ and
$(Z,m,n)$ and  $(Z^{\prime },m^{\prime },n^{\prime })$ are locally equivalent, by Theorem 2.33 and (37).◻
$(Z^{\prime },m^{\prime },n^{\prime })$ are locally equivalent, by Theorem 2.33 and (37).◻
By Corollary 2.34, instead of considering the relation given by chain local equivalence, we need only consider chain homotopy equivalences.
Definition 2.35. The connected ![]() $S^{1}$-homology of
$S^{1}$-homology of  $(Z,m,n)\in \mathfrak{CE}$, denoted by
$(Z,m,n)\in \mathfrak{CE}$, denoted by  $H_{\text{conn}}^{S^{1}}((Z,m,n))$, for
$H_{\text{conn}}^{S^{1}}((Z,m,n))$, for ![]() $Z$ a suspensionlike chain complex of type SWF, is the quotient
$Z$ a suspensionlike chain complex of type SWF, is the quotient  $(H_{\ast }^{S^{1}}(Z)/(H_{\ast }^{S^{1}}(Z^{S^{1}})+H_{\ast }^{S^{1}}(Z_{\text{iness}})))[m+4n]$, where
$(H_{\ast }^{S^{1}}(Z)/(H_{\ast }^{S^{1}}(Z^{S^{1}})+H_{\ast }^{S^{1}}(Z_{\text{iness}})))[m+4n]$, where  $Z_{\text{iness}}\subseteq Z$ is a maximal inessential subcomplex. By Theorem 2.33, the graded
$Z_{\text{iness}}\subseteq Z$ is a maximal inessential subcomplex. By Theorem 2.33, the graded ![]() $\mathbb{F}[U]$-module isomorphism class of
$\mathbb{F}[U]$-module isomorphism class of  $H_{\text{conn}}^{S^{1}}((Z,m,n))$ is an invariant of the chain local equivalence class of
$H_{\text{conn}}^{S^{1}}((Z,m,n))$ is an invariant of the chain local equivalence class of  $(Z,m,n)$.
$(Z,m,n)$.
Remark 2.36. We could have instead considered the quotient  $(H_{\ast }^{S^{1}}(Z)/H_{\ast }^{S^{1}}(Z_{\text{iness}}))[m+4n]$, which is isomorphic to
$(H_{\ast }^{S^{1}}(Z)/H_{\ast }^{S^{1}}(Z_{\text{iness}}))[m+4n]$, which is isomorphic to  $H_{\text{conn}}^{S^{1}}((Z,m,n))\oplus {\mathcal{T}}_{d}^{+}$, for some
$H_{\text{conn}}^{S^{1}}((Z,m,n))\oplus {\mathcal{T}}_{d}^{+}$, for some ![]() $d$. As defined above,
$d$. As defined above,  $H_{\text{conn}}^{S^{1}}((Z,m,n))$ has no infinite
$H_{\text{conn}}^{S^{1}}((Z,m,n))$ has no infinite ![]() $\mathbb{F}[U]$-tower.
$\mathbb{F}[U]$-tower.
3  $j$-split spaces
$j$-split spaces
In this section we introduce ![]() $j$-split spaces of type SWF, and compute their
$j$-split spaces of type SWF, and compute their ![]() $G$-Borel homology. We will see in Lemma 5.3 that the Seiberg–Witten Floer spectra of Seifert spaces are
$G$-Borel homology. We will see in Lemma 5.3 that the Seiberg–Witten Floer spectra of Seifert spaces are ![]() $j$-split. The computation of this section will then provide the
$j$-split. The computation of this section will then provide the ![]() $G$-equivariant Seiberg–Witten Floer homology of Seifert spaces.
$G$-equivariant Seiberg–Witten Floer homology of Seifert spaces.
Definition 3.1. We call a space ![]() $X$ of type SWF
$X$ of type SWF ![]() $j$-split if
$j$-split if ![]() $X/X^{S^{1}}$ may be written
$X/X^{S^{1}}$ may be written
 $$\begin{eqnarray}X/X^{S^{1}}=X_{+}\vee X_{-},\end{eqnarray}$$
$$\begin{eqnarray}X/X^{S^{1}}=X_{+}\vee X_{-},\end{eqnarray}$$ for some ![]() $S^{1}$-space
$S^{1}$-space ![]() $X_{+}$, where
$X_{+}$, where ![]() $j$ acts on the right-hand side by interchanging the factors (that is,
$j$ acts on the right-hand side by interchanging the factors (that is,  $jX_{+}=X_{-}$). Similarly, we call a
$jX_{+}=X_{-}$). Similarly, we call a ![]() ${\mathcal{G}}$-chain complex
${\mathcal{G}}$-chain complex ![]() $(Z,\unicode[STIX]{x2202})$ of type SWF
$(Z,\unicode[STIX]{x2202})$ of type SWF ![]() $j$-split if (i)–(iii) below are satisfied.
$j$-split if (i)–(iii) below are satisfied.
(i) There exists
 $f_{\text{red}}\in Z$ such that
$f_{\text{red}}\in Z$ such that  $\langle f_{\text{red}}\rangle$ is the fixed-point set,
$\langle f_{\text{red}}\rangle$ is the fixed-point set,  $Z^{S^{1}}$, of
$Z^{S^{1}}$, of  $Z$. Furthermore
$Z$. Furthermore  $sf_{\text{red}}=0,jf_{\text{red}}=f_{\text{red}}$. In particular,
$sf_{\text{red}}=0,jf_{\text{red}}=f_{\text{red}}$. In particular,  $Z$ is of type SWF at level
$Z$ is of type SWF at level  $0$.
$0$.(ii) The fixed-point set
 $Z^{S^{1}}$ is a subcomplex of
$Z^{S^{1}}$ is a subcomplex of  $Z$ (that is,
$Z$ (that is,  $\unicode[STIX]{x2202}(f_{\text{red}})=0$).
$\unicode[STIX]{x2202}(f_{\text{red}})=0$).(iii) We have
where $$\begin{eqnarray}Z/Z^{S^{1}}=(Z_{+}\oplus jZ_{+}),\end{eqnarray}$$
$$\begin{eqnarray}Z/Z^{S^{1}}=(Z_{+}\oplus jZ_{+}),\end{eqnarray}$$ $Z_{+}$ is a
$Z_{+}$ is a  $C_{\ast }^{\text{CW}}(S^{1})$ chain complex, and
$C_{\ast }^{\text{CW}}(S^{1})$ chain complex, and  $j$ acts on the right-hand side by interchanging the factors.
$j$ acts on the right-hand side by interchanging the factors.
Recall that ![]() $\tilde{\oplus }$ denotes a direct sum of
$\tilde{\oplus }$ denotes a direct sum of ![]() ${\mathcal{G}}$-modules that is not necessarily a direct sum of chain complexes. For a
${\mathcal{G}}$-modules that is not necessarily a direct sum of chain complexes. For a ![]() $j$-split chain complex
$j$-split chain complex ![]() $Z$ we may write, referring to
$Z$ we may write, referring to ![]() $jZ_{+}$ by
$jZ_{+}$ by ![]() $Z_{-}$,
$Z_{-}$,
 $$\begin{eqnarray}Z=(Z_{+}\oplus Z_{-})\,\tilde{\oplus }\,\langle f_{\text{red}}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}Z=(Z_{+}\oplus Z_{-})\,\tilde{\oplus }\,\langle f_{\text{red}}\rangle .\end{eqnarray}$$ In the above, ![]() $Z$ is to be thought of as the reduced CW chain complex of a
$Z$ is to be thought of as the reduced CW chain complex of a ![]() $G$-space
$G$-space ![]() $X$, and
$X$, and ![]() $f_{\text{red}}$ is to be thought of as the chain corresponding to the
$f_{\text{red}}$ is to be thought of as the chain corresponding to the ![]() $S^{1}$-fixed subset of
$S^{1}$-fixed subset of ![]() $X$. The requirement that
$X$. The requirement that ![]() $Z$ be a chain complex of type SWF at level
$Z$ be a chain complex of type SWF at level ![]() $0$ will be used in § 3.2 to calculate the chain local equivalence class of
$0$ will be used in § 3.2 to calculate the chain local equivalence class of ![]() $j$-split chain complexes.
$j$-split chain complexes.
A ![]() $j$-split space
$j$-split space ![]() $X$ with
$X$ with  $X^{S^{1}}=S^{0}$ admits a CW chain complex which is a
$X^{S^{1}}=S^{0}$ admits a CW chain complex which is a ![]() $j$-split chain complex. For
$j$-split chain complex. For ![]() $X$ a
$X$ a ![]() $j$-split space of type SWF at level
$j$-split space of type SWF at level ![]() $s$, we use the following lemma to relate the CW chain complex of
$s$, we use the following lemma to relate the CW chain complex of ![]() $X$ to
$X$ to ![]() $j$-split complexes.
$j$-split complexes.
Lemma 3.2. Let ![]() $X$ be a
$X$ be a ![]() $j$-split space of type SWF at level
$j$-split space of type SWF at level ![]() $s$. Then
$s$. Then
 $$\begin{eqnarray}[C_{\ast }^{\text{CW}}(X,\text{pt})]=[(Z,-s,0)]\in \mathfrak{CE},\end{eqnarray}$$
$$\begin{eqnarray}[C_{\ast }^{\text{CW}}(X,\text{pt})]=[(Z,-s,0)]\in \mathfrak{CE},\end{eqnarray}$$ for some ![]() $j$-split chain complex
$j$-split chain complex ![]() $Z$.
$Z$.
Proof. The chain complex  $C_{\ast }^{\text{CW}}(X,\text{pt})$ may be written
$C_{\ast }^{\text{CW}}(X,\text{pt})$ may be written
 $$\begin{eqnarray}C_{\ast }^{\text{CW}}(X,\text{pt})=R\,\tilde{\oplus }\,F,\end{eqnarray}$$
$$\begin{eqnarray}C_{\ast }^{\text{CW}}(X,\text{pt})=R\,\tilde{\oplus }\,F,\end{eqnarray}$$ where  $R=C_{\ast }^{\text{CW}}(X^{S^{1}},\text{pt})\cong C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$ is a subcomplex and
$R=C_{\ast }^{\text{CW}}(X^{S^{1}},\text{pt})\cong C_{\ast }^{\text{CW}}((\tilde{\mathbb{R}}^{s})^{+},\text{pt})$ is a subcomplex and ![]() $F$ is a free
$F$ is a free ![]() ${\mathcal{G}}$-chain complex. Since
${\mathcal{G}}$-chain complex. Since ![]() $X$ is
$X$ is ![]() $j$-split, the decomposition (38) may be chosen so that
$j$-split, the decomposition (38) may be chosen so that
 $$\begin{eqnarray}F=F_{+}\oplus jF_{+},\end{eqnarray}$$
$$\begin{eqnarray}F=F_{+}\oplus jF_{+},\end{eqnarray}$$ where ![]() $F_{+}$ is a
$F_{+}$ is a  $C_{\ast }^{\text{CW}}(S^{1})$-chain complex, and
$C_{\ast }^{\text{CW}}(S^{1})$-chain complex, and ![]() $j$ acts on
$j$ acts on ![]() $F$ by interchanging
$F$ by interchanging ![]() $F_{+}$ and
$F_{+}$ and ![]() $jF_{+}$.
$jF_{+}$.
We first show that we may choose ![]() $F$ satisfying (38) and (39) and so that, for
$F$ satisfying (38) and (39) and so that, for ![]() $x\in F$ homogeneous,
$x\in F$ homogeneous,
 $$\begin{eqnarray}(\unicode[STIX]{x2202}x)|_{R}=0,\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x2202}x)|_{R}=0,\end{eqnarray}$$ if  $\text{deg}\,x\neq s+1$.
$\text{deg}\,x\neq s+1$.
Indeed, fix some ![]() $F$ satisfying (38) and (39), and let
$F$ satisfying (38) and (39), and let ![]() $\{x_{i}\}$ be a homogeneous basis for
$\{x_{i}\}$ be a homogeneous basis for ![]() $F$. Let
$F$. Let ![]() $F(n)$ denote the
$F(n)$ denote the ![]() ${\mathcal{G}}$-chain complex generated by
${\mathcal{G}}$-chain complex generated by ![]() $x_{i}$ of degree less than or equal to
$x_{i}$ of degree less than or equal to ![]() $n$. We define new chain complexes
$n$. We define new chain complexes ![]() $F^{\prime }(n)$ so that
$F^{\prime }(n)$ so that  $R\,\tilde{\oplus }\,F^{\prime }(n)=R\,\tilde{\oplus }\,F(n)$, and so that
$R\,\tilde{\oplus }\,F^{\prime }(n)=R\,\tilde{\oplus }\,F(n)$, and so that  $F^{\prime }=\bigcup _{n}F^{\prime }(n)$ satisfies (38)–(40). Let
$F^{\prime }=\bigcup _{n}F^{\prime }(n)$ satisfies (38)–(40). Let ![]() $\unicode[STIX]{x1D70B}_{n}$ denote projection
$\unicode[STIX]{x1D70B}_{n}$ denote projection  $\unicode[STIX]{x1D70B}_{n}:R\,\tilde{\oplus }\,F^{\prime }(n)\rightarrow R$ onto the first factor. Set
$\unicode[STIX]{x1D70B}_{n}:R\,\tilde{\oplus }\,F^{\prime }(n)\rightarrow R$ onto the first factor. Set  $F^{\prime }(0)=F_{{\leqslant}0}$, the chain complex generated by all homogeneous elements of
$F^{\prime }(0)=F_{{\leqslant}0}$, the chain complex generated by all homogeneous elements of ![]() $F$ of degree at most
$F$ of degree at most ![]() $0$. Assume we have defined
$0$. Assume we have defined ![]() $F^{\prime }(n)$ for
$F^{\prime }(n)$ for  $n\leqslant N<s$, so that (40) holds for all
$n\leqslant N<s$, so that (40) holds for all  $x\in F^{\prime }(n)$.
$x\in F^{\prime }(n)$.
We define  $F^{\prime }(N+1)$ by defining generators
$F^{\prime }(N+1)$ by defining generators ![]() $x_{i}^{\prime }$ of
$x_{i}^{\prime }$ of  $F^{\prime }(N+1)/F^{\prime }(N)$ corresponding to the generators
$F^{\prime }(N+1)/F^{\prime }(N)$ corresponding to the generators ![]() $x_{i}$ of
$x_{i}$ of  $F(N+1)/F(N)$. For each
$F(N+1)/F(N)$. For each ![]() $x_{i}$ of degree
$x_{i}$ of degree ![]() $N+1$ so that
$N+1$ so that  $\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=0$, let
$\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=0$, let ![]() $x_{i}^{\prime }=x_{i}$. If instead
$x_{i}^{\prime }=x_{i}$. If instead ![]() $x_{i}$ is of degree
$x_{i}$ is of degree ![]() $N+1$ and
$N+1$ and  $\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})\neq 0$, then
$\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})\neq 0$, then
 $$\begin{eqnarray}\unicode[STIX]{x2202}(\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i}))=\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}^{2}(x_{i}))=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i}))=\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}^{2}(x_{i}))=0.\end{eqnarray}$$ So,  $\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=(1+j)c_{N}$, since
$\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=(1+j)c_{N}$, since  $(1+j)c_{N}$ is the only nonzero cycle of
$(1+j)c_{N}$ is the only nonzero cycle of ![]() $R$ in grading
$R$ in grading ![]() $N$ (or, when
$N$ (or, when ![]() $N=0$,
$N=0$,  $\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=c_{0}$). However, by assumption,
$\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=c_{0}$). However, by assumption, ![]() $N<s$, so
$N<s$, so  $\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=\unicode[STIX]{x2202}c_{N+1}$. Then, we let
$\unicode[STIX]{x1D70B}_{N}(\unicode[STIX]{x2202}x_{i})=\unicode[STIX]{x2202}c_{N+1}$. Then, we let  $x_{i}^{\prime }=x_{i}+c_{N+1}$.
$x_{i}^{\prime }=x_{i}+c_{N+1}$.
Let
 $$\begin{eqnarray}F^{\prime }(N+1)=\langle F^{\prime }(N),\mathop{\bigcup }_{\{i\mid \text{deg}\,x_{i}=N+1\}}x_{i}^{\prime }\rangle .\end{eqnarray}$$
$$\begin{eqnarray}F^{\prime }(N+1)=\langle F^{\prime }(N),\mathop{\bigcup }_{\{i\mid \text{deg}\,x_{i}=N+1\}}x_{i}^{\prime }\rangle .\end{eqnarray}$$ By construction  $R\,\tilde{\oplus }\,F^{\prime }(N+1)=R\,\tilde{\oplus }\,F(N+1)$, and (40) holds for all
$R\,\tilde{\oplus }\,F^{\prime }(N+1)=R\,\tilde{\oplus }\,F(N+1)$, and (40) holds for all  $x\in F^{\prime }(N+1)$.
$x\in F^{\prime }(N+1)$.
For ![]() $N\geqslant s$, define
$N\geqslant s$, define  $F^{\prime }(N+1)$ by
$F^{\prime }(N+1)$ by  $F^{\prime }(N+1)=\langle F^{\prime }(N),\bigcup _{\{i\mid \text{deg}\,x_{i}=N+1\}}x_{i}\rangle$.
$F^{\prime }(N+1)=\langle F^{\prime }(N),\bigcup _{\{i\mid \text{deg}\,x_{i}=N+1\}}x_{i}\rangle$.
From the construction, it is clear that ![]() $F^{\prime }$ satisfies (38)–(40), as needed.
$F^{\prime }$ satisfies (38)–(40), as needed.
Take ![]() $F$ satisfying (38)–(40). Consider the
$F$ satisfying (38)–(40). Consider the ![]() ${\mathcal{G}}$-chain complex
${\mathcal{G}}$-chain complex  $Z=C_{\ast }^{\text{CW}}(S^{0},\text{pt})\,\tilde{\oplus }\,F[s]$, where
$Z=C_{\ast }^{\text{CW}}(S^{0},\text{pt})\,\tilde{\oplus }\,F[s]$, where  $C_{\ast }^{\text{CW}}(S^{0},\text{pt})=\langle c_{0}\rangle$ is a subcomplex. To define the differentials from
$C_{\ast }^{\text{CW}}(S^{0},\text{pt})=\langle c_{0}\rangle$ is a subcomplex. To define the differentials from ![]() $F[s]$ to
$F[s]$ to  $C_{\ast }^{\text{CW}}(S^{0},\text{pt})$ in
$C_{\ast }^{\text{CW}}(S^{0},\text{pt})$ in ![]() $Z$, we set, for
$Z$, we set, for  $x[s]\in F[s]$,
$x[s]\in F[s]$,
 $$\begin{eqnarray}(\unicode[STIX]{x2202}x[s])|_{C_{\ast }^{\text{CW}}(S^{0},\text{pt})}=c_{0},\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x2202}x[s])|_{C_{\ast }^{\text{CW}}(S^{0},\text{pt})}=c_{0},\end{eqnarray}$$ if  $(\unicode[STIX]{x2202}x)|_{R}=(1+j)c_{s},$ and
$(\unicode[STIX]{x2202}x)|_{R}=(1+j)c_{s},$ and
 $$\begin{eqnarray}(\unicode[STIX]{x2202}x[s])|_{C_{\ast }^{\text{CW}}(S^{0},\text{pt})}=0\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x2202}x[s])|_{C_{\ast }^{\text{CW}}(S^{0},\text{pt})}=0\end{eqnarray}$$ if  $(\unicode[STIX]{x2202}x)|_{R}=0$.
$(\unicode[STIX]{x2202}x)|_{R}=0$.
By the construction of ![]() $F$, (41) and (42) determine the differential on
$F$, (41) and (42) determine the differential on ![]() $Z$.
$Z$.
Finally, consider the suspension
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z=\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}(C_{\ast }^{\text{CW}}(S^{0},\text{pt}))\,\tilde{\oplus }\,\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}(F[s])\simeq R\,\tilde{\oplus }\,\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F[s].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z=\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}(C_{\ast }^{\text{CW}}(S^{0},\text{pt}))\,\tilde{\oplus }\,\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}(F[s])\simeq R\,\tilde{\oplus }\,\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F[s].\end{eqnarray}$$ We note, as in the proof of Lemma 2.23, that  $\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F[s]\simeq F[0]=F.$ Then, there is a homotopy equivalence, constructed exactly as in the proofs of Lemmas 2.23 and 2.24:
$\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}F[s]\simeq F[0]=F.$ Then, there is a homotopy equivalence, constructed exactly as in the proofs of Lemmas 2.23 and 2.24:
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z\simeq R\,\tilde{\oplus }\,F.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\tilde{\mathbb{R}}^{s}}Z\simeq R\,\tilde{\oplus }\,F.\end{eqnarray}$$ It follows that  $[(Z,-s,0)]=[C_{\ast }^{\text{CW}}(X,\text{pt})]\in \mathfrak{CE}$, as needed.◻
$[(Z,-s,0)]=[C_{\ast }^{\text{CW}}(X,\text{pt})]\in \mathfrak{CE}$, as needed.◻
Note also that any ![]() $j$-split chain complex occurs as the CW chain complex of some
$j$-split chain complex occurs as the CW chain complex of some ![]() $j$-split space.
$j$-split space.
Remark 3.3. ![]() $j$-splitness is not the same as Floer
$j$-splitness is not the same as Floer ![]() $K_{G}$-splitness of [Reference ManolescuMan14].
$K_{G}$-splitness of [Reference ManolescuMan14].
3.1 Calculation of  $\tilde{H}_{\ast }^{G}(X)$
$\tilde{H}_{\ast }^{G}(X)$
In this section we will compute the ![]() $G$-equivariant homology of a
$G$-equivariant homology of a ![]() $j$-split space in terms of its
$j$-split space in terms of its ![]() $S^{1}$-homology.
$S^{1}$-homology.
Let ![]() $X$ be a
$X$ be a ![]() $j$-split space of type SWF at level
$j$-split space of type SWF at level ![]() $m$ with
$m$ with  $X/X^{S^{1}}=X_{+}\vee X_{-}$. The Puppe sequence
$X/X^{S^{1}}=X_{+}\vee X_{-}$. The Puppe sequence
 $$\begin{eqnarray}X^{S^{1}}\rightarrow X\rightarrow X/X^{S^{1}}\rightarrow \unicode[STIX]{x1D6F4}X^{S^{1}}\end{eqnarray}$$
$$\begin{eqnarray}X^{S^{1}}\rightarrow X\rightarrow X/X^{S^{1}}\rightarrow \unicode[STIX]{x1D6F4}X^{S^{1}}\end{eqnarray}$$leads to a commutative diagram, where the rows are cofibration sequences.

In (
44) the vertical maps are obtained by taking the quotient by the action of ![]() $j\in G$. The diagram (
$j\in G$. The diagram (
) itself yields a commutative diagram for Borel homology, where the rows are exact.

Specifically, we view (
45) as a diagram of  $\mathbb{F}[q,v]/(q^{3})$ modules, where
$\mathbb{F}[q,v]/(q^{3})$ modules, where ![]() $v$ acts on the top row by
$v$ acts on the top row by ![]() $U^{2}$ and
$U^{2}$ and ![]() $q$ annihilates the top row. An
$q$ annihilates the top row. An ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module ![]() $M$ viewed as an
$M$ viewed as an  $\mathbb{F}[q,v]/(q^{3})$-module this way is denoted
$\mathbb{F}[q,v]/(q^{3})$-module this way is denoted  $\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}M$. More precisely, let
$\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}M$. More precisely, let  $\unicode[STIX]{x1D719}:\mathbb{F}[q,v]/(q^{3})\rightarrow \mathbb{F}[U]$ be
$\unicode[STIX]{x1D719}:\mathbb{F}[q,v]/(q^{3})\rightarrow \mathbb{F}[U]$ be  $v\rightarrow U^{2},\,q\rightarrow 0$, and let
$v\rightarrow U^{2},\,q\rightarrow 0$, and let  $\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}$ be the corresponding restriction functor.
$\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}$ be the corresponding restriction functor.
Recall the notation  ${\mathcal{T}}^{+}(i)=\mathbb{F}[U^{-i+1},U^{-i+2},\ldots ]/U\mathbb{F}[U]$ and
${\mathcal{T}}^{+}(i)=\mathbb{F}[U^{-i+1},U^{-i+2},\ldots ]/U\mathbb{F}[U]$ and  ${\mathcal{V}}^{+}(i)=\mathbb{F}[v^{-i+1},v^{-i+2},\ldots ]/v\mathbb{F}[v]$, and set
${\mathcal{V}}^{+}(i)=\mathbb{F}[v^{-i+1},v^{-i+2},\ldots ]/v\mathbb{F}[v]$, and set  ${\mathcal{T}}_{d}^{+}(n)={\mathcal{T}}^{+}(n)[-d]$ and
${\mathcal{T}}_{d}^{+}(n)={\mathcal{T}}^{+}(n)[-d]$ and  ${\mathcal{V}}_{d}^{+}(n)={\mathcal{V}}^{+}(n)[-d]$. The restriction takes the simple
${\mathcal{V}}_{d}^{+}(n)={\mathcal{V}}^{+}(n)[-d]$. The restriction takes the simple ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module ![]() ${\mathcal{T}}_{d}^{+}(n)$ to
${\mathcal{T}}_{d}^{+}(n)$ to
 $$\begin{eqnarray}\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}{\mathcal{T}}_{d}^{+}(n)={\mathcal{V}}_{d}^{+}\biggl(\biggl\lfloor\frac{n+1}{2}\biggr\rfloor\biggr)\oplus {\mathcal{V}}_{d+2}^{+}\biggl(\biggl\lfloor\frac{n}{2}\biggr\rfloor\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}{\mathcal{T}}_{d}^{+}(n)={\mathcal{V}}_{d}^{+}\biggl(\biggl\lfloor\frac{n+1}{2}\biggr\rfloor\biggr)\oplus {\mathcal{V}}_{d+2}^{+}\biggl(\biggl\lfloor\frac{n}{2}\biggr\rfloor\biggr).\end{eqnarray}$$ We define the maps  $d_{S^{1}}:\tilde{H}_{\ast }^{S^{1}}(X_{+})\oplus \tilde{H}_{\ast }^{S^{1}}(X_{-})\rightarrow \tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})$ and
$d_{S^{1}}:\tilde{H}_{\ast }^{S^{1}}(X_{+})\oplus \tilde{H}_{\ast }^{S^{1}}(X_{-})\rightarrow \tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})$ and  $d_{G}:\tilde{H}_{\ast }^{G}(X/X^{S^{1}})\rightarrow \tilde{H}_{\ast }^{G}(X^{S^{1}})$ by shifting by
$d_{G}:\tilde{H}_{\ast }^{G}(X/X^{S^{1}})\rightarrow \tilde{H}_{\ast }^{G}(X^{S^{1}})$ by shifting by ![]() $1$ the degree of the horizontal maps on the right of diagram (45). (So that
$1$ the degree of the horizontal maps on the right of diagram (45). (So that ![]() $d_{S^{1}}$ and
$d_{S^{1}}$ and ![]() $d_{G}$ are maps of degree
$d_{G}$ are maps of degree ![]() $-1$.) Write
$-1$.) Write ![]() $d_{S^{1}}^{\pm }$ for the restriction of
$d_{S^{1}}^{\pm }$ for the restriction of ![]() $d_{S^{1}}$ to the
$d_{S^{1}}$ to the ![]() $X^{\pm }$ components.
$X^{\pm }$ components.
Fact 3.4. The map ![]() $\unicode[STIX]{x1D719}_{1}$ in (45) is precisely the corestriction map
$\unicode[STIX]{x1D719}_{1}$ in (45) is precisely the corestriction map ![]() $\text{cor}_{G}^{S^{1}}$, and is an isomorphism in degrees congruent to
$\text{cor}_{G}^{S^{1}}$, and is an isomorphism in degrees congruent to ![]() $m$ modulo
$m$ modulo ![]() $4$, and vanishes otherwise.
$4$, and vanishes otherwise.
Proof. This follows from the construction of the ![]() $\unicode[STIX]{x1D719}_{i}$ and the dual of Fact 2.1.◻
$\unicode[STIX]{x1D719}_{i}$ and the dual of Fact 2.1.◻
Fact 3.5. We have that
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{3}|_{\tilde{H}_{\ast }^{S^{1}}(X_{+})}:\tilde{H}_{\ast }^{S^{1}}(X_{+})\rightarrow \tilde{H}_{\ast }^{G}(X/X^{S^{1}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{3}|_{\tilde{H}_{\ast }^{S^{1}}(X_{+})}:\tilde{H}_{\ast }^{S^{1}}(X_{+})\rightarrow \tilde{H}_{\ast }^{G}(X/X^{S^{1}})\end{eqnarray}$$ is an isomorphism (of  $\mathbb{F}[q,v]/(q^{3})$-modules).
$\mathbb{F}[q,v]/(q^{3})$-modules).
Proof. Since ![]() $X$ is
$X$ is ![]() $j$-split, both domain and target are isomorphic, as vector spaces, to
$j$-split, both domain and target are isomorphic, as vector spaces, to  $\tilde{H}_{\ast }(X_{+}/S^{1})$. The map
$\tilde{H}_{\ast }(X_{+}/S^{1})$. The map ![]() $\unicode[STIX]{x1D719}_{3}$ is a bijection and an
$\unicode[STIX]{x1D719}_{3}$ is a bijection and an  $\mathbb{F}[q,v]/(q^{3})$-module map, and so is an isomorphism.◻
$\mathbb{F}[q,v]/(q^{3})$-module map, and so is an isomorphism.◻
In particular, Fact 3.5 shows that the ![]() $q$-action on
$q$-action on  $\tilde{H}_{\ast }^{G}(X/X^{S^{1}})$ is trivial. Since
$\tilde{H}_{\ast }^{G}(X/X^{S^{1}})$ is trivial. Since  $\unicode[STIX]{x1D719}_{3}|_{\tilde{H}^{S^{1}}(X_{+})}$ is an isomorphism, we have
$\unicode[STIX]{x1D719}_{3}|_{\tilde{H}^{S^{1}}(X_{+})}$ is an isomorphism, we have
 $$\begin{eqnarray}\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}\tilde{H}_{\ast }^{S^{1}}(X_{+})=\tilde{H}_{\ast }^{G}(X/X^{S^{1}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}\tilde{H}_{\ast }^{S^{1}}(X_{+})=\tilde{H}_{\ast }^{G}(X/X^{S^{1}}).\end{eqnarray}$$Fact 3.6. The maps ![]() $d_{S^{1}}$ and
$d_{S^{1}}$ and ![]() $d_{G}$ are
$d_{G}$ are ![]() $\mathbb{F}[U]$ and
$\mathbb{F}[U]$ and  $\mathbb{F}[q,v]/(q^{3})$-equivariant, respectively.
$\mathbb{F}[q,v]/(q^{3})$-equivariant, respectively.
Proof. The fact follows since the maps ![]() $d_{S^{1}}$ and
$d_{S^{1}}$ and ![]() $d_{G}$ are induced on Borel homology, respectively, from
$d_{G}$ are induced on Borel homology, respectively, from ![]() $S^{1}$ and
$S^{1}$ and ![]() $G$-equivariant maps.◻
$G$-equivariant maps.◻
By (45),
 $$\begin{eqnarray}d_{G}\unicode[STIX]{x1D719}_{3}=\unicode[STIX]{x1D719}_{1}d_{S^{1}}.\end{eqnarray}$$
$$\begin{eqnarray}d_{G}\unicode[STIX]{x1D719}_{3}=\unicode[STIX]{x1D719}_{1}d_{S^{1}}.\end{eqnarray}$$Lemma 3.7. We have
 $$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)=\text{coker}\,d_{S^{1}}\oplus \text{ker}\,d_{S^{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)=\text{coker}\,d_{S^{1}}\oplus \text{ker}\,d_{S^{1}}.\end{eqnarray}$$Proof. Using the top row of (45), we have an exact sequence,
 $$\begin{eqnarray}0\rightarrow \text{coker}\,d_{S^{1}}\rightarrow \tilde{H}_{\ast }^{S^{1}}(X)\rightarrow \text{ker}\,d_{S^{1}}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{coker}\,d_{S^{1}}\rightarrow \tilde{H}_{\ast }^{S^{1}}(X)\rightarrow \text{ker}\,d_{S^{1}}\rightarrow 0,\end{eqnarray}$$ so  $\tilde{H}_{\ast }^{S^{1}}(X)$ is an extension of
$\tilde{H}_{\ast }^{S^{1}}(X)$ is an extension of ![]() $\text{ker}\;d_{S^{1}}$ by
$\text{ker}\;d_{S^{1}}$ by  $\text{coker}\,d_{S^{1}}$. Note that
$\text{coker}\,d_{S^{1}}$. Note that  $\text{coker}\,d_{S^{1}}$ is isomorphic to
$\text{coker}\,d_{S^{1}}$ is isomorphic to ![]() ${\mathcal{T}}_{d}^{+}$ for some integer
${\mathcal{T}}_{d}^{+}$ for some integer ![]() $d$. A calculation shows
$d$. A calculation shows  $\text{Ext}_{\mathbb{F}[U]}^{1}({\mathcal{T}}_{d_{i}}^{+}(n_{i}),{\mathcal{T}}_{d}^{+})=0$ for all
$\text{Ext}_{\mathbb{F}[U]}^{1}({\mathcal{T}}_{d_{i}}^{+}(n_{i}),{\mathcal{T}}_{d}^{+})=0$ for all ![]() $d,d_{i},n_{i}$. Thus, any extension of
$d,d_{i},n_{i}$. Thus, any extension of ![]() $\text{ker}\;d_{S^{1}}$ by
$\text{ker}\;d_{S^{1}}$ by  $\text{coker}\,d_{S^{1}}$ is trivial, and we obtain the lemma.◻
$\text{coker}\,d_{S^{1}}$ is trivial, and we obtain the lemma.◻
We also write (50) as the homology of the complex  $\tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ with differential
$\tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ with differential ![]() $d_{S^{1}}$.
$d_{S^{1}}$.
Lemma 3.8. We have
 $$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X)\cong \text{coker}\,d_{G}\oplus \text{ker}\,d_{G},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X)\cong \text{coker}\,d_{G}\oplus \text{ker}\,d_{G},\end{eqnarray}$$ as ![]() $\mathbb{F}[v]$-modules. The subspace
$\mathbb{F}[v]$-modules. The subspace  $\text{coker}\,d_{G}$ is a
$\text{coker}\,d_{G}$ is a  $\mathbb{F}[q,v]/(q^{3})$-submodule, and
$\mathbb{F}[q,v]/(q^{3})$-submodule, and ![]() $q$ acts on
$q$ acts on  $x\in \text{ker}\,d_{G}$ by
$x\in \text{ker}\,d_{G}$ by ![]() $qx=0$ if
$qx=0$ if  $x\in \text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$ (using the decomposition of
$x\in \text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$ (using the decomposition of  $\tilde{H}_{\ast }^{S^{1}}(X)$ in Lemma 3.7). Also,
$\tilde{H}_{\ast }^{S^{1}}(X)$ in Lemma 3.7). Also,  $qx\neq 0\in \text{coker}\,d_{G}$ if
$qx\neq 0\in \text{coker}\,d_{G}$ if  $x\in \text{ker}\,d_{G}$ but
$x\in \text{ker}\,d_{G}$ but  $x\not \in \text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$. As there is at most one homogeneous element of each degree in
$x\not \in \text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$. As there is at most one homogeneous element of each degree in  $\text{coker}\,d_{G}$,
$\text{coker}\,d_{G}$, ![]() $qx$ is uniquely specified for all
$qx$ is uniquely specified for all  $x\in \text{ker}\,d_{G}$ in the decomposition (51).
$x\in \text{ker}\,d_{G}$ in the decomposition (51).
Proof. As in the proof of Lemma 3.7, we see that ![]() $\tilde{H}_{\ast }^{G}(X)$ is an extension of
$\tilde{H}_{\ast }^{G}(X)$ is an extension of
 $$\begin{eqnarray}\text{ker}\,d_{G}\subseteq \text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}\tilde{H}_{\ast }^{S^{1}}(X_{+})\end{eqnarray}$$
$$\begin{eqnarray}\text{ker}\,d_{G}\subseteq \text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}\tilde{H}_{\ast }^{S^{1}}(X_{+})\end{eqnarray}$$ by  $\text{coker}\,d_{G}=\tilde{H}_{\ast }^{G}(X^{S^{1}})/(\text{Im}\,d_{G})$. We will first show that the extension is trivial as an
$\text{coker}\,d_{G}=\tilde{H}_{\ast }^{G}(X^{S^{1}})/(\text{Im}\,d_{G})$. We will first show that the extension is trivial as an ![]() $\mathbb{F}[v]$-extension.
$\mathbb{F}[v]$-extension.
We construct  $M\subset \tilde{H}_{\ast }^{G}(X)$ a vector space lift of
$M\subset \tilde{H}_{\ast }^{G}(X)$ a vector space lift of  $\text{ker}\;d_{G}\subset \tilde{H}_{\ast }^{G}(X/X^{S^{1}})$, so that
$\text{ker}\;d_{G}\subset \tilde{H}_{\ast }^{G}(X/X^{S^{1}})$, so that  $\unicode[STIX]{x1D719}_{2}(\text{ker}\;d_{S^{1}}^{+})\subseteq M$, using the decomposition of
$\unicode[STIX]{x1D719}_{2}(\text{ker}\;d_{S^{1}}^{+})\subseteq M$, using the decomposition of  $\tilde{H}_{\ast }^{S^{1}}(X)$ in (50).
$\tilde{H}_{\ast }^{S^{1}}(X)$ in (50).
Specifically, we define ![]() $M$ in each degree
$M$ in each degree ![]() $i$ by
$i$ by
 $$\begin{eqnarray}M_{i}=\left\{\begin{array}{@{}l@{}}(\unicode[STIX]{x1D719}_{2}(\text{ker}\;d_{S^{1}}^{+}))_{i}\;\text{for}\;i\not \equiv 3+m\;\text{mod}\;4,\quad \\ \tilde{H}_{i}^{G}(X)\;\text{for}\;i\equiv 3+m\;\text{mod}\;4.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}M_{i}=\left\{\begin{array}{@{}l@{}}(\unicode[STIX]{x1D719}_{2}(\text{ker}\;d_{S^{1}}^{+}))_{i}\;\text{for}\;i\not \equiv 3+m\;\text{mod}\;4,\quad \\ \tilde{H}_{i}^{G}(X)\;\text{for}\;i\equiv 3+m\;\text{mod}\;4.\quad \end{array}\right.\end{eqnarray}$$ We next show that  $\unicode[STIX]{x1D70B}_{G}|_{M}:M\rightarrow \text{ker}\,d_{G}$ is an isomorphism.
$\unicode[STIX]{x1D70B}_{G}|_{M}:M\rightarrow \text{ker}\,d_{G}$ is an isomorphism.
We have  $(\text{coker}\,d_{G})_{i}=0$ for
$(\text{coker}\,d_{G})_{i}=0$ for  $i\equiv 3+m\;\text{mod}\;4$, since
$i\equiv 3+m\;\text{mod}\;4$, since  $\tilde{H}_{\ast }^{G}(X^{S^{1}})\cong H_{\ast }(BG)[-m]$, so
$\tilde{H}_{\ast }^{G}(X^{S^{1}})\cong H_{\ast }(BG)[-m]$, so
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{G}:\tilde{H}_{i}^{G}(X)\rightarrow (\text{ker}\;d_{G})_{i}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{G}:\tilde{H}_{i}^{G}(X)\rightarrow (\text{ker}\;d_{G})_{i}\end{eqnarray}$$ is an isomorphism for all  $i\equiv 3+m\;\text{mod}\;4$.
$i\equiv 3+m\;\text{mod}\;4$.
We now show that  $\unicode[STIX]{x1D70B}_{G}:(\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\;d_{S^{1}}^{+}})_{i}\rightarrow (\text{ker}\;d_{G})_{i}$ is an isomorphism for
$\unicode[STIX]{x1D70B}_{G}:(\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\;d_{S^{1}}^{+}})_{i}\rightarrow (\text{ker}\;d_{G})_{i}$ is an isomorphism for  $i\not \equiv 3+m\;\text{mod}\;4.$ It suffices to show
$i\not \equiv 3+m\;\text{mod}\;4.$ It suffices to show  $\text{ker}\,d_{G}\subseteq \text{Im}\,\unicode[STIX]{x1D719}_{3}|_{\text{ker}\,d_{S^{1}}^{+}}$ in degrees not congruent to
$\text{ker}\,d_{G}\subseteq \text{Im}\,\unicode[STIX]{x1D719}_{3}|_{\text{ker}\,d_{S^{1}}^{+}}$ in degrees not congruent to ![]() $3+m$ modulo
$3+m$ modulo ![]() $4$. Indeed,
$4$. Indeed, ![]() $\unicode[STIX]{x1D719}_{3}$ is surjective by (47). Furthermore, by Fact 3.4,
$\unicode[STIX]{x1D719}_{3}$ is surjective by (47). Furthermore, by Fact 3.4, ![]() $\unicode[STIX]{x1D719}_{1}$ is injective in degrees not congruent to
$\unicode[STIX]{x1D719}_{1}$ is injective in degrees not congruent to ![]() $2+m$ modulo
$2+m$ modulo ![]() $4$. By (49), if
$4$. By (49), if  $y\in \text{ker}\,d_{G}$ with
$y\in \text{ker}\,d_{G}$ with  $\text{deg}\,(y)\not \equiv 3+m\;\text{mod}\;4$, and
$\text{deg}\,(y)\not \equiv 3+m\;\text{mod}\;4$, and  $y=\unicode[STIX]{x1D719}_{3}(x)$, for
$y=\unicode[STIX]{x1D719}_{3}(x)$, for  $x\in \tilde{H}_{\ast }^{S^{1}}(X_{+})\subset \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$, then
$x\in \tilde{H}_{\ast }^{S^{1}}(X_{+})\subset \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$, then  $\unicode[STIX]{x1D719}_{1}(d_{S^{1}}x)=0$. By the injectivity of
$\unicode[STIX]{x1D719}_{1}(d_{S^{1}}x)=0$. By the injectivity of ![]() $\unicode[STIX]{x1D719}_{1}$, we have
$\unicode[STIX]{x1D719}_{1}$, we have  $d_{S^{1}}x=0$, and we obtain
$d_{S^{1}}x=0$, and we obtain
 $$\begin{eqnarray}y\in \text{Im}\,(\unicode[STIX]{x1D719}_{3}|_{\text{ker}\,d_{S^{1}}^{+}}).\end{eqnarray}$$
$$\begin{eqnarray}y\in \text{Im}\,(\unicode[STIX]{x1D719}_{3}|_{\text{ker}\,d_{S^{1}}^{+}}).\end{eqnarray}$$ That is,  $(\text{Im}\,\unicode[STIX]{x1D719}_{3}|_{\text{ker}\,d_{S^{1}}^{+}})_{i}=(\text{ker}\;d_{G})_{i}$ for
$(\text{Im}\,\unicode[STIX]{x1D719}_{3}|_{\text{ker}\,d_{S^{1}}^{+}})_{i}=(\text{ker}\;d_{G})_{i}$ for  $i\not \equiv 3+m\;\text{mod}\;4$. Then,
$i\not \equiv 3+m\;\text{mod}\;4$. Then,  $\unicode[STIX]{x1D70B}_{G}(\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\;d_{S^{1}}^{+}})_{i}=(\text{ker}\;d_{G})_{i}$, as needed.
$\unicode[STIX]{x1D70B}_{G}(\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\;d_{S^{1}}^{+}})_{i}=(\text{ker}\;d_{G})_{i}$, as needed.
We have then established that  $\tilde{H}_{\ast }^{G}(X)=\text{coker}\,d_{G}\oplus M$ as
$\tilde{H}_{\ast }^{G}(X)=\text{coker}\,d_{G}\oplus M$ as ![]() $\mathbb{F}$-vector spaces.
$\mathbb{F}$-vector spaces.
We next determine the  $\mathbb{F}[q,v]/(q^{3})$-action on
$\mathbb{F}[q,v]/(q^{3})$-action on  $M\subset \tilde{H}_{\ast }^{G}(X)$. Since
$M\subset \tilde{H}_{\ast }^{G}(X)$. Since  $\text{ker}\;d_{S^{1}}^{+}\subset \tilde{H}_{\ast }^{S^{1}}(X)$ is an
$\text{ker}\;d_{S^{1}}^{+}\subset \tilde{H}_{\ast }^{S^{1}}(X)$ is an  $\mathbb{F}[q,v]/(q^{3})$-submodule, so is its image in
$\mathbb{F}[q,v]/(q^{3})$-submodule, so is its image in ![]() $\tilde{H}_{\ast }^{G}(X)$. Then, for
$\tilde{H}_{\ast }^{G}(X)$. Then, for ![]() $x\in M$ homogeneous of degree not congruent to
$x\in M$ homogeneous of degree not congruent to ![]() $3+m$ modulo
$3+m$ modulo ![]() $4$, we have
$4$, we have  $qx,vx\in M$. In fact,
$qx,vx\in M$. In fact, ![]() $qx=0$, since
$qx=0$, since ![]() $q$ acts trivially on
$q$ acts trivially on  $\tilde{H}_{\ast }^{S^{1}}(X)$. Moreover, for
$\tilde{H}_{\ast }^{S^{1}}(X)$. Moreover, for ![]() $x\in M$ of degree congruent to
$x\in M$ of degree congruent to ![]() $3+m$ modulo
$3+m$ modulo ![]() $4$,
$4$,  $vx\in \tilde{H}_{\ast }^{G}(X)$ is also of degree congruent to
$vx\in \tilde{H}_{\ast }^{G}(X)$ is also of degree congruent to ![]() $3+m$, and, in particular, we see
$3+m$, and, in particular, we see  $vx\in M$. So we need only determine
$vx\in M$. So we need only determine ![]() $qx$ for
$qx$ for ![]() $x\in M$ with
$x\in M$ with  $\text{deg}\,x\equiv 3+m\;\text{mod}\;4$.
$\text{deg}\,x\equiv 3+m\;\text{mod}\;4$.
As in [Reference tom DiecktDie87, § III.2] there exists a Gysin sequence:

where ![]() $q\cup -$ denotes cup product with
$q\cup -$ denotes cup product with ![]() $q$. Dualizing, we obtain an exact sequence:
$q$. Dualizing, we obtain an exact sequence:

where  $(1+j)\cdot -$ denotes the map obtained from multiplication (on the chain level) by
$(1+j)\cdot -$ denotes the map obtained from multiplication (on the chain level) by  $1+j\in {\mathcal{G}}$, and
$1+j\in {\mathcal{G}}$, and ![]() $q\cap -$ denotes cap product with
$q\cap -$ denotes cap product with ![]() $q$.
$q$.
From (54), we have that if  $x\in M\subset \tilde{H}_{\ast }^{G}(X)$ is not in
$x\in M\subset \tilde{H}_{\ast }^{G}(X)$ is not in  $\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$, then
$\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$, then ![]() $qx\neq 0$. We will show that
$qx\neq 0$. We will show that  $qx\in \text{coker}\,d_{G}$.
$qx\in \text{coker}\,d_{G}$.
First, we see
 $$\begin{eqnarray}(1+j)\cdot \text{coker}\,d_{G}\subset \text{coker}\,d_{S^{1}}.\end{eqnarray}$$
$$\begin{eqnarray}(1+j)\cdot \text{coker}\,d_{G}\subset \text{coker}\,d_{S^{1}}.\end{eqnarray}$$Indeed, (55) follows from the commutativity of the following diagram.

Additionally, we see that

is injective by the ![]() $j$-splitness condition (Definition 3.1). Then
$j$-splitness condition (Definition 3.1). Then  $\text{ker}\;(1+j)\subset \tilde{H}_{\ast }^{G}(X)$ is, in fact, a subset of
$\text{ker}\;(1+j)\subset \tilde{H}_{\ast }^{G}(X)$ is, in fact, a subset of  $\text{coker}\,d_{G}$. Thus, if
$\text{coker}\,d_{G}$. Thus, if  $x\not \in \text{Im}\;\unicode[STIX]{x1D719}_{2}|_{\text{ker}\;d_{S^{1}}}$,
$x\not \in \text{Im}\;\unicode[STIX]{x1D719}_{2}|_{\text{ker}\;d_{S^{1}}}$, ![]() $qx$ must be the unique nonzero element in grading
$qx$ must be the unique nonzero element in grading  $\text{deg}\,x-1$ in
$\text{deg}\,x-1$ in  $\text{coker}\,d_{G}$, completing the proof.◻
$\text{coker}\,d_{G}$, completing the proof.◻
Our goal will be to relate (50) and (51), relying on (48) and (49). From this relationship we will be able to show that the ![]() $S^{1}$-homology (50) determines the
$S^{1}$-homology (50) determines the ![]() $G$-homology (51). In Lemmas 3.10 and 3.11 we compute
$G$-homology (51). In Lemmas 3.10 and 3.11 we compute  $\tilde{H}_{\ast }^{S^{1}}(X)$ from
$\tilde{H}_{\ast }^{S^{1}}(X)$ from  $\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ and
$\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ and ![]() $d_{S^{1}}$. In Lemmas 3.12–3.15, we show how to compute
$d_{S^{1}}$. In Lemmas 3.12–3.15, we show how to compute ![]() $\tilde{H}_{\ast }^{G}(X)$ from the same information. Then in Theorem 3.16 we compute
$\tilde{H}_{\ast }^{G}(X)$ from the same information. Then in Theorem 3.16 we compute ![]() $\tilde{H}_{\ast }^{G}(X)$ directly from
$\tilde{H}_{\ast }^{G}(X)$ directly from  $\tilde{H}_{\ast }^{S^{1}}(X)$.
$\tilde{H}_{\ast }^{S^{1}}(X)$.
We begin by noting that any finite graded ![]() $\mathbb{F}[U]$-module may be written as a direct sum of copies of
$\mathbb{F}[U]$-module may be written as a direct sum of copies of ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$, as
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$, as ![]() $\mathbb{F}[U]$ is a principal ideal domain. In particular,
$\mathbb{F}[U]$ is a principal ideal domain. In particular,  $\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$, since it has finite rank as an
$\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$, since it has finite rank as an ![]() $\mathbb{F}$-module, is a direct sum of copies of the
$\mathbb{F}$-module, is a direct sum of copies of the ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$.
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$.
Lemma 3.9. On  ${\mathcal{T}}_{d}^{+}(n)\subset \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$, the differential
${\mathcal{T}}_{d}^{+}(n)\subset \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$, the differential ![]() $d_{S^{1}}$ vanishes unless
$d_{S^{1}}$ vanishes unless  $2n+d\geqslant 3+m$ and
$2n+d\geqslant 3+m$ and  $d\leqslant m+1$.
$d\leqslant m+1$.
Proof. Let ![]() $U^{-k}$ denote the unique nonzero element of
$U^{-k}$ denote the unique nonzero element of ![]() ${\mathcal{T}}_{m}^{+}$ in degree
${\mathcal{T}}_{m}^{+}$ in degree ![]() $m+2k$. Let
$m+2k$. Let  $x_{d+2n-2}$ be an
$x_{d+2n-2}$ be an ![]() $\mathbb{F}[U]$-module generator of
$\mathbb{F}[U]$-module generator of ![]() ${\mathcal{T}}_{d}^{+}(n)$, with
${\mathcal{T}}_{d}^{+}(n)$, with  $\deg (x_{d+2n-2})=d+2n-2$. Then either
$\deg (x_{d+2n-2})=d+2n-2$. Then either ![]() $d_{S^{1}}$ vanishes on
$d_{S^{1}}$ vanishes on ![]() ${\mathcal{T}}_{d}^{+}(n)$ or
${\mathcal{T}}_{d}^{+}(n)$ or  $d_{S^{1}}(x_{d+2n-2})$ is nonzero. In this latter case, because of the grading,
$d_{S^{1}}(x_{d+2n-2})$ is nonzero. In this latter case, because of the grading,  $d_{S^{1}}(x_{d+2n-2})=U^{-(d+2n-m-3)/2}$. If
$d_{S^{1}}(x_{d+2n-2})=U^{-(d+2n-m-3)/2}$. If  $2n+d<3+m$, then
$2n+d<3+m$, then ![]() ${\mathcal{T}}_{d}^{+}(n)$ has no elements in degree greater than
${\mathcal{T}}_{d}^{+}(n)$ has no elements in degree greater than ![]() $m$, and so has no nontrivial maps to
$m$, and so has no nontrivial maps to ![]() ${\mathcal{T}}_{m}^{+}$. Similarly, for
${\mathcal{T}}_{m}^{+}$. Similarly, for  $d>m+1$,
$d>m+1$,  $d_{S^{1}}({\mathcal{T}}_{d}^{+}(n))=0$. Indeed, if
$d_{S^{1}}({\mathcal{T}}_{d}^{+}(n))=0$. Indeed, if  $d_{S^{1}}({\mathcal{T}}_{d}^{+}(n))\neq 0$, then
$d_{S^{1}}({\mathcal{T}}_{d}^{+}(n))\neq 0$, then
 $$\begin{eqnarray}d_{S^{1}}x_{d+2n-2}=U^{-(d+2n-m-3)/2}.\end{eqnarray}$$
$$\begin{eqnarray}d_{S^{1}}x_{d+2n-2}=U^{-(d+2n-m-3)/2}.\end{eqnarray}$$ Then, by Fact 3.6,  $d_{S^{1}}(U^{(d+2n-m-3)/2}x_{d+2n-2})=U^{0}\neq 0\in {\mathcal{T}}_{m}^{+}$; however, if
$d_{S^{1}}(U^{(d+2n-m-3)/2}x_{d+2n-2})=U^{0}\neq 0\in {\mathcal{T}}_{m}^{+}$; however, if  $d>m+1$, then
$d>m+1$, then  $U^{(d+2n-m-3)/2}x_{d+2n-2}=0$, a contradiction.◻
$U^{(d+2n-m-3)/2}x_{d+2n-2}=0$, a contradiction.◻
Lemma 3.10. There exists a decomposition
 $$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}\oplus J_{2},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}\oplus J_{2},\end{eqnarray}$$ as a direct sum of ![]() $\mathbb{F}[U]$-modules
$\mathbb{F}[U]$-modules ![]() $J_{1}$ and
$J_{1}$ and ![]() $J_{2}$, where
$J_{2}$, where ![]() $d_{S^{1}}$ vanishes on
$d_{S^{1}}$ vanishes on ![]() $J_{2}$ and
$J_{2}$ and
 $$\begin{eqnarray}J_{1}=\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i}),\end{eqnarray}$$
$$\begin{eqnarray}J_{1}=\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i}),\end{eqnarray}$$ with  $2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$, and
$2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$, and  $d_{i+1}>d_{i}$, for some
$d_{i+1}>d_{i}$, for some ![]() $N$. Moreover,
$N$. Moreover,  $d_{N}\leqslant 1+m,2n_{N}+d_{N}\geqslant 3+m$, and
$d_{N}\leqslant 1+m,2n_{N}+d_{N}\geqslant 3+m$, and ![]() $d_{S^{1}}$ is nonvanishing on each summand
$d_{S^{1}}$ is nonvanishing on each summand ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$.
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$.
Proof. To begin, set  $\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}\oplus J_{2}$ for some choices of
$\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}\oplus J_{2}$ for some choices of ![]() $J_{1}$ and
$J_{1}$ and ![]() $J_{2}$ so that
$J_{2}$ so that  $d_{S^{1}}|_{J_{2}}=0$, possibly by setting
$d_{S^{1}}|_{J_{2}}=0$, possibly by setting ![]() $J_{2}=0$. We introduce a partial ordering
$J_{2}=0$. We introduce a partial ordering ![]() $\succcurlyeq$ of (graded)
$\succcurlyeq$ of (graded) ![]() $\mathbb{F}[U]$-modules. We say
$\mathbb{F}[U]$-modules. We say
 $$\begin{eqnarray}{\mathcal{T}}_{d_{1}}^{+}(n_{1})\succcurlyeq {\mathcal{T}}_{d_{2}}^{+}(n_{2})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}_{d_{1}}^{+}(n_{1})\succcurlyeq {\mathcal{T}}_{d_{2}}^{+}(n_{2})\end{eqnarray}$$ if  $2n_{1}+d_{1}\geqslant 2n_{2}+d_{2}$ and
$2n_{1}+d_{1}\geqslant 2n_{2}+d_{2}$ and ![]() $d_{1}\geqslant d_{2}$. Our goal is to arrange that the summands of
$d_{1}\geqslant d_{2}$. Our goal is to arrange that the summands of ![]() $J_{1}$ are not comparable under this relation. Suppose we have
$J_{1}$ are not comparable under this relation. Suppose we have  ${\mathcal{T}}_{d_{1}}^{+}(n_{1})\oplus {\mathcal{T}}_{d_{2}}^{+}(n_{2})$ a summand of
${\mathcal{T}}_{d_{1}}^{+}(n_{1})\oplus {\mathcal{T}}_{d_{2}}^{+}(n_{2})$ a summand of ![]() $J_{1}$, and
$J_{1}$, and  ${\mathcal{T}}_{d_{1}}^{+}(n_{1})\succcurlyeq {\mathcal{T}}_{d_{2}}^{+}(n_{2})$. If one of the
${\mathcal{T}}_{d_{1}}^{+}(n_{1})\succcurlyeq {\mathcal{T}}_{d_{2}}^{+}(n_{2})$. If one of the ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ has
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ has  $d_{S^{1}}|_{{\mathcal{T}}_{d_{i}}^{+}(n_{i})}=0$, we move it to
$d_{S^{1}}|_{{\mathcal{T}}_{d_{i}}^{+}(n_{i})}=0$, we move it to ![]() $J_{2}$. Otherwise, we have that
$J_{2}$. Otherwise, we have that ![]() $d_{S^{1}}$ is nontrivial on both
$d_{S^{1}}$ is nontrivial on both ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$. Let
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$. Let ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ be generated by
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ be generated by ![]() $x_{i}$ for
$x_{i}$ for ![]() $i=1,2$. Then
$i=1,2$. Then  $\langle x_{1},U^{n_{1}-n_{2}+(d_{1}-d_{2})/2}x_{1}+x_{2}\rangle$ are new
$\langle x_{1},U^{n_{1}-n_{2}+(d_{1}-d_{2})/2}x_{1}+x_{2}\rangle$ are new ![]() $\mathbb{F}[U]$-generators for
$\mathbb{F}[U]$-generators for  ${\mathcal{T}}_{d_{1}}^{+}(n_{1})\oplus {\mathcal{T}}_{d_{2}}^{+}(n_{2})\subset J_{1}$, such that
${\mathcal{T}}_{d_{1}}^{+}(n_{1})\oplus {\mathcal{T}}_{d_{2}}^{+}(n_{2})\subset J_{1}$, such that ![]() $d_{S^{1}}$ vanishes on
$d_{S^{1}}$ vanishes on  $U^{n_{1}-n_{2}+(d_{1}-d_{2})/2}x_{1}+x_{2}$, i.e. so that
$U^{n_{1}-n_{2}+(d_{1}-d_{2})/2}x_{1}+x_{2}$, i.e. so that ![]() $d_{S^{1}}$ vanishes on the
$d_{S^{1}}$ vanishes on the ![]() ${\mathcal{T}}_{d_{2}}^{+}(n_{2})$ summand. So we may choose a new decomposition
${\mathcal{T}}_{d_{2}}^{+}(n_{2})$ summand. So we may choose a new decomposition  $\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}^{\prime }\oplus J_{2}^{\prime }$, where
$\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}^{\prime }\oplus J_{2}^{\prime }$, where  $J_{2}^{\prime }\cong J_{2}\oplus {\mathcal{T}}_{d_{2}}^{+}(n_{2})$. Thus, we may choose
$J_{2}^{\prime }\cong J_{2}\oplus {\mathcal{T}}_{d_{2}}^{+}(n_{2})$. Thus, we may choose ![]() $J_{1}$ such that there is no summand
$J_{1}$ such that there is no summand ![]() $X\oplus Y$ of
$X\oplus Y$ of ![]() $J_{1}$ with
$J_{1}$ with ![]() $X\succcurlyeq Y$. Say
$X\succcurlyeq Y$. Say  $J_{1}=\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})$ has been chosen so that all its summands are incomparable under
$J_{1}=\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})$ has been chosen so that all its summands are incomparable under ![]() $\succcurlyeq$ (and so that
$\succcurlyeq$ (and so that ![]() $d_{S^{1}}$ is nonvanishing on each
$d_{S^{1}}$ is nonvanishing on each ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$). Perhaps by reordering, let
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$). Perhaps by reordering, let  $d_{i+1}\geqslant d_{i}$. If
$d_{i+1}\geqslant d_{i}$. If  $d_{i+1}=d_{i}$,
$d_{i+1}=d_{i}$, ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ and
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ and  ${\mathcal{T}}_{d_{i+1}}^{+}(n_{i+1})$ would be comparable, contradicting our choice of
${\mathcal{T}}_{d_{i+1}}^{+}(n_{i+1})$ would be comparable, contradicting our choice of ![]() $J_{1}$. Thus
$J_{1}$. Thus  $d_{i+1}>d_{i}$. Again using that the
$d_{i+1}>d_{i}$. Again using that the ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ are incomparable, we obtain
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$ are incomparable, we obtain  $2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$. Finally, we saw in Lemma 3.9 that
$2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$. Finally, we saw in Lemma 3.9 that ![]() $d_{S^{1}}$ vanishes on any summand
$d_{S^{1}}$ vanishes on any summand ![]() ${\mathcal{T}}_{d}^{+}(n)$ with
${\mathcal{T}}_{d}^{+}(n)$ with  $d>1+m$ or
$d>1+m$ or  $2n+d<3+m,$ so by the condition that
$2n+d<3+m,$ so by the condition that ![]() $d_{S^{1}}$ is nonvanishing, we have
$d_{S^{1}}$ is nonvanishing, we have  $d_{N}\leqslant 1+m,2n_{N}+d_{N}\geqslant 3+m$.◻
$d_{N}\leqslant 1+m,2n_{N}+d_{N}\geqslant 3+m$.◻
Lemma 3.11. Let  $\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}\oplus J_{2}$, with
$\tilde{H}_{\ast }^{S^{1}}(X_{+})=J_{1}\oplus J_{2}$, with ![]() $J_{1}$ as in Lemma 3.10. Then
$J_{1}$ as in Lemma 3.10. Then
 $$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)={\mathcal{T}}_{d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J_{2}^{\oplus 2}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)={\mathcal{T}}_{d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J_{2}^{\oplus 2}.\end{eqnarray}$$ We interpret  $d_{N+1}=m+1,n_{N+1}=0$. The expression
$d_{N+1}=m+1,n_{N+1}=0$. The expression  $(d_{N+1}+2n_{N+1}-d_{N})/2$ may vanish, in which case
$(d_{N+1}+2n_{N+1}-d_{N})/2$ may vanish, in which case  ${\mathcal{T}}_{d_{N}}^{+}((d_{N+1}+2n_{N+1}-d_{N})/2)$ is the zero module.
${\mathcal{T}}_{d_{N}}^{+}((d_{N+1}+2n_{N+1}-d_{N})/2)$ is the zero module.
Proof. In the decomposition of Lemma 3.10, we write ![]() $x_{i}$ for the generator of
$x_{i}$ for the generator of ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$. We choose a basis for
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$. We choose a basis for ![]() $\text{ker}\,d_{S^{1}}$, given by
$\text{ker}\,d_{S^{1}}$, given by ![]() $\{{y_{i}\}}_{i}$ for
$\{{y_{i}\}}_{i}$ for  $y_{i}=x_{i+1}+U^{n_{i}-n_{i+1}+(d_{i}-d_{i+1})/2}x_{i}$ for
$y_{i}=x_{i+1}+U^{n_{i}-n_{i+1}+(d_{i}-d_{i+1})/2}x_{i}$ for  $i=1,\ldots ,N-1,$ and
$i=1,\ldots ,N-1,$ and  $y_{N}=U^{(d_{N}+2n_{N}-m-1)/2}x_{N}$. Note that
$y_{N}=U^{(d_{N}+2n_{N}-m-1)/2}x_{N}$. Note that ![]() $y_{N}$ may be zero.
$y_{N}$ may be zero.
We have seen that  $J_{2}\subset \text{ker}\,d_{S^{1}}$, and also
$J_{2}\subset \text{ker}\,d_{S^{1}}$, and also  $jJ_{2}\subset \text{ker}\,d_{S^{1}}$, giving the two copies of the
$jJ_{2}\subset \text{ker}\,d_{S^{1}}$, giving the two copies of the ![]() $J_{2}$ summand in (57). We see that
$J_{2}$ summand in (57). We see that  $\mathbb{F}[U]U^{-(d_{1}+2n_{1}-m-3)/2}=\text{Im}\;d_{S^{1}}\subset {\mathcal{T}}_{m}^{+}$, by Lemma 3.10. Then
$\mathbb{F}[U]U^{-(d_{1}+2n_{1}-m-3)/2}=\text{Im}\;d_{S^{1}}\subset {\mathcal{T}}_{m}^{+}$, by Lemma 3.10. Then  ${\mathcal{T}}_{d_{1}+2n_{1}-1}^{+}=\text{coker}\,d_{S^{1}}$. Further,
${\mathcal{T}}_{d_{1}+2n_{1}-1}^{+}=\text{coker}\,d_{S^{1}}$. Further,  $(1+j)J_{1}$ contributes the summand
$(1+j)J_{1}$ contributes the summand  $\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})$, since
$\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})$, since ![]() $d_{S^{1}}$ is
$d_{S^{1}}$ is ![]() $j$-invariant, and so vanishes on multiples of
$j$-invariant, and so vanishes on multiples of ![]() $(1+j)$. Finally, the set
$(1+j)$. Finally, the set ![]() $\{y_{i}\}$ generates the
$\{y_{i}\}$ generates the  $\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}((d_{i+1}+2n_{i+1}-d_{i})/2)$ summand.
$\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}((d_{i+1}+2n_{i+1}-d_{i})/2)$ summand.

Figure 2. An example of  $\tilde{H}_{\ast }^{S^{1}}(X)$ as in Lemma 3.11. The first four (finite) towers are
$\tilde{H}_{\ast }^{S^{1}}(X)$ as in Lemma 3.11. The first four (finite) towers are  ${\mathcal{T}}_{-1}^{+}(3)^{\oplus 2}\oplus {\mathcal{T}}_{1}^{+}(1)^{\oplus 2}$. Then
${\mathcal{T}}_{-1}^{+}(3)^{\oplus 2}\oplus {\mathcal{T}}_{1}^{+}(1)^{\oplus 2}$. Then  $J_{1}={\mathcal{T}}_{-1}^{+}(3)\oplus {\mathcal{T}}_{1}^{+}(1)$ and
$J_{1}={\mathcal{T}}_{-1}^{+}(3)\oplus {\mathcal{T}}_{1}^{+}(1)$ and  $J_{2}={\mathcal{T}}_{-1}^{+}(1)$ in (56) (keeping in mind that the action of
$J_{2}={\mathcal{T}}_{-1}^{+}(1)$ in (56) (keeping in mind that the action of ![]() $j$ interchanges the pairs of copies
$j$ interchanges the pairs of copies ![]() ${\mathcal{T}}_{d_{i}}^{+}(n_{i})$, so
${\mathcal{T}}_{d_{i}}^{+}(n_{i})$, so  $\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})\cong J_{1}\oplus J_{2}\oplus J_{1}\oplus J_{2}$ as an
$\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})\cong J_{1}\oplus J_{2}\oplus J_{1}\oplus J_{2}$ as an ![]() $\mathbb{F}[U]$-module). In particular,
$\mathbb{F}[U]$-module). In particular,  $d_{1}=-1,n_{1}=3,d_{2}=1,n_{2}=1$. Here
$d_{1}=-1,n_{1}=3,d_{2}=1,n_{2}=1$. Here ![]() $m=0$. The shaded-head arrows denote differentials while the open-head arrows denote
$m=0$. The shaded-head arrows denote differentials while the open-head arrows denote ![]() $U$-actions.
$U$-actions.
For an example of how the new basis gives the lemma, see Figures 2 and 3. ◻
We now compute  $\tilde{H}_{\ast }^{G}(X/X^{S^{1}})$. To find
$\tilde{H}_{\ast }^{G}(X/X^{S^{1}})$. To find ![]() $\text{ker}\,d_{G}$, we write
$\text{ker}\,d_{G}$, we write  $\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime }\oplus J_{2}^{\prime }$, where
$\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime }\oplus J_{2}^{\prime }$, where ![]() $d_{G}$ vanishes on
$d_{G}$ vanishes on ![]() $J_{2}^{\prime }$ (
$J_{2}^{\prime }$ (![]() $J_{2}^{\prime }$ need not be maximal, currently). To find
$J_{2}^{\prime }$ need not be maximal, currently). To find ![]() $J_{1}^{\prime }$ and
$J_{1}^{\prime }$ and ![]() $J_{2}^{\prime }$ in terms of
$J_{2}^{\prime }$ in terms of ![]() $J_{1}$ and
$J_{1}$ and ![]() $J_{2}$, we use the following lemma.
$J_{2}$, we use the following lemma.
Lemma 3.12. Let ![]() $J_{1},J_{2}$ and
$J_{1},J_{2}$ and ![]() $d_{i},n_{i}$ be as in Lemma 3.10. Then we may set
$d_{i},n_{i}$ be as in Lemma 3.10. Then we may set  $\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime }\oplus J_{2}^{\prime }$, where
$\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime }\oplus J_{2}^{\prime }$, where
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{1}^{\prime }=\bigoplus _{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle J_{2}^{\prime }=\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}{J_{2}\oplus \bigoplus }_{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{1}^{\prime }=\bigoplus _{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle J_{2}^{\prime }=\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}{J_{2}\oplus \bigoplus }_{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr). & \displaystyle \nonumber\end{eqnarray}$$ Moreover, ![]() $d_{G}$ is nonvanishing on each nontrivial summand of
$d_{G}$ is nonvanishing on each nontrivial summand of ![]() $J_{1}^{\prime }$, and
$J_{1}^{\prime }$, and  $d_{G}(J_{2}^{\prime })=0$.
$d_{G}(J_{2}^{\prime })=0$.
Proof. We use (46) and (48) to conclude that
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{3}J_{1}=\bigoplus _{i=1}^{N}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{3}J_{1}=\bigoplus _{i=1}^{N}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr).\end{eqnarray}$$We also use
 $$\begin{eqnarray}\text{cor}_{G}^{S^{1}}d_{S^{1}}=d_{G}\unicode[STIX]{x1D719}_{3},\end{eqnarray}$$
$$\begin{eqnarray}\text{cor}_{G}^{S^{1}}d_{S^{1}}=d_{G}\unicode[STIX]{x1D719}_{3},\end{eqnarray}$$ as in (49) to obtain that ![]() $d_{G}$ is nonvanishing on each of
$d_{G}$ is nonvanishing on each of  ${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )$, with
${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )$, with  $d_{i}\equiv m+1\;\text{mod}\;4$ and
$d_{i}\equiv m+1\;\text{mod}\;4$ and  ${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )$ with
${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )$ with  $d_{i}\equiv m+3\;\text{mod}\;4$. To find
$d_{i}\equiv m+3\;\text{mod}\;4$. To find ![]() $J_{2}^{\prime }$ we apply (48) again, to
$J_{2}^{\prime }$ we apply (48) again, to ![]() $J_{2}$, and we observe that
$J_{2}$, and we observe that ![]() $d_{G}$ is vanishing on each of
$d_{G}$ is vanishing on each of  ${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )$, with
${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )$, with  $d_{i}\equiv m+3\;\text{mod}\;4$ and
$d_{i}\equiv m+3\;\text{mod}\;4$ and  ${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )$ with
${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )$ with  $d_{i}\equiv m+1\;\text{mod}\;4$.◻
$d_{i}\equiv m+1\;\text{mod}\;4$.◻
Fact 3.13. The generators of the ![]() $\mathbb{F}[v]$-submodule
$\mathbb{F}[v]$-submodule
 $$\begin{eqnarray}\bigoplus _{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\end{eqnarray}$$ described in Lemma 3.12 are not in the image of  $\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$, while
$\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$, while  $\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J_{2}$ is in the image of
$\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J_{2}$ is in the image of  $\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$.
$\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$.
For an example of Lemma 3.12, see Figure 4. We define a partial order ![]() $\succcurlyeq$ on modules
$\succcurlyeq$ on modules ![]() ${\mathcal{V}}_{d}^{+}(n)$ with
${\mathcal{V}}_{d}^{+}(n)$ with  $d\equiv m+1\;\text{mod}\;4$. Note that all simple submodules
$d\equiv m+1\;\text{mod}\;4$. Note that all simple submodules ![]() ${\mathcal{V}}_{d}^{+}(n)$ of
${\mathcal{V}}_{d}^{+}(n)$ of ![]() $J_{1}^{\prime }$ in Lemma 3.12 have
$J_{1}^{\prime }$ in Lemma 3.12 have  $d\equiv m+1\,\text{mod}\,4$. Let
$d\equiv m+1\,\text{mod}\,4$. Let  ${\mathcal{V}}_{d_{1}}^{+}(n_{1})\succcurlyeq {\mathcal{V}}_{d_{2}}^{+}(n_{2})$ if
${\mathcal{V}}_{d_{1}}^{+}(n_{1})\succcurlyeq {\mathcal{V}}_{d_{2}}^{+}(n_{2})$ if ![]() $d_{1}\geqslant d_{2}$ and
$d_{1}\geqslant d_{2}$ and  $d_{1}+4n_{1}\geqslant d_{2}+4n_{2}$. Let
$d_{1}+4n_{1}\geqslant d_{2}+4n_{2}$. Let ![]() ${\mathcal{J}}$ denote the set of distinct pairs
${\mathcal{J}}$ denote the set of distinct pairs ![]() $(a,b)$ for which
$(a,b)$ for which ![]() ${\mathcal{V}}_{a}^{+}(b)$ is a maximal summand of
${\mathcal{V}}_{a}^{+}(b)$ is a maximal summand of ![]() $J_{1}^{\prime }$ as in Lemma 3.12. If
$J_{1}^{\prime }$ as in Lemma 3.12. If  $(a,b)\in {\mathcal{J}}$, set
$(a,b)\in {\mathcal{J}}$, set  $m(a,b)+1$ to be the multiplicity with which
$m(a,b)+1$ to be the multiplicity with which ![]() ${\mathcal{V}}_{a}^{+}(b)$ occurs as a summand of
${\mathcal{V}}_{a}^{+}(b)$ occurs as a summand of ![]() $J_{1}^{\prime }$. If
$J_{1}^{\prime }$. If  $(a,b)\not \in {\mathcal{J}}$, set
$(a,b)\not \in {\mathcal{J}}$, set ![]() $m(a,b)$ to be the multiplicity with which
$m(a,b)$ to be the multiplicity with which ![]() ${\mathcal{V}}_{a}^{+}(b)$ occurs in
${\mathcal{V}}_{a}^{+}(b)$ occurs in ![]() $J_{1}^{\prime }$. Then we define
$J_{1}^{\prime }$. Then we define
 $$\begin{eqnarray}J_{\text{rep}}=\bigoplus _{(a,b)}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)},\end{eqnarray}$$
$$\begin{eqnarray}J_{\text{rep}}=\bigoplus _{(a,b)}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)},\end{eqnarray}$$ where summands of multiplicity ![]() $0,-1$ do not contribute to the sum. That is,
$0,-1$ do not contribute to the sum. That is, ![]() $J_{\text{rep}}$ counts the repeated summands (whence the ‘rep’) in
$J_{\text{rep}}$ counts the repeated summands (whence the ‘rep’) in ![]() $J_{1}^{\prime }$, as well as those which are not contributing ‘new’ differentials targeting the reducible. In the example of Figure 4,
$J_{1}^{\prime }$, as well as those which are not contributing ‘new’ differentials targeting the reducible. In the example of Figure 4,  $J_{\text{rep}}={\mathcal{V}}_{1}^{+}(1)$.
$J_{\text{rep}}={\mathcal{V}}_{1}^{+}(1)$.
Arguing as in Lemma 3.10, we obtain the following result.
Lemma 3.14. Let  $\tilde{H}_{\ast }^{S^{1}}(X_{+})$ be decomposed as in Lemma 3.10, and let
$\tilde{H}_{\ast }^{S^{1}}(X_{+})$ be decomposed as in Lemma 3.10, and let ![]() ${\mathcal{J}}$ be as in the preceding paragraphs. Then we may set
${\mathcal{J}}$ be as in the preceding paragraphs. Then we may set  $\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime \prime }\oplus J_{2}^{\prime \prime }$ with
$\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime \prime }\oplus J_{2}^{\prime \prime }$ with
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{1}^{\prime \prime }\cong \bigoplus _{(a_{i},b_{i})\in {\mathcal{J}}}{\mathcal{V}}_{a_{i}}^{+}(b_{i}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle J_{2}^{\prime \prime }\cong \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}{J_{2}\oplus \bigoplus }_{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus J_{\text{rep}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{1}^{\prime \prime }\cong \bigoplus _{(a_{i},b_{i})\in {\mathcal{J}}}{\mathcal{V}}_{a_{i}}^{+}(b_{i}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle J_{2}^{\prime \prime }\cong \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}{J_{2}\oplus \bigoplus }_{\{i\mid d_{i}\equiv m+1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}\equiv m+3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus J_{\text{rep}}. & \displaystyle \nonumber\end{eqnarray}$$ Moreover, ![]() $d_{G}$ is nonvanishing on each nontrivial summand of
$d_{G}$ is nonvanishing on each nontrivial summand of ![]() $J_{1}^{\prime \prime }$, and
$J_{1}^{\prime \prime }$, and  $d_{G}(J_{2}^{\prime \prime })=0$. Further,
$d_{G}(J_{2}^{\prime \prime })=0$. Further,  $a_{i}<a_{i+1}$ and
$a_{i}<a_{i+1}$ and  $a_{i}+4b_{i}>a_{i+1}+4b_{i+1}$ for
$a_{i}+4b_{i}>a_{i+1}+4b_{i+1}$ for  $i=1,\ldots ,N_{0}-1$, where
$i=1,\ldots ,N_{0}-1$, where  $N_{0}=|{\mathcal{J}}|$.
$N_{0}=|{\mathcal{J}}|$.
Proof. We argue as in Lemma 3.10, starting with the decomposition
 $$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime }\oplus J_{2}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime }\oplus J_{2}^{\prime }\end{eqnarray}$$ given in Lemma 3.12. We will show that we may choose  $J_{1}^{\prime \prime }=\bigoplus _{(a_{i},b_{i})\in {\mathcal{J}}}{\mathcal{V}}_{a_{i}}^{+}(b_{i})$, so that
$J_{1}^{\prime \prime }=\bigoplus _{(a_{i},b_{i})\in {\mathcal{J}}}{\mathcal{V}}_{a_{i}}^{+}(b_{i})$, so that  $\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime \prime }\oplus J_{2}^{\prime \prime }$ with
$\tilde{H}_{\ast }^{G}(X/X^{S^{1}})=J_{1}^{\prime \prime }\oplus J_{2}^{\prime \prime }$ with  $d_{G}J_{2}^{\prime \prime }=0$. Fix a direct sum decomposition
$d_{G}J_{2}^{\prime \prime }=0$. Fix a direct sum decomposition  $J_{1}^{\prime }=\bigoplus _{i}{\mathcal{V}}_{a_{i}}^{+}(b_{i})$, for some
$J_{1}^{\prime }=\bigoplus _{i}{\mathcal{V}}_{a_{i}}^{+}(b_{i})$, for some ![]() $a_{i},b_{i}$. Say that
$a_{i},b_{i}$. Say that  ${\mathcal{V}}_{e_{1}}^{+}(f_{1})\subseteq J_{1}^{\prime }$, where
${\mathcal{V}}_{e_{1}}^{+}(f_{1})\subseteq J_{1}^{\prime }$, where  $(e_{1},f_{1})\not \in {\mathcal{J}}$ and choose
$(e_{1},f_{1})\not \in {\mathcal{J}}$ and choose  $(e_{2},f_{2})\in {\mathcal{J}}$, with
$(e_{2},f_{2})\in {\mathcal{J}}$, with  ${\mathcal{V}}_{e_{2}}^{+}(f_{2})\succcurlyeq {\mathcal{V}}_{e_{1}}^{+}(f_{1})$ and
${\mathcal{V}}_{e_{2}}^{+}(f_{2})\succcurlyeq {\mathcal{V}}_{e_{1}}^{+}(f_{1})$ and  ${\mathcal{V}}_{e_{1}}^{+}(f_{1})\oplus {\mathcal{V}}_{e_{2}}^{+}(f_{2})\subseteq J_{2}^{\prime }$. Further, assume that
${\mathcal{V}}_{e_{1}}^{+}(f_{1})\oplus {\mathcal{V}}_{e_{2}}^{+}(f_{2})\subseteq J_{2}^{\prime }$. Further, assume that ![]() $d_{G}$ is nontrivial on
$d_{G}$ is nontrivial on ![]() ${\mathcal{V}}_{e_{1}}^{+}(f_{1})$; if it were trivial, then we enlarge
${\mathcal{V}}_{e_{1}}^{+}(f_{1})$; if it were trivial, then we enlarge ![]() $J_{2}^{\prime }$ by setting
$J_{2}^{\prime }$ by setting  $J_{2}^{\prime \prime }=J_{2}^{\prime }\oplus {\mathcal{V}}_{e_{1}}^{+}(f_{1})$. Let
$J_{2}^{\prime \prime }=J_{2}^{\prime }\oplus {\mathcal{V}}_{e_{1}}^{+}(f_{1})$. Let ![]() $x_{i}$ be the generator of
$x_{i}$ be the generator of ![]() ${\mathcal{V}}_{e_{i}}^{+}(f_{i})$. We choose new
${\mathcal{V}}_{e_{i}}^{+}(f_{i})$. We choose new ![]() $\mathbb{F}[v]$-generators,
$\mathbb{F}[v]$-generators, ![]() $x_{2}$ of
$x_{2}$ of ![]() ${\mathcal{V}}_{e_{2}}^{+}(f_{2})$ and
${\mathcal{V}}_{e_{2}}^{+}(f_{2})$ and  $v^{f_{2}-f_{1}+(e_{2}-e_{1})/4}x_{2}+x_{1}$ of
$v^{f_{2}-f_{1}+(e_{2}-e_{1})/4}x_{2}+x_{1}$ of ![]() ${\mathcal{V}}_{e_{1}}^{+}(f_{1})$ so that
${\mathcal{V}}_{e_{1}}^{+}(f_{1})$ so that ![]() $d_{G}$ vanishes on
$d_{G}$ vanishes on ![]() ${\mathcal{V}}_{e_{1}}^{+}(f_{1})$. Again, then we may enlarge
${\mathcal{V}}_{e_{1}}^{+}(f_{1})$. Again, then we may enlarge ![]() $J_{2}^{\prime }$ by adding the
$J_{2}^{\prime }$ by adding the ![]() ${\mathcal{V}}_{e_{1}}^{+}(f_{1})$ factor. This shows that we can remove all summands
${\mathcal{V}}_{e_{1}}^{+}(f_{1})$ factor. This shows that we can remove all summands ![]() ${\mathcal{T}}_{a}^{+}(b)$ with
${\mathcal{T}}_{a}^{+}(b)$ with  $(a,b)\not \in {\mathcal{J}}$ from
$(a,b)\not \in {\mathcal{J}}$ from ![]() $J_{1}^{\prime }$. Similarly, if
$J_{1}^{\prime }$. Similarly, if  ${\mathcal{V}}_{a}^{+}(b)\oplus {\mathcal{V}}_{a}^{+}(b)\subseteq J_{1}^{\prime }$, with
${\mathcal{V}}_{a}^{+}(b)\oplus {\mathcal{V}}_{a}^{+}(b)\subseteq J_{1}^{\prime }$, with  $(a,b)\in {\mathcal{J}}$ and with generators
$(a,b)\in {\mathcal{J}}$ and with generators ![]() $x_{1}$ and
$x_{1}$ and ![]() $x_{2}$ such that
$x_{2}$ such that  $d_{G}(x_{1})=d_{G}(x_{2})\neq 0$, we choose the new basis
$d_{G}(x_{1})=d_{G}(x_{2})\neq 0$, we choose the new basis  $\langle x_{1},x_{2}+x_{1}\rangle$. The differential
$\langle x_{1},x_{2}+x_{1}\rangle$. The differential ![]() $d_{G}$ is nonzero on the copy of
$d_{G}$ is nonzero on the copy of ![]() ${\mathcal{V}}_{a}^{+}(b)$ generated by
${\mathcal{V}}_{a}^{+}(b)$ generated by ![]() $x_{1}$, while
$x_{1}$, while ![]() $d_{G}$ vanishes on the copy of
$d_{G}$ vanishes on the copy of ![]() ${\mathcal{V}}_{a}^{+}(b)$ generated by
${\mathcal{V}}_{a}^{+}(b)$ generated by ![]() $x_{1}+x_{2}$, and
$x_{1}+x_{2}$, and ![]() $J_{2}^{\prime }$ may be enlarged. Then we may choose
$J_{2}^{\prime }$ may be enlarged. Then we may choose  $J_{1}^{\prime \prime }\cong \bigoplus _{(a,b)\in {\mathcal{J}}}{\mathcal{V}}_{a}^{+}(b)$. The formula for
$J_{1}^{\prime \prime }\cong \bigoplus _{(a,b)\in {\mathcal{J}}}{\mathcal{V}}_{a}^{+}(b)$. The formula for ![]() $J_{2}^{\prime \prime }$ also follows once
$J_{2}^{\prime \prime }$ also follows once ![]() $J_{1}^{\prime \prime }$ is specified.◻
$J_{1}^{\prime \prime }$ is specified.◻
In Figures 5 and 6, we provide an example illustrating the proof of Lemma 3.14. We may now compute ![]() $\tilde{H}_{\ast }^{G}(X)$ in terms of
$\tilde{H}_{\ast }^{G}(X)$ in terms of  $\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ and the map
$\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ and the map ![]() $d_{S^{1}}$.
$d_{S^{1}}$.
Lemma 3.15. Let  $\tilde{H}_{\ast }^{S^{1}}(X_{+})$ be decomposed as in Lemma 3.10 and let
$\tilde{H}_{\ast }^{S^{1}}(X_{+})$ be decomposed as in Lemma 3.10 and let ![]() $J_{1}^{\prime \prime },J_{2}^{\prime \prime }$ be as in Lemma 3.14. Then
$J_{1}^{\prime \prime },J_{2}^{\prime \prime }$ be as in Lemma 3.14. Then
 $$\begin{eqnarray}\displaystyle \tilde{H}_{\ast }^{G}(X)={\mathcal{V}}_{a_{1}+4b_{1}-1}^{+}\oplus {\mathcal{V}}_{1+m}^{+}\oplus {\mathcal{V}}_{2+m}^{+}\oplus \mathop{\bigoplus }_{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus J_{2}^{\prime \prime }, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{H}_{\ast }^{G}(X)={\mathcal{V}}_{a_{1}+4b_{1}-1}^{+}\oplus {\mathcal{V}}_{1+m}^{+}\oplus {\mathcal{V}}_{2+m}^{+}\oplus \mathop{\bigoplus }_{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus J_{2}^{\prime \prime }, & & \displaystyle\end{eqnarray}$$ as an ![]() $\mathbb{F}[v]$-module. The
$\mathbb{F}[v]$-module. The ![]() $q$-action is given by the isomorphism
$q$-action is given by the isomorphism  $q:{\mathcal{V}}_{2+m}^{+}\rightarrow {\mathcal{V}}_{1+m}^{+}$ and the map
$q:{\mathcal{V}}_{2+m}^{+}\rightarrow {\mathcal{V}}_{1+m}^{+}$ and the map  ${\mathcal{V}}_{1+m}^{+}\rightarrow {\mathcal{V}}_{a_{1}+4b_{1}-1}^{+}$, which is an
${\mathcal{V}}_{1+m}^{+}\rightarrow {\mathcal{V}}_{a_{1}+4b_{1}-1}^{+}$, which is an ![]() $\mathbb{F}$-vector space isomorphism in all degrees at least
$\mathbb{F}$-vector space isomorphism in all degrees at least  $a_{1}+4b_{1}-1$. The action of
$a_{1}+4b_{1}-1$. The action of ![]() $q$ annihilates
$q$ annihilates  $\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)$ and
$\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)$ and  $\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J_{2}\oplus J_{\text{rep}}\subseteq J_{2}^{\prime \prime }$.
$\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J_{2}\oplus J_{\text{rep}}\subseteq J_{2}^{\prime \prime }$.

Figure 5. An example ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module  $\tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ for
$\tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ for ![]() $X$ with
$X$ with ![]() $m=0$. Here
$m=0$. Here  $d_{1}=-5,n_{1}=7$ and
$d_{1}=-5,n_{1}=7$ and  $d_{2}=-3,n_{2}=5$, and
$d_{2}=-3,n_{2}=5$, and ![]() $J_{2}=0$.
$J_{2}=0$.

Figure 6. Here we show how to compute  $(\tilde{H}_{\ast }^{G}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{G}(X/X^{S^{1}}),d_{G})$, given
$(\tilde{H}_{\ast }^{G}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{G}(X/X^{S^{1}}),d_{G})$, given  $(\tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}}),d_{S^{1}})$, for the example complex given in Figure 5. The curved arrows denote the
$(\tilde{H}_{\ast }^{S^{1}}(X^{S^{1}})\oplus \tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}}),d_{S^{1}})$, for the example complex given in Figure 5. The curved arrows denote the ![]() $v$-action. Here,
$v$-action. Here, ![]() $J_{\text{rep}}$ is
$J_{\text{rep}}$ is ![]() ${\mathcal{V}}_{-3}^{+}(3)$, and
${\mathcal{V}}_{-3}^{+}(3)$, and  $J_{1}^{\prime \prime }={\mathcal{V}}_{-3}^{+}(3)$. Then we have also
$J_{1}^{\prime \prime }={\mathcal{V}}_{-3}^{+}(3)$. Then we have also  $J_{2}^{\prime \prime }={\mathcal{V}}_{-3}^{+}(3)\oplus {\mathcal{V}}_{-1}^{+}(2)\oplus {\mathcal{V}}_{-5}^{+}(4)$. If we have a basis of
$J_{2}^{\prime \prime }={\mathcal{V}}_{-3}^{+}(3)\oplus {\mathcal{V}}_{-1}^{+}(2)\oplus {\mathcal{V}}_{-5}^{+}(4)$. If we have a basis of  $\text{cor}_{G}^{S^{1}}Ux_{1}$,
$\text{cor}_{G}^{S^{1}}Ux_{1}$,  $\text{cor}_{G}^{S^{1}}x_{2}$ for
$\text{cor}_{G}^{S^{1}}x_{2}$ for ![]() $J_{1}^{\prime }$, then
$J_{1}^{\prime }$, then  $\text{cor}_{G}^{S^{1}}Ux_{1}+\text{cor}_{G}^{S^{1}}x_{2}$ would be a basis for
$\text{cor}_{G}^{S^{1}}Ux_{1}+\text{cor}_{G}^{S^{1}}x_{2}$ would be a basis for ![]() $J_{\text{rep}}$ produced by Lemma 3.14.
$J_{\text{rep}}$ produced by Lemma 3.14.
To finish specifying the ![]() $q$-action, let
$q$-action, let ![]() $x_{i}$ be a generator of
$x_{i}$ be a generator of  ${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )$ for
${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )$ for ![]() $i$ such that
$i$ such that  $d_{i}\equiv m+1\;\text{mod}\;4$ (respectively, let
$d_{i}\equiv m+1\;\text{mod}\;4$ (respectively, let ![]() $x_{i}$ be a generator of
$x_{i}$ be a generator of  ${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )$ if
${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )$ if  $d_{i}\equiv m+3\;\text{mod}\;4$). Then
$d_{i}\equiv m+3\;\text{mod}\;4$). Then ![]() $qx_{i}$ is the unique nonzero element of
$qx_{i}$ is the unique nonzero element of  $\text{coker}(d_{G})\subset H_{\ast }^{G}(X/X^{S^{1}})$ in grading
$\text{coker}(d_{G})\subset H_{\ast }^{G}(X/X^{S^{1}})$ in grading  $\text{deg}\,x_{i}-1$, for all
$\text{deg}\,x_{i}-1$, for all ![]() $i$. In particular,
$i$. In particular,  $\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ and
$\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})$ and ![]() $d_{S^{1}}$ determine
$d_{S^{1}}$ determine ![]() $\tilde{H}_{\ast }^{G}(X)$. Here
$\tilde{H}_{\ast }^{G}(X)$. Here  $a_{N_{0}+1}=m+1,b_{N_{0}+1}=0$.
$a_{N_{0}+1}=m+1,b_{N_{0}+1}=0$.
Proof. The proof is analogous to that of Lemma 3.11. We choose a basis for ![]() $\text{ker}\,d_{G}$ as follows. Write the generator of
$\text{ker}\,d_{G}$ as follows. Write the generator of ![]() ${\mathcal{V}}_{a_{i}}^{+}(b_{i})$ as
${\mathcal{V}}_{a_{i}}^{+}(b_{i})$ as ![]() $x_{i}$. Then set
$x_{i}$. Then set  $y_{i}=x_{i+1}+v^{b_{i}-b_{i+1}+(a_{i}-a_{i+1})/4}x_{i}$ for
$y_{i}=x_{i+1}+v^{b_{i}-b_{i+1}+(a_{i}-a_{i+1})/4}x_{i}$ for  $i=1,\ldots ,N_{0}-1,$ and
$i=1,\ldots ,N_{0}-1,$ and  $y_{N_{0}}=v^{(a_{N_{0}}+4b_{N_{0}}-m-1)/4}x_{N_{0}}$. It is clear that
$y_{N_{0}}=v^{(a_{N_{0}}+4b_{N_{0}}-m-1)/4}x_{N_{0}}$. It is clear that  $y_{i}\in \text{ker}\,d_{G}$ for all
$y_{i}\in \text{ker}\,d_{G}$ for all ![]() $i$, and it is straightforward to check that
$i$, and it is straightforward to check that ![]() $\{y_{i}\}$ generates
$\{y_{i}\}$ generates  $\text{ker}\,d_{G}\cap J_{1}^{\prime \prime }$. The
$\text{ker}\,d_{G}\cap J_{1}^{\prime \prime }$. The ![]() $y_{i}$ generate the term
$y_{i}$ generate the term  $\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)$ in (59). Since
$\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)$ in (59). Since ![]() $d_{G}$ is
$d_{G}$ is ![]() $q$-equivariant and
$q$-equivariant and ![]() $q$ annihilates
$q$ annihilates  $\tilde{H}_{\ast }^{G}(X/X^{S^{1}})$, the modules
$\tilde{H}_{\ast }^{G}(X/X^{S^{1}})$, the modules ![]() ${\mathcal{V}}_{1+m}^{+}$ and
${\mathcal{V}}_{1+m}^{+}$ and  ${\mathcal{V}}_{2+m}^{+}\subset H_{\ast }(BG)$ are disjoint from the image of
${\mathcal{V}}_{2+m}^{+}\subset H_{\ast }(BG)$ are disjoint from the image of ![]() $d_{G}$. Moreover,
$d_{G}$. Moreover,  $v^{-(a_{1}+4b_{1}-5-m)/4}=d_{G}(x_{1})$, where
$v^{-(a_{1}+4b_{1}-5-m)/4}=d_{G}(x_{1})$, where ![]() $v^{-k}$ is the unique element
$v^{-k}$ is the unique element ![]() $x$ of
$x$ of  $H_{\ast }(BG)[-m]$ with
$H_{\ast }(BG)[-m]$ with ![]() $v^{k}x$ an
$v^{k}x$ an ![]() $\mathbb{F}$-generator of
$\mathbb{F}$-generator of  $H_{0}(BG)[-m]$. Since there are no elements
$H_{0}(BG)[-m]$. Since there are no elements ![]() $x\in J_{1}^{\prime \prime }$ with grading greater than
$x\in J_{1}^{\prime \prime }$ with grading greater than  $a_{1}+4b_{1}-4$, the maximal
$a_{1}+4b_{1}-4$, the maximal ![]() $k$ for which
$k$ for which  $v^{-k}\in \text{Im}\;d_{G}$ is
$v^{-k}\in \text{Im}\;d_{G}$ is  $(a_{1}+4b_{1}-5-m)/4$. It follows that
$(a_{1}+4b_{1}-5-m)/4$. It follows that
 $$\begin{eqnarray}\text{coker}\,d_{G}={\mathcal{V}}_{a_{1}+4b_{1}-1}^{+}\oplus {\mathcal{V}}_{1+m}^{+}\oplus {\mathcal{V}}_{2+m}^{+}.\end{eqnarray}$$
$$\begin{eqnarray}\text{coker}\,d_{G}={\mathcal{V}}_{a_{1}+4b_{1}-1}^{+}\oplus {\mathcal{V}}_{1+m}^{+}\oplus {\mathcal{V}}_{2+m}^{+}.\end{eqnarray}$$ Furthermore,  $J_{2}^{\prime \prime }\subseteq \text{ker}\,d_{G}$ by definition, contributing the
$J_{2}^{\prime \prime }\subseteq \text{ker}\,d_{G}$ by definition, contributing the ![]() $J_{2}^{\prime \prime }$ term of (59). To determine the
$J_{2}^{\prime \prime }$ term of (59). To determine the ![]() $q$-action on
$q$-action on ![]() $\text{ker}\,d_{G}$, we use Lemma 3.8. Indeed,
$\text{ker}\,d_{G}$, we use Lemma 3.8. Indeed, ![]() $q$ takes elements not in the image of
$q$ takes elements not in the image of  $\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$ to nontrivial elements of
$\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$ to nontrivial elements of  $\text{coker}\,d_{G}$, and
$\text{coker}\,d_{G}$, and ![]() $q$ vanishes on
$q$ vanishes on  $\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$. Using Fact 3.13, we obtain the
$\text{Im}\,\unicode[STIX]{x1D719}_{2}|_{\text{ker}\,d_{S^{1}}}$. Using Fact 3.13, we obtain the ![]() $q$-action on
$q$-action on ![]() $J_{2}^{\prime \prime }$ as in the Lemma. The
$J_{2}^{\prime \prime }$ as in the Lemma. The ![]() $q$-action on
$q$-action on  $\text{coker}\,d_{G}$ is given by that on
$\text{coker}\,d_{G}$ is given by that on  $H_{\ast }(BG)$.◻
$H_{\ast }(BG)$.◻
We combine Lemmas 3.10–3.15 to determine ![]() $\tilde{H}_{\ast }^{G}(X)$ from
$\tilde{H}_{\ast }^{G}(X)$ from  $\tilde{H}_{\ast }^{S^{1}}(X)$. We record this as the following theorem.
$\tilde{H}_{\ast }^{S^{1}}(X)$. We record this as the following theorem.
Theorem 3.16. Let  $X=(X^{\prime },p,h/4)\in \mathfrak{E}$ and
$X=(X^{\prime },p,h/4)\in \mathfrak{E}$ and ![]() $X^{\prime }$ be a
$X^{\prime }$ be a ![]() $j$-split space of type SWF. Then
$j$-split space of type SWF. Then
 $$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)={\mathcal{T}}_{s+d_{1}^{\prime }+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{s+d_{i}^{\prime }}^{+}\biggl(\frac{d_{i+1}^{\prime }+2n_{i+1}-d_{i}^{\prime }}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}^{\prime }}^{+}(n_{i})\oplus J^{\oplus 2}[-s],\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)={\mathcal{T}}_{s+d_{1}^{\prime }+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{s+d_{i}^{\prime }}^{+}\biggl(\frac{d_{i+1}^{\prime }+2n_{i+1}-d_{i}^{\prime }}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}^{\prime }}^{+}(n_{i})\oplus J^{\oplus 2}[-s],\end{eqnarray}$$ for some constants  $s,d_{i}^{\prime },n_{i},N$ and some
$s,d_{i}^{\prime },n_{i},N$ and some ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module ![]() $J$, where
$J$, where  $2n_{i}+d_{i}^{\prime }>2n_{i+1}+d_{i+1}^{\prime }$ and
$2n_{i}+d_{i}^{\prime }>2n_{i+1}+d_{i+1}^{\prime }$ and  $d_{i}^{\prime }<d_{i+1}^{\prime }$ for all
$d_{i}^{\prime }<d_{i+1}^{\prime }$ for all ![]() $i$,
$i$,  $2n_{N}+d_{N}^{\prime }\geqslant 3$,
$2n_{N}+d_{N}^{\prime }\geqslant 3$, ![]() $d_{N}^{\prime }\leqslant 1$, and
$d_{N}^{\prime }\leqslant 1$, and  $d_{N+1}^{\prime }=1,n_{N+1}=0$. Let
$d_{N+1}^{\prime }=1,n_{N+1}=0$. Let  ${\mathcal{J}}_{0}=\{(a_{k},b_{k})\}_{k}$ be the collection of pairs consisting of all
${\mathcal{J}}_{0}=\{(a_{k},b_{k})\}_{k}$ be the collection of pairs consisting of all  $(d_{i}^{\prime },\lfloor (n_{i}+1)/2\rfloor )$ for
$(d_{i}^{\prime },\lfloor (n_{i}+1)/2\rfloor )$ for  $d_{i}^{\prime }\equiv 1\;\text{mod}\;4$ and all
$d_{i}^{\prime }\equiv 1\;\text{mod}\;4$ and all  $(d_{i}^{\prime }+2,\lfloor n_{i}/2\rfloor )$ for
$(d_{i}^{\prime }+2,\lfloor n_{i}/2\rfloor )$ for  $d_{i}^{\prime }\equiv 3\;\text{mod}\;4$, counting multiplicity. Let
$d_{i}^{\prime }\equiv 3\;\text{mod}\;4$, counting multiplicity. Let  $(a,b)\succcurlyeq (c,d)$ if
$(a,b)\succcurlyeq (c,d)$ if  $a+4b\geqslant c+4d$ and
$a+4b\geqslant c+4d$ and ![]() $a\geqslant c$, and let
$a\geqslant c$, and let ![]() ${\mathcal{J}}$ be the subset of
${\mathcal{J}}$ be the subset of ![]() ${\mathcal{J}}_{0}$ consisting of pairs maximal under
${\mathcal{J}}_{0}$ consisting of pairs maximal under ![]() $\succcurlyeq$ (not counted with multiplicity). If
$\succcurlyeq$ (not counted with multiplicity). If  $(a,b)\in {\mathcal{J}}$, set
$(a,b)\in {\mathcal{J}}$, set  $m(a,b)+1$ to be the multiplicity of
$m(a,b)+1$ to be the multiplicity of ![]() $(a,b)$ in
$(a,b)$ in ![]() ${\mathcal{J}}_{0}$. If
${\mathcal{J}}_{0}$. If  $(a,b)\not \in {\mathcal{J}}$, set
$(a,b)\not \in {\mathcal{J}}$, set ![]() $m(a,b)$ to be the multiplicity of
$m(a,b)$ to be the multiplicity of ![]() $(a,b)$ in
$(a,b)$ in ![]() ${\mathcal{J}}_{0}$. Let
${\mathcal{J}}_{0}$. Let  $|{\mathcal{J}}|=N_{0}$ and order the elements of
$|{\mathcal{J}}|=N_{0}$ and order the elements of ![]() ${\mathcal{J}}$ so that
${\mathcal{J}}$ so that  ${\mathcal{J}}=\{(a_{i},b_{i})\}_{i}$, with
${\mathcal{J}}=\{(a_{i},b_{i})\}_{i}$, with  $a_{i}+4b_{i}>a_{i+1}+4b_{i+1}$. We interpret
$a_{i}+4b_{i}>a_{i+1}+4b_{i+1}$. We interpret  $a_{N_{0}+1}=1,b_{N_{0}+1}=0$. Then
$a_{N_{0}+1}=1,b_{N_{0}+1}=0$. Then
 $$\begin{eqnarray}\displaystyle \tilde{H}_{\ast }^{G}(X) & = & \displaystyle ({\mathcal{V}}_{4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus \bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\{i\mid d_{i}^{\prime }\equiv 1\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}^{\prime }+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}^{\prime }\equiv 3\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}^{\prime }}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\!)[-s].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{H}_{\ast }^{G}(X) & = & \displaystyle ({\mathcal{V}}_{4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus \bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\{i\mid d_{i}^{\prime }\equiv 1\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}^{\prime }+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i\mid d_{i}^{\prime }\equiv 3\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}^{\prime }}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\!)[-s].\end{eqnarray}$$ The ![]() $q$-action is given by the isomorphism
$q$-action is given by the isomorphism  $q:{\mathcal{V}}_{2}^{+}[-s]\rightarrow {\mathcal{V}}_{1}^{+}[-s]$ and the map
$q:{\mathcal{V}}_{2}^{+}[-s]\rightarrow {\mathcal{V}}_{1}^{+}[-s]$ and the map  $q:{\mathcal{V}}_{1}^{+}[-s]\rightarrow {\mathcal{V}}_{4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor }^{+}[-s]$ which is an
$q:{\mathcal{V}}_{1}^{+}[-s]\rightarrow {\mathcal{V}}_{4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor }^{+}[-s]$ which is an ![]() $\mathbb{F}$-vector space isomorphism in all degrees (in
$\mathbb{F}$-vector space isomorphism in all degrees (in ![]() ${\mathcal{V}}_{1}^{+}[-s]$) greater than or equal to
${\mathcal{V}}_{1}^{+}[-s]$) greater than or equal to  $4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor +s+1$, and vanishes on elements of
$4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor +s+1$, and vanishes on elements of ![]() ${\mathcal{V}}_{1}^{+}[-s]$ of degree less than
${\mathcal{V}}_{1}^{+}[-s]$ of degree less than  $4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor +s+1$.
$4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor +s+1$.
The action of ![]() $q$ annihilates
$q$ annihilates  $\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)[-s]$ and
$\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)[-s]$ and  $(\bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J)[-s]$.
$(\bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J)[-s]$.
To finish specifying the ![]() $q$-action, let
$q$-action, let ![]() $x_{i}$ be a generator of
$x_{i}$ be a generator of  ${\mathcal{V}}_{d_{i}^{\prime }+2}^{+}(\lfloor n_{i}/2\rfloor )[-s]$ for
${\mathcal{V}}_{d_{i}^{\prime }+2}^{+}(\lfloor n_{i}/2\rfloor )[-s]$ for ![]() $i$ such that
$i$ such that  $d_{i}^{\prime }\equiv 1\;\text{mod}\;4$ (respectively, let
$d_{i}^{\prime }\equiv 1\;\text{mod}\;4$ (respectively, let ![]() $x_{i}$ be a generator of
$x_{i}$ be a generator of  ${\mathcal{V}}_{d_{i}^{\prime }}^{+}(\lfloor (n_{i}+1)/2\rfloor )[-s]$ if
${\mathcal{V}}_{d_{i}^{\prime }}^{+}(\lfloor (n_{i}+1)/2\rfloor )[-s]$ if  $d_{i}^{\prime }\equiv 3\;\text{mod}\;4$). Then
$d_{i}^{\prime }\equiv 3\;\text{mod}\;4$). Then ![]() $qx_{i}$ is the unique nonzero element of
$qx_{i}$ is the unique nonzero element of  $({\mathcal{V}}_{4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+})[-s]$ in grading
$({\mathcal{V}}_{4\lfloor (d_{1}^{\prime }+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+})[-s]$ in grading  $\text{deg}\,x_{i}-1$, for all
$\text{deg}\,x_{i}-1$, for all ![]() $i$.
$i$.
Proof. We show that for ![]() $M$ an
$M$ an ![]() $\mathbb{F}[U]$-module of the form (57), the sets
$\mathbb{F}[U]$-module of the form (57), the sets ![]() $\{n_{i}\}$,
$\{n_{i}\}$, ![]() $\{d_{i}^{\prime }\}$, and the module
$\{d_{i}^{\prime }\}$, and the module ![]() $J_{2}$, are determined by the (graded) isomorphism type of
$J_{2}$, are determined by the (graded) isomorphism type of ![]() $M$, to establish that all the constants in (60) are well defined (independent of the choice of direct sum decomposition of
$M$, to establish that all the constants in (60) are well defined (independent of the choice of direct sum decomposition of  $\tilde{H}_{\ast }^{S^{1}}(X)$). For a fixed
$\tilde{H}_{\ast }^{S^{1}}(X)$). For a fixed ![]() $d$, there are at most two distinct isomorphism classes
$d$, there are at most two distinct isomorphism classes ![]() ${\mathcal{T}}_{d}^{+}(x)$, each appearing as summands of
${\mathcal{T}}_{d}^{+}(x)$, each appearing as summands of ![]() $M$ that occur an odd number of times in the decomposition of
$M$ that occur an odd number of times in the decomposition of ![]() $M$ into simple submodules (not including the infinite tower). Such a submodule
$M$ into simple submodules (not including the infinite tower). Such a submodule ![]() ${\mathcal{T}}_{d}^{+}(x)$ will be called a submodule occurring with odd multiplicity. For any
${\mathcal{T}}_{d}^{+}(x)$ will be called a submodule occurring with odd multiplicity. For any ![]() $d$ such that there is at least one isomorphism class
$d$ such that there is at least one isomorphism class ![]() ${\mathcal{T}}_{d}^{+}(x)$ with odd multiplicity, then
${\mathcal{T}}_{d}^{+}(x)$ with odd multiplicity, then  $d=s+d_{i}^{\prime }$ for some
$d=s+d_{i}^{\prime }$ for some ![]() $i$, using (57). Consider the case that there are exactly two such isomorphism classes
$i$, using (57). Consider the case that there are exactly two such isomorphism classes ![]() ${\mathcal{T}}_{d}^{+}(x_{1})$ and
${\mathcal{T}}_{d}^{+}(x_{1})$ and ![]() ${\mathcal{T}}_{d}^{+}(x_{2})$ with, say,
${\mathcal{T}}_{d}^{+}(x_{2})$ with, say,  $x_{1}<x_{2}$. Setting
$x_{1}<x_{2}$. Setting  $d=s+d_{i}^{\prime }$ for a fixed
$d=s+d_{i}^{\prime }$ for a fixed ![]() $i$, and using (57), we see that
$i$, and using (57), we see that ![]() $x_{2}=n_{i}$, since
$x_{2}=n_{i}$, since  $n_{i}>n_{i+1}+(d_{i+1}^{\prime }-d_{i}^{\prime })/2$ for all
$n_{i}>n_{i+1}+(d_{i+1}^{\prime }-d_{i}^{\prime })/2$ for all ![]() $i$. If instead there is one (graded) isomorphism class
$i$. If instead there is one (graded) isomorphism class ![]() $T_{d}(x)$ with odd multiplicity, Lemma 3.11 shows
$T_{d}(x)$ with odd multiplicity, Lemma 3.11 shows ![]() $x=n_{N}$. If, for a fixed
$x=n_{N}$. If, for a fixed ![]() $d$, there are no isomorphism classes
$d$, there are no isomorphism classes ![]() ${\mathcal{T}}_{d}^{+}(x)$ occurring with odd multiplicity, then
${\mathcal{T}}_{d}^{+}(x)$ occurring with odd multiplicity, then  $d\not \in \{s+d_{i}^{\prime }\}$. Thus, we see that
$d\not \in \{s+d_{i}^{\prime }\}$. Thus, we see that ![]() $\{d_{i}^{\prime }\}$ and
$\{d_{i}^{\prime }\}$ and ![]() $\{n_{i}\}$ are determined by the isomorphism type of
$\{n_{i}\}$ are determined by the isomorphism type of ![]() $M$ as a graded
$M$ as a graded ![]() $\mathbb{F}[U]$-module. It is then easy to see that
$\mathbb{F}[U]$-module. It is then easy to see that ![]() $J_{2}$ is also determined by the isomorphism type of
$J_{2}$ is also determined by the isomorphism type of ![]() $M$.
$M$.
In addition, we find that ![]() $s$ in (60) exists and is uniquely determined. First, we check that there is an
$s$ in (60) exists and is uniquely determined. First, we check that there is an ![]() $s$ so that (60) holds. Observe that
$s$ so that (60) holds. Observe that  $\tilde{H}_{\ast }^{S^{1}}(X)=\tilde{H}_{\ast }^{S^{1}}(X^{\prime })[p+h]$. Say that
$\tilde{H}_{\ast }^{S^{1}}(X)=\tilde{H}_{\ast }^{S^{1}}(X^{\prime })[p+h]$. Say that ![]() $X^{\prime }$ is a space of type SWF at level
$X^{\prime }$ is a space of type SWF at level ![]() $m$, and set
$m$, and set  $d_{i}^{\prime }=d_{i}-m$, where
$d_{i}^{\prime }=d_{i}-m$, where ![]() $d_{i}$ is as in (57). Then Lemma 3.11 shows that (60) holds for this choice of
$d_{i}$ is as in (57). Then Lemma 3.11 shows that (60) holds for this choice of ![]() $d_{i}^{\prime }$, and
$d_{i}^{\prime }$, and  $s=m-p-h$. We next show that there is a unique
$s=m-p-h$. We next show that there is a unique ![]() $s$ so that (60) holds. To see this, observe that
$s$ so that (60) holds. To see this, observe that  $\tilde{H}_{\ast ,\text{red}}^{S^{1}}(X)$, as in (60), is an
$\tilde{H}_{\ast ,\text{red}}^{S^{1}}(X)$, as in (60), is an ![]() $\mathbb{F}$-module of odd rank in degrees
$\mathbb{F}$-module of odd rank in degrees ![]() $d$ such that
$d$ such that  $d\equiv s+1\,\text{mod}\,2$, with
$d\equiv s+1\,\text{mod}\,2$, with  $s<d<s+d_{1}^{\prime }+2n_{1}$, and of even rank (possibly zero) in all other degrees (recall from (8) the definition of
$s<d<s+d_{1}^{\prime }+2n_{1}$, and of even rank (possibly zero) in all other degrees (recall from (8) the definition of ![]() $\tilde{H}_{\ast ,\text{red}}^{S^{1}}$). Then, for
$\tilde{H}_{\ast ,\text{red}}^{S^{1}}$). Then, for ![]() $M$ an
$M$ an ![]() $\mathbb{F}[U]$-module that is the homology of
$\mathbb{F}[U]$-module that is the homology of  $(X^{\prime },p,h/4)$ with
$(X^{\prime },p,h/4)$ with ![]() $X^{\prime }$
$X^{\prime }$![]() $j$-split, we have that
$j$-split, we have that  $s=m-p-h$ is determined by
$s=m-p-h$ is determined by ![]() $M$.
$M$.
As in (50),
 $$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)=\text{coker}\,d_{S^{1}}\oplus \text{ker}\,d_{S^{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}(X)=\text{coker}\,d_{S^{1}}\oplus \text{ker}\,d_{S^{1}}.\end{eqnarray}$$ Additionally, given ![]() $M$, we have determined the sets
$M$, we have determined the sets  $\{d_{i}^{\prime }\},\{n_{i}\}$ appearing in Lemma 3.10. Then Lemmas 3.12 and 3.14 show that
$\{d_{i}^{\prime }\},\{n_{i}\}$ appearing in Lemma 3.10. Then Lemmas 3.12 and 3.14 show that  $J_{1}^{\prime \prime }=\bigoplus _{(a_{i},b_{i})\in {\mathcal{J}}}{\mathcal{V}}_{a_{i}}^{+}(b_{i})$, for
$J_{1}^{\prime \prime }=\bigoplus _{(a_{i},b_{i})\in {\mathcal{J}}}{\mathcal{V}}_{a_{i}}^{+}(b_{i})$, for ![]() $a_{i},b_{i}$ as in the statement of the theorem, and that
$a_{i},b_{i}$ as in the statement of the theorem, and that
 $$\begin{eqnarray}J_{2}^{\prime \prime }=\text{res}_{\mathbb{ F}[v]}^{\mathbb{F}[U]}J\oplus \bigoplus _{\{i|d_{i}\equiv 1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i|d_{i}\equiv 3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}.\end{eqnarray}$$
$$\begin{eqnarray}J_{2}^{\prime \prime }=\text{res}_{\mathbb{ F}[v]}^{\mathbb{F}[U]}J\oplus \bigoplus _{\{i|d_{i}\equiv 1\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{\{i|d_{i}\equiv 3\,\text{mod}\,4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr)\oplus \bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}.\end{eqnarray}$$ Here we have replaced the notation  $\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}$ by
$\text{res}_{\mathbb{F}[q,v]/(q^{3})}^{\mathbb{F}[U]}$ by ![]() $\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}$ since
$\text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}$ since ![]() $q$ acts by
$q$ acts by ![]() $0$. Finally, Lemma 3.15 determines
$0$. Finally, Lemma 3.15 determines ![]() $\tilde{H}_{\ast }^{G}(X)$ given
$\tilde{H}_{\ast }^{G}(X)$ given ![]() $J_{1}^{\prime \prime }$ and
$J_{1}^{\prime \prime }$ and ![]() $J_{2}^{\prime \prime }$. This completes the proof of the theorem.◻
$J_{2}^{\prime \prime }$. This completes the proof of the theorem.◻
Remark 3.17. Since every ![]() $j$-split chain complex of type SWF is the cellular chain complex of some space of type SWF, Theorem 3.16 also applies to
$j$-split chain complex of type SWF is the cellular chain complex of some space of type SWF, Theorem 3.16 also applies to ![]() $j$-split chain complexes.
$j$-split chain complexes.
We give an example illustrating the steps of the proof of Theorem 3.16. Let ![]() $X$ be a
$X$ be a ![]() $j$-split space, and say that
$j$-split space, and say that  $\tilde{H}_{\ast }^{S^{1}}((X,p,h/4))$ is given as in Figure 7; that is,
$\tilde{H}_{\ast }^{S^{1}}((X,p,h/4))$ is given as in Figure 7; that is,
 $$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}((X,p,h/4))\cong {\mathcal{T}}_{6}^{+}\oplus {\mathcal{T}}_{-5}^{+}(6)\oplus {\mathcal{T}}_{-5}^{+}(5)\oplus {\mathcal{T}}_{-3}^{+}(4)\oplus {\mathcal{T}}_{-3}^{+}(3)\oplus {\mathcal{T}}_{-1}^{+}(2)\oplus {\mathcal{T}}_{-1}^{+}(1).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}_{\ast }^{S^{1}}((X,p,h/4))\cong {\mathcal{T}}_{6}^{+}\oplus {\mathcal{T}}_{-5}^{+}(6)\oplus {\mathcal{T}}_{-5}^{+}(5)\oplus {\mathcal{T}}_{-3}^{+}(4)\oplus {\mathcal{T}}_{-3}^{+}(3)\oplus {\mathcal{T}}_{-1}^{+}(2)\oplus {\mathcal{T}}_{-1}^{+}(1).\end{eqnarray}$$
Figure 7. The ![]() $S^{1}$-Borel homology of
$S^{1}$-Borel homology of  $(X,p,h/4)\in \mathfrak{E}$. The variables
$(X,p,h/4)\in \mathfrak{E}$. The variables ![]() $t_{i}$ stand for entries of the infinite tower in grading
$t_{i}$ stand for entries of the infinite tower in grading ![]() $i$.
$i$.
We calculate ![]() $d_{i}^{\prime },n_{i}$. As specified in the proof of Theorem 3.16, we see
$d_{i}^{\prime },n_{i}$. As specified in the proof of Theorem 3.16, we see  $\{d_{i}^{\prime }+m-p-h\}=\{-5,-3,-1\}$, and
$\{d_{i}^{\prime }+m-p-h\}=\{-5,-3,-1\}$, and  $\{n_{i}\}=\{6,4,2\}$. We see that
$\{n_{i}\}=\{6,4,2\}$. We see that  $m-p-h=0$ because
$m-p-h=0$ because  $\tilde{H}_{-1,\text{red}}^{S^{1}}((X,p,h/4))$ (i.e. the contribution in degree
$\tilde{H}_{-1,\text{red}}^{S^{1}}((X,p,h/4))$ (i.e. the contribution in degree ![]() $-1$ not coming from the tower) is of even rank, while
$-1$ not coming from the tower) is of even rank, while  $\tilde{H}_{1,\text{red}}^{S^{1}}((X,p,h/4))$ has odd rank. So
$\tilde{H}_{1,\text{red}}^{S^{1}}((X,p,h/4))$ has odd rank. So ![]() $s=0$ in Theorem 3.16. Then
$s=0$ in Theorem 3.16. Then  $\{d_{i}^{\prime }\}=\{-5,-3,-1\}$. Furthermore, we see
$\{d_{i}^{\prime }\}=\{-5,-3,-1\}$. Furthermore, we see ![]() $J_{2}=0$. Then we recover
$J_{2}=0$. Then we recover  $(\tilde{H}_{\ast }^{S^{1}}((X/X^{S^{1}},p,h/4))\oplus \tilde{H}_{\ast }^{S^{1}}((X^{S^{1}},p,h/4)),d_{S^{1}})$, as in Figure 8.
$(\tilde{H}_{\ast }^{S^{1}}((X/X^{S^{1}},p,h/4))\oplus \tilde{H}_{\ast }^{S^{1}}((X^{S^{1}},p,h/4)),d_{S^{1}})$, as in Figure 8.

Figure 8. The complex  $(\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})[p+h]\oplus \tilde{H}_{\ast }^{S^{1}}((X^{S^{1}},p,h/4)),d_{S^{1}})$ corresponding to Figure 7.
$(\tilde{H}_{\ast }^{S^{1}}(X/X^{S^{1}})[p+h]\oplus \tilde{H}_{\ast }^{S^{1}}((X^{S^{1}},p,h/4)),d_{S^{1}})$ corresponding to Figure 7.
Using Lemma 3.12, we have  $J_{1}^{\prime }={\mathcal{V}}_{-3}^{+}(3)\oplus {\mathcal{V}}_{-3}^{+}(2)\oplus {\mathcal{V}}_{1}^{+}(1)$ and
$J_{1}^{\prime }={\mathcal{V}}_{-3}^{+}(3)\oplus {\mathcal{V}}_{-3}^{+}(2)\oplus {\mathcal{V}}_{1}^{+}(1)$ and  $J_{2}^{\prime }={\mathcal{V}}_{-5}^{+}(3)\oplus {\mathcal{V}}_{-1}^{+}(2)\oplus {\mathcal{V}}_{-1}^{+}(1)$, as in Figure 9. We see that
$J_{2}^{\prime }={\mathcal{V}}_{-5}^{+}(3)\oplus {\mathcal{V}}_{-1}^{+}(2)\oplus {\mathcal{V}}_{-1}^{+}(1)$, as in Figure 9. We see that ![]() ${\mathcal{V}}_{-3}^{+}(2)$ is not maximal in
${\mathcal{V}}_{-3}^{+}(2)$ is not maximal in ![]() $J_{1}^{\prime }$, so
$J_{1}^{\prime }$, so  $m(-3,2)=1$, while
$m(-3,2)=1$, while  $m(-3,3)=0$, since
$m(-3,3)=0$, since ![]() ${\mathcal{V}}_{-3}^{+}(3)$ is maximal under
${\mathcal{V}}_{-3}^{+}(3)$ is maximal under ![]() $\succcurlyeq$. Similarly,
$\succcurlyeq$. Similarly, ![]() ${\mathcal{V}}_{1}^{+}(1)$ is maximal, so
${\mathcal{V}}_{1}^{+}(1)$ is maximal, so  $m(1,1)=0$. Then
$m(1,1)=0$. Then  $J_{\text{rep}}={\mathcal{V}}_{-3}^{+}(2)$, using (58).
$J_{\text{rep}}={\mathcal{V}}_{-3}^{+}(2)$, using (58).

Figure 9. The complex  $(\tilde{H}_{\ast }^{G}(X/X^{S^{1}})[p+h]\oplus \tilde{H}_{\ast }^{G}((X^{S^{1}},p,h/4)),d_{G})$ corresponding to Figure 7.
$(\tilde{H}_{\ast }^{G}(X/X^{S^{1}})[p+h]\oplus \tilde{H}_{\ast }^{G}((X^{S^{1}},p,h/4)),d_{G})$ corresponding to Figure 7.
In Figure 9,  $J_{1}^{\prime \prime }={\mathcal{V}}_{-3}^{+}(3)\oplus {\mathcal{V}}_{1}^{+}(1)$. Then Lemma 3.15 allows us to compute
$J_{1}^{\prime \prime }={\mathcal{V}}_{-3}^{+}(3)\oplus {\mathcal{V}}_{1}^{+}(1)$. Then Lemma 3.15 allows us to compute ![]() $\tilde{H}_{\ast }^{G}(X)$, as in Figure 10.
$\tilde{H}_{\ast }^{G}(X)$, as in Figure 10.

Figure 10. Finishing the calculation of ![]() $\tilde{H}_{\ast }^{G}(X)$ for the example of Figure 7. The curved arrows again represent the
$\tilde{H}_{\ast }^{G}(X)$ for the example of Figure 7. The curved arrows again represent the ![]() $v$-action. The straight arrows indicate a nontrivial
$v$-action. The straight arrows indicate a nontrivial ![]() $q$-action.
$q$-action.
We find  $\tilde{H}_{\ast }^{G}(X)={\mathcal{V}}_{8}^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+}\oplus {\mathcal{V}}_{-5}^{+}(3)\oplus {\mathcal{V}}_{-3}^{+}(2)^{\oplus 2}\oplus {\mathcal{V}}_{-1}^{+}(2)\oplus {\mathcal{V}}_{-1}^{+}(1)$, in accordance with Theorem 3.16.
$\tilde{H}_{\ast }^{G}(X)={\mathcal{V}}_{8}^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+}\oplus {\mathcal{V}}_{-5}^{+}(3)\oplus {\mathcal{V}}_{-3}^{+}(2)^{\oplus 2}\oplus {\mathcal{V}}_{-1}^{+}(2)\oplus {\mathcal{V}}_{-1}^{+}(1)$, in accordance with Theorem 3.16.
3.2 Chain local equivalence and  $j$-split spaces
$j$-split spaces
Using Theorem 3.16, we can determine the chain local equivalence class of ![]() $j$-split spaces. We start with some results on
$j$-split spaces. We start with some results on ![]() $j$-split chain complexes. First, write
$j$-split chain complexes. First, write ![]() ${\mathcal{S}}_{d}(n)$ for the free
${\mathcal{S}}_{d}(n)$ for the free ![]() ${\mathcal{G}}$-module generated by
${\mathcal{G}}$-module generated by
 $$\begin{eqnarray}\langle x_{d},x_{d+2},\ldots ,x_{d+2n-2}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\langle x_{d},x_{d+2},\ldots ,x_{d+2n-2}\rangle ,\end{eqnarray}$$ with ![]() $x_{i}$ of degree
$x_{i}$ of degree ![]() $i$ and
$i$ and  $\unicode[STIX]{x2202}(x_{i})=s(1+j^{2})x_{i-2}$. A quick computation gives
$\unicode[STIX]{x2202}(x_{i})=s(1+j^{2})x_{i-2}$. A quick computation gives  $H_{\ast }^{S^{1}}({\mathcal{S}}_{d}(n))={\mathcal{T}}_{d}^{+}(n)^{\oplus 2}$ as
$H_{\ast }^{S^{1}}({\mathcal{S}}_{d}(n))={\mathcal{T}}_{d}^{+}(n)^{\oplus 2}$ as ![]() $\mathbb{F}[U]$-modules, where
$\mathbb{F}[U]$-modules, where  $H_{\ast }^{S^{1}}(Z)$ is defined as in (20). Moreover, for an
$H_{\ast }^{S^{1}}(Z)$ is defined as in (20). Moreover, for an ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module  $J=\bigoplus _{i}{\mathcal{T}}_{e_{i}}^{+}(m_{i})$, let
$J=\bigoplus _{i}{\mathcal{T}}_{e_{i}}^{+}(m_{i})$, let  $S(J)=\bigoplus _{i}{\mathcal{S}}_{e_{i}}(m_{i})$.
$S(J)=\bigoplus _{i}{\mathcal{S}}_{e_{i}}(m_{i})$.
Proposition 3.18. Let  $C=\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,(C_{+}\oplus C_{-})$ be a
$C=\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,(C_{+}\oplus C_{-})$ be a ![]() $j$-split chain complex and
$j$-split chain complex and
 $$\begin{eqnarray}H_{\ast }^{S^{1}}(C)={\mathcal{T}}_{d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J^{\oplus 2},\end{eqnarray}$$
$$\begin{eqnarray}H_{\ast }^{S^{1}}(C)={\mathcal{T}}_{d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J^{\oplus 2},\end{eqnarray}$$ where  $d_{i+1}>d_{i}$ and
$d_{i+1}>d_{i}$ and  $2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$,
$2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$,  $2n_{N}+d_{N}\geqslant 3$, and
$2n_{N}+d_{N}\geqslant 3$, and ![]() $d_{N}\leqslant 1$. We interpret
$d_{N}\leqslant 1$. We interpret  $d_{N+1}=1$,
$d_{N+1}=1$,  $n_{N+1}=0$. Then
$n_{N+1}=0$. Then ![]() $C$ is homotopy equivalent to the chain complex
$C$ is homotopy equivalent to the chain complex
 $$\begin{eqnarray}\biggl(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\biggl(\mathop{\bigoplus }_{i}{\mathcal{S}}_{d_{i}}(n_{i})\biggr)\biggr)\oplus S(J),\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\biggl(\mathop{\bigoplus }_{i}{\mathcal{S}}_{d_{i}}(n_{i})\biggr)\biggr)\oplus S(J),\end{eqnarray}$$ where  $\unicode[STIX]{x2202}(f_{\text{red}})=0$,
$\unicode[STIX]{x2202}(f_{\text{red}})=0$,  $jf_{\text{red}}=f_{\text{red}},\,sf_{\text{red}}=0$, and
$jf_{\text{red}}=f_{\text{red}},\,sf_{\text{red}}=0$, and  $\text{deg}\,(f_{\text{red}})=0$. Furthermore, let each factor
$\text{deg}\,(f_{\text{red}})=0$. Furthermore, let each factor ![]() ${\mathcal{S}}_{d_{i}}(n_{i})$ have generators
${\mathcal{S}}_{d_{i}}(n_{i})$ have generators ![]() $x_{j}^{i}$, with
$x_{j}^{i}$, with  $\text{deg}\,x_{j}^{i}=j$. Then
$\text{deg}\,x_{j}^{i}=j$. Then  $\unicode[STIX]{x2202}x_{1}^{i}=f_{\text{red}}+s(1+j^{2})x_{-1}^{i}$ for all
$\unicode[STIX]{x2202}x_{1}^{i}=f_{\text{red}}+s(1+j^{2})x_{-1}^{i}$ for all ![]() $i$.
$i$.
Remark 3.19. By Lemma 3.10, for ![]() $C$ any
$C$ any ![]() $j$-split chain complex, a decomposition as in (63) is possible.
$j$-split chain complex, a decomposition as in (63) is possible.
Before giving the proof we establish a lemma.
Lemma 3.20. Let ![]() $F_{1},F_{2}$ be two free, finite
$F_{1},F_{2}$ be two free, finite  $C_{\ast }^{\text{CW}}(S^{1})$-complexes such that
$C_{\ast }^{\text{CW}}(S^{1})$-complexes such that  $H_{\ast }^{S^{1}}(F_{1})\cong H_{\ast }^{S^{1}}(F_{2})$ as
$H_{\ast }^{S^{1}}(F_{1})\cong H_{\ast }^{S^{1}}(F_{2})$ as ![]() $\mathbb{F}[U]$-modules. Then
$\mathbb{F}[U]$-modules. Then  $F_{1}\simeq F_{2}$, where
$F_{1}\simeq F_{2}$, where ![]() $\simeq$ denotes homotopy equivalence.
$\simeq$ denotes homotopy equivalence.
Proof. First, we note that  $C_{\ast }^{\text{CW}}(S^{1})$ is quasi-isomorphic to the algebra
$C_{\ast }^{\text{CW}}(S^{1})$ is quasi-isomorphic to the algebra  $\mathbb{F}[\bar{s}]/(\bar{s}^{2})$ where
$\mathbb{F}[\bar{s}]/(\bar{s}^{2})$ where  $\text{deg}(\bar{s})=1$ and
$\text{deg}(\bar{s})=1$ and  $\unicode[STIX]{x2202}(\bar{s})=0$. Koszul duality (see [Reference Goresky, Kottwitz and MacPhersonGKM98, Theorem 8.4]; there it is stated with
$\unicode[STIX]{x2202}(\bar{s})=0$. Koszul duality (see [Reference Goresky, Kottwitz and MacPhersonGKM98, Theorem 8.4]; there it is stated with ![]() $\mathbb{Z}$-coefficients, but also holds over
$\mathbb{Z}$-coefficients, but also holds over ![]() $\mathbb{F}$) is an equivalence of categories
$\mathbb{F}$) is an equivalence of categories ![]() $t$ from the derived category of bounded-below
$t$ from the derived category of bounded-below  $\mathbb{F}[s]/(s^{2})$-dgmodules to the derived category of bounded-below
$\mathbb{F}[s]/(s^{2})$-dgmodules to the derived category of bounded-below ![]() $\mathbb{F}[U]$-dgmodules, so that
$\mathbb{F}[U]$-dgmodules, so that  $H_{S^{1}}^{\ast }(X)=H^{\ast }(t(X))$ for
$H_{S^{1}}^{\ast }(X)=H^{\ast }(t(X))$ for ![]() $X$ a
$X$ a  $\mathbb{F}[s]/(s^{2})$-dgmodule. Then
$\mathbb{F}[s]/(s^{2})$-dgmodule. Then ![]() $F_{1}$ and
$F_{1}$ and ![]() $F_{2}$ are quasi-isomorphic as
$F_{2}$ are quasi-isomorphic as  $\mathbb{F}[\bar{s}]/(\bar{s}^{2})$ modules if and only if their Koszul duals
$\mathbb{F}[\bar{s}]/(\bar{s}^{2})$ modules if and only if their Koszul duals ![]() $t(F_{1})$ and
$t(F_{1})$ and ![]() $t(F_{2})$ are quasi-isomorphic. However,
$t(F_{2})$ are quasi-isomorphic. However, ![]() $t(F_{i})$ are, by construction, free, finitely-generated bounded-below
$t(F_{i})$ are, by construction, free, finitely-generated bounded-below ![]() $\mathbb{F}[U]$-dgmodules; such are quasi-isomorphic if and only if they have the same homology (as may be checked directly). By our original hypothesis,
$\mathbb{F}[U]$-dgmodules; such are quasi-isomorphic if and only if they have the same homology (as may be checked directly). By our original hypothesis,  $H_{\ast }^{S^{1}}(F_{1})$ and
$H_{\ast }^{S^{1}}(F_{1})$ and  $H_{\ast }^{S^{1}}(F_{2})$ are isomorphic as
$H_{\ast }^{S^{1}}(F_{2})$ are isomorphic as ![]() $\mathbb{F}[U]$-modules which also implies
$\mathbb{F}[U]$-modules which also implies  $H_{S^{1}}^{\ast }(F_{1})\cong H_{S^{1}}^{\ast }(F_{2})$, so we see that
$H_{S^{1}}^{\ast }(F_{1})\cong H_{S^{1}}^{\ast }(F_{2})$, so we see that ![]() $F_{1}$ and
$F_{1}$ and ![]() $F_{2}$ are quasi-isomorphic. Finally, by [Reference WeibelWei94, Theorem 10.4.8], quasi-isomorphic free chain complexes are chain homotopy equivalent, and so
$F_{2}$ are quasi-isomorphic. Finally, by [Reference WeibelWei94, Theorem 10.4.8], quasi-isomorphic free chain complexes are chain homotopy equivalent, and so ![]() $F_{1}$ and
$F_{1}$ and ![]() $F_{2}$ are chain homotopy equivalent. This establishes the lemma.◻
$F_{2}$ are chain homotopy equivalent. This establishes the lemma.◻
Proof of Proposition 3.18.
The proof is in two steps: first, we show that ![]() $C_{+}$ is chain homotopy equivalent to a chain complex of a certain form, and then we investigate differentials from
$C_{+}$ is chain homotopy equivalent to a chain complex of a certain form, and then we investigate differentials from ![]() $C_{+}$ to
$C_{+}$ to ![]() $\langle f_{\text{red}}\rangle$.
$\langle f_{\text{red}}\rangle$.
Note that the complex ![]() $C_{+}$ is a
$C_{+}$ is a  $C_{\ast }^{\text{CW}}(S^{1})$-complex. Let
$C_{\ast }^{\text{CW}}(S^{1})$-complex. Let ![]() ${\mathcal{S}}_{d}^{S^{1}}(n)$ be the
${\mathcal{S}}_{d}^{S^{1}}(n)$ be the  $C_{\ast }^{\text{CW}}(S^{1})$-submodule of
$C_{\ast }^{\text{CW}}(S^{1})$-submodule of ![]() ${\mathcal{S}}_{d}(n)$ generated (as a
${\mathcal{S}}_{d}(n)$ generated (as a  $C_{\ast }^{\text{CW}}(S^{1})$-module) by
$C_{\ast }^{\text{CW}}(S^{1})$-module) by  $\langle x_{d},x_{d+2},\ldots ,x_{d+2n-2}\rangle$. As for
$\langle x_{d},x_{d+2},\ldots ,x_{d+2n-2}\rangle$. As for ![]() ${\mathcal{S}}_{d}(n)$, a quick calculation shows
${\mathcal{S}}_{d}(n)$, a quick calculation shows  $H_{\ast }^{S^{1}}({\mathcal{S}}_{d}^{S^{1}}(n))={\mathcal{T}}_{d}^{+}(n)$. Similarly, for an
$H_{\ast }^{S^{1}}({\mathcal{S}}_{d}^{S^{1}}(n))={\mathcal{T}}_{d}^{+}(n)$. Similarly, for an ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module  $J=\bigoplus _{i}{\mathcal{T}}_{e_{i}}^{+}(m_{i})$, let
$J=\bigoplus _{i}{\mathcal{T}}_{e_{i}}^{+}(m_{i})$, let  $S^{S^{1}}(J)=\bigoplus _{i}{\mathcal{S}}_{e_{i}}^{S^{1}}(n_{i})$. We see
$S^{S^{1}}(J)=\bigoplus _{i}{\mathcal{S}}_{e_{i}}^{S^{1}}(n_{i})$. We see
 $$\begin{eqnarray}S(J)\cong S^{S^{1}}(J)\oplus S^{S^{1}}(J),\end{eqnarray}$$
$$\begin{eqnarray}S(J)\cong S^{S^{1}}(J)\oplus S^{S^{1}}(J),\end{eqnarray}$$ as ![]() ${\mathcal{G}}$-complexes, for all
${\mathcal{G}}$-complexes, for all ![]() $\mathbb{F}[U]$-modules
$\mathbb{F}[U]$-modules ![]() $J$, where the action of
$J$, where the action of ![]() $j$ on the right is given by interchanging the factors.
$j$ on the right is given by interchanging the factors.
Recall, by the proof of Theorem 3.16, that  $H_{\ast }^{S^{1}}(C_{+}\oplus C_{-})$ is determined by
$H_{\ast }^{S^{1}}(C_{+}\oplus C_{-})$ is determined by  $H_{\ast }^{S^{1}}(C)$ for
$H_{\ast }^{S^{1}}(C)$ for ![]() $C$ a
$C$ a ![]() $j$-split chain complex (see Remark 3.17). That is, from (63),
$j$-split chain complex (see Remark 3.17). That is, from (63),
 $$\begin{eqnarray}H_{\ast }^{S^{1}}(C_{+})=\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J.\end{eqnarray}$$
$$\begin{eqnarray}H_{\ast }^{S^{1}}(C_{+})=\bigoplus _{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J.\end{eqnarray}$$ Lemma 3.20 then implies  $C_{+}=\bigoplus _{i=1}^{N}\,{\mathcal{S}}_{d_{i}}^{S^{1}}(n_{i})\,\oplus \,S^{S^{1}}(J)$ as a
$C_{+}=\bigoplus _{i=1}^{N}\,{\mathcal{S}}_{d_{i}}^{S^{1}}(n_{i})\,\oplus \,S^{S^{1}}(J)$ as a  $C_{\ast }^{\text{CW}}(S^{1})$-complex. Since
$C_{\ast }^{\text{CW}}(S^{1})$-complex. Since  $j:C_{+}\rightarrow C_{-}$ is an isomorphism, we have, from (65),
$j:C_{+}\rightarrow C_{-}$ is an isomorphism, we have, from (65),
 $$\begin{eqnarray}C_{+}\oplus C_{-}\cong \bigoplus _{i}{\mathcal{S}}_{d_{i}}(n_{i})\oplus S(J).\end{eqnarray}$$
$$\begin{eqnarray}C_{+}\oplus C_{-}\cong \bigoplus _{i}{\mathcal{S}}_{d_{i}}(n_{i})\oplus S(J).\end{eqnarray}$$ Moreover,  $H_{\ast }^{S^{1}}(C)$ determines the map
$H_{\ast }^{S^{1}}(C)$ determines the map  $d_{S^{1}}:H_{\ast }^{S^{1}}(C_{+})\rightarrow H_{\ast }^{S^{1}}(\langle f_{\text{red}}\rangle )$. We compute
$d_{S^{1}}:H_{\ast }^{S^{1}}(C_{+})\rightarrow H_{\ast }^{S^{1}}(\langle f_{\text{red}}\rangle )$. We compute ![]() $d_{S^{1}}$ a different way, by using the differential from
$d_{S^{1}}$ a different way, by using the differential from ![]() $C_{+}$ to
$C_{+}$ to ![]() $\langle f_{\text{red}}\rangle$, and the form of
$\langle f_{\text{red}}\rangle$, and the form of ![]() $C_{+}$ determined by (66). Fix a pair of integers
$C_{+}$ determined by (66). Fix a pair of integers ![]() $(d,n)$. If
$(d,n)$. If ![]() $x_{i}$ is the generator of a copy of
$x_{i}$ is the generator of a copy of ![]() ${\mathcal{S}}_{d}(n)$ in degree
${\mathcal{S}}_{d}(n)$ in degree ![]() $i$ and
$i$ and  $x_{i}\in C_{+}$, then
$x_{i}\in C_{+}$, then  $d_{S^{1}}:H_{\ast }^{S^{1}}({\mathcal{S}}_{d}(n))\cong {\mathcal{T}}_{d}^{+}(n)\rightarrow {\mathcal{T}}^{+}$ is nontrivial if and only if
$d_{S^{1}}:H_{\ast }^{S^{1}}({\mathcal{S}}_{d}(n))\cong {\mathcal{T}}_{d}^{+}(n)\rightarrow {\mathcal{T}}^{+}$ is nontrivial if and only if  $\unicode[STIX]{x2202}(x_{1})=f_{\text{red}}+s(1+j^{2})x_{-1}$. Thus, since
$\unicode[STIX]{x2202}(x_{1})=f_{\text{red}}+s(1+j^{2})x_{-1}$. Thus, since ![]() $d_{S^{1}}$ is nonvanishing on the factors
$d_{S^{1}}$ is nonvanishing on the factors  ${\mathcal{T}}_{d_{i}}^{+}(n_{i})\subset H_{\ast }^{S^{1}}(C_{+})$ and vanishing elsewhere, each generator
${\mathcal{T}}_{d_{i}}^{+}(n_{i})\subset H_{\ast }^{S^{1}}(C_{+})$ and vanishing elsewhere, each generator ![]() $x_{1}^{i}$, with
$x_{1}^{i}$, with  $\text{deg}\,x_{1}^{i}=1$ of
$\text{deg}\,x_{1}^{i}=1$ of ![]() ${\mathcal{S}}_{d_{i}}(n_{i})$ in (66) must have
${\mathcal{S}}_{d_{i}}(n_{i})$ in (66) must have  $\unicode[STIX]{x2202}(x_{1}^{i})=f_{\text{red}}+s(1+j^{2})x_{-1}^{i}$, and all other differentials
$\unicode[STIX]{x2202}(x_{1}^{i})=f_{\text{red}}+s(1+j^{2})x_{-1}^{i}$, and all other differentials  $C_{+}\rightarrow \langle f_{\text{red}}\rangle$ vanish. Thus, in particular,
$C_{+}\rightarrow \langle f_{\text{red}}\rangle$ vanish. Thus, in particular,  $\unicode[STIX]{x2202}(S(J))\subset S(J)$. The decomposition (64) follows.◻
$\unicode[STIX]{x2202}(S(J))\subset S(J)$. The decomposition (64) follows.◻
Proposition 3.21. Let  $(X,p,h/4)\in \mathfrak{E}$ with
$(X,p,h/4)\in \mathfrak{E}$ with ![]() $X$ a
$X$ a ![]() $j$-split space of type SWF at level
$j$-split space of type SWF at level ![]() $m$, and
$m$, and
 $$\begin{eqnarray}\hspace{-5.0pt}\tilde{H}_{\ast }^{S^{1}}((X,p,h/4))={\mathcal{T}}_{s+d_{1}+2n_{1}+1}^{+}\,\oplus \,\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\,\oplus \,J^{\oplus 2}[-s],\hspace{-3.0pt}\end{eqnarray}$$
$$\begin{eqnarray}\hspace{-5.0pt}\tilde{H}_{\ast }^{S^{1}}((X,p,h/4))={\mathcal{T}}_{s+d_{1}+2n_{1}+1}^{+}\,\oplus \,\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\,\oplus \,J^{\oplus 2}[-s],\hspace{-3.0pt}\end{eqnarray}$$ where  $d_{i+1}>d_{i}$ and
$d_{i+1}>d_{i}$ and  $2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$, as well as
$2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$, as well as  $2n_{N}+d_{N}\geqslant 3$, and
$2n_{N}+d_{N}\geqslant 3$, and ![]() $d_{N}\leqslant 1$. Then the chain local equivalence type
$d_{N}\leqslant 1$. Then the chain local equivalence type  $[(C_{\ast }^{\text{CW}}(X,\text{pt}),p,h/4)]_{\text{cl}}\in \mathfrak{CLE}$ is the equivalence class of
$[(C_{\ast }^{\text{CW}}(X,\text{pt}),p,h/4)]_{\text{cl}}\in \mathfrak{CLE}$ is the equivalence class of
 $$\begin{eqnarray}C(p-m,h/4,\{{d_{i}\}}_{i},\{{n_{i}\}}_{i}):=\biggl(\biggl(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\biggl(\bigoplus _{i}{\mathcal{S}}_{d_{i}}(n_{i})\biggr)\biggr),p-m,h/4\biggr)\in \mathfrak{CLE}.\end{eqnarray}$$
$$\begin{eqnarray}C(p-m,h/4,\{{d_{i}\}}_{i},\{{n_{i}\}}_{i}):=\biggl(\biggl(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\biggl(\bigoplus _{i}{\mathcal{S}}_{d_{i}}(n_{i})\biggr)\biggr),p-m,h/4\biggr)\in \mathfrak{CLE}.\end{eqnarray}$$ The connected ![]() $S^{1}$-homology of
$S^{1}$-homology of  $(X,p,h/4)$ is given by
$(X,p,h/4)$ is given by
 $$\begin{eqnarray}H_{\text{conn}}^{S^{1}}((X,p,h/4))=\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i}).\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{conn}}^{S^{1}}((X,p,h/4))=\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i}).\end{eqnarray}$$ Further, ![]() $s$ in (67) is
$s$ in (67) is  $m-p-h$. Moreover,
$m-p-h$. Moreover,  $C(p,h/4,\{d_{i}\},\{n_{i}\})$ is chain locally equivalent to
$C(p,h/4,\{d_{i}\},\{n_{i}\})$ is chain locally equivalent to  $C(p^{\prime },h^{\prime }/4,\{d_{i}^{\prime }\},\{n_{i}^{\prime }\})$ if and only if
$C(p^{\prime },h^{\prime }/4,\{d_{i}^{\prime }\},\{n_{i}^{\prime }\})$ if and only if ![]() $p=p^{\prime }$,
$p=p^{\prime }$, ![]() $h=h^{\prime }$,
$h=h^{\prime }$,  $\{d_{i}\}=\{d_{i}^{\prime }\}$, and
$\{d_{i}\}=\{d_{i}^{\prime }\}$, and  $\{n_{i}\}=\{n_{i}^{\prime }\}$.
$\{n_{i}\}=\{n_{i}^{\prime }\}$.
Proof. Write  $[(A,b,c)]_{\text{cl}}$ for the chain local equivalence class of
$[(A,b,c)]_{\text{cl}}$ for the chain local equivalence class of  $(A,b,c)\in \mathfrak{CE}$. Let
$(A,b,c)\in \mathfrak{CE}$. Let  $[(Z,-m,0)]=[C_{\ast }^{\text{CW}}(X,\text{pt})]\in \mathfrak{CE}$ where
$[(Z,-m,0)]=[C_{\ast }^{\text{CW}}(X,\text{pt})]\in \mathfrak{CE}$ where ![]() $Z$ is a
$Z$ is a ![]() $j$-split chain complex, as allowed by Lemma 3.2. Using Proposition 3.18, we see
$j$-split chain complex, as allowed by Lemma 3.2. Using Proposition 3.18, we see
 $$\begin{eqnarray}[(Z,p,h/4)]_{\text{cl}}=\big(\big(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\bigoplus {\mathcal{S}}_{d_{i}}(n_{i})\big),p,h/4\big).\end{eqnarray}$$
$$\begin{eqnarray}[(Z,p,h/4)]_{\text{cl}}=\big(\big(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\bigoplus {\mathcal{S}}_{d_{i}}(n_{i})\big),p,h/4\big).\end{eqnarray}$$We have then
 $$\begin{eqnarray}C(p-m,h/4,\{d_{i}\},\{n_{i}\})=[(Z,p-m,h/4)]_{\text{cl}}=[(C_{\ast }^{\text{CW}}(X,\text{pt}),p,h/4)]_{\text{cl}},\end{eqnarray}$$
$$\begin{eqnarray}C(p-m,h/4,\{d_{i}\},\{n_{i}\})=[(Z,p-m,h/4)]_{\text{cl}}=[(C_{\ast }^{\text{CW}}(X,\text{pt}),p,h/4)]_{\text{cl}},\end{eqnarray}$$as in (68).
To prove (69) we consider the complex  $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})[4\lfloor (-d_{1}+3)/4\rfloor ]$ (we include the grading shift for convenience). We will see that it is homotopy equivalent to a suspensionlike complex, so we may apply the results of § 2.5. First, recall that
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})[4\lfloor (-d_{1}+3)/4\rfloor ]$ (we include the grading shift for convenience). We will see that it is homotopy equivalent to a suspensionlike complex, so we may apply the results of § 2.5. First, recall that  $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{N}}\langle f_{\text{red}}\rangle \simeq H_{n}$, as in the proof of Lemma 2.25, for a complex
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{N}}\langle f_{\text{red}}\rangle \simeq H_{n}$, as in the proof of Lemma 2.25, for a complex ![]() $H_{n}$ on generators
$H_{n}$ on generators ![]() $f,y_{4k+i}$ for
$f,y_{4k+i}$ for  $0\leqslant k\leqslant N-1$,
$0\leqslant k\leqslant N-1$,  $i=1,2,3$. Also, recall that for a free
$i=1,2,3$. Also, recall that for a free ![]() ${\mathcal{G}}$-module
${\mathcal{G}}$-module ![]() $M$,
$M$,  $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{N}}M\simeq M[-4N]$. Putting this together, there is then a homotopy equivalence:
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{N}}M\simeq M[-4N]$. Putting this together, there is then a homotopy equivalence:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})\bigg[4\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor\bigg]\nonumber\\ \displaystyle & & \displaystyle \qquad \simeq \langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\mathop{\bigoplus }_{k}\langle y_{k}\rangle \,\tilde{\oplus }\,\mathop{\bigoplus }_{i=1}^{N}\mathop{\bigoplus }_{\{k\equiv 1\;\text{mod}\;2,\;d_{i}\leqslant k\leqslant d_{i}+2n_{i}-2\}}\langle z_{k}^{i}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})\bigg[4\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor\bigg]\nonumber\\ \displaystyle & & \displaystyle \qquad \simeq \langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\mathop{\bigoplus }_{k}\langle y_{k}\rangle \,\tilde{\oplus }\,\mathop{\bigoplus }_{i=1}^{N}\mathop{\bigoplus }_{\{k\equiv 1\;\text{mod}\;2,\;d_{i}\leqslant k\leqslant d_{i}+2n_{i}-2\}}\langle z_{k}^{i}\rangle ,\end{eqnarray}$$where
 $$\begin{eqnarray}\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\mathop{\bigoplus }_{k}\langle y_{k}\rangle \simeq \unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}\langle f_{\text{red}}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\mathop{\bigoplus }_{k}\langle y_{k}\rangle \simeq \unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}\langle f_{\text{red}}\rangle ,\end{eqnarray}$$ and  $\text{deg}\,z_{k}^{i}=\text{deg}\,y_{k}=k$. Additionally,
$\text{deg}\,z_{k}^{i}=\text{deg}\,y_{k}=k$. Additionally,  $\unicode[STIX]{x2202}(z_{k}^{i})=s(1+j^{2})z_{k-2}^{i}$ if
$\unicode[STIX]{x2202}(z_{k}^{i})=s(1+j^{2})z_{k-2}^{i}$ if ![]() $k\neq 1$, and
$k\neq 1$, and  $\unicode[STIX]{x2202}(z_{1}^{i})=s(1+j^{2})z_{-1}^{i}+s(1+j)^{3}y_{-1}$. The
$\unicode[STIX]{x2202}(z_{1}^{i})=s(1+j^{2})z_{-1}^{i}+s(1+j)^{3}y_{-1}$. The ![]() $y_{k}$ are defined for
$y_{k}$ are defined for ![]() $k$ such that
$k$ such that  $k\not \equiv 0\;\text{mod}\;4$ and
$k\not \equiv 0\;\text{mod}\;4$ and  $-4\lfloor (-d_{1}+3)/4\rfloor +1\leqslant k\leqslant -1$. Also,
$-4\lfloor (-d_{1}+3)/4\rfloor +1\leqslant k\leqslant -1$. Also,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{4k+1}) & = & \displaystyle s(1+j)^{3}y_{4k-1},\quad k\neq -\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{4k+1}) & = & \displaystyle s(1+j)^{3}y_{4k-1},\quad k\neq -\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor,\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{4k+2}) & = & \displaystyle (1+j)y_{4k+1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{4k+2}) & = & \displaystyle (1+j)y_{4k+1},\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{4k+3}) & = & \displaystyle (1+j)y_{4k+2}+sy_{4k+1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{4k+3}) & = & \displaystyle (1+j)y_{4k+2}+sy_{4k+1},\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{-4\lfloor (-d_{1}+3)/4\rfloor +1}) & = & \displaystyle f_{\text{red}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(y_{-4\lfloor (-d_{1}+3)/4\rfloor +1}) & = & \displaystyle f_{\text{red}}.\end{eqnarray}$$ According to (71), the first two terms on the right of (70) account for the suspension of the reducible tower, and the ![]() $z_{k}^{i}$ correspond to the suspension of the free part. The
$z_{k}^{i}$ correspond to the suspension of the free part. The ![]() $z_{k}^{i}$ are suspensions of
$z_{k}^{i}$ are suspensions of  $x_{k}^{i}\in {\mathcal{S}}_{d_{i}}(n_{i})\subset C(0,0,\{d_{i}\},\{n_{i}\})$. From this presentation, it is clear that the chain complex
$x_{k}^{i}\in {\mathcal{S}}_{d_{i}}(n_{i})\subset C(0,0,\{d_{i}\},\{n_{i}\})$. From this presentation, it is clear that the chain complex  $\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})[4\lfloor (-d_{1}+3)/4\rfloor ]$ is irreducible (that is, it may not be written as a nontrivial direct sum of
$\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})[4\lfloor (-d_{1}+3)/4\rfloor ]$ is irreducible (that is, it may not be written as a nontrivial direct sum of ![]() ${\mathcal{G}}$-chain complexes). Then by Lemma 2.31 and Definition 2.32,
${\mathcal{G}}$-chain complexes). Then by Lemma 2.31 and Definition 2.32,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})\bigg[4\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor\bigg]\biggr)_{\text{conn}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})\bigg[4\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor\bigg].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})\bigg[4\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor\bigg]\biggr)_{\text{conn}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D6F4}^{\mathbb{H}^{\lfloor (-d_{1}+3)/4\rfloor }}C(0,0,\{d_{i}\},\{n_{i}\})\bigg[4\biggl\lfloor\frac{-d_{1}+3}{4}\biggr\rfloor\bigg].\end{eqnarray}$$ Then (69) follows from the definition of ![]() $H_{\text{conn}}^{S^{1}}$, applied to
$H_{\text{conn}}^{S^{1}}$, applied to  $C(0,0,\{d_{i}\},\{n_{i}\})$. The calculation of
$C(0,0,\{d_{i}\},\{n_{i}\})$. The calculation of  $H_{\text{conn}}^{S^{1}}((X,p,h/4))$ for nonzero
$H_{\text{conn}}^{S^{1}}((X,p,h/4))$ for nonzero ![]() $m,p,h$ follows, since
$m,p,h$ follows, since
 $$\begin{eqnarray}C(p-m,h/4,\{d_{i}\},\{n_{i}\})=\unicode[STIX]{x1D6F4}^{(m-p)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{-(h/4)\mathbb{H}}C(0,0,\{d_{i}\},\{n_{i}\}).\end{eqnarray}$$
$$\begin{eqnarray}C(p-m,h/4,\{d_{i}\},\{n_{i}\})=\unicode[STIX]{x1D6F4}^{(m-p)\tilde{\mathbb{R}}}\unicode[STIX]{x1D6F4}^{-(h/4)\mathbb{H}}C(0,0,\{d_{i}\},\{n_{i}\}).\end{eqnarray}$$ The assertion that  $s=m-p-h$ follows from the homology calculation of Theorem 3.16.
$s=m-p-h$ follows from the homology calculation of Theorem 3.16.
Recall that ![]() $H_{\text{conn}}^{S^{1}}$ is a chain local equivalence invariant. Hence, if
$H_{\text{conn}}^{S^{1}}$ is a chain local equivalence invariant. Hence, if  $[C(p,h/4,\{d_{i}\},\{n_{i}\})]_{\text{cl}}=[C(p^{\prime },h^{\prime }/4,\{d_{i}^{\prime }\},\{n_{i}^{\prime }\})]_{\text{cl}}$, we see from (69) that
$[C(p,h/4,\{d_{i}\},\{n_{i}\})]_{\text{cl}}=[C(p^{\prime },h^{\prime }/4,\{d_{i}^{\prime }\},\{n_{i}^{\prime }\})]_{\text{cl}}$, we see from (69) that  $\{d_{i}\}=\{d_{i}^{\prime }\},$
$\{d_{i}\}=\{d_{i}^{\prime }\},$ $\{n_{i}\}=\{n_{i}^{\prime }\}$, and
$\{n_{i}\}=\{n_{i}^{\prime }\}$, and  $p+h=p^{\prime }+h^{\prime }$. Furthermore, if
$p+h=p^{\prime }+h^{\prime }$. Furthermore, if  $C(p,h/4,\{d_{i}\},\{n_{i}\})$ and
$C(p,h/4,\{d_{i}\},\{n_{i}\})$ and  $C(p^{\prime },h^{\prime }/4,\{d_{i}^{\prime }\},\{n_{i}^{\prime }\})$ are chain locally equivalent, they must have chain homotopy equivalent fixed-point sets. That is,
$C(p^{\prime },h^{\prime }/4,\{d_{i}^{\prime }\},\{n_{i}^{\prime }\})$ are chain locally equivalent, they must have chain homotopy equivalent fixed-point sets. That is, ![]() $p=p^{\prime }$ and so also
$p=p^{\prime }$ and so also ![]() $h=h^{\prime }$, completing the proof.◻
$h=h^{\prime }$, completing the proof.◻
4 Seiberg–Witten Floer spectra and Floer homologies
4.1 Finite-dimensional approximation
In this section we review the finite-dimensional approximation to the Seiberg–Witten equations from Manolescu [Reference ManolescuMan03, Reference ManolescuMan16].
Let ![]() $\mathbb{S}$ be the spinor bundle of the three-manifold with spin structure
$\mathbb{S}$ be the spinor bundle of the three-manifold with spin structure ![]() $(Y,\mathfrak{s})$, and
$(Y,\mathfrak{s})$, and ![]() $\unicode[STIX]{x1D6E4}(\mathbb{S})$ its space of sections. Let
$\unicode[STIX]{x1D6E4}(\mathbb{S})$ its space of sections. Let ![]() $D$ denote the Dirac operator. Let
$D$ denote the Dirac operator. Let  $W=\text{ker}\,d^{\ast }\oplus \unicode[STIX]{x1D6E4}(\mathbb{S})$ be the global Coulomb slice, a vector subspace of an appropriate Sobolev completion of
$W=\text{ker}\,d^{\ast }\oplus \unicode[STIX]{x1D6E4}(\mathbb{S})$ be the global Coulomb slice, a vector subspace of an appropriate Sobolev completion of  $\unicode[STIX]{x1D6FA}^{1}(Y,i\mathbb{R})\oplus \unicode[STIX]{x1D6E4}(\mathbb{S})$. For
$\unicode[STIX]{x1D6FA}^{1}(Y,i\mathbb{R})\oplus \unicode[STIX]{x1D6E4}(\mathbb{S})$. For  $\unicode[STIX]{x1D706}\in (0,\infty )$, the Seiberg–Witten equations of
$\unicode[STIX]{x1D706}\in (0,\infty )$, the Seiberg–Witten equations of ![]() $(Y,\mathfrak{s},g)$ determine a sequence of vector fields
$(Y,\mathfrak{s},g)$ determine a sequence of vector fields ![]() ${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$ on finite-dimensional vector spaces
${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$ on finite-dimensional vector spaces ![]() $W^{\unicode[STIX]{x1D706}}$. Here
$W^{\unicode[STIX]{x1D706}}$. Here ![]() $W^{\unicode[STIX]{x1D706}}$ is the span of eigenvectors of the elliptic operator
$W^{\unicode[STIX]{x1D706}}$ is the span of eigenvectors of the elliptic operator  $\ell =\ast d+D$ acting on
$\ell =\ast d+D$ acting on ![]() $W$, with eigenvalue in
$W$, with eigenvalue in ![]() $(-\unicode[STIX]{x1D706},\unicode[STIX]{x1D706})$. The vector field
$(-\unicode[STIX]{x1D706},\unicode[STIX]{x1D706})$. The vector field ![]() ${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$ on
${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$ on ![]() $W^{\unicode[STIX]{x1D706}}$ is an approximation of the Seiberg–Witten equations restricted to
$W^{\unicode[STIX]{x1D706}}$ is an approximation of the Seiberg–Witten equations restricted to ![]() $W^{\unicode[STIX]{x1D706}}$. The action of
$W^{\unicode[STIX]{x1D706}}$. The action of  $G=\text{Pin}(2)$ on
$G=\text{Pin}(2)$ on ![]() $\unicode[STIX]{x1D6E4}(\mathbb{S})$ restricts to a smooth action on
$\unicode[STIX]{x1D6E4}(\mathbb{S})$ restricts to a smooth action on ![]() $W^{\unicode[STIX]{x1D706}}$ that commutes with the flow defined by
$W^{\unicode[STIX]{x1D706}}$ that commutes with the flow defined by ![]() ${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$, and we define an action of
${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$, and we define an action of ![]() $G$ on
$G$ on ![]() $\unicode[STIX]{x1D6FA}^{1}$ by letting
$\unicode[STIX]{x1D6FA}^{1}$ by letting ![]() $j$ act by
$j$ act by ![]() $-1$ and
$-1$ and ![]() $S^{1}$ act trivially. There is a distinguished subspace
$S^{1}$ act trivially. There is a distinguished subspace  $W(-\unicode[STIX]{x1D706},0)\subset W^{\unicode[STIX]{x1D706}}$ consisting of the span of the eigenvectors with eigenvalue in
$W(-\unicode[STIX]{x1D706},0)\subset W^{\unicode[STIX]{x1D706}}$ consisting of the span of the eigenvectors with eigenvalue in ![]() $(-\unicode[STIX]{x1D706},0)$. Following [Reference ManolescuMan03], we will use the sequence of flows on the spaces
$(-\unicode[STIX]{x1D706},0)$. Following [Reference ManolescuMan03], we will use the sequence of flows on the spaces ![]() $W^{\unicode[STIX]{x1D706}}$ to define an invariant of
$W^{\unicode[STIX]{x1D706}}$ to define an invariant of ![]() $(Y,\mathfrak{s})$.
$(Y,\mathfrak{s})$.
We next recall a few properties of the Conley Index. For a one-parameter family ![]() $\unicode[STIX]{x1D719}_{t}$ of diffeomorphisms of a manifold
$\unicode[STIX]{x1D719}_{t}$ of diffeomorphisms of a manifold ![]() $M$ and a compact subset
$M$ and a compact subset ![]() $A\subset M$, we define
$A\subset M$, we define
 $$\begin{eqnarray}\text{Inv}(A,\unicode[STIX]{x1D719})=\{x\in A\mid \unicode[STIX]{x1D719}_{t}(x)\in A\;\text{for}\;\text{all}\;t\in \mathbb{R}\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}(A,\unicode[STIX]{x1D719})=\{x\in A\mid \unicode[STIX]{x1D719}_{t}(x)\in A\;\text{for}\;\text{all}\;t\in \mathbb{R}\}.\end{eqnarray}$$ Then we say that a set ![]() $S\subset M$ is an isolated invariant set if there is some
$S\subset M$ is an isolated invariant set if there is some ![]() $A$ as above such that
$A$ as above such that  $S=\text{Inv}(A,\unicode[STIX]{x1D719})\subset \text{int}(A)$. Conley proved in [Reference ConleyCon78] that one may associate to any isolated invariant set
$S=\text{Inv}(A,\unicode[STIX]{x1D719})\subset \text{int}(A)$. Conley proved in [Reference ConleyCon78] that one may associate to any isolated invariant set ![]() $S$ a pointed homotopy type
$S$ a pointed homotopy type ![]() $I(S)$, an invariant of the triple
$I(S)$, an invariant of the triple  $(M,\unicode[STIX]{x1D719}_{t},S)$. Floer [Reference FloerFlo87] and Pruszko [Reference PruszkoPru99] defined an equivariant version, so that if a compact Lie group
$(M,\unicode[STIX]{x1D719}_{t},S)$. Floer [Reference FloerFlo87] and Pruszko [Reference PruszkoPru99] defined an equivariant version, so that if a compact Lie group ![]() $K$ acts smoothly on
$K$ acts smoothly on ![]() $M$ preserving the flow
$M$ preserving the flow ![]() $\unicode[STIX]{x1D719}_{t}$, then we may associate a pointed
$\unicode[STIX]{x1D719}_{t}$, then we may associate a pointed ![]() $K$-equivariant homotopy type
$K$-equivariant homotopy type ![]() $I_{K}(S)$. The Conley Index, as well as its equivariant refinement, are invariant under continuous changes of the flow, if
$I_{K}(S)$. The Conley Index, as well as its equivariant refinement, are invariant under continuous changes of the flow, if ![]() $S$ is isolated in an appropriate sense.
$S$ is isolated in an appropriate sense.
For ![]() $\unicode[STIX]{x1D706}$ sufficiently large, Manolescu showed in [Reference ManolescuMan16] that
$\unicode[STIX]{x1D706}$ sufficiently large, Manolescu showed in [Reference ManolescuMan16] that ![]() $S^{\unicode[STIX]{x1D706}}$, the set of all critical points of
$S^{\unicode[STIX]{x1D706}}$, the set of all critical points of ![]() ${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$, along with all trajectories of finite type between them contained in a certain sufficiently large ball in
${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$, along with all trajectories of finite type between them contained in a certain sufficiently large ball in ![]() $W^{\unicode[STIX]{x1D706}}$, is an isolated invariant set, and that the flow
$W^{\unicode[STIX]{x1D706}}$, is an isolated invariant set, and that the flow ![]() ${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$ is
${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$ is ![]() $G$-equivariant. We then write
$G$-equivariant. We then write  $I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g)=I_{G}(S^{\unicode[STIX]{x1D706}})$. To make this construction independent of
$I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g)=I_{G}(S^{\unicode[STIX]{x1D706}})$. To make this construction independent of ![]() $\unicode[STIX]{x1D706}$, we desuspend by
$\unicode[STIX]{x1D706}$, we desuspend by  $W(-\unicode[STIX]{x1D706},0)$. Then we can define a pointed stable homotopy type associated to a tuple
$W(-\unicode[STIX]{x1D706},0)$. Then we can define a pointed stable homotopy type associated to a tuple ![]() $(Y,\mathfrak{s},g)$:
$(Y,\mathfrak{s},g)$:
 $$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s},g)=\unicode[STIX]{x1D6F4}^{-W(-\unicode[STIX]{x1D706},0)}I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s},g)=\unicode[STIX]{x1D6F4}^{-W(-\unicode[STIX]{x1D706},0)}I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g).\end{eqnarray}$$ The desuspension in (77) is interpreted in ![]() $\mathfrak{E}$. That is,
$\mathfrak{E}$. That is,
 $$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s},g)=(I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g),\text{dim}_{\mathbb{R}}\;W(-\unicode[STIX]{x1D706},0)(\tilde{\mathbb{R}}),\text{dim}_{\mathbb{H}}\;W(-\unicode[STIX]{x1D706},0)(\mathbb{H})),\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s},g)=(I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g),\text{dim}_{\mathbb{R}}\;W(-\unicode[STIX]{x1D706},0)(\tilde{\mathbb{R}}),\text{dim}_{\mathbb{H}}\;W(-\unicode[STIX]{x1D706},0)(\mathbb{H})),\end{eqnarray}$$ where  $W(-\unicode[STIX]{x1D706},0)\cong W(-\unicode[STIX]{x1D706},0)(\tilde{\mathbb{R}})\oplus W(-\unicode[STIX]{x1D706},0)(\mathbb{H})$, and
$W(-\unicode[STIX]{x1D706},0)\cong W(-\unicode[STIX]{x1D706},0)(\tilde{\mathbb{R}})\oplus W(-\unicode[STIX]{x1D706},0)(\mathbb{H})$, and  $W(-\unicode[STIX]{x1D706},0)(\tilde{\mathbb{R}})$ is a direct sum of copies of
$W(-\unicode[STIX]{x1D706},0)(\tilde{\mathbb{R}})$ is a direct sum of copies of ![]() $\tilde{\mathbb{R}}$. Similarly,
$\tilde{\mathbb{R}}$. Similarly,  $W(-\unicode[STIX]{x1D706},0)(\mathbb{H})$ is a direct sum of copies of
$W(-\unicode[STIX]{x1D706},0)(\mathbb{H})$ is a direct sum of copies of ![]() $\mathbb{H}$.
$\mathbb{H}$.
Manolescu showed in [Reference ManolescuMan16] that  $\mathit{SWF}(Y,\mathfrak{s},g)$ is well defined, for
$\mathit{SWF}(Y,\mathfrak{s},g)$ is well defined, for ![]() $\unicode[STIX]{x1D706}$ sufficiently large. Further, we must remove the dependence on the choice of metric
$\unicode[STIX]{x1D706}$ sufficiently large. Further, we must remove the dependence on the choice of metric ![]() $g$. We use
$g$. We use  $n(Y,\mathfrak{s},g)$, a rational number which controls the spectral flow of the Dirac operator and may be expressed as a sum of eta invariants; for its definition, see [Reference ManolescuMan03]. We have
$n(Y,\mathfrak{s},g)$, a rational number which controls the spectral flow of the Dirac operator and may be expressed as a sum of eta invariants; for its definition, see [Reference ManolescuMan03]. We have
 $$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s})=\unicode[STIX]{x1D6F4}^{-(1/2)n(Y,\mathfrak{s},g)\mathbb{H}}\mathit{SWF}(Y,\mathfrak{s},g).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s})=\unicode[STIX]{x1D6F4}^{-(1/2)n(Y,\mathfrak{s},g)\mathbb{H}}\mathit{SWF}(Y,\mathfrak{s},g).\end{eqnarray}$$ Interpreted in ![]() $\mathfrak{E}$, if
$\mathfrak{E}$, if  $\mathit{SWF}(Y,\mathfrak{s},g)=(X,m,n)$, then
$\mathit{SWF}(Y,\mathfrak{s},g)=(X,m,n)$, then  $\mathit{SWF}(Y,\mathfrak{s})=(X,m,n+\frac{1}{2}n(Y,\mathfrak{s},g))$.
$\mathit{SWF}(Y,\mathfrak{s})=(X,m,n+\frac{1}{2}n(Y,\mathfrak{s},g))$.
In addition to the approximate flow above, we may also consider perturbations of the flow as in [Reference Kronheimer and MrowkaKM07].
For fixed ![]() $k\geqslant 1$, we call
$k\geqslant 1$, we call
 $$\begin{eqnarray}{\mathcal{C}}(Y,\mathfrak{s})=L_{k}^{2}\unicode[STIX]{x1D6FA}^{1}(Y,i\mathbb{R})\oplus L_{k}^{2}(Y;\mathbb{S})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(Y,\mathfrak{s})=L_{k}^{2}\unicode[STIX]{x1D6FA}^{1}(Y,i\mathbb{R})\oplus L_{k}^{2}(Y;\mathbb{S})\end{eqnarray}$$ the configuration space for the Seiberg–Witten equations, where  $L_{k}^{2}\unicode[STIX]{x1D6FA}^{1}(Y,i\mathbb{R})$ is the space of
$L_{k}^{2}\unicode[STIX]{x1D6FA}^{1}(Y,i\mathbb{R})$ is the space of ![]() $L_{k}^{2}$
$L_{k}^{2}$![]() $1$-forms. We write
$1$-forms. We write ![]() ${\mathcal{L}}$ for the Chern–Simons–Dirac functional and
${\mathcal{L}}$ for the Chern–Simons–Dirac functional and ![]() ${\mathcal{G}}$ for the
${\mathcal{G}}$ for the ![]() $L_{k+1}^{2}$-gauge transformations. Let
$L_{k+1}^{2}$-gauge transformations. Let ![]() ${\mathcal{X}}$ be the
${\mathcal{X}}$ be the ![]() $L^{2}$-gradient of
$L^{2}$-gradient of ![]() ${\mathcal{L}}$ on
${\mathcal{L}}$ on ![]() ${\mathcal{C}}(Y,\mathfrak{s})$. A map
${\mathcal{C}}(Y,\mathfrak{s})$. A map
 $$\begin{eqnarray}\mathfrak{q}:{\mathcal{C}}(Y,\mathfrak{s})\rightarrow {\mathcal{T}}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{q}:{\mathcal{C}}(Y,\mathfrak{s})\rightarrow {\mathcal{T}}_{0},\end{eqnarray}$$ where ![]() ${\mathcal{T}}_{j}$ denotes the
${\mathcal{T}}_{j}$ denotes the ![]() $L_{j}^{2}$ completion of the tangent bundle to
$L_{j}^{2}$ completion of the tangent bundle to ![]() ${\mathcal{C}}(Y,\mathfrak{s})$, is called a perturbation; we will only deal with very tame perturbations, in the sense of [Reference Lidman and ManolescuLM18]. Write
${\mathcal{C}}(Y,\mathfrak{s})$, is called a perturbation; we will only deal with very tame perturbations, in the sense of [Reference Lidman and ManolescuLM18]. Write
 $$\begin{eqnarray}{\mathcal{X}}_{\mathfrak{q}}={\mathcal{X}}+\mathfrak{q}:{\mathcal{C}}(Y,\mathfrak{s})\rightarrow {\mathcal{T}}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}_{\mathfrak{q}}={\mathcal{X}}+\mathfrak{q}:{\mathcal{C}}(Y,\mathfrak{s})\rightarrow {\mathcal{T}}_{0}.\end{eqnarray}$$ Let ![]() $W$ denote the global Coulomb slice in
$W$ denote the global Coulomb slice in ![]() ${\mathcal{C}}(Y,\mathfrak{s})$ and
${\mathcal{C}}(Y,\mathfrak{s})$ and ![]() ${\mathcal{T}}_{k}^{\text{gC}}$ the
${\mathcal{T}}_{k}^{\text{gC}}$ the ![]() $L_{k}^{2}$ completion of the tangent bundle to
$L_{k}^{2}$ completion of the tangent bundle to ![]() $W$. Lidman and Manolescu also consider a version of
$W$. Lidman and Manolescu also consider a version of ![]() ${\mathcal{X}}_{\mathfrak{q}}$, obtained by projecting trajectories of
${\mathcal{X}}_{\mathfrak{q}}$, obtained by projecting trajectories of ![]() ${\mathcal{X}}_{\mathfrak{q}}$ to
${\mathcal{X}}_{\mathfrak{q}}$ to ![]() $W$:
$W$:
 $$\begin{eqnarray}{\mathcal{X}}_{\mathfrak{q}}^{\text{gC}}:W\rightarrow {\mathcal{T}}_{0}^{\text{gC}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}_{\mathfrak{q}}^{\text{gC}}:W\rightarrow {\mathcal{T}}_{0}^{\text{gC}}.\end{eqnarray}$$ Lidman and Manolescu [Reference Lidman and ManolescuLM18] prove that there is a bijective correspondence between finite-energy trajectories of ![]() ${\mathcal{X}}_{\mathfrak{q}}^{\text{gC}}$ and those of
${\mathcal{X}}_{\mathfrak{q}}^{\text{gC}}$ and those of ![]() ${\mathcal{X}}_{\mathfrak{q}}$, modulo the appropriate gauges, for
${\mathcal{X}}_{\mathfrak{q}}$, modulo the appropriate gauges, for ![]() $\mathfrak{q}$ a very tame perturbation.
$\mathfrak{q}$ a very tame perturbation.
We write ![]() ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ for the finite-dimensional approximation of
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ for the finite-dimensional approximation of ![]() ${\mathcal{X}}_{\mathfrak{q}}^{\text{gC}}$ in
${\mathcal{X}}_{\mathfrak{q}}^{\text{gC}}$ in ![]() $W^{\unicode[STIX]{x1D706}}$ (recalling that
$W^{\unicode[STIX]{x1D706}}$ (recalling that ![]() $W^{\unicode[STIX]{x1D706}}$ are finite-dimensional subspaces of
$W^{\unicode[STIX]{x1D706}}$ are finite-dimensional subspaces of ![]() $W$). For very tame perturbations, we may define
$W$). For very tame perturbations, we may define  $I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g,\mathfrak{q})$ as above using
$I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g,\mathfrak{q})$ as above using ![]() ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ in place of
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ in place of ![]() ${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$. Furthermore, from
${\mathcal{X}}_{\unicode[STIX]{x1D706}}^{\text{gC}}$. Furthermore, from  $I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g,\mathfrak{q})$ we may also define
$I^{\unicode[STIX]{x1D706}}(Y,\mathfrak{s},g,\mathfrak{q})$ we may also define  $\mathit{SWF}(Y,\mathfrak{s},g,\mathfrak{q})$ analogously to the unperturbed case. Proposition 6.1.6 of [Reference Lidman and ManolescuLM18] shows that the spectrum is independent of
$\mathit{SWF}(Y,\mathfrak{s},g,\mathfrak{q})$ analogously to the unperturbed case. Proposition 6.1.6 of [Reference Lidman and ManolescuLM18] shows that the spectrum is independent of ![]() $\mathfrak{q}$. That is,
$\mathfrak{q}$. That is,
 $$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s},g,\mathfrak{q})=\mathit{SWF}(Y,\mathfrak{s},g).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWF}(Y,\mathfrak{s},g,\mathfrak{q})=\mathit{SWF}(Y,\mathfrak{s},g).\end{eqnarray}$$ We also have the attractor-repeller sequence of [Reference ManolescuMan16]. For a generic perturbation ![]() $\mathfrak{q}$ we may arrange that the reducible critical point of
$\mathfrak{q}$ we may arrange that the reducible critical point of ![]() ${\mathcal{X}}_{\mathfrak{q}}$, call it
${\mathcal{X}}_{\mathfrak{q}}$, call it ![]() $\unicode[STIX]{x1D6E9}$, is unique and nondegenerate and that there are no irreducible critical points
$\unicode[STIX]{x1D6E9}$, is unique and nondegenerate and that there are no irreducible critical points ![]() $x$ with
$x$ with  ${\mathcal{L}}_{\mathfrak{q}}(x)\in (0,\unicode[STIX]{x1D716})$ for some
${\mathcal{L}}_{\mathfrak{q}}(x)\in (0,\unicode[STIX]{x1D716})$ for some ![]() $\unicode[STIX]{x1D716}>0$, where
$\unicode[STIX]{x1D716}>0$, where ![]() ${\mathcal{L}}_{\mathfrak{q}}$ is the perturbed Chern–Simons–Dirac functional, and where we have imposed that
${\mathcal{L}}_{\mathfrak{q}}$ is the perturbed Chern–Simons–Dirac functional, and where we have imposed that  ${\mathcal{L}}_{\mathfrak{q}}(\unicode[STIX]{x1D6E9})=0$. Let
${\mathcal{L}}_{\mathfrak{q}}(\unicode[STIX]{x1D6E9})=0$. Let ![]() $T=T^{\unicode[STIX]{x1D706}}$ be the set of all critical points of
$T=T^{\unicode[STIX]{x1D706}}$ be the set of all critical points of ![]() ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ and points on flows of finite type between them. Then, for all
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ and points on flows of finite type between them. Then, for all ![]() $\unicode[STIX]{x1D714}>0$, we have the following isolated invariant sets:
$\unicode[STIX]{x1D714}>0$, we have the following isolated invariant sets:
∙
 $T_{{>}\unicode[STIX]{x1D714}}^{\text{irr}}$, the set of irreducible critical points
$T_{{>}\unicode[STIX]{x1D714}}^{\text{irr}}$, the set of irreducible critical points  $x$ with
$x$ with  ${\mathcal{L}}_{\mathfrak{q}}(x)>\unicode[STIX]{x1D714}$, together with all points on the flows between critical points of this type;
${\mathcal{L}}_{\mathfrak{q}}(x)>\unicode[STIX]{x1D714}$, together with all points on the flows between critical points of this type;∙
 $T_{{\leqslant}\unicode[STIX]{x1D714}}$, the same, but with
$T_{{\leqslant}\unicode[STIX]{x1D714}}$, the same, but with  ${\mathcal{L}}_{\mathfrak{q}}(x)\leqslant \unicode[STIX]{x1D714}$, and allowing
${\mathcal{L}}_{\mathfrak{q}}(x)\leqslant \unicode[STIX]{x1D714}$, and allowing  $x$ to be reducible.
$x$ to be reducible.
Then we have the coexact sequence
 $$\begin{eqnarray}I(T_{{\leqslant}\unicode[STIX]{x1D714}})\rightarrow I(T)\rightarrow I(T_{{>}\unicode[STIX]{x1D714}}^{\text{irr}})\rightarrow \unicode[STIX]{x1D6F4}I(T_{{\leqslant}\unicode[STIX]{x1D714}})\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}I(T_{{\leqslant}\unicode[STIX]{x1D714}})\rightarrow I(T)\rightarrow I(T_{{>}\unicode[STIX]{x1D714}}^{\text{irr}})\rightarrow \unicode[STIX]{x1D6F4}I(T_{{\leqslant}\unicode[STIX]{x1D714}})\rightarrow \cdots\end{eqnarray}$$We record a theorem of [Reference ManolescuMan16].
Theorem 4.1 (Manolescu [Reference ManolescuMan16], [Reference ManolescuMan14]).
Associated to a three-manifold with ![]() $b_{1}=0$ and a choice of spin structure
$b_{1}=0$ and a choice of spin structure ![]() $(Y,\mathfrak{s})$ there is an invariant
$(Y,\mathfrak{s})$ there is an invariant  $\mathit{SWF}(Y,\mathfrak{s})$, the Seiberg–Witten Floer spectrum class, in
$\mathit{SWF}(Y,\mathfrak{s})$, the Seiberg–Witten Floer spectrum class, in ![]() $\mathfrak{E}$. A spin cobordism
$\mathfrak{E}$. A spin cobordism ![]() $(W,\mathfrak{t})$ from
$(W,\mathfrak{t})$ from ![]() $Y_{1}$ to
$Y_{1}$ to ![]() $Y_{2}$, with
$Y_{2}$, with  $b_{2}(W)=0$, induces a map
$b_{2}(W)=0$, induces a map  $\mathit{SWF}(Y_{1},\mathfrak{t}|_{Y_{1}})\rightarrow \mathit{SWF}(Y_{2},\mathfrak{t}|_{Y_{2}})$. The induced map is a homotopy-equivalence on the
$\mathit{SWF}(Y_{1},\mathfrak{t}|_{Y_{1}})\rightarrow \mathit{SWF}(Y_{2},\mathfrak{t}|_{Y_{2}})$. The induced map is a homotopy-equivalence on the ![]() $S^{1}$-fixed-point set.
$S^{1}$-fixed-point set.
Remark 4.2. The three-manifold ![]() $Y$ in Theorem 4.1 may be disconnected.
$Y$ in Theorem 4.1 may be disconnected.
Definition 4.3. For  $[(X,m,n)]\in \mathfrak{E}$, we set
$[(X,m,n)]\in \mathfrak{E}$, we set
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}((X,m,n))={\displaystyle \frac{a(X)}{2}}-{\displaystyle \frac{m}{2}}-2n,\quad \unicode[STIX]{x1D6FD}((X,m,n))={\displaystyle \frac{b(X)}{2}}-{\displaystyle \frac{m}{2}}-2n,\\[5.0pt] \unicode[STIX]{x1D6FE}((X,m,n))={\displaystyle \frac{c(X)}{2}}-{\displaystyle \frac{m}{2}}-2n.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}((X,m,n))={\displaystyle \frac{a(X)}{2}}-{\displaystyle \frac{m}{2}}-2n,\quad \unicode[STIX]{x1D6FD}((X,m,n))={\displaystyle \frac{b(X)}{2}}-{\displaystyle \frac{m}{2}}-2n,\\[5.0pt] \unicode[STIX]{x1D6FE}((X,m,n))={\displaystyle \frac{c(X)}{2}}-{\displaystyle \frac{m}{2}}-2n.\end{array} & & \displaystyle\end{eqnarray}$$ The invariants ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ and ![]() $\unicode[STIX]{x1D6FE}$ do not depend on the choice of representative of the class
$\unicode[STIX]{x1D6FE}$ do not depend on the choice of representative of the class  $[(X,m,n)]$.
$[(X,m,n)]$.
The Manolescu invariants  $\unicode[STIX]{x1D6FC}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FD}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FE}(Y,\mathfrak{s})$ of a pair
$\unicode[STIX]{x1D6FC}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FD}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FE}(Y,\mathfrak{s})$ of a pair ![]() $(Y,\mathfrak{s})$ are then given by
$(Y,\mathfrak{s})$ are then given by  $\unicode[STIX]{x1D6FC}(\mathit{SWF}(Y,\mathfrak{s}))$,
$\unicode[STIX]{x1D6FC}(\mathit{SWF}(Y,\mathfrak{s}))$,  $\unicode[STIX]{x1D6FD}(\mathit{SWF}(Y,\mathfrak{s}))$, and
$\unicode[STIX]{x1D6FD}(\mathit{SWF}(Y,\mathfrak{s}))$, and  $\unicode[STIX]{x1D6FE}(\mathit{SWF}(Y,\mathfrak{s}))$, respectively.
$\unicode[STIX]{x1D6FE}(\mathit{SWF}(Y,\mathfrak{s}))$, respectively.
From Theorem 4.1, the local and chain local equivalence classes of  $\mathit{SWF}(Y,\mathfrak{s})$,
$\mathit{SWF}(Y,\mathfrak{s})$,  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{l}}$ and
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{l}}$ and  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$, respectively, are homology cobordism invariants of the pair
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$, respectively, are homology cobordism invariants of the pair ![]() $(Y,\mathfrak{s})$. Since a chain local equivalence induces a map of Borel homology which is an isomorphism in sufficiently high degrees, it is straightforward to check that
$(Y,\mathfrak{s})$. Since a chain local equivalence induces a map of Borel homology which is an isomorphism in sufficiently high degrees, it is straightforward to check that  $\unicode[STIX]{x1D6FC}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FD}(Y,\mathfrak{s}),$ and
$\unicode[STIX]{x1D6FC}(Y,\mathfrak{s}),\unicode[STIX]{x1D6FD}(Y,\mathfrak{s}),$ and ![]() $\unicode[STIX]{x1D6FE}(Y,\mathfrak{s})$ depend only on the chain local equivalence class
$\unicode[STIX]{x1D6FE}(Y,\mathfrak{s})$ depend only on the chain local equivalence class  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$.
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}$.
Fact 4.4. Let ![]() $Y_{1},Y_{2}$ be rational homology three-spheres with spin structures
$Y_{1},Y_{2}$ be rational homology three-spheres with spin structures ![]() $\mathfrak{t}_{1},\mathfrak{t}_{2}$ and
$\mathfrak{t}_{1},\mathfrak{t}_{2}$ and $(X_{i},m_{i},n_{i})=\mathit{SWF}(Y_{i},\mathfrak{t}_{i})$ for
$(X_{i},m_{i},n_{i})=\mathit{SWF}(Y_{i},\mathfrak{t}_{i})$ for ![]() $i=1,2$. Then
$i=1,2$. Then
 $$\begin{eqnarray}\mathit{SWF}(Y_{1}\#Y_{2},\mathfrak{t}_{1}\#\mathfrak{t}_{2})\equiv _{l}(X_{1}\wedge X_{2},m_{1}+m_{2},n_{1}+n_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWF}(Y_{1}\#Y_{2},\mathfrak{t}_{1}\#\mathfrak{t}_{2})\equiv _{l}(X_{1}\wedge X_{2},m_{1}+m_{2},n_{1}+n_{2}).\end{eqnarray}$$Proof. According to [Reference ManolescuMan16], the Seiberg–Witten Floer spectrum class of the disjoint union ![]() $Y_{1}\amalg Y_{2}$ is given by
$Y_{1}\amalg Y_{2}$ is given by
 $$\begin{eqnarray}\mathit{SWF}(Y_{1}\amalg Y_{2})\equiv _{l}(X_{1}\wedge X_{2},m_{1}+m_{2},n_{1}+n_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWF}(Y_{1}\amalg Y_{2})\equiv _{l}(X_{1}\wedge X_{2},m_{1}+m_{2},n_{1}+n_{2}).\end{eqnarray}$$ On the other hand ![]() $Y_{1}\amalg Y_{2}$ is homology cobordant to the connected sum
$Y_{1}\amalg Y_{2}$ is homology cobordant to the connected sum ![]() $Y_{1}\#Y_{2}$. Since the local equivalence class is a homology cobordism invariant, we obtain the claim.◻
$Y_{1}\#Y_{2}$. Since the local equivalence class is a homology cobordism invariant, we obtain the claim.◻
By Theorem 4.1 and Fact 4.4, we have a sequence of homomorphisms:
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{3}^{H}\xrightarrow[{}]{\mathit{SWF}}\mathfrak{LE}\xrightarrow[{}]{C_{\ast }}\mathfrak{CLE}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{3}^{H}\xrightarrow[{}]{\mathit{SWF}}\mathfrak{LE}\xrightarrow[{}]{C_{\ast }}\mathfrak{CLE}.\end{eqnarray}$$4.2 Approximate trajectories
Fix ![]() $\mathfrak{q}$ a very tame admissible perturbation, as in Definitions 4.9 and 4.19 of [Reference Lidman and ManolescuLM18]. Here we will record several results of Lidman and Manolescu [Reference Lidman and ManolescuLM18] for use in § 5. First, choose a sequence of real numbers
$\mathfrak{q}$ a very tame admissible perturbation, as in Definitions 4.9 and 4.19 of [Reference Lidman and ManolescuLM18]. Here we will record several results of Lidman and Manolescu [Reference Lidman and ManolescuLM18] for use in § 5. First, choose a sequence of real numbers ![]() $\unicode[STIX]{x1D706}_{i}$, none an eigenvalue of
$\unicode[STIX]{x1D706}_{i}$, none an eigenvalue of ![]() $\ell$, as in [Reference Lidman and ManolescuLM18, § 3.4]. The first result is a corollary of Proposition 9.11 of [Reference Lidman and ManolescuLM18].
$\ell$, as in [Reference Lidman and ManolescuLM18, § 3.4]. The first result is a corollary of Proposition 9.11 of [Reference Lidman and ManolescuLM18].
Proposition 4.5 [Reference Lidman and ManolescuLM18].
For ![]() $R>0$ large and fixed, and for
$R>0$ large and fixed, and for ![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{i}$ sufficiently large, there is a grading-preserving isomorphism between the set of irreducible critical points of the finite-dimensional approximation
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{i}$ sufficiently large, there is a grading-preserving isomorphism between the set of irreducible critical points of the finite-dimensional approximation  ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}/S^{1}$ in
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}/S^{1}$ in  $(B(R)\cap W^{\unicode[STIX]{x1D706}})/S^{1}$ and the set of irreducible critical points of
$(B(R)\cap W^{\unicode[STIX]{x1D706}})/S^{1}$ and the set of irreducible critical points of ![]() ${\mathcal{X}}_{\mathfrak{q}}$ on
${\mathcal{X}}_{\mathfrak{q}}$ on  ${\mathcal{C}}(Y,\mathfrak{s})/{\mathcal{G}}$.
${\mathcal{C}}(Y,\mathfrak{s})/{\mathcal{G}}$.
For ![]() $x,y$ critical points of
$x,y$ critical points of ![]() ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$, let
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$, let  $M_{\unicode[STIX]{x1D706}}([x],[y])$ denote the set of unparameterized trajectories of
$M_{\unicode[STIX]{x1D706}}([x],[y])$ denote the set of unparameterized trajectories of  ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}/S^{1}$ from
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}/S^{1}$ from ![]() $[x]$ to
$[x]$ to ![]() $[y]$ contained in the ball used to define
$[y]$ contained in the ball used to define ![]() $S^{\unicode[STIX]{x1D706}}$. Similarly, we let
$S^{\unicode[STIX]{x1D706}}$. Similarly, we let  $M([x],[y])$ be the set of unparameterized trajectories between critical points of
$M([x],[y])$ be the set of unparameterized trajectories between critical points of ![]() ${\mathcal{X}}_{\mathfrak{q}}$ on
${\mathcal{X}}_{\mathfrak{q}}$ on  ${\mathcal{C}}(Y,\mathfrak{s})/{\mathcal{G}}$.
${\mathcal{C}}(Y,\mathfrak{s})/{\mathcal{G}}$.
Proposition 4.6 [Reference Lidman and ManolescuLM18, Proposition 13.1].
For ![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{i}$ sufficiently large, there is a correspondence of degree
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{i}$ sufficiently large, there is a correspondence of degree ![]() $1$ trajectories compatible with Proposition 4.5. That is, if
$1$ trajectories compatible with Proposition 4.5. That is, if  $[x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}]$ are irreducible critical points, with
$[x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}]$ are irreducible critical points, with  $\text{gr}(x_{\unicode[STIX]{x1D706}})=\text{gr}(y_{\unicode[STIX]{x1D706}})+1$, of
$\text{gr}(x_{\unicode[STIX]{x1D706}})=\text{gr}(y_{\unicode[STIX]{x1D706}})+1$, of ![]() ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ corresponding to irreducible critical points
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$ corresponding to irreducible critical points ![]() $[x],[y]$ of
$[x],[y]$ of ![]() ${\mathcal{X}}_{\mathfrak{q}}$, respectively, then there is an identification
${\mathcal{X}}_{\mathfrak{q}}$, respectively, then there is an identification
 $$\begin{eqnarray}M([x],[y])=M_{\unicode[STIX]{x1D706}}([x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}]).\end{eqnarray}$$
$$\begin{eqnarray}M([x],[y])=M_{\unicode[STIX]{x1D706}}([x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}]).\end{eqnarray}$$ The condition  $\text{gr}(x)=\text{gr}(y)+1$ allows the application of an inverse function theorem. However, without the grading assumption, a compactness result still holds. That is, [Reference Lidman and ManolescuLM18, Proposition 12.17] implies the following.
$\text{gr}(x)=\text{gr}(y)+1$ allows the application of an inverse function theorem. However, without the grading assumption, a compactness result still holds. That is, [Reference Lidman and ManolescuLM18, Proposition 12.17] implies the following.
Proposition 4.7 [Reference Lidman and ManolescuLM18].
For ![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{i}$ sufficiently large, let
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{i}$ sufficiently large, let ![]() $[x]$ and
$[x]$ and ![]() $[y]$ be critical points of
$[y]$ be critical points of ![]() ${\mathcal{X}}_{\mathfrak{q}}$ corresponding to critical points
${\mathcal{X}}_{\mathfrak{q}}$ corresponding to critical points  $[x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}]$ of
$[x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}]$ of ![]() ${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$. If
${\mathcal{X}}_{\mathfrak{q},\unicode[STIX]{x1D706}}^{\text{gC}}$. If  $M([x],[y])=\emptyset$, then
$M([x],[y])=\emptyset$, then  $M_{\unicode[STIX]{x1D706}}([x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}])=\emptyset$.
$M_{\unicode[STIX]{x1D706}}([x_{\unicode[STIX]{x1D706}}],[y_{\unicode[STIX]{x1D706}}])=\emptyset$.
We will also need the following Theorem from [Reference Lidman and ManolescuLM18].
Theorem 4.8 [Reference Lidman and ManolescuLM18].
Let ![]() $(Y,\mathfrak{s})$ be a rational homology three-sphere with
$(Y,\mathfrak{s})$ be a rational homology three-sphere with ![]() $\text{spin}^{c}$ structure. Then
$\text{spin}^{c}$ structure. Then
 $$\begin{eqnarray}\check{HM}(Y,\mathfrak{s})=\mathit{SWFH}^{S^{1}}(Y,\mathfrak{s}),\end{eqnarray}$$
$$\begin{eqnarray}\check{HM}(Y,\mathfrak{s})=\mathit{SWFH}^{S^{1}}(Y,\mathfrak{s}),\end{eqnarray}$$ as absolutely graded ![]() $\mathbb{F}[U]$-modules, where
$\mathbb{F}[U]$-modules, where  $\check{HM}(Y,\mathfrak{s})$ denotes the ‘to’ version of monopole Floer homology defined in [Reference Kronheimer and MrowkaKM07].
$\check{HM}(Y,\mathfrak{s})$ denotes the ‘to’ version of monopole Floer homology defined in [Reference Kronheimer and MrowkaKM07].
4.3 Connected Seiberg–Witten Floer homology
Definition 4.9. Let ![]() $(Y,\mathfrak{s})$ be a rational homology three-sphere with spin structure, and
$(Y,\mathfrak{s})$ be a rational homology three-sphere with spin structure, and
 $$\begin{eqnarray}[\mathit{SWF}(Y,\mathfrak{s})]=(Z,m,n)\in \mathfrak{CE},\end{eqnarray}$$
$$\begin{eqnarray}[\mathit{SWF}(Y,\mathfrak{s})]=(Z,m,n)\in \mathfrak{CE},\end{eqnarray}$$ with ![]() $Z$ suspensionlike. The connected Seiberg–Witten Floer homology of
$Z$ suspensionlike. The connected Seiberg–Witten Floer homology of ![]() $(Y,\mathfrak{s})$,
$(Y,\mathfrak{s})$,  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$, is the quotient
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$, is the quotient  $(H_{\ast }^{S^{1}}(Z)/(H_{\ast }^{S^{1}}(Z^{S^{1}})+H_{\ast }^{S^{1}}(Z_{\text{iness}})))[m+4n]$, where
$(H_{\ast }^{S^{1}}(Z)/(H_{\ast }^{S^{1}}(Z^{S^{1}})+H_{\ast }^{S^{1}}(Z_{\text{iness}})))[m+4n]$, where  $Z_{\text{iness}}\subset Z$ is a maximal inessential subcomplex. By Theorems 2.33 and 4.1, the isomorphism class of
$Z_{\text{iness}}\subset Z$ is a maximal inessential subcomplex. By Theorems 2.33 and 4.1, the isomorphism class of  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ is a homology cobordism invariant.
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ is a homology cobordism invariant.
Remark 4.10. We could have instead considered the quotient  $(H_{\ast }^{S^{1}}(Z)/H_{\ast }^{S^{1}}(Z_{\text{iness}}))[m+4n]$, which is isomorphic to
$(H_{\ast }^{S^{1}}(Z)/H_{\ast }^{S^{1}}(Z_{\text{iness}}))[m+4n]$, which is isomorphic to  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})\oplus {\mathcal{T}}_{d}^{+}$ where
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})\oplus {\mathcal{T}}_{d}^{+}$ where ![]() $d$ is the Heegaard Floer correction term of
$d$ is the Heegaard Floer correction term of ![]() $(Y,\mathfrak{s})$. As defined above,
$(Y,\mathfrak{s})$. As defined above,  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ has no infinite
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ has no infinite ![]() $\mathbb{F}[U]$-tower, because of the quotient by
$\mathbb{F}[U]$-tower, because of the quotient by  $H_{\ast }^{S^{1}}(Z^{S^{1}})$. Further, let
$H_{\ast }^{S^{1}}(Z^{S^{1}})$. Further, let ![]() $Z_{\text{conn}}$ denote the connected complex (Definition 2.32) of
$Z_{\text{conn}}$ denote the connected complex (Definition 2.32) of ![]() $Z$. It is clear from the construction that
$Z$. It is clear from the construction that
 $$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})=(H_{\ast }^{S^{1}}(Z_{\text{conn}})/H_{\ast }^{S^{1}}(Z^{S^{1}}))[m+4n].\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})=(H_{\ast }^{S^{1}}(Z_{\text{conn}})/H_{\ast }^{S^{1}}(Z^{S^{1}}))[m+4n].\end{eqnarray}$$Remark 4.11. Using Theorem 4.8 and  $\check{HM}(Y,\mathfrak{s})\cong \mathit{HF}^{+}(Y,\mathfrak{s})$, as is shown by [Reference Colin, Ghiggini and HondaCGH11] and [Reference Kutluhan, Lee and TaubesKLT10], we have that
$\check{HM}(Y,\mathfrak{s})\cong \mathit{HF}^{+}(Y,\mathfrak{s})$, as is shown by [Reference Colin, Ghiggini and HondaCGH11] and [Reference Kutluhan, Lee and TaubesKLT10], we have that  $\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ can be viewed as an
$\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})$ can be viewed as an ![]() $\mathbb{F}[U]$-summand of
$\mathbb{F}[U]$-summand of  $HF_{\text{red}}(Y,\mathfrak{s})$.
$HF_{\text{red}}(Y,\mathfrak{s})$.
5 Floer spectra of Seifert fiber spaces
5.1 The Seiberg–Witten equations on Seifert spaces
In this section we record some results of [Reference Mrowka, Ozsváth and YuMOY97] to describe explicitly the monopole moduli space on Seifert fiber spaces. First we recall some notation associated with Seifert fiber spaces.
The standard fibered torus corresponding to a pair of integers ![]() $(a,b)$, for
$(a,b)$, for ![]() $a>0$, is the mapping torus of the automorphism of the disk
$a>0$, is the mapping torus of the automorphism of the disk ![]() $D^{2}$ given by rotation by
$D^{2}$ given by rotation by ![]() $2\unicode[STIX]{x1D70B}b/a$. Let
$2\unicode[STIX]{x1D70B}b/a$. Let ![]() $D_{a}^{2}$ be the standard disk, given an orbifold structure by letting
$D_{a}^{2}$ be the standard disk, given an orbifold structure by letting ![]() $\mathbb{Z}/a$ act by rotation by
$\mathbb{Z}/a$ act by rotation by ![]() $2\unicode[STIX]{x1D70B}/a$; the origin is then an orbifold point, with multiplicity
$2\unicode[STIX]{x1D70B}/a$; the origin is then an orbifold point, with multiplicity ![]() $a$. The standard fibered torus is naturally a circle bundle over the orbifold
$a$. The standard fibered torus is naturally a circle bundle over the orbifold ![]() $D_{a}^{2}$.
$D_{a}^{2}$.
Let  $f:Y\rightarrow P$ be a circle bundle over an orbifold
$f:Y\rightarrow P$ be a circle bundle over an orbifold ![]() $P$, and
$P$, and ![]() $x\in P$ an orbifold point with multiplicity
$x\in P$ an orbifold point with multiplicity ![]() $a$. If a neighborhood of the fiber over
$a$. If a neighborhood of the fiber over ![]() $x$ is equivalent, as an orbifold circle bundle, to the standard fibered torus corresponding to
$x$ is equivalent, as an orbifold circle bundle, to the standard fibered torus corresponding to ![]() $(a,b)$, we say that
$(a,b)$, we say that ![]() $Y$ has local invariant
$Y$ has local invariant ![]() $b$ at
$b$ at ![]() $x$.
$x$.
For  $a_{i}\in \mathbb{Z}_{{\geqslant}1}$, let
$a_{i}\in \mathbb{Z}_{{\geqslant}1}$, let  $S(a_{1},\ldots ,a_{k})$ denote the orbifold with underlying space
$S(a_{1},\ldots ,a_{k})$ denote the orbifold with underlying space ![]() $S^{2}$ and
$S^{2}$ and ![]() $k$ orbifold points, with corresponding multiplicities
$k$ orbifold points, with corresponding multiplicities  $a_{1},\ldots ,a_{k}$. Fix
$a_{1},\ldots ,a_{k}$. Fix ![]() $b_{i}\in \mathbb{Z}$ with
$b_{i}\in \mathbb{Z}$ with  $\gcd (a_{i},b_{i})=1$ for all
$\gcd (a_{i},b_{i})=1$ for all ![]() $i$. We let
$i$. We let  $\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ denote the circle bundle over
$\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ denote the circle bundle over  $S(a_{1},\ldots ,a_{k})$ with first Chern class
$S(a_{1},\ldots ,a_{k})$ with first Chern class ![]() $b$ and local invariants
$b$ and local invariants ![]() $b_{i}$. We define the degree of the Seifert space
$b_{i}$. We define the degree of the Seifert space  $\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ by
$\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ by  $b+\sum (b_{i}/a_{i})$. Finally, we call a space
$b+\sum (b_{i}/a_{i})$. Finally, we call a space  $\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ negative (positive) if
$\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ negative (positive) if  $b+\sum (b_{i}/a_{i})$ is negative (positive). The spaces
$b+\sum (b_{i}/a_{i})$ is negative (positive). The spaces  $\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ of nonzero degree are rational homology spheres. As orbifold circle bundles, the orientation reversal
$\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ of nonzero degree are rational homology spheres. As orbifold circle bundles, the orientation reversal  $-\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ is isomorphic to
$-\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ is isomorphic to  $\unicode[STIX]{x1D6F4}(-b,(-b_{1},a_{1}),\ldots ,(-b_{k},a_{k}))$. We write
$\unicode[STIX]{x1D6F4}(-b,(-b_{1},a_{1}),\ldots ,(-b_{k},a_{k}))$. We write  $\unicode[STIX]{x1D6F4}(a_{1},\ldots ,a_{k})$ for the unique negative Seifert integral homology sphere fibering over
$\unicode[STIX]{x1D6F4}(a_{1},\ldots ,a_{k})$ for the unique negative Seifert integral homology sphere fibering over  $S^{2}(a_{1},\ldots ,a_{k})$.
$S^{2}(a_{1},\ldots ,a_{k})$.
Let ![]() $Y$ be a negative Seifert rational homology three-sphere fibering over a base orbifold
$Y$ be a negative Seifert rational homology three-sphere fibering over a base orbifold ![]() $P$ with underlying space
$P$ with underlying space ![]() $S^{2}$. Equipping
$S^{2}$. Equipping ![]() $Y$ with the metric for which
$Y$ with the metric for which ![]() $Y$ has the Seifert geometry, Mrowka, Ozsváth and Yu [Reference Mrowka, Ozsváth and YuMOY97] show that the Seiberg–Witten moduli space
$Y$ has the Seifert geometry, Mrowka, Ozsváth and Yu [Reference Mrowka, Ozsváth and YuMOY97] show that the Seiberg–Witten moduli space ![]() ${\mathcal{M}}(Y)$ is composed of the following:
${\mathcal{M}}(Y)$ is composed of the following:
∙ a finite set of points forming the reducible critical set, in bijection with
 $\mathit{Hom}(H_{1}(Y),S^{1})$; and
$\mathit{Hom}(H_{1}(Y),S^{1})$; and∙ for each
 $(k+1)$-tuple of nonnegative integers
$(k+1)$-tuple of nonnegative integers  $\text{}\text{e}=(e,\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{k})$, such that
$\text{}\text{e}=(e,\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{k})$, such that  $0\leqslant \unicode[STIX]{x1D716}_{i}<a_{i}$ and two components, labeled
$0\leqslant \unicode[STIX]{x1D716}_{i}<a_{i}$ and two components, labeled $$\begin{eqnarray}e+\mathop{\sum }_{i=1}^{k}\frac{\unicode[STIX]{x1D716}_{i}}{a_{i}}\leqslant \biggl(\frac{k}{2}-1\biggr)-\mathop{\sum }_{i=1}^{k}\frac{1}{2a_{i}},\end{eqnarray}$$
$$\begin{eqnarray}e+\mathop{\sum }_{i=1}^{k}\frac{\unicode[STIX]{x1D716}_{i}}{a_{i}}\leqslant \biggl(\frac{k}{2}-1\biggr)-\mathop{\sum }_{i=1}^{k}\frac{1}{2a_{i}},\end{eqnarray}$$ $C^{+}(\text{}\text{e})$ and
$C^{+}(\text{}\text{e})$ and  $C^{-}(\text{}\text{e})$, in
$C^{-}(\text{}\text{e})$, in  ${\mathcal{M}}(Y)$.
${\mathcal{M}}(Y)$.
Here we work with the configuration space ![]() $W/S^{1}$, with
$W/S^{1}$, with ![]() $W$ as in § 4. The critical sets lying upstairs in
$W$ as in § 4. The critical sets lying upstairs in ![]() $W$, which we denote by
$W$, which we denote by ![]() ${\hat{C}}^{\pm }(\text{}\text{e})$, come with an
${\hat{C}}^{\pm }(\text{}\text{e})$, come with an ![]() $S^{1}$-action whose quotient is the moduli space as identified in [Reference Mrowka, Ozsváth and YuMOY97]. Each component
$S^{1}$-action whose quotient is the moduli space as identified in [Reference Mrowka, Ozsváth and YuMOY97]. Each component  $C^{+}(\text{}\text{e}),C^{-}(\text{}\text{e})$ is a copy of
$C^{+}(\text{}\text{e}),C^{-}(\text{}\text{e})$ is a copy of  $Sym^{e}(|\unicode[STIX]{x1D6F4}|)$, where
$Sym^{e}(|\unicode[STIX]{x1D6F4}|)$, where ![]() $\unicode[STIX]{x1D6F4}$ is the base orbifold and
$\unicode[STIX]{x1D6F4}$ is the base orbifold and ![]() $|\unicode[STIX]{x1D6F4}|$ its underlying manifold. Furthermore,
$|\unicode[STIX]{x1D6F4}|$ its underlying manifold. Furthermore, ![]() $C^{+}(\text{}\text{e})$ and
$C^{+}(\text{}\text{e})$ and ![]() $C^{-}(\text{}\text{e})$ are related by the action of
$C^{-}(\text{}\text{e})$ are related by the action of  $j\in \text{Pin}(2)$. That is, the restriction of
$j\in \text{Pin}(2)$. That is, the restriction of ![]() $j$ to
$j$ to ![]() $C^{+}(\text{}\text{e})$ acts as a diffeomorphism
$C^{+}(\text{}\text{e})$ acts as a diffeomorphism  $C^{+}(\text{}\text{e})\rightarrow C^{-}(\text{}\text{e})$, and vice versa.
$C^{+}(\text{}\text{e})\rightarrow C^{-}(\text{}\text{e})$, and vice versa.
Fact 5.1. All reducible critical points ![]() $x$ have
$x$ have  ${\mathcal{L}}(x)=0$, where
${\mathcal{L}}(x)=0$, where ![]() ${\mathcal{L}}$ is the Chern–Simons–Dirac functional. All irreducible critical points have
${\mathcal{L}}$ is the Chern–Simons–Dirac functional. All irreducible critical points have ![]() ${\mathcal{L}}>0$.
${\mathcal{L}}>0$.
Mrowka, Ozsváth and Yu do not use the Seiberg–Witten equations as in [Reference Kronheimer and MrowkaKM07]. Instead, they replace the Dirac operator ![]() $\hat{D}$ associated to the Seifert metric in the equations with
$\hat{D}$ associated to the Seifert metric in the equations with  $D=\hat{D}-\frac{1}{2}\unicode[STIX]{x1D709}$ for
$D=\hat{D}-\frac{1}{2}\unicode[STIX]{x1D709}$ for ![]() $\unicode[STIX]{x1D709}$ some constant depending on the Seifert fibration. It is then clear that the Seiberg–Witten equations they consider differ from the usual equations by a very tame perturbation
$\unicode[STIX]{x1D709}$ some constant depending on the Seifert fibration. It is then clear that the Seiberg–Witten equations they consider differ from the usual equations by a very tame perturbation ![]() $\mathfrak{q}_{0}$ in the sense of [Reference Kronheimer and MrowkaKM07]. Abusing notation somewhat, we call the Seiberg–Witten equations as in [Reference Mrowka, Ozsváth and YuMOY97] simply the Seiberg–Witten equations, or the unperturbed Seiberg–Witten equations subsequently.
$\mathfrak{q}_{0}$ in the sense of [Reference Kronheimer and MrowkaKM07]. Abusing notation somewhat, we call the Seiberg–Witten equations as in [Reference Mrowka, Ozsváth and YuMOY97] simply the Seiberg–Witten equations, or the unperturbed Seiberg–Witten equations subsequently.
We will further need the following.
Fact 5.2. There are no trajectories between ![]() $C^{+}(\text{}\text{e})$ and
$C^{+}(\text{}\text{e})$ and ![]() $C^{-}(\text{}\text{f})$ for any
$C^{-}(\text{}\text{f})$ for any ![]() $\text{}\text{e},\text{}\text{f}$. The Seiberg–Witten equations on
$\text{}\text{e},\text{}\text{f}$. The Seiberg–Witten equations on ![]() $Y$ is Morse-Bott, and if
$Y$ is Morse-Bott, and if ![]() $Y$ has four or fewer singular fibers, the critical points are isolated.
$Y$ has four or fewer singular fibers, the critical points are isolated.
Combining Propositions 4.5, 4.6, and Fact 5.2, we have the following result.
Lemma 5.3. Let  $Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology three-sphere. Then
$Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology three-sphere. Then  $\mathit{SWF}(Y,\mathfrak{s})$ has a representative
$\mathit{SWF}(Y,\mathfrak{s})$ has a representative  $(X,m,n)\in \mathfrak{E}$ with
$(X,m,n)\in \mathfrak{E}$ with ![]() $X$ a
$X$ a ![]() $j$-split space.
$j$-split space.
Proof. Throughout the proof, we work with the moduli spaces in ![]() $W$, so that the critical sets admit an
$W$, so that the critical sets admit an ![]() $S^{1}$-action.
$S^{1}$-action.
We first treat the case where ![]() $Y$ has at most four singular fibers. Then the
$Y$ has at most four singular fibers. Then the ![]() $S^{1}$ orbits of irreducibles are isolated, by Fact 5.2, and we make a perturbation away from the critical points to obtain that the flow lines are cut out transversely (in the case of five or more singular fibers to follow, we will explain how such a perturbation may be chosen, preserving the first property of Fact 5.2).
$S^{1}$ orbits of irreducibles are isolated, by Fact 5.2, and we make a perturbation away from the critical points to obtain that the flow lines are cut out transversely (in the case of five or more singular fibers to follow, we will explain how such a perturbation may be chosen, preserving the first property of Fact 5.2).
We recall the attractor–repeller sequence (80), which shows that  $\mathit{SWF}(Y,\mathfrak{s})$ is obtained by successively attaching stable cells
$\mathit{SWF}(Y,\mathfrak{s})$ is obtained by successively attaching stable cells  $G\times D^{\text{ind}\,C^{+}(\text{}\text{e})}$, corresponding to the irreducible critical point
$G\times D^{\text{ind}\,C^{+}(\text{}\text{e})}$, corresponding to the irreducible critical point ![]() $C^{+}(\text{}\text{e})$, to the union of cells of lower
$C^{+}(\text{}\text{e})$, to the union of cells of lower ![]() ${\mathcal{L}}$, and where the initial cell is that corresponding to the reducible (which has lowest
${\mathcal{L}}$, and where the initial cell is that corresponding to the reducible (which has lowest ![]() ${\mathcal{L}}$). Let
${\mathcal{L}}$). Let ![]() $S$ be set of all critical points and finite-energy trajectories between them, let
$S$ be set of all critical points and finite-energy trajectories between them, let ![]() $S_{\text{irr}}$ be the subset consisting of irreducible critical points and finite-energy trajectories between them, and let
$S_{\text{irr}}$ be the subset consisting of irreducible critical points and finite-energy trajectories between them, and let ![]() $S_{\text{red}}$ be the set of reducible critical points and trajectories between them. In particular,
$S_{\text{red}}$ be the set of reducible critical points and trajectories between them. In particular, ![]() $I(S)$ is obtained by attaching
$I(S)$ is obtained by attaching ![]() $I(S_{\text{irr}})$ to
$I(S_{\text{irr}})$ to ![]() $I(S_{\text{red}})$. To show that
$I(S_{\text{red}})$. To show that ![]() $I(S)$ has a
$I(S)$ has a ![]() $j$-split representative, we need only show that
$j$-split representative, we need only show that ![]() $I(S_{\text{irr}})$ is homotopy equivalent to a wedge of free
$I(S_{\text{irr}})$ is homotopy equivalent to a wedge of free ![]() $S^{1}$-CW complexes
$S^{1}$-CW complexes  $X_{+}\vee X_{-}$, so that
$X_{+}\vee X_{-}$, so that ![]() $j$ interchanges
$j$ interchanges ![]() $X_{+}$ and
$X_{+}$ and ![]() $X_{-}$. For this, we may choose an equivariant isolating neighborhood
$X_{-}$. For this, we may choose an equivariant isolating neighborhood ![]() $N$ of
$N$ of ![]() $S_{\text{irr}}$ so that
$S_{\text{irr}}$ so that ![]() $N$ is a disjoint union
$N$ is a disjoint union  $N_{+}\amalg N_{-}$ with
$N_{+}\amalg N_{-}$ with ![]() $j$ interchanging
$j$ interchanging ![]() $N_{+}$ and
$N_{+}$ and ![]() $N_{-}$. Then
$N_{-}$. Then  $I(S_{\text{irr}})=N_{+}/L_{+}\vee N_{-}/jL_{+}$ for
$I(S_{\text{irr}})=N_{+}/L_{+}\vee N_{-}/jL_{+}$ for  $(N_{+},L_{+})$ some choice of index pair. Then
$(N_{+},L_{+})$ some choice of index pair. Then ![]() $I(S)$ is homotopy-equivalent to a CW complex obtained by attaching
$I(S)$ is homotopy-equivalent to a CW complex obtained by attaching  $X_{+}\vee X_{-}$ to
$X_{+}\vee X_{-}$ to ![]() $I(S)^{S^{1}}$, and in particular
$I(S)^{S^{1}}$, and in particular  $\mathit{SWF}(Y,\mathfrak{s})=(X,m,n)$ with
$\mathit{SWF}(Y,\mathfrak{s})=(X,m,n)$ with ![]() $X$ a
$X$ a ![]() $j$-split space.
$j$-split space.
In the case of five or more singular fibers, we perturb the Seiberg–Witten equations to be nondegenerate. We can arrange that for a small perturbation ![]() $\mathfrak{q}$ the analogue of Fact 5.2 continues to hold. That is, there exists some very tame admissible perturbation
$\mathfrak{q}$ the analogue of Fact 5.2 continues to hold. That is, there exists some very tame admissible perturbation ![]() $\mathfrak{q}$ such that the set of irreducible critical points of
$\mathfrak{q}$ such that the set of irreducible critical points of ![]() ${\mathcal{X}}_{\mathfrak{q}}$ may be partitioned into two sets
${\mathcal{X}}_{\mathfrak{q}}$ may be partitioned into two sets ![]() $C^{+}$ and
$C^{+}$ and ![]() $C^{-}$, interchanged by the action of
$C^{-}$, interchanged by the action of ![]() $j$, so that for all
$j$, so that for all  $x\in C^{+},y\in C^{-}$, we have
$x\in C^{+},y\in C^{-}$, we have  $M(x,y)=\emptyset$.
$M(x,y)=\emptyset$.
We show the existence of such a ![]() $j$-equivariant perturbation
$j$-equivariant perturbation ![]() $\mathfrak{q}$. Choose a sequence of small
$\mathfrak{q}$. Choose a sequence of small ![]() $j$-equivariant very tame admissible perturbations
$j$-equivariant very tame admissible perturbations ![]() $\mathfrak{q}_{i}$, converging to
$\mathfrak{q}_{i}$, converging to ![]() $0$ in
$0$ in ![]() $C^{\infty }$, so that for each
$C^{\infty }$, so that for each ![]() $i$ the perturbed Seiberg–Witten equations have nondegenerate irreducible critical points. Lin establishes the existence of such perturbations in [Reference LinLin18]. Choose disjoint neighbourhoods
$i$ the perturbed Seiberg–Witten equations have nondegenerate irreducible critical points. Lin establishes the existence of such perturbations in [Reference LinLin18]. Choose disjoint neighbourhoods ![]() ${\mathcal{U}}^{\pm }(\text{}\text{e})$ of
${\mathcal{U}}^{\pm }(\text{}\text{e})$ of ![]() $C^{\pm }(\text{}\text{e})$ such that for
$C^{\pm }(\text{}\text{e})$ such that for ![]() $i$ sufficiently large all irreducible critical points of
$i$ sufficiently large all irreducible critical points of ![]() ${\mathcal{L}}_{\mathfrak{q}_{i}}$ lie in
${\mathcal{L}}_{\mathfrak{q}_{i}}$ lie in
 $$\begin{eqnarray}\mathop{\bigcup }_{\text{}\text{e}}({\mathcal{U}}^{+}(\text{}\text{e})\cup {\mathcal{U}}^{-}(\text{}\text{e})).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcup }_{\text{}\text{e}}({\mathcal{U}}^{+}(\text{}\text{e})\cup {\mathcal{U}}^{-}(\text{}\text{e})).\end{eqnarray}$$ Let ![]() $C_{i}^{+}$ denote the set of irreducible critical points of
$C_{i}^{+}$ denote the set of irreducible critical points of ![]() ${\mathcal{L}}_{\mathfrak{q}_{i}}$ in
${\mathcal{L}}_{\mathfrak{q}_{i}}$ in  $\bigcup _{\text{}\text{e}}{\mathcal{U}}^{+}(\text{}\text{e})$ and let
$\bigcup _{\text{}\text{e}}{\mathcal{U}}^{+}(\text{}\text{e})$ and let ![]() $C_{i}^{-}$ denote the set of irreducible critical points of
$C_{i}^{-}$ denote the set of irreducible critical points of ![]() ${\mathcal{L}}_{\mathfrak{q}_{i}}$ in
${\mathcal{L}}_{\mathfrak{q}_{i}}$ in  $\bigcup _{\text{}\text{e}}{\mathcal{U}}^{-}(\text{}\text{e})$. Let
$\bigcup _{\text{}\text{e}}{\mathcal{U}}^{-}(\text{}\text{e})$. Let ![]() $C^{\pm }$ denote the union
$C^{\pm }$ denote the union  $\bigcup _{\text{}\text{e}}C^{\pm }(\text{}\text{e})$.
$\bigcup _{\text{}\text{e}}C^{\pm }(\text{}\text{e})$.
Say, to obtain a contradiction, that for all ![]() $i$ there exists some pair of critical points
$i$ there exists some pair of critical points  $x_{i}\in C_{i}^{+}$,
$x_{i}\in C_{i}^{+}$,  $y_{i}\in C_{i}^{-}$, such that
$y_{i}\in C_{i}^{-}$, such that  $M(x_{i},y_{i})$ is nonempty. The sequences
$M(x_{i},y_{i})$ is nonempty. The sequences ![]() $x_{i},y_{i}$ have limit points
$x_{i},y_{i}$ have limit points  $x\in C^{+}(\text{}\text{e})$ and
$x\in C^{+}(\text{}\text{e})$ and  $y\in C^{-}(\text{}\text{f})$, by Proposition 11.6.4 of [Reference Kronheimer and MrowkaKM07]. Theorem 16.1.3 of [Reference Kronheimer and MrowkaKM07] shows that the moduli space of unparameterized broken trajectories (for a fixed perturbation) is compact. The proof of Theorem 16.1.3 can be applied to a sequence of trajectories
$y\in C^{-}(\text{}\text{f})$, by Proposition 11.6.4 of [Reference Kronheimer and MrowkaKM07]. Theorem 16.1.3 of [Reference Kronheimer and MrowkaKM07] shows that the moduli space of unparameterized broken trajectories (for a fixed perturbation) is compact. The proof of Theorem 16.1.3 can be applied to a sequence of trajectories ![]() $\breve{\unicode[STIX]{x1D6FE}}_{i}$ for perturbations
$\breve{\unicode[STIX]{x1D6FE}}_{i}$ for perturbations ![]() $\mathfrak{q}_{i}$ with
$\mathfrak{q}_{i}$ with ![]() $\mathfrak{q}_{i}\rightarrow 0$. That is, the sequence
$\mathfrak{q}_{i}\rightarrow 0$. That is, the sequence ![]() $\breve{\unicode[STIX]{x1D6FE}}_{i}$ has a limit point a broken trajectory
$\breve{\unicode[STIX]{x1D6FE}}_{i}$ has a limit point a broken trajectory  $(\breve{\unicode[STIX]{x1D70F}}_{1},\ldots ,\breve{\unicode[STIX]{x1D70F}}_{n})$ from
$(\breve{\unicode[STIX]{x1D70F}}_{1},\ldots ,\breve{\unicode[STIX]{x1D70F}}_{n})$ from ![]() $x$ to
$x$ to ![]() $y$, for the perturbation
$y$, for the perturbation ![]() $\mathfrak{q}=0$. Since
$\mathfrak{q}=0$. Since  $x\in C^{+},y\in C^{-}$, there exists a trajectory
$x\in C^{+},y\in C^{-}$, there exists a trajectory ![]() $\breve{\unicode[STIX]{x1D70F}}_{k}$ from
$\breve{\unicode[STIX]{x1D70F}}_{k}$ from ![]() $C^{+}$ to
$C^{+}$ to ![]() $C^{-}$, or there exists a trajectory
$C^{-}$, or there exists a trajectory ![]() $\breve{\unicode[STIX]{x1D70F}}_{k}$ from
$\breve{\unicode[STIX]{x1D70F}}_{k}$ from ![]() $C^{+}$ to the reducible and a trajectory
$C^{+}$ to the reducible and a trajectory ![]() $\breve{\unicode[STIX]{x1D70F}}_{l}$ from the reducible to
$\breve{\unicode[STIX]{x1D70F}}_{l}$ from the reducible to ![]() $C^{-}$. The first case contradicts Fact 5.2. The second case contradicts the minimality of
$C^{-}$. The first case contradicts Fact 5.2. The second case contradicts the minimality of ![]() ${\mathcal{L}}$ on the reducible (Fact 5.1). Thus, for some perturbation
${\mathcal{L}}$ on the reducible (Fact 5.1). Thus, for some perturbation ![]() $\mathfrak{q}$ as above we have the desired partition.
$\mathfrak{q}$ as above we have the desired partition.
The lemma then follows as in the case of three or four singular fibers. ◻
By Lemma 5.3, Theorem 3.16 applies to  $\mathit{SWF}(Y,\mathfrak{s})$ for
$\mathit{SWF}(Y,\mathfrak{s})$ for ![]() $Y$ a Seifert rational homology sphere, and we obtain the following corollary, from which Theorems 1.1 and 1.4 of the Introduction follow.
$Y$ a Seifert rational homology sphere, and we obtain the following corollary, from which Theorems 1.1 and 1.4 of the Introduction follow.
Corollary 5.4. Let  $Y=\unicode[STIX]{x1D6F4}(b,(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{1}),\ldots ,(\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FC}_{k}))$ be a negative Seifert rational homology sphere with a choice of spin structure
$Y=\unicode[STIX]{x1D6F4}(b,(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{1}),\ldots ,(\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FC}_{k}))$ be a negative Seifert rational homology sphere with a choice of spin structure ![]() $\mathfrak{s}$. Then
$\mathfrak{s}$. Then
 $$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\oplus J^{\oplus 2}[-s],\end{eqnarray}$$
$$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\oplus J^{\oplus 2}[-s],\end{eqnarray}$$ for some constants  $s,d_{i},n_{i},N$ and some
$s,d_{i},n_{i},N$ and some ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module ![]() $J$, all determined by
$J$, all determined by ![]() $(Y,\mathfrak{s})$. Furthermore,
$(Y,\mathfrak{s})$. Furthermore,  $2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$ for all
$2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$ for all ![]() $i$,
$i$,  $2n_{N}+d_{N}\geqslant 3$,
$2n_{N}+d_{N}\geqslant 3$, ![]() $d_{N}\leqslant 1$, and
$d_{N}\leqslant 1$, and  $d_{N+1}=1$,
$d_{N+1}=1$,  $n_{N+1}=0$. Let
$n_{N+1}=0$. Let  ${\mathcal{J}}_{0}=\{(a_{k},b_{k})\}_{k}$ be the collection of pairs consisting of all
${\mathcal{J}}_{0}=\{(a_{k},b_{k})\}_{k}$ be the collection of pairs consisting of all  $(d_{i},\lfloor (n_{i}+1)/2\rfloor )$ for
$(d_{i},\lfloor (n_{i}+1)/2\rfloor )$ for  $d_{i}\equiv 1\;\text{mod}\;4$ and all
$d_{i}\equiv 1\;\text{mod}\;4$ and all  $(d_{i}+2,\lfloor n_{i}/2\rfloor )$ for
$(d_{i}+2,\lfloor n_{i}/2\rfloor )$ for  $d_{i}\equiv 3\;\text{mod}\;4$, counting multiplicity. Let
$d_{i}\equiv 3\;\text{mod}\;4$, counting multiplicity. Let  $(a,b)\succcurlyeq (c,d)$ if
$(a,b)\succcurlyeq (c,d)$ if  $a+4b\geqslant c+4d$ and
$a+4b\geqslant c+4d$ and ![]() $a\geqslant c$, and let
$a\geqslant c$, and let ![]() ${\mathcal{J}}$ be the subset of
${\mathcal{J}}$ be the subset of ![]() ${\mathcal{J}}_{0}$ consisting of pairs maximal under
${\mathcal{J}}_{0}$ consisting of pairs maximal under ![]() $\succcurlyeq$ (not counted with multiplicity). If
$\succcurlyeq$ (not counted with multiplicity). If  $(a,b)\in {\mathcal{J}}$, set
$(a,b)\in {\mathcal{J}}$, set  $m(a,b)+1$ to be the multiplicity of
$m(a,b)+1$ to be the multiplicity of ![]() $(a,b)$ in
$(a,b)$ in ![]() ${\mathcal{J}}_{0}$. If
${\mathcal{J}}_{0}$. If  $(a,b)\not \in {\mathcal{J}}$, set
$(a,b)\not \in {\mathcal{J}}$, set ![]() $m(a,b)$ to be the multiplicity of
$m(a,b)$ to be the multiplicity of ![]() $(a,b)$ in
$(a,b)$ in ![]() ${\mathcal{J}}_{0}$. Let
${\mathcal{J}}_{0}$. Let  $|{\mathcal{J}}|=N_{0}$ and order the elements of
$|{\mathcal{J}}|=N_{0}$ and order the elements of ![]() ${\mathcal{J}}$ so that
${\mathcal{J}}$ so that  ${\mathcal{J}}=\{(a_{i},b_{i})\}_{i}$, with
${\mathcal{J}}=\{(a_{i},b_{i})\}_{i}$, with  $a_{i}+4b_{i}>a_{i+1}+4b_{i+1}$. Then
$a_{i}+4b_{i}>a_{i+1}+4b_{i+1}$. Then
 $$\begin{eqnarray}\displaystyle \mathit{SWFH}_{\ast }^{G}(Y,\mathfrak{s}) & = & \displaystyle ({\mathcal{V}}_{4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus \mathop{\bigoplus }_{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\{i\mid d_{i}\equiv 1\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \mathop{\bigoplus }_{\{i\mid d_{i}\equiv 3\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr))[-s].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{SWFH}_{\ast }^{G}(Y,\mathfrak{s}) & = & \displaystyle ({\mathcal{V}}_{4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+}\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}\biggl(\frac{a_{i+1}+4b_{i+1}-a_{i}}{4}\biggr)\oplus \mathop{\bigoplus }_{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J\nonumber\\ \displaystyle & & \displaystyle \oplus \mathop{\bigoplus }_{\{i\mid d_{i}\equiv 1\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}+2}^{+}\biggl(\biggl\lfloor\frac{n_{i}}{2}\biggr\rfloor\biggr)\oplus \mathop{\bigoplus }_{\{i\mid d_{i}\equiv 3\;\text{mod}\;4\}}{\mathcal{V}}_{d_{i}}^{+}\biggl(\biggl\lfloor\frac{n_{i}+1}{2}\biggr\rfloor\biggr))[-s].\end{eqnarray}$$ The ![]() $q$-action is given by the isomorphism
$q$-action is given by the isomorphism  ${\mathcal{V}}_{2}^{+}[-s]\rightarrow {\mathcal{V}}_{1}^{+}[-s]$ and the map
${\mathcal{V}}_{2}^{+}[-s]\rightarrow {\mathcal{V}}_{1}^{+}[-s]$ and the map  ${\mathcal{V}}_{1}^{+}[-s]\rightarrow {\mathcal{V}}_{4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}[-s]$ which is an
${\mathcal{V}}_{1}^{+}[-s]\rightarrow {\mathcal{V}}_{4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}[-s]$ which is an ![]() $\mathbb{F}$-vector space isomorphism in all degrees (in
$\mathbb{F}$-vector space isomorphism in all degrees (in ![]() ${\mathcal{V}}_{1}^{+}[-s]$) greater than or equal to
${\mathcal{V}}_{1}^{+}[-s]$) greater than or equal to  $4\lfloor (d_{1}+2n_{1}+1)/4\rfloor +s+1$, and vanishes on elements of
$4\lfloor (d_{1}+2n_{1}+1)/4\rfloor +s+1$, and vanishes on elements of ![]() ${\mathcal{V}}_{1}^{+}[-s]$ of degree less than
${\mathcal{V}}_{1}^{+}[-s]$ of degree less than  $4\lfloor (d_{1}+2n_{1}+1)/4\rfloor +s+1$. We interpret
$4\lfloor (d_{1}+2n_{1}+1)/4\rfloor +s+1$. We interpret  $a_{N_{0}+1}=1,b_{N_{0}+1}=0$.
$a_{N_{0}+1}=1,b_{N_{0}+1}=0$.
The action of ![]() $q$ annihilates
$q$ annihilates  $\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)[-s]$ and
$\bigoplus _{i=1}^{N_{0}}{\mathcal{V}}_{a_{i}}^{+}((a_{i+1}+4b_{i+1}-a_{i})/4)[-s]$ and  $(\bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J)[-s]$.
$(\bigoplus _{(a,b)\in {\mathcal{J}}_{0}}{\mathcal{V}}_{a}^{+}(b)^{\oplus m(a,b)}\oplus \text{res}_{\mathbb{F}[v]}^{\mathbb{F}[U]}J)[-s]$.
To finish specifying the ![]() $q$-action, let
$q$-action, let ![]() $x_{i}$ be a generator of
$x_{i}$ be a generator of  ${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )[-s]$ for
${\mathcal{V}}_{d_{i}+2}^{+}(\lfloor n_{i}/2\rfloor )[-s]$ for ![]() $i$ such that
$i$ such that  $d_{i}\equiv 1\;\text{mod}\;4$ (respectively, let
$d_{i}\equiv 1\;\text{mod}\;4$ (respectively, let ![]() $x_{i}$ be a generator of
$x_{i}$ be a generator of  ${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )[-s]$ if
${\mathcal{V}}_{d_{i}}^{+}(\lfloor (n_{i}+1)/2\rfloor )[-s]$ if  $d_{i}\equiv 3\;\text{mod}\;4$). Then
$d_{i}\equiv 3\;\text{mod}\;4$). Then ![]() $qx_{i}$ is the unique nonzero element of
$qx_{i}$ is the unique nonzero element of  $({\mathcal{V}}_{4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+})[-s]$ in grading
$({\mathcal{V}}_{4\lfloor (d_{1}+2n_{1}+1)/4\rfloor }^{+}\oplus {\mathcal{V}}_{1}^{+}\oplus {\mathcal{V}}_{2}^{+})[-s]$ in grading  $\text{deg}\,x_{i}-1$, for all
$\text{deg}\,x_{i}-1$, for all ![]() $i$.
$i$.
Theorem 1.4 follows by setting ![]() $N=1$ and
$N=1$ and ![]() $d_{1}=1$; these conditions imply that
$d_{1}=1$; these conditions imply that  $d_{2}+2n_{2}-d_{1}=0$, and so the term
$d_{2}+2n_{2}-d_{1}=0$, and so the term  $\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}((d_{i+1}+2n_{i+1}-d_{i})/2)$ in (83) is the zero module in this case.
$\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}((d_{i+1}+2n_{i+1}-d_{i})/2)$ in (83) is the zero module in this case.
The constant ![]() $s$ is the grading of the reducible critical point, where the metric on
$s$ is the grading of the reducible critical point, where the metric on ![]() $Y$ is that associated to the Seifert geometry on
$Y$ is that associated to the Seifert geometry on ![]() $Y$.
$Y$.
Proof. Let  $(X^{\prime },p,h/4)$ be a
$(X^{\prime },p,h/4)$ be a ![]() $j$-split representative for
$j$-split representative for  $\mathit{SWF}(Y,\mathfrak{s})$ at level
$\mathit{SWF}(Y,\mathfrak{s})$ at level ![]() $m$, and let
$m$, and let  $s=m-p-h$. We may choose such a representative for
$s=m-p-h$. We may choose such a representative for  $\mathit{SWF}(Y,\mathfrak{s})$ by Lemma 5.3. Then, using Lemma 3.11, we have
$\mathit{SWF}(Y,\mathfrak{s})$ by Lemma 5.3. Then, using Lemma 3.11, we have
 $$\begin{eqnarray}\displaystyle \mathit{SWFH}_{\ast }^{S^{1}}(Y,\mathfrak{s}) & = & \displaystyle \tilde{H}_{\ast }^{S^{1}}(X^{\prime })[-p-h]\nonumber\\ \displaystyle & = & \displaystyle \biggl(\mathop{\bigoplus }_{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \mathop{\bigoplus }_{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J_{2}^{\oplus 2}\oplus {\mathcal{T}}_{d_{1}+2n_{1}-1}^{+}\biggr)[-s].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{SWFH}_{\ast }^{S^{1}}(Y,\mathfrak{s}) & = & \displaystyle \tilde{H}_{\ast }^{S^{1}}(X^{\prime })[-p-h]\nonumber\\ \displaystyle & = & \displaystyle \biggl(\mathop{\bigoplus }_{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \mathop{\bigoplus }_{i=1}^{N}{\mathcal{T}}_{d_{i}}^{+}(n_{i})\oplus J_{2}^{\oplus 2}\oplus {\mathcal{T}}_{d_{1}+2n_{1}-1}^{+}\biggr)[-s].\nonumber\end{eqnarray}$$ Applying the equivalence of ![]() $\check{HM}$ and
$\check{HM}$ and  $\mathit{SWFH}^{S^{1}}$ of [Reference Lidman and ManolescuLM18], and the equivalence of
$\mathit{SWFH}^{S^{1}}$ of [Reference Lidman and ManolescuLM18], and the equivalence of ![]() $\check{HM}$ and
$\check{HM}$ and ![]() $\mathit{HF}^{+}$ of [Reference Colin, Ghiggini and HondaCGH11] and [Reference Kutluhan, Lee and TaubesKLT10], we obtain the expression (83). Then we apply Theorem 3.16 to obtain the calculation of
$\mathit{HF}^{+}$ of [Reference Colin, Ghiggini and HondaCGH11] and [Reference Kutluhan, Lee and TaubesKLT10], we obtain the expression (83). Then we apply Theorem 3.16 to obtain the calculation of  $\mathit{SWFH}_{\ast }^{G}$ of the corollary.◻
$\mathit{SWFH}_{\ast }^{G}$ of the corollary.◻
Further, using the results of § 3.2, we prove the results of the Introduction on homology cobordisms of Seifert spaces. Corollaries 1.6 and 1.7 of the Introduction follow from Proposition 5.5 below.
Proposition 5.5. Let  $Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology three-sphere with a choice of spin structure
$Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology three-sphere with a choice of spin structure ![]() $\mathfrak{s}$, and
$\mathfrak{s}$, and
 $$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\oplus J^{\oplus 2}[-s],\end{eqnarray}$$
$$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{s+d_{1}+2n_{1}-1}^{+_{}^{}\oplus \bigoplus }{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i})\oplus J^{\oplus 2}[-s],\end{eqnarray}$$ where  $d_{i+1}>d_{i}$ and
$d_{i+1}>d_{i}$ and  $2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$, as well as
$2n_{i}+d_{i}>2n_{i+1}+d_{i+1}$, as well as  $2n_{N}+d_{N}\geqslant 3$ and
$2n_{N}+d_{N}\geqslant 3$ and ![]() $d_{N}\leqslant 1$. Then the chain local equivalence type
$d_{N}\leqslant 1$. Then the chain local equivalence type  $[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}\in \mathfrak{CLE}$ is the equivalence class of
$[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}\in \mathfrak{CLE}$ is the equivalence class of
 $$\begin{eqnarray}C(s,\{{d_{i}\}}_{i},\{{n_{i}\}}_{i})=\biggl(\biggl(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\biggl(\bigoplus _{i}{\mathcal{S}}_{d_{i}}(n_{i})\biggr)\biggr),0,-s/4\biggr)\in \mathfrak{CLE}.\end{eqnarray}$$
$$\begin{eqnarray}C(s,\{{d_{i}\}}_{i},\{{n_{i}\}}_{i})=\biggl(\biggl(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,\biggl(\bigoplus _{i}{\mathcal{S}}_{d_{i}}(n_{i})\biggr)\biggr),0,-s/4\biggr)\in \mathfrak{CLE}.\end{eqnarray}$$ Further, the connected Seiberg–Witten Floer homology of ![]() $(Y,\mathfrak{s})$ is
$(Y,\mathfrak{s})$ is
 $$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})=\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i}).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{SWFH}_{\text{conn}}(Y,\mathfrak{s})=\bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}\biggl(\frac{d_{i+1}+2n_{i+1}-d_{i}}{2}\biggr)\oplus \bigoplus _{i=1}^{N}{\mathcal{T}}_{s+d_{i}}^{+}(n_{i}).\end{eqnarray}$$ Moreover, if ![]() $s\neq t$, or
$s\neq t$, or  $\{{d_{i}\}}_{i}\neq \{{e_{i}\}}_{i}$, or
$\{{d_{i}\}}_{i}\neq \{{e_{i}\}}_{i}$, or  $\{{n_{i}\}}_{i}\neq \{{m_{i}\}}_{i}$, the complexes
$\{{n_{i}\}}_{i}\neq \{{m_{i}\}}_{i}$, the complexes  $C(s,\{{d_{i}\}}_{i},\{{n_{i}\}}_{i})$ and
$C(s,\{{d_{i}\}}_{i},\{{n_{i}\}}_{i})$ and  $C(t,\{{e_{i}\}}_{i},\{{m_{i}\}}_{i})$ are not locally equivalent.
$C(t,\{{e_{i}\}}_{i},\{{m_{i}\}}_{i})$ are not locally equivalent.
Proof. Let  $\mathit{SWF}(Y,\mathfrak{s})=(X,p,h/4)\in \mathfrak{E}$ with
$\mathit{SWF}(Y,\mathfrak{s})=(X,p,h/4)\in \mathfrak{E}$ with ![]() $X$ a
$X$ a ![]() $j$-split space of type SWF. By the construction of
$j$-split space of type SWF. By the construction of  $\mathit{SWF}(Y,\mathfrak{s})$,
$\mathit{SWF}(Y,\mathfrak{s})$,  $X^{S^{1}}\simeq (\tilde{\mathbb{R}}^{p})^{+}$. By Lemma 3.2,
$X^{S^{1}}\simeq (\tilde{\mathbb{R}}^{p})^{+}$. By Lemma 3.2,  $[(X,p,h/4)]\in \mathfrak{CE}$ admits a representative
$[(X,p,h/4)]\in \mathfrak{CE}$ admits a representative  $(Z,p^{\prime },h^{\prime }/4)$ with
$(Z,p^{\prime },h^{\prime }/4)$ with ![]() $Z$ a
$Z$ a ![]() $j$-split chain complex, for some
$j$-split chain complex, for some ![]() $p^{\prime },h^{\prime }$. Since
$p^{\prime },h^{\prime }$. Since  $[(X,p,h/4)]\in \mathfrak{CE}$ and
$[(X,p,h/4)]\in \mathfrak{CE}$ and  $(Z,p^{\prime },h^{\prime }/4)$ must have chain homotopy equivalent fixed-point sets, we have
$(Z,p^{\prime },h^{\prime }/4)$ must have chain homotopy equivalent fixed-point sets, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{-\tilde{\mathbb{R}}^{p}}((\tilde{\mathbb{R}}^{p})^{+})=[(X^{S^{1}},p,0)]=(Z^{S^{1}},p^{\prime },0)\in \mathfrak{CE}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{-\tilde{\mathbb{R}}^{p}}((\tilde{\mathbb{R}}^{p})^{+})=[(X^{S^{1}},p,0)]=(Z^{S^{1}},p^{\prime },0)\in \mathfrak{CE}.\end{eqnarray}$$ However, by the requirement that ![]() $Z$ is
$Z$ is ![]() $j$-split,
$j$-split,  $Z^{S^{1}}\simeq \langle f_{\text{red}}\rangle$, where
$Z^{S^{1}}\simeq \langle f_{\text{red}}\rangle$, where  $jf_{\text{red}}=sf_{\text{red}}=\unicode[STIX]{x2202}(f_{\text{red}})=0$. Thus,
$jf_{\text{red}}=sf_{\text{red}}=\unicode[STIX]{x2202}(f_{\text{red}})=0$. Thus, ![]() $p^{\prime }=0$. Furthermore, by the proof of Corollary 5.4,
$p^{\prime }=0$. Furthermore, by the proof of Corollary 5.4,  $-p^{\prime }-h^{\prime }=-h^{\prime }=s$. Proposition 3.21 applied to
$-p^{\prime }-h^{\prime }=-h^{\prime }=s$. Proposition 3.21 applied to  $(Z,0,-s/4)$ yields (86) from (68) and (87) from (69).◻
$(Z,0,-s/4)$ yields (86) from (68) and (87) from (69).◻
5.2 Spaces of projective type
Let  $Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology three-sphere. Consider the case that
$Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology three-sphere. Consider the case that  $\mathit{HF}^{+}(Y,\mathfrak{s})$ is given by
$\mathit{HF}^{+}(Y,\mathfrak{s})$ is given by
 $$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{2\unicode[STIX]{x1D6FF}}^{+}\oplus {\mathcal{T}}_{d}^{+}(n)\oplus J^{\oplus 2},\end{eqnarray}$$
$$\begin{eqnarray}\mathit{HF}^{+}(Y,\mathfrak{s})={\mathcal{T}}_{2\unicode[STIX]{x1D6FF}}^{+}\oplus {\mathcal{T}}_{d}^{+}(n)\oplus J^{\oplus 2},\end{eqnarray}$$ for some ![]() $\mathbb{F}[U]$-module
$\mathbb{F}[U]$-module ![]() $J$, where possibly
$J$, where possibly ![]() $n=0$. In particular, by Corollary 5.4, this implies
$n=0$. In particular, by Corollary 5.4, this implies  $d+2n-1=2\unicode[STIX]{x1D6FF}$. Let
$d+2n-1=2\unicode[STIX]{x1D6FF}$. Let  $(Z,0,-s/4)=\mathit{SWF}(Y,\mathfrak{s})\in \mathfrak{CE}$. Then by Proposition 3.18, we may write
$(Z,0,-s/4)=\mathit{SWF}(Y,\mathfrak{s})\in \mathfrak{CE}$. Then by Proposition 3.18, we may write
 $$\begin{eqnarray}Z=(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,{\mathcal{S}}_{1}(n))\oplus S(J)\end{eqnarray}$$
$$\begin{eqnarray}Z=(\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,{\mathcal{S}}_{1}(n))\oplus S(J)\end{eqnarray}$$ as a direct sum of  $C_{\ast }^{\text{CW}}(S^{1})$-chain complexes, with
$C_{\ast }^{\text{CW}}(S^{1})$-chain complexes, with  $\unicode[STIX]{x2202}(x_{1})=f_{\text{red}}$,
$\unicode[STIX]{x2202}(x_{1})=f_{\text{red}}$,  $\unicode[STIX]{x2202}(x_{2i+1})=s(1+j^{2})x_{2i-1}$ for
$\unicode[STIX]{x2202}(x_{2i+1})=s(1+j^{2})x_{2i-1}$ for  $i=1,\ldots ,n-1$. Here
$i=1,\ldots ,n-1$. Here  $d=s+1$, by Corollary 5.4. The complex
$d=s+1$, by Corollary 5.4. The complex ![]() $Z$ is evidently chain locally equivalent to
$Z$ is evidently chain locally equivalent to  $\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,{\mathcal{S}}_{1}(n)$. For
$\langle f_{\text{red}}\rangle \,\tilde{\oplus }\,{\mathcal{S}}_{1}(n)$. For ![]() $X$ a
$X$ a ![]() $G$-space, let
$G$-space, let ![]() $\tilde{\unicode[STIX]{x1D6F4}}X$ denote the unreduced suspension of
$\tilde{\unicode[STIX]{x1D6F4}}X$ denote the unreduced suspension of ![]() $X$. The complex (89) with
$X$. The complex (89) with ![]() $J=0$, for
$J=0$, for ![]() $\unicode[STIX]{x1D6FF}>0$, may be realized as the
$\unicode[STIX]{x1D6FF}>0$, may be realized as the ![]() $G$-CW complex associated to
$G$-CW complex associated to
 $$\begin{eqnarray}(\tilde{\unicode[STIX]{x1D6F4}}(S^{2n-1}\amalg S^{2n-1}),0,-s/4),\end{eqnarray}$$
$$\begin{eqnarray}(\tilde{\unicode[STIX]{x1D6F4}}(S^{2n-1}\amalg S^{2n-1}),0,-s/4),\end{eqnarray}$$ where ![]() $S^{1}$ acts by complex multiplication on each of the two factors, and
$S^{1}$ acts by complex multiplication on each of the two factors, and ![]() $j$ interchanges the factors. Then
$j$ interchanges the factors. Then
 $$\begin{eqnarray}[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}\equiv [(\tilde{\unicode[STIX]{x1D6F4}}(S^{2n-1}\amalg S^{2n-1}),0,-s/4)]_{\text{cl}}.\end{eqnarray}$$
$$\begin{eqnarray}[\mathit{SWF}(Y,\mathfrak{s})]_{\text{cl}}\equiv [(\tilde{\unicode[STIX]{x1D6F4}}(S^{2n-1}\amalg S^{2n-1}),0,-s/4)]_{\text{cl}}.\end{eqnarray}$$ We call a negative Seifert rational homology sphere with spin structure ![]() $(Y,\mathfrak{s})$of projective type if (90) holds or if the chain local equivalence class of
$(Y,\mathfrak{s})$of projective type if (90) holds or if the chain local equivalence class of  $\mathit{SWF}(Y,\mathfrak{s})$ is
$\mathit{SWF}(Y,\mathfrak{s})$ is  $[\langle f_{\text{red}}\rangle ]_{\text{cl}}$. Indeed, we have established that
$[\langle f_{\text{red}}\rangle ]_{\text{cl}}$. Indeed, we have established that ![]() $(Y,\mathfrak{s})$ is of projective type if and only if
$(Y,\mathfrak{s})$ is of projective type if and only if  $\mathit{HF}^{+}(Y,\mathfrak{s})$ takes the form (88) (where perhaps
$\mathit{HF}^{+}(Y,\mathfrak{s})$ takes the form (88) (where perhaps ![]() $n=0$). The term of projective type refers to the fact
$n=0$). The term of projective type refers to the fact
 $$\begin{eqnarray}(S^{2n-1}\amalg S^{2n-1})/G\simeq \mathbb{C}P^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}(S^{2n-1}\amalg S^{2n-1})/G\simeq \mathbb{C}P^{n-1}.\end{eqnarray}$$ We can rephrase the projective type condition (88) in terms of the graded roots of [Reference NémethiNém05]. A graded root ![]() $(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D712})$ is an infinite tree
$(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D712})$ is an infinite tree ![]() $\unicode[STIX]{x1D6E4}$ with an action of
$\unicode[STIX]{x1D6E4}$ with an action of ![]() $\mathbb{F}[U]$, together with a grading function
$\mathbb{F}[U]$, together with a grading function  $\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{Z}$. Associated to any positive Seifert rational homology sphere with spin structure there is a graded root, which, additionally, has an involution
$\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{Z}$. Associated to any positive Seifert rational homology sphere with spin structure there is a graded root, which, additionally, has an involution  $\unicode[STIX]{x1D704}:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}$ that preserves the grading.
$\unicode[STIX]{x1D704}:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}$ that preserves the grading.
We have the following characterization of spaces of projective type in terms of graded roots as a consequence of Corollary 5.4.
Fact 5.6. Let  $Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology sphere with spin structure
$Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology sphere with spin structure ![]() $\mathfrak{s}$. Let
$\mathfrak{s}$. Let ![]() $(\unicode[STIX]{x1D6E4}_{Y},\unicode[STIX]{x1D712})$ be the graded root associated to
$(\unicode[STIX]{x1D6E4}_{Y},\unicode[STIX]{x1D712})$ be the graded root associated to ![]() $(-Y,\mathfrak{s})$, and let
$(-Y,\mathfrak{s})$, and let ![]() $\unicode[STIX]{x1D704}$ be the associated involution of
$\unicode[STIX]{x1D704}$ be the associated involution of ![]() $\unicode[STIX]{x1D6E4}_{Y}$. Let
$\unicode[STIX]{x1D6E4}_{Y}$. Let ![]() $v\in \unicode[STIX]{x1D6E4}_{Y}$ be the vertex of minimal grading which is invariant under
$v\in \unicode[STIX]{x1D6E4}_{Y}$ be the vertex of minimal grading which is invariant under ![]() $\unicode[STIX]{x1D704}$. The space
$\unicode[STIX]{x1D704}$. The space ![]() $(Y,\mathfrak{s})$ is of projective type if and only if there exists a vertex
$(Y,\mathfrak{s})$ is of projective type if and only if there exists a vertex ![]() $w$, and a path from
$w$, and a path from ![]() $v$ to
$v$ to ![]() $w$ in
$w$ in ![]() $\unicode[STIX]{x1D6E4}_{Y}$ which is grading-decreasing at each step, with
$\unicode[STIX]{x1D6E4}_{Y}$ which is grading-decreasing at each step, with  $\unicode[STIX]{x1D712}(w)=\text{min}_{x\in \unicode[STIX]{x1D6E4}_{Y}}\unicode[STIX]{x1D712}(x)$. Moreover,
$\unicode[STIX]{x1D712}(w)=\text{min}_{x\in \unicode[STIX]{x1D6E4}_{Y}}\unicode[STIX]{x1D712}(x)$. Moreover,  $\unicode[STIX]{x1D6FF}(Y,\mathfrak{s})-\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=\unicode[STIX]{x1D712}(v)-\unicode[STIX]{x1D712}(w)$.
$\unicode[STIX]{x1D6FF}(Y,\mathfrak{s})-\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=\unicode[STIX]{x1D712}(v)-\unicode[STIX]{x1D712}(w)$.
For instance, we refer to Figure 11. We call a graded root of projective type if its homology is of the form (88), so that a Seifert integral homology sphere is of projective type if and only if its graded root is.

Figure 11. Three graded roots. The roots ![]() $(a)$ and
$(a)$ and ![]() $(b)$ are of projective type, while
$(b)$ are of projective type, while ![]() $(c)$ is not.
$(c)$ is not.
More generally, the sets ![]() $\{d_{i}\}$ and
$\{d_{i}\}$ and ![]() $\{n_{i}\}$ may be read from the graded root, in terms of the minimal grading elements
$\{n_{i}\}$ may be read from the graded root, in terms of the minimal grading elements ![]() $w$ that are leaves of vertices
$w$ that are leaves of vertices ![]() $v$ that are invariant under
$v$ that are invariant under ![]() $\unicode[STIX]{x1D704}$.
$\unicode[STIX]{x1D704}$.
For spaces ![]() $Y$ of projective type, the homology cobordism invariants
$Y$ of projective type, the homology cobordism invariants ![]() $(d_{i},n_{i})$ are determined by
$(d_{i},n_{i})$ are determined by  $d(Y),\bar{\unicode[STIX]{x1D707}}(Y)$. The nice topological description of the Seiberg–Witten Floer spectrum of spaces of projective type simplifies calculations.
$d(Y),\bar{\unicode[STIX]{x1D707}}(Y)$. The nice topological description of the Seiberg–Witten Floer spectrum of spaces of projective type simplifies calculations.
The spaces  $\unicode[STIX]{x1D6F4}(p,q,pqn+1)$ and
$\unicode[STIX]{x1D6F4}(p,q,pqn+1)$ and  $\unicode[STIX]{x1D6F4}(p,q,pqn-1)$ are of projective type for all
$\unicode[STIX]{x1D6F4}(p,q,pqn-1)$ are of projective type for all ![]() $p,q,n$, as shown by Némethi [Reference NémethiNém07] and Tweedy [Reference TweedyTwe13], respectively, building on work of Borodzik and Némethi [Reference Borodzik and NémethiBN13].
$p,q,n$, as shown by Némethi [Reference NémethiNém07] and Tweedy [Reference TweedyTwe13], respectively, building on work of Borodzik and Némethi [Reference Borodzik and NémethiBN13].
However, not all Seifert fiber spaces are of projective type. The Brieskorn sphere  $\unicode[STIX]{x1D6F4}(5,8,13)$ is a Seifert space not of projective type, for instance, as one may confirm using graded roots. Indeed,
$\unicode[STIX]{x1D6F4}(5,8,13)$ is a Seifert space not of projective type, for instance, as one may confirm using graded roots. Indeed,  $\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(5,8,13))={\mathcal{T}}_{1}^{+}(2)\oplus {\mathcal{T}}_{1}^{+}(1)$. By Corollary 1.6, any space not of projective type is not homology cobordant to a space of projective type. In particular,
$\mathit{SWFH}_{\text{conn}}(\unicode[STIX]{x1D6F4}(5,8,13))={\mathcal{T}}_{1}^{+}(2)\oplus {\mathcal{T}}_{1}^{+}(1)$. By Corollary 1.6, any space not of projective type is not homology cobordant to a space of projective type. In particular,  $\unicode[STIX]{x1D6F4}(5,8,13)$ is not homology cobordant to any
$\unicode[STIX]{x1D6F4}(5,8,13)$ is not homology cobordant to any  $\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$.
$\unicode[STIX]{x1D6F4}(p,q,pqn\pm 1)$.
5.3 Calculation of beta
By the construction of  $\mathit{SWF}(Y,\mathfrak{s})$, the grading of the reducible element is
$\mathit{SWF}(Y,\mathfrak{s})$, the grading of the reducible element is  $-2n(Y,\mathfrak{s},g)$. We also saw that the constant
$-2n(Y,\mathfrak{s},g)$. We also saw that the constant ![]() $s$ (depending on
$s$ (depending on ![]() $(Y,\mathfrak{s})$) in Corollary 5.4 is the grading of the reducible (with respect to the Seifert metric). Also in Corollary 5.4, we saw
$(Y,\mathfrak{s})$) in Corollary 5.4 is the grading of the reducible (with respect to the Seifert metric). Also in Corollary 5.4, we saw  $s/2=\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})$ for Seifert rational homology spheres. We then obtain the following result.
$s/2=\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})$ for Seifert rational homology spheres. We then obtain the following result.
Corollary 5.7. Let  $Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology sphere and
$Y=\unicode[STIX]{x1D6F4}(b,(b_{1},a_{1}),\ldots ,(b_{k},a_{k}))$ be a negative Seifert rational homology sphere and ![]() $\mathfrak{s}$ a spin structure on
$\mathfrak{s}$ a spin structure on ![]() $Y$. Then
$Y$. Then  $\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=-n(Y,\mathfrak{s},g)$, where
$\unicode[STIX]{x1D6FD}(Y,\mathfrak{s})=-n(Y,\mathfrak{s},g)$, where ![]() $g$ is a metric for which
$g$ is a metric for which ![]() $Y$ has the Seifert geometry.
$Y$ has the Seifert geometry.
Ruberman and Saveliev [Reference Ruberman and SavelievRS11] show  $n(Y,g)=\bar{\unicode[STIX]{x1D707}}(Y)$ for Seifert integral homology spheres for the Seifert metric, from which we establish Theorem 1.3.
$n(Y,g)=\bar{\unicode[STIX]{x1D707}}(Y)$ for Seifert integral homology spheres for the Seifert metric, from which we establish Theorem 1.3.
We have established that ![]() $\bar{\unicode[STIX]{x1D707}}$ restricted to Seifert integral homology three-spheres extends to a homology cobordism invariant, but not necessarily that
$\bar{\unicode[STIX]{x1D707}}$ restricted to Seifert integral homology three-spheres extends to a homology cobordism invariant, but not necessarily that ![]() $\bar{\unicode[STIX]{x1D707}}$ extends to a homology cobordism invariant. In [Reference ManolescuMan13] it is shown that
$\bar{\unicode[STIX]{x1D707}}$ extends to a homology cobordism invariant. In [Reference ManolescuMan13] it is shown that ![]() $\unicode[STIX]{x1D6FD}$ is not additive; on the other hand,
$\unicode[STIX]{x1D6FD}$ is not additive; on the other hand, ![]() $\bar{\unicode[STIX]{x1D707}}$ is additive. Similarly,
$\bar{\unicode[STIX]{x1D707}}$ is additive. Similarly, ![]() $\unicode[STIX]{x1D6FD}$ does not agree with the Saveliev
$\unicode[STIX]{x1D6FD}$ does not agree with the Saveliev ![]() $\unicode[STIX]{x1D708}$ invariant of [Reference SavelievSav98, Reference SavelievSav99], although the two agree on Seifert fiber spaces.
$\unicode[STIX]{x1D708}$ invariant of [Reference SavelievSav98, Reference SavelievSav99], although the two agree on Seifert fiber spaces.
6 Applications and examples
First, we see that Corollary 1.2 follows from Corollary 5.4 and Theorem 1.3. Indeed, the negative fibration case follows immediately, and the positive fibration statement follows by using the properties of  $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\bar{\unicode[STIX]{x1D707}}$, and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\bar{\unicode[STIX]{x1D707}}$, and ![]() $d$ under orientation reversal.
$d$ under orientation reversal.
We also obtain the following result.
Theorem 6.1. Let ![]() $Y$ be a Seifert integral homology sphere. If
$Y$ be a Seifert integral homology sphere. If  $\bar{\unicode[STIX]{x1D707}}(Y)\neq -d(Y)/2$, then
$\bar{\unicode[STIX]{x1D707}}(Y)\neq -d(Y)/2$, then ![]() $Y$ is not homology cobordant to any Seifert integral homology sphere with fibration of sign opposite that of
$Y$ is not homology cobordant to any Seifert integral homology sphere with fibration of sign opposite that of ![]() $Y$.
$Y$.
Proof. If ![]() $Y$ is a negative Seifert fibration, and
$Y$ is a negative Seifert fibration, and  $\bar{\unicode[STIX]{x1D707}}(Y)\neq -d(Y)/2$, then
$\bar{\unicode[STIX]{x1D707}}(Y)\neq -d(Y)/2$, then  $\unicode[STIX]{x1D6FC}(Y)\neq \unicode[STIX]{x1D6FD}(Y)$, but for all positive fibrations
$\unicode[STIX]{x1D6FC}(Y)\neq \unicode[STIX]{x1D6FD}(Y)$, but for all positive fibrations ![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$. One performs a similar check for positive fibrations.◻
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$. One performs a similar check for positive fibrations.◻
This statement is expressed only in terms of ![]() $\bar{\unicode[STIX]{x1D707}}$ and
$\bar{\unicode[STIX]{x1D707}}$ and ![]() $d$, but the proof comes from the properties of
$d$, but the proof comes from the properties of ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$. As a particular example, we have
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$. As a particular example, we have  $\unicode[STIX]{x1D6F4}(2,3,12k-5)$ and
$\unicode[STIX]{x1D6F4}(2,3,12k-5)$ and  $\unicode[STIX]{x1D6F4}(2,3,12k-1)$, for all
$\unicode[STIX]{x1D6F4}(2,3,12k-1)$, for all ![]() $k\geqslant 1$, have
$k\geqslant 1$, have ![]() $\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$ and so are not homology cobordant to any positive Seifert fibration.
$\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$ and so are not homology cobordant to any positive Seifert fibration.
We remark that Némethi’s algorithm [Reference NémethiNém05] for Heegaard Floer homology of Seifert fiber spaces makes  $\mathit{SWFH}_{\ast }^{G}$ of Seifert spaces computable. Using Tweedy’s computations in [Reference TweedyTwe13], we provide calculations of
$\mathit{SWFH}_{\ast }^{G}$ of Seifert spaces computable. Using Tweedy’s computations in [Reference TweedyTwe13], we provide calculations of  $\mathit{SWFH}_{\ast }^{G}$ for the following infinite families as an example. In Tables 1 and 2, there are nontrivial
$\mathit{SWFH}_{\ast }^{G}$ for the following infinite families as an example. In Tables 1 and 2, there are nontrivial ![]() $q$-actions between infinite towers. The only other nontrivial
$q$-actions between infinite towers. The only other nontrivial ![]() $q$-actions are for
$q$-actions are for  $\unicode[STIX]{x1D6F4}(2,7,28k-1)$ and
$\unicode[STIX]{x1D6F4}(2,7,28k-1)$ and  $\unicode[STIX]{x1D6F4}(2,7,28k+15)$, where
$\unicode[STIX]{x1D6F4}(2,7,28k+15)$, where ![]() $q$ sends each summand of
$q$ sends each summand of  ${\mathcal{V}}_{3}^{+}(1)^{\oplus k}$ (respectively
${\mathcal{V}}_{3}^{+}(1)^{\oplus k}$ (respectively  ${\mathcal{V}}_{-1}^{+}(1)^{\oplus k+1}$) to
${\mathcal{V}}_{-1}^{+}(1)^{\oplus k+1}$) to ![]() ${\mathcal{V}}_{2}^{+}$ (respectively
${\mathcal{V}}_{2}^{+}$ (respectively ![]() ${\mathcal{V}}_{-2}^{+}$).
${\mathcal{V}}_{-2}^{+}$).
Table 1. The Seiberg–Witten Floer homology for some families of Brieskorn spheres ![]() $Y$.
$Y$.

Table 2. The Seiberg–Witten Floer homology for additional families of Brieskorn spheres.

Acknowledgements
The author is particularly grateful to Ciprian Manolescu for his guidance and constant encouragement. The author would also like to thank Cagri Karakurt, Tye Lidman, and Francesco Lin for helpful conversations, and an anonymous referee for several helpful suggestions on a previous version of this paper.