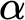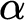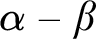1 Introduction
Prefix-free Kolmogorov complexity, which is perhaps the most prominent version of Kolmogorov complexity in the study of algorithmic randomness, is defined via prefix-free machines: A prefix-free machine is a partial computable function
$M: 2^{< \omega } \rightarrow 2^{< \omega }$
(
$2^{< \omega }$
being the set of finite binary strings) such that no two distinct elements of
$\operatorname {\mathrm {dom}}(M)$
are comparable under the prefix relation. The prefix-free Kolmogorov complexity of
$x \in 2^{< \omega }$
relative to the machine M is defined to be the quantity
$K_M(x)=\min \{|p| \, : \, M(p)=x\}$
. To get a machine-independent notion of Kolmogorov complexity, one needs to take an optimal prefix-free machine, that is, a prefix-free machine U such that for any prefix-free machine M, one has
$K_U \leq K_M + c_M$
for some constant
$c_M$
which depends solely on M. Then one defines the prefix-free Kolmogorov complexity K by setting
$K=K_U$
. The resulting function K only depends on the choice of U by an additive constant, because by definition, if U and V are optimal machines, then
$|K_U-K_V|=O(1)$
. To be complete, one needs to make sure optimal machines exist. One way to build one is to take a total computable function
$e \mapsto \sigma _e$
from
$\mathbb {N}$
to
$2^{< \omega }$
whose range is prefix-free (for example,
$\sigma _e=0^e1$
), and set
$U(\sigma _e \tau )=M_e(\tau )$
where
$(M_e)$
is an effective enumeration of all prefix-free machines. It is easy to see that U is prefix-free and for all e,
$K_U \leq K_{M_e} + |\sigma _e|$
, hence U is optimal. Machines U of this type are called universal by adjunction and they form a strict subclass of optimal prefix-free machines.Footnote
1
Remark. Often no distinction is made between optimal prefix-free machines and universal prefix-free machines. E.g., in [Reference Nies16] it is said that optimal prefix-free machines are often called universal prefix-free machines. In this paper, the distinction will be important. An optimal prefix-free machine is a prefix-free machine U such that for every prefix-free machine M, there is a constant
$c_M$
such that
$K_U \leq K_M + c_M$
. A universal prefix-free machine is one that is universal by adjunction. Thus every universal machine is optimal, but the converse is not true. Every machine in this paper will be prefix-free, and so we often omit the term ‘prefix-free’.
1.1 Omega numbers
Given a prefix-free machine M, one can consider the ‘halting probability’ of M, defined by
$$ \begin{align*} \Omega_M=\sum_{M(\sigma)\downarrow} 2^{-|\sigma|}. \end{align*} $$
The term ‘halting probability’ is justified by the following observation: a prefix-free machine M can be naturally extended to a partial functional from
$2^{ \omega }$
, the set of infinite binary sequences, to
$2^{< \omega }$
, where for
$X \in 2^{ \omega }$
,
$M(X)$
is defined to be
$M(\sigma )$
if some
$\sigma \in \operatorname {\mathrm {dom}}(M)$
is a prefix of X, and
$M(X) \uparrow $
otherwise. The prefix-freeness of M on finite strings ensures that this extension is well-defined. With this point of view,
$\Omega _M$
is simply
$\mu \{ X \in 2^{ \omega } : M(X) \downarrow \}$
, where
$\mu $
is the uniform probability measure (a.k.a. Lebesgue measure) on
$2^{ \omega }$
, that is, the measure where each bit of X is equal to
$0$
with probability
$1/2$
independently of all other bits.
For any machine M, the number
$\Omega _M$
is fairly simple from a computability-theoretic viewpoint, namely, it is the limit of a computable non-decreasing sequence of rationals (this is easy to see, because
$\Omega _M$
is the limit of
$\Omega _{M_s}=\sum _{M(\sigma )[s]\downarrow } 2^{-|\sigma |}$
). We call such a real left-c.e. It turns out that every left-c.e. real
$\alpha \in [0,1]$
can be represented in this way, i.e., for any left-c.e.
$\alpha \in [0,1]$
, there exists a prefix-free machine M such that
$\alpha = \Omega _M$
, as consequence of the Kraft–Chaitin theorem (see [Reference Downey and Hirschfeldt11, Theorem 3.6.1]).
One of the first major results in algorithmic randomness was Chaitin’s theorem [Reference Calude and Staiger10] that the halting probability
$\Omega _U$
of an optimal machine U is always an algorithmically random real, in the sense of Martin-Löf (for background on Martin-Löf randomness, one can consult [Reference Downey and Hirschfeldt11, Reference Nies16]). From here on we simply call a real random if it is random in the sense of Martin-Löf.
This is particularly interesting because this gives “concrete” examples of Martin-Löf random reals, which furthermore are, as we just saw, left-c.e. Whether the converse is true, that is, whether every random left-c.e. real
$\alpha \in [0,1]$
is equal to
$\Omega _U$
for some optimal machine U remained open for a long time. The answer turned out to be positive, a remarkable result with no less remarkable history. Shortly after the work of Chaitin and Solovay [Reference Solovay18] introduced a preorder on left-c.e. reals, which we now call Solovay reducibility: for
$\alpha , \beta $
left-c.e., we say that
$\alpha $
is Solovay-reducible to
$\beta $
, which we write
$\alpha \preceq _S \beta $
, if for some positive integer n,
$n \beta - \alpha $
is left-c.e.Footnote
2
Solovay showed that reals of type
$\Omega _U$
for optimal U are maximal with respect to the Solovay reducibility. While this did not fully settle the above question, Solovay reducibility turned out to be the pivotal notion towards its solution. Together with Solovay’s result, subsequent work lead to the following theorem.
Theorem 1.1. For
$\alpha \in [0,1]$
left-c.e., the following are equivalent.
-
(a)
$\alpha $
is Martin-Löf random -
(b)
$\alpha = \Omega _U$
for some optimal machine U -
(c)
$\alpha $
is maximal w.r.t Solovay reducibility.
The implication
$(b) \Rightarrow (a)$
is Chaitin’s result and the implication
$(b) \Rightarrow (c)$
is Solovay’s, as discussed above. Calude et al. [Reference Chaitin7] showed
$(c) \Rightarrow (b)$
, and the last crucial step
$(a) \Rightarrow (c)$
was made by Kučera and Slaman [Reference Kučera and Slaman14]. We refer the reader to the survey [Reference Bienvenu and Shen6] for an exposition of this result.
Summing up what we know so far, we have for any real
$\alpha \in [0,1]$
:
$$ \begin{align*} \alpha~\text{is left-c.e.} & \Leftrightarrow \alpha=\Omega_M~\text{for some machine}~M,\\ \alpha~\text{is left-c.e. and random} & \Leftrightarrow \alpha=\Omega_U~\text{for some optimal machine}~U. \end{align*} $$
The first equivalence is uniform: Given a prefix-free machine M (represented by its index in an effective enumeration of all prefix-free machines), we can pass in a uniform way to a left-c.e. index for
$\Omega _M$
; and moreover, given a left-c.e. index for a left-c.e. real
$\alpha \in [0,1]$
, we can pass uniformly to an index for a prefix-free machine M with
$\Omega _M = \alpha $
(a consequence of the so-called Kraft–Chaitin theorem, see [Reference Downey and Hirschfeldt11, Theorem 3.6.1]). By a left-c.e. index, we mean an index for a non-decreasing sequence of rationals
It was previously open however (see for example [Reference Barmpalias2, p. 11]) whether the second equivalence was uniform, that is: given an index for a random left-c.e.
$\alpha \in [0,1]$
, can we uniformly obtain an index for an optimal machine U such that
$\alpha =\Omega _U$
? Our first main result is a negative answer to this question.
Theorem 1.2. There is no partial computable function f such that if e is an index for a Martin-Löf random left-c.e. real
$\alpha \in [0,1]$
, then the value of
$f(e)$
is defined and is an index for an optimal Turing machine
$M_{f(e)}$
with halting probability
$\alpha $
.
Thus one cannot uniformly view a Martin-Löf random left-c.e. real as an
$\Omega $
number.
On the other hand, we show that given a left-c.e. random
$\alpha \in [0,1]$
, one can uniformly find a universal left-c.e. semi-measure m with
$\sum _i m(i) = \alpha $
. An interesting corollary is that one cannot uniformly turn a universal left-c.e. semi-measure m into a universal machine whose halting probability is
$\sum _i m(i)$
.
1.2 Differences of left-c.e. reals
The set of left-c.e. reals is closed under addition and multiplication, not under subtraction or inverse. However, the set
$\{\alpha - \beta \mid \alpha , \beta \ \text {left-c.e.}\}$
, of differences of two left-c.e. reals is algebraically much better behaved, namely it is a real closed field [Reference Ambos-Spies, Weihrauch and Zheng1, Reference Ng15, Reference Raichev17]. Barmpalias and Lewis-Pye proved the following theorem.
Theorem 1.3 (Barmpalias and Lewis-Pye) [Reference Bienvenu and Downey3]
If
$\alpha $
is a non-computable left-c.e. real there exists a left-c.e. real
$\beta $
such that
$\alpha - \beta $
is neither left-c.e. nor right-c.e.
The proof is non-uniform, and considers two separate cases depending on whether or not
$\alpha $
is Martin-Löf random (though it is uniform in each of these cases). Barmpalias and Lewis-Pye ask whether there is a uniform construction; we show that the answer is negative.
Theorem 1.4. There is no partial computable function f such that if e is an index for a non-computable left-c.e. real
$\alpha $
, then
$f(e)$
is defined and is an index for a left-c.e. real
$\beta $
such that
$\alpha - \beta $
is neither left-c.e. nor right-c.e.
Barmpalias and Lewis-Pye note that it follows from [Reference Downey, Hirschfeldt and Nies12, Theorem 3.5] that if
$\alpha $
and
$\beta $
are left-c.e. reals and
$\alpha $
is Martin-Löf random while
$\beta $
is not, then
$\alpha - \beta $
is a Martin-Löf random left-c.e. real. In particular, if
$\alpha $
in Theorem 1.3 is Martin-Löf random, then the corresponding
$\beta $
must be Martin-Löf random as well. Thus
$\alpha $
and
$\beta $
are the halting probabilities of universal machines.
Theorem 1.5 (Barmpalias and Lewis-Pye) [Reference Bienvenu and Downey3]
For every universal machine U, there is a universal machine V such that
$\Omega _U-\Omega _V$
is neither left-c.e. nor right-c.e.
Recall that the construction for Theorem 1.3 was uniform in the Martin-Löf random case. So it is not too surprising that Theorem 1.5 is uniform; but because we cannot pass uniformly from an arbitrary Martin-Löf random left-c.e. real to a universal machine (Theorem 1.2), this requires a new proof.
Theorem 1.6. Theorem 1.5 is uniform in the sense that there is a total computable function f such that if
$U=M_e$
is an optimal (respectively universal by adjunction) machine, then
$V=M_{f(e)}$
is optimal (respectively universal by adjunction) and
$\Omega _{U}-\Omega _{V}$
is neither left-c.e. nor right-c.e.
2 Omega numbers
2.1 No uniform construction of universal machines
We prove Theorem 1.2:
Theorem 1.2. There is no partial computable function f such that if e is an index for a random left-c.e. real
$\alpha \in [0,1]$
, then
$f(e)$
is defined and is an index for an optimal prefix-free machine
$M_{f(e)}$
with halting probability
$\alpha $
.
Proof First note that we can assume that the partial computable function f is total. Indeed, define a total function g as follows: for each input e,
$g(e)$
is an index for a machine which on input
$\sigma $
waits for
$f(e)$
to converge, and then copies
$M_{f(e)}(\sigma )$
.
Fix a partial computable function f taking indices for left-c.e. reals to indices for prefix-free machines. Using the recursion theorem, we will define a left-c.e. ML-random
$\alpha = \alpha _e \in [0,1]$
using, in its definition, the index
$f(e)$
of a prefix-free Turing machine
$M_{f(e)}$
. We must define
$\alpha $
even if
$M_{f(e)}$
is not optimal or
$f(e)$
does not converge. We can always assume that
$M_{f(e)}$
is prefix-free by not letting it converge on a string
$\sigma $
if it has already converged on a prefix of
$\sigma $
; we can also assume that
$f(e)$
converges by having
$\alpha $
follow some fixed left-c.e. random
$\beta $
(say the one chosen below) until
$f(e)$
converges. During the construction of
$\alpha $
we will also build an auxiliary machine Q. We will ensure that
$\alpha $
is a random left-c.e. real, but that either
$M_{f(e)}$
is not optimal (which will happen because for all d, there is
$\sigma $
such that
$K_{M_{f(e)}}(\sigma )> K_Q(\sigma ) + d$
), or
$\mu (\operatorname {\mathrm {dom}}(M_{f(e)}))$
is not
$\alpha $
. This will prove the theorem.
In the construction, we will build
$\alpha = \alpha _e$
(using the recursion theorem to know the index e in advance) while watching
$M = M_{f(e)}$
. (From now on, we drop the index e everywhere; we will write
$\alpha _s$
for the left-c.e. approximation to
$\alpha $
.) We will try to meet the requirements:
$$ \begin{align*} R_{d}\ \text{: For some}\ \sigma, K_{M}(\sigma)> K_Q(\sigma) + d.\end{align*} $$
If M is universal, then there must be some d such that, for all
$\sigma $
,
$K_M(\sigma ) \leq K_Q(\sigma ) + d$
. Thus meeting
$R_d$
for every d will ensure that M is not universal. At the same time, we will be trying to get a global win by having
$\mu (\operatorname {\mathrm {dom}}(M)) \neq \alpha $
.
We will define stage-by-stage rationals
$\alpha _0 < \alpha _1 < \alpha _2 < \cdots $
with
$\alpha = \lim _s \alpha _s$
. (Recall that an index for such a sequence is an index for
$\alpha $
.) Fix
$\beta $
a left-c.e. random,
$\frac {3}{4} < \beta < 1$
. We will have
$\alpha = q\beta +l$
for some
$q, l \in \mathbb {Q}$
,
$q> 0$
, so that
$\alpha $
will be random (indeed, multiplying by the denominator of q and subtracting
$\beta $
, we see that
$\beta \preceq _S \alpha $
, and since
$\beta $
is random, by Theorem 1.1, so is
$\alpha $
). It is quite possible that we will have
$\alpha = \beta $
. Let
$\beta _0 < \beta _1 < \beta _2 < \cdots $
be a computable sequence of rationals with limit
$\beta $
. At each stage s we will define
$\alpha _s = q_s\beta _s + l_s$
for some
$q_s, l_s \in \mathbb {Q}$
in such a way that
$q = \lim _s q_s$
and
$l = \lim _s l_s$
are reached after finitely many stages. We think of our opponent as defining the machine M with measure
$\gamma _s$
at stage s, with
$\gamma = \lim _s \gamma _s$
the measure of the domain of M. Our opponent must keep
$\gamma _s \leq \alpha _s$
, as if they ever have
$\gamma _s> \alpha _s$
then we can immediately abandon the construction and choose
$q,l$
such that
$\alpha = q \beta + l$
has
$\alpha _s < \alpha < \gamma $
and get a global win. Our opponent also has to (eventually) increase
$\gamma _s$
whenever we increase
$\alpha _s$
, or they will have
$\gamma < \alpha $
. However, they may wait to do this. But, intuitively speaking, whenever we increase
$\alpha _s$
, we can wait for our opponent to increase
$\gamma _s$
correspondingly (as long as, in the meantime, we work towards making
$\alpha $
random).
The requirements can be in one of four states: inactive, preparing, waiting, and restraining. Unless it is injured by a higher priority requirement, in which case it becomes inactive, a requirement will begin inactive, then be preparing, before switching back and forth between waiting and restraining.
Before giving the formal construction, we will give an overview. To start, each requirement will be inactive. When activated, a requirement will be in state preparing. When entering state preparing, a requirement
$R_d$
will have a reserved code
$\tau \in 2^{< \omega }$
and a restraint
$r_d = 2^{-(|\tau | + d)}$
. The reserved code
$\tau $
will be such that Q has not yet converged on input
$\tau $
nor on any prefix or extension of
$\tau $
, so that we can still use
$\tau $
as a code for some string
$\sigma $
to make
$K_Q(\sigma ) \leq |\tau |$
. While in this state, our left-c.e. approximation to
$\alpha $
will copy that of
$\beta $
. The requirement
$R_d$
will remain in this state until the measure of the domain of the machine M is close to our current approximation to
$\alpha $
, namely, within
$r_d$
. (If our opponent does not increase the measure of M as we increase the approximation to
$\alpha $
, then we win.) At this point, we will set
$Q(\tau ) = \sigma $
for some string
$\sigma $
for which
$K_M(\sigma )$
is currently greater than
$|\tau |+d$
. The requirement will move into state waiting. From now on, we are trying to ensure that M can never converge on a string of length
$\leq |\tau | + d$
, so that
$K_M(\sigma )$
will never drop below
$|\tau |+d$
, satisfying
$R_d$
. We do this by having the approximation to
$\alpha _s$
grow very slowly, so that M can only add a small amount of measure at each stage.
$R_d$
will now move between the states waiting and restraining. The requirement
$R_d$
will remain in state waiting at stages s when the measure of the domain of M is close (within
$r_d$
) to
$\beta _s$
, so that
$R_d$
is content to have
$\alpha $
approximate
$\beta $
. However, at some stages s, it might be that
$\beta _s$
is at least
$r_d$
greater than
$\gamma _s$
, the measure of the domain of M so far. In this case,
$R_d$
is in state restraining and has to actively restrain
$\alpha _s$
to not increase too much. Letting
$l=\alpha _{s-1}$
and
$q = r_d - (\alpha _{s-1} - \gamma _s)$
, where s is the stage when
$R_d$
enters the state restraining,
$R_d$
has
$\alpha $
temporarily approximate
$q \beta + l$
. Whenever the measure of the domain of M increases by
$\frac {1}{2} r_d$
,
$R_d$
updates the values of q and l (recall that
$\beta \geq \frac {3}{4}$
). Thus, each time the values of q and l are reset, the measure of the domain of M has increased by at least
$\frac {1}{2}r_d$
. (Again, if our opponent does not increase the measure of M as we increase the approximation to
$\alpha $
, then we win.) This can happen at most finitely many times until the measure of the domain of M is within
$r_d$
of the current approximation to
$\beta $
, and so the requirement re-enters state waiting.Footnote
3
The requirement may then later re-enter state restraining if the approximation to
$\beta _s$
increases too much faster than the measure of the domain of M, but since the measure of the domain of M will increase by at least
$\frac {1}{2} r_d$
every time
$R_d$
switches from restraining to waiting,
$R_d$
can only switch finitely many times.
Just considering one requirement, the possible outcomes of the construction are as follows:
-
•
$\gamma _s> \alpha _s$
at some stage s, in which case we can immediately ensure that
$\alpha < \gamma $
and that
$\alpha $
is random. -
•
$\gamma < \alpha $
; the requirement may get stuck in preparing or restraining. If it gets stuck in preparing, we have
$\alpha = \beta $
is random. If it gets stuck in restraining, we have
$\alpha = q \beta + l$
, with q and l rational, and this is random. -
•
$\gamma = \alpha $
; in this case, the requirement always leaves preparing, and every time it enters restraining it returns to waiting. After some stage, it is always in waiting and has
$\alpha = \beta $
, which is random. The requirement is satisfied by having
$K_Q(\sigma ) \leq |\tau |$
but
$K_M(\sigma )> |\tau | + d$
.
With multiple requirements, there is injury. A requirement only allows lower priority requirements to be active while it is waiting. Every stage at which a requirement is preparing or restraining, it injures all lower priority requirements. So, at any stage, there is at most one requirement—the lowest priority active requirement—which can be in a state other than waiting.
Construction.
Stage
$0$
. Begin with
$\alpha _0 = 0$
, all the requirements other than
$R_0$
inactive, and
$Q_0$
not converged on any input.
Set
$\alpha _{s} = \beta _{s}$
. Activate
$R_{0}$
and put it in state preparing. Choose a reserved code
$\tau _{0}$
such that
$Q_s(\tau _{0}) \uparrow $
and set the restraint
$r_{1} = 2^{-|\tau _{0}|}$
.
Stage
$s> 0$
. Let
$\gamma _s = \mu (\operatorname {\mathrm {dom}}(M_s))$
be the measure of the domain of M at stage s. If
$\gamma _s> \alpha _{s-1}$
, we can immediately end the construction, letting
$\alpha _{t} = \alpha _{s-1} + (\gamma _s - \alpha _{s-1}) \beta _t$
for
$t \geq s$
, so that
$$ \begin{align*} \alpha = \lim_{t \to \infty} \alpha_t = \alpha_{s-1} + (\gamma_s - \alpha_{s-1}) \beta < \gamma_s \leq \mu(\operatorname{\mathrm{dom}}(M_s)).\end{align*} $$
So for the rest of this stage, we may assume that
$\gamma _s \leq \alpha _{s-1}$
.
Find the highest-priority active requirement
$R_d$
, if it exists, such that
$\beta _s - \gamma _s \geq r_d$
. Cancel every lower priority requirement. Let
$R_d$
be the lowest priority active requirement. (Every higher priority requirement is in state waiting.)
Case 1.
$R_d$
is preparing.
Set
$\alpha _{s} = \beta _s$
.
$R_d$
has a reserved code
$\tau _d$
and restraint
$r_d$
. If
$\beta _s - \gamma _s> r_d$
,
$R_d$
remains preparing. Otherwise, if
$\beta _s - \gamma _s < r_d$
, find a string
$\sigma _d$
such that
$K_M(\sigma _d)[s]> |\tau _d| + d$
. Put
$Q(\tau _d) = \sigma _d$
.
$R_d$
is now waiting.
Case 2.
$R_d$
is waiting and
$\beta _s - \gamma _s < r_d$
.
Set
$\alpha _{s} = \beta _{s}$
. Requirement
$R_d$
remains in state waiting. Activate
$R_{d+1}$
and put it in state preparing. Choose a reserved code
$\tau _{d+1}$
such that
$Q_s(\tau _{d+1}) \uparrow $
and set the restraint
$r_{d+1} = 2^{-|\tau _{d+1}| - d - 1}$
.
Case 3.
$R_d$
is waiting and
$\beta _s - \gamma _s \geq r_d$
.
Set the reference values
$l_d = \alpha _{s-1}$
and
$q_{d}= r_d - (\alpha _{s-1} - \gamma _s)$
. (In Claim 1 we will show that
$q_d> 0$
.) Put
$R_d$
in state restraining. Set
$\alpha _{s} = q_d \beta _s + l_d$
.
Case 4.
$R_d$
is in state restraining.
$R_d$
has a restraint
$r_d$
and reference values
$q_d$
and
$l_d$
. If
$\gamma _s \leq l_d + \frac {1}{2} q_d$
, keep the same reference values, and set
$\alpha _{s} = q_d \beta _s + l_d$
. If
$\gamma _s> l_d + \frac {1}{2} q_d$
, then what we do depends on whether
$\beta _s - \gamma _s < r_d$
or
$\beta _s - \gamma _s \geq r_d$
. In either case, we call stage s incremental for
$R_d$
. If
$\beta _s - \gamma _s < r_d$
, then set
$\alpha _s = \beta _s$
and put
$R_d$
into state waiting. If
$\beta _s - \gamma _s \geq r_d$
, change the reference values
$l_d$
and
$q_d$
to
$l_d = \alpha _{s-1}$
and
$q_{d}= r_d - (\alpha _{s-1} - \gamma _s)$
, and set
$\alpha _{s} = q_d \beta _s + l_d$
.
$R_d$
remains restraining.
End construction.
Verification.
Claim 1. At every stage
$s>0$
,
$\alpha _{s-1}\leq \alpha _s \leq \beta _s$
, and for every requirement
$R_d$
which is active at stage s, either
$R_d$
is preparing or
$\alpha _s - \gamma _s < r_d$
.
Proof Assume the result holds for all
$t<s$
. Let d be the lowest priority active requirement at stage s (after the cancellation). By choice of d, for
$d' < d$
we have
$\beta _s - \gamma _s < r_{d'}$
. We now check that no matter which case of the construction was used to define
$\alpha _s$
, the result holds. In all cases we will have
$\alpha _s - \gamma _s \leq \beta _s - \gamma _s < r_{d'}$
, so it is really
$\alpha _s - \gamma _s < r_d$
that we must check.
-
(1) At stage s the construction was in Case 1 or Case 2. We set
$\alpha _s = \beta _s \geq \beta _{s-1} \geq \alpha _{s-1}$
. Either we are in Case 1 and
$R_d$
remains preparing, or
$\alpha _s - \gamma _s= \beta _s - \gamma _s < r_{d}$
. -
(2) At stage s the construction was in Case 3. We set
$\alpha _s = q_d\beta _s + l_d$
. Now in Case 3,
$l_d = \alpha _{s-1}$
and
$q_d = (r_d - (\alpha _{s-1} - \gamma _s))$
. Note that
$\alpha _{s-1} - \gamma _s \leq \alpha _{s-1} - \gamma _{s-1} < r_d$
by induction, so
$\alpha _s \geq \alpha _{s-1}$
. Also Finally, since we’ve just seen that
$$ \begin{align*}\alpha_s &= (r_d - (\alpha_{s-1} - \gamma_s))\beta_s +\alpha_{s-1} \\ & = r_d\beta_s - (\alpha_{s-1} - \gamma_s)\beta_s + (\alpha_{s-1} - \gamma_s) + \gamma_s \\ &= r_d\beta_s +(1-\beta_s)(\alpha_{s-1} - \gamma_s) +\gamma_s \\ & < r_d\beta_s +(1-\beta_s)r_d +\gamma_s \\ & = r_d + \gamma_s \\ & \leq \beta_s.\end{align*} $$
$\alpha _s < r_d + \gamma _s$
, we have that
$\alpha _s - \gamma _s < r_d$
.
-
(3) At stage s the construction was in Case 4. We set
$\alpha _s = q_d\beta _s + l_d$
. Then since
$R_d$
was in state restraining at stage s, we must have defined
$\alpha _{s-1}= q_d\beta _{s-1} + l_d$
unless s was an incremental stage, in which case
$q_d$
and
$l_d$
were reset at stage s before defining
$\alpha _s$
. If s was not incremental, then
$\alpha _s = q_d(\beta _s - \beta _{s-1}) + q_d\beta _{s-1} + l_d = q_d(\beta _s - \beta _{s-1})+\alpha _{s-1} \leq q_d(\beta _s - \beta _{s-1})+\beta _{s-1} \leq \beta _s$
. Also
$\alpha _{s-1}= q_d\beta _{s-1} + l_d \leq q_d\beta _{s} + l_d = \alpha _s$
. Finally, if we let
$\tilde {s}<s$
be the stage where
$q_d$
and
$l_d$
were last defined, then we see that Now suppose stage s was incremental for
$$ \begin{align*}\alpha_s - \gamma_s & = q_d\beta_s + l_d - \gamma_s \\ & = (r_d - (\alpha_{\tilde{s}-1} - \gamma_{\tilde{s}}))\beta_s + \alpha_{\tilde{s}-1} - \gamma_{s} \\ & \leq (r_d - (\alpha_{\tilde{s}-1} - \gamma_{\tilde{s}}))\beta_s + \alpha_{\tilde{s}-1} - \gamma_{\tilde{s}} \\ &= r_d\beta_s + (1-\beta_s)(\alpha_{\tilde{s}-1} - \gamma_{\tilde{s}}) \\ & < r_d. \end{align*} $$
$R_d$
. If
$\beta _s - \gamma _s < r_d$
, then the result follows as in (1), and if
$\beta _s - \gamma _s \geq r_d$
, then the result follows as in (3).⊣
Claim 2. Suppose that the requirement
$R_d$
is activated at stage s and never injured after stage s. Then
$R_d$
has only finitely many incremental stages.
Proof The restraint
$r_d$
is defined when
$R_d$
is activated, and never changes after stage s. Suppose to the contrary that there are incremental stages
$s_0 < s_1 < s_2 < \cdots $
after stage s. We claim that
$\gamma _{s_{i+1}} \geq \frac {1}{2}r_d + \gamma _{s_i}$
. From this it follows that there are at most
$2/r_d$
incremental stages for
$R_d$
, as if there were that many incremental stages, for some sufficiently large stage t we would have
$\gamma _t$
greater than
$1$
and hence greater than
$\alpha _{t-1}$
—and so the construction could immediately end, with finitely many incremental stages.
Fix i for which we will show that
$\gamma _{s_{i+1}} \geq \frac {1}{2}r_d + \gamma _{s_i}$
. Since stage
$s_i$
is incremental, at the start of that stage
$R_d$
is in stage restraining. There are two cases, depending on whether
$\beta _{s_i} - \gamma _{s_i} < r_d$
or
$\beta _{s_i} - \gamma _{s_i} \geq r_d$
.
Case 1.
$\beta _{s_i} - \gamma _{s_i} < r_d$
. During stage
$s_i$
, the requirement
$R_d$
enters state waiting. Since stage
$s_{i+1}$
is the next incremental stage, there must be some unique stage t,
$s_i < t < s_{i+1}$
, where
$R_d$
enters state restraining again and stays in that state until at least stage
$s_{i+1}$
. At stage t we define
$l_d = \alpha _{t-1}$
and
$q_d = r_d - (\alpha _{t-1} - \gamma _t)$
. These values cannot be redefined until the next incremental stage,
$s_{i+1}$
, where we have
$\gamma _{s_{i+1}}> l_d + \frac {1}{2} q_d$
. Then:
$$ \begin{align*} \gamma_{s_{i+1}} &> l_d + \frac{1}{2} q_d \\ & = \alpha_{t-1} + \frac{1}{2}(r_d - (\alpha_{t-1} - \gamma_{t}))\\ & = \frac{1}{2}r_d + \frac{1}{2}(\alpha_{t-1} +\gamma_{t})\\ & \geq \frac{1}{2}r_d + \gamma_{t} \\ & \geq \frac{1}{2}r_d + \gamma_{s_i}. \end{align*} $$
Case 2.
$\beta _{s_i} - \gamma _{s_i} \geq r_d$
. During stage
$s_i$
, the requirement
$R_d$
remains in state restraining, defining
$\ell _d = \alpha _{s_i - 1}$
and
$q_d = r_d - (\alpha _{s_{i-1}}-\gamma _{s_i - 1})$
. It stays in that state, with the same reference values
$q_d$
and
$l_d$
, until the next incremental stage
$s_{i+1}$
, where we have
$\gamma _{s_{i+1}}> l_d + \frac {1}{2} q_d$
. We get a similar computation to the previous case:
$$ \begin{align*} \gamma_{s_{i+1}} &> l_d + \frac{1}{2} q_d \\ & = \alpha_{s_i-1} + \frac{1}{2}(r_d - (\alpha_{s_i-1} - \gamma_{s_i}))\\ & = \frac{1}{2}r_d + \frac{1}{2}(\alpha_{s_i-1} +\gamma_{s_i})\\ & \geq \frac{1}{2}r_d + \gamma_{s_i}. \end{align*} $$
Thus for each i we have
$\gamma _{s_{i+1}} \geq \frac {1}{2}r_d + \gamma _{s_i}$
, completing the proof of the claim.⊣
Claim 3. Each requirement is injured only finitely many times.
Proof We argue by induction on the priority of the requirements. Suppose that each requirement of higher priority than
$R_d$
is only injured finitely many times. Fix a stage s after which none of them are injured. By the previous claim, by increasing s we may assume that no higher priority requirement has an incremental stage after stage s.
First of all,
$R_d$
can only be activated at stages when every higher priority requirement is waiting. If
$R_d$
is never activated after stage s, then it cannot be injured. Increasing s further, assume that
$R_d$
is activated at stage s. If
$R_d$
is injured after stage s, it is at the first stage
$t> s$
such that a requirement
$R_e$
of higher priority than
$R_d$
has
$\beta _t - \gamma _t> r_e$
. Moreover, the requirement
$R_e$
remains in the state waiting until such a stage. Suppose that
$t> s$
is the first such stage, if one exists. At the beginning of stage t,
$R_e$
is waiting, and so
$R_e$
enters the state restraining. Then
$R_e$
can only leave state restraining, and re-enter state waiting, at a stage which is incremental for
$R_e$
; since there are no such stages after stage s,
$R_e$
can never re-enter stage waiting. So even
$R_d$
is never again re-activated, and so cannot be injured. Thus
$R_d$
can be injured only once after stage s, proving the claim.⊣
Claim 4.
$\alpha = \lim _s \alpha _s$
is random.
Proof There are three possibilities.
-
(1) Some requirement enters state preparing at stage s, and is never injured nor leaves state preparing after stage s.
The requirement
$R_d$
is the lowest priority requirement which is active at any point after stage s. In this case, at each stage
$t \geq s$
, we set
$\alpha _{t} = \beta _t$
and so
$\alpha = \beta $
is random. -
(2) Some requirement enters state restraining at stage s, and is never injured nor leaves state restraining after stage s.
The requirement
$R_d$
is the lowest priority requirement which is active at any point after stage s. Increasing s, we may assume that this requirement
$R_d$
never has an incremental stage after stage s. Then the target value
$q_d \beta + l_d$
at stage s is also the target value at all stages
$t \geq s$
. At each such stage
$t \geq s$
, we set
$\alpha _{t+1} = q_d \beta _t + l_d$
. Thus
$\alpha = q_d \beta + l_d$
, with
$q_d,l_d \in \mathbb {Q}$
, and so is random. -
(3) For each requirement there is a stage s after which the requirement is never injured and is always in state waiting.
There are infinitely many stages s at which we are in Case 2 of the construction. At every stage, all requirements except possibly for the lowest priority requirement are in state waiting. For requirements
$R_1,\ldots ,R_n$
, there is some first stage t at which the lowest priority requirement is in state waiting and never again leaves state waiting. At stage t, we must be in Case 2 of the construction. Indeed, in Case 3 the requirement
$R_d$
leaves state waiting. In Case 2, we set
$\alpha _{t} = \beta _t$
. Moreover, we activate the next requirement, and the next requirement is never injured. So there is a greater corresponding first stage t at which that requirement is in state waiting and never again leaves that state. Continuing, there are infinitely many stages at which we set
$\alpha _{t} = \beta _t$
. It follows that
$\alpha = \beta $
, which is random. ⊣
Claim 5. Suppose that
$\mu (\operatorname {\mathrm {dom}}(M)) = \alpha $
. For each requirement
$R_d$
, there is a stage s after which the requirement is active, never injured, and is always in state waiting.
Proof We argue inductively that for each requirement
$R_d$
, there is a stage s after which the requirement is never injured and is always waiting.
By Claim 3 there is a stage s after which
$R_d$
is never injured, and (inductively) every higher priority requirement is always waiting after stage s. By Claim 2, by increasing s we may assume that
$R_d$
has no incremental stages after stage s.
Then
$R_d$
is activated at the least such stage s since each higher priority requirement is always waiting. Note that
$R_d$
can never be injured after stage s, as if
$R_d$
is injured by
$R_e$
, then
$R_e$
enters state restraining.
Now we claim that, if
$R_d$
is preparing, it leaves that state after stage s. Indeed, if
$R_d$
never left state preparing, we would have
$\alpha = \beta $
. By assumption,
$\alpha = \mu (\operatorname {\mathrm {dom}}(M)) = \lim _s \gamma _s$
. Thus for some stage t we must have that
$\beta _t - \gamma _t < r_d$
. At this stage t,
$R_d$
leaves state preparing.
Now we claim that
$R_d$
can never enter state restraining after stage s. Since
$R_d$
has no incremental stages after stage s, if
$R_d$
did enter state restraining, it would never be able to leave that state. Moreover,
$q_d$
and
$l_d$
can never change their values. So we end up with
$\alpha = q_d \beta + l_d$
. Moreover, for all
$t \geq s$
,
$\gamma _t < l_d + \frac {1}{2} q_d$
, as there are no more incremental stages. Then
$\gamma \leq l_d + \frac {1}{2}q_d < l_d + q_d \beta = \alpha $
, contradicting the hypotheses of the claim. Thus
$R_d$
can never enter state restraining after stage s.
Thus we have shown that for sufficiently large stages,
$R_d$
is in state waiting.⊣
Claim 6. Suppose that
$\mu (\operatorname {\mathrm {dom}}(M)) = \alpha $
. Then every requirement
$R_d$
is satisfied.
Proof Since
$\mu (\operatorname {\mathrm {dom}}(M)) = \alpha $
, at all stages s,
$\gamma _s \leq \alpha _{s-1}$
. As argued in the previous claim, there is a stage s at which
$R_d$
is activated, and after which
$R_d$
is never injured. At this stage s,
$R_d$
enters state preparing and we choose
$\tau _d$
such that
$Q(\tau _d) \uparrow $
and set
$r_d = 2^{-(|\tau _d| + d)}$
.
By the previous claim,
$R_d$
exits state preparing at some stage
$t> s$
. At this point, we have
$\beta _t - \gamma _t < r_d$
. We choose a string
$\sigma $
such that
$K_M(\sigma )> |\tau _d| + d$
and put
$Q(\tau _d) = \sigma $
. Thus
$K_Q(\sigma ) \leq |\tau _d|$
.
$R_d$
enters state waiting, and
$\alpha _s = \beta _s$
.
Since, at stage t,
$K_M(\sigma )> |\tau |_d + d$
, for every string
$\rho $
with
$|\rho | \leq |\tau _d| + d$
,
$M(\rho ) \neq \sigma $
. For each stage
$t' \geq t$
the requirement
$R_d$
is no longer in state preparing and so by Claim 1 we have
$\gamma _{t' + 1} - \gamma _{t'} \leq \alpha _{t'} - \gamma _{t'} < r_d$
. From this it follows that we can never have
$M(\rho ) = \sigma $
for any
$\rho $
with
$|\rho | \leq |\tau _d| + d$
; if
$M(\rho ) = \sigma $
for the first time at stage
$t' + 1> t$
, then we would have
$\gamma _{t'+1} - \gamma _{t'} \geq |\rho | = r_d$
, which as we just argued cannot happen.⊣
We can now use the claims to complete the verification. By Claim 4,
$\alpha = \lim _s \alpha _s$
is indeed random, and by Claim 1
$\alpha \leq \beta $
and so
$\alpha \in [0,1]$
. So the function f must output the index of a machine M with
$\mu (M) = \alpha $
. By Claim 6, each requirement is satisfied and so, for every d, there is
$\sigma $
such that
$K_{M}(\sigma )> K_Q(\sigma ) + d$
. Thus M is not optimal, a contradiction. This completes the proof of the theorem.⊣
2.2 Almost uniform constructions of optimal machines
We just established that there is no uniform procedure to turn a left-c.e. Martin-Löf random
$\alpha \in [0,1]$
into a universal machine M such that
$\Omega _M=\alpha $
. However, algorithmic randomness offers a notion of ‘almost uniformity’, known as layerwise computability, see [Reference Hoyrup and Rojas13]: Let
$(\mathcal {U}_k)$
be a fixed effectively optimal Martin-Löf test, i.e., a Martin-Löf test such that for any other Martin-Löf test
$(\mathcal {V}_k)$
, there exists a constant c such that
$\mathcal {V}_{k+c} \subseteq \mathcal {U}_k$
for all k, and this constant c can be uniformly computed in an index of the Martin-Löf test
$(\mathcal {V}_k)$
. Note that an effectively optimal Martin-Löf test is in particular universal, i.e., x is Martin-Löf random if and only if
$x \notin \mathcal {U}_d$
for some d. A function F from
$[0,1]$
(or more generally, from a computable metric space) to some represented space
$\mathcal {X}$
is layerwise computable if it is defined on every Martin-Löf random x and moreover there is a partial computable f from
$[0,1] \times \mathbb {N}$
to
$\mathcal {X}$
where
$f(x,d)=F(x)$
whenever
$x \notin \mathcal {U}_d$
.
Here we are in a different setting as we are dealing with indices of reals instead of reals, but by extension we could say that a partial function
$F: \mathbb {N} \rightarrow \mathcal {X}$
is layerwise computable on left-c.e. reals if
$F(e)$
is defined for every index e of a random left-c.e. real, and if there is a partial computable function
$f: \mathbb {N} \times \mathbb {N} \rightarrow \mathcal {X}$
such that
$f(e,d)=F(e)$
whenever the left-c.e. real
$\alpha _e$
of index e does not belong to
$\mathcal {U}_d$
(note that the definition remains the same if f is required to be total). Even with this weaker notion of uniformity, uniform construction of optimal machines from their halting probabilities remains impossible.
Theorem 2.1. There does not exist a layerwise computable mapping F from indices for random left-c.e. reals
$\alpha _e \in [0,1]$
to optimal machines such that
$\Omega _{M_{F(e)}}=\alpha _e$
.
Proof This is in fact a consequence of a stronger result: there is no
$\emptyset '$
-partial computable function F such that
$F(e)$
is defined whenever
$\alpha _e$
is Martin-Löf random and
$\Omega _{M_{F(e)}}=\alpha _e$
. Since a
$\emptyset '$
-partial computable function can be represented by a total computable function
$f(.,.)$
such that for every e on which F is defined,
$\lim _t f(e,t)=F(e)$
, we see that a layerwise computable function on left-c.e. reals is a particular case of
$\emptyset '$
-partial computable function.
Let now F be a
$\emptyset '$
-partial computable function and f a total computable such that
$\lim _t f(e,t) = F(e)$
whenever
$F(e)$
is defined.
The idea is to run the same construction as in Theorem 1.2, but instead of playing against the machine of index
$f(e)$
, we play against the machine of index
$f(e,s_0)$
, with
$s_0=0$
. If at some point we find a
$s_1>s_0$
such that
$f(e,s_1) \not = f(e,s_0)$
, we restart the entire construction, this time playing against the machine of index
$f(e,s_1)$
, until we find
$s_2>s_1$
such that
$f(e,s_2) \not = f(e,s_1)$
, then restart, etc. Of course when we restart the construction, we cannot undo the increases we have already made on
$\alpha $
. This problem is easily overcome as follows. First observe that the strategy presented in the proof of Theorem 1.2, is robust: instead of starting at
$\alpha =0$
, and staying in the interval
$[0,1]$
throughout the construction, for any rational interval
$[a,b] \subseteq [0,1]$
, we could have started the construction with
$\alpha _0=a$
and stayed within
$[a,b]$
by – for example – targeting the random real
$a+(b-a)\beta $
instead of
$\beta $
. Now, let
$\xi $
be a random left-c.e. real in
$[0,1]$
with computable lower approximation
$\xi _0 < \xi _1 < \cdots $
. We play against the machine of index
$f(e,s_i)$
by applying the strategy of Theorem 1.2 with the added constraint that
$\alpha $
must stay in the interval
$[\xi _i,\xi _{i+1}]$
. If we then find a
$s_{i+1}$
such that
$f(e,s_{i+1}) \not = f(e,s_i)$
, we then move to the next interval
$[\xi _{i+1},\xi _{i+2}]$
and apply the strategy to diagonalize against the machine of index
$f(e,s_{i+1})$
while keeping
$\alpha $
in this interval, etc.
There are two cases:
-
• Either
$f(e,t)$
eventually stabilizes to a value
$f(e,s_k)$
, in which case we get to fully implement the diagonalization against the machine of index
$f(e,s_k)=F(e)$
, which ensures that
$\alpha _e \not = \Omega _{M_{F(e)}}$
or that
$M_{F(e)}$
is not optimal. -
• Or
$f(e,t)$
does not stabilize, in which case we will infinitely often move
$\alpha $
from the interval
$[\xi _i,\xi _{i+1}]$
to
$[\xi _{i+1}, \xi _{i+2}]$
, which means that the limit value of
$\alpha =\alpha _e$
will be
$\xi $
, hence
$\alpha _e$
is random, while
$F(e)$
is undefined since
$f(e,t)$
does not converge.
In either case, we have shown what we wanted.⊣
Finally, we can consider a yet weaker type of non-uniformity. In the definition of layerwise computability on left-c.e. reals, we asked that for
$\alpha _e \notin \mathcal {U}_d$
, the machine of index
$f(e,d)$
has halting probability
$\alpha _e$
and
$f(e,d) = f(e,d')$
if
$\alpha _e \notin \mathcal {U}_d \cup \mathcal {U}_{d'}$
. Here we could try to remove this last condition by allowing
$f(e,d)$
and
$f(e,d')$
to be codes for different machines (but both with halting probabilities
$\alpha _e$
). In this setting, we do get a positive result.
Theorem 2.2. There exists a partial computable function
$f(.,.)$
such that if
$\alpha _e \notin \mathcal {U}_d$
,
$\alpha _e \in [0,1]$
, then
$f(e,d)$
is defined and
$\Omega _{M_{f(e,d)}}=\alpha _e$
.
Proof This follows from work of Calude et al. [Reference Chaitin7] and of Kučera and Slaman [Reference Kučera and Slaman14]. Let
$\Omega $
be the halting probability of an optimal machine. Kučera and Slaman showed how from the index of a left-c.e. real
$\alpha \in [0,1]$
one can build a Martin-Löf test
$(\mathcal {V}_k)$
such that if
$\alpha \notin (\mathcal {V}_k)$
then one can, uniformly in k, produce approximations
$\alpha _1 < \alpha _2 < \cdots $
of
$\alpha $
and
$\Omega _1 < \Omega _2 < \cdots $
of
$\Omega $
such that
$(\alpha _{s+1} - \alpha _s)> 2^{-k} (\Omega _{s+1}-\Omega _s)$
(see [Reference Downey and Hirschfeldt11, Theorem 9.2.3]). Then, by [Reference Chaitin7], one can use such approximations to uniformly build a uniform machine with halting probability
$\alpha $
, as long as
$\alpha \in (2^{-k},1-2^{-k})$
(see [Reference Downey and Hirschfeldt11, Theorem 9.2.2])
Thus, given an index for
$\alpha $
, if
$(\mathcal {V}_k)$
is the Martin-Löf test built as in [Reference Kučera and Slaman14], we can build the test
$\mathcal {V}^{\prime }_k = \mathcal {V}_{k+2} \cup (0,2^{-k-2}) \cup (1-2^{-k-2},1)$
(whose index can uniformly be computed from that of
$(\mathcal {V}_k)$
). Now, if
$\alpha \notin \mathcal {U}_d$
, then we can compute a constant c such that
$\alpha \notin \mathcal {V}^{\prime }_{d+c}$
, and apply the above argument with
$k=c+d+2$
.⊣
2.3 Uniform constructions of semi-measures
Another way to define Omega numbers, which is equivalent if one is not concerned about uniformity issues, is via left-c.e. semi-measures (see [Reference Downey and Hirschfeldt11, Section 3.9]).
Definition 2.3. A semi-measure is a function
$m: \mathbb {N} \rightarrow \mathbb {R}^+$
such that
$\sum _i m(i) \leq 1$
. It is left-c.e. if the set
$\{(i,q) \mid i \in \mathbb {N}, q \in \mathbb {Q}, \ m(i)>q\}$
is c.e., or equivalently, if m is the limit of a non-decreasing sequence
$(m_s)$
of uniformly computable functions such that
$\sum _s m_s(i) \leq 1$
for all s.
There exist universal left-c.e. semi-measures, i.e., left-c.e. semi-measures m such that for any other left-c.e. semi-measure
$\mu $
, there is a
$c>0$
such that
$m(i)>c \cdot \mu (i)$
for all i. The Levin coding theorem (see [Reference Downey and Hirschfeldt11, Theorem 3.9.4]) asserts that a left-c.e. semi-measure m is universal if and only if there are positive constants
$c_1,c_2$
such that
$c_1 \cdot 2^{-K(i)} < m(i) < c_2 \cdot 2^{-K(i)}$
for all i. An important result from Calude et al. [Reference Chaitin7] is that a left-c.e. real
$\alpha $
is an Omega number if and only if it is the sum
$\sum _i m(i)$
for some universal left-c.e. semi-measure m. Interestingly, with this representation of Omega numbers, uniform constructions are possible.
Theorem 2.4. There is a total computable function f such that if e is an index for a random left-c.e. real
$\alpha \in [0,1]$
, then
$f(e)$
is defined and is an index for a universal left-c.e. semi-measure
$m_{f(e)}$
with sum
$\alpha $
.
Proof Let
$\mu $
be a fixed universal semi-measure and
$\gamma \leq 1$
its sum. Suppose we are given (the index of) a left-c.e. real
$\alpha $
. We build our m by building uniformly, for each
$k>0$
, a left-c.e. semi-measure
$m_k$
of halting probability
$\alpha \cdot 2^{-k}$
and will take
$m = \sum _{k>0} m_k$
. While doing so, we also build an auxiliary Martin-Löf test
$(\mathcal {U}_k)_{k>0}$
.
The measure
$m_k$
is designed as follows. We monitor the semi-measure
$\mu $
and
$\alpha $
at the same time and run the following algorithm
-
1. Let
$s_0$
be the stage at which we entered step 1. Wait for the least stage
$s \geq s_0$
such that some value
$\mu (i)$
with
$i \leq s$
has increased since the last i-stage. If there is more than one such i at stage s, let i be the one whose most recent i-stage is least. Let x be the amount by which
$\mu (i)$
has increased since the previous i-stage, and say that s is an i-stage. Move to step 2. -
2. Put
$(\alpha _s,\alpha _s+2^{-k}x)$
into
$\mathcal {U}_k$
. Move to step 3. -
3. Increase
$m_k(i)$
by
$2^{-k}(\alpha _s - \alpha _{s_0})$
. At further stages
$t \geq s$
, when we see an increase
$\alpha _{t+1}>\alpha _t$
, we increase
$m_k(i)$
by
$2^{-k} (\alpha _{t+1}-\alpha _t)$
. Moreover, if we now have
$\alpha _{t+1}> \alpha _s+2^{-k}x$
, we go back to step 1, otherwise we stay in this step 3.
By construction we do have
$\sum _i m_k(i) = 2^{-k}\alpha $
. Still by construction, the measure of
$\; \mathcal {U}_k$
is bounded by
$\gamma \cdot 2^{-k} \leq 2^{-k}$
, so it is indeed a Martin-Löf test. Thus, if
$\alpha $
is indeed random, there is a j such that
$\alpha \notin \mathcal {U}_j$
. Looking at the above algorithm,
$\alpha \notin \mathcal {U}_j$
means that for this j, we enter step 1 of the algorithm infinitely often and thus whenever some
$\mu (i)$
is increased by x at step 1, this is met by a sum of increases of
$m_j(i)$
by strictly more than
$2^{-j}x$
during step 3. Thus,
$m_j> 2^{-j}\mu $
, which makes
$m_j$
a universal semi-measure, and thus
$m>m_j$
is universal.⊣
An interesting corollary is that one cannot uniformly turn a universal left-c.e. semi-measure m into a prefix-free machine whose halting probability is
$\sum _i m(i)$
. Indeed, if we could, then we could uniformly turn a random left-c.e.
$\alpha \in [0,1]$
into a prefix-free machine of halting probability
$\alpha $
by first applying the above theorem to get a universal left-c.e. semi-measure m of sum
$\alpha $
, and then we could turn m into a machine M of sum
$\alpha $
. This would contradict Theorem 1.2.
To summarize, for arbitrary (not necessarily random) left-c.e. reals, we can make all of the transformations uniformly:
For random left-c.e. reals, and optimal prefix-free machines, we can only make the following transformations uniformly:
3 Differences of left-c.e. reals
Theorem 1.4. There is no partial computable function f such that if e is an index for a non-computable left-c.e. real
$\alpha $
, then
$f(e)$
is defined and is an index for a left-c.e. real
$\beta $
such that
$\alpha - \beta $
is neither left-c.e. nor right-c.e.
Proof Using the recursion theorem, define a left-c.e. real
$\alpha $
while watching the left-c.e. real
$\beta $
produced from
$\alpha $
by a function f. We will also define a right-c.e. real
$\delta $
. Let
$\theta ^i$
be an enumeration of the right-c.e. reals with right-c.e. approximations
$(\theta ^i_s)$
. We will ensure that
$\alpha \neq \theta ^i$
for any i, so that
$\alpha $
is non-computable, and that either
$\alpha - \beta = \delta $
or for all sufficiently large stages,
$\alpha $
grows more than
$\beta $
(and so
$\alpha - \beta $
is left-c.e.).
Each stage of the construction will be in one of infinitely many possible states: wait and follow
$(i)$
for some i. In wait,
$\alpha $
will be held to the same value and we will begin decreasing the right-c.e. real
$\delta $
closer to
$\alpha - \beta $
; if there are infinitely many wait stages, then in fact we will have
$\delta = \alpha - \beta $
. At follow
$(i)$
stages,
$\alpha $
will increase as much as
$\beta $
, and possibly more, in an attempt to have
$\theta ^i < \alpha $
. Because
$\alpha $
will be increasing as much as and possibly more than
$\beta $
, if from some point on all stages are follow
$(i)$
stages, then
$\alpha - \beta $
will be left-c.e. We will only enter follow
$(i)$
when we have a reasonable chance of making
$\theta ^i < \alpha $
, i.e., when
$\theta ^i$
is not too much greater than
$\alpha $
, and we will only exit follow
$(i)$
when we have succeeded in making
$\theta ^i < \alpha $
. Since
$\theta ^i$
is right-c.e. and
$\alpha $
is left-c.e., this can never be injured. It is possible that we will never succeed in making
$\theta ^i < \alpha $
(because in fact
$\theta ^i> \alpha $
) but in this case we will still ensure that
$\alpha $
is not computable and make
$\alpha - \beta $
left-c.e. We just have to make sure that we never increase
$\alpha - \beta $
above
$\delta $
.
Note that technically when defining
$\alpha _s$
we cannot wait for
$\beta _s$
to converge. But we can do this by essentially the following argument. First, fix a non-computable left-c.e. real
$\gamma $
and let
$\alpha _s = \gamma _s$
until the uniform procedure provides us with a
$\beta $
and
$\beta _0$
converges at some stage
$s_0$
. Then we can restart the construction, considering the construction to begin with
$\alpha _0 = \gamma _{s_0}$
. We can also in a uniform way replace the given approximation to
$\beta $
(which might not even be total or left-c.e.) by a different one which is guaranteed to be left-c.e. and which converges in a known amount of time, and is equal to
$\beta $
in the case that
$\beta $
is in fact left-c.e.
Construction.
Stage
$s = 0$
. Begin with
$\alpha _0 = \gamma _{s_0}$
,
$\delta _0 = 1 + \alpha _0 - \beta _0$
. Say that stage 1 will be a wait stage.
Stage
$s+1$
. We will have determined in stage s whether stage
$s+1$
is a wait or follow stage.
wait: Let
$\alpha _{s+1} = \alpha _s$
and
$$ \begin{align*}\delta_{s+1} = \min\left(\delta_s,\alpha_{s+1}-\beta_{s+1} + \frac{1}{2^s}\right).\end{align*} $$
Check whether, for some
$i \leq s$
,
$\theta ^i_{s+1} \geq \alpha _{s+1}$
and
$\theta ^i_{s+1} - \alpha _{s+1} < \frac {1}{2^i}$
. If we find such an i, let i be the least such. The next stage is a follow
$(i)$
stage. If there is no such i, the next stage is a wait stage.
follow
$(i)$
: In all cases, let
$\delta _{s+1} = \delta _s$
. Then:
-
(1) Check whether
If so, set
$$ \begin{align*} \alpha_s + \beta_{s+1} - \beta_s> \theta^i_{s+1}.\end{align*} $$
where
$$ \begin{align*} \alpha_{s+1} = \theta^i_{s+1} + \epsilon \leq \alpha_s + \beta_{s+1} - \beta_s, \end{align*} $$
$\epsilon < \frac {1}{2^i}$
. The next stage is a wait stage.
-
(2) Otherwise, check whether for some j,
If we find such a j, choose the least such j, and let
$$ \begin{align*} 0 \leq \theta^j_s - \alpha_s < \frac{1}{2^{j+2}} \Big[ \delta_s - (\alpha_s-\beta_s) \Big]. \end{align*} $$
$\epsilon> 0$
be such that Let
$$ \begin{align*} \theta^j_s + \epsilon - \alpha_s < \frac{1}{2^{j+2}} \Big[ \delta_s - (\alpha_s-\beta_s) \Big]. \end{align*} $$
If
$$ \begin{align*}\alpha_{s+1} = \max(\theta^j_s + \epsilon,\alpha_s + \beta_{s+1}-\beta_s).\end{align*} $$
$j = i$
, the next stage is a wait stage. Otherwise, the next stage is a follow
$(i)$
stage.
-
(3) Finally, in any other case, let
The next stage is a follow
$$ \begin{align*}\alpha_{s+1} = \alpha_s + \beta_{s+1}-\beta_s.\end{align*} $$
$(i)$
stage.
End construction.
The verification will consist of five claims followed by a short argument.
Claim 1.
$\alpha = \mathop {\mathrm {sup}}\limits \alpha _s$
comes to a limit.
Proof In wait stages, we do not increase
$\alpha $
. If we enter follow
$(i)$
, then we can increase
$\alpha $
by at most
$\frac {2}{2^i}$
before we exit follow
$(i)$
. Thus
$$ \begin{align*} \alpha \leq \sum_{i \in \omega} \frac{2}{2^i} < \infty.\\[-40pt] \end{align*} $$
⊣
Claim 2. Suppose that, from some stage t on, every stage is a follow
$(i)$
stage. Then:
-
(1) for all
$s \geq t$
,
$\alpha _{s+1} - \alpha _s \geq \beta _{s+1} - \beta _s$
, -
(2)
$\alpha - \beta $
is left-c.e., and -
(3) for all
$s \geq t$
,
$$ \begin{align*}\delta_s - (\alpha_s-\beta_s) \geq \frac{1}{2}\Big[\delta_t - (\alpha_t-\beta_t)\Big].\end{align*} $$
Proof (1) follows from the fact that we either set the next stage to be a wait stage, or we have
$\alpha _{s+1} \geq \alpha _s + \beta _{s+1} - \beta _s$
. (2) follows easily from (1).
For (3), since
$\delta _s = \delta _t$
for all
$s \geq t$
, whenever we define
$$ \begin{align*}\alpha_{s+1} = \alpha_s + \beta_{s+1}-\beta_s \end{align*} $$
we maintain
$$ \begin{align*} \delta_{s+1} - (\alpha_{s+1}-\beta_{s+1}) = \delta_s - (\alpha_s-\beta_s).\end{align*} $$
The other possible case is when we find j such that
$$ \begin{align*} 0 \leq \theta^j_s - \alpha_s < \frac{1}{2^{j+2}} \Big[ \delta_s - (\alpha_s-\beta_s) \Big]. \end{align*} $$
and define
$$ \begin{align*}\alpha_{s+1} = \theta^j_s + \epsilon.\end{align*} $$
Note that in this case we permanently have
$\theta ^j - \alpha < 0$
so we can never do this again for the same j. We have
$$ \begin{align*} \delta_{s+1} - (\alpha_{s+1}-\beta_{s+1}) &= \delta_s - \theta^j_s - \epsilon + \beta_{s+1}\\ &\geq \delta_s - \alpha_s + \beta_s - \frac{1}{2^{j+2}}\Big[ \delta_s - (\alpha_s-\beta_s) \Big]\\ &= \frac{2^{j+2} - 1}{2^{j+2}} \Big[ \delta_s - (\alpha_s-\beta_s) \Big]. \end{align*} $$
Thus, for all stages
$s \geq t$
,
$$ \begin{align*} \delta_s - (\alpha_s-\beta_s) &\geq \prod_{j \in \omega} \frac{2^{j+2}-1}{2^{j+2}} \Big[\delta_t - (\alpha_t-\beta_t)\Big] \\ &\geq \frac{1}{2} \Big[\delta_t - (\alpha_t-\beta_t)\Big]. \\[-40pt]\end{align*} $$
⊣
Claim 3. For all stages s,
$\delta _s> \alpha _s - \beta _s$
.
Proof We argue by induction. This is true for
$s = 0$
.
If stage
$s+1$
is a wait stage, then there are two possible values for
$\delta _{s+1}$
:
$\delta _s$
or
$\alpha _{s+1} - \beta _{s+1} + \frac {1}{2^s}$
. It is clear that the second is strictly greater than
$\alpha _{s+1} - \beta _{s+1}$
. We also have, since
$\alpha _{s+1}=\alpha _s$
and
$\beta _{s+1} \geq \beta _s$
, that
$\delta _s> \alpha _s - \beta _s \geq \alpha _{s+1} - \beta _{s+1}$
.
If stage
$s+1$
is a follow stage, then
$\delta _{s+1} = \delta _s$
. There are two options for
$\alpha _{s+1}$
. First, we might set
$\alpha _{s+1} \leq \alpha _s + \beta _{s+1} - \beta _s$
so that
$\alpha _{s+1} - \beta _{s+1} \leq \alpha _s - \beta _s$
and
$\delta _{s+1}> \alpha _{s+1} - \beta _{s+1}$
follows from the induction hypothesis
$\delta _s> \alpha _s-\beta _s$
. Second, we might set
$$ \begin{align*}\alpha_{s+1} = \theta^j_s + \epsilon,\end{align*} $$
where
$$ \begin{align*} \theta^j_s + \epsilon - \alpha_s < \frac{1}{2^{j+2}} \Big[ \delta_s - (\alpha_s-\beta_s) \Big].\end{align*} $$
Then
$$ \begin{align*} \alpha_{s+1} - \beta_{s+1} &\leq \theta^j_s + \epsilon - \beta_s\\ &< \alpha_s - \beta_s + \frac{1}{2^{j+2}} \Big[ \delta_s - (\alpha_s-\beta_s) \Big]\\ &\leq \frac{1}{2^{j+2}} \delta_s + \frac{2^{j+2} - 1}{2^{j+2}} \Big[\alpha_s-\beta_s \Big]\\ &< \delta_s = \delta_{s+1}. \end{align*} $$
This completes the proof.⊣
Claim 4.
$\alpha $
is non-computable.
Proof If
$\alpha $
was computable, then it would be equal to a right-c.e. real
$\theta ^i$
. For all stages s,
$\alpha \leq \theta ^i_s$
. Let t be a stage such that
$\theta ^i_t - \alpha _t < \frac {1}{2^i}$
. Increasing t, we may assume that there is
$j \leq i$
such that we are in follow
$(j)$
from stage t on. Increasing t further, we can assume that for each
$i' < i$
, if
$\theta ^i < \alpha $
, then we have seen this by stage t. Consider the inequality
$$ \begin{align*} \theta^i_s - \alpha_s < \frac{1}{2^{i+2}} \Big[ \delta_s - (\alpha_s-\beta_s) \Big]. \end{align*} $$
By (3) of Claim 2, the right-hand-side has a lower bound, and this lower bound is strictly positive by Claim 3. Since
$\theta ^i = \alpha $
, there is a stage
$s \geq t$
where this inequality holds. Then by choice of t, i is the least value satisfying this inequality and we set
$\alpha _{s+1}> \theta ^i_s$
.⊣
Claim 5. If there are infinitely many wait stages, then
$\delta = \alpha - \beta $
.
Proof Using Claim 3, for each wait stage s, we have
$$ \begin{align*} \alpha_s - \beta_s \leq \delta_s \leq \alpha_s - \beta_s + \frac{1}{2^{s-1}}. \end{align*} $$
Thus
$\delta = \alpha - \beta $
.⊣
We are now ready to complete the proof. It follows from Claim 1 that
$\alpha $
is a left-c.e. real that comes to a limit, and by Claim 4,
$\alpha $
is a non-computable. If there are infinitely many wait stages, then by Claim 5
$\delta = \alpha - \beta $
is right-c.e. The other option is that there is j such that every stage from some point on is a follow
$(j)$
stage. In this case, by (2) of Claim 2,
$\alpha - \beta $
is left-c.e.⊣
We now turn to Theorem 1.6 which says that one can uniformly construct, from an optimal (respectively universal) machine U, an optimal (respectively universal) machine V such that
$\Omega _{U}-\Omega _{V}$
is neither left-c.e. nor right-c.e. We first prove this for optimal machines, and then obtain the result for universal machines as a corollary.
Theorem 3.1. Theorem 1.5 is uniform, in the sense that there is a total computable function f such that if
$U=M_e$
is an optimal machine, then
$V=M_{f(e)}$
is optimal and
$\Omega _{U}-\Omega _{V}$
is neither left-c.e. nor right-c.e.
Proof Let
$\gamma , \delta $
be two Solovay-incomparable left-c.e. reals. As explained in [Reference Bienvenu and Downey3], if
$\alpha $
is random, then
$\beta = \alpha + \gamma - \delta $
is left-c.e. and random, and
$\alpha -\beta $
is neither left-c.e. nor right-c.e. Our goal is to make this idea effective.
Let us first express
$\delta $
as the sum
$\sum _n 2^{-h(n)}$
where h is a computable function. In what follows, when we write
$h(\sigma )$
for a string
$\sigma $
, we mean
$h(n)$
where n is the integer associated to
$\sigma $
via a fixed computable bijection. Furthermore, let Q be a machine such that
$\mu (\operatorname {\mathrm {dom}}(Q))=\gamma $
.
We build a machine V from a machine U as follows. First, we wait for U to issue a description
$U(\sigma _0)=\tau _0$
. When this happens, V issues a description
$V(\sigma _0 0)=\tau _0$
and countably many descriptions by setting
$V(\sigma _0 1 p)=Q(p)$
for every
$p \in \operatorname {\mathrm {dom}}(Q)$
.
Now, for every string
$\tau \not = \tau _0$
in parallel, we enumerate all descriptions
${U(\sigma )=\tau }$
. As long as the enumerated descriptions are such that
$|\sigma | \geq h(\tau )$
, V copies these descriptions. If at some point we find a description
$U(\sigma ) = \tau $
with
$|\sigma | \leq h(\tau )-1$
, we then issue descriptions
$V(\sigma 0)=\tau $
, and
$V(\sigma ')=\tau $
for every
$\sigma '$
of length
$h(\tau )$
which extends
$\sigma 1$
, except for
$\sigma '=\sigma 1^{h(\tau )-|\sigma |}$
, for which we leave
$V(\sigma ')$
undefined. After having done that, V copies all further U-descriptions of
$\tau $
, regardless of the length of these descriptions.
By construction, V is prefix-free, because any U-description
$U(\sigma )=\tau $
is replaced in V by a set of descriptions
$V(\sigma ')=\tau '$
where the
$\sigma '$
form a prefix-free set of extensions of
$\sigma $
. Moreover, V is optimal because by construction, whenever a description
$U(\sigma )=\tau $
is enumerated, a V-description of
$\tau $
of length at most
$|\sigma |+1$
is issued. Let us now evaluate
$\Omega _U-\Omega _V$
. The very first description
$U(\sigma _0)=\tau _0$
of U gives rise to descriptions in V of total measure
$2^{-c-1}+2^{-c-1}\mu (\operatorname {\mathrm {dom}}(Q))$
, where
$c=|\sigma _0|$
. Thus this part of the construction contributes to
$\Omega _U-\Omega _V$
by an amount
$2^{-c}-2^{-c-1}-2^{-c-1}\mu (\operatorname {\mathrm {dom}}(Q))=2^{-c-1}-2^{-c-1}\gamma $
.
Now, for other strings
$\tau \not = \tau _0$
, there are two cases. Either a description
$U(\sigma )= \tau $
with
$|\sigma |<h(\tau )$
is found (which is equivalent to saying that
$K_U(\tau ) < h(\tau )$
), or no such description is found. Let A be the set of
$\tau $
for which such a description is found. For
$\tau \notin A$
, all U-descriptions of
$\tau $
are copied identically in V. For
$\tau \in A$
, all U-descriptions of
$\tau $
are copied except one description
$U(\sigma )=\tau $
(thus of measure
$2^{-|\sigma |}$
) which is mimicked in V by a set of descriptions of measure
$2^{-|\sigma |}-2^{-h(\tau )}$
.
Putting it all together:
$$ \begin{align*} \Omega_U-\Omega_V = 2^{-c-1}-2^{-c-1}\gamma + \sum_{\tau \in A} 2^{-h(\tau)}. \end{align*} $$
To finish the proof, we appeal to the theory of Solovay functions. When h is a computable positive function, the sum
$\sum _n 2^{-h(n)}$
is not random if and only if
$h(n) - K(n) \rightarrow \infty $
[Reference Bienvenu, Downey, Nies and Merkle4, Reference Barmpalias and Lewis-Pye5]. This is the case here as
$\delta =\sum _n 2^{-h(n)}$
is Solovay-incomplete hence not random. Suppose that the machine U is indeed an optimal machine. Then
$K_U = K +O(1)$
, and thus we have
$h(n) - K_U(n) \rightarrow \infty $
. In particular, for almost all n,
$h(n)> K_U(n)$
. This shows that the set A above is cofinite and therefore that
$\sum _{\tau \in A} 2^{-h(\tau )}=\delta -q$
for some (dyadic) rational q. Plugging this in the above equality, we get
$$ \begin{align*} \Omega_U-\Omega_V = 2^{-c-1}-2^{-c-1}\gamma + \delta - q. \end{align*} $$
Since
$\gamma $
and
$\delta $
are Solovay-incomparable, this shows that
$\Omega _U-\Omega _V$
is neither left-c.e. nor right-c.e.⊣
Corollary 3.2. There is a total computable function g such that if
$U=M_e$
is a universal machine, then
$W=M_{g(e)}$
is universal and
$\Omega _{U}-\Omega _{W}$
is neither left-c.e. nor right-c.e.
Proof Given
$U = M_e$
, construct
$V = M_{f(e)}$
as in the previous theorem. Define a machine
$W = M_{g(e)}$
by setting
$W(0 \sigma ) = U(0 \sigma )$
and
$W(1 \sigma ) = V(1 \sigma )$
. Then
$\Omega _W = \frac {1}{2} \Omega _U + \frac {1}{2} \Omega _V$
, and so
$\Omega _U - \Omega _W = \frac {1}{2}(\Omega _U - \Omega _V)$
. Thus if U is universal, then so is W, and
$\Omega _U - \Omega _W$
is neither left-c.e. nor right-c.e.⊣
Acknowledgment
Laurent Bienvenu was supported by the ANR ACTC-19-CE48-0012-01 grant. Barbara F. Csima was supported by an NSERC Discovery Grant.
