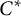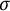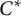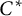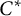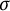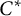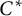1 Introduction
In the previous paper [Reference Kodaka and Teruya7], we discussed strong Morita equivalence for unital inclusions of unital
![]() $C^*$
-algebras induced by involutive equivalence bimodules. That is, let A and B be unital
$C^*$
-algebras induced by involutive equivalence bimodules. That is, let A and B be unital
![]() $C^*$
-algebras and X and Y an involutive
$C^*$
-algebras and X and Y an involutive
![]() $A-A$
-equivalence bimodule and an involutive
$A-A$
-equivalence bimodule and an involutive
![]() $B-B$
-equivalence bimodule, respectively. Let
$B-B$
-equivalence bimodule, respectively. Let
![]() $C_X$
and
$C_X$
and
![]() $C_Y$
be unital
$C_Y$
be unital
![]() $C^*$
-algebras induced by X and Y, respectively which are defined in [Reference Kodaka and Teruya9]. Then, we get the unital inclusions of unital
$C^*$
-algebras induced by X and Y, respectively which are defined in [Reference Kodaka and Teruya9]. Then, we get the unital inclusions of unital
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A\subset C_X$
and
$A\subset C_X$
and
![]() $B\subset C_Y$
, respectively. We suppose that
$B\subset C_Y$
, respectively. We suppose that
![]() $A' \cap C_X =\mathbf C 1$
. In the paper [Reference Kodaka and Teruya7], we showed that
$A' \cap C_X =\mathbf C 1$
. In the paper [Reference Kodaka and Teruya7], we showed that
![]() $A\subset C_X$
and
$A\subset C_X$
and
![]() $B\subset C_Y$
are strongly Morita equivalent if and only if there is an
$B\subset C_Y$
are strongly Morita equivalent if and only if there is an
![]() $A-B$
-equivalence bimodule M such that
$A-B$
-equivalence bimodule M such that
![]() $Y\cong \widetilde {M}\otimes _A X\otimes _A M$
as
$Y\cong \widetilde {M}\otimes _A X\otimes _A M$
as
![]() $B-B$
-equivalence bimodules. In the present paper, we will show the same result as above in the case of inclusions of
$B-B$
-equivalence bimodules. In the present paper, we will show the same result as above in the case of inclusions of
![]() $C^*$
-algebras induced by
$C^*$
-algebras induced by
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra equivalence bimodules.
$C^*$
-algebra equivalence bimodules.
Let A and B be
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebras and X and Y an
$C^*$
-algebras and X and Y an
![]() $A-A$
-equivalence bimodule and a
$A-A$
-equivalence bimodule and a
![]() $B-B$
-equivalence bimodule, respectively. Let
$B-B$
-equivalence bimodule, respectively. Let
![]() $A\rtimes _X \mathbf Z$
and
$A\rtimes _X \mathbf Z$
and
![]() $B\rtimes _Y \mathbf Z$
be the crossed products of A and B by X and Y, respectively, which are defined in [Reference Abadie, Eilers and Exel1]. Then, we get inclusions of
$B\rtimes _Y \mathbf Z$
be the crossed products of A and B by X and Y, respectively, which are defined in [Reference Abadie, Eilers and Exel1]. Then, we get inclusions of
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
with
$B\subset B\rtimes _Y \mathbf Z$
with
![]() $\overline {A(A\rtimes _X \mathbf Z)}=A\rtimes _X \mathbf Z$
and
$\overline {A(A\rtimes _X \mathbf Z)}=A\rtimes _X \mathbf Z$
and
![]() $\overline {B(B\rtimes _Y \mathbf Z)}=B\rtimes _Y \mathbf Z$
. We suppose that
$\overline {B(B\rtimes _Y \mathbf Z)}=B\rtimes _Y \mathbf Z$
. We suppose that
![]() $A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
. We will show that
$A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
. We will show that
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent if and only if there is an
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent if and only if there is an
![]() $A-B$
-equivalence bimodule M such that
$A-B$
-equivalence bimodule M such that
![]() $Y\cong \widetilde {M}\otimes _A X\otimes _A M$
or
$Y\cong \widetilde {M}\otimes _A X\otimes _A M$
or
![]() $\widetilde {Y}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
$\widetilde {Y}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
![]() $B-B$
-equivalence bimodules, where
$B-B$
-equivalence bimodules, where
![]() $\widetilde {M}$
and
$\widetilde {M}$
and
![]() $\widetilde {Y}$
are the dual
$\widetilde {Y}$
are the dual
![]() $B-A$
-equivalence bimodule and the dual
$B-A$
-equivalence bimodule and the dual
![]() $B-B$
-equivalence bimodule of M and Y, respectively. This is our main result (Theorem 3.6).
$B-B$
-equivalence bimodule of M and Y, respectively. This is our main result (Theorem 3.6).
In Section 3, we will prove it in the following way. First, we assume that there is an
![]() $A-B$
- equivalence bimodule M satisfying the above condition. Then, modifying the proof of [Reference Abadie, Eilers and Exel1, Theorem 4.2], we can show that
$A-B$
- equivalence bimodule M satisfying the above condition. Then, modifying the proof of [Reference Abadie, Eilers and Exel1, Theorem 4.2], we can show that
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent. We note that in this case, we do not need the assumption that
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent. We note that in this case, we do not need the assumption that
![]() $A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C1$
.
$A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C1$
.
Next, we assume that
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent. Then, there are automorphisms
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent. Then, there are automorphisms
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that
$\beta $
such that
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
and
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
and
![]() $B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
are isomorphic to
$B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
are isomorphic to
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
![]() $B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
as inclusions of
$B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
as inclusions of
![]() $C^*$
-algebras, respectively, in the sense of Definition 2.1 below. Applying [Reference Kodaka8, Theorem 5.5] to
$C^*$
-algebras, respectively, in the sense of Definition 2.1 below. Applying [Reference Kodaka8, Theorem 5.5] to
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, we can obtain the desired conclusion. When we do it, we need the assumption that
$\beta $
, we can obtain the desired conclusion. When we do it, we need the assumption that
![]() $A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
. As mentioned in [Reference Kodaka8], the condition
$A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
. As mentioned in [Reference Kodaka8], the condition
![]() $A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
holds if and only if the action of
$A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
holds if and only if the action of
![]() $\alpha $
on
$\alpha $
on
![]() $A\otimes \mathbf K$
is free. This freeness of
$A\otimes \mathbf K$
is free. This freeness of
![]() $\alpha $
plays an important role in proving [Reference Kodaka8, Theorem 5.5]. We refer to [Reference Kodaka8, Section 4] and the references therein for more details about the notion of free action on a
$\alpha $
plays an important role in proving [Reference Kodaka8, Theorem 5.5]. We refer to [Reference Kodaka8, Section 4] and the references therein for more details about the notion of free action on a
![]() $C^*$
-algebra. Furthermore, we remark that the same result as [Reference Kodaka8, Theorem 5.5] in the case of unital inclusions of unital
$C^*$
-algebra. Furthermore, we remark that the same result as [Reference Kodaka8, Theorem 5.5] in the case of unital inclusions of unital
![]() $C^*$
-algebras induced by coactions of a finite-dimensional
$C^*$
-algebras induced by coactions of a finite-dimensional
![]() $C^*$
-Hopf algebras is obtained in [Reference Kodaka and Teruya11].
$C^*$
-Hopf algebras is obtained in [Reference Kodaka and Teruya11].
In Section 4, we will give an application (Theorem 4.9) of the above result, that is, we will compute the Picard group of the inclusion of
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A\subset A\rtimes _X \mathbf Z$
under the assumption that
$A\subset A\rtimes _X \mathbf Z$
under the assumption that
![]() $A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
.
$A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
.
2 Preliminaries
Let
![]() $\mathbf K$
be the
$\mathbf K$
be the
![]() $C^*$
-algebra of all compact operators on a countably infinite-dimensional Hilbert space and
$C^*$
-algebra of all compact operators on a countably infinite-dimensional Hilbert space and
![]() $\{e_{ij}\}_{i, j\in \mathbf N}$
its system of matrix units.
$\{e_{ij}\}_{i, j\in \mathbf N}$
its system of matrix units.
For each
![]() $C^*$
-algebra A, we denote by
$C^*$
-algebra A, we denote by
![]() $M(A)$
the multiplier
$M(A)$
the multiplier
![]() $C^*$
-algebra of A. Let
$C^*$
-algebra of A. Let
![]() $\pi $
be an isomorphism of A onto a
$\pi $
be an isomorphism of A onto a
![]() $C^*$
-algebra B. Then, there is the unique strictly continuous isomorphism of
$C^*$
-algebra B. Then, there is the unique strictly continuous isomorphism of
![]() $M(A)$
onto
$M(A)$
onto
![]() $M(B)$
extending
$M(B)$
extending
![]() $\pi $
by Jensen and Thomsen [Reference Kodaka5, Corollary 1.1.15]. We denote it by
$\pi $
by Jensen and Thomsen [Reference Kodaka5, Corollary 1.1.15]. We denote it by
![]() $\underline {\pi }$
.
$\underline {\pi }$
.
For an algebra A, we denote by
![]() ${\mathrm {id}}_A$
the identity map on A. If A is unital, we denote by
${\mathrm {id}}_A$
the identity map on A. If A is unital, we denote by
![]() $1_A$
the unit element of A. If no confusion arises, we denote them by
$1_A$
the unit element of A. If no confusion arises, we denote them by
![]() ${\mathrm {id}}$
and
${\mathrm {id}}$
and
![]() $1$
, respectively.
$1$
, respectively.
Let A and B be
![]() $C^*$
-algebras and X an
$C^*$
-algebras and X an
![]() $A-B$
-bimodule. We denote its left A-action and right B-action on X by
$A-B$
-bimodule. We denote its left A-action and right B-action on X by
![]() $a\cdot x$
and
$a\cdot x$
and
![]() $x\cdot b$
for any
$x\cdot b$
for any
![]() $a\in A$
,
$a\in A$
,
![]() $b\in B$
,
$b\in B$
,
![]() $x\in X$
, respectively. We denote by
$x\in X$
, respectively. We denote by
![]() $\widetilde {X}$
the dual
$\widetilde {X}$
the dual
![]() $B-A$
-bimodule of X and let
$B-A$
-bimodule of X and let
![]() $\widetilde {x}$
denote the element in
$\widetilde {x}$
denote the element in
![]() $\widetilde {X}$
associated to an element
$\widetilde {X}$
associated to an element
![]() $x\in X$
. Furthermore, we regard X as a Hilbert
$x\in X$
. Furthermore, we regard X as a Hilbert
![]() $M(A)-M(B)$
-bimodule in the sense of [Reference Brown, Mingo and Shen4] in the same way as described before [Reference Kodaka8, Definition 2.4].
$M(A)-M(B)$
-bimodule in the sense of [Reference Brown, Mingo and Shen4] in the same way as described before [Reference Kodaka8, Definition 2.4].
Let
![]() $A\subset C$
and
$A\subset C$
and
![]() $B\subset D$
be inclusions of
$B\subset D$
be inclusions of
![]() $C^*$
-algebras. We give some definitions.
$C^*$
-algebras. We give some definitions.
Definition 2.1 We say that
![]() $A\subset C$
and
$A\subset C$
and
![]() $B\subset D$
are isomorphic as inclusions of
$B\subset D$
are isomorphic as inclusions of
![]() $C^*$
-algebras if there is an isomorphism
$C^*$
-algebras if there is an isomorphism
![]() $\pi $
of C onto D such that the restriction of
$\pi $
of C onto D such that the restriction of
![]() $\pi $
to A,
$\pi $
to A,
![]() $\pi |_A$
is an isomorphism of A onto B.
$\pi |_A$
is an isomorphism of A onto B.
Definition 2.2 [Reference Kodaka and Teruya10, Definition 2.1]
Let
![]() $A\subset C$
and
$A\subset C$
and
![]() $B\subset D$
be inclusions of
$B\subset D$
be inclusions of
![]() $C^*$
-algebras with
$C^*$
-algebras with
![]() $\overline {AC}=C$
and
$\overline {AC}=C$
and
![]() $\overline {BD}=D$
. Then, the inclusions
$\overline {BD}=D$
. Then, the inclusions
![]() $A\subset C$
and
$A\subset C$
and
![]() $B\subset D$
are strongly Morita equivalent with respect to a
$B\subset D$
are strongly Morita equivalent with respect to a
![]() $C-D$
-equivalence bimodule Y and its closed subspace X if there are a
$C-D$
-equivalence bimodule Y and its closed subspace X if there are a
![]() $C-D$
-equivalence bimodule Y and its closed subspace X satisfying the following conditions:
$C-D$
-equivalence bimodule Y and its closed subspace X satisfying the following conditions:
(1)
![]() $a\cdot x\in X$
,
$a\cdot x\in X$
,
![]() ${}_C \langle x, y \rangle \in A$
for any
${}_C \langle x, y \rangle \in A$
for any
![]() $a\in A$
,
$a\in A$
,
![]() $x, y\in X$
, and
$x, y\in X$
, and
![]() $\overline {{}_C \langle X, X \rangle }=A$
,
$\overline {{}_C \langle X, X \rangle }=A$
,
![]() $\overline {{}_C \langle Y, X \rangle }=C$
,
$\overline {{}_C \langle Y, X \rangle }=C$
,
(2)
![]() $x\cdot b\in X$
,
$x\cdot b\in X$
,
![]() $\langle x, y \rangle _D \in B$
for any
$\langle x, y \rangle _D \in B$
for any
![]() $b\in B$
,
$b\in B$
,
![]() $x, y\in X$
, and
$x, y\in X$
, and
![]() $\overline {\langle X, X \rangle _D }=B$
,
$\overline {\langle X, X \rangle _D }=B$
,
![]() $\overline {\langle Y, X \rangle _D}=D$
.
$\overline {\langle Y, X \rangle _D}=D$
.
We note that X can be regarded as an
![]() $A-B$
-equivalence bimodule. Furthermore, we give the following definition.
$A-B$
-equivalence bimodule. Furthermore, we give the following definition.
Definition 2.3 Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be actions of a discrete group G on A and B, respectively. We say that
$\beta $
be actions of a discrete group G on A and B, respectively. We say that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are strongly Morita equivalent with respect to
$\beta $
are strongly Morita equivalent with respect to
![]() $(X, \lambda )$
if there are an
$(X, \lambda )$
if there are an
![]() $A-B$
-equivalence bimodule X and a linear automorphism action
$A-B$
-equivalence bimodule X and a linear automorphism action
![]() $\lambda $
on X satisfying the following:
$\lambda $
on X satisfying the following:
(1)
![]() $\alpha _t ({}_A \langle x, y \rangle )={}_A \langle \lambda _t (x)\, , \, \lambda _t (y) \rangle $
,
$\alpha _t ({}_A \langle x, y \rangle )={}_A \langle \lambda _t (x)\, , \, \lambda _t (y) \rangle $
,
(2)
![]() $\beta _t (\langle x, y \rangle _B )=\langle \lambda _t (x) \, , \, \lambda _t (y) \rangle _B$
, for any
$\beta _t (\langle x, y \rangle _B )=\langle \lambda _t (x) \, , \, \lambda _t (y) \rangle _B$
, for any
![]() $x, y\in X$
and
$x, y\in X$
and
![]() $t\in G$
.
$t\in G$
.
Then, we have the following:
for any
![]() $a\in A$
,
$a\in A$
,
![]() $b\in B$
,
$b\in B$
,
![]() $x\in X$
, and
$x\in X$
, and
![]() $t\in G$
.
$t\in G$
.
Let A and B be
![]() $C^*$
-algebras and
$C^*$
-algebras and
![]() $\pi $
an isomorphism of B onto A. We construct an
$\pi $
an isomorphism of B onto A. We construct an
![]() $A-B$
-equivalence bimodule
$A-B$
-equivalence bimodule
![]() $X_{\pi }$
as follows: Let
$X_{\pi }$
as follows: Let
![]() $X_{\pi }=A$
as a
$X_{\pi }=A$
as a
![]() $\mathbf C$
-vector space. For any
$\mathbf C$
-vector space. For any
![]() $a\in A$
,
$a\in A$
,
![]() $b\in B$
, and
$b\in B$
, and
![]() $x, y\in X_{\pi }$
,
$x, y\in X_{\pi }$
,
 $$ \begin{align*} & a\cdot x=ax \, , \quad x\cdot b=x\pi(b), \\ & {}_A \langle x, y \rangle=xy^* \, , \quad \langle x, y \rangle_B=\pi^{-1}(x^* y). \end{align*} $$
$$ \begin{align*} & a\cdot x=ax \, , \quad x\cdot b=x\pi(b), \\ & {}_A \langle x, y \rangle=xy^* \, , \quad \langle x, y \rangle_B=\pi^{-1}(x^* y). \end{align*} $$
By easy computations, we can see that
![]() $X_{\pi }$
is an
$X_{\pi }$
is an
![]() $A-B$
-equivalence bimodule. We call
$A-B$
-equivalence bimodule. We call
![]() $X_{\pi }$
an
$X_{\pi }$
an
![]() $A-B$
-equivalence bimodule induced by
$A-B$
-equivalence bimodule induced by
![]() $\pi $
. Let
$\pi $
. Let
![]() $\alpha $
be an automorphism of A. Then, in the same way as above, we construct
$\alpha $
be an automorphism of A. Then, in the same way as above, we construct
![]() $X_{\alpha }$
, an
$X_{\alpha }$
, an
![]() $A-A$
-equivalence bimodule. Let
$A-A$
-equivalence bimodule. Let
![]() $u_{\alpha }$
be a unitary element in
$u_{\alpha }$
be a unitary element in
![]() $M(A\rtimes _{\alpha }\mathbf Z)$
implementing
$M(A\rtimes _{\alpha }\mathbf Z)$
implementing
![]() $\alpha $
. Hence,
$\alpha $
. Hence,
![]() $\alpha ={\mathrm {Ad}}(u_{\alpha })$
. We regard
$\alpha ={\mathrm {Ad}}(u_{\alpha })$
. We regard
![]() $Au_{\alpha }$
as an
$Au_{\alpha }$
as an
![]() $A-A$
-equivalence bimodule as follows:
$A-A$
-equivalence bimodule as follows:
 $$ \begin{align*} & a\cdot xu_{\alpha}=axu_{\alpha}\, , \quad xu_{\alpha}\cdot a =x\alpha(a), \\ & {}_A \langle xu_{\alpha} \, , \, yu_{\alpha} \rangle =xy^* \, , \quad \langle xu_{\alpha} \, , \, yu_{\alpha} \rangle_A =\alpha^{-1}(x^* y), \end{align*} $$
$$ \begin{align*} & a\cdot xu_{\alpha}=axu_{\alpha}\, , \quad xu_{\alpha}\cdot a =x\alpha(a), \\ & {}_A \langle xu_{\alpha} \, , \, yu_{\alpha} \rangle =xy^* \, , \quad \langle xu_{\alpha} \, , \, yu_{\alpha} \rangle_A =\alpha^{-1}(x^* y), \end{align*} $$
for any
![]() $a, x, y\in A$
.
$a, x, y\in A$
.
Lemma 2.1 With the above notation,
![]() $X_{\alpha }\cong Au_{\alpha }$
as
$X_{\alpha }\cong Au_{\alpha }$
as
![]() $A-A$
-equivalence bimodules.
$A-A$
-equivalence bimodules.
Proof. This is immediate by easy computations.▪
Let A be a
![]() $C^*$
-algebra and X an
$C^*$
-algebra and X an
![]() $A-A$
-equivalence bimodule. Let
$A-A$
-equivalence bimodule. Let
![]() $A\rtimes _X \mathbf Z$
be the crossed product of A by X defined in [Reference Abadie, Eilers and Exel1]. We regard the
$A\rtimes _X \mathbf Z$
be the crossed product of A by X defined in [Reference Abadie, Eilers and Exel1]. We regard the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathbf K$
as the trivial
$\mathbf K$
as the trivial
![]() $\mathbf K-\mathbf K$
-equivalence bimodule. Then, we obtain an
$\mathbf K-\mathbf K$
-equivalence bimodule. Then, we obtain an
![]() $A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodule
$A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodule
![]() $X\otimes \mathbf K$
, and we can also consider the crossed product
$X\otimes \mathbf K$
, and we can also consider the crossed product
of
![]() $A\otimes \mathbf K$
by
$A\otimes \mathbf K$
by
![]() $X\otimes \mathbf K$
. Hence, we have the following inclusions of
$X\otimes \mathbf K$
. Hence, we have the following inclusions of
![]() $C^*$
-algebras:
$C^*$
-algebras:
Because there is an isomorphism
![]() $\pi $
of
$\pi $
of
![]() $(A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
onto
$(A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
onto
![]() $(A\rtimes _X \mathbf Z)\otimes \mathbf K$
such that
$(A\rtimes _X \mathbf Z)\otimes \mathbf K$
such that
![]() $\pi |_{A\rtimes \mathbf K}={\mathrm {id}}$
on
$\pi |_{A\rtimes \mathbf K}={\mathrm {id}}$
on
![]() $A\otimes \mathbf K$
, we identify
$A\otimes \mathbf K$
, we identify
![]() $A\otimes \mathbf K \subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
with
$A\otimes \mathbf K \subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
with
![]() $A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z) \otimes \mathbf K$
. Thus,
$A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z) \otimes \mathbf K$
. Thus,
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z $
are strongly Morita equivalent.
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z $
are strongly Morita equivalent.
Let
![]() $H_A$
be the
$H_A$
be the
![]() $A\otimes \mathbf K-A$
-equivalence bimodule defined as follows: Let
$A\otimes \mathbf K-A$
-equivalence bimodule defined as follows: Let
![]() $H_A =(A\otimes \mathbf K)(1_{M(A)}\otimes e_{11})$
as a
$H_A =(A\otimes \mathbf K)(1_{M(A)}\otimes e_{11})$
as a
![]() $\mathbf C$
-vector space. For any
$\mathbf C$
-vector space. For any
![]() $a\in A$
,
$a\in A$
,
![]() $k\in \mathbf K$
, and
$k\in \mathbf K$
, and
![]() $x, y\in A\otimes \mathbf K$
,
$x, y\in A\otimes \mathbf K$
,
 $$ \begin{align*} & (a\otimes k)\cdot x(1\otimes e_{11})=(a\otimes k)x(1\otimes e_{11}) \, , \\ & x(1\otimes e_{11})\cdot a =x(a\otimes e_{11}) , \\ & {}_{A\otimes\mathbf K} \langle x(1\otimes e_{11}) \, , \, y(1\otimes e_{11}) \rangle =x(1\otimes e_{11})y^* \, , \\ & \langle x(1\otimes e_{11}) \, , \, y(1\otimes e_{11}) \rangle_A =(1\otimes e_{11})x^* y(1\otimes e_{11}) , \end{align*} $$
$$ \begin{align*} & (a\otimes k)\cdot x(1\otimes e_{11})=(a\otimes k)x(1\otimes e_{11}) \, , \\ & x(1\otimes e_{11})\cdot a =x(a\otimes e_{11}) , \\ & {}_{A\otimes\mathbf K} \langle x(1\otimes e_{11}) \, , \, y(1\otimes e_{11}) \rangle =x(1\otimes e_{11})y^* \, , \\ & \langle x(1\otimes e_{11}) \, , \, y(1\otimes e_{11}) \rangle_A =(1\otimes e_{11})x^* y(1\otimes e_{11}) , \end{align*} $$
where we identify A with
![]() $A\otimes e_{11}$
. Let B be a
$A\otimes e_{11}$
. Let B be a
![]() $C^*$
-algebra. Let
$C^*$
-algebra. Let
![]() $H_B$
be as above.
$H_B$
be as above.
Lemma 2.2 With the above notation, let M be an
![]() $A-B$
- equivalence bimodule. Then,
$A-B$
- equivalence bimodule. Then,
as
![]() $A-B$
-equivalence bimodules, where we regard
$A-B$
-equivalence bimodules, where we regard
![]() $M\otimes \mathbf K$
as an
$M\otimes \mathbf K$
as an
![]() $A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule.
$A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule.
Proof. Because the linear span of the set
is dense in
![]() $M\otimes \mathbf K$
,
$M\otimes \mathbf K$
,
![]() $(1\otimes e_{11})\cdot (M\otimes \mathbf K)\cdot (1\otimes e_{11}) \cong M\otimes e_{11}$
as
$(1\otimes e_{11})\cdot (M\otimes \mathbf K)\cdot (1\otimes e_{11}) \cong M\otimes e_{11}$
as
![]() $A-B$
-equivalence bimodules. Hence,
$A-B$
-equivalence bimodules. Hence,
as
![]() $A-B$
-equivalence bimodules.▪
$A-B$
-equivalence bimodules.▪
Lemma 2.3 With the above notation, let M be an
![]() $A-B$
-equivalence bimodule. Then,
$A-B$
-equivalence bimodule. Then,
as
![]() $A-B$
-equivalence bimodules.
$A-B$
-equivalence bimodules.
Proof. Let
![]() $\pi $
be the map from
$\pi $
be the map from
![]() $\widetilde {H_A}\otimes _{A\otimes \mathbf K}(M\otimes \mathbf K)\otimes _{B\otimes \mathbf K}H_B$
to
$\widetilde {H_A}\otimes _{A\otimes \mathbf K}(M\otimes \mathbf K)\otimes _{B\otimes \mathbf K}H_B$
to
![]() $(1\otimes e_{11})\cdot (M\otimes \mathbf K)\cdot (1\otimes e_{11})$
defined by
$(1\otimes e_{11})\cdot (M\otimes \mathbf K)\cdot (1\otimes e_{11})$
defined by
for any
![]() $a\in A\otimes \mathbf K$
,
$a\in A\otimes \mathbf K$
,
![]() $b\in B\otimes \mathbf K$
, and
$b\in B\otimes \mathbf K$
, and
![]() $x\in M\otimes \mathbf K$
. Then, by easy computations,
$x\in M\otimes \mathbf K$
. Then, by easy computations,
![]() $\pi $
is an
$\pi $
is an
![]() $A-B$
-equivalence bimodule isomorphism of
$A-B$
-equivalence bimodule isomorphism of
![]() $\widetilde {H_A}\otimes _{A\otimes \mathbf K}(M\otimes \mathbf K)\otimes _{B\otimes \mathbf K}H_B$
onto
$\widetilde {H_A}\otimes _{A\otimes \mathbf K}(M\otimes \mathbf K)\otimes _{B\otimes \mathbf K}H_B$
onto
![]() $(1\otimes e_{11})\cdot (M\otimes \mathbf K)\cdot (1\otimes e_{11})$
. Thus, by Lemma 2.2,
$(1\otimes e_{11})\cdot (M\otimes \mathbf K)\cdot (1\otimes e_{11})$
. Thus, by Lemma 2.2,
as
![]() $A-B$
-equivalence bimodules.▪
$A-B$
-equivalence bimodules.▪
We prepare the following lemma which is applied in the next section.
Lemma 2.4 Let A and B be
![]() $C^*$
-algebras and X and Y an
$C^*$
-algebras and X and Y an
![]() $A-A$
-equivalence bimodule and a
$A-A$
-equivalence bimodule and a
![]() $B-B$
-equivalence bimodule, respectively. Let
$B-B$
-equivalence bimodule, respectively. Let
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
be inclusions of
$B\subset B\rtimes _Y \mathbf Z$
be inclusions of
![]() $C^*$
algebras induced by X and Y, respectively. We suppose that there is an
$C^*$
algebras induced by X and Y, respectively. We suppose that there is an
![]() $A-B$
-equivalence bimodule M such that
$A-B$
-equivalence bimodule M such that
![]() $Y\cong \widetilde {M}\otimes _A X\otimes _A M$
or
$Y\cong \widetilde {M}\otimes _A X\otimes _A M$
or
![]() $\widetilde {Y}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
$\widetilde {Y}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
![]() $B-B$
-equivalence bimodules. Then, there is an
$B-B$
-equivalence bimodules. Then, there is an
![]() $A\rtimes _X \mathbf Z -B\rtimes _Y \mathbf Z$
-equivalence bimodule N satisfying the following:
$A\rtimes _X \mathbf Z -B\rtimes _Y \mathbf Z$
-equivalence bimodule N satisfying the following:
(1) M is included in N as a closed subspace,
(2)
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to N and its closed subspace M.
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to N and its closed subspace M.
Proof. Modifying the proof of [Reference Abadie, Eilers and Exel1, Theorem 4.2], we prove this lemma. We suppose that
![]() $Y\cong \widetilde {M}\otimes _A X\otimes _A M$
as
$Y\cong \widetilde {M}\otimes _A X\otimes _A M$
as
![]() $B-B$
-equivalence bimodules. Let
$B-B$
-equivalence bimodules. Let
![]() $L_M$
be the linking
$L_M$
be the linking
![]() $C^*$
-algebra for M defined by
$C^*$
-algebra for M defined by
 $$ \begin{align*}L_M =\begin{bmatrix} A & M \\ \widetilde{M} & B \end{bmatrix}. \end{align*} $$
$$ \begin{align*}L_M =\begin{bmatrix} A & M \\ \widetilde{M} & B \end{bmatrix}. \end{align*} $$
Furthermore, let W be the
![]() $L_M -L_M$
- equivalence bimodule defined in the proof of [Reference Abadie, Eilers and Exel1, Theorem 4.2], which is defined by
$L_M -L_M$
- equivalence bimodule defined in the proof of [Reference Abadie, Eilers and Exel1, Theorem 4.2], which is defined by
 $$ \begin{align*}W=\begin{bmatrix} X & X\otimes_A M \\ Y\otimes_B \widetilde{M} & Y \end{bmatrix}. \end{align*} $$
$$ \begin{align*}W=\begin{bmatrix} X & X\otimes_A M \\ Y\otimes_B \widetilde{M} & Y \end{bmatrix}. \end{align*} $$
Let
![]() $L_M \rtimes _W \mathbf Z$
be the crossed product of
$L_M \rtimes _W \mathbf Z$
be the crossed product of
![]() $L_M$
by W, and let
$L_M$
by W, and let
 $$ \begin{align*}p=\begin{bmatrix} 1_{M(A)} & 0 \\ 0 & 0 \end{bmatrix} \, , \quad q=\begin{bmatrix} 0 & 0 \\ 0 & 1_{M(B)} \end{bmatrix}. \end{align*} $$
$$ \begin{align*}p=\begin{bmatrix} 1_{M(A)} & 0 \\ 0 & 0 \end{bmatrix} \, , \quad q=\begin{bmatrix} 0 & 0 \\ 0 & 1_{M(B)} \end{bmatrix}. \end{align*} $$
Furthermore, let
![]() $N=p(L_M \rtimes _W \mathbf Z)q$
. Then, because
$N=p(L_M \rtimes _W \mathbf Z)q$
. Then, because
![]() $M=pL_M q$
, M is a closed subspace of N. Hence, by the proof of [Reference Abadie, Eilers and Exel1, Theorem 4.2],
$M=pL_M q$
, M is a closed subspace of N. Hence, by the proof of [Reference Abadie, Eilers and Exel1, Theorem 4.2],
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect N and its closed subspace M.
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect N and its closed subspace M.
Next, we suppose that
![]() $\widetilde {Y}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
$\widetilde {Y}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
![]() $B-B$
-equivalence bimodules. Let
$B-B$
-equivalence bimodules. Let
 $$ \begin{align*}W_0 =\begin{bmatrix} X & X\otimes_A M \\ \widetilde{Y}\otimes_B \widetilde{M} & \widetilde{Y} \end{bmatrix}. \end{align*} $$
$$ \begin{align*}W_0 =\begin{bmatrix} X & X\otimes_A M \\ \widetilde{Y}\otimes_B \widetilde{M} & \widetilde{Y} \end{bmatrix}. \end{align*} $$
Then,
![]() $W_0$
is an
$W_0$
is an
![]() $L_M -L_M$
-equivalence bimodule. Let
$L_M -L_M$
-equivalence bimodule. Let
![]() $N_0 =p(L_M \rtimes _{W_0}\mathbf Z)q$
. By the above discussions,
$N_0 =p(L_M \rtimes _{W_0}\mathbf Z)q$
. By the above discussions,
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _{\widetilde {Y}}\mathbf Z$
are strongly Morita equivalent with respect to
$B\subset B\rtimes _{\widetilde {Y}}\mathbf Z$
are strongly Morita equivalent with respect to
![]() $N_0$
and its closed subspace M. On the other hand, there is an isomorphism
$N_0$
and its closed subspace M. On the other hand, there is an isomorphism
![]() $\pi $
of
$\pi $
of
![]() $B\rtimes _Y \mathbf Z$
onto
$B\rtimes _Y \mathbf Z$
onto
![]() $B\rtimes _{\widetilde {Y}}\mathbf Z$
such that
$B\rtimes _{\widetilde {Y}}\mathbf Z$
such that
![]() $\pi |_{B}={\mathrm {id}}$
on B. Let
$\pi |_{B}={\mathrm {id}}$
on B. Let
![]() $X_{\pi }$
be the
$X_{\pi }$
be the
![]() $B\rtimes _{\widetilde {Y}}\mathbf Z-B\rtimes _Y \mathbf Z$
-equivalence bimodule induced by
$B\rtimes _{\widetilde {Y}}\mathbf Z-B\rtimes _Y \mathbf Z$
-equivalence bimodule induced by
![]() $\pi $
. Then, B is a closed subspace of
$\pi $
. Then, B is a closed subspace of
![]() $X_{\pi }$
, and we regard B as the trivial
$X_{\pi }$
, and we regard B as the trivial
![]() $B-B$
-equivalence bimodule, because
$B-B$
-equivalence bimodule, because
![]() $\pi |_{B} ={\mathrm {id}}$
on B. Thus,
$\pi |_{B} ={\mathrm {id}}$
on B. Thus,
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to
![]() $N_0 \otimes _{B\rtimes _{\widetilde {Y}}\mathbf Z}X_{\pi }$
and its closed subspace
$N_0 \otimes _{B\rtimes _{\widetilde {Y}}\mathbf Z}X_{\pi }$
and its closed subspace
![]() $M\otimes _B B(\cong M)$
. Therefore, we obtain the conclusion.▪
$M\otimes _B B(\cong M)$
. Therefore, we obtain the conclusion.▪
Lemma 2.5 With the above notation, we suppose that A is a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra. Then, there is an automorphism
$C^*$
-algebra. Then, there is an automorphism
![]() $\alpha $
of
$\alpha $
of
![]() $A\otimes \mathbf K$
such that
$A\otimes \mathbf K$
such that
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
is isomorphic to
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
is isomorphic to
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
as inclusions of
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
as inclusions of
![]() $C^*$
-algebras.
$C^*$
-algebras.
Proof. Because A is
![]() $\sigma $
-unital, by [Reference Brown, Green and Rieffel3, Corollary 3.5], there is an automorphism
$\sigma $
-unital, by [Reference Brown, Green and Rieffel3, Corollary 3.5], there is an automorphism
![]() $\alpha $
of
$\alpha $
of
![]() $A\otimes \mathbf K$
such that
$A\otimes \mathbf K$
such that
![]() $X\otimes \mathbf K\cong X_{\alpha }$
as
$X\otimes \mathbf K\cong X_{\alpha }$
as
![]() $A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodules, where
$A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodules, where
![]() $X_{\alpha }$
is the
$X_{\alpha }$
is the
![]() $A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodule induced by
$A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodule induced by
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $u_{\alpha }$
be a unitary element in
$u_{\alpha }$
be a unitary element in
![]() $M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
implementing
$M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
implementing
![]() $\alpha $
. We regard
$\alpha $
. We regard
![]() $(A\otimes \mathbf K)u_{\alpha }$
as an
$(A\otimes \mathbf K)u_{\alpha }$
as an
![]() $A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodule as above. Then, by Lemma 2.1,
$A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodule as above. Then, by Lemma 2.1,
![]() $X_{\alpha }\cong (A\otimes \mathbf K)u_{\alpha }$
as
$X_{\alpha }\cong (A\otimes \mathbf K)u_{\alpha }$
as
![]() $A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodules. Let
$A\otimes \mathbf K -A\otimes \mathbf K$
-equivalence bimodules. Let
![]() $(A\otimes \mathbf K)\rtimes _{(A\otimes \mathbf K)u_{\alpha }}\mathbf Z$
be the crossed product of
$(A\otimes \mathbf K)\rtimes _{(A\otimes \mathbf K)u_{\alpha }}\mathbf Z$
be the crossed product of
![]() $A\otimes \mathbf K$
by
$A\otimes \mathbf K$
by
![]() $(A\otimes \mathbf K)u_{\alpha }$
. Then, by the definition of the crossed product of a
$(A\otimes \mathbf K)u_{\alpha }$
. Then, by the definition of the crossed product of a
![]() $C^*$
-algebra by an equivalence bimodule, we can see that
$C^*$
-algebra by an equivalence bimodule, we can see that
as
![]() $C^*$
-algebras. Because
$C^*$
-algebras. Because
![]() $X_{\alpha }\cong X\otimes \mathbf K$
as
$X_{\alpha }\cong X\otimes \mathbf K$
as
![]() $A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodules, we obtain that
$A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodules, we obtain that
as
![]() $C^*$
-algebras. Because the above isomorphisms leave any element in
$C^*$
-algebras. Because the above isomorphisms leave any element in
![]() $A\otimes \mathbf K$
invariant, we can see that
$A\otimes \mathbf K$
invariant, we can see that
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha } \mathbf Z$
is isomorphic to
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha } \mathbf Z$
is isomorphic to
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
as inclusions of
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
as inclusions of
![]() $C^*$
-algebras.▪
$C^*$
-algebras.▪
3 Strong Morita equivalence
Let A and B be
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebras and X and Y an
$C^*$
-algebras and X and Y an
![]() $A-A$
-equivalence bimodule and a
$A-A$
-equivalence bimodule and a
![]() $B-B$
-equivalence bimodule, respectively. Let
$B-B$
-equivalence bimodule, respectively. Let
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
be the inclusions of
$B\subset B\rtimes _Y \mathbf Z$
be the inclusions of
![]() $C^*$
-algebras induced by X and Y, respectively. We suppose that
$C^*$
-algebras induced by X and Y, respectively. We suppose that
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to an
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to an
![]() $A\rtimes _X \mathbf Z -B\rtimes _Y \mathbf Z$
-equivalence bimodule N and its closed subspace M. We suppose that
$A\rtimes _X \mathbf Z -B\rtimes _Y \mathbf Z$
-equivalence bimodule N and its closed subspace M. We suppose that
![]() $A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
. Then, because the inclusion
$A' \cap M(A\rtimes _X \mathbf Z)=\mathbf C 1$
. Then, because the inclusion
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
is isomorphic to the inclusion
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
is isomorphic to the inclusion
![]() $A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z)\otimes \mathbf K$
as inclusions of
$A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z)\otimes \mathbf K$
as inclusions of
![]() $C^*$
-algebras, by [Reference Kodaka8, Lemma 3.1],
$C^*$
-algebras, by [Reference Kodaka8, Lemma 3.1],
Furthermore, by the above assumptions, the inclusion
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
is strongly Morita equivalent to the inclusion
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
is strongly Morita equivalent to the inclusion
![]() $B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
with respect to the
$B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
with respect to the
![]() $(A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z-(B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
-equivalence bimodule
$(A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z-(B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
-equivalence bimodule
![]() $N\otimes \mathbf K$
and its closed subspace
$N\otimes \mathbf K$
and its closed subspace
![]() $M\otimes \mathbf K$
. By Lemma 2.5, there are an automorphism
$M\otimes \mathbf K$
. By Lemma 2.5, there are an automorphism
![]() $\alpha $
of
$\alpha $
of
![]() $A\otimes \mathbf K$
and an automorphism
$A\otimes \mathbf K$
and an automorphism
![]() $\beta $
of
$\beta $
of
![]() $B\otimes \mathbf K$
such that
$B\otimes \mathbf K$
such that
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
and
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
and
![]() $B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
are isomorphic to
$B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{Y\otimes \mathbf K}\mathbf Z$
are isomorphic to
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
![]() $B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
as inclusions of
$B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
as inclusions of
![]() $C^*$
-algebras, respectively. Hence, we can assume that
$C^*$
-algebras, respectively. Hence, we can assume that
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
![]() $B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
are strongly Morita equivalent with respect to an
$B\otimes \mathbf K\subset (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
are strongly Morita equivalent with respect to an
![]() $(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z -(B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
-equivalence bimodule
$(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z -(B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
-equivalence bimodule
![]() $N\otimes \mathbf K$
and its closed subspace
$N\otimes \mathbf K$
and its closed subspace
![]() $M\otimes \mathbf K$
. Because A and B are
$M\otimes \mathbf K$
. Because A and B are
![]() $\sigma $
-unital, in the same way as in the proof of [Reference Kodaka and Teruya6, Proposition 3.5] or [Reference Brown, Green and Rieffel3, Proposition 3.1], there is an isomorphism
$\sigma $
-unital, in the same way as in the proof of [Reference Kodaka and Teruya6, Proposition 3.5] or [Reference Brown, Green and Rieffel3, Proposition 3.1], there is an isomorphism
![]() $\theta $
of
$\theta $
of
![]() $(B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
onto
$(B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
onto
![]() $(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
satisfying the following:
$(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
satisfying the following:
(1)
![]() $\theta |_{B\otimes \mathbf K}$
is an isomorphism of
$\theta |_{B\otimes \mathbf K}$
is an isomorphism of
![]() $B\otimes \mathbf K$
onto
$B\otimes \mathbf K$
onto
![]() $A\otimes \mathbf K$
,
$A\otimes \mathbf K$
,
(2) There is an
![]() $(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z-(B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
- equivalence bimodule isomorphism
$(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z-(B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
- equivalence bimodule isomorphism
![]() $\Phi $
of
$\Phi $
of
![]() $N\otimes \mathbf K$
onto
$N\otimes \mathbf K$
onto
![]() $Y_{\theta }$
such that
$Y_{\theta }$
such that
![]() $\Phi |_{M\otimes \mathbf K}$
is an
$\Phi |_{M\otimes \mathbf K}$
is an
![]() $A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule isomorphism of
$A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule isomorphism of
![]() $M\otimes \mathbf K$
onto
$M\otimes \mathbf K$
onto
![]() $X_{\theta }$
, where
$X_{\theta }$
, where
![]() $Y_{\theta }$
is the
$Y_{\theta }$
is the
![]() $(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z- (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
-equivalence bimodule induced by
$(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z- (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
-equivalence bimodule induced by
![]() $\theta $
and
$\theta $
and
![]() $X_{\theta }$
is the
$X_{\theta }$
is the
![]() $A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule induced by
$A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule induced by
![]() $\theta |_{B\otimes \mathbf K}$
.
$\theta |_{B\otimes \mathbf K}$
.
Let
and let
![]() $\lambda $
be the linear automorphism of
$\lambda $
be the linear automorphism of
![]() $X_{\theta }$
defined by
$X_{\theta }$
defined by
![]() $\lambda (x)=\gamma (x)$
for any
$\lambda (x)=\gamma (x)$
for any
![]() $x\in X_{\theta }(=A\otimes \mathbf K)$
.
$x\in X_{\theta }(=A\otimes \mathbf K)$
.
Lemma 3.1 With the above notation,
![]() $\gamma $
and
$\gamma $
and
![]() $\beta $
are strongly Morita equivalent with respect to
$\beta $
are strongly Morita equivalent with respect to
![]() $(X_{\theta }, \lambda )$
.
$(X_{\theta }, \lambda )$
.
Proof. For any
![]() $x, y\in X_{\theta }$
,
$x, y\in X_{\theta }$
,
 $$ \begin{align*} {}_{A\otimes\mathbf K}\langle \lambda(x) \, , \, \lambda(y) \rangle & =\gamma(xy^* )=\gamma({}_{A\otimes\mathbf K} \langle x \, , \, y \rangle) , \\ \langle \lambda(x) \, ,\, \lambda(y) \rangle _{B\otimes\mathbf K} & =\theta|_{B\otimes\mathbf K}^{-1}(\gamma(x^* y)) =\beta(\theta|_{B\otimes\mathbf K}^{-1}(x^* y))=\beta(\langle x \, \, y \rangle_{B\otimes\mathbf K}). \end{align*} $$
$$ \begin{align*} {}_{A\otimes\mathbf K}\langle \lambda(x) \, , \, \lambda(y) \rangle & =\gamma(xy^* )=\gamma({}_{A\otimes\mathbf K} \langle x \, , \, y \rangle) , \\ \langle \lambda(x) \, ,\, \lambda(y) \rangle _{B\otimes\mathbf K} & =\theta|_{B\otimes\mathbf K}^{-1}(\gamma(x^* y)) =\beta(\theta|_{B\otimes\mathbf K}^{-1}(x^* y))=\beta(\langle x \, \, y \rangle_{B\otimes\mathbf K}). \end{align*} $$
Hence,
![]() $\gamma $
and
$\gamma $
and
![]() $\beta $
are strongly Morita equivalent with respect to
$\beta $
are strongly Morita equivalent with respect to
![]() $(X_{\theta }, \lambda )$
.▪
$(X_{\theta }, \lambda )$
.▪
By the proof of [Reference Kodaka8, Theorem 5.5], there is an automorphism
![]() $\phi $
of
$\phi $
of
![]() $\mathbf Z$
satisfying that
$\mathbf Z$
satisfying that
![]() $\gamma ^{\phi }$
and
$\gamma ^{\phi }$
and
![]() $\alpha $
are exterior equivalent, that is, there is a unitary element
$\alpha $
are exterior equivalent, that is, there is a unitary element
![]() $z\in M(A\otimes \mathbf K)$
such that
$z\in M(A\otimes \mathbf K)$
such that
where
![]() $\gamma ^{\phi }$
is the automorphism of
$\gamma ^{\phi }$
is the automorphism of
![]() $A\otimes \mathbf K$
induced by
$A\otimes \mathbf K$
induced by
![]() $\gamma $
and
$\gamma $
and
![]() $\phi $
, that is,
$\phi $
, that is,
![]() $\gamma ^{\phi }$
is defined by
$\gamma ^{\phi }$
is defined by
![]() $\gamma ^{\phi }=\gamma ^{\phi (1)}$
. We note that
$\gamma ^{\phi }=\gamma ^{\phi (1)}$
. We note that
![]() $\gamma ^{\phi }=\gamma $
or
$\gamma ^{\phi }=\gamma $
or
![]() $\gamma ^{\phi }=\gamma ^{-1}$
. We regard
$\gamma ^{\phi }=\gamma ^{-1}$
. We regard
![]() $A\otimes \mathbf K$
as the trivial
$A\otimes \mathbf K$
as the trivial
![]() $A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodule. Let
$A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodule. Let
![]() $\mu $
be the linear automorphism of
$\mu $
be the linear automorphism of
![]() $A\otimes \mathbf K$
defined by
$A\otimes \mathbf K$
defined by
for any
![]() $x\in A\otimes \mathbf K$
.
$x\in A\otimes \mathbf K$
.
Lemma 3.2 With the above notation,
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma ^{\phi }$
are strongly Morita equivalent with respect to
$\gamma ^{\phi }$
are strongly Morita equivalent with respect to
![]() $(A\otimes \mathbf K, \mu )$
.
$(A\otimes \mathbf K, \mu )$
.
Proof. For any
![]() $x, y\in A\otimes \mathbf K$
,
$x, y\in A\otimes \mathbf K$
,
 $$ \begin{align*} {}_{A\otimes\mathbf K} \langle \mu(x) \, , \, \mu(y) \rangle & ={}_{A\otimes\mathbf K} \langle \alpha(x)z^* \, , \, \alpha(y)z^* \rangle =\alpha(xy^* )=\alpha({}_{A\otimes\mathbf K} \langle x \, , \, y \rangle) , \\ \langle \mu(x) \, , \, \mu(y) \rangle_{A\otimes\mathbf K} & =z\alpha(x^* y)z^* =\gamma^{\phi}(x^* y) =\gamma^{\phi}(\langle x \, ,\, y \rangle_{A\otimes\mathbf K}). \end{align*} $$
$$ \begin{align*} {}_{A\otimes\mathbf K} \langle \mu(x) \, , \, \mu(y) \rangle & ={}_{A\otimes\mathbf K} \langle \alpha(x)z^* \, , \, \alpha(y)z^* \rangle =\alpha(xy^* )=\alpha({}_{A\otimes\mathbf K} \langle x \, , \, y \rangle) , \\ \langle \mu(x) \, , \, \mu(y) \rangle_{A\otimes\mathbf K} & =z\alpha(x^* y)z^* =\gamma^{\phi}(x^* y) =\gamma^{\phi}(\langle x \, ,\, y \rangle_{A\otimes\mathbf K}). \end{align*} $$
Therefore, we obtain the conclusion.▪
Let
![]() $\nu $
be the linear automorphism of
$\nu $
be the linear automorphism of
![]() $X_{\theta }$
defined by
$X_{\theta }$
defined by
for any
![]() $x\in X_{\theta }(=A\otimes \mathbf K)$
.
$x\in X_{\theta }(=A\otimes \mathbf K)$
.
Lemma 3.3 With the above notation,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta ^{\phi }$
are strongly Morita equivalent with respect to
$\beta ^{\phi }$
are strongly Morita equivalent with respect to
![]() $(X_{\theta }, \nu )$
, where
$(X_{\theta }, \nu )$
, where
![]() $\beta ^{\phi }$
is the automorphism of
$\beta ^{\phi }$
is the automorphism of
![]() $B\otimes \mathbf K$
induced by
$B\otimes \mathbf K$
induced by
![]() $\beta $
and
$\beta $
and
![]() $\phi $
, that is,
$\phi $
, that is,
![]() $\beta ^{\phi }$
is defined by
$\beta ^{\phi }$
is defined by
![]() $\beta ^{\phi }=\beta ^{\phi (1)}$
.
$\beta ^{\phi }=\beta ^{\phi (1)}$
.
Proof. For any
![]() $x, y\in X_{\theta }$
,
$x, y\in X_{\theta }$
,
 $$ \begin{align*} {}_{A\otimes\mathbf K} \langle \nu(x) \, , \, \nu(y) \rangle & = {}_{A\otimes\mathbf K} \langle \gamma^{\phi}(z^* x) \, , \, \gamma^{\phi}(z^* y) \rangle=\gamma^{\phi}(z^* xy^* z) =z\alpha(z^* xy^* z)z^* \\ & =\alpha(xy^* )=\alpha({}_{A\otimes\mathbf K} \langle x \, , \, y \rangle) , \\ \langle \nu(x) \, , \, \nu(y) \rangle_{B\otimes\mathbf K} & = \langle \gamma^{\phi}(z^* x) \, , \, \gamma^{\phi}(z^* y) \rangle_{B\otimes\mathbf K} =\theta|_{B\otimes\mathbf K}^{-1}(\gamma^{\phi}(x^* y))=\beta^{\phi}(\theta|_{B\otimes\mathbf K}^{-1}(x^* y)) \\ & =\beta^{\phi}(\langle x \, , \, y \rangle_{B\otimes\mathbf K}). \end{align*} $$
$$ \begin{align*} {}_{A\otimes\mathbf K} \langle \nu(x) \, , \, \nu(y) \rangle & = {}_{A\otimes\mathbf K} \langle \gamma^{\phi}(z^* x) \, , \, \gamma^{\phi}(z^* y) \rangle=\gamma^{\phi}(z^* xy^* z) =z\alpha(z^* xy^* z)z^* \\ & =\alpha(xy^* )=\alpha({}_{A\otimes\mathbf K} \langle x \, , \, y \rangle) , \\ \langle \nu(x) \, , \, \nu(y) \rangle_{B\otimes\mathbf K} & = \langle \gamma^{\phi}(z^* x) \, , \, \gamma^{\phi}(z^* y) \rangle_{B\otimes\mathbf K} =\theta|_{B\otimes\mathbf K}^{-1}(\gamma^{\phi}(x^* y))=\beta^{\phi}(\theta|_{B\otimes\mathbf K}^{-1}(x^* y)) \\ & =\beta^{\phi}(\langle x \, , \, y \rangle_{B\otimes\mathbf K}). \end{align*} $$
Therefore, we obtain the conclusion.▪
Because
![]() $\beta ^{\phi }=\beta $
or
$\beta ^{\phi }=\beta $
or
![]() $\beta ^{\phi }=\beta ^{-1}$
, by Lemma 3.3,
$\beta ^{\phi }=\beta ^{-1}$
, by Lemma 3.3,
![]() $\alpha $
is strongly Morita equivalent to
$\alpha $
is strongly Morita equivalent to
![]() $\beta $
or
$\beta $
or
![]() $\beta ^{-1}$
.
$\beta ^{-1}$
.
(I) We suppose that
![]() $\alpha $
is strongly Morita equivalent to
$\alpha $
is strongly Morita equivalent to
![]() $\beta $
. Then, by Lemma 3.3, there is the linear automorphism
$\beta $
. Then, by Lemma 3.3, there is the linear automorphism
![]() $\nu $
of
$\nu $
of
![]() $X_{\theta }$
satisfying the following:
$X_{\theta }$
satisfying the following:
(1)
![]() $\nu (a\cdot x)=\alpha (a)\cdot \nu (x)$
,
$\nu (a\cdot x)=\alpha (a)\cdot \nu (x)$
,
(2)
![]() $\nu (x\cdot b)=\nu (x)\cdot \beta (b)$
,
$\nu (x\cdot b)=\nu (x)\cdot \beta (b)$
,
(3)
![]() ${}_{A\otimes \mathbf K} \langle \nu (x) \, , \, \nu (y)\rangle =\alpha ({}_{A\otimes \mathbf K} \langle x \, ,\, y \rangle )$
,
${}_{A\otimes \mathbf K} \langle \nu (x) \, , \, \nu (y)\rangle =\alpha ({}_{A\otimes \mathbf K} \langle x \, ,\, y \rangle )$
,
(4)
![]() $\langle \nu (x) \, , \, \nu (y)\rangle _{B\otimes \mathbf K}=\beta (\langle x \, ,\, y \rangle _{B\otimes \mathbf K})$
, for any
$\langle \nu (x) \, , \, \nu (y)\rangle _{B\otimes \mathbf K}=\beta (\langle x \, ,\, y \rangle _{B\otimes \mathbf K})$
, for any
![]() $a\in A\otimes \mathbf K$
,
$a\in A\otimes \mathbf K$
,
![]() $b\in B\otimes \mathbf K$
, and
$b\in B\otimes \mathbf K$
, and
![]() $x, y\in X_{\theta }$
.
$x, y\in X_{\theta }$
.
Lemma 3.4 With the above notation and assumptions, let
![]() $X_{\alpha }$
and
$X_{\alpha }$
and
![]() $X_{\beta }$
be the
$X_{\beta }$
be the
![]() $A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodule and the
$A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodule and the
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule induced by
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule induced by
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, respectively. Then,
$\beta $
, respectively. Then,
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules.
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules.
Proof. Let
![]() $\Psi $
be the map from
$\Psi $
be the map from
![]() $\widetilde {X_{\theta }}\otimes _{A\otimes \mathbf K}X_{\alpha }\otimes _{A\otimes \mathbf K}X_{\theta }$
to
$\widetilde {X_{\theta }}\otimes _{A\otimes \mathbf K}X_{\alpha }\otimes _{A\otimes \mathbf K}X_{\theta }$
to
![]() $X_{\beta }$
defined by
$X_{\beta }$
defined by
for any
![]() $x, y\in X_{\theta }$
and
$x, y\in X_{\theta }$
and
![]() $a\in X_{\alpha }$
. Then, for any
$a\in X_{\alpha }$
. Then, for any
![]() $x, x_1 , y, y_1 \in X_{\theta }$
and
$x, x_1 , y, y_1 \in X_{\theta }$
and
![]() $a, a_1 \in X_{\alpha }$
,
$a, a_1 \in X_{\alpha }$
,
 $$ \begin{align*} {}_{B\otimes\mathbf K} \langle \widetilde{x}\otimes a\otimes y \, , \, \widetilde{x_1}\otimes a_1 \otimes y_1 \rangle & ={}_{B\otimes\mathbf K} \langle \widetilde{x}\cdot {}_{A\otimes\mathbf K} \langle a\otimes y \, , \, a_1 \otimes y_1 \rangle \, , \, \widetilde{x_1} \rangle \\ & =\langle \, {}_{A\otimes\mathbf K} \langle a_1 \otimes y_1 \, , \, a \otimes y \rangle \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle \, {}_{A\otimes\mathbf K} \langle a_1 \cdot {}_{A\otimes\mathbf K} \langle y_ 1 \, , \, y \rangle \, , \, a \rangle \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle \, {}_{A\otimes\mathbf K} \langle a_1 \alpha({}_{A\otimes\mathbf K} \langle y_1 \, , \, y \rangle) \, , \, a \rangle \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle a_1 \alpha({}_{A\otimes\mathbf K} \langle y_1 \, ,\, y \rangle)a^* \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
$$ \begin{align*} {}_{B\otimes\mathbf K} \langle \widetilde{x}\otimes a\otimes y \, , \, \widetilde{x_1}\otimes a_1 \otimes y_1 \rangle & ={}_{B\otimes\mathbf K} \langle \widetilde{x}\cdot {}_{A\otimes\mathbf K} \langle a\otimes y \, , \, a_1 \otimes y_1 \rangle \, , \, \widetilde{x_1} \rangle \\ & =\langle \, {}_{A\otimes\mathbf K} \langle a_1 \otimes y_1 \, , \, a \otimes y \rangle \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle \, {}_{A\otimes\mathbf K} \langle a_1 \cdot {}_{A\otimes\mathbf K} \langle y_ 1 \, , \, y \rangle \, , \, a \rangle \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle \, {}_{A\otimes\mathbf K} \langle a_1 \alpha({}_{A\otimes\mathbf K} \langle y_1 \, , \, y \rangle) \, , \, a \rangle \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle a_1 \alpha({}_{A\otimes\mathbf K} \langle y_1 \, ,\, y \rangle)a^* \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
On the other hand,
 $$ \begin{align*} {}_{B\otimes\mathbf K} \langle \Psi(\widetilde{x}\otimes a\otimes y) \, , \, \Psi(\widetilde{x_1}\otimes a_1 \otimes y_1 )\rangle & ={}_{B\otimes\mathbf K} \langle \langle x\, , \, a\cdot \nu(y) \rangle_{B\otimes\mathbf K} \, , \, \langle x_1 \, , \, a_1 \cdot \nu(y_1 ) \rangle_{B\otimes\mathbf K} \rangle \\ & =\langle x\, , \, a\cdot\nu(y) \rangle_{B\otimes\mathbf K}\, \, \langle a_1 \cdot \nu(y_1 ) \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle x\, , \, a\cdot \nu(y)\cdot \langle a_1 \cdot \nu(y_1 ) \, , \, x_1 \rangle_{B\otimes\mathbf K} \, \, \rangle_{B\otimes\mathbf K} \\ & =\langle x \, , \, {}_{A\otimes\mathbf K} \langle a\cdot \nu(y) \, , \, a_1 \cdot \nu(y_1 ) \rangle \cdot x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle x\, , \, a \, {}_{A\otimes\mathbf K} \langle \nu(y) \, , \, \nu(y_1 ) \rangle a_1^* \cdot x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle a_1 \, {}_{A\otimes\mathbf K} \langle \nu(y_1 ) \, , \, \nu(y) \rangle a^* \cdot x\, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle a_1 \alpha({}_{A\otimes\mathbf K} \langle y_1 \, , \, y \rangle)a^* \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
$$ \begin{align*} {}_{B\otimes\mathbf K} \langle \Psi(\widetilde{x}\otimes a\otimes y) \, , \, \Psi(\widetilde{x_1}\otimes a_1 \otimes y_1 )\rangle & ={}_{B\otimes\mathbf K} \langle \langle x\, , \, a\cdot \nu(y) \rangle_{B\otimes\mathbf K} \, , \, \langle x_1 \, , \, a_1 \cdot \nu(y_1 ) \rangle_{B\otimes\mathbf K} \rangle \\ & =\langle x\, , \, a\cdot\nu(y) \rangle_{B\otimes\mathbf K}\, \, \langle a_1 \cdot \nu(y_1 ) \, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle x\, , \, a\cdot \nu(y)\cdot \langle a_1 \cdot \nu(y_1 ) \, , \, x_1 \rangle_{B\otimes\mathbf K} \, \, \rangle_{B\otimes\mathbf K} \\ & =\langle x \, , \, {}_{A\otimes\mathbf K} \langle a\cdot \nu(y) \, , \, a_1 \cdot \nu(y_1 ) \rangle \cdot x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle x\, , \, a \, {}_{A\otimes\mathbf K} \langle \nu(y) \, , \, \nu(y_1 ) \rangle a_1^* \cdot x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle a_1 \, {}_{A\otimes\mathbf K} \langle \nu(y_1 ) \, , \, \nu(y) \rangle a^* \cdot x\, , \, x_1 \rangle_{B\otimes\mathbf K} \\ & =\langle a_1 \alpha({}_{A\otimes\mathbf K} \langle y_1 \, , \, y \rangle)a^* \cdot x \, , \, x_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
Hence,
![]() $\Psi $
preserves the left
$\Psi $
preserves the left
![]() $B\otimes \mathbf K$
-valued inner products. Furthermore,
$B\otimes \mathbf K$
-valued inner products. Furthermore,
 $$ \begin{align*} \langle \widetilde{x}\otimes a\otimes y \, , \, \widetilde{x_1}\otimes a_1 \otimes y_1 \rangle_{B\otimes\mathbf K} & =\langle y \, , \, \langle \widetilde{x}\otimes a \, , \, \widetilde{x_1 }\otimes a_1 \rangle_{A\otimes\mathbf K}\cdot y_1 \rangle_{B\otimes\mathbf K} \\ & =\langle y \, , \, \langle a \, , \, {}_{A\otimes\mathbf K} \langle x\, , \, x_1 \rangle \cdot a_1 \rangle_{A\otimes\mathbf K}\cdot y_1 \rangle_{B\otimes\mathbf K} \\ & =\langle y \, , \, \langle a \, , \, {}_{A\otimes\mathbf K} \langle x\, , \, x_1 \rangle a_1 \rangle_{A\otimes\mathbf K}\cdot y_1 \rangle_{B\otimes\mathbf K} \\ & =\langle y\, , \, \alpha^{-1}(a^* \, {}_{A\otimes\mathbf K} \langle x\, , \, x_1 \rangle a_1 )\cdot y_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
$$ \begin{align*} \langle \widetilde{x}\otimes a\otimes y \, , \, \widetilde{x_1}\otimes a_1 \otimes y_1 \rangle_{B\otimes\mathbf K} & =\langle y \, , \, \langle \widetilde{x}\otimes a \, , \, \widetilde{x_1 }\otimes a_1 \rangle_{A\otimes\mathbf K}\cdot y_1 \rangle_{B\otimes\mathbf K} \\ & =\langle y \, , \, \langle a \, , \, {}_{A\otimes\mathbf K} \langle x\, , \, x_1 \rangle \cdot a_1 \rangle_{A\otimes\mathbf K}\cdot y_1 \rangle_{B\otimes\mathbf K} \\ & =\langle y \, , \, \langle a \, , \, {}_{A\otimes\mathbf K} \langle x\, , \, x_1 \rangle a_1 \rangle_{A\otimes\mathbf K}\cdot y_1 \rangle_{B\otimes\mathbf K} \\ & =\langle y\, , \, \alpha^{-1}(a^* \, {}_{A\otimes\mathbf K} \langle x\, , \, x_1 \rangle a_1 )\cdot y_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
On the other hand,
 $$ \begin{align*} \langle \Psi(\widetilde{x}\otimes a\otimes y)\, , \, \Psi(\widetilde{x_1}\otimes a_1 \otimes y_1 ) \rangle_{B\otimes\mathbf K} & =\langle \langle x\, , \, a\cdot\nu(y) \rangle_{B\otimes\mathbf K}\, , \, \langle x_1 \, , \, a_1 \cdot\nu(y_1 ) \rangle_{B\otimes\mathbf K} \rangle_{B\otimes\mathbf K} \\ & =\beta^{-1}(\langle a\cdot\nu(y) \, , \, x \rangle_{B\otimes\mathbf K}\, \langle x_1 \, , \, a_1 \cdot \nu(y_1 )\rangle_{B\otimes\mathbf K}) \\ & =\beta^{-1}(\langle a\cdot\nu(y) \, , \, x\cdot\langle x_1 \, , \, a_1 \cdot \nu(y_1 ) \rangle_{B\otimes\mathbf K} \, \rangle_{B\otimes\mathbf K}) \\ & =\beta^{-1}(\langle a\cdot\nu(y) \, , \, {}_{A\otimes\mathbf K} \langle x \, , \, x_1 \rangle a_1 \cdot\nu(y_1 ) \rangle_{B\otimes\mathbf K}) \\ & =\beta^{-1}(\langle \nu(y) \, , \, a^* {}_{A\otimes\mathbf K} \langle x \, ,\, x_1 \rangle a_1 \cdot \nu(y_1 ) \rangle_{B\otimes\mathbf K}) \\ & =\langle y \, , \, \alpha^{-1}(a^* \, {}_{A\otimes\mathbf K} \langle x \, , , x_1 \rangle a_1 )\cdot y_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
$$ \begin{align*} \langle \Psi(\widetilde{x}\otimes a\otimes y)\, , \, \Psi(\widetilde{x_1}\otimes a_1 \otimes y_1 ) \rangle_{B\otimes\mathbf K} & =\langle \langle x\, , \, a\cdot\nu(y) \rangle_{B\otimes\mathbf K}\, , \, \langle x_1 \, , \, a_1 \cdot\nu(y_1 ) \rangle_{B\otimes\mathbf K} \rangle_{B\otimes\mathbf K} \\ & =\beta^{-1}(\langle a\cdot\nu(y) \, , \, x \rangle_{B\otimes\mathbf K}\, \langle x_1 \, , \, a_1 \cdot \nu(y_1 )\rangle_{B\otimes\mathbf K}) \\ & =\beta^{-1}(\langle a\cdot\nu(y) \, , \, x\cdot\langle x_1 \, , \, a_1 \cdot \nu(y_1 ) \rangle_{B\otimes\mathbf K} \, \rangle_{B\otimes\mathbf K}) \\ & =\beta^{-1}(\langle a\cdot\nu(y) \, , \, {}_{A\otimes\mathbf K} \langle x \, , \, x_1 \rangle a_1 \cdot\nu(y_1 ) \rangle_{B\otimes\mathbf K}) \\ & =\beta^{-1}(\langle \nu(y) \, , \, a^* {}_{A\otimes\mathbf K} \langle x \, ,\, x_1 \rangle a_1 \cdot \nu(y_1 ) \rangle_{B\otimes\mathbf K}) \\ & =\langle y \, , \, \alpha^{-1}(a^* \, {}_{A\otimes\mathbf K} \langle x \, , , x_1 \rangle a_1 )\cdot y_1 \rangle_{B\otimes\mathbf K}. \end{align*} $$
Hence,
![]() $\Psi $
preserves the right
$\Psi $
preserves the right
![]() $B\otimes \mathbf K$
-valued inner products. Therefore, we obtain the conclusion.▪
$B\otimes \mathbf K$
-valued inner products. Therefore, we obtain the conclusion.▪
(II) We suppose that
![]() $\alpha $
is strongly Morita equivalent to
$\alpha $
is strongly Morita equivalent to
![]() $\beta ^{-1}$
. Then, by Lemma 3.4,
$\beta ^{-1}$
. Then, by Lemma 3.4,
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Thus, we obtain the following lemma.
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Thus, we obtain the following lemma.
Lemma 3.5 With the above notation and assumptions,
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules.
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules.
We recall that there is an
![]() $(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z- (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
- equivalence bimodule isomorphism
$(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z- (B\otimes \mathbf K)\rtimes _{\beta }\mathbf Z$
- equivalence bimodule isomorphism
![]() $\Phi $
of
$\Phi $
of
![]() $N\otimes \mathbf K$
onto
$N\otimes \mathbf K$
onto
![]() $Y_{\theta }$
such that
$Y_{\theta }$
such that
![]() $\Phi |_{M\otimes \mathbf K}$
is an
$\Phi |_{M\otimes \mathbf K}$
is an
![]() $A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule isomorphism of
$A\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodule isomorphism of
![]() $M\otimes \mathbf K$
onto
$M\otimes \mathbf K$
onto
![]() $X_{\theta }$
. We identify
$X_{\theta }$
. We identify
![]() $M\otimes \mathbf K$
with
$M\otimes \mathbf K$
with
![]() $X_{\theta }$
by
$X_{\theta }$
by
![]() $\Phi |_{M\otimes \mathbf K}$
. Then, by Lemmas 3.4 and 3.5,
$\Phi |_{M\otimes \mathbf K}$
. Then, by Lemmas 3.4 and 3.5,
or
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Furthermore, we recall that
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Furthermore, we recall that
![]() $X_{\alpha }\cong X\otimes \mathbf K$
as
$X_{\alpha }\cong X\otimes \mathbf K$
as
![]() $A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodules and that
$A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodules and that
![]() $X_{\beta }\cong Y\otimes \mathbf K$
as
$X_{\beta }\cong Y\otimes \mathbf K$
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Thus,
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Thus,
or
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Furthermore, by Lemma 2.3,
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Furthermore, by Lemma 2.3,
as
![]() $A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodules and
$A\otimes \mathbf K-A\otimes \mathbf K$
-equivalence bimodules and
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Thus,
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Thus,
 $$ \begin{align*} Y & \cong\widetilde{H_B}\otimes_{B\otimes\mathbf K}(Y\otimes\mathbf K)\otimes_{B\otimes\mathbf K}H_B \\ & \cong\widetilde{H_B}\otimes_{B\otimes\mathbf K}(\widetilde{M\otimes\mathbf K})\otimes_{A\otimes\mathbf K} (X\otimes\mathbf K)\otimes_{A\otimes\mathbf K}(M\otimes\mathbf K)\otimes_{B\otimes\mathbf K}H_B \\ & \cong\widetilde{H_B}\otimes_{B\otimes\mathbf K}(\widetilde{M\otimes\mathbf K})\otimes_{A\otimes\mathbf K} H_A \otimes_A X\otimes_A \widetilde{H_A}\otimes_{A\otimes\mathbf K}(M\otimes\mathbf K)\otimes_{B\otimes\mathbf K}H_B \end{align*} $$
$$ \begin{align*} Y & \cong\widetilde{H_B}\otimes_{B\otimes\mathbf K}(Y\otimes\mathbf K)\otimes_{B\otimes\mathbf K}H_B \\ & \cong\widetilde{H_B}\otimes_{B\otimes\mathbf K}(\widetilde{M\otimes\mathbf K})\otimes_{A\otimes\mathbf K} (X\otimes\mathbf K)\otimes_{A\otimes\mathbf K}(M\otimes\mathbf K)\otimes_{B\otimes\mathbf K}H_B \\ & \cong\widetilde{H_B}\otimes_{B\otimes\mathbf K}(\widetilde{M\otimes\mathbf K})\otimes_{A\otimes\mathbf K} H_A \otimes_A X\otimes_A \widetilde{H_A}\otimes_{A\otimes\mathbf K}(M\otimes\mathbf K)\otimes_{B\otimes\mathbf K}H_B \end{align*} $$
or similarly
as
![]() $B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Furthermore, by Lemma 2.3,
$B\otimes \mathbf K-B\otimes \mathbf K$
-equivalence bimodules. Furthermore, by Lemma 2.3,
as
![]() $A-B$
-equivalence bimodules. Hence,
$A-B$
-equivalence bimodules. Hence,
as
![]() $B-B$
-equivalence bimodules. Therefore, we obtain the following theorem.
$B-B$
-equivalence bimodules. Therefore, we obtain the following theorem.
Theorem 3.6 Let A and B be
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebras and X and Y an
$C^*$
-algebras and X and Y an
![]() $A-A$
-equivalence bimodule and a
$A-A$
-equivalence bimodule and a
![]() $B-B$
-equivalence bimodule, respectively. Let
$B-B$
-equivalence bimodule, respectively. Let
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
be the inclusions of
$B\subset B\rtimes _Y \mathbf Z$
be the inclusions of
![]() $C^*$
-algebras induced by X and Y, respectively. We suppose that
$C^*$
-algebras induced by X and Y, respectively. We suppose that
![]() $A' \cap M(A\rtimes _X \mathbf Z)\cong \mathbf C1$
. Then, the following conditions are equivalent:
$A' \cap M(A\rtimes _X \mathbf Z)\cong \mathbf C1$
. Then, the following conditions are equivalent:
(1)
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to an
$B\subset B\rtimes _Y \mathbf Z$
are strongly Morita equivalent with respect to an
![]() $A\rtimes _X \mathbf Z -B\rtimes _Y \mathbf Z$
-equivalence bimodule N and its closed subspace M,
$A\rtimes _X \mathbf Z -B\rtimes _Y \mathbf Z$
-equivalence bimodule N and its closed subspace M,
(2)
![]() $Y\cong \widetilde {M}\otimes _A X \otimes _A M$
or
$Y\cong \widetilde {M}\otimes _A X \otimes _A M$
or
![]() $\widetilde {Y}\cong \widetilde {M}\otimes _A X \otimes _A M$
as
$\widetilde {Y}\cong \widetilde {M}\otimes _A X \otimes _A M$
as
![]() $B-B$
-equivalence bimodules.
$B-B$
-equivalence bimodules.
Proof. (1)
![]() $\Rightarrow $
(2): This is immediate by the above discussions. (2)
$\Rightarrow $
(2): This is immediate by the above discussions. (2)
![]() $\Rightarrow $
(1): This is immediate by Lemma 2.4.▪
$\Rightarrow $
(1): This is immediate by Lemma 2.4.▪
Remark 3.7 The above theorem says that the inclusions
![]() $A\subset A\rtimes _X \mathbf Z$
and
$A\subset A\rtimes _X \mathbf Z$
and
![]() $B\subset B\rtimes _Y\mathbf Z$
are strongly Morita equivalent if and if X and Y are “flip” conjugate as equivalence bimodules. This is natural, because
$B\subset B\rtimes _Y\mathbf Z$
are strongly Morita equivalent if and if X and Y are “flip” conjugate as equivalence bimodules. This is natural, because
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, the corresponding actions on
$\beta $
, the corresponding actions on
![]() $A\otimes \mathbf K$
and
$A\otimes \mathbf K$
and
![]() $B\otimes \mathbf K$
to X and Y, respectively, are “flip” exterior equivalent, that is,
$B\otimes \mathbf K$
to X and Y, respectively, are “flip” exterior equivalent, that is,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
(or
$\beta $
(or
![]() $\beta ^{-1}$
) are exterior equivalent.
$\beta ^{-1}$
) are exterior equivalent.
4 The Picard groups
Let A be a unital
![]() $C^*$
-algebra and X an
$C^*$
-algebra and X an
![]() $A-A$
-equivalence bimodule. Let
$A-A$
-equivalence bimodule. Let
![]() $A\subset A\rtimes _X \mathbf Z$
be the inclusion of unital
$A\subset A\rtimes _X \mathbf Z$
be the inclusion of unital
![]() $C^*$
-algebras induced by X. We suppose that
$C^*$
-algebras induced by X. We suppose that
![]() $A' \cap (A\rtimes _X \mathbf Z)=\mathbf C 1$
. In this section, we shall compute
$A' \cap (A\rtimes _X \mathbf Z)=\mathbf C 1$
. In this section, we shall compute
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
, the Picard group of the inclusion
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
, the Picard group of the inclusion
![]() $A\subset A\rtimes _X \mathbf Z$
(See [Reference Kodaka and Teruya6]).
$A\subset A\rtimes _X \mathbf Z$
(See [Reference Kodaka and Teruya6]).
Let G be the subgroup of
![]() ${\mathrm {Pic}}(A)$
defined by
${\mathrm {Pic}}(A)$
defined by
 $$ \begin{align*} G=\{[M]\in{\mathrm{Pic}}(A) \, | \, X\cong\widetilde{M}\otimes_A X\otimes_A M \, \text{or} \, \widetilde{X} & \cong\widetilde{M}\otimes_A X\otimes_A M \\ & \text{as }A-A\text{-equivalence bimodules}\}. \end{align*} $$
$$ \begin{align*} G=\{[M]\in{\mathrm{Pic}}(A) \, | \, X\cong\widetilde{M}\otimes_A X\otimes_A M \, \text{or} \, \widetilde{X} & \cong\widetilde{M}\otimes_A X\otimes_A M \\ & \text{as }A-A\text{-equivalence bimodules}\}. \end{align*} $$
Let
![]() $f_A$
be the homomorphism of
$f_A$
be the homomorphism of
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
to
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
to
![]() ${\mathrm {Pic}}(A)$
defined by
${\mathrm {Pic}}(A)$
defined by
for any
![]() $[M, N]\in {\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
. First, we show
$[M, N]\in {\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
. First, we show
![]() ${\mathrm {Im}} f_A=G$
, where
${\mathrm {Im}} f_A=G$
, where
![]() ${\mathrm {Im}} f_A$
is the image of
${\mathrm {Im}} f_A$
is the image of
![]() $f_A$
.
$f_A$
.
Lemma 4.1 With the above notation,
![]() ${\mathrm {Im}} f_A =G$
.
${\mathrm {Im}} f_A =G$
.
Proof. Let
![]() $[M, N]\in {\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
. Then, by the definition of
$[M, N]\in {\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
. Then, by the definition of
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
, the inclusion
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
, the inclusion
![]() $A\subset A\rtimes _X \mathbf Z$
is strongly Morita equivalent to itself with respect to an
$A\subset A\rtimes _X \mathbf Z$
is strongly Morita equivalent to itself with respect to an
![]() $A\rtimes _X \mathbf Z -A\rtimes _X \mathbf Z$
-equivalence bimodule N and its closed subspace M. Hence, by Theorem 3.6,
$A\rtimes _X \mathbf Z -A\rtimes _X \mathbf Z$
-equivalence bimodule N and its closed subspace M. Hence, by Theorem 3.6,
![]() $X\cong \widetilde {M}\otimes _A X\otimes _A M$
or
$X\cong \widetilde {M}\otimes _A X\otimes _A M$
or
![]() $\widetilde {X}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
$\widetilde {X}\cong \widetilde {M}\otimes _A X\otimes _A M$
as
![]() $A-A$
-equivalence bimodules. Thus,
$A-A$
-equivalence bimodules. Thus,
![]() ${\mathrm {Im}} f_A \subset G$
. Next, let
${\mathrm {Im}} f_A \subset G$
. Next, let
![]() $[M]\in G$
. Then, by Lemma 2.4, there is an
$[M]\in G$
. Then, by Lemma 2.4, there is an
![]() $A\rtimes _X \mathbf Z- A\rtimes _X \mathbf Z$
-equivalence bimodule N satisfying the following:
$A\rtimes _X \mathbf Z- A\rtimes _X \mathbf Z$
-equivalence bimodule N satisfying the following:
(1) M is included in N as a closed subspace,
(2)
![]() $[M, N]\in {\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
.
$[M, N]\in {\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
.
Hence,
![]() $G\subset {\mathrm {Im}} f_A$
. Therefore, we obtain the conclusion.▪
$G\subset {\mathrm {Im}} f_A$
. Therefore, we obtain the conclusion.▪
Next, we compute
![]() ${\mathrm {Ker}} f_A$
, the kernel of
${\mathrm {Ker}} f_A$
, the kernel of
![]() $f_A$
. Let
$f_A$
. Let
![]() ${\mathrm {Aut}} (A, A\rtimes _X \mathbf Z)$
be the group of all automorphisms
${\mathrm {Aut}} (A, A\rtimes _X \mathbf Z)$
be the group of all automorphisms
![]() $\alpha $
of
$\alpha $
of
![]() $A\rtimes _X \mathbf Z$
such that
$A\rtimes _X \mathbf Z$
such that
![]() $\alpha |_A$
is an automorphism of A. Let
$\alpha |_A$
is an automorphism of A. Let
![]() ${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
be the group of all automorphisms
${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
be the group of all automorphisms
![]() $\alpha $
of
$\alpha $
of
![]() $A\rtimes _X \mathbf Z$
such that
$A\rtimes _X \mathbf Z$
such that
![]() $\alpha |_A ={\mathrm {id}}$
on A. It is clear that
$\alpha |_A ={\mathrm {id}}$
on A. It is clear that
![]() ${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
is a normal subgroup of
${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
is a normal subgroup of
![]() ${\mathrm {Aut}} (A, A\rtimes _X \mathbf Z)$
. Let
${\mathrm {Aut}} (A, A\rtimes _X \mathbf Z)$
. Let
![]() $\pi $
be the homomorphism of
$\pi $
be the homomorphism of
![]() ${\mathrm {Aut}}(A, A\rtimes _X \mathbf Z)$
to
${\mathrm {Aut}}(A, A\rtimes _X \mathbf Z)$
to
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
defined by
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
defined by
for any
![]() $\alpha \in {\mathrm {Aut}}(A, A\rtimes _X \mathbf Z)$
, where
$\alpha \in {\mathrm {Aut}}(A, A\rtimes _X \mathbf Z)$
, where
![]() $[M_{\alpha }, N_{\alpha }]$
is an element in
$[M_{\alpha }, N_{\alpha }]$
is an element in
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
induced by
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
induced by
![]() $\alpha $
(See [Reference Kodaka and Teruya6, Section 3]).
$\alpha $
(See [Reference Kodaka and Teruya6, Section 3]).
Lemma 4.2 With the above notation,
Proof. Let
![]() $[M, N]\in {\mathrm {Ker}} f_A$
. Then,
$[M, N]\in {\mathrm {Ker}} f_A$
. Then,
![]() $[M]=[A]$
in
$[M]=[A]$
in
![]() ${\mathrm {Pic}}(A)$
, and by [Reference Kodaka and Teruya6, Lemma 7.5], there is a
${\mathrm {Pic}}(A)$
, and by [Reference Kodaka and Teruya6, Lemma 7.5], there is a
![]() $\beta \in {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
such that
$\beta \in {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
such that
in
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
, where
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
, where
![]() $N_{\beta }$
is the
$N_{\beta }$
is the
![]() $A\rtimes _X \mathbf Z -A\rtimes _X \mathbf Z$
-equivalence bimodule induced by
$A\rtimes _X \mathbf Z -A\rtimes _X \mathbf Z$
-equivalence bimodule induced by
![]() $\beta $
. Therefore, we obtain the conclusion.▪
$\beta $
. Therefore, we obtain the conclusion.▪
Let
![]() ${\mathrm {Int}}(A, A\rtimes _X \mathbf Z)$
be the group of all
${\mathrm {Int}}(A, A\rtimes _X \mathbf Z)$
be the group of all
![]() ${\mathrm {Ad}}(u)$
such that u is a unitary element in A. By [Reference Kodaka and Teruya6, Lemma 3.4],
${\mathrm {Ad}}(u)$
such that u is a unitary element in A. By [Reference Kodaka and Teruya6, Lemma 3.4],
Hence,
 $$ \begin{align*} & {\mathrm{Ker}} \, \pi\cap{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) \\ &\quad =\{{\mathrm{Ad}}(u)\in{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) \, | \, u \text{ is a unitary element in }A\} \\ &\quad =\{{\mathrm{Ad}}(u)\in{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) \, | \, u \text{ is a unitary element in }A' \cap A\}. \end{align*} $$
$$ \begin{align*} & {\mathrm{Ker}} \, \pi\cap{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) \\ &\quad =\{{\mathrm{Ad}}(u)\in{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) \, | \, u \text{ is a unitary element in }A\} \\ &\quad =\{{\mathrm{Ad}}(u)\in{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) \, | \, u \text{ is a unitary element in }A' \cap A\}. \end{align*} $$
Because
![]() $A' \cap (A\rtimes _X \mathbf Z)=\mathbf C1$
,
$A' \cap (A\rtimes _X \mathbf Z)=\mathbf C1$
,
![]() $A' \cap A=\mathbf C1$
. Thus,
$A' \cap A=\mathbf C1$
. Thus,
It follows that we can obtain the following lemma.
Lemma 4.3 With the above notation,
![]() ${\mathrm {Ker}} f_A \cong {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
.
${\mathrm {Ker}} f_A \cong {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
.
Proof. Because
![]() ${\mathrm {Ker}} \, \pi \cap {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)=\{1\}$
, by Lemma 4.2,
${\mathrm {Ker}} \, \pi \cap {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)=\{1\}$
, by Lemma 4.2,
 $$ \begin{align*} {\mathrm{Ker}} f_A & =\pi({\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z))\cong{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z)/ ({\mathrm{Ker}} \, \pi\cap{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) )\\ & ={\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z). \end{align*} $$
$$ \begin{align*} {\mathrm{Ker}} f_A & =\pi({\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z))\cong{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z)/ ({\mathrm{Ker}} \, \pi\cap{\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z) )\\ & ={\mathrm{Aut}}_0 (A, A\rtimes_X \mathbf Z). \end{align*} $$
Therefore, we obtain the conclusion.▪
We recall that the inclusions of
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z)\otimes \mathbf K$
and
$A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z)\otimes \mathbf K$
and
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
are isomorphic as inclusions of
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
are isomorphic as inclusions of
![]() $C^*$
-algebras. Furthermore, there is an automorphism
$C^*$
-algebras. Furthermore, there is an automorphism
![]() $\alpha $
of
$\alpha $
of
![]() $A\otimes \mathbf K$
such that
$A\otimes \mathbf K$
such that
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
and
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{X\otimes \mathbf K}\mathbf Z$
and
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
are isomorphic as inclusions of
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
are isomorphic as inclusions of
![]() $C^*$
-algebras.
$C^*$
-algebras.
Lemma 4.4 With the above notation, the action
![]() $\alpha $
of
$\alpha $
of
![]() $\mathbf Z$
is free, that is, for any
$\mathbf Z$
is free, that is, for any
![]() $n\in \mathbf Z\setminus \{0\}$
,
$n\in \mathbf Z\setminus \{0\}$
,
![]() $\alpha ^n$
satisfies the following: If
$\alpha ^n$
satisfies the following: If
![]() $x\in M(A\otimes \mathbf K)$
satisfies that
$x\in M(A\otimes \mathbf K)$
satisfies that
![]() $xa=\alpha ^n (a)x$
for any
$xa=\alpha ^n (a)x$
for any
![]() $a\in A\otimes \mathbf K$
, then
$a\in A\otimes \mathbf K$
, then
![]() $x=0$
.
$x=0$
.
Proof. Because
![]() $A' \cap (A\rtimes _X \mathbf Z)=\mathbf C1$
, by [Reference Kodaka8, Lemma 3.1],
$A' \cap (A\rtimes _X \mathbf Z)=\mathbf C1$
, by [Reference Kodaka8, Lemma 3.1],
![]() $(A\otimes \mathbf K)' \cap M((A\rtimes _X \mathbf Z)\otimes \mathbf K)=\mathbf C1$
. Hence, because
$(A\otimes \mathbf K)' \cap M((A\rtimes _X \mathbf Z)\otimes \mathbf K)=\mathbf C1$
. Hence, because
![]() $A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z)\otimes \mathbf K$
is isomorphic to
$A\otimes \mathbf K\subset (A\rtimes _X \mathbf Z)\otimes \mathbf K$
is isomorphic to
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
as inclusions of
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
as inclusions of
![]() $C^*$
-algebras,
$C^*$
-algebras,
Thus, by [Reference Kodaka8, Corollary 4.2], the action
![]() $\alpha $
is free.▪
$\alpha $
is free.▪
For any
![]() $n\in \mathbf Z$
, let
$n\in \mathbf Z$
, let
![]() $\delta _n$
be the function on
$\delta _n$
be the function on
![]() $\mathbf Z$
defined by
$\mathbf Z$
defined by
 $$ \begin{align*}\delta_n (m) =\begin{cases} 1 & m=n \\ 0 & m\ne n \end{cases}. \end{align*} $$
$$ \begin{align*}\delta_n (m) =\begin{cases} 1 & m=n \\ 0 & m\ne n \end{cases}. \end{align*} $$
We regard
![]() $\delta _n$
as an element in
$\delta _n$
as an element in
![]() $M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
.
$M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
.
Let
![]() $E^{M(A\otimes \mathbf K)}$
be the canonical faithful conditional expectation from
$E^{M(A\otimes \mathbf K)}$
be the canonical faithful conditional expectation from
![]() $M(A\otimes \mathbf K)\rtimes _{\underline {\alpha }}\mathbf Z$
onto
$M(A\otimes \mathbf K)\rtimes _{\underline {\alpha }}\mathbf Z$
onto
![]() $M(A\otimes \mathbf K)$
defined in [Reference Bédos and Conti2, Section 3]. Then, we may let
$M(A\otimes \mathbf K)$
defined in [Reference Bédos and Conti2, Section 3]. Then, we may let
![]() $E^{A\otimes \mathbf K}$
be the restriction of
$E^{A\otimes \mathbf K}$
be the restriction of
![]() $E^{M(A\otimes \mathbf K)}$
to
$E^{M(A\otimes \mathbf K)}$
to
![]() $(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
, that is,
$(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
, that is,
![]() $E^{A\otimes \mathbf K}=E^{M(A\otimes \mathbf K)}|_{(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z}$
. Let
$E^{A\otimes \mathbf K}=E^{M(A\otimes \mathbf K)}|_{(A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z}$
. Let
![]() $\{u_i \}_{i\in I}$
be an approximate unit of
$\{u_i \}_{i\in I}$
be an approximate unit of
![]() $A\otimes \mathbf K$
. We fix the approximate unit
$A\otimes \mathbf K$
. We fix the approximate unit
![]() $\{u_i \}_{i\in I}$
of
$\{u_i \}_{i\in I}$
of
![]() $A\otimes \mathbf K$
. For any
$A\otimes \mathbf K$
. For any
![]() $x\in M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
, we define the Fourier coefficient of x at
$x\in M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
, we define the Fourier coefficient of x at
![]() $n\in \mathbf Z$
as in the same way as in [Reference Kodaka8, Section 2]. We show that
$n\in \mathbf Z$
as in the same way as in [Reference Kodaka8, Section 2]. We show that
![]() ${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)\cong \mathbf T$
.
${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)\cong \mathbf T$
.
Let
![]() $\beta \in {\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
. For any
$\beta \in {\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
. For any
![]() $a\in A\otimes \mathbf K$
,
$a\in A\otimes \mathbf K$
,
Hence,
![]() $\underline {\beta }(\delta _1 )a=\alpha (a)\underline {\beta }(\delta _1 )$
for any
$\underline {\beta }(\delta _1 )a=\alpha (a)\underline {\beta }(\delta _1 )$
for any
![]() $a\in A\otimes \mathbf K$
.
$a\in A\otimes \mathbf K$
.
Lemma 4.5 With the above notation, let
![]() $a_n$
be the Fourier coefficient of
$a_n$
be the Fourier coefficient of
![]() $\underline {\beta }(\delta _1 )$
at
$\underline {\beta }(\delta _1 )$
at
![]() $n\in \mathbf Z$
. Then, for any
$n\in \mathbf Z$
. Then, for any
![]() $a\in A\otimes \mathbf K$
,
$a\in A\otimes \mathbf K$
,
Proof. Let
![]() $a\in A\otimes \mathbf K$
. Then, because
$a\in A\otimes \mathbf K$
. Then, because
![]() $||au_i -u_i a||\to 0 (i\to \infty )$
, the Fourier coefficient of
$||au_i -u_i a||\to 0 (i\to \infty )$
, the Fourier coefficient of
![]() $\underline {\beta }(\delta _1 )a$
at
$\underline {\beta }(\delta _1 )a$
at
![]() $n\in \mathbf Z$
is given by
$n\in \mathbf Z$
is given by
 $$ \begin{align*} \lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )au_i \delta_n ) & = \lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )u_i a\delta_n ) \\ & =\lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )u_i \delta_n \alpha^n (a)) \\ & =\lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )u_i \delta_n ) \alpha^n (a) \\ & =a_n \alpha^n (a). \end{align*} $$
$$ \begin{align*} \lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )au_i \delta_n ) & = \lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )u_i a\delta_n ) \\ & =\lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )u_i \delta_n \alpha^n (a)) \\ & =\lim_i E^{A\otimes\mathbf K}(\underline{\beta}(\delta_1 )u_i \delta_n ) \alpha^n (a) \\ & =a_n \alpha^n (a). \end{align*} $$
Furthermore, the Fourier coefficient of
![]() $\alpha (a)\underline {\beta }(\delta _1 )$
at
$\alpha (a)\underline {\beta }(\delta _1 )$
at
![]() $n\in \mathbf Z$
is given by
$n\in \mathbf Z$
is given by
Because
![]() $\underline {\beta }(\delta _1 )a=\alpha (a)\underline {\beta }(\delta _1 )$
, we get that
$\underline {\beta }(\delta _1 )a=\alpha (a)\underline {\beta }(\delta _1 )$
, we get that
for any
![]() $a\in A\otimes \mathbf K$
. Because a is an arbitrary element in
$a\in A\otimes \mathbf K$
. Because a is an arbitrary element in
![]() $A\otimes \mathbf K$
, replacing a by
$A\otimes \mathbf K$
, replacing a by
![]() $\alpha ^{-1}(a)$
, we obtain the conclusion.▪
$\alpha ^{-1}(a)$
, we obtain the conclusion.▪
Lemma 4.6 With the above notation,
Proof. Let
![]() $\beta \in {\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
, and let
$\beta \in {\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
, and let
![]() $a_n$
be the Fourier coefficient of
$a_n$
be the Fourier coefficient of
![]() $\underline {\beta }(\delta _1 )$
at
$\underline {\beta }(\delta _1 )$
at
![]() $n\in \mathbf Z$
. Then, by Lemma 4.5,
$n\in \mathbf Z$
. Then, by Lemma 4.5,
![]() $a_n \alpha ^{n-1}(a)=aa_n$
for any
$a_n \alpha ^{n-1}(a)=aa_n$
for any
![]() $a\in A\otimes \mathbf K$
. Because the automorphism
$a\in A\otimes \mathbf K$
. Because the automorphism
![]() $\alpha ^{n-1}$
is free for any
$\alpha ^{n-1}$
is free for any
![]() $n\in \mathbf Z\setminus \{1\}$
by Lemma 4.4,
$n\in \mathbf Z\setminus \{1\}$
by Lemma 4.4,
![]() $a_n =0$
for any
$a_n =0$
for any
![]() $n\in \mathbf Z\setminus \{1\}$
. Thus,
$n\in \mathbf Z\setminus \{1\}$
. Thus,
![]() $\underline {\beta }(\delta _1 )=a_1 \delta _1$
. Because
$\underline {\beta }(\delta _1 )=a_1 \delta _1$
. Because
![]() $\underline {\beta }(\delta _1 )a\underline {\beta }(\delta _1^* )=\alpha (a)$
, for any
$\underline {\beta }(\delta _1 )a\underline {\beta }(\delta _1^* )=\alpha (a)$
, for any
![]() $a\in A\otimes \mathbf K$
,
$a\in A\otimes \mathbf K$
,
Because
![]() $\delta _1 a\delta _1^* =\alpha (a)$
,
$\delta _1 a\delta _1^* =\alpha (a)$
,
for any
![]() $a\in A\otimes \mathbf K$
. Because
$a\in A\otimes \mathbf K$
. Because
![]() $\delta _1$
and
$\delta _1$
and
![]() $\underline {\beta }(\delta _1 )$
are unitary elements in
$\underline {\beta }(\delta _1 )$
are unitary elements in
![]() $M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
,
$M((A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
,
![]() $a_1$
is a unitary element in
$a_1$
is a unitary element in
![]() $M(A\otimes \mathbf K)$
. Thus,
$M(A\otimes \mathbf K)$
. Thus,
for any
![]() $a\in A\otimes \mathbf K$
. Because
$a\in A\otimes \mathbf K$
. Because
![]() $(A\otimes \mathbf K)' \cap M(A\otimes \mathbf K)=\mathbf C1$
,
$(A\otimes \mathbf K)' \cap M(A\otimes \mathbf K)=\mathbf C1$
,
![]() $a_1 \in \mathbf C1$
. Because
$a_1 \in \mathbf C1$
. Because
![]() $a_1$
is a unitary element in
$a_1$
is a unitary element in
![]() $M(A\otimes \mathbf K)$
, there is the unique element
$M(A\otimes \mathbf K)$
, there is the unique element
![]() $c_{\beta }\in \mathbf T$
such that
$c_{\beta }\in \mathbf T$
such that
![]() $a_1 =c_{\beta }1$
. Let
$a_1 =c_{\beta }1$
. Let
![]() $\epsilon $
be the map from
$\epsilon $
be the map from
![]() ${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
onto
${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
onto
![]() $\mathbf T$
defined by
$\mathbf T$
defined by
![]() $\epsilon (\beta )=c_{\beta }$
. By routine computations, we can see that
$\epsilon (\beta )=c_{\beta }$
. By routine computations, we can see that
![]() $\epsilon $
is an isomorphism of
$\epsilon $
is an isomorphism of
![]() ${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
onto
${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z)$
onto
![]() $\mathbf T$
.▪
$\mathbf T$
.▪
Lemma 4.7 With the above notation,
Proof. Because
![]() $A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
$A\otimes \mathbf K\subset (A\otimes \mathbf K)\rtimes _{\alpha }\mathbf Z$
and
![]() $A\otimes \mathbf K\subset (A\rtimes _X\mathbf Z)\otimes \mathbf K$
are isomorphic as inclusions of
$A\otimes \mathbf K\subset (A\rtimes _X\mathbf Z)\otimes \mathbf K$
are isomorphic as inclusions of
![]() $C^*$
-algebras, it suffices to show that
$C^*$
-algebras, it suffices to show that
Let
![]() $\kappa $
be the homomorphism of
$\kappa $
be the homomorphism of
![]() ${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
to
${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
to
![]() ${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\rtimes _X \mathbf Z)\otimes \mathbf K)$
defined by
${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\rtimes _X \mathbf Z)\otimes \mathbf K)$
defined by
for any
![]() $\beta \in {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
. Then, it is clear that
$\beta \in {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
. Then, it is clear that
![]() $\kappa $
is a monomorphism of
$\kappa $
is a monomorphism of
![]() ${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
to
${\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf Z)$
to
![]() ${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\rtimes _X \mathbf Z)\otimes \mathbf K)$
. We show that
${\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\rtimes _X \mathbf Z)\otimes \mathbf K)$
. We show that
![]() $\kappa $
is surjective. Let
$\kappa $
is surjective. Let
![]() $\gamma \in {\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\rtimes _X \mathbf Z)\otimes \mathbf K)$
. Then,
$\gamma \in {\mathrm {Aut}}_0 (A\otimes \mathbf K, (A\rtimes _X \mathbf Z)\otimes \mathbf K)$
. Then,
for any
![]() $a\in A$
,
$a\in A$
,
![]() $i, j \in \mathbf N$
. Thus,
$i, j \in \mathbf N$
. Thus,
for any
![]() $x\in A\rtimes _X \mathbf Z$
. Hence, there is an automorphism
$x\in A\rtimes _X \mathbf Z$
. Hence, there is an automorphism
![]() $\beta $
of
$\beta $
of
![]() $A\rtimes _X \mathbf Z$
such that
$A\rtimes _X \mathbf Z$
such that
for any
![]() $x\in A\rtimes _X \mathbf Z$
. For any
$x\in A\rtimes _X \mathbf Z$
. For any
![]() $i, j\in \mathbf N$
and
$i, j\in \mathbf N$
and
![]() $x\in A\rtimes _X \mathbf Z$
,
$x\in A\rtimes _X \mathbf Z$
,
 $$ \begin{align*} \gamma(x\otimes e_{ij}) & =\gamma((1\otimes e_{i1})(x\otimes e_{11})(1\otimes e_{1j})) =(1\otimes e_{i1})(\beta(x)\otimes e_{11})(1\otimes e_{1j}) \\ & =\beta(x)\otimes e_{ij}. \end{align*} $$
$$ \begin{align*} \gamma(x\otimes e_{ij}) & =\gamma((1\otimes e_{i1})(x\otimes e_{11})(1\otimes e_{1j})) =(1\otimes e_{i1})(\beta(x)\otimes e_{11})(1\otimes e_{1j}) \\ & =\beta(x)\otimes e_{ij}. \end{align*} $$
Especially, if
![]() $a\in A$
,
$a\in A$
,
![]() $\beta (a)\otimes e_{ij}=\gamma (a\otimes e_{ij})=a\otimes e_{ij}$
, for any
$\beta (a)\otimes e_{ij}=\gamma (a\otimes e_{ij})=a\otimes e_{ij}$
, for any
![]() $i, j\in \mathbf N$
. Thus,
$i, j\in \mathbf N$
. Thus,
![]() $\beta (a)=a$
, for any
$\beta (a)=a$
, for any
![]() $a\in A$
. Therefore,
$a\in A$
. Therefore,
![]() $\gamma =\beta \otimes {\mathrm {id}}_{\mathbf K}$
and
$\gamma =\beta \otimes {\mathrm {id}}_{\mathbf K}$
and
![]() $\beta \in {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf K)$
. Hence, we have shown that
$\beta \in {\mathrm {Aut}}_0 (A, A\rtimes _X \mathbf K)$
. Hence, we have shown that
![]() $\kappa $
is surjective.▪
$\kappa $
is surjective.▪
Lemma 4.8 With the above notation,
![]() ${\mathrm {Ker}} f_A \cong \mathbf T$
.
${\mathrm {Ker}} f_A \cong \mathbf T$
.
By Lemmas 4.1 and 4.8, we have the following exact sequence:
where
 $$ \begin{align*} G=\{[M]\in{\mathrm{Pic}}(A) \, | \, X\cong\widetilde{M}\otimes_A X\otimes_A M \, \text{or} \, \widetilde{X} & \cong\widetilde{M}\otimes_A X\otimes_A M \\ & \text{as }A-A\text{-equivalence bimodules}\}. \end{align*} $$
$$ \begin{align*} G=\{[M]\in{\mathrm{Pic}}(A) \, | \, X\cong\widetilde{M}\otimes_A X\otimes_A M \, \text{or} \, \widetilde{X} & \cong\widetilde{M}\otimes_A X\otimes_A M \\ & \text{as }A-A\text{-equivalence bimodules}\}. \end{align*} $$
Let g be the map from G to
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
defined by
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
defined by
where N is the
![]() $A\rtimes _X \mathbf Z -A\rtimes _X \mathbf Z$
-equivalence bimodule defined in the proof of Lemma 2.4. Then, g is a homomorphism of G to
$A\rtimes _X \mathbf Z -A\rtimes _X \mathbf Z$
-equivalence bimodule defined in the proof of Lemma 2.4. Then, g is a homomorphism of G to
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
such that
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
such that
on G. Thus, we obtain the following theorem.
Theorem 4.9 Let A be a unital
![]() $C^*$
-algebra and X an
$C^*$
-algebra and X an
![]() $A-A$
-equivalence bimodule. Let
$A-A$
-equivalence bimodule. Let
![]() $A\subset A\rtimes _X \mathbf Z$
be the unital inclusion of unital
$A\subset A\rtimes _X \mathbf Z$
be the unital inclusion of unital
![]() $C^*$
-algebras induced by X. We suppose that
$C^*$
-algebras induced by X. We suppose that
![]() $A' \cap (A\rtimes _X \mathbf Z)=\mathbf C1$
. Then,
$A' \cap (A\rtimes _X \mathbf Z)=\mathbf C1$
. Then,
![]() ${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
is a semidirect product of G by
${\mathrm {Pic}}(A, A\rtimes _X \mathbf Z)$
is a semidirect product of G by
![]() $\mathbf T$
.
$\mathbf T$
.