2. Motor Insurance Rate-Making Framework

In this section, we provide a methodological overview of the motor insurance rate-making process. As our aim in this paper mainly focusses on the optimal design of a BMS itself, we shall only briefly discuss the modelling techniques of claim frequencies and residual heterogeneity that are required in the later sections for the determination of optimal relativities and the evaluation of transition rules. We refer interested readers to Lemaire (Reference Lemaire1995) and Denuit et al. (Reference Denuit, Maréchal, Pitrebois and Walhin2007) for more extensive details.

2.1. Modelling of a priori claim frequencies

Suppose we have a portfolio with n policies, where d_i is the length of exposure period and Y_i the number of claims reported by driver i during the period. The Poisson regression is widely used in the a priori classification of Y_i under the generalised linear models framework (see McCullagh & Nelder, Reference McCullagh and Nelder1989). In particular, we can express the predicted a priori claim frequency for driver i as

$$\lambda _{i} =d_{i} \,{\rm exp}\left( {\hat{\beta }_{0} {\plus}\mathop{\sum}\limits_{j=1}^q {\hat{\beta }_{j} x_{{ij}} } } \right)$$

where $$ \hat{\beta }_{0} ,\,\hat{\beta }_{1} ,\:\,\ldots\,\:,\,\hat{\beta }_{q} $$ are the estimated regression coefficients and $$(x_{{i1}} ,\,x_{{i{\rm 2}}} ,\:\,\ldots\,\:,\,x_{{iq}} )$$ represents the vector of observable risk classification variables for driver i. The purpose of this rate-making step is to classify the portfolio of drivers into a number of risk classes. However, it is well known that driving behaviours are influenced by other characteristics that are not observable by the insurer. As a result, the residual heterogeneity within the risk classes motivates the implementation of a posteriori rating via the BMS mechanism as the second step in the rate-making process.

2.2. Modelling of residual heterogeneity

Specifically, the residual heterogeneity is modelled by incorporating a random effect Θ_i into the conditional distribution of Y_i. Conditional on Θ_i=θ, Y_i is Poisson distributed with mean $\lambda _{i} \theta $ , that is

$${\rm Pr}\left[ {Y_{i} =k \! \mid \! \Theta _{i} =\theta } \right]={\rm exp}\left( {{\minus}\lambda _{i} \theta } \right){{\left( {\lambda _{i} \theta } \right)^{k} } \over {k\,!\,}},\,k=0,\,1,\,2,\,\,\ldots\,$$

We further suppose that all the Θ_i’s are independent and follow a Gamma distribution with parameters (a, a). The probability density function for Θ_i can be written as

$$f(\theta )={1 \over {\Gamma (a)}}a^{a} \theta ^{{a{\minus}1}} \,{\rm exp}\left( {{\minus}a\theta } \right),\,\theta \in {\Bbb R}^{{\plus}} $$

The use of a Poisson-Gamma mixture produces a negative binomial distribution for the number of claims reported Y_i. With these specifications, we have $${\Bbb E}[\Theta _{i} ]={\rm 1}$$ and ${\Bbb E}[Y_{i} ]={\Bbb E}\left[ {{\Bbb E}[Y_{i} \! \mid \! \Theta _{i} ]} \right]=\lambda _{i} $ . Note that other specifications of mixed Poisson models can also be used (see e.g. Yip & Yau, Reference Yip and Yau2005).

Now suppose that a motor vehicle driver is picked at random from the portfolio that has been subdivided into h risk classes. The actual expected annual claim frequency for this driver can be written as ΛΘ, where Λ is the unknown a priori expected annual claim frequency and Θ captures the random residual heterogeneity. We further denote n_g as the number of drivers in the g-th risk class whose expected claim frequency is $\lambda _{g} $ , so we have the proportion of drivers in the g-th risk class as $w_{g} ={\rm Pr}[\Lambda =\lambda _{g} ]={{n_{g} } \over n}$ .

As the current level occupied and the number of claims reported in the current period is sufficient to determine the next level occupied, the mechanism of BMS can be modelled as a Markov chain. Let us denote the transition probability of moving from level ${\ell }$ ₁ to level ${\ell }$ ₂ for a driver with expected claim frequency $\lambda \theta $ as $$p_{{\ell _{1} \ell _{2} }} (\lambda \theta )$$ , then the one-step transition matrix is ${\mib P}\left( {\lambda \theta } \right)=\{ p_{{\ell _{{\rm 1}} \ell _{{\rm 2}} }} (\lambda \theta )\} $ in a BMS with j levels. The row vector of the stationary distribution $$\bpi \left( {\lambda \theta } \right)=(\pi _{{\rm 1}} (\lambda \theta ),\,\pi _{{\rm 2}} (\lambda \theta ),\:\,\ldots\,\:,\,\pi _{j} (\lambda \theta ))$$ can be easily determined by solving the following two conditions:

$$\left\{ \matrix{ & {\bf \bpi }(\lambda \theta )={\bf \bpi }(\lambda \theta ){\mib P}(\lambda \theta ) \cr & {\bf \bpi }(\lambda \theta ){\bf 1}=1 \cr} \right.$$

where $\pi _{\ell } (\lambda \theta )$ is the stationary probability for a driver with expected claim frequency $\lambda \theta $ to be in level ${\ell }$ and 1 is the column vector of 1’s. With these setup, we obtain the following expression for the probability of drivers staying in level ${\ell }$

$$\eqalignno{ {\rm Pr}\,[L=\ell ] & =\mathop{\sum}\limits_{g=1}^h {{\rm Pr}\,[L=\ell \! \mid \!\Lambda =\lambda _{g} ]\,} {\rm Pr}\,[\Lambda =\lambda _{g} ] \cr & =\mathop{\sum}\limits_{g=1}^h {{\rm Pr}\,[\Lambda =\lambda _{g} ]\mathop{\int}\nolimits_0^{{\plus}\infty} {{\rm Pr}[L=\ell \! \mid \!\Lambda =\lambda _{g} ,\Theta =\theta ]f(\theta )} \,d\theta } \cr & =\mathop{\sum}\limits_{g=1}^h {w_{g} \mathop{\int}\nolimits_0^{{\plus}\infty} {\pi _{\ell } } (\lambda _{g} \theta )f(\theta )d\theta } $$

3. Determining Optimal Relativities of a BMS

In practice, the number of BMS levels is usually set in advance and the transition trajectory of drivers are governed by the chosen transition rules. Given these two inputs, the optimal relativities are determined and applied to all drivers independent of their a priori risk characteristics. To partially alleviate the unfairness towards the a priori more risky drivers, Tan et al. (Reference Tan, Li, Li and Balasooriya2015) proposed the minimisation of the objective function

(1) $${\Bbb E}\left[ {(\Lambda \Theta {\minus}\Lambda r_{L} )^{2} } \right]$$

under a financial equilibrium constraint ${\Bbb E}[r_{L} ]=1$ . They also derived an analytical formula for optimal relativity r _L that minimises the expected squared difference between the true premium and the actual premium in absolute terms, which is a generalisation of the asymptotic Norberg’s criterion (see Pitrebois et al., Reference Pitrebois, Denuit and Walhin2003) by incorporating the a priori base premiums directly into the objective function.

However, by allowing a general form for optimal relativity r _L in the optimisation, the obtained numerical values may be subject to irregular patterns from one BMS level to another, as pointed out by Pitrebois et al. (Reference Pitrebois, Denuit and Walhin2004). A more viable solution for commercial BMS in practice is to impose a linear restriction onto the values of optimal relativities, as proposed by Gilde & Sundt (Reference Gilde and Sundt1989). In more detail, the linear relativities can be written as $r_{L}^{{{\rm linear}}} =\alpha {\plus}\beta L$ , where it features a difference of a constant premium amount β for any two adjacent BMS levels.

In this paper, we analyse the determination of optimal relativities for a BMS when the linear restriction is imposed. As before, we take into account the financial balanced condition recommended by Coene & Doray (Reference Coene and Doray1996) and Baione et al. (Reference Baione, Levantesi and Menzieti2002). Hence we obtain the following constrained optimisation with an inequality constraint:

(2) $${\rm min}\,{\Bbb E}\left[ {(\Lambda \Theta {\minus}\Lambda \alpha {\minus}\lambda \beta L)^{2} } \right]\,{\rm subject}\,{\rm to}\,\alpha {\plus}\beta {\Bbb E}[L]\geq 1$$

We use the Lagrangian method to solve the optimisation problem in equation (2). In this case, the Lagrangian is defined as

(3) $${\cal L}\left( {\alpha {\rm ,}\,\beta {\rm ,}\,\gamma } \right)={\Bbb E}\left[ {(\Lambda \Theta {\minus}\Lambda \alpha {\minus}\lambda \beta L)^{2} } \right]{\plus}\gamma \left( {1{\minus}\alpha {\minus}\beta {\Bbb E}[L]} \right)$$

We can then derive the following Kuhn–Tucker conditions:

(4a) $${\minus}2\left( {{\Bbb E}[\Lambda ^{2} \Theta ]{\minus}\alpha {\Bbb E}[\Lambda ^{2} ]{\minus}\beta {\Bbb E}[\Lambda ^{2} L]} \right){\minus}\gamma =0$$

(4b) $${\minus}2\left( {{\Bbb E}[\Lambda ^{2} \Theta L]{\minus}\alpha {\Bbb E}[\Lambda ^{2} L]{\minus}\beta {\Bbb E}[\Lambda ^{2} L^{2} ]} \right){\minus}\gamma {\Bbb E}{\rm [}L{\rm ]}=0$$

(4c) $$\gamma \left( {1{\minus}\alpha {\minus}\beta {\Bbb E}[L]} \right)=0$$

(4d) $$1{\minus}\alpha {\minus}\beta {\Bbb E}[L]\leq 0$$

(4e) $$\gamma \geq 0$$

For brevity, let us define

(5) $$\eqalignno{ & A={\Bbb E}\left[ {\Lambda ^{2} } \right]=\mathop{\sum}\limits_{g=1}^h {\lambda _{g}^{2} } \mathop{\sum}\limits_{\ell =1}^j {{\rm Pr}\left[ {\Lambda =\lambda _{g} \! \mid \!L=\ell } \right]} \,{\rm Pr}\left[ {L=\ell } \right] \cr & =\mathop{\sum}\limits_{g=1}^h {\lambda _{g}^{2} } \mathop{\sum}\limits_{\ell =1}^j {{\rm Pr}\left[ {L=\ell \! \mid \!\Lambda =\lambda _{g} } \right]} \,{\rm Pr}\left[ {\Lambda =\lambda _{g} } \right] \cr & =\mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g}^{2} } \mathop{\sum}\limits_{\ell =1}^j {\mathop{\int}\nolimits_0^{{\plus}\infty} {{\rm Pr}} \left[ {L=\ell \! \mid \!\Lambda =\lambda _{g} ,\,\Theta =\theta } \right]f(\theta )d\theta } \cr & =\mathop{\sum}\limits_{\ell =1}^j {\mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g}^{2} \mathop{\int}\nolimits_0^{{\plus}\infty} {\pi _{\ell } (\lambda _{g} \theta )} f(\theta )d\theta } } $$

Similarly, we define the following notations:

(6) $$B={\Bbb E}[\Lambda ^{2} \Theta ]=\mathop{\sum}\limits_{\ell =1}^j {\mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g}^{2} \mathop{\int}\nolimits_0^{{\plus}\infty} {\theta \pi _{\ell } (\lambda _{g} \theta )f(\theta )d\theta } } } $$

(7) $$C={\Bbb E}[\Lambda ^{2} L]=\mathop{\sum}\limits_{\ell =1}^j {\ell \mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g}^{2} \mathop{\int}\nolimits_0^{{\plus}\infty} {\pi _{\ell } (\lambda _{g} \theta )f(\theta )d\theta } } } $$

(8) $$D={\Bbb E}[\Lambda ^{2} L^{2} ]=\mathop{\sum}\limits_{\ell =1}^j {\ell ^{2} \mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g}^{2} \mathop{\int}\nolimits_0^{{\plus}\infty} {\pi _{\ell } (\lambda _{g} \theta )f(\theta )d\theta } } } $$

(9) $$E={\Bbb E}[\Lambda ^{2} \Theta L]=\mathop{\sum}\limits_{\ell =1}^j {\ell \mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g}^{2} \mathop{\int}\nolimits_0^{{\plus}\infty} {\theta \pi _{\ell } (\lambda _{g} \theta )f(\theta )d\theta } } } $$

(10) $$F={\Bbb E}[L]=\mathop{\sum}\limits_{\ell =1}^j {\ell \mathop{\sum}\limits_{g=1}^h {w_{g} \mathop{\int}\nolimits_0^{{\plus}\infty} {\pi _{\ell } (\lambda _{g} \theta )f(\theta )d\theta } } } $$

The solution set (α, β, γ) is analysed as follows:

Case A1: γ=0 and if condition (4d) holds with the following solution set

(11a) $$\alpha ={{B{\minus}{\textstyle{{CE} \over D}}} \over {A{\minus}{\textstyle{{C^{2} } \over D}}}}$$

(11b) $$\beta ={{E{\minus}{\textstyle{{CB} \over A}}} \over {D{\minus}{\textstyle{{C^{2} } \over A}}}}$$

Otherwise, we have to select

Case A2: if γ>0 based on the following expression

(12a) $$\gamma ={{\left( {A{\minus}{{C^{2} } \over D}} \right)\left( {D{\minus}{{C^{2} } \over A}} \right){\minus}\left( {A{\minus}{{C^{2} } \over D}} \right)\left( {EF{\minus}{{BCF} \over A}} \right){\minus}\left( {D{\minus}{{C^{2} } \over A}} \right)\left( {B{\minus}{{EC} \over D}} \right)} \over {\left( {A{\minus}{{C^{2} } \over D}} \right)\left( {{{F^{2} } \over 2}{\minus}{{CF} \over {2A}}} \right){\plus}\left( {D{\minus}{{C^{2} } \over A}} \right)\left( {{1 \over 2}{\minus}{{CF} \over {2D}}} \right)}}$$

(12b) $$\alpha ={{B{\minus}{{C\left( {E{\plus}{\gamma \over 2}F} \right)} \over D}{\plus}{\gamma \over 2}} \over {A{\minus}{{C^{2} } \over D}}}$$

(12c) $$\beta ={{E{\minus}{{C\left( {B{\plus}{\gamma \over 2}} \right)} \over A}{\plus}{\gamma \over 2}F} \over {D{\minus}{{C^{2} } \over A}}}$$

If we relax the financial balanced inequality constraint, we have $\gamma ^{{{\rm unconstrained}}} =0$ and the solution set as shown in expressions (11a) and (11b) except that the condition (4d) may not be satisfied. In other words, the resulting unconstrained premium relativity may have an average of less than 100%, which may cause the insurer to be insolvent in the long run. Otherwise, the fulfilment of condition (4d) implies that it is not a binding constraint, such that solution set for the constrained optimisation is identical to that of the unconstrained optimisation.

Further constraints for a commercial BMS can be easily incorporated into the minimisation of (2). For instance, the insurer may want to set α=0 such that the drivers in the first BMS level are subject to a premium relativity of β instead of α+β. In this case, the Kuhn–Tucker condition (4a) is not required and the conditions (4b)–(4e) can be simplified by substituting α=0, where we obtain the following two cases:

Case B1: γ=0 and if condition (4d) holds with the following solution set

(13a) $$\alpha =0$$

(13b) $$\beta ={E \over D}$$

If Case B1 does not hold, we need to consider

Case B2: if γ>0 based on the following expression

(14a) $$\gamma ={{2(D{\minus}EF)} \over {F^{2} }}$$

(14b) $$\alpha =0$$

(14c) $$\beta ={{E{\plus}{\gamma \over 2}F} \over D}={1 \over F}$$

Alternatively, the insurer may wish to establish a minimum premium relativity of c _min, so we need to impose an additional inequality constraint of α+β≥c _min for the BMS level ${\ell }$ =1. The insurer may also want to impose a maximum relativity of c _max that introduces an extra constraint of α+βj≤c _max for the BMS level ${\ell }$ =j. The resulting set of optimal linear relativities can be derived accordingly to satisfy these commercial considerations. However, it should be noted that the minimised value of the objective function would increase with each additional constraint.

4. Choosing Effective Transition Rules for a BMS

In this section, we describe the measures of the interaction between the two rate-making steps and discuss how the varying extent of the a priori risk segmentation may affect the effectiveness of transition rules.

First, after the a priori rating step is carried out, the mean and variance of Λ can be expressed as

$$\eqalignno{ {\Bbb E}[\Lambda ]= & \mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g} } \cr {\Bbb V}[\Lambda ]= & {\Bbb E}[\Lambda ^{2} ]{\minus}\left[ {{\Bbb E}[\Lambda ]} \right]^{2} =\mathop{\sum}\limits_{g=1}^h {w_{g} \lambda _{g}^{2} } {\minus}\left( {\mathop{\sum}\limits_{g=1}^h {\omega _{g} \lambda _{g} } } \right)^{2} $$

Note that the value of $${\Bbb E}{\rm [}\Lambda {\rm ]}$$ for a portfolio of drivers is fixed, regardless of the choices of variables used to obtain the predicted claim frequencies λ _g’s. This is because of the following necessary condition in the estimation procedure:

$$\mathop{\sum}\limits_i {\lambda _{i} =\mathop{\sum}\limits_i {{{y_{i} } \over {d_{i} }}\to{{\mathop{\sum}\nolimits_{g=1}^h {n_{g} \lambda _{g} } } \over n}={{\mathop{\sum}\nolimits_i {{{y_{i} } \over {d_{i} }}} } \over n}} } $$

so we have $$\mathop{\sum}\nolimits_{g=1}^h {w_{g} } \lambda _{g} $$ equals to the average number of claims reported per unit exposure ${{\mathop{\sum}\nolimits_i {{{y_{i} } \over {d_{i} }}} } \over n}$ in all circumstances. On the other hand, the value of ${\Bbb V}[\Lambda ]$ would change according to the use of different a priori variables.

Pitrebois et al. (Reference Pitrebois, Denuit and Walhin2003) proposed to measure the interaction extent of the two rating mechanisms by

(15) $${\Bbb E}[\Lambda \! \mid \!L=\ell ]={{\mathop{\sum}\nolimits_{g=1}^h {w_{g} \mathop{\int}\nolimits_0^{{\plus}\infty} {\lambda _{g} \pi _{\ell } (\lambda _{g} \theta )f(\theta )d\theta } } } \over {\mathop{\sum}\nolimits_{g=1}^h {w_{g} \mathop{\int}\nolimits_0^{{\plus}\infty} {\pi _{\ell } (\lambda _{g} \theta )f(\theta )d\theta } } }}$$

Apart from conditional on the predicted claim frequencies λ _g’s, this measure is dependent on the stationary distribution of drivers in level ${\ell }$ – which in turn is reliant on the transition rules – therefore its value reflects how the two rate-making steps interact with one another. However, there are j values of ${\Bbb E}{\rm [}\Lambda \! \mid \!L=\ell ]\,{\rm for}\,\ell ={\rm 1},\,{\rm 2},\:\,\ldots\,\:,\,j$ , making them difficult to be used as a standard measure in the design of a BMS.

To address this problem, Tan et al. (Reference Tan, Li, Li and Balasooriya2015) suggested the following metric called effectiveness of transition rules

(16) $$\eqalignno{ \tau _{{{\rm rule}}} & ={{{\Bbb E}\left[ {{\Bbb V}[\Lambda \! \mid \!L]} \right]} \over {{\Bbb V}[\Lambda ]}}=1{\minus}{{{\Bbb V}\left[ {{\Bbb E}[\Lambda \! \mid \!L]} \right]} \over {{\Bbb V}[\Lambda ]}} \cr & =1{\minus}{{\mathop{\sum}\nolimits_{\ell =1}^j {\left( {{\Bbb E}[\Lambda \! \mid \! L=\ell ]{\minus}{\Bbb E}[\Lambda ]} \right)^{2} \,{\rm Pr}\,[L=\ell ]} } \over {{\Bbb E}[\Lambda ]^{2} {\minus}\left[ {{\Bbb E}[\Lambda ]} \right]^{2} }} $$

to compare the different sets of transition rules. Other things being equal, a larger value of $$\tau _{{{\rm rule}}} $$ is preferred in designing an optimal BMS.

Nonetheless, although the measure of $$\tau _{{{\rm rule}}} $$ utilises its denominator to normalise the impact of a priori rating in order to quantify the effectiveness of transition rules, we note that its numerical value would change based on the varying extent of risk classification. In particular, the value of ${\Bbb E}[\Lambda ^{2} ]$ (and hence ${\Bbb V}[\Lambda ]$ ) is expected to increase due to a finer risk segmentation if we include more observable variables in the Poisson regression. However, it is not clear analytically how this increment would be attributed to either of the two components ${\Bbb E}\left[ {{\Bbb V}[\Lambda \! \mid \! L]} \right]$ and ${\Bbb V}\left[ {{\Bbb E}[\Lambda \! \mid \! L]} \right]$ , respectively. Consequently, we may have to select different candidates of transition rules subject to the choices of risk segmentation variables. In this paper, we examine the sensitivity of the $$\tau _{{{\rm rule}}} $$ with respect to the use of a priori rating variables using numerical illustrations in section 5.

5. Numerical Illustrations

For our illustrations, we use the motor vehicle claims data as documented in De Jong & Heller (Reference De Jong and Heller2008). The data set contains the information of 67,856 1-year motor insurance policies of a portfolio in the period of 2004/2005. The distribution of the number of claims reported is shown in Table 1, whereby its mean and variance are 0.0728 and 0.0774, respectively.

Table 1 Distribution of the number of claims reported in the portfolio.

We make use of the following risk classification variables: driver’s age (“Age”, six categories), driver’s area of residence (“Area”, six categories) and vehicle’s age (“Vehicle”, four categories). For categorical variable s with v_s categories, we create v_s− 1 dummy variables. To investigate the impact of different a priori variables towards the effectiveness of transition rules, we consider all the possible subsets of the above three categorical variables except the case of not using any variables. In more detail, the seven subsets of variables are as follows: single categorical variable (three cases), combination of two categorical variables (three cases) and all three categorical variables (one case). For instance, the model with only driver’s age contains v _Age=5 dummy variables, whereas the model with driver’s area of residence and vehicle’s age consists of v _Area+v _Vehicle=5+3=8 dummy variables. The resulting number of risk classes is $\prod\nolimits_{s^{{\asterisk}} } \upsilon _{{s^{{\asterisk}} }} $ , where s ^∗ denotes the categorical variable included in the model. For example, the model that considers all three categorical variables has 6×6×4=144 risk classes. We can then evaluate the mean and variance of Λ from the predicted a priori claim frequencies.

For each of these models, we estimate the parameter a of the Gamma distribution for Θ accordingly via the following expression:

$$\alpha ={{\mathop{\sum}\nolimits_{i=1}^n {\left( {d_{i} {\rm exp}\left( {\hat{\beta }_{0} {\plus}\mathop{\sum}\nolimits_{j=1}^q {\hat{\beta }_{j} x_{{ij}} } } \right)} \right)^{2} } } \over {\mathop{\sum}\nolimits_{i=1}^n {\left[ {\left( {y_{i} {\minus}d_{i} {\rm exp}\left( {\hat{\beta }_{0} {\plus}\mathop{\sum}\nolimits_{j=1}^q {\hat{\beta }_{j} x_{{ij}} } } \right)} \right)^{2} {\minus}y_{i} } \right]} }}$$

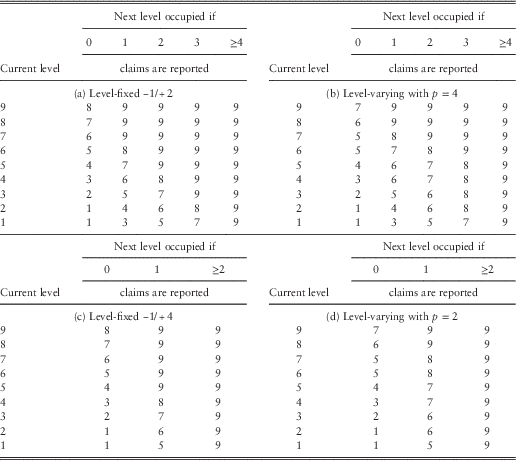
Similar to the BMS analysed by Taylor (Reference Taylor1997), we consider a BMS that comprises of j=9 levels with two sets of level-fixed rules of −1/+2 and −1/+4. We also examine the concept of level-varying rules as proposed by Tan et al. (Reference Tan, Li, Li and Balasooriya2015). In more detail, let t $_{\ell,k }$ be the level transition imposed on the drivers staying in level ${\ell }$ and making k claims in the current year, the proposed level-varying rulesFootnote ² can be represented as follows:

(17) $$\eqalignno{ & t_{{\ell ,0}} =\left\{ {\matrix{ {0,\quad } \hfill & {{\rm for}\,l=1} \hfill \cr {{\minus}1,\quad } \hfill & {{\rm for}\,2\leq \ell \leq \left\lceil {{\textstyle{j \over 2}}} \right\rceil {\plus}1} \hfill \cr {{\minus}2,\quad } \hfill & {{\rm for}\,\ell \,\gt \,\left\lceil {{\textstyle{j \over 2}}} \right\rceil {\plus}1} \hfill \cr } } \right. \cr & t_{{\ell ,k}} =\left\{ {\matrix{ {{\rm min}\left( {j{\minus}\ell ,\,{\rm max}\left( {k,\,\left\lceil {{\textstyle{{j{\minus}\ell } \over p}}{\times}k} \right\rceil } \right)} \right),\quad } \hfill & {{\rm for}\,k\geq 1,\,\ell \,\lt \,j} \hfill \cr {0,} \hfill & {{\rm for}\,k\geq 1,\,\ell =j} \hfill \cr } } \right. $$

where [x] is the ceiling function of x and the pre-specified parameter p is the smallest number of claims required for the drivers to move from level ${\ell }$ to level j. The specifications of the transition rules are illustrated in Table 2, where the level-fixed rules of −1/+2 are compared against the level-varying rules based on expression (17) with p=4. In particular, the basis of comparison is the smallest number of claims required for all drivers to move to the highest BMS level j. For instance, the rules of −1/+2 require p=4 claims for the drivers in level 1 to move to level 9. Similarly, the level-fixed rules of −1/+4 are compared against the level-varying rules with p=2. Note that the functional form of the level-varying transition rules in expression (17) may not be straightforward for motor vehicle drivers, but the representation in Table 2 should be much easier for their references. Hence, for a practical BMS, insurers should specify the specifications of transition rules using a table representation.

Table 2 Specifications of the four sets of transition rules under consideration.

With these details, we calculate the effectiveness of transition rules for each combination of a priori model and transition rules. The results are tabulated in Table 3. As expected, we observe that including additional variables into the model lead to an increase in the variability of Λ. In other words, using a richer set of a priori variables cause a higher variance in the predicted claim frequency relative to the reduced model. The values of $$\tau _{{{\rm rule}}} $$ are all highly satisfactory above 90% independent of the underlying a priori risk classification model.

Table 3 Effectiveness of transition rules for different combinations of a priori model and transition rules.

For each set of transition rules, the value of $$\tau _{{{\rm rule}}} $$ reduces with a larger variance of Λ, which indicates that the transition rules become less effective with a finer risk classification model. Moreover, the level-varying transition rules are more effective than the corresponding simple transition rules for each risk segmentation model, suggesting that the level-varying transition rules perform better, regardless of how the insurer specifies its risk classification model. In addition, it can be seen that the most effective transition rules are the level-varying rules with p=2, whereas the least effective rules are the level-fixed rules with −1/+2 consistently for all the models under consideration, implying that the varying extent of a priori risk segmentation is not a sensitive factor towards the ranking of the effectiveness of transition rules. More importantly, these results provide further empirical justifications for introducing the idea of level-varying transition rules into the design of BMS in practice.

In deciding the most suitable combination of a priori model and transition rules, we should take into account both the significance of a priori model as well as the effectiveness of transition rules instead of merely picking the combination that produces the highest value of $$\tau _{{{\rm rule}}} $$ . On the basis of the χ ² likelihood ratio test statistic based for nested models in Table 4, we find that the best model is the model that includes all three categorical variables. Hence, in our subsequent analysis we choose to design the BMS based on this model and the level-varying transition rules with p=2, where its estimated parameter a of the Gamma distribution for Θ is 2.7859.

Table 4 χ ² likelihood ratio test statistic for nested models.

Note: LL, value of log-likelihood; d.f., degrees of freedom.

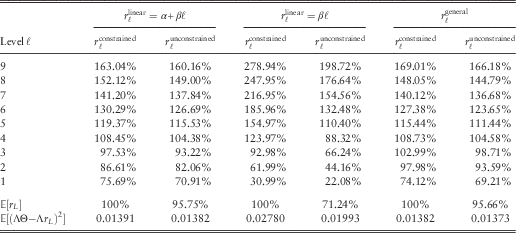
In our next step, we determine the optimal linear relativities for the BMS based on the analytical formulae presented in section 3. The results are shown in Table 5, where the corresponding value of ${\Bbb E}[r_{L} ]$ is also displayed. For comparison purpose, the optimal general relativities r $_{\ell }$ (i.e. without the constraint of linear form) and the optimised value of the objective function (1) are also provided to examine the extent of the deterioration in $${\Bbb E}[(\Lambda \Theta {\minus}\Lambda r_{L} )^{2} ]$$ when the linear restriction is imposed onto the BMS design.

Table 5 Optimal relativities for the bonus-malus system.

Note that $r_{\ell }^{{^{{{\rm constrained}}} }} $ and $r_{\ell }^{{^{{{\rm unconstrained}}} }} $ correspond to the optimal relativities with and without the financial balanced inequality constraint, respectively. We see that the values of r $_{\ell }$ are higher than $r_{\ell }^{{^{{{\rm unconstrained}}} }} $ for each BMS level ${\ell }$ under each form of optimal relativities. This finding can be explained by the values of ${\Bbb E}[r_{L} ]$ that are all below 100% for unconstrained optimal relativities. Put it differently, higher optimal relativities are needed such that the binding constraint of the financial balanced condition can be fulfilled.

Nonetheless, the constrained optimal relativities for both the values of $$r_{\ell }^{{{\rm linear}}} {\rm =}\alpha {\rm {\plus}}\beta \ell $$ and $r_{\ell }^{{{\rm general}}} $ are very close to that of their unconstrained versions, as further supported by the small difference between their values of $${\Bbb E}{\rm [}(\Lambda \Theta {\minus}\Lambda r_{L} )^{2} {\rm ]}$$ . More crucially, the optimised value of the objective function (1) for the optimal linear relativities is only about 0.7% higher relative to that of the optimal general relativities. These findings suggest that imposing a linear restriction to the numerical relativities do not cause a significant deterioration in the optimisation and hence optimal linear relativities should be preferred in designing a commercial BMS. However, the constrained linear relativities of the form $r_{\ell }^{{{\rm linear}}} =\beta \ell $ produce much larger differences in the optimised ${\Bbb E}{\rm [(}\Lambda \Theta {\minus}\Lambda r_{L} )^{{\rm 2}} {\rm ]}$ as compared with its unconstrained values as well as to the optimal general relativities. In summary, the numerical results in this section suggest that the insurer should consider using optimal linear relativities that are more viable in the practical implementation of BMS with a set of level-varying transition rules after a proper a priori risk classification model has been selected.

6. Concluding Remarks

In this paper, we study the determination of optimal relativities for a BMS when the set of relativities is a linear form of the BMS level. The analytical formulae for the optimal linear relativities are derived under the financial balanced inequality constraint. Moreover, it follows that further practical constraints can be easily taken into account in the optimisation procedure.

Our results indicate that imposing a set of linear relativities do not cause a significant change in the minimised objective function. This finding provides supporting justification for insurers in designing an optimal BMS that is both sufficiently optimal on a theoretical basis and commercially viable from a practical perspective. We also find that the varying extent of the a priori risk segmentation is not a sensitive factor towards the resulting effectiveness of transition rules. Furthermore, the numerical results also suggest that the level-varying transition rules are more effective than the level-fixed rules, regardless of the a priori risk classification model, hence insurers should definitely consider incorporating this idea into the design of an optimal BMS.

Throughout our analysis, we assume that the number of BMS levels is fixed in advance by the insurer. It is possible to relax this assumption by adding the number of BMS levels j as a parameter into the optimisation of (1). In future research, it is warranted to numerically examine the marginal improvement of incorporating j as an extra parameter into the optimal design of a BMS.