VARIABLE LABOR UTILIZATION AND ENDOGENOUS FLUCTUATIONS

This section shows that considering endogenous labor utilization and capital depreciation significantly alters the local dynamics of the Woodford (1986) infinite-horizon model. In particular, it turns out that local indeterminacy and expectations-driven fluctuations occur only if effort is not too elastic to the real wage. These results essentially arise from the fact that a more “intensive” use of labor reduces the elasticity of effective input substitution. Moreover, deterministic cycles appear to be less robust than stochastic equilibria (sunspots).

Technology

In each period t∈N, labor hours h_t≥0 and the capital stock k_t−1≥0 resulting from the previous period are combined in variable proportion to produce a consumption good under constant returns to scale at the firms level. Labor intensity e(ω) is interpreted as effort and is an increasing function of the real wage ω.

I make the simplest assumption that capitalists/entrepreneurs set the real wage and, thereby, workers' labor intensity. More precisely, we adopt the specification for technology suggested by Negishi (1979) and Solow (1979); that is, F[k, e(ω)h]₌^def e(ω)hAf[a/e(ω)], where A>0 is a scaling factor and a=k/h denotes the capital/labor(hours) ratio.

These assumptions are usual in the efficiency wage literature, according to which several informal arguments account for the fact that firms have the possibility to stimulate labor productivity by means of pecuniary incentives [see Akerlof and Yellen (1986), Weiss (1990)].¹

In addition, I assume that capital depreciation depends on effort: The depreciation function δ[e(ω)] varies with effort and, consequently, with the real wage. Here we view effort as measuring the quality of labor and, moreover, assume that capital depreciation decreases with effort. As shown below, the latter assumption implies that effort is (realistically) quite inelastic to the real wage, the corresponding elasticity being less than 1 at the optimum [see equation (2)], in contrast with the analysis by Solow (1979), which implies a unitary elasticity at the optimum. However, our analysis will be shown to be valid when depreciation is fairly inelastic to effort: δ′[e] is assumed to be arbitrarily close to zero. In that sense, this assumption is not critical to our analysis.

Finally, I assume that the economy benefits from external economies of scale and, more precisely, that total factor productivity A=A[k, e(ω)h], while given to any individual producer, is increasing in average capital and (efficient) labor. The following analysis does not rely on either any particular external effect (capital or labor) or the form of increasing returns (internal or external). In fact, as it clearly appears later, it is the presence of (negligible) increasing returns that is needed here to avoid that intertemporal equilibria degenerate, being stationary when returns to scale are constant [see also Pintus (2002, Sect. 3)]. Therefore, this second assumption is not critical either.

Assumption 1.

The intensive production function f(x)≥0 is continuous for x≥0, C^r for x>0 and r large enough, with f′(x)>0 and f′′(x)<0. The depreciation function 0≤δ(e)≤1 is continuous for e≥0, C^r for e>0 and r large enough, with δ′(e)<0 and δ′′(e)>0. The effort function e(ω)≥0 is continuous for ω≥0, C^r for ω>0 and r large enough, with e′(ω)>0 and e′′(ω)<0. Therefore, the function δ[e(ω)] is decreasing and convex.

The decision program solved by a typical entrepreneur/capitalist consists in maximizing profits given by he(ω)Af[a/e(ω)]-ωh-{r+δ[e(ω)]}k over k≥0, h≥0, and ω≥0, given the real interest rate r and total productivity A, and it follows that interior optima k>0, h>0, ω>0 satisfy

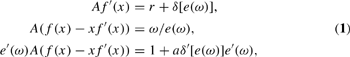
if x=^defa/e(ω).

In particular, it follows from the two last equalities in equations (1) that

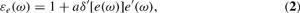
where ε_e(ω) is the elasticity of effort to the real wage.

Accordingly, one derives from equation (2), under appropriate assumptions, that the real wage depends, in an open neighborhood I of a steady state at which

to be defined below, on the capital/labor ratio. Moreover, the elasticity of real wage is then given by

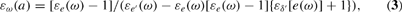
independently of the level of increasing returns.

In the absence of externalities, that is, when A is constant, equations (1) determine, under appropriate conditions, a, ω, and r: In that case, the dynamics of the model degenerate. Therefore, the assumption of increasing returns, that is, the assumption that A=A[k, e(ω)h] is increasing in k and eh, is intended, in this context, to allow the capital/labor ratio a, as well as the real wage and the rental price of capital, to be variable along nonstationary intertemporal equilibria. Consequently, the following analysis is carried over under the assumption that the level of increasing returns is arbitrarily small. To simplify the presentation, we may, therefore, abstract from the explicit presence of externalities and omit the arguments of A.

Moreover, as seen from equations (2), the configuration where the depreciation rate is constant—δ′[e]=0—leads to ε_e(ω)=1, that is, to wage rigidity and, consequently, to stationary intertemporal equilibria or degenerate dynamics with fixed labor [see Pintus (2002, Sect. 3] for a study of this limiting case). In contrast, endogenous depreciation—i.e. δ′[e]<0—allows for real wage variability, that is, ε_ω<1 under Assumption 1, in view of the previous equation, and, accordingly, for intertemporal substitution. Moreover, the assumption that depreciation decreases with effort implies, as seen from equations (2), that the elasticity of effort is smaller than one.²

Appendix B shows that the necessary and sufficient conditions for concavity of the Hessian of the profit function are met if, in addition to Assumption 1, δ[e] is sufficiently inelastic at the steady state to be defined later.

Finally, marginal productivities of (efficient) labor and capital are defined respectively, as

where ê(a)=^defe[ω(a)] and x=a/ê(a), while real wage ω(a) is implicitly defined under Assumption 1 by equations (2). Therefore, R(a) denotes the net interest factor and ωcirc;(x) denotes marginal productivity of efficient labor.

Variable Labor Utilization and Factor Substitution

The purpose of this section is to analyze the influence of a variable labor utilization on capital/labor substitution, a mechanism that is central to the occurrence of indeterminacy and endogenous fluctuations.

A natural and usual measure of input substitution possibilities is the (local) elasticity of capital over labor services with respect to the ratio of marginal productivities, that is, d ln(a/e)/d ln(ωcirc;/ρ). When labor utilization (e) is constant, this measure reduces to d lna/d ln(ωcirc;/ρ). As a consequence, d ln(a/e)/d ln(ωcirc;/ρ)≤d ln a/d ln(ωcirc;/ρ) if and only if d ln e/d ln(ωcirc;/ρ)≥0. Therefore, labor services (eh) are less substitutable to capital than labor hours (h) if and only if labor utilization increases with the relative rental price of labor: the more productive (or more expensive) labor is, the more intensively it is used.

In our framework, this general argument takes the following form. Define σ(a)=d ln[a/ê(a)]/d ln(ωcirc;/ρ) as the elasticity of effective input substitution and

(a)=d ln a/d ln(ωcirc;/ρ) as the elasticity of apparent (or measured) input substitution. It follows that σ(a)=[1–ε_e(ω)ε_ω(a)]

(a), where ε_e and ε_ω denote, respectively, the elasticities of the functions e(ω) and ω(a). In view of equation (2), σ(a)<

(a) if ε_e[ω(a)] is close to zero, for all a in I, since ε_ω(a) is then close to zero [see equation (3)].

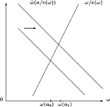
In that case, input substitution is reduced when effort is variable because both the wage and labor utilization increase when the capital/hours ratio moves up, under diminishing returns to labor hours, implying that the capital-efficient labor increases less than the capital/hours ratio: Labor is used more intensively when it is more productive. More precisely, efficient labor is optimal when its marginal productivity A{f[a/e(ω)]–af′[a/e(ω)]/e(ω)} equals its cost ω/e(ω) [see the second equality in equations (1)]. As a consequence, when the capital/labor ratio increases from a₀ to a₁>a₀, in Figure 1, that is, when capital is substituted for labor, the real wage increases from ω(a₀) to ω(a₁)>ω(a₀), in Figure 1, and, accordingly, effort e(ω) moves up. It follows, quite reasonably, as seen in Figure 1, that labor utilization is procyclical [as in the different model of Burnside et al. (1993)].

The above discussion is summarized in the following lemma.

LEMMA 1 (Variable Labor Utilization and Input Substitution).

Let σ(a)=^defd ln{a/e[ω(a)]}/d ln(ωcirc;/ρ)>0 be the elasticity of effective capital/labor substitution and

(a)=^defd ln a/d ln(ωcirc;/ρ)>0 be the elasticity of apparent (or measured) capital/labor substitution. It follows that σ(a)={1–ε_e[ω(a)]ε_ω(a)}

(a), where ε_e(ω)=^defωe′(ω)/e(ω)>0 and ε_ω(a)=^defaω′(a)/ω(a)>0 denote, respectively, the elasticities of utilization e(ω) and of real wage ω(a), whereas the latter function is implicitly defined, under Assumption 1, by equations (2). Then, one has ε_ω(a)=s(a)/(σ(a){1−ε_e[ω(a)]}+s(a)ε_e[ω(a)])>0, where 0<s(a)=^defxρ(x)/[Af(x)]<1 is the capital share in total income and x=^defa/e[ω(a)]. As a consequence, the elasticity of effective factor substitution σ(a)=

(a)−s(a)ε_e[ω(a)]/{1−ε_e[ω(a)]} is lower than the elasticity of measured factor substitution

(a), when labor utilization is variable, that is when ε_e(ω)>0. On the contrary, both definitions coincide, that is,

(a)≡σ(a), when labor utilization is constant, that is, when ε_e(ω)=0.

Proof.

Define σ(a)=d ln[a/ê(a)]/d ln(ωcirc;/ρ) as the elasticity of effective input substitution and

(a)=d ln a/d ln(ωcirc;/ρ) as the elasticity of apparent input substitution, with ê(a)=e[ω(a)]. It follows that σ(a)/

(a)=[1−ε_e(ω)ε_ω(a)], where ε_e and ε_ω denote, respectively, the elasticities of the functions e(ω) and ω(a), while real wage ω(a) is implicitly defined, under Assumption 1, by equations (2). I next derive the rental prices elasticities as functions of our underlying parameters, most notably the elasticity of effective input substitution. From 1/σ(a)=^defε_ωcirc;(x)−ε_ρ(x), where x=a/ê(a), and from the derivative of the identity Af(x)=xρ(x)+ωcirc;(x) [see equations (4)] with respect to x, one derives ε_ωcirc;(x)=s(a)/σ(a) and ε_ρ(x)=−[1−s(a)]/σ(a), where 0<s(a)=xρ(x)/[Af(x)]<1 denotes the capital share in total income while we denote ε_[phi](y) the elasticity of a given function [phi](y) with respect to y. Moreover, the second coordinate in equations (1) and the first definition in equations (4), that is, ωcirc;(x)=ω(a)/ê(a), yield ε_ωcirc;(x)=ε_ω(a)[1−ε_e(ω)]/[1−ε_e(ω)ε_ω(a)], where the dependence of ε_e on a is, for brevity, omitted. Therefore, we get

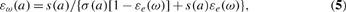
and

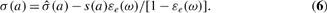
Finally, differentiating the definition of net interest factor R(a)=Aρ(a/ê(a)]+1−δ[ê(a) [see equations (4)] with respect to a leads to the following expression, to be used in the next section:

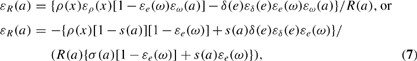
if we use equation (5).

To illustrate the main result of Lemma 1, I now turn to a simple example. If the production function is of the Cobb-Douglas type and both effort and capital depreciation are isoelastic functions, the profit is given by Ak^s[e(ω)h]^1−s−ωh−{r+δ[e(ω)]}k, with e(ω)=ω^ε, δ(e)=−e^α/α. The share of capital is given by 0<s<1, whereas 0<ε<1 and α<0 determine the convexity of labor utilization and capital depreciation, respectively.

At the unique optimum, the derivative of the profit function with respect to h vanishes, that is, A(1−s){k/[he(ω)]}^se(ω)=ω, with e(ω)=ω^ε. I derive from the latter equality the optimal real wage ω(a)=[A(1−s)a^s]^{1/[1−ε(1−s)]}, whose elasticity is given by s/[1−ε(1−s)]. It is then easily checked that ωcirc;(x)/ρ(x)=(1−s)a/[se(ω)]: Accordingly, the elasticity of effective input substitution σ=d ln[a/ê(a)]/d ln(ωcirc;/ρ) is equal to one while the elasticity of measured input substitution

=d ln a/d ln(ωcirc;/ρ)=1+sε/(1−ε), from equation (6), so that

=[1−ε(1−s)]/(1−ε)>1. In particular,

tends to +∞ when ε_e=ε tends to 1 from below: the possibilities to substituting one factor for another are reduced when the elasticity of labor utilization with respect to the real wage is high. On the contrary, σ and

coincide when both labor utilization and capital depreciation rates are constant, that is, when ε=0.

More generally, ε_e(ω)=0 corresponds to the case where the utilization rate of labor e as well as the depreciation rate for capital δ are constant, that is, where σ(a)≡

(a) in view of equation (6). Therefore, a moderate elasticity of effort may imply low input substitution. In other words, the assumption of constant utilization rate for labor overestimates input substitution: When the relative rental price of capital goes down, the “extensive” effect increases capital over labor, but an “intensive” effect goes in opposite direction by triggering an increase in labor utilization, implying that the elasticity of effective capital/labor substitution is lower than that considered when the utilization rate of labor is assumed to be fixed.

Intertemporal Equilibria

I now complete the description of the model, the detailed structure of which is presented by Woodford (1986). Specifically, a representative worker solves the following problem:

where B>0 is a scaling factor, c^w_t+1 is next-period consumption, h_t is labor supply, e(ω_t) is effort, p_t+1>0 is next-period price of consumption, assumed to be perfectly foreseen, and w_t>0 is nominal wage rate; that is, w_t=p_tω_t. I consider the case where leisure and consumption are gross substitutes and therefore assume the following.

Assumption 2.

The utility functions V₁(h) and V₂(c) are continuous for 0≤h≤h* and c≥0, where h*>0 is the (maybe infinite) workers' endowment of labor. They are C^r for, respectively, 0<h<h* and c>0, and r large enough, with V′₁(h)>0, V′′₁(h)>0, lim_h→h* V′₁(h)=+∞, and V′₂ (c)>0, V′′₂ (c)<0. Moreover, consumption and leisure are gross substitutes, that is −cV′′₂(c)<V′₂(c).

Since workers do not choose effort and are induced to provide the level of work intensity that is optimal for producers, it is natural to simplify as possible labor supply decisions. Therefore, we abstract from nonseparability issues and simply assume that labor disutility does not depend on effort. Then, the necessary conditions of the program in equations (8) describe the intertemporal substitution in terms of the functions V₁ and V₂ only and, therefore, we do not need more than what is stated in Assumption 2.³

It is easily shown that intertemporal competitive equilibria with perfect foresight (intertemporal equilibria thereafter) are summarized by the dynamics of two variables. Moreover, the discussion is conveniently amenable in terms of relevant parameters if the two variables are in fact chosen to be the capital/labor ratio a=k/h (a nonpredetermined variable) and the capital stock k (a predetermined variable).⁴

DEFINITION 1.

An intertemporal competitive equilibrium with perfect foresight of the Woodford model with capital/labor substitution is a sequence (a_t, k_t−1) of R²₊₊, t=0, 1, …, such that

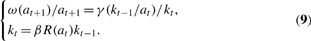
The first equality in equations (9) is the first-order condition of workers' optimization program (8), where γ is the function whose graph is the offer curve, that is, the locus described by workers' optimal choices in the (h_t, c_t+1) plane when the relative price w_t/p_t+1 varies. Under the assumption of gross substitutability, the elasticity of γ is larger than one or, equivalently, the labor supply elasticity with respect to the real wage is (given the expected inflation factor p_t+1/p_t) is ε_h(ω_tp_t/p_t+1)=1/[εγ(h_t)−1] and is positive. From equation (2), ω(a) denotes the equilibrium real wage.

The second equality in equations (9) summarizes capitalists' savings, under the assumption, made only for convenience since capitalists' preferences do not matter qualitatively here, of a logarithmic instantaneous utility function. The parameter 0<β<1 represents capitalists' discount factor while, in view of equations (4), R(a) denotes equilibrium gross returns to capital.

Robustness of Sunspots and Cycles

To ensure the existence of a (monetary) steady state, we appropriately scale the two parameters A and B. Moreover, the steady state is shown to be unique and is normalized, without loss of generality, at (

=(1, 1).

PROPOSITION 1 (Existence and Uniqueness of the Steady State).

Under Assumptions 1, 2, and lim_c→0 cV′₂ (c)<V′₁(1)<lim_c→+∞cV′₂(c), (

)=(1, 1) is the unique steady state of the dynamical system in equations (9) if and only if A=(1/β−1+δ′{e[ω(1)]})/f′{1/e[ω(1)]}, and B is the unique solution of ω(1)V′₂[ω(1)/B]/B=V′₁(1).

Proof.

In view of equations (9), the monetary steady states are the solutions (

,

) in R²₊₊ of ω(

) and β R(

)=1. By definition of R(a), in equations (4), the latter equation yields Af′[

)]+1−δ[ê(

)]=1/β, with ê(a)=e[ω(a)]. We set A={1/β−1+δ[ê(1)]}/f′[1/ê(1)] to ensure that

. Moreover, ω(1)=γ(1) or, equivalently, ω(1)V′₂[ω(1)/B]/B=V′₁(1) is achieved by scaling the unique solution B>0, under Assumption 2, implying that cV′₂(c) is continuous and increasing and lim_c→0 cV′₂ (c)<V′₁(1)<lim_c→+∞ cV′₂(c).

In the context of a non-Walrasian labor market in which the real wage is decided by entrepreneurs so as to provide the correct incentives, it is possible that labor demand is lower than labor supply, at the steady state. In other terms, it is possible that the real efficiency wage is larger than the market-clearing wage of the corresponding perfectly competitive economy and, accordingly, that the steady state is characterized by unemployment.

The introduction of efficiency wage is, as noticed above, natural in the present model and, more importantly, is consistent with an observed feature of modern labor markets. Under various forms, institutions or social norms—for example, minimum wage, unemployment benefits, or labor unions—have emerged and allow, to some extent, agents who have limited access to capital markets to reduce the volatility of labor income. The above formulation is consistent with this observation: As shown in equation (5), the wage elasticity is, ceteris paribus, lower when labor utilization varies with the real wage, that is, when ε_e(ω)>0, provided that the elasticity of input substitution is smaller than the capital share, that is, that σ(a)<s(a). Proposition 2 show that this condition is in fact necessary to the occurrence of endogenous fluctuations when labor utilization and capital depreciation are variable.

Accordingly, we study in the sequel the dynamics in the neighborhood of a steady state of the model with an efficiency wage fixed by capitalists and assume that a fraction of workers is unemployed and do not receive any compensation for that state. In particular, unemployed agents are chosen randomly and do not have the possibility of insuring themselves against unemployment risk.

Equations (9) define, near the steady state (

), a dynamical system of the form (a_t+1, k_t)=G(a_t, k_t−1), provided that ε_ω(

)≠1. We study the local dynamics as a function of the following parameters: The depreciation rate for capital 0<δ=^defδ[ê(

)]≤1, the elasticity of depreciation ε_δ=^defê(

)δ′[ê(

)]/δ[ê(

)]<0, the share of capital 0<s=^def

)]/{A

)]}<1, the elasticity of input substitution σ=^def

)>0, the capitalist's discount factor 0<β<1, the elasticity of effort ε_e=^defε_e[

)]>0, and the elasticity of the function whose graph is the offer curve εγ=^defεγ(

)>1, all evaluated at the steady state.

Straightforward algebra yields the following results.

LEMMA 2 (Dynamics near the Steady State).

Under Assumptions 2 and 1, let ε_R=

R′(

)/R(

)<0, ε_ω=

ω′(

)/ω(

)>0, εγ=

γ′(

)/γ(

)<1, and ε_e =ω(

)e′[ω(

)]/e[ω(

)]>0 be the elasticities of the functions R(a), ω(

), γ(h), and e(ω), evaluated at the steady state, and suppose ε_ω≠1. The Jacobian matrix of the map in equations (9), evaluated at the steady state, has trace T and determinant D given by

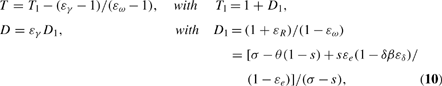
where[theta]=1−β(1−δ).

Moreover, slopeΔ_σ=1+ε_R=1−[[theta](1−s)+sδβε_δε_e/(1−ε_e)]/[σ+sε_e/(1−ε_e)].

Direct inspection of Lemma 2 shows that a half-line Δ_σ is generated from (T₁,D₁) in the (T,D) plane, when εγ increases from 1, while all other parameters, that is,

and ε_ω are held fixed.⁵

In the extreme case of constant utilization and depreciation (ε_e=0), the configuration in Figure 2 arises when σ (which equals

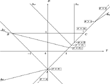
) is made to vary, under appropriate assumptions on the parameters [see Grandmont et al. (1998)]: D₁(σ) is a decreasing function, while the slope of Δ_σ increases with σ. It follows that local indeterminacy (when two eigenvalues are inside the unit circle) and endogenous fluctuations emerge only for low values of σ, that is, for σ<σ_I=[[theta](1−s)+s]/2, σ_I being defined as the value of σ such that [T₁(σ), D₁(σ)] coincides with point A (or equivalently D₁(σ)=−1] in Figure 2, and indeed for σ's that are significantly less than the share of capital s.

In particular, Hopf bifurcations are expected, implying the occurrence of an invariant closed curve surrounding the steady state, on which the dynamics is either periodic or quasiperiodic, when 0<σ<σ_H: At the intersection of Δ_σ and the interior of the segment (BC), the two complex eigenvalues have modulus one. Moreover, a flip bifurcation generally occurs when σ_F<σ<σ_I: An eigenvalue is equal to −1 when Δ_σ intersects the line (AB), that is, T=−1−D.

On the contrary, local determinacy is bound to prevail, that is, there exists a neighborhood in which no endogenous fluctuations occur, for larger values of σ, that is, when σ>σ_I [see Figure 2].

Most importantly, we are now going to show that when ε_e>0 is close to zero—when labor utilization varies with the real wage—local indeterminacy and expectations-driven fluctuations occur for even smaller elasticities of input substitution σ.

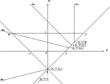
Starting from the configuration in Figure 2 for which labor utilization and capital depreciation are constant (for ε_e=0), the origin and the (absolute value of the) slope of the half-line Δ₀ (for σ=0) as well as the critical value σ_I decrease with ε_e. Even though indeterminacy still occurs for low σ's, the effect of variable utilization is, therefore, to reduce the range of input substitution elasticities that are consistent with local indeterminacy and endogenous fluctuations. However, if we fix ε_e at a positive value and vary σ, starting at a given Δ₀, we get the same qualitative picture: the origin and the (absolute value of the) slope of the half-line Δ_σ decrease with σ. Therefore, a convenient way to summarize the influence of ε_e is to represent how Δ₀ (for σ=0) moves with our key parameter, ε_e: this is the purpose of Figure 3.

More precisely, it is seen from Lemma 2 that D₁(σ) decreases, along the line (AC), and that slope_Δσ(σ) increases with both σ and ε_e, whenever[theta](1−s)<s. In particular, D₁(0)=[theta](1−s)/s−ε_e(1−δβε_δ)/(1−ε_e) decreases from[theta](1−s)/s<1 to −1, that is, σ_I=[s+[theta](1−s)−sε_e(1−δβε_δ)/(1−ε_e)]/2, defined by D₁(σ_I)=−1, decreases from [[theta](1−s)+s]/2 to zero, while slope_Δ0(0) increases from −∞ to a positive value, when ε_e increases from zero to ε_eI=[s+[theta](1−s)]/[[theta](1−s)+s(2−δβε_δ)], as summarized in Figure 3.

Accordingly, the intersection between the half-plane generated by the line Δ_σ, when σ moves up, and the indeterminacy triangle ABC gets smaller and smaller, in Figure 3, as ε_e is increased: The half-line Δ₀ (for σ=0) goes toward the negative orthant of the plane. This intersection may even become empty when ε_e is sufficiently high, that is, if ε_e>ε_eI=[s+[theta](1−s)]/[[theta](1−s)+s(2−δβε_δ)]. In that case, D₁(σ)<−1 and 0<slope_Δσ (σ)<1 when σ<σ₀, while D₁(σ)>1 and 0<slope_Δσ(σ)<1, when σ>σ₀: the steady state is a saddle (locally determinate) and there exists a neighborhood in which no endogenous fluctuations occur.

Figure 3 then summarizes the influence of variable labor utilization and capital depreciation rates, when[theta](1−s)<s. In particular, slope_Δ0(0)<−1 if ε_e is low enough, that is, if ε_e<ε_eF=[theta](1−s)/[[theta](1−s)+s(2−δβε_δ)]. Accordingly, the resulting local dynamics regimes are then similar to those appearing in Figure 2 (ε_e=0). When ε_e>ε_eF, however, the conclusion is different: The slope of Δ₀ (for σ=0) may be small enough so that the half-line Δ_σ (for σ close to zero) does not intersect the segment (BC). Figure 3 shows that this is indeed the case whenvever ε_e>ε_eH: Hopf bifurcations, that is, periodic and quasiperiodic intertemporal equilibria, no longer occur.

Appendix B derives lower and upper bounds for the expression of ε_eH, solution of slope_Δ0(0)=[D₁(0)−1]/[T₁(0)+2] [see Figure 3]. In particular, ε_eH tends to zero when [theta] tends to zero: If the period is short enough ([theta]≈ 0), the Hopf bifurcation disappears “quickly,” ceteris paribus, as ε_e increases from zero [see Figure 3]. For instance, ε_eF ≈ 3.5%<ε_eH<6.8% (resp. ε_eF ≈ 3.2%<ε_eH<5.6%) if s=1/3, β=0.988, δ=0.025, and ε_δ=−0.1 (resp. ε_δ=−10). This is the first notable departure from the model with constant labor utilization and constant capital depreciation: The existence of deterministic fluctuations due to self-fulfilling expectations (with period greater than three and quasiperiodic) is less likely because it is very sensitive to the elasticity of effort.

However, the existence of stochastic equilibria driven by self-fulfulling beliefs (sunspots) is still compatible with values of ε_e between ε_eH and ε_eI.⁶

Without additional information on higher-order derivatives of the Jacobian matrix, one cannot establish whether local deterministic cycles (originated through flip or Hopf bifurcations) are stable or unstable. However, for sake of brevity, I do not develop this analysis and focus on sunspots when discussing the plausibility of expectations-driven fluctuations.

Therefore, we have established the following results.

PROPOSITION 2 (Local Stability and Bifurcations of the Steady State).

Consider the monetary steady state

normalized by the procedure in Proposition 1, and suppose[theta](1−s)<s, where[theta]=1−β(1−δ), 0<β<1 is the capitalists ' discount factor, 0

is the depreciation rate for capital and

denotes the capital share in total income.

Under the assumptions of Lemma 1 and Proposition 1, the following results are generic.⁷

(i) if ε_eF<ε_e<ε_eH, then

• (a) 0<σ<σ_H: The steady state is a sink (locally indeterminate) when 1<εγ<ε_{γ H}, where ε_{γ H} is the value of εγ for which Δ_σ crosses [BC]. The steady state undergoes a Hopf bifurcation (the complex characteristic roots cross the unit circle) at εγ=ε_{γ H} and is a source when ε_{γ H}<εγ<ε_{γ F}, where ε_{γ F} is the value of εγ for which Δ_σ crosses the line (AB). A flip bifurcation occurs (one characteristic root goes through −1) at εγ=ε_{γ F} and the steady state is a saddle (locally determinate) if εγ>ε_{γ F}.
• (b) σ_H<σ<σ_I: The steady state is a sink when 1<εγ<ε_{γ F}. A flip bifurcation occurs at εγ=ε_{γ F} and the steady state is a saddle if εγ>ε_{γ F}.
• (c) σ_I<σ and σ ≠ σ₀: The steady state is a saddle for all ε_γ>1.

(ii) if ε_eH<ε_e<ε_eI, then

• (a) 0<σ<σ_I: The steady state is a sink when 1<εγ<ε_{γ F}. A flip bifurcation occurs at εγ=ε_{γ F} and the steady state is a saddle if εγ>ε_{γ F}.
• (b) σ_I<σ and σ≠σ₀: The steady state is a saddle for all εγ>1.

(iii) if ε_eI<ε_e, then the steady state is a saddle, independently of σ>0 and εγ>1.

The most important result of the above analysis is that variable labor utilization and capital depreciation rates reduce the range of effective input substitution elasticities 0<σ<σ_I for which deterministic and stochastic endogenous fluctuations occur. In particular, this range is small if effort is quite elastic to the real wage, that is, if ε_e(ω)=ω e′(ω)/e(ω) is large enough at the steady state and nearby. In fact, the critical elasticity σ_I decreases with ε_e and indeed becomes negative if ε_e>ε_eI=[s+[theta](1−s)]/[[theta](1−s)+s(2−δβε_δ)]. Other things being equal, the existence of endogenous fluctuations depends on more stringent conditions, in terms of parameter values involving the elasticity of effective substitution.

In the next section, however, I will argue that the plausibility of endogenous fluctuations, in the context of an “intensive” labor utilization reducing factor substitution, is indeed improved if the discussion is cast in terms of the apparent (or measured) elasticity.

Remark.

In the preceding subsection, I made σ increase from zero, given ε_e and ε_δ. Moreover, we have derived in equation (3) that ε_ω=(ε_e−1)/[ε_e′−ε_e(ε_e−1)(1+ε_δ′)]. In view of equation (5), therefore, the relation between all technology parameters (ε_e−1)/[ε_e′−ε_e(ε_e−1)(1+ε_δ′)]=s/[σ(1−ε_e)+sε_e] has to hold at the steady state. Given ε_e 1 and σ>0, we have therefore implicitly assumed that, for instance, ε_e′ is set at (ε_e−1)[σ(1−ε_e)/s+ε_e(2+ε_δ′)], which is negative if, in addition, 2+ε_δ′>0. In any case, these assumptions are not critical for the above qualitative results.

PLAUSIBILITY OF ENDOGENOUS FLUCTUATIONS WHEN LABOR UTILIZATION IS VARIABLE

Even though, as shown by Proposition 2 (and Figure 3), considering variable labor utilization and capital depreciation rates reduces the scope for endogenous fluctuations, in parameter space, it is argued in this section that their plausibility is, on the contrary, improved when variable intensity is taken into account. Section 2.2 has established that effective substitution is reduced when utilization (and depreciation) are variable. As a consequence, this has led, in Section 2.4, to conditions for local indeterminacy and endogenous fluctuations that are more restrictive.

The analysis also suggests that the elasticity of effective input substitution is, in this context, reduced and may be substantially lower than the elasticity of measured input substitution, which is in fact obtained under the assumption of constant utilization and depreciation. In summary, the more elastic utilization, the lower the elasticities of capital/labor substitution that are compatible with endogenous fluctuations, but, at the same time, the lower the elasticity of effective input substitution. Therefore, one has to assess more carefully, in this context, the plausibility of self-fulfilling cycles, which is the purpose of this section. I illustrate that a rather different conclusion is reached if the discussion is cast in terms of apparent substitution possibilities: Endogenous fluctuations are indeed compatible with higher elasticities of apparent substitution, when labor utilization is variable.

To simplify the discussion, suppose that the length of the period is short enough, so that we can neglect[theta]=1−β(1−δ) ≈ 0 (as β ≈ 1 and δ ≈ 0), and fix s=1/3. Proposition 2 [see also Figure 3] shows that endogenous fluctuations are possible only if ε_e<ε_eI ≈ 1/2 and σ<σ_I ≈ s(1/2−ε_e)/(1−ε_e). For instance, σ_I is, respectively, equal to 15%, 13% and 3% when ε_e=0.1, 0.2, and 0.45. Because direct estimates of the elasticity of effective input substitution are not available, we are forced to compare the range of measured substitution elasticities

with the corresponding estimates. By using Lemma 1, which provides the relation

, the condition σ<σ_I ≈ s(1/2−ε_e)/(1−ε_e) is rewritten as

]. Accordingly, the elasticity

has to be lower than, respectively, 19%, 21%, and 30% when ε_e=0.1, 0.2, and 0.45, to be consistent with the existence of expectations-driven cycles. On the contrary, when labor utilization is constant, that is, when

, the upper bound σ_I is approximatively equal to 17%.

Accordingly, the occurrence of local indeterminacy and endogenous fluctuations implies a less strigent condition—in terms of the elasticity of apparent factor substitution

—when labor utilization and capital depreciation are variable, in contrast to the model in which capital utilization is variable: The higher ε_e, the less restrictive the condition

<s/[2(1−ε_e)]. In particular, the values of the apparent elasticity that are consistent with endogenous fluctuations, that is,

<s (when ε_e=1/2 ≈ ε_eI), fall within the lowest end of the range of estimates [see, e.g., Hamermesh (1993, Ch. 3) or Rowthorn (1999, Table 2)].

We now examine the range of labor supply elasticities with respect to the real wage—that is, 1/(εγ−1)—that are consistent with local indeterminacy and bifurcations. The second part of Proposition 2 and Appendix B show that the steady state is locally indeterminate and, therefore, that stochastic equilibria do exist in its neighborhood, if ε_γ<ε_γF ≈ (s−σ)/[σ+sε_e/(1−ε_e)], when σ<σ_I. Imposing to the labor supply elasticity ε_l=1/(εγ−1) to be less than unity—that is, 2<εγ<ε_{γ F}–implies then σ<s(1/3−ε_e)/(1−ε_e), which is a stronger condition than σ<σ_I ≈ s(1/2−ε_e)/(1−ε_e); σ now has to be lower than 9% and 6%, respectively, if ε_e=0.1, 0.2. Equivalently,

<s/[3(1−ε_e)] has to hold: The measured elasticity

has to be smaller than 12%, 14%, and 20% when ε_e=0.1, 0.2, and 0.45, respectively, to be compatible with endogenous fluctuations when labor supply elasticity is less than unity (probably a strong requirement in view of most empirical studies). The existence of sunspots is therefore in agreement with the estimates of labor supply elasticity, provided that the elasticity of capital/labor substitution is low enough.

In summary, because the analysis of the model with variable utilization gives a precise framework to understand why input substitution possibilities may be low, the existence of endogenous fluctuations for small elasticities of capital/labor substitution may therefore be considered in this context as more plausible, even though direct estimates would allow us to assess more carefully this conclusion. In fact, the model with variable effort is compatible with larger elasticities of apparent input substitution, and it predicts that sunspots are more plausible than in the extreme case of constant labor utilization.