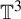1 Introduction
Let M be a closed
$C^{\infty }$
Riemannian manifold. Given a diffeomorphism
$f\in \operatorname {Diff}^r(M)$
and
$r\in [1,\infty ], s\in [0,r]$
, the
$C^s$
-centralizer of f is defined as
$$ \begin{align*} \mathcal{Z}^s(f)=\{g\in\operatorname{Diff}^s(M): g\circ f=f\circ g \}. \end{align*} $$
By definition, f is conjugate to itself by any element
$g\in \mathcal {Z}^s(f)$
. In other words, the centralizer of f is in fact the group of symmetries of f, where ‘symmetries’ can be interpreted classically as: changes of coordinates do not break the dynamics of the system. The centralizer of f always contains the integer powers of f. One says that f has trivial
$C^s$
-centralizer if
$\mathcal {Z}^s(f)=\{f^n\}_{n\in {\mathbb Z}}$
, and f has virtually trivial
$C^s$
-centralizer if the cyclic group
${<}f{>}:=\{f^n\}_{n\in {\mathbb Z}}$
is a finite index subgroup of
$\mathcal {Z}^s(f)$
.
The centralizers of diffeomorphisms play important roles in several topics of dynamical systems. For instance, people attempt to classify diffeomorphisms up to differentiable conjugacies, especially in the study of circle diffeomorphisms [Reference HermanHe]. On the other hand, the property of the centralizer of a diffeomorphism can give some consequences in foliation theory; see, for instance, [Reference BonattiB]. Moreover, the centralizer of a diffeomorphism is closely related to the study of higher-rank abelian actions on manifolds; see, for instance, [Reference Damjanovic and KatokDK, Reference Rodriguez HertzH, Reference Rodriguez Hertz and WangHW].
Smale [Reference SmaleSm1, Reference SmaleSm2] proposed the famous conjecture that typical diffeomorphisms have trivial centralizer, and considered it as one of the mathematical problems of this century.
Conjecture 1.1. There exists a residual subset
${\cal U}\subseteq \operatorname {Diff}^r(M)$
, such that every
$f\in {\cal U}$
has trivial
$C^r$
-centralizer.
The history of this conjecture goes back to the work of Kopell [Reference KopellKo] proving that
$\operatorname {Diff}^r(S^1)$
(
$r\geq 2$
) admits an open and dense subset in which each element has trivial centralizer. This conjecture has been solved for the case
$r=1$
in [Reference Bonatti, Crovisier and WilkinsonBCW, Reference Bonatti, Crovisier, Vago and WilkinsonBCVW]. It is still wide open for general case when
$r>1$
. Palis and Yoccoz studied Anosov diffeomorphisms [Reference Palis and YoccozPaYo2] and proved that
$C^{\infty }$
-open dense Anosov diffeomorphisms have trivial centralizer. See also [Reference FisherFi, Reference Palis and YoccozPaYo1, Reference Rocha and VarandasRV] for other related results.
Since hyperbolic systems are not dense, it is natural to study the centralizer problem for
$C^r, r>1$
, diffeomorphisms under a weaker hyperbolicity assumption. In 1970s, Brin and Pesin proposed the notion of partial hyperbolicity to weaken the notion of hyperbolicity; see §2.1 for a precise definition. There are only some partial results in this direction. Burslem [Reference BurslemBur] showed that
$C^1$
-open and dense partially hyperbolic diffeomorphisms have discrete centralizer. Recently, under a volume-preserving assumption, [Reference Damjanovic, Wilkinson and XuDWX] showed that for some classical
$C^1$
open class of
$C^r$
partially hyperbolic diffeomorphisms, the centralizer is either small (virtually trivial) or exceptionally large (contains a non-discrete Lie group); see related results in [Reference Barthelmé and GogolevBG]. It is still unknown whether the results in [Reference Damjanovic, Wilkinson and XuDWX] or [Reference Barthelmé and GogolevBG] can be generalized to the general non-volume-preserving case.
In this paper we will classify the centralizer for a classical open class of partially hyperbolic systems on
${\mathbb T}^3$
, without assuming a volume-preserving condition. More precisely, we consider derived-from-Anosov (DA) systems on
${\mathbb T}^3$
. For a partially hyperbolic diffeomorphism f on
${\mathbb T}^3$
, we denote its linear part
$L_f:\pi _1(\mathbb {T}^3)=\mathbb {Z}^3\rightarrow \mathbb {Z}^3$
induced by f on the fundamental group of
${\mathbb T}^3$
by
$L_f$
. If
$L_f\in \text {GL}(3,\mathbb {Z})$
is Anosov (hyperbolic), that is, f is homotopic to an Anosov automorphism, then f is called a DA diffeomorphism.
The study of partially hyperbolic DA diffeomorphisms originated from Mañé [Reference MañéM]. Partially hyperbolic DA diffeomorphisms have been studied extensively in their topological aspects (see. for instance. [Reference Brin, Burago and IvanovBBI1, Reference HammerlindlHa, Reference Hammerlindl and PotrieHaPo, Reference PotriePo]) as well as their measure-theoretic aspects (see, for instance, [Reference Buzzi, Fisher, Sambarino and VásquezBFSV, Reference Gan and ShiGS, Reference Hammerlindl and UresHaU, Reference Ponce, Tahzibi and VarãoPTV, Reference UresU, Reference Viana and YangVY]).
In this paper we essentially classify the centralizer of any
$C^r,1<r\leq \infty $
, partially hyperbolic DA diffeomorphisms on
${\mathbb T}^3$
.
Theorem 1.2. Let
$f\in \operatorname {Diff}^{\infty }({\mathbb T}^3)$
be a partially hyperbolic derived-from-Anosov diffeomorphism. Then one has the following dichotomy:
-
• either the
$C^{\infty }$
centralizer of f is virtually trivial, and
$$ \begin{align*} \#\{g\in\mathcal{Z}^{\infty}(f): g \text{ is homotopic to the identity} \}\leq |\!\operatorname{det}(L_f-\operatorname{Id})|; \end{align*} $$
-
• or f is
$C^{\infty }$
-conjugate to
$L_f$
, thus
$\mathcal {Z}^{\infty }(f)\cong \mathcal {Z}^{\infty }(L_f)$
.
For the centralizer of the partially hyperbolic DA diffeomorphisms with lower regularity, we get the following theorem. And Theorem 1.2 is a direct corollary of this theorem.
Theorem 1.3. Let
$f\in \operatorname {Diff}^r({\mathbb T}^3)$
(
$r>1$
) be a partially hyperbolic derived-from-Anosov diffeomorphism. Then f satisfies one of the following properties:
-
• the
$C^r$
centralizer of f is virtually trivial and
$$ \begin{align*} \#\{g\in\mathcal{Z}^r(f): g \text{ is homotopic to the identity} \}\leq |\!\operatorname{det}(L_f-\operatorname{Id})|;\end{align*} $$
-
• f is Anosov, and
$C^{r-{\varepsilon }}$
-conjugate to
$L_f$
for any
${\varepsilon }>0$
.
Unlike in [Reference Barthelmé and GogolevBG, Reference Damjanovic, Wilkinson and XuDWX], the proofs of our main results do not depend on the measure-theoretic properties of the center foliation. Instead we study the accessibility and topological information of the stable and unstable foliations, which allow us to get rid of the volume-preserving assumption in [Reference Barthelmé and GogolevBG, Reference Damjanovic, Wilkinson and XuDWX].
Remark 1.4.
-
(1) In the second case of Theorem 1.3, the loss of regularity comes from Journé’s theorem [Reference JournéJ]. If r is not an integer, then f is
$C^r$
-conjugate to
$L_f$
. Thus
$\mathcal {Z}^r(f)\cong \mathcal {Z}^r(L_f)=\mathcal {Z}^{\infty }(L_f)$
, which is virtually
${\mathbb Z}^2$
. -
(2) When
$\mathcal {Z}^r(f)$
is virtually trivial, one has
$\#\{g\in \mathcal {Z}^r(f): g \text{ is homotopic to the} \text{identity}\} \leq \#(\mathcal {Z}^r(f)/{<}f{>})$
, and the inequality could be strict provided that
$\mathcal {Z}^r(f)$
contains elements homotopic to
$-\!\operatorname {Id}_{{\mathbb T}^3}$
, or g with
$g^{n_0}=f$
and
$n_0>1. $
-
(3) From the proof, we can see that the dichotomy in both theorems comes from whether f is accessible. If f is accessible, then
$\mathcal {Z}^r(f)$
is virtually trivial. Otherwise, f is forced to be smoothly conjugate to its linear part
$L_f$
. -
(4) The reason why we discuss virtual triviality rather than triviality of the centralizer is that this property is more likely to be robust; for example, the class of systems which satisfies the dichotomy in our paper forms an open subset in the group of
$C^r$
diffeomorphisms on
${\mathbb T}^3$
. See [Reference Damjanovic, Wilkinson and XuDWX] and references therein for more results on ‘virtual triviality of centralizer or rigidity’ for partially hyperbolic diffeomorphisms.
In particular, our result implies that the centralizer of every diffeomorphism constructed by Mañé in [Reference MañéM] is virtually trivial. A direct corollary is that
$C^r$
-open densely, the
$C^r$
-centralizer of a partially hyperbolic diffeomorphism which is homotopic to an Anosov automorphism on
${\mathbb T}^3$
is trivial, which can be achieved by perturbing different fixed points to have different center Lyapunov exponents.
Question 1.5. Does Theorem 1.3 hold when
$r=1$
?
We do not know the answer to this question. Our proof strongly relies on the recent results in [Reference Gan and ShiGS, Reference Hammerlindl and ShiHaS] where
$r>1$
is crucial in their arguments.
Remark 1.6. If f is
$C^1$
-smooth and accessible, then
$\mathcal {Z}^1(f)$
is virtually trivial. See Remark 3.9 and Theorem 3.16 in §3. As accessible partially hyperbolic diffeomorphisms with one-dimensional center form a
$C^1$
-open and dense subset [Reference DidierDi, Reference Dolgopyat and WilkinsonDoW, Reference Rodriguez Hertz, Rodriguez Hertz and UresHHU], it follows that for a
$C^1$
-open dense set of partially hyperbolic DA diffeomorphisms on
${\mathbb T}^3$
, the
$C^1$
centralizer is trivial.
Question 1.7. Suppose that M is a closed 3-manifold and
$\text {PH}^r(M)$
is the set of
$C^r$
partially hyperbolic diffeomorphisms on M. Let
$\mathcal {U}^r\subset \text {PH}^r(M)$
be defined by
$$ \begin{align*}\mathcal{U}^r:=\{f\in \text{PH}^r(M): \mathcal{Z}^r(f) \text{~is trivial}\}.\end{align*} $$
Does
$\mathcal {U}^r$
contain an open dense subset in
$\text {PH}^r(M)$
for every
$r>1$
?
2 Preliminaries
In this section we collect the notions and results used in this paper.
2.1 Domination and partial hyperbolicity
A
$Df$
-invariant splitting
$TM=E\oplus F$
is dominated, if there exists
$N\in {\mathbb N}$
such that
$$ \begin{align*} \|Df^N|_{E(x)}\|\cdot \|Df^{-N}|_{F(f^n(x))}\|\leq \tfrac{1}{2}\quad \text{for any } x\in M.\end{align*} $$
$\operatorname {dim}(E)$
is called the index of the dominated splitting.
The following well-known result tells us that the dominated bundles are invariant under the diffeomorphisms in the centralizer.
Proposition 2.1. [Reference Damjanovic, Wilkinson and XuDWX, Lemma 13]
Let
$f\in \operatorname {Diff}^1(M)$
admit a dominated splitting of the form
$TM=E\oplus F$
. Then for any
$g\in \mathcal {Z}^1(f)$
, one has
$Dg(E)=E$
and
$Dg(F)=F$
.
A diffeomorphism
$f\in \operatorname {Diff}^r(M)$
is partially hyperbolic if there exist a
$Df$
-invariant splitting
$TM=E^{s}\oplus E^c\oplus E^{u}$
and
$N\in {\mathbb N}$
such that the following statements hold.
-
• Uniform contraction and expansion. For any
$x\in M$
, one has
$$ \begin{align*}\|Df^{N}|_{E^{s}(x)}\|\leq \tfrac{1}{2} \quad \text{ and } \quad \|Df^{-N}|_{E^{u}(x)}\|\leq \tfrac{1}{2}.\end{align*} $$
-
• Domination. For any
$x\in M$
, one has
$$ \begin{align*}\|Df^{N}|_{E^{s}(x)}\|\cdot\|Df^{-N}|_{E^c(f^N(x))}\|&\leq\tfrac{1}{2}, \\ \quad\|Df^N|_{E^c(x)}\|\cdot \|Df^{-N}|_{E^{u}(f^N(x))}\|&\leq \tfrac 12.\end{align*} $$
It is clear that the set of all
$C^r$
partially hyperbolic diffeomorphisms is an open subset of
$\operatorname {Diff}^r(M)$
in the
$C^r$
-topology. If either the strong stable bundle
$E^s$
or the strong unstable bundle
$E^u$
is trivial, we say f is weakly partially hyperbolic.
Not every manifold supports a partially hyperbolic diffeomorphism. For instance, there are no partially hyperbolic diffeomorphisms on
${\mathbb S}^3$
[Reference Burago and IvanovBI].
2.2 Dynamical coherence
For a partially hyperbolic diffeomorphism f, by [Reference Hirsch, Pugh and ShubHPS], there always exist f-invariant foliations
$\mathcal {F}^s$
and
$\mathcal {F}^u$
tangent to the bundles
$E^{s}$
and
$E^u$
respectively, and such foliations are unique. f is called dynamically coherent if there exist f-invariant foliations
$\mathcal {F}^{cs}$
and
$\mathcal {F}^{cu}$
tangent to
$E^{cs}:=E^{s}\oplus E^c$
and
$E^{cu}:=E^c\oplus E^u$
, respectively. By taking the intersection of
$\mathcal {F}^{cs}$
and
$\mathcal {F}^{cu}$
, one gets an invariant foliation
$\mathcal {F}^c$
tangent to
$E^c.$
The dynamical coherence of a partially hyperbolic DA diffeomorphism on
${\mathbb T}^3$
has been substantially investigated; see, for instance, [Reference Brin, Burago and IvanovBBI1, Reference Brin, Burago and IvanovBBI2, Reference Burago and IvanovBI, Reference Fisher, Potrie and SambarinoFiPoSa, Reference Hammerlindl and PotrieHaPo, Reference PotriePo].
Two transverse foliations
$\mathcal {F},\mathcal {G}$
on
${\mathbb R}^3$
have global product structure if for any
$x,y\in {\mathbb R}^3$
, the leaf
$\mathcal {F}(x)$
intersects the leaf
$\mathcal {G}(y)$
at a unique point. Following [Reference FenleyFe, Reference BrinBr], one says that a foliation
$\mathcal {F}$
on
${\mathbb R}^3$
is quasi-isometric if there exist
$a,b>0$
such that for any
$x\in {\mathbb R}^3$
and
$y\in \mathcal {F}(x)$
, one has
$\operatorname {d}_{\mathcal {F}}(x,y)\leq a\cdot \operatorname {d}(x,y)+b$
, where
$\operatorname {d}_{\mathcal {F}}(\cdot ,\cdot )$
denotes the distance on the leaves of
$\mathcal {F}$
and
$\operatorname {d}(\cdot ,\cdot )$
denotes the Euclidean distance. A foliation
$\mathcal {F}$
that satisfies this property is also called quasi-geodesic.
The following result gives the dynamical coherence of a partially hyperbolic hyperbolic DA diffeomorphism and further geometrical properties of the invariant foliations.
Theorem 2.2. [Reference Burago and IvanovBI, Reference HammerlindlHa, Reference PotriePo]
Let
$f\in \operatorname {Diff}^1({\mathbb T}^3)$
be a partially hyperbolic diffeomorphism with the partially hyperbolic splitting
$T{\mathbb T}^3=E^{s}\oplus E^c\oplus E^{u}$
. Assume that
$L_f$
is Anosov. Then one has the following statements:
-
• f has unique foliations
$\mathcal {F}^{cs}$
and
$\mathcal {F}^{cu}$
tangent to
$E^{s}\oplus E^c$
and
$E^c\oplus E^{u}$
, respectively; -
• the lifts of the foliations
$\mathcal {F}^{cs}$
and
$\mathcal {F}^u$
to
${\mathbb R}^3$
have global product structure; -
• the lifts of the foliations
$\mathcal {F}^s,\mathcal {F}^c,\mathcal {F}^u$
to
${\mathbb R}^3$
are quasi-isometric; -
• each leaf of
$\mathcal {F}^c$
is dense in
${\mathbb T}^3$
; -
•
$L_f$
has simple spectrum.
Remark 2.3. [Reference Burago and IvanovBI, Key Lemma 2.1]
gives the existence of two-dimensional foliations transverse to
$E^{u}$
and
$E^{s}$
respectively which is exactly the assumption of [Reference PotriePo, Theorem 1.2].
Notation 2.4. Throughout this paper, for any foliation
$\mathcal {F}$
on
${\mathbb T}^3$
, we will denote by
$\tilde {\mathcal {F}}$
the lift of
$\mathcal {F}$
to
${\mathbb R}^3.$
We denote by
$\operatorname {d}_{\tilde {\mathcal {F}}}(\cdot ,\cdot )$
the distance in a
$\tilde {\mathcal {F}}$
-leaf, and
$$ \begin{align*} \tilde{\mathcal{F}}_r(x)= \{y\in\tilde{\mathcal{F}}(x): \operatorname{d}_{\tilde{\mathcal{F}}}(x,y)<r\}. \end{align*} $$
And we assume the center Lyapunov exponent of
$L_f$
is larger than zero, that is, the stable dimension of
$L_f$
as an Anosov diffeomorphism is
$1$
. Otherwise, we only need to consider
$f^{-1}$
.
As a consequence of the global product structure for the lifted foliations, one has the following result whose proof can be found in [Reference PotriePo, Proposition 6.8].
Corollary 2.5. Let f be as in the assumption of Theorem 2.2. Then there exists a constant
$K>0$
such that for any
$r>0$
, any
$x\in {\mathbb R}^3$
, any
$y\in \tilde {\mathcal {F}}_{r}^{u}(x)$
and any
$w\in \tilde {\mathcal {F}}^{cs}(x)$
, one has that
$\tilde {\mathcal {F}}^u_{r+K}(w)\cap \tilde {\mathcal {F}}^{cs}(y)\neq \emptyset $
.
The analogous result with respect to the strong stable and center unstable foliations holds.
Combining with the result from the previous section, one has the following corollary.
Corollary 2.6. Let f be a
$C^1$
-partially hyperbolic diffeomorphism homotopic to a linear Anosov. Assume that f has the splitting of the form
$TM=E^s\oplus E^c\oplus E^u,$
then for any
$g\in \mathcal {Z}^1(f)$
, each invariant foliation
$\mathcal {F}^*$
of f is invariant under g for
$*=s,cs,c,cu,u.$
Proof By the classical stable manifold theorem and Theorem 2.2, there exist unique invariant foliations
$\mathcal {F}^s$
,
$\mathcal {F}^u$
,
$\mathcal {F}^{cs}$
and
$\mathcal {F}^{cu}$
tangent to
$E^s$
,
$E^u$
,
$E^{cs}$
, and
$E^{cu}$
respectively. For any
$g\in \mathcal {Z}^1(f)$
, by Proposition 2.1, one has that
$g(\mathcal {F}^*)$
is an f-invariant foliation tangent to
$E^*$
for
$*=s,u,cs,cu$
; therefore, one has
$g(\mathcal {F}^*)=\mathcal {F}^*$
for
$*=s,u,cs,cu$
. Finally, on has
$$ \begin{align*}g(\mathcal{F}^c)=g(\mathcal{F}^{cs})\cap g(\mathcal{F}^{cs})=\mathcal{F}^{cs} \cap\mathcal{F}^{cs}=\mathcal{F}^c. \\[-36pt] \end{align*} $$
For a diffeomorphism on the torus, if its linear part is Anosov, then it is semi-conjugate to its linear part.
Theorem 2.7. [Reference FranksFr, Reference WaltersW2]
Let
$f\in \operatorname {Diff}^1({\mathbb T}^d)$
and assume that
$L_f$
is Anosov. Consider a lift F of f to the universal cover
${\mathbb R}^d$
. Then there exists a unique continuous surjective map
$H: {\mathbb R}^d\to {\mathbb R}^d$
such that:
-
•
$H\circ F=L_f\circ H$
; -
•
$H(x+z)=H(x)+z$
, for any
$z\in {\mathbb Z}^d$
and any
$x\in {\mathbb R}^d$
.
As a consequence, one has the following corollary.
Corollary 2.8. Let
$f\in \operatorname {Diff}^1({\mathbb T}^d)$
whose linear part
$L_f$
is Anosov and F be a lift of f to
${\mathbb R}^d$
. Then there exists a continuous surjective map
$H:{\mathbb R}^d\to {\mathbb R}^d$
such that:
-
•
$H\circ F=L_f\circ H$
; -
•
$H(x+z)=H(x)+z$
for any
$x\in {\mathbb R}^d$
and any
$z\in {\mathbb Z}^d$
; -
• for any
$g\in \mathcal {Z}^1(f)$
and any lift G of g to
${\mathbb R}^d$
, if
$F\circ G=G\circ F,$
then
$H\circ G=L_g\circ H.$
Proof Let
$H:{\mathbb R}^d\to {\mathbb R}^d$
be the continuous surjective map given by Theorem 2.7 such that
$H\circ F=L_f\circ H$
and
$H-\operatorname {Id}_{{\mathbb R}^d}$
is
${\mathbb Z}^d$
-periodic. Consider the map
$\widehat {H}=L_g^{-1}\circ H\circ G$
which satisfies that
$\widehat H-\operatorname {Id}_{{\mathbb R}^d}$
is
${\mathbb Z}^d$
-periodic. Then one has
$$ \begin{align*}\widehat H\circ F=L_g^{-1}\circ H\circ G\circ F&=L_g^{-1}\circ H\circ F\circ G=L_g^{-1}\circ L_f\circ H\circ G\\ &=L_f\circ L_g^{-1} \circ H\circ G=L_f\circ \widehat H.\end{align*} $$
By the uniqueness property in Theorem 2.7, one has
$\widehat H=H$
which gives
$H\circ G=L_g\circ ~H$
.
Furthermore, the semi-conjugation preserves certain foliations.
Theorem 2.9. [Reference HammerlindlHa, Reference Hammerlindl and PotrieHaPo, Reference PotriePo, Reference UresU]
Let f be a
$C^1$
-partially hyperbolic diffeomorphism on
${\mathbb T}^3$
which is homotopic to an Anosov automorphism
$L_f$
with two positive Lyapunov exponents. Denote by
$\mathcal {F}^*$
and
$\mathcal {W}^*$
the foliations of f and
$L_f$
respectively, for
$*=s,u,cu,cs,c$
. Let h be the semi-conjugacy between f and
$L_f$
, in formula:
$L_f\circ h=h\circ f.$
Then one has the following properties.
-
(1) For any
$x\in {\mathbb T}^3$
and
$*=cu,cs,c$
, one has
$h(\mathcal {F}^*(x))=\mathcal {W}^*(h(x)).$
-
(2) For any
$x\in {\mathbb T}^3,$
the map
$h|_{\mathcal {F}^{s}(x)}:\mathcal {F}^{s}(x)\rightarrow \mathcal {W}^{s}(h(x))$
is a homeomorphism. -
(3) For any
$x\in {\mathbb T}^3$
, the pre-image
$h^{-1}(h(x))$
is a segment (could be trivial) contained in
$\mathcal {F}^c(x)$
. In particular, for any center leaf
$\mathcal {W}^c(y)$
, there exist at most countably many points whose pre-images under h are non-trivial center segments.
Remark 2.10.
-
(1) This result is obtained in [Reference HammerlindlHa, Reference UresU] assuming absolute partial hyperbolicity, and it is extended to general partially hyperbolic setting in [Reference PotriePo, Appendix A] (see also [Reference Hammerlindl and PotrieHaPo, §3]).
-
(2) The last item implies that f must have fixed points.
-
(3) Each center leaf of f is dense in
${\mathbb T}^3$
.
2.3 Centralizer of linear Anosov automorphisms
The following result comes from [Reference Adler and PalaisAP] (see also [Reference WaltersW1]).
Theorem 2.11. [Reference Adler and PalaisAP]
Let L be a linear Anosov map on
${\mathbb T}^3$
and h be a homeomorphism on
${\mathbb T}^3$
. If
$h\circ L=L\circ h$
, then h is affine.
In particular, Adler and Palais’ result implies that for each Anosov diffeomorphism f on
${\mathbb T}^3$
, there exists a homeomorphism h on
${\mathbb T}^3$
such that for any
$g\in \mathcal {Z}^0(f)$
, one has that
$h\circ g\circ h^{-1}$
is affine. Corollary 2.8 tells us that such results hold for semi-conjugacy to Anosov case.
The following result gives the rank of the group of linear automorphisms commuting with an Anosov automorphism, and it comes from [Reference Damjanovic, Wilkinson and XuDWX, Reference Katok, Katok and SchmidtKKS].
Lemma 2.12. [Reference Katok, Katok and SchmidtKKS, Proposition 3.7]
Consider a matrix
$L\in SL(n,{\mathbb Z})$
whose characteristic polynomial is irreducible over
${\mathbb Z}$
. Then the group
$\mathcal {G}(L)=\{L_1\in SL(n,{\mathbb Z}): LL_1=L_1L\}$
is abelian. Moreover,
$\mathcal {G}(L)$
is virtually
${\mathbb Z}^{r+c-1}$
, where r is the number of real eigenvalues of L and
$2c$
is the number of complex eigenvalues of L.
In our paper all the linear Anosov maps we consider have real simple spectrum. It is easy to see that these linear Anosov maps are irreducible in the sense that their characteristic polynomials are irreducible over
${\mathbb Z}$
.Footnote
1
Therefore, their centralizers are virtually
${\mathbb Z}^2$
by Theorem 2.11 and Lemma 2.12.
Corollary 2.13. Let
$f\in \text {Diff}^1(\mathbb {T}^3)$
be a partially hyperbolic diffeomorphism with Anosov linear part
$L_f\in \text {GL}(3,\mathbb {Z})$
. Then the
$C^0$
-centralizer
$\mathcal {Z}^0(L_f)$
of
$L_f$
is virtually
$\mathbb {Z}^2$
.
Moreover, the non-trivial elements in the centralizer is also Anosov.
Lemma 2.14. Let
$A\in SL(3,{\mathbb Z})$
be an Anosov automorphism. For any
$B\in SL(3,{\mathbb Z})$
, if
$AB=BA$
, then either
$B=\operatorname {Id}$
or B is Anosov.
Proof If
$B\in SL(3,{\mathbb Z})$
has eigenvalues of modulus
$1$
, then
$1$
is an eigenvalue of B since
$\operatorname {det}(B)=1$
. And there exists a rational vector
$0\neq v$
such that
$Bv=v$
. For any eigenvector w of B with respective to
$1$
, one has that
$BAw=ABw=Aw$
, which implies that the eigenvector space of B with respect to
$1$
is invariant under A; in particular. the rational vector
$Av$
is also an eigenvector of B with respect to the eigenvalue
$1$
and is not collinear to v, since A is Anosov and v is rational. Then the two-dimensional linear space generated by
$Av$
and v has rational slope and is contained in the eigenspace of B with respect to the eigenvalue
$1$
. Once again, as A is Anosov (in particular, irreducible), the linear space generated by
$Av$
and v is not A-invariant, which implies that each vector in
${\mathbb R}^3$
is in the eigenspace of B with respect to eigenvalue
$1$
. Hence B is the identity.
2.4 Regularity
Now, we collect some regularity lemmas showing that if a homeomorphism is differentiable along pairs of transverse foliations up to certain order, then the homeomorphism is differentiable.
Lemma 2.15. [Reference JournéJ]
Let M be a closed manifold and h be a homeomorphism on M. Assume that there exist two transverse continuous foliations
$\mathcal {F}$
and
$\mathcal {G}$
on M with
$C^r$
-leaves, and h is uniformly
$C^r$
when restricted to leaves of
$\mathcal {F}$
and
$\mathcal {G}$
. Then h is
$C^{r-{\varepsilon }}$
for any
${\varepsilon }>0$
.
Remark 2.16. If r is not an integer, then h is
$C^r$
. If r is an integer, then h is
$C^{r-1+\text {Lip}}$
.
One says that a foliation
$\mathcal {F}$
with
$C^1$
-leaves is expanding for
$f\in \operatorname {Diff}^1(M)$
if
$\mathcal {F}$
is f-invariant and there exists
$N\in {\mathbb N}$
such that
$\|Df^{-N}|_{T_x\mathcal {F}(x)}\|\leq \tfrac {1}{2},$
for any
$x\in M$
.
Lemma 2.17. [Reference GogolevGo2, Lemma 2.4]
Let
$f,g$
be two
$C^r$
-diffeomorphisms on a closed manifold
$M.$
Let
$\mathcal {F}, \mathcal {G}$
be one-dimensional expanding foliations with
$C^r$
-leaves for f and g, respectively. Assume that there exists a homeomorphism h on M such that:
-
•
$h\circ f=g\circ h$
and
$h(\mathcal {F})=\mathcal {G}$
; -
• h and its inverse are uniformly
$C^1$
along the leaves of
$\mathcal {F}$
and
$\mathcal {G}$
, respectively.
Then h is uniformly
$C^r$
along the leaves of
$\mathcal {F}$
and
$h^{-1}$
is uniformly
$C^r$
along the leaves of
$\mathcal {G}.$
2.5 Accessibility
Given a partially hyperbolic diffeomorphism
$f\in \operatorname {Diff}^1(M)$
and a point
$x\in M$
, the accessible class
$\operatorname {Acc}(x)$
of x is defined as the set of points which can be joined to x by paths which are concatenations of paths in a strong stable or strong unstable manifold. By definition,
$\operatorname {Acc}(x)$
is saturated by strong stable and strong unstable leaves. One says that f is accessible if any two points
$x,y\in M$
can be connected by a path
$\gamma $
which is a concatenation of paths in strong stable or strong unstable manifolds of f; in other words, the accessible class of a point is the whole manifold.
For a partially hyperbolic diffeomorphism f, the bundles
$E^s$
and
$E^u$
are jointly integrable, if there exists an f-invariant foliation tangent to
$E^s\oplus E^u$
everywhere. In this case, we call
$f\ su$
-integrable or
$su$
-jointly-integrable.
It has been proved in [Reference DidierDi] that if f is accessible, then
$E^s\oplus E^u$
is not jointly integrable. Moreover, if f has one-dimensional center, then there exists a point
$x\in M$
with the local accessibility property as follows.
Lemma 2.18. [Reference DidierDi, Reference Rodriguez Hertz, Rodriguez Hertz and UresHHU]
Let f be a
$C^1$
-partially hyperbolic diffeomorphism on M. If f is accessible and the center bundle is one-dimensional, then there exist
$r_0>0, r_1>0$
which can be arbitrarily small, and
$x\in M$
such that fir any center curve
$I_{r_1}^c(x)$
centered at x of radius
$r_1$
, there exist
$x^s,x^{su}, x^{sus}\in M$
and
$x^c\in I_{r_1}^c(x)$
such that:
-
•
$x^s\in \mathcal {F}^{s}_{r_0}(x)$
and
$x^{su}\in \mathcal {F}^{u}_{r_0}(x^s)$
, -
•
$x^{sus}\in \mathcal {F}^s_{r_0}(x^{su})$
and
$x^c\in \mathcal {F}^u_{r_0}(x^{sus})$
,
where
$\mathcal {F}^*_{r}(z)$
denotes the r-neighborhood of z in the leaf
$\mathcal {F}^*(z)$
for
$*=s,u$
.
Moreover, let
$I^c(x,x^c)$
denote the set of all points located between x and
$x^c$
in
$I_{r_1}^c(x)$
. Then
$\operatorname {Acc}(x)$
contains an open set U close to x, that is,
$$ \begin{align*} U~\subseteq~ \bigcup_{y\in I^c(x,x^c)} \bigcup_{z\in\mathcal{F}^s_{\text{loc}}(y)}\mathcal{F}^u_{\text{loc}}(z) ~\subseteq~ \operatorname{Acc}(x). \end{align*} $$
Each point in U can be connected to x by a local
$su$
-path contained in a small neighborhood of x.
If a diffeomorphism
$f:M\rightarrow M$
is partially hyperbolic, and
$\pi :\tilde M\rightarrow M$
is a covering map, then any lift
$\tilde f:\tilde M\rightarrow \tilde M$
is also partially hyperbolic. And the partially hyperbolic splitting on
$\tilde M$
is defined by pulling back the splitting on M:
$$ \begin{align*} T\tilde M=\pi^*(E^s)\oplus \pi^*(E^c)\oplus \pi^*(E^u). \end{align*} $$
The following result tells us that the accessibility is preserved under lifts of the manifold.
Lemma 2.19. Let
$f\in \operatorname {Diff}^1(M)$
be an accessible partially hyperbolic diffeomorphism, and assume that the center bundle is one-dimensional. Consider a covering map
$\pi : \tilde M\to M$
from a connected manifold
$\tilde M$
to M, and a lift
$\tilde f$
of f to
$\tilde M$
. Then
$\tilde f$
is accessible.
Proof Notice that the lifts of the strong stable and unstable foliations to
$\tilde M$
are the strong stable and unstable foliations of
$\tilde f$
. Since f is accessible, Lemma 2.18 shows that there exists
$x\in M$
with the local accessibility property.
This implies for every
$\tilde x\in \pi ^{-1}(x)$
, that the accessibility class
$\operatorname {Acc}(\tilde {x})$
with respect to
$\tilde f$
contains an open set close to
$\tilde x$
. If an accessible class contains an open set, then it is open. Thus
$\operatorname {Acc}(\tilde x)$
is open for every
$\tilde x\in \pi ^{-1}(x)$
.
On the other hand, for every
$\tilde y\in \tilde M$
, since
$\pi (y)\in M$
can be connected to x by an
$su$
-path,
$\tilde y$
can be connected to a point
$\tilde x\in \pi ^{-1}(x)$
by an
$su$
-path. This implies
$$ \begin{align*}\tilde M=\bigcup_{\tilde x\in\pi^{-1}(x)}\operatorname{Acc}(\tilde{x}). \end{align*} $$
Since
$\tilde M$
is connected and each
$\operatorname {Acc}(\tilde {x})$
is open, we must have
$\tilde M=\operatorname {Acc}(\tilde {x})$
for every
$\tilde x\in \pi ^{-1}(x)$
. Thus
$\tilde f$
is accessible.
The following result gives equivalence conditions for the joint integrability of strong stable and unstable distributions.
Theorem 2.20. ([Reference Gan and ShiGS, Theorem 1.1] and [Reference Hammerlindl and ShiHaS])
Let f be a
$C^r$
(
$r>1$
) partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov. The following statements are equivalent.
-
• Strong stable and unstable distributions of f are jointly integrable.
-
• Each periodic orbit of f has same center Lyapunov exponent as
$L_f$
, and f is Anosov. -
• f is not accessible.
Remark 2.21.
-
• Under the volume-preserving assumption, Hammerlindl and Ures [Reference Hammerlindl and UresHaU] proved that the first and third items are equivalent; in particular, f is topological Anosov;
-
• The equivalence of the first and second items is obtained in [Reference Gan and ShiGS] under the volume-preserving setting. Then the volume-preserving condition is removed by [Reference Hammerlindl and ShiHaS] and the third equivalent item is obtained in [Reference Hammerlindl and ShiHaS].
2.6 Equivalent conditions for
$su$
-integrability of an Anosov map
In this part, we collect the consequences of
$su$
-joint-integrability for Anosov diffeomorphisms on
${\mathbb T}^3$
, which is proved in [Reference Ren, Gan and ZhangGRZ, Reference Gan and ShiGS].
Theorem 2.22. [Reference Gan and ShiGS, Theorem 5.1]
Let f be a
$C^r$
(
$r>1$
) partially hyperbolic and Anosov diffeomorphism on
${\mathbb T}^3$
. Let h be the conjugacy between f and
$L_f$
. Then the following statements are equivalent:
-
• f is
$su$
-integrable; -
• f is not accessible;
-
• h preserves the strong stable and strong unstable foliations;
-
• the center Lyapunov exponent of any periodic point p of f coincides with the center Lyapunov exponent of
$L_f$
; -
• h is differentiable along the center leaves of f.
Remark 2.23. When the conjugacy preserves the strong foliations, one can show that h and
$h^{-1}$
is uniformly Hölder continuous along the leaves of strong foliations (see for instance Lemma 2.3 in [Reference Gan and ShiGS]).
Now, we state the following result which is essentially [Reference Gan and ShiGS, Proposition 4.1]. For completeness, we will give the proof in Appendix A.
Theorem 2.24. Let g be a
$C^r$
(
$r>1$
) Anosov diffeomorphism on
${\mathbb T}^3$
and let
$h\in \operatorname {Homeo}({\mathbb T}^3)$
such that
$h\circ g=L_g\circ h$
. Assume that:
-
• there exists a
$Dg$
-invariant continuous splitting
$E^s\oplus E^c\oplus E^u$
; -
• g is uniformly contracting along
$E^s$
and is uniformly expanding along
$E^c\oplus E^u$
; -
• there exist g-invariant foliations
$\mathcal {F}^c$
,
$\mathcal {F}^u$
and
$\mathcal {F}^{su}$
tangent to
$E^c$
,
$E^u$
and
$E^s\oplus E^u$
respectively; -
•
$L_g$
is partially hyperbolic; -
• h sends
$\mathcal {F}^c, \mathcal {F}^u$
to the center, strong unstable foliations of
$L_g$
respectively; -
• the holonomy map given by
$\mathcal {F}^u$
restricted to each unstable leaf between two local plaques tangent to
$E^c$
at a uniform bounded distance is uniformly
$C^1$
.
Then the Lyapunov exponent along
$E^c$
of any periodic point p is the same as the center Lyapunov exponent of
$L_g$
, and h is uniformly
$C^1$
along the leaves of
$\mathcal {F}^c$
.
Remark 2.25. In the statement of Theorem 2.24, we do not assume the splitting
$E^c\oplus E^u$
is dominated.
3 Centralizer of partially hyperbolic DA diffeomorphism: Proofs of Theorems 1.2 and 1.3
In this section we give the proof of our main theorems. We denote by
$\mathcal {L}:\text {Diff}^r(\mathbb {T}^3)\rightarrow \text {GL}(3,\mathbb {Z})$
the linearization operator, that is, for every
$g\in \text {Diff}^r(\mathbb {T}^3)$
,
$\mathcal {L}(g)=L_g$
is the action induced by g on
$\pi _1(\mathbb {T}^3)=\mathbb {Z}^3$
. For every
$f\in \text { Diff}^r(\mathbb {T}^3)$
,
$\mathcal {L}$
induces a group homomorphism
$$ \begin{align*} \mathcal{L}: ~\mathcal{Z}^r(f) &~\longrightarrow~ \text{GL}(3,\mathbb{Z}), \\ g &~\longmapsto~ L_g. \end{align*} $$
The image of
$\mathcal {Z}^r(f)$
by
$\mathcal {L}$
satisfies
$$ \begin{align*}\mathcal{L}(\mathcal{Z}^r(f))= \{L_g: g\in\mathcal{Z}^r(f)\} ~\subseteq~ \text{GL}(3,\mathbb{Z})\cap \mathcal{Z}^0(L_f), \end{align*} $$
which is a subgroup in both
$\text {GL}(3,\mathbb {Z})$
and
$\mathcal {Z}^0(L_f)$
.
Let
$$ \begin{align*} \mathcal{Z}^r_0(f)=\{g\in\mathcal{Z}^r(f): g \text{ is homotopic to the identity} \}. \end{align*} $$
Then
$\mathcal {Z}^r_0(f)$
is subgroup of
$\mathcal {Z}^r(f)$
. In particular, one has
$$ \begin{align*}\mathcal{Z}^r(f)/\mathcal{Z}^r_0(f)~\cong~\mathcal{L}(\mathcal{Z}^r(f)). \end{align*} $$
In §3.1, we show that
$\mathcal {L}(\mathcal {Z}^r(f))$
is abelian and virtually
$\mathbb {Z}^2$
or
$\mathbb {Z}$
. Then we prove that
$\mathcal {Z}^r_0(f)$
is finite in §3.2. The index of
$\mathcal {Z}^r_0(f)$
satisfies
$$ \begin{align*}\#\mathcal{Z}^r_0(f)\leq|\text{det}(L_f-\text{Id}_{\mathbb{R}^3})|. \end{align*} $$
Recall that
$\mathcal {L}(\mathcal {Z}^r(f))$
always contains
$<L_f>\cong \mathbb {Z}$
which is induced by
${<}f{>}\subseteq \mathcal {Z}^r(f)$
. If
$\mathcal {L}(\mathcal {Z}^r(f))$
is virtually
$\mathbb {Z}$
, then we show
$\mathcal {Z}^r(f)$
is virtually trivial, which is the first case of Theorem 1.3. Finally, we discuss the case where
$\mathcal {L}(\mathcal {Z}^r(f))$
is virtually
$\mathbb {Z}^2$
in §3.3, and we show that f is smoothly conjugate to
$L_f$
in this case.
3.1 Preliminary lemmas
The lifts of two commutable diffeomorphisms may not be commutable. The following result tells us that the lifts of the centralizer of partially hyperbolic DA diffeomorphisms, up to finite iterates, are still in the centralizer of the lifted diffeomorphism.
Lemma 3.1. Let f be a
$C^1$
-partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov, and let F be a lift of f to
${\mathbb R}^3$
.
Then for any
$g\in \mathcal {Z}^1(f)$
, there exist an integer
$0<l\leq |\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
and a lift
$\widehat G$
of
$g^l$
such that
$F\circ \widehat G=\widehat G\circ F.$
Furthermore, if g is homotopic to the identity, then l can be chosen as a factor of
$|\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
.
Proof Let
$p_1,\ldots ,p_k\in {\mathbb T}^3$
be all the fixed points of
$L_f.$
It is classical that
$k=|\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
. Let
$H:{\mathbb R}^3\to {\mathbb R}^3$
be the semi-conjuacy between F and
$L_f$
given by Theorem 2.7, and let
$h:{\mathbb T}^3\to {\mathbb T}^3$
be the map induced by H. Then the set of fixed points of f is contained in
$\bigcup _{i=1}^k h^{-1}(p_i)$
and each
$h^{-1}(p_i)$
is f-invariant. By Theorem 2.9, each
$h^{-1}(p_i)$
is a compact center segment (could be trivial). By the Brouwer fixed point theorem, f has fixed points in each
$h^{-1}(p_i)$
. Let
$I_i\subset h^{-1}(p_i)$
be the shortest connected and compact center segment (could be trivial) containing all fixed points of f in
$h^{-1}(p_i)$
. Then the two endpoints of
$I_i$
are fixed points of f.
Let
$\pi :{\mathbb R}^3\to {\mathbb T}^3$
be the canonical covering map. Without loss of generality, one can assume that
$p_1$
is the projection of
$0\in {\mathbb R}^3$
under
$\pi $
, that is,
$\pi (0)=p_1.$
Since
$g\in \mathcal {Z}^1(f)$
, by Corollary 2.6, g preserves the center foliation of f. As the set of fixed points of f is g-invariant, for each
$i\in \{1,\ldots ,k \}$
, there exists
$j\in \{1,\ldots , k \}$
such that
$g(I_i)=I_j$
which defines a permutation on
$\{1,\ldots , k\}.$
Therefore, there exists
$0<l\leq k$
such that
$g^{l}(I_1)=I_1$
. If
$g^l$
preserves the orientation of the center bundle, then the two endpoints of
$I_1$
are fixed points of f and
$g^l$
. If
$g^l$
reverses the orientation of the center bundle, then
$g^l$
has a unique fixed point in
$I_1$
which is also a fixed point of f since
$g^l(I_1)=f(I_1)=I_1$
and
$g\in \mathcal {Z}^1(f)$
. To summarize, f and
$g^l$
have a common fixed point
$q_1\in I_1$
. Notice that
$\widehat q_1=H^{-1}(0)\cap \pi ^{-1}(q_1)$
is a fixed point of F. Since
$q_1$
is a fixed point of
$g^l$
, there exists a lift
$\widehat G$
of
$g^l$
such that
$\widehat G(\widehat q_1)=\widehat q_1.$
Observe that
$F\circ \widehat G\circ F^{-1}\circ \widehat G^{-1}$
is a lift of the identity map on
${\mathbb T}^3$
and has a fixed point
$\widehat q_1$
, hence
$F\circ \widehat G=\widehat G\circ F.$
Now, we assume that g is homotopic to the identity. Let G be a lift of g to
${\mathbb R}^3.$
Since
$f\circ g=g\circ f$
, there exists
$n\in {\mathbb Z}^3$
such that
$F\circ G=G\circ F+n.$
Since
$L_f$
is Anosov, the linear map
$L_f-\operatorname {Id}_{{\mathbb R}^3}$
is invertible. Let
$m=(L_f-\operatorname {Id}_{{\mathbb R}^3})^{-1}n\in {\mathbb Q}^3$
. Then there exists an integer
$l>0$
which is a factor of
$|\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
such that
$l\cdot m\in {\mathbb Z}^3$
. Since g is homotopic to the identity, then
$F\circ G^l=G^l\circ F+ln$
. Now, let
$\widehat G=G^l-l\cdot m$
which is a lift of
$g^l$
, and one has
$$ \begin{align*} F\circ\widehat G=F\circ(G^l-lm)&=F\circ G^l-L_f(lm)=F\circ G^l-ln-lm \\ &=G^l\circ F-lm=\widehat G\circ F, \end{align*} $$
which ends the proof.
The following result discusses the existence of common fixed points for lifted dynamics.
Lemma 3.2. Let f be a
$C^1$
-partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov, and let
$g\in \mathcal {Z}^1(f)$
. Assume that there exist a lift F of f to
${\mathbb R}^3$
and a lift G of g to
${\mathbb R}^3$
such that
$F\circ G=G\circ F$
. Then F and G have a common fixed point, that is, there exists
$p\in {\mathbb R}^3$
such that
$F(p)=G(p)=p$
.
Proof By Corollary 2.6, the center foliation of F is G-invariant. Let
$H:{\mathbb R}^3\to {\mathbb R}^3$
be the continuous surjective map given by Corollary 2.8 such that:
-
•
$H\circ F= L_f\circ H$
and
$H\circ G=L_g\circ H;$
-
•
$H-\operatorname {Id}_{{\mathbb R}^3}$
is
${\mathbb Z}^3$
-periodic.
As
$L_f$
and
$L_g$
have a unique fixed point
$0\in {\mathbb R}^3$
, all the fixed points of F and G are contained in
$H^{-1}(0)$
. By Theorem 2.9,
$H^{-1}(0)$
is a compact and F-invariant center segment.
As F commutes with G, the set of fixed points of F is G-invariant and vice versa. If F reverses the orientation of the center bundle, by the fact that
$\operatorname {dim}(E^c)=1$
, F has a unique fixed point in
$H^{-1}(0)$
which is also a fixed point of G. If G reverses the orientation of the center bundle, one concludes analogously. If F and G preserve the orientation of the center bundle, the endpoints of
$H^{-1}(0)$
are the fixed points of F and G, proving the existence of common fixed points.
The following lemma tells us that the linearization of the centralizer is virtually
${\mathbb Z}$
or
${\mathbb Z}^2.$
Lemma 3.3. Let f be a partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part is Anosov. Then the group
$\{L_g\in GL(3,{\mathbb Z}): g\in \mathcal {Z}^r(f) \}$
is abelian and is virtually
${\mathbb Z}$
or
${\mathbb Z}^2.$
Proof Since f is partially hyperbolic, its linear part
$L_f$
has real simple spectrum. By Lemma 2.12, the group
$$ \begin{align*}\{L_g\in GL(3,{\mathbb Z}): g\in\mathcal{Z}^r(f) \}\subset\{B\in GL(3,{\mathbb Z}): L_fB=BL_f\}\end{align*} $$
is abelian and virtually
${\mathbb Z}^2$
or
${\mathbb Z}.$
3.2 The centralizer
$\mathcal {Z}^r(f)$
is virtually isomorphic to its linearization
In this part, we discuss the relationship between
$\mathcal {Z}^r(f)$
and its linearization
$\{L_g: g\in \mathcal {Z}^r(f) \}$
, and we prove that the centralizer
$\mathcal {Z}^r(f)$
is virtually isomorphic to
$\{L_g: g\in \mathcal {Z}^r(f) \}$
.
Theorem 3.4. Let f be a
$C^r$
(
$r>1$
) partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov. Then one has that:
-
• for each
$g\in \mathcal {Z}^r(f)$
which is homotopic to the identity, there exists an integer
$l=l_g$
which is a factor of
$|\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
such that
$g^l=\operatorname {Id}_{{\mathbb T}^3}$
; -
•
$\#\{g\in \mathcal {Z}^r(f): g \text { is homotopic to } \operatorname {Id}_{{\mathbb T}^3} \}\leq |\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|.$
Before giving the proof of Theorem 3.4, we need to make some preparations. We first show that if
$g\in \mathcal {Z}^r(f)$
is homotopic to the identity and a lift of g admits a fixed point on
${\mathbb R}^3$
, then g is the identity.
Proposition 3.5. Let
$f\in \operatorname {Diff}^r({\mathbb T}^3)$
(
$r>1$
) be a partially hyperbolic diffeomorphism and
$g\in \mathcal {Z}^r(f)$
. Make the following assumptions.
-
• The linear part
$L_f$
of f is Anosov. -
• There exists a lift
$G:{\mathbb R}^3\to {\mathbb R}^3$
of g with the following properties:-
–
$G(x+n)=G(x)+n$
for any
$x\in {\mathbb R}^3$
and
$n\in {\mathbb Z}^3$
; -
– G admits a fixed point
$q\in {\mathbb R}^3$
.
-
Then
$G=\operatorname {Id}_{{\mathbb R}^3}.$
Proof By Corollary 2.6 and the fact that
$G-\operatorname {Id}_{{\mathbb R}^3}$
is
${\mathbb Z}^3$
-periodic, one has
$$ \begin{align*}G(\tilde{\mathcal{F}}^c(q+n))=\tilde{\mathcal{F}}^c(q+n)=\tilde{\mathcal{F}}^c(q)+n\quad \text{ for any } n\in{\mathbb Z}^3.\end{align*} $$
By the third item of Remark 2.10, the set
$\{\tilde {\mathcal {F}}^c(q+n)\}_{n\in {\mathbb Z}^3}$
is dense in
${\mathbb R}^3$
.
The following claim tells us that G is center fixing.
Claim 3.6. For any
$x\in {\mathbb R}^3$
, the center leaf
$\tilde {\mathcal {F}}^c(x)$
is fixed by G.
Proof of the claim As the set
$\{\tilde {\mathcal {F}}^c(q+n)\}_{n\in {\mathbb Z}^3}$
is dense in
${\mathbb R}^3$
, for any
$x\in {\mathbb R}^3$
, there exists a sequence of points
$x_k\in \{\tilde {\mathcal {F}}^c(q+n)\}_{n\in {\mathbb Z}^3}$
such that
$x_k$
converges to x. Since
$G-\operatorname {Id}_{{\mathbb R}^3}$
is
${\mathbb Z}^3$
-periodic, there exists
$\ell _0>0$
such that
$\operatorname {d}(G(y),y)\leq \ell _0$
for any
$y\in {\mathbb R}^3$
. Since the center foliation
$\tilde {\mathcal {F}}^c$
is quasi-isometric, there exist
$a,b>0$
such that for any
$x,y\in {\mathbb R}^3$
with
$x\in \tilde {\mathcal {F}}^c(y)$
, one has
$\operatorname {d}_{\tilde {\mathcal {F}}^c}(x,y)\leq a\cdot \operatorname {d}(x,y)+b.$
Since the center leaf
$\tilde {\mathcal {F}}^c(x_k)$
is G-invariant, one has
$$ \begin{align*}\operatorname{d}_{\tilde{\mathcal{F}}^c}(G(x_k),x_k)\leq a\operatorname{d}(G(x_k),x_k)+b\leq a\ell_0+b.\end{align*} $$
Let
$\ell _1=a\ell _0+b.$
By the continuity of the center foliation,
$\tilde {\mathcal {F}}_{\ell _1}^c(x_k)$
converges to
$\tilde {\mathcal {F}}^c_{\ell _1}(x)$
. By the continuity of G and the fact that
$G(x_k)\in \tilde {\mathcal {F}}_{\ell _1}^c(x_k)$
, one has
$G(x)\in \tilde {\mathcal {F}}^c_{\ell _1}(x)$
, proving that the center leaf
$\tilde {\mathcal {F}}^c(x)$
is fixed by G.
Claim 3.7. For any fixed point
$x_0$
of G, one has
$$ \begin{align*}G|_{\tilde{\mathcal{F}}^s(x_0)\cup\tilde{\mathcal{F}}^u(x_0)}=\operatorname{Id}|_{\tilde{\mathcal{F}}^s(x_0)\cup\tilde{\mathcal{F}}^u(x_0)}.\end{align*} $$
Proof of the claim By Theorem 2.2, the foliations
$\tilde {\mathcal {F}}^{cu}$
and
$\tilde {\mathcal {F}}^{s}$
have global product structure, hence for any point
$x\in {\mathbb R}^3$
and any point
$y\in \tilde {\mathcal {F}}^{cs}(x)$
, the center leaf
$\tilde {\mathcal {F}}^c(y)$
intersects
$\tilde {\mathcal {F}}^s(x)$
at a unique point.
Now, let
$x_0$
be a fixed point of G. By Corollary 2.6, one has
$G(\tilde {\mathcal {F}}^s(x_0))=\tilde {\mathcal {F}}^s(x_0)$
and
$G(\tilde {\mathcal {F}}^u(x_0))=\tilde {\mathcal {F}}^u(x_0)$
. One only needs to show that G restricted to
$\tilde {\mathcal {F}}^s(x_0)$
is the identity, and the case for the strong unstable manifold works analogously. By Claim 3.6, for any
$z\in \tilde {\mathcal {F}}^s(x_0)\subset \tilde {\mathcal {F}}^{cs}(x_0)$
, one has
$G(\tilde {\mathcal {F}}^c(z))=\tilde {\mathcal {F}}^c(z)$
. As
$\tilde {\mathcal {F}}^c(z)$
intersects
$\tilde {\mathcal {F}}^s(x_0)$
at a unique point, by the fact that
$G(\tilde {\mathcal {F}}^s(x_0))=\tilde {\mathcal {F}}^s(x_0),$
one has
$\{G(z)\}=G(\tilde {\mathcal {F}}^c(z)\cap \tilde {\mathcal {F}}^s(x_0))=\tilde {\mathcal {F}}^c(z)\cap \tilde {\mathcal {F}}^s(x_0)=\{z\}.$
Now, we show that G is the identity. As
$\operatorname {Acc}(q)$
is saturated by strong stable and strong unstable leaves and q is a fixed point of G, by Claim 3.7, the map G coincides with the identity on
$\operatorname {Acc}(q)$
. There are two cases to discuss according to the accessibility property.
If f is accessible, by Lemma 2.19, each lift of f to the universal cover is also accessible, hence
$\operatorname {Acc}(q)={\mathbb R}^3$
which implies
$G=\operatorname {Id}_{{\mathbb R}^3}.$
If f is not accessible, by Theorem 2.20, f is Anosov. Consider a projection p of the fixed point G on
${\mathbb T}^3$
. Then g coincides with the identity on the union of the strong stable and unstable manifolds of p. As f is Anosov, then the union of the strong stable and unstable manifolds of p is dense in
${\mathbb T}^3$
, hence
$g=\operatorname {Id}_{{\mathbb T}^3}$
which in return implies
$G=\operatorname {Id}_{{\mathbb R}^3}$
since G has fixed points. Now the proof of Proposition 3.5 is completed.
As a consequence, one has the following corollary.
Corollary 3.8. Let
$f\in \operatorname {Diff}^r({\mathbb T}^3)$
(
$r>1$
) be a partially hyperbolic diffeomorphism whose linear part
$L_f$
is Anosov, and let
$g\in \mathcal {Z}^r(f)$
. If g is homotopic to the identity, then there exists
$l\in {\mathbb N}$
which is a factor of
$|\!\operatorname{det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
such that
$g^l=\operatorname {Id}_{{\mathbb T}^3}.$
Proof Consider a lift of F of f to
${\mathbb R}^3$
. Let
$g\in \mathcal {Z}^r(f)$
be a diffeomorphism homotopic to the identity. By Lemma 3.1, there exist a positive integer l which is a factor of
$|\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
and a lift
$\widehat G$
of
$g^l$
to
${\mathbb R}^3$
such that
$F\circ \widehat G=\widehat G\circ F.$
By Lemma 3.2,
$\widehat G$
admits fixed points, hence
$\widehat G$
satisfies the assumption of Proposition 3.5, which gives that
$ g^l=\operatorname {Id}_{{\mathbb T}^3}.$
Remark 3.9. Notice that Lemmas 3.1 and 3.2 are stated for
$C^1$
-partially hyperbolic DA diffeomorphisms. By the proof of Proposition 3.5, Corollary 3.8 holds for
$C^1$
-partially hyperbolic DA diffeomorphisms provided that they are accessible, as one only requires the regularity with
$r>1$
when dealing with the non-accessible case.
We have obtained the first item in Theorem 3.4. The following result completes the proof of Theorem 3.4.
Proposition 3.10. Let f be a
$C^r$
(
$r>1$
) partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov. Then
$$ \begin{align*} \#\{g\in\mathcal{Z}^r(f): g \text{ is homotopic to the identity}\}\leq |\!\operatorname{det}(L_f-\operatorname{Id}_{{\mathbb R}^3})|. \end{align*} $$
Proof Let
$p_1,\ldots , p_k$
be all the fixed points of
$L_f$
, where
$k=|\!\operatorname {det}(L_f-\operatorname {Id})|$
. Consider the semi-conjugacy
$h:{\mathbb T}^3\to {\mathbb T}^3$
between f and
$L_f$
which is homotopic to the identity. Then all the fixed points of f are contained in
$\bigcup _{i=1}^kh^{-1}(p_i)$
, and
$h^{-1}(p_i)$
is an f-invariant center segment. Let
$I_i$
be the smallest connected segments containing all fixed points of f in
$h^{-1}(p_i)$
. If f reverses the orientation of the center foliation, then each
$I_i$
is reduced to a single point. Since
$\mathcal {F}^c$
is orientable, we give it an orientation. Let
$I_i=[a_i,b_i]^c$
such that the direction from
$a_i$
to
$b_i$
gives the positive orientation. Let
$\mathcal {E}=\{a_i\}_{i=1}^k$
.
For any
$g\in \mathcal {Z}^r(f)$
which is homotopic to the identity, by Corollary 2.6, the center foliation
$\mathcal {F}^c$
is g-invariant and g preserves the orientation of
$\mathcal {F}^c.$
Therefore for each
$i\in \{1,\ldots , k\}$
, there exists
$j\in \{1,\ldots , k\}$
such that
$g(I_i)=I_j$
and
$g(a_i)=a_j$
.
Claim 3.11. For any
$g\in \mathcal {Z}^r(f)$
which is homotopic to the identity, if there exists some
$i\in \{1,\ldots , k\}$
such that
$g(a_i)=a_i$
, then
$g=\operatorname {Id}_{{\mathbb T}^3}.$
Proof of the claim Let
$\tilde {a}_i\in {\mathbb R}^3$
be lift of
$a_i$
. As
$a_i$
is a fixed point for g, there exists a lift G of g such that
$G(\tilde {a}_i)=\tilde {a}_i$
. Since
$g\in \mathcal {Z}^r(f)$
is homotopic to the identity, by Proposition 3.5, one has
$G=\operatorname {Id}_{{\mathbb R}^3},$
hence
$g=\operatorname {Id}_{{\mathbb T}^3}.$
Claim 3.12. For any
$i,j\in \{1,\ldots ,k\}$
, there exists at most one
$g\in \mathcal {Z}^r(f)$
such that:
-
•
$g(a_i)=a_j$
; -
• g is homotopic to the identity.
Proof of the claim Assume that there exist
$i,j\in \{1,\ldots , k\}$
and two diffeomorphisms
$g_1,g_2\in \mathcal {Z}^r(f)$
such that:
-
•
$g_1(a_i)=g_2(a_i)=a_j$
; -
•
$g_1$
and
$g_2$
are homotopic to the identity.
Let
$g=g_1\circ g^{-1}_2$
. Then
$g\in \mathcal {Z}^r(f)$
is homotopic to the identity and has
$a_j$
as a fixed point. By Claim 3.11,
$g=\operatorname {Id}_{{\mathbb T}^3},$
hence
$g_1=g_2.$
By Claims 3.11 and 3.12, and the fact that
$g\in \mathcal {Z}^r(f)$
which is homotopic to the identity must send
$a_1$
to some
$a_j$
, one has
$$ \begin{align*}\#\{g\in\mathcal{Z}^r(f): g \text{ is homotopic to the identity} \}\leq k=|\!\operatorname{det}(L_f-\operatorname{Id}_{{\mathbb R}^3})|. \\[-36pt] \end{align*} $$
3.3 The linearization of the centralizer is virtually
${\mathbb Z}^2$
: rigidity case
In this section we discuss the case where the linear part of the centralizer
$$ \begin{align*}\mathcal{L}(\mathcal{Z}^r(f))=\{L_g: g\in\mathcal{Z}^r(f) \} \end{align*} $$
is virtually
${\mathbb Z}^2$
. The following theorem is the main result of this section.
Theorem 3.13. Let f be a
$C^r$
(
$r>1$
) partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov. If there exists
$g\in \mathcal {Z}^r(f)$
such that
$L_g^m\notin \{ L_f^n\}_{n\in {\mathbb Z}}$
for any
$m\neq 0$
, then f is
$C^{r-{\varepsilon }}$
-conjugate to
$L_f$
for every
${\varepsilon }>0$
.
The proof of the following result is a standard fact for Cartan
$\mathbb {Z}^2$
-linear action on
$\mathbb {T}^3$
, and for completeness we give a sketch of the its proof.
Corollary 3.15. Let f be a
$C^1$
partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov. If there exists
$g\in \mathcal {Z}^1(f)$
such that
$L_g^m\notin \{ L_f^n\}_{n\in {\mathbb Z}}$
for any
$m\neq 0$
, then there exists
$\tilde {g}\in \mathcal {Z}^1(f)$
such that its linear part
$L_{\tilde {g}}$
satisfies the following properties:
-
•
$L_{\tilde {g}}$
is contracting along
$E^u_{L_f}$
and
$E^s_{L_f}$
; -
•
$L_{\tilde {g}}$
is uniformly expanding along
$E^c_{L_f}$
; -
• the splitting
$E^u_{L_f}\oplus _\prec E^s_{L_f}\oplus _\prec E^c_{L_f}$
is dominated for
$L_{\tilde {g}}$
.
Sketch of the proof.
By assumption, the rank of
$\mathcal {L}(\mathcal {Z}^1(f))$
is
$2$
. By Lemma 2.14, each element (except
$\operatorname {Id}$
and
$-\operatorname {Id}$
) in
$\mathcal {L}(\mathcal {Z}^1(f))$
is a hyperbolic automorphism on
${\mathbb T}^3.$
Hence
$\mathcal {L}(\mathcal {Z}^1(f))$
induces a
${\mathbb Z}^2$
-linear action on
${\mathbb T}^3$
which is a Cartan action.
By Proposition 2.1, the
$\mathbb {Z}^2$
-linear action on
${\mathbb T}^3$
given by
$\mathcal {L}(\mathcal {Z}^1(f))$
leaves
$E^{u}_{L_f}$
,
$E^{c}_{L_f}$
and
$E^{s}_{L_f}$
invariant. Then the Lyapunov exponents along
$E^{u}_{L_f}$
,
$E^{c}_{L_f}$
and
$E^{s}_{L_f}$
can be seen as linear functionals defined on
$\mathbb {Z}^2$
, and we denote them by
$\unicode{x3bb} ^{u}$
,
$\unicode{x3bb} ^{c}$
and
$\unicode{x3bb} ^{s}$
respectively. By Corollary 2.2.14 in [Reference Katok and NiticaKN], the Lyapunov hyperplanes (given by
$\ker \unicode{x3bb} ^{*}=0\subset \mathbb {R}^2$
with
$*=s,c,u$
) are in general position and are completely irrational. Since every element in the action has determinant
$\pm 1$
, one has
$\unicode{x3bb} ^s\oplus \unicode{x3bb} ^c\oplus \unicode{x3bb} ^u=0.$
Then using linear algebra one can find
$\tilde {g}\in \mathcal {Z}^1(f)$
satisfying the desired properties.
A priori, one does not know if the diffeomorphism g obtained in Corollary 3.15 is partially hyperbolic. To conclude, one needs further discussion.
Now, we show that the strong stable and unstable bundles are jointly integrable.
Theorem 3.16. Let f be a
$C^1$
partially hyperbolic diffeomorphism on
${\mathbb T}^3$
whose linear part
$L_f$
is Anosov. If there exists
$g\in \mathcal {Z}^1(f)$
such that
$L_g^m\notin \{ L_f^n\}_{n\in {\mathbb Z}}$
for any
$m\neq 0$
, then f is not accessible.
Proof Recall that we always assume
$L_f$
has two positive Lyapunov exponents. By Corollary 3.15, one can assume that
$g\in \mathcal {Z}^1(f)$
satisfies the following properties:
-
•
$ L_g$
is contracting along
$E^u_{L_f}$
and
$E^s_{L_f}$
; -
•
$ L_g$
is uniformly expanding along
$E^c_{L_f}$
; -
• the splitting
$E^u_{L_f}\oplus _\prec E^s_{L_f}\oplus _\prec E^c_{L_f}$
is dominated for
$ L_g$
.
Up to replacing f and g by
$f^2$
and
$g^2$
, one can assume that f and g preserve the orientation of
$E^s_{L_f}, E^c_{L_f}, E^u_{L_f}.$
Let
$\mathcal {F}^u,\mathcal {F}^s,\mathcal {F}^c$
be the strong unstable, strong stable and center foliations of f, respectively. Let
$\mathcal {W}^u,\mathcal {W}^s,\mathcal {W}^c$
be the strong unstable, strong stable and center foliations of
$L_f$
, respectively. Their corresponding center stable and center unstable foliations would be denoted by
$\mathcal {F}^{cs}, \mathcal {F}^{cu}, \mathcal {W}^{cs}, \mathcal {W}^{cu}$
.
Consider a lift F of f to
${\mathbb R}^3$
. By Lemma 3.1, there exists
$0<l\leq |\!\operatorname {det}(L_f-\operatorname {Id}_{{\mathbb R}^3})|$
such that
$g^l$
admits a lift to
${\mathbb R}^3$
which commutes with F. For simplicity, we will assume that
$l=1$
. Let G be the lift of g such that
$F\circ G=G\circ F.$
By Lemma 3.2, F and G have a common fixed point
$p\in {\mathbb R}^3.$
Let
$H:{\mathbb R}^3\to {\mathbb R}^3$
be the continuous surjective map given by Corollary 2.8 such that:
-
•
$H\circ F= L_f\circ H$
and
$H\circ G=L_g\circ H;$
-
•
$H-\operatorname {Id}_{{\mathbb R}^3}$
is
${\mathbb Z}^3$
-periodic.
Then
$H(p)=0.$
Claim 3.17.
G is topologically contracting along the foliation
$\tilde {\mathcal {F}}^s$
, that is, for any two points
$x,y$
on the same
$\tilde {\mathcal {F}}^s$
-leaf, one has
$\lim _{n\rightarrow +\infty }\operatorname {d}(G^n(x), G^n(y))=0.$
Proof of the claim By Theorem 2.9, the map H is injective along each leaf of
$\tilde {\mathcal {F}}^s$
and sends a leaf of
$\tilde {\mathcal {F}}^s$
to a leaf of
$\tilde {\mathcal {W}}^s$
. Recalling that
$L_g$
is uniformly contracting along
$\tilde {\mathcal {W}}^s$
and
$H\circ G=L_g\circ H$
, one deduces that G is topologically contracting along
$\tilde {\mathcal {F}}^s.$
Claim 3.18. There exists
$K>0$
such that for any
$x\in {\mathbb R}^3$
and
$y\in \tilde {\mathcal {F}}^u(x)$
, one has
$$ \begin{align*}\limsup_{n\rightarrow+\infty}\operatorname{d}_{\tilde{\mathcal{F}}^u}(G^n(x),G^n(y))\leq K.\end{align*} $$
Proof of the claim Recall that
$p\in {\mathbb R}^3$
is a fixed point of G and
$H(p)=0$
. Since the foliations
$\tilde {\mathcal {F}}^{cs}$
and
$\tilde {\mathcal {F}}^u$
have the global product structure, the space of
$\tilde {\mathcal {F}}^{cs}$
-leaves can be identified as
$\tilde {\mathcal {F}}^u(p)\cong {\mathbb R}.$
Similarly, the space of
$\tilde {\mathcal {W}}^{cs}$
-leaves of
$L_f$
can be identified as
$\tilde {\mathcal {W}}^u(0)$
:
$\mathbb {R}^3/\tilde {\mathcal {F}}^{cs}\cong \tilde {\mathcal {W}}^u(0)\cong \mathbb {R}$
.
Thanks to Corollary 2.6, one can consider the action
$G^{cs}$
, induced by G, on the space of
$\tilde {\mathcal {F}}^{cs}$
-leaves. Then one has the following commuting diagram, and
$G^{cs}$
can be identified as the diffeomorphism
$G:\tilde {\mathcal {F}}^u(p)\to \tilde {\mathcal {F}}^u(p)$
:
By Theorem 2.9, the map H sends a center stable leaf of F to a center stable leaf of
$L_f$
which induces a map
$H^{cs}$
from the space of
$\tilde {\mathcal {F}}^{cs}$
-leaves to the space of
$\tilde {\mathcal {W}}^{cs}$
-leaves.
Since
$H^{-1}(x)$
is contained in a single center leaf for any
$x\in {\mathbb R}^3$
, it follows that
$H^{cs}$
is a homeomorphism from the space of
$\tilde {\mathcal {F}}^{cs}$
-leaves to the space of
$\tilde {\mathcal {W}}^{cs}$
-leaves. Combining with the fact that
$H\circ G=L_g\circ H$
, one gets that the homeomorphism
$G^{cs}:\tilde {\mathcal {F}}^u(p)\to \tilde {\mathcal {F}}^u(p)$
is conjugate to
$L_g:\tilde {\mathcal {W}}^u(0)\to \tilde {\mathcal {W}}^u(0)$
:
By the choice of g, the linear map
$L_g$
is a contracting along
$\tilde {\mathcal {W}}^u(0)$
; therefore
$G^{cs}$
is topologically contracting, as is
$G:\tilde {\mathcal {F}}^u(p)\to \tilde {\mathcal {F}}^u(p).$
Let
$x\in {\mathbb R}^3$
and
$y\in \tilde {\mathcal {F}}^u(x)$
. By the global product structure, the leaves
$\tilde {\mathcal {F}}^{cs}(x)$
and
$\tilde {\mathcal {F}}^{cs}(y)$
intersect
$\tilde {\mathcal {F}}^{u}(p)$
at unique points
$\widehat x$
and
$\widehat y$
, respectively. Since
$\operatorname {d}(G^n(\widehat x), G^n(\widehat y))$
tends to
$0$
when n tends to infinity and the center stable foliation and strong unstable foliations are invariant under G, by Corollary 2.5, there exists a constant
$K>0$
such that
$$ \begin{align*}\operatorname{d}_{\tilde{\mathcal{F}}^u}(G^n(x), G^n(y))\leq K+\operatorname{d}(G^n(\widehat x), G^n(\widehat y)).\end{align*} $$
Letting n tend to
$+\infty $
, one gets the posited property.
Assume, to the contrary, that f is accessible. Lemma 2.19 shows that the lift
$F:{\mathbb R}^3\rightarrow {\mathbb R}^3$
is also accessible. For every point
$x\in {\mathbb R}^3$
, we choose
$y\in \mathcal {F}^c(x)$
such that
$H(x)\neq H(y)$
. Let
$I^c$
denote the segment between x and y contained in
$\mathcal {F}^c(x)$
.
Since F is accessible, there exists a sequence of segments
$I_1,I_2,\ldots ,I_k$
such that for every
$j=1,\ldots ,k$
, one has that:
-
•
$I_j$
is contained in a leaf of
$\tilde {\mathcal {F}}^s$
or
$\tilde {\mathcal {F}}^u$
; -
• the endpoints of
$I_j$
are
$x_{j-1}$
and
$x_j$
, where
$x_0=x$
and
$x_k=y$
.
$$ \begin{align*} \max_{j=1,\ldots,k}\{\limsup_{n\rightarrow+\infty}\ell(G^n(I_j))\}\leq K, \end{align*} $$
where
$\ell (\cdot )$
denotes the length of a
$C^1$
curve. This implies the two endpoints of
$G^n(I^c)$
are at uniformly bounded distance.
On the other hand, since
$H(x)\neq H(y)$
, by the choice of g, one has
$$ \begin{align*} \lim_{n\rightarrow+\infty}\ell(L_g^n\circ H(I^c))=\lim_{n\rightarrow+\infty} \ell(H\circ G^n(I^c))=+\infty. \end{align*} $$
Since
$H-\operatorname {Id}_{{\mathbb R}^3}$
is uniformly bounded on
${\mathbb R}^3$
, one has
$\lim _{n\rightarrow +\infty }\ell (G^n(I^c))=+\infty .$
This contradicts to the quasi-isometric property of the center foliation
$\tilde {\mathcal {F}}^c$
given by Theorem 2.2.
Now, we are ready to give the proof of Theorem 3.13.
Proof of Theorem 3.13 By Theorems 2.20 and 3.16, the strong stable and unstable bundles of f are jointly integrable, and f is Anosov. Let h be the homeomorphism such that
$h\circ f=L_f\circ h.$
Now, let us fix some notation. Recall that the partially hyperbolic splitting for f is denoted by
$E^s\oplus E^c\oplus E^u$
and the partially hyperbolic splitting for
$L_f$
is denoted by
$E^s_{L_f}\oplus E^c_{L_f}\oplus E^u_{L_f}$
. Let
$\mathcal {F}^s,\mathcal {F}^u,\mathcal {F}^c$
be the strong stable, strong unstable and center foliations of f respectively, and by Corollary 2.6, these foliations are invariant under each element of
$\mathcal {Z}^r(f)$
. Let
$\mathcal {W}^s,\mathcal {W}^u,\mathcal {W}^c$
be the strong stable, strong unstable and center foliations of
$L_f$
, respectively.
Since
$E^s\oplus E^u$
is integrable, by Theorem 2.22, one has that:
-
• the conjugacy h is uniformly
$C^1$
along the center leaves of f; -
• h sends the foliation
$\mathcal {F}^u$
to the foliation
$\mathcal {W}^u.$
In the following, we will show that h is uniformly
$C^1$
along the leaves of
$\mathcal {F}^s$
and
$\mathcal {F}^u.$
As per the discussion in Corollary 3.15, since the rank of the linearization of whole
$\mathcal {Z}^r(f)$
action is
$2$
(which is full rank), hence
$\mathcal {Z}^r(f)$
induces a maximal Cartan affine action on the torus, and there exist diffeomorphisms
$g, \widehat g\in \mathcal {Z}^r(f)$
whose linear parts satisfy the following properties:
-
•
$L_g$
is uniformly expanding along
$E^c_{L_f}$
, and
$L_g$
is uniformly contracting along
$E^u_{L_f}\oplus E^{s}_{L_f}$
; -
•
$L_{\widehat g}$
is uniformly expanding along
$E^s_{L_f}\oplus E^c_{L_f}$
, and
$L_{\widehat g}$
is uniformly contracting along
$E^u_{L_f}$
; -
• the splitting
$E^u_{L_f}\oplus E^s_{L_f}\oplus E^c_{L_f}$
is dominated for
$L_g$
and
$L_{\widehat g}$
.
Since both
$h\circ g\circ h^{-1}$
and
$h\circ \widehat g \circ h^{-1}$
belong to the centralizer of
$L_f$
, by Theorem 2.11, one has that
$$ \begin{align*}h\circ g\circ h^{-1}=L_g +w_g \quad \text{and} \quad h\circ \widehat g \circ h^{-1} =L_{\widehat g}+w_{\widehat g} \end{align*} $$
are both affine maps on
${\mathbb T}^3$
. Recall that h is uniformly
$C^1$
along the center leaves of f. Since
$h(\mathcal {F}^c)=\mathcal {W}^c$
,
$L_g$
and
$L_{\widehat g}$
are uniformly expanding along
$E^c_{L_f}$
, it follows that
$$ \begin{align*}g=h^{-1}\circ(L_g +w_g)\circ h \quad \text{and} \quad \widehat g=h^{-1}\circ(L_{\widehat g}+w_{\widehat g})\circ h \end{align*} $$
are uniformly expanding along
$E^c$
.
Claim 3.19. The diffeomorphisms g and
$\widehat g$
are Anosov. To be precise:
-
• g is uniformly contracting along
$E^u$
and
$E^s$
; -
•
$\widehat g$
is uniformly contracting along
$E^u$
, and uniformly expanding along
$E^s$
.
Proof of the claim We only prove the case for g (the case for
$\widehat g$
works analogously), since what we need are the conjugation through h to their linear parts and the Hölder continuity of h along the leaves of
$\mathcal {F}^u$
and
$\mathcal {F}^s$
.
Since g is topologically conjugate to
$(L_g+w_g)$
by h, it satisfies the shadowing lemma. In particular, every ergodic measure of g can be approximated by the atomic measures supported on periodic orbits. Thus to prove g is uniformly contracting along
$E^u$
and
$E^s$
, it suffices to show that the Lyapunov exponents of periodic points of g along
$E^u$
and
$ E^s$
are uniformly smaller than zero.
By the continuity of the bundle
$E^u$
, for any
${\varepsilon }>0$
, there exists
$\delta>0$
such that for any
$x,y\in {\mathbb T}^3$
with
$\operatorname {d}(x,y)<\delta $
, one has
$$ \begin{align} -{\varepsilon}\leq \log\|Dg|_{E^u(x)}\|-\log{\|Dg|_{E^u(y)}\|}\leq {\varepsilon}. \end{align} $$
Since g is conjugate to
$(L_g+w_g)$
and h sends the foliations
$\mathcal {F}^u,\mathcal {F}^s$
to the corresponding linear foliations of
$(L_g+w_g)$
, it follows that g is topologically contracting along the leaves of
$\mathcal {F}^u$
and
$\mathcal {F}^s$
. Let p be a periodic point of period k. Then
$g^k|_{\mathcal {F}^u(p)}:\mathcal {F}^u(p)\to \mathcal {F}^u(p)$
is topologically contracting and has a unique fixed point
$p.$
Let
$x\in \mathcal {F}^u_{\delta }(p)$
. Then
$g^{nk}(x)\in \mathcal {F}^u_{\delta }(p)$
for any
$n\in {\mathbb N}.$
By equation (1), one has
$$ \begin{align}~ \exp((\chi^u(p)-{\varepsilon})nk) \cdot \operatorname{d}(x,p)&\leq \operatorname{d}(g^{nk}(x),g^{nk}(p))\nonumber\\ &\leq \exp((\chi^u(p)+{\varepsilon})nk) \cdot \operatorname{d}(x,p), \end{align} $$
where
$\chi ^u(p)$
is the Lyapunov exponent of p for g along the direction
$E^u$
. Since
$h\circ g= (L_g+w_g)\circ h$
, one has
$$ \begin{align}~ \operatorname{d}(h\circ g^{nk}(x), h\circ g^{nk}(p)) &=\operatorname{d}((L_g+w_g)^{nk}(h(x)), (L_g+w_g)^{nk}(h(p)))\\ \notag &=\exp(\chi^u(L_g)\cdot{nk})\cdot\operatorname{d}(h(x),h(p)), \end{align} $$
where
$\chi ^u(L_g)$
is the Lyapunov exponent of
$L_g$
along
$E_{L_f}^u$
, which is the same as the Lyapunov exponent of
$(L_g+w_g)$
along
$E_{L_f}^u$
.
By Remark 2.23, the map h is uniformly Hölder continuous along the leaves of
$\mathcal {F}^u$
, that is, there exist
$C,\alpha>0$
such that for any two points
$x_1,x_2$
on the same
$\mathcal {F}^u$
-leaf, one has
$\operatorname {d}_{\mathcal {F}^u}(x_1,x_2) \leq C\cdot (\operatorname {d}_{\mathcal {W}^u}(h(x_1),h(x_2)))^{\alpha }.$
Hence one has
$$ \begin{align*}\operatorname{d}(hg^{nk}(x), hg^{nk}(p))\geq C^{-1/\alpha}\cdot (\operatorname{d}(g^{nk}(x), g^{nk}(p)))^{1/\alpha}. \end{align*} $$
Then, combining with Equations (2) and (3), for any
$n\in {\mathbb N}$
, one has
$$ \begin{align*}C^{-1/\alpha}\cdot \exp((\chi^u(p)-{\varepsilon})nk/\alpha) \cdot (\operatorname{d}(x,p))^{1/\alpha}\leq \exp(\chi^u(L_g)nk)\cdot\operatorname{d}(h(x),h(p)),\end{align*} $$
which implies that
$\chi ^u(p)-{\varepsilon }\leq \alpha \cdot \chi ^u(L_g)$
. The arbitrariness of
${\varepsilon }$
and p gives that the Lyapunov exponents of periodic points of g along
$E^u$
are uniformly bounded away from zero. Analogous argument gives that the Lyapunov exponents of periodic points of g along
$E^s$
are uniformly bounded away from zero. Hence g is also Anosov.
By [Reference Pinto and RandPiRa], which states that the codimension-one stable (or unstable) foliation of a
$C^r$
(
$r>1$
) codimension-one Anosov diffeomorphism is
$C^1$
-smooth, one has that:
-
• the unstable foliation of f, which is tangent to
$E^c\oplus E^u$
, is
$C^1$
-smooth; -
• the stable foliation of g, which is tangent to
$E^u\oplus E^s$
, is
$C^1$
-smooth; -
• the unstable foliation of
$\widehat g$
, which is tangent to
$E^s\oplus E^c$
, is
$C^1$
-smooth.
As a consequence, the foliations
$\mathcal {F}^{s},\mathcal {F}^c, \mathcal {F}^u$
are
$C^1$
. Now, both g and
$\widehat g$
satisfy the assumption of Theorem 2.24, hence h is uniformly
$C^1$
along the leaves of
$\mathcal {F}^s$
and
$\mathcal {F}^u$
. As
$f,g,\widehat g$
are Anosov diffeomorphisms, the leaves of
$\mathcal {F}^s,\mathcal {F}^c,\mathcal {F}^u$
are
$C^r.$
By Lemma 2.17, the map h is
$C^r$
along the leaves of
$\mathcal {F}^s,\mathcal {F}^c,\mathcal {F}^u$
. Finally, Journé’s theorem [Reference JournéJ] shows that
$h\in \operatorname {Diff}^{r-{\varepsilon }}({\mathbb T}^3)$
for any
${\varepsilon }>0.$
Acknowledgments
We would like to thank A. Gogolev and P. Varandas for useful comments. D.X. would like to thank Professor Amie Wilkinson for many useful discussions on general centralizer problems, and Claim 3.7 is partially inspired by discussion with her. Part of this work was done when D.X. served as Marie Curie fellow at Imperial College London. We thank the anonymous referees for helping us improve the presentation of this paper. S.G. is supported by NSFC 11771025 and 11831001. Y.S. is supported by NSFC 12071007, 11831001 and 12090015. D.X. is supported by NSFC 12090015. J.Z. is supported by NSFC 12001027.
A Appendix. Proof of Theorem 2.24
The aim of this section is to give the proof of Theorem 2.24 which essentially follows the argument in §A of [Reference Gan and ShiGS]. See also [Reference GogolevGo1].
Proof of Theorem 2.24 Assume, to the contrary, that there exist two periodic orbits whose Lyapunov exponents along the bundle
$E^c$
are different. For each periodic point p, we denote by
$\chi ^c(p)$
the Lyapunov exponent of p along the direction
$E^c.$
As g is Anosov, periodic measures (atomic probability measures equidistributed on a single periodic orbit) are dense among invariant measures [Reference SigmundSig]. Since g is uniformly expanding along the continuous bundle
$E^c$
, by the convexity of the set of invariant measures, there exist
$0<\chi _1<\chi _2$
such that
$\overline {\{\chi ^c(p): p \text { is a periodic point} \}}=[\chi _1,\chi _2].$
By the shadowing lemma, for each point
$x\in {\mathbb T}^3$
, one has
$$ \begin{align*} \chi_1\leq \liminf_{n\rightarrow\infty}\frac{1}{n}\log\|Dg^n|_{E^c(x)}\|\leq \limsup_{n\rightarrow\infty}\frac{1}{n}\log\|Dg^n|_{E^c(x)}\|\leq \chi_2. \end{align*} $$
Hence for any
${\varepsilon }>0$
, there exists an adapted metric
$\|\cdot \|_{{\varepsilon }}$
such that
$$ \begin{align*} \chi_1-{\varepsilon}\leq \log\|Dg|_{E^c(x)}\|_{{\varepsilon}}\leq \chi_2+{\varepsilon},\quad \text{for any } x\in{\mathbb T}^3. \end{align*} $$
By the continuity of the bundle
$E^{c}$
, there exists
$\delta>0$
such that for any
$z_1,z_2\in {\mathbb T}^3$
with
$\operatorname {d}(z_1,z_2)<3\delta $
, one has
$$ \begin{align*}-{\varepsilon}<\log\|Dg|_{E^c(z_1)}\|_{\varepsilon}-\log\|Dg|_{E^c(z_2)}\|_{\varepsilon}<{\varepsilon}.\end{align*} $$
Now, for
${\varepsilon }>0$
small (which will be fixed later), one fixes periodic points
$p,q$
such that
$\chi ^c(p)\leq \chi _1+{\varepsilon }$
and
$\chi ^c(q)\geq \chi _2-{\varepsilon }$
.
For the linear Anosov map
$L_g$
, let us denote by
$\mathcal {W}^{s}, \mathcal {W}^c,\mathcal {W}^u,\mathcal {W}^{su}$
the foliations tangent to
$E^{s}_{L_g}, E^c_{L_g}, E^u_{L_g}, E^{s}_{L_g}\oplus E^u_{L_g}$
, respectively.
Since the factors of unit eigenvectors of
$L_g$
are algebraic, there exists
$C_1>1$
such that for any
$l>0$
large, each strong unstable segment of
$L_g$
with length l is
$C_1/\sqrt {l}$
dense in
${\mathbb T}^3.$
For any
$l>0$
large, there exist
$x,y\in {\mathbb T}^3$
such that
$$ \begin{align}~ x\in \mathcal{W}^u_l(h(p)) \quad \text{ and } \quad y\in \mathcal{W}^s_{C_1/\sqrt{l}}(x)\cap \mathcal{W}^c_{C_1/\sqrt{l}}(h(q)). \end{align} $$
By the continuity of h, there exists
$\eta>0$
such that for any center segment for
$L_g$
of length no more than
$\eta $
, its pre-image under h has length no more than
$\delta .$
We will use
$\ell (I)$
denote the length of a
$C^1$
-curve. As
$\mathcal {W}^{su}$
is a linear foliation, the holonomy map given by
$\mathcal {W}^{su}$
is an isometry. Now, one chooses
$\mathcal {W}^c$
-center segments
$I_x$
and
$I_{h(p)}$
such that:
-
•
$\ell (I_x)=\ell (I_{h(p)})=\eta ;$
-
• x is an endpoint of
$I_x$
and
$h(p)$
is an endpoint of
$h(p)$
; -
•
$I_x$
is an image of
$I_{h(p)}$
under the holonomy map
$\mathcal {W}^{su}$
.
Then
$J_{\widehat x}=h^{-1}(I_x)$
and
$J_p=h^{-1}(I_{h(p)})$
are segments tangent to
$E^c$
with length no more than
$\delta $
, and
$J_p$
is the image of
$J_{\widehat x}$
under a holonomy map of
$\mathcal {F}^{su},$
where
$\widehat x=h^{-1}(x)$
.
By Remark 2.23, the homeomorphism h is uniformly Hölder continuous along the leaves of
$\mathcal {F}^u$
and
$\mathcal {F}^s$
, hence there exist constants
$C_2>1$
and
$\theta \in (0,\tfrac {1}{2})$
which is only determined by h such that
$\widehat x\in \mathcal {F}_d^u(p)$
and
$\widehat y\in \mathcal {F}^{s}_{C_2/d^{\theta }}(\widehat x)\cap \mathcal {F}^c_{\delta }(q)$
for d large, due to equation (4). As l can be chosen arbitrarily large, so is d.
As g is uniformly expanding and contracting along
$E^u$
and
$E^s$
respectively, let us denote
$$ \begin{align*}\tau=\sup_{x\in{\mathbb T}^3}\|Dg^{-1}|_{E^u(x)}\|_{\varepsilon}<1 \quad \text{and } \quad \kappa=\sup_{x\in{\mathbb T}^3}\|Dg^{-1}|_{E^s(x)}\|_{\varepsilon}>1. \end{align*} $$
Let
$N_d$
be the smallest integer such that
$\tau ^{N_d}\cdot d\leq 1.$
Then
$N_d\leq -({\log d}/{\log \tau })+1.$
Let
$N_d^1$
be the largest integer such that
$$ \begin{align*}\kappa^{N_d^1}C_2/d^{\theta}\leq \delta,\end{align*} $$
which implies that
$g^{-N_d^1}(J_{\widehat x})$
is contained in the
$3\delta $
-neighborhood of
$q.$
Then for d large enough, one has the following estimate:
$$ \begin{align*} \frac{N_d^1}{N_d}&\geq \frac{\theta\log d+\log\delta-\log C_2-1}{-({\log d}/{\log\tau})+1}\cdot \frac{1}{\log \kappa} \\ &= \frac{\theta\log d+\log\delta-\log C_2-1}{\log d-\log\tau}\cdot \frac{-\log\tau}{\log \kappa} \\ &\geq \frac{\theta}{2}\frac{-\log\tau}{\log \kappa}. \end{align*} $$
As g is uniformly expanding along
$E^c$
, by the choices of
$J_p$
and
$\delta $
, one has
$$ \begin{align*} \exp(-N_d(\chi^c(p)+{\varepsilon}))\cdot\ell(J_p)\leq \ell(g^{-N_d}(J_p)) \end{align*} $$
and
$$ \begin{align*} \ell(g^{-N_d}(J_x))\leq \ell(J_x)\cdot \exp(-N_d^1(\chi^c(q)-{\varepsilon}))\cdot \exp((N_d^1-N_d)\cdot(\chi_1-{\varepsilon})). \end{align*} $$
Then one has
$$ \begin{align*} \frac{\ell(g^{-N_d}(J_x))}{\ell(g^{-N_d}(J_p))}&\leq \frac{\ell(J_x)}{\ell(J_p)} \cdot \exp(-N_d^1(\chi^c(q)-{\varepsilon}))\\&\quad\cdot \exp((N_d^1-N_d)(\chi_1-{\varepsilon}))\cdot \exp(N_d(\chi^c(p)+{\varepsilon})) \\ &\leq \frac{\ell(J_x)}{\ell(J_p)} \cdot \exp(4N_d{\varepsilon})\cdot \exp(N_d^1(\chi^c(p)-\chi^c(q)))\\&\quad\cdot \exp((-N_d^1+N_d)\cdot(\chi^c(p)-\chi_1)) \\ & \leq \frac{\ell(J_x)}{\ell(J_p)} \cdot \exp(8N_d{\varepsilon})\cdot \exp(N_d^1(\chi_1-\chi_2)) \\ &\leq \frac{\ell(J_x)}{\ell(J_p)} \cdot \exp(8{\varepsilon} N_d)\cdot \exp\left( (\chi_1-\chi_2)\cdot \frac{\theta}{2}\frac{(-\log\tau)}{\log \kappa}\cdot N_d\right). \end{align*} $$
One only needs to choose
${\varepsilon }=({1}/{16})(\chi _2-\chi _1)\cdot ({\theta }/{-\!\log \tau })/{2}{\log \kappa },$
and one gets that
$ {\ell (g^{-N_d}(J_x))}/{\ell (g^{-N_d}(J_p))}$
tends to
$0$
when d tends to infinity. The holonomy map given by the foliation
$\mathcal {F}^u$
restricted to the unstable foliation of f is uniformly
$C^1$
; therefore
${\ell (g^{-N_d}(J_x))}/{\ell (g^{-N_d}(J_p))}$
is uniformly bounded from above and below, which gives the contradiction. This proves that all the periodic points have the same Lyapunov exponent along the bundle
$E^c$
. Applying [Reference Gan and ShiGS], one gets a periodic point whose Lyapunov exponent along
$E^c$
is the same as the center Lyapunov exponent of
$L_f.$
Finally, we apply [Reference Gan and ShiGS], which shows that h is
$C^1$
along each leaf of
$\mathcal {F}^c.$
