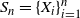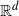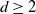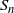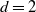1. Introduction
For any subset ![]() $A\subset\mathbb{R}^d$
(
$A\subset\mathbb{R}^d$
(![]() $d\ge 2$
), let
$d\ge 2$
), let ![]() ${{\rm conv}}(A)$
be the convex hull of A, i.e. the smallest convex set containing A. Most of the discussion below is for
${{\rm conv}}(A)$
be the convex hull of A, i.e. the smallest convex set containing A. Most of the discussion below is for ![]() $d=2$
, but when the results are valid for higher dimensions we use d for the dimension instead. Suppose
$d=2$
, but when the results are valid for higher dimensions we use d for the dimension instead. Suppose ![]() $S_n=\{X_i\}_{i=1}^{n}$
is a sequence of independent and identically distributed (i.i.d.) random points in
$S_n=\{X_i\}_{i=1}^{n}$
is a sequence of independent and identically distributed (i.i.d.) random points in ![]() $\mathbb{R}^d$
. The random convex polytopes (random convex hull)
$\mathbb{R}^d$
. The random convex polytopes (random convex hull) ![]() $K_n={{\rm conv}}(S_n)$
is the smallest convex set containing observations
$K_n={{\rm conv}}(S_n)$
is the smallest convex set containing observations ![]() $\{X_{i}\}_{i=1}^{n}$
. Random convex polytopes (in short, random polytopes) have been widely studied. For example, MacDonald et al. (Reference MacDonald, Ball, Hough, MacDonald and Amlaner1980) applied
$\{X_{i}\}_{i=1}^{n}$
. Random convex polytopes (in short, random polytopes) have been widely studied. For example, MacDonald et al. (Reference MacDonald, Ball, Hough, MacDonald and Amlaner1980) applied ![]() $K_n$
for the estimation of the territorial range of a wildlife species by tagging an individual of this species with a radio transmitter and recording the position as
$K_n$
for the estimation of the territorial range of a wildlife species by tagging an individual of this species with a radio transmitter and recording the position as ![]() $X_i$
after release. Ripley and Rasson (Reference Ripley and Rasson1977) applied
$X_i$
after release. Ripley and Rasson (Reference Ripley and Rasson1977) applied ![]() $K_n$
for the estimation of the homogeneous planar Poisson process support. Furthermore, in ordered statistics, the method of convex-hull peeling constructs a nested sequence of random polytopes based on the sample points. In this context, the number of convex layers for a sequence of given points is called convex-hull peeling depth, and the convex layers themselves are the depth contours for this notion of data depth. In other words
$K_n$
for the estimation of the homogeneous planar Poisson process support. Furthermore, in ordered statistics, the method of convex-hull peeling constructs a nested sequence of random polytopes based on the sample points. In this context, the number of convex layers for a sequence of given points is called convex-hull peeling depth, and the convex layers themselves are the depth contours for this notion of data depth. In other words ![]() ${{\rm conv}}(S_n)$
plays the role of the extreme layer, like the maximum of a sample, and the most internal layer can be considered as the multivariate median. For an extensive connection with the concept of data depth we refer the reader to Liu et al. (1979), Tukey (Reference Tukey1974), and Barnett (Reference Barnett1976).
${{\rm conv}}(S_n)$
plays the role of the extreme layer, like the maximum of a sample, and the most internal layer can be considered as the multivariate median. For an extensive connection with the concept of data depth we refer the reader to Liu et al. (1979), Tukey (Reference Tukey1974), and Barnett (Reference Barnett1976).
Throughout this paper we use the following notation. For any Borel set ![]() $A\subset\mathbb{R}^d$
(
$A\subset\mathbb{R}^d$
(![]() $d\ge 2$
), its volume is denoted by
$d\ge 2$
), its volume is denoted by ![]() $|A|$
(the Lebesgue measure of A). The sample points,
$|A|$
(the Lebesgue measure of A). The sample points, ![]() $S_n=\{X_i\}_{i=1}^{n}$
, are i.i.d. random elements taking values in
$S_n=\{X_i\}_{i=1}^{n}$
, are i.i.d. random elements taking values in ![]() $\mathbb{R}^d$
with the probability distribution F. Suppose F has the convex support K, which in this paper is referred to as the ‘underlying set’. When F is the uniform distribution, the set
$\mathbb{R}^d$
with the probability distribution F. Suppose F has the convex support K, which in this paper is referred to as the ‘underlying set’. When F is the uniform distribution, the set ![]() $K_n={{\rm conv}}(S_n)$
is called the uniform polytope. For functionals of
$K_n={{\rm conv}}(S_n)$
is called the uniform polytope. For functionals of ![]() $K_n$
, denote the volume by
$K_n$
, denote the volume by ![]() $|K_n|$
, the perimeter
$|K_n|$
, the perimeter ![]() $\partial (K_{n})$
(the boundary of
$\partial (K_{n})$
(the boundary of ![]() $K_{n}$
) by
$K_{n}$
) by ![]() $L_n$
, and the probability content by
$L_n$
, and the probability content by ![]() $F(K_n)={{\rm \mathrm{P}}\,}(X_{1}\in K_{n})$
. In addition, if K is the underlying set, we denote the set difference
$F(K_n)={{\rm \mathrm{P}}\,}(X_{1}\in K_{n})$
. In addition, if K is the underlying set, we denote the set difference ![]() $K\setminus K_n$
by
$K\setminus K_n$
by ![]() $D_n$
and the Hausdorff distance between K and
$D_n$
and the Hausdorff distance between K and ![]() $K_n$
by
$K_n$
by ![]() $H(K,K_n)$
. In the following section we provide a short list of some well-known results, which serve as the theoretical basis for this paper.
$H(K,K_n)$
. In the following section we provide a short list of some well-known results, which serve as the theoretical basis for this paper.
2. Preliminaries
In this section we review some existing results. Let F be the uniform distribution on the underlying convex set K. Suppose the underlying set ![]() $K\subset\mathbb{R}^d$
is a convex polygon with r (
$K\subset\mathbb{R}^d$
is a convex polygon with r (![]() $\ge 3$
) vertices. Problems related to convex hulls have received much attention from many authors. For
$\ge 3$
) vertices. Problems related to convex hulls have received much attention from many authors. For ![]() $d=2$, according to Cabo and Groeneboom (Reference Cabo and Groeneboom1994), we have, as
$d=2$, according to Cabo and Groeneboom (Reference Cabo and Groeneboom1994), we have, as ![]() $n\rightarrow \infty$
,
$n\rightarrow \infty$
,
where ![]() $\alpha_n=\frac{1}{n}\sqrt{\frac{28}{27}r\log{n}}$
,
$\alpha_n=\frac{1}{n}\sqrt{\frac{28}{27}r\log{n}}$
, ![]() $\beta_n=\frac{2}{3n}r\log{n}$
, and ‘
$\beta_n=\frac{2}{3n}r\log{n}$
, and ‘![]() $$\underrightarrow {\text{D}}$$
’ is convergence in distribution. For any convex set
$$\underrightarrow {\text{D}}$$
’ is convergence in distribution. For any convex set ![]() $K\subset\mathbb{R}^d$
,
$K\subset\mathbb{R}^d$
,
where ![]() $\kappa$
is the generalized Gaussian curvature and c(d) is a constant only depending on d. See Schütt (Reference Schütt1994) for details.
$\kappa$
is the generalized Gaussian curvature and c(d) is a constant only depending on d. See Schütt (Reference Schütt1994) for details.
Let K be a convex subset of ![]() $\mathbb{R}^2$
. Suppose the boundary of K, i.e.
$\mathbb{R}^2$
. Suppose the boundary of K, i.e. ![]() $\partial{K}$
, has curvature bounded away from 0 and
$\partial{K}$
, has curvature bounded away from 0 and ![]() $\infty$
, and
$\infty$
, and ![]() $\partial{K}\in\mathcal{C}^2(\mathbb{R})$
(the set of all functions with two continuous derivatives with domain
$\partial{K}\in\mathcal{C}^2(\mathbb{R})$
(the set of all functions with two continuous derivatives with domain ![]() $\mathbb{R}$
). For definitions and more details, see the Appendix A. Let L and
$\mathbb{R}$
). For definitions and more details, see the Appendix A. Let L and ![]() $L_n$
be the perimeters of K and
$L_n$
be the perimeters of K and ![]() $K_n$
respectively. Bräker and Hsing (Reference Bräker and Hsing1998) showed that, as
$K_n$
respectively. Bräker and Hsing (Reference Bräker and Hsing1998) showed that, as ![]() $n\to\infty$
,
$n\to\infty$
,
where ![]() $\boldsymbol{\Sigma}$
is a constant matrix. Convergence of expectations is given by
$\boldsymbol{\Sigma}$
is a constant matrix. Convergence of expectations is given by
and
where ![]() $c_1$
and
$c_1$
and ![]() $c_2$
are constants.
$c_2$
are constants.
Let ![]() $d\ (\!\ge2)$
and
$d\ (\!\ge2)$
and ![]() $s\ (\!\le d-1)$
be two nonnegative integers. Let
$s\ (\!\le d-1)$
be two nonnegative integers. Let ![]() $K\subset\mathbb{R}^d$
be a convex set with
$K\subset\mathbb{R}^d$
be a convex set with ![]() $\partial{K}\in\mathcal{C}^2(\mathbb{R}^{d-1})$
and positive Gaussian curvature bounded away from 0 and
$\partial{K}\in\mathcal{C}^2(\mathbb{R}^{d-1})$
and positive Gaussian curvature bounded away from 0 and ![]() $\infty$
. Let
$\infty$
. Let ![]() $\Phi$
be the cumulative distribution function of the standard normal distribution. Then Reitzner (Reference Reitzner2005) proved that there exists a sequence of constants
$\Phi$
be the cumulative distribution function of the standard normal distribution. Then Reitzner (Reference Reitzner2005) proved that there exists a sequence of constants ![]() $C_n$
, bounded between two positive constants, depending only on K, and another constant c, such that
$C_n$
, bounded between two positive constants, depending only on K, and another constant c, such that
where
Let K be a convex polygon with interior angles ![]() $\theta_1,\theta_2,\dots,\theta_r$
. Bräker et al. (Reference Bräker, Hsing and Bingham1998) derived that
$\theta_1,\theta_2,\dots,\theta_r$
. Bräker et al. (Reference Bräker, Hsing and Bingham1998) derived that
where
with
 \begin{equation}
p_k(x)=\left\{
\begin{aligned}
&\int_0^{\theta_k}h_k(x,\theta)\,{\rm d}\theta+\exp\Big\{\!-\frac{x^2}{2|K|}\tan\theta_k\Big\}, %\ \
\quad 0<\theta_k<\frac{\pi}{2}, \\
&\int_{\theta_k-\pi/2}^{\pi/2}h_k(x,\theta)\,{\rm d}\theta, %\ \
\quad \frac{\pi}{2}\le\theta_k<\pi,
\end{aligned}\right.
\label{eqn7}
\end{equation}
\begin{equation}
p_k(x)=\left\{
\begin{aligned}
&\int_0^{\theta_k}h_k(x,\theta)\,{\rm d}\theta+\exp\Big\{\!-\frac{x^2}{2|K|}\tan\theta_k\Big\}, %\ \
\quad 0<\theta_k<\frac{\pi}{2}, \\
&\int_{\theta_k-\pi/2}^{\pi/2}h_k(x,\theta)\,{\rm d}\theta, %\ \
\quad \frac{\pi}{2}\le\theta_k<\pi,
\end{aligned}\right.
\label{eqn7}
\end{equation}
and
Bräker et al. (Reference Bräker, Hsing and Bingham1998) also derived the limit theory for uniform polytopes, when the underlying set K satisfies a certain smoothness condition. Let K be a bounded convex set ![]() $K\subset\mathbb{R}^2$
. Suppose the boundary of K has length L and we parameterize it (positively oriented) as
$K\subset\mathbb{R}^2$
. Suppose the boundary of K has length L and we parameterize it (positively oriented) as ![]() $t\to c(t)$
, with t the arc length between c(0) and c(t). Suppose the curvature
$t\to c(t)$
, with t the arc length between c(0) and c(t). Suppose the curvature ![]() $\mathcal{K}(t)=|\ddot{c}(t)|$
is well defined, bounded away from 0 and
$\mathcal{K}(t)=|\ddot{c}(t)|$
is well defined, bounded away from 0 and ![]() $\infty$
, and has a bounded derivative. Define the function
$\infty$
, and has a bounded derivative. Define the function
and let ![]() $\lambda_0\,:\!=\max_{t\in[0,L)}\lambda(t)$
. Suppose that there exists some bounded sequence of nonnegative constants
$\lambda_0\,:\!=\max_{t\in[0,L)}\lambda(t)$
. Suppose that there exists some bounded sequence of nonnegative constants ![]() $\nu_n$
and positive constant
$\nu_n$
and positive constant ![]() $\mu$
such that, as
$\mu$
such that, as ![]() $n\to\infty$
,
$n\to\infty$
,
where
Denote
Then
for some constants ![]() $d_1$
and
$d_1$
and ![]() $d_2$
.
$d_2$
.
In practice, the statistical properties of different functionals of random polytopes are hard to use. For example, the limiting results in (2.6) are impossible to use. To assess the distributions of these functionals, a feasible idea is to apply the bootstrap method. In a general framework, let ![]() $S_n=\{X_i\}_{i=1}^{n}$
be a sequence of i.i.d. random points drawn from the underlying distribution F. Let
$S_n=\{X_i\}_{i=1}^{n}$
be a sequence of i.i.d. random points drawn from the underlying distribution F. Let ![]() $\phi_n(S_n;\,F)$
be a real-valued functional of interest. To draw a precise inference for
$\phi_n(S_n;\,F)$
be a real-valued functional of interest. To draw a precise inference for ![]() $\phi_n$
, we need to know the exact form of the underlying distribution F. The plug-in principle suggests using some other known approximate distribution to replace the underlying distribution F. Efron (Reference Efron1979) suggested replacing F with the empirical distribution
$\phi_n$
, we need to know the exact form of the underlying distribution F. The plug-in principle suggests using some other known approximate distribution to replace the underlying distribution F. Efron (Reference Efron1979) suggested replacing F with the empirical distribution ![]() $F_n$
, where
$F_n$
, where
with 1 the indicator function.
However, this plug-in principle will still need to be examined for consistency for every target functional. Specifically, suppose
for any continuity point ![]() $x\in\mathbb{R}$
of G. Conditional on
$x\in\mathbb{R}$
of G. Conditional on ![]() $S_n$
, draw a bootstrap sample of points
$S_n$
, draw a bootstrap sample of points ![]() $S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
from
$S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
from ![]() $F_n$
. For convenience, the regular bootstrap takes
$F_n$
. For convenience, the regular bootstrap takes ![]() $m=n$
; however, for generality we do not necessarily assume
$m=n$
; however, for generality we do not necessarily assume ![]() $m=n$
in the forthcoming sections. We would like to have
$m=n$
in the forthcoming sections. We would like to have
where ‘![]() $\xrightarrow{\,{\rm P}\,}$
’ is convergence in probability.
$\xrightarrow{\,{\rm P}\,}$
’ is convergence in probability.
However, the asymptotic failure of the regular bootstrap (![]() $m=n$
) for extremes is well known (see counterexamples in Bickel and Freedman (Reference Bickel and Freedman1981)). Obviously, this asymptotic failure will still be the case for random polytopes (see Zarepour (Reference Zarepour1999)). When the regular bootstrap fails, some authors suggest applying the m out of n resampling method, i.e. setting the resample size as
$m=n$
) for extremes is well known (see counterexamples in Bickel and Freedman (Reference Bickel and Freedman1981)). Obviously, this asymptotic failure will still be the case for random polytopes (see Zarepour (Reference Zarepour1999)). When the regular bootstrap fails, some authors suggest applying the m out of n resampling method, i.e. setting the resample size as ![]() $m=o(n)$
(
$m=o(n)$
(![]() $m/n\to 0$
as
$m/n\to 0$
as ![]() $n\to\infty$
). By assuming
$n\to\infty$
). By assuming ![]() $m=o(n)$
, Zarepour (Reference Zarepour1999) studied the bootstrapping point processes and proved the bootstrap consistency if the underlying distribution F satisfies the regularly varying condition:
$m=o(n)$
, Zarepour (Reference Zarepour1999) studied the bootstrapping point processes and proved the bootstrap consistency if the underlying distribution F satisfies the regularly varying condition: ![]() $nF({a_n}^{-1}X_1\in\cdot)\xrightarrow{\,{\rm V}\,}\mu(\!\cdot\!)$
, where
$nF({a_n}^{-1}X_1\in\cdot)\xrightarrow{\,{\rm V}\,}\mu(\!\cdot\!)$
, where ![]() $\mu$
is a Radon measure and ‘
$\mu$
is a Radon measure and ‘![]() $\xrightarrow{\,{\rm V}\,}$
’ is vague convergence (Kallenberg (Reference Kallenberg1983)). By the continuous mapping theorem, the conclusion can also be applied to the regular bootstrap for convex hulls when the underlying distribution has regularly varying tails.
$\xrightarrow{\,{\rm V}\,}$
’ is vague convergence (Kallenberg (Reference Kallenberg1983)). By the continuous mapping theorem, the conclusion can also be applied to the regular bootstrap for convex hulls when the underlying distribution has regularly varying tails.
In this paper we investigate the consistency of some bootstrapping schemes for convex hulls. In Section 3 we examine the consistency of the regular bootstrap for polygons. In Section 4, a semi-parametric bootstrapping scheme is introduced and with two simple examples (in which the underlying set K is either a circle or a rectangle) we discuss how this approach works. This new semi-parametric bootstrapping scheme is developed in more detail for more general underlying sets in Section 5. The bootstrapping consistency of the Hausdorff distance on the uniform polytopes is proved in this section. Moreover, we also derive results for the symmetric difference and the perimeter difference (see the forthcoming definitions) in Section 6. Since the technique is similar to Section 5, only concise proofs are given for these two examples.
3. The consistency of the regular bootstrap on the Euclidean distance
Suppose ![]() $S_n=\{X_i\}_{i=1}^{n}$
is a sequence of i.i.d. random points uniformly drawn from a polygon K with vertices
$S_n=\{X_i\}_{i=1}^{n}$
is a sequence of i.i.d. random points uniformly drawn from a polygon K with vertices ![]() ${c_{\bf{1}}},{c_{\bf{2}}}, \ldots ,{c_r}$
and interior angles
${c_{\bf{1}}},{c_{\bf{2}}}, \ldots ,{c_r}$
and interior angles ![]() $\theta_1,\theta_2,\dots,\theta_r$
. Let
$\theta_1,\theta_2,\dots,\theta_r$
. Let ![]() $d_{\rm e}$
be the Euclidean metric. Define the distance between a point
$d_{\rm e}$
be the Euclidean metric. Define the distance between a point ![]() $\bf{\it{x}}\in\mathbb{R}^2$
and a set
$\bf{\it{x}}\in\mathbb{R}^2$
and a set ![]() $A\subset\mathbb{R}^2$
by
$A\subset\mathbb{R}^2$
by ![]() $d_{\rm e}(\bf{\it{x}},A)\,:\!=\inf\{d_{\rm e}(\bf{\it{x}},\bf{\it{y}})\,:\,\bf{\it{y}}\in A\}$
, and as usual take
$d_{\rm e}(\bf{\it{x}},A)\,:\!=\inf\{d_{\rm e}(\bf{\it{x}},\bf{\it{y}})\,:\,\bf{\it{y}}\in A\}$
, and as usual take ![]() $K_n={{\rm conv}}(S_n)$
. Given the vertex
$K_n={{\rm conv}}(S_n)$
. Given the vertex ![]() $\bf{\it{c}}_{\bf{\it{k}}}$
, Bräker et al. (Reference Bräker, Hsing and Bingham1998) proved that
$\bf{\it{c}}_{\bf{\it{k}}}$
, Bräker et al. (Reference Bräker, Hsing and Bingham1998) proved that
where ![]() $p_k$
is defined in (2.7). See Figure 1 for a graphical description of
$p_k$
is defined in (2.7). See Figure 1 for a graphical description of ![]() $d_{\rm e}(\bf{\it{c}}_{\bf{\it{k}}},K_n)$
. Now, conditionally on
$d_{\rm e}(\bf{\it{c}}_{\bf{\it{k}}},K_n)$
. Now, conditionally on ![]() $S_n$
, the bootstrapping points
$S_n$
, the bootstrapping points ![]() $S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
are drawn from the empirical distribution
$S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
are drawn from the empirical distribution ![]() $F_n(\!-\!\infty,x]=\frac{1}{n}\sum_{i=1}^{n} %I
\mathbf{1}(X_i\le x)$
. Define
$F_n(\!-\!\infty,x]=\frac{1}{n}\sum_{i=1}^{n} %I
\mathbf{1}(X_i\le x)$
. Define ![]() $K_{n,m}^{*}\,:\!={{\rm conv}}(S_{n,m}^{*})$
. We would like to know whether bootstrapping is asymptotically valid for
$K_{n,m}^{*}\,:\!={{\rm conv}}(S_{n,m}^{*})$
. We would like to know whether bootstrapping is asymptotically valid for ![]() $d_{\rm e}(\bf{\it{c}}_{\bf{\it{k}}},K_{n,m}^{*})$
. To prove consistency, we will combine the point-process techniques in Zarepour (Reference Zarepour1999) and the results in Bräker et al. (Reference Bräker, Hsing and Bingham1998). Using the previously introduced notation, the following theorem is stated as follows.
$d_{\rm e}(\bf{\it{c}}_{\bf{\it{k}}},K_{n,m}^{*})$
. To prove consistency, we will combine the point-process techniques in Zarepour (Reference Zarepour1999) and the results in Bräker et al. (Reference Bräker, Hsing and Bingham1998). Using the previously introduced notation, the following theorem is stated as follows.

Figure 1. A representation of ![]() $d_{\rm e}(\bf{\it{c}}_{\bf{\it{k}}},K_n)$
, where the sample points are drawn uniformly from K, and
$d_{\rm e}(\bf{\it{c}}_{\bf{\it{k}}},K_n)$
, where the sample points are drawn uniformly from K, and ![]() $K_n$
is the convex hull of the sample.
$K_n$
is the convex hull of the sample.
Theorem 3.1. Under the assumptions above, suppose ![]() $m=o(n)$. Then for any integer k, where
$m=o(n)$. Then for any integer k, where ![]() $0\le k\le r$, we have
$0\le k\le r$, we have
as ![]() $n,m\to\infty$
, where
$n,m\to\infty$
, where ![]() $p_k$
is defined in (2.7).
$p_k$
is defined in (2.7).
Proof. We divide our proof into three steps as follows.
Step 1: Construction of the original point process. Here and later, the additions and subtractions between a set and a point are Minkowski sum and difference. In other words, if K is a nonempty subset of ![]() $\mathbb{R}^d$
and
$\mathbb{R}^d$
and ![]() ${\bf x}\in \mathbb{R}^d$
then
${\bf x}\in \mathbb{R}^d$
then
Let ![]() $\lambda$
be Lebesgue measure. For any measurable subset
$\lambda$
be Lebesgue measure. For any measurable subset ![]() $A\subset \mathbb{R}^2$
, we have
$A\subset \mathbb{R}^2$
, we have
 \begin{align}
n{{\rm \mathrm{P}}}(\sqrt{n}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A)&=n{{\rm \mathrm{P}}}\bigg(X_1\in\bigg(\frac{A}{\sqrt{n}}+\bf{\it{c}}_{\bf{\it{k}}}\bigg)\bigg)\notag\\
&=\frac{n}{|K|}\lambda\bigg(\frac{A}{\sqrt{n}}\cap (K-\bf{\it{c}}_{\bf{\it{k}}})\bigg)\notag\\
&=\frac{1}{|K|}\lambda(A\cap\sqrt{n}(K-\bf{\it{c}}_{\bf{\it{k}}}))\notag\\
&\xrightarrow{\ }\frac{1}{|K|}\lambda(A) %,\text{\ \ \ \ \ as }
\quad \text{as}\ n\to\infty.\notag
\end{align}
\begin{align}
n{{\rm \mathrm{P}}}(\sqrt{n}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A)&=n{{\rm \mathrm{P}}}\bigg(X_1\in\bigg(\frac{A}{\sqrt{n}}+\bf{\it{c}}_{\bf{\it{k}}}\bigg)\bigg)\notag\\
&=\frac{n}{|K|}\lambda\bigg(\frac{A}{\sqrt{n}}\cap (K-\bf{\it{c}}_{\bf{\it{k}}})\bigg)\notag\\
&=\frac{1}{|K|}\lambda(A\cap\sqrt{n}(K-\bf{\it{c}}_{\bf{\it{k}}}))\notag\\
&\xrightarrow{\ }\frac{1}{|K|}\lambda(A) %,\text{\ \ \ \ \ as }
\quad \text{as}\ n\to\infty.\notag
\end{align}
This is due to the fact that ![]() $\sqrt{n}(K-\bf{\it{c}}_{\bf{\it{k}}})\uparrow\mathbb{R}^2$
. Therefore, according to Resnick (Reference Resnick1987) we have
$\sqrt{n}(K-\bf{\it{c}}_{\bf{\it{k}}})\uparrow\mathbb{R}^2$
. Therefore, according to Resnick (Reference Resnick1987) we have
Define the point process ![]() $\xi_{n,k}=\sum_{i=1}^{n}\delta_{\sqrt{n}(X_i-\bf{\it{c}}_{\bf{\it{k}}})}$
. Here,
$\xi_{n,k}=\sum_{i=1}^{n}\delta_{\sqrt{n}(X_i-\bf{\it{c}}_{\bf{\it{k}}})}$
. Here, ![]() $\xi_{n,k}$
can be regarded as a random element in
$\xi_{n,k}$
can be regarded as a random element in ![]() $M_{p}(\text{Cone} \bf{\it{c}}_{\bf{\it{k}}})$
(the collection of all nonnegative point measures on the cone
$M_{p}(\text{Cone} \bf{\it{c}}_{\bf{\it{k}}})$
(the collection of all nonnegative point measures on the cone ![]() $\bf{\it{c}}_{\bf{\it{k}}}$
; see Resnick (Reference Resnick1987)) endowed with vague topology. The Laplace functional of
$\bf{\it{c}}_{\bf{\it{k}}}$
; see Resnick (Reference Resnick1987)) endowed with vague topology. The Laplace functional of ![]() $\xi_{n,k}$
will be
$\xi_{n,k}$
will be
 \begin{align}
\Phi_{\xi_{n,k}}(\kern2ptf)&=\bigg(\int_{\mathbb{R}^2} \exp\{\!-f(\sqrt{n}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))\}\frac{1}{|K|}\mu({\rm d}\bf{\it{x}})\bigg)^n\notag %\ \ \
\quad \bigg(\mu=\lambda(\cdot\cap K)\bigg)\\
&=\bigg(1-\frac{\int_{\mathbb{R}^2} (1-{\rm e}^{\:f(\bf{\it{y}})})\tilde{\mu}({\rm d}\bf{\it{y}})}{n}\bigg)^n %\ \ \
\quad (\bf{\it{y}}=\sqrt{n}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))\notag\\
&\to\exp\bigg\{\!-\int_{\mathbb{R}^2} (1-{\rm e}^{\:f(\bf{\it{y}})})\frac{1}{|K|}\lambda({\rm d}\bf{\it{y}})\bigg\},\notag
\end{align}
\begin{align}
\Phi_{\xi_{n,k}}(\kern2ptf)&=\bigg(\int_{\mathbb{R}^2} \exp\{\!-f(\sqrt{n}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))\}\frac{1}{|K|}\mu({\rm d}\bf{\it{x}})\bigg)^n\notag %\ \ \
\quad \bigg(\mu=\lambda(\cdot\cap K)\bigg)\\
&=\bigg(1-\frac{\int_{\mathbb{R}^2} (1-{\rm e}^{\:f(\bf{\it{y}})})\tilde{\mu}({\rm d}\bf{\it{y}})}{n}\bigg)^n %\ \ \
\quad (\bf{\it{y}}=\sqrt{n}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))\notag\\
&\to\exp\bigg\{\!-\int_{\mathbb{R}^2} (1-{\rm e}^{\:f(\bf{\it{y}})})\frac{1}{|K|}\lambda({\rm d}\bf{\it{y}})\bigg\},\notag
\end{align}
where
for any Borel set ![]() $A\subset\mathbb{R}^2$
. Hence, given the vertex
$A\subset\mathbb{R}^2$
. Hence, given the vertex ![]() $\bf{\it{c}}_{\bf{\it{k}}}$
, we have
$\bf{\it{c}}_{\bf{\it{k}}}$
, we have ![]() $\xi_{n,k}\xrightarrow{\,{\rm D}\,}\xi$
as
$\xi_{n,k}\xrightarrow{\,{\rm D}\,}\xi$
as ![]() $n\to\infty$
, where
$n\to\infty$
, where ![]() $\xi$
is a Poisson point process with intensity measure
$\xi$
is a Poisson point process with intensity measure ![]() $\frac{1}{|K|}\lambda$
.
$\frac{1}{|K|}\lambda$
.
Step 2: Construction of the bootstrapping point process. Conditionally on ![]() $S_n$
, let
$S_n$
, let ![]() $\xi_{n,m,k}^{*}=\sum_{i=1}^{m}\delta_{\sqrt{m}(X_{n,i}^{*}-\bf{\it{c}}_{\bf{\it{k}}})}$
, which is also a random element in
$\xi_{n,m,k}^{*}=\sum_{i=1}^{m}\delta_{\sqrt{m}(X_{n,i}^{*}-\bf{\it{c}}_{\bf{\it{k}}})}$
, which is also a random element in ![]() $M_{p}(\text{Cone} \bf{\it{c}}_{\bf{\it{k}}})$
. The Laplace functional of
$M_{p}(\text{Cone} \bf{\it{c}}_{\bf{\it{k}}})$
. The Laplace functional of ![]() $\xi_{n,m,k}^{*}$
is
$\xi_{n,m,k}^{*}$
is
 \begin{align}
\Phi_{\xi_{n,m,k}^{*}}(\it{f})&=\bigg(\int_{\mathbb{R}^2} {\rm e}^{-f(\sqrt{m}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))}F_n({\rm d}\bf{\it{x}})\bigg)^{m}\\
&=\bigg(\int_{\mathbb{R}^2} {\rm e}^{-f(\sqrt{m}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))}\frac{1}{n}\sum_{i=1}^{n}\delta_{X_i}({\rm d}\bf{\it{x}})\bigg)^{m}\\
&=\bigg(\frac{1}{n}\sum_{i=1}^{n}{\rm e}^{\:f(\sqrt{m}(X_i-\bf{\it{c}}_{\bf{\it{k}}}))}\bigg)^m\\
&=\bigg(\int_{\mathbb{R}^2}{\rm e}^{\:f(\bf{\it{y}})}\frac{1}{n}\sum_{i=1}^{n}\delta_{\sqrt{m}(X_i-\bf{\it{c}}_{\bf{\it{k}}})}({\rm d}\bf{\it{y}})\bigg)^m\\
&=\bigg(1-\frac{\int_{\mathbb{R}^2}(1-{\rm e}^{-f(\bf{\it{y}})})\frac{m}{n}\sum_{i=1}^{n}\delta_{\sqrt{m}(X_i-\bf{\it{c}}_{\bf{\it{k}}})}({\rm d}\bf{\it{y}})}{m}\bigg)^{m}.
\label{eqn10}\end{align}
\begin{align}
\Phi_{\xi_{n,m,k}^{*}}(\it{f})&=\bigg(\int_{\mathbb{R}^2} {\rm e}^{-f(\sqrt{m}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))}F_n({\rm d}\bf{\it{x}})\bigg)^{m}\\
&=\bigg(\int_{\mathbb{R}^2} {\rm e}^{-f(\sqrt{m}(\bf{\it{x}}-\bf{\it{c}}_{\bf{\it{k}}}))}\frac{1}{n}\sum_{i=1}^{n}\delta_{X_i}({\rm d}\bf{\it{x}})\bigg)^{m}\\
&=\bigg(\frac{1}{n}\sum_{i=1}^{n}{\rm e}^{\:f(\sqrt{m}(X_i-\bf{\it{c}}_{\bf{\it{k}}}))}\bigg)^m\\
&=\bigg(\int_{\mathbb{R}^2}{\rm e}^{\:f(\bf{\it{y}})}\frac{1}{n}\sum_{i=1}^{n}\delta_{\sqrt{m}(X_i-\bf{\it{c}}_{\bf{\it{k}}})}({\rm d}\bf{\it{y}})\bigg)^m\\
&=\bigg(1-\frac{\int_{\mathbb{R}^2}(1-{\rm e}^{-f(\bf{\it{y}})})\frac{m}{n}\sum_{i=1}^{n}\delta_{\sqrt{m}(X_i-\bf{\it{c}}_{\bf{\it{k}}})}({\rm d}\bf{\it{y}})}{m}\bigg)^{m}.
\label{eqn10}\end{align}
If
then (3.1) becomes
Since ![]() $m{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in\cdot)\xrightarrow{\,{\rm V}\,}\frac{1}{|K|}\lambda(\!\cdot\!)$
and
$m{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in\cdot)\xrightarrow{\,{\rm V}\,}\frac{1}{|K|}\lambda(\!\cdot\!)$
and ![]() $({{\text{e}}^x} - 1)/x \to 1$
as
$({{\text{e}}^x} - 1)/x \to 1$
as ![]() $x\to 0$
, we have
$x\to 0$
, we have
 \begin{align}
& {{\rm \mathrm{E}}}(\!\exp\{t\eta_{n,m,k}(A)\})\notag\\
&\qquad=({\rm e}^{tm/n}{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A)+1-{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A))^n\notag\\
&\qquad=\bigg(\frac{m{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A)(\frac{n}{tm}({\rm e}^{tm/n}-1))t}{n}+1\bigg)^n\notag\\
&\qquad\to\exp\Big\{\frac{t}{|K|}\lambda(A)\Big\} %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty. \notag
\end{align}
\begin{align}
& {{\rm \mathrm{E}}}(\!\exp\{t\eta_{n,m,k}(A)\})\notag\\
&\qquad=({\rm e}^{tm/n}{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A)+1-{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A))^n\notag\\
&\qquad=\bigg(\frac{m{{\rm \mathrm{P}}}(\sqrt{m}(X_1-\bf{\it{c}}_{\bf{\it{k}}})\in A)(\frac{n}{tm}({\rm e}^{tm/n}-1))t}{n}+1\bigg)^n\notag\\
&\qquad\to\exp\Big\{\frac{t}{|K|}\lambda(A)\Big\} %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty. \notag
\end{align}
Therefore, from Kallenberg (Reference Kallenberg1983), Theorem 4.2, page 32, we have
See also Zarepour (Reference Zarepour1999). Combining (3.3) with (3.2) implies that, as ![]() $n,m\to\infty$
,
$n,m\to\infty$
,
Step 3: The continuous mapping theorem. For any measure ![]() $\eta \in M_{p}(\text{Cone} \bf{\it{c}}_{\bf{\it{k}}})$
, suppose
$\eta \in M_{p}(\text{Cone} \bf{\it{c}}_{\bf{\it{k}}})$
, suppose ![]() $f_k$
maps
$f_k$
maps ![]() $\eta$
to the smallest distance between the origin and the convex hull of the points of
$\eta$
to the smallest distance between the origin and the convex hull of the points of ![]() $\eta$
. It is easy to find that
$\eta$
. It is easy to find that
Now apply Skorokhod’s representation theorem and the continuous mapping theorem on (3.4) to get
as ![]() $n\to\infty$
, noticing that
$n\to\infty$
, noticing that ![]() $m/n\rightarrow 0$
. From Bräker et al. (Reference Bräker, Hsing and Bingham1998), we have
$m/n\rightarrow 0$
. From Bräker et al. (Reference Bräker, Hsing and Bingham1998), we have
completing the proof.
This proves that the result in Bräker et al. (Reference Bräker, Hsing and Bingham1998), as stated in Theorem 3.1, is valid for the regular bootstrap when ![]() $m/n\rightarrow 0$
.
$m/n\rightarrow 0$
.
4. New bootstrapping scheme on uniform samples
Here we introduce the maximum likelihood estimator of the underlying set as follows.
Definition 4.1. Suppose ![]() $S_n=\{X_i\}_{i=1}^{n}$
is a sequence of i.i.d. random points drawn from F, where F has a nonempty, convex support
$S_n=\{X_i\}_{i=1}^{n}$
is a sequence of i.i.d. random points drawn from F, where F has a nonempty, convex support ![]() $K\subset\mathbb{R}^d$
and K is assumed to be unknown. We denote the maximum likelihood estimator of K by
$K\subset\mathbb{R}^d$
and K is assumed to be unknown. We denote the maximum likelihood estimator of K by ![]() $ML(S_n)$
.
$ML(S_n)$
.
Since ![]() $ML(S_n)$
is the maximum likelihood estimator for K, the geometric features of K determine the geometric features of
$ML(S_n)$
is the maximum likelihood estimator for K, the geometric features of K determine the geometric features of ![]() $ML(S_n)$
. For example, if we only know that K is a convex set, then
$ML(S_n)$
. For example, if we only know that K is a convex set, then ![]() $ML(S_n)={{\rm conv}}(S_n)=K_n$
(see Figure 2).
$ML(S_n)={{\rm conv}}(S_n)=K_n$
(see Figure 2).

Figure 2. K is a convex polygon. The sample size ![]() $n=100$
.
$n=100$
. ![]() $K_n$
is the convex hull of the sample points.
$K_n$
is the convex hull of the sample points.
Based on the maximum likelihood estimator of the underlying set, we introduce the following semi-parametric bootstrap method when we know F to a certain degree. Let F be the underlying distribution with nonempty convex support. Let ![]() $F_A$
be the restriction of F on a set
$F_A$
be the restriction of F on a set ![]() $A\subset\mathbb{R}^d$
, i.e. for any Borel set
$A\subset\mathbb{R}^d$
, i.e. for any Borel set ![]() $B\subset\mathbb{R}^d$
,
$B\subset\mathbb{R}^d$
,
Then in our semi-parametric bootstrapping scheme, points ![]() $S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
are independently drawn from
$S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
are independently drawn from ![]() $F_{ML(S_n)}$
when the sample points
$F_{ML(S_n)}$
when the sample points ![]() $S_n$
are given.
$S_n$
are given.
In the following two examples we consider two simple cases to explain how our approach works. In the first example we assume that the underlying set is a disk with an unknown radius R centered at the origin; in the second, we consider a rectangle as the underlying set. Additionally, the distribution on both sets is assumed to be uniform.
Example 4.1. Let ![]() $d_{\rm e}$
be the Euclidean metric on
$d_{\rm e}$
be the Euclidean metric on ![]() $\mathbb{R}^2$
. Define the Euclidean norm
$\mathbb{R}^2$
. Define the Euclidean norm ![]() $\|\bf{\it{x}}\|=d_{\rm e}(\textbf{0},\bf{\it{x}})\ %,\forall
\text{for all}\ \bf{\it{x}}\in\mathbb{R}^2$
. Denote
$\|\bf{\it{x}}\|=d_{\rm e}(\textbf{0},\bf{\it{x}})\ %,\forall
\text{for all}\ \bf{\it{x}}\in\mathbb{R}^2$
. Denote ![]() $B(\textbf{0},r)\,:\!=\{\bf{\it{x}}\in\mathbb{R}^2\,:\,\|\bf{\it{x}}\|\le r\}$
. Let
$B(\textbf{0},r)\,:\!=\{\bf{\it{x}}\in\mathbb{R}^2\,:\,\|\bf{\it{x}}\|\le r\}$
. Let ![]() $S_n=\{X_i\}_{i=1}^{n}$
be the i.i.d. random points uniformly drawn from the disk
$S_n=\{X_i\}_{i=1}^{n}$
be the i.i.d. random points uniformly drawn from the disk ![]() $C\,:\!=B(\textbf{0},R)$
. Let
$C\,:\!=B(\textbf{0},R)$
. Let ![]() $C_n\,:\!=B(\textbf{0},R_n)$
where
$C_n\,:\!=B(\textbf{0},R_n)$
where
i.e. ![]() $C_n$
is the smallest disk with its center at the origin and containing all the sample points (see Figure 3). It is easy to checkhat
$C_n$
is the smallest disk with its center at the origin and containing all the sample points (see Figure 3). It is easy to checkhat ![]() $C_n$
is the maximum likelihood estimator for C, i.e.
$C_n$
is the maximum likelihood estimator for C, i.e. ![]() $ML(S_n)=C_n$
. Since the sample points are drawn independently and uniformly from C, we have
$ML(S_n)=C_n$
. Since the sample points are drawn independently and uniformly from C, we have
 \begin{align}
{{\rm \mathrm{P}}}(|R_n-R|>\varepsilon)
&={{\rm \mathrm{P}}}(R_n<R-\varepsilon)\notag\\
&=\bigg(\frac{\pi (R-\varepsilon)^2}{\pi R^2}\bigg)^n\to 0 \quad \text{as}\ n\to\infty\notag,
\end{align}
\begin{align}
{{\rm \mathrm{P}}}(|R_n-R|>\varepsilon)
&={{\rm \mathrm{P}}}(R_n<R-\varepsilon)\notag\\
&=\bigg(\frac{\pi (R-\varepsilon)^2}{\pi R^2}\bigg)^n\to 0 \quad \text{as}\ n\to\infty\notag,
\end{align}

Figure 3. C is a disk centered at the origin.
which implies ![]() $R_n\xrightarrow{\,{\rm P}\,}R$
. Indeed,
$R_n\xrightarrow{\,{\rm P}\,}R$
. Indeed,
Therefore,
which implies ![]() $R_n$
converges to R completely (i.e.
$R_n$
converges to R completely (i.e. ![]() $R_n\xrightarrow{\,{\rm C}\,}R$
, which is stronger than almost sure convergence). See Hsu and Robins (1974) for the definition.
$R_n\xrightarrow{\,{\rm C}\,}R$
, which is stronger than almost sure convergence). See Hsu and Robins (1974) for the definition.
Now we can evaluate the asymptotic validity of a functional using our bootstrapping scheme on this sample. Given ![]() $S_n$
, define
$S_n$
, define
where ![]() $X_{n,i}^{*}$
,
$X_{n,i}^{*}$
, ![]() $1\le i\le m$
, are drawn uniformly from
$1\le i\le m$
, are drawn uniformly from ![]() $C_n$
. Notice that as
$C_n$
. Notice that as ![]() $n\to\infty$
we have
$n\to\infty$
we have
 \begin{align}
{{\rm \mathrm{P}}}(n(R-R_n)>x)
&={{\rm \mathrm{P}}}(R_n<R-x/n)\notag\\
&=\bigg(\frac{\pi (R-x/n)^2}{\pi R^2}\bigg)^n\to\exp\{\!-2x/R\},
\label{eqn14}\end{align}
\begin{align}
{{\rm \mathrm{P}}}(n(R-R_n)>x)
&={{\rm \mathrm{P}}}(R_n<R-x/n)\notag\\
&=\bigg(\frac{\pi (R-x/n)^2}{\pi R^2}\bigg)^n\to\exp\{\!-2x/R\},
\label{eqn14}\end{align}
and as ![]() $n,m\to\infty$
we have
$n,m\to\infty$
we have
 \begin{align}
{{\rm \mathrm{P}}}(m(R_n-R^*_{n,m})>x \mid C_n)
&={{\rm \mathrm{P}}}(R^*_{n,m}<R_n-x/m \mid C_n)\notag\\
&=\bigg(\frac{\pi (R_n-x/m)^2}{\pi R_n^2}\bigg)^m\xrightarrow{\,{\rm a.s.}\,}\exp\{\!-2x/R\}.
\label{eqn15}\end{align}
\begin{align}
{{\rm \mathrm{P}}}(m(R_n-R^*_{n,m})>x \mid C_n)
&={{\rm \mathrm{P}}}(R^*_{n,m}<R_n-x/m \mid C_n)\notag\\
&=\bigg(\frac{\pi (R_n-x/m)^2}{\pi R_n^2}\bigg)^m\xrightarrow{\,{\rm a.s.}\,}\exp\{\!-2x/R\}.
\label{eqn15}\end{align}
From (4.1) and (4.2), it can be seen that the bootstrap approximation is valid in this example. Notice that the standard condition of ![]() $m=o(n)$
(m out of n bootstrapping) is not required.
$m=o(n)$
(m out of n bootstrapping) is not required.
Example 4.2. Let ![]() $(X_i,Y_i)$
,
$(X_i,Y_i)$
, ![]() $1\le i\le n$
, be a sequence of i.i.d. random points uniformly distributed on a rectangle
$1\le i\le n$
, be a sequence of i.i.d. random points uniformly distributed on a rectangle ![]() $T=[0,a]\times[0,b]$
, where a and b are two unknown positive constants. Let
$T=[0,a]\times[0,b]$
, where a and b are two unknown positive constants. Let ![]() $T_n\,:\!=[\!\min_{1\le i\le
n}X_i,\max_{1\le i\le n}X_i]\times[\!\min_{1\le i\le
n}Y_i,\max_{1\le i\le n}Y_i]$
, i.e. the smallest rectangle containing all the sample points, and with all edges parallel to the coordinate axes (see Figure 4). Since
$T_n\,:\!=[\!\min_{1\le i\le
n}X_i,\max_{1\le i\le n}X_i]\times[\!\min_{1\le i\le
n}Y_i,\max_{1\le i\le n}Y_i]$
, i.e. the smallest rectangle containing all the sample points, and with all edges parallel to the coordinate axes (see Figure 4). Since ![]() $T_n$
is the maximum likelihood estimator for T, we have
$T_n$
is the maximum likelihood estimator for T, we have ![]() $ML(S_n)=T_n$
. Here,
$ML(S_n)=T_n$
. Here, ![]() $\partial{T}$
and
$\partial{T}$
and ![]() $\partial{T_n}$
consist of the four edges of T and
$\partial{T_n}$
consist of the four edges of T and ![]() $T_n$
, respectively. For any
$T_n$
, respectively. For any ![]() $A,B\subset\mathbb{R}^2$
, let h(A,B) be the shortest horizontal or vertical distance between A and B, i.e.
$A,B\subset\mathbb{R}^2$
, let h(A,B) be the shortest horizontal or vertical distance between A and B, i.e.

Figure 4. T is a rectangle with its edges parallel to the coordinate axes.
where
Therefore, as ![]() $n\to\infty$
we have
$n\to\infty$
we have
Given ![]() $S_n$
, let
$S_n$
, let ![]() $(X_{n,i}^{*},Y_{n,i}^{*})$
,
$(X_{n,i}^{*},Y_{n,i}^{*})$
, ![]() $1\le i\le m$
, be a sequence of i.i.d. random points uniformly drawn from
$1\le i\le m$
, be a sequence of i.i.d. random points uniformly drawn from ![]() $T_n$
. Denote
$T_n$
. Denote
 \begin{align*}
T_{n,m}^{*} & = [\!\min_{1\le i\le m}X_{n,i}^{*},\max_{1\le i\le m}X_{n,i}^{*}]\times[\!\min_{1\le i\le m}Y_{n,i}^{*},\max_{1\le i\le m}Y_{n,i}^{*}], \\
\Delta_{n,1} & \,:\!=\max_{1\le i\le n}X_i-\min_{1\le i\le n}X_i, \\ % \ \text{and}\ \
\Delta_{n,2} & \,:\!=\max_{1\le i\le n}Y_i-\min_{1\le i\le n}Y_i.
\end{align*}
\begin{align*}
T_{n,m}^{*} & = [\!\min_{1\le i\le m}X_{n,i}^{*},\max_{1\le i\le m}X_{n,i}^{*}]\times[\!\min_{1\le i\le m}Y_{n,i}^{*},\max_{1\le i\le m}Y_{n,i}^{*}], \\
\Delta_{n,1} & \,:\!=\max_{1\le i\le n}X_i-\min_{1\le i\le n}X_i, \\ % \ \text{and}\ \
\Delta_{n,2} & \,:\!=\max_{1\le i\le n}Y_i-\min_{1\le i\le n}Y_i.
\end{align*}
Since ![]() $\Delta_{n,1}$
and
$\Delta_{n,1}$
and ![]() $\Delta_{n,2}$
are both nondecreasing sequences and
$\Delta_{n,2}$
are both nondecreasing sequences and ![]() $\Delta_{n,1}\xrightarrow{\,{\rm P}\,}a$
,
$\Delta_{n,1}\xrightarrow{\,{\rm P}\,}a$
, ![]() $\Delta_{n,2}\xrightarrow{\,{\rm P}\,}b$
, then
$\Delta_{n,2}\xrightarrow{\,{\rm P}\,}b$
, then ![]() $\Delta_{n,1}\xrightarrow{\,{\rm a.s.}\,}a$
,
$\Delta_{n,1}\xrightarrow{\,{\rm a.s.}\,}a$
, ![]() $\Delta_{n,2}\xrightarrow{\,{\rm a.s.}\,}b$
. Therefore, as
$\Delta_{n,2}\xrightarrow{\,{\rm a.s.}\,}b$
. Therefore, as ![]() $n,m\to\infty$
, we have
$n,m\to\infty$
, we have
 \begin{align}
{{\rm \mathrm{P}}}(mh(\partial{T_n},\partial{T_{n,m}^{*}})>x \mid S_n)
&={{\rm \mathrm{P}}}^{m}(h(\partial{T_n},X_{n,1}^*)>x/m \mid S_n)\notag\\
&=\Delta_{n,1}^{-m}\Delta_{n,2}^{-m}\bigg(\Delta_{n,1}-\frac{2x}{m}\bigg)^m\bigg(\Delta_{n,2}-\frac{2x}{m}\bigg)^m \notag\\
&\xrightarrow{\,{\rm a.s.}\,}{\rm e}^{-2x(a^{-1}+b^{-1})}.
\label{eqn17}\end{align}
\begin{align}
{{\rm \mathrm{P}}}(mh(\partial{T_n},\partial{T_{n,m}^{*}})>x \mid S_n)
&={{\rm \mathrm{P}}}^{m}(h(\partial{T_n},X_{n,1}^*)>x/m \mid S_n)\notag\\
&=\Delta_{n,1}^{-m}\Delta_{n,2}^{-m}\bigg(\Delta_{n,1}-\frac{2x}{m}\bigg)^m\bigg(\Delta_{n,2}-\frac{2x}{m}\bigg)^m \notag\\
&\xrightarrow{\,{\rm a.s.}\,}{\rm e}^{-2x(a^{-1}+b^{-1})}.
\label{eqn17}\end{align}
From (4.3) and (4.4), we can conclude that our bootstrap approximation is valid for the functional h in this example. Again, the condition ![]() $m=o(n)$
is not necessary.
$m=o(n)$
is not necessary.
In the following sections we prove the consistency results for the Hausdorff distance when applying our semi-parametric bootstrapping scheme on uniform polytopes. In this case, the underlying distribution F is the uniform distribution on an unknown convex set K, which implies that ![]() $F_{ML(S_n)}$
is exactly the uniform distribution on
$F_{ML(S_n)}$
is exactly the uniform distribution on ![]() $ML(S_n)=K_n={{\rm conv}}(S_n)$
, and the bootstrapping points
$ML(S_n)=K_n={{\rm conv}}(S_n)$
, and the bootstrapping points ![]() $S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
are drawn from
$S_{n,m}^{*}=\{X_{n,i}^{*}\}_{i=1}^{m}$
are drawn from ![]() $F_{ML(S_n)}$
.
$F_{ML(S_n)}$
.
5. The bootstrap consistency of the Hausdorff distance on uniform polytopes with a semi-parametric bootstrapping scheme
5.1. Notation
Here and later the following notation is used. Suppose F is the uniform distribution on an unknown convex set K. Let ![]() $S_{n}\,:\!=\{X_i\}_{i=1}^{n}$
be a sequence of i.i.d. random points drawn from F and
$S_{n}\,:\!=\{X_i\}_{i=1}^{n}$
be a sequence of i.i.d. random points drawn from F and ![]() $K_n={{\rm conv}}(S_n)$
. Let
$K_n={{\rm conv}}(S_n)$
. Let ![]() $S_{n,m}^{*}\,:\!=\{X_{n,i}^{*}\}_{i=1}^{m}$
be a sequence of i.i.d. random points drawn from
$S_{n,m}^{*}\,:\!=\{X_{n,i}^{*}\}_{i=1}^{m}$
be a sequence of i.i.d. random points drawn from ![]() $F_{K_n}$
. Let
$F_{K_n}$
. Let ![]() $S_m'\,:\!=\{X_{i}'\}_{i=1}^{m}$
be another sequence of i.i.d. random points drawn from F and independent from
$S_m'\,:\!=\{X_{i}'\}_{i=1}^{m}$
be another sequence of i.i.d. random points drawn from F and independent from ![]() $S_n$
. For any set A, we denote
$S_n$
. For any set A, we denote ![]() $A^n=\underbrace{A\times\cdots\times A}_{n\
\text{times}}$
. For simplicity, we also use the following notation:
$A^n=\underbrace{A\times\cdots\times A}_{n\
\text{times}}$
. For simplicity, we also use the following notation:
The following convergences are equivalent:
 \begin{align}
% &(1)\
\begin{split}
m(1-F(K_n)) & \xrightarrow{\,{\rm P}\,}0 \quad %,\text{\ as\ }
\text{as}\ n,m\to\infty, \\ %;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\notag\\
% &(2)\
m\log{(F(K_n))} & \xrightarrow{\,{\rm P}\,}0 \quad %,\text{\ as\ }
\text{as}\ n,m\to\infty.
\end{split}
\label{eqn18}
\end{align}
\begin{align}
% &(1)\
\begin{split}
m(1-F(K_n)) & \xrightarrow{\,{\rm P}\,}0 \quad %,\text{\ as\ }
\text{as}\ n,m\to\infty, \\ %;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\notag\\
% &(2)\
m\log{(F(K_n))} & \xrightarrow{\,{\rm P}\,}0 \quad %,\text{\ as\ }
\text{as}\ n,m\to\infty.
\end{split}
\label{eqn18}
\end{align}
Note that ![]() ${{\rm \mathrm{P}}}(m(1-F(K_n))>m(1-\exp\{\!-\varepsilon/m\}))\to0$
if anf only if
${{\rm \mathrm{P}}}(m(1-F(K_n))>m(1-\exp\{\!-\varepsilon/m\}))\to0$
if anf only if ![]() ${{\rm \mathrm{P}}}(|m\log{(F(K_n))}|>\varepsilon)\to 0$
, where
${{\rm \mathrm{P}}}(|m\log{(F(K_n))}|>\varepsilon)\to 0$
, where ![]() $\varepsilon>0$
and
$\varepsilon>0$
and ![]() $m(1-\exp{(\!-\varepsilon/m)})\to\varepsilon$
as
$m(1-\exp{(\!-\varepsilon/m)})\to\varepsilon$
as ![]() $m\to\infty$
.
$m\to\infty$
.
5.2. The problem
For any functional ![]() $\phi$
, suppose we have
$\phi$
, suppose we have
where ![]() $\alpha_n$
and
$\alpha_n$
and ![]() $\beta_n$
are real numbers and Z is a random variable. Since F is the uniform distribution on K,
$\beta_n$
are real numbers and Z is a random variable. Since F is the uniform distribution on K, ![]() $F_{K_n}$
is the uniform distribution on
$F_{K_n}$
is the uniform distribution on ![]() $K_n$
. Then we will investigate the following two types of convergence:
$K_n$
. Then we will investigate the following two types of convergence:
 \begin{align*}
\text{Type\ I:} & \quad {\rm \mathrm{P}}\bigg(\frac{\phi(S^{*}_{n,m};\,F)-\beta_m}{\alpha_m}\le x \,|\, S_n\bigg) \xrightarrow{\,{\rm D}\,}{{\rm \mathrm{P}}}(Z\le x) \quad \text{as}\ n,m\to\infty. \\
\text{Type\ II:} & \quad {\rm \mathrm{P}}\bigg(\frac{\phi(S^{*}_{n,m};\,F_{K_n})-\beta_m}{\alpha_m}\le x \,|\, S_n\bigg) \xrightarrow{\,{\rm D}\,}{{\rm \mathrm{P}}}(Z\le x) \quad \text{as}\ n,m\to\infty.
\end{align*}
\begin{align*}
\text{Type\ I:} & \quad {\rm \mathrm{P}}\bigg(\frac{\phi(S^{*}_{n,m};\,F)-\beta_m}{\alpha_m}\le x \,|\, S_n\bigg) \xrightarrow{\,{\rm D}\,}{{\rm \mathrm{P}}}(Z\le x) \quad \text{as}\ n,m\to\infty. \\
\text{Type\ II:} & \quad {\rm \mathrm{P}}\bigg(\frac{\phi(S^{*}_{n,m};\,F_{K_n})-\beta_m}{\alpha_m}\le x \,|\, S_n\bigg) \xrightarrow{\,{\rm D}\,}{{\rm \mathrm{P}}}(Z\le x) \quad \text{as}\ n,m\to\infty.
\end{align*}
Type I convergence is used for derivation of type II convergence and also for theoretical interest. Of course, type II convergence establishes that the suggested bootstrap scheme works for the given functional ![]() $\phi$
.
$\phi$
.
According to (2.6) and (2.9), the convergence in (5.2) holds if we let
In this case, in the next section we will establish both type I convergence where
and type II convergence where
5.3. Uniform distribution on convex polygons
Suppose F is the uniform distribution on ![]() $K\subset\mathbb{R}^2$
, where K is a convex polygon with r vertices
$K\subset\mathbb{R}^2$
, where K is a convex polygon with r vertices ![]() $\bf{\it{c}}_{\textbf{1}},\bf{\it{c}}_{\textbf{2}},\dots,\bf{\it{c}}_{\bf{\it{r}}}$
and interior angles
$\bf{\it{c}}_{\textbf{1}},\bf{\it{c}}_{\textbf{2}},\dots,\bf{\it{c}}_{\bf{\it{r}}}$
and interior angles ![]() $\theta_1,\theta_2,\dots,\theta_r$
. From (2.6), we have
$\theta_1,\theta_2,\dots,\theta_r$
. From (2.6), we have
where ![]() $Z_1$
has the distribution function
$Z_1$
has the distribution function ![]() $G_1$
as in (2.6). Based on this result, we get the following theorem.
$G_1$
as in (2.6). Based on this result, we get the following theorem.
Theorem 5.1. Let ![]() $m\log{n}/n\rightarrow 0$
as
$m\log{n}/n\rightarrow 0$
as ![]() $n\to\infty$
. Then, as
$n\to\infty$
. Then, as ![]() $n,m\to\infty$
,
$n,m\to\infty$
,
Proof. Define the event
First, we show that, as ![]() $n,m\to\infty$
,
$n,m\to\infty$
,
This is equivalent to
Notice that ![]() ${{\rm \mathrm{P}}}(E_{n,m} \mid S_n)=(|K_n|/|K|)^m$
. Then we have
${{\rm \mathrm{P}}}(E_{n,m} \mid S_n)=(|K_n|/|K|)^m$
. Then we have
Let ![]() $|D_n|\,:\!=|K\setminus K_n|=|K|-|K_n|$
. Using the equivalence in (5.1), we only need to show that
$|D_n|\,:\!=|K\setminus K_n|=|K|-|K_n|$
. Using the equivalence in (5.1), we only need to show that
Notice that (2.1) shows that ![]() $$(|{D_n}|/|K| - {\beta _n})/{\alpha _n}$$
converges weakly where
$$(|{D_n}|/|K| - {\beta _n})/{\alpha _n}$$
converges weakly where ![]() $\beta_n=\frac{2}{3n}r\log{n}$
and
$\beta_n=\frac{2}{3n}r\log{n}$
and ![]() $\alpha_n=\frac{1}{n}\sqrt{\frac{28}{27}r\log{n}}$
, and also notice that as
$\alpha_n=\frac{1}{n}\sqrt{\frac{28}{27}r\log{n}}$
, and also notice that as ![]() $n,m\to\infty$
,
$n,m\to\infty$
, ![]() $m\alpha_n\to 0$
and
$m\alpha_n\to 0$
and ![]() $m\beta_n\to 0$
since
$m\beta_n\to 0$
since ![]() $m \log n/n\to 0$
. Then, as
$m \log n/n\to 0$
. Then, as ![]() $n,m\to\infty$
we have
$n,m\to\infty$
we have
 \begin{align}
m|D_n|/|K|
&=m\bigg(\alpha_n\frac{|D_n|/|K|-\beta_n}{\alpha_n}+\beta_n\bigg)\notag\\
&=m\alpha_n\bigg(\frac{|D_n|/|K|-\beta_n}{\alpha_n}\bigg)+m\beta_n\xrightarrow{\,{\rm P}\,} 0.\notag
\end{align}
\begin{align}
m|D_n|/|K|
&=m\bigg(\alpha_n\frac{|D_n|/|K|-\beta_n}{\alpha_n}+\beta_n\bigg)\notag\\
&=m\alpha_n\bigg(\frac{|D_n|/|K|-\beta_n}{\alpha_n}\bigg)+m\beta_n\xrightarrow{\,{\rm P}\,} 0.\notag
\end{align}
Now we develop our proof for Theorem 5.1. Define the function ![]() $f_n\,:\,\mathbb{R}^n\to\mathbb{R}$
such that
$f_n\,:\,\mathbb{R}^n\to\mathbb{R}$
such that
From (2.6), we get, as ![]() $n\to\infty$
,
$n\to\infty$
,
i.e. for any continuity point of ![]() $G_1$
, say
$G_1$
, say ![]() $x\in\mathbb{R}$
, as
$x\in\mathbb{R}$
, as ![]() $n\to\infty$
,
$n\to\infty$
,
Let ![]() $A_n\,:\!=(\kern2ptf_n^{-1}(\!-\!\infty,x])\cap K^n$
, where
$A_n\,:\!=(\kern2ptf_n^{-1}(\!-\!\infty,x])\cap K^n$
, where ![]() $f_{n}^{-1}(A)=
\{u\,:\,f_{n}(u)\in A\}$
for any subset A of the range of function
$f_{n}^{-1}(A)=
\{u\,:\,f_{n}(u)\in A\}$
for any subset A of the range of function ![]() $f_{n}$
. Since, given
$f_{n}$
. Since, given ![]() $S_n$
, the random vector
$S_n$
, the random vector ![]() $(X_{n,1}^{*},\dots,X_{n,m}^{*})$
is independent of
$(X_{n,1}^{*},\dots,X_{n,m}^{*})$
is independent of ![]() $E_{n,m}$
, we have
$E_{n,m}$
, we have
 \begin{align}
{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_{m} \mid S_n)
&={{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n,E_{n,m})\notag\\
&={{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m\cap K_n^m \mid S_n,E_{n,m})\notag\\
&={{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n,E_{n,m}).
\label{eqn22}\end{align}
\begin{align}
{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_{m} \mid S_n)
&={{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n,E_{n,m})\notag\\
&={{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m\cap K_n^m \mid S_n,E_{n,m})\notag\\
&={{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n,E_{n,m}).
\label{eqn22}\end{align}
The last equation holds because the joint distribution of ![]() $(X_{1}',\dots,X_{m}')$
is the same as that of
$(X_{1}',\dots,X_{m}')$
is the same as that of ![]() $(X_{n,1}^{*},\dots,X_{n,m}^{*})$
when its distribution is restricted on
$(X_{n,1}^{*},\dots,X_{n,m}^{*})$
when its distribution is restricted on ![]() $K_n$
. Applying the multiplication rule to the probability condition on
$K_n$
. Applying the multiplication rule to the probability condition on ![]() $S_{n}$
(Lemma B.1), we have
$S_{n}$
(Lemma B.1), we have
 \begin{align}
{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m& \mid S_n,E_{n,m}){{\rm \mathrm{P}}}(E_{n,m} \mid S_n)\notag\\ &={{\rm \mathrm{P}}}(\{(X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m\}\cap E_{n,m} \mid S_n)\notag\\
&={{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n).
\label{eqn23}\end{align}
\begin{align}
{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m& \mid S_n,E_{n,m}){{\rm \mathrm{P}}}(E_{n,m} \mid S_n)\notag\\ &={{\rm \mathrm{P}}}(\{(X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m\}\cap E_{n,m} \mid S_n)\notag\\
&={{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n).
\label{eqn23}\end{align}
From (5.3), we have ![]() $P(E_{n,m} \mid S_n)\xrightarrow{\,{\rm P}\,}1$
as
$P(E_{n,m} \mid S_n)\xrightarrow{\,{\rm P}\,}1$
as ![]() $n\to\infty$
. Therefore, (5.6) implies
$n\to\infty$
. Therefore, (5.6) implies
 \begin{align}
|{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n,E_{n,m})&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.
\label{eqn24}\end{align}
\begin{align}
|{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n,E_{n,m})&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_{m}\cap K_n^m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.
\label{eqn24}\end{align}
Since ![]() $(A_m\cap K_n^m)\subset A_m$
and
$(A_m\cap K_n^m)\subset A_m$
and ![]() $A_m\setminus(A_m\cap K_{n}^{m})\subset D_{n}^{m}$
, we have
$A_m\setminus(A_m\cap K_{n}^{m})\subset D_{n}^{m}$
, we have
 \begin{align}
|{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m\cap K_n^m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\le {{\rm \mathrm{P}}}((X_1',\dots,X_m')\in D_n^m \mid S_n)\notag\\
&=(|D_n|/|K|)^m\notag\\
&\xrightarrow{\,{\rm a.s.}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.
\label{eqn25}\end{align}
\begin{align}
|{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m\cap K_n^m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\le {{\rm \mathrm{P}}}((X_1',\dots,X_m')\in D_n^m \mid S_n)\notag\\
&=(|D_n|/|K|)^m\notag\\
&\xrightarrow{\,{\rm a.s.}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.
\label{eqn25}\end{align}
(Note that for almost all ![]() $\omega\in\Omega$
,
$\omega\in\Omega$
, ![]() $|D_n(\omega)|/|K|<|D_3(\omega)|/|K|<1$
implies
$|D_n(\omega)|/|K|<|D_3(\omega)|/|K|<1$
implies ![]() $(|D_n(\omega)|/|K|)^m$
$(|D_n(\omega)|/|K|)^m$
![]() $\to 0$
, as
$\to 0$
, as ![]() $n,m\to\infty$
.) Thus, combining (5.5), (5.7), and (5.8) implies that
$n,m\to\infty$
.) Thus, combining (5.5), (5.7), and (5.8) implies that
 \begin{align}
|{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.\notag
\end{align}
\begin{align}
|{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.\notag
\end{align}
This is equivalent to
 \begin{align}
|{{\rm \mathrm{P}}}(\kern2ptf_m(X_{n,1}^{*},\dots,X_{n,m}^{*})\le x \mid S_n)&-{{\rm \mathrm{P}}}(\kern2ptf_m(X_{1}',\dots,X_{m}')\le x \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.
\label{eqn26}\end{align}
\begin{align}
|{{\rm \mathrm{P}}}(\kern2ptf_m(X_{n,1}^{*},\dots,X_{n,m}^{*})\le x \mid S_n)&-{{\rm \mathrm{P}}}(\kern2ptf_m(X_{1}',\dots,X_{m}')\le x \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.
\label{eqn26}\end{align}
Since ![]() $f_m(X_{1}',\dots,X_{m}')$
is independent of
$f_m(X_{1}',\dots,X_{m}')$
is independent of ![]() $S_n$
, using (5.4) we have
$S_n$
, using (5.4) we have
Finally, (5.9) and (5.10) imply that
In the following theorem, we extend Theorem 5.1, which is of type I convergence, to type II convergence.
Theorem 5.2. Under the same conditions as Theorem 5.1, we have
Proof. In the proof of Theorem 5.1, given ![]() $S_n=\{X_i\}_{i=1}^{n}$
, we reset
$S_n=\{X_i\}_{i=1}^{n}$
, we reset ![]() $A_m=(g_m^{-1}(\!-\!\infty,x])\cap K^m$
, where
$A_m=(g_m^{-1}(\!-\!\infty,x])\cap K^m$
, where
Let x be a continuity point of ![]() $G_1$
. Then follow the steps of the proof of Theorem 5.1 to get
$G_1$
. Then follow the steps of the proof of Theorem 5.1 to get
 \begin{align}
|{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ } \quad \text{as}\ n,m\to\infty.\notag
\end{align}
\begin{align}
|{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ } \quad \text{as}\ n,m\to\infty.\notag
\end{align}
This is equivalent to
 \begin{align}
|{{\rm \mathrm{P}}}(g_m(X_{n,1}^{*},\dots,X_{n,m}^{*})\le x \mid S_n)&-{{\rm \mathrm{P}}}(g_m(X_{1}',\dots,X_{m}')\le x \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ } \quad \text{as}\ n,m\to\infty.\notag
\end{align}
\begin{align}
|{{\rm \mathrm{P}}}(g_m(X_{n,1}^{*},\dots,X_{n,m}^{*})\le x \mid S_n)&-{{\rm \mathrm{P}}}(g_m(X_{1}',\dots,X_{m}')\le x \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ } \quad \text{as}\ n,m\to\infty.\notag
\end{align}
So,
as ![]() $n,m\to\infty$
. From Theorem 5.1, we have
$n,m\to\infty$
. From Theorem 5.1, we have
and
as ![]() $n,m\to\infty$
. Notice that
$n,m\to\infty$
. Notice that ![]() $H(K,K_{n,m}^{*})\ge H(K_n,K_{n,m}^{*})$
. Suppose
$H(K,K_{n,m}^{*})\ge H(K_n,K_{n,m}^{*})$
. Suppose ![]() $G_{1,m}$
is the distribution function of
$G_{1,m}$
is the distribution function of ![]() $f_m(X_1',\dots,X_m')$
, where
$f_m(X_1',\dots,X_m')$
, where ![]() $f_m$
is the same as in the proof of Theorem 5.1. Then
$f_m$
is the same as in the proof of Theorem 5.1. Then ![]() $\lim_{m\to\infty}G_{1,m}(x)=G_1(x)$
. Since the Hausdorff distance satisfies the triangle inequality
$\lim_{m\to\infty}G_{1,m}(x)=G_1(x)$
. Since the Hausdorff distance satisfies the triangle inequality
we have
 \begin{align}
{{\rm \mathrm{P}}}(\sqrt{m}H(K_n,K_{m}')\le x \mid S_n)&\le {{\rm \mathrm{P}}}(\sqrt{m}(H(K,K_{m}')-H(K,K_n))\le x \mid S_n)\notag\\
&={{\rm \mathrm{P}}}(\sqrt{m}H(K,K_{m}')\le \sqrt{m}H(K,K_n)+x \mid S_n)\notag\\
&=G_{1,m}\bigg(\sqrt{\frac{m}{n}}(\sqrt{n}H(K,K_n))+x\bigg)\notag\\
&\xrightarrow{\,{\rm P}\,}G_1(x) %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty,
\label{eqn32}\end{align}
\begin{align}
{{\rm \mathrm{P}}}(\sqrt{m}H(K_n,K_{m}')\le x \mid S_n)&\le {{\rm \mathrm{P}}}(\sqrt{m}(H(K,K_{m}')-H(K,K_n))\le x \mid S_n)\notag\\
&={{\rm \mathrm{P}}}(\sqrt{m}H(K,K_{m}')\le \sqrt{m}H(K,K_n)+x \mid S_n)\notag\\
&=G_{1,m}\bigg(\sqrt{\frac{m}{n}}(\sqrt{n}H(K,K_n))+x\bigg)\notag\\
&\xrightarrow{\,{\rm P}\,}G_1(x) %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty,
\label{eqn32}\end{align}
where the last convergence follows from (2.6) and applying Skorokhod’s representation theorem. Then use Lemma B.4 with (5.11), (5.12), (5.13), and (5.14) to get
5.4. Uniform distribution on convex sets with a smooth boundary
A similar technique can also be applied to the smooth case. Let ![]() $K\subset\mathbb{R}^2$
be a convex set with
$K\subset\mathbb{R}^2$
be a convex set with ![]() $\partial{K}\subset\mathcal{C}^2(\mathbb{R})$
. Suppose the curvature of
$\partial{K}\subset\mathcal{C}^2(\mathbb{R})$
. Suppose the curvature of ![]() $\partial{K}$
is bounded away from 0 and
$\partial{K}$
is bounded away from 0 and ![]() $\infty$
and has a bounded derivative. Suppose our underlying distribution F is the uniform distribution on K. Also suppose F satisfies (2.8). From (2.9), we get
$\infty$
and has a bounded derivative. Suppose our underlying distribution F is the uniform distribution on K. Also suppose F satisfies (2.8). From (2.9), we get
where ![]() $Z_2$
has the distribution
$Z_2$
has the distribution ![]() $G_2$
. Based on this result, we have the following theorem.
$G_2$
. Based on this result, we have the following theorem.
Theorem 5.3. Let ![]() $m/n^{2/3}\rightarrow 0$
as
$m/n^{2/3}\rightarrow 0$
as ![]() $n\to\infty$
. Then we have
$n\to\infty$
. Then we have
where ![]() $G_2(x)=\exp\{\!-d_1{\rm e}^{-d_2x}\}$
, and
$G_2(x)=\exp\{\!-d_1{\rm e}^{-d_2x}\}$
, and ![]() $a_m$
,
$a_m$
, ![]() $b_m$
, and
$b_m$
, and ![]() $G_2$
are all defined in (2.9).
$G_2$
are all defined in (2.9).
Proof. The proof follows the same lines as in the case of Theorem 5.1. Define the events ![]() $E_{n,m} \buildrel \Delta \over = \{S_m'\subset K_n\}$
. First we need to show that, as
$E_{n,m} \buildrel \Delta \over = \{S_m'\subset K_n\}$
. First we need to show that, as ![]() $n,m\to\infty$
,
$n,m\to\infty$
,
Suppose ![]() $D_n=K\setminus K_n$
. Since
$D_n=K\setminus K_n$
. Since ![]() ${{\rm \mathrm{P}}}(E_{n,m} \mid S_n)=(|K_n|/|K|)^m$
, when taking
${{\rm \mathrm{P}}}(E_{n,m} \mid S_n)=(|K_n|/|K|)^m$
, when taking ![]() $\log$
s of both sides and using the equivalence in (5.1), (5.15) becomes
$\log$
s of both sides and using the equivalence in (5.1), (5.15) becomes
Notice that
where ![]() $mn^{-2/3}\to 0$
and
$mn^{-2/3}\to 0$
and ![]() $mn^{-5/6}\to 0$
according to our assumption about m. Finally, using (2.3) and (2.4), we complete the proof for
$mn^{-5/6}\to 0$
according to our assumption about m. Finally, using (2.3) and (2.4), we complete the proof for ![]() ${{\rm \mathrm{P}}}(E_{n,m} \mid S_n)\xrightarrow{\,{\rm P}\,}1$
.
${{\rm \mathrm{P}}}(E_{n,m} \mid S_n)\xrightarrow{\,{\rm P}\,}1$
.
Now, define the function ![]() $f_n\,:\,\mathbb{R}^n\to\mathbb{R}$
such that
$f_n\,:\,\mathbb{R}^n\to\mathbb{R}$
such that
We only need to follow the steps in the proof of Theorem 5.1 and use (2.9). Therefore, for any continuity point x of ![]() $G_2$
, we get
$G_2$
, we get
Again, in the following theorem we extend Theorem 5.3 (which is of type I convergence) to type II convergence.
Theorem 5.4. Under the same conditions as Theorem 5.3, we have
Proof. Here we use the same technique as for Theorem 5.1. Given ![]() $S_n=\{X_i\}_{i=1}^{n}$
, we reset
$S_n=\{X_i\}_{i=1}^{n}$
, we reset ![]() $A_m=(g_m^{-1}(\!-\!\infty,x])\cap K^m$
, where
$A_m=(g_m^{-1}(\!-\!\infty,x])\cap K^m$
, where
Let x be a continuity point of ![]() $G_2$
. Then follow the steps in the proof of Theorem 5.1 to get
$G_2$
. Then follow the steps in the proof of Theorem 5.1 to get
 \begin{align}
|{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.\notag
\end{align}
\begin{align}
|{{\rm \mathrm{P}}}((X_{n,1}^{*},\dots,X_{n,m}^{*})\in A_m \mid S_n)&-{{\rm \mathrm{P}}}((X_{1}',\dots,X_{m}')\in A_m \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.\notag
\end{align}
This is equivalent to
 \begin{align}
|{{\rm \mathrm{P}}}(g_m(X_{n,1}^{*},\dots,X_{n,m}^{*})\le x \mid S_n)&-{{\rm \mathrm{P}}}(g_m(X_{1}',\dots,X_{m}')\le x \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.\notag
\end{align}
\begin{align}
|{{\rm \mathrm{P}}}(g_m(X_{n,1}^{*},\dots,X_{n,m}^{*})\le x \mid S_n)&-{{\rm \mathrm{P}}}(g_m(X_{1}',\dots,X_{m}')\le x \mid S_n)|\notag\\
&\xrightarrow{\,{\rm P}\,}0 %,\text{\ \ as\ }
\quad \text{as}\ n,m\to\infty.\notag
\end{align}
Therefore, we have
as ![]() $n,m\to\infty$
. From Theorem 5.3, we have
$n,m\to\infty$
. From Theorem 5.3, we have
and
as ![]() $n,m\to\infty$
. Suppose
$n,m\to\infty$
. Suppose ![]() $G_{2,m}$
is the distribution function of
$G_{2,m}$
is the distribution function of ![]() $f_m(X_1',\dots,X_m')$
, where
$f_m(X_1',\dots,X_m')$
, where ![]() $f_m$
is the same as in the proof of Theorem 5.3. Then
$f_m$
is the same as in the proof of Theorem 5.3. Then ![]() $\lim_{m\to\infty}G_{2,m}(x)=G_2(x)$
. Since the Hausdorff distance satisfies the triangle inequality
$\lim_{m\to\infty}G_{2,m}(x)=G_2(x)$
. Since the Hausdorff distance satisfies the triangle inequality
we have
 \begin{align}
{{\rm \mathrm{P}}}\bigg(\frac{H(K_n,K_{m}')-b_m}{a_m}\le x \, | \, S_n\bigg)&\le {{\rm \mathrm{P}}}\bigg(\frac{H(K,K_{m}')-H(K,K_n)-b_m}{a_m}\le x \, | \, S_n\bigg)\notag\\
&={{\rm \mathrm{P}}}\bigg(\frac{H(K,K_{m}')-b_m}{a_m}\le \frac{H(K,K_n)}{a_m}+x \, | \, S_n\bigg)\notag\\
&=G_{2,m}\bigg(\frac{H(K,K_n)}{a_m}+x\bigg).
\label{eqn37}\end{align}
\begin{align}
{{\rm \mathrm{P}}}\bigg(\frac{H(K_n,K_{m}')-b_m}{a_m}\le x \, | \, S_n\bigg)&\le {{\rm \mathrm{P}}}\bigg(\frac{H(K,K_{m}')-H(K,K_n)-b_m}{a_m}\le x \, | \, S_n\bigg)\notag\\
&={{\rm \mathrm{P}}}\bigg(\frac{H(K,K_{m}')-b_m}{a_m}\le \frac{H(K,K_n)}{a_m}+x \, | \, S_n\bigg)\notag\\
&=G_{2,m}\bigg(\frac{H(K,K_n)}{a_m}+x\bigg).
\label{eqn37}\end{align}
Since ![]() $a_n/a_m\to0$
and
$a_n/a_m\to0$
and ![]() $b_n/a_m\to0$
, we get
$b_n/a_m\to0$
, we get
Therefore, according to (5.20) and Skorokhod’s representation theorem, we have
Finally, use Lemma B.4 and (5.16), (5.17), (5.18), (5.19), and (5.21) to get
Remark 5.1. We can also get another bonus convergence result:
(This result is only a by-product of our proof and has nothing to do with our bootstrapping scheme.) By Lemma B.3 and (2.9), it is sufficient to prove
which is similar to (5.20).
6. Two more examples
In addition to the Hausdorff distance, the same technique can also be applied to other functionals. Two noticeable examples are the symmetric difference and the perimeter difference.
The following example is the symmetric difference on ![]() $\mathbb{R}^d$
. Suppose
$\mathbb{R}^d$
. Suppose ![]() $d\ (\!\ge2)$
is a fixed integer and K is a convex set in
$d\ (\!\ge2)$
is a fixed integer and K is a convex set in ![]() $\mathbb{R}^d$
such that
$\mathbb{R}^d$
such that ![]() $\partial{K}\in\mathcal{C}^2(\mathbb{R}^{d-1})$
with positive Gaussian curvature (see Appendix A for details) bounded away from 0 and
$\partial{K}\in\mathcal{C}^2(\mathbb{R}^{d-1})$
with positive Gaussian curvature (see Appendix A for details) bounded away from 0 and ![]() $\infty$
. With these assumptions, we can use the results in (2.5) and (2.2).
$\infty$
. With these assumptions, we can use the results in (2.5) and (2.2).
Example 6.1. Let ![]() $\phi_1(A,B)$
be the area of the symmetric difference between A and B, i.e.
$\phi_1(A,B)$
be the area of the symmetric difference between A and B, i.e. ![]() $\phi_1(A,B)=|(A\setminus B)\cup (B\setminus A)|$
. Since
$\phi_1(A,B)=|(A\setminus B)\cup (B\setminus A)|$
. Since ![]() $K_n\subset K$
, we have
$K_n\subset K$
, we have ![]() $\phi_1(K,K_n)=|D_n|$
. From (2.5) we have
$\phi_1(K,K_n)=|D_n|$
. From (2.5) we have
and (2.2) gives
where ![]() $\sigma$
and c are constants. Rewrite (6.1) using
$\sigma$
and c are constants. Rewrite (6.1) using ![]() $\phi_1$
to get
$\phi_1$
to get
where ![]() $a_n=\sigma C_{n}^{1/2} n^{-\frac{1}{2}-\frac{1}{d+1}}$
and
$a_n=\sigma C_{n}^{1/2} n^{-\frac{1}{2}-\frac{1}{d+1}}$
and ![]() $b_n={{\rm \mathrm{E}}}{(|D_n|)}=\Theta(n^{-\frac{2}{d+1}})$
. Let
$b_n={{\rm \mathrm{E}}}{(|D_n|)}=\Theta(n^{-\frac{2}{d+1}})$
. Let ![]() $\Phi$
be the cumulative distribution function for the standard normal distribution. Our goal is to find a proper assumption about m such that the type I convergence holds for
$\Phi$
be the cumulative distribution function for the standard normal distribution. Our goal is to find a proper assumption about m such that the type I convergence holds for ![]() $\phi_1$
, i.e., as
$\phi_1$
, i.e., as ![]() $n,m\to\infty$
we have
$n,m\to\infty$
we have
As before, define the events ![]() $E_{n,m} \buildrel \Delta \over = \{S_m'\subset K_n\}$
for the positive integers m and n. To impose a proper assumption on m, we must ensure that
$E_{n,m} \buildrel \Delta \over = \{S_m'\subset K_n\}$
for the positive integers m and n. To impose a proper assumption on m, we must ensure that
Taking ![]() $\log$
s of both sides and using the equivalence in (5.1), we have
$\log$
s of both sides and using the equivalence in (5.1), we have
Since
 \begin{align}
m|D_n|
&=m\phi_1(K,K_n)\notag\\
&=m\bigg[a_n\frac{\phi_1(K,K_n)-b_n}{a_n}+b_n\bigg]\notag\\
&=m a_n\bigg[\frac{\phi_1(K,K_n)-b_n}{a_n}\bigg]+m b_n,\notag
\end{align}
\begin{align}
m|D_n|
&=m\phi_1(K,K_n)\notag\\
&=m\bigg[a_n\frac{\phi_1(K,K_n)-b_n}{a_n}+b_n\bigg]\notag\\
&=m a_n\bigg[\frac{\phi_1(K,K_n)-b_n}{a_n}\bigg]+m b_n,\notag
\end{align}
the assumption required for m is
as ![]() $n,m\to\infty$
. So, the resample size m should satisfy
$n,m\to\infty$
. So, the resample size m should satisfy ![]() $m=o(n^{\frac{2}{d+1}})$
. We omit the details for getting type I convergence in (6.2) as the proof mimics those for Theorems 5.1 and 5.3.
$m=o(n^{\frac{2}{d+1}})$
. We omit the details for getting type I convergence in (6.2) as the proof mimics those for Theorems 5.1 and 5.3.
Furthermore, to prove type II convergence for ![]() $\phi_1$
, i.e.
$\phi_1$
, i.e.
notice that
and
which are easy to verify. On the other hand, observe that
as ![]() $n,m\to\infty$
.
$n,m\to\infty$
.
Now we can consider the perimeter difference (defined below) on ![]() $\mathbb{R}^2$
. To use the result in (2.3), suppose K satisfies
$\mathbb{R}^2$
. To use the result in (2.3), suppose K satisfies ![]() $\partial{K}\in\mathcal{C}^2(\mathbb{R})$
with positive curvature bounded away from 0 and
$\partial{K}\in\mathcal{C}^2(\mathbb{R})$
with positive curvature bounded away from 0 and ![]() $\infty$
.
$\infty$
.
Example 6.2. Let ![]() $d=2$
and define
$d=2$
and define ![]() $\phi_2(A,B)=|\text{perimeter of\ }A-\text{perimeter of\ }B|$
. From (2.3) we have
$\phi_2(A,B)=|\text{perimeter of\ }A-\text{perimeter of\ }B|$
. From (2.3) we have
and
where ![]() $\sigma'$
and c’ are two constants. Rewriting (6.8) in terms of
$\sigma'$
and c’ are two constants. Rewriting (6.8) in terms of ![]() $\phi_2$
, we have
$\phi_2$
, we have
where ![]() $a'_n=\sigma' n^{-5/6}$
and
$a'_n=\sigma' n^{-5/6}$
and ![]() $b'_n={{\rm \mathrm{E}}}{(L-L_n)}=\Theta(n^{-2/3})$
. To prove type I convergence, i.e.
$b'_n={{\rm \mathrm{E}}}{(L-L_n)}=\Theta(n^{-2/3})$
. To prove type I convergence, i.e.
we need to show that
As in Example 6.1, m should satisfy the condition
Thus, our assumption for m should follow ![]() $m=o(n^{2/3)})$
. (Notice that
$m=o(n^{2/3)})$
. (Notice that ![]() $d=2$
.)
$d=2$
.)
To prove type II convergence, i.e.
notice that
and
which are easy to verify using Lemma B.2. Obviously,
as ![]() $n,m\to\infty$
.
$n,m\to\infty$
.
Appendix A. Basic definitions and notation
A.1. Curvature and Gaussian curvature
Let the planar curve ![]() $c(t)=(x(t),y(t))$
, where
$c(t)=(x(t),y(t))$
, where ![]() $x,
y\in\mathcal{C}^2(\mathbb{R})$
and t is the arc length between c(0) and c(t). Then the curvature
$x,
y\in\mathcal{C}^2(\mathbb{R})$
and t is the arc length between c(0) and c(t). Then the curvature ![]() $\kappa(t)=|\ddot{c}(t)|$
.
$\kappa(t)=|\ddot{c}(t)|$
.
Let S be a surface in Euclidean space with second fundamental form ![]() ${\displaystyle II}$
(see Kobayashi and Nomizu (Reference Kobayashi and Nomizu1996)). Given a point z on S, suppose
${\displaystyle II}$
(see Kobayashi and Nomizu (Reference Kobayashi and Nomizu1996)). Given a point z on S, suppose ![]() $\{v_1,v_2\}$
is an orthonormal basis of tangent vectors at z. Suppose
$\{v_1,v_2\}$
is an orthonormal basis of tangent vectors at z. Suppose ![]() $\kappa_1$
and
$\kappa_1$
and ![]() $\kappa_2$
are the eigenvalues of the following matrix:
$\kappa_2$
are the eigenvalues of the following matrix:
Then the Gaussian curvature at the point z is given by ![]() $\kappa=\kappa_1\kappa_2$
.
$\kappa=\kappa_1\kappa_2$
.
Appendix B. Some lemmas
The following multiplication rule is obvious, but we mention it for completeness.
Lemma B.1. For any events A, B, and C we have
Lemma B.2. If ![]() $P\subset K\subset\mathbb{R}^2$
such that P is a convex polygon and K is a convex set, we have
$P\subset K\subset\mathbb{R}^2$
such that P is a convex polygon and K is a convex set, we have
where L(P) and L(K) are the perimeters of P and K, respectively.
Proof. We refer the reader to Figure 5 in the proof of this lemma. Suppose P has r vertices. Let ![]() $e_1,e_2,\dots,e_r$
be the edges of P. It is enough to show that disjoint segments
$e_1,e_2,\dots,e_r$
be the edges of P. It is enough to show that disjoint segments ![]() $s_1,s_2,\dots,s_r$
on the boundary of K exist such that
$s_1,s_2,\dots,s_r$
on the boundary of K exist such that

Figure 5. The edges ![]() $e_1,e_2,\dots,e_r$
and the segments
$e_1,e_2,\dots,e_r$
and the segments ![]() $s_1,s_2,\dots,s_r$
.
$s_1,s_2,\dots,s_r$
.
Consider the segments ![]() $s_1,s_2,\dots,s_r$
in Figure 5. Since the length of
$s_1,s_2,\dots,s_r$
in Figure 5. Since the length of ![]() $e_i$
, for any
$e_i$
, for any ![]() $1\le i\le r$
, is the distance between the two parallel lines, the length of
$1\le i\le r$
, is the distance between the two parallel lines, the length of ![]() $s_i$
is not shorter than the length of
$s_i$
is not shorter than the length of ![]() $e_i$
. Hence,
$e_i$
. Hence,
Lemma B.3. (Billingsley (Reference Billingsley1999), Theorem 3.1, page 27) Suppose d is the metric on S. If ![]() $(X_n,Y_n)$
are random elements of
$(X_n,Y_n)$
are random elements of ![]() $S\times S$
such that
$S\times S$
such that ![]() $X_n\xrightarrow{\,{\rm D}\,}X_0$
and
$X_n\xrightarrow{\,{\rm D}\,}X_0$
and ![]() $d(X_n,Y_n)\xrightarrow{\,{\rm D}\,}0$
, then
$d(X_n,Y_n)\xrightarrow{\,{\rm D}\,}0$
, then ![]() $Y_n\xrightarrow{\,{\rm D}\,}X_0$
.
$Y_n\xrightarrow{\,{\rm D}\,}X_0$
.
Lemma B.4. If ![]() $|A_n-B_n|\xrightarrow{\,{\rm P}\,}0$
,
$|A_n-B_n|\xrightarrow{\,{\rm P}\,}0$
, ![]() $A_n\ge C_n$
,
$A_n\ge C_n$
, ![]() $C_n\xrightarrow{\,{\rm P}\,}Z$
,
$C_n\xrightarrow{\,{\rm P}\,}Z$
, ![]() $B_n\le D_n$
, and
$B_n\le D_n$
, and ![]() $D_n\xrightarrow{\,{\rm P}\,}Z$
, then we have
$D_n\xrightarrow{\,{\rm P}\,}Z$
, then we have ![]() $A_n\xrightarrow{\,{\rm P}\,}Z$
and
$A_n\xrightarrow{\,{\rm P}\,}Z$
and ![]() $B_n\xrightarrow{\,{\rm P}\,}Z$
.
$B_n\xrightarrow{\,{\rm P}\,}Z$
.
Proof. For any given ![]() $\varepsilon>0$
, as
$\varepsilon>0$
, as ![]() $n\to\infty$
,
$n\to\infty$
,
 \begin{align}
{{\rm \mathrm{P}}}(A_n-Z>\varepsilon)&= {{\rm \mathrm{P}}}(A_n-B_n+B_n-D_n+D_n-Z>\varepsilon)\notag\\
&\le {{\rm \mathrm{P}}}(A_n-B_n>\varepsilon/3)+{{\rm \mathrm{P}}}(B_n-D_n>\varepsilon/3)+{{\rm \mathrm{P}}}(D_n-Z>\varepsilon/3)\to 0;\notag\\
{{\rm \mathrm{P}}}(Z-A_n>\varepsilon)&={{\rm \mathrm{P}}}(Z-C_n+C_n-A_n)\notag\\
&\le {{\rm \mathrm{P}}}(Z-C_n>\varepsilon/2)+{{\rm \mathrm{P}}}(C_n-A_n>\varepsilon/2)\to 0.
\end{align}
\begin{align}
{{\rm \mathrm{P}}}(A_n-Z>\varepsilon)&= {{\rm \mathrm{P}}}(A_n-B_n+B_n-D_n+D_n-Z>\varepsilon)\notag\\
&\le {{\rm \mathrm{P}}}(A_n-B_n>\varepsilon/3)+{{\rm \mathrm{P}}}(B_n-D_n>\varepsilon/3)+{{\rm \mathrm{P}}}(D_n-Z>\varepsilon/3)\to 0;\notag\\
{{\rm \mathrm{P}}}(Z-A_n>\varepsilon)&={{\rm \mathrm{P}}}(Z-C_n+C_n-A_n)\notag\\
&\le {{\rm \mathrm{P}}}(Z-C_n>\varepsilon/2)+{{\rm \mathrm{P}}}(C_n-A_n>\varepsilon/2)\to 0.
\end{align}
Acknowledgements
The authors are greatly indebted to the referees and the associate editors for several corrections and helpful suggestions. Financial support from the Natural Sciences and Engineering Research Council of Canada (RGPIN-2018-04008) is gratefully acknowledged.