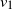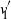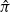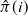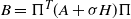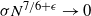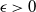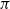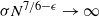1. Introduction
The graph alignment problem
Graph alignment (or graph matching, or network alignment) consists in recovering the underlying vertex correspondence between two correlated graphs, and hence can be viewed as the noisy version of the isomorphism problem. Many questions can be phrased as graph alignment problems. They are found in various fields, such as network privacy and data de-anonymization [Reference Narayanan and Shmatikov15, Reference Narayanan and Shmatikov16], biology and protein–protein interaction networks [Reference Singh, Xu and Berger20], natural language processing [Reference Haghighi, Ng and Manning13], and pattern recognition in image processing [Reference Conte, Foggia, Vento and Sansone6].
For two graphs of size N with adjacency matrices A and B, the graph matching problem can be formalized as an optimization problem:
\begin{equation}\mathop{\mathop{\textrm{arg max}}}_{P \in \mathcal{S}_N} \langle A, P B P^T \rangle ,\end{equation}
where the maximum is taken over all
$N \times N$
permutation matrices, and
$\langle \cdot,\cdot \rangle$
is the canonical matrix inner product. Note that for each
$P \in \mathcal{S}_N, \; P B P^T $
is the matrix obtained from B by relabeling the nodes according to
$P^{-1}$
. This formulation is a special case of the well studied quadratic assignment problem [Reference Pardalos, Rendl, Wolkowicz, Pardalos and Wolkowicz19], which is known to be NP-hard in the worst case, as well as some of its approximations [Reference Makarychev, Manokaran and Sviridenko14]. A natural idea is then to study the average-case version of this problem, when A and B are random instances. Following a recent line of work [Reference Ding, Ma, Wu and Xu7, Reference Fan, Mao, Wu and Xu9, Reference Feizi11], this paper focuses on the case where the signal lies in the weights of edges between all pairs of nodes.
Related work
Some general spectral methods for random graph alignment are introduced in [Reference Feizi11], based on representation matrices and low-rank approximations. These methods are tested over synthetic graphs and real data; however, no precise theoretical guarantee—e.g. an error control of the inferred mapping depending on the signal-to-noise ratio—can be found for such techniques.
Most recently, a spectral method for matrix and graph alignment (GRAMPA) was proposed in [Reference Fan, Mao, Wu and Xu9, Reference Fan, Mao, Wu and Xu10], which computes a similarity matrix which takes into account all pairs of eigenvalues
$(\lambda_i, \mu_j)$
and eigenvectors
$(u_i,v_j)$
of matrices A and B. The authors study the regime in which the method exactly recovers the underlying vertex correspondence, meeting the state-of-the-art performances for alignment of Erdös–Ri graphs in polynomial time, and improving the performances among spectral methods for matrix alignment. This method can tolerate a noise
$\sigma$
up to
$O\left(1/\log N\right)$
to recover the entire underlying vertex correspondence. Since the computation of all eigenvectors is required, the time complexity of GRAMPA is at least
$O(N^3)$
.
It is important to note that the signs of eigenvectors are ambiguous: in order to optimize the cost function in practice, it is necessary to test over all possible signs of eigenvectors. This additional complexity has no consequence when reducing A and B to rank-one matrices, but becomes costly when the reduction made is of rank
$k \gg 1$
. This combinatorial observation makes implementation and analysis of general rank-reduction methods (such as the ones proposed in [Reference Feizi11]) more difficult. We therefore focus on the analysis of the rank-one reduction (EIG1 hereafter) which is the simplest and most natural spectral alignment method, where only the leading eigenvectors of A and B are computed, with time complexity
$O(N^2)$
, which is significantly less than that of GRAMPA.
Gaussian weighted graph matching: model and method
As mentioned above, we focus on the case where the graphs are complete, weight-correlated. Matrices A and B are thus symmetric, with correlated entries. A natural model recently studied in [Reference Ding, Ma, Wu and Xu7, Reference Fan, Mao, Wu and Xu9, Reference Feizi11] is as follows: A and H are two
$N \times N$
independent normalized matrices of the Gaussian orthogonal ensemble (GOE), i.e. such that for all
$1 \leq i \leq j \leq N$
,
$\left\{A_{i,j}\right\}_{i<j}$
are independent,
\begin{equation}A_{i,j} = A_{j,i} \sim \begin{cases}\frac{1}{\sqrt{N}} \mathcal{N}(0,1) & \text{if $i \neq j$}, \\[4pt] \frac{\sqrt{2}}{\sqrt{N}} \mathcal{N}(0,1) & \text{if $i = j$},\end{cases}\end{equation}
and H is an independent copy of A. We define
$B=\Pi^T \left(A+\sigma H\right) \Pi$
, where
$\Pi$
is the matrix of some permutation
$\pi$
—e.g. random uniform—of
$\left\lbrace 1,\ldots,N\right\rbrace$
(i.e. such that
$\Pi_{i,j}=1$
if and only if
$i = \pi(j)$
), and
$\sigma = \sigma(N)$
is the noise parameter.
Given two vectors
$x=\left(x_1,\ldots,x_n\right)$
and
$y=\left(y_1,\ldots,y_n\right)$
whose coordinates are all distinct, the permutation
$\rho$
which aligns x and y is the permutation such that for all
$1 \leq i \leq n$
, the rank (for the usual order) of
$x_{\rho(i)}$
in x is the rank of
$y_{i}$
in y.
Remark 1.1. Note that in our model, all the probability distributions are absolutely continuous with respect to Lebesgue measure; thus the eigenvectors of A and B all have almost surely pairwise distinct coordinates.
We recall that the aim is to infer the underlying permutation
$\Pi$
given the observation of A and B. We now introduce our simple spectral algorithm EIG1, derived from [Reference Feizi11], which computes and aligns the leading eigenvectors
$v_1$
and
$v'_{\!\!1}$
of A and B. This very natural method can be thought of as the relaxation of the quadratic assignment problem formulation (1.1) when reducing A and B to rank-one matrices
$\lambda_1 v_1 v_1^T$
and
$\lambda'_1 v'_{\!\!1} v_1^{{}^{\prime}T}$
. Indeed, as soon as
$v_1$
and
$v'_{\!\!1}$
have pairwise distinct coordinates, it is easy to see that
\begin{equation*}\mathop{\textrm{arg max}}_{P \in \mathcal{S}_N} \Big\langle \lambda_1 v_1 v_1^T, P \lambda'_1 v'_{\!\!1} v_1^{{}^{\prime}T} P^T \Big\rangle = \mathop{\textrm{arg max}}_{P \in \mathcal{S}_N} \pm v_1^T P v'_{\!\!1} = \rho,\end{equation*}
where
$\rho$
is the aligning permutation of
$v_1$
and
$\pm v'_{\!\!1}$
. Computing the two normalized leading eigenvectors (i.e. those corresponding to the highest eigenvalues)
$v_1$
and
$v'_{\!\!1}$
of A and B, the EIG1 algorithm (Algorithm 1) returns the aligning permutation of
$v_1$
and
$\pm v'_{\!\!1}$
. The method then decides which permutation to output according to the scores.
The aim of this paper is to find the regime in which EIG1 achieves almost exact recovery, i.e. recovers all but a vanishing fraction of nodes of the planted truth
$\Pi$
.
2. Notation, main results, and proof scheme
In this section we introduce some notation that will be used throughout this paper; we also mention the main results and the proof scheme.
2.1 Notation
-
Recall that A and H are two
$N \times N$
matrices drawn under the model (1.2). The matrix B is defined as
$\Pi^T \left(A+\sigma H\right) \Pi $
, where
$\Pi$
is a uniform
$N \times N$
permutation matrix and
$\sigma$
is the noise parameter, depending on N. -
In the following,
$\left(v_1, v_2, \ldots, v_N\right)$
(resp.
$\left(v'_{\!\!1}, v'_{\!\!2}, \ldots, v'_N\right)$
) denotes an orthonormal basis of eigenvectors of A (resp. of B) with respect to the (real) eigenvalues
$\lambda_1\;\geq\;\lambda_2\;\geq\;\ldots\;\geq\;\lambda_N$
of A (resp.
$\lambda'_1\;\geq\;\lambda'_2\;\geq\;\ldots\;\geq\;\lambda'_N$
of B). Throughout the paper, the sign of
$v'_{\!\!1}$
is fixed so that
$\langle \Pi v_1,v'_{\!\!1} \rangle >0$
. -
Denote by
$\| \cdot \|$
the Euclidean norm of
$\mathbb{R}^N$
. Let
$\langle \cdot, \cdot \rangle$
denote the corresponding inner product. -
For any estimator
$\hat{\Pi}$
of
$\Pi$
, define its overlap: (2.1)This metric is used to quantify the quality of a given estimator of
\begin{equation}\mathcal{L}(\hat{\Pi},\Pi) \;:\!=\; \frac{1}{N} \sum_{i=1}^{N} \mathbf{1}_{\hat{\Pi}(i)=\Pi(i)}.\end{equation}
$\Pi$
.
-
The equality
$\overset{(d)}{=}$
will refer to equality in distribution. An event
$A_N$
is said to hold with high probability (w.h.p.) if
$\mathbb{P}(A_N)$
converges to 1 when
$N \to \infty$
. -
For two random variables
$u=u(N)$
and
$v=v(N)$
, we will use the notation
$u=o_{\mathbb{P}}\left(v\right)$
if
$\frac{u(N)}{v(N)} \overset{\mathbb{P}}{\longrightarrow} 0$
when
$N \to \infty$
. We also use this notation when
$X=X(N)$
and
$Y=Y(N)$
are N-dimensional random vectors:
$X=o_{\mathbb{P}}\left(Y\right)$
if
$\frac{\| X(N) \|}{\| Y(N) \|} \overset{\mathbb{P}}{\longrightarrow} 0$
when
$N \to \infty$
. -
Define
For two random variables
\begin{equation*}\mathcal{F} \;:\!=\; \left\lbrace f \;:\;\mathbb{N} \to \mathbb{R}_+ \; | \; \forall t>0, N^t f(N) \to \infty, \frac{f(N)}{N^t} \to 0 \right\rbrace.\end{equation*}
$u=u(N)$
and
$v=v(N)$
,
$u \asymp v$
refers to equivalence w.h.p. up to some sub-polynomial factor, meaning that there exists a function
$f \in \mathcal{F}$
such that
\begin{equation*}\mathbb{P}\left(\frac{v(N)}{f(N)} \leq u(N) \leq f(N) v(N)\right) \to 1.\end{equation*}
Throughout the paper, all limits are taken as
$N \to \infty$
, and the dependency on N will most of the time be elided, as an abuse of notation.
2.2 Main results, proof scheme
The result shown can be stated as follows: there exists a condition—a threshold—on
$\sigma$
and N under which the EIG1 method enables us to recover
$\Pi$
almost exactly, in terms of the overlap
$\mathcal{L}$
defined in (2.1). Above this threshold, we show that EIG1 cannot recover more than a vanishing part of
$\Pi$
.
Theorem 2.1. (Zero--one law for the method.) For all N, let
$\Pi_N$
denote an arbitrary permutation of size N, and let
$\hat{\Pi}_N$
be the estimator obtained with the algorithm EIG1, for A and B of the model (1.2), with permutation
$\Pi_N$
and noise parameter
$\sigma$
. We have the following zero–one law:
-
(i) If there exists
$\epsilon>0$
such that
$\sigma = o(N^{-7/6-\epsilon})$
, then
\begin{align*}\mathcal{L}(\hat{\Pi}_N,\Pi_N) \overset{L^1}{\longrightarrow} 1.\end{align*}
-
(ii) If there exists
$\epsilon>0$
such that
$\sigma = \omega(N^{-7/6+\epsilon})$
, then
\begin{align*}\mathcal{L}(\hat{\Pi}_N,\Pi_N) \overset{L^1}{\longrightarrow} 0.\end{align*}
The results of Theorem 2.1 are illustrated in Figure 1, which shows the zero–one law at
$\sigma \asymp N^{-7/6}$
. Note that the convergence to the step function appears to be slow.
Figure 1. Estimated overlap
$\mathcal{L}(\hat{\Pi},\Pi)$
reached by EIG1 in the model (1.2), for varying N and
$\sigma$
. (With 95% confidence intervals.)
Remark 2.1. We now underline that without loss of generality, we can assume that
$\Pi = \textrm{Id}$
, the identity mapping. Indeed, one can return to the general case by applying the transformations
$A \rightarrow \Pi A \Pi^T$
and
$H \rightarrow \Pi H \Pi^T$
. From now on we will assume that
$\Pi = \textrm{Id}$
.
In order to prove this theorem, it is necessary to establish two intermediate results along the way, which may also be of independent interest. First, we study the behavior of
$v'_{\!\!1}$
with respect to
$v_1$
, showing that under some conditions on
$\sigma$
and N, the difference
$v_1 - v'_{\!\!1}$
can be approximated by a renormalized Gaussian standard vector, multiplied by a variance term
$\mathbf{S}$
, where
$\mathbf{S}$
is a random variable whose behavior is well understood in terms of N and
$\sigma$
when
$N \to \infty$
. For this we work under the following assumption:
\begin{equation}\exists \, \alpha >0, \quad \;\sigma = o \left(N^{-1/2-\alpha}\right).\end{equation}
Proposition 2.1. Under the assumption (2.2), there exist a standard Gaussian vector
$Z \sim \mathcal{N}\left(0,I_N\right)$
, independent of
$v_1$
, and a random variable
$\mathbf{S} \asymp \sigma N^{1/6}$
such that
\begin{equation*}v'_{\!\!1} = \left(1 + o_{\mathbb{P}}(1)\right) \left(v_1+ \mathbf{S} \frac{Z}{\|Z\|}\right).\end{equation*}
Remark 2.2. The assumption (2.2) (or a tighter formulation) arises when studying the diffusion trajectories of eigenvalues and eigenvectors in random matrices, and corresponds to the microscopic regime in [Reference Allez, Bun and Bouchaud2]. This assumption ensures that all eigenvalues of B are close enough to the eigenvalues of A. The comparison term is justified from random matrix theory:
$N^{-1/2}$
is the typical amplitude of the spectral gaps
$\sqrt{N}(\lambda_i - \lambda_{i+1})$
in the bulk—i.e. for i of order
$\eta n$
with
$\eta \in (0,1)$
—which are the smaller ones.
Eigenvector diffusions in similar models (diffusion processes drawn with the scaling
$\sigma = \sqrt{t}$
) are studied in [Reference Allez, Bun and Bouchaud2], where the main tool is the Dyson Brownian motion (see e.g. [Reference Anderson, Guionnet and Zeitouni3]) and its formulation for eigenvector trajectories, giving stochastic differential equations for the evolutions of
$v'_{\!\!j(t)}$
with respect to vectors
$v_i=v'_{\!\!i(0)}$
. These equations lead to a system of stochastic differential equations for the overlaps
$\langle v_i, v'_{\!\!j(t)} \rangle$
, which is quite difficult to analyze rigorously. In this work we use a more elementary method to get an expansion of
$v'_{\!\!1}$
around
$v_1$
, for which this very condition (2.2) also appears.
Note that here, spectral gaps at the edge—i.e. for
$i = O(1)$
—are of order
$N^{-1/6}$
, so the assumption (2.2) may not optimal for our study, and we expect Proposition 2.1 to hold up to
$\sigma = o \left(N^{-1/6-\alpha}\right)$
. However, since the positive result of Theorem 2.1 holds in a much more restrictive regime (see the condition (i)), the condition (2.2) is enough for our purposes and allows a short and simple proof.
Proposition 2.1 suggests the study of
$v'_{\!\!1}$
as a Gaussian perturbation of
$v_1$
. The main question is now formulated as follows: what is the probability that the perturbation on
$v_1$
has an impact on the overlap of the estimator
$\hat{\Pi}$
from the EIG1 method? To answer this question, we introduce a correlated Gaussian vectors model (referred to hereafter as the toy model) of parameters N and
$s>0$
. In this model, we draw a standard Gaussian vector X of size N and
$Y= X + s Z$
where Z is an independent copy of X. We will use the notation
$(X,Y) \sim \mathcal{J}(N,s)$
.
Define
$r_1$
as the function that associates to any vector
$T=(t_1,\ldots,t_p)$
the rank of
$t_1$
in T (for the usual decreasing order). For
$(X,Y) \sim \mathcal{J}(N,s)$
we evaluate
\begin{equation*}p(N,s) \;:\!=\; \mathbb{P}\left(r_1(X)=r_1(Y)\right).\end{equation*}
Our second result shows that there is a zero–one law for the property of rank preservation in the toy model
$\mathcal{J}(N,s)$
.
Proposition 2.2. (Zero--one law for p(N,s).) In the correlated Gaussian vectors model we have the following:
-
(i) If
$s = o(1/N)$
then
\begin{align*}p(N,s) \underset{N \to \infty}{\longrightarrow} 1.\end{align*}
-
(ii) If
$s = \omega(1/N)$
then
\begin{align*}p(N,s) \underset{N \to \infty}{\longrightarrow} 0.\end{align*}
These results are illustrated in Figure 2, which shows the zero–one law at
$s \asymp N^{-1}$
.
Organization of paper.
The Gaussian approximation of
$v_1 - v'_{\!\!1}$
is established in Section 3 with the proof of Proposition 2.1. The toy model defined above is studied in Section 4, where Proposition 2.2 is established. Finally, we gather results of Propositions 2.1 and 2.2 in Section 5 to prove Theorem 2.1. Some additional proofs are deferred to Appendices A and B.
Figure 2. Estimated p(N, s) in the toy model
$\mathcal{J}(N,s)$
. (With 95% confidence intervals.)
3. Behavior of the leading eigenvectors of correlated matrices
The main idea of this section is to find a first-order expansion of
$v'_{\!\!1}$
around
$v_1$
. Recall that we use the notation
$\left(v_1, v_2, \ldots, v_N\right)$
for normalized eigenvectors of A, corresponding to the eigenvalues
$\lambda_1\;\geq\;\lambda_2\;\geq\;\ldots\;\geq\;\lambda_N$
. Similarly,
$\left(v'_{\!\!1}, v'_{\!\!2}, \ldots, v'_N\right)$
and
$\lambda'_1\;\geq\;\lambda'_2\;\geq\;\ldots\;\geq\;\lambda'_N$
will refer to eigenvectors and eigenvalues of
$B = A + \sigma H$
. Since A and B are symmetric, all these eigenvalues are real and the vectors
$\left\{v_i\right\}_i$
(resp.
$\left\{v'_{\!\!i}\right\}_i$
) are pairwise orthogonal. We also recall that
$v'_{\!\!1}$
is taken such that
$\langle v_1,v'_{\!\!1} \rangle >0$
.
3.1 Computation of a leading eigenvector of B
Recall now that we are working under the assumption (2.2):
\begin{equation*}\exists \, \alpha >0, \quad \;\sigma = o \left(N^{-1/2-\alpha}\right).\end{equation*}
Let w
′ be a (non-normalized) eigenvector of B for the eigenvalue
$\lambda'_1$
of the form
\begin{equation*}w' \;:\!=\; \sum_{i=1}^{N} \theta_i v_i,\end{equation*}
where we assume that
$\theta_1 =1$
. Such an assumption can be made almost surely since any hyperplane of
$\mathbb{R}^N$
has a null Lebesgue measure in
$\mathbb{R}^N$
(see Remark 1.1).
The defining eigenvector equations projected on vectors
$v_i$
give
\begin{equation}\left \{\begin{array}{c c c}\theta_1 & = & 1,\\[4pt] \forall i>1, \; \theta_i \;\;\; & = & \;\; \dfrac{\sigma}{\lambda'_1 - \lambda_i} \sum_{j=1}^{N} \theta_j \langle H v_j,v_i \rangle, \\[4pt] \lambda'_1 - \lambda_1 & = & \sigma \sum_{j=1}^{N} \theta_j \langle H v_j,v_1 \rangle. \\\end{array}\right.\end{equation}
The strategy is then to approximately solve (3.1) with an iterative scheme, leading to the following expansion.
Proposition 3.1. Under the assumption (2.2) one has the following:
\begin{equation}w' = v_1 + \sigma \sum_{i=2}^{N} \frac{\langle Hv_i,v_1 \rangle }{\lambda_1 - \lambda_i} v_i + o_{\mathbb{P}}\left(\sigma \sum_{i=2}^{N} \frac{\langle Hv_i,v_1 \rangle }{\lambda_1 - \lambda_i} v_i \right).\end{equation}
We refer to Appendix A.1 for the details regarding the definition of the mentioned iterative scheme, as well as a proof of Proposition 3.1. The proof uses the assumption (2.2) and builds upon some standard results on the distribution of eigenvalues in the GOE.
Remark 3.1. The above proposition could easily be extended to all eigenvectors of B, under the assumption (2.2). Based on the studies of the trajectories of the eigenvalues and eigenvectors in the Gaussian unitary ensemble (GUE) [Reference Allez, Bun and Bouchaud2] and the GOE [Reference Allez and Bouchaud1], since we are only interested here in the leading eigenvectors, we expect the conclusion of Proposition 3.1 to hold under the weaker assumption
$\sigma N^{1/6+\alpha} \to 0$
, for
$N^{-1/6}$
is the typical spectral gap
$\sqrt{N}(\lambda_1-\lambda_2)$
at the edge. However, as explained before (see Remark 2.2), our analysis does not require this less restrictive assumption. We also know that the expansion (3.2) fails to hold as soon as
$\sigma = \omega(N^{-1/6})$
. A result proved by Chatterjee [Reference Chatterjee5, Theorem 3.8] shows that the eigenvectors corresponding to the highest eigenvalues
$v_1$
of A and
$v'_{\!\!1}$
of
$B=A+\sigma H$
, when A and H are two independent matrices from the GUE, are delocalized (in the sense that
$\langle v_1,v'_{\!\!1} \rangle$
converges in probability to 0 as
$N \to \infty$
), when
$\sigma = \omega(N^{-1/6})$
.
3.2 Gaussian representation of
$v'_{\!\!1} - v_1$
We continue to work under the assumption (2.2). After renormalization, we have
$v'_{\!\!1} = \frac{w'}{\| w' \|}$
. We are now able to study the behavior of the overlap
$\langle v'_{\!\!1}, v_1 \rangle$
:
\begin{equation*}\langle v'_{\!\!1}, v_1 \rangle = \left(1+\sigma^2 (1+o_{\mathbb{P}}(1)) \sum_{i=2}^{N} \dfrac{\langle H v_i,v_1 \rangle ^2 }{\left(\lambda_1 - \lambda_i\right)^2}\right)^{-1/2}.\end{equation*}
Hence
\begin{equation}\langle v'_{\!\!1}, v_1 \rangle = 1-\frac{\sigma^2}{2} \sum_{i=2}^{N} \frac{\langle H v_i,v_1 \rangle ^2 }{\left(\lambda_1 - \lambda_i\right)^2} + o_{\mathbb{P}}\left(\sigma^2 \sum_{i=2}^{N} \frac{\langle H v_i,v_1 \rangle ^2 }{\left(\lambda_1 - \lambda_i\right)^2} \right).\end{equation}
Let us give the heuristic to evaluate the first sum in the right-hand side of (3.3): since the GOE distribution is invariant by rotation (see e.g. [Reference Anderson, Guionnet and Zeitouni3]), the random variables
$\langle H v_i,v_1 \rangle$
are zero-mean Gaussian, with variance
$1/N$
. Moreover, it is well known [Reference Anderson, Guionnet and Zeitouni3] that the eigenvalue gaps
$\lambda_1 - \lambda_i$
are of order
$N^{-1/6}$
when i is small, and
$N^{-1/2}$
in the bulk (when i is typically of order N). These considerations lead to the following.
Lemma 3.1. We have the following concentration:
\begin{equation}\sum_{i=2}^{N} \frac{\langle H v_i,v_1 \rangle ^2 }{\left(\lambda_1 - \lambda_i\right)^2} \asymp N^{1/3}.\end{equation}
We refer to Appendix A.2 for a rigorous proof of this result. With this lemma, we are now able to give the first-order expansion of
$\langle v'_{\!\!1}, v_1 \rangle$
with respect to
$\sigma$
:
\begin{equation*}\langle v'_{\!\!1}, v_1 \rangle = 1-\frac{\sigma^2}{2} N^{1/3} + o_{\mathbb{P}}\left(\sigma^2 N^{1/3} \right).\end{equation*}
Remark 3.2. The comparison between
$\sigma $
and
$N^{1/6}$
made in [Reference Chatterjee5] naturally reappears here, as
$\sigma^2 N^{1/3}$
is the typical shift of
$v'_{\!\!1}$
with respect to
$v_1$
.
The intuition is that the scalar product
$\langle v'_{\!\!1}, v_1 \rangle$
is sufficient to derive a Gaussian representation of
$v'_{\!\!1}$
with respect to
$v_1$
. We formalize this in the following lemma.
Lemma 3.2. Given
$v_1$
, when writing the decomposition
$w' = v_1 + w$
, with
\begin{equation*}w \;:\!=\;\sum_{i=2}^{N} \theta_i v_i,\end{equation*}
the distribution of w is invariant by rotation in the orthogonal complement of
$v_1$
. This implies in particular that given
$v_1$
,
$\|w\|$
and
$\frac{w}{\|w\|}$
are independent, and that
$\frac{w}{\|w\|}$
is uniformly distributed on
$\mathbb{S}^{N-2}$
, the unit sphere of
$v_1^\perp$
.
Proof of Lemma 3.2. We work conditionally on
$v_1$
. Let O be an orthogonal transformation of the hyperplane
$v_1^{\perp}$
(such that
$Ov_1=v_1$
). Since the GOE distribution is invariant by rotation and A and H are independent,
$\widetilde{B} \;:\!=\; O^TAO + \sigma O^THO$
has the same distribution as
$B = A+\sigma H$
.
Note that
$Ow' = v_1 + Ow$
is an eigenvector of
$\widetilde{B}$
for the eigenvalue
$\lambda_{1}$
. Since the distribution of the matrix of eigenvectors
$(v_2, \ldots, v_n)$
is the Haar measure on the orthogonal group
$\mathcal{O}_{n-1}\left(v_1^{\perp}\right)$
, denoted by
$d\mathcal{H}$
, the distribution of w is also invariant by rotation in the orthogonal complement of
$v_1$
. Furthermore, for any bounded continuous functions f, g and
$O \in \mathcal{O}_{n-1}\left(v_1^{\perp}\right)$
,
\begin{align*}\mathbb{E}\left[f(\|w\|)g\left(\frac{w}{\|w\|}\right)\right] &= \mathbb{E}\left[f(\|w\|)g\left(\frac{Ow}{\|Ow\|}\right)\right] \\[4pt]& = \mathbb{E}\left[f(\|w\|) \int_{\mathcal{O}_{n-1}\left(v_1^{\perp}\right)} d\mathcal{H}(O) g\left(\frac{Ow}{\|Ow\|}\right)\right] \\[4pt]&= \mathbb{E}\left[f(\|w\|) \int_{\mathbb{S}^{n-2}} \frac{g(u) du}{\textrm{Vol}\left(\mathbb{S}^{n-2}\right)}\right] = \mathbb{E}\left[f(\|w\|)\right]\mathbb{E}\left[g\left(\frac{w}{\|w\|}\right)\right].\end{align*}
This completes the proof of Lemma 3.2.
We can now prove the main result of this section, Proposition 2.1.
Proof of Proposition 2.1. Recall the decomposition
$w'= v_1 + w$
with
$w =\sum_{i=2}^{N} \theta_i v_i$
. According to Lemma 3.2, conditioned to
$v_1$
,
$\frac{w}{\|w\|}$
is uniformly distributed on
$\mathbb{S}^{N-2}$
, the unit sphere of
$v_1^\perp$
. We now state a classical result about sampling uniform vectors on a sphere.
Lemma 3.3. Let E be p-dimensional Euclidean space, endowed with an orthogonal basis
$\mathcal{B} = (e_1, \ldots, e_p)$
. Let u be a random vector uniformly distributed on the unit sphere
$\mathbb{S}^{p-1}$
of E. Then, in the basis
$\mathcal{B}$
, u has the same distribution as
\begin{align*}\left( \frac{\xi_1}{\sqrt{\sum_{i=1}^{p} \xi_i^2}}, \ldots, \frac{\xi_p}{\sqrt{\sum_{i=1}^{p} \xi_i^2}} \right), \end{align*}
where
$\xi_1, \ldots, \xi_p$
are independent and identically distributed standard normal random variables.
We refer e.g. to [Reference O’Rourke, Vu and Wang18, Lemma 10.1] for the proof of this result. In our context, this proves that the joint distribution of the coordinates
$w_2, \ldots, w_n$
of w along
$v_2, \ldots, v_n$
is always that of a normalized standard Gaussian vector (on
$\mathbb{R}^{N-1}$
). This joint probability does not depend on
$v_1$
. Hence, there exist standard Gaussian independent variables
$Z_2, \ldots, Z_N$
, independent from
$v_1$
(and from
$\| w\|$
by Lemma 3.2), such that
\begin{equation*}w' = v_1 + \frac{\|w\|}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2}} \sum_{i=2}^{N} Z_i v_i.\end{equation*}
Let
$Z_1$
be another standard Gaussian variable, independent from everything else. Then
\begin{equation*}w' = \left(1 - \frac{\|w\| Z_1}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2}}\right) v_1 + \frac{\|w\|}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2}} \sum_{i=1}^{N} Z_i v_i.\end{equation*}
Let
$Z =\sum_{i=1}^{N} Z_i v_i$
, which is a standard Gaussian vector. Since the distribution of Z is invariant by permutation of the
$\left(Z_i\right)_{1 \leq i \leq N}$
, Z and
$v_1$
are independent. We have
\begin{align*}v'_{\!\!1} &= \frac{w'}{\| w'\|} = \frac{w'}{\sqrt{1+\|w\|^2}} \\[4pt] &= \frac{1}{\sqrt{1+\|w\|^2}} \left(1 - \frac{\|w\| Z_1}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2}}\right) v_1+ \frac{\|w\| \|Z\|}{\sqrt{1+\|w\|^2} \left(\sum_{i=2}^{N} Z_i^2\right)^{1/2}} \frac{Z}{\|Z\|}.\end{align*}
Taking
\begin{equation*}\mathbf{S}=\frac{\|w\| \|Z\|}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2} - \|w\| Z_1},\end{equation*}
we get
\begin{equation}v'_{\!\!1} = \frac{1}{\sqrt{1+\|w\|^2}} \left(1 - \frac{\|w\| Z_1}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2}}\right) \left(v_1+ \mathbf{S} \frac{Z}{\|Z\|}\right).\end{equation}
Proposition 3.1 together with Lemma 3.1 yields
\begin{equation*}\|w\|^2=\|w'-v_1\|^2 = (1+o_{\mathbb{P}}(1)) \cdot \sigma^2 \sum_{i=2}^{N} \frac{\langle H v_i,v_1 \rangle ^2 }{\left(\lambda_1 - \lambda_i\right)^2} \asymp \sigma^2 N^{1/3},\end{equation*}
the last quantity being o(1) under the assumption (2.2). With the previous computation, Equation (3.5) becomes
\begin{align*}v'_{\!\!1} = \left(1 + o_{\mathbb{P}}(1)\right) \left(v_1+ \mathbf{S} \frac{Z}{\|Z\|}\right),\end{align*}
with
$\mathbf{S} = (1+o_{\mathbb{P}}(1)) \|w\|\; {\asymp} \; \sigma N^{1/6}$
.
4. Definition and analysis of a toy model
Now that we have established an expansion of
$v'_{\!\!1}$
with respect to
$v_1$
, our main question boils down to the study of the effect of a random Gaussian perturbation of a Gaussian vector in terms of the ranks of its coordinates: if these ranks are preserved, the permutation that aligns these two vectors will be
$\hat{\Pi}=\Pi = \textrm{Id}$
. Otherwise we want to understand the error between
$\hat{\Pi}$
and
${\Pi}=\textrm{Id}$
.
4.1 Definitions and notation
We refer to Section 2.1 for the definition of the toy model
$\mathcal{J}(N,s)$
. Recall that we want to compute, when
$(X,Y) \sim \mathcal{J}(N,s)$
, the probability
\begin{equation*}p(N,s) \;:\!=\; \mathbb{P}\left(r_1(X)=r_1(Y)\right).\end{equation*}
In this section, we denote by E the probability density function of a standard Gaussian variable, and by F its cumulative distribution function. Namely,
\begin{equation*}E(u) \;:\!=\; \frac{1}{\sqrt{2 \pi}} e^{-u^2 /2} \quad \mbox{and} \quad F(u) \;:\!=\; \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^{u} e^{-z^2 /2} dz.\end{equation*}
We hereafter elaborate on the link between this toy model and our first matrix model (1.2) in Section 3. Since
$v_1$
is uniformly distributed on the unit sphere, we have the equality in distribution
$v_1 = \frac{X}{\|X\|}$
, where X is a standard Gaussian vector of size N, independent of Z by Proposition 2.1. We write
\begin{align*}v_1 &= \frac{X}{\|X\|}, \\[5pt] v'_{\!\!1} &= \left( 1 + o_{\mathbb{P}}(1) \right)\left( \frac{X}{\|X\|} + \mathbf{S} \frac{Z}{\|Z\|}\right).\end{align*}
Note that for all
$\lambda>0$
,
$r_1(\lambda T) = r_1(T)$
; hence
\begin{equation}r_1(v_1) = r_1(X), \quad r_1(v'_{\!\!1}) = r_1 \left(X + \mathbf{s} Z \right),\\\end{equation}
where
\begin{equation*}\mathbf{s} = \frac{\mathbf{S} \|X\|}{\|Z\|} \asymp \sigma N^{1/6};\end{equation*}
here we use the law of large numbers (
$\|X\|/\|Z\| \to 1$
almost surely) as well as Proposition 2.1 in the last expansion. Equation (4.1) shows that this toy model is relevant for our initial problem, up to the fact that the noise term
$\mathbf{s}$
is random in the matrix model (though we know its order of magnitude to be
$\asymp \sigma N^{1/6}$
).
Remark 4.1. The intuition for the zero–one law for p(N, s) is as follows. If we sort the N coordinates of X on the real axis, all coordinates being typically perturbed by a factor s, it seems natural to compare s with the typical gap between two coordinates of order
$1/N$
to decide whether the rank of the first coordinate of X is preserved in Y.
Let us show that this intuition is rigorously justified. For every pair (x, y) of real numbers, define
\begin{equation*}\mathcal{N}_{N,s}^{+}(x,y) \;:\!=\; \sharp \left\lbrace 1 \leq i \leq N, \; X_i > x, Y_i < y \right\rbrace,\end{equation*}
\begin{equation*}\mathcal{N}^{-}_{N,s}(x,y) \;:\!=\; \sharp \left\lbrace 1 \leq i \leq N, \; X_i < x, Y_i > y \right\rbrace.\end{equation*}
In the following, we omit all dependencies on N and s, using the notation
$\mathcal{N}^{+}$
and
$\mathcal{N}^{-}$
. The corresponding regions are shown in Figure 3. We will also need the following probabilities:
\begin{align*}S^{+}(x,y) &\;:\!=\; \mathbb{P}\left(X_1 > x, Y_1 < y\right), \mbox{ and}\\S^{-}(x,y) &\;:\!=\; \mathbb{P}\left(X_1 < x, Y_1 > y\right) = S^{+}(-x,-y).\end{align*}
In terms of distribution, the random vector
\begin{equation*}\left(\mathcal{N}^{+}(x,y), \mathcal{N}^{-}(x,y), N-1-\mathcal{N}^{+}(x,y)-\mathcal{N}^{+}(x,y)\right)\end{equation*}
follows a multinomial distribution of parameters
\begin{equation*}\left(N-1,S^{+}(x,y),S^{-}(x,y),1-S^{+}(x,y)-S^{-}(x,y)\right).\end{equation*}
Figure 3. Areas corresponding to
$\mathcal{N}^{+} (x,y)$
and
$\mathcal{N}^{-} (x,y)$
.
In order to have
$r_1(X)=r_1(Y)$
, there must be the same number of points in the two domains in Figure 3, for
$x=X_1$
and
$y=Y_1$
. We then have the following expression for p(N, s):
\begin{align*}p(N,s) &= \mathbb{E}\left[\mathbb{P}\left(\mathcal{N}^{+}(X_1,Y_1)=\mathcal{N}^{-}(X_1,Y_1)\right)\right] \\[4pt]&= \int_{\mathbb{R}} \int_{\mathbb{R}} \mathbb{P}(dx,dy) \mathbb{P}(\mathcal{N}^{+}(x,y)=\mathcal{N}^{-}(x,y)) \\[4pt] &= \int_{\mathbb{R}} \int_{\mathbb{R}} E(x) E(z) \phi_{x,z}(N,s) \, dx \, dz,\end{align*}
with
\begin{equation}\phi_{x,z}(N,s) \;:\!=\; \sum_{k=0}^{\lfloor(N-1)/2\rfloor} \binom{N-1}{k} \binom{N-1-k}{k} \left(S^{+}_{x,z}\right)^k \left(S^{-}_{x,z}\right)^k \left(1-S^{+}_{x,z}-S^{-}_{x,z}\right)^{N-1-2k},\end{equation}
using the notation
$S^{+}_{x,z} = S^{+}(x,x+sz)$
and
$S^{-}_{x,z} = S^{-}(x,x+sz)$
. A simple computation shows that
\begin{align}S^{+}(x,x+sz) &= \int_{x}^{+ \infty} \frac{1}{\sqrt{2\pi}} e^{-u^2 /2} \left( \int_{- \infty}^{z+\frac{x-u}{s}} \frac{1}{ \sqrt{2\pi}} e^{-v^2 / 2} \, dv \right) du \nonumber \\&= \int_{x}^{+ \infty} E(u) \, F \left(z-\frac{u-x}{s}\right) du, \end{align}
\begin{align} = s\int_{0}^{+ \infty} E(x+vs) \, F \left(z-v\right) dv. \end{align}
We have the classical integration result
\begin{equation}\int_{- \infty}^{z} F(u) du = z F(z) + E(z).\end{equation}
From (4.3), (4.4), and (4.5) we derive the following easy lemma.
Lemma 4.1. For all x and z,
\begin{align*}S^{+}(x,x+s z) & \underset{s \to 0}{=} s \left[E(x) \left(z F(z) +E(z)\right)\right] + o(s),\\S^{+}(x,x+s z) & \underset{s \to \infty}{\longrightarrow} F(z) \left(1-F(x)\right),\\S^{-}(x,x+s z) & \underset{s \to 0}{=} s \left[E(x) \left(-z+ z F(z) +E(z)\right)\right] + o(s),\\S^{-}(x,x+s z) & \underset{s \to \infty}{\longrightarrow} F(x) \left(1-F(z)\right).\end{align*}
Moreover, both
$s \mapsto S^{+}(x,x+s z)$
and
$s \mapsto S^{-}(x,x+s z)$
are increasing.
4.2. Zero-one law for
$p(N,s)$
In this section we give a proof of Proposition 2.2.
Proof of Proposition 2.2. In the first case (
i
), if
$s = o(1/N)$
, we have the following inequality:
\begin{equation}p(N,s) \geq \int_{\mathbb{R}} \int_{\mathbb{R}} dx dz E(x) E(z) \mathbb{P} \left(\mathcal{N}^{+}(x,x+sz)=\mathcal{N}^{-}(x,x+sz)=0\right).\end{equation}
According to Lemma 4.1, for all
$x,z \in \mathbb{R}$
\begin{align*}\mathbb{P} \left(\mathcal{N}^{+}(x,x+sz)=\mathcal{N}^{-}(x,x+sz)=0\right)&= \left(1-S^{+}(x,x+sz)-S^{-}(x,x+sz)\right)^{N-1}\\ & \sim \exp\left(- NsE(x)\left[z(2F(z)-1)+2E(z)\right]\right) \\& \underset{N \to \infty}{\longrightarrow} 1.&&\end{align*}
By applying the dominated convergence theorem in (4.6), we conclude that
$p(N,s) \to 1$
.
In the second case (ii)
, if
$s N \to \infty$
, recall that
\begin{equation}p(N,s)= \int_{\mathbb{R}} \int_{\mathbb{R}} dx dz E(x) E(z) \phi_{x,z}(N,s),\end{equation}
with
$\phi_{x,z}$
defined in Equation (4.2). In the rest of the proof, we fix two real numbers x and z. Let
\begin{equation*}b(N,s,k) \;:\!=\; \binom{N-1}{k} \left(S^{+}_{x,z}\right)^k \left(1- S^{+}_{x,z}\right)^{N-1-k}\end{equation*}
and
\begin{equation*}M(N,s) \;:\!=\; \underset{0 \leq k \leq N-1}{\max} b(N,s,k).\end{equation*}
Note that by Lemma 4.1, there exists
$C = C(x,z) <1$
such that for N large enough,
$S^{+}_{x,z}<C<1$
. Moreover, combining this lemma with the assumption (ii) gives that
$ N S^{+}_{x,z} \to \infty$
. It is also known that
$M(N,s) = b(N,s,\lfloor N S^{+}_{x,z} \rfloor)$
, and a classical computation shows that in this case (see e.g. [Reference Bollobás4, Formula 1.5]),
\begin{align*}M(N,s) & = \binom{N-1}{\lfloor N S^{+}_{x,z} \rfloor} \left(S^{+}_{x,z}\right)^{\lfloor N S^{+}_{x,z} \rfloor} \left(1- S^{+}_{x,z}\right)^{N-1-{\lfloor N S^{+}_{x,z} \rfloor}}\\& \sim \frac{1}{\sqrt{2 \pi N t(1-t)}} t^{-(N-1)t} (1-t)^{-(N-1)(1-t)} \left(S^{+}_{x,z}\right)^{(N-1)t} \left(1- S^{+}_{x,z}\right)^{(N-1)(1-t)}\\& = \left(N S^{+}_{x,z}\right)^{-1/2} (1+O(1)) \to 0,\end{align*}
where
\begin{align*}t \;:\!=\; \frac{\lfloor N S^{+}_{x,z} \rfloor}{N-1} \sim S^{+}_{x,z}.\end{align*}
Working with Equation (4.2), we obtain the following control:
\begin{align*}\phi_{x,z}(N,s) & \leq M(N,s) \times \sum_{k=0}^{\lfloor(N-1)/2\rfloor} \binom{N-1-k}{k} \left(S^{-}_{x,z}\right)^k \frac{\left(1-S^{+}_{x,z}-S^{-}_{x,z}\right)^{N-1-2k}}{\left(1-S^{+}_{x,z}\right)^{N-1-k}}\\& \overset{(a)}{=} M(N,s) \times \frac{(1-S^{+}_{x,z})\left(1-\left(\frac{-S^{+}_{x,z}}{1-S^{-}_{x,z}} \right)^N\right)}{1+S^{-}_{x,z}-S^{+}_{x,z}}\\& \overset{(b)}{=} M(N,s) \times O(1) \underset{N \to \infty}{\longrightarrow} 0. &&\end{align*}
We used in (b) the facts that
$S^{+}_{x,z}+S^{-}_{x,z}$
is increasing in s, and that given x and z, for all
$s>0$
, by Lemma 4.1,
\begin{align*}S^{+}_{x,z}+S^{-}_{x,z}< F(x)\left(1-F(z)\right)+F(z)\left(1-F(x)\right)<1.\end{align*}
We used in (a) the following combinatorial result.
Lemma 4.2. For all
$\alpha>0$
,
\begin{equation}\sum_{k=0}^{\lfloor(N-1)/2\rfloor} \binom{N-1-k}{k} \alpha^k = \frac{1}{\sqrt{1+4 \alpha}} \left[\left(\frac{1+\sqrt{1+4 \alpha}}{2}\right)^N - \left(\frac{1-\sqrt{1+4 \alpha}}{2}\right)^N\right].\end{equation}
We refer to Appendix B.1 for a proof of this result. To obtain (a) from Lemma 4.2, we apply (4.8) to
\begin{align*}\alpha = \frac{S^{-}_{x,z} \left(1-S^{+}_{x,z}\right)}{\left(1-S^{+}_{x,z}-S^{-}_{x,z}\right)^2},\end{align*}
with
\begin{align*}\sqrt{1+4 \alpha} = \frac{1-S^{+}_{x,z}+S^{-}_{x,z}}{1-S^{+}_{x,z}-S^{-}_{x,z}}.\end{align*}
Some straightforward simplifications then give the claimed result. The dominated convergence theorem in (4.7) shows that
$p(N,s) \to 0$
and ends the proof.
Remark 4.2. The above computations also imply the existence of a non-degenerate limit of p(N, s) in the critical case where
$s N \to c>0$
: in this case, previous discussions as well as Lemma 4.1 show that the joint distribution of
$(\mathcal{N}^+(x,x+sz), \mathcal{N}^-(x,x+sz))$
is asymptotically
\begin{align*}\textrm{Poi}(c \left[E(x) \left(z F(z) +E(z)\right)\right]) \otimes \textrm{Poi}(c \left[E(x) \left(-z+z F(z) +E(z)\right)\right]).\end{align*}
Therefore, p(N, s) has a non-degenerate limit given by
\begin{equation}\int_{\mathbb{R}} \int_{\mathbb{R}} E(x) E(z) \cdot \mathbf{G}\left(c \left[E(x) \left(z F(z) +E(z)\right)\right],c \left[E(x) \left(-z+z F(z) +E(z)\right)\right] \right) \, dx \, dz,\end{equation}
where
\begin{equation}\mathbf{G}(a,b) \;:\!=\; \mathbb{P}(\textrm{Poi}(a)=\textrm{Poi}(b)) = e^{-(a+b)} \sum_{k \geq 0} \frac{a^k b^k}{(k!)^2}.\end{equation}
Note that
$\mathbf{G}(a,b) \to 1$
when
$a,b \to 0$
, and
$\mathbf{G}(a,b) \to 0$
when
$a,b \to + \infty$
.
5. Analysis of the EIG1 method for matrix alignment
We now come back to our initial problem, which is the analysis of the EIG1 method. Recall that for any estimator
$\hat{\Pi}$
of
$\Pi$
, its overlap is defined as follows:
\begin{equation*}\mathcal{L}(\hat{\Pi},\Pi) \;:\!=\; \frac{1}{N} \sum_{i=1}^{N} \mathbf{1}_{\hat{\Pi}(i)=\Pi(i)}.\end{equation*}
The aim of this section is to show how Propositions 2.1 and 2.2 can be assembled to prove the main result of our study, namely Theorem 2.1.
Proof of Theorem 2.1. In the first case (
i
)
, assuming
$\sigma = o(N^{-7/6-\epsilon})$
for some
$\epsilon>0$
, we have in particular that the condition (2.2) holds. Proposition 2.1 and Equation (4.1) in Section 4 enable us to identify
$v_1$
and
$v'_{\!\!1}$
with the following vectors:
\begin{equation}v_1 \sim X, \quad v'_{\!\!1} \sim X + \mathbf{s} Z,\end{equation}
where X and Z are two independent Gaussian vectors from the toy model, and where
$\mathbf{s} \asymp \sigma N^{1/6} $
w.h.p. Recall that we work under the assumptions
$\Pi=\textrm{Id}$
and
$\langle v_1, v'_{\!\!1} \rangle >0$
. In this case, we expect
$\Pi_{+}$
to be very close to Id.
We will use the notation of Section 4 hereafter. Let us take
$f \in \mathcal{F}$
such that w.h.p.,
$\sigma N^{1/6}f(N)^{-1} \leq \mathbf{s} \leq \sigma N^{1/6 }f(N)$
. For all
$1 \leq i \leq N$
, we have
\begin{align*}\mathbb{P}\left({\Pi_{+}}(i)=\Pi(i)\right) &= \mathbb{P}\left({\Pi_{+}}(1)=\Pi(1)\right) \\& = \mathbb{E}\left[\iint dx dz E(x) E(z) \phi_{x,z}\left(N, \mathbf{s} \right)\mathbf{1}_{\sigma N^{1/6}f(N)^{-1} \leq \mathbf{s} \leq \sigma N^{1/6 }f(N)}\right] + o(1)\\& = \iint dx dz E(x) E(z) \mathbb{E}\left[\phi_{x,z}\left(N, \mathbf{s} \right)\mathbf{1}_{\sigma N^{1/6}f(N)^{-1} \leq \mathbf{s} \leq \sigma N^{1/6 }f(N)}\right] + o(1).&&\end{align*}
When conditioning on the event
$\mathcal{A}$
where
$\sigma N^{1/6}f(N)^{-1} \leq \mathbf{s} \leq \sigma N^{1/6 }f(N)$
, we know that
$\mathbf{s}N \to 0$
by the condition (i), and for all x, z, we have
$\mathbb {E}\left[\phi_{x,z}\left(N, \mathbf{s} \right) \, | \, \mathcal{A} \right] \to 1$
as shown in Section 4. Since
$\mathcal{A}$
occurs w.h.p. we have
\begin{align*}\mathbb {E}\left[\phi_{x,z}\left(N, \mathbf{s} \right)\mathbf{1}_{\mathcal{A}}\right] {\longrightarrow} 1,\end{align*}
which implies, together with the dominated convergence theorem, that
\begin{equation}\mathbb{E}\left[\mathcal{L}({\Pi_{+}},\Pi)\right] \underset{N \to \infty}{\longrightarrow} 1\end{equation}
and thus
\begin{equation*}\mathcal{L}({\Pi_{+}},\Pi) \overset{L^1}{\rightarrow} 1.\end{equation*}
We now check that w.h.p.,
$\Pi_{+}$
is preferred to
$\Pi_{-}$
in the EIG1 method.
Lemma 5.1. In the case (i), if
$\langle v_1,v'_{\!\!1} \rangle >0$
, we have w.h.p.
\begin{equation*}\langle A, \Pi_{+} B \Pi_{+}^T \rangle > \langle A, \Pi_{-} B \Pi_{-}^T \rangle;\end{equation*}
in other words, the algorithm EIG1 returns w.h.p.
$\hat{\Pi}=\Pi_{+}$
.
This lemma is proved in Appendix B.3 and implies, together with (5.2), that
\begin{align*}\mathbb{E}\left[\mathcal{L}(\hat{\Pi},\Pi)\right] & \geq \mathbb{E}\left[\mathcal{L}(\hat{\Pi},\Pi)\mathbf{1}_{\hat{\Pi}=\Pi_{+}}\right] = \mathbb{E}\left[\mathcal{L}(\Pi_{+},\Pi)\mathbf{1}_{\hat{\Pi}=\Pi_{+}}\right] \\& = \mathbb{E}\left[\mathcal{L}(\Pi_{+},\Pi)\right] - \mathbb{E}\left[\mathcal{L}(\Pi_{+},\Pi)\mathbf{1}_{\hat{\Pi}=\Pi_{-}}\right] \\& = 1 -o(1),\end{align*}
and thus
\begin{equation}\mathcal{L}(\hat{\Pi},\Pi) \underset{N \to \infty}{\overset{L^1}{\longrightarrow}} 1.\end{equation}
In the second case (ii)
, if the condition (2.2) is verified, then the identification (5.1) still holds and the proof of the case (i) adapts well. However, if (2.2) is not verified, we can still make a link to the toy model studied in Section 4. We use a simple coupling argument: if
$\sigma = \omega(N^{-1/2-\alpha})$
for some
$\alpha \geq 0$
, let us take
$\sigma_1, \sigma_2 >0$
such that
\begin{align*}\sigma^2 = \sigma_1^2 + \sigma_2^2 \end{align*}
and
\begin{align*} N^{-7/6+\epsilon} \ll \sigma_1 \ll N^{-1/2-\alpha}, \end{align*}
fixing for instance
$\sigma_1 = N^{-1}$
. We will use the notation
$\widetilde{v}_1$
, now viewed as the leading eigenvector of the matrix
\begin{equation*}\widetilde{B} = A + \sigma_1 H + \sigma_2 \widetilde{H},\end{equation*}
where
$\widetilde{H}$
is an independent copy of H. This has no consequence in terms of distribution:
$(A,\widetilde{B})$
is still drawn under the model (1.2). Let us denote by
$v'_{\!\!1}$
the leading eigenvector of
$B_1=A+\sigma_1 H$
, chosen so that
$\langle v_1,v'_{\!\!1}\rangle >0$
. It is clear that the condition (2.2) holds for
$\sigma_1$
. We have the following result, based on the invariance by rotation of the GOE distribution.
Lemma 5.2. We still have the following equality in distribution:
\begin{equation*}\left(r_1(v_1),r_1(\widetilde{v}_1)\right) \overset{(d)}{=} \left(r_1(X),r_1(X+\mathbf{s}Z) \right),\end{equation*}
where X, Z are two standard Gaussian vectors from the toy model, with w.h.p.
\begin{equation*}\mathbf{s} \geq \mathbf{s^1} \asymp \sigma_1 N^{1/6}.\end{equation*}
We refer to Appendix B.2 for a proof. Since w.h.p.
$\mathbf{s} \geq \mathbf{s^1}$
and
$\mathbf{s^1} N \asymp \sigma_1 N^{7/6} \to \infty$
, for all
$1 \leq i \leq N$
we have
\begin{align*}\mathbb{P}\left(\Pi_{+}(i)=\Pi(i)\right) &= \mathbb{P}\left(\Pi_{+}(1)=\Pi(1)\right) \\& = \mathbb{E} \left[\iint dx dz E(x) E(z) \phi_{x,z}(N,\mathbf{s}) \mathbf{1}_{\mathbf{s} N \to \infty} \right] + o(1)\\& = \iint dx dz E(x) E(z) \mathbb{E} \left[\phi_{x,z}(N,\mathbf{s}) \mathbf{1}_{\mathbf{s} N \to \infty} \right] + o(1).\end{align*}
With the same arguments as in the case (i), we show that
$\phi_{x,z}(N,\mathbf{s}) \mathbf{1}_{\mathbf{s} N \to \infty} \overset{L^1}{\longrightarrow} 0,$
which implies
\begin{equation*}\mathbb{E}\left[\mathcal{L}(\Pi_{+},\Pi)\right] \underset{N \to \infty}{\longrightarrow} 0,\end{equation*}
and hence
$\mathcal{L}(\Pi_{+},\Pi) \underset{N \to \infty}{\overset{L^1}{\longrightarrow}} 0.$
The last step is to verify that the overlap achieved by
$\Pi_{-}$
does not outperform that of
$\Pi_{+}$
. We prove the following lemma in Appendix B.4.
Lemma 5.3. In the case (ii), if
$\langle v_1,v'_{\!\!1} \rangle >0$
, we also have
\begin{equation*}\mathcal{L}(\Pi_{-},\Pi) \underset{N \to \infty}{\overset{L^1}{\longrightarrow}} 0.\end{equation*}
Lemma 5.3 then gives
\begin{equation*}\mathbb{E}\left[\mathcal{L}(\hat{\Pi},\Pi)\right] \leq \mathbb{E}\left[\mathcal{L}(\Pi_{+},\Pi)\right] + \mathbb{E}\left[\mathcal{L}(\Pi_{-},\Pi)\right] \underset{N \to \infty}{\longrightarrow} 0,\end{equation*}
and thus
\begin{equation}\mathcal{L}(\hat{\Pi},\Pi) \underset{N \to \infty}{\overset{L^1}{\longrightarrow}} 0.\end{equation}
Of course, the convergences in (5.3) and (5.4) also hold in probability, by Markov’s inequality.
Remark 5.1. We conclude this work with a remark about the critical case in Theorem 2.1. In the light of Remark 4.2, if
$\sigma \asymp N^{7/6}$
, we expect
$\mathcal{L}(\hat{\Pi},\Pi)$
to have a non-degenerate limit
$\mathcal{L}_\infty$
in probability, whose behavior is random in [0,1]. Since our estimates are always made up to a sub-polynomial factor, it is nontrivial to establish such a result for Theorem 2.1 in the critical case without substantial additional work. However, we can make a guess about the expected result when
$\sigma N^{7/6} \to c>0$
: in this case we conjecture that the expected value of
$\mathcal{L}_\infty$
is given by
\begin{equation}\int_{\mathbb{R}} \int_{\mathbb{R}} E(x) E(z) \cdot \mathbf{G}\left(c \left[E(x) \left(z F(z) +E(z)\right)\right],c \left[E(x) \left(-z+z F(z) +E(z)\right)\right] \right) \, dx \, dz,\end{equation}
Appendix A. Additional proofs for Section 3
Throughout the proofs, all variables denoted by
$C_i$
with
$i=1,2,\ldots$
are unspecified, independent, positive constants.
A.1 Proof of Proposition 3.1
Proof of Proposition 3.1. Let us establish a first inequality: since the GOE distribution is invariant by rotation (see e.g. [Reference Anderson, Guionnet and Zeitouni3]), the random variables
$\langle H v_j,v_i \rangle$
are zero-mean Gaussian, with variance
$1/N$
if
$i \neq j$
and
$2/N$
if
$i=j$
. Hence, w.h.p.
\begin{equation}\underset{1 \leq i,j \leq N}{\sup} \left|\langle H v_j,v_i \rangle \right|\leq C_1 \sqrt{\frac{\log N}{N}}.\end{equation}
We will use the following shorthand notation for
$1 \leq i,j \leq N$
:
\begin{equation*}m_{i,j} \;:\!=\; \langle H v_j,v_i \rangle.\end{equation*}
The defining eigenvector equations projected on vectors
$v_i$
are written as follows:
\begin{equation}\left \{\begin{array}{c @{=} c}\theta_i & \dfrac{\sigma}{\lambda'_1 - \lambda_i} \sum_{j=1}^{N} \theta_j m_{i,j}, \\\lambda'_1 - \lambda_1 & \sigma \sum_{j=1}^{N} \theta_j m_{1,j}. \\\end{array}\right.\end{equation}
In order to approximate the
$\theta_i$
variables, we define the following iterative scheme:
\begin{equation}\left \{\begin{array}{c @{\; = } c}\theta_i^k & \dfrac{\sigma}{\lambda_1^{k-1} - \lambda_i} \sum_{j=1}^{N} \theta_j^{k-1} m_{i,j} ,\\\lambda^{k}_1 - \lambda_1 & \sigma \sum_{j=1}^{N} \theta_j^{k-1} m_{1,j} ,\end{array}\right.\end{equation}
with initial conditions
$\left(\theta_i^{0}\right)_{2 \leq i \leq N}=0$
and
$\lambda_{1}^0 = \lambda_1$
, and setting
$\theta_1^{k}=1$
for all k. For
$k \geq 1$
, define
\begin{equation*}\Delta_k \;:\!=\; \sum_{i \geq 2} \left|\theta_i^k - \theta_i^{k-1}\right|,\end{equation*}
and for
$k \geq 0$
,
\begin{equation*}S_k \;:\!=\; \sum_{i \geq 1} \left|\theta_i^k \right|.\end{equation*}
Recall that under the assumption (2.2), there exists
$\alpha>0$
such that
$\sigma = o \left(N^{-1/2-\alpha}\right)$
. We define
$\epsilon$
as follows:
\begin{equation*}\epsilon = \epsilon(N) = \sqrt{\sigma N^{1/2+\alpha}}.\end{equation*}
The idea is to show that the sequence
$\left\{\Delta_k \right\}_{k \geq 1}$
decreases geometrically with k at rate
$\epsilon$
. More specifically, we show the following result.
Lemma A.1. With the same notation and under the assumption (2.2) of Proposition 3.1, one has w.h.p.
-
(i)
$\forall k \geq 1$
,
$\Delta_k \leq \Delta_1 \epsilon^{k-1}$
; -
(ii)
$\forall k \geq 0, \ \forall \, 2 \leq i \leq N$
,
$\left|\lambda_{1}^k - \lambda_i\right| \geq \frac{1}{2} \left|\lambda_{1} - \lambda_i\right| \left(1- \epsilon - \ldots - \epsilon^{k-1}\right)$
; -
(iii)
$\forall k \geq 0$
,
$S_k \leq 1 +(1+\ldots+\epsilon^{k-1}) \Delta_1$
; -
(iv)
$\sum_{i=2}^{N} \left| \theta_i - \theta_i^{1} \right|^2 = o\left(\sum_{i=2}^{N} \left| \theta_i^{1} \right|^2 \right)$
.
This lemma is proved in the next section. Equation (iv) of Lemma A.1 yields
\begin{align*}w' & = v_1 + \sum_{i=2}^{N} \theta_i^1 v_i + \sum_{i=2}^{N} \left(\theta_i - \theta_i^1\right) v_i\\& = v_1 + \sigma \sum_{i=2}^{N} \frac{\langle Hv_i,v_1 \rangle }{\lambda_1 - \lambda_i} v_i + o_{\mathbb{P}}\left(\sigma \sum_{i=2}^{N} \frac{\langle Hv_i,v_1 \rangle }{\lambda_1 - \lambda_i} v_i \right).\end{align*}
Proof of Lemma A.1
Proof of Lemma A.1. In this proof we will use the same notation as defined in the proof of Proposition 3.1, and we make the assumption (2.2). We now state three technical lemmas controlling some statistics of eigenvalues in the GOE which will be useful hereafter.
Lemma A.2. W.h.p., for all
$\delta>0$
,
\begin{equation}\sum_{j = 2}^{N} \frac{1}{\lambda_1 - \lambda_j} \leq O\left( N ^{1+\delta}\right).\end{equation}
Lemma A.3. We have
\begin{equation}\; \sum_{j = 2}^{N} \frac{1}{\left(\lambda_1 - \lambda_j \right)^2} \asymp N^{4/3}.\end{equation}
Lemma A.4. For any
$C>0$
, w.h.p.
\begin{equation}\lambda_1 - \lambda_2 \geq N^{-2/3} \left(\log N\right)^{-C \log \log N}.\end{equation}
Proofs of these three lemmas can be found in the next sections. We will work under the event (that occurs w.h.p.) on which the equations (A.4), (A.5), (A.6), (3.4), and (A.1) are satisfied. We show the following inequalities:
-
(i)
$\forall k \geq 1$
,
$\Delta_k \leq \Delta_1 \epsilon^{k-1}$
; -
(ii)
$\forall k \geq 0, \ \forall \, 2 \leq i \leq N$
,
$\left|\lambda_{1}^k - \lambda_i\right| \geq \frac{1}{2} \left|\lambda_{1} - \lambda_i\right| \left(1- \epsilon - \ldots - \epsilon^{k-1}\right)$
; -
(iii)
$\forall k \geq 0$
,
$S_k \leq 1 + (1+\ldots+\epsilon^{k-1}) \Delta_1$
.
Recall that
$\epsilon$
is given by
\begin{equation*}\epsilon = \epsilon(N) = \sqrt{\sigma N^{1/2+\alpha}}.\end{equation*}
We will denote by
$f_{i}(N)$
, with i an integer, functions as defined in Lemma A.3. All of the following inequalities will be valid for N large enough (uniformly in i and in k).
Step 1: Propagation of the first equation. Let
$k \geq 3$
. We work by induction, assuming that (i), (ii), and (iii) are verified up to
$k-1$
. We have the following:
\begin{align*}\left| \theta_i^k - \theta_i^{ k-1} \right| & \leq \left| \frac{\sigma}{\lambda_1^{k-1}-\lambda_i} \sum_{j=2}^{N} \left(\theta_j^{k-1} - \theta_j^{k-2}\right)m_{i,j} \right| + \left| \frac{\sigma \left(\lambda_1^{k-2}-\lambda_1^{k-1}\right)}{\left(\lambda_1^{k-1}-\lambda_i\right)\left(\lambda_1^{k-2}-\lambda_i\right)} \sum_{j=1}^{N} \theta_j^{k-2} m_{i,j} \right|\\[5pt]& \leq \frac{ \sigma}{\left|\lambda_1^{k-1}-\lambda_i\right|} C_1 \sqrt{\frac{\log N}{N}} \Delta_{k-1} + \sigma C_1 \sqrt{\frac{\log N}{N}} S_{k-2} \frac{\left|\lambda_1^{k-2}-\lambda_1^{k-1}\right|}{\left|\lambda_1^{k-1}-\lambda_i\right|\left|\lambda_1^{k-2}-\lambda_i\right|} \\[5pt]& \overset{(a)}{\leq} \sigma \frac{3}{\left|\lambda_1-\lambda_i\right|} C_1 \sqrt{\frac{\log N}{N}} \Delta_{k-1} + \sigma C_1 \sqrt{\frac{\log N}{N}} S_{k-2} \frac{9 \left|\lambda_1^{k-2}-\lambda_1^{k-1}\right|}{\left|\lambda_1-\lambda_i\right|^2} \\[5pt]& \overset{(b)}{\leq} \sigma \frac{3}{\left|\lambda_1-\lambda_i\right|} C_1 \sqrt{\frac{\log N}{N}} \Delta_{k-1} + \sigma C_1 \sqrt{\frac{\log N}{N}} 2 \frac{9 \left|\lambda_1^{k-2}-\lambda_1^{k-1}\right|}{\left|\lambda_1-\lambda_i\right|^2},\end{align*}
where we applied (ii) to
$k-1$
,
$k-2$
in (a) and (iii) to
$k-2$
in (b). Note that
\begin{align*}\left|\lambda_1^{k-2}-\lambda_1^{k-1}\right| & = \left|\sigma \sum_{j=1}^{N} \left(\theta_j^{k-2}-\theta_j^{k-3}\right) m_{i,j}\right| \leq \sigma C_1 \sqrt{\frac{\log N}{N}} \Delta_{k-2},\end{align*}
which yields the inequality
\begin{align*}\left| \theta_i^k - \theta_i^{ k-1} \right| & \leq \frac{\sigma}{\left|\lambda_1-\lambda_i\right|} f_1(N) N^{-1/2} \Delta_{k-1} + \frac{\sigma^2 }{\left|\lambda_1-\lambda_i\right|^2} f_2(N) N^{-1} \Delta_{k-2}.\end{align*}
We choose
$\delta $
such that
$0 < \delta < \alpha$
(where
$\alpha$
is fixed by (2.2)), and we sum from
$i=2$
to N:
\begin{align*}\Delta_k & \leq \sigma f_1(N) N^{1/2 + \delta} \Delta_{k-1} + \sigma^2 f_3(N) N^{1/3} \Delta_{k-2} \\[5pt]& \overset{(a)}{\leq} o(\epsilon) \epsilon^{k-2} \Delta_1 + o(\epsilon^2) \epsilon^{k-3} \Delta_1 \\[5pt]& \leq \epsilon^{k-1} \Delta_1.\end{align*}
Here we used
$\sigma f_1(N) N^{1/2 + \delta} =o(\epsilon)$
,
$\sigma^2 f_3(N) N^{1/3} = o(\epsilon^2)$
, and we applied (i) to
$k-1$
and
$k-2$
in (a).
Step 2: Propagation of the second equation. Let
$k \geq 2$
, and
$0 < \delta < \alpha$
. We work by induction, assuming that (i), (ii), and (iii) are verified up to
$k-1$
. We have the following:
\begin{align*}\left| \lambda_1^k - \lambda_1^{ k-1} \right| & \leq \sigma f_1(N) N^{-1/2} \Delta_{k-1} \\& \overset{(a)}{\leq} \sigma f_1(N) N^{-1/2} {\epsilon^{k-2} \Delta_1}\\& \leq N^{-2/3} (\log N)^{-C \log \log N} \epsilon^{k-2} \Delta_1\\& \leq \frac{\lambda_1-\lambda_2}{2} \epsilon^{k-2} \Delta_1\\& \leq \frac{\lambda_1-\lambda_i}{2} \epsilon^{k-2} \Delta_1.\end{align*}
We applied (i) to
$k-1$
in (a). Note that
\begin{align*}\Delta_1 & = \sum_{j=2}^{N} \frac{\sigma}{\lambda_1 - \lambda_i} \left| m_{i,1} \right| \leq \sigma f_1(N) N^{1/2+\delta} \leq o(\epsilon).\end{align*}
Applying (ii) to
$k-1$
, we get
\begin{align*}\left| \lambda_1^k - \lambda_i \right| & \geq \left| \lambda_1 - \lambda_1^{k-1} \right| - \left| \lambda_1^k - \lambda_1^{k-1} \right| \\& \geq \frac{\lambda_1-\lambda_i}{2} \left(1-\epsilon-\ldots-\epsilon^{k-2}\right) - \frac{\lambda_1-\lambda_i}{2} \epsilon^{k-1}\\& \geq \frac{\lambda_1-\lambda_i}{2} \left(1-\epsilon-\ldots-\epsilon^{k-1}\right).\end{align*}
Step 3: Propagation of the third equation. Let
$k \geq 1$
. Here again, we work by induction, assuming that (i), (ii), and (iii) are verified up to
$k-1$
. We have the following:
\begin{align*}S_k &= 1 + \sum_{j=2}^{N} \left|\theta^k_j\right|\\& \leq 1 + \Delta_k + S_{k-1} - 1\\& \overset{(a)}{\leq} \epsilon^{k-1} \Delta_1 + 1 + \left(1+\ldots+\epsilon^{k-2}\right)\Delta_1\\& \leq 1 + \left(1+\epsilon+\ldots+\epsilon^{k-1}\right) \Delta_1.\end{align*}
We applied (i) to k and (iii) to
$k-1$
in (a).
Step 4: Proof of
(i)
for
$k=1,2$
,
(ii)
for
$k=0,1$
, and
(iii)
for
$k=0,1$
. The equation (i) for
$k=1$
is obvious. For
$k=2$
, we have
\begin{align*}\left| \theta_i^2 - \theta_i^1 \right| & \leq \left| \frac{\sigma}{\lambda_1^1-\lambda_i} \sum_{j=2}^{N} \left(\theta_j^{1} - \theta_j^{0}\right)m_{i,j} \right| + \left| \frac{\sigma \left(\lambda_1^{0}-\lambda_1^{1}\right)}{\left(\lambda_1^{1}-\lambda_i\right)\left(\lambda_1^{0}-\lambda_i\right)} \sum_{j=1}^{N} \theta_j^{0} m_{i,j} \right|.\end{align*}
We have
\begin{align*}\left| \lambda_1^1 - \lambda_i \right| & \geq \left| \lambda_1 - \lambda_i \right| - \left| \lambda_1 - \lambda_1^1 \right|\geq \left| \lambda_1 - \lambda_i \right| - \sigma \left|m_{1,1}\right|\\& \geq \left| \lambda_1 - \lambda_i \right| - \frac{1}{2} \left| \lambda_1 - \lambda_2 \right|\geq \frac{1}{2} \left| \lambda_1 - \lambda_i \right|,\end{align*}
which shows (ii) for
$k=0,1$
. Thus, for
$0<\delta < \alpha$
,
\begin{align*}\left| \theta_i^2 - \theta_i^1 \right| &\leq \frac{2 \sigma}{\lambda_1-\lambda_i} C_1 \sqrt{\frac{\log N}{N}} \Delta_1 + \frac{4 \sigma}{\left(\lambda_{1}-\lambda_i\right)^2 } \sigma \left|m_{1,1}\right| \left|m_{i,1}\right|,\end{align*}
and
\begin{align*}\Delta_2 & \leq \sigma f_1(N) N^{1/2 + \delta} \Delta_1 + 4 \sigma \left|m_{1,1}\right| \sum_{i=2}^{N} \frac{\sigma \left|m_{i,1}\right|}{\left(\lambda_1 - \lambda_i\right)^2}\\& \leq \sigma f_1(N) N^{1/2 + \delta} \Delta_1 + 4 \sigma f_4(N) N^{-1/2} N^{2/3} \sum_{i=2}^{N} \frac{\sigma \left|m_{i,1}\right|}{\left(\lambda_1 - \lambda_i\right)}\\& \leq \sigma f_1(N) N^{1/2 + \delta} \Delta_1 + 4 \sigma f_4(N) N^{1/6} \Delta_1\\& \leq \epsilon \Delta_1.\end{align*}
The proof of (iii) for
$k=0,1$
is obvious.
Step 5: Proof of Equation (iv). Let
$k \geq 2$
and
$2 \leq i \leq N$
. In the same way as in Step 1, we have
\begin{align*}\left| \theta_i^k - \theta_i^{ k-1} \right| & \leq \frac{2 \sigma C_1}{\lambda_1-\lambda_i} \sqrt{\frac{\log N}{N}} \epsilon^{k-2} \Delta_1 + \frac{8 \sigma^2 C_1^2}{\left(\lambda_1-\lambda_i\right)^2} \frac{\log N}{N} \epsilon^{(k-3)_+}\Delta_1.\end{align*}
In the right-hand term, the ratio of the second term to the first one is smaller than
\begin{equation*}\frac{4 \sigma C_1}{\lambda_1 - \lambda_i} \sqrt{\frac{\log N}{N}} \epsilon^{-1} \leq \sigma N^{1/6} f(N) \epsilon^{-1} \leq \epsilon \to 0,\end{equation*}
using Lemma A.4, with
$f \in \mathcal{F}$
. It follows that for N big enough (uniformly in k and i) one has
\begin{equation}\left| \theta_i^k - \theta_i^{ k-1} \right| \leq \frac{\sigma f(N) }{\lambda_1-\lambda_i} N^{-1/2} \epsilon^{k-2} \Delta_1.\end{equation}
Equation (A.7) shows that the scheme (A.3) converges, and that the limits are indeed the solutions
$\theta_1=1, \theta_2, \ldots, \theta_N$
of the fixed-point equations. By a simple summation of (A.7) over
$k \geq 2$
, applying Lemma A.2 and the inequality (A.1), we have
\begin{align*}\left| \theta_i - \theta_i^{1} \right| & \leq \frac{2 \sigma f(N) }{\lambda_1-\lambda_i} N^{-1/2} \Delta_1 \leq \frac{2 \sigma^2 f(N) }{\lambda_1-\lambda_i} N^{\delta},\end{align*}
where
$\delta>0$
is a positive quantity as in Lemma A.2, to be specified later. Using Lemma A.3 one has the following control:
\begin{equation*}\sum_{i=2}^{N} \left| \theta_i - \theta_i^{1} \right|^2 \leq 4 \sigma^4 N^{2 \delta} f(N) N^{4/3}.\end{equation*}
Moreover, Lemma 3.1 shows that
\begin{equation*}\sum_{i=2}^{N} \left| \theta_i^{1} \right|^2 \asymp \sigma^2 N^{1/3} \geq g(N)^{-1} \sigma^2 N^{1/3},\end{equation*}
where g is another function in
$\mathcal{F}$
. This yields
\begin{equation*}\sum_{i=2}^{N} \left| \theta_i - \theta_i^{1} \right|^2 \leq \sum_{i=2}^{N} \left| \theta_i^{1} \right|^2 4 \sigma^2 N^{2 \delta+1} {f(N)}{g(N)}.\end{equation*}
The proof is completed by taking
$\delta = \alpha/2$
and applying (2.2).
Proof of Lemma A.4
Proof of Lemma A.4. This lemma provides a control of the spectral gap
$\lambda_1 - \lambda_2$
. Given a good rescaling (in
$N^{2/3}$
), the asymptotic joint law of the eigenvalues in the edge has been investigated in a great deal of research, for Gaussian ensembles and for more general Wigner matrices. The GOE case has mainly been studied by Tracy, Widom, and Forrester, among many others; in [Reference Forrester12, Reference Tracy and Widom21], the convergence of the joint distribution of the first k eigenvalues towards a density distribution is established, as stated in the following proposition.
Proposition A.1. ([Reference Forrester12, Reference Tracy and Widom21].) For a given
$k\geq 1$
, and all
$s_1, \ldots, s_k$
real numbers,
\begin{equation}\mathbb{P}\left(N^{2/3} \left(\lambda_1 - 2\right) \leq s_1, \ldots, N^{2/3} \left(\lambda_k - 2\right) \leq s_k \right) \underset{N \to \infty}{\longrightarrow} \mathcal{F}_{1,k}(s_1, \ldots, s_k),\end{equation}
where the
$\mathcal{F}_{1,k}$
are continuous and can be expressed as solutions of nonlinear partial differential equations. Thus the rescaled spectral gap
$N^{2/3}\left(\lambda_{1}-\lambda_2\right)$
has a limit probability density law supported by
$\mathbb{R_+}$
, which implies that
\begin{equation*}\mathbb{P}\left(N^{2/3} \left(\lambda_1 - \lambda_2\right) \geq \left(\log N\right)^{-C \log \log N} \right) \underset{N \to \infty}{\longrightarrow} 1.\end{equation*}
Of course, the choice of the function
$N \mapsto \left(\log N\right)^{-C \log \log N}$
here is arbitrary, and the result is also true for any function tending to 0.
Proof of Lemma A.3
Proof of Lemma A.3. This result needs an understanding of the behavior of the spectral gaps of the matrix A, in the bulk and in the edges (left and right). The eigenvalues in the edges correspond to indices i such that
$i=o(N)$
(left) or
$i = N-o(N)$
(right). The eigenvalues in the bulk are the remaining eigenvalues. For this, we use a result on rigidity of eigenvalues, due to L. Erdös et al. [Reference Erdös, Yau and Yin8], which consists in a control of the probability of the gap between the eigenvalues of A and the typical eigenvalues
$\gamma_j$
of the semicircle law, defined as follows:
\begin{equation}\forall i \in \left\lbrace 1, \dots, n\right\rbrace , \qquad \frac{1}{2 \pi} \int_{-2}^{\gamma_j} \sqrt{4-x^2} dx =1- \frac{j}{N}.\end{equation}
Proposition A.2. ([Reference Erdös, Yau and Yin8].) For some positive constants
$C_5>0$
and
$C_6>0$
, for N large enough,
\begin{align}\mathbb{P}\left( \exists j \in \left\lbrace 1, \dots, n\right\rbrace \, | \, \left|\lambda_j - \gamma_j \right| \geq \left(\log N\right)^{C_5 \log \log N} \left(\min \left(j, N+1-j\right)\right)^{-1/3} N^{-2/3} \right) \end{align}
\begin{align*} \leq C_5 \exp \left(- \left(\log N\right)^{C_6 \log \log N} \right).\end{align*}
Remark A.1. Another similar result that goes in the same direction for the GOE is already known: it has been shown by O’Rourke in [Reference O’Rourke17] that the variables
$\lambda_i - \gamma_i$
behave as Gaussian variables when
$N \to \infty$
. However, the rigidity result in (A.10) obtained in [8] can be applied in more general models. This quantitative probabilistic statement was not previously known even for the GOE case.
Remark A.2. Let us note that one of the assumptions made in [Reference Erdös, Yau and Yin8] is that variances of each column sum to 1, which is not directly the case in our model (1.2). Nevertheless, one may use (A.10) for the rescaled matrix
$\tilde{A} \;:\!=\; A \left(1+\frac{1}{N}\right)^{-1/2}$
, then easily check that there is a possible step back to A:
\begin{align*}|\lambda_j - \gamma_j|\leq \left|\lambda_j \left(1+\frac{1}{N}\right)^{-1/2}- \gamma_j \right|+ N^{-1} + o(N^{-1}),\end{align*}
and
$ N^{-1} + o(N^{-1}) \leq 2\left(\min \left(j, N+1-j\right)\right)^{-1/3} N^{-2/3}$
for N big enough. Tolerating a slight increase of the constant
$C_5$
, the result (A.10) is thus valid in the GOE.
Let us now compute an asymptotic expansion of
$\gamma_j$
in the right edge, which is for
$j = o(N)$
. Define
\begin{equation}G(x) \;:\!=\; \frac{1}{2 \pi} \int_{-2}^{x} \sqrt{4-t^2} dt = \frac{x\sqrt{4-x^2}+4 \arcsin(x/2)}{4 \pi}+\frac{1}{2} ,\end{equation}
for all
$x \in [-2,2]$
. We have
$\gamma_j = G^{-1}(1-j/N) = - G^{-1}(j/N)$
, observing that the integrand in (A.11) is an even function. We get the following expansion when
$x \to -2$
:
\begin{equation*}G(x) \underset{x \to -2}{=} \frac{2(x+2)^{3/2}}{3 \pi} + o\left((x+2)^{3/2}\right),\end{equation*}
which implies that
\begin{equation*}G^{-1}(y) \underset{y \to 0}{=} -2 + \left(\frac{3 \pi y}{2}\right)^{2/3} + o\left(y^{2/3}\right),\end{equation*}
and hence
\begin{equation}\gamma_j \underset{j/N \to 0}{=} 2 - \left(\frac{3 \pi j}{2 N}\right)^{2/3} + o\left((j/N)^{2/3}\right).\end{equation}
Remark A.3. One can observe the coherence of this result that arises naturally in [Reference O’Rourke17] as the expectation of the eigenvalues in the edge.
Let
$\epsilon>0$
, to be specified later. To establish our result we will split the variables j into three sets:
\begin{align*}A_1 &\;:\!=\; \left\lbrace 2 \leq j \leq \left(\log N\right)^{(C_5+1)\log \log N} \right\rbrace \; \mbox{(a small part of the right edge)},\\ A_2 &\;:\!=\; \left\lbrace \left(\log N\right)^{(C_5+1)\log \log N} < j \leq N^{1-\epsilon} \right\rbrace \; \mbox{(a larger part of the right edge)}, \\ A_3 &\;:\!=\; \left\lbrace N^{1-\epsilon} < j \leq N \right\rbrace \; \mbox{(everything else)}.\end{align*}
We show that the sum over
$A_1$
is the major contribution in (A.5). The split in the right edge between
$A_1$
and
$A_2$
is driven by the error term of (A.10): this term is small compared to
$\gamma_j$
if and only if
$\left(\log N\right)^{C_5 \log \log N} = o(j)$
.
Step 1: Estimation of the sum over
$A_1$
. According to (A.10) and Lemma (A.4), w.h.p.
\begin{equation*}N^{-4/3} \left(\log N\right)^{-C_6 \log \log N} \leq \left(\lambda_1 - \lambda_2 \right)^2 \leq C_7 N^{-4/3} \left( \log N \right)^{C_6 \log \log N},\end{equation*}
where
$C_6, C_7$
are positive constants. Hence, w.h.p.
\begin{align*}\frac{N^{4/3}}{C_7 \left( \log N \right)^{C_6 \log \log N}} &\leq \sum_{j \in A_1} \frac{1}{\left(\lambda_1 - \lambda_j\right)^2} \\ & \leq \sum_{j \in A_1} \frac{1}{\left(\lambda_1- \lambda_2\right)^2}\\ & \leq N^{4/3} \left( \log N \right)^{(C_5+C_6+1) \log \log N}.\end{align*}
Step 2: Estimation of the sum over
$A_2$
. Let us show that the sum over
$A_2$
is asymptotically small compared to the sum over
$A_1$
: using (A.10) and (A.13), we know that there exists
$C_8>0$
such that for all
$j \in A_2$
, w.h.p.
\begin{equation*}\lambda_j = 2 - C_8 \left(\frac{j}{N}\right)^{2/3} + o\left((j/N)^{2/3}\right),\end{equation*}
and we know furthermore (se e.g. [Reference Anderson, Guionnet and Zeitouni3]) that w.h.p.
\begin{equation}\lambda_1 = 2 + o\left((j/N)^{2/3}\right) \qquad \forall j \in A_2;\end{equation}
hence w.h.p.
\begin{align*}\sum_{j \in A_2} \frac{1}{\left(\lambda_1 - \lambda_j\right)^2} &= N^{4/3} \sum_{j \in A_2} \frac{1}{C_9 j^{4/3}(1+o(1))}\\& = N^{4/3} (1+o(1)) \sum_{j \in A_2} \frac{1}{C_9 j^{4/3}} = o\left(N^{4/3}\right),\end{align*}
using in the last line the fact that the Riemann series
$\sum j^{-4/3}$
converges.
Step 3: Estimation of the sum under
$A_3$
. From the previous results (A.10), (A.13), and (A.14), assuming that
$\epsilon<1$
, we get w.h.p.
\begin{equation*}\lambda_1 - \lambda_{N^{1-\epsilon}} = C_8 N^{-2\epsilon/3} + O\left(N^{-2\epsilon/3}\right),\end{equation*}
which gives w.h.p. the following control:
\begin{align*}\sum_{j \in A_3} \frac{1}{\left(\lambda_1- \lambda_j\right)^2} &\leq \left(N-N^{1-\epsilon}\right) \frac{1}{\left(\lambda_1 - \lambda_{N^{1-\epsilon}}\right)^2}\\& = \left(N-N^{1-\epsilon}\right) \frac{N^{4\epsilon/3}}{C_9 (1+o(1))} = O\left(N^{1+4\epsilon/3}\right) = o\left(N^{4/3}\right),&&\end{align*}
as long as
$\epsilon < 1/4$
. Taking such an
$\epsilon$
, these three controls complete the proof.
Proof of Lemma A.2
Proof of Lemma A.2. We follow the same steps as in the proof of Lemma A.3. Let us take
$\delta>0$
. We split the j variables into three sets:
\begin{align*}A_1 &\;:\!=\; \left\lbrace 2 \leq j \leq N^{1/3} \right\rbrace,\\ A_2 &\;:\!=\; \left\lbrace N^{1/3} < j \leq N^{1-\delta} \right\rbrace,\\ A_3 &\;:\!=\; \left\lbrace N^{1-\delta} < j \leq N \right\rbrace.\end{align*}
We use Lemma A.4 to obtain the following control: w.h.p.
\begin{align*}\sum_{j \in A_1} \frac{1}{\lambda_1 - \lambda_j} \leq N^{1/3} N^{2/3} \left(\log N\right)^{C_5 \log \log N} = O(N^{1+\delta}).\end{align*}
Similarly, for
$A_2$
,
\begin{align*}\sum_{j \in A_2} \frac{1}{\lambda_1 - \lambda_j} &\leq \sum_{j \in A_2} \frac{1}{o(N^{-2/3}) + C_8(j/N)^{2/3} + O\left(\left(\log N\right)^{C_5 \log \log N}N^{-2/3}j^{-1/3}\right)} \\ &= N^{2/3} \sum_{j \in A_2} \frac{1}{o(1)+C_8j^{2/3}} \leq C_{10} N^{2/3} N^{(1-\delta)/3} \leq O\big(N^{1+\delta}\big).\end{align*}
Finally, using the Cauchy–Schwarz inequality,
\begin{align*}\sum_{j \in A_3} \frac{1}{\lambda_1 - \lambda_j} \leq \sqrt{N} \left(\sum_{j \in A_3} \frac{1}{\left(\lambda_1 - \lambda_j\right)^2}\right)^{1/2} \leq \sqrt{N} O\big(N^{1/2+2\delta/3}\big) = O\big(N^{1+\delta}\big).\end{align*}
A.2 Proof of Lemma 3.1
Proof of Lemma 3.1. We show that w.h.p.
\begin{equation}\sum_{i=2}^{N} \frac{\langle Hv_i,v_1 \rangle ^2 }{\left(\lambda_1 - \lambda_i\right)^2} - \frac{1}{N} \sum_{i=2}^{N} \frac{1}{\left(\lambda_1 - \lambda_i\right)^2}= o\left(\frac{1}{N} \sum_{i=2}^{N} \frac{1}{\left(\lambda_1 - \lambda_i\right)^2}\right).\end{equation}
Let us recall that H is drawn according to the GOE; hence its law is invariant by rotation. This implies that the
$\langle Hv_i,v_1 \rangle$
are independent variables with variance
$1/N$
, independent of
$\lambda_1, \ldots, \lambda_N$
. Define
\begin{equation*}M_N \;:\!=\; \sum_{i=2}^{N} \frac{\langle Hv_i,v_1 \rangle ^2 - 1/N }{\left(\lambda_1 - \lambda_i\right)^2}.\end{equation*}
Computing the second moment of
$M_N$
, we get
\begin{align*}\mathbb{E}\left[M_N ^2 \Big| \lambda_1, \ldots, \lambda_N \right]& = \textrm{Var}(M_N | \lambda_1, \ldots, \lambda_N) = \frac{1}{N^4} \sum_{i=2}^{N} \frac{2 }{\left(\lambda_1 - \lambda_i\right)^4}.\end{align*}
Adapting the proof of Lemma A.3, following the same steps, one can also show that w.h.p.
\begin{equation}\sum_{i=2}^{N} \frac{1}{\left(\lambda_1 - \lambda_i\right)^4} \asymp N^{8/3}.\end{equation}
Let
$\epsilon = \epsilon(N)>0$
to be specified later. By Markov’s inequality
\begin{align*}\mathbb{P}\left(\left|M_N\right| \geq \frac{\epsilon}{N} \left. \sum_{i=2}^{N} \frac{1}{\left(\lambda_1 - \lambda_i\right)^2} \right| \lambda_1, \ldots, \lambda_N \right)& \leq \frac{N^2}{\epsilon^2} \frac{\mathbb{E}\left[M_N ^2 | \lambda_1, \ldots, \lambda_N \right]}{\left(\sum_{i=2}^{N} \frac{1}{\left(\lambda_1 - \lambda_i\right)^2}\right)^2} \\& \asymp \frac{1}{\epsilon^2 N^2},\end{align*}
by Lemma A.3 and Equation (A.16). Taking e.g.
$\epsilon(N)=N^{-1/2}$
concludes the proof.
Appendix B. Additional proofs for Sections 4 and 5
B.1 Proof of Lemma 4.2
Proof of Lemma 4.2. We fix
$\alpha>0$
, and we want to prove
\begin{equation}\sum_{k=0}^{\lfloor(N-1)/2\rfloor} \binom{N-1-k}{k} \alpha^k = \frac{1}{\sqrt{1+4 \alpha}} \left[\left(\frac{1+\sqrt{1+4 \alpha}}{2}\right)^N - \left(\frac{1-\sqrt{1+4 \alpha}}{2}\right)^N\right].\end{equation}
In the following, we define
\begin{align*}\phi_+ \;:\!=\; \frac{1+\sqrt{1+4 \alpha}}{2}, \qquad \phi_- \;:\!=\; \frac{1-\sqrt{1+4 \alpha}}{2},\end{align*}
and for all
$N \geq 1$
,
\begin{equation*}u_N = u_N(\alpha) \;:\!=\; \sum_{k=0}^{\lfloor(N-1)/2\rfloor} \binom{N-1-k}{k} \alpha^k.\end{equation*}
We clearly have
$u_N(\alpha) \leq \left(1+\alpha\right)^N$
. For all
$t>0$
small enough (e.g.
$t < {1}/{(1+\alpha)}$
), define
\begin{equation*}f(t) \;:\!=\; \sum_{N =1}^{\infty} u_N t^N.\end{equation*}
On the one hand,
\begin{align*}\frac{t}{1-t-\alpha t^2} & = t \sum_{m=0}^{\infty} \big(t+\alpha t^2\big)^m = \sum_{m=0}^{\infty} \sum_{l=0}^{m} \binom{m}{l} \alpha ^l t^{l + m + 1}\\& = \sum_{N=1}^{\infty} \left(\sum_{\substack{0 \leq l \leq m \\ l+m = N-1}} \binom{m}{l} \alpha^l \right) t^N = \sum_{N=1}^{\infty} u_N t^N = f(t).\end{align*}
On the other hand,
\begin{align*}\frac{t}{1-t-\alpha t^2} & = \frac{t}{\left(1-\phi_{-}t\right)\left(1-\phi_{+}t\right)} = \frac{1}{\phi_{+}-\phi_{-}}\left(\frac{1}{1-\phi_{+}t}-\frac{1}{1-\phi_{-}t}\right)\\& = \frac{1}{\sqrt{1+4\alpha}} \sum_{N=1}^{\infty}\left(\phi_{+}^N - \phi_{-}^N\right) t^N.\end{align*}
This proves (B.1).
B.2 Proof of Lemma 5.2
Proof of Lemma 5.2. Let us represent the situation in the plane spanned by
$v_1$
and
$v'_{\!\!1}$
, as shown in Figure 4.
Figure 4. Orthogonal projection of
$\widetilde{v}_1$
on
$\mathcal{P} \;:\!=\; \textrm{span}(v'_{\!\!1}, v_1)$
.
Since
$\widetilde{v}_1$
is taken such that
$\langle v_1,\widetilde{v}_1 \rangle >0$
and
$\sigma_1$
satisfies (2.2), we have
$\langle \widetilde{v}_1,v'_{\!\!1} \rangle >0$
for N large enough by Proposition (2.1). Let
$p \;:\!=\; \langle \widetilde{v}_1,v'_{\!\!1} \rangle^2$
and
$\widetilde{w} \;:\!=\; \widetilde{v}_1 - \sqrt{p} v'_{\!\!1} \in \left(v'_{\!\!1}\right)^{\perp}$
. By invariance by rotation we obtain that
\begin{align*}\frac{\widetilde{w}}{\| \widetilde{w}\|}=\frac{\widetilde{w}}{\sqrt{1-p}}\end{align*}
is uniformly distributed on the unit sphere
$\mathbb{S}^{N-2}$
of
$\left(v'_{\!\!1}\right)^{\perp}$
, and independent of p,
$v_1$
, and
$v'_{\!\!1}$
. Hence
\begin{equation*}\langle b,\widetilde{v}_1 \rangle = \langle b, \widetilde{w} \rangle \overset{(d)}{=} \sqrt{1-p} \cdot \frac{\widetilde{Z}_1}{\sqrt{\sum_{i=1}^{N-1} \left(\widetilde{Z}_i\right)^2}},\end{equation*}
where the
$\widetilde{Z}_i$
are independent Gaussian standard variables, independent from everything else. From Section 3 we know that
$1 - \langle v_1,v'_{\!\!1} \rangle \asymp \sigma_1^2 N^{1/3} $
and thus
$\langle v_1,b \rangle \asymp \sigma_1 N^{1/6}$
. This yields, for N large enough, w.h.p.
\begin{align*}0 < \langle \widetilde{v}_1, v_1 \rangle & \leq \sqrt{p} \langle v_1, v'_{\!\!1} \rangle + \sqrt{\frac{1-p}{N}} \widetilde{Z}_1 \sigma_1 N^{1/6} f(N)\\& \leq \sqrt{p} \langle v_1, v'_{\!\!1} \rangle + \sqrt{1-p} N^{-4/3} g(N) \\& \leq \max \left(\sqrt{p},\sqrt{1-p}\right) \langle v_1, v'_{\!\!1} \rangle \\& \leq \langle v_1, v'_{\!\!1} \rangle,\end{align*}
where f and g are two functions as defined in Lemma A.3. From this point one can still make the link to the toy model, as done at the beginning of Section 4. By invariance by rotation, letting
$t \;:\!=\; \widetilde{v}_1 - \langle \widetilde{v}_1,v_1 \rangle v_1$
, we know that
$\|t\|$
and
$\frac{t}{\| t\|}$
are independent, and that
$\frac{t}{\| t\|}$
is uniformly distributed on the unit sphere in
$v_1^{\perp}$
. We have the following equality in distribution:
\begin{equation*}\left(r_1(v_1),r_1(\widetilde{v}_1)\right) \overset{(d)}{=} \left(r_1(X),r_1(X+\mathbf{s}Z) \right),\end{equation*}
with w.h.p.
\begin{align*}\mathbf{s} \geq \mathbf{s^1} = \frac{\|w\| \|X\|}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2} \left(1 - \frac{\|w\| Z_1}{\left(\sum_{i=2}^{N} Z_i^2\right)^{1/2}}\right)} \asymp \sigma_1 N^{1/6},\end{align*}
where the
$X_i$
,
$Z_i$
, and w are defined in Section 4, for
$\sigma=\sigma_1$
.
B.3 Proof of Lemma 5.1
Proof of Lemma 5.1. Recall that we work in the case (i) (
$\sigma = o(N^{-7/6-\epsilon})$
for some
$\epsilon>0$
), with
$\langle v_1,v'_{\!\!1} \rangle >0$
and
$\Pi = \textrm{Id}$
. We want to show that w.h.p.
\begin{equation}\langle A, \Pi_{+} B \Pi_{+}^T \rangle > \langle A, \Pi_{-} B \Pi_{-}^T \rangle.\end{equation}
Define
\begin{equation*}\mathcal{G} \;:\!=\; \left\lbrace i, \Pi_{+}(i)=\Pi(i)=i \right\rbrace\end{equation*}
and
\begin{equation*}\mathcal{A} \;:\!=\; \left\lbrace \sigma N^{1/6}f(N)^{-1} \leq \mathbf{s} \leq \sigma N^{1/6 }f(N) \right\rbrace,\end{equation*}
with
$f \in \mathcal{F}$
such that
$\mathbb{P} \left(\mathcal{A}\right) \to 1$
. For N large enough, on the event
$\mathcal{A}$
, we have
$ 0 \leq \mathbf{s}N \leq N^{-\epsilon }f(N)$
. Hence, repeating the proof of Proposition 2.2, we have
\begin{align*}\phi_{x,z}\left(N, \mathbf{s} \right) & \geq \mathbb{P} \left(\mathcal{N}^{+}(x,x+\mathbf{s}z)=\mathcal{N}^{-}(x,x+\mathbf{s}z)=0\right) \\& \sim \exp\left(- \mathbf{s}NE(x)\left[z(2F(z)-1)+2E(z)\right]\right) = 1 - O(N^{-\epsilon}f(N)).&&\end{align*}
Thus, with dominated convergence, for N large enough,
\begin{align}\mathbb{P}\left({\Pi_{+}}(i)=\Pi(i) | \mathcal{A} \right) = \iint dx dz E(x) E(z) \mathbb{E}\left[\phi_{x,z}\left(N, \mathbf{s} \right)| \mathcal{A}\right] \geq 1 - O(N^{-\epsilon}f(N)).\end{align}
We use Markov’s inequality with (B.3) to show that
$\mathbb{P}\left(\sharp \mathcal{G} \leq N- N^{1-\epsilon/2} \; | \; \mathcal{A} \right) \leq O\left(N^{-\epsilon/2}f(N)\right) $
, and hence w.h.p.
\begin{equation}\sharp \mathcal{G} \geq N- N^{1-\epsilon/2}.\end{equation}
Splitting the sum
\begin{align*}\langle A, \Pi_{+} B \Pi_{+}^T \rangle & = \sum_{i,j} A_{i,j} B_{\Pi_{+}(i),\Pi_{+}(j)} = \sum_{(i,j) \in \mathcal{G}^2 } A_{i,j} B_{i,j} + \sum_{(i,j) \notin \mathcal{G}^2 } A_{i,j} B_{\Pi_{+}(i),\Pi_{+}(j)},\end{align*}
one has, w.h.p.,
\begin{multline*}\langle A, \Pi_{+} B \Pi_{+}^T \rangle = \sum_{(i,j) \in \mathcal{G}^2 } A_{i,j}^2 + \sum_{\substack{(i,j) \notin \mathcal{G}^2\\ (\Pi_{+}(i),\Pi_{+}(j)) \neq (j,i) } } A_{i,j} A_{\Pi_{+}(i),\Pi_{+}(j)} \\+ \sum_{\substack{(i,j) \notin \mathcal{G}^2\\ (\Pi_{+}(i),\Pi_{+}(j)) = (j,i) } } A_{i,j}^2 + \sigma \sum_{1 \leq i,j \leq N } A_{i,j} H_{\Pi_{+}(i),\Pi_{+}(j)} \\\geq C_1 \frac{(\sharp \mathcal{G})^2}{N} - C_2 \left(N^2-(\sharp \mathcal{G})^2\right)\frac{\log N}{N} - C_2 \sigma N^2 \frac{\log N}{N}.\end{multline*}
Here we applied the law of large numbers for the first sum, lower-bounded the third sum by zero, and used the classical inequality
\begin{align*}\max_{i,j}\left\lbrace A_{i,j}, H_{i,j} \right\rbrace \leq C_2 \frac{\log N}{N}\end{align*}
(which holds w.h.p.) for the two others.
The inequality (B.4) and the condition (i) lead to, w.h.p.,
\begin{equation*}\langle A, \Pi_{+} B \Pi_{+}^T \rangle \geq C_1 N - 2 C_1 N^{1- \epsilon/2} - 2 C_2 N^{1- \epsilon/2} \log N - C_2 N^{-1/6-\epsilon}\log N \geq C_3 N.\end{equation*}
On the other hand, since by definition
$\Pi_{-}(i)=\Pi_{+}(N+1-i)$
, w.h.p.,
\begin{multline*}\langle A, \Pi_{-} B \Pi_{-}^T \rangle = \sum_{(i,j) \in \mathcal{G}^2 } A_{i,j}B_{N+1-i,N+1-j} + \sum_{\substack{(i,j) \notin \mathcal{G}^2 } } A_{i,j} B_{\Pi_{-}(i),\Pi_{-}(j)} \\\leq O(\log N) + \frac{(\sharp \mathcal{G})^2 }{N}o(1) + C_2 \left(N^2-(\sharp \mathcal{G})^2\right)\frac{\log N}{N}.\end{multline*}
For the first sum, we used the law of large numbers: the variables
$A_{i,j}$
and
$B_{N+1-i,N+1-j}$
are independent in all cases but at most
$N+1$
, and this part of the sum is bounded by
$O(\log N) $
. We used the same control on Gaussian variables as above.
This gives
\begin{equation*}\left(\langle A, \Pi_{-} B \Pi_{-}^T \rangle \right)_{+} = o_{\mathbb{P}}(N),\end{equation*}
where
$(x)_{+} \;:\!=\; \max (0,x)$
, which proves (B.2).
B.4 Proof of Lemma 5.3
Proof of Lemma 5.3. Recall that we work in the case (ii) (
$\sigma = \omega(N^{-7/6+\epsilon})$
for some
$\epsilon>0$
), with
$\langle v_1,v'_{\!\!1} \rangle >0$
and
$\Pi = \textrm{Id}$
. We want to show that the aligning permutation between
$v_1$
and
$-v'_{\!\!1}$
has a very bad overlap. Taking the pair
$(X,-Y)$
where
$(X,Y) \sim \mathcal{J}(N,s)$
, one can adapt the proof of Proposition 2.2, with the new definitions
\begin{align*}\widetilde{S^{+}}(x,y) &\;:\!=\; \mathbb{P}\left(X_1 > x, -Y_1 < -y\right) \quad \mbox{ and}\\\widetilde{S^{-}}(x,y) &\;:\!=\; \mathbb{P}\left(X_1 < x, -Y_1 > -y\right).\end{align*}
The analysis is even easier since for all x, z, there exist two constants c, C such that
\begin{align*}0 < c \leq \widetilde{S^{+}}(x,x+s z) , \, \widetilde{S^{-}}(x,x+ sz) \leq C <1.\end{align*}
It is then easy to check that the proof of Proposition 2.2, case (ii), adapts well.
Funding Information
This work was partially supported by the French government under the management of the Agence Nationale de la Recherche, as part of the Investissements d‘Avenir program, reference ANR19-P3IA-0001 (PRAIRIE 3IA Institute).
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process for this article.
